Bài tập trắc nghiệm sự đồng biến và nghịch biến của hàm số – Ngọc Đàn Toán 12

Bài tập trắc nghiệm sự đồng biến và nghịch biến của hàm số – Ngọc Đàn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

96 48 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

44 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 1
VẤN ĐỀ 1. XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Phương pháp
Bước 1. Tìm tập xác định của hàm số
Bước 2. Tính đạo hàm
y
. Tìm nghiệm (nếu có ) của phương trình
0y
Bước 3. Lập bảng biến thiên (Xét dấu đạo hàm)
Bước 4. Dựa vào bảng biến thiên để kết luận
+) Nếu
0fx
với mọi
;x a b
thì hàm số
y f x
đồng biến trên khoảng
;ab
.
+) Nếu
0fx
với mọi
;x a b
thì hàm số
y f x
đồng biến trên khoảng
;ab
.
A- VẬN DỤNG
Ví dụ 1. Xét chiều biến thiên của các hàm số sau
Mẫu:
1)
32
11
21
32
y x x x
2)
32
6 9 2y x x x
3)
32
3 4 3y x x x
4)
32
4y x x x
5)
6)
32
6 12 1y x x x
7)
3
31y x x
8)
3
1
4 10
3
y x x
Ví dụ 2. Xét chiều biến thiên của các hàm số sau Mẫu:
21
1
x
y
x
1)
31
12
x
y
x
2)
1
12
x
y
x


3)
1
1
x
y
x
4)
2
1
x
y
x
Ví dụ 3. Xét chiều biến thiên của các hàm số sau Mẫu:
2
22
1
xx
y
x

1)
2
1
21
xx
y
x

2)
2
22
1
xx
y
x

3)
4
yx
x

4)
1
4
x
y
x
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 2
Ví dụ 4. Xét chiều biến thiên của các hàm số sau.
1)
32
4
23
3
y x x x
2)
32
2 6 6 9y x x x
3)
5 4 3
33
42
54
y x x x
4)
42
3
5
2
y x x x
5)
43
1
42
4
y x x x
Chú ý. Giả sử hàm số
y f x
có đạo hàm trên khoảng
;ab
+) Nếu
0, ;f x x a b
và
0fx
chỉ tại hữu hạn điểm trên khoảng
;ab
thì hàm
số đồng biến trên khoảng .
+) Nếu
0, ;f x x a b
và
0fx
chỉ tại hữu hạn điểm trên khoảng
;ab
thì hàm
số nghịch biến trên khoảng .
B- BÀI TẬP RÈN LUYỆN
Bài tập 1. Xét chiều biến thiên của các hàm số sau
1)
32
3 9 10y x x x
2)
3
36y x x
3)
32
3 5 5y x x x
4)
32
31y x x
5)
3
6
3
x
yx
6)
3
2
2
2
33
x
y x x
7)
32
3 3 5y x x x
8)
4
2
2
2
x
yx
9)
42
25y x x
10)
42
22y x x
11)
42
81y x x
12)
42
34y x x
13)
42
8 10y x x
14)
42
23y x x
Bài tập 2. Xét chiều biến thiên của các hàm số sau
1)
1
12
x
y
x
2)
25
3
x
y
x
3)
24
1
x
y
x
4)
1
x
y
x
5)
2
22
1
xx
y
x

6)
2
2
1
xx
y
x
7)
2
4 5 2
1
xx
y
x

8)
2
4
x
y
x
9)
2
2
1
1
xx
y
xx


DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 3
Bài tập 3. Xét chiều biến thiên của các hàm số sau
1)
32
2 6 6 9y x x x
2)
5 4 3
3
3 4 2
5
y x x x
3)
42
3
5
2
y x x x
4)
35
4
36
5
y x x
5)
32
24y x x x
6)
32
1
3 9 1
3
y x x x
Bài tập 4. Xét chiều biến thiên của hàm số:
1)
2
2y x x
2)
2
4y x x
3)
3 2 2y x x
4)
23
3y x x
C - BÀI TẬP TRẮC NGHIỆM
ĐỀ 01. [1]
Câu 1. Hàm số
32
7y x x x
A. Luôn đồng biến trên B. Luôn nghịch biến trên
C. Có khoảng đồng biến và nghịch biến. D. Nghịch biến trên khoảng
.1;3
Câu 2. Hàm số
32
7y x x x
A. Luôn đồng biến trên B. Luôn nghịch biến trên
C. Có khoảng đồng biến và nghịch biến. D. Đồng biến trên khoảng
.1;3
Câu 3. Hàm số
32
y x x x
có khoảng đồng biến là
A.
1;3
B.
1
;1
3


C.
1;3
D.
1
( ; ) (1; )
3
Câu 4. Hàm số
5
22
x
y
x

luôn
A. Nghịch biến trên từng khoảng xác định của nó. B. Đồng biến trên
C. Đồng biến trên khoảng
( 4;6).
D. Nghịch biến trên
Câu 5. Hàm số
42
23y x x
đồng biến trên khoảng nào sau đây?
A.
;1
và
0;1
B.
1;0
và
1; 
C.
;0
D.
1;1
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 4
Câu 6. Hàm số nào sau đây đồng biến trên ?
A.
1
3
x
y
x
B.
32
21y x x x
C.
42
23y x x
D.
3
2y x x
Câu 7. Cho hàm số
1
3
x
y
x
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
;3
và
3; 
B. Hàm số nghịch biến trên
;3
và
3; 
C. Tập xác định của hàm số là
D. Tiệm cận ngang của đồ thị hàm số là y = 3
Câu 8. Khoảng đồng biến của hàm số
42
81y x x
là:
A.
;2
và
0;2
B.
;0
và
0;2
C.
;2
và
2;
D.
2;0
và
2;
Câu 9. Khoảng đồng biến của hàm số
32
31y x x
là:
A.
1;3
B.
0;2
C.
2;0
D.
0;1
Câu 10. Hàm số:
32
34y x x
nghịch biến khi x thuộc khoảng nào sau đây:
A.
( 2;0)
B.
( 3;0)
C.
( ; 2)
D.
(0; )
Câu 11. Hàm số nào sau đây đồng biến trên
A.
2
1
x
y
x
B.
42
21y x x
C.
32
3 3 2y x x x
D.
sin 2y x x
Câu 12. Kết luận nào sau đây về tính đơn điệu của hàm số
21
1
x
y
x
là đúng?
A. Hàm số luôn nghịch biến trên
\1
;
B. Hàm số luôn đồng biến trên
\1
;
C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +);
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 5
D. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +).
Câu 13. Hàm số
3
4yx
đồng biến trên:
A. B.
0;
C.
3; 
D.
;0
Câu 14. Hàm số
3
32y x x
nghịch biến trên:
A.
; 1 ; 1; 
B.
1; 
C.
1;1
D. .
Câu 15. Đồ thị của hàm số nào luôn nghịch biến trên
:
A.
42
21y x x
B.
2
3 4 1y x x
C.
2
21yx
D.
3
3 2 1y x x
Câu 16. Hàm số
42
22y x x
nghịch biến trên:
A.
; 1 ; 0;1
B.
1;0 ; 1; 
C.
1;1
D. .
Câu 17. Hàm số
42
4y x x
đồng biến trên:
A.
0;
B.
;0
C.
1;1
D. .
Câu 18. Khoảng nghịch biến của hàm số
32
1
2 3 2
3
y x x x
là:
A.
;3
B.
3; 1
C.
; 3 1; 
D.
;3
Câu 19. Hàm số
3
21
x
y
x
:
A. Đồng biến trên khoảng
; 
B. Nghịch biến trên khoảng
; 
C. Đồng biến trên từng khoảng xác định D. Nghịch biến trên từng khoảng xác định
Câu 20. Hàm số
2
2 4 3y x x
tăng trên khoảng nào?
A.
1; 
B.
;1
C.
; 
D. Một kết quả khác
Câu 21.
Hàm số nào sau đây luôn đồng biến trên
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 6
A.
42
23y x x
B.
3
21y x x
C.
32
7y x x
D.
32
1
32
3
y x x x
Câu 22. Trong các hàm số sau, những hàm số nào luôn đồng biến trên từng khoảng
xác định của nó:
21
3
x
y
x
(I),
42
21y x x
(II),
3
33y x x
(III)
A. (I) và (II) B. Chỉ (I) C. (II) và (III) D. (I) và (III)
Câu 23. Hàm số y = f(x) có bảng biến thiên như sau. Khẳng định nào sau đây là đúng?
x
2
,
y
- -
y
2
2
A. Hàm số nghịch biến trên
󰇛

󰇜
󰇛 󰇜 B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên
󰇛

󰇜
󰇛 󰇜 D. Hàm số nghịch biến trên R\{2}
Câu 24. Hàm số nào trong các hàm số sau đây nghịch biến trên khoảng
1;3
A.
32
2
4 6 1
3
y x x x
B.
2
1
1
xx
y
x

C.
2
42y x x
D.
21
1
x
y
x
Câu 25. Cho hàm số
3
1
2017.
3
y x x
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên R
B. Hàm số đồng biến trên
󰇛
 
󰇜
󰇛 󰇜 và nghịch biến trên (-1;1)
C. Hàm số đồng biến trên R
D. Hàm số nghịch biến trên 󰇛 󰇜
Câu 26. Hàm số
42
21y x x
đồng biến trên các khoảng:
A.
;1
và
(0;1)
B.
(0;1)
C.
1;0
và
(1; )
D.
( 1;1)
Câu 27. Khoảng nghịch biến của hàm số
32
34y x x
là:
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 7
A.(-2; 0)
B.
;2
và
(0 ; )
C.
2 ;0
và
(2 ; )
D.
0;
Câu 28. Hàm số
32
6 9 7y x x x
đồng biến trên các khoảng nào ?
A.
;1 & 3; 
B.
;1 3;
C.
1;3
D.
; 
Câu 29. Hàm số
3
32y x x
nghịch biến trên các khoảng nào ?
A.
; 1 & 1; 
B.
1;1
C.
;1
D.
1; 
Câu 30. Hàm số nào sau đây đồng biến trên
A.
32
31y x x x
B.
3
33y x x
C.
2
28
1
xx
y
x

D.
1
x
y
x
Câu 31. Hàm số
42
22y x x
đồng biến trên :
A. B. C. D.
Câu 32. Các khoảng đồng biến của hàm số
32
2 9 12 3y x x x
là :
A. (1;2) B. (-1;2) C. (-
;-1) và (2 ;+∞) D. (-∞;1) và (2;+
)
Câu 33. Hàm số
42
2 4 2y x x
đồng biến trên khoảng
A.
( ;1)
B.
(1; )
C.
( ;0)
D.
(0; )
Câu 34. Hàm số
25
3
x
y
x
đồng biến trên khoảng:
A. B.
;3
C.
3; 
D.
;3
và
3; 
Câu 35. Cho hàm số
32
3
6
3 2 4
xx
f x x
A. Hàm số đồng biến trên khoảng
2;3
. B. Hàm số nghịch biến trên khoảng
2;3
.
C. Hàm số nghịch biến trên
;2
D. Hàm số đồng biến trên
2; 
.
( ; 1),(0,1)
( 1,0),(1; ) 
( 1;1)
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 8
ĐỀ 02. [1]
Câu 1. Cho hàm số
5 4 3
6 15 10 22y x x x
. Khẳng định nào sau đây là đúng:
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên
;0
và nghịch biến trên
0;
.
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên
0;1
và đồng biến trên
0;
.
Câu 2. Hàm số
42
21y x x
đồng biến trên các khoảng:
A.
; 1 ,(0;1)
B.
(0;1)
C.
1;0 ,(1; ) 
D.
( 1;1)
Câu 3. Hàm số nào sau đây nghịch biến trên ?
A.
32
3 4y x x
B.
42
2 2y x x
C.
32
2 1y x x x
D.
42
3 2y x x
Câu 4. Khoảng đồng biến của hàm số
42
81y x x
là
A.
;2
,
0;2
B.
;0
,
0;2
C.
;2
,
2;
D.
2;0
,
2;
Câu 5. Khoảng nghịch biến của hàm số
32
1
3
3
y x x x
là
A.
;1
B.
1;3
C.
3; 
D.
;1
,
3; 
Câu 6. Hàm số nào sau đây đồng biến trên mỗi khoảng xác đinh của nó ?
A.
2
2
x
y
x
B.
2
2
x
y
x

C.
2
2
x
y
x

D.
2
2
x
y
x

”
Câu 7.
Hàm số
32
11
61
32
y x x x
A. Đồng biến trên khoảng (-2; 3) B. Nghịch biến trên khoảng (-2; 3)
C. Đồng biến trên khoảng
3; 
D. Nghịch biến trên khoảng
;2
”
Câu 8. Khoảng nghịch biến của hàm số
32
34y x x
là:
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 9
A. (-2; 0)
B.
; 2 ,(0 ; ) 
C.
2 ;0 ;(2 ; ) 
D.
0;
Câu 9.
Khoảng nghịch biến của hàm số
42
1
25
4
y x x
là
A.
2 ;0 ,(2; )
B.
; 2 ,(0 ; ) 
C.
; 2 ,(0 ;2)
D.
0;
Câu 10. Hàm số y = –x
3
+ 6x
2
– 9x + 4 đồng biến trên khoảng:
A. (1;3) B.
(3; )
C.
( ;3)
D.
(1; )
Câu 11. Cho hàm số
1
1
x
y
x
. Khẳng định nào sau đây là đúng
A. Hàm số đồng biến trên
\1
B. Hàm số nghịch biến trên
\1
C. Hàm số nghịch biến trên khoảng
;1
, đồng biến trên khoảng
1; 
D. Hàm số nghịch biến trên các khoảng
;1
và
1; 
”
Câu 12. Hàm số
32
6 9 7y x x x
đồng biến trên các khoảng:
A.
( ;1) (3;va 
) B.
1;3
C.
3; 1
D.
; 
.
Câu 13. Kết luận nào sau đây về tính đơn điệu của hàm số
21
1
x
y
x
là đúng?
A. Hàm số đồng biến trên các khoảng
;1
và
1; 
B. Hàm số luôn luôn đồng biến trên
\1
C. Hàm số nghịch biến trên các khoảng
;1
và
1; 
D. Hàm số luôn luôn nghịch biến trên
\1
Câu 14. Cho hàm số
32
3 9 5y x x x
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên
( 1;3)
B. Hàm số nghịch biến trên khoảng
( ; 1)
.
C. Hàm số đồng biến trên mỗi khoảng
( ; 1)
,
(3; )
;
D. Hàm số chỉ đồng biến trên khoảng
(3; )
.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 10
Câu 15. Bảng biến thiên sau đây là của hàm số nào?
A.
21
2
x
y
x
B.
3
2
x
y
x
C.
3
2
x
y
x
D.
3
21
x
y
x
Câu 16. Bảng biến thiên sau là của hàm số nào?
A.
32
32y x x
B.
32
32y x x
C.
32
32y x x
D.
32
32y x x
x
0 2
,
y
- 0 + 0 -
y
6
2
Câu 17. Kết luận nào sau đây về tính đơn điệu của hàm số
21
1
x
y
x

là đúng?
A. Hàm số luôn nghịch biến trên
\1
.
B. Hàm số luôn đồng biến trên
\1
.
C. Hàm số luôn nghịch biến trên
;1
và
1; 
.
D. Hàm số luôn đồng biến trên
;1
và
1; 
.
Câu 18. Hàm số
23
4
x
y
x
. Chọn phát biểu đúng:
A. Luôn đồng biến trên B. Luôn nghịch biến trên từng khoảng xác định
C. Luôn nghịch biến trên D. Đồng biến trên từng khoảng xác định
Câu 19. Cho hàm số y = –x
3
+ 3x
2
– 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại x = 1. B. Hàm số đạt cực đại tại x = 1;
C. Hàm số luôn luôn đồng biến; D. Hàm số luôn luôn nghịch biến;
Câu 20. Hàm số
25
3
x
y
x
đồng biến trên khoảng:
-
-
2
1
1
+
-
+
-
y
y'
x
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 11
A. B.
;3
C.
3; 
D.
;3
và
3; 
Câu 21. Cho hàm số
32
3
6
3 2 4
xx
f x x
A. Hàm số đồng biến trên
2;3
B. Hàm số nghịch biến trên
2;3
C. Hàm số nghịch biến trên
;2
D. Hàm số đồng biến trên
2; 
.
Câu 22. Cho hàm số
5 4 3
6 15 10 22y x x x
. Khẳng định nào sau đây là đúng:
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên
;0
và nghịch biến trên
0;
.
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên
0;1
và đồng biến trên
0;
.
Câu 23. Hàm số nào sau đây có bảng biến thiên như hình bên:
x
2
,
y
- -
y
2
2
A.
25
2
x
y
x
B.
23
2
x
y
x
C.
3
2
x
y
x
D.
21
2
x
y
x
Câu 24. Hàm số nào sau đây là đồng biến trên ?
A.
3
31y x x
B.
2
1
x
y
x
C.
1
2
x
y
x
D.
4
2yx
Câu 25. Hàm số
2
1
1
xx
y
x

đồng biến trên:
A.
;0
và
1;2
B.
0;1
và
2;
C.
0;1
và
1;2
D.
;0
và
2;
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 12
Câu 26. Hàm số
21
1
x
y
x
:
A. Hàm số luôn nghịch biến trên
B. Hàm số luôn đồng biến trên
C. Hàm số nghịch biến trên các khoảng
;1
và
1;
D. Hàm số đồng biến trên các khoảng
;1
và
1;
Câu 27. Hàm số
32
3 3 2y x x x
:
A. Hàm số luôn nghịch biến trên D. Hàm số nghịch biến trên khoảng
;1
B. Hàm số luôn đồng biến trên C. Hàm số đồng biến trên khoảng
1; 
Câu 28. Bảng biến thiên sau đây là của hàm số nào? Chọn 1 câu đúng.
x
2
,
y
- -
y
1
1
A.
1
2
x
y
x
B.
21
2
x
y
x
C.
3
2
x
y
x
D.
1
21
x
y
x
Câu 29. Bảng biến thiên sau đây của hàm số nào?
A.
32
31y x x
B.
32
31y x x
C.
32
31y x x
D.
32
31y x x
x
0 2
,
y
- 0 + 0 -
y
3
-1
Câu 30. Hàm số
32
1
31
3
y x x x
đồng biến trên các khoảng:
A.
;3
và
1; 
B.
3;1
C.
1;3
D.
;1
và
3; 
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 13
Câu 31. Hàm số
32
34y x x
nghịch biến trên các khoảng nào sau đây:
A.
2;0
B.
3;0
C.
;2
D.
0;
Câu 32. Hàm số
42
23y x x
nghịch biến trên các khoảng khoảng nào sau đây:
A.
1;
B. C.
;0
D.
0;
Câu 33. Hàm số
2
2
3
7
xx
y
xx


A. Đồng biến trên khoảng
5;0
và
0;5
B. Nghịch biến trên khoảng
5;1
C. Đồng biến trên khoảng
1;0
và
1; 
D. Nghịch biến trên khoảng
6;0
Câu 34. Cho hàm số
2
1
x
y
x
. Khi đó:
A.
25y
B. Hàm số luôn đồng biến trên
C. Hàm số luôn nghịch biến trên
D. Hàm số luôn nghịch biến trên từng khoảng xác định của nó.
Câu 35. Trong mỗi hàm số sau hàm số nào nghịch biến trên từng khoảng xác định
của nó?
A.
2
1
x
y
x
B.
cotyx
C.
1
5
x
y
x
D.
tanyx
ĐỀ 03. [2]
Câu 1. Cho hàm số
1
sin2 3
2
y x x
. Khẳng định nào sau đây là đúng:
A. Hàm số đồng biến trên .
B. Hàm số đồng biến trên
;0
.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 14
C. Hàm số nghịch biến trên
;0
và đồng biến trên
0;
.
D. Hàm số nghịch biến trên .
Câu 2. Hàm số nào sau đây đồng biến trên
A.
3
1yx
B.
tanyx
C.
21
1
x
y
x
D.
42
1y x x
Câu 3. Hàm số
2
25yx
A. Đồng biến trên khoảng
( 5;0)
và
(0;5).
B. Đồng biến trên khoảng
( 5;0)
và nghịch biến trên khoảng
(0;5).
C. Nghịch biến trên khoảng
( 5;0)
và đồng biến trên khoảng
(0;5).
D. Nghịch biến trên khoảng
( 6;6).
Câu 4. Hàm số
24y x x
nghịch biến trên khoảng
A.
2;3
B.
2;3
C.
2;4
D.
3;4
Câu 5. Hàm số
43
1
3
y x x
có khoảng đồng biến là:
A.
1
;
4




B.
1
;
4




C.
0;
D.
1
;0
4



Câu 6. Hàm số
2
2y x x
nghịch biến trên khoảng nào sau đây?
A.
1;2
B.
0;1
C.
;1
D.
1; 
Câu 7. Hàm số
15y x x
đồng biến trên khoảng nào sau đây?
A.
5; 3
B.
3; 
C.
5; 
D.
;3
Câu 8. Hàm số nào sau đây luôn đồng biến trên từng khoảng xác định của chúng
A.
1
y
x
B.
2
1
x
y
x
C.
2
2
1
xx
y
x
D.
9
yx
x

Câu 9. Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó ?
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 15
A.
2
21
x
y
x
B.
21
3
x
y
x
C.
1
1
x
y
x
D.
5
1
x
y
x

Câu 10. Trong các khẳng định sau về hàm số
24
1
x
y
x
, hãy tìm khẳng định đúng?
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định.
Câu 11. Hàm số
2
2y x x
đồng biến trên:
A.
1;2
B.
0;2
C.
0;1
D.
Câu 12. Hàm số
cosy x x
A. Đồng biến trên B. Đồng biến trên
;0
C. Nghịch biến trên D. Nghịch biến trên
0;
Câu 13. Hàm số
siny x x
A. Đồng biến trên B. Đồng biến trên
;0
C. Nghịch biến trên D. Nghịch biến trên
0;
Câu 14. Khoảng nghịch biến của hàm số
2
24y x x
A.
11
;
42



B.
11
;
42



C.
1
0;
2



D.
1
0;
4



Câu 15. Cho hàm số
2
1
1
xx
y
x

. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
0;2
B. Hàm số nghịch biến trên khoảng
1;2
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 16
C. Hàm số nghịch biến trên khoảng
0;1
D. Hàm số đồng biến trên khoảng
;2
và
2;
Câu 16. Cho hàm số
32
3 3 9 11y x x x
. Độ dài khoảng đồng biến là:
A. 2 B. 4 C. 0 D. 1
Câu 17. Hàm số
42
33y x x
đồng biến trên khoảng nào trong các khoảng sau:
. 1;0 ; . 1;1 ; . 2;I II III 
A. (I) và (II) B. (I) và (III) C. chỉ (I) D. (II) và (III)
Câu 18. Kết luận nào sau đây về tính đơn điệu của hàm số
21
1
x
y
x
là đúng
A. Hàm số luôn luôn nghịch biến trên
\1
.
B. Hàm số luôn luôn đồng biến trên
\1
.
C. Hàm số nghịch biến trên các khoảng
;1
và
1;
D. Hàm số đồng biến trên các khoảng
;1
và
1;
Câu 19. Cho hàm số
42
24y x x
. Hãy chọn mệnh đề sai trong bốn phát biểu sau:
A. Hàm số nghịch biến trên các khoảng
;1
và
0;1
B. Trên các khoảng
;1
và
0;1
, y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
C. Hàm số đồng biến trên các khoảng
;1
và
1;
D. Trên các khoảng
1;0
và
1; 
, y’ > 0 nên hàm số đồng biến trên mỗi khoảng đó
Câu 20. Hàm số nào sau đây nghịch biến trên từng khoảng xác định của nó ?
A.
2
12
x
y
x

B.
21
3
x
y
x

C.
1
1
x
y
x
D.
5
1
x
y
x

Câu 21. Hàm số
3
54
4
1
53
x
y x x
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 17
A. Đồng biến trên khoảng
;0
và
1
;
2




B. Đồng biến trên
C. Nghịch biến trên
1
;
2




và đồng biến trên
1
;
2




D. Nghịch biến trên
1
0;
2



Câu 22. Bảng biến thiên sau đây của hàm số nào?
A.
3
2
1
3
x
yx
B.
3
2
2
3
x
yx
C.
2
1
1
xx
y
x


D.
2
1
1
xx
y
x

x
- 2 0
,
y
- 0 + 0 -
y
Câu 23. Hàm số
42
21y x x
đồng biến trên các khoảng nào sau đây :
A.
1;0 ; 1; 
B.
1;0 ; 0;1
C.
; 1 ; 0;1
D.
Câu 24. Cho hàm số
35
2
x
y
x
. Chọn khẳng định đúng:
A. Hàm số đồng biến trên khoảng
2;
B. Hàm số nghịch biến trên
C. Hàm số đồng biến trên khoảng
;2 ; 2; 
D. Hàm số đồng biến trên
\2
Câu 25. Trong các hàm số sau, hàm số nào không đồng biến trên ?
A.
3
4yx
x

B.
4 3sin cosy x x x
C.
32
3 2 7y x x x
D.
3
y x x
Câu 26. Cho hàm số
32
2 3 12 5f x x x x
.Trong các mệnh đề sau, tìm mệnh đề
đúng?
A. Hàm số tăng trong khoảng
3;1
B. Hàm số tăng trong khoảng
1;1
C. Hàm số tăng trong khoảng
5;10
D. Hàm số giảm trong khoảng
1;3
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 18
Câu 27. Cho hàm số
23
1
x
y
x
. Khẳng định nào sau đây là đúng:
A. Hàm số đồng biến trên B. Hàm số đồng biến trên khoảng
1; 
C. Hàm số đồng biến trên
;1 ; 1; 
D. Hàm số đồng biến trên
\1
Câu 28. Trong các hàm số sau , hàm số nào đồng biến trên các khoảng
;1 ; 1; 
:
A.
2
32y x x
B.
42
1
3
2
y x x
C.
2
1
x
y
x
D.
2
1
1
xx
y
x

Câu 29. Hàm số
32
3y x x
đồng biến trên các khoảng là
A.
;0 ; 2; 
B.
;0
C.
2;
D.
; 2 ; 0; 
Câu 30. Hàm số
32
31y x x
nghịch biến trên các khoảng là
A.
;0 ; 2; 
B.
; 
C.
2;
D.
; 2 ; 0; 
Câu 31. Hàm số
42
21y x x
nghịch biến trên các khoảng nào sau đây?
A.
; 1 ; 0;1
B.
;0 ; 1; 
C.
; 1 ; 0; 
D.
1;0 ; 1; 
Câu 32. Cho hàm số
1
2
x
y
x
.Chọn phương án đúng dưới đây:
A. Hàm số đồng biến trên các khoảng
;2
và
2;
B. Hàm số đồng biến trên các khoảng
;2 2;
C. Hàm số nghịch biến trên các khoảng
;2
và
2;
D. Hàm số nghịch biến trên các khoảng
; 2 2;
Câu 33. Cho hàm số
2
1
1
x
y
x
. Chọn phương án đúng dưới đây:
A. Hàm số nghịch biến trên các khoảng
1; 
B. Hàm số nghịch biến trên các khoảng
; 1 1;
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 19
C. Hàm số nghịch biến trên khoảng
;1
D. Hàm số nghịch biến trên toàn trục số (trên )
Câu 34. Hàm số
32
34y x x
đồng biến trên các khoảng là
A.
;0 ; 2; 
B.
;0
C.
2;
D.
; 2 ; 0; 
Câu 35. Các khoảng nghịch biến của hàm số
42
1
25
4
y x x
là:
A.
2;0 ; 2; 
B.
;2 ; 0;2
C.
1;0 ; 1; 
D.
;0 ; 0; 
Câu 36. Cho hàm số
32
3 3 5y x x x
. Tìm tất cả giá trị của số thực x để hàm số
đồng biến.
A.
;x  
B.
;1x 
C.
1;x 
D.
;1 1;x 
Câu 37. Hàm số
4
2
3
22
x
yx
nghịch biến trên khoảng :
A.
0;
B.
; 
C.
3;5
D.
;0
Câu 38. Cho hàm số
21
2
x
y
x
. Tìm tất cả giá trị của số thực x để hàm số đồng biến.
A.
; 2 ; 2;xx  
B.
;2x 
C.
2;x 
D.
;x  
Câu 39. Hàm số
2
2y x x
nghịch biến trên khoảng
A.
1
;2
2



B.
1
1;
2



C.
1;2
D.
2;
Câu 40. Trong các hàm số sau, hàm số nào nghịch biến trên ?
A.
3
100yx
B.
2
21y x x
C.
42
21y x x
D.
1
1
x
y
x
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 20
ĐỀ 04 [2]
Câu 1. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
3
99yx
B.
4
16yx
C.
3
3 999y x x
D.
4
43y x x
Câu 2. Trong các hàm số sau, những hàm số nào luôn đồng biến trên từng khoảng
xác định của nó:
4 2 3
21
; 2 ; 3 5
1
x
y I y x x II y x x III
x
A. ( I ) và ( II ) B. Chỉ ( I ) C. ( II ) và ( III ) D. ( I ) và ( III)
Câu 3. Khoảng đồng biến của hàm số
2
2y x x
là
A.
;1
B.
0;1
C.
1;2
D.
1; 
Câu 4. Hàm số
43
2
10
2 16 15
23
xx
y x x
đồng biến trên khoảng nào sau đây?
A.
2;
B.
;1
C.
4;
D.
2;4
Câu 5. Hàm số
2
2y x x
nghịch biến trên khoảng
A.
2;
B.
1
1;
2



C.
1
;2
2



D.
1;2
Câu 6. Hàm số
2
1
x
y
x
đồng biến trên các khoảng
A.
;1
và
2;
B.
;1
và
1;2
C.
0;1
và
1;2
D.
;1
và
1; 
Câu 7. Hàm số
2
yx
x
A. Đồng biến trên khoảng
;0
B. Nghịch biến trên
C. Đồng biến trên khoảng
0;
D. Nghịch biến trên các khoảng
;0 ; 0; 
Câu 8. Hàm số nào sau đây nghịch biến trên khoảng
1;3
A.
2
1
23
2
y x x
B.
32
2
4 6 10
3
y x x x
C.
25
1
x
y
x
D.
2
1
1
xx
y
x

DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 21
Câu 9. Cho hàm số
2
53
1
xx
y
x

. Chọn phát biểu đúng trong các phát biểu sau:
A. Nghịch biến trên các khoảng
; 2 ; 4; 
B. Nghịch biến trên khoảng
2;4
C. Nghịch biến trên các khoảng
2;1 ; 1;4
D. Nghịch biến trên
\1
Câu 10. Hàm số
3
54
4
1
53
x
y x x
A. Đồng biến trên khoảng
;1
và nghịch biến trên khoảng
1; 
B. Nghịch biến trên khoảng
;1
và đồng biến trên khoảng
1; 
C. Nghịch biến trên
D. Đồng biến trên
Câu 11. Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó ?
A.
1
1
x
y
x
B.
1
1
x
y
x
C.
1
1
x
y
x

D.
1
1
x
y
x


Câu 12. Hàm số nào sau đây đồng biến trên ?
A.
tanyx
B.
3
2yx
C.
42
2y x x
D.
3
31y x x
Câu 13. Hàm số
2
2y x x
đồng biến trên khoảng
A.
2;
B.
1
1;
2



C.
1
;2
2



D.
1;2
Câu 14. Hàm số
32
32y x x
đồng biến trên khoảng nào sau đây:
A.
2;
B.
0;
C.
;0
D.
0;2
Câu 15. Hàm số
42
23y x x
nghịch biến trên các khoảng nào sau đây:
A.
;1
và
1; 
B.
1;0
và
1; 
C.
1;0
và
0;1
D.
;1
và
0;1
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 22
Câu 16. Hàm số
25
3
x
y
x
đồng biến trên:
A.
3; 
B. C.
;3
D.
\3
Câu 17. Cho hàm số
2
1yx
. Khẳng định nào sao đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng
0;1
B. Hàm số đồng biến trên khoảng
0;1
C. Hàm số nghịch biến trên khoảng
0;
D. Hàm số đồng biến trên khoảng
0;
Câu 18. Hàm số nào sau đây đồng biến trên
A.
32
33y x x x
B.
1 x
y
x
C.
1y
D.
2
1yx
Câu 19. Cho hàm số
1
2
x
y
x
. Khẳng định nào sau đây đúng:
A. Hàm số đã cho nghịch biến trên
B. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó
C. Hàm số đã cho đồng biến trên từng khoảng xác định của nó
D. Hàm số đã cho đồng biến trên khoảng
;2 2;
Câu 20. Bảng biến thiên sau đây là bảng biến thiên của một hàm số trong 4 hàm số
được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
x
1
0 1
,
y
- 0 + 0 - 0 +
y
- 3
4
4
A.
42
23y x x
B.
42
1
33
4
y x x
C.
42
33y x x
D.
42
23y x x
Câu 21. Cho hàm số
2
2y x x
. Các khoảng đồng biến, nghịch biến của hàm số là:
A. Đồng biến trên
0;1
và nghịch biến
1;2
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 23
B. Đồng biến trên
;1
và nghịch biến
1; 
C. Đồng biến trên
1;2
và nghịch biến
0;1
D. Đồng biến trên
1; 
và nghịch biến
;1
Câu 22. Các khoảng đơn điệu của hàm số
2
1
1
xx
y
x

là:
A. Đồng biến trên các khoảng
;0
và
2;
Nghịch biến trên các khoảng
0;1
và
1;2
B. Đồng biến trên khoảng
;1
; Nghịch biến trên khoảng
1;2
C. Đồng biến trên khoảng
2;
; Nghịch biến trên khoảng
0;2
D. Đồng biến trên khoảng
2;
; Nghịch biến trên khoảng
0;1
Câu 23. Hàm số
42
21y x x
đồng biến trên các khoảng nào?
A.
1;0
và
1; 
B.
1;1
C.
1;
D.
x
Câu 24. Các khoảng nghịch biến của hàm số
32
31y x x
là:
A.
;0
và
2;
B.
0;2
C.
0;
D.
Câu 25. Hàm số nào sau đây là hàm số đồng biến trên
A.
1
x
y
x
B.
2
1 3 2y x x
C.
2
1
x
y
x
D.
tanyx
Câu 26. Hàm số
2
1yx
A. Đồng biến trên
0;1
B. Đồng biến trên
0;1
C. Nghịch biến trên
0;1
D. Nghịch biến trên
1;0
Câu 27. Cho hàm số
32
4
23
3
y x x x
. Khẳng định nào sau đây sai:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 24
A. Hàm số đã cho nghịch biến trên
1
;
2



B. Hàm số đã cho nghịch biến trên
1
;
2



C. Hàm số đã cho nghịch biến trên
1
;
2




và
1
;
2




D. Hàm số đã cho nghịch biến trên
Câu 28. (Đề thi minh họa THPT Quốc Gia lần 1) Hàm số
4
21yx
đồng biến trên
khoảng nào?
A.
1
;
2




B.
0;
C.
1
;
2




D.
;0
Câu 29. (Chuyên KHTN lần 2) Cho hàm số
42
21y x x
. Mệnh đề nào dưới đây là
đúng?
A. Hàm số đồng biến trên
;1
B. Hàm số đồng biến trên
;0
C. Hàm số đồng biến trên
0;
D. Hàm số đồng biến trên
1; 
Câu 30. (THPT Lê Hồng Phong lần 1) Khoảng đồng biến của hàm số
32
34y x x
là
A.
; 2 2;
B.
;0 2;
C.
2;0
D.
0;2
Câu 31. (THPT Kim Liên lân 1) Cho hàm số
2
1
x
y
x
. Trong các khẳng định sau,
khẳng định nào là đúng?
A. Hàm số nghịch biến trên B. Hàm số đồng biến trên từng khoảng xác định
C. Hàm số đồng biến trên D. Hàm số có duy nhất một cực trị
Câu 32. (THPT Nguyễn Thị Minh Khai) Hàm số
fx
liên tục trên và có đạo hàm
2
2
' 1 2f x x x x
. Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
2; 
B. Hàm số nghịch biến trên các khoảng
2; 1 ; 0; 
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 25
C. Hàm số đồng biến trên khoảng
;2
D. Hàm số đồng biến trên các khoảng
; 2 ; 0; 
Câu 33. (Sở GD và ĐT Vĩnh Phúc lần 2) Hàm số
2
2y x x
đồng biến trên khoảng
nào?
A.
0;2
B.
1;2
C.
0;1
D.
;1
Câu 34. (Chuyên KHTN lần 3) Cho hàm số
1
x
y
x
. Mệnh đề nào đúng
A. Hàm số đồng biến trên khoảng
0;1
B. Hàm số nghịch biến trên
\1
C. Hàm số nghịch biến trên
;1 1;
D. Hàm số nghịch biến trên từng khoảng
;1
và
1; 
Câu 35. (Lương Tài –Bắc Ninh lần 1) Trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây, hàm số nào là hàm số đồng biến trên khoảng
; 
A.
21
2
x
y
x
B.
3
32y x x
C.
42
1
4
y x x
D.
3
2y x x
Câu 36. (Chuyên KHTN lần 4) Cho hàm số
fx
có đạo hàm
23
' 1 1 2f x x x x
. Hàm số
fx
đồng biến trên khoảng nào dưới đây?
A.
;1
B.
1;1
C.
2;
D.
1;2
Câu 37. (Chuyên KHTN lần 4) Cho hàm số
42
43y x x
. Mệnh đề nào sau đây
đúng?
A. Hàm số đồng biến trên
;0
và nghịch biến trên
0;
B. Hàm số đồng biến trên
; 
C. Hàm số nghịch biến trên
;0
và đồng biến trên
0;
D. Hàm số nghịc biến trên
; 
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 26
Câu 38. (THPT Gia Lộc II, Hải Dương) Tìm khoảng đồng biến của hàm số
32
4 4 2y x x x
A.
12
;
23



B.
1
;
2




C.
2
;
3




D.
1
;
2




và
2
;
3




Câu 39. (THPT Gia Lộc II, Hải Dương) Cho hàm số
2
6y x x
. Hãy chọn đáp án
đúng
A. Hàm số đồng biến trên
1
;
2




và
1
;2
2



B. Hàm số đồng biến trên
;3
và
2;
C. Hàm số nghịch biến trên
1
;
2




và
1
;2
2



D. Hàm số đồng biến trên
1
;
2




Câu 40. (Chu Văn An- HN lần 2) Hàm số
32
3y x x
nghịch biến trên khoảng nào
dưới đây?
A.
1;1
B.
;1
C.
0;2
D.
2;
Câu 41. (Chuyên Lê Quý Đôn – Đà Nẵng) Cho hàm số
1
1
xm
f x m
x

A. Hàm số luôn giảm trên
;1
và
1; 
với
1m
B. Hàm số luôn giảm trên Tập xác định
C. Hàm số luôn tăng trên
;1
và
1; 
với
1m
D. Hàm số luôn tăng trên
;1
và
1; 
Câu 42. (Quốc học Quy Nhơn- Bình Định) Cho hàm số
32
2 6 6 2017y x x x
.
Mệnh đề nào sau đây sai?
A. Hàm số đã cho đồng biến trên
B. Hàm số đã cho nghịch biến trên
C. Trên khoảng
;2
hàm số đã cho đồng biến
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 27
D. Trên khoảng
2;
hàm số đã cho đồng biến
Câu 43. (Chuyên Lê Thánh Tông – Quảng Nam) Cho hàm số
2
2f x x x
. Trong
các khẳng định sau, khẳng định nào đúng?
A. Hàm số nghịch biến trên khoảng
1;2
B. Hàm số nghịch biến trên khoảng
;1
C. Hàm số đồng biến trên khoảng
2;2
D. Hàm số đồng biến trên khoảng
2;
VẤN ĐỀ 2. TÌM THAM SỐ M ĐỂ HÀM SỐ LUÔN TĂNG (HOẶC GIẢM)
TRÊN TẬP XÁC ĐỊNH D
Phương pháp
Các hàm số :
32
0y ax bx cx d a
và
2
0
ax bx c
ya
Ax B


luôn tăng (giảm) trên
từng khoảng xác định của nó khi và chỉ khi
0y
0y
xD
Hàm số:
ax b
y
cx d
luôn tăng (giảm) trên từng khoảng xác định của nó khi và chỉ khi
0y
0y
xD
A - VẬN DỤNG
Ví dụ 1. Cho hàm số
32
1
22
3
y x mx m x
. Tìm m để hàm số nghịch biến trên
tập xác định
Ví dụ 2. Tìm m để các hàm số sau luôn đồng biến trên tập xác định của nó
1)
32
3 2 1 12 5 2y x m x m x
Đs:
11
66
m
2)
3 2 2
1 4 9y x m x m x
Đs:
1 3 3 1 3 3
22
mm
Ví dụ 3. Tìm m để hàm số đồng biến trên tập xác định của nó?
1)
32
1
1 3 2
3
y m x mx m x
Đs:
2m
Ví dụ 4. Tìm m để hàm số sau luôn đồng biến trên tập xác định của nó?
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 28
1)
2 3 2
1
2 3 1
3
y m m x mx x
Đs:
30m
2)
2 3 2
1
1 1 3 5
3
y m x m x x
Đs:
12m
Ví dụ 5. Tìm m để hàm số đồng biến trên từng khoảng xác định của nó?
1)
xm
y
xm
Đs:
0m
2)
4mx
y
xm
Đs:
22m
Ví dụ 6. Tìm m để hàm số đồng biến trên từng khoảng xác định của nó?
1)
2
23
2
x x m
y
x

Đs:
2m 
2)
22
1
x x m
y
x

Đs:
0m
B- BÀI TẬP ÁP DỤNG
Bài tập 1. Tìm m để hàm số sau luôn nghịch biến trên ?
1)
32
3 2 2y x m x mx
Đs:
6 3 3 6 3 3m
2)
32
1
2 2 1 3 2
3
y x x m x m
Đs:
5
2
m 
3)
32
1
27
3
y x m x mx
Đs:
41m
4)
32
1
3 2 1
3
y x mx m x
Đs:
21m
Bài tập 2. Tìm m để hàm số sau luôn đồng biến trên ?
1)
3 2 2
2 4 9y x m x m x
Đs:
42mm
2)
32
5y x mx x
Đs:
33m
3)
32
1
43
3
y x mx x
Đs:
22m
4)
32
3y x x mx m
Đs:
3m
Bài tập 3. Tìm m để hàm số sau giảm trên ?
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 29
1)
3
22
2 2 8 1
3
x
y m m x m x m
Đs:
2m 
2)
32
1
1 2 2 2 2 5
3
y m x m x m x
Đs:
23m
3)
32
11
1 3 2
33
y mx m x m x
Đs:
26
2
m
4)
32
3 3 1y mx mx x
Đs:
1m 
Bài tập 4. Tìm m để hàm số sau đồng biến trên ?
1)
2 3 2
1
4 2 2 3
3
m x m x x
Đs:
26mm
2)
3
22
1 1 3 1
3
x
m m x x
Đs:
12mm
3)
32
11m x m x x m
Đs:
1;4m
4)
32
2 3 2 3 3 9m x m x m x
Đs:
2m 
Bài tập 5. Tìm m để hàm số đồng biến trên từng khoảng xác định của nó?
1)
1m x m
y
xm

Đs:
02m
2)
2
3
mx
y
xm

Đs:
12mm
3)
43mx m
y
xm

Đs:
41m
4)
12mx
y
xm

Đs:
2;1m
Bài tập 6. Tìm m để hàm số nghịch biến trên từng khoảng xác định của nó?
1)
1x
y
xm
Đs:
1m
2)
32mx m
y
xm

Đs:
31m
3)
5
1
mx
y
x
Đs:
5m
Bài tập 7. Tìm m để hàm số nghịch biến trên từng khoảng xác định của nó?
1)
2
2 1 5
1
x m x m
y
x
Đs:
4m
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 30
2)
2 3 2
1 2 2m x mx m m
y
xm
Đs:
1m 
Bài tập 8. Tìm m để hàm số luôn đồng biến trên từng khoảng xác định của nó
1)
2
21
1
mx x
y
x

Đs:
01m
2)
2
1
m
yx
x
Đs:
0m
Bài tập 9. Cho hàm số
3 2 2
1
1 2 3
3
y x m x m x m
. Chứng minh rằng hàm số
luôn nghịch biến trên tập xác định cuả nó?
Bài tập 10. Cho hàm số
32
2 3 2 1 6 1 1y x m x m m x
. Chứng minh hàm số không
thể luôn đồng biến trên tập xác định của nó?
C - BÀI TẬP TRẮC NGHIỆM
ĐỀ 01
Câu 1. Tất cả giá trị của tham số m để hàm số
2
2
mx
y
xm
luôn nghịch biến trên từng
khoảng xác định của nó là:
A.
2 2m
B.
2m 
hoặc
2m
C.
2 2m
D.
2m 
hoặc
2m
Câu 2. Hàm số
32
3 2 1y x mx x
đồng biến trên khi và chỉ khi:
A.
m
B.
32m
C.
m
D.
3 2 3 2m
Câu 3. Hàm số
2
2
1
x mx
y
x
giảm trên từng khoảng xác định khi:
A.
3m 
B.
3m
C.
3m 
D.
m
Câu 4. Hàm số
3
1
kx
y
x
giảm trên từng khoảng xác định khi
A.
3k
B.
3k 
C.
3k
D.
3k 
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 31
Câu 5. Hàm số
1mx
y
xm
nghịch biến trên từng khoảng xác định khi giá trị của m
bằng
A.
1m
B.
1m
C.
m
D.
11m
Câu 6. Tìm tất cả các giá trị của tham số m sao cho hàm số
32
3 3 1y x x mx
đồng
biến trên . Chọn kết quả đúng:
A.
1m
B.
1m
C.
1m
D.
1m
Câu 7. Tìm tất cả các giá trị của tham số m sao cho hàm số
3
2
1 4 5
3
x
y m x x
đồng biến trên . Chọn kết quả đúng:
A.
31m
B.
31mm
C.
22m
D.
22m
Câu 8. Hàm số
32
1
1 3 2
3
y m x mx m x
luôn đồng biến trên tập xác định khi:
A.
1
2
m
B.
2m
C.
1m
D.
2m
Câu 9. Hàm số
78mx m
y
xm

luôn đồng biến trên từng khoảng xác định khi:
A.
81m
B.
81m
C.
41m
D.
41m
Câu 10. Cho hàm số
cosy x ax
. Với giá trị nào của a thì hàm số đồng biến trên
A.
1a
B.
1a 
C.
01a
D.
10a
Câu 11. Cho hàm số
32
1
2 2 1 3 2
3
y x x m x m
. Để hàm số nghịch biến trên
thì điều kiện tham số m là
A.
5
2
m
B.
5
2
m 
C.
1m
D.
1m 
Câu 12. Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số
4mx
y
xm
đồng
biến trên từng khoảng xác định
A.
2;2
B.
;2
C.
2; 
D.
;2
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 32
Câu 13. Tìm tập hợp các giá trị tham số thực m để hàm số
sin 7 5 3y m x x m
đồng
biến trên
A.
7m 
B.
77m
C.
7m
D.
1m 
Câu 14. Tìm tát cả các giá trị của tham số m để hàm số
32
12y mx mx m m x
đồng biến trên
A.
4
3
m
B.
4
3
m
và
0m
C.
0m
hoặc
4
3
m
D.
4
3
m
Câu 15. Tìm tập các giá trị của tham số thực m để hàm số
2
11y x mx
đồng
biến trên
; 
A.
;1
B.
1; 
C.
1;1
D.
;1
Câu 16. (THPT Ngô Sĩ Liên- Bắc Giang) Hàm số
32
1
1 1 1
3
y x m x m x
đồng
biến trên tập xác định của nó khi và chỉ khi
A.
1
2
m
m


B.
1
2
m
m

C.
21m
D.
21m
Câu 17. (THPT chuyên Lê Hồng Phong- HCM) Tìm tất cả các giá trị của tham số m
để hàm số
1mx
y
xm
đồng biến trên từng khoảng xác định của nó
A.
1m 
hoặc
1m
B.
1m 
hoặc
1m
C.
1m 
hoặc
1m
D.
11m
Câu 18. (THPT Đông Quan) Hàm số
1mx
y
xm
đồng biến trên khoảng
1; 
khi
A.
11m
B.
1m
C.
\ 1;1m
D.
1m
Câu 19. (THPT Hà Trung- Thanh Hóa) Tìm tất cả các giá trị của m để hàm số
2
2
mx
y
xm
đồng biến trên mỗi khoảng xác định
A.
2
2
m
m

B.
22m
C.
2
2
m
m

D.
22m
Câu 20. (THPT Ngô Gia Tự) Tìm tất cả các giá trị thực của tham số m để hàm số
cosy x m x
đồng biến trên
A.
1m
B.
1m
C.
1;1 \ 0m
D.
11m
Câu 21. (THPT Ninh Giang- Hải Dương) Hàm số
32
23
3
m
y x x m x m
luôn
đồng biến trên thì giá trị nhỏ nhất của m là
A.
1m
B.
2m 
C.
4m 
D.
0m
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 33
Câu 22. (Chuyên ĐH Vinh) Các giá trị của tham số m để hàm số
32
3 3 2y mx mx x
nghịch biến trên và đồ thị của nó không có tiếp tuyến song song với trục hoành là
A.
10m
B.
10m
C.
10m
D.
10m
Câu 23. (THPT Dịu Hiền- Cần Thơ) Tìm m để hàm số
sin 3y mx x
đồng biến trên
A.
1m
B.
1m
C.
1m 
D.
1m
VẤN ĐỀ 3. TÌM THAM SỐ M ĐỂ HÀM SỐ LUÔN TĂNG (HOẶC GIẢM)
TRÊN MỘT KHOẢNG
A. VẬN DỤNG
Ví dụ 1. Cho hàm số :
32
3 2 4y x x mx
. Tìm m để hàm số đồng biến trên khoảng
;0
.
Cách 1. Giải biện luận theo phương trình
'y
.
Cách 2. Cô lập m. Đs:
3
2
m 
Ví dụ 2. Cho hàm số:
3 2 2
3 3 1 2 3y x mx m x m
. Xác định m để hàm số nghịch
biến trên khoảng
1;2
? Đs:
12m
Ví dụ 3. Cho hàm số
32
32y x x mx
. Xác định m để hàm số đồng biến trên khoảng
0;
Đs:
3m 
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Cho hàm số
3 2 2
1 2 3 2 1y x m x m m x
. Tìm m để hàm số đồng biến
trên khoảng
2;
? Đs:
3
2
2
m
Bài tập 2. Cho hàm số
32
3 3 1y mx x x
. Tìm m để hàm số nghịch biến trên khoảng
1;2
Đs: Không tồn tại m
Bài tập 3. Cho hàm số
32
3 1 4y x x m x m
. Tìm m để hàm số nghịch biến trên
khoảng
1;1
? Đs:
10m 
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 34
Bài tập 4. Cho hàm số
32
y x mx m
. Tìm m để hàm số đồng biến trên khoảng
1;2
?
Đs:
3m
Bài tập 5. Cho hàm số
32
1
1 3 4
3
y x m x m x
. Tìm m để hàm số đồng biến
trên khoảng
0;3
? Đs:
12
7
m
Bài tập 6. Cho hàm số
32
1
1 2 7
3
y x m x m m x
. Tìm m để hàm số đồng biến
trên khoảng
4;9
? Đs:
2; 9mm
Bài tập 7. Cho hàm số
3 2 2
2 7 7 2 1 2 3y x mx m m x m m
. Tìm m để hàm số
đồng biến trên khoảng
2;
? Đs:
5
1
2
m
Bài tập 8. Cho hàm số
3 2 2
2 7 7 2 1 2 3y x mx m m x m m
. Tìm m để hàm số
đồng biến trên khoảng
3; 
? Đs:
17
12
m
Bài tập 9. Cho hàm số
32
3 2 1 12 5 2y x m x m x
. Tìm m để hàm số đồng biến
trên khoảng
2;
? Đs:
5
12
m
Bài tập 10. Cho hàm số
32
11
1 3 2
33
y mx m x m x
. Tìm m để hàm số đồng biến
trên khoảng
2;
? Đs:
2
3
m
Bài tập 11. Cho hàm số
32
1
2 1 1
3
y mx m x m x m
. Tìm m để hàm số đồng biến
trên khoảng
2;
? Đs:
9
13
m
Bài tập 12. Cho hàm số
3 2 2
3 3 1 1y x mx m x m
. Tìm m để hàm số đồng biến trên
mỗi khoảng
;2
và
4;
? Đs:
3m
Bài tập 13. Cho hàm số
32
3 2 1 12 5 2y x m x m x
. Tìm m để hàm số đồng biến
trên mỗi khoảng
;1
và
2;
? Đs:
75
12 12
m
C. BÀI TẬP TRẮC NGHIỆM
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 35
Câu 1. Tìm tham số m để hàm số
3
2
13
3
x
f x m x m x
tăng trên khoảng
0;3
A.
12
7
m
B.
12
7
m
C.
12
7
m
D.
12
7
m
Câu 2. Tìm tham số m để hàm số
4mx
fx
xm
tăng trên khoảng
2;
A.
2m
B.
2m
C.
2m
D.
0m
Câu 3. Tìm tham số m để hàm số
4mx
fx
xm
giảm trên khoảng
;1
A.
21m
B.
21m
C.
21m
D.
21m
Câu 4. Tìm tham số m để hàm số
3
2
1
23
33
x
y m x m m x
nghịch biến
trên khoảng
1; 
A.
4
55
2
m
m
B.
4
55
2
m
m
C.
4
55
2
m
m
D.
4
55
2
m
m
Câu 5. Với giá trị nào của m thì hàm số
32
2 15 2y x mx m x
đồng biến trên
1;3
?
A.
3m
B.
18
5
m
C.
18
3
5
m
D.
18
5
m
Câu 6. Tìm m để hàm số
32
3 3 1y x x mx
nghịchbiến trên khoảng
0;
A.
0m
B.
1m 
C.
1m
D.
2m
Câu 7. Hàm số
2x
y
xm
đồng biến trên khoảng
2;
khi
A.
2m
B.
2m
C.
2m 
D.
2m 
Câu 8. Hàm số
32
61y x x mx
đồng biến trên khoảng
0;
khi:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 36
A.
0m
B.
0m
C.
0m
D.
0m
Câu 9. Với giá trị nào của m thì hàm số
22
23y x mx m
đồng biến trên khoảng
2;
A.
2m
B.
2m 
C.
2m
D.
0m
Câu 10. Cho hàm số
3 2 2
1 2 3 2 1y x m x m m x
. Kết luận nào sau đây đúng
A. Hàm số luôn đồng biến trên
B. Hàm số luôn đồng biến trên
C. Hàm số không đơn điệu trên
D. Hàm số có hai cực trị và khoảng cách giữa hai điểm cực trị bằng 1 với mọi m
Câu 11. Cho hàm số
1mx
y
xm
đồng biến trên khoảng
1; 
khi
A.
11m
B.
1m
C.
\ 1;1m
D.
1m
Câu 12. Tìm tất cả các giá trị của tham số m sao cho hàm số
32
1
1
32
m
y x x x
đồng
biến trên khoảng
1; 
. Chọn kết quả đúng:
A.
2m 
B.
2m
C.
22m
D.
22m
Câu 13. Tìm tất cả các giá trị thực của tham số m để hàm số
32
1
1 3 1
3
m
y x m x x



nghịch biến trên tập xác định của nó
A.
4; 1
B.
4; 1
C.
4;1
D.
41mm
Câu 14. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
32
34y x x mx
nghịch biến trên khoảng
0;
.
A.
;0m 
B.
0;m 
C.
0;m 
D.
;1m 
Câu 15. Cho hàm số
2
2
1
x x m
y
x

với m là tham số . Hàm số luôn đồng biến trên các
khoảng xác định của nó khi và chỉ khi:
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 37
A.
3m 
B.
3m
C.
6m 
D.
1m
Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
32
3 3 1y x mx mx
nghịch biến trên khoảng
0;
.
A.
3m 
B.
3m
C.
6m 
D.
1m
Câu 17. Giá trị của tham số m để hàm số
32
3 3 2 3 2y x mx m x
đồng biến trên
khoảng
2;
là
A.
1
2
m
B.
m
C.
1
2
m
D.
1
2
m
Câu 18. Hàm số
32
61y x x mx
đồng biến trên khoảng
0;
. Giá trị của m là:
A.
12m
B.
0m
C.
0 12m
D.
0m
Câu 19. Hàm số
32
1
3
y x x mx
đồng biến trên khoảng
1; 
thì m thuộc khoảng
nào sau
A.
1;
B.
1;3
C.
;3
D.
3; 
Câu 20. Tìm m để hàm số
2
4
2
xx
y
xm
đồng biến trên nửa khoảng
1; 
A.
1
;
3
m



B.
1
;
3
m




C.
1
;
3
m



D.
1
; \ 0
3
m



Câu 21. Tìm tất cả các giá trị của m để hàm số
1mx
y
xm
tăng trên khoảng
1; 
A.
1m 
B.
1m 
C.
1m
D. Đáp án khác
Câu 22. Tìm tất cả các giá trị của m để hàm số
32
1
1 3 10
3
y x m x m x
đồng biến trên khoảng
0;3
A.
12
3
m
B.
12
3
m
C.
12
3
m
D.
m
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 38
Câu 23. Cho hàm số
78mx m
y
xm

. Tìm tất cả các giá trị của m để hàm số luôn đồng
biến trên trên khoảng
0;
.
A.
80m
B.
81m
C.
80m
D.
80m
Câu 24. Tìm tất cả các giá trị của m để hàm số
32
1
1 3 2
33
m
y x m x m x
đồng
biến trên
2;
.
A.
2
;
3
m



B.
2
;
3
m




C.
2
;
3
m



D.
2
;
3
m




Câu 25. Tìm giá trị nhỏ nhất của tham số m sao cho hàm số
32
3 3 1y x x mx
nghịch
biến trên
0;
A.
1m 
B.
1m
C.
2m
D.
2m 
Câu 26. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
sin 3
sin
x
y
xm
đồng biến
trên khoảng
0;
2



A.
1 0 3mm
B.
1m 
C.
03m
D.
3m
Câu 27. Tìm tất cả các giá trị của tham số m sao cho hàm số
32
3 3 1y x x mx
nghịch
biến trên
0;
A.
1m 
B.
1m 
C.
1m
D.
01m
Câu 28. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
sin 2
sin
x
y
xm
đồng biến
trên khoảng
0;
2



A.
0 1 2mm
B.
0m
C.
12m
D.
2m
Câu 29. Tìm tất cả giá trị m để hàm số
32
61y x x mx
đồng biến trên khoảng
0;
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 39
A.
12m
B.
0m
C.
12m
D.
0m
Câu 30. Tìm tất cả giá trị m để hàm số
4mx
y
xm
nghịch biến trên
;1
A.
21m
B.
22m
C.
22m
D.
21m
ĐỀ 02
Câu 1. Cho hàm số
2
4
2
xx
y
xm
. Để hàm số đồng biến trên
1; 
thì m phải thỏa
A.
1
4;
2
m



B.
1;4 \ 2m
C.
1
;1 \ 0
2
m



D.
1
1; \ 0
2
m



Câu 2. Để hàm số
32
5
32
x mx
yx
đồng biến trên khoảng
1; 
thì các giá trị
thích hợp của tham số m là
A.
2m 
B.
2m 
C.
2m
D.
2m
Câu 3. Để hàm số
3
14
3
x
y a x
đồng biến trên
0;3
thì tham số a phải thỏa
A.
3a 
B.
3a 
C.
12
7
a
D.
12
7
a
Câu 4. Cho hàm số
32
3 2 1 12 5 2y x m x m x
. Để hàm số đồng biến trên
khoảng
2;
thì tham số m phải thỏa
A.
11
66
m
B.
5
12
m
C.
1
6
m 
D.
5
12
m
Câu 5. Cho hàm số
2
22
1
x mx m
y
xm
. Để hàm số này nghịch biến trong khoảng
2;
thì giá trị của tham số m là
A.
4 3 2 4 3 2m
B.
4 3 2m
C.
1m
D.
4 3 2m 
Câu 6. Cho hàm số
32
2 3 6 1y x x mx
. Để hàm số nghịch biến trên
0;2
thì tham
số m thỏa mãn điều kiện
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 40
A.
6m
B.
1
4
m
C.
6m 
D.
1
4
m
Câu 7. Tìm m để hàm số
22
56
3
x x m
fx
x
đồng biến trên
1; 
.
A.
44m
B.
42m
C.
22m
D.
24m
Câu 8. Với các giá trị nào của tham số m thì hàm số
32
3 2 2f x x x mx
nghịch
biến trên khoảng
0;
A.
4
3
m
B.
3
2
m 
C.
16
3
m 
D.
32
27
m 
Câu 9. Tìm tất cả các giá trị thực của tham số m để hàm số
1 2 1y mx m x
nghịch biến trên khoảng
2;D 
A.
0m
B.
1m 
C.
1m 
D.
21m
Câu 10. (THPT AMSTERDAM HN) Trong tất cả các giá trị của tham số m để hàm số
32
1
3
y x mx mx m
đồng biến trên , giá trị nhỏ nhất của m là
A.
4
B.
1
C.
0
D.
1
Câu 11. (THPT AMSTERDAM HN) Xác định các giá trị của tham số m để hàm số
32
3y x mx m
nghịch biến trên khoảng
0;1
?
A.
1
2
m
B.
1
2
m
C.
0m
D.
0m
Câu 12. (THPT chuyên Hạ Long) Tìm các giá trị thực của tham số m để hàm số
2
sin
cos
mx
y
x
nghịch biến trên khoảng
0;
6



A.
5
2
m
B.
5
2
m
C.
5
4
m
D.
5
4
m
Câu 13. (THPT Hàm Rồng) Tìm tất cả các giá trị thực của tham số m sao cho hàm số
tan 2
tan
x
y
xm
đồng biến trên khoảng
0;
4



A.
0m
B.
12m
C.
0
12
m
m

D.
2m
Câu 14. (THPT Kiến An) Tìm tất cả các giá trị m để hàm số
2sin 1
sin
x
y
xm
nghịch biến
trên khoảng
0;
2



A.
1m 
B.
0m
C.
4m
D.
0m
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 41
Câu 15. (THPT Kiến An) Tìm tất cả các giá trị m để hàm số
32
1
22
3
y x x mx
nghịch biến trên khoảng
0;3
A.
3m
B.
0m
C.
4m
D.
0m
Câu 16. (THPT Lê Quý Đôn- Bình Phước) Tập hợp các giá trị của m để hàm số
32
1
1 3 2 1
3
y mx m x m x
đồng biến trên khoảng
2;
là
A.
2
;1
3
S



B.
2
;
3
S



C.
;1S 
D.
2
;1
3
S



Câu 17. (THPT Lục Ngạn 1- Bắc Ninh) Hãy chọn câu trả lời đúng. Hàm số
2 siny x x
A. Nghịch biến trên tập xác định B. Đồng biến trên
;0
C. Đồng biến trên tập xác định D. Đồng biến trên
0;
Câu 18. (Sở GD Bình Định) Tìm tất cả các giá trị thực của tham số m sao cho hàm số
1 2 2m x m
y
xm
nghịch biến trên khoảng
1;
A.
;1 2;m 
B.
1m
C.
12m
D.
12m
Câu 19. (THPT Nghĩa Hưng- Nam Định) Cho hàm số
2
22x mx m
y
xm
. Với giá trị
nào của m thì hàm số đồng biến trên khoảng
1; 
A.
3 17
2
4
m

B.
2m
C.
3 17
4
m
D.
3 17
2
4
mm
Câu 20. (THPT Phù Cát- Binh Định) Tất cả các giá trị thực của tham số m để hàm số
32
11
32
y x mx mx
đồng biến trên khoảng
1; 
A.
4m
B.
4m
C.
4m
D.
0m
Câu 21. (THPT Yên Lạc- Vĩnh Phúc) Cho hàm số
1 1 2
1
mx
y
xm

. Tìm tất cả các
giá trị của tham số m để hàm số đồng biến trên khoảng
17;37
A.
41m
B.
2
6
m
m

C.
2
4
m
m

D.
12m
Câu 22. (THPT Yên Lạc- Vĩnh Phúc) Cho hàm số
1 sin 2
sin
mx
y
xm

. Tìm tất cả các
giá trị của tham số m để hàm số nghịch biến trên khoảng
0;
2



DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 42
A.
12m
B.
1
2
m
m

C.
1
2
m
m

D.
0
1
m
m
Câu 23. (THPT Ninh Giang – Hải Dương) Tìm tâph hợp các giá trị của tham số m để
hàm số
2
2
x
y x x m
đồng biến trên
;2
A.
1
4
m
B.
1
4
m
C.
2m
D.
7m
Câu 24. (THPT chuyên Vĩnh Phúc) Tìm tất cả các giá trị của tham số m để hàm số
32
12
1 2 3
33
y x m x m x
đồng biến trên
1; 
A.
2m
B.
2m
C.
1m
D.
1m
Câu 25. (THPT Phạm Văn Đồng- Phú Yên) Tìm tập hợp tất cả các giá trị cuẩ tham
số thực m để hàm số
3 2 2
1
41
3
y x mx x m m
đồng biến trên
1;3
A.
;1
B.
;1
C.
10
;
3




D.
10
;
3



Câu 26. (THPT Phả Lại) Tìm tất cả các giá trị của tham số m để hàm số
32
2 3 1 6 2 2017y x m x m x
nghịch biến trên khoảng
;ab
sao cho
3ba
A.
9m
B.
0
6
m
m
C.
6m
D.
0m
Câu 27. (Chuyên Bắc Giang) Tìm m để hàm số
2cos 1
cos
x
y
xm
đồng biến trên
0;
A.
1m 
B.
1
2
m 
C.
1m 
D.
1m
Câu 28. (Chuyên ĐH Vinh) Tìm tất cả các giá trị của tham số m để hàm số
2 4 2
12y m x x mx
đồng biến trên
1; 
A.
1m 
hoặc
1m
B.
1m 
hoặc
15
2
m
C.
1m 
hoặc
15
2
m
D.
1m 
Câu 29. (Chuyên Lê Hồng Phong- Nam Định) Tìm tất cả các giá trị thực của tham số
m để hàm số
cot 1
cot 1
x
y
mx
đồng biến trên khoảng
;
42




A.
;0 1;m
B.
;0m 
C.
1;m 
D.
;1m 
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 43
VẤN ĐỀ 4. TÌM THAM SỐ M ĐỂ HÀM SỐ LUÔN TĂNG (HOẶC GIẢM)
TRÊN ĐOẠN DÀI L
A. VẬN DỤNG
Ví dụ 1. Cho hàm số
32
3y x x mx m
. Tìm m để hàm số nghịch biến trên đoạn có
độ dài bằng 1. Đs:
9
4
m
Ví dụ 2. Cho hàm số
32
11
2 3 4
32
y x mx mx m
. Tìm m để hàm số đồng biến trên
đoạn có độ dài bằng 3. Đs:
1; 9mm
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Cho hàm số
32
3y x x mx m
. Tìm m để hàm số nghịch biến trên đoạn có
độ dài bằng 3. Đs:
15
4
m 
Bài tập 2. Cho hàm số
32
3 2 2 3 1y x mx m x
. Tìm m để hàm số nghịch biến trên
đoạn có độ dài bằng
2 11
. Đs:
15
4
m 
C. BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm m để hàm số
32
3y x m x
nghịch biến trên khoảng có độ dài bằng 2
A.
11m
B.
1m 
C.
22m
D.
2m 
Câu 2. Cho hàm số
3 2 2
2 3 3 1 6 2 3y x m x m m x
. Tìm m để hàm số nghịch
biến trên đoạn có độ dài bằng 4
A.
53mm
B.
53mm
C.
53mm
D.
53mm
Câu 3. Hàm số
32
3y x x mx m
nghịch biến trên một khoảng có độ dài bằng 1
khi:
A.
9
4
m
B.
9
4
m 
C.
9
2
m
D.
9
2
m 
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 44
Câu 4. Cho hàm số
32
1
1 2 1 3 2
3
y m x m x m x m
. Giá trị m làm cho hàm số
có khoảng nghịch biến có độ dài bằng 4 là?
A.
7 61
6
m
B.
7 61
6
m
C.
7 61
6
m
D.
7 62
6
m
Câu 5. Tìm tham số m để hàm số
32
3y x x mx m
nghịch biến trên một khoảng
có độ dài bằng 1
A.
9
4
m
B.
9
4
m
C.
9
4
m
D.
9
4
m
Câu 6. Với giá trị nào của m thì hàm số
32
1
1 4 2
3
y x m x x
có độ dài khoảng
nghịch biến là
25
A.
2; 4m
B.
2;4m
C.
1;3m
D.
3;1m
Câu 7. (THPT Hùng Vương- Bình Định) Xác định m để hàm số
32
1 4 7y x m x x
có độ dài khoảng nghịch biến bằng 12
A.
2, 4mm
B.
1, 3mm
C.
0, 1mm
D.
2, 4mm
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
VẤN ĐỀ 1. XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ Phương pháp
Bước 1. Tìm tập xác định của hàm số
Bước 2. Tính đạo hàm y . Tìm nghiệm (nếu có ) của phương trình y  0
Bước 3. Lập bảng biến thiên (Xét dấu đạo hàm)
Bước 4. Dựa vào bảng biến thiên để kết luận
+) Nếu f x  0 với mọi x ;
a b thì hàm số y f x đồng biến trên khoảng a;b .
+) Nếu f x  0 với mọi x ;
a b thì hàm số y f x đồng biến trên khoảng a;b . A- VẬN DỤNG Ví dụ 1.
Xét chiều biến thiên của các hàm số sau Mẫu: 1 1 3 2
y x  3x  9x  2 1) 3 2 y x x  2x 1 2) 3 2
y  x  6x  9x  2 3 2 3) 1 3 2
y  x  3x  4x  3 4) 3 2
y x x x  4 5) 3 2 y
x x  3x 1 3 1 6) 3 2
y  x  6x 12x 1 7) 3
y x  3x 1 8) 3
y   x  4x 10 3 Ví dụ 2. x
Xét chiều biến thiên của các hàm số sau Mẫu: 2 1 y x1 3x 1 x 1 x 1 x  2 1) y y y y  1 2) 2x 1   3) 2x x  4) 1 x 1 2 Ví dụ 3. x  2x  2
Xét chiều biến thiên của các hàm số sau Mẫu: y x 1 2 x x 1 2 x  2x  2 4 x 1 1) y y y x  4) y    2x  2) 1 1 3) x x 4 x
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 1
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Ví dụ 4.
Xét chiều biến thiên của các hàm số sau. 4 3 3 1) 3 2 y
x  2x x  3 2) 3 2 y  2
x  6x  6x  9 3) 5 4 3 y x x  4x  2 3 5 4 3 1 4) 4 2 y x x x  5 5) 4 3 y  
x x  4x  2 2 4
Chú ý. Giả sử hàm số y f x có đạo hàm trên khoảng a;b
+) Nếu f x  0, x   ;
a b và f  x  0 chỉ tại hữu hạn điểm trên khoảng a;b thì hàm
số đồng biến trên khoảng .
+) Nếu f x  0, x   ;
a b và f  x  0 chỉ tại hữu hạn điểm trên khoảng a;b thì hàm
số nghịch biến trên khoảng .
B- BÀI TẬP RÈN LUYỆN
Bài tập 1. Xét chiều biến thiên của các hàm số sau 1) 3 2
y x  3x  9x 10 2) 3
y  x  3x  6 3) 3 2
y  x  3x  5x  5 3 x 3 x 2 4) 3 2
y x  3x 1 5) y    x  6 6) 2 y    x  2x  3 3 3 4 x 7) 3 2
y x  3x  3x  5 8) 2 y   x  2 9) 4 2
y x  2x  5 2 10) 4 2
y  x  2x  2 11) 4 2
y  x  8x 1 12) 4 2
y x  3x  4 13) 4 2
y x  8x 10 14) 4 2
y x  2x  3
Bài tập 2. Xét chiều biến thiên của các hàm số sau    1) x 1 x x x y  2) 2 5 y  3) 2 4 y  4) y  1 2x x  3 1 x x 1 2   2  2   5) x 2x 2 x 2x 4x 5x 2 x y  6) y  7) y  8) y x 1 x 1 x 1 2 x  4 2   9) x x 1 y  2 x x 1
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 2
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
Bài tập 3. Xét chiều biến thiên của các hàm số sau 1) 3 3 3 2
y  2x  6x  6x  9 2) 5 4 3
y   x  3x  4x  2 3) 4 2 y x x x  5 5 2 4) 4 1 3 5 y  3x x  6 5) 3 2
y x x  2x  4 6) 3 2 y
x  3x  9x 1 5 3
Bài tập 4. Xét chiều biến thiên của hàm số: 1) 2
y  2x x 2) 2
y x 4  x
3) y x  3 2 2  x 4) 2 3
y  3x x
C - BÀI TẬP TRẮC NGHIỆM ĐỀ 01. [1] Câu 1. Hàm số 3 2
y x x  7x
A. Luôn đồng biến trên
B. Luôn nghịch biến trên
C. Có khoảng đồng biến và nghịch biến.
D. Nghịch biến trên khoảng 1;3. Câu 2. Hàm số 3 2
y  x x  7x
A. Luôn đồng biến trên
B. Luôn nghịch biến trên
C. Có khoảng đồng biến và nghịch biến.
D. Đồng biến trên khoảng 1;3. Câu 3. Hàm số 3 2
y  x x x có khoảng đồng biến là  A.   1   1;3 B. ;1   C.  1  ;3 D. 1 ( ;  )  (1;  )   3  3 Câu 4. x Hàm số 5 y  luôn 2  x  2
A. Nghịch biến trên từng khoảng xác định của nó. B. Đồng biến trên
C. Đồng biến trên khoảng ( 4  ;6).
D. Nghịch biến trên Câu 5. Hàm số 4 2
y  x  2x  3 đồng biến trên khoảng nào sau đây? A.  ;    1 và 0;  1
B. 1;0 và 1;  C.  ;  0 D.  1   ;1
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 3
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 6.
Hàm số nào sau đây đồng biến trên ?  A. x 1 y B. 3 2
y x x  2x 1 C. 4 2
y x  2x  3 D. 3
y  x x  2 x  3 Câu 7. x Cho hàm số 1 y
. Khẳng định nào sau đây đúng? x  3
A. Hàm số đồng biến trên  ;3   và 3; 
B. Hàm số nghịch biến trên  ;3   và 3; 
C. Tập xác định của hàm số là
D. Tiệm cận ngang của đồ thị hàm số là y = 3 Câu 8.
Khoảng đồng biến của hàm số 4 2
y  x  8x 1 là: A.  ;  2   và 0;2 B.  ;  0 và 0;2 C.  ;  2   và 2; D. 2  ;0 và 2; Câu 9.
Khoảng đồng biến của hàm số 3 2
y  x  3x 1 là: A.  1  ;3 B. 0;2 C.  2  ;0 D. 0;  1 Câu 10. Hàm số: 3 2
y x  3x  4 nghịch biến khi x thuộc khoảng nào sau đây: A. ( 2  ;0) B. ( 3  ;0) C. ( ;  2  ) D. (0;) Câu 11.
Hàm số nào sau đây đồng biến trên A. 2x y B. 4 2
y x  2x 1 C. 3 2
y x  3x  3x  2
D. y  sin x  2x x 1 Câu 12. x
Kết luận nào sau đây về tính đơn điệu của hàm số 2 1 y  là đúng? x 1
A. Hàm số luôn nghịch biến trên \  1 ;
B. Hàm số luôn đồng biến trên \  1 ;
C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +);
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 4
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
D. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +). Câu 13. Hàm số 3
y x  4 đồng biến trên: A. B. 0; C. 3; D.  ;  0 Câu 14. Hàm số 3
y x  3x  2 nghịch biến trên: A.  ;    1 ;1;  B. 1; C.  1   ;1 D. . Câu 15.
Đồ thị của hàm số nào luôn nghịch biến trên : A. 4 2
y x  2x 1 B. 2
y  3x  4x 1
C. y   x  2 2 1 D. 3 y  3
x  2x 1 Câu 16. Hàm số 4 2
y  x  2x  2 nghịch biến trên: A.  ;    1 ;0  ;1 B.  1  ;0;1; C.  1   ;1 D. . Câu 17. Hàm số 4 2
y x x  4 đồng biến trên: A. 0; B.  ;  0 C.  1   ;1 D. . Câu 18. 1
Khoảng nghịch biến của hàm số 3 2 y
x  2x  3x  2 là: 3 A.  ;  3   B.  3  ;  1 C.  ;  3    1  ; D.  ;3   Câu 19. x Hàm số 3 y  : 2x 1
A. Đồng biến trên khoảng  ;  
B. Nghịch biến trên khoảng  ;  
C. Đồng biến trên từng khoảng xác định D. Nghịch biến trên từng khoảng xác định Câu 20. Hàm số 2
y  2x  4x  3 tăng trên khoảng nào? A. 1; B.   ;1  C.  ;  
D. Một kết quả khác Câu 21.
Hàm số nào sau đây luôn đồng biến trên
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 5
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 1 4 2
y  2x x  3 B. 3
y  2x x 1 C. 3 2
y x x  7 D. 3 2
y   x  3x x  2 3 Câu 22.
Trong các hàm số sau, những hàm số nào luôn đồng biến trên từng khoảng  xác định của nó: 2x 1 y  (I), 4 2
y  x  2x 1(II), 3
y  3x x  3 (III) x  3 A. (I) và (II) B. Chỉ (I) C. (II) và (III) D. (I) và (III) Câu 23.
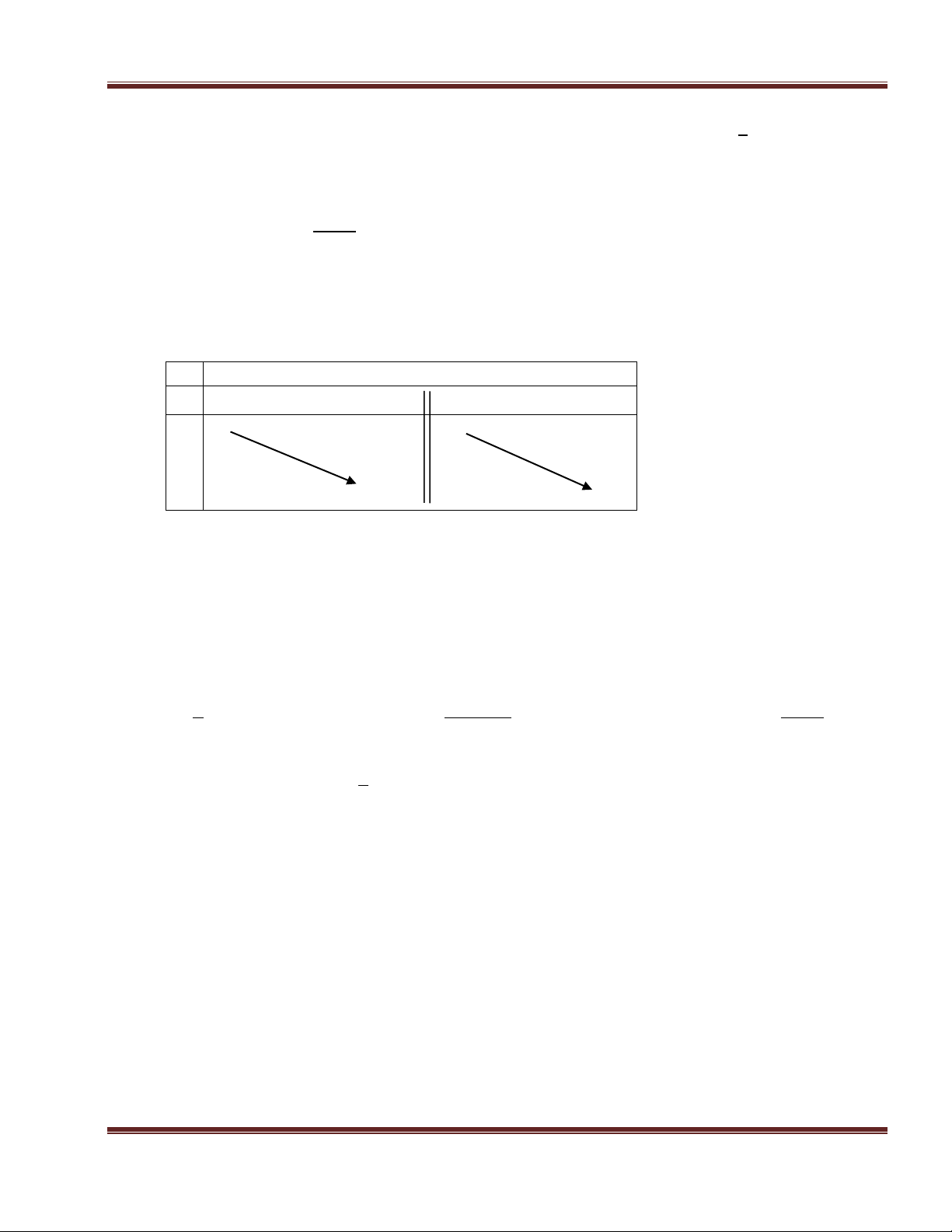
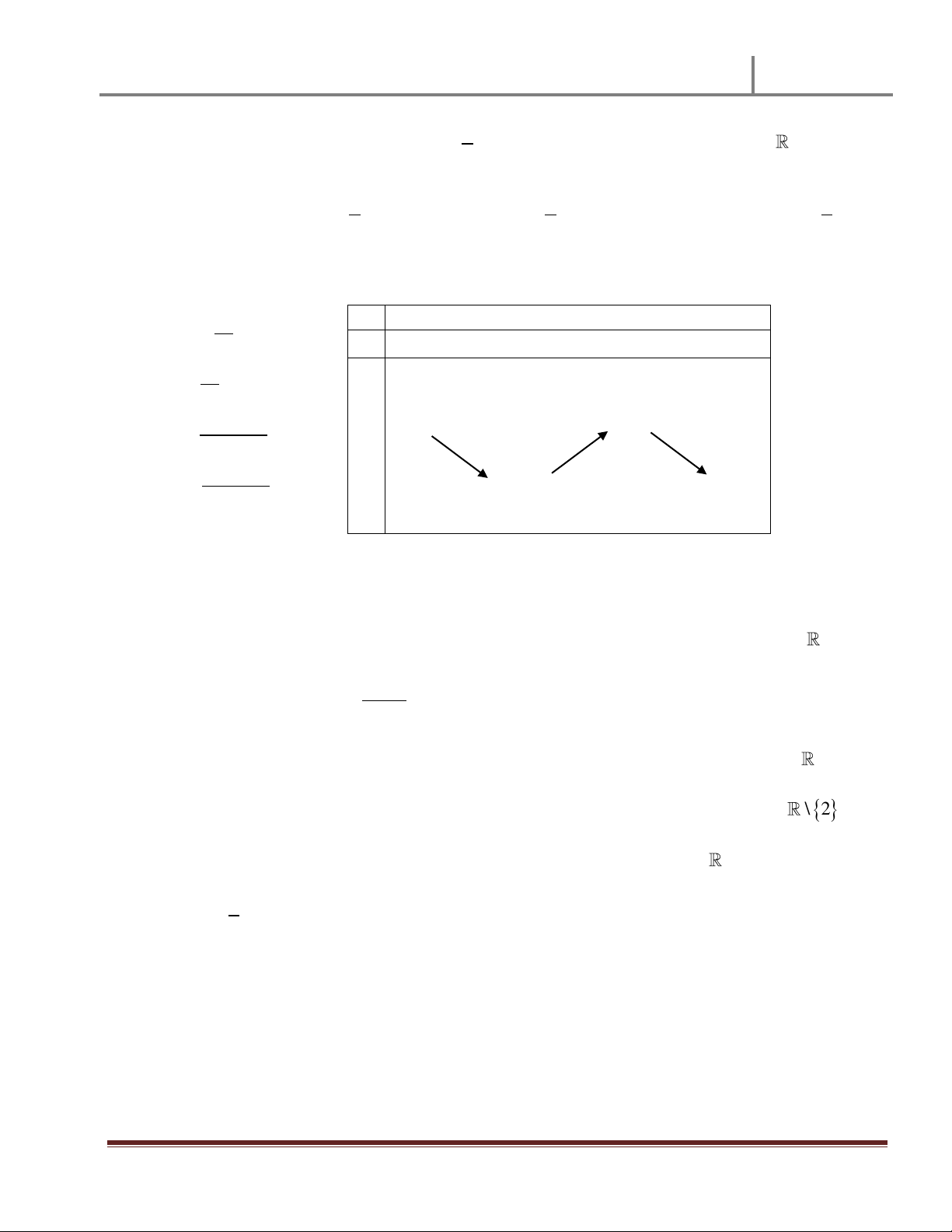
Hàm số y = f(x) có bảng biến thiên như sau. Khẳng định nào sau đây là đúng? x   2   , y - - 2   y   2
A. Hàm số nghịch biến trên ( ) ( ) B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên ( ) ( )
D. Hàm số nghịch biến trên R\{2} Câu 24.
Hàm số nào trong các hàm số sau đây nghịch biến trên khoảng 1;3 2    A. 2 x x 1 x 3 2 y
x  4x  6x 1 B. y C. 2
y x  4x  2 D. 2 1 y  3 x 1 x 1 Câu 25. 1 Cho hàm số 3 y
x x  2017. Mệnh đề nào sau đây đúng? 3
A. Hàm số nghịch biến trên R
B. Hàm số đồng biến trên ( ) ( ) và nghịch biến trên (-1;1)
C. Hàm số đồng biến trên R
D. Hàm số nghịch biến trên ( ) Câu 26. Hàm số 4 2
y x  2x 1 đồng biến trên các khoảng: A.  ;    1 và (0;1) B. (0;1)
C.1;0 và (1;) D. ( 1  ;1) Câu 27.
Khoảng nghịch biến của hàm số 3 2
y x  3x  4 là:
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 6
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A.(-2; 0) B.  ; 2   và (0 ;) C. 2  ;0 và (2 ;) D.0; Câu 28. Hàm số 3 2
y x  6x  9x  7 đồng biến trên các khoảng nào ? A.   ;1 & 3;  B.   ;1 3; C. 1;3 D.  ;   Câu 29. Hàm số 3
y  x  3x  2 nghịch biến trên các khoảng nào ? A.  ;    1 & 1;  B.  1   ;1 C.  ;    1 D. 1; Câu 30.
Hàm số nào sau đây đồng biến trên 2   A. x 2x 8 x 3 2
y x x  3x 1 B. 3
y x  3x  3 C. y D. y x 1 x 1 Câu 31. Hàm số 4 2
y  x  2x  2 đồng biến trên : A. ( ;  1  ),(0,1) B. ( 1  ,0),(1; )  C. D. ( 1  ;1) Câu 32.
Các khoảng đồng biến của hàm số 3 2 y  2
x  9x 12x  3 là : A. (1;2) B. (-1;2)
C. (- ;-1) và (2 ;+∞)
D. (-∞;1) và (2;+ ) Câu 33. Hàm số 4 2
y  2x  4x  2 đồng biến trên khoảng A. ( ;1  ) B. (1;) C. ( ;  0) D. (0;) Câu 34. x Hàm số 2 5 y
đồng biến trên khoảng: x  3 A. B.  ;3   C.  3;   D.  ;  3   và  3;   Câu 35. x x
Cho hàm số f x 3 2 3    6x  3 2 4
A. Hàm số đồng biến trên khoảng 2;3 . B. Hàm số nghịch biến trên khoảng 2;3 .
C. Hàm số nghịch biến trên  ;  2  
D. Hàm số đồng biến trên  2;   .
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 7
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 ĐỀ 02. [1] Câu 1. Cho hàm số 5 4 3
y  6x 15x 10x  22 . Khẳng định nào sau đây là đúng:
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên  ;
 0 và nghịch biến trên 0;.
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên 0; 
1 và đồng biến trên 0;  . Câu 2. Hàm số 4 2
y x  2x 1 đồng biến trên các khoảng: A.  ;    1 , (0;1) B. (0;1) C.  1  ;0,(1;) D. ( 1  ;1) Câu 3.
Hàm số nào sau đây nghịch biến trên ? A. 3 2
y   x  3x  4 B. 4 2
y  x  2x  2 C. 3 2
y  x x  2x 1 D. 4 2
y x  3x  2 Câu 4.
Khoảng đồng biến của hàm số 4 2
y  x  8x 1 là A.  ;  2   ,0;2 B.  ;  0,0;2 C.  ;  2   ,2; D. 2  ;0 ,2; Câu 5. 1
Khoảng nghịch biến của hàm số 3 2 y
x x  3x là 3 A.  ;    1 B.  1  ;3 C. 3; D. ;    1 , 3;  Câu 6.
Hàm số nào sau đây đồng biến trên mỗi khoảng xác đinh của nó ?      A. x 2 x x x y B. 2 y C. 2 y D. 2 y  ” x  2 x  2 x  2 x  2 1 1 Câu 7. Hàm số 3 2 y x x  6x 1 3 2
A. Đồng biến trên khoảng (-2; 3)
B. Nghịch biến trên khoảng (-2; 3)
C. Đồng biến trên khoảng  3  ;
D. Nghịch biến trên khoảng  ;  2   ” Câu 8.
Khoảng nghịch biến của hàm số 3 2
y x  3x  4 là:
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 8
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. (-2; 0) B.  ; 2  ,(0 ;) C.  2  ;0;(2 ;) D. 0; 1 Câu 9.
Khoảng nghịch biến của hàm số 4 2 y  
x  2x  5 là 4 A.  2  ;0,(2; ) B.  ; 2  ,(0 ;) C. ; 2
 ,(0 ;2) D. 0; Câu 10.
Hàm số y = –x3 + 6x2 – 9x + 4 đồng biến trên khoảng: A. (1;3) B. (3;) C. ( ;  3) D. (1;) Câu 11. x Cho hàm số 1 y
. Khẳng định nào sau đây là đúng x 1
A. Hàm số đồng biến trên \  1
B. Hàm số nghịch biến trên \  1
C. Hàm số nghịch biến trên khoảng   ;1
 , đồng biến trên khoảng 1;
D. Hàm số nghịch biến trên các khoảng   ;1  và 1; ” Câu 12. Hàm số 3 2
y x  6x  9x  7 đồng biến trên các khoảng: A. ( ;  1) va (3; ) B. 1;3 C.  3  ;  1 D. ;   . Câu 13. x
Kết luận nào sau đây về tính đơn điệu của hàm số 2 1 y  là đúng? x 1
A. Hàm số đồng biến trên các khoảng  ;    1 và 1; 
B. Hàm số luôn luôn đồng biến trên \  1 
C. Hàm số nghịch biến trên các khoảng  ;    1 và 1; 
D. Hàm số luôn luôn nghịch biến trên \  1  Câu 14. Cho hàm số 3 2
y x  3x  9x  5 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên ( 1  ;3)
B. Hàm số nghịch biến trên khoảng ( ;  1  ) .
C. Hàm số đồng biến trên mỗi khoảng ( ;  1  ) , (3;) ;
D. Hàm số chỉ đồng biến trên khoảng (3;) .
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 9
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 15.
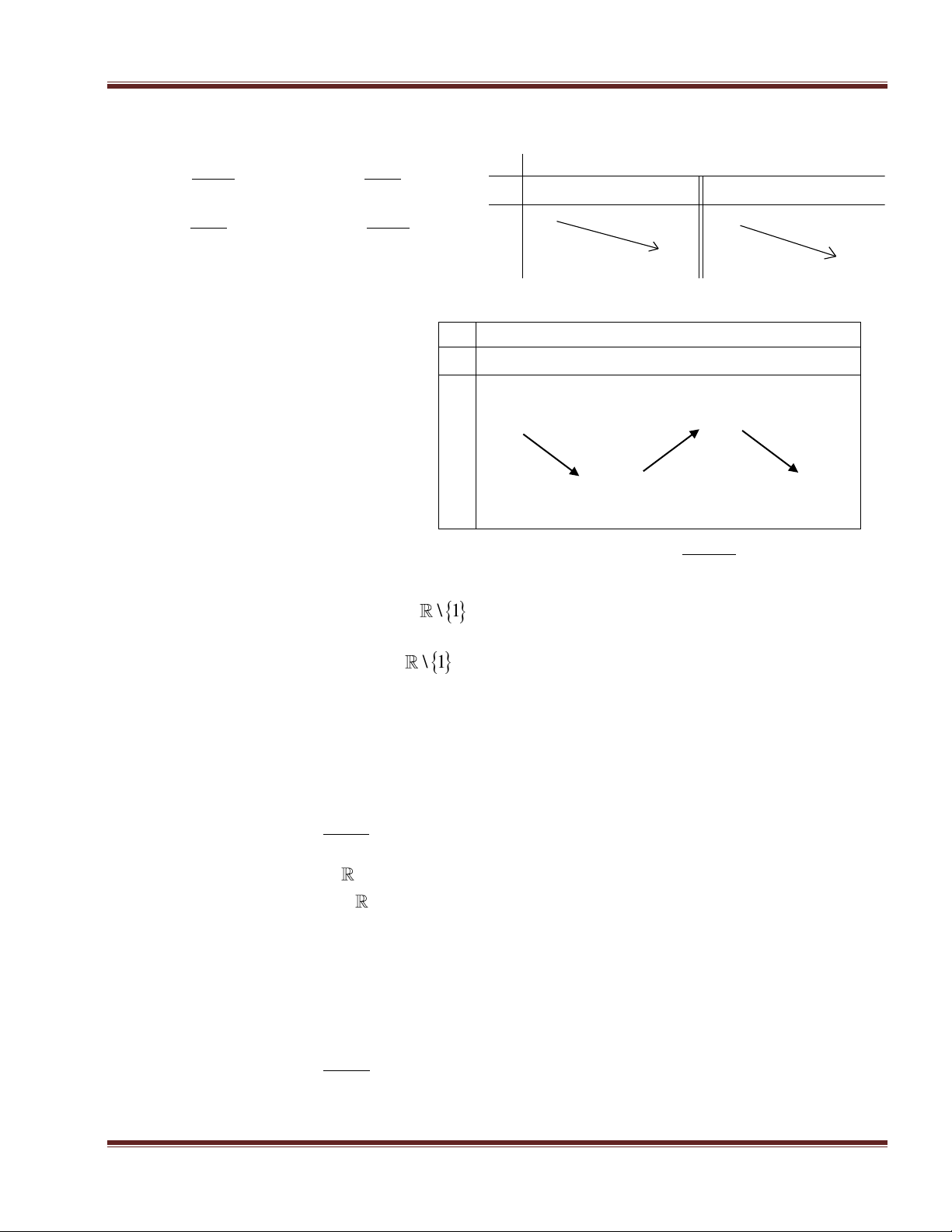
Bảng biến thiên sau đây là của hàm số nào?   x 2 A. 2x 1 x -  +  y B. 3 y x  2 x  2 y' - -   C. x 3 x 1 +  y D. 3 y  y x  2 2x 1 -  1 Câu 16.
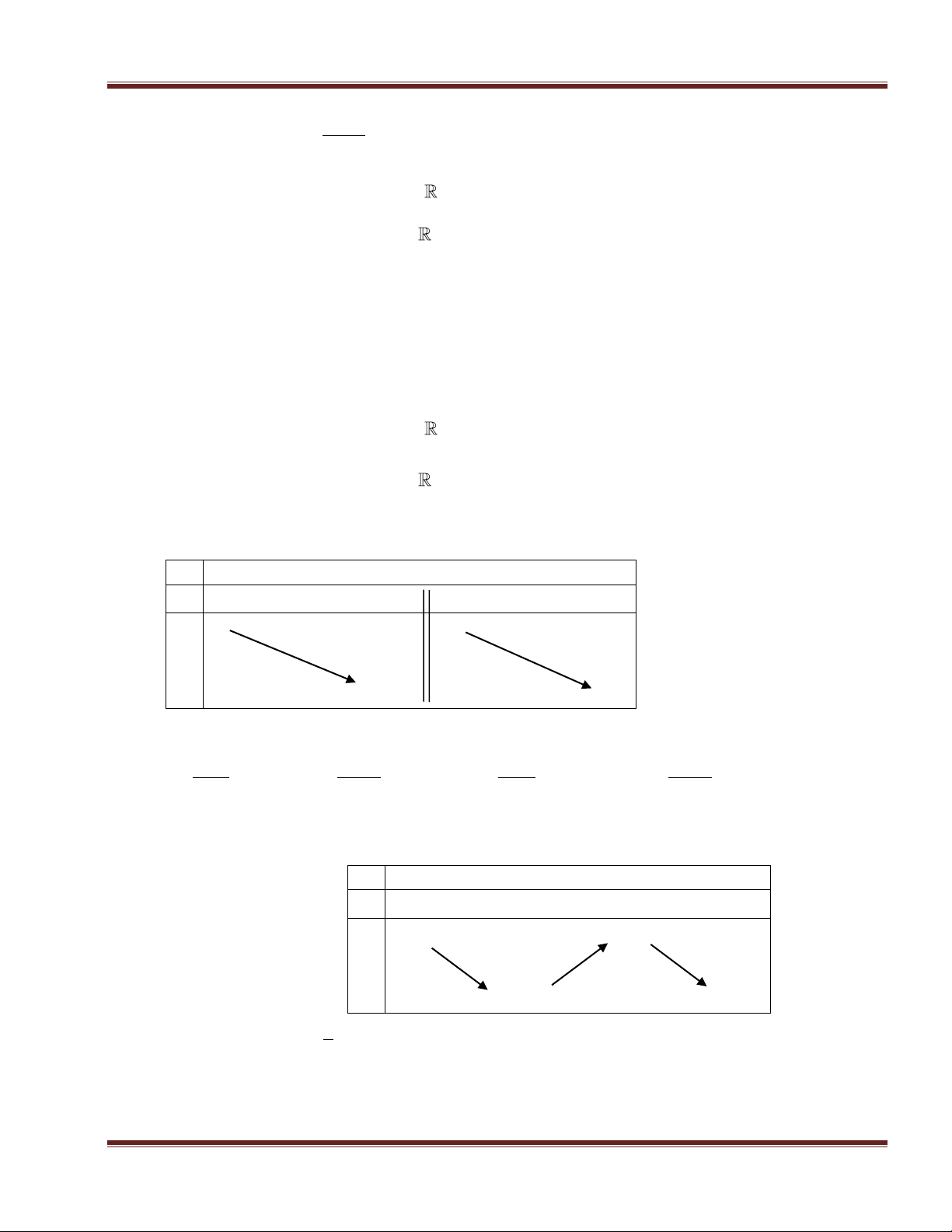
Bảng biến thiên sau là của hàm số nào? A. 3 2
y x  3x  2 x   0 2   , y - 0 + 0 - B. 3 2
y  x  3x  2   6 C. 3 2
y x  3x  2 y D. 3 2
y  x  3x  2 2   Câu 17.x
Kết luận nào sau đây về tính đơn điệu của hàm số 2 1 y  là đúng? 1 x
A. Hàm số luôn nghịch biến trên \  1 .
B. Hàm số luôn đồng biến trên \  1 .
C. Hàm số luôn nghịch biến trên   ;1  và 1;.
D. Hàm số luôn đồng biến trên   ;1  và 1; . Câu 18. x Hàm số 2 3 y
. Chọn phát biểu đúng: 4  x
A. Luôn đồng biến trên
B. Luôn nghịch biến trên từng khoảng xác định
C. Luôn nghịch biến trên
D. Đồng biến trên từng khoảng xác định Câu 19.
Cho hàm số y = –x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại x = 1.
B. Hàm số đạt cực đại tại x = 1;
C. Hàm số luôn luôn đồng biến;
D. Hàm số luôn luôn nghịch biến; Câu 20. x Hàm số 2 5 y
đồng biến trên khoảng: x  3
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 10
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. B.  ;3   C.  3;   D.  ;  3   và  3;   Câu 21. x x
Cho hàm số f x 3 2 3    6x  3 2 4
A. Hàm số đồng biến trên 2;3
B. Hàm số nghịch biến trên 2;3
C. Hàm số nghịch biến trên  ;  2  
D. Hàm số đồng biến trên  2;   . Câu 22. Cho hàm số 5 4 3
y  6x 15x 10x  22 . Khẳng định nào sau đây là đúng:
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên  ;
 0 và nghịch biến trên 0;.
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên 0; 
1 và đồng biến trên 0;  . Câu 23.
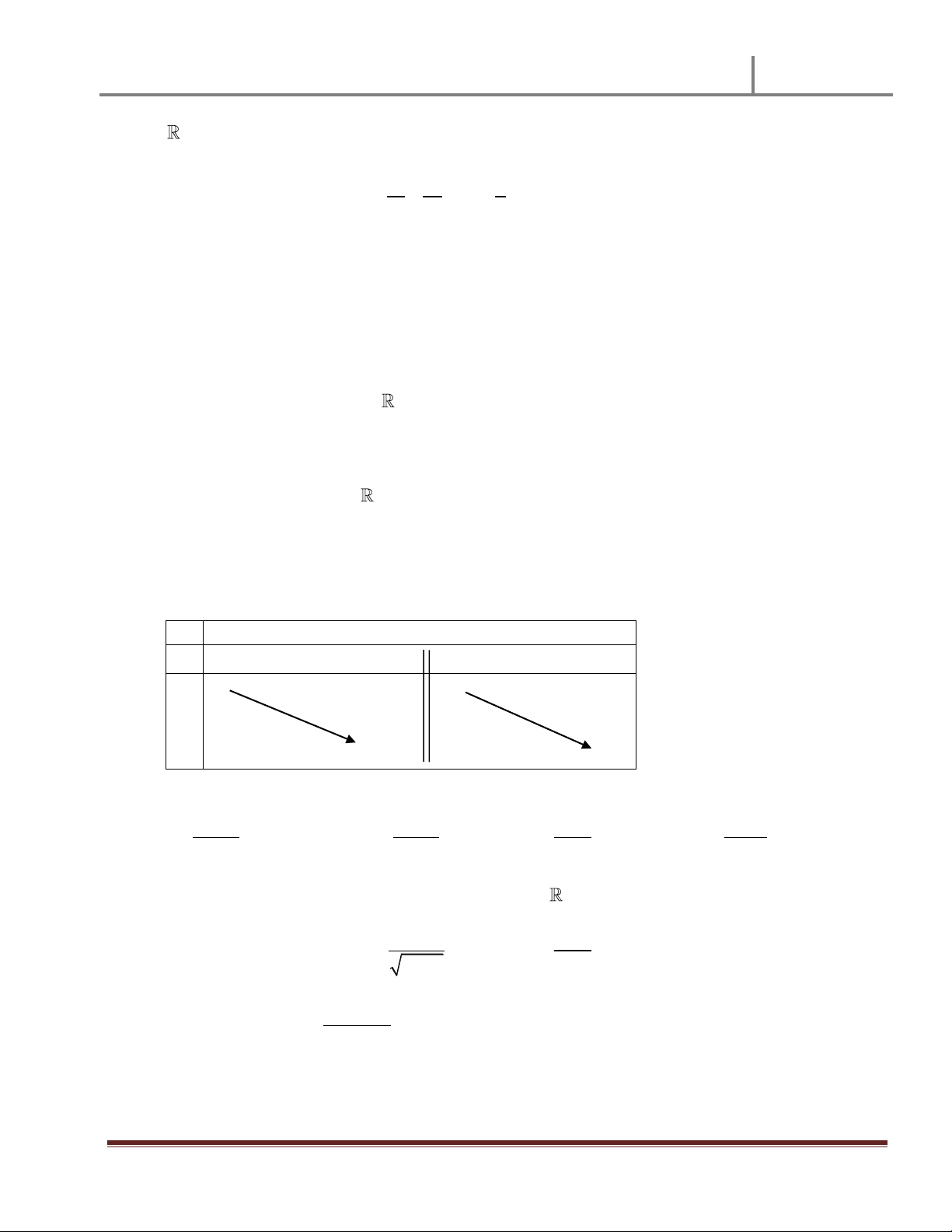
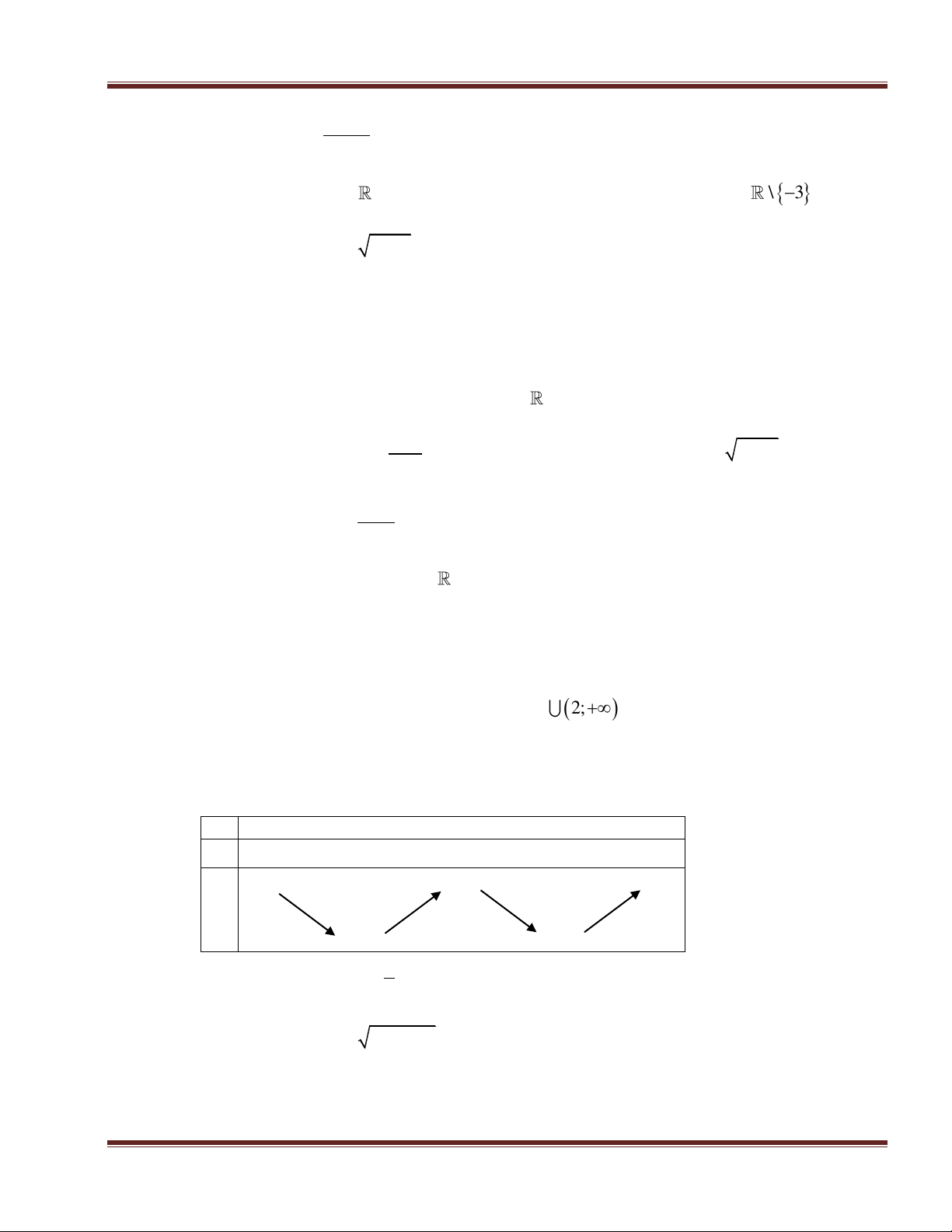
Hàm số nào sau đây có bảng biến thiên như hình bên: x   2   , y - - 2   y   2     A. 2x 5 x x x y B. 2 3 y C. 3 y D. 2 1 y x  2 x  2 x  2 x  2 Câu 24.
Hàm số nào sau đây là đồng biến trên ? A. x x 3
y x  3x 1 B. y C. 1 y D. 4 y x  2 2 x 1 x  2 2 Câu 25. x x 1 Hàm số y  đồng biến trên: x 1 A.  ;  0 và 1;2 B. 0; 
1 và 2;  C. 0;  1 và 1; 2 D.  ;  0 và 2;
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 11
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 26. x Hàm số 2 1 y  : x 1
A. Hàm số luôn nghịch biến trên
B. Hàm số luôn đồng biến trên
C. Hàm số nghịch biến trên các khoảng  ;   
1 và 1; 
D. Hàm số đồng biến trên các khoảng  ;   
1 và 1;  Câu 27. Hàm số 3 2
y x  3x  3x  2 :
A. Hàm số luôn nghịch biến trên
D. Hàm số nghịch biến trên khoảng   ;1 
B. Hàm số luôn đồng biến trên
C. Hàm số đồng biến trên khoảng 1; Câu 28.
Bảng biến thiên sau đây là của hàm số nào? Chọn 1 câu đúng. x   2   , y - - 1   y   1     A. x 1 x x x y B. 2 1 y C. 3 y D. 1 y x  2 x  2 x  2 2x 1 Câu 29.
Bảng biến thiên sau đây của hàm số nào? A. 3 2
y  x  3x 1 x   0 2   B. 3 2 ,
y x  3x 1 y - 0 + 0 - C. 3 2
y x  3x 1   3 D. 3 2
y  x  3x 1 y -1   Câu 30. 1 Hàm số 3 2 y
x x  3x 1 đồng biến trên các khoảng: 3 A.  ;  3
  và 1; B.  3   ;1 C.  1  ;3 D.  ;    1 và 3; 
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 12
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 31. Hàm số 3 2
y x  3x  4 nghịch biến trên các khoảng nào sau đây: A.  2  ;0 B. 3;0 C.  ;  2   D. 0; Câu 32. Hàm số 4 2
y  x  2x  3 nghịch biến trên các khoảng khoảng nào sau đây: A. 1; B. C.  ;  0
D. 0; 2 Câu 33. x x  3 Hàm số y  2 x x  7
A. Đồng biến trên khoảng 5;0 và 0;5
B. Nghịch biến trên khoảng  5   ;1
C. Đồng biến trên khoảng 1;0 và 1;
D. Nghịch biến trên khoảng  6  ;0 Câu 34. x Cho hàm số 2 y  . Khi đó: x 1
A. y 2  5
B. Hàm số luôn đồng biến trên
C. Hàm số luôn nghịch biến trên
D. Hàm số luôn nghịch biến trên từng khoảng xác định của nó. Câu 35.
Trong mỗi hàm số sau hàm số nào nghịch biến trên từng khoảng xác định của nó? 2  A. x x y
B. y  cot x C. 1 y
D. y  tan x x 1 x  5 ĐỀ 03. [2] Câu 1. Cho hàm số 1 y
sin 2x  3x . Khẳng định nào sau đây là đúng: 2
A. Hàm số đồng biến trên .
B. Hàm số đồng biến trên  ;  0.
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 13
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
C. Hàm số nghịch biến trên  ;
 0 và đồng biến trên 0;.
D. Hàm số nghịch biến trên . Câu 2.
Hàm số nào sau đây đồng biến trên  A. x 3 y x 1
B. y  tan x C. 2 1 y D. 4 2
y x x 1 x 1 Câu 3. Hàm số 2 y  25  x
A. Đồng biến trên khoảng ( 5  ;0) và (0;5).
B. Đồng biến trên khoảng ( 5
 ;0) và nghịch biến trên khoảng (0;5).
C. Nghịch biến trên khoảng ( 5
 ;0) và đồng biến trên khoảng (0;5).
D. Nghịch biến trên khoảng ( 6  ;6). Câu 4.
Hàm số y x  2  4  x nghịch biến trên khoảng A. 2;3 B.  2;3 C. 2;4 D. 3;4 Câu 5. 1 Hàm số 4 3
y x x
có khoảng đồng biến là: 3 A.  1       ;     B. 1  ;   C. 0; D. 1  ;0    4   4   4  Câu 6. Hàm số 2
y  2x x nghịch biến trên khoảng nào sau đây? A. 1;2 B. 0;  1 C.   ;1  D. 1; Câu 7.
Hàm số y 1 x x  5 đồng biến trên khoảng nào sau đây? A.  5  ; 3   B.  3;   C.  5;   D.  ;  3   Câu 8.
Hàm số nào sau đây luôn đồng biến trên từng khoảng xác định của chúng  2 A. 1 x x  2x y B. 2 y C. y D. 9 y x x x 1 x 1 x Câu 9.
Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó ?
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 14
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12     A. x 2 x x x y B. 2 1 y C. 1 y D. 5 y  2x 1 x  3 x 1 x 1 Câu 10. x
Trong các khẳng định sau về hàm số 2 4 y
, hãy tìm khẳng định đúng? x 1
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định. Câu 11. Hàm số 2
y  2x x đồng biến trên: A. 1;2 B. 0;2 C. 0;  1 D. Câu 12.
Hàm số y x  cos x A. Đồng biến trên
B. Đồng biến trên  ;  0
C. Nghịch biến trên
D. Nghịch biến trên 0; Câu 13.
Hàm số y  sin x x A. Đồng biến trên
B. Đồng biến trên  ;  0
C. Nghịch biến trên
D. Nghịch biến trên 0; Câu 14.
Khoảng nghịch biến của hàm số 2
y  2x  4x A.  1 1        ;   B. 1 1  ;   C. 1 0;   D. 1 0;    4 2   4 2   2   4  2 Câu 15. x x 1 Cho hàm số y
. Khẳng định nào sau đây sai? x 1
A. Hàm số nghịch biến trên khoảng 0;2
B. Hàm số nghịch biến trên khoảng 1;2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 15
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
C. Hàm số nghịch biến trên khoảng 0;  1
D. Hàm số đồng biến trên khoảng  ;  2 và 2; Câu 16. Cho hàm số 3 2
y  3x  3x  9x 11 . Độ dài khoảng đồng biến là: A. 2 B. 4 C. 0 D. 1 Câu 17. Hàm số 4 2
y x  3x  3 đồng biến trên khoảng nào trong các khoảng sau: I . 1
 ;0; II . 1  
;1 ;  III .2;  A. (I) và (II) B. (I) và (III) C. chỉ (I) D. (II) và (III) Câu 18. x
Kết luận nào sau đây về tính đơn điệu của hàm số 2 1 y  là đúng x 1
A. Hàm số luôn luôn nghịch biến trên \  1  .
B. Hàm số luôn luôn đồng biến trên \  1  .
C. Hàm số nghịch biến trên các khoảng  ;   
1 và 1; 
D. Hàm số đồng biến trên các khoảng  ;   
1 và 1;  Câu 19. Cho hàm số 4 2
y  2x  4x . Hãy chọn mệnh đề sai trong bốn phát biểu sau:
A. Hàm số nghịch biến trên các khoảng  ;    1 và 0;  1
B. Trên các khoảng  ;    1 và 0; 
1 , y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
C. Hàm số đồng biến trên các khoảng  ;   
1 và 1; 
D. Trên các khoảng 1;0 và 1;, y’ > 0 nên hàm số đồng biến trên mỗi khoảng đó Câu 20.
Hàm số nào sau đây nghịch biến trên từng khoảng xác định của nó ?     A. x 2 x x x y B. 2 1 y C. 1 y D. 5 y  1   2x 3   x x 1 x 1 3 Câu 21. 4 x Hàm số 5 4 y x x  1 5 3
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 16
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
A. Đồng biến trên khoảng    ;  0 và 1 ;   B. Đồng biến trên  2 
C. Nghịch biến trên  1      ;  
 và đồng biến trên 1 ; 
D. Nghịch biến trên 1 0;    2   2   2  Câu 22.
Bảng biến thiên sau đây của hàm số nào? 3  - 2 0   A. x x  2 y    x 1 , 3 y - 0 + 0 - 3 B. x 2 y   x  2 3 2 C. x x 1 y  x 1 y 2 D. x x 1 y x 1 Câu 23. Hàm số 4 2
y x  2x 1 đồng biến trên các khoảng nào sau đây : A.  1  ;0;1; B.  1  ;0;0  ;1 C.  ;    1 ;0  ;1 D. Câu 24. x Cho hàm số 3 5 y
. Chọn khẳng định đúng: 2  x
A. Hàm số đồng biến trên khoảng 2;
B. Hàm số nghịch biến trên
C. Hàm số đồng biến trên khoảng  ;
 2;2; D. Hàm số đồng biến trên \  2 Câu 25.
Trong các hàm số sau, hàm số nào không đồng biến trên ? A. 3 y  4x
B. y  4x 3sin x  cos x C. 3 2
y  3x x  2x  7 D. 3
y x x x Câu 26.
Cho hàm số f x 3 2  2
x  3x 12x  5 .Trong các mệnh đề sau, tìm mệnh đề đúng?
A. Hàm số tăng trong khoảng  3   ;1
B. Hàm số tăng trong khoảng  1   ;1
C. Hàm số tăng trong khoảng 5;10
D. Hàm số giảm trong khoảng  1  ;3
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 17
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 27. x Cho hàm số 2 3 y
. Khẳng định nào sau đây là đúng: x 1
A. Hàm số đồng biến trên
B. Hàm số đồng biến trên khoảng 1;
C. Hàm số đồng biến trên  
;1 ;1;  D. Hàm số đồng biến trên \   1 Câu 28.
Trong các hàm số sau , hàm số nào đồng biến trên các khoảng   ;1 ;1;  :  2 A. 1 x x x 1 2
y x  3x  2 B. 4 2 y x x  3 C. 2 y D. y  2 x 1 x 1 Câu 29. Hàm số 3 2
y x  3x đồng biến trên các khoảng là A.  ;  0;2; B.  ;  0 C. 2; D.  ;  2  ;0; Câu 30. Hàm số 3 2
y  x  3x 1 nghịch biến trên các khoảng là A.  ;  0;2; B.  ;   C. 2; D.  ;  2  ;0; Câu 31. Hàm số 4 2
y x  2x 1 nghịch biến trên các khoảng nào sau đây? A.  ;    1 ;0  ;1 B.  ;  0;1; C.  ;   
1 ;0;  D.  1
 ;0;1; Câu 32.x Cho hàm số 1 y
.Chọn phương án đúng dưới đây: x  2
A. Hàm số đồng biến trên các khoảng  ;  2 và 2;
B. Hàm số đồng biến trên các khoảng  ;  2 2;
C. Hàm số nghịch biến trên các khoảng  ;  2 và 2;
D. Hàm số nghịch biến trên các khoảng  ;  2    2  ; Câu 33. x 1 Cho hàm số y
. Chọn phương án đúng dưới đây: 2 x 1
A. Hàm số nghịch biến trên các khoảng 1;
B. Hàm số nghịch biến trên các khoảng  ;    1 1;
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 18
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
C. Hàm số nghịch biến trên khoảng   ;1 
D. Hàm số nghịch biến trên toàn trục số (trên ) Câu 34. Hàm số 3 2
y x  3x  4 đồng biến trên các khoảng là A.  ;  0;2; B.  ;  0 C. 2; D.  ;  2  ;0; Câu 35. 1
Các khoảng nghịch biến của hàm số 4 2 y  
x  2x  5 là: 4 A.  2  ;0;2; B.  ;  2;0;2 C.  1  ;0;1; D.  ;  0;0; Câu 36. Cho hàm số 3 2
y x  3x  3x  5 . Tìm tất cả giá trị của số thực x để hàm số đồng biến. A. x  ;  
B. x   ;1
C. x 1;
D. x   ;1 1; 4 Câu 37. x 3 Hàm số 2 y  
x  nghịch biến trên khoảng : 2 2 A. 0; B.  ;   C. 3;5 D.  ;  0 Câu 38. x Cho hàm số 2 1 y
. Tìm tất cả giá trị của số thực x để hàm số đồng biến. x  2 A. x  ;  2  ; x 2  ; B. x  ;  2   C. x  2;   D. x  ;   Câu 39. Hàm số 2
y  2  x x nghịch biến trên khoảng A.  1    ; 2   B. 1 1;   C. 1;2 D. 2;  2   2  Câu 40.
Trong các hàm số sau, hàm số nào nghịch biến trên ?  A. x 3
y  x 100 B. 2
y  x  2x 1 C. 4 2
y  x  2x 1 D. 1 y x1
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 19
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 ĐỀ 04 [2] Câu 1.
Trong các hàm số sau, hàm số nào đồng biến trên ? A. 3 y x  99 B. 4 y x 16 C. 3
y x  3x  999 D. 4
y x  4x  3 Câu 2.
Trong các hàm số sau, những hàm số nào luôn đồng biến trên từng khoảng  xác định của nó: 2x 1 y  I 4 2
; y  x x  2 II  3
; y x  3x  5 III x 1 A. ( I ) và ( II ) B. Chỉ ( I ) C. ( II ) và ( III ) D. ( I ) và ( III) Câu 3.
Khoảng đồng biến của hàm số 2
y  2x x là A.   ;1  B. 0;  1 C. 1;2 D. 1; 4 3 Câu 4. x 10x Hàm số 2 y  
 2x 16x 15 đồng biến trên khoảng nào sau đây? 2 3 A. 2; B.  ;    1 C. 4; D. 2;4 Câu 5. Hàm số 2
y  2  x x
nghịch biến trên khoảng A.      2;  B. 1 1;   C. 1 ;2   D. 1;2  2   2  2 Câu 6. x Hàm số y
đồng biến trên các khoảng 1 x A.   ;1  và 2; B.   ;1 
và 1;2 C. 0;  1 và 1; 2 D.   ;1  và 1; Câu 7. Hàm số 2
y  x x
A. Đồng biến trên khoảng  ;
 0 B. Nghịch biến trên
C. Đồng biến trên khoảng 0; D. Nghịch biến trên các khoảng  ;  0;0; Câu 8.
Hàm số nào sau đây nghịch biến trên khoảng 1;3  2 A. 1 2 x   2 x x 1 y x  2x  3 B. 3 2 y
x  4x  6x 10 C. 2 5 y D. y  2 3 x 1 x 1
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 20
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 2 Câu 9. x  5x  3 Cho hàm số y
. Chọn phát biểu đúng trong các phát biểu sau: x 1
A. Nghịch biến trên các khoảng  ;  2  ;4;
B. Nghịch biến trên khoảng  2  ;4
C. Nghịch biến trên các khoảng  2  ;  1 ;1; 4
D. Nghịch biến trên \  1 3 Câu 10. 4 x Hàm số 5 4 y x x  1 5 3
A. Đồng biến trên khoảng   ;1
 và nghịch biến trên khoảng 1;
B. Nghịch biến trên khoảng   ;1
 và đồng biến trên khoảng 1;
C. Nghịch biến trên D. Đồng biến trên Câu 11.
Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó ?       A. x 1 x x x y B. 1 y C. 1 y D. 1 y x 1 x 1 x 1 x 1 Câu 12.
Hàm số nào sau đây đồng biến trên ?
A. y  tan x B. 3 y x  2 C. 4 2
y  2x x D. 3
y x  3x 1 Câu 13. Hàm số 2
y  2  x x
đồng biến trên khoảng A.      2;  B. 1 1;   C. 1 ;2   D. 1;2  2   2  Câu 14. Hàm số 3 2
y  x  3x  2 đồng biến trên khoảng nào sau đây: A. 2; B. 0; C.  ;  0 D. 0;2 Câu 15. Hàm số 4 2
y x  2x  3 nghịch biến trên các khoảng nào sau đây: A.  ;    1 và 1; 
B. 1;0 và 1;
C. 1;0 và 0;  1 D.  ;    1 và 0;  1
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 21
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 16. x Hàm số 2 5 y  đồng biến trên: x  3 A.  3;   B. C.  ;3   D. \  3  Câu 17. Cho hàm số 2 y  1 x
. Khẳng định nào sao đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng 0;  1
B. Hàm số đồng biến trên khoảng 0;  1
C. Hàm số nghịch biến trên khoảng 0; D. Hàm số đồng biến trên khoảng 0; Câu 18.
Hàm số nào sau đây đồng biến trên  A. 3 2
y x  3x  3x B. 1 x y
C. y 1 D. 2 y x 1 x Câu 19. x Cho hàm số 1 y
. Khẳng định nào sau đây đúng: 2  x
A. Hàm số đã cho nghịch biến trên
B. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó
C. Hàm số đã cho đồng biến trên từng khoảng xác định của nó
D. Hàm số đã cho đồng biến trên khoảng  ;  2 2; Câu 20.
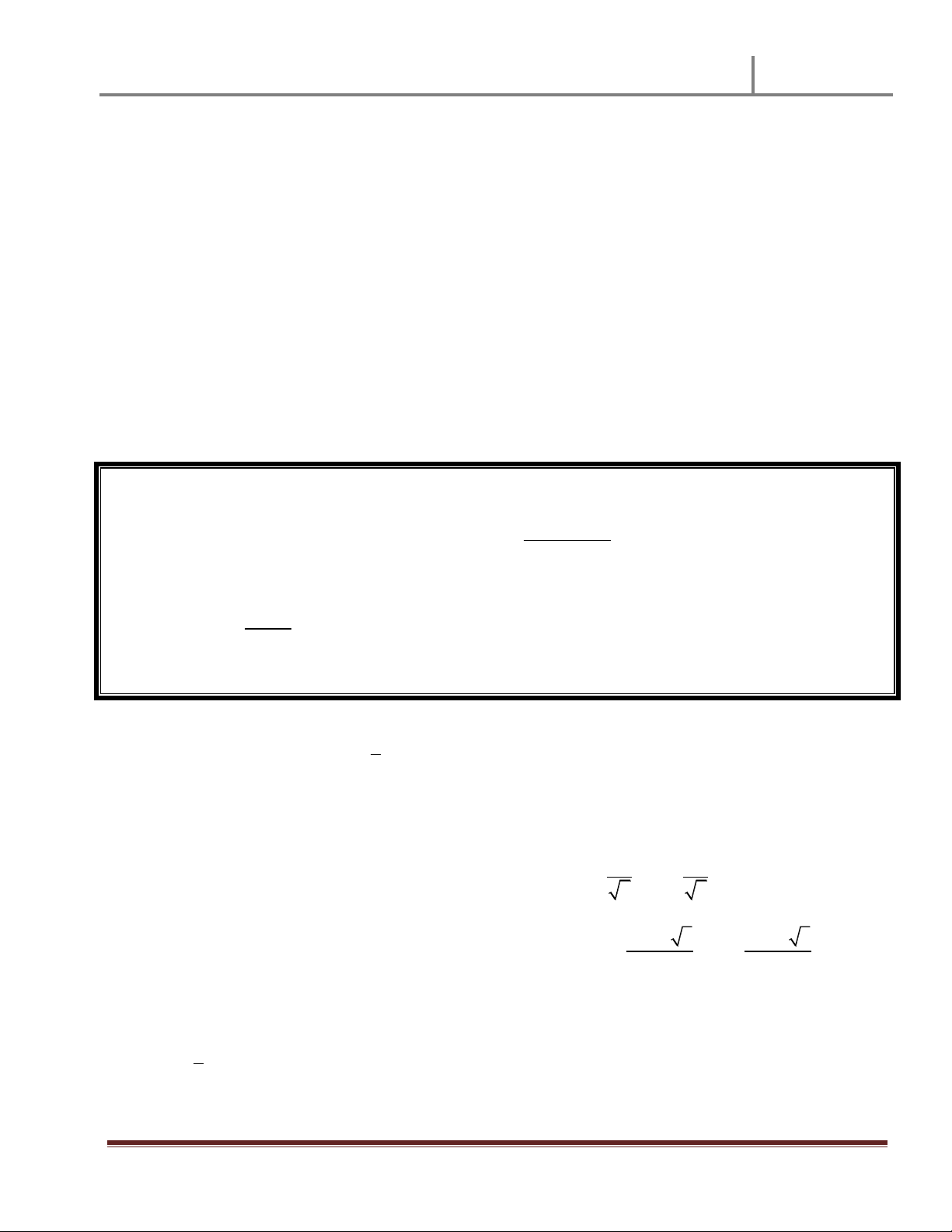
Bảng biến thiên sau đây là bảng biến thiên của một hàm số trong 4 hàm số
được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x   1 0 1   , y - 0 + 0 - 0 +   - 3   y 4 4 A. 1 4 2
y x  2x  3 B. 4 2 y x  3x  3 C. 4 2
y x  3x  3 D. 4 2
y x  2x  3 4 Câu 21. Cho hàm số 2
y  x  2x . Các khoảng đồng biến, nghịch biến của hàm số là:
A. Đồng biến trên0; 
1 và nghịch biến 1; 2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 22
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
B. Đồng biến trên   ;1
 và nghịch biến 1;
C. Đồng biến trên 1;2 và nghịch biến 0;  1
D. Đồng biến trên 1; và nghịch biến   ;1  2 Câu 22. x x 1
Các khoảng đơn điệu của hàm số y  là: x 1
A. Đồng biến trên các khoảng  ;  0 và 2;
Nghịch biến trên các khoảng 0;  1 và 1; 2
B. Đồng biến trên khoảng   ;1
 ; Nghịch biến trên khoảng 1;2
C. Đồng biến trên khoảng 2; ; Nghịch biến trên khoảng 0;2
D. Đồng biến trên khoảng 2; ; Nghịch biến trên khoảng 0;  1 Câu 23. Hàm số 4 2
y x  2x 1 đồng biến trên các khoảng nào?
A. 1;0 và 1; B.  1   ;1 C. 1; D. x   Câu 24.
Các khoảng nghịch biến của hàm số 3 2
y  x  3x 1 là: A.  ;  0 và 2; B. 0;2 C. 0; D. Câu 25.
Hàm số nào sau đây là hàm số đồng biến trên A. x x y B. y   2 x   1  3x  2 C. y
D. y  tan x x 1 2 x 1 Câu 26. Hàm số 2 y  1 x
A. Đồng biến trên 0;  1
B. Đồng biến trên 0;  1
C. Nghịch biến trên 0;  1
D. Nghịch biến trên 1;0 Câu 27. 4 Cho hàm số 3 2 y  
x  2x x  3 . Khẳng định nào sau đây sai: 3
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 23
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
A. Hàm số đã cho nghịch biến trên  1   ;      2 
B. Hàm số đã cho nghịch biến trên  1   ;    2 
C. Hàm số đã cho nghịch biến trên  1     ;     và 1  ;    2   2 
D. Hàm số đã cho nghịch biến trên Câu 28.
(Đề thi minh họa THPT Quốc Gia lần 1) Hàm số 4
y  2x 1 đồng biến trên khoảng nào? A.  1     ;     B. 0; C. 1  ;   D.  ;  0  2   2  Câu 29.
(Chuyên KHTN lần 2) Cho hàm số 4 2
y  x  2x 1. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên  ;    1
B. Hàm số đồng biến trên  ;  0
C. Hàm số đồng biến trên 0;
D. Hàm số đồng biến trên 1; Câu 30.
(THPT Lê Hồng Phong lần 1) Khoảng đồng biến của hàm số 3 2
y x  3x  4 là A.  ;  2   2; B.  ;  0 2; C.  2  ;0 D. 0;2 Câu 31. x
(THPT Kim Liên lân 1) Cho hàm số 2 y
. Trong các khẳng định sau, x 1
khẳng định nào là đúng?
A. Hàm số nghịch biến trên
B. Hàm số đồng biến trên từng khoảng xác định
C. Hàm số đồng biến trên
D. Hàm số có duy nhất một cực trị Câu 32.
(THPT Nguyễn Thị Minh Khai) Hàm số f x liên tục trên và có đạo hàm
f x  x x  2 2 '
1  x  2 . Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng  2;  
B. Hàm số nghịch biến trên các khoảng  2  ;  1 ;0; 
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 24
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
C. Hàm số đồng biến trên khoảng  ;  2  
D. Hàm số đồng biến trên các khoảng  ;  2  ;0; Câu 33.
(Sở GD và ĐT Vĩnh Phúc lần 2) Hàm số 2 y  2x x đồng biến trên khoảng nào? A. 0;2 B. 1;2 C. 0;  1 D.   ;1  Câu 34. x
(Chuyên KHTN lần 3) Cho hàm số y
. Mệnh đề nào đúng x 1
A. Hàm số đồng biến trên khoảng 0;  1
B. Hàm số nghịch biến trên \  1
C. Hàm số nghịch biến trên   ;1 1;
D. Hàm số nghịch biến trên từng khoảng   ;1  và 1; Câu 35.
(Lương Tài –Bắc Ninh lần 1) Trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây, hàm số nào là hàm số đồng biến trên khoảng  ;   A. 2x 1 1 y B. 3
y x  3x  2 C. 4 2 y x x D. 3
y  x x  2 x  2 4 Câu 36.
(Chuyên KHTN lần 4) Cho hàm số f x có đạo hàm
f x   x  2  x  3 ' 1
1 2  x . Hàm số f x đồng biến trên khoảng nào dưới đây? A.  ;    1 B.  1   ;1 C. 2; D. 1;2 Câu 37.
(Chuyên KHTN lần 4) Cho hàm số 4 2
y x  4x  3 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên  ;
 0 và nghịch biến trên 0;
B. Hàm số đồng biến trên  ;  
C. Hàm số nghịch biến trên  ;
 0 và đồng biến trên 0;
D. Hàm số nghịc biến trên  ;  
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 25
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 38.
(THPT Gia Lộc II, Hải Dương) Tìm khoảng đồng biến của hàm số 3 2
y  4x x  4x  2 A.  1 2           ;   B. 1  ;     C. 2 ;   D. 1  ;     và 2 ;    2 3   2   3   2   3  Câu 39.
(THPT Gia Lộc II, Hải Dương) Cho hàm số 2
y  6  x x . Hãy chọn đáp án đúng
A. Hàm số đồng biến trên  1     ;     và 1  ;2    2   2 
B. Hàm số đồng biến trên  ;  3
  và 2;
C. Hàm số nghịch biến trên  1     ;     và 1  ;2    2   2 
D. Hàm số đồng biến trên  1   ;      2  Câu 40.
(Chu Văn An- HN lần 2) Hàm số 3 2
y x  3x nghịch biến trên khoảng nào dưới đây? A.  1   ;1 B.   ;1  C. 0;2 D. 2; Câu 41. x m
(Chuyên Lê Quý Đôn – Đà Nẵng) Cho hàm số f x  m   1 x 1
A. Hàm số luôn giảm trên   ;1 
và 1; với m 1
B. Hàm số luôn giảm trên Tập xác định
C. Hàm số luôn tăng trên   ;1 
và 1; với m 1
D. Hàm số luôn tăng trên   ;1  và 1; Câu 42.
(Quốc học Quy Nhơn- Bình Định) Cho hàm số 3 2
y  2x  6x  6x  2017 .
Mệnh đề nào sau đây sai?
A. Hàm số đã cho đồng biến trên
B. Hàm số đã cho nghịch biến trên
C. Trên khoảng  ;  2
  hàm số đã cho đồng biến
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 26
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
D. Trên khoảng 2; hàm số đã cho đồng biến Câu 43.
(Chuyên Lê Thánh Tông – Quảng Nam) Cho hàm số f x 2
 x  2x . Trong
các khẳng định sau, khẳng định nào đúng?
A. Hàm số nghịch biến trên khoảng 1;2 B. Hàm số nghịch biến trên khoảng   ;1 
C. Hàm số đồng biến trên khoảng  2
 ;2 D. Hàm số đồng biến trên khoảng 2;
VẤN ĐỀ 2. TÌM THAM SỐ M ĐỂ HÀM SỐ LUÔN TĂNG (HOẶC GIẢM)
TRÊN TẬP XÁC ĐỊNH D Phương pháp 2    Các hàm số : 3 2 ax bx c
y ax bx cx d a  0 và y
a  0 luôn tăng (giảm) trên Ax B
từng khoảng xác định của nó khi và chỉ khi y  0  y  0 x   D   Hàm số: ax b y
luôn tăng (giảm) trên từng khoảng xác định của nó khi và chỉ khi cx d
y  0  y  0 x   D A - VẬN DỤNG Ví dụ 1. 1 Cho hàm số 3 2
y   x mx  m  2 x  2 . Tìm m để hàm số nghịch biến trên 3 tập xác định Ví dụ 2.
Tìm m để các hàm số sau luôn đồng biến trên tập xác định của nó 1) 3
y x   m   2 3 2
1 x  12m  5 x  2 Đs: 1 1   m  6 6 2)     3
y x  m   2 x   2 1
m  4 x  9 Đs: 1 3 3 1 3 3 m   m  2 2 Ví dụ 3.
Tìm m để hàm số đồng biến trên tập xác định của nó? 1) 1
y  m   3 2
1 x mx  3m  2 x Đs: m  2 3 Ví dụ 4.
Tìm m để hàm số sau luôn đồng biến trên tập xác định của nó?
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 27
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 1) 1 y   2 m m 3 2
x  2mx  3x 1 Đs: 3   m  0 3 2) 1 y   2 m   3
1 x  m   2 1 x  3x  5
Đs: 1 m  2 3 Ví dụ 5.
Tìm m để hàm số đồng biến trên từng khoảng xác định của nó?   1) x m mx y
Đs: m  0 2) 4 y Đs: 2
  m  2 x m x m Ví dụ 6.
Tìm m để hàm số đồng biến trên từng khoảng xác định của nó? 2 2 2 1)
2x  3x m
x x m y Đs: m  2  2) y Đs: m  0 x  2 x 1
B- BÀI TẬP ÁP DỤNG
Bài tập 1. Tìm m để hàm số sau luôn nghịch biến trên ? 1) 3
y  x    m 2 3 x  2mx  2
Đs: 6  3 3  m  6  3 3 2) 1 3 2
y   x  2x  2m   1 x  3m  2 Đs: 5 m   3 2 3) 1 3
y   x  m  2 2 x mx  7 Đs: 4   m  1  3 4) 1 3 2
y   x mx  3m  2 x 1 Đs: 2   m  1  3
Bài tập 2. Tìm m để hàm số sau luôn đồng biến trên ? 1) 3
y x  m   2 x   2 2
m  4 x  9 Đs: m  4   m  2 2) 3 2
y x mx x  5
Đs:  3  m  3 3) 1 3 2 y
x mx  4x  3 Đs: 2   m  2 3 4) 3 2
y x  3x mx m Đs: m  3
Bài tập 3. Tìm m để hàm số sau giảm trên ?
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 28
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 3 1)     x y m m   2
x  m   2 2 2 8 x m 1 Đs: m  2  3 2) 1
y  1 m 3
x  22  m 2
x  22  mx  5
Đs: 2  m  3 3 3) 1 1  3
y mx  m   2
1 x  3m  2 x Đs: 2 6 m  3 3 2 4) 3 2
y mx  3mx  3x 1 Đs: m  1 
Bài tập 4. Tìm m để hàm số sau đồng biến trên ? 1) 1  2 m  4 3
x  m  2 2 x  2x  3 Đs: m  2   m  6 3 3 2)  x 2 m    m   2 1 1 x  3x 1 Đs: m  1   m  2 3 3) m   3
x  m   2 1
1 x x m
Đs: m 1;4 4) m   3
x  m   2 2 3
2 x  3m  3 x  9 Đs: m  2 
Bài tập 5. Tìm m để hàm số đồng biến trên từng khoảng xác định của nó? m    1) 1 x m mx y
Đs: 0  m  2 2) 2 y
Đs: m 1 m  2 x m x m  3 m   3) mx  4  3m 1 x 2 y Đs: 4   m 1 4) y Đs: m 2   ;1 x m x m
Bài tập 6. Tìm m để hàm số nghịch biến trên từng khoảng xác định của nó?    1) x 1 mx m y
Đs: m 1 2) 3 2 y Đs: 3   m 1 x m x m  3) mx 5 y
Đs: m  5 x 1
Bài tập 7. Tìm m để hàm số nghịch biến trên từng khoảng xác định của nó? 2
x  2m     1) 1 x m 5 y Đs: m  4 x 1
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 29
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
m   2x mx  3 2 1 2 m m  2 2) y Đs: m  1  x m
Bài tập 8. Tìm m để hàm số luôn đồng biến trên từng khoảng xác định của nó 2 1) mx  2x 1 m y
Đs: 0  m 1
2) y x  2  Đs: m  0 x 1 x 1 Bài tập 9. 1 Cho hàm số 3
y   x  m   2 1 x  2 2
m  3 x m . Chứng minh rằng hàm số 3
luôn nghịch biến trên tập xác định cuả nó?
Bài tập 10. Cho hàm số 3
y x   m   2 2 3 2
1 x  6m m  
1 x 1 . Chứng minh hàm số không
thể luôn đồng biến trên tập xác định của nó?
C - BÀI TẬP TRẮC NGHIỆM ĐỀ 01 Câu 1. mx
Tất cả giá trị của tham số m để hàm số 2 y
luôn nghịch biến trên từng 2x m
khoảng xác định của nó là: A. 2   m  2 B. m  2  hoặc m  2 C. 2   m  2 D. m  2  hoặc m  2 Câu 2. Hàm số 3 2
y  3x mx  2x 1 đồng biến trên khi và chỉ khi: A. mB. m  3 2 C. m D. 3  2  m  3 2 2 Câu 3.
x mx  2 Hàm số y
giảm trên từng khoảng xác định khi: x 1 A. m  3  B. m  3 C. m  3  D. m Câu 4. kx Hàm số 3 y
giảm trên từng khoảng xác định khi x 1 A. k  3 B. k  3  C. k  3 D. k  3 
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 30
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 5. mx Hàm số 1 y
nghịch biến trên từng khoảng xác định khi giá trị của m x m bằng A. m 1 B. m 1 C. mD. 1   m 1 Câu 6.
Tìm tất cả các giá trị của tham số m sao cho hàm số 3 2
y x  3x  3mx 1 đồng
biến trên . Chọn kết quả đúng: A. m 1 B. m 1 C. m 1 D. m 1 3 Câu 7. x
Tìm tất cả các giá trị của tham số m sao cho hàm số y   m   2 1 x  4x  5 3
đồng biến trên . Chọn kết quả đúng: A. 3   m 1 B. m  3   m 1 C. 2   m  2 D. 2   m  2 Câu 8. 1
Hàm số y  m   3 2
1 x mx  3m  2 x luôn đồng biến trên tập xác định khi: 3 A. 1 m B. m  2 C. m 1 D. m  2 2 Câu 9. mx m Hàm số 7 8 y
luôn đồng biến trên từng khoảng xác định khi: x m A. 8   m 1 B. 8   m 1 C. 4   m 1 D. 4   m 1 Câu 10.
Cho hàm số y  cos x ax . Với giá trị nào của a thì hàm số đồng biến trên A. a 1 B. a  1  C. 0  a 1 D. 1   a  0 Câu 11. 1 Cho hàm số 3 2
y   x  2x  2m  
1 x  3m  2 . Để hàm số nghịch biến trên 3
thì điều kiện tham số m là A. 5 m B. 5 m   C. m 1 D. m  1  2 2 Câu 12. mx
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số 4 y  đồng x m
biến trên từng khoảng xác định A.  2  ;2 B.  ;  2 C. 2; D.  ;  2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 31
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 13.
Tìm tập hợp các giá trị tham số thực m để hàm số y msin x  7x 5m  3 đồng biến trên A. m  7  B. 7   m  7 C. m  7 D. m  1  Câu 14.
Tìm tát cả các giá trị của tham số m để hàm số 3 2
y mx mx m m   1 x  2 đồng biến trên A. 4 m B. 4 m
và m  0 C. m  0 hoặc 4 m D. 4 m  3 3 3 3 Câu 15.
Tìm tập các giá trị của tham số thực m để hàm số 2 y
x 1  mx 1 đồng biến trên  ;   A.   ;1  B. 1; C.  1   ;1 D.  ;    1 Câu 16. 1
(THPT Ngô Sĩ Liên- Bắc Giang) Hàm số 3 y
x  m   2
1 x  m   1 x 1 đồng 3
biến trên tập xác định của nó khi và chỉ khi       A. m 1 mB. 1  C. 2   m  1  D. 2   m  1  m  2  m  2 Câu 17.
(THPT chuyên Lê Hồng Phong- HCM) Tìm tất cả các giá trị của tham số m để hàm số mx 1 y
đồng biến trên từng khoảng xác định của nó x m A. m  1  hoặc m 1 B. m  1
 hoặc m 1 C. m  1
 hoặc m 1 D. 1   m 1 Câu 18. mx
(THPT Đông Quan) Hàm số 1 y
đồng biến trên khoảng 1; khi x m A. 1   m 1 B. m 1 C. m \ 1   ;1 D. m 1 Câu 19.
(THPT Hà Trung- Thanh Hóa) Tìm tất cả các giá trị của m để hàm số mx  2 y
đồng biến trên mỗi khoảng xác định 2x m       A. m 2 mB. 2   m  2 C. 2  D. 2   m  2 m  2 m  2 Câu 20.
(THPT Ngô Gia Tự) Tìm tất cả các giá trị thực của tham số m để hàm số
y x mcos x đồng biến trên A. m 1 B. m 1 C. m 1   ;1 \   0 D. 1   m 1 Câu 21. m
(THPT Ninh Giang- Hải Dương) Hàm số 3 2 y
x  2x  m  3 x m luôn 3
đồng biến trên thì giá trị nhỏ nhất của m là A. m 1 B. m  2  C. m  4  D. m  0
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 32
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 22.
(Chuyên ĐH Vinh) Các giá trị của tham số m để hàm số 3 2
y mx  3mx  3x  2
nghịch biến trên và đồ thị của nó không có tiếp tuyến song song với trục hoành là A. 1   m  0 B. 1   m  0 C. 1   m  0 D. 1   m  0 Câu 23.
(THPT Dịu Hiền- Cần Thơ) Tìm m để hàm số y mx sin x  3 đồng biến trên A. m 1 B. m 1 C. m  1  D. m 1
VẤN ĐỀ 3. TÌM THAM SỐ M ĐỂ HÀM SỐ LUÔN TĂNG (HOẶC GIẢM) TRÊN MỘT KHOẢNG A. VẬN DỤNG Ví dụ 1. Cho hàm số : 3 2
y x  3x  2mx  4 . Tìm m để hàm số đồng biến trên khoảng  ;  0 .
Cách 1. Giải biện luận theo phương trình y ' . Cách 2. Cô lập m. Đs: 3 m   2 Ví dụ 2. Cho hàm số: 3 2
y x mx   2 3 3 m  
1 x  2m  3 . Xác định m để hàm số nghịch
biến trên khoảng 1;2 ?
Đs: 1 m  2 Ví dụ 3. Cho hàm số 3 2
y x  3x mx  2 . Xác định m để hàm số đồng biến trên khoảng 0; Đs: m  3 
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Cho hàm số 3
y x  m   2 x   2 1
2m  3m  2 x 1 . Tìm m để hàm số đồng biến
trên khoảng 2; ? Đs: 3 2   m  2
Bài tập 2. Cho hàm số 3 2
y mx  3x  3x 1 . Tìm m để hàm số nghịch biến trên khoảng 1;2
Đs: Không tồn tại m
Bài tập 3. Cho hàm số 3 2
y x  3x  m  
1 x  4m . Tìm m để hàm số nghịch biến trên khoảng  1   ;1 ? Đs: m  10 
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 33
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
Bài tập 4. Cho hàm số 3 2
y  x mx m . Tìm m để hàm số đồng biến trên khoảng 1; 2 ? Đs: m  3 Bài tập 5. 1 Cho hàm số 3
y   x  m   2
1 x  m  3 x  4 . Tìm m để hàm số đồng biến 3 trên khoảng 0;3 ? Đs: 12 m  7 Bài tập 6. 1 Cho hàm số 3 y
x  m   2
1 x mm  2 x  7 . Tìm m để hàm số đồng biến 3 trên khoảng 4;9 ?
Đs: m  2;m  9
Bài tập 7. Cho hàm số 3 2
y x mx   2
2m  7m  7 x  2m  
1 2m  3 . Tìm m để hàm số
đồng biến trên khoảng 2; ? Đs: 5 1   m  2
Bài tập 8. Cho hàm số 3 2
y x mx   2
2m  7m  7 x  2m  
1 2m  3 . Tìm m để hàm số
đồng biến trên khoảng 3; ? Đs: 17 m  12
Bài tập 9. Cho hàm số 3
y x   m   2 3 2
1 x  12m  5 x  2 . Tìm m để hàm số đồng biến
trên khoảng 2; ? Đs: 5 m  12 Bài tập 10. 1 1 Cho hàm số 3
y mx  m   2
1 x  3m  2 x
. Tìm m để hàm số đồng biến 3 3
trên khoảng 2; ? Đs: 2 m  3 Bài tập 11. 1 Cho hàm số 3
y mx  2m   2
1 x  m  
1 x m . Tìm m để hàm số đồng biến 3
trên khoảng 2; ? Đs: 9 m  13
Bài tập 12. Cho hàm số 3 2
y x mx   2 3 3 m  
1 x 1 m . Tìm m để hàm số đồng biến trên mỗi khoảng  ;
 2 và 4; ? Đs: m  3
Bài tập 13. Cho hàm số 3
y x   m   2 3 2
1 x  12m  5 x  2 . Tìm m để hàm số đồng biến trên mỗi khoảng  ;    1 và 2;  ? Đs: 7 5   m  12 12
C. BÀI TẬP TRẮC NGHIỆM
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 34
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 3 Câu 1. x
Tìm tham số m để hàm số f x   m   2
1 x  m  3 x tăng trên khoảng 3 0;3 A. 12 m B. 12 m C. 12 m D. 12 m  7 7 7 7 Câu 2. mx
Tìm tham số m để hàm số f x 4 
tăng trên khoảng 2; x m A. m  2 B. m  2 C. m  2 D. m  0 Câu 3. mx
Tìm tham số m để hàm số f x 4 
giảm trên khoảng   ;1  x m A. 2   m  1  B. 2   m  1  C. 2   m  1  D. 2   m  1  3 Câu 4. x 1
Tìm tham số m để hàm số y    m  2 2
x mm  3 x  nghịch biến 3 3 trên khoảng 1; m  4 m  4 m  4 m  4 A.      5  5 B.  5  5 C.  5  5 D.  5  5 m  m  m  m   2  2  2  2 Câu 5.
Với giá trị nào của m thì hàm số 3 2
y  x  2mx  m 15 x  2 đồng biến trên 1;3 ? A. m  3 B. 18 m C. 18 3  m D. 18 m  5 5 5 Câu 6.
Tìm m để hàm số 3 2
y  x  3x  3mx 1 nghịchbiến trên khoảng 0;  A. m  0 B. m  1  C. m 1 D. m  2 Câu 7. x Hàm số 2 y
đồng biến trên khoảng 2; khi x m A. m  2 B. m  2 C. m  2  D. m  2  Câu 8. Hàm số 3 2
y x  6x mx 1 đồng biến trên khoảng 0;  khi:
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 35
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. m  0 B. m  0 C. m  0 D. m  0 Câu 9.
Với giá trị nào của m thì hàm số 2 2 y
x  2mx m  3 đồng biến trên khoảng 2; A. m  2 B. m  2  C. m  2 D. m  0 Câu 10. Cho hàm số 3
y x  m   2 x   2 1
2m  3m  2 x 1 . Kết luận nào sau đây đúng
A. Hàm số luôn đồng biến trên
B. Hàm số luôn đồng biến trên
C. Hàm số không đơn điệu trên
D. Hàm số có hai cực trị và khoảng cách giữa hai điểm cực trị bằng 1 với mọi m Câu 11. mx Cho hàm số 1 y
đồng biến trên khoảng 1; khi x m A. 1   m 1 B. m 1 C. m \ 1   ;1 D. m 1 Câu 12. 1 m
Tìm tất cả các giá trị của tham số m sao cho hàm số 3 2 y x
x x 1 đồng 3 2
biến trên khoảng 1; . Chọn kết quả đúng: A. m  2  B. m  2 C. 2   m  2 D. 2   m  2 Câu 13.
Tìm tất cả các giá trị thực của tham số m để hàm số  m 1 3 y x    m   2
1 x  3x 1 nghịch biến trên tập xác định của nó  3  A.  4  ;  1 B.  4  ;  1 C. 4  ;1
D. m  4 m  1  Câu 14.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y  x  3x mx  4 nghịch biến trên khoảng 0;  . A. m ;  0
B. m0;
C. m0; D. m ;    1 2 Câu 15.
x  2x m Cho hàm số y
với m là tham số . Hàm số luôn đồng biến trên các x 1
khoảng xác định của nó khi và chỉ khi:
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 36
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. m  3  B. m  3 C. m  6  D. m 1 Câu 16.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y  x  3mx  3mx 1 nghịch biến trên khoảng 0;  . A. m  3  B. m  3 C. m  6  D. m 1 Câu 17.
Giá trị của tham số m để hàm số 3 2
y x  3mx  32m  3 x  2 đồng biến trên khoảng 2; là A. 1 m B. mC. 1 m D. 1 m  2 2 2 Câu 18. Hàm số 3 2
y x  6x mx 1 đồng biến trên khoảng 0;  . Giá trị của m là:
A. m 12 B. m  0 C. 0  m 12 D. m  0 Câu 19. 1 Hàm số 3 2 y
x x mx đồng biến trên khoảng 1;  thì m thuộc khoảng 3 nào sau A. 1; B.  1  ;3 C.   ;3 
D. 3; 2 Câu 20. x  4x
Tìm m để hàm số y
đồng biến trên nửa khoảng 1; 2x m A.  1       1  m   ;     B. 1 m   ;    C. 1 m   ;   
D. m  ; \     0  3  3   3   3  Câu 21. mx
Tìm tất cả các giá trị của m để hàm số 1 y
tăng trên khoảng 1; x m A. m  1  B. m  1  C. m 1 D. Đáp án khác Câu 22. 1
Tìm tất cả các giá trị của m để hàm số 3
y   x  m   2
1 x  m  3 x 10 3
đồng biến trên khoảng 0;3 A. 12 m B. 12 m C. 12 m D. m 3 3 3
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 37
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 23. mx m Cho hàm số 7 8 y
. Tìm tất cả các giá trị của m để hàm số luôn đồng x m
biến trên trên khoảng 0; . A. 8   m  0 B. 8   m 1 C. 8   m  0 D. 8   m  0 Câu 24. m 1
Tìm tất cả các giá trị của m để hàm số 3 y
x  m   2
1 x  3m  2 x  đồng 3 3 biến trên 2; . A.  2        m  ;    B. 2 m  ;    C. 2 m   ;   D. 2 m   ;      3   3   3   3 
Câu 25. Tìm giá trị nhỏ nhất của tham số m sao cho hàm số 3 2
y  x  3x  3mx 1 nghịch biến trên 0; A. m  1  B. m 1 C. m  2 D. m  2  Câu 26. x
Tìm tất cả các giá trị thực của tham số m sao cho hàm số sin 3 y  đồng biến sin x m   trên khoảng  0;    2  A. m  1   0  m  3 B. m  1  C. 0  m  3 D. m  3
Câu 27. Tìm tất cả các giá trị của tham số m sao cho hàm số 3 2
y  x  3x  3mx 1 nghịch biến trên 0; A. m  1  B. m  1  C. m 1 D. 0  m 1 Câu 28. x
Tìm tất cả các giá trị thực của tham số m sao cho hàm số sin 2 y  đồng biến sin x m   trên khoảng  0;    2 
A. m  01 m  2 B. m  0 C. 1 m  2 D. m  2
Câu 29. Tìm tất cả giá trị m để hàm số 3 2
y x  6x mx 1 đồng biến trên khoảng 0; 
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 38
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. m 12 B. m  0 C. m 12 D. m  0 Câu 30. mx
Tìm tất cả giá trị m để hàm số 4 y  nghịch biến trên   ;1  x m A. 2   m  1  B. 2   m  2 C. 2   m  2 D. 2   m 1 ĐỀ 02 2 Câu 1. x  4x Cho hàm số y
. Để hàm số đồng biến trên 1; thì m phải thỏa 2 x mA.  1   1   1  m  4;   
B. m1;4\  2 C. m  ;1 \    0 D. m 1  ; \    0    2   2   2  3 2 Câu 2. x mx Để hàm số y  
x  5 đồng biến trên khoảng 1; thì các giá trị 3 2
thích hợp của tham số m là A. m  2  B. m  2  C. m  2 D. m  2 3 Câu 3. x
Để hàm số y    a  
1 x  4 đồng biến trên 0;3 thì tham số a phải thỏa 3 A. a  3  B. a  3  C. 12 a D. 12 a  7 7 Câu 4. Cho hàm số 3
y x   m   2 3 2
1 x  12m  5 x  2 . Để hàm số đồng biến trên
khoảng 2; thì tham số m phải thỏa A. 1 1   m B. 5 m C. 1 m   D. 5 m  6 6 12 6 12 2 Câu 5.
2x mx m  2 Cho hàm số y
. Để hàm số này nghịch biến trong khoảng x m 1
2; thì giá trị của tham số m là
A. 43 2  m  43 2 B. m  43 2 C. m 1
D. m  4 3 2 Câu 6. Cho hàm số 3 2
y  2x  3x  6mx 1. Để hàm số nghịch biến trên 0; 2 thì tham
số m thỏa mãn điều kiện
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 39
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. m  6 B. 1 m C. m  6  D. 1 m  4 4 Câu 7.
x x m
Tìm m để hàm số f x 2 2 5 6 
đồng biến trên 1; . x  3 A. 4   m  4 B. 4   m  2 C. 2   m  2 D. 2   m  4 Câu 8.
Với các giá trị nào của tham số m thì hàm số f x 3 2
 x  3x  2mx  2 nghịch
biến trên khoảng 0; A. 4 m B. 3 m   C. 16 m   D. 32 m   3 2 3 27 Câu 9.
Tìm tất cả các giá trị thực của tham số m để hàm số y mx  m   1 x  2 1
nghịch biến trên khoảng D  2; A. m  0 B. m  1  C. m  1  D. 2   m 1 Câu 10.
(THPT AMSTERDAM HN) Trong tất cả các giá trị của tham số m để hàm số 1 3 2 y
x mx mx m đồng biến trên
, giá trị nhỏ nhất của m là 3 A. 4 B. 1  C. 0 D. 1 Câu 11.
(THPT AMSTERDAM HN) Xác định các giá trị của tham số m để hàm số 3 2
y x  3mx m nghịch biến trên khoảng 0;  1 ? A. 1 m B. 1 m
C. m  0
D. m  0 2 2 Câu 12.
(THPT chuyên Hạ Long) Tìm các giá trị thực của tham số m để hàm số m  sin x    y
nghịch biến trên khoảng 0;   2 cos x  6  A. 5 m B. 5 m C. 5 m D. 5 m  2 2 4 4 Câu 13.
(THPT Hàm Rồng) Tìm tất cả các giá trị thực của tham số m sao cho hàm số tan x  2    y
đồng biến trên khoảng 0;   tan x m  4    A. m m  0 B. 1 m  2 C. 0  D. m  2 1   m  2 Câu 14. x
(THPT Kiến An) Tìm tất cả các giá trị m để hàm số 2sin 1 y  nghịch biến sin x m   trên khoảng  0;    2  A. m  1  B. m  0 C. m  4 D. m  0
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 40
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 15. 1
(THPT Kiến An) Tìm tất cả các giá trị m để hàm số 3 2 y
x  2x mx  2 3
nghịch biến trên khoảng 0;3 A. m  3 B. m  0 C. m  4 D. m  0 Câu 16.
(THPT Lê Quý Đôn- Bình Phước) Tập hợp các giá trị của m để hàm số 1 3 y
mx  m   2
1 x  3m  2 x 1 đồng biến trên khoảng 2;  là 3 A.  2      S  ;1   B. 2 S  ;   
C. S    ;1 D. 2 S  ;1    3  3   3  Câu 17.
(THPT Lục Ngạn 1- Bắc Ninh) Hãy chọn câu trả lời đúng. Hàm số y  2  x  sin x
A. Nghịch biến trên tập xác định
B. Đồng biến trên  ;  0
C. Đồng biến trên tập xác định
D. Đồng biến trên 0; Câu 18.
(Sở GD Bình Định) Tìm tất cả các giá trị thực của tham số m sao cho hàm số m  1 x  2m  2 y
nghịch biến trên khoảng 1; x m
A. m  ;1 2; B. m 1 C. 1   m  2 D. 1 m  2 2 Câu 19.
x  2mx m  2
(THPT Nghĩa Hưng- Nam Định) Cho hàm số y  . Với giá trị x m
nào của m thì hàm số đồng biến trên khoảng 1; A. 3 17    m  2
B. m  2 C. 3 17 m D. 3 17 m   m  2 4 4 4 Câu 20.
(THPT Phù Cát- Binh Định) Tất cả các giá trị thực của tham số m để hàm số 1 1 3 2 y x
mx mx đồng biến trên khoảng 1;  3 2 A. m  4 B. m  4 C. m  4 D. m  0 m    Câu 21. 1 x 1 2
(THPT Yên Lạc- Vĩnh Phúc) Cho hàm số y  . Tìm tất cả các x 1  m
giá trị của tham số m để hàm số đồng biến trên khoảng 17;37     A. m m 4   m  1  B. 2  C. 2  D. 1   m  2 m  6  m  4  m  Câu 22. 1 sin x  2
(THPT Yên Lạc- Vĩnh Phúc) Cho hàm số y  . Tìm tất cả các sin x m  
giá trị của tham số m để hàm số nghịch biến trên khoảng  0;    2 
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 41
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953         A. m m m 1   m  2 B. 1  C. 1  D. 0  m  2 m  2 m  1 Câu 23.
(THPT Ninh Giang – Hải Dương) Tìm tâph hợp các giá trị của tham số m để hàm số x 2 y
x x m đồng biến trên  ;  2 2 A. 1 m B. 1 m
C. m  2
D. m  7 4 4 Câu 24.
(THPT chuyên Vĩnh Phúc) Tìm tất cả các giá trị của tham số m để hàm số 1 2 3 y
x  m   2
1 x  2m  3 x
đồng biến trên 1; 3 3 A. m  2 B. m  2 C. m 1 D. m 1 Câu 25.
(THPT Phạm Văn Đồng- Phú Yên) Tìm tập hợp tất cả các giá trị cuẩ tham số thực m để hàm số 1 3 2 2 y
x mx x m  4m 1 đồng biến trên 1;  3 3 A.       ;1  B.   ;1  C. 10 ;    D. 10 ;     3   3  Câu 26.
(THPT Phả Lại) Tìm tất cả các giá trị của tham số m để hàm số 3
y x  m   2 2 3
1 x  6 m  2 x  2017 nghịch biến trên khoảng a;b sao cho b a  3   A. m m  9 B. 0 
C. m  6
D. m  0 m  6 Câu 27. x
(Chuyên Bắc Giang) Tìm m để hàm số 2cos 1 y
đồng biến trên 0;  cos x m A. m  1  B. 1 m   C. m  1  D. m 1 2 Câu 28.
(Chuyên ĐH Vinh) Tìm tất cả các giá trị của tham số m để hàm số y m  2 x   4 2
1 x  2mx đồng biến trên 1;  A.m  1
 hoặc m 1 B. m  1  hoặc 1 5 m  2 C.m  1  hoặc 1 5 m D. m  1  2 Câu 29.
(Chuyên Lê Hồng Phong- Nam Định) Tìm tất cả các giá trị thực của tham số    m để hàm số cot x 1  y
đồng biến trên khoảng ;   m cot x 1  4 2  A. m ;  0 1; B. m ;  0
C. m1;
D. m  ;1
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 42
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
VẤN ĐỀ 4. TÌM THAM SỐ M ĐỂ HÀM SỐ LUÔN TĂNG (HOẶC GIẢM) TRÊN ĐOẠN DÀI L A. VẬN DỤNG Ví dụ 1. Cho hàm số 3 2
y x  3x mx m . Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 1. Đs: 9 m  4 Ví dụ 2. 1 1 Cho hàm số 3 2 y
x mx  2mx  3m  4 . Tìm m để hàm số đồng biến trên 3 2
đoạn có độ dài bằng 3. Đs: m  1  ;m  9
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Cho hàm số 3 2
y x  3x mx m . Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 3. Đs: 15 m   4
Bài tập 2. Cho hàm số 3 2
y x  3mx  22m  3 x 1 . Tìm m để hàm số nghịch biến trên
đoạn có độ dài bằng 2 11 . Đs: 15 m   4
C. BÀI TẬP TRẮC NGHIỆM Câu 1. Tìm m để hàm số 3 2
y x  3m x nghịch biến trên khoảng có độ dài bằng 2 A. 1   m 1 B. m  1  C. 2   m  2 D. m  2  Câu 2. Cho hàm số 3
y x   m   2 x   2 2 3 3 1
6 2m mx  3 . Tìm m để hàm số nghịch
biến trên đoạn có độ dài bằng 4
A. m  5 m  3 B. m  5   m  3
C. m  5 m  3  D. m  5   m  3  Câu 3. Hàm số 3 2
y x  3x mx m nghịch biến trên một khoảng có độ dài bằng 1 khi: A. 9 m B. 9 m   C. 9 m D. 9 m   4 4 2 2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 43
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 4. 1
Cho hàm số y  m   3
1 x  2m   2
1 x  3m  2 x m . Giá trị m làm cho hàm số 3
có khoảng nghịch biến có độ dài bằng 4 là? A. 7  61    m B. 7 61 m C. 7 61 m D. 7 62 m  6 6 6 6 Câu 5.
Tìm tham số m để hàm số 3 2
y x  3x mx m nghịch biến trên một khoảng có độ dài bằng 1 A. 9 m B. 9 m C. 9 m D. 9 m  4 4 4 4 Câu 6. 1
Với giá trị nào của m thì hàm số 3 y
x  m   2
1 x  4x  2 có độ dài khoảng 3 nghịch biến là 2 5
A. m2;  4 B. m 2  ;  4 C. m1;  3 D. m 3   ;1 Câu 7.
(THPT Hùng Vương- Bình Định) Xác định m để hàm số 3
y x  m   2
1 x  4x  7 có độ dài khoảng nghịch biến bằng 12 A. m  2  ,m  4
B. m 1,m  3
C. m  0,m  1 
D. m  2,m  4 
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 44