124 trang 30 lượt tải

Bài tập trắc nghiệm tích phân hàm ẩn có đáp án và lời giải Toán 12

60

Bài tập trắc nghiệm tích phân hàm ẩn có đáp án và lời giải Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/124
https://toanmath.com/
TÍCH PHÂN CỦA HÀM ẨN
BÀI TẬP
DẠNG 1: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT NGUYÊN HÀM
Câu 1: Cho hàm số
( )
fx
xác định trên
{ }
\1
thỏa mãn
( )
1
1
fx
x
′
=
−
,
( )
0 2017f =
,
( )
2 2018f =
. Tính
( ) ( )
31Sf f= −−
.
A.
1S =
. B.
ln 2S =
. C.
. D.
4S =
.
Câu 2: Cho hàm số
( )
fx
xác định trên
1
\
2



thỏa mãn
( )
2
21
fx
x
′
=
−
và
(
)
01f =
. Giá trị của
biểu thức
( ) ( )
13ff−+
bằng
A.
4 ln15+
. B.
3 ln15+
. C.
2 ln15+
. D.
ln15
.
Câu 3: Cho hàm số
()
fx
xác định trên
1
\
2



thỏa mãn
2
()
21
fx
x
′
=
−
,
(0) 1f =
và
(1) 2f =
. Giá
trị của biểu thức
( 1) (3)ff−+
bằng
A.
4 ln5+
. B.
2 ln15+
. C.
3 ln15+
. D.
ln15.
Câu 4: Cho hàm số
( )
fx
xác định trên
thỏa mãn
( )
21fx x
′
= +
và
( )
15f =
. Phương trình
( )
5
fx=
có hai nghiệm
1
x
,
2
x
. Tính tổng
21 22
log logSx x= +
.
A.
1S =
. B.
2S =
. C.
0S =
. D.
4S =
.
Câu 5: Cho hàm số
()fx
xác định trên
1
\
3



thỏa mãn
(
)
( )
3
,01
31
fx f
x
′
= =
−
và
2
2
3
f

=


.
Giá trị của biểu thức
( ) ( )
13ff−+
bằng
A.
3 5ln 2+
. B.
2 5ln 2−+
. C.
4 5ln 2
+
. D.
2 5ln 2
+
.
Câu 6: Cho hàm số
( )
fx
xác định trên
{ }
\ 2;2−
và thỏa mãn
( ) ( )
2
4
; 30
4
fx f
x
′
= −=
−
;
( )
01f =
và
( )
32f =
. Tính giá trị biểu thức
( ) ( ) ( )
4 14Pf f f= −+ −+
.
A.
3
3 ln
25
P
= +
. B.
3 ln3P = +
. C.
5
2 ln
3
P
= +
. D.
5
2 ln
3
P = −
.
Câu 7: Cho hàm số
( )
fx
xác định trên
{ }
\ 2;1−
thỏa mãn
( )
2
1
2
fx
xx
′
=
+−
;
(
) ( )
3 30ff
−− =
và
( )
1
0
3
f =
. Giá trị của biểu thức
( ) ( ) ( )
4 14fff−+ −−
bằng
A.
11
ln 2
33
+
. B.
1 ln80+
. C.
14
1 ln 2 ln
35
++
. D.
18
1 ln
35
+
.
Câu 8: Cho hàm số
( )
fx
xác định trên
{ }
\ 1;1−
và thỏa mãn
( )
2
1
1
fx
x
′
=
−
;
( ) ( )
3 30ff−+ =
và
11
2
22
ff

−+ =


. Tính giá trị của biểu thức
( )
( )
04Pf f= +
.
A.
3
2 ln
5
P = +
. B.
3
1 ln
5
P = +
. C.
13
1 ln
25
P = +
. D.
13
ln
25
P
=
.
Câu 9: Cho hàm số
(
)
fx
xác định trên
{ }
\1±
thỏa mãn
( )
2
1
1
fx
x
′
=
−
. Biết
( ) ( )
3 30ff−+ =
và
11
2
22
ff

−+ =


. Giá trị
( ) ( ) ( )
204Tf f f= −+ +
bằng:
https://toanmath.com/
A.
15
2 ln
29
T = +
. B.
19
1 ln
25
T
= +
. C.
19
3 ln
25
T = +
. D.
19
ln
25
T
=
.
Câu 10: Cho hàm số
( )
fx
nhận giá trị dương, có đạo hàm liên tục trên
(
)
0;+∞
thỏa mãn
( )
1
2
15
f
=
và
( ) ( ) (
)
2
24 0
fx x f x
′
++ =
. Tính
( )
(
) (
)
123
ff f
++
.
A.
7
15
. B.
11
15
. C.
11
30
. D.
7
30
.
Câu 11: Cho hàm số
( )
fx
xác định và liên tục trên
. Biết
( ) ( )
6
. 12 13f xfx x
′
= +
và
( )
02f =
.
Khi đó phương trình
( )
3fx=
có bao nhiêu nghiệm?
A.
2
. B.
3
. C.
7
. D.
1
.
Câu 12: Cho hàm số
( )
fx
xác định trên
thỏa mãn
( )
ee 2
xx
fx
−
′
= +−
,
( )
05f =
và
1
ln 0
4
f

=


. Giá trị của biểu thức
( ) ( )
ln16 ln 4Sf f=−+
bằng
A.
31
2
S =
. B.
9
2
S =
. C.
5
2
S =
. D.
( ) ( )
0. 2 1ff=
.
Câu 13: Cho hàm số
( )
fx
liên tục, không âm trên đoạn
0;
2
π



, thỏa mãn
( )
03f =
và
( ) ( ) ( )
2
. cos . 1fxf x x f x
′
= +
,
0;
2
x
π

∀∈


. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
( )
fx
trên đoạn
;
62
ππ



.
A.
21
2
m =
,
22M
=
. B.
5
2
m =
,
3M =
.
C.
5
2
m
=
,
3M
=
. D.
3m =
,
22M =
.
Câu 14: Cho hàm số
( )
fx
có đạo hàm liên tục trên
và thỏa mãn
( )
0fx>
,
x∀∈
. Biết
( )
01
f =
và
( )
( )
'
22
fx
x
fx
= −
. Tìm các giá trị thực của tham số
m
để phương trình
( )
fx m
=
có hai
nghiệm thực phân biệt.
A.
me>
. B.
01
m<≤
. C.
0 me<<
. D.
1 me<<
.
Câu 15: Cho hàm số
( )
fx
liên tục trên
và
( )
0fx≠
với mọi
x∈
.
( ) (
) ( )
2
21fx x f x
′
= +
và
( )
1 0,5f = −
. Biết rằng tổng
( ) ( ) ( ) ( )
1 2 3 ... 2017
a
ff f f
b
+ + ++ =
;
( )
,ab∈∈
với
a
b
tối giản. Mệnh đề nào dưới đây đúng?
A.
1ab+=−
. B.
( )
2017;2017a∈−
. C.
1
a
b
<−
. D.
4035ba−=
.
Câu 16: Cho hàm số
( )
0fx≠
thỏa mãn điều kiện
( ) ( ) ( )
'2
2 3.fx x fx
= +
và
( )
1
0
2
f
−
=
. Biết tổng
( )
( ) ( )
( )
1 2 ... 2017 2018
a
ff f f
b
+ ++ + =
với
*
,ab∈∈
và
a
b
là phân số tối giản. Mệnh
đề nào sau đây đúng?
A.
1
a
b
<−
. B.
1
a
b
>
.
C.
1010ab+=
. D.
3029
ba−=
.
https://toanmath.com/
Câu 17: Cho hàm số
( )
y fx
=
,
0x∀≥
, thỏa mãn
( ) ( ) ( ) ( )
( ) ( )
2
3
.2 0
0 0; 0 1
f x f x f x xf x
ff
′′ ′
− +=


′
= =
. Tính
( )
1f
.
A.
2
3
. B.
3
2
. C.
6
7
. D.
7
6
.
Câu 18: Giả sử hàm số
()fx
liên tục, dương trên
; thỏa mãn
( )
01
f =
và
( )
( )
2
1
fx
x
fx x
′
=
+
. Khi đó
hiệu
(
)
(
)
22 2 1Tf f= −
thuộc khoảng
A.
( )
2;3
. B.
( )
7;9
. C.
(
)
0;1
. D.
( )
9;12
.
Câu 19: Khi đó
(
)
( )
1
4
2
00
tan
dd
cos
ft
t fx x
t
π
=
∫∫
. Vậy
( )
1
0
d6fx x=
∫
.Cho hàm số
( )
y fx=
đồng biến trên
( )
0;+∞
;
( )
y fx=
liên tục, nhận giá trị dương trên
( )
0;+∞
và thỏa mãn
(
)
2
3
3
f =
và
( ) ( ) ( )
2
' 1.f x x fx= +


. Mệnh đề nào dưới đây đúng?
A.
( )
2
2613 8 2614f
<<
. B.
( )
2
2614 8 2615f<<
.
C.
( )
2
2618 8 2619f<<
. D.
( )
2
2616 8 2617f<<
.
Câu 20: Giả sử hàm số
( )
y fx=
liên tục, nhận giá trị dương trên
(
)
0; +∞
và thỏa mãn
( )
11f =
,
( )
( )
31fx f x x
=′+
, với mọi
0x >
. Mệnh đề nào sau đây đúng?
A.
( )
4 55f<<
. B.
( )
2 53f<<
.
C.
(
)
3 54f<<
. D.
( )
1 52f<<
.
Câu 21: Cho hàm số
( )
fx
thỏa mãn
(
) (
) ( )
2
4
. 15 12f x fxf x x x
′ ′′
+=+


,
x∀∈
và
( )
( )
0 01
ff
′
= =
. Giá trị của
( )
2
1
f
bằng
A.
9
2
. B.
5
2
. C.
10
. D.
8
.
Câu 22: Cho hàm số
(
)
fx
liên tục trên
và thỏa mãn
( )
( )
1 2 13
d
5
1
fx x
xC
x
x
+ ++
= +
+
+
∫
. Nguyên
hàm của hàm số
( )
2fx
trên tập
+
là:
A.
(
)
2
3
24
x
C
x
+
+
+
. B.
2
3
4
x
C
x
+
+
+
. C.
(
)
2
23
41
x
C
x
+
+
+
. D.
( )
2
23
81
x
C
x
+
+
+
.
DẠNG 2: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT, GIẢI HỆ TÍCH PHÂN
Câu 23: Cho
( )
5
2
d 10fx x=
∫
. Kết quả
(
)
2
5
24 dfx x−


∫
bằng:
A.
34
. B.
36
. C.
40
. D.
32
.
Câu 24: Cho hàm số
(
)
fx
liên tục trên
và
(
)
Fx
là nguyên hàm của
( )
fx
, biết
( )
9
0
d9fx x=
∫
và
( )
03F =
. Tính
( )
9F
.
A.
( )
96F = −
. B.
( )
96F
=
. C.
( )
9 12F =
. D.
( )
9 12F = −
.
https://toanmath.com/
Câu 25: Cho
(
)
2
0
d3I fx x
= =
∫
. Khi đó
( )
2
0
4 3dJ fx x= −


∫
bằng:
A.
2
. B.
6
. C.
8
. D.
4
.
Câu 26: Cho
( )
4
2
d 10fx x=
∫
và
( )
4
2
d5gx x=
∫
. Tính
( ) ( )
4
2
3 5dI fx gx x= −


∫
A.
5I =
. B.
15I =
. C.
5I = −
. D.
10I =
.
Câu 27: Giả sử
( )
9
0
d 37fx x=
∫
và
( )
0
9
d 16gx x=
∫
. Khi đó,
( )
9
0
2 3()dI f x gx x= +


∫
bằng:
A.
26
I =
. B.
58I =
. C.
143I =
. D.
122
I =
.
Câu 28: Nếu
(
)
2
1
d3fx x
=
∫
,
( )
5
2
d1fx x= −
∫
thì
( )
5
1
dfx x
∫
bằng
A.
2−
. B.
2
. C.
3
. D.
4
.
Câu 29: Cho
( )
2
1
d1fx x
=
∫
và
( )
3
2
d2fx x= −
∫
. Giá trị của
( )
3
1
dfx x
∫
bằng
A.
1
. B.
3−
. C.
1−
. D.
3
.
Câu 30: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
và
( )
10
0
d7fx x=
∫
và
( )
6
2
d3fx x=
∫
. Tính
( ) ( )
2 10
06
ddP fx x fx x= +
∫∫
.
A.
7
P =
. B.
4
P
= −
. C.
4P =
. D.
10
P =
.
Câu 31: Cho
( )
1
0
d2fx x=
∫
,
( )
2
1
d4
fx x=
∫
, khi đó
(
)
2
0
dfx x=
∫
?
A.
6
. B.
2
. C.
1
. D.
3
.
Câu 32: Cho hàm số
( )
fx
liên tục trên
và có
( )
1
0
d2fx x
=
∫
;
( )
3
1
d6fx x=
∫
. Tính
( )
3
0
dI fx x
=
∫
.
A.
8I =
. B.
12I =
. C.
36I =
. D.
4I =
.
Câu 33: Cho
( )
2
1
d2fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x fx gx x
−
=++


∫
bằng
A.
11
2
I =
. B.
7
2
I =
. C.
17
2
I =
. D.
5
2
I =
.
Câu 34: Biết
( )
8
1
d2fx x= −
∫
;
( )
4
1
d3fx x=
∫
;
( )
4
1
d7gx x=
∫
. Mệnh đề nào sau đây sai?
A.
( )
8
4
d1
fx x=
∫
. B.
( ) ( )
4
1
d 10fx gx x+=


∫
.
C.
( )
8
4
d5fx x= −
∫
. D.
( )
( )
4
1
4 2 d2fx gx x−=−


∫
.
Câu 35: Cho hàm số
( )
fx
có
( )
fx
′
liên tục trên đoạn
[ ]
1; 3−
,
( )
13f −=
và
3
1
( )d 10fxx
−
′
=
∫
giá trị
của
( )
3f
bằng
A.
13−
. B.
7
−
. C.
13
. D.
7
.
https://toanmath.com/
Câu 36: Cho
(
)
2
0
d3fx x
=
∫
. Tính
( )
( )
2
0
1d
fx x
+
∫
?
A.
4
. B.
5
. C.
7
. D.
1
.
Câu 37: Cho
(
)
y fx
=
,
(
)
y gx=
là các hàm số có đạo hàm liên tục trên
[
]
0;2
và
( )
(
)
2
0
. d2
gx f x x
′=
∫
,
( ) ( )
2
0
. d3gxfx x′=
∫
. Tính tích phân
( ) ( )
2
0
.dI fxgx x
′
=


∫
.
A.
1I = −
. B.
6I =
. C.
5I =
. D.
1I =
.
Câu 38: Cho hai tích phân
(
)
5
2
d8fx x
−
=
∫
và
( )
2
5
d3
gx x
−
=
∫
. Tính
( ) ( )
5
2
4 1dI fx gx x
−
= −−


∫
.
A.
11I = −
. B.
13I
=
. C.
27I =
. D.
3
I =
.
Câu 39: Cho hàm số
( )
432
42 1fx x x x x= − + −+
,
x∀∈
. Tính
( ) ( )
1
2
0
.df xfxx
′
∫
.
A.
2
3
. B.
2
. C.
2
3
−
. D.
2−
.
Câu 40: Cho hàm số
( )
fx
liên tục trên đoạn [0; 6] thỏa mãn
(
)
6
0
10f x dx
=
∫
và
( )
4
2
6f x dx =
∫
. Tính
giá trị của biểu thức
( ) ( )
26
04
P f x dx f x dx= +
∫∫
.
A.
4P
=
.` B.
16
P =
. C.
8P =
. D.
10P =
.
Câu 41: Cho hàm số
( )
fx
liên tục trên đoạn [0; 1] và có
(
)
1
0
32 5
f x dx−=


∫
. Tính
( )
1
0
f x dx
∫
.
A.
1−
. B. 2. C. 1. D.
2−
.
Câu 42: Cho hai hàm số
( )
fx
và
( )
gx
liên tục trên đoạn [0; 1], có
( )
1
0
4f x dx
=
∫
và
( )
1
0
2
g x dx = −
∫
. Tính tích phân
( ) ( )
3I f x g x dx= −


∫
.
A.
10−
. B.
10
. C. 2. D.
2−
.
Câu 43: Cho hàm số
(
)
2
ln 1fx x x
=++
. Tính tích phân
( )
1
0
'I f x dx
=
∫
.
A.
ln 2I =
. B.
( )
ln 1 2I = +
. C.
ln 2
I =
D.
2ln 2
I =
Câu 44: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn [1; ln3] và thỏa mãn
( )
2
1fe
=
,
( )
ln3
2
1
'9f x dx e= −
∫
. Tính
( )
ln3If=
.
A.
2
92Ie= −
. B.
9I =
. C.
9I = −
. D.
2
29Ie= −
.
Câu 45: Cho hai hàm số
( )
y fx=
và
( )
y gx=
có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn
( ) ( )
1
0
'. 1f x g x dx =
∫
,
( ) ( )
1
0
.' 1f x g x dx = −
∫
. Tính
( )
( )
1
/
0
.I f x g x dx
=


∫
.
A.
2I = −
. B.
0I =
. C.
3I =
. D.
2I =
.
https://toanmath.com/
Câu 46: Cho hàm số
( )
fx
liên tục trên
(
)
0;
+∞
và thỏa
( )
2
0
.cos
x
f t dt x x
π
=
∫
. Tính
( )
4f
.
A.
( )
4 123f
=
. B.
( )
2
4
3
f =
. C.
(
)
3
4
4
f
=
. D.
( )
1
4
4
f =
.
Câu 47: Cho hàm số
(
)
fx
thỏa mãn
( )
2
0
. .cos
fx
t dt x x
π
=
∫
. Tính
( )
4f
.
A.
( )
4 23f =
. B.
( )
41f
= −
. C.
(
)
1
4
2
f =
. D.
( )
3
4 12f =
.
Câu 48: Cho hàm số
( ) ( )
0
.cos .
x
G x t x t dt= −
∫
. Tính
'
2
G
π



.
A.
'1
2
G
π

= −


. B.
'1
2
G
π

=


. C.
'0
2
G
π

=


. D.
'2
2
G
π

=


.
Câu 49: Cho hàm số
( )
2
0
cos .
x
G x t dt=
∫
(
0x >
). Tính
( )
'Gx
.
A.
( )
2
' .cosGx x x=
. B.
( )
' 2 .cosGx x x=
. C.
( )
' cos
Gx x=
. D.
( )
' cos 1Gx x= −
.
Câu 50: Cho hàm số
( )
2
1
1
x
G x t dt
= +
∫
. Tính
( )
'Gx
.
A.
2
1
x
x+
. B.
2
1 x+
. C.
2
1
1 x+
. D.
( )
22
11xx
++
.
Câu 51: Cho hàm số
( )
2
1
sin .
x
F x t dt=
∫
(
0x
>
). Tính
( )
'Fx
.
A.
sin x
. B.
sin
2
x
x
. C.
2sin x
x
. D.
sin x
.
Câu 52: Tính đạo hàm của
( )
fx
, biết
( )
fx
thỏa
( ) ( )
0
.
x
ft fx
t e dt e=
∫
.
A.
( )
'fx x=
. B.
(
)
2
'1fx x= +
. C.
( )
1
'fx
x
=
. D.
( )
1
'
1
fx
x
=
−
.
Câu 53: Cho hàm số
( )
y fx=
liên tục trên
[
)
0;+∞
và
( ) ( )
2
0
d .sin
x
ft t x x
π
=
∫
. Tính
( )
4
f
A.
( )
4
f
π
π
−1
=
. B.
( )
2
f
π
π
=
. C.
( )
4
f
π
π
=
. D.
( )
1
2
f
π
=
.
Câu 54: Cho hàm số
( )
fx
liên tục trên khoảng
( )
2; 3−
. Gọi
( )
Fx
là một nguyên hàm của
( )
fx
trên
khoảng
( )
2; 3−
. Tính
( )
2
1
2dI fx x x
−
= +


∫
, biết
( )
11F −=
và
( )
24F =
.
A.
6I =
. B.
10
I =
. C.
3I =
. D.
9I =
.
Câu 55: Cho
( )
2
1
d2fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x fx gx x
−
=+−


∫
A.
11
2
I =
. B.
7
2
I =
. C.
17
2
I =
. D.
5
2
I
=
.
Câu 56: Cho
( ) ( )
2
1
3 2 d1fx gx x+=


∫
,
(
) ( )
2
1
2 d3fx gx x−=−


∫
. Khi đó,
( )
2
1
dfx x
∫
bằng
https://toanmath.com/
A.
11
7
. B.
5
7
−
. C.
6
7
. D.
16
7
.
Câu 57: Cho
( )
fx
,
(
)
gx
là hai hàm số liên tục trên đoạn
[ ]
1;1−
và
( )
fx
là hàm số chẵn,
( )
gx
là
hàm số lẻ. Biết
( )
1
0
d5fx x=
∫
;
(
)
1
0
d7gx x=
∫
. Mệnh đề nào sau đây là sai?
A.
( )
1
1
d 10fx x
−
=
∫
. B.
( ) ( )
1
1
d 10fx gx x
−
+=


∫
.
C.
( ) ( )
1
1
d 10f x gx x
−
−=


∫
. D.
( )
1
1
d 14gx x
−
=
∫
.
Câu 58: Cho
( )
fx
,
(
)
gx
là hai hàm số liên tục trên đoạn
[ ]
1;1−
và
( )
fx
là hàm số chẵn,
( )
gx
là
hàm số lẻ. Biết
( )
1
0
d5fx x=
∫
;
( )
1
0
d7gx x=
∫
. Mệnh đề nào sau đây là sai?
A.
( )
1
1
d 10fx x
−
=
∫
. B.
( ) ( )
1
1
d 10fx gx x
−
+=


∫
.
C.
( ) ( )
1
1
d 10f x gx x
−
−=


∫
. D.
( )
1
1
d 14gx x
−
=
∫
.
Câu 59: Nếu
( )
10
0
d 17fz z=
∫
và
( )
8
0
d 12ft t=
∫
thì
( )
10
8
3dfx x−
∫
bằng
A.
15
−
. B.
29
. C.
15
. D.
5
.
Câu 60: Cho
( )
2
1
d2fx x
−
=
∫
,
( )
7
1
d9ft t
−
=
∫
. Giá trị của
( )
7
2
dfz z
∫
là
A.
11
. B.
5
. C.
7
. D.
9
.
Câu 61: Cho hàm số
( )
y fx=
liên tục, luôn dương trên
[ ]
0;3
và thỏa mãn
( )
3
0
d4I fx x= =
∫
. Khi đó
giá trị của tích phân
( )
( )
( )
3
1 ln
0
4d
fx
Ke x
+
= +
∫
là:
A.
4 12e+
. B.
12 4e
+
. C.
3e 14+
. D.
14 3e+
.
Câu 62: Cho hàm số
( )
y fx=
có đạo hàm trên
thỏa
( ) ( )
( ) ( ) ( ) ( )
0 0 1;
3 1, x,y
ff
fx y fx fy xyx y
′
= =
+= + + +−∀∈
.
Tính
( )
1
0
1dfx x−
∫
.
A.
1
2
. B.
1
4
−
. C.
1
4
. D.
7
4
.
Câu 63: Cho hàm số
( )
fx
là hàm bậc nhất thỏa mãn
( ) ( )
1
0
1 d 10x fxx
′
+=
∫
và
( ) ( )
21 0 2ff−=
.
Tính
( )
1
0
dI fx x=
∫
.
A.
1I =
. B.
8I =
. C.
12I = −
. D.
8I = −
.
https://toanmath.com/
Câu 64: Cho hàm số
( )
fx
xác định trên
{ }
\0
, thỏa mãn
( )
35
1
fx
xx
′
=
+
,
( )
1fa=
và
(
)
2fb−=
. Tính
( ) ( )
12ff−+
.
A.
(
) (
)
12f f ab− + =−−
. B.
( ) ( )
12f f ab−+ =−
.
C.
(
) ( )
12f f ab
−+ =+
. D.
( ) ( )
12f f ba−+ =−
.
Câu 65: Cho hàm số
(
)
fx
xác định trên
{ }
\0
và thỏa mãn
( )
24
1
fx
xx
′
=
+
,
( )
1fa=
,
( )
2fb−=
. Giá trị của biểu thức
( ) ( )
12ff−−
bằng
A.
ba−
. B.
ab+
. C.
ab−
. D.
ab−−
.
Câu 66: Cho hàm số
( )
y fx=
xác định và liên tục trên
thỏa mãn đồng thời các điều kiện
( )
0fx>
,
x∀∈
;
( )
(
)
2
.
x
f x ef x
′
= −
,
x∀∈
và
( )
1
0
2
f =
. Tính giá trị của
( )
ln 2f
.
A.
( )
2
ln 2
9
f =
. B.
( )
2
ln 2
9
f
= −
. C.
( )
2
ln 2
3
f =
. D.
( )
1
ln 2
3
f =
.
Câu 67: Cho hàm số
( )
y fx=
có đồ thị
(
)
C
, xác định và liên tục trên
thỏa mãn đồng thời các
điều kiện
( )
0fx x> ∀∈
,
( ) ( )
( )
2
.,f x xf x x
′
= ∀∈
và
( )
02f =
. Phương trình tiếp
tuyến tại điểm có hoành độ
1x =
của đồ thị
( )
C
là.
A.
6 30yx= +
. B.
6 30yx=−+
. C.
36 30yx= −
. D.
36 42yx=−+
.
Câu 68: Cho hàm số
( )
0y fx= >
xác định, có đạo hàm trên đoạn
[ ]
0;1
và thỏa mãn:
( ) ( )
0
1 2018 dt
x
gx ft= +
∫
,
( )
( )
2
gx f x=
. Tính
( )
1
0
dgx x
∫
.
A.
1011
2
. B.
1009
2
. C.
2019
2
. D.
505
.
Câu 69: Cho hàm số
( )
y fx=
có đạo hàm và liên tục trên đoạn
[ ]
1;1−
, thỏa mãn
( )
0,fx x> ∀∈
và
(
) ( )
'2 0f x fx+=
. Biết
( )
11f =
, tính
( )
1
f −
.
A.
( )
2
1fe
−
−=
. B.
( )
3
1fe−=
. C.
( )
4
1fe−=
. D.
( )
13f −=
.
Câu 70: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
đồng thời thỏa mãn
( )
09f
′
=
và
( ) ( )
2
99f x fx x
′′ ′
+ −=


. Tính
( ) (
)
10Tf f
= −
.
A.
2 9ln 2
T = +
. B.
9T =
. C.
1
9ln 2
2
T = +
. D.
2 9ln 2T = −
.
Câu 71: Cho hàm số
( )
y fx=
thỏa mãn
( ) ( )
42
'.f xfx x x= +
. Biết
( )
02f =
. Tính
( )
2
2f
.
A.
( )
2
313
2
15
f =
. B.
( )
2
332
2
15
f =
. C.
( )
2
324
2
15
f
=
. D.
( )
2
323
2
15
f =
.
Câu 72: Cho
()fx
xác định, có đạo hàm, liên tục và đồng biến trên
[ ]
1; 4
thỏa mãn
(
) ( )
[ ]
( )
2
3
2 , 1; 4 , 1
2
x xf x f x x f
′
+ = ∀∈ =


. Giá trị
( )
4f
bằng:
A.
391
18
B.
361
18
C.
381
18
D.
371
18
Câu 73: Cho hàm số
( )
y fx=
có
( )
fx
′
liên tục trên nửa khoảng
[
)
0;+∞
thỏa mãn
( ) ( )
2
3 1 3.e
x
fx f x
−
′
+=+
. Khi đó:
https://toanmath.com/
A.
( ) ( )
3
2
11
e1 0
2
e3
ff−= −
+
. B.
(
)
( )
3
2
11
e1 0
4
2e 3
ff
−= −
+
.
C.
( )
(
)
( )
22
3
e3e38
e1 0
3
ff
+ +−
−=
. D.
( )
(
)
(
)
3 22
e1 0 e3e38
ff
− = + +−
.
Câu 74: Cho hàm số
f
liên tục,
( )
1fx>−
,
( )
00f =
và thỏa
( ) ( )
2
12 1f x x xfx
′
+= +
. Tính
( )
3
f
.
A.
0
. B.
3
. C.
7
. D.
9
.
Câu 75: Cho hàm số
( )
0fx≠
thỏa mãn điều kiện
( ) ( ) ( )
2
23fx x f x
′
= +
và
(
)
1
0
2
f
= −
. Biết rằng
tổng
( )
(
)
(
) (
) (
)
1 2 3 ... 2017 2018
a
ff f f f
b
+ + ++ + =
với
( )
*
,ab∈∈
và
a
b
là phân số
tối giản. Mệnh đề nào sau đây đúng?
A.
1
a
b
<−
. B.
1
a
b
>
. C.
1010ab+=
. D.
3029
ba−=
.
Câu 76: Biết luôn có hai số
a
và
b
để
( )
4
ax b
Fx
x
+
=
+
( )
40ab−≠
là nguyên hàm của hàm số
(
)
fx
và thỏa mãn:
( ) ( ) ( )
2
21f x Fx f x
′
= −


.
Khẳng định nào dưới đây đúng và đầy đủ nhất?
A.
1a =
,
4b =
. B.
1a =
,
1b = −
. C.
1a =
,
{ }
\4b∈
. D.
a∈
,
b∈
.
Câu 77: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
1; 2
thỏa mãn
( )
14f =
và
(
) ( )
32
23f x xf x x x
′
= −−
. Tính
(
)
2f
A.
5
. B.
20
. C.
10
. D.
15
.
Câu 78: Cho
( )
2
cos
x
fx
x
=
trên
;
22
ππ

−


và
( )
Fx
là một nguyên hàm của
( )
xf x
′
thỏa mãn
( )
00F
=
. Biết
;
22
a
ππ

∈−


thỏa mãn
tan 3a =
. Tính
(
)
2
10 3
Fa a a
−+
.
A.
1
ln10
2
−
. B.
1
ln10
4
−
. C.
1
ln10
2
. D.
ln10
.
Câu 79: Cho hàm số
( )
y fx=
xác định và liên tục trên
thỏa mãn đồng thời các điều kiện sau
( )
0fx>
,
x∀∈
,
( ) ( )
2
e.
x
fx f x
′
= −
x
∀∈
và
( )
1
0
2
f =
. Phương trình tiếp tuyến của
đồ thị tại điểm có hoành độ
0
ln 2x =
là
A.
2 9 2ln 2 3 0xy+ − −=
. B.
2 9 2ln 2 3 0xy− − +=
.
C.
2 9 2ln 2 3 0xy− + −=
. D.
2 9 2ln 2 3 0xy+ + −=
.
Câu 80: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
,
( )
fx
và
( )
fx
′
đều nhận giá trị
dương trên đoạn
[ ]
0;1
và thỏa mãn
( )
02f =
,
( ) ( ) ( )
( )
11
2
00
. 1d 2 . df x fx x f xfx x

′′
+=



∫∫
. Tính
( )
1
3
0
dfx x


∫
.
A.
15
4
. B.
15
2
. C.
17
2
. D.
19
2
.
https://toanmath.com/
Câu 81: Cho
()fx
không âm thỏa mãn điều kiện
2
(). '() 2 () 1fxf x x f x= +
và
(0) 0f =
. Tổng giá trị
lớn nhất và nhỏ nhất của hàm số
()y fx=
trên
[ ]
1; 3
là
A.
22
B.
4 11 3
+
C.
20 2+
D.
3 11 3
+
Câu 82: Cho hàm số
( )
fx
có đạo hàm và đồng biến trên
thỏa mãn
( )
01
f
=
và
( )
( )
( )
2
,
x
f x ef x x
′
= ∀∈
. Tính tích phân
(
)
1
0
f x dx
∫
bằng
A.
2e −
. B.
1e −
. C.
2
2e −
. D.
2
1
e −
.
Câu 83: Cho hàm số
( )
y fx=
xác định và liên tục trên
{ }
\0
thỏa mãn
( ) ( )
( ) ( )
22
21 1x f x x f x xf x
′
+− = −
với
{ }
\0x∀∈
và
(
)
12
f
= −
. Tính
( )
2
1
f x dx
∫
.
A.
1
ln 2
2
−−
. B.
3
ln 2
2
−−
. C.
ln 2
1
2
−−
. D.
3 ln 2
22
−−
.
Câu 84: Cho hàm số
( )
y fx=
. Có đạo hàm liên tục trên
. Biết
( )
1ef =
và
( ) ( ) ( )
3
2x f x xf x x
′
+=−
,
x∀∈
. Tính
( )
2f
.
A.
2
4e 4e 4
−+
. B.
2
4e 2e 1−+
. C.
3
2e 2e 2
−+
. D.
2
4e 4e 4+−
.
Câu 85: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( )
00f =
. Biết
(
)
1
2
0
9
d
2
f xx
=
∫
và
( )
1
0
3
cos d
24
x
fx x
ππ
′
=
∫
. Tích phân
(
)
1
0
dfx x
∫
bằng
A.
1
π
. B.
4
π
. C.
6
π
. D.
2
π
.
Câu 86: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
0; 1
, thỏa mãn
( ) ( )
11
00
d d1fx x xfx x
= =
∫∫
và
( )
1
2
0
d4fx x=


∫
. Giá trị của tích phân
( )
1
3
0
dfx x


∫
bằng
A.
1
. B.
8
. C.
10
. D.
80
.
Câu 87: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn [1, 2] và thỏa mãn
( )
0fx>
khi
[ ]
1, 2x∈
.
Biết
(
)
2
1
' 10
f x dx =
∫
và
( )
( )
2
1
'
ln 2
fx
dx
fx
=
∫
. Tính
( )
2f
.
A.
(
)
2 10f
= −
. B.
( )
2 20f =
. C.
( )
2 10f =
. D.
( )
2 20f = −
.
Câu 88: Cho hàm số
( )
fx
có đạo hàm và liên tục trên đoạn
[ ]
4;8
và
( )
00f ≠
với
[ ]
4;8x
∀∈
. Biết
rằng
( )
( )
2
8
4
4
1
fx
dx
fx
′


=


∫
và
( ) ( )
11
4 ,8
42
ff= =
. Tính
( )
6f
.
A.
5
8
. B.
2
3
. C.
3
8
. D.
1
3
.
Câu 89: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục trên đoạn
[ ]
0;1
đồng thời thỏa mãn các điều
kiện
( )
01
f
′
= −
và
( ) ( )
2
fx f x
′ ′′
=


. Đặt
( ) ( )
10Tf f= −
, hãy chọn khẳng định đúng?
A.
21T
− ≤ <−
. B.
10T−≤ <
. C.
01T≤<
. D.
12T≤<
.
https://toanmath.com/
Câu 90: Cho hàm số
( )
y fx=
có đạo hàm cấp
2
liên tục trên
thoả
( )
(
)
(
)
22
0, ,
0 0 1,
,.
fx x
ff
xy y yy x
> ∀∈
′
= =
′ ′′
+ = ∀∈
.
Mệnh đề nào sau đây đúng?
A.
( )
1
ln 1 1
2
f<<
. B.
( )
1
0 ln 1
2
f<<
. C.
( )
3
ln 1 2
2
f<<
. D.
(
)
3
1 ln 1
2
f<<
.
Câu 91: Cho
,
fg
là hai hàm liên tục trên
[
]
1;3
thỏa mãn điều kiện
( ) ( )
3
1
3 d 10fx gx x
+=


∫
đồng
thời
( ) (
)
3
1
2 d6f x gx x−=


∫
. Tính
( ) ( )
3
1
df x gx x+


∫
.
A.
9
. B.
6
. C.
7
. D.
8
.
Câu 92: Cho hàm số
( )
y fx
=
liên tục trên
[
]
;
ab
, nếu
( )
d5
d
a
fx x=
∫
và
( )
d2
d
b
fx x
=
∫
(với
adb<<
) thì
( )
d
b
a
fx x
∫
bằng.
A.
3
. B.
7
. C.
5
2
. D.
10
.
Câu 93: Cho
( )
fx
và
( )
gx
là hai hàm số liên tục trên đoạn
[
]
1; 3
, thỏa mãn:
( ) ( )
3
1
3 d 10fx gx x+=


∫
và
( ) ( )
3
1
2 d6f x gx x−=


∫
. Tính
( ) ( )
3
1
dI f x gx x= +


∫
A.
8
I =
. B.
9I =
. C.
6I =
. D.
7I
=
.
Câu 94: Cho hàm số
( )
y fx=
có đạo hàm
( )
fx
′
liên tục trên đoạn
[ ]
0;5
và đồ thị hàm số
( )
y fx
′
=
trên đoạn
[ ]
0;5
được cho như hình bên.
Tìm mệnh đề đúng
A.
( ) ( ) ( )
053fff= <
. B.
( ) ( ) ( )
305fff<=
.
C.
( ) ( )
( )
305fff<<
. D.
( ) ( ) ( )
350fff<<
.
Câu 95: Cho hàm số liên tục và có đạo hàm tại mọi đồng thời thỏa mãn điều kiện:
và Khi đó, nằm trong khoảng
nào?
A. . B. . C. . D. .
( )
fx
( )
0;x∈ +∞
( ) ( )
(
)
sin ' cosfx x x f x x= ++
( )
3
2
2
sin d 4.f x xx
π
π
= −
∫
( )
f
π
( )
6;7
( )
5;6
( )
12;13
( )
11;12
5−
3
5
1
x
O
y
https://toanmath.com/
Câu 96: Cho hàm số
( )
fx
xác định trên
0;
2
π



thỏa mãn
(
)
(
)
2
2
0
2
2 2 sin d
42
f x fx x x
π
ππ
−

− −=




∫
. Tích phân
(
)
2
0
d
fx x
π
∫
bằng
A.
4
π
. B.
0
. C.
1
. D.
2
π
.
Câu 97: Cho hàm số
()y fx
=
liên tục trên thỏa mãn
(
) (
)
( )
2
21
3 2 2 1e 4
xx
fx f x x
−+
+ −= − +
. Tính
tích phân
( )
2
0
d
I fx x
=
∫
ta được kết quả:
A.
e4I = +
. B.
8I =
. C.
2I =
. D.
e2I
= +
.
Câu 98: Suy ra
( ) ( )
22
00
4 d8 d2fx x fx x=⇔=
∫∫
. Cho hàm số
( )
y fx=
liên tục trên
{ }
\ 0; 1−
thỏa
mãn điều kiện
( )
1 2ln 2f = −
và
( ) ( ) ( )
2
1.xx f x f x x x
′
+ +=+
. Giá trị
( )
2 ln3f ab= +
, với
,ab
∈
. Tính
22
ab+
.
A.
25
4
. B.
9
2
. C.
5
2
. D.
13
4
.
Câu 99: Cho hàm số
( )
y fx=
có đạo hàm trên
và
( )
4
2
2
2
fx x x
x
′
≥+−
0x∀>
và
( )
11f = −
.
Khẳng định nào sau đây đúng?
A. Phương trình
( )
0fx=
có
1
nghiệm trên
( )
0;1
.
B. Phương trình
( )
0fx=
có đúng
3
nghiệm trên
( )
0;+∞
.
C. Phương trình
( )
0fx=
có
1
nghiệm trên
( )
1; 2
.
C. Phương trình
( )
0fx
=
có
1
nghiệm trên
(
)
2;5
.
Hươngd dẫn giải
Chọn C
( )
4
2
2
2fx x x
x
′
≥+−
63
2
22xx
x
−+
=
(
)
2
3
2
11
0
x
x
−+
= >
,
0x∀>
.
(
)
y fx⇒=
đồng biến trên
( )
0;+∞
.
( )
0fx⇒ =
có nhiều nhất
1
nghiệm trên khoảng
( )
0;+∞
( )
1
.
Mặt khác ta có:
( )
4
2
2
20
fx x x
x
′
≥+−>
,
0x∀>
( )
22
4
2
11
2 21
d 2d
5
fxx x xx
x

′
⇒ ≥ +− =


∫∫
( ) ( )
21
21
5
ff⇒ −≥
( )
17
2
5
f⇒≥
.
Kết hợp giả thiết ta có
( )
y fx=
liên tục trên
[ ]
1; 2
và
( ) ( )
2. 1 0ff<
( )
2
.
Từ
(
)
1
và
( )
2
suy ra phương trình
( )
0fx=
có đúng
1
nghiệm trên khoảng
( )
1; 2 .
Câu 100: Cho hàm số
( )
fx
có đạo hàm
( )
fx
′
liên tục trên
và thỏa mãn
( )
[ ]
1;1fx
′
∈−
với
( )
0;2x∀∈
. Biết
( ) ( )
0 21ff= =
. Đặt
(
)
2
0
dI fx x=
∫
, phát biểu nào dưới đây đúng?
A.
(
]
;0I ∈ −∞
. B.
(
]
0;1I ∈
. C.
[
)
1;I ∈ +∞
. D.
( )
0;1I
∈
.
https://toanmath.com/
Câu 101: Cho hàm số
( )
y fx=
liên tục trên
[ ]
0; 1
thỏa mãn
( )
1
0
d0xf x x =
∫
và
( )
[0; 1]
max 1.fx=
Tích
phân
(
)
1
0
ed
x
I fx x
=
∫
thuộc khoảng nào trong các khoảng sau đây?
A.
5
;.
4

−∞ −


B.
3
;e 1 .
2

−


C.
53
;.
42

−


D.
( )
e 1; .− +∞
Câu 102: Cho hàm số
( )
fx
có đạo hàm dương, liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
01f =
và
(
)
( )
( ) (
)
11
2
00
1
3 d2 d
9
f x fx x f xfx x

′′
+≤




∫∫
. Tính tích phân
(
)
1
3
0
d
fx x


∫
:
A.
3
2
. B.
5
4
. C.
5
6
. D.
7
6
.
Câu 103: Cho hai hàm số
( )
fx
và
( )
gx
có đạo hàm trên đoạn
[
]
1; 4
và thỏa mãn hệ thức
( ) ( )
( ) ( ) ( ) ( )
1 14
.; .
fg
gxxfxfxxgx
+=
′′
=−=−
. Tính
( ) ( )
4
1
dI f x gx x= +


∫
.
A.
8ln 2
. B.
3ln 2
. C.
6ln 2
. D.
4ln 2
.
https://toanmath.com/
HƯỚNG DẪN GIẢI
DẠNG 1: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT NGUYÊN HÀM
Câu 1: Cho hàm số
( )
fx
xác định trên
{ }
\1
thỏa mãn
( )
1
1
fx
x
′
=
−
,
(
)
0 2017f =
,
(
)
2 2018f =
. Tính
(
)
( )
31Sf f
= −−
.
A.
1S =
. B.
ln 2S =
. C.
ln4035S =
. D.
4S =
.
Hươngd dẫn giải
Chọn A
Cách 1: Ta có
( )
( )
1
d d ln 1
1
fx x x x C
x
= = −+
−
∫∫
.
Theo giả thiết
( )
0 2017f =
,
(
)
2 2018f =
nên
(
)
(
)
( )
( )
ln 1 2017 khi 1
ln 1 2018 khi 1
fx x x
fx x x
= −+ <
= −+ >
.
Do đó
( )
(
)
31Sf f= −−
ln2 2018 ln 2 2017 1=+ −− =
.
Cách 2:
Ta có:
00
0
1
11
33
3
2
22
1
(0) ( 1) '( ) ln 1 | ln (1)
12
(3) (2) '( ) ln 1 | ln 2 (2)
1
dx
f f f x dx x
x
dx
f f f x dx x
x
−
−−
− −= = = − =
−
− = = = −=
−
∫∫
∫∫
Lấy (1)+(2), ta được
(3) (2) (0) ( 1) 0 S 1ffff−+−−=⇒=
.
Câu 2: Cho hàm số
(
)
fx
xác định trên
1
\
2



thỏa mãn
( )
2
21
fx
x
′
=
−
và
( )
01f =
. Giá trị của
biểu thức
( ) ( )
13ff−+
bằng
A.
4 ln15
+
. B.
3 ln15+
. C.
2 ln15+
. D.
ln15
.
Hươngd dẫn giải
Chọn C
Ta có
( ) ( )
( )
1
2. 2 1
2
2
ln 2 1
21 21
dx
f x f x dx dx x c
xx
−
′
= = = = −+
−−
∫∫∫
.
( )
01f =
1c⇔=
( )
ln 2 1 1fx x⇔ = −+
.
( )
( )
1 ln3 1
3 ln5 1
f
f
−= +
= +
( )
( )
1 3 2 ln15ff⇔ −+ =+
.
Câu 3: Cho hàm số
()fx
xác định trên
1
\
2



thỏa mãn
2
()
21
fx
x
′
=
−
,
(0) 1f =
và
(1) 2f =
.
Giá trị của biểu thức
( 1) (3)ff
−+
bằng
A.
4 ln5+
. B.
2 ln15
+
. C.
3 ln15+
. D.
ln15.
Hươngd dẫn giải
Chọn C
Cách 1: • Trên khoảng
1
;
2

+∞


:
1
2
( ) ln(2 1) .
21
f x dx x C
x
= = −+
−
∫
Lại có
1
(1) 2 2.fC=⇒=
• Trên khoảng
1
;
2

−∞


:
2
2
( ) ln(1 2 ) .
21
f x dx x C
x
= =−+
−
∫
https://toanmath.com/
Lại có
2
(0) 1 1.fC=⇒=
Vậy
1
ln(2 1) 2
2
()
1
ln(1 2 ) 1
2
x khi x
fx
x khi x
−+ >
=
−+ <
.
Suy ra
( 1) (3) 3 ln15.ff−+ =+
Cách 2:
Ta có:
00
0
1
11
33
3
1
11
21
(0) ( 1) '( ) ln 2 1 | ln (1)
21 3
2
(3) (1) '( ) ln 2 1 | ln 5 (2)
21
dx
f f f x dx x
x
dx
f f f x dx x
x
−
−−
− −= = = − =
−
− = = = −=
−
∫∫
∫∫
Lấy (2)-(1), ta được
(3) (1) (0) ( 1) ln15 ( 1) (3) 3 ln15fff f f f
− − + −= ⇒ −+ =+
.
Câu 4: Cho hàm số
( )
fx
xác định trên
thỏa mãn
( )
21fx x
′
= +
và
( )
15f =
. Phương trình
(
)
5
fx=
có hai nghiệm
1
x
,
2
x
. Tính tổng
21 22
log logSx x= +
.
A.
1S =
. B.
2S =
. C.
0
S
=
. D.
4S
=
.
Hướng dẫn giải
Chọn A
Ta có:
(
) (
) (
)
2
d 2 1d
fx f x x x x x xC
′
= = + = ++
∫∫
.
Mà
( ) ( )
2
1 5 11 5 3 3f C C fx x x
= ⇔++ = ⇔ = ⇒ = + +
.
Xét phương trình:
( )
22
1
5 35 20
2
x
fx xx xx
x
=
=⇔ ++=⇔ +−=⇔
= −
.
21 22 2 2
log log log 1 log 2 1
Sx x= + = + −=
.
Câu 5: Cho hàm số
()fx
xác định trên
1
\
3



thỏa mãn
( ) (
)
3
,01
31
fx f
x
′
= =
−
và
2
2
3
f

=


.
Giá trị của biểu thức
( )
( )
13
ff−+
bằng
A.
3 5ln 2+
. B.
2 5ln 2−+
. C.
4 5ln 2+
. D.
2 5ln 2+
.
Hươngd dẫn giải
Chọn A
Cách 1: Từ
( ) ( )
1
1
1
ln 3 1 khi x ;
3
33
dx=
31 31
1
ln 3 1 khi x ;
3
xC
f x fx
xx
xC

− + ∈ −∞


′
= ⇒=
−−

− + ∈ +∞


∫
.
Ta có:
( )
11
22
01
01 1
2
02 2
2
3
f
CC
CC
f
=
+= =

⇒⇔


+= =
=



( )
1
ln 3 1 1 khi x ;
3
1
ln 3 1 2 khi x ;
3
x
fx
x

− + ∈ −∞


⇒=

− + ∈ +∞


.
Khi đó:
( ) ( )
1 3 ln 4 1 ln8 2 3 ln32 3 5ln 2ff− + = ++ + = + = +
.
Cách 2: Ta có
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
00
0
0
1
1
11
33
3
3
2
2
3
3
22
33
31
0 1 dx dx ln 3 1 ln 1
31 4
23
3 dx dx ln 3 1 ln8 2
3 31
f f fx f x x
x
f f fx f x x
x
−
−
−−
′
− −= = = = − =
−

′
− = = = = −=

−

∫∫
∫∫
https://toanmath.com/
Lấy
( ) ( )
21−
, ta được:
( ) ( ) ( ) ( ) ( )
2
3 1 0 ln32 1 3 3 5ln 2
3
ff ff f f

+ −− − = ⇒ −+ =+


.
Câu 6: Cho hàm số
( )
fx
xác định trên
{
}
\ 2;2
−
và thỏa mãn
( ) ( )
2
4
; 30
4
fx f
x
′
= −=
−
;
( )
01f =
và
( )
32f
=
. Tính giá trị biểu thức
(
)
(
)
(
)
4 14
Pf f f= −+ −+
.
A.
3
3 ln
25
P
= +
. B.
3 ln3P = +
. C.
5
2 ln
3
P = +
. D.
5
2 ln
3
P = −
.
Hươngd dẫn giải
Chọn B
Từ
( )
2
4
4
fx
x
′
=
−
( )
2
4
4
dx
fx
x
⇒=
−
∫
(
)(
)
4
22
dx
xx
=
−+
∫
( )
( )
( )
1
2
3
2
ln ; 2
2
2
ln 2; 2
2
2
ln 2;
2
x
C khi x
x
x
C khi x
x
x
C khi x
x
−
+ ∈ −∞ −
+
−
= + ∈−
+
−
+ ∈ +∞
+
Ta có
(
)
(
)
( )
30
01
22
f
f
f
−=
=
=
1
2
3
ln5 0
01
1
ln 2
5
C
C
C
+=
⇒+=
+=
1
2
3
ln5
1
2 ln5
C
C
C
= −
⇔=
= +
( )
fx
⇒
( )
( )
( )
2
ln -ln5 ; 2
2
2
ln 1 2; 2
2
2
ln 2 ln 5 2;
2
x
khi x
x
x
khi x
x
x
khi x
x
−
∈ −∞ −
+
−
= + ∈−
+
−
+ + ∈ +∞
+
.
Khi đó
(
) ( )
( )
4 14
Pf f f
= −+ −+
1
ln3 ln5 ln3 1 ln 2 ln5
3
=−+++ ++
3 ln3= +
.
Câu 7: Cho hàm số
( )
fx
xác định trên
{ }
\ 2;1−
thỏa mãn
( )
2
1
2
fx
xx
′
=
+−
;
(
) ( )
3 30
ff−− =
và
( )
1
0
3
f =
. Giá trị của biểu thức
(
) ( ) ( )
4 14fff−+ −−
bằng
A.
11
ln 2
33
+
. B.
1 ln80+
. C.
14
1 ln 2 ln
35
++
. D.
18
1 ln
35
+
.
Hươngd dẫn giải
Chọn A
( )
2
1
2
fx
xx
′
=
+−
( )
( )(
)
( )
(
)
( )
1
2
2
3
11
ln ; 2
32
d d 11
ln 2;1
2 1 23 2
11
ln 1;
32
x
C khi x
x
xxx
f x C khi x
xx x x x
x
C khi x
x
−
+ ∈ −∞ −
+
−
⇒ = = = + ∈−
+− − + +
−
+ ∈ +∞
+
∫∫
Do đó
( ) ( )
1 3 31
1 12 1
3 3 0 ln 4 ln ln10
3 35 3
f f C C CC−− =⇒ + − − ⇒ = +
.
https://toanmath.com/
Và
(
)
22
1 1 1 1 11
0 ln ln 2
3 3 2 3 33
f CC
=⇒ +=⇒=+
.
( )
(
)
( )
( )
1
1
11
ln ; 2
32
1 1 11
ln ln 2 2;1
3 2 33
11 1
ln ln10 1;
32 3
x
C khi x
x
x
f x khi x
x
x
C khi x
x
−
+ ∈ −∞ −
+
−
⇒ = + + ∈−
+
−
+ + ∈ +∞
+
.
Khi đó:
( )
(
) (
)
11
1 5 1 11 1 1 1 11
4 1 4 ln ln 2 ln 2 ln ln10 ln 2
3 2 3 33 3 2 3 33
fff C C
 
−+−−= ++++− ++ =+
 
 
.
Câu 8: Cho hàm số
( )
fx
xác định trên
{ }
\ 1;1−
và thỏa mãn
( )
2
1
1
fx
x
′
=
−
;
( ) ( )
3 30ff−+ =
và
11
2
22
ff

−+ =


. Tính giá trị của biểu thức
( ) ( )
04Pf f= +
.
A.
3
2 ln
5
P = +
. B.
3
1 ln
5
P = +
. C.
13
1 ln
25
P = +
. D.
13
ln
25
P =
.
Hươngd dẫn giải
Chọn C
( )
( )( )
(
) ( )
( )
1
22
2
11
ln ; 1 1;
21
1d d
1 1 11
11
ln 1;1
21
x
C khi x
x
xx
fx
x x xx
x
C khi x
x
−
+ ∈ −∞ − ∪ +∞
+
′
=⇒= =
− − −+
−
+ ∈−
+
∫∫
.
Ta có
( ) ( )
1 11
1 11
3 3 0 ln 2 ln 0 0
2 22
ff C CC−+ =⇒ + + + =⇒ =
.
Và
2 22
1 1 1 11
2 ln3 ln 2 1
2 2 2 23
f f C CC

−+ =⇒ ++ +=⇒=


.
Suy ra
( )
( ) ( )
( )
11
ln ; 1 1;
21
11
ln 1 1;1
21
x
khi x
x
fx
x
khi x
x
−
∈ −∞ − ∪ +∞
+
=
−
+ ∈−
+
.
Vậy
(
) ( )
04Pf f= +
=
13
1 ln
25
+
.
Câu 9: Cho hàm số
( )
fx
xác định trên
{ }
\1±
thỏa mãn
(
)
2
1
1
fx
x
′
=
−
. Biết
( ) ( )
3 30ff−+ =
và
11
2
22
ff

−+ =


. Giá trị
( ) ( ) ( )
204Tf f f= −+ +
bằng:
A.
15
2 ln
29
T = +
. B.
19
1 ln
25
T = +
. C.
19
3 ln
25
T = +
. D.
19
ln
25
T =
.
Hươngd dẫn giải
Chọn B
Ta có
(
)
2
1
dd
1
fxx x
x
′
=
−
∫∫
11 1
d
2 11
x
xx

= −

−+

∫
11
ln
21
x
C
x
−
= +
+
.
https://toanmath.com/
Do đó
( )
1
2
11
ln khi 1, 1
21
11
ln khi 1 1
21
x
Cxx
x
Cx
f
x
x
x
−
+ <− >
+
−
+−
=
<<
+
.
Do
( )
(
)
3 30ff−+ =
nên
1
0C =
,
11
2
22
ff

−+ =


nên
2
1C =
.
Nên
( )
11
ln khi 1, 1
21
11
ln 1 khi 1 1
21
x
xx
x
x
x
x
x
f
−
<− >
+
−
+
=
−< <
+
.
( ) ( ) ( )
204Tf f f= −+ +
19
1 ln
25
= +
.
Câu 10: Cho hàm số
( )
fx
nhận giá trị dương, có đạo hàm liên tục trên
( )
0;+∞
thỏa mãn
( )
1
2
15
f =
và
( ) ( ) ( )
2
24 0fx x f x
′
++ =
. Tính
( ) ( ) ( )
123ff f++
.
A.
7
15
. B.
11
15
. C.
11
30
. D.
7
30
.
Hươngd dẫn giải
Chọn D
Vì
( ) ( )
( )
2
24 0fx x f x
′
++ =
và
( )
0fx>
, với mọi
( )
0;x∈ +∞
nên ta có
( )
( )
2
24
fx
x
fx
′
−=+
.
Suy ra
( )
2
1
4x xC
fx
=++
. Mặt khác
( )
1
2
15
f =
nên
3C
=
hay
(
)
2
1
43
fx
xx
=
++
.
Do đó
( ) ( ) ( )
123ff f++
11 1
8 15 24
=++
7
30
=
.
Câu 11: Cho hàm số
( )
fx
xác định và liên tục trên
. Biết
( ) (
)
6
. 12 13
f xfx x
′
= +
và
( )
02f =
.
Khi đó phương trình
( )
3
fx=
có bao nhiêu nghiệm?
A.
2
. B.
3
. C.
7
. D.
1
.
Hươngd dẫn giải
Chọn A
Từ
( ) ( )
6
. 12 13
f xfx x
′
= +
( )
( )
( )
6
. 12 13
f x f x dx x dx
′
⇒=+
∫∫
( )
( )
62
6 13f x df x x x C⇔ =++
∫
(
)
7
2
6 13
7
fx
x xC⇔ =++
( )
02
2
7
f
C
=
→ =
.
Suy ra:
(
)
72
42 91 2fx x x= ++
.
Từ
(
)
3fx=
( )
7
2187fx⇔=
2
42 91 2 2187
xx⇒ + +=
( )
2
42 91 2185 0 *
xx⇔ +− =
.
Phương trình
( )
*
có
2
nghiệm trái dầu do
0ac <
.
Câu 12: Cho hàm số
(
)
fx
xác định trên
thỏa mãn
(
)
ee 2
xx
fx
−
′
= +−
,
( )
05f =
và
1
ln 0
4
f

=


. Giá trị của biểu thức
(
) ( )
ln16 ln 4Sf f=−+
bằng
A.
31
2
S =
. B.
9
2
S =
. C.
5
2
S =
. D.
( ) ( )
0. 2 1ff=
.
Hươngd dẫn giải
Chọn C
https://toanmath.com/
Ta có
( )
ee 2
xx
fx
−
′
= +−
e1
e
x
x
−
=
22
22
e e khi 0
e e khi 0
xx
xx
x
x
−
−
−≥
=
−<
.
Do đó
( )
22
1
22
2
2e 2e khi 0
2e 2e khi 0
xx
xx
Cx
fx
Cx
−
−
++ ≥
=
− −+ <
.
Theo đề bài ta có
(
)
05f =
nên
00
1
2e 2e 5C+ +=
1
1C⇔=
.
( )
ln 4 ln 4
22
ln4 2e 2e 1f
−
⇒ =++
6=
Tương tự
1
ln 0
4
f

=


nên
11
ln ln
44
22
2
2e 2e 0C
 
 
 
−
− − +=
2
5C⇔=
.
( )
( )
( )
ln16 ln16
22
ln16 2e 2e 5f
−−
−
⇒− =− − +
7
2
= −
.
Vậy
( )
(
)
5
ln16 ln 4
2
Sf f=−+ =
.
Câu 13: Cho hàm số
( )
fx
liên tục, không âm trên đoạn
0;
2
π



, thỏa mãn
( )
03f =
và
(
) (
)
(
)
2
. cos . 1fxf x x f x
′
= +
,
0;
2
x
π

∀∈


. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
( )
fx
trên đoạn
;
62
ππ



.
A.
21
2
m =
,
22M =
. B.
5
2
m =
,
3M =
.
C.
5
2
m =
,
3M =
. D.
3m =
,
22
M =
.
Hươngd dẫn giải
Chọn A
Từ giả thiết
(
) ( ) ( )
2
. cos . 1fxf x x f x
′
= +
( ) ( )
( )
2
.
d sin
1
fxf x
x xC
fx
′
⇒=+
+
∫
Đặt
( )
(
)
2 22
11t fx t fx
= + ⇒=+
( ) (
)
ddtt f x f x x
′
⇒=
.
Thay vào ta được
d sin sint xC t xC= + ⇒= +
∫
( )
2
1 sinf x xC
⇒+ = +
.
Do
( )
03f =
2C⇒=
.
Vậy
(
) ( )
2 22
1 sin 2 sin 4sin 3fx x fx x x+ = +⇒ = + +
( )
2
sin 4sin 3fx x x⇒= + +
, vì hàm số
( )
fx
liên tục, không âm trên đoạn
0;
2
π



.
Ta có
1
sin 1
6 22
xx
ππ
≤≤ ⇒≤ ≤
, xét hàm số
( )
2
43gt t t=++
có hoành độ đỉnh
2t = −
loại.
Suy ra
( ) ( )
1
;1
2
18max g t g



= =
,
( )
1
;1
2
1 21
min
24
gt g




= =


.
( ) ( )
( )
2
.
cos
1
′
⇒=
+
fxf x
x
fx
https://toanmath.com/
Suy ra
(
)
;
62
22
2
max f x f
ππ
π




= =


,
(
)
;
62
21
min
62
fx g
ππ
π




= =


.
Câu 14: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
và thỏa mãn
(
)
0fx
>
,
x∀∈
. Biết
(
)
01
f
=
và
( )
( )
'
22
fx
x
fx
= −
. Tìm các giá trị thực của tham số
m
để phương trình
( )
fx m=
có hai nghiệm thực phân biệt.
A.
me>
. B.
01
m
<≤
. C.
0 me<<
. D.
1 me<<
.
Hươngd dẫn giải
Chọn C
Ta có
(
)
(
)
22
fx
x
fx
′
= −
( )
(
)
(
)
d 22d
fx
x xx
fx
′
⇒=−
∫∫
.
( )
2
ln 2
fx x x C
⇔ = −+
( )
2
2
.
xx
f x Ae
−
⇔=
. Mà
( )
01f
=
suy ra
( )
2
2xx
fx e
−
=
.
Ta có
(
)
22
2 1 21xx x x−=− −+
( )
2
1 11x
=−− ≤
. Suy ra
2
2
0
xx
ee
−
<≤
và ứng với một giá trị thực
1t <
thì phương trình
2
2xx t
−=
sẽ có hai nghiệm phân biệt.
Vậy để phương trình
(
)
fx m=
có
2
nghiệm phân biệt khi
1
0
me e
<<=
.
Câu 15: Cho hàm số
( )
fx
liên tục trên
và
(
)
0fx≠
với mọi
x
∈
.
( ) ( ) ( )
2
21fx x f x
′
= +
và
( )
1 0,5f = −
. Biết rằng tổng
( ) ( ) (
) ( )
1 2 3 ... 2017
a
ff f f
b
+ + ++ =
;
( )
,ab∈∈
với
a
b
tối giản. Mệnh đề nào dưới đây đúng?
A.
1
ab+=−
. B.
(
)
2017;2017
a
∈−
. C.
1
a
b
<−
. D.
4035ba−=
.
Hươngd dẫn giải
Chọn D
Ta có
( ) ( ) ( )
2
21fx x f x
′
= +
( )
( )
( )
2
21
fx
x
fx
′
⇔=+
(
)
(
)
(
)
2
d 2 1d
fx
x xx
fx
′
⇒=+
∫∫
( )
2
1
x xC
fx
⇔− = + +
Mà
( )
1
1
2
f = −
nên
0C =
( )
2
1 11
1
fx
xxx x
⇒=− =−
++
.
Mặt khác
(
)
( )
( )
( )
1 11 11 1 1
1 2 3 ... 2017 1 ...
2 3 2 4 3 2018 2017
ff f f
 
+ + ++ = − + − + − ++ −
 
 
( ) (
) ( ) (
)
1 2017
1 2 3 ... 2017 1
2018 2018
ff f f
−
⇔ + + + + =−+ =
2017
a⇒=−
;
2018b =
.
Khi đó
4035ba−=
.
Câu 16: Cho hàm số
( )
0fx≠
thỏa mãn điều kiện
(
) ( ) ( )
'2
2 3.fx x fx= +
và
( )
1
0
2
f
−
=
. Biết tổng
( ) ( ) ( ) ( )
1 2 ... 2017 2018
a
ff f f
b
+ ++ + =
với
*
,ab∈∈
và
a
b
là phân số tối giản.
Mệnh đề nào sau đây đúng?
A.
1
a
b
<−
. B.
1
a
b
>
.
C.
1010ab+=
. D.
3029ba−=
.
Hươngd dẫn giải
Chọn D
https://toanmath.com/
Biến đổi
( ) ( ) ( )
'2
2 3.fx x f x= +
( )
( )
'
2
23
fx
x
fx
⇔=+
( )
( )
( )
'
2
23
fx
dx x dx
fx
⇔=+
∫∫
(
)
(
)
2
2
11
3
3
x xC fx
fx x xC
⇔− = + + ⇒ =−
++
. Mà
(
)
1
0
2
f
−
=
nên
2
=
.
Do đó
(
)
( )
(
)
2
11
32 1 2
fx
xx x x
=−=−
++ + +
.
Khi đó
(
) (
) ( )
(
)
1 2 ... 2017 2018
a
ff f f
b
= + ++ +
11 1 1
.....
2.3 3.4 2018.2019 2019.2020

=− + ++ +


1111 1 1 1
.....
2 3 3 4 2018 2019 2020

=−−+−++−−


11
2 2020

=−−


1009
2020
−
=
.
Với điều kiện
,ab
thỏa mãn bài toán, suy ra:
1009
2020
a
b
= −
=
3029
ba⇒−=
.
Câu 17: Cho hàm số
( )
y fx=
,
0x
∀≥
, thỏa mãn
( ) ( ) ( )
( )
( ) ( )
2
3
.2 0
0 0; 0 1
f x f x f x xf x
ff
′′ ′
− +=


′
= =
. Tính
( )
1f
.
A.
2
3
. B.
3
2
. C.
6
7
. D.
7
6
.
Hươngd dẫn giải
Chọn C
Ta có:
( ) (
) (
)
( )
2
3
.2 0f x f x f x xf x
′′ ′
− +=


( ) ( ) ( )
( )
2
3
.2f xfx f x
x
fx
′′ ′
−


⇔=−
( )
( )
2
fx
x
fx
′

′
⇒=−


(
)
( )
2
2
2
fx
x
C
fx
′
⇒ =−+
( )
( )
2
2
0
0
02
f
C
f
′
⇒ =−+
0C⇒=
.
Do đó
( )
( )
2
2
2
fx
x
fx
′
= −
( )
( )
11
2
2
00
dd
2
fx
x
xx
fx
′
⇒=−
∫∫
(
)
1
1
3
0
0
1
6
x
fx

⇒− = −


( ) (
)
111
1 06ff
⇒− + =−
( )
6
1
7
f
⇒=
.
Câu 18: Giả sử hàm số
()fx
liên tục, dương trên
; thỏa mãn
( )
01f =
và
(
)
( )
2
1
fx
x
fx x
′
=
+
. Khi đó
hiệu
( )
( )
22 2 1
Tf f= −
thuộc khoảng
A.
( )
2;3
. B.
( )
7;9
. C.
( )
0;1
. D.
( )
9;12
.
Hươngd dẫn giải
Chọn C
Ta có
( )
( )
d
fx
x
fx
′
=
∫
2
d
1
x
x
x
⇔
+
∫
( )
( )
( )
( )
2
2
d1
d
1
21
x
fx
fx x
+
=
+
∫∫
.
Vậy
( )
( )
( )
2
1
ln ln 1
2
fx x C= ++
, mà
( )
01 0fC
=⇔=
. Do đó
( )
2
1fx x= +
.
Nên
(
)
2 2 3;f =
( )
2 1 22f =
( )
( ) ( )
22 2 1 322 0;1ff⇒ − =−∈
.
https://toanmath.com/
Câu 19: Khi đó
(
)
(
)
1
4
2
00
tan
dd
cos
ft
t fx x
t
π
=
∫∫
. Vậy
( )
1
0
d6
fx x=
∫
.Cho hàm số
( )
y fx=
đồng biến trên
(
)
0;+∞
;
(
)
y fx=
liên tục, nhận giá trị dương trên
( )
0;+∞
và thỏa mãn
(
)
2
3
3
f
=
và
( ) ( ) (
)
2
' 1.
f x x fx= +


. Mệnh đề nào dưới đây đúng?
A.
( )
2
2613 8 2614
f
<<
. B.
( )
2
2614 8 2615f<<
.
C.
(
)
2
2618 8 2619f<<
. D.
(
)
2
2616 8 2617
f
<<
.
Hươngd dẫn giải
Chọn A
Hàm số
( )
y fx
=
đồng biến trên
(
)
0;+∞
nên suy ra
( ) ( )
0, 0;fx x
′
≥ ∀ ∈ +∞
.
Mặt khác
( )
y fx=
liên tục, nhận giá trị dương trên
( )
0;+∞
nên
( ) ( ) ( ) ( ) ( ) ( )
2
11f x x fx f x x fx
′′
=+ ⇒=+


,
( )
0;x∀ ∈ +∞
( )
( )
( )
1
fx
x
fx
′
⇒=+
,
( )
0;x∀ ∈ +∞
;
( )
( )
( )
1
fx
dx x dx
fx
′
⇒=+
∫∫
( )
( )
3
1
1
3
fx x C⇒ = ++
;
Từ
(
)
3
3
2
f =
suy ra
28
33
C = −
Như vậy
( )
( )
2
3
1 28
1
3 33
fx x

= ++ −



Bởi thế:
( )
(
)
22
3
1 28 28
8 81 9
3 33 33
f

= ++−=+−



( )
4
2
28
8 9 2613,26
33
f

⇒ =+−≈



.
Câu 20: Giả sử hàm số
( )
y fx=
liên tục, nhận giá trị dương trên
( )
0; +∞
và thỏa mãn
( )
11f =
,
( ) ( )
31fx f x x=′+
, với mọi
0x >
. Mệnh đề nào sau đây đúng?
A.
( )
4 55f<<
. B.
( )
2 53f<<
.
C.
( )
3 54f<<
. D.
( )
1 52f<<
.
Hươngd dẫn giải
Chọn C
Cách 1:
Với điều kiện bài toán ta có
( ) ( )
31fx f x x=′+
( )
( )
( )
( )
11
dd
31 31
fx fx
xx
fx fx
xx
′′
⇔= ⇔ =
++
∫∫
( )
( )
( )
( ) ( )
1
2
d
1
31d31
3
fx
xx
fx
−
′
⇔ =++
∫∫
(
)
2
ln 3 1
3
fx x C⇔ = ++
( )
2
31
3
e
xC
fx
++
⇔=
.
Khi đó
( )
4
3
4
11 e 1
3
C
fC
+
=⇔ =⇔=−
( )
24
31
33
e
x
fx
+−
⇒=
( ) ( )
4
3
5 e 3, 79 3; 4f⇒ =≈∈
.
Vậy
( )
3 54f<<
.
https://toanmath.com/
Chú ý: Các bạn có thể tính
d
31
x
x +
∫
bằng cách đặt
31tx= +
.
Cách 2:
Với điều kiện bài toán ta có
(
)
( )
31fx f x x
=′+
( )
( )
1
31
fx
fx
x
′
⇔=
+
( )
( )
55
11
1
dd
31
fx
xx
fx
x
′
⇔=
+
∫∫
( )
( )
( )
5
1
d
4
3
fx
fx
⇔=
∫
( )
5
1
4
ln
3
fx⇔=
( )
(
)
5
4
ln
13
f
f
⇔=
( ) ( ) ( )
4
3
5 1 .e 3, 79 3; 4ff⇔ = ≈∈
.
Câu 21: Cho hàm số
( )
fx
thỏa mãn
( ) ( ) ( )
2
4
. 15 12f x fxf x x x
′ ′′
+=+


,
x∀∈
và
( ) ( )
0 01ff
′
= =
. Giá trị của
( )
2
1f
bằng
A.
9
2
. B.
5
2
. C.
10
. D.
8
.
Hươngd dẫn giải
Chọn D
Ta có:
( )
( )
( )
( )
2
4
. 15 12f x fxf x x x
′ ′′
+=+
,
x∀∈
.
( ) ( )
4
. 15 12f xfx x x
′
′
⇔=+


,
x∀∈
( ) ( )
52
1
. 36f xfx x x C
′
⇔ =++
Do
( ) ( )
0 01ff
′
= =
nên ta có
1
1.C =
Do đó:
(
) ( )
52
. 361f xfx x x
′
=++
(
)
2 52
1
361
2
fx x x
′

⇔ =++


( )
2 63
2
42 .
f x x x xC⇔ =+ ++
Mà
(
)
01f =
nên ta có
2
1.C =
Do đó
(
)
2 63
4 21fx x x x
=+ ++
.
Vậy
( )
2
1 8.f =
Câu 22: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
( )
1 2 13
d
5
1
fx x
xC
x
x
+ ++
= +
+
+
∫
. Nguyên
hàm của hàm số
( )
2fx
trên tập
+
là:
A.
( )
2
3
24
x
C
x
+
+
+
. B.
2
3
4
x
C
x
+
+
+
. C.
(
)
2
23
41
x
C
x
+
+
+
. D.
( )
2
23
81
x
C
x
+
+
+
.
Hươngd dẫn giải
Chọn D
Theo đề ra ta có:
( )
(
)
(
)
( )
(
)
( )
2
1 2 13 2 13
d 2 1d 1
5
1
14
fx x x
x C fx x C
x
x
x
+ ++ ++
= +⇔ + += +
+
+
++
∫∫
.
Hay
( )
( )
( )
22
23
3
2d d
44
t
t
ft t C ft t C
tt
+
+
′
= +⇒ = +
++
∫∫
.
Suy ra
( ) ( ) ( )
( )
1
2
2
1 123 23
2d 2d2
2 2 88
24
xx
fxx fx x C C
x
x

++
= = += +


+
+

∫∫
https://toanmath.com/
DẠNG 2: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT, GIẢI HỆ TÍCH PHÂN
Câu 23: Cho
( )
5
2
d 10fx x
=
∫
. Kết quả
( )
2
5
24 dfx x−


∫
bằng:
A.
34
. B.
36
. C.
40
. D.
32
.
Hươngd dẫn giải
Chọn A
Tacó
( ) ( )
2 22
5 55
2 4 d 2d 4 dfx x x fx x−=−


∫ ∫∫
(
) (
)
5
5
2
2
2 4 d 2. 5 2 4.10 34
x fx x=− + =− −+ =
∫
.
Câu 24: Cho hàm số
( )
fx
liên tục trên
và
(
)
Fx
là nguyên hàm của
(
)
fx
, biết
(
)
9
0
d9
fx x=
∫
và
( )
03
F
=
. Tính
( )
9F
.
A.
( )
96F = −
. B.
( )
96F =
. C.
( )
9 12F =
. D.
( )
9 12
F = −
.
Hươngd dẫn giải
Chọn C
Ta có:
( ) (
)
9
9
0
0
dI fx x Fx= =
∫
( ) ( )
9 09FF=−=
( )
9 12
F⇔=
.
Câu 25: Cho
( )
2
0
d3I fx x= =
∫
. Khi đó
( )
2
0
4 3dJ fx x= −


∫
bằng:
A.
2
. B.
6
. C.
8
. D.
4
.
Hươngd dẫn giải
Chọn B
Ta có
(
)
( )
2 22
2
0
0 00
4 3 d 4 d 3 d 4.3 3 6J fx x fx x x x= − = − =−=


∫ ∫∫
.
Câu 26: Cho
( )
4
2
d 10fx x=
∫
và
(
)
4
2
d5
gx x=
∫
. Tính
( ) ( )
4
2
3 5dI fx gx x= −


∫
A.
5I
=
. B.
15I =
. C.
5I
= −
. D.
10I =
.
Hươngd dẫn giải
Chọn A
Có:
( ) (
)
4
2
3 5dI fx gx x= −


∫
(
) ( )
44
22
3 d5 d5fxx gxx=−=
∫∫
.
Câu 27: Giả sử
( )
9
0
d 37fx x=
∫
và
( )
0
9
d 16gx x=
∫
. Khi đó,
( )
9
0
2 3()dI f x gx x= +


∫
bằng:
A.
26I =
. B.
58I =
. C.
143I =
. D.
122I =
.
Hươngd dẫn giải
Chọn A
Ta có:
( ) ( ) ( ) ( ) ( )
9 99 90
0 00 09
2 3()d 2 d 3 d2 d3 d26I fx gx x fxx gxx fxx gxx=+= + = − =


∫ ∫∫ ∫∫
.
Câu 28: Nếu
( )
2
1
d3fx x=
∫
,
( )
5
2
d1fx x= −
∫
thì
( )
5
1
dfx x
∫
bằng
A.
2−
. B.
2
. C.
3
. D.
4
.
Hươngd dẫn giải
Chọn B
https://toanmath.com/
Ta có
( ) ( ) ( )
5 25
1 12
31 2f x dx f x dx f x dx= + =−=
∫ ∫∫
.
Câu 29: Cho
(
)
2
1
d1fx x
=
∫
và
(
)
3
2
d2fx x
= −
∫
. Giá trị của
(
)
3
1
dfx x
∫
bằng
A.
1
. B.
3−
. C.
1−
. D.
3
.
Hươngd dẫn giải
Chọn C
( ) ( )
23
12
ddfx x fx x+
∫∫
1= −
.
Câu 30: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
và
(
)
10
0
d7fx x=
∫
và
(
)
6
2
d3
fx x
=
∫
. Tính
(
)
( )
2 10
06
dd
P fx x fx x
= +
∫∫
.
A.
7P =
. B.
4P
= −
. C.
4P =
. D.
10P =
.
Hươngd dẫn giải
Chọn C
Ta có
( )
10
0
d7fx x
=
∫
( ) ( )
( )
2 6 10
026
d d d7fx x fx x fx x⇔++ =
∫∫∫
(
)
(
)
2 10
06
d d 734
fx x fx x
⇔ + =−=
∫∫
.
Vậy
4P =
.
Câu 31: Cho
( )
1
0
d2fx x=
∫
,
( )
2
1
d4fx x=
∫
, khi đó
?
A.
6
. B.
2
. C.
1
. D.
3
.
Hươngd dẫn giải
Chọn A
(
) (
) (
)
212
0 01
d d d6fx x fx x fx x=+=
∫∫∫
.
Câu 32: Cho hàm số
( )
fx
liên tục trên
và có
( )
1
0
d2
fx x=
∫
;
( )
3
1
d6fx x=
∫
. Tính
( )
3
0
d
I fx x=
∫
.
A.
8I =
. B.
12I =
. C.
36I =
. D.
4I =
.
Hươngd dẫn giải
Chọn A
( )
3
0
d
I fx x=
∫
(
) ( )
13
01
dd
fx x fx x= +
∫∫
268=+=
.
Câu 33: Cho
( )
2
1
d2fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x fx gx x
−
=++


∫
bằng
A.
11
2
I =
. B.
7
2
I =
. C.
17
2
I =
. D.
5
2
I =
.
Hươngd dẫn giải
Chọn D
https://toanmath.com/
Ta có:
( ) ( )
22
2
11
2
35
2 d 3 d 43
1
2 22
x
I fxx gxx
−−
= + + = +−=
−
∫∫
.
Câu 34: Biết
( )
8
1
d2fx x= −
∫
;
( )
4
1
d3fx x=
∫
;
( )
4
1
d7gx x=
∫
. Mệnh đề nào sau đây sai?
A.
( )
8
4
d1fx x=
∫
. B.
(
) (
)
4
1
d 10fx gx x
+=


∫
.
C.
( )
8
4
d5fx x= −
∫
. D.
( ) ( )
4
1
4 2 d2fx gx x−=−


∫
.
Hươngd dẫn giải
Chọn A
Ta có
( ) ( )
( )
8 84
4 11
d d d 23 5fx x fx x fx x= − =−− =−
∫∫∫
Câu 35: Cho hàm số
( )
fx
có
( )
fx
′
liên tục trên đoạn
[ ]
1; 3−
,
( )
13f −=
và
3
1
( )d 10fxx
−
′
=
∫
giá trị
của
( )
3f
bằng
A.
13
−
. B.
7−
. C.
13
. D.
7
.
Hươngd dẫn giải
Chọn C
Ta có
3
1
( )d 10fxx
−
′
=
∫
( )
3
1
10
fx
−
⇒=
( ) ( )
3 1 10ff
⇔ − −=
( ) ( )
3 1 10 13ff⇔ = −+ =
.
Câu 36: Cho
(
)
2
0
d3fx x=
∫
. Tính
( )
( )
2
0
1dfx x+
∫
?
A.
4
. B.
5
. C.
7
. D.
1
.
Hươngd dẫn giải.
Chọn B
Ta có
(
)
( )
( )
2 22
0 00
1d d d 3 2 5fx x fx x x
+ = + =+=
∫ ∫∫
.
Câu 37: Cho
( )
y fx=
,
( )
y gx=
là các hàm số có đạo hàm liên tục trên
[
]
0;2
và
( ) (
)
2
0
. d2gx f x x
′=
∫
,
( ) (
)
2
0
. d3
gxfx x′=
∫
. Tính tích phân
( ) ( )
2
0
.dI fxgx x
′
=


∫
.
A.
1I = −
. B.
6I =
. C.
5I
=
. D.
1I =
.
Hươngd dẫn giải
Chọn C
Xét tích phân
( ) ( ) ( ) ( ) ( ) ( )
22
00
.d . .dI fxgx x f xgx fxgx x
′
′′
= = +


∫∫
( ) ( ) (
) ( )
22
0
0
. d . d5gxfxx gxfxx=′ + ′=
∫∫
.
Câu 38: 46TCho hai tích phân
( )
5
2
d8fx x
−
=
∫
và
( )
2
5
d3gx x
−
=
∫
46T. Tính
( ) ( )
5
2
4 1dI fx gx x
−
= −−


∫
46T.
A.
11I = −
. B.
13I =
. C.
27I =
. D.
3I =
.
Hươngd dẫn giải
Chọn B
https://toanmath.com/
Ta có:
( ) ( )
5
2
4 1dI fx gx x
−
= −−


∫
( ) ( )
52
5
2
25
d4 dfxx gxxx
−
−
−
=+−
∫∫
( )
8 4.3 5 2 13=+ −+=
46T.
Câu 39: Cho hàm số
( )
432
42 1fx x x x x
= − + −+
,
x∀∈
. Tính
(
) (
)
1
2
0
.df xfxx
′
∫
.
A.
2
3
. B.
2
. C.
2
3
−
. D.
2−
.
Hươngd dẫn giải
Chọn C
Ta có
( )
(
) ( ) ( )
11
22
00
. d .dfxfxx fx fx
′
=


∫∫
( )
1
3
0
3
fx
=
( ) ( )
33
10
3
ff
−
=
2
3
= −
.
Câu 40: Cho hàm số
( )
fx
liên tục trên đoạn [0; 6] thỏa mãn
( )
6
0
10f x dx
=
∫
và
( )
4
2
6f x dx =
∫
. Tính
giá trị của biểu thức
( ) ( )
26
04
P f x dx f x dx= +
∫∫
.
A.
4P =
.` B.
16P =
. C.
8P =
. D.
10P =
.
Hươngd dẫn giải:
Ta có:
( ) ( ) ( ) ( ) ( )
26 62 6
04 06 4
P f x dx f x dx f x dx f x dx f x dx

=+= + +


∫∫ ∫∫ ∫
( )
(
)
(
) (
) (
) (
)
6 42 6 62
0 64 4 04
f x dx f x dx f x dx f x dx f x dx f x dx

=+++=+


∫ ∫∫ ∫∫∫
Chọn A
Câu 41: Cho hàm số
( )
fx
liên tục trên đoạn [0; 1] và có
( )
1
0
32 5f x dx
−=


∫
. Tính
( )
1
0
f x dx
∫
.
A.
1
−
. B. 2. C. 1. D.
2−
.
Hươngd dẫn giải:
Ta có:
( )
1
0
32 5f x dx−=


∫
( )
(
)
11 1
1
0
00 0
325325dx f x dx x f x dx
⇔−=⇔−=
∫∫ ∫
(
) (
)
11
00
2 532 1f x dx f x dx
⇔− = − = ⇒ =−
∫∫
Chọn A
Câu 42: Cho hai hàm số
( )
fx
và
( )
gx
liên tục trên đoạn [0; 1], có
( )
1
0
4f x dx
=
∫
và
( )
1
0
2
g x dx = −
∫
. Tính tích phân
( ) ( )
3I f x g x dx= −


∫
.
A.
10−
. B.
10
. C. 2. D.
2−
.
Hươngd dẫn giải:
( ) ( ) ( ) ( ) ( )
1 11
0 00
3 3 4 3 2 10I f x g x dx f x dx g x dx= − = − =−−=


∫ ∫∫
Chọn B
Câu 43: Cho hàm số
( )
2
ln 1fx x x=++
. Tính tích phân
(
)
1
0
'I f x dx=
∫
.
A.
ln 2I =
. B.
( )
ln 1 2I = +
. C.
ln 2I =
D.
2ln 2
I =
https://toanmath.com/
Hươngd dẫn giải:
Ta có:
(
)
(
)
( )
1
1
1
2
0
0
0
' ln 1 ln 1 2I f x dx f x x x
= = = + += +
∫
Chọn B
Câu 44: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn [1; ln3] và thỏa mãn
( )
2
1fe=
,
( )
ln3
2
1
'9f x dx e= −
∫
. Tính
( )
ln3If=
.
A.
2
92Ie= −
. B.
9I =
. C.
9I = −
. D.
2
29Ie= −
.
Hươngd dẫn giải:
Ta có:
( ) (
)
( )
( )
ln3
ln3
2
1
1
' ln3 1 9f x dx f x f f e= = −=−
∫
(gt)
( ) ( )
22
ln3 9 ln3 9f e ef⇒ −=−⇒ =
Chọn B
Câu 45: Cho hai hàm số
( )
y fx=
và
( )
y gx=
có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn
( )
( )
1
0
'. 1
f x g x dx =
∫
,
( ) ( )
1
0
.' 1f x g x dx = −
∫
. Tính
( ) ( )
1
/
0
.I f x g x dx=


∫
.
A.
2I
= −
. B.
0I =
. C.
3I =
. D.
2I =
.
Hươngd dẫn giải:
(
)
( ) ( )
( ) (
)
( )
11
/
00
.g . ' ' .gI f x x dx f x g x f x x dx= = +


∫∫
( )
( ) ( )
( )
11
00
.' ' . 11 0f x g x dx f x g x dx= + =−=
∫∫
Chọn B
Câu 46: Cho hàm số
( )
fx
liên tục trên
( )
0;+∞
và thỏa
(
)
2
0
.cos
x
f t dt x x
π
=
∫
. Tính
( )
4f
.
A.
( )
4 123f =
. B.
( )
2
4
3
f =
. C.
( )
3
4
4
f =
. D.
( )
1
4
4
f =
.
Hươngd dẫn giải:
Ta có:
( ) ( ) ( )
( )
'
Ft ftdt Ft ft= ⇒=
∫
Đặt
( ) ( )
( )
( )
2
2
0
0
x
G x f t dt F x F= = −
∫
( )
( ) (
)
/
22
' 2.G x F x xf x

⇒= =

(Tính chất đạo hàm hợp:
( ) ( ) ( )
' ' .'f ux f uu x=


)
Mặt khác, từ gt:
( )
( )
2
0
.cos
x
G x f t dt x x
π
= =
∫
( ) ( )
' .cos ' sin cos
Gx x x x x x
π ππ π
⇒= =− +
( )
2
2 . sin cosxf x x x x
ππ π
⇒ =−+
(1)
Tính
( )
4f
⇒ ứng với
2x =
Thay
2x =
vào (1)
( )
4. 4 2 sin 2 cos2 1f
ππ π
⇒ =− +=
( )
1
4
4
f⇒=
Chọn D
https://toanmath.com/
Câu 47: Cho hàm số
( )
fx
thỏa mãn
( )
2
0
. .cos
fx
t dt x x
π
=
∫
. Tính
( )
4f
.
A.
( )
4 23f =
. B.
( )
41f = −
. C.
(
)
1
4
2
f
=
. D.
( )
3
4 12f =
.
Hươngd dẫn giải:
( )
( )
( )
( )
3
3
3
2
0
0
cos 3 .cos
33
fx
fx
fx
t
t dt x x f x x x
ππ


== =⇒=


∫
( ) ( )
3
3
3 cos 4 12fx x x f
π
⇒= ⇒=
Chọn D
Câu 48: Cho hàm số
(
) (
)
0
.cos .
x
G x t x t dt= −
∫
. Tính
'
2
G
π



.
A.
'1
2
G
π

= −


. B.
'1
2
G
π

=


. C.
'0
2
G
π

=


. D.
'2
2
G
π

=


.
Hươngd dẫn giải:
Cách 1: Ta có:
( ) (
) (
)
( )
.cos ' .cosFt t xtdt Fx t xt= −⇒ = −
∫
Đặt
( ) ( ) ( ) ( )
0
.cos 0
x
G x t x t dt F x F= −= −
∫
( ) ( ) ( ) ( ) ( ) ( )
//
' 0 ' ' 0 cos 0 ' 1Gx FxF FxF x xx x⇒ = − = − = −− ==


'1
2
G
π

⇒=


Chọn B
Cách 2: Ta có
( )
( )
0
.cos
x
G x t x t dt= −
∫
. Đặt
u t du dt=⇒=
,
( )
cos
dv x t dx= −
chọn
( )
sinv xt=−−
( ) ( ) ( ) ( ) ( )
00
00
.sin sin sin cos cos0 cos 1 cos
xx
xx
Gx t xt xtdt xtdt xt x x⇒ =− −+ −= −= −= − =−
∫∫
(
)
' sin ' sin 1
22
Gx x G
ππ

⇒=⇒ ==


Chọn B
Câu 49: Cho hàm số
( )
2
0
cos .
x
G x t dt=
∫
(
0x >
). Tính
( )
'
Gx
.
A.
( )
2
' .cosGx x x=
. B.
( )
' 2 .cosGx x x=
. C.
( )
' cosGx x=
. D.
( )
' cos 1Gx x= −
.
Hươngd dẫn giải:
Ta có
( )
( )
cos ' cosF t tdt F t t= ⇒=
∫
( )
( )
( )
2
2
0
cos 0
x
G x tdt F x F⇒= = −
∫
( )
( )
( )
( )
( )
( ) ( )
// /
/
2 2 22
' 0 0 2 .F'G x Fx F Fx F Fx x x
 
⇒= − = − = =


 
2
2 .cos 2 .cosx x xx= =
Chọn B
Câu 50: Cho hàm số
( )
2
1
1
x
G x t dt= +
∫
. Tính
( )
'Gx
.
A.
2
1
x
x+
. B.
2
1 x+
. C.
2
1
1 x+
. D.
( )
22
11xx++
.
https://toanmath.com/
Hươngd dẫn giải:
Đặt
( )
( )
22
1 '1F t t dt F t t=+⇒ =+
∫
( ) ( ) ( ) ( ) ( ) ( ) ( )
2
2
1
1 1 ' ' '1 '
1
x
x
Gx tdtFx F Gx Fx F Fx
x
=+= − ⇒ = − = =
+
∫
Chọn A
Câu 51: Cho hàm số
( )
2
1
sin .
x
F x t dt=
∫
(
0x >
). Tính
( )
'Fx
.
A.
sin x
. B.
sin
2
x
x
. C.
2sin x
x
. D.
sin
x
.
Hươngd dẫn giải:
Đặt
( )
2
sinF t t dt=
∫
,
( )
( )
( )
2
1
sin 1
x
G x t dt F x F= = −
∫
( )
( )
(
)
( ) ( ) ( )
2
sin
' ' ' 1 ' '.sin
2
x
GxFxF Fx x x
x
⇒ = −= = =
Chọn B
Câu 52: Tính đạo hàm của
( )
fx
, biết
( )
fx
thỏa
( ) (
)
0
.
x
ft fx
t e dt e
=
∫
.
A.
( )
'fx x=
. B.
( )
2
'1fx x= +
. C.
( )
1
'fx
x
=
. D.
(
)
1
'
1
fx
x
=
−
.
Hươngd dẫn giải:
Đặt
( )
( )
( )
( )
. '.
ft ft
F t te dt F t te= ⇒=
∫
( )
(
)
(
) (
)
0
.0
x
ft
G x t e dt F x F
⇒= =−
∫
(
) ( )
( )
''
fx
Gx Fx e⇒==
(gt)
(
) ( )
.
fx fx
xe e⇔=
( ) ( )
/
.
fx fx
xe e

⇒=

( )
( )
( )
( )
( )
.'.e '.
fx fx fx
e xfx fxe⇒+ =
(
)
( )
(
)
1
1 .' ' '
1
xfx fx fx
x
⇒+ = ⇒ =
−
Chọn D
Câu 53: Cho hàm số
( )
y fx=
liên tục trên
[
)
0;+∞
và
( ) ( )
2
0
d .sin
x
ft t x x
π
=
∫
. Tính
( )
4f
A.
( )
4
f
π
π
−1
=
. B.
( )
2
f
π
π
=
. C.
( )
4
f
π
π
=
. D.
( )
1
2
f
π
=
.
Hươngd dẫn giải
Chọn B
Ta có
( ) ( )
dft t Ft=
∫
(
) ( )
Ft ft
′
⇒=
Khi đó
( )
( )
2
0
d .sin
x
ft t x x
π
=
∫
( ) ( )
2
0
.sin
x
Ft x x
π
⇔=
( )
( ) ( )
2
0 .sinFx F x x
π
⇔ −=
( )
( ) ( )
2
.2 sin .cosFx x x x x
ππ π
′
⇒=+
( )
( ) ( )
2
.2 sin .cosfx x x x x
ππ π
⇔=+
( )
4
2
f
π
⇒=
.
46TCâu 54: Cho hàm số
( )
fx
liên tục trên khoảng
( )
2; 3−
. Gọi
( )
Fx
là một nguyên hàm của
( )
fx
trên khoảng
(
)
2; 3
−
. Tính
( )
2
1
2dI fx x x
−
= +


∫
, biết
( )
11F −=
và
( )
24F =
.
https://toanmath.com/
46TA.
6I =
. B.
10I =
. C.
3I =
. D.
9I =
.
Hươngd dẫn giải
Chọn A
( )
2
1
2dI fx x x
−
= +


∫
(
)
2
2
2
1
1
Fx x
−
−
= +
46T
( ) ( ) ( )
2 1 41FF= − −+ −
413 6= −+ =
.
Câu 55: Cho
( )
2
1
d2fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x fx gx x
−
=+−


∫
A.
11
2
I =
. B.
7
2
I =
. C.
17
2
I =
. D.
5
2
I =
.
Hươngd dẫn giải
Chọn C
Ta có:
( ) ( )
2
1
2 3dI x fx gx x
−
=+−


∫
( ) ( )
22 2
11 1
xd 2 f d 3 g d
x xx xx
−− −
=+−
∫∫ ∫
2
2
1
17
43
22
x
−
= ++=
.
Câu 56: Cho
( ) ( )
2
1
3 2 d1fx gx x+=


∫
,
( ) ( )
2
1
2 d3fx gx x−=−


∫
. Khi đó,
( )
2
1
dfx x
∫
bằng
A.
11
7
. B.
5
7
−
. C.
6
7
. D.
16
7
.
Hươngd dẫn giải
Chọn B
Đặt
( )
2
1
da fx x=
∫
,
( )
2
1
d
b fx x=
∫
, ta có hệ phương trình
321
23
ab
ab
+=
−=−
5
7
11
7
a
b
= −
⇔
=
Vậy
(
)
2
1
5
d
7
fx x
= −
∫
.
Câu 57: Cho
( )
fx
,
( )
gx
là hai hàm số liên tục trên đoạn
[ ]
1;1−
và
( )
fx
là hàm số chẵn,
( )
gx
là
hàm số lẻ. Biết
( )
1
0
d5
fx x=
∫
;
( )
1
0
d7gx x=
∫
. Mệnh đề nào sau đây là sai?
A.
(
)
1
1
d 10fx x
−
=
∫
. B.
( ) (
)
1
1
d 10fx gx x
−
+=


∫
.
C.
(
) (
)
1
1
d 10f x gx x
−
−=


∫
. D.
( )
1
1
d 14gx x
−
=
∫
.
Hươngd dẫn giải
Chọn D
Vì
( )
fx
là hàm số chẵn nên
( ) ( )
11
10
d2 dfx x fx x
−
=
∫∫
2.5=
10=
.
Vì
( )
gx
là hàm số lẻ nên
( )
1
1
d0gx x
−
=
∫
.
⇒
( ) ( )
1
1
d 10fx gx x
−
+=


∫
và
( )
( )
1
1
d 10f x gx x
−
−=


∫
.
Vậy đáp án D sai.
https://toanmath.com/
Câu 58: Cho
( )
fx
,
( )
gx
là hai hàm số liên tục trên đoạn
[
]
1;1
−
và
( )
fx
là hàm số chẵn,
( )
gx
là
hàm số lẻ. Biết
(
)
1
0
d5fx x=
∫
;
(
)
1
0
d7gx x=
∫
. Mệnh đề nào sau đây là sai?
A.
(
)
1
1
d 10
fx x
−
=
∫
. B.
(
) (
)
1
1
d 10fx gx x
−
+=


∫
.
C.
(
) (
)
1
1
d 10
fx gx x
−
−=


∫
. D.
( )
1
1
d 14gx x
−
=
∫
.
Hươngd dẫn giải
Chọn D
Vì
( )
fx
là hàm số chẵn nên
( ) ( )
11
10
d 2 d 2.5 10
fx x fx x
−
= = =
∫∫
.
Vì
( )
gx
là hàm số lẻ nên
( )
1
1
d0gx x
−
=
∫
.
⇒
( ) ( )
1
1
d 10fx gx x
−
+=


∫
và
( ) ( )
1
1
d 10f x gx x
−
−=


∫
.
Câu 59: Nếu
( )
10
0
d 17fz z=
∫
và
( )
8
0
d 12ft t=
∫
thì
( )
10
8
3dfx x
−
∫
bằng
A.
15−
. B.
29
. C.
15
. D.
5
.
Hươngd dẫn giải
Chọn A
( ) ( ) ( ) ( )
10 0 10
8 80
3 d 3 d d 3 12 17 15I fx x fx x fx x

=− =− + =−− + =−


∫ ∫∫
.
Câu 60: Cho
(
)
2
1
d2fx x
−
=
∫
,
( )
7
1
d9ft t
−
=
∫
. Giá trị của
( )
7
2
dfz z
∫
là
A.
11
. B.
5
. C.
7
. D.
9
.
Hươngd dẫn giải
Chọn C
Ta có
( ) ( )
77
11
ddft t fx x
−−
=
∫∫
và
( ) ( )
77
22
ddfz z fx x=
∫∫
nên
( )
( ) ( )
7 27
1 12
d ddfx x fx x fx x
−−
= +
∫∫∫
.
Vậy
( )
7
2
d7fz z=
∫
.
Câu 61: Cho hàm số
( )
y fx=
liên tục, luôn dương trên
[ ]
0;3
và thỏa mãn
( )
3
0
d4
I fx x= =
∫
. Khi
đó giá trị của tích phân
( )
( )
( )
3
1 ln
0
4d
fx
Ke x
+
= +
∫
là:
A.
4 12e+
. B.
12 4e+
. C.
3e 14+
. D.
14 3e+
.
Hươngd dẫn giải
Chọn B
Ta có
( )
( )
( )
(
)
( )
( )
3 3 33 3
3
1 ln 1 ln
0
0 0 00 0
e 4 d e d 4d e. d 4d 4e 4 4e 12
|
fx fx
K x xxfxxx x
++
= += += +=+=+
∫ ∫ ∫∫ ∫
.
Vậy
.
Câu 62: Cho hàm số
( )
y fx=
có đạo hàm trên
thỏa
https://toanmath.com/
( )
( )
( ) ( ) ( )
( )
0 0 1;
3 1, x,y
ff
fx y fx fy xyx y
′
= =
+= + + +−∀∈
.
Tính
( )
1
0
1d
fx x−
∫
.
A.
1
2
. B.
1
4
−
. C.
1
4
. D.
7
4
.
Hươngd dẫn giải
Chọn C
Lấy đạo hàm theo hàm số
y
( ) ( )
2
36f x y f y x xy
′′
+= + +
,
x∀∈
.
Cho
( ) ( )
2
0 03y fx f x
′′
=⇒=+
( )
2
13fx x
′
⇒=+
Vậy
( ) ( )
3
f x f x dx x x C
′
= = ++
∫
mà
( )
01f =
1
C⇒=
suy ra
( )
3
1fx x x= ++
.
( )
1
0
1dfx x−=
∫
(
)
0
3
1
1
x x dx
−
++
∫
0
42
1
42
xx
x
−

= ++


11
1
42
=−−+
1
4
=
.
Câu 63: Cho hàm số
( )
fx
là hàm bậc nhất thỏa mãn
( ) ( )
1
0
1 d 10x fxx
′
+=
∫
và
( ) ( )
21 0 2
ff
−=
.
Tính
( )
1
0
dI fx x=
∫
.
A.
1I =
. B.
8
I =
. C.
12I = −
. D.
8I = −
.
Hươngd dẫn giải
Chọn D
Gọi
( )
f x ax b= +
,
( )
0
a ≠
( )
fx a
′
⇒=
.
Theo giả thiết ta có:
+)
( ) ( )
1
0
1 d 10x fxx
′
+=
∫
( )
1
0
1 d 10ax x
⇔ +=
∫
( )
1
0
10
1dxx
a
⇔+ =
∫
3 10 20
23
a
a
⇔ = ⇒=
.
+)
( )
( )
21 0 2ff−=
20
2. 2
3
bb

⇔ + −=


34
3
b⇔=−
.
Do đó,
(
)
20 34
33
fx x= −
.
Vậy
(
)
1
0
dI fx x=
∫
1
0
20 34
d8
33
xx

= −=−


∫
.
Câu 64: Cho hàm số
( )
fx
xác định trên
{ }
\0
, thỏa mãn
( )
35
1
fx
xx
′
=
+
,
( )
1fa=
và
(
)
2fb
−=
. Tính
( ) ( )
12ff−+
.
A.
( ) ( )
12f f ab− + =−−
. B.
(
) ( )
12f f ab−+ =−
.
C.
( ) ( )
12
f f ab−+ =+
. D.
( ) ( )
12f f ba−+ =−
.
Hươngd dẫn giải
Chọn C
Ta có
(
)
( ) ( )
35
1
fx
xx
′
−=
− +−
35
1
xx
= −
+
( )
fx
′
= −
nên
( )
fx
′
là hàm lẻ.
Do đó
( ) ( ) ( )
2 12
2 21
d0 d dfxx fxx fxx
−
−−
′ ′′
=⇔=−
∫ ∫∫
.
https://toanmath.com/
Suy ra
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
1 2 21 12 21f f f f f f f f ab−− − =− + ⇒ −+ = −+ =+
.
Câu 65: Cho hàm số
(
)
fx
xác định trên
{ }
\0
và thỏa mãn
( )
24
1
fx
xx
′
=
+
,
(
)
1fa
=
,
( )
2fb−=
. Giá trị của biểu thức
( ) ( )
12ff−−
bằng
A.
ba−
. B.
ab+
. C.
ab−
. D.
ab−−
.
Hươngd dẫn giải
Chọn A
Ta có
( )
(
) ( )
24
1
fx
xx
′
−=
− +−
24
1
xx
=
+
( )
fx
′
=
nên
( )
fx
′
là hàm chẵn.
Do đó
( ) ( )
12
21
ddfxx fxx
−
−
′′
=
∫∫
.
Suy ra
( ) ( ) ( )
(
) (
) (
)
( ) ( )
12 1 2 2112ffffffff−− = −− −+ −− + −
( ) ( )
12
21
ddfxxba fxx
−
−
′′
= +−−
∫∫
ba= −
.
Câu 66: Cho hàm số
(
)
y fx=
xác định và liên tục trên
thỏa mãn đồng thời các điều kiện
( )
0fx>
,
x∀∈
;
( )
( )
2
.
x
f x ef x
′
= −
,
x∀∈
và
(
)
1
0
2
f =
. Tính giá trị của
( )
ln 2f
.
A.
( )
2
ln 2
9
f =
. B.
( )
2
ln 2
9
f = −
. C.
( )
2
ln 2
3
f =
. D.
( )
1
ln 2
3
f =
.
Hươngd dẫn giải
Chọn D
(
) (
)
2
.
x
f x ef x
′
= −
(
)
( )
2
x
fx
e
fx
′
⇔=−
( )
( )
ln 2 1
2
00
d ed
x
fx
xx
fx
′
⇔=−
∫∫
( )
(
)
ln 2
ln 2
2
0
0
d
x
fx
e
fx
⇔=−
∫
(
)
ln 2
0
1
1
fx
⇔− =−
(
)
( )
11
1
ln 2 0ff
⇔ −=
( )
1
3
ln 2f
⇔=
( )
1
ln 2
3
f⇔=
.
Câu 67: Cho hàm số
( )
y fx=
có đồ thị
( )
C
, xác định và liên tục trên
thỏa mãn đồng thời các
điều kiện
( )
0fx x> ∀∈
,
( ) ( )
( )
2
.,f x xf x x
′
= ∀∈
và
( )
02f =
. Phương trình tiếp
tuyến tại điểm có hoành độ
1
x =
của đồ thị
(
)
C
là.
A.
6 30yx= +
. B.
6 30
yx=−+
. C.
36 30yx= −
. D.
36 42yx=−+
.
Hươngd dẫn giải
Chọn C
( ) ( )
( )
2
.f x xf x
′
=
( )
( )
2
2
fx
x
fx
′
⇔=
( )
( )
11
2
2
00
dd
fx
x xx
fx
′
⇔=
∫∫
( )
( )
1
1
3
2
0
0
d
3
fx
x
fx
⇔=
∫
( )
1
0
11
3fx
⇔− =
( )
( )
111
1 03ff
⇔− =−
( )
11
16f
⇔=
( )
16f⇔=
.
( ) ( )
( )
2
1 1. 1 36ff
′
= =
.
Vậy phương trình tiếp tuyến cần lập là
36 30yx= −
.
Câu 68: Cho hàm số
( )
0
y fx= >
xác định, có đạo hàm trên đoạn
[ ]
0;1
và thỏa mãn:
( ) ( )
0
1 2018 dt
x
gx ft= +
∫
,
( ) ( )
2
gx f x
=
. Tính
( )
1
0
dgx x
∫
.
https://toanmath.com/
A.
1011
2
. B.
1009
2
. C.
2019
2
. D.
505
.
Hươngd dẫn giải
Chọn A
Ta có
( ) ( )
0
1 2018 dt
x
gx ft
= +
∫
( ) ( ) ( )
2018 2018g x f x gx
′
⇒= =
( )
( )
2018
gx
gx
′
⇒=
(
)
( )
00
d 2018 d
tt
gx
xx
gx
′
⇒=
∫∫
( )
( )
0
0
2 2018
t
t
gx x⇒=
( )
( )
2 1 2018gt t⇒ −=
(do
( )
01g =
)
( )
1009 1gt t⇒=+
( )
1
1
2
0
0
1009 1011
dt
22
gt t t

⇒ = +=


∫
.
Câu 69: Cho hàm số
( )
y fx=
có đạo hàm và liên tục trên đoạn
[ ]
1;1−
, thỏa mãn
(
)
0,fx x
> ∀∈
và
( ) ( )
'2 0f x fx+=
. Biết
( )
11
f =
, tính
( )
1f −
.
A.
( )
2
1fe
−
−=
. B.
( )
3
1fe−=
. C.
( )
4
1fe−=
. D.
( )
13
f −=
.
Hươngd dẫn giải
Chọn C
Biến đổi:
( ) (
)
( )
( )
( )
( )
( )
( )
( )
1 11
1
1
1 11
''
' 2 0 2 2 4 ln 4
fx fx dfx
f x f x dx dx f x
fx fx fx
−
− −−
+ = ⇔ =−⇔ = − ⇔ =−⇔ =−
∫ ∫∫
( )
( )
( )
( )
( ) (
)
4 44
11
ln 4 1 1 .
11
ff
e f f ee
ff
−
=−⇔ = ⇔ − = =
−−
.
Câu 70: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
đồng thời thỏa mãn
( )
09f
′
=
và
( )
( )
2
99f x fx x
′′ ′
+ −=


. Tính
(
) ( )
10Tf f= −
.
A.
2 9ln 2
T = +
. B.
9T =
. C.
1
9ln 2
2
T = +
. D.
2 9ln 2T = −
.
Hươngd dẫn giải
Chọn C
Ta có
( ) ( )
2
99f x fx x
′′ ′
+ −=


( )
(
)
( )
2
91
f x fx x
′′ ′
⇒ −=− −


( )
( )
2
1
1
9
fx
fx x
′′
−
⇒− =
′
−


.
Lấy nguyên hàm hai vế
(
)
( )
2
1
1
dd
9
'
fx
xx
fx x
′′
−
−=
−


∫∫
( )
1
9
x
C
fx x
⇒=+
′
−
.
Do
( )
09f
′
=
nên
1
9
C =
suy ra
( )
9
1
fx x
x
′
−=
+
( )
9
1
fx x
x
′
⇒=+
+
Vậy
(
) ( )
1
0
9
10 d
1
T f f xx
x

=−= +

+

∫
1
2
0
9ln 1
2
x
x

= ++


1
9ln 2
2
= +
.
Câu 71: Cho hàm số
( )
y fx=
thỏa mãn
( ) ( )
42
'.
f xfx x x= +
. Biết
( )
02f =
. Tính
( )
2
2f
.
A.
( )
2
313
2
15
f =
. B.
( )
2
332
2
15
f =
. C.
( )
2
324
2
15
f =
. D.
( )
2
323
2
15
f =
.
Hươngd dẫn giải
https://toanmath.com/
Chọn B
Ta có
( ) ( ) (
) (
)
( )
( ) ( )
( )
2
2 22
42 42 2
0
0 00
136 136
'. '.
15 2 15
fx
f xfx x x f xfxdx x x dx fxdfx=+⇒ = + ⇔ = ⇔ =
∫ ∫∫
( )
(
)
2
2
24
136 332
2
2 15 15
f
f
−
=⇔=
.
Câu 72: Cho
()fx
xác định, có đạo hàm, liên tục và đồng biến trên
[ ]
1; 4
thỏa mãn
( )
( )
[
]
( )
2
3
2 , 1; 4 , 1
2
x xf x f x x f
′
+ = ∀∈ =


. Giá trị
( )
4f
bằng:
A.
391
18
B.
361
18
C.
381
18
D.
371
18
Hươngd dẫn giải
Chọn A
Biến đổi:
(
)
( )
2
2x xf x f x
′
+=


( )
( )
( )
2
12x fx f x
′
⇔+ =


( )
( )
( )
( )
2
12
12
fx
fx
xx
fx
fx
′

′

⇔=⇒ =
+
+
.
( )
( )
44
11
12
fx
dx xdx
fx
′
⇒=
+
∫∫
( )
4
1
14
12
3
fx⇔+ =
( ) (
)
14 391
12 4 2 4
3 18
ff⇔ + −= ⇔ =
.
Chọn A
Chú ý: Nếu không nhìn được ra luôn
( )
( )
( )
4
4
1
1
12
12
fx
I dx f x
fx
′
= = +
+
∫
( )
12 4 2f=+−
thì ta có
thể sử dụng kỹ thuật vi phân hoặc đổi biến (bản chất là một).
+ Vi phân:
( )
( )
( )
( )
44
11
'
12 12
f x df x
dx
fx fx
=
++
∫∫
( )
( )
( )
( )
( )
4
1
4
2
1
1
1
12 12 12
2
fx d fx fx
−
=+ +=+
∫
.
+ Đổi biến: Đặt
(
)
12t fx= +
(
)
2
12t fx⇒=+
(
)
tdt f x dx
′
⇔=
với
( ) ( )
1 12 1 2; 4 12 4xtfxtf=⇒= + = = ⇒= +
.
Khi đó
( )
12 4
2
f
tdt
I
t
+
= =
∫
( )
( )
12 4
12 4
2
2
f
f
dt t
+
+
=
∫
( )
12 4 2f=+−
.
Câu 73: Cho hàm số
( )
y fx=
có
( )
fx
′
liên tục trên nửa khoảng
[
)
0;+∞
thỏa mãn
( ) ( )
2
3 1 3.e
x
fx f x
−
′
+=+
. Khi đó:
A.
( ) ( )
3
2
11
e1 0
2
e3
ff−= −
+
. B.
( ) ( )
3
2
11
e1 0
4
2e 3
ff−= −
+
.
C.
( ) ( )
( )
22
3
e3e38
e1 0
3
ff
+ +−
−=
. D.
( ) ( )
( )
3 22
e1 0 e3e38ff− = + +−
.
Hươngd dẫn giải
Chọn C
Ta có:
( ) ( )
2
2
e3
3 1 3.e
e
x
x
x
fx f x
−
+
′
+=+=
( ) ( )
3 3 22
3e e e e 3
x x xx
fx f x
′
⇒ +=+
.
( )
3 22
e ee 3
x xx
fx
′

⇔=+

.
https://toanmath.com/
Lấy tích phân từ
0
đến
1
hai vế ta được
(
)
11
3 22
00
e d e e 3 d
x xx
fx x x
′

= +

∫∫
(
)
(
)
1
3
1
32
0
0
1
e e3
3
xx
fx

⇔=+

( ) ( )
( )
22
3
e3e38
e1 0
3
ff
+ +−
⇔ −=
.
Câu 74: Cho hàm số
f
liên tục,
( )
1fx>−
,
( )
00f =
và thỏa
( ) (
)
2
12 1f x x xfx
′
+= +
. Tính
( )
3
f
.
A.
0
. B.
3
. C.
7
. D.
9
.
Hươngd dẫn giải
Chọn B
Ta có
( )
( )
( )
( )
2
2
2
12 1
1
1
fx
x
f x x xfx
fx
x
′
′
+= +⇔ =
+
+
( )
( )
( ) ( )
33
3
33
2
2
00
0
00
2
d d 1 1 11
1
1
fx
x
x x fx x fx
fx
x
′
⇔ = ⇔ += +⇔ +=
+
+
∫∫
(
)
(
)
( )
( )
31 011 312 3 3ff f f⇔ +− +=⇔ += ⇔ =
.
Câu 75: Cho hàm số
( )
0fx≠
thỏa mãn điều kiện
(
) (
) (
)
2
23
fx x f x
′
= +
và
( )
1
0
2
f = −
. Biết rằng
tổng
( )
( ) (
) (
) (
)
1 2 3 ... 2017 2018
a
ff f f f
b
+ + ++ + =
với
(
)
*
,ab∈∈

và
a
b
là phân
số tối giản. Mệnh đề nào sau đây đúng?
A.
1
a
b
<−
. B.
1
a
b
>
. C.
1010ab+=
. D.
3029
ba
−=
.
Hươngd dẫn giải
Chọn D
Ta có
( ) ( ) ( )
2
23fx x f x
′
= +
(
)
(
)
2
23
fx
x
fx
′
⇔=+
( )
( )
( )
d 2 3d
fx
x xx
fx
′
⇔=+
∫∫
( )
2
1
3x xC
fx
⇔− = + +
.
Vì
( )
1
02
2
fC=−⇒ =
.
Vậy
( )
( )( )
1 11
12 21
fx
xx x x
=−=−
++ + +
.
Do đó
( ) ( ) ( ) ( ) ( )
1 1 1009
1 2 3 ... 2017 2018
2020 2 2020
ff f f f+ + ++ + = −=−
.
Vậy
1009a = −
;
2020b =
. Do đó
3029ba−=
.
Câu 76: Biết luôn có hai số
a
và
b
để
( )
4
ax b
Fx
x
+
=
+
( )
40ab−≠
là nguyên hàm của hàm số
(
)
fx
và thỏa mãn:
(
) ( )
( )
2
21f x Fx f x
′
= −


.
Khẳng định nào dưới đây đúng và đầy đủ nhất?
A.
1a =
,
4b =
. B.
1a =
,
1b
= −
. C.
1a =
,
{ }
\4b∈
. D.
a∈
,
b∈
.
Hươngd dẫn giải
Chọn C
https://toanmath.com/
Ta có
(
)
4
ax b
Fx
x
+
=
+
là nguyên hàm của
( )
fx
nên
(
)
( )
(
)
2
4
4
ab
fx Fx
x
−
′
= =
+
và
(
)
(
)
3
28
4
ba
fx
x
−
′
=
+
.
Do đó:
( ) ( )
(
)
( )
2
21f x Fx f x
′
= −
(
)
( )
(
)
2
43
24
28
1
4
44
ab
ax b b a
x
xx
−
+−

⇔=−

+

++
( )
44
a b ax b x
⇔ −=− +−−
(
)
( )
41 0 1xaa
⇔ + − =⇔=
(do
40x +≠
)
Với
1a =
mà
40ab−≠
nên
4b ≠
.
Vậy
1a =
,
{ }
\4
b∈
.
Chú ý: Ta có thể làm trắc nghiệm như sau:
+ Vì
40ab−≠
nên loại được ngay phương án A:
1a =
,
4b =
và phương án D:
a∈
,
b∈
.
+ Để kiểm tra hai phương án còn lại, ta lấy
0b =
,
1a =
. Khi đó, ta có
( )
4
x
Fx
x
=
+
,
(
)
( )
2
4
4
fx
x
=
+
,
( )
( )
3
8
4
fx
x
′
= −
+
.
Thay vào
( )
( )
( )
( )
2
21f x Fx f x
′
= −
thấy đúng nên
Chọn C
Câu 77: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
1; 2
thỏa mãn
( )
14
f
=
và
( ) ( )
32
23f x xf x x x
′
= −−
. Tính
( )
2
f
A.
5
. B.
20
. C.
10
. D.
15
.
Hươngd dẫn giải
Chọn B
Do
[ ]
1; 2x∈
nên
(
) (
)
(
)
( )
(
)
32
2
2 3 23 23
xf x fx fx
f x xf x x x x x
xx
′
′
−

′
= − − ⇔ = +⇔ = +


( )
2
3
fx
x xC
x
⇔ =++
.
Do
( )
14f =
nên
0C =
⇒
( )
32
3fx x x= +
.
Vậy
( )
2 20f =
.
Câu 78: Cho
( )
2
cos
x
fx
x
=
trên
;
22
ππ

−


và
( )
Fx
là một nguyên hàm của
( )
xf x
′
thỏa mãn
( )
00F =
. Biết
;
22
a
ππ

∈−


thỏa mãn
tan 3a =
. Tính
( )
2
10 3Fa a a−+
.
A.
1
ln10
2
−
. B.
1
ln10
4
−
. C.
1
ln10
2
. D.
ln10
.
Hươngd dẫn giải
Chọn C
Ta có:
( ) ( )
dF x xf x x
′
=
∫
( )
d
xfx=
∫
( ) ( )
dxfx fx x
= −
∫
Ta lại có:
( )
2
dd
cos
x
fx x x
x
=
∫∫
( )
= d tanxx
∫
tan tan dx x xx= −
∫
sin
tan d
cos
x
xx x
x
= −
∫
( )
1
tan d cos
cos
xx x
x
= +
∫
tan ln cosx x xC=++
( ) ( )
tan ln cosF x xf x x x x C⇒= − − +
Lại có:
( )
00F =
0C⇒=
, do đó:
( ) ( )
tan ln cosF x xf x x x x=−−
.
( ) ( )
tan ln cosF a af a a a a⇒= − −
https://toanmath.com/
Khi đó
(
)
2
cos
a
fa
a
=
(
)
2
1 tanaa= +
10a=
và
2
2
1
1 tan
cos
a
a
= +
10=
2
1
cos
10
a
⇔=
1
cos
10
a
⇔=
.
Vậy
( )
2
10 3Fa a a−+
22
1
10 3 ln 10 3
10
aa aa= −− − +
1
ln10
2
=
.
Câu 79: Cho hàm số
( )
y fx
=
xác định và liên tục trên
thỏa mãn đồng thời các điều kiện sau
( )
0fx>
,
x
∀∈
,
( ) ( )
2
e.
x
fx f x
′
= −
x∀∈
và
( )
1
0
2
f
=
. Phương trình tiếp tuyến của
đồ thị tại điểm có hoành độ
0
ln 2x =
là
A.
2 9 2ln 2 3 0xy+ − −=
. B.
2 9 2ln 2 3 0xy− − +=
.
C.
2 9 2ln 2 3 0xy
− + −=
. D.
2 9 2ln 2 3 0xy
+ + −=
.
Hươngd dẫn giải
Chọn A
Ta có
( ) ( )
2
e.
x
fx f x
′
= −
(
)
(
)
2
e
x
fx
fx
′
⇔− =
( )
( )
ln 2 ln 2
2
00
d ed
x
fx
xx
fx

′
⇒− =


∫∫
(
)
(
)
ln 2
ln 2
0
0
1
e
x
fx

⇒=



( ) ( )
11
1
ln 2 0ff
⇒ −=
( )
1
ln 2
3
f⇒=
.
Từ đó ta có
( ) (
)
ln 2 2
ln 2 e ln 2ff
′
= −
2
1
2.
3

= −


2
9
= −
.
Vậy phương trình tiếp tuyến cần tìm là
( )
21
ln 2
93
yx=−− +
2 9 2ln 2 3 0xy⇔ + − −=
.
Câu 80: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
,
( )
fx
và
( )
fx
′
đều nhận giá trị
dương trên đoạn
[
]
0;1
và thỏa mãn
(
)
02f =
,
( ) ( ) (
) ( )
11
2
00
. 1d 2 . df x fx x f xfx x

′′
+=



∫∫
. Tính
( )
1
3
0
dfx x


∫
.
A.
15
4
. B.
15
2
. C.
17
2
. D.
19
2
.
Hươngd dẫn giải
Chọn D
Theo giả thiết, ta có
( ) ( ) ( ) ( )
11
2
00
. 1d 2 . d
f x fx x f xfx x

′′
+=



∫∫
( ) ( ) ( ) ( )
11
2
00
. 1d 2 . d 0f x fx x f xfx x

′′
⇔ +− =



∫∫
( ) ( ) (
)
( )
1
2
0
. 2 . 1d 0f x fx f xfx x

′′
⇔ − +=



∫
( )
( )
2
1
0
. 1d 0f xfx x

′
⇔ −=

∫
( ) ( )
. 10f xfx
′
⇒ −=
( ) ( )
2
.1f xfx
′
⇒=
( )
3
3
fx
xC⇒=+
. Mà
( )
8
02
3
fC=⇒=
.
Vậy
( )
3
38fx x= +
.
Vậy
( ) ( )
1
11
2
3
00
0
3 19
d 3 8d 8
22
x
fx x x x x

= += + =




∫∫
.
https://toanmath.com/
Câu 81: Cho
()fx
không âm thỏa mãn điều kiện
2
(). '() 2 () 1fxf x x f x
= +
và
(0) 0f =
. Tổng giá
trị lớn nhất và nhỏ nhất của hàm số
()y fx=
trên
[ ]
1; 3
là
A.
22
B.
4 11 3+
C.
20 2+
D.
3 11 3
+
Hươngd dẫn giải
Chọn D
Biến đổi:
2
22
(). '() (). '()
(). '() 2 () 1 2 2
() 1 () 1
fxf x fxf x
f x f x x f x x dx xdx
fx fx
= +⇔ = ⇒ =
++
∫∫
22
() 1
fx x C
⇔ += +
Với
2 2 2 42
(0) 0 1 () 1 1 () 2 ()
f C fx x fx x x gx= ⇒ =⇒ += +⇒ = + =
Ta có:
[ ]
3
'( ) 4 4 0, 1; 3gx x x x
= + > ∀∈
. Suy ra
()gx
đồng biến trên
[ ]
1; 3
Suy ra:
( )
()0
22
(1) () () 3 3 () 99 3 () 311
fx
g gx fx g fx fx
≥
≤ = ≤ ⇒ ≤ ≤ → ≤ ≤
[ ]
1;3
3
min ( ) 3
( ) 3 11
fx
Max f x
=
⇒
=
Chú ý: Nếu không tìm được ra luôn
2
2
(). '()
() 1
() 1
fxf x
dx f x C
fx
= ++
+
∫
thì ta có thể sử dụng kĩ thuật
vi phân hoặc đổi biến (bản chất là một)
+) Vi phân:
( )
( )
( )
1
2 22
2
22
(). '() () 1
() () 1 () 1 () 1
2
() 1 () 1
fxf x fx
dx dfx fx dfx fx C
fx fx
−
= = + + = ++
++
∫∫ ∫
+ Đổi biến: Đặt
2 22
() 1 () 1 () '()
t f x t f x tdt f x f x dx= +⇒ = +⇒ =
Suy ra:
2
2
(). '()
() 1
() 1
f x f x tdt
dx dt t C f x C
t
fx
= = =+ = ++
+
∫ ∫∫
Câu 82: Cho hàm số
( )
fx
có đạo hàm và đồng biến trên
thỏa mãn
(
)
01f =
và
( )
(
)
( )
2
,
x
f x ef x x
′
= ∀∈
. Tính tích phân
( )
1
0
f x dx
∫
bằng
A.
2e
−
. B.
1e −
. C.
2
2e −
. D.
2
1e −
.
Hươngd dẫn giải
Chọn B
Biến đổi
( )
(
)
( )
2
x
f x ef x
′
=
( )
( )
( )
2
x
fx
e
fx
′
⇔=
( )
( )
x
fx
e
fx
′
⇔=
( )
( )
x
fx
dx e dx
fx
′
⇒=
∫∫
( )
(
)
( )
1
2
2
x
f x df x e dx
−
⇔=
∫∫
( )
2
22
x
fx e C
⇔=+
Vì
( )
01 0
fC=⇒=
( )
2
x
fx e⇒=
( )
x
fx e⇔=
Suy ra
( )
1
11
00
0
1
x
f x dx edx e e= = = −
∫∫
Câu 83: Cho hàm số
( )
y fx=
xác định và liên tục trên
{ }
\0
thỏa mãn
( ) ( ) ( ) ( )
22
21 1x f x x f x xf x
′
+− = −
với
{ }
\0x∀∈
và
( )
12f = −
. Tính
( )
2
1
f x dx
∫
.
https://toanmath.com/
A.
1
ln 2
2
−−
. B.
3
ln 2
2
−−
. C.
ln 2
1
2
−−
. D.
3 ln 2
22
−−
.
Hươngd dẫn giải
Chọn A
Ta có
( ) ( ) (
) (
)
22
21 1x f x x f x xf x
′
+− = −
( )
( )
( ) ( )( )
2
1*xf x f x xf x
′
⇔ += +
Đặt
(
) (
)
( )
h x f x xf x
′
= +
( ) ( ) ( )
h x f x xf x
′′
⇒=+
, khi đó
( )
*
có dạng
( ) ( )
2
h x hx
′
=
(
)
(
)
2
1
hx
hx
′
⇒=
( )
( )
2
1
hx
dx dx
hx
′
⇒=
∫∫
( )
( )
2
dh x
xC
hx
⇒=+
∫
( )
1
xC
hx
⇔− = +
( )
1
hx
xC
⇒=−
+
( )
1
1xf x
xC
⇒ +=−
+
Vì
(
)
12f
= −
nên
1
21
1 C
−+=−
+
0C⇒=
Khi đó
( )
1
1xf x
x
+=−
( )
2
11
fx
xx
⇒ =−−
Suy ra:
(
)
22
2
11
11
f x dx dx
xx

=−−


∫∫
2
1
1
ln x
x

= −


1
ln 2
2
=−−
Câu 84: Cho hàm số
( )
y fx=
. Có đạo hàm liên tục trên
. Biết
(
)
1ef
=
và
( ) ( ) ( )
3
2x f x xf x x
′
+=−
,
x∀∈
. Tính
( )
2f
.
A.
2
4e 4e 4−+
. B.
2
4e 2e 1−+
. C.
3
2e 2e 2−+
. D.
2
4e 4e 4+−
.
Hươngd dẫn giải
Chọn D
Ta có:
( )
( ) (
)
3
2x f x xf x x
′
+=−
( ) (
) ( )
3
2
1
xf x x f x
x
′
−+
⇔=
( )
2
e
e
x
x
fx
x
−
−
′

⇔=


Suy ra
( )
22
2
11
e
d ed
x
x
fx
xx
x
−
−
′

=


∫∫
(
)
( )
21
21
22
e 2e 1
ee
21
ff
−−
−−

⇔ − =−−

( )
( )
21
12
e 2e 1
ee
41
ff
−−
−−
⇔ −=−
( ) ( )
2 4e 1 e 1
ff⇔ = +−


2
4e 4e 4
= +−
.
Câu 85: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và thỏa mãn
(
)
00f =
. Biết
( )
1
2
0
9
d
2
f xx=
∫
và
( )
1
0
3
cos d
24
x
fx x
ππ
′
=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
1
π
. B.
4
π
. C.
6
π
. D.
2
π
.
Hươngd dẫn giải
Chọn C
Ta có
(
)
( )
( )
11
00
cos d cos d
22
xx
f x x fx
ππ
′
=
∫∫
( ) ( )
1
1
0
0
cos . sin . d
2 22
xx
fx fx x
π ππ
= +
∫
( )
1
0
sin . d
22
x
fx x
ππ
=
∫
.
https://toanmath.com/
Suy ra
(
)
1
0
3
sin . d
22
x
fx x
π
=
∫
Mặt khác
( )
2
11
00
11
sin d 1-cos d
22 2
x
x xx
π
π

= =


∫∫
.
Do đó
( ) (
)
2
11 1
2
00 0
d 2 3sin d 3sin d 0
22
xx
f xx fxx x
ππ

− +=


∫∫ ∫
.
hay
(
)
2
1
0
3sin d 0
2
x
fx x
π

−=


∫
suy ra
(
)
3sin
2
x
fx
π
=
.
Vậy
(
)
1
11
0
00
66
d 3sin d cos
22
xx
fx x x
ππ
ππ
= =−=
∫∫
.
Câu 86: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
0; 1
, thỏa mãn
(
) (
)
11
00
d d1fx x xfx x= =
∫∫
và
( )
1
2
0
d4fx x
=


∫
. Giá trị của tích phân
( )
1
3
0
dfx x


∫
bằng
A.
1
. B.
8
. C.
10
. D.
80
.
Hươngd dẫn giải
Chọn C
Xét
( ) ( )
1
2
0
df x ax b x++


∫
( ) (
) ( ) ( )
11 1
2
2
00 0
d2 . d d
f x x f x ax b x ax b x= + + ++


∫∫ ∫
( ) ( )
(
)
1
11
3
00
0
1
42 d 2 d
3
axfx x bfx x axb
a
=+ + ++
∫∫
( )
2
2
42
3
a
a b ab b=+ ++ + +
.
Cần xác định
,ab
để
( )
2
2
2 2 40
3
a
ba b b+ + + + +=
Ta có:
( )
22
4
44 24
3
bb bb∆=++− ++
( )
2
2
0
3
b−−
= ≤
26
ba⇒=⇒=−
.
Khi đó:
( ) ( )
1
2
0
62d0
fx x x+− + =


∫
( )
62
fx x⇒=−
Suy ra
( ) ( )
11
3
3
00
d 6 2dfx x x x= −


∫∫
( )
1
4
0
1
6 2 10
24
x= −=
.
Câu 87: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn [1, 2] và thỏa mãn
( )
0fx>
khi
[ ]
1, 2x
∈
.
Biết
(
)
2
1
' 10
f x dx =
∫
và
(
)
( )
2
1
'
ln 2
fx
dx
fx
=
∫
. Tính
( )
2f
.
A.
( )
2 10f = −
. B.
( )
2 20f =
. C.
( )
2 10f =
. D.
( )
2 20f = −
.
Hươngd dẫn giải:
Ta có:
( )
( ) ( ) ( )
2
2
1
1
' 2 1 10f x dx f x f f= = −=
∫
(gt)
( )
( )
( ) ( ) ( )
( )
( )
2
2
1
1
'2
ln ln 2 ln 1 ln ln 2
1
fx f
dx f x f f
fx f
= = −==


∫
(gt)
https://toanmath.com/
Vậy ta có hệ:
( ) ( )
( )
(
)
( )
( )
2 1 10
2 20
2
2
1 10
1
ff
f
f
f
f
−=
=
⇔

=
=
Chọn B
Câu 88: Cho hàm số
( )
fx
có đạo hàm và liên tục trên đoạn
[ ]
4;8
và
( )
00f ≠
với
[ ]
4;8x∀∈
. Biết
rằng
( )
( )
2
8
4
4
1
fx
dx
fx
′


=


∫
và
( ) ( )
11
4 ,8
42
ff= =
. Tính
( )
6f
.
A.
5
8
. B.
2
3
. C.
3
8
. D.
1
3
.
Hươngd dẫn giải
Chọn D
+) Xét
( )
(
)
( )
( ) ( ) ( ) ( )
( )
88
22
44
8
1 11
24 2
4
84
f x df x
dx
fx fx fx f f

′
= =− =− − =−−=



∫∫
.
+) Gọi
k
là một hằng số thực, ta sẽ tìm
k
để
( )
( )
2
8
2
4
0
fx
k dx
fx

′
+=



∫
.
Ta có:
( )
( )
( )
( )
( )
( )
( )
2
2
8 8 88
2
22
4
22
4 4 44
2 14 4 2 1
fx
fx fx
k dx dx k dx k dx k k k
fx fx
fx
′


′′

+ = + + =++ = +





∫ ∫ ∫∫
.
Suy ra:
1
2
k = −
thì
( )
( )
( )
( )
( )
( )
2
8 66
2 22
4 44
1 11
0
2 22
fx fx fx
dx dx dx
fx fx fx

′ ′′
−=⇔ =⇔ =



∫ ∫∫
(
)
( )
( ) (
) ( )
( )
( )
6
2
4
6
1 11 1 1
1 1 14 1 6
4
46 6 3
df x
f
f x fx f f f
⇔ =⇔− =⇔−=⇔−=⇔=
∫
.
Chú ý:
(
)
0
b
a
f x dx =
∫
không được phép suy ra
( )
0fx=
, nhưng
( ) ( )
2
00
b
k
a
f x dx f x=⇔=
∫
.
Câu 89: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục trên đoạn
[
]
0;1
đồng thời thỏa mãn các
điều kiện
( )
01f
′
= −
và
( ) ( )
2
fx f x
′ ′′
=


. Đặt
( ) ( )
10Tf f= −
, hãy chọn khẳng định
đúng?
A.
21
T− ≤ <−
. B.
10T−≤ <
. C.
01T≤<
. D.
12T≤<
.
Hươngd dẫn giải
Chọn A
Ta có:
( )
( )
10Tf f
= −
( )
1
0
dfxx
′
=
∫
Lại có:
( )
( )
2
fx f x
′ ′′
=


( )
( )
2
1
fx
fx
′′
⇔− =−
′


( )
1
1
fx
′

⇔− =

′

( )
1
xc
fx
⇔− + =
′
( )
1
fx
xc
′
⇔=
−+
.
Mà
( )
01f
′
= −
nên
1c = −
.
Vậy
( )
1
0
dT fxx
′
=
∫
1
0
1
d
1
x
x
=
−−
∫
1
0
ln 1x=− −−
ln 2= −
.
https://toanmath.com/
Câu 90: Cho hàm số
(
)
y fx=
có đạo hàm cấp
2
liên tục trên
thoả
( )
(
)
(
)
22
0, ,
0 0 1,
,.
fx x
ff
xy y yy x
> ∀∈
′
= =
′ ′′
+ = ∀∈
.
Mệnh đề nào sau đây đúng?
A.
( )
1
ln 1 1
2
f<<
. B.
( )
1
0 ln 1
2
f<<
. C.
( )
3
ln 1 2
2
f<<
. D.
(
)
3
1 ln 1
2
f
<<
.
Hươngd dẫn giải
Chọn D
Ta có
22
xy y yy
′ ′′
+=
2
2
yy y
x
y
′′ ′
−
⇔=
y
x
y
′
′

⇔=


2
2
yx
C
y
′
⇔=+
hay
( )
(
)
2
2
fx
x
C
fx
′
= +
.
Lại có
( ) ( )
0 01ff
′
= =
1C⇒=
.
Ta có
( )
( )
2
1
2
fx
x
fx
′
= +
( )
(
)
11
2
00
d 1d
2
fx
x
xx
fx
′

⇔=+


∫∫
( )
( )
1
0
7
ln
6
fx⇔=
( )
7
ln 1
6
f⇔=
.
(
)
(
)
3
1 ln 1
2
f⇒< <
.
Câu 91: Cho
,
fg
là hai hàm liên tục trên
[ ]
1;3
thỏa mãn điều kiện
( ) ( )
3
1
3 d 10
fx gx x+=


∫
đồng
thời
( ) (
)
3
1
2 d6f x gx x
−=


∫
. Tính
(
)
( )
3
1
d
fx gx x+


∫
.
A.
9
. B.
6
. C.
7
. D.
8
.
Hươngd dẫn giải
Chọn B
Đặt
( )
3
1
da fx x=
∫
,
( )
3
1
db gx x=
∫
. Khi đó
( ) ( )
3
1
3 d 10fx gx x+=


∫
3 10ab
⇔+ =
,
( ) ( )
3
1
2 d6f x gx x−=


∫
26
ab⇔ −=
.
Do đó:
3 10
26
ab
ab
+=
−=
4
2
a
b
=
⇔
=
. Vậy
( )
( )
3
1
df x gx x
+


∫
6ab=+=
.
Câu 92: Cho hàm số
( )
y fx=
liên tục trên
[ ]
;ab
, nếu
( )
d5
d
a
fx x=
∫
và
(
)
d2
d
b
fx x=
∫
(với
adb<<
) thì
(
)
d
b
a
fx x
∫
bằng.
A.
3
. B.
7
. C.
5
2
. D.
10
.
Hươngd dẫn giải
Chọn A
(
)
( )
d5
d2
d
a
d
b
fx x
fx x
=
=
∫
∫
( )
( )
( ) (
)
5
2
Fd Fa
Fd Fb
−=
⇒
−=
( ) ( ) ( )
3d
b
a
Fb Fa f x x⇒−==
∫
.
Câu 93: Cho
( )
fx
và
( )
gx
là hai hàm số liên tục trên đoạn
[ ]
1; 3
, thỏa mãn:
https://toanmath.com/
( ) ( )
3
1
3 d 10fx gx x
+=


∫
và
(
) (
)
3
1
2 d6f x gx x
−=


∫
. Tính
( ) ( )
3
1
dI f x gx x= +


∫
A.
8I =
. B.
9I =
. C.
6I =
. D.
7I =
.
Hươngd dẫn giải
Chọn C
Ta có:
( ) ( )
( ) ( )
3
1
3
1
3 d 10
2 d6
fx gx x
fx gx x
+=


−=


∫
∫
(
)
( )
3
1
3
1
d4
d2
fx x
gx x
=
⇒
=
∫
∫
( ) ( )
3
1
d6I f x gx x⇒= + =


∫
.
Câu 94: Cho hàm số
( )
y fx=
có đạo hàm
( )
fx
′
liên tục trên đoạn
[ ]
0;5
và đồ thị hàm số
(
)
y fx
′
=
trên đoạn
[ ]
0;5
được cho như hình bên.
Tìm mệnh đề đúng
A.
( )
(
) (
)
053fff= <
. B.
( ) ( ) ( )
305fff<=
.
C.
( ) ( ) ( )
305fff<<
. D.
( ) ( ) (
)
350fff<<
.
Hươngd dẫn giải
Chọn C
Ta có
( ) ( ) ( )
5
3
d 5 30fxx f f
′
=−>
∫
, do đó
( ) (
)
53ff>
.
( ) ( ) ( )
3
0
d 3 00fxx f f
′
=−<
∫
, do đó
( ) ( )
30ff<
( ) ( )
( )
5
0
d 5 00fxx f f
′
=−<
∫
, do đó
( ) ( )
50ff<
Câu 95: Cho hàm số
( )
fx
liên tục và có đạo hàm tại mọi
(
)
0;x∈ +∞
đồng thời thỏa mãn điều kiện:
(
) ( )
(
)
sin ' cosfx x x f x x=++
và
( )
3
2
2
sin d 4.f x xx
π
π
= −
∫
Khi đó,
( )
f
π
nằm trong khoảng
nào?
A.
( )
6;7
. B.
( )
5;6
. C.
( )
12;13
. D.
( )
11;12
.
Hươngd dẫn giải
Chọn B
Ta có:
( ) ( )
( )
sin cosfx x x f x x
′
= ++
( ) ( )
22
sin cos
f x xf x
xx
x xx
′
−
⇒=+
( ) ( )
11
cos cos
fx fx
x xc
x x xx
′
′


⇒ = ⇒= +




5
−
3
5
1
x
O
y
https://toanmath.com/
(
)
cos
f x x cx
⇒=+
Khi đó:
( )
3
2
2
sin d 4f x xx
π
π
= −
∫
( )
3
2
2
cos sin d 4
x cx x x
π
π
⇔+ =−
∫
33
22
22
cos sin d sin d 4xxxcxxx
ππ
ππ
⇔ +=−
∫∫
(
)
0 24
c⇔+ − =−
2c⇔=
(
)
cos 2fx x x⇒=+
( ) ( )
2 1 5; 6f
ππ
⇒ = −∈
.
Câu 96: Cho hàm số
(
)
fx
xác định trên
0;
2
π



thỏa mãn
(
)
( )
2
2
0
2
2 2 sin d
42
f x fx x x
π
ππ
−

− −=




∫
. Tích phân
( )
2
0
dfx x
π
∫
bằng
A.
4
π
. B.
0
. C.
1
. D.
2
π
.
Hươngd dẫn giải
Chọn B
Ta có:
2
2
0
2sin d
4
xx
π
π

−


∫
2
0
1 cos 2 d
2
xx
π
π


=−−




∫
( )
2
0
1 sin 2 dxx
π
= −
∫
2
0
1
cos2
2
xx
π

= +


2
2
π
−
=
.
Do đó:
( ) ( )
2
2
0
2 2 sin d
4
f x fx x x
π
π


−−




∫
2
2
0
2sin d
4
xx
π
π

+−


∫
22
0
22
ππ
−−
=+=
( )
( )
2
22
0
2 2 sin 2sin d 0
44
f x fx x x x
π
ππ

 
⇔ − −+ − =
 

 

∫
( )
2
2
0
2 sin d 0
4
fx x x
π
π


⇔− − =




∫
Suy ra
( )
2 sin 0
4
fx x
π

− −=


, hay
( )
2 sin
4
fx x
π

= −


.
Bởi vậy:
( )
22
00
d 2 sin d
4
fx x x x
ππ
π

= −


∫∫
2
0
2 cos 0
4
x
π
π

=− −=


.
Câu 97: Cho hàm số
()y fx=
liên tục trên thỏa mãn
( ) ( ) ( )
2
21
3 2 2 1e 4
xx
fx f x x
−+
+ −= − +
. Tính
tích phân
( )
2
0
d
I fx x=
∫
ta được kết quả:
A.
e4I = +
. B.
8I =
. C.
2I =
. D.
e2I = +
.
Đề ban đầu bị sai vì khi thay
0x =
và
2x =
vào ta thấy mâu thuẫn nên tôi đã sửa lại đề
Hươngd dẫn giải
Chọn C
https://toanmath.com/
Theo giả thuyết ta có
(
)
( )
(
) (
)
2
22
21
00
3 2 d 2 1e 4 d *
xx
fx f x x x x
−+

+− = − +



∫∫
.
Ta tính
( )
( ) ( ) (
)
22 2
00 0
2d 2d2 d
f xx f x x fxx− =− − −=
∫∫ ∫
.
Vì vậy
( )
(
) ( )
22
00
3 2 d4 d
fx f x x fx x+− =


∫∫
.
Hơn nữa
(
)
( )
22 2
22
2
21 21 2 21
0
00
2 1 d e d 21e 0
xx xx xx
xe x x x
−+ −+ −+
− = − += =
∫∫
và
2
0
4d 8x =
∫
.
Câu 98: Suy ra
( )
( )
22
00
4 d8 d2fx x fx x
=⇔=
∫∫
. Cho hàm số
( )
y fx=
liên tục trên
{ }
\ 0; 1−
thỏa
mãn điều kiện
( )
1 2ln 2
f = −
và
( ) ( ) ( )
2
1.xx f x f x x x
′
+ +=+
. Giá trị
( )
2 ln3f ab= +
,
với
,ab∈
. Tính
22
ab+
.
A.
25
4
. B.
9
2
. C.
5
2
. D.
13
4
.
Hươngd dẫn giải
Chọn B
Từ giả thiết, ta có
( ) ( ) ( )
2
1.xx f x f x x x
′
+ +=+
⇔
( )
( )
( )
2
1
.
11
1
xx
f x fx
xx
x
′
+=
++
+
( )
.
11
xx
fx
xx
′

⇔=

++

, với
{ }
\ 0; 1
x∀∈ −
.
Suy ra
( )
.
1
x
fx
x +
d
1
x
x
x
=
+
∫
hay
( )
.
1
x
fx
x +
ln 1
xx C=− ++
.
Mặt khác, ta có
( )
1 2ln 2f = −
nên
1C = −
. Do đó
( )
.
1
x
fx
x +
ln 1 1
xx=− +−
.
Với
2x =
thì
( )
2
. 2 1 ln3
3
f = −
⇔
(
)
33
2 ln 3
22
f = −
. Suy ra
3
2
a =
và
3
2
b = −
.
Vậy
22
9
2
ab
+=
.
Câu 99: Cho hàm số
( )
y fx=
có đạo hàm trên
và
(
)
4
2
2
2fx x x
x
′
≥+−
0x∀>
và
( )
11f = −
.
Khẳng định nào sau đây đúng?
A. Phương trình
( )
0fx=
có
1
nghiệm trên
( )
0;1
.
B. Phương trình
( )
0fx=
có đúng
3
nghiệm trên
( )
0;+∞
.
C. Phương trình
( )
0fx
=
có
1
nghiệm trên
( )
1; 2
.
C. Phương trình
( )
0fx=
có
1
nghiệm trên
( )
2;5
.
Hươngd dẫn giải
Chọn C
( )
4
2
2
2fx x x
x
′
≥+−
63
2
22xx
x
−+
=
( )
2
3
2
11
0
x
x
−+
= >
,
0x∀>
.
( )
y fx⇒=
đồng biến trên
( )
0;+∞
.
( )
0fx⇒ =
có nhiều nhất
1
nghiệm trên khoảng
( )
0;+∞
( )
1
.
Mặt khác ta có:
https://toanmath.com/
( )
4
2
2
20fx x x
x
′
≥+−>
,
0x
∀>
( )
22
4
2
11
2 21
d 2d
5
fxx x xx
x

′
⇒ ≥ +− =


∫∫
(
)
(
)
21
21
5
ff
⇒ −≥
( )
17
2
5
f⇒≥
.
Kết hợp giả thiết ta có
(
)
y fx=
liên tục trên
[ ]
1; 2
và
( ) ( )
2. 1 0ff<
( )
2
.
Từ
( )
1
và
( )
2
suy ra phương trình
( )
0fx=
có đúng
1
nghiệm trên khoảng
(
)
1; 2 .
Câu 100: Cho hàm số
(
)
fx
có đạo hàm
( )
fx
′
liên tục trên
và thỏa mãn
( )
[ ]
1;1fx
′
∈−
với
(
)
0;2x∀∈
. Biết
(
)
( )
0 21ff= =
. Đặt
(
)
2
0
d
I fx x=
∫
, phát biểu nào dưới đây đúng?
A.
(
]
;0
I ∈ −∞
. B.
(
]
0;1I ∈
. C.
[
)
1;I ∈ +∞
. D.
( )
0;1
I ∈
.
Hươngd dẫn giải
Chọn C
Ta có
( )
( ) ( )
212
0 01
ddd
I fx x fx x fx x= = +
∫∫∫
.
( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
1 111
1
0
0 000
1
d 1 1 d1 1 d1 1 d
2
fxx x fx x fxx xfxx xx
′′
= − − − =+ − ≥− − =
∫ ∫∫∫
( )
1
.
(
) ( ) ( )
( ) ( ) (
) ( )
2 22
2
1
1 11
d 1 1d1 1d
fxx x fx x fxx x fxx
′′
=− −− =−−
∫ ∫∫
(
)
2
1
1
11d
2
xx≥− − =
∫
( )
2
.
Từ
( )
1
và
(
)
2
suy ra
11
1
22
I ≥+=
.
Câu 101: Cho hàm số
( )
y fx=
liên tục trên
[ ]
0; 1
thỏa mãn
( )
1
0
d0xf x x =
∫
và
(
)
[0; 1]
max 1.fx=
Tích
phân
( )
1
0
ed
x
I fx x=
∫
thuộc khoảng nào trong các khoảng sau đây?
A.
5
;.
4

−∞ −


B.
3
;e 1 .
2

−


C.
53
;.
42

−


D.
( )
e 1; .− +∞
Hươngd dẫn giải
Chọn C
Với mọi
[ ]
0;1a∈
, ta có
( )
1
0
0dxf x x=
∫
(
)
1
0
da xf x x=
∫
(
)
1
0
daxf x x
=
∫
Kí hiệu
( )
( )
1
0
ed
x
I a ax x= −
∫
.
Khi đó, với mọi
[ ]
0;1a∈
ta có
( )
1
0
ed
x
fx x
∫
( ) ( )
11
00
ed d
x
fx x axfx x= −
∫∫
( )
( )
1
0
ed
x
ax f x x= −
∫
( )
1
0
e.d
x
ax f x x≤−
∫
[ ]
( )
1
0;1
0
e .max d
x
x
ax f x x
∈
≤−
∫
( )
1
0
ed
x
ax x I a=−=
∫
.
Suy ra
( )
[
]
( )
1
0;1
0
e d min
x
a
f x x Ia
∈
≤
∫
Mặt khác
Với mọi
[ ]
0;1a∈
ta có
( )
( )
11
00
ede d
xx
I a ax x ax x=−=−
∫∫
1
2
0
e
2
x
a
x

= −


e1
2
a
=−−
https://toanmath.com/
[
]
( )
0;1
3
min e
2
a
Ia
∈
= −
(
)
1
0
3
e d e 1, 22
2
x
fx x⇒ ≤− ≈
∫
.
Vậy
53
;
42
I

∈−


.
Câu 102: Cho hàm số
( )
fx
có đạo hàm dương, liên tục trên đoạn
[ ]
0;1
thỏa mãn
(
)
01
f
=
và
( )
( )
( )
( )
11
2
00
1
3 d2 d
9
f x fx x f xfx x

′′
+≤




∫∫
. Tính tích phân
( )
1
3
0
d
fx x


∫
:
A.
3
2
. B.
5
4
. C.
5
6
. D.
7
6
.
Hươngd dẫn giải
Chọn D
Từ giả thiết suy ra:
( ) ( )
( )
( ) ( )
1
2
0
3 2.3 1 d 0f xf x f xf x x

′′
− +≤


∫
( ) ( )
1
2
0
3 1d 0f xf x x

′
⇔ −≤

∫
.
Suy ra
( ) ( )
3 10f xf x
′
−=
( )
( )
1
3
f xf x
′
⇔=
( ) ( )
2
1
.
9
fxf x
′
⇔=
.
Vì
( ) ( ) ( )
32
3.f x f xf x
′
′

=

nên suy ra
( )
3
1
3
fx
′

=

( )
3
1
3
f x xC⇒=+
.
Vì
(
)
01f =
nên
( )
3
01
f =
1C
⇒=
.
Vậy
( )
3
1
1
3
fx x⇒=+
.
Suy ra
( )
1
3
0
dfx x


∫
1
0
17
1d
36
xx

= +=


∫
.
Câu 103: Cho hai hàm số
( )
fx
và
( )
gx
có đạo hàm trên đoạn
[ ]
1; 4
và thỏa mãn hệ thức
( ) ( )
( ) ( ) ( ) ( )
1 14
.; .
fg
gxxfxfxxgx
+=
′′
=−=−
. Tính
( ) ( )
4
1
dI f x gx x= +


∫
.
A.
8ln 2
. B.
3ln 2
. C.
6ln 2
. D.
4ln 2
.
Hươngd dẫn giải
Chọn A
Cách 1: Ta có
( ) (
) ( )
( )
fxgx xfxgx
′′
+=− +


( ) ( )
( ) ( )
1
fx gx
fx gx x
+
⇔=−
′′
+
( ) ( )
( ) ( )
1
dd
fx gx
xx
fx gx x
+
⇔=−
′′
+
∫∫
( ) ( )
ln f x gx⇒+
ln xC
=−+
Theo giả thiết ta có
( ) ( )
ln 1 ln 1 1C fg−= +
ln 4C⇒=
.
Suy ra
(
) ( )
( ) ( )
4
4
fx gx
x
fx gx
x
+=
+=−
, vì
( ) ( )
1 14
fg+=
nên
( ) ( )
4
fx gx
x
+=
( ) (
)
4
1
d 8ln 2I fx gx x⇒= + =


∫
.
Cách 2: Ta có
( ) ( ) ( ) ( )
fxgx xfxgx
′′
+=− +


( ) ( )
( ) ( )
dd
fxgxx xfxgxx
′′
⇒+ =− +


∫∫
.
https://toanmath.com/
(
) (
)
( )
(
) (
) (
)
ddfx gx x x fx gx fx gx x
⇒ + =− ++ +


∫∫
.
( ) ( ) (
)
( )
C
xf x gx C f x gx
x
⇒− + = ⇒ + =−


. Vì
( )
( )
11 4
f g CC
+ =−⇒ =−
Do đó
( ) ( )
4
fx gx
x
+=
. Vậy
(
) (
)
4
1
d 8ln 2I fx gx x
=+=


∫
.
https://toanmath.com/
DẠNG 3: PHƯƠNG PHÁP ĐỔI BIẾN
BÀI TẬP
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 1
Câu 104: Cho
(
)
4
0
d 16fx x=
∫
. Tính
( )
2
0
2d
f xx
∫
A.
16
. B.
4
. C.
32
. D.
8
.
Câu 105: Nếu
( )
6
0
d 12fx x=
∫
thì
( )
2
0
3df xx
∫
bằng
A.
6
. B.
36
. C.
2
. D.
4
.
Câu 106: Cho
( )
2
2
1
1d 2f x xx+=
∫
. Khi đó
( )
5
2
dI fxx=
∫
bằng:
A.
2
. B.
1
. C.
1−
. D.
4
.
Câu 107: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
1
5
d9fx x
−
=
∫
. Tính tích phân
(
)
2
0
1 3 9dfx x−+


∫
.
A.
27
. B.
21
. C.
15
. D.
75
.
Câu 108: Biết
(
)
fx
làm hàm liên tục trên
và
( )
9
0
d9fx x=
∫
. Khi đó giá trị của
( )
4
1
3 3dfx x−
∫
là
A.
27
. B.
3
. C.
0
. D.
24
.
Câu 109: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
d 10fx x
=
∫
. Tính
2
0
d
2
x
fx



∫
.
A.
2
0
5
d
22
x
fx

=


∫
. B.
2
0
d 20
2
x
fx

=


∫
. C.
2
0
d 10
2
x
fx

=


∫
. D.
2
0
d5
2
x
fx

=


∫
.
Câu 110: Cho
( )
5
1
d4
fx x
−
=
∫
. Tính
(
)
2
1
2 1d
I fx x
−
= +
∫
.
A.
2I =
. B.
5
2
I =
. C.
4I =
. D.
3
2
I =
.
Câu 111: Giả sử hàm số
( )
y fx=
liên tục trên
và
( )
5
3
dfx x a=
∫
,
( )
a∈
. Tích phân
( )
2
1
2 1dI fx x= +
∫
có giá trị là
A.
1
1
2
Ia= +
. B.
21Ia= +
. C.
2Ia=
. D.
1
2
Ia=
.
Câu 112: Cho
( )
2
2
1
1d 2f x xx+=
∫
. Khi đó
( )
5
2
dI fx x=
∫
bằng
A.
2
. B.
1
. C.
1−
. D.
4
.
Câu 113: Cho hàm số
( )
fx
liên tục trên
[
)
1;
+∞
và
( )
3
0
1d 8fx x+=
∫
. Tích phân
( )
2
1
dI xf x x=
∫
bằng:
A.
16I =
. B.
2I =
. C.
8I =
. D.
4I =
Câu 114: Biết
( )
11
1
d 18fx x
−
=
∫
. Tính
( )
( )
2
2
0
2 3 1dI x fx x=+−
∫
.
https://toanmath.com/
A.
5I
=
. B.
7I =
. C.
8I =
D.
10
I
=
.
Câu 115: Cho hàm số
( )
y fx=
liên tục trên
và
(
)
1
0
2d 8
f xx
=
∫
. Tính
( )
2
2
0
dI xf x x=
∫
A.
4
. B.
16
. C.
8
. D.
32
.
Câu 116: Cho hàm số
( )
fx
liên tục trên
và có
(
)
( )
13
00
d 2; d 6fx x fx x
= =
∫∫
. Tính
( )
1
1
2 1dI fx x
−
= −
∫
.
A.
2
3
I
=
. B.
4I =
. C.
3
2
I =
. D.
6I =
.
Câu 117: Cho hàm số
( )
y fx=
liên tục trên
[ ]
0;4
và
( )
2
0
d1
fx x
=
∫
;
;
( )
4
0
d3fx x=
∫
. Tính
( )
1
1
3 1dfx x
−
−
∫
.
A.
4
. B.
2
. C.
4
3
. D.
1
.
Câu 118: Cho
( )
fx
là hàm số liên tục trên
và
( )
1
0
d4fx x=
∫
,
( )
3
0
d6fx x=
∫
. Tính
( )
1
1
2 1dI fx x
−
= +
∫
.
A.
3
I =
. B.
5I =
. C.
6I =
. D.
4I =
.
Câu 119: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
2d 2f xx=
∫
và
( )
2
0
6 d 14f xx=
∫
. Tính
( )
2
2
5 2dfx x
−
+
∫
.
A.
30
. B.
32
. C.
34
. D.
36
.
Câu 120: Cho tích phân
( )
2
0
cos . sin 8I x f x dx= =
∫
π
. Tính tích phân
( )
2
0
sin . cosK x f x dx
=
∫
π
.
A.
8K = −
. B.
4
K =
. C.
8K
=
. D.
16
K =
.
Câu 121: Cho hàm số
( )
y fx=
liên tục trên R, thỏa mãn
(
)
1
0
1
f x dx =
∫
. Tính
( )
( )
4
2
0
tan 1 . tanI f x dx= +
∫
π
.
A.
1I =
. B.
1I = −
. C.
4
I =
π
. D.
4
I = −
π
.
Câu 122: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
23f x fx=
,
x∀∈
. Biết rằng
( )
1
0
d1fx x=
∫
. Giá trị của tích phân
( )
2
1
dI fx x=
∫
bằng bao nhiêu?
A.
5I =
. B.
3I =
. C.
8I =
. D.
2I =
.
https://toanmath.com/
Câu 123: Cho hàm số
( )
y fx=
liên tục và có đạo hàm trên
thỏa mãn
( )
22
f = −
;
( )
2
0
d1fxx=
∫
. Tính
tích phân
(
)
4
0
dI f xx
′
=
∫
.
A.
10
I = −
. B.
5I = −
. C.
0I =
. D.
18I = −
.
Câu 124: Cho
( )
2
1
d2fx x=
∫
. Tính
( )
4
1
d
fx
Ix
x
=
∫
bằng
A.
1
I
=
. B.
2I =
. C.
4I =
. D.
1
2
I =
.
Câu 125: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
16
1
d6
fx
x
x
=
∫
và
( )
2
0
sin cos d 3f x xx
π
=
∫
. Tính
tích phân
( )
4
0
dI fx x=
∫
.
A.
2
I = −
. B.
6I =
. C.
9I =
. D.
2I =
.
Câu 126: Cho
( )
fx
liên tục trên
thỏa
( )
9
1
d4
fx
x
x
=
∫
và
( )
2
0
sin cos d 2f x xx
π
=
∫
. Tính
( )
3
0
dI fx x
=
∫
.
A.
10I
=
. B.
6I =
. C.
4I =
. D.
2I =
.
Câu 127: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
1; 4
và thỏa mãn
( )
( )
21
ln
fx
x
fx
x
x
−
= +
. Tính tích
phân
( )
4
3
dI fx x=
∫
.
A.
2
3 2ln 2I
= +
. B.
2
2ln 2I =
. C.
2
ln 2
I =
. D.
2ln 2I =
.
Câu 128: Cho hàm số
( )
fx
liên tục trên
[
)
4;− +∞
và
( )
5
0
4d 8fx x+=
∫
. Tính
( )
2
3
.d
I xf x x
=
∫
.
A.
8I =
. B.
4I =
. C.
16I = −
. D.
4
I = −
.
Câu 129: Cho và . Tính .
A. . B. . C. . D. .
Câu 130: Cho hàm
( )
fx
liên tục trên
thỏa mãn
( )
4
0
tan d 3f xx
π
=
∫
và
( )
2
1
2
0
d1
1
xf x
x
x
=
+
∫
. Tính
( )
1
0
dfx x
∫
.
A.
4
. B.
2
. C.
5
. D.
1
.
Câu 131: Cho hàm số
( )
fx
liên tục trên R và
(
)
( )
2
1
4
2
00
tand4; d2
1
xf x
f xx x
x
π
= =
+
∫∫
. Tính
( )
1
0
dI fx x=
∫
.
A.
6I =
. B.
2I =
. C.
3I =
. D.
1I =
.
( )
1
0
2 1 d 12fx x+=
∫
( )
2
2
0
sin sin 2 d 3f x xx
π
=
∫
( )
3
0
dfx x
∫
26
22
27
15
https://toanmath.com/
Câu 132: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
2018
0
d2fx x=
∫
. Khi đó tích phân
(
)
(
)
2018
e1
2
2
0
ln 1 d
1
x
fx x
x
−
+
+
∫
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 133: Tìm tất cả các giá trị dương của
m
để
( )
3
0
10
3
9
m
x x dx f

′′
−=−


∫
, với
( )
15
lnfx x=
.
A.
20m =
. B.
4m =
. C.
5m =
. D.
3m =
.
Câu 134: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
4f x fx−=
. Biết
(
)
3
1
d5
xf x x =
∫
.
Tính
( )
3
1
d
I fx x
=
∫
.
A.
5
2
I =
. B.
7
2
I =
. C.
9
2
I =
. D.
11
2
I =
.
Câu 135: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
1; 3
thỏa mãn
( ) ( )
[ ]
4 , 1; 3f x fx x− = ∀∈
và
(
)
3
1
d2
xf x x
= −
∫
. Giá trị
( )
3
1
dfx x
∫
bằng
A.
2
. B.
1−
. C.
2
−
. D.
1
.
Câu 136: Cho hàm số
f
liên tục trên đoạn
[ ]
6;5−
, có đồ thị gồm hai đoạn thẳng và nửa đường tròn
như hình vẽ. Tính giá trị
(
)
5
6
2d
I fx x
−
= +


∫
.
A.
2 35I
π
= +
. B.
2 34I
π
= +
. C.
2 33I
π
= +
. D.
2 32I
π
= +
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 2
Cho hàm số
( )
fx
thỏa mãn :
( ) ( ) (
)
( )
. .. .A f x Bu f u C f a b x g x
′
+ + +− =
+) Với
(
)
( )
ua a
ub b
=
=
thì
( ) ( )
1
bb
aa
f x dx g x dx
ABC
=
++
∫∫
.
+) Với
( )
( )
ua b
ub a
=
=
thì
( ) ( )
1
bb
aa
f x dx g x dx
ABC
=
−+
∫∫
.
Trong đề bài thường sẽ bị khuyết một trong các hệ số
,,
ABC
.
Nếu
( )
fx
liên tục trên
[ ]
;
ab
thì
( )
( )
bb
aa
f a b x dx f x dx
+− =
∫∫
.
Câu 137: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
thỏa mãn
( )
( )
23
6
6
31
f x xf x
x
= −
+
. Tính
( )
1
0
dfx x
∫
A.
2
. B.
4
. C.
1−
. D.
6
.
O
x
y
5
4−
6−
1−
3
https://toanmath.com/
Câu 138: Xét hàm số
(
)
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
( )
( )
22
4 3 11xf x f x x+ −= −
.
Tích phân
(
)
1
0
d
I fx x
=
∫
bằng
A.
4
I
π
=
. B.
6
I
π
=
. C.
20
I
π
=
. D.
16
I
π
=
Câu 139: Cho hàm số
()fx
liên tục trên
[ ]
0;2
và thỏa mãn điều kiện
( ) ( )
22fx f x x+ −=
. Tính giá
trị của tích phân
(
)
2
0
I f x dx
=
∫
.
A.
4I = −
. B.
1
2
I =
. C.
4
3
I =
. D.
2
I
=
.
Câu 140: Xét hàm số
(
)
fx
liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( ) ( )
2 31 1fx f x x+ −=−
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
2
3
. B.
1
6
. C.
2
15
. D.
3
5
.
Câu 141: Xét hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
và thỏa mãn điều kiện
( ) (
)
2 31 1fx f x x x− −= −
. Tính tích phân
( )
1
0
dI fx x
=
∫
.
A.
1
25
I =
. B.
4
15
I = −
. C.
1
15
I = −
. D.
4
75
I
=
.
Câu 142: Xét hàm số
( )
fx
liên tục trên
[
]
1; 2−
và thỏa mãn
( )
( )
( )
23
2 231 4
f x xf x f x x+ −+ −=
.
Tính giá trị của tích phân
( )
2
1
I f x dx
−
=
∫
.
A.
5I =
. B.
5
2
I =
. C.
3
I =
. D.
15I =
.
Câu 143: Hàm số
( )
fx
liên tục trên
[ ]
1; 2−
và thỏa mãn điều kiện
( )
( )
2
2 3.
f x x xf x= ++ −
Tính
giá trị của
( )
2
1
dI fxx
−
=
∫
A.
14
3
I =
. B.
28
3
I =
. C.
4
3
I =
. D.
2I =
.
Câu 144: Xét hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn
( )
( )
( )
2
1
1 31
1
f x xf x f x
x
+ − + −=
+
. Tính
giá trị của tích phân
(
)
1
0
d
I fx x=
∫
.
A.
9
ln 2
2
I =
. B.
2
ln 2
9
I =
. C.
4
3
I =
. D.
3
2
I
=
.
Câu 145: Cho hàm số
( )
y fx=
và thỏa mãn
( )
( )
3
34
2
80
1
x
f x xf x
x
− +=
+
. Tích phân
(
)
1
0
2ab
I f x dx
c
−
= =
∫
với
,,abc∈
và
;
ab
cc
tối giản. Tính
abc++
A.
6
. B.
4−
. C.
4
. D.
10−
.
https://toanmath.com/
Câu 146: Cho hàm số
( )
fx
liên tục trên đoạn
[
]
ln 2;ln 2
−
và thõa mãn
( )
(
)
1
1
x
fx f x
e
+ −=
+
. Biết
(
)
ln 2
ln 2
d ln 2 ln3fx x a b
−
= +
∫
, với
,ab
∈
. Tính giá trị của
Pab= +
.
A.
1
2
P =
. B.
2P = −
. C.
1P = −
. D.
2P =
.
Câu 147: Biết hàm số
2
y fx

= +


π
là hàm số chẵn trên đoạn
;
22

−


ππ
và
( )
sin cos
2
fx fx x x

+ += +


π
. Tính
(
)
2
0
I f x dx
=
∫
π
.
A.
0I =
. B.
1I =
. C.
1
2
I =
. D.
1I = −
.
Câu 148: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
,
( )
00f =
và
( )
sin .cos
2
fx f x x x
π

+ −=


với
x∀∈
. Giá trị của tích phân
( )
2
0
xf x dx
π
′
∫
bằng
A.
4
π
−
. B.
1
4
. C.
4
π
. D.
1
4
−
.
Câu 149: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
(
)
2
2
1 2x 1 2x ,
1
x
ff x
x
+ + − = ∀∈
+
. tính tích
phân
( )
3
1
I f x dx
−
=
∫
.
A.
2
2
I
π
= −
. B.
1
4
I
π
= −
. C.
1
28
I
π
= −
. D.
4
I
π
=
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 3
Cách giải: Lần lượt đặt
(
)
t ux=
và
( )
t vx=
để giải hệ phương trình hai ẩn (trong đó có ẩn
( )
fx
) để
suy ra hàm số
( )
fx
(nếu
( )
ux x=
thì chỉ cần đặt một lần
( )
t vx=
).
Các kết quả đặc biệt:
Cho
( ) ( )
( )
..A f ax b B f ax c g x++ −+=
với
22
AB≠
) khi đó
(
)
22
..
xb xc
Ag Bg
aa
fx
AB
−−

−

−

=
−
(*)
+)Hệ quả 1 của (*):
( )
( ) (
) (
)
( ) ( )
22
..
..
Ag x Bg x
Afx Bf x gx fx
AB
−−
+ −= ⇒ =
−
+)Hệ quả 2 của (*):
( ) ( ) ( ) ( )
( )
..
gx
Afx Bf x gx fx
AB
+ −= ⇒ =
+
với
(
)
gx
là hàm số chẵn.
Câu 150: Cho hàm số
( )
y fx=
liên tục trên
và
( )
1
23fx f x
x

+=


. Tính
( )
2
1
2
fx
I dx
x
=
∫
.
A.
3
2
I
=
. B.
1
I =
. C.
1
2
I =
. D.
1I = −
.
Câu 151: Cho hàm số
(
)
y fx=
liên tục trên
{ }
\0
và thỏa mãn
( )
2 15
23 3
2
x
fx f
x

+=−


,
( )
9
3
dfx x k=
∫
. Tính
3
2
1
2
1
dIf x
x

=


∫
theo
k
.
A.
45
9
k
I
+
= −
. B.
45
9
k
I
−
=
. C.
45
9
k
I
+
=
. D.
45 2
9
k
I
−
=
.
https://toanmath.com/
Câu 152: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
2018 2 sinf x fx x x−+ =
. Tính giá
trị của
( )
2
2
dI fx x
π
π
−
=
∫
.
A.
2
2019
I =
. B.
2
1009
I =
. C.
4
2019
I =
. D.
1
1009
I =
.
Câu 153: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) (
)
2018
x
f x fx e−+ =
. Tính giá trị của
(
)
1
1
I f x dx
−
=
∫
A.
2
1
2019e
e
I
−
=
. B.
2
1
2018e
e
I
−
=
. C.
0I =
. D.
2
1e
I
e
−
=
.
Câu 154: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
, thỏa mãn
( ) ( )
2
2 2 1 12fx f x x+ −=
.
Phương trình tiếp tuyến của đồ thị hàm số
( )
y fx=
tại điểm có hoành độ bằng
1
là
A.
22
yx= +
. B.
46
yx= −
. C.
26
yx= −
. D.
42yx= −
.
Câu 155: Cho
( )
fx
là hàm số chẵn, liên tục trên
thỏa mãn
( )
1
0
2018=
∫
f x dx
và
(
)
gx
là hàm số
liên tục trên
thỏa mãn
( )
( )
1+ −=gx g x
,
∀∈x
. Tính tích phân
( )
( )
1
1−
=
∫
I f x g x dx
.
A.
2018
=I
. B.
1009
2
=I
. C.
4036
=I
. D.
1008=I
.
Câu 156: Cho số dương
a
và hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
fx f x a+ −=
,
x∀∈
. Giá
trị của biểu thức
( )
d
a
a
fx x
−
∫
bằng
A.
2
2a
. B.
a
. C.
2
a
. D.
2a
.
Câu 157: Cho hàm số
(
)
fx
liên tục trên
thỏa điều kiện
( ) ( )
2sinfx f x x+ −=
. Tính
( )
2
2
dfx x
π
π
−
∫
A.
1
−
. B.
0
. C.
1
. D.
2
.
Câu 158: Cho
()fx
là một hàm số liên tục trên thỏa mãn
(
) ( )
2 2cos2fx f x x+ −= −
. Tính tích
phân
( )
3
2
3
2
dI fx x
π
π
−
=
∫
.
A.
3I =
. B.
4I =
. C.
6I =
. D.
8I =
.
Câu 159: Cho hàm số
( )
y fx=
liên tục trên R và thỏa mãn
(
) ( )
2 2cos2fx f x x
+ −= +
. Tính
( )
2
2
I f x dx
−
=
∫
π
π
.
A.
1I = −
. B.
1I =
. C.
2
I = −
. D.
2I =
.
https://toanmath.com/
Câu 160: Cho hàm số liên tục trên và . Tính
A. . B. . C. . D. .
Câu 161: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
ln 2;ln 2−
và thỏa mãn
(
)
(
)
1
1
x
fx f x
e
+ −=
+
.
Biết
(
)
ln 2
ln 2
d ln 2 ln3fx x a b
−
= +
∫
( )
;
ab∈
. Tính
Pab= +
.
A.
1
2
P =
. B.
2P = −
. C.
1P = −
. D.
2
P
=
.
Câu 162: Xét hàm số
( )
fx
liên tục trên
[
]
0;1
và thỏa mãn điều kiện
(
) (
)
2 31 1+ −= −fx f x x x
. Tính
tích phân
( )
1
0
=
∫
I f x dx
.
A.
4
15
= −I
. B.
1
15
=I
. C.
4
75
=I
. D.
1
25
=
I
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 4
Câu 163: Cho
( )
fx
và
( )
gx
là hai hàm số liên tục trên
[ ]
1,1−
và
( )
fx
là hàm số chẵn,
( )
gx
là hàm
số lẻ. Biết
( )
1
0
5
f x dx =
∫
và
( )
1
0
7
g x dx =
∫
. Mệnh đề nào dưới đây sai?
A.
(
)
1
1
10
f x dx
−
=
∫
. B.
(
)
1
1
14g x dx
−
=
∫
.
C.
( ) ( )
1
1
10f x g x dx
−
+=


∫
. D.
( ) ( )
1
1
10f x g x dx
−
−=


∫
.
Câu 164: Nếu hàm
( )
fx
CHẴN thì
( ) ( )
0
2
aa
a
f x dx f x dx
−
=
∫∫
2. Nếu hàm
( )
fx
LẺ thì
( )
0
a
a
f x dx
−
=
∫
Nếu chứng minh thì như sau:
Đặt
( ) (
) ( )
1
2
1 01
1 10
A
A
A f x dx f x dx f x dx
−−
= = +
∫∫∫


( )
0
1
1
A f x dx
−
=
∫
. Đặt
tx= −
dt dx⇒=−
Đổi cận:
( )
( ) ( ) ( )
0 11
1
1 00
.A f t dt f t dt f x dx⇒= − −= − = −
∫ ∫∫
(Do tích phân xác định không phụ thuộc
vào biến số tích phân)
( )
1
0
f x dx=
∫
(Do
( )
fx
là hàm chẵn
( ) ( )
f x fx⇒ −=
)
Vậy
( ) ( ) ( )
1 11
100
10A f x dx f x dx f x dx
−
= =+=
∫∫∫
(1)
Đặt
( ) ( ) ( )
1
2
1 01
1 10
B
B
B g x dx g x dx g x dx
−−
= = +
∫∫∫


( )
fx
( ) ( )
2
3 2 tanf x fx x−− =
( )
π
4
π
4
dfx x
−
∫
π
1
2
−
π
1
2
−
π
1
4
+
π
2
2
−
https://toanmath.com/
( )
0
1
1
B g x dx
−
=
∫
. Đặt
tx= −
dt dx⇒=−
Đổi cận:
( ) (
) (
)
( )
0 11
1
1 00
.
B g t dt g t dt g x dx⇒= −−= − = −
∫ ∫∫
(Do tích phân xác định không phụ thuộc
vào biến số tích phân)
( )
1
0
g x dx
= −
∫
(Do
( )
fx
là hàm chẵn
( )
( )
g x gx⇒ −=−
)
Vậy
(
)
( )
( )
1 11
1 00
0B g x dx g x dx g x dx
−
= =−+ =
∫ ∫∫
(2)
Từ (1) và (2)
Chọn B
Câu 165: Cho hàm số
( )
y fx=
là hàm lẻ và liên tục trên
[ ]
4;4−
biết
( )
0
2
d2f xx
−
−=
∫
và
( )
2
1
2d 4
f xx−=
∫
. Tính
( )
4
0
dI fx x=
∫
.
A.
10I = −
. B.
6I = −
. C.
6
I =
. D.
10I =
.
Câu 166: Cho hàm số chẵn
(
)
y fx=
liên tục trên
và
( )
1
1
2
d8
12
x
fx
x
−
=
+
∫
. Tính
( )
2
0
dfx x
∫
.
A.
2
. B.
4
. C.
8
. D.
16
.
Câu 167: Cho
( )
fx
là hàm số chẵn liên tục trong đoạn
[ ]
1; 1−
và
(
)
1
1
d2fx x
−
=
∫
. Kết quả
( )
1
1
d
1e
x
fx
Ix
−
=
+
∫
bằng
A.
1I =
. B.
3
I =
. C.
2
I
=
. D.
4I =
.
Câu 168: Cho
( )
y fx=
là hàm số chẵn và liên tục trên
.
Biết
( ) ( )
12
01
1
d d1
2
fx x fx x= =
∫∫
. Giá trị của
( )
2
2
d
31
x
fx
x
−
+
∫
bằng
A.
1
. B.
6
. C.
4
. D.
3
.
Câu 169: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
3
,fxfxxx+ = ∀∈
. Tính
( )
2
0
I f x dx=
∫
A.
2I =
. B.
3
2
I =
. C.
1
2
I =
. D.
5
4
I =
.
Câu 170: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( ) ( )
32
236f x f x fx x− +=
,
x
∀∈
. Tính tích
phân
( )
5
0
d
I fx x=
∫
.
A.
5
4
I =
. B.
5
2
I =
. C.
5
12
I
=
. D.
5
3
I =
.
Câu 171: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
3
21x f x fx++ =
,
x∀∈
. Tính
( )
1
2
dI fx x
−
=
∫
.
A.
7
4
I =
. B.
7
2
I =
. C.
7
3
I =
. D.
5
4
I =
.
https://toanmath.com/
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5
Bài toán: “ Cho
( ) ( )
2
.fxfab x k+− =
, khi đó
( )
d
2
b
a
x ba
I
k fx k
−
= =
+
∫
Chứng minh:
Đặt
t abx=+−
( )
(
)
2
dt dx
k
fx
ft
= −
⇒
=
và
xa tb= ⇒−
;
xb ta=⇒=
.
Khi đó
(
)
(
)
( )
(
)
2
fd
d d1
bb b
aa a
xx
xx
I
k
k fx k k fx
k
ft
= = =
++
+
∫∫ ∫
.
( )
( )
( )
fd
d1
2
bb
aa
xx
x
I
k fx k k fx
=+=
++
∫∫
( )
11
d
b
a
x ba
kk
= −
∫
2
ba
I
k
−
⇒=
.
Câu 172: Cho hàm số
( )
fx
liên tục và nhận giá trị dương trên
[ ]
0;1
. Biết
( )
( )
.1 1fxf x−=
với
[ ]
0;1x∀∈
. Tính giá trí
(
)
1
0
d
1
x
I
fx
=
+
∫
A.
3
2
. B.
1
2
. C.
1
. D.
2
.
Câu 173: Cho hàm số
( )
fx
liên tục trên
, ta có
( )
0fx>
và
( ) ( )
0 . 2018 1ff x−=
. Giá trị của tích
phân
( )
2018
0
d
1
x
I
fx
=
+
∫
A.
2018I =
. B.
0I
=
C.
1009I
=
D.
4016
Câu 174: Cho hàm số
( )
y fx=
có đạo hàm, liên tục trên
và
(
)
0
fx>
khi
[ ]
0;5x∈
.
Biết
( ) ( )
.5 1fxf x−=
,
tính tích phân
( )
5
0
d
1
x
I
fx+
=
∫
.
A.
5
4
I =
. B.
5
3
I =
. C.
5
2
I =
. D.
10I =
.
Câu 175: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
4f x fx−=
. Biết
( )
3
1
d5xf x x =
∫
.
Tính tích phân
( )
3
1
dfx x
∫
.
A.
5
2
. B.
7
2
. C.
9
2
. D.
11
2
.
Câu 176: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên R và
( )
0fx>
khi x ∈ [0; a] (
0a >
). Biết
( ) (
)
.1fxfa x−=
, tính tích phân
( )
0
1
a
dx
I
fx
=
+
∫
.
A.
2
a
I =
. B.
2Ia=
. C.
3
a
I =
. D.
4
a
I =
.
Câu 177: Cho
( )
fx
là hàm liên tục trên đoạn
[ ]
0;a
thỏa mãn
( ) ( )
( )
[ ]
.1
0, 0;
fxfa x
fx x a
−=
> ∀∈
và
( )
0
d
,
1
a
x ba
fx c
=
+
∫
trong đó
b
,
c
là hai số nguyên dương và
b
c
là phân số tối giản. Khi đó
bc+
có giá trị thuộc khoảng nào dưới đây?
https://toanmath.com/
A.
( )
11;22 .
B.
( )
0;9 .
C.
( )
7;21 .
D.
(
)
2017;2020 .
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 6
Câu 178: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 4
, đồng biến trên đoạn
[ ]
1; 4
và thỏa
mãn đẳng thức
( )
2.x xf x+
(
)
2
fx
′
=


,
[ ]
1; 4x∀∈
. Biết rằng
( )
3
1
2
f =
, tính
(
)
4
1
dI fx x=
∫
?
A.
1186
45
I =
. B.
1174
45
I =
. C.
1222
45
I =
. D.
1201
45
I =
.
Câu 179: Cho hàm số
( )
y fx=
có đạo hàm trên
thỏa mãn
( )
( )
(
)
32
1
2
2
3 .e 0
fxx
x
fx
fx
−−
′
−=
và
( )
01f =
. Tích phân
( )
7
0
.dxf x x
∫
bằng
A.
27
3
. B.
15
4
. C.
45
8
. D.
57
4
.
Câu 180: Cho hàm số
( )
432
43 1fx x x x x
= + − −+
,
x∀∈
. Tính
( ) ( )
1
2
0
.dI f xfxx
′
=
∫
.
A.
2
. B.
2
−
. C.
7
3
−
. D.
7
3
.
Câu 181: Cho hàm số
( )
fx
có đạo hàm liên tục trên khoảng
( )
0;1
và
( )
0fx≠
,
( )
0;1x∀∈
. Biết rằng
1
2
fa

=


,
3
2
fb

=



và
( ) ( )
24x xf x f x
′
+=−
,
(
)
0;1x∀∈
. Tính tích phân
( )
2
3
2
6
sin .cos 2sin 2
sin
d
xx x
Ix
fx
π
π
+
=
∫
theo
a
và
b
.
A.
3
4
ab
I
ab
.
B.
3
4
ba
I
ab
. C.
3
4
ba
I
ab
. D.
3
4
ab
I
ab
.
Câu 182: Cho hàm số
f
liên tục,
( )
1fx
>−
,
( )
00f
=
và thỏa
( )
( )
2
12 1f x x xfx
′
+= +
. Tính
( )
3f
.
A.
0
. B.
3
. C.
7
. D.
9
.
Câu 183: Cho hàm số
( )
fx
liên tục trên
và
( )
5
2
d4fx x=
∫
,
( )
53f =
,
( )
22f =
. Tính
( )
2
32
1
1dI xf x x
′
= +
∫
A.
3
. B.
4
. C.
1
. D.
6
.
Câu 184: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
1; 4
và thỏa mãn
( )
( )
21
ln
fx
x
fx
x
x
−
= +
. Tính tích
phân
(
)
4
3
dI fx x=
∫
.
A.
2
3 2ln 2I = +
. B.
2
2ln 2I =
. C.
2
ln 2I
=
. D.
2ln 2
I =
.
https://toanmath.com/
Câu 185: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
( )
16
2
2
1
4
cot . sin d d 1
fx
xf x x x
x
π
π
= =
∫∫
. Tính
tích phân
( )
1
1
8
4
d
fx
x
x
∫
.
A.
3I =
. B.
3
2
I =
. C.
2I =
. D.
5
2
I =
.
Câu 186: Xét hàm số
(
)
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
( )
( )
22
4. 3 1 1xf x f x x+ −=−
.
Tích phân
( )
1
0
d
I fx x
=
∫
bằng:
A.
4
I
π
=
. B.
6
I
π
=
. C.
20
I
π
=
. D.
16
I
π
=
.
Câu 187: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
11f =
,
(
)
1
2
0
9
d
5
fx x
′
=


∫
và
(
)
1
0
2
d
5
f xx=
∫
. Tính tích phân
( )
1
0
dI fx x
=
∫
.
A.
3
5
I =
. B.
1
4
I
=
. C.
3
4
I
=
. D.
1
5
I =
.
https://toanmath.com/
HƯỚNG DẪN GIẢI
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 1
Câu 104: Cho
( )
4
0
d 16
fx x
=
∫
. Tính
(
)
2
0
2d
f xx
∫
A.
16
. B.
4
. C.
32
. D.
8
.
17THướng dẫn giải
17TChọn D
17TXét tích phân 17T
(
)
2
0
2df xx
∫
ta có
Đặt
2xt=
1
d dt
2
x⇒=
. Khi
0x =
thì
0t =
; khi
2
x =
thì
4t =
.
Do đó
( ) ( )
24
00
1
2 d dt
2
f x x ft=
∫∫
( )
4
0
1
d
2
fx x=
∫
1
.16
2
=
8=
.
Câu 105: Nếu
(
)
6
0
d 12fx x=
∫
thì
(
)
2
0
3df xx
∫
bằng
A.
6
. B.
36
. C.
2
. D.
4
.
Hướng dẫn giải
Chọn D
Đặt
3 d 3dtx t x=⇒=
. Đổi cận:
00xt= ⇒=
,
26xt= ⇒=
Khi đó:
( )
( )
26
00
11
3 d d .12 4
33
f x x ft t
= = =
∫∫
.
Câu 106: Cho
(
)
2
2
1
1d 2
f x xx+=
∫
. Khi đó
( )
5
2
dI fxx=
∫
bằng:
A.
2
. B.
1
. C.
1−
. D.
4
.
Hướng dẫn giải
Chọn D
Đặt
2
12t x dt xdx= +⇒ =
.
Đổi cận:
12xt=⇒=
,
25xt
= ⇒=
.
Khi đó:
( )
( )
25
2
12
1
1d d
2
f x xx f t t
+=
∫∫
( )
( )
52
2
21
d 2 1d 4f t t f x xx⇒ = +=
∫∫
.
Mà tích phân không phụ thuộc vào biến nên:
( ) ( )
55
22
d d4I fxx ft t= = =
∫∫
.
Câu 107: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
1
5
d9fx x
−
=
∫
. Tính tích phân
( )
2
0
1 3 9dfx x−+


∫
.
A.
27
. B.
21
. C.
15
. D.
75
.
Hướng dẫn giải
Chọn B
Đặt
13tx= −
d 3dtx⇒=−
.
Với
01xt= →=
và
25xt= →=−
.
Ta có
( )
2
0
1 3 9dfx x−+


∫
( )
22
00
1 3 d 9df xx x=−+
∫∫
( )
5
2
0
1
d
9
3
t
ft x
−
= +


−
∫
( )
1
5
1
d 18
3
fx x
−
= +


∫
https://toanmath.com/
1
.9 18 21
3
= +=
.
Câu 108: Biết
( )
fx
làm hàm liên tục trên
và
( )
9
0
d9
fx x
=
∫
. Khi đó giá trị của
( )
4
1
3 3dfx x−
∫
là
A.
27
. B.
3
. C.
0
. D.
24
.
Hướng dẫn giải
Chọn B
( )
4
1
3 3dI fx x= −
∫
. Đặt
33
tx= −
d 3dtx⇒=
Đổi cận:
10
9
4
xt
x t
=⇒=
= ⇒=
( )
9
0
1
d
3
I ft t
=
∫
(
)
9
0
1
d
3
fx x
=
∫
3=
.
Câu 109: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
d 10fx x=
∫
. Tính
2
0
d
2
x
fx



∫
.
A.
2
0
5
d
22
x
fx

=


∫
. B.
2
0
d 20
2
x
fx

=


∫
. C.
2
0
d 10
2
x
fx

=


∫
. D.
2
0
d5
2
x
fx

=


∫
.
Hướng dẫn giải
Chọn B
Đặt
2
x
t =
1
dd
2
tx⇒=
.
Đổi cận:
0
x =
0t⇒=
;
2
x =
1t⇒=
.
Ta có:
2
0
d
2
x
fx



∫
( )
1
0
2. dft t=
∫
2.10=
20=
.
Câu 110: Cho
( )
5
1
d4fx x
−
=
∫
. Tính
(
)
2
1
2 1d
I fx x
−
= +
∫
.
A.
2I =
. B.
5
2
I =
. C.
4I =
. D.
3
2
I =
.
Hướng dẫn giải
Chọn A
Đặt
21tx= +
2ddt x⇒=
1
dd
2
xt
⇒=
.
Với
11xt=−⇒ =−
, với
25xt= ⇒=
.
Khi đó ta có
(
)
2
1
2 1dI fx x
−
= +
∫
( )
5
1
1
.d
2
I ft t
−
⇒=
∫
( )
5
1
1
d
2
ft t
−
=
∫
(
)
5
1
1
d
2
fx x
−
=
∫
1
.4 2
2
= =
.
Câu 111: Giả sử hàm số
( )
y fx=
liên tục trên
và
( )
5
3
dfx x a=
∫
,
( )
a∈
. Tích phân
( )
2
1
2 1dI fx x= +
∫
có giá trị là
A.
1
1
2
Ia
= +
. B.
21Ia= +
. C.
2Ia=
. D.
1
2
Ia=
.
Hướng dẫn giải
Chọn D
Đặt
21d2dtx t x= +⇒ =
.
Đổi cận:
13xt=⇒=
;
25xt= ⇒=
.
https://toanmath.com/
(
)
( )
55
33
11 1
dd
22 2
I ft t fx x a⇒= = =
∫∫
.
Câu 112: Cho
(
)
2
2
1
1d 2f x xx
+=
∫
. Khi đó
(
)
5
2
dI fx x
=
∫
bằng
A.
2
. B.
1
. C.
1−
. D.
4
.
Hướng dẫn giải
Chọn D
Đặt
2
1 d 2d
t x t xx= +⇒ =
Đổi cận:
12
xt
=⇒=
;
25xt= ⇒=
.
Khi đó:
( ) (
) (
)
55 5
22 2
11
2 d d d 4.
22
ft t fx x I fx x= = ⇒= =
∫∫ ∫
.
Câu 113: Cho hàm số
( )
fx
liên tục trên
[
)
1; +∞
và
(
)
3
0
1d 8fx x+=
∫
. Tích phân
( )
2
1
dI xf x x=
∫
bằng:
A.
16I =
. B.
2I =
. C.
8I =
. D.
4I =
Hướng dẫn giải
Chọn D
( )
3
0
1d 8I fx x= +=
∫
. Đặt
2
1 12ddt x t x tt x= +⇒ = +⇒ =
;
đổi cận:
01xt= ⇒=
;
32
xt=⇒=
.
Khi đó
( )
2
1
2 d8I tf t t= =
∫
( )
2
1
d4tf t t⇒=
∫
. Vậy
(
)
2
1
d4I xf x x
= =
∫
.
Câu 114: Biết
( )
11
1
d 18fx x
−
=
∫
. Tính
(
)
( )
2
2
0
2 3 1d
I x fx x=+−
∫
.
A.
5I =
. B.
7I =
. C.
8I =
D.
10I =
.
Hướng dẫn giải
Chọn B
Đặt
2
31tx= −
d 6dt xx⇒=
. Đổi cận
01xt=⇒=−
,
2 11xt= ⇒=
( )
(
)
( )
( )
2 2 2 11
22
0 00 1
11
2 3 1 d 2 d 3 1 d 4 d 4 .18 7
66
I x fx x xx xfx x ftt
−
= + − = + −=+ =+ =
∫ ∫∫ ∫
.
Câu 115: Cho hàm số
( )
y fx=
liên tục trên
và
( )
1
0
2d 8f xx=
∫
. Tính
( )
2
2
0
d
I xf x x=
∫
A.
4
. B.
16
. C.
8
. D.
32
.
Hướng dẫn giải
Chọn C
Đặt
2
2 2 d 2d d dx t xx t xx t=⇒ =⇒=
. Đổi cận:
00xt= ⇒=
,
21xt= ⇒=
.
Ta có:
( )
1
0
2d 8I f tt= =
∫
.
Câu 116: Cho hàm số
( )
fx
liên tục trên
và có
( ) ( )
13
00
d 2; d 6fx x fx x= =
∫∫
. Tính
( )
1
1
2 1d
I fx x
−
= −
∫
.
A.
2
3
I =
. B.
4I =
. C.
3
2
I =
. D.
6I =
.
Hướng dẫn giải
https://toanmath.com/
Chọn B
Có
(
)
(
) (
)
1
11
2
12
1
11
2
21d 12d 21dI f x x f xx f x xI I
−−
= − = − + −=+
∫ ∫∫
Tính
( )
1
2
1
1
12 dI f xx
−
= −
∫
.Đặt
1 2 d 2du xu x=−⇒=−
. Đổi cận:
13
1
0
2
xu
xu
=−⇒ =
=⇒=
.
(
)
( )
03
1
30
11
du du 3
22
I fu fu
−
⇒= = =
∫∫
Tính
(
)
1
2
1
2
2 1dI fx x= −
∫
. Đặt
2 1 d 2dux u x= −⇒ =
. Đổi cận:
11
1
0
2
xu
xu
=⇒=
=⇒=
.
(
)
( )
11
2
00
11
du du 1
22
I fu fu⇒= = =
∫∫
Vậy
12
4III=+=
.
Câu 117: Cho hàm số
( )
y fx=
liên tục trên
[ ]
0;4
và
( )
2
0
d1fx x=
∫
;
;
( )
4
0
d3fx x=
∫
. Tính
( )
1
1
3 1dfx x
−
−
∫
.
A.
4
. B.
2
. C.
4
3
. D.
1
.
Hướng dẫn giải
Chọn C
( )
( ) (
)
1 1/3 1
1 1 1/3
31d 13d 31df x x f xx f x x
−−
−= − + −
∫ ∫∫
.
( ) ( ) ( ) ( )
1/3 1
1 1/3
11
13d13 3 1d3 1
33
fxxfxx
−
=− −−+ −−
∫∫
.
( )
( ) ( )
02
40
11
dd
33
ftt ft t=−+
∫∫
( )
1 14
3 .1
3 33
=− −+ =
.
Câu 118: Cho
( )
fx
là hàm số liên tục trên
và
( )
1
0
d4fx x=
∫
,
( )
3
0
d6fx x=
∫
. Tính
( )
1
1
2 1d
I fx x
−
= +
∫
.
A.
3I =
. B.
5I =
. C.
6I =
. D.
4I =
.
Hướng dẫn giải
Chọn B
Đặt
21ux= +
1
dd
2
xu⇒=
. Khi
1x = −
thì
1u = −
. Khi
1x
=
thì
3u =
.
Nên
( )
3
1
1
d
2
I fu u
−
=
∫
( )
( )
03
10
1
dd
2
fu u fu u
−

= +


∫∫
( ) ( )
03
10
1
dd
2
fuu fuu
−

= −+


∫∫
.
https://toanmath.com/
Xét
( )
1
0
d4
fx x
=
∫
. Đặt
xu
= −
ddxu⇒=−
.
Khi
0x =
thì
0u =
. Khi
1x =
thì
1u = −
.
Nên
( )
1
0
4dfx x= =
∫
( )
1
0
dfuu
−
−−
∫
(
)
0
1
dfuu
−
= −
∫
.
Ta có
(
)
3
0
d6fx x=
∫
( )
3
0
d6fu u⇒=
∫
.
Nên
( )
(
)
03
10
1
dd
2
I fuu fuu
−

= −+


∫∫
( )
1
46 5
2
= +=
.
Câu 119: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
2d 2
f xx=
∫
và
( )
2
0
6 d 14f xx=
∫
. Tính
(
)
2
2
5 2d
fx x
−
+
∫
.
A.
30
. B.
32
. C.
34
. D.
36
.
Hướng dẫn giải
Chọn B
+ Xét
( )
1
0
2d 2f xx=
∫
.
Đặt
2 d 2dux u x=⇒=
;
00xu=⇒=
;
12
xu=⇒=
.
Nên
( )
1
0
2 2d
f xx=
∫
( )
2
0
1
d
2
fu u=
∫
( )
2
0
d4fu u⇒=
∫
.
+ Xét
(
)
2
0
6 d 14f xx
=
∫
.
Đặt
6 d 6dvx v x=⇒=
;
00xv=⇒=
;
2 12xv
=⇒=
.
Nên
( )
2
0
14 6 df xx=
∫
( )
12
0
1
d
6
fv v=
∫
( )
12
0
d 84fv v⇒=
∫
.
+ Xét
(
)
2
2
5 2d
fx x
−
+
∫
(
)
( )
02
20
5 2d 5 2d
fx x fx x
−
= ++ +
∫∫
.
Tính
( )
0
1
2
5 2dI fx x
−
= +
∫
.
Đặt
52tx= +
.
Khi
20x−< <
,
52tx=−+
d 5dtx⇒=−
;
2 12xt=−⇒=
;
02xt= ⇒=
.
( )
2
1
12
1
d
5
I ft t
−
=
∫
(
) ( )
12 2
00
1
dd
5
ft t ft t

= −


∫∫
( )
1
84 4 16
5
= −=
.
Tính
( )
2
1
0
5 2dI fx x= +
∫
.
Đặt
52tx= +
.
Khi
02x<<
,
52tx= +
d 5dtx⇒=
;
2 12xt= ⇒=
;
02xt= ⇒=
.
( )
12
2
2
1
d
5
I ft t=
∫
( ) ( )
12 2
00
1
dd
5
ft t ft t

= −


∫∫
( )
1
84 4 16
5
= −=
.
Vậy
( )
2
2
5 2 d 32fx x
−
+=
∫
.
https://toanmath.com/
Câu 120: Cho tích phân
( )
2
0
cos . sin 8I x f x dx= =
∫
π
. Tính tích phân
( )
2
0
sin . cosK x f x dx=
∫
π
.
A.
8
K
= −
. B.
4K =
. C.
8K =
. D.
16K
=
.
Hướng dẫn giải:
( )
2
0
cos . sin
I x f x dx
=
∫
π
Đặt
2
tx= −
π
dt dx⇒=−
Đổi cận:
( )
(
)
( )
0
22
00
2
cos . sin . sin . cos . sin . cos .
22
I t f t dt t f x dt x f x dt

 
⇒= − − − = =
 

 

∫ ∫∫
ππ
π
ππ
(Tích phân xác
định không phụ thuộc vào biến số tích phân)
K
=
8KI⇒==
Chọn C
Câu 121: Cho hàm số
( )
y fx=
liên tục trên R, thỏa mãn
( )
1
0
1f x dx =
∫
. Tính
( )
(
)
4
2
0
tan 1 . tanI f x dx= +
∫
π
.
A.
1I
=
. B.
1I = −
. C.
4
I =
π
. D.
4
I
= −
π
.
Hướng dẫn giải:
Đặt
( )
2
tan 1 tan
t x dt x dx
= ⇒=+
. Đổi cận:
( )
( )
11
00
I f t dt f x dx⇒= =
∫∫
(Tích phân xác định không phụ thuộc vào biến số tích phân)
1
=
Chọn A
Câu 122: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
23f x fx=
,
x∀∈
. Biết rằng
( )
1
0
d1fx x=
∫
. Giá trị của tích phân
(
)
2
1
d
I fx x
=
∫
bằng bao nhiêu?
A.
5I
=
. B.
3I =
. C.
8I =
. D.
2I =
.
Hướng dẫn giải
Chọn A
Xét tích phân
( )
2
0
dJ fx x=
∫
, đặt
2 d 2dxt x t=⇒=
.
Với
21xt= ⇒=
,
00xt= ⇒=
.
Ta có
( ) ( )
11
00
2 2d 2 2 dJ ft t ftt= =
∫∫
( ) ( )
11
00
23 d 6 dft t ft t= = =
∫∫
( )
1
0
6 d6fx x
=
∫
.
Mặt khác, ta có
( ) ( ) ( )
212
0 01
dddJ fx x fx x fx x= = +
∫∫∫
( ) ( ) ( ) ( )
2 21 1
1 00 0
d d d d5I fx x fx x fx x J fx x⇒==−=−=
∫∫∫ ∫
.
Câu 123: Cho hàm số
( )
y fx=
liên tục và có đạo hàm trên
thỏa mãn
( )
22f = −
;
( )
2
0
d1fxx=
∫
.
Tính tích phân
( )
4
0
dI f xx
′
=
∫
.
https://toanmath.com/
A.
10I = −
. B.
5I = −
. C.
0I
=
. D.
18
I
= −
.
Hướng dẫn giải
Chọn A
Đặt
tx=
, ta có:
2
tx=
và
2d d
tt x=
. Khi
00xt= ⇒=
;
42
xt
= ⇒=
.
( )
4
0
d
I f xx
′
=
∫
( )
2
0
2dtf t t
′
=
∫
.
Đặt
( )
2 ; d du t v ftt
′
= =
ta được:
d 2dut=
;
( )
v ft=
.
Khi đó:
( )
( )
(
)
2
2
0
0
2 2dI tft ftt
= −
∫
( )
4 2 2.1f= −
( )
4. 2 2 10= − −=−
.
Câu 124: Cho
( )
2
1
d2fx x=
∫
. Tính
( )
4
1
d
fx
Ix
x
=
∫
bằng
A.
1I =
. B.
2I =
. C.
4I =
. D.
1
2
I =
.
Hướng dẫn giải
Chọn C
Đặt
1
dd
2
tx t x
x
= ⇒=
; đổi cận:
11xt=⇒=
,
42xt= ⇒=
( )
( ) ( )
4 22
1 11
d 2d 2 d 2.2 4
fx
I x ft t ft t
x
= = = = =
∫∫∫
.
Câu 125: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
16
1
d6
fx
x
x
=
∫
và
( )
2
0
sin cos d 3f x xx
π
=
∫
.
Tính tích phân
(
)
4
0
dI fx x=
∫
.
A.
2I = −
. B.
6I =
. C.
9I =
. D.
2I =
.
Hướng dẫn giải
Chọn B
•Xét
(
)
16
1
d6
fx
Ix
x
= =
∫
, đặt
d
d
2
x
xt t
x
=⇒=
Đổi cận:
11xt=⇒=
;
16 4xt= ⇒=
( )
4
1
2 d6I ft t= =
∫
( )
4
1
6
d3
2
ft t⇒==
∫
.
•
( )
2
0
sin cos d 3J f x xx
π
= =
∫
, đặt
sin cos d dx u xx u=⇒=
Đổi cận:
00xu=⇒=
;
1
2
xu
π
= ⇒=
( )
1
0
d3J fu u= =
∫
Vậy
( )
( ) ( )
414
0 01
d d d 336
I fx x fx x fx x= = + =+=
∫∫∫
.
https://toanmath.com/
Câu 126: Cho
( )
fx
liên tục trên
thỏa
( )
9
1
d4
fx
x
x
=
∫
và
( )
2
0
sin cos d 2f x xx
π
=
∫
. Tính
( )
3
0
dI fx x
=
∫
.
A.
10I =
. B.
6I =
. C.
4I =
. D.
2I =
.
Hướng dẫn giải
Chọn C
Ta có:
( )
9
1
d4
fx
x
x
=
∫
, đặt
tx
=
2
tx
⇒=
2d dtt x⇒=
đổi cận
11xt=⇒=
,
93
xt=⇒=
Do đó ta có:
(
)
3
1
2 dt 4
ft
t
t
=
∫
( )
3
1
dt 2ft⇔=
∫
(1)
Ta có:
( )
2
0
sin cos .d 4f x xx
π
=
∫
, đặt
sintx=
d cos .dt xx⇒=
đổi cận
00xt= ⇒=
,
1
2
xt
π
= ⇒=
Do đó ta có:
( )
2
0
sin cos .d 2f x xx
π
=
∫
(
)
1
0
d2
ft t
⇔=
∫
(2)
Từ (1) và (2) ta có:
( ) ( )
33
00
d d 4.fx x ft t= =
∫∫
.
Câu 127: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
1; 4
và thỏa mãn
( )
( )
21
ln
fx
x
fx
x
x
−
= +
. Tính tích
phân
( )
4
3
dI fx x
=
∫
.
A.
2
3 2ln 2I = +
. B.
2
2ln 2I =
. C.
2
ln 2I =
. D.
2ln 2
I
=
.
Hướng dẫn giải
Chọn B
Ta có
( )
4
1
dfx x
∫
( )
4
1
21
ln
d
fx
x
x
x
x

−

= +


∫
(
)
44
11
21
ln
dd
fx
x
xx
x
x
−
= +
∫∫
.
Xét
( )
4
1
21
d
fx
Kx
x
−
=
∫
.
Đặt
21
xt−=
1
2
t
x
+
⇒=
d
d
x
t
x
⇒=
.
( )
3
1
d
K ft t⇒=
∫
( )
3
1
dfx x=
∫
.
Xét
4
1
ln
d
x
Mx
x
=
∫
( )
4
1
ln d lnxx=
∫
4
2
1
ln
2
x
= =
2
2ln 2
.
Do đó
( ) ( )
43
2
11
d d 2ln 2fx x fx x= +
∫∫
( )
4
2
3
d 2ln 2fx x⇒=
∫
.
https://toanmath.com/
Câu 128: Cho hàm số
( )
fx
liên tục trên
[
)
4;− +∞
và
( )
5
0
4d 8
fx x+=
∫
. Tính
(
)
2
3
.dI xf x x=
∫
.
A.
8I =
. B.
4
I =
. C.
16I = −
. D.
4I = −
.
Hướng dẫn giải
Chọn D
Đặt
2
44
x t xt
+=⇒= −
.
Khi
02
53
xt
xt
=⇒=
=⇒=
( )
( )
( )
33
2
22
8 d 4 2. d 8
ft t tft t
⇒= − ⇔ =
∫∫
.
Mà
( ) ( ) ( )
33 3
22 2
2.d2.d .d4 4
tf t t xf x x xf x x I= ⇒ =⇒=−
∫∫ ∫
.
Câu 129: Cho và . Tính .
A. . B. . C. . D. .
Hướng dẫn giải
Chọn C
Đặt .
Ta có
.
Câu 130: Cho hàm
( )
fx
liên tục trên
thỏa mãn
( )
4
0
tan d 3f xx
π
=
∫
và
(
)
2
1
2
0
d1
1
xf x
x
x
=
+
∫
. Tính
(
)
1
0
dfx x
∫
.
A.
4
. B.
2
. C.
5
. D.
1
.
Hướng dẫn giải
Chọn A
( )
( )
( )
2
1 11
22
0 00
ddd
11
xfx fx
x fx x x
xx
= −
++
∫ ∫∫
( )
( )
( )
2
1 11
22
0 00
ddd
11
xfx fx
x x fx x
xx
⇔ +=
++
∫ ∫∫
.
Đặt
tan xt
=
suy ra
(
)
(
)
2
2
1
d tan d d d 1 tan d d
cos
x t xt xxt
x
= ⇔ = ⇔+ =
.
( )
2
2
dd
d
1
1 tan
tt
x
t
x
⇔= =
+
+
.
( ) ( )
1
4
2
00
d
tan d
1
t
f x x ft
t
π
= =
+
∫∫
( )
1
2
0
d
1
fx
x
x +
∫
=3.
Vậy
( )
1
0
4f x dx =
∫
.
( )
1
0
2 1 d 12
fx x+=
∫
( )
2
2
0
sin sin 2 d 3f x xx
π
=
∫
( )
3
0
d
fx x
∫
26
22
27
15
21xt+=
( )
3
1
1
12 d
2
t
ft
−

⇒=


∫
( )
3
1
1
d
2
ft t=
∫
( )
3
1
1
d
2
fx x=
∫
( )
3
1
d 24fx x
⇒=
∫
( )
2
2
0
sin sin 2 df x xx
π
∫
(
)
2
2
0
sin .2sin cos d
f x x xx
π
=
∫
( )
( )
2
2
0
2sin . sin d sinxf x x
π
=
∫
(
) ( )
2
22
0
sin d sinfx x
π
=
∫
( )
1
0
dfu u=
∫
( )
1
0
d3fx x= =
∫
( )
3
0
d
fx x⇒
∫
( ) ( )
13
01
d d 3 24 27fx x fx x= + =+=
∫∫
https://toanmath.com/
Câu 131: Cho hàm số
( )
fx
liên tục trên R và
( )
( )
2
1
4
2
00
tand4; d2
1
xf x
f xx x
x
π
= =
+
∫∫
. Tính
( )
1
0
d
I fx x=
∫
.
A.
6
I
=
. B.
2I =
. C.
3I =
. D.
1I =
.
Hướng dẫn giải
Chọn A
Từ
( )
4
0
t anx d 4
fx
π
=
∫
; Ta đặt
tantx
=
ta được
(
)
1
2
0
d4
1
ft
t
t
=
+
∫
Từ
(
)
( )
( )
( )
(
)
2
2
1 1 11
22 2
0 0 00
11
d2 d2 d d2
11 1
x fx
xfx fx
x x fx x x
xx x
+−
=⇔ =⇔− =
++ +
∫ ∫ ∫∫
( )
(
)
11
2
00
d2 d246
1
fx
fx x x
x
⇒ =+ =+=
+
∫∫
.
Câu 132: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
2018
0
d2
fx x=
∫
. Khi đó tích phân
( )
(
)
2018
e1
2
2
0
ln 1 d
1
x
fx x
x
−
+
+
∫
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
Chọn B
Xét
( )
( )
2018
e1
2
2
0
ln 1 d
1
x
I fx x
x
−
= +
+
∫
.
Đặt
( )
2
ln 1
tx
= +
2
2
dd
1
x
tx
x
⇒=
+
. Đổi cận:
0x
=
0t⇒=
;
2018
e1x = −
2018t⇒=
.
Suy ra
( )
( )
2018 2018
00
11 1
d d .2 1
22 2
I ft t fx x= = = =
∫∫
.
Câu 133: Tìm tất cả các giá trị dương của
m
để
(
)
3
0
10
3
9
m
x x dx f

′′
−=−


∫
, với
( )
15
lnfx x=
.
A.
20m =
. B.
4m =
. C.
5m =
. D.
3m =
.
Hướng dẫn giải
Chọn D
+ Từ
( )
15
lnfx x=
( )
14
15
15 15x
fx
xx
′
⇒==
( )
2
15
fx
x
−
′′
⇒=
do đó
10 243
9 20
f
−

′′
=


.
+ Tính tích phân
( )
3
0
3d
m
I x xx= −
∫
:
• Đặt
3tx= −
3xt⇒=−
,
ddxt= −
,
03
30
x
t
• Do đó
( ) ( )
0
3
3d
m
I tt t=−−
∫
( )
3
1
0
3d
mm
tt t
+
= −
∫
3
12
0
3
12
mm
tt
mm
++
= −
++
( )( )
2
3
12
m
mm
+
=
++
+ Ta có
( )
3
0
10
3
9
m
x x dx f

′′
−=−


∫
( )( )
2
3 243
1 2 20
m
mm
+
⇔=
++
( )( )
25
33
1 2 4.5
m
mm
+
⇔=
++
Thay lần lượt các giá trị
m
ở 4 đáp án, nhận giá trị
3m =
.
Chú ý:
https://toanmath.com/
-Việc giải phương trình
( )( )
3
33
1 2 4.5
m
mm
=
++
không cần thiết nên chọn phương pháp thế đáp để làm
trắc nghiệm trong bài này.
-Để giải phương trình
(
)
(
)
3
33
1 2 4.5
m
mm
=
++
ta xét hàm trên
(
)
(
)(
)
3
33
1 2 4.5
m
fm
mm
= −
++
với
0m >
thì chứng minh được phương trình có nghiệm duy nhất
3m
=
.
Câu 134: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
(
)
( )
4f x fx−=
. Biết
( )
3
1
d5
xf x x =
∫
.
Tính
( )
3
1
dI fx x=
∫
.
A.
5
2
I =
. B.
7
2
I =
. C.
9
2
I =
. D.
11
2
I
=
.
Hướng dẫn giải
Chọn A
Cách 1: Dùng tính chất để tính nhanh
Cho hàm số
( )
fx
liên tục trên
[ ]
;ab
và thỏa mãn điều kiện
(
) ( )
[
]
,;
f a b x f x xab
+− = ∀
. Khi đó
( )
( )
dd
2
bb
aa
ab
xfx x fx x
+
=
∫∫
Chứng minh:
Đặt
t abx=+−
ddxt⇒=−
, với
[ ]
;x ab∈
. Đổi cận: khi
xa tb= ⇒=
; khi
xb tb= ⇒=
Ta có
( )
( ) (
) (
)
dd d
bb a
aa b
xf x x xf a b x x a b t f t t= +− =− +−
∫∫ ∫
( ) (
) ( )
( ) ( )
( ) ( )
( )
d dd d d
b bb b b
a aa a a
a btft t a b ft t tft t a b fx x xfx x= +− = + − = + −
∫ ∫∫ ∫ ∫
(
)
( )
(
) (
)
(
)
2d d d d
2
b bb b
a aa a
ab
xfx x ab fx x xfx x fx x
+
⇒ =+ ⇒=
∫ ∫∫ ∫
.
Áp dụng tính chất trên với
1a =
,
3b =
.
( )
fx
liên tục trên
[ ]
;ab
và thỏa mãn
(
) ( )
13f x fx+− =
.
Khi đó
( ) ( ) ( )
3 33
1 11
13 5
d dd
42
xfx x fx x fx x
+
= ⇒=
∫ ∫∫
.
Cách 2: Đổi biến trực tiếp:
Đặt
4tx= −
, với
[ ]
1; 3x∈
.
Ta có
( ) (
) ( )
( ) (
) ( )
3 3 3 33
1 1 1 11
d 4 d 4 d4 d . dxfx x xf x x tft t ft t tft t= −=− = −
∫ ∫ ∫ ∫∫
( ) ( )
33
11
5
54 d 5 d
2
ft t ft t⇒= −⇒ =
∫∫
.
Câu 135: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
1; 3
thỏa mãn
( ) ( )
[ ]
4 , 1; 3f x fx x− = ∀∈
và
( )
3
1
d2
xf x x = −
∫
. Giá trị
( )
3
1
dfx x
∫
bằng
A.
2
. B.
1−
. C.
2−
. D.
1
.
Hướng dẫn giải
https://toanmath.com/
Chọn B
Xét
3
1
( )dI xf x x=
∫
(1).
Đặt
4xt= −
, ta có
ddxt= −
;
13xt=⇒=
,
31xt=⇒=
.
Suy ra
( )
3
1
4 (4 )dI tf tt=−−
∫
(
)
3
1
4 ( )dt ft t
= −
∫
, hay
( )
3
1
4 ()I x f x dx= −
∫
(2).
Cộng (1) và (2) vế theo vế ta được
3
1
2 4 ()I f x dx
=
∫
3
1
() 1
2
I
f x dx⇒==−
∫
.
Câu 136: Cho hàm số
f
liên tục trên đoạn
[ ]
6;5−
, có đồ thị gồm hai đoạn thẳng và nửa đường tròn
như hình vẽ. Tính giá trị
( )
5
6
2d
I fx x
−
= +


∫
.
17TA. 17T
2 35I
π
= +
. 17TB. 17T
2 34I
π
= +
. 17TC. 17T
2 33
I
π
= +
. 17TD. 17T
2 32I
π
= +
.
Hướng dẫn giải
17TChọn D
17TTa có 17T
( )
2
1
2 khi 6 2
2
1 4 khi 2 2
21
khi 2 5
33
xx
fx x x
xx
+ − ≤ ≤−
= + − −≤≤
− ≤≤
17T.
(
) ( )
5 55
6 66
2d d 2 d
I fx x fx x x
− −−
= += +


∫ ∫∫
(
)
22 5
2
62 2
1 21
2 d 1 4 d d 22
2 33
x x xx x x
−
−−

= + + +− + − +


∫∫ ∫
25
22
62
11
2 22 28
4 33
x
xx J x J
−
−

= + ++ − + =+


.
Tính
(
)
2
2
2
14 dJ xx
−
= +−
∫
Đặt
2sinxt
=
d 2cos dx tt⇒=
.
Đổi cận: Khi
2x =
thì
2
t
π
= −
; khi
2x =
thì
2
t
π
=
.
(
)
( )
2
22
22
2
22
1 4 d 44cosd 42 1cos2d 42J x x tt t t
ππ
ππ
π
−
−−
= +− =+ =+ + =+
∫ ∫∫
. Vậy
32 2I
π
= +
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 2
Cho hàm số
( )
fx
thỏa mãn :
( ) ( ) ( )
( )
. .. .A f x Bu f u C f a b x g x
′
+ + +− =
O
x
y
5
4−
6−
1−
3
https://toanmath.com/
+) Với
( )
( )
ua a
ub b
=
=
thì
( ) ( )
1
bb
aa
f x dx g x dx
ABC
=
++
∫∫
.
+) Với
( )
( )
ua b
ub a
=
=
thì
( ) ( )
1
bb
aa
f x dx g x dx
ABC
=
−+
∫∫
.
Trong đề bài thường sẽ bị khuyết một trong các hệ số
,,
ABC
.
Nếu
(
)
fx
liên tục trên
[ ]
;ab
thì
(
) (
)
bb
aa
f a b x dx f x dx
+− =
∫∫
.
Câu 137: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
thỏa mãn
( )
( )
23
6
6
31
f x xf x
x
= −
+
. Tính
( )
1
0
dfx x
∫
A.
2
. B.
4
. C.
1−
. D.
6
.
Hướng dẫn giải
Chọn B
Cách 1: (Dùng công thức)
Biến đổi
( )
( )
23
6
6
31
f x xf x
x
= −
+
( )
( )
23
6
2.3 .
31
fx xfx
x
⇔− =−
+
với
1A
=
,
2
B = −
.
Áp dụng công thức ta có:
( )
( )
11
00
16
d d4
12
31
fx x x
x
=−=
+−
+
∫∫
.
Cách 2: (Dùng công thức biến đổi – nếu không nhớ công thức)
Từ
( )
( )
23
6
6
31
f x xf x
x
= −
+
( )
( )
11 1
23
00 0
1
d 23 d 6 d
31
f x x xf x x x
x
⇒− =−
+
∫∫ ∫
Đặt
32
3 dxu x du x=⇒=
; Với
00
xu
=⇒=
và
11xu=⇒=
.
Khi đó
( )
( ) ( )
1 11
23
0 00
3d d d
xf x x fu u f x x= =
∫ ∫∫
thay vào
( )
*
, ta được:
( ) (
)
11 1
00 0
1
d2 d 6 d
31
fx x fx x x
x
−=−
+
∫∫ ∫
( )
11
00
1
d6 d4
31
fx x x
x
⇔= =
+
∫∫
.
Câu 138: Xét hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
( )
( )
22
4 3 11xf x f x x+ −= −
.
Tích phân
( )
1
0
dI fx x=
∫
bằng
A.
4
I
π
=
. B.
6
I
π
=
. C.
20
I
π
=
. D.
16
I
π
=
Hướng dẫn giải
Chọn C
Từ
( )
( )
( )
( )
1 11
2 22 2
0 00
4. 3 1 1 22 d 3 1 d 1 dxfx fx x xfx x f x x x x+ −= − ⇒ + − = −
∫ ∫∫
( )
∗
+) Đặt
2
d 2du x u xx=⇒=
; Với
00xu=⇒=
và
11
xu=⇒=
.
Khi đó
( )
( ) ( ) ( )
1 11
2
0 00
2 d d d1xf x x f u u f x x= =
∫ ∫∫
+) Đặt
1 ddt xt x=−⇒ =−
; Với
01xt=⇒=
và
10
xt
=⇒=
.
Khi đó
( )
( ) ( ) ( )
1 11
0 00
1d d d 2f xx ftt fxx−= =
∫ ∫∫
Thay
( ) ( )
1,2
vào
( )
∗
ta được:
https://toanmath.com/
( ) ( )
1 11
2
0 00
2 d3 d 1 dfx x fx x xx+=−
∫ ∫∫
(
)
11
2
00
1
d 1d
5 20
fxx x x
π
⇔ = −=
∫∫
.
Câu 139: Cho hàm số
()fx
liên tục trên
[
]
0;2
và thỏa mãn điều kiện
( ) ( )
22fx f x x+ −=
. Tính giá
trị của tích phân
( )
2
0
I f x dx=
∫
.
A.
4I = −
. B.
1
2
I =
. C.
4
3
I =
. D.
2I =
.
Hướng dẫn giải
Chọn D
Cách 1: (Dùng công thức)
Với
( ) ( )
22fx f x x
+ −=
ta có
1A =
;
1B =
, suy ra:
(
)
2
0
I f x dx=
∫
2
0
1
2
11
xdx=
+
∫
2
2
0
2
x
=
2=
.
Cách 2: (Dùng phương pháp đổi biến – nếu không nhớ công thức)
Từ
( ) ( )
22fx f x x+ −=
(
) (
)
22 2
00 0
22f x dx f x dx xdx⇒ +−=
∫∫ ∫
4=
(*)
Đặt
2ux= −
du dx⇒=−
; Với
0
x =
2u⇒=
và
2x =
0u⇒=
.
Suy ra
( )
2
0
2f x dx
−
∫
( )
2
0
f u du=
∫
( )
2
0
f x dx=
∫
.
Thay vào (*), ta được
( )
2
0
24f x dx =
∫
( )
2
0
2f x dx
⇔=
∫
.
Câu 140: Xét hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( )
( )
2 31 1
fx f x x+ −=−
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
2
3
. B.
1
6
. C.
2
15
. D.
3
5
.
Hướng dẫn giải
Chọn C
Đặt
1 ddt xx t=−⇒ =−
.
Suy ra
( ) ( )
( ) ( )
1 011
0 100
1d d d df x x ft t ft t fx x−=− = =
∫ ∫∫∫
( ) ( )
2 31 1fx f x x
+ −=−
( )
11
00
5 d 1df x x xx⇔=−
∫∫
( )
1
3
0
22
1
33
x=−−=
.
Suy ra
( )
1
0
2
d
15
fx x=
∫
.
Chú ý: Ta có thể dùng công thức
( ) ( )
22
11
dd
x ax b
x ax b
f ax b x f x x
+
+
+=
∫∫
. Khi đó:
Từ
( ) ( )
2 31 1fx f x x+ −=−
suy ra:
( ) ( )
11 1
00 0
2 d3 1 d 1dfxx f xx xx+ −=−
∫∫ ∫
(
) ( )
10 1
01 0
2 d3 1 d 1dfxx f xx xx⇔ − −=−
∫∫ ∫
( ) ( )
11
00
22
5d d
3 15
fx x fx x⇔ =⇔=
∫∫
.
Câu 141: Xét hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
và thỏa mãn điều kiện
( ) ( )
2 31 1fx f x x x− −= −
. Tính tích phân
( )
1
0
dI fx x=
∫
.
https://toanmath.com/
A.
1
25
I
=
. B.
4
15
I
= −
. C.
1
15
I = −
. D.
4
75
I
=
.
Hướng dẫn giải
Chọn B
Do
( ) ( )
2 31 1fx f x x x− −= −
(
) (
)
(
)
12
11 1
00 0
2 d 31 d 1 d 1
II
fxx f xx x xx
⇒ − −=−
∫∫ ∫
  
.
+ Xét
( )
1
1
0
31d
I f xx= −
∫
:
Đặt
1 ddt xx t
=−⇒ =−
. Khi
0 1; 1 0
x tx t
=⇒= =⇒=
.
Khi đó
(
)
1
1
0
3 d3
I ft t I= =
∫
.
+ Xét
1
2
0
1dI x xx
= −
∫
. Đặt
2
1 1 d 2 dtt xx t x t= −⇒=− ⇒ =−
.
Khi
0 1; 1 0x tx t=⇒= =⇒=
.
Khi đó
( )
( )
0
0
53
2
2
1
1
22 4
1 2d
5 3 15
tt
I tt tt

=−− =− =


∫
.
Thây vào
(
)
44
1 :2 3
15 15
II I
− = ⇔=−
.
Câu 142: Xét hàm số
(
)
fx
liên tục trên
[
]
1; 2−
và thỏa mãn
(
)
(
)
( )
23
2 231 4
f x xf x f x x+ −+ −=
.
Tính giá trị của tích phân
( )
2
1
I f x dx
−
=
∫
.
A.
5I =
. B.
5
2
I =
. C.
3I =
. D.
15I =
.
Hướng dẫn giải
Chọn C
Cách 1: (Dùng công thức – Dạng 2)
Với:
( )
( )
( )
( )
23
2 2 31 4fx xfx f x x+ −+ −=
. Ta có:
1; 1; 3ABC= = =
và
2
2ux= −
thỏa mãn
( )
( )
11
22
u
u
−=−
=
.
Khi đó áp dụng công thức có:
( )
2
22
4
3
11
1
1
4 dx 3
113 5
x
I fx x
−−
−
= = = =
++
∫∫
.
Cách 2: (Dùng phương pháp đổi biến – nếu không nhớ công thức)
Từ
( )
(
)
( )
23
2 231 4f x xf x f x x+ −+ −=
.
( )
( )
( ) ( )
22 2 2
23
11 1 1
dx 2 . 2 dx 3 1 dx 4 dx *f x xf x f x x
−− − −
⇒ + −+ −=
∫∫ ∫ ∫
+) Đặt
2
2 du 2 dxux x= −⇒ =
; với
11xu=−⇒ =−
và
22xu=⇒=
.
Khi đó
( )
( ) ( ) ( )
2 22
2
1 11
2 . 2 dx du dx 1xf x f u f x
− −−
−= =
∫ ∫∫
+) Đặt
1 dt dxtx=−⇒ =−
; Với
12xt=−⇒ =
và
21xt= ⇒=−
.
Khi đó
( ) ( ) ( ) ( )
2 22
1 11
1 dx dt dx 2f x ft fx
− −−
−= =
∫ ∫∫
https://toanmath.com/
Thay
( )
(
)
1,2
vào
( )
*
ta được:
( ) ( )
22
11
5 dx 15 dx 3fx fx
−−
=⇒=
∫∫
.
Câu 143: Hàm số
(
)
fx
liên tục trên
[ ]
1; 2−
và thỏa mãn điều kiện
( )
( )
2
2 3.
f x x xf x= ++ −
Tính
giá trị của
(
)
2
1
d
I fxx
−
=
∫
A.
14
3
I =
. B.
28
3
I =
. C.
4
3
I =
. D.
2I =
.
Hướng dẫn giải
Chọn B
Cách 1: ( Dùng công thức).
Với
( )
( )
2
23f x x xf x
= ++ −
( ) ( )
( )
2
1
. 2x . 3 2
2
fx f x x⇒ +− −=+
1
1; ; 0
2
AB C= = =
và
2
3
ux= −
thỏa mãn
( )
( )
12
21
u
u
−=
= −
Khi đó áp dụng công thức ta có:
( )
22
11
1 28
d 2d =
1
3
10
2
I fxx x x
−−
= = +
−+
∫∫
.
Cách 2: ( Dùng phương pháp đổi biến).
Từ
( )
( )
2
32f x xf x x− −=+
( )
( )
22 2
2
11 1
14
d 3 d 2d
3
f x x xf x x x x
−− −
⇒ − − = +=
∫∫ ∫
(*)
Đặt
2
3 d 2du x u xx=−⇒ =−
với
12
21
xu
xu
=−⇒ =
=⇒=−
Khi đó
( )
2
2
1
3dxf x x
−
−=
∫
(
) ( )
22
11
11
dd
22
fu u fx x
−−
=
∫∫
thay vào (*) ta được
( ) ( ) ( )
22 2
11 1
1 14 28
dx d d =
23 3
fx fx x fx x
−− −
−=⇔
∫∫ ∫
.
Câu 144: Xét hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn
( )
(
)
( )
2
1
1 31
1
f x xf x f x
x
+ − + −=
+
. Tính
giá trị của tích phân
( )
1
0
d
I fx x=
∫
.
A.
9
ln 2
2
I
=
. B.
2
ln 2
9
I =
. C.
4
3
I =
. D.
3
2
I =
.
Hướng dẫn giải
Chọn B
Cách 1: (Dùng công thức)
Với:
( ) ( )
( )
( )
2
1
.2 1 31 2
2
fx xf x f x x− − − + −=
. Ta có:
1A =
;
1
2
B
−
=
; và
2
2ux= −
thỏa mãn
( )
( )
01
10
u
u
=
=
.
Khi đó áp dụng công thức ta có:
( )
1
0
dI fx x=
∫
1
0
1d
1
1
13
2
x
x
=
+

−− +


∫
1
2
ln 1
0
9
x= +
2
ln 2
9
=
.
Cách 2: (Dùng công thức đổi biến nếu không nhớ công thức)
https://toanmath.com/
Từ
( )
( )
(
)
2
1
1 31
1
f x xf x f x
x
+ − + −=
+
( )
(
)
(
)
11 1
2
00 0
d 1 d3 1 d
fxx xf x x f xx
⇒ + −+ −
∫∫ ∫
1
0
1
d
1
x
x
=
+
∫
1
0
ln 1 ln 2
x
= +=
. (*)
+) Đặt
2
1
ux= −
2du xdx
⇒=−
; Với
01xu=⇒=
và
10
xu=⇒=
.
Khi đó
( )
( ) ( )
1 11
2
0 00
11
1d d d
22
xf x x f u u f x x−= =
∫ ∫∫
(1).
+) Đặt
1ux= −
dd
u xx⇒=−
; Với
01xt=⇒=
và
10xt=⇒=
.
Khi đó
( ) ( ) ( )
1 11
0 00
1d d dxf xx ftt ft t−= =
∫ ∫∫
(2).
Thay (1), (2) vào (*) ta được:
(
)
( )
( )
1 11
0 00
1
d d 3 d ln 2
2
fxx fxx fxx+ +=
∫ ∫∫
(
)
1
0
9
d ln 2
2
fxx⇒=
∫
( )
1
0
2
d ln 2
9
fxx⇔=
∫
.
Câu 145: Cho hàm số
( )
y fx=
và thỏa mãn
( )
( )
3
34
2
80
1
x
f x xf x
x
− +=
+
. Tích phân
(
)
1
0
2ab
I f x dx
c
−
= =
∫
với
,,abc∈
và
;
ab
cc
tối giản. Tính
abc++
A.
6
. B.
4−
. C.
4
. D.
10−
.
Hướng dẫn giải
Chọn A
Cách 1: (Dùng công thức).
Biến đổi
( )
( )
3
34
2
80
1
x
f x xf x
x
− +=
+
( )
( ) ( )
3
34
2
2. 4
1
x
fx x fx
x
⇔− =−
+
với
1; 2AB
= = −
Áp dụng công thức ta có:
(
)
(
)
1 11
33
22
0 00
1
12
11
x x dx
f x dx dx
xx

=−=

+−
++

∫ ∫∫
.
Đặt
2 22
11t x t x tdt xdx= +⇒ = +⇒ =
; Với
01xt=⇒=
và
12xt=⇒=
.
Khi đó:
( )
11
2
2
00
.
1
x
f x dx xdx
x
=
+
∫∫
2
2
1
1
.
t
tdt
t
−
=
∫
(
)
2
2
1
1t dt= −
∫
2
3
1
3
t
t

= −


22
3
−
=
2ab
c
−
=
Suy ra
2; 1; 3 6a b c abc= = =⇒++=
.
Cách 2: (Dùng phương pháp đổi biến – nếu không nhớ công thức)
Từ
( )
( )
3
34
2
80
1
x
f x xf x
x
− +=
+
(
)
(
)
11 1
3
34
2
00 0
2 4 0 (*)
1
x
f x dx x f x dx dx
x
⇔− + =
+
∫∫ ∫
Đặt
43
4u x du x dx=⇒=
; Với
00xu=⇒=
và
11xu
=⇒=
.
Khi đó
( )
( ) ( )
1 11
34
0 00
4x f x dx f u du f x dx= =
∫ ∫∫
thay vào (*), ta được:
( )
( )
1 11
3
2
0 00
20
1
x
f x dx f x dx dx
x
−+ =
+
∫ ∫∫
( )
11
3
2
00
1
x
f x dx dx
x
⇔=
+
∫∫
Đặt
2 22
11t x t x tdt xdx= +⇒ = +⇒ =
; Với
01xt=⇒=
và
12xt=⇒=
.
Khi đó:
( )
11
2
2
00
.
1
x
f x dx xdx
x
=
+
∫∫
2
2
1
1
.
t
tdt
t
−
=
∫
( )
2
2
1
1t dt= −
∫
2
3
1
3
t
t

= −


22
3
−
=
2ab
c
−
=
Suy ra
2; 1; 3 6a b c abc= = =⇒++=
.
https://toanmath.com/
Câu 146: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
ln 2;ln 2−
và thõa mãn
( ) (
)
1
1
x
fx f x
e
+ −=
+
. Biết
(
)
ln 2
ln 2
d ln 2 ln3fx x a b
−
= +
∫
, với
,ab
∈
. Tính giá trị của
Pab= +
.
A.
1
2
P
=
. B.
2P = −
. C.
1P = −
. D.
2P =
.
Hướng dẫn giải
Chọn A
Cách 1: Dùng công thức
Với
( ) ( )
1
1
x
fx f x
e
+ −=
+
ta có
1; 1AB= =
, suy ra
( )
ln 2 ln 2 ln2
ln 2 ln 2 ln2
1 d1d
d
11 1 2 1
xx
xx
fx x
ee
− −−
= =
++ +
∫ ∫∫
Cách 2: Dùng phương pháp dồn biến nếu không nhớ công thức
Từ
(
) (
) ( ) ( ) (
)
ln 2 ln 2 ln 2
ln 2 ln 2 ln 2
1d
dd*
11
xx
x
fx f x fx x f x x
ee
−− −
+ −= ⇒ + − =
++
∫∫ ∫
Đặt
ddux u x=−⇒ =−
( )
( ) ( )
ln 2 ln 2 ln 2
ln 2 ln 2 ln 2
d du d
f xx fu fxx
− −−
⇒ −= =
∫ ∫∫
thay vào
( )
*
ta được:
( ) ( )
ln 2 ln 2 ln 2 ln 2
ln 2 ln 2 ln 2 ln 2
d 1d
2d d
1 21
xx
xx
fx x fx x
ee
− −− −
=⇔=
++
∫ ∫∫ ∫
Đặt
d
xx
te dtex=⇒=
Với
1
ln 2 , ln 2 2
2
x tx t=− ⇒= = ⇒=
( )
(
)
2
ln 2 ln 2 2
1
1
ln 2 ln 2
2
2
d dd
ln ln 2
1 11
1
x
x
xx
x ex t t
e tt t
ee
−−
⇒= ===
+ ++
+
∫∫ ∫
Khi đó:
( )
ln 2
,
ln 2
11
d ln 2 ln 2 ln3 , 0
22
ab
fx x a b a b
∈
−
= = + →= =
∫
1
2
Pab⇒ =+=
.
Câu 147: Biết hàm số
2
y fx

= +


π
là hàm số chẵn trên đoạn
;
22

−


ππ
và
( )
sin cos
2
fx fx x x

+ += +


π
. Tính
( )
2
0
I f x dx=
∫
π
.
A.
0I =
. B.
1I =
. C.
1
2
I =
. D.
1I = −
.
Hướng dẫn giải:
Đặt
2
t x dt dx= −⇒ =−
π
Đổi cận:
( )
0
22
00
2
.
2 22
I f t dt f t dt f x dx
 
⇒= − − = − = −
 
 
∫ ∫∫
ππ
π
π ππ
(Tích
phân xác định không phụ thuộc vào biến số tích phân)
2
0
2
fx

= +


∫
π
π
Vì
2
fx

+


π
là hàm số chẵn
22
f xf x

⇒ += −


ππ
https://toanmath.com/
Vậy
(
)
(
)
(
)
22
2
00
0
2 sin cos cos sin 1 1 2
2
I f x f x dx x x dx x x


= + + = + = − =−−=−




∫∫
ππ
π
π
1I⇒=−
⇒ Chọn D
Câu 148: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
,
(
)
00f =
và
( )
sin .cos
2
fx f x x x
π

+ −=


với
x∀∈
. Giá trị của tích phân
( )
2
0
xf x dx
π
′
∫
bằng
A.
4
π
−
. B.
1
4
. C.
4
π
. D.
1
4
−
.
Hướng dẫn giải
Cách 1: (Dùng công thức)
Với
( )
sin .cos
2
fx f x x x
π

+ −=


, ta có
1; 1AB= =
.
Suy ra
( )
22
00
11
sin .cos .
11 4
f x dx x x dx
ππ
= =
+
∫∫
.
Cách 2: (Dùng phương pháp đổi biến – nếu nhớ công thức)
Từ
( )
sin .cos
2
fx f x x x
π

+ −=


(
)
22 2
00 0
1
sin .cos
22
f x f x dx x xdx
ππ π
π

⇒ + −= =


∫∫ ∫
(*)
Đặt
2
u x du dx
π
= −⇒ =−
Với
0; 0
22
x ux u
ππ
=⇒= = ⇒=
.
Suy ra
( ) ( )
2 22
0 00
2
f x dx f u du f x dx
π ππ
π

−= =


∫ ∫∫
, thay vào (*) ta được
( ) ( )
22
00
11
2
24
f x dx f x dx
ππ
=⇔=
∫∫
(1)
Đặt
(
) ( )
u x du dx
dv f x dx v f x
= =


⇒

′
= =


( )
( )
( )
( )
2
2 22
0 00
0
22
xf x dx xf x f x dx f f x dx
π
π ππ
ππ

′
⇒ =−=−


∫ ∫∫
(*)
Từ điều kiện
( )
sin .cos
2
fx f x x x
π

+ −=


suy ra
( )
( )
00
2
0
2
00
2
ff
f
ff
π

−=

π


⇒=

π


+=


(2).
Thay (1), (2) vào (*), ta được
(
)
2
0
1
4
xf x dx
π
′
= −
∫
.
Chọn D
Câu 149: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( ) ( )
2
2
1 2x 1 2x ,
1
x
ff x
x
+ + − = ∀∈
+
. tính
tích phân
( )
3
1
I f x dx
−
=
∫
.
A.
2
2
I
π
= −
. B.
1
4
I
π
= −
. C.
1
28
I
π
= −
. D.
4
I
π
=
.
Hướng dẫn giải.
Đặt
12 12 2t x xt=+ ⇒− = −
và
1
2
t
x
−
=
, khi đó điều kiện trở thành
https://toanmath.com/
( ) ( )
( ) ( )
22
22
21 2 1
22
25 2 5
tt xx
ft f t fx f x
tt xx
−+ − +
+−= ⇒ +−=
−+ − +
(*)
Cách 1: (Dùng công thức)
Với
(
) (
)
2
2
21
2
25
xx
fx f x
xx
−+
+ −=
−+
ta có
1; 1AB= =
.
Suy ra
( )
2
33
2
11
1 21
0,429 2
11 2 5 2
xx
f x dx dx
xx
−−
−+ π
= ≈=−
+ −+
∫∫
Chọn A
Cách 2: (Dùng công thức đổi biến – nếu nhớ công thức)
Từ (*), ta có
( ) ( )
2
2
21
2
25
xx
fx f x
xx
−+
+ −=
−+
( ) ( )
2
33 3
2
11 1
21
2
25
xx
f x dx f x dx dx
xx
−− −
−+
⇒ + −=
−+
∫∫ ∫
(2*)
Đặt
2
u x du dx
=−⇒ =−
. Với
1 3; 3 1x ux u=−⇒= =⇒=−
.
Suy ra
( ) ( ) ( )
3 33
1 11
2f x dx f u du f x dx
− −−
−= =
∫ ∫∫
, thay vào (*), ta được:
( )
2
33
2
11
21
2
25
xx
f x dx dx
xx
−−
−+
=
−+
∫∫
( )
2
33
2
11
1 21
0,429 2 -
2 25 2
xx
f x dx dx
xx
−−
−+ π
⇒ = ≈=
−+
∫∫
https://toanmath.com/
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 3
Cách giải: Lần lượt đặt
( )
t ux=
và
( )
t vx=
để giải hệ phương trình hai ẩn (trong đó có ẩn
( )
fx
) để
suy ra hàm số
(
)
fx
(nếu
( )
ux x=
thì chỉ cần đặt một lần
( )
t vx=
).
Các kết quả đặc biệt:
Cho
(
) ( ) ( )
..A f ax b B f ax c g x++ −+=
với
22
AB≠
) khi đó
( )
22
..
xb xc
Ag Bg
aa
fx
AB
−−

−

−

=
−
(*)
+)Hệ quả 1 của (*):
( ) (
)
( )
( )
( ) ( )
22
..
..
Ag x Bg x
Afx Bf x gx fx
AB
−−
+ −= ⇒ =
−
+)Hệ quả 2 của (*):
( ) ( )
(
) (
)
( )
..
gx
Afx Bf x gx fx
AB
+ −= ⇒ =
+
với
( )
gx
là hàm số chẵn.
Câu 150: Cho hàm số
( )
y fx=
liên tục trên
và
( )
1
23fx f x
x

+=


. Tính
(
)
2
1
2
fx
I dx
x
=
∫
.
A.
3
2
I =
. B.
1I =
. C.
1
2
I
=
. D.
1I = −
.
Hướng dẫn giải
Chọn A
Đặt,
11
tx
xt
=⇒=
khi đó điều kiện trở thành
( ) ( )
1 3 13
22 .f ft fx f
t t xx

+=⇒ +=


Hay
( )
16
42fx f
xx

+=


, kết hợp với điều kiện
( )
1
23fx f x
x

+=


. Suy ra :
( )
( )
2
62
3 3x 1
fx
fx
x xx
= − ⇒ = −⇒
( )
22
2
11
22
2
2 23
1
1
2
2
fx
I dx dx x
xx x
−

= = −=−=
∫∫


.
Chọn B
Câu 151: Cho hàm số
( )
y fx=
liên tục trên
{ }
\0
và thỏa mãn
( )
2 15
23 3
2
x
fx f
x

+=−


,
(
)
9
3
dfx x k=
∫
. Tính
3
2
1
2
1
dIf x
x

=


∫
theo
k
.
A.
45
9
k
I
+
= −
. B.
45
9
k
I
−
=
. C.
45
9
k
I
+
=
. D.
45 2
9
k
I
−
=
.
Hướng dẫn giải
Chọn A
Đặt
2tx=
⇒
1
dd
2
xt=
. Đổi cận
1
1
2
3
3
2
xt
xt
= ⇒=
= ⇒=
.
Khi đó
3
1
12
d
2
Ifx
t

=


∫
.
Mà
( )
2 15
23 3
2
x
fx f
x

+=−


⇔
( )
2 52
3
23
x
f fx
x

=−−


Nên
( ) ( ) ( )
3 33 3
1 11 1
1 52 5 1 1
3 d d 3d 5 3d
2 23 4 3 3
x
I fx x xx fxx fxx

= − − =− − =−−


∫ ∫∫ ∫
(*)
https://toanmath.com/
Đặt
3
ux=
⇒
1
dd
3
xx=
. Đổi cận
13
39
xu
xt
=⇒=
=⇒=
.
Khi đó
(
)
9
3
1 45
5 d5
9 99
kk
I ft t
+
=−− =−− =−
∫
.
Câu 152: Cho hàm số
(
)
y fx=
liên tục trên
và thỏa mãn
( ) ( )
2018 2 sinf x fx x x−+ =
. Tính giá
trị của
( )
2
2
dI fx x
π
π
−
=
∫
.
A.
2
2019
I =
. B.
2
1009
I
=
. C.
4
2019
I =
. D.
1
1009
I
=
.
Hướng dẫn giải
Chọn C
Cách 1: (Dùng công thức)
Với
(
)
(
)
2018 2 sin
f x fx x x−+ =
ta có
1; 2018AB
= =
Suy ra
( )
2
2
dI fx x
π
π
−
=
∫
2
2
1
2 sin d
1 2018
x xx
π
π
−
=
+
∫
4
2019
Casio
=
⇒
Đáp án C
Cách 2:
Áp dụng Hệ quả 2:
( ) ( ) ( )
.A f x Bf x g x+ −=
( )
(
)
gx
fx
AB
⇒=
+
với
(
)
gx
là hàm số chẵn.
Ta có
( ) ( )
2018 2 sinf x fx x x
−+ =
( )
2 sin
2019
xx
fx⇒=
( )
2
2
dI fx x
π
π
−
=
∫
2
2
2
sin d
2019
x xx
π
π
−
=
∫
4
2019
Casio
=
⇒
Đáp án C
Câu 153: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
2018
x
f x fx e−+ =
. Tính giá trị
của
( )
1
1
I f x dx
−
=
∫
A.
2
1
2019e
e
I
−
=
. B.
2
1
2018e
e
I
−
=
. C.
0I =
. D.
2
1e
I
e
−
=
.
Hướng dẫn giải
Chọn A
Cách 1: (Dùng công thức).
Với
( ) (
)
2018
x
f x fx e
−+ =
ta có
1; 2018AB= =
.
Suy ra
( )
1
1
I f x dx
−
=
∫
1
1
1
1 2018
x
e dx
−
=
+
∫
1
1
1
2019
x
e
−
=
2
1
2019e
e −
=
.
Cách 2: (Dùng công thức)
Áp dụng Hệ quả 1:
( ) ( ) ( )
..Af x Bf x g x+ −=
( )
( ) ( )
22
..Ag x Bg x
fx
AB
−−
⇒=
−
.
Ta có:
( ) ( )
2018
x
f x fx e−+ =
( )
2
2018
2018 1
xx
ee
fx
−
−
⇒=
−
( )
( )
11
11
1
2018
2019.2017
xx
f x dx e e dx
−
−−
⇒= −
∫∫
https://toanmath.com/
2
3
1
1,164.10
2019e
e
−
−
≈≈
(Casio).
Câu 154: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
, thỏa mãn
( ) ( )
2
2 2 1 12fx f x x+ −=
.
Phương trình tiếp tuyến của đồ thị hàm số
( )
y fx=
tại điểm có hoành độ bằng
1
là
A.
22yx= +
. B.
46
yx
= −
. C.
26
yx
= −
. D.
42yx
= −
.
Hướng dẫn giải
Chọn C
Áp dụng kết quả
“Cho
( ) ( ) ( )
..A f ax b B f ax c g x++ −+=
(với
22
AB≠
) khi đó
( )
22
. .g
xb xc
Ag B
aa
fx
AB
−−

−


=
−
”.
Ta có
( ) (
)
( )
2
2 2 1 12f x f x x gx+ −= =
(
)
2
1
2.
22
21
xx
gg
fx
−

−

−

⇔=
−
( )
2
2
2
631
21
3
xx
xx
−−
= =+−
.
Suy ra
( )
( )
12
14
f
f
=
′=
, khi đó phương trình tiếp tuyến cần lập là:
42yx= −
.
Câu 155: Cho
( )
fx
là hàm số chẵn, liên tục trên
thỏa mãn
( )
1
0
2018=
∫
f x dx
và
( )
gx
là hàm số
liên tục trên
thỏa mãn
( ) ( )
1+ −=gx g x
,
∀∈x
. Tính tích phân
( ) ( )
1
1−
=
∫
I f x g x dx
.
A.
2018
=I
. B.
1009
2
=I
. C.
4036=I
. D.
1008=
I
.
Hướng dẫn giải
Chọn A
Áp dụng Hệ quả
(
) ( )
(
)
..
+ −=Ag x Bg x h x
( )
( )
⇒=
+
hx
gx
AB
với
(
)
hx
là hàm số chẵn.
Ta có:
( ) ( ) ( )
1+ −==gx g x hx
( )
11
11 2
⇒==
+
gx
.
Kết hợp với điều kiện
( )
fx
là hàm số chẵn, ta có:
( ) ( )
( )
11
11
1
2
−−
= =
∫∫
I f x g x dx f x dx
( )
1
0
2018= =
∫
f x dx
.
Chú ý: Nếu
(
)
fx
là hàm số chẵn, liên tục trên
[ ]
( ) ( )
0
;2
−
−⇒ =
∫∫
aa
a
a a f x dx f x dx
.
Câu 156: Cho số dương
a
và hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
fx f x a+ −=
,
x∀∈
.
Giá trị của biểu thức
( )
d
a
a
fx x
−
∫
bằng
A.
2
2a
. B.
a
. C.
2
a
. D.
2a
.
Hướng dẫn giải
Chọn C
https://toanmath.com/
Đặt
(
)
( )
(
) (
) (
)
d d dd
aa aa
aa a a
x t fxx f t t f tt f xx
−
− −−
=−⇒ = − − = − = −
∫∫ ∫ ∫
(
)
( ) ( ) ( ) (
)
22
2d dd2d2 d
a a aa a
a a aa a
fx x fx f x x ax fx x a fx x a
− − −− −
⇒ = +− = ⇔ = ⇔ =


∫ ∫ ∫∫ ∫
.
Câu 157: Cho hàm số
( )
fx
liên tục trên
thỏa điều kiện
( ) ( )
2sinfx f x x+ −=
. Tính
( )
2
2
dfx x
π
π
−
∫
A.
1−
. B.
0
. C.
1
. D.
2
.
Hướng dẫn giải
Chọn B
Giả sử
( )
2
2
dI fx x
π
π
−
=
∫
.
Đặt
tx= −
ddtx⇒=−
, đổi cận
22
xt
ππ
=− →=
22
xt
ππ
= →=−
.
Khi đó
( )
( )
22
22
ddI ft t ft t
ππ
ππ
−
−
=−=
∫∫
.
Suy ra
( ) ( )
2
2
2
dI fx f x x
π
π
−
= +−


∫
2
2
2sin 0
dxx
π
π
−
= =
∫
20I⇒=
0I⇒=
Câu 158: Cho
()fx
là một hàm số liên tục trên thỏa mãn
( ) ( )
2 2cos2fx f x x+ −= −
. Tính tích
phân
(
)
3
2
3
2
dI fx x
π
π
−
=
∫
.
A.
3I =
. B.
4I =
. C.
6I =
. D.
8I =
.
Hướng dẫn giải
Chọn C
Ta có
( )
( )
( )
33
0
22
33
0
22
d ddI fx x fx x fx x
ππ
ππ
−−
= = +
∫ ∫∫
.
Xét
(
)
0
3
2
d
fx x
π
−
∫
Đặt
ddtx t x=−⇒ =−
; Đổi cận:
33
22
xt
ππ
=− ⇒=
;
00xt= ⇒=
.
Suy ra
( ) ( ) ( ) ( )
33
00
22
33
00
22
d dt d dfxx f t f tt f xx
ππ
ππ
−
=− −= −= −
∫ ∫∫∫
.
https://toanmath.com/
Theo giả thiết ta có:
(
) (
)
( )
( )
( )
33
22
00
2 2cos 2 d 2 2cos dfx f x x fx f x x xx
ππ
+−= − ⇔ +− = −
∫∫
( )
( )
33 3
22 2
00 0
d d 2 sin dfxx f xx xx
ππ π
⇔ +−=
∫∫ ∫
( ) ( )
33
0
22
3
0 00
2
d d 2 sin d 2 sin dfx x f x x xx xx
ππ
π
π
−
⇔+ =−
∫∫ ∫∫
Câu 159: Cho hàm số
( )
y fx=
liên tục trên R và thỏa mãn
( ) ( )
2 2cos2fx f x x+ −= +
. Tính
( )
2
2
I f x dx
−
=
∫
π
π
.
A.
1I = −
. B.
1I =
. C.
2I = −
. D.
2I =
.
Hướng dẫn giải
(
)
2
2
I f x dx
−
=
∫
π
π
(1) Đặt
t x dt dx=−⇒ =−
Đổi cận:
( ) ( )
( )
( )
2 22
2 22
.I f t dt f t dt f x dx
−
−−
⇒= − − = − = −
∫ ∫∫
π ππ
π ππ
(2) (Tích phân xác định không phụ thuộc vào
biến số tích phân)
(1) + (2)
( ) ( )
22
22
2 2 2cos 2I f x f x dx xdx
−−
⇒= +− = +


∫∫
ππ
ππ
( )
2
2
2 1 cos2x dx
−
=+=
∫
π
π
( )
2 22
2
2
2
2 22
2 2cos 2 cos 2 cos 2sin 2 1 1 4xdx x dx xdx x
−
− −−
= = = = −− =


∫ ∫∫
π ππ
π
π
π ππ
2I⇒=
Chọn D
Câu 160: Cho hàm số liên tục trên và . Tính
A. . B. . C. . D. .
Hướng dẫn giải
Chọn D
( )
fx
( ) (
)
2
3 2 tanf x fx x−− =
( )
π
4
π
4
dfx x
−
∫
π
1
2
−
π
1
2
−
π
1
4
+
π
2
2
−
https://toanmath.com/
Cách 1: Ta có
.
Đặt , đổi cận , .
Suy ra,
Vậy
Cách 2: ( Trắc nghiệm)
Chọn (Thỏa mãn giả thiết).
Khi đó
Câu 161: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
ln 2;ln 2−
và thỏa mãn
( ) (
)
1
1
x
fx f x
e
+ −=
+
.
Biết
( )
ln 2
ln 2
d ln 2 ln3fx x a b
−
= +
∫
(
)
;ab∈
. Tính
Pab= +
.
A.
1
2
P =
. B.
2P = −
. C.
1P = −
. D.
2P
=
.
Hướng dẫn giải
Chọn A
Gọi
( )
ln 2
ln 2
dI fx x
−
=
∫
.
Đặt
tx
= −
⇒
d dt x= −
.
Đổi cận: Với
ln 2x = −
⇒
ln 2
t =
; Với
ln 2
x =
⇒
ln 2t = −
.
Ta được
( )
ln 2
ln 2
dI f tt
−
=−−
∫
( )
ln 2
ln 2
df tt
−
= −
∫
( )
ln 2
ln 2
df xx
−
= −
∫
.
Khi đó ta có:
2I
( )
( )
ln 2 ln 2
ln 2 ln 2
ddfxx f xx
−−
= +−
∫∫
( ) ( )
ln 2
ln 2
dfx f x x
−
== +−


∫
ln 2
ln 2
1
d
e1
x
x
−
=
+
∫
.
Xét
ln 2
ln 2
1
d
e1
x
x
−
+
∫
. Đặt
e
x
u =
⇒
d ed
x
ux=
Đổi cận: Với
ln 2x = −
⇒
1
2
u =
;
ln 2x =
2u⇒=
.
π
4
2
π
4
tan d
xx
−
∫
4
2
4
1
1d
cos
x
x
π
π
−

= −


∫
( )
π
4
π
4
tan xx
−
= −
ππ
11
44

=− −−+


π
2
2
= −
( )
( )
π
4
π
4
π
2 3 2d
2
f x fx x
−
⇒− = − −


∫
dd
tx t x
=−⇒ =−
ππ
44
xt
=− ⇒=
ππ
44
xt= ⇒=−
( ) ( )
π
4
π
4
3 2df x fx x
−
−−


∫
( ) ( )
π
4
π
4
32 dft f t t
−
= −−


∫
( ) ( )
π
4
π
4
32 dfx f x x
−
= −−


∫
(
)
( )
ππ
44
ππ
44
ddfxx f xx
−−
= −
∫∫
( ) ( )
π
4
π
4
π
2 3 2d
2
fx fx x
−
⇒− = −


∫
(
)
π
4
π
4
π
2d
2
fx x
−
⇔− =
∫
( )
π
4
π
4
π
d2
2
fx x
−
= −
∫
( ) ( )
2
tanfx f x x= −=
( )
ππ π
44 4
2
2
ππ π
44 4
1
d tan x d 1 d 2
cos 2
fx x x x
x
π
−− −

= = −=−


∫∫∫
https://toanmath.com/
Ta được
ln 2
ln 2
1
d
e1
x
x
−
+
∫
(
)
ln 2
ln 2
e
d
ee 1
x
xx
x
−
=
+
∫
( )
ln 2
ln 2
1
d
1
u
uu
−
=
+
∫
ln 2
ln 2
11
d
1
u
uu
−

= −

+

∫
( )
2
1
2
ln ln 1
uu
= −+
ln 2=
Vậy ta có
1
2
a =
,
1
0
2
b ab=⇒+=
.
Câu 162: Xét hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
( ) ( )
2 31 1+ −= −fx f x x x
.
Tính tích phân
( )
1
0
=
∫
I f x dx
.
A.
4
15
= −I
. B.
1
15
=I
. C.
4
75
=I
. D.
1
25
=I
.
Hướng dẫn giải
Chọn C
Cách 1: (Dùng công thức)
Với
( ) ( )
2 31 1+ −= −fx f x x x
ta có
2; 3
= =AB
.
Suy ra:
( )
11
00
1
1
23
= −
+
∫∫
f x dx x xdx
( )
4
0,05 3
75
= =
Casio
.
Áp dụng kết quả
“Cho
( ) ( ) ( )
..++ −+=A f ax b B f ax c g x
(Với
22
≠
AB
) khi đó
( )
22
..
−−

−

−

=
−
xb xc
Ag Bg
aa
fx
AB
”
.
Ta có:
( ) ( ) ( )
2 31 1+ − = −=f x f x x x gx
( )
( ) ( )
22
2 31
23
−−
⇒=
−
gx g x
fx
( )
2 1 31
5
−− −
=
−
x x xx
.
Suy ra:
( )
( )
11
00
2 1 31
5
−− −
= =
−
∫∫
x x xx
I f x dx dx
(
)
4
0,05 3
75
= =
Casio
.
Cách 3: (Dùng phương pháp đổi biến – nếu không nhớ công thức)
Từ
( ) ( )
2 31 1+ −= −fx f x x x
( ) ( )
11 1
00 0
2 31 1⇒ + −=−
∫∫ ∫
f x dx f x dx x xdx
( ) ( )
4
0,2 6
15
= = ∗
Casio
Đặt
1=−⇒ =−u x du dx
; Với
01=⇒=xu
và
10=⇒=xu
.
Suy ra
( ) ( ) (
)
1 11
0 00
1−= =
∫ ∫∫
f x dx f u du f x dx
thay vào
( )
∗
, ta được:
( ) ( )
22
00
44
5
15 75
=⇔=
∫∫
f x dx f x dx
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 4
Câu 163: Cho
( )
fx
và
( )
gx
là hai hàm số liên tục trên
[ ]
1,1−
và
( )
fx
là hàm số chẵn,
( )
gx
là
hàm số lẻ. Biết
( )
1
0
5f x dx =
∫
và
( )
1
0
7g x dx =
∫
. Mệnh đề nào dưới đây sai?
A.
( )
1
1
10f x dx
−
=
∫
. B.
( )
1
1
14g x dx
−
=
∫
.
https://toanmath.com/
C.
( ) ( )
1
1
10f x g x dx
−
+=


∫
. D.
(
) (
)
1
1
10f x g x dx
−
−=


∫
.
Hướng dẫn giải
Nhớ 2 tích chất sau để làm trắc nghiệm nhanh:
Câu 164: Nếu hàm
( )
fx
CHẴN thì
(
)
( )
0
2
aa
a
f x dx f x dx
−
=
∫∫
2. Nếu hàm
( )
fx
LẺ thì
(
)
0
a
a
f x dx
−
=
∫
Nếu chứng minh thì như sau:
Đặt
(
) ( ) ( )
1
2
1 01
1 10
A
A
A f x dx f x dx f x dx
−−
= = +
∫∫∫


( )
0
1
1
A f x dx
−
=
∫
. Đặt
tx= −
dt dx
⇒=−
Đổi cận:
( ) ( ) (
)
( )
0 11
1
1 00
.
A f t dt f t dt f x dx⇒= − −= − = −
∫ ∫∫
(Do tích phân xác định không phụ thuộc vào biến
số tích phân)
( )
1
0
f x dx=
∫
(Do
( )
fx
là hàm chẵn
( ) ( )
f x fx⇒ −=
)
Vậy
( )
( ) (
)
1 11
100
10A f x dx f x dx f x dx
−
= =+=
∫∫∫
(1)
Đặt
( )
( ) (
)
1
2
1 01
1 10
B
B
B g x dx g x dx g x dx
−−
= = +
∫∫∫


( )
0
1
1
B g x dx
−
=
∫
. Đặt
tx= −
dt dx⇒=−
Đổi cận:
( ) ( ) ( ) ( )
0 11
1
1 00
.B g t dt g t dt g x dx⇒= −−= − = −
∫ ∫∫
(Do tích phân xác định không phụ thuộc vào biến
số tích phân)
( )
1
0
g x dx= −
∫
(Do
( )
fx
là hàm chẵn
( ) ( )
g x gx⇒ −=−
)
Vậy
( ) ( ) ( )
1 11
1 00
0B g x dx g x dx g x dx
−
= =−+ =
∫ ∫∫
(2)
Từ (1) và (2)
Chọn B
Câu 165: 17TCho hàm số 17T
( )
y fx=
17T là hàm lẻ và liên tục trên 17T
[ ]
4;4−
17T biết 17T
( )
0
2
d2f xx
−
−=
∫
17T và 17T
( )
2
1
2d 4
f xx−=
∫
17T. Tính 17T
( )
4
0
dI fx x=
∫
17T.
17TA. 17T
10I = −
. 17TB. 17T
6I = −
. 17TC. 17T
6I =
. 17TD. 17T
10I =
.
17THướng dẫn giải
17TChọn B
17TCách 1: Sử dụng công thức: 17T
( ) ( )
22
11
1
dd
xx
xx
f ax b x f ax x
a
+=
∫∫
17T và tính chất 17T
( )
d0
a
a
fx x
−
=
∫
17T với 17T
( )
fx
17T là
hàm số lẻ trên đoạn 17T
[ ]
;aa−
17T.
https://toanmath.com/
Áp dụng, ta có:
•
( )
(
)
( )
2
42
24
1
11
4 2d d d
22
f xx fxx fxx
−−
−−
=−=− =
∫ ∫∫
(
)
2
4
d8
fx x
−
−
⇔=
∫
.
•
(
)
(
)
(
)
0
02
20
2
2df x x fx fx
−
=−=− =
∫ ∫∫
( )
2
0
2fx⇔=
∫
Suy ra:
( )
( ) ( ) ( )
4 20 4
4 4 20
0d d d dfx x fx x fx x fx x
−
−−−
== ++
∫∫∫∫
( ) (
)
(
)
22
20
08 d d
fx x fx x I
−
⇔=+ − +
∫∫
( )
08 02 6II⇔=+ − +⇔=−
.
Cách 2: Xét tích phân
(
)
0
2
d2f xx
−
−=
∫
.
Đặt
xt−=
d dtx⇒=−
.
Đổi cận: khi
2x = −
thì
2t =
; khi
0x =
thì
0t =
do đó
( ) ( )
00
22
d dtf x x ft
−
−=−
∫∫
( )
2
0
dtft=
∫
(
)
2
0
dt 2
ft
⇒=
∫
( )
2
0
d2fx x⇒=
∫
.
Do hàm số
(
)
y fx=
là hàm số lẻ nên
(
) (
)
22f x fx
−=−
.
Do đó
( ) ( )
22
11
2d 2df xx f xx−=−
∫∫
( )
2
1
2d 4f xx⇒=−
∫
.
Xét
( )
2
1
2df xx
∫
.
Đặt
2xt=
1
d dt
2
x⇒=
.
Đổi cận: khi
1x =
thì
2t =
; khi
2x =
thì
4t =
do đó
( ) ( )
24
12
1
2 d dt 4
2
f x x ft= = −
∫∫
(
)
4
2
dt 8ft⇒=−
∫
( )
4
2
d8
fx x⇒=−
∫
.
Do
( )
4
0
d
I fx x=
∫
(
) ( )
24
02
ddfx x fx x
= +
∫∫
28 6=−=−
.
Câu 166: Cho hàm số chẵn
( )
y fx=
liên tục trên
và
( )
1
1
2
d8
12
x
fx
x
−
=
+
∫
. Tính
( )
2
0
dfx x
∫
.
A.
2
. B.
4
. C.
8
. D.
16
.
Hướng dẫn giải
Chọn D
Ta có
( )
( )
12
12
2
d 8 d 16
12
12
x
x
f x fx
xx
−−
=⇔=
+
+
∫∫
.
Đặt
ddtx t x=−⇒ =−
, khi đó
( )
( )
( )
2 22
2 22
2
16 d dt d
12 12 12
t
x tt
fx f t ft
Ix t
−−
−
−
−
===−=
+ ++
∫ ∫∫
.
Suy ra
( ) ( )
( ) ( )
2 2 22
2 2 20
2
2 d d d2 d
12 12
x
xx
fx fx
I x x fx x fx x
−
−−
=+==
++
∫ ∫ ∫∫
.
Vậy
( )
2
0
d 16fx x=
∫
.
https://toanmath.com/
Câu 167: Cho
( )
fx
là hàm số chẵn liên tục trong đoạn
[ ]
1; 1−
và
(
)
1
1
d2
fx x
−
=
∫
. Kết quả
( )
1
1
d
1e
x
fx
Ix
−
=
+
∫
bằng
A.
1
I =
. B.
3I =
. C.
2
I =
. D.
4I =
.
Hướng dẫn giải
Chọn A
(
)
(
)
(
)
1 01
12
1 10
d dd
1e 1e 1e
x xx
fx fx fx
I x x xI I
−−
= =+=+
+ ++
∫∫∫
Xét
( )
0
1
1
d
1e
x
fx
Ix
−
=
+
∫
Đặt
dd
xt x t=−⇒ =−
,
đổi cận:
00xt= ⇒=
,
11xt=−⇒ =
( )
( )
( )
01
1
10
e.
dd
1e 1e
t
tt
fx fx
Itt
−
= −=
++
∫∫
.
Lại có
( )
(
)
11
00
e. e.
dd
1e 1e
tx
tx
ft fx
tx
=
++
∫∫
.
Suy ra:
(
) ( ) ( )
( )
( )
( ) ( )
1 1 11 1 1
10 00 0 1
1e.
e.
1
d d d d d d1
1e 1e 1e 1e 2
t
t
x tt t
ft
fx ft ft
I x t x t ft t ft t
−−
+
= = += == =
+ ++ +
∫ ∫ ∫∫ ∫ ∫
.
Câu 168: Cho
( )
y fx=
là hàm số chẵn và liên tục trên
.
Biết
( )
( )
12
01
1
d d1
2
fx x fx x= =
∫∫
. Giá trị
của
(
)
2
2
d
31
x
fx
x
−
+
∫
bằng
A.
1
. B.
6
. C.
4
. D.
3
.
Hướng dẫn giải
Chọn D
Cách 1: Sử dụng tính chất của hàm số chẵn
Ta có:
( )
(
)
0
dd
1
aa
x
a
fx
x fx x
b
−
=
+
∫∫
, với
(
)
fx
là hàm số chẵn và liên tục trên
[
]
;
aa−
.
Áp dụng ta có:
( )
( )
( ) ( )
2 2 12
2 0 01
dddd123
31
x
fx
x fx x fx x fx x
−
= = + =+=
+
∫ ∫∫∫
Cách 2: Do
( )
1
0
dfx x=
∫
( )
2
1
1
d1
2
fx x=
∫
( )
1
0
d1fx x⇒=
∫
và
( )
2
1
d2fx x=
∫
( ) ( )
12
01
ddfx x fx x⇒+
∫∫
( )
2
0
d3fx x= =
∫
.
Mặt khác
( )
2
2
d
31
x
fx
x
−
=
+
∫
( )
( )
02
20
dd
31 31
xx
fx fx
xx
−
+
++
∫∫
và
( )
y fx=
là hàm số chẵn, liên tục trên
( ) ( )
f x fx x⇒ − = ∀∈
.
Xét
( )
0
2
d
31
x
fx
Ix
−
=
+
∫
. Đặt
ddtx x t=−⇒ =−
https://toanmath.com/
Suy ra
( )
0
2
d
31
x
fx
Ix
−
= =
+
∫
(
)
0
2
d =
31
t
ft
t
−
−
−
+
∫
( )
2
0
d =
1
1
3
t
ft
t
−
+
∫
( )
2
0
3
d =
31
t
t
ft
t
+
∫
(
)
2
0
3
d
31
x
x
fx
x
+
∫
(
)
2
2
d
31
x
fx
x
−
⇒=
+
∫
( )
( )
02
20
dd
31 31
xx
fx fx
xx
−
+=
++
∫∫
( )
( )
22
00
3
dd
31 31
x
xx
fx fx
xx+=
++
∫∫
( )
(
)
2
0
31
d
31
x
x
fx
x
+
=
+
∫
( )
2
0
d3fx x=
∫
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5
“ Cho hàm số
( )
y fx=
thỏa mãn
( )
gfx x

=

và
( )
gt
là hàm đơn điệu ( luôn đồng biến hoặc
nghịch biến) trên
.Hãy tính tích phân
( )
b
a
I f x dx=
∫
“
Cách giải: Đặt
( )
( ) ( )
y f x x g y dx g y dy
′
= ⇒= ⇒ =
Đổi cận
( )
(
)
x a gy a y
x b gy b y
α
β
=→ =⇔=
=→ =⇔=
Suy ra
(
) (
)
b
a
I f x dx yg y dy
β
α
= =
∫∫
Câu 169: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
(
) (
)
3
,fxfxxx+ = ∀∈
. Tính
( )
2
0
I f x dx=
∫
A.
2I =
. B.
3
2
I =
. C.
1
2
I =
. D.
5
4
I =
.
Hướng dẫn giải
Chọn D
Đặt
(
)
( )
32
31
y f x x y y dx y dy= ⇒= +⇒ = +
Đổi cận
3
3
0 00
2 21
x yy y
x yy y
=→ +=⇔=
=→ +=⇔=
Khi đó
(
)
( )
( )
21 1
23
00 0
5
31 3
4
I f x dx y y dy y y dy
= = += + =⇒
∫∫ ∫
đáp án D
Câu 170: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( ) ( )
32
236f x f x fx x− +=
,
x∀∈
. Tính
tích phân
( )
5
0
dI fx x=
∫
.
A.
5
4
I =
. B.
5
2
I
=
. C.
5
12
I =
. D.
5
3
I =
.
Hướng dẫn giải
Chọn B
Đặt
( )
32
236y fx x y y y= ⇒= − +
( )
2
d 6 1dx yy y⇒ = −+
.
Đổi cận: với
32
02 3 6 0 0x yyy y
=⇒ − + =⇔=
và
32
52 3 6 5 1x yyy y=⇒ − + =⇔=
.
Khi đó
( )
( )
11
2
00
d .6 1 dI fx x y y y y= = −+
∫∫
( )
1
32
0
5
6d
2
y y yy= −+ =
∫
.
https://toanmath.com/
Câu 171: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
3
21x f x fx++ =
,
x∀∈
. Tính
( )
1
2
dI fx x
−
=
∫
.
A.
7
4
I =
. B.
7
2
I =
. C.
7
3
I
=
. D.
5
4
I =
.
Hướng dẫn giải
Chọn A
Đặt
( )
(
)
32
2 1 d 3 2d
y fx x y y x y y= ⇒ =− − +⇒ =− −
.
Đổi cận: Với
3
2 212 1x yy y=−⇒− − +=−⇔ =
;
3
1 2 11 0x yy y= ⇒− − + = ⇔ =
.
Khi đó:
( )
0
2
1
7
3 2d
4
Iyy y= −− =
∫
.
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5
Bài toán: “ Cho
( ) ( )
2
.fxfab x k
+− =
, khi đó
( )
d
2
b
a
x ba
I
k fx k
−
= =
+
∫
Chứng minh:
Đặt
t abx=+−
( )
( )
2
dt dx
k
fx
ft
= −
⇒
=
và
xa tb= ⇒−
;
xb ta=⇒=
.
Khi đó
( )
(
)
( )
( )
2
fd
d d1
bb b
aa a
xx
xx
I
k
k fx k k fx
k
ft
= = =
++
+
∫∫ ∫
.
( )
( )
( )
fd
d1
2
bb
aa
xx
x
I
k fx k k fx
=+=
++
∫∫
(
)
11
d
b
a
x ba
kk
= −
∫
2
ba
I
k
−
⇒=
.
Câu 172: Cho hàm số
( )
fx
liên tục và nhận giá trị dương trên
[ ]
0;1
. Biết
( ) ( )
.1 1fxf x−=
với
[ ]
0;1x∀∈
. Tính giá trí
( )
1
0
d
1
x
I
fx
=
+
∫
A.
3
2
. B.
1
2
. C.
1
. D.
2
.
Hướng dẫn giải
Chọn B
Ta có:
( ) ( ) ( ) ( )
11fx fxf x fx+ = −+
(
)
(
) ( )
1
1 11
fx
fx f x
=⇒
+ −+
Xét
( )
1
0
d
1
x
I
fx
=
+
∫
.
Đặt
11t xx t=−⇔=−
ddxt⇒=−
. Đổi cận:
01xt=⇒=
;
10xt=⇒=
.
Khi đó
( ) ( )
( )
( )
( )
011 1
100 0
d
ddd
11 11 11 1
fx x
ttx
I
ft ft fx fx
=−= = =
+− +− +− +
∫∫∫∫
Mặt khác
( )
( )
( )
( )
11 1 1
00 0 0
d1
d
d d1
1 1 1 ()
fx x fx
x
xx
fx fx ft
+
+= ==
++ +
∫∫∫ ∫
hay
21I =
. Vậy
1
2
I =
.
Câu 173: Cho hàm số
( )
fx
liên tục trên
, ta có
( )
0fx>
và
( ) ( )
0 . 2018 1ff x−=
. Giá trị của
tích phân
( )
2018
0
d
1
x
I
fx
=
+
∫
https://toanmath.com/
A.
2018
I =
. B.
0I =
C.
1009I =
D.
4016
Hướng dẫn giải
Chọn C
ta có
I
=
( )
2018
0
1 2018 0
d 1009
1 2.1
x
fx
−
= =
+
∫
.
Câu 174: Cho hàm số
(
)
y fx
=
có đạo hàm, liên tục trên
và
( )
0fx>
khi
[
]
0;5x∈
.
Biết
( ) ( )
.5 1
fxf x
−=
,
tính tích phân
( )
5
0
d
1
x
I
fx+
=
∫
.
A.
5
4
I
=
. B.
5
3
I
=
. C.
5
2
I
=
. D.
10I =
.
Hướng dẫn giải
Chọn C
Đặt
5xt= −
ddxt⇒=−
0 5x t= ⇒=
;
5 0x t= ⇒=
( )
( )
( )
05
50
d
d
15 1
I
ft t
t
f t ft
=
++
= −
−
∫∫
(do
( )
( )
1
5f
f
t
t
−=
)
5
0
2 d5It⇒= =
∫
5
2
I⇒=
.
Câu 175: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
4f x fx−=
. Biết
( )
3
1
d5xf x x =
∫
.
Tính tích phân
( )
3
1
dfx x
∫
.
A.
5
2
. B.
7
2
. C.
9
2
. D.
11
2
.
Hướng dẫn giải
Chọn A
Đặt
4tx= −
ddtx⇒=−
và
13xt=⇒=
;
31
xt=⇒=
.
Khi đó:
( )
(
) ( )
33
11
5 d 4 4d
xf x x t f t t= =−−
∫∫
( ) ( ) ( ) ( )
33
11
4 4d 4 dxf x x xfx x=− −=−
∫∫
.
Suy ra:
(
) ( ) ( )
33
11
10 d 4 dxfx x xfx x= +−
∫∫
(
)
3
1
5
4d
2
fx x= =
∫
.
Câu 176: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên R và
( )
0fx>
khi x ∈ [0; a] (
0a >
). Biết
( ) ( )
.1fxfa x−=
, tính tích phân
( )
0
1
a
dx
I
fx
=
+
∫
.
A.
2
a
I =
. B.
2Ia=
. C.
3
a
I
=
. D.
4
a
I =
.
Hướng dẫn giải:
( )
0
1
a
dx
I
fx
=
+
∫
(1) Đặt
t a x dt dx=−⇒ =−
Đổi cận:
( )
( ) ( )
0
00
11
11 1
aa
a
dt
I dt dx
fat fat fa x
⇒=− = =
+− +− +−
∫∫ ∫
(2) (Tích phân xác định không phụ
thuộc vào biến số tích phân)
(1) + (2)
( ) ( )
0
11
2
11
a
I dx
fx fa x

⇒= +

+ +−

∫
https://toanmath.com/
( ) (
)
( ) ( ) (
)
( )
( )
( )
( ) ( )
2
00
11 2
1. 2
a
fa x fx fa x fx
dx dx dx a
fxfa x fx fa x fa x fx
+ −++ + −+
= = = =
+ −+ + − + −+
∫∫
2
a
I⇒=
Chọn A
Câu 177: Cho
( )
fx
là hàm liên tục trên đoạn
[ ]
0;a
thỏa mãn
( ) ( )
( )
[ ]
.1
0, 0;
fxfa x
fx x a
−=
> ∀∈
và
( )
0
d
,
1
a
x ba
fx c
=
+
∫
trong đó
b
,
c
là hai số nguyên dương và
b
c
là phân số tối giản. Khi đó
bc
+
có giá trị thuộc khoảng nào dưới đây?
A.
(
)
11;22 .
B.
( )
0;9 .
C.
( )
7;21 .
D.
( )
2017;2020 .
Hướng dẫn giải
Chọn B
Cách 1. Đặt
dd
tax t x=−⇒ =−
Đổi cận
0 ; 0.x t ax a t= ⇒= = ⇒=
Lúc đó
( ) ( ) ( )
( )
( )
( )
0
0 0 00
d
dddd
1
11 1 1
1
a a aa
a
fx x
x t xx
I
fx fat fa x fx
fx
−
= = = = =
+ +− +− +
+
∫∫ ∫ ∫∫
Suy ra
( )
( )
( )
00 0
d
d
2 1d
11
aa a
fx x
x
III xa
fx fx
=+= + = =
++
∫∫∫
Do đó
1
1; 2 3.
2
I a b c bc= ⇒= =⇒+=
Cách 2. Chọn
(
)
1fx=
là một hàm thỏa các giả thiết.
Dễ dàng tính được
1
1; 2 3.
2
I a b c bc
= ⇒= =⇒+=
https://toanmath.com/
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 6
Câu 178: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 4
, đồng biến trên đoạn
[ ]
1; 4
và thỏa
mãn đẳng thức
( )
2.x xf x+
(
)
2
fx
′
=


,
[ ]
1; 4x∀∈
. Biết rằng
( )
3
1
2
f =
, tính
( )
4
1
dI fx x
=
∫
?
A.
1186
45
I =
. B.
1174
45
I =
. C.
1222
45
I
=
. D.
1201
45
I
=
.
Hướng dẫn giải
Chọn A
Ta có
( )
2.x xf x+
( )
2
fx
′
=


( ) ( )
.1 2x fx f x
′
⇒+ =
(
)
(
)
12
fx
x
fx
′
⇒=
+
,
[ ]
1; 4x∀∈
.
Suy ra
( )
( )
dd
12
fx
x xx C
fx
′
= +
+
∫∫
( )
( )
d
dd
12
fx
x xx C
fx
⇔=+
+
∫∫
( )
3
2
2
12
3
fx x C⇒+ = +
. Mà
( )
3
1
2
f =
4
3
C⇒=
. Vậy
( )
2
3
2
24
1
33
2
x
fx

+−


=
.
Vậy
( )
4
1
1186
d
45
I fx x= =
∫
.
Câu 179: Cho hàm số
( )
y fx=
có đạo hàm trên
thỏa mãn
( )
( )
( )
32
1
2
2
3 .e 0
fxx
x
fx
fx
−−
′
−=
và
( )
01f =
. Tích phân
( )
7
0
.dxf x x
∫
bằng
A.
27
3
. B.
15
4
. C.
45
8
. D.
57
4
.
Hướng dẫn giải
Chọn C
Ta có
( )
( )
( )
32
1
2
2
3 .e 0
fxx
x
fx
fx
−−
′
−=
⇔
( ) ( )
( )
3
2
21
3 . .e 2 .e
fx
x
f xfx x
+
′
=
Suy ra
( )
3
2
1
ee
fx
x
C
+
= +
. Mặt khác, vì
( )
01f =
nên
0C =
.
Do đó
( )
3
2
1
ee
fx
x +
=
(
)
32
1fx x⇔=+
( )
3
2
1fx x⇔=+
.
Vậy
( )
7
0
.dxf x x
∫
7
3
2
0
. 1dxx x= +
∫
(
)
7
3
22
0
1
1d 1
2
xx= ++
∫
( )
7
3
22
0
3
11
8
xx

=++

45
8
=
.
Câu 180: Cho hàm số
( )
432
43 1fx x x x x= + − −+
,
x∀∈
. Tính
( )
( )
1
2
0
.dI f xfxx
′
=
∫
.
A.
2
. B.
2−
. C.
7
3
−
. D.
7
3
.
Hướng dẫn giải
Chọn D
Đặt
( ) ( )
ddtfx tfxx
′
= ⇒=
. Đổi cận:
( )
0 01x tf=⇒= =
,
( )
1 12x tf=⇒= =
.
Khi đó
2
2
3
2
1
1
817
d
3 33 3
t
I tt= = =−=
∫
.
https://toanmath.com/
Câu 181: Cho hàm số
( )
fx
có đạo hàm liên tục trên khoảng
( )
0;1
và
( )
0fx≠
,
( )
0;1x∀∈
. Biết
rằng
1
2
fa

=


,
3
2
fb

=



và
( ) ( )
24x xf x f x
′
+=−
,
( )
0;1x∀∈
. Tính tích phân
( )
2
3
2
6
sin .cos 2sin 2
sin
d
xx x
Ix
fx
π
π
+
=
∫
theo
a
và
b
.
A.
3
4
ab
I
ab
.
B.
3
4
ba
I
ab
. C.
3
4
ba
I
ab
. D.
3
4
ab
I
ab
.
Hướng dẫn giải
Chọn D
( )
0;1x∀∈
ta có:
( )
(
)
24
x xf x f x
′
+=−
(
) ( )
42x f x xf x
′
⇔+= −
( ) ( )
22
42x x xf x x f x
′
⇒+= −
( )
( ) ( )
( )
2
2
22
2
4
xf x x f x
xx
fx fx
′
−
+
⇔=
(
)
(
)
22
2
4xx x
f x fx
′

+
⇔=



.
Tính
( ) ( )
22
33
22
66
sin .cos 2sin 2 sin .cos 4sin .cos
sin sin
dd
xx x xx xx
Ix x
fx fx
ππ
ππ
++
= =
∫∫
Đặt
sin cosddt x t xx= ⇒=
, đổi cận
1
62
xt
π
= ⇒=
,
3
32
xt
π
= ⇒=
.
Ta có
( )
3
2
2
2
1
2
4
d
tt
It
ft
+
=
∫
( )
3
2
2
1
2
t
ft
=
2
2
3
1
2
2
1
3
2
2
f
f





= −





313
44 4
ab
b a ab
−
=−=
.
Câu 182: Cho hàm số
f
liên tục,
( )
1fx>−
,
( )
00f =
và thỏa
( )
( )
2
12 1f x x xfx
′
+= +
. Tính
( )
3f
.
A.
0
. B.
3
. C.
7
. D.
9
.
Hướng dẫn giải
Chọn B
Ta có
( ) ( )
( )
( )
2
2
2
12 1
1
1
fx
x
f x x xfx
fx
x
′
′
+= +⇔ =
+
+
(
)
( )
( )
( )
33
3
33
2
2
00
0
00
2
d d 1 1 11
1
1
fx
x
x x fx x fx
fx
x
′
⇔ = ⇔ += +⇔ +=
+
+
∫∫
( )
( )
( )
( )
31 011 312 3 3ff f f⇔ +− +=⇔ +=⇔ =
.
Câu 183: Cho hàm số
( )
fx
liên tục trên
và
( )
5
2
d4
fx x=
∫
,
( )
53f =
,
( )
22f =
. Tính
( )
2
32
1
1dI xf x x
′
= +
∫
A.
3
. B.
4
. C.
1
. D.
6
.
https://toanmath.com/
Hướng dẫn giải
Chọn A
Đặt
2
1tx= +
d 2dt xx⇒=
.
12xt=⇒=
;
25
xt= ⇒=
. Khi đó
( )
( )
5
2
1
1d
2
I t ftt
′
= −
∫
.
Đặt
1d dut u t=−⇒ =
;
( )
d d,
v ftt
′
=
chọn
( )
v ft=
.
( )
(
)
( )
5
5
2
2
11
1d
22
I t ft ft t
=−−
∫
(
)
( )
(
)
1
4 5 2 23
2
ff
= − −=
.
Câu 184: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
1; 4
và thỏa mãn
( )
( )
21
ln
fx
x
fx
x
x
−
= +
. Tính tích
phân
(
)
4
3
d
I fx x
=
∫
.
A.
2
3 2ln 2
I = +
. B.
2
2ln 2I
=
. C.
2
ln 2I =
. D.
2ln 2I =
.
Hướng dẫn giải
Chọn B
Ta có
( )
4
1
dfx x
∫
( )
4
1
21
ln
d
fx
x
x
x
x

−

= +


∫
( )
44
11
21
ln
dd
fx
x
xx
x
x
−
= +
∫∫
.
Xét
( )
4
1
21
d
fx
Kx
x
−
=
∫
.
Đặt
21xt−=
1
2
t
x
+
⇒=
d
d
x
t
x
⇒=
.
( )
3
1
d
K ft t⇒=
∫
( )
3
1
dfx x
=
∫
.
Xét
4
1
ln
d
x
Mx
x
=
∫
( )
4
1
ln d lnxx=
∫
4
2
1
ln
2
x
= =
2
2ln 2
.
Do đó
( ) ( )
43
2
11
d d 2ln 2fx x fx x= +
∫∫
( )
4
2
3
d 2ln 2fx x⇒=
∫
.
Câu 185: Cho hàm số
(
)
fx
liên tục trên
và thỏa mãn
( )
( )
16
2
2
1
4
cot . sin d d 1
fx
xf x x x
x
π
π
= =
∫∫
. Tính
tích phân
( )
1
1
8
4
d
fx
x
x
∫
.
A.
3I =
. B.
3
2
I =
. C.
2I =
. D.
5
2
I =
.
Hướng dẫn giải
Chọn D
Đặt
( )
2
2
1
4
cot . sin d 1I xf x x
π
π
= =
∫
,
( )
16
2
1
d1
fx
Ix
x
== =
∫
.
Đặt
2
sintx=
d 2sin .cos dt x xx⇒=
2
2sin .cot dx xx=
2 .cot dt xx=
.
https://toanmath.com/
x
4
π
2
π
t
1
2
1
(
)
2
2
1
4
cot . sin dI xf x x
π
π
=
∫
( )
1
1
2
1
.d
2
ft t
t
=
∫
( )
1
1
2
1
d
2
ft
t
t
=
∫
(
)
( )
1
4
1
8
4
1
d4
24
fx
x
x
=
∫
( )
1
4
1
8
4
1
d
2
fx
x
x
=
∫
.
Suy ra
( )
1
4
1
1
8
4
d2 2
fx
xI
x
= =
∫
Đặt
tx=
2d dtt x⇒=
.
x
1
16
t
1
4
( )
16
2
1
d
fx
Ix
x
=
∫
(
)
4
2
1
2d
ft
tt
t
=
∫
(
)
4
1
2d
ft
t
t
=
∫
(
)
(
)
1
1
4
4
2 d4
4
fx
x
x
=
∫
( )
1
1
4
4
2d
fx
x
x
=
∫
.
Suy ra
( )
1
2
1
4
4
11
d
22
fx
xI
x
= =
∫
Khi đó, ta có:
( )
( ) ( )
1
11
4
1 11
8 84
444
ddd
fx fx fx
xxx
xxx
= +
∫∫∫
15
2
22
=+=
.
Câu 186: Xét hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
(
)
(
)
22
4. 3 1 1xf x f x x+ −=−
.
Tích phân
( )
1
0
d
I fx x=
∫
bằng:
A.
4
I
π
=
. B.
6
I
π
=
. C.
20
I
π
=
. D.
16
I
π
=
.
Hướng dẫn giải
Chọn C
Vì
( )
fx
liên tục trên
[ ]
0;1
và
( )
( )
22
4. 3 1 1xf x f x x+ −=−
nên ta có
( )
( )
11
22
00
4. 3 1 d 1 dxf x f x x x x

+− =−

∫∫
( )
( )
11 1
22
00 0
4. d 3 1 d 1 dxf x x f x x x x⇔ + −=−
∫∫∫
( )
1
.
Mà
( )
1
2
0
4. dxf x x
∫
( ) ( )
1
22
0
2dfx x=
∫
(
)
2
1
0
2d
tx
ft t
=
→
∫
2I=
và
( )
1
0
31 d
f xx−
∫
( ) ( )
1
0
3 1 d1fx x=−−−
∫
( )
1
1
0
3d
ux
fu u
= −
→
∫
3I=
Đồng thời
1
2
0
1dxx−
∫
2
sin
2
0
1 sin .cos d
xt
t tt
π
=
→ −
∫
2
2
0
cos dtt
π
=
∫
( )
2
0
1
1 cos2 d
2
tt
π
= +
∫
4
π
=
.
Do đó,
( )
1 ⇔
23
4
II
π
+=
hay
20
I
π
=
.
https://toanmath.com/
Câu 187: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
11f =
,
( )
1
2
0
9
d
5
fx x
′
=


∫
và
( )
1
0
2
d
5
f xx
=
∫
. Tính tích phân
(
)
1
0
dI fx x=
∫
.
A.
3
5
I =
. B.
1
4
I =
. C.
3
4
I =
. D.
1
5
I
=
.
Hướng dẫn giải
Chọn B
Đặt
2
d 2d
t x t x x tt= ⇒=⇒ =
. Đổi cận
0 0; 1 1x tx t= ⇒= =⇒=
Suy ra
( )
( )
11
00
d 2. d
f x x tf t t
=
∫∫
( )
1
0
1
.d
5
tf t t⇔=
∫
. Do đó
( )
1
0
1
.d
5
xf x x⇔=
∫
Mặt khác
( )
( ) ( )
1
11
22
00
0
.d d
22
xx
xfx x fx f x x
′
= −
∫∫
(
)
1
2
0
1
d
22
x
fxx
′
= −
∫
.
Suy ra
( )
1
2
0
11 3
d
2 2 5 10
x
fxx
′
=−=
∫
( )
1
2
0
3
d
5
xf x x
′
⇒=
∫
Ta tính được
( )
1
2
2
0
9
3d
5
xx=
∫
.
Do đó
( ) ( )
( )
1 11
2
2
22
0 00
d 23 d 3 d 0fx x xfxx x x
′′
− +=


∫ ∫∫
( )
( )
1
2
2
0
3 d0fx x x
′
⇔−=
∫
( )
2
30fx x
′
⇔ −=
( )
2
3fx x
′
⇔=
( )
3
fx x C⇔=+
.
Vì
( )
11f =
nên
( )
3
fx x=
Vậy
( )
11
3
00
1
dd
4
I fx x xx
= = =
∫∫
.
https://toanmath.com/
DẠNG 4: PHƯƠNG PHÁP TỪNG PHẦN
BÀI TẬP
Câu 188. Cho hàm số
( )
y fx
=
có đạo hàm
( )
fx
′
liên tục trên
[ ]
0;2
và
( )
23f =
,
(
)
2
0
d3fx x=
∫
.
Tính
(
)
2
0
.dxf x x
′
∫
.
A.
3−
. B.
3
. C.
0
. D.
6
.
Câu 189. Cho hàm số
( )
y fx=
có đạo hàm là
( )
'fx
liên tục trên đoạn [0; 1] và
( )
12f =
. Biết
( )
1
0
1
f x dx =
∫
, tính tích phân
( )
1
0
.'I x f x dx=
∫
.
A.
1I =
. B.
1I = −
. C.
3I =
. D.
3I = −
.
Câu 190. Cho hàm số
( )
fx
thỏa mãn
( ) ( )
1
0
1 ' 10x f x dx+=
∫
và
( ) ( )
21 0 2ff−=
. Tính
( )
1
0
I f x dx=
∫
.
A.
8
I
=
. B.
8I = −
. C.
4I =
. D.
4
I = −
.
Câu 191. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;2
và thỏa mãn
( )
2 16f =
,
(
)
2
0
d4fx x=
∫
. Tính tích phân
( )
1
0
. 2dI xf x x
′
=
∫
.
A.
12I =
. B.
7
I =
. C.
13I =
. D.
20I =
.
Câu 192. Cho hàm số có đạo hàm liên tục trên và thỏa mãn ,
. Tính .
A. . B. . C. . D. .
Câu 193. Cho hàm số
y fx
thỏa mãn
3
3 1 3 2, .fx x x x 
Tính
5
1
.I x f x dx
.
A.
5
4
. B.
17
4
. C.
33
4
. D.
1761−
.
Câu 194. Cho hàm số
( )
fx
liên tục trong đoạn
[ ]
1; e
, biết
( )
e
1
d1
fx
x
x
=
∫
,
( )
e1f =
. Khi đó
( )
e
1
.ln dI f x xx
′
=
∫
bằng
A.
4I =
. B.
3
I =
. C.
1I =
. D.
0I =
.
Câu 195. Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
thỏa mãn
( )
π
sin .cos
2
fx f x x x

+ −=


, với mọi
x∈
và
( )
00f =
. Giá trị của tích phân
( )
π
2
0
.dxf x x
′
∫
bằng
A.
π
4
−
. B.
1
4
. C.
π
4
. D.
1
4
−
.
( )
y fx
=
(
)
21f −=
(
)
2
1
2 4d 1
fx x
−=
∫
(
)
0
2
dxf x x
−
′
∫
1I =
0I =
4I = −
4I =
https://toanmath.com/
Câu 196. Cho hàm số
(
)
fx
thỏa
( ) ( )
0 11ff= =
. Biết
( ) ( )
1
0
'
x
e f x f x dx ae b+=+


∫
. Tính biểu
thức
2018 2018
Qa b= +
.
A.
8Q =
. B.
6Q =
. C.
4
Q =
. D.
2
Q =
.
Câu 197. Cho hàm số
( )
fx
có đạo hàm trên
thỏa mãn
( ) ( )
2017 2018
2018 2018. .e
x
f x fx x
′
−=
với
mọi
x∈
và
( )
0 2018.f =
Tính giá trị
( )
1.f
A.
(
)
2018
1 2019ef
=
. B.
(
)
2018
1 2018.e
f
−
=
. C.
(
)
2018
1 2018.ef
=
. D.
(
)
2018
1 2017.e
f =
.
Câu 198. Cho hàm số
( )
y fx=
với
( ) ( )
0 11ff= =
. Biết rằng:
( )
(
)
1
0
e de
x
fx f x x a b
′
+=+


∫
Tính
2017 2017
Qa b= +
.
A.
2017
21Q = +
. B.
2Q =
. C.
0Q =
. D.
2017
21
Q
= −
.
Câu 199. Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
0;5
và
( )
5 10f =
,
( )
5
0
d 30xf x x
′
=
∫
. Tính
( )
5
0
d
fx x
∫
.
A.
20
. B.
30−
. C.
20−
. D.
70
.
Câu 200. Cho hai hàm số liên tục
f
và
g
có nguyên hàm lần lượt là
F
và
G
trên đoạn
[ ]
1; 2
. Biết
rằng
( )
11F
=
,
( )
24F =
,
( )
3
1
2
G =
,
( )
22G =
và
( ) ( )
2
1
67
d
12
f xGx x
=
∫
. Tính
( ) ( )
2
1
dFxgx x
∫
A.
11
12
. B.
145
12
−
. C.
11
12
−
. D.
145
12
.
Câu 201. Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( ) ( )
1
0
2d 1
xf x x f
′

−=

∫
. Giá
trị của
( )
1
0
dI fx x
=
∫
bằng
A.
2−
. B.
2
. C.
1
−
. D.
1
.
Câu 202. Cho hàm số
( )
y fx=
liên tục trên đoạn
[
]
1; 2
và
( )
( )
2
1
1dx fxxa
′
−=
∫
. Tính
( )
2
1
dfx x
∫
theo
a
và
( )
2bf=
.
A.
ba−
. B.
ab
−
. C.
ab+
. D.
ab−−
.
Câu 203. Cho hàm số
( )
fx
liên tục trên
và
( )
2 16f =
,
( )
2
0
d4fx x=
∫
. Tính tích phân
( )
1
0
. 2dI xf x x
′
=
∫
.
A.
13I =
. B.
12I =
. C.
20
I =
. D.
7I =
.
Câu 204. Cho
( )
y fx=
là hàm số chẵn, liên tục trên
biết đồ thị hàm số
( )
y fx=
đi qua điểm
1
;4
2
M

−


và
( )
1
2
0
dt 3ft =
∫
, tính
( )
0
6
sin 2 . sin dI xf x x
π
−
′
=
∫
.
https://toanmath.com/
A.
10I =
. B.
2
I = −
. C.
1I =
. D.
1I = −
.
Câu 205. Cho hàm số
( )
y fx=
thỏa mãn
(
) (
)
2
0
sin . d 0
xf x x f
π
=
∫
1=
. Tính
( )
2
0
cos . dI xf x x
π
′
=
∫
.
A.
1I
=
. B.
0I =
. C.
2
I
=
. D.
1I
= −
.
Câu 206. Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
2018 2 sinf x fx x x−+ =
. Tính
( )
2
2
dI fx x
π
π
−
=
∫
?
A.
2
2019
. B.
2
2018
. C.
2
1009
. D.
4
2019
.
Câu 207. Cho hàm số
(
)
fx
và
(
)
gx
liên tục, có đạo hàm trên
và thỏa mãn
( ) ( )
0. 2 0ff
′′
≠
và
( ) ( ) ( )
2e
x
gxf x xx
′
= −
. Tính giá trị của tích phân
( ) ( )
2
0
.d
I fxgx x
′
=
∫
?
A.
4−
. B.
e2−
. C.
4
. D.
2e−
.
Câu 208. Cho hàm số
( )
y fx=
có đạo hàm và liên tục trên
0;
4
π



thỏa mãn
3
4
f
π

=


,
( )
4
0
d1
cos
fx
x
x
π
=
∫
và
( )
4
0
sin .tan . d 2x xf x x
π

=
∫
. Tích phân
( )
4
0
sin . dxf x x
π
′
∫
bằng:
A.
4
. B.
2 32
2
+
. C.
132
2
+
. D.
6
.
Câu 209. Cho hàm số
( )
fx
liên tục trên
và
( )
2 16f =
,
(
)
2
0
d4fx x
=
∫
. Tính
4
0
d
2
x
I xf x

′
=


∫
A.
12I =
. B.
112I =
. C.
28I =
. D.
144I =
.
Câu 210. Cho hàm số
( )
fx
có đạo hàm cấp hai
( )
fx
′′
liên tục trên đoạn
[
]
0;1
thoả
mãn
( ) ( )
1 01ff= =
,
(
)
0 2018f
′
=
. Mệnh đề nào dưới đây đúng?
A.
( )( )
1
0
1 2018fx xx
′′
−=−
∫
d
.
B.
( )( )
1
0
11fx xx−−
′′
=
∫
d
.
C.
( )( )
1
0
1 2018fx xx−=
′′
∫
d
. D.
( )( )
1
0
11fx xx−
′′
=
∫
d
.
Câu 211. Cho hàm số
( )
fx
có đạo hàm liên tục thỏa mãn
0
2
f
π

=


,
( )
2
2
d
4
fx x
π
π
π
′
=


∫
và
( )
2
cos d
4
xf x x=
∫
π
π
π
. Tính
( )
2018f
π
.
A.
1−
. B.
0
. C.
1
2
. D.
1
.
Câu 212. Cho hàm số
( )
fx
nhận giá trị dương, có đạo hàm liên tục trên đoạn
[ ]
0; 2
. Biết
( )
01f =
và
( ) ( )
2
24
.2 e
xx
fxf x
−
−=
, với mọi
[ ]
0; 2x∈
. Tính tích phân
( )
(
)
( )
32
2
0
3
d
x xfx
Ix
fx
−′
=
∫
.
https://toanmath.com/
A.
16
3
I = −
. B.
16
5
I = −
. C.
14
3
I = −
. D.
32
5
I = −
.
Câu 213. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
thỏa mãn
( )
10f =
và
( ) ( ) ( )
11
2
2
00
e1
d 1e d
4
x
f x x x fx x
−
′
=+=


∫∫
. Tính tích phân
( )
1
0
dI fx x=
∫
.
A.
2eI
= −
. B.
e2I = −
. C.
e
2
I =
. D.
e1
2
I
−
=
.
Câu 214. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1; 2
thỏa mãn
( ) ( )
2
2
1
1
1d
3
x fx x−=−
∫
,
( )
20f =
và
(
)
2
2
1
d7
fx x
′
=


∫
. Tính tích phân
( )
2
1
dI fx x=
∫
.
A.
7
5
I =
. B.
7
5
I = −
. C.
7
20
I = −
. D.
7
20
I =
.
Câu 215. Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
thỏa mãn
( )
11
f
=
,
( )
1
2
0
d9fx x
′
=


∫
và
( )
1
3
0
1
d
2
xf x x=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
2
3
. B.
5
2
. C.
7
4
. D.
6
5
.
Câu 216. Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
0;
4
π



và
0
4
f
π

=


. Biết
( )
4
2
0
d
8
f xx
π
π
=
∫
,
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Tính tích phân
( )
8
0
2d
I f xx
π
=
∫
A.
1I =
. B.
1
2
I =
. C.
2I =
. D.
1
4
I =
.
Câu 217. . Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[
]
0;1
và
( ) ( )
0 10ff+=
. Biết
( )
1
2
0
1
d
2
f xx=
∫
,
( ) ( )
1
0
cos d
2
fx xx
π
π
′
=
∫
. Tính
( )
1
0
dfx x
∫
.
A.
π
. B.
1
π
. C.
2
π
. D.
3
2
π
.
Câu 218. Cho hàm số
( )
fx
có đạo hàm
( )
fx
′
liên tục trên đoạn
[
]
0;1
thỏa
( )
10f =
,
( )
(
)
1
2
2
0
dx
8
fx
π
′
=
∫
và
( )
1
0
1
cos d
22
xfx x
π

=


∫
. Tính
( )
1
0
dfx x
∫
.
A.
2
π
. B.
π
. C.
1
π
. D.
2
π
.
Câu 219. Xét hàm số
( )
fx
có đạo hàm liên tục trên
và thỏa mãn điều kiện
( )
11f =
và
( )
24f =
. Tính
( ) ( )
2
2
1
21
d
f x fx
Jx
xx
′
++

= −


∫
.
A.
1 ln 4J = +
. B.
4 ln 2J = −
. C.
1
ln 2
2
J = −
. D.
1
ln 4
2
J = +
.
https://toanmath.com/
Câu 220. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
thỏa mãn
( ) ( ) ( )
11
2
2
00
e1
d 1e d
4
x
f x x x fx x
−
′
=+=


∫∫
và
(
)
10
f =
. Tính
( )
1
0
dfx x
∫
A.
e1
2
−
. B.
2
e
4
. C.
e2−
. D.
e
2
.
Câu 221. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
10f =
,
( )
1
2
0
d7fx x
′
=


∫
và
( )
1
2
0
1
d
3
xf x x
=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
7
5
. B.
1
. C.
7
4
. D.
4
.
https://toanmath.com/
HƯỚNG DẪN GIẢI
Câu 188. Cho hàm số
( )
y fx=
có đạo hàm
( )
fx
′
liên tục trên
[ ]
0;2
và
( )
23f =
,
(
)
2
0
d3fx x=
∫
.
Tính
( )
2
0
.dxf x x
′
∫
.
A.
3−
. B.
3
. C.
0
. D.
6
.
Hướng dẫn giải
Chọn B
Ta có
( )
2
0
.dxf x x
′
∫
(
)
( )
2
0
dx fx=
∫
( )
( )
2
2
0
0
.dxfx fx x= −
∫
( )
2233f= −=
.
Câu 189. Cho hàm số
( )
y fx=
có đạo hàm là
(
)
'
fx
liên tục trên đoạn [0; 1] và
( )
12f =
. Biết
( )
1
0
1f x dx
=
∫
, tính tích phân
(
)
1
0
.'I x f x dx=
∫
.
A.
1I =
. B.
1I = −
. C.
3I =
. D.
3I = −
.
Hướng dẫn giải
Ta có:
(
)
1
0
.'I x f x dx=
∫
Đặt
u x du dx=⇒=
,
( )
'dv f x dx=
chọn
( )
(
)
'
v f x dx f x
= =
∫
( ) ( ) ( ) ( ) ( )
11
1
0
00
. 1. 1 0. 0 2 1 1I xfx fxdx f f fxdx⇒=−=−−=−=
∫∫
Chọn A
Câu 190. Cho hàm số
( )
fx
thỏa mãn
( ) ( )
1
0
1 ' 10x f x dx+=
∫
và
( ) ( )
21 0 2ff−=
. Tính
(
)
1
0
I f x dx=
∫
.
A.
8I =
. B.
8I = −
. C.
4I =
. D.
4I = −
.
Hướng dẫn giải
(
) (
)
1
0
1'A x f x dx= +
∫
Đặt
1u x du dx= +⇒ =
,
( )
'dv f x dx=
chọn
( )
v fx=
( )
( )
( )
( )
( ) (
)
1 11 1
1
0
0 00 0
1 . 2 (1) (0) 2 10 8
A x fx fxdx f f fxdx fxdx fxdx⇒=+−=−−=−=⇒=−
∫ ∫∫ ∫
Chọn B
Câu 191. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;2
và thỏa mãn
( )
2 16f =
,
( )
2
0
d4fx x=
∫
. Tính tích phân
( )
1
0
. 2dI xf x x
′
=
∫
.
A.
12I
=
. B.
7I =
. C.
13I =
. D.
20I =
.
Hướng dẫn giải
Chọn B
https://toanmath.com/
Đặt
( )
( )
dd
2
d 2d
2
ux
ux
fx
v f xx
v
=
=

⇒

′
=
=
.
Khi đó:
(
)
( )
( )
( )
12
1
0
00
.2 2
1 1 16 1
2 d d .4 7
2 2 2 4 24
xf x f
I f x x ft t= − = − =−=
∫∫
.
Câu 192. Cho hàm số có đạo hàm liên tục trên và thỏa mãn ,
. Tính .
A. . B. . C. . D. .
Hướng dẫn giải
Chọn B
Đặt , đổi cận , .
.
Đặt , .
Vậy .
Câu 193. Cho hàm số
y fx
thỏa mãn
3
3 1 3 2, .
fx x x x 
Tính
5
1
.
I x f x dx
.
A.
5
4
. B.
17
4
. UC. U
33
4
. D.
1761−
.
Hướng dẫn giải
Chọn C
Đặt
5
5
1
1
u x du dx
I xfx fxdx
dv f x dx v f x










.
Từ
3
55 1
313 2
12 0
fx
fx x x
fx



, suy ra
5
1
23 .I f x dx
Đặt
2
3
33
31
32
dt x dx
tx x
ft x



Đổi cận: Với
3
11 3 1 0
t xx x 
và
3
5 3 15 1t xx x 
.
Khi đó
51
2
10
33
23 23 3 2 3 3
4
Casio
I f x dx x x dx 

Chọn C
Câu 194. Cho hàm số
( )
fx
liên tục trong đoạn
[ ]
1; e
, biết
( )
e
1
d1
fx
x
x
=
∫
,
( )
e1
f =
. Khi đó
( )
e
1
.ln dI f x xx
′
=
∫
bằng
A.
4I =
. B.
3I =
. C.
1I =
. D.
0I =
.
Hướng dẫn giải
Chọn D
( )
y fx=
( )
21f −=
( )
2
1
2 4d 1
fx x
−=
∫
( )
0
2
dxf x x
−
′
∫
1I
=
0
I
=
4I
= −
4I =
2 4 d 2dtx t x= −⇒ =
12xt=⇒=−
20xt= ⇒=
( )
( )
20
12
1
1 2 4d d
2
f x x ft t
−
= −=
∫∫
( )
0
2
d2ft t
−
⇒=
∫
( )
0
2
d2fx x
−
⇒=
∫
ddux u x=⇒=
( ) ( )
ddvfxx vfx
′
= ⇒=
( )
0
2
dxf x x
−
′
∫
( ) ( )
0
0
2
2
d
xfx fx x
−
−
= −
∫
( )
2 22
f= −−
2.1 2 0= −=
https://toanmath.com/
Cách 1: Ta có
(
) (
)
(
)
(
)
ee
e
1
11
1
.ln d .ln . d e 1 1 1 0
I f x xx fx x fx x f
x
′
= = − = −=−=
∫∫
.
Cách 2: Đặt
( )
( )
d
ln
d
dd
x
ux
u
x
v fxx
v fx
=
=

→

′
=
=
.
Suy ra
( ) ( )
( )
( )
ee
e
1
11
.ln d ln d e 1 1 1 0
fx
I fx xxfx x xf
x
′
= = − = −=−=
∫∫
.
Câu 195. Cho hàm số
( )
y fx
=
có đạo hàm liên tục trên
thỏa mãn
( )
π
sin .cos
2
fx f x x x

+ −=


, với mọi
x∈
và
( )
00f =
. Giá trị của tích phân
( )
π
2
0
.d
xf x x
′
∫
bằng
A.
π
4
−
. B.
1
4
. C.
π
4
. D.
1
4
−
.
Hướng dẫn giải
Chọn D
Theo giả thiết,
(
)
00
f =
và
( )
π
sin .cos
2
fx f x x x

+ −=


nên
( )
π
00
2
ff

+=


π
0
2
f

⇔=


.
Ta có:
( )
π
2
0
.dI xf x x
′
=
∫
( )
π
2
0
dx fx=


∫
(
)
(
)
π
π
2
2
0
0
dxfx fx x
= −


∫
Suy ra:
( )
π
2
0
dI fx x= −
∫
.
Mặt khác, ta có:
( )
π
sin .cos
2
fx f x x x

+ −= ⇒


( )
22 2
00 0
1
d d sin .cos d
22
fx x f x x x xx
ππ π
π

+ −= =


∫∫ ∫
Suy ra:
( )
( )
0
22
00
2
11
dd d
22 4
fx x f x x fx x
ππ
π
π

− −=⇔ =


∫∫ ∫
Vậy
(
)
π
2
0
1
d
4
I fx x=−=−
∫
.
Câu 196. Cho hàm số
( )
fx
thỏa
(
) ( )
0 11
ff= =
. Biết
( )
( )
1
0
'
x
e f x f x dx ae b+=+


∫
. Tính biểu
thức
2018 2018
Qa b= +
.
A.
8Q =
. B.
6Q =
. C.
4Q =
. D.
2Q =
.
Hướng dẫn giải
( ) (
) ( ) ( )
12
1 11
0 00
''
x xx
AA
A e f x f x dx e f x dx e f x dx= += +


∫ ∫∫
 
( )
1
1
0
x
A e f x dx=
∫
https://toanmath.com/
Đặt
(
) (
)
'
u f x du f x dx
= ⇒=
,
x
dv e dx=
chọn
x
ve=
(
)
( )
2
1
1
1
0
0
.'
xx
A
A e f x e f x dx
⇒= −
∫

Vậy
( ) ( ) ( ) ( )
11
22
00
.1 0 1
xx
A ef x A A ef x ef f e= −+= = − =−
2018 2018
1
11 2
1
a
ab
b
=
⇒ ⇒ + =+=
= −
Chọn D
Câu 197. Cho hàm số
( )
fx
có đạo hàm trên
thỏa mãn
( ) ( )
2017 2018
2018 2018. .e
x
f x fx x
′
−=
với
mọi
x∈
và
(
)
0 2018.f
=
Tính giá trị
( )
1.
f
A.
( )
2018
1 2019ef =
. B.
(
)
2018
1 2018.e
f
−
=
. C.
( )
2018
1 2018.e
f
=
. D.
( )
2018
1 2017.ef =
.
Hướng dẫn giải
Chọn A
Ta có:
( ) (
)
2017 2018
2018 2018. .e
x
f x fx x
′
−=
( ) ( )
2017
2018
2018.
2018.
e
x
f x fx
x
′
−
⇔=
( ) ( )
11
2017
2018
00
2018.
d 2018. d
e
x
f x fx
x xx
′
−
⇔=
∫∫
( )
1
Xets
( ) ( )
1
2018
0
2018.
d
e
x
f x fx
Ix
′
−
=
∫
( ) ( )
11
2018 2018
00
.e d 2018. .e d
xx
fxx fxx
−−
′
= −
∫∫
Xét
( )
1
2018
1
0
2018. .e d
x
I fx x
−
=
∫
. Đặt
( ) ( )
2018 2018
dd
d 2018.e d e
xx
ufx ufxx
v xv
−−
′
= =

⇒

= = −


.
Do đó
( )
( )
( ) ( )
1
2018 1 2018 2018
10
0
. e .e d 1 .e 2018
xx x
I fx f x x I f
−− −
′
= − + ⇒= −
∫
Khi đó
( )
1
( )
2018 2018 1
0
1 .e 2018
x
fx
−
⇔ −=
( )
2018
1 2019.ef⇒=
.
Câu 198. Cho hàm số
( )
y fx=
với
( ) ( )
0 11ff= =
. Biết rằng:
( ) (
)
1
0
e de
x
fx f x x a b
′
+=+


∫
Tính
2017 2017
Qa b= +
.
A.
2017
21Q = +
. B.
2
Q =
. C.
0Q =
. D.
2017
21Q = −
.
Hướng dẫn giải
Chọn C
Đặt
( ) ( )
dd
d ed e
xx
ufx ufxx
v xv
′
= =

⇒

= =


.
( ) ( ) ( ) ( ) ( )
1 11
2
1
0 00
e de eded
x xx x
fx fx x fx fxx fxx
′ ′′
+=− +


∫ ∫∫
(
) ( )
e1 0ff
= −
e1
= −
.
Do đó
1a =
,
1b = −
.
Suy ra
2017 2017
Qa b= +
( )
2017
2017
1 10= +− =
.
Vậy
0Q
=
.
https://toanmath.com/
45TCâu 199. 45TCho45T hàm số 45T
(
)
y fx=
có đạo hàm liên tục trên đoạn
[ ]
0;5
và
( )
5 10f =
,
(
)
5
0
d 30
xf x x
′
=
∫
. Tính
( )
5
0
dfx x
∫
.
45TA. 45T
20
45T. B. 45T
30−
45T. C. 45T
20
−
45T. D. 45T
70
45T.
Hướng dẫn giải
Chọn A
Đặt
(
) ( )
dd
dd
ux u x
vfxx vfx
=⇒=
′
= ⇒=
( ) ( )
( )
( )
55
5
0
00
.d. dxf x x xf x f x x
′
= −
∫∫
( ) ( )
5
0
30 5 5 df fx x⇔= −
∫
(
) (
)
5
0
d 5 5 30 20fx x f⇔ = −=
∫
.
Câu 200. Cho hai hàm số liên tục
f
và
g
có nguyên hàm lần lượt là
F
và
G
trên đoạn
[ ]
1; 2
. Biết
rằng
( )
11
F =
,
( )
24F =
,
( )
3
1
2
G =
,
( )
22G =
và
( ) ( )
2
1
67
d
12
f xGx x=
∫
. Tính
( ) ( )
2
1
dFxgx x
∫
A.
11
12
. B.
145
12
−
. C.
11
12
−
. D.
145
12
.
Hướng dẫn giải
Chọn A
Đặt
(
)
( )
d
u Fx
dv g x x
=
=
(
)
( )
ddu fx x
v Gx
=
⇒
=
( ) ( )
2
1
dFxgx x
∫
( ) ( )
( )
( ) ( )
2
2
1
1
dFxGx f xGx x= −
∫
( ) ( ) ( ) ( ) ( ) ( )
2
1
22 11 dF G F G f xGx x= −−
∫
3 67
4.2 1.
2 12
=−−
11
12
=
.
Câu 201. Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
(
) (
)
1
0
2d 1xf x x f
′

−=

∫
. Giá
trị của
( )
1
0
dI fx x
=
∫
bằng
A.
2−
. B.
2
. C.
1−
. D.
1
.
Hướng dẫn giải
Chọn C
Ta có
( )
1
0
2dxf x x
′

−

∫
( )
11
00
. d 2dxf x x xx
′
= −
∫∫
( )
1
1
2
0
0
dx fx x

= −

∫
( ) ( )
1
1
0
0
. d1xfx fx x=−−
∫
( )
11fI= −−
.
Theo đề bài
( ) ( )
1
0
2d 1xf x x f
′

−=

∫
1I⇒=−
.
https://toanmath.com/
Câu 202. Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
1; 2
và
( ) ( )
2
1
1dx fxxa
′
−=
∫
. Tính
( )
2
1
dfx x
∫
theo
a
và
( )
2bf=
.
A.
ba−
. B.
ab−
. C.
ab+
. D.
ab−−
.
Hướng dẫn giải
Chọn A
Đặt
1d dux u x
= −⇒ =
;
(
)
ddv fxx
′
=
chọn
( )
v fx=
.
( ) ( )
2
1
1dx fxx
′
−
∫
( ) ( ) ( )
2
2
1
1
1dx fx fx x=−−
∫
( ) ( )
2d
b
a
f fx x= −
∫
( )
2
1
b fx= −
∫
.
Ta có
( )
( )
2
1
1dx fxxa
′
−=
∫
( )
2
1
db fx x a⇔− =
∫
( )
2
1
dfx x ba⇔=−
∫
.
Câu 203. Cho hàm số
( )
fx
liên tục trên
và
( )
2 16f =
,
( )
2
0
d4fx x=
∫
. Tính tích phân
( )
1
0
. 2dI xf x x
′
=
∫
.
A.
13I =
. B.
12I =
. C.
20I =
. D.
7I =
.
Hướng dẫn giải
Chọn D
Đặt
( )
( )
dd
1
d 2d
2
2
ux
ux
v f xx
v fx
=
=

⇒

′
=
=
.
Khi đó,
( ) ( )
( ) ( ) ( )
1
1 11
0
0 00
1 1 11 1
. 2 2d 2 2d 8 2d
2 2 22 2
Ixfx fxx f fxx fxx=−=−=−
∫ ∫∫
.
Đặt
2 d 2dtx t x= ⇒=
.
Với
00xt= ⇒=
;
12xt
=⇒=
.
Suy ra
(
)
2
0
1
8 d 817
4
I ft t
=− =−=
∫
.
Câu 204. Cho
( )
y fx=
là hàm số chẵn, liên tục trên
biết đồ thị hàm số
(
)
y fx=
đi qua điểm
1
;4
2
M

−


và
(
)
1
2
0
dt 3ft =
∫
, tính
( )
0
6
sin 2 . sin dI xf x x
π
−
′
=
∫
.
A.
10I =
. B.
2I = −
. C.
1I
=
. D.
1
I = −
.
Hướng dẫn giải
Chọn B
Xét tích phân
( ) ( )
00
66
sin 2 . sin d 2sin . sin .cos d
I xf x x xf x xx
ππ
−−
′′
= =
∫∫
.
Đặt:
sin d cos dt x t xx= ⇒=
. Đổi cận:
1
62
00
xt
xt
π
=− ⇒=−
=⇒=
.
( )
0
1
2
2. dI tf t t
−
′
⇒=
∫
.
https://toanmath.com/
Đăt:
( ) ( )
2 d 2d
dd
ut u t
vftt vft
= =


⇒

′
= =


.
( )
(
)
( )
00
11
22
0
1
2. 2d 2d
1
2
2
I tft ft t f ft t
−−

⇒= − = − −

−

∫∫
.
Đồ thị hàm số
( )
y fx=
đi qua điểm
1
;4
2
M

−


1
4
2
f

⇒−=


.
Hàm số
( )
y fx=
là hàm số chẵn, liên tục trên
⇒
( ) ( ) ( )
11
0
22
1
00
2
d d d3ft t ft t fx x
−
= = =
∫∫∫
.
Vậy
4 2.3 2I =−=−
.
Câu 205. Cho hàm số
( )
y fx
=
thỏa mãn
( )
(
)
2
0
sin . d 0xf x x f
π
=
∫
1=
. Tính
( )
2
0
cos . dI xf x x
π
′
=
∫
.
A.
1I =
. B.
0I =
. C.
2I =
. D.
1I = −
.
Hướng dẫn giải
Chọn C
Đặt
( )
d ( )d
d sin d cos
′
= ⇒=
= ⇒=−
ufx ufxx
v xx v x
(
) ( )
( )
(
)
22
2
0
00
sin . d cos . cos . dxf x x xf x xf x x
ππ
π
′
⇒ =−+
∫∫
.
( )
2
0
cos . dI xf x x
π
′
⇒=
∫
(
) ( )
2
2
0
0
sin . d cos .xf x x xf x
π
π
= +
∫
11= −
0=
.
Câu 206. Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
( ) ( )
2018 2 sinf x fx x x−+ =
. Tính
( )
2
2
dI fx x
π
π
−
=
∫
?
A.
2
2019
. B.
2
2018
. C.
2
1009
. D.
4
2019
.
Hướng dẫn giải
Chọn D
Ta có
( )
( )
( )
22
22
2018 d 2 sin df x f x x x xx
ππ
ππ
−−
−+ =
∫∫
( ) ( )
2 22
2 22
d 2018 d 2 sin df xx fxx x xx
π ππ
π ππ
− −−
⇔ −+ =
∫ ∫∫
( )
22
22
2019 d 2 sin df x x x xx
ππ
ππ
−−
⇔=
∫∫
( )
1
+ Xét
2
2
2 sin dP x xx
π
π
−
=
∫
https://toanmath.com/
Đặt
2
d sin d
ux
v xx
=
=
d 2d
cos
ux
vx
=
⇒
= −
( )
22
22
2 . cos sin 4Px x x
ππ
ππ
−−
=− +=
Từ
( )
1
suy ra
( )
2
2
dI fx x
π
π
−
=
∫
4
2019
=
.
Câu 207. Cho hàm số
(
)
fx
và
(
)
gx
liên tục, có đạo hàm trên
và thỏa mãn
( ) ( )
0. 2 0ff
′′
≠
và
( )
(
) (
)
2e
x
gxf x xx
′
= −
. Tính giá trị của tích phân
( ) ( )
2
0
.dI fxgx x
′
=
∫
?
A.
4−
. B.
e2−
. C.
4
. D.
2e−
.
Hướng dẫn giải
Chọn C
Ta có
(
)
( )
( )
2e
x
gxf x xx
′
= −
(
) (
)
0 20gg
⇒==
(vì
(
) ( )
0. 2 0ff
′′
≠
)
( )
( )
2
0
.dI fxgx x
′
=
∫
( ) ( )
2
0
df x gx=
∫
( ) ( )
(
)
2
0
.f xgx=
( )
( )
2
0
.dgx f x x
′
−
∫
( )
2
2
0
2 ed 4
x
xxx=−− =
∫
.
Câu 208. Cho hàm số
( )
y fx
=
có đạo hàm và liên tục trên
0;
4
π



thỏa mãn
3
4
f
π

=


,
(
)
4
0
d1
cos
fx
x
x
π
=
∫
và
(
)
4
0
sin .tan . d 2
x xf x x
π

=

∫
. Tích phân
( )
4
0
sin . dxf x x
π
′
∫
bằng:
A.
4
. B.
2 32
2
+
. C.
132
2
+
. D.
6
.
Hướng dẫn giải
Chọn B
Ta có:
(
)
4
0
sin . dI xf x x
π
′
=
∫
. Đặt
(
) ( )
sin d cos d
dd
u x u xx
vfxx vfx
= =


⇒

′
= =


.
( ) ( )
4
4
0
0
sin . cos . dI xf x xf x x
π
π
= −
∫
1
32
2
I= −
.
( )
4
0
2 sin .tan . dx xf x x
π

=

∫
( )
4
2
0
sin . d
cos
fx
xx
x
π

=


∫
( )
( )
4
2
0
1 cos . d
cos
fx
xx
x
π

= −


∫
.
( )
( )
44
00
d cos . d
cos
fx
x xf x x
x
ππ

= −


∫∫
1
1 I= −
.
1
1I⇒=−
32
1
2
I⇒= +
32 2
2
+
=
.
Câu 209. Cho hàm số
( )
fx
liên tục trên
và
( )
2 16f =
,
( )
2
0
d4fx x=
∫
. Tính
4
0
d
2
x
I xf x

′
=


∫
A.
12I =
. B.
112I =
. C.
28I =
. D.
144I =
.
Hướng dẫn giải
Chọn B
https://toanmath.com/
Đặt
dd
2
ux
x
vf x
=

′
=


dd
2
2
ux
x
vf
=
⇒

=


.
Khi đó
4
0
d
2
x
I xf x

′
=


∫
4
4
0
0
2 2d
22
xx
xf f x
 
= −
 
 
∫
1
128 2I= −
với
4
1
0
d
2
x
If x

=


∫
.
Đặt
d 2d
2
x
u xu=⇒=
, khi đó
4
1
0
d
2
x
If x

=


∫
( )
2
0
2dfu u=
∫
( )
2
0
2 d8fx x= =
∫
.
Vậy
1
128 2II= −
128 16 112
= −=
.
Câu 210. Cho hàm số
( )
fx
có đạo hàm cấp hai
(
)
fx
′′
liên tục trên đoạn
[ ]
0;1
thoả
mãn
(
)
( )
1 01ff
= =
,
(
)
0 2018
f
′
=
. Mệnh đề nào dưới đây đúng?
A.
( )( )
1
0
1 2018fx xx
′′
−=−
∫
d
.
B.
( )( )
1
0
11fx xx−−
′′
=
∫
d
.
C.
( )( )
1
0
1 2018fx xx−=
′′
∫
d
. D.
( )( )
1
0
11fx xx−
′′
=
∫
d
.
Hướng dẫn giải
Chọn A
Xét
( )( )
1
0
1I fx xx
′′
= −
∫
d
( ) ( )
( )
1
0
1dx fx
′
−=
∫
Đặt
( )
( )
1
dd
ux
v fx
= −
′
=
( )
ddux
v fx
= −
⇔
′
=
(
) ( ) ( )
1
0
1
0
1
dI xf x fxx
′
⇔
′
=−+
∫
( ) ( ) ( ) ( )
1
0
11 1 0f f fx
′′
=− −+


( ) ( ) ( )
0 10f ff
′
=−+ −


( )
2018 1 1 2018=− +−=−
.
Câu 211. Cho hàm số
( )
fx
có đạo hàm liên tục thỏa mãn
0
2
f
π

=


,
( )
2
2
d
4
fx x
π
π
π
′
=


∫
và
( )
2
cos d
4
xf x x=
∫
π
π
π
. Tính
( )
2018f
π
.
A.
1−
. B.
0
. C.
1
2
. D.
1
.
Hướng dẫn giải
Chọn D
Bằng công thức tích phân từng phần ta có
( )
( ) ( )
2
22
cos d sin sin dxf x x xf x xf x x
ππ
π
π
ππ
′
= −


∫∫
. Suy ra
( )
2
sin d
4
xf x x
π
π
π
′
= −
∫
.
Hơn nữa ta tính được
2
2
22
1 cos 2 2 sin 2
sin d d
2 44
x xx
xx x
π
ππ
π
ππ
π
−−

= = =


∫∫
.
https://toanmath.com/
Do đó:
( )
(
)
( )
2 22 2
22
2
0 00 0
d 2 sin d sin d 0 sin d 0
fx x xfxx xx fx x x
π ππ π
′′ ′
+ + =⇔+ =


∫ ∫∫ ∫
.
Suy ra
( )
sinfx x
′
= −
. Do đó
( )
cosfx xC= +
. Vì
0
2
f
π

=


nên
0=C
.
Ta được
( )
cosfx x
=
(
)
( )
2018 cos 2018 1f
ππ
⇒= =
.
Câu 212. Cho hàm số
(
)
fx
nhận giá trị dương, có đạo hàm liên tục trên đoạn
[
]
0; 2
. Biết
( )
01f =
và
( ) ( )
2
24
.2 e
xx
fxf x
−
−=
, với mọi
[ ]
0; 2x∈
. Tính tích phân
( )
( )
( )
32
2
0
3
d
x xfx
Ix
fx
−′
=
∫
.
A.
16
3
I = −
. B.
16
5
I = −
. C.
14
3
I = −
. D.
32
5
I
= −
.
Hướng dẫn giải
Chọn B
Cách 1: Theo giả thiết, ta có
( ) ( )
2
24
.2 e
xx
fxf x
−
−=
và
( )
fx
nhận giá trị dương nên
( ) ( )
2
24
ln . 2 ln e
xx
fxf x
+
−=


⇔
( ) ( )
2
ln ln 2 2 4fx f x x x+ −= −
.
Mặt khác, với
0x
=
, ta có
(
)
( )
0. 2 1ff=
và
(
)
01
f =
nên
( )
21f =
.
Xét
( )
( )
( )
32
2
0
3
d
x xfx
Ix
fx
−′
=
∫
, ta có
( )
( )
( )
2
32
0
3. d
fx
I xx x
fx
′
= −
∫
Đặt
( )
( )
32
3
dd
ux x
fx
vx
fx
= −
′
=
(
)
( )
2
d 3 6d
ln
u x xx
v fx
= −
⇒
=
Suy ra
( )
( )
( )
( )
2
2
32 2
0
0
3 ln 3 6 .ln dI x x fx x x fx x

=− −−

∫
( )
( )
2
2
0
3 6 .ln dx x fx x=−−
∫
( )
1
.
Đến đây, đổi biến
2xt= −
ddxt⇒=−
. Khi
02xt= →=
và
20xt= →=
.
Ta có
( )
( )( )
0
2
2
3 6 .ln 2 dI ttf t t=− − −−
∫
(
)
(
)
2
2
0
3 6 .ln 2 dt t f tt=−− −
∫
Vì tích phân không phụ thuộc vào biến nên
( )
( )
2
2
0
3 6 .ln 2 dI x x f xx=−− −
∫
( )
2
.
Từ
( )
1
và
( )
2
ta cộng vế theo vế, ta được
( )
( ) ( )
2
2
0
2 3 6 . ln ln 2 dI x x fx f x x=−− + −


∫
Hay
( ) ( )
2
22
0
1
3 6 .2 4 d
2
I x x x xx=−− −
∫
16
5
= −
.
Cách 2 (Trắc nghiệm)
Chọn hàm số
( )
2
2
e
xx
fx
−
=
, khi đó:
( )
( )
( )
( )
2
2
32 2
22
32
2
00
3 .e . 2 2
16
d 3 .2 2d
5
e
xx
xx
xx x
I x xx x x
−
−
−−
−
= =− −=
∫∫
.
Câu 213. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
10f =
và
( ) ( ) ( )
11
2
2
00
e1
d 1e d
4
x
f x x x fx x
−
′
=+=


∫∫
. Tính tích phân
( )
1
0
dI fx x=
∫
.
https://toanmath.com/
A.
2e
I = −
. B.
e2I = −
. C.
e
2
I
=
. D.
e1
2
I
−
=
.
Hướng dẫn giải
Chọn B
Xét
( ) ( )
1
0
1e d
x
A x fx x= +
∫
. Đặt
(
)
(
)
d 1ed
x
u fx
vx x
=
= +
( )
dd
e
x
u fxx
vx
′
=
⇒
=
Suy ra
( ) ( )
1
1
0
0
e ed
xx
Axfx xfxx
′
= −
∫
( )
1
0
ed
x
xfxx
′
= −
∫
( )
1
2
0
1e
ed
4
x
xfxx
−
′
⇒=
∫
Xét
1
1
2
22 2 2
0
0
1 1 1 e1
ed e
2 24 4
xx
xx xx
−

= −+ =


∫
.
Ta có
( )
(
)
1 11
2
22
0 00
d 2 e d ed 0
xx
fx x xfxx x x
′′
+ +=


∫ ∫∫
(
)
( )
1
2
0
ed0
x
fx x x
′
⇔+=
∫
Suy ra
( )
e0
x
fx x
′
+=
[
]
0;1
x∀∈
(do
( )
( )
2
e0
x
fx x
′
+≥
[ ]
0;1x∀∈
)
( )
e
x
fx x
′
⇒=−
( ) ( )
1e
x
fx x C⇒ =−+
Do
( )
10f
=
nên
( )
( )
1e
x
fx x= −
Vậy
( ) ( ) ( )
11
1
0
00
d 1 ed 2 e e 2
xx
I fx x x x x= =− =−=−
∫∫
.
Câu 214. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1; 2
thỏa mãn
( ) ( )
2
2
1
1
1d
3
x fx x−=−
∫
,
( )
20f =
và
(
)
2
2
1
d7
fx x
′
=


∫
. Tính tích phân
( )
2
1
dI fx x=
∫
.
A.
7
5
I =
. B.
7
5
I = −
. C.
7
20
I = −
. D.
7
20
I =
.
Hướng dẫn giải
Chọn B
Đặt
( ) ( )
ddufx ufxx
′
= ⇒=
,
(
)
( )
3
2
1
d 1d
3
x
vx xv
−
= − ⇒=
Ta có
( ) ( )
2
2
1
1
1d
3
x fx x−= −
∫
( )
( )
( )
( )
2
33
2
1
1
11
.d
33
xx
fx f x x
−−
′
= −
∫
( ) ( )
2
3
1
11
1d
33
x fxx
′
⇔− =− −
∫
( ) ( )
2
3
1
1 d1x fxx
′
⇔− =
∫
(
) ( )
2
3
1
2.7 1 d 14x fxx
′
⇒− − =−
∫
Tính được
( )
2
6
1
49 1 d 7xx−=
∫
( )
2
2
1
dfx x
′
⇒


∫
( ) ( )
2
3
1
2.7 1 dx fxx
′
−−
∫
( )
2
6
1
49 1 d 0xx+ −=
∫
( ) ( )
2
2
3
1
7 1 d0x fx x

′
⇒ −− =

∫
( ) ( )
3
71fx x
′
⇒=−
( )
( )
4
71
4
x
fx C
−
⇒= +
.
Do
( )
20f =
( )
( )
4
71
7
44
x
fx
−
⇒= −
.
Vậy
( )
2
1
dI fx x=
∫
( )
4
2
1
71
7
d
44
x
x

−
= −



∫
7
5
= −
.
https://toanmath.com/
Câu 215. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
11f =
,
(
)
1
2
0
d9
fx x
′
=


∫
và
( )
1
3
0
1
d
2
xf x x
=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
2
3
. B.
5
2
. C.
7
4
. D.
6
5
.
Hướng dẫn giải
Chọn B
Ta có:
(
)
1
2
0
d9
fx x
′
=


∫
(
)
1
- Tính
( )
1
3
0
1
d.
2
xf x x=
∫
Đặt
( )
4
dd
4
u fxx
x
v
′
=
⇒
=
( )
1
3
0
1
d
2
xf x x
⇒=
∫
( )
1
4
0
.
4
x
fx

=


(
)
1
4
0
1
.d
4
xf x x
′
−
∫
( )
1
4
0
11
.d
44
xf x x
′
= −
∫
( )
1
4
0
. d1xf x x
′
⇒=−
∫
( )
1
4
0
18 . d 18xf x x
′
⇒=−
∫
( )
2
- Lại có:
1
1
9
8
0
0
1
d
99
x
xx= =
∫
1
8
0
81 d 9xx⇒=
∫
( )
3
- Cộng vế với vế các đẳng thức
( )
1
,
(
)
2
và
( )
3
ta được:
( ) (
)
1
2
48
0
18 . 81 d 0fx xfx x x

′′
+ +=



∫
( )
1
4
0
9d0fx x x
′

⇔ +=

∫
( )
1
4
0
. 9d0fx x x
π
′

⇔ +=

∫
Hay thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hàm số
( )
4
9y fx x
′
= +
, trục
hoành
Ox
, các đường thẳng
0
x =
,
1
x =
khi quay quanh
Ox
bằng
0
( )
4
90fx x
′
⇒ +=
( )
4
9fx x
′
⇒=−
( ) ( )
.dfx f x x
′
⇒=
∫
4
9
5
xC
=−+
.
Lại do
( )
11f =
14
5
C⇒=
(
)
5
9 14
55
fx x⇒ =−+
( )
1
0
dfx x⇒=
∫
1
5
0
9 14
d
55
xx

−+


∫
1
6
0
3 14 5
10 5 2
xx

=−+ =


.
Câu 216. Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
0;
4
π



và
0
4
f
π

=


. Biết
( )
4
2
0
d
8
f xx
π
π
=
∫
,
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Tính tích phân
(
)
8
0
2dI f xx
π
=
∫
A.
1I =
. B.
1
2
I =
. C.
2I =
. D.
1
4
I =
.
Hướng dẫn giải
Chọn D
https://toanmath.com/
17TTính 17T
(
)
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Đặt
(
) ( )
sin 2 2cos 2 d d
dd
x u xx u
f x x v fx v
= =


⇒

′
= =


, khi đó
( )
( )
( )
44
4
0
00
sin 2 d sin 2 . 2 cos2 d
f x xx xf x f x xx
ππ
π
′
= −
∫∫
(
)
( )
4
0
sin . sin0. 0 2 cos2 d
24
f f f x xx
π
ππ

= −−


∫
(
)
4
0
2 cos2 d
f x xx
π
= −
∫
.
Theo đề bài ta có
(
)
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
⇒
( )
4
0
cos2 d
8
f x xx
π
π
=
∫
.
Mặt khác ta lại có
4
2
0
cos 2 d
8
xx
π
π
=
∫
.
Do
( )
( ) ( )
44
2
22
00
cos2 d 2 .cos2 cos 2 dfx x x f x fx x x x
ππ

−=− +



∫∫
20
8 88
π ππ

=−+=


nên
( )
cos2fx x=
.
Ta có
8
8
0
0
11
cos4 d sin 4
44
I xx x
π
π
= = =
∫
.
Câu 217. . Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và
( ) ( )
0 10ff+=
. Biết
( )
1
2
0
1
d
2
f xx
=
∫
,
( ) ( )
1
0
cos d
2
fx xx
π
π
′
=
∫
. Tính
( )
1
0
dfx x
∫
.
A.
π
. B.
1
π
. C.
2
π
. D.
3
2
π
.
Hướng dẫn giải
17TChọn C
Đặt
(
)
( )
cos
dd
ux
v fxx
π
=
′
=
( )
( )
d sin du xx
v fx
ππ
= −
⇒
=
.
Khi đó:
( ) ( ) ( ) ( )
( ) ( )
11
1
0
00
cos d cos sin df x x x xfx fx x x
π πππ
′
= +
∫∫
( ) ( )
( )
( ) ( ) ( ) ( )
11
00
1 0 sin d sin df f fx x x fx x x
ππππ
=−+ + =
∫∫
( ) ( )
1
0
1
sin d
2
fx x x
π
⇒=
∫
.
Cách 1: Ta có
Tìm
k
sao cho
(
) ( )
1
2
0
sin d 0fx k x x
π
−=


∫
Ta có:
( ) ( ) ( ) ( ) ( ) ( )
1 11 1
2
2 22
0 00 0
sin d d 2 sin d sin dfx k x x f xx kfx xxk xx
π ππ
−=− +


∫ ∫∫ ∫
https://toanmath.com/
2
1
01
22
k
kk= −+ =⇔ =
.
Do đó
(
)
( )
1
2
0
sin d 0fx x x
π
−=


∫
( ) ( )
sinfx x
π
⇒=
(do
( ) ( )
2
sin 0fx x
π
−≥


x∀∈
).
Vậy
(
)
( )
11
00
2
d sin dfxx xx
π
π
= =
∫∫
.
Cách 2: Sử dụng BĐT Holder.
( )
(
) (
) ( )
2
22
d d. d
b bb
a aa
fxgxx f xxgxx

≤


∫ ∫∫
.
Dấu “
=
” xảy ra
(
)
( )
.f x kg x⇔=
,
[
]
;x ab
∀∈
.
Áp dụng vào bài ta có
(
) (
) ( ) ( )
2
1 11
22
0 00
11
sin d d . sin d
44
fx xx f xx xx
ππ

=≤=


∫ ∫∫
,
suy ra
( ) ( )
.sinfx k x
π
=
,
k
∈
.
Mà
( ) ( ) ( )
11
2
00
11
sin d sin d 1
22
fx xx k xx k
ππ
=⇔ =⇔=
∫∫
( ) ( )
sinfx x
π
⇒=
Vậy
(
) ( )
11
00
2
d sin d
fxx xx
π
π
= =
∫∫
.
Câu 218. Cho hàm số
( )
fx
có đạo hàm
( )
fx
′
liên tục trên đoạn
[ ]
0;1
thỏa
( )
10f =
,
( )
( )
1
2
2
0
dx
8
fx
π
′
=
∫
và
( )
1
0
1
cos d
22
xfx x
π

=


∫
. Tính
(
)
1
0
d
fx x
∫
.
A.
2
π
. B.
π
. C.
1
π
. D.
2
π
.
Hướng dẫn giải
Chọn D
Đặt
( )
( )
dd
2
sin
d cos d
2
2
u fxx
u fx
x
x
v
vx
π
π
π
′
=
=

⇒

=
=

Do đó
( )
1
0
1
cos d
22
xfx x
π

=


∫
( )
( )
1
1
0
0
22 1
sin sin d
2 22
x
fx xf x x
ππ
ππ

′
⇔− =


∫
( )
1
0
sin d
24
xf x x
ππ

′
⇔=−


∫
.
Lại có:
1
2
0
1
sin d
22
xx
π

=


∫
( )
( )
2
1 11
2
0 00
22
. d 2 sin d sin d
22
I fx x xfxx xx
ππ
ππ
 
′′
⇒= − − − +
 
 
∫ ∫∫
( )
2
1
2
2
0
2 4 21
sin d . 0
2 8 22
fx x x
π ππ
π ππ


′
= − − = − +=




∫
Vì
( )
2
2
sin 0
2
fx x
π
π


′
−− ≥




trên đoạn
[ ]
0;1
nên
https://toanmath.com/
( )
2
1
0
2
sin d 0
2
fx x x
π
π


′
−− =




∫
( )
2
=sin
2
fx x
π
π

′
⇔−


( )
= sin
22
fx x
ππ

′
⇔−


.
Suy ra
( )
=cos
2
fx x C
π

+


mà
( )
10f
=
do đó
( )
=cos
2
fx x
π



.
Vậy
( )
11
00
2
d cos d
2
fx x x x
π
π

= =


∫∫
.
Câu 219. Xét hàm số
( )
fx
có đạo hàm liên tục trên
và thỏa mãn điều kiện
( )
11f =
và
( )
24f =
. Tính
( )
( )
2
2
1
21
d
f x fx
Jx
xx
′
++

= −


∫
.
A.
1 ln 4J = +
. B.
4 ln 2J = −
. C.
1
ln 2
2
J = −
. D.
1
ln 4
2
J = +
.
Hướng dẫn giải
Chọn D
Cách 1: Ta có
( )
( )
2
2
1
21
d
f x fx
Jx
xx
′
++

= −


∫
( ) ( )
2 22
22
1 11
21
dd d
f x fx
xx x
x x xx
′

= − +−


∫∫∫
.
Đặt
( )
(
)
2
11
dd
dd
u ux
xx
vfxx vfx

= = −

⇒


′
= =

( )
( )
2
2
1
21
d
f x fx
Jx
xx
′
++

= −


∫
( )
( ) ( )
2
222
22 2
1
111
1 21
. dd d
fx fx
fx x x x
x x x xx

= + − +−


∫∫∫
( ) ( )
2
1
1 11
2 1 2ln ln 4
22
ff x
x

= −+ +=+


.
Cách 2:
( )
( )
2
2
1
21
d
f x fx
Jx
xx
′
++

= −


∫
( )
(
)
2
22
1
21
d
xf x f x
x
x xx
′
−

= +−


∫
(
)
22
2
11
21
dd
fx
xx
x xx
′


= +−




∫∫
( )
2
1
11
2ln ln 4
2
fx
x
xx

= + +=+


.
Cách 3: ( Trắc nghiệm)
Chọn hàm số
( )
f x ax b= +
. Vì
( )
( )
11
3
2
24
f
a
b
f
=
=
⇒

= −
=
, suy ra
( )
32fx x= −
.
Vậy
2
2
2
1
1
53 1 1 1
d 2ln ln 4
2
x
J xx
xx x
−

=− = −=+


∫
.
Câu 220. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( ) ( )
( )
11
2
2
00
e1
d 1e d
4
x
f x x x fx x
−
′
=+=


∫∫
và
( )
10f =
. Tính
( )
1
0
dfx x
∫
A.
e1
2
−
. B.
2
e
4
. C.
e2−
. D.
e
2
.
Hướng dẫn giải
Chọn C
- Tính:
( ) ( )
1
0
1e d
x
I x fx x=+=
∫
( ) ( )
11
00
eded
xx
x fx x fx x J K+=+
∫∫
.
https://toanmath.com/
Tính
( )
1
0
ed
x
K fx x=
∫
Đặt
( )
( ) ( )
de e d
e
dd
xx
x
u fx f x x
u fx
vx
vx
′

= +
=


⇒

=
=
(
)
( )
( ) ( )
1
1
0
0
e e ed
x xx
K xfx xfx xfx x
′

⇒= − +

∫
( ) ( )
11
00
e de d
xx
xfxx xfxx
′
=−−
∫∫
( )
( )
do 1 0f =
( )
1
0
ed
x
K J xfxx
′
⇒ =−−
∫
( )
1
0
ed
x
I JK xfxx
′
⇒=+ =−
∫
.
- Kết hợp giả thiết ta được:
( )
(
)
1
2
2
0
1
2
0
e1
d
4
e1
d
4
x
fx x
xe f x x
−
′
=


−
′
−=
∫
∫
(
)
(
)
1
2
2
0
1
2
0
e1
d (1)
4
e1
2 e d (2)
2
x
fx x
xfxx
−
′
=


⇒
−
′
= −
∫
∫
- Mặt khác, ta tính được:
1
2
22
0
e1
e d (3)
4
x
xx
−
=
∫
.
- Cộng vế với vế các đẳng thức (1), (2), (3) ta được:
( ) ( )
(
)
1
2
22
0
2e e d 0
xx
fx xfx x x
′′
+ +=


∫
( )
( )
1
2
ed0
x
o
fx x x
′
⇔+=
∫
( )
(
)
1
2
ed0
x
o
fx x x
π
′
⇔ +=
∫
hay thể tích hình phẳng giới hạn bởi đồ thị hàm số
( )
e
x
y fx x
′
= +
, trục
Ox
, các đường thẳng
0
x =
,
1x =
khi quay quanh trục
Ox
bằng
0
( )
e0
x
fx x
′
⇒ +=
( )
e
x
fx x
′
⇔=−
( ) ( )
ed 1 e C
xx
fx x x x⇒ =− =−+
∫
.
- Lại do
( ) ( ) ( )
1 0 C0 1 e
x
f fx x=⇒=⇒ =−
( ) ( )
11
00
d 1 ed
x
fx x x x⇒=−
∫∫
( )
( )
1
1
0
0
1 e ed
xx
xx=−+
∫
1
0
1e e2
x
=−+ = −
.
Vậy
( )
1
0
d e2fx x= −
∫
.
Câu 221. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
10f =
,
( )
1
2
0
d7fx x
′
=


∫
và
( )
1
2
0
1
d
3
xf x x=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
7
5
. B.
1
. C.
7
4
. D.
4
.
Hướng dẫn giải
Chọn A
Cách 1: Tính:
( )
1
2
0
dxf x x
∫
. Đặt
( )
( )
3
2
dd
dd
3
u fxx
u fx
x
v xx
v
′
=
=

⇒

=
=
.
Ta có:
( )
( )
( )
1
3
11
23
00
0
1
d .d
33
xf x
xfxx xfxx
′
= −
∫∫
https://toanmath.com/
( )
(
)
(
)
(
)
11
33
00
1. 1 0. 0
11
.d .d
33 3
ff
xf x x xf x x
−
′′
= −=−
∫∫
.
Mà
( )
1
2
0
1
d
3
xf x x=
∫
( )
( )
11
33
00
11
.d .d1
33
xf x x xf x x
′′
⇒− = ⇒ =−
∫∫
.
Ta có
( )
1
2
0
d7fx x
′
=


∫
(1).
1
1
7
6
0
0
1
d
77
x
xx
= =
∫
1
6
0
1
49 d .49 7
7
xx⇒==
∫
(2).
( ) (
)
11
33
00
. d 1 14 . d 14xf x x xf x x
′′
=−⇒ =−
∫∫
(3).
Cộng hai vế (1) (2) và (3) suy ra
( ) ( )
1 11
2
63
0 00
d 49 d 14 . d 7 7 14 0fx x xx xfxx
′′
+ + =+− =


∫ ∫∫
.
( ) (
)
{ }
1
2
36
0
14 49 d 0fx xfx x x
′′
⇒ + +=


∫
( )
1
2
3
0
7 d0fx x x
′

⇒+=

∫
.
Do
( )
2
3
70fx x
′

+≥

( )
1
2
3
0
7 d0fx x x
′

⇒+≥

∫
. Mà
( )
1
2
3
0
7 d0fx x x
′

+=

∫
( )
3
7fx x
′
⇒=−
.
( )
4
7
4
x
fx C=−+
. Mà
( )
77
10 0
44
f CC= ⇒− + = ⇒ =
.
Do đó
( )
4
77
44
x
fx=−+
.
Vậy
( )
1
11
45
00
0
77 77 7
dd
4 4 20 4 5
xx
fx x x x

=−+ =−+ =


∫∫
.
Cách 2: Tương tự như trên ta có:
( )
1
3
0
. d1xf x x
′
= −
∫
Áp dụng BĐT Cauchy-Schwarz, ta có:
(
)
(
)
( )
( ) ( )
2
1 11 1 1
2
2 22
33
0 00 0 0
1
77 d 7 d d 7 d d
7
xfxx x x fx x fx x fx x

′ ′ ′′
= ≤ ⋅ =⋅⋅ =
  

  

∫ ∫∫ ∫ ∫
Dấu bằng xảy ra khi và chỉ khi
( )
3
f x ax
′
=
, với
a
∈
.
Ta có
( )
1
11
7
3 33
00
0
. d1 .d1 1 7
7
ax
x f x x x ax x a
′
=−⇒ =−⇒ =−⇒ =−
∫∫
.
Suy ra
( )
( )
4
3
7
7
4
x
f x x fx C
′
=−⇒ =− +
, mà
( )
10f
=
nên
7
4
C =
Do đó
( )
(
)
4
7
1
4
fx x x
= − ∀∈
.
Vậy
( )
11
45
00
1
77 77 7
dd
0
4 4 20 4 5
xx
fx x x x

=−+ =−+ =


∫∫
.
Chú ý: Chứng minh bất đẳng thức Cauchy-Schwarz
Cho hàm số
( )
fx
và
( )
gx
liên tục trên đoạn
[ ]
;
ab
.
https://toanmath.com/
Khi đó, ta có
(
)
( ) ( ) ( )
2
22
d dd
b bb
a aa
fxgxx f xx gxx

≤⋅


∫ ∫∫
.
Chứng minh:
Trước hết ta có tính chất:
Nếu hàm số
( )
hx
liên tục và không âm trên đoạn
[
]
;ab
thì
( )
d0
b
a
hx x≥
∫
Xét tam thức bậc hai
( )
(
) (
) (
)
(
)
(
)
2
22 2
20
fx gx f x f xgx g x
λ λλ
+ = + +≥


, với mọi
λ
∈
Lấy tích phân hai vế trên đoạn
[
]
;
ab
ta được
( ) ( ) ( ) ( )
22 2
d2 g d d0
bb b
aa a
f xx fx xx gxx
λλ
+ +≥
∫∫ ∫
, với mọi
λ
∈
( )
*
Coi
( )
*
là tam thức bậc hai theo biến
λ
nên ta có
0
′
∆≤
( )
( ) ( )
2
2 22
d d d0
b bb
a aa
f xx f xx gxx

⇔− ≤


∫ ∫∫
( ) ( ) ( )
2
2 22
d dd
b bb
a aa
f xx f xx gxx

⇔≤


∫ ∫∫
(đpcm)

Tài liệu khác của Toán 12

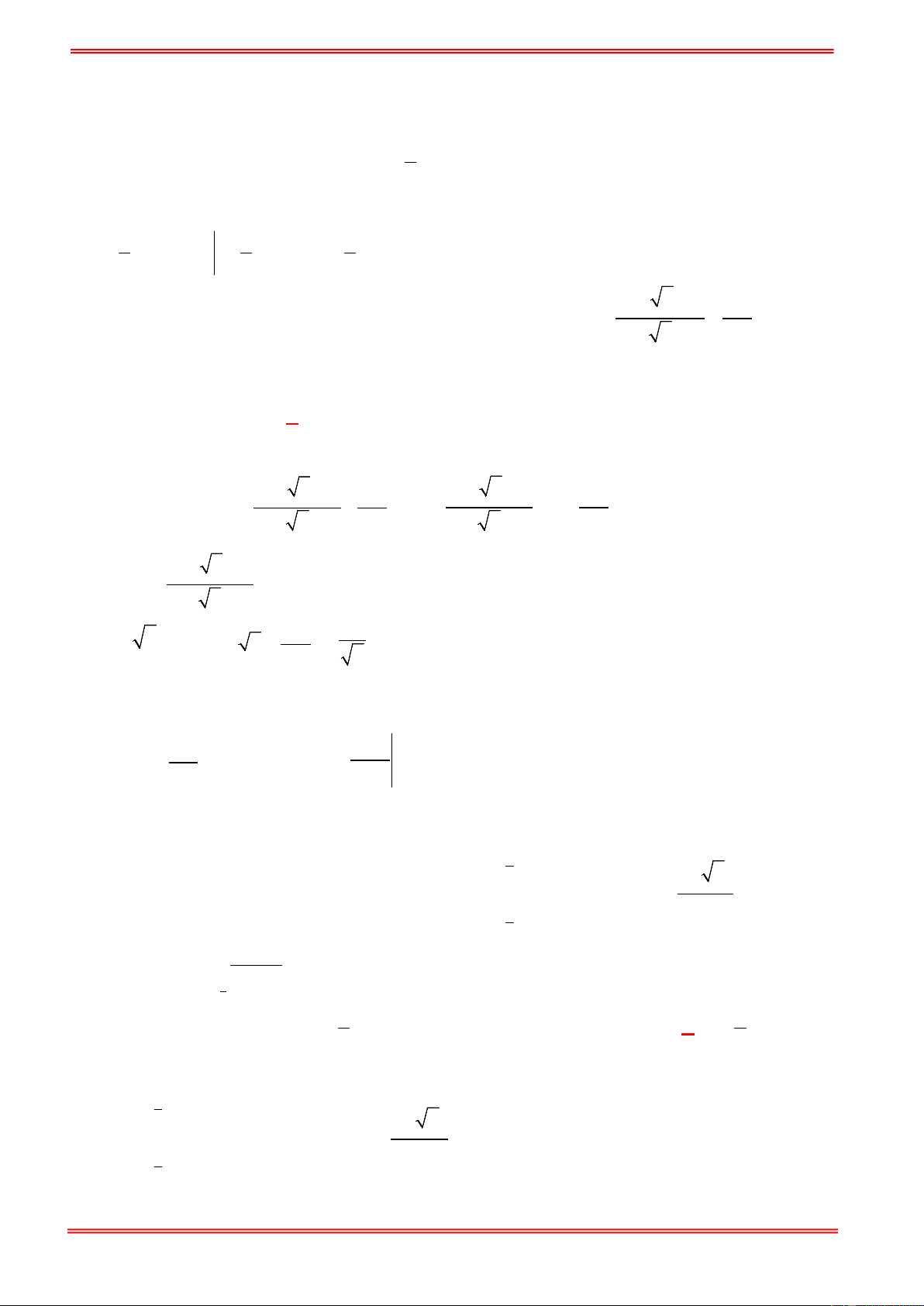
Preview text:


TÍCH PHÂN CỦA HÀM ẨN BÀI TẬP
DẠNG 1: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT NGUYÊN HÀM f ( x)  \{ } 1
f (0) = 2017 f (2) = 2018 Câu 1: Cho hàm số xác định trên
thỏa mãn f ′( x) 1 = , , x −1
S = f (3) − f (− ) 1 . Tính .
A. S = 1 .
B. S = ln 2 .
C. S = ln 4035 . D. S = 4 . 1  Câu 2:
Cho hàm số f ( x) xác định trên  \   thỏa mãn f ′( x) 2 =
và f (0) = 1. Giá trị của 2 2x −1 biểu thức f (− )
1 + f (3) bằng A. 4 + ln15 . B. 3 + ln15 . C. 2 + ln15 . D. ln15 . 1  2 Câu 3:
Cho hàm số f (x) xác định trên  \   thỏa mãn f ( ′ x) =
, f (0) = 1 và f (1) = 2 . Giá 2 2x −1
trị của biểu thức f ( 1)
− + f (3) bằng A. 4 + ln 5 . B. 2 + ln15 . C. 3 + ln15 . D. ln15. Câu 4:
Cho hàm số f ( x) xác định trên  thỏa mãn f ′( x) = 2x +1 và f ( ) 1 = 5 . Phương trình
f ( x) = 5 có hai nghiệm x , x . Tính tổng S = log x + log x . 1 2 2 1 2 2
A. S = 1 .
B. S = 2 .
C. S = 0 . D. S = 4 . 1 3  2  Câu 5:
Cho hàm số f (x) xác định trên  \   thỏa mãn f ′( x) =
, f (0) = 1 và f = 2   . 3 3x −1  3 
Giá trị của biểu thức f (− )
1 + f (3) bằng A. 3 + 5 ln 2 . B. 2 − + 5ln 2 . C. 4 + 5 ln 2 . D. 2 + 5 ln 2 . f ( x)  \{ 2; − } 2 4 f (0) = 1 Câu 6: Cho hàm số xác định trên
và thỏa mãn f ′( x) = ; f 3 − = 0 ; 2 ( ) x − 4 f (3) = 2 P = f ( 4 − ) + f (− ) 1 + f (4) và
. Tính giá trị biểu thức . 3 5 5 A. P = 3 + ln .
B. P = 3 + ln 3 . C. P = 2 + ln . D. P = 2 − ln . 25 3 3 1 Câu 7:
Cho hàm số f ( x) xác định trên  \ { 2; − }
1 thỏa mãn f ′( x) = ; f ( 3 − ) − f (3) = 0 2 x + x − 2 và f ( ) 1 0 =
. Giá trị của biểu thức f ( 4 − ) + f (− )
1 − f (4) bằng 3 1 1 1 4 1 8 A. + ln 2 . B. 1+ ln 80 . C. 1+ ln 2 + ln . D. 1+ ln . 3 3 3 5 3 5 1 Câu 8:
Cho hàm số f ( x) xác định trên  \ { 1 − ; }
1 và thỏa mãn f ′( x) = ; f ( 3 − ) + f (3) = 0 2 x −1  1   1  và f − + f = 2    
. Tính giá trị của biểu thức P = f (0) + f (4) .  2   2  3 3 1 3 1 3 A. P = 2 + ln . B. P = 1+ ln . C. P = 1+ ln . D. P = ln . 5 5 2 5 2 5 1 Câu 9:
Cho hàm số f ( x) xác định trên  \ { } 1
± thỏa mãn f ′(x) = . Biết f ( 3 − ) + f (3) = 0 2 x −1  1   1  và f − + f = 2    
. Giá trị T = f ( 2
− ) + f (0) + f (4) bằng:  2   2  https://toanmath.com/ 1 5 1 9 1 9 1 9 A. T = 2 + ln . B. T = 1+ ln . C. T = 3 + ln . D. T = ln . 2 9 2 5 2 5 2 5
Câu 10: Cho hàm số f ( x) nhận giá trị dương, có đạo hàm liên tục trên (0; +∞) thỏa mãn f ( ) 1 2 = 15
và f ′( x) + ( x + ) 2 2
4 f ( x) = 0 . Tính f ( )
1 + f (2) + f (3) . 7 11 11 7 A. . B. . C. . D. . 15 15 30 30
Câu 11: Cho hàm số f ( x) xác định và liên tục trên  . Biết 6
f ( x). f ′( x) = 12x +13 và f (0) = 2 .
Khi đó phương trình f (x) = 3 có bao nhiêu nghiệm? A. 2 . B. 3 . C. 7 . D. 1.
Câu 12: Cho hàm số f ( x) xác định trên  thỏa mãn ( ) ex e x f x − ′ = + − 2 , f (0) = 5 và  1  f ln = 0  
. Giá trị của biểu thức S = f (− ln16) + f (ln 4) bằng  4  31 9 5 A. S = . B. S = . C. S = .
D. f (0). f (2) = 1. 2 2 2  π 
Câu 13: Cho hàm số f ( x) liên tục, không âm trên đoạn 0; 
 , thỏa mãn f (0) = 3 và  2   π 
f ( x) f ′( x) 2 . = cos .
x 1+ f ( x) , x ∀ ∈ 0; 
 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M  2  π π 
của hàm số f ( x) trên đoạn ;   .  6 2  21 5 A. m =
, M = 2 2 . B. m = , M = 3 . 2 2 5 C. m = , M = 3 .
D. m = 3 , M = 2 2 . 2
Câu 14: Cho hàm số f ( x) có đạo hàm liên tục trên  và thỏa mãn f ( x) > 0 , x
∀ ∈  . Biết f (0) =1 f '( x) và
( ) = 2− 2x . Tìm các giá trị thực của tham số m để phương trình f (x) = m có hai f x
nghiệm thực phân biệt.
A. m > e .
B. 0 < m ≤ 1 .
C. 0 < m < e .
D. 1 < m < e .
Câu 15: Cho hàm số f ( x) liên tục trên  và f ( x) ≠ 0 với mọi x ∈  . f ′( x) = ( x + ) 2 2 1 f ( x) và a a f ( ) 1 = 0,
− 5 . Biết rằng tổng f ( )
1 + f (2) + f (3) + ... + f (2017) =
; (a ∈ ,b ∈ ) với b b
tối giản. Mệnh đề nào dưới đây đúng? a
A. a + b = 1 − . B. a ∈ ( 2017 − ; 2017) . C. < 1 − .
D. b − a = 4035 . b −
Câu 16: Cho hàm số f ( x) ≠ 0 thỏa mãn điều kiện '
f ( x) = ( x + ) 2 2
3 . f ( x) và f ( ) 1 0 = . Biết tổng 2 ( ) a a
f 1 + f (2) + ... + f (2017) + f (2018) = với *
a ∈ ,b ∈  và là phân số tối giản. Mệnh b b
đề nào sau đây đúng? a a A. < 1 − . B. >1. b b
C. a + b = 1010 .
D. b − a = 3029 . https://toanmath.com/
 f ′′(x) f (x)−  f ′  ( x) 2 3 . 2  + xf  (x) = 0
Câu 17: Cho hàm số y = f ( x) , x ∀ ≥ 0 , thỏa mãn  . Tính  f ′  (0) = 0; f (0) = 1 f ( ) 1 . 2 3 6 7 A. . B. . C. . D. . 3 2 7 6 f ′( x) x
Câu 18: Giả sử hàm số f (x) liên tục, dương trên  ; thỏa mãn f (0) = 1 và = . Khi đó f ( x) 2 x +1
hiệu T = f (2 2 ) − 2 f ( ) 1 thuộc khoảng A. (2;3) . B. (7;9) . C. (0; ) 1 . D. (9;12) . π 4 f (tan t ) 1 1 Câu 19: Khi đó dt = f x dx ∫ ∫ . Vậy f
∫ (x)dx = 6.Cho hàm số y = f (x) đồng biến trên 2 ( ) cos t 0 0 0
(0;+∞); y = f (x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f ( ) 2 3 = và 3  f  ( x) 2 '  =  (x + )
1 . f ( x) . Mệnh đề nào dưới đây đúng? A. 2
2613 < f (8) < 2614 . B. 2
2614 < f (8) < 2615 . C. 2
2618 < f (8) < 2619 . D. 2
2616 < f (8) < 2617 .
Câu 20: Giả sử hàm số y = f ( x) liên tục, nhận giá trị dương trên (0; +
 ∞) và thỏa mãn f ( ) 1 = 1,
f ( x) = f ′( x) 3x +1 , với mọi x > 0 . Mệnh đề nào sau đây đúng?
A. 4 < f (5) < 5 .
B. 2 < f (5) < 3 .
C. 3 < f (5) < 4 .
D. 1 < f (5) < 2 . 2 Câu 21: Cho hàm số
f ( x) thỏa mãn  f ′  ( x) + f
(x) f ′′(x) 4 . = 15x +12x , x ∀ ∈  và
f (0) = f ′(0) = 1. Giá trị của 2 f ( ) 1 bằng 9 5 A. . B. . C. 10 . D. 8 . 2 2 f ( x +1) 2 ( x +1 + 3)
Câu 22: Cho hàm số f ( x) liên tục trên  và thỏa mãn dx = + C ∫ . Nguyên x +1 x + 5
hàm của hàm số f (2x) trên tập +  là: x + 3 x + 3 2x + 3 2x + 3 A. + C . B. + C . C. + C . D. + C . 2 ( 2 x + 4) 2 x + 4 4 ( 2 x + ) 1 8( 2 x + ) 1
DẠNG 2: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT, GIẢI HỆ TÍCH PHÂN 5 2 Câu 23: Cho f
∫ (x)dx =10. Kết quả 2−4 f ∫ (x)dx  bằng: 2 5 A. 34 . B. 36 . C. 40 . D. 32 . 9 f ( x) F ( x) f ( x) Câu 24: Cho hàm số liên tục trên  và là nguyên hàm của , biết f
∫ (x)dx = 9 và 0 F (0) = 3 F (9) . Tính . A. F (9) = 6 − .
B. F (9) = 6 .
C. F (9) = 12 . D. F (9) = 12 − . https://toanmath.com/ 2 2 I = f ∫ (x)dx = 3 J = 4 f
∫ (x)−3dxCâu 25: Cho 0 . Khi đó 0 bằng: A. 2 . B. 6 . C. 8 . D. 4 . 4 4 4 f ∫ (x)dx =10 g ∫ (x)dx = 5 I = 3 f
∫ (x)−5g(x)dxCâu 26: Cho 2 và 2 . Tính 2
A. I = 5 .
B. I = 15 . C. I = 5 − . D. I = 10 . 9 0 9 f ∫ (x)dx = 37 g ∫ (x)dx =16 I = 2 f
∫ (x)+3g(x)dxCâu 27: Giả sử 0 và 9 . Khi đó, 0 bằng:
A. I = 26 .
B. I = 58 .
C. I = 143 . D. I = 122 . 2 5 5 f
∫ (x)dx = 3 f (x)dx = 1 − ∫ f ( x) dx ∫ Câu 28: Nếu 1 , 2 thì 1 bằng A. 2 − . B. 2 . C. 3 . D. 4 . 2 3 3 f ∫ (x)dx =1
f ( x) dx = 2 − ∫ f ( x) dx ∫ Câu 29: Cho 1 và 2 . Giá trị của 1 bằng A. 1. B. 3 − . C. 1 − . D. 3 . 10 6
Câu 30: Cho hàm số f ( x) liên tục trên đoạn [0;10] và f
∫ (x)dx = 7 và f
∫ (x)dx = 3. Tính 0 2 2 10 P = f
∫ (x)dx+ f
∫ (x)dx. 0 6
A. P = 7 . B. P = 4 − .
C. P = 4 .
D. P = 10 . 1 2 f ∫ (x)dx = 2
f ( x) dx = ∫ 2 Câu 31: Cho 0 , f
∫ (x)dx = 4, khi đó 0 ? 1 A. 6 . B. 2 . C. 1. D. 3 . 1 3 3
Câu 32: Cho hàm số f ( x) liên tục trên  và có f
∫ (x)dx = 2; f
∫ (x)dx = 6. Tính I = f
∫ (x)dx . 0 1 0
A. I = 8 .
B. I = 12 .
C. I = 36 . D. I = 4 . 2 2 2 f ∫ (x)dx = 2
g ( x) dx = 1 − ∫ I = x + 2 f ∫ 
(x)+3g (x)dxCâu 33: Cho 1 − và 1 − . Tính 1 − bằng 11 7 17 5 A. I = . B. I = . C. I = . D. I = . 2 2 2 2 8 4 4
f ( x) dx = 2 − ∫ f
∫ (x)dx = 3 g ∫ (x)dx = 7 Câu 34: Biết 1 ; 1 ; 1
. Mệnh đề nào sau đây sai? 8 4 A. f
∫ (x)dx =1. B. f
∫ (x)+ g(x)dx =10  . 4 1 8 4 C.
f ( x) dx = 5 − ∫ . D. 4 f
∫ (x)−2g(x)dx = 2 −  . 4 1 3 f ( x) f ′( x) [ 1 − ; ] 3 f (− ) 1 = 3 Câu 35: Cho hàm số có liên tục trên đoạn , và f ( ′ x)dx =10 ∫ giá trị 1 − f (3) của bằng A. 13 − . B. 7 − . C. 13 . D. 7 . https://toanmath.com/ 2 2 f ∫ (x)dx = 3 ( f (x)+ ∫ )1dx Câu 36: Cho 0 . Tính 0 ? A. 4 . B. 5 . C. 7 . D. 1. 2
Câu 37: Cho y = f ( x) , y = g ( x) là các hàm số có đạo hàm liên tục trên [0; 2] và g
∫ (x).f ′(x)dx = 2 0 2 2 ′ , g′
∫ (x).f (x)dx = 3. Tính tích phân I =  f
∫ (x).g(x) dx  . 0 0 A. I = 1 − .
B. I = 6 .
C. I = 5 . D. I = 1. 5 2 − f ∫ (x)dx = 8 g ∫ (x)dx = 3 5
Câu 38: Cho hai tích phân 2 − và 5 . Tính I =  f
∫  (x)−4g(x)−1dx  . 2 − A. I = 11 − .
B. I = 13 .
C. I = 27 . D. I = 3 . 1
Câu 39: Cho hàm số f ( x) 4 3 2
= x − 4x + 2x − x +1, x ∀ ∈  . Tính 2
f ( x). f ′ ∫ (x)dx. 0 2 2 A. . B. 2 . C. − . D. 2 − . 3 3 6 4
Câu 40: Cho hàm số f ( x) liên tục trên đoạn [0; 6] thỏa mãn f
∫ (x)dx =10 và f
∫ (x)dx = 6. Tính 0 2 2 6
giá trị của biểu thức P = f
∫ (x)dx+ f
∫ (x)dx. 0 4
A. P = 4 .`
B. P = 16 .
C. P = 8 . D. P = 10 . 1 1
Câu 41: Cho hàm số f ( x) liên tục trên đoạn [0; 1] và có 3 − 2 f ∫ (x) dx = 5  . Tính f ( x) dx ∫ . 0 0 A. 1 − . B. 2. C. 1. D. 2 − . 1 1
Câu 42: Cho hai hàm số f ( x) và g ( x) liên tục trên đoạn [0; 1], có f
∫ (x)dx = 4 và g(x)dx = 2 − ∫ 0 0
. Tính tích phân I =  f
∫ (x)−3g(x)dx  . A. 10 − . B. 10 . C. 2. D. 2 − . 1
Câu 43: Cho hàm số f ( x) 2
= ln x + x +1 . Tính tích phân I = f '
∫ (x)dx. 0
A. I = ln 2 .
B. I = ln (1+ 2 ) .
C. I = ln 2 D. I = 2 ln 2
Câu 44: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [1; ln3] và thỏa mãn f ( ) 2 1 = e , ln 3 f ' ∫ (x) 2
dx = 9 − e . Tính I = f (ln 3) . 1 A. 2
I = 9 − 2e .
B. I = 9 . C. I = 9 − . D. 2 I = 2e − 9 .
Câu 45: Cho hai hàm số y = f ( x) và y = g ( x) có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn 1 1 1 / f '
∫ (x).g(x)dx =1, f (x).g '(x)dx = 1 − ∫
. Tính I =  f
∫ (x).g(x) dx  . 0 0 0 A. I = 2 − .
B. I = 0 .
C. I = 3 . D. I = 2 . https://toanmath.com/ 2 x
Câu 46: Cho hàm số f ( x) liên tục trên (0; +∞) và thỏa f
∫ (t)dt = .xcosπ x . Tính f (4). 0
A. f (4) = 123 . B. f ( ) 2 4 = . C. f ( ) 3 4 = . D. f ( ) 1 4 = . 3 4 4 f ( x)
Câu 47: Cho hàm số f ( x) thỏa mãn 2 t .dt = . x cosπ x ∫ . Tính f (4) . 0
A. f (4) = 2 3 . B. f (4) = 1 − . C. f ( ) 1 4 = . D. f ( ) 3 4 = 12 . 2 x  π 
Câu 48: Cho hàm số G ( x) = t.cos ∫
(x −t).dt . Tính G'  .  2  0  π   π   π   π  A. G ' = 1 −   . B. G ' = 1   . C. G ' = 0   . D. G ' = 2   .  2   2   2   2  2 x
Câu 49: Cho hàm số G ( x) = cos t.dt ∫
( x > 0 ). Tính G '( x) . 0 A. G ( x) 2 '
= x .cos x .
B. G '( x) = 2 .
x cos x . C. G '( x) = cos x .
D. G '( x) = cos x −1. x
Câu 50: Cho hàm số G ( x) 2 = 1+ t dt ∫
. Tính G '( x) . 1 x 1 A. . B. 2 1+ x . C. . D. ( 2 x + ) 2 1 x +1 . 2 1+ x 2 1+ x x
Câu 51: Cho hàm số F ( x) 2 = sin t .dt ∫
( x > 0 ). Tính F '( x) . 1 sin x 2 sin x
A. sin x . B. . C. . D. sin x . 2 x x x f (t ) f ( x)
Câu 52: Tính đạo hàm của f ( x) , biết f ( x) thỏa t.e dt = e ∫ . 0
A. f '( x) = x . B. f ( x) 2 ' = x +1. C. f ( x) 1 ' = . D. f ( x) 1 ' = . x 1− x 2 x
y = f ( x) [0;+ ∞) f (4) Câu 53: Cho hàm số liên tục trên và f
∫ (t)dt = .xsin(π x). Tính 0 π −1 π π A. f (π ) = . B. f (π ) = . C. f (π ) = . D. f (π ) 1 = . 4 2 4 2 f ( x) ( 2; − 3) F ( x) f ( x) Câu 54: Cho hàm số liên tục trên khoảng . Gọi là một nguyên hàm của trên 2 ( I =  f
∫  (x)+ 2xdx  2; − 3) F (− ) 1 = 1 F (2) = 4 khoảng . Tính 1 − , biết và .
A. I = 6 .
B. I = 10 .
C. I = 3 . D. I = 9 . 2 2 2 f ∫ (x)dx = 2
g ( x) dx = 1 − ∫ I = x + 2 f ∫ 
(x)−3g (x)dxCâu 55: Cho 1 − và 1 − . Tính 1 − 11 7 17 5 A. I = . B. I = . C. I = . D. I = . 2 2 2 2 2 2 2 3 f
∫ (x)+ 2g(x)dx =1  2 f
∫ (x)− g(x)dx = 3 −  f ( x) dx ∫ Câu 56: Cho 1 , 1 . Khi đó, 1 bằng https://toanmath.com/ 11 5 6 16 A. . B. − . C. . D. . 7 7 7 7
Câu 57: Cho f ( x) , g ( x) là hai hàm số liên tục trên đoạn [ 1 − ; ]
1 và f ( x) là hàm số chẵn, g ( x) là 1 1
hàm số lẻ. Biết f
∫ (x)dx = 5; g
∫ (x)dx = 7 . Mệnh đề nào sau đây là sai? 0 0 1 1 A. f
∫ (x)dx =10. B. f
∫  (x)+ g(x)dx =10  . 1 − 1 − 1 1 C. f
∫  (x)− g(x)dx =10  . D. g ∫ (x)dx =14. 1 − 1 −
Câu 58: Cho f ( x) , g ( x) là hai hàm số liên tục trên đoạn [ 1 − ; ]
1 và f ( x) là hàm số chẵn, g ( x) là 1 1
hàm số lẻ. Biết f
∫ (x)dx = 5; g
∫ (x)dx = 7. Mệnh đề nào sau đây là sai? 0 0 1 1 A. f
∫ (x)dx =10. B. f
∫  (x)+ g(x)dx =10  . 1 − 1 − 1 1 C. f
∫  (x)− g(x)dx =10  . D. g ∫ (x)dx =14. 1 − 1 − 10 8 10 f ∫ (z)dz =17 f ∫ (t)dt =12 3 − f ∫ (x)dx Câu 59: Nếu 0 và 0 thì 8 bằng A. 15 − . B. 29 . C. 15 . D. 5 . 2 7 7 f
∫ (x)dx = 2 f ∫ (t)dt = 9 f ( z) dz ∫ Câu 60: Cho 1 − , 1 − . Giá trị của 2 là A. 11. B. 5 . C. 7 . D. 9 . 3
Câu 61: Cho hàm số y = f ( x) liên tục, luôn dương trên [0; ] 3 và thỏa mãn I = f
∫ (x)dx = 4. Khi đó 0 3 1+ln( f ( x))
giá trị của tích phân K = ∫(e + 4)dx là: 0 A. 4 +12e . B. 12 + 4e . C. 3e +14 . D. 14 + 3e .
Câu 62: Cho hàm số y = f ( x) có đạo hàm trên  thỏa  f  (0) = f ′(0) = 1;  .  f
 ( x + y) = f ( x) + f ( y) + 3xy ( x + y) −1, x,y ∀ ∈  1 Tính f ( x − ∫ ) 1 dx . 0 1 1 1 7 A. . B. − . C. . D. . 2 4 4 4 1
Câu 63: Cho hàm số f ( x) là hàm bậc nhất thỏa mãn ∫(x + )
1 f ′( x) dx = 10 và 2 f ( ) 1 − f (0) = 2 . 0 1 Tính I = f
∫ (x)dx. 0
A. I = 1.
B. I = 8 . C. I = 12 − . D. I = 8 − . https://toanmath.com/ f ( x)  \{ } 0 1 f ( ) 1 = a f ( 2 − ) = b Câu 64: Cho hàm số xác định trên
, thỏa mãn f ′( x) = , và 3 5 x + x f (− ) 1 + f (2) . Tính . A. f (− )
1 + f (2) = −a − b . B. f (− )
1 + f (2) = a − b . C. f (− )
1 + f (2) = a + b . D. f (− )
1 + f (2) = b − a . f ( x)  \{ } 0 1 f ( ) 1 = a f ( 2 − ) = b Câu 65: Cho hàm số xác định trên
và thỏa mãn f ′( x) = , , 2 4 x + x f (− ) 1 − f (2)
. Giá trị của biểu thức bằng
A. b − a .
B. a + b .
C. a − b .
D. −a − b .
Câu 66: Cho hàm số y = f ( x) xác định và liên tục trên  thỏa mãn đồng thời các điều kiện f ( x) > 0 , x
∀ ∈  ; f ′(x) x 2
= −e . f (x), x ∀ ∈  và f ( ) 1 0 =
. Tính giá trị của f (ln 2) . 2 A. f ( ) 2 ln 2 = . B. f ( ) 2 ln 2 = − . C. f ( ) 2 ln 2 = . D. f ( ) 1 ln 2 = . 9 9 3 3
Câu 67: Cho hàm số y = f ( x) có đồ thị (C ) , xác định và liên tục trên  thỏa mãn đồng thời các
điều kiện f (x) > 0 x
∀ ∈  , f ′(x) = (x f (x))2 . , x
∀ ∈  và f (0) = 2 . Phương trình tiếp
tuyến tại điểm có hoành độ x = 1 của đồ thị (C ) là.
A. y = 6x + 30 . B. y = 6 − x + 30 .
C. y = 36x − 30 . D. y = 36 − x + 42 .
Câu 68: Cho hàm số y = f ( x) > 0 xác định, có đạo hàm trên đoạn [0; ] 1 và thỏa mãn: x 1
g ( x) = 1+ 2018 f ∫ (t)dt , ( ) 2
g x = f ( x) . Tính g ( x)dx ∫ . 0 0 1011 1009 2019 A. . B. . C. . D. 505 . 2 2 2
y = f ( x) [ 1 − ; ] 1
f ( x) > 0, x ∀ ∈  Câu 69: Cho hàm số
có đạo hàm và liên tục trên đoạn , thỏa mãn
f '( x) + 2 f ( x) = 0 f ( ) 1 = 1 f (− ) 1 và . Biết , tính . A. f ( ) 2 1 e− − = . B. f (− ) 3 1 = e . C. f (− ) 4 1 = e . D. f (− ) 1 = 3 .
Câu 70: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 đồng thời thỏa mãn f ′(0) = 9 và
f ′′( x) +  f ′  ( x) 2 9 − x = 9 
. Tính T = f ( ) 1 − f (0) . 1
A. T = 2 + 9 ln 2 .
B. T = 9 . C. T = + 9ln 2 .
D. T = 2 − 9 ln 2 . 2
y = f ( x)
f ( x) f ( x) 4 2 ' . = x + x f (0) = 2 2 f (2) Câu 71: Cho hàm số thỏa mãn . Biết . Tính . 313 332 324 323 A. 2 f (2) = . B. 2 f (2) = . C. 2 f (2) = . D. 2 f (2) = . 15 15 15 15
Câu 72: Cho f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1; 4] thỏa mãn
x + xf ( x) =  f ′  ( x) 2  x ∀ ∈  [ ] f ( ) 3 2 , 1; 4 , 1 =
. Giá trị f (4) bằng: 2 391 361 381 371 A. B. C. D. 18 18 18 18
y = f ( x) f ′( x) [0;+∞) Câu 73: Cho hàm số có
liên tục trên nửa khoảng thỏa mãn ( )+ ( ) 2 3 = 1+ 3.e x f x f x − ′ . Khi đó: https://toanmath.com/ 1 1 1 1 A. 3 e f ( ) 1 − f (0) = − . B. 3 e f ( ) 1 − f (0) = − . 2 + 2 e 3 2 + 4 2 e 3 e + 3 e + 3 − 8 3 ( 2 ) 2 C. e f ( ) 1 − f (0) = .
D. 3 f ( ) − f ( ) = ( 2 + ) 2 e 1 0 e 3 e + 3 − 8 . 3
Câu 74: Cho hàm số f liên tục, f ( x) > 1
− , f (0) = 0 và thỏa f ′(x) 2 x +1 = 2x
f ( x) +1 . Tính f ( 3) . A. 0 . B. 3 . C. 7 . D. 9 .
Câu 75: Cho hàm số f ( x) ≠ 0 thỏa mãn điều kiện f ′( x) = ( x + ) 2 2
3 f ( x) và f ( ) 1 0 = − . Biết rằng 2 a a tổng f ( )
1 + f (2) + f (3) + ... + f (2017) + f (2018) = với ( *
a ∈ , b ∈  ) và là phân số b b
tối giản. Mệnh đề nào sau đây đúng? a a A. < 1 − . B. >1.
C. a + b = 1010 .
D. b − a = 3029 . b b ax + b
Câu 76: Biết luôn có hai số a và b để F ( x) =
(4a −b ≠ 0) là nguyên hàm của hàm số f (x) x + 4 và thỏa mãn: 2
2 f ( x) = F
 ( x) −1 f ′  ( x) .
Khẳng định nào dưới đây đúng và đầy đủ nhất?
A. a = 1, b = 4 .
B. a = 1, b = 1 − .
C. a = 1, b ∈  \ { }
4 . D. a ∈  , b ∈  .
y = f ( x) [1;2] f ( ) 1 = 4 Câu 77: Cho hàm số
có đạo hàm liên tục trên thỏa mãn và
f ( x) = xf ′( x) 3 2 − 2x − 3x f (2) . Tính A. 5 . B. 20 . C. 10 . D. 15 . x  π π 
Câu 78: Cho f ( x) = trên − ; 
 và F ( x) là một nguyên hàm của xf ′( x) thỏa mãn 2 cos x  2 2   π π 
F (0) = 0 . Biết a ∈ − ; 
 thỏa mãn tan a = 3. Tính F (a) 2
−10a + 3a .  2 2  1 1 1 A. − ln10 . B. − ln10 . C. ln10 . D. ln10 . 2 4 2
Câu 79: Cho hàm số y = f ( x) xác định và liên tục trên  thỏa mãn đồng thời các điều kiện sau
f ( x) > 0 , x
∀ ∈  , f ′(x) x 2
= −e . f (x) x ∀ ∈  và f ( ) 1 0 =
. Phương trình tiếp tuyến của 2
đồ thị tại điểm có hoành độ x = ln 2 là 0
A. 2x + 9 y − 2 ln 2 − 3 = 0 .
B. 2x − 9 y − 2 ln 2 + 3 = 0 .
C. 2x − 9 y + 2 ln 2 − 3 = 0 .
D. 2x + 9 y + 2 ln 2 − 3 = 0 .
Câu 80: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 , f ( x) và f ′( x) đều nhận giá trị 1 1 dương trên đoạ 2 n [  ′  0; ]
1 và thỏa mãn f (0) = 2 , f
∫ (x). f (x) +1 dx = 2 f ′  ∫
(x).f (x)dx   0 0 1 3 . Tính  f ∫ (x) dx  . 0 15 15 17 19 A. . B. . C. . D. . 4 2 2 2 https://toanmath.com/
Câu 81: Cho f (x) không âm thỏa mãn điều kiện 2
f (x). f '(x) = 2x
f (x) +1 và f (0) = 0 . Tổng giá trị
lớn nhất và nhỏ nhất của hàm số y = f (x) trên [1; ] 3 là A. 22 B. 4 11 + 3 C. 20 + 2 D. 3 11 + 3
Câu 82: Cho hàm số f ( x) có đạo hàm và đồng biến trên  thỏa mãn f (0) = 1 và ( 1 ′( ))2 x f x
= e f (x), x
∀ ∈  . Tính tích phân f (x)dx ∫ bằng 0
A. e − 2 .
B. e −1. C. 2 e − 2 . D. 2 e −1. y = f x  \{ } 0 Câu 83: Cho hàm số
( ) xác định và liên tục trên thỏa mãn 2 2 2
x f ( x) + (2x − )
1 f ( x) = xf ′( x) −1 x ∀ ∈  \{ } 0 f ( ) 1 = 2 − với và . Tính f ( x) dx ∫ . 1 1 3 ln 2 3 ln 2 A. − − ln 2. B. − − ln 2. C. 1 − − . D. − − . 2 2 2 2 2
Câu 84: Cho hàm số y = f ( x) . Có đạo hàm liên tục trên  . Biết f ( ) 1 = e và
(x + ) f (x) = xf ′(x) 3 2 − x , x
∀ ∈  . Tính f (2) . A. 2 4e − 4e + 4 . B. 2 4e − 2e +1 . C. 3 2e − 2e + 2 . D. 2 4e + 4e − 4 .
Câu 85: Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 và thỏa mãn f (0) = 0 . Biết 1 9 1 π x 3π 1 2
f ( x) dx = ∫ và f ′( x) cos dx = ∫ . Tích phân f ( x) dx ∫ bằng 2 2 4 0 0 0 1 4 6 2 A. π . B. π . C. π . D. π . 1 1
Câu 86: Cho hàm số y = f ( x) liên tục trên đoạn [0; ] 1 , thỏa mãn f
∫ (x)dx = xf
∫ (x)dx =1 và 0 0 1 1  3 f
∫ (x) 2 dx = 4 
. Giá trị của tích phân  f ∫ (x) dx  bằng 0 0 A. 1. B. 8 . C. 10 . D. 80 .
Câu 87: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [1, 2] và thỏa mãn f ( x) > 0 khi x ∈[1, 2] . 2 2 f '( x) Biết f '
∫ (x)dx =10 và dx = ln 2 ∫ . Tính f (2) . f x 1 ( ) 1 A. f (2) = 10 − .
B. f (2) = 20 .
C. f (2) = 10 . D. f (2) = 20 − .
Câu 88: Cho hàm số f ( x) có đạo hàm và liên tục trên đoạn [4;8] và f (0) ≠ 0 với x ∀ ∈[4;8]. Biết  f ′(x) 2 8    1 1 rằng = ∫
và f (4) = , f (8) = . Tính f (6) . f  ( x) dx 1 4  4 2 4  5 2 3 1 A. . B. . C. . D. . 8 3 8 3
Câu 89: Cho hàm số f ( x) có đạo hàm xác định, liên tục trên đoạn [0; ]
1 đồng thời thỏa mãn các điều 2 kiện f ′(0) = 1 − và  f ′
 ( x) = f ′′ 
(x). Đặt T = f ( )
1 − f (0) , hãy chọn khẳng định đúng? A. 2 − ≤ T < 1 − . B. 1
− ≤ T < 0 .
C. 0 ≤ T < 1.
D. 1 ≤ T < 2 . https://toanmath.com/
f (x) > 0,∀ x∈, 
Câu 90: Cho hàm số y = f ( x) có đạo hàm cấp 2 liên tục trên  thoả  f (0) = f ′(0) = 1, .  2 2
xy + y′ = yy , ′′ ∀ x ∈ .  
Mệnh đề nào sau đây đúng? 1 3 A. < ln f ( ) 1 < 1. B. < f ( ) 1 0 ln 1 < . C. < ln f ( ) 1 < 2 . D. < f ( ) 3 1 ln 1 < . 2 2 2 2 3
Câu 91: Cho f , g là hai hàm liên tục trên [1; ]
3 thỏa mãn điều kiện  f
∫ (x)+3g(x)dx =10  đồng 1 3 3 thời 2 f
∫ (x)− g(x)dx = 6  . Tính  f
∫ (x)+ g(x)dx  . 1 1 A. 9 . B. 6 . C. 7 . D. 8 . d d
Câu 92: Cho hàm số y = f ( x) liên tục trên [ ; a b] , nếu f
∫ (x)dx = 5 và f
∫ (x)dx = 2 (với a < d < b a b b ) thì f ( x) dx ∫ bằng. a 5 A. 3 . B. 7 . C. . D. 10 . 2
Câu 93: Cho f ( x) và g ( x) là hai hàm số liên tục trên đoạn [1; ] 3 , thỏa mãn: 3 3 3  f
∫ (x)+3g(x)dx =10  và 2 f
∫ (x)− g(x)dx = 6 
. Tính I =  f
∫ (x)+ g(x)dx 1 1 1
A. I = 8 .
B. I = 9 .
C. I = 6 . D. I = 7 .
Câu 94: Cho hàm số y = f ( x) có đạo hàm f ′( x) liên tục trên đoạn [0;5] và đồ thị hàm số y = f ′( x)
trên đoạn [0;5] được cho như hình bên. y 1 O 3 5 x 5 −
Tìm mệnh đề đúng
A. f (0) = f (5) < f (3) . B. f (3) < f (0) = f (5) .
C. f (3) < f (0) < f (5) . D. f (3) < f (5) < f (0) .
Câu 95: Cho hàm số f ( x) liên tục và có đạo hàm tại mọi x ∈(0; +∞) đồng thời thỏa mãn điều kiện: 3π 2
f ( x) = x (sin x + f '( x)) + cos x và f ∫ (x)sin d x x = 4.
− Khi đó, f (π ) nằm trong khoảng π 2 nào? A. (6;7) . B. (5;6) . C. (12;13) . D. (11;12) . https://toanmath.com/  π  Câu 96: Cho hàm số f ( x) xác định trên 0;   thỏa mãn  2  π π 2   π  2 − π 2 2 f
∫  (x)−2 2 f (x)sin x− d x =   . Tích phân f
∫ (x)d x bằng   4  2 0 0 π π A. . B. 0 . C. 1. D. . 4 2 Câu 97: Cho hàm số − +
y = f (x) liên tục trên  thỏa mãn f ( x) + f ( − x) = ( x − ) 2x 2x 1 3 2 2 1 e + 4 . Tính 2 tích phân I = f
∫ (x)dx ta được kết quả: 0
A. I = e + 4 .
B. I = 8 .
C. I = 2 . D. I = e + 2 . 2 2
Câu 98: Suy ra 4 f
∫ (x)dx = 8 ⇔ f
∫ (x)dx = 2. Cho hàm số y = f (x) liên tục trên  \{0; − }1 thỏa 0 0
mãn điều kiện f ( ) 1 = 2
− ln 2 và x(x + ) f ′(x) + f (x) 2 1 .
= x + x . Giá trị f (2) = a + bln 3 , với
a, b ∈  . Tính 2 2 a + b . 25 9 5 13 A. . B. . C. . D. . 4 2 2 4 2
Câu 99: Cho hàm số y = f ( x) có đạo hàm trên  và f ′( x) 4 ≥ x + − 2x x ∀ > 0 và f ( ) 1 = 1 − . 2 x
Khẳng định nào sau đây đúng?
A. Phương trình f ( x) = 0 có 1 nghiệm trên (0; ) 1 .
B. Phương trình f ( x) = 0 có đúng 3 nghiệm trên (0; +∞) .
C. Phương trình f ( x) = 0 có 1 nghiệm trên (1; 2) .
C. Phương trình f ( x) = 0 có 1 nghiệm trên (2;5) . Hươngd dẫn giải Chọn C 6 3 x − 2x + 2 (x − )2 3 1 +1 f ′( x) 2 4 ≥ x + − 2x = = > 0 , x ∀ > 0 . 2 x 2 x 2 x
⇒ y = f (x) đồng biến trên (0;+∞).
⇒ f (x) = 0 có nhiều nhất 1 nghiệm trên khoảng (0;+∞) ( ) 1 . Mặt khác ta có: 2 2  2  21 f ′( x) 2 4 ≥ x +
− 2x > 0 , x ∀ > 0 ⇒ f ′ ∫ (x) 4 dx ≥ x + − 2x dx = ∫  2 x 2  x  5 1 1
⇒ f ( ) − f ( ) 21 2 1 ≥ ⇒ f ( ) 17 2 ≥ . 5 5
Kết hợp giả thiết ta có y = f ( x) liên tục trên [1; 2] và f (2). f ( ) 1 < 0 (2) . Từ ( )
1 và (2) suy ra phương trình f ( x) = 0 có đúng 1 nghiệm trên khoảng (1; 2).
Câu 100: Cho hàm số f ( x) có đạo hàm f ′( x) liên tục trên  và thỏa mãn f ′( x) ∈[ 1 − ; ] 1 với 2 x
∀ ∈(0;2) . Biết f (0) = f (2) =1. Đặt I = f
∫ (x)dx , phát biểu nào dưới đây đúng? 0 A. I ∈ ( ; −∞ 0]. B. I ∈ (0; ] 1 .
C. I ∈[1; +∞) . D. I ∈ (0; ) 1 . https://toanmath.com/ 1
Câu 101: Cho hàm số y = f ( x) liên tục trên [0; ] 1 thỏa mãn xf
∫ (x)dx = 0 và max f (x) =1. Tích [0; 1] 0 1 phân = ex I f
∫ (x)dx thuộc khoảng nào trong các khoảng sau đây? 0  5   3   5 3  A. ; −∞ − .   B. ; e −1 .   C. − ; .   D. (e −1; + ∞).  4   2   4 2 
Câu 102: Cho hàm số f ( x) có đạo hàm dương, liên tục trên đoạn [0; ]
1 thỏa mãn f (0) = 1 và 1 1   1 3 f ′ ∫ (x) f   ( x) 2 1 3  + dx ≤ 2 f ′  ∫
(x) f (x)dx
. Tính tích phân  f
∫ (x) dx:   9  0 0 0 3 5 5 7 A. . B. . C. . D. . 2 4 6 6
Câu 103: Cho hai hàm số f ( x) và g ( x) có đạo hàm trên đoạn [1; 4] và thỏa mãn hệ thức  f  ( ) 1 + g ( ) 1 = 4 4 
. Tính I =  f
∫ (x)+ g(x)dx  . g  ( x) = − . x f ′( x); f ( x) = − . x g′( x) 1 A. 8 ln 2 . B. 3ln 2 . C. 6 ln 2 . D. 4 ln 2 . https://toanmath.com/ HƯỚNG DẪN GIẢI
DẠNG 1: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT NGUYÊN HÀM f ( x)  \{ } 1 f (0) = 2017 Câu 1: Cho hàm số xác định trên
thỏa mãn f ′( x) 1 = , , x −1 f (2) = 2018
S = f (3) − f (− ) 1 . Tính .
A. S = 1 .
B. S = ln 2 .
C. S = ln 4035 . D. S = 4 . Hươngd dẫn giải Chọn A 1 Cách 1: Ta có f ∫ (x)dx = dx = ln ∫ ( x−1)+C . x −1  f
 ( x) = ln ( x −1 ) + 2017 khi x < 1
Theo giả thiết f (0) = 2017 , f (2) = 2018 nên  .  f ( x) = ln 
( x −1)+ 2018 khi x >1
Do đó S = f (3) − f (− )
1 = ln 2 + 2018 − ln 2 − 2017 = 1 . Cách 2: 0 0  dx 1 0
f (0) − f ( 1)
− = f '(x)dx = = ln x −1 | = ln (1) ∫ ∫ 1 −  x −1 2 − − Ta có: 1 1  3 3  dx 3
f (3) − f (2) =
f '(x)dx =
= ln x −1 | = ln 2 (2) ∫ ∫ 2  x −1  2 2
Lấy (1)+(2), ta được f (3) − f (2) + f (0) − f ( 1 − ) = 0 ⇒ S = 1. 1 
Câu 2: Cho hàm số f ( x) xác định trên  \   thỏa mãn f ′( x) 2 =
và f (0) = 1. Giá trị của 2 2x −1 biểu thức f (− )
1 + f (3) bằng A. 4 + ln15 . B. 3 + ln15 . C. 2 + ln15 . D. ln15 . Hươngd dẫn giải Chọn C 1 2. d (2x − ) 1 2
Ta có f ( x) = f ′ ∫ (x) 2 dx = dx = = ln 2x −1 + c ∫ ∫ . 2x −1 2x −1
f (0) = 1 ⇔ c = 1 ⇔ f ( x) = ln 2x −1 +1 .  f  (− ) 1 = ln 3 +1  ⇔ f (− ) 1 + f (3) = 2 + ln15 .  f  (3) = ln 5 +1 1  2
Câu 3: Cho hàm số f (x) xác định trên  \   thỏa mãn f ( ′ x) =
, f (0) = 1 và f (1) = 2 . 2 2x −1
Giá trị của biểu thức f ( 1)
− + f (3) bằng A. 4 + ln 5 . B. 2 + ln15 . C. 3 + ln15 . D. ln15. Hươngd dẫn giải Chọn C  1  2
Cách 1: • Trên khoảng ; +∞   : f (x) =
dx = ln(2x −1) + C . ∫  2  1 2x −1
Lại có f (1) = 2 ⇒ C = 2. 1  1  2 • Trên khoảng ; −∞   : f (x) =
dx = ln(1− 2x) + C . ∫  2  2 2x −1 https://toanmath.com/
Lại có f (0) = 1 ⇒ C = 1. 2  1
ln(2x −1) + 2 khi x >  2
Vậy f (x) =  . 1
ln(1− 2x) +1khi x <  2 Suy ra f ( 1
− ) + f (3) = 3 + ln15. Cách 2: 0 0  2dx 1 0
f (0) − f ( 1)
− = f '(x)dx = =ln 2x −1 | = ln (1) ∫ ∫ 1 −  2x −1 3 − − Ta có: 1 1  3 3  2dx 3
f (3) − f (1) =
f '(x)dx =
=ln 2x −1 | = ln 5 (2) ∫ ∫ 1  2x −1  1 1
Lấy (2)-(1), ta được f (3) − f (1) − f (0) + f ( 1) − = ln15 ⇒ f ( 1)
− + f (3) = 3 + ln15 .
Câu 4: Cho hàm số f ( x) xác định trên  thỏa mãn f ′( x) = 2x +1 và f ( ) 1 = 5 . Phương trình
f ( x) = 5 có hai nghiệm x , x . Tính tổng S = log x + log x . 1 2 2 1 2 2
A. S = 1 .
B. S = 2 .
C. S = 0 . D. S = 4 . Hướng dẫn giải Chọn A
Ta có: f ( x) = f ′
∫ (x) x = ∫( x+ ) 2 d 2
1 dx = x + x + C .
Mà f ( ) = ⇔ + + C = ⇔ C = ⇒ f ( x) 2 1 5 1 1 5 3 = x + x + 3.  =
Xét phương trình: f (x) x 1 2 2
= 5 ⇔ x + x + 3 = 5 ⇔ x + x − 2 = 0 ⇔  . x = 2 −
S = log x + log x = log 1 + log 2 − = 1. 2 1 2 2 2 2 1 3  2 
Câu 5: Cho hàm số f (x) xác định trên  \   thỏa mãn f ′( x) =
, f (0) = 1 và f = 2   . 3 3x −1  3 
Giá trị của biểu thức f (− )
1 + f (3) bằng A. 3 + 5 ln 2 . B. 2 − + 5ln 2 . C. 4 + 5 ln 2 . D. 2 + 5 ln 2 . Hươngd dẫn giải Chọn A   1 
ln 3x −1 + C khi x ∈ ; −∞  1   3 3   3 
Cách 1: Từ f ′( x) = ⇒ f (x) = dx= ∫  . 3x −1 3x −1   1 
ln 3x −1 + C khi x ∈ ; +∞ 1     3     1  f (0) = 1 ln 3x −1 +1 khi x ∈ ; −∞     0 + C =1 C  = 1   3  Ta có: 1 1   2 ⇒   ⇔ 
⇒ f ( x) =  . f = 2 0 + C = 2 C = 2       1  2  2   3 
ln 3x −1 + 2 khi x ∈ ; +∞     3  Khi đó: f (− )
1 + f (3) = ln 4 +1+ ln 8 + 2 = 3 + ln 32 = 3 + 5ln 2 . 0 0 
f ( ) − f (− ) = f ( x) 0 = f ′ ∫ (x) 3 0 1 0 1 dx = dx = ln 3x −1 = ln ∫ ( )1 1 − 1 3x −1 − 4  1 − 1 − Cách 2: Ta có  3 3    f ( ) 2 − f = f   (x) 3 3 3 = ′ = = − = 2 f ∫ (x) 3 dx dx ln 3x 1 2 ln 8 ∫ (2)   3  − 3 3x 1 2 2 3  3 3 https://toanmath.com/  2  Lấy (2) − ( )
1 , ta được: f (3) + f (− )
1 − f (0) − f = ln 32 ⇒ f   (− )
1 + f (3) = 3 + 5ln 2 .  3  f ( x)  \{ 2; − } 2 4 Câu 6: Cho hàm số xác định trên
và thỏa mãn f ′( x) = ; f 3 − = 0 ; 2 ( ) x − 4 f (0) = 1 f (3) = 2 P = f ( 4 − ) + f (− ) 1 + f (4) và
. Tính giá trị biểu thức . 3 5 5 A. P = 3 + ln .
B. P = 3 + ln 3 . C. P = 2 + ln . D. P = 2 − ln . 25 3 3 Hươngd dẫn giải Chọn B x − 2 ln + C khi x ∈ ; −∞ 2 −  1 ( ) x + 2  4 4dx 4dxx − 2 Từ f ′( x) =
⇒ f ( x) = ∫ = ∫ = ln + C khi x ∈ 2; − 2 2 ( ) 2 x − 4 2 x − 4 (x − 2)(x + 2) x + 2   x − 2 ln + C khi x ∈ 2; +∞ 3 ( )  x + 2   f ( 3 − ) = 0 ln 5 + C = 0 C  = − ln 5  1  1 
Ta có  f (0) = 1 ⇒ 0 + C = 1 ⇔ C  = 1 2 2    f  (2) = 2 1  C = 2 + ln 5  ln + C = 2 3 3  5  x − 2 ln -ln5 khi x ∈ ( ; −∞ 2 −  ) x + 2   − ⇒ x 2 f ( x) = ln +1 khi x ∈( 2; − 2) . x + 2   x − 2 ln + 2 + ln 5 khi x ∈ (2; +∞)  x + 2
Khi đó P = f ( 4 − ) + f (− ) 1 + 1
f (4) = ln 3 − ln 5 + ln 3 +1+ ln + 2 + ln 5 = 3 + ln 3. 3 1
Câu 7: Cho hàm số f ( x) xác định trên  \ { 2; − }
1 thỏa mãn f ′( x) = ; f ( 3 − ) − f (3) = 0 2 x + x − 2 và f ( ) 1 0 =
. Giá trị của biểu thức f ( 4 − ) + f (− )
1 − f (4) bằng 3 1 1 1 4 1 8 A. + ln 2 . B. 1+ ln 80 . C. 1+ ln 2 + ln . D. 1+ ln . 3 3 3 5 3 5 Hươngd dẫn giải Chọn A 1 x −1 ln + C khi x ∈ ; −∞ 2 −  1 ( ) 3 x + 2  dx dx 1 x −1 f ′( x) 1 = ⇒ f (x) = = = ∫ ∫  ln + C khi x ∈ 2; − 1 2 2 ( ) 2 x + x − 2 x + x − 2 (x − ) 1 ( x + 2) 3 x + 2  1 x −1  ln + C khi x ∈ 1; +∞ 3 ( ) 3 x + 2
Do đó f (− ) − f ( ) 1 1 2 1 3 3 = 0 ⇒ ln 4 + C − ln
− C ⇒ C = C + ln10 . 1 3 3 1 3 3 5 3 https://toanmath.com/ 1 1 1 1 1 1
Và f (0) = ⇒ ln + C = ⇒ C = + ln 2 . 2 2 3 3 2 3 3 3  1 x −1 ln + C khi x ∈ ; −∞ 2 −  1 ( ) 3 x + 2   − ⇒ f (x) 1 x 1 1 1 =  ln + + ln 2 khi x ∈ ( 2 − ; ) 1 . 3 x + 2 3 3  1 x −1 1  ln + C + ln10 khi x ∈ 1; +∞ 1 ( ) 3 x + 2 3 Khi đó:      
f (− ) + f (− ) − f ( ) 1 5 1 1 1 1 1 1 1 1 4 1 4 = ln + C + ln 2 + + ln 2 − ln + C + ln10 = + ln 2  . 1     1   3 2   3 3 3   3 2 3  3 3 1
Câu 8: Cho hàm số f ( x) xác định trên  \ { 1 − ; }
1 và thỏa mãn f ′( x) = ; f ( 3 − ) + f (3) = 0 2 x −1  1   1  và f − + f = 2    
. Tính giá trị của biểu thức P = f (0) + f (4) .  2   2  3 3 1 3 1 3 A. P = 2 + ln . B. P = 1+ ln . C. P = 1+ ln . D. P = ln . 5 5 2 5 2 5 Hươngd dẫn giải Chọn C 1 x −1 ln + C khi x ∈ ; −∞ 1 − ∪ 1;+∞  1 ( ) ( )  + f ′( x) 1 dx dx 2 x 1 = ⇒ = = ∫ ∫  . 2 2 x −1 x −1 (x − ) 1 ( x + ) 1 1 x −1  ln + C khi x ∈ 1 − ;1 2 ( ) 2 x +1 1 1 1 Ta có f ( 3
− ) + f (3) = 0 ⇒ ln 2 + C + ln + C = 0 ⇒ C = 0 . 1 1 1 2 2 2  1   1  1 1 1 Và f − + f
= 2 ⇒ ln 3 + C + ln + C = 2 ⇒ C = 1     . 2 2 2  2   2  2 2 3 1 x −1 ln khi x ∈ ( ; −∞ − ) 1 ∪ (1; +∞  ) 2 x +1
Suy ra f ( x) =  . 1 x −1  ln +1 khi x ∈( 1 − ; ) 1 2 x +1 1 3
Vậy P = f (0) + f (4) =1+ ln . 2 5 1
Câu 9: Cho hàm số f ( x) xác định trên  \ { } 1
± thỏa mãn f ′(x) = . Biết f ( 3 − ) + f (3) = 0 2 x −1  1   1  và f − + f = 2    
. Giá trị T = f ( 2
− ) + f (0) + f (4) bằng:  2   2  1 5 1 9 1 9 1 9 A. T = 2 + ln . B. T = 1+ ln . C. T = 3 + ln . D. T = ln . 2 9 2 5 2 5 2 5 Hươngd dẫn giải Chọn B 1   x − Ta có f ′ ∫ (x)dx = dx ∫ 1 1 1 = − dx ∫ 1 1   = ln + C . 2 x −1 2  x −1 x +1  2 x +1 https://toanmath.com/ 1 x −1 ln + C khi x < 1 − , x > 1  Do đó  + f ( x) 1 2 x 1 =  . 1 1− x  ln
+ C khi −1 < x < 1 2 2 x +1  1   1  Do f ( 3
− ) + f (3) = 0 nên C = 0 , f − + f = 2 nên C = 1. 1      2 2   2  1 x −1 ln khi x < 1 − , x > 1 2 x +1
Nên f ( x) =  . T = f ( 2 − ) + f (0) + 1 9 f (4) = 1+ ln . 1 1− x  2 5 ln
+1 khi −1 < x < 1 2 x +1
Câu 10: Cho hàm số f ( x) nhận giá trị dương, có đạo hàm liên tục trên (0; +∞) thỏa mãn f ( ) 1 2 =
và f ′( x) + ( x + ) 2 2
4 f ( x) = 0 . Tính f ( )
1 + f (2) + f (3) . 15 7 11 11 7 A. . B. . C. . D. . 15 15 30 30 Hươngd dẫn giải Chọn D f ′( x)
Vì f ′( x) + ( x + ) 2 2
4 f ( x) = 0 và f ( x) > 0 , với mọi x ∈(0; +∞) nên ta có − = 2x + 4 . 2 f ( x) 1 1 Suy ra 2
( ) = x + 4x +C . Mặt khác f ( ) 1 2 =
nên C = 3 hay f ( x) = . f x 15 2 x + 4x + 3 Do đó f ( ) 1 + f (2) + 1 1 1 f (3) = + + 7 = . 8 15 24 30
Câu 11: Cho hàm số f ( x) xác định và liên tục trên  . Biết 6
f ( x). f ′( x) = 12x +13 và f (0) = 2 .
Khi đó phương trình f (x) = 3 có bao nhiêu nghiệm? A. 2 . B. 3 . C. 7 . D. 1. Hươngd dẫn giải Chọn A Từ 6
f ( x). f ′( x) = 12x +13 6 ⇒ f
∫ (x).f ′(x)dx = ∫(12x+13)dx 6 ⇔ f
∫ (x)df (x) 2
= 6x +13x + C 7 f ( x) 2 ⇔ = = 6x +13x + f (0) C 2 2 →C = . 7 7 Suy ra: 7 f ( x) 2
= 42x + 91x + 2 . Từ f ( x) = 3 7 ⇔ f (x) = 2187 2
⇒ 42x + 91x + 2 = 2187 2
⇔ 42x + 91x − 2185 = 0(*) .
Phương trình (*) có 2 nghiệm trái dầu do ac < 0 .
Câu 12: Cho hàm số f ( x) xác định trên  thỏa mãn ( ) ex e x f x − ′ = + − 2 , f (0) = 5 và  1  f ln = 0  
. Giá trị của biểu thức S = f (− ln16) + f (ln 4) bằng  4  31 9 5 A. S = . B. S = . C. S = .
D. f (0). f (2) = 1. 2 2 2 Hươngd dẫn giải Chọn C https://toanmath.com/ x x  − ex −1 2 2 e − e khi x ≥ 0 Ta có ( ) ex e x f x − ′ = + − 2 = =  . x x ex −  2 2 e − e khi x < 0 x x  −  + + ≥ Do đó f (x) 2 2 2e 2e C khi x 0 1 =  . x x −  2 2 2e − − 2e + C khi x < 0  2
Theo đề bài ta có f (0) = 5 nên 0 0
2e + 2e + C = 5 ⇔ C = 1. 1 1 ln 4 ln 4 − ⇒ f ( ) 2 2 ln 4 = 2e + 2e +1 = 6  1   1  ln ln      4   4  Tương tự  1  − f ln = 0   nên 2 2 2e − − 2e
+ C = 0 ⇔ C = 5.  2 4  2 (−ln16) (−ln16) − ⇒ 7 f (− ) 2 2 ln16 = 2e − − 2e + 5 = − . 2 Vậy S = f (− )+ f ( ) 5 ln16 ln 4 = . 2  π 
Câu 13: Cho hàm số f ( x) liên tục, không âm trên đoạn 0; 
 , thỏa mãn f (0) = 3 và  2   π 
f ( x) f ′( x) 2 . = cos .
x 1+ f ( x) , x ∀ ∈ 0; 
 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M  2  π π 
của hàm số f ( x) trên đoạn ;   .  6 2  21 5 A. m =
, M = 2 2 . B. m = , M = 3 . 2 2 5 C. m = , M = 3 .
D. m = 3 , M = 2 2 . 2 Hươngd dẫn giải Chọn A
Từ giả thiết f ( x) f ′( x) 2 . = cos .
x 1+ f ( x)
f ( x). f ′( x)
f ( x). f ′( x) ⇒ = cos x ⇒
dx = sin x + C 2 ∫ 2 1+ f ( x) 1+ f ( x) Đặt 2 t = + f (x) 2 2 1
⇒ t = 1+ f (x) ⇒ tdt = f (x) f ′(x)dx .
Thay vào ta được dt = sin x + C ⇒ t = sin x + C ∫ 2
⇒ 1+ f (x) = sin x + C .
Do f (0) = 3 ⇒ C = 2 . Vậy 2 + f (x) 2 =
x + ⇒ f ( x) 2 1 sin 2
= sin x + 4sin x + 3 ⇒  π  f ( x) 2
= sin x + 4sin x + 3 , vì hàm số f (x) liên tục, không âm trên đoạn 0;   .  2  π π 1 Ta có
≤ x ≤ ⇒ ≤ sin x ≤ 1, xét hàm số g (t) 2
= t + 4t + 3 có hoành độ đỉnh t = 2 − loại. 6 2 2  1  21
Suy ra max g (t ) = g ( )
1 = 8 , min g (t ) = g =   . 1  1    ;1   ;1 2 4    2  2  https://toanmath.com/  π   π  21
Suy ra max f ( x) = f = 2 2  
, min f ( x) = g =   . π π    π π    ; 2 6 2   ;    6 2   6 2 
Câu 14: Cho hàm số f ( x) có đạo hàm liên tục trên  và thỏa mãn f ( x) > 0 , x ∀ ∈  . Biết f '( x) f (0) = 1 và
( ) = 2− 2x . Tìm các giá trị thực của tham số m để phương trình f (x) = m f x
có hai nghiệm thực phân biệt.
A. m > e .
B. 0 < m ≤ 1 .
C. 0 < m < e .
D. 1 < m < e . Hươngd dẫn giải Chọn C f ′( x) f ′( x) Ta có ( ) = 2− 2x ⇒ dx = 2 − 2x dx ∫ ∫ . f x f ( x) ( ) ⇔ f ( x) 2 ln
= 2x − x + C ( ) 2 2 . x x f x A e − ⇔ =
. Mà f (0) = 1 suy ra ( ) 2 2 x x f x e − = . 2 − Ta có 2
x − x = − ( 2 2 1 x − 2x + ) 1 = − ( x − )2 1 1 ≤ 1. Suy ra 2 0 x x < e
≤ e và ứng với một giá trị thực
t < 1 thì phương trình 2
2x − x = t sẽ có hai nghiệm phân biệt.
Vậy để phương trình f ( x) = m có 2 nghiệm phân biệt khi 1
0 < m < e = e .
Câu 15: Cho hàm số f ( x) liên tục trên  và f ( x) ≠ 0 với mọi x ∈  . f ′( x) = ( x + ) 2 2 1 f ( x) và a a f ( ) 1 = 0,
− 5 . Biết rằng tổng f ( )
1 + f (2) + f (3) + ... + f (2017) =
; (a ∈ ,b ∈ ) với b b
tối giản. Mệnh đề nào dưới đây đúng? a
A. a + b = 1 − . B. a ∈ ( 2017 − ; 2017) . C. < 1 − .
D. b − a = 4035 . b Hươngd dẫn giải Chọn D f ′( x) f ′( x)
Ta có f ′( x) = ( x + ) 2 2 1 f ( x) ⇔ = 2x +1 ⇒ dx = 2x +1 dx ∫ ∫ 2 f ( x) ( ) 2 f ( x) ( ) 1 2
⇔ − ( ) = x + x+C f x 1 1 1 Mà f ( ) 1 1 = −
nên C = 0 ⇒ f ( x) = − = − . 2 2 x + x x +1 x        
Mặt khác f ( ) + f ( ) + f ( ) + + f ( ) 1 1 1 1 1 1 1 1 2 3 ... 2017 = −1 + − + − + ...+ −          2   3 2   4 3   2018 2017  −
⇔ f ( ) + f ( ) + f ( ) + + f ( ) 1 2017 1 2 3 ... 2017 = 1 − + = ⇒ a = 2017 − ; b = 2018 . 2018 2018
Khi đó b − a = 4035. −
Câu 16: Cho hàm số f ( x) ≠ 0 thỏa mãn điều kiện '
f ( x) = ( x + ) 2 2
3 . f ( x) và f ( ) 1 0 = . Biết tổng 2 ( ) a a
f 1 + f (2) + ... + f (2017) + f (2018) = với *
a ∈ ,b ∈  và là phân số tối giản. b b
Mệnh đề nào sau đây đúng? a a A. < 1 − . B. >1. b b
C. a + b = 1010 .
D. b − a = 3029 . Hươngd dẫn giải Chọn D https://toanmath.com/ ' f ( x) ' f ( x) Biến đổi '
f ( x) = ( x + ) 2 2 3 . f ( x) ⇔ = 2x + 3 ⇔ dx = 2x + 3 dx ∫ ∫ 2 f ( x) 2 f ( x) ( ) 1 1 − 2 ⇔ − = + + ⇒ = − . Mà f ( ) 1 0 = nên = 2 . f ( x) x 3x C f ( x) 2
x + 3x + C 2 Do đó f (x) 1 1 = − = − . 2 x + 3x + 2 (x + )1(x + 2) Khi đó a =   f ( )
1 + f (2) + ... + f (2017) + 1 1 1 1 f (2018) = − + + .....+ +   b  2.3 3.4 2018.2019 2019.2020   1 1 1 1 1 1 1  − = − − + − +  1 1  1009 ..... + − −   = − −   = .  2 3 3 4 2018 2019 2020   2 2020  2020 a = 1009 −
Với điều kiện a,b thỏa mãn bài toán, suy ra: 
⇒ b − a = 3029 . b  = 2020
 f ′′(x) f (x)−  f ′  ( x) 2 3 . 2  + xf  (x) = 0
Câu 17: Cho hàm số y = f ( x) , x ∀ ≥ 0 , thỏa mãn  . Tính  f ′  (0) = 0; f (0) = 1 f ( ) 1 . 2 3 6 7 A. . B. . C. . D. . 3 2 7 6 Hươngd dẫn giải Chọn C
f ′′( x). f ( x) − 2  f ′  ( x) 2  2 
Ta có: f ′ ( x) f ( x) −  f ′  ( x) 3 . 2  + xf  (x) = 0 ⇔ = −x 3 f ( x) ′  f ′(x)  f ′( x) 2 f ′(0) 2 ⇒ x 0   = −x ⇒ = − + C ⇒ = − + C ⇒ C = 0 . 2 f  (x) 2 f ( x) 2 2 f (0) 2 f ′( x) 2 Do đó x = − 2 f ( x) 2 1 1 1 f ′( x) 1 2 x 3   ⇒ 1 x 1 1 1 dx = − dx ∫ ∫ ⇒ − = −  ⇒ − + = − ⇒ f ( ) 6 1 = . 2 f x 2 f ( x)  6  f ( ) 1 f (0) 6 7 0 ( ) 0 0 0 f ′( x) x
Câu 18: Giả sử hàm số f (x) liên tục, dương trên  ; thỏa mãn f (0) = 1 và = . Khi đó f ( x) 2 x +1
hiệu T = f (2 2 ) − 2 f ( ) 1 thuộc khoảng A. (2;3) . B. (7;9) . C. (0; ) 1 . D. (9;12) . Hươngd dẫn giải Chọn C 2 f ′( x) d f x d 1 (x + ) x ( ( )) 1 Ta có ( ) dx = ∫ dx ⇔ ∫ = ∫ ∫ . f x 2 x +1 f ( x) 2 2 x +1 1
Vậy ln ( f ( x)) = ln ( 2 x + )
1 + C , mà f (0) = 1 ⇔ C = 0 . Do đó f ( x) 2 = x +1 . 2
Nên f (2 2 ) = 3; 2 f ( )
1 = 2 2 ⇒ f (2 2 ) − 2 f ( ) 1 = 3 − 2 2 ∈ (0; ) 1 . https://toanmath.com/ π 4 f (tan t ) 1 1 Câu 19: Khi đó dt = f x dx ∫ ∫ . Vậy f
∫ (x)dx = 6.Cho hàm số y = f (x) đồng biến trên 2 ( ) cos t 0 0 0
(0;+∞); y = f (x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f ( ) 2 3 = và 3  f  ( x) 2 '  =  (x + )
1 . f ( x) . Mệnh đề nào dưới đây đúng? A. 2
2613 < f (8) < 2614 . B. 2
2614 < f (8) < 2615 . C. 2
2618 < f (8) < 2619 . D. 2
2616 < f (8) < 2617 . Hươngd dẫn giải Chọn A
Hàm số y = f ( x) đồng biến trên (0; +∞) nên suy ra f ′( x) ≥ 0, x ∀ ∈(0;+∞).
Mặt khác y = f ( x) liên tục, nhận giá trị dương trên (0; +∞) nên  f ′  ( x) 2  =  (x + )
1 f ( x) ⇒ f ′( x) = ( x + )
1 f ( x) , x ∀ ∈(0;+∞) f ′( x) ⇒ = (x + ) , x ∀ ∈(0;+∞) ; f ( x) 1 f ′( x) ⇒ 1 dx = (x + ∫ ∫ ) ⇒ = + + ( ) 1 dx f ( x) (x )3 1 C ; f x 3 2 8 Từ f ( ) 3 3 = suy ra C = − 2 3 3 2   Như vậ 1 3 2 8 y f ( x) =  (x + ) 1 + −    3 3 3   Bởi thế: 2 2     4  2 8  f ( ) 1 =  ( + )3 2 8 2 8 8 8 1 + −  = 9 + −  2     ⇒ f (8) = 9 + −  ≈ 2613,26   . 3 3 3 3 3     3 3  
Câu 20: Giả sử hàm số y = f ( x) liên tục, nhận giá trị dương trên (0; +
 ∞) và thỏa mãn f ( ) 1 = 1,
f ( x) = f ′( x) 3x +1 , với mọi x > 0 . Mệnh đề nào sau đây đúng?
A. 4 < f (5) < 5 .
B. 2 < f (5) < 3 .
C. 3 < f (5) < 4 .
D. 1 < f (5) < 2 . Hươngd dẫn giải Chọn C Cách 1:
Với điều kiện bài toán ta có f ′( x) 1 f ′( x) 1
f ( x) = f ′( x) 3x +1 ⇔ ( ) = ⇔ = ∫ ∫ x + f ( x) dx dx f x 3 1 3x +1 d ( f ′( x)) 1 1 2 − ⇔ = + + ∫ ∫ 3x 1 + +C ⇔ f ( x) 2 ln =
3x +1 + C ⇔ f ( x) 3 = e . f ( x) (3x ) 2 1 d (3x ) 1 3 3 4 2 4 4 Khi đó + 3x 1 + − f ( ) C 4 3 1 = 1 ⇔ e
=1 ⇔ C = − ⇒ f (x) 3 3 = e ⇒ f ( ) 3 5 = e ≈ 3, 79 ∈ (3; 4  ) . 3
Vậy 3 < f (5) < 4 . https://toanmath.com/ dx
Chú ý: Các bạn có thể tính ∫
bằng cách đặt t = 3x +1 . 3x +1 Cách 2:
Với điều kiện bài toán ta có f ′( x) 1 5 f ′( x) 5 1 5 d ( f ( x)) 4
f ( x) = f ′( x) 3x +1 ⇔ = ⇔ dx = dx ∫ ∫ ⇔ = ∫ f ( x) 3x +1 f x 3x +1 f x 3 1 ( ) 1 ( ) 1 f (5) 4 ⇔ 4 f ( x) 5 4 ln = ⇔ ln
= ⇔ f ( ) = f ( ) 3 5 1 .e ≈ 3, 79 ∈ (3; 4  ) . f ( ) 1 3 1 3 2
Câu 21: Cho hàm số f ( x) thỏa mãn  f ′  ( x) + f
(x) f ′′(x) 4 .
= 15x +12x , x ∀ ∈  và
f (0) = f ′(0) = 1. Giá trị của 2 f ( ) 1 bằng 9 5 A. . B. . C. 10 . D. 8 . 2 2 Hươngd dẫn giải Chọn D 2
Ta có: ( f ′( x)) + f ( x) f ′′( x) 4 .
=15x +12x , x ∀ ∈  . ′ ⇔  f ′
 ( x) f ( x) 4 .  = 15x +12x  , x
∀ ∈  ⇔ f ′(x). f (x) 5 2
= 3x + 6x + C 1
Do f (0) = f ′(0) = 1 nên ta có C = 1. Do đó: f ′( x) f ( x) 5 2 . = 3x + 6x +1 1 ′  1  2 ⇔ f  (x) 5 2 = 3x + 6x +1  2 ⇔ f (x) 6 3
= x + 4x + 2x + C .  2  2
Mà f (0) = 1 nên ta có C = 1. Do đó 2 f ( x) 6 3
= x + 4x + 2x +1. 2 Vậy 2 f ( ) 1 = 8. f ( x +1) 2 ( x +1 + 3)
Câu 22: Cho hàm số f ( x) liên tục trên  và thỏa mãn dx = + C ∫ . Nguyên x +1 x + 5
hàm của hàm số f (2x) trên tập +  là: x + 3 x + 3 2x + 3 2x + 3 A. + C . B. + C . C. + C . D. + C . 2 ( 2 x + 4) 2 x + 4 4 ( 2 x + ) 1 8( 2 x + ) 1 Hươngd dẫn giải Chọn D Theo đề ra ta có: f ( x +1) 2 ( x +1 + 3) x + + dx = + C ⇔ 2 f ∫
∫ ( x+1)d( x+1) 2( 1 3) = + C . x +1 x + 5 ( x+1)2 +4 2 t + 3 t + 3 Hay 2 f ∫ (t) ( ) dt =
+ C ⇒ f t dt = + C′ ∫ . 2 ( ) 2 t + 4 t + 4 1 1  2x 3  + 2x + 3 Suy ra f
∫ (2x)dx = f
∫ (2x)d(2x) =  + C  = + C 2 2  (2x)2 1 2 + 4  8x +8  https://toanmath.com/
DẠNG 2: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT, GIẢI HỆ TÍCH PHÂN 5 2 Câu 23: Cho f
∫ (x)dx =10. Kết quả 2−4 f ∫ (x)dx  bằng: 2 5 A. 34 . B. 36 . C. 40 . D. 32 . Hươngd dẫn giải Chọn A 2 2 2 5 5 Tacó 2 − 4 f ∫
(x)dx = 2 dx − 4 f  ∫ ∫ (x)dx = 2 − x + 4 f ∫ (x)dx = 2. − (5 − 2) + 4.10 = 34 . 2 5 5 5 2 9
Câu 24: Cho hàm số f ( x) liên tục trên  và F ( x) là nguyên hàm của f ( x) , biết f ∫ (x)dx = 9 0
và F (0) = 3. Tính F (9) . A. F (9) = 6 − .
B. F (9) = 6 .
C. F (9) = 12 . D. F (9) = 12 − . Hươngd dẫn giải Chọn C 9 9 Ta có: I = f
∫ (x)dx = F (x) = F (9)− F (0) = 9 ⇔ F (9) =12. 0 0 2 2 I = f ∫ (x)dx = 3 J = 4 f
∫ (x)−3dxCâu 25: Cho 0 . Khi đó 0 bằng: A. 2 . B. 6 . C. 8 . D. 4 . Hươngd dẫn giải Chọn B 2 2 2 2
Ta có J = 4 f
∫ (x)−3dx = 4 f
∫ (x)dx−3 dx = 4.3−3x = 6 ∫ . 0 0 0 0 4 4 4 f ∫ (x)dx =10 g ∫ (x)dx = 5 I = 3 f
∫ (x)−5g(x)dxCâu 26: Cho 2 và 2 . Tính 2
A. I = 5 .
B. I = 15 . C. I = 5 − . D. I = 10 . Hươngd dẫn giải Chọn A 4 4 4 Có: I = 3 f
∫ (x)−5g(x)dx  = 3 f
∫ (x)dx−5 g ∫ (x)dx = 5. 2 2 2 9 0 9 f ∫ (x)dx = 37 g ∫ (x)dx =16 I = 2 f
∫ (x)+3g(x)dxCâu 27: Giả sử 0 và 9 . Khi đó, 0 bằng:
A. I = 26 .
B. I = 58 .
C. I = 143 . D. I = 122 . Hươngd dẫn giải Chọn A 9 9 9 9 0
Ta có: I = 2 f
∫ (x)+3g(x)dx = 2 f
∫ (x)dx+ 3g
∫ (x)dx = 2 f
∫ (x)dx−3 g ∫ (x)dx = 26. 0 0 0 0 9 2 5 5 f
∫ (x)dx = 3 f (x)dx = 1 − ∫ f ( x) dx ∫ Câu 28: Nếu 1 , 2 thì 1 bằng A. 2 − . B. 2 . C. 3 . D. 4 . Hươngd dẫn giải Chọn B https://toanmath.com/ 5 2 5 Ta có f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 3−1= 2. 1 1 2 2 3 3 f ∫ (x)dx =1
f ( x) dx = 2 − ∫ f ( x) dx ∫ Câu 29: Cho 1 và 2 . Giá trị của 1 bằng A. 1. B. 3 − . C. 1 − . D. 3 . Hươngd dẫn giải Chọn C 3 2 3
f ( x) dx = ∫ f
∫ (x)dx+ f ∫ (x)dx = 1 − . 1 1 2 10 6
Câu 30: Cho hàm số f ( x) liên tục trên đoạn [0;10] và f
∫ (x)dx = 7 và f
∫ (x)dx = 3. Tính 0 2 2 10 P = f
∫ (x)dx+ f
∫ (x)dx. 0 6
A. P = 7 . B. P = 4 − .
C. P = 4 .
D. P = 10 . Hươngd dẫn giải Chọn C 10 2 6 10 Ta có f
∫ (x)dx = 7 ⇔ f
∫ (x)dx+ f
∫ (x)dx+ f ∫ (x)dx = 7 0 0 2 6 2 10 ⇔ f
∫ (x)dx+ f
∫ (x)dx = 7−3 = 4. 0 6 Vậy P = 4 . 1 2 f ∫ (x)dx = 2
f ( x) dx = ∫ 2 Câu 31: Cho 0 , f
∫ (x)dx = 4, khi đó 0 ? 1 A. 6 . B. 2 . C. 1. D. 3 . Hươngd dẫn giải Chọn A 2 1 2 f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx = 6. 0 0 1 1 3 3
Câu 32: Cho hàm số f ( x) liên tục trên  và có f
∫ (x)dx = 2; f
∫ (x)dx = 6. Tính I = f
∫ (x)dx . 0 1 0
A. I = 8 .
B. I = 12 .
C. I = 36 . D. I = 4 . Hươngd dẫn giải Chọn A 3 1 3 I = f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 2+6 = 8. 0 0 1 2 2 2 f ∫ (x)dx = 2
g ( x) dx = 1 − ∫ I = x + 2 f ∫ 
(x)+3g (x)dxCâu 33: Cho 1 − và 1 − . Tính 1 − bằng 11 7 17 5 A. I = . B. I = . C. I = . D. I = . 2 2 2 2 Hươngd dẫn giải Chọn D https://toanmath.com/ 2 2 2 x 2 3 5 Ta có: I =
+ 2 f (x)dx + 3 g (x)dx = + 4 − 3 = 2 1 − ∫ ∫ . 2 2 1 − 1 − 8 4 4
f ( x) dx = 2 − ∫ f
∫ (x)dx = 3 g ∫ (x)dx = 7 Câu 34: Biết 1 ; 1 ; 1
. Mệnh đề nào sau đây sai? 8 4 A. f
∫ (x)dx =1. B. f
∫ (x)+ g(x)dx =10  . 4 1 8 4 C.
f ( x) dx = 5 − ∫ . D. 4 f
∫ (x)−2g(x)dx = 2 −  . 4 1 Hươngd dẫn giải Chọn A 8 8 4 Ta có
f ( x) dx = f ( x) dx − f ( x) dx = 2 − − 3 = 5 − ∫ ∫ ∫ 4 1 1 3 f ( x) f ′( x) [ 1 − ; ] 3 f (− ) 1 = 3 Câu 35: Cho hàm số có liên tục trên đoạn , và f ( ′ x)dx =10 ∫ giá trị 1 − f (3) của bằng A. 13 − . B. 7 − . C. 13 . D. 7 . Hươngd dẫn giải Chọn C 3 Ta có f ( ′ x)dx =10 ∫
⇒ f (x) 3 =10 ⇔ f (3) − f (− )
1 = 10 ⇔ f (3) = f (− ) 1 +10 = 13 . 1 − 1 − 2 2 f ∫ (x)dx = 3 ( f (x)+ ∫ )1dx Câu 36: Cho 0 . Tính 0 ? A. 4 . B. 5 . C. 7 . D. 1. Hươngd dẫn giải. Chọn B 2 2 2
Ta có ∫( f (x) + ) 1 dx = f
∫ (x)dx+ dx = 3+ 2 = 5 ∫ . 0 0 0
Câu 37: Cho y = f ( x) , y = g ( x) là các hàm số có đạo hàm liên tục trên [0; 2] và 2 2 2 ′ g
∫ (x).f ′(x)dx = 2, g′
∫ (x).f (x)dx = 3. Tính tích phân I =  f
∫ (x).g(x) dx  . 0 0 0 A. I = 1 − .
B. I = 6 .
C. I = 5 . D. I = 1. Hươngd dẫn giải Chọn C 2 2 ′
Xét tích phân I =  f
∫ (x).g(x) dx =  f ′ 
∫ (x).g(x)+ f (x).g′(x)dx  0 0 2 2 = g′
∫ (x).f (x)dx+ g
∫ (x).f ′(x)dx = 5. 0 0 5 2 − f ∫ (x)dx = 8 g ∫ (x)dx = 3 5
Câu 38: Cho hai tích phân 2 − và 5 . Tính I =  f
∫  (x)−4g(x)−1dx. 4 6 T 4 6 T  4 6 T 2 − A. I = 11 − .
B. I = 13 .
C. I = 27 . D. I = 3 . Hươngd dẫn giải Chọn B https://toanmath.com/ 5 5 2 − 5 Ta có: I =  f
∫  (x)−4g(x)−1dx  = f
∫ (x)dx+ 4 g
∫ (x)dx− x = 8+ 4.3−(5+ 2) =13. 46T 2 − 2 − 2 − 5 1
Câu 39: Cho hàm số f ( x) 4 3 2
= x − 4x + 2x − x +1, x ∀ ∈  . Tính 2
f ( x). f ′ ∫ (x)dx. 0 2 2 A. . B. 2 . C. − . D. 2 − . 3 3 Hươngd dẫn giải Chọn C 1 1 f ( x) 1 3 3 f ( ) 3 1 − f (0) 2 Ta có 2 f
∫ (x).f ′(x) 2 dx = f
∫ (x).d f (x)   = = = − . 3 3 3 0 0 0 6 4
Câu 40: Cho hàm số f ( x) liên tục trên đoạn [0; 6] thỏa mãn f
∫ (x)dx =10 và f
∫ (x)dx = 6. Tính 0 2 2 6
giá trị của biểu thức P = f
∫ (x)dx+ f
∫ (x)dx. 0 4
A. P = 4 .`
B. P = 16 .
C. P = 8 . D. P = 10 . Hươngd dẫn giải: 2 6 6 2 6   Ta có: P = f
∫ (x)dx+ f
∫ (x)dx =  f
∫ (x)dx+ f
∫ (x)dx+ f ∫ (x)dx 0 4  0 6  4 6 4 2 6 6 2   = f
∫ (x)dx+ f
∫ (x)dx+ f
∫ (x)dx+ f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx =10−6 = 4 0  6 4  4 0 4 Chọn A 1 1
Câu 41: Cho hàm số f ( x) liên tục trên đoạn [0; 1] và có 3 − 2 f ∫ (x) dx = 5  . Tính f ( x) dx ∫ . 0 0 A. 1 − . B. 2. C. 1. D. 2 − . Hươngd dẫn giải: 1 1 1 1 1 Ta có: 3 − 2 f ∫ (x) dx = 5  ⇔ 3dx − 2 f ∫
∫ (x)dx = 5 ⇔ 3x −2 f ∫ (x)dx = 5 0 0 0 0 0 1 1 ⇔ 2 −
f ( x) dx = 5 − 3 = 2 ⇒ f ( x) dx = 1 − ∫ ∫ 0 0 Chọn A 1 1
Câu 42: Cho hai hàm số f ( x) và g ( x) liên tục trên đoạn [0; 1], có f
∫ (x)dx = 4 và g(x)dx = 2 − ∫ 0 0
. Tính tích phân I =  f
∫ (x)−3g(x)dx  . A. 10 − . B. 10 . C. 2. D. 2 − . Hươngd dẫn giải: 1 1 1 I =  f
∫ (x)−3g(x)dx = f
∫ (x)dx−3 g
∫ (x)dx = 4−3( 2 − ) =10 0 0 0 Chọn B 1
Câu 43: Cho hàm số f ( x) 2
= ln x + x +1 . Tính tích phân I = f '
∫ (x)dx. 0
A. I = ln 2 .
B. I = ln (1+ 2 ) .
C. I = ln 2 D. I = 2 ln 2 https://toanmath.com/ Hươngd dẫn giải: 1 1 1 Ta có: I = f '
∫ (x)dx = f (x) 2
= ln x + x +1 = ln 1+ 2 0 ( ) 0 0 Chọn B
Câu 44: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [1; ln3] và thỏa mãn f ( ) 2 1 = e , ln 3 f ' ∫ (x) 2
dx = 9 − e . Tính I = f (ln 3) . 1 A. 2
I = 9 − 2e .
B. I = 9 . C. I = 9 − . D. 2 I = 2e − 9 . Hươngd dẫn giải: ln 3 ln 3 Ta có: f '
∫ (x)dx = f (x) = f (ln3)− f ( ) 2 1 = 9 − e (gt) 1 1 ⇒ f ( ) 2 2
ln 3 − e = 9 − e ⇒ f (ln 3) = 9 Chọn B
Câu 45: Cho hai hàm số y = f ( x) và y = g ( x) có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn 1 1 1 / f '
∫ (x).g(x)dx =1, f (x).g '(x)dx = 1 − ∫
. Tính I =  f
∫ (x).g(x) dx  . 0 0 0 A. I = 2 − .
B. I = 0 .
C. I = 3 . D. I = 2 . Hươngd dẫn giải: 1 1 I =  f
∫ (x).g(x) / dx =  f
∫ (x).g '(x)+ f '(x).g(x)dx 0 0 1 1 = f
∫ (x).g '(x)dx+ f '
∫ (x).g(x)dx =1−1= 0 0 0 Chọn B 2 x
Câu 46: Cho hàm số f ( x) liên tục trên (0; +∞) và thỏa f
∫ (t)dt = .xcosπ x . Tính f (4). 0
A. f (4) = 123 . B. f ( ) 2 4 = . C. f ( ) 3 4 = . D. f ( ) 1 4 = . 3 4 4 Hươngd dẫn giải:
Ta có: F (t ) = f
∫ (t)dt ⇒ F '(t) = f (t) 2 x
Đặt G (x) = f
∫ (t)dt = F ( 2x)− F (0) 0
⇒ G (x) = F  ( x ) / 2  = x f  ( 2 ' 2 .
x ) (Tính chất đạo hàm hợp: f ' u
 ( x) = f ' 
(u).u'(x) ) 2 x
Mặt khác, từ gt: G ( x) = f
∫ (t)dt = .xcosπ x 0 ⇒ G '(x) = ( .
x cosπ x) ' = −xπ sin π x + cosπ x ⇒ x f ( 2 2 .
x ) = −xπ sinπ x + cosπ x (1)
Tính f (4) ⇒ ứng với x = 2
Thay x = 2 vào (1) ⇒ 4. f (4) = 2
− π sin 2π + cos 2π = 1 ⇒ f ( ) 1 4 = 4 Chọn D https://toanmath.com/ f ( x)
Câu 47: Cho hàm số f ( x) thỏa mãn 2 t .dt = . x cosπ x ∫ . Tính f (4) . 0
A. f (4) = 2 3 . B. f (4) = 1 − . C. f ( ) 1 4 = . D. f ( ) 3 4 = 12 . 2 Hươngd dẫn giải: f ( x) f ( x) tf (x) 3 3    t dt = =
= x cosπ x ⇒  f ∫  ( x) 3 2  = 3 . x cosπ x 3 3 0 0 ⇒ f (x) 3
= 3x cosπ x ⇒ f (4) 3 = 12 Chọn D x  π 
Câu 48: Cho hàm số G ( x) = t.cos ∫
(x −t).dt . Tính G'  .  2  0  π   π   π   π  A. G ' = 1 −   . B. G ' = 1   . C. G ' = 0   . D. G ' = 2   .  2   2   2   2  Hươngd dẫn giải:
Cách 1: Ta có: F (t ) = t.cos ∫
(x −t)dt ⇒ F '(x) = t.cos(x −t) x
Đặt G (x) = t.cos ∫
(x −t)dt = F (x)− F (0) 0  π ⇒ 
G ( x) = F
 ( x) − F ( ) /  = F
(x) − F ( ) = x  (x − x) / ' 0 ' ' 0 cos − 0 = x ' = 1  ⇒ G ' = 1    2  Chọn B x
Cách 2: Ta có G ( x) = t.cos ∫
(x −t)dt . Đặt u = t ⇒ du = dt , dv = cos(x −t)dx chọn 0
v = − sin ( x − t ) x x ⇒ ( ) x x G x = t
− .sin (x − t) + sin
∫ (x−t)dt = sin
∫ (x−t)dt = cos(x−t) = cos0−cos x =1−cos x 0 0 0 0  π  π
⇒ G '(x) = sin x ⇒ G ' = sin = 1    2  2 Chọn B 2 x
Câu 49: Cho hàm số G ( x) = cos t.dt ∫
( x > 0 ). Tính G '( x) . 0 A. G ( x) 2 '
= x .cos x .
B. G '( x) = 2 .
x cos x .
C. G '( x) = cos x .
D. G '( x) = cos x −1. Hươngd dẫn giải: 2 x
Ta có F (t ) = cos tdt ⇒ F ' ∫
(t) = cos t ⇒ G(x) = cos tdt = F ∫ ( 2x)− F (0) 0
⇒ G (x) = F
 ( x ) − F ( ) /  = F   ( x ) /  − F   ( ) = F   ( x ) / / 2 2 2  = x  ( 2 ' 0 0 2 .F' x ) 2 = 2 . x cos x = 2 . x cos x Chọn B x
Câu 50: Cho hàm số G ( x) 2 = 1+ t dt ∫
. Tính G '( x) . 1 x 1 A. . B. 2 1+ x . C. . D. ( 2 x + ) 2 1 x +1 . 2 1+ x 2 1+ x https://toanmath.com/ Hươngd dẫn giải: Đặt F (t) 2 = + t dt ⇒ F ∫ (t) 2 1 ' = 1+ t x G ( x) x 2 = 1+ t dt = F ∫ (x)− F ( )
1 ⇒ G '( x) = F '( x) − F '( ) 1 = F '( x) = 2 + 1 1 x Chọn A x
Câu 51: Cho hàm số F ( x) 2 = sin t .dt ∫
( x > 0 ). Tính F '( x) . 1 sin x 2 sin x
A. sin x . B. . C. . D. sin x . 2 x x Hươngd dẫn giải: x Đặt F (t) 2 = sin t dt ∫ , G ( x) 2 = sin t dt = F ∫ ( x)−F( )1 1 ⇒
(x) = F ( x)− F ( ) = F ( x) = ( x) ( x)2 sinx G ' ' ' 1 ' '.sin = 2 x Chọn B x f (t ) f ( x)
Câu 52: Tính đạo hàm của f ( x) , biết f ( x) thỏa t.e dt = e ∫ . 0
A. f '( x) = x . B. f ( x) 2 ' = x +1. C. f ( x) 1 ' = . D. f ( x) 1 ' = . x 1− x Hươngd dẫn giải: x Đặt F (t) f (t ) = t e dt ⇒ F ∫ (t) f (t ) . '
= t.e ⇒ G (x) f (t )
= t.e dt = F ∫ (x)− F (0) 0 ⇒ ( ) = ( ) ( ) ( ) ( ) ( ) / ( ) ' ' f x G x F x = e (gt) ⇔ . f x f x x e = e ⇒  . f x f x x e  = e      f ( x) ⇒ e
+ x f (x) f (x) = f (x) f (x) . ' .e ' .e
⇒ + x f ( x) = f ( x) ⇒ f ( x) 1 1 . ' ' ' = 1− x Chọn D 2 x
y = f ( x) [0;+ ∞) f (4) Câu 53: Cho hàm số liên tục trên và f
∫ (t)dt = .xsin(π x). Tính 0 π −1 π π A. f (π ) = . B. f (π ) = . C. f (π ) = . D. f (π ) 1 = . 4 2 4 2 Hươngd dẫn giải Chọn B Ta có f
∫ (t)dt = F (t) ⇒ F′(t) = f (t) 2 x Khi đó 2 x f
∫ (t)dt = .xsin(π x) ⇔ F (t) = .xsin(π x) ⇔ F ( 2x)− F (0) = .xsin(π x) 0 0 ⇒ F′( 2
x ).2x = sin (π x) + π .
x cos (π x) ⇔ f ( 2
x ).2x = sin (π x) + π . x cos (π x) π ⇒ f (4) = . 2 f ( x) ( 2; − 3) F ( x) f ( x) Câu 54: Cho hàm số liên tục trên khoảng . Gọi là một nguyên hàm của 4 6 T 2 ( I =  f
∫  (x)+ 2xdx  2; − 3) F (− ) 1 = 1 F (2) = 4 trên khoảng . Tính 1 − , biết và . https://toanmath.com/
A. I = 6 .
B. I = 10 .
C. I = 3 . D. I = 9 . 4 6 T Hươngd dẫn giải Chọn A 2 2
= F (2) − F (− ) 1 + (4 − ) 1 I =  f ∫ = − + =
 ( x) + 2x dx  = F (x) 2 2 + x 4 1 3 6 . 4 6 T 1 − 1 − 1 − 2 2 2 f ∫ (x)dx = 2
g ( x) dx = 1 − ∫ I = x + 2 f ∫ 
(x)−3g (x)dxCâu 55: Cho 1 − và 1 − . Tính 1 − 11 7 17 5 A. I = . B. I = . C. I = . D. I = . 2 2 2 2 Hươngd dẫn giải Chọn C 2 2 2 2 2 2 x 17 Ta có: I = x + 2 f ∫ 
(x)−3g (x)dx  = xdx + 2 f ∫ ∫ (x)dx−3 g ∫ (x)dx = + 4 + 3 = . 2 2 1 − 1 − 1 − 1 − 1 − 2 2 2 3 f
∫ (x)+ 2g(x)dx =1  2 f
∫ (x)− g(x)dx = 3 −  f ( x) dx ∫ Câu 56: Cho 1 , 1 . Khi đó, 1 bằng 11 5 6 16 A. . B. − . C. . D. . 7 7 7 7 Hươngd dẫn giải Chọn B  5 = − 2 2  + = a  Đặ a b  7 t a = f
∫ (x)dx, b = f
∫ (x)dx , ta có hệ phương trình 3 2 1  ⇔  2a − b = 3 − 11 1 1 b  =  7 2 5
Vậy f ( x) dx = − ∫ . 7 1
Câu 57: Cho f ( x) , g ( x) là hai hàm số liên tục trên đoạn [ 1 − ; ]
1 và f ( x) là hàm số chẵn, g ( x) là 1 1
hàm số lẻ. Biết f
∫ (x)dx = 5; g
∫ (x)dx = 7 . Mệnh đề nào sau đây là sai? 0 0 1 1 A. f
∫ (x)dx =10. B. f
∫  (x)+ g(x)dx =10  . 1 − 1 − 1 1 C. f
∫  (x)− g(x)dx =10  . D. g ∫ (x)dx =14. 1 − 1 − Hươngd dẫn giải Chọn D 1 1
Vì f ( x) là hàm số chẵn nên f
∫ (x)dx = 2 f
∫ (x)dx = 2.5 =10. 1 − 0 1
Vì g ( x) là hàm số lẻ nên g ∫ (x)dx = 0. 1 − 1 1 ⇒  f
∫  (x)+ g(x)dx =10  và  f
∫  (x)− g(x)dx =10  . 1 − 1 − Vậy đáp án D sai. https://toanmath.com/
Câu 58: Cho f ( x) , g ( x) là hai hàm số liên tục trên đoạn [ 1 − ; ]
1 và f ( x) là hàm số chẵn, g ( x) là 1 1
hàm số lẻ. Biết f
∫ (x)dx = 5; g
∫ (x)dx = 7. Mệnh đề nào sau đây là sai? 0 0 1 1 A. f
∫ (x)dx =10. B. f
∫  (x)+ g(x)dx =10  . 1 − 1 − 1 1 C. f
∫  (x)− g(x)dx =10  . D. g ∫ (x)dx =14. 1 − 1 − Hươngd dẫn giải Chọn D 1 1
Vì f ( x) là hàm số chẵn nên f
∫ (x)dx = 2 f
∫ (x)dx = 2.5 =10. 1 − 0 1
Vì g ( x) là hàm số lẻ nên g ∫ (x)dx = 0. 1 − 1 1 ⇒  f
∫  (x)+ g(x)dx =10  và  f
∫  (x)− g(x)dx =10  . 1 − 1 − 10 8 10 f ∫ (z)dz =17 f ∫ (t)dt =12 3 − f ∫ (x)dx Câu 59: Nếu 0 và 0 thì 8 bằng A. 15 − . B. 29 . C. 15 . D. 5 . Hươngd dẫn giải Chọn A 10 0 10   I = 3 − f ∫ (x)dx = 3 −  f
∫ (x)dx+ f ∫ (x)dx = 3 − ( 12 − +17) = 15 − . 8  8 0  2 7 7 f
∫ (x)dx = 2 f ∫ (t)dt = 9 f ( z) dz ∫ Câu 60: Cho 1 − , 1 − . Giá trị của 2 là A. 11. B. 5 . C. 7 . D. 9 . Hươngd dẫn giải Chọn C 7 7 7 7 7 2 7 Ta có f
∫ (t)dt = f
∫ (x)dx và f
∫ (z)dz = f
∫ (x)dx nên f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx. 1 − 1 − 2 2 1 − 1 − 2 7 Vậy f ∫ (z)dz = 7. 2 3
Câu 61: Cho hàm số y = f ( x) liên tục, luôn dương trên [0; ] 3 và thỏa mãn I = f
∫ (x)dx = 4. Khi 0 3 đó giá trị 1+ln( f ( x))
của tích phân K = ∫(e + 4)dx là: 0 A. 4 +12e . B. 12 + 4e . C. 3e +14 . D. 14 + 3e . Hươngd dẫn giải Chọn B 3 1+ln( 3 3 3 3 f ( x)) 1+ln( f x ) 3 Ta có K = ∫(e + 4) ( ) dx = e
dx + 4dx = e. f ∫ ∫
∫ (x)dx+ 4dx = 4e+ 4x = 4e+12 ∫ | . 0 0 0 0 0 0 Vậy K = 4e +12 .
Câu 62: Cho hàm số y = f ( x) có đạo hàm trên  thỏa https://toanmath.com/ f  (0) = f ′(0) = 1;  .  f
 ( x + y) = f ( x) + f ( y) + 3xy ( x + y) −1, x,y ∀ ∈  1 Tính f ( x − ∫ ) 1 dx . 0 1 1 1 7 A. . B. − . C. . D. . 2 4 4 4 Hươngd dẫn giải Chọn C
Lấy đạo hàm theo hàm số y
f ′( x + y) = f ′( y) 2
+ 3x + 6xy , x ∀ ∈  .
Cho y = ⇒ f ′( x) = f ′( ) 2 0
0 + 3x ⇒ f ′( x) 2 = 1+ 3x Vậy ( ) = ′ ∫ ( ) 3 f x f
x dx = x + x + C mà f (0) = 1 ⇒ C = 1 suy ra f ( x) 3 = x + x +1. 0 1 0 0 4 2  x x  1 1 f ( x − ) 1 dx = ∫
f ( x)dx = ∫ ( 3x + x+ ∫
)1dx =  + + x = − − + 1 1 = .  4 2  4 2 4 0 1 − 1 − 1 − 1
Câu 63: Cho hàm số f ( x) là hàm bậc nhất thỏa mãn ∫(x + )
1 f ′( x) dx = 10 và 2 f ( ) 1 − f (0) = 2 . 0 1 Tính I = f
∫ (x)dx. 0
A. I = 1.
B. I = 8 . C. I = 12 − . D. I = 8 − . Hươngd dẫn giải Chọn D
Gọi f ( x) = ax + b , (a ≠ 0) ⇒ f ′( x) = a . Theo giả thiết ta có: 1 1 1 10 3 10 20 +) ∫(x + )
1 f ′( x) dx = 10 ⇔ a∫(x + )
1 dx = 10 ⇔ ( x + ) 1 dx = ∫ ⇔ = ⇒ a = . a 2 a 3 0 0 0   34 +) 2 f ( ) 1 − f (0) = 20 2 ⇔ 2. + b − b = 2   ⇔ b = − .  3  3
Do đó, f (x) 20 34 = x − . 3 3 1 1  20 34  Vậy I = f ∫ (x)dx = x − dx = 8 − ∫   . 0 0  3 3  f ( x)  \{ } 0 1 f ( ) 1 = a Câu 64: Cho hàm số xác định trên
, thỏa mãn f ′( x) = , và 3 5 x + x f ( 2 − ) = b f (− ) 1 + f (2) . Tính . A. f (− )
1 + f (2) = −a − b . B. f (− )
1 + f (2) = a − b . C. f (− )
1 + f (2) = a + b . D. f (− )
1 + f (2) = b − a . Hươngd dẫn giải Chọn C 1 1
Ta có f ′(−x) = = − = − f ′( x) ′ (
nên f ( x) là hàm lẻ. −x)3 + (− 3 5 x)5 x + x 2 1 − 2 Do đó f ′
∫ (x)dx = 0 ⇔ f ′
∫ (x)dx = − f ′ ∫ (x)dx. 2 − 2 − 1 https://toanmath.com/ Suy ra f (− ) 1 − f ( 2
− ) = − f (2) + f ( ) 1 ⇒ f (− )
1 + f (2) = f ( 2 − ) + f ( ) 1 = a + b . f ( x)  \{ } 0 1 f ( ) 1 = a Câu 65: Cho hàm số xác định trên
và thỏa mãn f ′( x) = , , 2 4 x + x f ( 2 − ) = b f (− ) 1 − f (2)
. Giá trị của biểu thức bằng
A. b − a .
B. a + b .
C. a − b .
D. −a − b . Hươngd dẫn giải Chọn A 1 1
Ta có f ′(−x) = = = f ′(x) ′ (
nên f ( x) là hàm chẵn. −x)2 + (− 2 4 x)4 x + x 1 − 2 Do đó f ′
∫ (x)dx = f ′ ∫ (x)dx . 2 − 1 Suy ra f (− )
1 − f (2) = f (− ) 1 − f ( 2 − ) + f ( 2 − ) − f ( ) 1 + f ( ) 1 − f (2) 1 − 2 = f ′
∫ (x)dx+b−a − f ′
∫ (x)dx = b−a . 2 − 1
Câu 66: Cho hàm số y = f ( x) xác định và liên tục trên  thỏa mãn đồng thời các điều kiện
f ( x) > 0 , x
∀ ∈  ; f ′(x) x 2
= −e . f (x), x ∀ ∈  và f ( ) 1 0 =
. Tính giá trị của f (ln 2) . 2 A. f ( ) 2 ln 2 = . B. f ( ) 2 ln 2 = − . C. f ( ) 2 ln 2 = . D. f ( ) 1 ln 2 = . 9 9 3 3 Hươngd dẫn giải Chọn D f ′( x) ln 2 f ′( x) 1 ln 2 df ( x) ln 2 f ′( x) x 2
= −e . f (x) x ⇔ = −e ⇔
dx = − exdx ∫ ∫ x ⇔ = −e ∫ 2 f ( x) 2 f x 2 f x 0 ( ) 0 0 ( ) 0 ln 2 1 ⇔ − 1 1 1 ⇔ f (ln 2) 1 ( ) = 1 − ⇔ − = 1 ⇔ = 3 = . f x f (ln 2) f (0) f (ln 2) 3 0
Câu 67: Cho hàm số y = f ( x) có đồ thị (C ) , xác định và liên tục trên  thỏa mãn đồng thời các
điều kiện f (x) > 0 x
∀ ∈  , f ′(x) = (x f (x))2 . , x
∀ ∈  và f (0) = 2 . Phương trình tiếp
tuyến tại điểm có hoành độ x = 1 của đồ thị (C ) là.
A. y = 6x + 30 . B. y = 6 − x + 30 .
C. y = 36x − 30 . D. y = 36 − x + 42 . Hươngd dẫn giải Chọn C 1 1 f ′( x) 1 f ′( x) 1 1 df ( x) 3 x 1 1
f ′( x) = ( x f ( x))2 . 2 ⇔ = x 2 ⇔ dx = x dx ∫ ∫ ⇔ = ∫ ⇔ − = 2 f ( x) 2 f x 2 f x 3 f ( x) 3 0 ( ) 0 ( ) 0 0 0 1 1 1 ⇔ − = − 1 1 ⇔ = ⇔ f ( ) 1 = 6 . f ( ) 1 f (0) 3 f ( ) 1 6
f ′( ) = ( f ( ))2 1 1. 1 = 36 .
Vậy phương trình tiếp tuyến cần lập là y = 36x − 30 .
Câu 68: Cho hàm số y = f ( x) > 0 xác định, có đạo hàm trên đoạn [0; ] 1 và thỏa mãn: x 1
g ( x) = 1+ 2018 f ∫ (t)dt , ( ) 2
g x = f ( x) . Tính g ( x)dx ∫ . 0 0 https://toanmath.com/ 1011 1009 2019 A. . B. . C. . D. 505 . 2 2 2 Hươngd dẫn giải Chọn A x
Ta có g ( x) = 1+ 2018 f
∫ (t)dt ⇒ g′(x) = 2018 f (x) = 2018 g(x) 0 g′( x) t g′( x) t t ⇒ = ⇒ t dx = 2018 dx ∫
∫ ⇒ 2( g(x)) = 2018x g ( x) 2018 0 0 0 g ( x) 0
⇒ 2( g (t) − )1 = 2018t (do g (0) =1)
⇒ g (t) =1009t +1 1 1   ⇒ g ∫ (t) 1009 1011 2 dt = t + t =   .  2  2 0 0
y = f ( x) [ 1 − ; ] 1
f ( x) > 0, x ∀ ∈  Câu 69: Cho hàm số
có đạo hàm và liên tục trên đoạn , thỏa mãn
f '( x) + 2 f ( x) = 0 f ( ) 1 = 1 f (− ) 1 và . Biết , tính . A. f ( ) 2 1 e− − = . B. f (− ) 3 1 = e . C. f (− ) 4 1 = e . D. f (− ) 1 = 3 . Hươngd dẫn giải Chọn C Biến đổi: 1 1 1 f x f x df x
f '( x) + 2 f ( x) '( ) '( ) ( ) 1 = 0 ⇔ = − ⇔ = − ⇔ = − ⇔ = − ∫ ∫ ∫ − f ( x) 2 f − (x)dx 2dx f − − (x) 4 ln f ( x) 4 1 1 1 1 f ( ) 1 f ( ) 1 4 − 4 4 ln ( ) = 4 − ⇔ = ⇔ − = = . − f (− ) e f ( ) 1 f ( ) 1 .e e f 1 1
Câu 70: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 đồng thời thỏa mãn f ′(0) = 9 và
f ′′( x) +  f ′  ( x) 2 9 − x = 9 
. Tính T = f ( ) 1 − f (0) . 1
A. T = 2 + 9 ln 2 .
B. T = 9 . C. T = + 9ln 2 .
D. T = 2 − 9 ln 2 . 2 Hươngd dẫn giải Chọn C
f ′′( x) −1 1
Ta có f ′′( x) +  f ′  ( x) 2 9 − x = 9 
⇒ ( f ′′(x) − ) = −  f ′(x) 2 9 1 − x   ⇒ − = .  f ′  ( x) 2 −  9 x
f ′′( x) −1 1 1 x
Lấy nguyên hàm hai vế − = ∫ ∫ ⇒ = + C .  f  ( x) dx dx 2 −  9 ' x
f ′( x) − x 9 1
Do f ′(0) = 9 nên C = suy ra f ′( x) 9 − x = ⇒ f ′( x) 9 = + x 9 x +1 x +1 1 1  9  2  x  1 Vậy T = f ( ) 1 − f (0) = + x dx ∫  = 9 ln x  +1 +  = 9ln 2 + .  x +1   2  2 0 0
y = f ( x)
f ( x) f ( x) 4 2 ' . = x + x f (0) = 2 2 f (2) Câu 71: Cho hàm số thỏa mãn . Biết . Tính . 313 332 324 323 A. 2 f (2) = . B. 2 f (2) = . C. 2 f (2) = . D. 2 f (2) = . 15 15 15 15 Hươngd dẫn giải https://toanmath.com/ Chọn B Ta có 2 2 2 2 f x
f '( x). f ( x) 136 136 4 2
= x + x ⇒ f '(x). f (x)dx = ( 4 2
x + x ) dx ⇔ f ( x) df ( x) ( ) 2 = ⇔ = ∫ ∫ ∫ 0 15 2 15 0 0 0 2 f (2) − 4 136 332 2 = ⇔ f (2) = . 2 15 15
Câu 72: Cho f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1; 4] thỏa mãn
x + xf ( x) =  f ′  ( x) 2  x ∀ ∈  [ ] f ( ) 3 2 , 1; 4 , 1 =
. Giá trị f (4) bằng: 2 391 361 381 371 A. B. C. D. 18 18 18 18 Hươngd dẫn giải Chọn A Biến đổi:  f ′(x) 2  f ′   (x)
x + xf ( x) =  f ′( x) 2 2  
 ⇔ x( + f ( x)) =  f ′( x) 2 1 2    ⇔ = x ⇒ = x . 1+ 2 f ( x) 1+ 2 f ( x) 4 f ′( x) 4 ⇒ 14 14 391 dx = xdx ∫ ∫
⇔ 1+ 2 f ( x) 4 = ⇔ 1+ 2 f (4) − 2 = ⇔ f (4) = . + 1 3 3 18 1 1 2 f ( x) 1 Chọn A 4 f ′( x) 4
Chú ý: Nếu không nhìn được ra luôn I = dx = 1+ 2 f ∫
(x) = 1+ 2 f (4) − 2 thì ta có 1+ 2 f ( x) 1 1
thể sử dụng kỹ thuật vi phân hoặc đổi biến (bản chất là một). 4 f '( x) 4 df ( x) 4 1 4 1 − + Vi phân: dx = ∫ ∫ =
∫(1+ 2 f (x)) 2 d (1+ 2 f (x)) = 1+ 2 f (x) . + + 1 2 1 1 2 f ( x) 1 1 2 f ( x) 1
+ Đổi biến: Đặt t = 1+ 2 f (x) 2
⇒ t = 1+ 2 f (x) ⇔ tdt = f ′(x)dx
với x = 1 ⇒ t = 1+ 2 f ( )
1 = 2; x = 4 ⇒ t = 1+ 2 f (4) . 1+2 f (4) 1+2 f (4) Khi đó tdt 1+2 f (4) I = = ∫ dt = t ∫ = 1+ 2 f (4) − 2. t 2 2 2
y = f ( x) f ′( x) [0;+∞) Câu 73: Cho hàm số có
liên tục trên nửa khoảng thỏa mãn ( )+ ( ) 2 3 = 1+ 3.e x f x f x − ′ . Khi đó: 1 1 1 1 A. 3 e f ( ) 1 − f (0) = − . B. 3 e f ( ) 1 − f (0) = − . 2 + 2 e 3 2 + 4 2 e 3 e + 3 e + 3 − 8 3 ( 2 ) 2 C. e f ( ) 1 − f (0) = .
D. 3 f ( ) − f ( ) = ( 2 + ) 2 e 1 0 e 3 e + 3 − 8 . 3 Hươngd dẫn giải Chọn C − e x + x 3
Ta có: 3 f ( x) + f ′( x) 2 2 = 1+ 3.e = 3x ⇒ ( ) 3x + ′( ) 2 x 2 3e e = e e x f x f x + 3 . ex ′ 3x ⇔  ( ) 2 x 2 e  = e e x f x + 3   . https://toanmath.com/ 1 1 ′
Lấy tích phân từ 0 đến 1 hai vế ta được 3 e x ∫ ( ) 2 x 2  d = e e x f x x + 3 dx   ∫ 0 0 e + 3 e + 3 − 8 3 ( 2 ) 2 x ⇔  ( ) 1 e  =   ( e x f x + 3) 13 1 3 2 ⇔ e f ( ) 1 − f (0) = . 0 3 3 0
Câu 74: Cho hàm số f liên tục, f ( x) > 1
− , f (0) = 0 và thỏa f ′(x) 2 x +1 = 2x
f ( x) +1 . Tính f ( 3) . A. 0 . B. 3 . C. 7 . D. 9 . Hươngd dẫn giải Chọn B f ′ x 2x Ta có f ′( x) 2 x +1 = 2x f ( x) ( ) +1 ⇔ = f ( x) 2 +1 x +1 3 f ′( x) 3 2x ⇔ dx = dx ⇔ f ∫ ∫ (x) 3 3
+1 = x +1 ⇔ f (x) 3 2 +1 = 1 + + 0 f ( x) 2 0 0 0 1 0 x 1
⇔ f ( 3) +1 − f (0) +1 =1⇔ f ( 3) +1 = 2 ⇔ f ( 3) = 3.
Câu 75: Cho hàm số f ( x) ≠ 0 thỏa mãn điều kiện f ′( x) = ( x + ) 2 2
3 f ( x) và f ( ) 1 0 = − . Biết rằng 2 a a tổng f ( )
1 + f (2) + f (3) + ... + f (2017) + f (2018) = với ( *
a ∈ , b ∈  ) và là phân b b
số tối giản. Mệnh đề nào sau đây đúng? a a A. < 1 − . B. >1.
C. a + b = 1010 .
D. b − a = 3029 . b b Hươngd dẫn giải Chọn D f ′( x)
Ta có f ′( x) = ( x + ) 2 2 3 f ( x) ⇔ = 2x + 3 2 f ( x) f ′( x) ⇔ ∫ 1 2
( )dx = ∫(2x +3)dx ⇔ −
= x + 3x + C . f x f ( x) Vì f ( ) 1 0 = − ⇒ C = 2 . 2 1 1 1
Vậy f ( x) = − ( = − . x + ) 1 ( x + 2) x + 2 x +1
Do đó f ( ) + f ( ) + f ( ) + + f ( )+ f ( ) 1 1 1009 1 2 3 ... 2017 2018 = − = − . 2020 2 2020 Vậy a = 1009 −
; b = 2020 . Do đó b − a = 3029 . ax + b
Câu 76: Biết luôn có hai số a và b để F ( x) =
(4a −b ≠ 0) là nguyên hàm của hàm số f (x) x + 4 và thỏa mãn: 2
2 f ( x) = F
 ( x) −1 f ′  ( x) .
Khẳng định nào dưới đây đúng và đầy đủ nhất?
A. a = 1, b = 4 .
B. a = 1, b = 1 − .
C. a = 1, b ∈  \ { } 4 .
D. a ∈  , b ∈  . Hươngd dẫn giải Chọn C https://toanmath.com/ ax + b 4a − b 2b − 8a Ta có F ( x) =
là nguyên hàm của f ( x) nên f ( x) = F′( x) = và f ′( x) = . x + 4 (x + 4)2 (x + 4)3 2 (4a − b)2 Do đó:  ax + b  2b − 8a 2
2 f ( x) = ( F ( x) − ) 1 f ′( x) ⇔ = − (   x + 4) 1 4  x + 4  (x + 4)3
⇔ 4a − b = −(ax + b − x − 4) ⇔ (x + 4)(1− a) = 0 ⇔ a =1 (do x + 4 ≠ 0 )
Với a = 1 mà 4a − b ≠ 0 nên b ≠ 4 .
Vậy a = 1, b ∈  \ { } 4 .
Chú ý: Ta có thể làm trắc nghiệm như sau:
+ Vì 4a − b ≠ 0 nên loại được ngay phương án A: a = 1, b = 4 và phương án D: a ∈  , b ∈  .
+ Để kiểm tra hai phương án còn lại, ta lấy b = 0, a =1. Khi đó, ta có ( ) x 4 8 F x = , f ( x) =
, f ′( x) = − . x + 4 (x + 4)2 (x + 4)3 Thay vào 2
2 f ( x) = ( F ( x) − )
1 f ′( x) thấy đúng nên Chọn C
y = f ( x) [1;2] f ( ) 1 = 4 Câu 77: Cho hàm số
có đạo hàm liên tục trên thỏa mãn và
f ( x) = xf ′( x) 3 2 − 2x − 3x f (2) . Tính A. 5 . B. 20 . C. 10 . D. 15 . Hươngd dẫn giải Chọn B ′
xf ′ x − f xf x
Do x ∈[1; 2] nên f ( x) = xf ′( x) 3 2 ( ) ( ) ( )
− 2x − 3x ⇔ = 2x + 3 ⇔   = 2x + 3 2 x x   f ( x) 2 ⇔
= x + 3x + C . x Do f ( )
1 = 4 nên C = 0 ⇒ f ( x) 3 2 = x + 3x . Vậy f (2) = 20 . x  π π 
Câu 78: Cho f ( x) = trên − ; 
 và F ( x) là một nguyên hàm của xf ′( x) thỏa mãn 2 cos x  2 2   π π 
F (0) = 0 . Biết a ∈ − ; 
 thỏa mãn tan a = 3. Tính F (a) 2
−10a + 3a .  2 2  1 1 1 A. − ln10 . B. − ln10 . C. ln10 . D. ln10 . 2 4 2 Hươngd dẫn giải Chọn C
Ta có: F ( x) = xf ′ ∫ (x)dx = d x f ∫
(x) = xf (x)− f ∫ (x)dx x sin x Ta lại có: f ∫ (x)dx = dx ∫ = d x (tan x ∫
) = x tan x − tan d x x ∫ = x tan x − dx ∫ 2 cos x cos x 1 = x tan x + d ∫
(cos x) = x tan x + ln cos x +C ⇒ F (x) = xf (x)− x tan x −ln cos x +C cos x
Lại có: F (0) = 0 ⇒ C = 0 , do đó: F ( x) = xf ( x) − x tan x − ln cos x .
⇒ F (a) = af (a) − a tan a − ln cos a https://toanmath.com/ Khi đó ( ) a 1 1 f a = = a ( 2
1+ tan a) = 10a và 2 =1+ tan a =10 2 ⇔ cos a = 2 cos a 2 cos a 10 1 ⇔ cos a = . 10 1 Vậy F (a) 2 −10a + 3a 2 2
= 10a − 3a − ln −10a + 1 3a = ln10 . 10 2
Câu 79: Cho hàm số y = f ( x) xác định và liên tục trên  thỏa mãn đồng thời các điều kiện sau
f ( x) > 0 , x
∀ ∈  , f ′(x) x 2
= −e . f (x) x ∀ ∈  và f ( ) 1 0 =
. Phương trình tiếp tuyến của 2
đồ thị tại điểm có hoành độ x = ln 2 là 0
A. 2x + 9 y − 2 ln 2 − 3 = 0 .
B. 2x − 9 y − 2 ln 2 + 3 = 0 .
C. 2x − 9 y + 2 ln 2 − 3 = 0 .
D. 2x + 9 y + 2 ln 2 − 3 = 0 . Hươngd dẫn giải Chọn A ln 2 f ′( x) ln 2  f ′( x) ln 2    ln 2 1 Ta có f ′( x) x 2
= −e . f (x) ⇔ − = ex ⇒ ∫ −
 dx = exdx ∫ ⇒   =   (ex) 2 f ( x) 2 f x f  ( x) 0 0  ( ) 0  0 1 1 ⇒ − = ⇒ f ( ) 1 ln 2 = . f ( ) f ( ) 1 ln 2 0 3 2  1  2 Từ đó ta có f ′( ) ln 2 2 ln 2 = −e f (ln 2) = 2. −   = − .  3  9 2 1
Vậy phương trình tiếp tuyến cần tìm là y = − ( x − ln 2) +
⇔ 2x + 9y − 2ln 2 − 3 = 0 . 9 3
Câu 80: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 , f ( x) và f ′( x) đều nhận giá trị dương trên đoạn [0; ]
1 và thỏa mãn f (0) = 2 , 1 1  1 3 f ′
∫ (x). f (x) 2 +1dx = 2 f ′  ∫
(x).f (x)dx     . Tính f ∫ (x) dx  . 0 0 0 15 15 17 19 A. . B. . C. . D. . 4 2 2 2 Hươngd dẫn giải Chọn D 1 1 2
Theo giả thiết, ta có  f ′
∫ (x). f (x) +1dx = 2 f ′  ∫
(x).f (x)dx   0 0 1 1  ⇔ f ′
∫ (x). f (x) 2 +1dx−2 f ′  ∫
(x).f (x)dx = 0   0 0 1 2  1 ⇔ f ′
∫ (x). f (x) 2 −2 f ′ 
(x).f (x)+1dx = 0 ⇔  ′ −  =   f ∫
(x).f (x) 1 dx 0   0 0 3 f ( x)
⇒ f ′(x). f (x) −1 = 0 2
⇒ f (x). f ′(x) =1 ⇒
= x + C . Mà f ( ) 8 0 = 2 ⇒ C = . 3 3 Vậy 3
f ( x) = 3x + 8 . 1 1 1 2 3  3x  19 Vậy  f
∫ (x) dx = 
∫(3x+8)dx =  + 8x  = .  2  2 0 0 0 https://toanmath.com/
Câu 81: Cho f (x) không âm thỏa mãn điều kiện 2
f (x). f '(x) = 2x
f (x) +1 và f (0) = 0 . Tổng giá
trị lớn nhất và nhỏ nhất của hàm số y = f (x) trên [1; ] 3 là A. 22 B. 4 11 + 3 C. 20 + 2 D. 3 11 + 3 Hươngd dẫn giải Chọn D Biến đổi:
f (x). f '(x)
f (x). f '(x) 2
f (x). f '(x) = 2x f (x) +1 ⇔ = 2x ⇒ dx = 2xdx ∫ ∫ 2 2
⇔ f (x) +1 = x + C 2 2 f (x) +1 f (x) +1 Với 2 2 2 4 2
f (0) = 0 ⇒ C = 1 ⇒
f (x) +1 = x +1 ⇒ f (x) = x + 2x = g(x) Ta có: 3
g '(x) = 4x + 4x > 0, x ∀ ∈[1; ]
3 . Suy ra g(x) đồng biến trên [1; ] 3 Suy ra: 2
g(1) ≤ g(x) = f (x) ≤ g (3) 2 f ( x)≥0
⇒ 3 ≤ f (x) ≤ 99 → 3 ≤ f (x) ≤ 3 11 min f (x) = 3  [1; ]3 ⇒ 
Max f (x) = 3 11  3
f (x). f '(x)
Chú ý: Nếu không tìm được ra luôn 2 dx =
f (x) +1 + C ∫
thì ta có thể sử dụng kĩ thuật 2 f (x) +1
vi phân hoặc đổi biến (bản chất là một) 1 −
f (x). f '(x) f (x) 1 +) Vi phân: dx = d ∫ ∫
( f (x)) = ∫( 2f(x)+ )1 d ( 2f(x)+ ) 2 2 1 =
f (x) +1 + C 2 2 + + 2 f (x) 1 f (x) 1
+ Đổi biến: Đặt 2 2 2 t =
f (x) +1 ⇒ t = f (x) +1 ⇒ tdt = f (x) f '(x)dx
f (x). f '(x) tdt Suy ra: 2 dx =
= dt = t + C = f (x) +1 + C ∫ ∫ ∫ 2 ( ) +1 t f x
Câu 82: Cho hàm số f ( x) có đạo hàm và đồng biến trên  thỏa mãn f (0) = 1 và ( 1 ′( ))2 x f x
= e f (x), x
∀ ∈  . Tính tích phân f (x)dx ∫ bằng 0
A. e − 2 .
B. e −1. C. 2 e − 2 . D. 2 e −1. Hươngd dẫn giải Chọn B ( f ′(x))2 f ′( x) f ′( x) 2 Biến đổi ( ′( )) x f x = e f (x) x ⇔ x x ( ) = e ⇔ = e ⇒ dx = e dx ∫ ∫ f x f ( x) f ( x) x ∫( x − ⇔
f ( x)) 12df ( x) 2 = e dx ∫ ⇔ f ( x) 2 2 = 2e + C x
Vì f (0) = 1 ⇒ C = 0 ⇒ f ( x) 2 = e ⇔ ( ) x f x = e 1 1 1 Suy ra ∫ ( ) x
f x dx = edx = e = e −1 ∫ 0 0 0 y = f x  \{ } 0 Câu 83: Cho hàm số
( ) xác định và liên tục trên thỏa mãn 2 2 2
x f ( x) + (2x − )
1 f ( x) = xf ′( x) −1 x ∀ ∈  \{ } 0 f ( ) 1 = 2 − với và . Tính f ( x) dx ∫ . 1 https://toanmath.com/ 1 3 ln 2 3 ln 2 A. − − ln 2. B. − − ln 2. C. 1 − − . D. − − . 2 2 2 2 2 Hươngd dẫn giải Chọn A 2 Ta có 2 2
x f ( x) + (2x − )
1 f ( x) = xf ′( x) −1 ⇔ ( xf ( x) + ) 1
= f (x) + xf ′(x)(*)
Đặt h(x) = f (x) + xf ′(x) ⇒ h′(x) = f (x) + xf ′(x) , khi đó (*) có dạng h′( x) h′( x) dh ( x) 1 2
h ( x) = h′( x) ⇒ =1 ⇒ dx = 1dx ∫ ∫ ⇒ = x + C ∫ ⇔ − = x + C 2 h ( x) 2 h ( x) 2 h ( x) h ( x) ⇒ ( ) 1 h x = − ⇒ xf ( x) 1 +1 = − x + C x + C 1 Vì f ( ) 1 = 2 − nên 2 − +1 = − ⇒ C = 0 1+ C Khi đó 1 1 xf ( x) 1
+1 = − ⇒ f (x) = − − x 2 x x 2 2  2 1 1   1  1 Suy ra: f
∫ (x)dx = − − dx ∫  = − ln x   = − − ln 2 2  x x   x  2 1 1 1
Câu 84: Cho hàm số y = f ( x) . Có đạo hàm liên tục trên  . Biết f ( ) 1 = e và
(x + ) f (x) = xf ′(x) 3 2 − x , x
∀ ∈  . Tính f (2) . A. 2 4e − 4e + 4 . B. 2 4e − 2e +1 . C. 3 2e − 2e + 2 . D. 2 4e + 4e − 4 . Hươngd dẫn giải Chọn D ′
xf ′( x) − ( x + 2) f ( x)
e−x f (x) Ta có: ( −
x + ) f ( x) = xf ′( x) 3 2 − x ⇔ =1 ⇔   = e x 3 x 2 x   ′
2  e−x f ( x) 2  Suy ra ∫ 
 dx = e−xdx ∫ 2 x 1   1 2 e− f (2) 1 e− f ( ) 1 2 − 1 ⇔ − = − e − e−   2 2   2 1 2 e− f (2) 1 e− f ( ) 1 1 − 2 e e− ⇔ − = − 4 1
⇔ f (2) = 4 ef ( ) 1 + e −1   2 = 4e + 4e − 4 .
Câu 85: Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 và thỏa mãn f (0) = 0 . Biết 1 9 1 π x 3π 1 2
f ( x) dx = ∫ và f ′( x) cos dx = ∫ . Tích phân f ( x) dx ∫ bằng 2 2 4 0 0 0 1 4 6 2 A. π . B. π . C. π . D. π . Hươngd dẫn giải Chọn C 1 1 π 1 x π x 1 π x π π x Ta có f ′
∫ (x)cos dx = cos d ∫
( f (x)) = cos .f (x) + sin .f ∫ (x)dx 2 2 2 2 2 0 0 0 0 1 π π x = sin .f ∫ (x)dx. 2 2 0 https://toanmath.com/ 1 π x 3 Suy ra sin
.f ( x) dx = ∫ 2 2 0 1 2 1  π x  1 1 Mặt khác sin dx = ∫
∫(1-cosπ x)dx =   .  2  2 2 0 0 1 1 1 2 Do đó π x  π x  2 f
∫ (x)dx−2 3sin f ∫ (x)dx + 3sin dx = 0 ∫  . 2  2  0 0 0 1 2  π x  π x hay f ∫ (x)−3sin dx = 0  
suy ra f ( x) = 3sin .  2  2 0 1 1 1 π x 6 π x 6
Vậy f ( x) dx = 3sin dx = − cos = ∫ ∫ . 2 π 2 π 0 0 0 1 1
Câu 86: Cho hàm số y = f ( x) liên tục trên đoạn [0; ] 1 , thỏa mãn f
∫ (x)dx = xf
∫ (x)dx =1 và 0 0 1 1  3 f
∫ (x) 2 dx = 4 
. Giá trị của tích phân  f ∫ (x) dx  bằng 0 0 A. 1. B. 8 . C. 10 . D. 80 . Hươngd dẫn giải Chọn C 1 1 1 1 2 2 2 Xét  f
∫ (x)+(ax+b) dx  =  f
∫ (x) dx+ 2  f
∫ (x).(ax+b)dx+ 
∫(ax+b) dx 0 0 0 0 1 1 1 = + a a xf
∫ (x) x+ b f ∫ (x) 1 4 2 d 2 dx +
(ax +b)3 = + (a +b) 2 2 4 2 + + ab + b . 3a 3 0 0 0 2 a
Cần xác định a, b để + ( + b) 2 2
a + b + 2b + 4 = 0 3 4 −(b − )2 2 Ta có: 2
∆ = b + 4b + 4 − ( 2 b + 2b + 4) =
≤ 0 ⇒ b = 2 ⇒ a = 6 − . 3 3 1 Khi đó:  f ∫ (x)+( 6 − x + 2) 2  dx = 0 
⇒ f ( x) = 6x − 2 0 1 1 1 3 3 1 4 Suy ra  f
∫ (x) dx = 
∫(6x−2) dx = (6x−2) =10. 24 0 0 0
Câu 87: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [1, 2] và thỏa mãn f ( x) > 0 khi x ∈[1, 2] . 2 2 f '( x) Biết f '
∫ (x)dx =10 và dx = ln 2 ∫ . Tính f (2) . f x 1 ( ) 1 A. f (2) = 10 − .
B. f (2) = 20 .
C. f (2) = 10 . D. f (2) = 20 − . Hươngd dẫn giải: 2 2 Ta có: f '
∫ (x)dx = f (x) = f (2)− f ( )1 =10 (gt) 1 1 2 f '( x) 2 f 2 =   =   −   = = ∫       (gt)
f ( x) dx ln f ( x) ln f (2) ln f ( ) ( ) 1 ln ln 2 1 f 1 1 ( ) https://toanmath.com/
f (2) − f ( ) 1 = 10   f  (2) = 20
Vậy ta có hệ:  f (2) ⇔  =   =  f  ( ) 2 f ( ) 1 10 1 Chọn B
Câu 88: Cho hàm số f ( x) có đạo hàm và liên tục trên đoạn [4;8] và f (0) ≠ 0 với x ∀ ∈[4;8]. Biết  f ′(x) 2 8    1 1 rằng = ∫
và f (4) = , f (8) = . Tính f (6) . f  ( x) dx 1 4  4 2 4  5 2 3 1 A. . B. . C. . D. . 8 3 8 3 Hươngd dẫn giải Chọn D 8 f ′( x) 8 df ( x) 1 8  1 1  +) Xét dx = = − = − ∫ ∫  −  = − 2 − 4 = 2 . 2 f ( x) 2 f x f x 4  f 8 f 4  4 4 ( ) ( )  ( ) ( ) ( )   f ′(x) 2 8 
+) Gọi k là một hằng số thực, ta sẽ tìm k để ∫
+ k dx = 0 . 2  f x  4  ( )   f ′(x) 2 8 8   f ′(x) 2 8  f ′   (x) 8 2 Ta có: 2 2 ∫ + k dx = dx + 2k dx + k
dx = 1+ 4k + 4k = 2k +1 ∫ ∫ ∫ . 2  f  (x)    f  ( x) 4 2  f x 4 4 4 ( ) ( ) 4  2 1
8  f ′( x) 1  f ′( x) 6 1 f ′( x) 6 1 Suy ra: k = − thì ∫ −  dx = 0 ⇔ = ⇔ dx = dx ∫ ∫ 2 2  f  (x) 2 2  f  (x) 2 2 f x 2 4 4 ( ) 4 6 df ( x) 1 6 1 1 1 1 ⇔ = 1 ⇔ − = 1 ⇔ − = 1 ⇔ 4 − = 1 ⇔ f 6 = ∫ . 2 f x f x 4 f 4 f 6 f 6 3 4 ( ) ( ) ( ) ( ) ( ) ( ) b b Chú ý: f
∫ (x)dx = 0 không được phép suy ra f (x) = 0, nhưng 2k f
∫ (x)dx = 0 ⇔ f (x) = 0 . a a
Câu 89: Cho hàm số f ( x) có đạo hàm xác định, liên tục trên đoạn [0; ]
1 đồng thời thỏa mãn các điề 2 u kiện f ′(0) = 1 − và  f ′
 ( x) = f ′′ 
(x). Đặt T = f ( )
1 − f (0) , hãy chọn khẳng định đúng? A. 2 − ≤ T < 1 − . B. 1
− ≤ T < 0 .
C. 0 ≤ T < 1.
D. 1 ≤ T < 2 . Hươngd dẫn giải Chọn A 1
Ta có: T = f ( )
1 − f (0) = f ′ ∫ (x)dx 0 ′ f ′′( x)   2 1 Lại có:  f ′
 ( x) = f ′′  (x) ⇔ 1 − = − ⇔ 1 − =    f ′(x) 2    f ′  ( x) 1 ⇔ −x + c = ⇔ ′( ) 1 f x = . f ′( x) −x + c Mà f ′(0) = 1 − nên c = 1 − . 1 1 1 Vậy T = f ′ ∫ (x)dx = dx ∫ 1 = − − − = −ln 2. − ln x 1 x −1 0 0 0 https://toanmath.com/
f (x) > 0,∀ x∈, 
Câu 90: Cho hàm số y = f ( x) có đạo hàm cấp 2 liên tục trên  thoả  f (0) = f ′(0) = 1, .  2 2
xy + y′ = yy , ′′ ∀ x ∈ .  
Mệnh đề nào sau đây đúng? 1 3 A. < ln f ( ) 1 < 1. B. < f ( ) 1 0 ln 1 < . C. < ln f ( ) 1 < 2 . D. < f ( ) 3 1 ln 1 < . 2 2 2 2 Hươngd dẫn giải Chọn D ′ 2 y y ′′ − y′  ′  2 y′ x f ′( x) 2 x Ta có 2 2
xy + y′ = yy′′ ⇔ = y x ⇔ = x   ⇔ = + C hay = + C . 2 yy y 2 f ( x) 2
Lại có f (0) = f ′(0) = 1 ⇒ C = 1. f ′( x) 2 1 1 x f ′( x) 2  x  7 Ta có = + ⇔ dx = ∫ ∫ +1 dx
⇔ ln ( f (x))1 = ⇔ f ( ) 7 ln 1 = . f ( x) 1 2 f x  2  0 6 6 0 ( ) 0 ⇒ < ( f ( )) 3 1 ln 1 < . 2 3
Câu 91: Cho f , g là hai hàm liên tục trên [1; ]
3 thỏa mãn điều kiện  f
∫ (x)+3g(x)dx =10  đồng 1 3 3 thời 2 f
∫ (x)− g(x)dx = 6  . Tính  f
∫ (x)+ g(x)dx  . 1 1 A. 9 . B. 6 . C. 7 . D. 8 . Hươngd dẫn giải Chọn B 3 3 3 Đặt a = f
∫ (x)dx, b = g
∫ (x)dx . Khi đó  f
∫ (x)+3g(x)dx =10 
⇔ a + 3b =10 , 1 1 1 3 2 f
∫ (x)− g(x)dx = 6 
⇔ 2a − b = 6 . 1  + =  = 3 Do đó: a 3b 10 a 4  ⇔  . Vậy  f
∫ (x)+ g(x)dx  = a + b = 6 . 2a − b = 6 b  = 2 1 d d
Câu 92: Cho hàm số y = f ( x) liên tục trên [a;b] , nếu f
∫ (x)dx = 5 và f
∫ (x)dx = 2 (với a b b
a < d < b ) thì f ( x) dx ∫ bằng. a 5 A. 3 . B. 7 . C. . D. 10 . 2 Hươngd dẫn giải Chọn A d   f ∫ (x)dx = 5  F
 (d ) − F (a) = 5 b a  ⇒ 
⇒ F (b) − F (a) = 3 = f ∫ (x)dx . d  F
 (d ) − F (b) = 2 f ∫ (x)dx = 2 a b
Câu 93: Cho f ( x) và g ( x) là hai hàm số liên tục trên đoạn [1; ] 3 , thỏa mãn: https://toanmath.com/ 3 3 3  f
∫ (x)+3g(x)dx =10  và 2 f
∫ (x)− g(x)dx = 6 
. Tính I =  f
∫ (x)+ g(x)dx 1 1 1
A. I = 8 .
B. I = 9 .
C. I = 6 . D. I = 7 . Hươngd dẫn giải Chọn C 3  3    f
∫ (x)+3g(x)dx =10   f ∫ (x)dx = 4   3 Ta có: 1  1 ⇒  ⇒ I =  f
∫ (x)+ g(x)dx = 6  . 3  3   2 f 1 ∫ 
(x)− g (x)dx = 6  g ∫ (x)dx = 2   1 1
Câu 94: Cho hàm số y = f ( x) có đạo hàm f ′( x) liên tục trên đoạn [0;5] và đồ thị hàm số
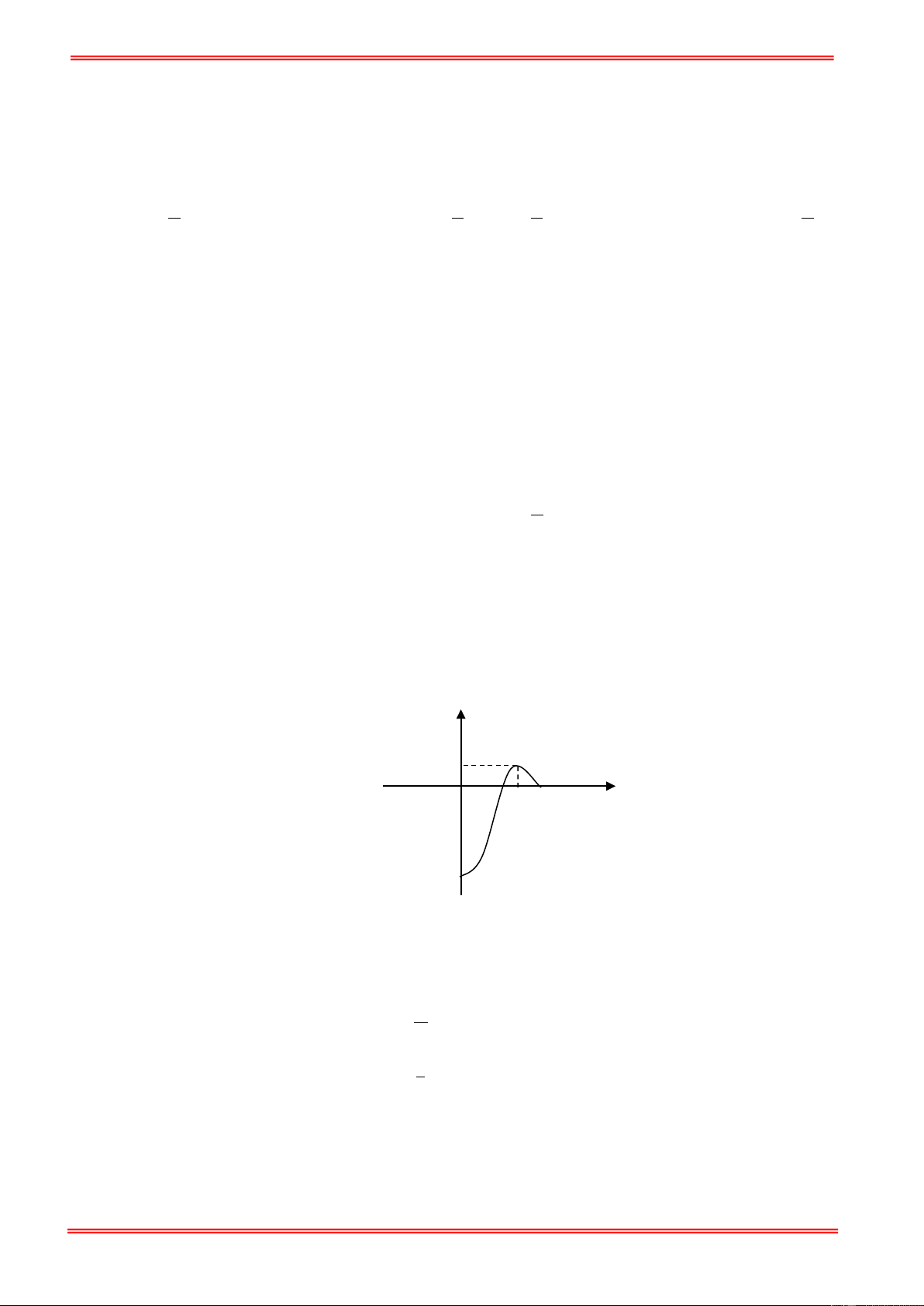
y = f ′( x) trên đoạn [0;5] được cho như hình bên. y 1 O 3 5 x 5 − Tìm mệnh đề đúng
A. f (0) = f (5) < f (3) .
B. f (3) < f (0) = f (5) .
C. f (3) < f (0) < f (5) .
D. f (3) < f (5) < f (0) . Hươngd dẫn giải Chọn C 5 Ta có f ′
∫ (x)dx = f (5)− f (3) > 0, do đó f (5) > f (3) . 3 3 f ′
∫ (x)dx = f (3)− f (0) < 0, do đó f (3) < f (0) 0 5 f ′
∫ (x)dx = f (5)− f (0) < 0, do đó f (5) < f (0) 0
Câu 95: Cho hàm số f ( x) liên tục và có đạo hàm tại mọi x ∈(0; +∞) đồng thời thỏa mãn điều kiện: 3π 2
f ( x) = x (sin x + f '( x)) + cos x và f ( x)sin d x x = 4. − ∫
Khi đó, f (π ) nằm trong khoảng π 2 nào? A. (6;7) . B. (5;6) . C. (12;13) . D. (11;12) . Hươngd dẫn giải Chọn B Ta có:
f ( x) = x (sin x + f ′( x)) + cos x ′ ′
f ( x) − xf ′( x) sin x cos x
f (x)   1  f ( x) ⇒ = + 1 ⇒   = cos x ⇒ = cos x + c   2 2 x x x x    xx x https://toanmath.com/
⇒ f ( x) = cos x + cx Khi đó: 3π 3π 2 2 f ( x)sin d x x = 4 − ∫
⇔ (cos x + cx)sin d x x = 4 − ∫ π π 2 2 3π 3π 2 2 ⇔ cos xsin d x x + c x sin d x x = 4 − ∫ ∫ ⇔ 0 + c ( 2 − ) = 4 − ⇔ c = 2 π π 2 2
⇒ f ( x) = cos x + 2x ⇒ f (π ) = 2π −1∈(5;6) .  π 
Câu 96: Cho hàm số f ( x) xác định trên 0;   thỏa mãn  2  π π 2   π  2 − π 2 2 f
∫  (x)−2 2 f (x)sin x− d x =   . Tích phân f
∫ (x)d x bằng   4  2 0 0 π π A. . B. 0 . C. 1. D. . 4 2 Hươngd dẫn giải Chọn B π π π 2  π  2   π  2 Ta có: 2 2 sin x − d x ∫   = 1− cos 2x − d x ∫   
= ∫(1−sin 2x)d x   4    2  0 0 0 π 2  1  π − = 2 x + cos 2x   = .  2  2 0 π π 2   π 2  π Do đó:   −π π − 2 f
∫  (x)−2 2 f (x)sin x− d x   2 + 2sin x − d x ∫ 2 2   = + = 0   4   4  2 2 0 0 π 2   π   π  2 ⇔ f
∫  (x)−2 2 f (x) 2 sin x − + 2sin x − d x = 0       4   4  0 π 2 2   π  ⇔ f
∫  (x)− 2sin x− d x = 0     4  0  π   π 
Suy ra f ( x) − 2 sin x − = 0  
, hay f ( x) = 2 sin x −   .  4   4  π π π 2 2  π   π  Bởi vậy: f
∫ (x)d x = 2sin x− d x ∫ 2   = − 2 cos x − = 0   .  4   4  0 0 0 Câu 97: Cho hàm số − +
y = f (x) liên tục trên  thỏa mãn f ( x) + f ( − x) = ( x − ) 2x 2x 1 3 2 2 1 e + 4 . Tính 2 tích phân I = f
∫ (x)dx ta được kết quả: 0
A. I = e + 4 .
B. I = 8 .
C. I = 2 . D. I = e + 2 .
Đề ban đầu bị sai vì khi thay x = 0 và x = 2 vào ta thấy mâu thuẫn nên tôi đã sửa lại đề Hươngd dẫn giải Chọn C https://toanmath.com/ 2 2 2
Theo giả thuyết ta có 3 f
∫ (x)+ f (2− x)dx = 2 
∫ (x− ) x −2x 1 1 e +  + 4 dx (*)   . 0 0 2 2 2 Ta tính f
∫ (2− x)dx = − f
∫ (2− x)d(2− x) = f ∫ (x)dx . 0 0 0 2 2 Vì vậy 3 f
∫ (x)+ f (2− x)dx = 4 f  ∫ (x)dx. 0 0 2 2 2 Hơn nữ 2 2 2 2 a 2
∫ (x ) x −2x 1+ x −2 x 1 1 e dx e + d ∫
( 2x 2x ) x −2x 1 1 e + − = − + = = 0 và 4dx = 8 ∫ . 0 0 0 0 2 2
Câu 98: Suy ra 4 f
∫ (x)dx = 8 ⇔ f
∫ (x)dx = 2. Cho hàm số y = f (x) liên tục trên  \{0; − }1 thỏa 0 0
mãn điều kiện f ( ) 1 = 2
− ln 2 và x(x + ) f ′(x) + f (x) 2 1 .
= x + x . Giá trị f (2) = a + bln 3 ,
với a,b ∈  . Tính 2 2 a + b . 25 9 5 13 A. . B. . C. . D. . 4 2 2 4 Hươngd dẫn giải Chọn B x 1 x
Từ giả thiết, ta có x ( x + ) f ′( x) + f ( x) 2 1 . = x + x ⇔ . f ′( x) + f x = 2 ( ) x +1 (x + )1 x +1 ′  xx ⇔ . f ( x) =   , với x ∀ ∈  \{0; − } 1 .  x +1  x +1 x x x Suy ra . f ( x) = dx ∫ hay
. f ( x) = x − x + + C . x +1 x +1 x + ln 1 1 x
Mặt khác, ta có f ( ) 1 = 2 − ln 2 nên C = 1 − . Do đó
. f ( x) = x − x + − . x + ln 1 1 1 2 3 3
Với x = 2 thì . f (2) = 1− ln 3 ⇔ f ( ) 3 3 2 =
− ln 3 . Suy ra a = và b = − . 3 2 2 2 2 9 Vậy 2 2 a + b = . 2 2
Câu 99: Cho hàm số y = f ( x) có đạo hàm trên  và f ′( x) 4 ≥ x + − 2x x ∀ > 0 và f ( ) 1 = 1 − . 2 x
Khẳng định nào sau đây đúng?
A. Phương trình f ( x) = 0 có 1 nghiệm trên (0; ) 1 .
B. Phương trình f ( x) = 0 có đúng 3 nghiệm trên (0; +∞) .
C. Phương trình f ( x) = 0 có 1 nghiệm trên (1; 2) .
C. Phương trình f ( x) = 0 có 1 nghiệm trên (2;5) . Hươngd dẫn giải Chọn C 6 3 x − 2x + 2 (x − )2 3 1 +1 f ′( x) 2 4 ≥ x + − 2x = = > 0 , x ∀ > 0 . 2 x 2 x 2 x
⇒ y = f (x) đồng biến trên (0;+∞).
⇒ f (x) = 0 có nhiều nhất 1 nghiệm trên khoảng (0;+∞) ( ) 1 . Mặt khác ta có: https://toanmath.com/ 2 2  2  21 f ′( x) 2 4 ≥ x +
− 2x > 0 , x ∀ > 0 ⇒ f ′ ∫ (x) 4 dx ≥ x + − 2x dx = ∫  2 x 2  x  5 1 1
⇒ f ( ) − f ( ) 21 2 1 ≥ ⇒ f ( ) 17 2 ≥ . 5 5
Kết hợp giả thiết ta có y = f ( x) liên tục trên [1; 2] và f (2). f ( ) 1 < 0 (2) . Từ ( )
1 và (2) suy ra phương trình f ( x) = 0 có đúng 1 nghiệm trên khoảng (1; 2).
Câu 100: Cho hàm số f ( x) có đạo hàm f ′( x) liên tục trên  và thỏa mãn f ′( x) ∈[ 1 − ; ] 1 với 2 x
∀ ∈(0;2) . Biết f (0) = f (2) =1. Đặt I = f
∫ (x)dx , phát biểu nào dưới đây đúng? 0 A. I ∈ ( ; −∞ 0]. B. I ∈ (0; ] 1 .
C. I ∈[1; +∞) . D. I ∈ (0; ) 1 . Hươngd dẫn giải Chọn C 2 1 2 Ta có I = f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx. 0 0 1 1 1 1 1  1 1
f ( x) dx = ( x − )
1 f ( x) − ( x − )
1 f ′( x) dx = 1+ (1− x) f ′( x) dx ≥ 1− (1− x) dx = ∫ ∫ ∫ ∫ ( )1 . 0 2 0 0 0 0 2 2 2 2  2 1
f ( x) dx = ( x − )
1 f ( x) − ( x − )
1 f ′( x) dx = 1− ( x − ∫ ∫ ∫ )
1 f ′( x) dx ≥ 1− (1− x) dx = ∫ (2) . 1 2 1 1 1 1 1 1 Từ ( ) 1 và (2) suy ra I ≥ + =1. 2 2 1
Câu 101: Cho hàm số y = f ( x) liên tục trên [0; ] 1 thỏa mãn xf
∫ (x)dx = 0 và max f (x) =1. Tích [0; 1] 0 1 phân = ex I f
∫ (x)dx thuộc khoảng nào trong các khoảng sau đây? 0  5   3   5 3  A. ; −∞ − .   B. ; e −1 .   C. − ; .   D. (e −1; + ∞).  4   2   4 2  Hươngd dẫn giải Chọn C 1 1 1 Với mọi a ∈[0; ] 1 , ta có 0 = xf
∫ (x)dx = a xf
∫ (x)dx = axf ∫ (x)dx 0 0 0 1 Kí hiệu ( ) = ∫(ex I a − ax)dx . 0 1 1 1 1
Khi đó, với mọi a ∈[0; ] 1 ta có
ex f ( x) dx ∫ = ex f
∫ (x)dx− axf
∫ (x)dx = ∫(ex −ax) f (x)dx 0 0 0 0 1 1 1
≤ ex − ax . f ∫
(x) dx ≤ ex − ax .max f ∫
(x) dx = ex − ax dx = I ∫ (a). x [ ∈ 0 ] ;1 0 0 0 1 Suy ra ex f
∫ (x)dx ≤ min I (a) a [ ∈ 0 ] ;1 0 Mặt khác 1 1 1  aa Với mọi a ∈[0; ] 1 ta có ( ) = ex − d = ∫ ∫(ex I a ax x − ax)dx x 2 = e − x   = e − −1  2  2 0 0 0 https://toanmath.com/ 1 x 3 I (a) 3 min = e − ⇒ e f
∫ (x)dx ≤ e− ≈1,22. a [ ∈ 0 ] ;1 2 2 0  5 3  Vậy I ∈ − ;   .  4 2 
Câu 102: Cho hàm số f ( x) có đạo hàm dương, liên tục trên đoạn [0; ]
1 thỏa mãn f (0) = 1 và 1 1   1 3 f ′ ∫ (x) f   ( x) 2 1 3  + dx ≤ 2 f ′  ∫
(x) f (x)dx
. Tính tích phân  f
∫ (x) dx:   9  0 0 0 3 5 5 7 A. . B. . C. . D. . 2 4 6 6 Hươngd dẫn giải Chọn D Từ giả thiết suy ra: 1  1 ∫ 2 ⇔  ′ −  ( 
3 f ′( x) f ( x))2 − 2.3 f ′(x) f (x) +1 dx ≤ 0  3 f ∫
(x) f (x) 1 dx ≤ 0.     0 0 1
Suy ra 3 f ′( x) f ( x) −1 = 0 ⇔
f ′( x) f ( x) 1 = ⇔ f ′(x) 2 . f ( x) = . 3 9 ′ ′ 1 1 Vì 3  f (x) 2
 = 3. f (x) f ′(x)   nên suy ra 3  f (x) =   3
⇒ f (x) = x + C . 3 3 Vì f (0) = 1 nên 3
f (0) = 1 ⇒ C = 1. 1 Vậy 3
⇒ f (x) = x +1. 3 1 1 3  1  7 Suy ra  f ∫ (x) dx  = x +1 dx = ∫  .  3  6 0 0
Câu 103: Cho hai hàm số f ( x) và g ( x) có đạo hàm trên đoạn [1; 4] và thỏa mãn hệ thức  f  ( ) 1 + g ( ) 1 = 4 4 
. Tính I =  f
∫ (x)+ g(x)dx  . g  ( x) = − . x f ′( x); f ( x) = − . x g′( x) 1 A. 8 ln 2 . B. 3ln 2 . C. 6 ln 2 . D. 4 ln 2 . Hươngd dẫn giải Chọn A
f ( x) + g ( x) 1
Cách 1: Ta có f ( x) + g ( x) = −x f ′( x) + g′( x)   ⇔ = −
f ′( x) + g′( x) x
f ( x) + g ( x) 1 ⇔ ∫ ⇒ + = − + ′( ) ∫
ln f ( x) g ( x) + ′( ) dx = − dx ln x C f x g x x
Theo giả thiết ta có C − ln 1 = ln f ( ) 1 + g ( ) 1 ⇒ C = ln 4 .
f (x)+ g(x) 4 =  x Suy ra  , vì f ( ) 1 + g ( ) 1 = 4 nên ( )+ ( ) 4 f x g x =  x
f ( x) + g ( x) 4 = −  x 4 ⇒ I =  f
∫ (x)+ g(x)dx = 8ln2  . 1
Cách 2: Ta có f ( x) + g ( x) = −x f ′( x) + g′( x)   ⇒  f
∫ (x)+ g(x)dx = − xf ′ 
∫  (x)+ g′(x)dx  . https://toanmath.com/ ⇒  f
∫ (x)+ g(x)dx = −xf
 ( x) + g ( x) +  f
 ∫  (x) + g (x) dx  .
⇒ −  ( ) + ( ) = ⇒  ( )+ ( ) C x f x g x C f x g x = − . Vì f ( ) 1 + g ( ) 1 = C − ⇒ C = 4 − x 4 Do đó ( ) + ( ) 4 f x g x =
. Vậy I =  f
∫ (x)+ g(x)dx = 8ln2  . x 1 https://toanmath.com/
DẠNG 3: PHƯƠNG PHÁP ĐỔI BIẾN BÀI TẬP
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 1 4 2 Câu 104: Cho f
∫ (x)dx =16 . Tính f (2x)dx ∫ 0 0 A. 16 . B. 4 . C. 32 . D. 8 . 6 2
Câu 105: Nếu f
∫ (x)dx =12 thì f (3x)dx ∫ bằng 0 0 A. 6 . B. 36 . C. 2 . D. 4 . 2 5 Câu 106: Cho f ∫ ( 2x + )1 d
x x = 2 . Khi đó I = f
∫ (x)dx bằng: 1 2 A. 2 . B. 1. C. 1 − . D. 4 . 1
Câu 107: Cho hàm số f ( x) liên tục trên  và thỏa mãn f
∫ (x)dx = 9 . Tính tích phân 5 − 2  f
∫ (1−3x)+9dx  . 0 A. 27 . B. 21 . C. 15 . D. 75 . 9 4
Câu 108: Biết f ( x) làm hàm liên tục trên  và f
∫ (x)dx = 9 . Khi đó giá trị của f
∫ (3x −3)dx là 0 1 A. 27 . B. 3 . C. 0 . D. 24 . 1 2  x
Câu 109: Cho hàm số f ( x) liên tục trên  thỏa f
∫ (x)dx =10 . Tính f dx ∫   .  2  0 0 2  x  5 2  x  2  x  2  x A. f dx = ∫   . B. f dx = 20 ∫   . C. f dx = 10 ∫   . D. f dx = 5 ∫   .  2  2  2   2   2  0 0 0 0 5 2 f ∫ (x)dx = 4 I = f (2x + ∫ )1dx Câu 110: Cho 1 − . Tính 1 − . 5 3
A. I = 2 . B. I = .
C. I = 4 . D. I = . 2 2 5
Câu 111: Giả sử hàm số y = f ( x) liên tục trên  và f
∫ (x)dx = a, (a∈) . Tích phân 3 2 I = f (2x + ∫
)1dx có giá trị là 1 1 1 A. I = a +1 .
B. I = 2a +1 .
C. I = 2a . D. I = a . 2 2 2 5 Câu 112: Cho f ∫ ( 2x + )1 d
x x = 2 . Khi đó I = f
∫ (x)dx bằng 1 2 A. 2 . B. 1. C. 1 − . D. 4 . 3 2
Câu 113: Cho hàm số f ( x) liên tục trên [1; +∞) và f
∫ ( x +1)dx = 8. Tích phân I = xf ∫ (x)dx 0 1 bằng: A. I = 16 .
B. I = 2 .
C. I = 8 . D. I = 4 11 2 Câu 114: Biết f
∫ (x)dx =18. Tính I = x(2+ f ( 2 3x − ∫ )1)dx. 1 − 0 https://toanmath.com/
A. I = 5 .
B. I = 7 .
C. I = 8 D. I = 10 . 1 2
Câu 115: Cho hàm số y = f ( x) liên tục trên  và f
∫ (2x)dx = 8. Tính I = xf
∫ ( 2x)dx 0 0 A. 4 . B. 16 . C. 8 . D. 32 . 1 3
Câu 116: Cho hàm số f ( x) liên tục trên và có f
∫ (x)dx = 2; f
∫ (x)dx = 6 . Tính 0 0 1 I = f
∫ ( 2x−1)dx . 1 − 2 3 A. I = .
B. I = 4 . C. I = . D. I = 6 . 3 2 2 4
Câu 117: Cho hàm số y = f ( x) liên tục trên [0; 4] và f
∫ (x)dx =1; f
∫ (x)dx = 3. Tính 0 ; 0 1 f
∫ ( 3x−1)dx . 1 − 4 A. 4 . B. 2 . C. . D. 1. 3 1 3
Câu 118: Cho f ( x) là hàm số liên tục trên  và f
∫ (x)d x = 4, f
∫ (x)d x = 6. Tính 0 0 1 I = f
∫ ( 2x+1)d x. 1 −
A. I = 3 .
B. I = 5 .
C. I = 6 . D. I = 4 . 1 2
Câu 119: Cho hàm số f ( x) liên tục trên  thỏa f
∫ (2x)dx = 2 và f
∫ (6x)dx =14 . Tính 0 0 2 f
∫ (5 x + 2)dx . 2 − A. 30 . B. 32 . C. 34 . D. 36 . π π 2 2
Câu 120: Cho tích phân I = cos . x f ∫
(sin x)dx = 8. Tính tích phân K = sin .x f ∫
(cos x)dx . 0 0 A. K = 8 − .
B. K = 4 .
C. K = 8 . D. K = 16 . 1
Câu 121: Cho hàm số
y = f ( x) liên tục trên R, thỏa mãn f
∫ (x)dx =1. Tính 0 π 4 I = ( 2 tan + ∫
)1.f (tan x)dx . 0 π π
A. I = 1. B. I = 1 − . C. I = . D. I = − . 4 4 1
Câu 122: Cho hàm số f ( x) liên tục trên  thỏa mãn f (2x) = 3 f ( x) , x
∀ ∈ . Biết rằng f ∫ (x)dx =1 0 2
. Giá trị của tích phân I = f
∫ (x)dx bằng bao nhiêu? 1
A. I = 5 .
B. I = 3 .
C. I = 8 . D. I = 2 . https://toanmath.com/ 2
Câu 123: Cho hàm số y = f ( x) liên tục và có đạo hàm trên  thỏa mãn f (2) = 2 − ; f
∫ (x)dx =1. Tính 0 4 tích phân I = f ′
∫ ( x)dx. 0 A. I = 10 − . B. I = 5 − .
C. I = 0 . D. I = 18 − . 2 4 f ( x ) f ∫ (x)dx = 2 I = dx ∫ Câu 124: Cho x 1 . Tính 1 bằng 1
A. I = 1.
B. I = 2 .
C. I = 4 . D. I = . 2 π 16 f ( x ) 2
Câu 125: Cho hàm số f ( x) liên tục trên  thỏa mãn dx = 6 ∫ và f ∫ (sin x)cos d x x = 3 . Tính x 1 0 4 tích phân I = f ∫ (x)dx . 0 A. I = 2 − . B. I = 6 .
C. I = 9 . D. I = 2 . π 9 f ( x ) 2
Câu 126: Cho f ( x) liên tục trên  thỏa dx = 4 ∫ và f ∫ (sin x)cos d x x = 2 . Tính x 1 0 3 I = f
∫ (x)dx . 0
A. I = 10 .
B. I = 6 .
C. I = 4 . D. I = 2 . f (2 x − ) 1 ln x
Câu 127: Cho hàm số f ( x) liên tục trên đoạn [1;4] và thỏa mãn f ( x) = + . Tính tích x x 4 phân I = f
∫ (x)dx . 3 A. 2
I = 3 + 2 ln 2 . B. 2 I = 2 ln 2 . C. 2 I = ln 2 . D. I = 2 ln 2 . 5 2
Câu 128: Cho hàm số f ( x) liên tục trên [ 4; − + ∞) và f
∫ ( x + 4)dx = 8. Tính I = .xf
∫ (x)dx. 0 3
A. I = 8 .
B. I = 4 . C. I = 16 − . D. I = 4 − . π 1 2 3 Câu 129: Cho f
∫ (2x+ )1dx =12 và f ∫ ( 2 sin x)sin 2 d
x x = 3 . Tính f
∫ (x)dx . 0 0 0 A. 26 . B. 22 . C. 27 . D. 15 . π 4 1 2 x f ( x)
Câu 130: Cho hàm f ( x) liên tục trên  thỏa mãn f
∫ (tan x)dx = 3 và dx = 1 ∫ . Tính 2 x +1 0 0 1 f ( x) dx ∫ . 0 A. 4 . B. 2 . C. 5 . D. 1. π 4 1 2 x f x 1
Câu 131: Cho hàm số f ( x) liên tục trên R và f ∫ (tan x) ( ) dx = 4; dx = 2 ∫ . Tính I = f
∫ (x)dx . 2 x +1 0 0 0
A. I = 6 .
B. I = 2 .
C. I = 3 . D. I = 1. https://toanmath.com/ 2018
Câu 132: Cho hàm số f ( x) liên tục trên  thỏa f
∫ (x)dx = 2 . Khi đó tích phân 0 2018 e 1 − x f ∫
(ln( 2x +1 dx bằng 2 ) x +1 0 A. 4 . B. 1. C. 2 . D. 3 . 3 m 10 
Câu 133: Tìm tất cả các giá trị dương của m để x
∫ (3− x) dx = − f ′′ , với f (x) 15 = ln x .  9  0
A. m = 20 .
B. m = 4 .
C. m = 5 . D. m = 3 . 3
Câu 134: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn f (4 − x) = f ( x) . Biết xf ∫ (x)dx = 5. 1 3 Tính I = f
∫ (x)dx. 1 5 7 9 11 A. I = . B. I = . C. I = . D. I = . 2 2 2 2
Câu 135: Cho hàm số y = f ( x) liên tục trên đoạn [1; ]
3 thỏa mãn f (4 − x) = f ( x), x ∀ ∈[1; ] 3 và 3 3
xf ( x) dx = 2 − ∫
. Giá trị f ( x) dx ∫ bằng 1 1 A. 2 . B. 1 − . C. 2 − . D. 1.
Câu 136: Cho hàm số f liên tục trên đoạn [ 6;
− 5] , có đồ thị gồm hai đoạn thẳng và nửa đường tròn 5
như hình vẽ. Tính giá trị I =  f
∫  (x)+ 2dx  . 6 − y 3 6 − 4 − O x 5 1 −
A. I = 2π + 35 .
B. I = 2π + 34 .
C. I = 2π + 33 .
D. I = 2π + 32 .
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 2
Cho hàm số f ( x) thỏa mãn : . A f ( x) + .
B u .′ f (u) + C. f (a + b − x) = g ( x) u  (a) =a b 1 b +) Với  thì f ∫ (x)dx = g ∫ (x)dx. u  (b)=b A + B + C a a u  (a) =b b 1 b +) Với  thì f ∫ (x)dx = g ∫ (x)dx. u  (b)=a
A − B + C a a
Trong đề bài thường sẽ bị khuyết một trong các hệ số , A B, C . f ( x) [ ;ab] b b Nếu liên tục trên thì f
∫ (a +b− x)dx = f ∫ (x)dx. a a 6 1 2 3
Câu 137: Cho hàm số f ( x) liên tục trên [0; ]
1 thỏa mãn f ( x) = 6x f ( x ) − f x dx ∫ 3x + . Tính ( ) 1 0 A. 2 . B. 4 . C. 1 − . D. 6 . https://toanmath.com/
Câu 138: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn điều kiện xf ( 2
x ) + f ( x − ) 2 4 3 1 = 1− x . 1 Tích phân I = f
∫ (x)dx bằng 0 π π π π A. I = . B. I = . C. I = . D. I = 4 6 20 16
Câu 139: Cho hàm số f (x) liên tục trên [0; 2] và thỏa mãn điều kiện f ( x) + f (2 − x) = 2x . Tính giá 2
trị của tích phân I = f
∫ (x)dx . 0 1 4 A. I = 4 − . B. I = . C. I = .
D. I = 2 . 2 3
Câu 140: Xét hàm số f ( x) liên tục trên đoạn [0; ]
1 và thỏa mãn 2 f ( x) + 3 f (1− x) = 1− x . Tích phân 1 f ( x) dx ∫ bằng 0 2 1 2 3 A. . B. . C. . D. . 3 6 15 5
Câu 141: Xét hàm số f ( x) liên tục trên đoạn [0; ]
1 và thỏa mãn điều kiện 2 f ( x) − 3 f (1− x) = x 1− x 1 . Tính tích phân I = f
∫ (x)dx . 0 1 4 1 4 A. I = . B. I = − . C. I = − . D. I = . 25 15 15 75
Câu 142: Xét hàm số f ( x) liên tục trên[ 1
− ;2] và thỏa mãn f (x) + xf ( 2x − )+ f ( − x) 3 2 2 3 1 = 4x . 2
Tính giá trị của tích phân I = f
∫ (x)dx . 1 − 5
A. I = 5 . B. I = .
C. I = 3 . D. I = 15 . 2
Câu 143: Hàm số f ( x) liên tục trên [ 1
− ;2] và thỏa mãn điều kiện f (x) = x + + xf ( 2 2 3 − x ). Tính 2 giá trị của I = f
∫ (x)dx 1 − 14 28 4 A. I = . B. I = . C. I = .
D. I = 2 . 3 3 3 1
Câu 144: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn f ( x) + xf ( 2
1− x ) + 3 f (1− x) = . Tính x +1 1
giá trị của tích phân I = f
∫ (x)dx . 0 9 2 4 3 A. I = ln 2 . B. I = ln 2 . C. I = . D. I = . 2 9 3 2 x
Câu 145: Cho hàm số y = f ( x) và thỏa mãn f ( x) − 8x f ( x ) 3 3 4 + = 0 . Tích phân 2 x +1 1 − a b I = f ( x) a b 2 dx = ∫
với a,b, c ∈  và ; tối giản. Tính a + b + c c c c 0 A. 6 . B. 4 − . C. 4 . D. 10 − . https://toanmath.com/
Câu 146: Cho hàm số f ( x) liên tục trên đoạn [− ln 2;ln 2] và thõa mãn f ( x) + f (−x) 1 = . Biết x e +1 ln 2 f
∫ (x)dx = aln2+bln3, với a,b∈. Tính giá trị của P = a +b . −ln 2 1 A. P = . B. P = 2 − . C. P = 1 − . D. P = 2 . 2  π   π π 
Câu 147: Biết hàm số y = f x + 
 là hàm số chẵn trên đoạn − ; và    2   2 2  π  π  2
f ( x) + f x + = sin x + cos x   . Tính I = f ∫ (x) . dx 2  0 1
A. I = 0 .
B. I = 1. C. I = . D. I = 1 − . 2  π 
Câu 148: Cho hàm số y = f ( x) có đạo hàm liên tục trên  , f (0) = 0 và f ( x) + f
− x = sin x.cos x  2    π với x
∀ ∈ . Giá trị của tích phân 2 xf ′ ∫
(x)dx bằng 0 π 1 π 1 A. − . B. . C. . D. − . 4 4 4 4 x
Câu 149: Cho hàm số f ( x ) liên tục trên  và thỏa mãn f (1+ 2x) + f (1− 2x) 2 = , x ∀ ∈  . tính tích 2 x + 1 3 phân I = f
∫ (x)dx . 1 − π π 1 π π A. I = 2 − . B. I = 1 − . C. I = − . D. I = . 2 4 2 8 4
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 3
Cách giải: Lần lượt đặt t = u( x) và t = v( x) để giải hệ phương trình hai ẩn (trong đó có ẩn f ( x ) ) để
suy ra hàm số f ( x ) (nếu u( x ) = x thì chỉ cần đặt một lần t = v( x) ).
Các kết quả đặc biệt:  x − b   x − c  . A g − .   B ga    a  −  Cho .
A f (ax + b) + .
B f (−ax + c) = g(x) với 2 2
A ≠ B ) khi đó f (x) = (*) 2 2 A − B . A g x − . B g −x +)Hệ quả 1 của (*): . A f ( x) + .
B f (−x) = g ( x) ⇒ f ( x) ( ) ( ) = 2 2 A − B g x
+)Hệ quả 2 của (*): A f ( x) + B f (−x) = g ( x) ⇒ f ( x) ( ) . . =
với g ( x) là hàm số chẵn. A + B   2 f ( x)
Câu 150: Cho hàm số y = f ( x) liên tục trên  và f ( x) 1 + 2 f = 3x   . Tính I = ∫ dx . x  1 x 2 3 1 A. I = .
B. I = 1. C. I = . D. I = 1 − . 2 2   x
Câu 151: Cho hàm số y = f ( x) liên tục trên  \ { }
0 và thỏa mãn f ( x) 2 15 2 3 + 3 f = −   ,  x  2 3 9 2  1  f
∫ (x)dx = k . Tính I = f dx ∫    theo k . x  3 1 2 45 + k 45 − k 45 + k 45 − 2k A. I = − . B. I = . C. I = . D. I = . 9 9 9 9 https://toanmath.com/
Câu 152: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn f (−x) + 2018 f ( x) = 2x sin x . Tính giá π 2 trị của I = f ∫ (x)dx. π − 2 2 2 4 1 A. I = . B. I = . C. I = . D. I = . 2019 1009 2019 1009
Câu 153: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn (− ) + 2018 ( ) x f x
f x = e . Tính giá trị của 1 I = f
∫ (x)dx 1 − 2 e −1 2 e −1 2 e −1 A. I = . B. I = .
C. I = 0 . D. I = . 2019e 2018e e
Câu 154: Cho hàm số y = f ( x) có đạo hàm liên tục trên  , thỏa mãn f ( x) + f ( − x) 2 2 2 1 =12x .
Phương trình tiếp tuyến của đồ thị hàm số y = f ( x) tại điểm có hoành độ bằng 1 là
A. y = 2x + 2 .
B. y = 4x − 6 .
C. y = 2x − 6 .
D. y = 4x − 2 . 1
Câu 155: Cho f ( x) là hàm số chẵn, liên tục trên  thỏa mãn ∫ f (x)dx = 2018 và g (x) là hàm số 0 1
liên tục trên  thỏa mãn g ( x) + g (−x) = 1, ∀x ∈  . Tính tích phân I = ∫ f (x)g (x)dx . 1 − 1009
A. I = 2018 . B. I = .
C. I = 4036 . D. I = 1008 . 2
Câu 156: Cho số dương a và hàm số f ( x) liên tục trên  thỏa mãn f ( x) + f (−x) = a , x ∀ ∈ . Giá a
trị của biểu thức f
∫ (x)dx bằng −a A. 2 2a . B. a . C. 2 a . D. 2a . π 2
Câu 157: Cho hàm số f ( x) liên tục trên  thỏa điều kiện f ( x) + f (−x) = 2sin x . Tính f
∫ (x)dx π − 2 A. 1 − . B. 0 . C. 1. D. 2 .
Câu 158: Cho f (x) là một hàm số liên tục trên  thỏa mãn f ( x) + f (−x) = 2 − 2cos 2x . Tính tích 3π 2 phân I = f
∫ (x)dx. 3π − 2
A. I = 3 .
B. I = 4 .
C. I = 6 .
D. I = 8 .
Câu 159: Cho hàm số y = f ( x) liên tục trên R và thỏa mãn f ( x) + f (−x) = 2 + 2 cos 2x . Tính π 2 I = f
∫ (x)dx . π − 2 A. I = 1 − .
B. I = 1. C. I = 2 − . D. I = 2 . https://toanmath.com/ π 4
Câu 160: Cho hàm số f ( x) liên tục trên  và f (−x) − f ( x) 2 3 2
= tan x . Tính f
∫ (x)dx π − 4 π A. 1− π . B. − π 1 . C. 1+ π . D. 2 − . 2 2 4 2
Câu 161: Cho hàm số f ( x) liên tục trên đoạn [− ln 2;ln 2] và thỏa mãn f ( x) + f (−x) 1 = . x e +1 ln 2 Biết f
∫ (x)dx = aln2+bln3 (a;b∈). Tính P = a +b . −ln 2 1 A. P = . B. P = 2 − . C. P = 1 − . D. P = 2 . 2
Câu 162: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn điều kiện 2 f ( x) + 3 f (1− x) = x 1− x . Tính 1
tích phân I = ∫ f (x)dx . 0 4 1 4 1 A. I = − . B. I = . C. I = . D. I = . 15 15 75 25
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 4
Câu 163: Cho f ( x) và g ( x) là hai hàm số liên tục trên [ 1,
− ]1 và f (x) là hàm số chẵn, g (x) là hàm 1 1 số lẻ. Biết f
∫ (x)dx = 5 và g
∫ (x)dx = 7. Mệnh đề nào dưới đây sai? 0 0 1 1 A. f
∫ (x)dx =10. B. g
∫ (x)dx =14. 1 − 1 − 1 1 C. f
∫  (x)+ g(x)dx =10  . D. f
∫  (x)− g(x)dx =10  . 1 − 1 − a a a
Câu 164: Nếu hàm f ( x) CHẴN thì f
∫ (x)dx = 2 f
∫ (x)dx 2. Nếu hàm f (x) LẺ thì f ∫ (x)dx = 0 −a 0 −a
Nếu chứng minh thì như sau: 1 0 1 Đặt A = f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx 1 − 1 − 0
  1 A 2 A 0 A = f x dx ∫
. Đặt t = −x ⇒ dt = −dx 1 ( ) 1 − Đổi cận: 0 1 1 ⇒ A = f t − . −dt = f t
− dt = f −x dx ∫ ∫ ∫
(Do tích phân xác định không phụ thuộc 1 ( ) ( ) ( ) ( ) 1 0 0 1
vào biến số tích phân) = f
∫ (x)dx (Do f (x) là hàm chẵn ⇒ f (−x) = f (x) ) 0 1 1 1 Vậy A = f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx =10 (1) 1 − 0 0 1 0 1 Đặt B = g
∫ (x)dx = g
∫ (x)dx+ g ∫ (x)dx 1 − 1 − 0
  1 B 2 B https://toanmath.com/ 0 B = g x dx ∫
. Đặt t = −x ⇒ dt = −dx 1 ( ) 1 − Đổi cận: 0 1 1 ⇒ B = g t
− . −dt = g t
− dt = g −x dx ∫ ∫ ∫
(Do tích phân xác định không phụ thuộc 1 ( ) ( ) ( ) ( ) 1 0 0 1
vào biến số tích phân) = − g
∫ (x)dx (Do f (x) là hàm chẵn ⇒ g(−x) = −g(x) ) 0 1 1 1 Vậy B = g
∫ (x)dx = − g
∫ (x)dx + g
∫ (x)dx = 0 (2) 1 − 0 0 Từ (1) và (2) Chọn B 0
Câu 165: Cho hàm số y = f ( x) là hàm lẻ và liên tục trên [ 4; − 4] biết f
∫ (−x)dx = 2 và 2 − 2 4 f ∫ ( 2
− x)dx = 4 . Tính I = f
∫ (x)dx . 1 0 A. I = 10 − . B. I = 6 − .
C. I = 6 . D. I = 10 . 1 f (2x) 2
Câu 166: Cho hàm số chẵn y = f ( x) liên tục trên  và dx = 8 ∫ . Tính f ( x) dx ∫ . 1+ 2x 1 − 0 A. 2 . B. 4 . C. 8 . D. 16 . 1
Câu 167: Cho f ( x) là hàm số chẵn liên tục trong đoạn [ 1 − ; ] 1 và f
∫ (x)dx = 2 . Kết quả 1 − 1 f ( x) I = dx ∫ bằng 1+ ex 1 −
A. I = 1.
B. I = 3 .
C. I = 2 . D. I = 4 . 1 2 1
Câu 168: Cho y = f ( x) là hàm số chẵn và liên tục trên .  Biết f
∫ (x)dx = f
∫ (x)dx =1. Giá trị của 2 0 1 2 f ( x) dx ∫ bằng 3x +1 2 − A. 1. B. 6 . C. 4 . D. 3 . f (x) 3
f (x) + f (x) = x, x ∀ ∈ 2
Câu 169: Cho hàm số
liên tục trên thỏa mãn . Tính I = f ∫ (x)dx 0 3 1 5
A. I = 2 . B. I = . C. I = . D. I = . 2 2 4
Câu 170: Cho hàm số f ( x) liên tục trên  thỏa mãn 3 f ( x) 2 2
− 3 f (x) + 6 f (x) = x, x ∀ ∈ . Tính tích 5 phân I = f
∫ (x)dx . 0 5 5 5 5 A. I = . B. I = . C. I = . D. I = . 4 2 12 3
Câu 171: Cho hàm số f ( x) liên tục trên  thỏa mãn 3
x + f ( x) + 2 f ( x) = 1 , x ∀ ∈ . Tính 1 I = f
∫ (x)dx . 2 − 7 7 7 5 A. I = . B. I = . C. I = . D. I = . 4 2 3 4 https://toanmath.com/
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5 b dx b − a
Bài toán: “ Cho f ( x) f (a + b − x) 2 .
= k , khi đó I = = ∫ k + f x k a ( ) 2 Chứng minh:dt = −dx
Đặt t = a + b − x ⇒  ( ) 2 k
và x = a ⇒ t − b ; x = b ⇒ t = a . f x =  f  (t) b b b Khi đó dx dx 1 f ( x) dx I = = = ∫ ∫ ∫ . k + f x k k k + f x a ( ) 2 a a ( ) k + f (t) b dx
1 b f ( x) dx 1 b 1 b − a 2I = + = ∫ ∫ dx = ∫
(b − a) ⇒ I = . k + f x k k + f x k k 2k a ( ) a ( ) a
Câu 172: Cho hàm số f ( x) liên tục và nhận giá trị dương trên [0; ]
1 . Biết f ( x). f (1− x) = 1 với 1 dx x ∀ ∈[0; ]
1 . Tính giá trí I = ∫ 1+ f x 0 ( ) 3 1 A. . B. . C. 1. D. 2 . 2 2
Câu 173: Cho hàm số f ( x) liên tục trên  , ta có f ( x) > 0 và f (0). f (2018 − x) = 1. Giá trị của tích 2018 dx phân I = ∫ 1+ f x 0 ( )
A. I = 2018 .
B. I = 0
C. I = 1009 D. 4016
Câu 174: Cho hàm số y = f ( x) có đạo hàm, liên tục trên  và f ( x) > 0 khi x ∈[0;5] Biết . 5 dx
f ( x). f (5 − x) = 1 tính tích phân I = ∫ . , 0 1+ f ( x) 5 5 5 A. I = . B. I = . C. I = . D. I = 10 . 4 3 2 3
Câu 175: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn f (4 − x) = f ( x) . Biết xf ∫ (x)dx = 5. 1 3 Tính tích phân f ( x) dx ∫ . 1 5 7 9 11 A. . B. . C. . D. . 2 2 2 2
Câu 176: Cho hàm số y = f ( x) có đạo hàm liên tục trên R và f ( x) > 0 khi x ∈ [0; a] ( a > 0 ). Biết a dx
f ( x). f (a − x) = 1, tính tích phân I = ∫ . 1+ f x 0 ( ) a a a A. I = .
B. I = 2a . C. I = . D. I = . 2 3 4
 f (x). f (a − x) =1
Câu 177: Cho f ( x) là hàm liên tục trên đoạn [0; a] thỏa mãn  và  f
 ( x) > 0, x ∀ ∈[0;a] a dx ba = , ∫
trong đó b , c là hai số nguyên dương và b là phân số tối giản. Khi đó 1+ f x c c 0 ( )
b + c có giá trị thuộc khoảng nào dưới đây? https://toanmath.com/ A. (11; 22). B. (0;9). C. (7; 2 ) 1 . D. (2017; 2020).
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 6
Câu 178: Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [1;4], đồng biến trên đoạn [1;4] và thỏa 4
mãn đẳng thức x + 2 .x f (x) =  ′( ) 2 f x    , x
∀ ∈[1;4] . Biết rằng f ( ) 3 1 = , tính I = f
∫ (x)dx ? 2 1 1186 1174 1222 1201 A. I = . B. I = . C. I = . D. I = . 45 45 45 45 3 2 f x − x 1 − 2x
Câu 179: Cho hàm số y = f ( x) có đạo hàm trên thỏa mãn 3 f ′( x) ( ) .e − = 0 và 2 f ( x) 7 f (0) = 1. Tích phân .
x f ( x) dx ∫ bằng 0 2 7 15 45 5 7 A. . B. . C. . D. . 3 4 8 4 1
Câu 180: Cho hàm số f ( x) 4 3 2
= x + 4x − 3x − x +1, x ∀ ∈ . Tính 2 I = f
∫ (x).f ′(x)dx. 0 7 7 A. 2 . B. 2 − . C. − . D. . 3 3
Câu 181: Cho hàm số f ( x) có đạo hàm liên tục trên khoảng (0; )
1 và f ( x) ≠ 0 , x ∀ ∈(0; ) 1 . Biết rằng  1   3  f = a   , f
 = b và x + xf ′( x) = 2 f ( x) − 4 , x ∀ ∈(0; ) 1 . Tính tích phân    2  2   π 3 2 sin .
x cos x + 2sin 2x I = dx ∫
theo a và b . 2 π f (sin x) 6 3a b 3b a 3b a 3a b A. I  . B. I  . C. I  . D. I  . 4ab 4ab 4ab 4ab
Câu 182: Cho hàm số f liên tục, f ( x) > 1
− , f (0) = 0 và thỏa f ′(x) 2 x +1 = 2x
f ( x) +1 . Tính f ( 3) . A. 0 . B. 3 . C. 7 . D. 9 . 5
Câu 183: Cho hàm số f ( x) liên tục trên  và f
∫ (x)dx = 4, f (5) = 3, f (2) = 2. Tính 2 2 3 I = x f ′( 2 x + ∫ )1dx 1 A. 3 . B. 4 . C. 1. D. 6 . f (2 x − ) 1 ln x
Câu 184: Cho hàm số f ( x) liên tục trên đoạn [1;4] và thỏa mãn f ( x) = + . Tính tích x x 4 phân I = f
∫ (x)dx . 3 A. 2
I = 3 + 2 ln 2 . B. 2 I = 2 ln 2 . C. 2 I = ln 2 . D. I = 2 ln 2 . https://toanmath.com/ π 2 16 f x 2 ( )
Câu 185: Cho hàm số f ( x) liên tục trên  và thỏa mãn cot . x f ∫ (sin x)dx = dx = 1 ∫ . Tính π x 1 4 1 f (4x) tích phân dx ∫ . x 1 8 3 5
A. I = 3 . B. I = .
C. I = 2 . D. I = . 2 2
Câu 186: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn điều kiện x f ( 2
x ) + f ( − x) 2 4 . 3 1 = 1− x . 1 Tích phân I = f
∫ (x)dx bằng: 0 π π π π A. I = . B. I = . C. I = . D. I = . 4 6 20 16 1 2 9
Câu 187: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 1,  f ′
∫ (x) dx =  5 0 1 2 1 và
f ( x )dx = ∫ . Tính tích phân I = f
∫ (x)dx . 5 0 0 3 1 3 1 A. I = . B. I = . C. I = . D. I = . 5 4 4 5 https://toanmath.com/ HƯỚNG DẪN GIẢI
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 1 4 2 Câu 104: Cho f
∫ (x)dx =16 . Tính f (2x)dx ∫ 0 0 A. 16 . B. 4 . C. 32 . D. 8 . Hướng dẫn giải 1 7 T Chọn D 1 7 T 2 Xét tích phân f (2x) dx ∫ ta có 1 7 T 1 7 T 0 Đặt 2x = 1
t ⇒ dx = dt . Khi x = 0 thì t = 0 ; khi x = 2 thì t = 4. 2 2 4 4 Do đó 1 1 f ∫ ( x) 1 2 dx = f ∫ (t)dt = f
∫ (x)dx = .16 = 8. 2 2 2 0 0 0 6 2
Câu 105: Nếu f
∫ (x)dx =12 thì f (3x)dx ∫ bằng 0 0 A. 6 . B. 36 . C. 2 . D. 4 . Hướng dẫn giải Chọn D
Đặt t = 3x ⇒ dt = 3dx . Đổi cận: x = 0 ⇒ t = 0 , x = 2 ⇒ t = 6 2 6 Khi đó: f ∫ ( x) 1 x = f ∫ (t) 1 3 d dt = .12 = 4 . 3 3 0 0 2 5 Câu 106: Cho f ∫ ( 2x + )1 d
x x = 2 . Khi đó I = f
∫ (x)dx bằng: 1 2 A. 2 . B. 1. C. 1 − . D. 4 . Hướng dẫn giải Chọn D Đặt 2
t = x +1 ⇒ dt = 2xdx .
Đổi cận: x =1⇒ t = 2, x = 2 ⇒ t = 5 . 2 5 5 2 Khi đó: f ∫ ( 1 2 x + ) 1 d x x = f
∫ (t)dt ⇒ f
∫ (t)dt = 2 f ∫ ( 2x + )1 d x x = 4 . 2 1 2 2 1 5 5
Mà tích phân không phụ thuộc vào biến nên: I = f
∫ (x)dx = f ∫ (t)dt = 4 . 2 2 1
Câu 107: Cho hàm số f ( x) liên tục trên  và thỏa mãn f
∫ (x)dx = 9 . Tính tích phân 5 − 2  f
∫ (1−3x)+9dx  . 0 A. 27 . B. 21. C. 15 . D. 75 . Hướng dẫn giải Chọn B
Đặt t =1−3x ⇒ dt = 3d − x .
Với x = 0 → t = 1 và x = 2 → t = 5 − . 2 2 2 5 − dt 1 1 Ta có  f
∫ (1−3x)+9dx  = f
∫ (1−3x)dx + 9dx ∫ =  f ∫  (t) 2  + 9x  =  f
∫  (x)dx +18 0  3 − 3 0 0 0 1 5 − https://toanmath.com/ 1 = .9 +18 = 21. 3 9 4
Câu 108: Biết f ( x) làm hàm liên tục trên  và f
∫ (x)dx = 9 . Khi đó giá trị của f
∫ (3x −3)dx là 0 1 A. 27 . B. 3 . C. 0 . D. 24 . Hướng dẫn giải Chọn B 4 I = f
∫ (3x−3)dx. Đặt t = 3x −3 ⇒ dt = 3dx 1  = ⇒ =
Đổi cận: x 1 t 0 
x = 4 ⇒ t = 9 9 1 9 1 I = f
∫ (t)dt = f ∫ (x)dx = 3. 3 3 0 0 1 2  x
Câu 109: Cho hàm số f ( x) liên tục trên  thỏa f
∫ (x)dx =10 . Tính f dx ∫   .  2  0 0 2  x  5 2  x  2  x  2  x A. f dx = ∫   . B. f dx = 20 ∫   . C. f dx = 10 ∫   . D. f dx = 5 ∫   .  2  2  2   2   2  0 0 0 0 Hướng dẫn giải Chọn B Đặ x t t = 1 ⇒ dt = dx . 2 2
Đổi cận: x = 0 ⇒ t = 0 ; x = 2 ⇒ t =1. 2  x  1 Ta có: f dx ∫   = 2. f
∫ (t)dt = 2.10 = 20.  2  0 0 5 2 f ∫ (x)dx = 4 I = f (2x + ∫ )1dx Câu 110: Cho 1 − . Tính 1 − . 5 3
A. I = 2 . B. I = .
C. I = 4 . D. I = . 2 2 Hướng dẫn giải Chọn A
Đặt t = 2x +1 ⇒ dt = 1
2dx ⇒ dx = dt . 2 Với x = 1 − ⇒ t = 1
− , với x = 2 ⇒ t = 5 . 2 5 5 5 Khi đó ta có 1 1 1 1 I = f (2x + ∫
)1dx ⇒ I = f ∫ (t). dt = f ∫ (t)dt = f
∫ (x)dx = .4 = 2. 2 2 2 2 1 − 1 − 1 − 1 − 5
Câu 111: Giả sử hàm số y = f ( x) liên tục trên  và f
∫ (x)dx = a, (a∈) . Tích phân 3 2 I = f (2x + ∫
)1dx có giá trị là 1 1 1 A. I = a +1 .
B. I = 2a +1 .
C. I = 2a . D. I = a . 2 2 Hướng dẫn giải Chọn D
Đặt t = 2x +1⇒ dt = 2dx .
Đổi cận: x =1⇒ t = 3 ; x = 2 ⇒ t = 5 . https://toanmath.com/ 5 5 1 ⇒ I = f ∫ (t) 1 t = f ∫ (x) 1 d dx = a . 2 2 2 3 3 2 5 Câu 112: Cho f ∫ ( 2x + )1 d
x x = 2 . Khi đó I = f
∫ (x)dx bằng 1 2 A. 2 . B. 1. C. 1 − . D. 4 . Hướng dẫn giải Chọn D Đặt 2
t = x +1 ⇒ dt = 2 d x x
Đổi cận: x =1⇒ t = 2; x = 2 ⇒ t = 5 . 5 5 5 Khi đó: 1 = f ∫ (t) 1 2 dt = f
∫ (x)dx ⇒ I = f ∫ (x)dx = 4.. 2 2 2 2 2 3 2
Câu 113: Cho hàm số f ( x) liên tục trên [1; +∞) và f
∫ ( x +1)dx = 8. Tích phân I = xf ∫ (x)dx 0 1 bằng:
A. I = 16 .
B. I = 2 .
C. I = 8 . D. I = 4 Hướng dẫn giải Chọn D 3 2 I = f
∫ ( x +1)dx = 8 . Đặt t = x +1 ⇒ t = x +1⇒ 2tdt = dx; 0
đổi cận: x = 0 ⇒ t =1; x = 3 ⇒ t = 2 . 2 2 2 Khi đó I = 2tf
∫ (t)dt = 8 ⇒ tf
∫ (t)dt = 4. Vậy I = xf ∫ (x)dx = 4. 1 1 1 11 2 Câu 114: Biết f
∫ (x)dx =18. Tính I = x(2+ f ( 2 3x − ∫ )1)dx. 1 − 0
A. I = 5 .
B. I = 7 .
C. I = 8 D. I = 10 . Hướng dẫn giải Chọn B Đặt 2
t = 3x −1 ⇒ dt = 6 d
x x . Đổi cận x = 0 ⇒ t = 1
− , x = 2 ⇒ t =11 2 I = x
∫ (2+ f (3x − )1) 2 2 dx = 2 d x x + xf ∫ ∫ (3x − ) 11 1 1 2 2 1 dx = 4 + f
∫ (t)dt = 4+ .18 = 7 . 6 6 0 0 0 1 − 1 2
Câu 115: Cho hàm số y = f ( x) liên tục trên  và f
∫ (2x)dx = 8. Tính I = xf
∫ ( 2x)dx 0 0 A. 4 . B. 16 . C. 8 . D. 32 . Hướng dẫn giải Chọn C Đặt 2 x = 2t ⇒ 2 d x x = 2dt ⇒ d
x x = dt . Đổi cận: x = 0 ⇒ t = 0 , x = 2 ⇒ t = 1. 1 Ta có: I = f ∫ (2t)dt = 8. 0 1 3
Câu 116: Cho hàm số f ( x) liên tục trên và có f
∫ (x)dx = 2; f
∫ (x)dx = 6 . Tính 0 0 1 I = f
∫ ( 2x−1)dx . 1 − 2 3 A. I = .
B. I = 4 . C. I = . D. I = 6 . 3 2 Hướng dẫn giải https://toanmath.com/ Chọn B 1 1 2 1 Có I = f
∫ ( 2x−1)dx = f
∫ (1−2x)dx+ f
∫ (2x− )1dx = I + I 1 2 1 − 1 − 1 2 1 x = 1 − ⇒ u = 3 2  Tính I =
f 1− 2x dx ∫
.Đặt u =1− 2x ⇒ du = 2
− dx . Đổi cận:  1 . 1 ( ) x = ⇒ u = 0 1 −  2 0 3 1 − 1 ⇒ I = f u du = f u du = 3 ∫ ∫ 1 ( ) ( ) 2 2 3 0
x = 1⇒ u = 1 1 
Tính I = f 2x −1 dx ∫
. Đặt u = 2x −1⇒ du = 2dx . Đổi cận:  1 . 2 ( ) x = ⇒ u = 0 1  2 2 1 1 1 1 ⇒ I = f u du = f u du = 1 ∫ ∫ 2 ( ) ( ) 2 2 0 0
Vậy I = I + I = 4 1 2 . 2 4
Câu 117: Cho hàm số y = f ( x) liên tục trên [0; 4] và f
∫ (x)dx =1; f
∫ (x)dx = 3. Tính 0 ; 0 1 f
∫ ( 3x−1)dx . 1 − 4 A. 4 . B. 2 . C. . D. 1. 3 Hướng dẫn giải Chọn C 1 f ( 3x −1 ) 1/3 1 dx =
f (1− 3x)dx + f (3x − ∫ ∫ ∫ ) 1 dx . 1 − 1 − 1/3 1/3 1 1 = −
f ( − x) ( − x) 1 1 3 d 1 3 + f (3x − ) 1 d (3x − ∫ ∫ ) 1 . 3 3 1 − 1/3 0 2 1 = − 1 1 4 f ∫ (t) 1 dt + f
∫ (t)d(t) = − ( 3 − ) + .1 = . 3 3 3 3 3 4 0 1 3
Câu 118: Cho f ( x) là hàm số liên tục trên  và f
∫ (x)d x = 4, f
∫ (x)d x = 6. Tính 0 0 1 I = f
∫ ( 2x+1)d x. 1 −
A. I = 3 .
B. I = 5 .
C. I = 6 . D. I = 4 . Hướng dẫn giải Chọn B
Đặt u = 2x + 1
1 ⇒ d x = d u . Khi x = 1 − thì u = 1
− . Khi x = 1 thì u = 3. 2 3 1 0 3 1   Nên I = f
∫ ( u )du =  f
∫ ( u )du + f ∫ ( u )du 2 2 1 −  1 − 0  0 3 1   =  f ∫ ( u − )du + f ∫ (u)du . 2  1 − 0  https://toanmath.com/ 1 Xét f
∫ (x)d x = 4. Đặt x = u
− ⇒ d x = −du . 0
Khi x = 0 thì u = 0 . Khi x = 1 thì u = 1 − . 1 1 − 0 Nên 4 =
f ( x) d x = ∫ − f ( u − ∫
)du = f ( u − ∫ )du . 0 0 1 − 3 3 Ta có f
∫ (x)d x = 6 ⇒ f ∫ (u)du = 6 . 0 0 0 3 1   1 Nên I =  f ∫ ( u − )du + f
∫ (u)du = (4+6) = 5. 2  2 1 − 0  1 2
Câu 119: Cho hàm số f ( x) liên tục trên  thỏa f
∫ (2x)dx = 2 và f
∫ (6x)dx =14 . Tính 0 0 2 f
∫ (5 x + 2)dx . 2 − A. 30 . B. 32 . C. 34 . D. 36 . Hướng dẫn giải Chọn B 1 + Xét f ∫ (2x)dx = 2. 0
Đặt u = 2x ⇒ du = 2dx ; x = 0 ⇒ u = 0 ; x =1⇒ u = 2 . 1 2 1 2 Nên 2 = f ∫ (2x)dx = f
∫ (u)du ⇒ f ∫ (u)du = 4. 2 0 0 0 2 + Xét f
∫ (6x)dx =14 . 0
Đặt v = 6x ⇒ dv = 6dx ; x = 0 ⇒ v = 0 ; x = 2 ⇒ v =12 . 2 12 1 12 Nên 14 = f
∫ (6x)dx = f
∫ (v)dv ⇒ f ∫ (v)dv = 84. 6 0 0 0 2 0 2 + Xét f
∫ (5 x + 2)dx = f
∫ (5 x + 2)dx + f
∫ (5 x + 2)dx. 2 − 2 − 0 0
 Tính I = f 5 x + 2 dx ∫ . 1 ( ) 2 −
Đặt t = 5 x + 2 . Khi 2
− < x < 0 , t = 5
− x + 2 ⇒ dt = 5d − x ; x = 2
− ⇒ t =12 ; x = 0 ⇒ t = 2. 2 1 − 12 2 1   1 I = f t dt ∫ =  f
∫ (t)dt − f
∫ (t)dt = (84−4) =16. 1 ( )  5 5 5 12  0 0  2
 Tính I = f 5 x + 2 dx ∫ . 1 ( ) 0
Đặt t = 5 x + 2 .
Khi 0 < x < 2 , t = 5x + 2 ⇒ dt = 5dx ; x = 2 ⇒ t = 12 ; x = 0 ⇒ t = 2 . 12 1 12 2 1   1 I = f t dt ∫ =  f
∫ (t)dt − f
∫ (t)dt = (84−4) =16. 2 ( )  5 5 5 2  0 0  2 Vậy f
∫ (5 x +2)dx = 32. 2 − https://toanmath.com/ π π 2 2
Câu 120: Cho tích phân I = cos . x f ∫
(sin x)dx = 8. Tính tích phân K = sin .x f ∫
(cos x)dx . 0 0 A. K = 8 − .
B. K = 4 .
C. K = 8 . D. K = 16 . Hướng dẫn giải: π 2 π I = cos . x f ∫
(sin x)dx Đặt t = − x ⇒ dt = −dx Đổi cận: 2 0 π π 0  π    π  ⇒ I = cos − t . f sin − t . ∫      (−dt) 2 = sin t. f ∫ (cos x) 2 .dt = sin . x f ∫
(cos x).dt (Tích phân xác π  2    2  0 0 2
định không phụ thuộc vào biến số tích phân) = K ⇒ K = I = 8 Chọn C 1
Câu 121: Cho hàm số y = f ( x) liên tục trên R, thỏa mãn f
∫ (x)dx =1. Tính 0 π 4 I = ( 2 tan + ∫
)1.f (tan x)dx . 0 π π
A. I = 1. B. I = 1 − . C. I = . D. I = − . 4 4 Hướng dẫn giải: Đặt t = x ⇒ dt = ( 2 tan
1+ tan x) dx . Đổi cận: 1 1 ⇒ I = f
∫ (t)dt = f
∫ (x)dx (Tích phân xác định không phụ thuộc vào biến số tích phân)=1 0 0 Chọn A
Câu 122: Cho hàm số f ( x) liên tục trên  thỏa mãn f (2x) = 3 f ( x) , x ∀ ∈ . Biết rằng 1 2 f
∫ (x)dx =1. Giá trị của tích phân I = f
∫ (x)dx bằng bao nhiêu? 0 1
A. I = 5 .
B. I = 3 .
C. I = 8 . D. I = 2 . Hướng dẫn giải Chọn A 2 Xét tích phân J = f
∫ (x)dx , đặt x = 2t ⇒ dx = 2dt . 0
Với x = 2 ⇒ t = 1, x = 0 ⇒ t = 0 . 1 1 1 1 1 Ta có J = f
∫ (2t)2dt = 2 f
∫ (2t)dt = 2 3f (t)dt = 6 f (t)dt = ∫ ∫ 6 f ∫ (x)dx = 6. 0 0 0 0 0 2 1 2 Mặt khác, ta có J = f
∫ (x)dx = f
∫ (x)dx + f ∫ (x)dx 0 0 1 2 2 1 1 ⇒ I = f
∫ (x)dx = f
∫ (x)dx − f
∫ (x)dx = J − f ∫ (x)dx = 5. 1 0 0 0 2
Câu 123: Cho hàm số y = f ( x) liên tục và có đạo hàm trên  thỏa mãn f (2) = 2 − ; f ∫ (x)dx =1. 0 4 Tính tích phân I = f ′
∫ ( x)dx. 0 https://toanmath.com/ A. I = 10 − . B. I = 5 − .
C. I = 0 . D. I = 18 − . Hướng dẫn giải Chọn A
Đặt t = x , ta có: 2t = x và 2tdt = dx. Khi x = 0 ⇒ t = 0 ; x = 4 ⇒ t = 2 . 4 2 I = f ′
∫ ( x)dx = 2tf ′ ∫ (t)dt . 0 0
Đặt u = 2t; dv = f ′(t)dt ta được: du = 2dt ; v = f (t) . 2
Khi đó: I = (2tf (t)) 2 − 2 f
∫ (t)dt = 4 f (2)−2.1 = 4.( 2 − ) − 2 = 10 − . 0 0 2 4 f ( x ) Câu 124: Cho f
∫ (x)dx = 2. Tính I = dx ∫ bằng x 1 1 1
A. I = 1.
B. I = 2 .
C. I = 4 . D. I = . 2 Hướng dẫn giải Chọn C 1
Đặt t = x ⇒ dt =
dx ; đổi cận: x = 1⇒ t = 1, x = 4 ⇒ t = 2 2 x 4 f ( x ) 2 2 I = dx = f ∫
∫ (t)2dt = 2 f
∫ (t)dt = 2.2 = 4. x 1 1 1 π 16 f ( x ) 2
Câu 125: Cho hàm số f ( x) liên tục trên  thỏa mãn dx = 6 ∫ và f ∫ (sin x)cos d x x = 3 . x 1 0 4 Tính tích phân I = f
∫ (x)dx . 0 A. I = 2 − .
B. I = 6 .
C. I = 9 . D. I = 2 . Hướng dẫn giải Chọn B 16 f ( x ) dx •Xét I = dx = 6 ∫
, đặt x = t ⇒ = dt x 2 x 1
Đổi cận: x =1⇒ t =1; x =16 ⇒ t = 4 4 4 6 I = 2 f
∫ (t)dt = 6 ⇒ f
∫ (t)dt = = 3. 2 1 1 π 2 • J = f ∫ (sin x)cos d
x x = 3 , đặt sin x = u ⇒ cos d x x = du 0 Đổ π
i cận: x = 0 ⇒ u = 0 ; x = ⇒ u = 1 2 1 J = f ∫ (u)du = 3 0 4 1 4 Vậy I = f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx = 3+3 = 6. 0 0 1 https://toanmath.com/ π 9 f ( x ) 2
Câu 126: Cho f ( x) liên tục trên  thỏa dx = 4 ∫ và f ∫ (sin x)cos d x x = 2 . Tính x 1 0 3 I = f
∫ (x)dx . 0
A. I = 10 .
B. I = 6 .
C. I = 4 . D. I = 2 . Hướng dẫn giải Chọn C 9 f ( x ) Ta có: dx = 4 ∫ , đặt t = x 2
⇒ t = x ⇒ 2t dt = dx x 1
đổi cận x =1⇒ t =1, x = 9 ⇒ t = 3 3 f (t) 3 Do đó ta có: 2t dt = 4 ∫ ⇔ f ∫ (t)dt = 2 (1) t 1 1 π 2 Ta có: f ∫ (sin x)cos .d
x x = 4 , đặt t = sin x ⇒ dt = cos .d x x 0 đổ π
i cận x = 0 ⇒ t = 0 , x = ⇒ t = 1 2 π 1 Do đó ta có: 2 f ∫ (sin x)cos .d x x = 2 ⇔ f
∫ (t)dt = 2 (2) 0 0 3 3
Từ (1) và (2) ta có: f
∫ (x)dx = f ∫ (t)dt = 4.. 0 0 f (2 x − ) 1 ln x
Câu 127: Cho hàm số f ( x) liên tục trên đoạn [1;4] và thỏa mãn f ( x) = + . Tính tích x x 4 phân I = f
∫ (x)dx . 3 A. 2
I = 3 + 2 ln 2 . B. 2 I = 2 ln 2 . C. 2 I = ln 2 . D. I = 2 ln 2 . Hướng dẫn giải Chọn B  −  4 4 f (2 x )1 4 f (2 x − ) ln x 4 1 ln x Ta có f ( x) dx ∫ =  +  dx ∫ = +  dx dx ∫ ∫ . x x x x 1 1   1 1 4 f (2 x − ) 1 Xét K = dx ∫ . x 1 Đặ t +1 dx
t 2 x −1 = t ⇒ x = ⇒ = dt . 2 x 3 3 ⇒ K = f
∫ (t)dt = f ∫ (x)dx. 1 1 4 4 2 ln x 4 ln x Xét M = dx ∫ = ln d x ∫ (ln x) = = 2 2 ln 2 . x 2 1 1 1 4 3 4 Do đó f
∫ (x)dx = f ∫ (x) 2 dx + 2 ln 2 ⇒ f ∫ (x) 2 dx = 2 ln 2 . 1 1 3 https://toanmath.com/ 5 2
Câu 128: Cho hàm số f ( x) liên tục trên [ 4; − + ∞) và f
∫ ( x + 4)dx = 8. Tính I = .xf
∫ (x)dx. 0 3
A. I = 8 .
B. I = 4 . C. I = 16 − . D. I = 4 − . Hướng dẫn giải Chọn D Đặ 2 t
x + 4 = t ⇒ x = t − 4 .
x = 0 ⇒ t = 2 3 3 Khi  ⇒ 8 = f
∫ (t)d( 2t −4) ⇔ 2t.f ∫ (t)dt = 8.
x = 5 ⇒ t = 3 2 2 3 3 3
Mà 2t. f (t ) dt = 2 .
x f ( x) dx ⇒ .
x f ( x) dx = 4 ⇒ I = 4 − ∫ ∫ ∫ . 2 2 2 π 1 2 3 Câu 129: Cho f
∫ (2x+ )1dx =12 và f ∫ ( 2 sin x)sin 2 d
x x = 3 . Tính f
∫ (x)dx . 0 0 0 A. 26 . B. 22 . C. 27 . D. 15 . Hướng dẫn giải Chọn C 3  − 3 3 3 Đặ t 1  1 1
t 2x +1 = t ⇒ 12 = f ∫ (t)d  = f
∫ (t)dt = f
∫ (x)dx ⇒ f ∫ (x)dx = 24.  2  2 2 1 1 1 1 π π π 2 2 2 Ta có f ∫ ( 2 sin x)sin 2 d x x = f ∫ ( 2
sin x).2sin x cos d x x = 2 sin . x f ∫ ( 2 sin x)d (sin x) 0 0 0 π 2 1 1 = f ∫ ( 2 sin x)d ( 2 sin x) = f
∫ (u)du = f ∫ (x)dx = 3 0 0 0 3 1 3 ⇒ f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 3+ 24 = 27 . 0 0 1 π 4 1 2 x f ( x)
Câu 130: Cho hàm f ( x) liên tục trên  thỏa mãn f
∫ (tan x)dx = 3 và dx = 1 ∫ . Tính 2 x +1 0 0 1 f ( x) dx ∫ . 0 A. 4 . B. 2 . C. 5 . D. 1. Hướng dẫn giải Chọn A 1 2 x f ( x) 1 1 f x 1 2 x f ( x) 1 f ( x) 1 dx = f x dx − dx ∫ ∫ ∫ ⇔ dx + dx = f x dx ∫ ∫ ∫ . 2 2 ( ) 2 ( ) ( ) 2 x +1 x +1 x +1 x +1 0 0 0 0 0 0 Đặ 1
t tan x = t suy ra d (tan x) = dt ⇔ dx = dt ⇔ ( 2
1+ tan x dx = dt . 2 ) cos x dt dt ⇔ dx = ( = . 2 1+ tan x) 2 1+ t π 4 1 1 f ( x)
∫ ( x) x = f ∫ (t) dt f tan d = dx ∫ =3. 2 1+ t 2 x +1 0 0 0 1 Vậy f ∫ (x)dx = 4. 0 https://toanmath.com/ π 4 1 2 x f x 1
Câu 131: Cho hàm số f ( x) liên tục trên R và f ∫ (tan x) ( ) dx = 4; dx = 2 ∫ . Tính I = f
∫ (x)dx . 2 x +1 0 0 0
A. I = 6 .
B. I = 2 .
C. I = 3 . D. I = 1. Hướng dẫn giải Chọn A π 4 1 f (t ) Từ f
∫ (tanx)dx = 4; Ta đặt t = tan x ta được dt = 4 ∫ 2 t +1 0 0 1 x f ( x) 1 ( 2 2 x +1− ) 1 f ( x) 1 1 f x Từ dx = 2 ⇔ dx = 2 ⇔ f x dx − dx = 2 ∫ ∫ ∫ ∫ 2 2 ( ) ( ) 2 x +1 x +1 x +1 0 0 0 0 1 1 ⇒ f ∫ (x) f ( x) dx = 2 + dx = 2 + 4 = 6 ∫ . 2 x +1 0 0 2018
Câu 132: Cho hàm số f ( x) liên tục trên  thỏa f
∫ (x)dx = 2 . Khi đó tích phân 0 2018 e 1 − x f ∫
(ln( 2x +1 dx bằng 2 ) x +1 0 A. 4 . B. 1. C. 2 . D. 3 . Hướng dẫn giải Chọn B 2018 e 1 − x Xét I = f ∫ (ln( 2x +1 dx. 2 ) x +1 0 Đặ 2x t t = ( 2 ln x + ) 1 ⇒ dt =
dx . Đổi cận: x = 0 ⇒ t = 0 ; 2018 x = e −1 ⇒ t = 2018 . 2 x +1 2018 2018 1 1 1 Suy ra I = f ∫ (t)dt = f
∫ (x)dx = .2 =1. 2 2 2 0 0 3 m 10 
Câu 133: Tìm tất cả các giá trị dương của m để x
∫ (3− x) dx = − f ′′ , với f (x) 15 = ln x .  9  0
A. m = 20 .
B. m = 4 .
C. m = 5 . D. m = 3 . Hướng dẫn giải Chọn D 15x 15   − 15 − 10 243 + Từ f ( x) 15
= ln x ⇒ f ′(x) 14 = = ⇒ ′′ f ′′( x) = do đó f   = 15 x x 2 x  9  . 20 3 + Tính tích phân = ∫ ( m I
x 3 − x) dx : 0 • x 0 3
Đặt t = 3 − x ⇒ x = 3 − t , dx = −dt , t 3 0 0 3 3 m 1 + m+2 m+2 • 3t t 3 Do đó = ∫(3− ) m I t t (−dt ) ( m m 1 3t t + = − ∫ )dt = − = m +1 m + 2 (m + ) 1 (m + 2) 3 0 0 3 m+2 m+2 5 m 10  3 243 3 3 + Ta có x
∫ (3− x) dx = − f ′′  ⇔ = ⇔ =  9  (m + ) 1 (m + 2) 20 (m + ) 1 (m + 2) 4.5 0
Thay lần lượt các giá trị m ở 4 đáp án, nhận giá trị m = 3 . Chú ý: https://toanmath.com/ m 3 3 3
-Việc giải phương trình ( =
không cần thiết nên chọn phương pháp thế đáp để làm m + ) 1 (m + 2) 4.5
trắc nghiệm trong bài này. m 3 3 3 m 3 3 3
-Để giải phương trình ( =
ta xét hàm trên f (m) = − với m > 0 m + ) 1 (m + 2) 4.5 (m + ) 1 (m + 2) 4.5
thì chứng minh được phương trình có nghiệm duy nhất m = 3 . 3
Câu 134: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn f (4 − x) = f ( x) . Biết xf ∫ (x)dx = 5. 1 3 Tính I = f
∫ (x)dx. 1 5 7 9 11 A. I = . B. I = . C. I = . D. I = . 2 2 2 2 Hướng dẫn giải Chọn A
Cách 1: Dùng tính chất để tính nhanh
Cho hàm số f ( x) liên tục trên [ ;
a b] và thỏa mãn điều kiện f (a + b − x) = f ( x), x
∀ [a;b]. Khi đó b b ∫ ( ) a + b xf x dx = f ∫ (x)dx 2 a a Chứng minh:
Đặt t = a + b − x ⇒ dx = −dt , với x∈[ ;
a b] . Đổi cận: khi x = a ⇒ t = b ; khi x = b ⇒ t = b b b a Ta có xf
∫ (x)dx = xf
∫ (a +b− x)dx = −∫(a +b−t) f (t)dt a a b b b b b b
= ∫(a +b −t) f (t)dt = (a +b) f
∫ (t)dt − tf
∫ (t)dt = (a +b) f
∫ (x)dx − xf ∫ (x)dx a a a a a b b b b a + b ⇒ 2 xf
∫ (x)dx = (a+b) f
∫ (x)dx ⇒ xf ∫ (x)dx = f ∫ (x)dx . 2 a a a a
Áp dụng tính chất trên với a = 1 , b = 3 .
f ( x) liên tục trên [ ;
a b] và thỏa mãn f (1+ 3 − x) = f ( x) . 3 3 3 Khi đó + xf ( x) 1 3 x =
f ( x) x ⇒ f ( x) 5 d d dx = ∫ ∫ ∫ . 4 2 1 1 1
Cách 2: Đổi biến trực tiếp:
Đặt t = 4 − x , với x ∈[1; ] 3 . 3 3 3 3 3 Ta có xf
∫ (x)dx = xf
∫ (4− x)dx = ∫(4−t) f (t)dt = 4 f
∫ (t)dt − t.f ∫ (t)dt 1 1 1 1 1 3 3 ⇒ =
f (t ) t − ⇒ f (t ) 5 5 4 d 5 dt = ∫ ∫ . 2 1 1
Câu 135: Cho hàm số y = f ( x) liên tục trên đoạn [1; ]
3 thỏa mãn f (4 − x) = f ( x), x ∀ ∈[1; ] 3 và 3 3
xf ( x) dx = 2 − ∫
. Giá trị f ( x) dx ∫ bằng 1 1 A. 2 . B. 1 − . C. 2 − . D. 1. Hướng dẫn giải https://toanmath.com/ Chọn B 3
Xét I = xf (x)dx ∫ (1). 1
Đặt x = 4 − t , ta có dx = −dt ; x =1⇒ t = 3 , x = 3 ⇒ t =1. 3 3 3
Suy ra I = ∫(4 − t) f (4 − t)dt = ∫(4 − t) f (t)dt , hay I = ∫(4 − x) f (x)dx (2). 1 1 1 3 3 I
Cộng (1) và (2) vế theo vế ta được 2I = 4 f (x)dx ∫
⇒ f (x)dx = = 1 − ∫ . 2 1 1
Câu 136: Cho hàm số f liên tục trên đoạn [ 6;
− 5] , có đồ thị gồm hai đoạn thẳng và nửa đường tròn 5
như hình vẽ. Tính giá trị I =  f
∫  (x)+ 2dx  . 6 − y 3 6 − 4 − O x 5 1 −
A. I = 2π + 35 .
B. I = 2π + 34 .
C. I = 2π + 33 .
D. I = 2π + 32 . 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T Hướng dẫn giải Chọn D 1 7 T
1 x + 2 khi −6 ≤ x ≤ 2 − 2  f ( x) 2 = 1
 + 4 − x khi − 2 ≤ x ≤ 2 2 1
x − khi 2 ≤ x ≤ 5 3 3  Ta có . 1 7 T 1 7 T 1 7 T 5 5 5 I =  f
∫  (x)+ 2dx = f
∫ (x)dx + 2 dx ∫ 6 − 6 − 6 − 2 − 2  1    = x + 2 dx + ∫   ∫ (1+ 4− x ) 5 2 1 2 dx + x − dx + 22 ∫   2   3 3  6 − 2 − 2 2 − 5  1   1 x  2 2 = x + 2x + J + x − + 22 = J + 28     .  4   3 3  6 − 2 2 Tính J = ∫ ( 2 1+ 4 − x )dx 2 −
Đặt x = 2sin t ⇒ dx = 2costdt . Đổ π π
i cận: Khi x = 2 thì t = −
; khi x = 2 thì t = . 2 2 π π 2
J = ∫ (1+ 4 − x ) 2 2 2 2
dx = 4 + 4 cos tdt = 4 + 2 ∫
∫ (1+cos2t)dt = 4+2π . Vậy I = 32+2π . 2 − π π − − 2 2
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 2
Cho hàm số f ( x) thỏa mãn : . A f ( x) + .
B u .′ f (u) + C. f (a + b − x) = g ( x) https://toanmath.com/ u  (a) =a b 1 b +) Với  thì f ∫ (x)dx = g ∫ (x)dx. u  (b)=b A + B + C a a u  (a) =b b 1 b +) Với  thì f ∫ (x)dx = g ∫ (x)dx. u  (b)=a
A − B + C a a
Trong đề bài thường sẽ bị khuyết một trong các hệ số , A B, C . f ( x) [a;b] b b Nếu liên tục trên thì f
∫ (a +b− x)dx = f ∫ (x)dx. a a 6 1 2 3
Câu 137: Cho hàm số f ( x) liên tục trên [0; ]
1 thỏa mãn f ( x) = 6x f ( x ) − f x dx ∫ 3x + . Tính ( ) 1 0 A. 2 . B. 4 . C. 1 − . D. 6 . Hướng dẫn giải Chọn B
Cách 1: (Dùng công thức) 6 6 2 3 2 3
Biến đổi f ( x) = 6x f ( x ) −
⇔ f x − 2.3x . f x = − A = , B = 2 − . 3x + ( ) ( ) 1 3x + với 1 1 1 1 1 6
Áp dụng công thức ta có: f ∫ (x)dx = − dx = 4 ∫ . 1+ 2 − 3x +1 0 ( ) 0
Cách 2: (Dùng công thức biến đổi – nếu không nhớ công thức) 6 1 1 1 2 3 1
Từ f ( x) = 6x f ( x ) − 2 3
⇒ f x dx − 2 3x f x dx = 6 − dx ∫ ∫ ∫ 3x + ( ) ( ) 1 3x +1 0 0 0 Đặt 3 2
u = x ⇒ du = 3x dx ; Với x = 0 ⇒ u = 0 và x = 1 ⇒ u = 1. 1 1 1 Khi đó 2 3x f ∫
( 3x)dx = f
∫ (u)du = f
∫ (x)dxthay vào (*) , ta được: 0 0 0 1 1 1 1 1 1 f
∫ (x) x − f ∫ (x) 1 d 2 dx = 6 − dx ∫ ⇔ f ∫ (x)dx = 6 dx = 4 ∫ . 3x +1 3x +1 0 0 0 0 0
Câu 138: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn điều kiện xf ( 2
x ) + f ( x − ) 2 4 3 1 = 1− x . 1 Tích phân I = f
∫ (x)dx bằng 0 π π π π A. I = . B. I = . C. I = . D. I = 4 6 20 16 Hướng dẫn giải Chọn C 1 1 1 Từ 4 . x f ( 2
x ) + 3 f ( x − ) 2
1 = 1− x ⇒ 2 2xf
∫ ( 2x)dx +3 f ∫ (1− x) 2 dx = 1− x dx ∫ (∗) 0 0 0 +) Đặt 2
u = x ⇒ du = 2 d
x x ; Với x = 0 ⇒ u = 0 và x = 1 ⇒ u = 1. 1 1 1 Khi đó 2xf ∫
( 2x)dx = f
∫ (u)du = f ∫ (x)dx ( )1 0 0 0
+) Đặt t =1− x ⇒ dt = −dx ; Với x = 0 ⇒ t =1 và x =1⇒ t = 0 . 1 1 1 Khi đó f
∫ (1− x)dx = f
∫ (t)dt = f ∫ (x)dx (2) 0 0 0 Thay ( )
1 ,(2) vào (∗) ta được: https://toanmath.com/ 1 1 1 1 1 1 π 2 f
∫ (x)dx +3 f ∫ (x) 2 dx = 1− x dx ∫ ⇔ f (x) 2 dx = 1− x dx = ∫ ∫ . 5 20 0 0 0 0 0
Câu 139: Cho hàm số f (x) liên tục trên [0; 2] và thỏa mãn điều kiện f ( x) + f (2 − x) = 2x . Tính giá 2
trị của tích phân I = f
∫ (x)dx . 0 1 4 A. I = 4 − . B. I = . C. I = .
D. I = 2 . 2 3 Hướng dẫn giải Chọn D
Cách 1: (Dùng công thức) 2 2 1 2 2
Với f ( x) + f (2 − x) = 2x ta có A = 1 ; B = 1 , suy ra: x I = f ∫ (x)dx = 2x dx ∫ = = 2 . 1+1 2 0 0 0
Cách 2: (Dùng phương pháp đổi biến – nếu không nhớ công thức) 2 2 2
Từ f ( x) + f (2 − x) = 2x ⇒ f
∫ (x)dx+ f
∫ (2− x)dx = 2xdx ∫ = 4 (*) 0 0 0
Đặt u = 2 − x ⇒ du = − dx ; Với x = 0 ⇒u = 2 và x = 2 ⇒ u = 0 . 2 2 2 Suy ra f
∫ (2− x)dx = f
∫ (u)du = f ∫ (x)dx. 0 0 0 2 2
Thay vào (*), ta được 2 f
∫ (x)dx = 4 ⇔ f ∫ (x)dx = 2. 0 0
Câu 140: Xét hàm số f ( x) liên tục trên đoạn [0; ]
1 và thỏa mãn 2 f ( x) + 3 f (1− x) = 1− x . Tích phân 1 f ( x) dx ∫ bằng 0 2 1 2 3 A. . B. . C. . D. . 3 6 15 5 Hướng dẫn giải Chọn C
Đặt t =1− x ⇒ dx = −dt . 1 0 1 1 Suy ra f
∫ (1− x)dx = − f
∫ (t)dt = f
∫ (t)dt = f ∫ (x)dx 0 1 0 0 1 1 1 2 2
2 f ( x) + 3 f (1− x) = 1− x ⇔ 3 5 f
∫ (x)dx = 1− xdx ∫ = − (1− x) = . 3 3 0 0 0 1 2 Suy ra
f ( x) dx = ∫ . 15 0 + 2 x 2 ax b
Chú ý: Ta có thể dùng công thức f
∫ (ax+b)dx = f ∫
(x)dx . Khi đó: + 1 x 1 ax b 1 1 1
Từ 2 f ( x) + 3 f (1− x) = 1− x suy ra: 2 f
∫ (x)dx+3 f
∫ (1− x)dx = 1− xdx ∫ 0 0 0 1 ⇔ 2 f ∫ (x) 0 dx − 3 f ∫ (1− x) 1 dx = 1− xdx ∫ 1 ⇔ f ( x) 1 2 x = ⇔ f ( x) 2 5 d dx = ∫ ∫ . 0 1 0 0 0 3 15
Câu 141: Xét hàm số f ( x) liên tục trên đoạn [0; ]
1 và thỏa mãn điều kiện 1
2 f ( x) − 3 f (1− x) = x 1− x . Tính tích phân I = f
∫ (x)dx . 0 https://toanmath.com/ 1 4 1 4 A. I = . B. I = − . C. I = − . D. I = . 25 15 15 75 Hướng dẫn giải Chọn B 1 1 1
Do 2 f ( x) − 3 f (1− x) = x 1− x ⇒ 2 f
∫ (x)dx − 3f
∫ (1− x)dx = x 1− xdx ∫ ( ) 1 . 0 0 0    1 I I2 1
+ Xét I = 3 f 1− x dx ∫ : 1 ( ) 0
Đặt t =1− x ⇒ dx = −dt . Khi x = 0 ⇒ t =1; x =1⇒ t = 0 . 1
Khi đó I = 3 f t dt = 3I ∫ . 1 ( ) 0 1 2
+ Xét I = x 1− xdx ∫
. Đặt t = 1− x ⇒ x =1− t ⇒ dx = 2 − tdt . 2 0
Khi x = 0 ⇒ t = 1; x = 1 ⇒ t = 0 . 0 0 5 3   Khi đó I = ∫( 2t 2t 4 2 1− t t 2 − t dt =  −  = . 2 ) ( )  5 3  15 1 1 Thây vào ( ) 4 4 1 : 2I − 3I = ⇔ I = − . 15 15
Câu 142: Xét hàm số f ( x) liên tục trên[ 1
− ;2] và thỏa mãn f (x) + xf ( 2x − )+ f ( − x) 3 2 2 3 1 = 4x . 2
Tính giá trị của tích phân I = f
∫ (x)dx . 1 − 5
A. I = 5 . B. I = .
C. I = 3 . D. I = 15 . 2 Hướng dẫn giải Chọn C
Cách 1: (Dùng công thức – Dạng 2)
Với: f ( x) + ( x) f ( 2
x − ) + f ( − x) 3 2 2 3 1 = 4x . Ta có: u  (− )1 = 1 −
A = 1; B = 1;C = 3 và 2
u = x − 2 thỏa mãn  . u  (2) = 2
Khi đó áp dụng công thức có: 2 2 2 I = f ∫ (x) 4 1 x 3 = 4x dx = = 3 ∫ . 1+1+ 3 5 1 − 1 − 1 −
Cách 2: (Dùng phương pháp đổi biến – nếu không nhớ công thức)
Từ f ( x) + xf ( 2
x − ) + f ( − x) 3 2 2 3 1 = 4x . 2 2 2 2 ⇒ f
∫ (x)dx + 2 .xf ∫
( 2x −2)dx +3 f ∫ (1− x) 3 dx = 4x dx ∫ (*) 1 − 1 − 1 − 1 − +) Đặt 2
u = x − 2 ⇒ du = 2 dx x ; với x = 1 − ⇒ u = 1
− và x = 2 ⇒ u = 2 . 2 2 2 Khi đó 2 .x f ∫ ( 2x −2)dx = f ∫ (u)du = f ∫ (x)dx ( )1 1 − 1 − 1 −
+) Đặt t =1− x ⇒ dt = −dx ; Với x = 1
− ⇒ t = 2 và x = 2 ⇒ t = 1 − . 2 2 2 Khi đó f
∫ (1− x)dx = f ∫ (t)dt = f ∫ (x)dx (2) 1 − 1 − 1 − https://toanmath.com/ 2 2 Thay ( )
1 ,(2) vào (*) ta được: 5 f
∫ (x)dx =15⇒ f ∫ (x)dx = 3. 1 − 1 −
Câu 143: Hàm số f ( x) liên tục trên [ 1
− ;2] và thỏa mãn điều kiện f (x) = x + + xf ( 2 2 3 − x ). Tính 2 giá trị của I = f
∫ (x)dx 1 − 14 28 4 A. I = . B. I = . C. I = .
D. I = 2 . 3 3 3 Hướng dẫn giải Chọn B
Cách 1: ( Dùng công thức). 1
Với f ( x) = x + + xf ( 2 2
3 − x ) ⇒ f ( x) + .( 2x − ). f ( 2
3 − x ) = x + 2 2 1 u  (− ) 1 = 2 A = 1; B = ;C = 0 và 2
u = 3 − x thỏa mãn  2 u  (2) = 1 − 2 2 Khi đó áp dụ 1 28
ng công thức ta có: I = f ∫ (x)dx = x + 2dx= ∫ . 1 3 1 − 1 1− + 0 − 2
Cách 2: ( Dùng phương pháp đổi biến). 2 2 2 14
Từ f ( x) − xf ( 2
3 − x ) = x + 2 ⇒
f ( x) dx − xf ( 2 3 − x )dx = x + 2dx = ∫ ∫ ∫ (*) 3 1 − 1 − 1 −  = − ⇒ = Đặ x 1 u 2 t 2
u = 3 − x ⇒ du = 2 − d x x với 
x = 2 ⇒ u = 1 − 2 2 2 Khi đó 1 1 xf ( 2 3 − x )dx = ∫ f ∫ (u)du = f
∫ (x)dx thay vào (*) ta được 2 2 1 − 1 − 1 − 2 2 2 f ∫ (x) 1 − f ∫ (x) 14 x = ⇔ f ∫ (x) 28 dx d dx= . 2 3 3 1 − 1 − 1 − 1
Câu 144: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn f ( x) + xf ( 2
1− x ) + 3 f (1− x) = . Tính x +1 1
giá trị của tích phân I = f
∫ (x)dx . 0 9 2 4 3 A. I = ln 2 . B. I = ln 2 . C. I = . D. I = . 2 9 3 2 Hướng dẫn giải Chọn B
Cách 1: (Dùng công thức) 1
Với: f ( x) − .( 2 − x) f ( 2
1− x ) + 3 f (1− x) = 2x . Ta có: 2 − u  (0) =1 A = 1 1 ; B = ; và 2
u = x − 2 thỏa mãn  . 2 u  ( ) 1 = 0
Khi đó áp dụng công thức ta có: 1 1 1 dx 2 I = f ∫ (x)dx = ∫ 1 = ln x + 2 1 = .  ln 2 1  x +1 9 0 9 0 0 1− − + 3    2 
Cách 2: (Dùng công thức đổi biến nếu không nhớ công thức) https://toanmath.com/ 1
Từ f ( x) + xf ( 2
1− x ) + 3 f (1− x) = x +1 1 1 1 1 ⇒ 1 f
∫ (x)dx + xf ∫ ( 2
1− x )dx + 3 f ∫ (1− x)dx = dx ∫ 1 = ln x +1 = ln 2. (*) x +1 0 0 0 0 0 +) Đặt 2
u = 1 − x ⇒ du = 2
− xdx ; Với x = 0 ⇒ u =1 và x =1⇒ u = 0 . 1 1 1 Khi đó xf ∫ ( 1 1 2 1− x )dx = f ∫ (u)du = f ∫ (x)dx (1). 2 2 0 0 0
+) Đặt u =1− x ⇒ du = − d
x x ; Với x = 0 ⇒ t = 1 và x = 1 ⇒ t = 0 . 1 1 1 Khi đó xf
∫ (1− x)dx = f
∫ (t)dt = f ∫ (t)dt (2). 0 0 0
Thay (1), (2) vào (*) ta được: 1 1 1 1 9 1 2 f ∫ (x) 1 dx + f
∫ (x)dx+3 f
∫ (x)dx = ln2 ⇒ f
∫ (x)dx = ln2 ⇔ f
∫ (x)dx = ln2. 2 2 9 0 0 0 0 0 x
Câu 145: Cho hàm số y = f ( x) và thỏa mãn f ( x) − 8x f ( x ) 3 3 4 + = 0 . Tích phân 2 x +1 1 − a b I = f ( x) a b 2 dx = ∫
với a,b, c ∈  và ; tối giản. Tính a + b + c c c c 0 A. 6 . B. 4 − . C. 4 . D. 10 − . Hướng dẫn giải Chọn A
Cách 1: (Dùng công thức). x x
Biến đổi f ( x) − 8x f ( x ) 3 3 4 +
= 0 ⇔ f (x) − 2.(4x ) f (x ) 3 3 4 = −
với A = 1; B = 2 − 2 x +1 2 x +1 1 1 3 1 3 1  xx dx
Áp dụng công thức ta có: f ∫ (x)dx = ∫−  dx = ∫ . 1+ ( 2 − ) 2 2  +  + 0 0 x 1 0 x 1 Đặt 2 2 2 t =
x +1 ⇒ t = x +1 ⇒ tdt = xdx ; Với x = 0 ⇒ t = 1 và x = 1 ⇒ t = 2 . 2 1 1 2 2 2 2 3   − − Khi đó: ∫ ( ) x t −1 t 2 2 a b 2 f x dx = .xdx ∫ = .tdt ∫ = ( 2t − ∫
)1dt =  −t = = 2 + t  3  3 c 0 0 x 1 1 1 1
Suy ra a = 2;b = 1; c = 3 ⇒ a + b + c = 6 .
Cách 2: (Dùng phương pháp đổi biến – nếu không nhớ công thức) x 1 1 1 3 x
Từ f ( x) − 8x f ( x ) 3 3 4 + = 0 ⇔ f ∫ (x) 3 dx − 2 4x f ∫ ( 4x)dx+ dx = 0 (*) ∫ 2 x +1 2 + 0 0 0 x 1 Đặt 4 3
u = x ⇒ du = 4x dx ; Với x = 0 ⇒ u = 0 và x = 1 ⇒ u = 1. 1 1 1 Khi đó 3 4x f ∫
( 4x)dx = f
∫ (u)du = f
∫ (x)dx thay vào (*), ta được: 0 0 0 1 1 1 1 1 3 ∫ ( ) x x f x dx − 2 f ∫ (x) 3 dx + dx = 0 ∫ ⇔ f ∫ (x)dx = dx ∫ 2 + 2 + 0 0 0 x 1 0 0 x 1 Đặt 2 2 2 t =
x +1 ⇒ t = x +1 ⇒ tdt = xdx ; Với x = 0 ⇒ t = 1 và x = 1 ⇒ t = 2 . 2 1 1 2 2 2 2 3   − − Khi đó: ∫ ( ) x t −1 t 2 2 a b 2 f x dx = .xdx ∫ = .tdt ∫ = ( 2t − ∫
)1dt =  −t = = 2 + t  3  3 c 0 0 x 1 1 1 1
Suy ra a = 2;b = 1; c = 3 ⇒ a + b + c = 6 . https://toanmath.com/
Câu 146: Cho hàm số f ( x) liên tục trên đoạn [− ln 2;ln 2] và thõa mãn f ( x) + f (−x) 1 = . Biết x e +1 ln 2 f
∫ (x)dx = aln2+bln3, với a,b∈. Tính giá trị của P = a +b . −ln 2 1 A. P = . B. P = 2 − . C. P = 1 − . D. P = 2 . 2 Hướng dẫn giải Chọn A
Cách 1: Dùng công thức ln 2 ln 2 ln 2 1 dx 1 dx
Với f ( x) + f (−x) 1 =
ta có A = 1; B = 1 , suy ra f ∫ (x)dx = = ∫ ∫ x e +1 1+1 x e +1 2 x e +1 −ln 2 −ln 2 −ln 2
Cách 2: Dùng phương pháp dồn biến nếu không nhớ công thức ln 2 ln 2 ln 2 1 dx
Từ f ( x) + f (−x) = ⇒ f x x + f −x x = ∫ ∫ ∫ x ( )d ( )d x (*) e +1 e +1 −ln 2 −ln 2 −ln 2
Đặt u = −x ⇒ du = −dx ln 2 ln 2 ln 2 ⇒ f
∫ (−x)dx = f ∫ (u)du = f
∫ (x)dx thay vào (*) ta được: −ln 2 −ln 2 −ln 2 ln 2 ln 2 ln 2 ln 2 ∫ ( ) dx x f x x = ⇔ f x x = ∫ ∫ ∫ x ( ) 1 d 2 d d e +1 2 x e +1 −ln 2 −ln 2 −ln 2 −ln 2 Đặt x x
t = e ⇒ dt = e dx 1
Với x = − ln 2 ⇒ t = , x = ln 2 ⇒ t = 2 2 2 ln 2 ln 2 x 2 dx e dx dt t ⇒ = = = ln = ln 2 ∫ ∫ ∫ x e +1 x x e e +1 t t +1 t +1 −ln 2 −ln 2 ( ) ( ) 1 1 2 2 ln 2 a,b∈ Khi đó: f ∫ (x) 1 1 dx =
ln 2 = a ln 2 + b ln 3 → a = , b = 0 2 2 −ln 2 1
⇒ P = a + b = . 2  π   π π 
Câu 147: Biết hàm số y = f x + 
 là hàm số chẵn trên đoạn − ; và    2   2 2  π  π  2
f ( x) + f x + = sin x + cos x   . Tính I = f ∫ (x) . dx 2  0 1
A. I = 0 .
B. I = 1. C. I = . D. I = 1 − . 2
Hướng dẫn giải: π π 0 2 2  π   π   π  Đặ π t t =
− x ⇒ dt = −dx Đổi cận: ⇒ I = f − t . ∫   (−dt) = f − t dt = f − x dx ∫   ∫   (Tích 2 π  2   2   2  0 0 2 π   π  phân xác đị 2  π 
nh không phụ thuộc vào biến số tích phân) = f + x ∫    Vì f + x   là hàm số chẵn  2    2  0  π   π  ⇒ f + x = f − x      2   2  https://toanmath.com/ π π π 2 2 2   π  Vậy 2I = f
∫  (x)+ f x + dx = 
∫(sin x +cos x)dx = (cos x −sin x) = 1 − −1 = 2 −   ⇒ I = 1 −   2  0 0 0 ⇒ Chọn D  π 
Câu 148: Cho hàm số y = f ( x) có đạo hàm liên tục trên  , f (0) = 0 và f ( x) + f
− x = sin x.cos x  2    π với x
∀ ∈ . Giá trị của tích phân 2 xf ′ ∫
(x)dx bằng 0 π 1 π 1 A. − . B. . C. . D. − . 4 4 4 4 Hướng dẫn giải
Cách 1: (Dùng công thức)  π 
Với f ( x ) + f
− x = sin x.cos xA = B = 2  , ta có 1; 1.   π 1 π 1 Suy ra 2 f ∫ (x) 2 dx =
sin x.cos x.dx = ∫ . 0 0 1 + 1 4
Cách 2: (Dùng phương pháp đổi biến – nếu nhớ công thức)  π  π π π  π  1
Từ f ( x ) + f
− x = sin x.cos x  2 2 2 ⇒ f x + f
− x dx = sin x.cos xdx = ∫ ∫ ∫ 2  ( )   (*)   0 0 0  2  2 Đặ π t u =
− x ⇒ du = −dx 2 π π
Với x = 0 ⇒ u = ; x = ⇒ u = 0 . 2 2 π π π  π  Suy ra 2 2 f − x dx = f ∫   ∫ (u) 2 du = f
∫ (x)dx , thay vào (*) ta được 0 0 0  2  π 1 π 1 2 2 f (x) 2 dx = ⇔ f (x)dx = ∫ ∫ (1) 0 0 2 4  = π π π π   = π  π  Đặ u xdu dx t  ⇒  2 ⇒ xf ′ ∫
(x)dx = xf (x) 2 2 − f ∫ (x) 2 dx = f − f
  ∫ (x)dx (*) dv = f ′ 
(x)dx v = f  (x) 0 0 0 0 2  2   π 
Từ điều kiện f ( x ) + f
− x = sin x.cos x  2  suy ra     π  f − f    (0) = 0   2   π   ⇒ f = 0   (2).   π    f ( ) 2 0 + f = 0   2     π
Thay (1), (2) vào (*), ta đượ 1
c 2 xf ′( x)dx = − ∫ . 0 4 Chọn D x
Câu 149: Cho hàm số f ( x ) liên tục trên  và thỏa mãn f (1+ 2x) + f (1− 2x) 2 = , x ∀ ∈  . tính 2 x + 1 3 tích phân I = f
∫ (x)dx . 1 − π π 1 π π A. I = 2 − . B. I = 1 − . C. I = − . D. I = . 2 4 2 8 4 Hướng dẫn giải. Đặ t −1
t t = 1 + 2x ⇒ 1 − 2x = 2 − t và x =
, khi đó điều kiện trở thành 2 https://toanmath.com/ − + − +
f (t) + f ( − t) 2 t 2t 1 =
⇒ f (x) + f ( − x) 2 x 2x 1 2 2 = (*) 2 2 t − 2t + 5 x − 2x + 5
Cách 1: (Dùng công thức) x − 2x + 1
Với f ( x) + f (2 − x) 2 =
ta có A = 1; B = 1 . 2 x − 2x + 5 1 x − 2x + 1 π Suy ra f ∫ (x) 2 3 3 dx = dx ≈ 0,429 = 2 − ∫ − − 2 1 1 1 + 1 x − 2x + 5 2 Chọn A
Cách 2: (Dùng công thức đổi biến – nếu nhớ công thức) x − 2x + 1 x − 2x + 1
Từ (*), ta có f ( x) + f (2 − x) 2 = ⇒ f
∫ (x)dx + f ∫ (2 − x) 2 3 3 3 dx = dx ∫ (2*) 2 x − 2x + 5 − − − 2 1 1 1 x − 2x + 5
Đặt u = 2 − x ⇒ du = −dx . Với x = 1
− ⇒ u = 3;x = 3 ⇒ u = 1 − . 3 3 3 Suy ra f
∫ (2 − x)dx = f
∫ (u)du = f
∫ (x)dx , thay vào (*), ta được: 1 − 1 − 1 − − + 1 x − 2x + 1 π f ∫ (x) 2 3 3 x 2x 1 2 dx = dx ∫ ⇒ f ∫ (x) 2 3 3 dx = dx ≈ 0,429 = 2 - ∫ − − 2 1 1 x − 2x + 5 − − 2 1 1 2 x − 2x + 5 2 https://toanmath.com/
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 3
Cách giải: Lần lượt đặt t = u( x) và t = v( x) để giải hệ phương trình hai ẩn (trong đó có ẩn f ( x ) ) để
suy ra hàm số f ( x ) (nếu u( x ) = x thì chỉ cần đặt một lần t = v( x) ).
Các kết quả đặc biệt:  x − b   x − c  . A g − .   B ga    a  −  Cho .
A f (ax + b) + .
B f (−ax + c) = g(x) với 2 2
A ≠ B ) khi đó f (x) = (*) 2 2 A − B . A g x − . B g −x +)Hệ quả 1 của (*): . A f ( x) + .
B f (−x) = g ( x) ⇒ f ( x) ( ) ( ) = 2 2 A − B g x
+)Hệ quả 2 của (*): A f ( x) + B f (−x) = g ( x) ⇒ f ( x) ( ) . . =
với g ( x) là hàm số chẵn. A + B   2 f ( x)
Câu 150: Cho hàm số y = f ( x) liên tục trên  và f ( x) 1 + 2 f = 3x   . Tính I = ∫ dx . x  1 x 2 3 1 A. I = .
B. I = 1. C. I = . D. I = 1 − . 2 2 Hướng dẫn giải Chọn A     Đặ 1 1 1 3 1 3 t, t =
⇒ x = khi đó điều kiện trở thành f + 2 f  
(t) = ⇒ 2 f (x)+ f = .   x tt tx x     Hay f ( x) 1 6 4 + 2 f =  
, kết hợp với điều kiện f ( x) 1 + 2 f = 3x   . Suy ra :  x xx  2 2 f ( x) 2    −  f ( x) 6 f ( x) 2 3 = − 3x ⇒ = −1⇒ 2 2 3 I = ∫ dx = ∫ −1 dx = − x = . 2     1 x x x 2 1 x 1  x   x  2 2 2 2 Chọn B   x
Câu 151: Cho hàm số y = f ( x) liên tục trên  \ { }
0 và thỏa mãn f ( x) 2 15 2 3 + 3 f = −   ,  x  2 3 9 2  1  f
∫ (x)dx = k . Tính I = f dx ∫    theo k . x  3 1 2 45 + k 45 − k 45 + k 45 − 2k A. I = − . B. I = . C. I = . D. I = . 9 9 9 9 Hướng dẫn giải Chọn A 1 x = ⇒ t = 1 Đặ 1 t t = 2x ⇒ 2 dx = dt . Đổi cận . 2 3 x = ⇒ t = 3 2 3 Khi đó 1  2  I = f dx ∫   . 2  t  1   x  2  5x 2 Mà f ( x) 2 15 2 3 + 3 f = −   ⇔ f = − − f   (3x)  x  2  x  2 3 3 3 3 3 1  5x 2  5 1 1 Nên I = − − f ∫
(3x) dx = − xdx − f ∫ ∫ (3x)dx = 5 − − f ∫ (3x)dx   (*) 2  2 3  4 3 3 1 1 1 1 https://toanmath.com/ = ⇒ = Đặ 1 x 1 u 3
t u = 3x ⇒ dx = dx . Đổi cận 3 x = 3⇒ t = . 9 9 Khi đó 1 + = − − f (t ) k 45 k I 5 dt = 5 − − = − ∫ . 9 9 9 3
Câu 152: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn f (−x) + 2018 f ( x) = 2x sin x . Tính giá π 2 trị của I = f
∫ (x)dx. π − 2 2 2 4 1 A. I = . B. I = . C. I = . D. I = . 2019 1009 2019 1009 Hướng dẫn giải Chọn C Cách 1: (Dùng công thức)
Với f (−x) + 2018 f ( x) = 2x sin x ta có A = 1; B = 2018 π π 2 2 1 Casio Suy ra = I = f ∫ (x)dx 2x sin d x x ∫ 4 = ⇒ Đáp án C 1+ 2018 π π 2019 − − 2 2 Cách 2: g x Áp dụng Hệ quả 2: .
A f ( x) + Bf (−x) = g ( x) ⇒ f ( x) ( ) =
g x là hàm số chẵn. A + với ( ) B x x
Ta có f (−x) + 2018 f ( x) = 2x sin x ⇒ f ( x) 2 sin = 2019 π π 2 2 2 = Casio I = f ∫ (x)dx x sin d x x ∫ 4 = ⇒ Đáp án C 2019 π π 2019 − − 2 2
Câu 153: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn (− ) + 2018 ( ) x f x
f x = e . Tính giá trị 1 của I = f
∫ (x)dx 1 − 2 e −1 2 e −1 2 e −1 A. I = . B. I = .
C. I = 0 . D. I = . 2019e 2018e e Hướng dẫn giải Chọn A
Cách 1: (Dùng công thức). Với (− ) + 2018 ( ) x f x
f x = e ta có A = 1; B = 2018 . 1 1 2 1 1 1 e −1 Suy ra I = f ∫ (x)dx x = e dx ∫ x = e = . 1+ 2018 2019 2019e 1 − 1 − 1 −
Cách 2: (Dùng công thức) . A g x − . B g −x Áp dụng Hệ quả 1: . A f ( x) + .
B f (−x) = g ( x) ⇒ f ( x) ( ) ( ) = 2 2 A − . B Ta có: x −x ( − 1 1 − ) + 2018e e 1 2018 ( ) x f x
f x = e ⇒ f ( x) = ⇒ ∫ ( ) = ∫ (2018 x −x f x dx
e − e ) dx 2 2018 −1 2019.2017 1 − 1 − https://toanmath.com/ 2 − e −1 3 ≈1,164.10 ≈ (Casio). 2019e
Câu 154: Cho hàm số y = f ( x) có đạo hàm liên tục trên  , thỏa mãn f ( x) + f ( − x) 2 2 2 1 =12x .
Phương trình tiếp tuyến của đồ thị hàm số y = f ( x) tại điểm có hoành độ bằng 1 là
A. y = 2x + 2 .
B. y = 4x − 6 .
C. y = 2x − 6 .
D. y = 4x − 2 . Hướng dẫn giải Chọn C Áp dụng kết quả x − b   x − c  . A g − . B g      a   a  “Cho .
A f (ax + b) + .
B f (−ax + c) = g ( x) (với 2 2
A ≠ B ) khi đó f ( x) = 2 2 A − B ”. Ta có  x   x −1 2.g − g      2   2 − 
6x − 3( x − )2 2 1
f ( x) + f ( − x) 2 2 2 1
=12x = g (x) ⇔ f (x) = 2 = = x + 2x −1. 2 2 − 1 3  f  ( ) 1 = 2 Suy ra 
, khi đó phương trình tiếp tuyến cần lập là: y = 4x − 2 .  f ′  ( ) 1 = 4 1
Câu 155: Cho f ( x) là hàm số chẵn, liên tục trên  thỏa mãn ∫ f (x)dx = 2018 và g (x) là hàm số 0 1
liên tục trên  thỏa mãn g ( x) + g (−x) = 1, ∀x ∈  . Tính tích phân I = ∫ f (x)g (x)dx . 1 − 1009
A. I = 2018 . B. I = .
C. I = 4036 . D. I = 1008 . 2 Hướng dẫn giải Chọn A Áp dụng Hệ quả h x . A g ( x) + .
B g (−x) = h( x) g ( x) ( ) ⇒ =
với h ( x) là hàm số chẵn. A + B
Ta có: g ( x) + g (−x) = 1 = h ( x) ⇒ g ( x) 1 1 = = . 1+1 2
Kết hợp với điều kiện f ( x) là hàm số chẵn, ta có: 1 1 1 I =
f ( x) g ( x) 1 dx = ∫
∫ f (x)dx = ∫ f (x)dx = 2018. 2 1 − 1 − 0 a a
Chú ý: Nếu f ( x) là hàm số chẵn, liên tục trên [− ;
a a] ⇒ ∫ f ( x)dx = 2∫ f (x)dx . −a 0
Câu 156: Cho số dương a và hàm số f ( x) liên tục trên  thỏa mãn f ( x) + f (−x) = a , x ∀ ∈ . a
Giá trị của biểu thức f
∫ (x)dx bằng −a A. 2 2a . B. a . C. 2 a . D. 2a . Hướng dẫn giải Chọn C https://toanmath.com/ a −a a a Đặt x = t − ⇒ f
∫ (x)dx = f
∫ ( t−)(−dt) = f
∫ ( t−)dt = f ∫ (−x)dx −a a −a −a a a a a a ⇒ f
∫ (x) x =  f
∫  (x)+ f (−x) x = a x ⇔ f  ∫ ∫ (x) 2 x = a ⇔ f ∫ (x) 2 2 d d d 2 d 2 dx = a . −a −a −a −a −a π 2
Câu 157: Cho hàm số f ( x) liên tục trên  thỏa điều kiện f ( x) + f (−x) = 2sin x . Tính f
∫ (x)dx π − 2 A. 1 − . B. 0 . C. 1. D. 2 . Hướng dẫn giải Chọn B π 2 Giả sử I = f ∫ (x)dx . π − 2 Đặ π π π π
t t = −x ⇒ dt = −dx , đổi cận x = − → t = x = → t = − . 2 2 2 2 π π − 2 2
Khi đó I = − f
∫ (t)dt = f ∫ (t)dt . π π − 2 2 π π 2 2 Suy ra 2I =  f
∫  (x)+ f (−x)dx  = 2sin d x x = 0 ∫
⇒ 2I = 0 ⇒ I = 0 π π − − 2 2
Câu 158: Cho f (x) là một hàm số liên tục trên  thỏa mãn f ( x) + f (−x) = 2 − 2cos 2x . Tính tích 3π 2 phân I = f
∫ (x)dx. 3π − 2
A. I = 3 .
B. I = 4 .
C. I = 6 .
D. I = 8 . Hướng dẫn giải Chọn C 3π 3π 2 0 2 Ta có I = f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx. 3π 3π 0 − − 2 2 0 3π 3π Xét f
∫ (x)dx Đặt t = −x ⇒ dt = −dx ; Đổi cận: x = − ⇒ t = ; x = 0 ⇒ t = 0. 2 2 3π − 2 3π 3π 0 0 2 2 Suy ra f
∫ (x)dx = − f
∫ ( t−)dt = f
∫ ( t−)dt = f ∫ (−x)dx. 3π 3π 0 0 − 2 2 https://toanmath.com/ 3π 3π 2 2
Theo giả thiết ta có: f ( x) + f (−x) = 2 − 2cos 2x ⇔ ∫ ( f (x) + f (−x))dx = 2 − 2 cos xdx ∫ 0 0 3π 3π 3π 2 ⇔ f ∫ (x) 2 dx + f ∫ (−x) 2 dx = 2 sin x dx ∫ 0 0 0 3π 3π 2 0 π ⇔ f
∫ (x)dx+ f ∫ (x) 2
dx = 2 sin x dx − 2 sin x dx ∫ ∫ 0 3π 0 0 − 2
Câu 159: Cho hàm số y = f ( x) liên tục trên R và thỏa mãn f ( x) + f (−x) = 2 + 2 cos 2x . Tính π 2 I = f
∫ (x)dx . π − 2 A. I = 1 − .
B. I = 1. C. I = 2 − . D. I = 2 . Hướng dẫn giải π 2 I = f
∫ (x)dx (1) Đặt t = −x ⇒ dt = −dx Đổi cận: π − 2 π π π − 2 ⇒ I = f
∫ ( t−).(−dt) 2 = f ∫ ( t−) 2 dt = f
∫ (−x)dx(2) (Tích phân xác định không phụ thuộc vào π π π − − 2 2 2 biến số tích phân) π π 2 2 (1) + (2) ⇒ 2I =  f
∫  (x)+ f (−x)dx = 2+2cos2xdx  ∫ π π − − 2 2 π 2 = 2(1+ cos 2x)dx = ∫π−2 π π π π 2 2 2 2 2 2 2 cos xdx = 2 cos x dx = 2 cos xdx = 2sin x = 2 1  − ∫ ∫ ∫  (− ) 1  = 4  π π π π − − − − 2 2 2 2 ⇒ I = 2 Chọn D π 4
Câu 160: Cho hàm số f ( x) liên tục trên  và f (−x) − f ( x) 2 3 2
= tan x . Tính f
∫ (x)dx π − 4 π A. 1− π . B. − π 1 . C. 1+ π . D. 2 − . 2 2 4 2 Hướng dẫn giải Chọn D https://toanmath.com/ π π 4 4  π 1    π Cách 1: Ta có 2 tan d x x = −1 dx ∫   = ( tan x − π π x) 4π = 1− − 1 − +   = 2 − ∫ 2 − π π  cos x  4  4  2 − − 4 4 4 π 4 π ⇒ 2 − = 3 f
∫  (−x)−2 f (x)dx.  2 π − 4
Đặt t = −x ⇒ dt = − π π
dx , đổi cận x = − ⇒ t = π π , x = ⇒ t = − . 4 4 4 4 π π π 4 4 4 3 f
∫  (−x)−2 f (x)dx = 3f
∫  (t)−2 f ( t−)dt = 3f
∫  (x)−2 f (−x)dx    π − π − π − 4 4 4 π π π π 4 4 4 π 4 π Suy ra, f
∫ (x)dx = f
∫ (−x)dx ⇒ 2− = 3f
∫  (x)−2 f (x)dx ⇔ 2− = f ∫ (x)dx  π π 2 2 − − π − π − 4 4 4 4 π 4 π Vậy f
∫ (x)dx = 2− π 2 − 4
Cách 2: ( Trắc nghiệm)
Chọn f ( x) = f (−x) 2
= tan x (Thỏa mãn giả thiết). π π π 4 4 4   π Khi đó f ∫ (x) 1 2 dx = tan x dx = −1 dx = 2 − ∫ ∫   2 π π π  cos x  2 − − − 4 4 4
Câu 161: Cho hàm số f ( x) liên tục trên đoạn [− ln 2;ln 2] và thỏa mãn f ( x) + f (−x) 1 = . x e +1 ln 2 Biết f
∫ (x)dx = aln2+bln3 (a;b∈). Tính P = a +b . −ln 2 1 A. P = . B. P = 2 − . C. P = 1 − . D. P = 2 . 2 Hướng dẫn giải Chọn A ln 2 Gọi I = f ∫ (x)dx . −ln 2
Đặt t = −x ⇒ dt = −dx .
Đổi cận: Với x = −ln 2 ⇒ t = ln 2 ; Với x = ln 2 ⇒ t = −ln 2 . −ln 2 ln 2 ln 2 Ta được I = − f ( t − ∫ )dt = f ( t − ∫ )dt = f ∫ (−x)dx. ln 2 −ln 2 −ln 2 ln 2 ln 2 ln 2 ln 2 Khi đó ta có: 1 2I = f
∫ (x)dx+ f
∫ (−x)dx ==  f
∫  (x)+ f (−x)dx  = dx ∫ . x + − e 1 ln 2 −ln 2 −ln 2 −ln 2 ln 2 1 Xét dx ∫ . Đặt ex u = ⇒ d = ex u dx ex +1 −ln 2
Đổi cận: Với x = −ln 2 ⇒ 1 u =
; x = ln 2 ⇒ u = 2 . 2 https://toanmath.com/ ln 2 ln 2 ln 2 Ta đượ 1 x 1 c dx ∫ e = dx ∫ = du ∫ ex +1 ex ex +1 u u +1 −ln 2 ( ) −ln 2 ( ) −ln 2 ln 2  1 1  = − du ∫  
= (ln u − ln u +1) 2 = ln 2  u u +1 1 −  ln 2 2 1 1 Vậy ta có a =
, b = 0 ⇒ a + b = . 2 2
Câu 162: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn điều kiện 2 f ( x) + 3 f (1− x) = x 1− x . 1
Tính tích phân I = ∫ f (x)dx . 0 4 1 4 1 A. I = − . B. I = . C. I = . D. I = . 15 15 75 25 Hướng dẫn giải Chọn C Cách 1: (Dùng công thức)
Với 2 f ( x) + 3 f (1− x) = x 1− x ta có A = 2; B = 3. 1 1 1 Casio
Suy ra: ∫ f (x)dx = x 1− ∫ xdx = ( ) 4 0, 05 3 = . 2 + 3 75 0 0 Áp dụng kết quả “Cho .
A f (ax + b) + .
B f (−ax + c) = g ( x) (Với 2 2
A ≠ B ) khi đó  x − b   x − c  . A g − .   B g   f ( x)  a   −a  = 2 2 ”. A − B
2g x − 3g 1− x
2x 1− x − 3(1− x) x
Ta có: 2 f ( x) + 3 f (1− x) = x 1− x = g ( x) ⇒ f ( x) ( ) ( ) = = . 2 2 2 − 3 5 − 1 1 2 1− − 3 1− Casio Suy ra: = ∫ ( ) ( ) = ∫ x x x x I f x dx dx = ( ) 4 0, 05 3 = . 5 − 75 0 0
Cách 3: (Dùng phương pháp đổi biến – nếu không nhớ công thức) 1 1 1 Casio 4
Từ 2 f ( x) + 3 f (1− x) = x 1− x ⇒ 2 f ( x) dx + 3 f (1− x) dx = x 1− ∫ ∫ ∫ xdx = 0, 2 (6) = (∗)Đặt 15 0 0 0
u = 1− x ⇒ du = −dx ; Với x = 0 ⇒ u = 1 và x = 1 ⇒ u = 0 . 1 1 1 Suy ra
f (1− x) dx = f (u) du = ∫ ∫
∫ f (x)dx thay vào (∗) , ta được: 0 0 0 2 2 f ( x) 4 dx = ⇔ f (x) 4 5 dx = ∫ ∫ . 15 75 0 0
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 4
Câu 163: Cho f ( x) và g ( x) là hai hàm số liên tục trên [ 1,
− ]1 và f (x) là hàm số chẵn, g (x) là 1 1
hàm số lẻ. Biết f
∫ (x)dx = 5 và g
∫ (x)dx = 7. Mệnh đề nào dưới đây sai? 0 0 1 1 A. f
∫ (x)dx =10. B. g
∫ (x)dx =14. 1 − 1 − https://toanmath.com/ 1 1 C. f
∫  (x)+ g(x)dx =10  . D. f
∫  (x)− g(x)dx =10  . 1 − 1 − Hướng dẫn giải
Nhớ 2 tích chất sau để làm trắc nghiệm nhanh: a a a
Câu 164: Nếu hàm f ( x) CHẴN thì f
∫ (x)dx = 2 f
∫ (x)dx 2. Nếu hàm f (x) LẺ thì f ∫ (x)dx = 0 −a 0 −a
Nếu chứng minh thì như sau: 1 0 1 Đặt A = f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx 1 − 1 − 0
  1 A 2 A 0 A = f x dx ∫
. Đặt t = −x ⇒ dt = −dx 1 ( ) 1 − Đổi cận: 0 1 1 ⇒ A = f t − . −dt = f t
− dt = f −x dx ∫ ∫ ∫
(Do tích phân xác định không phụ thuộc vào biến 1 ( ) ( ) ( ) ( ) 1 0 0 1 số tích phân) = f
∫ (x)dx (Do f (x) là hàm chẵn ⇒ f (−x) = f (x) ) 0 1 1 1 Vậy A = f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx =10 (1) 1 − 0 0 1 0 1 Đặt B = g
∫ (x)dx = g
∫ (x)dx+ g ∫ (x)dx 1 − 1 − 0
  1 B 2 B 0 B = g x dx ∫
. Đặt t = −x ⇒ dt = −dx 1 ( ) 1 − Đổi cận: 0 1 1 ⇒ B = g t
− . −dt = g t
− dt = g −x dx ∫ ∫ ∫
(Do tích phân xác định không phụ thuộc vào biến 1 ( ) ( ) ( ) ( ) 1 0 0 1
số tích phân) = − g
∫ (x)dx (Do f (x) là hàm chẵn ⇒ g(−x) = −g(x) ) 0 1 1 1 Vậy B = g
∫ (x)dx = − g
∫ (x)dx + g
∫ (x)dx = 0 (2) 1 − 0 0 Từ (1) và (2) Chọn B 0
Câu 165: Cho hàm số y = f ( x) là hàm lẻ và liên tục trên [ 4; − 4] biết f
∫ (−x)dx = 2 và 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 2 − 2 4 f ∫ ( 2
− x)dx = 4 . Tính I = f
∫ (x)dx . 1 7 T 1 7 T 1 7 T 1 0 A. I = 10 − . B. I = 6 − .
C. I = 6 . D. I = 10 . 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T Hướng dẫn giải 1 7 T Chọn B 1 7 T a 2 x 2 x
Cách 1: Sử dụng công thức: f ( x) f ∫ (ax +b) 1 dx = f
∫ (ax)dx và tính chất f
∫ (x)dx = 0 với là 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T 1 7 T a −a 1 x 1 x
hàm số lẻ trên đoạn [− ; a a]. 1 7 T 1 7 T https://toanmath.com/ Áp dụng, ta có: 2 2 − • − − = f ∫ (− x) 4 1 x = − f ∫ (x) 2 1 4 2 d dx = f
∫ (x)dx ⇔ f ∫ (x)dx =8. 2 − 4 2 2 − 4 − 1 0 2 • 2 = f ∫ (−x) 0 dx = − f ∫ (x) 2 = f ∫ (x) ⇔ f ∫ (x) = 2 2 0 0 2 − 4 2 − 0 4 Suy ra: 0 = f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx+ f ∫ (x)dx 4 − 4 − 2 − 0 ⇔ 0 = 8 + ( 2 f ∫ (x) 2 dx − f
∫ (x)dx + I ⇔ 0 = 8+(0−2)+ I ⇔ I = 6 − . 2 − 0 ) 0
Cách 2: Xét tích phân f
∫ (−x)dx = 2. 2 −
Đặt −x = t ⇒ dx = −dt . 0 0 2 Đổi cận: khi x = 2
− thì t = 2; khi x = 0 thì t = 0 do đó f
∫ (−x)dx =− f ∫ (t)dt = f ∫ (t)dt 2 − 2 0 2 2 ⇒ f
∫ (t)dt = 2 ⇒ f ∫ (x)dx = 2. 0 0
Do hàm số y = f ( x) là hàm số lẻ nên f ( 2
− x) = − f (2x). 2 2 2 Do đó f ∫ ( 2
− x)dx = − f
∫ (2x)dx ⇒ f (2x)dx = 4 − ∫ . 1 1 1 2 Xét f (2x) dx ∫ . 1 Đặt 2x = 1 t ⇒ dx = dt . 2 2 4 Đổ 1
i cận: khi x = 1 thì t = 2; khi x = 2 thì t = 4 do đó f (2x) dx = f (t ) dt = 4 − ∫ ∫ 2 1 2 4 4 ⇒ f (t)dt = 8 − ∫
⇒ f (x)dx = 8 − ∫ . 2 2 4 2 4 Do I = f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx = 2−8 = 6 − . 0 0 2 1 f (2x) 2
Câu 166: Cho hàm số chẵn y = f ( x) liên tục trên  và dx = 8 ∫ . Tính f ( x) dx ∫ . 1+ 2x 1 − 0 A. 2 . B. 4 . C. 8 . D. 16 . Hướng dẫn giải Chọn D 1 f (2x) 2 f ( x) Ta có dx = 8 ⇔ dx = 16 ∫ ∫ . 1+ 2x x + 1 − 2 − 1 2 t 2 f ( x) 2 − f ( t − ) 2 − 2 f (t )
Đặt t = −x ⇒ dt = −dx , khi đó 16 = I = dx = − dt = dt ∫ ∫ ∫ . x −t t + + + 2 − 1 2 2 1 2 2 1 2 x 2 f ( x) 2 − 2 f ( x) 2 2 Suy ra 2I = dx + dx = f x x = f x x ∫ ∫ ∫ ∫ . x x ( )d 2 ( )d + + 2 − 1 2 2 1 2 2 − 0 2 Vậy f ∫ (x)dx =16 . 0 https://toanmath.com/ 1
Câu 167: Cho f ( x) là hàm số chẵn liên tục trong đoạn [ 1 − ; ] 1 và f
∫ (x)dx = 2 . Kết quả 1 − 1 f ( x) I = dx ∫ bằng 1+ ex 1 −
A. I = 1.
B. I = 3 .
C. I = 2 . D. I = 4 . Hướng dẫn giải Chọn A 1 f ( x) 0 f ( x) 1 f ( x) I = dx = dx +
dx = I + I ∫ ∫ ∫ x x x 1 2 1+ e 1+ e 1+ e 1 − 1 − 0 0 f ( x) Xét I = dx ∫ 1 1+ ex 1 − Đặt x = t
− ⇒ dx = −dt , đổi cận: x = 0 ⇒ t = 0, x = 1 − ⇒ t =1 0 f ( x) 1 et . f x I = −dt = dt ∫ ∫ . 1 −t ( ) ( ) 1+ e 1+ et 1 0
1 et . f (t )
1 ex. f ( x) Lại có dt = dx ∫ ∫ . 1+ et 1+ ex 0 0 1 f ( x) 1 t
et . f (t ) 1 f (t) 1 (1+ e ). f (t) 1 1 1 Suy ra: I = dx = dt + dx = dt = f t t = f t t = ∫ ∫ ∫ ∫ ∫ ∫ . x t t t ( )d ( )d 1 1+ e 1+ e 1+ e 1+ e 2 1 − 0 0 0 0 1 − 1 2 1
Câu 168: Cho y = f ( x) là hàm số chẵn và liên tục trên .  Biết f
∫ (x)dx = f
∫ (x)dx =1. Giá trị 2 0 1 2 f ( x) của dx ∫ bằng 3x +1 2 − A. 1. B. 6 . C. 4 . D. 3 . Hướng dẫn giải Chọn D
Cách 1: Sử dụng tính chất của hàm số chẵn a f ( x) a Ta có: dx = f x x ∫ ∫
, với f ( x) là hàm số chẵn và liên tục trên [− ; a a]. x ( )d b +1 −a 0 Áp dụng ta có: 2 f ( x) 2 1 2 dx = f x x = f x x + f x x = + = ∫ ∫ ∫ ∫ x ( )d ( )d ( )d 1 2 3 3 +1 2 − 0 0 1 1 2 1 1 2 Cách 2: Do
f ( x) dx = ∫ f
∫ (x)dx =1 ⇒ f (x)dx 1 = ∫ và f ∫ (x)dx = 2 2 0 1 0 1 1 2 2 ⇒ f
∫ (x)dx+ f
∫ (x)dx = f ∫ (x)dx = 3. 0 1 0 2 f ( x) 0 f ( x) 2 f ( x) Mặt khác dx = ∫ dx + dx ∫ ∫
và y = f ( x) là hàm số chẵn, liên tục trên  3x +1 3x +1 3x +1 2 − 2 − 0
⇒ f (−x) = f (x) x ∀ ∈  . 0 f ( x) Xét I = dx ∫
. Đặt t = −x ⇒ dx = −dt 3x +1 2 − https://toanmath.com/ 0 2 f ( x) 0 f ( t − ) f ( t − ) 2 3t f t 2 3x f ( x) Suy ra I = dx = ∫ − dt = ∫ dt = ∫ ( ) dt = ∫ dx ∫ 3x +1 3−t +1 1 3t +1 3x +1 2 − 2 0 +1 0 0 3t 2 (3x + ) 2 1 f ( x) f ( x) 0 2 2 x 2 ⇒ f x f x 3 f x f x dx = ∫ ( ) ( ) dx + dx = ∫ ∫ ( ) ( ) dx + dx = ∫ ∫ dx = ∫ 3x +1 x 3x +1 3x +1 3x +1 3x +1 3 +1 2 − 2 − 0 0 0 0 2 f ∫ (x)dx = 3. 0
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5
“ Cho hàm số y = f ( x ) thỏa mãn g f  ( x) = x
và g (t) là hàm đơn điệu ( luôn đồng biến hoặc b
nghịch biến) trên .Hãy tính tích phân I = f
∫ (x)dx “ a
Cách giải: Đặt y = f ( x ) ⇒ x = g ( y) ⇒ dx = g′( y) dy
x = a → g
(y) = a ⇔ y =α Đổi cận 
x = b → g
(y) = b ⇔ y = β b β Suy ra I = f
∫ (x)dx = yg ∫ (y)dy a α f (x) 3
f (x) + f (x) = x, x ∀ ∈
Câu 169: Cho hàm số
liên tục trên thỏa mãn . Tính 2 I = f
∫ (x)dx 0 3 1 5
A. I = 2 . B. I = . C. I = . D. I = . 2 2 4 Hướng dẫn giải Chọn D
Đặt y = f (x) 3
⇒ x = y + y ⇒ dx = ( 2 3y + ) 1 dy 3 Đổ
x = 0 → y + y = 0 ⇔ y = 0 i cận  3
x = 2 → y + y = 2 ⇔ y = 1 Khi đó 2 I = f ( x) 1 dx = y (3y + ) 1 5 2 1 dy = ( 3
3y + y)dy = ⇒ ∫ ∫ ∫ đáp án D 0 0 0 4
Câu 170: Cho hàm số f ( x) liên tục trên  thỏa mãn 3 f ( x) 2 2
− 3 f (x) + 6 f (x) = x, x ∀ ∈ . Tính 5 tích phân I = f
∫ (x)dx . 0 5 5 5 5 A. I = . B. I = . C. I = . D. I = . 4 2 12 3 Hướng dẫn giải Chọn B
Đặt y = f (x) 3 2
⇒ x = 2y − 3y + 6y ⇒ x = ( 2 d 6 y − y + ) 1 dy . Đổ 3 2 3 2
i cận: với x = 0 ⇒ 2 y − 3y + 6 y = 0 ⇔ y = 0 và x = 5 ⇒ 2 y − 3y + 6 y = 5 ⇔ y = 1. 1 1 1 Khi đó 5 I =
f ( x) dx = .6 y ( 2 y − y + ∫ ∫ )1dy = 6 ( 3 2
y − y + y )dy = ∫ . 2 0 0 0 https://toanmath.com/
Câu 171: Cho hàm số f ( x) liên tục trên  thỏa mãn 3
x + f ( x) + 2 f ( x) = 1 , x ∀ ∈ . Tính 1 I = f
∫ (x)dx . 2 − 7 7 7 5 A. I = . B. I = . C. I = . D. I = . 4 2 3 4 Hướng dẫn giải Chọn A
Đặt y = f (x) 3
⇒ x = − y − y + ⇒ x = ( 2 2 1 d 3
− y − 2)dy . Đổ 3 3 i cận: Với x = 2
− ⇒ −y − 2y +1= 2
− ⇔ y =1; x =1⇒ −y − 2y +1=1⇔ y = 0 . 0
Khi đó: I = y ( 7 2 3 − y − 2)dy = ∫ . 4 1
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5 b dx b − a
Bài toán: “ Cho f ( x) f (a + b − x) 2 .
= k , khi đó I = = ∫ k + f x k a ( ) 2 Chứng minh:dt = −dx
Đặt t = a + b − x ⇒  ( ) 2 k
và x = a ⇒ t − b ; x = b ⇒ t = a . f x =  f  (t) b b b Khi đó dx dx 1 f ( x) dx I = = = ∫ ∫ ∫ . k + f x k k k + f x a ( ) 2 a a ( ) k + f (t) b dx
1 b f ( x) dx 1 b 1 b − a 2I = + = ∫ ∫ dx = ∫
(b − a) ⇒ I = . k + f x k k + f x k k 2k a ( ) a ( ) a
Câu 172: Cho hàm số f ( x) liên tục và nhận giá trị dương trên [0; ]
1 . Biết f ( x). f (1− x) = 1 với 1 dx x ∀ ∈[0; ]
1 . Tính giá trí I = ∫ 1+ f x 0 ( ) 3 1 A. . B. . C. 1. D. 2 . 2 2 Hướng dẫn giải Chọn B f x 1
Ta có: 1+ f ( x) = f ( x) f (1− x) + ( ) f ( x) ⇒ = 1+ f ( x) f (1− x) +1 1 dx Xét I = ∫ . 1+ f x 0 ( )
Đặt t =1− x ⇔ x =1− t ⇒ dx = −dt . Đổi cận: x = 0 ⇒ t =1; x =1⇒ t = 0 . 0 1 1 1 dt dt dx f ( x) Khi đó dx I = − = = = ∫ ∫ ∫ ∫ 1+ f 1− t 1+ f 1− t 1+ f 1− x 1+ f x 1 ( ) 0 ( ) 0 ( ) 0 ( ) 1 1 dx f ( x) 1 dx 1+ f ( x) 1 1 Mặt khác + = dx = dx = 1 ∫ ∫ ∫ ∫
hay 2I = 1. Vậy I = . 1+ f x 1+ f x 1+ f (t) 2 0 ( ) 0 ( ) 0 0
Câu 173: Cho hàm số f ( x) liên tục trên  , ta có f ( x) > 0 và f (0). f (2018 − x) = 1. Giá trị của 2018 dx tích phân I = ∫ 1+ f x 0 ( ) https://toanmath.com/
A. I = 2018 .
B. I = 0
C. I = 1009 D. 4016 Hướng dẫn giải Chọn C 2018 1 2018 − 0 ta có I = dx = = 1009 ∫ . 1+ f x 2.1 0 ( )
Câu 174: Cho hàm số y = f ( x) có đạo hàm, liên tục trên  và f ( x) > 0 khi x ∈[0;5] Biết . 5 dx
f ( x). f (5 − x) = 1 tính tích phân I = ∫ . , 0 1+ f ( x) 5 5 5 A. I = . B. I = . C. I = . D. I = 10 . 4 3 2 Hướng dẫn giải Chọn C
Đặt x = 5 − t ⇒ dx = −dt
x = 0 ⇒ t = 5 ; x = 5 ⇒ t = 0 0 5 dt f (t ) dt 1 I = − = ∫ ∫
(do f (5 − t ) = )
5 1+ f (5 − t ) 0 1+ f (t ) f (t ) 5 ⇒ 2I = dt = 5 ∫ 5 ⇒ I = . 0 2 3
Câu 175: Cho hàm số y = f ( x) liên tục trên  và thỏa mãn f (4 − x) = f ( x) . Biết xf ∫ (x)dx = 5. 1 3 Tính tích phân f ( x) dx ∫ . 1 5 7 9 11 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải Chọn A
Đặt t = 4 − x ⇒ dt = −dx và x =1⇒ t = 3 ; x = 3 ⇒ t =1. 3 3 3 3 Khi đó: 5 = xf
∫ (x)dx = ∫(4−t) f (4−t)dt = ∫(4− x) f (4− x)dx = ∫(4− x) f (x)dx . 1 1 1 1 3 3 3 5 Suy ra: 10 = xf
∫ (x)dx+ ∫(4− x) f (x)dx = 4 f (x)dx = ∫ . 2 1 1 1
Câu 176: Cho hàm số y = f ( x) có đạo hàm liên tục trên R và f ( x) > 0 khi x ∈ [0; a] ( a > 0 ). Biết a dx
f ( x). f (a − x) = 1, tính tích phân I = ∫ . 1+ f x 0 ( ) a a a A. I = .
B. I = 2a . C. I = . D. I = . 2 3 4 Hướng dẫn giải: a dx I = ∫
(1) Đặt t = a − x ⇒ dt = −dx Đổi cận: 1+ f x 0 ( ) 0 a dt 1 a 1 ⇒ I = − = dt = dx ∫ ∫ ∫
(2) (Tích phân xác định không phụ 1+ f a − t + f a − t + f a − x a ( ) 1 1 0 ( ) 0 ( )
thuộc vào biến số tích phân) a  1 1 
(1) + (2) ⇒ 2I = ∫  +  dx 1+ f x 1+ f a − x 0  ( ) ( ) https://toanmath.com/ 1+ ( − ) +1+ ( ) 2 2 + ( − ) + ( ) a f a x f x f a x f x = a dx =
dx = dx = a ∫ ∫ ⇒ I =
1+ f ( x). f (a − x) + f ( x) + f (a − x)
2 + f a − x + f x 2 0 ( ) ( ) 0 Chọn A
 f (x). f (a − x) =1
Câu 177: Cho f ( x) là hàm liên tục trên đoạn [0; a] thỏa mãn  và  f
 ( x) > 0, x ∀ ∈[0;a] a dx ba = , ∫
trong đó b , c là hai số nguyên dương và b là phân số tối giản. Khi đó 1+ f x c c 0 ( )
b + c có giá trị thuộc khoảng nào dưới đây? A. (11; 22). B. (0;9). C. (7; 2 ) 1 . D. (2017; 2020). Hướng dẫn giải Chọn B
Cách 1. Đặt t = a − x ⇒ dt = −dx
Đổi cận x = 0 ⇒ t = ;
a x = a ⇒ t = 0. a 0 dx −d a t d a x d a x f ( x) Lúc đó dx I = = = = = ∫ ∫ ∫ ∫ ∫ 1+ f x 1+ f a − t 1+ f a − x 1 1+ f x 0 ( ) a ( ) 0 ( ) 0 0 ( ) 1+ f (x) a d a x ( )d a f x x
Suy ra 2I = I + I = + = 1dx = a ∫ ∫ ∫ 1+ f x 1+ f x 0 ( ) 0 ( ) 0 Do đó 1 I =
a ⇒ b = 1; c = 2 ⇒ b + c = 3. 2
Cách 2. Chọn f ( x) = 1 là một hàm thỏa các giả thiết. 1
Dễ dàng tính được I =
a ⇒ b = 1; c = 2 ⇒ b + c = 3. 2 https://toanmath.com/
TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 6
Câu 178: Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [1;4], đồng biến trên đoạn [1;4] và thỏa 4
mãn đẳng thức x + 2 .x f (x) =  ′( ) 2 f x    , x
∀ ∈[1;4] . Biết rằng f ( ) 3 1 = , tính I = f
∫ (x)dx ? 2 1 1186 1174 1222 1201 A. I = . B. I = . C. I = . D. I = . 45 45 45 45 Hướng dẫn giải Chọn A f ′( x) Ta có x + 2 .
x f ( x) =  ′( ) 2 ⇒ = f x  
 ⇒ x. 1+ 2 f ( x) = f ′( x) x , x ∀ ∈[1;4] . 1+ 2 f ( x) f ′( x) df ( x) Suy ra = + ∫ ∫ ⇔ dx = xdx + C ∫ ∫
+ f (x) dx xdx C 1 2 1+ 2 f ( x) 2 3  2 4  2  x +  −1 3 ⇒ 3 3   1+ 2 f ( x) 2 2
= x + C . Mà f ( ) 3 1 = 4
⇒ C = . Vậy f ( x) = . 3 2 3 2 4 1186
Vậy I = f ( x) dx = ∫ . 45 1 3 2 f x − x 1 − 2x
Câu 179: Cho hàm số y = f ( x) có đạo hàm trên thỏa mãn 3 f ′( x) ( ) .e − = 0 và 2 f ( x) 7 f (0) = 1. Tích phân .
x f ( x) dx ∫ bằng 0 2 7 15 45 5 7 A. . B. . C. . D. . 3 4 8 4 Hướng dẫn giải Chọn C 3 2 f x − x 1 − 2x 3 2
Ta có 3 f ′( x) ( ) .e − = 0 ⇔ 2
f ( x) f ( x) f (x) x 1 3 . .e 2 .e x + ′ = 2 f ( x) 3 f (x) 2 x 1 + Suy ra e
= e + C . Mặt khác, vì f (0) =1 nên C = 0. 3 Do đó f (x) 2 x 1 e e + = 3 ⇔ f (x) 2
= x +1 ⇔ f (x) 3 2 = x +1 . 7 7 7 1 3 2 2   45 Vậy = (x + ) 7 3 .
x f ( x) dx ∫ 3 2 = . x x +1 dx ∫ 3 2 = x +1 d ( 2 x + ∫ )1 1 x +1   = . 2 8 0 8 0 0 0 1
Câu 180: Cho hàm số f ( x) 4 3 2
= x + 4x − 3x − x +1, x ∀ ∈ . Tính 2 I = f
∫ (x).f ′(x)dx. 0 7 7 A. 2 . B. 2 − . C. − . D. . 3 3 Hướng dẫn giải Chọn D
Đặt t = f (x) ⇒ dt = f ′(x)dx . Đổi cận: x = 0 ⇒ t = f (0) =1, x =1⇒ t = f ( ) 1 = 2 . 2 2 3 Khi đó t 8 1 7 2
I = t dt = = − = ∫ . 3 3 3 3 1 1 https://toanmath.com/
Câu 181: Cho hàm số f ( x) có đạo hàm liên tục trên khoảng (0; )
1 và f ( x) ≠ 0 , x ∀ ∈(0; ) 1 . Biết  1   3  rằng f = a   , f
 = b và x + xf ′( x) = 2 f ( x) − 4 , x ∀ ∈(0; ) 1 . Tính tích phân    2  2   π 3 2 sin .
x cos x + 2sin 2x I = dx ∫
theo a và b . 2 π f (sin x) 6 3a b 3b a 3b a 3a b A. I  . B. I  . C. I  . D. I  . 4ab 4ab 4ab 4ab Hướng dẫn giải Chọn D x ∀ ∈(0; ) 1 ta có:
x + xf ′( x) = 2 f ( x) − 4 ⇔ x + 4 = 2 f ( x) − xf ′( x) 2
⇒ x + x = xf (x) 2 4 2 − x f ′(x) ′ 2 x + 4x 2xf ( x) 2 − x f ′( x) 2 2 +   ⇔ = x 4x x ⇔ =   . 2 f ( x) 2 f ( x) 2 f ( x)  f (x)    π π 3 2 3 2 sin .
x cos x + 2sin 2x sin . x cos x + 4sin . x cos x Tính I = dx = dx ∫ ∫ 2 π f (sin x) 2 π f (sin x) 6 6 π Đặ π 1 3
t t = sin x ⇒ dt = cos d
x x , đổi cận x = ⇒ t = , x = ⇒ t = . 6 2 3 2 2 2  3  3 3  1    2 2 2   t + 4t 2 t 2    2  3 1 3a − b Ta có I = dt ∫ = = − = − = . 2 f t f (t )    1  1 ( ) 1 3 4b 4a 4ab f f     2 2  2 2   
Câu 182: Cho hàm số f liên tục, f ( x) > 1
− , f (0) = 0 và thỏa f ′(x) 2 x +1 = 2x
f ( x) +1 . Tính f ( 3) . A. 0 . B. 3 . C. 7 . D. 9 . Hướng dẫn giải Chọn B f ′ x 2x 2
Ta có f ′( x) x +1 = 2x f ( x) ( ) +1 ⇔ = f ( x) 2 +1 x +1 3 f ′( x) 3 2x ⇔ dx = dx ⇔ f ∫ ∫ (x) 3 3
+1 = x +1 ⇔ f (x) 3 2 +1 =1 + + 0 f ( x) 2 0 0 0 1 0 x 1
⇔ f ( 3)+1− f (0)+1 =1⇔ f ( 3)+1 = 2 ⇔ f ( 3) = 3. 5
Câu 183: Cho hàm số f ( x) liên tục trên  và f
∫ (x)dx = 4, f (5) = 3, f (2) = 2. Tính 2 2 3 I = x f ′( 2 x + ∫ )1dx 1 A. 3 . B. 4 . C. 1. D. 6 . https://toanmath.com/ Hướng dẫn giải Chọn A Đặt 2
t = x +1 ⇒ dt = 2 d x x . 5 1
x = 1 ⇒ t = 2 ; x = 2 ⇒ t = 5 . Khi đó I = (t − ∫
)1 f ′(t)dt . 2 2
Đặt u = t −1⇒ du = dt ; dv = f ′(t)dt, chọn v = f (t) . 5 5 1 1 I =
(t − ) f (t) 1 1 − f
∫ (t)dt = (4 f (5)− f (2))−2 = 3. 2 2 2 2 2 f (2 x − ) 1 ln x
Câu 184: Cho hàm số f ( x) liên tục trên đoạn [1;4] và thỏa mãn f ( x) = + . Tính tích x x 4 phân I = f
∫ (x)dx . 3 A. 2
I = 3 + 2 ln 2 . B. 2 I = 2 ln 2 . C. 2 I = ln 2 . D. I = 2 ln 2 . Hướng dẫn giải Chọn B  −  4 4 f (2 x )1 4 f (2 x − ) ln x 4 1 ln x Ta có f ( x) dx ∫ =  +  dx ∫ = +  dx dx ∫ ∫ . x x x x 1 1   1 1 4 f (2 x − ) 1 Xét K = dx ∫ . x 1 Đặ t +1 dx
t 2 x −1 = t ⇒ x = ⇒ = dt . 2 x 3 3 ⇒ K = f
∫ (t)dt = f ∫ (x)dx. 1 1 4 4 2 ln x 4 ln x Xét M = dx ∫ = ln d x ∫ (ln x) = = 2 2 ln 2 . x 2 1 1 1 4 3 4 Do đó f
∫ (x)dx = f ∫ (x) 2 dx + 2 ln 2 ⇒ f ∫ (x) 2 dx = 2 ln 2 . 1 1 3 π 2 16 f x 2 ( )
Câu 185: Cho hàm số f ( x) liên tục trên  và thỏa mãn cot . x f ∫ (sin x)dx = dx = 1 ∫ . Tính π x 1 4 1 f (4x) tích phân dx ∫ . x 1 8 3 5
A. I = 3 . B. I = .
C. I = 2 . D. I = . 2 2 Hướng dẫn giải Chọn D π 2 16 f ( x ) Đặ 2 t I = cot .
x f sin x dx = 1 ∫ == = 1 ( ) , I dx 1 ∫ . 2 π x 1 4  Đặt 2
t = sin x ⇒ dt = 2 sin . x cos d x x 2 = 2sin . x cot d x x = 2t.cot d x x . https://toanmath.com/ π π x 4 2 1 t 1 2 π 1 1 2 4 4 1 1 1 f (4x) 1 f (4x) 1 f (t ) I = cot . x f ∫ ( 2 sin x dx = = d ∫ (4x) f ∫ (t) 1 = = dx ∫ 1 ) . dt dt ∫ . π 2t 2 t 2 4x 2 x 1 1 1 1 4 2 2 8 8 1 4 f (4x) Suy ra dx = 2I = 2 ∫ 1 x 1 8
Đặt t = x ⇒ 2tdt = dx . x 1 16 t 1 4 16 f ( x ) 4 f (t) 4 f (t ) 1 f (4x) 1 f (4x) I = dx ∫ = 2tdt ∫ = 2 dt ∫ = 2 d ∫ (4x) = 2 2 dx ∫ . x 2 t t 4x x 1 1 1 1 1 4 4 1 f (4x) 1 1 Suy ra dx = I = ∫ 2 x 2 2 1 4 Khi đó, ta có: 1 1 f (4x) 4 f (4x) 1 f (4x) dx = dx + dx ∫ ∫ ∫ 1 5 = 2 + = . x x x 1 1 1 2 2 8 8 4
Câu 186: Xét hàm số f ( x) liên tục trên [0; ]
1 và thỏa mãn điều kiện x f ( 2
x ) + f ( − x) 2 4 . 3 1 = 1− x . 1 Tích phân I = f
∫ (x)dx bằng: 0 π π π π A. I = . B. I = . C. I = . D. I = . 4 6 20 16 Hướng dẫn giải Chọn C
Vì f ( x) liên tục trên [0; ] 1 và x f ( 2
x ) + f ( − x) 2 4 . 3 1 = 1− x nên ta có 1 1 1 1 4 . x f ∫ 2 2  (x ) 1 2 + 3 f (1− x) 2  dx = 1− x dx  ∫ ⇔ 4 . x f ∫
(x )dx+ 3f
∫ (1− x)dx = 1− x dx ∫ ( ) 1 . 0 0 0 0 0 1 1 1 2 Mà 4 . x f ( 2 x )dx ∫ = 2 f
∫ ( 2x)d( 2x) t=x  →2 f
∫ (t)dt = 2I 0 0 0 1 1 1 và 3 f
∫ (1− x)dx = 3 − f
∫ (1− x)d(1− x) u 1=−x →3 f
∫ (u)du = 3I 0 0 0 π π π 1 Đồ 2 2 1 π ng thời 2 1− x dx ∫ 2 x=sin t 2 →
1− sin t .cos tdt ∫ 2 = cos tdt ∫
= ∫(1+ cos2t)dt = . 2 4 0 0 0 0 Do đó, ( ) π π 1 ⇔ 2I + 3I = hay I = . 4 20 https://toanmath.com/ 1 2 9
Câu 187: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 1,  f ′
∫ (x) dx =  5 0 1 2 1 và
f ( x )dx = ∫ . Tính tích phân I = f
∫ (x)dx . 5 0 0 3 1 3 1 A. I = . B. I = . C. I = . D. I = . 5 4 4 5 Hướng dẫn giải Chọn B Đặ 2 t t =
x ⇒ t = x ⇒ dx = 2tdt . Đổi cận x = 0 ⇒ t = 0; x = 1⇒ t = 1 1 1 1 1 1 1 Suy ra f
∫ ( x)dx = 2 t.f
∫ (t)dt ⇔ t.f (t)dt = ∫ . Do đó ⇔ .
x f ( x) dx = ∫ 5 5 0 0 0 0 1 1 2 1 2 x x 1 2 1 x Mặt khác . x f
∫ (x)dx = f (x) − f ′ ∫ (x)dx = − f ′ ∫ (x)dx . 2 2 2 2 0 0 0 0 1 2 x 1 1 3 1 3 Suy ra
f ′( x) dx = − = ∫ 2
⇒ x f ′(x)dx = ∫ 2 2 5 10 5 0 0 1 Ta tính đượ 2 9 c ( 2 3x ) dx = ∫ . 5 0 1 1 1 1 Do đó  2 f ′ ∫ (x) 2 2
 dx − 2 3x f ′  ∫ (x)dx + ∫( 2
3x )2dx = 0 ⇔ ∫( f ′( x) 2 − 3x ) dx = 0 0 0 0 0 ⇔ f ′(x) 2
− 3x = 0 ⇔ f ′(x) 2 = 3x ⇔ ( ) 3
f x = x + C . Vì f ( ) 1 = 1 nên ( ) 3 f x = x 1 1 1 Vậy I = f ( x) 3 dx = x dx = ∫ ∫ . 4 0 0 https://toanmath.com/
DẠNG 4: PHƯƠNG PHÁP TỪNG PHẦN BÀI TẬP 2
Câu 188. Cho hàm số y = f ( x) có đạo hàm f ′( x) liên tục trên [0; 2] và f (2) = 3 , f ∫ (x)dx = 3. 0 2 Tính . x f ′ ∫ (x)dx . 0 A. 3 − . B. 3 . C. 0 . D. 6 .
Câu 189. Cho hàm số y = f ( x) có đạo hàm là f '( x) liên tục trên đoạn [0; 1] và f ( ) 1 = 2 . Biết 1 1 f
∫ (x)dx =1, tính tích phân I = .xf ' ∫ (x)dx. 0 0
A. I = 1. B. I = 1 − .
C. I = 3 . D. I = 3 − . 1
Câu 190. Cho hàm số f ( x) thỏa mãn ∫(x + )
1 f '( x) dx = 10 và 2 f ( )
1 − f (0) = 2 . Tính 0 1 I = f ∫ (x)dx. 0
A. I = 8 . B. I = 8 − .
C. I = 4 . D. I = 4 − .
Câu 191. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; 2] và thỏa mãn f (2) = 16 , 2 1 f
∫ (x)dx = 4. Tính tích phân I = .x f ′ ∫ (2x)dx . 0 0
A. I = 12 .
B. I = 7 .
C. I = 13 . D. I = 20 .
Câu 192. Cho hàm số y = f ( x) có đạo hàm liên tục trên  và thỏa mãn f ( 2 − ) =1, 2 0 f
∫ (2x−4)dx =1. Tính xf ′
∫ (x)dx. 1 2 −
A. I = 1 .
B. I = 0 . C. I = 4 − . D. I = 4 . 5
Câu 193. Cho hàm số y f x thỏa mãn f  3 x  3x  
1  3x  2, x  .  Tính I  .
x f xdx  . 1 5 17 33 A. . B. . C. . D. 1761 − . 4 4 4 e f ( x)
Câu 194. Cho hàm số f ( x) liên tục trong đoạn [1;e] , biết dx = 1 ∫ , f (e) = 1. Khi đó x 1 e I = f ′ ∫ (x).ln d x x bằng 1
A. I = 4 .
B. I = 3 .
C. I = 1. D. I = 0 .
Câu 195. Cho hàm số y = f ( x) có đạo hàm liên tục trên thỏa mãn π   2 f ( x) π + f − x = sin . x cos x  
, với mọi x ∈ và f (0) = 0 . Giá trị của tích phân . x f ′ ∫
(x)dx bằng  2  0 π 1 π 1 A. − . B. . C. . D. − . 4 4 4 4 https://toanmath.com/ 1
Câu 196. Cho hàm số f ( x) thỏa f (0) = f ( ) 1 = 1. Biết x e f
∫  (x)+ f '(x)dx = ae+b  . Tính biểu 0 thức 2018 2018 Q = a + b .
A. Q = 8 .
B. Q = 6 .
C. Q = 4 . D. Q = 2 .
Câu 197. Cho hàm số f ( x) có đạo hàm trên  thỏa mãn ′( ) − ( ) 2017 2018 2018 = 2018. .e x f x f x x với
mọi x ∈  và f (0) = 2018. Tính giá trị f ( ) 1 . A. f ( ) 2018 1 = 2019e . B. f ( ) 2018 1 2018.e− = . C. f ( ) 2018 1 = 2018.e . D. f ( ) 2018 1 = 2017.e . 1
Câu 198. Cho hàm số y = f ( x) với f (0) = f ( )
1 = 1. Biết rằng: ex f
∫  (x)+ f ′(x)dx = ae+b  Tính 0 2017 2017 Q = a + b . A. 2017 Q = 2 +1.
B. Q = 2 .
C. Q = 0 . D. 2017 Q = 2 −1. 5
Câu 199. Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [0;5] và f (5) = 10 , xf ′ ∫ (x)dx = 30 0 5 . Tính f ( x) dx ∫ . 0 A. 20 . B. 30 − . C. 20 − . D. 70 .
Câu 200. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2]. Biết 2 67 2 rằng F ( )
1 = 1, F (2) = 4 , G ( ) 3 1 =
, G (2) = 2 và f ( x)G ( x) dx = ∫
. Tính F ( x) g ( x) dx ∫ 2 12 1 1 11 145 11 145 A. . B. − . C. − . D. . 12 12 12 12 1
Câu 201. Cho hàm số f ( x) có đạo hàm liên tục trên [0; ]
1 thỏa mãn x f ′
∫  (x)−2dx = f  ( )1. Giá 0 1 trị của I = f
∫ (x)dx bằng 0 A. 2 − . B. 2 . C. 1 − . D. 1. 2 2
Câu 202. Cho hàm số y = f ( x) liên tục trên đoạn [1;2] và ∫(x − )
1 f ′( x) dx = a . Tính f ( x)dx ∫ 1 1
theo a và b = f (2) .
A. b − a .
B. a − b .
C. a + b .
D. −a − b . 2
Câu 203. Cho hàm số f ( x) liên tục trên  và f (2) = 16 , f
∫ (x)dx = 4. Tính tích phân 0 1 I = . x f ′ ∫ (2x)dx . 0
A. I = 13 .
B. I = 12 .
C. I = 20 . D. I = 7 .
Câu 204. Cho y = f ( x) là hàm số chẵn, liên tục trên  biết đồ thị hàm số y = f ( x) đi qua điểm 1  0 1  2 M − ; 4   và f
∫ (t)dt = 3, tính I = sin2 .xf ′ ∫
(sin x)dx .  2  0 π − 6 https://toanmath.com/
A. I = 10 . B. I = 2 − .
C. I = 1. D. I = 1 − . π π 2 2
Câu 205. Cho hàm số y = f ( x) thỏa mãn sin . x f ∫
(x)dx = f (0) =1. Tính I = cos .xf ′ ∫ (x)dx . 0 0
A. I = 1.
B. I = 0 .
C. I = 2 . D. I = 1 − .
Câu 206. Cho hàm số y = f ( x) liên tục trên và thỏa mãn f (−x) + 2018 f ( x) = 2x sin x . Tính π 2 I = f
∫ (x)dx? π − 2 2 2 2 4 A. . B. . C. . D. . 2019 2018 1009 2019
Câu 207. Cho hàm số f ( x) và g ( x) liên tục, có đạo hàm trên  và thỏa mãn f ′(0). f ′(2) ≠ 0 và 2 ( ) ′( ) = ( − 2)ex g x f x x x
. Tính giá trị của tích phân I = f
∫ (x).g′(x)dx? 0 A. 4 − . B. e − 2 . C. 4 . D. 2 − e .  π   π 
Câu 208. Cho hàm số y = f ( x) có đạo hàm và liên tục trên 0;   thỏa mãn f = 3   ,  4   4  π π π 4 f ( x) 4 4 dx = 1 ∫ và sin . x tan . x f ∫  (x)dx = 2  . Tích phân sin . x f ′ ∫
(x)dx bằng: cos x 0 0 0 2 + 3 2 1+ 3 2 A. 4 . B. . C. . D. 6 . 2 2 2 4  x
Câu 209. Cho hàm số f ( x) liên tục trên  và f (2) = 16 , f
∫ (x)dx = 4. Tính I = xf ′ dx ∫    2  0 0
A. I = 12 .
B. I = 112 .
C. I = 28 . D. I = 144 .
Câu 210. Cho hàm số f ( x) có đạo hàm cấp hai f ′ ( x) liên tục trên đoạn [0; ] 1 thoả mãn f ( )
1 = f (0) = 1, f ′(0) = 2018 . Mệnh đề nào dưới đây đúng? 1 1
A. f ′′( x)(1− x) x = 2018 − ∫ d . B. f ′′
∫ (x)(1− x)dx = 1 − . 0 0 1 1 C. f ′′
∫ (x)(1− x)dx = 2018. D. f ′′
∫ (x)(1− x)dx =1. 0 0  π  π π
Câu 211. Cho hàm số f ( x) có đạo hàm liên tục thỏa mãn f = 0   ,  f ′
∫ (x) 2 dx = và   2  π 4 2 π π
cos x f ( x) dx = ∫
. Tính f (2018π ) . π 4 2 1 A. 1 − . B. 0 . C. . D. 1. 2
Câu 212. Cho hàm số f ( x) nhận giá trị dương, có đạo hàm liên tục trên đoạn [0; 2  ]. Biết f (0) =1 ( 3 2 2
x − 3x ) f ′( x) và ( ) ( ) 2 2 4 . 2 e x x f x f x − − =
, với mọi x ∈[0; 2
 ] . Tính tích phân I = dx ∫ . f x 0 ( ) https://toanmath.com/ 16 16 14 32 A. I = − . B. I = − . C. I = − . D. I = − . 3 5 3 5
Câu 213. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 0 và 1 1 1  ′ ∫ ( ) =  ∫( + ) − x f x x x f ( x) 2 2 e 1 d 1 e dx = . Tính tích phân I = f
∫ (x)dx . 4 0 0 0 e e −1
A. I = 2 − e .
B. I = e − 2 . C. I = . D. I = . 2 2 2 2 1
Câu 214. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [1; 2] thỏa mãn ( x − ) 1
f ( x) dx = − ∫ , 3 1 2 2 2
f (2) = 0 và  f ′
∫ (x) dx = 7  . Tính tích phân I = f
∫ (x)dx . 1 1 7 7 7 7 A. I = . B. I = − . C. I = − . D. I = . 5 5 20 20
Câu 215. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 1, 1 1 1  1 f ′
∫ (x) 2 dx = 9  và 3
x f ( x) dx = ∫ . Tích phân f ( x) dx ∫ bằng 2 0 0 0 2 5 7 6 A. . B. . C. . D. . 3 2 4 5  π   π 
Câu 216. Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn 0;   và f = 0   . Biết  4   4  π π π 4 π 4 π 8 2
f ( x) dx = ∫ , f ′( x)sin 2 d x x = − ∫ . Tính tích phân I = f
∫ (2x)dx 8 4 0 0 0 1 1
A. I = 1. B. I = .
C. I = 2 . D. I = . 2 4
Câu 217. . Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 và f (0) + f ( ) 1 = 0 . Biết 1 1 1 π 1 2
f ( x) dx = ∫ ,
f ′( x) cos (π x) dx = ∫ . Tính f ( x) dx ∫ . 2 2 0 0 0 1 2 3π A. π . B. π . C. π . D. . 2
Câu 218. Cho hàm số f ( x) có đạo hàm f ′( x) liên tục trên đoạn [0; ] 1 thỏa f ( ) 1 = 0 , 1 ( π 1  π  1 1 f ′( x)) 2 2 dx = ∫ và cos x f ∫ (x)dx =   . Tính f ( x) dx ∫ . 8  2  2 0 0 0 π 1 2 A. . B. π . C. 2 π . D. π .
Câu 219. Xét hàm số f ( x) có đạo hàm liên tục trên  và thỏa mãn điều kiện f ( ) 1 = 1 và
2  f ′( x) + 2 f ( x) +1
f (2) = 4 . Tính J = ∫ − dx . 2 x x   1 1 1
A. J = 1+ ln 4 .
B. J = 4 − ln 2 . C. J = ln 2 − . D. J = + ln 4 . 2 2 https://toanmath.com/
Câu 220. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn 1 1 1  ′ ∫ ( ) =  ∫( + ) − x f x x x f ( x) 2 2 e 1 d 1 e dx = và f ( ) 1 = 0 . Tính f ( x) dx ∫ 4 0 0 0 e −1 2 e e A. . B. . C. e − 2 . D. . 2 4 2
Câu 221. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 0 , 1 1 1  1 f ′
∫ (x) 2 dx = 7  và 2
x f ( x) dx = ∫ . Tích phân f ( x) dx ∫ bằng 3 0 0 0 7 7 A. . B. 1. C. . D. 4 . 5 4 https://toanmath.com/ HƯỚNG DẪN GIẢI 2
Câu 188. Cho hàm số y = f ( x) có đạo hàm f ′( x) liên tục trên [0; 2] và f (2) = 3 , f ∫ (x)dx = 3. 0 2 Tính . x f ′ ∫ (x)dx . 0 A. 3 − . B. 3 . C. 0 . D. 6 . Hướng dẫn giải Chọn B 2 2 2 2 Ta có . x f ′ ∫ (x)dx = d x
∫ ( f (x)) = .xf (x) − f
∫ (x)dx = 2 f (2)−3 = 3. 0 0 0 0
Câu 189. Cho hàm số y = f ( x) có đạo hàm là f '( x) liên tục trên đoạn [0; 1] và f ( ) 1 = 2 . Biết 1 1 f
∫ (x)dx =1, tính tích phân I = .xf ' ∫ (x)dx. 0 0
A. I = 1. B. I = 1 − .
C. I = 3 . D. I = 3 − . Hướng dẫn giải 1 Ta có: I = . x f ' ∫ (x)dx 0
Đặt u = x ⇒ du = dx , dv = f '(x)dx chọn v = f '
∫ (x)dx = f (x) 1 1 ⇒ I = .
x f ( x) 1 − f
∫ (x)dx =1.f ( )1−0.f (0)− f
∫ (x)dx = 2−1=1 0 0 0 Chọn A 1
Câu 190. Cho hàm số f ( x) thỏa mãn ∫(x + )
1 f '( x) dx = 10 và 2 f ( )
1 − f (0) = 2 . Tính 0 1 I = f ∫ (x)dx. 0
A. I = 8 . B. I = 8 − .
C. I = 4 . D. I = 4 − . Hướng dẫn giải 1 A = ( x + ∫
)1 f '(x)dx Đặt u = x +1⇒ du = dx , dv = f '(x)dx chọn v = f (x) 0 1 1 1 1 ⇒ A = (x + )
1 . f ( x) 1 − f ( x) dx = 2 f (1) − f (0) − f ( x) dx = 2 − f ( x) dx = 10 ⇒ f ( x) dx = 8 − ∫ ∫ ∫ ∫ 0 0 0 0 0 Chọn B
Câu 191. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; 2] và thỏa mãn f (2) = 16 , 2 1 f
∫ (x)dx = 4. Tính tích phân I = .x f ′ ∫ (2x)dx. 0 0
A. I = 12 .
B. I = 7 .
C. I = 13 . D. I = 20 . Hướng dẫn giải Chọn B https://toanmath.com/ du = dx u  = x Đặ   t  ⇒  f x . dv = f ′  (2x) (2 ) dxv =  2 . x f (2x) 1 2 1 Khi đó: 1 I = − f ∫ ( x) f (2) 1 x = − f ∫ (t) 16 1 2 d dt = − .4 = 7 . 2 0 2 2 4 2 4 0 0
Câu 192. Cho hàm số y = f ( x) có đạo hàm liên tục trên  và thỏa mãn f ( 2 − ) =1, 2 0 f
∫ (2x−4)dx =1. Tính xf ′
∫ (x)dx. 1 2 −
A. I = 1 .
B. I = 0 . C. I = 4 − . D. I = 4 . Hướng dẫn giải Chọn B
Đặt t = 2x − 4 ⇒ dt = 2dx , đổi cận x =1⇒ t = 2
− , x = 2 ⇒ t = 0. 2 0 0 0 = f ∫ ( x− ) 1 1 2 4 dx = f
∫ (t)dt ⇒ f
∫ (t)dt = 2 ⇒ f ∫ (x)dx = 2 . 2 1 2 − 2 − 2 −
Đặt u = x ⇒ du = dx , dv = f ′(x)dx ⇒ v = f (x) . 0 0 Vậy 0 xf ′
∫ (x)dx = xf (x) − f
∫ (x)dx = 2 f ( 2
− ) − 2 = 2.1− 2 = 0 . 2 − 2 − 2 − 5
Câu 193. Cho hàm số y f x thỏa mãn f  3 x  3x  
1  3x  2, x  .  Tính I  .
x f xdx  . 1 5 17 33 A. . B. . C. . D. 1761 − . U U 4 4 4 Hướng dẫn giải Chọn C 5     Đặ u x du dx 5 t     
I xf x  f x   .
dv f xdx v
  f xdx 1   1
 f 5  5 x 1 5  Từ f  3 x  3x       1  3x  2      , suy ra I 23 f x . dxf    1  2 x  0  1 dt    2 3x  3 dx 3  Đặ 
t t x  3x 1  
f t 3x  2  Đổi cận: Với 3
t  1 1 x  3x 1  x  0 và 3
t  5  x  3x 1  5  x  1. 5 1 Casio
Khi đó I  23 f xdx  23 3x  2 33 2 3x   3 dx    4 1 0 Chọn C e f ( x)
Câu 194. Cho hàm số f ( x) liên tục trong đoạn [1;e] , biết dx = 1 ∫ , f (e) = 1. Khi đó x 1 e I = f ′ ∫ (x).ln d x x bằng 1
A. I = 4 .
B. I = 3 .
C. I = 1. D. I = 0 . Hướng dẫn giải Chọn D https://toanmath.com/ e e e 1 Cách 1: Ta có I = f ′
∫ (x).ln dxx = f (x).ln x − f
∫ (x). dx = f (e)−1=1−1= 0 . 1 x 1 1  dx u  = ln x  du = Cách 2: Đặt  →  x . dv = f ′ 
(x)dx v = f  (x) e e e f x Suy ra I = f ′
∫ (x).ln dxx = f (x) ( ) ln x − dx = f ∫ (e)−1=1−1= 0. 1 x 1 1
Câu 195. Cho hàm số y = f ( x) có đạo hàm liên tục trên thỏa mãn π   2 f ( x) π + f − x = sin . x cos x  
, với mọi x ∈ và f (0) = 0 . Giá trị của tích phân . x f ′ ∫
(x)dx bằng  2  0 π 1 π 1 A. − . B. . C. . D. − . 4 4 4 4 Hướng dẫn giải Chọn D  
Theo giả thiết, f (0) = 0 và f ( x) π + f − x = sin . x cos x   nên  2     π  f ( ) π 0 + f = 0   ⇔ f = 0   .  2   2  Ta có: π π π 2 2 π 2 I = . x f ′ ∫ (x)dx = d x f ∫ (x)   = xf  ( x) 2  − f  ∫ (x)dx 0 0 0 0 π 2
Suy ra: I = − f ∫ (x)dx . 0 Mặt khác, ta có:   π π π  π  1 f ( x) π + f − x = sin . x cos x ⇒   2 f ∫ (x) 2 2 dx + f − x dx = sin .
x cos x dx = ∫   ∫  2  0 0 0  2  2 π π 0  π  1 1 Suy ra: 2 f ∫ (x) 2 dx − π f − x dx = ⇔ f ∫ ∫ (x)dx =   0 0  2  2 4 2 π 2 1
Vậy I = − f ( x) dx = − ∫ . 4 0 1
Câu 196. Cho hàm số f ( x) thỏa f (0) = f ( ) 1 = 1. Biết x e f
∫  (x)+ f '(x)dx = ae+b  . Tính biểu 0 thức 2018 2018 Q = a + b .
A. Q = 8 .
B. Q = 6 .
C. Q = 4 . D. Q = 2 . Hướng dẫn giải 1 1 1 x
A = e f
∫  (x)+ f '(x) xdx = e f  ∫ (x) x dx + e f ' ∫ (x)dx 0 0 0
  1 A 2 A 1 x A = e f x dx ∫ 1 ( ) 0 https://toanmath.com/ 1 Đặ 1
t u = f ( x) ⇒ du = f '( x) dx , x
dv = e dx chọn x v = e x ⇒ A = e . x f x − e f ' x dx ∫ 1 ( ) ( ) 0 0  2 A 1 1 Vậy x = ( ) x A e f x
− A + A = e f x = .
e f 1 − f 0 = e −1 2 2 ( ) ( ) ( ) 0 0 a = 1 2018 2018 ⇒  ⇒ a + b =1+1 = 2 b  = 1 − Chọn D
Câu 197. Cho hàm số f ( x) có đạo hàm trên  thỏa mãn ′( ) − ( ) 2017 2018 2018 = 2018. .e x f x f x x với
mọi x ∈  và f (0) = 2018. Tính giá trị f ( ) 1 . A. f ( ) 2018 1 = 2019e . B. f ( ) 2018 1 2018.e− = . C. f ( ) 2018 1 = 2018.e . D. f ( ) 2018 1 = 2017.e . Hướng dẫn giải Chọn A
f ′( x) − 2018. f ( x) Ta có: ′( ) − ( ) 2017 2018 2018 = 2018. .e x f x f x x 2017 ⇔ = 2018.x 2018 e x
1 f ′( x) − 2018. f ( x) 1 2017 ⇔ dx = 2018.x dx ∫ ∫ ( ) 1 2018 e x 0 0
1 f ′( x) − 2018. f ( x) 1 1 Xets I = dx ∫ = ′ ∫ ( ) 2018 .e− xd − 2018. ∫ ( ) 2018 .e− x f x x f x dx 2018 e x 0 0 0 1 u  = f (x)
du = f ′(x)dx Xét = 2018. ∫ ( ) 2018 .e− x I f x dx . Đặt  ⇒  . 1 2018 − x 2018 dv = 2018.e dx
v = −e− x 0 1 Do đó = ( ).( 2018 −e− x ) 1 + ′ ∫ ( ) 2018 .e− xd ⇒ = ( ) 2018 1 .e− x I f x f x x I f − 2018 1 0 0 Khi đó ( ) 1 ⇔ f ( ) 2018 − x 2018 1 1 .e − 2018 = x ⇒ f ( ) 2018 1 = 2019.e . 0 1
Câu 198. Cho hàm số y = f ( x) với f (0) = f ( )
1 = 1. Biết rằng: ex f
∫  (x)+ f ′(x)dx = ae+b  Tính 0 2017 2017 Q = a + b . A. 2017 Q = 2 +1.
B. Q = 2 .
C. Q = 0 . D. 2017 Q = 2 −1. Hướng dẫn giải Chọn C u
 = f (x) du = f ′(x)dx Đặt  ⇒  .
dv = exdx v = ex 1 1 1 ex
∫  ( )+ ′( )d = ex  ( ) 2 − ex ′ ∫ ( )d + ex f x f x x f x f x x f ′ ∫
(x)dx = ef ( )1− f (0) = e −1. 1 0 0 0
Do đó a =1, b = 1 − . Suy ra 2017 2017 Q = a + b = + (− )2017 2017 1 1 = 0. Vậy Q = 0 . https://toanmath.com/ 5
Câu 199. Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [0;5] và f (5) = 10 , xf ′ ∫ (x)dx = 30 4 5 T 4 5 T 4 5 T 4 5 T 0 5 . Tính f ( x) dx ∫ . 0 A. 20 . B. 30 − . C. 20 − . D. 70 . 4 5 T 4 5 T 4 5 T 4 5 T 4 5 T 4 5 T 4 5 T 4 5 T 4 5 T Hướng dẫn giải Chọn A u
 = x ⇒ du = dx Đặ  t  dv = f ′ 
(x)dx ⇒ v = f (x) 5 5 5 . x f ′ ∫
(x)dx = ( .xf (x))5 − f
∫ (x)dx ⇔ 30 = 5 f (5)− f ∫ (x)dx 0 0 0 0 5 ⇔ f
∫ (x)dx = 5 f (5)−30 = 20. 0
Câu 200. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2]. Biết 2 67 2 rằng F ( )
1 = 1, F (2) = 4 , G ( ) 3 1 =
, G (2) = 2 và f ( x)G ( x) dx = ∫
. Tính F ( x) g ( x) dx ∫ 2 12 1 1 11 145 11 145 A. . B. − . C. − . D. . 12 12 12 12 Hướng dẫn giải Chọn A u  = F  (x) du = f  (x)dx Đặt  ⇒  dv = g
(x)dx v = G  (x) 2 2 2 2
F ( x) g ( x) dx ∫
= (F (x)G(x)) − f
∫ (x)G(x)dx = F (2)G(2)− F (1)G(1)− f
∫ (x)G(x)dx 1 1 1 1 3 67 = 4.2 −1. − 11 = . 2 12 12 1
Câu 201. Cho hàm số f ( x) có đạo hàm liên tục trên [0; ]
1 thỏa mãn x f ′
∫  (x)−2dx = f  ( )1. Giá 0 1 trị của I = f
∫ (x)dx bằng 0 A. 2 − . B. 2 . C. 1 − . D. 1. Hướng dẫn giải Chọn C 1 1 1
Ta có x f ′
∫  (x)−2dx  = . x f ′ ∫ (x)dx − 2 d x x ∫ 0 0 0 1 1 1 1 = d x f ∫  (x) 2  − x  = .
x f ( x) − f
∫ (x)dx−1 = f ( )1− I −1. 0 0 0 0 1
Theo đề bài x f ′
∫  (x)−2dx = f  ( )1 ⇒ I = 1 − . 0 https://toanmath.com/ 2 2
Câu 202. Cho hàm số y = f ( x) liên tục trên đoạn [1;2] và ∫(x − )
1 f ′( x) dx = a . Tính f ( x)dx ∫ 1 1
theo a và b = f (2) .
A. b − a .
B. a − b .
C. a + b .
D. −a − b . Hướng dẫn giải Chọn A
Đặt u = x −1⇒ du = dx ; dv = f ′(x)dx chọn v = f (x). 2 2 2 ( b 2 x − ∫
)1 f ′(x)dx = (x − )1 f (x) − f
∫ (x)dx = f (2)− f
∫ (x)dx = b− f ∫ (x). 1 1 1 a 1 2 2 2 Ta có ∫(x − )
1 f ′( x) dx = a ⇔ b − f
∫ (x)dx = a ⇔ f
∫ (x)dx = b−a. 1 1 1 2
Câu 203. Cho hàm số f ( x) liên tục trên  và f (2) = 16 , f
∫ (x)dx = 4. Tính tích phân 0 1 I = . x f ′ ∫ (2x)dx . 0
A. I = 13 .
B. I = 12 .
C. I = 20 . D. I = 7 . Hướng dẫn giải Chọn D du = dx u  = x Đặ   t  ⇒  .  v = f ′  ( x) 1 d 2 dx v = f  (2x)  2 1 1 1 1 Khi đó, 1 I = x f ( x) 1 − f ∫ ( x) 1 x = f ( ) 1 − f ∫ ( x) 1 . 2 2 d 2 2 dx = 8 − f ∫ (2x)dx . 2 2 2 2 2 0 0 0 0
Đặt t = 2x ⇒ dt = 2dx .
Với x = 0 ⇒ t = 0 ; x = 1 ⇒ t = 2 . 2 1 Suy ra I = 8 − f
∫ (t)dt = 8−1= 7 . 4 0
Câu 204. Cho y = f ( x) là hàm số chẵn, liên tục trên  biết đồ thị hàm số y = f ( x) đi qua điểm 1  0 1  2 M − ; 4   và f
∫ (t)dt = 3, tính I = sin2 .xf ′ ∫
(sin x)dx .  2  0 π − 6
A. I = 10 . B. I = 2 − .
C. I = 1. D. I = 1 − . Hướng dẫn giải Chọn B 0 0 Xét tích phân I = sin 2 . x f ′ ∫
(sin x)dx = 2sin .xf ′ ∫ (sin x).cos d x x . π π − − 6 6  π 1  = − ⇒ = − Đặ x t
t: t = sin x ⇒ dt = cos d x x . Đổi cận:  6 2 .
x = 0 ⇒ t = 0 0
⇒ I = 2 t. f ′ ∫ (t)dt . 1 − 2 https://toanmath.com/ u  = 2t  du = 2dt Đăt:   ⇒  . dv = f ′ 
(t)dt v = f  (t) 0 0 0  
⇒ I = t f (t) 1 − f ∫ (t) 1 2 . 2 dt = f − − 2 f   ∫ (t)dt. −  2  1 1 2 − − 2 2   1   1 
Đồ thị hàm số y = f ( x) đi qua điểm M − ; 4   ⇒ f − = 4   .  2   2  1 1 0 2 2
 Hàm số y = f (x) là hàm số chẵn, liên tục trên  ⇒ f
∫ (t)dt = f
∫ (t)dt = f ∫ (x)dx = 3. 1 0 0 − 2 Vậy I = 4 − 2.3 = 2 − . π π 2 2
Câu 205. Cho hàm số y = f ( x) thỏa mãn sin . x f ∫
(x)dx = f (0) =1. Tính I = cos .xf ′ ∫ (x)dx . 0 0
A. I = 1.
B. I = 0 .
C. I = 2 . D. I = 1 − . Hướng dẫn giải Chọn C
u = f (x) ⇒ u = f ′ Đặ d (x)dx t  dv = sin d
x x ⇒ v = − cos x π π 2 π ⇒ sin . x f ∫
(x)dx = (−cos .xf (x)) 2 2 + cos . x f ′ ∫ (x)dx . 0 0 0 π π 2 2 π ⇒ I = cos . x f ′ ∫
(x)dx = sin .xf ∫
(x)dx+cos .xf (x) 2 =1−1 = 0. 0 0 0
Câu 206. Cho hàm số y = f ( x) liên tục trên và thỏa mãn f (−x) + 2018 f ( x) = 2x sin x . Tính π 2 I = f
∫ (x)dx? π − 2 2 2 2 4 A. . B. . C. . D. . 2019 2018 1009 2019 Hướng dẫn giải Chọn D π π 2 2
Ta có ∫ ( f (−x) + 2018 f (x))dx = 2xsin d x x ∫ π π − − 2 2 π π π π π 2 2 2 ⇔ f ∫ (−x) 2 dx + 2018 f ∫ (x) 2 dx = 2x sin d x x ∫ ⇔ 2019 f
∫ (x)dx = 2xsin d x x ∫ ( ) 1 π π π π π − − − − − 2 2 2 2 2 π 2 + Xét P = 2x sin d x x ∫ π − 2 https://toanmath.com/  =  = Đặ u 2x du 2dx t  ⇒  dv = sin d x xv = −cos x π π P = 2 . x (− cos x) 2 2 +sin x = 4 π π − − 2 2 π 2 4 Từ ( ) 1 suy ra I = f ∫ (x)dx = . π 2019 − 2
Câu 207. Cho hàm số f ( x) và g ( x) liên tục, có đạo hàm trên  và thỏa mãn f ′(0). f ′(2) ≠ 0 và 2 ( ) ′( ) = ( − 2)ex g x f x x x
. Tính giá trị của tích phân I = f
∫ (x).g′(x)dx? 0 A. 4 − . B. e − 2 . C. 4 . D. 2 − e . Hướng dẫn giải Chọn C
Ta có ( ) ′( ) = ( − 2) ex g x f x x x
⇒ g (0) = g (2) = 0 (vì f ′(0). f ′(2) ≠ 0) 2 2 2 2 I = f
∫ (x).g′(x)dx = f
∫ (x)dg(x) = ( f (x).g(x))2 − g
∫ (x).f ′(x)dx = −∫( 2 −2 )ex x x dx = 4 . 0 0 0 0 0  π   π 
Câu 208. Cho hàm số y = f ( x) có đạo hàm và liên tục trên 0;   thỏa mãn f = 3   ,  4   4  π π π 4 f ( x) 4 4 dx = 1 ∫ và sin . x tan . x f ∫  (x)dx = 2  . Tích phân sin . x f ′ ∫
(x)dx bằng: cos x 0 0 0 2 + 3 2 1+ 3 2 A. 4 . B. . C. . D. 6 . 2 2 Hướng dẫn giải Chọn B π 4 u  = sin x  du = cos d x x  Ta có: I = sin . x f ′ ∫
(x)dx . Đặt  ⇒  . dv = f ′ 
(x)dx v = f  (x) 0 π π 3 2 I = sin . x f ( x) 4 4 − cos . x f ∫ (x)dx = − I . 0 1 2 0 π π π 4 4  f x  4  f x  2 ( ) 2 = sin . x tan . x f ∫  (x)dx  = ∫ sin .x  dx = ∫ ( 2 1− cos x) ( ) .  dx . cos x cos x 0 0   0   π π 4  f ( x) 4  = ∫   dx − cos . x f ∫
(x)dx =1− I . cos x 1 0   0 ⇒ + I = 1 − 3 2 ⇒ I = + 3 2 2 1 = . 1 2 2 2 4  x
Câu 209. Cho hàm số f ( x) liên tục trên  và f (2) = 16 , f
∫ (x)dx = 4. Tính I = xf ′ dx ∫    2  0 0
A. I = 12 .
B. I = 112 .
C. I = 28 . D. I = 144 . Hướng dẫn giải Chọn B https://toanmath.com/ u  = x du = dx Đặ   t   x  ⇒   x  . dv = f ′ dx    v = 2 f      2    2  Khi đó 4  x  4  x  4 4  x   x I = xf ′ dx ∫   = 2xf − 2 f dx  
∫   =128−2I với I = f dx ∫   .  2  0  2   2  1 1  2  0 0 0 4 2 2 Đặ xx  t u =
⇒ dx = 2du , khi đó I = f dx ∫   = 2 f
∫ (u)du = 2 f ∫ (x)dx =8. 2 1  2  0 0 0
Vậy I = 128 − 2I = 128 −16 = 112 . 1
Câu 210. Cho hàm số f ( x) có đạo hàm cấp hai f ′ ( x) liên tục trên đoạn [0; ] 1 thoả mãn f ( )
1 = f (0) = 1, f ′(0) = 2018 . Mệnh đề nào dưới đây đúng? 1 1
A. f ′′( x)(1− x) x = 2018 − ∫ d . B. f ′′
∫ (x)(1− x)dx = 1 − . 0 0 1 1 C. f ′′
∫ (x)(1− x)dx = 2018. D. f ′′
∫ (x)(1− x)dx =1. 0 0 Hướng dẫn giải Chọn A 1 1
Xét I = f ′′
∫ (x)(1− x)dx = ∫(1− x)d( f ′(x)) 0 0 u  =1− x du = −dx Đặ   t  ⇔  dv = d  ( f ′(x)) v = f ′  (x) 1
⇔ I = (1− x) f ′(x)1 + f ′
∫ (x)dx = (1− )1 f ′( )1− f ′(0) + f
(x)1 = − f ′(0) +  f ( ) 1 − f (0)   0 0 0 = 2018 − + (1− ) 1 = 2018 − .  π  π π
Câu 211. Cho hàm số f ( x) có đạo hàm liên tục thỏa mãn f = 0   ,  f ′
∫ (x) 2 dx = và   2  π 4 2 π π
cos x f ( x) dx = ∫
. Tính f (2018π ) . π 4 2 1 A. 1 − . B. 0 . C. . D. 1. 2 Hướng dẫn giải Chọn D
Bằng công thức tích phân từng phần ta có π π π π π cos xf ∫
(x)dx = sin xf  (x) − ′ π sin xf  ∫
(x)dx . Suy ra sin xf ′(x)dx = − ∫ . π π 4 2 π 2 2 2 π π π −  −  π Hơn nữa ta tính đượ 1 cos 2x 2x sin 2x c 2 sin d x x = dx = = ∫ ∫   . 2  4 π π π  4 2 2 2 https://toanmath.com/ π π π π 2 2 2 2 Do đó:  f ′
∫  (x) 2 dx+ 2 sin xf ′  ∫ (x)dx + sin d
x x = 0 ⇔  f ′ ∫ ∫  (x) 2 2
+ sin x dx = 0  . 0 0 0 0  π 
Suy ra f ′( x) = − sin x . Do đó f ( x) = cos x + C . Vì f = 0   nên C = 0 .  2 
Ta được f (x) = cos x ⇒ f (2018π ) = cos(2018π ) =1.
Câu 212. Cho hàm số f ( x) nhận giá trị dương, có đạo hàm liên tục trên đoạn [0; 2  ]. Biết f (0) =1 ( 3 2 2
x − 3x ) f ′( x) và ( ) ( ) 2 2 4 . 2 e x x f x f x − − =
, với mọi x ∈[0; 2
 ] . Tính tích phân I = dx ∫ . f x 0 ( ) 16 16 14 32 A. I = − . B. I = − . C. I = − . D. I = − . 3 5 3 5 Hướng dẫn giải Chọn B
Cách 1: Theo giả thiết, ta có ( ) ( ) 2 2 4 . 2 e x x f x f x − − =
và f ( x) nhận giá trị dương nên  ( ) ( ) 2 2 4 ln . 2  ln e x x f x f x + − =  ⇔ f ( x) + f ( − x) 2 ln ln 2 = 2x − 4x .
Mặt khác, với x = 0 , ta có f (0). f (2) = 1 và f (0) = 1 nên f (2) = 1 . ( 3 2 2
x − 3x ) f ′( x) 2 f ′ x Xét I = dx ∫ , ta có I = ∫( 3 2 x − 3x ) ( ) . dx f x f x 0 ( ) 0 ( ) 3 2 u  = x − 3xu =  ( 2 d
3x − 6x)dx Đặ  t  f ′( x) ⇒  dv =  v = ln f  (x)  ( ) dx f x 2 2 2 Suy ra I =  2 ( 3 2
x − 3x )ln f ( x) −  ∫( 2
3x − 6x).ln f ( x)dx = −∫(3x − 6x).ln f (x)dx ( ) 1 . 0 0 0
Đến đây, đổi biến x = 2 − t ⇒ dx = −dt . Khi x = 0 → t = 2 và x = 2 → t = 0. 0 2 Ta có I = −∫( 2
3t − 6t ).ln f (2 − t)(−dt ) = −∫( 2
3t − 6t ).ln f (2 − t )dt 2 0 2
Vì tích phân không phụ thuộc vào biến nên I = −∫( 2
3x − 6x).ln f (2 − x)dx (2) . 0 2 Từ ( )
1 và (2) ta cộng vế theo vế, ta được 2I = −∫( 2
3x − 6x).ln f
(x)+ ln f (2− x)dx  0 2 1 16 Hay I = − ∫( 2 3x − 6x).( 2
2x − 4x)dx = − . 2 5 0
Cách 2 (Trắc nghiệm) Chọn hàm số ( ) 2 2 ex x f x − = , khi đó: ( 3 2
x − 3x ) 2x−2 2 .e x .(2x − 2) 2 16 − 3 2 I = dx =
x − 3x . 2x − 2 dx = ∫ ∫ . 2 − ( ) ( ) x 2 e x 5 0 0
Câu 213. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 0 và 1 1 1  ′ ∫ ( ) =  ∫( + ) − x f x x x f ( x) 2 2 e 1 d 1 e dx = . Tính tích phân I = f
∫ (x)dx . 4 0 0 0 https://toanmath.com/ e e −1
A. I = 2 − e .
B. I = e − 2 . C. I = . D. I = . 2 2 Hướng dẫn giải Chọn B 1 u  = f  (x)
du = f ′(x)dx Xét = ( + ∫ )1ex A x
f ( x) dx . Đặt  ⇒  dv =  (x + ) 1 exdx  = 0 v ex x 1 1 1 2 1 − x 1 e Suy ra = ex ( ) − ex A x f x x f ′ ∫
(x)dx = − ex x f ′ ∫ (x)dx ⇒ e x
f ′( x) dx = ∫ 0 4 0 0 0 1 1 2   − x x 1 1 1 e 1 Xét 2 2 2 2 x e dx = e x − x + = ∫   .  2 2 4  4 0 0 1 1 1 1 2 2 Ta có  ′
∫ ( ) d +2 ex ′  ∫ ( ) 2 2 d + e x f x x x f x x x dx = 0 ∫ ⇔ ∫( ′( )+ ex f x x ) dx = 0 0 0 0 0 Suy ra ′( ) + ex f x x = 0 x ∀ ∈[0; ] 1 (do ( ′( ) x f x + x )2 e ≥ 0 x ∀ ∈[0; ] 1 ) ⇒ ′( ) = − ex f x x ⇒ ( ) = (1− )ex f x x + C Do f ( ) 1 = 0 nên ( ) = (1− )ex f x x 1 1 1
Vậy = ∫ ( )d = ∫(1− )exd = (2 − )ex I f x x x x x = e − 2 . 0 0 0 2 2 1
Câu 214. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [1; 2] thỏa mãn ( x − ) 1
f ( x) dx = − ∫ , 3 1 2 2 2
f (2) = 0 và  f ′
∫ (x) dx = 7  . Tính tích phân I = f
∫ (x)dx . 1 1 7 7 7 7 A. I = . B. I = − . C. I = − . D. I = . 5 5 20 20 Hướng dẫn giải Chọn B − Đặ x
t u = f ( x) ⇒ du = f ′( x) dx , v = ( x − ) ( )3 2 1 d 1 dx ⇒ v = 3 2 2 3 3 1 (x − ) 2 − 2 1 x 1 Ta có − = (x − ∫
)1 f (x)dx = . f ( x) ( ) − f ′ ∫ (x)dx 3 3 3 1 1 1 2 1 1 2 2 ⇔ − = − ( 3 3 x − ∫ )3 1
f ′( x) dx ⇔ ∫(x − ) 1
f ′( x) dx = 1 ⇒ − 2.7 ( x − ) 1
f ′( x) dx = 14 − ∫ 3 3 1 1 1 2 2 2 2 Tính đượ 6 2 3 6 c 49
∫ (x− )1 dx = 7 ⇒  f ′ ∫ (x) dx  − 2.7(x − ∫
)1 f ′(x)dx + 49
∫ (x− )1 dx = 0 1 1 1 1 2 − ⇒  x 7
∫ (x− )1 − f ′(x) 2 3  dx = 0  
⇒ f ′(x) = (x − )3 7 1 ⇒ f ( x) ( )4 7 1 = + C . 4 1 x −
Do f (2) = 0 ⇒ f ( x) ( )4 7 1 7 = − . 4 4 2 7(x − )4 2 1 7  Vậy I = f ∫ (x)dx =  −  dx ∫ 7 = − .  4 4  5 1 1   https://toanmath.com/
Câu 215. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 1, 1 1 1  1 f ′
∫ (x) 2 dx = 9  và 3
x f ( x) dx = ∫ . Tích phân f ( x) dx ∫ bằng 2 0 0 0 2 5 7 6 A. . B. . C. . D. . 3 2 4 5 Hướng dẫn giải Chọn B 1 2 Ta có:  f ′
∫ (x) dx = 9  ( ) 1 0 1 1 - Tính 3 x f ∫ (x)dx = . 2 0
du = f ′(x)dx u  = f (x) Đặ  t  ⇒ 4  3  x
dv = x .dxv =  4 1 1 1 4  x  1 1 1 1 1 3 ⇒ = x f
∫ (x)dx =  .f (x) 4 − x . f ′ ∫ (x)dx 4 = − x . f ′ ∫ (x)dx 2  4  4 4 4 0 0 0 0 1 1 4
⇒ x . f ′(x)dx = 1 − ∫ 4
⇒ 18 x . f ′(x)dx = 18 − ∫ (2) 0 0 1 1 9 x 1 1 - Lại có: 8 x dx = = ∫ 8 ⇒ 81 x dx = 9 ∫ (3) 9 9 0 0 0
- Cộng vế với vế các đẳng thức ( ) 1 , (2) và (3) ta được: 1  1 1  f ′ ∫  (x) 2 4  +18x . f ′  (x) 8
+ 81x  dx = 0 ⇔  f ′ ∫ (x) 4 +  = ⇔ π.  f ′ ∫ (x) 4 +  =   9x dx 0   9x dx 0   0 0 0
Hay thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hàm số y = f ′( x) 4 + 9x , trục
hoành Ox , các đường thẳng x = 0 , x = 1 khi quay quanh Ox bằng 0 ⇒ 9 f ′( x) 4
+ 9x = 0 ⇒ f ′(x) 4 = 9
− x ⇒ f (x) = f ′ ∫ (x).dx 4 = − x + C . 5 9 14 Lại do f ( ) 1 = 14 1 ⇒ C = ⇒ f (x) 5 = − x + 5 5 5 1 1 1 ⇒  9 14   3 14  5
f ( x) dx = ∫ 5 − x + dx ∫  6 = − x + x = .    5 5   10 5  2 0 0 0  π   π 
Câu 216. Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn 0;   và f = 0   . Biết  4   4  π π π 4 π 4 π 8 2
f ( x) dx = ∫ , f ′( x)sin 2 d x x = − ∫ . Tính tích phân I = f
∫ (2x)dx 8 4 0 0 0 1 1
A. I = 1. B. I = .
C. I = 2 . D. I = . 2 4 Hướng dẫn giải Chọn D https://toanmath.com/ π 4 π s  in 2x = u  2cos 2 d x x = du  Tính f ′( x)sin 2 d x x = − ∫ . Đặt  ⇒  , khi đó 1 7 T 1 7 T 4  f ′
 ( x)dx = dvf  ( x) = v 0 π π π 4 π 4 π  π  f ′ ∫ (x)sin 2 d x x = sin 2 . x f ( x) 4 4 − 2 f ∫ (x)cos2 d x x = sin . f − sin 0. f   (0)− 2 f ∫ (x)cos2 d x x 0 2  4  0 0 0 π 4 = 2 − f ∫ (x)cos2 d x x . 0 π π 4 π 4 π
Theo đề bài ta có f ′(x)sin 2 d x x = − ∫ ⇒ f ( x)cos2 d x x = ∫ . 4 8 0 0 π 4 π Mặt khác ta lại có 2 cos 2 d x x = ∫ . 8 0 π π 4 4 2  π π π  Do  f ∫  (x) 2
− cos2x dx =  f
∫ (x)−2f (x) 2
.cos2x + cos 2x dx   = − 2 + = 0   nên  8 8 8  0 0
f ( x) = cos 2x . π π 8 8 1 1 Ta có I = cos 4 d x x = sin 4x = ∫ . 4 4 0 0
Câu 217. . Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn [0; ]
1 và f (0) + f ( ) 1 = 0 . Biết 1 1 1 π 1 2
f ( x) dx = ∫ ,
f ′( x) cos (π x) dx = ∫ . Tính f ( x) dx ∫ . 2 2 0 0 0 1 2 3π A. π . B. π . C. π . D. . 2 Hướng dẫn giải Chọn C 1 7 T u  = cos  (π x) du = π − sin  (π x)dx Đặt  ⇒  . dv = f ′ 
(x)dx v = f  (x) 1 1 Khi đó: f ′
∫ (x)cos(πx)dx = cos(πx) f (x)1 +π f
∫ (x)sin(πx)dx 0 0 0 = −( 1 1 f ( )
1 + f (0)) + π f
∫ (x)sin(πx)dx =π f
∫ (x)sin(πx)dx 0 0 1 ⇒ f (x) (π x) 1 sin dx = ∫ . 2 0 Cách 1: Ta có 1 2
Tìm k sao cho  f
∫ (x)−ksin(πx) dx = 0  0 1 1 1 1 2 Ta có:  f
∫ (x)−ksin(πx) 2  dx = f
∫ (x)dx−2k f ∫ (x)sin(πx) 2 2 dx + k sin ∫ (πx)dx 0 0 0 0 https://toanmath.com/ 2 1 k = − k + = 0 ⇔ k =1. 2 2 1 Do đó  f
∫ (x)−sin(πx) 2 dx = 0 
⇒ f (x) = sin (π x) (do  f  ( x) − (π x) 2 sin  ≥ 0  x ∀ ∈  ). 0 1 1 2
Vậy f ( x) dx = sin (π x) dx = ∫ ∫ π . 0 0
Cách 2: Sử dụng BĐT Holder. 2 b b b    f
∫ (x)g(x) 2 x ≤ f ∫ (x) 2 d d . x g ∫ (x)dx . aa a
Dấu “ = ” xảy ra ⇔ f ( x) = k.g ( x) , x ∀ ∈[ ; a b] . 2 1 1 1 1   1 Áp dụng vào bài ta có =  f ∫ (x)sin(π x) 2 dx ≤ f ∫ (x) 2 d . x sin ∫ (π x)dx = , 4 4 0  0 0
suy ra f ( x) = k.sin (π x) , k ∈  . 1 1 1 1 Mà f ∫ (x)sin(πx) 2 dx = ⇔ k sin
∫ (πx)dx = ⇔ k =1 ⇒ f (x) = sin(πx) 2 2 0 0 1 1 2
Vậy f ( x) dx = sin (π x) dx = ∫ ∫ π . 0 0
Câu 218. Cho hàm số f ( x) có đạo hàm f ′( x) liên tục trên đoạn [0; ] 1 thỏa f ( ) 1 = 0 , 1 ( π 1  π  1 1 f ′( x)) 2 2 dx = ∫ và cos x f ∫ (x)dx =   . Tính f ( x) dx ∫ . 8  2  2 0 0 0 π 1 2 A. . B. π . C. 2 π . D. π . Hướng dẫn giải Chọn D u  = f (x)
du = f ′(x)dx Đặ   t  π x ⇒  2 π x dv = cos dx v = sin    2  π 2 1  π Do đó  x f ∫ (x) 1 cos dx =    2  2 0 1 1 1 2 π x  π   π  π ⇔ f ( x) 2 − x f ′ ∫   (x) 1 sin sin dx = ⇔ sin x f ′ ∫   (x) = − π dx . 2 π  2  2  2  4 0 0 0 1  π  1 Lại có: 2 sin x dx = ∫    2  2 0 1 2 1 1  2     π   π  ⇒ I = − f ′ ∫ (x) 2 . dx − 2 − sin x f ′    ∫   ( x) 2 dx + sin x dx π π ∫        2   2  0 0 0 2 1  2  π  π π = − f ′ ∫ (x) 2 4 2 1 − sin x dx = − . + = 0   2  π  2  π 8 π 2 2 0 2  2  π  Vì − f ′ 
(x)−sin x ≥ 0 trên đoạn [0; ]1 nên  π    2  https://toanmath.com/ 2 1  2  π   π π  π − 2   f ′ ∫ (x)−sin x dx = 0 ⇔ − f ′( x) =sin x
 ⇔ f ′( x) = − sin x   .  π    2  π  2  2  2  0  π   π 
Suy ra f ( x) =cos x + C   mà f ( )
1 = 0 do đó f ( x) =cos x   .  2   2  1 1  π  2 Vậy f
∫ (x)dx = cos x dx = ∫   .  2  π 0 0
Câu 219. Xét hàm số f ( x) có đạo hàm liên tục trên  và thỏa mãn điều kiện f ( ) 1 = 1 và
2  f ′( x) + 2 f ( x) +1
f (2) = 4 . Tính J = ∫ − dx . 2 x x   1 1 1
A. J = 1+ ln 4 .
B. J = 4 − ln 2 . C. J = ln 2 − . D. J = + ln 4 . 2 2 Hướng dẫn giải Chọn D
2  f ′( x) + 2 f ( x) +1 2 f ′( x) 2 f ( x) 2  2 1 
Cách 1: Ta có J = ∫ − dx = dx − dx + − dx ∫ ∫ ∫  . 2 x x   2 2 x xx x  1 1 1 1  1  1 u  = du = − dx Đặt 2  x ⇒  x dv = f ′ 
(x)dx v = f  (x)
2  f ′( x) + 2 f ( x) +1 2 2 2 2 1 f x f x  2 1  J = ∫ −
dx = . f ( x) ( ) ( ) + dx − dx + − dx ∫ ∫ ∫  2 x x   2 2 2 x x xx x  1 1 1 1 1 2 1  
= f ( ) − f ( ) 1 1 2 1 + 2 ln x + = + ln 4   . 2  x  2 1
2  f ′( x) + 2 f ( x) +1
2  xf ′( x) − f ( x) 2 1 
Cách 2: J = ∫ − dx = ∫ + − dx 2 x x   2 2 x x x   1 1 2 ′  f (x) 2   2 1   f (x) 2  = ∫ 1 1   dx + − dx ∫  = 
+ 2ln x +  = + ln 4 . 2 x    x x x x 2   1 1 1
Cách 3: ( Trắc nghiệm)  f  ( ) 1 = 1 a = 3
Chọn hàm số f ( x) = ax + b . Vì  ⇒ 
, suy ra f ( x) = 3x − 2 .  f  (2) = 4 b  = 2 − 2 2  5 3x −1  1  1 Vậy J = − dx = 2 ln x − = ln 4 + ∫    . 2  x x   x  2 1 1
Câu 220. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn 1 1 1  ′ ∫ ( ) =  ∫( + ) − x f x x x f ( x) 2 2 e 1 d 1 e dx = và f ( ) 1 = 0 . Tính f ( x) dx ∫ 4 0 0 0 e −1 2 e e A. . B. . C. e − 2 . D. . 2 4 2 Hướng dẫn giải Chọn C 1 1 1 - Tính: = ( + ) 1 ex I x
f ( x) dx = ∫ ex ∫ ( )d + ex x f x x f
∫ (x)dx = J + K . 0 0 0 https://toanmath.com/ 1 Tính = ex K f ∫ (x)dx 0 u
 = ex f (x) du = ex f (x) + ex f ′(x) Đặ dx   t  ⇒  dv = dx v = x 1 1 ⇒ = ( 1
ex ( )) 1 −  ex ∫ ( )+ ex K x f x x f x x
f ′( x) dx   = − ex ∫ ( )d − ex x f x x x f ′ ∫
(x)dx ( f ( ) do 1 = 0) 0 0 0 0 1 1 ⇒ = − − ex K J x f ′ ∫
(x)dx ⇒ = + = − ex I J K x f ′ ∫ (x)dx. 0 0
- Kết hợp giả thiết ta được: 1  − 1 2  2 e −1   f ′ ∫ (x) 2 2 e 1  dx =    f ′
∫ (x) dx = (1)   4  4 0  0 ⇒  1  − 1 2  − x e 1 x − xe f ′ ∫ (x) 2 e 1 dx =  2 e x f ′ ∫ (x)dx = − (2) 4   2 0  0 1 2 − x e 1
- Mặt khác, ta tính được: 2 2 x e dx = (3) ∫ . 4 0
- Cộng vế với vế các đẳng thức (1), (2), (3) ta được: 1 1 1 ∫( ′ 2 2  ( ) 2  + 2 ex ′  ( ) 2 2 + e x f x x f x x
)dx=0 ⇔ ∫( f′(x)+ exx) dx=0 ⇔π∫( f′(x)+ exx) dx=0 0 o o
hay thể tích hình phẳng giới hạn bởi đồ thị hàm số = ′( ) + ex y f x x
, trục Ox , các đường thẳng x = 0
, x = 1 khi quay quanh trục Ox bằng 0 ⇒ ′( ) + ex f x x = 0 ⇔ ′( ) = − ex f x x ⇒ ( ) = − exd = ∫ (1− )ex f x x x x + C. - Lại do ( ) 1 = 0 ⇒ C = 0 ⇒ ( ) = (1− )ex f f x x 1 1 ⇒ ( )d = (1− ∫ ∫ )ex f x x x
dx = ( 1− )ex ) 1 1 + ex x dx ∫ 1 1 ex = − + = e − 2 . 0 0 0 0 0 1 Vậy f
∫ (x)dx = e−2. 0
Câu 221. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn f ( ) 1 = 0 , 1 1 1  1 f ′
∫ (x) 2 dx = 7  và 2
x f ( x) dx = ∫ . Tích phân f ( x) dx ∫ bằng 3 0 0 0 7 7 A. . B. 1. C. . D. 4 . 5 4 Hướng dẫn giải Chọn A
du = f ′ x dx 1 u  = f (x) ( )  Cách 1: Tính: 2
x f ( x) dx ∫ . Đặt  ⇒ 3  . 2 x  =  = 0 dv x dx v  3 1 1 3 1 x f x 1 Ta có: 2 x f ∫ (x) ( ) 3 dx = − x . f ′ ∫ (x)dx 3 3 0 0 0 https://toanmath.com/ 1. f ( ) 1 − 0. f (0) 1 1 1 1 3 = − x . f ′ ∫ (x) 3 dx = − x . f ′ ∫ (x)dx . 3 3 3 0 0 1 1 1 1 1 1 Mà 2
x f ( x) dx = ∫ 3 ⇒ −
x . f ′( x) 3 dx =
⇒ x . f ′(x)dx = 1 − ∫ ∫ . 3 3 3 0 0 0 1 2 Ta có  f ′
∫ (x) dx = 7  (1). 0 1 1 7 x 1 1 6 1 x dx = = ∫ 6
⇒ 49x dx = .49 = 7 ∫ (2). 7 7 7 0 0 0 1 1 3
x . f ′( x) 3 dx = 1
− ⇒ 14x . f ′(x)dx = 14 − ∫ ∫ (3). 0 0 1 1 1 2
Cộng hai vế (1) (2) và (3) suy ra  f ′ ∫ (x) 6 3
 dx + 49x dx + 14x . f ′  ∫ ∫
(x)dx = 7 + 7 −14 = 0. 0 0 0 1 1 ⇒ ∫{ 2 f ′  ( x) 2 3  +14x f ′  (x) 6
+ 49x }dx = 0 ⇒  f ′ ∫ (x) 3 + 7x  dx = 0   . 0 0 1 1 2 2 Do  f ′( x) 2 3 + 7x  ≥ 0 3 3   ⇒  f ′
∫ (x)+7x  dx ≥ 0   . Mà  f ′
∫ (x)+7x  dx = 0   ⇒ f ′( x) 3 = 7 − x . 0 0 ( ) 4 7x f x = − + C . Mà f ( ) 7 7 1 = 0 ⇒ −
+ C = 0 ⇒ C = . 4 4 4 Do đó f (x) 4 7x 7 = − + . 4 4 1 1 1 4 5  7x 7   7x 7  7 Vậy f
∫ (x)dx = ∫− + dx  = − + x  = .  4 4   20 4  5 0 0 0 1
Cách 2: Tương tự như trên ta có: 3
x . f ′( x) dx = 1 − ∫ 0
Áp dụng BĐT Cauchy-Schwarz, ta có: 2 1 1 1 1 1       =  x f ′ ∫
(x) x ≤ ∫(x )2 x⋅  f ′ ∫ (x) 2 1 7 7 d 7 d  dx
 = 7 ⋅ ⋅  f ′
∫ (x) 2 dx =  f ′  ∫ (x) 2 3 3  dx  7  0   0   0  0 0
Dấu bằng xảy ra khi và chỉ khi ′( ) 3 f
x = ax , với a ∈  . 1 1 1 7 ax Ta có 3
x . f ′( x) 3 3 dx = 1
− ⇒ x .ax dx = 1 − ⇒ = 1 − ⇒ a = 7 − ∫ ∫ . 7 0 0 0 7x 7
Suy ra f ′( x) = 7
− x ⇒ f (x) 4 3 = − + C , mà f ( ) 1 = 0 nên C = 4 4 Do đó f (x) 7 = ( 4 1− x ) x ∀ ∈  . 4 1 1 4 5  7x 7   7x 7  1 7 Vậy f
∫ (x)dx = ∫− + dx  = − + x  = .  4 4   20 4 0  5 0 0
Chú ý: Chứng minh bất đẳng thức Cauchy-Schwarz
Cho hàm số f ( x) và g ( x) liên tục trên đoạn [ ; a b] . https://toanmath.com/ 2 b b b       Khi đó, ta có  f
∫ (x)g(x) 2 x  ≤  f ∫ (x) 2 d dx  ⋅ g ∫ (x)dx .  a   a   a  Chứng minh:
Trước hết ta có tính chất: b
Nếu hàm số h ( x) liên tục và không âm trên đoạn [a;b] thì h ∫ (x)dx ≥ 0 a 2
Xét tam thức bậc hai λ f
(x) + g (x) 2 2  = λ f
(x) + λ f (x) g (x) 2 2
+ g (x) ≥ 0 , với mọi λ ∈
Lấy tích phân hai vế trên đoạn [a;b] ta được b b b 2 2 λ f
∫ (x) x+ λ f ∫ (x) (x) 2 d 2 g dx + g
∫ (x)dx ≥ 0, với mọi λ∈ (*) a a a
Coi (*) là tam thức bậc hai theo biến λ nên ta có ∆′ ≤ 0 2 b b b      2 ⇔  f ∫ (x) 2 x  −  f ∫ (x) 2 d dx  g
∫ (x)dx ≤ 0  a   a  a  2 b b b      2 ⇔  f ∫ (x) 2 x  ≤  f ∫ (x) 2 d dx  g
∫ (x)dx (đpcm)  a   a  a https://toanmath.com/
Document Outline

  • 8.1 TÍCH PHÂN HÀM ẨN ÁP DỤNG TÍNH CHẤT- P1_ĐÔNG NQA
    • TÍCH PHÂN CỦA HÀM ẨN
    • BÀI TẬP
      • DẠNG 1: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT NGUYÊN HÀM
      • DẠNG 2: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT, GIẢI HỆ TÍCH PHÂN
    • HƯỚNG DẪN GIẢI
      • DẠNG 1: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT NGUYÊN HÀM
      • DẠNG 2: ÁP DỤNG ĐỊNH NGHĨA, TÍNH CHẤT, GIẢI HỆ TÍCH PHÂN
  • 8.2 TÍCH PHÂN HÀM ẨN ÁP DỤNG ĐỔI BIẾN - P2_ĐÔNG NQA
    • DẠNG 3: PHƯƠNG PHÁP ĐỔI BIẾN
    • BÀI TẬP
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 1
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 2
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 3
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 4
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 6
    • HƯỚNG DẪN GIẢI
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 1
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 2
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 3
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 4
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 5
      • TÍCH PHÂN HÀM ẨN ĐỔI BIẾN DẠNG 6
  • 8.3 TÍCH PHÂN HÀM ẨN ÁP DỤNG TỪNG PHẦN- P3_ĐÔNG NQA
    • DẠNG 4: PHƯƠNG PHÁP TỪNG PHẦN
    • BÀI TẬP
    • HƯỚNG DẪN GIẢI

Tài liệu liên quan: