Thông tin
Quiz

Bài tập trắc nghiệm tích phân và ứng dụng của tích phân vận dụng cao Toán 12

Bài tập trắc nghiệm tích phân và ứng dụng của tích phân vận dụng cao Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

125 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập trắc nghiệm tích phân và ứng dụng của tích phân vận dụng cao Toán 12

61 31 lượt tải Tải xuống

TÍCH PHÂN VẬN DỤNG CAO

Vấn đề 1. Tính tích phân theo định nghĩa

Câu 1. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa

   

2 31 1 .fx f x x 

Giá

trị của tích phân





fxx



bằng

Câu 2. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 1 1.ff

Biêt rằng

   

e f x f x x ae b





 





Tính

2018 2018

.Qa b

2017

21Q 

. B.

2Q 

. C.

Q 

. D.

2017



Câu 3. Cho các hàm số

 

,y fx

 

y gx

có đạo hàm liên tục trên

 

0;2

và thỏa mãn

   

' d 2,

f xgx x





   

' d 3.f xg x x





Tính tích phân

   

d.I f xgx x









1.I



1.I



5.I 

6.I 

Câu 4. Cho hàm số





y fx



liên tục trên

 

0;

và thỏa

   

d .sin

ft t x x





. Tính





























































































Câu 5. Cho hàm số

 

liên tục trên

 

;a 

với

0a 

và thỏa

 

d 62





với mọi

.xa

Tính

 

4.f

 

4 2.f 

 

4 4.f 

 

4 8.f 





4 16.

f 

Vấn đề 2. Kỹ thuật đổi biến

Câu 6. Cho

 

2017

d2fx x



. Tính tích phân

 

2017

. ln 1 d .

I fx x















1.I



2.I 

4.I 

5.I 

Câu 7. Cho hàm số

 

liên tục trên



và

 

d 4, sin cos d 2.

x f x xx







Tính tích

phân

 

d.I fx x



2.I 

6.I 

4.I



10.I 

Câu 8. Cho hàm số

 

liên tục trên



và

 

tan d 4, d 2.

xfx

f xx x









Tính tích

phân

 

d.I fx x



6.I 

2.I 

3.I 

1.I 

Câu 9. Cho hàm số

 

liên tục trên



và thỏa mãn





tan . cos d 1,

xf x x







 

d 1.





Tính tích phân









1.I 

2.I 

3.I 

4.I 

Câu 10. Cho hàm số

 

y fx

xác định và liên tục trên

;2 ,







thỏa

 

2.fx f x







 











Tính tích phân











I 

2.I 

I 

Câu 11. Cho hàm số

 

liên tục trên



và thỏa

   

2 2 cos 2fx f x x  

với mọi

x  

Tính





dI fx x









6I 

. B.

I 

. C.

2I 

. D.

6I 

Câu 12. Cho hàm số

 

y fx

xác định và liên tục trên

,

thỏa

 

4 321fx x x  

với

mọi

.x  

Tích phân





dfx x





bằng

10.

72.

Câu 13. Cho các hàm số

 

,fx

 

liên tục trên

 

0;1 ,

thỏa

  

 



. .1mf x nf x g x 

với

,mn

là số thực khác

và

   

d d 1.fxx gxx



Tính

.mn

0.mn

mn

1.mn

2.mn

Câu 14. Cho hàm số

 

xác định và liên tục trên

 

0;1 ,

thỏa mãn

   

' '1fx f x

với mọi

 

0;1 .x 

Biết rằng

   

0 1, 1 41.ff

Tính tích phân

 

d.I fx x



41.I 

21.I 

41.I 

42.I 

Câu 15. Cho hàm số

 

y fx

liên tục trên



và thỏa mãn

   

f x fx x

với mọi

.x  

Tính

 

d.I fx x



I 

I 

I 

I 

Vấn đề 3. Kỹ thuật tích phân từng phần

Câu 16. Cho hàm số

 

thỏa mãn





 

. .d8

xf x e x







và

 

3 ln 3f 

. Tính

 

I ex



1.I



11.I 

8 ln 3.I 

8 ln 3.I 

Câu 17. Cho hàm số

 

có đạo hàm liên tục trên

0; ,









thỏa mãn

 

' cos d 10f x xx







và





0 3.

f 

Tích phân





sin 2 df x xx





bằng

13.I 

7.I 

7.I



13.I 

Câu 18. Cho hàm số





y fx



có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

1d 3fx x



và

 

1 4.f 

Tích phân

 

'dxf x x



bằng



Câu 19. Cho hàm số

 

nhận giá trị dương, có đạo hàm liên tục trên

 

0;2 .

Biết

 

01f 

và





 

fxf x e





với mọi

 

0;2 .x 

Tính tích phân

 

x x fx









I 



I 

Câu 20. Cho biểu thức

 

2 cot

ln 1 2 sin 2 d ,

S xe x























 

























với số thực

0.m



Chọn khẳng định

đúng trong các khẳng định sau.

5.S 

9.S



2 cot 2 ln sin .



  















  



2 tan 2 ln .























Vấn đề 4. Tính a, b, c trong tích phân

Câu 21. Biết

 

ln 9 d ln 5 ln 2x xa b c 



với

, , .abc



Tính

.Pabc

13.

P 

18.

P 

26.

P 

34.

P 

Câu 22. Biết

2 2 11

d .ln

x ex e

men e











 















với

, , mnp

là các số nguyên

dương. Tính tổng

.P mn p 

5.P



6.P 

7.P 

8.P 

Câu 23. Biết

 

2 cos cos 1 sin

d ln

cos

x x xx x

xa b



  

 





với

, , abc

là các số hữu tỉ.

Tính

.P ac b

P 

Câu 24. Biết

ln 8

ln 3

d 1 ln

x aa b

  





với

, .



 

Tính

.P ab

1.P





3.P 

5.P 

Câu 25. Biết

 

a bc

x x xx



 



với

, , .

abc







Tính

P abc

P 

. B.

18P 

. C.

24P 

. D.

46P



Câu 26. Biết

sin 4 2 6

cos 1 sin 1

x abc







 



với

, , .abc

 

Tính

.Pabc

10.P 

12.P 

14.P 

36.P 

Câu 27. Biết

x ae e



  



với

, , .abc 

Tính

.P abc

5.P 

4.P 

3.P 

3.P 

Câu 28. Biết

xa b c





 





với

, , .

abc



Tính

.P abc

P 

2.P 

3.P 

4.P 

Câu 29. Biết

   

ln ln 1

ln 1 2

xx b

xx e



 

 



với

, .ab



 

Tính

P ba

8.P 

6.P





10.

P 

Câu 30. Biết

cos 3







 





với

, , abc

là các số nguyên. Tính

P abc

37.P 

35.P 

35.P 

41.P 

Vấn đề 5. Tính tích phân hàm phân nhánh

Câu 31. Cho hàm sô

 

1 khi 0

khi 0



















Tính tích phân

 

d.I fx x



















11 11





Câu 32. Cho hàm số

 

xác định trên













thỏa



  

, 0 1

fx f







và





1 2.f 

Giá trị của biểu thức

   

13ff

bằng

ln15.

2 ln15.



3 ln15.

4 ln15.

Câu 33. Cho hàm số

 

xác định trên

 

,\ 2;1

thỏa mãn

 









  

3 30ff 

và





f 

Giá trị biểu thức

 

   

4 14f ff 

bằng

ln 20 .



ln 2 .



ln 80 1.

ln 1.



Câu 34. Cho hàm số

 

xác định trên

   

0; \ ,e

thỏa mãn

 

ln 1







ln 6f



















và

 

3.fe 

Giá trị biểu thức

 

f fe



















bằng

 

3 ln 2 1 .

2 ln 2.

3 ln 2 1.

ln 2 3.

Câu 35. Cho

 

là một nguyên hàm của hàm số

1 sin 2





với

\ ,.

x kk







  









Biết

   

0 1, 0FF

, tính giá trị biểu thức

12 12

PF F



 





 









 

0.P 

2 3.P 

1.P 

D. Không tồn tại

Vấn đề 6. Tính tích phân dựa vào tính chất

Câu 36. Cho hàm số





là hàm số lẻ, liên tục trên

 

4;4 .

Biết rằng

 

d2f xx







và

 

2 d 4.

f xx





Tính tích phân

 

d.I fx x



10.

I 

6.I 

6.I 

10.I 

Câu 37. Cho hàm số

 

là hàm số chẵn, liên tục trên





1; 6 .

Biết rằng

 

d8fx x







và

 

2 d 3.f xx



Tính tích phân





d.I fx x







I 

11.I 

14.I 

Câu 38. Cho hàm số

 

liên tục trên

 

3;7 ,

thỏa mãn





 

10fx f x



với mọi

 

3;7x 

và

 

d 4.fx x



Tính tích phân

 

d.I xf x x





20.I



40.I 

60.I 

80.I



Câu 39. Cho hàm số

 

y fx

là hàm số chẵn và liên tục trên đoạn







thỏa mãn

 

d 2018.fx x







Giá trị của tích phân





2018 1











bằng

0.I



2018



2018.I 

4036.I 

Câu 40. Biết

2018

2018 2018

sin

sin cos

x xb









với

,.ab



 

Tính

2.P ab

6.P



P 

10.P 

12.P 

Vấn đề 7. Kỹ thuật phương trình hàm

Câu 41. Cho hàm số

 

y fx

liên tục trên

;













và thỏa mãn

  



2 cos .fx f x x 

Tính

tích phân

 

I fx x









2.I 

I 

Câu 42. Cho hàm số





y fx

liên tục trên

 

2;2

và thỏa mãn

   

23 .

fx f x

 



Tính tích phân





d.I fx x























Câu 43. Cho hàm số





y fx

liên tục trên

 

0;1

và thỏa mãn

   

1 2.xfx f x x x  

Tính tích phân

 

d.I fx x





I 

Câu 44. Cho hàm số

 

liên tục trên







và thỏa mãn

 

2 3.fx f x



















Tính tích

phân

 





I 



I 

Câu 45. Cho hàm số

 

liên tục trên

 

0;1

và thỏa mãn





 

2 31 1 .fx f x x 

Tính

tích phân

 

d.I fx x





Vấn đề 8. Kỹ thuật biến đổi

Câu 46. Cho hàm số

 

thỏa



 



3 6.

fxf x x x





Biết rằng

 

0 2,f 

tính

 

2.f

 

2 64.f 

 

2 81.f 

 

2 100.f 

 

2 144.f 

Câu 47. Cho hàm số

 

có đạo hàm

 

liên tục và nhận giá trị không âm trên

 

1; ,



thỏa

 

1 0,f 

 





. 4 41

e fx x x





 



với mọi

 

1; .x  

Mệnh đề nào sau đây đúng?

 

1 4 0.f



 

 

0 4 1.f





 

1 4 2.f





 

2 4 3.





Câu 48. Cho hàm số

 

thỏa mãn

   

 

. 15 12

f x fx f x x x



 

 



với mọi

 

và

 

0 0 1.





Giá trị của





bằng

10.

Câu 49. Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

1; 2

và thỏa mãn

   

0, 1; 2 .fx x 

Biết rằng

 

d 10fxx







và

 

d ln 2.







Tính

 

2.f

 

2 20.

f 

 

2 10.f 

 

2 10.f 

 

2 20.f 

Câu 50. Cho hàm số

 

có đạo hàm liên tục trên

 

1;1

, thỏa mãn

 

0, fx x 

và

   

'2 0f x fx

. Biết rằng

 

11f 

, giá trị của

 

1f 

bằng



Câu 51. Cho hàm số

 

xác định và liên tục trên



đồng thời thỏa mãn

 

' , .

fx x

f x ef x x





 



  













Tính giá trị của

 

ln 2 .f

 

ln 2 .

f 

 

ln 2 .



 

ln 2 ln 2 .



 

ln 2 ln 2 .

f 

Câu 52. Cho hàm số

 

có đạo hàm liên tục trên

 

0;

, biết

     

' 2 3 0,fx x f x 

 

0fx

với mọi



và

 

f 

Tính

     

1 1 2 ... 2018 .P ff f   

1009

2020



2019

2020

P 

3029

2020

P 

4039

2020

P 

Câu 53. Cho hàm số

 

liên tục trên

0; 3 ,







thỏa mãn

 

1,fx

 

00f 

và

   

1 2 1.f x x x fx



 

Giá trị của

 

bằng

Câu 54. Cho hàm số

 

có đạo hàm và liên tục trên

 

1; 4 ,

đồng biến trên

 

1; 4 ,

thoản mãn

   

2x xf x f x









với mọi

 

1; 4 .x 

Biết rằng

 

f 

tính tích phân

 

d.I fx x



1186

I 

1187

I 

1188

I 

Câu 55. Cho hàm số





liên tục, không âm trên









, thỏa

   

 

. ' cos 1fx f x x f x

với mọi













và

 

0 3.f 

Giá trị của



















bằng

2 2.

Câu 56. Cho hàm số

 

liên tục, không âm trên

 

0;3 ,

thỏa

    



.2 1fx f x x f x





với

mọi

 

0;3x 

và

 

0 0.f 

Giá trị của

 

bằng

3 11.

Câu 57. Cho hàm số

 

có đạo hàm không âm trên





0;1 ,

thỏa mãn

 

0fx

với mọi

 

0;1x 

và

   

 

42 3

.' . 1 1 .fx f x x fx

  

 

  

Biết

 

0 2,f 

hãy chọn khẳng định đúng

trong các khẳng định sau đây.

 

1 2.

f

 

21.

f

 

1 3.



 

31.



Câu 58. Cho hàm số

 

liên tục trên

 

,\ 0; 1

thỏa mãn

    



1.xx f x f x x x



  

với mọi

 

0; 1\x 

và

 

1 2 ln 2.f 

Biết

 

2 ln 3f ab

với

, ab 

, tính

.Pa b

P 

Câu 59. Cho hàm số

 

có đạo hàm xác định, liên tục trên

 

0;1 ,

thỏa mãn

 

01f





và

   

 

fx f x







 



















với mọi

 

0;1 .x 

Đặt

   

10Pf f

, khẳng định nào sau đây đúng?

2 1.P  

1 0.P 

0 1.P

1 2.P

Câu 60. Cho hai hàm số

 

và

 

có đạo hàm liên tục trên

 

0;2 ,

thỏa mãn

   

'0. '2 0ff

và

     

.' 2 .

gx f x xx e

Tính tích phân

   

. ' d.I fxgx x



4.I 

4.I 

2.Ie

Câu 61. Cho hàm số

 

0fx



xác định và có đạo hàm trên đoạn

 

0;1 ,

thỏa mãn

   

1 2018 d

gx f t t

gx f x





















Tính





I gx x





1009



505.I 

1011



2019



Câu 62. Cho hai hàm





và





có đạo hàm trên

 

1; 4 ,

thỏa mãn

   

1 14fg

g x xf x

f x xg x

























với mọi

 

1; 4 .x 

Tính tích phân

   

d.I f x gx x









3 ln 2.I 

4 ln 2.I 

6 ln 2.I 

8 ln 2.I 

Câu 63. Cho hai hàm

 

và

 

có đạo hàm trên

 

1; 2 ,

thỏa mãn

   

1 10fg

và

 

     

   

 

2017 1

, 1; 2 .

2018

gx x x f x

gx fx x







 

























Tính tích phân

   

I gx f x x



















1.I



I 

2.I 

Câu 64. Cho hàm số





y fx

có đạo hàm trên

 

0;3 ,

thỏa mãn

   

 

3. 1

f x fx



















với mọi

 

0;3

x 

và

 

f 

Tính tích phân





 





13 .

xf x

f x fx











I 

1.I



I 

Câu 65. Cho hàm số

 

y fx

liên tục trên đoạn

 

0;1

và thỏa mãn

   

af b bf a



với mọi





, 0;1 .ab

Tính tích phân

 

d.I fx x





I 









Vấn đề 9. Kỹ thuật đạo hàm đúng

Câu 66. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thoả mãn



 



2018

3 f x xf x x





với

mọi

 

0;1 .x 

Tính

 

dI fx x



2018 2021

I 



2019 2020

I 



2019 2021

I 



2018 2019

I 



Câu 67. Cho hàm số

 

có đạo hàm liên tục trên

 

0;4 ,

thỏa mãn

   

fx f x e x





 

với mọi

 

0;4 .x 

Khẳng định nào sau đây là đúng?

   

40 .

ef f

   

4 0 3.ef f e

   

4 0 1.

ef f e 

   

4 0 3.

ef f

Câu 68. Cho hàm số

 

có đạo hàm trên



thỏa mãn

   

2017 2018

' 2018 2018

f x fx x e

với

mọi

x  

và

 

0 2018.f



Tính giá trị

 

1.f





2018

1 2018 .









2018

1 2017 .fe

 

2018

1 2018 .fe

 

2018

1 2019 .fe

Câu 69. Cho hàm số

 

có đạo hàm và liên tục trên

,

thỏa mãn

   

f x xf x xe







và

 

0 2.

f 

Tính

 

1.f

 

1.fe

 

1.f



 

1.f



 

1.f



Câu 70. Cho hàm số





liên tục và có đạo hàm trên

0; ,



















thỏa mãn hệ thức





 

tan .

cos

f x xf x





Biết rằng

3 3 ln 3

f fab





 















 

trong đó

, .ab 

Tính giá

trị của biểu thức

P ab

P 

P 

Vấn đề 10. Kỹ thuật đưa về bình phương loại 1

Câu 71. Cho hàm số

 

liên tục trên

0; ,









thỏa

  



2 2 sin d .

f x fx x x

















 

















Tính tích phân





I fx x







0.I 





1.I 





Câu 72. Cho hàm số





liên tục trên

 

0;1

thỏa

 





 

2 ln d 2 ln 1 d .f x x fx x x





 









Tích phân

 

d.I fx x



I 

. B.

lnI



. C.

I 

. D.

lnI



Câu 73. Cho hàm số

 

có đạo liên tục trên

 

0;1 ,





và

 

'fx

đều nhận giá trị dương

trên

 

0;1

và thỏa mãn

 

02f 

và

     

 

' . 1d 2 ' . d .f x fx x f x fx x











Tính

 

d.I fx x









I 

Câu 74. Cho hàm số

 

có đạo hàm dương, liên tục trên đoạn

 

0;1

và thỏa mãn

 

0 1,f 

 

     

3 ' . d 2 ' . d.

f x fx x f xfx x















Tính

 

d.I fx x









I 

Câu 75. Cho hàm số





y fx

có đạo hàm dương, liên tục trên đoạn

 

0;1 ,

thỏa





 

1 01

ff

và

     

 

' 1d 2 ' d .fxf x x fxfxx











Giá trị của tích phân

 

dfx x







bằng

5 33 27



5 33

5 33 54



Vấn đề 11. Kỹ thuật đưa về bình phương loại 2

Kỹ thuật Holder

Câu 76. Cho hàm số

 

y fx

liên tục trên đoạn

 

0;1 ,

thỏa mãn

  



d d1

fx x xfx x





và

 

d4fx x









. Giá trị của tích phân

 

dfx x







bằng

10.

80.

Câu 77. Cho hàm số

 

y fx

liên tục trên đoạn





0;1 ,

thỏa mãn

 

d d1xfx x xfx x





và

 

d 5.fx x









Giá trị của tích phân





fx x







bằng

10.

Câu 78. Cho hàm số

 

y fx

liên tục trên đoạn

 

0;1 ,

thỏa mãn

   

d d.

xfxx xfxx



Giá trị của tích phân

 

dfx x



bằng

Câu 79. Cho hàm số

 

có đạo hàm liên tục trên

 

1; 8

và thỏa mãn

   

 

2 28

1 11

2 38

d2 d d .

3 15

fx x fx x fx x



 





 

Tích phân

 

dfx x



bằng

8 ln 2

ln 2

Câu 80. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

10f



 

d7fx x











và

 

xfx x



Tích phân

 

dfx x



bằng

. B.

. C.

. D.

Câu 81. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

11f 

 

xf x x



và

   

 

f x fx







Tính

 

2.f

 

2 2.f 





251

f 

 

256

f 





261

f 

Câu 82. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 





1 2, 0 0ff

và

 

' d 4.fx x









. Tích phân

 

2018 d .

f x xx











bằng

1011.

2018.

2022.

Câu 83. Cho hàm số





có đạo hàm liên tục trên

 

1; 2 ,

thỏa mãn

 





1d ,

x fx x 



 

20f 

và

 

' d 7.fx x









Tích phân

 

dfx x



bằng



Câu 84. Cho hàm số





có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

1 1, ' d

f fx x









và

 

f x x





Tích phân

 

dfx x



bằng

I 

Câu 85. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn



  

0 1 0,ff

   

' cos d

fx xx



 



và

 

f xx



Tích phân





fx x



bằng



.



Câu 86. Cho hàm số

 

có đạo hàm liên tục trên

 

0; ,

thỏa mãn





' sin d 1f x xx







và

 

d.f xx







Tích phân

 

dxf x x





bằng











Câu 87. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa

   

1 0, ' d

f fx x











và

 

cos d .

fx x























Tích phân

 

dfx x



bằng



.

Câu 88. Cho hàm số





có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn



  

' sin d

fx xx



và

 

d 2.f xx



Tích phân



















bằng











Câu 89. Cho hàm số

 

có đạo hàm liên tục trên

0; ,









thỏa

 

0, d 3

f f xx























và

 

sin d 6 .

x xf x

























Tích phân

 

dfx x











bằng





3.

9.

Câu 90. Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

0;1 ,

thỏa mãn

 



và

 

'd 1 d .

f x x x ef x x





 





Tính tích phân

 

d.I fx x







I 

2.Ie

I 

Câu 91. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 0, 1 1ff

và















Tích phân

 

dfx x



bằng



  



Câu 92. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 0, 1 1ff

và





 

1 'd .

ln 1 2

x fx x











Tích phân

 

x



bằng

 

ln 1 2 .



 

ln 1 2 .





 

ln 1 2 .



   

2 1 ln 1 2 .

Câu 93. Cho hàm số

 

có đạo hàm liên tục trên

 

1;1 ,

thỏa mãn

 

1 0,f 

 

' d 112fx x











và

 

xfx x







Tính tích phân

 

d.I fx x









I 

168

I 

Câu 94. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

1 0,f 

 

' d 2 ln 2

fx x









và









d 2 ln 2 .







Tích phân





fx x



bằng

1 ln 2



1 2 ln 2



3 2 ln 2



3 4 ln 2



Câu 95. Cho hàm số

 

có đạo hàm liên tục trên





1; 2 ,

đồng biến trên





1; 2 ,

thỏa mãn

 

10f 

 

d2fx x











và



  

. ' d 1.

fxf x x



Tích phân

 

dfx x



bằng

2 2.

Câu 96. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

10f 

 

d1f xx



và

   

fx f xx











Giá trị của

 

bằng



 

31 2



 

31 2



Câu 97. Cho hàm số





có đạo hàm liên tục trên

 

0;2 ,

thỏa mãn

 

21f 

 

xfx x



và

 

'd .

fx x









Giá trị của tích phân

 

dfx x



bằng



Vấn đề 12. Kỹ thuật đánh giá AM-GM

Câu 98. Cho hàm số

 

nhận giá trị dương và có đạo hàm

 

'fx

liên tục trên

 

0;1 ,

thỏa

mãn

   

f ef

và









' d 2.

fx x









Mệnh đề nào sau đây đúng ?

 





 















 







Câu 99. Cho hàm số

 

nhận giá trị dương trên





0;1 ,

có đạo hàm dương và liên tục trên

 

0;1 ,

thỏa mãn







và



 

    

4 ' d 3 ' d.f x fx x fxf xx











Tính





I fx x





 

2 1.Ie

 

2 1.

Ie









Câu 100. Cho hàm số

 

nhận giá trị dương trên





0;1 ,

có đạo hàm dương liên và tục trên

 

0;1 ,

thỏa mãn

 

xf x





và

 

0 1,f 

 

1.fe

Tính giá trị của

























































































Câu 101. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

' d1fxf x x









và

 

0 1,f 





1 3.

f 

Tính giá trị của

























































































Câu 102. Cho hàm số

 

nhận giá trị dương và có đạo hàm

 

'fx

liên tục trên





1; 2 ,

thỏa

mãn

 

d 24

xf x









và

 

1 1,f 





2 16.f



Tính giá trị của

 

2.f

 

2 1.f 

 

2 2.f 

 

2 2.f 

 

2 4.f 

Vấn đề 13. Tìm GTLN-GTNN của tích phân

Câu 103. Cho hàm số

 

liên tục trên

,

có đạo hàm cấp hai thỏa mãn

 

xf x e x





và

 

2 2,fe





 

0.fe

Mệnh đề nào sau đây là đúng?

 

2 4 1.fe

 

22 .f ee

 

2 2.f ee

 

2 12.f 

Câu 104. Cho hàm số

 

dương và liên tục trên

 

1; 3 ,

thỏa

 





1;3

max 2,fx

 

 

1;3

min

fx

và

biểu thức

 

d. dS fx x x





đạt giá trị lớn nhất, khi đó hãy tính

 

d.I fx x



Câu 105. Cho hàm số

 

có đạo hàm liên tục trên

,

thỏa mãn

   

1fx f x





với mọi

x  

và

 

0 0.f 

Giá trị lớn nhất của

 

bằng

1.e 



e 

Câu 106. Cho hàm số

 

nhận giá trị dương và có đạo hàm

 



liên tục trên

 

0;1 ,

thỏa

mãn

   

1 2018 0 .ff

Giá trị nhỏ nhất của biểu thức

 

M x fx x















bằng

ln 2018.

2 ln 2018.

2.me

2018 .me

Câu 107. Cho hàm số





có đạo hàm liên tục trên

 

0;1

và

   

1 d.

x fxx



 



Giá trị

nhỏ nhật của biểu thức

 





d0fx x f









bằng



Câu 108. Cho hàm số

()fx

liên tục trên

[0; 1]

thỏa mãn

 

d0xf x x 



và

 

[0; 1]

max 1.



Tích phân

 

efx x



thuộc khoảng nào trong các khoảng sau đây?







 











; 1.





































 

1; .e  

Câu 109. Cho hàm số

 

nhận giá trị không âm và liên tục trên

 

0;1 .

Đặt

   

1 d.

gx f t t



Biết

   

gx f x

với mọi

 

0;1x 

, tích phân

 



có giá trị lớn nhất

bằng

Câu 110. Cho hàm số

 

nhận giá trị không âm và liên tục trên đoạn

 

0;1 ,

thỏa mãn

     

13 d

f x f t t gx 



với mọi





0;1x 

, tích phân

 

dgx x



có giá trị lớn nhất bằng

Câu 111. Cho hàm số

 

nhận giá trị không âm và liên tục trên đoạn

 

0;1 ,

thỏa mãn



 



2018 2 d

fx ft t





với mọi

 

0;1 .x 

Biết giá trị lớn nhất của tích phân

 

dfx x



có

dạng

ae b

với

, .ab 

Tính

.ab

1009.

2018.

2020.

Câu 112. Cho hàm số

 

nhận giá trị không âm và liên tục trên đoạn

 

0;1 .

Đặt

   

1 d.

gx f t t



Biết

 

2g x xf x

với mọi

 

0;1x 

, tích phân

 

dgx x



có giá trị lớn

nhất bằng

1.e 

1.e 

Câu 113. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa

 

   

' 0, 0;1 .

f x fx x  

Giá trị lớn nhất của biểu thức

 

0. dfx



bằng





1.e 

Câu 114. Cho hàm số

 

liên tục trên

 

0; ,

thỏa mãn

 

d cos d 1.

fx x xfx x







Giá

trị nhỏ nhất của tích phân

 

f xx





bằng



Câu 115. Cho hàm số

 

liên tục trên

 

0; ,

thỏa mãn

   

sin d cos d 1.xf x x xf x x







Giá trị nhỏ nhất của tích phân

 

f xx





bằng



2

Câu 116. Cho hàm số

 

liên tục trên

 

0;1 ,

thỏa mãn

   

d d 1.

fx x efx x



Gọi

là giá trị nhỏ nhất của tích phân

 

d.fx x







Mệnh đề nào sau đây đúng?

0 1.m

1 2.m



2 3.m

3 4.

m

Câu 117. Cho hàm số

 

liên tục trên

 

0;1

thỏa mãn

   

d d 1.fx x xfx x



Giá trị

nhỏ nhất của tích phân

 

df xx



bằng

Câu 118. Cho hàm số

 

y fx

có đạo hàm liên tục trên

 

1; 2 ,

thỏa

 

d 31.xf x x



Giá trị

nhỏ nhất của tích phân

 

df xx



bằng

961.

3875.

148955.

923521.

Câu 119. Cho hàm số

 

liên tục và có đạo hàm đến cấp

trên

 

0;2

thỏa

     

0 2 1 2 1.f ff 

Giá trị nhỏ nhất của tích phân

 

'' dfx x







bằng

Câu 120. Cho hàm số

 

có đạo hàm trên

 

1; 3

và

 

1 0,f 

 

 

1;3

max 10.fx



Giá trị nhỏ

nhất của tích phân

 

'dfx x







bằng

10.

20.

TÍCH PHÂN VẬN DỤNG CAO

Mục lục

1. Tính tích phân theo định nghĩa…………………………………….………………… 02

2. Kỹ thuật đổi biến…………………………………………………………………………………. 03

3. Kỹ thuật tích phân từng phần………………………………………….……………… 07

4. Tính a, b, c trong tích phân………………………………………………………………. 09

5. Tính tích phân hàm phân nhánh………………………………………….………… 12

6. Tính tích phân dựa vào tính chất……………………………………….…………… 14

7. Kỹ thuật phương trình hàm…………………………………………………….………. 15

8. Kỹ thuật biến đổi…………………………………………………………………………………. 18

9. Kỹ thuật đưa về đạo hàm đúng……………………………………...……………… 24

10. Kỹ thuật đưa về bình phương loại 1……………………………………………… 25

11. Kỹ thuật đưa về bình phương loại 2 – Kỹ thuật Holder……………27

12. Kỹ thuật đánh giá AM-GM……………………………………………………………. 38

13. Tìm GTLN-GTNN của tích phân…………………………………………….……. 42

Vấn đề 1. Tính tích phân theo định nghĩa

Câu 1. Cho hàm số





có đạo hàm liên tục trên

 

0;1 ,

thỏa

   

2 31 1 .fx f x x 

Giá

trị của tích phân

 

'dfxx



bằng

Lời giải. Ta có

   

d 1 0.f x x fx f f



 



Từ

  



   

 

20 31 1

2 31 1 .

21 30 0

fx f x x

















      

















Vậy

     

' d 1 0 1.

I fxx f f   



Chọn C.

Câu 2. Cho hàm số





có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 1 1.ff

Biêt rằng

   

e f x f x x ae b





 





Tính

2018 2018

.Qa b

2017

21Q 

. B.



. C.

0Q 

. D.

2017

21Q 

Lời giải. Ta có

 

    

   



  



0 11

d d 1 0 1.

x xx

e fx f x x efx x efx ef f e









     









Suy ra

 

2018

2018 2018 2018

1 1 2.

Qa b







       











Chọn B.

Câu 3. Cho các hàm số

 

,y fx



 

y gx

có đạo hàm liên tục trên

 

0;2

và thỏa mãn

 

' d 2,f xgx x



   

' d 3.f xg x x



Tính tích phân

   

d.I f xgx x









1.I



1.I



5.I 

I 

Lời giải. Ta có



 



 



 



d ' 'd

I f xgx x f xgx f xg x x

  

 

  



       

' d ' d 2 3 5.f xgx x f xg x x  



Chọn C.

Câu 4. Cho hàm số





y fx



liên tục trên

 

0;

và thỏa

   

d .sin

ft t x x



. Tính





























































































Lời giải. Từ

   

d .sin

ft t x x





, đạo hàm hai vế ta được





   

2 sin cos .xf x x x x 

Cho

x 

ta được

11 1

2. . sin cos 1 1.

2 4 22 2 4

 

 





     









 

Chọn C.

Câu 5. Cho hàm số

 

liên tục trên

 

;a 

với

0a 

và thỏa

 

d 62





với mọi

.xa

Tính

 

4.f

 

4 2.f 

 

4 4.f 

 

4 8.f 

 

4 16.f 

Lời giải. Từ

 

d 62





, đạo hàm hai vế ta được

 



Suy ra

   

4 4 4 8.

fx xx f    

Chọn C.

Vấn đề 2. Kỹ thuật đổi biến

Câu 6. Cho





2017

d2fx x



. Tính tích phân

 

2017

. ln 1 d .

I fx x















1.I 



5.I 

Lời giải. Đặt

 

ln 1 ,

tx

suy ra

2d d d

xx xx t

   



Đổi cận:

2017

1 2017

xe t











 





Khi đó

 

2017 2017

11 1

d d .2 1.

22 2

I ft t fx x

  



Chọn A.

Câu 7. Cho hàm số

 

liên tục trên



và

 

d 4, sin cos d 2.

x f x xx







Tính tích

phân

 

d.I fx x



2.I



I 

4.I



10.I 

Lời giải.  Xét

 

d 4.





Đặt

t xt x 

suy ra

2d d .tt x

Đổi cận

















Suy ra





 





933

111

4 d 2 2d d 2.

x ft t ft t

    



 Xét

 

sin cos d 2.f x xx







Đặt

sin ,ux

suy ra

d cos d .u xx

Đổi cận













 





Suy ra

   

2 sin cos d d .f x xx f t t







Vậy

 

   

3 13

0 01

d d d 4.

I fx x fx x fx x



Chọn C.

Câu 8. Cho hàm số

 

liên tục trên



và

 

tan d 4, d 2.

xfx

f xx x









Tính tích

phân

 

d.I fx x



6.I 

2.I 

3.I 

1.I 

Lời giải. Xét

 

tan d 4.f xx







Đặt

tan ,tx

suy ra

 

d d tan 1 d d .

cos 1

t x xx x

     



Đổi cận:













 





Khi đó

 

   

0 00

4tanddd.

ft fx

f xx t x



 



 

Từ đó suy ra

 

11 1

00 0

d d d 4 2 6.

fx xfx

I fx x x x

   



 

Chọn A.

Câu 9. Cho hàm số

 

liên tục trên



và thỏa mãn





tan . cos d 1,

xf x x







 

d 1.





Tính tích phân

 





1.I 

2.I 

3.I 

4.I 

Lời giải. ● Xét

 

tan . cos d 1A xf x x







. Đặt

cos .tx

Suy ra

d 2 sin cos d 2cos tan d 2 .tan d tan d .

t x xx x xx t xx xx

    

Đổi cận:







   







   





Khi đó









 





11 1

22 2

111

1 d d d d 2.

222

ft ft fx fx

A tt x x

ttx x

       

 

● Xét

 

d 1.





Đặt

ln .

ux

Suy ra

2 ln 2 ln 2 d du

dd dd .

ln ln ln 2

x xu x

ux x x

x xx xx xx u

     

Đổi cận:

xe u





   







   





Khi đó

     

44 4

11 1

1 d d d 2.

fu fx fx

Bux x

ux x

     

 

● Xét tích phân cần tính

 





Đặt

2,vx

suy ra



















Đổi cận:





   







   





Khi đó









 

44 1 4

11 1

22 2

d d d d 2 2 4.

fv fx fx fx

Iv x xx

vx x x

    

  

Chọn D.

Câu 10. Cho hàm số

 

y fx

xác định và liên tục trên

;2 ,







thỏa

 

2.fx f x







 











Tính tích phân

 







I 

2.I 

I 

3.I 

Lời giải. Đặt



suy ra

d d.xt



Đổi cận:





   







   





Khi đó

22 2

1 11

. d d d.

f ff

t tx

I tt x

tt x

   

 

 

 

 

 

 



   





  















 

Suy ra

 





22 2 2

11 1 1

22 2 2

2 dd d d

11 1 1

f fx f

I xx x x

xx x x

 

















 

 

  

 

1 11 3

d 1d 3 .

x xx I

 







        









 



Chọn A.

Câu 11. Cho hàm số

 

liên tục trên



và thỏa

   

2 2 cos 2fx f x x  

với mọi

x  

Tính





I fx x











. B.

0I 

. C.

2I 

. D.

6I 

Lời giải. Đặt

d d.tx x t  

Đổi cận:







  







  





Khi đó

     

33 3

22 2

3 33

2 22

d d d.I f tt f tt f xx

 

 





   



Suy ra

  



3 33

2 22

CASIO

3 33

2 22

2 d 2 2 cos 2 d 2 cos d 12 6.

I ft f t t tt t t I

 

 



         



 

Chọn D.

Câu 12. Cho hàm số

 

y fx

xác định và liên tục trên



thỏa

 

4 321fx x x  

với

mọi

.x  

Tích phân

 

dfx x





bằng

10.

72.

Lời giải. Đặt

4 3,xt t

suy ra

 

d 5 4 d.xt t

Đổi cận



  













Khi đó

 

 



 

81 1

54 4

21 1

d 4 3 5 4 d 2 1 5 4 d 10.fxxfttttttt

 

    

 

Chọn B.

Câu 13. Cho các hàm số

 

,fx

 

liên tục trên

 

0;1 ,

thỏa

     

. .1mf x nf x g x 

với

,mn

là số thực khác

và

   

d d 1.fxx gxx



Tính

.mn

0.mn

mn

2.mn

Lời giải. Từ giả thiết



    

. .1mf x nf x g x 

, lấy tích phân hai vế ta được

 





. . 1 d ( )dmf x nf x x gx x









Suy ra

 

1 d1mn f xx 



(do

   

d d1

fxx gxx









Xét tích phân

 

1 d.f xx





Đặt

1tx



, suy ra

d d.tx

Đổi cận:

















Khi đó

   



  

1 011

0 100

1 d d d d 1.f x x ft t ft t fx x    

 

 

Từ

 

và

 

suy ra

mn

. Chọn C.

Câu 14. Cho hàm số

 

xác định và liên tục trên

 

0;1 ,

thỏa mãn

   

' '1fx f x

với mọi

 

0;1 .x 

Biết rằng

   

0 1, 1 41.ff

Tính tích phân

 

d.I fx x



41.I



21.I 

41.I 

42.I 

Lời giải. Ta có



   



 

' '1 1 .f x f x fx f x C

       

Suy ra



  



 



0 1, 1 41.

0 1 42.

f fC C



   

Suy ra



  

   

1 42 1 42fx f x fx f x        

   

1 d 42d 42.fx f x x x



     





 

Vì

       

' '1 d 1 d .fx f x fxx f xx     



 

Từ

 

và

 

suy ra

   

d 1 d 21.fxx f xx 



Chọn B.

Câu 15. Cho hàm số

 

y fx

liên tục trên



và thỏa mãn

   

f x fx x

với mọi

.x 



Tính

 

d.I fx x



I 



I 

I 

Lời giải. Đặt

 

u fx

, ta thu được

.u ux

Suy ra

 

3 1d d .u ux

Từ

u ux

, ta đổi cận

















Khi đó

 

3 1d .

I uu u 



Chọn D.

Cách khác. Nếu bài toán cho

 

có đạo hàm liên tục thì ta làm như sau:

Từ giả thiết

 

   



  

 





0 00 00

2 22

ff f

f x fx x





 



    

















 

Cũng từ giả thiết

   

f x fx x

, ta có

         

'. '. .'.fxf x fxfx xfx

Lấy tích phân hai vế

         

'. '. d .'dfxf x fxfx x xfxx











   





 

d d.

42 4

fx fx

xfx fx x fx x

















        



















Vấn đề 3. Kỹ thuật tích phân từng phần

Câu 16. Cho hàm số

 

thỏa mãn





 

. .d8

xf x e x







và

 

3 ln 3f 

. Tính

 

I ex



1.I



11.I 

8 ln 3.I 

8 ln 3.I 

Lời giải. Đặt

 

d .d

v f xe x





















Khi đó

 





 

. . d . d.

fx fx fx

xfxexxe ex







Suy ra

   

 

8 3. d d 9 8 1.

f fx fx

e ex ex      



Chọn A.

Câu 17. Cho hàm số

 

có đạo hàm liên tục trên

0; ,









thỏa mãn

 

' cos d 10f x xx







và

 

0 3.

f 

Tích phân





sin 2 df x xx





bằng

13.



7.I



7.I 

13.I 

Lời giải. Xét

 

' cos d 10f x xx







, đặt









d sin 2 d

cos

d ' cos d

u xx

v fx

v f x xx























Khi đó

   

 

10 ' cos d cos sin 2 df x xx xf x f x xx





 



   

 

10 0 sin 2 d sin 2 d 10 0 13.f f x xx f x xx f



        



Chọn D.

Câu 18. Cho hàm số

 

y fx

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

1d 3fx x



và

 

1 4.f



Tích phân

 

xf x x



bằng



Lời giải. Ta có

   

1d 3 d 3

fx x ft t



     



hay

 

d 3.fx x



Xét

 

   

1 11

0 00

' d ' d ' d.

xfx x tftt xfxx



   

 

Đặt

   

d 'd

ux u x

vfxx vfx



















Khi đó







  

  



111

000

1 1 11

' d ' d d 43 .

2 2 22

xf x x tf t t xfx fx x







       







Chọn C.

Câu 19. Cho hàm số

 

nhận giá trị dương, có đạo hàm liên tục trên

 

0;2 .

Biết

 

01f 

và

 

fxf x e





với mọi

 

0;2 .x 

Tính tích phân

 

x x fx







I 

Lời giải. Từ giả thiết

 

   

24 2

2 2 1.

xx x

fxf x e f



     

Ta có

 





x x fx







Đặt

















d 3 6d

ux x

u x xx

v fx



































Khi đó

 





 





 

32 2 2

3 ln 3 6 ln d 3 2 ln d 3 .

I x x fx x x fx x x x fx x J



   



Ta có

 



 



 

2 ln d 2 2 2 ln 2 d 2

J x x fx x t t f t t





      







    

 



 

2 2 2 ln 2 d 2 2 ln 2 d .x xfx x xxfxx



       







Suy ra

 

   

22 2

00 0

2 2 ln d 2 ln 2 d 2 ln 2 dJ x x fxx x x f xx x x fxf xx   

 

  





2 24 2 2

32 16

2ln d 2 2 4d .

15 15

xxe x xxx xx J



   



Vậy

IJ 

Chọn D.

Câu 20. Cho biểu thức

 

2 cot

ln 1 2 sin 2 d ,

S xe x























 

























với số thực

0.m



Chọn khẳng định

đúng trong các khẳng định sau.

5.S



9.S



2 cot 2 ln sin .



  















  



2 tan 2 ln .























Lời giải. Ta có

 

2 22

2 cot 2 cot 2 cot

4 44

2 sin 2 d 2 d sin 2 d .

xx x

m mm

xex ex xex

 

 

 

 

 

Xét

 

22 2

2 cot 2 cot 2 2 2 cot 2 2 cot

44 4

sin 2 d d sin sin . sin d

sin

xx x x

mm m

xex e x xe x ex

 



 



 







  











 

2 2 cot 2 cot

sin . 2 d .

xe e x









 

Từ

 

và

 

suy ra

2 cot

2 2 cot 2

sin . 1 sin . .

I xe e





  



2 cot

2 22

ln sin . 2 cot 2 ln sin .

4 44

m mm



 





  







 



    

















  



 





Chọn C.

Vấn đề 4. Tính a, b, c trong tích phân

Câu 21. Biết





ln 9 d ln 5 ln 2

x xa b c

 



với

, , .

abc





Tính

.Pabc

13.P 

18.P 

26.P 

34.P 

Lời giải. Đặt





ln 9

du dx

dv dx







































Khi đó

 









3 ln 9 2 d 5 ln 5 4 ln 8 2 1 d

Ix x x x









       



















5 ln 5 12 ln 2 2 3 ln 3 5ln 5 6 ln 2 2 6 13.

x x bP







 











Chọn A.

Nhận xét. Ở đây chọn

3vx



thay bởi

để rút gọn cho

9 x

, giảm thiểu biến đổi.

Câu 22. Biết

2 2 11

d .ln

x ex e

men e











 















với

, , mnp

là các số nguyên

dương. Tính tổng

.P mn p 

5.P 

6.P



7.P 

8.P



Lời giải. Ta có

22 2 1 1

dd .

.2 .2

xx x

x ex

I x x xx A A















    

















Tính









Đặt

.2 d .ln 2.2 d 2 d d .

ln 2

x xx

t e te x x t



       

Đổi cận:

x te

xt e





 







 





Khi đó

1 d1 1 21

. ln ln ln 1 .

.ln 2 .ln 2 ln 2 ln 2

t ee

e te e ee e















   















Vậy

ln 1 2 7.

4 ln 2

I n P mn p

















          

























Chọn C.

Câu 23. Biết

 

2 cos cos 1 sin

d ln

cos

x x xx x

xa b



  

 





với

, , abc

là các số hữu tỉ.

Tính

.P ac b

P 

Lời giải. Ta có

 

2 cos cos 1 sin

cos

x xx x x



  











 

2 22 2

0 00 0

cos d cos

1 sin

d d cos d

cos cos cos

xx xx

x x x xx

xx xx xx

  





   

 

  

2 22

1 1 12

sin ln cos 1 ln 1 ln

2 8 28

x xx x













  











1 2.

b P ac b









       











Chọn C.

Câu 24. Biết

ln 8

ln 3

d 1 ln

x aa b

  





với

, .







Tính

P ab

1.P 

1.P



3.P



5.P 

Lời giải. Ta có

 

ln 8 ln 8 ln 8 ln 8

ln 3 ln 3 ln 3 ln 3

d 1 d 1d d .

xx x x

I x e e x e x e x

     



  



ln 8

ln 3

d 2 2 3.

ex e

 





ln 8

ln 3

1d .

ex



Đặt

2 22

t e te

   

, suy ra

2d 2 d d .

tt tt

tt e x x

  



Đổi cận:

ln 3 2

ln 8 3





 







 





Khi đó

ln 8 3 3

ln 3

d 1 1 1 13

1d 1 d ln 1 ln .

2 1 22

tt t

e x dt t t













      





















 

Vậy

1 ln 2 2 3 5.

I P ab







          











Chọn D.

Câu 25. Biết

 

a bc

x x xx



 



với

, , .abc



 

Tính

P abc



12P



. B.

18P 

. C.

P 

. D.

46P



Lời giải. Ta có

 





 

x xx

xx x x





 



Đặt

ux x 

, suy ra

 

11 1

d d 2d d .

2 12

u xu x











    















Đổi cận

2 32

1 21





 







  





Khi đó

d2 1 1

3 2 21











   

















3 2 21

2 32 12 2 12 46.

32 21























           



























Chọn D.

Câu 26. Biết

sin 4 2 6

cos 1 sin 1

x abc







 



với

, , .abc 

Tính

.Pabc

10.P 

12.P 

14.P 

36.P 

Lời giải. Ta có

sin 4 2 sin 2 cos 2

d 2 d.

3 cos2 3 cos2

cos 1 sin 1

x xx

Ix x





 

 



Đặt

cos 2 d 2 sin 2 d .t x t xx

    

Đổi cận:













 





Khi đó

 

01 1

10 0

2d2d33d

33 33 2

I t t t tt

tt tt

     

   

 

 

1 2 2 16 2 12 6 8

3 3 12 36.

33 6

t t bP















          

















Chọn D.

Câu 27. Biết

x ae e



  



với

, , .abc 

Tính

.P abc

5.P 

4.P



3.P 

3.P



Lời giải. Ta có

 

44 4

11 1

1 44

d dd

x xx

xe e x ex

x xx



 

 

 

2 1 1 1 11

d d 11

x x x ee

e ee

ex x













        

















1 4.

b P abc







          











Chọn B.

Câu 28. Biết

xa b c





 





với

, , .

abc

 

Tính

P abc

1.P



2.P



3.P



4.P



Lời giải. Đặt

2 cosxu

với













. Suy ra

4 cos d 4 sin 2 d .x u x uu    

Đổi cận







   







   





Khi đó

cos

2 2 cos

4 sin 2 d 8 .sin .cos d

2 2 cos

sin

I uu u uu











   

2 2 22

4 4 44

16 cos .cos d 8 1 cos .cos d 8 cos d 4 1 cos 2 d

uu u uu uu u u

  

   

  

 

8sin 4 2.sin 2 4 2 6 4 3.

ux u b P











            











Chọn C.

Câu 29. Biết

 

ln ln 1

ln 1 2

xx b

xx e



 

 



với

, .ab



 

Tính

.P ba

P 

6.P



10.P 

Lời giải. Ta có

   

ln ln ln 1 ln

d . d.

ln 1

ln 1 ln 1

xx x x

xx xx







 



Đặt

 

ln 1 ln 1 ln

d d d.

ln 1 ln 1

ln 1

xx x

t tx x

xx xx









     











 



Đổi cận:

xe t























Khi đó

 

1 12

I tt t



   





Chọn B.

Câu 30. Biết

cos 3







 





với

, , abc

là các số nguyên. Tính

P abc

37.P 

35.P 

35.P 

41.P 

Lời giải. Ta có

   

66 6

cos

d cos 1 d 1 cos d .

I x x x xxx x xx xx

 

 

    



 

Lại có





 

66 6

2 22

66 6

cos

cos cos

d dd

xx tt

I x tt

xx tt

 









  

  

 

 

 

1 cos d 1 cos d .t t t tt x x x xx





     



Suy ra

 

66 6

2 22

66 6

2 1 cos d 1 cos d 2 cos d

I x x x xx x x x xx x xx

 

 

      

 

cos d .I x xx





   



Tích phân từng phần hai lần ta được

36 3



 



36 35.

b P abc







         











Chọn C.

Vấn đề 5. Tính tích phân hàm phân nhánh

Câu 31. Cho hàm sô

 

1 khi 0

khi 0



















Tính tích phân

 

d.I fx x



















11 11





Lời giải. Ta có

     

0 2 02

1 0 10

d d d 1d .

I fx x fx x e x x x





   

  

Chọn C.

Câu 32. Cho hàm số

 

xác định trên













thỏa

 

, 0 1

fx f







và





1 2.f



Giá trị của biểu thức

   

13ff

bằng

ln15.

2 ln15.

3 ln15.

4 ln15.

Lời giải. Ta có

 







 





ln 1 2 ;

d ln 2 1

n2 1 ;

xC x

fx x x C

x Cx

 

      





















   

0 1 ln 1 2.0 1 1.f CC       



   

1 2 ln 2.1 1 2 2.f CC   

Do đó

 





 

ln 1 2 1 khi

1 ln 3 1

3 ln 5 2

ln 2 1 2 khi





 





 















 





   

1 3 3 ln 5 ln 3 3 ln15.ff    

Chọn C.

Câu 33. Cho hàm số

 

xác định trên





\ 2;1



thỏa mãn

 







   

3 30ff 

và

 

f 

Giá trị biểu thức

     

4 14f ff 

bằng

ln 20 .



ln 2 .



ln 80 1.



ln 1.



Lời giải. Ta có

 

1 11 1

31 2









 















 

   

ln 1 ln 2 ; 2

d ln 1 ln 2 ; 2 1

ln 1 ln 2 ; 1

x x Cx

fx x x x C x

x x Cx



     





          







































  

 



11 1 1 1

0 ln 1 0 ln 0 2 ln 2 .

33 3 3 3

f CC



           





 

3 3 0 ln .

3 10

f f CC      

Ta có



 



2 13

151 11 1 1

4 1 4 ln ln 2 ln ln 2 .

323 32 3 3

f f f C CC

     

Chọn B.

Câu 34. Cho hàm số

 

xác định trên

   

0; \ ,e

thỏa mãn

 

ln 1







ln 6f



















và





3.fe



Giá trị biểu thức

 

f fe



















bằng

 

3 ln 2 1 .

2 ln 2.

3 ln 2 1.

ln 2 3.

Lời giải. Ta có









ln 1







 

   

ln 1 ln khi 0;

d ln 1

d ln ln 1 .

ln 1 ln 1

ln ln 1 khi ;

xC x e

fx x x C

xx x

x C xe





 





       







   









ln 6 ln 1 ln ln 6 ln 2.

f CC

  





       









  



   

3 ln ln 1 3 3.fe e C C       

Do đó

 



  

   

 

ln 2 ln 2

ln 1 ln ln 2 khi 0;

ln ln 1 3 khi ;

ln 2 3

x xe





















 

















   











 

3 ln 2 1 .f fe







    











Chọn C.

Câu 35. Cho

 

là một nguyên hàm của hàm số

1 sin 2





với

\ ,.

x kk







  









Biết

   

0 1, 0FF

, tính giá trị biểu thức

12 12

PF F



 





 









 

0.P 

2 3.

P 

1.P 

D. Không tồn tại

Lời giải. Với

thuộc vào mỗi khoảng

; ,

k kk









  













ta có

 

d d d1

tan .

1 sin 2 2 4

sin cos

2 cos

xx x

Fx x C









    































 



0; ;

12 4 4

 







 











nên

 

1 13 33

0 tan .

12 2 4 2 2 12 2 2

FF x F



 





   

 

 

  

 

 

 

 

   



11 5

;;

12 4 4

 





















nên

 

11 1 1 3 11 1 3

tan .

12 2 4 2 2 12 2 2

FF x F



 





   

 

 

          

 

 

 

 

   

Vậy

12 12

PF F



 





  









 

Chọn C.

Vấn đề 6. Tính tích phân dựa vào tính chất

Câu 36. Cho hàm số





là hàm số lẻ, liên tục trên





4;4 .

Biết rằng

 

d2f xx







và

 

2 d 4.

f xx



Tính tích phân

 

d.I fx x



10.I



6.I 

6.I 

10.I 

Lời giải. Do

 

là hàm lẻ nên

 





f x fx 

 Xét

 

d 2.A f xx







Đặt

d d.tx t x  

Đổi cận:



  













Khi đó

     

022

200

d d d.A ft t ft t fx x  



 Xét

   

2d 2d.B f xx f xx  



Đặt

2 d 2d .ux u x   

Đổi cận:



 













Khi đó

     

4 44

2 22

d d d 2 2.4 8.

B fu u fx x fx x B     



Vậy

    



424

002

d d d 2 8 6.I fx x fx x fx x     



Chọn B.

Câu 37. Cho hàm số

 

là hàm số chẵn, liên tục trên

 

1; 6 .

Biết rằng

 

fx x







và





2 d 3.f xx





Tính tích phân

 

d.I fx x







I 

5.I



11.

I 

14.

I 

Lời giải. Vì

 

là hàm số chẵn nên

 

2d 2d 3.f xx f xx

 



Xét

 

2 d 3.K f xx



Đặt

2 d 2d .tx t x

   

Đổi cận:

















Khi đó

     

66 6

22 2

d d d 2 6.

K ft t fx x fx x K

     

 

Vậy

    



626

1 12

d d d 8 6 14.I fx x fx x fx x



   



Chọn D.

Câu 38. Cho hàm số

 

liên tục trên

 

3;7 ,

thỏa mãn

   

10fx f x

với mọi

 

3;7

x 

và

 

d 4.fx x



Tính tích phân

 

d.I xf x x



20.I 

40.I 

60.I 

80.I 

Lời giải. Đặt

 

3 7 d d.t x tx      

Đổi cận

















Khi đó

           

377

733

10 10 d 10 10 d 10 10 dI tf t t tf t t xf x x      



 



   

 



 

7 77 7

3 33 3

10 d 10 d d 10 d .

fx f x

xfx x fx x xfx x fx x I





  

Suy ra

 

2 10 d 10.4 40 20.

I fx x I     



Chọn A.

Câu 39. Cho hàm số





y fx



là hàm số chẵn và liên tục trên đoạn

 

;,

thỏa mãn

 

d 2018.fx x







Giá trị của tích phân

 

2018 1











bằng

I 

2018

I 

2018.I 

4036.I 

Lời giải. Đặt

d d.

xt x t  

Đổi cận





  







  





Khi đó

       

2018 2018

d d d d.

2018 1 2018 1 1 2018 1 2018

tt t x

ft ft ft fx

I tt t x

  

  





 

  

   

  

 

Vì

 

y fx

là hàm số chẵn trên đoạn

 

;

nên

   

 

2018

2018 1

f x fx I x





    





Vậy

  



 

2018

2 d d d 2 d 2.2018 2018.

2018 1 2018 1

fx fx

I x x fx x fx x I

  

 

 

     



  

Chọn C.

Câu 40. Biết

2018

2018 2018

sin

sin cos

x xb









với



 

Tính

P ab

6.P 

8.P 

10.P 

12.P 

Lời giải. Gọi

2018

2018 2018

sin

sin cos









Đặt

d d.t x tx

     

Đổi cận













 





Khi đó

 







 







 

2018 2018 2018

2018 2018 2018 2018 2018 2018

sin sin sin

d d d.

sin cos sin cos sin cos

t t tt xx

I tt x

t t tt xx





  



  

  

   

 

Suy ra

 

2018

2018 2018

2018 2018 2018 2018 2018 2018

000

sin

sin sin

2ddd

sin cos sin cos sin cos

xx x

I xxx

xx xx xx

 











2018 2018 2018

2018 2018 2018 2018 2018 2018

sin sin sin

d d d.

2 sin cos 2 sin cos sin cos

x xx

I x xx

xx xx xx













    



 





 

Đặt





ta suy ra

2018 2018 2018

2018 2018 2018 2018 2018 2018

sin cos cos

d d d.

sin cos sin cos sin cos

xux

xx uu xx











Vậy

d 8.

Ix P











      













Chọn B.

Vấn đề 7. Kỹ thuật phương trình hàm

Câu 41. Cho hàm số

 

y fx

liên tục trên

;













và thỏa mãn

   

2 cos .

fx f x x 

Tính

tích phân

 

d.I fx x









2.I 

I 

2.I 

Lời giải. Từ giả thiết, thay

bằng



ta được

   

2 cos .f x fx x 

Do đó ta có hệ

   

 

2 cos 4 2 2 cos

cos .

2 cos 2 cos

fx f x x fx f x x

fx x

f x fx x fx f x x





   



   





   





Khi đó

 

1 12

d cos d sin .

3 33

I f x x xx x











  



Chọn B.

Câu 42. Cho hàm số

 

y fx

liên tục trên

 

2;2

và thỏa mãn

   

23 .

fx f x

 



Tính tích phân

 

d.I fx x























Lời giải. Từ giả thiết, thay

bằng

x

ta được



  

23 .

f x fx

 



Do đó ta có hệ





 

   

 

   

 

23 46

2 3 96

fx f x fx f x

f x fx fx f x





   







   









   









Khi đó

 

d d.

5 20

I fx x x





 





Chọn C.

Câu 43. Cho hàm số

 

y fx

liên tục trên

 

0;1

và thỏa mãn

  



1 2.xfx f x x x  

Tính tích phân

 

d.I fx x



I 



I 



Lời giải. Từ giả thiết, thay

bằng

x

ta được

 



 

  

1 1 21 1x f x fx x x     

 

   

2 2 34

2 1 1 12 6 4 .x x f x fx x x x x

     

 

Ta có

       

2 4 42

12 12xfx f x x x f x x x xfx    

. Thay vào

 

ta được

 

   

2 42 2 34

2 12 1 2 6 4x x x x xfx fx x x x x



     





 

2 34 6 5 3 2

1 2 2221x x x fx x x x x

 

 





 

2 34 2 2 34

12 112

x xxfx x x xx

fx x

    

   

Vậy

 

d 1d .

I fx x x x x x







    













Chọn C.

Câu 44. Cho hàm số





liên tục trên







và thỏa mãn

 

2 3.fx f x



















Tính tích

phân

 





I 

Lời giải. Từ giả thiết, thay

bằng

ta được

 

2.f fx



















Do đó ta có hệ

 

23 23

1 3 16

2 42

fx f x fx f x

fx x

f fx fx f

x x xx



 









 



 







 



    





 







 













 





Khi đó

 

2 23

I dx dx x

  





     









  



Chọn B.

Cách khác. Từ

   

2 3 32 .fx f x fx x f

 





     









 

Khi đó

 

2 2 22

1 1 11

2 2 22

d 3 2 d 3 d 2 d.

I x xx x

xx x



 



 



















 









   























  

Xét





















Đặt



, suy ra

d d d d d.t x tx x t

   

Đổi cận:





 













Khi đó

 





d dt d .

ft fx

J tf t t x I







   











 

Vậy

3d 2 d .

I xI I x     



Câu 45. Cho hàm số

 

liên tục trên

 

0;1

và thỏa mãn

   

2 31 1 .fx f x x 

Tính

tích phân

 

d.I fx x





Lời giải. Từ giả thiết, thay

bằng

x

ta được

   

21 3 2 .f x fx x x  

Do đó ta có hệ

  



   

 

   

2 3 1 1 4 6 1 21

21 3 2 9 61 32

fx f x x fx f x x

f x fx x x fx f x x x





    









     





 

32 21

xx x

 

  

Vậy

 

32 21 d .

5 20

I xx x x



   



Chọn A.

Cách khác. Từ

   

2 31 1 1 31 .

fx f x x fx x f x



         





Khi đó

   

11 1

00 0

d 1 d 3 1 d.

I fxx xx f xx





   







Xét

 

1 d.J f xx



Đặt

1 d d.t x tx

     

Đổi cận:

















Khi đó

     

011

100

dt dt d .J ft ft fx x I   



Vậy

1d3 1d .

2 5 20

I xx I I xx







       







Vấn đề 8. Kỹ thuật biến đổi

Câu 46. Cho hàm số

 

thỏa

   

3 6.fxf x x x





Biết rằng

 

0 2,f 

tính





2.f

 

2 64.

f 

 

2 81.f 

 

2 100.f 

 

2 144.f 

Lời giải. Từ giả thiết ta có

 













52 3

. d 3 6d 2 .

fx f x x x x x x C



    



Thay

0x 

vào hai vế, ta được

 

CC

Suy ra

   

2 63 2 6 3

4 4 2 2 4.2 4 100.fx x x f

        

Chọn C.

Câu 47. Cho hàm số





có đạo hàm

 

'fx

liên tục và nhận giá trị không âm trên

 

1; ,



thỏa

 

1 0,f



 





. 4 41

e fx x x





 



với mọi

 

1; .x  

Mệnh đề nào sau đây đúng?

 

1 4 0.



 

 

0 4 1.f





 

1 4 2.f





 

2 4 3.f





Lời giải. Từ giả thiết suy ra

 

e fx x





(do

 

'fx

không âm trên

 

1; 

)







  

 

d 2 1d .

fx fx

e fxx x x e x xC



       



Thay

1x 

vào hai vế, ta được

 

1 1 1.

e CC   

Suy ra

 





   

21 7

1 ln 1 4 .

e xx fx xx fx f





       



Chọn B.

Câu 48. Cho hàm số

 

thỏa mãn

     

. 15 12f x fx f x x x



 

 



với mọi

x 



và

   

0 0 1.ff





Giá trị của

 

bằng

10.

Lời giải. Nhận thấy được

    

    

. ..

f x fx f x fx f x



  

  



  

Do đó giả thiết tương đương với

   

. 15 12 .fx f x x x











Suy ra

 





 

0 0 1.

4 52

. 15 12 d 3 6 1

fx f x x x x x x C C







      



   

. 361fx f x x x



 

   

 

52 3

. d 3 6 1 d 2 '.

fx f x x x x x x x C



         



Thay



vào hai vế ta được

 

' '.



Vậy

   

2 63 2

4 2 1 1 8.fx x x x f      

Chọn C.

Câu 49. Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

1; 2

và thỏa mãn

   

0, 1; 2 .fx x 

Biết rằng

 

d 10fxx







và

 

d ln 2.







Tính

 

2.f

 

2 20.f 

 

2 10.f 

 

2 10.f 

 

2 20.f 

Lời giải. Ta có

       

d 10 10 2 1 10.f x x fx f f



   



 

Lại có

 

   

d ln 2 ln ln 2 ln ln 2

x fx fx





  





(do

   

0, 1; 2fx x 

)

   

 

ln 2 ln 1 ln 2 ln ln 2 2.

    

 

Từ

 

và

 

, suy ra





2 20.f 

Chọn B.

Câu 50. Cho hàm số





có đạo hàm liên tục trên

 

1;1

, thỏa mãn

 

0, fx x 

và

 





'2 0f x fx

. Biết rằng

 

11f



, giá trị của

 

1f 

bằng



Lời giải. Ta có

       

 

' 2 0' 2 2

f x fx f x fx

     

(do

 

fx

)

 

d 2d ln 2

x x fx x C

       



(do

 

0fx

Mà



 



 





22 4

1 1 2 ln 2 2 1 .

f C fx x fx e f e



             

Chọn C.

Câu 51. Cho hàm số

 

xác định và liên tục trên



đồng thời thỏa mãn

 

   

 

' , .

fx x

f x ef x x





 



  













Tính giá trị của

 

ln 2 .f

 

ln 2 .







ln 2 .



 

ln 2 ln 2 .

f 

 

ln 2 ln 2 .

f 

Lời giải. Ta có

   

 

f x ef x e

  

(do

 

0fx

)

 





dd .

x e x e C fx

fx e C

          





Thay



ta được

 

0 1.



     



Vậy

   

ln 2

1 1 11

ln 2 .

21 3

fx f

     





Chọn B.

Câu 52. Cho hàm số

 

có đạo hàm liên tục trên

 

0;

, biết

   

 

' 2 3 0,fx x f x 

 

0fx

với mọi

0x 

và

 

f 

Tính

     

1 1 2 ... 2018 .P ff f   

1009

2020

P 

2019

2020

P 

3029

2020

P 

4039

2020

P 

Lời giải. Ta có





   

 

' 23 0 23

fx x f x x

     

(do

 

0fx

)

 

d 2 3d 3 .

x x x x x C fx

f x x xC

             





Mà



  

11 1 1 11

12 .

66 12

1 3.1 3 2

f C fx

C xx

           



 

Suy ra

1 1 1 1 1 1 3029

1 ... .

2 3 3 4 2019 2020 2020

    

 

 

  

 

 

 

 

    

Chọn C.

Câu 53. Cho hàm số

 

liên tục trên

0; 3 ,







thỏa mãn

 

1,fx

 

00f 

và

   

1 2 1.f x x x fx



 

Giá trị của

 

bằng

Lời giải. Từ giả thiết suy ra

 

fx fx



   





 

2 d 2 d 2 12 1

x x fx x C





    





Mà

   

 

0 0 0 3 3.f C fx x f   

Chọn B.

Câu 54. Cho hàm số

 

có đạo hàm và liên tục trên

 

1; 4 ,

đồng biến trên

 

1; 4 ,

thoản mãn





 

2x xf x f x









với mọi

 

1; 4 .x 

Biết rằng

 

f  tính tích phân

 

d.I fx x





1186

I 

1187

I 

1188



I 

Lời giải. Nhận xét: Do





đồng biến trên

 

1; 4

nên

 

 

' 0, 1; 4fx x

 

Từ giả thiết ta có

 

       

12 ' .12 , 1;4

x fx f x f x x fx x

  



       

  

 

d d 12 .

21 2 21 2

fx fx

x x xx f x x x C

fx fx



         





Mà

  



3 4 28 7

2 3 2 9 9 18

f C fx x xx



















        

 

1186

fx x  



Chọn A.

Câu 55. Cho hàm số

 

liên tục, không âm trên









, thỏa

   

 

. ' cos 1fx f x x f x

với mọi













và

 

0 3.f 

Giá trị của



















bằng

2 2.

Lời giải. Từ giả thiết ta có

   

 

cos , 0;

fx f x









 







   

 

d cos d 1 sin .

fx f x

x xx f x x C



      





Mà

 

   

0 3 2 sin 2 1 sin 4 sin 3, 0;

f C fx x x x x







            





2 2.









  











Chọn D.

Câu 56. Cho hàm số

 

liên tục, không âm trên

 

0;3 ,

thỏa

     

.2 1fx f x x f x





với

mọi

 

0;3x 

và

 

0 0.f 

Giá trị của

 

bằng

3 11.

Lời giải. Từ giả thiết ta có

   

 

 

2 , 0;3

fx f x



 



 

d 2d 1 .

fx f x

x xx f x x C



      





Mà

   

 

 

2 42

0 0 1 1 1 2 , 0;3f C fx x x x x

 

3 3 11.f  

Chọn D.

Câu 57. Cho hàm số

 

có đạo hàm không âm trên

 

0;1 ,

thỏa mãn

 

0fx

với mọi

 

0;1

x 

và

 













42 3

.' . 1 1 .

fx f x x fx

  

 

  

Biết





0 2,

f 

hãy chọn khẳng định đúng

trong các khẳng định sau đây.

 

1 2.

f

 

21.

f

 

1 3.



 

31.



Lời giải. Từ giả thiết ta có

 

   

 

.' . 1 1

fx f x

fx f x x fx





 

   

 









   

 

1 1 11

3 2 32

0 0 00

12 1

dd d

1 21

fx f x

xx x

fx fx









     



 



 

  

 





1 ln 1 1 2,605.

fx x x f





         



Chọn C.

Câu 58. Cho hàm số

 

liên tục trên

 

,\ 0; 1



thỏa mãn



 



 

1.xx f x f x x x



  

với mọi





0; 1

\x 



và

 

1 2 ln 2.f 

Biết





2 ln 3f ab



với

, ab 

, tính

.Pa b

P 

Lời giải. Từ giả thiết ta có

















, 0; 1 .

f x fx x



   







Nhận thấy









 





f x fx fx



















Do đó giả thiết tương đương với

   

. , 0; .

\ 1

fx x







  









Suy ra

 

. d 1 d ln 1 .

11 1

fx x x x x C

xx x







    











 



Mà



 



1 2 ln 2 1 . ln 1 1.

f C fx x x

       



Cho

2x 

ta được

 





2 33 9

2 . 2 ln 3 1 2 ln 3 .

3 22 2

ff P









         











Chọn D.

Câu 59. Cho hàm số

 

có đạo hàm xác định, liên tục trên

 

0;1 ,

thỏa mãn





01f





và

   

 

fx f x







 



















với mọi

 

0;1 .x 

Đặt

   

10Pf f



, khẳng định nào sau đây đúng?

2 1.P  

1 0.P 

0 1.P

1 2.P

Lời giải. Nhận thấy

     

10 dP f f fxx







nên ta cần tìm





.fx



Từ giả thiết ta có

 

1 d 1d .

fx fx

x x xC fx

fx xC

fx fx

 



          





 



 



Mà

   

01 1 .

f C fx



    



Vậy

 

d d ln 2 0,69.

P fxx x



   





Chọn B.

Câu 60. Cho hai hàm số

 

và





có đạo hàm liên tục trên

 

0;2 ,

thỏa mãn

   

'0. '2 0ff

và

     

.' 2 .

gx f x xx e

Tính tích phân

   

. ' d.I fxgx x





4.I 

4.I 

2.Ie

2.Ie



Lời giải. Từ giả thiết

   

 

'0 0

'0. '2 0 .

'2 0









  











Do đó từ



 

  

.' 2

gx f x xx e

, suy ra

 





22 2

00 2



























Tích phân từng phần ta được

   

. .dI f x gx gx f x x











       

   

2. 2 0. 0 2 d 2 d 4.

f g f g xx e x xx e x  



Chọn B.

Câu 61. Cho hàm số

 

0fx

xác định và có đạo hàm trên đoạn

 

0;1 ,

thỏa mãn

  



  



1 2018 d

gx f t t

gx f x





















Tính

 

d.I gx x



1009

I 

505.

I 

1011

I 

2019

I 

Lời giải. Từ giả thiết, ta có

   

     

' 2018

2018 2 ' .

' 2' .

gx fx

fx f x fx

gx f x fx









  











   

2 1009 ' 0 .

' 1009 1009

fx f x

f x fx x C









  





    





loaïi

Thay ngược lại, ta được

   

1 2018 1009 d 1009

tCt xC  



 

1009

1 2018 1009 1.

t Ct x C C







     











Suy ra

 

1009 1fx x

hoặc

 

1009 1fx x

(loại vì

   

0 0;1fx x 

Khi đó

     

1 11

0 00

1011

d d 1009 1 d .

I gx x f x x x x   

 

Chọn C.

Câu 62. Cho hai hàm

 

và

 

có đạo hàm trên

 

1; 4 ,

thỏa mãn



  

   

1 14fg

g x xf x

f x xg x

























với mọi

 

1; 4 .x 

Tính tích phân

  



d.I f x gx x









3 ln 2.

I 

4 ln 2.I 

6 ln 2.I 

8 ln 2.I 

Lời giải. Từ giả thiết ta có

       

..f x g x x f x xg x



  

           

. . 0. . 0f x x f x g x xg x x f x xg x



      



      

      

    



 

.. .

xf x xgx C f x gx

      

Mà

    



 

1 1 4 4 d d 8 ln 2.f g C I f x gx x x



         





Chọn A.

Câu 63. Cho hai hàm

 

và

 

có đạo hàm trên

 

1; 2 ,

thỏa mãn

   

1 10fg

và

 





 

   

 

2017 1

, 1; 2 .

2018

gx x x f x

gx fx x







 

























Tính tích phân



 



I gx f x x

















I 

1.I



I 

2.I 

Lời giải. Từ giả thiết ta có

 





 





 

 

2017

, 1; 2 .

2018

gx f x

gx fx











 

























Suy ra

 

  



 





gx g x f x f x gx f x

x xx x x







  







  





     



  











  



 





gx f x x C



    



Mà

       

 

1 1 0 1 d 1d .

f g C I gx f x x x x







           









Chọn A.

Câu 64. Cho hàm số

 

y fx



có đạo hàm trên





0;3 ,

thỏa mãn

 





 

3. 1

f x fx



















với mọi

 

0;3x 

và

 



Tính tích phân





 





13 .

xf x

f x fx













1.I



I 

Lời giải. Từ giả thiết

   

 

3. 1

3 2.

f x fx











   











Ta có

   

 

3. 1

13 . 1 .

f x fx

f x f x fx



  

  

  

Tích phân

 

33 3

00 0

d d d 1.

11 1

xf x

I xx x J

fx fx fx











     









 









 

Tính

       

3 033

0 300

1 11 1

d d d d.

1 13 13 13

Jx t t x

fx ft ft fx



   

   

 

Suy ra

   

33 3

3. 1

00 0

11 3

2 d d 1.d 3 .

1 13 2

f x fx

J x x xJ

fx f x



   

 

 

Vậy

I 

Chọn A.

Câu 65. Cho hàm số

 

y fx

liên tục trên đoạn

 

0;1

và thỏa mãn

   

1af b bf a

với mọi

 

, 0;1 .ab

Tính tích phân

 

d.I fx x



I 









Lời giải. Đặt

sin , cosa xb x

với

0; .













Từ giả thiết, suy ra

   

sin cos cos sin 1xf x xf x



  

22 2

00 0

sin cos d cos sin d 1d .

xf x x xf x x x

 



    



 

Ta có

     

cos

0 10

sin

0 00

sin cos d d d

cos sin d d d

xf xx ftt fxx









 













 

Do đó

   

1 d.

fx x







Chọn D.

Vấn đề 9. Kỹ thuật đạo hàm đúng

Câu 66. Cho hàm số





có đạo hàm liên tục trên

 

0;1 ,

thoả mãn

  



2018

f x xf x x





với

mọi

 

0;1 .x 

Tính

 

I fx x



2018 2021

I 



2019 2020

I 



2019 2021





2018 2019





Lời giải. Từ giả thiết

   

2018

3,f x xf x x





nhân hai vế cho

ta được



 







2 3 2020 3 2020

xf x xf x x xf x x







    





Suy ra





2021

3 2020

2021

xf x x x C 



Thay

x 

vào hai vế ta được

 

2018

2021

C fx   

Vậy

 

2018 2019

1 11 1

d d. .

2021 2021 2019 2021 2019

fx x x x x 





Chọn C.

Nhận xét: Ý tưởng nhân hai vế cho

là để thu được đạo hàm đúng dạng

 

' ' '.uv u v uv

Câu 67. Cho hàm số

 

có đạo hàm liên tục trên

 

0;4 ,

thỏa mãn

  



fx f x e x





 

với mọi





0;4 .x 

Khẳng định nào sau đây là đúng?

 

40 .

ef f

   

4 0 3.ef f e

   

4 0 1.ef f e 

  



4 0 3.ef f

Lời giải. Nhân hai vế cho

để thu được đạo hàm đúng, ta được

   

 

' 21 21.

xx x

efx ef x x efx x



  





Suy ra



  

21d 2121.

efx x x x x C    



Vậy

 

40 .

ef f

Chọn A.

Câu 68. Cho hàm số

 

có đạo hàm trên

,

thỏa mãn

   

2017 2018

' 2018 2018

f x fx x e

với

mọi

 

và

 

0 2018.

f 

Tính giá trị

 

1.f

 

2018

1 2018 .fe





 

2018

1 2017 .fe

 

2018

1 2018 .fe

 

2018

1 2019 .fe

Lời giải. Nhân hai vế cho

2018



để thu được đạo hàm đúng, ta được

   

 

2018 2018 2017 2018 2017

2018 2018 2018 .

xx x

f xe f xe x f xe x

 







  





Suy ra

 

2018 2017 2018

2018 d .

f xe x x x C



 



Thay

0x 

vào hai vế ta được

 

2018 2018

2018 2018 .

C fx x e    

Vậy

 

2018

1 2019 .fe

Chọn D.

Câu 69. Cho hàm số

 

có đạo hàm và liên tục trên

,

thỏa mãn

   

f x xf x xe







và

 

0 2.f



Tính

 

1.f

 



 

1.f



 

1.f



 

1.f



Lời giải. Nhân hai vế cho

để thu được đạo hàm đúng, ta được

 

2 2 22 2

2 2.

x x xx x

f x e f x xe xe e f x xe











  





Suy ra

 

2 22

2d 2 .

x xx

e f x xe x e C



  



Thay

0x 

vào hai vế ta được

 

0 2.

C fx e



    

Vậy





12 .fe



 

Chọn D.

Câu 70. Cho hàm số

 

liên tục và có đạo hàm trên

0; ,



















thỏa mãn hệ thức

   

tan .

cos

f x xf x





Biết rằng

3 3 ln 3

f fab





 















 

trong đó

, .ab

 

Tính giá

trị của biểu thức

P ab



P 

P 

Lời giải. Từ giả thiết, ta có

   

 

cos sin sin .

cos cos

xf x xf x xf x







  



Suy ra

 

sin d tan ln cos .

cos

xf x x x x x C

  



 Với

. 3 ln 2 3 . 3 2 ln 2 2 .

3 2 33 33

xf f C

  



 





         









 

 Với

1 31 1

. ln 3 ln 2 . 3 ln 3 2 ln 2 2 .

6 2 6 63 2 6 9

x f Cf C

  



 





            









 

Suy ra

3 3 ln 3 .

3 69 9

f f P ab









 









          













 









Chọn A.

Vấn đề 10. Kỹ thuật đưa về bình phương loại 1

Câu 71. Cho hàm số

 

liên tục trên

0; ,









thỏa

   

2 2 sin d .

f x fx x x

















 

















Tính tích phân

 

d.I fx x







0.I 





1.I 





Lời giải. Ta có

2 sin d .













 













Do đó giả thiết tương đương với

   

2 2 sin 2 sin d 0

f x fx x x x







 







   











 





 





2 sin d 0 2 sin 0, 0; .

4 42

fx x x fx x x



 



  



















 





Suy ra

   

2 sin d 2 sin d 0.

fx x I fx x x x



 





       









 



Chọn A.

Câu 72. Cho hàm số





liên tục trên

 

0;1

thỏa

   





2 ln d 2 ln 1 d .f x x fx x x





 









Tích phân

 

d.I fx x



I 

. B.



. C.

I 

. D.

lnI



Lời giải. Bằng phương pháp tích phân từng phần ta tính được

 

2 22

ln 1 d 2 ln 2 ln d .xx x

 



Do đó giả thiết tương đương với

         

ln 1 d 0 ln 1 , 0;1 .fx x x fx x x



      





Suy ra

 





d ln 1 d ln

fxx xx

 



. Chọn B.

Câu 73. Cho hàm số

 

có đạo liên tục trên

 

0;1 ,





và

 

'fx

đều nhận giá trị dương

trên

 

0;1

và thỏa mãn

 

02f 

và

     

 

' . 1d 2 ' . d .f x fx x f x fx x











Tính

 

d.I fx x









I 

Lời giải. Giả thiết tương đương với

   

' . 1d 0f xfx x











             

' . 1, 0;1 ' 1 ' d dfxfx x fxf x fxf xx x          



 

xC C



        

Vậy

   

38 d .

f x x I fx x



     





Chọn D.

Câu 74. Cho hàm số

 

có đạo hàm dương, liên tục trên đoạn

 

0;1

và thỏa mãn

 

0 1,f 

       

3 ' . d 2 ' . d.

f x fx x f xfx x















Tính

 

d.I fx x









I 

Lời giải. Giả thiết

 





3 '. d 2 '. d

f x fx x f xfx x



 







     

 

   

1 1 11

0 0 00

3'. d 23'. d d 0 3'. 1d 0f x fx x f x fx x x f x fx x

  

     

  

  

  

 



 

 



 





3 ' . 1 0, 0;1 9' . 1 9' . d d

fxfx x fxf x fxf xx x           



 





9. 3.

xC C



        

Vậy

   

1 d.

f x x fx x



    





Chọn D.

Câu 75. Cho hàm số

 

y fx

có đạo hàm dương, liên tục trên đoạn

 

0;1 ,

thỏa

 





1 01ff

và

       

' 1d 2 ' d .fxf x x fxfxx











Giá trị của tích phân

 

dfx x







bằng

5 33 27



5 33

5 33 54



Lời giải. Nhóm hằng đẳng thức ta có

       

' 1d 2 ' dfxf x x fxfxx













 







 



  



 



0 vi 1 0 1

' ' d2 ' d 0

' 1 d ' 1d 0

fxf x fx x fxfxx

fxfx x fx x

 



  







   









             

' . 1, 0;1 ' 1 ' d dfxfx x fxf x fxf xx x          



 



  

1 01

5 33 27

33 .

3 54

xC f x x C C





             

Vậy

   

5 33 27 5 33

3 d.

18 18

f x x fx x





    





Chọn C.

Vấn đề 11. Kỹ thuật đưa về bình phương loại 2

Kỹ thuật Holder

Câu 76. Cho hàm số

 

y fx

liên tục trên đoạn

 

0;1 ,

thỏa mãn

   

d d1fx x xfx x



và

 

d4fx x









. Giá trị của tích phân





dfx x







bằng

10.

80.

Lời giải. Ở đây các hàm xuất hiện dưới dấu tích phân là

     

, , fx xfx fx





nên ta sẽ liên kết

với bình phương





.fx x









Với mỗi số thực

, 

ta có

         

1 11 1

0 00 0

d d2 d dfx x x fx x x fx x x x  

  

     

  

  

 

42 .



       

Ta cần tìm

, 

sao cho

 

d0fx x x



 





hay

 

42 0



      

 

3 6 3 6 12 0.        

Để tồn tại



thì

 

3 6 4 3 6 12 0      





3 12 12 0 3 2 0 2 6.

   

     

Vậy

  



 

 

6 2 d 0 6 2, 0;1 d 10.fx x x fx x x fx x

  

           

  



Chọn C.

Câu 77. Cho hàm số





y fx

liên tục trên đoạn

 

0;1 ,

thỏa mãn

 

d d1xfx x xfx x



và

 

d 5.fx x









Giá trị của tích phân

 

dfx x







bằng

10.

Lời giải. Ở đây các hàm xuất hiện dưới dấu tích phân là

   

 

, , fx xfx xfx





nên ta sẽ liên

kết với bình phương

 

.fx x x









Với mỗi số thực

, 

ta có

   

 









1 11 1

0 00 0

d d2 d dfx x x x fx x x xfx x x x x  



     





  

 

52 .

352

  

    

Ta cần tìm

, 

sao cho

 

d0fx x x x



 







hay





5 2 0.

352

  

    

Tương tự như bài trước, ta tìm được

15, 10. 

Vậy

  

    

15 10 d 0 15 10 , 0;1 d .

fx x x x fx x x x fx x



           







Chọn A.

Câu 78. Cho hàm số

 

y fx

liên tục trên đoạn

 

0;1 ,

thỏa mãn

   

d d.

xfxx xfxx



Giá trị của tích phân

 

dfx x



bằng

Lời giải. Hàm bình phương không như thông thường là

 





hoặc

 

'.fx





Ở đây các hàm xuất hiện dưới dấu tích phân là

   

, xfx xfx







nên ta sẽ liên kết với bình

phương

  



 

??? 2??? ??? .xf x xf x xf x



  





So sánh ta thấy được

??? .



Do đó giả thiết được viết lại

 

d d 0.

2 2 16

xx xx

xf x x x

  









  









  



Suy ra

       

, 0;1 d .

2 24

xx x

xfx x fx fx x        



Chọn B.

Câu 79. Cho hàm số

 

có đạo hàm liên tục trên

 

1; 8

và thỏa mãn

   

 

2 28

1 11

2 38

d2 d d .

3 15

fx x fx x fx x



 





 

Tích phân

 

dfx x



bằng

8 ln 2

ln 2

Lời giải. Nhận thấy có một tích phân khác cận là

 

d.fx x



Bằng cách đổi biến

xt

thu được tích phân

   

23 2 3

3 d 3 d.tft t xfx x





Do đó giả thiết được viết lại

 





2 22

3 3 23

1 11

d2 d 2 d .

fx x fx x xfx x



 





 





Ở đây các hàm xuất hiện dưới dấu tích phân là

     

3 32 3

, , fx fx xfx







nên ta sẽ liên kết với

bình phương

 

.fx x









Tương tự như các bài trên ta tìm được

1, 1. 

Do đó

 



  

32 2

* 1d 1 d 0

fx x x x x



      







 

   

32 2

1, 1; 2 1, 1; 8 d .

fx x x fx x x fx x              



Chọn D.

Câu 80. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

10f 





d7fx x











và

 

xfx x



Tích phân

 

dfx x



bằng

. B.

. C.

. D.

Lời giải. Hàm dưới dấu tích phân là

   

, f x xf x







không có mối liên hệ với nhau.

Dùng tích phân từng phần ta có

     

d ' d.

xfx x fx xf x x



Kết hợp với giả thiết

 

10f 

, ta suy ra





' d 1.xf x x



Bây giờ giả thiết được đưa về

 

'd 1

fx x

xf x x





























Hàm dưới dấu tích phân bây giờ là

   

, 'f x xf x







nên ta sẽ liên kết với bình phương

 

'.fx x









Với mỗi số thực



ta có

     

1 111

3 3 26

0 000

' d ' d2 'd dfx x x fx x xfxx xx 



  





 

 

7 2 7.



   

Ta cần tìm



sao cho

 

' d0fx x x











hay

 

7 0 7.

 

Vậy

       

33 4

' 7 d 0 ' 7 , 0;1

fx x x fx x x fx x C



            







 

   

7 77 7

4 44 5

C fx x fx x



            



Chọn B.

Cách 2. Dùng tích phân từng phần ta có

     

d ' d.

xfx x fx xf x x



Kết hợp với

giả thiết

 

10f 

, ta suy ra

 

' d 1.xf x x



Theo Holder

    



1 11

0 00

1 ' d d . ' d .7 1.

xfxx xx fx x













   















 

Vậy đẳng thức xảy ra nên ta có

 

',f x kx

thay vào

 

'd 1

xf x x



ta được

7.k 

Suy ra

 

fx x

(làm tiếp như trên)

Câu 81. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

11f 

 

xf x x



và



 



 

f x fx







Tính

 

2.f

 

2 2.f 

 

251

f 

 

256

f 

 

261

f 

Lời giải. Viết lại





 

d d.

13 13

fx fx fx x





 





Dùng tích phân từng phần ta có

     

d d.

xfx x fx xf x x







Kết hợp với giả

thiết

 

11f 

, ta suy ra

 

xf x x







Bây giờ giả thiết được đưa về

 

fx x

xf x x





























Hàm dưới dấu tích phân bây giờ là

   

, 'f x xf x







nên ta sẽ liên kết với bình phương

 

'.fx x









Tương tự như bài trên ta

tìm được

   

 

22 .

f x x fx x C C





             

Vậy





 

2 5 261

77 7

fx x f    

Chọn D.

Cách 2. Theo Holder



  

1 11

6 12

0 00

2 14 4

d . d. .

13 13 13 169

xfxx xdx fx x



















  



















 

Câu 82. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

1 2, 0 0

ff

và

 

' d 4.fx x









. Tích phân

 

2018 d .f x xx











bằng

1011.

2018.

2022.

Lời giải. Từ giả thiết

   

1 2, 0 0

ff

suy ra

   

' d 2.f x x fx



Hàm dưới dấu tích phân là

   

' , 'fx fx





nên sẽ liên kết với bình phương

 

'.fx









Ta tìm được

   

 

2 ' 2 2 0.

f x fx x C C



             

Vậy

   

2 2018 d 1011.fx x f x x x



    







Chọn B.

Cách 2. Theo Holder

   

1 11

0 00

2 ' d d . ' d 1.4 4.fxx x fx x













  















 

Câu 83. Cho hàm số

 

có đạo hàm liên tục trên

 

1; 2 ,

thỏa mãn

   

1d ,

x fx x 



 

f 

và

 

' d 7.fx x









Tích phân

 

fx x



bằng



Lời giải. Chuyển thông tin



 



1dx fx x





sang





'fx

bằng cách tích phân từng phần, ta

được

   

1 ' d 1.x fxx



Hàm dưới dấu tích phân là

     

' , 1 'fx x fx







nên liên kết với

   

' 1.fx x











Ta tìm được

       





7 ' 71 1 .

f x x fx x C C



                

Vậy

   

 

77 7

1 d.

44 5

fx x fx x      



Chọn C.

Cách 2. Theo Holder





 

  



2 22

1 11

1 1 ' d 1 d ' d .7 1.

x fxx x x fx x







    









 

Câu 84. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

1 1, ' d

f fx x









và





f x x





Tích phân

 

dfx x



bằng

I 

Lời giải. Chuyển thông tin

 

f x x



sang

 

'fx

bằng cách:

 Đặt





t x tf t t   



hay

 

xf x x 



 Tích phân từng phần

 

d,xf x x



ta được

 

'd .

xf x x



Hàm dưới dấu tích phân là

   

' , 'fx xfx





nên liên kết với

 

'.fx x









Ta tìm được

 

3 ' 3 0.

f x x fx x C C



             

Vậy

   

fx x fx x   



Chọn B.

Cách 2. Theo Holder

   

1 11

0 00

3 19 9

'd d ' d . .

5 5 5 25

xfxx xx fx x













  



















 

Câu 85. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 1 0,ff

   

' cos d

fx xx



 



và

 

f xx



Tích phân

 

dfx x



bằng



.



Lời giải. Hàm dưới dấu tích phân là

 

và

   

' cosfx x

, không thấy liên kết.

Do đó ta chuyển thông tin của

   

' cosfx x

về

 

bằng cách tích phân từng phần của

   

' cos d

fx xx



 



cùng với kết hợp

   

0 1 0,ff

ta được



 



sin d .

fx x x







Hàm dưới dấu tích phân bây giờ là





và



 



sinfx x

nên ta sẽ liên kết với bình phương

  



sin .fx x







Ta tìm được

     

1 sin d .fx x fx x



       



Chọn B.

Cách 2. Theo Holder

       

1 11

0 00

1 11

sin d d . sin . .

2 22

fx xx f xx x dx

















 



















 

Câu 86. Cho hàm số

 

có đạo hàm liên tục trên

 

0; ,

thỏa mãn

 

' sin d 1

f x xx







và

 

d.f xx







Tích phân

 

xf x x





bằng











Lời giải. Hàm dưới dấu tích phân là

 

và





' sin

fx x

, không thấy liên kết.

Do đó ta chuyển thông tin của

 

' sinfx x

về

 

bằng cách tích phân từng phần của

 

' sin d 1,

f x xx







ta được





cos d 1.f x xx







Hàm dưới dấu tích phân bây giờ là

 

và

 

cosfx x

nên ta sẽ liên kết với bình phương

 

cos .fx x







Ta tìm được



  

2 2 2 cos 4

cos d d .

fx x xfx x x





  

         



Chọn B.

Cách 2. Theo Holder

     

0 00

1 cos d d cos d . 1.

f x xx f x x xx

 



  

 

Câu 87. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa

   

1 0, ' d

f fx x











và

 

cos d .

fx x























Tích phân

 

dfx x



bằng



.

Lời giải. Hàm dưới dấu tích phân là

 

'fx





và

 

cos



















, không thấy liên kết.

Do đó ta chuyển thông tin của

 

cos



















về

 

'fx

bằng cách tích phân từng phần của

 

cos d

fx x























cùng với kết hợp

 

1 0,f 

ta được

 

sin ' d .

fxx























Hàm dưới dấu tích phân bây giờ là

 

'fx





và

 

sin '



















nên ta sẽ liên kết với bình

phương

 

' sin .































Ta tìm được

   

 

' sin cos 0.

2 22 2

f x fx C C

  





 





             









 

Vậy

  



cos d .

fx fx x









   













Chọn B.

Cách 2. Theo Holder

   

1 11

0 00

sin ' d sin d . ' d . .

4 2 2 28

fxx x fx x

  



   





 

 







  

 



 





 



 

   







 

Câu 88. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

' sin dfx xx



và

 

d 2.f xx



Tích phân



















bằng











Lời giải. Chuyển thông tin của

   

' sin

fx x

về

 

bằng cách tích phân từng phần của

   

' sin d ,fx xx



ta được

   

cos d 1.fx x x 



Hàm dưới dấu tích phân bây giờ là

 

và

   

cos xfx

nên ta sẽ liên kết với bình phương

   

cos .fx x







Ta tìm được

   

2 2 cos d 2 cos d .

fx x f x x







  





     









  



Chọn B.

Cách 2. Theo Holder

 

  



1 11

0 00

1 cos d cos d d .2.

fx x x x x fx x







  









 

Câu 89. Cho hàm số

 

có đạo hàm liên tục trên

0; ,









thỏa

 

0, d 3

f f xx























và

 

sin d 6 .

x xf x

























Tích phân

 

dfx x











bằng





3.

9.

Lời giải. Tích phân từng phần của

 

sin d 6 ,

x xf x

























kết hợp với





















ta được

 

sin d .

xf x x







Hàm dưới dấu tích phân bây giờ là

 

và

 

sin xf x

nên ta sẽ liên kết với bình phương

 

sin .fx x









Ta tìm được

     

4 4 sin ' 4 sin 2 '' 8 cos 2 .

fx xfx xfx x         

Vậy

  



d 8cos 2 d 0.fx x xx













Chọn B.

Cách 2. Theo Holder

 

2 22

2 42

0 00

sin d sin d d .3 .

4 16

xfxx xx f xx

 

























 























 

Câu 90. Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

0;1 ,

thỏa mãn

 

10f 

và

   





'd 1 d .

f x x x ef x x





 





Tính tích phân

 

d.I fx x







I 

Ie

I 

Lời giải. Tích phân từng phần của



  

1 d,

x efx x





kết hợp với

 

10f 

ta được





'd .

xe f x x







Hàm dưới dấu tích phân bây giờ là









và

 

xe f x

nên ta sẽ liên kết với

 

f x xe









Ta tìm được

     

 

1 ' d 1 0.

x xx

f x xe f x xe x x e C C



                



Vậy

       

1 d 1 d 2.

f x xe f x x xe x e       



Chọn C.

Cách 2. Theo Holder



  

1 11

2 22

0 00

1 11

' d d. ' d . .

4 44

e ee

xefxx xe x fx x



 

















  



















 

Câu 91. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 0, 1 1ff

và

 











Tích phân

 

dfx x



bằng



  

12ee

Lời giải. Hàm dưới dấu tích phân là

 





nên ta cần tìm một thông tin liên quan

 

'.fx

Từ giả thiết

   

0 0, 1 1

ff

ta nghĩ đến

 

   

 

' d 1 0 1. f x x fx f f  



Do đó ta có hàm dưới dấu tích phân là

 





và

 

'fx

nên sẽ liên kết với bình phương

 













Với mỗi số thực



ta có

 

1 1 11

0 0 00

d d2 'd d

e x x fxx ex

 







  





  

   

2 1 1 1.

 



     





Ta cần tìm



sao cho

 















hay

 

1 10 .





    





Với

 



thì

   

 

d 0 , 0;1 .

fx fx

e x ex





    











Suy ra

   

0 0, 1 1

'd .

1 11 1

x xx

e ee

f x fx x C C

e ee e



      

  



Vậy

   

fx fx x



   





Chọn A.

Cách 2. Theo Holder

 





2 22

1 1 11

0 0 00

1 ' d . d d d . 1 1.

fxx ex xex e

    



  

    

  



  

  

  

Câu 92. Cho hàm số





có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

   

0 0, 1 1ff

và





 

1 'd .

ln 1 2

x fx x











Tích phân

 

x



bằng

 

ln 1 2 .



 

ln 1 2 .



 C.

 

ln 1 2 .







 

2 1 ln 1 2 .

Lời giải. Tương tự bài trước, ta có

   

' d 1 0 1.f x x fx f f 



Do đó ta có hàm dưới dấu tích phân là

 

1'x fx







và

 

'fx

nên sẽ liên kết với bình

phương

 

1' .

xf x

















Ta tìm được

 

1 11

ln 1 2 ln 1 2

     





 

11 1

. d ln 1 .

ln 1 2 ln 1 2

fx x x x C

      







Mà

 



 







 

ln 1

0 0, 1 1 0 .

ln 1 2

f f C fx



      



Vậy

 

   

11 1

00 0

ln 1

d d ln 1 d ln 1

ln 1 2 ln 1 2

x x xxxx





   







 

 

ln 1

. ln 1 2 .

ln 1 2

xx

 



Chọn C.

Cách 2. Theo Holder

 





11 1 1

22 2

00 0 0

1 ' d 1 ' . d 1 ' d.

fxx xfx x x fx x













  

















  

 

.ln 1 2 1.

ln 1 2

 



Câu 93. Cho hàm số

 

có đạo hàm liên tục trên





1;1 ,

thỏa mãn

 

1 0,f 

 

' d 112fx x











và

 

xfx x







Tính tích phân

 

d.I fx x







I 

168

I 

Lời giải. Như các bài trước, ta chuyển

 

xfx x







về thông tin của

 

'fx

bằng cách

tích phân từng phần. Đặt

 

d 'd

u fxx

u fx

v xx

































Khi đó

 









 

11 1

23 3

11 1

1 11 1

d 'd 1 1 'd.

3 3 33 3

xfxx fx xfxx f f xfxx



 

    

 

Tới đây ta

bị vướng

 

vì giả thiết không cho. Do đó ta điều chỉnh lại như sau

 

d 'd

u fxx

u fx

v xx



































với

là hằng số.

Khi đó

   

 

d 'd

xfx x kfx kf x x





 







  











 



  



 





0 do 1 0

1 1 ' d.

33 3

kf kf kf x x



 



  











      

 















  







Ta chọn

sao cho

kk   

Khi đó





 





 

11 1

23 3

11 1

16 1

d 1 ' d 1 ' d 16.

xfxx x fxx x fxx

 

     

 

Hàm dưới dấu tích phân là

 

' , 1 'fx x fx







nên ta liên kết với

 

'1fx x









Ta tìm được

 

3 34

7 ' 7 1 7 1d 7

f x x fx x x x x C          



 

35 7 35

4 44

C fx x x



          

Vậy

 

I fx x







Cách 2. Theo Holder

 

1 11

16 1 ' d 1 d . ' d .112 256.

x fxx x x fx x

 













     















 

Câu 94. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

1 0,

f 

 

' d 2 ln 2

fx x









và

 

d 2 ln 2 .







Tích phân

 

dfx x



bằng

1 ln 2



1 2 ln 2



3 2 ln 2



3 4 ln 2



Lời giải. Như các bài trước, ta chuyển

 

d 2 ln 2







về thông tin của

 

'fx

bằng

cách tích phân từng phần. Đặt

 

d 'd

u fx

u fxx







































Khi đó





 

         

11 1

00 0

' 10 '

d d d.

1 1 21 1

fx fx f x f f f x

xx x

    

 



 

Tới đây ta bị vướng

 

vì giả thiết không cho. Do đó ta điều chỉnh lại như sau





 

d 'd

u fx

u fxx

























 













với

là hằng số.

Khi đó

 



  

d 'd

x kfx kf x x

 





  









 







 

     

1 0 ' d.

kf kf x x









     















Ta chọn

sao cho

1 0 1.kk   

Khi đó









   

11 1

00 0

2 ln 2 d ' d ' d 2 ln 2.

2 1 12

x fxx fxx

       





 

Hàm dưới dấu tích phân là

 

' , '

fx fx







nên ta liên kết với

 















Ta tìm được

 

1 ' d ln 1

f x fx x x x C

           











 



ln 2 1 ln 1 ln 2 1.

C fx x x



            

Vậy

 

1 2 ln 2

fx x







Chọn B.

Cách 2. Theo Holder

 

1 11

0 00

3 33

2 ln 2 ' d d ' d 2 ln 2 2 ln 2 .

2 1 1 22

fxx x fx x



  



  

  



    

  

  





  

  

  







 

Câu 95. Cho hàm số

 

có đạo hàm liên tục trên

 

1; 2 ,

đồng biến trên

 

1; 2 ,

thỏa mãn

 

10f 

 

d2fx x











và

 





. ' d 1.

fxf x x



Tích phân

 

dfx x



bằng

2 2.

Lời giải. Hàm dưới dấu tích phân là

     

, .fx fxfx







nên ta sẽ liên kết với bình phương

   

.f x fx









Nhưng khi khai triển thì vướng

 

fx x







nên hướng này không khả thi.

Ta có

   



      

 

2 22 2

2 1 20

1 .' d 2 2

222

fx f f f

fxf x x f



      



(do đồng biến

trên

 

1; 2

nên

 

2 10



)

Từ

 

10f 

và

 

22f 

ta nghĩ đến

       

' d 2 1 2 0 2.f x x fx f f    



Hàm dưới dấu tích phân bây giờ là

   

fx fx







nên ta sẽ liên kết với





fx 









Ta tìm được

 





2 ' 2 2 2.

f x fx x C C



              

Vậy

   

22 d .

fx x fx x    



Chọn A.

Câu 96. Cho hàm số

 

có đạo hàm liên tục trên





0;1 ,

thỏa mãn

 

10f 

 

d1f xx



và

   

fx f xx











Giá trị của

 

bằng



 

31 2



 

31 2



Lời giải. Hàm dưới dấu tích phân là

   

fx f x







và

 

nên ta sẽ liên kết với bình

phương



    

.f xfx fx









Nhưng khi khai triển thì vướng

   

'df xf x x



nên hướng

này không khả thi.

Tích phân từng phần

 

d1f xx



kết hợp với

 

1 0,f 

ta được

   

'd .

xf x f x x 



Hàm dưới dấu tích phân bây giờ là

 

fx f x







và

   

'xf x f x

nên ta sẽ liên kết với bình

phương





 

fxf x x









Ta tìm được



 





 







3 3 33

' 'd d

2 2 2 24

fxf x x fxf x x xx x C

        



 









 

2 22

33 3

1 2.

42 2

C fx x f



            

Chọn A.

Câu 97. Cho hàm số

 

có đạo hàm liên tục trên





0;2 ,

thỏa mãn

 

21f 

 

xfx x



và

 

'd .

fx x









Giá trị của tích phân

 

dfx x



bằng



Lời giải. Hàm dưới dấu tích phân





'fx





và





xfx

. Lời khuyên là đừng có cố liên kết với

bình phương nào, vì có tìm cũng không ra.

Tích phân từng phần





xfx x





kết hợp với

 

21f 

, ta được

 

xf x x







Áp dụng Holder

lần ta được

   

 

4 42 2

2 2 22

3 2 42

0 0 00

d . d d 'd

xfx x xxfxx xx xfx x

      



  

  





  





  

 



  



  





  





  

  

      

  

 





2 22

0 00

d d. ' d

1048576 32

d 'd .

625 5

xx xx fx x

xx fx x

  

























  

















  



















 



Dấu

'' ''

xảy ra, tức là

   

''xf x kx f x kx 

thay vào

 

fx x









tìm được

1k 

   

 

' d 1.

f x x f x xx C C



            



Vậy



  

1 d.

fx fx x     



Chọn B.

Cách 2. Áp dụng bất đẳng thức AM – GM ta có

   

444 3

' 4 '.fx x x x xfx







Do vậy

   

2 22

0 00

' d 3 d 4 d.f x x x x xf x x









 

Mà giá trị của hai vế bằng nhau, có nghĩa là

dấu

'' ''

xảy ra nên

 

'.fx x

(Làm tiếp như trên).

Vấn đề 12. Kỹ thuật đánh giá AM-GM

Câu 98. Cho hàm số

 

nhận giá trị dương và có đạo hàm

 

liên tục trên

 

0;1 ,

thỏa

mãn

   

10f ef

và

 

' d 2.

fx x









Mệnh đề nào sau đây đúng ?

 





 







 





 







Lời giải. Ta có

 





 

11 1 1

AM GM

00 0 0

'd ' d 2 d

fx x fx x x

fx fx







 

  

 





  



    

 

2 ln 2 ln 1 2 ln 0 2 ln 2 ln 2.

fx f f e

    

Mà

 





' d2

fx x









nên dấu

'' ''

xảy ra, tức là

 



 



' '1

fx fxfx

 

   

 

' d d 2 2.

fxf x x xx x C fx x C

         



Theo giả thiết



  

10f ef

nên ta có

22 2 22 2

C e C C eC C

     











2 22

2 12 .

1 11

fx x f

e ee



 

Chọn C.

Câu 99. Cho hàm số

 

nhận giá trị dương trên

 

0;1 ,

có đạo hàm dương và liên tục trên

 

0;1 ,

thỏa mãn





01f 

và



 

    

4 ' d 3 ' d.

f x fx x fxf xx











Tính





I fx x



 

2 1.Ie

 

2 1.

Ie









Lời giải. Áp dụng bất đẳng thức

AM GM

cho ba số dương ta có

    



   

 

   

3 3 33

33 3

4' 4' 34' . . 3' .

2 2 22

fx fx fxfx

f x fx fx fx fxf x

 

   

 

Suy ra



 







4 ' d 3 ' d.

f x fx x fxf xx











Mà

     

 

4' d 3 ' df x fx x fxf xx











nên dấu

'' ''



xảy ra, tức là

 

   

4' '

22 2

fx fx

fx fx fx



  



 

   

11 1

d d ln .

22 2

fx fx

x x fx x C fx e

fx fx



          



Theo giả thiết



 







0 1 0 d 2 1.

f C fx e fx x e

        



Chọn A.

Câu 100. Cho hàm số

 

nhận giá trị dương trên

 

0;1 ,

có đạo hàm dương liên và tục trên

 

0;1 ,

thỏa mãn

 

xf x





và

 

0 1,f 

 

1.fe

Tính giá trị của

























































































Lời giải. Hàm dưới dấu tích phân là

 





 

 

. , 0;1 .

xfx fx

fx fx

 

Điều này làm ta liên

tưởng đến đạo hàm đúng

 





'fx

, muốn vậy ta phải đánh giá theo

AM GM

như sau:

 

fx xfx

mx m

fx fx



với

0m 

và

 

0;1 .x 

Do đó ta cần tìm tham số

m 

sao cho

 

d 2. d

fx xfx

mx x m x

fx fx













hay

 

ln 2 .1 ln 1 ln 0 2 2 0 2 .

2 22

x mm

fx m m f f m m

     

Để dấu

'' ''

xảy ra thì ta cần có

2 0 2 4.

mm   

Với



thì đẳng thức xảy ra nên

 



 



  

d 4 d ln 2 .

x xx fx x C fx e



       



Theo giả thiết

 

C fx e f e















       





















Chọn C.

Cách 2. Theo Holder

 





 

1 1 11

0 0 00

' ' '1

1 d . d d . d . ln 1.

xfx fx fx f

x x x xx x

fx fx fx f

  









   













  

  

Vậy đẳng thức xảy ra nên ta có

 







thay vào

 

xf x





ta được

k 

Suy ra

 



(làm tiếp như trên)

Câu 101. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa mãn

 

' d1fxf x x









và

 

0 1,f 





1 3.

f 

Tính giá trị của

























































































Lời giải. Nhận thấy bài này ngược dấu bất đẳng thức với bài trên.

Hàm dưới dấu tích phân là

  



'.fxf x





Điều này làm ta liên tưởng đến đạo hàm đúng

 

'fxf x

, muốn vậy ta phải đánh giá theo

AM GM

như sau:

       

' 2. 'fxf x m mfxf x







với

0.m



Do đó ta cần tìm tham số

m 

sao cho

  



 

   

' d 2 ' d.

fxf x m x m fxf x x









hay

 

1 2. 1 2.

mm mm 

Để dấu

'' ''

xảy ra thì ta cần có

1 2 1.m mm 

Với

1m 

thì đẳng thức xảy ra nên

   

'1 .

fxf x























       

 

' 1 ' d d 1 1.

fxf x fxf x x x x      



(vô lý)



       

 

' 1 ' d d 2 2.

fxf x fxf x x x x C fx x C          



Theo giả thiết

 

2 1 2.

C fx x f















        





















Chọn A.

Cách 2. Ta có

 







  

' d 1 0 1.

fxf x x f f



  







Theo Holder





 









1 11

0 00

1 1. ' d 1 d . ' d 1.1 1.

fxf x x x fxf x x













  















 

Vậy đẳng thức xảy ra nên ta có

   

',f xfx k

thay vào





 

'd 1fxf x x





ta được

1.k



Suy ra

   

' 1.f xf x

(làm tiếp như trên)

Câu 102. Cho hàm số

 

nhận giá trị dương và có đạo hàm

 

'fx

liên tục trên

 

1; 2 ,

thỏa

mãn

 

d 24

xf x









và

 

1 1,f 

 

2 16.f 

Tính giá trị của





2.f

 

2 1.f 

 

2 2.f 

 

2 2.f 

 

2 4.f 

Lời giải. Hàm dưới dấu tích phân là

 

fx fx

xfx x fx

 

 



Điều này làm ta liên tưởng đến

đạo hàm đúng

 

'fx

, muốn vậy ta phải đánh giá theo

AM GM

như sau:





 









mx m

xf x







với

0m 

và

 

1; 2 .x 

Do đó ta cần tìm tham số

0m 

sao cho

 

d2 d

mx x m x

xf x





































hay

 









22 2

24 4 24 4 2 1 24 12 16.

33 3

mm m

m fx m f f m m



    





Để dấu

'' ''

xảy ra thì ta cần có

24 12 16.

mm  

Với

m 

thì đẳng thức xảy ra nên

 





16 2

xf x





 

 





d 2d .

x xx fx x C fx x C

         



Theo giả thiết

 





0 2 4.

2 16

C fx x f









       











Chọn D.

Cách 2. Ta có

 





 

d 2. d 2 2 2 1 6.

fx fx

x x fx f f

fx fx



   







Theo Holder

 

2 1 22

1 1 11

6 d . d d . d .24 36.

fx fx

x x x xx x

xf x

fx xfx

  















   















  

  

Vậy đẳng thức xảy ra nên ta có





 

fx fx

k x kx

xfx fx

 

thay vào

 





được

4.k 

Suy ra

 



(làm tiếp như trên)

Vấn đề 13. Tìm GTLN-GTNN của tích phân

Câu 103. Cho hàm số

 

liên tục trên



có đạo hàm cấp hai thỏa mãn

 

xf x e x





và

 

2 2,fe





 

fe

Mệnh đề nào sau đây là đúng?

 

2 4 1.fe

 

22 .f ee

 

2 2.f ee

 

2 12.f 

Lời giải. Từ giả thiết

 

xf x e x





ta có

 

. d d.

xf xx e xx







 

Đặt

   

ux u x

vfx vfx











   







Khi đó

   

 

1. d

xfx fxx e











  















   

       

22 2

00 0

2. 2 0. 0 2 0 2 1

xf x f x e

f f ff e











  













  



     

  

 

2 41fe

 

(do

 

2 2,





 

0fe

). Chọn A

Câu 104. Cho hàm số

 

dương và liên tục trên

 

1; 3 ,

thỏa

 

 

1;3

max 2,fx

 

 

1;3

min

fx

và

biểu thức

 

d. dS fx x x





đạt giá trị lớn nhất, khi đó hãy tính

 

d.I fx x



Lời giải. Từ giả thiết ta có





fx

, suy ra

 







Suy ra





 





   

 

3 33 3 3 3

1 11 1 1 1

15 1 1

d d d d5 d5 d.

fx x x fx x x x fx x

fx fx fx





     





    

Khi đó

 

   

33 3 3

11 1 1

1 25

d. d d.5 d .

S fx x x fx x fx x











  













  

(dạng

 

5 25 25

2 44

tt tt t







      











)

Dấu



xảy ra khi và chỉ khi

 

fx x



Chọn D.

Câu 105. Cho hàm số

 

có đạo hàm liên tục trên



thỏa mãn

  



1fx f x





với mọi

x  

và

 

0 0.f 

Giá trị lớn nhất của

 

bằng

1.e 



e 

Lời giải. Từ giả thiết

   

1fx f x





, nhân thêm hai vế cho

để thu được đạo hàm đúng

là

     

, ,.

xx x x x

efx ef x e x efx e x







     







Suy ra

       

d d 1 1 1. 0 1

x xx

efx x e x efx e ef f e



 



    

 



 



 





   

Chọn B.

Câu 106. Cho hàm số

 

nhận giá trị dương và có đạo hàm

 



liên tục trên

 

0;1 ,

thỏa

mãn

   

1 2018 0 .ff

Giá trị nhỏ nhất của biểu thức

 

M x fx x















bằng

ln 2018.

2 ln 2018.

2.me

2018 .me

Lời giải. Áp dụng bất đẳng thức Cauchy, ta được





 













 

11 1

00 0

d d 2 d 2 ln 2 ln 2 ln 2018.

fx f

M x f x x x fx

fx f







    







 

Chọn B.

Câu 107. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1

và

   

1 d.

x fxx



 



Giá trị

nhỏ nhật của biểu thức



 



d0fx x f









bằng



Lời giải. Tích phân từng phần



 



x fxx



 



, ta được

 

   

0 2 1 d.

f xfx x 



Áp dụng bất đẳng thức Cauchy, ta được

 

     

1 11

0 00

2 1 d 1 d d.

xfx x x x fx x



  



 

Từ đó suy ra



 







11 1

00 0

d 21 d 1 dfx x xfx x x x



  



 

   

 

d0 .

fx x f





  





Vậy

   

d0 .

fx x f



 





Chọn D.

Câu 108. Cho hàm số

()fx

liên tục trên

[0; 1]

thỏa mãn

 

d0xf x x 



và





[0; 1]

max 1.fx

Tích phân

 

efx x



thuộc khoảng nào trong các khoảng sau đây?







 











; 1.





































 

1; .

e  

Lời giải. Với mỗi số thực

  

ta có

     

1 11

0 00

d dd

efx x efx x xfx x

 

 

11 1

00 0

d . d d.

x xx

fxexx fxexx exx

     



Suy ra

 

   

11 1

0;1 0 ;1

00 0

d min d min d min 1 .

xx x

efx x e xx e xx e e

 





 





       







 



Chọn C.

Câu 109. Cho hàm số

 

nhận giá trị không âm và liên tục trên

 

0;1 .

Đặt

   

1 d.

gx f t t



Biết

   

gx f x

với mọi

 

0;1x 

, tích phân

 



có giá trị lớn nhất

bằng

Lời giải. Từ giả thiết

 





1 d,

gx f t t



ta có

 

   

gx fx



















và

   

0, 0;1 .gx x 

Theo giả thiết

   

 

' 1 1.

gx f x gx g x

       

Suy ra

 





 

 





 

1 11 1

d 1d , 0;1 1 .

x xt x t t

gx gt g gt

             



Do đó

 





d 1d .

x xx

 



Chọn B.

Câu 110. Cho hàm số

 

nhận giá trị không âm và liên tục trên đoạn





0;1 ,

thỏa mãn

     

13 d

f x f t t gx 



với mọi

 

0;1x 

, tích phân

 

dgx x



có giá trị lớn nhất bằng

Lời giải. Từ giả thiết

   

1 3 d,

gx f t t



ta có

 

   

gx fx



















và

   

0, 0;1 .gx x 

Theo giả thiết

 

   









 

gx f x gx





     

Suy ra

 

   

     

3 3 33

d d , 0;1 0 1.

2 2 22

x x t gx x gt g t gt t

           



Do đó

 

d 1d .

gx x x x







 













Chọn B.

Câu 111. Cho hàm số





nhận giá trị không âm và liên tục trên đoạn

 

0;1 ,

thỏa mãn

   

2018 2 d

fx ft t



với mọi

 

0;1 .x 

Biết giá trị lớn nhất của tích phân

 

dfx x



có

dạng

ae b

với

, .ab 

Tính

.ab

1009.

2018.

2020.

Lời giải. Đặt

   

2018 2 d ,

gx f t t



ta có

 

   

0 2018

gx fx



















và

   

0, 0;1 .gx x 

Theo giả thiết

     

 

gx gx

gx f x gx

     

Suy ra

 

   

d 2d , 0;1 ln 2

x x t gx x

     



   

  



ln ln 0 2 ln 2 ln 2018 2018.

gt g t gt t gt e     

Do đó

   

11 1

2 22

00 0

d d 2018 d 1009 1009 1009.

fxx gxx e x e e   

 

Chọn A.

Câu 112. Cho hàm số

 

nhận giá trị không âm và liên tục trên đoạn

 

0;1 .

Đặt

   

1 d.

gx f t t



Biết

 

2g x xf x

với mọi

 

0;1x 

, tích phân

 

dgx x



có giá trị lớn

nhất bằng

1.e 

1.e 

Lời giải. Từ giả thiết

   

1 d,

gx f t t



ta có

 

g x xf x



















và

   

0, 0;1 .gx x 

Theo giả thiết

 

   

 

2 ' 1.

gx xf x gx g x

     

Suy ra

 



 



d 1d , 0;1 ln

x x t gx x

     



       

ln ln 0 ln .

gt g t gt t gt e    

Do đó

 

d d 1.

gx x e x e 



Chọn B.

Nhận xét. Gọi

 

là một nguyên hàm của hàm số

 

trên đoạn

0; .







Khi đó



  

 

  



 



 



2 2 2 /2 2

1 1 0 ' 2.

gx Ft Fx F g x Fx x F x xf x



      





Câu 113. Cho hàm số

 

có đạo hàm liên tục trên

 

0;1 ,

thỏa

     

' 0, 0;1 .f x fx x  

Giá trị lớn nhất của biểu thức

 

0. dfx



bằng





1.e 

Lời giải. Từ giả thiết

   

 

' 0, 0;1

f x fx x  

ta có









 

1, 0; 1 .

 

Suy ra

 

           

d 1d , 0;1 ln ln ln 0 0 .

x x t fx x ft f t ft f e

          



Do đó

 

1 11

0. d d .

f xx

fx e







Chọn B.

Câu 114. Cho hàm số

 

liên tục trên

 

0; ,

thỏa mãn

   

d cos d 1.fx x xfx x







Giá

trị nhỏ nhất của tích phân

 

df xx





bằng



Lời giải. Theo Holder

  

    

22 2

0 00 0

1 cos d cos d . d . d .

xfxx xx f xx f xx

  







 





  

Suy ra

 

d.f xx







(Đến đây bạn đọc có thể chọn A)

Dấu

'' ''



xảy ra khi

 

cosfx k x

thay vào

 

d1fx x







ta được

 

1 d cos d .sin 0.fxxk xxk x





  



Điều này hoàn toàn vô lý.

Lời giải đúng. Ta có

   

 

cos d

d cos d 1

a a xf x x

fx x xfx x

b bf x x















   

















với



















Theo Holder

  

 



 

0 00

cos d cos d d .ab a xbfxx a xb x f xx

 





   





 

Lại có

 





cos d 2 .

a xb x a b



 



Từ đó suy ra

 

f xx











với mọi

ab



và

0.ab

Do đó









d .max .

f xx



























Chọn B.

Nhận xét:  Ta nhân thêm

, ab

vào giả thiết được gọi là phương pháp biến thiên hằng số.

 Cách tìm giá trị lớn nhất của

 







ta làm như sau:

Nếu

0 1.bP   

(chính là đáp án sai mà mình đã làm ở trên)

Nếu

 

22 2 2

0 .

ab t

























     





















Tới đây ta khảo sát hàm số hoặc

dùng MODE 7 dò tìm. Kết quả thu được GTLN của

bằng

khi

2 2 2.

t ab



Vậy dấu

'' ''

để bài toán xảy ra khi

   

2 cos 1

fx b x

















thay ngược lại điều kiện, ta được

   

1 2 cos 1

2 cos 1 d 1 .

b x x b fx







      



Lúc này

 

2 cos 1 3

d d.

f xx x

























Cách khác. Đưa về bình phương

Hàm dưới dấu tích phân là

     

, , cosf x fx xfx

nên ta liến kết với

 

cos .fx x







Với mỗi số thực

, 

ta có

         

0 00 0

cos d 2 cos d cos dfx x f x x x fx x x x

  

  



     



  

  



2 22

d2 .

f xx



      



Ta cần tìm

, 

sao cho

 



    

đạt giá trị nhỏ nhất. Ta có





2 1 33

2 .



      

  

 





        









 

Vậy với

; 



 

thì ta có

  



21 3

cos d .fx x f x x



 





  







Suy ra

   

2 1 33

d cos .f x x fx x



  





   







Dấu

'' ''

xảy ra khi

 

2 cos 1







Câu 115. Cho hàm số

 

liên tục trên

 

0; ,

thỏa mãn

   

sin d cos d 1.xf x x xf x x







Giá trị nhỏ nhất của tích phân

 

f xx





bằng



Lời giải. Liên kết với bình phương

 

sin cos .fx x x







Ta có





sin cos dfx x x x













       

   

00 0

d 2 sin cos d sin cos d

d2 .

fx x x xfx x x x x

fx x

 



 

 





   





   



 



Phân tích

 

2 24

2 22 2

   

  

 

  





      









  

Chọn C.

Câu 116. Cho hàm số

 

liên tục trên





0;1 ,

thỏa mãn

   

d d 1.

fx x efx x



Gọi

là giá trị nhỏ nhất của tích phân

 

d.fx x







Mệnh đề nào sau đây đúng?

0 1.m

1 2.m



2 3.

m

3 4.m

Lời giải. Từ giả thiết, ta có

 





a ae f x x

b bf x x





















Theo Holder

 













1 11

0 00

d d d.

a b ae b f x x ae b x f x x





   





 

Lại có

   

 

22 2 2 2 2

d 2 d 1 21 .

x xx

ae b x a e abe b x e a e ab b     



Suy ra

 

22 2

1 21

f xx

e a e ab b









với mọi

, ab 

và

0.ab

Do đó

 

22 2

d max 1 3,1316.

1 21

f xx

e a e ab b









    

















Chọn D.

Câu 117. Cho hàm số

 

liên tục trên

 

0;1

thỏa mãn

   

d d 1.fx x xfx x



Giá trị

nhỏ nhất của tích phân

 

df xx



bằng

Lời giải. Từ giả thiết, ta có









a a xf x x

b bf x x





















Theo Holder





 





 

1 11

0 00

d d. d.a b ax bfx x ax b x f x x











   













 

Lại có

 

a ab

ax b x b  



Suy ra

 

f xx

a ab









với mọi

ab



và

0.ab

Do đó





 

d max 3.

f xx

a ab























Chọn D.

Cách 2. Liên kết với bình phương

 

.fx x









Ta có

 

dfx x x















 

   

00 0

d2 d d

d2 .

fx x x fx x x x

fx x

 



 



   



   





    



 



Phân tích

 

4 21

2 1 6 3.

2 3 3 18



      







       











Câu 118. Cho hàm số

 

y fx

có đạo hàm liên tục trên

 

1; 2 ,

thỏa

 

d 31.xf x x



Giá trị

nhỏ nhất của tích phân

 

df xx



bằng

961.

3875.

148955.

923521.

Lời giải. Ta có áp dụng hai lần liên tiếp bất đẳng thức Holder ta được

       

4 2 2 23

2 2 2 2 22

4 3 2 4 22 4 4

1 1 1 1 11

31 d . d d d d d .

xfxx xxfxx xx xf xx xx f xx



   





  

  







  



  

  



  



  





  



  

  





   









    

Suy ra

 

d 3875.

f xx



























Dấu

'' ''

xảy ra khi





f x kx

nên

 

d 31 5 5 .k x x k fx x     



Chọn B.

Câu 119. Cho hàm số

 

liên tục và có đạo hàm đến cấp

trên

 

0;2

thỏa





 

0 2 1 2 1.f ff

 

Giá trị nhỏ nhất của tích phân

 

'' dfx x







bằng

Lời giải. Ta có

     

1 11 1

Holder

0 00 0

'' d 3 d . '' d 3 . '' dfx x xx fx x xfxx









 









 









  

 



     

d '' d

3 '1 0 1 ;

vf xx

f ff





 







       

2 22 2

Holder

1 11 1

'' d 3 2 d . '' d 3 2 . '' d 2

fx x x x fx x x fxx









 



  





 









  

 



     

d '' d

3 '1 2 1 .

vf xx

f ff







 



Suy ra

             

2 22

'' d 3 '1 0 1 3 '1 2 1fxxf ff f ff

    

  

    



     

0 21 2

3. .

f ff









Chọn B.

Nhận xét: Lời giải trên sử dụng bất đẳng thức ở bước cuối là

 





Câu 120. Cho hàm số

 

có đạo hàm trên

 

1; 3

và





1 0,f 

 

 

1;3

max 10.fx



Giá trị nhỏ

nhất của tích phân

 

'dfx x







bằng

10.

20.

Lời giải. Vì

 

  



1;3

max 10 1; 3fx x     

sao cho

 











1; 3



    

sao cho

 

10.fx 

Theo Holder



  

   

0 00 0

1 11 1

' d 1d. ' d 1. ' d.

x xx x

fxx x fx x x fx x









 



 





 











  

Mà





     

 

' d 1 10.

f x x fx fx f

















  























Từ đó suy ra





fx x











 

10 10

'd 'd

1 31

fx x fx x

 

    

 





. Chọn B.

ỨNG DỤNG TÍCH PHÂN

Phần 1. Áp dụng công thức…………………………………………………………

Phần 2. Đồ thị hàm

 

………………………………………………………………

Phần 3. Đồ thị hàm

 



……………………………………………………..…….

Phần 4. Diện tích hình phẳng …………………………………………….……

Phần 5. Thể tích khối tròn xoay ………………………………….………….

Phần 6. Bài toán vận tốc …………………….……………………………………..

Phần 1. Áp dụng công thức

Câu 1.

Cho hàm số

 

y fx

liên tục trên

 

;ab

và có

đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

 





fxx

là độ dài đoạn thẳng

.NM

 





fxx

là độ dài đường cong

.AB

 





fxx

là độ dài đoạn thẳng

.BP

 





fxx

là diện tích hình thang cong

ABMN

Câu 2. Cho hàm số

 

y fx



liên tục trên

 

0;4

và có đồ thị như

hình bên. Tích phân

 



dfx x

bằng

Câu 3.

Cho hàm số

 

y fx

liên tục trên

 

0;3

và có đồ thị

như hình bên. Biết

 

d 2,3fx x



và

  

 



, 0; 4 .F x fx x



 

Hiệu



  

30FF

bằng

0,3.

1, 3.

3, 3.

4,3.

Câu 4. Cho hàm số

 

y fx



liên tục trên

 

2;2

và có đồ thị

đối xứng qua gốc tọa độ như hình bên. Biết

 

d 2.fx x







Tích

phân

 



dfx x

bằng

2.

Câu 5.

Cho hàm số

 

y fx

liên tục trên

 

2;2

và có đồ thị

đối xứng qua trục tung như hình bên. Biết

 

fx x



Tích phân

 





dfx x

bằng

I 

Câu 6. Cho hàm số

 

y fx

liên tục trên

 

3;5

và có đồ

thị như hình bên (phần cong của đồ thị là một phần của

Parabol

 

y ax bx c

). Tích phân

 





dfx x

bằng

Câu 7.

Cho hàm số

 

y fx

có đạo hàm liên tục trên

 

1; 4

và có

đồ thị như hình bên. Tích phân

 





fx x

bằng

Câu 8. Cho hàm số

 

y fx

liên tục trên



và hàm số

 

y gx xf x

có đồ thị trên đoạn

 

1; 2

như hình vẽ bên.

Biết phần diện tích miền được tô màu là



giá trị của tích

phân

 





dI fx x

bằng

10.

Câu 9.

Cho hàm số

 

y fx

có đạo hàm liên tục trên

 



1; 2 .

Đồ thị của hàm số

 

y fx





được cho như hình bên. Diện tích

các hình phẳng

  



,KH

lần lượt là

và

Biết

 

f 

tính

 

2.f







 



 



 

2 3.f 

Câu 10.

Cho hàm số

 

y fx

có đạo hàm liên tục trên

 

2;4 .

Đồ thị của hàm số

 

y fx





được cho như hình

bên. Diện tích hình phẳng giới hạn bởi trục

và đồ thị

hàm số

 

y fx





trên đoạn

 

2;1

và

 

1; 4

lần lượt bằng

và

12.

Cho

 

1 3.f 

Tổng

   

24ff

bằng

21.

Phần 2. Đồ thị hàm

 

.fx

Câu 1. Cho hàm số

 

y fx



có đạo hàm liên tục trên



và có

đồ thị như hình bên. Giá trị của biểu thức

  



2d 2dfx x fx x



 



bằng

2.

10.

Câu 2. Cho hàm số

 

y fx

xác định và liên tục

trên





0;2

và có bảng biến thiên như hình bên.

Hỏi có bao nhiêu giá trị nguyên của

để thỏa

mãn điều kiện

 









d0fx m x

11.

12.

13.

14.

Câu 3. Cho hai hàm số





f x ax bx cx  

và

 

1g x dx ex 

 

 ,,, , .abcde

Biết rằng đồ thị hàm số

 

y fx



và

 

y gx

cắt nhau tại ba điểm có hoành độ lần

lượt là

3; 1; 1

(tham khảo hình vẽ). Hình phẳng giới hạn

bởi hai đồ thị đã cho có diện tích bằng

Câu 4.

Cho hai hàm số

 

1f x ax bx cx  

và

 

g x dx ex 

 

 ,,, , .abcde

Biết rằng đồ thị hàm số

 

y fx



và

 

y gx

cắt nhau tại ba điểm có hoành độ lần

lượt

3; 1; 2

(tham khảo hình vẽ). Hình phẳng giới hạn bởi

hai đồ thị đã cho có diện tích bằng

125

253

125

253

Câu 5.

Cho hai hàm số

 

 

2bxfx cxxa

và

 

2xg x dx e



 

 ,,, , .abcde

Biết rằng đồ thị hàm số

 

y fx

và

 

y gx

cắt nhau tại ba điểm có hoành độ lần lượt

là

2; 1; 1

(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ

thị đã cho có diện tích bằng

Câu 6. Cho hai hàm số





f x ax bx cx

  

và

 

g x dx ex 

 

 ,,, , .abcde

Biết rằng đồ thị hàm số

 

y fx

và

 

y gx

cắt nhau tại ba điểm có hoành độ lần

lượt là

2; 1; 3

(tham khảo hình vẽ). Hình phẳng giới hạn

bởi hai đồ thị đã cho có diện tích bằng

125

253

125

253

Câu 7.

Cho hàm số





y fx



xác định và liên tục

trên đoạn

 

5;3

và có đồ thị như hình vẽ. Biết

rằng diện tích hình phẳng

123

,,SSS

giới hạn bởi

đồ thị hàm số

 

y fx

và đường cong

 

y g x ax bx c  

lần lượt là

,,.mn p

Tích phân

 

fx x





bằng

208

mn p

208

mn p



208

mnp

208

mnp

Câu 8.

Cho hàm số





y fx

xác định và liên tục

trên đoạn

 

3;3

và có đồ thị như hình vẽ. Biết rằng

diện tích hình phẳng

,SS

giới hạn bởi đồ thị hàm

số

 

y fx



và đường thẳng

yx 

lần lượt là

;.Mm

Tích phân





dfx x





bằng

6.mM

6.mM

6.Mm



6.mM

Câu 9. Cho hàm số

 

y fx

có đạo hàm liên tục trên



và có đồ thị như hình bên. Đặt

   

. . d,K xf x f x x







khi đó

thuộc khoảng nào sau đây?

 

3; 2 .

2; .





































;0 .



















Câu 10*. Cho Parabol

 

Pyx



Hai điểm

di dộng

trên

 

sao cho

2AB 

. Khi diện tích phần mặt phẳng giới

hạn bởi

 

và cát tuyến

đạt giá trị lớn nhất thì hai

điểm

, AB

có tọa độ xác định

 

;

Ax y

và

 

Bx y

Giá trị

của biểu thức

22 22

AB AB

T xx yy

bằng

Phần 3. Đồ thị hàm

 



.fx

Câu 1.

Cho hàm số

 

y fx



có đạo hàm

 



liên tục trên

.

Hình bên là đồ thị của hàm số

 



y fx

trên

 

5; 4 .

Giá

trị nhỏ nhất của

 

trên

 

5; 4

là

 



 

4.f

 

1.f

 

4.f

Câu 2.

Cho hàm số

 

y fx



có đao hàm

 



liên tuc trên



và đồ thị của hàm số

 

y fx





cắt trục hoành tại ba điểm có

hoành độ

,,abc

(hình bên). Khẳng định nào sau đây đúng?

   

 

.fc fa fb

     

.fa fc fb

     

.fb fc fa

     

.fa fb fc

Câu 3.

Cho hàm số

 

y fx

có đạo hàm

 



liên

tục trên

.

Hình bên là đồ thị của hàm số

 



trên

đoạn

 

2; .d

Giá trị nhỏ nhất và giá trị lớn nhất của

hàm số

 

y fx

trên đoạn

 

2;d

lần lượt là

 

và

 

.fb

 

và

 

2.f

 

và

 

.fb

 

và

 

Câu 4. Cho hàm số

 

y fx

có đạo hàm

 



liên tục trên



Miền hình phẳng trong hình vẽ được giới hạn bởi đồ thị hàm số

 

y fx





và trục hoành đồng thời có diện tích

.Sa

Biết rằng

   

1dx fxx b







và

 

3.fc

Tính

 

d.I fx x



.I abc

.I abc  

.I abc  

.I abc

Câu 5.

Cho hàm số

 

y fx

có đạo hàm

 



liên tục

trên

 

2;1 .

Hình bên là đồ thị của hàm số







 .y fx

Đặt



 





gx f x

Khẳng định nào sau đây đúng?



 

  

210.g gg

 



 





1 2 0.gg g

     

 0 1 2.g gg

 

   

0 2 1.gg g

Câu 6. Cho hàm số





y fx

có đạo hàm







liên tục

trên

 

3;3 .

Hình bên là đồ thị của hàm số

 



 .

y fx

Đặt

  



2.gx f x x



Khẳng định nào sau đây đúng?

     

3 3 1.gg g

     

3 3 1.g gg 

     

1 3 3.gg g 

     

1 3 3.gg g 

Câu 7.

Cho hàm số

 

y fx

có đạo hàm

 



liên tục

trên

 

3;3 .

Hình bên là đồ thị của hàm số









y fx

Đặt

  

  

 

2 1.gx f x x

Gọi

là số thực thỏa mãn

 

d 0.

gx x















Khẳng định nào sau đây đúng?



 



6 1 3.

g mg

   

6 1 6 3.g mg 

   

3 1 3 3.g mg 

   

3 1 3 3.g mg  

Câu 8. Cho hàm số





y fx



có đạo hàm







liên tục trên

 

3;3 .

Hình bên là đồ thị của hàm số

 



 .y fx

Biết

 

16f



và

   

 

gx f x





. Khẳng định nào sau đây là đúng?

A. Phương trình

 

0gx

không có nghiệm thuộc

 

3;3 .

B. Phương trình

 

0gx

có đúng một nghiệm thuộc

 

3;3 .

C. Phương trình

 

0gx

có đúng hai nghiệm thuộc

 

3;3 .

D. Phương trình

 

0gx

có đúng ba nghiệm thuộc

 

3;3 .

Câu 9. Cho hàm số

 

y fx

có đạo hàm

 



liên tục trên

 

2;1 .

Hình bên là đồ thị của hàm số

 



 .y fx

Đặt

   



gx f x

Điều kiện cần và đủ để phương trình

 

 0gx

có bốn nghiệm phân biệt là

 



















 























 



















 





















1 0.

Câu 10. Cho hàm số





y fx

có đạo hàm

 



liên tục

trên



Hàm số







y fx

có đồ thị như hình bên. Tổng giá

trị lớn nhất và giá trị nhỏ nhất của hàm số

 



gx f x

trên

đoạn

 

2;2

bằng

   

1 0.ff

   



4 0.ff

   

1 4.ff

 

   



1 0 4.fff

Phần 4. Diện tích hình phẳng

Câu 1.

Cho Parabol như hình vẽ bên. Diện tích hình phẳng

giới hạn bởi Parabol và trục hoành bằng

16.

Câu 2.

Tính diện tích hình phẳng được tô đậm ở hình bên.



S 

Câu 3. Ông An xây dựng một sân bóng đá mini

hình chữ nhật có chiều rộng

30 m

và chiều dài

50 m.

Để giảm bớt chi phí cho việc trồng cỏ nhân

tạo, ông An chia sân bóng ra làm hai phần (tô đen

và không tô đen) như hình bên. Phần tô đen gồm

hai miền diện tích bằng nhau và đường cong

AIB

là một Parabol đỉnh

Phần tô đen được trồng cỏ nhân tạo với giá cỏ nhân tạo với giá

130 000

đồng

và

phần còn lại được trồng cỏ nhân tạo với giá

90 000

đồng

/m .

Hỏi ông An phải trả bao

nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?

135

triệu đồng. B.

151

triệu đồng.

165

triệu đồng. D.

195

triệu đồng.

Câu 4. Nhà ông An cần sơn mặt trước của cổng có dạng như

hình bên, các đường cong có dạng là Parabol với các kích

thước được cho như hình. Biết giá thuê nhân công là

100.000

đồng

. Hỏi ông An phải trả cho bên thi công bao nhiêu

tiền để sơn cổng?

2 468650

đồng. B.

1866 667

đồng.

1775361

đồng. D.

1668 653

đồng.

Câu 5.

Một hoa văn trang trí được tạo ra từ một miếng bìa

mỏng hình vuông cạnh

10 cm

bằng cách khoét bỏ đi bốn

phần bằng nhau có hình dạng Parabol (như hình vẽ). Biết

 5 cmAB

 4 cmOH

. Diện tích bề mặt hoa văn đó bằng

cm .

140

cm .

160

cm .

50 cm .

Câu 6. Một mảnh vườn toán học có dạng hình chữ nhật,

chiều dài là

16 m

và chiều rộng là

8 m.

Các nhà Toán học

dùng hai đường Parabol, mỗi Parabol có đỉnh là trung

điểm của một cạnh dài và đi qua hai mút của cạnh đối

diện, phần mảnh vườn nằm ở miền trong của cả hai

Parabol (phần tô đậm như hình vẽ) được trồng hoa hồng. Biết chi phí để trồng hoa

hồng là

45000

đồng

/m .

Hỏi các nhà Toán học phải chi bao nhiêu tiền để trồng hoa

trên phần mảnh vườn đó? (Số tiền được làm tròn đến hàng nghìn).

1920 000

đồng. B.

2159 000

đồng. C.

2715000

đồng. D.

3322 000

đồng.

Câu 7. Một công ty quảng cáo muốn làm một bức tranh trang trí hình

MNEIF

ở

chính giữa của một bức tường hình chữ nhật

ABCD

có chiều cao

 6 mBC

, chiều dài

12 mCD

(hình vẽ bên). Cho biết

MNEF

là hình chữ nhật có

 4 m;MN

cung

EIF

có hình dạng là một phần của cung Parabol có đỉnh

là trung điểm của cạnh

và

đi qua hai điểm

Kinh phí làm bức tranh là

900.000

đồng

/m .

Hỏi công ty cần

bao nhiêu tiền để làm bức tranh đó?

20.400.000

đồng. B.

20.600.000

đồng.

20.800.000

đồng. D.

21.200.000

đồng.

Câu 8.

Một chiếc cổng có hình dạng là một Parabol có khoảng cách

giữa hai chân cổng là

8 m.AB



Người ra treo một tâm phông hình

chữ nhật có hai đỉnh

,MN

nằm trên Parabol và hai đỉnh

,PQ

nằm

trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô

đen) người ta mua hoa để trang trí với chi phí cho

cần số tiền

mua hoa là

200.000

đồng, biết

4 m, 6 m.MN MQ

Hỏi số tiền dùng để mua hoa

trang trí chiếc cổng gần với số tiền nào sau đây?

3373 400

đồng. B.

3434 300

đồng. C.

3437 300

đồng. D.

3733300

đồng.

Câu 9. Cho

là hình phẳng giới hạn bởi đồ thị

 

:4Cy xx

và

trục hoành (hình vẽ bên). Đường thẳng

ym

chia

thành hai

phần có diện tích bằng nhau. Biết

ma b



với

,ab

là các số hữu

tỉ, tính

S ab

64.S 

32.S 

32.

S 

64.S 

Câu 10.

Cho

là hình phẳng giới hạn bởi đồ thị

 

của hàm

số

y xx

và trục hoành. Hai đường thẳng

ym

và

yn

chia hình

thành ba phần có diện tích bằng nhau. Tính

  



9 9.

Pm n 

 403.P

 405.P

407.P 

 409.P

Câu 11.

Cho hình phẳng

(phần tô đậm) được giới hạn bởi

các đường



4,yx

yx

và

 2

có diện tích là

S ab

với

 , .ab

Khẳng định nào sau đây đúng?



1.ab

2 3.ab



4 5.ab

1a

và



1.b

Câu 12. Cho đường tròn tâm

đường kính

 8.AB

Trên

lấy hai điểm

đối xứng nhau qua

sao cho

 4.MN

Qua

kẻ hai dây cung

và

cùng vuông góc với

.AB

Diện tích phần giới hạn bởi đường tròn và hai dây cung

,PQ

(phần tô đậm như hình vẽ) bằng

 5 5.

 6 8 3.

 12 7.

 

8 3.

Câu 13. Biết rằng đường Parabol





:2Py x

chia đường

tròn

 

:8Cx y

thành hai phần lần lượt có diện tích là

, SS

(hình bên). Khi đó

SS a

 

với

, , abc

nguyên

dương và

là phân số tối giản. Tổng

abc

bằng

13.

14.

15.

16.

Câu 14.

Một khuôn viên dạng nửa hình tròn có đường

kính bằng

4 5 m.

Trên đó người thiết kế hai phần để

trồng hoa có dạng của một cánh hoa hình Parabol có

đỉnh trùng với tâm nửa hình tròn và hai đầu mút của

cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng

4 m,

phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết

các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là

100 000

đồng

/m .

Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn

đến hàng nghìn).

1194 000

đồng. B.

1948 000

đồng. C.

2388 000

đồng. D.

3895000

đồng.

Câu 15. Một viên gạch hoa hình vuông cạnh

40 cm.

Người

thiết kế đã sử dụng bốn đường Parabol có chung đỉnh tại tâm

của viên gạch để tạo ra bốn cánh hoa (được tô màu như hình

bên). Diện tích mỗi cánh hoa của viên gạch bằng

250 cm .

400

cm .

800

cm .

1600

cm .

Câu 16. Gọi

là diện tích của hình phẳng giới hạn bởi Elip



và

là

diện tích của hình thoi có các đỉnh là đỉnh của Elip đó. Tỉ số

bằng

.



2

Câu 17.

Một sân chơi cho trẻ em hình chữ nhật có

chiều dài

100 m

và chiều rộng là

60 m

người ta

làm một con đường nằm trong sân (như hình vẽ).

Biết rằng viền ngoài và viền trong của con đường là

hai đường elip, Elip của đường viền ngoài có trục

lớn và trục bé lần lượt song song với các cạnh hình

chữ nhật và chiều rộng của mặt đường là

2 m.

Kinh

phí cho mỗi

làm đường

600 000

đồng. Tính tổng số tiền làm con đường đó. (Số tiền

được làm tròn đến hàng nghìn).

293804 000

đồng. B.

293904 000

đồng.

294 053000

đồng. D.

294153000

đồng.

Câu 18.

Một mảnh vườn hình chữ nhật có chiều dài

10 m

và chiều rộng

6 m,

được phân chia thành các phần

bởi một đường chéo và một đường Elip nội tiếp bên trong

như hình vẽ bên. Hãy tính diện tích phần tô đậm (theo

đơn vị

 

5 2. 

 

54 .





45 4



 

45 4



Câu 19.

Một biển quảng cáo có dạng hình Elip với bốn đỉnh

1212

, ,,AABB

như hình vẽ bên. Biết chi phí sơn phần tô đậm

là

200 000

đồng

và phần còn lại là

100 000

đồng

/m .

Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào

dưới đây, biết

12 12

8 m, 6 mAA BB

và tứ giác

MNPQ

là

hình chữ nhật có

 3m

5.526.000

đồng. B.

5.782.000

đồng.

7 213000

đồng. D.

7322 000

đồng.

Câu 20.

Nhà trường dự định làm một vườn hoa

dạng hình Elip được chia ra làm bốn phần bởi hai

đường Parabol có chung đỉnh, đối xứng với nhau

qua trục của Elip như hình vẽ bên. Biết độ dài trục

lớn, trục nhỏ của Elip lần lượt là

và

4 m; ,FF

là hai tiêu điểm của Elip. Phần

,AB

dùng để trồng hoa; phần

dùng để trồng cỏ.

Kinh phí để trồng mỗi mét vuông trồng hoa và trồng cỏ lần lượt là

250 000

đồng và

150 000

đồng. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).

4 656 000

đồng. B.

4766 000

đồng.

5455000

đồng. D.

5676 000

đồng.

Câu 21.

Cho hình phẳng giới hạn bởi các

đường

 sin ,yx

 cosyx

và

là

diện tích của các phần được gạch chéo như

hình vẽ. Tổng



bằng

10 2 2.

10 2 2.

11 12 2.

11 2 2.

Câu 22. Kí hiệu

là hình phẳng giới hạn bởi các đường

 ,

 0,y



và

1.x

Đường thẳng

 

01xk k

 

chia

thành hai phần có diện tích tương ứng

, SS

như hình vẽ bên,

biết



.SS

Mệnh đề nào sau đây là đúng?

















Câu 23. Cho hình phẳng

giới hạn bởi các đường

,yx

0,y 

0,x 

4.x 

Đường thẳng



 

0 16



chia hình

thành hai phần có diện tích

, SS

(hình vẽ). Tìm

để



.SS

k 

. B.

4k 

5.k 

8k 

Câu 24. Xét hình phẳng

giới hạn bởi đồ thị hàm số







3,yx

trục hoành và đường thẳng

0.x 

Gọi

 

0;9 ,

 

;0Bb

 

 3 0.

Tìm giá trị của tham số

để đoạn thẳng

chia

thành hai phần có diện tích bằng nhau.

2b 

. B.

b 

. C.

b 

Câu 25.

Trong mặt phẳng tọa độ, cho hình chữ nhật

có một cạnh nằm trên trục hoành và có hai đỉnh trên một

đường chéo là

 

1; 0A

và





;Ca a

với

 0.a

Biết rằng

đồ thị hàm số

yx

chia hình

thành hai phần có

diện tích bằng nhau, tìm



 3.a

 4.a

 9.a

Phần 5. Thể tích khối tròn xoay

Câu 1.

Cho hình phẳng

giới hạn bởi các đồ thị hàm

số

4yx



và



2.yx

Tính thể tích

của khối

tròn xoay tạo thành khi quay

quanh trục hoành.

10 .V 

12 .V 

14 .V 

16 .V 

Câu 2. Thể tích

của khối tròn xoay khi cho hình

phẳng

giới hạn bởi các đường

1yx

và

1yx

quay quanh trục

được xác định bởi công thức nào sau

đây?

   

1 1 d.V xx x



  



   

1 1d.V xx x





 



 

1 d.V xx







   

1 1 d.V x xx





  







Câu 3. Cho hình vuông

OABC

có cạnh bằng

được chia

thành hai phần bởi đường cong

 

có phương trình



Gọi

là hình phẳng không bị gạch (như hình vẽ).

Tính thể tích

của vật thể tròn xoay khi cho phần

qua

quanh trục

.Ox









128





128





256

Câu 4. Cho hình phẳng

giới hạn bởi

đường tròn có

bán kính

2,R 

đường cong

4yx

và trục hoành

(miên tô đậm như hình vẽ). Tính thể tích

của khối tạo

thành khi cho hình

quay quanh trục

.Ox

















Câu 5.

Cho hình phẳng

giới hạn bởi các đường

2, 2, 1.y x yx x

    

Tính thể tích

của vật thể

tròn xoay khi quay hình phẳng

quanh trục

.Ox

 9.V













Câu 6.

Gọi

là thể tích khối tròn xoay tạo

thành khi quay hình phẳng giới hạn bởi các

đường

 ,yx

0y 

và

4x 

quanh trục

Đường thẳng

 

xa a 

cắt đồ thị hàm số

yx

tại

(hình vẽ bên). Gọi

là thể tích

khối tròn xoay tạo thành khi quay tam giác

OMH

quanh trục

. Biết rằng

2VV

. Khi đó

2a 

. B.

a 

. C.

22a 

. D.

3a 

Câu 7. Gọi

là thể tích khối tròn xoay tạo thành khi

quay hình phẳng giới hạn bởi các đường

 sin ,yx

hai

trục tọa độ và



quanh trục hoành. Đường thẳng



 

0 k

cắt đồ thị hàm số

 sinyx

tại điểm

và trục hoành tại điểm

(hình vẽ bên).

Gọi

là thể tích khối tròn xoay tạo thành khi quay tam giác

OMN

quanh trục

.Ox

Biết rằng



Khi đó



 .



 .

 2.k

 3.k

Câu 8. Có một vật thể là hình tròn xoay có dạng giống như một

cái ly như hình vẽ bên. Người ta đo được đường kính của miệng

ly là

4 cm

và chiều cao là

6 cm.

Biết rằng thiết diện của chiếc

ly cắt bởi mặt phẳng đối xứng là một Parabol. Thể tích của vật

thể đã cho bằng

 



12 cm .





12 cm .

 



cm .

 

cm .

Câu 9. Trong mặt phẳng cho đường Elip

 

có độ dài trục

lớn là

8AA





và độ dài trục nhỏ



 6;BB

đường tròn tâm

đường kính



như hình vẽ. Tính thể tích

của khối

tròn xoay có được bằng cách cho miền hình phẳng giới hạn

bởi đường Elip và đường tròn (được tô đậm trên hình vẽ)

quay xung quanh trục

.AA



12 .

V 

16 .V



28 .V

36 .V



Câu 10. Một thùng chứa rượu làm bằng gỗ là một hình tròn

xoay như hình bên có hai đáy là hai hình tròn bằng nhau,

khoảng cách giữa hai đáy bằng

8 dm.

Đường cong mặt bên của

thùng là một phần của đường Elip có độ dài trục lớn bằng

10 dm

, độ dài trục bé bằng

6 dm.

Hỏi chiếc thùng gỗ đó đựng

được bao nhiêu lít rượu?

1316

(lít). B.

1416

(lít). C.

1516

(lít). D.

1616

(lít).

Câu 11. Bên trong hình vuông cạnh

dựng hình sao

bốn cánh đều như hình vẽ bên (các kích thước cần thiết

cho như ở trong hình). Tính thể tích

của khối tròn

xoay sinh ra khi quay hình sao đó quanh trục

















Câu 12. Cho hình phẳng

gồm nửa hình tròn đường kính

và tam giác

ABC

đều (như hình vẽ). Gọi



là đường thẳng qua

và song song với

.AB

Biết

 2 3 cm.AB

Thể tích khối tròn

xoay tạo bởi hình

quay quanh trục



bằng

 



8 3 9 cm .

 



 

8 3 cm .

 



32 3 18 cm .









16 3 9 cm .

Câu 13. Cho hình vẽ bên, biết cung tròn

nằm trên đường tròn

bán kính

4.R 

Cạnh

4.AB BC CD DA

Thể tích vật tròn

xoay tạo thành khi quay hình bên quanh trục

nằm trong

khoản nào sau đây?





165;170 .





160;165 .

 

155;160 .

 

150;155 .

Câu 14.

Cho hình tròn tâm

có bán kính

2R 

và hình vuông

OABC

có cạnh bằng

(như hình vẽ bên). Tính thể tích

của vật

thể tròn xoay khi quay mô hình bên xung quanh trục là đường

thẳng

.OB

 

83 4 2





 

82 5 2





 

83 5 2





 

32 1 2





Câu 15.

Cho hình vuông có độ dài cạnh bằng

8cm

và một hình

tròn có bán kính

5cm

được xếp chồng lên nhau sao cho tâm

của hình tròn trùng với tâm của hình vuông như hình vẽ bên.

Tính thể tích

của vật thể tròn xoay tạo thành khi quay mô

hình trên quanh trục

.XY

260

cm .





290

cm .





520

cm .





580

cm .





Câu 16. Cho hai tam giác cân có chung đường cao

40cmXY 

và cạnh đáy lần lượt là

40cm

và

60cm

, được

xếp chồng lên nhau sao cho đỉnh của tam giác này là trung

điểm cạnh đáy của tam giác kia như hình vẽ bên. Tính thể

tích

của vật thể tròn xoay được tạo thành khi quay mô

hình trên quanh trục

40480

cm .





52000

cm .





46240

cm .





1920 cm .



Câu 17.

Cho khối cầu có bán kính

. Một mặt phẳng cắt

khối cầu thành hai nửa. Nửa bé có khoảng cách từ đỉnh đến

đáy bằng

(tham khảo hình vẽ bên). Tính thể tích nửa bé.





















V hR





















V hR





















V hR





















V hR

Câu 18.

Cho hai mặt cầu





 

có cùng bán kính

thỏa mãn tính chất: tâm của

 

thuộc

 

và ngược lại.

Tính thể tích phần chung

của hai khối cầu tạo bởi

 

và

 















Câu 19.

Cho hai đường tròn





;5O

và

 

;3O

cắt nhau tại

hai điểm

và

sao cho

là một đường kính của

đường tròn

 

Gọi

là diện tích hình phẳng giới hạn

bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch

chéo như hình vẽ). Quay hình

quanh trục

,OO

được một khối tròn xoay. Thể tích của khối tròn xoay được

tạo thành bằng









68

36 .

Câu 20.

Ta vẽ hai nửa đường tròn như hình vẽ bên,

trong đó đường kính của nửa đường tròn lớn gấp đôi

đường kính của nửa đường tròn nhỏ. Biết rằng nửa

hình tròn đường kính

có diện tích là

8

và



30 .BAC

Thể tích của vật thể tròn xoay được tạo

thành khi quay hình

(phần tô đậm) xung quanh

đường thẳng

bằng



220



224

Phần 6. Bài toán vận tốc

Câu 1. (ĐỀ MINH HỌA 2016 – 2017) Một ô tô đang chạy với vận tốc

10m/s

thì

người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

 5 10 m/s ,vt t

trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu

đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

0, 2m.

2m.

10m.

20m.

Câu 2. Một ô tô đang đi với vận tốc lớn hơn

72km/h,

phía trước là đoạn đường chỉ cho

phép chạy với tốc độ tối đa là

72km/h,

vì thế người lái xe đạp phanh để ô tô chuyển

động chậm dần đều với vận tốc

   

30 2 m/s ,vt t

trong đó

là khoảng thời gian

tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt

tốc độ

72km/h,

ô tô đã di chuyển quãng đường là bao nhiêu mét?

100m.

125m.

150m.

175m.

Câu 3. Hai viên đạn cùng rời khỏi nòng súng thời điểm

 0t

với những vận tốc khác

nhau: viên đạn thứ nhất có vận tốc

  





3 1 m/s ,vt t

viên đạn thứ hai có vận tốc

   



2 4 m/s .vt t

Hỏi từ giây thứ mấy thì viên đạn thứ nhất xa điểm xuất phát hơn

viên đạn thứ hai?

A. Giây thứ nhất. B. Giây thứ hai.

C. Giây thứ ba. D. Giây thứ tư.

Câu 4. Một ô tô đang chạy với vận tốc

 

10 m/s

thì người lái xe đạp phanh. Từ thời

điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

 2 10 m/s ,vt t

trong đó

là khoảng thời gian được tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quảng

đường ô tô di chuyển được trong

giây cuối cùng.

16m.

25m.

50m.

55m.

Câu 5. Một vật đang chuyển động với vận tốc

6m/s

thì tăng tốc với gia tốc

 





m/s ,

trong đó

là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng

tốc. Hỏi vận tốc của vật sau

giây gần nhất với kết quả nào sau đây?

11m/s

. B.

12 m/s

. C.

13m/s

. D.

14 m/s

Câu 6. Một vật đang chuyển động với vận tốc

10m/s

thì tăng tốc với gia tốc

 



3 m/s ,

at t t

trong đó

là khoảng thời gian tính bằng giây kể từ lúc bắt đầu

tăng tốc. Hỏi quãng đường vật đi được trong khoảng thời gian

giây kể từ lúc bắt

đầu tăng tốc bằng bao nhiêu mét?

1900

2200

4000

4300

Câu 7. Một ô tô đang chạy thẳng đều với vận tốc

 

m/sv

thì người đạp phanh, từ

thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc

 

5 m/s ,vt t v 

trong

đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp

phanh đến lúc dừng hẳn ô tô di chuyển được

40m

thì vận tốc ban đầu

bằng bao

nhiêu?

20m/s.v 

25m/s.

v 

40m/s.v



80m/s.v 

Câu 8. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao

162m

với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng,

khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật

 

10 m/svt t t

, trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu

chuyển động. Hỏi lúc vừa tiếp đất, vận tốc

của khí cầu bằng bao nhiêu?

3m/s.v 

5m/s.v 

7m/s.v 

9m/s.v 

Câu 9. (ĐỀ THI CHÍNH THỨC 2016 – 2017) Một vật chuyển động theo quy luật

s tt 

với

(giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động

và

(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong

khoảng thời gian

giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt

được bằng bao nhiêu?

18m/s.

24m/s.

64m/s.

108m/s.

Câu 10. Một tàu lửa đang chạy với vận tốc

200 m/s

thì người lái tàu đạp phanh. Từ

thời điểm đó, tàu chuyển động chậm dần đều với vận tốc

   

t 200 m/s ,v at

trong

đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh và





m/sa

là

gia tốc. Biết rằng khi đi được

1500m

thì tàu dừng, hỏi gia tốc của tàu bằng bao

nhiêu?

200

m/s .

a 

100

m/s .

a 

m/s .

a 

 

m/s .

a 

Câu 11.

Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu tăng tốc

với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường

cong Parabol có hình bên. Biết rằng sau

10s

thì xe đạt đến vận

tốc cao nhất

50m/s

và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu

tăng tốc đến lúc đạt vận tốc cao nhất thì xe đã đi được quãng

đường bao nhiêu mét?

1000

1100

1400

300m.

Câu 12.

Một vật chuyển động trong

giờ với vận tốc

 

km/hv

phụ

thuộc thời gian

 

có đồ thị là một phần của đường Parabol có

đỉnh

 

2;9I

và trục đối xứng song song với trục tung như hình bên.

Tính quãng đường

mà vật di chuyển được trong

giờ đó.

24,25km.

s 

24,75km.

s 

25,25km.s 

26,75km.s 

Câu 13.

Một vật chuyển động trong

giờ với vận tốc

 

km/hv

phụ thuộc thời gian

 

có đồ thị của vận tốc như hình bên.

Trong khoảng thời gian

giờ kể từ khi bắt đầu chuyển động,

đồ thị đó là một phần của đường Parabol có đỉnh

 

2;9I

với

trục đối xứng song song với trục tung, khoảng thời gian còn lại

đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng

đuờng

mà vật chuyển động trong

giờ đó.

24km.

s 

26,5km.s 

27km.

s 

28,5km.s 

Câu 14.

Một vật chuyển động trong

giờ với vận tốc





km/h

phụ thuộc thời gian

 

có đồ thị của vận tốc

như hình bên. Trong khoảng thời gian

giờ kể từ khi

bắt đầu chuyển động, đồ thị đó là một phần của đường

Parabol có đỉnh

 

1; 2I

và trục đối xứng song song với

trục tung, khoảng thời gian còn lại đồ thị là một phần

đường thẳng. Tính quãng đường

mà vật di chuyển được

trong

giờ đó (kết quả làm tròn đến hàng phần trăm).



5, 44km.s

 8,67km.s

 9,27km.s

11,35km.s

Câu 15.

Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi

hành cùng một lúc, bên cạnh nhau và trên cùng một con

đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường

Parabol, đồ thị biểu diễn vận tốc của xe B là một đường

thẳng ở hình bên. Hỏi sau khi đi được

giây khoảng cách

giữa hai xe là bao nhiêu mét?

0 m.

60 m.

90 m.

270 m.

---------- HẾT ----------

ỨNG DỤNG TÍCH PHÂN

Phần 1. Áp dụng công thức…………………………………………………………

Phần 2. Đồ thị hàm

 

………………………………………………………………

Phần 3. Đồ thị hàm

 



……………………………………………………..…….

Phần 4. Diện tích hình phẳng …………………………………………….……

Phần 5. Thể tích khối tròn xoay …………………….……………………….

Phần 6. Bài toán vận tốc …………………….……………………………………..

Phần 1. Áp dụng công thức

Câu 1.

Cho hàm số

 

y fx

liên tục trên

 

;ab

và có

đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

 





fxx

là độ dài đoạn thẳng

.NM

 





fxx

là độ dài đường cong

.AB

 





fxx

là độ dài đoạn thẳng

.BP

 





fxx

là diện tích hình thang cong

ABMN

Lời giải. Ta có

      





   



f x x f x f b f a BM MP BP

Chọn C.

Câu 2. Cho hàm số

 

y fx



liên tục trên

 

0;4

và có đồ thị như

hình bên. Tích phân

 



dfx x

bằng

Lời giải. Kí hiệu các điểm như trên hình vẽ.

Ta có:



  

 

4 24

0 02

d dd .

ABCO CDE

fx x fx x fx x S S  



Diện tích hình thang

ABCO

là:

 

2. 1 2

ABCO





Diện tích hình tam giác

CDE

là:

2.2

CDE

S 

Vậy

 

d 3 2 1.

ABCO CDE

fx x S S  



Chọn B.

Câu 3.

Cho hàm số

 

y fx

liên tục trên

 

0;3

và có đồ thị

như hình bên. Biết

 

d 2,3fx x



và



    

, 0; 4 .F x fx x



 

Hiệu

   

30FF

bằng

0,3.

1, 3.

3, 3.

4,3.

Lời giải. Kí hiệu các điểm như trên hình vẽ. Ta có

     

3 13

0 01

d d d 2,3 2 2,3 4,3.

ABCO

fx x fx x fx x S

   



Lại có

    



   

d d 3 0.fxx Fxx Fx F F



  



Suy ra

   

3 0 4,3.FF

Chọn D.

Câu 4.

Cho hàm số

 

y fx

liên tục trên

 

2;2

và có đồ thị

đối xứng qua gốc tọa độ như hình bên. Biết





d 2.fx x







Tích

phân

 



dfx x

bằng

2.

Lời giải. Vì đồ thị hàm số





y fx



đối xứng qua gốc tọa độ nên hàm số

 

y fx

là

hàm số lẻ. Áp dụng tính chất hàm lẻ, ta có

 







d 0.fx x

Mà





 







2 02

2 20

d d d 0.

fx x fx x fx x

Suy ra

 





d 2.fx x

Chọn A.

Câu 5. Cho hàm số

 

y fx

liên tục trên

 

2;2



và có đồ thị

đối xứng qua trục tung như hình bên. Biết

 

fx x



Tích phân









dfx x

bằng

0.I 

Lời giải. Vì đồ thị hàm số

 

y fx

đối xứng qua trục tung nên hàm số

 

y fx

là

hàm số chẵn. Áp dụng tính chất hàm chẵn, ta có

   







d d.

fx x fx x

Chọn A.

Câu 6. Cho hàm số

 

y fx

liên tục trên







3;5

và có đồ

thị như hình bên (phần cong của đồ thị là một phần của

Parabol

 

y ax bx c

). Tích phân

 





dfx x

bằng

Lời giải. Dựa vào đồ thị hàm số ta suy ra





















   











  

30 1 3

22 0 1

4 97

d 4d4d4 d.

fxx x x xx xx x

Chọn D.

Câu 7. Cho hàm số





y fx

có đạo hàm liên tục trên

 

1; 4

và có

đồ thị như hình bên. Tích phân

 





dfx x

bằng

Lời giải. Dựa vào đồ thị ta thấy:

●

     

1 4 0; 2 3.ff f 

● Hàm số

 

y fx

đồng biến trên khoảng

 

1; 2

và nghịch biến trên khoảng





2;4

nên suy ra

 







 









 





0 khi 1 2

0 khi 2 4

fx x

Do đó

    

    

 

  

 

4 24

1 12

d ddfx x fxx fxx fx fx

  

 





   



2 1 4 2 6.ffff

Chọn D.

Câu 8. Cho hàm số





y fx



liên tục trên



và hàm số

 

.y gx xf x

có đồ thị trên đoạn

 

1; 2

như hình vẽ bên.

Biết phần diện tích miền được tô màu là



giá trị của tích

phân

 





dI fx x

bằng

10.

Lời giải. Diện tích phần tô màu là:

 

d.S gx x



Theo giả thiết

 

. d.

S xf x x 



Đặt

d 2d

t x t xx   

. Đổi cận:

















Khi đó

 

   

2 44

1 11

. d d d5

xfx x ft t ft t    

 

hay

 

d 5.fx x



Chọn C.

Câu 9.

Cho hàm số

 

y fx

có đạo hàm liên tục trên

 



1; 2 .

Đồ thị của hàm số

 

y fx





được cho như hình bên. Diện tích

các hình phẳng

   

,KH

lần lượt là

và

Biết

 

f 

tính

 

2.f







 









 

2 3.f



Lời giải. Dựa vào đồ thị ta thấy:

     

2 02

1 10

58 9

d dd .

12 3 4

fxx fxx fxx





    



Mặt khác:





  

 



 

d 2 1 2.

f x x fx f f f





 



Từ đó suy ra





 

     

19 9 9 19 2

2 2.

12 4 4 12 3

Chọn A.

Câu 10. Cho hàm số





y fx

có đạo hàm liên tục trên

 

2;4 .

Đồ thị của hàm số

 

y fx





được cho như hình

bên. Diện tích hình phẳng giới hạn bởi trục

và đồ thị

hàm số

 

y fx





trên đoạn

 

2;1

và

 

1; 4

lần lượt bằng

và

12.

Cho

 

1 3.f 

Tổng

   

24ff

bằng

21.

Lời giải. Theo giả thiết, ta có





d9fxx









và

 

d 12.fxx







•

         

d 9 1 2 9 3 2 9 2 12.

fxx f f f f





           



•

  



 

  



d 12 4 1 12 4 3 12 4 9.fxx f f f f



        



Vậy

     

2 4 12 9 3.ff    

Chọn B.

Phần 2. Đồ thị hàm

 

.fx

Câu 1.

Cho hàm số

 

y fx



có đạo hàm liên tục trên



và có

đồ thị như hình bên. Giá trị của biểu thức

  



2d 2dfx x fx x



 



bằng

2.

10.

Lời giải. Ta có

   











2d d

fx x ftt

và

   









2 d d.

fx x ftt

Khi đó

         



   

   

  

4 2 24 4

0 0 22 2

2d 2d d d dfx x fx x ftt ftt ftt

  

    



   

4 2 4 2 6.ft f f

Chọn C.

Câu 2. Cho hàm số





y fx

xác định và liên tục

trên

 

0;2

và có bảng biến thiên như hình bên.

Hỏi có bao nhiêu giá trị nguyên của

để thỏa

mãn điều kiện

 









fx m x

11.

12.

13.

14.

Lời giải: Dựa vào bảng biến thiên ta có

 

 





 





 











  













22 2

0;2

00 0

0;2

max 7

5 d d 7d

min 5

x fx x x

hay

 

 



10 d 14.fx x

Từ giả thiết

 



  





d 0 2 d.fx m x m fx x

Do đó để phương trình có nghiệm

     10 2 14 5 7

. Vậy có

giá trị

nguyên thỏa mãn. Chọn C.

Câu 3. Cho hai hàm số





f x ax bx cx  

và

 

g x dx ex 

 

 ,,, , .abcde

Biết rằng đồ thị hàm số

 

y fx



và

 

y gx

cắt nhau tại ba điểm có hoành độ lần

lượt là

3; 1; 1

(tham khảo hình vẽ). Hình phẳng giới hạn

bởi hai đồ thị đã cho có diện tích bằng

Lời giải. Phương trình hoành độ giao điểm của đồ thị

 

và

 

là

  

  

        

32 2 3 2

1 0.

ax bx cx dx ex ax b d x c d x

Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình

 



có ba nghiệm

là

3; 1; 1.

Ta được

 

   

 

311 .

ax x x ax b dx c dx     

Đồng nhất

hai vế ta suy ra

   

Vậy diện tích hình phẳng cần tìm là

   



 



311

d 4.xx xx

Chọn A.

Câu 4. Cho hai hàm số

 

1f x ax bx cx  

và





g x dx ex 

 

 ,,, , .abcde

Biết rằng đồ thị hàm số

 

y fx

và

 

y gx

cắt nhau tại ba điểm có hoành độ lần

lượt

3; 1; 2

(tham khảo hình vẽ). Hình phẳng giới hạn bởi

hai đồ thị đã cho có diện tích bằng

125

253

125

253

Lời giải. Tương tự như bài trên ta được



Vậy diện tích hình phẳng cần tìm là









 



1 253

312

4 48

xxxx

Chọn D.

Câu 5. Cho hai hàm số

 

 

2bxfx cxxa

và

 

g x dx e



 

 ,,, , .abcde

Biết rằng đồ thị hàm số





y fx



và

 

y gx

cắt nhau tại ba điểm có hoành độ lần lượt

là

2; 1; 1

(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ

thị đã cho có diện tích bằng

Lời giải. Tương tự như bài trên ta được



Vậy diện tích hình phẳng cần tìm là

   

d21 .

21xx xx



 



Chọn C.

Câu 6. Cho hai hàm số

 

f x ax bx cx  

và

 

g x dx ex 

 

 ,,, , .abcde

Biết rằng đồ thị hàm số





y fx

và

 

y gx

cắt nhau tại ba điểm có hoành độ lần

lượt là

2; 1; 3

(tham khảo hình vẽ). Hình phẳng giới hạn

bởi hai đồ thị đã cho có diện tích bằng

125

253

125

253

Lời giải. Tương tự như bài trên ta được



Vậy diện tích hình phẳng cần tìm là

   



  



1 253

213d .

4 48

xx xx

Chọn D.

Câu 7. Cho hàm số

 

y fx

xác định và liên tục

trên đoạn

 

5;3

và có đồ thị như hình vẽ. Biết

rằng diện tích hình phẳng

123

,,SSS

giới hạn bởi

đồ thị hàm số

 

y fx



và đường cong

 

y g x ax bx c  

lần lượt là

,,.mn p

Tích phân

 

dfx x





bằng

208

mn p

208

mn p

208

mnp



208

mnp



Lời giải. Đồ thị hàm

 

  

y g x ax bx c

đi qua các điểm

     

0;0 , 2;0 , 3;2OA B

nên suy ra

 



15 15

gx x x

Dựa vào đồ thị, ta có

   

 

     

20 3

5 20

ddd

m n p f x gx x gx f x x f x gx x







      





   

d d.fxx gxx







Suy ra

   

208

d d.

fxx mn p gxx mn p



   



Chọn B.

Câu 8.

Cho hàm số

 

y fx

xác định và liên tục

trên đoạn

 



3;3

và có đồ thị như hình vẽ. Biết rằng

diện tích hình phẳng

,SS

giới hạn bởi đồ thị hàm

số

 

y fx

và đường thẳng

1yx 

lần lượt là

;.Mm

Tích phân

 

dfx x





bằng

6.mM

6.mM

6.Mm

6.mM

Lời giải. Ta có

 

     

  



      



  

1 11 1

3 33 3

1 d 1d d 0 d ;M x fx x x x fx x fx x



        







  

3 33 3

1 11 1

1dd1dd6.m fx x x fx x x x fx x

Suy ra



    



   



31 3

1 33

d6d6d.m M fx x fx x fx x

Suy ra

 



 



d 6.fx x m M

Chọn D.

Câu 9. Cho hàm số

 

y fx



có đạo hàm liên tục trên



và có đồ thị như hình bên. Đặt

   

. . d,K xf x f x x







khi đó

thuộc khoảng nào sau đây?

 

3; 2 .

2; .





































;0 .



















Lời giải. Đặt

   























 











d .d

v fx f x x

Khi đó

 





 

1 11

0 00

1 11

. . d d d.

2 2 22

xf x

K xfxfxx f xx f xx



   

 

Từ đồ thị, ta thấy:

●

   



 

  



          

 

11 1

00 0

71 2

2 , 0;1 d d d .

2 2 6 22 3

fx x fx

fx x x x x K x

●

  











         

 

11 1

00 0

2, 0;1 d 2 d 2 d .

2 22 2

fx fx

fx x x x K x

Chọn C.

Câu 10*. Cho Parabol

 

Pyx

Hai điểm

di dộng

trên

 

sao cho

2AB



. Khi diện tích phần mặt phẳng giới

hạn bởi

 

và cát tuyến

đạt giá trị lớn nhất thì hai

điểm

, AB

có tọa độ xác định

 

;

Ax y

và

 

Bx y

Giá trị

của biểu thức

22 22

AB AB

T xx yy

bằng

Lời giải. Do

 

, AB P

nên giả sử

 

; , ;Aaa B bb

với



Phương trình đường thẳng







xa ya

hay

 

 .y a b x ab

Ta có

 

   



     





2 22

2 44 4AB ba b a ba ba

 

  



Suy ra

2.ba

Ta có

   





      











2 23

S a b x ab x dx a b x abx x

   

 

  

  

          

  

  

2 2 3 22 3

1 1 1 1 1 84

2 3 2 3 6 63

abb ab b aba ab a ba

Dấu

""

xảy ra

   



  



    





 





1;1 , 1;1 2.

ba a

ABT

ba b

Chọn B.

Phần 3. Đồ thị hàm

 



.fx

Câu 1.

Cho hàm số

 

y fx

có đạo hàm

 



liên tục trên

.

Hình bên là đồ thị của hàm số

 



y fx

trên

 

5; 4 .

Giá

trị nhỏ nhất của

 

trên

 

5; 4

là

 



5.f

 

4.f

 

1.f

 

4.f

Lời giải. Dựa vào đồ thị hàm số

 



,fx

ta suy ra

bảng biến thiên như hình bên. Khi đó:











 







5;4

min min 4 ; 4 .

fx f f





Dựa vào đồ thị

 



,fx

ta có













d 0.

fxx

Suy ra





 



4 4.

Vậy

 

   

5;4

min 4 .

fx f





Chọn B.

Câu 2. Cho hàm số

 

y fx



có đao hàm

 



liên tuc trên



và đồ thị của hàm số

 

y fx





cắt trục hoành tại ba điểm có

hoành độ

,,abc

(hình bên). Khẳng định nào sau đây đúng?

     

.fc fa fb

     

.fa fc fb





 







.fb fc fa







 





fa fb fc

Lời giải. Dựa vào đồ thị hàm số

 



,fx

ta suy

ra bảng biến thiên như hình bên. Khi đó:

  

 



 

 

min ; ; .

fa fb fc fb

Dựa vào đồ thị

 



ta có

 







d 0.

fxx

Suy ra

   

 .fc fa

Vậy

 

  



.

fc fa fb

Chọn A.

Câu 3. Cho hàm số





y fx

có đạo hàm

 



liên

tục trên



Hình bên là đồ thị của hàm số

 



trên

đoạn

 

2; .d

Giá trị nhỏ nhất và giá trị lớn nhất của

hàm số







y fx

trên đoạn

 

2;d

lần lượt là

 

và

 

.fb

 

và

 

2.f

 

và

 

.fb

 

và

 

.fd

Lời giải. Dựa vào đồ thị hàm số







,fx

ta suy ra bảng biến thiên

Dựa vào bảng biến thiên, suy ra

   

 

 min ; ,m fa fc

    



 

max 2 ; ; .M f fb fd

Dựa vào đồ thị

 



,fx

ta có

•

           



    



d0 0 0 .

f x x fx fc fa fc fa

•





   





    



d0 2

f x x fb f

và

     



   



d0 .

f x x fb fd

Vậy

   

, .m f a M fb

Chọn A.

Câu 4.

Cho hàm số

 

y fx

có đạo hàm

 



liên tục trên

.

Miền hình phẳng trong hình vẽ được giới hạn bởi đồ thị hàm số

 

y fx





và trục hoành đồng thời có diện tích

.Sa

Biết rằng

   

1dx fxx b







và

 

3.fc

Tính

 

d.I fx x



.I abc

.I abc  

I abc  

.I abc

Lời giải. Đặt

   



 







 







1 dd

ux u x

vfxx vfx

Khi đó

 



  

 



      



1 d 1 d 21 0 .

b x f x x x fx fx x f f I

Mặt khác, ta có

           





     





d d 10 31aS fxx fxx f f f f

  

      

  21 0 3 21 0 .ff f ffc

Suy ra

   

 21 0 .f f ac

Vậy

   

   21 0 .I f f b acb

Chọn A.

Câu 5.

Cho hàm số

 

y fx

có đạo hàm

 



liên tục

trên

 

2;1 .

Hình bên là đồ thị của hàm số

 



 .y fx

Đặt



  



gx f x

Khẳng định nào sau đây đúng?

     

210.g gg 

     

1 2 0.gg g

  

  

 

0 1 2.g gg

     

0 2 1.gg g

Lời giải. Ta có

 



;gx f x x

   



 0.gx f x x

Suy ra nghiệm của phương

trình

 



 0

là hoành độ giao điểm của đồ thị hàm số

 



y fx

và đường thẳng

 .yx

Dựa vào đồ thị ta thấy đường

yx

cắt đồ thị hàm số

 

y fx





tại các điểm

có hoành độ

2; 0; 1

(tham khảo hình vẽ)

Dựa vào bảng biến thiên, suy ra

  

  

 

 

max 2 ; 1 ; 0 0 .g gg g

Dựa vào đồ thị, ta có

   







 





ddfx xx x fx x

hay

   









ddgx x gx x

 



 

    

    0 2 0 1 2 1.gg gg g g

Chọn A.

Câu 6.

Cho hàm số

 

y fx

có đạo hàm

 



liên tục

trên

 



3;3 .

Hình bên là đồ thị của hàm số







 .

y fx

Đặt

   

2.gx f x x

Khẳng định nào sau đây đúng?

     

3 3 1.gg g





 

3 3 1.

g gg

 

     

1 3 3.gg g 

     

1 3 3.gg g 

Lời giải. Ta có

   



2 2;gx f x x



  



  0.gx f x x

Ta thấy đường thẳng

yx

cắt đồ thị hàm số

 

y fx





tại các điểm có hoành độ

3; 1; 3.

Dựa vào bảng biến thiên, suy ra

 



  





 



min 3 ; 1 ; 3 1 .g gg g

Dựa vào đồ thị, ta có

   







 





d 2 2 d 0.gx x f x x x

Suy ra

  



3 3.gg

Vậy

     

1 3 3.gg g 

Chọn C.

Câu 7.

Cho hàm số

 

y fx

có đạo hàm







liên tục

trên





3;3 .

Hình bên là đồ thị của hàm số

 



 .y fx

Đặt

  

  

 

2 1.gx f x x

Gọi

là số thực thỏa mãn

 

d 0.

gx x















Khẳng định nào sau đây đúng?

   

6 1 3.

g mg



  

6 1 6 3.g mg 

   

3 1 3 3.g mg 

   

3 1 3 3.g mg  

Lời giải. Từ giả thiết

 















d 0,

gx x

suy ra

 







2 d.m gx x

Ta có

   



 2 2 2;gx f x x

   



   0 1.gx f x x

Ta thấy đường

yx 

cắt đồ thị hàm số

 

y fx





tại các điểm có hoành độ

3; 1; 3.

Dựa vào bảng biến thiên, suy ra

 



  





 

min 3 ; 1 ; 3 1 .g gg g

Dựa vào đồ thị, ta có





 



  



     

  



1 d 1d

S S x fx x fx x x

   

    

      



  



    

  



 



       





2 1 d 2 1d

1 3 3 1 3 3.

x fx x fx x x

gx x gx x

gg g g g g

Suy ra

 

   

 

   

       











       











3;3

min 1

1 3 , 3; 3 .

max 3

gx g

g gx g x

gx g

Suy ra

     

 

   









      



6 1 d 6 3 3 1 3 3.

m gx x

g gx x g g m g

Chọn C.

Câu 8. Cho hàm số

 

y fx

có đạo hàm







liên tục trên

 

3;3 .

Hình bên là đồ thị của hàm số

 





.y fx

Biết





16f 

và

 

gx f x





. Khẳng định nào sau đây là đúng?

A. Phương trình

 

0gx



không có nghiệm thuộc

 

3;3 .

B. Phương trình

 

gx

có đúng một nghiệm thuộc

 

3;3 .



C. Phương trình

 

0gx

có đúng hai nghiệm thuộc

 

3;3 .

D. Phương trình

 

0gx

có đúng ba nghiệm thuộc

 

3;3 .

Lời giải. Từ giả thiết

 

1 6 1 4.fg   

Ta có

    





 

1;gx f x x

   



 0 1.gx f x x

Ta thấy đường thẳng

1yx

cắt đồ thị hàm số

 

y fx





tại các điểm có hoành độ

3; 1; 3.

Dựa vào đồ thị, ta có

•

       

   







    





1d4 d4 1 34 30.f x x x gx x g g g

•

           

  



         

  



1 d4 d4 3 14 30.x f x x gx x g g g

Từ BBT suy ra phương trình

 

0gx

có đúng một nghiệm thuộc

 

3;3 .

Chọn B.

Câu 9. Cho hàm số

 

y fx



có đạo hàm

 



liên tục trên

 

2;1 .

Hình bên là đồ thị của hàm số









y fx

Đặt

   



gx f x

Điều kiện cần và đủ để phương trình

 

 0gx

có bốn nghiệm phân biệt là

 























 



















 



















 





















1 0.

Lời giải.

Ta có

   



;gx f x x

  





 0.

gx f x x

thấy đường thẳng

yx

cắt đồ thị hàm số

 

y fx





tại các

điểm có hoành độ

2; 0; 1.

Dựa vào đồ thị, ta có

   







 





ddfx xx x fx x

hay



  









ddgx x gx x



       

  



       



0 2 1 0 2 1.g g gg g g

Từ đó ta có bảng biến thiên như hình bên.

Dựa vào bảng biến thiên, suy ra đồ thị hàm số

 

y gx

cắt trục hoành tại

điểm phân biệt

 





















Chọn A.

Câu 10.

Cho hàm số





y fx

có đạo hàm

 



liên tục

trên

.

Hàm số

 



y fx

có đồ thị như hình bên. Tổng giá

trị lớn nhất và giá trị nhỏ nhất của hàm số

 



gx f x

trên

đoạn

 

2;2

bằng

   

1 0.ff

   

4 0.ff

   

1 4.ff

     

1 0 4.fff

Lời giải. Ta có

 





2;g x xf x

 





















Dựa vào đồ thị ta suy ra

 









 





   

















01 .

fx x

• Dựa vào bảng biến thiên suy ra

 

   





2;2

max 1 .gx f

• Dựa vào đồ thị hàm số







ta thấy

       



   



d 0 0 4 00f x x fx f f

   

4 0.ff

Kết hợp với bảng biến thiên ta suy ra

 

   





2;2

min 4 .gx f

Vậy

 

 

 

     



 

2;2

max min 1 4 .gx gx f f

Chọn C.

Phần 4. Diện tích hình phẳng

Câu 1. Cho Parabol như hình vẽ bên. Diện tích hình phẳng giới

hạn bởi Parabol và trục hoành bằng

16.

Lời giải. Dựa vào đồ thị, ta xác đinh được phương trình của

 

 

: 4.Py x

Khi đó diện tích hình phẳng cần tính bằng:





4d .

S xx



  



Chọn D.

Cách 2. Áp dụng công tính nhanh

2 2 32

.4.4

33 3

S Bh

= = =

(với

 4

là chiều dài của

đáy,

 4h

là chiều cao).

Câu 2. Tính diện tích hình phẳng được tô đậm ở hình bên.



S 



9.S



Lời giải. Áp dụng công thức tính nhanh, ta có diện tích miền khép kín giới hạn bởi

Parabol và đường

 4y

là

 

2 2 32

.4.4 .

33 3

AOB

S Bh

Diện tích tam giác

ABC

là



 4.

ABC

Suy ra diện tích phần tô đậm



 

AOB ABC

SS S

Chọn B.

Câu 3. Ông An xây dựng một sân bóng đá mini hình

chữ nhật có chiều rộng

30 m

và chiều dài

50 m.

Để

giảm bớt chi phí cho việc trồng cỏ nhân tạo, ông An

chia sân bóng ra làm hai phần (tô đen và không tô đen)

như hình bên. Phần tô đen gồm hai miền diện tích

bằng nhau và đường cong

AIB

là một Parabol đỉnh

Phần tô đen được trồng cỏ nhân tạo với giá cỏ nhân tạo với giá

130 000

đồng

và

phần còn lại được trồng cỏ nhân tạo với giá

90 000

đồng

/m .

Hỏi ông An phải trả bao

nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?

135

triệu đồng. B.

151

triệu đồng.

165

triệu đồng. D.

195

triệu đồng.

Lời giải. Diện tích hình chữ nhật:



30 50 1500 m .S

Diện tích hai phần tô đen:

  

2 2 .30.10 400 m .

S Bh

Suy ra diện tích phần không tô đen:



2 01

1100 m .S SS

Vậy tổng chi phí:

 

130 000. 90 000. 151000000

T SS

đồng. Chọn B.

Câu 4.

Nhà ông An cần sơn mặt trước của cổng có dạng như

hình bên, các đường cong có dạng là Parabol với các kích

thước được cho như hình. Biết giá thuê nhân công là

100.000

đồng

. Hỏi ông An phải trả cho bên thi công bao nhiêu

tiền để sơn cổng?

2 468650

đồng. B.

1866 667

đồng.

1775361

đồng. D.

1668 653

đồng.

Lời giải. Công thức tính nhanh, ta có diện tích cần sơn:

 

 

2 56

. 8.8 6.6 m .

Vậy số tiền cần phải trả:

100000. 1866667



(đồng). Chọn B.

Câu 5. Một hoa văn trang trí được tạo ra từ một miếng bìa

mỏng hình vuông cạnh

10 cm

bằng cách khoét bỏ đi bốn

phần bằng nhau có hình dạng Parabol (như hình vẽ). Biết

 5 cmAB

 4 cm

. Diện tích bề mặt hoa văn đó bằng

cm .

140

cm .

160

cm .

50 cm .

Lời giải. Diện tích hình vuông:



10 100 cm .S

Diện tích của bốn hình Parabol được khoét bỏ là:

  





 









  

2 2 160

4 4 .5.4 cm .

3 33

S Bh

Suy ra diện tích bề mặt hoa văn là:

  

2 01

160 140

100 cm .

S SS

Chọn B.

Câu 6. Một mảnh vườn toán học có dạng hình chữ nhật,

chiều dài là

16 m

và chiều rộng là

8 m.

Các nhà Toán học

dùng hai đường Parabol, mỗi Parabol có đỉnh là trung

điểm của một cạnh dài và đi qua hai mút của cạnh đối

diện, phần mảnh vườn nằm ở miền trong của cả hai

Parabol (phần tô đậm như hình vẽ) được trồng hoa hồng. Biết chi phí để trồng hoa

hồng là

45000

đồng

/m .

Hỏi các nhà Toán học phải chi bao nhiêu tiền để trồng hoa

trên phần mảnh vườn đó? (Số tiền được làm tròn đến hàng nghìn).

1920 000

đồng. B.

2159 000

đồng. C.

2715000

đồng. D.

3322 000

đồng.

Lời giải. Chọn hệ trục tọa độ

Oxy

và gọi tên các đỉnh

như hình vẽ bên. Dễ dàng xác định được

• Parabol đi qua ba điểm

AI B

là

 

 

: 8.

Py x

• Parabol đi qua ba điểm

,,COD

là

 





Py x

Phương trình hoành độ giao điểm:

8 4 2.

x xx    

Suy ra diện tích trồng hoa là:

 

22 2

1 1 128 2

8 d m.

88 3

S x xx



   



Vậy chi phí trồng hoa là:

128 2

45000. 45000. 2715000

TS 

đồng. Chọn C.

Câu 7. Một công ty quảng cáo muốn làm một bức tranh trang trí hình

MNEIF

ở

chính giữa của một bức tường hình chữ nhật

ABCD

có chiều cao

 6 mBC

, chiều dài

12 mCD

(hình vẽ bên). Cho biết

MNEF

là hình chữ nhật có

 4 m;MN

cung

EIF

có hình dạng là một phần của cung Parabol có đỉnh

là trung điểm của cạnh

và

đi qua hai điểm

Kinh phí làm bức tranh là

900.000

đồng

/m .

Hỏi công ty cần

bao nhiêu tiền để làm bức tranh đó?

20.400.000

đồng. B.

20.600.000

đồng.

20.800.000

đồng. D.

21.200.000

đồng.

Lời giải. Gắn hệ trục tọa độ như hình vẽ bên dưới

Dễ dàng xác định được Parabol đi qua ba điểm

, , , ,

DFIEC

là

 



Hai điểm

, MF

nằm trên đường thẳng

2;x

, NE

nằm trên đường thẳng



Khi đó diện tích hình

MNEIF

là:











 















208

6d m.

MNEIF

Kinh phí làm bức tranh:



208

900000. 20800000

(đồng). Chọn C.

Câu 8.

Một chiếc cổng có hình dạng là một Parabol có khoảng cách

giữa hai chân cổng là

8 m.

AB 

Người ra treo một tâm phông hình

chữ nhật có hai đỉnh

,MN

nằm trên Parabol và hai đỉnh

,PQ

nằm

trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô

đen) người ta mua hoa để trang trí với chi phí cho

cần số tiền

mua hoa là

200.000

đồng, biết



4 m, 6 m.MN MQ

Hỏi số tiền dùng để mua hoa

trang trí chiếc cổng gần với số tiền nào sau đây?

3373 400

đồng. B.

3434 300

đồng. C.

3437 300

đồng. D.

3733300

đồng.

Lời giải. Chọn hệ trục tọa độ

Oxy

như hình vẽ.

Parabol đối xứng qua

nên có dạng

 



P y ax c

Vì

 

đi qua

 

4;0B

và

 

2;6N

nên





 

: 8.

Py x

Diện tích hình phẳng giới hạn bởi

 

và trục

là







 













1 128

2 8d m.

S xx

Diện tích phần trồng hoa là

   

128 56

24 m .

MNPQ

SSS

Do đó số tiền cần dùng để mua hoa là



200000 3733300

đồng. Chọn D.

Câu 9. Cho

là hình phẳng giới hạn bởi đồ thị

 

:4Cy xx

và

trục hoành (hình vẽ bên). Đường thẳng

ym

chia

thành hai

phần có diện tích bằng nhau. Biết

ma b



với

,ab

là các số hữu

tỉ, tính

..S ab

64.S 

32.S 

32.S 

64.S 

Lời giải. Diện tích hình phẳng

là

 

2 2 32

.4.4 .

33 2

S Bh

Phương trình hoành độ giao điểm:

 



 



   



 





4 ; 0;4 .

xx m m

Suy ra

   

 24;, 24;;A mm B mm

 

là trung

điểm

;AB

 

2;4I

là đỉnh của

 

Khi đó diện tích miền

khép kín giới hạn bởi Parabol và đường

ym

(phần gạch

sọc) là

 



   

. .2 4 . 4 .

33 3

S AB IM m m

Theo giả thiết, ta có

 









       











1 16

4 16 .

2 33

SS m

Chọn D.

Câu 10.

Cho

là hình phẳng giới hạn bởi đồ thị

 

của hàm

số

y xx

và trục hoành. Hai đường thẳng

ym

và



chia hình

thành ba phần có diện tích bằng nhau. Tính

  



9 9.Pm n 

 403.P

 405.P

407.P 

 409.P

Lời giải. Như bài trên, ta được





















9 33

405.

9 3 12

Chọn B.

Câu 11.

Cho hình phẳng

(phần tô đậm) được giới hạn bởi

các đường



4,yx

yx

và

 2

có diện tích là



S ab

với

 , .ab

Khẳng định nào sau đây đúng?

1.ab

2 3.ab



4 5.ab



và

1.

Lời giải. Dựa vào hình vẽ, ta có

 



     



24 d 2 d2 .

S x x xx

Suy ra

 

2, .

Chọn C.

Câu 12. Cho đường tròn tâm

đường kính



8.AB

Trên

lấy hai điểm

đối xứng nhau qua

sao cho

 4.MN

Qua

kẻ hai dây cung

và

cùng vuông góc với

.AB

Diện tích phần giới hạn bởi đường tròn và hai dây cung

,PQ

(phần tô đậm như hình vẽ) bằng

 5 5.

 6 8 3.

 12 7.

 

8 3.

Lời giải. Chọn hệ trục tọa độ như hình vẽ

Dễ dàng xác định phương trình đường tròn là



16.

Suy ra cung

có phương trình



16 .

Diện tích hình phẳng cần tính





   



2 16 d 8 3.

S xx

Chọn D.

Câu 13.

Biết rằng đường Parabol





:2Py x



chia đường

tròn

 

:8Cx y

thành hai phần lần lượt có diện tích là

(hình bên). Khi đó

SS a

 

với

, ,

abc

nguyên

dương và

là phân số tối giản. Tổng

abc

bằng

13.

14.

15.

16.

Lời giải.

Diện tích hình tròn

S 

Phương trình hoành độ giao điểm của

 

và





là













 











Suy ra













   

















2 22

2. 2 d 8 d 2 .

S xx x x

Suy ra

  

S SS

SS b









       











. Chọn C.

Câu 14.

Một khuôn viên dạng nửa hình tròn có đường

kính bằng

4 5 m.

Trên đó người thiết kế hai phần để

trồng hoa có dạng của một cánh hoa hình Parabol có

đỉnh trùng với tâm nửa hình tròn và hai đầu mút của

cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng

4 m,

phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết

các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là

100 000

đồng

/m .

Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn

đến hàng nghìn).

1194 000

đồng. B.

1948 000

đồng. C.

2388 000

đồng. D.

3895000

đồng.

Lời giải. Hình tròn có diện tích

 



2 5 20 .S

Chọn hệ trục tọa độ

Oxy

như hình vẽ.

Khi đó phương trình nửa đường tròn là:



20yx

Parabol có đỉnh là gốc

và đi qua điểm

 

2;4

nên có phương trình

 



:.Pyx

Khi đó diện tích phần tô đậm:

 



 





22 2

11,94 m20 .S x x dx

Diện tích phần trồng cỏ Nhật Bản (phần không tô màu):

19, 47592654.

SS= −≈

Vậy số tiền cần dùng:

100 000 1948 000TS=×≈

(đồng). Chọn B.

Câu 15.

Một viên gạch hoa hình vuông cạnh

40 cm.

Người

thiết kế đã sử dụng bốn đường Parabol có chung đỉnh tại tâm

của viên gạch để tạo ra bốn cánh hoa (được tô màu như hình

bên). Diện tích mỗi cánh hoa của viên gạch bằng

250 cm .

400

cm .

800

cm .

1600

cm .

Lời giải.

Gắn hệ trục tọa độ như hình bên (ta chuyển về

đơn vị tính là

)

Xét cánh hoa ở góc phần tư thứ nhất. Đường cong trên ứng

với

 2,yx

đường cong dưới ứng với



Khi đó diện tích cần tính

   









  















4 400

2 d dm cm .

23 3

S xx

Chọn B.

Câu 16. Gọi

là diện tích của hình phẳng giới hạn bởi Elip



và

là

diện tích của hình thoi có các đỉnh là đỉnh của Elip đó. Tỉ số

bằng

.



2

Lời giải.

Từ phương trình Elip



suy ra đường Elip nằm trong góc phần tư thứ nhất

có phương trình



Suy ra diện tích Elip

  



4 1 d 3.

Diện tích hình thoi có các đỉnh là đỉnh của elip:



.6.2 6.

Khi đó





. Chọn B.

Chú ý: Ta có công thức nhanh:

 



có diện tích

 .

S ab

Câu 17. Một sân chơi cho trẻ em hình chữ nhật có

chiều dài

100 m

và chiều rộng là

60 m

người ta

làm một con đường nằm trong sân (như hình vẽ).

Biết rằng viền ngoài và viền trong của con đường là

hai đường elip, Elip của đường viền ngoài có trục

lớn và trục bé lần lượt song song với các cạnh hình

chữ nhật và chiều rộng của mặt đường là

2 m.

Kinh

phí cho mỗi

làm đường

600 000

đồng. Tính tổng số tiền làm con đường đó. (Số tiền

được làm tròn đến hàng nghìn).

293804 000

đồng. B.

293904 000

đồng.

294 053000

đồng. D.

294153000

đồng.

Lời giải. Diện tích Elip lớn là:



50.30 1500 m .S

Diện tích Elip lớn là:



48.28 1344 m .S

Suy ra diện tích cần trang trí là:

 

3 12

1500 1344 156 m .S SS

Vậy chi phí cần:



  

600 000 156 600 000 294 053 000S

đồng. Chọn C.

Câu 18.

Một mảnh vườn hình chữ nhật có chiều dài

10 m

và chiều rộng

6 m,

được phân chia thành các phần

bởi một đường chéo và một đường Elip nội tiếp bên trong

như hình vẽ bên. Hãy tính diện tích phần tô đậm (theo

đơn vị

 

5 2. 

 

54 .

 

45 4



 

45 4



Lời giải. Chọn hệ trục tọa độ và gọi các điểm như hình.

Phương trình Elip là:

25 9



Suy ra

• đường Elip nằm trên trục

là:

 





3 25

• đường Elip nằm dưới trục

là:

 

3 25





Phương trình đường thẳng

OD y 

Phường trình đường thẳng

: 3.AB y 

Tọa độ giao điểm của

 

và

là:

5232





















Do đó diện tích phần tô đậm là:

 



  













    













  



45 4

3 3 25 3 25

d 3d .

55 5 8

xx x

S xx

Chọn D.

Câu 19. Một biển quảng cáo có dạng hình Elip với bốn đỉnh

1212

, ,,AABB

như hình vẽ bên. Biết chi phí sơn phần tô đậm

là

200 000

đồng

và phần còn lại là

100 000

đồng

/m .

Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào

dưới đây, biết

12 12

8 m, 6 mAA BB

và tứ giác

MNPQ

là

hình chữ nhật có

 3m

5.526.000

đồng. B.

5.782.000

đồng.

7 213000

đồng. D.

7322 000

đồng.

Lời giải. Chọn hệ trục tọa độ và gọi các điểm như hình.

Diện tích Elip:



.4.3 12 m .S

Phương trình Elip là:

 

: 1.

16 9

E 

Suy ra đường

Elip nằm trên trục

là:



16 .

Từ giả thiết

 3mMQ

suy ra

,MN

nằm trên đường thẳng

dy

2 3; .







 











Diện tích phần tô màu:









   













4 16 d 8 6 3 m .

S xx

Suy ra diện tích phần không tô màu:

  

4 6 3m.S SS

Vậy số tiền cần chi phí

   

    200000 8 6 3 100000 4 6 3 7 322 000T

đồng. Chọn D.

Câu 20. Nhà trường dự định làm một vườn hoa

dạng hình Elip được chia ra làm bốn phần bởi hai

đường Parabol có chung đỉnh, đối xứng với nhau

qua trục của Elip như hình vẽ bên. Biết độ dài trục

lớn, trục nhỏ của Elip lần lượt là

và

4 m; ,FF

là hai tiêu điểm của Elip. Phần

,AB

dùng để trồng hoa; phần

,CD

dùng để trồng cỏ.

Kinh phí để trồng mỗi mét vuông trồng hoa và trồng cỏ lần lượt là

250 000

đồng và

150 000

đồng. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).

4 656 000

đồng. B.

4766 000

đồng.

5455000

đồng. D.

5676 000

đồng.

Lời giải. Diện tích Elip:



.4.2 8 m .

Chọn hệ trục tọa độ và gọi các điểm như hình.

Phương trình Elip là:

 



: 1.

16 4

Suy ra đường

Elip nằm trên trục

là:





Giao điểm của đường thẳng

: 23dx

đi qua tiêu điểm

và nửa Elip nằm bên trên

trục

là

 

2 3;1M

 

2 3;1 .N  

Parabol đi qua các điểm

 





 

2 3;1 , 0;0 , 2 3;1M ON

có phương trình





Py

Khi đó diện tích

















 

















16 8 2 3

2 12 3

Vậy số tiền cần chi phí:

 

    2 250000 2 150000 5676 000

T S SS

đồng. Chọn D.

Câu 21.

Cho hình phẳng giới hạn bởi các

đường

 sin ,

 cosyx

và

là

diện tích của các phần được gạch chéo như

hình vẽ. Tổng



bằng



10 2 2.

10 2 2.

11 12 2.

11 2 2.

Lời giải. Ta có:

 



  cos 0 , .

x x kk

 











     











sin cos sin 0 , .

x x x x kk

Dựa vào hình vẽ ta có

 





  



cos sin d 1 2;S x xx

 



 



sin cos d 2 2.S x xx

Suy ra

   

    

1 2 22 11 22SS

. Chọn D.

Câu 22. Kí hiệu

là hình phẳng giới hạn bởi các đường

 ,

 0,y

0x 

và

1.x

Đường thẳng

 

01xk k 

chia

thành hai phần có diện tích tương ứng

, SS

như hình vẽ bên,

biết



.SS

Mệnh đề nào sau đây là đúng?

















Lời giải. Ta có

x xk

S ex e e  



và

  



xx k

S ex e ee

Theo giả thiết

k kk

S S e ee e



    

Chọn B.

Câu 23. Cho hình phẳng

giới hạn bởi các đường

,yx

0,y 

0,x 

4.x



Đường thẳng

yk

 

0 16k

chia hình

thành hai phần có diện tích

, SS

(hình vẽ). Tìm

để



.SS

3k 

. B.



5.k 

8k 

Lời giải. Phương trình hoành độ giao điểm:



    

20x

xk x k

. Ta có:

●

S S xx  



●

 

2 64

d 4.

3 33

x kk

S x k x kx k









      















Theo giả thiết

 

1 2 1 12

1 2 64 32

2 3 33

S S S SS k         

 

2 12 32 0 2 12 32 0 2 4.

tk t

kk k t t t k

 

           

Chọn B.

Câu 24. Xét hình phẳng

giới hạn bởi đồ thị hàm số

 



trục hoành và đường thẳng

0.x 

Gọi





0;9 ,A

 

;0Bb

 

 3 0.b

Tìm giá trị của tham số

để đoạn thẳng

chia

thành hai phần có diện tích bằng nhau.

2b 

. B.

b 

. C.

1.b 

b 

Lời giải. Phương trình hoành độ giao điểm:

 

3 0 3.xx   

Do đó

 



 



CASIO

3 d 9.S xx

Diện tích tam giác

OAB

bằng:



OAB

S OA OB b

Ycbt

 







     

1 99

2 22

OAB

SS b b

Chọn C.

Câu 25. Trong mặt phẳng tọa độ, cho hình chữ nhật

có một cạnh nằm trên trục hoành và có hai đỉnh trên một

đường chéo là

 

1; 0A

và

 

;Ca a

với

 0.a

Biết rằng

đồ thị hàm số

yx

chia hình

thành hai phần có

diện tích bằng nhau, tìm



 3.a

 4.a

 9.a

Lời giải. Từ hình vẽ ta suy ra

 

;0 .Ba

Hình chữ nhật

ACBD

có

1AB a

và

AD a

nên có diện tích

 

1.S aa

Diện tích miền gạch sọc:







S xx

Theo giả thiết, ta có

 







      

23 2

S aa

Chọn B.

Phần 5. Thể tích khối tròn xoay

Câu 1. Cho hình phẳng

giới hạn bởi các đồ thị hàm

số

4yx



và



2.yx

Tính thể tích

của khối

tròn xoay tạo thành khi quay

quanh trục hoành.

10 .V



12 .V 

14 .V 



16 .V 



Lời giải. Phương trình hoành độ giao điểm:

42 1x xx    

Thể tích cần tính

   

CASIO

22 2

4 2 d 12 12 d 16 .V x x x xx

 



     



Chọn D.

Câu 2.

Thể tích

của khối tròn xoay khi cho hình

phẳng

giới hạn bởi các đường

1yx

và

1yx

quay quanh trục

được xác định bởi công thức nào sau

đây?

   

1 1 d.V xx x



  



   

1 1d.V xx x



 



 

1 d.V xx







   

1 1 d.V x xx





  







Lời giải. Phương trình hoành độ giao điểm:

1 1 1.xx x    

Vì đồ thị hàm số

1yx

đối xứng với đồ thị hàm số

1yx

qua trục hoành nên

thể tích khối tròn xoay cần tính bằng thể tích khối tròn xoay khi cho hình phẳng giới

hạn bởi các đường

1 , 0, 1, 1y xy x x

    

quay quanh trục

.Ox

Vậy công thức tính thể tích là

 









1 d.V xx

Chọn C.

Câu 3. Cho hình vuông

OABC

có cạnh bằng

được chia

thành hai phần bởi đường cong

 

có phương trình



Gọi

là hình phẳng không bị gạch (như hình vẽ).

Tính thể tích

của vật thể tròn xoay khi cho phần

qua

quanh trục

.Ox









128





128





256

Lời giải. Thể tích vật thể khi quay hình vuông

OABC

quanh trục

là



.4 .4 64 .

Thể tích vật thể khi quay phần gạch sọc quanh

là























1 64

. d.

Vậy thể tích vật thể tròn xoay cần tính bằng



 

64 256

64 .

Chọn D.

Câu 4. Cho hình phẳng

giới hạn bởi

đường tròn có

bán kính

2,R



đường cong

4yx



và trục hoành

(miên tô đậm như hình vẽ). Tính thể tích

của khối tạo

thành khi cho hình

quay quanh trục

.Ox

















Lời giải. Phương trình hoành độ giao điểm:

4 0 4.xx

 Thể tích vật thể khi quay phần

quanh trục hoành là nửa khối cầu bán kính



nên có thể tích bằng





1 4 2 16

.2 .

23 3 3

 Thể tích vật thể khi quay phần

quanh trục hoành là

 





4 d 8.xx

Vậy thể tích cần tính





16 40

Chọn A.

Câu 5. Cho hình phẳng

giới hạn bởi các đường

2, 2, 1.y x yx x    

Tính thể tích

của vật thể

tròn xoay khi quay hình phẳng

quanh trục

.Ox

 9.V













Lời giải. Sai lầm hay gặp là chúng ta sử dụng công thức

 

2 2d .

V x xx







    







Lấy đối xứng phần đồ thị hàm số

2yx 

qua trục hoành ta được đồ thị hàm số



(tham khảo hình vẽ). Khi đó thể tích cần tính bằng tổng của miền tô đậm

và miền gạch sọc quay quanh trục

.Ox

Thể tích vật thể khi quay miền

• Gạch sọc quanh

là

 









2 d 9.V xx

• Tô đậm quanh

là

 





   



2 2d .

V x xx

Vậy thể tích cần tính

VVV



  

Chọn D.

Câu 6. Gọi

là thể tích khối tròn xoay tạo

thành khi quay hình phẳng giới hạn bởi các

đường



,yx

0y 

và

x 

quanh trục

Đường thẳng

 

04xa a 

cắt đồ thị hàm số

yx

tại

(hình vẽ bên). Gọi

là thể tích

khối tròn xoay tạo thành khi quay tam giác

OMH

quanh trục

. Biết rằng

2VV

. Khi đó

2a 

. B.

a 

. C.

22a 

. D.

3a 

Lời giải. Phương trình hoành độ giao điểm:

0 0.xx

 Thể tích

d 8.V xx



 Tính

Gọi

 

;.Ma a

Khi quay tam giác

OMH

quanh trục

tạo thành hai

hình nón có chung đáy:

ð Hình nón

 

có đỉnh là

chiều cao

 ,OK a

bán kính đáy

R MK a

nên có thể tích bằng

 

. ..

33 3

R OK a a





ð Hình nón

 

có đỉnh là

chiều cao

4,

HK a

bán kính đáy

R MK a



nên có thể tích bằng

 

11 4

.4 .

33 3

R HK a a





 

Suy ra

33 3

a aa a

  

 

Theo giả thiết



2VV

nên suy ra



Chọn D.

Câu 7. Gọi

là thể tích khối tròn xoay tạo thành khi

quay hình phẳng giới hạn bởi các đường

 sin ,yx

hai

trục tọa độ và



quanh trục hoành. Đường thẳng

xk

 



0 k

cắt đồ thị hàm số

 sinyx

tại điểm

và trục hoành tại điểm

(hình vẽ bên).

Gọi

là thể tích khối tròn xoay tạo thành khi quay tam giác

OMN

quanh trục

.Ox

Biết rằng



.VV

Khi đó



 .



 .



 3.

Lời giải. Ta có



   



sin d cos 2 .V xx x

Khi quay tam giác

OMN

quanh trục

tạo thành hình nón có đỉnh là

chiều cao

 ,ON k

bán kính đáy

sinR MN k

nên có thể tích bằng



 

1 .sin

R ON

Theo giả thiết



nên suy ra



   

sin

(vì

0

). Chọn A.

Câu 8.

Có một vật thể là hình tròn xoay có dạng giống như một

cái ly như hình vẽ bên. Người ta đo được đường kính của miệng

ly là

4 cm

và chiều cao là

6 cm.

Biết rằng thiết diện của chiếc

ly cắt bởi mặt phẳng đối xứng là một Parabol. Thể tích của vật

thể đã cho bằng

 



12 cm .





12 cm .

 



cm .

 

cm .

Lời giải.

Xét phần mặt cắt và chọn hệ trục

Ixy

như hình vẽ.

(trong đó

là gốc tọa độ).

Khi đó Parabol

 

đi qua các điểm

   

2;6 , 2;6AB

và

 

0;0I

nên Parabol

 

có phương trình:

yx x   

Khi đó thể tích của vật thể đã cho là:

 

d d 12 cm .

V x y yy 







 













Chọn A.

Câu 9. Trong mặt phẳng cho đường Elip

 

có độ dài trục

lớn là

8AA





và độ dài trục nhỏ





đường tròn tâm

đường kính



như hình vẽ. Tính thể tích

của khối

tròn xoay có được bằng cách cho miền hình phẳng giới hạn

bởi đường Elip và đường tròn (được tô đậm trên hình vẽ)

quay xung quanh trục



12 .

V 



16 .V 



 28 .V

36 .V 

Lời giải. Elip

 

có

4, 3.ab

Suy ra

 



: 1.

16 9

Thể tích khối elip

 

quay quanh trục



là:













 















. 9. 1 d 48 .

Thể tích khối cầu là:

 

.3 36 .

Vậy thể tích cần tính





12 .VVV

Chọn A.

Câu 10.

Một thùng chứa rượu làm bằng gỗ là một hình tròn

xoay như hình bên có hai đáy là hai hình tròn bằng nhau,

khoảng cách giữa hai đáy bằng

8 dm.

Đường cong mặt bên của

thùng là một phần của đường Elip có độ dài trục lớn bằng

10 dm

, độ dài trục bé bằng

6 dm.

Hỏi chiếc thùng gỗ đó đựng

được bao nhiêu lít rượu?

1316

(lít). B.

1416

(lít). C.

1516

(lít). D.

1616

(lít).

Lời giải. Elip có



5, 3.ab

Suy ra

 



: 1.

25 9

Chọn hệ trục tọa độ đi qua hai trục của thùng rượu

như hình vẽ.

Vì thùng rượu có tính đối xứng nên thể tích thùng rượu

gấp hai lần thể tích khối tròn xoay khi quay hình

quanh trục

.Ox

Thể tích cần tính:





 



225 9 1416

2 d.

25 25

Chọn B.

Câu 11. Bên trong hình vuông cạnh

dựng hình sao

bốn cánh đều như hình vẽ bên (các kích thước cần thiết

cho như ở trong hình). Tính thể tích

của khối tròn

xoay sinh ra khi quay hình sao đó quanh trục

.Ox

















Lời giải. Xét hình nằm ở góc phần tư thứ nhất.

Gọi

là thể tích khối tròn xoay cần tính.

Gọi

là thể tích khối tròn xoay khi quay hình phẳng được tô

màu trong hình bên (chỉ xét ở góc phần tư thứ nhất) quanh

trục hoành. Khi đó

2.VV

Ta có

d 2d .

2 4 2 96

xa a a

V x xx





  





 









  



Suy ra thể tích cần tính





Chọn C.

Câu 12.

Cho hình phẳng

gồm nửa hình tròn đường kính

và tam giác

ABC

đều (như hình vẽ). Gọi



là đường thẳng qua

và song song với

.AB

Biết

 2 3 cm.AB

Thể tích khối tròn

xoay tạo bởi hình

quay quanh trục



bằng

 



8 3 9 cm .

 



 

8 3 cm .

 



32 3 18 cm .







16 3 9 cm .

Lời giải. Chọn

 ,CO



như hình vẽ.

Khi đó

 

 3;3A

 

3;3 .B

Suy ra

 : 3 , : 3 .

AC y x BC y x

Phương trình đường tròn đường kính

là

 

 

3 3.xy

Suy ra phần phía trên của nửa đường tròn có phương trình

 

33 .yx

Thể tích khi quay phần tô đậm quanh trục hoành là

 

    



3 3 3 d 83 .

x xx

Suy ra thể tích cần tính









 











2 83 .

Chọn D.

Câu 13.

Cho hình vẽ bên, biết cung tròn

nằm trên đường tròn

bán kính

4.R 

Cạnh

4.AB BC CD DA

Thể tích vật tròn

xoay tạo thành khi quay hình bên quanh trục

nằm trong

khoản nào sau đây?

 

165;170 .

 

160;165 .

 

155;160 .

 

150;155 .

Lời giải. Chọn hệ trục tọa độ như hình vẽ bên.

Gọi

là tâm đường tròn

 

chứa cung

.BC

Khi đó

nằm

trên đường thẳng

2.x 

Gọi

là trung điểm của

Ta có

OBC

là tam giác đều, nên

2 3.

OH 

Do đó

cách

là một khoảng

4 23

 

2;4 2 3 .O  

Phương trình đường tròn



  

 

: 2 4 2 3 16 4 2 3 16 2 .Cx y y x           

Dựa vào đồ thị ta thấy cung

nằm bên dưới đường thẳng

4 2 3,y 

nên đường

cong chứa cung

có phương trình

 

   

4 2 3 16 2 .

Khi đó thể tích vật tròn xoay:

 

4 2 3 16 2 d 166,6.

V xx    



Chọn A.

Câu 14.

Cho hình tròn tâm

có bán kính

2R 

và hình vuông

OABC

có cạnh bằng

(như hình vẽ bên). Tính thể tích

của vật

thể tròn xoay khi quay mô hình bên xung quanh trục là đường

thẳng

.OB

 

83 4 2





 

82 5 2





 

83 5 2





 

32 1 2





Lời giải.

Chọn hệ trục tọa độ

Oxy

có gốc tọa độ trùng

tia

có giá là

và tia

song song

(như hình vẽ).

Khi đó đường tròn

 

có phương trình

4xy

và đường

thẳng

có phương trình

.yx

Phương trình hoành độ giao điểm của đường thẳng

và

đường tròn

 

là:

4 2.x xx 

Thể tích vật thể tròn xoay khi quay phần tô đen quanh

là:

 

   

16 10 2 16 8 2

.4 .

33 3

V x dx x









    



Thể tích khối tròn xoay khi quay

 

quanh

là khối cầu có

4 32

.2 .

V 

Thể tích khối tròn xoay khi quay

OABC

quanh

là (tổng của hai khối nón)

 







 





1 32 2

2 .22 .22 .

Vậy thể tích cần tính

 

2 31

8 2 52

16 40 2

VVVV





 

Chọn B.

Câu 15. Cho hình vuông có độ dài cạnh bằng

8cm

và một hình

tròn có bán kính

5cm

được xếp chồng lên nhau sao cho tâm

của hình tròn trùng với tâm của hình vuông như hình vẽ bên.

Tính thể tích

của vật thể tròn xoay tạo thành khi quay mô

hình trên quanh trục

260

cm .





290

cm .





520

cm .





580

cm .





Lời giải. Chọn hệ trục tọa độ như hình vẽ.

● Thể tích khối cầu

4 4 500

33 3





 

● Gọi

là thể tích khối tròn xoay khi quay hình

phẳng

(phần tô màu) được giới hạn bởi đường

thẳng

4y 

, đường tròn

yx

và

x 

quanh trục hoành

 

4 25 d .

V xx



     



Vậy thể tích cần tính

520

2 cm .

VV V



 

Chọn C.

Câu 16.

Cho hai tam giác cân có chung đường cao

40cmXY 

và cạnh đáy lần lượt là

40cm

và

60cm

, được

xếp chồng lên nhau sao cho đỉnh của tam giác này là trung

điểm cạnh đáy của tam giác kia như hình vẽ bên. Tính thể

tích

của vật thể tròn xoay được tạo thành khi quay mô

hình trên quanh trục

40480

cm .





52000

cm .





46240

cm .





1920 cm .V 



Lời giải. Chọn hệ trục tọa độ như hình vẽ, khi đó:

       

0;0 , 40;0 , 0;20 , 40;30YO X A M

Phương trình đường

:3 4 0 .

YM x y y 

Phương trình

: 2 40 0 .

AX x y y



  

Phương trình hoành độ giao điểm của hai đường

và

là:

3 40

16.



 

Thể tích vật thể được tạo ra bằng cách quay hình phẳng (phần tô đậm như hình).

Thể tích vật thể cần tính

16 40

0 16

40 3 46240

d d cm .

2 43

V xx





  







 









  



Chọn C.

Câu 17. Cho khối cầu có bán kính

. Một mặt phẳng cắt

khối cầu thành hai nửa. Nửa bé có khoảng cách từ đỉnh đến

đáy bằng

(tham khảo hình vẽ bên). Tính thể tích nửa bé.





















V hR





















V hR





















V hR





















V hR

Lời giải.

Xét phần mặt cắt và gắn tọa độ như hình vẽ

Khi đó

 

0;0 ,O

 

;0AR

và

 

;0IR h

là tâm của đường

tròn thiết diện. Thể tích chỏm cầu bị cắt chính là vật thể

tròn xoay tạo bởi phần đường tròn

y Rx

quay

xung quanh trục

từ

Rh

đến

. Do đó

 











  













22 2

V R x x hR

Chọn B.

Câu 18. Cho hai mặt cầu

 

có cùng bán kính

thỏa mãn tính chất: tâm của

 

thuộc

 

và ngược lại.

Tính thể tích phần chung

của hai khối cầu tạo bởi

 

và

 



.VR













Lời giải. Thể tích cần tính là tổng của hai chỏm cầu bằng nhau.

Áp dụng công thức bài trước, thể tích mỗi chỏm cầu bằng























3 24

Vậy thể tích phần chung

của hai khối cầu là



 

24 12

Chọn D.

Câu 19. Cho hai đường tròn

 

;5O

và





;3O

cắt nhau tại

hai điểm

và

sao cho

là một đường kính của

đường tròn

 

Gọi

là diện tích hình phẳng giới hạn

bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch

chéo như hình vẽ). Quay hình

quanh trục

,OO

được một khối tròn xoay. Thể tích của khối tròn xoay được

tạo thành bằng









68

36 .

Lời giải. Xét phần mặt cắt như hình vẽ. Ta thấy thể tích cần

tính bằng thể tích

trừ đi thể tích

trong đó

•

là thể tích nửa khối cầu

 

nên









 











.3 18 .

•

là thể tích của chỏm cầu (khi quay miền gạch sọc quanh

trục

). Áp dụng công thức bài trước, ta được













   











h OM

V hR V

Vậy thể tích vật thể cần tính:



VVV

Chọn B.

Câu 20.

Ta vẽ hai nửa đường tròn như hình vẽ bên,

trong đó đường kính của nửa đường tròn lớn gấp đôi

đường kính của nửa đường tròn nhỏ. Biết rằng nửa

hình tròn đường kính

có diện tích là

8

và



30 .BAC

Thể tích của vật thể tròn xoay được tạo

thành khi quay hình

(phần tô đậm) xung quanh

đường thẳng

bằng



220



224

Lời giải.

Ta có:



2.8 R

suy ra

 4

và

 2.r

Vì

IHC

vuông tại



60

CIH

nên ta có





 



   











sin 60 4. 2 3

16 12 2.

CH IC

IH IC CH

AL AH

Cách 1. (Dùng công thức thuần túy)

• Thể tích khối nón đỉnh

bán kính đáy

là:



. 24 .

V HC AH

• Thể tích chỏm cầu (hình cầu lớn) có

2

h HB

là:









 











V HB R

• Thể tích khối nón đỉnh

bán kính đáy

là:



. 3.

V LD AL

• Thể tích chỏm cầu (hình cầu nhỏ) có

1h LI

là:









 











V LI r

Suy ra thể tích cần tìm

   



12 34

V VV VV

Chọn B.

Cách 2. (Dùng tích phân) Dễ dàng viết được phương trình

:

AC y

và hai phương

trình đường tròn là

 

 

16 4yx

và

 

 

4 2.yx

Thể tích cần tìm



  





  



     

  



  





 

64 8

33 6

.d42d164d .

V x xx xx

Phần 6. Bài toán vận tốc

Giả sử

 

là vận tốc của vật

tại thời điểm

và

 

là quãng đường vật đi được

sau khoảng thời gian

tính từ lúc bắt đầu chuyển động. Ta có mối liên hệ giữa





và

 

như sau:

● Đạo hàm của quãng đường là vận tốc:

   

.s t vt





● Nguyên hàm của vận tốc là quãng đường

   

d.st vt t



 

từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian

 

 ;

t ab

là

  

  

vt t sb sa





Nếu gọi

 

là gia tốc của vật

thì ta có mối liên hệ giữa

 

và

 

như sau:

● Đạo hàm của vận tốc là gia tốc:

   

v t at





● Nguyên hàm của gia tốc là vận tốc:

   

d.vt at t



Câu 1. (ĐỀ MINH HỌA 2016 – 2017) Một ô tô đang chạy với vận tốc

10m/s

thì

người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

 5 10 m/s ,vt t

trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu

đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

0, 2m.

2m.

10m.

20m.

Lời giải. Lúc dừng hẳn thì

 

0 5 10 0 2.vt t t       

Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô đi được quãng đường là

 

5 10 d 10 10m.

s t t tt







     













Chọn C.

Câu 2. Một ô tô đang đi với vận tốc lớn hơn

72km/h,

phía trước là đoạn đường chỉ cho

phép chạy với tốc độ tối đa là

72km/h,

vì thế người lái xe đạp phanh để ô tô chuyển

động chậm dần đều với vận tốc

   

30 2 m/s ,vt t



trong đó

là khoảng thời gian

tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt

tốc độ

72km/h,

ô tô đã di chuyển quãng đường là bao nhiêu mét?

100m.

125m.

150m.

175m.

Lời giải. Ta có

72km/h 20m/s

Từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ

72km/h,

ta có phương trình

30 2 20 5.tt  

Vậy từ lúc đạp phanh đến khi ô tô đạt tốc độ

72km/h,

ô tô đi được quãng đường là

 

30 2 d 125m.s tt



Chọn B.

Câu 3. Hai viên đạn cùng rời khỏi nòng súng thời điểm

 0t

với những vận tốc khác

nhau: viên đạn thứ nhất có vận tốc

   



3 1 m/s ,vt t

viên đạn thứ hai có vận tốc

   



2 4 m/s .vt t

Hỏi từ giây thứ mấy thì viên đạn thứ nhất xa điểm xuất phát hơn

viên đạn thứ hai?

A. Giây thứ nhất. B. Giây thứ hai.

C. Giây thứ ba. D. Giây thứ tư.

Lời giải. Quảng đường

 



        



1 11

3 1 d 0.

st t t t t C C

Do đó

 



.st t t



  

 



        



2 22

2 4 d 4 0.

st t t t t C C

Do đó

 



4.st t t

Xét

 





  

3 2 32 0

1 13

4 3 0 2,3.

st st t t t t t t t t

Ta có

 

 

3 30 3 21

 

từ giây thứ ba trở đi thì viên đạn thứ nhất xa điểm

xuất phát hơn viên đạn thứ hai. Chọn C.

Câu 4. Một ô tô đang chạy với vận tốc

 

10 m/s

thì người lái xe đạp phanh. Từ thời

điểm đó, ô tô chuyển động chậm dần đều với vận tốc



  

 2 10 m/s ,

vt t

trong đó

là khoảng thời gian được tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quảng

đường ô tô di chuyển được trong

giây cuối cùng.

16m.

25m.

50m.

55m.

Lời giải. Ta có phương trình:

   2 10 0 5.tt

Suy ra thời gian tính từ lúc bắt đầu đạp phanh đến khi dừng là

giây. Vậy trong

giây cuối cùng thì có

giây ô tô chuyển động với vận tốc

10m/s

và

giây chuyển

động chậm dần đều với vận tốc

   

 2 10 m/s .vt t

Suy ra quảng đường ô tô di

chuyển là





     



3.10 2 10 d 30 25 55 m.s tt

Chọn D.

Câu 5. Một vật đang chuyển động với vận tốc

6m/s

thì tăng tốc với gia tốc

 





m/s ,

trong đó

là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng

tốc. Hỏi vận tốc của vật sau

giây gần nhất với kết quả nào sau đây?

11m/s

. B.

12 m/s

. C.

13m/s

. D.

14 m/s

Lời giải. Ta có

 

d 3 ln 1 .

vt t t C

  





Tại thời điểm lúc bắt đầu tăng tốc

0t 

thì

6m/sv 

nên ta có

3 ln1 6 6.CC 

Suy ra

 

3 ln 1 6 m/s .vt t 

Tại thời điểm

 

10 10 3ln11 6 13m/s.ts v     

Chọn C.

Câu 6. Một vật đang chuyển động với vận tốc

10m/s

thì tăng tốc với gia tốc

 



3 m/s ,

at t t

trong đó

là khoảng thời gian tính bằng giây kể từ lúc bắt đầu

tăng tốc. Hỏi quãng đường vật đi được trong khoảng thời gian

giây kể từ lúc bắt

đầu tăng tốc bằng bao nhiêu mét?

1900

2200

4000

4300

Lời giải. Ta có

 

3d .

vt t t t C   



Tại thời điểm lúc bắt đầu tăng tốc

0t 

thì

10m/sv 

nên suy ra

10.C 

Suy ra

   

10 m/s .

 

Vậy quãng đường vật đi được trong khoảng thời gian

giây kể từ lúc bắt đầu tăng

tốc bằng

  







     











  



23 34

3 4300

10 10 m.

2 3 2 12 3

tt tt

s dt t

Chọn D.

Câu 7. Một ô tô đang chạy thẳng đều với vận tốc

 

m/sv

thì người đạp phanh, từ

thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

5 m/s ,vt t v 

trong

đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp

phanh đến lúc dừng hẳn ô tô di chuyển được

40m

thì vận tốc ban đầu

bằng bao

nhiêu?

20m/s.

v 

25m/s.

v 

40m/s.

v 

80m/s.

v 

Lời giải. Lúc dừng hẳn thì





05 0 .

vt t v t

       

Theo giả thiết, ta có:

 

22 2

00 0

40m= 5 d

2 10 5 10

vv v

t v t t vt







       













     

40m 20m/s.

Chọn A.

Câu 8. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao

162m

với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng,

khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật

   

10 m/svt t t

, trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu

chuyển động. Hỏi lúc vừa tiếp đất, vận tốc

của khí cầu bằng bao nhiêu?

3m/s.v 

5m/s.v 

7m/s.

v 

9m/s.v 

Lời giải. Do

 

10 0 10.vt t t t     

Giả sử chiếc khí cầu chạm đất kể từ lúc bắt đầu chuyển động là

giây

 

0 10t

Theo đề bài ta có phương trình

 

22 2

162 10 d 5 5

tt t t t









    



















0 10

5 162 0 9 9 9m/s.

t tv



            

Chọn D.

Câu 9. (ĐỀ THI CHÍNH THỨC 2016 – 2017) Một vật chuyển động theo quy luật

s tt 

với

(giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động

và

(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong

khoảng thời gian

giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt

được bằng bao nhiêu?

18m/s.

24m/s.

64m/s.

108m/s.

Lời giải. Vận tốc

   

  

' 12 .

vt s t t t

Ycbt là đi tìm GTLN của hàm số

 

vt t t

 

với

0 8.t

Đạo hàm và lập bảng biến thiên ta tìm được

 

 

0;8

max 4 24m/s.

vt v

Chọn B.

Câu 10. Một tàu lửa đang chạy với vận tốc

200 m/s

thì người lái tàu đạp phanh. Từ

thời điểm đó, tàu chuyển động chậm dần đều với vận tốc

   

t 200 m/s ,v at

trong

đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh và

 

m/sa

là

gia tốc. Biết rằng khi đi được

1500m

thì tàu dừng, hỏi gia tốc của tàu bằng bao

nhiêu?

200

m/s .



100

m/s .

a 

m/s .

a 

 

m/s .

a 

Lời giải. Khi tàu dừng hẳn thì





200

0 200 0 m/s .v at t

       

Theo đề bài, ta có:















     















200

40000 40000

1500 200 d 200 .

at t t

Suy ra

 

m/s .

a 

Chọn C.

Câu 11.

Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu tăng tốc

với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường

cong Parabol có hình bên. Biết rằng sau

10s

thì xe đạt đến vận

tốc cao nhất

50m/s

và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu

tăng tốc đến lúc đạt vận tốc cao nhất thì xe đã đi được quãng

đường bao nhiêu mét?

1000

1100

1400

300m.

Lời giải. Dựa vào đồ thị suy ra

   

 

10 m/s .

vt t t

Quảng đường:

 







   













10 10

1 1000

d 10 d m.

s vtt t tt

Chọn A.

Câu 12. Một vật chuyển động trong

giờ với vận tốc

 

km/h

phụ

thuộc thời gian





có đồ thị là một phần của đường Parabol có

đỉnh

 

2;9I

và trục đối xứng song song với trục tung như hình bên.

Tính quãng đường

mà vật di chuyển được trong

giờ đó.

24,25km.



24,75km.



25,25km.s 

26,75km.s 

Lời giải. Dựa vào đồ thị suy ra

   

  

3 6 m/s .

vt t t

Quảng đường người đó đi được trong khoảng thời gian

giờ là:

3 6 d 24,75km.

s tt t







   













Chọn B.

Câu 13.

Một vật chuyển động trong

giờ với vận tốc

 

km/hv

phụ thuộc thời gian

 

có đồ thị của vận tốc như hình bên.

Trong khoảng thời gian

giờ kể từ khi bắt đầu chuyển động,

đồ thị đó là một phần của đường Parabol có đỉnh

 

2;9I

với

trục đối xứng song song với trục tung, khoảng thời gian còn lại

đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng

đuờng

mà vật chuyển động trong

giờ đó.

24km.s 

26,5km.s 

27km.s 

28,5km.s 

Lời giải. Dựa vào đồ thị suy ra

 











  





9 m/s khi 0 t 3

m/s khi 3 4

Quảng đường người đó đi được trong khoảng thời gian

giờ là:

9 27

9 d d 27km.

s t tt t







   













Chọn C.

Câu 14. Một vật chuyển động trong

giờ với vận tốc

 

km/h

phụ thuộc thời gian

 

có đồ thị của vận tốc

như hình bên. Trong khoảng thời gian

giờ kể từ khi

bắt đầu chuyển động, đồ thị đó là một phần của đường

Parabol có đỉnh

 

1; 2I

và trục đối xứng song song với

trục tung, khoảng thời gian còn lại đồ thị là một phần

đường thẳng. Tính quãng đường

mà vật di chuyển được

trong

giờ đó (kết quả làm tròn đến hàng phần trăm).

 5,44km.s

 8,67km.s

 9,27km.s

11,35km.s

Lời giải. Dựa vào đồ thị suy ra

 

  

















2 3 khi 0 t 2

5 khi

2 4

Quảng đường người đó đi được trong khoảng thời gian

giờ là:

 





     



2 3 d 5 d 8, 67k m.

s t t t tt

Chọn B.

Câu 15. Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi

hành cùng một lúc, bên cạnh nhau và trên cùng một con

đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường

Parabol, đồ thị biểu diễn vận tốc của xe B là một đường

thẳng ở hình bên. Hỏi sau khi đi được

giây khoảng cách

giữa hai xe là bao nhiêu mét?

0 m.

60 m.

90 m.

270 m.

Lời giải. Dựa vào đồ thị suy ra

   





 













20 80 m/s

20 m/s

vt t t

vt t

Quãng đường đi được sau

giây của xe A là:

 

20 80 d 180m.

s t tt  



Quãng đường đi được sau

giây của xe B là:

20 d 90m.

s tt





Vậy khoảng cách giữa hai xe sau

giây sẽ bằng:

90 m.

ss

Chọn C.

Bấm Tải xuống để xem toàn bộ.

| 1/125

| | Tải xuống

Preview text:

TÍCH PHÂN VẬN DỤNG CAO
Vấn đề 1. Tính tích phân theo định nghĩa
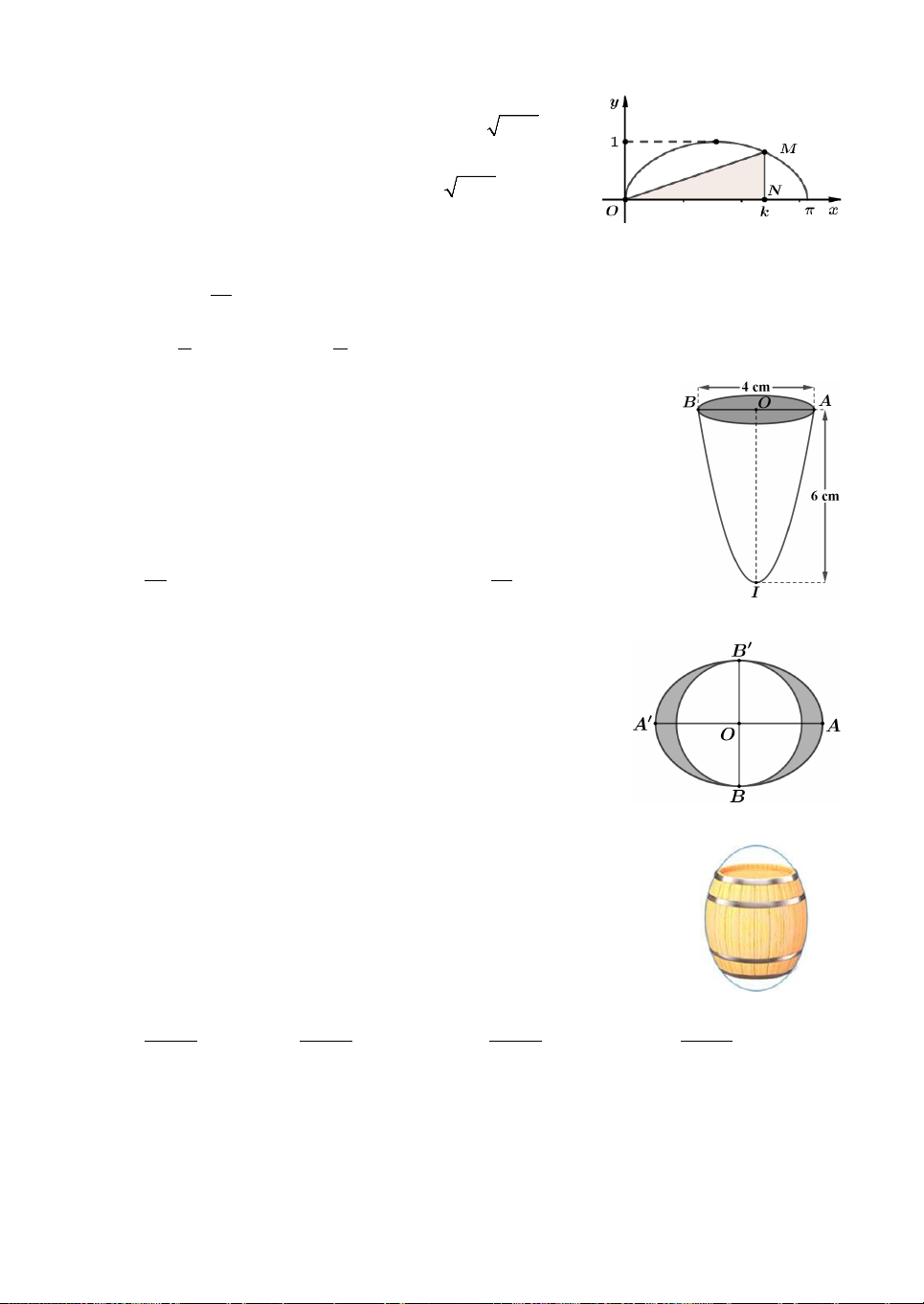
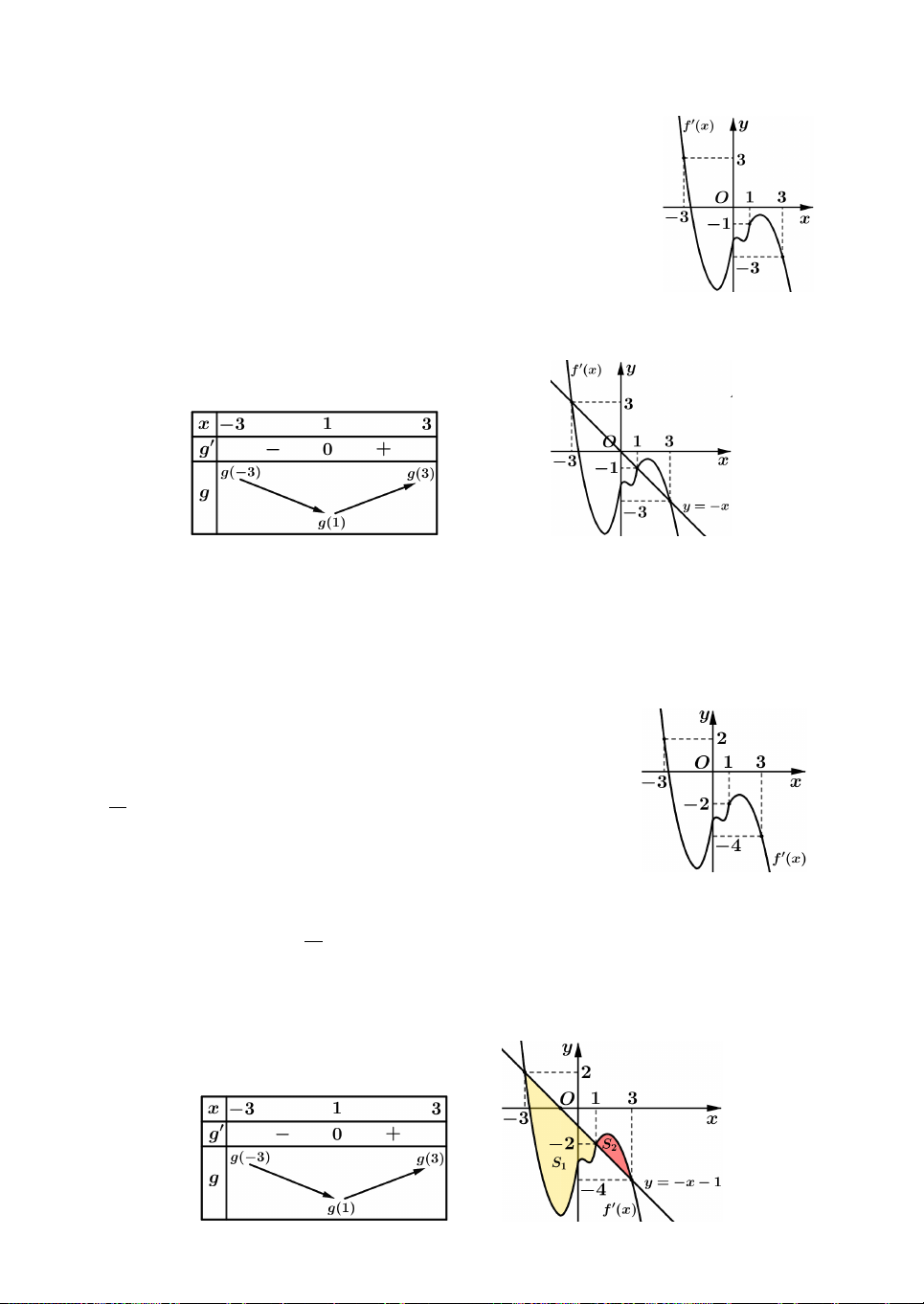
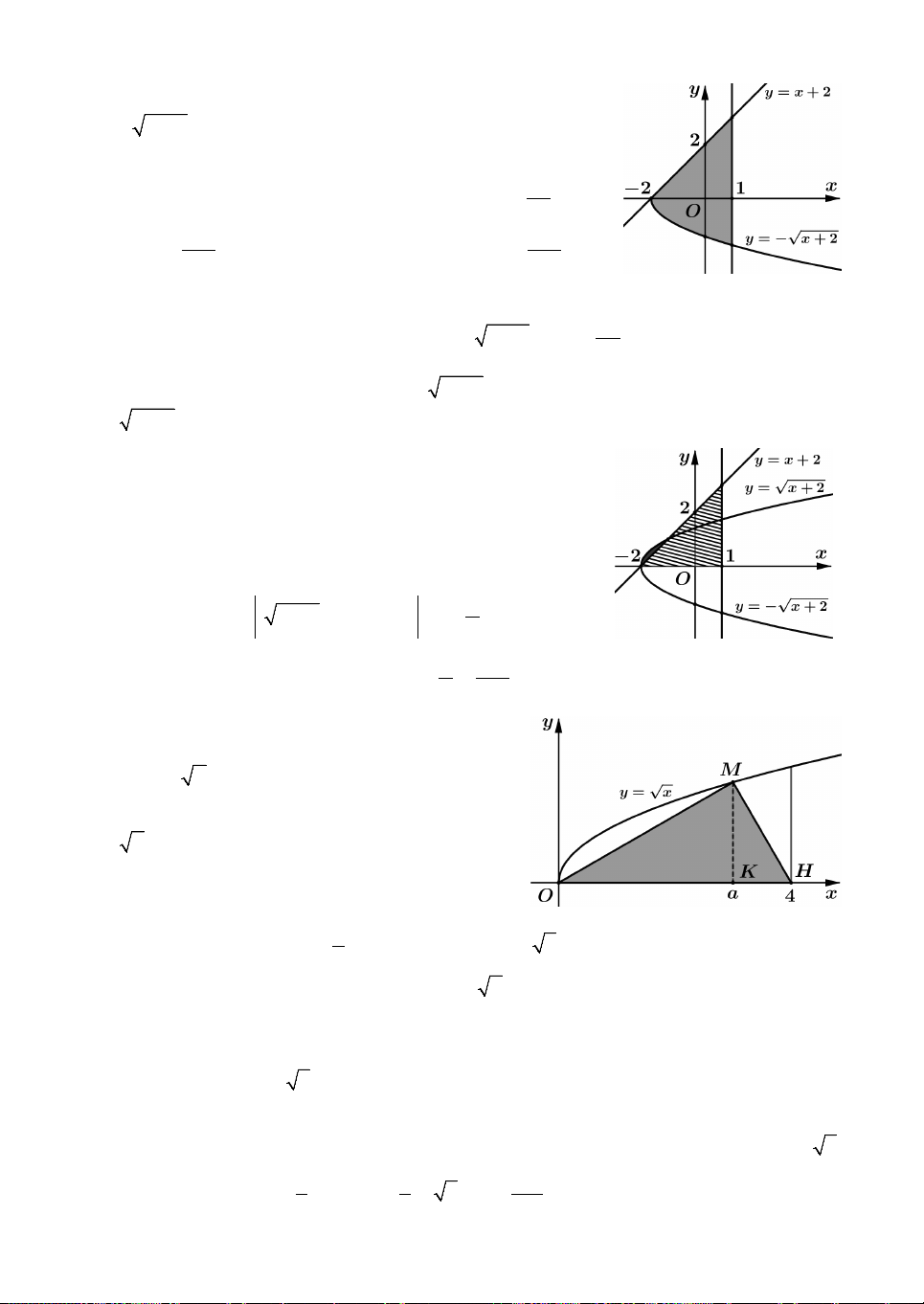
Câu 1. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa f x f   x 2 2 3 1  1 x . Giá 1 trị của tích phân
f 'xdx  bằng 0 A. 0. B. 1 . C. 1. D. 3 . 2 2
Câu 2. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0  f   1  1. Biết rằng 1 x
e  f x f x dx  ae  . b    Tính 2018 2018 Q  a b . 0 A. 2017 Q  2 1 . B. Q  2 . C. Q  0 . D. 2017 Q  2 1 .
Câu 3. Cho các hàm số y  f x, y  gx có đạo hàm liên tục trên 0;2 và thỏa mãn 2 2 2
f 'x gxdx  2, 
f x g 'xdx  3. 
Tính tích phân I   f x gx / dx.    0 0 0 A. I  1. B. I  1. C. I  5. D. I  6. 2 x  
Câu 4. Cho hàm số y  f x liên tục trên 0; và thỏa
f tdt  x.sinx  . Tính 1 f      . 4 0         A. 1   f       .        B. 1 1 f    . C. 1 f   1. D. 1 f   1 . 4 2 4 2 4 4 2 x f t
Câu 5. Cho hàm số f x liên tục trên a; với a  0 và thỏa dt  6  2 x  với mọi 2 t a x  .
a Tính f 4.
A. f 4 2.
B. f 4 4.
C. f 4 8.
D. f 416.
Vấn đề 2. Kỹ thuật đổi biến 2017 2017 e 1  Câu 6. Cho x
f xdx  2  . Tính tích phân I . f ln    2 x 1    dx. 2  x 1    0 0 A. I  1. B. I  2. C. I  4. D. I  5.  9 f  x  2
Câu 7. Cho hàm số f x liên tục trên  và dx  4, f 
sin xcos xdx  2.   Tính tích x 1 0 3 phân I 
f xdx.  0 A. I  2. B. I  6. C. I  4.
D. I  10.  4 1 2 x f x
Câu 8. Cho hàm số f x liên tục trên  và
f tan xdx  4, dx  2.   Tính tích 2 x 1 0 0 1 phân I 
f xdx.  0 A. I  6. B. I  2. C. I  3.
D. I  1. 1  4
Câu 9. Cho hàm số f x liên tục trên  và thỏa mãn tan x. f   2
cos xdx 1, 0 2 e f  2 ln x 2 f 2x dx  1. 
Tính tích phân I  dx.  x ln x x e 1 4 A. I  1. B. I  2. C. I  3. D. I  4.  
Câu 10. Cho hàm số y  f x xác định và liên tục trên 1  ;2, thỏa 2      2 f x f x 1 1 2  f      x   2.  
Tính tích phân I  dx. 2   x  x 2 x 1 1 2 A. 3 I  . B. I  2. C. 5 I  . D. I  3. 2 2
Câu 11. Cho hàm số f x liên tục trên  và thỏa f x f x 2 2cos2x với mọi x   . 3 2 Tính I 
f xd x  . 3  2 A. I  6 . B. I  0 . C. I  2 . D. I  6 .
Câu 12. Cho hàm số y  f x xác định và liên tục trên ,  thỏa f  5 x  4x   3  2x 1 với 8 mọi x  .  Tích phân
f xdx  bằng 2 A. 2. B. 10. C. 32 . D. 72. 3
Câu 13. Cho các hàm số f x, gx liên tục trên 0;  1 , thỏa . m f x .
n f 1 x  gx với 1 1 ,
m n là số thực khác 0 và
f xdx 
g xdx  1.   Tính m  . n 0 0
A. m  n  0. B. 1 m  n  .
C. m  n  1.
D. m  n  2. 2
Câu 14. Cho hàm số f x xác định và liên tục trên 0; 
1 , thỏa mãn f 'x  f '1 x với mọi 1 x 0; 
1 . Biết rằng f 0  1, f  
1  41. Tính tích phân I 
f xdx.  0 A. I  41. B. I  21. C. I  41. D. I  42.
Câu 15. Cho hàm số y  f x liên tục trên  và thỏa mãn 3
f x f x  x với mọi x  .  2 Tính I 
f xdx.  0 A. 4 I   . B. 4 I  . C. 5 I   . D. 5 I  . 5 5 4 4 2
Vấn đề 3. Kỹ thuật tích phân từng phần 3 3
Câu 16. Cho hàm số f x thỏa mãn x. f x f x .e dx  8  và f   3  ln 3 . Tính f x I  e dx.  0 0 A. I  1. B. I  11.
C. I  8ln 3.
D. I  8  ln 3.    2 Câu 17. Cho hàm số 
f x có đạo hàm liên tục trên 0; , thỏa mãn f 'x 2 cos xdx  10   và 2    0  2
f 0  3. Tích phân
f xsin 2xdx  bằng 0 A. I  13. B. I  7. C. I  7. D. I  13. 2
Câu 18. Cho hàm số y  f x có đạo hàm liên tục trên 0;  1 , thỏa mãn f x   1 dx  3  và 1 1 f   1  4. Tích phân 3 x f ' 2 x dx  bằng 0 A. 1. B. 1  . C. 1 . D. 1. 2 2
Câu 19. Cho hàm số f x nhận giá trị dương, có đạo hàm liên tục trên 0;2. Biết f 01 2  3 2
x 3x  f 'x và     2 2 4 2 x x f x f x e   
với mọi x 0;2. Tính tích phân I  dx.  f x 0 A. 14 I   . B. 32 I   . C. 16 I   . D. 16 I   . 3 5 3 5      2  
Câu 20. Cho biểu thức   S  ln 1   
2sin 2x 2cotx e dx, 
 với số thực m  0. Chọn khẳng định    n     2 4m 
đúng trong các khẳng định sau. A. S  5. B. S  9.         C.     S  2 cot    2 ln          sin . D. S 2 tan 2 ln    . 2 2 4  m   4  m  2 2 4  m  4 m 
Vấn đề 4. Tính a, b, c trong tích phân 2 Câu 21. Biết ln   2
9  x dx  a ln5b ln 2 c với ,
a b, c  .
 Tính P  a  b  c . 1 A. P  13. B. P  18. C. P  26. D. P  34. 1 3 x 3 x     Câu 22. Biết x 2 ex 2 1 1 e dx   .ln  p    với , m ,
n p là các số nguyên
  e.2x m e ln n  e   0
dương. Tính tổng P  m  n  . p A. P  5. B. P  6. C. P  7. D. P  8.  2 2
x 2x  cos xcos x 1sin x Câu 23. Biết 2 c
dx  a b ln  với ,
a b, c là các số hữu tỉ. x  cos x  0 Tính 3 P  ac  . b A. 5 P  . B. 3 P  . C. P  2. D. P  3. 4 2 3 ln 8 Câu 24. Biết 1 1 b
dx  1 ln  a a  b  với , a b 
  . Tính P  a  . b 2 x e 1 x 2 e a ln 3 A. P  1. B. P  1. C. P  3. D. P  5. 2 Câu 25. Biết dx
 a  b c  với , a b, c 
  . Tính P  a b  c .
x 1 x  x x 1 1   A. P  12 . B. P  18 .
C. P  24 . D. P  46 .  4 Câu 26. Biết sin 4x
a 2  b 6  c dx   với ,
a b, c  .
 Tính P  a  b  c . 2 2
cos x 1  sin x 1 6 0 A. P  10. B. P  12. C. P  14. D. P  36. 4 x Câu 27. Biết 1 x  e  d b c
x  a  e e  với ,
a b, c  .
 Tính P  a b  c. 2 4 x x xe 1 A. P  5. B. P  4. C. P  3. D. P  3. 2 Câu 28. Biết
2  x dx  ab 2 c  với ,
a b, c  .
 Tính P  a b  c. 2  x 0 A. P  1. B. P  2. C. P  3. D. P  4. e 2 Câu 29. Biết ln x  ln x 1 b I  dx    với , a b 
  . Tính P  b  . a
ln x  x  3 1 a e 22 1 A. P  8. B. P  6. C. P  6. D. P  10.  6 2 Câu 30. Biết x cos x  3 dx  a    với ,
a b, c là các số nguyên. Tính P  a b  c. 2  1 x  x b c  6 A. P  37. B. P  35. C. P  35. D. P  41.
Vấn đề 5. Tính tích phân hàm phân nhánh x 1 khi x  0 2
Câu 31. Cho hàm số f x   
. Tính tích phân I 
f xdx.  2 x e  khi x  0  1 2 2 2 2 A. 3e 1 7e 1 9e 1 11e 11 I  . B. I  . C. I  . D. I  . 2 2e 2 2e 2 2e 2 2e   Câu 32. Cho hàm số 2
f x xác định trên 1  \ 
 , thỏa f x  , f 
0  1 và f   1  2. 2   2x 1
Giá trị của biểu thức f   1  f   3 bằng A. ln15. B. 2  ln15. C. 3 ln15. D. 4  ln15. Câu 33. Cho hàm số 1
f x xác định trên \2; 
1 , thỏa mãn f x  , 2 x  x 2 f   3  f   3  0 và f   1
0  . Giá trị biểu thức f 4 f   1  f 4 bằng 3 A. 1 1 ln 20  . B. 1 1 ln 2  . C. ln 80 1. D. 1 8 ln 1. 3 3 3 3 3 5 Câu 34. Cho hàm số 1
f x xác định trên 0;\e, thỏa mãn f x  ,
x ln x   1  1  1 f  
   ln 6 và f  2
e  3. Giá trị biểu thức f     f    3e bằng 2 e  e  A. 3ln 2   1 . B. 2 ln 2. C. 3ln 2 1. D. ln 2 3. 4   Câu 35. Cho  
F x là một nguyên hàm của hàm số 1  y  với x  \ k ,  k       . 1 sin 2x  4        Biết  
F 0  1, F  0
 , tính giá trị biểu thức 11 P  F      F      .  12  12  A. P  0.
B. P  2 3. C. P  1.
D. Không tồn tại P.
Vấn đề 6. Tính tích phân dựa vào tính chất 0
Câu 36. Cho hàm số f x là hàm số lẻ, liên tục trên 4;4 . Biết rằng
f xdx  2  và 2 2 4
f 2xdx  4. 
Tính tích phân I  f xdx.  1 0 A. I  10. 
B. I  6.
C. I  6.
D. I 10. 2
Câu 37. Cho hàm số f x là hàm số chẵn, liên tục trên 1;6. Biết rằng
f xdx  8  và 1 3 6
f 2xdx  3. 
Tính tích phân I  f xdx.  1 1 A. I  2. B. I  5. C. I 11. D. I 14.
Câu 38. Cho hàm số f x liên tục trên 3;7, thỏa mãn f x f 10 x với mọi x 3;7 và 7 7
f xdx  4. 
Tính tích phân I  xf xdx.  3 3 A. I  20. B. I  40. C. I  60. D. I  80.
Câu 39. Cho hàm số y  f x là hàm số chẵn và liên tục trên đoạn  
 ;, thỏa mãn   f x
f xdx  2018.  Giá trị của tích phân   I  dx  bằng 2018x 1 0  A. I  0. B. 1 I  . C. I  2018. D. I  4036. 2018  2018 a Câu 40. Biết x sin x  dx   với a,b 
  . Tính P  2a  . b 2018 2018 sin x  cos x b 0 A. P  6. B. P  8. C. P 10. D. P 12.
Vấn đề 7. Kỹ thuật phương trình hàm   Câu 41. Cho hàm số  
y  f x liên tục trên  ;  và thỏa mãn 2 f x f x  cos x. Tính  2 2     2 tích phân I 
f xdx.    2 A. I  2. B. 2 I  . C. 3 I  . D. I  2. 3 2 Câu 42. Cho hàm số 1
y  f x liên tục trên 2;2 và thỏa mãn 2 f x3 f x  . 2 4  x 2 Tính tích phân I 
f xdx.  2 A.     I   . B. I   . C. I  . D. I  . 10 20 20 10 5
Câu 43. Cho hàm số y  f x liên tục trên 0;  1 và thỏa mãn 2
x f x f   x 4 1  2x  x . 1 Tính tích phân I 
f xdx.  0 A. 1 I  . B. 3 I  . C. 2 I  . D. 4 I  . 2 5 3 3    
Câu 44. Cho hàm số f x liên tục trên 1
 ;2 và thỏa mãn f x 1  2 f  
   3x. Tính tích 2    x  2 f x phân I  dx.  x 1 2 A. 1 I  . B. 3 I  . C. 5 I  . D. 7 I  . 2 2 2 2
Câu 45. Cho hàm số f x liên tục trên 0; 
1 và thỏa mãn f x f   x 2 2 3 1  1 x . Tính 1 tích phân I 
f xdx.  0 A.     . B. .
C. . D. . 20 16 6 4
Vấn đề 8. Kỹ thuật biến đổi
Câu 46. Cho hàm số f x thỏa f x f x 5 2
 3x  6x . Biết rằng f 0  2, tính 2 f 2. A. 2 f 2  64. B. 2
f 2  81. C. 2 f 2  100. D. 2 f 2  144.
Câu 47. Cho hàm số f x có đạo hàm f 'x liên tục và nhận giá trị không âm trên 1;, thỏa f  
1  0, f x e
 f x 2 2 2 .
  4x 4x 1  
với mọi x 1;. Mệnh đề nào sau đây đúng?
A. 1 f 4 0. B. 0  f 41.
C. 1 f 4 2.
D. 2  f 4 3.
Câu 48. Cho hàm số f x thỏa mãn  f x 2  f x f  x 4 .  15x 12x  
với mọi x   và
f 0  f 0  1. Giá trị của 2 f   1 bằng A. 5 . B. 9 . C. 8. D. 10. 2 2
Câu 49. Cho hàm số f x có đạo hàm liên tục trên đoạn 1;2 và thỏa mãn 2 2 f x
f x 0,x 1;2. Biết rằng
f xdx  10  và dx  ln 2.  Tính f 2. f x 1 1
A. f 2 20.
B. f 2 10.
C. f 210.
D. f 2 20.
Câu 50. Cho hàm số f x có đạo hàm liên tục trên 1; 
1 , thỏa mãn f x 0, x   và
f 'x 2 f x  0 . Biết rằng f  
1  1 , giá trị của f   1 bằng A. 2 e . B. 3 e . C. 4 e . D. 3.
Câu 51. Cho hàm số f x xác định và liên tục trên  đồng thời thỏa mãn
f x0, x   
f 'x x 2  e  f x, x  .
f   1 0   2
Tính giá trị của f ln 2. 6 A. f   1 ln 2  . B. f   1 ln 2  . 4 3 C. 1 f   1 ln 2  ln 2  . D. f ln 2 2  ln 2  . 2 2
Câu 52. Cho hàm số f x có đạo hàm liên tục trên 0; , biết f x x   2 ' 2
3 f x  0,
f x 0 với mọi x  0 và f   1
1  . Tính P  1 f  
1  f 2... f 2018. 6 A. 1009 P  . B. 2019 P  . C. 3029 P  . D. 4039 P  . 2020 2020 2020 2020
Câu 53. Cho hàm số f x liên tục trên 0; 3,  thỏa mãn và  
f x 1, f 0  0 f x 2
x 1  2x f x1. Giá trị của f  3 bằng A. 0. B. 3. C. 7. D. 9.
Câu 54. Cho hàm số f x có đạo hàm và liên tục trên 1;4, đồng biến trên 1;4, thoản mãn 4
x  xf x   f x 2 2  
 với mọi x 1;4. Biết rằng f   3
1  , tính tích phân I 
f xdx.  2 1 A. 1186 I  . B. 1187 I  . C. 1188 I  . D. 9 I  . 45 45 45 2   Câu 55. Cho hàm số 
f x liên tục, không âm trên 0;  , thỏa f x f x 2 . '
 cos x 1 f x  2        với mọi  
x  0;  và f 0  3. Giá trị của f   bằng    2    2 A. 0. B. 1. C. 2. D. 2 2.
Câu 56. Cho hàm số f x liên tục, không âm trên 0;3, thỏa f x f x 2 .
 2x f x1 với
mọi x 0;3 và f 0 0. Giá trị của f   3 bằng A. 0. B. 1. C. 3. D. 3 11.
Câu 57. Cho hàm số f x có đạo hàm không âm trên 0; 
1 , thỏa mãn f x 0 với mọi x 0; 
1 và  f x 4  f x 2   
 x      f x 3 2 . ' . 1 1  . 
 Biết f 0  2, hãy chọn khẳng định đúng
trong các khẳng định sau đây. A. 3 5  f   1  2.
B.  f   5 2 1  . C.  f   1  3.
D.  f   7 3 1  . 2 2 2 2
Câu 58. Cho hàm số f x liên tục trên \0; 
1 , thỏa mãn x x   f x f x 2 1 .  x  x
với mọi x  \0;  1 và f  
1  2 ln 2. Biết f 2  a b ln 3 với ,
a b   , tính 2 2
P  a  b . A. 1 P  . B. 3 P  . C. 13 P  . D. 9 P  . 2 4 4 2
Câu 59. Cho hàm số f x có đạo hàm xác định, liên tục trên 0; 
1 , thỏa mãn f 0  1 và
 f x 2  f  x   
với mọi x 0; 
1 . Đặt P  f  
1  f 0 , khẳng định nào sau đây đúng?
 f x 0 
A. 2  P  1.
B. 1 P  0.
C. 0  P 1.
D. 1 P  2.
Câu 60. Cho hai hàm số f x và gx có đạo hàm liên tục trên 0;2, thỏa mãn 2
f '0. f '2  0 và  . '    2 x g x f x x x
e . Tính tích phân I 
f x.g 'xdx.  0 A. I  4. B. I  4.
C. I  e 2.
D. I  2e. 7
Câu 61. Cho hàm số f x 0 xác định và có đạo hàm trên đoạn 0;  1 , thỏa mãn x
gx12018 f tdt 1    . Tính I 
g xdx. 0    0 gx 2  f x  A. 1009 I  . B. I  505. C. 1011 I  . D. 2019 I  . 2 2 2  f   1  g   1  4 
Câu 62. Cho hai hàm f x và gx có đạo hàm trên 1;4, thỏa mãn gx xf x với mọi
f xxgx  4
x 1;4. Tính tích phân I   f x gx dx.    1 A. I  3ln 2.
B. I  4 ln 2.
C. I  6 ln 2.
D. I  8 ln 2.
Câu 63. Cho hai hàm f x và gx có đạo hàm trên 1;2, thỏa mãn f   1  g   1  0 và  x 
g x  2017x  x 1 f  x  2       x   1  , x  1;2.  3  x  g 
x f x 2  2018x x 1 2    Tính tích phân x I  
g x x 1 
f x dx.   x 1 x  1  A. 1 I  .
B. I  1. C. 3 I  . D. I  2. 2 2
 f 3 x. f x1
Câu 64. Cho hàm số y  f x có đạo hàm trên 0;3, thỏa mãn  với mọi
 f x1  3 xf 'x
x 0;3 và f   1
0  . Tính tích phân I  dx.  2 1
  f 3 x 2 2  0 . f x   A. 1 I  . B. I  1. C. 3 I  . D. 5 I  . 2 2 2
Câu 65. Cho hàm số y  f x liên tục trên đoạn 0; 
1 và thỏa mãn af bbf a  1 với mọi 1 , a b  0; 
1 . Tính tích phân I 
f xdx.  0 A. 1   I  . B. 1 I  . C. I  . D. I  . 2 4 2 4
Vấn đề 9. Kỹ thuật đạo hàm đúng
Câu 66. Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thoả mãn     2018 3 f x xf x  x với 1 mọi x 0;  1 . Tính I 
f xdx  . 0 A. 1 I  . B. 1 I  . C. 1 I  . D. 1 I  . 20182021 20192020 20192021 20182019
Câu 67. Cho hàm số f x có đạo hàm liên tục trên 0;4, thỏa mãn     x f x f x  e
2x 1 với mọi x 0;4. Khẳng định nào sau đây là đúng? A. 26 4
e f 4 f 0  . B. 4
e f 4 f 0  3e. 3 C. 4
e f   f   4 4 0  e 1. D. 4
e f 4 f 0  3. 8
Câu 68. Cho hàm số f x có đạo hàm trên ,  thỏa mãn     2017 2018 ' 2018  2018 x f x f x x e với
mọi x   và f 0 2018. Tính giá trị f   1 . A. f   2018 1 2018e  . B. f   2018 1  2017e . C. f   2018 1  2018e . D. f   2018 1  2019e .
Câu 69. Cho hàm số f x có đạo hàm và liên tục trên ,  thỏa mãn     2 2 x f x xf x xe    và
f 0  2. Tính f   1 . A. f   1  e. B. f   1 1  . C. f   2 1  . D. f   2 1   . e e e   Câu 70. Cho hàm số 
f x liên tục và có đạo hàm trên 0; ,  thỏa mãn hệ thức  2        x  
f x  tan xf x 
. Biết rằng 3 f     f    
   a 3 b ln 3 trong đó a, b  .  Tính giá 3 cos x  3 6
trị của biểu thức P  a  . b A. 4 P   . B. 2 P   . C. 7 P  . D. 14 P  . 9 9 9 9
Vấn đề 10. Kỹ thuật đưa về bình phương loại 1    2    Câu 71. Cho hàm số   2 
f x liên tục trên 0; , thỏa 2
 f x2 2 f xsin  x    dx  .  2      4  2 0    2 Tính tích phân I 
f xdx.  0 A.   I  0. B. I  . C. I  1. D. I  . 4 2 1 1   Câu 72. Cho hàm số 2
f x liên tục trên 0;  1 thỏa 2  f x 2  2 ln
 dx  2  f xlnx   1  dx.    e     0  0 1 Tích phân I 
f xdx.  0 A. e e I  ln . B. 4 I  ln . C. I  ln . D. 2 I  ln . 4 e 2 e
Câu 73. Cho hàm số f x có đạo liên tục trên 0; 
1 , f x và f 'x đều nhận giá trị dương 1 1 trên 0; 
1 và thỏa mãn f 0  2 và  f '
  x. f x 2 1    dx  2 f '   
x. f xdx.    Tính 0 0 1 I 
 f x 3 dx.    0 A. 15 I  . B. 15 I  . C. 17 I  . D. 19 I  . 4 2 2 2
Câu 74. Cho hàm số f x có đạo hàm dương, liên tục trên đoạn 0; 
1 và thỏa mãn f 0  1, 1 1   1
 f x  f x 2 1 3 ' .    dx  2
f 'x. f xdx.  3   I   f x  dx.   Tính     9   0  0 0 A. 3 I  . B. 5 I  . C. 5 I  . D. 7 I  . 2 4 6 6 9
Câu 75. Cho hàm số y  f x có đạo hàm dương, liên tục trên đoạn 0;  1 , thỏa 1 1 1 f  
1  f 0  1 và f 'x 2  f  3 
x1 dx  2 f '    
x f xdx.   Giá trị của tích phân
f x dx    0 0 0 bằng A. 3   . B. 5 33 27 . C. 5 33 . D. 5 33 54 . 2 18 18 18
Vấn đề 11. Kỹ thuật đưa về bình phương loại 2 Kỹ thuật Holder 1 1
Câu 76. Cho hàm số y  f x liên tục trên đoạn 0; 1, thỏa mãn
f xdx  xf xdx 1   và 0 0 1 1
 f x 2 dx  4  3  
. Giá trị của tích phân  f x dx    bằng 0 0 A. 1. B. 8. C. 10. D. 80. 1 1
Câu 77. Cho hàm số y  f x liên tục trên đoạn 0; 1, thỏa mãn xf xdx 
x f xdx 1   và 0 0 1 1
 f x 2 dx  5.  3  
Giá trị của tích phân  f x dx    bằng 0 0 A. 5. B. 6. C. 8. D. 10. 6 5 1 1 Câu 78. Cho hàm số 1
y  f x liên tục trên đoạn 0;  1 , thỏa mãn 2 xf x 2 dx 
x f xdx  .   16 0 0 1
Giá trị của tích phân f xdx  bằng 0 A. 1. B. 1. C. 1. D. 2. 5 4 3 5
Câu 79. Cho hàm số f x có đạo hàm liên tục trên 1;8 và thỏa mãn 2 2 8  f   x  2 2 38 3  dx  2 f  
  3xdx 
f xdx  .   3 15 1 1 1 8 Tích phân
f xdx  bằng 1 A. 8 ln 2 . B. ln 2 . C. 4 . D. 3 . 27 27 3 2
Câu 80. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0 , 1 1 1  1
f x 2 dx  7  2  
và x f xdx  .  Tích phân
f xdx  bằng 3 0 0 0 A. 1. B. 7 . C. 7 . D. 4 . 5 4
Câu 81. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  1 , 1 11 1 4 5
x f xdx   và f xd 
 f x . Tính f 2. 78 13 0 0
A. f 2 2. B. f   251 2  . C. f   256 2  . D. f   261 2  . 7 7 7 10
Câu 82. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  2, f  0  0 và 1 1
 f 'x 2 dx  4.  3      . Tích phân f
  x 2018x dx.   bằng 0 0 A. 0. B. 1011. C. 2018. D. 2022. 2 Câu 83. Cho hàm số 1
f x có đạo hàm liên tục trên 1;2, thỏa mãn x  2
1 f xdx   ,  3 1 2 2
f 2  0 và  f 'x 2 dx  7.    Tích phân
f xdx  bằng 1 1 A. 7  . B. 7 . C. 7  . D. 7 . 20 20 5 5 1 Câu 84. Cho hàm số 9
f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  1, '
 f x 2 dx     5 0 1 1 và f   x 2 dx  . Tích phân
f xdx  bằng 5 0 0 A. 1 I  . B. 1 I  . C. 3 I  . D. 3 I  . 5 4 5 4
Câu 85. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0 f   1  0, 1  1 1 1
f 'xcosxdx   và 2
f xdx  .  Tích phân
f xdx  bằng 2 2 0 0 0 A. 1  . B. 2 . C. .  D. 3 .   2 
Câu 86. Cho hàm số f x có đạo hàm liên tục trên 0;, thỏa mãn
f 'xsin xdx  1  và 0  2  2
f xdx  . 
Tích phân xf xdx  bằng  0 0 A. 6  . B. 4  . C. 2 . D. 4 .     1 2 Câu 87. Cho hàm số 
f x có đạo hàm liên tục trên 0;  1 , thỏa f   1  0, '
 f x 2 dx     và 8 0 1 x  1  
   f x 1 cos dx  . Tích phân 
f xdx   bằng 2  2 0 0 A. 1  . B. 2 . C. . D. .    2 1
Câu 88. Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thỏa mãn
f 'xsinxdx    và 0 1 1   2 x
f xdx  2.  Tích phân f     dx bằng 2 0 0 A. 6  . B. 4  . C. 4 . D. 6 .        2   Câu 89. Cho hàm số  
f x có đạo hàm liên tục trên 0; , thỏa 2 f      0, f x dx  3  2    2  và 0   2   x 
sin x  x f    3  dx  6 .
 Tích phân    
f x dx   bằng 2    0 0 11 A. 2  . B. 0. C. 3 .  D. 9 .  
Câu 90. Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
1 , thỏa mãn f   1  0 và 1 1 2  1
 f x 2 x  x   xe f x e 1 ' d 1 dx  .    
Tính tích phân I 
f xdx.  4 0 0 0 2 A. e 1 e e I  . B. I  .
C. I  e 2. D. I  . 2 4 2
Câu 91. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0  0, f   1  1 và  f 'x 2 1  1 1   dx  .  Tích phân
f xdx x  bằng e e 1 0 0 A. e 2 e  1 . B. 1 . D. . C. 1. e 1 e 2 e   1 e 2
Câu 92. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0  0, f   1  1 và 1 1 f x
1 x  f 'x 2 1 2  dx  .    Tích phân dx  bằng ln 1 2 2 0   0 1 x A. 1 2 1 1 2 ln 1 2. B. 2
ln 1 2. C. ln1 2. D.  2   1 ln1 2. 2 2 2
Câu 93. Cho hàm số f x có đạo hàm liên tục trên 1; 
1 , thỏa mãn f   1  0, 1 1 1  16
f 'x 2 dx  112  2  
và x f xdx  . 
Tính tích phân I 
f xdx.  3 1 1 1 A. 84 I  . B. 35 I  . C. 35 I  . D. 168 I  . 5 2 4 5
Câu 94. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0, 1 1 1  f x 3 f x 2 3 '  dx  2 ln 2    và dx  2 ln 2  .  Tích phân
f xdx  bằng 2 x 1 2 0  2 0 0 A. 1ln 2    . B. 1 2 ln 2 . C. 3 2 ln 2 . D. 3 4 ln 2 . 2 2 2 2
Câu 95. Cho hàm số f x có đạo hàm liên tục trên 1;2, đồng biến trên 1;2, thỏa mãn 2 2 2 f   1  0 ,
 f x 2 dx  2    và
f x.f 'xdx  1.  Tích phân
f xdx  bằng 1 1 1 A. 2 . B. 2. C. 2. D. 2 2. 2 1
Câu 96. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0 , 2
f xdx  1  0 1
và  f x 2 3 2
 f xdx  .  2  
Giá trị của f  2 bằng 4 0 31 2 31 2 A. 3  . B. 3 . C. . D.  . 2 2 2 2
Câu 97. Cho hàm số f x có đạo hàm liên tục trên 0;2, thỏa mãn f 21 , 2 8 2 32 2 2
x f xdx  
và  f 'x 4 dx  .  Giá trị của tích phân
f xdx  bằng 15   5 0 0 0 A. 3  . B. 2  . C. 7  . D. 7 . 2 3 3 3 12
Vấn đề 12. Kỹ thuật đánh giá AM-GM
Câu 98. Cho hàm số f x nhận giá trị dương và có đạo hàm f 'x liên tục trên 0;  1 , thỏa 1 1 mãn dx f   1  ef 0 và
  f 'x 2 dx  2.  2 
Mệnh đề nào sau đây đúng ? f x   0 0 2e 2 2 2e 2 A.   2e 2e f 1  . B. f   1  . C. f   1  . D. f   1  . e 1 e 1 2 e 1 e 1
Câu 99. Cho hàm số f x nhận giá trị dương trên 0; 
1 , có đạo hàm dương và liên tục trên 1 1 1 0; 
1 , thỏa mãn f 0  1 và  f
  x4 f 'x 3 3    dx  3 f '    x 2
f xdx. I  f x dx.    Tính    0 0 0 2 A. e  e 1
I  2 e   1 . B. I   2 2 e   1 . C. 1 I  . D. I  . 2 2
Câu 100. Cho hàm số f x nhận giá trị dương trên 0; 
1 , có đạo hàm dương liên và tục trên 1 xf 'x    0;  1 , thỏa mãn dx 1 
và f 01, f   2
1  e . Tính giá trị của 1 f    . f x 2 0         A. 1 f      1.        B. 1 f    4. C. 1
f    e. D. 1
f    e. 2 2 2 2 1
Câu 101. Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thỏa mãn
 f x f 'x 2 dx 1    và 0  
f 0  1, f  
1  3. Tính giá trị của 1 f    .  2         A. 1 f      2.        B. 1 f    3. C. 1
f    e. D. 1
f    e. 2 2 2 2
Câu 102. Cho hàm số f x nhận giá trị dương và có đạo hàm f 'x liên tục trên 1;2, thỏa  f 'x 2 2  mãn   dx  24  và f  
1  1, f 2  16. Tính giá trị của f  2. xf x 1
A. f  21.
B. f  2 2.
C. f  2 2.
D. f  2 4.
Vấn đề 13. Tìm GTLN-GTNN của tích phân
Câu 103. Cho hàm số f x liên tục trên ,
 có đạo hàm cấp hai thỏa mãn .   x x f
x  e  x
và f 2 2e, f   2
0  e . Mệnh đề nào sau đây là đúng?
A. f 2 4e 1. B. f   2
2  2e  e . C. f   2
2  e 2e.
D. f 212.
Câu 104. Cho hàm số 1
f x dương và liên tục trên 1;3, thỏa max f x  2, min f x  và 1;3 1;3 2 3 3 3 biểu thức S  f x 1 dx. dx  
đạt giá trị lớn nhất, khi đó hãy tính I 
f xdx.  f x 1 1 1 A. 3. B. 7 . C. 7 . D. 5 . 5 5 2 2
Câu 105. Cho hàm số f x có đạo hàm liên tục trên ,
 thỏa mãn f x f x1 với mọi
x   và f 0  0. Giá trị lớn nhất của f   1 bằng A. e  e e 1. B. 1. C. . D. e. e e 1 13
Câu 106. Cho hàm số f x nhận giá trị dương và có đạo hàm f x liên tục trên 0;  1 , thỏa 1 1 mãn 1 f  
1  2018 f 0. Giá trị nhỏ nhất của biểu thức M  dx 
 f  x  dx  bằng 2   2      0 f x 0   A. ln 2018. B. 2 ln 2018.
C. m  2e.
D. m  2018e. 1
Câu 107. Cho hàm số 1
f x có đạo hàm liên tục trên 0;  1 và
1 x2 f xdx   .  Giá trị 3 0 1
nhỏ nhật của biểu thức  f x 2 dx  f 0    bằng 0 A. 1. B. 2 . C. 1  . D. 2  . 3 3 3 3 1
Câu 108. Cho hàm số f (x) liên tục trên [0; 1] thỏa mãn
xf xdx  0 
và max f x 1. [0; 1] 0 1 Tích phân x
e f xdx 
thuộc khoảng nào trong các khoảng sau đây? 0       A. 5  ;    .      B. 3  ; e 1. C. 5 3   ; .
D. e 1; .  4 2   4 2
Câu 109. Cho hàm số f x nhận giá trị không âm và liên tục trên 0;  1 . Đặt x 1 1 gx1
f tdt. 
Biết gx f x với mọi x 0;  1 , tích phân dx  có giá trị lớn nhất g x 0 0 bằng A. 1. B. 1 . C. 2 . D. 1. 3 2 2
Câu 110. Cho hàm số f x nhận giá trị không âm và liên tục trên đoạn 0;  1 , thỏa mãn x 1 2
f x13 f tdt  gx 
với mọi x 0;  1 , tích phân
g xdx 
có giá trị lớn nhất bằng 0 0 A. 4 . B. 7 . C. 9 . D. 5 . 3 4 5 2
Câu 111. Cho hàm số f x nhận giá trị không âm và liên tục trên đoạn 0;  1 , thỏa mãn x 1
f x 2018  2 f tdt 
với mọi x 0; 
1 . Biết giá trị lớn nhất của tích phân
f xdx  có 0 0 dạng 2
ae  b với , a b  .  Tính a  . b A. 0. B. 1009. C. 2018. D. 2020.
Câu 112. Cho hàm số f x nhận giá trị không âm và liên tục trên đoạn 0;  1 . Đặt 2 x 1
g x  1
f tdt. 
Biết gx xf  2 2
x  với mọi x 0;  1 , tích phân
g xdx  có giá trị lớn 0 0 nhất bằng A. 1. B. e 1. C. 2. D. e 1.
Câu 113. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa f 'x f x 0, x  0;  1 . 1
Giá trị lớn nhất của biểu thức f   1 0 . dx  bằng f x 0 A. e  e  1. B. 1. C. 1. D. e 1. e e 14  
Câu 114. Cho hàm số f x liên tục trên 0;, thỏa mãn
f xdx  cos xf xdx  1.   Giá 0 0 
trị nhỏ nhất của tích phân 2
f xdx  bằng 0 A. 2 . B. 3 . C. 4 . D. 3 .    2  
Câu 115. Cho hàm số f x liên tục trên 0;, thỏa mãn sin xf xdx  cos xf xdx 1.   0 0 
Giá trị nhỏ nhất của tích phân 2
f xdx  bằng 0 A. 2 . B. 3 . C. 4 . D. 3 .    2 1 1
Câu 116. Cho hàm số f x liên tục trên 0;  1 , thỏa mãn  d x f x x 
e f xdx  1.   Gọi m 0 0 1
là giá trị nhỏ nhất của tích phân  f x 2 dx.   
Mệnh đề nào sau đây đúng? 0
A. 0  m 1.
B. 1 m  2.
C. 2  m  3.
D. 3  m  4. 1 1
Câu 117. Cho hàm số f x liên tục trên 0;  1 thỏa mãn
f xdx 
x f xdx  1.   Giá trị 0 0 1
nhỏ nhất của tích phân 2
f xdx  bằng 0 A. 2 . B. 1. C. 8 . D. 3. 3 3 2
Câu 118. Cho hàm số y  f x có đạo hàm liên tục trên 1;2, thỏa 3
x f xdx  31.  Giá trị 1 2
nhỏ nhất của tích phân 4
f xdx  bằng 1 A. 961. B. 3875. C. 148955. D. 923521.
Câu 119. Cho hàm số f x liên tục và có đạo hàm đến cấp 2 trên 0;2 thỏa 2
f 02 f  
1  f 2  1. Giá trị nhỏ nhất của tích phân  f ''x 2 dx    bằng 0 A. 2 . B. 3 . C. 4 . D. 5 . 3 2 5 4
Câu 120. Cho hàm số f x có đạo hàm trên 1;3 và f  
1  0, max f x  10. Giá trị nhỏ 1;3 3
nhất của tích phân  f 'x 2 dx    bằng 1 A. 1. B. 5. C. 10. D. 20. 15
TÍCH PHÂN VẬN DỤNG CAO Mục lục
1. Tính tích phân theo định nghĩa…………………………………….………………… 02
2. Kỹ thuật đổi biến…………………………………………………………………………………. 03
3. Kỹ thuật tích phân từng phần………………………………………….……………… 07
4. Tính a, b, c trong tích phân………………………………………………………………. 09
5. Tính tích phân hàm phân nhánh………………………………………….………… 12
6. Tính tích phân dựa vào tính chất……………………………………….…………… 14
7. Kỹ thuật phương trình hàm…………………………………………………….………. 15
8. Kỹ thuật biến đổi…………………………………………………………………………………. 18
9. Kỹ thuật đưa về đạo hàm đúng……………………………………...……………… 24
10. Kỹ thuật đưa về bình phương loại 1……………………………………………… 25
11. Kỹ thuật đưa về bình phương loại 2 – Kỹ thuật Holder……………27
12. Kỹ thuật đánh giá AM-GM……………………………………………………………. 38
13. Tìm GTLN-GTNN của tích phân…………………………………………….……. 42 1
Vấn đề 1. Tính tích phân theo định nghĩa
Câu 1. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa f x f   x 2 2 3 1  1 x . Giá 1 trị của tích phân
f 'xdx  bằng 0 A. 0. B. 1 . C. 1. D. 3 . 2 2 1 1 Lời giải. Ta có
f xdx  f x  f   1  f 0.  0 0  2  2
 f 03 f   f 0 1  1    Từ  
f x f   x 2 5 2 3 1  1 x     . 2  f   1  3 f 0  0    f   3 1   5 1 Vậy I 
f x x  f   f   3 2 ' d 1 0    1.  Chọn C. 5 5 0
Câu 2. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0  f   1  1. Biết rằng 1 x
e  f x f x dx  ae  . b    Tính 2018 2018 Q  a b . 0 A. 2017 Q  2 1 . B. Q  2 . C. Q  0 . D. 2017 Q  2 1 . 1 1 1
f 0 f   1 1  Lời giải. Ta có
x      d x         / d x e f x f x x e f x x  e f   
x  ef     1  f 0  e 1.  0 0 0 a  1 Suy ra   Q  a b  1  2018 2018 2018 2018 1  2. Chọn B. b   1 
Câu 3. Cho các hàm số y  f x, y  gx có đạo hàm liên tục trên 0;2 và thỏa mãn 2 2 2
f 'x gxdx  2, 
f x g 'xdx  3. 
Tính tích phân I   f x gx / dx.    0 0 0 A. I  1. B. I  1. C. I  5. D. I  6. 2 2
Lời giải. Ta có I   f x gx / dx   f 'x gx f x g 'x dx       0 0 2 2 
f 'x gxdx 
f x g 'xdx  2 3  5.   Chọn C. 0 0 2 x  
Câu 4. Cho hàm số y  f x liên tục trên 0; và thỏa
f tdt  x.sinx  . Tính 1 f      . 4 0         A. 1   f       .        B. 1 1 f    . C. 1 f   1. D. 1 f   1 . 4 2 4 2 4 4 2 2 x Lời giải. Từ
f tdt  x.sinx 
, đạo hàm hai vế ta được xf  2 2
x  sinxx cosx. 0     Cho 1    x  ta được 1 1 1 2. . f  
   sin  cos  1   f    
   1. Chọn C. 2 2 4 2 2 2 4 x f t
Câu 5. Cho hàm số f x liên tục trên a; với a  0 và thỏa dt  6  2 x  với mọi 2 t a x  .
a Tính f 4.
A. f 4 2.
B. f 4 4.
C. f 4 8.
D. f 416. x f t f x Lời giải. Từ 1 dt  6  2 x 
, đạo hàm hai vế ta được  . 2 t 2 x x a 2
Suy ra f x x x 
 f 4  4 4  8. Chọn C.
Vấn đề 2. Kỹ thuật đổi biến 2017 2017 e 1  Câu 6. Cho x
f xdx  2  . Tính tích phân I . f ln    2 x 1    dx. 2  x 1    0 0 A. I  1. B. I  2. C. I  4. D. I  5. Lời giải. Đặt 2xdx xdx dt t   2 ln x   1 , suy ra dt     . 2 2 x 1 x 1 2
x  0  t  0 Đổi cận:  . 2017
x  e 1  t  2017  2017 2017 Khi đó 1 I  f t 1 t  f x 1 d dx  .2  1.   Chọn A. 2 2 2 0 0  9 f  x  2
Câu 7. Cho hàm số f x liên tục trên  và dx  4, f 
sin xcos xdx  2.   Tính tích x 1 0 3 phân I 
f xdx.  0 A. I  2. B. I  6. C. I  4.
D. I  10. 9 f  x  Lời giải.  Xét dx  4.  Đặt 2
t  x  t  x, suy ra 2tdt  dx. x 1
x 1 t 1 9 f  x  3 3 Đổi cận  . Suy ra 4  dx  2
f t2dt  
f tdt  2.    
x  9  t  3  x 1 1 1  2  Xét
f sin xcos xdx  2. 
Đặt u  sin x, suy ra du  cos xdx. 0
x  0  u  0   2 1 Đổi cận   . Suy ra 2 
f sin xcos xdx 
f tdt.   
x   u  1  2 0 0 3 1 3 Vậy I 
f xdx 
f xdx 
f xdx  4.    Chọn C. 0 0 1  4 1 2 x f x
Câu 8. Cho hàm số f x liên tục trên  và
f tan xdx  4, dx  2.   Tính tích 2 x 1 0 0 1 phân I 
f xdx.  0 A. I  6. B. I  2. C. I  3.
D. I  1.  4 Lời giải. Xét
f tan xdx  4.  0 Đặt 1 dt
t  tan x, suy ra dt  dx   2
tan x 1 dx  dx  . 2  2 cos x 1 t
x  0  t  0   4 1 f t 1 f x Đổi cận:   . Khi đó 4 
f tan xdx  dt  dx.    
x   t  1  2 2 t 1 x 1  4 0 0 0 3 1 1 f x 1 2 x f x Từ đó suy ra I 
f xdx  dx  dx  4  2  6.   2  Chọn A. 2 x 1 x 1 0 0 0  4
Câu 9. Cho hàm số f x liên tục trên  và thỏa mãn tan x. f   2
cos xdx 1, 0 2 e f  2 ln x 2 f 2x dx  1. 
Tính tích phân I  dx.  x ln x x e 1 4 A. I  1. B. I  2. C. I  3. D. I  4.  4
Lời giải. ● Xét A  tan x. f   2
cos xdx 1. Đặt 2 t  cos x. 0 Suy ra d 2 t
dt  2 sin x cos xdx  2 cos x tan xdx  2t.tan xdx 
 tan xdx   . 2t x  0  t  1  Đổi cận:  .  1
x  t   4 2 1 2 1 f t 1 1 f t 1 1 f x 1 f x
Khi đó 1  A   dt  dt  dx   dx  2.     2 t 2 t 2 x x 1 1 1 1 2 2 2 2 e f  2 ln x ● Xét B  dx  1.  Đặt 2 u  ln x. x ln x e 2 Suy ra 2 ln x 2 ln x 2u dx du du  dx  dx  dx    . x x ln x x ln x x ln x 2u
x  e  u  1 Đổi cận:  . 2
x  e u  4  4 1 f u 4 1 f x 4 f x Khi đó 1  B  du  dx   dx  2.    2 u 2 x x 1 1 1 2 f 2x
● Xét tích phân cần tính I  dx.  x 1 2  1 d  x  dv   1 1 x   v  Đặt 
v  2x, suy ra 2  . Đổi cận:  4 2 .  v   x    x  2  v  4  2  4 f v 4 f x 1 f x 4 f x Khi đó I  dv  dx  dx  dx  2  2  4.     Chọn D. v x x x 1 1 1 1 2 2 2  
Câu 10. Cho hàm số y  f x xác định và liên tục trên 1  ;2, thỏa 2      2 f x f x 1 1 2  f      x   2.  
Tính tích phân I  dx. 2   x  x 2 x 1 1 2 A. 3 I  . B. I  2. C. 5 I  . D. I  3. 2 2 4  1 x   t  2  Lời giải. Đặt 1 1 
x  , suy ra dx   dt. Đổi cận: 2  . t 2 t  1
x  2 t   2 1 1 1 1 f     f       f   2 2 2             Khi đó t 1 t  x  I  .     dt  dt  dx. 2    2  2 1  t  t 1 x 1 2 1 1 1 2 2 2 t 1 1        1 f x f f x 2 2 2 2 f     2 x   2     2 Suy ra x  x  2  d  d  d x I x x x  dx  2  2  2  2 x 1 x 1 x 1 x 1 1 1 1 1 2 2 2 2 2 2 2 2 x 1  1   1  3  dx  1   
   dx    x     3 
 I  . Chọn A. 2 2 1 x  x   x  2 1 1 2 2 2
Câu 11. Cho hàm số f x liên tục trên  và thỏa f x f x 2 2cos2x với mọi x   . 3 2 Tính I 
f xd x  . 3  2 A. I  6 . B. I  0 . C. I  2 . D. I  6 .  3 3 x    t   Lời giải. Đặt 
t  x  dx  d  t. Đổi cận: 2 2  .  3 3 x   t    2 2 3 3 3  2 2 2 Khi đó I   f  t  dt  f  t  dt 
f xdx.    3 3 3   2 2 2 3 3 3 2 2 2 CASIO Suy ra 2I 
 f t f  t   dt 
2  2 cos 2tdt 
2 cos t dt  12   I  6.      Chọn D. 3 3 3    2 2 2
Câu 12. Cho hàm số y  f x xác định và liên tục trên ,  thỏa f  5 x  4x   3  2x 1 với 8 mọi x  .  Tích phân
f xdx  bằng 2 A. 2. B. 10. C. 32 . D. 72. 3
x  2  t  1 Lời giải. Đặt 5
x  t  4t  3, suy ra x   4 d
5t  4dt. Đổi cận  .
x  8  t  1  8 1 1 Khi đó
f xdx  f 
  5t 4t  3 4
5t  4dt  2t   1   4
5t  4dt 10. Chọn B. 2 1 1
Câu 13. Cho các hàm số f x, gx liên tục trên 0;  1 , thỏa . m f x .
n f 1 x  gx với 1 1 ,
m n là số thực khác 0 và
f xdx 
g xdx  1.   Tính m  . n 0 0
A. m  n  0. B. 1 m  n  .
C. m  n  1.
D. m  n  2. 2 5
Lời giải. Từ giả thiết . m f x .
n f 1 x  gx, lấy tích phân hai vế ta được 1 1  . m f x .
n f 1 xd
 x  g(x)dx     0 0 1 1 1
Suy ra m  n f 1 xdx 1  (do
f xdx 
g xdx  1   ).   1 0 0 0 1
x  0  t 1 Xét tích phân
f 1 xdx. 
Đặt t  1 x , suy ra dt  d
 x. Đổi cận:  .
x  1  t  0 0  1 0 1 1 Khi đó
f 1 xdx   f tdt 
f tdt 
f xdx  1.     2 0 1 0 0 Từ  
1 và 2, suy ra m  n  1 . Chọn C.
Câu 14. Cho hàm số f x xác định và liên tục trên 0; 
1 , thỏa mãn f 'x  f '1 x với mọi 1 x 0; 
1 . Biết rằng f 0  1, f  
1  41. Tính tích phân I 
f xdx.  0 A. I  41. B. I  21. C. I  41. D. I  42.
Lời giải. Ta có f 'x f '1 x 
 f x   f 1 xC.
Suy ra f    f   f 0 1  , f   1 41. 0
1 C  C  42.
Suy ra f x  f 1 x 42 
 f x f 1 x  42 1 1 
  f x f 1 x dx  42dx  42.       1 0 0 1 1
Vì f 'x f '1 x  
f xdx 
f 1 xdx.   2 0 0 1 1 Từ   1 và 2, suy ra
f xdx 
f 1 xdx  21.   Chọn B. 0 0
Câu 15. Cho hàm số y  f x liên tục trên  và thỏa mãn 3
f x f x  x với mọi x  .  2 Tính I 
f xdx.  0 A. 4 I   . B. 4 I  . C. 5 I   . D. 5 I  . 5 5 4 4
Lời giải. Đặt u  f x , ta thu được 3
u  u  x. Suy ra  2 3u   1 du  dx.
x  0  u  0 1 Từ 5 3
u  u  x , ta đổi cận  . Khi đó I  u   2 3u  
1 du  . Chọn D.
x  2  u  1  4 0
Cách khác. Nếu bài toán cho f x có đạo hàm liên tục thì ta làm như sau: 3
 f 0 f 0 0  f 0 0 Từ giả thiết 3
f x f x  x       . * 3
 f 2 f 2 2    f 2  1  Cũng từ giả thiết 3
f x f x  x , ta có f x 3 '
. f x f 'x. f x  x. f 'x. 2 2
Lấy tích phân hai vế  f '   x 3
. f x f 'x. f x dx  x. f '   xdx   0 0
 f x 4  f x 2  2 2  2 2            xf  
x  f x * x  f x 5 d dx  .   4 2   0 0   4   0 0 6
Vấn đề 3. Kỹ thuật tích phân từng phần 3 3
Câu 16. Cho hàm số f x thỏa mãn x. f x f x .e dx  8  và f   3  ln 3 . Tính f x I  e dx.  0 0 A. I  1. B. I  11.
C. I  8ln 3.
D. I  8  ln 3. u   x d  u  dx 3 3 3
Lời giải. Đặt      . Khi đó
x. f x f x f x f x .e
dx  x.e  e dx.   d  v  f  
x f x f x .e dx v     e  0 0 0 3 3 Suy ra f   3 f x f x 8  3.e  e dx   e dx  9 8  1.   Chọn A. 0 0    2 Câu 17. Cho hàm số 
f x có đạo hàm liên tục trên 0; , thỏa mãn f 'x 2 cos xdx  10   và 2    0  2
f 0  3. Tích phân
f xsin 2xdx  bằng 0 A. I  13. B. I  7. C. I  7. D. I  13.  2 2 u   cos x d
 u  sin 2xdx Lời giải. Xét f 'x 2 cos xdx  10  , đặt      . d  v  f '  x 2 cos xdx v   f   x 0    2  2 Khi đó 10  f 'x 2 2
cos xdx  cos xf x 2 
f xsin 2xdx   0 0 0   2 2
 10   f 0
f xsin 2xdx  
f xsin 2xdx  10  f 0  13.   Chọn D. 0 0 2
Câu 18. Cho hàm số y  f x có đạo hàm liên tục trên 0;  1 , thỏa mãn f x   1 dx  3  và 1 1 f   1  4. Tích phân 3 x f ' 2 x dx  bằng 0 A. 1. B. 1  . C. 1 . D. 1. 2 2 2 1 1 Lời giải. Ta có f x  tx 1 1 dx 3    
f tdt  3   hay
f xdx  3.  1 0 0 1 1 1 u   x d  u  dx Xét tx 1 1 3 x f '   2x 2 dx  
tf 'tdt 
xf 'xdx.   Đặt      . 2 2 d  v  f '  xdx v   f   x 0 0 0  1 1 1  1  Khi đó tx 1 1 1 1 3 x f '   2x 2 dx
tf 'tdt xf   x
f xdx       
43 . Chọn C. 2 2 0 2 2 0 0  0   
Câu 19. Cho hàm số f x nhận giá trị dương, có đạo hàm liên tục trên 0;2. Biết f 01 2  3 2
x 3x  f 'x và     2 2 4 2 x x f x f x e   
với mọi x 0;2. Tính tích phân I  dx.  f x 0 A. 14 I   . B. 32 I   . C. 16 I   . D. 16 I   . 3 5 3 5
Lời giải. Từ giả thiết f x f   x 2 2 x 4 x x 2 2  e   f 2  1. 7 3 2 u
  x 3x 2  3 2
x 3x  f 'x  d  u    2
3x 6xdx Ta có I  dx.  Đặt  f 'x    . f x d  v  dx  v
  ln f x 0  f x   2 2 f 2 2 1  Khi đó I   3 2
x 3x ln f x   2
3x 6xln f x dx  3  2
x 2xln f x dx  3J. 0 0 0 2 0 x 2t Ta có J
 x 2xln f x dx  2  t   2 2 22 t       ln f 
2t d2t   0 2 0 2 2 x   2 22 x     ln f 
2 x d2 x   2x 2xln f 2x dx.   2 0 2 2 2
Suy ra 2J    2x 2xln f x dx   2x 2xln f 2x dx    2x 2xln f x f 2x dx 0 0 0 2 2    x  x 32 16 2 x 2x 2 2 4 ln e dx    2 x 2x 2
2x  4xdx    J  . 15 15 0 0 Vậy 16
I  3J   . Chọn D. 5      2  
Câu 20. Cho biểu thức   S  ln 1   
2sin 2x 2cotx e dx, 
 với số thực m  0. Chọn khẳng định    n     2 4m 
đúng trong các khẳng định sau. A. S  5. B. S  9.         C.     S  2 cot    2 ln          sin . D. S 2 tan 2 ln    . 2 2 4  m   4  m  2 2 4  m  4 m     2 2 2 Lời giải. Ta có
2sin 2x 2cotx 2 cot x 2 cot e dx  2 e dx  sin 2 x xe dx.      1    2 2 2 4m 4m 4m    2 2  2   Xét x x x 2 2 cot 2 cot sin 2xe dx  e d    2 sin x 2 2 cot 2 2 cot 2  sin x.e  sin x x      e dx  2  sin x  2   4m  2 2 2 4m 4m 4m   2 2 2 cot x 2 cot 2  sin x.e  2 x e dx. 2     2 4m  2 4m   2 cot Từ    1 và 2, suy ra 2 2 2 cot x 2 2 4
I  sin x.e  1 sin . m e .  2 4  m 2 4m   2 cot        2 2   4    lnsin . m S e     2 cot    2 ln Chọn C.     sin . 2 2 2  4   m  4   m   4  m  8
Vấn đề 4. Tính a, b, c trong tích phân 2 Câu 21. Biết ln   2
9  x dx  a ln5b ln 2 c với ,
a b, c  .
 Tính P  a  b  c . 1 A. P  13. B. P  18. C. P  26. D. P  34.      2    x  2x u ln 9  Lời giải. Đặt du  dx  2    9  x . dv  dx    v   x 3  2 2 2 x x  3  
Khi đó I  x   3 ln 3 2 9  x     2
dx  5ln 5 4 ln 8  2     1   dx 2   1 9  x  3 x  1 1 a   5 2 
5 ln 5 12 ln 2 2x 3ln 3 x  5 ln 5 6 ln 2 2 b          
  6  P 13. Chọn A. 1 c 2 
Nhận xét. Ở đây chọn v  x 3 thay bởi x để rút gọn cho 2
9  x , giảm thiểu biến đổi. 1 3 x 3 x     Câu 22. Biết x 2 ex 2 1 1 e dx   .ln  p    với , m ,
n p là các số nguyên
  e.2x m e ln n  e   0
dương. Tính tổng P  m  n  . p A. P  5. B. P  6. C. P  7. D. P  8. 1 1 3 x 3 x x 1     Lời giải. Ta có x 2 ex 2 2 1 1 3   4 I  dx  x  dx  x  A   . A  
  e.2x 
  e.2x  4 4 0 0 0 1 x Tính 2 A  dx.  Đặt x x x 1
t    e.2 
dt  e.ln 2.2 dx  2 dx  dt.
  e.2x e ln 2 0
x  0  t   e Đổi cận:  .
x  1  t    2e  2e 2e    Khi đó 1 dt 1 1  2e 1 e A  .  ln t  ln  ln 1      . e.ln 2 t e.ln 2   e e ln 2   e e ln 2  e   e m   4    Vậy 1 1 e  I   ln 1        n
  2  P  mn p  7. Chọn C. 4 e ln 2  e   p 1   2 2
x 2x  cos xcos x 1sin x Câu 23. Biết 2 c
dx  a b ln  với ,
a b, c là các số hữu tỉ. x  cos x  0 Tính 3 P  ac  . b A. 5 P  . B. 3 P  . C. P  2. D. P  3. 4 2   2 2 2
x  2x cos x  cos x1sin x
Lời giải. Ta có I  dx  x  cos x 0    
x cos x2 2 2 2 2 1sin x
dx  cos x  dx 
dx  x  cos xdx      x  cos x x  cos x x  cos x 0 0 0 0  1  2 1  1 2 2 2 2
  x sin x  ln x cos x    1 ln   1ln 2  8 2 8  0 9  1 a    8  3   b   1 
 P  ac b  2. Chọn C. c  2  ln 8 Câu 24. Biết 1 1 b
dx  1 ln  a a  b  với , a b 
  . Tính P  a  . b 2 x e 1 x 2 e a ln 3 A. P  1. B. P  1. C. P  3. D. P  5. ln 8 ln 8 ln 8 ln 8 Lời giải. Ta có 1 I  dx  e   e x  e  x  e x     x x  2x 1 x 2 d x 1d x d . 2 e 1 e ln 3 ln 3 ln 3 ln 3 ln 8 ln 8  x d x e x  e  2 2  3.  ln 3 ln 3 ln 8 x tdt d t t  2 x e 1dx.  Đặt 2 x 2 2  1 x t e
 t  e 1 , suy ra 2
2tdt  2e dx  dx   . 2 x 2 e t 1 ln 3
x  ln 3  t  2 Đổi cận:  .
x  ln 8  t  3  ln 8 3 3 2 3      Khi đó x t dt 1 1 t 1 1 3 2 e 1dx  dt  1        dt   t  ln  1 ln . 2 2 t 1  t 1  2 t 1  2 2 ln 3 2 2 2 1 3 a   2 Vậy I 1 ln 2 2 3        
 P  a b  5. Chọn D. 2 2 b   3  2 Câu 25. Biết dx
 a  b c  với , a b, c 
  . Tính P  a b  c .
x 1 x  x x 1 1   A. P  12 . B. P  18 .
C. P  24 . D. P  46 . 2 2 Lời giải. Ta có dx x 1  x I   dx.   x x  
1  x 1  x  x x  
1  x 1  x 2 1 1   Đặt 1 1   x  x 1
u  x 1  x , suy ra du    dx  2du  dx.  
2 x 1 2 x  x x   1
x  2  u  3  2 3 2 3 2   Đổi cận  du 2 1 1  . Khi đó I  2    2        
x  1  u  2 1 2   u u    2 1  3 2 2 1 2 1  a   32  3   2 2 1     2      32  12 2   b
 12 P  46. Chọn D.  32 2 1    c   2   4 Câu 26. Biết sin 4x
a 2  b 6  c dx   với ,
a b, c  .
 Tính P  a  b  c . 2 2
cos x 1  sin x 1 6 0 A. P  10. B. P  12. C. P  14. D. P  36.   4 4 Lời giải. Ta có sin 4x 2 sin 2x cos 2x I  dx  2 dx.   2 2
cos x 1  sin x 1
3  cos 2x  3cos 2x 0 0
x  0  t 1 
Đặt t  cos 2x 
dt  2 sin 2xdx. Đổi cận:   .
x   t  0  4 0 1 1 Khi đó t t 1 I   2 dt  2 dt   
  3t  3tdt
3  t  3t
3  t  3t 2 1 0 0 10 a  16 1 1 2          t3 2   t3 16 2 12 6 8 3 3    b   
  12  P  36. Chọn D. 2 3 3  0  6 c 8  4 x Câu 27. Biết 1 x  e  d b c
x  a  e e 
với a, b, c  .
 Tính P  a b  c. 2 4 x x xe 1 A. P  5. B. P  4. C. P  3. D. P  3.     x x x x e  2 1 4 4 x x e e x e x 2 4 4 4 2 Lời giải. Ta có  dx  dx  dx    2 x 2 4x xe 4 x xe x 1 1 1 2e x2 4 4 x 4 e  2 x  1 1   1  1 1   1 4  dx      dx      x     1
  1 e e x x x     4 2e x 2 x e   e  e e 1 1 1 a  1 b    1 
 P  a b  c  4. Chọn B. c 4  2 Câu 28. Biết
2  x dx  ab 2 c  với ,
a b, c  .
 Tính P  a b  c. 2  x 0 A. P  1. B. P  2. C. P  3. D. P  4.   Lời giải. Đặt 
x  2 cosu với u  0;  . Suy ra 2
x  4 cos u 
dx  4 sin 2ud . u  2      x  0  u    u  2 2 cos Đổi cận  2 2  2 cosu  . Khi đó 2 I  4 sin 2udu  8 .sin . u cosudu      2 2 cosu u x  2  u    sin  4 4 4 2     2 2 2 2 2 u  16 cos
.cos udu  8 1 cosu.cosudu  8 cosudu  4 1 cos 2udu     2     4 4 4 4 a  1    2 8 sin u               Chọn C. 
4x 2.sin 2u 2 4 2 6 b 4 P 3.   4 4 c   6  e 2 Câu 29. Biết ln x  ln x 1 b I  dx    với , a b 
  . Tính P  b  . a
ln x  x  3 1 a e 22 1 A. P  8. B. P  6. C. P  6. D. P  10. e 2 e Lời giải. Ta có ln x  ln x ln x 1 ln x dx  . dx.  
ln x  x  3 1
ln x  x 1 ln x  x  2 1 1 1 /     Đặt ln x 1 ln x 1 ln x t   dt      dx   dx. ln x  x 1
ln x  x 1
ln x  x  2 1  1
x 1 t  2 2  e2 e2 Đổi cận:  2 1 1 2  . Khi đó 2 I  
tdt   t   .  2  Chọn B.  2 2 8
x  e  t  1 1 e 2  e  2 2 2  6 2 Câu 30. Biết x cos x  3 dx  a    với ,
a b, c là các số nguyên. Tính P  a b  c. 2  1 x  x b c  6 A. P  37. B. P  35. C. P  35. D. P  41. 11    6 6 6 Lời giải. Ta có x cos x I  dx  x cos x    2
1 x  xdx  x   2
1 x  x cos xdx. 2   1 x  x      6 6 6      6 6 x cos x t x  t  cos t   6 Lại có  x   t   t cos t I d d  dt    2  1 x  x  1       t2 2 t  1 t t 6 6 6   6   t
  1t t 6 2
cos tdt   x   2
1 x  xcos xdx.     6 6    6 6 6 Suy ra 2I  x   2
1 x  xcos xdx  x   2 1 x  x 2
cos xdx  2 x cos xdx        6 6 6  6 2  3 2  
 I   x cos xdx. 
Tích phân từng phần hai lần ta được I  2   36 3   6 a   2 b    36 
 P  a b  c  35. Chọn C. c 3 
Vấn đề 5. Tính tích phân hàm phân nhánh x 1 khi x  0 2
Câu 31. Cho hàm số f x   
. Tính tích phân I 
f xdx.  2 x e  khi x  0  1  2 2 2 2 A. 3e 1 7e 1 9e 1 11e 11 I  . B. I  . C. I  . D. I  . 2 2e 2 2e 2 2e 2 2e 0 2 0 2 2
Lời giải. Ta có    e  I f x dx  f x x 9 1 2 dx 
e dx  x   1 dx  .     Chọn C. 2 2e 1  0 1  0   Câu 32. Cho hàm số 2
f x xác định trên 1  \ 
 , thỏa f x  , f 
0  1 và f   1  2. 2   2x 1
Giá trị của biểu thức f   1  f   3 bằng A. ln15. B. 2  ln15. C. 3 ln15. D. 4  ln15.
Lời giải. Ta có f x 2  2x 1
   x 1 ln 1 2 C ; x  1    f x 2 2 
dx  ln 2x 1 C    . 2x 1 ln2x  1 1 C ; x  2  2
 f 0  1 
 ln12.0C  1  C  1. 1 1  f   1  2   ln2.1 
1 C  2  C  2. 2 2
   x 1 ln 1 2 1 khi x   2  f   1  ln 3 1
Do đó f x          x   1  f   3  ln 5  2 ln 2 1  2 khi x    2   f   1  f  
3  3  ln 5  ln 3  3  ln15. Chọn C. 12 Câu 33. Cho hàm số 1
f x xác định trên \2; 
1 , thỏa mãn f x  , 2 x  x 2 f   3  f   3  0 và f   1
0  . Giá trị biểu thức f 4 f   1  f 4 bằng 3 A. 1 1 ln 20  . B. 1 1 ln 2  . C. ln 80 1. D. 1 8 ln 1. 3 3 3 3 3 5  
Lời giải. Ta có f x 1 1 1 1        2 x  x 2
3  x 1 x  2 1  ln 
1 xlnx 2 C ;x 2 1 3      f x 1 1  dx    
 ln 1 x ln x  2  C ;2  x 1. 2     2 x x 2 3    
1lnx 1lnx2C ;x1 3 3    1 1 1 1 1
 f 0  
 ln10ln0  2 C   C  ln 2  . 2 2 3 3   3 3 3 1 1  f   3  f   3  0  C C  ln . 1 3 3 10
Ta có f   f   f   1 5 1 1 1 1 1 4 1
4  ln  ln 2  ln C C C  ln 2  . Chọn B. 2 1 3 3 2 3 3 2 3 3 Câu 34. Cho hàm số 1
f x xác định trên 0;\e, thỏa mãn f x  ,
x ln x   1  1  1 f  
   ln 6 và f  2
e  3. Giá trị biểu thức f     f    3e bằng 2 e  e  A. 3ln 2   1 . B. 2 ln 2. C. 3ln 2 1. D. ln 2 3.
Lời giải. Ta có f x 1 
x ln x   1 1 dln x   1
ln1ln xC khi x  0;e 1   f x dx ln ln x 1 C             .
x ln x   1 ln x   1 ln  ln x  
1 C khi x  e; 2     1   1   f      ln 6   ln 1   
 ln C  ln 6  C  ln 2. 2 2 1 1 e   e   f  2 e  3   ln 2 ln e  
1 C  3  C  3. 2 2  1
ln1ln x ln 2 khi x 0;e  f      ln 2  ln 2
Do đó f x       e   ln  ln x  
1  3 khi x  e;    f   3 e  ln 2 3  1   f     f  
 3e 3ln2 1. Chọn C. e    Câu 35. Cho  
F x là một nguyên hàm của hàm số 1  y  với x  \ k ,  k       . 1 sin 2x  4        Biết  
F 0  1, F  0
 , tính giá trị biểu thức 11 P  F      F      .  12  12  A. P  0.
B. P  2 3. C. P  1.
D. Không tồn tại P.   Lời giải. Với  
x thuộc vào mỗi khoảng  
 k;  k, k    ta có  4 4    F x dx dx dx 1     tan    x   C. 1 sin 2x
sin x cos x2     2  2  4  2 cos x     4  13     0    1   1 3   F   3 3  0;   ;  nên F 0 0 1  F       tan   x        F            . 12  4 4  12 2  4      2 2  12 2 2 12
   11 1    1 3   F   11 1 3  11 5 ;
 ;  nên F    0  F      tan   x        F           . 12 4 4  11 12 2  4   2 2  12  2 2 12     Vậy  11 P  F      F        1. Chọn C.  12  12 
Vấn đề 6. Tính tích phân dựa vào tính chất 0
Câu 36. Cho hàm số f x là hàm số lẻ, liên tục trên 4;4 . Biết rằng
f xdx  2  và 2 2 4
f 2xdx  4. 
Tính tích phân I  f xdx.  1 0 A. I  10. 
B. I  6.
C. I  6.
D. I 10.
Lời giải. Do f x là hàm lẻ nên f x  f x. 0
x    t   Xét A 
f xdx  2. 
Đặt t  x  dt  d  x. Đổi cận: 2 2  .
x  0  t  0 2  0 2 2
Khi đó A   f tdt  f tdt  f xdx.    2 0 0 2 2
x   u   Xét B 
f 2xdx   f 2xdx.  
Đặt u  2x 
du  2dx. Đổi cận: 1 2  .
x  2  u  4 1 1  4 4 4 Khi đó 1 B   f u 1 du  
f xdx  
f xdx  2B  2.4  8.    2 2 2 2 2 4 2 4
Vậy I  f xdx  f xdx  f xdx  28  6.    Chọn B. 0 0 2 2
Câu 37. Cho hàm số f x là hàm số chẵn, liên tục trên 1;6. Biết rằng
f xdx  8  và 1 3 6
f 2xdx  3. 
Tính tích phân I  f xdx.  1 1 A. I  2. B. I  5. C. I 11. D. I 14. 3 3
Lời giải. Vì f x là hàm số chẵn nên f 2xdx  f 2xdx  3.   1 1 3  Xét
x   t  K 
f 2xdx  3. 
Đặt t  2x 
dt  2dx. Đổi cận: 1 2  .
x  3  t  6 1  6 6 6 Khi đó 1 K  f t 1 dt 
f xdx  
f xdx  2K  6.    2 2 2 2 2 6 2 6
Vậy I  f xdx  f xdx  f xdx  8  6 14.    Chọn D. 1 1 2
Câu 38. Cho hàm số f x liên tục trên 3;7, thỏa mãn f x f 10 x với mọi x 3;7 và 7 7
f xdx  4. 
Tính tích phân I  xf xdx.  3 3 A. I  20. B. I  40. C. I  60. D. I  80.  Lời giải. Đặt
x   t 
t  3  7 x  dt  d  x. Đổi cận 7 3  .
x  3  t  7  3 7 7
Khi đó I   10t f 10tdt  10t f 10tdt  10 x f 10 xdx    7 3 3 14
f x f  x 7 7 7 7 10 
10  x f xdx 10 f xdx  xf xdx 10 f xdx  I.     3 3 3 3 7
Suy ra 2I 10 f xdx 10.4  40  I  20.  Chọn A. 3
Câu 39. Cho hàm số y  f x là hàm số chẵn và liên tục trên đoạn  
 ;, thỏa mãn   f x
f xdx  2018.  Giá trị của tích phân   I  dx  bằng 2018x 1 0  A. I  0. B. 1 I  . C. I  2018. D. I  4036. 2018  Lời giải. Đặt x  
  t   x  t   dx  d
 t. Đổi cận  .
x    t        t  x Khi đó f  t   f  t   2018 f  t  
2018 f x I   dt  dt  dt  dx.     2018t 1 2018t 1 1 2018t 1 2018x      x Vì 2018 f x
y  f x là hàm số chẵn trên đoạn  
 ; nên f x f x I  dx.  2018x 1    x   Vậy f x 2018 f x 2I  dx  dx 
f xdx  2 f xdx  2.2018  I  2018.     Chọn C. 2018x 1 2018x 1    0  2018 a Câu 40. Biết x sin x  dx   với a,b 
  . Tính P  2a  . b 2018 2018 sin x  cos x b 0 A. P  6. B. P  8. C. P 10. D. P 12.  2018 Lời giải. Gọi x sin x I  dx  2018 2018 sin x  cos x 0  Đặt
x   t  
t    x  dt  d  x. Đổi cận 0  .
x    t  0  0 2018  2018  2018 Khi đó
 tsin  t
 tsin t
  xsin x I   dt  dt  dx.  2018   sin  t 2018  cos  t 2018 2018 2018 2018 sin t  cos t sin x  cos x  0 0  2018   2018 Suy ra x sin x
  x 2018 sin x  sin x 2I  dx  dx  dx  2018 2018  2018 2018  2018 2018 sin x  cos x sin x  cos x sin x  cos x 0 0 0     2018  2 2018  2018  sin x  sin x sin x  I dx  dx dx      .  2018 2018  2018 2018  2018 2018 2 sin x cos x 2 sin  x cos x sin x cos x     0 0      2    2018 2 2018  2018 Đặt  sin x cos u cos x
x  u  ta suy ra dx  du  dx.    2 2018 2018 2018 2018 2018 2018 sin x  cos x sin u  cos u sin x  cos x  0  2 2  2 2  Vậy   a   2 I dx        
P  8. Chọn B. 2 4 b   4 0 
Vấn đề 7. Kỹ thuật phương trình hàm   Câu 41. Cho hàm số  
y  f x liên tục trên  ;  và thỏa mãn 2 f x f x  cos x. Tính  2 2     2 tích phân I 
f xdx.    2 A. I  2. B. 2 I  . C. 3 I  . D. I  2. 3 2 15
Lời giải. Từ giả thiết, thay x bằng x ta được 2 f x f x cos x. 2
 f x f x cos x
4 f x2 f x 2cos x Do đó ta có hệ        f x 1  cos x. 2
 f x f x cos x  
 f x 2 f x  cos x 3    2 2  Khi đó I  f x 1 1 2 2 dx 
cos xdx  sin x  .   Chọn B. 3 3   3   2   2 2 Câu 42. Cho hàm số 1
y  f x liên tục trên 2;2 và thỏa mãn 2 f x3 f x  . 2 4  x 2 Tính tích phân I 
f xdx.  2 A.     I   . B. I   . C. I  . D. I  . 10 20 20 10
Lời giải. Từ giả thiết, thay 1
x bằng x ta được 2 f x3 f x  . 2 4  x  
 f x f x 1  2 2 3 
4 f x  6 f x   2      2 Do đó ta có hệ  4  x  4  x      f x 1  . 2        1 3 5 4 2 3 9       6  x f x f x f x f x  2       2  4 x    4  x 2 2 Khi đó  I  f x 1 1 dx  dx  .   Chọn C. 2 5 4  x 20 2 2
Câu 43. Cho hàm số y  f x liên tục trên 0;  1 và thỏa mãn 2
x f x f   x 4 1  2x  x . 1 Tính tích phân I 
f xdx.  0 A. 1 I  . B. 3 I  . C. 2 I  . D. 4 I  . 2 5 3 3
Lời giải. Từ giả thiết, thay x bằng 1 x ta được   x2 f   x f x   x  x4 1 1 2 1 1   2
x  x   f   x f x 2 3 4 2 1 1
 1 2x 6x  4x  x .   1 Ta có 2
x f x f   x 4
 x  x 
 f   x 4 2 1 2 1
 2x  x  x f x. Thay vào   1 ta được
 2x  x   4 2
 x  x  x f  x  f   x 2 3 4 2 1 2
 1 2x 6x  4x  x    2 3 4
 x  x  x  f x 6 5 3 2 1 2
 x 2x  2x 2x 1   2 3 4
1 x  2x  x  f x  2 1 x  2 3 4
1 x  2x  x    f x 2  1 x . 1 1 1   Vậy I 
f xdx     1 2 2 1 x  3
dx  x  x   .  Chọn C.  3  3 0 0 0    
Câu 44. Cho hàm số f x liên tục trên 1
 ;2 và thỏa mãn f x 1  2 f  
   3x. Tính tích 2    x  2 f x phân I  dx.  x 1 2 A. 1 I  . B. 3 I  . C. 5 I  . D. 7 I  . 2 2 2 2  
Lời giải. Từ giả thiết, thay 1 3
x bằng 1 ta được f  
  2 f x  . x x  x 16        f x 1  f      x      f x 1 2 3  2 f      3x        Do đó ta có hệ x x        f x 2   x.  1      
   f x 3    f x 1 6 x f 2 4  2 f           x  x     x  x  2 f x 2 2     Khi đó 2 2 3 I  dx   
  1dx    
 x  . Chọn B. 2 1 x  x   x  2 1 1 2 2 2    
Cách khác. Từ f x 1  f      x   f x 1 2 3
 3x 2 f      .  x  x   1 1         2   2 f 2 2 f f x           Khi đó x  x  I  dx  32  
dx  3 dx 2 dx.     x  x  x 1 1   1 1   2 2   2 2   1   2 f     Xét  x  1 1 J  dx.  Đặt 1 t  , suy ra 2 dt   dx  t  dx 
dx   dt. x x 2 2 x t 1 2  1
x   t  2 1  2 2  1  f t 2 f x Đổi cận:  2  . Khi đó J  tf t     dt  dt  dx  I.    1    2  t  t x
x  2  t  2 1 1  2 2 2 2 2 Vậy 3
I  3 dx 2I   I  dx  .   2 1 1 2 2
Câu 45. Cho hàm số f x liên tục trên 0; 
1 và thỏa mãn f x f   x 2 2 3 1  1 x . Tính 1 tích phân I 
f xdx.  0 A.     . B. .
C. . D. . 20 16 6 4
Lời giải. Từ giả thiết, thay x bằng 1 x ta được f   x f x 2 2 1 3  2x  x . 2
 f x 3 f 1 x 2 1 x     
4 f x 6 f 1 x 2  2 1 x Do đó ta có hệ      2
 f 1x3 f x 2  2x  x 9  
 f x 6 f 1 x 2  3 2x  x   2 2 
   3 2x  x 2 1 x f x  . 5 1 Vậy 1  I    2 2
3 2x  x 2 1 x dx  . Chọn A. 5 20 0
Cách khác. Từ 2 f x 3 f 1 x 1 2 1 x f x  2 1 x 3 f  1 x           . 2    1 1 1   Khi đó I f x 1 2 dx  1 x dx 3
f 1 xdx      .    2   0  0 0  1 Xét J 
f 1 xdx. 
Đặt t  1 x  dt  d  x. 0
x  0  t 1 0 1 1 Đổi cận: 
. Khi đó J   f tdt  f tdt 
f xdx  I.    
x  1  t  0  1 0 0 1 1   Vậy 1 1 2 2  I 
1 x dx 3I       I  1 x dx  .   2   5 20  0  0 17
Vấn đề 8. Kỹ thuật biến đổi
Câu 46. Cho hàm số f x thỏa f x f x 5 2
 3x  6x . Biết rằng f 0  2, tính 2 f 2. A. 2 f 2  64. B. 2
f 2  81. C. 2 f 2  100. D. 2 f 2  144. 2 6 f x
Lời giải. Từ giả thiết ta có
f x f x x     5 2 x  x    x 3 . d 3 6 dx    2x C. 2 2 2 f 0
Thay x  0 vào hai vế, ta được
 C  C  2. 2 Suy ra 2 f x 6 3 2
 x  x    f   6 3 4 4
2  2  4.2  4  100. Chọn C.
Câu 47. Cho hàm số f x có đạo hàm f 'x liên tục và nhận giá trị không âm trên 1;, thỏa f  
1  0, f x e
 f x 2 2 2 .
  4x 4x 1  
với mọi x 1;. Mệnh đề nào sau đây đúng?
A. 1 f 4 0. B. 0  f 41.
C. 1 f 4 2.
D. 2  f 4 3.
Lời giải. Từ giả thiết suy ra f x e
f x  2x 1 (do f 'x không âm trên 1; ) f x   e
f x x   x   f x 2 d 2 1 dx  e
 x  x C.  
Thay x  1 vào hai vế, ta được f  1 2 e
 1 1C  C  1. Suy ra f x 2x 1 7 2 e
 x  x 1  f x  ln 2 x  x  
1  f x    f  4  . Chọn B. 2   x  x 1 13
Câu 48. Cho hàm số f x thỏa mãn  f x 2  f x f  x 4 .  15x 12x  
với mọi x   và
f 0  f 0  1. Giá trị của 2 f   1 bằng A. 5 . B. 9 . C. 8. D. 10. 2 2
Lời giải. Nhận thấy được f x 2  f x. f  x f x. f x      .    
Do đó giả thiết tương đương với  f x f x  4 .
 15x 12x.  
Suy ra f x. f x   4 15x 12x 5 2
f 0 f 0 1  .
dx  3x  6x C C  1 
 f x f x 5 2 .
 3x  6x 1 2 6  
f x f x x     f x 5 2 x  x     x 3 . d 3 6 1 dx  
 2x  x C '. 2 2 2 f 0 Thay 1
x  0 vào hai vế ta được
 C '  C '  . 2 2 Vậy 2 f x 6 3 2
 x  4x  2x 1   f   1  8. Chọn C.
Câu 49. Cho hàm số f x có đạo hàm liên tục trên đoạn 1;2 và thỏa mãn 2 2 f x
f x 0,x 1;2. Biết rằng
f xdx  10  và dx  ln 2.  Tính f 2. f x 1 1
A. f 2 20.
B. f 2 10.
C. f 210.
D. f 2 20. 2 2 Lời giải. Ta có
f xdx  10  f x  10  f 2 f   1  10.    1 1 1 2 f x 2 2 Lại có
dx  ln 2  ln f x  ln 2  ln  f x  ln 2 
(do f x 0,x 1;2) f x   1 1 1 f 2 f 2
 ln f 2ln f   1  ln 2  ln  ln 2   2. 2 f   1 f   1 18 Từ  
1 và 2 , suy ra f 2  20. Chọn B.
Câu 50. Cho hàm số f x có đạo hàm liên tục trên 1; 
1 , thỏa mãn f x 0, x   và
f 'x 2 f x  0 . Biết rằng f  
1  1 , giá trị của f   1 bằng A. 2 e . B. 3 e . C. 4 e . D. 3. f 'x
Lời giải. Ta có f 'x2 f x 0  f 'x 2 f x 
 2 (do f x 0 ) f x f 'x  
dx  2dx  ln f x  2x C  
(do f x 0 ). f x
Mà f    C   f x  x    f x 2x 2  e   f   4 1 1 2 ln 2 2
1  e . Chọn C.
Câu 51. Cho hàm số f x xác định và liên tục trên  đồng thời thỏa mãn
f x0, x   
f 'x x 2  e  f x, x  .
f   1 0   2
Tính giá trị của f ln 2. A. f   1 ln 2  . B. f   1 ln 2  . 4 3 C. 1 f   1 ln 2  ln 2  . D. f ln 2 2  ln 2  . 2 2 f ' x x 2  
Lời giải. Ta có f 'x e  f x x   e
 (do f x 0 ) 2 f x f 'x x 1 x 1   dx  e  dx    e
 C  f x  .  2    f x f x x e C Thay 1 f 
x  0 ta được f 0   1 0 2 
C  1. 0 e C Vậy f x 1    f   1 1 1 ln 2    . Chọn B. x ln 2 e 1 e 1 2 1 3
Câu 52. Cho hàm số f x có đạo hàm liên tục trên 0; , biết f x x   2 ' 2
3 f x  0,
f x 0 với mọi x  0 và f   1
1  . Tính P  1 f  
1  f 2... f 2018. 6 A. 1009 P  . B. 2019 P  . C. 3029 P  . D. 4039 P  . 2020 2020 2020 2020 f ' x 2  
Lời giải. Ta có f 'x2x  
3 f x  0 
  2x 3 (do f x 0 ) 2   f x f 'x  
dx   2x   1 1 2 3 dx  
 x 3x C   f x  .  2    f x f x 2
x  3x C Mà f   1 1 1 1 1 1 1      C  2   f x    . 2   2 6 6 1  3.1C x  3x  2 x 1 x  2       Suy ra 1 1 1 1 1 1 3029 P  1          ...  Chọn C.         . 2 3 3 4 2019 2020 2020
Câu 53. Cho hàm số f x liên tục trên 0; 3,  thỏa mãn và  
f x 1, f 0  0 f x 2
x 1  2x f x1. Giá trị của f  3 bằng A. 0. B. 3. C. 7. D. 9. 19 f x 2x f x
Lời giải. Từ giả thiết suy ra 2x    dx  dx   f x 2 1 x 1 f x 2 1 x 1 f x x  / 2 1  2 dx  2
dx  2 f x 2
1  2 x 1 C   2 f x 2 1 2 x 1
Mà f    C   f x 2 0 0 0  x 
 f  3 3. Chọn B.
Câu 54. Cho hàm số f x có đạo hàm và liên tục trên 1;4, đồng biến trên 1;4, thoản mãn 4
x  xf x   f x 2 2  
 với mọi x 1;4. Biết rằng f   3
1  , tính tích phân I 
f xdx.  2 1 A. 1186 I  . B. 1187 I  . C. 1188 I  . D. 9 I  . 45 45 45 2
Lời giải. Nhận xét: Do f x đồng biến trên 1;4 nên f 'x 0, x  1;4 .
Từ giả thiết ta có x   f x   f x 2 1 2  
 f 'x  x. 1 2 f x, x 1;4     2 f x 2 f x    x   x  x x   f x 2 d d 1 2  x x C.  
2 1 2 f x
2 1 2 f x 3 2 2 4  x x    1   Mà   f   3 4 1   C    f x 3 3 2 8 7 3 
 x  x x  2 3 2 9 9 18 4   f x 1186 dx  .  Chọn A. 45 1   Câu 55. Cho hàm số 
f x liên tục, không âm trên 0;  , thỏa f x f x 2 . '
 cos x 1 f x  2        với mọi  
x  0;  và f 0  3. Giá trị của f   bằng    2    2 A. 0. B. 1. C. 2. D. 2 2.
2 f x. f x  
Lời giải. Từ giả thiết ta có   cos x, 0 x   ;  2 2 1 f x  2   
2 f x. f x 2   dx 
cos xdx  1 f x  sin x C.   2 2 1 f x   Mà  f     C  
 f x   x  2 2 0 3 2 sin
2 1  sin x  4 sin x  3, 0 x   ;   2       f      2 2.  Chọn D.  2 
Câu 56. Cho hàm số f x liên tục, không âm trên 0;3, thỏa f x f x 2 .
 2x f x1 với
mọi x 0;3 và f 0 0. Giá trị của f   3 bằng A. 0. B. 1. C. 3. D. 3 11.
2 f x. f x
Lời giải. Từ giả thiết ta có
 2x, x  0;3 2 2 1 f x
2 f x. f x 2   dx 
2xdx  1 f x 2  x C.   2 2 1 f x
Mà f    C  
 f x  x  2 2 4 2 0 0 1
1 1  x  2x , x  0;3   f   3  3 11. Chọn D. 20
Câu 57. Cho hàm số f x có đạo hàm không âm trên 0; 
1 , thỏa mãn f x 0 với mọi x 0; 
1 và  f x 4  f x 2   
 x      f x 3 2 . ' . 1 1  . 
 Biết f 0  2, hãy chọn khẳng định đúng
trong các khẳng định sau đây. A. 3 5  f   1  2.
B.  f   5 2 1  . C.  f   1  3.
D.  f   7 3 1  . 2 2 2 2
 f x 2 2 3 . f 'x
Lời giải. Từ giả thiết ta có  f x . f 'x 1 2
. x 1  1  f x        
  f x 3 2  x 1 1   3    2 1    1 1 d    1 2 1 . ' f x f x f x     1 1     dx  dx    dx    
  f x 3 2  x 1 3
  f x 3 2 0 0 0  0 x 1 1 2 1     1 1 2
  1  f x 3  ln    2 x  x 1 f 02  f   1  2,605. Chọn C. 3 0 0
Câu 58. Cho hàm số f x liên tục trên \0; 
1 , thỏa mãn x x   f x f x 2 1 .  x  x
với mọi x  \0;  1 và f  
1  2 ln 2. Biết f 2  a b ln 3 với ,
a b   , tính 2 2
P  a  b . A. 1 P  . B. 3 P  . C. 13 P  . D. 9 P  . 2 4 4 2
Lời giải. Từ giả thiết ta có x   1 x f x  f x  , x  \ 0;1 . 2     x 1 x   1 x 1    Nhận thấy x   1 x f x 
f x   f x .
 . Do đó giả thiết tương đương với 2     x 1 x   1  x 1      x  x f x .   , x  \ 0;  1 .  x 1 x 1   Suy ra   x x f x .  dx  1      
dx  x ln x 1 C. x 1 x 1  x 1 Mà   x
f 1  2 ln 2  C  1   f x.
 x ln x 1 1. x 1  3 a    Cho 2 3 3  2 9
x  2 ta được f 2.  2ln 31  f 2   ln 3  
 P  . Chọn D. 3 2 2  3 2 b     2
Câu 59. Cho hàm số f x có đạo hàm xác định, liên tục trên 0; 
1 , thỏa mãn f 0  1 và
 f x 2  f  x   
với mọi x 0; 
1 . Đặt P  f  
1  f 0 , khẳng định nào sau đây đúng?
 f x 0 
A. 2  P  1.
B. 1 P  0.
C. 0  P 1.
D. 1 P  2. 1
Lời giải. Nhận thấy P  f   1  f 0 
f xdx 
nên ta cần tìm f x. 0 f  x f  x Từ giả thiết ta có 1 1  1  
dx  1dx  
 x C  f  x   . 2  2   
 f x
 f x f x x C    
Mà f     C    f x 1 0 1 1   . x 1 21 1 1 Vậy P  f x 1 dx  
dx  ln 2  0,69.   Chọn B. x 1 0 0
Câu 60. Cho hai hàm số f x và gx có đạo hàm liên tục trên 0;2, thỏa mãn 2
f '0. f '2  0 và  . '    2 x g x f x x x
e . Tính tích phân I 
f x.g 'xdx.  0 A. I  4. B. I  4.
C. I  e 2.
D. I  2e.  f '0 0
Lời giải. Từ giả thiết f '0. f '2 0     .  f '2 0   222 x   e g 2   0  f '2
Do đó từ  . '   2 x g x f x x x e , suy ra  .  002 x   e g 0   0  f '  0  2 2
Tích phân từng phần ta được I   f x.gx  gx. f xdx    0 0 2 2
 2. 2 0. 0  2 xd    2 x f g f g x x e x x x e dx  4.   Chọn B. 0 0
Câu 61. Cho hàm số f x 0 xác định và có đạo hàm trên đoạn 0;  1 , thỏa mãn x
gx12018 f tdt 1    . Tính I 
g xdx. 0    0 gx 2  f x  A. 1009 I  . B. I  505. C. 1011 I  . D. 2019 I  . 2 2 2
g 'x 2018 f x
Lời giải. Từ giả thiết, ta có  
2018 f x  2 f 'x. f x
g 'x 2 f 'x. f x
f x0 loaïi
 2 f x 1009 
 f 'x  0   .   
 f 'x  1009 
 f x  1009x C  x
Thay ngược lại, ta được 1 2018 1009t C dt  1009x C2  0 x   1009  1 2018
t Ct  1009x C 2 2 2  C  1.   2  0
Suy ra f x1009x 1 hoặc f x1009x 1 (loại vì f x 0 x  0;  1 ). 1 1 1 Khi đó I 
g x x 
f x x   x   1011 d d 1009 1 dx  .    Chọn C. 2 0 0 0  f   1  g   1  4 
Câu 62. Cho hai hàm f x và gx có đạo hàm trên 1;4, thỏa mãn gx xf x với mọi
f xxgx  4
x 1;4. Tính tích phân I   f x gx dx.    1 A. I  3ln 2.
B. I  4 ln 2.
C. I  6 ln 2.
D. I  8 ln 2.
Lời giải. Từ giả thiết ta có f x gx x. f x x.gx
 f x x. f x  gx x.gx  0  x. f x   x.gx           0         22 C 
 x. f x x.gx  C  f x gx  . x 4 4
Mà f   g   C    I 
 f x gx 4 1 1 4 4  dx  dx  8 ln 2.     Chọn A. x 1 1
Câu 63. Cho hai hàm f x và gx có đạo hàm trên 1;2, thỏa mãn f   1  g   1  0 và  x 
g x  2017x  x 1 f  x  2       x   1  , x  1;2.  3  x  g 
x f x 2  2018x x 1 2    Tính tích phân x I  
g x x 1 
f x dx.   x 1 x  1  A. 1 I  .
B. I  1. C. 3 I  . D. I  2. 2 2  1 x   1  g x 
f  x  2017 2     
Lời giải. Từ giả thiết ta có x   1 x  , x  1;2.  x  gx 1  f x  2018 2   x 1 x           Suy ra 1 x   x  1 1 x x  1 g x  g x   f  x  f x   1   g x    f x   1  2       2       x   1 x 1   x x        x 1    x    x x   1   g x
f x  x C. x 1 x 2 2   
Mà f   g  x
  C     I  
g x x 1 
f x x  x   1 1 1 0 1 d 1 dx  .    Chọn A.  x 1 x  2 1 1
 f 3 x. f x1
Câu 64. Cho hàm số y  f x có đạo hàm trên 0;3, thỏa mãn  với mọi
 f x1  3 xf 'x
x 0;3 và f   1
0  . Tính tích phân I  dx.  2 1
  f 3 x 2 2  0 . f x   A. 1 I  . B. I  1. C. 3 I  . D. 5 I  . 2 2 2
 f 3 x. f x1 
Lời giải. Từ giả thiết  x 3  1   f   3  2.  f 0  2
f 3x. f x 1 
Ta có   f   x 2 f x    1
  f x 2 2 1 3 .  .     3 xf 'x 3 3   3 Tích phân  1  x 1 I  dx   xd        
dx  1 J .     1 f x  f x  1 f x 1 f x 0 1   2     0   0 0   3 0 3 3 t3x Tính 1 1 1 1 J  dx   dt  dt  dx.     1 f x
1 f 3t
1 f 3t
1 f 3 x 0 3 0 0 3 3
f  x f x 3 3 . 1  Suy ra 1 1 3 2J  dx  dx 
1.dx  3  J  .    Vậy 1
I  . Chọn A. 1 f x
1 f 3 x 2 2 0 0 0
Câu 65. Cho hàm số y  f x liên tục trên đoạn 0; 
1 và thỏa mãn af bbf a  1 với mọi 1 a, b  0; 
1 . Tính tích phân I 
f xdx.  0 A. 1   I  . B. 1 I  . C. I  . D. I  . 2 4 2 4 23   Lời giải. Đặt  a  sin x, cos b 
x với x  0; .  2   
Từ giả thiết, suy ra sin xf cos xcos xf sin x1    2 2 2  
 sin xf cos xdx  cos xf sin xdx  1dx  .      1 2 0 0 0   2 0 1 tcos x
 sinxf cosxdx   f tdt  f xdx     1 Ta có 0 1 0    . Do đó   1 
f xdx  .  Chọn D.   4 2 1 1  0 tsin x
 cos xf sin xdx 
f tdt 
f xdx     0 0 0
Vấn đề 9. Kỹ thuật đạo hàm đúng
Câu 66. Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thoả mãn     2018 3 f x xf x  x với 1 mọi x 0;  1 . Tính I 
f xdx  . 0 A. 1 I  . B. 1 I  . C. 1 I  . D. 1 I  . 20182021 20192020 20192021 20182019
Lời giải. Từ giả thiết f x xf x 2018 3  x , nhân hai vế cho 2 x ta được 2 x f x 3
 x f x 2020 3  x  x f  x 2020 3  x .   2021 Suy ra 3   2020 x x f x  x dx  C.  2021 2018 Thay x
x  0 vào hai vế ta được C  0 
 f x  . 2021 1 1 1 Vậy f x 1 1 1 1 2018 2019 dx  x dx  . x  .   Chọn C. 2021 2021 2019 20212019 0 0 0
Nhận xét: Ý tưởng nhân hai vế cho 2
x là để thu được đạo hàm đúng dạng uv'  u 'v uv '.
Câu 67. Cho hàm số f x có đạo hàm liên tục trên 0;4, thỏa mãn     x f x f x  e
2x 1 với mọi x 0;4. Khẳng định nào sau đây là đúng? A. 26 4
e f 4 f 0  . B. 4
e f 4 f 0  3e. 3 C. 4
e f   f   4 4 0  e 1. D. 4
e f 4 f 0  3.
Lời giải. Nhân hai vế cho x
e để thu được đạo hàm đúng, ta được x   x    x e f x e f x  x   e f  x / ' 2 1   2x 1.   Suy ra x e f x 1 
2x 1dx  2x   1 2x 1 C.  3 Vậy 26 4
e f 4 f 0  . Chọn A. 3
Câu 68. Cho hàm số f x có đạo hàm trên ,  thỏa mãn     2017 2018 ' 2018  2018 x f x f x x e với
mọi x   và f 0 2018. Tính giá trị f   1 . A. f   2018 1 2018e  . B. f   2018 1  2017e . C. f   2018 1  2018e . D. f   2018 1  2019e .
Lời giải. Nhân hai vế cho 2018x e
để thu được đạo hàm đúng, ta được 24
f x 2018x e 
f x 2018x 2017 e  x   f
 x 2018x  2017 2018 2018 e   2018x .  
Suy ra f x 2018x 2017 2018 e  2018x dx  x C. 
Thay x  0 vào hai vế ta được        2018   2018 2018 2018 x C f x x e . Vậy f   2018 1  2019e . Chọn D.
Câu 69. Cho hàm số f x có đạo hàm và liên tục trên ,  thỏa mãn     2 2 x f x xf x xe    và
f 0  2. Tính f   1 . A. f   1  e. B. f   1 1  . C. f   2 1  . D. f   2 1   . e e e 2 x
Lời giải. Nhân hai vế cho 2
e để thu được đạo hàm đúng, ta được 2 2 2 2 2 x x x x    x   f x 2
e  f x 2 2  2 xe  xe
 e f x 2 2  2xe .     2 2 2 x x x Suy ra   2 e f x 2 2  2xe dx  2e C. 
Thay x  0 vào hai vế ta được   2 0 2 x C f x e      . Vậy f    2 1
1  2e   . Chọn D. e   Câu 70. Cho hàm số 
f x liên tục và có đạo hàm trên 0; ,  thỏa mãn hệ thức  2        x  
f x  tan xf x 
. Biết rằng 3 f     f    
   a 3 b ln 3 trong đó , a b  .  Tính giá 3 cos x  3 6
trị của biểu thức P  a  . b A. 4 P   . B. 2 P   . C. 7 P  . D. 14 P  . 9 9 9 9
Lời giải. Từ giả thiết, ta có x  x
cos xf x sin xf x   sin xf x   . 2     2 cos x cos x Suy ra x
sin xf x 
dx  x tan x  ln cos x C.  2 cos x      Với 3 2 x    f      . 3 ln 2   3 f    
   . 3 2 ln 2  2C. 3 2  3 3 3 3      Với 1 3 1 1 x    f      .
 ln 3ln 2 C   f    
   . 3  ln 32 ln 2  2C. 6 2  6  6 3 2 6 9  5      Suy ra   5 a  4 3 f     f    
    3 ln 3    9 
 P  a b   . Chọn A.  3 6 9  9 b   1 
Vấn đề 10. Kỹ thuật đưa về bình phương loại 1    2    Câu 71. Cho hàm số   2 
f x liên tục trên 0; , thỏa 2
 f x2 2 f xsin  x    dx  .  2      4  2 0    2 Tính tích phân I 
f xdx.  0 A.   I  0. B. I  . C. I  1. D. I  . 4 2 25  2   Lời giải. Ta có  2  2  2 sin   x   dx   .   4  2 0  2     
Do đó giả thiết tương đương với 2  
 f x2 2 f x 2 sin  x    2 sin     x    dx  0  4   4  0    2 2         
 f x 2 sin  x  
 dx  0  f x 2 sin    x     0, 0 x   ; .  4   4      2  0    2 2     Suy ra  
f x  2 sinx      I 
f xdx  2 sin     x 
 dx  0. Chọn A.  4   4  0 0 1 1   Câu 72. Cho hàm số 2
f x liên tục trên 0;  1 thỏa 2  f x 2  2 ln
 dx  2  f xlnx   1  dx.    e     0  0 1 Tích phân I 
f xdx.  0 A. e e I  ln . B. 4 I  ln . C. I  ln . D. 2 I  ln . 4 e 2 e
Lời giải. Bằng phương pháp tích phân từng phần ta tính được 1 1 2 2 2 ln x   2 2 1 dx  2 ln  2 ln dx.   e e 0 0 1
Do đó giả thiết tương đương với  f xln1 x 2dx  0  f x ln1 x, x  0;  1 .    0 1 1 Suy ra
f x x    x 4 d ln 1 dx  ln   . Chọn B. e 0 0
Câu 73. Cho hàm số f x có đạo liên tục trên 0; 
1 , f x và f 'x đều nhận giá trị dương 1 1 trên 0; 
1 và thỏa mãn f 0  2 và  f '
  x. f x 2 1    dx  2 f '   
x. f xdx.    Tính 0 0 1 I 
 f x 3 dx.    0 A. 15 I  . B. 15 I  . C. 17 I  . D. 19 I  . 4 2 2 2 1 2
Lời giải. Giả thiết tương đương với  f '
  x.f x 1  dx  0    0 
 f x f x  x     f x 2
f x    f x 2 ' . 1, 0;1 ' 1 '
f xdx  dx   3 f x f 02 8  
 x C C  . 3 3 1
Vậy f x 3x 8   I   f x 3 19 3  dx  .    Chọn D. 2 0
Câu 74. Cho hàm số f x có đạo hàm dương, liên tục trên đoạn 0; 
1 và thỏa mãn f 0  1, 1 1   1
 f x  f x 2 1 3 ' .    dx  2
f 'x. f xdx.  3   I   f x  dx.   Tính     9   0  0 0 A. 3 I  . B. 5 I  . C. 5 I  . D. 7 I  . 2 4 6 6 26 1 1 2
Lời giải. Giả thiết  f
  x f x 1 3 ' .   dx   2 f ' 
x. f xdx    3 0 0 1 1 1 1 2 2 3 f '  
x. f x dx 2 3 f ' 
x. f xdx dx 0 3 f '    
x. f x 1       dx  0      0 0 0 0  
f x f x  x    f x 2
f x    f x 2 3 ' . 1 0, 0;1 9 ' . 1 9 '
. f xdx  dx   3 f x f 0 1 9. x C   
  C  3. 3 1
Vậy f x 1  x 1 
  f x 3 7 3  dx  .  Chọn D. 3   6 0
Câu 75. Cho hàm số y  f x có đạo hàm dương, liên tục trên đoạn 0;  1 , thỏa 1 1 1 f  
1  f 0  1 và f 'x 2  f  3 
x1 dx  2 f '    
x f xdx.   Giá trị của tích phân
f x dx    0 0 0 bằng A. 3   . B. 5 33 27 . C. 5 33 . D. 5 33 54 . 2 18 18 18 1 1
Lời giải. Nhóm hằng đẳng thức ta có f 'x 2  f  
x1 dx  2 f '  
x f xdx   0 0 1 1   f '
  x 2f x f 'xdx 2 f '  
x f xdx  0   0 0 1 1 2   f '
  xf x1 dx   f ' 
x1 dx  0      0 0
 0 vi f   1  f 0 1  
 f x f x  x     f x 2
f x    f x 2 ' . 1, 0;1 ' 1 '
f xdx  dx   3 f x f  f  5 33 27 3  
 x C   f x   1 0 1
 3x 3C  C  . 3 54 1 Vậy  f x 5 33 27  3x  
  f x 3 5 33 3  dx  .  Chọn C. 18   18 0
Vấn đề 11. Kỹ thuật đưa về bình phương loại 2 Kỹ thuật Holder 1 1
Câu 76. Cho hàm số y  f x liên tục trên đoạn 0; 1, thỏa mãn
f xdx  xf xdx 1   và 0 0 1 1
 f x 2 dx  4  3  
. Giá trị của tích phân  f x dx    bằng 0 0 A. 1. B. 8. C. 10. D. 80.
Lời giải. Ở đây các hàm xuất hiện dưới dấu tích phân là  f x 2 , xf x , f x   nên ta sẽ liên kết
với bình phương  f x 2
x   .   1 1 1 1 Với mỗi số thực ,
  ta có  f x 2
 x   dx   f x 2 dx  2 x   f xdx  x  2 dx         0 0 0 0 2
      2 4 2 
    . 3 1 2 Ta cần tìm  ,
  sao cho  f x 2
 x   dx  0  2  
hay 4  2  
     0 3 0 27 2
      2 3
6   3  6 12  0. Để tồn tại  thì      2   2 3 6
4 3  6 12 0
     
     2 2 3 12 12 0 3
2  0    2    6. 1 1
Vậy  f x 2
 6x  2 dx  0 
 f x 6x 2, x  0;  1 
  f x 3 dx 10.       Chọn C. 0 0 1 1
Câu 77. Cho hàm số y  f x liên tục trên đoạn 0; 1, thỏa mãn xf xdx 
x f xdx 1   và 0 0 1 1
 f x 2 dx  5.  3  
Giá trị của tích phân  f x dx    bằng 0 0 A. 5. B. 6. C. 8. D. 10. 6 5
Lời giải. Ở đây các hàm xuất hiện dưới dấu tích phân là  f x 2 , xf x , x f  x   nên ta sẽ liên
kết với bình phương  f x 2 x  x    .    Với mỗi số thực ,
  ta có 1 1 1 1  f x 2
 x   x  dx   f x dx  2       
 x  x  f xdx   x  x 2 2 dx 0 0 0 0 2 2
      4  5 2    . 3 5 2 1 2 2 Ta cần tìm 2  4  ,
  sao cho  f x x  x    dx  0   hay  
5  2      0. 3 5 2 0
Tương tự như bài trước, ta tìm được   15, 10.   1 1
Vậy  f x 2  x 
x  x  
 f x x 
x x  
  f x 3 5 15 10 d 0 15 10 , 0;1  dx  .   Chọn A.      6 0 0 1 1 Câu 78. Cho hàm số 1
y  f x liên tục trên đoạn 0;  1 , thỏa mãn 2 xf x 2 dx 
x f xdx  .   16 0 0 1
Giá trị của tích phân f xdx  bằng 0 A. 1. B. 1. C. 1. D. 2. 5 4 3 5
Lời giải. Hàm bình phương không như thông thường là    2 f x  
 hoặc  f x 2 '  .  
Ở đây các hàm xuất hiện dưới dấu tích phân là  x f x 2 2
 , x f x 
nên ta sẽ liên kết với bình   phương  x x x f x 2  
 xf x
x f x 2 2 ??? 2??? ??? .  So sánh ta thấy được   ???  . 2 2 2 1 1    
Do đó giả thiết được viết lại  x f x x x   x x  1      dx         dx   0.  2   2  16 0 0 1 Suy ra   x x        x x f x x f x    f x 1 , 0;1 dx  .  Chọn B. 2 2 4 0
Câu 79. Cho hàm số f x có đạo hàm liên tục trên 1;8 và thỏa mãn 2 2 8  f   x  2 2 38 3  dx  2 f  
  3xdx 
f xdx  .   3 15 1 1 1 8 Tích phân
f xdx  bằng 1 A. 8 ln 2 . B. ln 2 . C. 4 . D. 3 . 27 27 3 2 28 8
Lời giải. Nhận thấy có một tích phân khác cận là
f xdx.  Bằng cách đổi biến 3 x  t ta 1 2 2 thu được tích phân 2 3 t f   3t 2 dt  3 x f   3xdx. 1 1 2 2 2
Do đó giả thiết được viết lại  f   x  2 38 3  dx  2 f     3x 2 dx  2 x f 
 3xdx  .  * 15 1 1 1
Ở đây các hàm xuất hiện dưới dấu tích phân là  f x  2 3  f
nên ta sẽ liên kết với  
 3x 2x f  3 , , x  
bình phương  f x  2 3 2 x    .  
Tương tự như các bài trên ta tìm được   1, 1   . 2 2 Do đó    f   x  2 38 * x 1    dx       1x 2 3 2 2 dx  0  15 1 1 8   f  3 3 x  2
 x 1, x  1;2 
 f x 3 2
 x 1, x  1;8  
f xdx  .  Chọn D. 2 1
Câu 80. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0 , 1 1 1  1
f x 2 dx  7  2  
và x f xdx  .  Tích phân
f xdx  bằng 3 0 0 0 A. 1. B. 7 . C. 7 . D. 4 . 5 4
Lời giải. Hàm dưới dấu tích phân là  f x 2 2
 , x f x  
không có mối liên hệ với nhau. 1 1 3 1
Dùng tích phân từng phần ta có x 1 2
x f xdx  f x 3 
x f 'xdx.  
Kết hợp với giả thiết 3 0 3 0 0 1 f   1  0 , ta suy ra 3
x f 'xdx  1.  0 1
  f x2 dx 7    
Bây giờ giả thiết được đưa về  0 
. Hàm dưới dấu tích phân bây giờ là 1  3  x f ' 
xdx  1   0
 f x 2 3  , x f 'x     
nên ta sẽ liên kết với bình phương f  x 2 3 ' x .   1 1 1 1
Với mỗi số thực  ta có  f '   x 2
x  dx   f '   x 2 3 3
 dx 2 x f 'x 2 6 dx   x dx       0 0 0 0 2  1  7 2    72 . 7 7 1 Ta cần tìm 1
 sao cho  f '   x 2 3
x  dx  0  
hay 72  0    7. 7 0 1 Vậy  f '   x 2 7 3
7x  dx  0   f '   x 3
 7x , x 0;  1   f x 4   x C  4 0 1 f   1 0 7
C    f x 7 7 7 4   x   
f xdx  .  Chọn B. 4 4 4 5 0 1 1 3 1
Cách 2. Dùng tích phân từng phần ta có x 1 2
x f xdx  f x 3 
x f 'xdx.   Kết hợp với 3 0 3 0 0 1 giả thiết f   1  0 , ta suy ra 3
x f 'xdx  1.  0 29 Theo Holder 2 1 1 1   7 1  2  3  x
1   x f 'x 6 dx   
x dx.  f 'x 2 dx  .7  1.         7 0 0  0 0 1
Vậy đẳng thức xảy ra nên ta có f x 3 '  kx , thay vào 3
x f 'xdx  1 
ta được k  7. 0 Suy ra f x 3 '
 7x (làm tiếp như trên)
Câu 81. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  1 , 1 11 1 4 5
x f xdx   và f xd 
 f x . Tính f 2. 78 13 0 0
A. f 2 2. B. f   251 2  . C. f   256 2  . D. f   261 2  . 7 7 7 1 1
Lời giải. Viết lại f x 
 f x 4  
 f x 2 4 d  dx  .  13   13 0 0 1 1 6 1
Dùng tích phân từng phần ta có x 1 5
x f xdx  f x 6 
x f xdx.   Kết hợp với giả 6 0 6 0 0 1 thiết 2 f   1  1 , ta suy ra 6
x f xdx  .  13 0 1
  f x2 4  dx      13
Bây giờ giả thiết được đưa về  0 
. Hàm dưới dấu tích phân bây giờ là 1  2 6
 x f 'xdx   13  0
 f x 2 6  , x f 'x     
nên ta sẽ liên kết với bình phương f  x 2 6 ' x . 
 Tương tự như bài trên ta
tìm được   2   f x 2 f  5 6  2x   f x 7   1 1
 x C C  . 7 7
Vậy f x 2 5 261 7  x    f 2  . Chọn D. 7 7 7 Cách 2. Theo Holder 2 2 1 1 1 2       
    x f xdx     
x dx.  f x 2 1 4 4 6 12  dx  .  .    13       13 13 169 0  0 0
Câu 82. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  2, f  0  0 và 1 1
 f 'x 2 dx  4.  3      . Tích phân f
  x 2018x dx.   bằng 0 0 A. 0. B. 1011. C. 2018. D. 2022. 1 1
Lời giải. Từ giả thiết f   1  2, f  0  0 suy ra
f 'xdx  f x  2.  0 0
Hàm dưới dấu tích phân là  f x 2 '  , f'x  
nên sẽ liên kết với bình phương  f x 2 '  .  
Ta tìm được    
 f x    f x f 00 2 ' 2
 2x C C  0. 1 Vậy f x 3  2x    f
  x2018xdx 1011.   Chọn B. 0 Cách 2. Theo Holder 2 1 1 1   2   
f 'xdx 
  dx.  f 'x 2 2  dx 1.4  4.         0  0 0 30 2 Câu 83. Cho hàm số 1
f x có đạo hàm liên tục trên 1;2, thỏa mãn x  2
1 f xdx   ,  3 1 2 2
f 2  0 và  f 'x 2 dx  7.    Tích phân
f xdx  bằng 1 1 A. 7  . B. 7 . C. 7  . D. 7 . 20 20 5 5 2
Lời giải. Chuyển thông tin x  2
1 f xdx 
sang f 'x bằng cách tích phân từng phần, ta 1 2 được x  3
1 f 'xdx  1.  1
Hàm dưới dấu tích phân là  f x 2 x  3 ' , 1 f 'x    
nên liên kết với f xx    2 3 ' 1 .   
Ta tìm được    
 f x  x  3   f x 7  x  4 f 20 7 7 ' 7 1
1 C C   . 4 4 2
Vậy f x 7  x  4 7    f x 7 1 dx   .  Chọn C. 4 4 5 1 Cách 2. Theo Holder 2 2 2 2   1   x  3
1 f 'xdx  x  6 1 1
1 dx  f 'x 2 dx  .7  1.       7  1  1 1 1 Câu 84. Cho hàm số 9
f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  1, '
 f x 2 dx     5 0 1 1 và f   x 2 dx  . Tích phân
f xdx  bằng 5 0 0 A. 1 I  . B. 1 I  . C. 3 I  . D. 3 I  . 5 4 5 4 1
Lời giải. Chuyển thông tin
f  x dx 
sang f 'x bằng cách: 0 1 1 1 1
 Đặt t  x 
 tf tdt  
hay xf xdx  .  5 5 0 0 1 1 3  Tích phân từng phần
xf xdx,  ta được 2
x f 'xdx  .  5 0 0
Hàm dưới dấu tích phân là  f x 2 2 '  , x f 'x     
nên liên kết với f  x 2 2 ' x .   Ta tìm được  3 f 'x 2 3x f x 3 f   1 1 x C         
 C  0. 1 Vậy f x 1 3  x  
f xdx  .  Chọn B. 4 0 Cách 2. Theo Holder 2 2 1 1 1 3          
x f 'xdx  x dx  f 'x 2 1 9 9 2 4  dx  .  .     5      5 5 25  0  0 0
Câu 85. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0 f   1  0, 1  1 1 1
f 'xcosxdx   và 2
f xdx  .  Tích phân
f xdx  bằng 2 2 0 0 0 A. 1  . B. 2 . C. .  D. 3 .   2
Lời giải. Hàm dưới dấu tích phân là 2
f x và f 'xcosx, không thấy liên kết. 31
Do đó ta chuyển thông tin của f 'xcosx về f x bằng cách tích phân từng phần của 1  1 1
f 'xcosxdx  
cùng với kết hợp f 0 f   1  0, ta được
f xsinxdx  .  2 2 0 0
Hàm dưới dấu tích phân bây giờ là 2
f x và f xsinx nên ta sẽ liên kết với bình phương
 f x x 2 sin  .   1
Ta tìm được    
 f x  x   f x 2 1 sin dx  .  Chọn B.  0 Cách 2. Theo Holder 2 2 1 1 1 1           
f xsinxdx     
f xdx. sinx 2 1 1 2  dx  . .    2       2 2 0  0 0 
Câu 86. Cho hàm số f x có đạo hàm liên tục trên 0;, thỏa mãn
f 'xsin xdx  1  và 0  2  2
f xdx  . 
Tích phân xf xdx  bằng  0 0 A. 6  . B. 4  . C. 2 . D. 4 .    
Lời giải. Hàm dưới dấu tích phân là 2
f x và f 'xsin x , không thấy liên kết.
Do đó ta chuyển thông tin của f 'xsin x về f x bằng cách tích phân từng phần của  
f 'xsin xdx  1,  ta được
f xcos xdx  1.  0 0
Hàm dưới dấu tích phân bây giờ là 2
f x và f xcos x nên ta sẽ liên kết với bình phương  f x 2
 cos x .     Ta tìm được 2      f x 2  x   xf x 2x cos x 4 cos dx  dx   .   Chọn B.     0 0 Cách 2. Theo Holder 2     2  1  f x 2 2 cos xdx  f x 2
dx cos xdx  .  1.     2 0 0 0 1 2 Câu 87. Cho hàm số 
f x có đạo hàm liên tục trên 0;  1 , thỏa f   1  0, '
 f x 2 dx     và 8 0 1 x  1  
   f x 1 cos dx  .  Tích phân
f xdx   bằng 2  2 0 0 A. 1  . B. 2 . C. . D. .    2  
Lời giải. Hàm dưới dấu tích phân là  x f x 2 '      và cos  f x  , không thấy liên kết.  2   
Do đó ta chuyển thông tin của x cos    f x 
về f 'x bằng cách tích phân từng phần của  2  1 x  1      x    f x 1 cos
dx  cùng với kết hợp ta được    f   1  0, sin
   f 'xdx  .  2  2  2  4 0 0  
Hàm dưới dấu tích phân bây giờ là  x f x 2 '      và sin  f 'x 
nên ta sẽ liên kết với bình  2  2    phương x
 f 'x sin    .   2    32     Ta tìm được         f x x         f x x f   1 0 ' sin  cos    
C C  0. 2 2  2   2  1   Vậy   x f x        f x 2 cos dx  .  2   Chọn B.  0
Cách 2. Theo Holder 2 2 1 1 1   2       x   x        sin     
 f 'xdx  sin         
dx.  f 'x 2 1 2  dx  . .  4  2     2     2 8 0  0 0 1
Câu 88. Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thỏa mãn
f 'xsinxdx    và 0 1 1   2 x
f xdx  2.  Tích phân f     dx bằng 2 0 0 A. 6  . B. 4  . C. 4 . D. 6 .    
Lời giải. Chuyển thông tin của f 'xsinx về f x bằng cách tích phân từng phần của 1 1
f 'xsinxdx  ,   ta được
f xcosxdx  1.  0 0
Hàm dưới dấu tích phân bây giờ là 2
f x và cosx f x nên ta sẽ liên kết với bình phương
 f x x 2 cos  .   1 1     Ta tìm được    
 f x   x x x 4 2 2 cos   f  
  dx 2 cos   
  dx  . Chọn B. 2  2   0 0
Cách 2. Theo Holder 2 1 1 1    2 1  
f xcosx 1 2 dx 
cos xdx  f x 2 dx  .2.       2  0  0 0    2   Câu 89. Cho hàm số  
f x có đạo hàm liên tục trên 0; , thỏa 2 f      0, f x dx  3  2    2  và 0   2   x 
sin x  x f    3  dx  6 .  Tích phân    
f x dx   bằng 2    0 0 A. 2  . B. 0. C. 3 .  D. 9 .       
Lời giải. Tích phân từng phần của  x 
sin x  x f     dx  6 ,
 kết hợp với   ta được  f    0 2  2 0  2 ta được 3 2 
sin xf xdx  .  4 0
Hàm dưới dấu tích phân bây giờ là 2 f x và 2
sin xf x nên ta sẽ liên kết với bình phương  f x 2 2
 sin x .  
Ta tìm được      f x 2 4
 4 sin x  f 'x  4 sin 2x  f ' x  8cos 2x.   2 2
Vậy  f x 3 dx  8cos2x3 dx  0.     Chọn B. 0 0
Cách 2. Theo Holder 33 2      2  2  2 2 3       3 2  
   sin xf x 4 2 dx    sin xdx
f xdx  .3 .     4       16  0  0 0  
Câu 90. Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
1 , thỏa mãn f   1  0 và 1 1 2  1
 f x 2 x  x   xe f x e 1 ' d 1 dx  .    
Tính tích phân I 
f xdx.  4 0 0 0 2 A. e 1 e e I  . B. I  .
C. I  e 2. D. I  . 2 4 2 1
Lời giải. Tích phân từng phần của    1 x x
e f xdx, 
kết hợp với f   1  0 ta được 0 1 2  x xe f x e 1 ' dx   .  4 0
Hàm dưới dấu tích phân bây giờ là  f x 2 '  x x    
 và xe f 'x nên ta sẽ liên kết với f  x 2 xe .  
Ta tìm được     f x x  xe   f x x
  xe x    x x f   1 0 1 ' d 1
e C C  0.  1 1
Vậy   1  x  
 d  1  x f x x e f x x
x e dx  e 2.   Chọn C. 0 0 Cách 2. Theo Holder 2 2 1 1 1 2      2 2 e 1       x e e      xe f '   xd x x   
x e dx.  f 'x 2 1 1 2 2  dx  . .     4        4 4 0  0 0
Câu 91. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0  0, f   1  1 và  f 'x 2 1  1 1   dx  .  Tích phân
f xdx x  bằng e e 1 0 0 A. e 2 e  1 . B. 1 . D. . C. 1. e 1 e 2 e   1 e 2  f x 2 ' 
Lời giải. Hàm dưới dấu tích phân là 
 nên ta cần tìm một thông tin liên quan f 'x. x e 1 1
Từ giả thiết f 0 0, f   1  1 ta nghĩ đến
f 'xdx  f x  f   1  f 0  1.  0 0  f x 2 ' 
Do đó ta có hàm dưới dấu tích phân là 
 và f 'x nên sẽ liên kết với bình phương x e  f x 2 '  x   e  . 
Với mỗi số thực  ta có x  e     f 'x 2 1 1   f 'x 2 1 1  x   e  dx    dx  2 f 'x 2 d x x   e dx     x   x  e  e 0  0 0 0 1 
   e   1 2 1  e   2 2 1  1 . e 1 e 1      f 'x 2 1  Ta cần tìm 1 1  sao cho x 
 e  dx  0       hay e  2
1  1  0     . x  e 1    e 1 0  e   f 'x 2 1 1  f ' x x   Với 1 1    thì   e  dx  0 x   e , x  0;  1 .  e 1  x  e e 1  x  e e 1 0 x x x Suy ra f x e    f x e e
f 00, f   1 1  1 '  dx 
C C   .  e 1 e 1 e 1 e 1 34 1 x Vậy  
f x e 1    f x e 2 dx  .  Chọn A. e 1 e 1 0 Cách 2. Theo Holder 2    f 'x 2   f 'x 2 1 1 1 1  x       x 1 2 1 
f 'xdx  . e dx  dx e dx  .e   1  1.      x  x    e e e 1 0 0  0 0
Câu 92. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f 0  0, f   1  1 và 1 1 f x
1 x  f 'x 2 1 2  dx  .    Tích phân dx  bằng ln 1 2 2 0   0 1 x A. 1 2 1 1 2 ln 1 2. B. 2
ln 1 2. C. ln1 2. D.  2   1 ln1 2. 2 2 2 1 1
Lời giải. Tương tự bài trước, ta có
f 'xdx  f x  f   1  f 0  1.  0 0
Do đó ta có hàm dưới dấu tích phân là
 x  f x 2 2 1 '  
 và f 'x nên sẽ liên kết với bình 2   phương  4 2
 1 x f 'x    .   4 2  1   x  Ta tìm được 1 1 1      f x  ln1 2 '  ln1 2. 2 1 x   f x 1 1 1  . dx  ln   2
x  1 x C. 2  ln1 2 1 x ln1 2  2
ln x  1 x 
Mà f 0 0, f  
1  1  C  0 
 f x     . ln 1 2 ln 2 1 1 x  1 1  x f x  1 Vậy   1 2  2 dx dx ln x 1 x d    ln x 1 x         2 1 x ln1 2 2 1 x ln 1 2   0 0       0 2 ln  2 x  1 1  x  1 1    Chọn C. ln1 2. ln1 2. 2 2 0 Cách 2. Theo Holder 2 1 1 1 1     x 1   f 'x 1 d 4 dx   
1 x f 'x. dx 
1 x  f 'x 2 2 2 2  dx.      4 2   2   0  0 1 x 0 0 1 x 1    .ln1 21. ln 1 2
Câu 93. Cho hàm số f x có đạo hàm liên tục trên 1; 
1 , thỏa mãn f   1  0, 1 1 1  16
f 'x 2 dx  112  2  
và x f xdx  . 
Tính tích phân I 
f xdx.  3 1 1 1  A. 84 I  . B. 35 I  . C. 35 I  . D. 168 I  . 5 2 4 5 1
Lời giải. Như các bài trước, ta chuyển 16 2
x f xdx  
về thông tin của f 'x bằng cách 3 1      d
 u  f 'xdx u f x 
tích phân từng phần. Đặt   3    . 2 x d  v x dx v       3 35 1 1 1 3 1 Khi đó x 1 1 1 1 2
x f xdx  f x 3 
x f 'xdx  f   1  f   3 1 
x f 'xdx.    Tới đây ta 3 1 3 3 3 3 1 1 1 bị vướng f  
1 vì giả thiết không cho. Do đó ta điều chỉnh lại như sau      d
 u  f 'xdx u f x    3   
với k là hằng số. 2 x d  v x dx v       k  3 1 1 3 1 3     Khi đó 2   x   x x f x dx    k f    x      k f '       xdx 3    1 3  1 1 1 3       1         1 x k f 1    
 k f   1     k f '        xdx. 3  3   3 
 1 0 do f   1 0 Ta chọn k sao cho 1 1
 k  0  k   . 3 3 1 1 1 Khi đó 16 1 2 
x f xdx   
  3x  1 f 'xdx   3x  1 f 'xdx 16. 3 3 1 1 1
Hàm dưới dấu tích phân là  f x 2  3 ' , x     
1 f 'x nên ta liên kết với f xx    2 3 ' 1 .  
Ta tìm được   7 
 f 'x  7 7 3 x  
1  f x  7  3 x   4
1 dx   x 7x C 4 1 f   1 0 35 84  C    f x 7 35 4
  x 7x  . Vậy I 
f xdx  .  4 4 4 5 1  Cách 2. Theo Holder 2 1 1 1   162      16 3 x  
1 f 'xdx    3 x  2
1 dx.  f 'x 2 dx  .112  256.        7 1   1  1 
Câu 94. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0, 1 1 1  f x 3 f x 2 3 '  dx  2 ln 2    và dx  2 ln 2  .  Tích phân
f xdx  bằng 2 x 1 2 0  2 0 0 A. 1ln 2    . B. 1 2 ln 2 . C. 3 2 ln 2 . D. 3 4 ln 2 . 2 2 2 2 1 f x
Lời giải. Như các bài trước, ta chuyển 3 dx  2 ln 2  
về thông tin của f 'x bằng x  2 1 2 0 u
  f x d  
 u  f 'xdx  
cách tích phân từng phần. Đặt  1    1 . d  v  dx     2 v    x 1    x 1 1 f x f x 1 f 'x f   1 f 0 1 1 f 'x Khi đó dx    dx     dx.    Tới đây ta bị vướng x  2 1 x 1 0 x 1 2 1 x 1 0 0 0
f 0 vì giả thiết không cho. Do đó ta điều chỉnh lại như sau u
  f x d  
 u  f 'xdx    1    1
với k là hằng số. d  v  dx     2 v     k x 1    x 1 1 f x 1 1     Khi đó 1 1 dx      k f x      
 k f ' x dx  2     x   1  x 1    0  x 1  0 0 f   1 1 0  
   k f   1 1 0    
 k f 'xdx.   x 1  0
Ta chọn k sao cho 1 k  0  k  1. 36 1 3 f x 1 1 Khi đó x x 3 2 ln 2   dx  
f ' x dx  
f ' x dx  2 ln 2.  2       2 x 1 x 1 x 1 2 0   0 0 2  
Hàm dưới dấu tích phân là   x x 2 x f '  , f'x  
nên ta liên kết với  f 'x  . x 1  x 1 Ta tìm được x x   1 
 f 'x 
 f x 
dx  x  ln x 1 C  x 1 x 1 1 f   1 0 12 ln 2
C  ln 2 1 
 f x  x lnx   1  ln 2 1. Vậy
f xdx  .  Chọn B. 2 0 Cách 2. Theo Holder 2 2 1 1 2 1 3  x             x      f x x         
 x  f x 2 3 3 2 ln 2 ' d d '  dx           2 ln 2        2 ln 2. 2 x 1 x 1 2 2   0  0 0
Câu 95. Cho hàm số f x có đạo hàm liên tục trên 1;2, đồng biến trên 1;2, thỏa mãn 2 2 2 f   1  0 ,
 f x 2 dx  2    và
f x.f 'xdx  1.  Tích phân
f xdx  bằng 1 1 1 A. 2 . B. 2. C. 2. D. 2 2. 2
Lời giải. Hàm dưới dấu tích phân là  f x 2 , f x . f x  
nên ta sẽ liên kết với bình phương 2
 f x f x 2 . 2 
 Nhưng khi khai triển thì vướng  f x dx   
nên hướng này không khả thi. 1 2 2 f x 2 f 2 2  f   2 2 1 f 20 Ta có 1 
f x.f 'xdx      f 2  2  (do đồng biến 2 1 2 2 1
trên 1;2 nên f 2 f   1  0 ) 2 2 Từ f  
1  0 và f 2  2 ta nghĩ đến
f 'xdx  f x  f 2 f   1  2 0  2.  1 1
Hàm dưới dấu tích phân bây giờ là  f x 2 , f x  
nên ta sẽ liên kết với  f x 2  .  
Ta tìm được    
 f x    f x f   1 0 2 ' 2
 2x C C   2. 2
Vậy f x x    f x 2 2 2 dx  .  Chọn A. 2 1 1
Câu 96. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0 , 2
f xdx  1  0 1
và  f x 2 3 2
 f xdx  .  2  
Giá trị của f  2 bằng 4 0 31 2 31 2 A. 3  . B. 3 . C. . D.  . 2 2 2 2
Lời giải. Hàm dưới dấu tích phân là    2 2
f x  f x 2  
và f x nên ta sẽ liên kết với bình 1
phương  f x f x f x 2 . 2 
 Nhưng khi khai triển thì vướng
f x f 'xdx  nên hướng 0 này không khả thi. 1 1 Tích phân từng phần 1 2
f xdx  1 
kết hợp với f   1  0, ta được
xf x f 'xdx   .  2 0 0 37
Hàm dưới dấu tích phân bây giờ là    2 2
f x  f x  
và xf x f 'x nên ta sẽ liên kết với bình
phương  f x f x 2 ' x .   2 3 3 3 f x
Ta tìm được   
 f x f 'x   x 
f x f 'x 3 2 dx   xdx    x C   2 2 2 2 4 f   1 0 3 3 3 2
C  
 f x   2 1 x  2 
 f  2  . Chọn A. 4 2 2
Câu 97. Cho hàm số f x có đạo hàm liên tục trên 0;2, thỏa mãn f 21 , 2 8 2 32 2 2
x f xdx  
và  f 'x 4 dx  .  Giá trị của tích phân
f xdx  bằng 15   5 0 0 0 A. 3  . B. 2  . C. 7  . D. 7 . 2 3 3 3
Lời giải. Hàm dưới dấu tích phân  f x 4 '  2 
 và x f x. Lời khuyên là đừng có cố liên kết với
bình phương nào, vì có tìm cũng không ra. 2 2 Tích phân từng phần 8 32 2
x f xdx  
kết hợp với f 21 , ta được 3
x f xdx  .  15 5 0 0
Áp dụng Holder 2 lần ta được 4 4 2 2 4 2 2 2 2           32   
    x f xdx     
   x .xf xdx       
  x dx         
  x  f 'x 2 3 2 4 2  dx        5          0 0 0 0  2 2 2 2     
 x dx      
x dx.  f 'x 4 4 4  dx               0 0 0 3 2 2 4         x dx 
   f 'x 4 1048576 32 4  dx            .   625  5  0  0 2 Dấu 32
''  '' xảy ra, tức là xf x 2 '
 kx  f 'x  kx thay vào  f 'x 4 dx     tìm được k  1 5 0 2
f x x f x x f 2 1 ' xdx C       
 C  1.  2 2 2 Vậy   x f x     f x 2 1 dx   .  Chọn B. 2 3 0
Cách 2. Áp dụng bất đẳng thức AM – GM ta có  f x 4 4 4 4 3 '
  x  x  x  4x f 'x.   2 2 2 Do vậy  f 'x 4 4 3
 dx 3 x dx  4 x f xdx.     
Mà giá trị của hai vế bằng nhau, có nghĩa là 0 0 0
dấu ''  '' xảy ra nên f 'x x. (Làm tiếp như trên).
Vấn đề 12. Kỹ thuật đánh giá AM-GM
Câu 98. Cho hàm số f x nhận giá trị dương và có đạo hàm f 'x liên tục trên 0;  1 , thỏa 1 1 mãn dx f   1  ef 0 và
  f 'x 2 dx  2.  2 
Mệnh đề nào sau đây đúng ? f x   0 0 2e 2 2 2e 2 A.   2e 2e f 1  . B. f   1  . C. f   1  . D. f   1  . e 1 e 1 2 e 1 e 1 38 1 1 1 1   AM G  M dx 2 1 2 f 'x Lời giải. Ta có
  f ' x  dx  
  f ' x   dx  2 dx  2        2    f x f  x    f   x 0 0 0  0 1 f   1
 2 ln f x  2 ln f  
1 2 ln f 0  2 ln  2 ln e  2. f 0 0   1 1 Mà dx 1
  f 'x 2 dx  2 
 xảy ra, tức là f 'x 
 f x f 'x  1 2  nên dấu '' '' f x   f x 0 0 2 f x  
f x f 'xdx  xdx 
 x C 
 f x  2x  2C .   2 Theo giả thiết 1 f  
1  ef 0 nên ta có 2
2  2C  e 2C  2  2C  e 2C  C  2 e 1 2     2 2 2e f x  2x   f 1  2   . Chọn C. 2   2 2 e 1 e 1 e 1
Câu 99. Cho hàm số f x nhận giá trị dương trên 0; 
1 , có đạo hàm dương và liên tục trên 1 1 1 0; 
1 , thỏa mãn f 0  1 và  f
  x4 f 'x 3 3    dx  3 f '    x 2
f xdx. I  f x dx.    Tính    0 0 0 2 A. e  e 1
I  2 e   1 . B. I   2 2 e   1 . C. 1 I  . D. I  . 2 2
Lời giải. Áp dụng bất đẳng thức AM GM cho ba số dương ta có 3 f x 3 f x 3 f x 3 3 3 3 f x 3  
f x  f x   f x     f x  f x 2 3 4 ' 4 ' 3 4 ' . . 3 ' f x.     2 2   2 2 1 1 Suy ra  f
  x4 f 'x 3 3    dx  3 f '    x 2
f xdx.    0 0 1 1 Mà  f
  x4 f 'x 3 3    dx  3 f '    x 2
f xdx  xảy ra, tức là    nên dấu '' '' 0 0 3 f x 3 3 f x
 f x    f x 1 4 ' '  f x   2 2 2 f 'x 1 f 'x 1 1      x  x  f x 1 x C d d ln
 x C   f x 2  e .   f x 2 f x 2 2 1 1 Theo giả thiết  x
f 0  1  C  0  f x 2  e  
f xdx  2 e   1. Chọn A. 0
Câu 100. Cho hàm số f x nhận giá trị dương trên 0; 
1 , có đạo hàm dương liên và tục trên 1 xf 'x    0;  1 , thỏa mãn dx 1 
và f 01, f   2
1  e . Tính giá trị của 1 f    . f x 2 0         A. 1 f      1.        B. 1 f    4. C. 1
f    e. D. 1
f    e. 2 2 2 2 xf 'x f 'x
Lời giải. Hàm dưới dấu tích phân là  x. , x  0; 
1 . Điều này làm ta liên f x f x f 'x
tưởng đến đạo hàm đúng
, muốn vậy ta phải đánh giá theo AM GM như sau: f x f 'x xf 'x  mx  2 m.
với m  0 và x 0;  1 . f x f x
Do đó ta cần tìm tham số m  0 sao cho 1  f 'x 1  xf 'x  mx  dx  2 m. dx    f  x  f   x 0  0 39 hay 1 2 1 x m m
ln f x  m
 2 m.1  ln f  
1  ln f 0   2 m  20   2 m. 0 2 0 2 2 Để dấu m
''  '' xảy ra thì ta cần có 2 0 
 2 m  m  4. 2 f 'x
Với m  4 thì đẳng thức xảy ra nên  4x f x
f 'x dx 4xdx ln f x 2x C f x 2 2 2 x C e          .   f x  f 01   Theo giả thiết   C  0   f x 2 x 1 2  e   f  
   e. Chọn C.  f   2 1  e 2  Cách 2. Theo Holder 2 2  1  xf 'x   1   f 'x  1 1  f ' x 1 f 1 2     1  dx      x. dx  xdx. dx  .ln  1.     f x      f x   f x 2 f 0 0 0  0 0 f 'x 1 xf 'x
Vậy đẳng thức xảy ra nên ta có  kx, thay vào dx  1  ta được k  4. f x f x 0 f 'x Suy ra
 4x. (làm tiếp như trên) f x 1
Câu 101. Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thỏa mãn
 f x f 'x 2 dx 1    và 0  
f 0  1, f  
1  3. Tính giá trị của 1 f    .  2         A. 1 f      2.        B. 1 f    3. C. 1
f    e. D. 1
f    e. 2 2 2 2
Lời giải. Nhận thấy bài này ngược dấu bất đẳng thức với bài trên.
Hàm dưới dấu tích phân là  f x f x 2 '  . 
 Điều này làm ta liên tưởng đến đạo hàm đúng
f x f 'x , muốn vậy ta phải đánh giá theo AM GM như sau:
 f x f x 2 '
 m  2 m. f x f 'x   với m  0.
Do đó ta cần tìm tham số m  0 sao cho 1   1
 f x f 'x 2 m  
dx 2 m f x f 'xdx.  0 0 hay 2 f x 1 1 m  2 m.
 1 m  2 m. 2 0
Để dấu ''  '' xảy ra thì ta cần có 1 m  2 m  m  1.  2
f x f 'x  1
Với m  1 thì đẳng thức xảy ra nên  f x f 'x 1   .    f
 x f 'x  1  1 1 2 f x 1 1
 f x f 'x  1  
f x f 'xdx   dx 
 x  1  1.   (vô lý) 2 0 0 0 0 2 f x
 f x f 'x  1  
f x f 'xdx  dx 
 x C 
 f x  2x  2C .   2  f 01    Theo giả thiết 1   C    f x 1  2x 1   f  
   2. Chọn A.  f   1  3 2 2  40 1 2 f x 1 Cách 2. Ta có
f x f 'x 1 2 dx    f     2
1  f 0  1. 2   0 2 0 Theo Holder 2 1 1 1   1 
  1. f x f 'xdx 
  1 dx.  f x f 'x 2 2 2  dx 1.11.         0  0 0 1
Vậy đẳng thức xảy ra nên ta có f 'x f x k, thay vào
f x f 'xdx  1  ta được k  1. 0
Suy ra f 'x f x1.(làm tiếp như trên)
Câu 102. Cho hàm số f x nhận giá trị dương và có đạo hàm f 'x liên tục trên 1;2, thỏa  f 'x 2 2  mãn   dx  24  và f  
1  1, f 2  16. Tính giá trị của f  2. xf x 1
A. f  21.
B. f  2 2.
C. f  2 2.
D. f  2 4.
 f x 2
1  f x 2 ' ' 
Lời giải. Hàm dưới dấu tích phân là   .   
. Điều này làm ta liên tưởng đến xf x x f x f 'x đạo hàm đúng
, muốn vậy ta phải đánh giá theo AM GM như sau: f x  f x 2 '  f 'x 
 mx  2 m
với m  0 và x 1;2. xf x f x
Do đó ta cần tìm tham số m  0 sao cho
 f 'x 2 2  2   f '    x 
 mxdx  2 m dx    xf  x    1   1 f x hay 2 2m m f x 2m m  f    f   2m 24 4 24 4 2 1         24 
12 m  m  16. 3    1 3 3 Để dấu m
''  '' xảy ra thì ta cần có 2 24 
 12 m  m  16. 3  f x 2 '  f 'x
Với m  16 thì đẳng thức xảy ra nên   16x   2x xf x 2 f x f 'x   dx 
2xdx  f x  x C 
 f x    x C2 2 2 . 2 f x  f   1  1 Theo giả thiết   C  0   f x 4  x 
 f  2 4. Chọn D.  f 216  2 f 'x 2 f 'x 2 Cách 2. Ta có dx 2. dx 2 f x 2  f    2 f   1       6.  f x 2 f x   1 1 1 Theo Holder 2 2
 f 'x     f '   x   f 'x 2 2 1 2 2  2 2 2        x 6 dx     x. dx  xdx. dx  .24  36.       f  x   xf  x     xf x 2 1 1 1  1 1 f 'x f 'x 2 f 'x
Vậy đẳng thức xảy ra nên ta có  k x   kx, thay vào dx  6  ta xf x f x 1 f x f 'x
được k  4. Suy ra
 4x. (làm tiếp như trên) f x 41
Vấn đề 13. Tìm GTLN-GTNN của tích phân
Câu 103. Cho hàm số f x liên tục trên ,
 có đạo hàm cấp hai thỏa mãn .   x x f
x  e  x
và f 2 2e, f   2
0  e . Mệnh đề nào sau đây là đúng?
A. f 2 4e 1. B. f   2
2  2e  e . C. f   2
2  e 2e.
D. f 212.
Lời giải. Từ giả thiết 2 2 .   x x f
x  e  x ta có .  d     x x f x x
e  xdx.   1 0 0 u   x d  u  dx Đặt      . d
 v  f   x v   f    x  2 2 2   Khi đó   1  .   2   d  x x x f x f x x e       0   0 2  0 2 2 2 2    .       x x x f x f x e        0 0 2  0
 2. f 20. f 0   f 2 f 0 2   e 21    
 f 2 4e 1 (do f 2 2e, f   2
0  e ). Chọn A
Câu 104. Cho hàm số 1
f x dương và liên tục trên 1;3, thỏa max f x  2, min f x  và 1;3 1;3 2 3 3 3 biểu thức S  f x 1 dx. dx  
đạt giá trị lớn nhất, khi đó hãy tính I 
f xdx.  f x 1 1 1 A. 3. B. 7 . C. 7 . D. 5 . 5 5 2 2
Lời giải. Từ giả thiết ta có 1 1 5
 f x 2 , suy ra f x  . 2 f x 2 3 3 3 3 3 3  
Suy ra  f x 1 5   x  x  f x 1 1 d d dx  dx  5  dx  5
f xdx.        f  x 2 f   x f x 1  1 1 1 1 1 3 3 3 3   Khi đó S  f x 1 x x 
f x x   f x  25 d . d d . 5 dx        . f x    4 1 1 1 1  2  
(dạng t 5t 5 25 25 2  t
 5t  t      )  2 4 4 3 Dấu 5
"  " xảy ra khi và chỉ khi
f xdx  .  Chọn D. 2 1
Câu 105. Cho hàm số f x có đạo hàm liên tục trên ,
 thỏa mãn f x f x1 với mọi
x   và f 0  0. Giá trị lớn nhất của f   1 bằng A. e  e e 1. B. 1. C. . D. e. e e 1
Lời giải. Từ giả thiết f x f x1, nhân thêm hai vế cho x
e để thu được đạo hàm đúng là x   x    x  ,     x     x e f x e f x e x
e f x   e , x  .    1 1 1 1 Suy ra x        d x  d x e f x x e x  e f    
x  e 1  ef    
1 1. f 0  e 1    0 0 0 0 f 00 
 f   e 1 1  . Chọn B. e 42
Câu 106. Cho hàm số f x nhận giá trị dương và có đạo hàm f x liên tục trên 0;  1 , thỏa 1 1 mãn 1 f  
1  2018 f 0. Giá trị nhỏ nhất của biểu thức M  dx 
 f  x  dx  bằng 2   2      0 f x 0   A. ln 2018. B. 2 ln 2018.
C. m  2e.
D. m  2018e.
Lời giải. Áp dụng bất đẳng thức Cauchy, ta được 1 1 1 1 f x 1 2 f   1 M  dx 
 f  x  dx  2 dx  2 ln f x  2 ln  2 ln 2018.  2         Chọn B.  f x  f x f 0 0     0   0 0   1
Câu 107. Cho hàm số 1
f x có đạo hàm liên tục trên 0;  1 và
1 x2 f xdx   .  Giá trị 3 0 1
nhỏ nhật của biểu thức  f x 2 dx  f 0    bằng 0 A. 1. B. 2 . C. 1  . D. 2  . 3 3 3 3 1 1
Lời giải. Tích phân từng phần  1
 x2 f x 1 1 dx   
, ta được f 0  2 1 x f xdx.  3 3 0 0
Áp dụng bất đẳng thức Cauchy, ta được 1 1 1
2 1 x f xdx  1 x2 dx   f x 2 dx.      0 0 0 1 1 1
Từ đó suy ra  f x 2 dx  2 1 x f xdx  1 x2 dx      0 0 0 1 2 1 1 x3 1
  f x dx  f 0  .    3 3 0 0 1
Vậy  f x 2 x  f   2 d 0   .    Chọn D. 3 0 1
Câu 108. Cho hàm số f (x) liên tục trên [0; 1] thỏa mãn
xf xdx  0 
và max f x 1. [0; 1] 0 1 Tích phân x
e f xdx 
thuộc khoảng nào trong các khoảng sau đây? 0       A. 5  ;    .      B. 3  ; e 1. C. 5 3   ; .
D. e 1; .  4 2   4 2 1 1 1
Lời giải. Với mỗi số thực    ta có x  d x e f x x 
e f xdx  xf xdx    0 0 0 1 1 1    
 x  d 
  . x  d x f x e x x f x e x x 
e x dx.   0 0 0 1 1 1   Suy ra x   e f x x x  3 dx min e x dx min e x dx min e  Chọn C.     1           e  .     0  ;1    0  ;1   2    2 0 0 0
Câu 109. Cho hàm số f x nhận giá trị không âm và liên tục trên 0;  1 . Đặt x 1 1 gx1
f tdt. 
Biết gx f x với mọi x 0;  1 , tích phân dx  có giá trị lớn nhất g x 0 0 bằng A. 1. B. 1 . C. 2 . D. 1. 3 2 2 43 x g01
Lời giải. Từ giả thiết gx1 f tdt,  ta có 
và gx 0, x  0;  1 .
g 'x f x 0  g 'x g 'x
Theo giả thiết gx f x 
 gx g 'x  1  1. g x 2 g x t '  t t t g x Suy ra 1 1 1 1 dx  1dx,
t  0;1   x     t  1t.  2    g x g x 0 0
g t g0 g t 0 0 1 1 Do đó 1
x    x 1 d 1 dx  .   Chọn B. g x 2 0 0
Câu 110. Cho hàm số f x nhận giá trị không âm và liên tục trên đoạn 0;  1 , thỏa mãn x 1 2
f x13 f tdt  gx 
với mọi x 0;  1 , tích phân
g xdx 
có giá trị lớn nhất bằng 0 0 A. 4 . B. 7 . C. 9 . D. 5 . 3 4 5 2 x g01
Lời giải. Từ giả thiết gx13 f tdt,  ta có 
và gx 0, x  0;  1 .
g 'x 3 f x 0 
 g 'x 2 g ' x 3 2  
Theo giả thiết gx f x g x         . 9 2 g x 2 t t t t Suy ra g 'x 3 x 
x t   gx 3
 x  gt  g  3
 t  gt 3 d d , 0;1 0  t 1.   2 gx 2 0 2 0 2 2 0 0 1 1   Do đó g x 3 7 dx   
  x 1dx  .  Chọn B. 2  4 0 0
Câu 111. Cho hàm số f x nhận giá trị không âm và liên tục trên đoạn 0;  1 , thỏa mãn x 1
f x 2018  2 f tdt 
với mọi x 0; 
1 . Biết giá trị lớn nhất của tích phân
f xdx  có 0 0 dạng 2
ae  b với , a b  .  Tính a  . b A. 0. B. 1009. C. 2018. D. 2020. x g0 2018
Lời giải. Đặt gx 20182 f tdt,  ta có 
và gx 0, x  0;  1 .
g 'x 2 f x 0  g 'x g 'x
Theo giả thiết gx f x   gx   2. 2 g x t '  t t t g x Suy ra dx  2dx, t  0; 
1  ln g x  2x   g x 0 0 0 0             2 ln ln 0 2 ln 2 ln 2018  2018. t g t g t g t t g t e 1 1 1 1 Do đó
f xdx  g x 2 x 2 x 2
dx  2018 e dx  1009e  1009e 1009.    Chọn A. 0 0 0 0
Câu 112. Cho hàm số f x nhận giá trị không âm và liên tục trên đoạn 0;  1 . Đặt 2 x 1
g x  1
f tdt. 
Biết gx xf  2 2
x  với mọi x 0;  1 , tích phân
g xdx  có giá trị lớn 0 0 nhất bằng A. 1. B. e 1. C. 2. D. e 1. 2 x g01
Lời giải. Từ giả thiết gx1 f tdt,  ta có 
và gx 0, x  0;  1 .
g 'x 2xf  2 x  0  44 g ' x 2  
Theo giả thiết gx 2xf x 
 gx g 'x  1. g x t '  t t t g x Suy ra
dx  1dx, t  0; 
1  ln g x  x   g x 0 0 0 0
 ln  ln 0  ln      t g t g t g t t g t  e . 1 1 Do đó  d x g x x 
e dx  e 1.   Chọn B. 0 0
Nhận xét. Gọi F t là một nguyên hàm của hàm số f t trên đoạn 2 0;x .   2 x
Khi đó gx 1 F t
1 F x  F 0
g 'x F  x  /            x / 2 2 2 / F  2
x  2xf  2 x .  0
Câu 113. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 , thỏa f 'x f x 0, x  0;  1 . 1
Giá trị lớn nhất của biểu thức f   1 0 . dx  bằng f x 0 A. e  e  1. B. 1. C. 1. D. e 1. e e f 'x
Lời giải. Từ giả thiết f 'x f x 0, x  0;  1 ta có 1, x  0;  1 . f x t f 'x t t t Suy ra
dx  1dx, t  0; 
1  ln f x  x  ln f tln f 0 t  f t f 0 te.   f x 0 0 0 0 1 1 Do đó  f   1 1 e 1 0 . dx  dx  .   Chọn B. f x x e e 0 0  
Câu 114. Cho hàm số f x liên tục trên 0;, thỏa mãn
f xdx  cos xf xdx  1.   Giá 0 0 
trị nhỏ nhất của tích phân 2
f xdx  bằng 0 A. 2 . B. 3 . C. 4 . D. 3 .    2
Lời giải. Theo Holder 2        2  1
 cos xf x 2 2 dx 
 cos xdx. f x 2 dx  .
f xdx.      2  0  0 0 0  Suy ra 2 2
f xdx  . 
(Đến đây bạn đọc có thể chọn A)  0 
Dấu ''  '' xảy ra khi f x k cos x thay vào f xdx 1  ta được 0    1 
f xdx  k cos xdx  k.sin x  0.   0 0 0
Điều này hoàn toàn vô lý. 
a  acosxf xdx      , a b  
Lời giải đúng. Ta có
f xdx  cos xf x  0 dx  1      với  .   2 2 a  b  0 0 0   b   bf   xdx    0 Theo Holder 45 2     
a b2  a cos x b f xdx   
 a cos x b2 2 dx
f xdx.      0  0 0 Lại có
 a x b2 1 cos dx     2 2 a  2b . 2 0  2 a  b 2  2 Từ đó suy ra
f xdx   với mọi ,
a b   và 2 2 a  b  0.  2 2 a  2b 0   2
 ab    3 2  2 Do đó
f xdx .max       . Chọn B. 2 2 
a  2b   0    
Nhận xét:  Ta nhân thêm ,
a b vào giả thiết được gọi là phương pháp biến thiên hằng số. a b2
 Cách tìm giá trị lớn nhất của P  ta làm như sau: 2 2 a  2b Nếu b  0 
 P  1. (chính là đáp án sai mà mình đã làm ở trên) 2 a a   a      a  b2 2 1 t 2   Nếu b b  b t  2t 1 b  0   P   
. Tới đây ta khảo sát hàm số hoặc 2 2 2 2 a  2b a t  2      2 b
dùng MODE 7 dò tìm. Kết quả thu được GTLN của a
P bằng 3 khi t  2    2  a  2 . b 2 b a   2b
Vậy dấu ''  '' để bài toán xảy ra khi 
thay ngược lại điều kiện, ta được
 f x b2cos x    1    b x   1 x   b  
 f x 2 cos x 1 2 cos 1 d 1  .    0      Lúc này 2 cos x 1 3 2
f xdx        dx  .      0 0
Cách khác. Đưa về bình phương
Hàm dưới dấu tích phân là 2
f x, f x, cos xf x nên ta liến kết với  f x 2
 cos x   .   Với mỗi số thực ,
  ta có      f x 2
 cos x   
f xdx  2  cos x   f xdx   cos x  2 2 dx       0 0 0 0  2  
f xdx  2   2 2
    .  2 0 Ta cần tìm  ,
  sao cho    2 2 2
    đạt giá trị nhỏ nhất. Ta có 2 2 2      
2                        2 1 3 3 2 2   . 2 2       Vậy với 2 1
   ;    thì ta có    2     f x 2 1 3 2  cos x   
f xdx  .          0 0   2   Suy ra 2 1 3 3  2 x
f xdx   f x cos x     .  
Dấu ''  '' xảy ra khi f x 2cos 1  .          0 0 46  
Câu 115. Cho hàm số f x liên tục trên 0;, thỏa mãn sin xf xdx  cos xf xdx 1.   0 0 
Giá trị nhỏ nhất của tích phân 2
f xdx  bằng 0 A. 2 . B. 3 . C. 4 . D. 3 .    2
Lời giải. Liên kết với bình phương  f x 2
 sin x   cos x .   
Ta có  f x 2
 sin x   cos x dx    0    
 f x 2 dx 2 sin x  cos x f xdx  sin x  cos x2 dx      0 0 0  2 2   
 f x 2 dx 2   .    2 2 0 2 2 2 2    
Phân tích      2  2 4 2               
   . Chọn C. 2 2 2   2    1 1
Câu 116. Cho hàm số f x liên tục trên 0;  1 , thỏa mãn  d x f x x 
e f xdx  1.   Gọi m 0 0 1
là giá trị nhỏ nhất của tích phân  f x 2 dx.   
Mệnh đề nào sau đây đúng? 0
A. 0  m 1.
B. 1 m  2.
C. 2  m  3.
D. 3  m  4. 1  x a  
ae f xdx   
Lời giải. Từ giả thiết, ta có  0  . 1
b  bf  xdx    0 Theo Holder 2 1 1 1   
2   x   d         x a b ae b f x x ae  b2 2 dx
f xdx.   0  0 0 Lại có 1 1   x
ae  b2 dx    x x 1 2 2 2
a e  2abe  b dx   2 e   2
1 a  2e   2 1 ab  b . 2 0 0 1 a  b 2  2 Suy ra
f xdx   với mọi ,
a b   và 2 2 a  b  0. 1  2e   2
1 a  2e   2 0 1 ab  b 2   1  a  b      1 1 2  2 Do đó
f xdx max       1   3,1316. Chọn D.  1   2  e   2
1 a  2e   2 3e e 1 0 1 ab  b   2    1 1
Câu 117. Cho hàm số f x liên tục trên 0;  1 thỏa mãn
f xdx 
x f xdx  1.   Giá trị 0 0 1
nhỏ nhất của tích phân 2
f xdx  bằng 0 A. 2 . B. 1. C. 8 . D. 3. 3 3 47 1
a  a x f xdx   
Lời giải. Từ giả thiết, ta có  0  . 1
b  bf  xdx    0 Theo Holder 2 1 1 1   a b 
  a x b f xdx   
 a x b2 2 2 dx.
f xdx.    0  0 0 Lại có 1
 a x b 2 2 a 4ab 2 dx   b . 2 3 0 1 a  b 2  2 Suy ra
f xdx   với mọi ,
a b   và 2 2 a  b  0. 2 a 4ab 2 0  b 2 3     1  a b   2  2 Do đó  
f xdx max      3. Chọn D. 2  a 4ab  2 0  b      2 3   
Cách 2. Liên kết với bình phương  f x 2  x    .    
Ta có  f x 2  x    dx     0    
 f x dx 2   
  x  f xdx   x 2 2 dx 0 0 0  2  
 f x 2 dx 2  4 2 
    .    2 3 0 2 2  
Phân tích    4 2 1 2 
        1   62 2 3. 2 3  3  18 2
Câu 118. Cho hàm số y  f x có đạo hàm liên tục trên 1;2, thỏa 3
x f xdx  31.  Giá trị 1 2
nhỏ nhất của tích phân 4
f xdx  bằng 1 A. 961. B. 3875. C. 148955. D. 923521.
Lời giải. Ta có áp dụng hai lần liên tiếp bất đẳng thức Holder ta được 2 4 2 2 2 3 2  2  2 2 2 2               4 3
31   x f x   2 dx     
x .xf x    4   2 2
dx   x dx      
  x f x   4  4 dx             
  x dx      
f xdx.        1 1   1 1 1  1 2 4 Suy ra 31 4
f xdx   3875.  3 2   1  4  x dx      1  2
Dấu ''  '' xảy ra khi f x kx nên 4
k x dx  31  k  5   f x 2  5x .  Chọn B. 1 48
Câu 119. Cho hàm số f x liên tục và có đạo hàm đến cấp 2 trên 0;2 thỏa 2
f 02 f  
1  f 2  1. Giá trị nhỏ nhất của tích phân  f ''x 2 dx    bằng 0 A. 2 . B. 3 . C. 4 . D. 5 . 3 2 5 4 2 1 1 1 1 Holder   Lời giải. Ta có
 f ''x 2 dx  3 x dx.  f ''x 2 2
 dx  3 x. f ''xdx             0 0 0 0  ux
dv f ''xdx 
 f   f   f   2 3 ' 1 0 1  ;   2 2 2 2 Holder  
 f ''x 2 dx  3 x 22 dx.  f ''x 2 dx  3 x 2. f ''xdx         2    1 1 1 1  ux2
dv f ''xdx 
 f   f   f   2 3 ' 1 2 1  .   2
Suy ra  f ' x 2 dx  3 f ' 
1  f 0 f   2
1   3  f ' 
1  f 2 f   2 1         0
 f   f   f   2 0 2 1 2  3 3.     . Chọn B. 2 2 a  b 2 2  2
Nhận xét: Lời giải trên sử dụng bất đẳng thức ở bước cuối là a b  . 2
Câu 120. Cho hàm số f x có đạo hàm trên 1;3 và f  
1  0, max f x  10. Giá trị nhỏ 1;3 3
nhất của tích phân  f 'x 2 dx    bằng 1 A. 1. B. 5. C. 10. D. 20.
Lời giải. Vì max f x
 10 x  1;3 sao cho f x  10 0  0   1;3 f   1 0
x  1;3 sao cho f x  10. 0  0   Theo Holder 2 x0 x0 x0 x0      f ' 
xdx  1 dx.  f 'x 2 dx  x  
1 .  f 'x 2 2  dx.    0           1  1 1 1 2 x 2 0   x   Mà    f '  xdx 
   f x 0      
 f x  f   1 2 10. 0        1  1 x0
Từ đó suy ra  f x 2 10 '  dx     x 1 1 0 3 x0 
  f x 2 x   f x 2 10 10 ' d '  dx         . Chọn B. x 1 31 1 1 0 49
ỨNG DỤNG TÍCH PHÂN
Phần 1. Áp dụng công thức…………………………………………………………
Phần 2. Đồ thị hàm f x………………………………………………………………
Phần 3. Đồ thị hàm f x ……………………………………………………..…….
Phần 4. Diện tích hình phẳng …………………………………………….……
Phần 5. Thể tích khối tròn xoay ………………………………….………….
Phần 6. Bài toán vận tốc …………………….……………………………………..
Phần 1. Áp dụng công thức
Câu 1. Cho hàm số y  f x liên tục trên a;b và có
đồ thị như hình bên. Mệnh đề nào dưới đây đúng? b A. f x 
dx là độ dài đoạn thẳng NM. a b B. f x 
dx là độ dài đường cong AB. a b C. f x 
dx là độ dài đoạn thẳng BP. a b D. f x 
dx là diện tích hình thang cong ABMN. a
Câu 2. Cho hàm số y  f x liên tục trên 0;4 và có đồ thị như 4 hình bên. Tích phân f x  dx bằng 0 A. 0. B. 1. C. 5. D. 8.
Câu 3. Cho hàm số y  f x liên tục trên 0;3 và có đồ thị 3 như hình bên. Biết
f xdx  2,3 
và F x f x, x 0;4. 1 Hiệu F   3  F 0 bằng A. 0,3. B. 1,3. C. 3,3. D. 4,3.
Câu 4. Cho hàm số y  f x liên tục trên 2;2 và có đồ thị 0
đối xứng qua gốc tọa độ như hình bên. Biết
f xdx  2.  Tích 2 2 phân f x  dx bằng 0 A. 2. B. 0. C. 2. D. 4.
Câu 5. Cho hàm số y  f x liên tục trên 2;2 và có đồ thị 2
đối xứng qua trục tung như hình bên. Biết f x 12 dx  .  5 0 0 Tích phân f x  dx bằng 2 A. 12 . B. 24 . 5 5 C. 5 .
D. I  0. 12
Câu 6. Cho hàm số y  f x liên tục trên 3;5 và có đồ
thị như hình bên (phần cong của đồ thị là một phần của 3 Parabol  2 y
ax  bx  c ). Tích phân f x  dx bằng 2 A. 43. B. 53. 2 3 C. 95. D. 97 . 6 6
Câu 7. Cho hàm số y  f x có đạo hàm liên tục trên 1;4 và có 4
đồ thị như hình bên. Tích phân f x  dx bằng 1 A. 0. B. 2. C. 4. D. 6.
Câu 8. Cho hàm số y  f x liên tục trên  và hàm số
y  g x  x f  2 .
x  có đồ thị trên đoạn 1;2 như hình vẽ bên.
Biết phần diện tích miền được tô màu là 5
S  , giá trị của tích 2 4 phân I  f x  dx bằng 1 A. 5 . B. 5 . C. 5. D. 10. 4 2
Câu 9. Cho hàm số y  f x có đạo hàm liên tục trên 1;2.
Đồ thị của hàm số y  f x được cho như hình bên. Diện tích
các hình phẳng K , H  lần lượt là 5 và 8. Biết f   19 1  , 12 3 12 tính f 2. A. 2 11 f   2
2   . B. f 2  .
C. f 2 .
D. f 2 3. 3 3 6
Câu 10. Cho hàm số y  f x có đạo hàm liên tục trên
2;4. Đồ thị của hàm số y  f x được cho như hình
bên. Diện tích hình phẳng giới hạn bởi trục Ox và đồ thị
hàm số y  f x trên đoạn 2; 
1 và 1;4 lần lượt bằng 9 và 12. Cho f  
1  3. Tổng f 2 f 4 bằng A. 2. B. 3. C. 9. D. 21.
Phần 2. Đồ thị hàm f x.
Câu 1. Cho hàm số y  f x có đạo hàm liên tục trên  và có
đồ thị như hình bên. Giá trị của biểu thức 4 2
f x 2dx 
f x  2dx   bằng 0 0 A. 2. B. 2. C. 6. D. 10.
Câu 2. Cho hàm số y  f x xác định và liên tục
trên 0;2 và có bảng biến thiên như hình bên.
Hỏi có bao nhiêu giá trị nguyên của m để thỏa 2
mãn điều kiện  f xm dx     0 ? 0 A. 11. B. 12. C. 13. D. 14.
Câu 3. Cho hai hàm số f x 1 3 2
 ax bx  cx  và 2 g x 2
 dx  ex 1  ,
a b, c, d, e  . Biết rằng đồ thị hàm số
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần
lượt là 3; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng A. 4. B. 9 . C. 5. D. 8. 2
Câu 4. Cho hai hàm số f x 3 2
 ax bx  cx 1 và g x 1 2
 dx  ex  a, b, c, d, e  . Biết rằng đồ thị hàm số 2
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần
lượt 3; 1; 2 (tham khảo hình vẽ). Hình phẳng giới hạn bởi
hai đồ thị đã cho có diện tích bằng A. 125. B. 253. C. 125. D. 253. 12 12 48 48
Câu 5. Cho hai hàm số f x  3 ax  2
bx  cx 2 và g x 2  dx  x e  2  ,
a b, c, d, e  . Biết rằng đồ thị hàm số
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần lượt
là 2; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ
thị đã cho có diện tích bằng A. 9 . B. 13. C. 37 . D. 37 . 2 2 6 12
Câu 6. Cho hai hàm số f x 3 3 2
 ax bx  cx  và 4 g x 3 2
 dx  ex   ,
a b, c, d, e  . Biết rằng đồ thị hàm số 4
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần
lượt là 2; 1; 3 (tham khảo hình vẽ). Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng A. 125. B. 253. C. 125. D. 253. 24 24 48 48
Câu 7. Cho hàm số y  f x xác định và liên tục
trên đoạn 5;3 và có đồ thị như hình vẽ. Biết
rằng diện tích hình phẳng S , S , S giới hạn bởi 1 2 3
đồ thị hàm số y  f x và đường cong    2 y
g x  ax  bx  c lần lượt là , m , n . p 3 Tích phân
f xdx  bằng 5 A. 208
m n  p  . B. 208
m n  p  . 45 45 C. 208 m
  n  p  . D. 208 m
  n  p  . 45 45
Câu 8. Cho hàm số y  f x xác định và liên tục
trên đoạn 3;3 và có đồ thị như hình vẽ. Biết rằng
diện tích hình phẳng S , S giới hạn bởi đồ thị hàm 1 2
số y  f x và đường thẳng y  x 1 lần lượt là 3 M ; . m Tích phân
f xdx  bằng 3
A. 6  m  M.
B. 6m  M.
C. M m  6.
D. m  M 6.
Câu 9. Cho hàm số y  f x có đạo hàm liên tục trên 1
 và có đồ thị như hình bên. Đặt K  x. f x. f xdx,  0
khi đó K thuộc khoảng nào sau đây?      
A. 3;2. B. 3   2;   .      C. 3 2   ; . D. 2   ;0.  2  2 3  3 
Câu 10*. Cho Parabol P 2
: y  x . Hai điểm A , B di dộng
trên P sao cho AB  2 . Khi diện tích phần mặt phẳng giới
hạn bởi P và cát tuyến AB đạt giá trị lớn nhất thì hai điểm ,
A B có tọa độ xác định Ax ; y và Bx ; y Giá trị B B . A A  của biểu thức 2 2 2 2
T  x x  y y bằng A B A B A. 1. B. 2. C. 3. D. 4.
Phần 3. Đồ thị hàm f x.
Câu 1. Cho hàm số y  f x có đạo hàm f x liên tục trên .
 Hình bên là đồ thị của hàm số y  f x trên 5;4. Giá
trị nhỏ nhất của f x trên 5;4 là A. f   5 .
B. f 4. C. f   1 . D. f 4.
Câu 2. Cho hàm số y  f x có đạo hàm f x liên tục trên 
và đồ thị của hàm số y  f x cắt trục hoành tại ba điểm có hoành độ ,
a b, c (hình bên). Khẳng định nào sau đây đúng?
A. f c f a f b.
B. f a f c f b.
C. f b f c f a.
D. f a f b f c.
Câu 3. Cho hàm số y  f x có đạo hàm f x liên tục trên .
 Hình bên là đồ thị của hàm số f x trên
đoạn 2;d. Giá trị nhỏ nhất và giá trị lớn nhất của
hàm số y  f x trên đoạn 2;d lần lượt là
A. f a và f b. B. f a và f 2.
C. f c và f b. D. f c và f d.
Câu 4. Cho hàm số y  f x có đạo hàm f x liên tục trên .
Miền hình phẳng trong hình vẽ được giới hạn bởi đồ thị hàm số
y  f x và trục hoành đồng thời có diện tích S  . a Biết rằng 1 1 x  
1 f xdx  b  và f  
3  c. Tính I 
f xdx.  0 0
A. I  a b  c. B. I  a  b c.
C. I  a
 b  c. D. I  a b c.
Câu 5. Cho hàm số y  f x có đạo hàm f x liên tục trên 2; 
1 . Hình bên là đồ thị của hàm số y  f x. Đặt 2   x
g x  f x
. Khẳng định nào sau đây đúng? 2
A. g2 g 
1  g 0. B. g 
1  g 2 g0.
C. g0 g 
1  g 2. D. g0 g2 g  1 .
Câu 6. Cho hàm số y  f x có đạo hàm f x liên tục
trên 3;3. Hình bên là đồ thị của hàm số y  f x. Đặt
g x  f x 2 2
 x . Khẳng định nào sau đây đúng? A. g  3  g   3  g  
1 . B. g   3  g   3  g   1 . C. g  1  g   3  g   3 . D. g   1  g   3  g   3 .
Câu 7. Cho hàm số y  f x có đạo hàm f x liên tục
trên 3;3. Hình bên là đồ thị của hàm số y  f x.
Đặt gx f xx  2 2
1 . Gọi m là số thực thỏa mãn 3 m 
  gx dx  0. 
Khẳng định nào sau đây đúng?  3  3  A. 6g 
1  m  g   3 . B. 6g 
1  m  6g   3 . C. 3g 
1  m  3g  
3 . D. 3g  
1  m  3g   3 .
Câu 8. Cho hàm số y  f x có đạo hàm f x liên tục trên
3;3. Hình bên là đồ thị của hàm số y  f x. Biết f   1  6 x  2 1
và gx f x
. Khẳng định nào sau đây là đúng? 2
A. Phương trình gx 0 không có nghiệm thuộc 3;3.
B. Phương trình gx 0 có đúng một nghiệm thuộc 3;3.
C. Phương trình gx 0 có đúng hai nghiệm thuộc 3;3.
D. Phương trình gx 0 có đúng ba nghiệm thuộc 3;3.
Câu 9. Cho hàm số y  f x có đạo hàm f x liên tục trên 2; 
1 . Hình bên là đồ thị của hàm số y  f x. Đặt 2   x
g x  f x
. Điều kiện cần và đủ để phương trình g x  0 2
có bốn nghiệm phân biệt là g0 0 g0 0 g0 0 g0 0  A.  . B.  . C.  .
D. g  1  0 .    g  1      0 g  1   0 g2  0 g2  0
Câu 10. Cho hàm số y  f x có đạo hàm f x liên tục
trên . Hàm số y  f x có đồ thị như hình bên. Tổng giá
trị lớn nhất và giá trị nhỏ nhất của hàm số    2 g x f x  trên đoạn 2;2 bằng A. f  
1  f 0. B. f 4 f 0. C. f  
1  f 4. D. f  
1  f 0 f 4.
Phần 4. Diện tích hình phẳng
Câu 1. Cho Parabol như hình vẽ bên. Diện tích hình phẳng
giới hạn bởi Parabol và trục hoành bằng A. 16. B. 16 . 3 C. 28 . D. 32 . 3 3
Câu 2. Tính diện tích hình phẳng được tô đậm ở hình bên. A. 10 S  . B. 20 S  . 3 3 C. 25 S  . D. S  9. 6
Câu 3. Ông An xây dựng một sân bóng đá mini
hình chữ nhật có chiều rộng 30 m và chiều dài
50 m. Để giảm bớt chi phí cho việc trồng cỏ nhân
tạo, ông An chia sân bóng ra làm hai phần (tô đen
và không tô đen) như hình bên. Phần tô đen gồm
hai miền diện tích bằng nhau và đường cong AIB
là một Parabol đỉnh I.
Phần tô đen được trồng cỏ nhân tạo với giá cỏ nhân tạo với giá 130 000 đồng 2 /m và
phần còn lại được trồng cỏ nhân tạo với giá 90 000 đồng 2
/m . Hỏi ông An phải trả bao
nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?
A. 135 triệu đồng.
B. 151 triệu đồng.
C. 165 triệu đồng.
D. 195 triệu đồng.
Câu 4. Nhà ông An cần sơn mặt trước của cổng có dạng như
hình bên, các đường cong có dạng là Parabol với các kích
thước được cho như hình. Biết giá thuê nhân công là 100.000 đồng 2
/m . Hỏi ông An phải trả cho bên thi công bao nhiêu tiền để sơn cổng? A. 2 468650 đồng. B. 1866 667 đồng. C. 1775361 đồng.
D. 1668653 đồng.
Câu 5. Một hoa văn trang trí được tạo ra từ một miếng bìa
mỏng hình vuông cạnh 10 cm bằng cách khoét bỏ đi bốn
phần bằng nhau có hình dạng Parabol (như hình vẽ). Biết
AB  5 cm , OH  4 cm . Diện tích bề mặt hoa văn đó bằng A. 40 140 2 cm . B. 2 cm . 3 3 C. 160 2 cm . D. 2 50 cm . 3
Câu 6. Một mảnh vườn toán học có dạng hình chữ nhật,
chiều dài là 16 m và chiều rộng là 8 m. Các nhà Toán học
dùng hai đường Parabol, mỗi Parabol có đỉnh là trung
điểm của một cạnh dài và đi qua hai mút của cạnh đối
diện, phần mảnh vườn nằm ở miền trong của cả hai
Parabol (phần tô đậm như hình vẽ) được trồng hoa hồng. Biết chi phí để trồng hoa hồng là 45000 đồng 2
/m . Hỏi các nhà Toán học phải chi bao nhiêu tiền để trồng hoa
trên phần mảnh vườn đó? (Số tiền được làm tròn đến hàng nghìn).
A. 1920 000 đồng. B. 2159 000 đồng.
C. 2715000 đồng. D. 3322 000 đồng.
Câu 7. Một công ty quảng cáo muốn làm một bức tranh trang trí hình MNEIF ở
chính giữa của một bức tường hình chữ nhật ABCD có chiều cao BC  6 m , chiều dài
CD  12 m (hình vẽ bên). Cho biết MNEF là hình chữ nhật có MN  4 m; cung EIF
có hình dạng là một phần của cung Parabol có đỉnh I là trung điểm của cạnh AB và
đi qua hai điểm C, D. Kinh phí làm bức tranh là 900.000 đồng 2 /m . Hỏi công ty cần
bao nhiêu tiền để làm bức tranh đó? A. 20.400.000 đồng. B. 20.600.000 đồng. C. 20.800.000 đồng. D. 21.200.000 đồng.
Câu 8. Một chiếc cổng có hình dạng là một Parabol có khoảng cách
giữa hai chân cổng là AB  8 m. Người ra treo một tâm phông hình
chữ nhật có hai đỉnh M , N nằm trên Parabol và hai đỉnh P, Q nằm
trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô
đen) người ta mua hoa để trang trí với chi phí cho 2 1 m cần số tiền
mua hoa là 200.000 đồng, biết MN  4 m, MQ  6 m. Hỏi số tiền dùng để mua hoa
trang trí chiếc cổng gần với số tiền nào sau đây?
A. 3373400 đồng. B. 3434 300 đồng. C. 3437300 đồng. D. 3733300 đồng.
Câu 9. Cho H là hình phẳng giới hạn bởi đồ thị C 2
: y  4x  x và
trục hoành (hình vẽ bên). Đường thẳng y  m chia H thành hai
phần có diện tích bằng nhau. Biết 3
m  a  b với ,
a b là các số hữu tỉ, tính S  . a . b A. S  64. B. S  32. C. S  32. D. S  64.
Câu 10. Cho H là hình phẳng giới hạn bởi đồ thị P của hàm số 2
y  6x  x và trục hoành. Hai đường thẳng y  m và y  n
chia hình H thành ba phần có diện tích bằng nhau. Tính
P   m3  n3 9 9 . A. P  403. B. P  405. C. P  407. D. P  409.
Câu 11. Cho hình phẳng H (phần tô đậm) được giới hạn bởi các đường y   2
4 x , y  x và y  2 có diện tích là
S  a  b với , a b  
. Khẳng định nào sau đây đúng?
A. a b 1.
B. a  2b  3. C. 2 a  2
4b  5. D. a 1 và b 1.
Câu 12. Cho đường tròn tâm O đường kính AB  8. Trên AB
lấy hai điểm M , N đối xứng nhau qua O sao cho MN  4.
Qua M , N kẻ hai dây cung PQ và EF cùng vuông góc với AB.
Diện tích phần giới hạn bởi đường tròn và hai dây cung PQ, EF
(phần tô đậm như hình vẽ) bằng A. 16  5  5. B. 6 8 3.
C. 12 7. D.  8 3. 3
Câu 13. Biết rằng đường Parabol P 2
: y  2x chia đường tròn C 2 2
: x  y  8 thành hai phần lần lượt có diện tích là b
S , S (hình bên). Khi đó S S  a  với ,
a b, c nguyên 1 2 2 1 c
dương và b là phân số tối giản. Tổng a b  c bằng c A. 13. B. 14. C. 15. D. 16.
Câu 14. Một khuôn viên dạng nửa hình tròn có đường
kính bằng 4 5 m. Trên đó người thiết kế hai phần để
trồng hoa có dạng của một cánh hoa hình Parabol có
đỉnh trùng với tâm nửa hình tròn và hai đầu mút của
cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng 4 m,
phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết
các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100 000 đồng 2 /m .
Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn).
A. 1194 000 đồng. B. 1948000 đồng. C. 2388000 đồng. D. 3895000 đồng.
Câu 15. Một viên gạch hoa hình vuông cạnh 40 cm. Người
thiết kế đã sử dụng bốn đường Parabol có chung đỉnh tại tâm
của viên gạch để tạo ra bốn cánh hoa (được tô màu như hình
bên). Diện tích mỗi cánh hoa của viên gạch bằng A. 400 2 250 cm . B. 2 cm . 3 C. 800 1600 2 cm . D. 2 cm . 3 3 2 2 Câu 16. Gọi x y
S là diện tích của hình phẳng giới hạn bởi Elip   1 và S là 1 9 1 2
diện tích của hình thoi có các đỉnh là đỉnh của Elip đó. Tỉ số S1 bằng S2 A. 2 . B.  . C.  . D.  . 2 3 3
Câu 17. Một sân chơi cho trẻ em hình chữ nhật có
chiều dài 100 m và chiều rộng là 60 m người ta
làm một con đường nằm trong sân (như hình vẽ).
Biết rằng viền ngoài và viền trong của con đường là
hai đường elip, Elip của đường viền ngoài có trục
lớn và trục bé lần lượt song song với các cạnh hình
chữ nhật và chiều rộng của mặt đường là 2 m. Kinh phí cho mỗi 2
m làm đường 600 000 đồng. Tính tổng số tiền làm con đường đó. (Số tiền
được làm tròn đến hàng nghìn). A. 293804 000 đồng. B. 293904 000 đồng. C. 294 053000 đồng. D. 294153000 đồng.
Câu 18. Một mảnh vườn hình chữ nhật có chiều dài
10 m và chiều rộng 6 m, được phân chia thành các phần
bởi một đường chéo và một đường Elip nội tiếp bên trong
như hình vẽ bên. Hãy tính diện tích phần tô đậm (theo đơn vị 2 m )? 454  454 
A. 52.
B. 54. C. . D. . 7 8
Câu 19. Một biển quảng cáo có dạng hình Elip với bốn đỉnh
A , A , B , B như hình vẽ bên. Biết chi phí sơn phần tô đậm 1 2 1 2 là 200 000 đồng 2
/m và phần còn lại là 100 000 đồng 2 /m .
Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào
dưới đây, biết A A  8 m, B B  6 m và tứ giác MNPQ là 1 2 1 2
hình chữ nhật có MQ  3 m ? A. 5.526.000 đồng. B. 5.782.000 đồng.
C. 7 213000 đồng. D. 7322 000 đồng.
Câu 20. Nhà trường dự định làm một vườn hoa
dạng hình Elip được chia ra làm bốn phần bởi hai
đường Parabol có chung đỉnh, đối xứng với nhau
qua trục của Elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của Elip lần lượt là 8 m và 4 m; F , F 1 2
là hai tiêu điểm của Elip. Phần ,
A B dùng để trồng hoa; phần C, D dùng để trồng cỏ.
Kinh phí để trồng mỗi mét vuông trồng hoa và trồng cỏ lần lượt là 250 000 đồng và
150 000 đồng. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 4 656 000 đồng. B. 4766 000 đồng. C. 5455000 đồng. D. 5676 000 đồng.
Câu 21. Cho hình phẳng giới hạn bởi các
đường y  sin x, y  cos x và S , S là 1 2
diện tích của các phần được gạch chéo như hình vẽ. Tổng 2 S  2 S bằng 1 2 A. 102 2. B. 10  2 2. C. 1112 2. D. 11 2 2.
Câu 22. Kí hiệu H là hình phẳng giới hạn bởi các đường  x y e ,
y  0, x  0 và x  1. Đường thẳng x  k 0  k   1 chia H
thành hai phần có diện tích tương ứng S , S như hình vẽ bên, 1 2
biết S  S . Mệnh đề nào sau đây là đúng? 1 2 A. k e 1 k e 1 e  . B.  e  . 2 2 C. k e 3 k e  2 e  . D.  e  . 2 2
Câu 23. Cho hình phẳng H giới hạn bởi các đường 2
y  x , y  0, x  0, x  4. Đường thẳng y  k
0  k 16 chia hình H thành hai phần có diện tích
S , S (hình vẽ). Tìm k để S  S . 1 2 1 2 A. k  3 . B. k  4 . C. k  5. D. k  8 .
Câu 24. Xét hình phẳng H giới hạn bởi đồ thị hàm số
y  x  2
3 , trục hoành và đường thẳng x  0. Gọi A0;9,
Bb;0 3  b  0. Tìm giá trị của tham số b để đoạn thẳng
AB chia H thành hai phần có diện tích bằng nhau.
A. b  2 . B. 3 b   . C. b  1. D. 1 b   . 2 2
Câu 25. Trong mặt phẳng tọa độ, cho hình chữ nhật H
có một cạnh nằm trên trục hoành và có hai đỉnh trên một
đường chéo là A1;0 và C a; a với a  0. Biết rằng
đồ thị hàm số y  x chia hình H thành hai phần có
diện tích bằng nhau, tìm . a A. 1 a  .
B. a  3. C. a  4. D. a  9. 2
Phần 5. Thể tích khối tròn xoay
Câu 1. Cho hình phẳng H giới hạn bởi các đồ thị hàm số 2
y  4  x và y   2
2 x . Tính thể tích V của khối
tròn xoay tạo thành khi quay H quanh trục hoành. A. V  10 .  B. V  12 .  C. V  14 .  D. V  16 . 
Câu 2. Thể tích V của khối tròn xoay khi cho hình
phẳng H giới hạn bởi các đường 2
y  1 x và 2 y  x 1
quay quanh trục Ox được xác định bởi công thức nào sau đây? 1 1
A. V   1x 2 x   2 2 2 1 dx.
B. V    2 1 x  2 x   1 dx. 1 1 1 1 C. 2 2
V   1x 2 2 dx. D. V   2  x 1  2 1 x       d  x.   1 1
Câu 3. Cho hình vuông OABC có cạnh bằng 4 được chia
thành hai phần bởi đường cong P có phương trình 1 y  2
x . Gọi S là hình phẳng không bị gạch (như hình vẽ). 4
Tính thể tích V của vật thể tròn xoay khi cho phần S qua quanh trục Ox. A. 64 128 128 256 V  . B.  V  . C.  V  . D.  V  . 5 3 5 5
Câu 4. Cho hình phẳng H giới hạn bởi 1 đường tròn có 4
bán kính R  2, đường cong y  4  x và trục hoành
(miền tô đậm như hình vẽ). Tính thể tích V của khối tạo
thành khi cho hình H quay quanh trục Ox. A. 40    V   B. 53 V   C. 67 V   D. 77 V   3 6 6 6
Câu 5. Cho hình phẳng H giới hạn bởi các đường
y   x  2, y  x  2,
x  1. Tính thể tích V của vật thể
tròn xoay khi quay hình phẳng H quanh trục Ox. A. 9 V  9. B.  V  . 2 C.  25 55 V  . D.  V  . 3 6
Câu 6. Gọi V là thể tích khối tròn xoay tạo
thành khi quay hình phẳng giới hạn bởi các
đường y  x, y  0 và x  4 quanh trục Ox .
Đường thẳng x  a 0  a  4 cắt đồ thị hàm số
y  x tại M (hình vẽ bên). Gọi V là thể tích 1
khối tròn xoay tạo thành khi quay tam giác
OMH quanh trục Ox . Biết rằng V  2V . Khi đó 1 A. a  2 . B. 5 a  . C. a  2 2 . D. a  3 . 2
Câu 7. Gọi V là thể tích khối tròn xoay tạo thành khi
quay hình phẳng giới hạn bởi các đường y  sin x, hai
trục tọa độ và x   quanh trục hoành. Đường thẳng
x  k 0  k   cắt đồ thị hàm số y  sin x tại điểm
M và trục hoành tại điểm N (hình vẽ bên).
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác OMN quanh trục Ox. 1 Biết rằng 12 V  V . Khi đó 1 k A.  k  . B.  k  . C. k  2.
D. k  3. 6 3
Câu 8. Có một vật thể là hình tròn xoay có dạng giống như một
cái ly như hình vẽ bên. Người ta đo được đường kính của miệng
ly là 4 cm và chiều cao là 6 cm. Biết rằng thiết diện của chiếc
ly cắt bởi mặt phẳng đối xứng là một Parabol. Thể tích của vật thể đã cho bằng A.   3 12 cm . B.  3 12 cm . C. 72 72   3 cm . D.  3 cm . 5 5
Câu 9. Trong mặt phẳng cho đường Elip E có độ dài trục
lớn là AA  8 và độ dài trục nhỏ BB  6; đường tròn tâm
O đường kính BB như hình vẽ. Tính thể tích V của khối
tròn xoay có được bằng cách cho miền hình phẳng giới hạn
bởi đường Elip và đường tròn (được tô đậm trên hình vẽ)
quay xung quanh trục AA . A. V  12 .  B. V  16 . 
C. V  28. D. V  36 . 
Câu 10. Một thùng chứa rượu làm bằng gỗ là một hình tròn
xoay như hình bên có hai đáy là hai hình tròn bằng nhau,
khoảng cách giữa hai đáy bằng 8 dm. Đường cong mặt bên của
thùng là một phần của đường Elip có độ dài trục lớn bằng
10 dm , độ dài trục bé bằng 6 dm. Hỏi chiếc thùng gỗ đó đựng
được bao nhiêu lít rượu?
A. 1316 (lít). B. 1416 (lít).
C. 1516 (lít).
D. 1616 (lít). 25 25 25 25
Câu 11. Bên trong hình vuông cạnh , a dựng hình sao
bốn cánh đều như hình vẽ bên (các kích thước cần thiết
cho như ở trong hình). Tính thể tích V của khối tròn
xoay sinh ra khi quay hình sao đó quanh trục Ox. A.  5 3
V  a . B.  V  3 a . 8 24 C. 5 5 3 V  a . D.  V  3 a . 48 96
Câu 12. Cho hình phẳng H gồm nửa hình tròn đường kính AB
và tam giác ABC đều (như hình vẽ). Gọi  là đường thẳng qua
C và song song với AB. Biết AB  2 3 cm. Thể tích khối tròn
xoay tạo bởi hình H quay quanh trục  bằng 2 A. 9
  2  3 8 3 9 cm . B. 8  3   3 cm . 2 C.
  2  3 32 3 18 cm . D.
  2  3 16 3 9 cm .
Câu 13. Cho hình vẽ bên, biết cung tròn BC nằm trên đường tròn
bán kính R  4. Cạnh AB  BC  CD  DA  4. Thể tích vật tròn
xoay tạo thành khi quay hình bên quanh trục AD nằm trong
khoản nào sau đây? A. 165;170. B. 160;  165 . C. 155;160. D. 150;  155 .
Câu 14. Cho hình tròn tâm O có bán kính R  2 và hình vuông
OABC có cạnh bằng 4 (như hình vẽ bên). Tính thể tích V của vật
thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng OB. 83 4 2 82 5 2 A. V  . B. V  . 3 3 835 2 321 2 C. V  . D. V  . 3 3
Câu 15. Cho hình vuông có độ dài cạnh bằng 8cm và một hình
tròn có bán kính 5cm được xếp chồng lên nhau sao cho tâm
của hình tròn trùng với tâm của hình vuông như hình vẽ bên.
Tính thể tích V của vật thể tròn xoay tạo thành khi quay mô
hình trên quanh trục XY . A. 260 290 520 580 3    V  cm . B. 3 V  cm . C. 3 V  cm . D. 3 V  cm . 3 3 3 3
Câu 16. Cho hai tam giác cân có chung đường cao
XY  40cm và cạnh đáy lần lượt là 40cm và 60cm , được
xếp chồng lên nhau sao cho đỉnh của tam giác này là trung
điểm cạnh đáy của tam giác kia như hình vẽ bên. Tính thể
tích V của vật thể tròn xoay được tạo thành khi quay mô
hình trên quanh trục XY . A. 40480 52000 3  V  cm . B. 3 V  cm . 3 3 C. 46240 3 V  cm . D. 3
V  1920cm . 3
Câu 17. Cho khối cầu có bán kính R . Một mặt phẳng cắt
khối cầu thành hai nửa. Nửa bé có khoảng cách từ đỉnh đến
đáy bằng h (tham khảo hình vẽ bên). Tính thể tích nửa bé.  h  h
A. V   2 h   R   V  2 h    . B.
 R  .  2    3  h  h
C. V   2 h   R   V  2 h    . D.
 R  .  4    3
Câu 18. Cho hai mặt cầu S , S có cùng bán kính R 2  1 
thỏa mãn tính chất: tâm của S thuộc S và ngược lại. 2  1 
Tính thể tích phần chung V của hai khối cầu tạo bởi S 1  và S . 2  3 3 3 A. R 2 R 5 R V   3 R . B.  V  . C.  V  . D.  V  . 2 5 12
Câu 19. Cho hai đường tròn O ;5 và O ;3 cắt nhau tại 2  1 
hai điểm A và B sao cho AB là một đường kính của
đường tròn O . Gọi H là diện tích hình phẳng giới hạn 2 
bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch
chéo như hình vẽ). Quay hình H quanh trục O O , ta 1 2
được một khối tròn xoay. Thể tích của khối tròn xoay được tạo thành bằng A. 14 40 68  B.  
C.  .
D. 36. 3 3 3
Câu 20. Ta vẽ hai nửa đường tròn như hình vẽ bên,
trong đó đường kính của nửa đường tròn lớn gấp đôi
đường kính của nửa đường tròn nhỏ. Biết rằng nửa
hình tròn đường kính AB có diện tích là 8 và 
BAC  30. Thể tích của vật thể tròn xoay được tạo
thành khi quay hình H (phần tô đậm) xung quanh
đường thẳng AB bằng A. 98 220 224 2 4 . B. . C. . D. . 3 3 3
Phần 6. Bài toán vận tốc
Câu 1. (ĐỀ MINH HỌA 2016 – 2017) Một ô tô đang chạy với vận tốc 10m/s thì
người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc
vt  5t 10m/s, trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m. B. 2m. C. 10m. D. 20m.
Câu 2. Một ô tô đang đi với vận tốc lớn hơn 72km/h, phía trước là đoạn đường chỉ cho
phép chạy với tốc độ tối đa là 72km/h, vì thế người lái xe đạp phanh để ô tô chuyển
động chậm dần đều với vận tốc vt 302t  m/s, trong đó t là khoảng thời gian
tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt
tốc độ 72km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét? A. 100m. B. 125m. C. 150m. D. 175m.
Câu 3. Hai viên đạn cùng rời khỏi nòng súng thời điểm t  0 với những vận tốc khác
nhau: viên đạn thứ nhất có vận tốc v t 3t
1 m/s , viên đạn thứ hai có vận tốc 1    2   
v t  2t  4 m/s . Hỏi từ giây thứ mấy thì viên đạn thứ nhất xa điểm xuất phát hơn 2   viên đạn thứ hai? A. Giây thứ nhất. B. Giây thứ hai. C. Giây thứ ba. D. Giây thứ tư.
Câu 4. Một ô tô đang chạy với vận tốc 10 
m/s thì người lái xe đạp phanh. Từ thời
điểm đó, ô tô chuyển động chậm dần đều với vận tốc vt 2t 10  m/s, trong đó t
là khoảng thời gian được tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quảng
đường ô tô di chuyển được trong 8 giây cuối cùng. A. 16m. B. 25m. C. 50m. D. 55m.
Câu 5. Một vật đang chuyển động với vận tốc 6m/s thì tăng tốc với gia tốc at 3  2
m/s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng t 1
tốc. Hỏi vận tốc của vật sau 10 giây gần nhất với kết quả nào sau đây? A. 11m/s . B. 12 m/s . C. 13m/s . D. 14 m/s .
Câu 6. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc
at  t  2 t  2 3
m/s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu
tăng tốc. Hỏi quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt
đầu tăng tốc bằng bao nhiêu mét? A. 1900 m. B. 2200 m. C. 4000 m. D. 4300 m. 3 3 3 3
Câu 7. Một ô tô đang chạy thẳng đều với vận tốc v m/s thì người đạp phanh, từ 0  
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc vt 5t v m/s , trong 0  
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp
phanh đến lúc dừng hẳn ô tô di chuyển được 40m thì vận tốc ban đầu v bằng bao 0 nhiêu?
A. v  20m/s. B. v  25m/s. C. v  40m/s. D. v  80m/s. 0 0 0 0
Câu 8. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162m so
với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng,
khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật vt 2
 10t t m/s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
chuyển động. Hỏi lúc vừa tiếp đất, vận tốc v của khí cầu bằng bao nhiêu? A. v  3m/s. B. v  5m/s. C. v  7m/s. D. v  9m/s.
Câu 9. (ĐỀ THI CHÍNH THỨC 2016 – 2017) Một vật chuyển động theo quy luật 1 3 2
s   t  6t với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động 2
và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian 8 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. 18m/s. B. 24m/s. C. 64m/s. D. 108m/s.
Câu 10. Một tàu lửa đang chạy với vận tốc
200 m/s thì người lái tàu đạp phanh. Từ
thời điểm đó, tàu chuyển động chậm dần đều với vận tốc vt 200 at  m/s, trong
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh và a 2 m/s  là
gia tốc. Biết rằng khi đi được 1500m thì tàu dừng, hỏi gia tốc của tàu bằng bao nhiêu? A. 200 100 40 40 a   2
m/s . B. a   2
m/s . C. a   2 m/s . D. a   2 m/s . 13 13 3 3
Câu 11. Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu tăng tốc
với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường
cong Parabol có hình bên. Biết rằng sau 10s thì xe đạt đến vận
tốc cao nhất 50m/s và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu
tăng tốc đến lúc đạt vận tốc cao nhất thì xe đã đi được quãng
đường bao nhiêu mét? A. 1000 m. B. 1100 m. C. 1400 m. D. 300m. 3 3 3
Câu 12. Một vật chuyển động trong 3 giờ với vận tốc vkm/h phụ
thuộc thời gian t h có đồ thị là một phần của đường Parabol có
đỉnh I 2;9 và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
A. s  24,25km. B. s  24,75km.
C. s  25,25km.
D. s  26,75km.
Câu 13. Một vật chuyển động trong 4 giờ với vận tốc vkm/h
phụ thuộc thời gian t h có đồ thị của vận tốc như hình bên.
Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động,
đồ thị đó là một phần của đường Parabol có đỉnh I 2;9 với
trục đối xứng song song với trục tung, khoảng thời gian còn lại
đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng
đuờng s mà vật chuyển động trong 4 giờ đó.
A. s  24km.
B. s  26,5km. C. s  27km.
D. s  28,5km.
Câu 14. Một vật chuyển động trong 4 giờ với vận tốc
v km/h phụ thuộc thời gian t h có đồ thị của vận tốc
như hình bên. Trong khoảng thời gian 2 giờ kể từ khi
bắt đầu chuyển động, đồ thị đó là một phần của đường
Parabol có đỉnh I 1;2 và trục đối xứng song song với
trục tung, khoảng thời gian còn lại đồ thị là một phần
đường thẳng. Tính quãng đường s mà vật di chuyển được
trong 4 giờ đó (kết quả làm tròn đến hàng phần trăm).
A. s  5,44km. B. s  8,67km.
C. s  9,27km.
D. s  11,35km.
Câu 15. Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi
hành cùng một lúc, bên cạnh nhau và trên cùng một con
đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường
Parabol, đồ thị biểu diễn vận tốc của xe B là một đường
thẳng ở hình bên. Hỏi sau khi đi được 3 giây khoảng cách
giữa hai xe là bao nhiêu mét? A. 0 m. B. 60 m. C. 90 m. D. 270 m.
---------- HẾT ----------
ỨNG DỤNG TÍCH PHÂN
Phần 1. Áp dụng công thức…………………………………………………………
Phần 2. Đồ thị hàm f x………………………………………………………………
Phần 3. Đồ thị hàm f x ……………………………………………………..…….
Phần 4. Diện tích hình phẳng …………………………………………….……
Phần 5. Thể tích khối tròn xoay …………………….……………………….
Phần 6. Bài toán vận tốc …………………….……………………………………..
Phần 1. Áp dụng công thức
Câu 1. Cho hàm số y  f x liên tục trên a;b và có
đồ thị như hình bên. Mệnh đề nào dưới đây đúng? b A. f x 
dx là độ dài đoạn thẳng NM. a b B. f x 
dx là độ dài đường cong AB. a b C. f x 
dx là độ dài đoạn thẳng BP. a b D. f x 
dx là diện tích hình thang cong ABMN. a b Lời giải. Ta có
f x x  f xb  f b f a  BM  MP   d BP. Chọn C. a a
Câu 2. Cho hàm số y  f x liên tục trên 0;4 và có đồ thị như 4 hình bên. Tích phân f x  dx bằng 0 A. 0. B. 1. C. 5. D. 8.
Lời giải. Kí hiệu các điểm như trên hình vẽ. 4 2 4 Ta có:
f xdx 
f xdx 
f xdx  S S .    ABCO CDE 0 0 2 2.1 2
Diện tích hình thang ABCO là: S   3. ABCO 2
Diện tích hình tam giác CDE là: 2.2 S   2 CDE 2 4 Vậy
f xdx  S S  32  1.  Chọn B. ABCO CDE 0
Câu 3. Cho hàm số y  f x liên tục trên 0;3 và có đồ thị 3 như hình bên. Biết
f xdx  2,3 
và F x f x, x 0;4. 1 Hiệu F   3  F 0 bằng A. 0,3. B. 1,3. C. 3,3. D. 4,3.
Lời giải. Kí hiệu các điểm như trên hình vẽ. Ta có 3 1 3
f xdx 
f xdx 
f xdx  S  2,3  2  2,3  4,3.    ABCO 0 0 1 3 3 Lại có
f xdx  F xdx  F x3  F   3  F 0.   0 0 0 Suy ra F  
3  F 0  4,3. Chọn D.
Câu 4. Cho hàm số y  f x liên tục trên 2;2 và có đồ thị 0
đối xứng qua gốc tọa độ như hình bên. Biết
f xdx  2.  Tích 2 2 phân f x  dx bằng 0 A. 2. B. 0. C. 2. D. 4.
Lời giải. Vì đồ thị hàm số y  f x đối xứng qua gốc tọa độ nên hàm số y  f x là 2
hàm số lẻ. Áp dụng tính chất hàm lẻ, ta có
f xdx   0. 2 2 0 2 2 Mà
f xdx 
f xdx 
f xdx     0. Suy ra
f xdx    2. Chọn A. 2 2 0 0
Câu 5. Cho hàm số y  f x liên tục trên 2;2 và có đồ thị 2
đối xứng qua trục tung như hình bên. Biết f x 12 dx  .  5 0 0 Tích phân f x  dx bằng 2 A. 12 . B. 24 . 5 5 C. 5 .
D. I  0. 12
Lời giải. Vì đồ thị hàm số y  f x đối xứng qua trục tung nên hàm số y  f x là 0 2
hàm số chẵn. Áp dụng tính chất hàm chẵn, ta có f x 12 dx 
f xdx    . Chọn A. 5 2 0
Câu 6. Cho hàm số y  f x liên tục trên 3;5 và có đồ
thị như hình bên (phần cong của đồ thị là một phần của 3 Parabol  2 y
ax  bx  c ). Tích phân f x  dx bằng 2 A. 43. B. 53. 2 3 C. 95. D. 97 . 6 6
Lời giải. Dựa vào đồ thị hàm số ta suy ra 3 0 1 3 f x 4  97 dx    
  x 4dx  4xdx  2   
 4x x dx  . Chọn D. 3  6 2 2 0 1
Câu 7. Cho hàm số y  f x có đạo hàm liên tục trên 1;4 và có 4
đồ thị như hình bên. Tích phân f x  dx bằng 1 A. 0. B. 2. C. 4. D. 6.
Lời giải. Dựa vào đồ thị ta thấy: ● f  
1  f 4  0; f 2  3.
● Hàm số y  f x đồng biến trên khoảng 1;2 và nghịch biến trên khoảng 2;4
 f x 0 khi 1 x  2 nên suy ra  .  f 
 x 0 khi 2  x   4 4 2 4 2 4 Do đó
f x dx 
f xdx 
f xdx  f x  f x    1 2 1 1 2
 f 2 f  
1   f 4 f 2    6. Chọn D.
Câu 8. Cho hàm số y  f x liên tục trên  và hàm số
y  g x  x f  2 .
x  có đồ thị trên đoạn 1;2 như hình vẽ bên.
Biết phần diện tích miền được tô màu là 5
S  , giá trị của tích 2 4 phân I  f x  dx bằng 1 A. 5 . B. 5 . C. 5. D. 10. 4 2 2
Lời giải. Diện tích phần tô màu là: S 
g xdx.  1 2 Theo giả thiết 5 S   x. f   5 2 x dx  . 2 2 1
x 1 t 1 Đặt 2 t  x 
dt  2xdx . Đổi cận:  .
x  2  t  4  2 4 4 4
Khi đó 5  x. f   1 2 x dx 
f tdt  
f tdt  5   hay
f xdx  5.  Chọn C. 2 2 1 1 1 1
Câu 9. Cho hàm số y  f x có đạo hàm liên tục trên 1;2.
Đồ thị của hàm số y  f x được cho như hình bên. Diện tích
các hình phẳng K , H  lần lượt là 5 và 8. Biết f   19 1  , 12 3 12 tính f 2. A. 2 11 f   2
2   . B. f 2  .
C. f 2 .
D. f 2 3. 3 3 6 2 0 2
Lời giải. Dựa vào đồ thị ta thấy:
f x x 
f x x  f x 5 8 9 d d dx     .    12 3 4 1 1  0 2 Mặt khác:
f x x  f x 2  f   f    f   19 d 2 1 2  .  1 12 1
Từ đó suy ra f   19 9 9 19 2 2    
 f 2      . Chọn A. 12 4 4 12 3
Câu 10. Cho hàm số y  f x có đạo hàm liên tục trên
2;4. Đồ thị của hàm số y  f x được cho như hình
bên. Diện tích hình phẳng giới hạn bởi trục Ox và đồ thị
hàm số y  f x trên đoạn 2; 
1 và 1;4 lần lượt bằng 9 và 12. Cho f  
1  3. Tổng f 2 f 4 bằng A. 2. B. 3. C. 9. D. 21. 1 4
Lời giải. Theo giả thiết, ta có
f xdx  9  và
f xdx  12.  2 1 1 •
f xdx  9  f  
1  f 2  9  3 f 2  9 
 f 2  12.  2 4 •
f xdx  12  f 4 f  
1  12  f 43  12   f 4  9.  1
Vậy f 2 f 412 9 3. Chọn B.
Phần 2. Đồ thị hàm f x.
Câu 1. Cho hàm số y  f x có đạo hàm liên tục trên  và có
đồ thị như hình bên. Giá trị của biểu thức 4 2
f x 2dx 
f x  2dx   bằng 0 0 A. 2. B. 2. C. 6. D. 10. 4 tx 2 2 2 tx  4 2 Lời giải. Ta có
f x 2dx  f t   dt và
f x  2dx  f t   dt. 0 2 0 2 4 2 2 4 4 Khi đó
f x 2dx 
f x  2dx  f  tdt 
f tdt  f t      dt 0 0 2 2 2 4  f t
 f 4 f 2  4 2  6. Chọn C. 2
Câu 2. Cho hàm số y  f x xác định và liên tục
trên 0;2 và có bảng biến thiên như hình bên.
Hỏi có bao nhiêu giá trị nguyên của m để thỏa 2
mãn điều kiện  f xm dx     0 ? 0 A. 11. B. 12. C. 13. D. 14.
Lời giải: Dựa vào bảng biến thiên ta có
max f x  7  2 2 2 2 x   0;2     5 dx 
f xdx  7dx hay 10 
f xdx 14.     
min f x 5  0 0 0 0  x   0;2  2 2
Từ giả thiết  f xm dx  0  2m  f x    
dx. Do đó để phương trình có nghiệm 0 0
 10  2m 14  5  m  7 . Vậy có 13 giá trị m nguyên thỏa mãn. Chọn C.
Câu 3. Cho hai hàm số f x 1 3 2
 ax bx  cx  và 2 g x 2
 dx  ex 1  ,
a b, c, d, e  . Biết rằng đồ thị hàm số
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần
lượt là 3; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng A. 4. B. 9 . C. 5. D. 8. 2
Lời giải. Phương trình hoành độ giao điểm của đồ thị f x và gx là 1 3 3 ax  2
bx  cx   2
dx  ex 1  3
ax b d 2
x c dx   0    . 2 2
Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình    có ba nghiệm là 3
3; 1; 1. Ta được ax   3 x   1 x   3
1  ax b d 2
x c dx  . Đồng nhất 2 hai vế ta suy ra 3 1
3a    a  . 2 2 1
Vậy diện tích hình phẳng cần tìm là
1 x  3x  1x  1dx   4. Chọn A. 2 3
Câu 4. Cho hai hàm số f x 3 2
 ax bx  cx 1 và g x 1 2
 dx  ex  a, b, c, d, e  . Biết rằng đồ thị hàm số 2
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần
lượt 3; 1; 2 (tham khảo hình vẽ). Hình phẳng giới hạn bởi
hai đồ thị đã cho có diện tích bằng A. 125. B. 253. C. 125. D. 253. 12 12 48 48
Lời giải. Tương tự như bài trên ta được 1 a  . 4 2
Vậy diện tích hình phẳng cần tìm là 1  253 x   3 x  
1 x 2 dx   . Chọn D. 4 48 3
Câu 5. Cho hai hàm số f x  3 ax  2
bx  cx 2 và g x 2  dx  x e  2  ,
a b, c, d, e  . Biết rằng đồ thị hàm số
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần lượt
là 2; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ
thị đã cho có diện tích bằng A. 9 . B. 13. C. 37 . D. 37 . 2 2 6 12
Lời giải. Tương tự như bài trên ta được a  2. 1
Vậy diện tích hình phẳng cần tìm là
2x  2x   1 x   37 1 dx  .  Chọn C. 6 2
Câu 6. Cho hai hàm số f x 3 3 2
 ax bx  cx  và 4 g x 3 2
 dx  ex  a, b, c, d, e  . Biết rằng đồ thị hàm số 4
y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần
lượt là 2; 1; 3 (tham khảo hình vẽ). Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng A. 125. B. 253. C. 125. D. 253. 24 24 48 48
Lời giải. Tương tự như bài trên ta được 1 a  . 4 3
Vậy diện tích hình phẳng cần tìm là 1  253
x  2x   1 x   3 dx   . Chọn D. 4 48 2
Câu 7. Cho hàm số y  f x xác định và liên tục
trên đoạn 5;3 và có đồ thị như hình vẽ. Biết
rằng diện tích hình phẳng S , S , S giới hạn bởi 1 2 3
đồ thị hàm số y  f x và đường cong    2 y
g x  ax  bx  c lần lượt là , m , n . p 3 Tích phân
f xdx  bằng 5 A. 208
m n  p  . B. 208
m n  p  . 45 45 C. 208 m
  n  p  . D. 208 m
  n  p  . 45 45
Lời giải. Đồ thị hàm    2 y g x
ax  bx  c đi qua các điểm O 0;0, A2;0, B3;2
nên suy ra gx 2 4  2 x  x. 15 15
Dựa vào đồ thị, ta có 2 0 3
m n  p 
 f x gx dx  gx f x dx   f x gx dx          5 2 0 3 3 
f xdx  gxdx.   5 5 3 3 Suy ra
f x x  m n  p  gx 208 d
dx  m n  p  .   Chọn B. 45 5 5
Câu 8. Cho hàm số y  f x xác định và liên tục
trên đoạn 3;3 và có đồ thị như hình vẽ. Biết rằng
diện tích hình phẳng S , S giới hạn bởi đồ thị hàm 1 2
số y  f x và đường thẳng y  x 1 lần lượt là 3 M ; . m Tích phân
f xdx  bằng 3
A. 6  m  M.
B. 6m  M.
C. M m  6.
D. m  M 6. 1 1 1 1
Lời giải. Ta có M  x 1 f x dx  x   1 dx 
f xdx  0 f x       dx; 3 3 3 3 3 3 3 3
m   f xx   1  dx 
f xdx  x   1 dx 
f xdx        6. 1 1 1 1 3 1 3
Suy ra m  M 
f xdx  6 
f xdx  6  f x    dx. 1 3 3 3 Suy ra
f xdx  m  M   6. Chọn D. 3
Câu 9. Cho hàm số y  f x có đạo hàm liên tục trên 1
 và có đồ thị như hình bên. Đặt K  x. f x. f xdx,  0
khi đó K thuộc khoảng nào sau đây?      
A. 3;2. B. 3   2;   .      C. 3 2   ; . D. 2   ;0.  2  2 3  3  du   dx u  x 
Lời giải. Đặt     2 f x . dv  
f x. f x    dx   v   2 2 x f x 1 1 1 1
Khi đó K  x. f x. f x 1 1 1 2 dx   f x 2 dx  
f xdx.    2 2 2 2 0 0 0 0 Từ đồ thị, ta thấy: 1 2 f x 1 2 x2 1 2 7 1 f x ● f x 2
 2  x, x 0;  1  dx 
dx   K   dx      . 2 2 6 2 2 3 0 0 0 1 2 f x 1 1 2 1 f x ● f x 3
 2, x 0;  1  dx 
2 dx  2  K   dx      . Chọn C. 2 2 2 2 0 0 0
Câu 10*. Cho Parabol P 2
: y  x . Hai điểm A , B di dộng
trên P sao cho AB  2 . Khi diện tích phần mặt phẳng giới
hạn bởi P và cát tuyến AB đạt giá trị lớn nhất thì hai điểm ,
A B có tọa độ xác định Ax ; y và Bx ; y Giá trị B B . A A  của biểu thức 2 2 2 2
T  x x  y y bằng A B A B A. 1. B. 2. C. 3. D. 4. Lời giải. Do ,
A B  P nên giả sử A 2 a a  B 2 ;
, b;b  với b  . a 2
Phương trình đường thẳng x a y a AB : 
hay y  a bx  . ab b  2 a b  2 a Ta có AB 2
b a2 b a 2 4 b a2 4 b a2 2 2               4   4
 b a2 
 4. Suy ra b a  2.
1b  a2 b 1 1  b Ta có S  a   2 2 3 
bx ab  x  dx    
a bx abx  x   2 3  a   a 1 1  1 1  1 8 4
  a bb ab  b    a ba a b  a   b a3 2 2 3 2 2 3   . 2 3  2 3      6 6 3
b a  2 a  1 Dấu "  " xảy ra        A1;  1 , B1; 
1 T  2. Chọn B. b  a  0 b    1
Phần 3. Đồ thị hàm f x.
Câu 1. Cho hàm số y  f x có đạo hàm f x liên tục trên .
 Hình bên là đồ thị của hàm số y  f x trên 5;4. Giá
trị nhỏ nhất của f x trên 5;4 là A. f   5 .
B. f 4. C. f   1 . D. f 4.
Lời giải. Dựa vào đồ thị hàm số f x, ta suy ra
bảng biến thiên như hình bên. Khi đó:
min f x  min f 4; f 4. x   5;4 4
Dựa vào đồ thị f x, ta có f xdx   0. 4
Suy ra f 4 f 4. Vậy min f x f 4. Chọn B. x   5;4
Câu 2. Cho hàm số y  f x có đạo hàm f x liên tục trên 
và đồ thị của hàm số y  f x cắt trục hoành tại ba điểm có
hoành độ a, b, c (hình bên). Khẳng định nào sau đây đúng?
A. f c f a f b.
B. f a f c f b.
C. f b f c f a.
D. f a f b f c.
Lời giải. Dựa vào đồ thị hàm số f x, ta suy
ra bảng biến thiên như hình bên. Khi đó:
min f a; f b; f c  f b . c
Dựa vào đồ thị f x, ta có f x x   d 0. a
Suy ra f c f a. Vậy f c f a f b. Chọn A.
Câu 3. Cho hàm số y  f x có đạo hàm f x liên tục trên .
 Hình bên là đồ thị của hàm số f x trên
đoạn 2;d. Giá trị nhỏ nhất và giá trị lớn nhất của
hàm số y  f x trên đoạn 2;d lần lượt là
A. f a và f b. B. f a và f 2.
C. f c và f b. D. f c và f d.
Lời giải. Dựa vào đồ thị hàm số f x, ta suy ra bảng biến thiên
Dựa vào bảng biến thiên, suy ra m  min f a; f c, M  max f 2; f b; f d.
Dựa vào đồ thị f x, ta có c c •
f x x   f x   f c f a  f c f a  d 0 0 0 . a a b d •
f xdx  0 
 f b f 2  và
f x x  
 f b f d  d 0 . 2 b
Vậy m  f a, M  f b . Chọn A.
Câu 4. Cho hàm số y  f x có đạo hàm f x liên tục trên .
Miền hình phẳng trong hình vẽ được giới hạn bởi đồ thị hàm số
y  f x và trục hoành đồng thời có diện tích S  . a Biết rằng 1 1 x  
1 f xdx  b  và f  
3  c. Tính I 
f xdx.  0 0
A. I  a b  c. B. I  a  b c.
C. I  a
 b  c. D. I  a b c.
u  x 1 du  dx
Lời giải. Đặt     .
dv  f x    dx v    f x  1 1 1
Khi đó b  x  
1 f xdx  x   1 f x 
f xdx  2 f   1  f 0   I. 0 0 0 1 3
Mặt khác, ta có a  S 
f xdx 
f xdx  f  
1  f 0  f   3  f   1      0 1  2 f  
1  f 0 f   3  2 f  
1  f 0c. Suy ra 2 f  
1  f 0  a  c. Vậy I  2 f  
1  f 0b  a  c  . b Chọn A.
Câu 5. Cho hàm số y  f x có đạo hàm f x liên tục trên 2; 
1 . Hình bên là đồ thị của hàm số y  f x. Đặt 2   x
g x  f x
. Khẳng định nào sau đây đúng? 2
A. g2 g 
1  g 0. B. g 
1  g 2 g0.
C. g0 g 
1  g 2. D. g0 g2 g  1 .
Lời giải. Ta có gx f x x; gx 0  f x x. Suy ra nghiệm của phương
trình gx 0 là hoành độ giao điểm của đồ thị hàm số y  f x và đường thẳng
y  x. Dựa vào đồ thị ta thấy đường y  x cắt đồ thị hàm số y  f x tại các điểm
có hoành độ 2; 0; 1 (tham khảo hình vẽ)
Dựa vào bảng biến thiên, suy ra maxg2 g  ; 1 g 
; 0  g0. 0 1 0 1
Dựa vào đồ thị, ta có  f x x dx  x  f x       dx hay
gxdx   gx   dx 2 0 2 0
 g0 g2 g0 g 
1  g 2 g  1 . Chọn A.
Câu 6. Cho hàm số y  f x có đạo hàm f x liên tục
trên 3;3. Hình bên là đồ thị của hàm số y  f x. Đặt
g x  f x 2 2
 x . Khẳng định nào sau đây đúng? A. g  3  g   3  g  
1 . B. g   3  g   3  g   1 . C. g  1  g   3  g   3 . D. g   1  g   3  g   3 .
Lời giải. Ta có gx 2 f x2x; gx 0  f x x. Ta thấy đường thẳng
y  x cắt đồ thị hàm số y  f x tại các điểm có hoành độ 3; 1; 3.
Dựa vào bảng biến thiên, suy ra ming  3 g   ; 1 g  ;  3   g  1 . 3 3
Dựa vào đồ thị, ta có
gxdx  2 f x 2x dx      0. Suy ra g   3  g   3 . 3 3 Vậy g  1  g   3  g   3 . Chọn C.
Câu 7. Cho hàm số y  f x có đạo hàm f x liên tục
trên 3;3. Hình bên là đồ thị của hàm số y  f x.
Đặt gx f xx  2 2
1 . Gọi m là số thực thỏa mãn 3 m 
  gx dx  0. 
Khẳng định nào sau đây đúng?  3  3  A. 6g 
1  m  g   3 . B. 6g 
1  m  6g   3 . C. 3g 
1  m  3g  
3 . D. 3g  
1  m  3g   3 . 3 m  3
Lời giải. Từ giả thiết   gx dx   0, suy ra 2m 
g xdx.   3  3   3
Ta có gx 2 f x2x 2; gx 0  f x x 1. Ta thấy đường y  x 1
cắt đồ thị hàm số y  f x tại các điểm có hoành độ 3; 1; 3.
Dựa vào bảng biến thiên, suy ra ming  3 g   ; 1 g  ;  3   g  1 . 1 3
Dựa vào đồ thị, ta có S  S  x 1 f  x dx f x x 1 dx 1 2
              3 1 1 3
 2 x 1 f x dx  2  f x x         1 dx 3 1 1 3
  gxdx  gx   dx 3 1   g  1  g   3   g   3  g   1  g   3  g     3 .
min gx g   1 Suy ra 3;3    g 
1  g x g  3 , x  3;3.
max gx g   3  3;3  3 3 2m gx  dx Suy ra 6g  1 
g xdx  6g   3  3 3g 
1  m  3g    3 . Chọn C. 3
Câu 8. Cho hàm số y  f x có đạo hàm f x liên tục trên
3;3. Hình bên là đồ thị của hàm số y  f x. Biết f   1  6 x  2 1
và gx f x
. Khẳng định nào sau đây là đúng? 2
A. Phương trình gx 0 không có nghiệm thuộc 3;3.
B. Phương trình gx 0 có đúng một nghiệm thuộc 3;3.
C. Phương trình gx 0 có đúng hai nghiệm thuộc 3;3.
D. Phương trình gx 0 có đúng ba nghiệm thuộc 3;3.
Lời giải. Từ giả thiết f   1  6   g  1  4.
Ta có gx f xx  
1 ; gx  0  f x  x 1. Ta thấy đường thẳng y  x 1
cắt đồ thị hàm số y  f x tại các điểm có hoành độ 3; 1; 3.
Dựa vào đồ thị, ta có 1 1
•  f xx   1  dx  4 
gxdx  4  g  1  g   3  4   g  3      0. 3 3 3 3 • x  
1  f x dx  4   gxdx  4  g  3  g   1   4   g  3        0. 1 1
Từ BBT suy ra phương trình gx 0 có đúng một nghiệm thuộc 3;3. Chọn B.
Câu 9. Cho hàm số y  f x có đạo hàm f x liên tục trên 2; 
1 . Hình bên là đồ thị của hàm số y  f x. Đặt 2   x
g x  f x
. Điều kiện cần và đủ để phương trình g x  0 2
có bốn nghiệm phân biệt là g0 0 g0 0 g0 0 g0 0  A.  . B.  . C.  .
D. g  1  0 .    g  1      0 g   1   0 g2  0 g2  0
Lời giải. Ta có gx f x x; gx 0  f x x. Ta
thấy đường thẳng y  x cắt đồ thị hàm số y  f x tại các
điểm có hoành độ 2; 0; 1. 0 1
Dựa vào đồ thị, ta có  f x x dx  x  f x       dx 2 0 0 1 hay
gxdx   gx   dx 2 0
 g0 g2 g 
1  g 0  g2 g    1 .
Từ đó ta có bảng biến thiên như hình bên.
Dựa vào bảng biến thiên, suy ra đồ thị hàm số
y  g x cắt trục hoành tại 4 điểm phân biệt g0  0   . Chọn A. g  1   0
Câu 10. Cho hàm số y  f x có đạo hàm f x liên tục
trên . Hàm số y  f x có đồ thị như hình bên. Tổng giá
trị lớn nhất và giá trị nhỏ nhất của hàm số    2 g x f x  trên đoạn 2;2 bằng A. f  
1  f 0. B. f 4 f 0. C. f  
1  f 4. D. f  
1  f 0 f 4. x  0
Lời giải. Ta có gx xf  2 2
x ; g x    0   . f  2 x   0  2 x    1  2 x  1 x  1
Dựa vào đồ thị ta suy ra f  2 x   2 0 x 1          . 2   x 4 x 2 2       x   4
• Dựa vào bảng biến thiên suy ra max gx f   1 . 2;2 4 4
• Dựa vào đồ thị hàm số f x, ta thấy
f xdx  0  f x  0  f 4 f 0  0 0 0
 f 4 f 0. Kết hợp với bảng biến thiên ta suy ra min gx  f 4. 2;2
Vậy max gxmin gx f  
1  f 4. Chọn C. 2;2 2;2
Phần 4. Diện tích hình phẳng
Câu 1. Cho Parabol như hình vẽ bên. Diện tích hình phẳng giới
hạn bởi Parabol và trục hoành bằng A. 16. B. 16 . 3 C. 28 . D. 32 . 3 3
Lời giải. Dựa vào đồ thị, ta xác đinh được phương trình của P y   2 : x  4. 2
Khi đó diện tích hình phẳng cần tính bằng: S    32 2
x  4dx  . Chọn D. 3 2
Cách 2. Áp dụng công tính nhanh 2 2 32 S = Bh = .4.4 =
(với B  4 là chiều dài của 3 3 3
đáy, h  4 là chiều cao).
Câu 2. Tính diện tích hình phẳng được tô đậm ở hình bên. A. 10 S  . B. 20 S  . 3 3 C. 25 S  . D. S  9. 6
Lời giải. Áp dụng công thức tính nhanh, ta có diện tích miền khép kín giới hạn bởi Parabol và đường 2 2 32 y  4 là S  Bh  .4.4  . AOB 3 3 3
Diện tích tam giác ABC là S  4. ABC
Suy ra diện tích phần tô đậm 20 S  S S  . Chọn B. AOB ABC 3
Câu 3. Ông An xây dựng một sân bóng đá mini hình
chữ nhật có chiều rộng 30 m và chiều dài 50 m. Để
giảm bớt chi phí cho việc trồng cỏ nhân tạo, ông An
chia sân bóng ra làm hai phần (tô đen và không tô đen)
như hình bên. Phần tô đen gồm hai miền diện tích
bằng nhau và đường cong AIB là một Parabol đỉnh I.
Phần tô đen được trồng cỏ nhân tạo với giá cỏ nhân tạo với giá 130 000 đồng 2 /m và
phần còn lại được trồng cỏ nhân tạo với giá 90 000 đồng 2
/m . Hỏi ông An phải trả bao
nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?
A. 135 triệu đồng.
B. 151 triệu đồng.
C. 165 triệu đồng.
D. 195 triệu đồng.
Lời giải. Diện tích hình chữ nhật: S  3050  2 1500 m . 0
Diện tích hai phần tô đen: 2 2
S  2 Bh  2 .30.10  2 400 m . 1 3 3
Suy ra diện tích phần không tô đen: S  S S  2 1100 m . 2 0 1
Vậy tổng chi phí: T  130000.S  90000.S  151000000 đồng. Chọn B. 1 2
Câu 4. Nhà ông An cần sơn mặt trước của cổng có dạng như
hình bên, các đường cong có dạng là Parabol với các kích
thước được cho như hình. Biết giá thuê nhân công là 100.000 đồng 2
/m . Hỏi ông An phải trả cho bên thi công bao nhiêu tiền để sơn cổng? A. 2 468650 đồng. B. 1866 667 đồng. C. 1775361 đồng.
D. 1668653 đồng.
Lời giải. Công thức tính nhanh, ta có diện tích cần sơn: 2 56
S  .8.86.6  2 m . 3 3
Vậy số tiền cần phải trả: 56 100000.
 1866667 (đồng). Chọn B. 3
Câu 5. Một hoa văn trang trí được tạo ra từ một miếng bìa
mỏng hình vuông cạnh 10 cm bằng cách khoét bỏ đi bốn
phần bằng nhau có hình dạng Parabol (như hình vẽ). Biết
AB  5 cm , OH  4 cm . Diện tích bề mặt hoa văn đó bằng A. 40 140 2 cm . B. 2 cm . 3 3 C. 160 2 cm . D. 2 50 cm . 3
Lời giải. Diện tích hình vuông: S  2 10  2 100 cm . 0 2  2 
Diện tích của bốn hình Parabol được khoét bỏ là: 160 S  4   Bh  4  2 .5.4 cm . 1      3    3  3
Suy ra diện tích bề mặt hoa văn là: 160 140
S  S S  100   2 cm . Chọn B. 2 0 1 3 3
Câu 6. Một mảnh vườn toán học có dạng hình chữ nhật,
chiều dài là 16 m và chiều rộng là 8 m. Các nhà Toán học
dùng hai đường Parabol, mỗi Parabol có đỉnh là trung
điểm của một cạnh dài và đi qua hai mút của cạnh đối
diện, phần mảnh vườn nằm ở miền trong của cả hai
Parabol (phần tô đậm như hình vẽ) được trồng hoa hồng. Biết chi phí để trồng hoa hồng là 45000 đồng 2
/m . Hỏi các nhà Toán học phải chi bao nhiêu tiền để trồng hoa
trên phần mảnh vườn đó? (Số tiền được làm tròn đến hàng nghìn).
A. 1920 000 đồng. B. 2159 000 đồng.
C. 2715000 đồng. D. 3322 000 đồng.
Lời giải. Chọn hệ trục tọa độ Oxy và gọi tên các đỉnh
như hình vẽ bên. Dễ dàng xác định được
• Parabol đi qua ba điểm 1 ,
A I, B là P: y   2 x  8. 8
• Parabol đi qua ba điểm 1
C, O, D là P : y  2 x . 8
Phương trình hoành độ giao điểm: 1 1 2 2
 x 8  x  x  4 2. 8 8 4 2
Suy ra diện tích trồng hoa là: 1 1 128 2 2 2 S 
 x 8 x dx    2 m . 8 8 3 4  2
Vậy chi phí trồng hoa là: 128 2
T  45000.S  45000.
 2715000 đồng. Chọn C. 3
Câu 7. Một công ty quảng cáo muốn làm một bức tranh trang trí hình MNEIF ở
chính giữa của một bức tường hình chữ nhật ABCD có chiều cao BC  6 m , chiều dài
CD  12 m (hình vẽ bên). Cho biết MNEF là hình chữ nhật có MN  4 m; cung EIF
có hình dạng là một phần của cung Parabol có đỉnh I là trung điểm của cạnh AB và
đi qua hai điểm C, D. Kinh phí làm bức tranh là 900.000 đồng 2 /m . Hỏi công ty cần
bao nhiêu tiền để làm bức tranh đó? A. 20.400.000 đồng. B. 20.600.000 đồng. C. 20.800.000 đồng. D. 21.200.000 đồng.
Lời giải. Gắn hệ trục tọa độ như hình vẽ bên dưới 2
Dễ dàng xác định được Parabol đi qua ba điểm x
D, F , I, E, C là P: y   . 6
Hai điểm M , F nằm trên đường thẳng x  2; N, E nằm trên đường thẳng x  2. 2  2 x  Khi đó diện tích hình 208 MNEIF là:   S   x MNEIF   6d   2   m .  6  9 2 Kinh phí làm bức tranh: 208 900000.
 20800000 (đồng). Chọn C. 9
Câu 8. Một chiếc cổng có hình dạng là một Parabol có khoảng cách
giữa hai chân cổng là AB  8 m. Người ra treo một tâm phông hình
chữ nhật có hai đỉnh M , N nằm trên Parabol và hai đỉnh P, Q nằm
trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô
đen) người ta mua hoa để trang trí với chi phí cho 2 1 m cần số tiền
mua hoa là 200.000 đồng, biết MN  4 m, MQ  6 m. Hỏi số tiền dùng để mua hoa
trang trí chiếc cổng gần với số tiền nào sau đây?
A. 3373400 đồng. B. 3434 300 đồng. C. 3437300 đồng. D. 3733300 đồng.
Lời giải. Chọn hệ trục tọa độ Oxy như hình vẽ.
Parabol đối xứng qua Oy nên có dạng P y  2 : ax  c. Vì  1
P  đi qua B4;0 và N 2;6 nên P: y   2 x  8. 2
Diện tích hình phẳng giới hạn bởi P và trục Ox là 4  1  128 S  2  2  
  x  8dx  2   m .  2  3 0
Diện tích phần trồng hoa là 128 56
S  S S  24  2 m . 1 MNPQ 3 3
Do đó số tiền cần dùng để mua hoa là 56200000  3733300 đồng. Chọn D. 3
Câu 9. Cho H là hình phẳng giới hạn bởi đồ thị C 2
: y  4x  x và
trục hoành (hình vẽ bên). Đường thẳng y  m chia H thành hai
phần có diện tích bằng nhau. Biết 3
m  a  b với ,
a b là các số hữu tỉ, tính S  . a . b A. S  64. B. S  32. C. S  32. D. S  64.
Lời giải. Diện tích hình phẳng H là 2 2 32
S  Bh  .4.4  . 3 3 2
x  2  4m
Phương trình hoành độ giao điểm: 2 
4x  x  m  ; m  0;4  . x  2  4   m
Suy ra A2 4m;m , B2 4m;m; M 2;m là trung
điểm AB; I 2;4 là đỉnh của C. Khi đó diện tích miền
khép kín giới hạn bởi Parabol và đường y  m (phần gạch 4 2 2  3 4 m
sọc) là S  AB.IM  .2 4 m. 4 m . 1    3 3 3 4 1  3 4 m 16 a 4 3   Theo giả thiết, ta có  S  S  
 m  4  16   . Chọn D. 1  2 3 3 b   16
Câu 10. Cho H là hình phẳng giới hạn bởi đồ thị P của hàm số 2
y  6x  x và trục hoành. Hai đường thẳng y  m và y  n
chia hình H thành ba phần có diện tích bằng nhau. Tính
P   m3  n3 9 9 . A. P  403. B. P  405. C. P  407. D. P  409. m  9 3 3 3
Lời giải. Như bài trên, ta được 
 P  405. Chọn B. n  9  3 3 12
Câu 11. Cho hình phẳng H (phần tô đậm) được giới hạn bởi các đường y   2
4 x , y  x và y  2 có diện tích là
S  a  b với , a b  
. Khẳng định nào sau đây đúng?
A. a b 1.
B. a  2b  3. C. 2 a  2
4b  5. D. a 1 và b 1. 2 2
Lời giải. Dựa vào hình vẽ, ta có S  2 2 4 x dx 2 x       dx  2    . 2 0 2 Suy ra 1
a  2, b   . Chọn C. 2
Câu 12. Cho đường tròn tâm O đường kính AB  8. Trên AB
lấy hai điểm M , N đối xứng nhau qua O sao cho MN  4.
Qua M , N kẻ hai dây cung PQ và EF cùng vuông góc với AB.
Diện tích phần giới hạn bởi đường tròn và hai dây cung PQ, EF
(phần tô đậm như hình vẽ) bằng A. 16  5  5. B. 6 8 3.
C. 12 7. D.  8 3. 3
Lời giải. Chọn hệ trục tọa độ như hình vẽ
Dễ dàng xác định phương trình đường tròn là 2 x  2 y  16.
Suy ra cung PE có phương trình y   2 16 x .
Diện tích hình phẳng cần tính 2 16 S  2 16  2 x dx     8 3. Chọn D. 3 2
Câu 13. Biết rằng đường Parabol P 2
: y  2x chia đường tròn C 2 2
: x  y  8 thành hai phần lần lượt có diện tích là b
S , S (hình bên). Khi đó S S  a  với ,
a b, c nguyên 1 2 2 1 c
dương và b là phân số tối giản. Tổng a b  c bằng c A. 13. B. 14. C. 15. D. 16.
Lời giải. Diện tích hình tròn S  8 . 
Phương trình hoành độ giao điểm của P và C là 2 y  2x x  0       x  2. 2 2 2
x  y  8 x 2x  8    2 2 2  Suy ra  4 2  S  2.  2xdx 8 x dx 2 . 1              3 0 2  a   4  Suy ra 4 8 
S  S S  6  S S 4 b       
  8 . Chọn C. 2 1 3 2 1 3 c 3 
Câu 14. Một khuôn viên dạng nửa hình tròn có đường
kính bằng 4 5 m. Trên đó người thiết kế hai phần để
trồng hoa có dạng của một cánh hoa hình Parabol có
đỉnh trùng với tâm nửa hình tròn và hai đầu mút của
cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng 4 m,
phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết
các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100 000 đồng 2 /m .
Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn).
A. 1194 000 đồng. B. 1948000 đồng. C. 2388000 đồng. D. 3895000 đồng.
Lời giải. Hình tròn có diện tích 2 S  2 5 20 . 1    
Chọn hệ trục tọa độ Oxy như hình vẽ.
Khi đó phương trình nửa đường tròn là: y   2 20 x .
Parabol có đỉnh là gốc O và đi qua điểm 2;4 nên có phương trình P y  2 : x . 2
Khi đó diện tích phần tô đậm: S  20 x x dx 11,94 m . 2       2 2 2 2
Diện tích phần trồng cỏ Nhật Bản (phần không tô màu): S1 S = − S ≈ 19,47592654. 2 2
Vậy số tiền cần dùng: T = S ×100000 ≈ 1948000 (đồng). Chọn B.
Câu 15. Một viên gạch hoa hình vuông cạnh 40 cm. Người
thiết kế đã sử dụng bốn đường Parabol có chung đỉnh tại tâm
của viên gạch để tạo ra bốn cánh hoa (được tô màu như hình
bên). Diện tích mỗi cánh hoa của viên gạch bằng A. 400 2 250 cm . B. 2 cm . 3 C. 800 1600 2 cm . D. 2 cm . 3 3
Lời giải. Gắn hệ trục tọa độ như hình bên (ta chuyển về đơn vị tính là dm )
Xét cánh hoa ở góc phần tư thứ nhất. Đường cong trên ứng 2 với x
y  2x , đường cong dưới ứng với y  . 2
Khi đó diện tích cần tính 2  2 x    4 400 S   2x  dx   2 2   dm  cm . Chọn B.  2  3 3 0 2 2 Câu 16. Gọi x y
S là diện tích của hình phẳng giới hạn bởi Elip   1 và S là 1 9 1 2
diện tích của hình thoi có các đỉnh là đỉnh của Elip đó. Tỉ số S1 bằng S2 A. 2 . B.  . C.  . D.  . 2 3 3 Lời giải. 2 2
Từ phương trình Elip x y 
 1, suy ra đường Elip nằm trong góc phần tư thứ nhất 9 1 2 3 2 có phương trình x x y  1
. Suy ra diện tích Elip S  4 1 dx  3 . 1   9 9 0
Diện tích hình thoi có các đỉnh là đỉnh của elip: 1 S  .6.2  6. 2 2 Khi đó S 3 1     . Chọn B. S 6 2 2 2 2
Chú ý: Ta có công thức nhanh:   x y E : 
 1 có diện tích S   . ab 2 2 a b
Câu 17. Một sân chơi cho trẻ em hình chữ nhật có
chiều dài 100 m và chiều rộng là 60 m người ta
làm một con đường nằm trong sân (như hình vẽ).
Biết rằng viền ngoài và viền trong của con đường là
hai đường elip, Elip của đường viền ngoài có trục
lớn và trục bé lần lượt song song với các cạnh hình
chữ nhật và chiều rộng của mặt đường là 2 m. Kinh phí cho mỗi 2
m làm đường 600 000 đồng. Tính tổng số tiền làm con đường đó. (Số tiền
được làm tròn đến hàng nghìn). A. 293804 000 đồng. B. 293904 000 đồng. C. 294 053000 đồng. D. 294153000 đồng.
Lời giải. Diện tích Elip lớn là: S  50.30 1500 2 m . 1
Diện tích Elip lớn là: S  48.28 1344 2 m . 2
Suy ra diện tích cần trang trí là: S  S S  1500 1344  156 2 m . 3 1 2
Vậy chi phí cần: S 600 000  156600000  294 053000 đồng. Chọn C. 3
Câu 18. Một mảnh vườn hình chữ nhật có chiều dài
10 m và chiều rộng 6 m, được phân chia thành các phần
bởi một đường chéo và một đường Elip nội tiếp bên trong
như hình vẽ bên. Hãy tính diện tích phần tô đậm (theo đơn vị 2 m )? 454  454 
A. 52.
B. 54. C. . D. . 7 8
Lời giải. Chọn hệ trục tọa độ và gọi các điểm như hình. 2 2
Phương trình Elip là: x y   1. Suy ra 25 9 2
• đường Elip nằm trên trục 3 25 x
Ox là: E : y ; 1    5 2
• đường Elip nằm dưới trục 3 25 x
Ox là: E : y   . 2  5
Phương trình đường thẳng 3x OD : y 
. Phường trình đường thẳng AB : y  3. 5  
Tọa độ giao điểm của E và OD là: 5 2 3 2 E  ; . 1     2 2 
Do đó diện tích phần tô đậm là: 5   5 2  2  3x 3 25 x   3 25 x  454  S       dx     3 dx . Chọn D.        5 5    5 8 5 2     0   3
Câu 19. Một biển quảng cáo có dạng hình Elip với bốn đỉnh
A , A , B , B như hình vẽ bên. Biết chi phí sơn phần tô đậm 1 2 1 2 là 200 000 đồng 2
/m và phần còn lại là 100 000 đồng 2 /m .
Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào
dưới đây, biết A A  8 m, B B  6 m và tứ giác MNPQ là 1 2 1 2
hình chữ nhật có MQ  3 m ? A. 5.526.000 đồng. B. 5.782.000 đồng.
C. 7 213000 đồng. D. 7322 000 đồng.
Lời giải. Chọn hệ trục tọa độ và gọi các điểm như hình.
Diện tích Elip: S     2 .4.3 12 m . 2 2
Phương trình Elip là:   x y E :   1. Suy ra đường 16 9 Elip nằm trên trục 3 Ox là: y  16  2 x . 4   Từ giả thiết 3
MQ  3 m suy ra M , N nằm trên đường thẳng 3 d : y  
 N 2 3; . 2  2 2 3 3 
Diện tích phần tô màu: S  4  2 
  16x dx  8 2 6 3 m . 1   4  0
Suy ra diện tích phần không tô màu: S  S S  4  2 6 3 m . 2 2
Vậy số tiền cần chi phí T  200000 
 8  6 3100000 
 4 6 3  7322000 đồng. Chọn D.
Câu 20. Nhà trường dự định làm một vườn hoa
dạng hình Elip được chia ra làm bốn phần bởi hai
đường Parabol có chung đỉnh, đối xứng với nhau
qua trục của Elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của Elip lần lượt là 8 m và 4 m; F , F 1 2
là hai tiêu điểm của Elip. Phần ,
A B dùng để trồng hoa; phần C, D dùng để trồng cỏ.
Kinh phí để trồng mỗi mét vuông trồng hoa và trồng cỏ lần lượt là 250 000 đồng và
150 000 đồng. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 4 656 000 đồng. B. 4766 000 đồng. C. 5455000 đồng. D. 5676 000 đồng.
Lời giải. Diện tích Elip: S     2 .4.2 8 m .
Chọn hệ trục tọa độ và gọi các điểm như hình. 2 2
Phương trình Elip là:   x y E :   1. Suy ra đường 16 4 2 Elip nằm trên trục 16 x Ox là:  y  . 2
Giao điểm của đường thẳng d : x  2 3 đi qua tiêu điểm F và nửa Elip nằm bên trên 2
trục Ox là M 2 3;  1   N 2 3;  1 . 2 Parabol đi qua các điểm x M 2 3;  1 , O  0;0, N  2 3; 
1 có phương trình P: y  . 12 2 3  2 2  Khi đó diện tích  16  x x  8  2 3 S     x A   d  .    2 12  3 2 3  
Vậy số tiền cần chi phí:
T  2S 250000  
S 2S 150000  5676 000 đồng. Chọn D. A A
Câu 21. Cho hình phẳng giới hạn bởi các
đường y  sin x, y  cos x và S , S là 1 2
diện tích của các phần được gạch chéo như hình vẽ. Tổng 2 S  2 S bằng 1 2 A. 102 2. B. 10  2 2. C. 1112 2. D. 11 2 2. Lời giải. Ta có: 
cos x  0  x   k, k  . 2    
sin x  cos x  sin 
x    0  x   k, k     .  4  4  5 4 4
Dựa vào hình vẽ ta có S 
cos x sin x dx 1 2; S 
sin x cos x dx 2 2. 2     1           2 4 Suy ra 2 2 2 S  2 S  1 2 2 2 11 2 2 . Chọn D. 1 2       
Câu 22. Kí hiệu H là hình phẳng giới hạn bởi các đường  x y e ,
y  0, x  0 và x  1. Đường thẳng x  k 0  k   1 chia H
thành hai phần có diện tích tương ứng S , S như hình vẽ bên, 1 2
biết S  S . Mệnh đề nào sau đây là đúng? 1 2 A. k e 1 k e 1 e  . B.  e  . 2 2 C. k e 3 k e  2 e  . D.  e  . 2 2 k k 1 1 Lời giải. Ta có x  d x k S e x  e  e 1 x S e d x k x e e e . 1  và     2  0 0 k k Theo giả thiết  k k k e 1
S  S  e 1 e e  e  . Chọn B. 1 2 2
Câu 23. Cho hình phẳng H giới hạn bởi các đường 2
y  x , y  0, x  0, x  4. Đường thẳng y  k
0  k 16 chia hình H thành hai phần có diện tích
S , S (hình vẽ). Tìm k để S  S . 1 2 1 2 A. k  3 . B. k  4 . C. k  5. D. k  8 .
Lời giải. Phương trình hoành độ giao điểm: 2 x
x  k 
0 x  k . Ta có: 4 3 4 ● x 64 2 S S  x dx   . 1 2  3 3 0 0 4 4 3   ● S    x 2   k k 64 2
x  k dx   kx  4k   . 1   3  3 3 k k Theo giả thiết 1 2k k 64 32 S  S  S 
S S  4k    1 2 1  1 2  2 3 3 3
t k 0t4 3 2
 2k k 12k 32  0 2t 12t 32  0  t  2 
 k  4. Chọn B.
Câu 24. Xét hình phẳng H giới hạn bởi đồ thị hàm số
y  x  2
3 , trục hoành và đường thẳng x  0. Gọi A0;9,
Bb;0 3  b  0. Tìm giá trị của tham số b để đoạn thẳng
AB chia H thành hai phần có diện tích bằng nhau.
A. b  2 . B. 3 b   . C. b  1. D. 1 b   . 2 2
Lời giải. Phương trình hoành độ giao điểm: x  2
3  0  x  3. 0 CASIO Do đó S  H x  2 3 dx   9. 3 Diện tích tam giác 1 9 OAB bằng: S  O . A OB  b . OAB 2 2 Ycbt 1 9 9   3 b0  S  S  b  
b  1. Chọn C. OAB H  2 2 2
Câu 25. Trong mặt phẳng tọa độ, cho hình chữ nhật H
có một cạnh nằm trên trục hoành và có hai đỉnh trên một
đường chéo là A1;0 và C a; a với a  0. Biết rằng
đồ thị hàm số y  x chia hình H thành hai phần có
diện tích bằng nhau, tìm . a A. 1 a  .
B. a  3. C. a  4. D. a  9. 2
Lời giải. Từ hình vẽ ta suy ra Ba;0.
Hình chữ nhật ACBD có AB  a 1 và AD  a nên có diện tích S  a a   1 . a
Diện tích miền gạch sọc:  2a a S  xdx   . 3 0 S 2a a a a   1 Theo giả thiết, ta có a S     
0a  3. Chọn B. 2 3 2
Phần 5. Thể tích khối tròn xoay
Câu 1. Cho hình phẳng H giới hạn bởi các đồ thị hàm số 2
y  4  x và y   2
2 x . Tính thể tích V của khối
tròn xoay tạo thành khi quay H quanh trục hoành. A. V  10 .  B. V  12 .  C. V  14 .  D. V  16 . 
Lời giải. Phương trình hoành độ giao điểm: 2 2
4  x  2  x  x  1 . 1 1 CASIO
Thể tích cần tính V   4x 2 2 x 2 2 2 2
dx   12 12x dx  16 .   Chọn D. 1 1
Câu 2. Thể tích V của khối tròn xoay khi cho hình
phẳng H giới hạn bởi các đường 2
y  1 x và 2 y  x 1
quay quanh trục Ox được xác định bởi công thức nào sau đây? 1 1
A. V   1x 2 x   2 2 2 1 dx.
B. V    2 1 x  2 x   1 dx. 1 1 1 1 C. 2 2
V   1x 2 2 dx. D. V   2  x 1  2 1 x       d  x.   1 1
Lời giải. Phương trình hoành độ giao điểm: 2 2
1 x  x 1  x  1. Vì đồ thị hàm số 2
y  1 x đối xứng với đồ thị hàm số 2
y  x 1 qua trục hoành nên
thể tích khối tròn xoay cần tính bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đường 2
y  1 x , y  0, x  1
 , x  1 quay quanh trục Ox. 1
Vậy công thức tính thể tích là V   1  x 2 2 dx. Chọn C. 1
Câu 3. Cho hình vuông OABC có cạnh bằng 4 được chia
thành hai phần bởi đường cong P có phương trình 1 y  2
x . Gọi S là hình phẳng không bị gạch (như hình vẽ). 4
Tính thể tích V của vật thể tròn xoay khi cho phần S qua quanh trục Ox. A. 64 128 128 256 V  . B.  V  . C.  V  . D.  V  . 5 3 5 5
Lời giải. Thể tích vật thể khi quay hình vuông OABC quanh trục Ox là  2
.4 .4  64. 4 1 2
Thể tích vật thể khi quay phần gạch sọc quanh 64 Ox là 2  .  
  x  dx    . 4  5 0
Vậy thể tích vật thể tròn xoay cần tính bằng 64 256 64   . Chọn D. 5 5
Câu 4. Cho hình phẳng H giới hạn bởi 1 đường tròn có 4
bán kính R  2, đường cong y  4  x và trục hoành
(miền tô đậm như hình vẽ). Tính thể tích V của khối tạo
thành khi cho hình H quay quanh trục Ox. A. 40    V   B. 53 V   C. 67 V   D. 77 V   3 6 6 6
Lời giải. Phương trình hoành độ giao điểm: 4  x  0  x  4.
 Thể tích vật thể khi quay phần S quanh trục hoành là nửa khối cầu bán kính 1 1 4 2 16
R  2 nên có thể tích bằng 3 3 
 R  .2  . 2 3 3 3 4
 Thể tích vật thể khi quay phần S quanh trục hoành là  4  xdx  8. 2 0
Vậy thể tích cần tính 16 40 8  . Chọn A. 3 3
Câu 5. Cho hình phẳng H giới hạn bởi các đường
y   x  2, y  x  2,
x  1. Tính thể tích V của vật thể
tròn xoay khi quay hình phẳng H quanh trục Ox. A. 9 V  9. B.  V  . 2 C.  25 55 V  . D.  V  . 3 6
Lời giải. Sai lầm hay gặp là chúng ta sử dụng công thức 1   
V   x    x  2 2 9 2 2  dx  .   2 2
Lấy đối xứng phần đồ thị hàm số y   x  2 qua trục hoành ta được đồ thị hàm số
y  x  2 (tham khảo hình vẽ). Khi đó thể tích cần tính bằng tổng của miền tô đậm
và miền gạch sọc quay quanh trục Ox.
Thể tích vật thể khi quay miền 1
• Gạch sọc quanh Ox là V  x 2 dx 9 . 1    2   2
• Tô đậm quanh Ox là 1 2 V  x 2 x 2 dx . 2      2     6 2 Vậy thể tích cần tính  55
V V V  9   . Chọn D. 1 2 6 6
Câu 6. Gọi V là thể tích khối tròn xoay tạo
thành khi quay hình phẳng giới hạn bởi các
đường y  x, y  0 và x  4 quanh trục Ox .
Đường thẳng x  a 0  a  4 cắt đồ thị hàm số
y  x tại M (hình vẽ bên). Gọi V là thể tích 1
khối tròn xoay tạo thành khi quay tam giác
OMH quanh trục Ox . Biết rằng V  2V . Khi đó 1 A. a  2 . B. 5 a  . C. a  2 2 . D. a  3 . 2
Lời giải. Phương trình hoành độ giao điểm: x  0  x  0. 4
 Thể tích V   xdx  8 .   0
 Tính V : Gọi M a; a. Khi quay tam giác OMH quanh trục Ox tạo thành hai 1 hình nón có chung đáy:
ð Hình nón N có đỉnh là O, chiều cao OK  ,
a bán kính đáy R  MK  a 1  nên có thể tích bằng 1 1 a
R .OK   a 2 2 2 .a  . 3 3 3
ð Hình nón N có đỉnh là H, chiều cao HK  4a, bán kính đáy 2  2 2 1 1 4a a
R  MK  a nên có thể tích bằng 2
R HK   a .4a . 3 3 3 2 2 Suy ra a 4a a 4a V   
. Theo giả thiết V  2V nên suy ra a  3. Chọn D. 1 3 3 3 1
Câu 7. Gọi V là thể tích khối tròn xoay tạo thành khi
quay hình phẳng giới hạn bởi các đường y  sin x, hai
trục tọa độ và x   quanh trục hoành. Đường thẳng
x  k 0  k   cắt đồ thị hàm số y  sin x tại điểm
M và trục hoành tại điểm N (hình vẽ bên).
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác OMN quanh trục Ox. 1 Biết rằng 12 V  V . Khi đó 1 k A.  k  . B.  k  . C. k  2.
D. k  3. 6 3  
Lời giải. Ta có V   sin xdx  
 cos x  2  . 0 0
Khi quay tam giác OMN quanh trục Ox tạo thành hình nón có đỉnh là O, chiều cao 1 k.sin k
ON  k, bán kính đáy R  MN  sin k nên có thể tích bằng 2  R .ON  . 3 3 Theo giả thiết 12 1 V  V nên suy ra  sin k  
 k  (vì 0  k   ). Chọn A. 1 k 2 6
Câu 8. Có một vật thể là hình tròn xoay có dạng giống như một
cái ly như hình vẽ bên. Người ta đo được đường kính của miệng
ly là 4 cm và chiều cao là 6 cm. Biết rằng thiết diện của chiếc
ly cắt bởi mặt phẳng đối xứng là một Parabol. Thể tích của vật thể đã cho bằng A.   3 12 cm . B.  3 12 cm . C. 72 72   3 cm . D.  3 cm . 5 5
Lời giải. Xét phần mặt cắt và chọn hệ trục Ixy như hình vẽ.
(trong đó I là gốc tọa độ).
Khi đó Parabol P đi qua các điểm A2;6, B2;6 và I 0;0 nên Parabol  3 2 y
P  có phương trình: 2 2 y  x   x  . 2 3
Khi đó thể tích của vật thể đã cho là: 6 6 2  2
V   x dy    
  ydy 12    3 cm . Chọn A. 3  0 0
Câu 9. Trong mặt phẳng cho đường Elip E có độ dài trục
lớn là AA  8 và độ dài trục nhỏ BB  6; đường tròn tâm
O đường kính BB như hình vẽ. Tính thể tích V của khối
tròn xoay có được bằng cách cho miền hình phẳng giới hạn
bởi đường Elip và đường tròn (được tô đậm trên hình vẽ)
quay xung quanh trục AA . A. V  12 .  B. V  16 . 
C. V  28. D. V  36 .  2 2 Lời giải. Elip  x y
E có a  4, b  3. Suy ra E:   1. 16 9 4  2 x 
Thể tích khối elip E quay quanh trục AA là: V  . 9. 1 dx 48 . 1             16 4 Thể tích khối cầu là: 4 4 V  R .3 36 . 2
 3   3   3 3
Vậy thể tích cần tính V V V  12 . Chọn A. 1 2 
Câu 10. Một thùng chứa rượu làm bằng gỗ là một hình tròn
xoay như hình bên có hai đáy là hai hình tròn bằng nhau,
khoảng cách giữa hai đáy bằng 8 dm. Đường cong mặt bên của
thùng là một phần của đường Elip có độ dài trục lớn bằng
10 dm , độ dài trục bé bằng 6 dm. Hỏi chiếc thùng gỗ đó đựng
được bao nhiêu lít rượu?
A. 1316 (lít). B. 1416 (lít).
C. 1516 (lít).
D. 1616 (lít). 25 25 25 25 2 2 Lời giải. Elip có x y a  5, b  3. Suy ra E:   1. 25 9
Chọn hệ trục tọa độ đi qua hai trục của thùng rượu như hình vẽ.
Vì thùng rượu có tính đối xứng nên thể tích thùng rượu
gấp hai lần thể tích khối tròn xoay khi quay hình S 1 quanh trục Ox. 4 2 Thể tích cần tính: 2259x 1416 V  2 dx   . Chọn B. 25 25 0
Câu 11. Bên trong hình vuông cạnh , a dựng hình sao
bốn cánh đều như hình vẽ bên (các kích thước cần thiết
cho như ở trong hình). Tính thể tích V của khối tròn
xoay sinh ra khi quay hình sao đó quanh trục Ox. A.  5 3
V  a . B.  V  3 a . 8 24 C. 5 5 3 V  a . D.  V  3 a . 48 96
Lời giải. Xét hình nằm ở góc phần tư thứ nhất.
Gọi V là thể tích khối tròn xoay cần tính.
Gọi V là thể tích khối tròn xoay khi quay hình phẳng được tô 1
màu trong hình bên (chỉ xét ở góc phần tư thứ nhất) quanh
trục hoành. Khi đó V  2V . 1 a a 2 2 2 2 3     Ta có x a a 5a V    
    dx      2x    dx  . 1 2 4  2 96 0 a 4 3
Suy ra thể tích cần tính 5a V  2V  . Chọn C. 1 48
Câu 12. Cho hình phẳng H gồm nửa hình tròn đường kính AB
và tam giác ABC đều (như hình vẽ). Gọi  là đường thẳng qua
C và song song với AB. Biết AB  2 3 cm. Thể tích khối tròn
xoay tạo bởi hình H quay quanh trục  bằng 2 A. 9
  2  3 8 3 9 cm . B. 8  3   3 cm . 2 C.
  2  3 32 3 18 cm . D.
  2  3 16 3 9 cm .
Lời giải. Chọn C  O,   Ox như hình vẽ. Khi đó A 3;  3 , B 3; 
3 . Suy ra AC : y   3x,
BC : y  3x.
Phương trình đường tròn đường kính AB là x y  2 2 3  3.
Suy ra phần phía trên của nửa đường tròn có phương trình y    2 3 3 x .
Thể tích khi quay phần tô đậm quanh trục hoành là 3 2 2 9  3 3 2
x   3x dx  8  3  2. 2 0  9 
Suy ra thể tích cần tính V  2  8  3  2   . Chọn D.  2 
Câu 13. Cho hình vẽ bên, biết cung tròn BC nằm trên đường tròn
bán kính R  4. Cạnh AB  BC  CD  DA  4. Thể tích vật tròn
xoay tạo thành khi quay hình bên quanh trục AD nằm trong
khoản nào sau đây? A. 165;170. B. 160;  165 . C. 155;160. D. 150;  155 .
Lời giải. Chọn hệ trục tọa độ như hình vẽ bên.
Gọi O là tâm đường tròn C chứa cung BC . Khi đó O nằm
trên đường thẳng x  2. Gọi H là trung điểm của BC .
Ta có OBC là tam giác đều, nên 4 3 OH   2 3. 2
Do đó O cách Ox là một khoảng 4  2 3  O 2;4 2 3.
Phương trình đường tròn
C x   y  2 2    y    x  2 : 2 4 2 3 16 4 2 3 16 2 .
Dựa vào đồ thị ta thấy cung BC nằm bên dưới đường thẳng y  4  2 3 , nên đường
cong chứa cung BC có phương trình y    x  2 4 2 3 16 2 . 4 2
Khi đó thể tích vật tròn xoay: V   42 3 16x 22  dx 166,6. Chọn A. 0
Câu 14. Cho hình tròn tâm O có bán kính R  2 và hình vuông
OABC có cạnh bằng 4 (như hình vẽ bên). Tính thể tích V của vật
thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng OB. 83 4 2 82 5 2 A. V  . B. V  . 3 3 835 2 321 2 C. V  . D. V  . 3 3
Lời giải. Chọn hệ trục tọa độ Oxy có gốc tọa độ trùng O, tia
Ox có giá là OB và tia Oy song song AC (như hình vẽ).
Khi đó đường tròn O có phương trình 2 2
x  y  4 và đường
thẳng OA có phương trình y  x.
Phương trình hoành độ giao điểm của đường thẳng OA và
đường tròn C là: 2
4  x  x  x  2.
Thể tích vật thể tròn xoay khi quay phần tô đen quanh Ox là: 2 2 16 10 2  16 8 2 2 2  2 2     
V   x dx  .  4  x    . 1     3 3 3 0 2
Thể tích khối tròn xoay khi quay  4 32
O quanh Ox là khối cầu có 3 V  .  2  .  2 3 3
Thể tích khối tròn xoay khi quay OABC quanh Ox là (tổng của hai khối nón)  2 1 32 2 V  2 . 2 2 .2 2 . 3        3    3 8  25 2 16 40 2 
Vậy thể tích cần tính V V V V     . Chọn B. 2 3 1 3 3
Câu 15. Cho hình vuông có độ dài cạnh bằng 8cm và một hình
tròn có bán kính 5cm được xếp chồng lên nhau sao cho tâm
của hình tròn trùng với tâm của hình vuông như hình vẽ bên.
Tính thể tích V của vật thể tròn xoay tạo thành khi quay mô
hình trên quanh trục XY . A. 260 290 520 580 3    V  cm . B. 3 V  cm . C. 3 V  cm . D. 3 V  cm . 3 3 3 3
Lời giải. Chọn hệ trục tọa độ như hình vẽ. ● Thể tích khối cầu 4 4 500 3 3 
V  R  5  . 1 3 3 3
● Gọi V là thể tích khối tròn xoay khi quay hình 2
phẳng H (phần tô màu) được giới hạn bởi đường
thẳng y  4 , đường tròn 2 2
y  25 x và x  4 quanh trục hoành 4 10 2   V    4    2 25 x dx  . 2  3 3 Vậy thể tích cần tính 520 3
V V  2V  cm . Chọn C. 1 2 3
Câu 16. Cho hai tam giác cân có chung đường cao
XY  40cm và cạnh đáy lần lượt là 40cm và 60cm , được
xếp chồng lên nhau sao cho đỉnh của tam giác này là trung
điểm cạnh đáy của tam giác kia như hình vẽ bên. Tính thể
tích V của vật thể tròn xoay được tạo thành khi quay mô
hình trên quanh trục XY . A. 40480 52000 3  V  cm . B. 3 V  cm . 3 3 C. 46240 3 V  cm . D. 3
V  1920cm . 3
Lời giải. Chọn hệ trục tọa độ như hình vẽ, khi đó:
Y  O 0;0, X  40;0, A 0;20, M  40;30 . Phương trình đường 3x
YM : 3x  4 y  0  y  . 4 Phương trình 40  x
AX : x  2y  40  0  y  . 2
Phương trình hoành độ giao điểm của hai đường YM và AX là: 3x 40  x   x  16. 4 2
Thể tích vật thể được tạo ra bằng cách quay hình phẳng (phần tô đậm như hình). 16 2 40 2     
Thể tích vật thể cần tính 40 x 3x 46240 3 V      
 dx          dx  cm . Chọn C.  2   4  3 0 16
Câu 17. Cho khối cầu có bán kính R . Một mặt phẳng cắt
khối cầu thành hai nửa. Nửa bé có khoảng cách từ đỉnh đến
đáy bằng h (tham khảo hình vẽ bên). Tính thể tích nửa bé.  h  h
A. V   2 h   R   V  2 h    . B.
 R  .  2    3  h  h
C. V   2 h   R   V  2 h    . D.
 R  .  4    3
Lời giải. Xét phần mặt cắt và gắn tọa độ như hình vẽ
Khi đó O0;0, AR;0 và I R h;0 là tâm của đường
tròn thiết diện. Thể tích chỏm cầu bị cắt chính là vật thể
tròn xoay tạo bởi phần đường tròn 2 2
y  R  x quay
xung quanh trục Ox từ R h đến R . Do đó R  h
V     2 R  2
x  x   2 d h   R    . Chọn B.  3 Rh
Câu 18. Cho hai mặt cầu S , S có cùng bán kính R 2  1 
thỏa mãn tính chất: tâm của S thuộc S và ngược lại. 2  1 
Tính thể tích phần chung V của hai khối cầu tạo bởi S 1  và S . 2  3 3 3 A. R 2 R 5 R V   3 R . B.  V  . C.  V  . D.  V  . 2 5 12
Lời giải. Thể tích cần tính là tổng của hai chỏm cầu bằng nhau. R h  h 3
Áp dụng công thức bài trước, thể tích mỗi chỏm cầu bằng 2 5 2 R h   R      .  3 24 3 3
Vậy thể tích phần chung 5 R 5 R
V của hai khối cầu là   V  2  . Chọn D. 24 12
Câu 19. Cho hai đường tròn O ;5 và O ;3 cắt nhau tại 2  1 
hai điểm A và B sao cho AB là một đường kính của
đường tròn O . Gọi H là diện tích hình phẳng giới hạn 2 
bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch
chéo như hình vẽ). Quay hình H quanh trục O O , ta 1 2
được một khối tròn xoay. Thể tích của khối tròn xoay được tạo thành bằng A. 14 40 68  B.  
C.  .
D. 36. 3 3 3
Lời giải. Xét phần mặt cắt như hình vẽ. Ta thấy thể tích cần
tính bằng thể tích V trừ đi thể tích V , trong đó 1 2 1 4 
• V là thể tích nửa khối cầu O nên V    .3 18 . 1
  3   2  1 2   3 
• V là thể tích của chỏm cầu (khi quay miền gạch sọc quanh 2  h trục R 14
O O ). Áp dụng công thức bài trước, ta được 2 5  V  h R V . 2          1 2   hO M  3 1 2 2 3
Vậy thể tích vật thể cần tính: 40
V V V  . Chọn B. 1 2  3
Câu 20. Ta vẽ hai nửa đường tròn như hình vẽ bên,
trong đó đường kính của nửa đường tròn lớn gấp đôi
đường kính của nửa đường tròn nhỏ. Biết rằng nửa
hình tròn đường kính AB có diện tích là 8 và 
BAC  30. Thể tích của vật thể tròn xoay được tạo
thành khi quay hình H (phần tô đậm) xung quanh
đường thẳng AB bằng A. 98 220 224 2 4 . B. . C. . D. . 3 3 3 Lời giải. Ta có:    2 2.8
R suy ra R  4 và r  2.
Vì IHC vuông tại H, 
CIH  60 nên ta có  3 CH  o IC sin 60  4.   2 3  2 IH  2 IC  2 CH  16 12  2.  1
AL  AH  3  2 
Cách 1. (Dùng công thức thuần túy)
• Thể tích khối nón đỉnh 1 ,
A bán kính đáy HC là: V  HC .AH 24 . 1  2   3  HB 
• Thể tích chỏm cầu (hình cầu lớn) có 40
h  HB  2 là: 2  V  HB R . 2           3  3
• Thể tích khối nón đỉnh 1 ,
A bán kính đáy LD là: V  LD .AL 3 . 3  2   3  LI 
• Thể tích chỏm cầu (hình cầu nhỏ) có 5
h  LI  1 là: 2  V  LI r . 4           3  3 Suy ra thể tích cần tìm 98
V  V V V V   . Chọn B. 1 2 3 4  3
Cách 2. (Dùng tích phân) Dễ dàng viết được phương trình x AC : y  và hai phương 3
trình đường tròn là y  x  2 16 4 và y  x  2 4 2 .  6 4 8 2  Thể tích cần tìm  x  V . dx 4 x 22   dx 16 x 42 98           dx         . 3       3 3 3 6 
Phần 6. Bài toán vận tốc
Giả sử vt là vận tốc của vật M tại thời điểm t và st là quãng đường vật đi được
sau khoảng thời gian t tính từ lúc bắt đầu chuyển động. Ta có mối liên hệ giữa st
và vt như sau:
● Đạo hàm của quãng đường là vận tốc: st vt.
● Nguyên hàm của vận tốc là quãng đường st vtdt.  
 từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian t  a;b là b
vtdt  sb sa.  a
Nếu gọi at là gia tốc của vật M thì ta có mối liên hệ giữa vt và at như sau:
● Đạo hàm của vận tốc là gia tốc: vt at.
● Nguyên hàm của gia tốc là vận tốc: vt atdt. 
Câu 1. (ĐỀ MINH HỌA 2016 – 2017) Một ô tô đang chạy với vận tốc 10m/s thì
người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc
vt  5t 10m/s, trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m. B. 2m. C. 10m. D. 20m.
Lời giải. Lúc dừng hẳn thì vt 0 
5t 10  0  t  2.
Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô đi được quãng đường là 2 2  
s  5t 10 5 2 dt    
t 10t  10m.  Chọn C.  2  0 0
Câu 2. Một ô tô đang đi với vận tốc lớn hơn 72km/h, phía trước là đoạn đường chỉ cho
phép chạy với tốc độ tối đa là 72km/h, vì thế người lái xe đạp phanh để ô tô chuyển
động chậm dần đều với vận tốc vt 302t  m/s, trong đó t là khoảng thời gian
tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt
tốc độ 72km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét? A. 100m. B. 125m. C. 150m. D. 175m.
Lời giải. Ta có 72km/h  20m/s .
Từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72km/h, ta có phương trình
30 2t  20  t  5.
Vậy từ lúc đạp phanh đến khi ô tô đạt tốc độ 72km/h, ô tô đi được quãng đường là 5
s  302tdt  125m.  Chọn B. 0
Câu 3. Hai viên đạn cùng rời khỏi nòng súng thời điểm t  0 với những vận tốc khác
nhau: viên đạn thứ nhất có vận tốc v t 3t
1 m/s , viên đạn thứ hai có vận tốc 1    2   
v t  2t  4 m/s . Hỏi từ giây thứ mấy thì viên đạn thứ nhất xa điểm xuất phát hơn 2   viên đạn thứ hai? A. Giây thứ nhất. B. Giây thứ hai. C. Giây thứ ba. D. Giây thứ tư.
Lời giải. Quảng đường 3 1 d s s t t t t t C C 0. Do đó s t t t. 1    3  1    2  3           1 0 0 1 1 s t 2t 4 s   
 dt  t  4t C C   2 0 0 0. Do đó s t t 4t. 2    2  2 2 2 Xét t 1 13 s t s t t t t 4t t t 3t 0 t 2,3. 1   2   3 2 3 2 0              2 Ta có s   3  30  s   3  21 
 từ giây thứ ba trở đi thì viên đạn thứ nhất xa điểm 1 2
xuất phát hơn viên đạn thứ hai. Chọn C.
Câu 4. Một ô tô đang chạy với vận tốc 10 
m/s thì người lái xe đạp phanh. Từ thời
điểm đó, ô tô chuyển động chậm dần đều với vận tốc vt 2t 10  m/s, trong đó t
là khoảng thời gian được tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quảng
đường ô tô di chuyển được trong 8 giây cuối cùng. A. 16m. B. 25m. C. 50m. D. 55m.
Lời giải. Ta có phương trình: 2t 10  0  t  5.
Suy ra thời gian tính từ lúc bắt đầu đạp phanh đến khi dừng là 5 giây. Vậy trong 8
giây cuối cùng thì có 3 giây ô tô chuyển động với vận tốc 10m/s và 5 giây chuyển
động chậm dần đều với vận tốc vt 2t 10m/s. Suy ra quảng đường ô tô di 5
chuyển là s  3.10  2t 10dt  30 25   55 m. Chọn D. 0
Câu 5. Một vật đang chuyển động với vận tốc 6m/s thì tăng tốc với gia tốc at 3  2
m/s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng t 1
tốc. Hỏi vận tốc của vật sau 10 giây gần nhất với kết quả nào sau đây? A. 11m/s . B. 12 m/s . C. 13m/s . D. 14 m/s .
Lời giải. Ta có vt 3 
dt  3ln t 1 C.  t 1
Tại thời điểm lúc bắt đầu tăng tốc t  0 thì v  6m/s nên ta có 3ln1C  6  C  6.
Suy ra vt 3ln t 1 6m/s.
Tại thời điểm t  10 s 
v10  3ln11 6  13m/s. Chọn C.
Câu 6. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc
at  t  2 t  2 3
m/s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu
tăng tốc. Hỏi quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt
đầu tăng tốc bằng bao nhiêu mét? A. 1900 m. B. 2200 m. C. 4000 m. D. 4300 m. 3 3 3 3 2 3
Lời giải. Ta có     3 2 t t v t
3t  t dt   C. 2 3
Tại thời điểm lúc bắt đầu tăng tốc t  0 thì v  10m/s nên suy ra C  10. 2 3 Suy ra   3t t v t   10m/s. 2 3
Vậy quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng 10  2 3 3t t   3 4 t t  10 tốc bằng     4300 s    10dt       10t  m. Chọn D.  2 3      2 12  0 3 0
Câu 7. Một ô tô đang chạy thẳng đều với vận tốc v m/s thì người đạp phanh, từ 0  
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc vt 5t v m/s , trong 0  
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp
phanh đến lúc dừng hẳn ô tô di chuyển được 40m thì vận tốc ban đầu v bằng bao 0 nhiêu?
A. v  20m/s. B. v  25m/s. C. v  40m/s. D. v  80m/s. 0 0 0 0
Lời giải. Lúc dừng hẳn thì vt v0  0 
5t v  0  t  . 0 5 v0 5 v0 2 2 2   Theo giả thiết, ta có:  5 v v v 40m=
5t v dt     t  v t     0  2 5 0 0 0 0  2  0 10 5 10 0 2 v   40m  0 
v  20m/s. Chọn A. 0 10
Câu 8. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162m so
với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng,
khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật vt 2
 10t t m/s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
chuyển động. Hỏi lúc vừa tiếp đất, vận tốc v của khí cầu bằng bao nhiêu? A. v  3m/s. B. v  5m/s. C. v  7m/s. D. v  9m/s.
Lời giải. Do vt 2
 10t t  0  t 10.
Giả sử chiếc khí cầu chạm đất kể từ lúc bắt đầu chuyển động là t giây 0  t 10 . 1  1 1 t 3 t 3  
Theo đề bài ta có phương trình t t 162    2 10t t  1 2   2 1 dt  5
 t    5t    1  3  0 3 0 3 t1 2 0 1t 1  0
  5t 162  0  t  9 
v 9  9m/s. Chọn D. 1 1   3
Câu 9. (ĐỀ THI CHÍNH THỨC 2016 – 2017) Một vật chuyển động theo quy luật 1 3 2
s   t  6t với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động 2
và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian 8 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. 18m/s. B. 24m/s. C. 64m/s. D. 108m/s.
Lời giải. Vận tốc vt 3
 s 't   2 t 12t. 2
Ycbt là đi tìm GTLN của hàm số vt 3 2
  t 12t với 0  t  8. 2
Đạo hàm và lập bảng biến thiên ta tìm được max vt v4 24m/s. Chọn B. 0;8
Câu 10. Một tàu lửa đang chạy với vận tốc
200 m/s thì người lái tàu đạp phanh. Từ
thời điểm đó, tàu chuyển động chậm dần đều với vận tốc vt 200 at  m/s, trong
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh và a 2 m/s  là
gia tốc. Biết rằng khi đi được 1500m thì tàu dừng, hỏi gia tốc của tàu bằng bao nhiêu? A. 200 100 40 40 a   2
m/s . B. a   2
m/s . C. a   2 m/s . D. a   2 m/s . 13 13 3 3
Lời giải. Khi tàu dừng hẳn thì v    at 200 0 200  0  t   m/s. a 200  a  2 at  200 Theo đề bài, ta có: 40000 40000 1500  200 at   
dt  200t   a       .  2  0 a 2a 0 Suy ra 40 a    2 m/s . Chọn C. 3
Câu 11. Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu tăng tốc
với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường
cong Parabol có hình bên. Biết rằng sau 10s thì xe đạt đến vận
tốc cao nhất 50m/s và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu
tăng tốc đến lúc đạt vận tốc cao nhất thì xe đã đi được quãng
đường bao nhiêu mét? A. 1000 m. B. 1100 m. C. 1400 m. D. 300m. 3 3 3
Lời giải. Dựa vào đồ thị suy ra vt 1   2 t 10t  m/s. 2 10 10 Quảng đường: 1 1000 s  vt   dt   2   
  t 10tdt    m. Chọn A.  2  3 0 0
Câu 12. Một vật chuyển động trong 3 giờ với vận tốc vkm/h phụ
thuộc thời gian t h có đồ thị là một phần của đường Parabol có
đỉnh I 2;9 và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
A. s  24,25km. B. s  24,75km.
C. s  25,25km.
D. s  26,75km.
Lời giải. Dựa vào đồ thị suy ra vt 3   2
t  3t  6  m/s. 4
Quảng đường người đó đi được trong khoảng thời gian 3 giờ là: 3  3  2 s  
  t 3t 6dt 24  ,75km.  Chọn B.  4  0
Câu 13. Một vật chuyển động trong 4 giờ với vận tốc vkm/h
phụ thuộc thời gian t h có đồ thị của vận tốc như hình bên.
Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động,
đồ thị đó là một phần của đường Parabol có đỉnh I 2;9 với
trục đối xứng song song với trục tung, khoảng thời gian còn lại
đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng
đuờng s mà vật chuyển động trong 4 giờ đó.
A. s  24km.
B. s  26,5km. C. s  27km.
D. s  28,5km.  9  2
t  9t m/s khi 0  t  3
Lời giải. Dựa vào đồ thị suy ra vt   4  . 27  m/s  khi 3  t  4  4
Quảng đường người đó đi được trong khoảng thời gian 4 giờ là: 3 4  9  27 2 s  
  t 9tdt  dt 27  km.   Chọn C. 4  4 0 3
Câu 14. Một vật chuyển động trong 4 giờ với vận tốc
v km/h phụ thuộc thời gian t h có đồ thị của vận tốc
như hình bên. Trong khoảng thời gian 2 giờ kể từ khi
bắt đầu chuyển động, đồ thị đó là một phần của đường
Parabol có đỉnh I 1;2 và trục đối xứng song song với
trục tung, khoảng thời gian còn lại đồ thị là một phần
đường thẳng. Tính quãng đường s mà vật di chuyển được
trong 4 giờ đó (kết quả làm tròn đến hàng phần trăm).
A. s  5,44km. B. s  8,67km.
C. s  9,27km.
D. s  11,35km.  2
Lời giải. Dựa vào đồ thị suy ra vt
t 2t  3 khi 0  t  2   . 5t khi 2   t   4
Quảng đường người đó đi được trong khoảng thời gian 4 giờ là: 2 4 26
s   2t 2t  
3 dt  5tdt     8,67k m. Chọn B. 3 0 2
Câu 15. Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi
hành cùng một lúc, bên cạnh nhau và trên cùng một con
đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường
Parabol, đồ thị biểu diễn vận tốc của xe B là một đường
thẳng ở hình bên. Hỏi sau khi đi được 3 giây khoảng cách
giữa hai xe là bao nhiêu mét? A. 0 m. B. 60 m. C. 90 m. D. 270 m. v t t t A     2 20  80  m/s
Lời giải. Dựa vào đồ thị suy ra  . v t t B    20  m/s  3
Quãng đường đi được sau 3 giây của xe A là: s    2
20t 80tdt 180m. A 0 3
Quãng đường đi được sau 3 giây của xe B là: s  20t dt  90m. B  0
Vậy khoảng cách giữa hai xe sau 3 giây sẽ bằng: s  s  90 m. Chọn C. A B
Document Outline

TÍCH PHÂN VẬN DỤNG CAO
- DE1
- DAP AN1
DE
DAP AN