Bài tập trắc nghiệm tìm số nghiệm của phương trình hàm hợp Toán 12

Bài tập trắc nghiệm tìm số nghiệm của phương trình hàm hợp Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

65 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Strong Team Toán VD – VDC Trang 1/67
BÀI TẬP TRẮC NGHIỆM
TÌM SỐ NGHIỆM CỦA PHƯƠNG TRÌNH HÀM HỢP
ĐỀ BÀI
Câu 1. Cho hàm số
y f x
xác định trên R và có bảng biến thiên như sau:
x
-1 1

y
0
0
y
1

-1
Số nghiệm của phương trình
2
2 2
f x x
là
A.
4
. B.
2
C.
3
D.
8
Câu 2. Cho hàm số
y f x
xác định trên R và có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;
của phương trình
os2 0
f f c x
là
A.
4
. B.
2
C.
3
D.
8
Câu 3. Cho hàm số
( )f x
liên tục trên đoạn
1;3
và có bảng biến thiên như sau:
Tổng tất cả các số nguyên m để phương trình
2
( 1)
6 12
m
f x
x x
có hai nghiệm phân biệt
trên đoạn
2;4
bằng
A.
75
. B.
72
. C.
294
. D.
297
.
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;2
của phương trình
3 sin 2 2 0f x
là:
0
+∞
+ 0 – 0 + 0 –
1
0
1
Strong Team Toán VD – VDC Trang 2/67
A.
7
. B.
8
. C.
5
. D.
6
.
Câu 5. Cho hàm số
3 2
( ) ( 0)y f x ax bx cx d a
có đồ thị như hình vẽ. Phương trình
( ( )) 0f f x có bao nhiêu nghiệm thực?
A.
3
. B.
7
. C.
9
. D.
5
.
Câu 6. Cho hàm số
( )y f x
có đồ thị như hình vẽ và
lim
x
y


. Hỏi có bao nhiêu điểm trên
đường tròn lượng giác biểu diễn nghiệm của phương trình
cos 2 0f f x
?
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 7. Cho hàm số
y f x
có đồ thị như hình vẽ:
Khi đó phương trình
4
4 3 3 0f x
có bao nhiêu nghiệm dương?
A. 2. B. 4. C. 5. D. 1.
Câu 8. Cho hàm số
y f x
có đồ thị như hình vẽ:
Strong Team Toán VD – VDC Trang 3/67
Phương trình
2 cos 1 0f x
có bao nhiêu nghiệm trong đoạn
;2
đồng thời
tan 0x
?
A.
3
. B. 4. C. 5. D. 6.
Câu 9. Cho hàm số
y f x
có đồ thị như hình vẽ.
Số nghiệm của phương trình
2 sin 1 0f x
trên đoạn
5
;
2 2
là
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 10. Cho hàm số
y f x
có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn
0;5
của phương trình
cos 1f x
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 11. Cho hàm số
f x
xác định trên
\ 0
và có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình
3 2 1 10 0f x
là.
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 12. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ
O
1
1
1
1
x
y
Strong Team Toán VD – VDC Trang 4/67
Tập hợp các giá trị
m
để phương trình
cos 2 2 1 0
f x m
có nghiệm thuộc khoảng
;
3 4
là:
A.
1
0;
2
B.
1
0;
2
C.
1 1
;
4 2
D.
2 2 1
;
4 4
Câu 13. Cho hàm số liên tục trên có đồ thị như hình vẽ bên. Phương trình
3 2 1
f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A. . B. . C. . D. .
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;2
của phương trình
2 cos 1 0
f x
là:
A.
7
. B.
4
. C.
5
. D.
6
.
Câu 15. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
4 2
3 6 1 1
f x x
là
A.
4
. B.
5
. C.
6
. D.
3
.
Câu 16. Cho hàm số
f x
có bảng biến thiên như sau:
y f x
6
5
7
4
Strong Team Toán VD – VDC Trang 5/67
Số nghiệm thuộc đoạn
7
0;
3
của phương trình
2. cos 5 0
f x
là
A.
8
. B.
7
. C.
5
. D.
6
.
Câu 17. Cho hàm số
( )f x
có bảng biến thiên bảng biến thiên như sau
Số nghiệm thuộc
[ ;2 ]
2
của phương trình
(sinx) 1 0
f
là
A.
3
. B.
6
. C.
4
. D.
5
.
Câu 18. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới
Tìm số giá trị nguyên của tham số m để phương trình
2
( 4 )
f x m
có hai nghiệm phân
biệt
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 19. Cho hàm số
3 2
f x ax bx bx c
có đồ thị như hình vẽ:
Strong Team Toán VD – VDC Trang 6/67
Số nghiệm nằm trong
9
;
2 2
của phương trình
cos 1 cos 1f x x
là
A.
6
. B.
10
. C.
4
. D.
8
.
Câu 20. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;5
của phương trình
sin 1
f x
là
A.
6
. B.
4
. C.
10
. D.
8
.
Câu 21. Cho hàm số
f x
liên tục trên
có đồ thị
y f x
như hình vẽ dưới đây.
Strong Team Toán VD – VDC Trang 7/67
Số nghiệm thực của phương trình
4 2 2
x
f f
là
A. 1. B. 2. C. 3. D. 4.
Câu 22. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm nhiều nhất thuộc đoạn
3
0;
2
của phương trình
2cos 1 0f x
là:
A.
7
. B.
5
. C.
4
. D.
6
.
Câu 23. Cho hàm số
y f x
có bảng biến thiên sau:
Hỏi có bao nhiêu giá trị
m
nguyên để phương trình
2 2 1f tan2x m
có nghiệm thuộc
khoảng
0;
8
là:
A.
1
. B.
3
. C. Vô số. D.
0
.
Câu 24. Cho hàm số
y f x
liên tục trên
có đồ thị như hình vẽ. Phương trình
1 0f f x
có
tối đa bao nhiêu nghiệm thực phân biệt?
A.
7
. B.
9
. C.
6
. D.
5
.
Câu 25. Cho hàm số
f x
liên tục trên
có bảng biến thiên như sau:
Strong Team Toán VD – VDC Trang 8/67
Số nghiệm thuộc đoạn
;
của phương trình
2
2cos 3 3f x
là:
A.
8
. B.
2
. C.
6
. D.
4
.
Câu 26. Cho hàm số
f x
liên tục trên
có bảng biến thiên như sau:
Số nghiệm của phương trình
2
2f x x là:
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 27. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;3
của phương trình
cos 2f x
là
A.
3
. B.
4
. C.
6
. D.
8
.
Câu 28. Cho hàm số
y f x
có bảng biến thiên như sau :
Số nghiệm thuộc đoạn
0;2
của phương trình
3 2 sin 2 0f x
là :
Strong Team Toán VD – VDC Trang 9/67
A.
2
. B.
3
. C.
4
. D.
6
.
Câu 29. Cho hàm số
f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
1;3
của phương trình
2
3 1 0f x x
là
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 30. Cho hàm số
f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
5
;3
6
của phương trình
4 cos2 1 0f x
là
A.
5
. B.
9
. C.
4
. D.
10
.
Câu 31. Cho hàm số
y f x
liên tục, có đạo hàm trên
2; 4
và có bảng biến thiên như hình vẽ
Số nghiệm của phương trình
3
3 2 1 8 6f x x x
trên đoạn
3 3
;
2 2
là
A.
1
. B.
2
. C.
3
. D. 5 .
Câu 32. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.
Strong Team Toán VD – VDC Trang 10/67
Số nghiệm thuộc đoạn
;2
của phương trình
2 2 sin 1 0f x là
A.
6
. B.
2
. C.
8
. D.
12
.
Câu 33. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
Gọi
m
là số nghiệm của phương trình
1f f x
. Khẳng định nào sau đây là đúng ?
A.
6m
. B.
7m
. C.
5m
. D.
9m
.
Câu 34. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ dưới. Gọi
S
là tập hợp tất cả
các giá trị nguyên của
m
để phương trình
(sin ) 2sin 2f x x m
có nghiệm thuộc khoảng
(0; )
. Tổng các phần tử của
S
bằng:
A.
2
B.
0
. C.
1
. D.
5
.
Câu 35. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
2 ;2
của phương trình
2 2sin 1 0
f x
là
A.
8
. B.
5
. C.
2
. D.
6
.
Strong Team Toán VD – VDC Trang 11/67
Câu 36. Cho hàm số
3
3 1y f x x x
. Số nghiệm của phương trình
3
3 1 0f x f x
là:
A. 1. B. 6. C. 5. D. 7.
Câu 37. Cho hàm số
( )y f x
là hàm số bậc 3 có đồ thị như hình vẽ dưới đây
Số nghiệm thuộc đoạn
0;3
của phương trình
3 1
2 sin 1 0
2 2
f x
là
A.
5
. B.
3.
C.
4.
D.
6.
Câu 38. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
4 4
sin cosf x x m
có nghiệm
0; .
4
x
A.
1
. B.
3.
C.
2.
D.
4.
Câu 39. Cho hàm số
( )y f x
có đồ thị như hình vẽ.
Số nghiệm của phương trình
2 (cos 2 ) 1 0f x
trên đoạn
5
0;
4
là
∞
+
∞
1
+
2
1
∞
∞
+
+
y
y'
x
1
0
0
2
Strong Team Toán VD – VDC Trang 12/67
A. 3. B. 4. C. 5. D. 6.
Câu 40. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m
để phương trình
3 ( )f f x m
có đúng 6 nghiệm phân biệt
[ 5;0].x
A.
2.
B.
3.
C.
4.
D.
5.
Câu 41. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
2019;1
của phương trình
ln 4f x
A. 2020 B. 4. C. 2019. D. 3.
Câu 42. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;
4
của phương trình
sin cos 1f x x
A. 1 B. 3 C. 2 D. 0.
Câu 43. Cho hàm số
( )y f x
liên tục trên
có đồ thị như hình vẽ
Strong Team Toán VD – VDC Trang 13/67
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
(sin ) 2sin 0
f x x m
có
nghiệm thuộc khoảng
0;
?
A.
9
. B.
4
. C.
5
. D.
6
.
Câu 44. Cho hàm số
( )f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
;2
của phương trình
2 (sin ) 3 0
f x
là
A.
6
. B.
3
. C.
4
. D.
8
.
Câu 45. Cho hàm số
y f x
có bảng biến thiên như sau
Số nghiệm của phương trình
4 1 0
x
f e
trong đoạn
ln 2 ; ln 6
là
A. 1. B. 2. C. 3. D.
4
.
Câu 46. Cho hàm số
y f x
là hàm đa thức bậc 3 và có bảng biến thiên như sau
Số nghiệm của phương trình
sin 3 cos 0
f x x
trong đoạn
5
0 ;
2
là
A. 1. B. 4. C. 3. D.
2
.
Câu 47. Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình
3 2 2 3 2
1 3 1 2 3 1 2
f x x f x x
là
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 48. Cho hàm số
y f x
là hàm bậc 3 và có bảng biến thiên như sau
Strong Team Toán VD – VDC Trang 14/67
Phương trình
2
sin cos 1 sin 2 2 2 sin sin cos
4
f x x x x f x x
có mấy nghiệm
thực thuộc đoạn
5 5
;
4 4
?
A.
1
. B.
3
. C.
4
. D.
6
.
Câu 49. Cho
y f x
là hàm số bậc ba và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên
5;5
m
để hàm số
g x f f x m
có
4
điểm cực trị?
A. 5. B. 6. C. 7. D. 8.
Câu 50. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc khoảng
;
của phương trình
2
cos cos 2
f x f x
là
A.
5
. B.
6
. C.
7
. D.
9
.
Câu 51. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm
0;x
của phương trình
2020 2 0
x
f e x
là
A.1. B.2. C.
0
. D.
2020
.
Câu 52. Cho hàm số
f x
có đồ thị như hình vẽ:
Strong Team Toán VD – VDC Trang 15/67
Số nghiệm thuộc đoạn
3
;2
2
của phương trình
2 cos 5 0
f x
là
A.
5
. B.
1
. C.
3
. D.
4
.
Câu 53. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của
m
để phương trình
2
2
f x x m
có đúng
4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
.
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 54. Cho hàm số
y f x
có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin
f x m
có đúng hai nghiệm thuộc đoạn
0;
?
A.
4
. B.
7
. C.
5
. D.
6
.
Câu 55. Cho hàm số bậc bốn
y f x
có đồ thị như hình bên:
Strong Team Toán VD – VDC Trang 16/67
Số điểm cực trị của hàm số
3 2
3 4
g x f x x
là
A.
5
. B.
3
. C.
7
. D.
11
.
Câu 56. Cho hàm số
y f x
có đồ thị như hình bên
Số nghiệm thuộc đoạn
0;3
của phương trình :
2 cos 1 0
f x
A.
12
. B.
6
. C.
10
. D.
8
.
Câu 57. Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây. Số nghiệm thuộc đoạn
3
;
2 2
của phương trình
cot 1 1
f x
là
x

1
1
2

f x
0
0
0
f x

1
1
2

A. 7. B. 6. C. 8. D. 5.
Câu 58. Cho hàm số
y f x
có bảng biến thiên như hình vẽ
x

0
1
2

f x
0
0
0
f x

0
3
1

3
2
1
1
2
2 2
x
y
-1
-1
1
1
Strong Team Toán VD – VDC Trang 17/67
Số nghiệm của phương trình
sin 1 2
f x
trên
;2
là
A. 6. B. 7. C. 5. D. 4.
-------------------- HẾT --------------------
Strong Team Toán VD – VDC Trang 18/67
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho hàm số
y f x
xác định trên R và có bảng biến thiên như sau
x
-1 1

y
0
0
y
1

-1
Số nghiệm của phương trình
2
2 2
f x x
là
A.
4
. B.
2
C.
3
D.
8
Lời giải
Chọn B
Phương trình
2
2 3
f x x
2
2
2 2
2 2
f x x
f x x
Dựa vào bảng biến thiên
x
-1 1 a

y
0
0
y
1

-1
phương trình
2
2 2
f x x
2 2
2 1 2 0
x x a a x x a
có
1 0
a
phương trình có 2 nghiệm.
Tương tự, dựa vào bảng biến thiên
x
b
-1 1

y
0
0
y
1

-1
Phương trình
2
2 2
f x x
2 2
2 1 2 0
x x b b x x b
có
1 0
b
phương trình vô nghiệm.
Vậy phương trình
2
2 2
f x x
có 2 nghiệm.
Câu 2. Cho hàm số
y f x
xác định trên R và có bảng biến thiên như sau
Số nghiệm thuộc đoạn
0;
của phương trình
os2 0
f f c x
là
A.
4
. B.
2
C.
3
D.
8
Lời giải
Chọn B
0
+∞
+ 0 – 0 + 0 –
1
0
1
a
2
y
2
y
Strong Team Toán VD – VDC Trang 19/67
Dựa và bảng biến thiên ta có
1,f x x R
và
os2 0f f c x
os2
os2
os2 0
f c x a
f c x a
f c x
với
1a
Với
os2f c x a
thì phương trình vô nghiệm.
Với
os2f c x a
os2x =c b
với
1b
nên phương trình vô nghiệm.
Với
os2 0f c x
os2x =0 2x .
2 4 2
c k x k
Vậy phương trình
os2 0f f c x
có 2 nghiệm thuộc đoạn
0;
.
Câu 3. Cho hàm số
( )f x
liên tục trên đoạn
1;3
và có bảng biến thiên như sau:
Tổng tất cả các số nguyên m để phương trình
2
( 1)
6 12
m
f x
x x
có hai nghiệm phân biệt
trên đoạn
2;4
bằng
A.
75
. B.
72
. C.
294
. D.
297
.
Lời giải
Chọn B.
Phương trình tương đương với:
2
( ) 6 12 ( 1).m g x x x f x
Ta có
2
'( ) (2 6) ( 1) ( 6 12) '( 1)g x x f x x x f x
+) Nếu
2
2 6 0; ( 1) 0
2 3 '( ) 0
6 12 0; '( 1) 0
x f x
x g x
x x f x
+) Nếu 3 '(3) 0. (2) 3. '(2) 0x g f f
+) Nếu
2
2 6 0; ( 1) 0
3 4 '( ) 0.
6 12 0; '( 1) 0
x f x
x g x
x x f x
Vậy trên đoạn
2;4
ta có
'( ) 0 3.g x x
Bảng biến thiên:
x
– ∞
-1 0 1
+ ∞
y'
+
0
–
0
+
0
–
y
– ∞
1
0
1
–
∞
-a
Strong Team Toán VD – VDC Trang 20/67
Vậy phương trình có hai nghiệm phân biệt trên đoạn
[2;4] 12 3 12,..., 4 .m m
Tổng các số nguyên cần tìm bằng
12 ( 11) ... ( 5) ( 4) 72
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;2
của phương trình
3 sin 2 2 0f x
là:
A.
7
. B.
8
. C.
5
. D.
6
.
Lời giải
Chọn B.
Đặt
sin 2x t
,
0;2 1;1x t
.
Phương trình trở thành:
2
3
f t
.
Từ bảng biến thiên ta có:
2
3
t a
f t
t b
Với
1 0a
và
0 1b
Xét BBT của hàm số
sin 2y x
trên
0;2
:
Strong Team Toán VD – VDC Trang 21/67
Dựa vào BBT của hàm số ta có
+) Phương trình
sin 2x a
có
4
nghiệm.
+) Phương trình
sin 2x b
có
4
nghiệm
Vậy phương trình
3 sin 2 2 0f x
có
8
nghiệm.
Câu 5. Cho hàm số
3 2
( ) ( 0)y f x ax bx cx d a
có đồ thị như hình vẽ. Phương trình
( ( )) 0f f x
có bao nhiêu nghiệm thực?
B.
3
. B.
7
. C.
9
. D.
5
.
Lời giải
Chọn C
Đặt
t f x
, phương trình
0f f x
trở thành
0 *f t
(số nghiệm phương trình
*
là số giao điểm của đồ thị
f x
với trục
Ox
) . Nhìn vào đồ thị ta thấy phương trình
*
có 3 nghiệm
t
thuộc khoảng
2;2
, với mỗi giá trị
t
như vậy phương trình
f x t
có 3
nghiệm phân biệt. Vậy phương trình
0f f x
có 9 nghiệm. Vậy chọn C
Câu 6. Cho hàm số
( )y f x
có đồ thị như hình vẽ và
lim
x
y


. Hỏi có bao nhiêu điểm trên
đường tròn lượng giác biểu diễn nghiệm của phương trình
cos2 0f f x
?
Strong Team Toán VD – VDC Trang 22/67
B.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn B
Từ đồ thị ta có
1,f x x
và suy ra được
cos2 1f x a a
hoặc
cos2 0f x
TH1: Nếu
cos 2 1f x a
thì phương trình này vô nghiệm.
TH2: Nếu
cos2 1f x a
thì
cos2 1x
, phương trình này vô nghiệm.
TH3: Nếu
cos2 ( )
cos2 0
cos2 0
x a VN
f x
x
cos 2 0 ( )
4 2
k
x x k Z
nên có 4 điểm trên đường tròn lượng giác. Vậy có 4 điểm.
Câu 7. Cho hàm số
y f x
có đồ thị như hình vẽ:
Khi đó phương trình
4
4 3 3 0f x
có bao nhiêu nghiệm dương?
A. 2. B. 4. C. 5. D. 1.
Lời giải
Chọn A
Bảng biến thiên của hàm số
4
3y x
:
Ta có:
4
1 1
4 4 4
2 2
4
3 3
3 , 1;0
3
4 3 3 0 3 3 , 0;1
4
3 , 1;2
x x x
f x f x x x x
x x x
.
Dựa vào bảng biến thiên ta có
4
1
3x x
vô nghiệm;
4
2
3x x
có một nghiệm âm một nghiệm
dương;
4
3
3x x
có một nghiệm âm một nghiệm dương.
Vậy phương trình
4
4 3 3 0f x
có 2 nghiệm dương.
Câu 8. Cho hàm số
y f x
có đồ thị như hình vẽ:
Strong Team Toán VD – VDC Trang 23/67
Phương trình
2 cos 1 0f x
có bao nhiêu nghiệm trong đoạn
;2
đồng thời
tan 0x
?
A.
3
. B. 4. C. 5. D. 6.
Lời giải
Chọn A
1 1
2 2
3 3
4 4
cos , ; 1 VN
cos , 1;0
1
2 cos 1 0 cos
2
cos , 0;1
cos , 1; VN
x x x
x x x
f x f x
x x x
x x x


.
Vì
tan 0x
và
;2x
nên khi đó
3
; 0; ; *
2 2 2
x
.
Bảng biến thiên của hàm số
cosy x
trên
3
; 0; ;
2 2 2
x
Dựa vào bảng biến thiên ta có:
Phương trình
2
cos x x
với
2
1;0x
có
2
nghiệm thỏa
*
.
Phương trình
3
cos x x
với
3
0;1x
có
1
nghiệm thỏa
*
.
Vậy có
3
nghiệm
x
thỏa yêu cầu bài toán.
Câu 9. Cho hàm số
y f x
có đồ thị như hình vẽ.
O
1
1
1
1
x
y
Strong Team Toán VD – VDC Trang 24/67
Số nghiệm của phương trình
2 sin 1 0
f x
trên đoạn
5
;
2 2
là
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn D
Đặt
sint x
,
1;1
t
ta được:
1
2
f t
.
Dựa vào đồ thị ta có
,( 1 0)
, 0 1
t a a
t b b
Xét hàm số
sing x x
trên đoạn
5
;
2 2
Đồ thị của hàm số
sing x x
tên đoạn
5
;
2 2
là
Dựa vào đồ thị ta có
sin
x a
có
3
nghiệm trên
5
;
2 2
,
sin
x b
có
3
nghiệm trên
5
;
2 2
.
Vậy phương trình
2 sin 1 0
f x
có
6
nghiệm trên
5
;
2 2
.
Câu 10. Cho hàm số
y f x
có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn
0;5
của phương trình
cos 1
f x
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn C
Đặt
cost x
,
1;1
t
ta được
1
f t
t a
với
0;1
a
Strong Team Toán VD – VDC Trang 25/67
Xét hàm số
cosg x x
trên đoạn
0;5
Đồ thị của hàm số
cosg x x
tên đoạn
0;5
là
Dựa vào đồ thị ta có
cos x a
có
5
nghiệm trên
0;5
Vậy phương trình
cos 1f x
có
5
nghiệm trên
0;5
.
Câu 11. Cho hàm số
f x
xác định trên
\ 0
và có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình
3 2 1 10 0f x
là.
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn C
Đặt
2 1t x
, ta có phương trình trở thành
10
3
f t
. Với mỗi nghiệm
t
thì có một nghiệm
1
2
t
x
nên số nghiệm
t
của phương trình
10
3
f t
bằng số nghiệm của
3 2 1 10 0f x
.
Bảng biến thiên của hàm số
y f x
là
Suy ra phương trình
10
3
f t
có
4
nghiệm phân biệt nên phương trình
3 2 1 10 0f x
có
4
nghiệm phân biệt.
Câu 12. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình vẽ
Strong Team Toán VD – VDC Trang 26/67
Tập hợp các giá trị
m
để phương trình
cos 2 2 1 0
f x m
có nghiệm thuộc khoảng
;
3 4
là:
A.
1
0;
2
B.
1
0;
2
C.
1 1
;
4 2
D.
2 2 1
;
4 4
Lời giải
Chọn A
Đặt
1
cos2 , ; ;1
3 4 2
x t x t
.
Yêu cầu đề bài tương đương với phương trình
2 1
f t m
có nghiệm
1
;1
2
t
.
Từ bảng biến thiên suy ra yêu cầu
1
1 2 1 2 0
2
m m
.
Câu 13. Cho hàm số liên tục trên có đồ thị như hình vẽ bên. Phương trình
3 2 1
f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A. . B. . C. . D. .
Lời giải
Chọn D
Dựa vào đồ thị ta có:
3 2 1
f f x
2
3 2 1
1
3 2 2
2
f x
f x
f x
f x
.
Mà
2
f x
có 1 nghiệm duy nhất lớn hơn
2
.
Và
1
2
f x
có 3 nghiệm phân biệt
1
2; 1
x
,
2
1;0
x
,
3
1;2
x
y f x
6
5
7
4
Strong Team Toán VD – VDC Trang 27/67
Vậy phương trình có 4 nghiệm thực phân biệt.
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;2
của phương trình
2 cos 1 0
f x
là:
A.
7
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn D
Đặt
cos x t
,
;2 1;1
x t
.
Phương trình trở thành:
1
2
f t
.
Từ bảng biến thiên ta có:
1
2
t a
f t
t b
Với
1 0
a
và
0 1b
Dựa vào đồ thị
cosy x
ta có :
+)
cos x a
có
3
nghiệm.
+)
cos
x b
có
3
nghiệm
Vậy phương trình
2 cos 1 0
f x
có
6
nghiệm.
Câu 15. Cho hàm số
f x
có bảng biến thiên như sau:
Strong Team Toán VD – VDC Trang 28/67
Số nghiệm của phương trình
4 2
3 6 1 1
f x x
là
A.
4
. B.
5
. C.
6
. D.
3
.
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta có
; 2
1 2;1
1;
x a
f x x b
x c


.
Do đó
4 2
4 2 4 2
4 2
3 6 1 (1)
3 6 1 1 3 6 1 (2)
3 6 1 (3)
x x a
f x x x x b
x x c
Xét hàm số
4 2
3 6 1
g x x x
Có
3
1
12 12 0 0
1
x
g x x x x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên, có:
- Phương trình (1) vô nghiệm.
- Phương trình (2) có đúng 4 nghiệm phân biệt.
- Phương trình (3) có đúng 2 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 6 nghiệm.
Câu 16. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
7
0;
3
của phương trình
2. cos 5 0
f x
là
A.
8
. B.
7
. C.
5
. D.
6
.
Lời giải
Strong Team Toán VD – VDC Trang 29/67
Chọn B
Xét phương trình
5
2. 5 0
2
f x f x
.
Dựa vào bảng biến thiên, ta có
1;0
1
0;
2
5
2
1
;1
2
1;
x a
x b
f x
x c
x d

.
Do đó
cos 1;0 (1)
1
cos 0; (2)
2
5
2. cos 5 0 cos
2
1
cos ;1 (3)
2
cos 1; (4)
x a
x b
f x f x
x c
x d

.
Dựa vào đường tròn lượng giác, trên đoạn
7
0;
3
ta có:
- Phương trình (1) có đúng 2 nghiệm phân biệt.
- Phương trình (2) có đúng 2 nghiệm phân biệt.
- Phương trình (3) có đúng 3 nghiệm phân biệt.
- Phương trình (4) vô nghiệm.
Vậy phương trình đã cho có tất cả 7 nghiệm.
Câu 17. Cho hàm số
( )f x
có bảng biến thiên bảng biến thiên như sau
Số nghiệm thuộc
[ ;2 ]
2
của phương trình
(sinx) 1 0
f
là
A.
3
. B.
6
. C.
4
. D.
5
.
Lời giải
Chọn C
Strong Team Toán VD – VDC Trang 30/67
Ta có
sin 1
(sin ) 1 0 (sin ) 1 sin ( 1;0)
sin 1
x
f x f x x a
x b
2
sin 0 cos 0
2
3
2
x
g x x g x x x
x
Ta có bảng biến thiên hàm
g x
trên
; 2
2
như sau:
Từ bảng biến thiên trên, ta thấy các phương trình
sin
x b
vô nghiệm.
Phương trình
sin
x a
có 3 nghiệm phân biệt thuộc
; 2
2
Phương trình
sin 1x
có 1 nghiệm
; 2
2
Và các nghiệm trên phân biệt.
Vậy phương trình
sin 1 0
f x
có 4 nghiệm phân biệt thuộc
; 2
2
.
Câu 18. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới
Tìm số giá trị nguyên của tham số m để phương trình
2
( 4 )
f x m
có hai nghiệm phân
biệt
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn B
Strong Team Toán VD – VDC Trang 31/67
Đặt
2
4
t x
, phương trình thành
( )
f t m
Lập BBT của hàm số
2
( ) 4 , [ 2;2]
u x x x
BBT của hàm số
2
( ) 4 , [ 2;2]
u x x x
Ta được
[0; 2]
t
Ta thấy rằng
[0 ;2)
t
nghiệm mỗi t tạo ra 2 nghiệm nghiệm
x
2t
thì nghiệm
0
x
Từ hình vẽ ta thấy :
+
0
m
: được nghiệm
2t
tạo ra 1 nghiệm
x
+
1, 2,3
m
thỏa
Vây có ba giá trị
m
nguyên của tham số thỏa mãn
Câu 19. Cho hàm số
3 2
f x ax bx bx c
có đồ thị như hình vẽ:
Số nghiệm nằm trong
9
;
2 2
của phương trình
cos 1 cos 1f x x
là
A.
6
. B.
10
. C.
4
. D.
8
.
Lời giải
Chọn B
Strong Team Toán VD – VDC Trang 32/67
Từ đồ thị ta có
;0
0;1
2
x a
f x x x b
x

Do đó
cos 1 ;0
cos 1 cos 1 cos 1 0;1
cos 1 2
x a
f x x x b
x

1
2
cos 1 ; 1 ( )
cos 1 1;0 (1)
cos 1 (2)
x a t VN
x b t
x

Dựa vào đường tròn lượng giác, phương trình (1) có
4
nghiệm nằm trong
9
;
2 2
.
Phương trình (2) có
6
nghiệm nằm trong
9
;
2 2
.
Vậy phương trình ban đầu có tất cả
10
nghiệm nằm trong
9
;
2 2
.
Câu 20. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;5
của phương trình
sin 1
f x
là
A.
6
. B.
4
. C.
10
. D.
8
.
Lời giải
Chọn C
Từ bảng biến thiên ta được
Strong Team Toán VD – VDC Trang 33/67
1
2 2
3
sin ; 1 ( )
sin 1 sin 1;0 sin 1;0 (1)
sin 1; ( )
x t VN
f x x t x t
x t VN
.
Dựa vào đường tròn lượng giác, phương trình (1) có 4 nghiệm nằm trong đoạn
0;5
.
4
5 5
6
sin ; 1 ( )
sin 1 sin 0;1 sin 0;1 (2)
sin 1; ( )
x t VN
f x x t x t
x t VN
.
Dựa vào đường tròn lượng giác, ta được phương trình (2) có
6
nghiệm nằm trong đoạn
0;5
.
Vậy phương trình ban đầu có tất cả
10
nghiệm.
Câu 21. Cho hàm số
f x
liên tục trên
có đồ thị
y f x
như hình vẽ dưới đây.
Số nghiệm thực của phương trình
4 2 2
x
f f
là
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn B
Ta có:
Theo đồ thị :
Strong Team Toán VD – VDC Trang 34/67
4 2 2
4 2 2
4 2 , 4 6
x
x
x
f
f f
f a a
TH1)
4 2 2
x
f
2 6
x
f
2 2
1
2 2
x
x
x
b KTM
.
TH2)
4 2
x
f a
2 4,
x
f a
0 4 2
a
2
2 2
2 0 log
2 4
x
x
x
c KTM
d KTM x t
t
.
Vì
4t
nên
2 2
log log 4 2 1
t
nên phương trình đã cho có 2 nghiệm phân biệt.
Câu 22. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm nhiều nhất thuộc đoạn
3
0;
2
của phương trình
2cos 1 0
f x
là:
A.
7
. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn C
Đặt
2cos 1t x
,
3
0; 1;3
2
x t
.
Xét phương trình:
0
f t
, với
1;3
t
.
Từ bảng biến thiên ta có:
Trên đoạn
1;3
, phương trình
0
f t
có nghiệm
t a
t b
, với
1 0
a
và
0 3
b
Vẽ đồ thị
2cos 1y x
trên đoạn
3
0;
2
, ta có :
Strong Team Toán VD – VDC Trang 35/67
Với
2cos 1
x a
Đường thẳng
y a
cắt đồ thị hàm số
2cos 1y x
tại 2 điểm
3
0;
2
x
.
Với
2cos 1
x b
Đường thẳng
y b
cắt đồ thị hàm số
2cos 1y x
tại tối đa 2 điểm
3
0;
2
x
.
Vậy phương trình
2cos 1 0
f x
có nhiều nhất
4
nghiệm.
Câu 23. Cho hàm số
y f x
có bảng biến thiên sau:
Hỏi có bao nhiêu giá trị
m
nguyên để phương trình
2 2 1
f tan2x m
có nghiệm thuộc
khoảng
0;
8
là:
A.
1
. B.
3
. C. Vô số. D.
0
.
Lời giải
Chọn A
Đặt
2 2 0 2t tan x, t ;
. Khi đó
2 1 0 2
f t m , t ; *
.
Số nghiệm của phương trình (*) chính là số giao điểm của đồ thị hàm số
y f x
và đường
thẳng
2 1
y m
.
Dựa vào bảng biến thiên ta có phương trình (*) có nghiệm
1 2 1 5 2 0
m m
.
Câu 24. Cho hàm số
y f x
liên tục trên
có đồ thị như hình vẽ. Phương trình
1 0
f f x
có
tối đa bao nhiêu nghiệm thực phân biệt?
Strong Team Toán VD – VDC Trang 36/67
A.
7
. B.
9
. C.
6
. D.
5
.
Lời giải
Chọn A
Từ đồ thị hàm số ta có
1 0f f x
1 2 1
1 0 1
1 1 2
f x m m
f x n n
f x p p
1
1
1
f x m
f x n
f x p
.
+) Do
2 1 m 2 1 3m
. Từ đồ thị hàm số ta suy ra phương trình
1f x m
có
đúng một nghiệm
1
2 x
.
+) Do
0 1 n 0 1 1n
. Từ đồ thị hàm số ta suy ra phương trình
1f x n
có đúng
ba nghiệm
2 3 4
2 0 1 2x x x
.
+) Do
1 2 p 1 1 0p
. Từ đồ thị hàm số ta suy ra phương trình
1f x p
có
đúng ba nghiệm
5 6 7
2 1 1 2x x x
khác
2 3 4
, ,x x x
.
Vậy phương trình đã cho có tối đa
7
nghiệm phân biệt.
Strong Team Toán VD – VDC Trang 37/67
Câu 25 . Cho hàm số
f x
liên tục trên
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;
của phương trình
2
2cos 3 3f x
là:
A.
8
. B.
2
. C.
6
. D.
4
.
Lời giải
Chọn D
Đặt
2
2cos 3t x
, vì
;x
nên
3; 1t
Ta có phương trình
3 , 3; 1f t t
Dựa vào BBT ta có:
Vậy
3f t
, 3, 2t a a
Ta có:
2
2cos 3 , 3, 2x a a
Suy ra
2
1
cos , 0;
2
x b b
Strong Team Toán VD – VDC Trang 38/67
Suy ra
cos
cos
x b
x b
với
2
0,
2
b
Với mọi
;
x
thì phương trình cos
x b
có 2 nghiệm và phương trình cos
x b
có
2 nghiệm (dựa vào đường tròn lượng giác hoặc đồ thị hàm số
cosy x
để kiểm tra nghiệm).
Vậy có 4 nghiệm thỏa yêu cầu bài toán.
Câu 26. Cho hàm số
f x
liên tục trên
có bảng biến thiên như sau:
Số nghiệm của phương trình
2
2
f x x
là:
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn D
2
2
f x x
2
2
2
2
f x x
f x x
Dựa vào BBT ta có:
Suy ra
2 2
2
2 2
2
2
, 1; , 1;
2
, ; 1 , ; 1
2
1
1 5
2
x x a a x x a a
f x x
x x b b x x b b
f x x
x x
x
 
 
Xét phương trình:
2
0
x x a
có
1 4 0
a
vì
1
a
Nên phương trình
2
0
x x a
có hai nghiệm phân biệt khác
1 5
2
Xét phương trình:
2
0
x x b
có
1 4 0
b
vì
1
b
Strong Team Toán VD – VDC Trang 39/67
Nên phương trình
2
0
x x b
vô nghiệm.
Vậy có 4 nghiệm đã cho thõa yêu cầu bài toán.
Câu 27. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm
0;x
của phương trình
2020 2 0
x
f e x
là
A.1. B.2. C.
0
. D.
2020
.
Lời giải
Tác giả: Trần Tường; Fb: Trần Tường
Chọn A
Ta có
2020 ; 1
2020 2 0 2020 2
2020 1;
x
x x
x
e x a
f e x f e x
e x b

Vì
0;x
nên
2020 1;
x
e x
nên
2020 ; 1
x
e x a
vô nghiệm.
Xét phương trình
2020 1;
x
e x b
trên
0;

Ta có hàm số
2020
x
g x e x
đồng biến trên
0;

và
1; 0;g x x
nên phương
trình
2020 1;
x
e x b
luôn có 1 nghiệm duy nhất trên
0;

.
Vậy phương trình đã cho có
1
nghiệm thuộc
0;

.
Câu 28. Cho hàm số
f x
có đồ thị như hình vẽ:
Số nghiệm thuộc đoạn
3
;2
2
của phương trình
2 cos 5 0
f x
là
A.
5
. B.
1
. C.
3
. D.
4
.
Lời giải
Tác giả:Trần Tường ; Fb: Trần Tường
Chọn C
Strong Team Toán VD – VDC Trang 40/67
Ta có
cos 0;1
5
2 cos 5 0 cos cos 1;3
2
cos 3;
x a
f x f x x b
x c
.
Vì
cos 1;1
x
3
;2
2
x
nên
cos 1;3
x b
và
cos 3;x c
vô nghiệm.
Xét đồ thị hàm số
cosy x
trên
3
;2
2
Phương trình
cos 0;1
x a
có 3 nghiệm phân biệt.
Vậy phương trình đã cho có
3
nghiệm phân biệt thuộc đoạn
3
;2
2
.
Câu 29. Cho hàm số
f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
1;3
của phương trình
2
3 1 0
f x x
là
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn D
Đặt
2
3t x x
, ta có
2
3 1 0
f x x
1 0
f t
1
f t
.
, 2;0
, 0;1
, 1;4
t a a
t b b
t c c
Khảo sát hàm số
2
3t x x
trên
1;3
.
Ta có
2 3t x
Cho
0
t
2 3 0
x
3
1;3
2
x
.
Strong Team Toán VD – VDC Trang 41/67
Ta có BBT của hàm
2
3t x x
như sau:
Từ BBT trên ta thấy:
Với
, 2;0
t a a
phương trình có
2
nghiệm phân biệt.
Với
, 0;1
t b b
phương trình có
1
nghiệm.
Với
, 1;4
t c c
phương trình có
1
nghiệm.
Vậy phương trình ban đầu có
4
nghiệm.
Câu 30. Cho hàm số
f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
5
;3
6
của phương trình
4 cos2 1 0
f x
là
A.
5
. B.
9
. C.
4
. D.
10
.
Lời giải
Chọn B
Đặt
cos2t x
, ta có
4 1 0
f t
1
4
f t
.
, ; 1
1
, 1;
2
1
, ;1
2
, 1;
t a a
t b b
t c c
t d d

Khảo sát hàm số
cos2t x
trên
5
;3
6
.
Ta có
2sin2t x
Strong Team Toán VD – VDC Trang 42/67
Cho
0t
sin2 0x
2
k
x
,
k
.
Vì
5
;3
6
x
3 5
; ;2 ; ;3
2 2
x
.
Ta có BBT của hàm
cos2t x
như sau:
Từ BBT trên ta thấy:
Với
, ; 1t a a 
phương trình vô nghiệm.
Với
1
, 1;
2
t b b
phương trình có
4
nghiệm.
Với
1
, ;1
2
t c c
phương trình có
5
nghiệm.
Với
, 1;t d d
phương trình vô nghiệm.
Vậy phương trình ban đầu có
9
nghiệm.
Câu 31. Cho hàm số
y f x
liên tục, có đạo hàm trên
2;4
và có bảng biến thiên như hình vẽ
Số nghiệm của phương trình
3
3 2 1 8 6f x x x
trên đoạn
3 3
;
2 2
là
A.
1
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn A
Đặt
2 1t x
.Với
3 3
; 2; 4
2 2
x t
.
Mỗi nghiệm của
t
cho duy nhất một nghiệm của
x
.
Strong Team Toán VD – VDC Trang 43/67
Biến đổi
3 3
3 3 2
8 6 2 3 2 1 3 1 3 2x x x x t t t t
.
Phương trình trở thành
3 2
3 3 2 0f t t t
.
Xét hàm số
3 2
3 3 2g t f t t t
2 2
3 3 6 3 2g t f t t t f t t t
2
0 2g t f t t t
Ta có
0
0
2
x
f t
x
2
0
2 0
2
x
t t
x
Ta có bảng xét dấu
g t
Từ đó ta có bảng biến thiên sau:
Dựa vào bảng biến thiên ta có phương trình
0g t
có
1
nghiệm nên phương trình ban đầu
có
1
nghiệm.
Câu 32. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn
;2
của phương trình
2 2 sin 1 0f x
là
Strong Team Toán VD – VDC Trang 44/67
A.
6
. B.
2
. C.
8
. D.
12
.
Lời giải
Chọn D
Đặt
2 sint x
. Xét hàm
2 sint g x x
trên đoạn
;2
Ta có bảng biến thiên của hàm số
2 siny g x x
trên đoạn
;2
Dựa vào BBT ta có
0,2 ;2t x
Nếu
0,2t
thì mỗi giá trị
t
cho
6
giá trị
x
thuộc đoạn
;2
Phương trình
2 2 sin 1 0f x
trở thành
1
2
f t
với
0,2t
Dựa vào đồ thị ta có phương trình
1
2
f t
có
2
nghiệm
t
phân biệt thuộc khoảng
0,2
nên phương trình ban đầu có 12 nghiệm phân biệt thuộc đoạn
;2
Câu 33. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
Gọi
m
là số nghiệm của phương trình
1f f x
. Khẳng định nào sau đây là đúng ?
A.
6m
. B.
7m
. C.
5m
. D.
9m
.
Lời giải
Chọn B
Đặt
f x u
khi đó nghiệm của phương trình
1f f x
chính là hoành độ giao điểm của
đồ thị
f u
với đường thẳng
1y
.
Strong Team Toán VD – VDC Trang 45/67
Dựa vào đồ thị ta có ba nghiệm
1
2
3
f x u
f x u
f x u
với
1
1;0u
,
2
0;1u
,
3
5
;3
2
u
.
Tiếp tục xét số giao điểm của đồ thị hàm số
f x
với từng đường thẳng
1
y u
,
2
y u
,
3
y u
.
Dựa vào đồ thị ta có được
7
giao điểm. Suy ra phương trình ban đầu
1f f x
có
7
nghiệm.
Câu 34. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ dưới. Gọi
S
là tập hợp tất cả
các giá trị nguyên của
m
để phương trình
(sin ) 2sin 2f x x m
có nghiệm thuộc khoảng
(0; )
. Tổng các phần tử của
S
bằng:
A.
2
B.
0
. C.
1
. D.
5
.
Lời giải
Chọn C
Đặt
sint x
với
0; 0;1x t
.
Strong Team Toán VD – VDC Trang 46/67
Xét phương trình
( ) 2 2f t t m
.
Để phương trình có nghiệm thì đồ thị hàm
y f t
cắt đồ thị hàm số
2 2y t m
tại ít nhất
một điểm có hoành độ
t
thuộc
0;1
.
Từ đồ thị ta suy ra đồ thị hàm số
2 2y t m
nằm ở phần hình phẳng giới hạn bởi đồ thị 2 hàm
số
2 1y t
và
2 3y t
.
Từ đó suy ra
3 2 1 1;0
m m
.
Vậy tổng các phần tử bằng
1
.
Câu 35. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
2 ;2
của phương trình
2 2sin 1 0
f x
là
A.
8
. B.
5
. C.
2
. D.
6
.
Lời giải
Chọn A
Đặt
2sint x
. Vì
2 ;2 2;2
x t
. Ta có pt:
1
2 1 0
2
f t f t
.
Từ BBT suy ra pt có nghiệm:
sin 1
0 2
2sin
2
2 0
2sin
sin 2
2
a
x
t a a
x a
t b b
x b b
x
PT
1
có 4 nghiệm, pt
2
có 4 nghiệm. Vậy pt đã cho có 8 nghiệm thuộc đoạn
2 ;2
Câu 36. Cho hàm số
3
3 1y f x x x
. Số nghiệm của phương trình
3
3 1 0
f x f x
là:
A. 1. B. 6. C. 5. D. 7.
Lời giải
Chọn D
Đồ thị hàm số
3
3 1y f x x x
có dạng:
Strong Team Toán VD – VDC Trang 47/67
Dựa vào đồ thị ta thấy phương trình
0f x
có 3 nghiệm
1 2 3
2; 1 , 0;1 , 1;2x x x
Nếu phương trình
3
3 1 0f x f x
có nghiệm
0
x
thì
0 1 2 3
, ,f x x x x
.
Dựa vào đồ thị ta có:
+
1 1
, 2; 1f x x x
có 1 nghiệm duy nhất.
+
2 2
, 0;1f x x x
có 3 nghiệm phân biệt.
+
3 3
( ) , 1;2f x x x
có 3 nghiệm phân biệt.
Vậy phương trình
3
3 1 0f x f x
có 7 nghiệm phân biệt.
Câu 37. Cho hàm số
( )y f x
là hàm số bậc 3 có đồ thị như hình vẽ dưới đây
Số nghiệm thuộc đoạn
0;3
của phương trình
3 1
2 sin 1 0
2 2
f x
là
A.
5
. B.
3.
C.
4.
D.
6.
Lời giải
Chọn D
Đặt
3 1
sin
2 2
t x
vì
0;3x
nên
1;2 .t
Ta được phương trình
1
2
f t
với
1;2 .t
Quan sát đồ thị ta thấy phương trình
1
2
f t
có 3 nghiệm
Strong Team Toán VD – VDC Trang 48/67
; 1 ; 1;0 ; 1;2 .
t a t b t c 
Bảng biến thiên của hàm số
3 1
sin
2 2
t x
trên đoạn
0;3 .
Từ bảng biến thiên ta thấy
+) Với
; 1
t a
thì phương trình
3 1
sin
2 2
x a
vô nghiệm.
+) Với
1;0
t b
thì phương trình
3 1
sin
2 2
x b
có 2 nghiệm.
+) Với
1;2
t c
thì phương trình
3 1
sin
2 2
x c
có 4 nghiệm.
Cả 6 nghiệm của phương trình trong các trường hợp trên là khác nhau. Vậy phương trình có 6
nghiệm phân biệt.
Câu 38. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
4 4
sin cos
f x x m
có nghiệm
0; .
4
x
A.
1
. B.
3.
C.
2.
D.
4.
Lời giải
Chọn D
Đặt
4 4
3 cos4
sin cos
4
x
t x x
vì
0;
4
x
nên
1
;1 .
2
t
Ta được phương trình
f t m
với
1
;1 .
2
t
Quan sát bảng biến thiên ta thấy với
1
;1
2
t
thì
2;1
f t
2;1 2; 1;0;1 .
m m
Vậy số các giá trị nguyên của tham số
m
là
4.
Câu 39. Cho hàm số
( )y f x
có đồ thị như hình vẽ.
1
2
5π
2
3π
2
1
2
1
+00
x
t'
t
π
2
+
0
0
3π
2
2
∞
+
∞
1
+
2
1
∞
∞
+
+
y
y'
x
1
0
0
2
Strong Team Toán VD – VDC Trang 49/67
Số nghiệm của phương trình
2 (cos2 ) 1 0f x
trên đoạn
5
0;
4
là
A. 3. B. 4. C. 5. D. 6.
Lời giải
Chọn C
Ta có:
cos 2 1;0 1
1
2 (cos 2 ) 1 0 (cos 2 ) cos 2 0;1 2
2
cos 2 2;3
x a
f x f x x b
x c VN
Bảng biến thiên của hàm số
5
cos 2 , 0;
4
y x x
Từ bảng biến thiên suy ra: (1) có 2 nghiệm phân biệt, (2) có 3 nghiệm phân biệt không trùng
với nghiệm của phương trình (1).
Câu 40. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m
để phương trình
3 ( )f f x m
có đúng 6 nghiệm phân biệt
[ 5;0].x
A.
2.
B.
3.
C.
4.
D.
5.
Lời giải
Strong Team Toán VD – VDC Trang 50/67
Chọn A
Đặt
( ), 5;0 t 1; 3 0;4
t f x x f t
Phương trình đã cho có dạng
, t 1;3
3
m
f t
TH1:
0;4
3
m
phương trình đã cho vô nghiệm
TH2:
1
1 1
0 :
3
3 2
3
t
f x
m
m f t
t
f x
Phương trình (1) Có 1 nghiệm, (2) có 1 nghiệm trong miền
[ 5;0].x
Do đó phương trình ban
đầu có 2 nghiệm
[ 5;0].x
TH3:
0 3 hay 0<m<9
3
m
1
1;0 3
3
2; 3 4
3
t
f x a
m
f t
t
f x b
Phương trình (1) Có 1 nghiệm, (2) có 1 nghiệm trong miền
[ 5;0].x
Do đó phương trình ban
đầu có 2 nghiệm
[ 5;0].x
TH4:
3 4 hay 9<m<12
3
m
0;2 0;2 5
0;2 , 0;2 6
3
t c f x c
m
f t
t d c d f x d
Hệ (3), (4) có 6 nghiệm phân biệt trong miền
[ 5;0].x
Do đó phương trình ban đầu có 6
nghiệm
[ 5;0].x
TH5:
3 4
3 3
m m
phương trình ban đầu lần lượt có 4 nghiệm, 3 nghiệm trong miền
[ 5;0].x
Vậy để phương trình
3 ( )
f f x m
có đúng 6 nghiệm phân biệt
[ 5;0].x
thì
9<m<12
hay
m 10;11
.
Câu 41. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
2019;1
của phương trình
ln 4
f x
A. 2020 B. 4. C. 2019. D. 3.
Lời giải
Chọn D
Strong Team Toán VD – VDC Trang 51/67
Đặt
ln , ( 0)t x x
mà
2019;1x
nên
0;1x
.
Do hàm
( ) lnf x x
là hàm đồng biến trên khoảng
0;
nên
;0t 
.
Khi đó phương trình
ln 4f x
trở thành
4f t
với
;0t 
Đây là phương trình hoành độ giao điểm của hàm số
( )y f t
với đường thẳng
1y
Ứng với mỗi giá trị
;0t 
ta có một nghiệm
0;1x
nên số giao điểm của đồ thị hàm số
( )y f t
và đồ thị hàm số
4y
trên
;0
là số nghiệm của phương trình.
Bảng biến thiên
Dựa vào bảng biến thiên, phương trình đã cho có 3 nghiệm
Câu 42. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;
4
của phương trình
sin cos 1f x x
A. 1 B. 3 C. 2 D. 0.
Lời giải
Chọn D
Đặt
sin cos 2 sin
4
t x x x
, với
0; 1; 2
4
x t
Đây là phương trình hoành độ giao điểm của hàm số
( )y f t
với đường thẳng
1y
.
Bảng biến thiên
Strong Team Toán VD – VDC Trang 52/67
+ Ứng với
; 2
t a 
,
1;0
t b
,
0;1
t c
,
2;t d

loại vì không thỏa
1; 2
t
Câu 43. Cho hàm số
( )y f x
liên tục trên
có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
(sin ) 2sin 0
f x x m
có
nghiệm thuộc khoảng
0;
?
A.
9
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn B
Đặt
sint x
, với
0; 0;1
x t
Phương trình đã cho trở thành
( ) 2 , 0;1
f t t m t
(1).
Yêu cầu bài toán tương đương phương trình (1) có nghiệm trong nửa khoảng
0;1
Dựa vào đồ thị, để phương trình (1) có nghiệm trong nửa khoảng
0;1
4 0
m
, mà
m
nên
1; 2; 3; 4
m
là các giá trị cần tìm.
Câu 44. Cho hàm số
( )f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
;2
của phương trình
2 (sin ) 3 0
f x
là
A.
6
. B.
3
. C.
4
. D.
8
.
Lời giải
Strong Team Toán VD – VDC Trang 53/67
Chọn A
Đặt
sint x
, lúc đó
cost x
Cho
0 ,
2
t x k k
. Do
3
;2 ;
2 2
x x
Bảng biến thiên
Từ bảng biến thiên ta thấy
;2 1;1
x t
Nhận xét: Với mỗi giá trị
1;0
t
ta có 4 nghiệm
;2
x
;
0;1 1
t
ta có 2
nghiệm
;2
x
và
1t
ta có 1 nghiệm
;2
x
Khi đó phương trình trở thành
3
2 ( ) 3 0 ( ) , 1;1
2
f t f t t
Từ bảng biến thiên ta có đồ thị hàm số
( ) , 1;1
y f t t
Dựa vào đồ thị, ta thấy
1;0
3
( ) , 1;1
2
0;1
t a
f t t
t b
Với
1;0
t a
ta có 4 nghiệm
;2
x
Với
0;1
t b
ta có 2 nghiệm
;2
x
Vậy phương trình đã cho có 6 nghiệm.
Câu 45. Cho hàm số
y f x
có bảng biến thiên như sau
Strong Team Toán VD – VDC Trang 54/67
Số nghiệm của phương trình
4 1 0
x
f e
trong đoạn
ln 2 ; ln 6
là
A. 1. B. 2. C. 3. D.
4
.
Lời giải
Chọn B
Đặt
4
x
t e
. Với
ln 2 ; ln 6 2 ; 2
x t
. Ta được PT
1
f t
.
Dựa vào bảng biến thiên, ta thấy phương trình
1
f t
có 2 nghiệm là
1
2 ; 0
t t
và
2
0 ; 2
t t
.
Với
1
t t
ta được
1 1
4 ln 4
x
e t x t
.
Với
2
t t
ta được
2 2
4 ln 4
x
e t x t
.
Vì
1 2
t t
nên
1 2
ln 4 ln 4
t t
.
Vậy PT đã cho có 2 nghiệm phân biệt.
Câu 46. Cho hàm số
y f x
là hàm đa thức bậc 3 và có bảng biến thiên như sau
Số nghiệm của phương trình
sin 3 cos 0
f x x
trong đoạn
5
0 ;
2
là
A. 1. B. 4. C. 3. D.
2
.
Lời giải
Chọn D
Đặt
sin 3 cost x x
. Ta có
2cos 2 2
6
t x t
. Ta được PT
0
f t
.
Dựa vào BBT ta thấy đồ thị hàm số có 2 điểm cực trị là
2; 4
và
2;4
nên đồ thị có điểm
uốn là gốc tọa độ
O
. Do đó đồ thị cắt trục hoành tại 3 điểm có hoành độ lần lượt là
2, 0, 2
x a x x b
. Mà
2 2
t
nên PT
0
f t
có 1 nghiệm là
0t
.
Với
0t
ta được
2
2cos 0
6 6 2 3
x x k k x k k
.
Theo yêu cầu bài:
5 2 5 2 11
0 0
2 3 2 3 6
x k k
.
Vì
0; 1k k k
. Ta được 2 nghiệm
2
3
x
và
5
3
x
thỏa yêu cầu bài toán.
Strong Team Toán VD – VDC Trang 55/67
Câu 47. Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình
3 2 2 3 2
1 3 1 2 3 1 2
f x x f x x
là
A.
5
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn B
Đặt
3 2
3 1
a f x x
ta được bất phương trình
2
2
2 2
1
1 0
1 2 2 1
1 2 2 2
1 0
a
a
a a a
a a a
a
.
Với
1
a
ta được
3 2
3 1 1
f x x
. Đặt
3 2
3 1
t x x
ta được PT
1 *
f t
.
Vẽ đường thẳng
1y
lên đồ thị đã cho ta được PT
*
có 1 nghiệm
1
2; 1
t t
và 1
nghiệm
2
1;2
t t
.
Ta có BBT của hàm số
3 2
3 1
y x x
như sau
Với
1
t t
ta được PT
3 2
1
3 1
x x t
. Dựa vào BBT ta thấy PT này có 3 nghiệm phân biệt.
Với
2
t t
ta được PT
3 2
2
3 1
x x t
. Dựa vào BBT ta thấy PT này có 1 nghiệm.
Vậy BPT đã cho có 4 nghiệm thực.
Câu 48. Cho hàm số
y f x
là hàm bậc 3 và có bảng biến thiên như sau
Phương trình
2
sin cos 1 sin 2 2 2 sin sin cos
4
f x x x x f x x
có mấy nghiệm
thực thuộc đoạn
5 5
;
4 4
?
A.
1
. B.
3
. C.
4
. D.
6
.
Strong Team Toán VD – VDC Trang 56/67
Lời giải
Chọn B
Vì hàm số có 2 điểm cực trị là
1
x
nên
2 3
' 3 3 3
f x ax a f x ax ax d
. Theo
BBT thì đồ thị hàm số đi qua 2 điểm
1;2
và
1; 2
nên
2 2 1
2 2 0
a d a
a d d
Suy ra
3
3f x x x
.
Ta có
2
sin cos 1 sin 2 2 2 sin sin cos
4
f x x x x f x x
2
2
sin cos sin cos 2 sin cos sin cosf x x x x x x f x x
2
sin cos sin cos 0 sin cos sin cosf x x x x f x x x x
Đặt
sin cos 2 sin , 2; 2
4
t x x x t
ta được phương trình
3
0
3
2
loaïi
t
f t t t t t
t
Với
0t
ta được
2 sin 0 ,
4 4
x x k k
Ta có
5 5 3
1 1, 0, 1
4 4 4 2
k k k k k
. Vậy PT có 3 nghiệm.
Câu 49. Cho
y f x
là hàm số bậc ba và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên
5;5
m
để hàm số
g x f f x m
có
4
điểm cực trị?
B. 5. B. 6. C. 7. D. 8.
Lời giải
Chọn B
. .g x f x f f x m
0
0
0
f x
g x
f f x m
2 2
2 2
,
2 2
2 2
x x
x x
f x m f x m
f x m f x m
trong đó
2
x
và
2
x
là hai nghiệm bội lẻ.
Đặt
1
2
f x f x
và
2
2
f x f x
, ta có đồ thị sau
Strong Team Toán VD – VDC Trang 57/67
Với
5;5m
m
và nhìn vào đồ thị, ta thấy hàm số
g x
có
4
điểm cực trị
0g x
có 4
nghiệm bội lẻ
4; 3; 1;1;3;4 .m
Câu 50. Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc khoảng
;
của phương trình
2
cos cos 2f x f x
là
A.
5
. B.
6
. C.
7
. D.
9
.
Lời giải
Chọn A
Đặt
cos ,t x
; .x
Ta có bảng biến thiên (*)
1;1 .t
Phương trình đã cho trở thành
2
2 (1)
2 0 .
1 (2)
f t
f t f t
f t
Từ bảng biến thiên của đề bài, với
1;1t
ta có nghiệm của phương trình (1) là
1;0t a
hay
0;1t b
và nghiệm của phương trình (2) là
1t
.
Strong Team Toán VD – VDC Trang 58/67
Từ bảng biến thiên (*), ta có:
1;0t a
1
2
;0
.
0;
x x
x x
0;1t b
3
4
;0
.
0;
x x
x x
1
t
0.
x
Vậy, phương trình đã cho có 5 nghiệm phân biệt thuộc khoảng
; .
Câu 51. Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm
0;x
của phương trình
2020 2 0
x
f e x
là
A.1. B.2. C.
0
. D.
2020
.
Lời giải
Chọn A
Ta có
2020 ; 1
2020 2 0 2020 2
2020 1;
x
x x
x
e x a
f e x f e x
e x b

Vì
0;x
nên
2020 1;
x
e x
nên
2020 ; 1
x
e x a
vô nghiệm.
Xét phương trình
2020 1;
x
e x b
trên
0;

Ta có hàm số
2020
x
g x e x
đồng biến trên
0;

và
1; 0;g x x
nên phương
trình
2020 1;
x
e x b
luôn có 1 nghiệm duy nhất trên
0;

.
Vậy phương trình đã cho có
1
nghiệm thuộc
0;

.
Câu 52. Cho hàm số
f x
có đồ thị như hình vẽ:
Số nghiệm thuộc đoạn
3
;2
2
của phương trình
2 cos 5 0
f x
là
Strong Team Toán VD – VDC Trang 59/67
A.
5
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn C
Ta có
cos 0;1
5
2 cos 5 0 cos cos 1;3
2
cos 3;
x a
f x f x x b
x c
.
Vì
cos 1;1
x
3
;2
2
x
nên
cos 1;3
x b
và
cos 3;x c
vô nghiệm.
Xét đồ thị hàm số
cosy x
trên
3
;2
2
Phương trình
cos 0;1
x a
có 3 nghiệm phân biệt.
Vậy phương trình đã cho có
3
nghiệm phân biệt thuộc đoạn
3
;2
2
.
Câu 53. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của
m
để phương trình
2
2
f x x m
có đúng
4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
.
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn C
Đặt
2
2t x x
,
3 7
;
2 2
x
Bảng biến thiên:
Strong Team Toán VD – VDC Trang 60/67
Dựa vào bảng biến thiên
21
1;
4
t
.
Ta có:
2
2
f x x m
1
f t m
2
.
Ta thấy, với mỗi giá trị
21
1;
4
t
ta tìm được hai giá trị của
3 7
;
2 2
x
.
Do đó, phương trình
1
có
4
nghiệm thực phân biệt thuộc
3 7
;
2 2
Phương trình
2
có hai nghiệm thực phân biệt thuộc
21
1;
4
Đường thẳng
y m
cắt đồ thị hàm số
y f t
tại hai điểm phân biệt có hoành độ thuộc
21
1;
4
.
Dựa vào đồ thị ta thấy có hai giá trị nguyên của
m
thỏa yêu cầu là
3
m
và
5
m
.
Câu 54. Cho hàm số
y f x
có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin
f x m
có đúng hai nghiệm thuộc đoạn
0;
?
A.
4
. B.
7
. C.
5
. D.
6
.
Lời giải
Chọn C
Đặt
sint x
,
0;
x
thì
0;1
t
. Để phương trình
sin
f x m
có đúng hai nghiệm
0;
x
thì phương trình
f t m
có đúng một nghiệm
0;1
t
. Dựa vào đồ thị ta có
7; 2
m
, do
m
nguyên nên
7; 6; 5; 4; 3
m
. Vậy có
5
giá trị.
Câu 55. Cho hàm số bậc bốn
y f x
có đồ thị như hình bên
Strong Team Toán VD – VDC Trang 61/67
++
4
∞ 0
+∞
x
∞ +∞0 2
0 0
h'
h
Số điểm cực trị của hàm số
3 2
3 4
g x f x x
là
A.
5
. B.
3
. C.
7
. D.
11
.
Lời giải
Chọn C
Tập xác định của hàm số:
D
.
2 3 2
3 6 3 4
g x x x f x x
.
3 2
0
0 2
3 4 0 *
x
g x x
f x x
Khi đó
3 2
3 2
3 2
3 4 2;0
* 3 4 0;4
3 4 4;6
x x a
x x b
x x c
Xét hàm số
3 2
3 4
h x x x
trên
.
Ta có:
2
0
3 6 0
2
x
h x x x
x
. Từ đó ta có BBT của hàm
h x
như sau:
Từ BBT của hàm
h x
ta thấy phương trình
h x a
có 1 nghiệm duy nhất nhỏ hơn
1
,
h x b
có
3
nghiệm lần lượt thuộc các khoảng
1;0 ; 0;2 ; 2;3
,
h x c
có duy nhất
1
nghiệm lớn hơn 3.
Vậy
0
g x
có đúng 7 nghiệm đơn phân biệt nên hàm số có
7
cực trị.
Câu 56. Cho hàm số
y f x
có đồ thị như hình bên
Strong Team Toán VD – VDC Trang 62/67
Số nghiệm thuộc đoạn
0;3
của phương trình :
2 cos 1 0
f x
.
A.
12
. B.
6
. C.
10
. D.
8
.
Lời giải
Chọn A
1
cos
2
2 cos 1 0
1
cos
2
f x
f x
f x
Căn cứ vào đồ thị ta thấy:
1
cos , 1 1
2
1 1
cos cos , 0 2
2 2
cos , 1 3
x a a
f x x b b
x c c
cos , 1 4
1 1
cos cos ,0 5
2 2
1
cos , 1 6
2
x d d
f x x e e
x g g
Các phương trình
3 , 4
đều vô nghiệm.
Xét đồ thị hàm số
cosy x
trên đoạn
0;3
3
2
1
1
2
2 2
x
y
-1
-1
1
1
2
1
1
y
π 2π 3π
O
x
Strong Team Toán VD – VDC Trang 63/67
Ta thấy các phương trình
1 , 2 , 5 , 6
lần lượt có
3
nghiệm phân biệt và trong số chúng
không có
2
nghiệm nào trùng nhau. Vậy phương trình ban đầu có
12
nghiệm.
Câu 57. Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây. Số nghiệm thuộc đoạn
3
;
2 2
của phương trình
cot 1 1
f x
là
x

1
1
2

f x
0
0
0
f x

1
1
2

A. 7. B. 6. C. 8. D. 5.
Lời giải
Chọn A
Đặt
cot 1,t x
phương trình tương đương với
1.
f t
Dựa vào bảng biến thiên, ta thấy
1
cot 1 cot 1 0
1 1 cot 1 cot 1 0
cot 1 1 cot 0
2
t a a
x a x a
f t t x b x b
x x
t b b
Xét
2
1
0
sin
t
x
nên ta có bảng biến thiên hàm
t x
trên
3
;
2 2
như sau
x
2
0
3
2
t
t
0




0
Từ đó, phương trình
cot 1x a
có đúng 2 nghiệm, phương trình
cot 1x b
có đúng 2
nghiệm và phương trình
cot 0x
có đúng 3 nghiệm thuộc
3
;
2 2
nên phương trình đã
cho có
7
nghiệm.
Câu 58. Cho hàm số
y f x
có bảng biến thiên như hình vẽ
x

0
1
2

f x
0
0
0
f x

0
3
1

Số nghiệm của phương trình
sin 1 2
f x
trên
;2
là
A. 6. B. 7. C. 5. D. 4.
Lời giải
Strong Team Toán VD – VDC Trang 64/67
Chọn A
Dựa vào bảng biến thiên hàm số
,f x
ta thấy
0
0 1
2 .
1 2
2
x a a
x b b
f x
x c c
x d d
Đặt
sin 1.t x
Phương trình đã cho tương đương với
1
2
2
3
4
t a
t b
f t
t c
t d
Ta có:
cos 0 .
2
t x x t x x k k
Ta có bảng biến thiên hàm số
t x
trên
;2
là:
x
2
2
3
2
2
t x
0
0
0
t x
1
0
2
0
1
Từ bảng biến thiên này, ta thấy các phương trình
1
và
4
vô nghiệm, phương trình
2
có 4
nghiệm và phương trình
3
có đúng 2 nghiệm. Vậy phương trình đã cho có 6 nghiệm phân
biệt.
-------------------- HẾT --------------------
Strong Team Toán VD – VDC Trang 65/67
| 1/65
| | Tải xuống

Có thể bạn quan tâm:

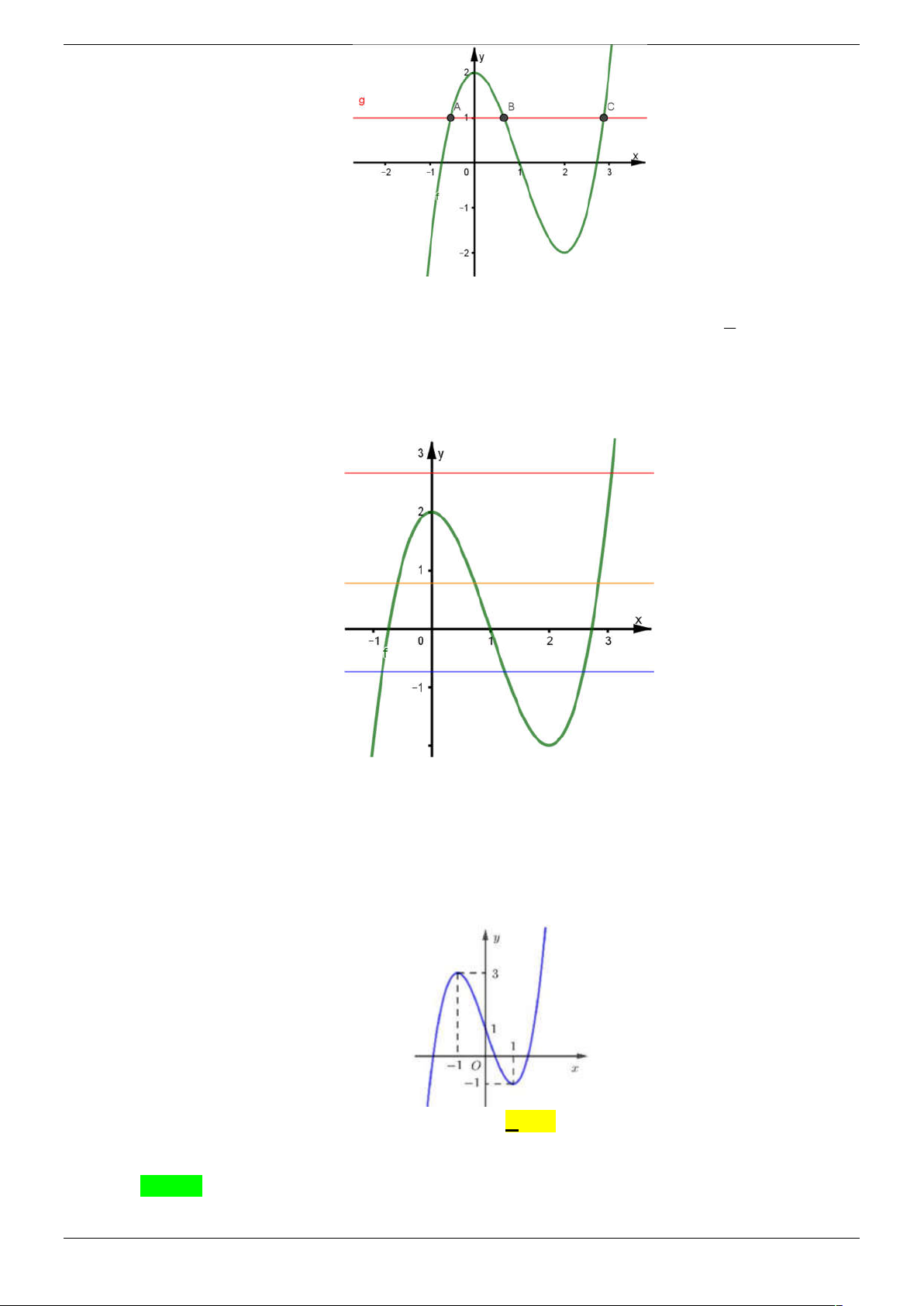
Preview text:

BÀI TẬP TRẮC NGHIỆM
TÌM SỐ NGHIỆM CỦA PHƯƠNG TRÌNH HÀM HỢP ĐỀ BÀI Câu 1.
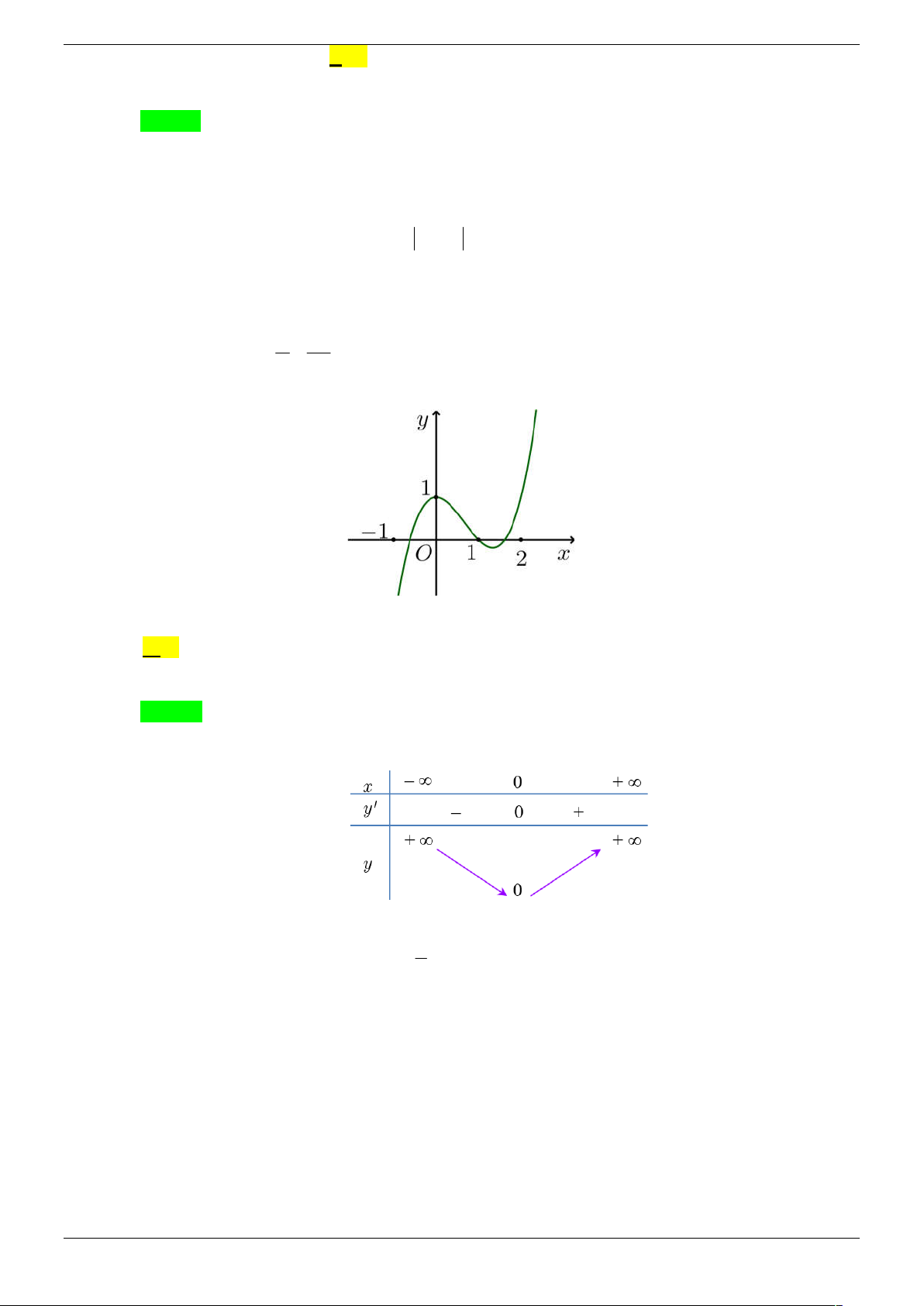
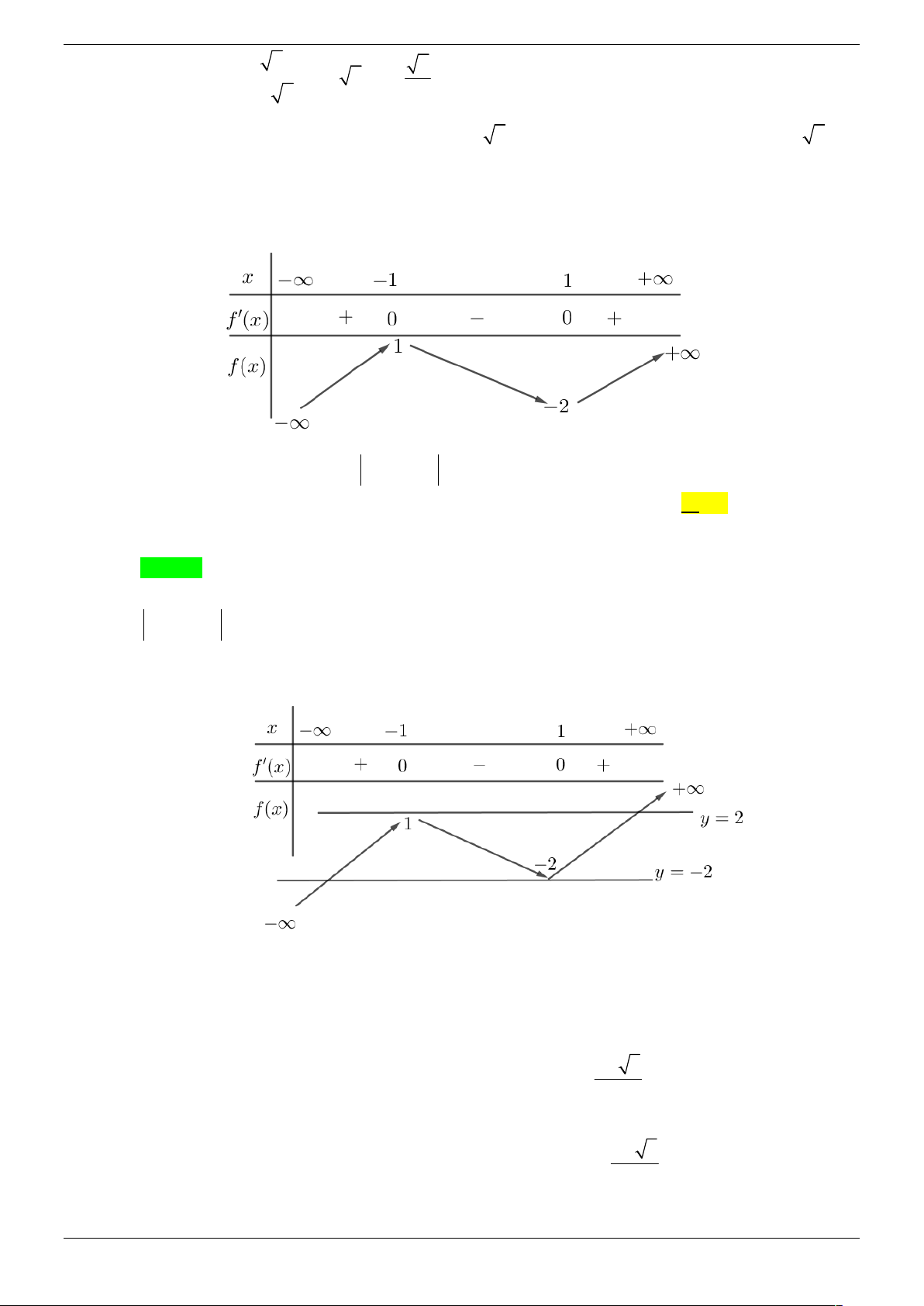
Cho hàm số y f x xác định trên R và có bảng biến thiên như sau: x  -1 1  y  0  0  y 1   -1
Số nghiệm của phương trình f  2
x  2x  2 là A. 4 . B. 2 C. 3 D. 8 Câu 2.
Cho hàm số y f x xác định trên R và có bảng biến thiên như sau: –∞ 0 +∞ + 0 – 0 + 0 – 1 1 0
Số nghiệm thuộc đoạn 0;  của phương trình f f  os
c 2x  0 là A. 4 . B. 2 C. 3 D. 8
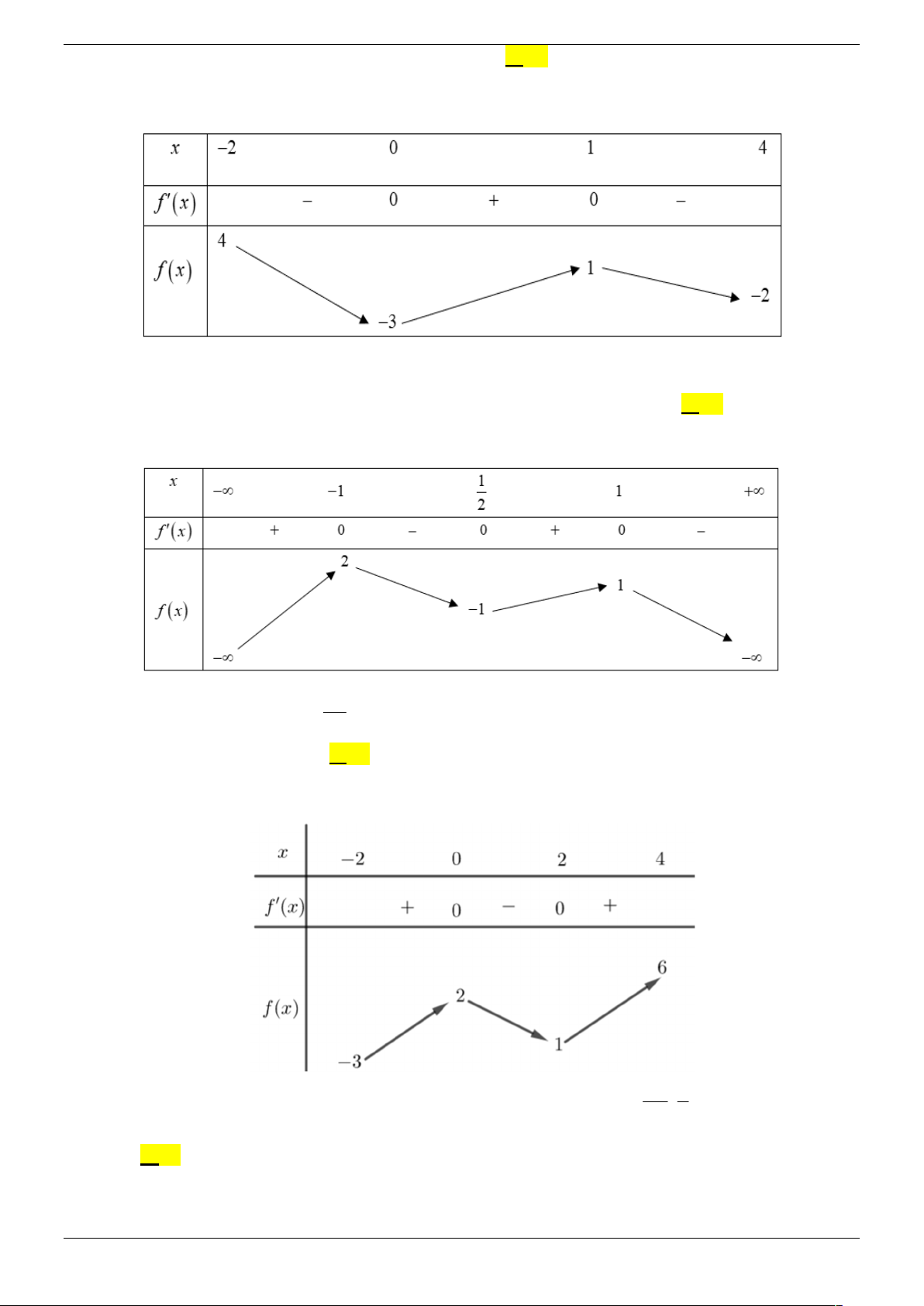
Câu 3. Cho hàm số f (x) liên tục trên đoạn 1; 
3 và có bảng biến thiên như sau: m
Tổng tất cả các số nguyên m để phương trình f (x 1) 
có hai nghiệm phân biệt 2 x  6x 12
trên đoạn 2; 4 bằng A. 75  . B. 72  . C. 294  . D. 29  7 . Câu 4.
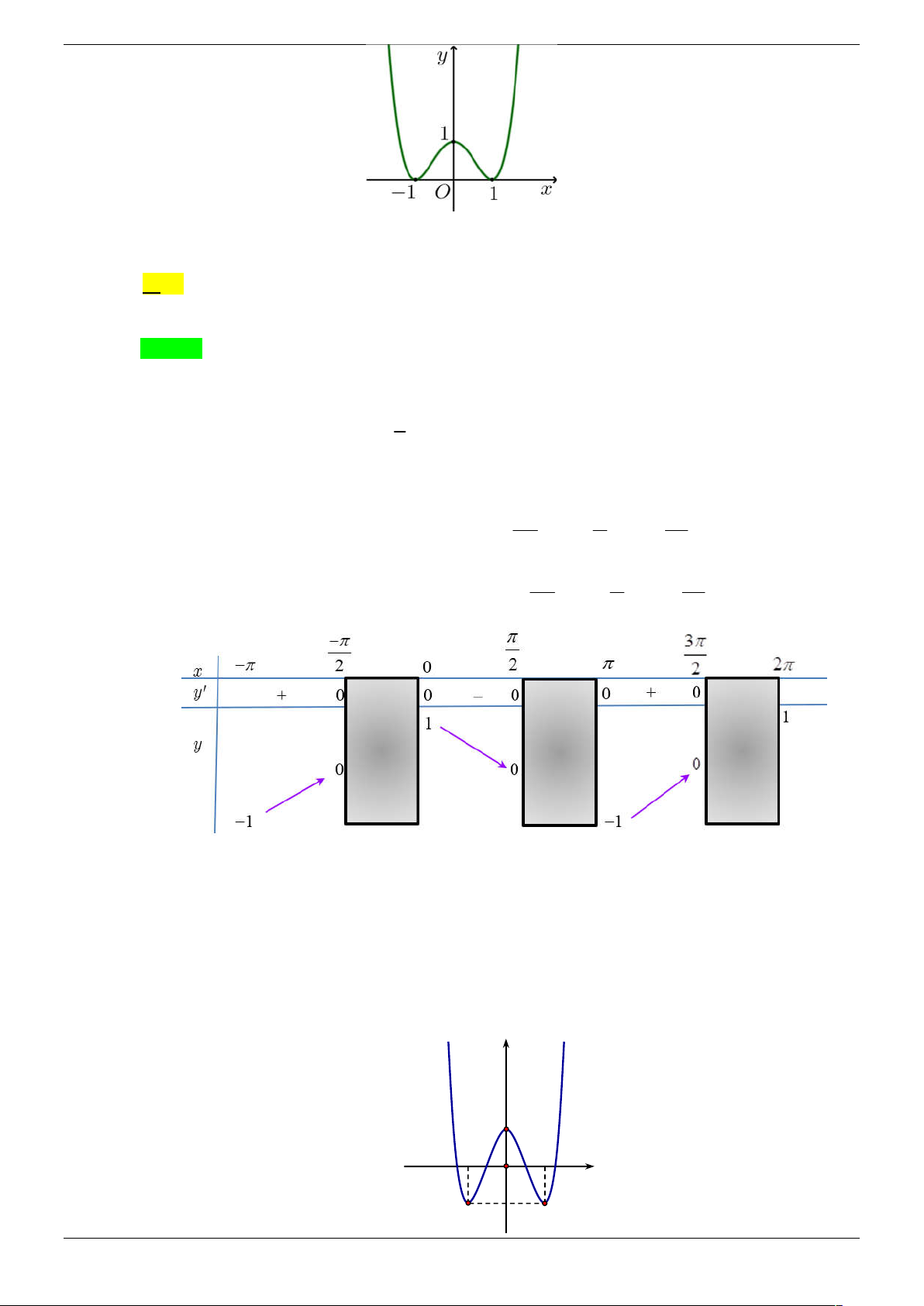
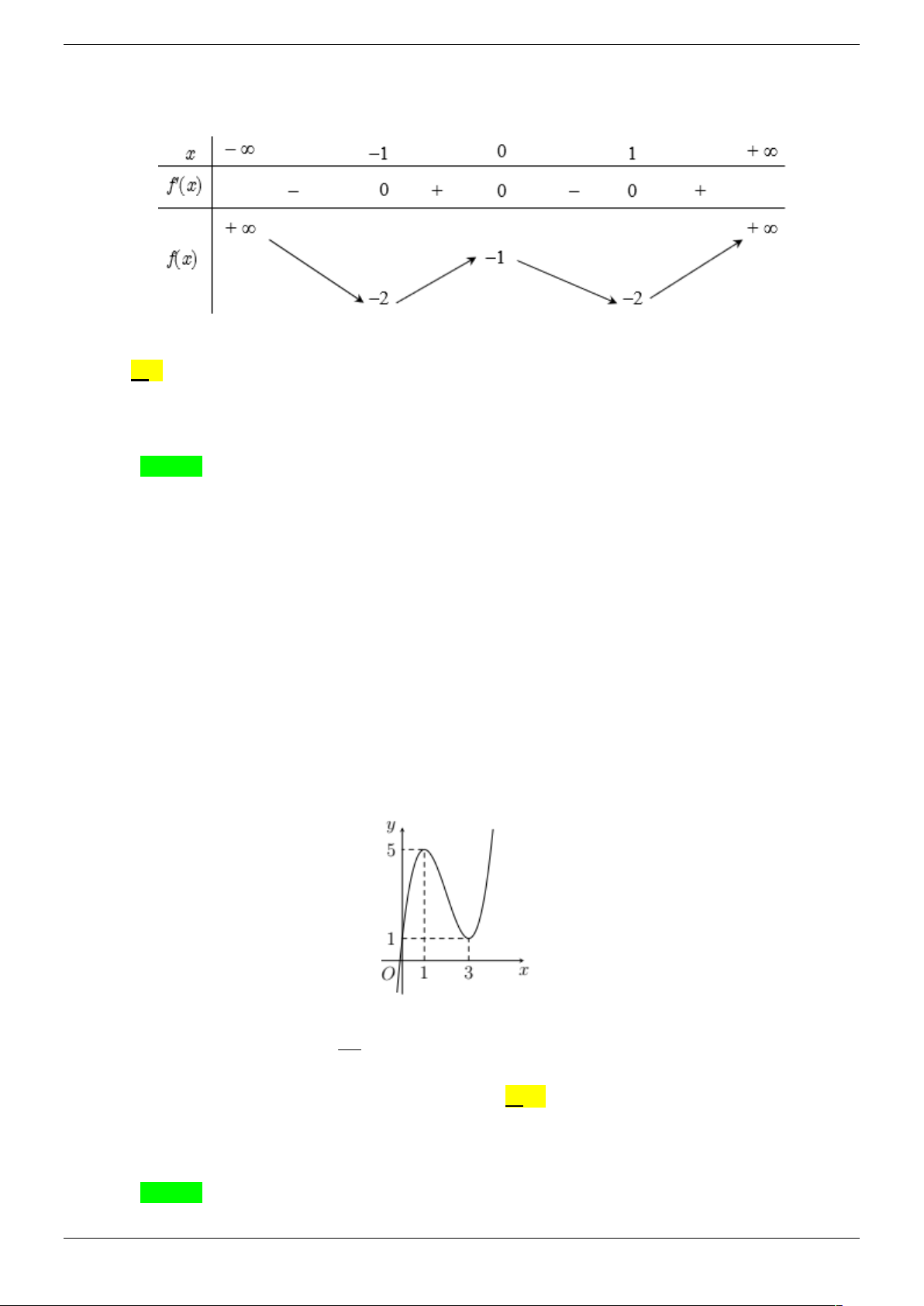
Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0; 2  của phương trình 3 f sin 2x  2  0 là: Strong Team Toán VD – VDC Trang 1/67 A. 7 . B. 8 . C. 5 . D. 6 . Câu 5. Cho hàm số 3 2
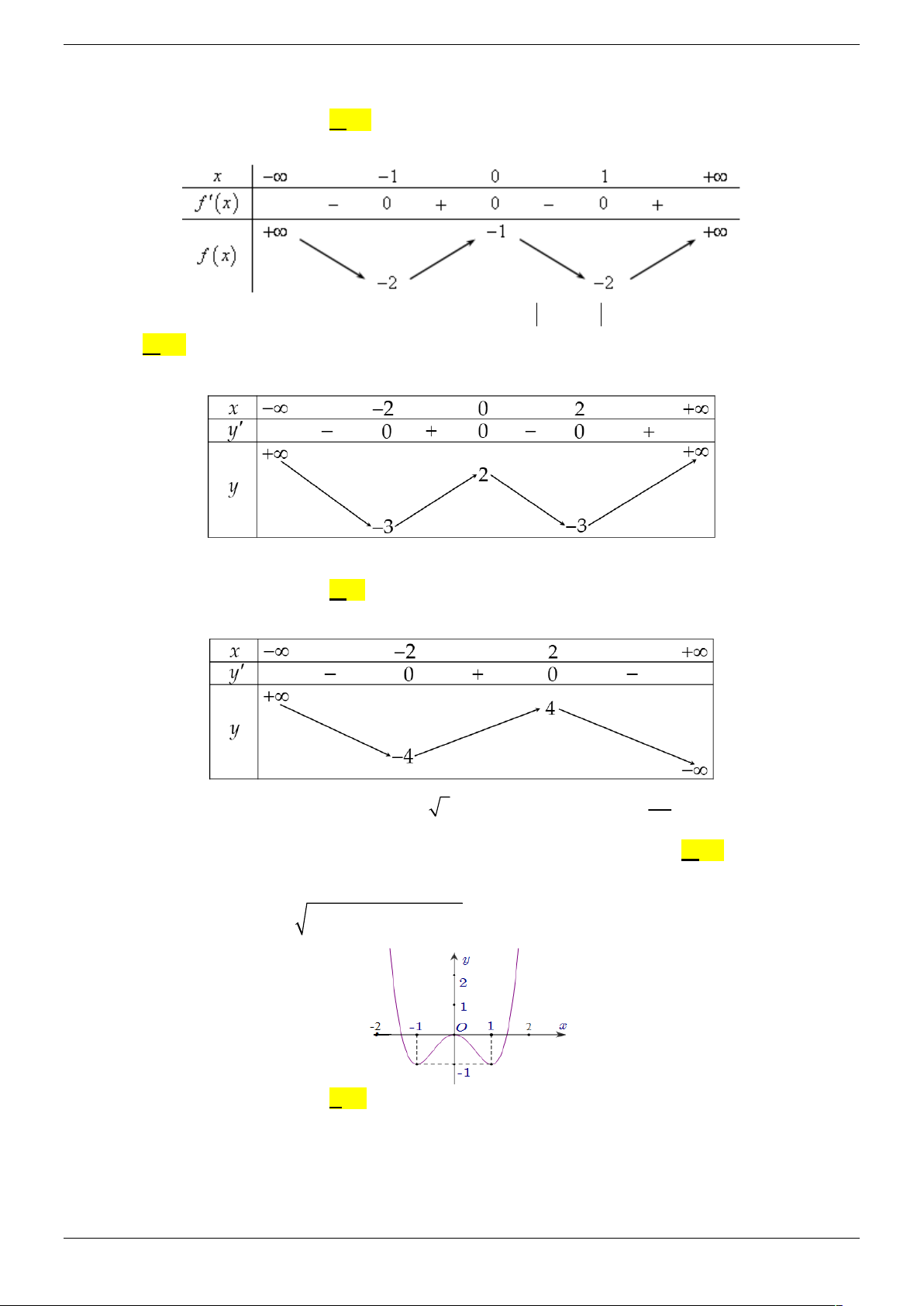
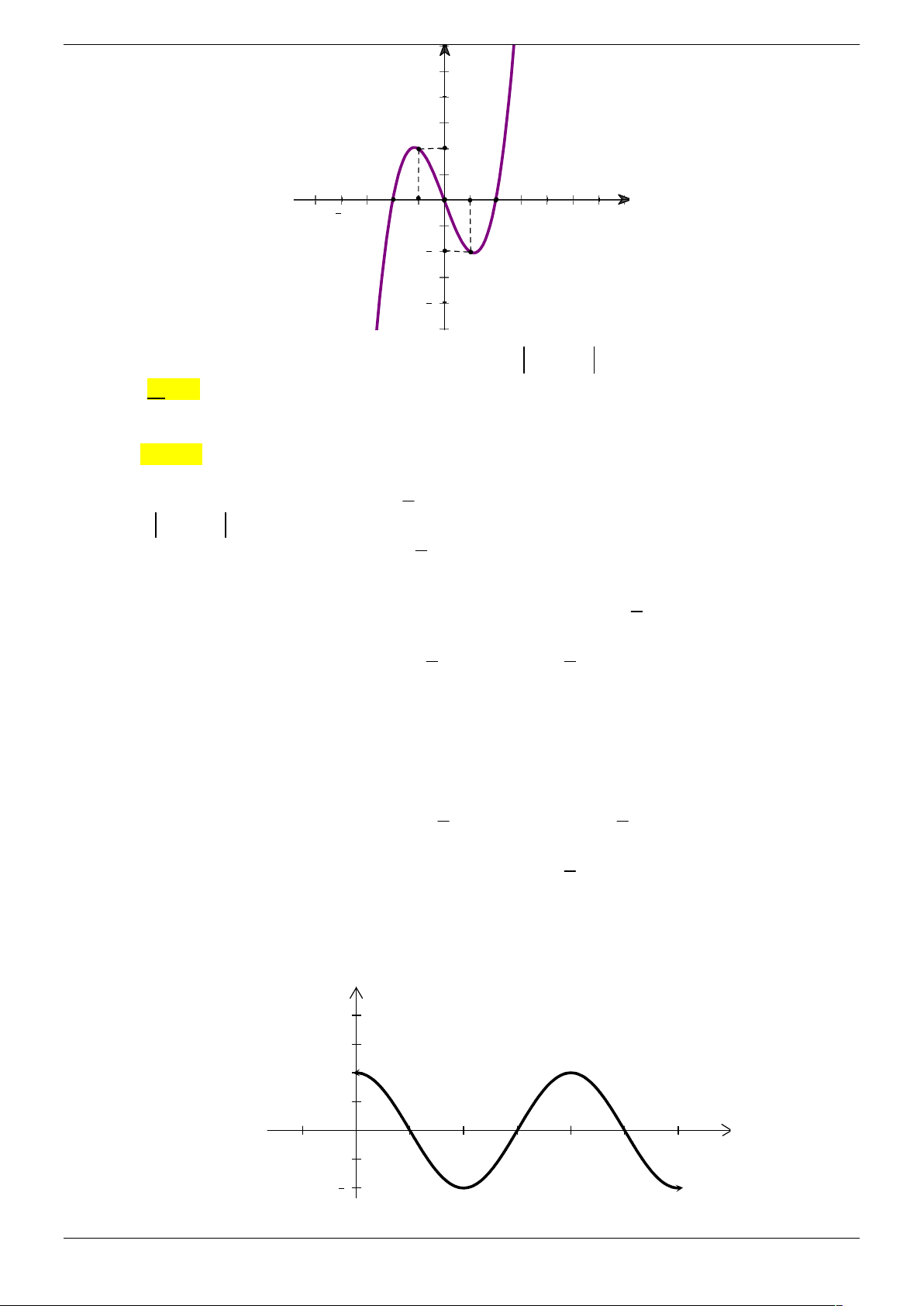
y f (x)  ax bx cx d (a  0) có đồ thị như hình vẽ. Phương trình
f ( f (x))  0 có bao nhiêu nghiệm thực? A. 3 . B. 7 . C. 9 . D. 5 .
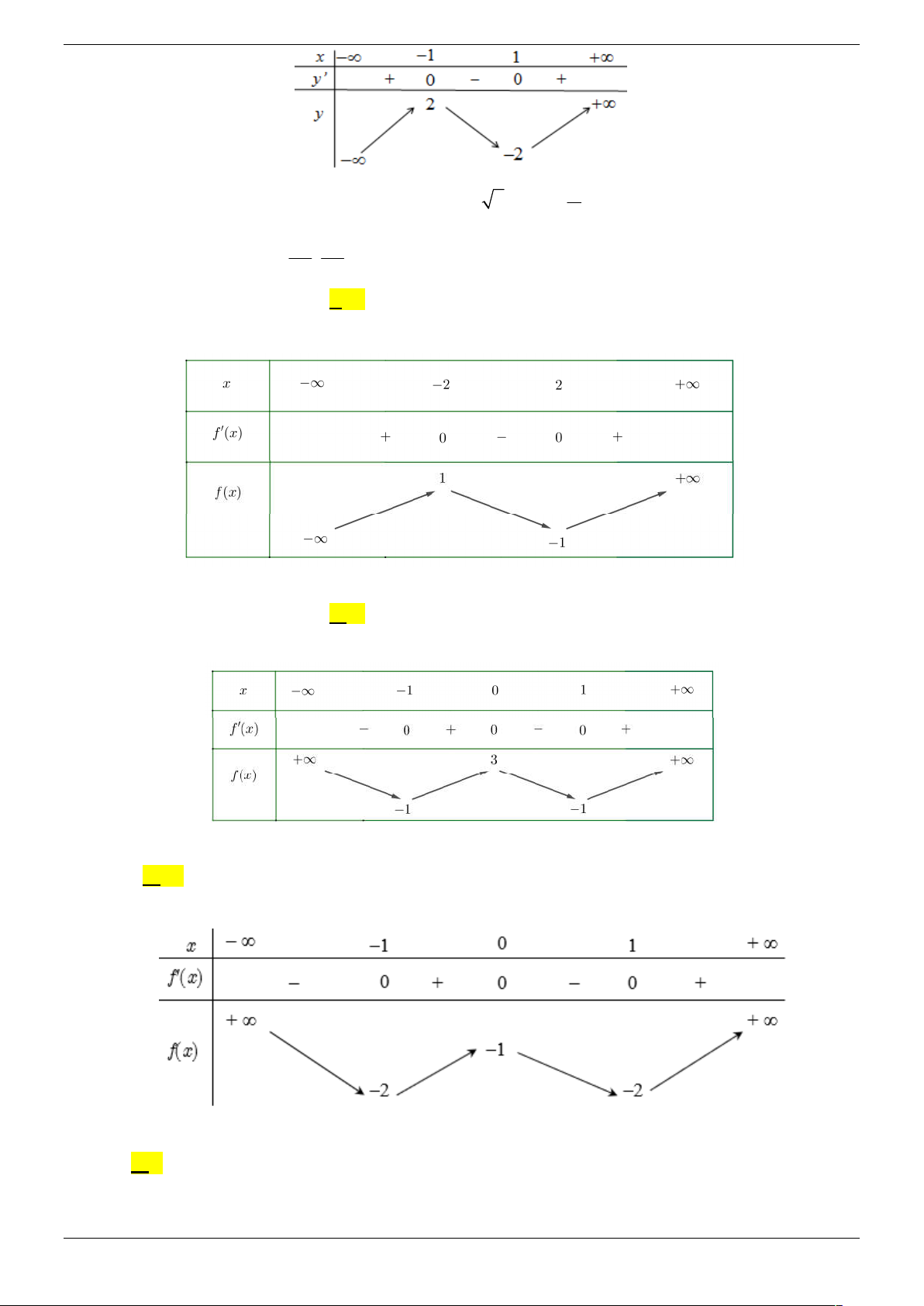
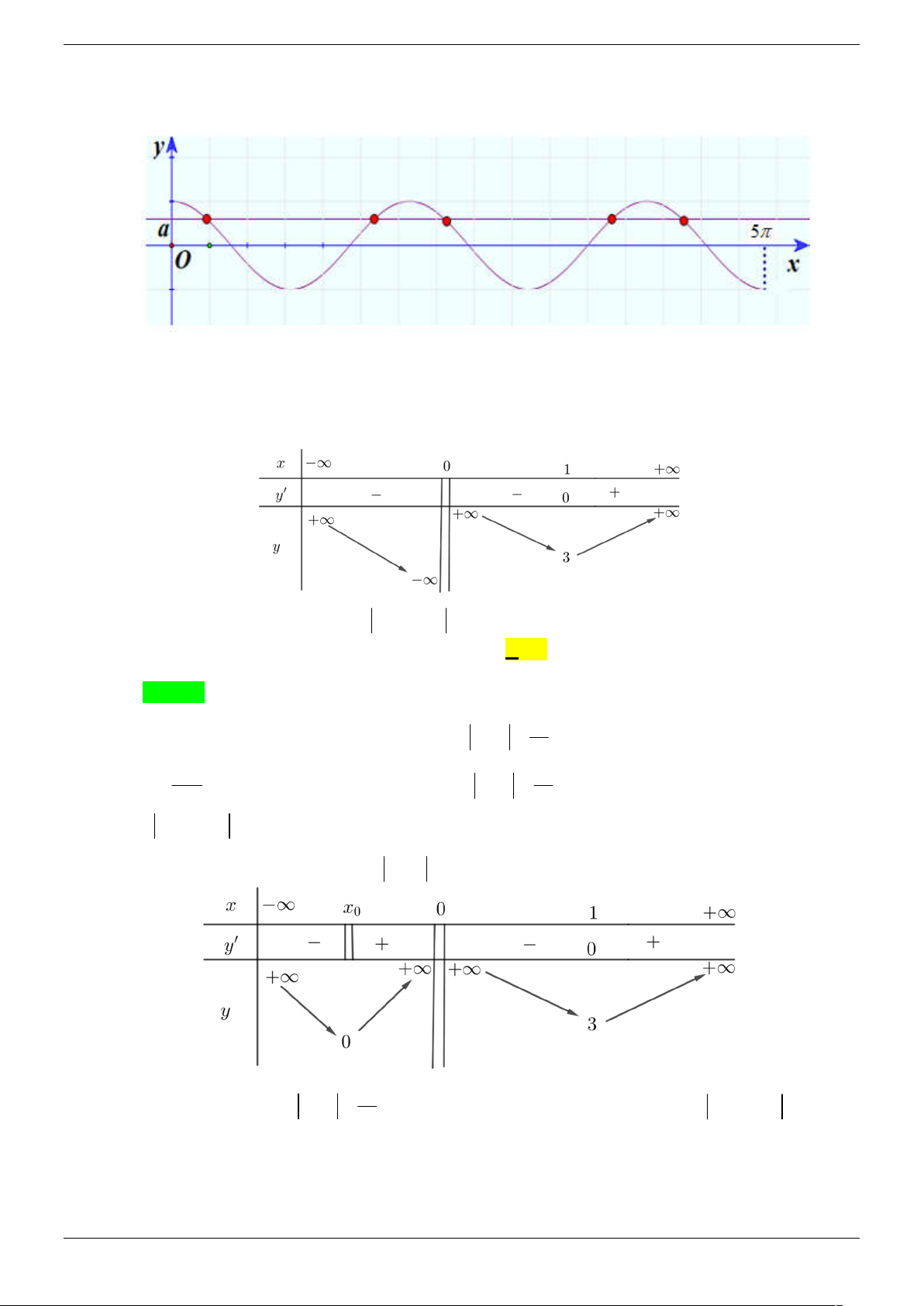
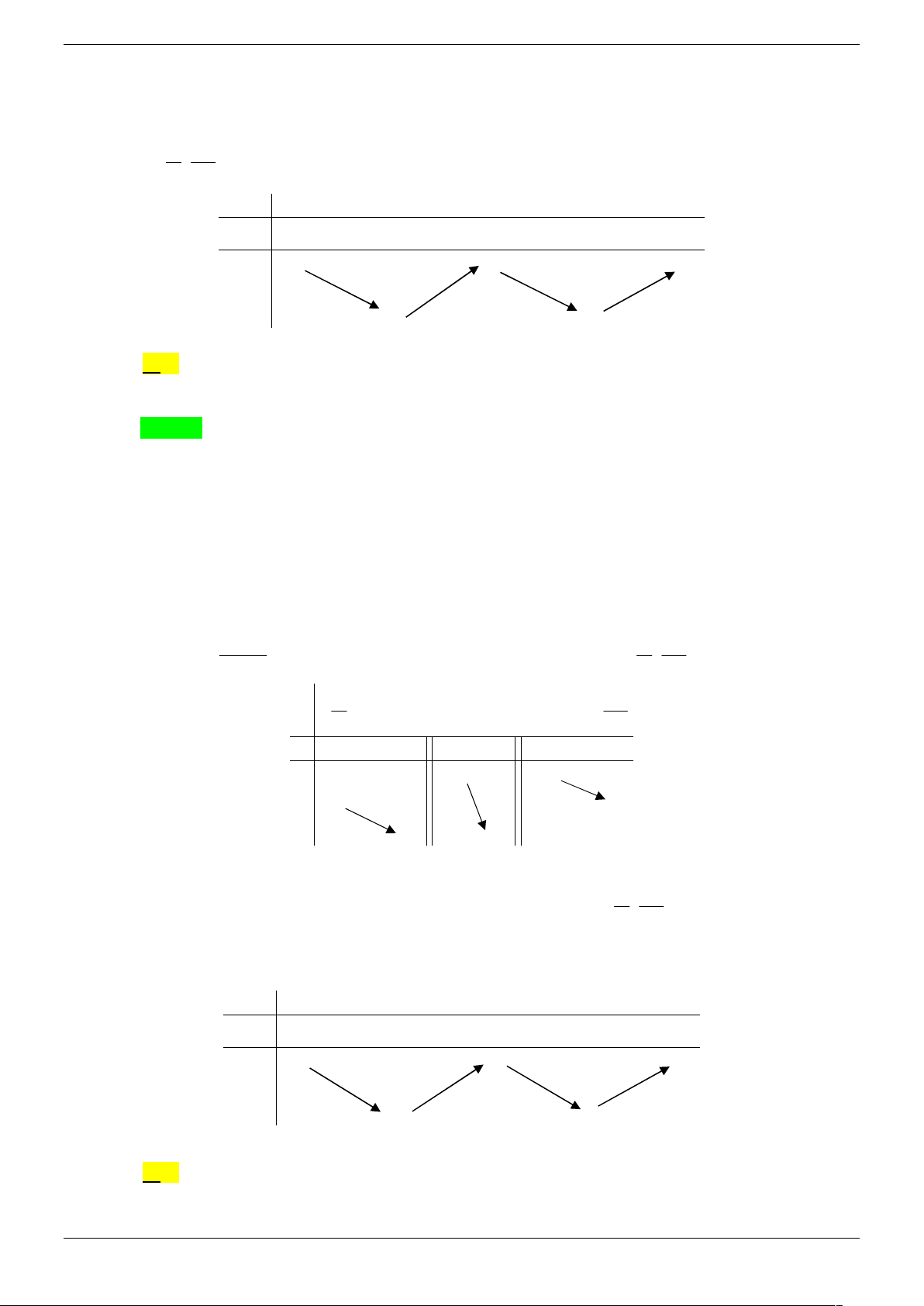
Câu 6. Cho hàm số y f (x) có đồ thị như hình vẽ và lim y   . Hỏi có bao nhiêu điểm trên x
đường tròn lượng giác biểu diễn nghiệm của phương trình f f cos 2x  0 ? A. 3 . B. 4 . C. 2 . D.1. Câu 7.
Cho hàm số y f x có đồ thị như hình vẽ:
Khi đó phương trình f  4 4
3x   3  0 có bao nhiêu nghiệm dương? A. 2. B. 4. C. 5. D. 1.
Câu 8. Cho hàm số y f x có đồ thị như hình vẽ: Strong Team Toán VD – VDC Trang 2/67
Phương trình 2 f cos x  1  0 có bao nhiêu nghiệm trong đoạn  
 ; 2  đồng thời tan x  0 ? A. 3 . B. 4. C. 5. D. 6. Câu 9.
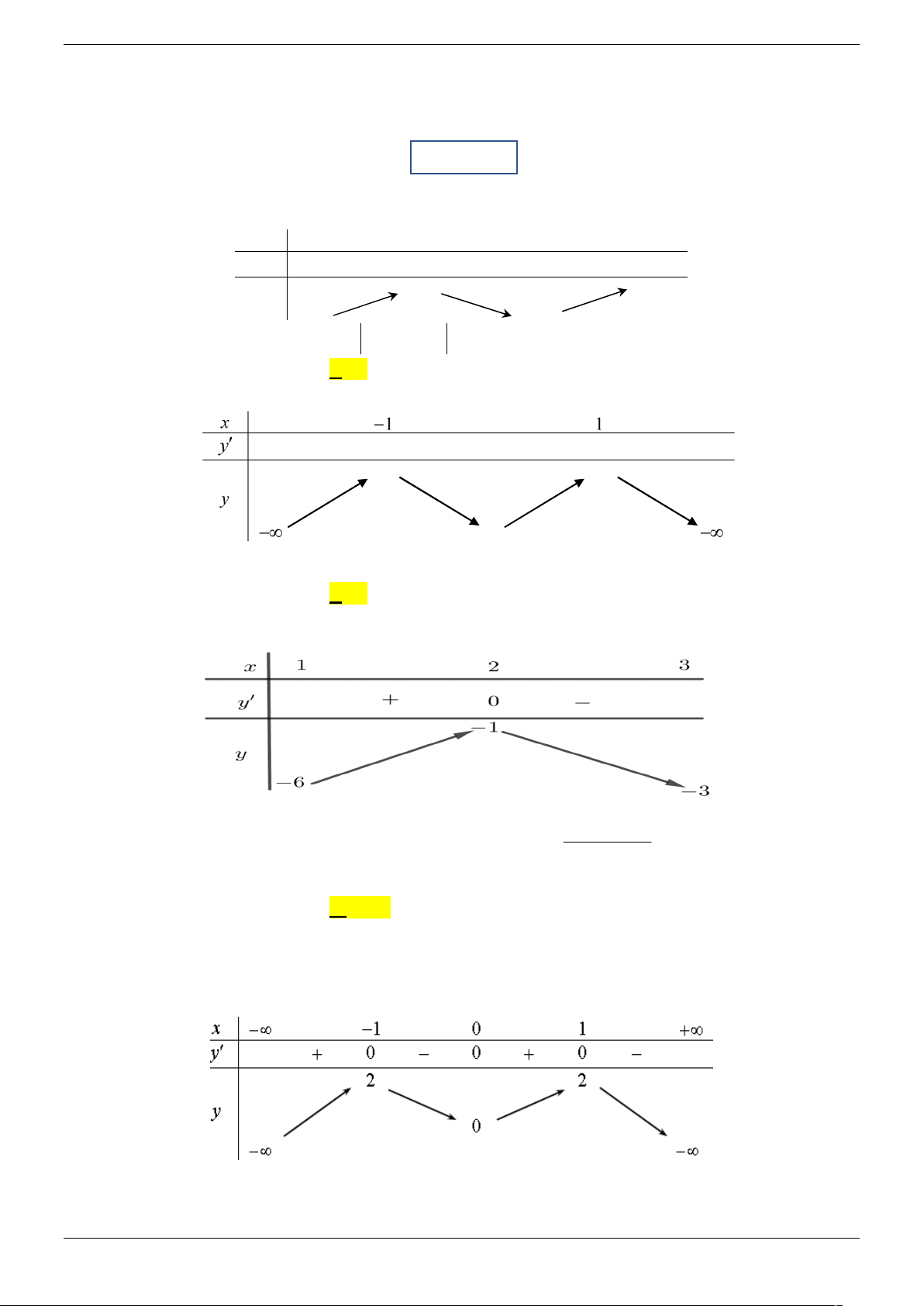
Cho hàm số y f x có đồ thị như hình vẽ. y 1 1  1 O x 1    5 
Số nghiệm của phương trình 2 f sin x 1  0 trên đoạn  ;  là 2 2    A. 3 . B. 4 . C. 5 . D. 6 .
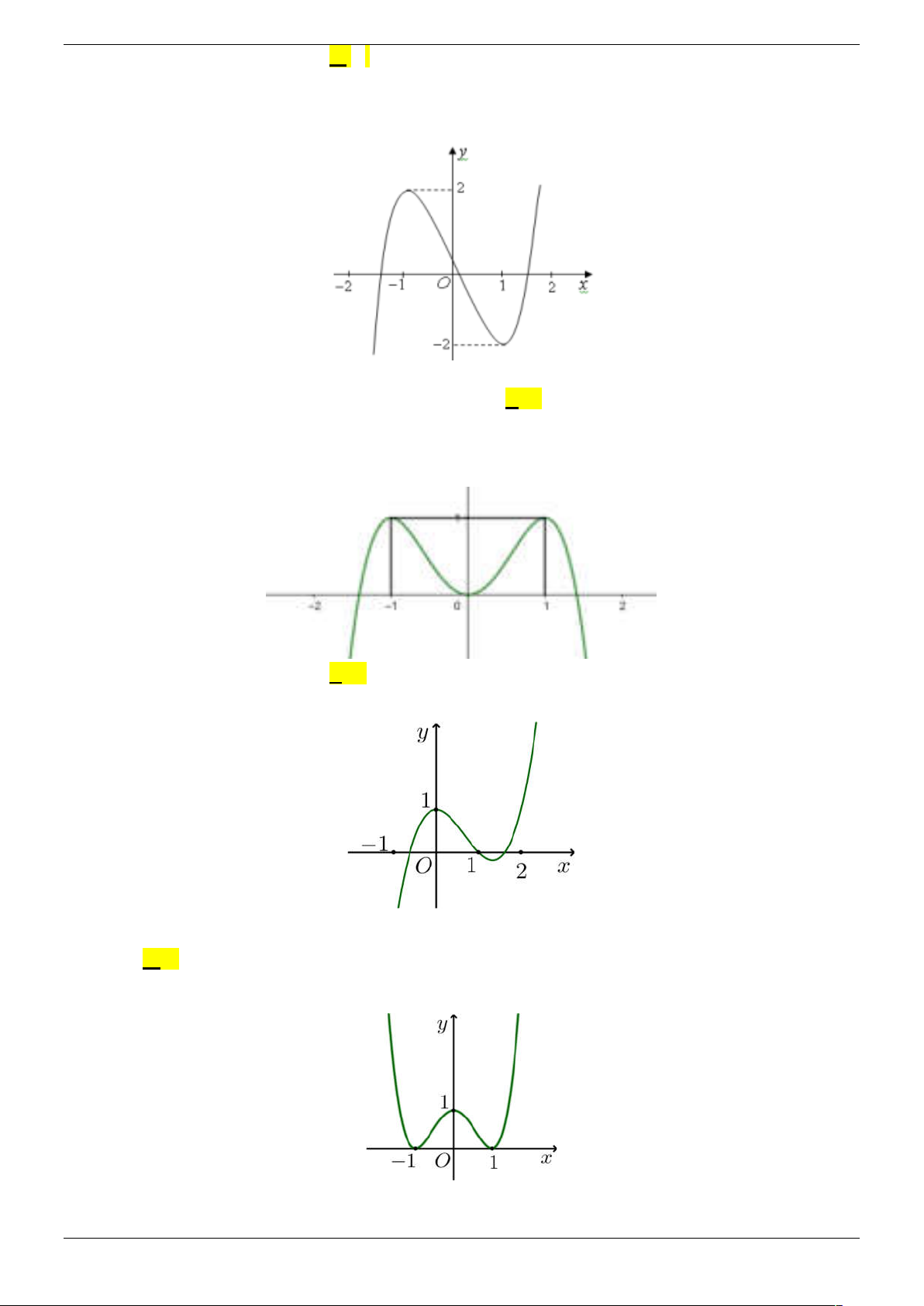
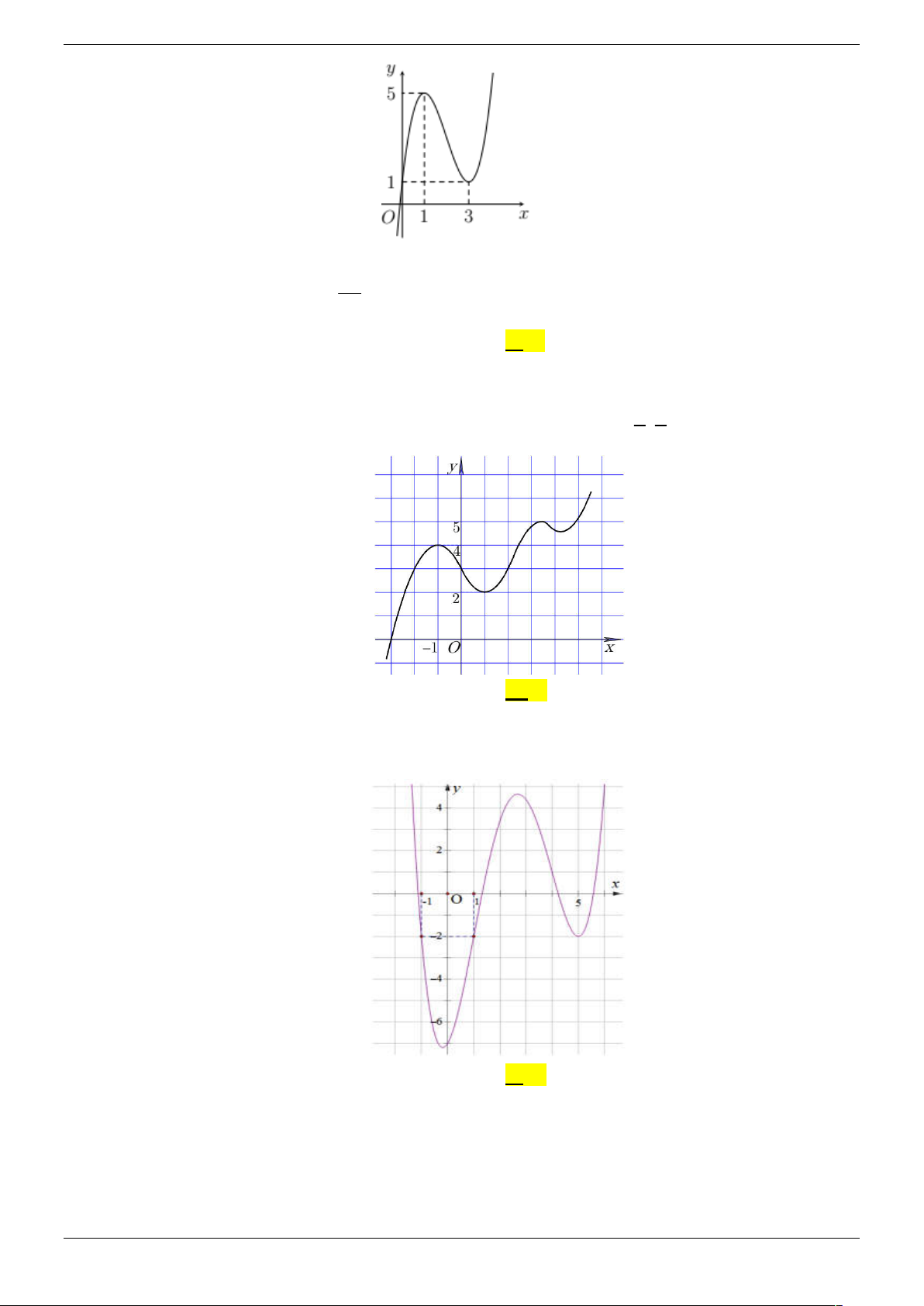
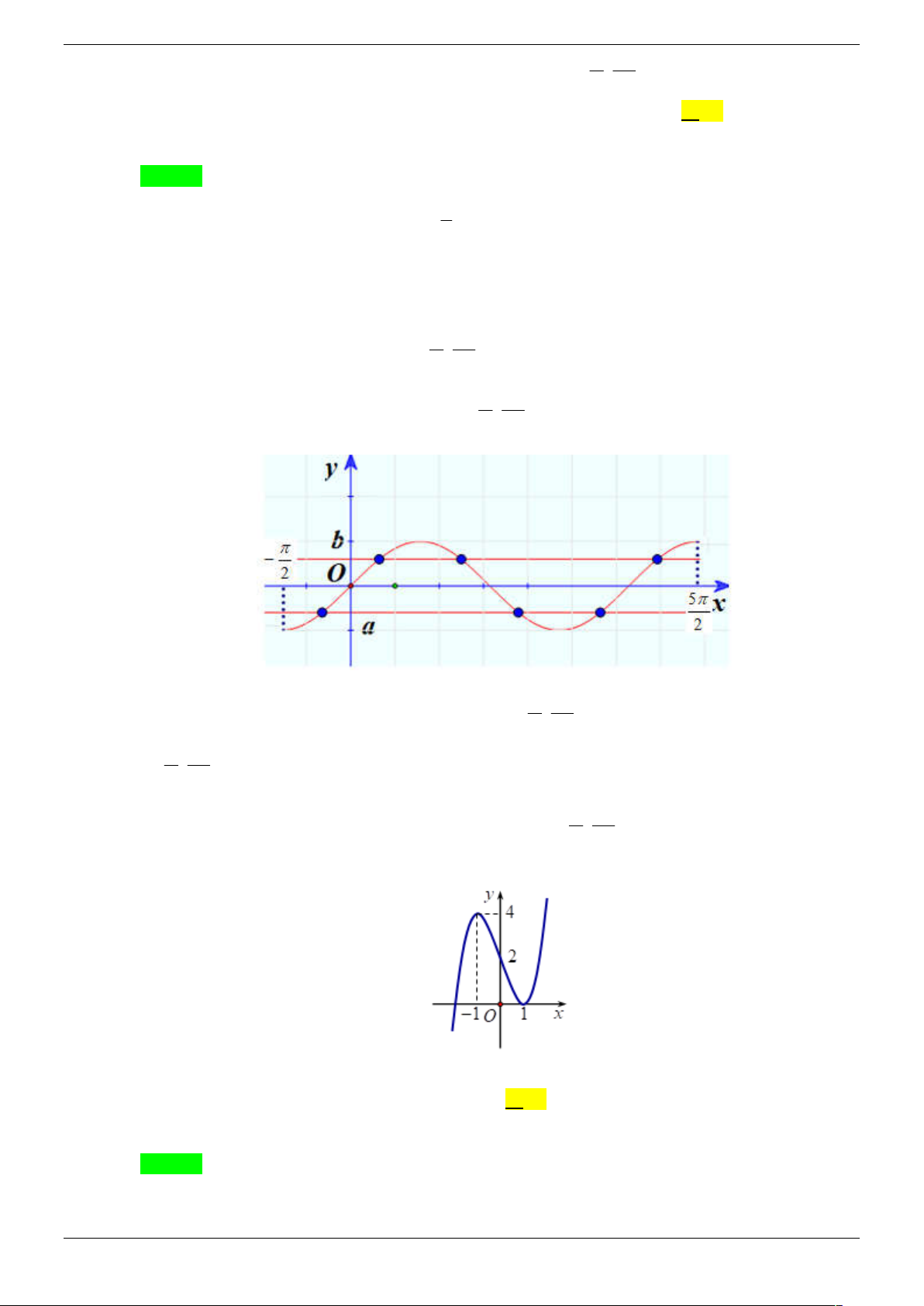
Câu 10. Cho hàm số y f x có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn 0;5  của phương trình f cos x  1 A. 3 . B. 4 . C. 5 . D. 6 .
Câu 11. Cho hàm số f x xác định trên  \  
0 và có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình 3 f 2x   1 10  0 là. A. 2 . B. 1. C. 4 . D. 3 .
Câu 12. Cho hàm số y f x liên tục trên  và có bảng biến thiên như hình vẽ Strong Team Toán VD – VDC Trang 3/67
Tập hợp các giá trị m để phương trình f cos 2x  2m 1  0 có nghiệm thuộc khoảng      ;   là:  3 4   1   1   1 1   2   2 1  A. 0;  B. 0;  C. ;  D.  ;  2       2   4 2   4 4   
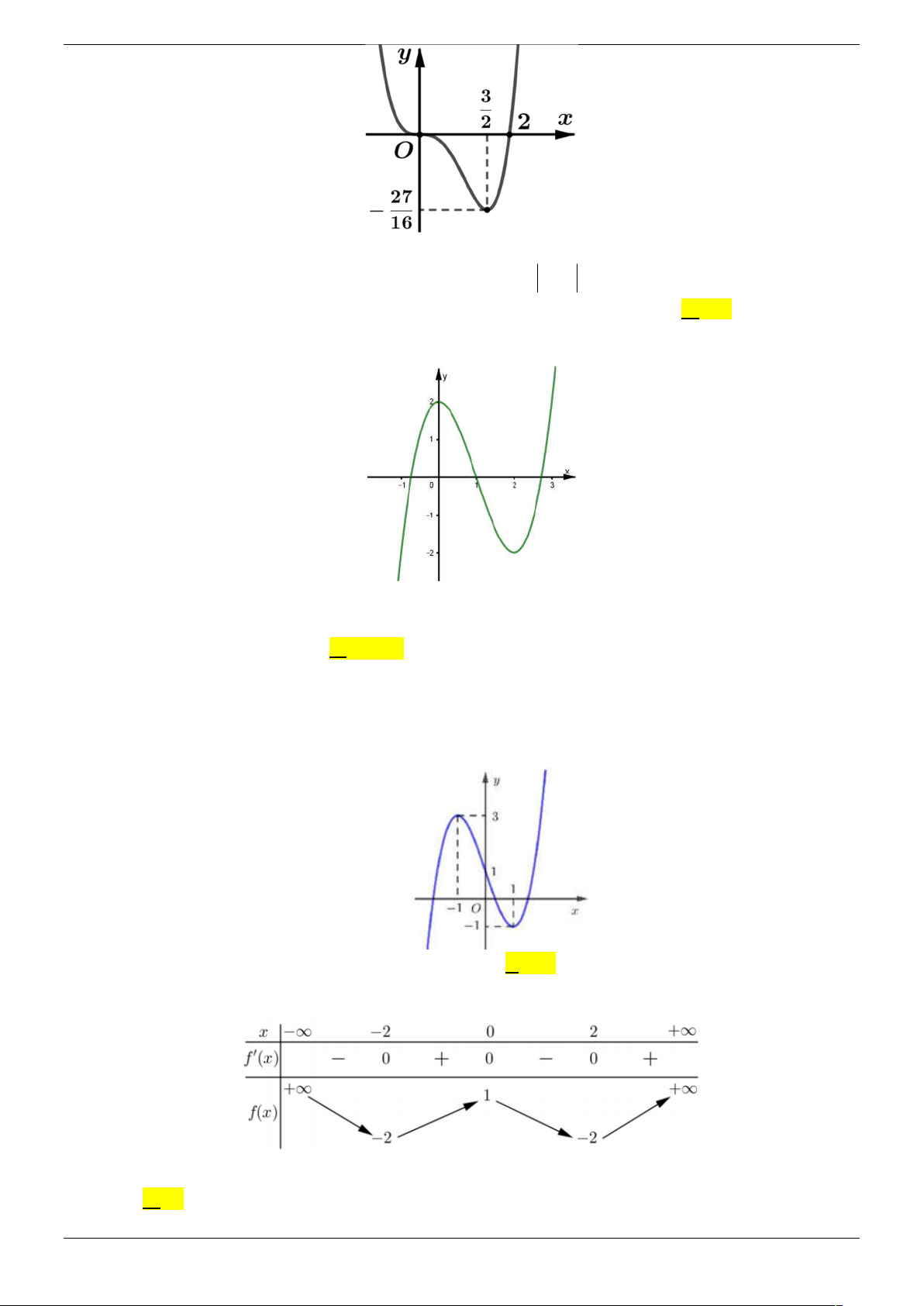
Câu 13. Cho hàm số y f x liên tục trên  có đồ thị như hình vẽ bên. Phương trình
f 3  2 f x 1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6 . B. 5 . C. 7 . D. 4.
Câu 14. Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  
 ; 2  của phương trình 2 f cos x 1  0 là: A. 7 . B. 4 . C. 5 . D. 6 .
Câu 15. Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm của phương trình f  4 2
3x  6x   1 1 là A. 4 . B. 5 . C. 6 . D. 3.
Câu 16. Cho hàm số f x có bảng biến thiên như sau: Strong Team Toán VD – VDC Trang 4/67  7 
Số nghiệm thuộc đoạn 0;
2. f cos x 5  0  của phương trình   là 3    A. 8 . B. 7 . C. 5 . D. 6 .
Câu 17. Cho hàm số f (x) có bảng biến thiên bảng biến thiên như sau Số nghiệm thuộc [ 
; 2 ] của phương trình f (s inx) 1  0 là 2 A. 3 . B. 6 . C. 4 . D. 5 .
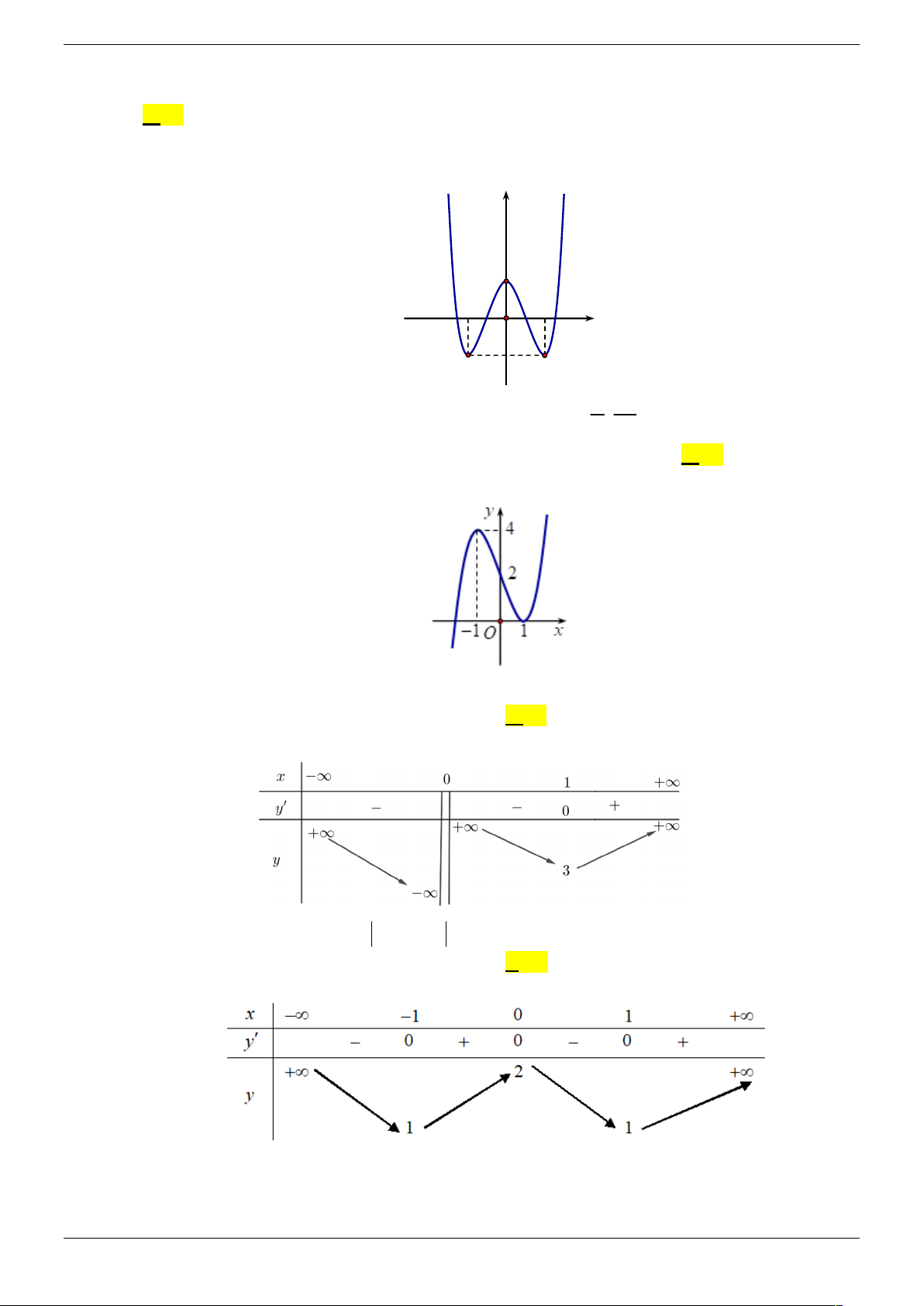
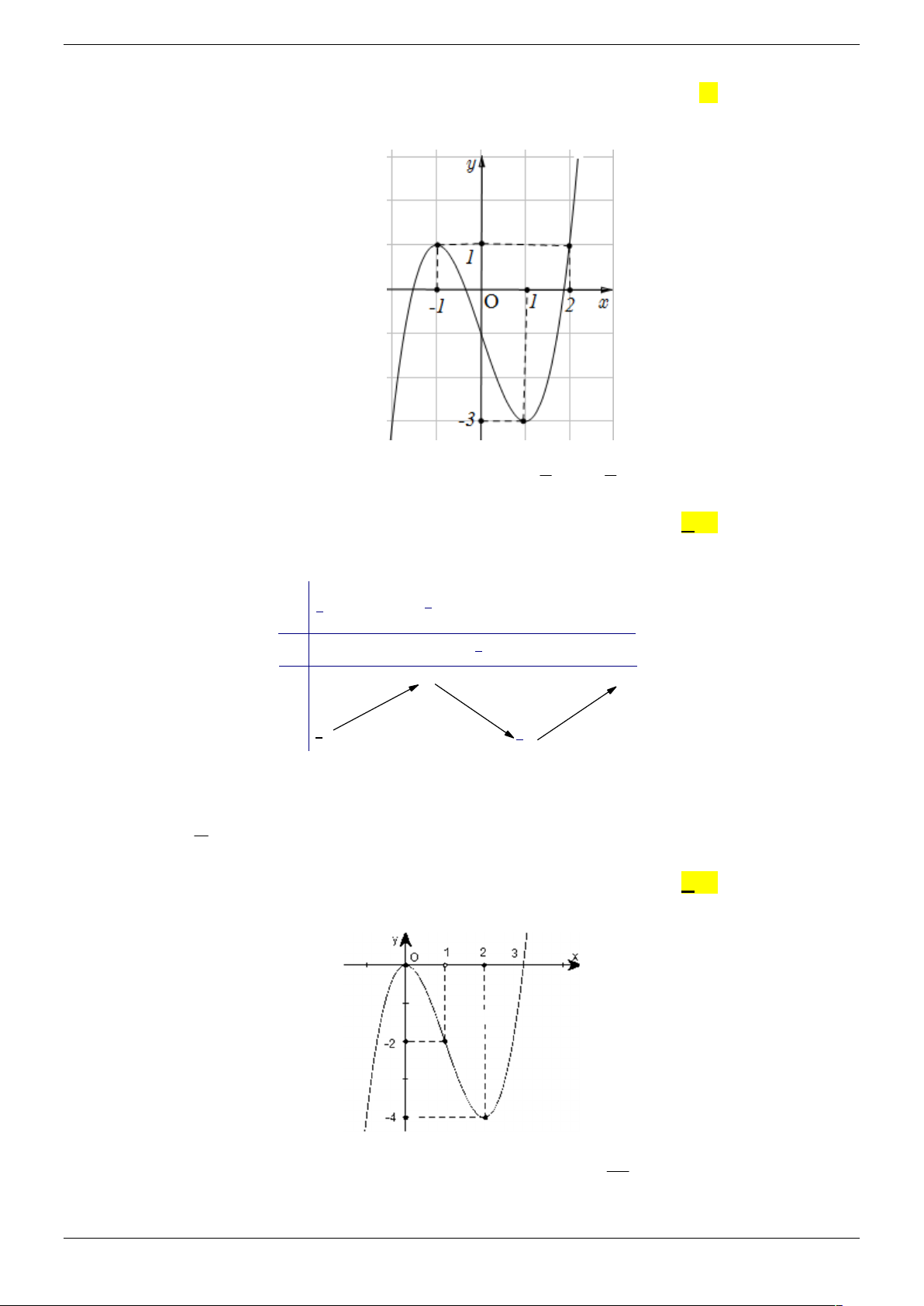
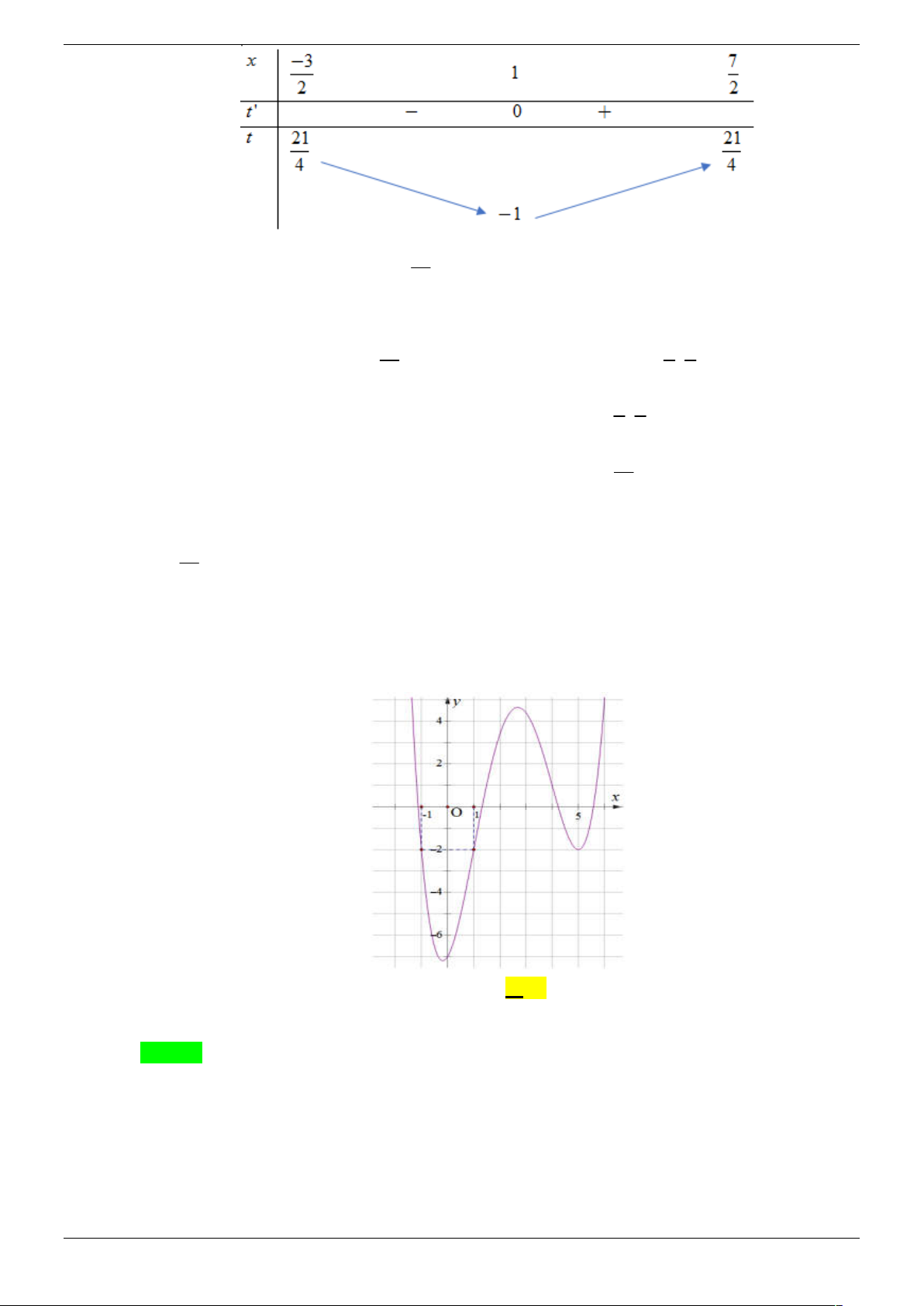
Câu 18. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới
Tìm số giá trị nguyên của tham số m để phương trình 2
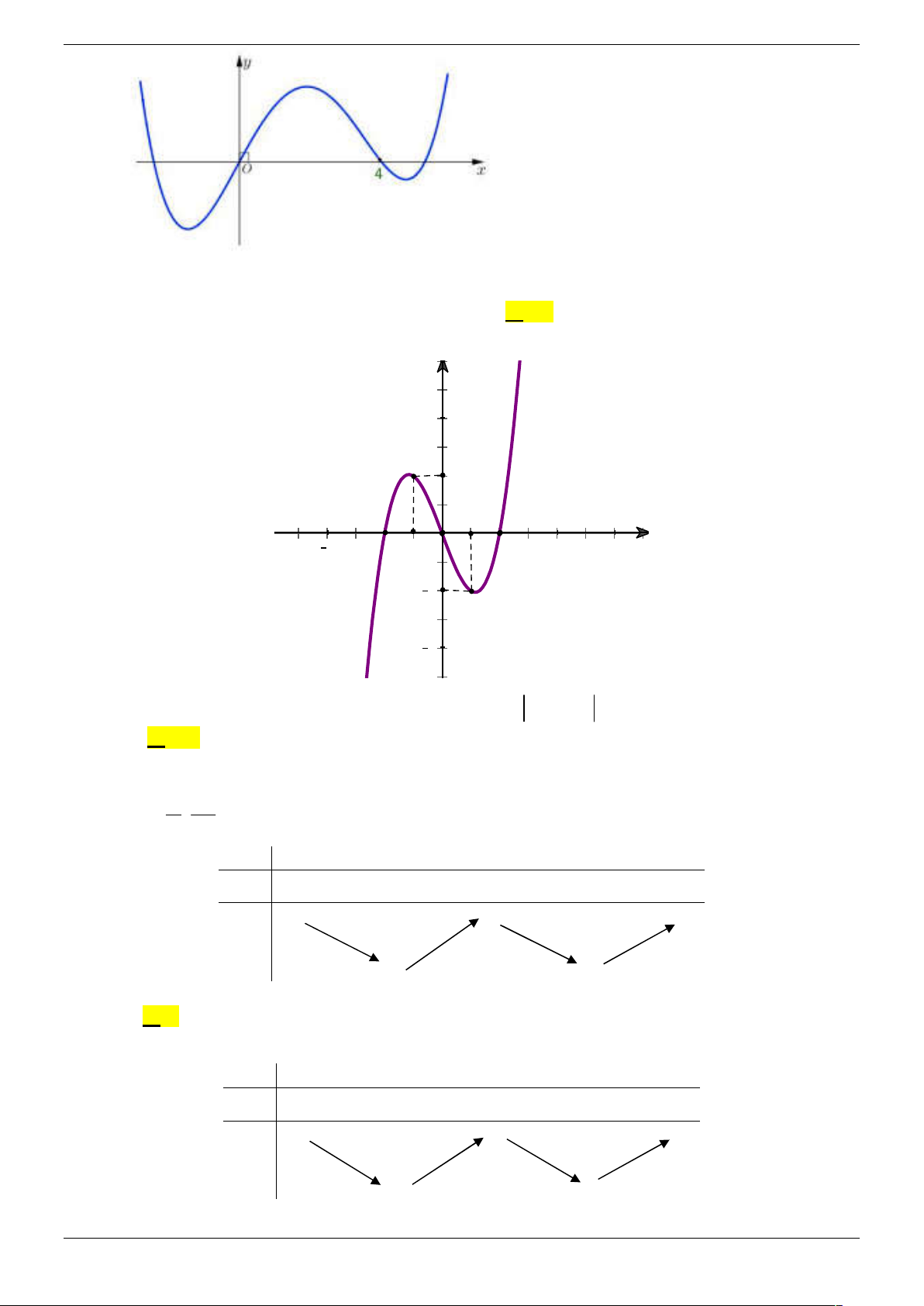
f ( 4  x )  m có hai nghiệm phân biệt A. 2 . B. 3 . C. 1. D. 4 . Câu 19. Cho hàm số   3 2
f x ax bx bx c có đồ thị như hình vẽ: Strong Team Toán VD – VDC Trang 5/67    9  Số nghiệm nằm trong ; 
 của phương trình f cos x  
1  cos x 1 là  2 2  A. 6 . B. 10. C. 4 . D. 8 .
Câu 20. Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0;5  của phương trình f sin x 1 là A. 6 . B. 4 . C. 10 . D. 8 .
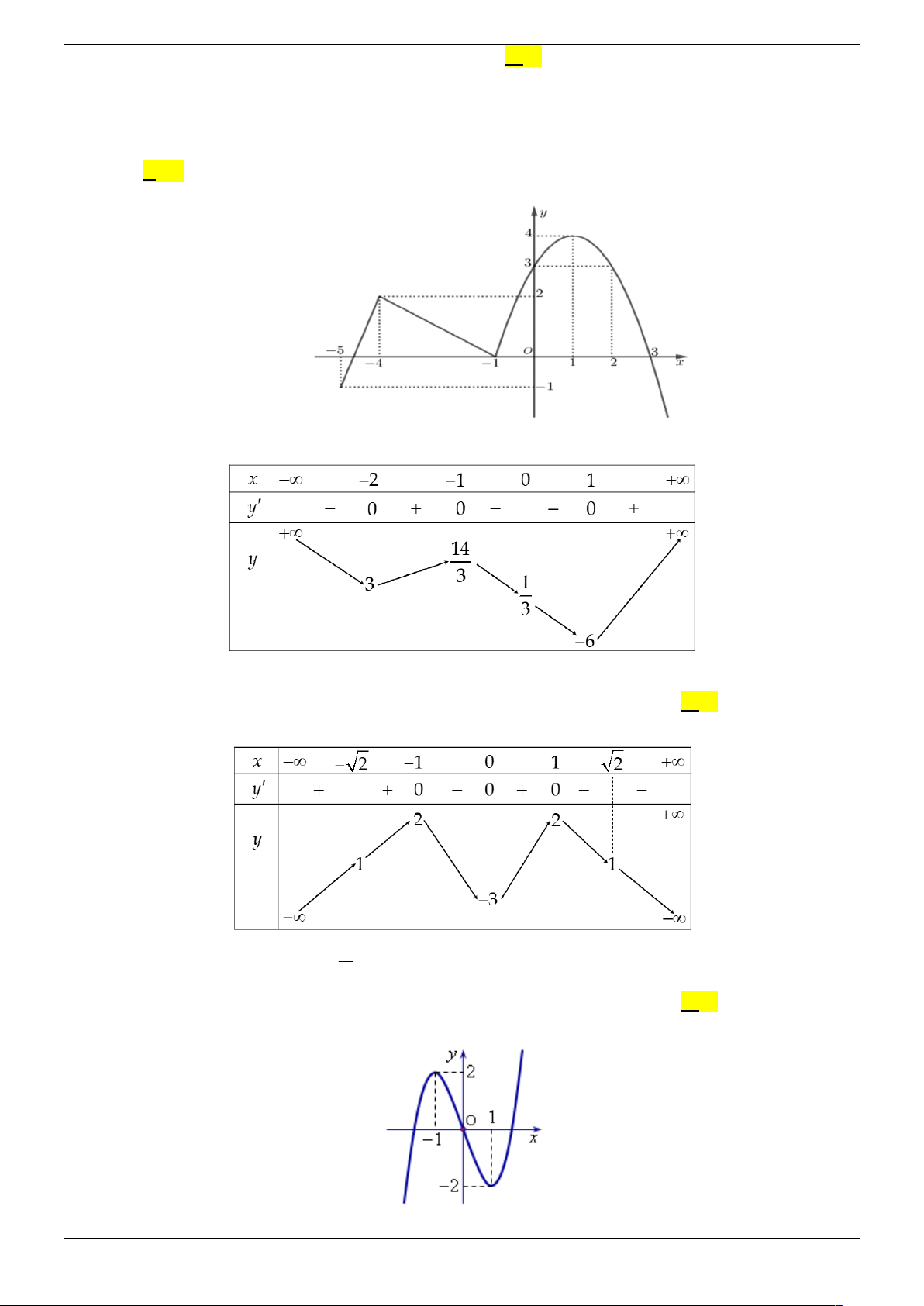
Câu 21. Cho hàm số f x liên tục trên  có đồ thị y f x như hình vẽ dưới đây. Strong Team Toán VD – VDC Trang 6/67
Số nghiệm thực của phương trình 4 2x f f   2 là A. 1. B. 2. C. 3. D. 4.
Câu 22. Cho hàm số y f x có bảng biến thiên như sau:  3 
Số nghiệm nhiều nhất thuộc đoạn 0; 
của phương trình f 2cos x   1  0 là: 2    A. 7 . B. 5. C. 4 . D. 6 .
Câu 23. Cho hàm số y f x có bảng biến thiên sau:
Hỏi có bao nhiêu giá trị m nguyên để phương trình f 2tan2x  2
m 1 có nghiệm thuộc    khoảng 0;   là:  8  A. 1. B. 3 . C. Vô số. D. 0 .
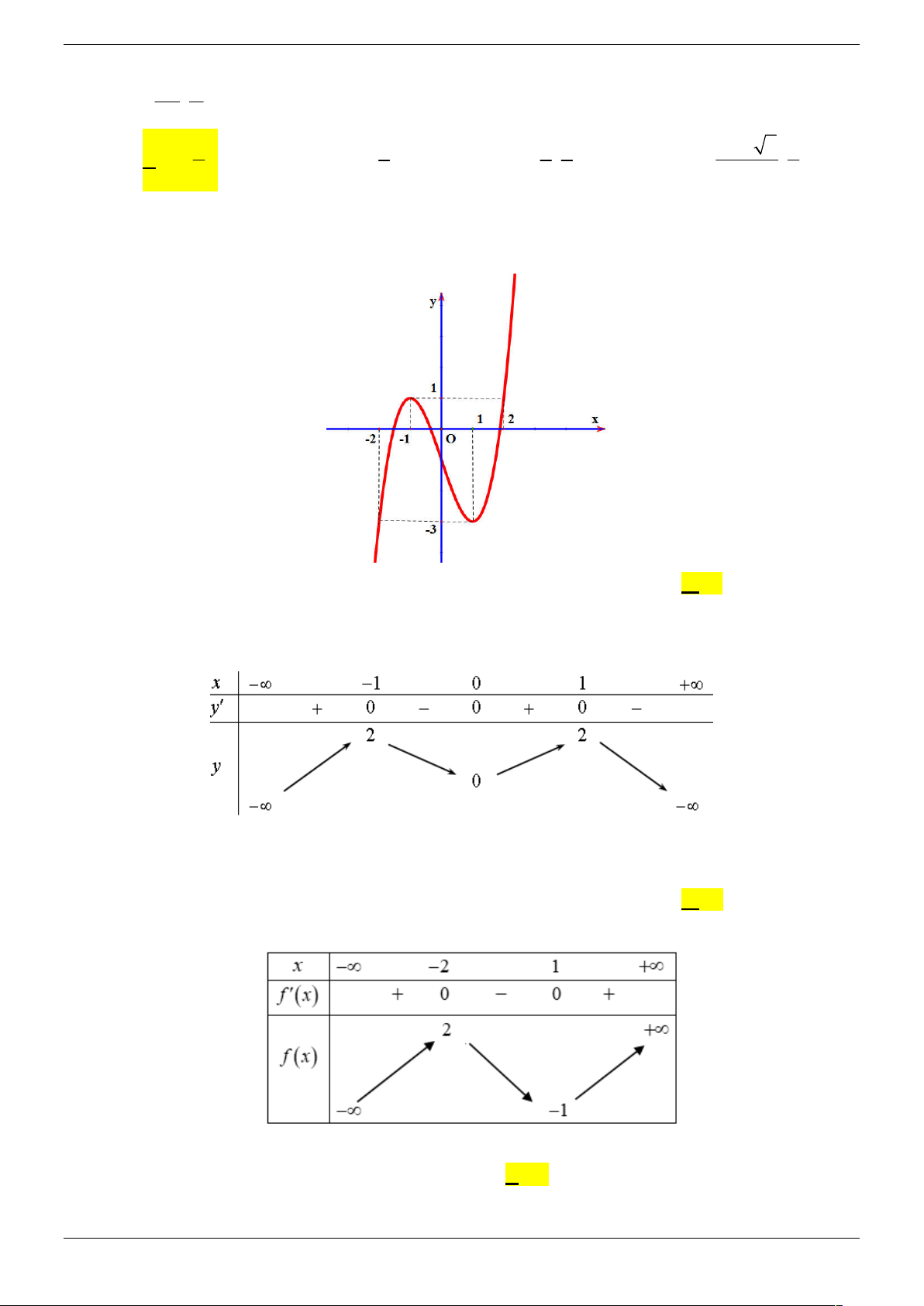
Câu 24. Cho hàm số y f x liên tục trên  có đồ thị như hình vẽ. Phương trình f 1 f x  0 có
tối đa bao nhiêu nghiệm thực phân biệt? A. 7 . B. 9 . C. 6 . D. 5.
Câu 25. Cho hàm số f x liên tục trên  có bảng biến thiên như sau: Strong Team Toán VD – VDC Trang 7/67
Số nghiệm thuộc đoạn  
 ;  của phương trình f  2
2 cos x  3  3 là: A. 8 . B. 2 . C. 6 . D. 4 .
Câu 26. Cho hàm số f x liên tục trên  có bảng biến thiên như sau:
Số nghiệm của phương trình f  2
x x  2 là: A. 1 . B. 3 . C. 2 . D. 4 .
Câu 27. Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0;3  của phương trình f cos x  2 là A. 3 . B. 4 . C. 6 . D. 8 . Câu 28.
Cho hàm số y f x có bảng biến thiên như sau :
Số nghiệm thuộc đoạn 0; 2  của phương trình 3 f 2 sin x   2  0 là : Strong Team Toán VD – VDC Trang 8/67 A. 2 . B. 3 . C. 4 . D. 6 .
Câu 29. Cho hàm số f x có bảng biến thiên như sau
Số nghiệm thuộc đoạn 1; 
3 của phương trình f  2
x  3x 1  0 là A. 5 . B. 3 . C. 2 . D. 4 .
Câu 30. Cho hàm số f x có bảng biến thiên như sau 5  Số nghiệm thuộc đoạn ;3 
của phương trình 4 f cos2x 1  0 là 6    A. 5 . B. 9 . C. 4 . D. 10 .
Câu 31. Cho hàm số y f x liên tục, có đạo hàm trên  2; 4  
 và có bảng biến thiên như hình vẽ  3 3 
Số nghiệm của phương trình f  x   3 3 2
1  8x  6x trên đoạn  ;  là  2 2   A. 1 . B. 2 . C. 3 . D. 5 .
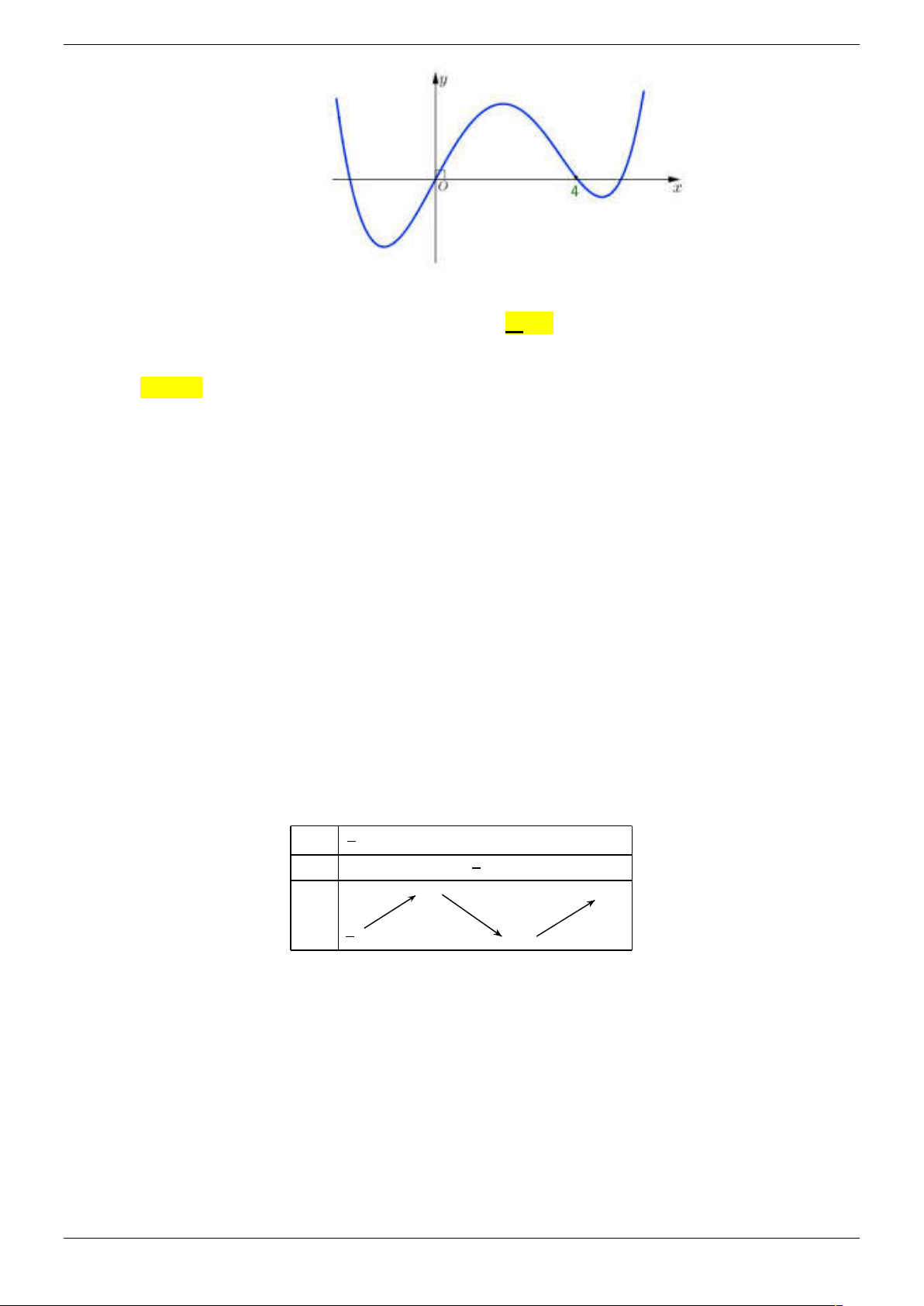
Câu 32. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Strong Team Toán VD – VDC Trang 9/67  
Số nghiệm thuộc đoạn  ; 2    
 của phương trình 2f 2 sinx  1 0 là A. 6 . B. 2 . C. 8 . D. 12 .
Câu 33. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ
Gọi m là số nghiệm của phương trình f f x  1. Khẳng định nào sau đây là đúng ? A. m  6 . B. m  7 . C. m  5 . D. m  9 .
Câu 34. Cho hàm số yf x liên tục trên  và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả
các giá trị nguyên của m để phương trình f (sin x)  2 sin x  2m có nghiệm thuộc khoảng
(0; ) . Tổng các phần tử của S bằng: A. 2 B. 0 . C. 1. D. 5 .
Câu 35. Cho hàm số f  
x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  2  ;
2 của phương trình 2 f 2sin x 1   0 là A. 8 . B. 5 . C. 2 . D. 6 . Strong Team Toán VD – VDC Trang 10/67 3
Câu 36. Cho hàm số y f x 3
x  3x 1. Số nghiệm của phương trình  f x  3 f x 1  0   là: A. 1. B. 6. C. 5. D. 7.
Câu 37. Cho hàm số y f (x) là hàm số bậc 3 có đồ thị như hình vẽ dưới đây  3 1 
Số nghiệm thuộc đoạn 0;3  của phương trình 2 f sin x  1  0   là  2 2  A. 5 . B. 3. C. 4. D. 6.
Câu 38. Cho hàm số y f (x) có bảng biến thiên như sau: 1 x ∞ 1 + ∞ 2 y' + 0 0 + 1 ∞ + y ∞ 2
Có bao nhiêu giá trị nguyên của tham số m để phương trình f  4 4
sin x  cos x  m có nghiệm    x  0; .  4    A. 1. B. 3. C. 2. D. 4.
Câu 39. Cho hàm số y f (x) có đồ thị như hình vẽ.  5
Số nghiệm của phương trình 2f (cos 2x)  1  0 trên đoạn 0;   là 4    Strong Team Toán VD – VDC Trang 11/67 A. 3. B. 4. C. 5. D. 6.
Câu 40. Cho hàm số y f (x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình
3f f (x
)  m có đúng 6 nghiệm phân biệt x  [ 5  ;0]. A. 2. B. 3. C. 4. D. 5.
Câu 41. Cho hàm số f (x) có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  201  9; 
1 của phương trình f ln x  4 A. 2020 B. 4. C. 2019. D. 3.
Câu 42. Cho hàm số f (x) có bảng biến thiên như sau:   
Số nghiệm thuộc đoạn 0; 
của phương trình f sin x  cos x  1  4    A. 1 B. 3 C. 2 D. 0.
Câu 43. Cho hàm số y f (x) liên tục trên  có đồ thị như hình vẽ Strong Team Toán VD – VDC Trang 12/67
Có bao nhiêu giá trị nguyên của tham số m để phương trình f (sin x)  2 sin x m  0 có
nghiệm thuộc khoảng 0;  ? A. 9 . B. 4 . C. 5 . D. 6 .
Câu 44. Cho hàm số f (x) có bảng biến thiên như sau
Số nghiệm thuộc đoạn  
 ; 2  của phương trình 2 f (sin x)  3  0 là A. 6 . B. 3 . C. 4 . D. 8 .
Câu 45. Cho hàm số y f x có bảng biến thiên như sau
Số nghiệm của phương trình  x
f e  4 1  0 trong đoạn ln 2 ; ln 6 là A. 1. B. 2. C. 3. D. 4 .
Câu 46. Cho hàm số y f x là hàm đa thức bậc 3 và có bảng biến thiên như sau  5 
Số nghiệm của phương trình f sin x  3 cos x  0 trong đoạn 0 ;  là 2    A. 1. B. 4. C. 3. D. 2 .
Câu 47. Cho hàm số y f x có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình  f  3 2 x x   2  f  3 2 1 3 1 2 x  3x   1  2 là A. 5 . B. 4 . C. 3 . D. 2 .
Câu 48. Cho hàm số y f x là hàm bậc 3 và có bảng biến thiên như sau Strong Team Toán VD – VDC Trang 13/67    Phương trình 2
f sin x  cos x 1 sin 2x  2 2 sin x f  
sin x  cos x có mấy nghiệm  4   5 5  thực thuộc đoạn  ;  ? 4 4    A.1. B. 3 . C. 4 . D. 6 .
Câu 49. Cho y f x là hàm số bậc ba và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên m   5
 ;5 để hàm số g x  f f x  m có 4 điểm cực trị? A. 5. B. 6. C. 7. D. 8.
Câu 50. Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc khoảng  
 ;  của phương trình 2
f cos x  f cos x  2 là A. 5 . B. 6 . C. 7 . D. 9 .
Câu 51. Cho hàm số f (x) có bảng biến thiên như sau:
Số nghiệm x  0;   của phương trình  x
f e  2020 x   2  0 là A.1. B.2. C. 0 . D. 2020 .
Câu 52. Cho hàm số f x có đồ thị như hình vẽ: Strong Team Toán VD – VDC Trang 14/67  3 
Số nghiệm thuộc đoạn  ; 2
2 f cos x 5  0  của phương trình   là 2    A. 5. B. 1. C. 3. D. 4 .
Câu 53. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình  3 7  f  2
x  2x  m có đúng 4 nghiệm thực phân biệt thuộc đoạn  ;  . 2 2    A. 1. B. 4 . C. 2 . D. 3 .
Câu 54. Cho hàm số y f x có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số m
để phương trình f sin x  m có đúng hai nghiệm thuộc đoạn 0;  ? A. 4 . B. 7 . C. 5 . D. 6 .
Câu 55. Cho hàm số bậc bốn y f x có đồ thị như hình bên: Strong Team Toán VD – VDC Trang 15/67
Số điểm cực trị của hàm số g x  f  3 2
x  3x  4 là A. 5 . B. 3 . C. 7 . D. 11 .
Câu 56. Cho hàm số y f x có đồ thị như hình bên 3y 1 2 1 -1 x 2 1 2 1 -1 2
Số nghiệm thuộc đoạn 0;3của phương trình : 2 f cos x 1  0 A. 12 . B. 6 . C. 10 . D. 8 .
Câu 57. Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. Số nghiệm thuộc đoạn   3   ; 
của phương trình f cot x   1  1 là 2 2    x  1 1 2  f  x  0  0  0   1  f x 1 2 A. 7. B. 6. C. 8. D. 5.
Câu 58. Cho hàm số y f x có bảng biến thiên như hình vẽ x  0 1 2  f  x  0  0  0   3  f x 0 1 Strong Team Toán VD – VDC Trang 16/67
Số nghiệm của phương trình f sin x   1  2 trên    ; 2  là A. 6. B. 7. C. 5. D. 4.
-------------------- HẾT -------------------- Strong Team Toán VD – VDC Trang 17/67
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1.
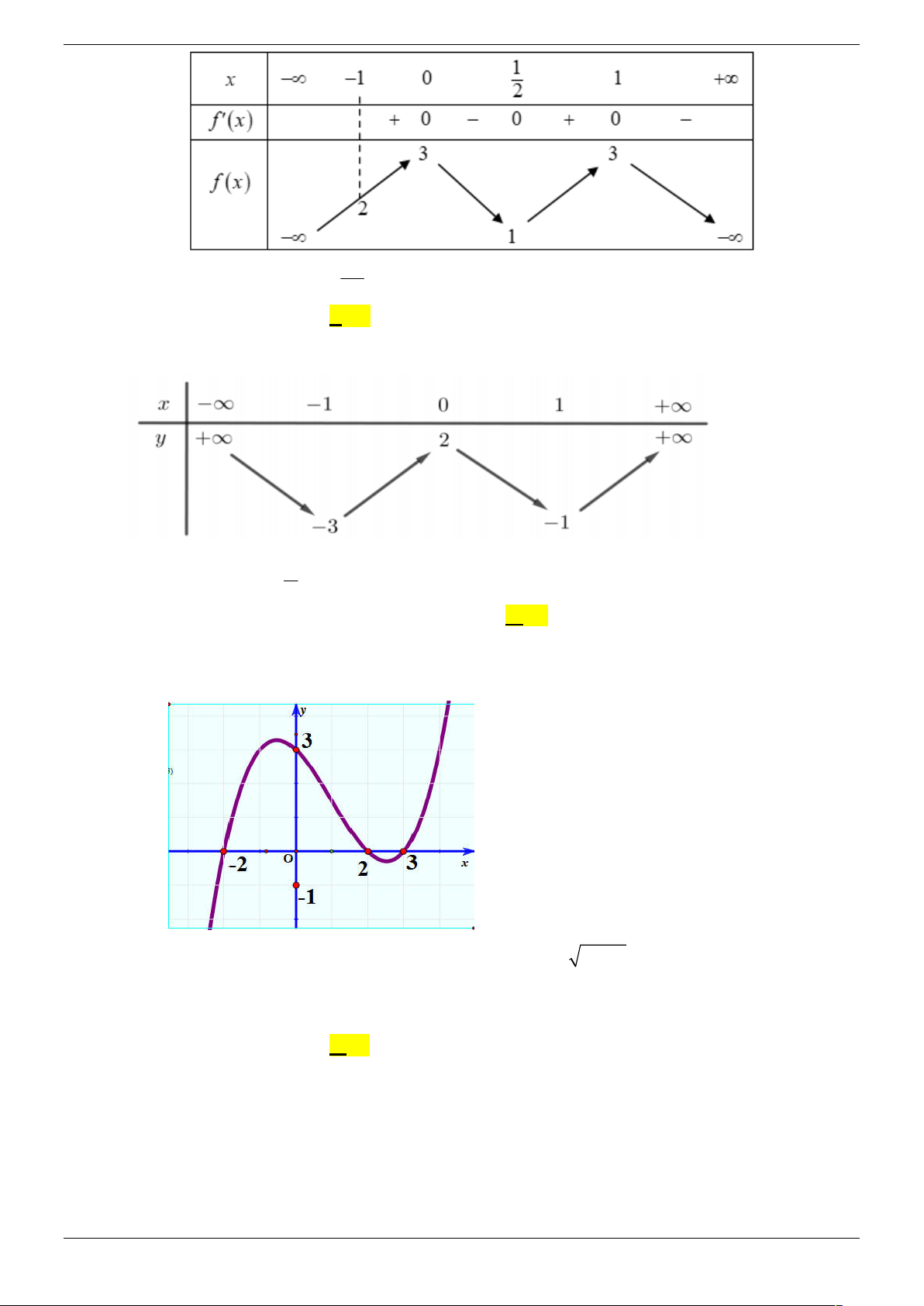
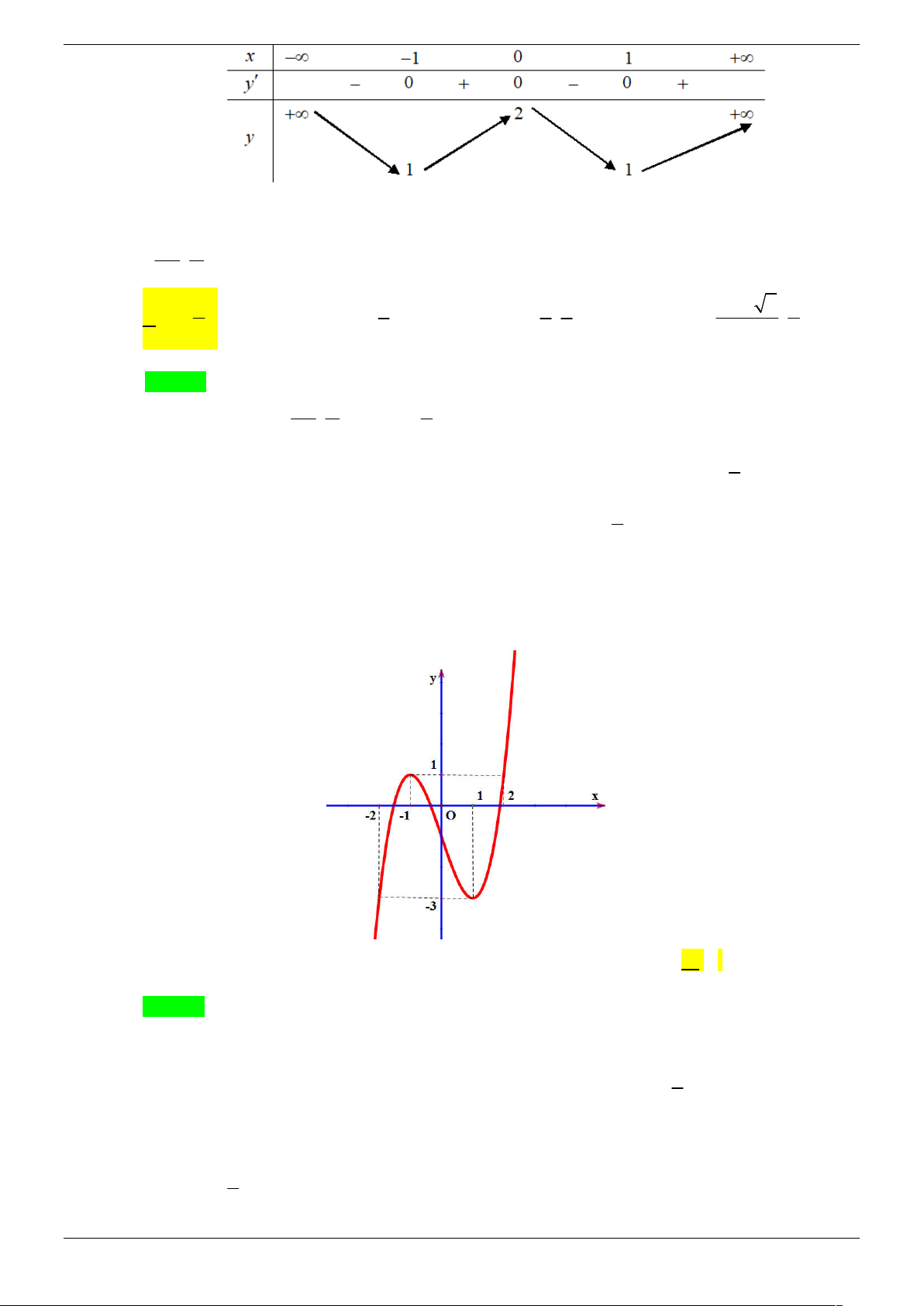
Cho hàm số y f x xác định trên R và có bảng biến thiên như sau x  -1 1  y  0  0  y 1   -1
Số nghiệm của phương trình f  2
x  2x  2 là A. 4 . B. 2 C. 3 D. 8 Lời giải Chọn Bf  2
x  2x  2 Phương trình f  2
x  2x  3    f  2
x  2x  2  
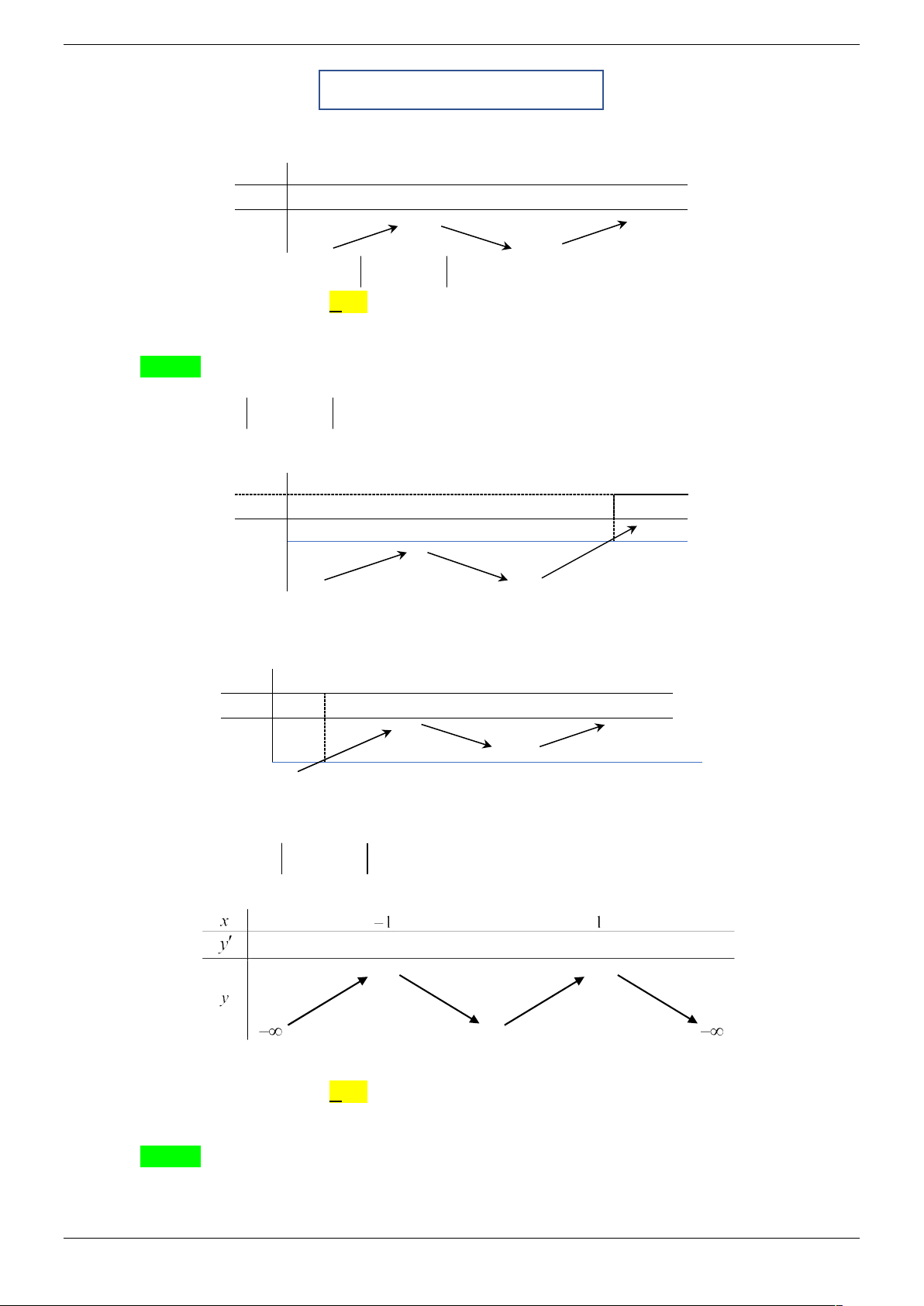
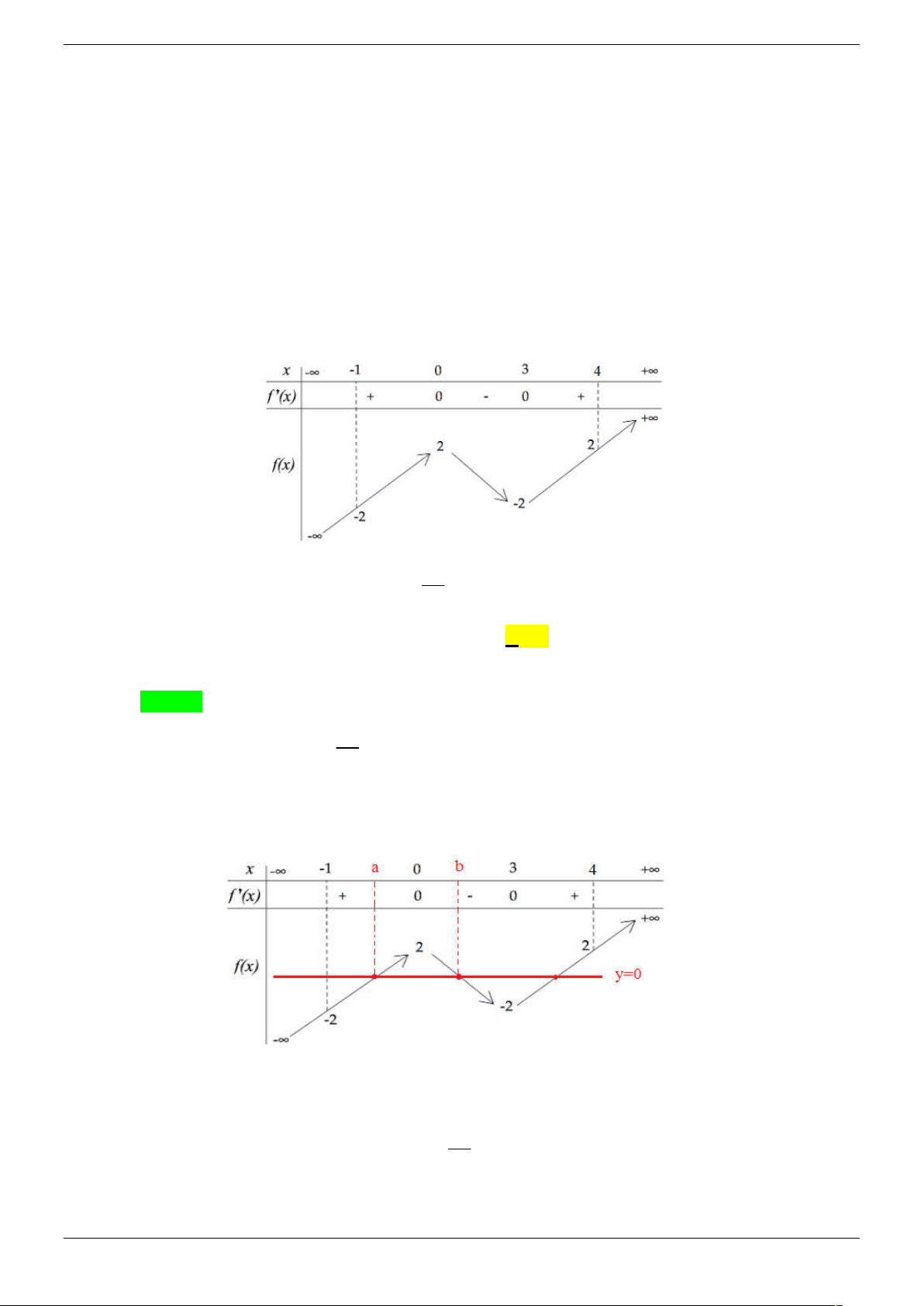
Dựa vào bảng biến thiên x  -1 1 a  y  0  0  y  2 y 1   -1 phương trình f  2
x  2x  2 2
x x a a   2 2
1  x  2x a  0
có   1 a  0  phương trình có 2 nghiệm.
Tương tự, dựa vào bảng biến thiên x  b -1 1  y  0  0  y 1  -1 y  2  
Phương trình f  2
x  2x  2 2
x x b b    2 2
1  x  2x b  0
có   1 b  0  phương trình vô nghiệm.
Vậy phương trình f  2
x  2x  2 có 2 nghiệm. Câu 2.
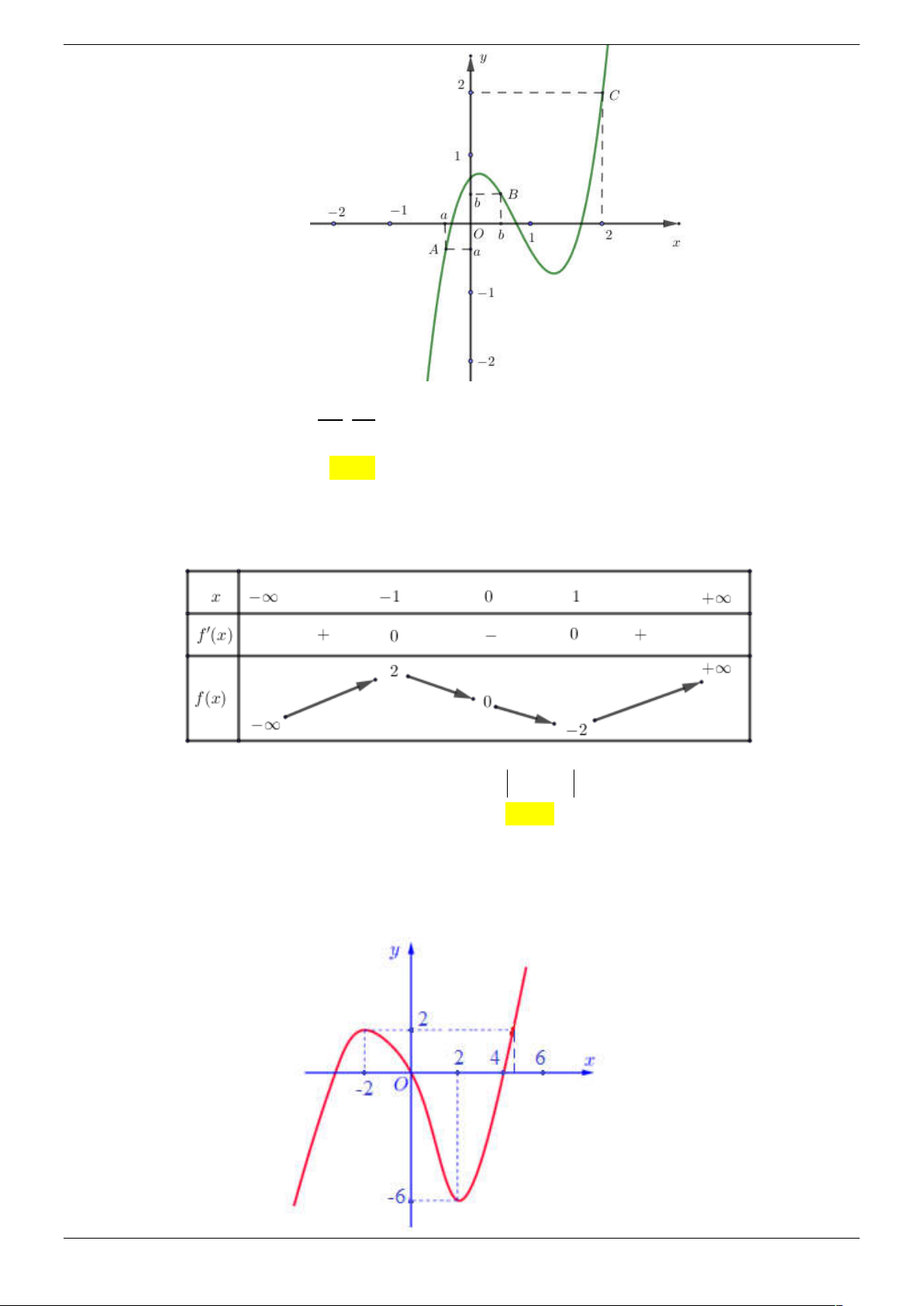
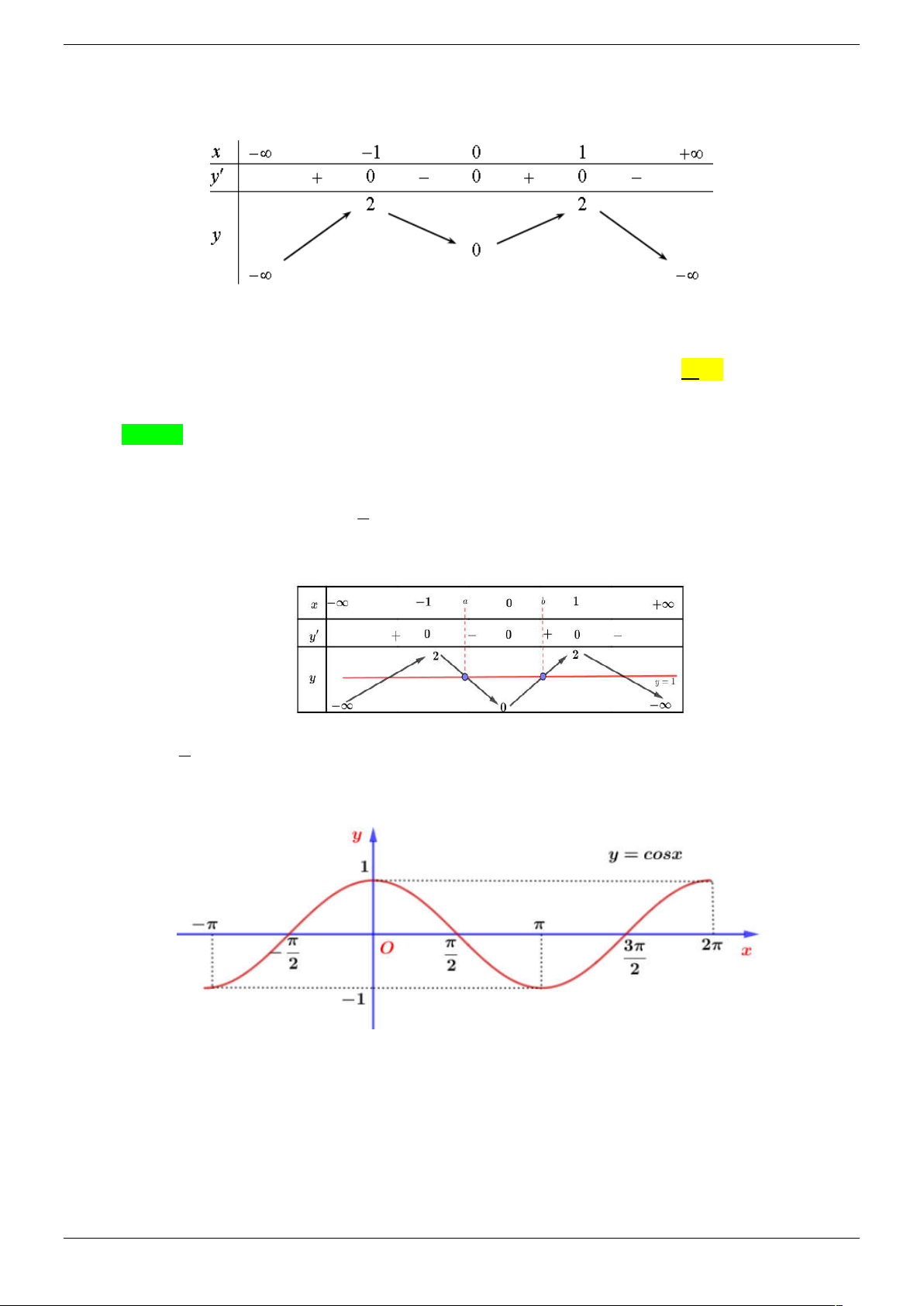
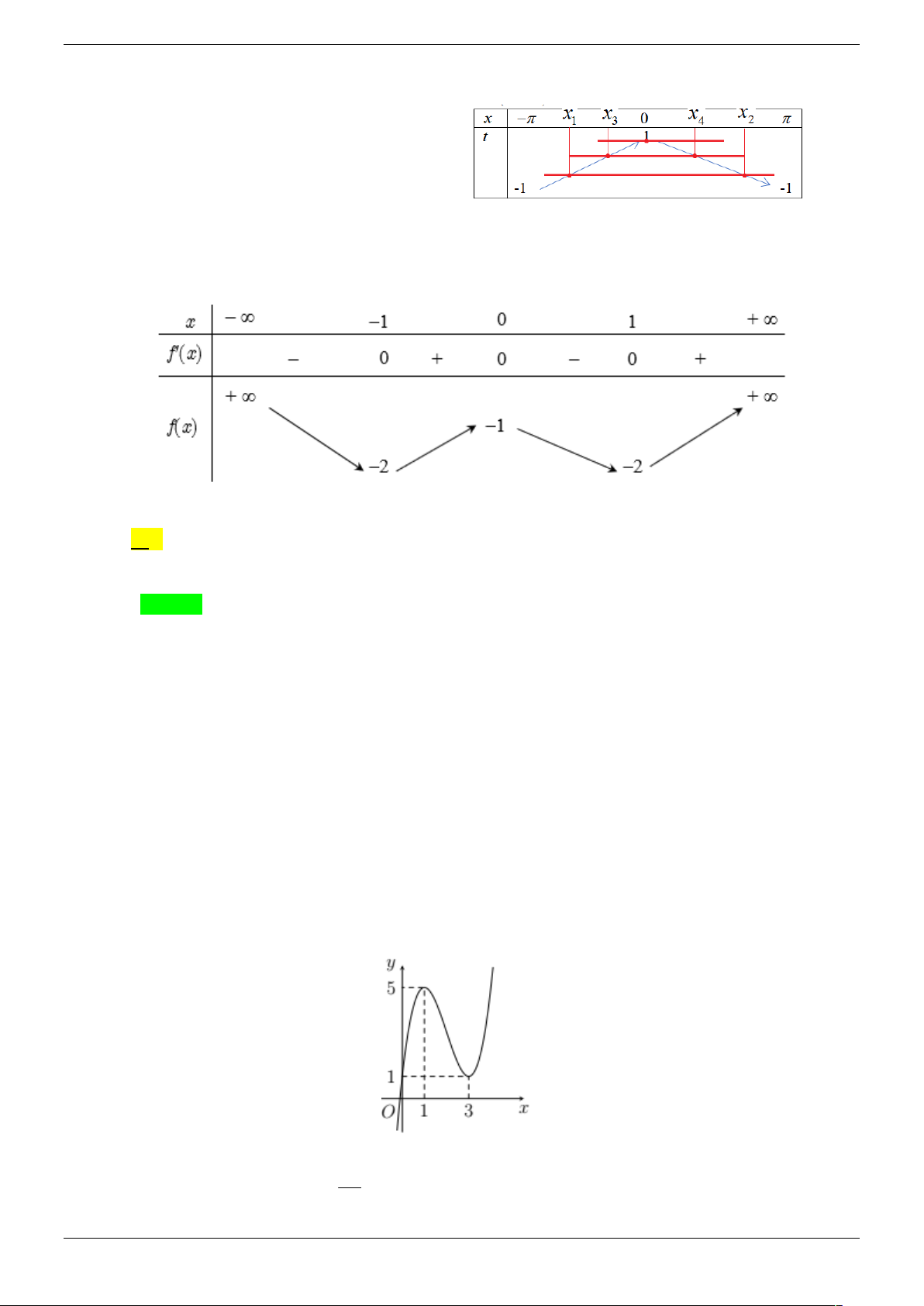
Cho hàm số y f x xác định trên R và có bảng biến thiên như sau –∞ 0 +∞ + 0 – 0 + 0 – 1 1 0
Số nghiệm thuộc đoạn 0;  của phương trình f f  o
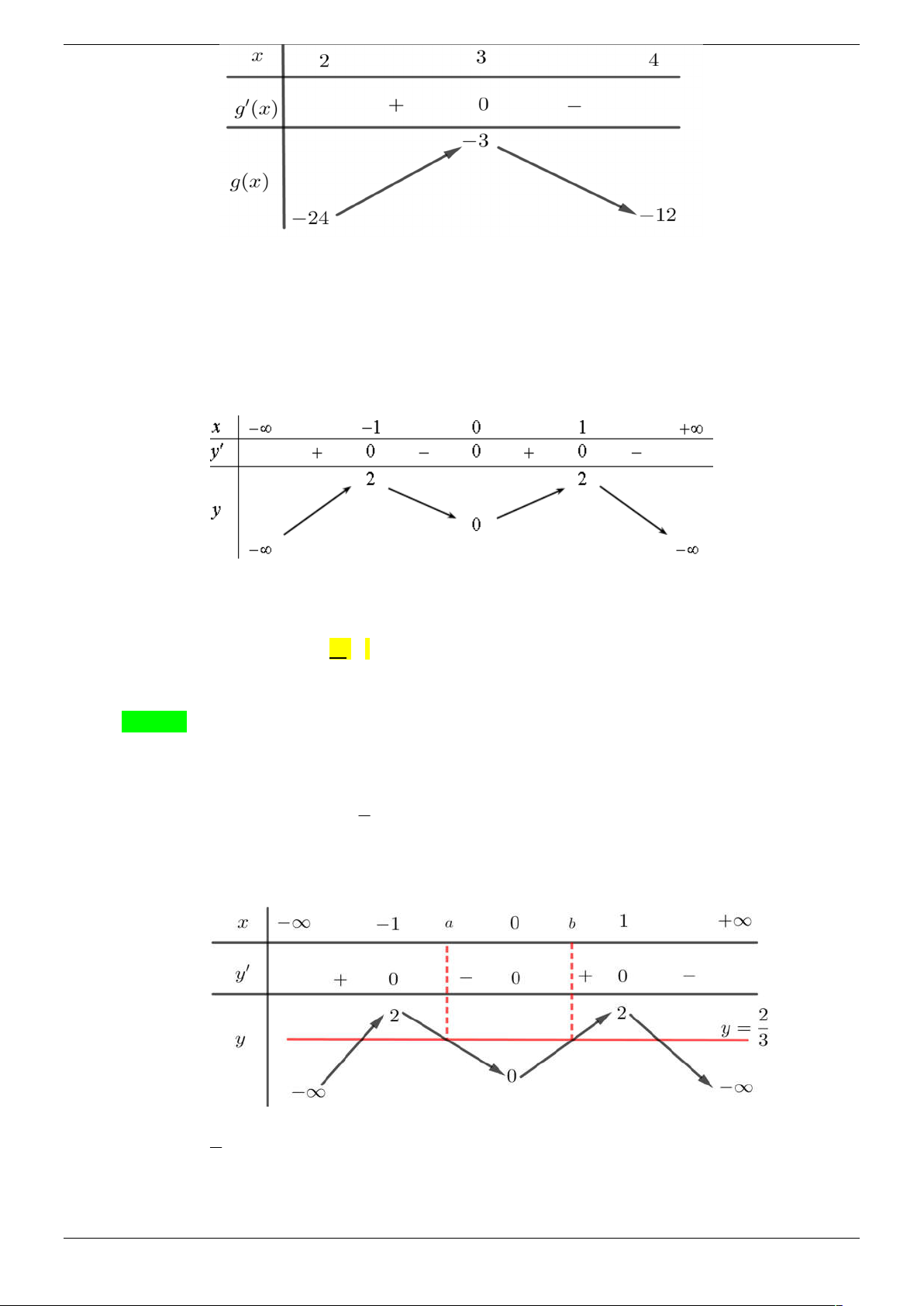
c s2x  0 là A. 4 . B. 2 C. 3 D. 8 Lời giải Chọn B a Strong Team Toán VD – VDC Trang 18/67 x – ∞ -1 0 1 + ∞ -a y' + 0 – 0 + 0 – 1 1 y 0 – ∞ – ∞
Dựa và bảng biến thiên ta có f x  1, x   R và  f  o
c s2x  af f  o
c s2x  0  f  os c 2x  a  với a  1  f  os c 2x  0  Với f  os
c 2x  a thì phương trình vô nghiệm. Với f  o
c s2x  a  o
c s2x =  b với b  1nên phương trình vô nghiệm.    Với f  o
c s2x  0  os2 c x =0  2x 
k  x   k . 2 4 2
Vậy phương trình f f  o
c s2x  0 có 2 nghiệm thuộc đoạn 0; .
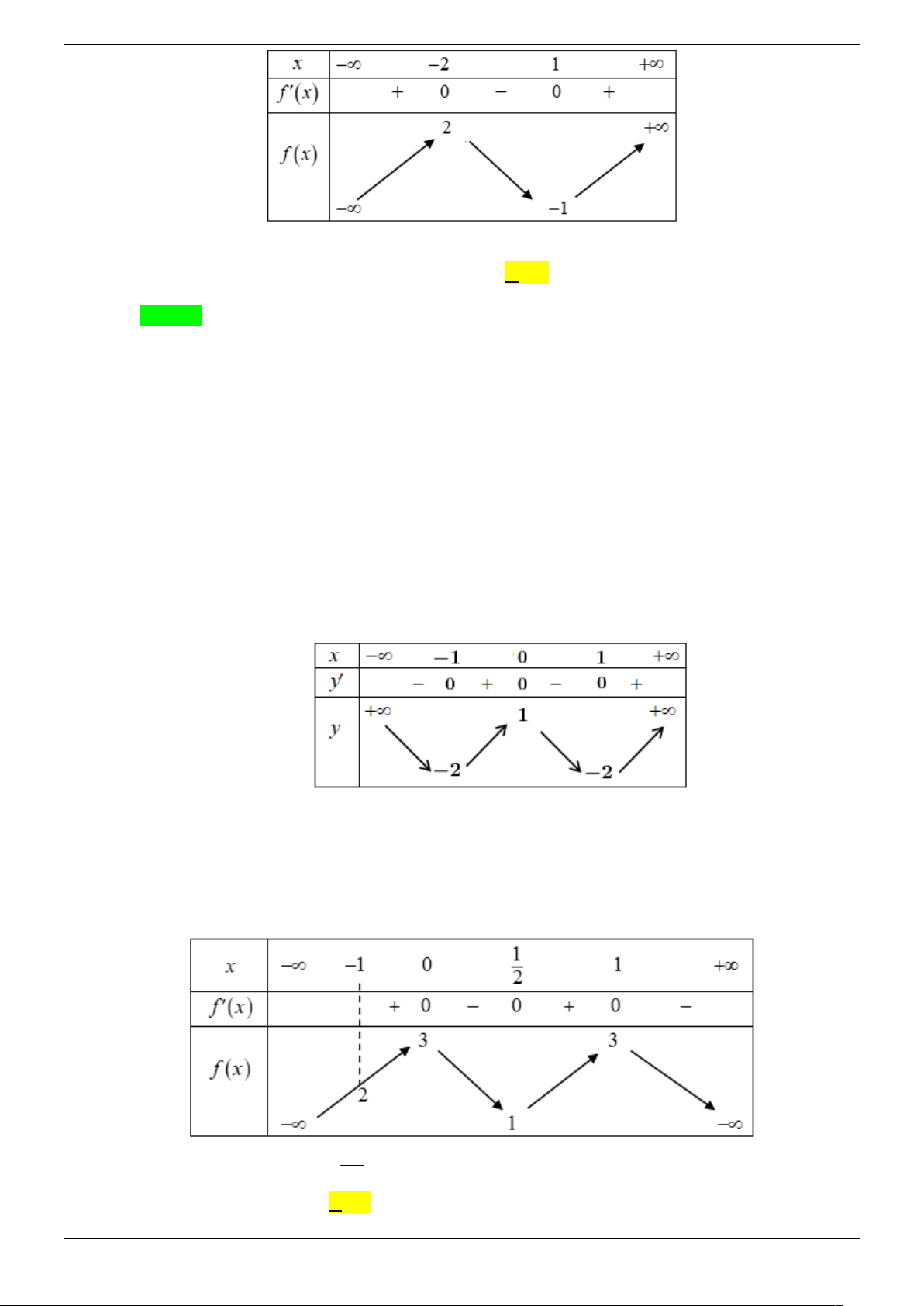
Câu 3. Cho hàm số f (x) liên tục trên đoạn 1; 
3 và có bảng biến thiên như sau: m
Tổng tất cả các số nguyên m để phương trình f (x 1) 
có hai nghiệm phân biệt 2 x  6x 12
trên đoạn 2;4 bằng A. 75  . B. 72  . C. 294  . D. 297  . Lời giải Chọn B.
Phương trình tương đương với: m g x   2 ( )
x  6x 12 f (x 1). Ta có 2
g '(x)  (2x  6) f (x 1)  (x  6x 12) f '(x 1)
2x  6  0; f (x 1)  0
+) Nếu 2  x  3  
g '(x)  0 2
x  6x 12  0; f '(x 1)  0 
+) Nếu x  3  g '(3)  0. f (2)  3. f '(2)  0
2x  6  0; f (x 1)  0
+) Nếu 3  x  4  
g '(x)  0. 2
x  6x 12  0; f '(x 1)  0 
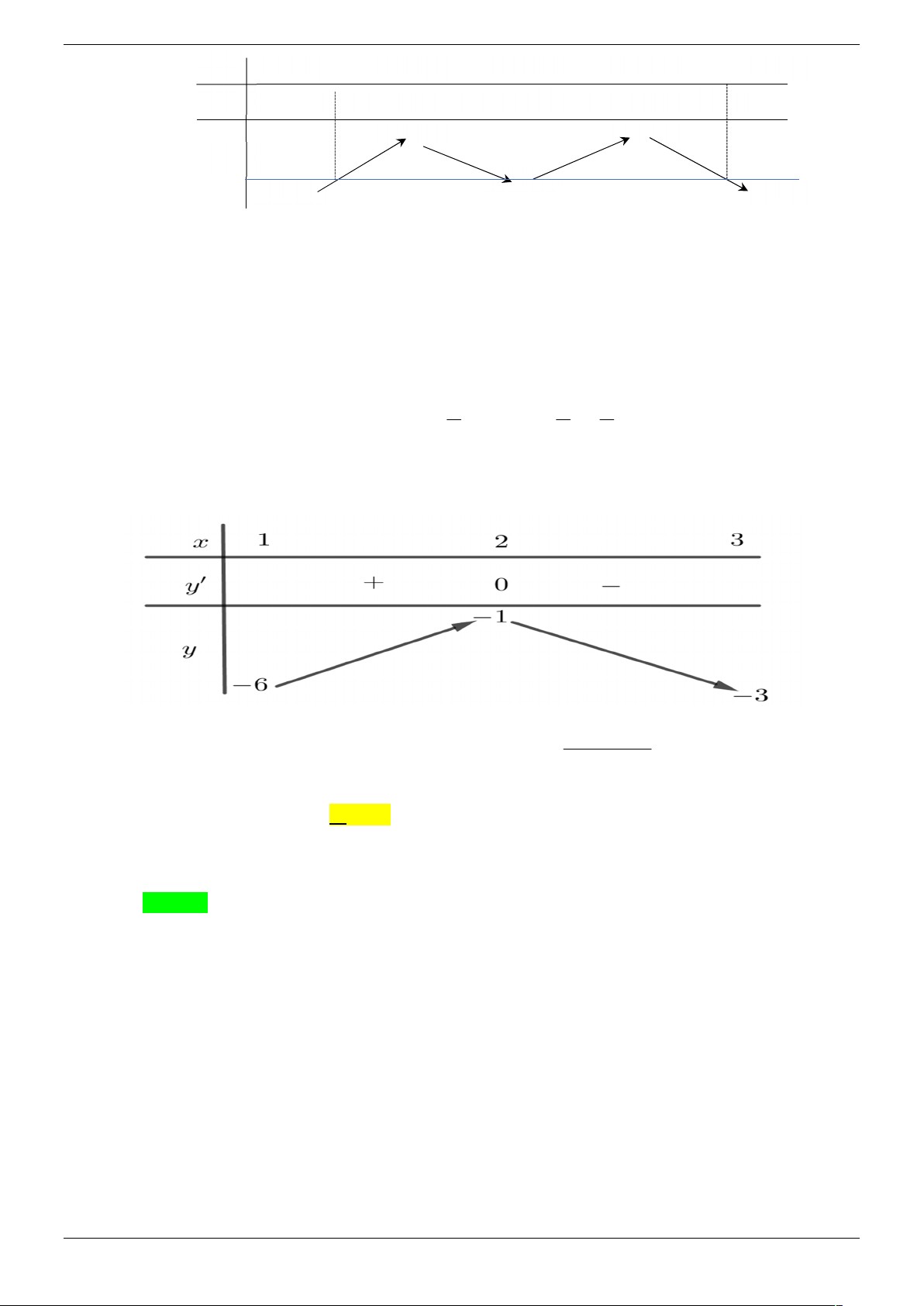
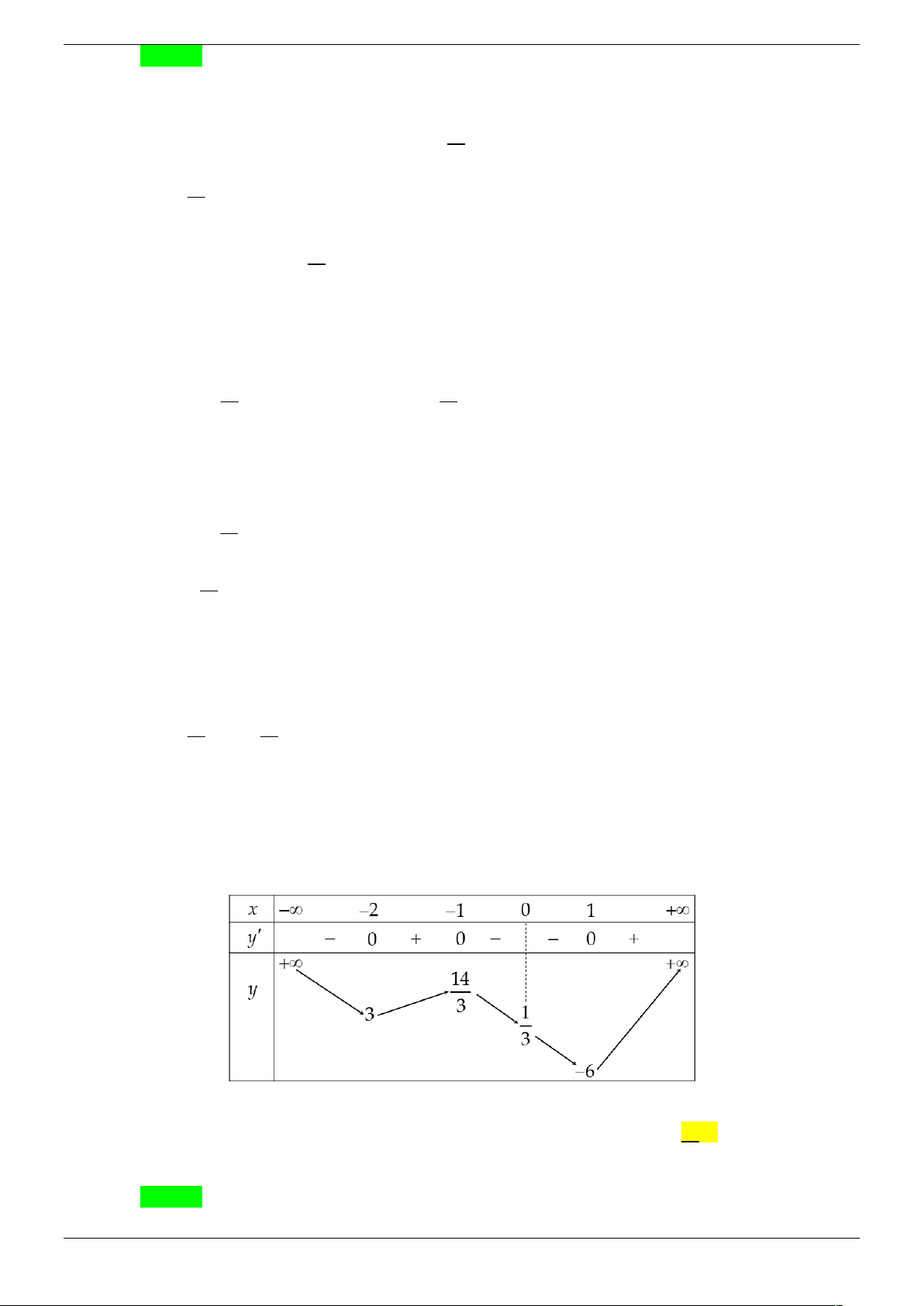
Vậy trên đoạn 2;4 ta có g '(x)  0  x  3. Bảng biến thiên: Strong Team Toán VD – VDC Trang 19/67
Vậy phương trình có hai nghiệm phân biệt trên đoạn
[2; 4]  12  m  3
  m 12,...,   4 .
Tổng các số nguyên cần tìm bằng 1  2  ( 1  1)  ...  ( 5  )  ( 4  )  7  2 Câu 4.
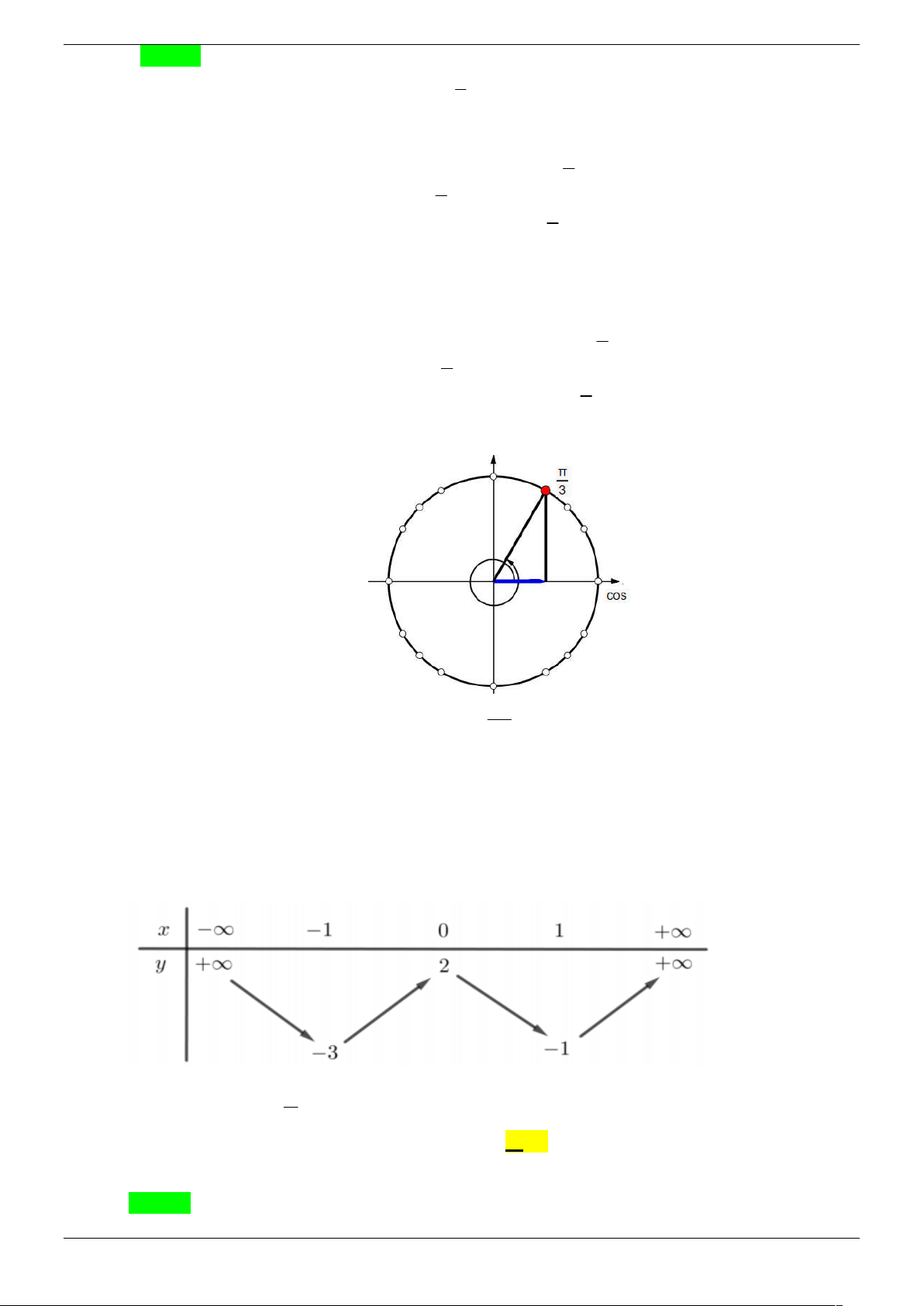
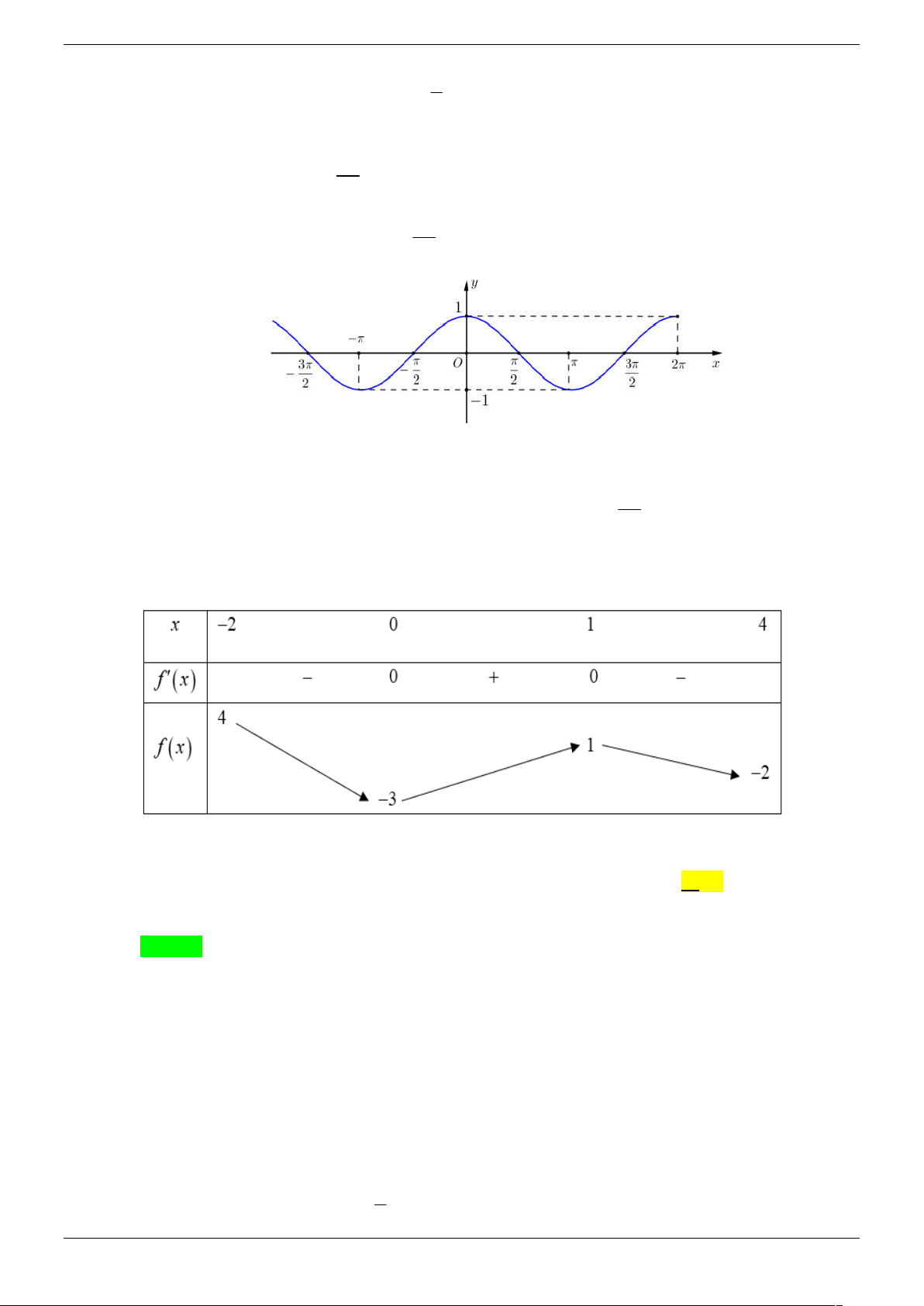
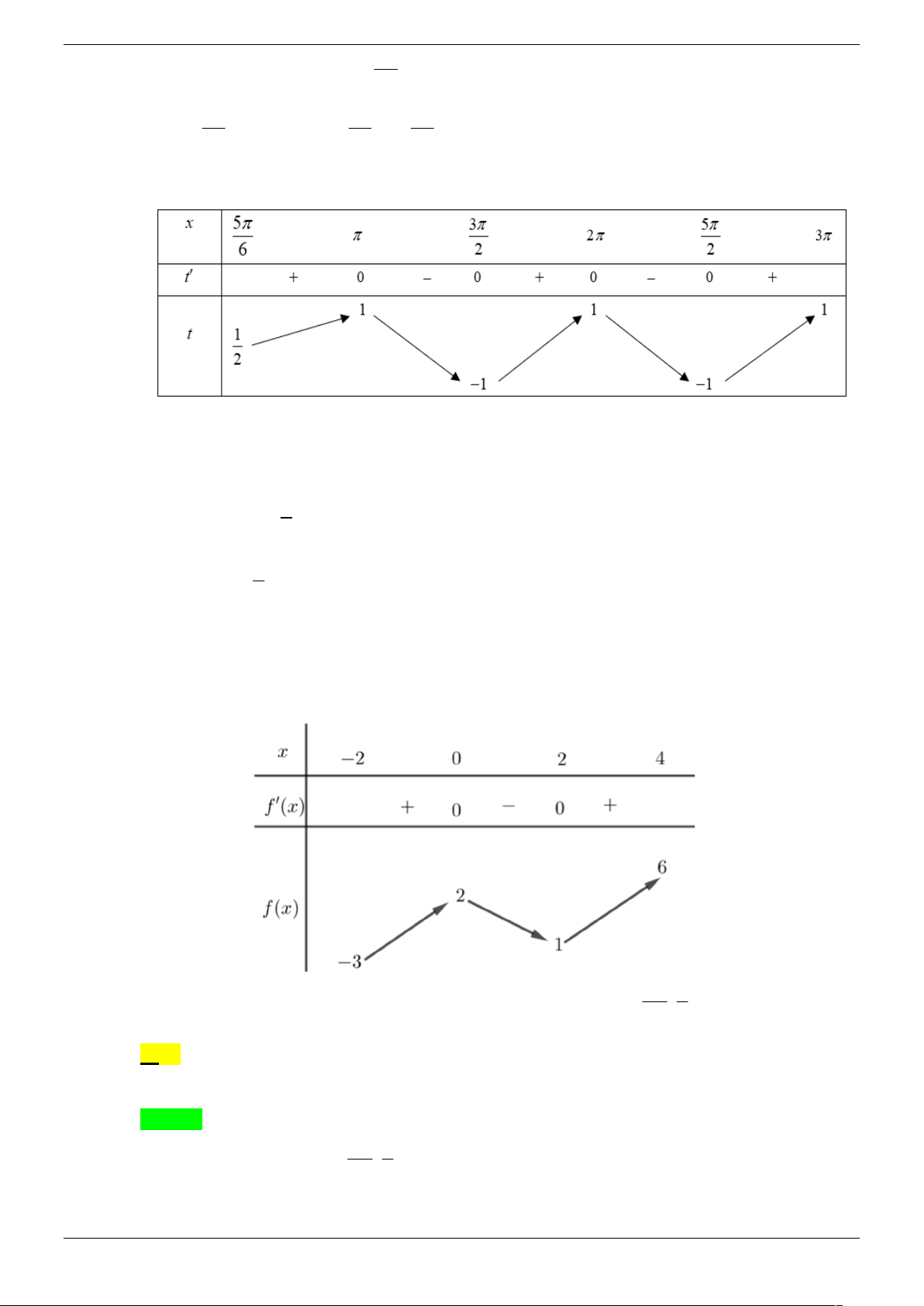
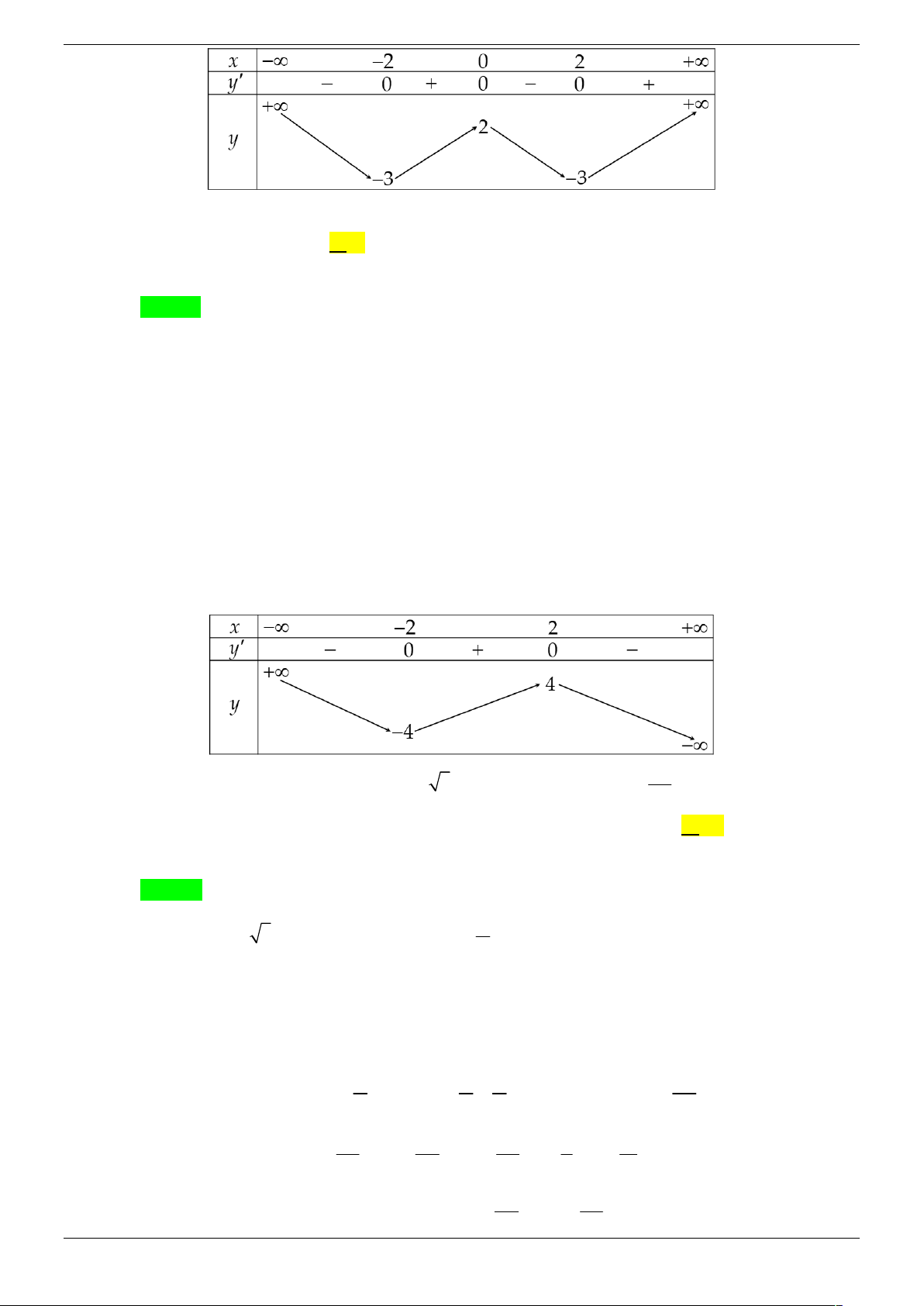
Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0; 2  của phương trình 3 f sin 2x  2  0 là: A. 7 . B. 8 . C. 5 . D. 6 . Lời giải Chọn B.
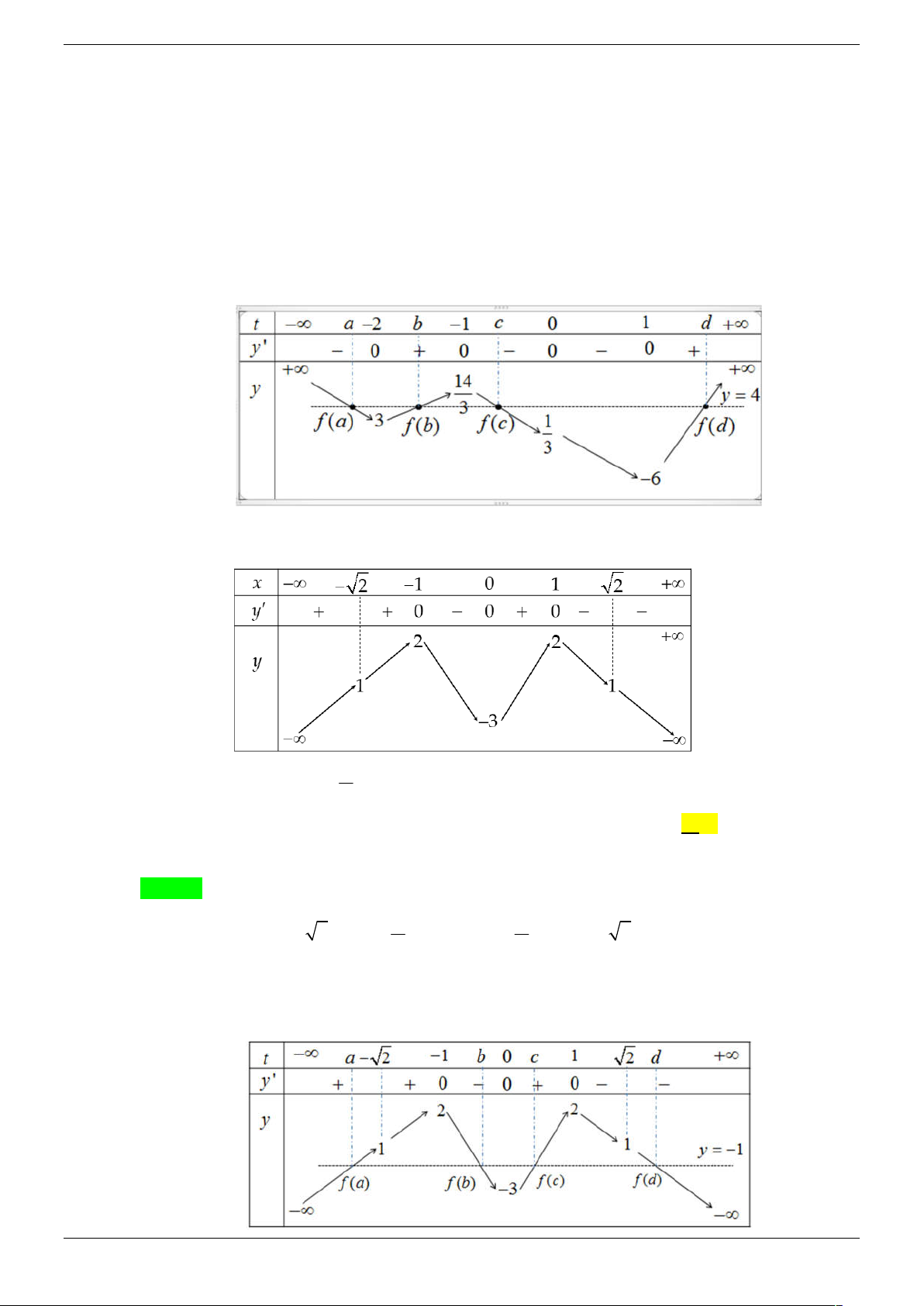
Đặt sin 2x t , x 0; 2   t 1;  1 . 2
Phương trình trở thành: f t   . 3
Từ bảng biến thiên ta có: 2 t a f t     Với 1
  a  0 và 0  b  1 3 t b
Xét BBT của hàm số y  sin 2x trên 0; 2  : Strong Team Toán VD – VDC Trang 20/67
Dựa vào BBT của hàm số ta có
+) Phương trình sin 2x a có 4 nghiệm.
+) Phương trình sin 2x b có 4 nghiệm
Vậy phương trình 3 f sin 2x  2  0 có 8 nghiệm. Câu 5. Cho hàm số 3 2
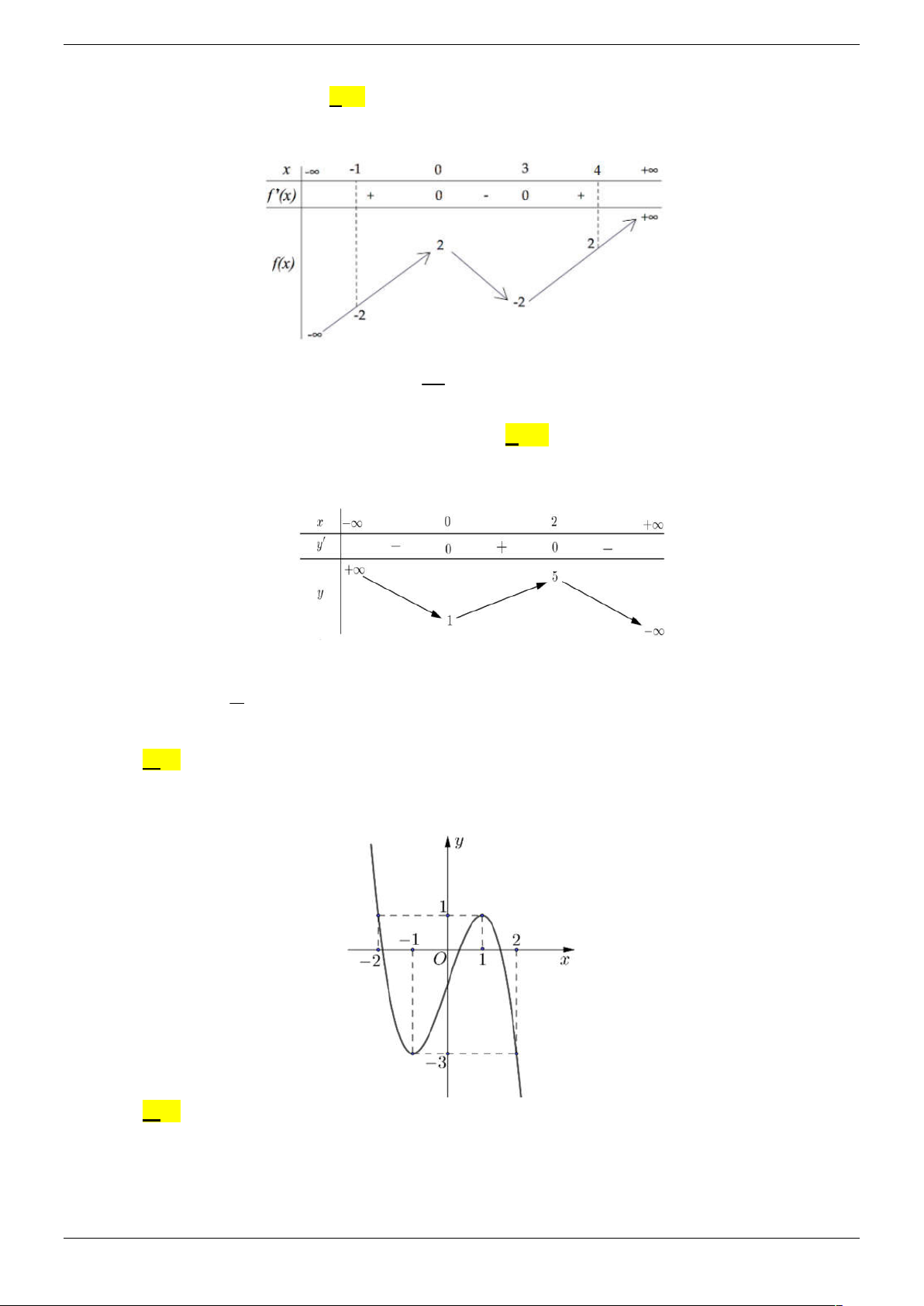
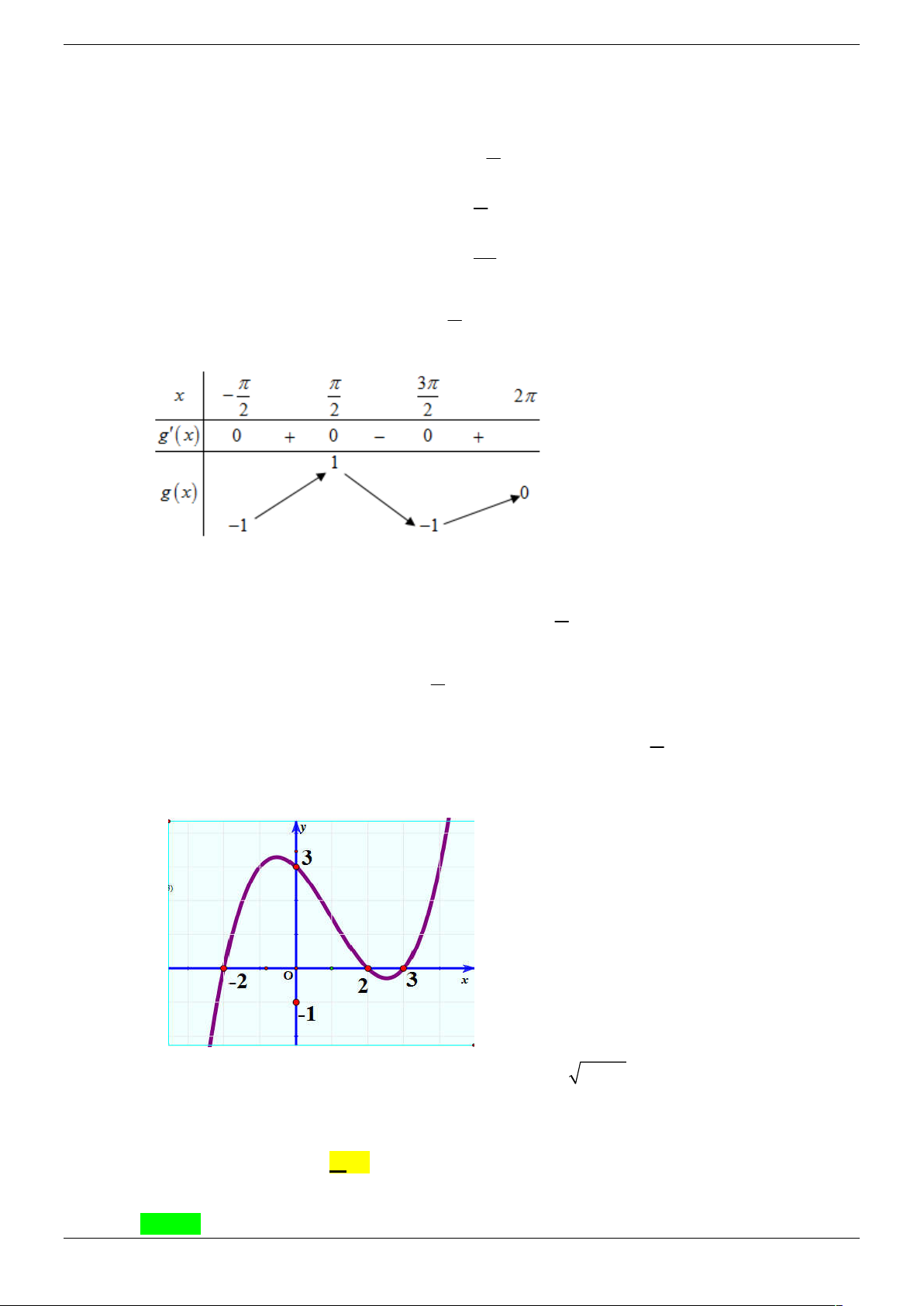
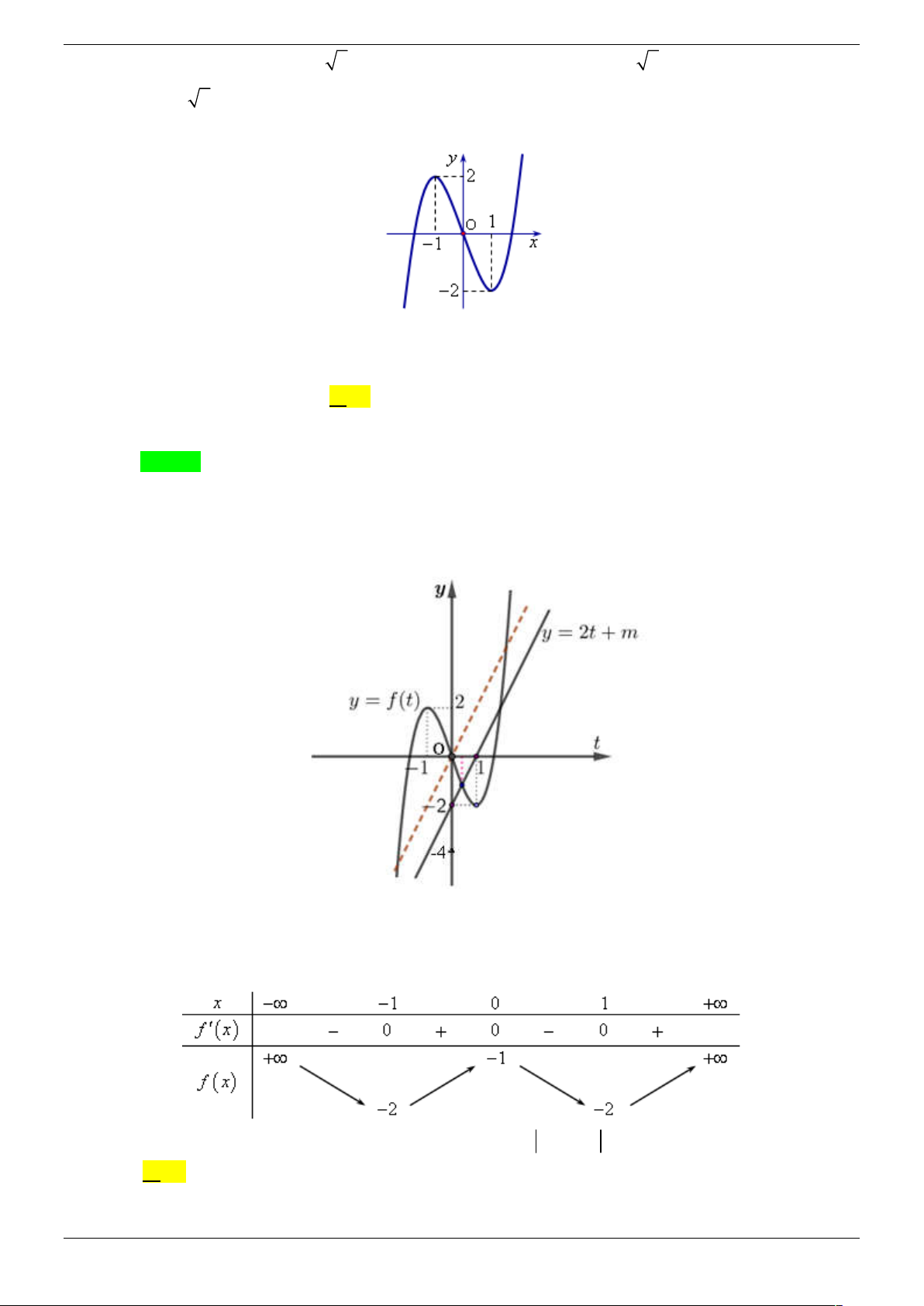
y f (x)  ax bx cx d (a  0) có đồ thị như hình vẽ. Phương trình
f ( f (x))  0 có bao nhiêu nghiệm thực? B. 3 . B. 7 . C. 9 . D. 5 . Lời giải Chọn C
Đặt t f x , phương trình f f x  0 trở thành f t   0  
* (số nghiệm phương trình
* là số giao điểm của đồ thị f x với trục Ox ) . Nhìn vào đồ thị ta thấy phương trình *
có 3 nghiệm t thuộc khoảng  2
 ; 2 , với mỗi giá trị t như vậy phương trình f x  t có 3
nghiệm phân biệt. Vậy phương trình f f x  0 có 9 nghiệm. Vậy chọn C
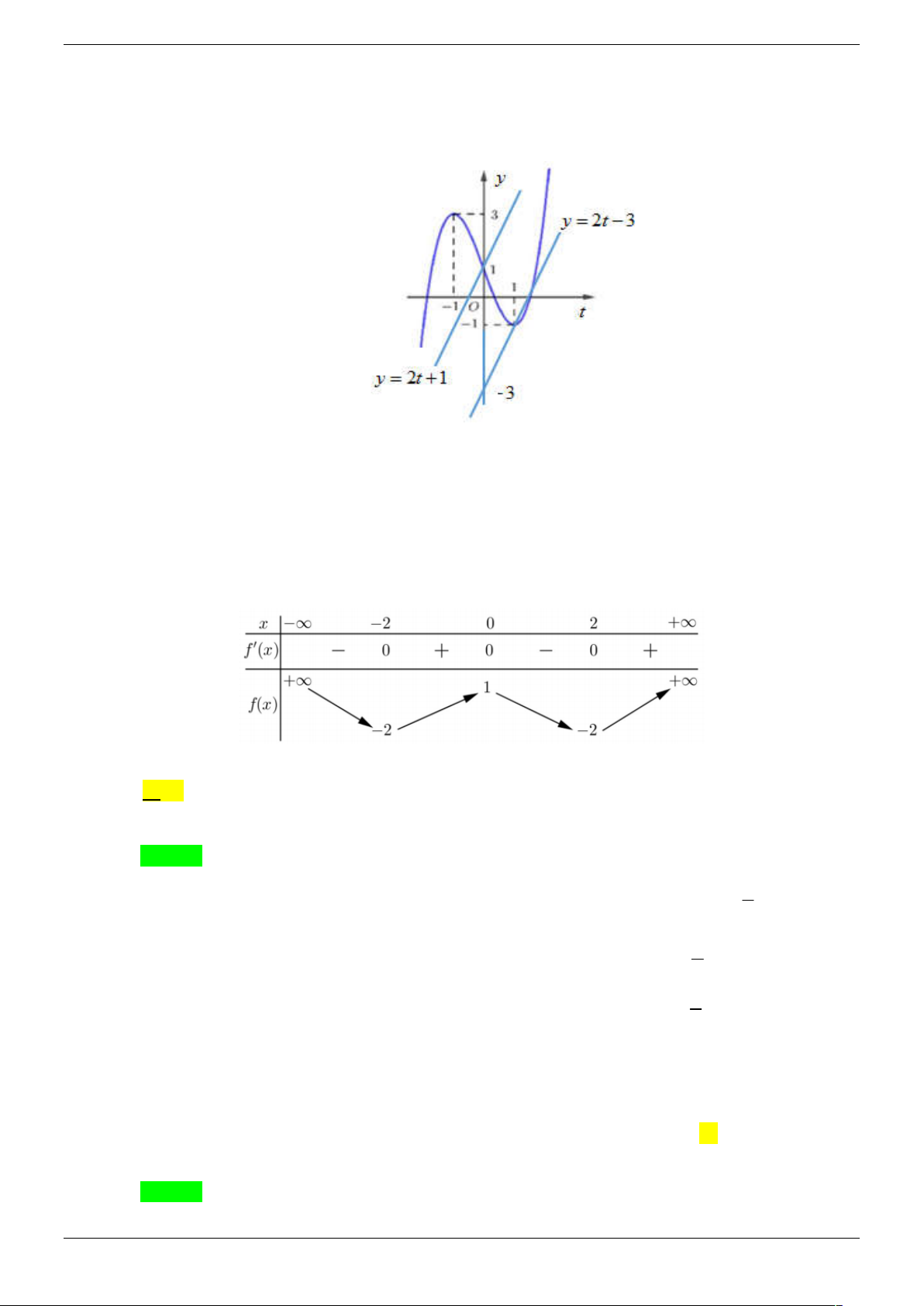
Câu 6. Cho hàm số y f (x) có đồ thị như hình vẽ và lim y   . Hỏi có bao nhiêu điểm trên x
đường tròn lượng giác biểu diễn nghiệm của phương trình f f cos 2x  0 ? Strong Team Toán VD – VDC Trang 21/67 B. 3 . B. 4 . C. 2 . D.1. Lời giải Chọn B
Từ đồ thị ta có f x  1, x
   và suy ra được f cos 2x   a a  
1 hoặc f cos 2x  0
TH1: Nếu f cos 2x  a  1 thì phương trình này vô nghiệm.
TH2: Nếu f cos 2x  a  1
 thì cos 2x  1, phương trình này vô nghiệm.
cos 2x  a (VN )
TH3: Nếu f cos 2x  0   cos 2x  0   k
cos 2x  0  x  
(k Z ) nên có 4 điểm trên đường tròn lượng giác. Vậy có 4 điểm. 4 2 Câu 7.
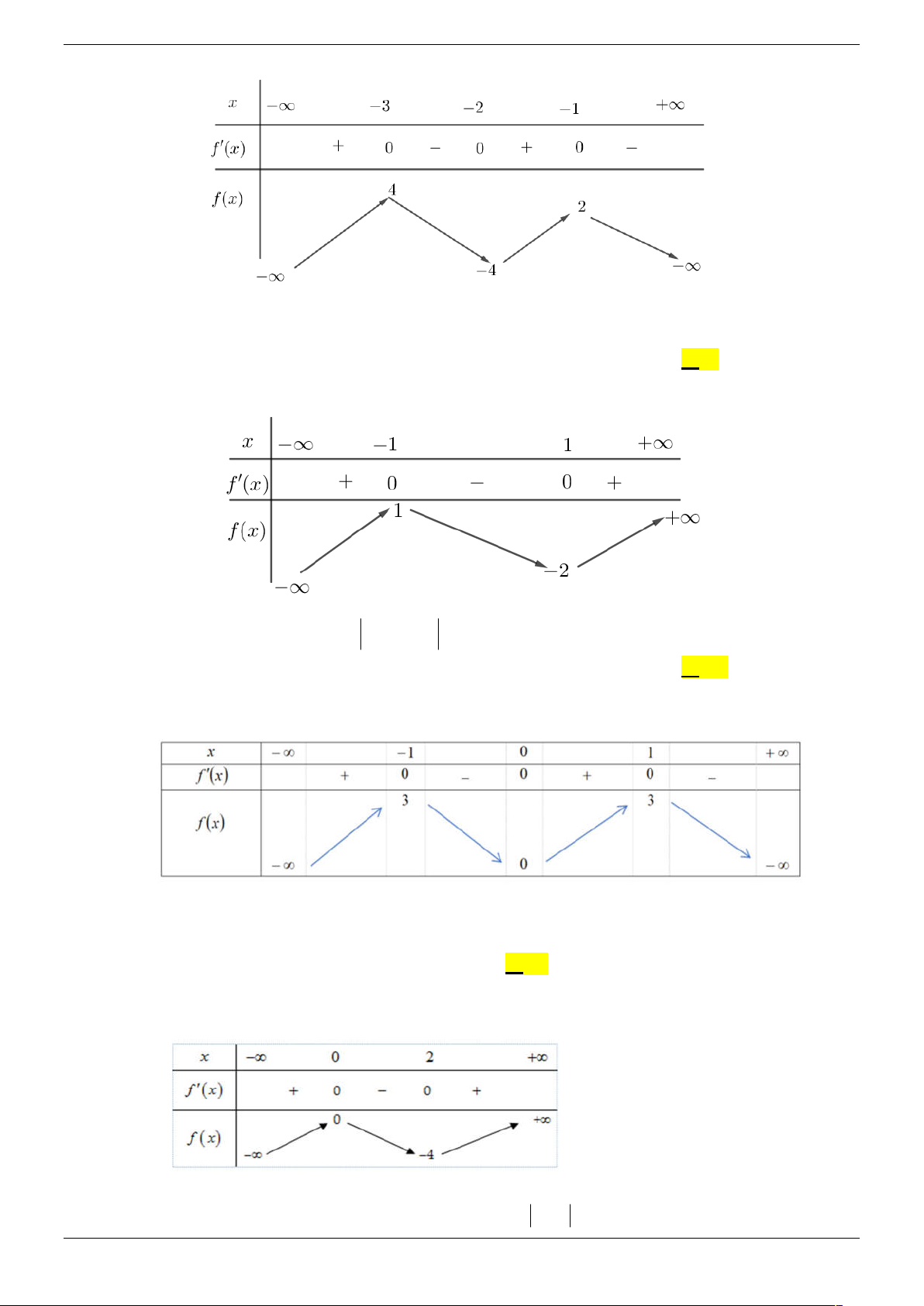
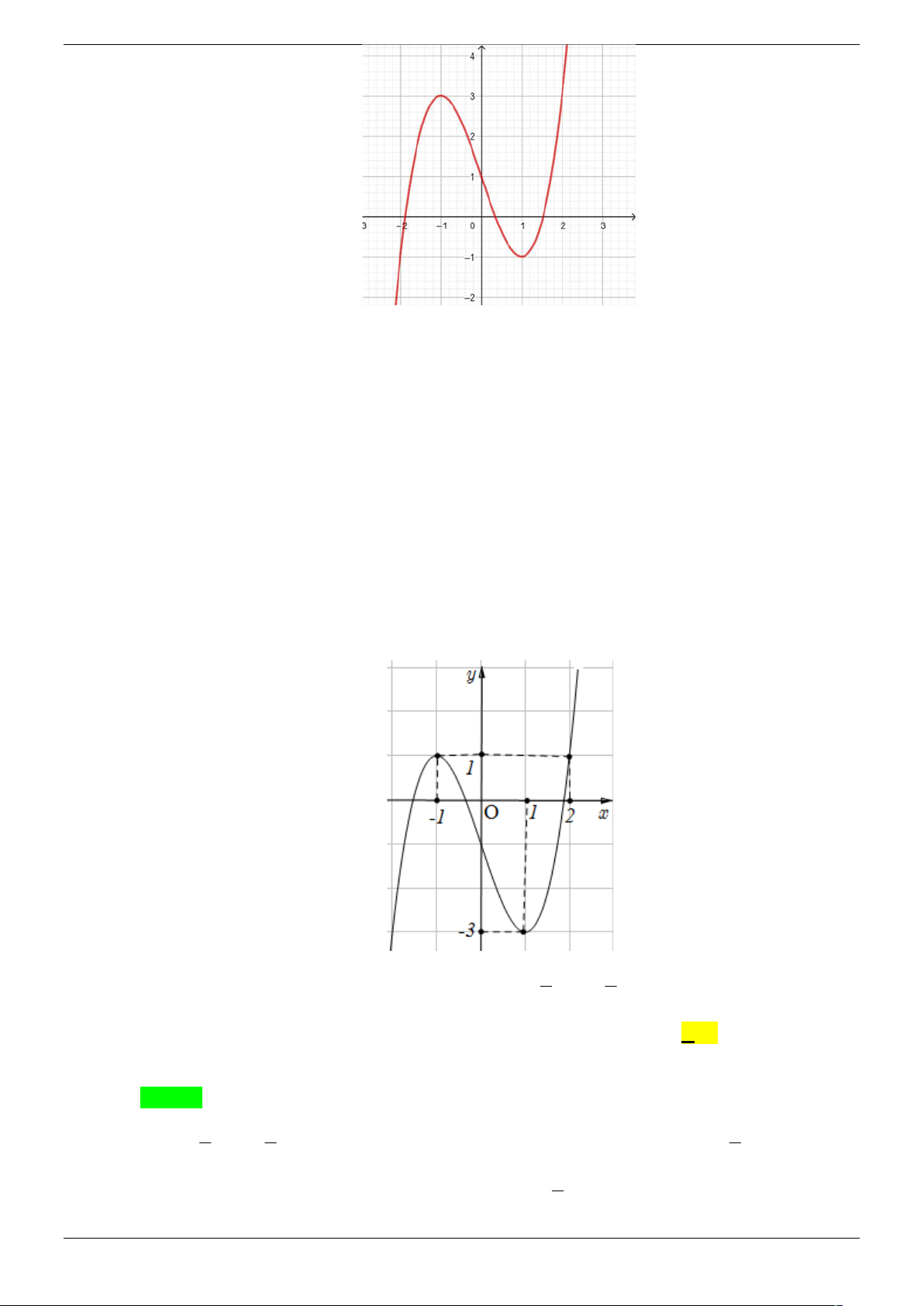
Cho hàm số y f x có đồ thị như hình vẽ:
Khi đó phương trình f  4 4
3x   3  0 có bao nhiêu nghiệm dương? A. 2. B. 4. C. 5. D. 1. Lời giải Chọn A
Bảng biến thiên của hàm số 4 y  3x : 4
3x x , x  1;0 1 1   3  Ta có: 4 f  4
3x   3  0  f  4 3x  4 
 3x x , x  0;1 . 2 2   4  4
3x x , x  1; 2  3 3   
Dựa vào bảng biến thiên ta có 4
3x x vô nghiệm; 4
3x x có một nghiệm âm một nghiệm 1 2 dương; 4
3x x có một nghiệm âm một nghiệm dương. 3
Vậy phương trình f  4 4
3x   3  0 có 2 nghiệm dương.
Câu 8. Cho hàm số y f x có đồ thị như hình vẽ: Strong Team Toán VD – VDC Trang 22/67
Phương trình 2 f cos x  1  0 có bao nhiêu nghiệm trong đoạn  
 ; 2  đồng thời tan x  0 ? A. 3 . B. 4. C. 5. D. 6. Lời giải Chọn A cos x x , x  ; 1  VN 1 1    
cos x x , x  1;0 1  2 2  
2 f cos x 1  0  f cos x   . 2
cos x x , x  0;1 3 3   
cos x x , x  1; VN  4 4             3 
Vì tan x  0 và x  
 ; 2  nên khi đó x    ;  0;   ;       * .  2   2   2          3 
Bảng biến thiên của hàm số y  cos x trên x    ;  0;   ;        2   2   2 
Dựa vào bảng biến thiên ta có:
Phương trình cos x x với x  1;0 có 2 nghiệm thỏa * . 2   2
Phương trình cos x x với x  0;1 có 1 nghiệm thỏa * . 3   3
Vậy có 3 nghiệm x thỏa yêu cầu bài toán. Câu 9.
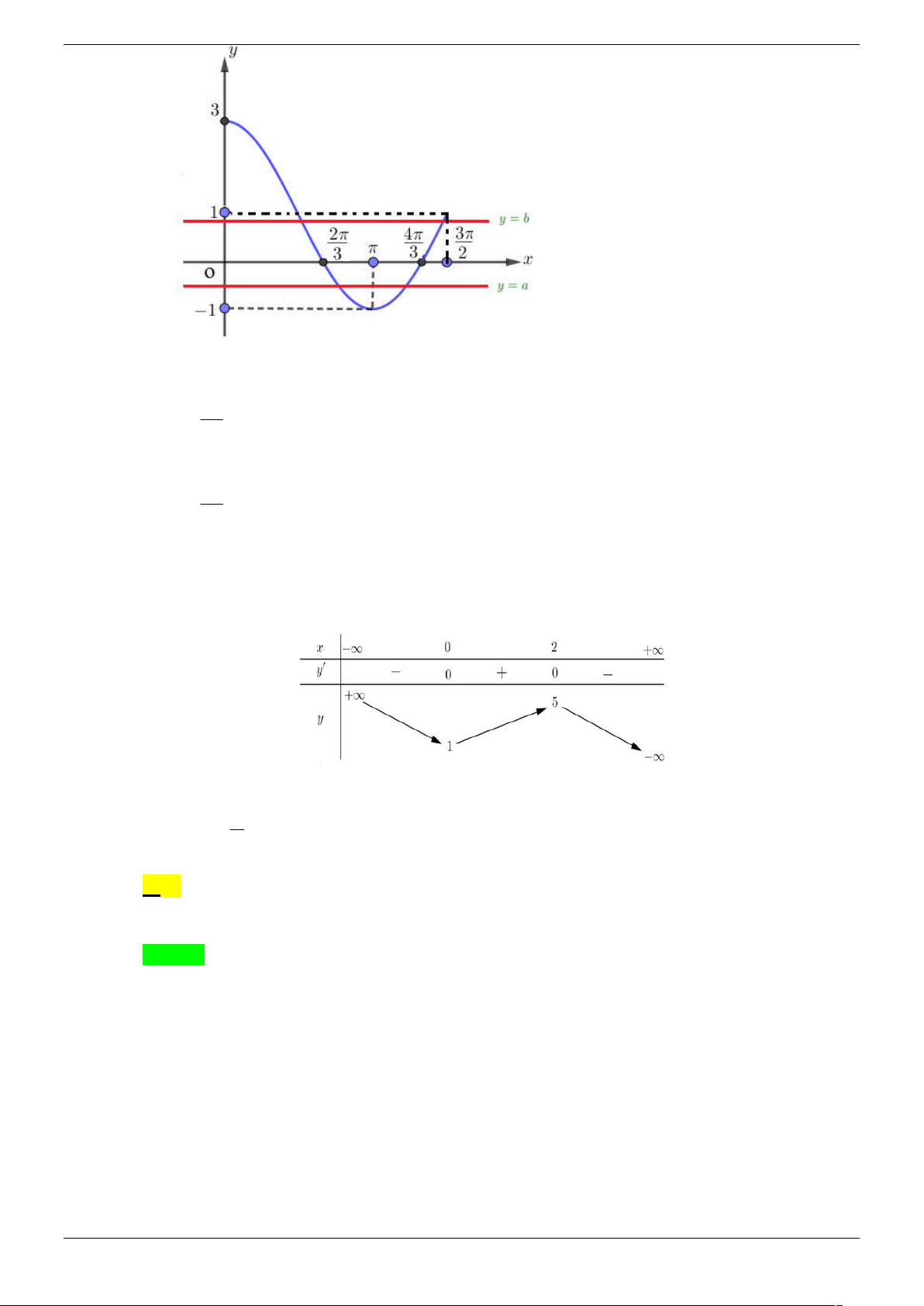
Cho hàm số y f x có đồ thị như hình vẽ. y 1 1  1 O x 1  Strong Team Toán VD – VDC Trang 23/67   5 
Số nghiệm của phương trình 2 f sin x 1  0 trên đoạn  ;  là 2 2    A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn D 1
Đặt t  sin x , t  1  ; 
1 ta được: f t  . 2
t a, (1  a  0)
Dựa vào đồ thị ta có  t  ,
b 0  b   1    5 
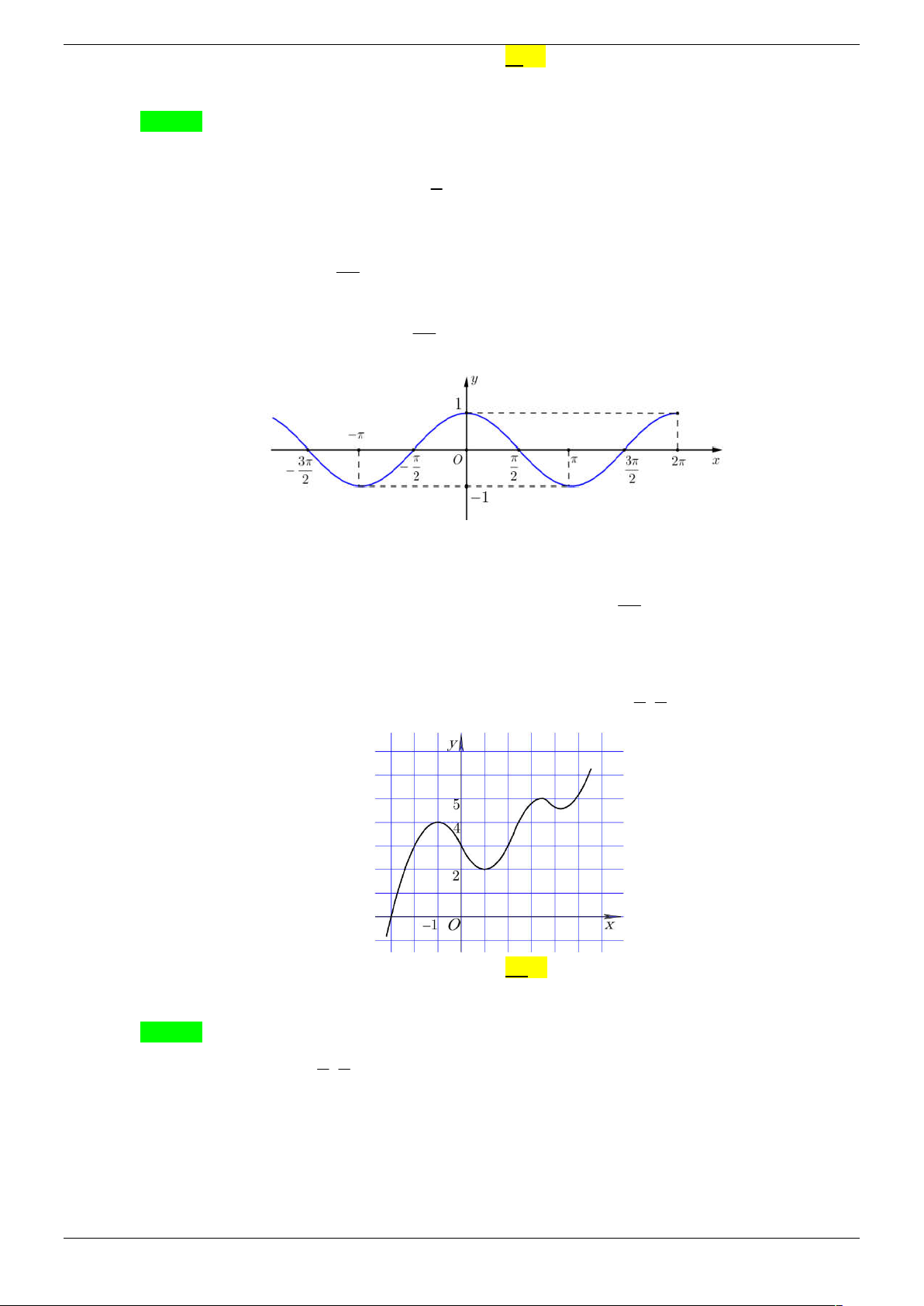
Xét hàm số g x  sin x trên đoạn  ;  2 2      5 
Đồ thị của hàm số g x  sin x tên đoạn  ;  là 2 2      5 
Dựa vào đồ thị ta có sin x a có 3 nghiệm trên  ; 
, sin x b có 3 nghiệm trên 2 2      5   ;  . 2 2      5 
Vậy phương trình 2 f sin x 1  0 có 6 nghiệm trên  ;  . 2 2   
Câu 10. Cho hàm số y f x có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn 0;5  của phương trình f cos x  1 A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn C
Đặt t  cos x , t  1  ; 
1 ta được f t   1  t a với a 0  ;1 Strong Team Toán VD – VDC Trang 24/67
Xét hàm số g x  cos x trên đoạn 0;5 
Đồ thị của hàm số g x  cos x tên đoạn 0;5  là
Dựa vào đồ thị ta có cos x a có 5 nghiệm trên 0;5 
Vậy phương trình f cos x  1 có 5 nghiệm trên 0;5  .
Câu 11. Cho hàm số f x xác định trên  \  
0 và có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình 3 f 2x   1 10  0 là. A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn C 10
Đặt t  2x 1, ta có phương trình trở thành f t  
. Với mỗi nghiệm t thì có một nghiệm 3 t 1 10 x
nên số nghiệm t của phương trình f t   bằng số nghiệm của 2 3
3 f 2x   1 10  0 .
Bảng biến thiên của hàm số y f x là 10
Suy ra phương trình f t  
có 4 nghiệm phân biệt nên phương trình 3 f 2x   1 10  0 3 có 4 nghiệm phân biệt.
Câu 12. Cho hàm số y f x liên tục trên  và có bảng biến thiên như hình vẽ Strong Team Toán VD – VDC Trang 25/67
Tập hợp các giá trị m để phương trình f cos 2x  2m 1  0 có nghiệm thuộc khoảng      ;   là:  3 4   1   1   1 1   2  2 1  A. 0;  B. 0;  C. ;  D.  ;  2       2   4 2   4 4    Lời giải Chọn A       1 
Đặt cos 2x t, x  ;  t   ;1    . 3 4 2       1 
Yêu cầu đề bài tương đương với phương trình f t   2m 1 có nghiệm t   ;1  . 2    1
Từ bảng biến thiên suy ra yêu cầu  1  2m 1  2  0  m  . 2
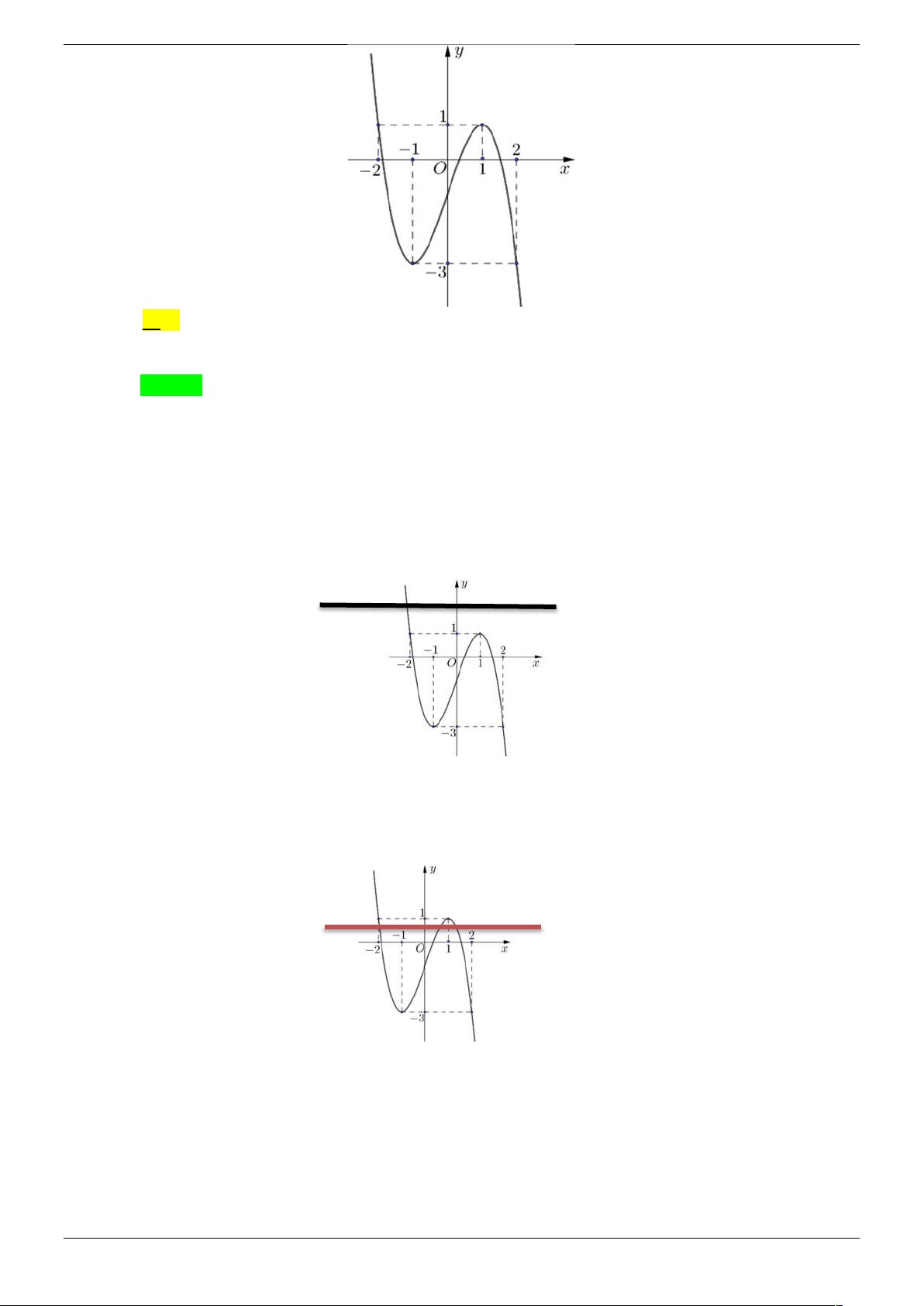
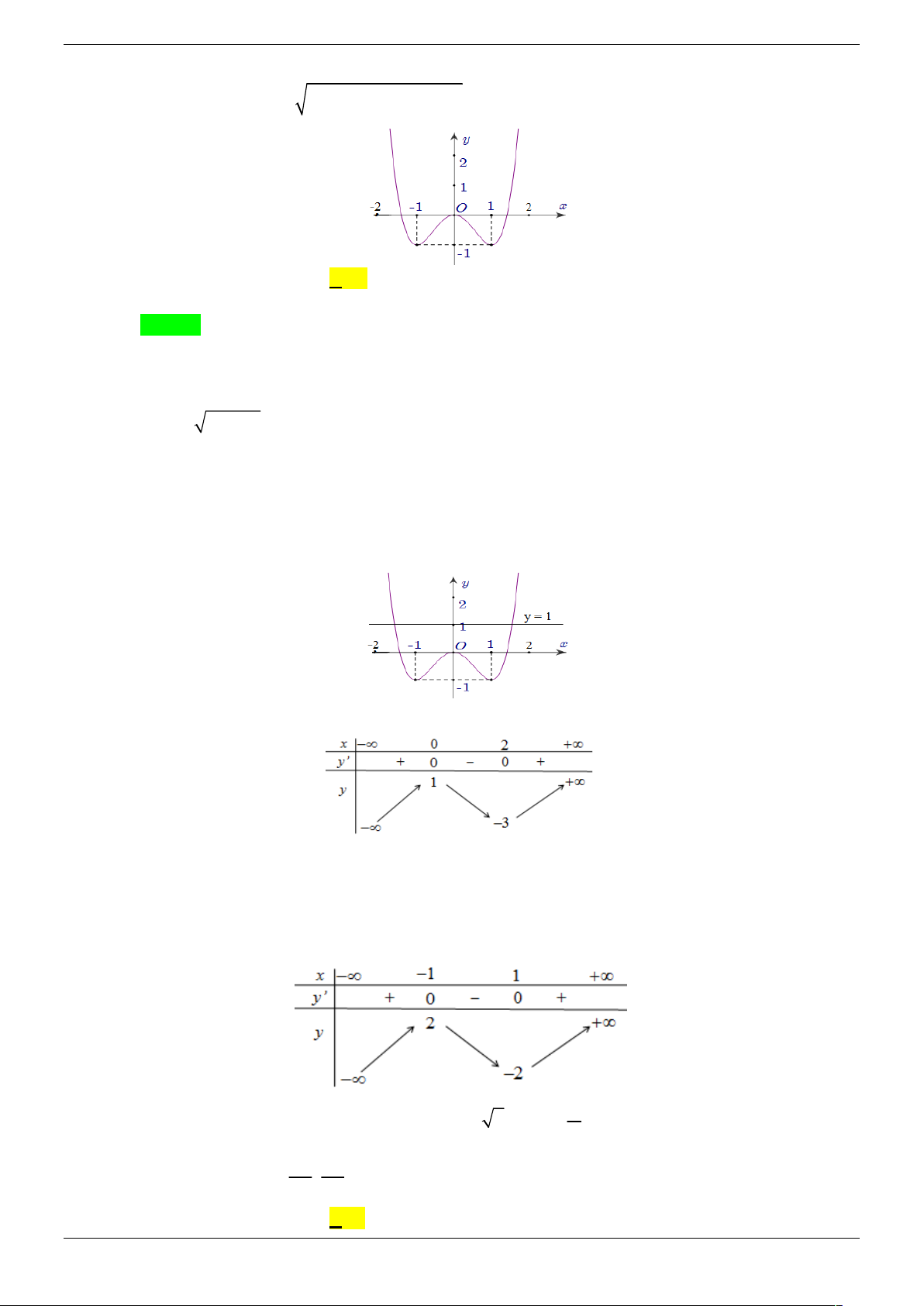
Câu 13. Cho hàm số y f x liên tục trên  có đồ thị như hình vẽ bên. Phương trình
f 3  2 f x 1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6 . B. 5 . C. 7 . D. 4. Lời giải Chọn D  
  f xf x 2 3 2  1 
Dựa vào đồ thị ta có: f 3  2 f x 1     .  f x 1 3 2 2    f   x   2
Mà f x  2 có 1 nghiệm duy nhất lớn hơn 2 . 1
Và f x  có 3 nghiệm phân biệt x  2  ; 1  , x  1  ;0 , x  1; 2 3   2   1   2 Strong Team Toán VD – VDC Trang 26/67
Vậy phương trình có 4 nghiệm thực phân biệt.
Câu 14. Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  
 ; 2  của phương trình 2 f cos x 1  0 là: A. 7 . B. 4 . C. 5 . D. 6 . Lời giải Chọn D
Đặt cos x t , x  
 ; 2   t 1;  1 . 1
Phương trình trở thành: f t   . 2
Từ bảng biến thiên ta có: 1 t a f t     Với 1
  a  0 và 0  b  1 2 t b
Dựa vào đồ thị y  cos x ta có :
+) cos x a có 3 nghiệm.
+) cos x b có 3 nghiệm
Vậy phương trình 2 f cos x 1  0 có 6 nghiệm.
Câu 15. Cho hàm số f x có bảng biến thiên như sau: Strong Team Toán VD – VDC Trang 27/67
Số nghiệm của phương trình f  4 2
3x  6x   1 1 là A. 4 . B. 5 . C. 6 . D. 3 . Lời giải Chọn C
x a   ;  2 
Dựa vào bảng biến thiên, ta có f x  1  x b   2  ;1 .
x c1;  4 2
3x  6x 1  a (1)  Do đó f  4 2
3x  6x   4 2
1  1  3x  6x 1  b (2)   4 2
3x  6x 1  c (3) 
Xét hàm số g x 4 2
 3x  6x 1 x  1 Có g x 3 12x 12x 0       x  0 . x 1  Bảng biến thiên:
Dựa vào bảng biến thiên, có:
- Phương trình (1) vô nghiệm.
- Phương trình (2) có đúng 4 nghiệm phân biệt.
- Phương trình (3) có đúng 2 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 6 nghiệm.
Câu 16. Cho hàm số f x có bảng biến thiên như sau:  7 
Số nghiệm thuộc đoạn 0;
2. f cos x 5  0  của phương trình   là 3    A. 8 . B. 7 . C. 5 . D. 6 . Lời giải Strong Team Toán VD – VDC Trang 28/67 Chọn B Xét phương trình
f x    f x 5 2. 5 0  . 2
x a   1  ; 0    1  x b  0;   5   2 
Dựa vào bảng biến thiên, ta có f x    . 2   1  x c  ;1     2  
x d  1;  
cos x a  1;0 (1)    1 
cos x b  0; (2)   5   2 
Do đó 2. f cos x  5  0  f cos x    . 2   1  cos x c  ;1 (3)     2  
cos x d  1;  (4)   7 
Dựa vào đường tròn lượng giác, trên đoạn 0;  ta có: 3   
- Phương trình (1) có đúng 2 nghiệm phân biệt.
- Phương trình (2) có đúng 2 nghiệm phân biệt.
- Phương trình (3) có đúng 3 nghiệm phân biệt.
- Phương trình (4) vô nghiệm.
Vậy phương trình đã cho có tất cả 7 nghiệm.
Câu 17. Cho hàm số f (x) có bảng biến thiên bảng biến thiên như sau Số nghiệm thuộc [ 
; 2 ] của phương trình f (s inx) 1  0 là 2 A. 3 . B. 6 . C. 4 . D. 5 . Lời giải Chọn C Strong Team Toán VD – VDC Trang 29/67 sin x  1 
Ta có f (s inx) 1  0  f (sin x)  1
  sin x a  ( 1  ; 0) 
sin x b  1     x    2  
g x  sin x g x  0  cos x  0    x   2  3 x   2   
Ta có bảng biến thiên hàm g x trên  ; 2  như sau: 2   
Từ bảng biến thiên trên, ta thấy các phương trình sin x b vô nghiệm.   
Phương trình sin x a có 3 nghiệm phân biệt thuộc  ; 2  2      
Phương trình sin x  1 có 1 nghiệm  ; 2 
Và các nghiệm trên phân biệt. 2      
Vậy phương trình f sin x 1  0 có 4 nghiệm phân biệt thuộc  ; 2  . 2   
Câu 18. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới
Tìm số giá trị nguyên của tham số m để phương trình 2
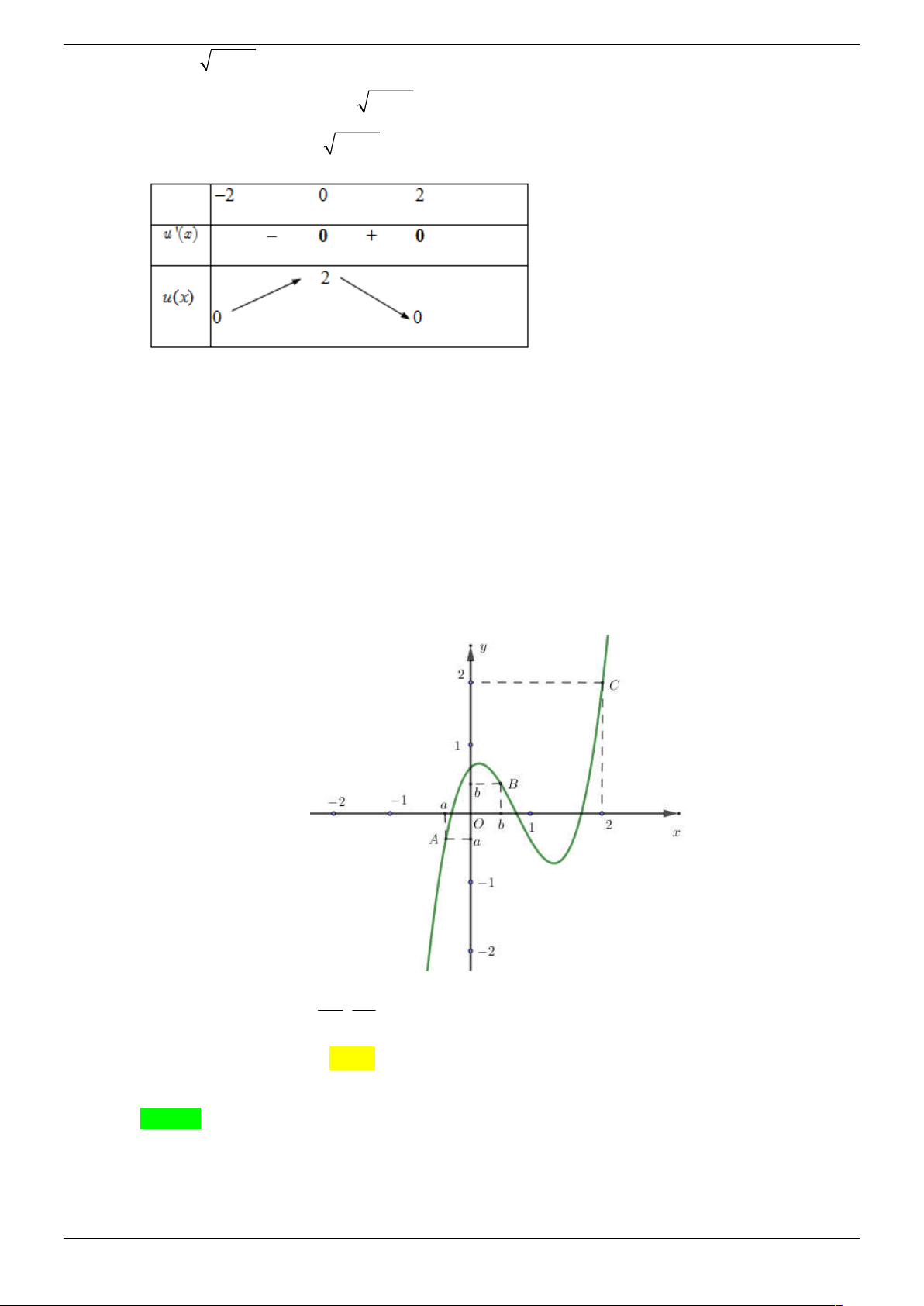
f ( 4  x )  m có hai nghiệm phân biệt A. 2 . B. 3 . C. 1. D. 4 . Lời giải Chọn B Strong Team Toán VD – VDC Trang 30/67 Đặt 2 t
4  x , phương trình thành f (t)  m Lập BBT của hàm số 2 u(x) 
4  x , x [  2; 2] BBT của hàm số 2 u(x) 
4  x , x [  2; 2]
Ta được t  [0; 2]
Ta thấy rằng t [0 ; 2) nghiệm mỗi t tạo ra 2 nghiệm nghiệm x
t  2 thì nghiệm x  0 Từ hình vẽ ta thấy :
+ m  0 : được nghiệm t  2 tạo ra 1 nghiệm x
+ m  1, 2, 3 thỏa
Vây có ba giá trị m nguyên của tham số thỏa mãn Câu 19. Cho hàm số   3 2
f x ax bx bx c có đồ thị như hình vẽ:    9  Số nghiệm nằm trong ; 
 của phương trình f cos x  
1  cos x 1 là  2 2  A. 6 . B. 10. C. 4 . D. 8 . Lời giải Chọn B Strong Team Toán VD – VDC Trang 31/67
x a  ;0 
Từ đồ thị ta có f x  x x b   0  ;1 x  2 
cos x 1  a   ;  0
cos x a 1  t   ;  1 (VN ) 1    
Do đó f cos x  
1  cos x 1  cos x 1  b   0  ;1
 cos x b 1  t  1  ; 0 (1)  2   cos x 1  2   cos x  1 (2)     9 
Dựa vào đường tròn lượng giác, phương trình (1) có 4 nghiệm nằm trong ;   .  2 2     9 
Phương trình (2) có 6 nghiệm nằm trong ;   .  2 2     9 
Vậy phương trình ban đầu có tất cả 10 nghiệm nằm trong ;   .  2 2 
Câu 20. Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0;5  của phương trình f sin x 1 là A. 6 . B. 4 . C. 10 . D. 8 . Lời giải Chọn C
Từ bảng biến thiên ta được Strong Team Toán VD – VDC Trang 32/67 s
 in x t   ;  1  (VN) 1   
f sin x 1 sin x t  1  ;0
 sin x t  1  ;0 (1)  2   2   .
sin x t  1; (VN)  3  
Dựa vào đường tròn lượng giác, phương trình (1) có 4 nghiệm nằm trong đoạn 0;5  . s
 in x t   ;  1  (VN) 4   
f sin x  1
  sin x t  0;1
 sin x t  0;1 (2)  5   5   .
sin x t  1; (VN)  6  
Dựa vào đường tròn lượng giác, ta được phương trình (2) có 6 nghiệm nằm trong đoạn 0;5  .
Vậy phương trình ban đầu có tất cả 10 nghiệm.
Câu 21. Cho hàm số f x liên tục trên  có đồ thị y f x như hình vẽ dưới đây.
Số nghiệm thực của phương trình 4 2x f f   2 là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B Ta có: Theo đồ thị : Strong Team Toán VD – VDC Trang 33/67
4  f 2x   2
f 4  f 2x   2  4 f 2x  a,4  a  6  2x  2 TH1) 4  2x f   2  2x f   6    x  1.
2x b  2   KTM  
2x c  2   KTM   TH2) 4  2x f
  a  2x f
  a  4, 0  a  4  2  2x d  0KTM   x  log t . 2
2x t  4 
Vì t  4 nên log t  log 4  2  1 2 2
nên phương trình đã cho có 2 nghiệm phân biệt.
Câu 22. Cho hàm số y f x có bảng biến thiên như sau:  3 
Số nghiệm nhiều nhất thuộc đoạn 0; 
của phương trình f 2 cos x   1  0 là: 2    A. 7 . B. 5 . C. 4 . D. 6 . Lời giải Chọn C  3 
Đặt t  2 cos x 1, x  0;  t 1;  3  . 2   
Xét phương trình: f t   0 , với t 1;  3 .
Từ bảng biến thiên ta có: t a Trên đoạn 1; 
3 , phương trình f t   0 có nghiệm  , với 1
  a  0 và 0  b  3 t b   3 
Vẽ đồ thị y  2cos x 1 trên đoạn 0;  , ta có : 2    Strong Team Toán VD – VDC Trang 34/67
Với 2 cos x 1  a  Đường thẳng y a cắt đồ thị hàm số y  2 cos x 1 tại 2 điểm  3  x  0;  . 2   
Với 2 cos x 1  b  Đường thẳng y b cắt đồ thị hàm số y  2 cos x 1 tại tối đa 2 điểm  3  x  0;  . 2   
Vậy phương trình f 2 cos x  
1  0 có nhiều nhất 4 nghiệm.
Câu 23. Cho hàm số y f x có bảng biến thiên sau:
Hỏi có bao nhiêu giá trị m nguyên để phương trình f 2tan2x  2
m 1 có nghiệm thuộc    khoảng 0;   là:  8  A. 1. B. 3 . C. Vô số. D. 0 . Lời giải Chọn A
Đặt t  2tan 2x, t 0;2 . Khi đó f t   2
m 1, t 0;2 * .
Số nghiệm của phương trình (*) chính là số giao điểm của đồ thị hàm số y f x và đường thẳng y  2  m 1 .
Dựa vào bảng biến thiên ta có phương trình (*) có nghiệm  1  2  m 1  5  2   m  0 .
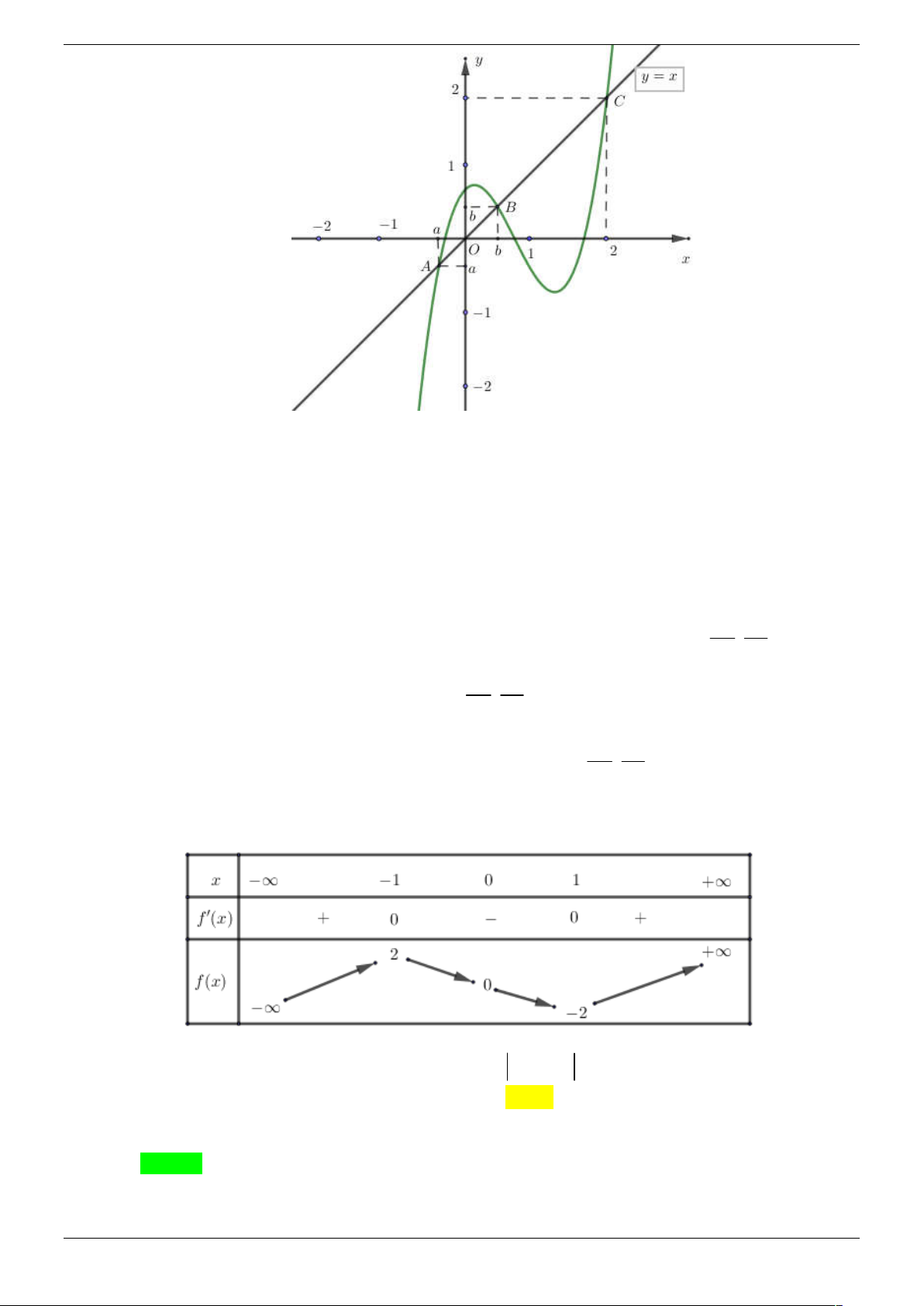
Câu 24. Cho hàm số y f x liên tục trên  có đồ thị như hình vẽ. Phương trình f 1 f x  0 có
tối đa bao nhiêu nghiệm thực phân biệt? Strong Team Toán VD – VDC Trang 35/67 A. 7 . B. 9 . C. 6 . D. 5 . Lời giải Chọn A 1
  f x  m  2   m    1
f x  1 m  
Từ đồ thị hàm số ta có f 1 f x  0  1 f x  n 0  n    1  f
  x  1 n .  
1 f x  p 1 p  2 
f x  1 p  +) Do 2   m  1
  2  1 m  3 . Từ đồ thị hàm số ta suy ra phương trình f x  1 m có
đúng một nghiệm x  2  . 1
+) Do 0  n  1  0  1 n  1 . Từ đồ thị hàm số ta suy ra phương trình f x  1 n có đúng
ba nghiệm 2  x  0  x  1  x  2 . 2 3 4
+) Do 1  p  2  1  1 p  0 . Từ đồ thị hàm số ta suy ra phương trình f x  1 p có
đúng ba nghiệm 2  x  1  x  1  x  2 khác x , x , x . 5 6 7 2 3 4
Vậy phương trình đã cho có tối đa 7 nghiệm phân biệt. Strong Team Toán VD – VDC Trang 36/67
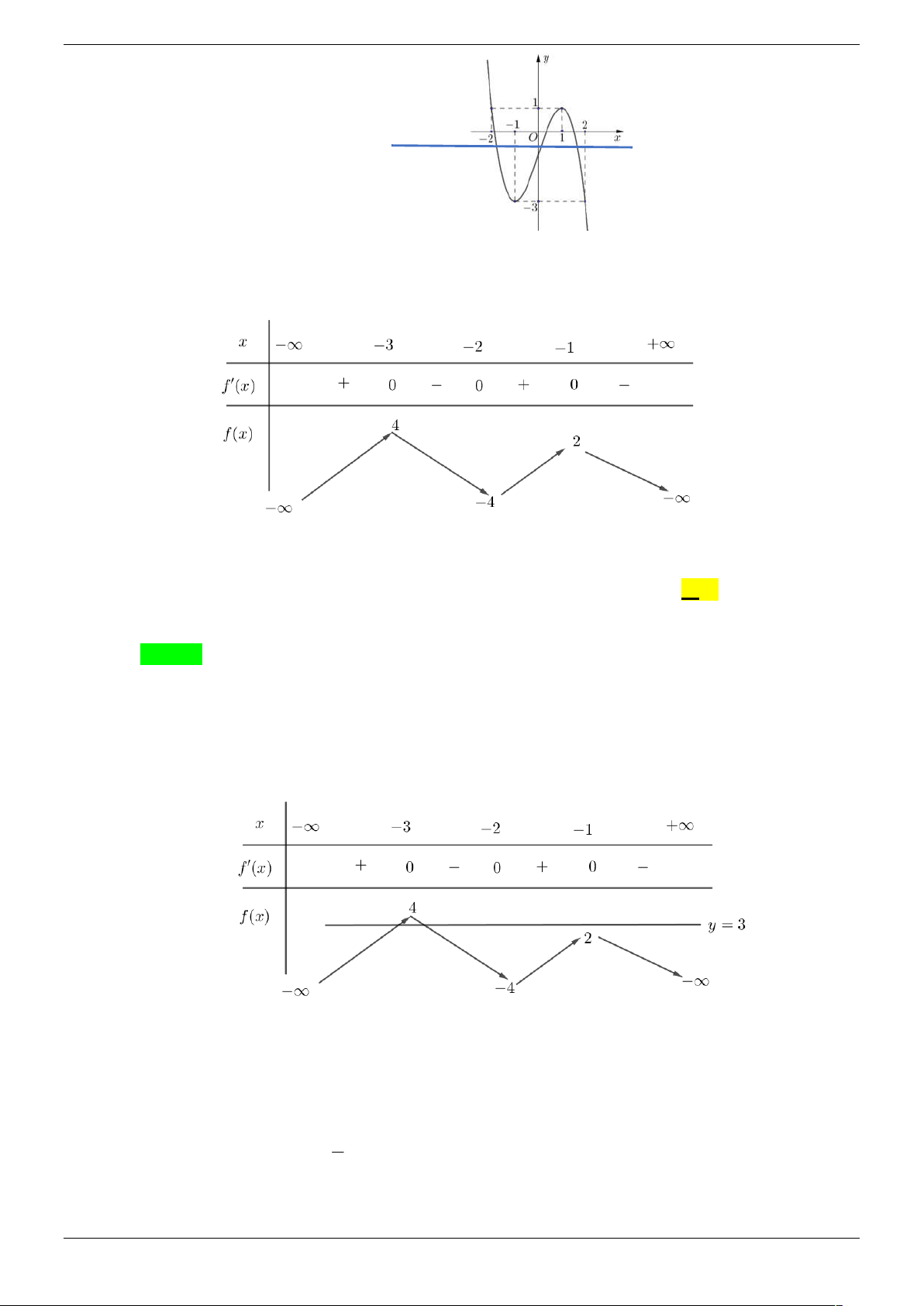
Câu 25 . Cho hàm số f x liên tục trên  có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  
 ;  của phương trình f  2
2 cos x  3  3 là: A. 8 . B. 2 . C. 6 . D. 4 . Lời giải Chọn D Đặt 2
t  2 cos x  3 , vì x  
 ;  nên t  3  ;   1
Ta có phương trình f t   3 , t  3  ;   1 Dựa vào BBT ta có:
Vậy f t   3  t a, a  3  , 2   Ta có: 2
2 cos x  3  a , a   3  , 2    1  Suy ra 2
cos x b , b  0;    2  Strong Team Toán VD – VDC Trang 37/67 cos x b  2  Suy ra  với b   0,   
cos x   b  2  
Với mọi x  
 ;  thì phương trình cos x b có 2 nghiệm và phương trình cos x   b có
2 nghiệm (dựa vào đường tròn lượng giác hoặc đồ thị hàm số y  cos x để kiểm tra nghiệm).
Vậy có 4 nghiệm thỏa yêu cầu bài toán.
Câu 26. Cho hàm số f x liên tục trên  có bảng biến thiên như sau:
Số nghiệm của phương trình f  2
x x  2 là: A. 1 . B. 3 . C. 2 . D. 4 . Lời giải Chọn D f  2 x x  2 f  2
x x  2    f  2
x x  2  Dựa vào BBT ta có:  2
x x a , a 1;  2
x x a , a  1; 2  
f x x  2   Suy ra 2 
 x x b , b  ;    2
1   x x b , b  ;    1 f  2 x x  2    2  x x  1   1 5  x   2 Xét phương trình: 2
x x a  0 có   1  4a  0 vì a  1 1 5 Nên phương trình 2
x x a  0 có hai nghiệm phân biệt khác 2 Xét phương trình: 2
x x b  0 có   1  4b  0 vì b  1 Strong Team Toán VD – VDC Trang 38/67 Nên phương trình 2
x x b  0 vô nghiệm.
Vậy có 4 nghiệm đã cho thõa yêu cầu bài toán.
Câu 27. Cho hàm số f (x) có bảng biến thiên như sau:
Số nghiệm x  0;   của phương trình  x
f e  2020 x   2  0 là A.1. B.2. C. 0 . D. 2020 . Lời giải
Tác giả: Trần Tường; Fb: Trần Tường Chọn A x
e  2020x a ;   1 Ta có f x
e  2020x  2  0  f x
e  2020x  2   x
e  2020x b  1;   
Vì x0; nên x
e  2020x1; nên x
e  2020x a;  1 vô nghiệm. Xét phương trình x
e  2020x b  1;  trên 0;  Ta có hàm số   x
g x e  2020x đồng biến trên 0;  và g x 1; x
 0; nên phương trình x
e  2020x b  1;  luôn có 1 nghiệm duy nhất trên 0;  .
Vậy phương trình đã cho có 1 nghiệm thuộc 0;  .
Câu 28. Cho hàm số f x có đồ thị như hình vẽ:  3 
Số nghiệm thuộc đoạn  ; 2
2 f cos x 5  0  của phương trình   là 2    A. 5. B. 1. C. 3 . D. 4 . Lời giải
Tác giả:Trần Tường ; Fb: Trần Tường Chọn C Strong Team Toán VD – VDC Trang 39/67
cos x a 0  ;1 5 
Ta có 2 f cos x  5  0  f cos x   cos x b   1;3 . 2
cos x c3;    3  Vì cos x 1  ;  1 x   ; 2
cos x b 1;3
cos x c 3;   nên   và   vô nghiệm. 2     3 
Xét đồ thị hàm số y  cos x trên  ; 2  2   
Phương trình cos x a 0; 
1 có 3 nghiệm phân biệt.  3 
Vậy phương trình đã cho có 3 nghiệm phân biệt thuộc đoạn  ; 2 .  2   
Câu 29. Cho hàm số f x có bảng biến thiên như sau
Số nghiệm thuộc đoạn 1; 
3 của phương trình f  2
x  3x 1  0 là A. 5 . B. 3 . C. 2 . D. 4 . Lời giải Chọn D Đặt 2
t x  3x , ta có f  2
x  3x 1  0  f t 1  0  f t  1  .
t a , a  2;0  
t b ,b  0;  1 
t c,c 1;4  Khảo sát hàm số 2
t x  3x trên 1;  3 .
Ta có t  2x  3 3
Cho t  0  2x  3  0  x  1;  3 . 2 Strong Team Toán VD – VDC Trang 40/67 Ta có BBT của hàm 2
t x  3x như sau: Từ BBT trên ta thấy:
Với t a , a  2
 ;0  phương trình có 2 nghiệm phân biệt.
Với t b,b 0; 
1  phương trình có 1 nghiệm.
Với t c , c 1;4  phương trình có 1 nghiệm.
Vậy phương trình ban đầu có 4 nghiệm.
Câu 30. Cho hàm số f x có bảng biến thiên như sau 5  Số nghiệm thuộc đoạn ;3 
của phương trình 4 f cos2x 1  0 là 6    A. 5 . B. 9 . C. 4 . D. 10 . Lời giải Chọn B 1
Đặt t  cos2x , ta có 4 f t  1  0  f t   . 4
t a , a   ;  1   1 
t b,b  1;     2     1 
t c,c  ;1     2  
t d , d  1;    5 
Khảo sát hàm số t  cos2x trên ;3  . 6    Ta có t  2  sin2x Strong Team Toán VD – VDC Trang 41/67 k
Cho t  0  sin2x  0  x  , k  . 2 5   3 5  Vì x  ;3   x    ; ; 2 ; ;3 . 6     2 2 
Ta có BBT của hàm t  cos2x như sau: Từ BBT trên ta thấy:
Với t a , a ; 
1  phương trình vô nghiệm.  1 
Với t b,b  1  ; 
  phương trình có 4 nghiệm.  2   1 
Với t c ,c  ;1 
  phương trình có 5 nghiệm.  2 
Với t d , d 1;   phương trình vô nghiệm.
Vậy phương trình ban đầu có 9 nghiệm.
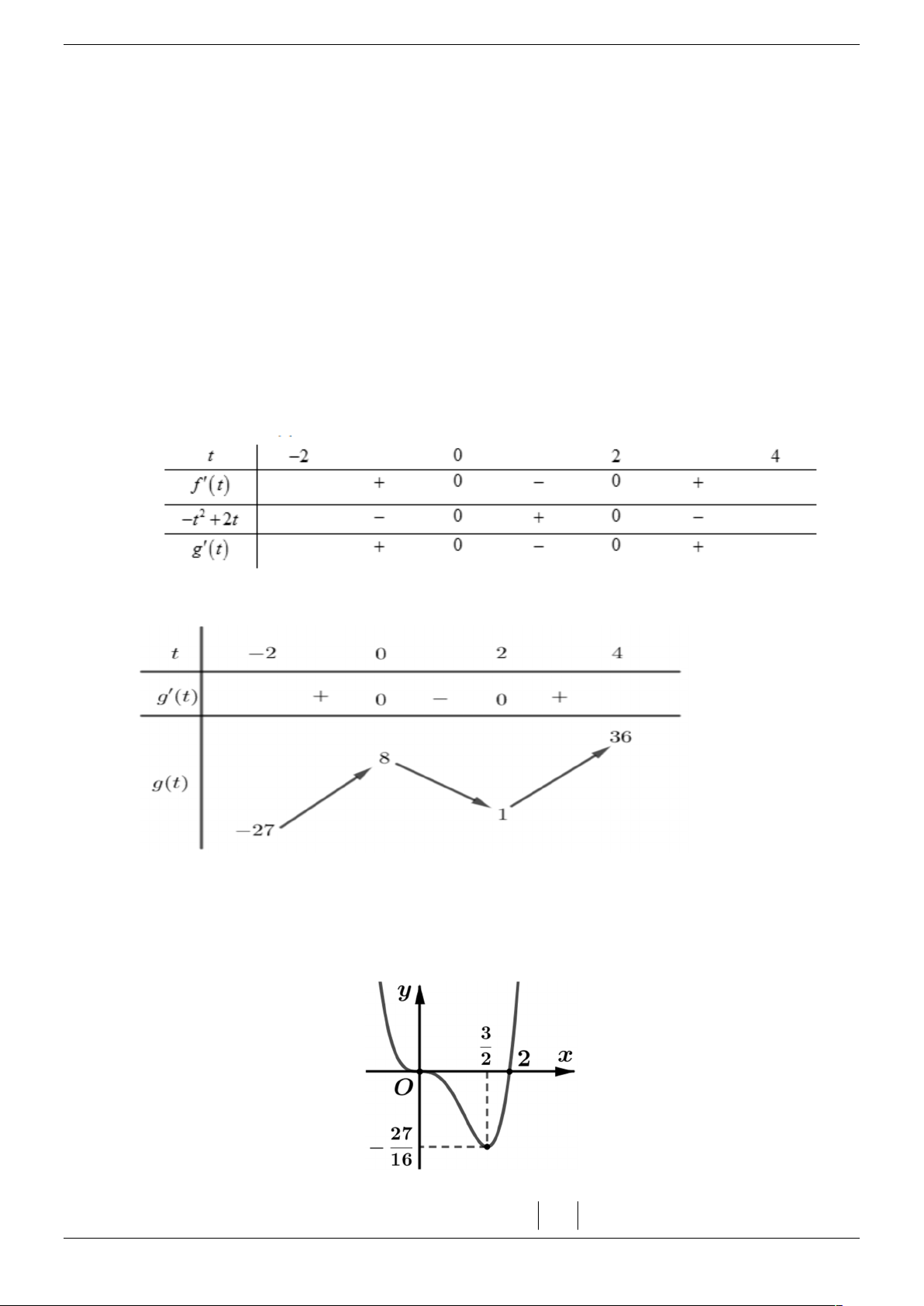
Câu 31. Cho hàm số y f x liên tục, có đạo hàm trên  2; 4  
 và có bảng biến thiên như hình vẽ  3 3 
Số nghiệm của phương trình f  x   3 3 2
1  8x  6x trên đoạn  ;  là  2 2   A. 1 . B. 2 . C. 3 . D. 5 . Lời giải Chọn A  3 3  Đặt t  2
x  1 .Với x   ;   t   2;4  . 2 2    
Mỗi nghiệm của t cho duy nhất một nghiệm của x . Strong Team Toán VD – VDC Trang 42/67 3 3 Biến đổi 3
x x   x   x   t   t 3 2 8 6 2 3 2 1 3 1  t   3t  2 .
Phương trình trở thành f t  3 2 3 t   3t   2  0 . Xét hàm số
g t  f t 3 2 3 t   3t   2  
gt  f t  2
t t  f   t 2 3 3 6 3 t   2t  
gt  f t 2 0  t   2t x  
Ta có f  t 0  0   x  2  x   0 2 t 2t 0      x   2 
Ta có bảng xét dấu g  t
Từ đó ta có bảng biến thiên sau:
Dựa vào bảng biến thiên ta có phương trình g t  0 có 1 nghiệm nên phương trình ban đầu có 1 nghiệm.
Câu 32. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ.  
Số nghiệm thuộc đoạn  ; 2   
 của phương trình 2f 2 sin x  1  0 là Strong Team Toán VD – VDC Trang 43/67 A. 6 . B. 2 . C. 8 . D. 12 . Lời giải Chọn D  
Đặt t  2 sin x . Xét hàm t g x   2 sin x trên đoạn  ; 2      
Ta có bảng biến thiên của hàm số y g x   2 sin x trên đoạn  ; 2        
Dựa vào BBT ta có t  0,2  x   ; 2           Nếu t  0, 
2 thì mỗi giá trị t cho 6 giá trị x thuộc đoạn  ; 2     
Phương trình 2f 2 sin x  1  0 trở thành f t 1   với t   0,2 2    
Dựa vào đồ thị ta có phương trình f t 1
  có 2 nghiệm t phân biệt thuộc khoảng 0,  2 2  
nên phương trình ban đầu có 12 nghiệm phân biệt thuộc đoạn  ; 2    
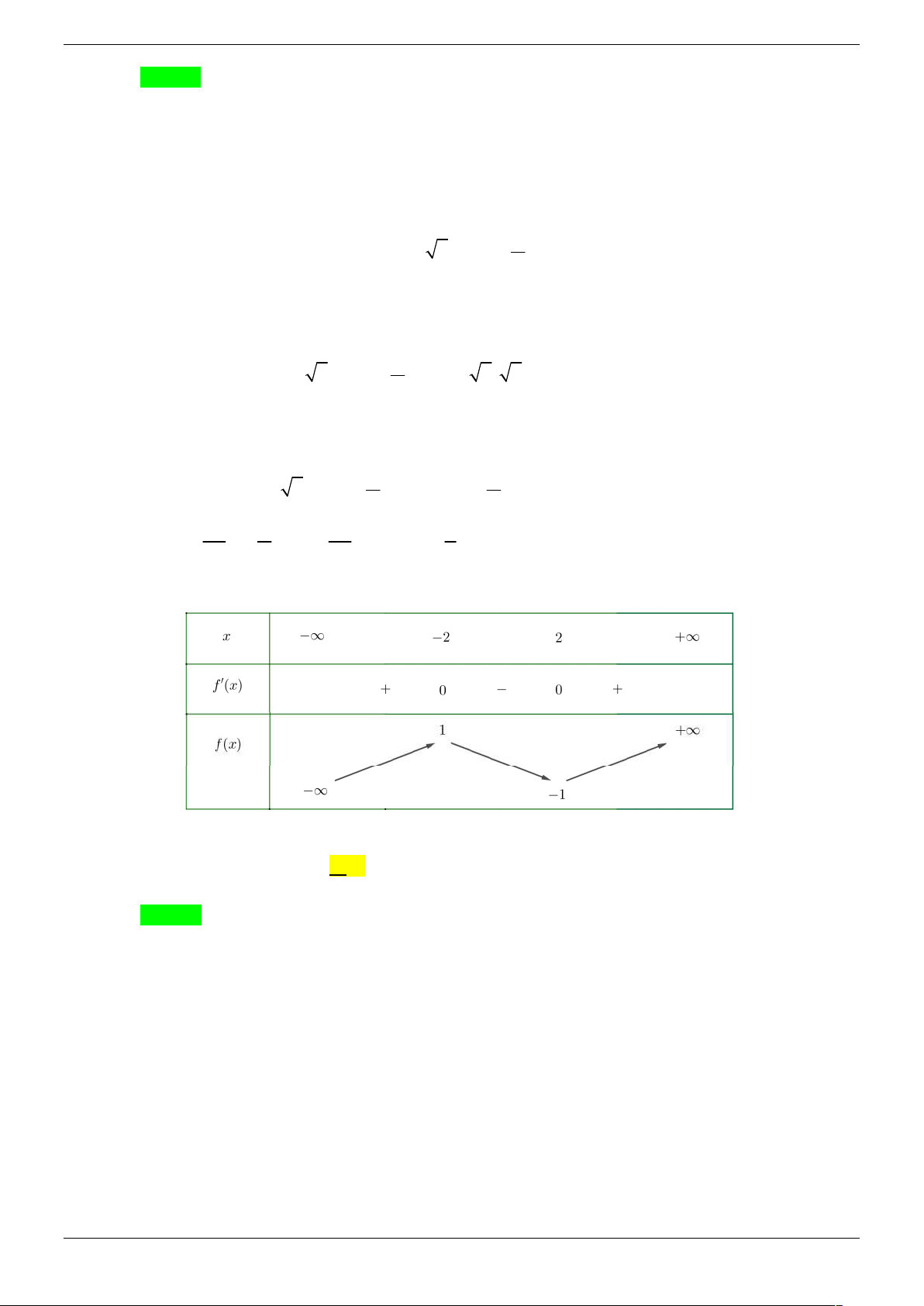
Câu 33. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ
Gọi m là số nghiệm của phương trình f f x 1. Khẳng định nào sau đây là đúng ? A. m  6 . B. m  7 . C. m  5 . D. m  9 . Lời giải Chọn B
Đặt f x  u khi đó nghiệm của phương trình f f x 1 chính là hoành độ giao điểm của
đồ thị f u với đường thẳng y  1. Strong Team Toán VD – VDC Trang 44/67
f x  u1   5 
Dựa vào đồ thị ta có ba nghiệm f
  x  u với u  1
 ;0 , u  0;1 , u  ;3 . 2   1   2 3     2 
f x  u  3
Tiếp tục xét số giao điểm của đồ thị hàm số f x với từng đường thẳng y u , y u , y u 1 2 3 .
Dựa vào đồ thị ta có được 7 giao điểm. Suy ra phương trình ban đầu f f x 1 có 7 nghiệm.
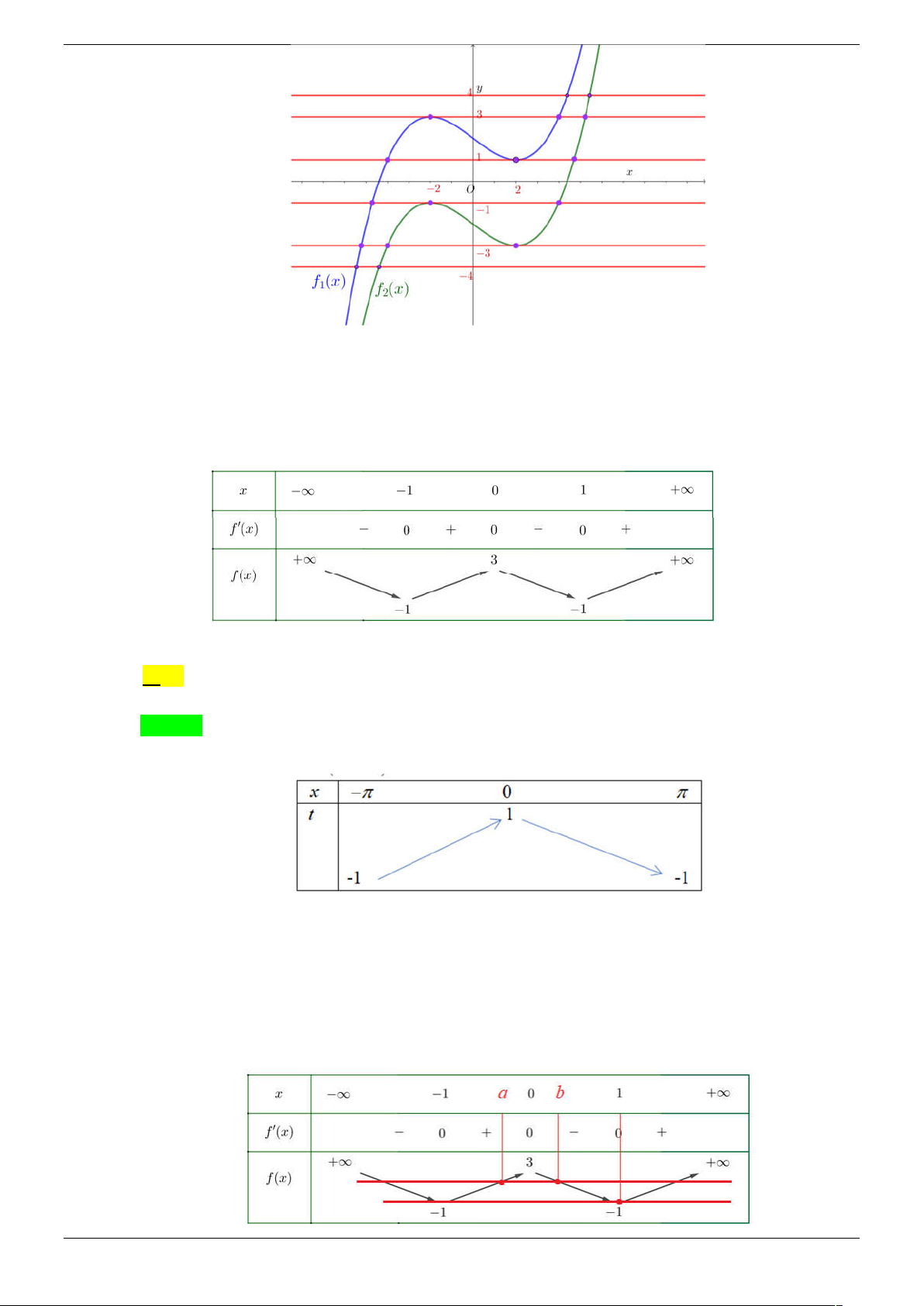
Câu 34. Cho hàm số yf x liên tục trên  và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả
các giá trị nguyên của m để phương trình f (sin x)  2 sin x  2m có nghiệm thuộc khoảng
(0; ) . Tổng các phần tử của S bằng: A. 2  B. 0 . C. 1. D. 5  . Lời giải Chọn C
Đặt t  sin x với x 0;   t 0  ;1 . Strong Team Toán VD – VDC Trang 45/67
Xét phương trình f (t)  2t  2m .
Để phương trình có nghiệm thì đồ thị hàm y f t  cắt đồ thị hàm số y  2t  2m tại ít nhất
một điểm có hoành độ t thuộc 0  ;1 .
Từ đồ thị ta suy ra đồ thị hàm số y  2t  2m nằm ở phần hình phẳng giới hạn bởi đồ thị 2 hàm
số y  2t 1 và y  2t  3 . Từ đó suy ra 3
  2m  1  m  1  ;  0 .
Vậy tổng các phần tử bằng 1.
Câu 35. Cho hàm số f  
x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  2  ;
2 của phương trình 2 f 2sin x 1   0 là A. 8 . B. 5 . C. 2 . D. 6 . Lời giải Chọn A 1
Đặt t  2sin x . Vì x  2
  ; 2   t  2
 ; 2 . Ta có pt: 2 f t  1  0  f t   . 2  a
t a   a   sin x   1 0 2 2 sin x a  2
Từ BBT suy ra pt có nghiệm:     t b  2 b 0      2 sin x b b   sin x  2  2 PT  
1 có 4 nghiệm, pt 2 có 4 nghiệm. Vậy pt đã cho có 8 nghiệm thuộc đoạn  2  ; 2 3
Câu 36. Cho hàm số y f x 3
x  3x 1. Số nghiệm của phương trình  f x  3 f x 1  0   là: A. 1. B. 6. C. 5. D. 7. Lời giải Chọn D
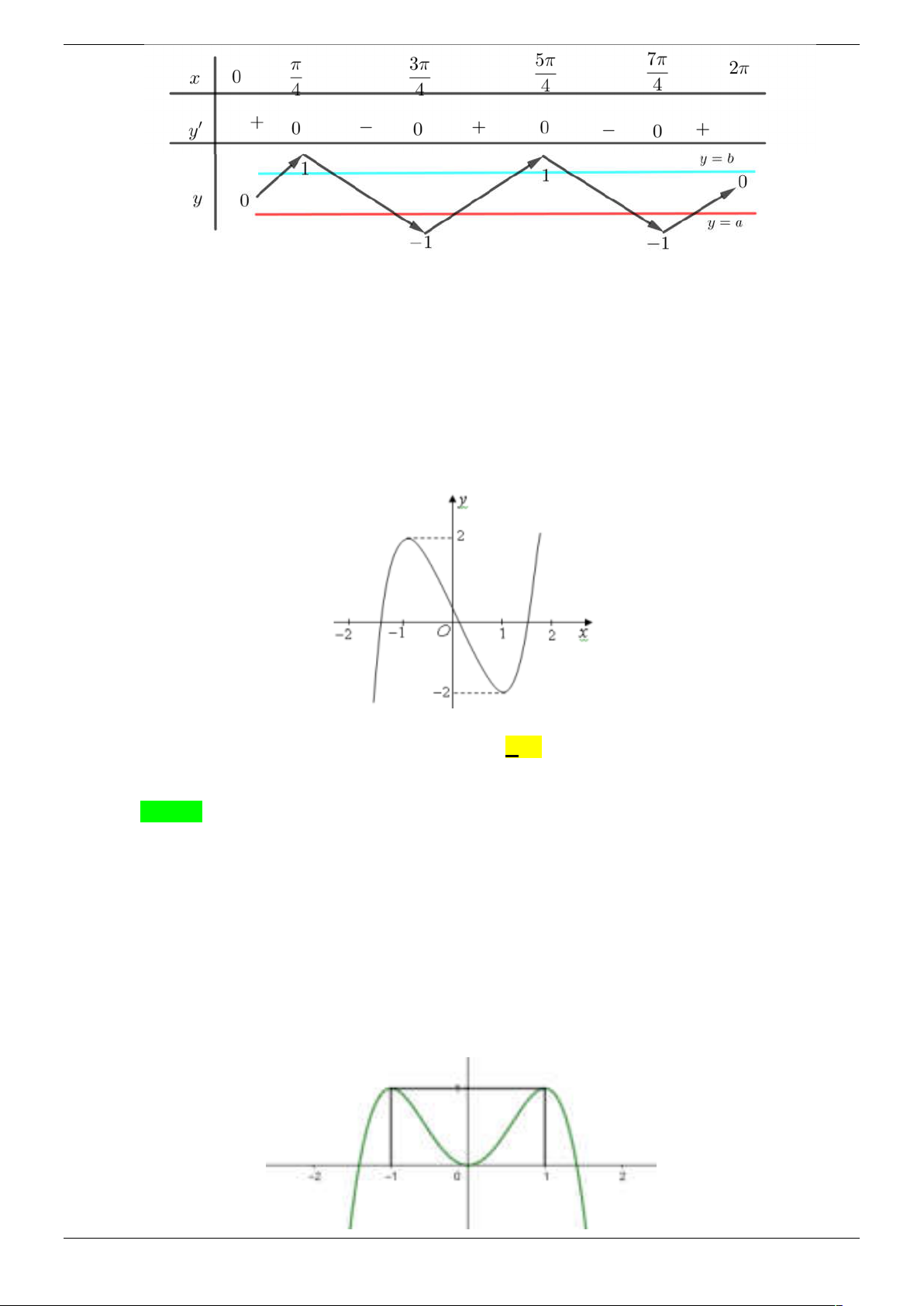
Đồ thị hàm số y f x 3
x  3x 1 có dạng: Strong Team Toán VD – VDC Trang 46/67
Dựa vào đồ thị ta thấy phương trình f x  0 có 3 nghiệm x  2  ; 1
 , x  0;1 , x  1; 2 1   2   3   3
Nếu phương trình  f x  3 f x 1  0  
có nghiệm x thì f x x , x , x . 0   1 2 3 0
Dựa vào đồ thị ta có:
+ f x  x , x  2  ; 1  có 1 nghiệm duy nhất. 1 1  
+ f x  x , x  0;1 có 3 nghiệm phân biệt. 2 2  
+ f (x)  x , x  1; 2 có 3 nghiệm phân biệt. 3 3   3
Vậy phương trình  f x  3 f x 1  0   có 7 nghiệm phân biệt.
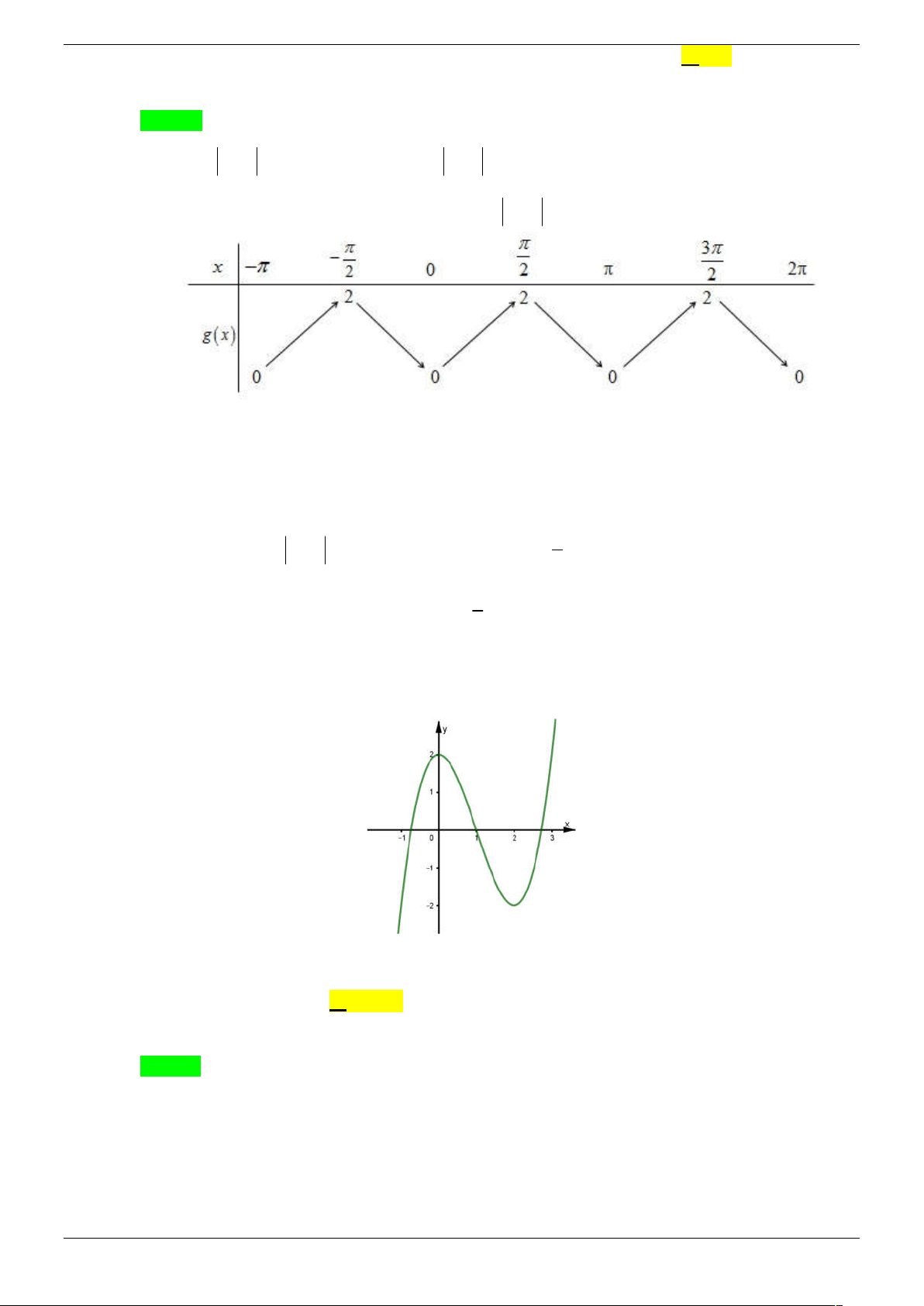
Câu 37. Cho hàm số y f (x) là hàm số bậc 3 có đồ thị như hình vẽ dưới đây  3 1 
Số nghiệm thuộc đoạn 0;3  của phương trình 2 f sin x  1  0   là  2 2  A. 5 . B. 3. C. 4. D. 6. Lời giải Chọn D 3 1 1 Đặt t  sin x
vì x 0;3  nên t  1
 ; 2. Ta được phương trình f t   với 2 2 2 1 t  1
 ; 2. Quan sát đồ thị ta thấy phương trình f t   có 3 nghiệm 2 Strong Team Toán VD – VDC Trang 47/67
t a   ;   
1 ;t b  1;0;t c  1; 2. 3 1
Bảng biến thiên của hàm số t  sin x  trên đoạn 0;3 . 2 2 π 3π 5π x 0 3π 2 2 2 t' + 0 0 + 0 2 2 t 1 1 2 2 1
Từ bảng biến thiên ta thấy 3 1
+) Với t a  ;   
1 thì phương trình sin x   a vô nghiệm. 2 2 3 1
+) Với t b   1
 ;0 thì phương trình sin x   b có 2 nghiệm. 2 2 3 1
+) Với t c 1; 2 thì phương trình sin x   c có 4 nghiệm. 2 2
Cả 6 nghiệm của phương trình trong các trường hợp trên là khác nhau. Vậy phương trình có 6 nghiệm phân biệt.
Câu 38. Cho hàm số y f (x) có bảng biến thiên như sau: 1 x ∞ 1 + ∞ 2 y' + 0 0 + 1 ∞ + y ∞ 2
Có bao nhiêu giá trị nguyên của tham số m để phương trình f  4 4
sin x  cos x  m có nghiệm    x  0; .  4    A. 1. B. 3. C. 2. D. 4. Lời giải Chọn D 3  cos 4x     1  Đặt 4 4
t  sin x  cos x  vì x  0; nên t
;1 . Ta được phương trình 4  4       2   1   1 
f t   m với t  ;1 . 
Quan sát bảng biến thiên ta thấy với t
;1 thì f t   2   ;1 2       2   m  2   ;1  m  2  ; 1  ;0 
;1 . Vậy số các giá trị nguyên của tham số m là 4.
Câu 39. Cho hàm số y f (x) có đồ thị như hình vẽ. Strong Team Toán VD – VDC Trang 48/67  5
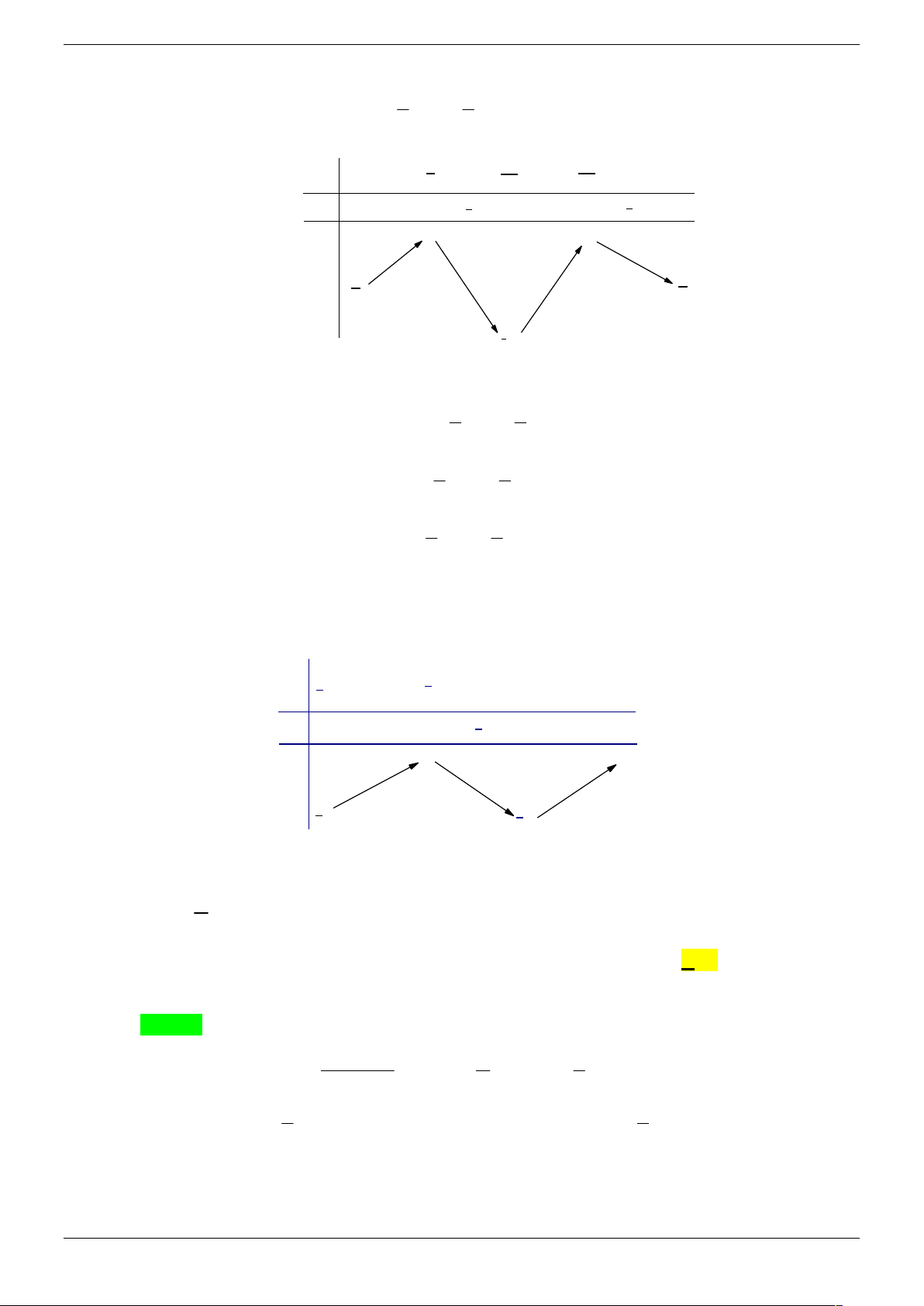
Số nghiệm của phương trình 2f (cos 2x)  1  0 trên đoạn 0;   là 4    A. 3. B. 4. C. 5. D. 6. Lời giải Chọn C
 cos 2x a   1  ; 0   1 1 
Ta có: 2 f (cos 2x) 1  0  f (cos 2x)  
cos 2x b  0;  1 2 2 
 cos 2x c  2;3 VN    5 
Bảng biến thiên của hàm số y  cos 2x, x  0;  4   
Từ bảng biến thiên suy ra: (1) có 2 nghiệm phân biệt, (2) có 3 nghiệm phân biệt không trùng
với nghiệm của phương trình (1).
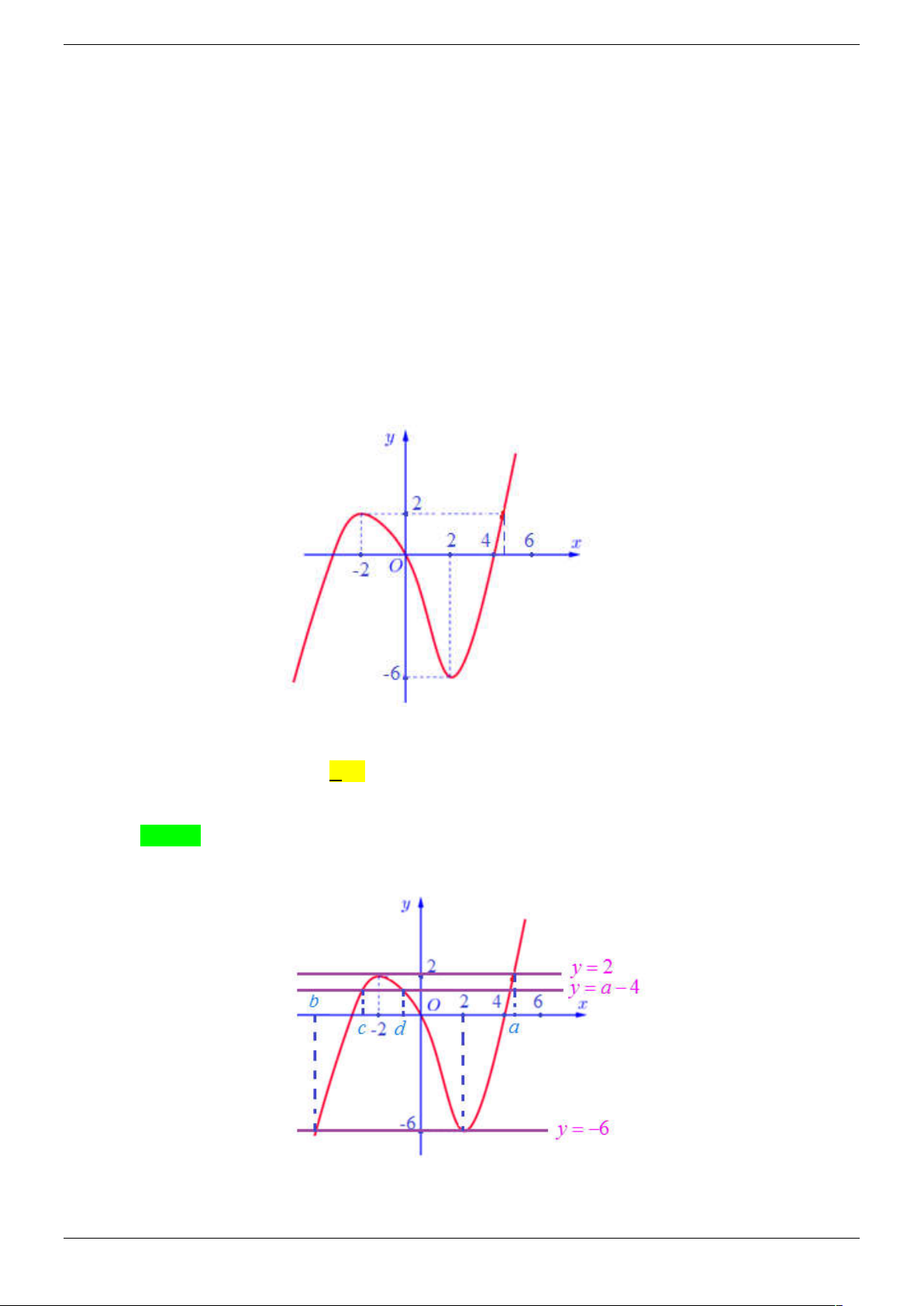
Câu 40. Cho hàm số y f (x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình
3f f (x
)  m có đúng 6 nghiệm phân biệt x  [ 5  ;0]. A. 2. B. 3. C. 4. D. 5. Lời giải Strong Team Toán VD – VDC Trang 49/67 Chọn A Đặt t f (x),x  5;0 t  1;3
f t 0;4               m
Phương trình đã cho có dạng f t , t  1;3    3   m TH1: 0;4  3 
 phương trình đã cho vô nghiệm m t  1   f x  1  1  
TH2: m  0 : f t        3  t  3  f
 x  3   2  
Phương trình (1) Có 1 nghiệm, (2) có 1 nghiệm trong miền x  [ 5
 ;0]. Do đó phương trình ban
đầu có 2 nghiệm x  [ 5  ;0]. m m t  1   f x a  1  ;0 3   TH3: 0   3 hay 0f t          3 3  t  3  f
x  b   2;  3 4  
Phương trình (1) Có 1 nghiệm, (2) có 1 nghiệm trong miền x  [ 5
 ;0]. Do đó phương trình ban
đầu có 2 nghiệm x  [ 5  ;0]. m TH4: 3   4 hay 93      
f tm t c  0;2 f  x c 0;2 5    3 td 0;  2 ,c d    
f x  d    0;  2 6  
Hệ (3), (4) có 6 nghiệm phân biệt trong miền x  [ 5
 ;0]. Do đó phương trình ban đầu có 6 nghiệm x  [ 5  ;0]. m m TH5:  3 
 4 phương trình ban đầu lần lượt có 4 nghiệm, 3 nghiệm trong miền 3 3 x  [ 5  ;0].
Vậy để phương trình 3f f (x
)  m có đúng 6 nghiệm phân biệt x  [ 5
 ;0]. thì 9m  10;1  1 .
Câu 41. Cho hàm số f (x) có bảng biến thiên như sau:
Số nghiệm thuộc đoạn  20  19; 
1 của phương trình f ln x  4 A. 2020 B. 4. C. 2019. D. 3. Lời giải Chọn D Strong Team Toán VD – VDC Trang 50/67
Đặt t  ln x, (x  0) mà x  2  019  ;1 nên x 0  ;1 .
Do hàm f (x)  ln x là hàm đồng biến trên khoảng 0;  nên t  ;  0 .
Khi đó phương trình f ln x  4 trở thành f t   4 với t  ;  0
Đây là phương trình hoành độ giao điểm của hàm số y f (t) với đường thẳng y  1
Ứng với mỗi giá trị t   ;
 0 ta có một nghiệm x 0 
;1 nên số giao điểm của đồ thị hàm số
y f (t) và đồ thị hàm số y  4 trên  ;
 0 là số nghiệm của phương trình. Bảng biến thiên
Dựa vào bảng biến thiên, phương trình đã cho có 3 nghiệm
Câu 42. Cho hàm số f (x) có bảng biến thiên như sau:   
Số nghiệm thuộc đoạn 0; 
của phương trình f sin x  cos x  1  4    A. 1 B. 3 C. 2 D. 0. Lời giải Chọn D      
Đặt t  sin x  cos x  2 sin x    , với x  0;  t  1  ; 2     4  4    
Đây là phương trình hoành độ giao điểm của hàm số y f (t) với đường thẳng y  1. Bảng biến thiên Strong Team Toán VD – VDC Trang 51/67
+ Ứng với t a  ;
  2  ,t b 1
 ;0 , t c 0 
;1 , t d  2; loại vì không thỏa t  1  ; 2   
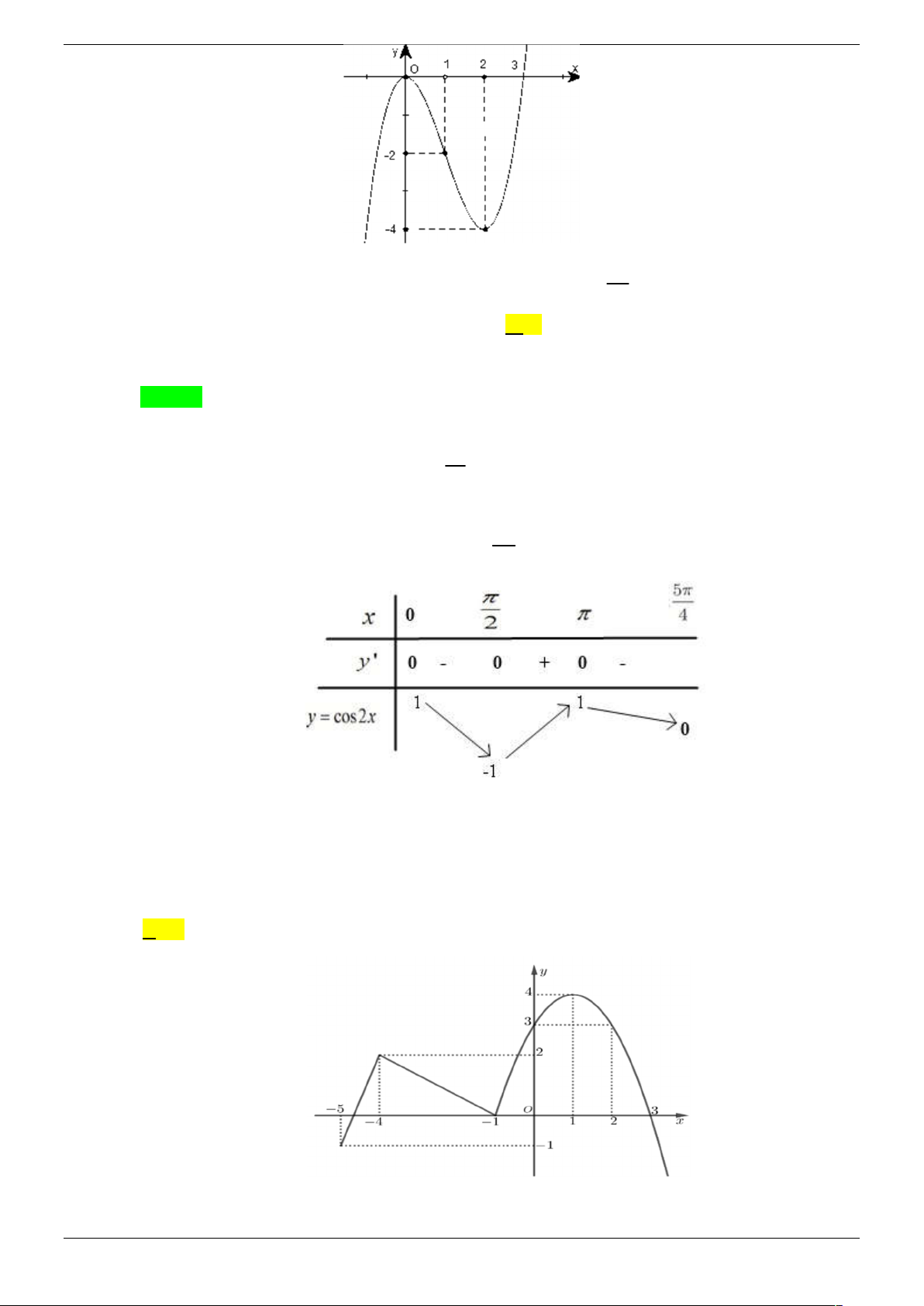
Câu 43. Cho hàm số y f (x) liên tục trên  có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số m để phương trình f (sin x)  2 sin x m  0 có
nghiệm thuộc khoảng 0;  ? A. 9 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B
Đặt t  sin x , với x  0;   t  0;  1
Phương trình đã cho trở thành f (t)  2t m , t  0;  1 (1).
Yêu cầu bài toán tương đương phương trình (1) có nghiệm trong nửa khoảng 0  ;1
Dựa vào đồ thị, để phương trình (1) có nghiệm trong nửa khoảng 0  ;1
 4  m  0 , mà m   nên m 1;  2;  3;  
4 là các giá trị cần tìm.
Câu 44. Cho hàm số f (x) có bảng biến thiên như sau
Số nghiệm thuộc đoạn  
 ; 2  của phương trình 2 f (sin x)  3  0 là A. 6 . B. 3 . C. 4 . D. 8 . Lời giải Strong Team Toán VD – VDC Trang 52/67 Chọn A
Đặt t  sin x , lúc đó t  cos x    3 
Cho t  0  x
k , k   . Do x  
 ; 2   x   ;  2  2 2  Bảng biến thiên
Từ bảng biến thiên ta thấy x  
 ; 2   t  1  ;  1
Nhận xét: Với mỗi giá trị t   1;
 0 ta có 4 nghiệm x  
 ; 2  ; t 0  ;1   1 ta có 2 nghiệm x  
 ; 2  và t  1 ta có 1 nghiệm x    ; 2  3
Khi đó phương trình trở thành 2 f (t)  3  0  f (t)  , t  1;  1 2
Từ bảng biến thiên ta có đồ thị hàm số y f (t) , t    1;1
t a   1;  0 3 
Dựa vào đồ thị, ta thấy f (t)    , t   1;   1 2
t b  0  ;1 
Với t a   1
 ;0 ta có 4 nghiệm x    ; 2 
Với t b 0 
;1 ta có 2 nghiệm x    ; 2 
Vậy phương trình đã cho có 6 nghiệm.
Câu 45. Cho hàm số y f x có bảng biến thiên như sau Strong Team Toán VD – VDC Trang 53/67
Số nghiệm của phương trình  x
f e  4 1  0 trong đoạn ln 2 ; ln 6 là A. 1. B. 2. C. 3. D. 4 . Lời giải Chọn B Đặt x
t e  4 . Với x ln 2 ; ln 6  t 2 ; 2. Ta được PT f t   1.
Dựa vào bảng biến thiên, ta thấy phương trình f t   1 có 2 nghiệm là t t  2  ; 0 và 1  
t t  0 ; 2 . 2  
Với t t ta được x
e  4  t x  ln 4  t . 1  1  1
Với t t ta được x
e  4  t x  ln 4  t . 2  2  2
Vì t t nên ln 4  t  ln 4  t . 1   2  1 2
Vậy PT đã cho có 2 nghiệm phân biệt.
Câu 46. Cho hàm số y f x là hàm đa thức bậc 3 và có bảng biến thiên như sau  5 
Số nghiệm của phương trình f sin x  3 cos x  0 trong đoạn 0 ;  là 2    A. 1. B. 4. C. 3. D. 2 . Lời giải Chọn D   
Đặt t  sin x  3 cos x . Ta có t  2 cos x   2   t  2  
. Ta được PT f t   0 .  6 
Dựa vào BBT ta thấy đồ thị hàm số có 2 điểm cực trị là  2  ; 4
  và 2;4 nên đồ thị có điểm
uốn là gốc tọa độ O . Do đó đồ thị cắt trục hoành tại 3 điểm có hoành độ lần lượt là x a  2
 , x  0, x b  2 . Mà 2  t  2 nên PT f t   0 có 1 nghiệm là t  0 .      2
Với t  0 ta được 2 cos x   0  x    k
k   x
k k     .  6  6 2 3 5 2 5 2 11
Theo yêu cầu bài: 0  x   0   k     k  . 2 3 2 3 6 2 5
Vì k    k  0; k  1. Ta được 2 nghiệm x  và x
thỏa yêu cầu bài toán. 3 3 Strong Team Toán VD – VDC Trang 54/67
Câu 47. Cho hàm số y f x có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình  f  3 2 x x   2  f  3 2 1 3 1 2 x  3x   1  2 là A. 5 . B. 4 . C. 3 . D. 2 . Lời giải Chọn B
Đặt a f  3 2 x  3x  
1 ta được bất phương trình 1   a  0 a  1   2
1 a  2a  2      a  1 .
1 2a a  2a  2  a   2 2 2 1  0 
Với a  1 ta được f  3 2 x  3x   1  1. Đặt 3 2
t x  3x 1 ta được PT f t   1 * .
Vẽ đường thẳng y  1 lên đồ thị đã cho ta được PT * có 1 nghiệm t t  2  ; 1 và 1 1  
nghiệm t t  1; 2 . 2   Ta có BBT của hàm số 3 2
y x  3x 1 như sau
Với t t ta được PT 3 2
x  3x 1  t . Dựa vào BBT ta thấy PT này có 3 nghiệm phân biệt. 1 1
Với t t ta được PT 3 2
x  3x 1  t . Dựa vào BBT ta thấy PT này có 1 nghiệm. 2 2
Vậy BPT đã cho có 4 nghiệm thực.
Câu 48. Cho hàm số y f x là hàm bậc 3 và có bảng biến thiên như sau    Phương trình 2
f sin x  cos x 1 sin 2x  2 2 sin x f  
sin x  cos x có mấy nghiệm  4   5 5  thực thuộc đoạn  ;  ? 4 4    A.1. B. 3 . C. 4 . D. 6 . Strong Team Toán VD – VDC Trang 55/67 Lời giải Chọn B
Vì hàm số có 2 điểm cực trị là x  1
 nên f x 2
ax a f x 3 ' 3 3
ax  3ax d . Theo
2a d  2 a  1
BBT thì đồ thị hàm số đi qua 2 điểm 1; 2 và 1; 2 nên   
2a d  2 d  0  
Suy ra f x 3  x  3x .    Ta có 2
f sin x  cos x 1 sin 2x  2 2 sin x f  
sin x  cos x  4  2 2
f sin x  cos x  sin x  cos x  2sin x  cos xf sin x  cos x 2
  f sin x  cos x  sin x  cos x  0  f sin x  cos x  sin x  cos x     
Đặt t  sin x  cos x  2 sin x  , t   2; 2    ta được phương trình 4     t  0 f t  3
t t  3t t   t  2  loaïi     
Với t  0 ta được 2 sin x   0  x    k , k      4  4 5  5 3 Ta có     k   1   k   k  1
 , k  0, k  1. Vậy PT có 3 nghiệm. 4 4 4 2
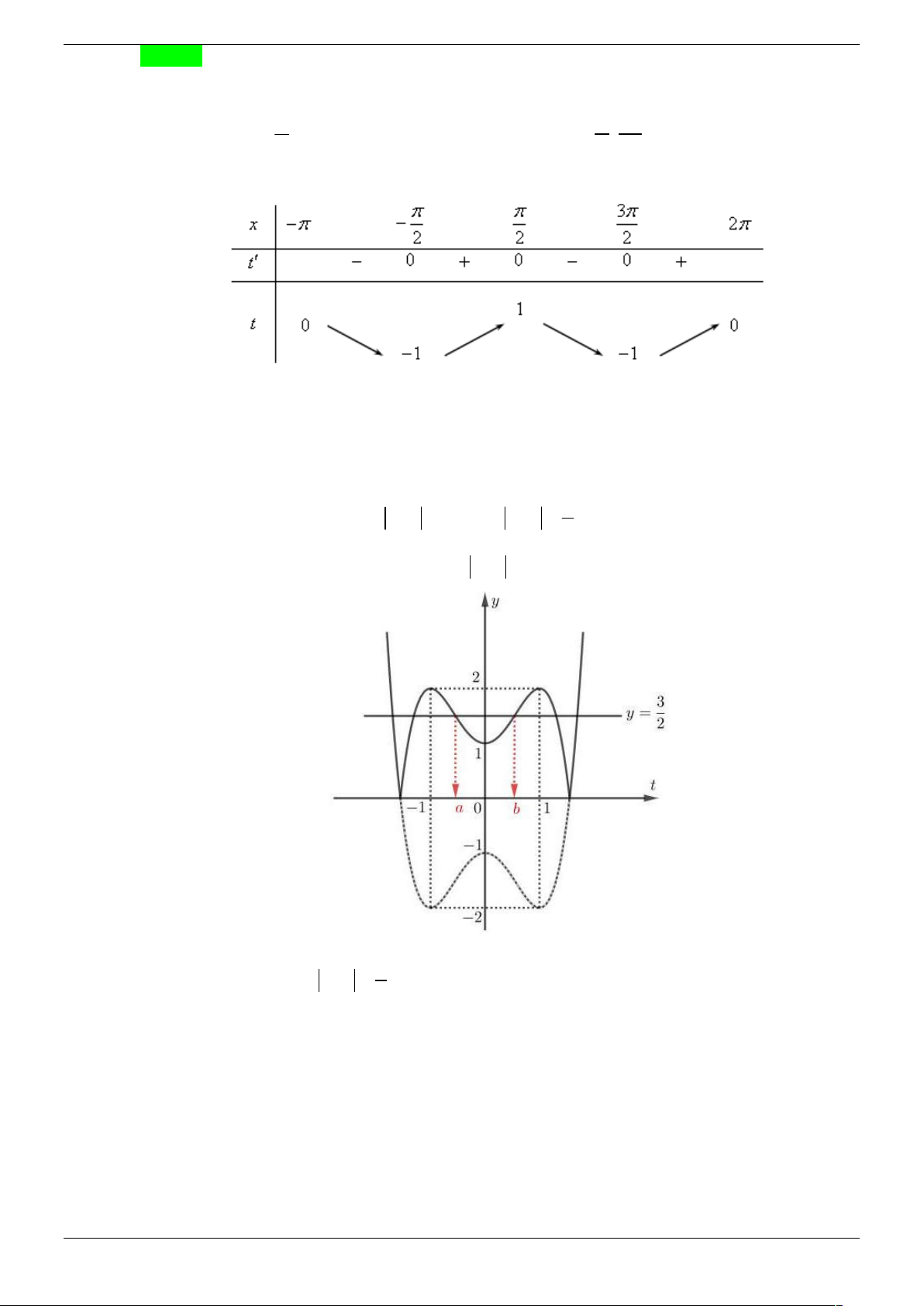
Câu 49. Cho y f x là hàm số bậc ba và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên m   5
 ;5 để hàm số g x  f f x  m có 4 điểm cực trị? B. 5. B. 6. C. 7. D. 8. Lời giải Chọn B
g x  f  x. f  f x  m.
f  x  0
g x  0  
f  f x  m  0  x  2 x  2    x  2 x  2    
, trong đó x  2 và x  2 là hai nghiệm bội lẻ.
f x  m  2 
f x  2  m  
f x  m  2
f x  2  m  
Đặt f x f x  2 và f
x f x  2 , ta có đồ thị sau 2     1     Strong Team Toán VD – VDC Trang 56/67  m   5  ;5 Với 
và nhìn vào đồ thị, ta thấy hàm số g x có 4 điểm cực trị  g x  0 có 4 m   
nghiệm bội lẻ  m  4  ; 3  ; 1  ;1;3;  4 .
Câu 50. Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc khoảng  
 ;  của phương trình 2
f cos x  f cos x  2 là A. 5 . B. 6 . C. 7 . D. 9 . Lời giải Chọn A
Đặt t  cos x, x   
 ; . Ta có bảng biến thiên (*)  t  1  ;  1 .
f t   2 (1)
Phương trình đã cho trở thành 2
f t   f t   2  0   .
f t   1 (2) 
Từ bảng biến thiên của đề bài, với t  1  
;1 ta có nghiệm của phương trình (1) là t a  1
 ; 0 hay t b 0 
;1 và nghiệm của phương trình (2) là t  1. Strong Team Toán VD – VDC Trang 57/67
Từ bảng biến thiên (*), ta có: x x    ; 0 1   t a  1  ;0   .
x x  0;  2   x x    ; 0 3  
t b 0  ;1   .
x x  0;  4  
t  1  x  0.
Vậy, phương trình đã cho có 5 nghiệm phân biệt thuộc khoảng    ; .
Câu 51. Cho hàm số f (x) có bảng biến thiên như sau:
Số nghiệm x  0;   của phương trình  x
f e  2020 x   2  0 là A.1. B.2. C. 0 . D. 2020 . Lời giải Chọn A x
e  2020x a ;   1 Ta có f x
e  2020x  2  0  f x
e  2020x  2   x
e  2020x b  1;   
Vì x0; nên x
e  2020x1; nên x
e  2020x a;  1 vô nghiệm. Xét phương trình x
e  2020x b  1;  trên 0;  Ta có hàm số   x
g x e  2020x đồng biến trên 0;  và g x 1; x
 0; nên phương trình x
e  2020x b  1;  luôn có 1 nghiệm duy nhất trên 0;  .
Vậy phương trình đã cho có 1 nghiệm thuộc 0;  .
Câu 52. Cho hàm số f x có đồ thị như hình vẽ:  3 
Số nghiệm thuộc đoạn  ; 2
2 f cos x 5  0  của phương trình   là 2    Strong Team Toán VD – VDC Trang 58/67 A. 5. B. 1. C. 3 . D. 4 . Lời giải Chọn C
cos x a 0  ;1 5 
Ta có 2 f cos x  5  0  f cos x   cos x b   1;3 . 2
cos x c3;    3  Vì cos x 1  ;  1 x   ; 2
cos x b 1;3
cos x c 3;   nên   và   vô nghiệm. 2     3 
Xét đồ thị hàm số y  cos x trên  ; 2  2   
Phương trình cos x a 0; 
1 có 3 nghiệm phân biệt.  3 
Vậy phương trình đã cho có 3 nghiệm phân biệt thuộc đoạn  ; 2 .  2   
Câu 53. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình  3 7  f  2
x  2x  m có đúng 4 nghiệm thực phân biệt thuộc đoạn  ;  . 2 2    A. 1. B. 4 . C. 2 . D. 3 . Lời giải Chọn C  3 7  Đặt 2
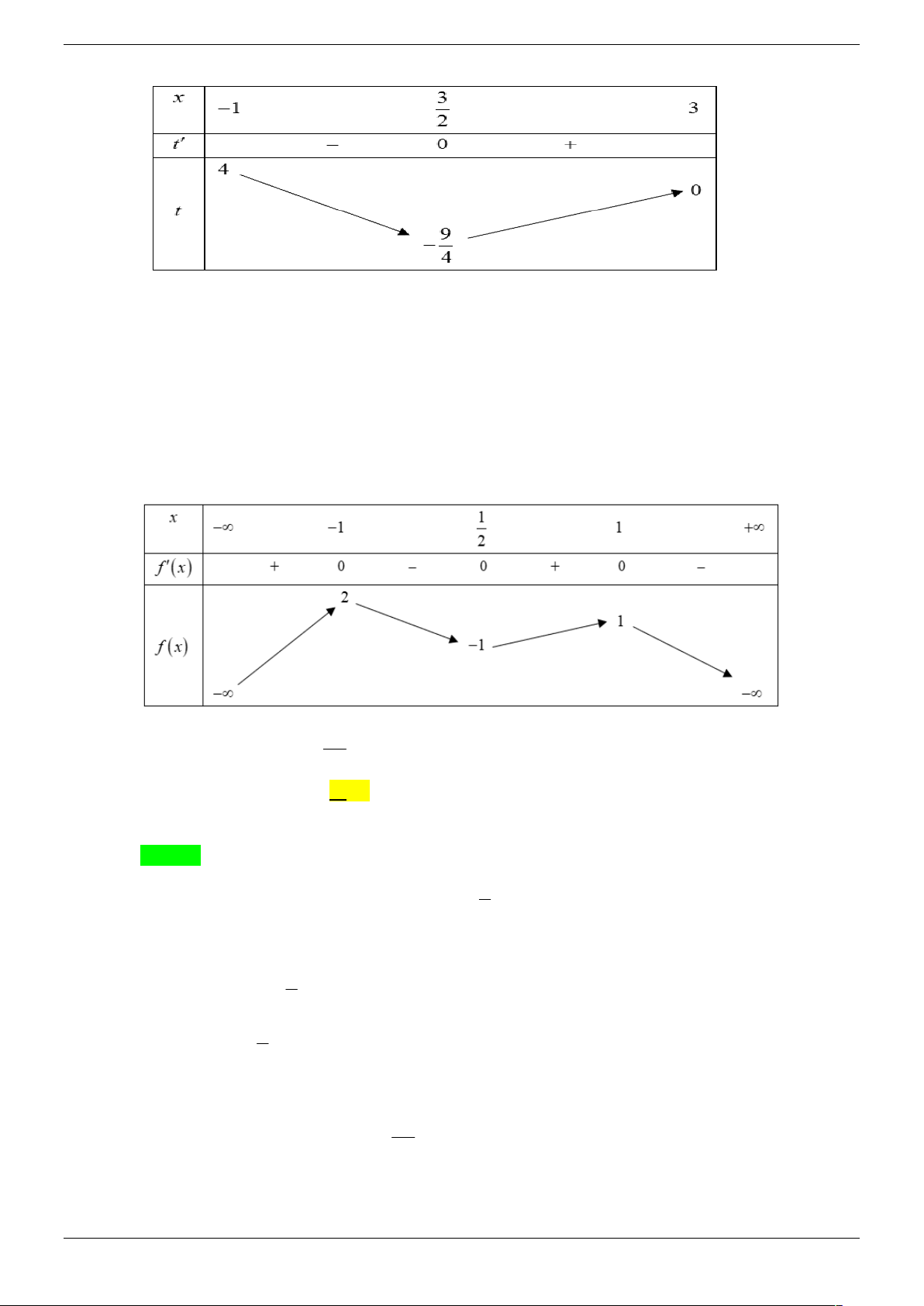
t x  2x , x   ;  2 2    Bảng biến thiên: Strong Team Toán VD – VDC Trang 59/67  21
Dựa vào bảng biến thiên  t  1  ;  . 4    Ta có: f  2
x  2x  m  
1  f t   m 2 .  21  3 7 
Ta thấy, với mỗi giá trị t  1; 
ta tìm được hai giá trị của x   ; . 4       2 2   3 7 
Do đó, phương trình  
1 có 4 nghiệm thực phân biệt thuộc  ;  2 2     21
 Phương trình 2 có hai nghiệm thực phân biệt thuộc 1;  4   
 Đường thẳng y m cắt đồ thị hàm số y f t tại hai điểm phân biệt có hoành độ thuộc  21 1;  . 4   
Dựa vào đồ thị ta thấy có hai giá trị nguyên của m thỏa yêu cầu là m  3 và m  5 .
Câu 54. Cho hàm số y f x có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số m
để phương trình f sin x  m có đúng hai nghiệm thuộc đoạn 0;  ? A. 4 . B. 7 . C. 5 . D. 6 . Lời giải Chọn C
Đặt t  sin x , x 0;  thì t 0 
;1 . Để phương trình f sin x  m có đúng hai nghiệm
x 0;  thì phương trình f t  m có đúng một nghiệm t 0 
;1 . Dựa vào đồ thị ta có m  7  ; 2
  , do m nguyên nên m 7; 6; 5; 4;   3 . Vậy có 5 giá trị.
Câu 55. Cho hàm số bậc bốn y f x có đồ thị như hình bên Strong Team Toán VD – VDC Trang 60/67
Số điểm cực trị của hàm số g x  f  3 2
x  3x  4 là A. 5 . B. 3 . C. 7 . D. 11 . Lời giải Chọn C
Tập xác định của hàm số: D   .
g x   2
x xf  3 2 3 6
x  3x  4 .  x  0 
g  x  0  x  2  f    3 2
x  3x  4  0  *  3 2
x  3x  4  a   2  ; 0  Khi đó * 3 2
 x  3x  4  b  0; 4  3 2
x  3x  4  c   4;6 
Xét hàm số h x 3 2
x  3x  4 trên  . x  0
Ta có: h x 2
 3x  6x  0  
. Từ đó ta có BBT của hàm h x như sau: x  2  x ∞ 0 2 +∞ h' + 0 0 + 4 +∞ h ∞ 0
Từ BBT của hàm h x ta thấy phương trình hx  a có 1 nghiệm duy nhất nhỏ hơn 1  ,
h x  b có 3 nghiệm lần lượt thuộc các khoảng  1
 ;0;0; 2;2;3 , hx  c có duy nhất 1 nghiệm lớn hơn 3.
Vậy g x  0 có đúng 7 nghiệm đơn phân biệt nên hàm số có 7 cực trị.
Câu 56. Cho hàm số y f x có đồ thị như hình bên Strong Team Toán VD – VDC Trang 61/67 3y 1 2 1 -1 x 2 1 2 1 -1 2
Số nghiệm thuộc đoạn 0;3của phương trình : 2 f cos x 1  0. A. 12 . B. 6 . C. 10 . D. 8 . Lời giải Chọn A  1
f cos x   f x 2 2 cos  1  0   1
f cos x    2  1 cos x a , 1
  a     1  2  1 1
Căn cứ vào đồ thị ta thấy: f cos x  
 cos x b ,   b  0 2 2  2
cos x c,c  13   
cos x d , d  1  4  1 1 f cos x   
 cos x e , 0  e  5 2  2  1 cos x g ,  g  16  2
Các phương trình 3 , 4 đều vô nghiệm.
Xét đồ thị hàm số y  cos x trên đoạn 0;3y 2 1 O π 2π 3π x 1 Strong Team Toán VD – VDC Trang 62/67
Ta thấy các phương trình  
1 ,2,5,6 lần lượt có 3 nghiệm phân biệt và trong số chúng
không có 2 nghiệm nào trùng nhau. Vậy phương trình ban đầu có 12 nghiệm.
Câu 57. Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. Số nghiệm thuộc đoạn   3   ; 
của phương trình f cot x   1  1 là 2 2    x  1 1 2  f  x  0  0  0   1  f x 1 2 A. 7. B. 6. C. 8. D. 5. Lời giải Chọn A
Đặt t  cot x 1, phương trình tương đương với f t   1.
Dựa vào bảng biến thiên, ta thấy
t a a    1
cot x 1  a
cot x a 1  0   
f t   1  t  1
 cot x 1  b  cot x b 1  0   
t b b  2 cot x 1  1 cot x  0    1   3  Xét t  
 0 nên ta có bảng biến thiên hàm t x trên  ; như sau 2 sin x  2 2     3 x  0  2 2 t      t 0 0  
Từ đó, phương trình cot x a 1 có đúng 2 nghiệm, phương trình cot x b 1 có đúng 2   3 
nghiệm và phương trình cot x  0 có đúng 3 nghiệm thuộc  ;  nên phương trình đã 2 2    cho có 7 nghiệm.
Câu 58. Cho hàm số y f x có bảng biến thiên như hình vẽ x  0 1 2  f  x  0  0  0   3  f x 0 1
Số nghiệm của phương trình f sin x   1  2 trên    ; 2  là A. 6. B. 7. C. 5. D. 4. Lời giải Strong Team Toán VD – VDC Trang 63/67 Chọn A
x a a  0
x b 0  b    1
Dựa vào bảng biến thiên hàm số f x, ta thấy f x  2  . 
x c 1  c  2 
x d d  2 
t a   1 t b  2
Đặt t  sin x 1. Phương trình đã cho tương đương với f t   2   t c 3 
t d 4  
Ta có: t x  cos x t x  0  x
k k  . 2
Ta có bảng biến thiên hàm số t x trên    ; 2  là:   3 x    2 2 2 2 t x  0  0  0  1 2 1 t x 0 0
Từ bảng biến thiên này, ta thấy các phương trình  
1 và 4 vô nghiệm, phương trình 2 có 4
nghiệm và phương trình 3 có đúng 2 nghiệm. Vậy phương trình đã cho có 6 nghiệm phân biệt.
-------------------- HẾT -------------------- Strong Team Toán VD – VDC Trang 64/67 Strong Team Toán VD – VDC Trang 65/67