Bài tập trắc nghiệm ứng dụng tích phân để tính diện tích hình phẳng Toán 12

Tài liệu gồm 99 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tuyển chọn các bài tập trắc nghiệm chủ đề ứng dụng tích phân để tính diện tích hình phẳng, có đáp án và lời giải chi tiết; giúp học sinh lớp 12 rèn luyện khi học chương trình môn Toán 12 phần Giải tích chương 3: Nguyên Hàm, Tích Phân Và Ứng Dụng.

31 16 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

DIỆN TÍCH HÌNH PHẲNG

TOÁN 12

LÊ BÁ BẢO

TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ

ỨNG DỤNG TÍCH PHÂN

 LUYỆN THI THPT QUỐC GIA

 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 1_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

y f x

liên tục trên đoạn

;ab





. Gọi

là diện tích hình phẳng giới hạn bởi đồ

thị

   

:C y f x

, trục hoành, hai đường thẳng

xa

xb

(như hình vẽ dưới đây).

Giả sử

là diện tích hình phẳng

. Mệnh đề nào dưới đây đúng?

   

S f x x f x x



. B.

   

S f x x f x x  



   

S f x x f x x



. D.

   

S f x x f x x  



Câu 2: Gọi

là diện tích hình phẳng giới hạn bởi các đường

y 

0y 

0x 

2x 

. Mệnh đề

nào dưới đây đúng?

e d .







e d .

Sx



e d .







e d .

Sx



Câu 3: Gọi

là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số

3yx

và

4yx

. Khẳng

định nào dưới đây đúng?

4 3 d  



S x x x

. B.

 

4 3 d  



S x x x

 

3 4 d  



S x x x

. D.

4 3 d  



S x x x

Câu 4: Cho hàm số

 

y f x

xác định, liên tục và có nguyên hàm trên

2;4





đồng thời có đồ thị như

hình vẽ dưới đây.

Tính

 

I f x x







8I 

. B.

4I 

. C.

6I 

. D.

2I 

Câu 5: Diện tích hình phẳng giới hạn bởi hai đồ thị

 

32f x x x  

;

 

2g x x

là

8S 

. B.

4S 

. C.

12S 

. D.

16S 

Câu 6: Diện tích

của hình phẳng giới hạn bởi các đường

2yx

πy 

4x 

và trục tung được

tính bởi công thức nào dưới đây ?

 

2 πdS x x



. B.

π 2 dS x x







 

2 πdS x x



. D.

2dS x x







Câu 7: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên. Đặt

   

2.g x f x x

Khẳng định nào sau đây đúng?

     

3 3 1 .g g g  

     

1 3 3 .g g g  

     

1 3 3 .g g g  

     

3 3 1 .g g g   

Câu 8: Tính diện tích

của hình phẳng giới hạn bởi

 

:4P y x

, tiếp tuyến của

 

tại

 

2;0M

và trục

là

S 

. B.

2S 

. C.

S 

. D.

S 

Câu 9: Cho hình phẳng

 

giới hạn bởi đồ thị của hai hàm số

 

và

 

liên tục trên đoạn

 

;ab

và hai đường thẳng

xa

xb

(tham khảo hình vẽ dưới).

Công thức tính diện tích của hình

 

là

   

S f x f x x



   

 

S f x f x x



   

S f x f x x



   

d d .

S f x x f x x



Câu 10: Cho hàm số

ye

, gọi

là diện tích hình phẳng giới hạn bởi các đường

; 1;

y e x x k   

và

là diện tích hình phẳng giới hạn bởi các đường

; ; 1

y e x k x  

. (tham khảo hình vẽ).

Xác định

để

.SS

ln ln2ke



  





. B.

2ln 1ke



  





. C.

2ln 2 1k 

. D.

ln 2k 

Câu 11: Trong mặt phẳng cho đường tròn

 

(tham khảo hình vẽ dưới đây).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

2,01.

2,46.

C. 1,81. D.

3,13.

Câu 12: Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên đoạn

 

;ab

với

ab

. Kí hiệu

là diện

tích hình phẳng giới hạn bởi các đường

 

3y f x

 

3y g x

xa

xb

;

là diện tích

hình phẳng giới hạn bởi các đường

 

2y f x

 

2y g x

xa

xb

. Khẳng định nào

sau đây đúng?

2.SS

3.SS

2 2.SS

2 2.SS

Câu 13: Cho hàm số bậc ba

()f x ax bx cx d   

và đường thẳng

: ( )d g x mx n

có đồ thị như

hình vẽ bên dưới:

Nếu diện tích phần tô bằng bằng

thì diện tích phần gạch bằng

. B.

. C.

. D.

Câu 14: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

   

1 0 0ff  

. Gọi

là diện tích hình

phẳng giới hạn bởi các đường

 

y f x

0y 

1x 

và

1x 

. Mệnh đề nào sau đây đúng?

 

dS f x x







   

ddS f x x f x x







ye

1

2

 

dS f x x







 

dS f x x







Câu 15: Một sân bóng hình chữ nhật với diện tích

200m

. Người ta muốn trồng cỏ trên sân bóng theo

hình một parabol bậc hai sao cho đỉnh của parabol trùng với trung điểm một cạnh của sân

bóng như hình vẽ bên. Biết chi phí trồng cỏ là 300 ngàn đồng cho mỗi mét vuông. Xác định

chi phí trồng cỏ cần có cho sân bóng trên?

triệu đồng. B.

triệu đồng. C.

triệu đồng. D.

triệu đồng.

Câu 16: Diện tích hình phẳng giới hạn bởi đường cong

4yx

và trục hoành là

. B.

. C.

. D.

Câu 17: Tính diện tích

của hình phẳng

 

giới hạn bởi đồ thị hàm số

yx

, trục hoành và

đường thẳng

2yx

2S 

. B.

S 

. C.

S 

. D.

S 

Câu 18: Một viên gạch hoa hình vuông cạnh

40cm

. Người thiết kế đã sử dụng bốn đường parabol có

chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ).

Diện tích mỗi cánh hoa của viên gạch bằng

800cm

. B.

800

. C.

400

. D.

250cm

Câu 19: Cho hai hàm số

 

 

2bxfx cxxa

và

 

2xg x dx e

(

e 

). Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

2

;

1

;

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

1

2

Câu 20: Cho hàm số

y x mx

 

04m

có đồ thị

 

. Gọi

SS

là diện tích của hình phẳng giới

hạn bởi

 

, trục hoành, trục tung và đường thẳng

4x 

(phần tô đậm trong hình vẽ bên

dưới). Giá trị của

sao cho

SS

là

3.m 

m 

2.m 

m 

____________________________HẾT____________________________

Huế, 11h00’ Ngày 09 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 1_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

y f x

liên tục trên đoạn

;ab





. Gọi

là diện tích hình phẳng giới hạn bởi đồ

thị

   

:C y f x

, trục hoành, hai đường thẳng

xa

xb

(như hình vẽ dưới đây).

Giả sử

là diện tích hình phẳng

. Mệnh đề nào dưới đây đúng?

   

S f x x f x x



. B.

   

S f x x f x x  



   

S f x x f x x



. D.

   

S f x x f x x  



Lời giải:

+ Nhìn đồ thị ta thấy:

 Đồ thị

()C

cắt trục hoành tại

 

0;0O

 Trên đoạn

;0a





, đồ thị

()C

ở dưới trục hoành nên

   

f x f x

 Trên đoạn

0;b





, đồ thị

 

ở trên trục hoành nên

   

f x f x

+ Do đó:

 

S f x x



   

f x x f x x



   

f x x f x x  





Chọn đáp án B.

Câu 2: Gọi

là diện tích hình phẳng giới hạn bởi các đường

y 

0y 

0x 

2x 

. Mệnh đề

nào dưới đây đúng?

e d .







e d .

Sx



e d .







e d .

Sx



Lời giải:

Diện tích hình phẳng giới hạn bởi các đường

y 

0y 

0x 

2x 

là

S e x





Chọn đáp án B.

Câu 3: Gọi

là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số

3yx

và

4yx

. Khẳng

định nào dưới đây đúng?

4 3 d  



S x x x

. B.

 

4 3 d  



S x x x

 

3 4 d  



S x x x

. D.

4 3 d  



S x x x

Lời giải:

Ta có phương trình hoành độ giao điểm của các đồ thị hàm số

3yx

và

4yx

là:

34xx

4 3 0   xx













Diện tích của hình phẳng cần tìm là:

4 3 d  



S x x x



Chọn đáp án A.

Câu 4: Cho hàm số

 

y f x

xác định, liên tục và có nguyên hàm trên

2;4





đồng thời có đồ thị như

hình vẽ dưới đây.

Tính

 

I f x x







8I 

. B.

4I 

. C.

6I 

. D.

2I 

Lời giải:

Ta có giá trị của tích phân

 

I f x x







là hiệu của diện tích hình thang với diện tích tam

giác.

Từ hình vẽ ta có hình thang cân, độ dài đáy lớn bằng

, độ dài đáy bé bằng

, chiều cao

bằng

. Diện tích hình thang là

Tam giác cân có cạnh đáy bằng

, chiều cao bằng

. Diện tích của tam giác là

Vậy

 



   



6 2 4.I f x x



Chọn đáp án B.

Câu 5: Diện tích hình phẳng giới hạn bởi hai đồ thị

 

32f x x x  

;

 

2g x x

là

8S 

. B.

4S 

. C.

12S 

. D.

16S 

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị

3 2 2 4 0

x x x x x





       







Diện tích cần tìm

4 d 4 dS x x x x x x



   



   

4 d 4 dx x x x x x



   



2 2 8

   

    

   



   



Chọn đáp án A.

Câu 6: Diện tích

của hình phẳng giới hạn bởi các đường

2yx

πy 

4x 

và trục tung được

tính bởi công thức nào dưới đây ?

 

2 πdS x x



. B.

π 2 dS x x







 

2 πdS x x



. D.

2dS x x







Lời giải:

Diện tích

của hình phẳng được tính bởi công thức:

 

2 π d 2 π dS x x x x   





Chọn đáp án C.

Câu 7: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên. Đặt

   

2.g x f x x

Khẳng định nào sau đây đúng?

     

3 3 1 .g g g  

     

1 3 3 .g g g  

     

1 3 3 .g g g  

     

3 3 1 .g g g   

Lời giải:

Ta có

       

2 2 0 3;1;3g x f x x g x x

  

      

Từ đồ thị của

 

y f x





ta có bảng biến thiên.(Chú ý là hàm

 

và

 



)

Suy ra

   

31gg

. Kết hợp với đồ thị ta có:

 

g x x g x x









               

3 1 3 1 3 3g x x g x x g g g g g g





         



Vậy ta có

     

3 3 1g g g  



Chọn đáp án B.

Câu 8: Tính diện tích

của hình phẳng giới hạn bởi

 

:4P y x

, tiếp tuyến của

 

tại

 

2;0M

và trục

là

S 

. B.

2S 

. C.

S 

. D.

S 

Lời giải:

Ta có:

2yx





;

 

24y





Phương trình tiếp tuyến của

 

tại

 

2;0 :M

 

4 2 4 8y x x   

Diện tích hình phẳng cần tìm là

 

4 4 8 d 4 4 dS x x x x x x      



 

x 





Chọn đáp án C.

Câu 9: Cho hình phẳng

 

giới hạn bởi đồ thị của hai hàm số

 

và

 

liên tục trên đoạn

 

;ab

và hai đường thẳng

xa

xb

(tham khảo hình vẽ dưới).

Công thức tính diện tích của hình

 

là

   

S f x f x x



   

 

S f x f x x



   

S f x f x x



   

d d .

S f x x f x x



Câu 10: Cho hàm số

ye

, gọi

là diện tích hình phẳng giới hạn bởi các đường

; 1;

y e x x k   

và

là diện tích hình phẳng giới hạn bởi các đường

; ; 1

y e x k x  

. (tham khảo hình vẽ).

Xác định

để

.SS

ln ln2ke



  





. B.

2ln 1ke



  





. C.

2ln 2 1k 

. D.

ln 2k 

Lời giải:

Ta có

SS

d d ln ln2

x x k k

e x e x e e e k e





         









Chọn đáp án A.

ye

1

2

Câu 11: Trong mặt phẳng cho đường tròn

 

(tham khảo hình vẽ dưới đây).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

2,01.

2,46.

C. 1,81. D.

3,13.

Lời giải:

Phương trình đường tròn là







  



  



Xét hệ phương trình:











  

















Diện tích cần tính là





2 4 1 2,46.S x x   





Chọn đáp án B.

Câu 12: Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên đoạn

 

;ab

với

ab

. Kí hiệu

là diện

tích hình phẳng giới hạn bởi các đường

 

3y f x

 

3y g x

xa

xb

;

là diện tích

hình phẳng giới hạn bởi các đường

 

2y f x

 

2y g x

xa

xb

. Khẳng định nào

sau đây đúng?

2.SS

3.SS

2 2.SS

2 2.SS

Lời giải:

Ta có

   

3 3 d

S f x g x x



   

f x g x x



 

3 2 2 d

f x g x x



   





3S



Chọn đáp án B.

Câu 13: Cho hàm số bậc ba

()f x ax bx cx d   

và đường thẳng

: ( )d g x mx n

có đồ thị như

hình vẽ bên dưới:

Nếu diện tích phần tô bằng bằng

thì diện tích phần gạch bằng

. B.

. C.

. D.

Lời giải:

Cách 1:

Dựa vào đồ thị



đường thẳng

: ( ) 1.d g x x

Phương trình hoành độ giao điểm của của hai đồ thị hàm số

   

,f x g x

là

   

3 2 3 2

1 1 1 0 1ax bx cx d x ax bx c x d           

Dựa vào đồ thị ta thấy đồ thị hàm số

   

,f x g x

cắt nhau tại ba điểm

0, 1, 2x x x  

    

 

1 1 2 0 3 2 0ax x x a x x x       

Diện tích phần tô màu:

 

3 2 2

a x x x dx a a     



Diện tích phần không tô màu giới hạn bởi đồ thị hàm số

   

,f x g x

và hai đường thẳng

1, 2xx

là

 

2 3 2

S x x x dx    



Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

1, , 1, 2g x x Ox x x   

là

S 

Diện tích phần gạch chéo là

S S S    

Cách 2:

Diện tích phần không tô màu giới hạn bởi đồ thị hàm số

   

,f x g x

và hai đường thẳng

1, 2xx

là

Diện tích phần tô màu là

S 

. Dựa vào đồ thị ta thấy

SS

Dựa vào đồ thị



đường thẳng

: ( ) 1d g x x

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

1, , 1, 2g x x Ox x x   

là

S 

Diện tích phần gạch chéo là

S S S    



Chọn đáp án B.

Câu 14: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

   

1 0 0ff  

. Gọi

là diện tích hình

phẳng giới hạn bởi các đường

 

y f x

0y 

1x 

và

1x 

. Mệnh đề nào sau đây đúng?

 

dS f x x







   

ddS f x x f x x







 

dS f x x







 

dS f x x







Lời giải:

Từ giả thiết ta có diện tích hình phẳng cần tìm được giới hạn bởi đồ thị hàm số

 

y f x

liên

tục trên ,

0y 

1x 

và

1x 

, nên:

 

dS f x x









Chọn đáp án D.

Câu 15: Một sân bóng hình chữ nhật với diện tích

200m

. Người ta muốn trồng cỏ trên sân bóng theo

hình một parabol bậc hai sao cho đỉnh của parabol trùng với trung điểm một cạnh của sân

bóng như hình vẽ bên. Biết chi phí trồng cỏ là 300 ngàn đồng cho mỗi mét vuông. Xác định

chi phí trồng cỏ cần có cho sân bóng trên?

triệu đồng. B.

triệu đồng. C.

triệu đồng. D.

triệu đồng.

Lời giải:

Gọi chiều dài của hình chữ nhật là

, chiều rộng là

(

0mn

Ta có diện tích hình chữ nhật là

200S mn

(

Chọn hệ trục tọa độ Đề các vuông góc Oxy sao cho đỉnh của parabol là

(0; ).In

Parabol đi qua

2 điểm









và







Do đó parabol có dạng

y x n





Vậy phần diện tích trồng cỏ là

S x n x















Vậy số tiền trồng cỏ cần là:

2 2.200

.300000 .300000



40000000.



Chọn đáp án D.

Câu 16: Diện tích hình phẳng giới hạn bởi đường cong

4yx

và trục hoành là

. B.

. C.

. D.

Lời giải:

Phương trình hoành độ giao điểm:





  







Diện tích hình phẳng là.

   

d d d d d

4 0 4 0 4

4 4 0 4 0

4 4 4 4 4 16S x x x x x x x x x x

  

          

    



Chọn đáp án C.

Câu 17: Tính diện tích

của hình phẳng

 

giới hạn bởi đồ thị hàm số

yx

, trục hoành và

đường thẳng

2yx

2S 

. B.

S 

. C.

S 

. D.

S 

Lời giải:

Hoành độ giao điểm

2xx

4( 0)xx  

00xx  

;

2 0 2xx   

Diện tích

S x dx



2x x dx   



xdx 



 

x x dx  





Chọn đáp án B.

Câu 18: Một viên gạch hoa hình vuông cạnh

40cm

. Người thiết kế đã sử dụng bốn đường parabol có

chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ).

Diện tích mỗi cánh hoa của viên gạch bằng

800cm

. B.

800

. C.

400

. D.

250cm

Lời giải:

Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng

10 1cm dm

), các cánh hoa tạo bởi các

đường parabol có phương trình

y 

y 

x 

x 

Diện tích một cánh hoa (nằm trong góc phàn tư thứ nhất) bằng diện tích hình phẳng giới hạn

bởi hai đồ thị hàm số

y 

2yx

và hai đường thẳng

0; 2xx

Do đó diện tích một cánh hoa bằng











 









   

4 400

dm cm



   

4 400

dm cm





Chọn đáp án C.

Câu 19: Cho hai hàm số

 

 

2bxfx cxxa

và

 

2xg x dx e

(

e 

). Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

2

;

1

;

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Lời giải:

Phương trình hoành độ giao điểm của đồ thị

 

và

 

là

     

3 2 2 3 2

2 3 2 4 0. *bx cx dx x a b d x c e xax             

Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình

 

có ba nghiệm

2x 

;

1x 

;

1x 

. Ta được

       

4 2 1 1ax b d x c e x k x x x      

. Khi đó

4 2 2kk    

Vậy diện tích hình phẳng cần tìm là

   

2 2 1 1

xxxx



  





Chọn đáp án A.

1

2

Câu 20: Cho hàm số

y x mx

 

04m

có đồ thị

 

. Gọi

SS

là diện tích của hình phẳng giới

hạn bởi

 

, trục hoành, trục tung và đường thẳng

4x 

(phần tô đậm trong hình vẽ bên

dưới). Giá trị của

sao cho

SS

là

3.m 

m 

2.m 

m 

Lời giải:

Phương trình hoành độ giao điểm của

 

và trục

là:

 

x mx

x m m





  



  





 

2 3 3

2 3 6

x x m

S x mx x mx x x m



      







 

3 2 3

3 2 3 6

x x m

S x mx x x mx x m m



        







Ta có:

64 8

S S m m     



Chọn đáp án D.

____________________________HẾT____________________________

Huế, 11h00’ Ngày 09 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 2_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Diện tích của hình phẳng

 

được giới hạn bởi đồ thị hàm số

 

y f x

, trục hoành và hai

đường thẳng

xa

xb

 

ab

(phần tô đậm trong hình vẽ dưới đây) tính theo công thức:

 

S f x x



. B.

   

S f x x f x x  



 

S f x x



. D.

   

S f x x f x x



Câu 2: Diện tích

của hình phẳng giới hạn bởi các đường

2 , 3, 1, 2y x x y x x      

được tính bởi công thức nào dưới đây ?

 

2 3 dS x x x



   



. B.

 

2 3 dS x x x   



 

2 3 dS x x x   



. D.

 

2 3 dS x x x  



Câu 3: Diện tích hình phẳng giới hạn bởi các đường

72yx

4yx

bằng

. B.

. C.

. D.

Câu 4: Diện tích hình phẳng giới hạn bởi các đường





, trục hoành và đường thẳng

1x 

là

S a b

. Khi đó

ab

bằng:

. B.

. C.

. D.

Câu 5: Hình phẳng

()H

được giới hạn bởi đồ thị

()C

của hàm đa thức bậc ba và parabol

()P

có trục

đối xứng vuông góc với trục hoành.

Phần tô đậm của hình vẽ có diện tích bằng



Câu 6: Phần hình phẳng

 

được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm

số

 

y f x

4y x x

và hai đường thẳng

2 ; 0xx  

Biết

 

f x x







. Diện tích hình

 

bằng

. B.

. C.

. D.

Câu 7: Tính diện tích miền hình phẳng giới hạn bởi các đường

2y x x

0y 

10x 

10x 

2000

S 

. B.

2008S 

. C.

2008

S 

. D.

2000

Câu 8: Gi

 

là hình phẳng giới hạn bởi các đường

 

3yx

, trục tung và trục hoành. Gi

 

kk

là hệ số góc của hai đường thẳng cng đi qua đim

 

0;9A

và chia

 

làm ba phần

có diện tích bằng nhau. Tính

kk

. B.

. C.

. D.

Câu 9: Anh Toàn có một cái ao hình elip với độ dài trục lớn và độ dài trục bé lần lượt là

100m

và

80m

. Anh chia ao ra hai phần theo một đường thẳng từ một đỉnh của trục lớn đến một đỉnh

của trục bé (Bề rộng không đáng k). Phần rộng hơn anh nuôi cá lấy thịt, phần nhỏ anh nuôi

cá giống. Biết lãi nuôi cá lấy thịt và lãi nuôi cá giống trong 1 năm lần lượt là

20.000

đồng/m

và

40.000

đồng/m

. Hỏi trong 1 năm anh Toàn có bao nhiêu tiền lãi từ nuôi cá trong ao đã nói

trên (Lấy làm tròn đến hàng nghìn)?

176350000

đồng. B.

137080000

đồng. C.

139043000

đồng. D.

105664000

đồng.

Câu 10: Diện tích hình phẳng giới hạn bởi các đường

;

y e y e

và

0x 

bằng

. B.

. C.

. D.

Câu 11: Trong mặt phẳng cho đường tròn

 

và parabol

 

(tham khảo hình vẽ dưới đây).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

1,04.

0,21.

0,67.

0,45.

Câu 12: Diện tích

của hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới

đây?

 

3 3 d .S x x x x



    



 

3 3 d .S x x x x



   



 

3 3 d .S x x x x



   



 

3 3 d .S x x x x



   



Câu 13: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ dưới đây:

Biết phương trình

 

0fx





có bốn nghiệm phân biệt

với

0a b c  

. Mệnh đề nào

dưới đây đúng?

     

f a f c f b

. B.

     

f a f b f c

     

f c f a f b

. D.

     

f b f a f c

Câu 14: Cho hàm số

   

, , , , 0y f x ax bx cx d a b c a      

có đồ thị

 

. Biết rằng đồ thị

 

tiếp

xúc với đường thẳng

4y 

tại đim có hoành độ âm và đồ thị hàm số

 

y f x





cho bởi hình

vẽ dưới đây:

Tính diện tích

của hình phẳng giới hạn bởi đồ thị

 

và trục hoành.

9S 

. B.

S 

. C.

. D.

Câu 15: Cho hai hàm số

2()f x ax bx cx   

và

2()gdxxxe 

( , , , , ).a b c d e

Biết rằng

đồ thị của hàm số

()y f x

và

()y g x

cắt nhau tại ba đim có hoành độ lần lượt là

2;

1;

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Câu 16: Diện tích hình phẳng

giới hạn các đồ thị hàm số

,2y x y x  

và trục hoành

(như

hình vẽ dưới đây) được tính bởi công thức nào sau đây ?

S x x



(2 ) d .S x x x  



(2 ) d .S x x x  



d ( 2)d .S x x x x  



Câu 17: Cho hình vuông

ABCD

tâm

, độ dài cạnh là

cm. Đường cong

BOC

là một phần của

parabol đỉnh

chia hình vuông thành hai hình phẳng có diện tích lần lượt là

và

(tham

khảo hình vẽ).

4 cm

Tỉ số

bằng

. B.

. C.

. D.

Câu 18: Cho hàm số

3 3 1y x x mx m    

. Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục

có diện tích phần nằm phía trên trục

và phần nằm dưới trục

bằng nhau. Giá trị

của

là:

. B.

. C.

. D.

Câu 19: Diện tích của hình phẳng giới hạn bởi

2yx

;

yx

;

1y 

trên miền

0x 

;

1,y 

bằng

Câu 20: Cho hàm số

 

y f x

. Đồ thị của hàm số

 

y f x





như hình dưới đây.

Đặt

     

21g x f x x  

. Mệnh đề nào dưới đây đúng?

     

3 3 1g g g  

. B.

     

3 3 1g g g  

     

1 3 3g g g  

. D.

     

1 3 3g g g  

____________________________HẾT____________________________

Huế, 21h00’ Ngày 09 tháng 02 năm 2022

2

3

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 2_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

LỜI GIẢI CHI TIẾT

Câu 1: Diện tích của hình phẳng

 

được giới hạn bởi đồ thị hàm số

 

y f x

, trục hoành và hai

đường thẳng

xa

xb

 

ab

(phần tô đậm trong hình vẽ dưới đây) tính theo công thức:

 

S f x x



. B.

   

S f x x f x x  



 

S f x x



. D.

   

S f x x f x x



Lời giải:

Áp dụng công thức tính diện tích hình phẳng ta có:

         

d d d d d00

b c b c b

a a c a c

S f x x f x x f x x f x x f x x

   

       

   

    



Chọn đáp án B.

Câu 2: Diện tích

của hình phẳng giới hạn bởi các đường

2 , 3, 1, 2y x x y x x      

được tính bởi công thức nào dưới đây ?

 

2 3 dS x x x



   



. B.

 

2 3 dS x x x   



 

2 3 dS x x x   



. D.

 

2 3 dS x x x  



Lời giải:

Diện tích

của hình phẳng giới hạn bởi các đường

2 , 3, 1, 2y x x y x x      

là:

 

2 3 d 2 3 .S x x x x x dx       





Chọn đáp án C.

Câu 3: Diện tích hình phẳng giới hạn bởi các đường

72yx

4yx

bằng

. B.

. C.

. D.

Lời giải:

Phương trình hoành độ giao đim của các đường

72yx

4yx

là

2 2 2

7 2 4 3 3 1x x x x       

Khi đó diện tích hình phẳng cần tìm là

     

1 1 1

2 2 2 2

1 1 1

7 2 4 d 3 3 d 3 3 d 4S x x x x x x x

  

        

  



Chọn đáp án C.

Câu 4: Diện tích hình phẳng giới hạn bởi các đường





, trục hoành và đường thẳng

1x 

là

S a b

. Khi đó

ab

bằng:

. B.

. C.

. D.

Lời giải:

Xét phương trình





0x

Vậy diện tích cần tính bằng

1 2 1

S x x

    





Vậy

2a 

;

1b 

nên

3ab



Chọn đáp án D.

Câu 5: Hình phẳng

()H

được giới hạn bởi đồ thị

()C

của hàm đa thức bậc ba và parabol

()P

có trục

đối xứng vuông góc với trục hoành.

Phần tô đậm của hình vẽ có diện tích bằng



Lời giải:

Vì đồ thị hàm số

   

:C f x ax bx cx d   

và

   

:P g x mx nx p  

có

hoành độ

giao đim là

1,1,2

nên

       

1 1 2f x g x a x x x    

Ta có

   

0 2, 0 0fg

nên

      

0 0 .1. 1 2 2 2 1f g a a a       

Vậy phần diện tích tô đậm là

   

1 1 2

S x x x dx



    





Chọn đáp án A.

Câu 6: Phần hình phẳng

 

được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm

số

 

y f x

4y x x

và hai đường thẳng

2 ; 0xx  

Biết

 

f x x







. Diện tích hình

 

bằng

. B.

. C.

. D.

Lời giải:

Diện tích hình

 

là :

 

4dS f x x x x





  





 

d 4 df x x x x x



  





  







 

4 20

3 3 3



    

Vậy diện tích hình

 

là

S 



Chọn đáp án D.

Câu 7: Tính diện tích miền hình phẳng giới hạn bởi các đường

2y x x

0y 

10x 

10x 

2000

S 

. B.

2008S 

. C.

2008

S 

. D.

2000

Lời giải:

Phương trình hoành độ giao đim của đồ thị

2y x x

và

0y 

là

20xx













Trên đoạn

10;10







ta có:

20xx

10;0x



  



và

2;10





;

20xx

0;2x







Do đó

2S x x x







     

d d d

0 2 10

2 2 2

10 0 2

2 2 2x x x x x x x x x



     

  

2008



( đvdt).



Chọn đáp án C.

Nhận xét:

Nếu hc sinh sử dụng MTCT tính tích phân mà không chia khoảng thì có sự sai khác về kết

quả giữa máy casio và vinacal. Trong trường hợp này máy vinacal cho đáp số đúng.

Câu 8: Gi

 

là hình phẳng giới hạn bởi các đường

 

3yx

, trục tung và trục hoành. Gi

 

kk

là hệ số góc của hai đường thẳng cng đi qua đim

 

0;9A

và chia

 

làm ba phần

có diện tích bằng nhau. Tính

kk

. B.

. C.

. D.

Lời giải:

Gi

:9d y k x

 

kk

Gi

;0M d Ox M



   





;

;0N d Ox N



   







  





Giao đim của

   

:3P y x

với hai trục ta độ lần lượt là

 

3;0C

 

0;9A

Theo giả thiết ta có

9 18

AON ANM

S S OM N k k



        

Lại có

 

1 243 27

3 3 3. . . 9

2 2 2

AON

S x x OA ON k



         



Suy ra

k 

kk  



Chọn đáp án D.

Câu 9: Anh Toàn có một cái ao hình elip với độ dài trục lớn và độ dài trục bé lần lượt là

100m

và

80m

. Anh chia ao ra hai phần theo một đường thẳng từ một đỉnh của trục lớn đến một đỉnh

của trục bé (Bề rộng không đáng k). Phần rộng hơn anh nuôi cá lấy thịt, phần nhỏ anh nuôi

cá giống. Biết lãi nuôi cá lấy thịt và lãi nuôi cá giống trong 1 năm lần lượt là

20.000

đồng/m

và

40.000

đồng/m

. Hỏi trong 1 năm anh Toàn có bao nhiêu tiền lãi từ nuôi cá trong ao đã nói

trên (Lấy làm tròn đến hàng nghìn)?

176350000

đồng. B.

137080000

đồng. C.

139043000

đồng. D.

105664000

đồng.

Lời giải:

Diện tích toàn bộ ao là

 

.40.50 2000 mS





Diện tích phần nuôi cá giống là:

 

500 1000 m

OAB





   

Diện tích phần nuôi cá thịt là:

 

1500 1000 mS S S



   

Tiền lãi từ nuôi cá là:

40000. 20000. 137080000SS



Chọn đáp án B.

Câu 10: Diện tích hình phẳng giới hạn bởi các đường

;

y e y e

và

0x 

bằng

. B.

. C.

. D.

Lời giải:

Ta có:

e e e e x     

Xét dấu

ee

–

∞

–

∞

– e

Diện tích hình phẳng giới hạn bởi các đường

;

y e y e

và

0; 1xx

là

   

 

x x x

S e edx e e dx ex e e e e          





Chọn đáp án C.

Câu 11: Trong mặt phẳng cho đường tròn

 

và parabol

 

(tham khảo hình vẽ dưới đây).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

1,04.

0,21.

0,67.

0,45.

Lời giải:

Phương trình đường tròn là

 

1 1 .

y x x







   



  



Phương trình parabol là

.yx

Diện tích cần tính là





2 0,45.S x x x x   





Chọn đáp án D.

Câu 12: Diện tích

của hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới

đây?

 

3 3 d .S x x x x



    



 

3 3 d .S x x x x



   



 

3 3 d .S x x x x



   



 

3 3 d .S x x x x



   



Lời giải:

Diện tích phần gạch chéo được tính bở công thức :

3 2 3 2

3 2 1 ( 3 3) .S x x x dx x x x dx



        





Chọn đáp án B.

Câu 13: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ dưới đây:

Biết phương trình

 

0fx





có bốn nghiệm phân biệt

với

0a b c  

. Mệnh đề nào

dưới đây đúng?

     

f a f c f b

. B.

     

f a f b f c

     

f c f a f b

. D.

     

f b f a f c

Lời giải:

Ta có bảng biến thiên

f(c)

f(b)

f(0)

f(a)



f(x)

(x)

Suy ra

   

f c f b

(1)

Gi

là diện tích hình phẳng giới hạn bởi đồ thị

 

y f x





, đường thẳng

xa

0x 

là diện tích hình phẳng giới hạn bởi đồ thị

 

y f x





, đường thẳng

0x 

xb

là diện tích hình phẳng giới hạn bởi đồ thị

 

y f x





, đường thẳng

xb

xc

Vì

1 3 2

S S S



     

d d d

f x x f x x f x x

  



  



     

d d d

f x x f x x f x x

  

  

  



           

00f f a f c f b f b f     



   

f a f c

(2)

Từ (1) và (2)



     

f a f c f b



Chọn đáp án A.

Câu 14: Cho hàm số

   

, , , , 0y f x ax bx cx d a b c a      

có đồ thị

 

. Biết rằng đồ thị

 

tiếp

xúc với đường thẳng

4y 

tại đim có hoành độ âm và đồ thị hàm số

 

y f x





cho bởi hình

vẽ dưới đây:

Tính diện tích

của hình phẳng giới hạn bởi đồ thị

 

và trục hoành.

9S 

. B.

S 

. C.

. D.

Lời giải:

Từ đồ thị suy ra

 

33f x x





   

 

3 3 3f x f x dx x dx x x C



     



 

tiếp xúc với đường thẳng

4y 

tại đim có hoành độ

âm nên

 

0 0 0

0 3 3 0 1f x x x



      

. Suy ra

 

1 4 2fC   

 

: 3 2C y x x   

Xét phương trình

3 2 0





   







Diện tích hình phẳng cần tìm là:

 

x x dx



  





Chọn đáp án B.

Câu 15: Cho hai hàm số

2()f x ax bx cx   

và

2()gdxxxe 

( , , , , ).a b c d e

Biết rằng

đồ thị của hàm số

()y f x

và

()y g x

cắt nhau tại ba đim có hoành độ lần lượt là

2;

1;

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Lời giải:

Ta có phương trình hoành độ giao đim:

   

f x g x

   

0f x g x  

   

40b d x cax ex      

(1).

Vì phương trình (1) là phương trình bậc 3 và

2; 1; 1x x x    

là 3 nghiệm phân biệt của

phương trình (1) nên ta suy ra

       

2 1 1f x g x a x x x    

(2).

Ta có

 

02f 

 

02g 

nên

   

0 0 4fg  

Mặt khác từ (2) ta có

         

0 0 0 2 . 0 1 . 0 1 2f g a a      

Suy ra

2 4 2aa    

Do đó

         

 

2. 2 1 1 2 2 1f x g x x x x x x       

Diện tích hình phẳng cần tìm là

     

 

d 2 2 1 d

S f x g x x x x x



     





Chọn đáp án A.

Câu 16: Diện tích hình phẳng

giới hạn các đồ thị hàm số

,2y x y x  

và trục hoành

(như

hình vẽ dưới đây) được tính bởi công thức nào sau đây ?

S x x



(2 ) d .S x x x  



(2 ) d .S x x x  



d ( 2)d .S x x x x  



Lời giải:

1 2 1

0 1 0

(2 ) .

S x dx x dx x dx    

  



Chọn đáp án A.

Câu 17: Cho hình vuông

ABCD

tâm

, độ dài cạnh là

cm. Đường cong

BOC

là một phần của

parabol đỉnh

chia hình vuông thành hai hình phẳng có diện tích lần lượt là

và

(tham

khảo hình vẽ).

4 cm

Tỉ số

bằng

. B.

. C.

. D.

Lời giải:

-2

Gắn hệ trục toạ độ như hình vẽ.

Ta có phương trình parabol

 

P y x

Suy ra

1 16

S x dx





  







(đvdt).

Diện tích hình vuông

ABCD

là

4 16

ABCD

S 

(đvdt).

Do đó diện tích

là

16 32

ABCD

S S S    

(đvdt).

Vậy tỉ số

16 32 1

3 3 2





Chọn đáp án B.

Câu 18: Cho hàm số

3 3 1y x x mx m    

. Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục

có diện tích phần nằm phía trên trục

và phần nằm dưới trục

bằng nhau. Giá trị

của

là:

. B.

. C.

. D.

Lời giải:

TXĐ:

D 

 

3 6 3 3 2y x x m x x m



     

Yêu cầu bài toán suy ra đồ thị hàm số cắt trục

tại

đim phân biệt nên.

20x x m  

có hai nghiệm phân biệt

0 1 0 1



       

Khi đó đồ thị hàm số đối xứng qua tâm

 

1; 3 4Im

Yêu cầu bài toán tương đương với

 

t/m

3 4 0

I Ox m m      



Chọn đáp án A.



Chọn đáp án A.

Câu 19: Diện tích của hình phẳng giới hạn bởi

2yx

;

yx

;

1y 

trên miền

0x 

;

1,y 

bằng

Lời giải:

Phương trình hoành động giao đim

1x 

1x

;

21x 

x

Hình phẳng cần tính được tạo từ hai hình

 

và

 

Trong đó

 

H y x

















2dS x x x  





Và

 

H y x

















1dS x x  





Vậy diện tích hình phẳng cần tính là

5 5 5

24 24 12

S S S    



Chọn đáp án C.

Câu 20: Cho hàm số

 

y f x

. Đồ thị của hàm số

 

y f x





như hình dưới đây.

Đặt

     

21g x f x x  

. Mệnh đề nào dưới đây đúng?

     

3 3 1g g g  

. B.

     

3 3 1g g g  

     

1 3 3g g g  

. D.

     

1 3 3g g g  

Lời giải:

Ta có

     

2 2 1g x f x x



  

   

g x f x x







    







Bảng biến thiên

Suy ra

   

31gg

và

   

31gg

Theo hình vẽ

           

d d d d

1 3 1 3

3 1 3 1

f x x x x f x x g x x g x x



   

   

       

   

   

               

1 3 3 1 3 3g x g x g g g g g g



           

Vậy

     

1 3 3g g g  



Chọn đáp án D.

____________________________HẾT____________________________

Huế, 21h00’ Ngày 09 tháng 02 năm 2022



1



 











 



 

1g 

 

2

3

2

3

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 3_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

y f x

liên tục trên

Gọi

là diện tích hình phẳng giới hạn bởi đồ thị

   

:C y f x

, trục hoành, hai đường thẳng

2x

 4x

(tham khảo hình vẽ bên dưới).

(

)

-2

Giả sử

là diện tích hình phẳng

. Mệnh đề nào dưới đây sai?

 







S f x x

 







S f x x

   







S f x x f x x

   







S f x x f x x

Câu 2: Diện tích hình phẳng giới hạn bởi các đường

y x x

22yx

0x 

3x 

được tính bởi

công thức

 

3 2 dS x x x  



. B.

3 2 dS x x x  



3 2 dS x x x  



. D.

2dS x x x  



Câu 3: Diện tích của hình phẳng giới hạn bởi các đường

cos ; 0y x y

và





bằng





. B.





. C.





. D.



Câu 4: Diện tích hình phẳng giới hạn bởi các đường

yx

và

2yx

là

9S 

. B.

S 

. C.

S 

. D.

S 

Câu 5: Cho hàm số

 

có đồ thị trên đoạn

 

3;3

là đường gấp khúc

ABCD

như hình vẽ.

-2

Tính

 

df x x





. B.

. C.



. D.



Câu 6: Cho hàm số

 

y f x

liên tục trên đoạn







2;2

, có đồ thị tạo với trục hoành một hình phẳng

gồm

phần có diện tích

;

như hình vẽ bên dưới:

(

)

-2

Tích phân

 





f x x

bằng

2 3 1

S S S

. B.

1 2 3

S S S

. C.

1 2 3

S S S

. D.

  

1 2 3

S S S

Câu 7: Cho hàm số

 

có đạo hàm

 



liên tục trên và đồ thị của

 



trên đoạn

 

2;6

như hình bên dưới. Khẳng định nào dưới đây đúng?

(C): y = f(x)

       

2 1 2 6f f f f    

. B.

       

2 2 1 6f f f f    

       

2 2 1 6f f f f    

. D.

       

6 2 2 1f f f f    

Câu 8: Tính diện tích

của hình phẳng giới hạn bởi đồ thị các hàm số

yx

2yx

S

3.S

S

Câu 9: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên.

Đặt

     

2 1 .g x f x x   

Khẳng định nào sau đây đúng?

     

3 1 0 .g g g

     

1 0 3 .g g g

     

0 3 1 .ggg

     

1 3 0 .g g g

(

)

-2

Câu 10: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

 

1y e x

và

 

y e x

là.



. B.



. C.

. D.



Câu 11: Cho

()y f x

là hàm số đa thức bậc ba có đồ thị như hình vẽ bên dưới:

Tính diện tích hình phẳng được tô đậm.

. B.

. C.

. D.

Câu 12: Cho hàm số

3y x x m  

có đồ thị

 

, với

là tham số thực. Giả sử

 

cắt trục

tại bốn điểm phân biệt như hình vẽ

Gọi

là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của

để

1 3 2

S S S

là



Câu 13: Cho hàm số

()y f x

có đồ thị trên đoạn

[ 2;6]

như hình vẽ bên dưới. Biết các miền

,,A B C

có diện tích lần lượt là

32, 2

và

Tích phân

(3 4) 1 2 5 d

I x f x x x





     







bằng

I 

82I 

. C.

66I 

. D.

50I 

Câu 14: Biết rằng hình phẳng

 

giới hạn bởi các đường thẳng

2yx

0y 

xk

3x 

 

2k 

và có diện tích bằng

. Xác định giá trị

để

S 

2 15k   

. B.

2 31k 

. C.

2 15k 

. D.

2 31k   

Câu 15: Trong mặt phẳng cho hai đường tròn

 

và

 

(tham khảo hình vẽ dưới đây).





( )

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) gần nhất với giá trị bằng

1,04.

2,21.

1,71.

1,45.

Câu 16: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao

4GH m

, chiều rộng

4AB m

0,9AC BD m

. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật

CDEF

tô đậm có

giá là

1200000

đồng

, còn các phần để trắng làm xiên hoa có giá là

900000

đồng

. Hỏi

tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?

11445000

đồng. B.

4077000

đồng. C.

7368000

đồng. D.

11370000

đồng.

Câu 17: Tính diện tích hình phẳng giới hạn bởi các đường

yx

yx  

và trục hoành.

. B.

. C.

343

162

. D.

Câu 18: Trong mặt phẳng cho elip và đường tròn như hình vẽ.

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

593,92.

602,22.

570,14.

613,02.

Câu 19: Cho đường thẳng

yx

và parabol

y x a

(

là tham số thực dương). Gọi

,SS

lần

lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.

Khi

SS

thì

thuộc khoảng nào dưới đây?

;

4 32







. B.

;

32 4







. C.

;

16 32







. D.







Câu 20: Cho hình phẳng

()H

giới hạn bởi đồ thị hàm số

( ) 4f x x x

trục hoành và hai đường

thẳng

0, 2xx

(tham khảo hình vẽ bên dưới).

Đường thẳng

()y a b x

(với

,ab

là các số nguyên dương) chia

()H

thành hai phần có

diện tích bằng nhau. Giá trị của biểu thức

bằng

. B.

. C.

. D.

____________________________HẾT____________________________

Huế, 11h00’ Ngày 11 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 3_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

y f x

liên tục trên

Gọi

là diện tích hình phẳng giới hạn bởi đồ thị

   

:C y f x

, trục hoành, hai đường thẳng

2x

 4x

(tham khảo hình vẽ bên dưới).

(

)

-2

Giả sử

là diện tích hình phẳng

. Mệnh đề nào dưới đây sai?

 







S f x x

 







S f x x

   







S f x x f x x

   







S f x x f x x

Câu 2: Diện tích hình phẳng giới hạn bởi các đường

y x x

22yx

0x 

3x 

được tính bởi

công thức

 

3 2 dS x x x  



. B.

3 2 dS x x x  



3 2 dS x x x  



. D.

2dS x x x  



Lời giải:

Ta có

 

2 2 d 3 2 dS x x x x x x x      





Chọn đáp án C.

Câu 3: Diện tích của hình phẳng giới hạn bởi các đường

cos ; 0y x y

và





bằng





. B.





. C.





. D.



Lời giải:

Diện tích hình phẳng cần tìm là:

 

4 4 4

0 0 0

1 1 1 1

cos cos 1 cos2 sin 2

2 2 2 8 4

S x dx xdx x dx x x



  





       





  



Chọn đáp án C.

Câu 4: Diện tích hình phẳng giới hạn bởi các đường

yx

và

2yx

là

9S 

. B.

S 

. C.

S 

. D.

S 

Lời giải:

Phương trình hoành độ giao điểm là:

2xx













Ta có

2dS x x x



  



3 2 2





   







Chọn đáp án C.

Câu 5: Cho hàm số

 

có đồ thị trên đoạn

 

3;3

là đường gấp khúc

ABCD

như hình vẽ.

-2

Tính

 

df x x





. B.

. C.



. D.



Lời giải:

-2

Phương trình đường thẳng

đi qua

 

1;1C

và nhận

 

2; 3CD 

làm véctơ chỉ phương.

Phương trình chính tắc

 

: 3 2 5

CD x y



     



Đặt

 

E CD Ox

Ta được

3 2 5



   



























Do đó

 

df x x







       

2 1 3

3 2 1

d d d df x x f x x f x x f x x





  

   

1 1 2 2 3

ABA A BCA A CE EDA

S S S S   

   

1 1 2 1 4

1 1 3 1 1 2

2 2 3 2 3

   

       

   

   

1 1 4 5

2 3 3 2

    



Chọn đáp án A.

Câu 6: Cho hàm số

 

y f x

liên tục trên đoạn







2;2

, có đồ thị tạo với trục hoành một hình phẳng

gồm

phần có diện tích

;

như hình vẽ bên dưới:

(

)

-2

Tích phân

 





f x x

bằng

2 3 1

S S S

. B.

1 2 3

S S S

. C.

1 2 3

S S S

. D.

  

1 2 3

S S S

Lời giải:

Ta có đồ thị hàm số

 

y f x

cắt trục hoành tại điểm có hoành độ

2x

;

0x 

;

 1x

;

 2x

Ta có:

       

d d d d



  

   

2 0 1 2

2 2 0 1

f x x f x x f x x f x x

   

1 2 3

S S S



Chọn đáp án D.

Câu 7: Cho hàm số

 

có đạo hàm

 



liên tục trên và đồ thị của

 



trên đoạn

 

2;6

như hình bên dưới. Khẳng định nào dưới đây đúng?

(C): y = f(x)

       

2 1 2 6f f f f    

. B.

       

2 2 1 6f f f f    

       

2 2 1 6f f f f    

. D.

       

6 2 2 1f f f f    

Lời giải:

Dựa vào đồ thị của hàm

 



trên đoạn

 

2;6

ta suy ra bảng biến thiên của hàm số

 

trên đoạn

 

2;6

như sau:

Dựa vào bảng biến thiên ta có

   

  















nên A, D sai.

(C): y = f(x)

Ta cần so sánh

 

2f 

và

 

2.f

Gọi

là diện tích hình phẳng được tô đậm như trên hình vẽ.

Ta có:

 

dS f x x









 

f x dx









   

12ff   

 

dS f x x









 

df x x









   

12ff  

Dựa vào đồ thị ta thấy

SS

nên

       

1 2 1 2f f f f     

   

22ff  



Chọn đáp án B.

Câu 8: Tính diện tích

của hình phẳng giới hạn bởi đồ thị các hàm số

yx

2yx

S

3.S

S

Lời giải:

Xét phương trình:

2xx

5 4 0











  

















Diện tích hình phẳng cần tìm:



   



S x x x



Chọn đáp án D.

Câu 9: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên.

Đặt

     

2 1 .g x f x x   

Khẳng định nào sau đây đúng?

     

3 1 0 .g g g

     

1 0 3 .g g g

     

0 3 1 .ggg

     

1 3 0 .g g g

(

)

-2

Lời giải:

Ta có

         

2 2 1 2 1 ;g x f x x f x x





       



   

0 1 1

g x f x x x









      







Bảng biến thiên:

Suy ra

   

01gg

và

   

31gg

(

)

-2

Theo hình vẽ

           

d d d d

1 3 1 3

0 1 0 1

f x x x x f x x g x x g x x

   

   

         

   

   

               

         

1 0 3 1 3 0g x g x g g g g g g

. Vậy

     

1 0 3 .g g g



Chọn đáp án B.

Câu 10: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

 

1y e x

và

 

y e x

là.



. B.



. C.

. D.



Lời giải:

Ta có: Phương trình hoành độ giao điểm của hai đường cong là

 

e x e x  

Suy ra

0; 1xx

Do đó

 

1 1 d ... 1

S e x e x x      





Chọn đáp án D.

Câu 11: Cho

()y f x

là hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng được

tô đậm.





 











 



 



. B.

. C.

. D.

Lời giải:

Giả sử

()f x ax bx cx d   

có đồ thị

()C

như hình vẽ trên.

Điểm

(0;0) ( ) d 0 ( )O C f x ax bx cx      

Các điểm

(1;0), (2;2), (3;0) (C) 4 2 1 4 ( ) 4 3

9 3 0 3

a b c a

A B D a b c b f x x x x

a b c c

    





           





    



Diện tích hình phẳng cần tìm là

   

1 3 1 3

3 2 3 2

0 1 0 1

0 ( ) ( ) 0 ( 4 3 ) ( 4 3 ) .

S f x dx f x dx x x x dx x x x dx           

   



Chọn đáp án B.

Câu 12: Cho hàm số

3y x x m  

có đồ thị

 

, với

là tham số thực. Giả sử

 

cắt trục

tại bốn điểm phân biệt như hình vẽ

Gọi

là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của

để

1 3 2

S S S

là



Lời giải:

Gọi

là nghiệm dương lớn nhất của phương trình

30x x m  

, ta có

3m x x  

 

Vì

1 3 2

S S S

và

SS

nên

2SS

hay

 

f x x 



Mà

 

f x x



 

x x m x  



x mx



  





x mx  

x x m



  





Do đó,

x x m



  







xm  

 

Từ

 

và

 

, ta có phương trình

2 4 2

1 1 1

x x x   



4 10 0xx  



x 

Vậy

3m x x  





Chọn đáp án B.

Câu 13: Cho hàm số

()y f x

có đồ thị trên đoạn

[ 2;6]

như hình vẽ bên dưới. Biết các miền

,,A B C

có diện tích lần lượt là

32, 2

và

Tích phân

(3 4) 1 2 5 d

I x f x x x





     







bằng

I 

82I 

. C.

66I 

. D.

50I 

Lời giải:

Đặt

 

2 5 2 3 4 2

t x x dt x dx x dx dt



           





Đổi cận: - Với

22xt    

-Với

26xt  

Ta được:

   

6 6 6

2 2 2

2 1 2 2 16 2I f t dt dt f t dt M

  

        





  

Với

       

6 2 4 6

2 2 2 4

32 2 3 33M f t dt f t dt f t dt f t dt



         

   

Vậy:

 

16 2. 33 50I     



Chọn đáp án D.

Câu 14: Biết rằng hình phẳng

 

giới hạn bởi các đường thẳng

2yx

0y 

xk

3x 

 

2k 

và có diện tích bằng

. Xác định giá trị

để

S 

2 15k   

. B.

2 31k 

. C.

2 15k 

. D.

2 31k   

Lời giải:

3 2 3

2 d 2 d 2 d

S x x x x x x     

  

   

2 d 2 d

x x x x   



   

    

   

   

kk  

x x x x

   

   

   

   

Mà

S 

nên suy ra

2 16

kk  

1 27

kk   

2 31















Vì

2k 

nên

2 31k 



Chọn đáp án B.

Câu 15: Trong mặt phẳng cho hai đường tròn

 

và

 

(tham khảo hình vẽ dưới đây).





( )

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) gần nhất với giá trị bằng

1,04.

2,21.

1,71.

1,45.

Lời giải:





( )

Phương trình đường tròn

 

là







  



  



Phương trình đường tròn

 

là

 

2 1 .



  



   



  



Xét hệ phương trình:

 

























  





  











Diện tích cần tính là

 





2 2 4 2 1 1,71.

S S S x x x





        







Cách 2:





2 2 1 4 1,71S x x x



     









Chọn đáp án C.

Câu 16: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao

4GH m

, chiều rộng

4AB m

0,9AC BD m

. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật

CDEF

tô đậm có

giá là

1200000

đồng

, còn các phần để trắng làm xiên hoa có giá là

900000

đồng

. Hỏi

tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?

11445000

đồng. B.

4077000

đồng. C.

7368000

đồng. D.

11370000

đồng.

Lời giải:

Gắn hệ trục tọa độ Oxy sao cho

trùng

khi đó parabol có đỉnh

 

2;4G

và đi qua gốc tọa độ.

Giả sử phương trình của parabol có dạng

 

0y ax bx c a   

Vì parabol có đỉnh là

 

2;4G

và đi qua điểm

 

0;0O

nên ta có

.2 .2 4













  



















Suy ra phương trình parabol là

() 4y f x x x

Diện tích của cả cổng là

   

2 2 2

4 d 2 m

S x x x x



      







Mặt khác chiều cao

 

0,9 2,79(m)CF DE f  

;

 

4 2.0,9 2,2 mCD   

Diện tích hai cánh cổng là

 

. 6,138 m

CDEF

S CD CF

Diện tích phần xiên hoa là

 

32 6793

6,14 m

3 1500

xh CDEF

S S S    

Vậy tổng số tiền để làm cổng là

6793

6,138.1200000 .900000 11441400

1500



đồng.



Chọn đáp án A.

Câu 17: Tính diện tích hình phẳng giới hạn bởi các đường

yx

yx  

và trục hoành.

. B.

. C.

343

162

. D.

Lời giải:

Phương trình hoành độ giao điểm của các đường

yx

yx  

là

xx  

3 4 0xx   















Hoành độ giao điểm của đường thẳng

yx  

với trục hoành là

4x 

Hoành độ giao điểm của parabol

yx

với trục hoành là

0x 

Diện tích hình phẳng cần tìm là:

S x x x x



   







3 6 3



   









Chọn đáp án A.

Câu 18: Trong mặt phẳng cho elip và đường tròn như hình vẽ.

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

593,92.

602,22.

570,14.

613,02.

Lời giải:

Đường tròn có phương trình là:

 

20 400

20 400 .

20 400



  



   



  



Elip có phương trình là:

400 1

1600

1600 400

400 1

1600















  







  









Xét hệ phương trình:

 

20 400

1 1600 1

1600 400 400



  







    













 

20 20 13

17,37

1600 1 20 400 3 40 1600 0 .

400

20 20 13

y y y













          















Xét

20 20 13

19,83.



  

Lúc đó:





g¹ch

19,83

2 400 1 20 400 593,92.

1600

S x x







     













Chọn đáp án A.

Câu 19: Cho đường thẳng

yx

và parabol

y x a

(

là tham số thực dương). Gọi

,SS

lần

lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.

Khi

SS

thì

thuộc khoảng nào dưới đây?

;

4 32







. B.

;

32 4







. C.

;

16 32







. D.







Lời giải:

Xét phương trình hoành độ giao điểm

1 3 1 3

2 4 2 4

x a x x x a     

 

Do đường thẳng

yx

cắt parabol

y x a

tại hai điểm phân biệt có hoành độ dương

nên phương trình

 

có hai nghiệm dương phân biệt

0 xx









     









Ta có:

S x a x x



  







;

3 1 1 3

4 2 2 4

S x x a x x a x x

   

      

   

   



1 2 1 2

1 3 1 3

0 d d 0

2 4 2 4

S S S S x a x x x a x x

   

          

   

   



1 3 3

d 0 0

2 4 6 8

x a x x ax x



       







3 2 2

2 2 2 2

1 3 1 3

6 8 6 8

x ax x x a x       

Mà

là nghiệm phương trình

 

nên

x x a  

Trừ vế với vế hai phương trình được:

 

x TM







   









Với

x 

128

a

(tm). Vậy

27 3 7

;

128 16 32











Chọn đáp án C.

Câu 20: Cho hình phẳng

()H

giới hạn bởi đồ thị hàm số

( ) 4f x x x

trục hoành và hai đường

thẳng

0, 2xx

(tham khảo hình vẽ bên dưới).

Đường thẳng

()y a b x

(với

,ab

là các số nguyên dương) chia

()H

thành hai phần có

diện tích bằng nhau. Giá trị của biểu thức

bằng

. B.

. C.

. D.

Lời giải:

Phương trình hoành độ giao điểm:

( ) 0 4 0 0, 2f x x x x x

Diện tích miền

()H

là:

(4 ) 4S x x dx

Giả sử đường thẳng

y kx

chia miền

()H

thành

phần có diện tích bằng nhau và bằng

Xét phương trình hoành độ giao điểm:

4 0, 4x x kx x x k

Ta có:

2 4 2 2 2

(4 ) (4 ) (4 )

2 ((4 ) ) (4 ).

2 4 2 4 4

x x k k k

k x x dx k

4 2 2

(4 ) 8 4 2 2 4, 8 12

4 2 2

k k a b a b



Chọn đáp án A.

____________________________HẾT____________________________

Huế, 11h00’ Ngày 11 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 4_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên đoạn

 

;ba

. Gọi

là diện tích hình

phẳng giới hạn bởi các đồ thị hàm số

 

y f x

 

y g x

và hai đường thẳng

 

,x a x b a b  

, diện tích của

được tính theo công thức nào dưới đây?

   

 

f x g x x



. B.

   

S f x x g x x



.C.

   

f x g x x



.D.

   

f x g x x



Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

4yx  

, trục hoành và các đường thẳng

0x 

3x 

là:

. B. 3. C.

. D.

Câu 3: Cho hàm số bậc bốn

 

y f x

liên tục trên

Gọi

là hình phẳng giới hạn bởi đồ thị

   

:C y f x

(tham khảo hình vẽ bên dưới).

-2

Mệnh đề nào dưới đây sai?

 







S f x x

     

ddd



  

  

0 1 2

2 0 1

S f x x f x x f x x

     

d d d



   

  

0 1 2

2 0 1

S f x x f x x f x x

   







S f x x f x x

Câu 4: Trong mặt phẳng cho đường tròn

 

và parabol

 

(tham khảo hình vẽ dưới đây).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

11,04.

12,04.

9,13.

13,13.

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số:

2 2 1y x x x   

và đường thẳng

1yx  

là:

. B.

. C.

. D.

Câu 6: Diện tích

của hình phẳng

được giới hạn bởi parabol

 

: 2P y x x

và đường thẳng

:4d y x

xác định bởi công thức nào dưới đây?

 

3 4 dS x x x





  



. B.

 

3 4 dS x x x



   



 

3 4 dS x x x



  



. D.

 

3 4 dS x x x   



Câu 7: Biết đồ thị hàm số bậc ba

 

cắt đường thẳng

 

tạo thành các hình phẳng có diện tích

,SS

như hình vẽ bên dưới:

(

)

(

)

-2

Tính

   

 

2.dI f x g x x



  



2.I S S  

8.I S S  

8.I S S  

2.I S S  

Câu 8: Kí hiệu

 

là diện tích hình phẳng giới hạn bởi các đường

 

2 1, 0, 1, , 1y x y x x t t     

. Tìm

để

 

10St

4t 

. B.

13t 

. C.

3t 

. D.

14t 

Câu 9: Cho mảnh đất hình vuông

ABCD

có cạnh bằng

40 ,m

,,M N I

lần lượt là trung điểm

, , .AD BC AB

Biết đường cong là parabol đỉnh

(tham khảo hình vẽ).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

203,15 .m

487,59 .m

601,25 .m

450,35 .m

Câu 10: Cho hàm

 

y F x

là một nguyên hàm của hàm số

 

y f x

, biết đồ thị hàm số

 

y f x

trên đoạn

 

2;2

như hình vẽ ở bên dưới và có diện tích

1 2 3

22 76

15 15

S S S  

Giá trị của biểu thức

       

2 1 1 2F F F F    

bằng

I 

. B.

I 

. C.

I 

. D.

I 

Câu 11: Tính diện tích hình phẳng được đánh dấu trên hình dưới:

S 

. B.

S 

. C.

S 

. D.

S 

Câu 12: Cho hình phẳng

 

giới hạn bởi đồ thị hàm số







và hai đường thẳng

2y 

1yx  

(tham khảo hình vẽ).

Tính diện tích

của hình phẳng

 

8 3ln3S 

. B.

8 3ln3S 

. C.

3ln3S 

. D.

4 3ln3S   

Câu 13: Trong mặt phẳng cho elip và hai đường thẳng như hình vẽ bên dưới:

-10

Diện tích phần không tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

1203,15 .m

1350,25 .m

1530,58 .m

1450,35 .m

Câu 14: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện

một dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.

Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật

ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000

đồng cho 1

. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ?

1.230.000

đồng. B.

900.000

đồng. C.

1.232.000

đồng. D.

902.000

đồng.

Câu 15: Cho hình phẳng

()H

(phần gạch đậm) như hình vẽ bên dưới:

Tính diện tích hình phẳng

( ).H

ln3 2.



ln3 .



ln3 2.



Câu 16: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên.

Đặt

     

2 2 .g x f x x  

Khẳng định nào sau đây đúng?

     

0 2 1 .g g g  

     

1 2 0 .g g g  

     

2 1 0 .g g g  

     

0 1 2 .g g g  

(

)

-2

Câu 17: Cho hàm số

4 3 2

, ( 0)y ax bx cx dx e a     

có đồ thị

()C

và đường

:d y mx n

cắt đồ

thị

()C

tại các điểm có hoành độ lần lượt là

2; 1; 0; 1.

Biết rằng hình phẳng giới hạn bởi

( ), Cd

và đường thẳng

2, 0xx  

có diện tích bằng

Diện tích hình phẳng giới hạn bởi đồ thị

( ),C

đường thẳng

trục tung và đường

1x 

bằng



Câu 18: Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của

hai hình tròn lần lượt là

20m

và

15m

. Khoảng cách giữa hai tâm của hai hình tròn là

30m

.Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là

300

nghìn đồng và chi

phí làm mỗi mét vuông còn lại là

100

nghìn đồng. Hỏi số tiền làm mặt sàn sân khấu gần với

số nào trong các số dưới đây?

202

triệu đồng. B.

208

triệu đồng. C.

218

triệu đồng. D.

200

triệu đồng.

Câu 19: Với mọi

thì đường thẳng

:2d y mx

luôn cắt parabol

( ) : 1P y x

tại hai điểm phân

biệt có hoành độ

,xx

. Tìm

để diện tích của hình phẳng giới hạn bởi

và

()P

là nhỏ

nhất.

0m 

. B.

m 

4.m 

Câu 20: Cho hàm số bậc ba

()y f x

có đồ thị là đường cong trong hình bên dưới:

Biết hàm số

()fx

đạt cực trị tại hai điểm

, xx

thỏa mãn

4xx

và

( ) ( ) 0.f x f x

Gọi

và

là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số

bằng

. B.

. C.

. D.

____________________________HẾT____________________________

Huế, 15h00’ Ngày 11 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 4_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

LỜI GIẢI CHI TIẾT

Câu 1: Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên đoạn

 

;ba

. Gọi

là diện tích hình

phẳng giới hạn bởi các đồ thị hàm số

 

y f x

 

y g x

và hai đường thẳng

 

,x a x b a b  

, diện tích của

được tính theo công thức nào dưới đây?

   

 

f x g x x



. B.

   

S f x x g x x



   

f x g x x



. D.

   

f x g x x



Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

4yx  

, trục hoành và các đường thẳng

0x 

3x 

là:

. B. 3. C.

. D.

Lời giải:

Phương trình hoành độ giao điểm giữa

( ): 4P y x  

và trục hoành:

 

2 0;3





   



  





Vậy diện tích hình phẳng là:

   

2 3 2 3

2 2 2 2

0 2 0 2

4 4 4 4d d d dS x x x x x x x x           

   

16 16 23

4 4 3

3 3 3 3 3

   

         

   

   



Chọn đáp án D.

Câu 3: Cho hàm số bậc bốn

 

y f x

liên tục trên

Gọi

là hình phẳng giới hạn bởi đồ thị

   

:C y f x

(tham khảo hình vẽ bên dưới).

-2

Mệnh đề nào dưới đây sai?

 







S f x x

     

ddd



  

  

0 1 2

2 0 1

S f x x f x x f x x

     

d d d



   

  

0 1 2

2 0 1

S f x x f x x f x x

   







S f x x f x x

Câu 4: Trong mặt phẳng cho đường tròn

 

và parabol

 

(tham khảo hình vẽ dưới đây).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

11,04.

12,04.

9,13.

13,13.

Lời giải:

-4+2

Phương trình đường tròn là







  



  



Gọi

 

:P y ax c

(Do

 

đối xứng qua

)

Ta có:

   

0;1 1

2;3 4 3

A P c

B P a c



  









   









Vậy

 

: 1.

P y x

Xét hệ phương trình:

4 2 7 0

1 4 .

4 2 7 0







   





    













   







4 2 7



  







   



Diện tích cần tính là

4 2 7

4 2 4 1 11,04.

S x x x









     













Chọn đáp án A.

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số:

2 2 1y x x x   

và đường thẳng

1yx  

là:

. B.

. C.

. D.

Lời giải:

Xét phương trình

2 2 1 1x x x x     

2 2 0 1

x x x x







       







Ta có diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số

()hx

và

()gx

bằng

2 2 dxS x x x



    



8 5 37

3 12 12

  



Chọn đáp án A.

Câu 6: Diện tích

của hình phẳng

được giới hạn bởi parabol

 

: 2P y x x

và đường thẳng

:4d y x

xác định bởi công thức nào dưới đây?

 

3 4 dS x x x





  



. B.

 

3 4 dS x x x



   



 

3 4 dS x x x



  



. D.

 

3 4 dS x x x   



Lời giải:

Phương trình hoành độ giao điểm của

 

và

2 4 3 4 0

x x x x x





       







Suy ra

 

3 4 d 3 4 dS x x x x x x



      



(do

 

3 4 0, 1;4x x x     



Chọn đáp án B.

Câu 7: Biết đồ thị hàm số bậc ba

 

cắt đường thẳng

 

tạo thành các hình phẳng có diện tích

,SS

như hình vẽ bên dưới:

(

)

(

)

-2

Tính

   

 

2.dI f x g x x



  



2.I S S  

8.I S S  

8.I S S  

2.I S S  

Lời giải:

Ta có:

   

 

   

 

2 2 2

22d d dI f x g x x f x g x x x

  

     

  

   

 

   

 

8 8.ddf x g x x f x g x x S S



       





Chọn đáp án C.

Câu 8: Kí hiệu

 

là diện tích hình phẳng giới hạn bởi các đường

 

2 1, 0, 1, , 1y x y x x t t     

. Tìm

để

 

10St

4t 

. B.

13t 

. C.

3t 

. D.

14t 

Lời giải:

Ta có

 

S t x dx



. Do

 

1; , 1x t t

nên

2 1 0x 

Khi đó:

   

 

2 1 | 2

S t x dx x x t t      



Để

 

10St

thì

2 10 12 0

t t t t





       







1t 

nên

3t 

thỏa mãn.



Chọn đáp án C.

Câu 9: Cho mảnh đất hình vuông

ABCD

có cạnh bằng

40 ,m

,,M N I

lần lượt là trung điểm

, , .AD BC AB

Biết đường cong là parabol đỉnh

(tham khảo hình vẽ).

Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

203,15 .m

487,59 .m

601,25 .m

450,35 .m

Lời giải:

 

có đỉnh là

 

0;40A

và qua

 

20;0B

nên

 

: 40.

P y x  

Xét hệ phương trình:

10 2

200 .

10 2







  



  

















Diện tích cần tính là

10 2 20

2 2 2

10 2

2 40 20 20 40 487,59 .

10 10

S x x x x m





   

        





   

   











Chọn đáp án B.

Câu 10: Cho hàm

 

y F x

là một nguyên hàm của hàm số

 

y f x

, biết đồ thị hàm số

 

y f x

trên đoạn

 

2;2

như hình vẽ ở bên dưới và có diện tích

1 2 3

22 76

15 15

S S S  

Giá trị của biểu thức

       

2 1 1 2F F F F    

bằng

I 

. B.

I 

. C.

I 

. D.

I 

Lời giải:

Ta có:

     

2 1 d

F F f x x S     



     

1 1 d

F F f x x S



    



     

1 2 d

F F f x x S



       



Vậy có :

           

2 1 2 1 1 1 2F F F F F F       





22 76 22 108

15 15 15 15

    

       

108 36

2 1 1 2

15 5

F F F F       



Chọn đáp án A.

Câu 11: Tính diện tích hình phẳng được đánh dấu trên hình dưới:

S 

. B.

S 

. C.

S 

. D.

S 

Lời giải:

Ta có

y x x y   

, từ hình vẽ ta thấy

0x x y   

 

2 2 2

d d 3 3 1 2 3

3 3 3

S y y x x x       





Chọn đáp án D.

Câu 12: Cho hình phẳng

 

giới hạn bởi đồ thị hàm số







và hai đường thẳng

2y 

1yx  

(tham khảo hình vẽ).

Tính diện tích

của hình phẳng

 

8 3ln3S 

. B.

8 3ln3S 

. C.

3ln3S 

. D.

4 3ln3S   

Lời giải:

Dựa vào đồ thị ta có

   

 

3 1 3 1

5 3 5 3

2 d 1 2 d 1 d 1 d

3ln 2 3ln3.

S x x x x x x

x x x

   



   

           

   



   



       





   



Chọn đáp án C.

Câu 13: Trong mặt phẳng cho elip và hai đường thẳng như hình vẽ bên dưới:

-10

Diện tích phần không tô đậm (làm tròn đến chữ số hàng phần trăm) bằng

1203,15 .m

1350,25 .m

1530,58 .m

1450,35 .m

Lời giải:

Elip có phương trình là:

400 1

1600

1600 400

400 1

1600















  







  









Xét hệ phương trình:

20 3

1600 400





























Lúc đó:

g¹ch

20 3

40.20 4 400 1 10 1530,58.

1600









    













Chọn đáp án C.

Câu 14: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện

một dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.

Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật

ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000

đồng cho 1

. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ?

1.230.000

đồng. B.

900.000

đồng. C.

1.232.000

đồng. D.

902.000

đồng.

Lời giải:

Chọn hệ trục tọa độ

Oxy

như hình vẽ, khi đó ta được phương trình của parabol là

4.yx  

Gọi

    

   

;0 0 2 ;0 , ; 4 , ; 4 .C x x D x B x x A x x        

Ta có diện tích của Pano là

   

4 d .

x x m



  



Diện tích hình chữ nhật

ABCD

là

 

. 2 . 4 .

ABCD

S CD BC x x   

Chi phí dán hoa văn thấp nhất khi và chỉ khi diện tích hình chữ nhật

ABCD

lớn nhất.

Xét hàm số

 

( ) 2 . 4 , 0;2f x x x x   

có

 

0;2

32 3

M ( ) .

ax f x





Chi phí thấp nhất cho việc dán hoa văn là

32 32 3

.200000 902.000









đồng.



Chọn đáp án D.

Câu 15: Cho hình phẳng

()H

(phần gạch đậm) như hình vẽ bên dưới:

Tính diện tích hình phẳng

( ).H

ln3 2.



ln3 .



ln3 2.



Lời giải:

Ta có: diện tích cần tìm là

lnS x xdx



Đặt

du dx

dv xdx





























khi đó:

2 2 2

1 9 1 9

ln ln3 ln3 2.

2 2 2 2 2 2

x x x

S x dx

     





Chọn đáp án B.

Câu 16: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên.

Đặt

     

2 2 .g x f x x  

Khẳng định nào sau đây đúng?

     

0 2 1 .g g g  

     

1 2 0 .g g g  

     

2 1 0 .g g g  

     

0 1 2 .g g g  

(

)

-2

Lời giải:

Ta có

         

2 2 2 2 2 ;g x f x x f x x





     



   

0 2 0

g x f x x x









     







Bảng biến thiên:

Suy ra

   

20gg

và

   

10gg

(

)

-2

Theo hình vẽ

           

d d d d

0 1 0 1

2 0 2 0

f x x x x f x x g x x g x x



   

   

       

   

   

               

0 2 1 0 1 2g x g x g g g g g g



           

. Vậy

     

0 1 2g g g  



Chọn đáp án D.

Câu 17: Cho hàm số

4 3 2

, ( 0)y ax bx cx dx e a     

có đồ thị

()C

và đường

:d y mx n

cắt đồ

thị

()C

tại các điểm có hoành độ lần lượt là

2; 1; 0; 1.

Biết rằng hình phẳng giới hạn bởi

( ), Cd

và đường thẳng

2, 0xx  

có diện tích bằng



2



 











 



 

2g 

 



Diện tích hình phẳng giới hạn bởi đồ thị

( ),C

đường thẳng

trục tung và đường

1x 

bằng



Lời giải:

Theo bài ra phương trình

4 3 2

ax bx cx dx e mx n     

có

nghiệm phân biệt

2; 1;0;1.

   

4 32

0f x ax bx cx d m x e n        

có

nghiệm phân biệt

2; 1;0;1.

Suy ra

 

( 2)( 1)( 0)( 1) ( 2)( 1)( 1)f x a x x x x ax x x x        

Gọi

là diện tích hình phẳng giới hạn bởi

( ), Cd

và đường thẳng

2, 0xx  

ta có

     

d 2 1 1 dS f x x a x x x x x



    



1 .1 1 1aa    

Vậy diện tích

cần tìm là

     

d 2 1 1 d

S f x x x x x x x     





Chọn đáp án B.

Câu 18: Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của

hai hình tròn lần lượt là

20m

và

15m

. Khoảng cách giữa hai tâm của hai hình tròn là

30m

.Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là

300

nghìn đồng và chi

phí làm mỗi mét vuông còn lại là

100

nghìn đồng. Hỏi số tiền làm mặt sàn sân khấu gần với

số nào trong các số dưới đây?

202

triệu đồng. B.

208

triệu đồng. C.

218

triệu đồng. D.

200

triệu đồng.

Lời giải:

Gọi

,IJ

lần lượt là tâm của hai đường tròn bán kính

20m

15m

Gọi

,AB

là giao của hai đường tròn.

Chọn hệ trục tọa độ

Oxy

sao cho

trùng

và

song song với

và

là gốc tọa độ

(như hình vẽ).

Khi đó đường tròn tâm

bán kính

20Rm

có phương trình

400xy

Vì khoảng cách giữa hai tâm của hai hình tròn là

30m

nên

 

0;30J

. Do đó đường tròn

tâm

 

0;30J

bán kính

15Rm

có phương trình

 

30 225xy  

Khi đó phần chung của hai đường tròn giới hạn bởi

 

400 ; 30 225y x y x    

Xét hệ

4 455

400

215

30 225



















  









Diện tích phần chung của hai đường tròn là





5 455

400 225 30 60,2S x x dx



     



Diện tích riêng của hai đường tròn là

625 2 625 120,4SS



   

Số tiền chi phí là

 

300000 100000 300000.60,2 100000. 625 120,4 202369540SS



    

Vậy số tiền làm mặt sàn sân là gần

202

triệu đồng.



Chọn đáp án A.

Câu 19: Với mọi

thì đường thẳng

:2d y mx

luôn cắt parabol

( ) : 1P y x

tại hai điểm phân

biệt có hoành độ

,xx

. Tìm

để diện tích của hình phẳng giới hạn bởi

và

()P

là nhỏ

nhất.

0m 

. B.

m 

4.m 

Lời giải:

Ta có

,xx

là hai nghiệm của phương trình

10x mx   

. Khi

đó

 

   

 

2 1 1 2 1 2 1 2

2 1 1

2 3 3 2

mx x m

S mx x dx x x x x x x x x x





              











   

2 2 2 2 2

1 1 4

4 2 1 3 6 4 4

6 6 6

m m m m m



         



min

0Sm  



Chọn đáp án A.

Câu 20: Cho hàm số bậc ba

()y f x

có đồ thị là đường cong trong hình bên dưới:

Biết hàm số

()fx

đạt cực trị tại hai điểm

, xx

thỏa mãn

4xx

và

( ) ( ) 0.f x f x

Gọi

và

là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số

bằng

. B.

. C.

. D.

Lời giải:

Cách 1:

Gọi

 

,f x ax bx cx d   

(với

0, , , ,a a b c d

)



 

32f x ax bx c



  

Theo giả thiết ta có:

           

   

1 2 1 2 1 1

0 3 3 4

3 12 .

f x f x f x a x x x x a x x x x

a x x a x x

  

         

   

       

6f x f x dx a x x a x x C



      



     

1 2 1 1

( ) ( ) 0 4 0 64 96 0 16 .f x f x f x f x C a a C C a            

Vậy

     

6 16f x a x x a x x a    

SS

là diện tích hình chữ nhật có các kích thước là 2 và

 

1 1 2

16 32f x a S S a   

 

S f x dx a







. Suy ra

12Sa

. Vậy



Cách 2:

Kết quả bài toán sẽ không đổi nếu ta tịnh tiến đồ thị của hàm số đã cho sang trái sao cho

điểm uốn trùng với gốc tọa độ

Gọi

 

,0g x ax bx cx d a    

là hàm số đó và ta thấy đồ thị của hàm số

 

đối xứng

nhau qua gốc tọa độ

nên

 

là hàm số lẻ

 

0b d g x ax cx     

 

có hai cực trị là

2, 2

nên

   

2 2 0 12 0 12g g a c c a



        

Vậy

 

12g x ax ax

SS

là diện tích hình chữ nhật có các kích thước là 2 và

 

2 16 32g a S S a    

 

20S g x dx a







. Suy ra

12Sa

. Vậy





Chọn đáp án B.

____________________________HẾT____________________________

Huế, 15h00’ Ngày 11 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 5_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho đồ thị

()y f x

như hình vẽ sau đây:

Diện tích của hình phẳng được gạch chéo trong hình vẽ là

( )dS f x x







. B.

( )d ( )dS f x x f x x







( )d ( )dS f x x f x x



  



. D.

( )d ( )dS f x x f x x







Câu 2: Cho hàm số

 

y f x

liên tục trên đoạn

 

5;6

có đồ thị như hình vẽ bên dưới:

-1

-2

-5

Giá trị của

 

df x x





bằng

. B.

. C.

. D.

Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số

, trục hoành và hai đường thẳng

là

. B.

. C.

. D.

Câu 4: Cho hàm số

   

,y f x y g x

liên tục trên đoạn

 

;ab

. Diện tích hình phẳng giới hạn bởi

đồ thị hàm số

   

,y f x y g x

và các đường thẳng

,x a x b

là

   

 

S f x g x x



. B.

   

S f x g x x



   

 

S f x g x x



. D.

   

 

S f x g x x



Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

13yx

, trục

và hai đường thẳng

0, 1xx

bằng

 

1 3 dxx



1 3 dxx



. C.

1 3 dxx







. D.

 

1 3 dxx







Câu 6: Cho hàm số

()y f x

liên tục và có đồ thị trên

[ 3;5]

như hình bên.

Biết các miền

,,A B C

có diện tích lần lượt là

1377 2673

188, ,

A B C

S S S  

. Khi đó

 

1df x x











bằng

A. 520. B.

2417

. C. -504. D.

2401

Câu 7: Cho đồ thị

 

y f x

như hình vẽ sau đây. Biết rằng

 

df x x a







và

 

df x x b



. Tính

diện tích S của phần hình phẳng được tô đậm.

S a b  

. B.

S a b

. C.

S b a

. D.

S a b

Câu 8: Gọi

là diện tích hình phẳng giới hạn bởi các đường

 

2 1; 0y x x y m m    

và

0; 1.xx

Tìm

sao cho

4.S 

m 

. B.

m 

. C.

m 

. D.

4m 

Câu 9: Ông A đã cải tạo một miếng đất thành hình elip. Elip này có độ dài trục lớn là 12 mét. Trong

elip có một đường tròn đi qua các đỉnh trên trục nhỏ và các tiêu điểm

,FF

.Ông A muốn

trồng cỏ May Mắn cho mảnh đất là phần bên trong Elip và bên ngoài đường tròn. Biết rằng

chi phí cho việc trồng cỏ May Mắn là 60 nghìn đồng trên một mét vuông. Hỏi tổng chi phí

trồng cỏ May Mắn gần nhất với số tiền nào sau đây?

A. 2811 nghìn đồng. B. 1405 nghìn đồng. C. 447 nghìn đồng. D. 895 nghìn đồng.

Câu 10: Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai đường

2 , 4 .y x y x





. B.





. C.

S 

. D.

S 

Câu 11: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

21y x x  

và

1yx

là

189

S 

. B.

S 

. C.

6S 

. D.

S 

Câu 12: Cho hàm số bậc ba

 

có đồ thị như hình vẽ bên. Biết đồ thị hàm số

 

cắt trục

hoành tại ba điểm phân biệt có hoành độ

1 2 3

,,x x x

thoả mãn

23xx

và

1 2 3

,,x x x

theo

thứ tự lập thành một cấp số cộng. Diện tích hình phẳng gạch sọc trong hình vẽ bằng

. B.

. C.

. D.

Câu 13: Cho hai hàm số

 

y f x

 

y g x

có đạo hàm liên tục trên . Biết rằng đồ thị của hai hàm

số này cắt nhau tại hai điểm có hoành độ lần lượt là

và

, phần hình phẳng gạch sọc giới

hạn bởi hai đồ thị đã cho và hai đường thẳng

1x 

2x 

có diện tích bằng

và

 

d7g x x 



Mệnh đề nào sau đây đúng?

 

d 15f x x 



. B.

 

d 11f x x 



. C.

 

d 22f x x 



. D.

 

d3f x x 



Câu 14: Hình giới hạn bởi một đường parabol và một nửa đường tròn tâm

bán kính bằng

(phần gạch sọc) trong hình vẽ bên có diện tích bằng





. B.





. C.





. D.





Câu 15: Cho đường cong

 



:C y x

. Xét điểm

có hoành độ dương thuộc

 

, tiếp tuyến của

 

tại

tạo với

 

một hình phẳng có diện tích bằng

. Hoành độ điểm

thuộc khoảng

nào dưới đây?







. B.







. C.







. D.







;2 .

Câu 16: Diện tích hình phẳng giới hạn vởi đồ thị hai hàm số

43y x x  

và

3yx

bằng

Câu 17: Cho hai hàm số

( ) , ( ) , ( 0)f x ax bx c g x bx ax c a      

có đồ thị như hình vẽ bên dưới:

Gọi

,SS

là diện tích hình phẳng được gạch trong hình vẽ. Khi

3SS

thì

()df x x



bằng

. B.

3

. C.

. D.

6

Câu 18: Cho hàm số

, ( 0)y ax bx c a   

có đồ thị

()C

và tiếp tuyến

của đồ thị

()C

tại điểm có

hoành độ

1,x 

cắt

()C

tại hai giao điểm còn lại có hoành bằng

0, 2xx

(tham khảo

hình vẽ).

Biết rằng hình phẳng giới hạn bởi

( ), Cd

và đường thẳng

0, 2xx

có diện tích bằng

28/5.

Tính diện tích hình phẳng giới hạn bởi đồ thị

( ),C

đường thẳng

và

0, 1.xx  



Câu 19: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của

một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường

kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và

cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không tô màu) dành để

trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản

tương ứng là

150.000

đồng/

và

100.000

đồng/

. Hỏi số tiền cần để trồng hoa và trồng cỏ

Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây?

3.739.000

(đồng). B.

1.948.000

(đồng). C.

3.926.000

(đồng). D.

4.115.000

(đồng).

Câu 20: Cho hàm số

y x mx  

có đồ thị

 

với tham số

0m 

được cho như hình vẽ. Giả sử

 

cắt trục

tại ba điểm phân biệt như hình vẽ bên dưới:

Gọi

và

là diện tích các miền được giới hạn bởi đồ thị

 

và trục

. Biết

là giá trị

để

10 5

SS

, hỏi

thuộc khoảng nào sau đây?

 

15;30

. B.

 

5;10

. C.

 

0;3

. D.

 

2;6

____________________________HẾT____________________________

Huế, 11h00’ Ngày 14 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 5_TrNg 2022

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

LỜI GIẢI CHI TIẾT

Câu 1: Cho đồ thị

()y f x

như hình vẽ sau đây:

Diện tích của hình phẳng được gạch chéo trong hình vẽ là

( )dS f x x







. B.

( )d ( )dS f x x f x x







( )d ( )dS f x x f x x



  



. D.

( )d ( )dS f x x f x x







Lời giải:

 Có

2 1 2 1 2

1 1 1 1 1

( ) ( ) ( ) ( ) ( ( )) .S f x dx f x dx f x dx f x dx f x dx

  

     

    



Chọn đáp án D.

Câu 2: Cho hàm số

 

y f x

liên tục trên đoạn

 

5;6

có đồ thị như hình vẽ bên dưới:

-1

-2

-5

Giá trị của

 

df x x





bằng

. B.

. C.

. D.

Lời giải:

-1

-2

-5

Ta có

. .6.3 9;

ABC

S BC AB  

. .1.2 1.

DEE

S DF EF  

 

1 1 3

.3.1 .

2 2 2

FEGO

S GO EF DO   

Khi đó:

       

0 2 1 0

5 5 2 1

3 13

dx dx dx dx 9 1 .

ABC DEE FEGO

f x f x f x f x S S S



   

         

   



Chọn đáp án D.

Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số

, trục hoành và hai đường thẳng

là

. B.

. C.

. D.

Lời giải:

Xét phương trình hoành độ giao điểm của đồ thị hàm số

, trục hoành

Diện tích hình phẳng cần tính là

 

2 2 2 6

1 1 1

2 2 2 2

x x x

S e dx e dx e e      





Chọn đáp án C.

Câu 4: Cho hàm số

   

,y f x y g x

liên tục trên đoạn

 

;ab

. Diện tích hình phẳng giới hạn bởi

đồ thị hàm số

   

,y f x y g x

và các đường thẳng

,x a x b

là

   

 

S f x g x x



. B.

   

S f x g x x



   

 

S f x g x x



. D.

   

 

S f x g x x



Lời giải:

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

   

,y f x y g x

và các đường thẳng

,x a x b

được tính theo công thức

   

S f x g x x





Chọn đáp án B.

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

13yx

, trục

và hai đường thẳng

0, 1xx

bằng

 

1 3 dxx



1 3 dxx



. C.

1 3 dxx







. D.

 

1 3 dxx







Lời giải:

1 3 d 1 3 dS x x x x   





Chọn đáp án B.

Câu 6: Cho hàm số

()y f x

liên tục và có đồ thị trên

[ 3;5]

như hình bên.

Biết các miền

,,A B C

có diện tích lần lượt là

1377 2673

188, ,

A B C

S S S  

. Khi đó

 

1df x x











bằng

A. 520. B.

2417

. C. -504. D.

2401

Lời giải:

         

5 5 5 5

3 3 3 3

1 8 8

A B C

f x dx f x dx dx f x dx f x dx f x dx S S S

   

          





     

1377 2673

188 8 520.

    



Chọn đáp án A.

Câu 7: Cho đồ thị

 

y f x

như hình vẽ sau đây. Biết rằng

 

df x x a







và

 

df x x b



. Tính

diện tích S của phần hình phẳng được tô đậm.

S a b  

. B.

S a b

. C.

S b a

. D.

S a b

Lời giải:

Ta có

   

S f x dx f x dx a b



     





Chọn đáp án C.

Câu 8: Gọi

là diện tích hình phẳng giới hạn bởi các đường

 

2 1; 0y x x y m m    

và

0; 1.xx

Tìm

sao cho

4.S 

m 

. B.

m 

. C.

m 

. D.

4m 

Lời giải:

Diện tích hình phẳng giới hạn bởi các đường

 

2 1; 0y x x y m m    

và

0; 1xx

là

 

2 1 d 2 1 d do 0 .S x x m x x x m x m        



Suy ra

 

4 2 1 d 4 4

S x x m x x x mx



          







1 1 4 .

mm       



Chọn đáp án B.

Câu 9: Ông A đã cải tạo một miếng đất thành hình elip. Elip này có độ dài trục lớn là 12 mét. Trong

elip có một đường tròn đi qua các đỉnh trên trục nhỏ và các tiêu điểm

,FF

.Ông A muốn

trồng cỏ May Mắn cho mảnh đất là phần bên trong Elip và bên ngoài đường tròn. Biết rằng

chi phí cho việc trồng cỏ May Mắn là 60 nghìn đồng trên một mét vuông. Hỏi tổng chi phí

trồng cỏ May Mắn gần nhất với số tiền nào sau đây?

A. 2811 nghìn đồng. B. 1405 nghìn đồng. C. 447 nghìn đồng. D. 895 nghìn đồng.

Lời giải:

Gắn hệ trục tọa độ

Oxy

như hình vẽ.

Phương trình elip



với

0ab

và phương trình đường tròn

2 2 2

x y R

Độ dài trục lớn là 12 mét, suy ra

6a 

Vì đường tròn đi qua các đỉnh trên trục nhỏ và tiêu điểm của elip nên

b c R

Do đó

2 2 2 2 2 2

2 2 36 3 2c a b c a c c       

Tổng chi phí để trồng cỏ May Mắn là

6 3 2

4. 3 2 1 18 .60000 1405

T dx x dx



    







nghìn đồng.



Chọn đáp án B.

Câu 10: Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai đường

2 , 4 .y x y x





. B.





. C.

S 

. D.

S 

Lời giải:

Theo hình vẽ ta có

42y x y x  

Xét phương trình hoành độ giao điểm của hai đường

2 , 2y x y x







  











Dựa vào đồ thị, diện tích của hình phẳng cần tính là

 

4 2 2

2 2 d

3 3 3

S x x x x x x



    









Chọn đáp án D.

Câu 11: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

21y x x  

và

1yx

là

189

S 

. B.

S 

. C.

6S 

. D.

S 

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị đã cho là

3 2 2 3 2

2 1 1 3 0

x x x x x





       







. Vậy diên tích hình phẳng cần tìm là:

     

3 2 2 3 2 4 3

1 27

2 1 1 3

S x x x x x x x x x



           









Chọn đáp án B.

Câu 12: Cho hàm số bậc ba

 

có đồ thị như hình vẽ bên. Biết đồ thị hàm số

 

cắt trục

hoành tại ba điểm phân biệt có hoành độ

1 2 3

,,x x x

thoả mãn

23xx

và

1 2 3

,,x x x

theo

thứ tự lập thành một cấp số cộng. Diện tích hình phẳng gạch sọc trong hình vẽ bằng

. B.

. C.

. D.

Lời giải:

Diện tích phần gạch sọc trên hình là hình phẳng giới hạn bởi các đường

 

3, ,y y f x

,x x x x

. Do đó,

 

       

3 3 3 3 3

1 1 1 1 1

3 3 3 6        

    

x x x x x

S f x dx dx f x dx x x f x dx f x dx

Xét

 

.   f x ax bx cx d

Theo viet có

1 2 3

   

x x x

Mặt khác

1 2 3

,,x x x

theo thứ tự lập thành cấp số cộng nên

   

1 2 3 1 3 2 2 2 2 2 2

2 3 ;0

             

x x x x x x x x x x U x

là điểm uốn của đồ thị

hàm số đã cho. Vì vậy, trục hoành cùng với đồ thị hàm số

 

tạo thành hai hình có

diện tích bằng nhau tức

     

1 2 1

0.   

  

x x x

f x dx f x dx f x dx

Vậy

6S



Chọn đáp án D.

Câu 13: Cho hai hàm số

 

y f x

 

y g x

có đạo hàm liên tục trên . Biết rằng đồ thị của hai hàm

số này cắt nhau tại hai điểm có hoành độ lần lượt là

và

, phần hình phẳng gạch sọc giới

hạn bởi hai đồ thị đã cho và hai đường thẳng

1x 

2x 

có diện tích bằng

và

 

d7g x x 



Mệnh đề nào sau đây đúng?

 

d 15f x x 



. B.

 

d 11f x x 



. C.

 

d 22f x x 



. D.

 

d3f x x 



Lời giải:

Từ hình vẽ suy ra

           

2 2 2 2

1 1 1 1

d d 4 d d 4f x g x x f x g x x f x x g x x      





   

   

d 4 d 4 7 11f x x g x x     





Chọn đáp án B.

Câu 14: Hình giới hạn bởi một đường parabol và một nửa đường tròn tâm

bán kính bằng

(phần gạch sọc) trong hình vẽ bên có diện tích bằng





. B.





. C.





. D.





Lời giải:

Phương trình nhánh trên đường tròn

2yx

11xy   

Parabol có đỉnh

 

0; 1

và đi qua hai điểm

 

1;1

 

1;1

có phương trình :

21yx

 

2 2 1 d

S x x x







     







Chọn đáp án A.

Câu 15: Cho đường cong

 



:C y x

. Xét điểm

có hoành độ dương thuộc

 

, tiếp tuyến của

 

tại

tạo với

 

một hình phẳng có diện tích bằng

. Hoành độ điểm

thuộc khoảng

nào dưới đây?







. B.







. C.







. D.







;2 .

Lời giải:

Ta có





3yx

 

  

; , 0A C A a a a

Phương trình tiếp tuyến

của

 

tại

là

 

  

:3d y a x a a

hay

 

  

:3d y a x a a

Ta có phương trình hoành độ giao điểm của

và

 

là

     

      

3 2 3

3 2 0x a x a a x a x a











Gọi

là diện tích của hình phẳng giới hạn bởi tiếp tuyến

và

 

Ta có

 



     



3 2 3

27 3 27

S x a x a a dx

 



   



3 2 3

3 2 d 27

x a x a x





   





4 2 2

2 27

x a x





  



  



2 ( 0)

a ktma

Vậy

 2a



Chọn đáp án C.

Câu 16: Diện tích hình phẳng giới hạn vởi đồ thị hai hàm số

43y x x  

và

3yx

bằng

Lời giải:

Xét phương trình hoành độ giao điểm:

4 3 3 2

x x x x







     







Khi đó diện tích hình phẳng giới hạn bởi hai đồ thị là:

   

1 13

3 4 3 4 3 3 2

S x x x dx x x x dx            





Chọn đáp án C.

Câu 17: Cho hai hàm số

( ) , ( ) , ( 0)f x ax bx c g x bx ax c a      

có đồ thị như hình vẽ bên dưới:

Gọi

,SS

là diện tích hình phẳng được gạch trong hình vẽ. Khi

3SS

thì

()df x x



bằng

. B.

3

. C.

. D.

6

Lời giải:

Phương trình hoành độ giao điểm:

 

( ) ( ) 0 ( ) 0

a b x b a x a b x x





        







Ký hiệu

là diện tích hình phẳng như hình vẽ dưới.

Cách 1: Ta có:

 

( ( ) ( )) ( ) ( )

S f x g x dx a b x x dx a b

S g x f x dx a b x x dx a b





      









       







Vậy

1 1 1

1 2 3 2

0 0 0

3 3 ( ( ) ( )) ( ) 3 ( ) 3.S S S S g x f x dx g x dx f x dx            

  

Cách 2:

 

( ( ) ( )) ( ) ( )

S f x g x dx a b x x dx a b



      



;

 

()

S g x dx bx ax c dx c



         







Vi vậy

3 ( ) 3 2 4 12

4 4 2

S S a b c a b c            

Suy ra

 

( ) 3.

4 2 4

a b a b c

f x dx ax bx c dx c



        





Chọn đáp án B.

Câu 18: Cho hàm số

, ( 0)y ax bx c a   

có đồ thị

()C

và tiếp tuyến

của đồ thị

()C

tại điểm có

hoành độ

1,x 

cắt

()C

tại hai giao điểm còn lại có hoành bằng

0, 2xx

(tham khảo

hình vẽ).

Biết rằng hình phẳng giới hạn bởi

( ), Cd

và đường thẳng

0, 2xx

có diện tích bằng

28/5.

Tính diện tích hình phẳng giới hạn bởi đồ thị

( ),C

đường thẳng

và

0, 1.xx  



Lời giải:

Phương trình tiếp tuyến có dạng

:d y mx n

Phương trình hoành độ giao điểm của đồ thị

()C

và đường thẳng

là

   

4 2 4 2

01ax bx c mx n f x ax bx mx c n          

Theo bài ra phương trình

 

có

nghiệm

1 , 0, 2x x x   

trong đó

1x 

là nghiệm

kép, suy ra

          

1 0 2 1 2f x ax bx mx c n a x x x ax x x           

Gọi

là diện tích hình phẳng giới hạn bởi

( ), Cd

và đường thẳng

0, 2xx

ta có

       

1 2 d 1 2 d 1

S ax x x x a x x x x a         



Vậy diện tích

cần tìm là

    

d 2 1 d

S f x x x x x x



    





Chọn đáp án C.

Câu 19: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của

một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường

kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và

cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không tô màu) dành để

trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản

tương ứng là

150.000

đồng/

và

100.000

đồng/

. Hỏi số tiền cần để trồng hoa và trồng cỏ

Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây?

3.739.000

(đồng). B.

1.948.000

(đồng). C.

3.926.000

(đồng). D.

4.115.000

(đồng).

Lời giải:

Kết hợp vào hệ trục tọa độ, ta được:

Gọi parabol là

 

:P y ax

. Do

   

2;4FP

nên

 

:P y x

Gọi đường tròn có tâm ở gốc tọa độ là

 

2 2 2

:C x y R

. Do

   

2;4FC

nên nửa đường

tròn trên là

20yx

Đặt

là diện tích phần tô đậm. Khi đó:





2. 20 d 20arcsin

S x x x



    







Đặt

là diện tích phần không tô đậm. Khi đó:

1 5 8

. . 10 20arcsin

2 5 3

S R S





    





Vậy: Số tiền cần để trồng hoa và cỏ Nhật Bản là:

150000. 100000. 3738574T S S  

(đồng).



Chọn đáp án A.

Câu 20: Cho hàm số

y x mx  

có đồ thị

 

với tham số

0m 

được cho như hình vẽ. Giả sử

 

cắt trục

tại ba điểm phân biệt như hình vẽ bên dưới:

Gọi

và

là diện tích các miền được giới hạn bởi đồ thị

 

và trục

. Biết

là giá trị

để

10 5

SS

, hỏi

thuộc khoảng nào sau đây?

 

15;30

. B.

 

5;10

. C.

 

0;3

. D.

 

2;6

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là

x mx









    











Do đồ thị hàm số nhận trục tung làm trục đối xứng nên

SS

Ta có

1 2 2 2

10 5 10 5 5 5

3 3 3

S S S S     

Mà

 

5 5 5 5

3 5 3 3

x mx

S x mx dx



       







   

5 5 25 5 5

3,78

5 3 3 2

m m m

mm        



Chọn đáp án D.

____________________________HẾT____________________________

Huế, 11h00’ Ngày 14 tháng 02 năm 2022

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 6_TrNg 2024

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

y f x

và

 

y g x

có đồ thị như hình vẽ bên dưới:

Diện tích

của phần gạch chéo trong hình vẽ trên được tính bằng công thức nào dưới đây?

   

S g x f x x







. B.

   

S f x g x x



   

S f x g x x







. D.

   

S f x g x x







Câu 2: Cho hình phẳng

 

giới hạn bởi đồ thị của ba hàm số

()y f x

()y g x

()y h x

như hình

bên dưới.

Diện tích hình phẳng

 

là

. Mệnh đề nào sau đây đúng?

   

( ) ( ) ( ) ( )

S f x g x dx g x h x dx   



. B.

   

( ) ( ) ( ) ( )

S f x g x dx g x h x dx   



 

( ) ( )

S f x g x dx



. D.

   

( ) ( ) ( ) ( )

S f x h x dx g x h x dx   



Câu 3: Cho hàm số

 

liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các đường

 

, 0, 1, 2y f x y x x    

(như hình vẽ).

Mệnh đề nào dưới đây đúng?

   

d dS f x x f x x







. B.

   

d dS f x x f x x



  



   

d dS f x x f x x



  



. D.

   

d dS f x x f x x







Câu 4: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới

đây?

 

2 2 dxx







. B.

 

2 2 dxx





 

2 2 4 dx x x







. D.

 

2 2 4 dx x x



  



Câu 5: Gọi

là diện tích hình phẳng

 

giới hạn bởi đồ thị của hai hàm số

yx

và

yx

. Mệnh

đề nào sau đây đúng?

 

dS x x x







. B.

 

dS x x x



. C.

 

dS x x x



. D.

 

dS x x x



Câu 6: Cho hàm số

 

y f x

liên tục trên đoạn

 

0;8

và có đồ thị như hình vẽ bên dưới:

Trong các giá trị sau, giá trị nào lớn nhất?

 



f x x

. B.

 



f x x

. C.

 



f x x

. D.

 



f x x

Câu 7: Diện tích

của hình phẳng giới hạn bởi đồ thị hàm số

31yx

, trục hoành và hai đường

thẳng

0, 2xx

là

11S 

. B.

12S 

. C.

10S 

. D.

9S 

Câu 8: Cho hàm số

 

y f x

liên tục trên và có đồ thị như hình vẽ, diện tích hai phần

S ,S

lần

lượt bằng 12 và 3.

Giá trị của

 

I f x dx







bằng

A. 15. B. 9. C. 36. D. 27.

Câu 9: Gọi

là hình phẳng giới hạn bởi đồ thị hàm số

( ):







và các trục tọa độ. Khi đó, giá

trị của

bằng

ln 2 1

. B.

2ln 2 1

. C.

ln 2 1

. D.

2ln 2 1

Câu 10: Cho

 

là hình phẳng giới hạn bởi các đường

yx

2yx

và trục hoành. Diện tích

của

 

bằng

yx

2yx

yx

2yx

yx

2yx

. B.

. C.

. D.

Câu 11: Diện tích hình phẳng

giới hạn bởi đồ thị của hai hàm số

yx

và

32yx

được xác

định bởi công thức nào sau đây?

 

2 16 dS x x







. B.

 

16 dS x x







. C.

 

4 16 dS x x



. D.

 

2 16 dS x x



Câu 12: Gọi

là diện tích hình phẳng giới hạn bởi các đồ thị hàm số:

3y x x

yx

. Tính

4S 

. B.

8S 

. C.

2S 

. D.

0S 

Câu 13: Một biển quảng cáo có dạng hình elip với bốn đỉnh

1 2 1 2

, , ,A A B B

như hình vẽ bên dưới. Biết

chi phí để sơn phần tô đậm là

200.000 nđv / m

và phần còn lại

100.000 nđv / m

. Hỏi số tiền

để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết

8mAA 

6mBB 

và tứ giác

MN PQ

là hình chữ nhật có

3mMQ 

5.526.000

đồng. B.

5.782.000

đồng C.

7.322.000

đồng. D.

7.213.000

đồng.

Câu 14: Cho đường thẳng

y x a

và parabol

yx

(

là tham số thực). Gọi

,SS

lần lượt là

diện tích của hai hình phẳng được tô đậm và gạch chéo trong hình vẽ bên dưới:

Khi

SS

thì

thuộc khoảng nào dưới đây?







. B.

;

16 2









. C.







. D.







Câu 15: Cho hàm số bậc bốn

 

có đồ thị

   

;'f x f x

như hình vẽ bên dưới:

Gọi

;SS

là diện tích hai hình phẳng được gạch trong hình vẽ, khi

1S 

thì

bằng

104

. B.

. C.

. D.

Câu 16: Cho hàm số

 

y f x

có đồ thị như hình vẽ và diện tích hai phần

,AB

lần lượt bằng

và

Giá trị của

 

3 1 dI f x x







bằng

13.

Câu 17: Cho parabol

 

:P y x

và một đường thẳng

thay đổi cắt

 

tại hai điểm

sao cho

2018AB 

. Gọi

là diện tích hình phẳng giới hạn bởi

 

và đường thẳng

. Tìm giá trị

lớn nhất

max

của

2018 1

max





. B.

2018

max

S 

. C.

2018 1

max





. D.

2018



max

Câu 18: Trong mặt phẳng

Oxy

cho là hình phẳng

 

giới hạn bởi parabol

4yx

và trục hoành.

Đường thẳng

 

, 2 2x k k   

chia

 

thành hai phần

   

,HH

như hình vẽ bên dưới:

Biết rằng diện tích

 

gấp

lần diện tích

 

, hỏi giá trị

thuộc khoảng nào sau đây?

 

2; 1

. B.

 

0;1

. C.

 

1;0

. D.

 

1;2

Câu 19: Cho hai hàm số

 

4 3 2

2f x ax bx cx x   

và

 

2g x mx nx x  

với

, , , ,a b c m n

. Biết

hàm số

   

y f x g x

có ba điểm cực trị là

1; 2

và

. Diện tích hình phẳng giới hạn bởi

hai đường

 

y f x





và

 

y g x





bằng

. B.

. C.

. D.

Câu 20: Cho hàm số

 

4 3 2

f x x bx cx dx e    

(

, , ,b c d e

) có các giá trị cực trị là

1,4

và

. Diện

tích hình phẳng giới hạn bởi đồ thị hàm số

 





và trục hoành bằng

____________________________HẾT____________________________

Huế, 11h00’ Ngày 13 tháng 01 năm 2024

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

ĐỀ ÔN TẬP SỐ 6_TrNg 2024

§Ò KIÓM TRA §ÞNH Kú

M«n:

To¸n 12

Chñ ®Ò: Ứng dụng tích phân

DIỆN TÍCH HÌNH PHẲNG

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

y f x

và

 

y g x

có đồ thị như hình vẽ bên dưới:

Diện tích

của phần gạch chéo trong hình vẽ trên được tính bằng công thức nào dưới đây?

   

S g x f x x







. B.

   

S f x g x x



   

S f x g x x







. D.

   

S f x g x x







Lời giải:

Áp dụng công thức tính diện tích hình phẳng giới hạn bởi hai đường cong

 

y f x

 

y g x

và hai dường thẳng

xa

xc

ta có

   

S f x g x x



Câu 2: Cho hình phẳng

 

giới hạn bởi đồ thị của ba hàm số

()y f x

()y g x

()y h x

như hình

bên dưới.

Diện tích hình phẳng

 

là

. Mệnh đề nào sau đây đúng?

   

( ) ( ) ( ) ( )

S f x g x dx g x h x dx   



. B.

   

( ) ( ) ( ) ( )

S f x g x dx g x h x dx   



 

( ) ( )

S f x g x dx



. D.

   

( ) ( ) ( ) ( )

S f x h x dx g x h x dx   



Lời giải:

Dựa vào hình trên, ta thấy

( ) ( ) ( ) ( )

S f x g x dx g x h x dx   



Trên đoạn

;ab

( ) ( )f x g x

nên

 

( ) ( ) ( ) ( )

f x g x dx f x g x dx  



Trên đoạn

;bc

( ) ( )g x h x

nên

 

( ) ( ) ( ) ( )

g x h x dx g x h x dx   



Vậy

   

( ) ( ) ( ) ( )

S f x g x dx g x h x dx   



Câu 3: Cho hàm số

 

liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các đường

 

, 0, 1, 2y f x y x x    

(như hình vẽ).

Mệnh đề nào dưới đây đúng?

   

d dS f x x f x x







. B.

   

d dS f x x f x x



  



   

d dS f x x f x x



  



. D.

   

d dS f x x f x x







Lời giải:

Dựa vào đồ thị, ta có

   

d dS f x x f x x







Câu 4: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới

đây?

 

2 2 dxx







. B.

 

2 2 dxx





 

2 2 4 dx x x







. D.

 

2 2 4 dx x x



  



Lời giải:

Phương trình hoành độ giao điểm:

2 2 2

2 1 3 2 2 4 0

x x x x x





         







Diện tích hình phẳng cần tìm là

     

2 2 2

3 2 1 d 2 2 4 dS x x x x x x x





         





Câu 5: Gọi

là diện tích hình phẳng

 

giới hạn bởi đồ thị của hai hàm số

yx

và

yx

. Mệnh

đề nào sau đây đúng?

 

dS x x x







. B.

 

dS x x x



. C.

 

dS x x x



. D.

 

dS x x x



Lời giải:

Xét phương trình hoành độ giao điểm:





  







Suy ra:

 

ddS x x x x x x   



Câu 6: Cho hàm số

 

y f x

liên tục trên đoạn

 

0;8

và có đồ thị như hình vẽ bên dưới:

Trong các giá trị sau, giá trị nào lớn nhất?

 



f x x

. B.

 



f x x

. C.

 



f x x

. D.

 



f x x

Lời giải:

Ta có:

 

1 2 3

f x dx S S S  



 

3 2 2 3 1 2 3 1

0S S S S f x dx S S S S         



   

f x dx f x dx



(1)

 

1 2 2 1 1 2 3 3

0S S S S f x dx S S S S         



   

f x dx f x dx



(2)

Ta có

     

5 3 5

1 2 1

0 0 0

f x dx S S S f x dx f x dx    

  

(2)

Từ (1), (2) và (3) suy ra trong các giá trị trên, giá trị nào lớn nhất là

 

f x dx



Câu 7: Diện tích

của hình phẳng giới hạn bởi đồ thị hàm số

31yx

, trục hoành và hai đường

thẳng

0, 2xx

là

11S 

. B.

12S 

. C.

10S 

. D.

9S 

Lời giải:

Ta có

   

2 3 2

3 1 d 8 2 10S x x x x      



Câu 8: Cho hàm số

 

y f x

liên tục trên và có đồ thị như hình vẽ, diện tích hai phần

S ,S

lần

lượt bằng 12 và 3.

Giá trị của

 

I f x dx







bằng

A. 15. B. 9. C. 36. D. 27.

Lời giải:

 

I f x dx S S 9



   



Câu 9: Gọi

là hình phẳng giới hạn bởi đồ thị hàm số

( ):







và các trục tọa độ. Khi đó, giá

trị của

bằng

ln 2 1

. B.

2ln 2 1

. C.

ln 2 1

. D.

2ln 2 1

Lời giải:

Phương trình trục

()Ox

và

()Oy

lần lượt là

0y 

và

0x 

Phương trình hoành độ giao điểm của hàm số

()H

và trục Ox:



  



Ta có:









. Vì

 

0, 0;1



  



nên diện tích cần tìm là:

 

d 1 d 2ln 1 2ln2 1

S x x x x





          









Câu 10: Cho

 

là hình phẳng giới hạn bởi các đường

yx

2yx

và trục hoành. Diện tích

của

 

bằng

yx

2yx

yx

2yx

yx

2yx

. B.

. C.

. D.

Lời giải:

Xét các hình phẳng

 

0, 4

















và

 

2, 4

















Ta có

     

\H H H

H H H















Do đó

       

2 16 10

d 2 d 2 2

3 2 3 3

S H S H S H x x x x x x x



          







Cách khác: Ta có

 

0, 2

H x y

















. Suy ra

   

S H y y y   



Câu 11: Diện tích hình phẳng

giới hạn bởi đồ thị của hai hàm số

yx

và

32yx

được xác

định bởi công thức nào sau đây?

 

2 16 dS x x







. B.

 

16 dS x x







. C.

 

4 16 dS x x



. D.

 

2 16 dS x x



Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số

yx

và

32yx

4 4 4

32 16

x x x





    







Diện tích hình phẳng giới hạn bởi đồ thị các hàm số là:

   

2 2 2 2

4 4 4 4 4

2 2 2 2

32 d 2 32d 32 2 d 2 16 dS x x x x x x x x x

   

        

   

Mặt khác vì hàm số

16yx

là hàm số chẵn nên

   

16 d 2 16 dx x x x



  



Vậy

 

4 16 dS x x



Câu 12: Gọi

là diện tích hình phẳng giới hạn bởi các đồ thị hàm số:

3y x x

yx

. Tính

4S 

. B.

8S 

. C.

2S 

. D.

0S 

Lời giải:

Ta có

3x x x

40xx  















Vậy

   

2 0 2

3 3 3

2 2 0

4 d 4 d 4 dS x x x x x x x x x



     

  

4 4 8  

Câu 13: Một biển quảng cáo có dạng hình elip với bốn đỉnh

1 2 1 2

, , ,A A B B

như hình vẽ bên dưới. Biết

chi phí để sơn phần tô đậm là

200.000 nđv / m

và phần còn lại

100.000 nđv / m

. Hỏi số tiền

để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết

8mAA 

6mBB 

và tứ giác

MN PQ

là hình chữ nhật có

3mMQ 

5.526.000

đồng. B.

5.782.000

đồng C.

7.322.000

đồng. D.

7.213.000

đồng.

Lời giải:

Gọi phương trình chính tắc của elip

 

có dạng:



Với

6 2 3

A A a

B B b b











  



 

: 1 16

16 9 4

E y x      

Suy ra diên tích của hình elip là

 

. 12 m

S a b





Vì

MN PQ

là hình chữ nhật và

 

MQ M x E



  





1 3 3

1 12 2 3; ; 2 3;

16 4 2 2

x M N

   

      

   

   

Gọi

;SS

lần lượt là diện tích phần bị tô màu và không bị tô màu

Ta có:

 

4sin

2 2 2

2 3 2 3

4. 16 d 3 16 d 4 6 3 m

S x x x x S





      



Suy ra:

 

8 6 3

S S S



   

. Gọi

là tổng chi phí. Khi đó ta có

   

4 6 3 .100 8 6 3 .200 7.322.000T



   

(đồng).

Câu 14: Cho đường thẳng

y x a

và parabol

yx

(

là tham số thực). Gọi

,SS

lần lượt là

diện tích của hai hình phẳng được tô đậm và gạch chéo trong hình vẽ bên dưới:

Khi

SS

thì

thuộc khoảng nào dưới đây?







. B.

;

16 2









. C.







. D.







Lời giải:

Phương trình hoành độ giao điểm của của hai đồ thị:

2 2 0

x a x x x a     

Theo giả thiết, phương trình có hai nghiệm phân biệt

1 16 0

aa       

Khi đó, phương trình có hai nghiệm

 

1 2 1 2

,x x x x

thỏa:



  







  



S x x

P x x a

Lưu ý:

   

2 1 2 1 1 2 1 2

4 4 .

x x x x x x x x a       

Diện tích hình phẳng:

2 4 3

x x x

S a dx x dx ax





     







2 2 2 3 3 2 2

1 1 1 1 1 1

1 1 1 1 1

.4 2

4 4 3 3 4

x ax a a x x x ax a         

Diện tích hình phẳng

 

S x a x dx





   







Theo giả thiết,

 

1 2 1 1

4 3 6

S S x a a x a



      

 

3 3 2

1 2 1 2 2 1 1

. . 0

6 2 4

x x x x x x a x a        

 

1 1 16

1 1 3 1 1 1 16

4 . 0

6 8 2 2 4 64 4

a a a





        





3,684a

Câu 15: Cho hàm số bậc bốn

 

có đồ thị

   

;'f x f x

như hình vẽ bên dưới:

Gọi

;SS

là diện tích hai hình phẳng được gạch trong hình vẽ, khi

1S 

thì

bằng

104

. B.

. C.

. D.

Lời giải:

Đặt

     

5 2 , 0f x k x x k   

Khi đó

            

2 5 2 2 5 2 5 2 4 14f x k x x k x x k x x x



         

Xét hàm

        

 

5 2 3 4g x f x f x k x x x x



      

Suy ra

 























Từ đó ta suy ra:

      

 

2 4 4

5 5 5

5 2 3 4S g x dx g x dx k x x x x dx

  

        

  

23 10

10 23

kk   

Vậy

    

 

10 104

5 2 3 4

23 23

S g x dx x x x x dx



      



Câu 16: Cho hàm số

 

y f x

có đồ thị như hình vẽ và diện tích hai phần

,AB

lần lượt bằng

và

Giá trị của

 

3 1 dI f x x







bằng

13.

Lời giải:

+) Xét

 

3 1 dI f x x







, đặt

 

3 1 3

x t dt dx dx     

+) Đổi cận

    





  



         

1 0 1

2 2 0

1 1 1 1

dt= dt + dt 11 2 3.

3 3 3 3

I f t f t f t S S





      





  

Câu 17: Cho parabol

 

:P y x

và một đường thẳng

thay đổi cắt

 

tại hai điểm

sao cho

2018AB 

. Gọi

là diện tích hình phẳng giới hạn bởi

 

và đường thẳng

. Tìm giá trị

lớn nhất

max

của

2018 1

max





. B.

2018

max

S 

. C.

2018 1

max





. D.

2018



max

Lời giải:

Giả sử

( ; )A a a

;

( ; )( )B b b b a

sao cho

2018AB 

Phương trình đường thẳng

là:

()y a b x ab  

Khi đó:

 

( ) d d

S a b x ab x x a b x ab x x b a         



Vì

 

   

 

2 2 2

2 2 2 2

2018 2018 1 2018AB b a b a b a b a          

 

2018ba  

2018

b a b a S      

Vậy

max

2018

S 

khi

1009a 

và

1009b 

Câu 18: Trong mặt phẳng

Oxy

cho là hình phẳng

 

giới hạn bởi parabol

4yx

và trục hoành.

Đường thẳng

 

, 2 2x k k   

chia

 

thành hai phần

   

,HH

như hình vẽ bên dưới:

Biết rằng diện tích

 

gấp

lần diện tích

 

, hỏi giá trị

thuộc khoảng nào sau đây?

 

2; 1

. B.

 

0;1

. C.

 

1;0

. D.

 

1;2

Lời giải:

Gọi

,,S S S

lần lượt là diện tích của hình phẳng

   

,HH

và

 

Ta có

1 2 1 2 2

20 27

S S S S S S S    

Mặt khác

 

32 7 32 224

4 d .

3 27 3 81

S x x S



     



Mà

 

1 16

4 d 4 4

3 3 3

S x x x x k



      







nên ta được

16 224

3 3 81

k  

208

3 81

k   

27 324 208 0kk   

 

3 2 9 6 104 0

k k k k      

(do

 

2;2k 

Câu 19: Cho hai hàm số

 

4 3 2

2f x ax bx cx x   

và

 

2g x mx nx x  

với

, , , ,a b c m n

. Biết

hàm số

   

y f x g x

có ba điểm cực trị là

1; 2

và

. Diện tích hình phẳng giới hạn bởi

hai đường

 

y f x





và

 

y g x





bằng

. B.

. C.

. D.

Lời giải:

Ta có:

     

y h x f x g x  

     

3 2 2

4 3 2 2 3 2 2h x f x g x ax bx cx mx nx

  

         

     

4 3 3 2 2 4h x ax b m x c n x



      

Do hàm số

     

h x f x g x

có ba cực trị là

1; 2

và

nên

 



có dạng

     

4 1 2 3h x a x x x



   

;

    

0 4 4 .1. 2 3 4

h a a



      

       

1 2 3

f x g x x x x



    

Vậy

       

2 71

d 1 2 3 d

S f x g x x x x x x





      



Câu 20: Cho hàm số

 

4 3 2

f x x bx cx dx e    

(

, , ,b c d e

) có các giá trị cực trị là

1,4

và

. Diện

tích hình phẳng giới hạn bởi đồ thị hàm số

 





và trục hoành bằng

Lời giải:

+) Gọi

1 2 3

x x x

là ba điểm cực trị của hàm số

 

. Ta có bảng biến thiên:

+) Phương trình hoành độ giao điểm của đồ thị hàm số

 

và trục hoành là:

 

0 ( 1,2,3)

0 (TM)

f x x x i



  









   









+) Diện tích cần tìm là:

 

         

213

d d 2 2 4 2 2 6.

f x f x

S x x f x f x f x f x f x

f x f x



       



____________________________HẾT____________________________

Huế, 11h00’ Ngày 13 tháng 01 năm 2024

Bấm Tải xuống để xem toàn bộ.

| 1/99

| | Tải xuống

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 ỨNG DỤNG TÍCH PHÂN DIỆN TÍCH HÌNH PHẲNG
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 1_TrNg 2022 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
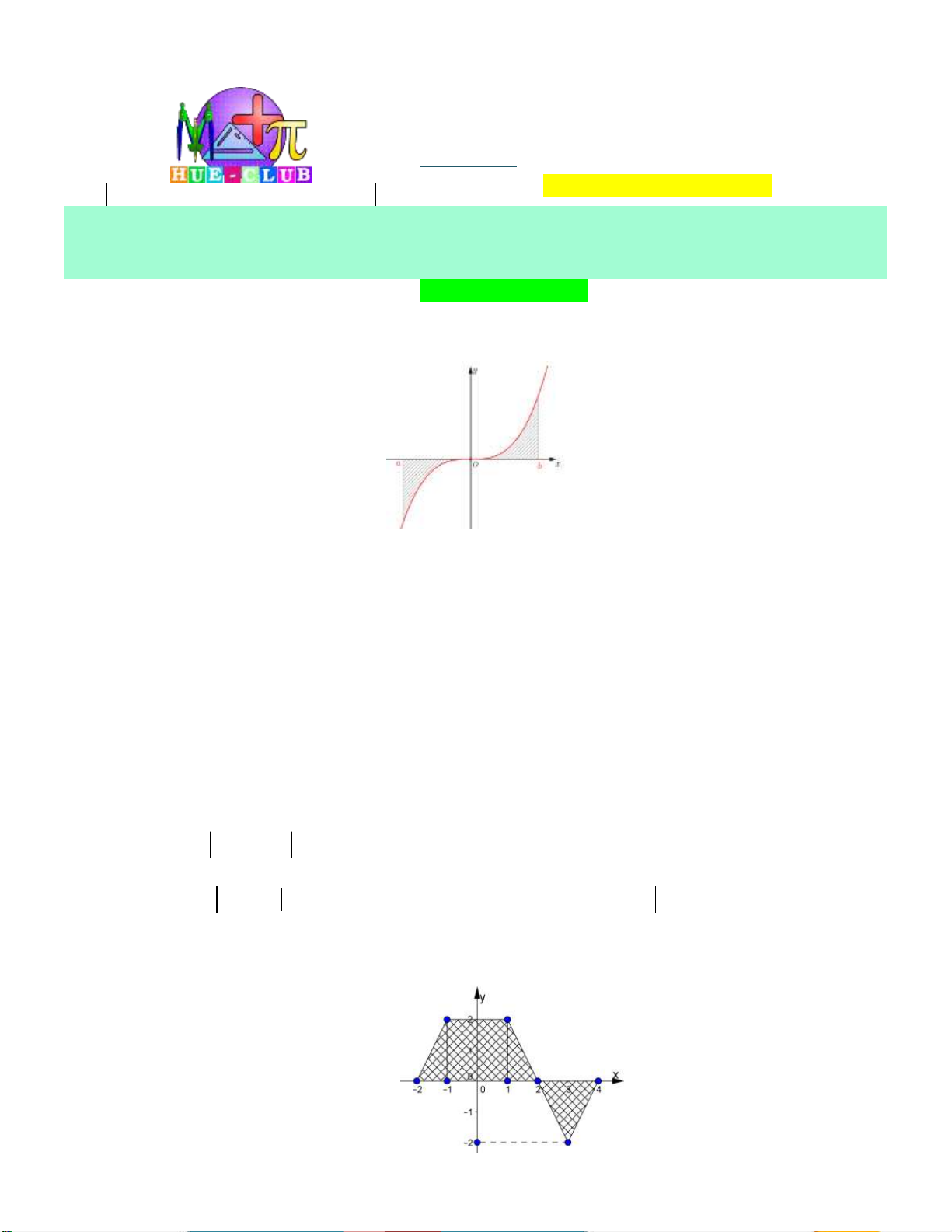
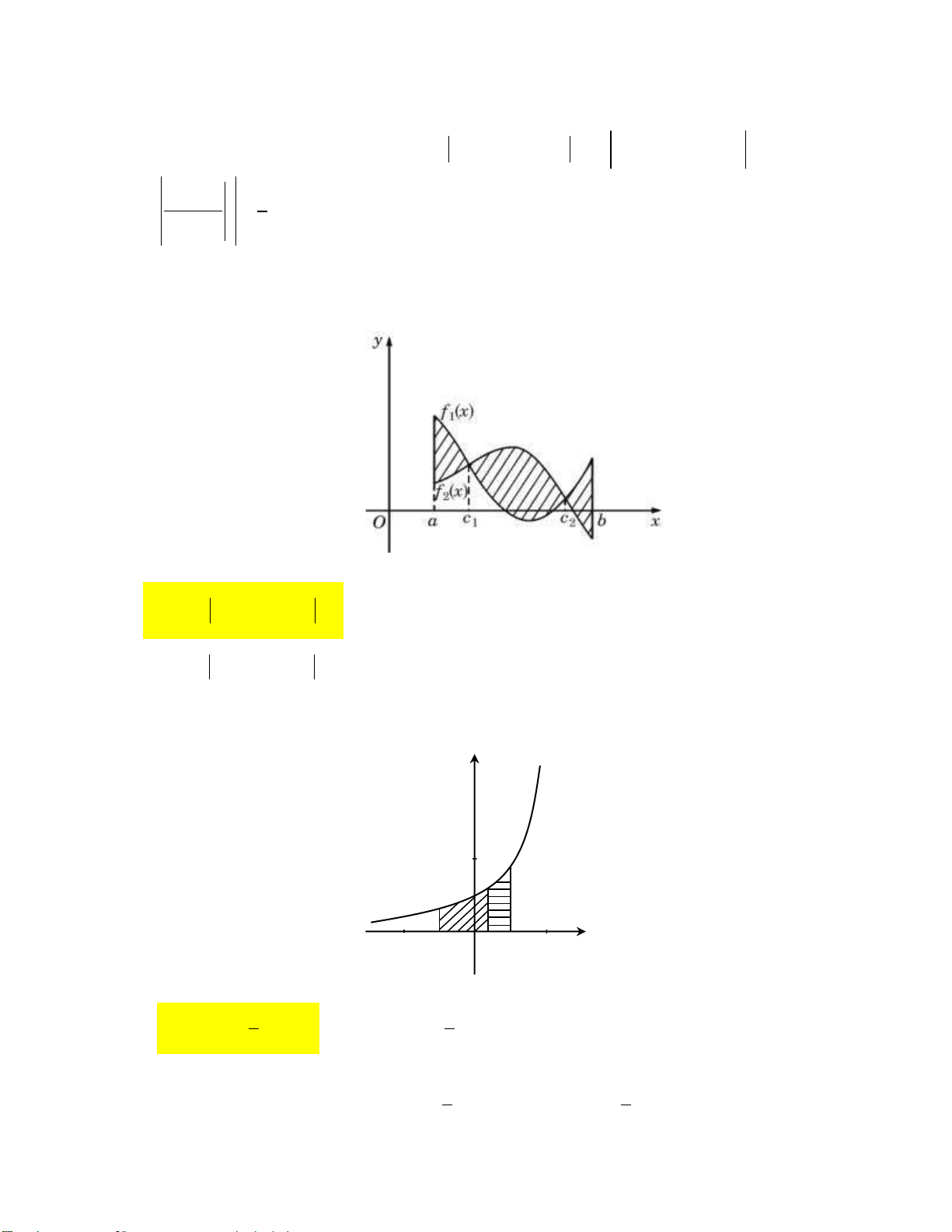
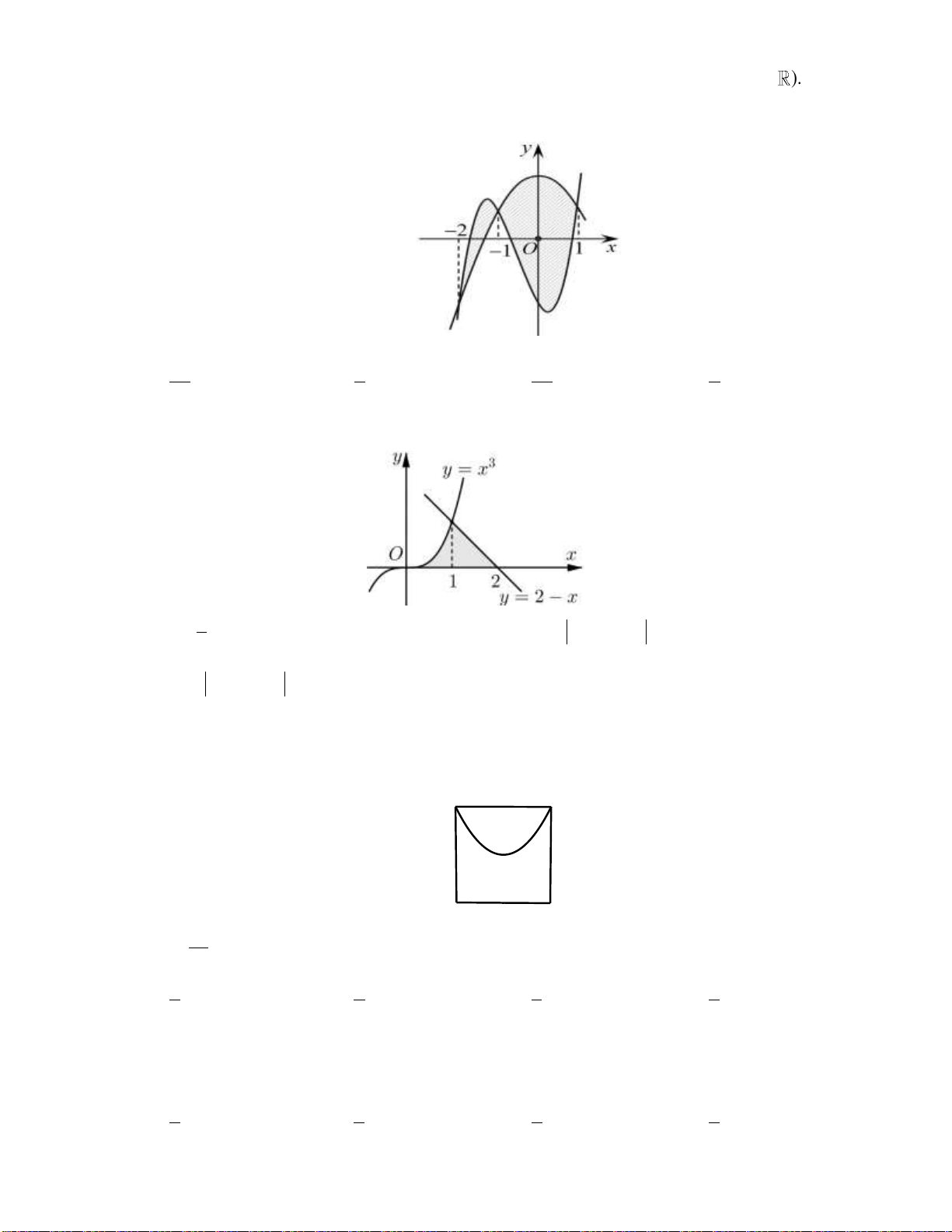
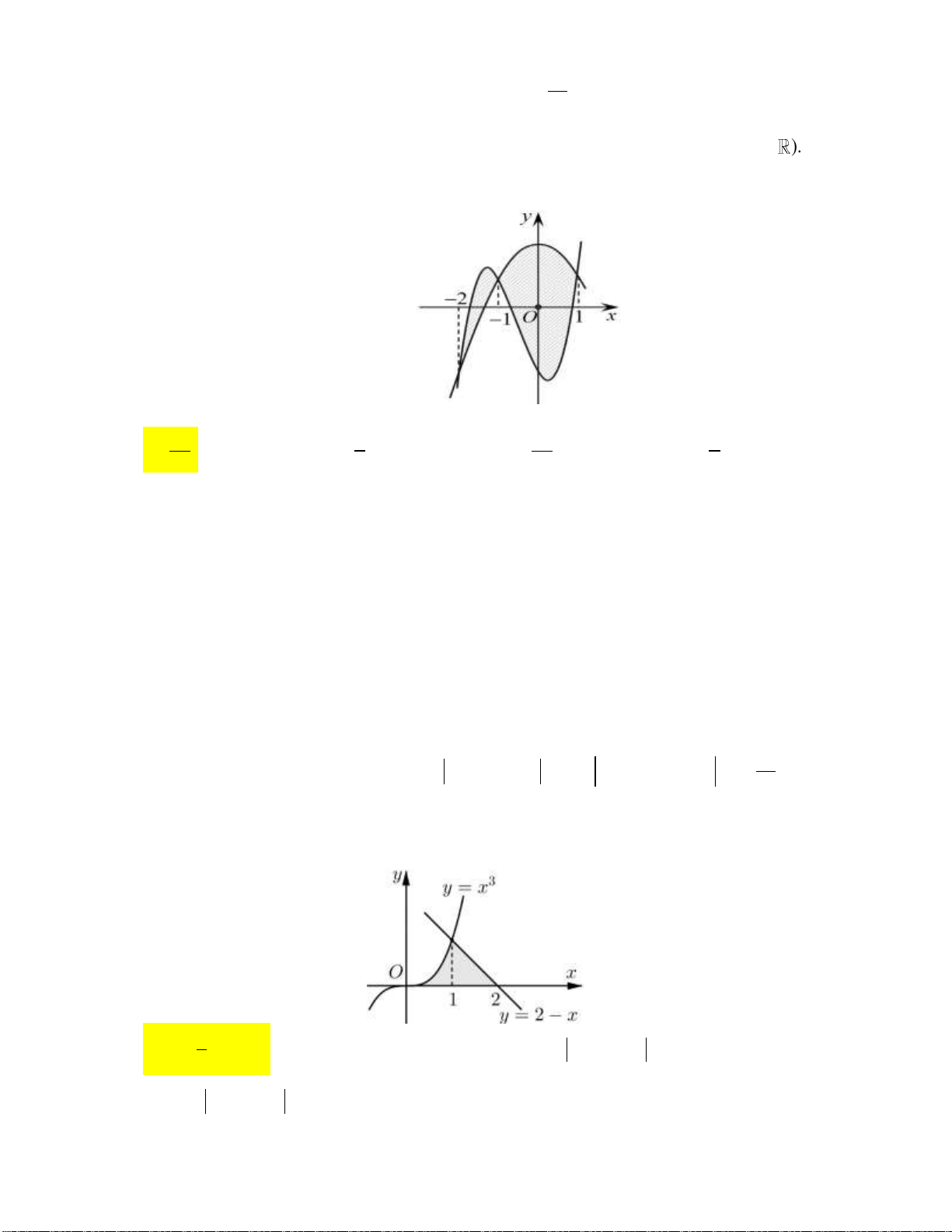
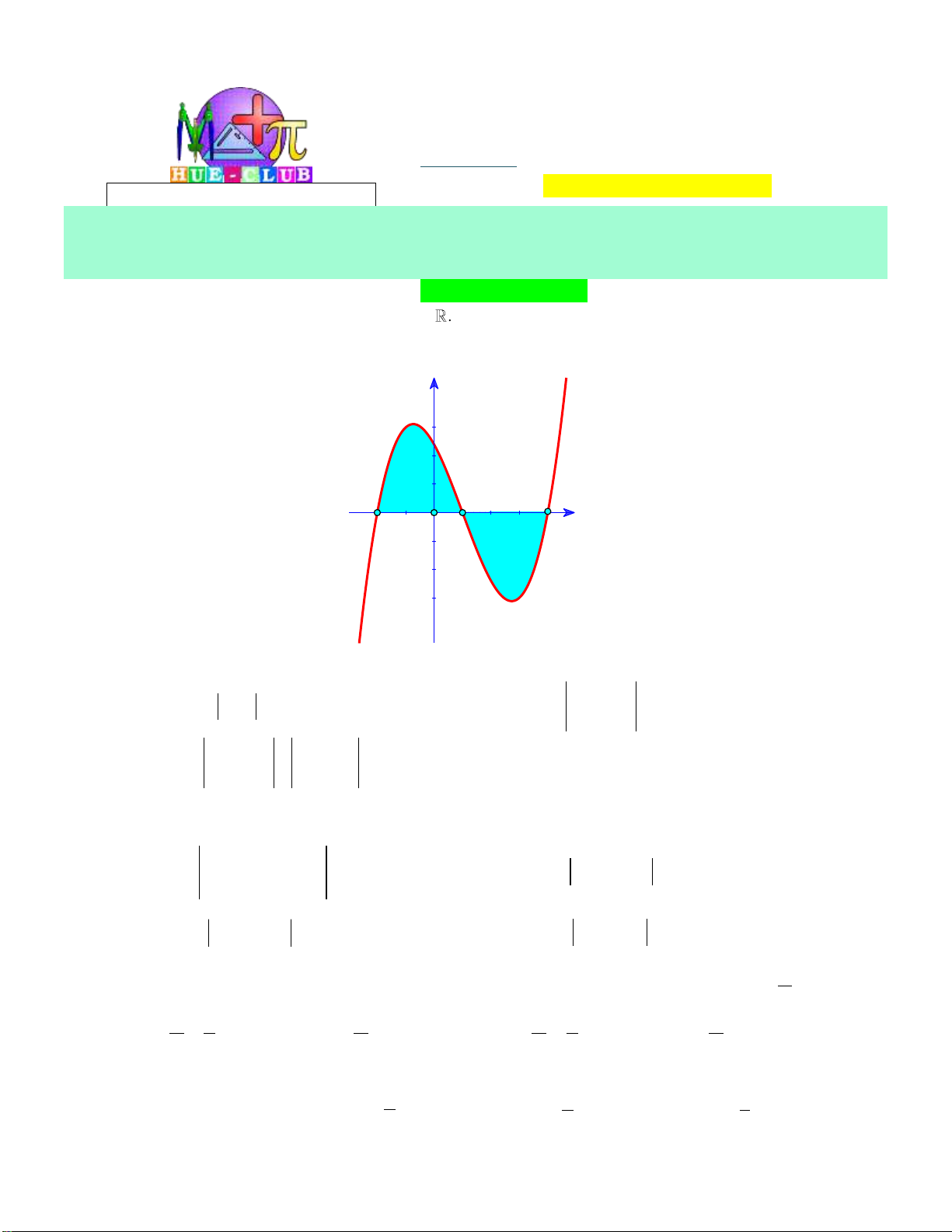
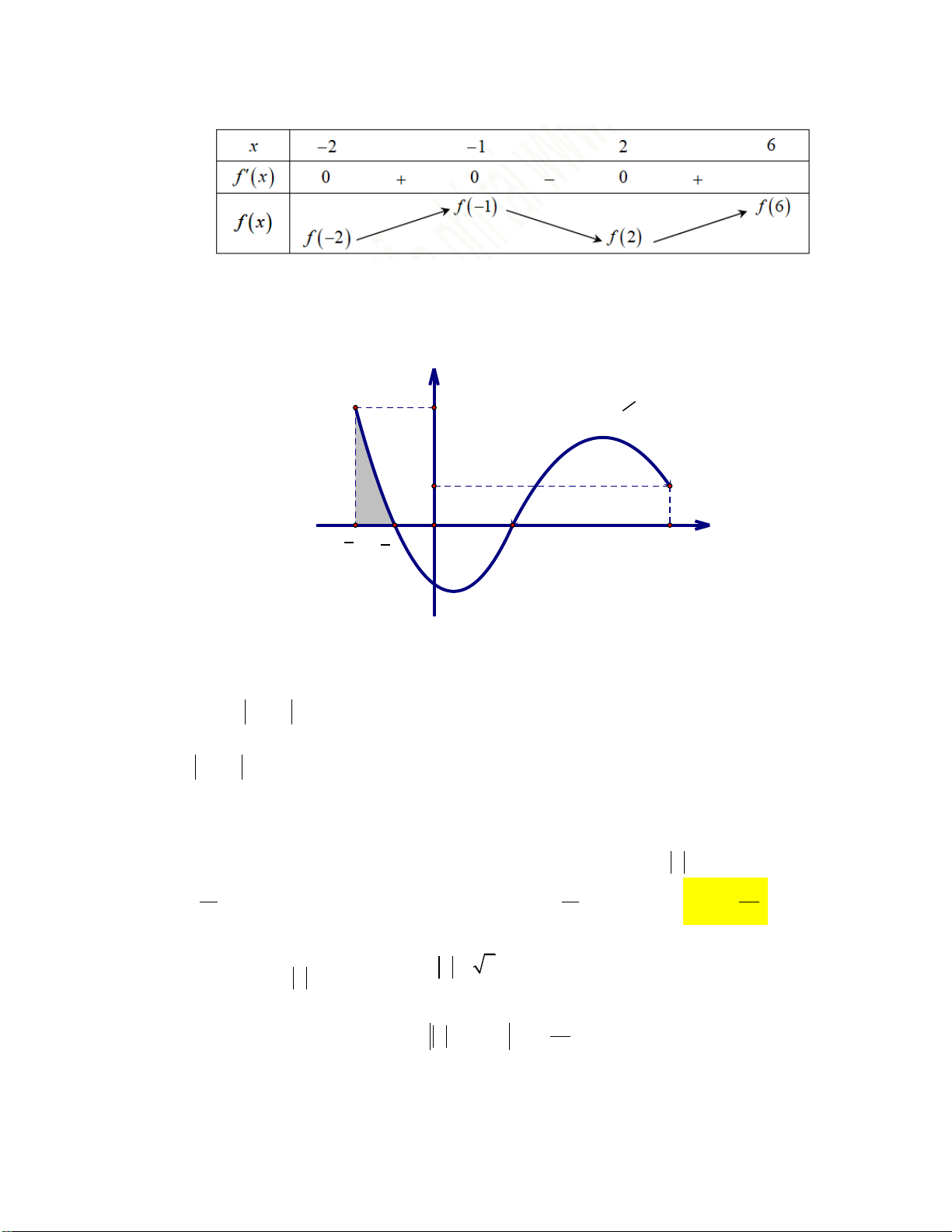
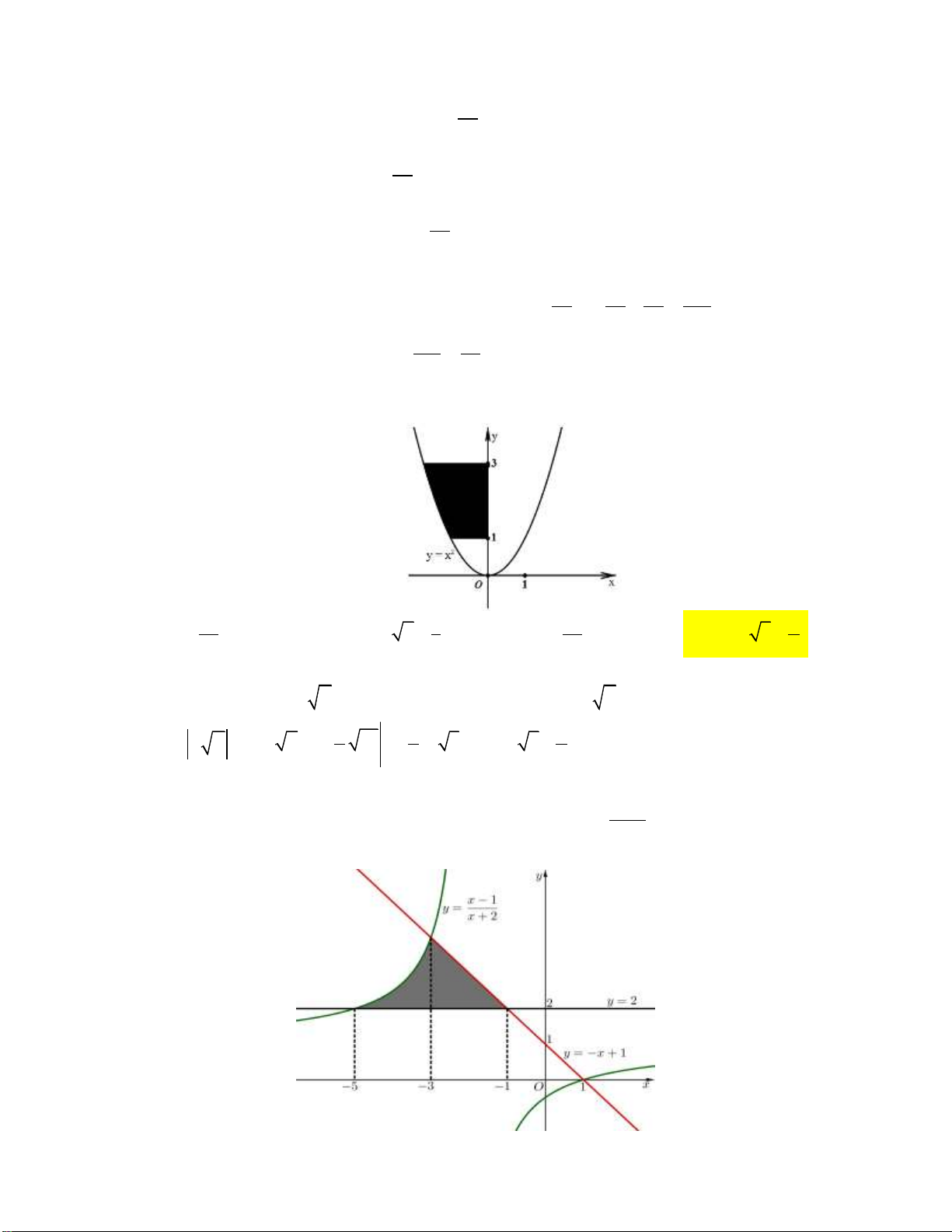
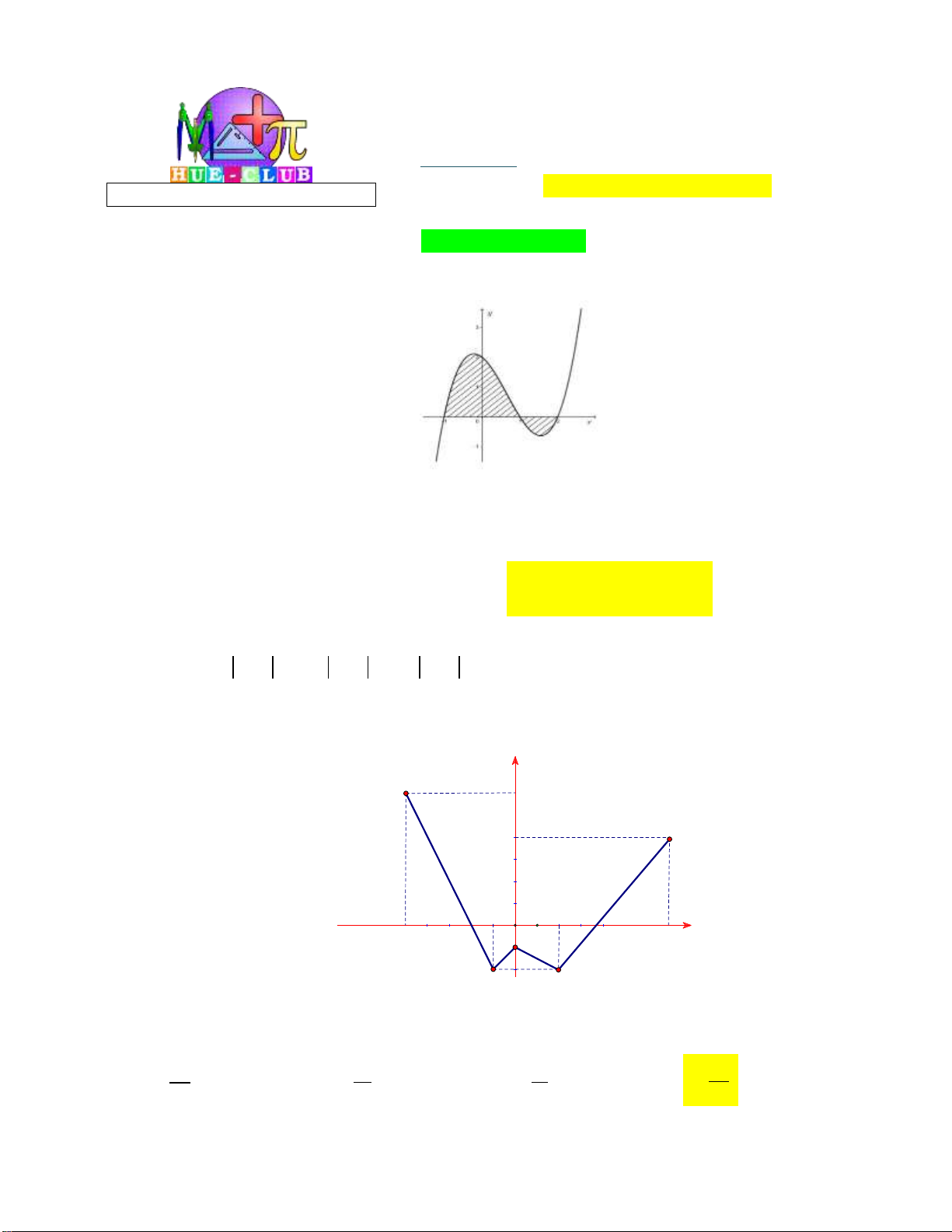
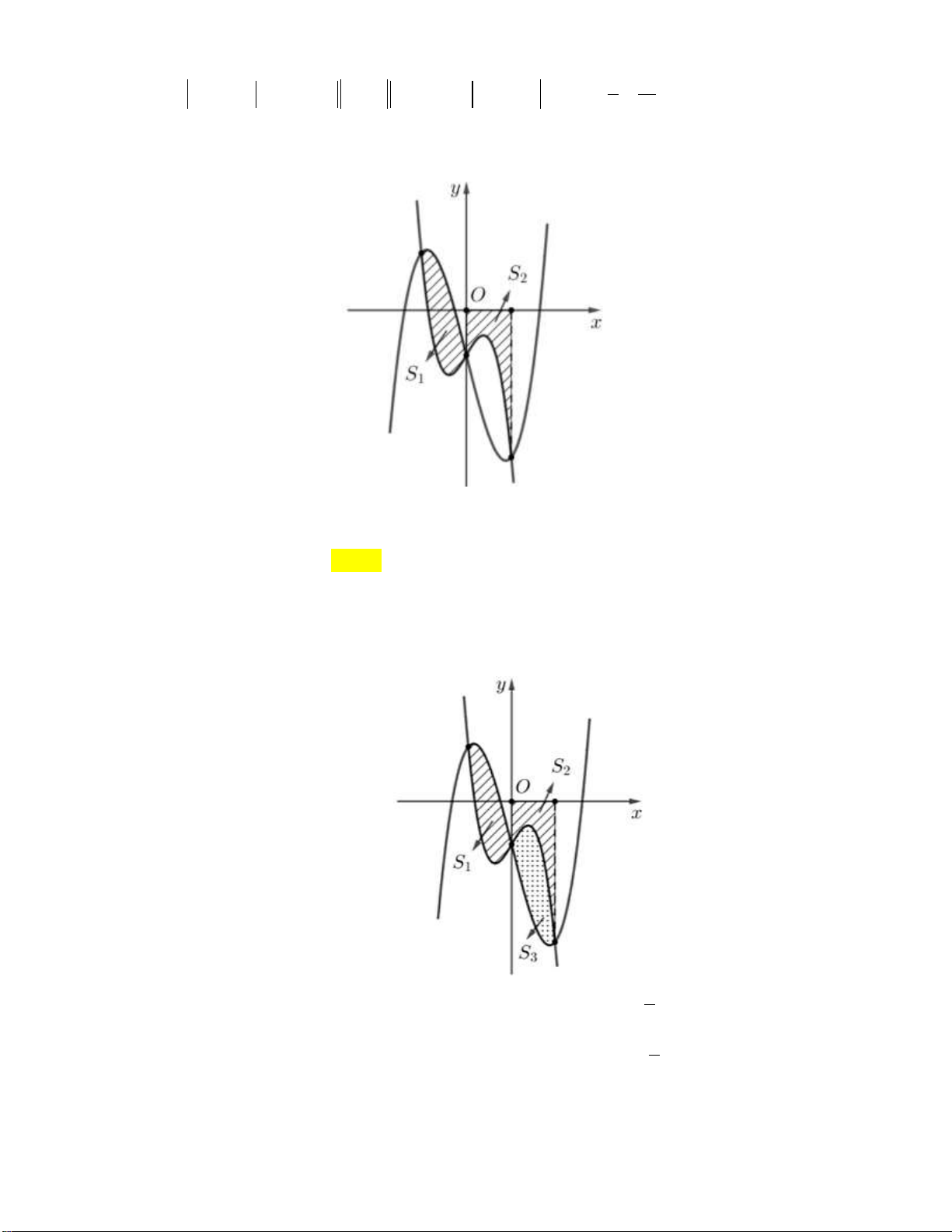
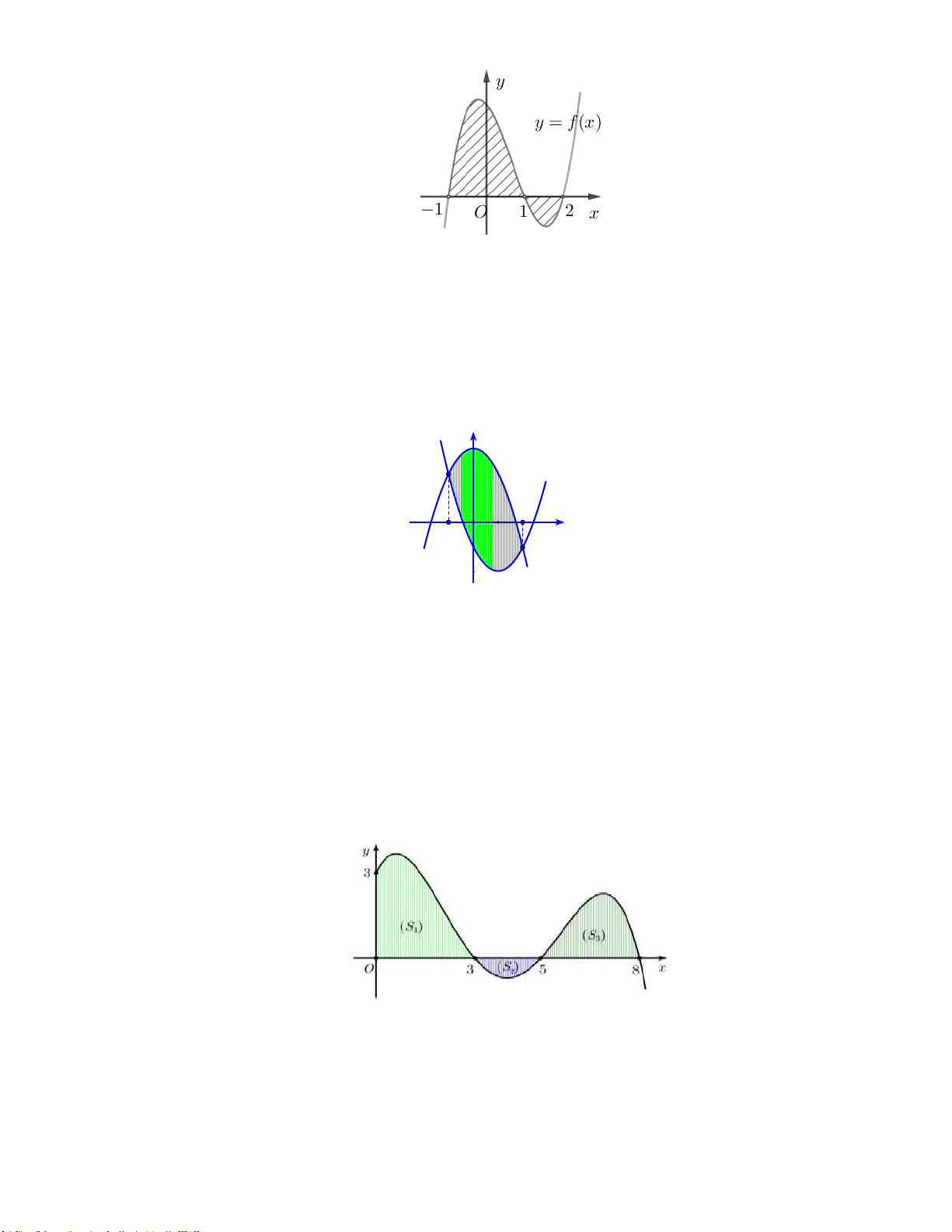
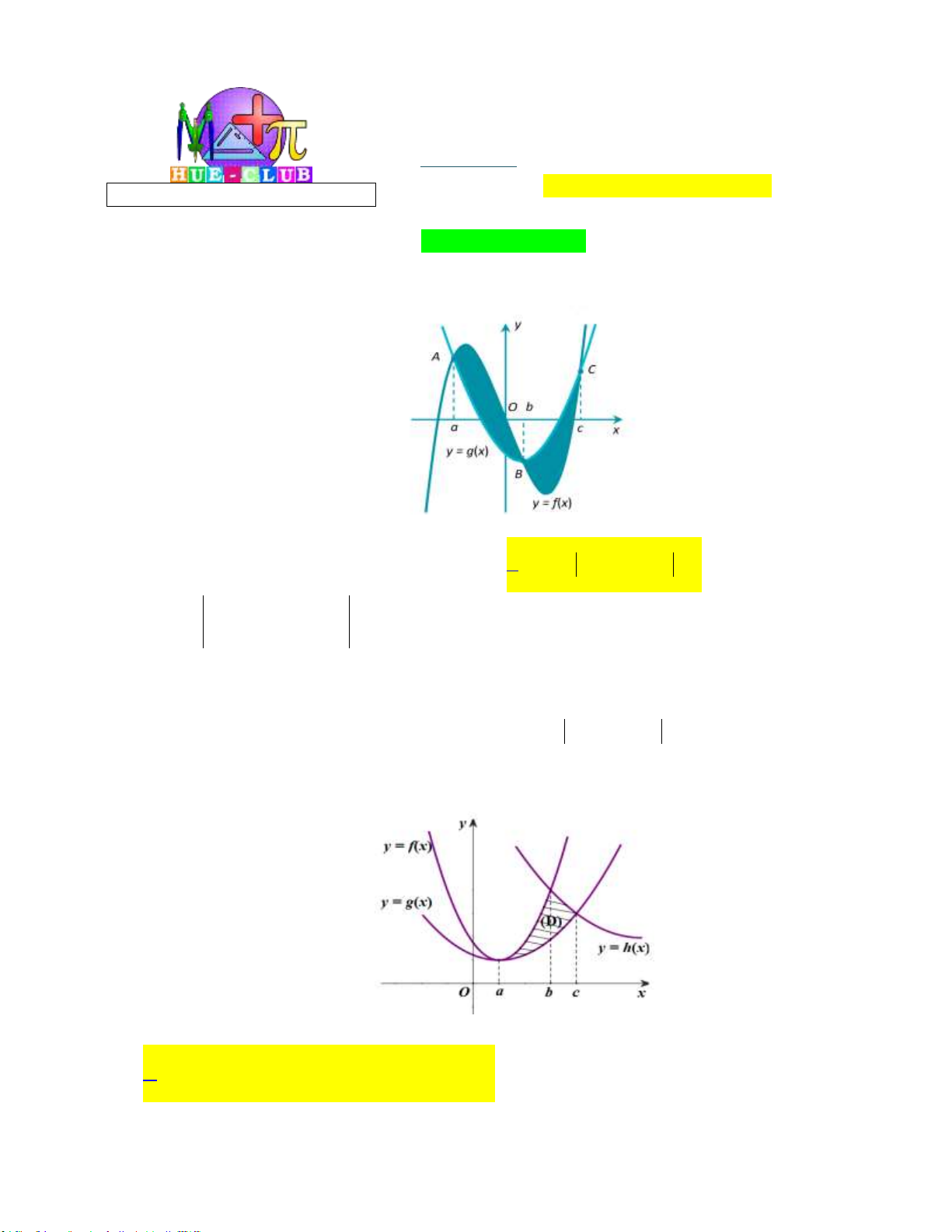
Câu 1: Cho hàm số y  f x liên tục trên đoạn a;b 
 . Gọi D là diện tích hình phẳng giới hạn bởi đồ
thị C : y  f x , trục hoành, hai đường thẳng x  a , x  b (như hình vẽ dưới đây).
Giả sử S là diện tích hình phẳng D . Mệnh đề nào dưới đây đúng? D 0 b 0 b
A. S  f x x  f x x   .
B. S   f x x  f x x   . D  d  d D  d  d a 0 a 0 0 b 0 b
C. S  f x x  f x x   .
D. S   f x x  f x x   . D  d  d D  d  d a 0 a 0
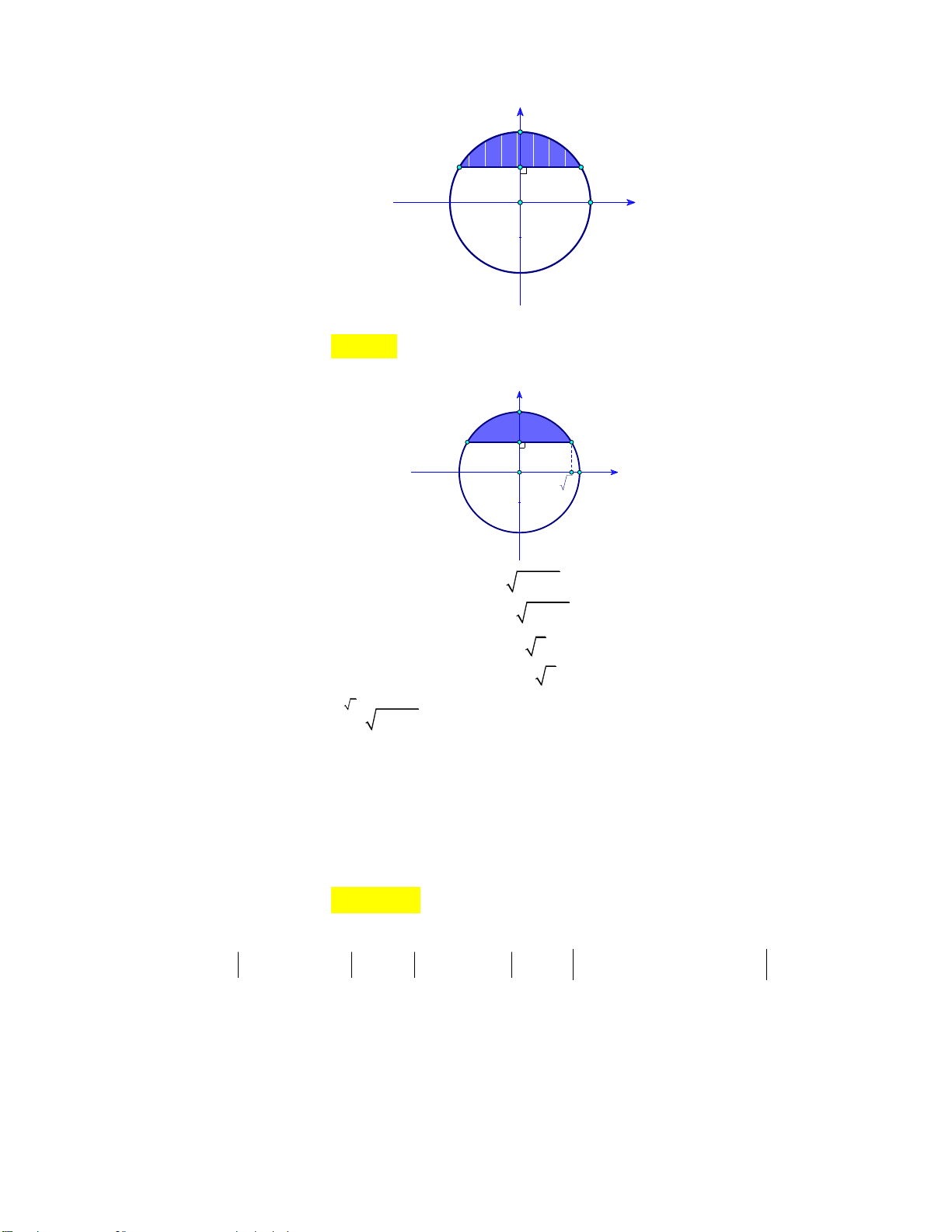
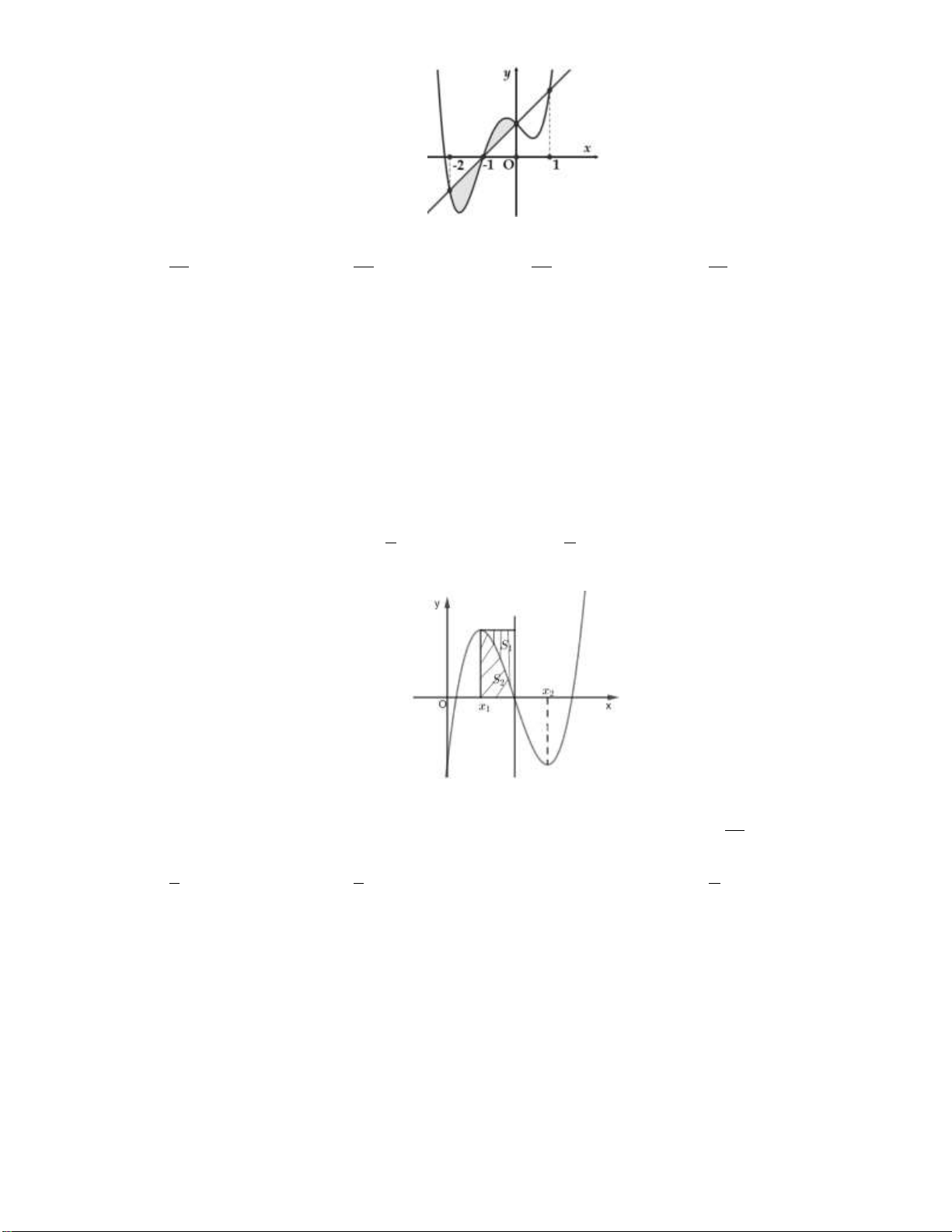
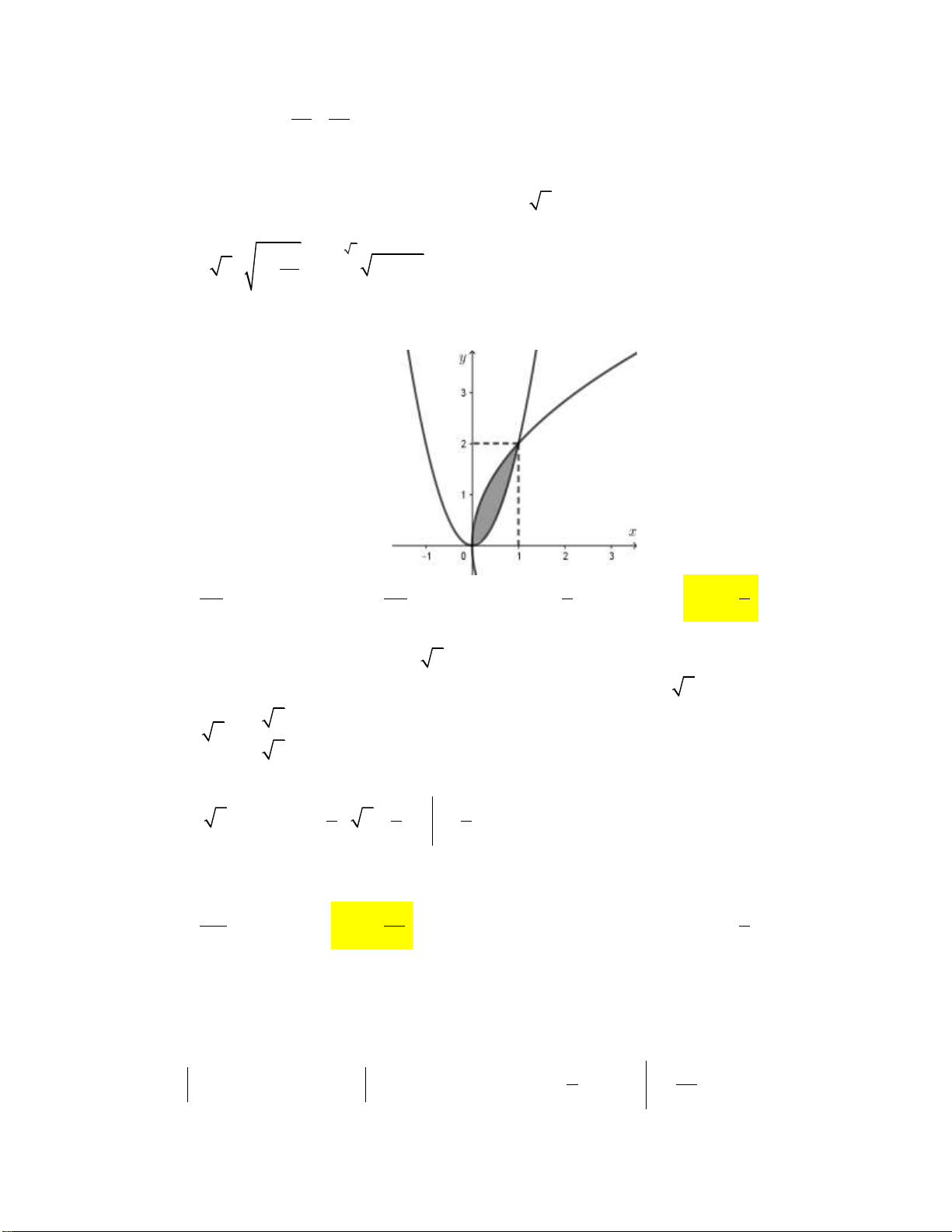
Câu 2: Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y 
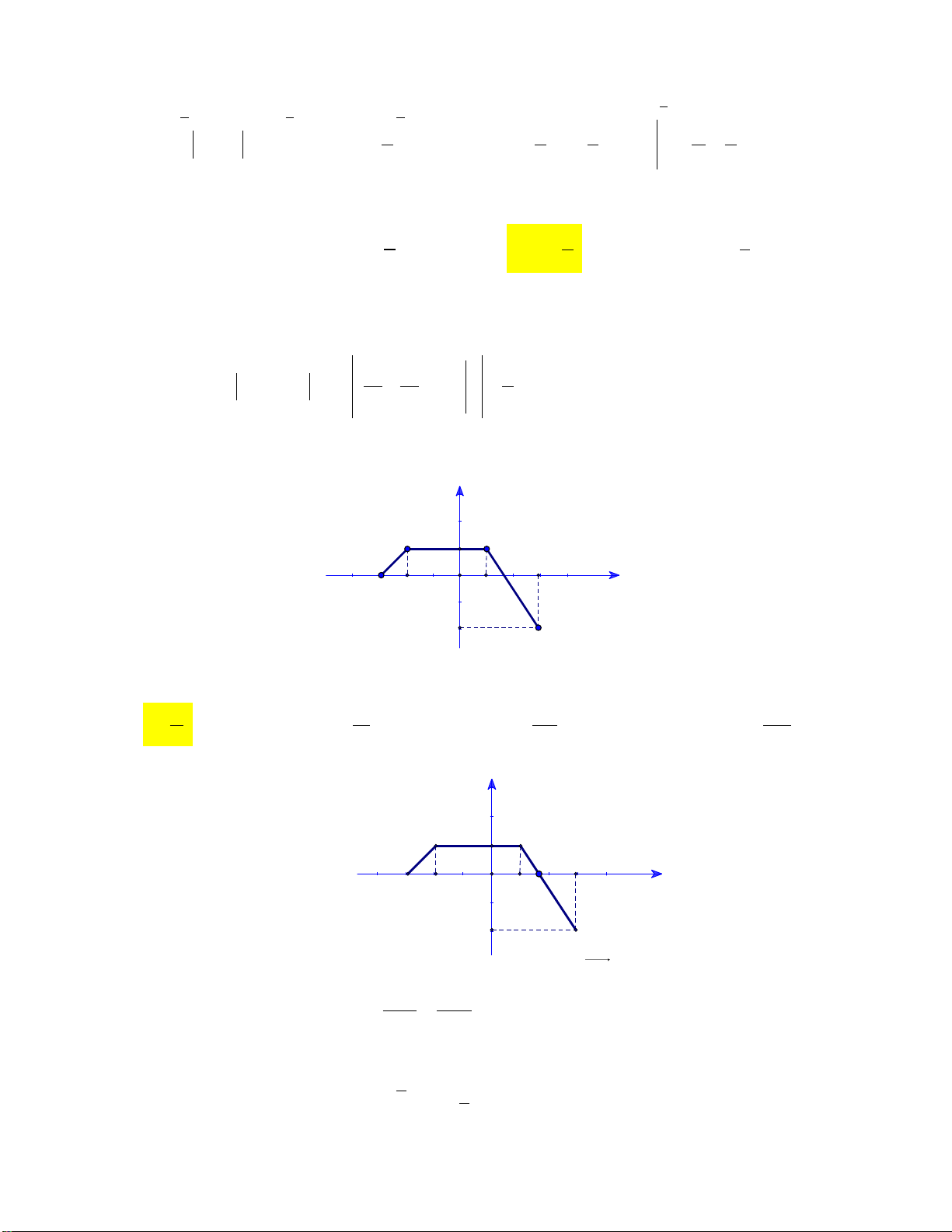
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e x S d . x  B.  ex S d . x  C.   ex S d . x  D. 2  e x S d . x  0 0 0 0
Câu 3: Gọi S là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số 2
y  x  3 và y  4x . Khẳng
định nào dưới đây đúng? 3 3 A. 2 S  x  4x  3 d  x . B. S   2
x  4x  3dx . 1 1 3 3 C. S   2
x  3  4x dx . D. 2 S  x  4x  3 d  x . 1 1
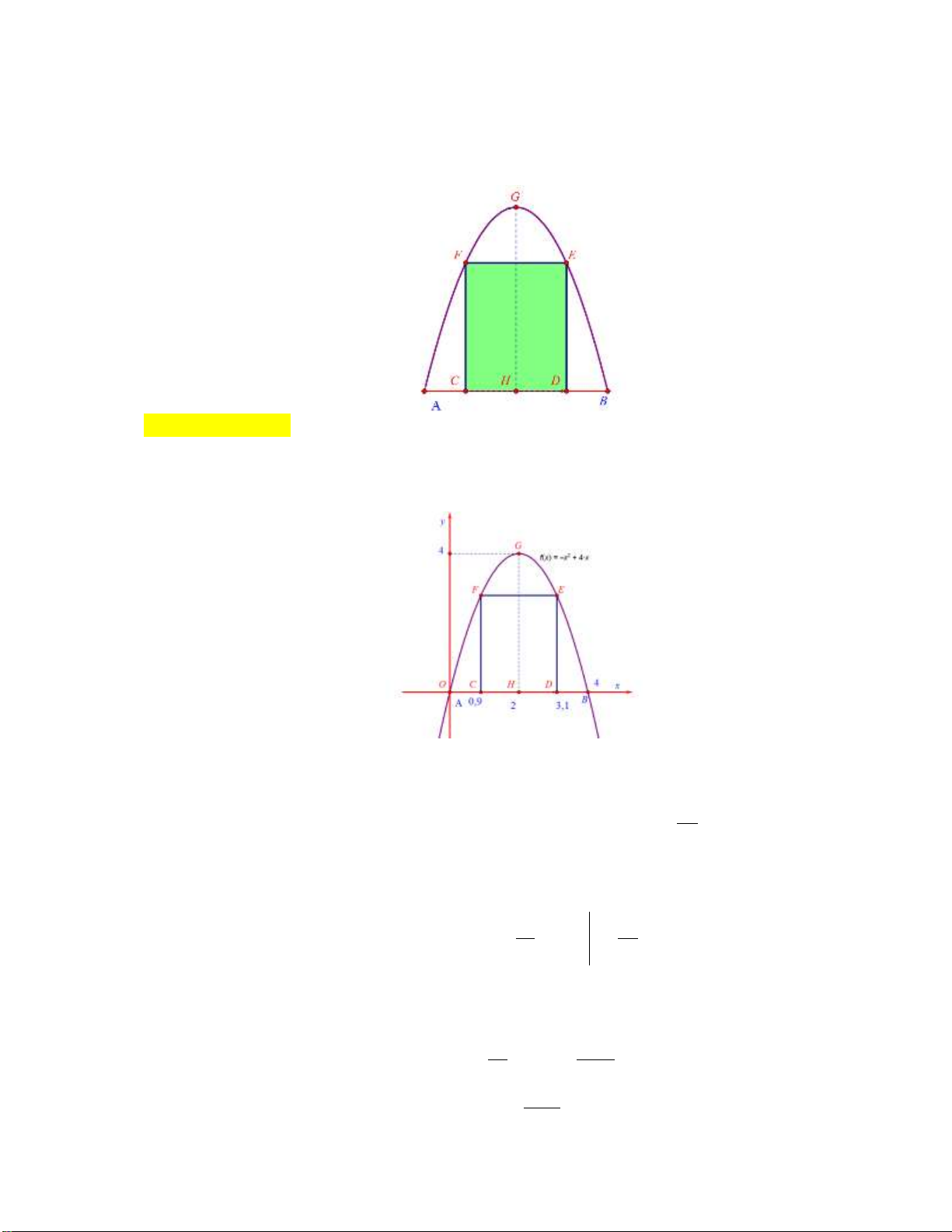
Câu 4: Cho hàm số y  f x xác định, liên tục và có nguyên hàm trên 2; 4 
 đồng thời có đồ thị như hình vẽ dưới đây. 4 Tính I  f  xdx 2  A. I  8 . B. I  4 . C. I  6 . D. I  2 .
Câu 5: Diện tích hình phẳng giới hạn bởi hai đồ thị f  x 3
 x  3x  2 ; g x  x  2 là A. S  8 . B. S  4 . C. S  12 . D. S  16 .
Câu 6: Diện tích S của hình phẳng giới hạn bởi các đường 3
y  2x , y  π , x  4 và trục tung được
tính bởi công thức nào dưới đây ? 4 4 A. S   3
2x  πdx . B. 3 S  π 2x dx  . 0 π 4 4 C. S   3
2x  πdx . D. 3 S  2x dx  . 0 π
Câu 7: Cho hàm số y  f x. Đồ thị hàm số y  f x như hình bên. Đặt
gx  f x 2 2
 x . Khẳng định nào sau đây đúng?
A. g3  g 3
   g1. B. g 
1  g3  g 3  . C. g  1  g 3
   g3. D. g 3
   g3  g 1  .
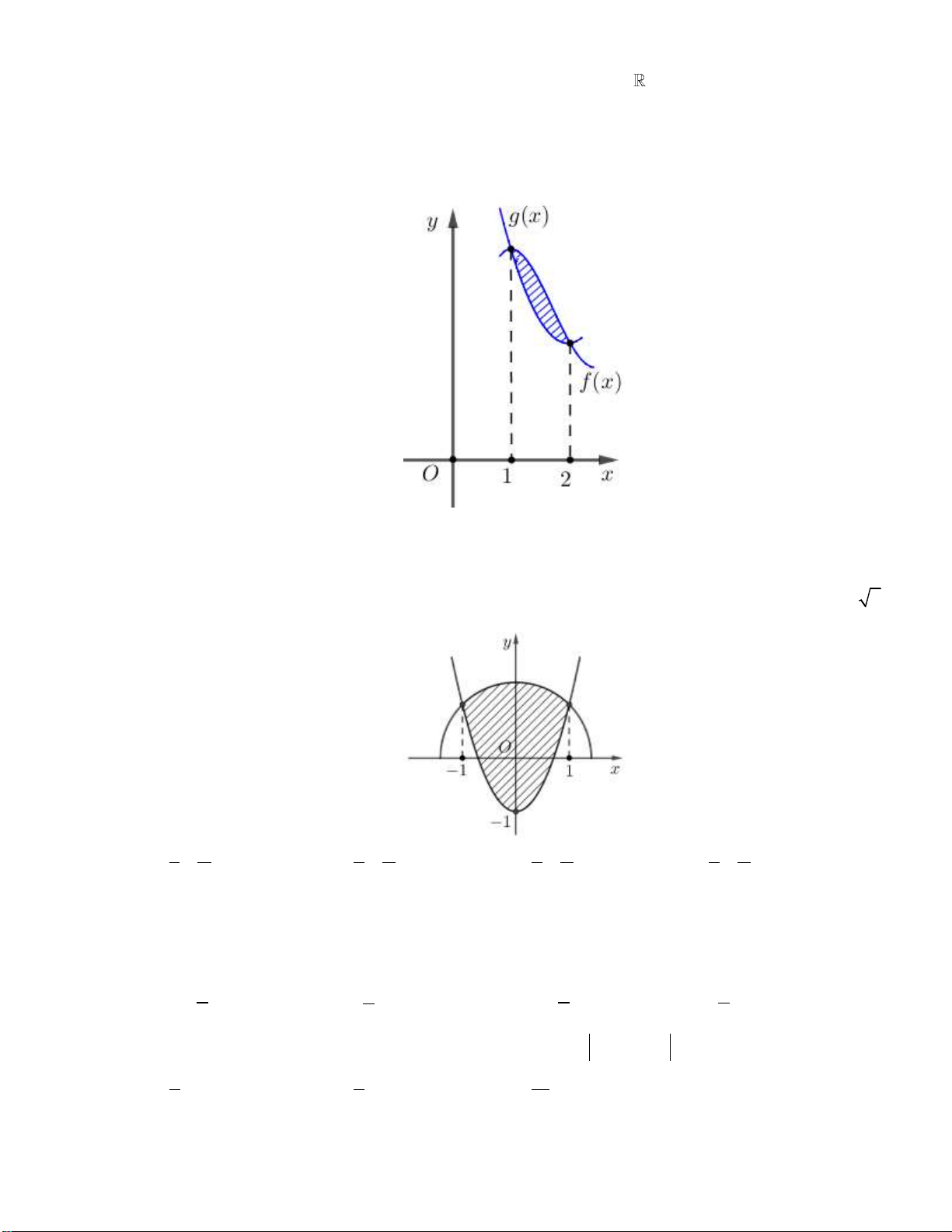
Câu 8: Tính diện tích S của hình phẳng giới hạn bởi  P 2
: y  x  4 , tiếp tuyến của  P tại M 2;0 và trục Oy là 4 8 7 A. S  . B. S  2 . C. S  . D. S  . 3 3 3
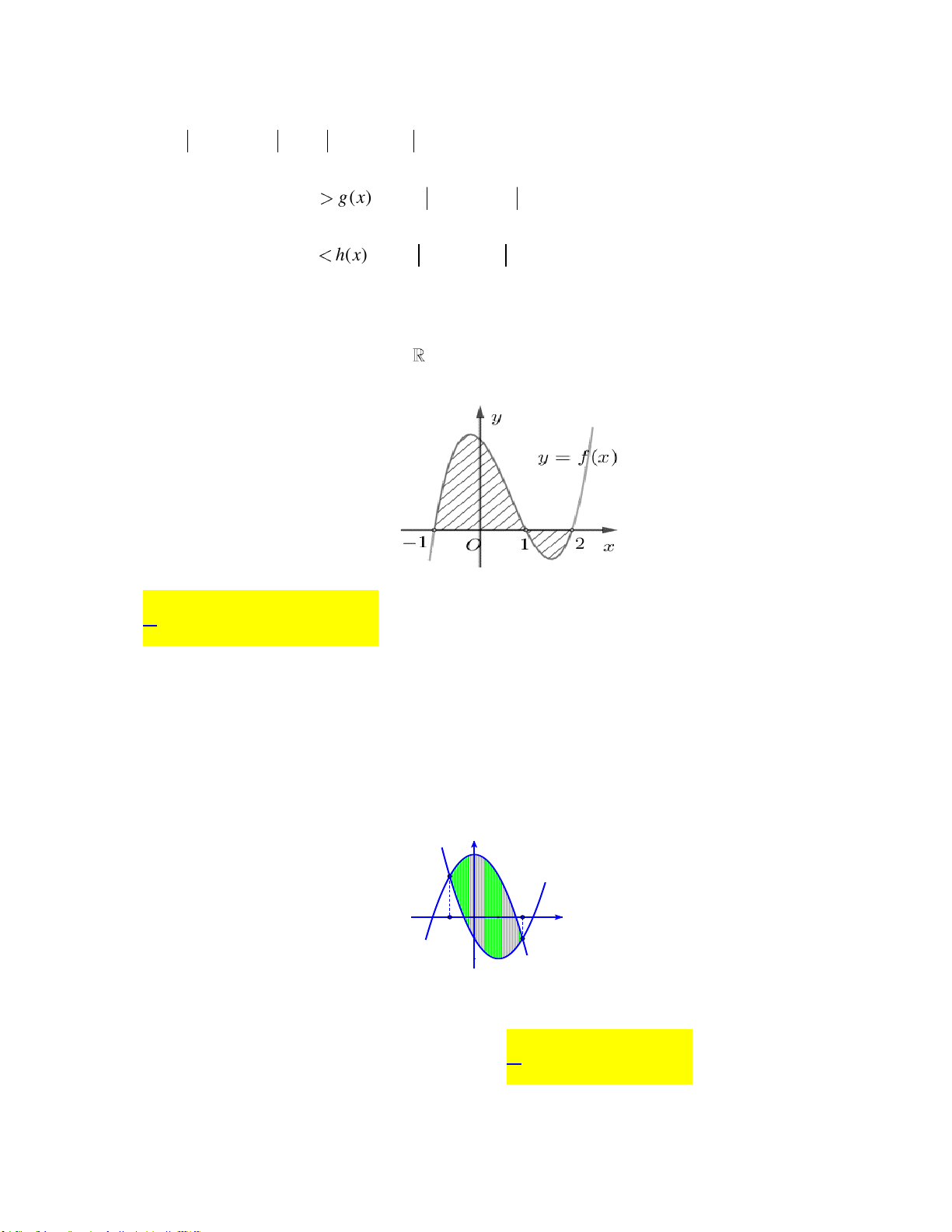
Câu 9: Cho hình phẳng  H  giới hạn bởi đồ thị của hai hàm số f x và f x liên tục trên đoạn 2   1  
a; b và hai đường thẳng x  a, x  b (tham khảo hình vẽ dưới).
Công thức tính diện tích của hình  H  là b b A. S  f x  f x d . x 
B. S   f x  f x d .x 1   2   1   2   a a b b b C. S  f x  f x d . x  D. S  f x dx  f x d . x   2   1   1   2   a a a Câu 10: Cho hàm số x
y  e , gọi S là diện tích hình phẳng giới hạn bởi các đường x
y  e ; x  1  ; x  k 1
và S là diện tích hình phẳng giới hạn bởi các đường x
y  e ; x  k; x  1. (tham khảo hình vẽ). 2 y x y  e 2 1 2  1  O 1 2 x
Xác định k để S  S . 1 2  1   1 
A. k  ln e   ln 2  
. B. k  2 ln e  1  
. C. k  2 ln 2 1. D. k  ln 2 .  e   e 
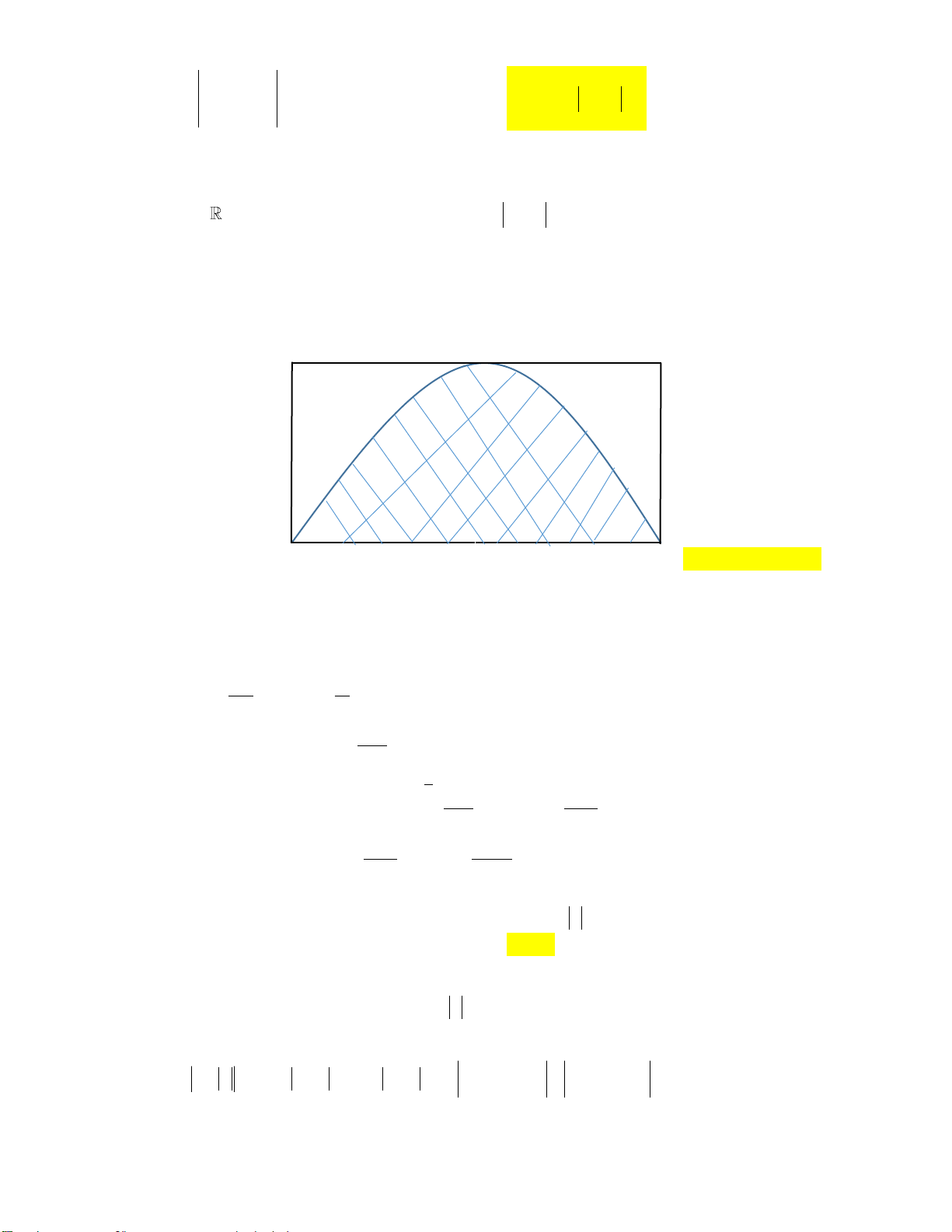
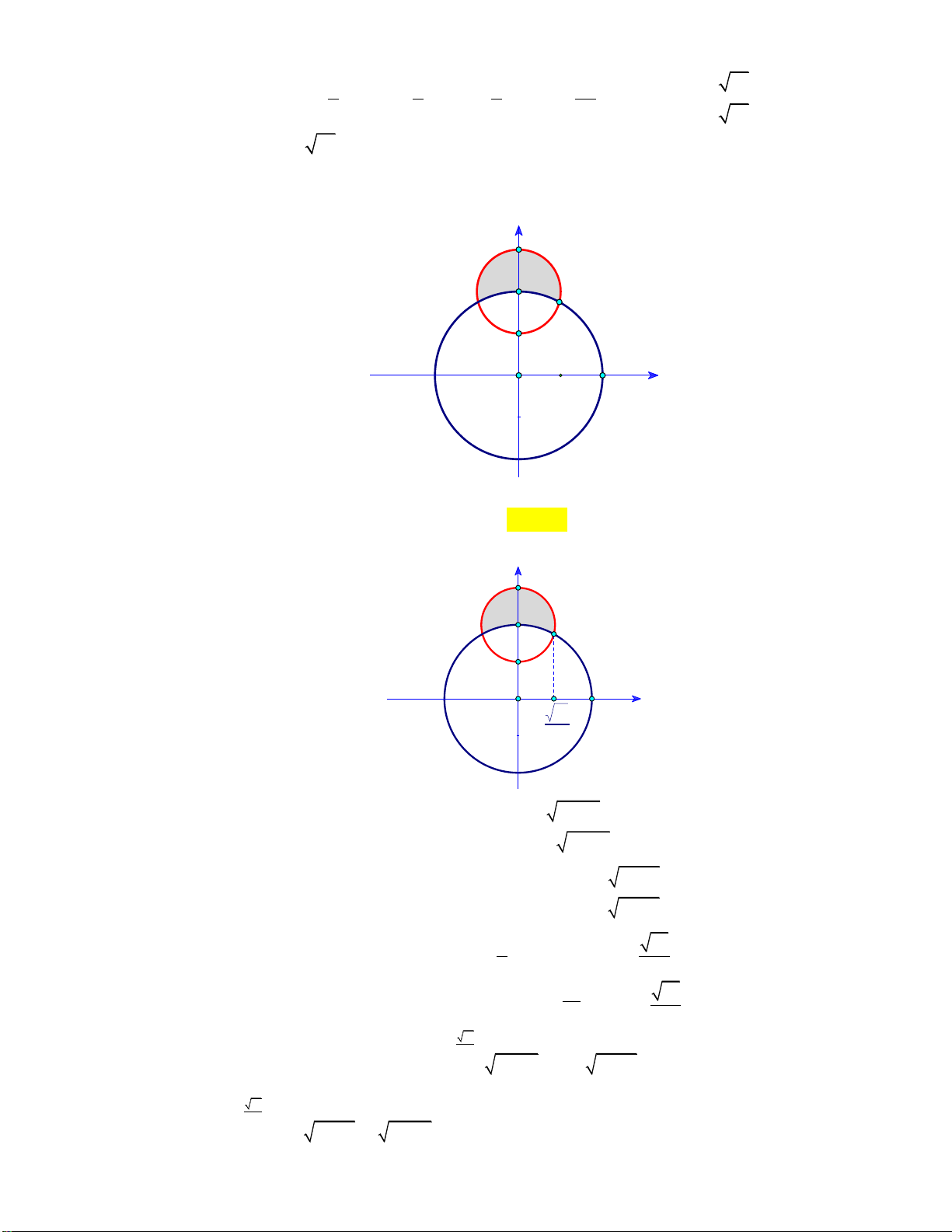
Câu 11: Trong mặt phẳng cho đường tròn C (tham khảo hình vẽ dưới đây). y 2 1 O 2 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 2,01. B. 2,46. C. 1,81. D. 3,13.
Câu 12: Cho hai hàm số y  f  x và y  g  x liên tục trên đoạn a;b với a  b . Kí hiệu S là diện 1
tích hình phẳng giới hạn bởi các đường y  3 f  x , y  3g  x , x  a , x  b ; S là diện tích 2
hình phẳng giới hạn bởi các đường y  f  x  2 , y  g  x  2 , x  a , x  b . Khẳng định nào sau đây đúng? A. S  2S . B. S  3S .
C. S  2S  2.
D. S  2S  2. 1 2 1 2 1 2 1 2
Câu 13: Cho hàm số bậc ba 3 2
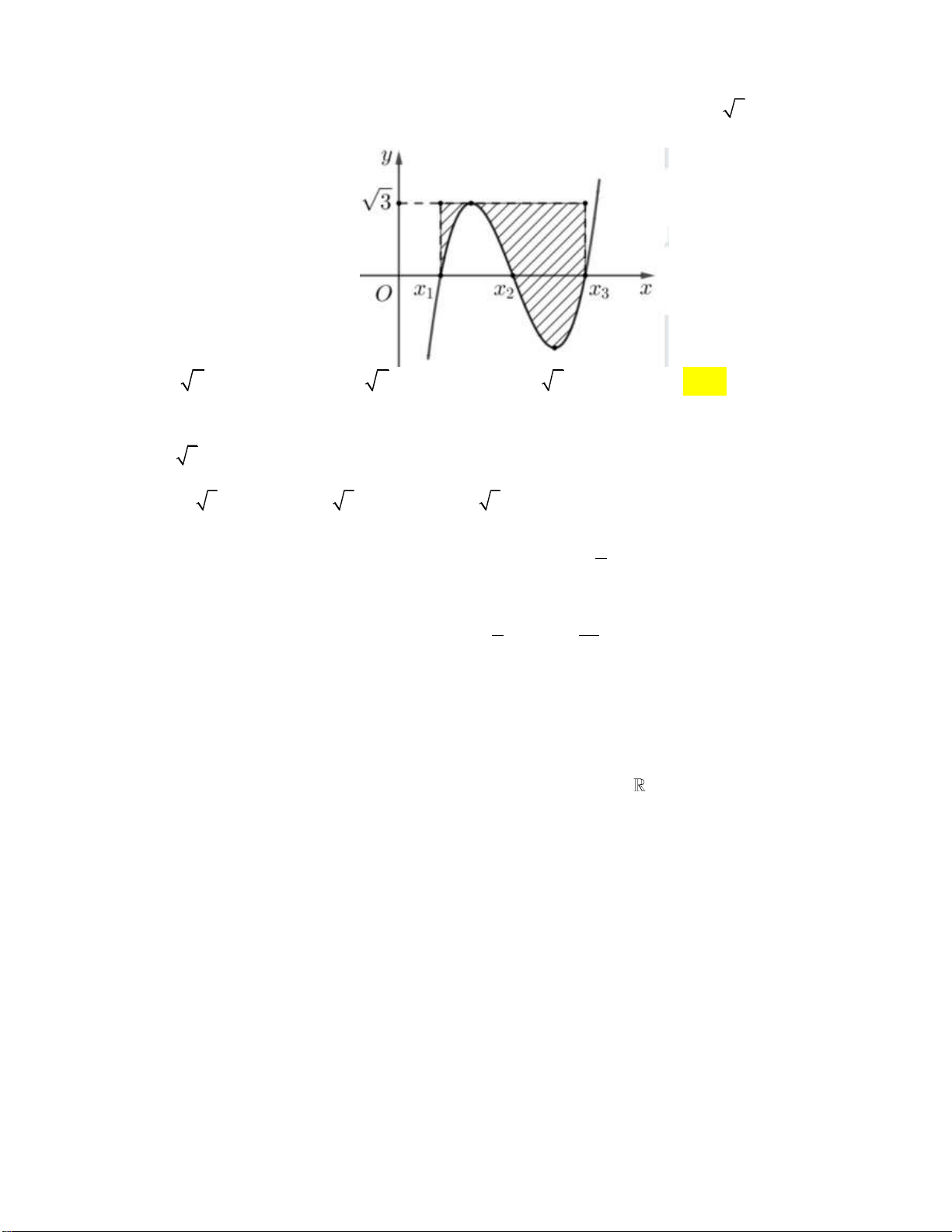
f (x)  ax  bx  cx  d và đường thẳng d : g(x)  mx  n có đồ thị như hình vẽ bên dưới: 1
Nếu diện tích phần tô bằng bằng
thì diện tích phần gạch bằng 2 5 3 A. . B. 2 . C. 1. D. . 2 2
Câu 14: Cho hàm số y  f  x liên tục trên
và thỏa mãn f  
1  0  f 0 . Gọi S là diện tích hình
phẳng giới hạn bởi các đường y  f  x , y  0 , x  1 và x  1 . Mệnh đề nào sau đây đúng? 1 0 1 A. S  f  xdx B. S  f
 xdx f  x dx 1  1  0 1 1 C. S  f  xdx D. S  f  x dx 1 1 
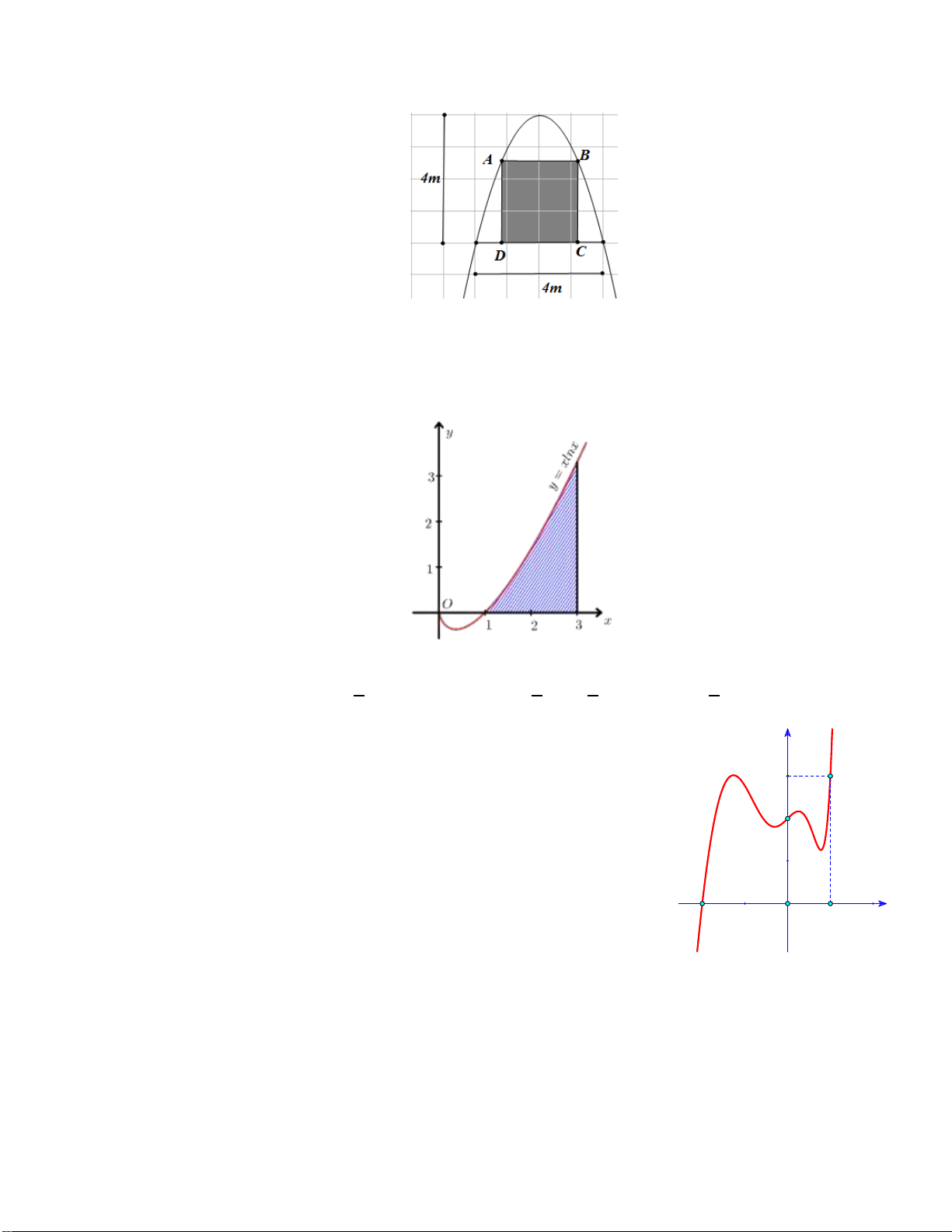
Câu 15: Một sân bóng hình chữ nhật với diện tích 2
200m . Người ta muốn trồng cỏ trên sân bóng theo
hình một parabol bậc hai sao cho đỉnh của parabol trùng với trung điểm một cạnh của sân
bóng như hình vẽ bên. Biết chi phí trồng cỏ là 300 ngàn đồng cho mỗi mét vuông. Xác định
chi phí trồng cỏ cần có cho sân bóng trên? A. 30 triệu đồng. B. 60 triệu đồng. C. 50 triệu đồng. D. 40 triệu đồng.
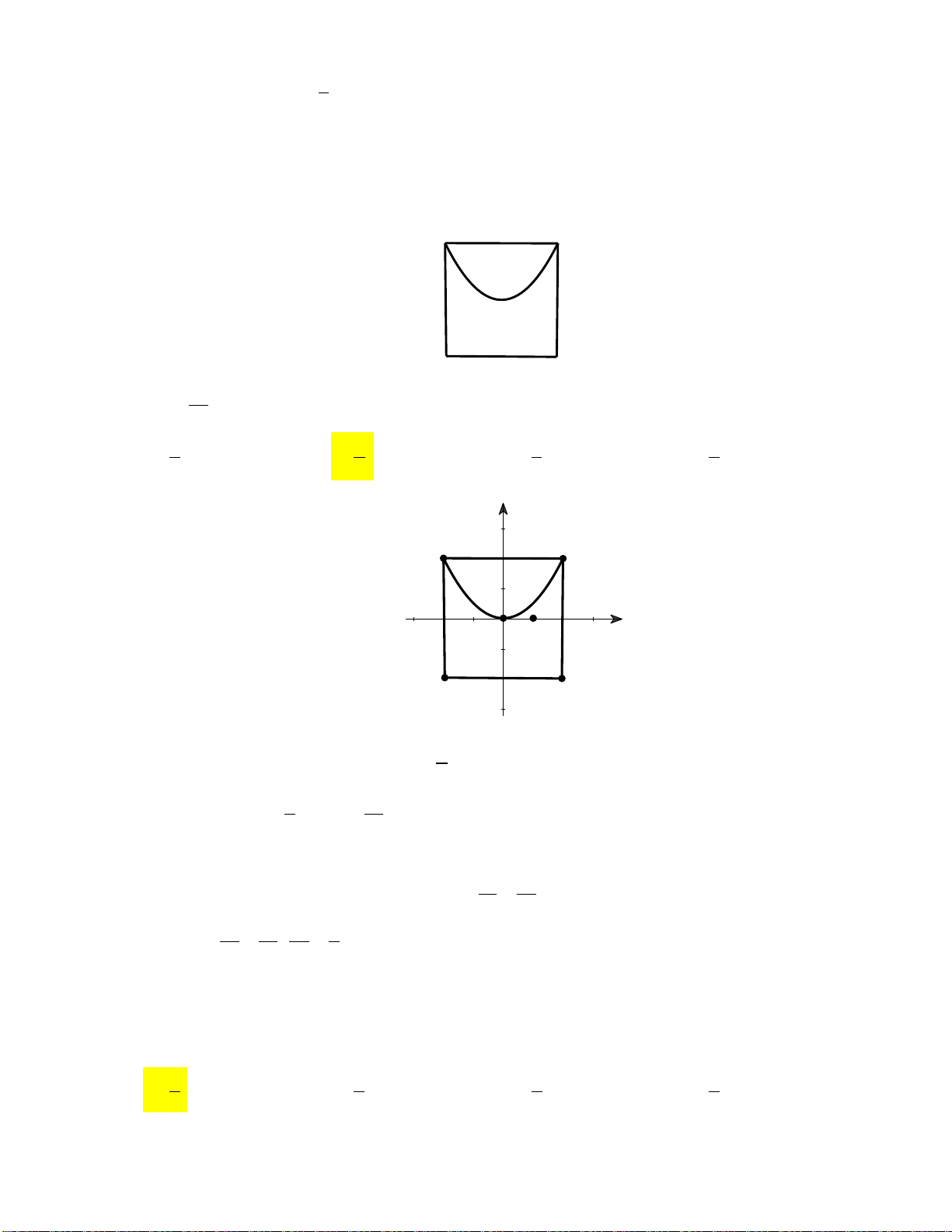
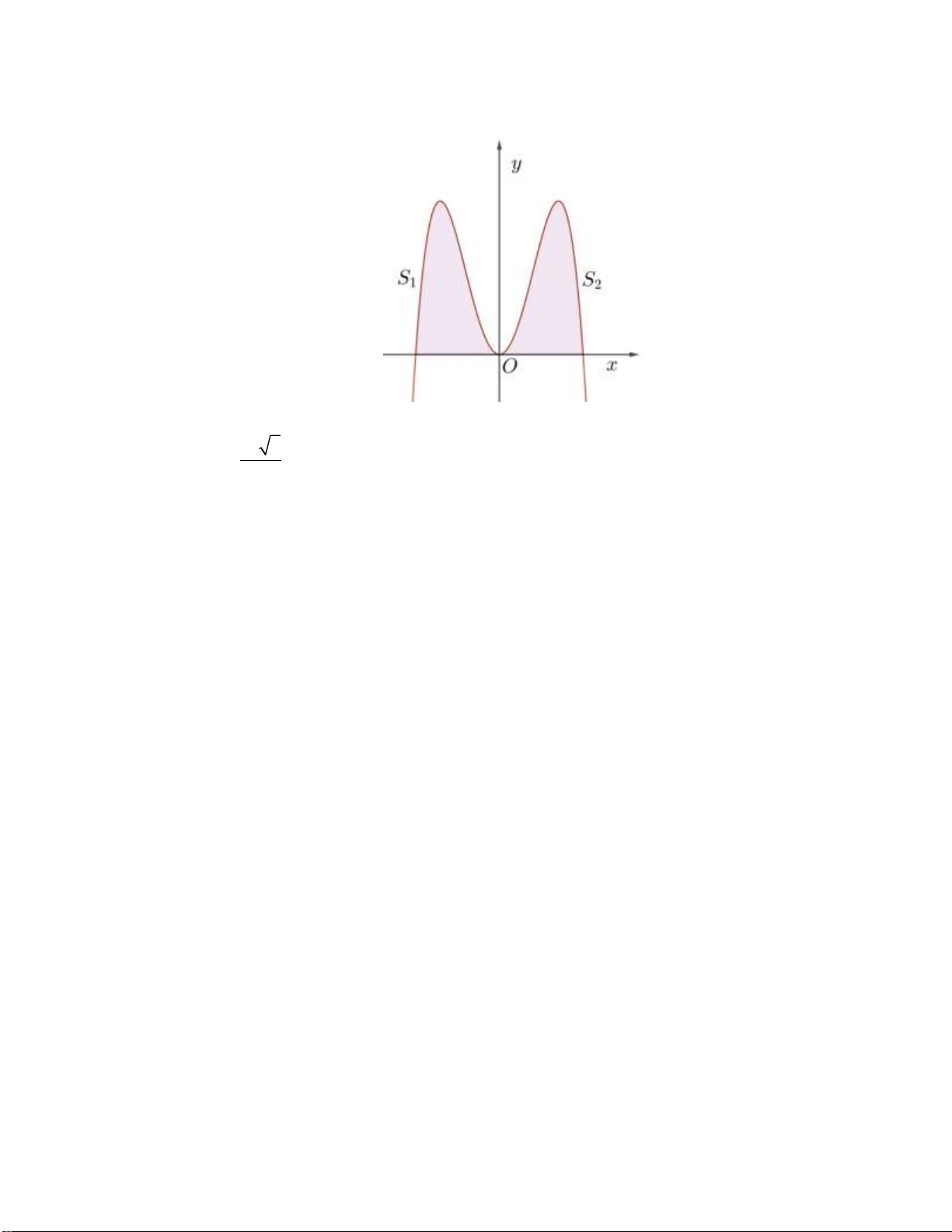
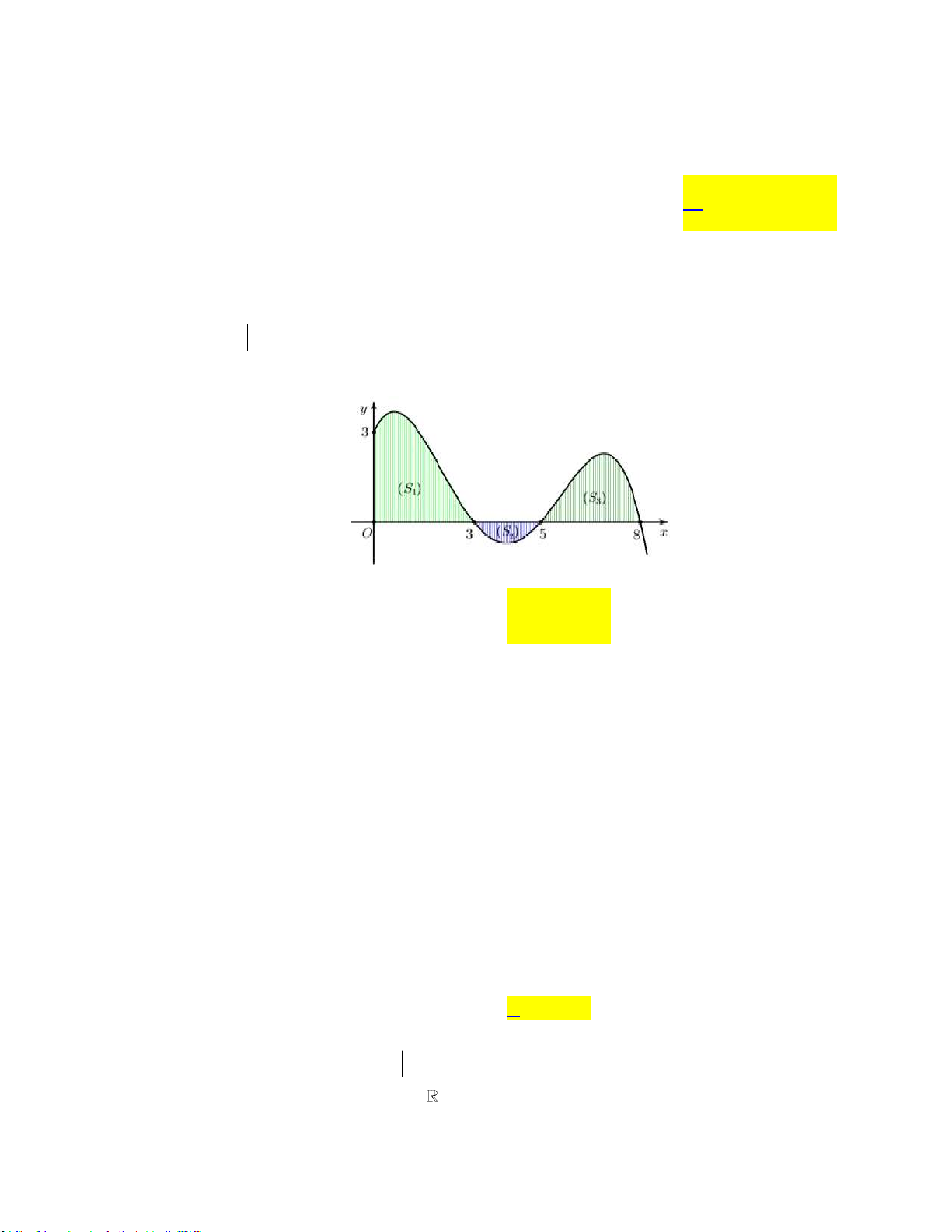
Câu 16: Diện tích hình phẳng giới hạn bởi đường cong y  4  x và trục hoành là A. 4 . B. 0 . C. 16 . D. 8 .
Câu 17: Tính diện tích S của hình phẳng  H  giới hạn bởi đồ thị hàm số y  x , trục hoành và
đường thẳng y  x  2 . 10 16 22 A. S  2 . B. S  . C. S  . D. S  . 3 3 3
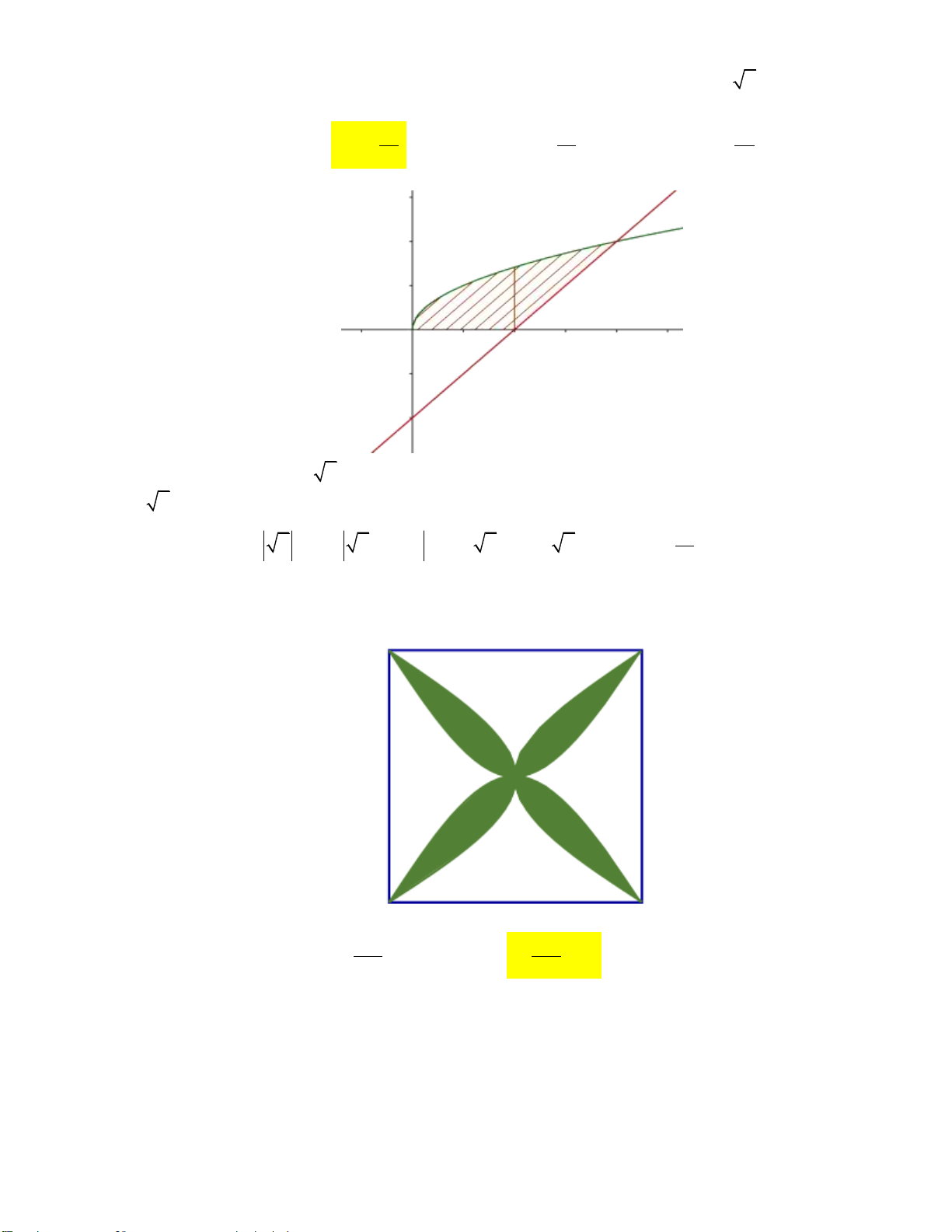
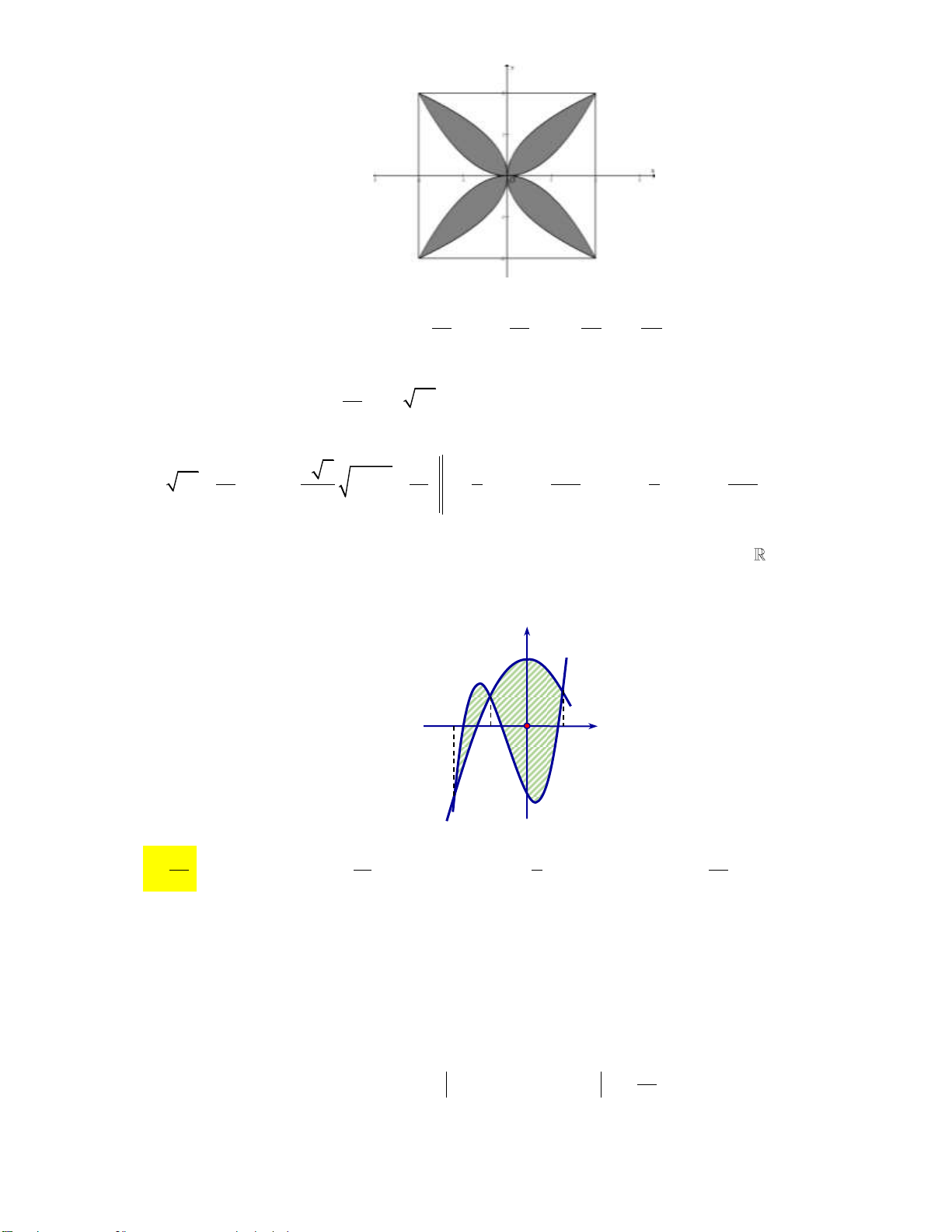
Câu 18: Một viên gạch hoa hình vuông cạnh 40cm . Người thiết kế đã sử dụng bốn đường parabol có
chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ).
Diện tích mỗi cánh hoa của viên gạch bằng 800 400 A. 2 800 cm . B. 2 cm . C. 2 cm . D. 2 250 cm . 3 3
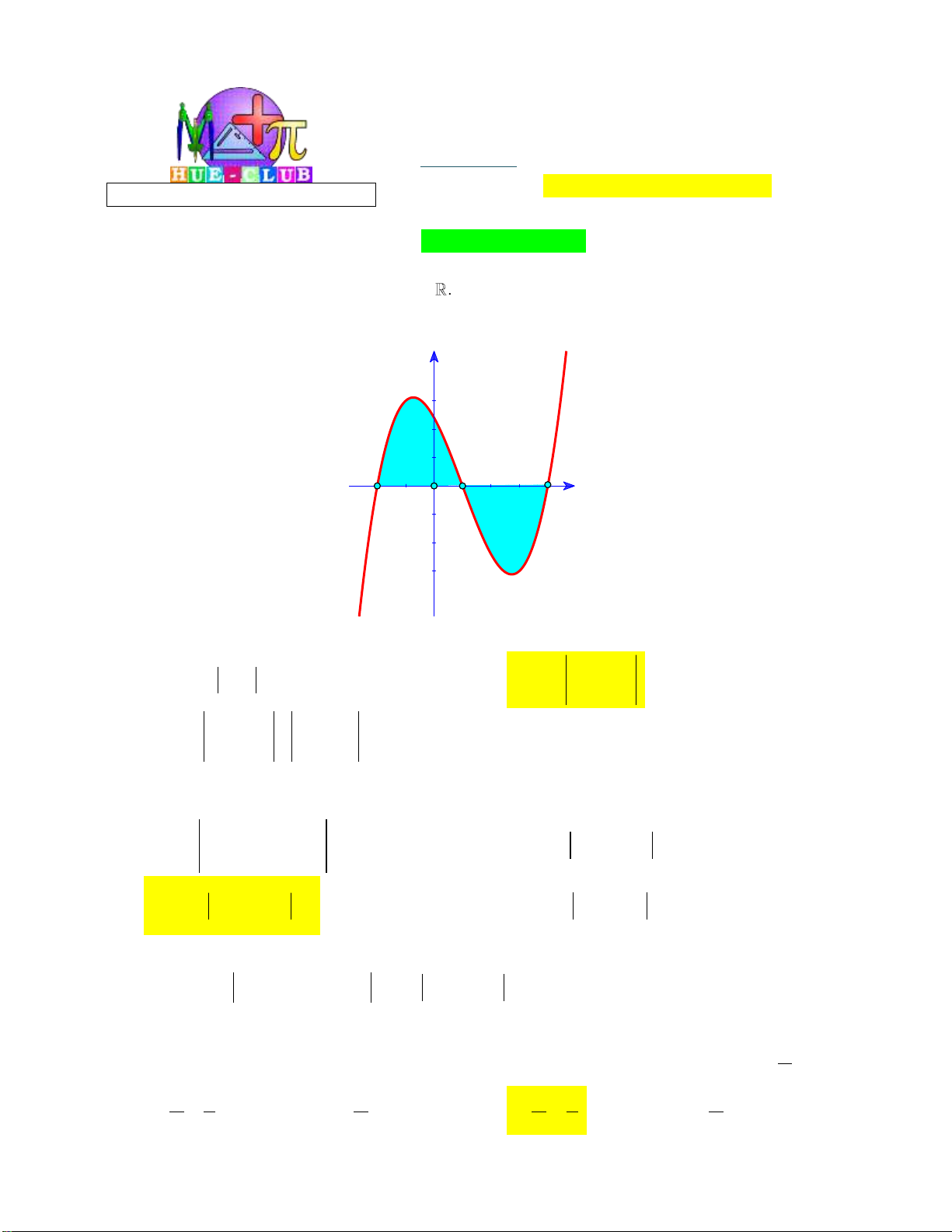
Câu 19: Cho hai hàm số f x  3 x a  2
bx  cx  2 và g x 2  dx  x
e  2 ( a , b , c , d , e  ). Biết rằng đồ
thị của hàm số y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần lượt là 2  ; 1  ; 1 (tham khảo hình vẽ). y 2 1  O 1 x
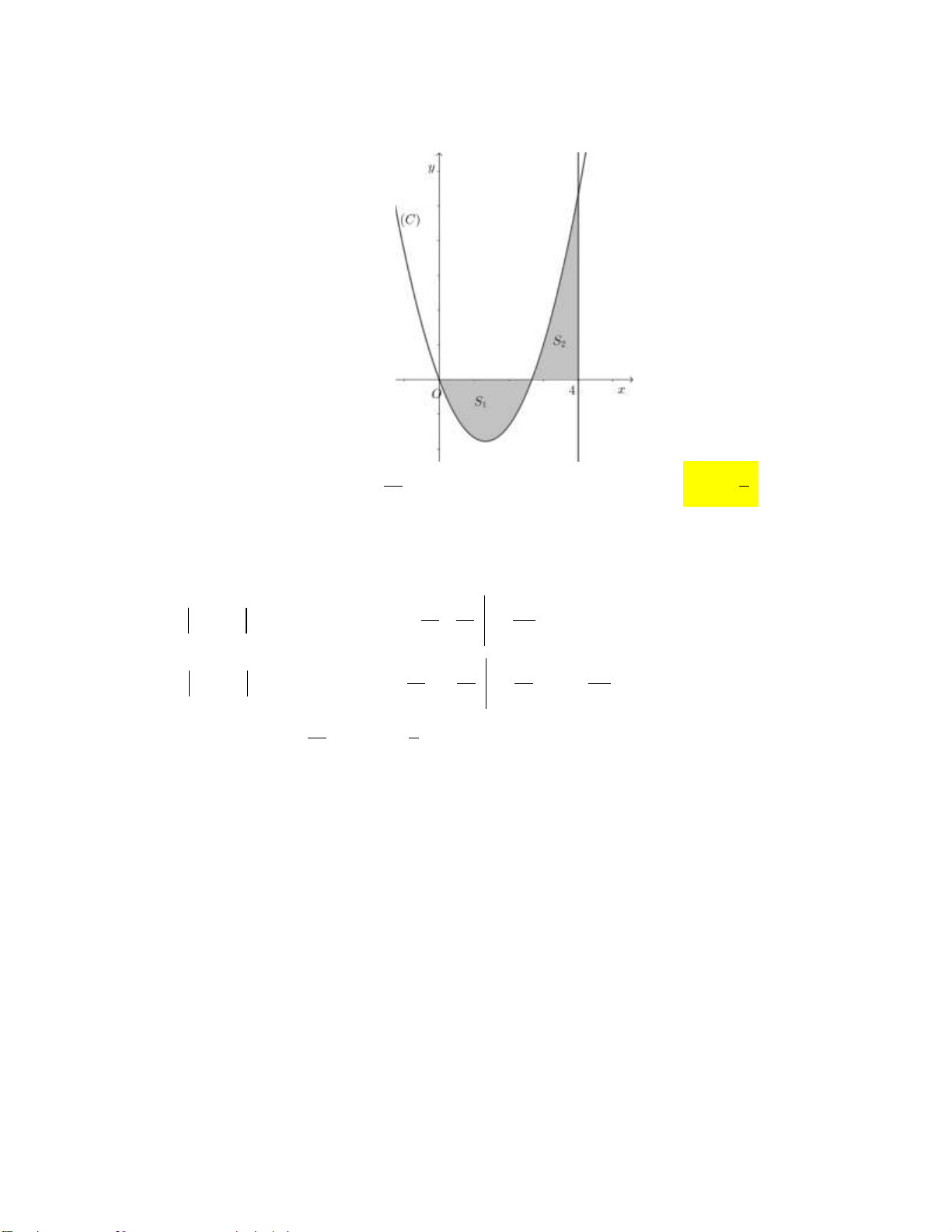
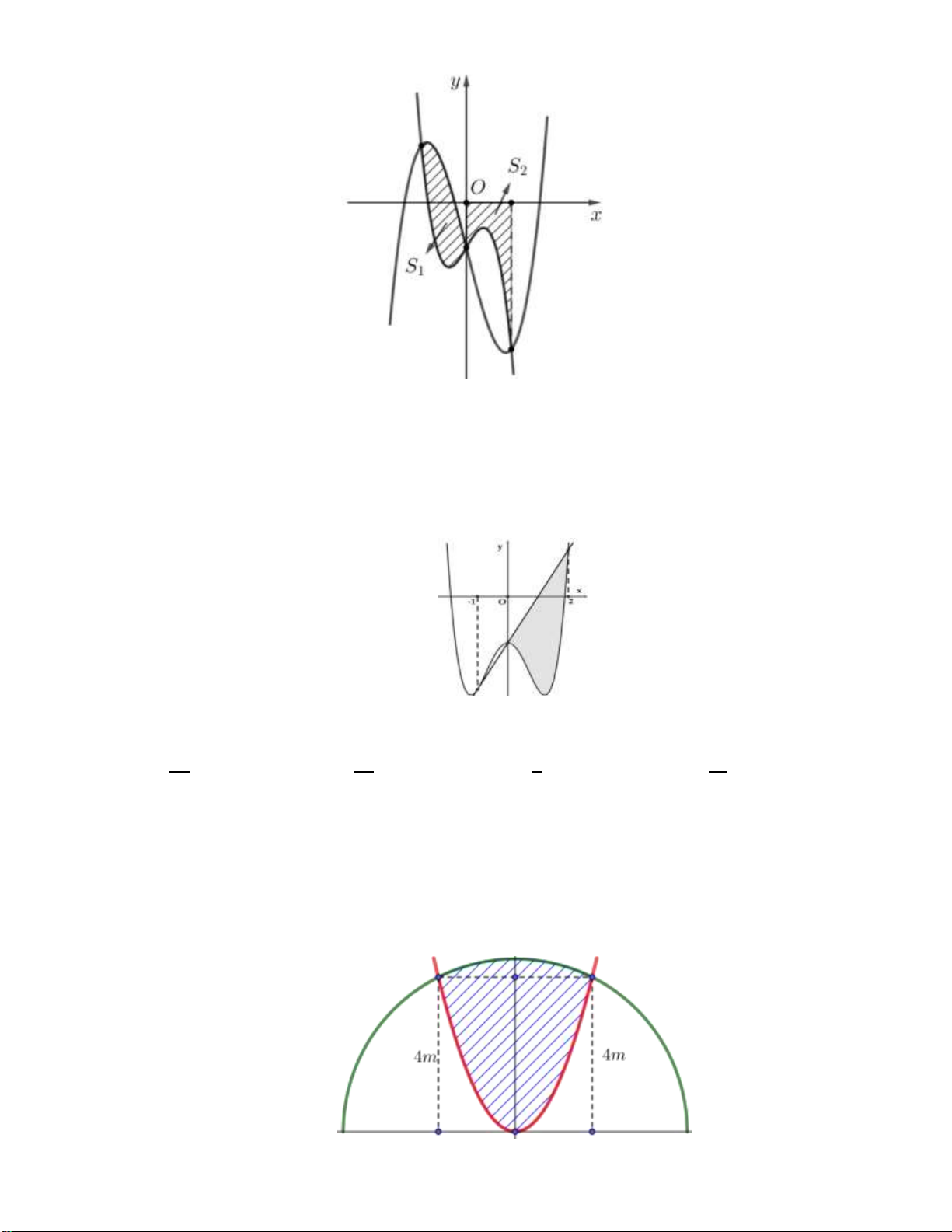
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 13 9 37 A. . B. . C. . D. . 6 2 2 12 Câu 20: Cho hàm số 2
y  x  mx 0  m  4 có đồ thị C . Gọi S  S là diện tích của hình phẳng giới 1 2
hạn bởi C , trục hoành, trục tung và đường thẳng x  4 (phần tô đậm trong hình vẽ bên
dưới). Giá trị của m sao cho S  S là 1 2 10 8 A. m  3. B. m  . C. m  2. D. m  . 3 3
____________________________HẾT____________________________
Huế, 11h00’ Ngày 09 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 1_TrNg 2022
LỜI GIẢI CHI TIẾT
Câu 1: Cho hàm số y  f x liên tục trên đoạn a;b 
 . Gọi D là diện tích hình phẳng giới hạn bởi đồ
thị C : y  f x , trục hoành, hai đường thẳng x  a , x  b (như hình vẽ dưới đây).
Giả sử S là diện tích hình phẳng D . Mệnh đề nào dưới đây đúng? D 0 b 0 b
A. S  f x x  f x x   .
B. S   f x x  f x x   . D  d  d D  d  d a 0 a 0 0 b 0 b
C. S  f x x  f x x   .
D. S   f x x  f x x   . D  d  d D  d  d a 0 a 0 Lời giải:
+ Nhìn đồ thị ta thấy:
 Đồ thị (C) cắt trục hoành tại O0;0
 Trên đoạn a;0 
 , đồ thị (C) ở dưới trục hoành nên f x   f x
 Trên đoạn 0;b 
 , đồ thị C ở trên trục hoành nên f x  f x b 0 b 0 b + Do đó: S  f x x   f
 x dx  f
 x dx   f
 xdx  f  xdx D   d a a 0 a 0
 Chọn đáp án B.
Câu 2: Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y 
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e x S d . x  B.  ex S d . x  C.   ex S d . x  D. 2  e x S d . x  0 0 0 0 Lời giải: 2
Diện tích hình phẳng giới hạn bởi các đường ex y 
, y  0 , x  0 , x  2 là x
S  e dx  . 0
 Chọn đáp án B.
Câu 3: Gọi S là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số 2
y  x  3 và y  4x . Khẳng
định nào dưới đây đúng? 3 3 A. 2 S  x  4x  3 d  x . B. S   2
x  4x  3dx . 1 1 3 3 C. S   2
x  3  4x dx . D. 2 S  x  4x  3 d  x . 1 1 Lời giải:
Ta có phương trình hoành độ giao điểm của các đồ thị hàm số 2
y  x  3 và y  4x là:  x 1 2 x  3  4x 2
 x  4x  3  0   . x  3 3
Diện tích của hình phẳng cần tìm là: 2 S  x  4x  3 d  x . 1
 Chọn đáp án A.
Câu 4: Cho hàm số y  f x xác định, liên tục và có nguyên hàm trên 2; 4 
 đồng thời có đồ thị như hình vẽ dưới đây. 4 Tính I  f  xdx 2  A. I  8 . B. I  4 . C. I  6 . D. I  2 . Lời giải: 4
Ta có giá trị của tích phân I  f
 xdx là hiệu của diện tích hình thang với diện tích tam 2  giác.
Từ hình vẽ ta có hình thang cân, độ dài đáy lớn bằng 4 , độ dài đáy bé bằng 2 , chiều cao
bằng 2 . Diện tích hình thang là 6
Tam giác cân có cạnh đáy bằng 2 , chiều cao bằng 2 . Diện tích của tam giác là 2 Vậy I 
f xdx  6  2  4 4. 2
 Chọn đáp án B.
Câu 5: Diện tích hình phẳng giới hạn bởi hai đồ thị f  x 3
 x  3x  2 ; g x  x  2 là A. S  8 . B. S  4 . C. S  12 . D. S  16 . Lời giải: x  0
Phương trình hoành độ giao điểm của hai đồ thị 3 3
x  3x  2  x  2  x  4x  0   x  2  Diện tích cần tìm 0 2 0 2 4 4  x  0  x  2 3 3 S 
x  4x dx 
x  4x dx  
   3x 4xdx   3x 4xdx 2 2    2x 
   2x   8. 4 2     4 0  2  0 2  0
 Chọn đáp án A.
Câu 6: Diện tích S của hình phẳng giới hạn bởi các đường 3
y  2x , y  π , x  4 và trục tung được
tính bởi công thức nào dưới đây ? 4 4 A. S   3
2x  πdx . B. 3 S  π 2x dx  . 0 π 4 4 C. S   3
2x  πdx . D. 3 S  2x dx  . 0 π Lời giải: 4 4
Diện tích S của hình phẳng được tính bởi công thức: 3 S  2x  π dx    3
2x  πdx . 0 0
 Chọn đáp án C.
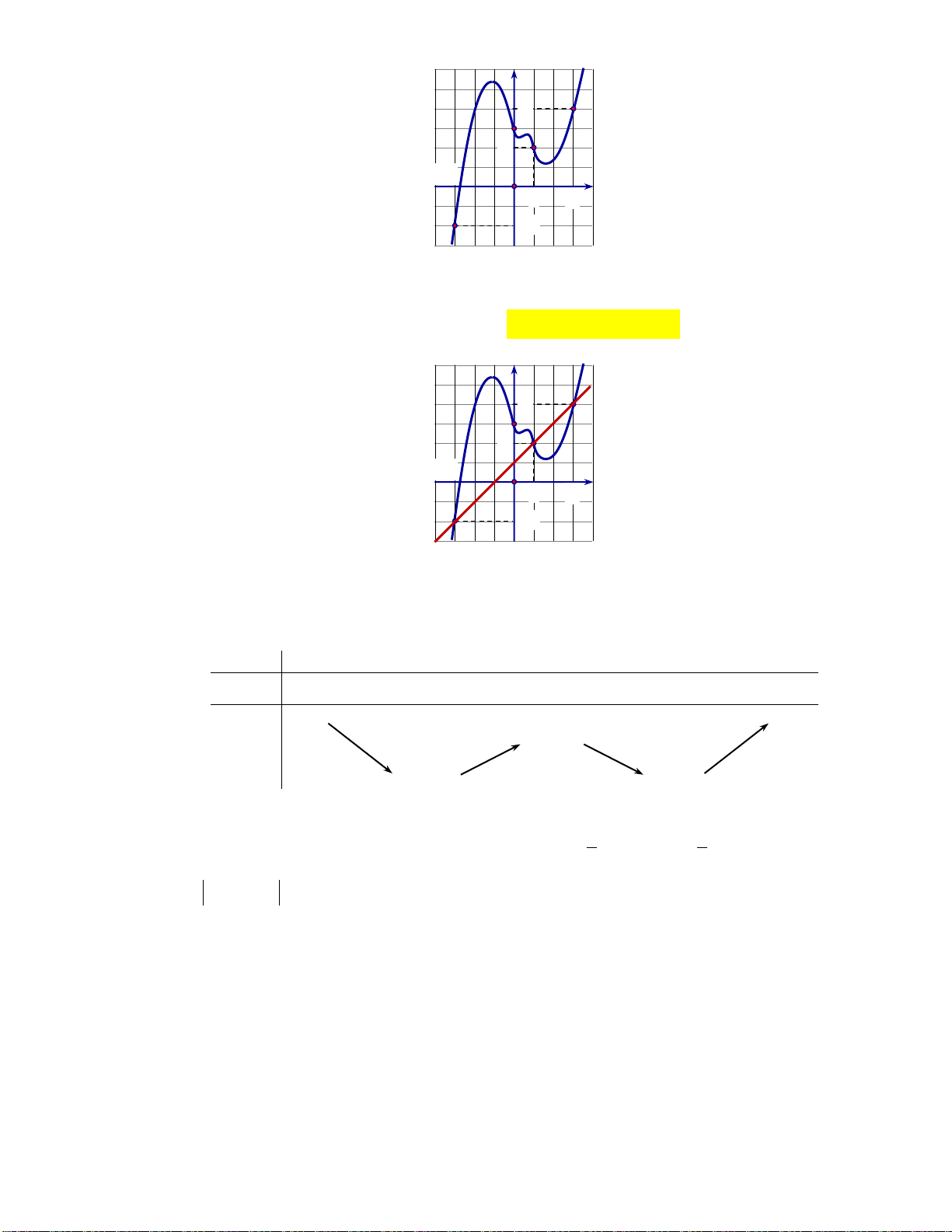
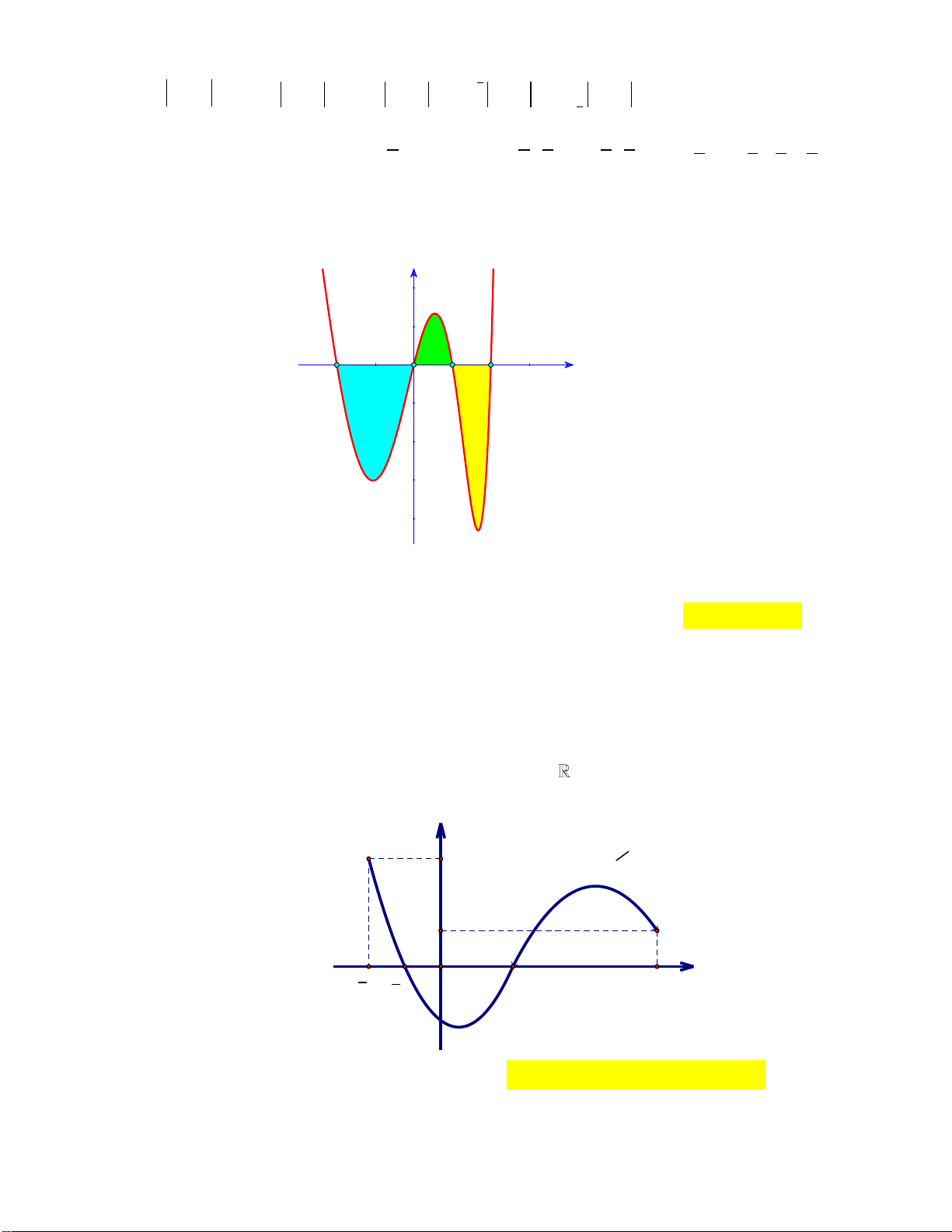
Câu 7: Cho hàm số y  f x. Đồ thị hàm số y  f x như hình bên. Đặt
gx  f x 2 2
 x . Khẳng định nào sau đây đúng?
A. g3  g 3
   g1. B. g 
1  g3  g 3  . C. g  1  g 3
   g3. D. g 3
   g3  g 1  . Lời giải:
Ta có gx  2 f x  2x  gx  0  x  3  ;1;  3 .
Từ đồ thị của y  f x ta có bảng biến thiên.(Chú ý là hàm
g x và gx ) 1 3
Suy ra g3  g 
1 . Kết hợp với đồ thị ta có:  gxdx  g  xdx 3  1 3   g  x 3 dx  g
 xdx  g 3    g 
1  g3  g  1  g 3    g3 . 1 1 Vậy ta có g 3
   g3  g1 .
 Chọn đáp án B.
Câu 8: Tính diện tích S của hình phẳng giới hạn bởi  P 2
: y  x  4 , tiếp tuyến của  P tại M 2;0 và trục Oy là 4 8 7 A. S  . B. S  2 . C. S  . D. S  . 3 3 3 Lời giải:
Ta có: y  2x ; y2  4 .
Phương trình tiếp tuyến của  P tại M 2;0 : y  4 x  2  4x  8 . 2 2
Diện tích hình phẳng cần tìm là 2 S  x  4  
4x 8 dx    2x 4x4dx 0 0 x  2 2 3  8  . 3 3 0
 Chọn đáp án C.
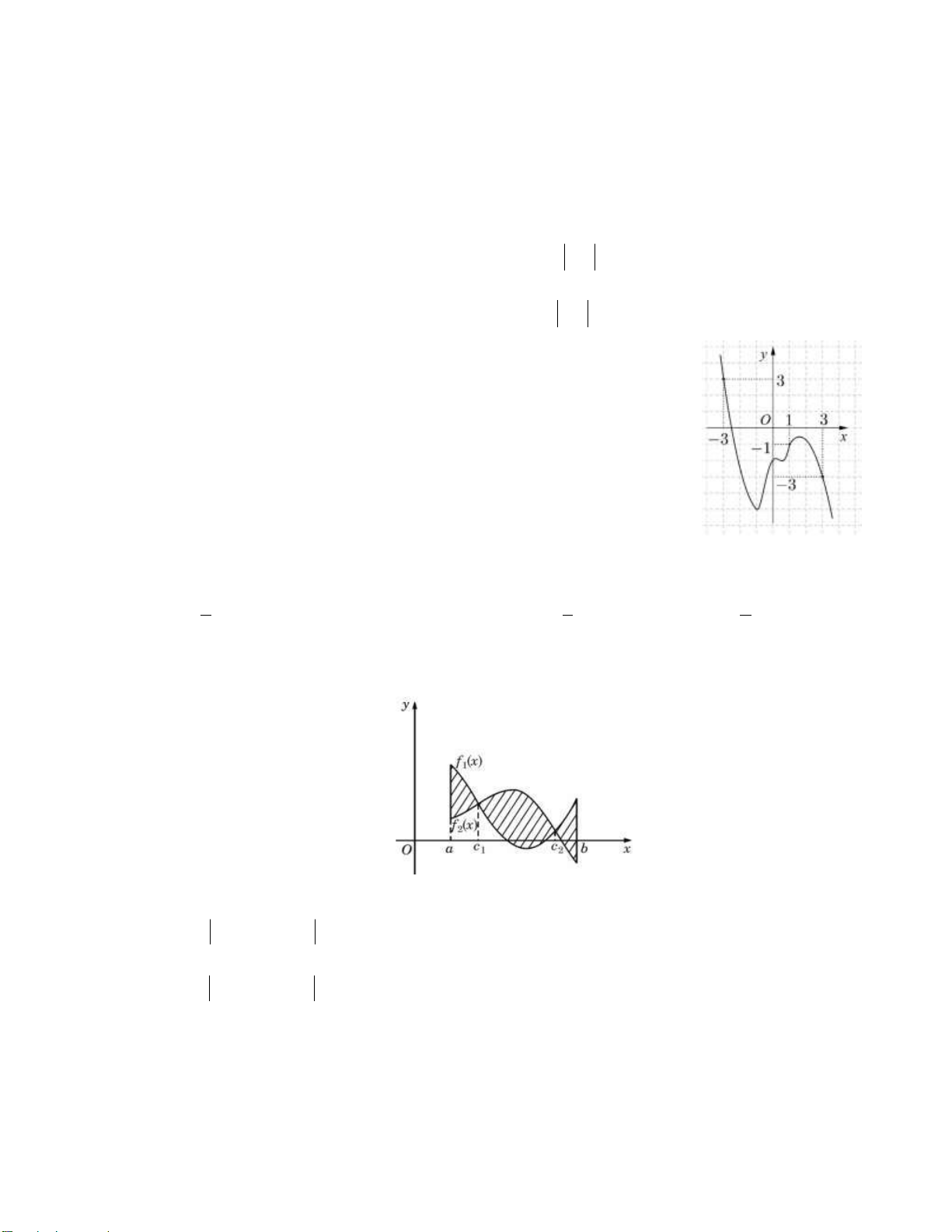
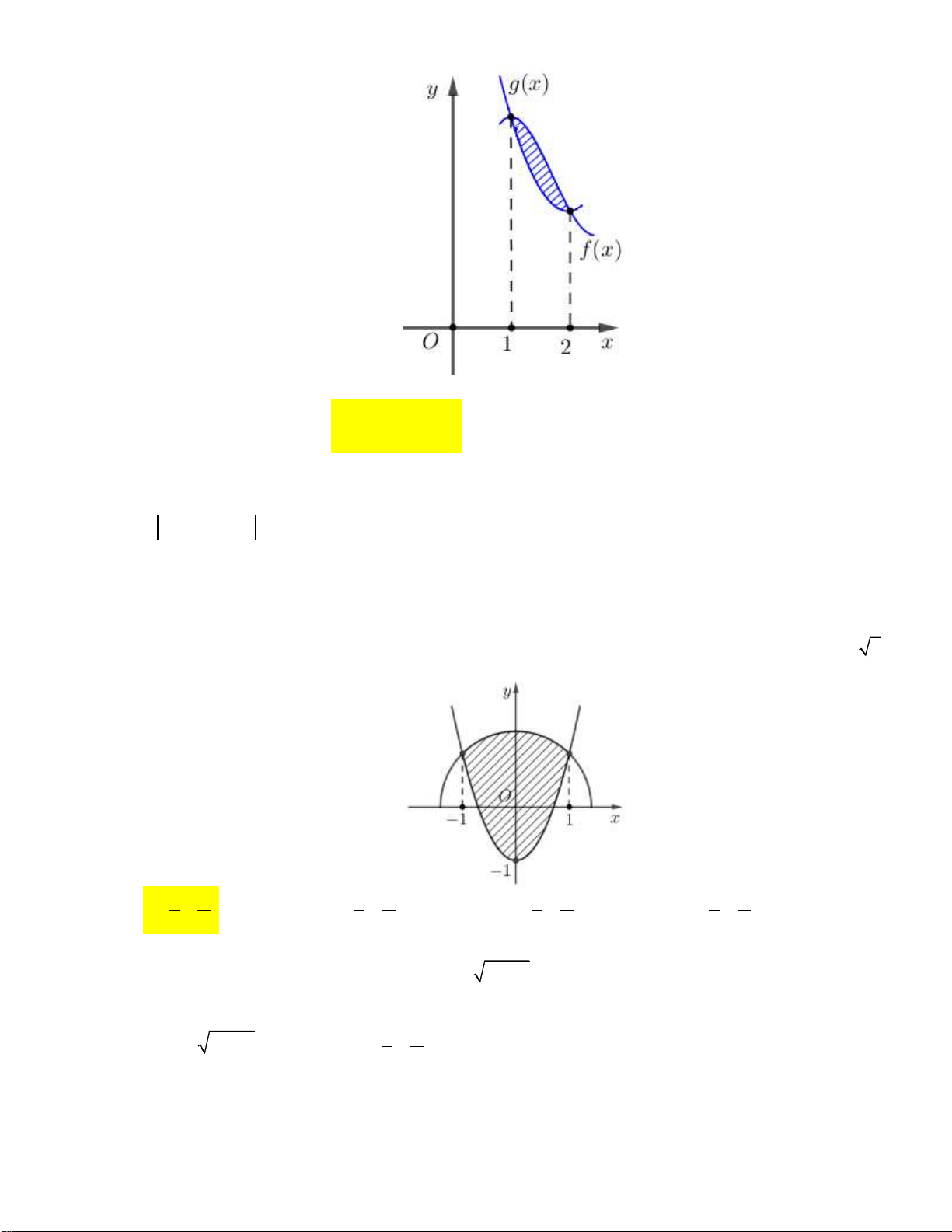
Câu 9: Cho hình phẳng  H  giới hạn bởi đồ thị của hai hàm số f x và f x liên tục trên đoạn 2   1  
a; b và hai đường thẳng x  a, x  b (tham khảo hình vẽ dưới).
Công thức tính diện tích của hình  H  là b b A. S  f x  f x d . x 
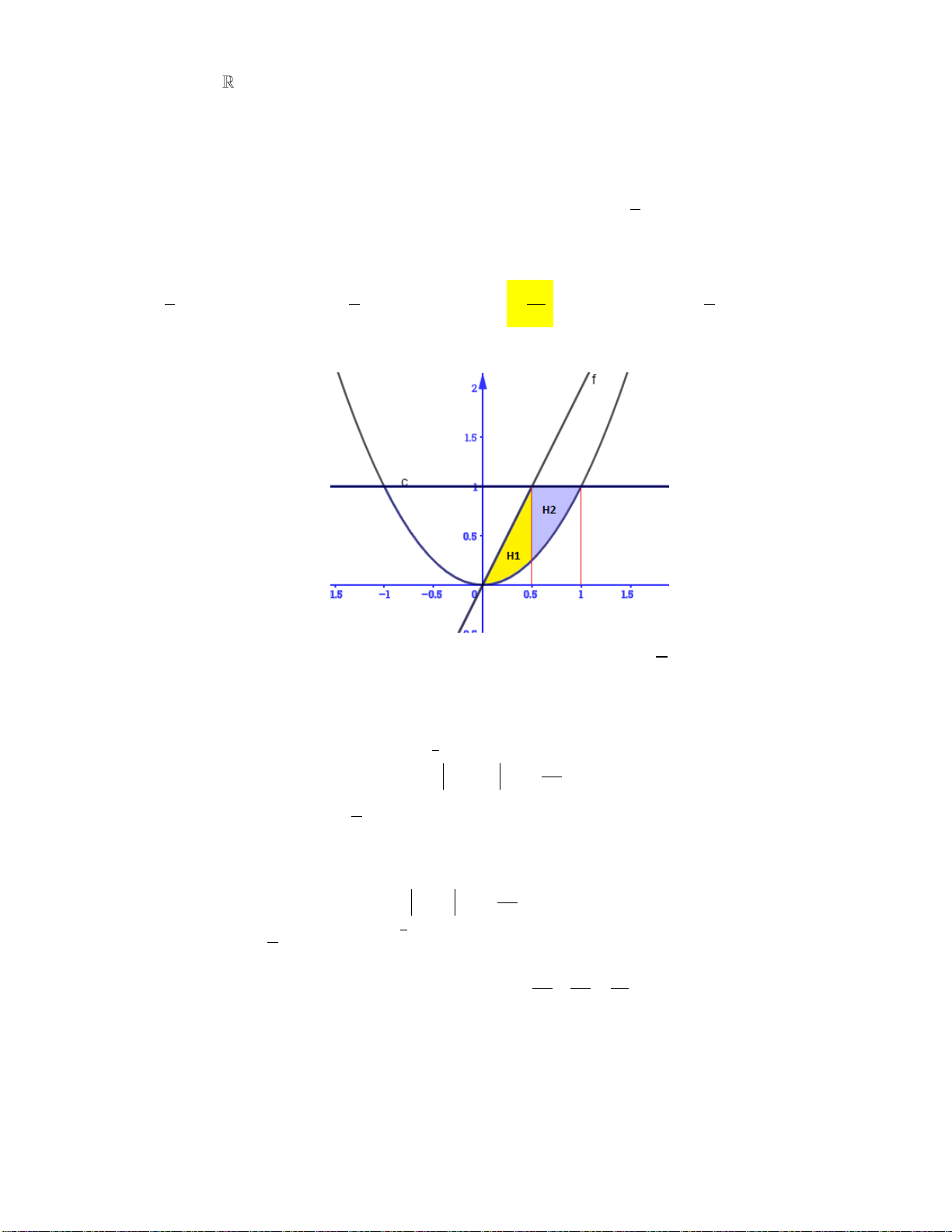
B. S   f x  f x d .x 1   2   1   2   a a b b b C. S  f x  f x d . x  D. S  f x dx  f x d . x   2   1   1   2   a a a Câu 10: Cho hàm số x
y  e , gọi S là diện tích hình phẳng giới hạn bởi các đường x
y  e ; x  1  ; x  k 1
và S là diện tích hình phẳng giới hạn bởi các đường x
y  e ; x  k; x  1. (tham khảo hình vẽ). 2 y x y  e 2 1 2  1  O 1 2 x
Xác định k để S  S . 1 2  1   1 
A. k  ln e   ln 2  
. B. k  2 ln e  1  
. C. k  2 ln 2 1. D. k  ln 2 .  e   e  Lời giải: k 1   x x k 1 k 1
Ta có S  S  e dx  e dx  e   e  e  k  ln e   ln 2   . 1 2   e  e  1  k
 Chọn đáp án A.
Câu 11: Trong mặt phẳng cho đường tròn C (tham khảo hình vẽ dưới đây). y 2 1 O 2 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 2,01. B. 2,46. C. 1,81. D. 3,13. Lời giải: y 2 1 O 3 2 x  2 y  4  x
Phương trình đường tròn là 2 2
x  y  4   . 2 y   4   x 2 2
x  y  4 x  3 Xét hệ phương trình: 2   x  3   . y  1 x   3 3
Diện tích cần tính là S  2   2
4  x  1dx  2,46. 0
Chọn đáp án B.
Câu 12: Cho hai hàm số y  f  x và y  g  x liên tục trên đoạn a;b với a  b . Kí hiệu S là diện 1
tích hình phẳng giới hạn bởi các đường y  3 f  x , y  3g  x , x  a , x  b ; S là diện tích 2
hình phẳng giới hạn bởi các đường y  f  x  2 , y  g  x  2 , x  a , x  b . Khẳng định nào sau đây đúng? A. S  2S . B. S  3S .
C. S  2S  2.
D. S  2S  2. 1 2 1 2 1 2 1 2 Lời giải: b b b
Ta có S  3 f x  3g x dx   3 f
 x gx dx  3 
  f x2gx2 dx  3S . 1      2 a a a
 Chọn đáp án B.
Câu 13: Cho hàm số bậc ba 3 2
f (x)  ax  bx  cx  d và đường thẳng d : g(x)  mx  n có đồ thị như hình vẽ bên dưới: 1
Nếu diện tích phần tô bằng bằng
thì diện tích phần gạch bằng 2 5 3 A. . B. 2 . C. 1. D. . 2 2 Lời giải: Cách 1:
Dựa vào đồ thị đường thẳng d : g(x)  x 1.
Phương trình hoành độ giao điểm của của hai đồ thị hàm số f  x, g  x là 3 2 3 2
ax  bx  cx  d  x 1  ax  bx  c  
1 x  d 1  0   1
Dựa vào đồ thị ta thấy đồ thị hàm số f  x, g  x cắt nhau tại ba điểm x  0, x  1, x  2 .
   axx  x     a 3 2 1 1 2 0
x  3x  2x  0 . 1 1 1
Diện tích phần tô màu: a   3 2
x  3x  2x dx  a   a  2 . 4 2 0
Diện tích phần không tô màu giới hạn bởi đồ thị hàm số f  x, g  x và hai đường thẳng 2 1
x  1, x  2 là S  2   3 2
x  3x  2x dx   . 1  2 1 5
Diện tích hình phẳng giới hạn bởi đồ thị hàm số g  x  x 1, Ox, x  1, x  2 là S  . 2 2 5 1
Diện tích phần gạch chéo là S  S  S    2 . 2 1 2 2 Cách 2:
Diện tích phần không tô màu giới hạn bởi đồ thị hàm số f  x, g  x và hai đường thẳng
x  1, x  2 là S . 1 1 1
Diện tích phần tô màu là S 
. Dựa vào đồ thị ta thấy S  S  . 2 2 1 2 2
Dựa vào đồ thị đường thẳng d : g(x)  x 1 5
Diện tích hình phẳng giới hạn bởi đồ thị hàm số g  x  x 1, Ox, x  1, x  2 là S  . 3 2 5 1
Diện tích phần gạch chéo là S  S  S    2 . 3 1 2 2
 Chọn đáp án B.
Câu 14: Cho hàm số y  f  x liên tục trên
và thỏa mãn f  
1  0  f 0 . Gọi S là diện tích hình
phẳng giới hạn bởi các đường y  f  x , y  0 , x  1 và x  1 . Mệnh đề nào sau đây đúng? 1 0 1 A. S  f  xdx B. S  f
 xdx f  x dx 1  1  0 1 1 C. S  f  xdx D. S  f  x dx 1 1  Lời giải:
Từ giả thiết ta có diện tích hình phẳng cần tìm được giới hạn bởi đồ thị hàm số y  f  x liên 1 tục trên
, y  0 , x  1 và x  1 , nên: S  f  x dx. 1 
 Chọn đáp án D.
Câu 15: Một sân bóng hình chữ nhật với diện tích 2
200m . Người ta muốn trồng cỏ trên sân bóng theo
hình một parabol bậc hai sao cho đỉnh của parabol trùng với trung điểm một cạnh của sân
bóng như hình vẽ bên. Biết chi phí trồng cỏ là 300 ngàn đồng cho mỗi mét vuông. Xác định
chi phí trồng cỏ cần có cho sân bóng trên? A. 30 triệu đồng. B. 60 triệu đồng. C. 50 triệu đồng. D. 40 triệu đồng. Lời giải:
Gọi chiều dài của hình chữ nhật là m , chiều rộng là n ( m  n  0 ).
Ta có diện tích hình chữ nhật là S  mn  200 ( 2 m ) .
Chọn hệ trục tọa độ Đề các vuông góc Oxy sao cho đỉnh của parabol là I(0; ). n Parabol đi qua  m   m  2 điểm A
; 0  và B ;0 .  2   2  4  n Do đó parabol có dạng 2 y  x  . n 2 m m 2  4n  mn
Vậy phần diện tích trồng cỏ là 2 S  2 x   2  n d  x  . 2  m  3 0 2mn 2.200
Vậy số tiền trồng cỏ cần là: .300000  .300000  40000000. 3 3
 Chọn đáp án D.
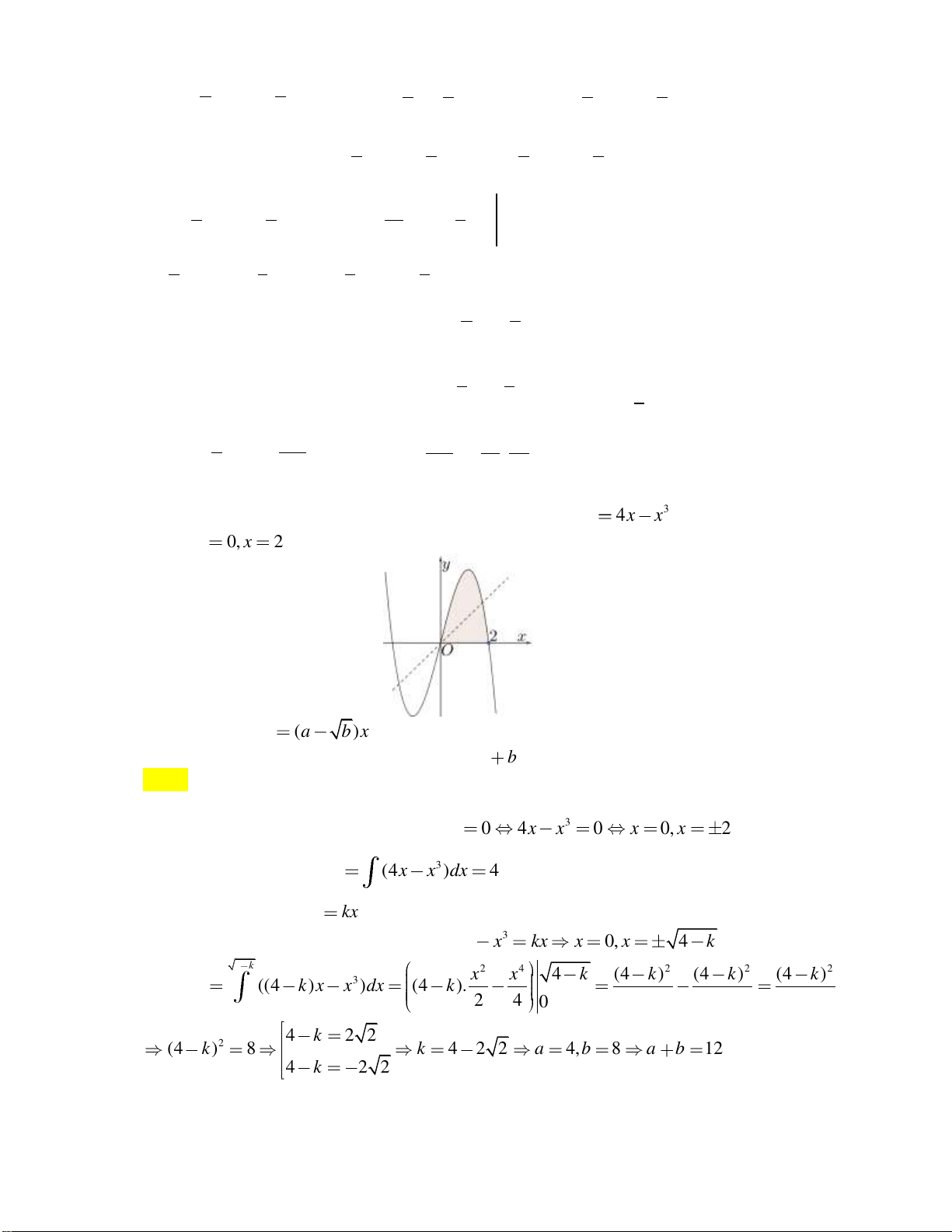
Câu 16: Diện tích hình phẳng giới hạn bởi đường cong y  4  x và trục hoành là A. 4 . B. 0 . C. 16 . D. 8 . Lời giải: x  4
Phương trình hoành độ giao điểm: 4  x  0   . x  4  
Diện tích hình phẳng là. 4 0 4 0 4 S  4  x dx  4  x dx  4  x dx    
 4 xdx   4 xdx 16 . 4  4  0 4  0
 Chọn đáp án C.
Câu 17: Tính diện tích S của hình phẳng  H  giới hạn bởi đồ thị hàm số y  x , trục hoành và
đường thẳng y  x  2 . 10 16 22 A. S  2 . B. S  . C. S  . D. S  . 3 3 3 Lời giải: .
Hoành độ giao điểm x  x  2  x  4( x  0) .
x  0  x  0 ; x  2  0  x  2 . 2 4 2 4 10 Diện tích S  x d x  
x  x  2dx   xdx  
 x  x2dx   . 3 0 2 0 2
 Chọn đáp án B.
Câu 18: Một viên gạch hoa hình vuông cạnh 40cm . Người thiết kế đã sử dụng bốn đường parabol có
chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ).
Diện tích mỗi cánh hoa của viên gạch bằng 800 400 A. 2 800 cm . B. 2 cm . C. 2 cm . D. 2 250 cm . 3 3 Lời giải:
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng 10cm  1dm ), các cánh hoa tạo bởi các 2 x 2 x 2 y 2 y
đường parabol có phương trình y  , y   , x   , x  . 2 2 2 2
Diện tích một cánh hoa (nằm trong góc phàn tư thứ nhất) bằng diện tích hình phẳng giới hạn 2 x
bởi hai đồ thị hàm số y 
, y  2x và hai đường thẳng x  0; x  2 . 2
Do đó diện tích một cánh hoa bằng 2 2 2  x  3    2 2 x 4 400 4 400  3 2x  dx  
2x     2 dm    2 cm    2 dm    2 cm  .    2  3 6 3 3 3 3 0   0
 Chọn đáp án C.
Câu 19: Cho hai hàm số f x  3 x a  2
bx  cx  2 và g x 2  dx  x
e  2 ( a , b , c , d , e  ). Biết rằng đồ
thị của hàm số y  f x và y  gx cắt nhau tại ba điểm có hoành độ lần lượt là 2  ; 1  ; 1 (tham khảo hình vẽ). y 2 1  O 1 x
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 13 9 37 A. . B. . C. . D. . 6 2 2 12 Lời giải:
Phương trình hoành độ giao điểm của đồ thị f x và gx là 3 2 2 3
ax  bx  cx   dx  x   a  b  d 2 2 3 2
x  c  ex  4  0. *
Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình * có ba nghiệm x  2 ;
x  1; x  1 . Ta được 3
ax  b  d 2
x  c  e x  4  k x  2x  1x  1 . Khi đó 4  2k  k  2 . 1 37
Vậy diện tích hình phẳng cần tìm là
2x  2x   1 x   1 dx  .  6 2
 Chọn đáp án A. Câu 20: Cho hàm số 2
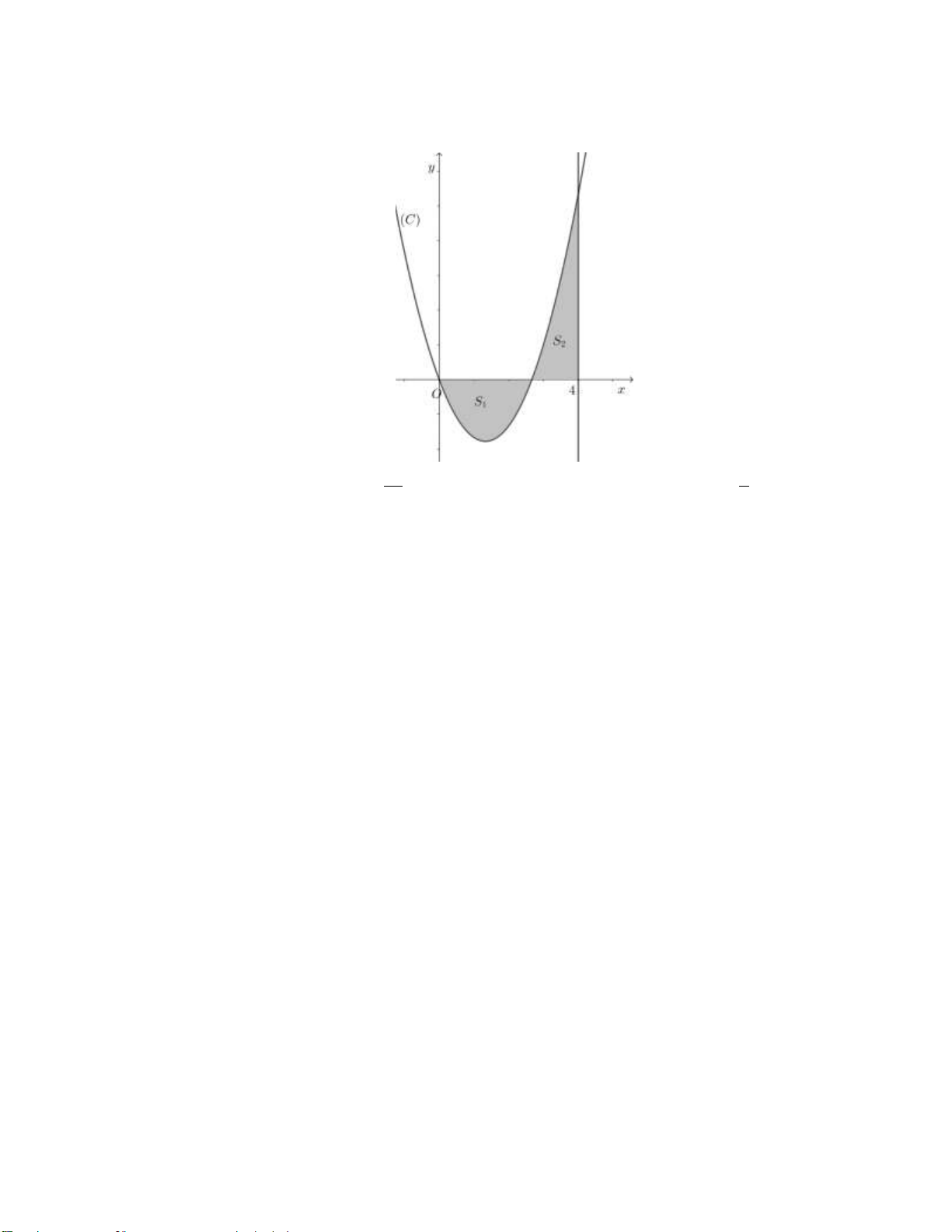
y  x  mx 0  m  4 có đồ thị C . Gọi S  S là diện tích của hình phẳng giới 1 2
hạn bởi C , trục hoành, trục tung và đường thẳng x  4 (phần tô đậm trong hình vẽ bên
dưới). Giá trị của m sao cho S  S là 1 2 10 8 A. m  3. B. m  . C. m  2. D. m  . 3 3 Lời giải: x  0
Phương trình hoành độ giao điểm của C và trục Ox là: 2
x  mx  0   x  m  0  m   4 m m m 2 3 3   2 x x m
S  x  mx dx    2 mx  x x   m    . 1 d  2 3  6 0 0 0 4 4 4 3 2 3   2 x x 64 m
S  x  mx dx  
 2x  mx x    m    8m  . 2 d  3 2  3 6 m m m 64 8
Ta có: S  S  8m   0  m  . 1 2 3 3
 Chọn đáp án D.
____________________________HẾT____________________________
Huế, 11h00’ Ngày 09 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 2_TrNg 2022 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
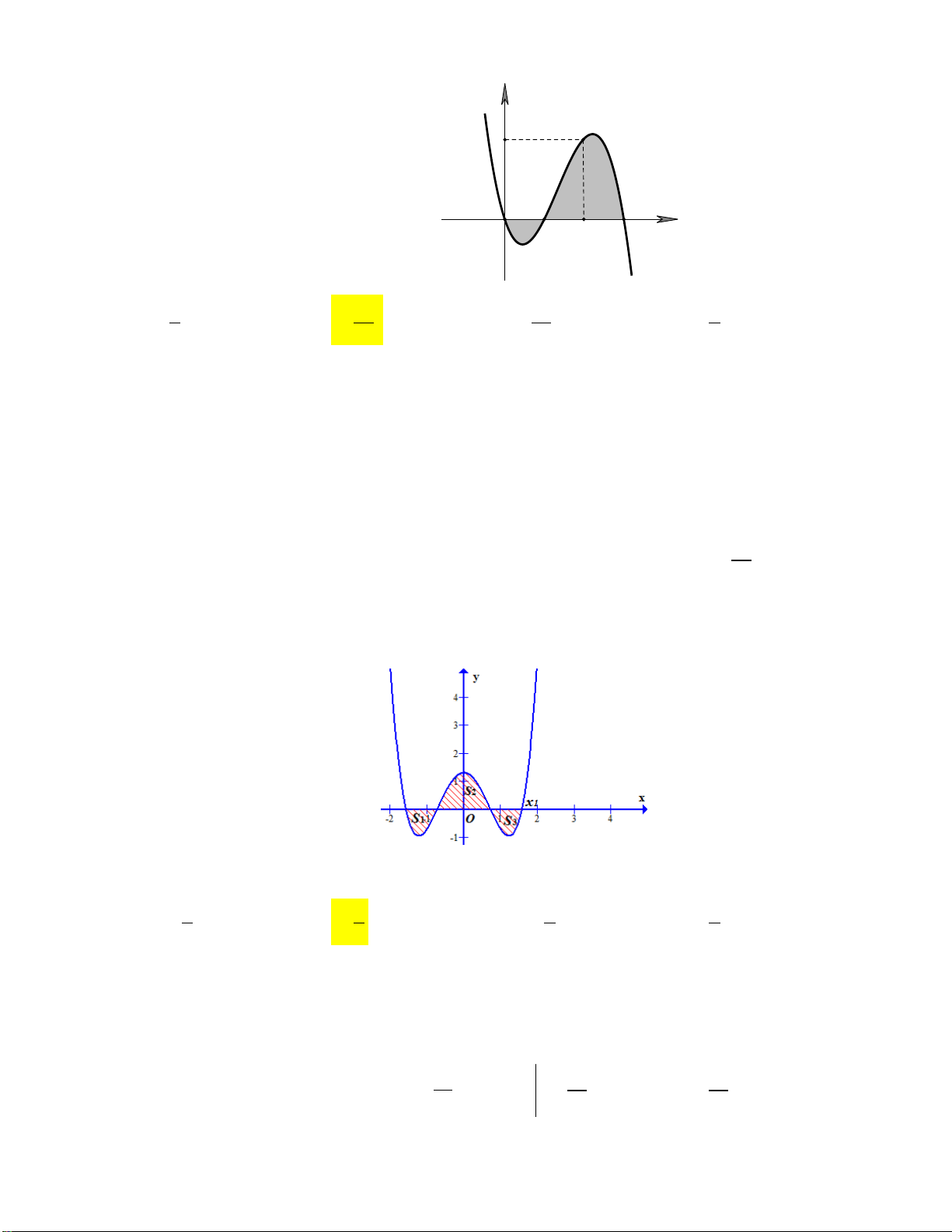
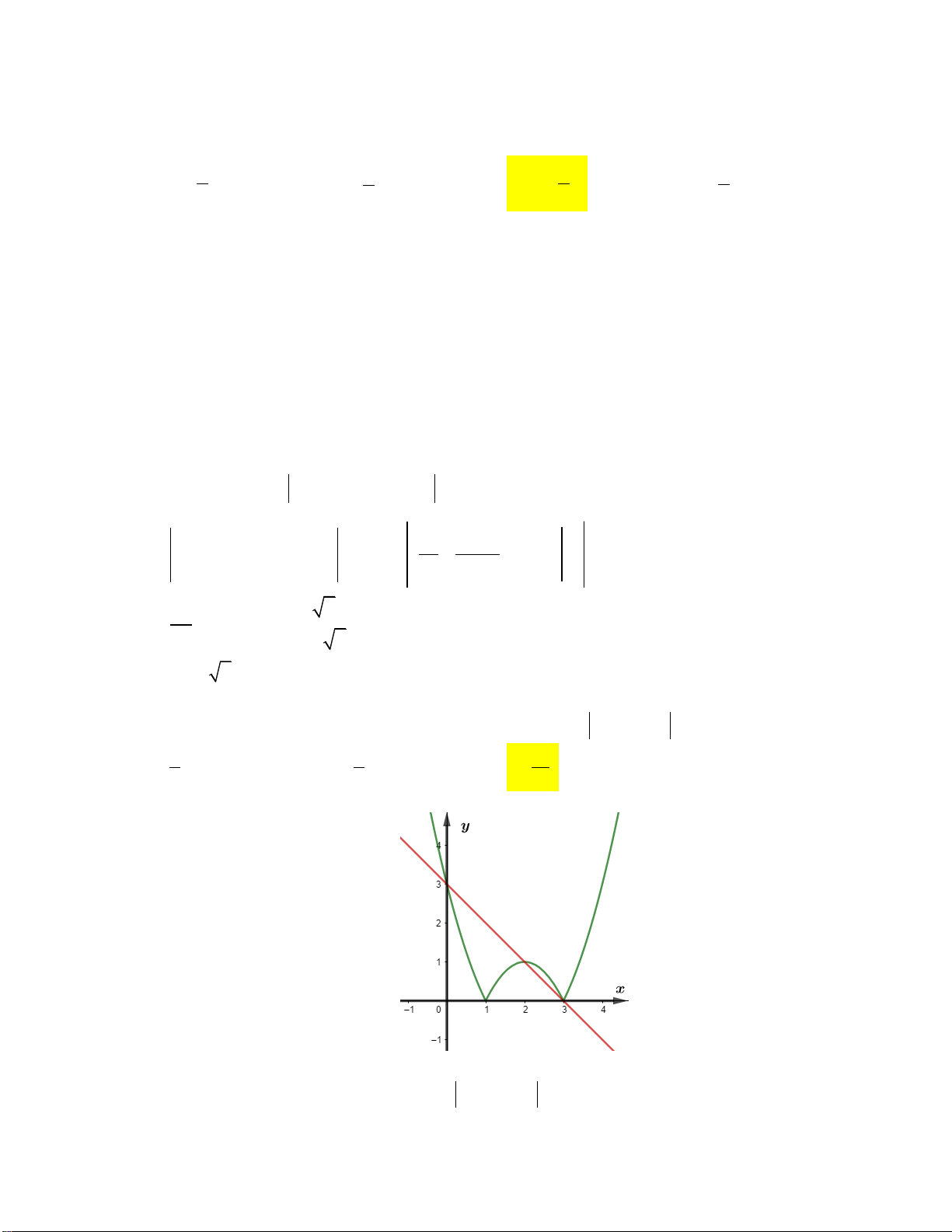
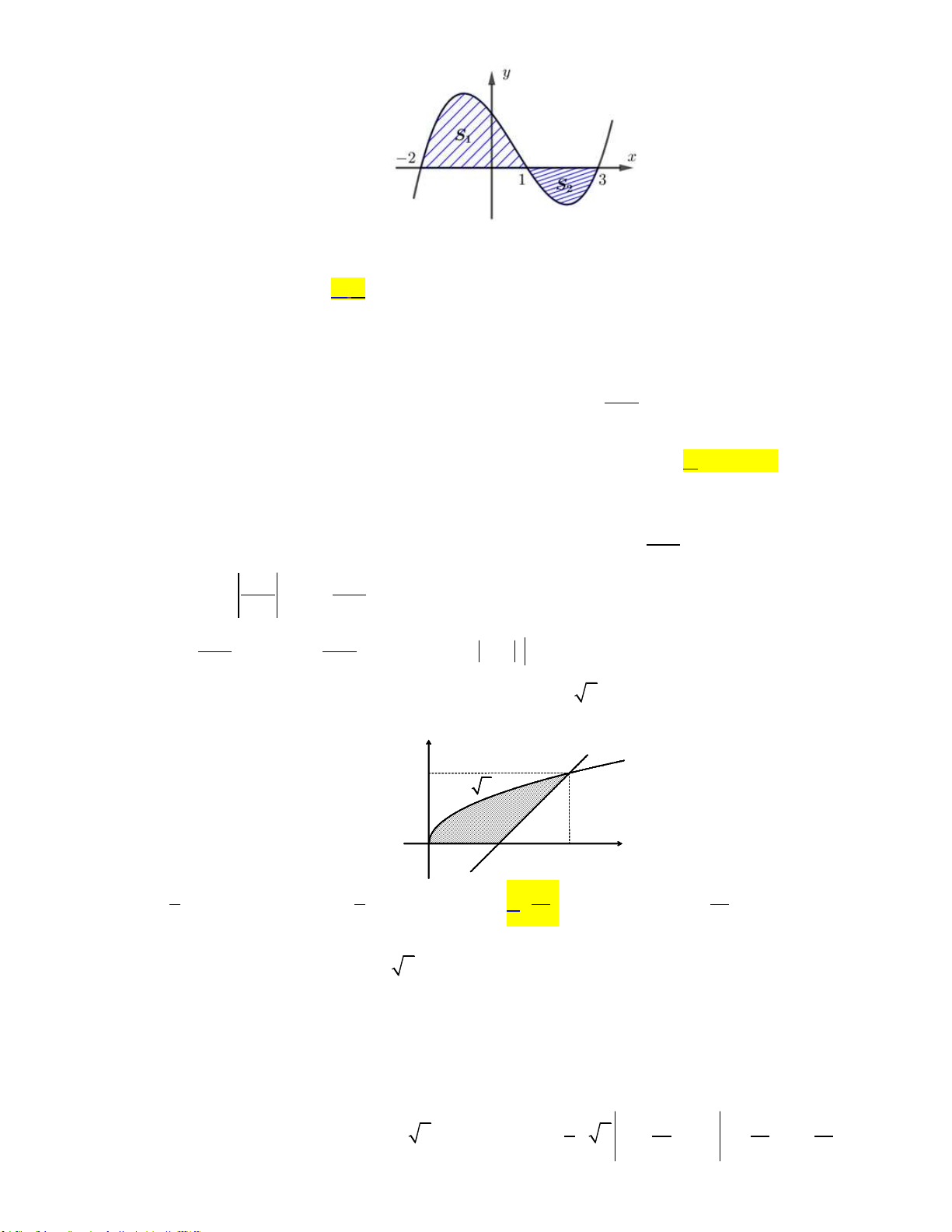
Câu 1: Diện tích của hình phẳng H được giới hạn bởi đồ thị hàm số y  f x , trục hoành và hai
đường thẳng x  a , x  b a  b (phần tô đậm trong hình vẽ dưới đây) tính theo công thức: b c b A. S  f  xdx . B. S   f
 xdx  f  xdx. a a c b c b C. S  f  xdx . D. S  f
 xdx  f  xdx. a a c
Câu 2: Diện tích S của hình phẳng giới hạn bởi các đường 2
y   x  2x, y  3, x  1, x  2
được tính bởi công thức nào dưới đây ? 2 2 2 A. S     2
x  2x  3 dx . B. S   2
x  2x  3dx . 1 1 2 2 C. S   2 x  2x   3dx. D. S    2
x  2x  3dx . 1 1
Câu 3: Diện tích hình phẳng giới hạn bởi các đường 2
y  7  2x , 2
y  x  4 bằng 5 A. 5 . B. 3 . C. 4 . D. . 2 x
Câu 4: Diện tích hình phẳng giới hạn bởi các đường y 
, trục hoành và đường thẳng x  1 là 2 1  x
S  a  b . Khi đó a  b bằng: A. 4 . B. 5 . C. 6 . D. 3 .
Câu 5: Hình phẳng (H ) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục
đối xứng vuông góc với trục hoành.
Phần tô đậm của hình vẽ có diện tích bằng 37 7 11 5 A. . B.  C.  D.  12 12 12 12
Câu 6: Phần hình phẳng  H  được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm
số y  f  x , 2
y  x  4x và hai đường thẳng x  2 ; x  0 . 0 4 Biết
f  xdx  
. Diện tích hình  H  bằng 3 2  7 16 4 20 A. . B. . C. . D. . 3 3 3 3
Câu 7: Tính diện tích miền hình phẳng giới hạn bởi các đường 2
y  x  2x , y  0 , x  10 , x  10 . 2000 2008 A. S  . B. S  2008 . C. S  . D. 2000 . 3 3
Câu 8: Gọi H là hình phẳng giới hạn bởi các đường y  x  2
3 , trục tung và trục hoành. Gọi k , k 1 2
k  k là hệ số góc của hai đường thẳng cùng đi qua điểm A0;9 và chia H làm ba phần 1 2 
có diện tích bằng nhau. Tính k  k . 1 2 13 25 27 A. . B. 7 . C. . D. . 2 4 4
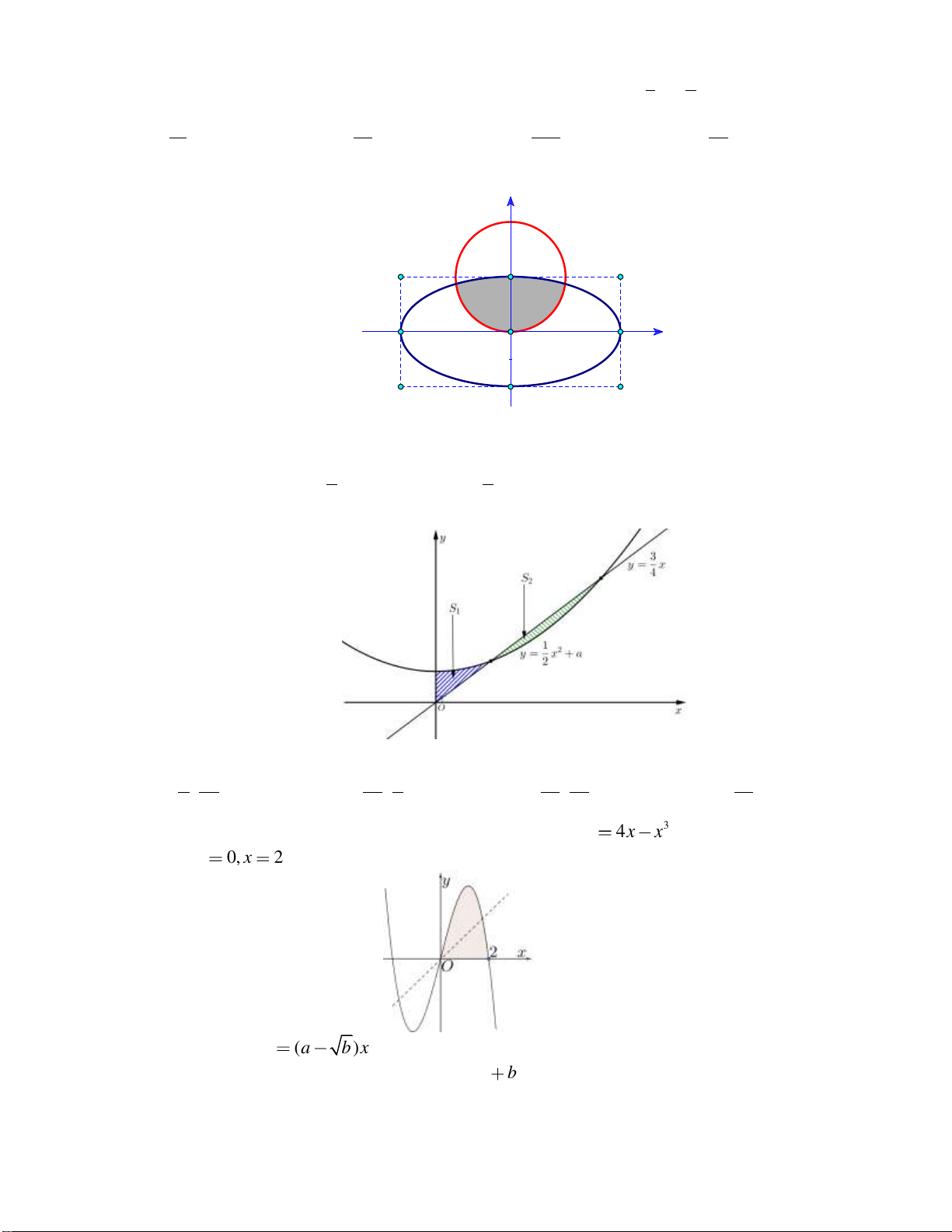
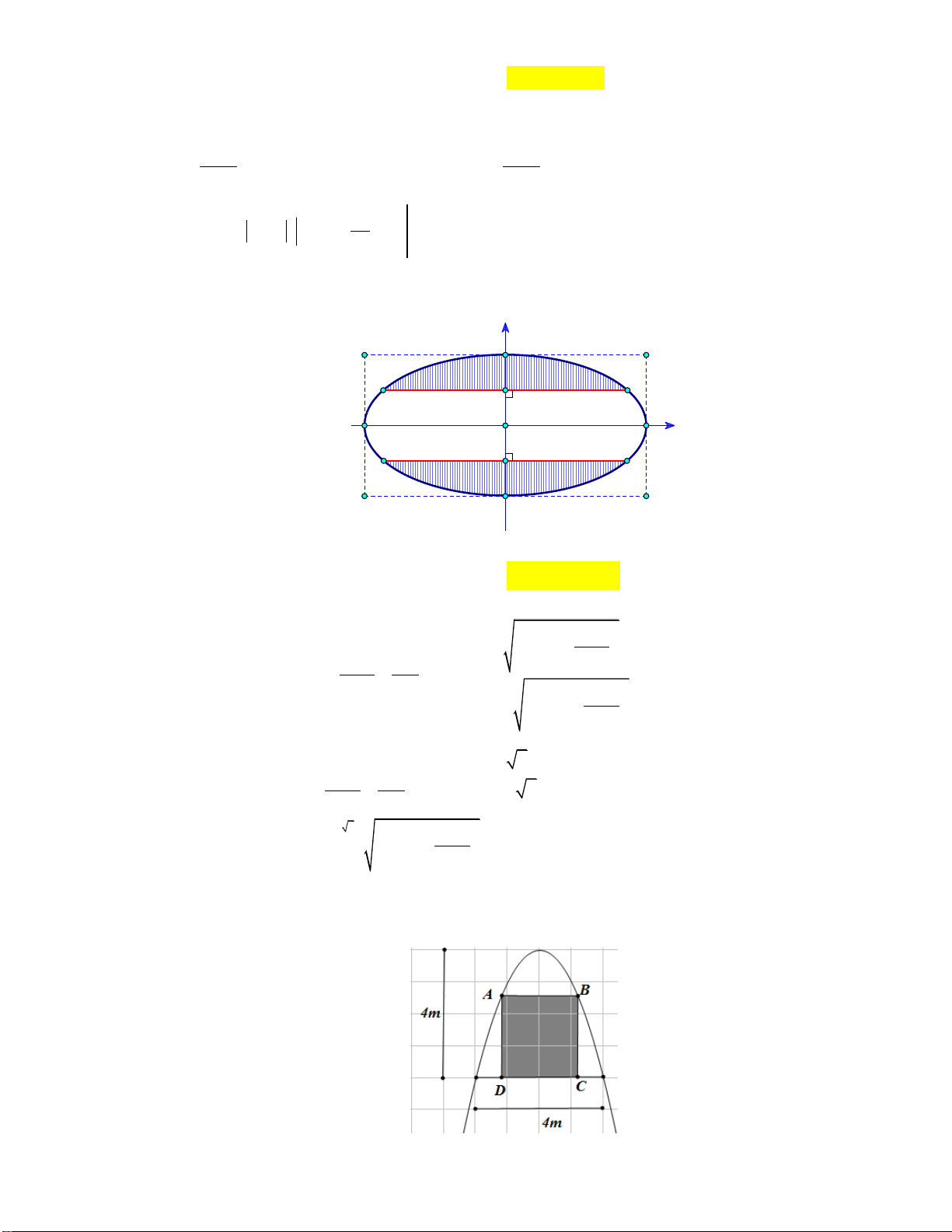
Câu 9: Anh Toàn có một cái ao hình elip với độ dài trục lớn và độ dài trục bé lần lượt là 100 m và
80 m . Anh chia ao ra hai phần theo một đường thẳng từ một đỉnh của trục lớn đến một đỉnh
của trục bé (Bề rộng không đáng kể). Phần rộng hơn anh nuôi cá lấy thịt, phần nhỏ anh nuôi
cá giống. Biết lãi nuôi cá lấy thịt và lãi nuôi cá giống trong 1 năm lần lượt là 20.000 đồng/m2
và 40.000 đồng/m2. Hỏi trong 1 năm anh Toàn có bao nhiêu tiền lãi từ nuôi cá trong ao đã nói
trên (Lấy làm tròn đến hàng nghìn)? A. 176 350 000 đồng. B. 137 080 000 đồng. C. 139 043000 đồng. D. 105664000 đồng.
Câu 10: Diện tích hình phẳng giới hạn bởi các đường x
y  e ; y  e và x  0 bằng 2 e 2 e 1 A. . B. . C. 1. D. . 2 3 2
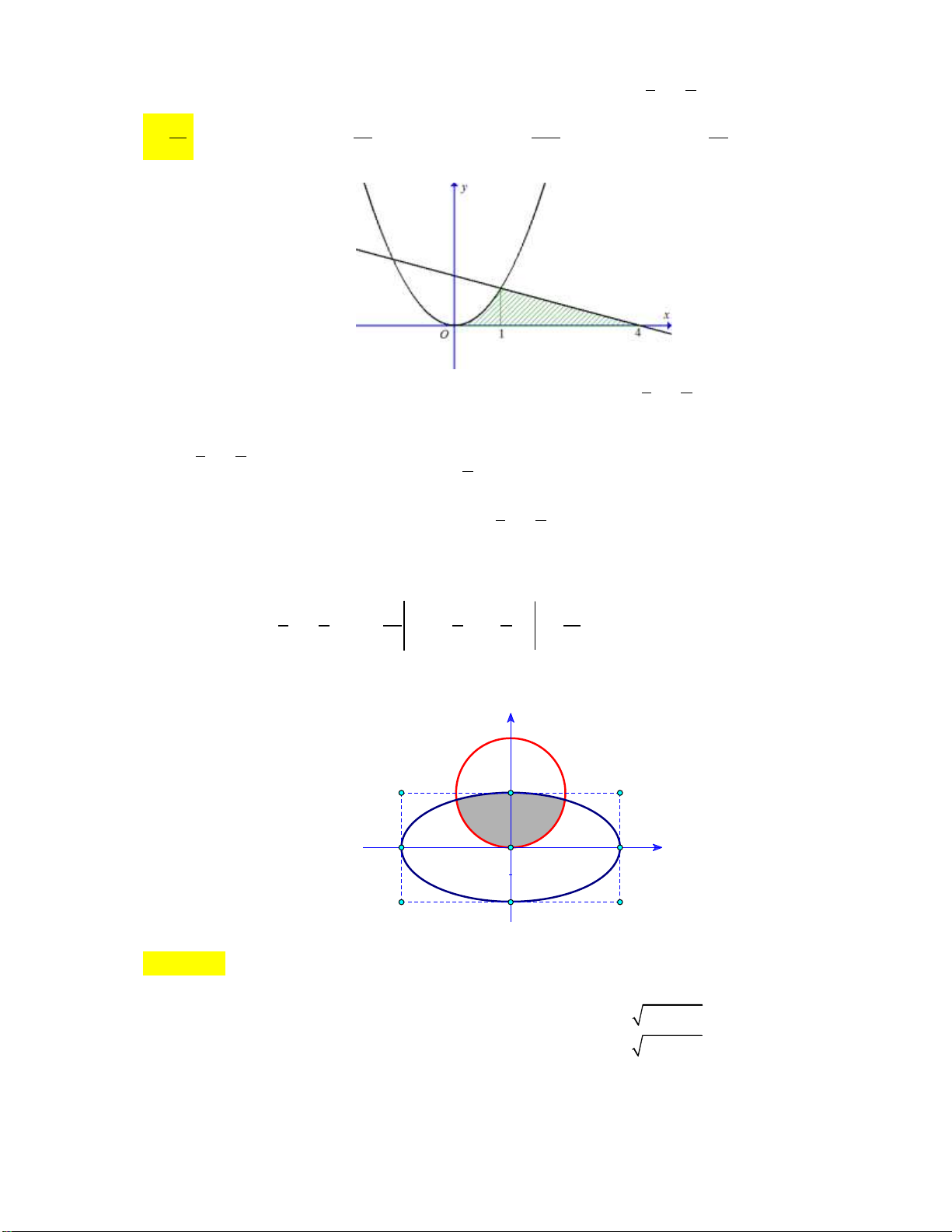
Câu 11: Trong mặt phẳng cho đường tròn C và parabol P (tham khảo hình vẽ dưới đây). y 1 O 1 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 1,04. B. 0,21. C. 0,67. D. 0,45.
Câu 12: Diện tích S của hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 1 1 A. S    3 2
x  3x  x  3d .x B. S    3 2
x  3x  x  3d . x 1  1  1 3 C. S    3 2
x  3x  x  3d . x D. S    3 2
x  3x  x  3d . x 1  1 
Câu 13: Cho hàm số y  f x . Hàm số y  f x có đồ thị như hình vẽ dưới đây:
Biết phương trình f x  0 có bốn nghiệm phân biệt a , 0 , b , c với a  0  b  c . Mệnh đề nào dưới đây đúng?
A. f a  f c  f b .
B. f a  f b  f c .
C. f c  f a  f b .
D. f b  f a  f c .
Câu 14: Cho hàm số y  f x 3 2
 ax  bx  cx  d,a,b,c ,a  0 có đồ thị C . Biết rằng đồ thị C tiếp
xúc với đường thẳng y  4 tại điểm có hoành độ âm và đồ thị hàm số y  f x cho bởi hình vẽ dưới đây:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị C và trục hoành. 27 21 5 A. S  9 . B. S  . C. . D. . 4 4 4
Câu 15: Cho hai hàm số 3 2
f (x)  ax  bx  cx  2 và 2
g(x)  dx  x
e  2 (a, b, c, d, e  ). Biết rằng
đồ thị của hàm số y  f (x) và y  g(x) cắt nhau tại ba điểm có hoành độ lần lượt là 2; 1  ; 1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 8 37 4 A. . B. . C. . D. . 6 3 12 3
Câu 16: Diện tích hình phẳng S giới hạn các đồ thị hàm số 3
y  x , y  2  x và trục hoành Ox (như
hình vẽ dưới đây) được tính bởi công thức nào sau đây ? 1 1 2 A. 3 S   x d . x  B. 3 S 
x  (2  x) d . x  2 0 0 2 1 2 C. 3 S 
(2  x)  x d . x  D. 3
S  x dx  (x  2)d . x   0 0 1
Câu 17: Cho hình vuông ABCD tâm O , độ dài cạnh là 4 cm. Đường cong BOC là một phần của
parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham 1 2 khảo hình vẽ). 4 cm B C S1 4 cm O S2 A D S Tỉ số 1 bằng S2 2 1 1 3 A. . B. . C. . D. . 5 2 3 5 Câu 18: Cho hàm số 3 2
y  x  3x  3mx  m  1 . Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục
Ox có diện tích phần nằm phía trên trục Ox và phần nằm dưới trục Ox bằng nhau. Giá trị của m là: 3 3 2 4 A. . B. . C. . D. . 4 5 3 5
Câu 19: Diện tích của hình phẳng giới hạn bởi y  2x ; 2
y  x ; y  1 trên miền x  0 ; y  1, bằng 1 1 5 2 A. . B. . C. . D. . 3 2 12 3
Câu 20: Cho hàm số y  f x . Đồ thị của hàm số y  f x như hình dưới đây. y 4 2 3  x O 1 3 2
Đặt g x  f x  x  2 2
1 . Mệnh đề nào dưới đây đúng?
A. g3  g 3    g1 . B. g 3
   g3  g1 .
C. g1  g 3    g3 .
D. g1  g3  g 3   .
____________________________HẾT____________________________
Huế, 21h00’ Ngày 09 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 2_TrNg 2022
LỜI GIẢI CHI TIẾT
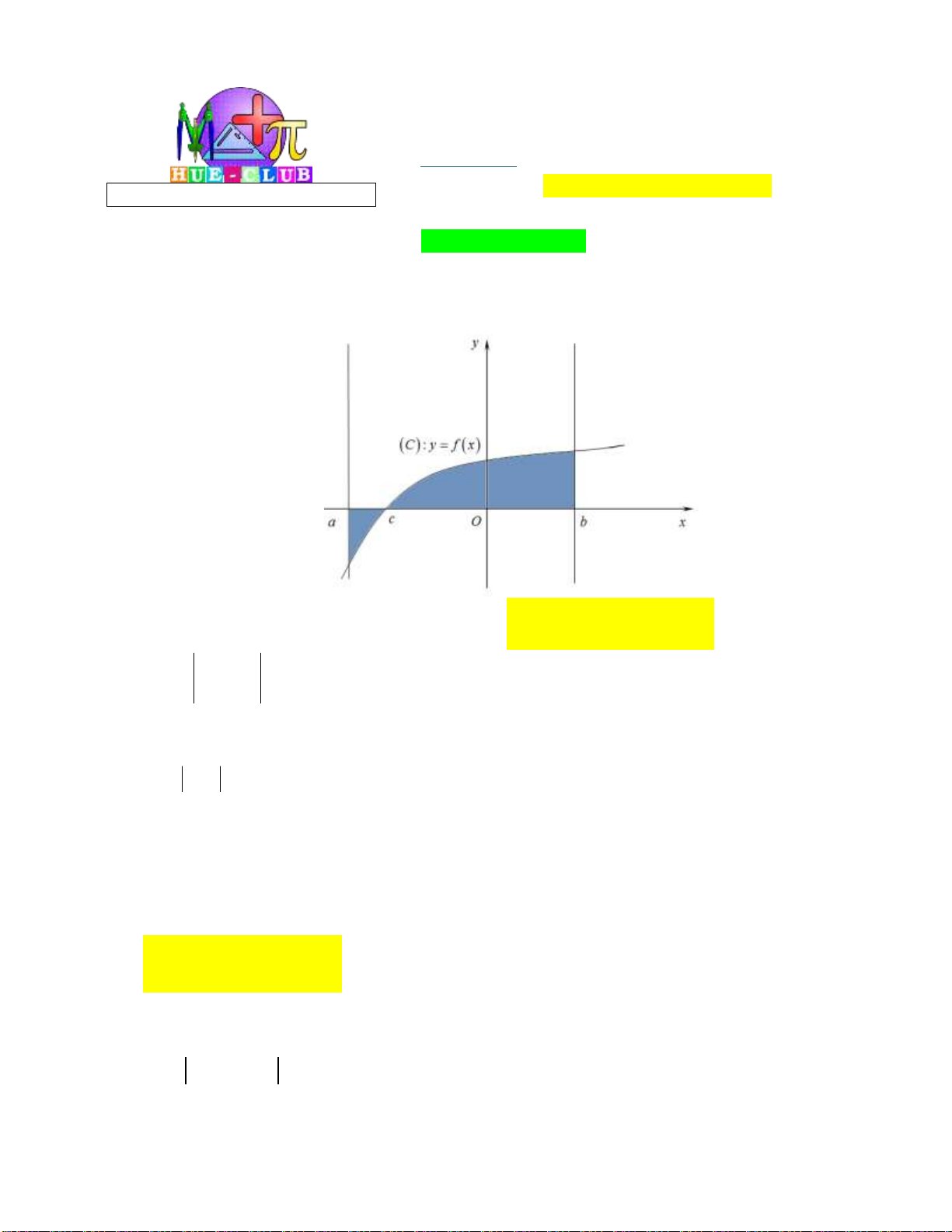
Câu 1: Diện tích của hình phẳng H được giới hạn bởi đồ thị hàm số y  f x , trục hoành và hai
đường thẳng x  a , x  b a  b (phần tô đậm trong hình vẽ dưới đây) tính theo công thức: b c b A. S  f  xdx . B. S   f
 xdx  f  xdx. a a c b c b C. S  f  xdx . D. S  f
 xdx  f  xdx. a a c Lời giải:
Áp dụng công thức tính diện tích hình phẳng ta có: b S  f  x c b c b
dx  0  f 
xdx   f 
 x0dx  f 
 xdx  f  xdx. a a c a c
 Chọn đáp án B.
Câu 2: Diện tích S của hình phẳng giới hạn bởi các đường 2
y   x  2x, y  3, x  1, x  2
được tính bởi công thức nào dưới đây ? 2 2 2 A. S     2
x  2x  3 dx . B. S   2
x  2x  3dx . 1 1 2 2 C. S   2 x  2x   3dx. D. S    2
x  2x  3dx . 1 1 Lời giải:
Diện tích S của hình phẳng giới hạn bởi các đường 2
y   x  2x, y  3, x  1, x  2 là: 2 2 2 S 
x  2x  3 dx    2
x  2x  3.dx . 1 1
 Chọn đáp án C.
Câu 3: Diện tích hình phẳng giới hạn bởi các đường 2
y  7  2x , 2
y  x  4 bằng 5 A. 5 . B. 3 . C. 4 . D. . 2 Lời giải:
Phương trình hoành độ giao điểm của các đường 2
y  7  2x , 2
y  x  4 là 2 2 2
7  2x  x  4  3x  3  x  1  .
Khi đó diện tích hình phẳng cần tìm là 1
S   7  2x  x  4 1 1 2 2 2 dx  3  3x dx     2
3  3x dx  4 . 1  1  1 
 Chọn đáp án C. x
Câu 4: Diện tích hình phẳng giới hạn bởi các đường y 
, trục hoành và đường thẳng x  1 là 2 1  x
S  a  b . Khi đó a  b bằng: A. 4 . B. 5 . C. 6 . D. 3 . Lời giải: x Xét phương trình  0  x  0 . 2 1  x 1 1 x
Vậy diện tích cần tính bằng S  d 2 x  1  x  2  1  . 2 0  0 1 x
Vậy a  2 ; b  1 nên a  b  3 .
 Chọn đáp án D.
Câu 5: Hình phẳng (H ) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục
đối xứng vuông góc với trục hoành.
Phần tô đậm của hình vẽ có diện tích bằng 37 7 11 5 A. . B.  C.  D.  12 12 12 12 Lời giải:
Vì đồ thị hàm số C  f  x 3 2 :
 ax  bx  cx  d và P g  x 2 :
 mx  nx  p có 3 hoành độ
giao điểm là 1,1, 2 nên f  x  g  x  a  x   1  x   1  x  2 .
Ta có f 0  2, g 0  0 nên f 0  g 0  .1 a .  1  2
   2  2a  a 1. 2 37
Vậy phần diện tích tô đậm là S 
x  1x  1x  2 dx   . 12 1 
 Chọn đáp án A.
Câu 6: Phần hình phẳng  H  được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm
số y  f  x , 2
y  x  4x và hai đường thẳng x  2 ; x  0 . 0 4 Biết
f  xdx  
. Diện tích hình  H  bằng 3 2  7 16 4 20 A. . B. . C. . D. . 3 3 3 3 Lời giải:
Diện tích hình  H  là : 0 0 0 S   f  x 2 
 2x 4x dx   f
 xdx  x 4xdx 2  2  2  3 3 4  x  0 4  2   20 2     2 2x     2 2    . 3 3 2    3 3 3 20
Vậy diện tích hình  H  là S  . 3
 Chọn đáp án D.
Câu 7: Tính diện tích miền hình phẳng giới hạn bởi các đường 2
y  x  2x , y  0 , x  10 , x  10 . 2000 2008 A. S  . B. S  2008 . C. S  . D. 2000 . 3 3 Lời giải: x 
Phương trình hoành độ giao điểm của đồ thị 2
y  x  2x và y  0 là 2 x  2x  0 0   . x   2 Trên đoạn 10;10   ta có: 2
x  2x  0 , x    10  ;0   và 2;10   ; 2
x  2x  0 , x   0;2   . 10 0 2 10 2008 Do đó 2 S 
x  2x dx 
   2x  2xdx   2x  2xdx    2
x  2xdx  ( đvdt). 3 10  1  0 0 2
 Chọn đáp án C. Nhận xét:
Nếu học sinh sử dụng MTCT tính tích phân mà không chia khoảng thì có sự sai khác về kết
quả giữa máy casio và vinacal. Trong trường hợp này máy vinacal cho đáp số đúng.
Câu 8: Gọi H là hình phẳng giới hạn bởi các đường y  x  2
3 , trục tung và trục hoành. Gọi k , k 1 2
k  k là hệ số góc của hai đường thẳng cùng đi qua điểm A0;9 và chia H làm ba phần 1 2 
có diện tích bằng nhau. Tính k  k . 1 2 13 25 27 A. . B. 7 . C. . D. . 2 4 4 Lời giải:
Gọi d : y  k x  9 , d : y  k x  9 k  k . 1 2  1 1 2 2  9   9   9 9 
Gọi M  d  Ox  M  
; 0  ; N  d  Ox  N   ; 0       1  k 2  k  k k 1  2  2 1 
Giao điểm của P y  x  2 :
3 với hai trục tọa độ lần lượt là C 3;0 , A0;9 . 9 18
Theo giả thiết ta có S  S
 OM  2ON      k  2k . A  ON A  NM 2 1 k k 1 2 3 2 1 243 27 Lại có S  S 3  x  x  OA ON     k    . H A  ON  3   d 3. . . 9 2 2 2k 2 0 2 27 27 Suy ra k    k  k  . 1 4 1 2 4
 Chọn đáp án D.
Câu 9: Anh Toàn có một cái ao hình elip với độ dài trục lớn và độ dài trục bé lần lượt là 100 m và
80 m . Anh chia ao ra hai phần theo một đường thẳng từ một đỉnh của trục lớn đến một đỉnh
của trục bé (Bề rộng không đáng kể). Phần rộng hơn anh nuôi cá lấy thịt, phần nhỏ anh nuôi
cá giống. Biết lãi nuôi cá lấy thịt và lãi nuôi cá giống trong 1 năm lần lượt là 20.000 đồng/m2
và 40.000 đồng/m2. Hỏi trong 1 năm anh Toàn có bao nhiêu tiền lãi từ nuôi cá trong ao đã nói
trên (Lấy làm tròn đến hàng nghìn)? A. 176 350 000 đồng. B. 137 080 000 đồng. C. 139 043000 đồng. D. 105664000 đồng. Lời giải: .
Diện tích toàn bộ ao là S      2 .40.50 2000 m  . S
Diện tích phần nuôi cá giống là: S   S  500  1000   2 m . 1  4 OAB
Diện tích phần nuôi cá thịt là: S  S  S  1500  1000 2 m . 2 1 
Tiền lãi từ nuôi cá là: 40000.S  20000.S  137 080000 . 1 2
 Chọn đáp án B.
Câu 10: Diện tích hình phẳng giới hạn bởi các đường x
y  e ; y  e và x  0 bằng 2 e 2 e 1 A. . B. . C. 1. D. . 2 3 2 Lời giải:
Ta có: x   0 x e e
 e  e  x  1. Xét dấu x e  e x – ∞ 1 + ∞ ex – e – 0 +
Diện tích hình phẳng giới hạn bởi các đường x
y  e ; y  e và x  0; x  1 là 1 1 x      x     x S e e dx e e dx
ex  e  1  e  e   0 0  e   1. 0 0 0
 Chọn đáp án C.
Câu 11: Trong mặt phẳng cho đường tròn C và parabol P (tham khảo hình vẽ dưới đây). y 1 O 1 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 1,04. B. 0,21. C. 0,67. D. 0,45. Lời giải:
y  2x  x
Phương trình đường tròn là x  1 2 2 2  y  1   . 2
y   2x   x Phương trình parabol là 2 y  x . 1
Diện tích cần tính là S   2 2
2x  x  x dx  0,45. 0
Chọn đáp án D.
Câu 12: Diện tích S của hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 1 1 A. S    3 2
x  3x  x  3d .x B. S    3 2
x  3x  x  3d . x 1  1  1 3 C. S    3 2
x  3x  x  3d . x D. S    3 2
x  3x  x  3d . x 1  1  Lời giải:
Diện tích phần gạch chéo được tính bở công thức : 1 1 3 2 3 2 S 
x  3x  2  x 1 dx 
(x  3x  x  3)d . x   1  1 
 Chọn đáp án B.
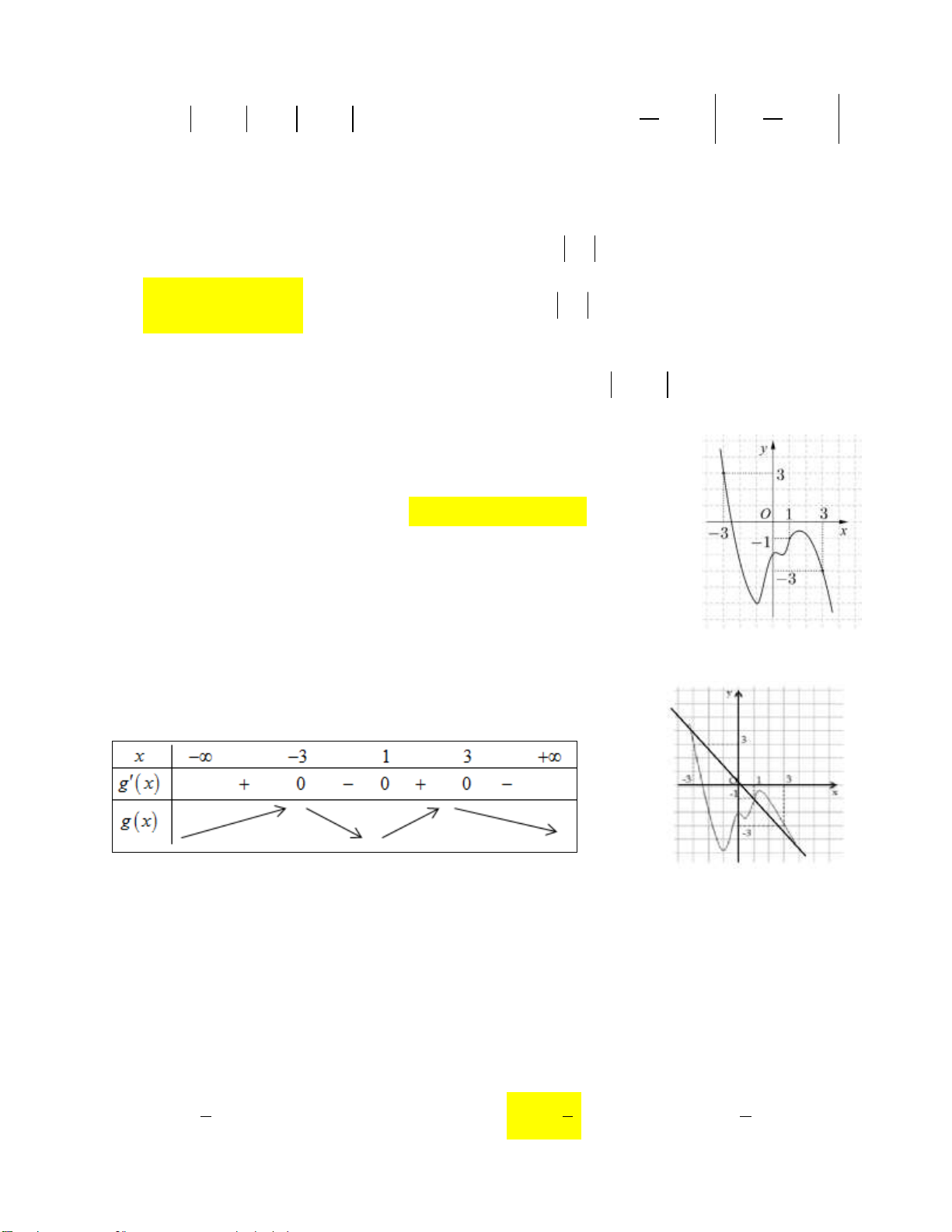
Câu 13: Cho hàm số y  f x . Hàm số y  f x có đồ thị như hình vẽ dưới đây:
Biết phương trình f x  0 có bốn nghiệm phân biệt a , 0 , b , c với a  0  b  c . Mệnh đề nào dưới đây đúng?
A. f a  f c  f b .
B. f a  f b  f c .
C. f c  f a  f b .
D. f b  f a  f c . Lời giải:
Ta có bảng biến thiên x -  a 0 b c +  f / (x) - 0 + 0 - 0 + 0 - f(0) f(c) f(x) f(a) f(b)
Suy ra f c  f b (1)
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị y  f x , đường thẳng x  a , x  0 . 1
S là diện tích hình phẳng giới hạn bởi đồ thị y  f x , đường thẳng x  0 , x  b . 2
S là diện tích hình phẳng giới hạn bởi đồ thị y  f x , đường thẳng x  b , x  c . 3 0 c b
Vì S  S  S  f 
 x dx  f
 x dx  f  x dx 1 3 2 a b 0 0 c b  f 
 xdx  f
 xdx   f  xdx a b 0
 f 0  f a  f c  f b   f b  f 0
 f a  f c (2)
Từ (1) và (2)  f a  f c  f b .
 Chọn đáp án A.
Câu 14: Cho hàm số y  f x 3 2
 ax  bx  cx  d,a,b,c ,a  0 có đồ thị C . Biết rằng đồ thị C tiếp
xúc với đường thẳng y  4 tại điểm có hoành độ âm và đồ thị hàm số y  f x cho bởi hình vẽ dưới đây:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị C và trục hoành. 27 21 5 A. S  9 . B. S  . C. . D. . 4 4 4 Lời giải:
Từ đồ thị suy ra f x 2  3x  3 .
f x  f 
 xdx   2x   3 3
3 dx  x  3x  C .
Do C tiếp xúc với đường thẳng y  4 tại điểm có hoành độ x âm nên 0 f x  2
 0  3x  3  0  x  1  . Suy ra f  1
   4  C  2  C 3
: y  x  3x  2 0 0 0 x  2  Xét phương trình 3
x  3x  2  0   . x   1 1 27
Diện tích hình phẳng cần tìm là:     .   3 x 3x 2dx 2 4
 Chọn đáp án B.
Câu 15: Cho hai hàm số 3 2
f (x)  ax  bx  cx  2 và 2
g(x)  dx  x
e  2 (a, b, c, d, e  ). Biết rằng
đồ thị của hàm số y  f (x) và y  g(x) cắt nhau tại ba điểm có hoành độ lần lượt là 2; 1  ; 1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 8 37 4 A. . B. . C. . D. . 6 3 12 3 Lời giải:
Ta có phương trình hoành độ giao điểm:
f  x  g  x  f  x  g  x  0 3
 ax  b  d  2
x  c  e x  4  0 (1).
Vì phương trình (1) là phương trình bậc 3 và x  2; x  1; x  1 là 3 nghiệm phân biệt của
phương trình (1) nên ta suy ra
f  x  g  x  a  x  2  x   1  x   1 (2). Ta có f 0  2
 , g 0  2 nên f 0  g 0  4  .
Mặt khác từ (2) ta có f 0  g 0  a 0  2.0   1 .0   1  2  a .
Suy ra 2a  4  a  2 . 2
Do đó f  x  g  x  2. x  2 x   1  x  
1  2 x  2x   1 . 2 1 37
Diện tích hình phẳng cần tìm là S 
f  x  g  x dx  2 x  2 2 x   1 dx    . 6 2  2 
 Chọn đáp án A.
Câu 16: Diện tích hình phẳng S giới hạn các đồ thị hàm số 3
y  x , y  2  x và trục hoành Ox (như
hình vẽ dưới đây) được tính bởi công thức nào sau đây ? 1 1 2 A. 3 S   x d . x  B. 3 S 
x  (2  x) d . x  2 0 0 2 1 2 C. 3 S 
(2  x)  x d . x  D. 3
S  x dx  (x  2)d . x   0 0 1 Lời giải: 1 2 1 1 3 3
S  x dx  (2  x)dx   x d . x    2 0 1 0
 Chọn đáp án A.
Câu 17: Cho hình vuông ABCD tâm O , độ dài cạnh là 4 cm. Đường cong BOC là một phần của
parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham 1 2 khảo hình vẽ). 4 cm B C S1 4 cm O S2 A D S Tỉ số 1 bằng S2 2 1 1 3 A. . B. . C. . D. . 5 2 3 5 Lời giải: y 2 B C -2 1 2 x O D A -2
Gắn hệ trục toạ độ như hình vẽ. 1
Ta có phương trình parabol  P 2 : y  x . 2 2  1  16 Suy ra 2 S  2  x dx   (đvdt). 1    2  3 2 
Diện tích hình vuông ABCD là 2 S  4  16 (đvdt). ABCD 16 32
Do đó diện tích S là S  S  S 16   (đvdt). 2 2 ABCD 1 3 3 S 16 32 1 Vậy tỉ số 1  :  . S 3 3 2 2
 Chọn đáp án B. Câu 18: Cho hàm số 3 2
y  x  3x  3mx  m  1 . Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục
Ox có diện tích phần nằm phía trên trục Ox và phần nằm dưới trục Ox bằng nhau. Giá trị của m là: 3 3 2 4 A. . B. . C. . D. . 4 5 3 5 Lời giải: TXĐ: D  . 2
y  x  x  m   2 3 6 3
3 x  2x  m .
Yêu cầu bài toán suy ra đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt nên. 2
x  2x  m  0 có hai nghiệm phân biệt          0 1 m 0 m 1. y
Khi đó đồ thị hàm số đối xứng qua tâm I 1; 3   4m . 3
Yêu cầu bài toán tương đương với I Ox  3
  4m  0  m  t/m. Chọn đáp án A. 4
 Chọn đáp án A.
Câu 19: Diện tích của hình phẳng giới hạn bởi y  2x ; 2
y  x ; y  1 trên miền x  0 ; y  1, bằng 1 1 5 2 A. . B. . C. . D. . 3 2 12 3 Lời giải:
Phương trình hoành động giao điểm 2
x  1  x  1; 2x  1 1  x  . 2
Hình phẳng cần tính được tạo từ hai hình  H và  H 2  1   y  2x 1  2 Trong đó  H  2 y  x 2
 S  2x  x dx  5  . 1 1  24 1 0
x  0; x   2   y  1  1 Và  H  2  y  x 2
 S  1 x dx  5  . 2 2  24 1 1
x  ; x 1 2  2 5 5 5
Vậy diện tích hình phẳng cần tính là S  S  S    . 1 2 24 24 12
 Chọn đáp án C.
Câu 20: Cho hàm số y  f x . Đồ thị của hàm số y  f x như hình dưới đây. y 4 2 3  x O 1 3 2
Đặt g x  f x  x  2 2
1 . Mệnh đề nào dưới đây đúng?
A. g3  g 3    g1 . B. g 3
   g3  g1 .
C. g1  g 3    g3 .
D. g1  g3  g 3   . Lời giải: y 4 2 3  x O 1 3 d 2
Ta có gx  2 f x  2x  1  
gx   f x x 1 0  x  1   . x  3   Bảng biến thiên x  1  3 5 
g x  0  0  0   
g  x g 3 g   1 g 5 Suy ra g 3
   g1 và g3  g1 . 1 3 1 3 1 1
Theo hình vẽ  f 
  xx  1dx   
x  1 fxdx  g 
 xdx   g  xdx  2  2 3 1 3 1
 gx 1  gx 3  g  1  g  3
   g3  g1  g3  g 3   . 3  1
Vậy g1  g3  g 3   .
 Chọn đáp án D.
____________________________HẾT____________________________
Huế, 21h00’ Ngày 09 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 3_TrNg 2022 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
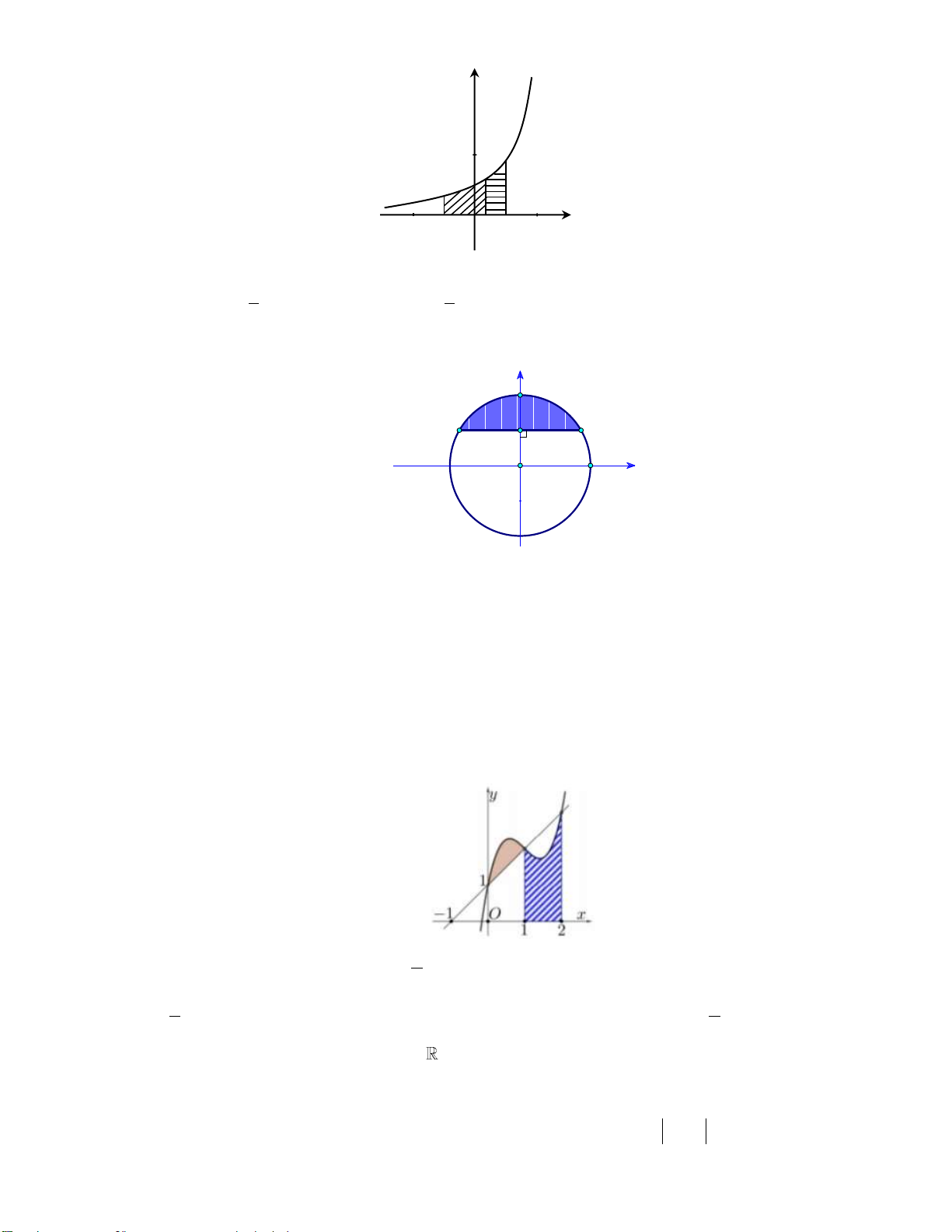
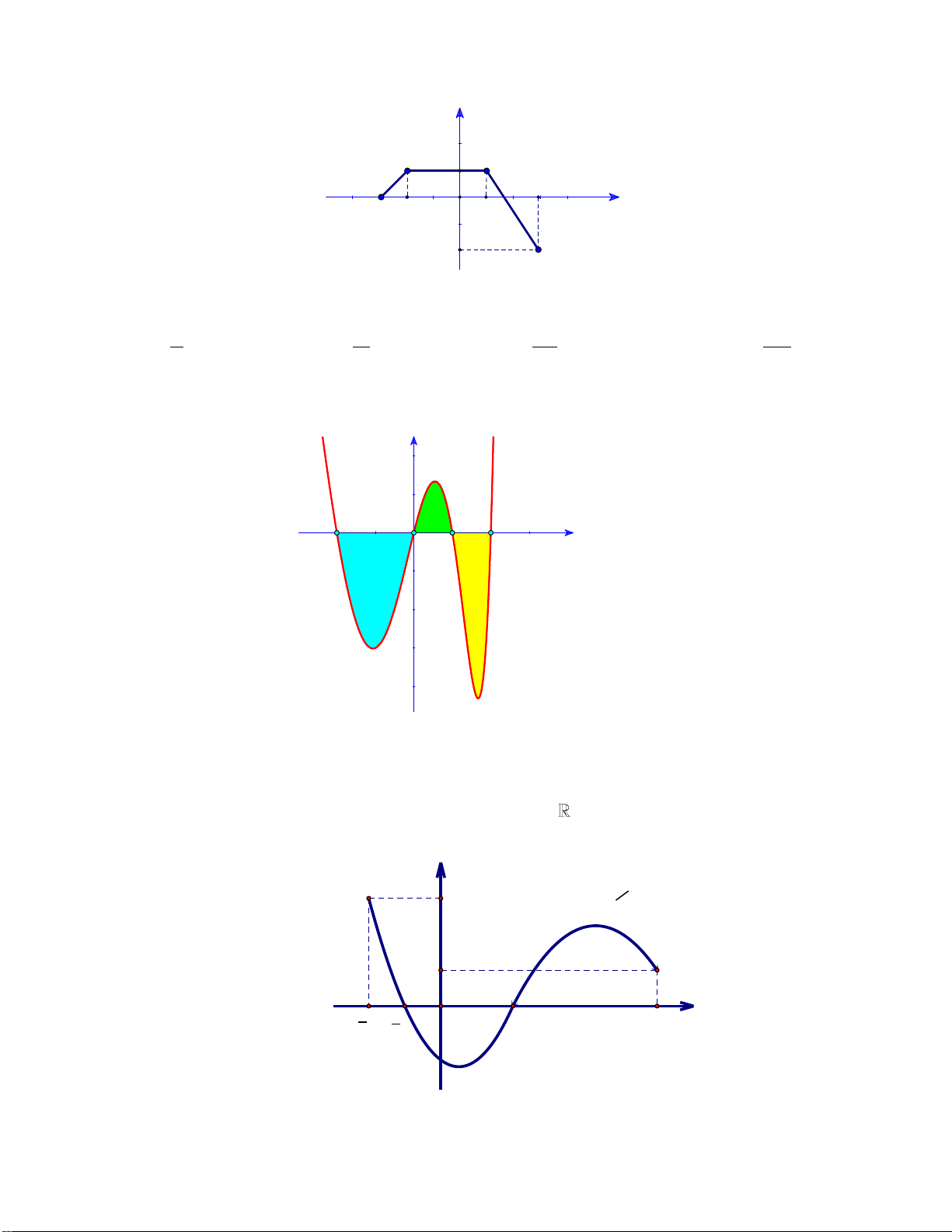
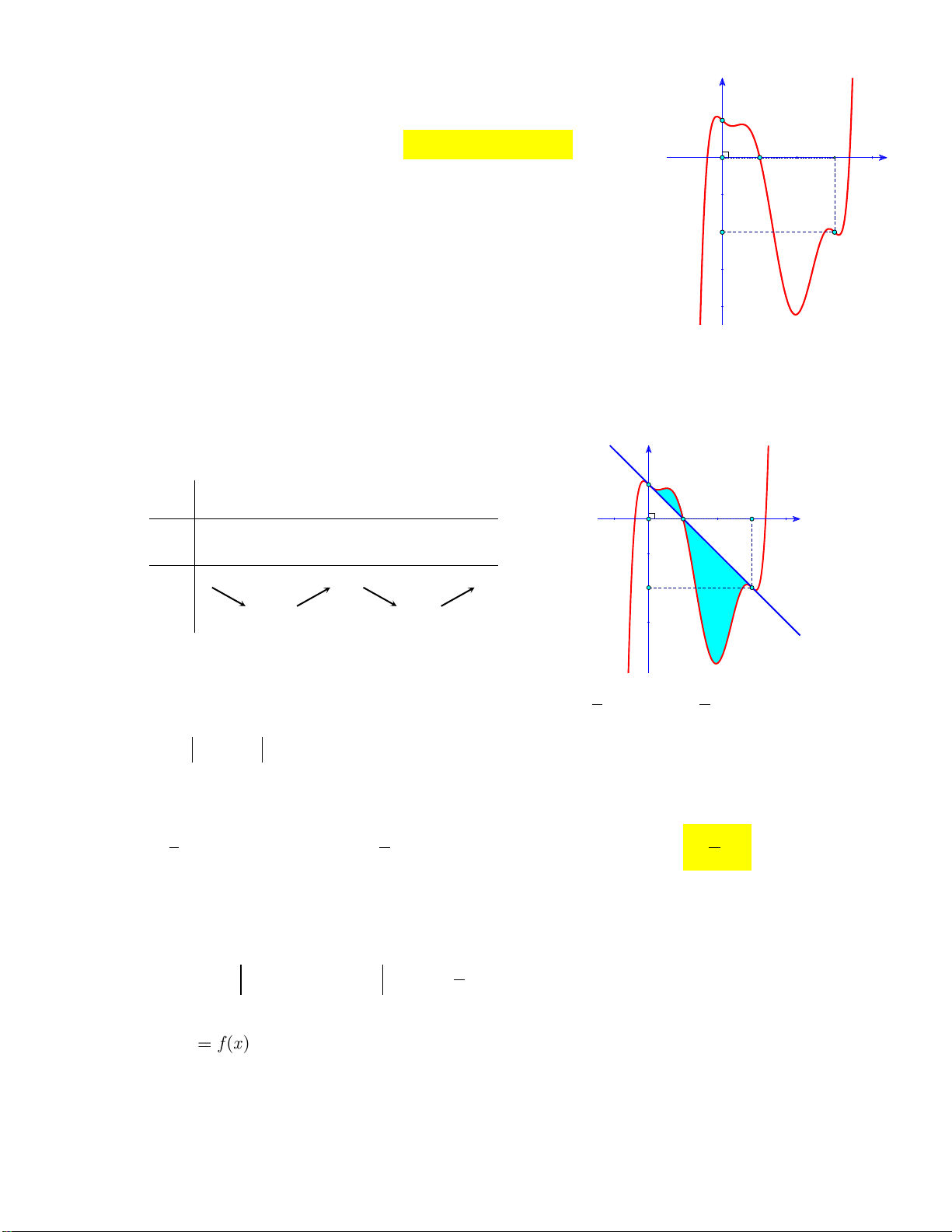
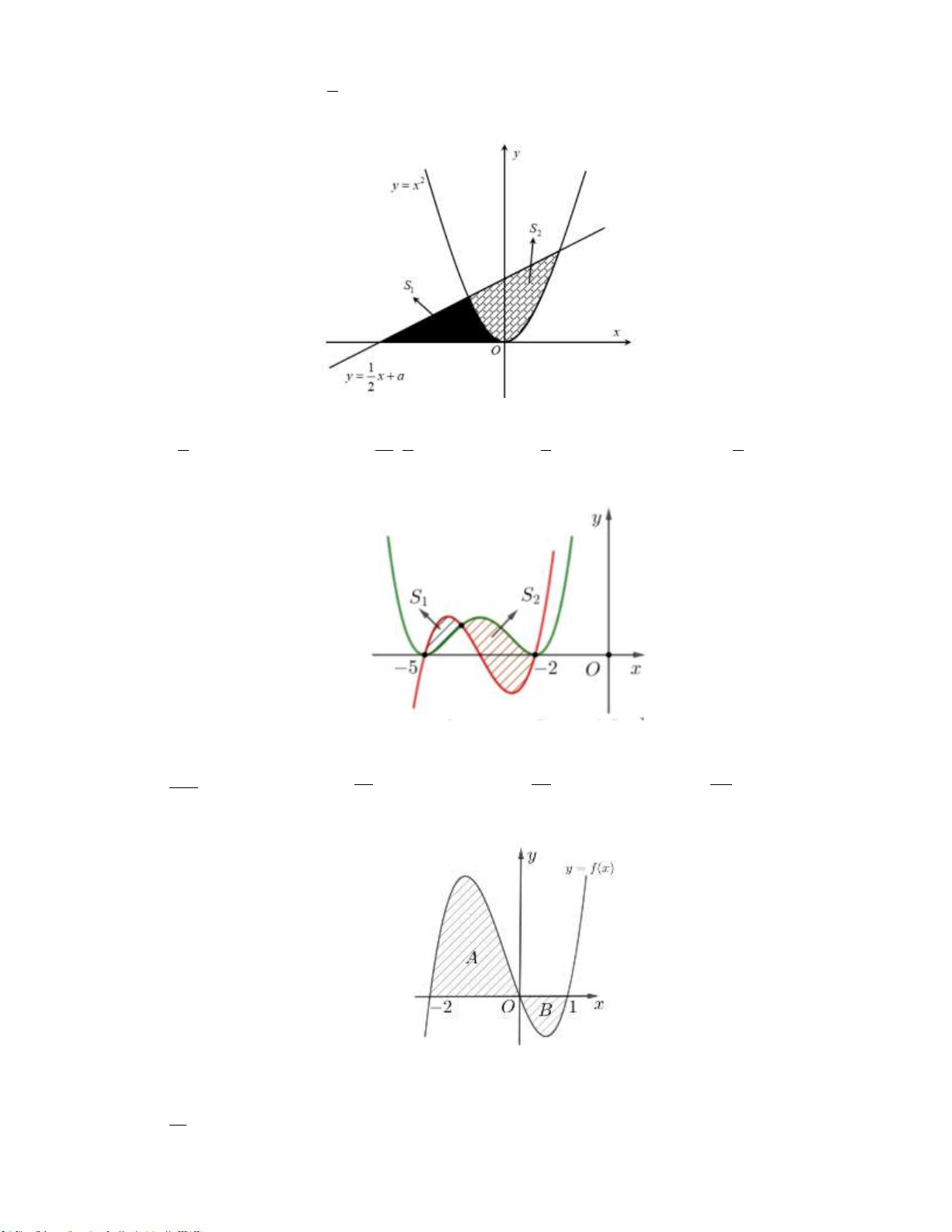
Câu 1: Cho hàm số y  f x liên tục trên . Gọi D là diện tích hình phẳng giới hạn bởi đồ thị
C: y  f x, trục hoành, hai đường thẳng x  2 , x  4 (tham khảo hình vẽ bên dưới). y
f(x) -2 1 4 x O
Giả sử S là diện tích hình phẳng D . Mệnh đề nào dưới đây sai? D 4 4
A. S   f x d . x B. S  f x x D   d . D 2 2 1 4 1 4 C. S 
f xdx  
 f xdx . D. S  f x x f x x . D  d     d D 2 1 2 1
Câu 2: Diện tích hình phẳng giới hạn bởi các đường 2
y  x  x , y  2x  2 , x  0 , x  3 được tính bởi công thức 3 2 A. S   2
x  3x  2dx . B. 2 S 
x  3x  2 dx  . 0 1 3 2 C. 2 S 
x  3x  2 dx  . D. 2 S 
x  x  2 dx  . 0 1 
Câu 3: Diện tích của hình phẳng giới hạn bởi các đường 2
y  cos x ; y  0 và x  0; x  bằng 4  1   1  A.  . B. 1. C.  . D. . 4 2 4 8 4 8
Câu 4: Diện tích hình phẳng giới hạn bởi các đường 2
y  x và y  x  2 là 9 9 8 A. S  9 . B. S  . C. S  . D. S  . 4 2 9
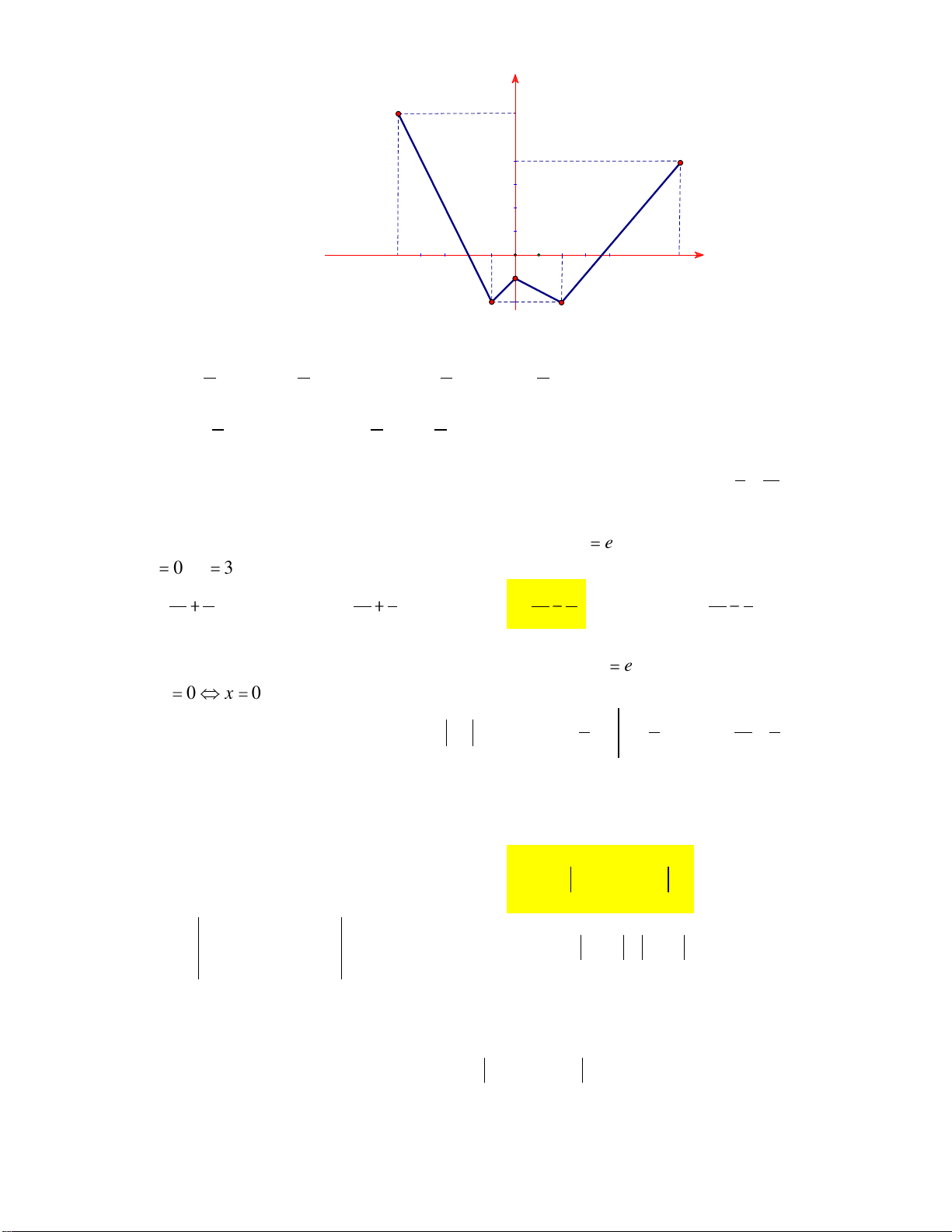
Câu 5: Cho hàm số f  x có đồ thị trên đoạn 3; 
3 là đường gấp khúc ABCD như hình vẽ. y B 1 C 3 A x -2 1 -2 D 3 Tính f  xdx . 3    A. 5 . B. 35 . C. 5 . D. 35 . 2 6 2 6
Câu 6: Cho hàm số y  f x liên tục trên đoạn 2; 2 
 , có đồ thị tạo với trục hoành một hình phẳng
gồm 3 phần có diện tích S ; S ; S như hình vẽ bên dưới: 1 2 3 y
f(x) S2 1 2 x -2 O S1 S3 2
Tích phân  f xdx bằng 2
A. S  S  S .
B. S  S  S .
C. S  S  S .
D. S  S  S . 2 3 1 1 2 3 1 2 3 1 2 3
Câu 7: Cho hàm số f  x có đạo hàm f  x liên tục trên
và đồ thị của f  x trên đoạn 2;6
như hình bên dưới. Khẳng định nào dưới đây đúng? y 3 (C): y = f(x) 1 x 2 1 O 2 6 A. f  2
   f  
1  f 2  f 6 .
B. f 2  f  2
   f   1  f 6 . C. f  2
   f 2  f   1  f 6 .
D. f 6  f 2  f  2
   f   1 .
Câu 8: Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y  x , 2
y  x  2 . 13 11 20 A. S  . B. S  3. C. S  . D. S  . 3 2 3
Câu 9: Cho hàm số y  f x. Đồ thị hàm số y  f x như hình bên. y
Đặt gx  f x  x  2 2
1 . Khẳng định nào sau đây đúng? 1
f ('x)
A. g3  g1  g0. B. g 
1  g0  g3. 3 x
C. g0  g3  g1. D. g 
1  g3  g0. O 1 -2
Câu 10: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y  e   1 x và  1 x y
 e  x là. 3 e e A. 1. B. 2  . C. 2 . D. 1 . e 2 2 Câu 11: Cho y
f (x) là hàm số đa thức bậc ba có đồ thị như hình vẽ bên dưới: y 2 O 1 2 3 x
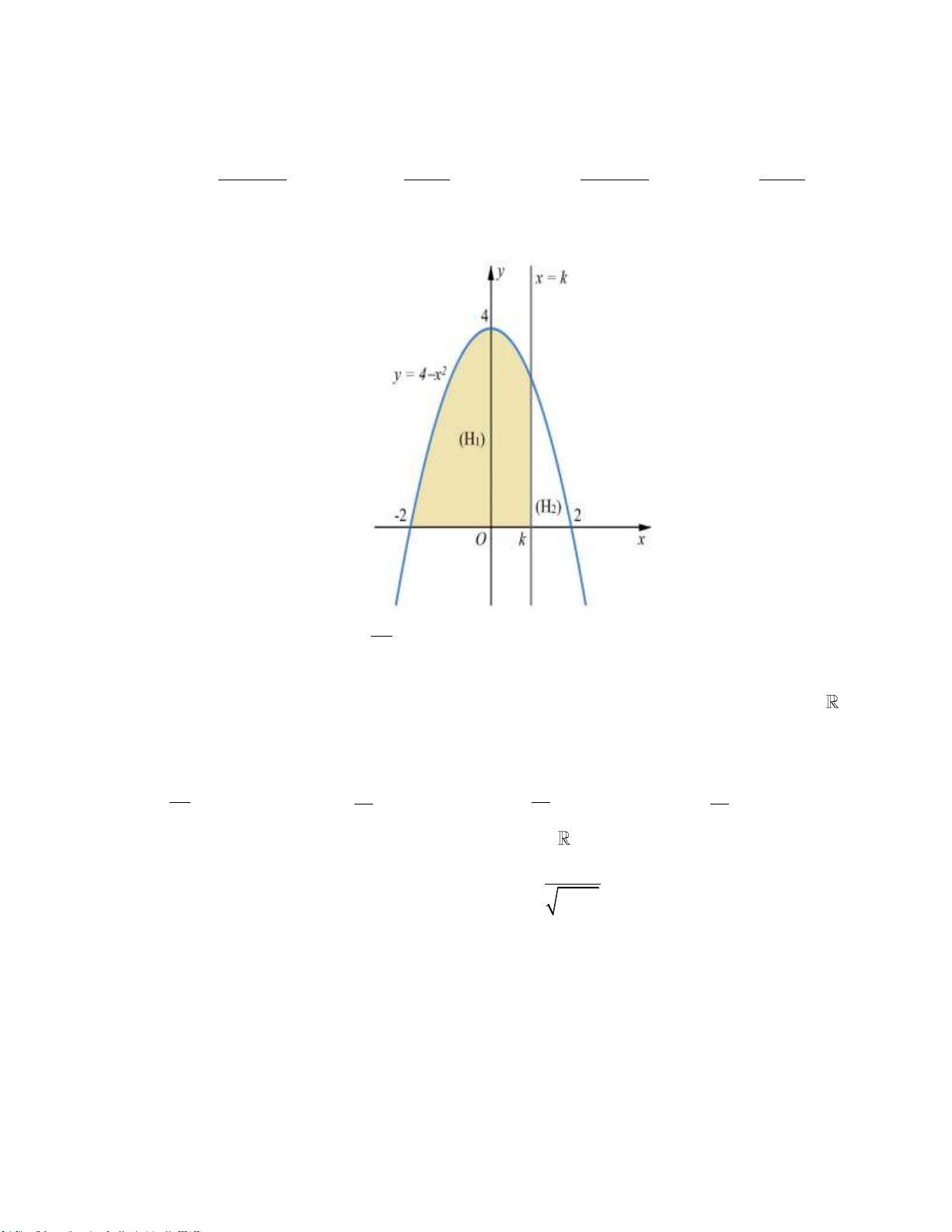
Tính diện tích hình phẳng được tô đậm. 9 37 5 8 A. . B. . C. . D. . 4 12 12 3 Câu 12: Cho hàm số 4 2
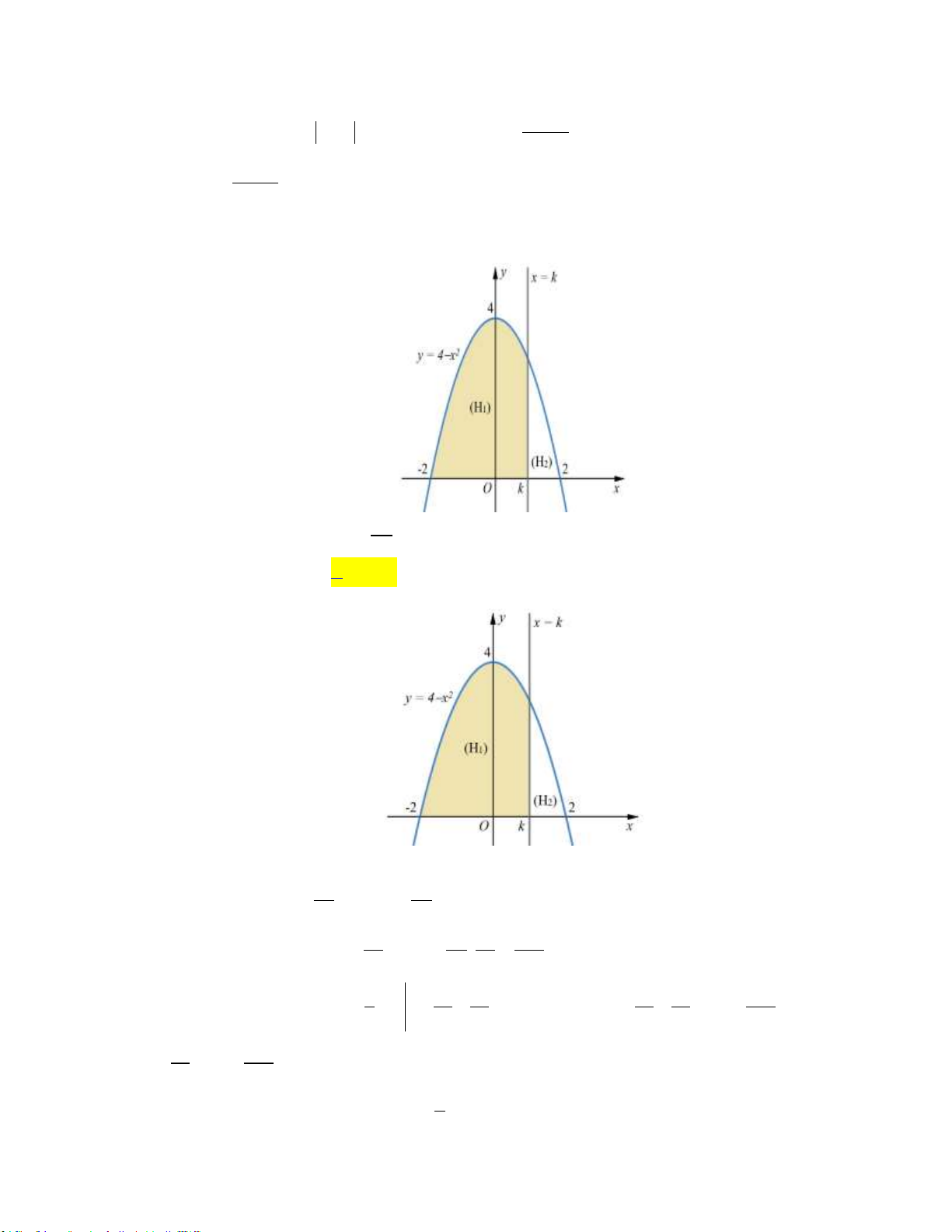
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox m  m 
tại bốn điểm phân biệt như hình vẽ
Gọi S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để 1 2 3
S  S  S là 1 3 2 5 5 5 5 A.  B. C.  D. 2 4 4 2
Câu 13: Cho hàm số y  f (x) có đồ thị trên đoạn [  2;6] như hình vẽ bên dưới. Biết các miền , A B, C
có diện tích lần lượt là 32, 2 và 3 . 2   3  Tích phân 2 I 
(3x  4) 1 f  x  2x  5 dx     bằng   4  2  1 A. I  B. I  82 . C. I  66 . D. I  50 . 2
Câu 14: Biết rằng hình phẳng  H  giới hạn bởi các đường thẳng y  2  x , y  0 , x  k , x  3 k  2
và có diện tích bằng S . Xác định giá trị k để S  16 . k k A. k  2   15 . B. k  2  31 . C. k  2  15 . D. k  2   31 .
Câu 15: Trong mặt phẳng cho hai đường tròn C và C (tham khảo hình vẽ dưới đây). 2  1  y C 2 2 (C1) 1 2 O 1 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) gần nhất với giá trị bằng A. 1,04. B. 2,21. C. 1,71. D. 1,45.
Câu 16: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao GH  4m , chiều rộng AB  4m ,
AC  BD  0, 9m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng 2
/m , còn các phần để trắng làm xiên hoa có giá là 900000 đồng 2 /m . Hỏi
tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000 đồng. B. 4077000 đồng. C. 7368000 đồng. D. 11370000 đồng. 1 4
Câu 17: Tính diện tích hình phẳng giới hạn bởi các đường 2
y  x , y   x  và trục hoành. 3 3 11 61 343 39 A. . B. . C. . D. . 6 3 162 2
Câu 18: Trong mặt phẳng cho elip và đường tròn như hình vẽ. y 20 40 O x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 593,92. B. 602,22. C. 570,14. D. 613,02. 3 1
Câu 19: Cho đường thẳng y  x và parabol 2 y 
x  a ( a là tham số thực dương). Gọi S , S lần 1 2 4 2
lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.
Khi S  S thì a thuộc khoảng nào dưới đây? 1 2  1 9   7 1   3 7   3  A. ;  . B. ;  . C. ;   . D. 0;   .  4 32   32 4  16 32   16 
Câu 20: Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 3 f (x) 4x
x trục hoành và hai đường thẳng x 0, x
2 (tham khảo hình vẽ bên dưới). Đường thẳng y (a
b )x (với a, b là các số nguyên dương) chia (H ) thành hai phần có
diện tích bằng nhau. Giá trị của biểu thức a b bằng A.12 . B. 4 . C.16 . D.14 .
____________________________HẾT____________________________
Huế, 11h00’ Ngày 11 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 3_TrNg 2022
LỜI GIẢI CHI TIẾT
Câu 1: Cho hàm số y  f x liên tục trên . Gọi D là diện tích hình phẳng giới hạn bởi đồ thị
C: y  f x, trục hoành, hai đường thẳng x  2 , x  4 (tham khảo hình vẽ bên dưới). y
f(x) -2 1 4 x O
Giả sử S là diện tích hình phẳng D . Mệnh đề nào dưới đây sai? D 4 4
A. S   f x d . x B. S  f x x D   d . D 2 2 1 4 1 4 C. S 
f xdx  
 f xdx . D. S  f x x f x x . D  d     d D 2 1 2 1
Câu 2: Diện tích hình phẳng giới hạn bởi các đường 2
y  x  x , y  2x  2 , x  0 , x  3 được tính bởi công thức 3 2 A. S   2
x  3x  2dx . B. 2 S 
x  3x  2 dx  . 0 1 3 2 C. 2 S 
x  3x  2 dx  . D. 2 S 
x  x  2 dx  . 0 1 Lời giải: 3 3 Ta có S    2
x  x  2x  2 2 dx 
x  3x  2 dx  . 0 0
Chọn đáp án C. 
Câu 3: Diện tích của hình phẳng giới hạn bởi các đường 2
y  cos x ; y  0 và x  0; x  bằng 4  1   1  A.  . B. 1. C.  . D. . 4 2 4 8 4 8 Lời giải:
Diện tích hình phẳng cần tìm là:     4 4 4 4 1 1  1   1 2 2 S 
cos x dx  cos xdx   
1 cos2xdx  x  sin2x     . 2 2  2  8 4 0 0 0 0
Chọn đáp án C.
Câu 4: Diện tích hình phẳng giới hạn bởi các đường 2
y  x và y  x  2 là 9 9 8 A. S  9 . B. S  . C. S  . D. S  . 4 2 9 Lời giải:  x  
Phương trình hoành độ giao điểm là: 2 x  x  1 2   . x  2 2 2 3 2  x x  9 Ta có 2 S 
x  x  2 dx 
    2x  .  3 2  2 1  1 
 Chọn đáp án C.
Câu 5: Cho hàm số f  x có đồ thị trên đoạn 3; 
3 là đường gấp khúc ABCD như hình vẽ. y B 1 C 3 A x -2 1 -2 D 3 Tính f  xdx . 3  5 35 5  35  A. . B. . C. . D. . 2 6 2 6 Lời giải: y B 1 C E A A 3 2 1 A A3 x -2 1 -2 D
Phương trình đường thẳng CD đi qua C 1; 
1 và nhận CD  2; 3
  làm véctơ chỉ phương. x  y 
Phương trình chính tắc CD 1 1 :   3
 x  2y  5  . 2 3 
Đặt E  CD  Ox .  5  3
 x  2y  5 x   5  Ta được    3  E ; 0   .  y  0   3   y  0 Do đó 3 5 2  1 3
f  x dx   f
 x dx f  x 3 dx  f
 x dx f x dx  5   3  3  2  1 3  1 1  2  1  4  S  S  S  S  11  31  1   2 1 1 4 5      AB         3 . 1 A 1 A B 2 CA 2 A CE ED 3 A 2 2  3  2  3  2 3 3 2
Chọn đáp án A.
Câu 6: Cho hàm số y  f x liên tục trên đoạn 2; 2 
 , có đồ thị tạo với trục hoành một hình phẳng
gồm 3 phần có diện tích S ; S ; S như hình vẽ bên dưới: 1 2 3 y
f(x) S2 1 2 x -2 O S1 S3 2
Tích phân  f xdx bằng 2
A. S  S  S .
B. S  S  S .
C. S  S  S .
D. S  S  S . 2 3 1 1 2 3 1 2 3 1 2 3 Lời giải:
Ta có đồ thị hàm số y  f x cắt trục hoành tại điểm có hoành độ x  2 ; x  0 ; x  1 ; x  2 . 2 0 1 2 Ta có:
f xdx  f xdx  f xdx    
 f xdx  S S S . 1 2 3 2 2 0 1
Chọn đáp án D.
Câu 7: Cho hàm số f  x có đạo hàm f  x liên tục trên
và đồ thị của f  x trên đoạn 2;6
như hình bên dưới. Khẳng định nào dưới đây đúng? y 3 (C): y = f(x) 1 x 2 1 O 2 6 A. f  2
   f  
1  f 2  f 6 .
B. f 2  f  2
   f   1  f 6 . C. f  2
   f 2  f   1  f 6 .
D. f 6  f 2  f  2
   f   1 . Lời giải:
Dựa vào đồ thị của hàm f  x trên đoạn 2;6 ta suy ra bảng biến thiên của hàm số f  x
trên đoạn 2;6 như sau:  f  2
   f   1 
Dựa vào bảng biến thiên ta có  f 2  f   1 nên A, D sai.  f
 2  f 6 y 3 (C): y = f(x) 1 S1 x 2 1 O S 2 6 2
Ta cần so sánh f 2 và f 2.
Gọi S , S là diện tích hình phẳng được tô đậm như trên hình vẽ. 1 2 1  1  Ta có: S 
f  x dx   f 
 xdx  f  1 f  2   . 1   2  2  2 2 S 
f  x dx    f 
 xdx  f  1 f 2. 2   1  1 
Dựa vào đồ thị ta thấy S  S nên f   1  f  2
   f  
1  f 2  f  2
   f 2 . 1 2
Chọn đáp án B.
Câu 8: Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y  x , 2
y  x  2 . 13 11 20 A. S  . B. S  3. C. S  . D. S  . 3 2 3 Lời giải:  x  2 x  2  Xét phương trình: 2
x  x  2     . 4 2
x 5x  4  0  x  2 2 20
Diện tích hình phẳng cần tìm: 2 S 
x  x  2 dx   . 3 2 
Chọn đáp án D.
Câu 9: Cho hàm số y  f x. Đồ thị hàm số y  f x như hình bên. y
Đặt gx  f x  x  2 2
1 . Khẳng định nào sau đây đúng? 1
f ('x)
A. g3  g1  g0. B. g 
1  g0  g3. 3 x
C. g0  g3  g1. D. g 
1  g3  g0. O 1 -2 Lời giải: x  0 
Ta có gx  2 f x  2x  1  2  f 
 x  x  1 ;
 gx  0  f x  x  1  x  1  . x  3  Bảng biến thiên: y 1
f '(x) x  0 1 3  3 x O 1
gx  0  0  0   g1  -2
g x g 0 g 3 d
Suy ra g0  g 
1 và g 3  g1 . 1 3 1 3 1 1
Theo hình vẽ  f 
 xx  1dx   
x  1 fxdx  g 
 xdx   g  xdx 2 2 0 1 0 1
 gx 1  gx 3  g 
1  g 0  g3  g1  g3  g0 . Vậy g 
1  g0  g3. . 0 1
Chọn đáp án B.
Câu 10: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y  e   1 x và  1 x y
 e  x là. 3 e e A. 1. B. 2  . C. 2 . D. 1 . e 2 2 Lời giải:
Ta có: Phương trình hoành độ giao điểm của hai đường cong là    1  1 x e x  e  x .
Suy ra x  0; x  1 . 1 e
Do đó S   1 e x 1 x
 e  x dx  ...  1. 2 0
Chọn đáp án D. Câu 11: Cho y
f (x) là hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng được tô đậm. y 2 O 1 2 3 x 9 37 5 8 A. . B. . C. . D. . 4 12 12 3 Lời giải: Giả sử 3 2
f (x)  ax  bx  cx  d có đồ thị (C) như hình vẽ trên. Điểm 3 2
O(0; 0)  (C)  d  0  f (x)  ax  bx  cx .
a  b  c  0 a  1    Các điểm 3 2 (
A 1; 0), B(2; 2), D(3; 0)  (C)  4a  2b  c  1  b
  4  f (x)  x  4x  3x .  
9a  3b  c  0 c  3   
Diện tích hình phẳng cần tìm là 1
S  0  f (x) 3
dx   f (x)  0 1 3 37 3 2 3 2
dx  (x  4x  3x)dx  (x  4x  3x)dx  .   12 0 1 0 1
Chọn đáp án B. Câu 12: Cho hàm số 4 2
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox m  m 
tại bốn điểm phân biệt như hình vẽ
Gọi S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để 1 2 3
S  S  S là 1 3 2 5 5 5 5 A.  B. C.  D. 2 4 4 2 Lời giải:
Gọi x là nghiệm dương lớn nhất của phương trình 4 2
x  3x  m  0 , ta có 4 2
m  x  3x   1 . 1 1 1 x1
Vì S  S  S và S  S nên S  2S hay f
 xdx  0. 1 3 2 1 3 2 3 0 x x 1 x 1 1 5  x  5 x 4  x 
Mà f  xdx    4 2
x  3x  mdx 3
   x  mx 1 3   x  mx 1 2
 x   x  m .  5  1 1 5 1 1  5  0 0 0 4  x  4 x Do đó, 1 2 x 
 x  m  0  1 2
 x  m  0 2 . 1 1  5  1 5 4 x 5 Từ  
1 và 2 , ta có phương trình 1 2 4 2
 x  x  3x  0  4 2
4x 10x  0  2 x  . 1 1 1 5 1 1 1 2 Vậy 4 2 m  x  5 3x  . 1 1 4
Chọn đáp án B.
Câu 13: Cho hàm số y  f (x) có đồ thị trên đoạn [  2;6] như hình vẽ bên dưới. Biết các miền , A B, C
có diện tích lần lượt là 32, 2 và 3 . 2   3  Tích phân 2 I 
(3x  4) 1 f  x  2x  5 dx     bằng   4  2  1 A. I  B. I  82 . C. I  66 . D. I  50 . 2 Lời giải: 3  3  Đặt 2 t  
x  2x  5  dt   x  2 dx   
3x  4dx  2  dt 4  2 
Đổi cận: - Với x  2   t  2 
-Với x  2  t  6 6 6 6 Ta được: I  2  1   f  
tdt  2  dt  2 f  
 tdt  1  6  2M . 2  2  2  6 2 4 6 Với M  f
 tdt  f
 tdt  f
 tdt  f
 tdt  3  2  2  3  3  3 . 2  2  2 4 Vậy: I  16   2. 33    50 .
Chọn đáp án D.
Câu 14: Biết rằng hình phẳng  H  giới hạn bởi các đường thẳng y  2  x , y  0 , x  k , x  3 k  2
và có diện tích bằng S . Xác định giá trị k để S  16 . k k A. k  2   15 . B. k  2  31 . C. k  2  15 . D. k  2   31 . Lời giải: 3 2 3 2 3 S  2  x dx 
2  x dx  2  x dx   
 2 xdx  2 xdx k k k 2 k 2  1   1  1 5 2
 2  2k  k       2
 k  2k   2   2  2 2 2 3  1   1  2 2  2x  x  2x  x      2   2  k 2 1 5 1 27 k  2  31
Mà S  16 nên suy ra 2 k  2k   16 2  k  2k   0   . k 2 2 2 2 k  2  31
Vì k  2 nên k  2  31 .
Chọn đáp án B.
Câu 15: Trong mặt phẳng cho hai đường tròn C và C (tham khảo hình vẽ dưới đây). 2  1  y C 2 2 (C1) 1 2 O 1 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) gần nhất với giá trị bằng A. 1,04. B. 2,21. C. 1,71. D. 1,45. Lời giải: y C 2 2 S1 (C1) 1 2 O 15 x 4  2 y  4  x
Phương trình đường tròn C là 2 2
x  y  4   . 1  2 y   4   x
y  2  1 x
Phương trình đường tròn C là x  y  2 2 2 2  1   . 2  2 y  2  1  x  7  15 2 2    4 y   x x y    Xét hệ phương trình: 4      4 x   y  2 . 2 2  1   2 2 15 15
x  4  y  x    16  4 15 4 Diện tích cần tính là 2 S S 2S        2 4  x     2 2  1  x x  1,71. C 1    d  2  0 15 4  
Cách 2: S  2   2 2  1  x  2
 4  x dx  1,71  . 0
Chọn đáp án C.
Câu 16: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao GH  4m , chiều rộng AB  4m ,
AC  BD  0, 9m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng 2
/m , còn các phần để trắng làm xiên hoa có giá là 900000 đồng 2 /m . Hỏi
tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000 đồng. B. 4077000 đồng. C. 7368000 đồng. D. 11370000 đồng. Lời giải:
Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox , A trùng O khi đó parabol có đỉnh G 2; 4
và đi qua gốc tọa độ.
Giả sử phương trình của parabol có dạng 2
y  ax  bx  c a  0 . c  0  a  1   b 
Vì parabol có đỉnh là G 2; 4 và đi qua điểm O 0;0 nên ta có   2  b  4 . 2a  c  0 2    .2 a  .2 b  c  4
Suy ra phương trình parabol là 2
y  f (x)  x  4x . 4 4 3  x  32
Diện tích của cả cổng là S   2 x  4x 2 dx     2x    2 m  .  3  3 0 0
Mặt khác chiều cao CF  DE  f 0,9  2,79(m) ; CD  4  2.0,9  2, 2 m . 2
Diện tích hai cánh cổng là S  . CD CF  6,138 m CDEF . 32 6793
Diện tích phần xiên hoa là S  S  S   6,14  . xh CDEF  2 m  3 1500 6793
Vậy tổng số tiền để làm cổng là 6,138.1200000  .900000  11441400 đồng. 1500
Chọn đáp án A. 1 4
Câu 17: Tính diện tích hình phẳng giới hạn bởi các đường 2
y  x , y   x  và trục hoành. 3 3 11 61 343 39 A. . B. . C. . D. . 6 3 162 2 Lời giải: 1 4
Phương trình hoành độ giao điểm của các đường 2
y  x , y   x  là 3 3 x  1 1 4 2  x   x  2
 3x  x  4  0  4 . 3 3 x    3 1 4
Hoành độ giao điểm của đường thẳng y   x 
với trục hoành là x  4 . 3 3
Hoành độ giao điểm của parabol 2
y  x với trục hoành là x  0 .
Diện tích hình phẳng cần tìm là: 1 4  1 4 1 4  3 x  1 4  11 2
S  x d x   x  d x    2    x  x    .  3 3  3  6 3  6 0 1 0 1
Chọn đáp án A.
Câu 18: Trong mặt phẳng cho elip và đường tròn như hình vẽ. y 20 40 O x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 593,92. B. 602,22. C. 570,14. D. 613,02. Lời giải:
y  20  400  x
Đường tròn có phương trình là: x  y  20 2 2 2  400   . 2 y  20  400   x  2  x  y  4001  2 2   1600 x y  Elip có phương trình là:   1   . 1600 400 2   x 
y   4001     1600 
x  y  202 2  400  Xét hệ phương trình: 2 2 2  x y  y  2  
 1  x  16001  1600 400  400      2  0  20 13    2 y 17,37  y       y  2 2         3 1600 1 20 400 3y 40y 1600 0 .  400     2  0  20 13 y   3 2  0  20 13 Xét y   x  19,83. 3 19 ,83  2   x  Lúc đó: 2 S  2  400  1 
  20  400  x  dx  593,92. g¹ch     1600   0  
Chọn đáp án A. 3 1
Câu 19: Cho đường thẳng y  x và parabol 2 y 
x  a ( a là tham số thực dương). Gọi S , S lần 1 2 4 2
lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.
Khi S  S thì a thuộc khoảng nào dưới đây? 1 2  1 9   7 1   3 7   3  A. ;  . B. ;  . C. ;   . D. 0;   .  4 32   32 4  16 32   16  Lời giải: 1 3 1 3
Xét phương trình hoành độ giao điểm 2 2 x  a  x  x 
x  a  0 * . 2 4 2 4 3 1
Do đường thẳng y  x cắt parabol 2 y 
x  a tại hai điểm phân biệt có hoành độ dương 4 2
nên phương trình * có hai nghiệm dương phân biệt 0  x  x 1 2   0  9    2a  0 9  S  0  16   0  a  . 32   P  0  2a  0 Ta có: 1 x  1 3  2 x 2 x     2 3 1 1 3 S  x  a  x dx  ; 2 2 S  x 
x  a dx   x  a  x dx   . 1        2 4  2  4 2   2 4  0 1 x 1 x 1 x 2 x  1 3   1 3  2 2
S  S  S  S  0  x  a  x dx  x  a  x dx  0   1 2 1 2      2 4   2 4  0 1 x x 2 x 2 3  1 3   x 3  2 2  x  a  x dx  0     
 ax  x   0  2 4   6 8  0 0 1 3 1 3 3 2 2
 x  ax  x  0  x  a  x  0 . 2 2 2 2 2 6 8 6 8 1 3
Mà x là nghiệm phương trình * nên 2 x  x  a  0 . 2 2 2 2 4 x  0 L 2   1 3 
Trừ vế với vế hai phương trình được: 2
 x  x  0  . 2 2 9 3 8 x  TM 2    8 9 27  3 7  Với x  27  a  (tm). Vậy a   ; . 2   8 128 128 16 32 
Chọn đáp án C.
Câu 20: Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 3 f (x) 4x
x trục hoành và hai đường thẳng x 0, x
2 (tham khảo hình vẽ bên dưới). Đường thẳng y (a
b )x (với a, b là các số nguyên dương) chia (H ) thành hai phần có
diện tích bằng nhau. Giá trị của biểu thức a b bằng A.12 . B. 4 . C.16 . D.14 . Lời giải:
Phương trình hoành độ giao điểm: 3 f (x) 0 4x x 0 x 0, x 2 . 2
Diện tích miền (H ) là: 3 S (4x x )dx 4 . 0
Giả sử đường thẳng y
kx chia miền (H ) thành 2 phần có diện tích bằng nhau và bằng 2 .
Xét phương trình hoành độ giao điểm: 3 4x x kx x 0, x 4 k . 4 k 2 4 2 2 2 x x 4 k (4 k) (4 k) (4 k) Ta có: 3 2 ((4 k)x x )dx (4 k). 2 4 0 2 4 4 0 4 k 2 2 2 (4 k) 8 k 4 2 2 a 4, b 8 a b 12 . 4 k 2 2
Chọn đáp án A.
____________________________HẾT____________________________
Huế, 11h00’ Ngày 11 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
ĐỀ ÔN TẬP SỐ 4_TrNg 2022
DIỆN TÍCH HÌNH PHẲNG Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Cho hai hàm số y  f  x và y  g  x liên tục trên đoạn  ;
b a . Gọi D là diện tích hình
phẳng giới hạn bởi các đồ thị hàm số y  f  x , y  g  x và hai đường thẳng
x  a, x  b a  b , diện tích của D được tính theo công thức nào dưới đây? b b b b a
A.  f x  g xdx . B. S  f
 xdx g
 xdx .C. f
 x gxdx .D. f
 x gxdx . a a a a b
Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  4 , trục hoành và các đường thẳng
x  0 , x  3 là: 32 25 23 A. . B. 3. C. . D. . 3 3 3
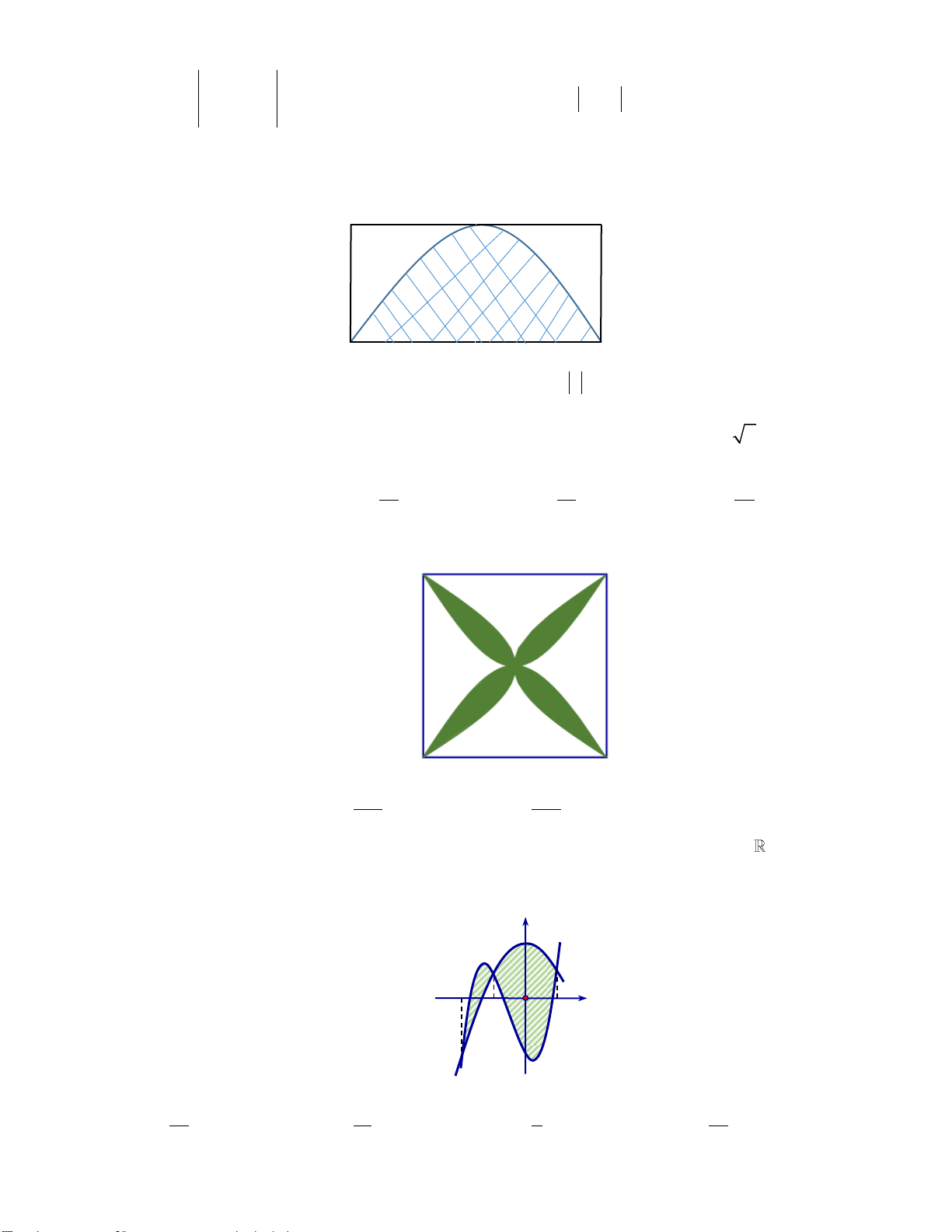
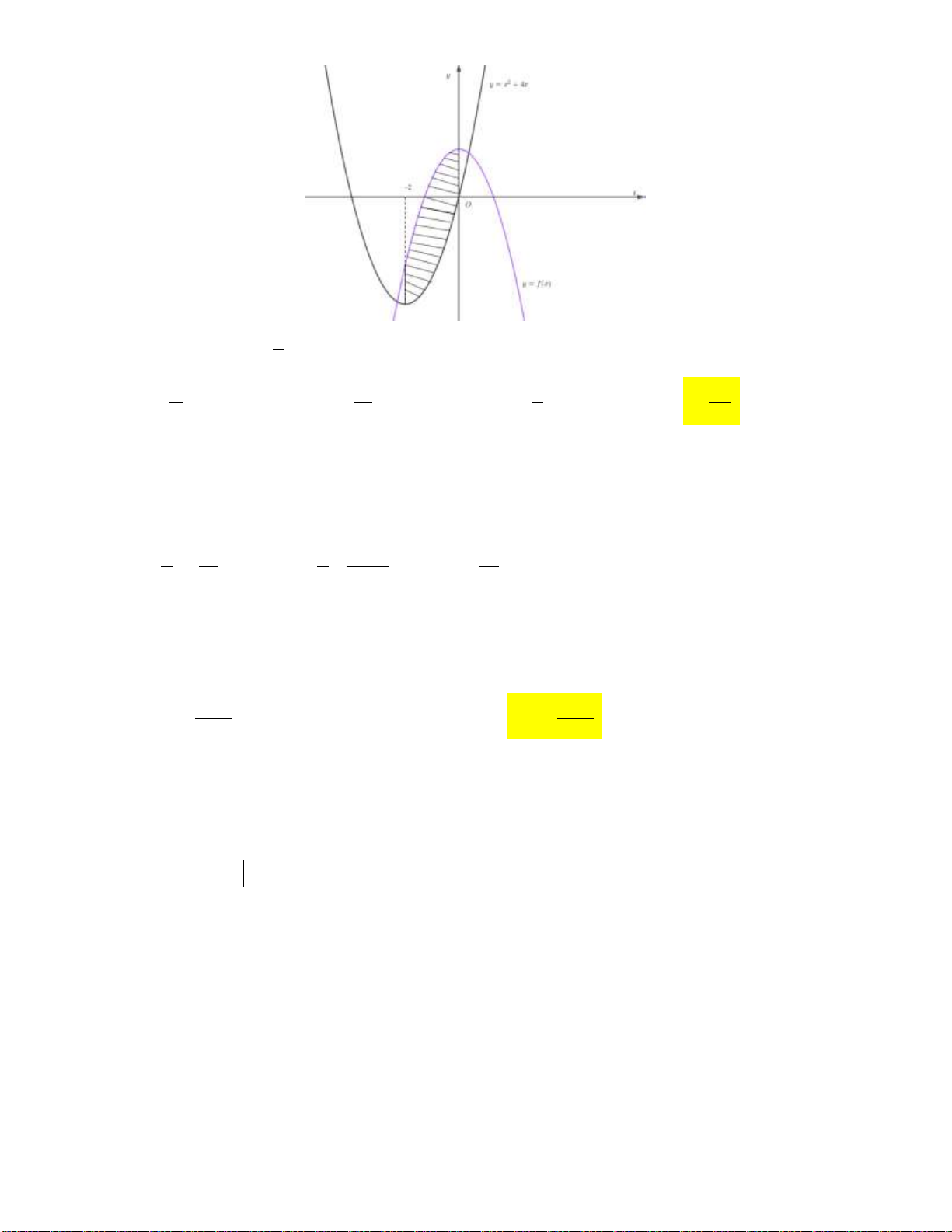
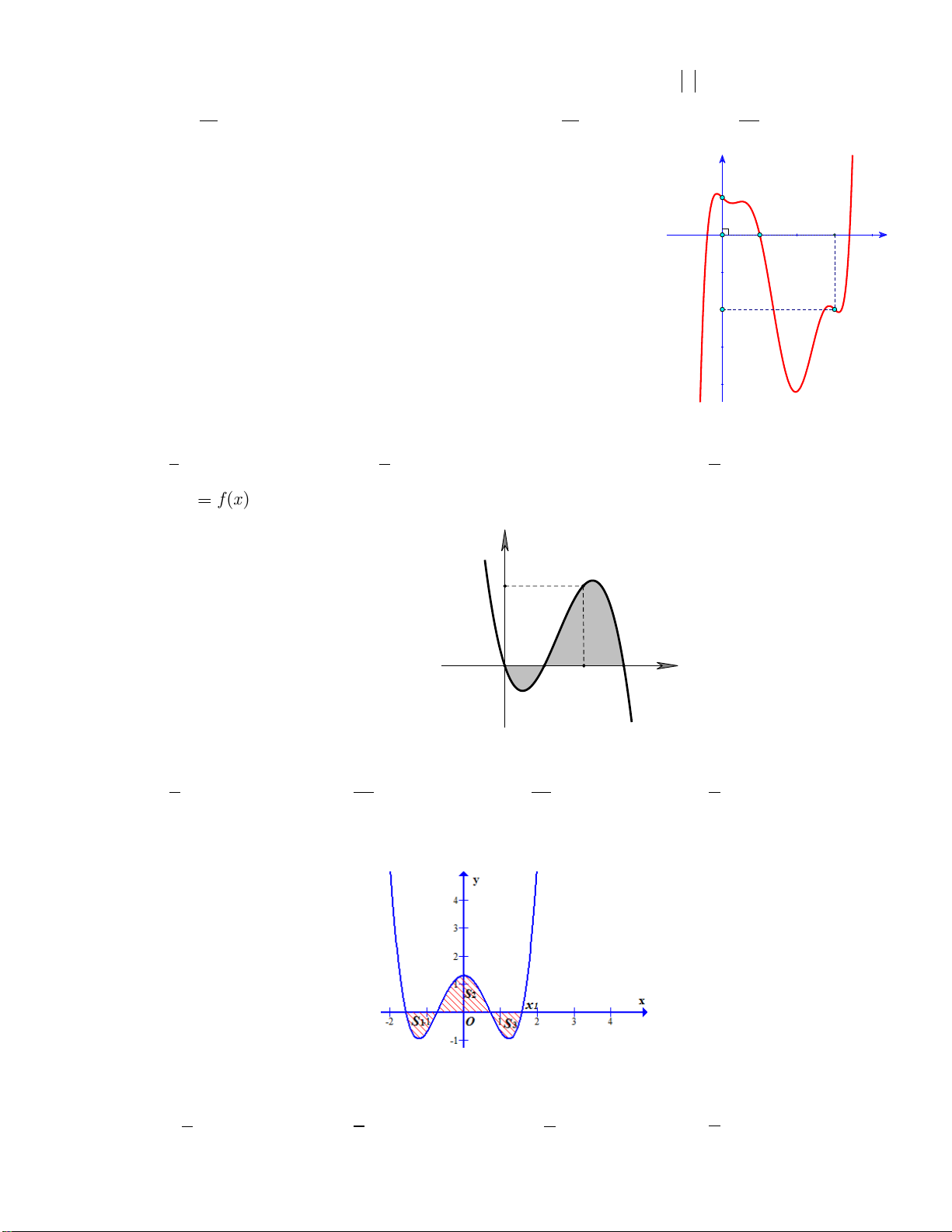
Câu 3: Cho hàm số bậc bốn y  f x liên tục trên . Gọi H là hình phẳng giới hạn bởi đồ thị
C: y  f x (tham khảo hình vẽ bên dưới). y 1 2 x -2 O
Mệnh đề nào dưới đây sai? 2 0 1 2
A. S   f x d . x B. S  f x x f x x f x x H   d    d       d . H 2 2 0 1 0 1 2 0 2
C. S   f xdx  f xdx   
 f xd .x D. S  f x x f x x H  d     d . H 2 0 1 2 0
Câu 4: Trong mặt phẳng cho đường tròn C và parabol P (tham khảo hình vẽ dưới đây). y 3 2 1 O 1 2 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 11,04. B. 12,04. C. 9,13. D. 13,13.
Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số: 3 2
y  x  2x  2x 1 và đường thẳng
y  x 1 là: 37 9 8 5 A. . B. . C. . D. . 12 4 3 12
Câu 6: Diện tích S của hình phẳng D được giới hạn bởi parabol  P 2
: y  x  2x và đường thẳng
d : y  x  4 xác định bởi công thức nào dưới đây? 4 4 2 A. S     2
x  3x  4 dx . B. S    2
x  3x  4dx . 1  1  4 4 C. S    2
x  3x  4dx . D. S   2
x  3x  4dx. 1  1
Câu 7: Biết đồ thị hàm số bậc ba f  x cắt đường thẳng g  x tạo thành các hình phẳng có diện tích
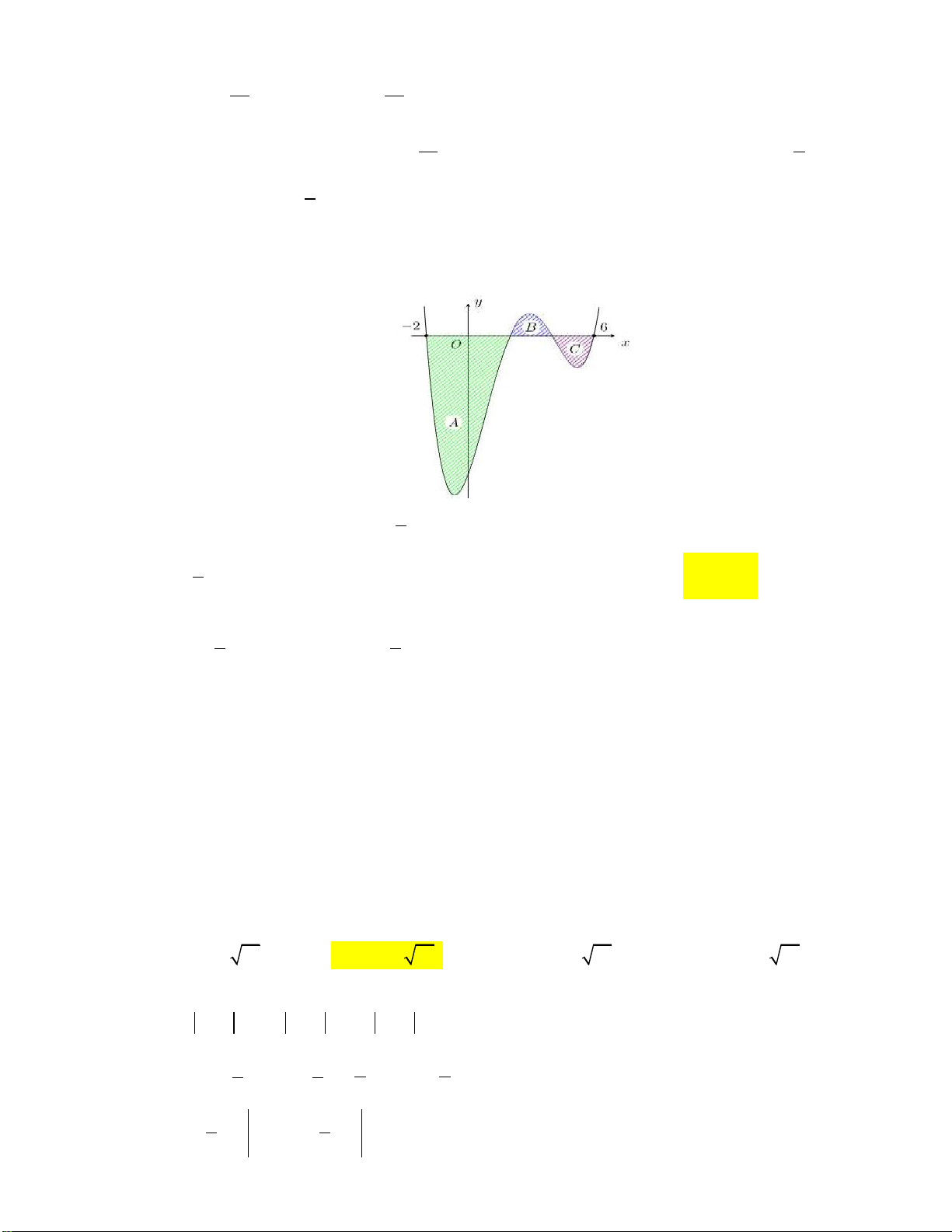
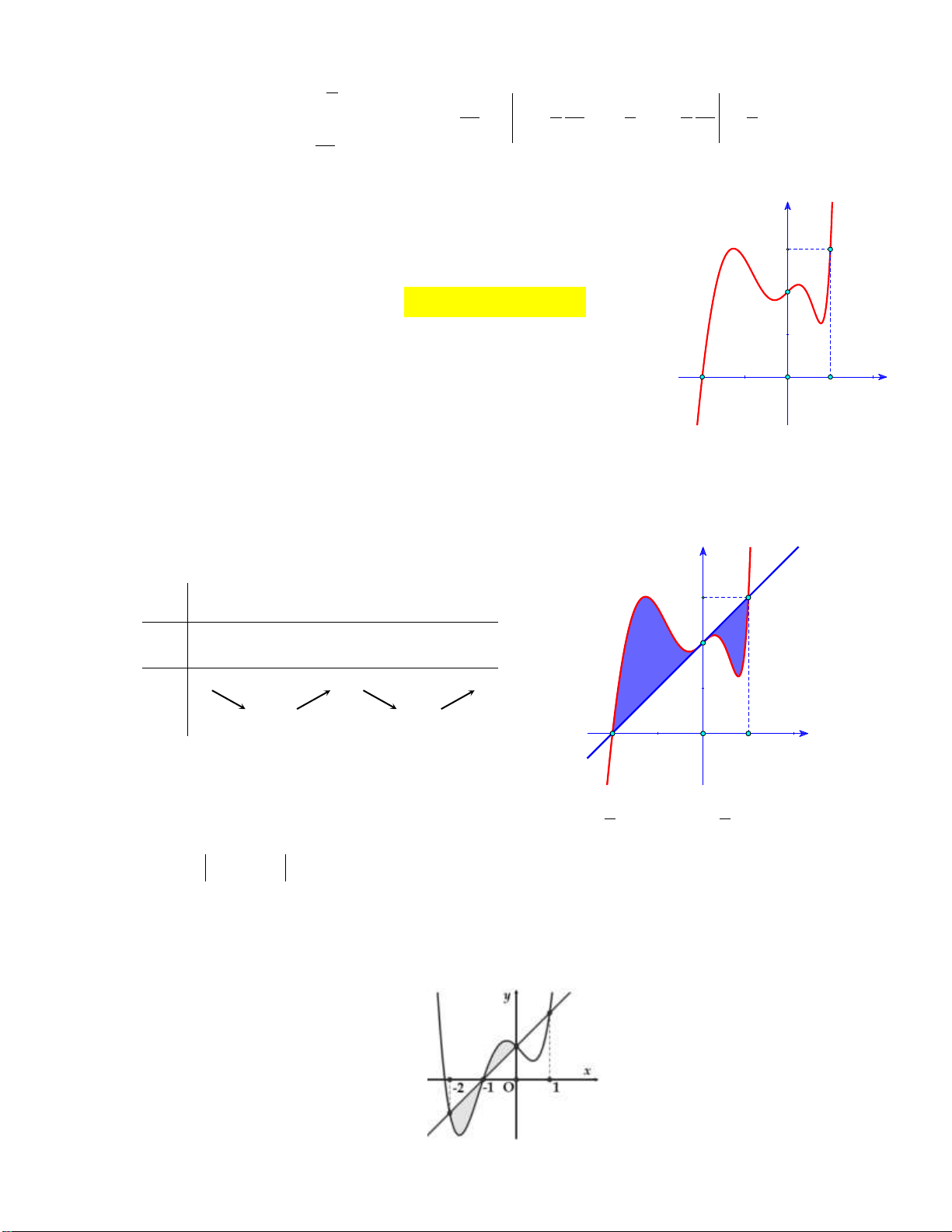
S , S như hình vẽ bên dưới: 1 2 y
f(x) S1 S2 -2 x O 2
g(x) 2
Tính I    f x  g x  2d .x 2 
A. I  S  S  2.
B. I  S  S  8.
C. I  S  S  8.
D. I  S  S  2. 1 2 1 2 1 2 1 2 Câu 8: Kí hiệu S t  là diện tích hình phẳng giới hạn bởi các đường
y  2x 1, y  0, x  1, x  t, t  
1 . Tìm t để S t   10 . A. t  4 . B. t  13 . C. t  3 . D. t  14 .
Câu 9: Cho mảnh đất hình vuông ABCD có cạnh bằng 40 m, M, N , I lần lượt là trung điểm AD, BC, .
AB Biết đường cong là parabol đỉnh I (tham khảo hình vẽ). I A B M N D C
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 2 203,15 m . B. 2 487,59 m . C. 2 601,25 m . D. 2 450,35 m .
Câu 10: Cho hàm y  F  x là một nguyên hàm của hàm số y  f  x , biết đồ thị hàm số y  f  x 22 76
trên đoạn 2; 2 như hình vẽ ở bên dưới và có diện tích S  S  , S  . 1 2 3 15 15
Giá trị của biểu thức F 2  F   1  F   1  F  2   bằng 36 32 18 32 A. I  . B. I  . C. I  . D. I   . 5 15 5 15
Câu 11: Tính diện tích hình phẳng được đánh dấu trên hình dưới: 28 1 18 2 A. S  . B. S  3 2  . C. S  . D. S  2 3  . 3 3 3 3 x 1
Câu 12: Cho hình phẳng  H  giới hạn bởi đồ thị hàm số y  y  ,
x  và hai đường thẳng 2 2
y  x 1 (tham khảo hình vẽ).
Tính diện tích S của hình phẳng  H  . A. S  8  3ln 3 . B. S  8  3ln 3 . C. S  3ln 3 .
D. S  4  3ln 3 .
Câu 13: Trong mặt phẳng cho elip và hai đường thẳng như hình vẽ bên dưới: y 20 10 O 40 x -10
Diện tích phần không tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 2 1203,15 m . B. 2 1350,25 m . C. 2 1530,58 m . D. 2 1450,35 m .
Câu 14: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện
một dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.
Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật
ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho 1 2
m . Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ? A. 1.230.000 đồng. B. 900.000 đồng. C. 1.232.000 đồng. D. 902.000 đồng.
Câu 15: Cho hình phẳng (H ) (phần gạch đậm) như hình vẽ bên dưới:
Tính diện tích hình phẳng (H ). 9 9 3 9 A. 1. B. ln 3  2. C. ln 3  . D. ln 3  2. 2 2 2 2
Câu 16: Cho hàm số y  f x. Đồ thị hàm số y  f x như hình bên. y
Đặt g x  f x  x  2 2
2 . Khẳng định nào sau đây đúng? 3
A. g0  g 2
   g1. B. g  1  g 2    g0.
f '(x) 2 C. g 2
   g1  g0. D. g0  g1  g 2  . x -2 O 1 Câu 17: Cho hàm số 4 3 2
y  ax  bx  cx  dx  ,
e (a  0) có đồ thị (C) và đường d : y  mx  n cắt đồ
thị (C) tại các điểm có hoành độ lần lượt là 2; 1; 0; 1. Biết rằng hình phẳng giới hạn bởi
(C), d và đường thẳng x  2, x  0 có diện tích bằng 1.
Diện tích hình phẳng giới hạn bởi đồ thị (C), đường thẳng d , trục tung và đường x  1 bằng 11 19 49 19 A.  B.  C.  D.  30 30 30 15
Câu 18: Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của
hai hình tròn lần lượt là 20 m và 15 m . Khoảng cách giữa hai tâm của hai hình tròn là
30 m .Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 nghìn đồng và chi
phí làm mỗi mét vuông còn lại là 100 nghìn đồng. Hỏi số tiền làm mặt sàn sân khấu gần với
số nào trong các số dưới đây? A. 202 triệu đồng. B. 208 triệu đồng. C. 218 triệu đồng. D. 200 triệu đồng.
Câu 19: Với mọi m thì đường thẳng d : y  mx  2 luôn cắt parabol 2
(P) : y  x 1 tại hai điểm phân
biệt có hoành độ x , x . Tìm m để diện tích của hình phẳng giới hạn bởi d và (P) là nhỏ 1 2 nhất. 4 3 A. m  0 . B. m  . C. m  . D. m  4. 3 4
Câu 20: Cho hàm số bậc ba y  f (x) có đồ thị là đường cong trong hình bên dưới:
Biết hàm số f (x) đạt cực trị tại hai điểm x , x thỏa mãn x  x  4 và f (x )  f (x )  0. Gọi 1 2 2 1 1 2 S
S và S là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số 1 bằng 1 2 S2 5 3 3 A. . B. . C. 1. D. . 3 5 4
____________________________HẾT____________________________
Huế, 15h00’ Ngày 11 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
ĐỀ ÔN TẬP SỐ 4_TrNg 2022
DIỆN TÍCH HÌNH PHẲNG
LỜI GIẢI CHI TIẾT
Câu 1: Cho hai hàm số y  f  x và y  g  x liên tục trên đoạn  ;
b a . Gọi D là diện tích hình
phẳng giới hạn bởi các đồ thị hàm số y  f  x , y  g  x và hai đường thẳng
x  a, x  b a  b , diện tích của D được tính theo công thức nào dưới đây? b b b
A.  f x  g xdx . B. S  f
 xdx g  xdx . a a a b a C. f
 x gxdx . D. f
 x gxdx . a b
Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  4 , trục hoành và các đường thẳng
x  0 , x  3 là: 32 25 23 A. . B. 3. C. . D. . 3 3 3 Lời giải:
Phương trình hoành độ giao điểm giữa 2
(P) : y  x  4 và trục hoành: x  20;3 2
x  4  0   . x  2  0;3
Vậy diện tích hình phẳng là: 2 3 2 S 
x  4 dx  x  4 dx    x 4 3 2 2 2 dx   2 x  4dx 0 2 0 2 2 3 3 3  x   x  16 16 23
   4x    4x   3  .  3   3  3 3 3 0 2
Chọn đáp án D.
Câu 3: Cho hàm số bậc bốn y  f x liên tục trên . Gọi H là hình phẳng giới hạn bởi đồ thị
C: y  f x (tham khảo hình vẽ bên dưới). y 1 2 x -2 O
Mệnh đề nào dưới đây sai? 2 0 1 2
A. S   f x d . x B. S  f x x f x x f x x H   d    d       d . H 2 2 0 1 0 1 2 0 2
C. S   f xdx  f xdx   
 f xd .x D. S  f x x f x x H  d     d . H 2 0 1 2 0
Câu 4: Trong mặt phẳng cho đường tròn C và parabol P (tham khảo hình vẽ dưới đây). y 3 2 1 O 1 2 x
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 11,04. B. 12,04. C. 9,13. D. 13,13. Lời giải: y 3 2 1 O 2 x -4+2 7  2 y  4  x
Phương trình đường tròn là 2 2
x  y  4   . 2 y   4   x Gọi P 2
: y  ax  c (Do P đối xứng qua Oy ) 
A P 1 0;1  c  1 a  1 Ta có:    Vậy P 2
: y  x  1. B
 2; 3P 2 .  4a  c   3  2 c   1 2 2 x  y  4 2 2   1   x  4   2 7  0 Xét hệ phương trình: 2 2 
 x   x  1   4   . 1 2 2 y  x  1  2  x  4   2 7  0  2 x  4  2 7   .  x   4   2 7 4  2 7   1  Diện tích cần tính là 2 2 S  4  2
  4  x  x 1dx 11,04.   2  0 
Chọn đáp án A.
Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số: 3 2
y  x  2x  2x 1 và đường thẳng
y  x 1 là: 37 9 8 5 A. . B. . C. . D. . 12 4 3 12 Lời giải: x 1  Xét phương trình 3 2
x  2x  2x 1  x 1 3 2
 x  2x  x  2  0  x  1  . x  2 
Ta có diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số h(x) và g(x) bằng 2 3 2 S 
x  2x  x  2 dx   8 5 37    . 3 12 12 1 
Chọn đáp án A.
Câu 6: Diện tích S của hình phẳng D được giới hạn bởi parabol  P 2
: y  x  2x và đường thẳng
d : y  x  4 xác định bởi công thức nào dưới đây? 4 4 2 A. S     2
x  3x  4 dx . B. S    2
x  3x  4dx . 1  1  4 4 C. S    2
x  3x  4dx . D. S   2
x  3x  4dx. 1  1 Lời giải:
Phương trình hoành độ giao điểm của  P và d x  1  2 2
x  2x  x  4  x  3x  4  0   . x  4 4 4 Suy ra 2 S 
x  3x  4 dx    2
x  3x  4dx (do 2
x  3x  4  0, x   1;  4). 1  1 
Chọn đáp án B.
Câu 7: Biết đồ thị hàm số bậc ba f  x cắt đường thẳng g  x tạo thành các hình phẳng có diện tích
S , S như hình vẽ bên dưới: 1 2 y
f(x) S1 S2 -2 x O 2
g(x) 2
Tính I    f x  g x  2d .x 2 
A. I  S  S  2.
B. I  S  S  8.
C. I  S  S  8.
D. I  S  S  2. 1 2 1 2 1 2 1 2 Lời giải: 2 2 2
Ta có: I    f x  g x  2dx    f x  g xdx  2dx  2  2  2  0    2
f  x  g  xdx   f x  g xdx  8  S  S  8. 1 2 2  0
Chọn đáp án C. Câu 8: Kí hiệu S t  là diện tích hình phẳng giới hạn bởi các đường
y  2x 1, y  0, x  1, x  t, t  
1 . Tìm t để S t   10 . A. t  4 . B. t  13 . C. t  3 . D. t  14 . Lời giải: t
Ta có S t   2x 1 dx 
. Do x 1;t, t  1 nên 2x 1  0 . 1 t
Khi đó: S t   2x   1 dx   2
x  x t 2
|  t  t  2 . 1 1 t  3
Để S t   10 thì 2 2
t  t  2  10  t  t 12  0   . t  4 
Do t  1nên t  3 thỏa mãn.
Chọn đáp án C.
Câu 9: Cho mảnh đất hình vuông ABCD có cạnh bằng 40 m, M, N , I lần lượt là trung điểm AD, BC, .
AB Biết đường cong là parabol đỉnh I (tham khảo hình vẽ). I A B M N D C
Diện tích phần tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 2 203,15 m . B. 2 487,59 m . C. 2 601,25 m . D. 2 450,35 m . Lời giải: y A 40 I B M N 20 D C O 20 x 10 2 1
Do P có đỉnh là A0; 40 và qua B20;0 nên P 2 : y   x  40. 10  1 2 y   x  40 x  10 2 Xét hệ phương trình: 2  10  x  200   .    x  10  2 y 20 10 2 20   1    1   Diện tích cần tính là 2 S  2     x  40  20 d 2
 x   20    x  40d 2
x  487,59 m .   10     10   0 10 2 
Chọn đáp án B.
Câu 10: Cho hàm y  F  x là một nguyên hàm của hàm số y  f  x , biết đồ thị hàm số y  f  x 22 76
trên đoạn 2; 2 như hình vẽ ở bên dưới và có diện tích S  S  , S  . 1 2 3 15 15
Giá trị của biểu thức F 2  F   1  F   1  F  2   bằng 36 32 18 32 A. I  . B. I  . C. I  . D. I   . 5 15 5 15 Lời giải: 2 22
Ta có: F 2  F   1 
f  xdx  S    . 2 15 1 1
F    F    f  x 76 1 1 dx  S   . 3 15 1  1 
F    F    f  x 22 1 2
dx  S    . 1 15 2  Vậy có : 22 76 22 108
F 2  F   1  2 F    1  F   1   F    1  F  2      2.   15 15 15 15
 F    F    F    F   108 36 2 1 1 2   . 15 5
Chọn đáp án A.
Câu 11: Tính diện tích hình phẳng được đánh dấu trên hình dưới: 28 1 18 2 A. S  . B. S  3 2  . C. S  . D. S  2 3  . 3 3 3 3 Lời giải: Ta có 2
y  x  x   y , từ hình vẽ ta thấy x  0  x   y . 3 3 3 2 2 2 3 S   y dy  xdx  x  3 3   1  2 3    . 3 3 3 1 1 1
Chọn đáp án D. x 1
Câu 12: Cho hình phẳng  H  giới hạn bởi đồ thị hàm số y  y  ,
x  và hai đường thẳng 2 2
y  x 1 (tham khảo hình vẽ).
Tính diện tích S của hình phẳng  H  . A. S  8  3ln 3 . B. S  8  3ln 3 . C. S  3ln 3 .
D. S  4  3ln 3 . Lời giải: Dựa vào đồ thị ta có 3  1  3  1   x 1    S   x    x   3 2 d 1 2 dx  1 dx    x      1 dx  x  2   x  2  5  3  5  3  1     x 
 x  3ln x  2  2
3    x  3ln3. 5   2  3
Chọn đáp án C.
Câu 13: Trong mặt phẳng cho elip và hai đường thẳng như hình vẽ bên dưới: y 20 10 O 40 x -10
Diện tích phần không tô đậm (làm tròn đến chữ số hàng phần trăm) bằng A. 2 1203,15 m . B. 2 1350,25 m . C. 2 1530,58 m . D. 2 1450,35 m . Lời giải:  2  x  y  4001  2 2   1600 x y  Elip có phương trình là:   1   . 1600 400 2   x 
y   4001     1600  y  10   x  20 3 Xét hệ phương trình: 2 2    . x y    1 x  20  3 1600 400 20 3  2   x  Lúc đó: S  40.20  4  400  1 
  10 dx  1530,58. g¹ch   1600   0  
Chọn đáp án C.
Câu 14: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện
một dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.
Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật
ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho 1 2
m . Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ? A. 1.230.000 đồng. B. 900.000 đồng. C. 1.232.000 đồng. D. 902.000 đồng. Lời giải:
Chọn hệ trục tọa độ Oxy như hình vẽ, khi đó ta được phương trình của parabol là 2
y  x  4.
Gọi C  x   x    D x  B  2
x x   A 2 ; 0 0 2 ; 0 , ; 4 ,  ;
x x  4. 2 32
Ta có diện tích của Pano là  2
x  4dx    2 m . 3 2 
Diện tích hình chữ nhật ABCD là S
 CD BC  x  2 . 2 . x  4. ABCD
Chi phí dán hoa văn thấp nhất khi và chỉ khi diện tích hình chữ nhật ABCD lớn nhất. 32 3
Xét hàm số f x  x  2 ( )
2 . x  4, x 0;2 có Max f (x)  . x   0;2 9  32 32 3 
Chi phí thấp nhất cho việc dán hoa văn là   .200000  902.000   đồng. 3 9  
Chọn đáp án D.
Câu 15: Cho hình phẳng (H ) (phần gạch đậm) như hình vẽ bên dưới:
Tính diện tích hình phẳng (H ). 9 9 3 9 A. 1. B. ln 3  2. C. ln 3  . D. ln 3  2. 2 2 2 2 Lời giải: 3
Ta có: diện tích cần tìm là S  x ln xdx  1  1 du  dx u   ln x  2 3 x 2 2 x 3 1 x 9 1 x 3 9 Đặt    khi đó: S  ln x  dx  ln 3   ln 3 2.  2 dv  xdx x  2 1 x 2 2 2 2 1 2 v  1  2
Chọn đáp án B.
Câu 16: Cho hàm số y  f x. Đồ thị hàm số y  f x như hình bên. y
Đặt g x  f x  x  2 2
2 . Khẳng định nào sau đây đúng? 3
A. g0  g 2
   g1. B. g  1  g 2    g0.
f '(x) 2 C. g 2
   g1  g0. D. g0  g1  g 2  . x -2 O 1 Lời giải: x  2  
Ta có gx  2 f x  2x  2  2  f 
 x  x  2;
 gx  0  f x  x  2  x  0  . x  1  Bảng biến thiên: y d x   3 2 0 1 
gx f  ('x) 2 0  0  0   g0 
g x g  2   g1 x -2 O 1 Suy ra g 2
   g0 và g  1  g0 . 0 1 0 1 1 1
Theo hình vẽ  f 
  xx 2dx   
x 2 fxdx  g 
 xdx   g  xdx  2  2 2 0 2 0
 gx 0  gx 1  g0  g 2    g 
1  g0  g1  g 2
 . Vậy g0  g1  g 2   . 2  0
Chọn đáp án D. Câu 17: Cho hàm số 4 3 2
y  ax  bx  cx  dx  ,
e (a  0) có đồ thị (C) và đường d : y  mx  n cắt đồ
thị (C) tại các điểm có hoành độ lần lượt là 2; 1; 0; 1. Biết rằng hình phẳng giới hạn bởi
(C), d và đường thẳng x  2, x  0 có diện tích bằng 1.
Diện tích hình phẳng giới hạn bởi đồ thị (C), đường thẳng d , trục tung và đường x  1 bằng 11 19 49 19 A.  B.  C.  D.  30 30 30 15 Lời giải:
Theo bài ra phương trình 4 3 2
ax  bx  cx  dx  e  mx  n có 4 nghiệm phân biệt 2  ;1;0;1.  f x 4 3 2
 ax  bx  cx  d  m x  e  n  0 có 4 nghiệm phân biệt 2  ;1;0;1.
Suy ra f  x  a(x  2)(x 1)(x  0)(x 1)  ax(x  2)(x 1)(x 1) .
Gọi S là diện tích hình phẳng giới hạn bởi (C), d và đường thẳng x  2, x  0 ta có 1 0 0 S 
f x dx  a x x  2
x 1 x 1 dx  
1  a .1 1  a 1. 1       2  2  1 1 19
Vậy diện tích S cần tìm là S 
f  xdx  x  x  2 x   1  x   1 dx    . 30 0 0
Chọn đáp án B.
Câu 18: Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của
hai hình tròn lần lượt là 20 m và 15 m . Khoảng cách giữa hai tâm của hai hình tròn là
30 m .Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 nghìn đồng và chi
phí làm mỗi mét vuông còn lại là 100 nghìn đồng. Hỏi số tiền làm mặt sàn sân khấu gần với
số nào trong các số dưới đây? A. 202 triệu đồng. B. 208 triệu đồng. C. 218 triệu đồng. D. 200 triệu đồng. Lời giải:
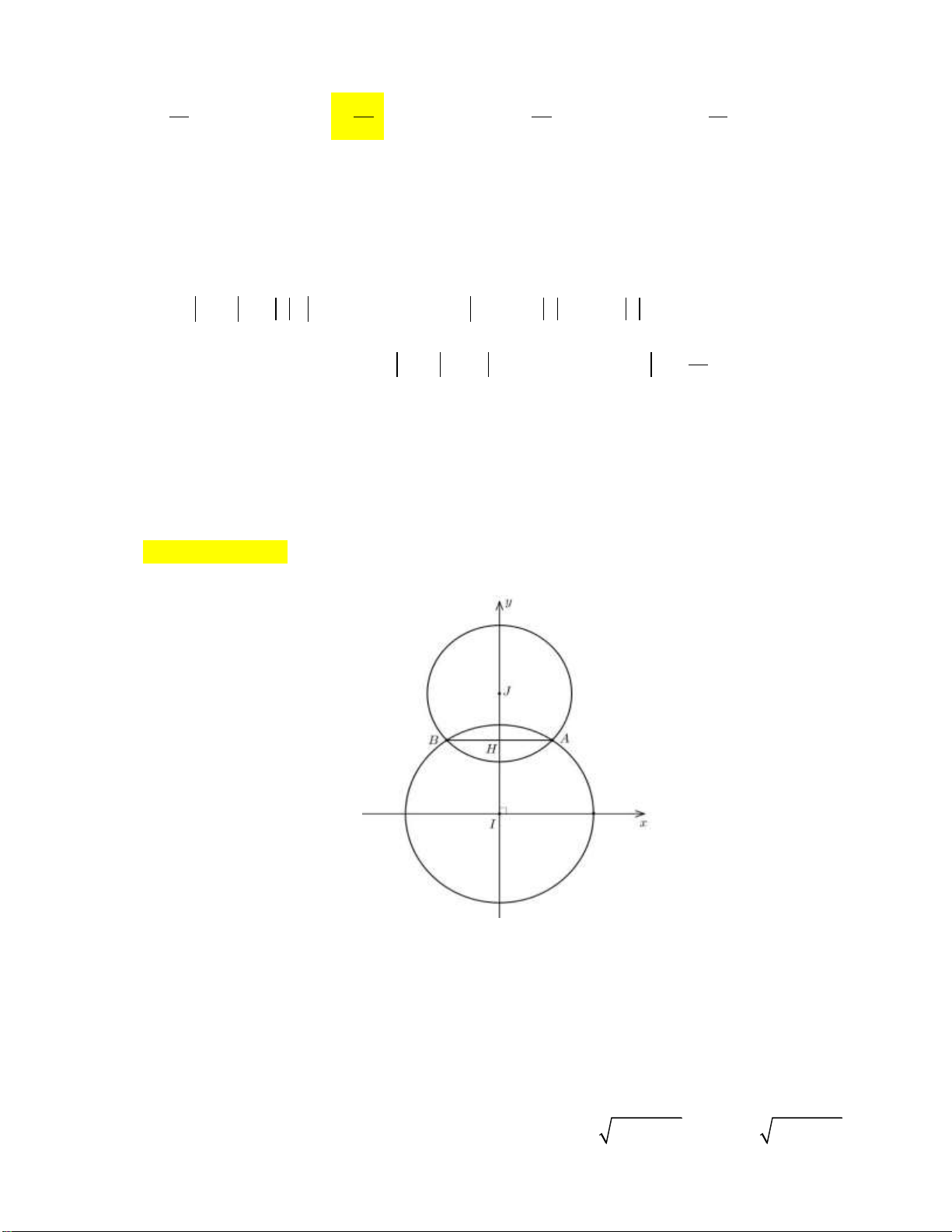
Gọi I , J lần lượt là tâm của hai đường tròn bán kính 20 m , 15 m . Gọi ,
A B là giao của hai đường tròn.
Chọn hệ trục tọa độ Oxy sao cho Oy trùng IJ và Ox song song với AB và I là gốc tọa độ (như hình vẽ).
Khi đó đường tròn tâm I bán kính R  20 m có phương trình 2 2
x  y  400 .
Vì khoảng cách giữa hai tâm của hai hình tròn là 30 m nên J 0;30 . Do đó đường tròn
tâm J 0;30 bán kính R  15 m có phương trình x   y  2 2 30  225 .
Khi đó phần chung của hai đường tròn giới hạn bởi  2 2 y 
400  x ; y  30  225  x  .  4 455  2      400 x y  x  Xét hệ 12    . 2 215
y  30  225  x  y   12
Diện tích phần chung của hai đường tròn là 5 455 12 S    2 2
400  x  225  x  30 dx  60, 2 1  . 5  455 12
Diện tích riêng của hai đường tròn là S  625  2S  625 120, 4 2 1 .
Số tiền chi phí là 300000S 100000S  300000.60, 2 100000. 625 120, 4  202369540 1 2   .
Vậy số tiền làm mặt sàn sân là gần 202 triệu đồng.
Chọn đáp án A.
Câu 19: Với mọi m thì đường thẳng d : y  mx  2 luôn cắt parabol 2
(P) : y  x 1 tại hai điểm phân
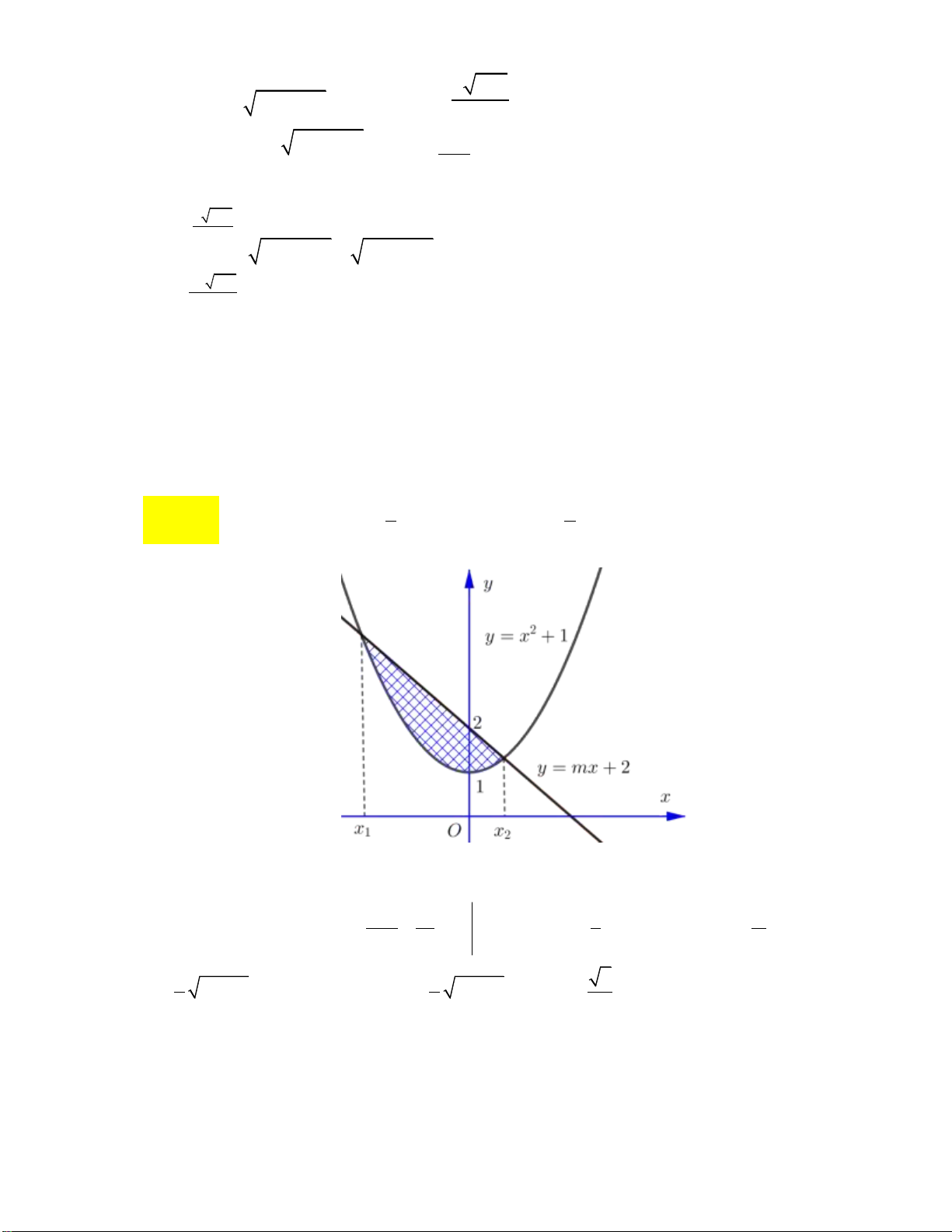
biệt có hoành độ x , x . Tìm m để diện tích của hình phẳng giới hạn bởi d và (P) là nhỏ 1 2 nhất. 4 3 A. m  0 . B. m  . C. m  . D. m  4. 3 4 Lời giải:
Ta có x , x là hai nghiệm của phương trình 2
x  mx 1  0 . Khi 1 2 đó x x          x   2 2 3 2 mx x dx   
 x   x  x  1 m S mx 2 1  x  x  x x  x  x    x  2 2 1 2 1 1 2 1 2   1 2  1  2 3   3 2  1 x 1  
m  4 2m   1 1  3m  6 
m  4 m  4 3 4 2 2 2 2 2    6 6 6  S  m  0 . min
Chọn đáp án A.
Câu 20: Cho hàm số bậc ba y  f (x) có đồ thị là đường cong trong hình bên dưới:
Biết hàm số f (x) đạt cực trị tại hai điểm x , x thỏa mãn x  x  4 và f (x )  f (x )  0. Gọi 1 2 2 1 1 2 S
S và S là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số 1 bằng 1 2 S2 5 3 3 A. . B. . C. 1. D. . 3 5 4 Lời giải: Cách 1:
Gọi f  x 3 2
 ax  bx  cx  d, (với a  0,a,b,c,d  ) f x 2
 3ax  2bx  c . Theo giả thiết ta có:
f  x  f  x  0  f  x  3a x  x x  x  3a x  x x  x  4 1   2     1   2   1   1 
 3a x  x 2 12a x  x . 1  1 
 f x  f 
 xdx ax x 3 6ax x 2 C . 1 1
f (x )  f (x )  0  f x  f x  4  0  C  64a  96a  C  0  C  16 . a 1 2  1  1    3 2
Vậy f  x  a  x  x  6a x  x 16a . 1   1 
S  S là diện tích hình chữ nhật có các kích thước là 2 và f  x  16a  S  S  32a . 1  1 2 1 2  1 x 2 S 3 S  f x dx  20a 
. Suy ra S  12a . Vậy 1  . 2   1 S 5 2 1 x Cách 2:
Kết quả bài toán sẽ không đổi nếu ta tịnh tiến đồ thị của hàm số đã cho sang trái sao cho
điểm uốn trùng với gốc tọa độ O . Gọi g  x 3 2
 ax  bx  cx  d, a  0 là hàm số đó và ta thấy đồ thị của hàm số g  x đối xứng
nhau qua gốc tọa độ O nên g  x là hàm số lẻ  b  d   g  x 3 0  ax  cx .
g  x có hai cực trị là 2, 2 nên g2  g 2
   0 12a  c  0  c  12  a . Vậy g  x 3
 ax 12ax .
S  S là diện tích hình chữ nhật có các kích thước là 2 và g  2
  16a  S  S  32a . 1 2 1 2 0 S 3 S  g x dx  20a 
. Suy ra S  12a . Vậy 1  . 2   1 S 5 2  2
Chọn đáp án B.
____________________________HẾT____________________________
Huế, 15h00’ Ngày 11 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 5_TrNg 2022 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
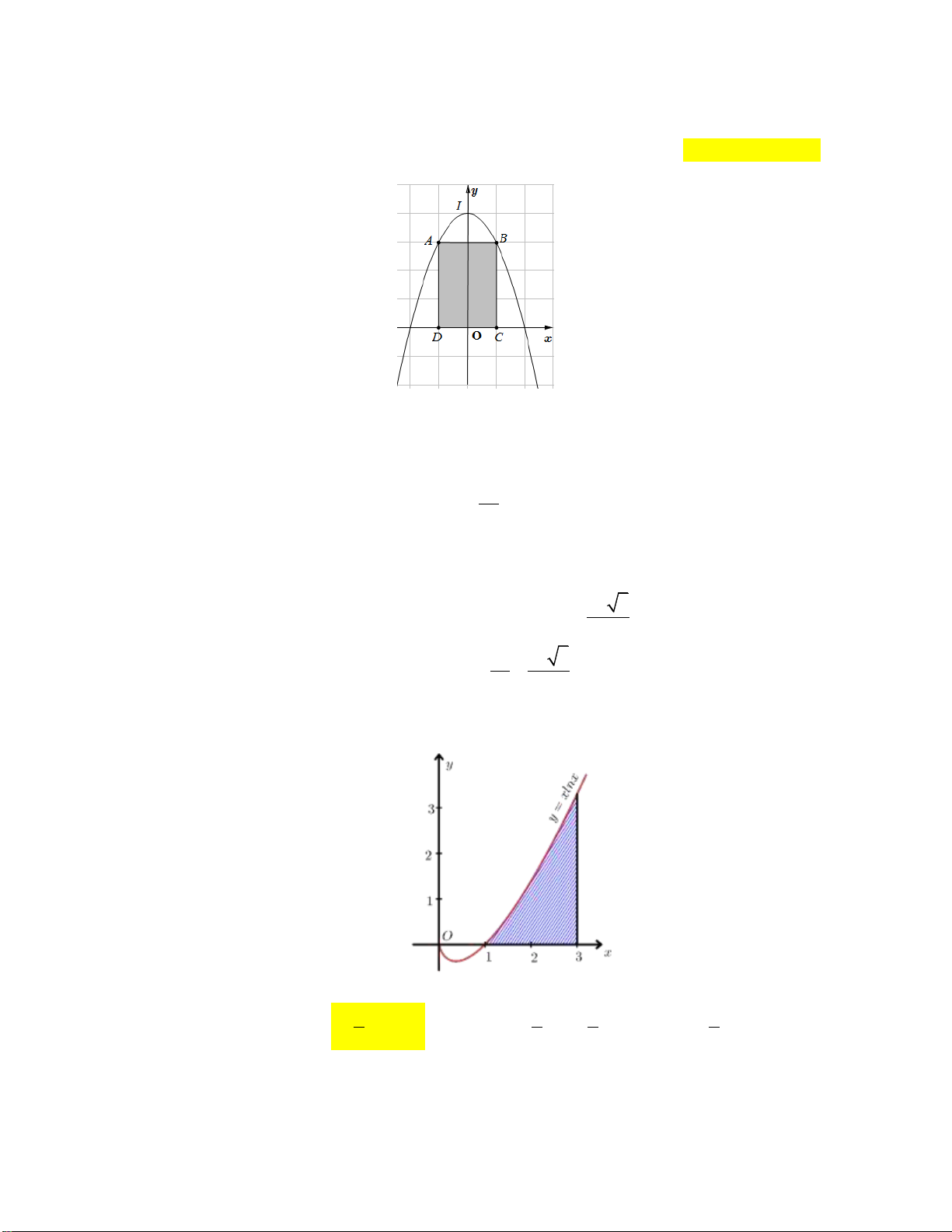
Câu 1: Cho đồ thị y  f (x) như hình vẽ sau đây:
Diện tích của hình phẳng được gạch chéo trong hình vẽ là 2 1 2 A. S  f (x)dx  . B. S 
f (x)dx  f (x)dx   . 1  1  1 1 2 1 2
C. S   f (x)dx  f (x)dx   . D. S 
f (x)dx  f (x)dx   . 1  1 1  1
Câu 2: Cho hàm số y  f  x liên tục trên đoạn 5;6có đồ thị như hình vẽ bên dưới: y 6 4 -1 O 1 2 x -5 -2 -1 6 -2 0 Giá trị của f
 xdx bằng 5  25 19 11 13 A. . B. . C. . D. . 2 2 2 2
Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 2 x y
e , trục hoành và hai đường thẳng x 0 , x 3 là 6 e 1 6 e 1 6 e 1 6 e 1 A. . B. . C. . D. . 2 2 3 3 2 2 3 3
Câu 4: Cho hàm số y  f  x, y  g  x liên tục trên đoạn a;b . Diện tích hình phẳng giới hạn bởi
đồ thị hàm số y  f  x, y  g  x và các đường thẳng x  a, x  b là b b
A. S   f x  g xdx . B. S  f
 x gxdx . a a b b
C. S   f x  g xdx .
D. S   f x  g x dx . a a
Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  1 3x , trục Ox và hai đường thẳng
x  0, x  1 bằng 1 1 1 1
A. 1 3xdx B. 1 3xdx  . C.  1 3xdx  .
D.  1 3xdx . 0 0 0 0
Câu 6: Cho hàm số y  f (x) liên tục và có đồ thị trên [3;5] như hình bên. 1377 2673 Biết các miền ,
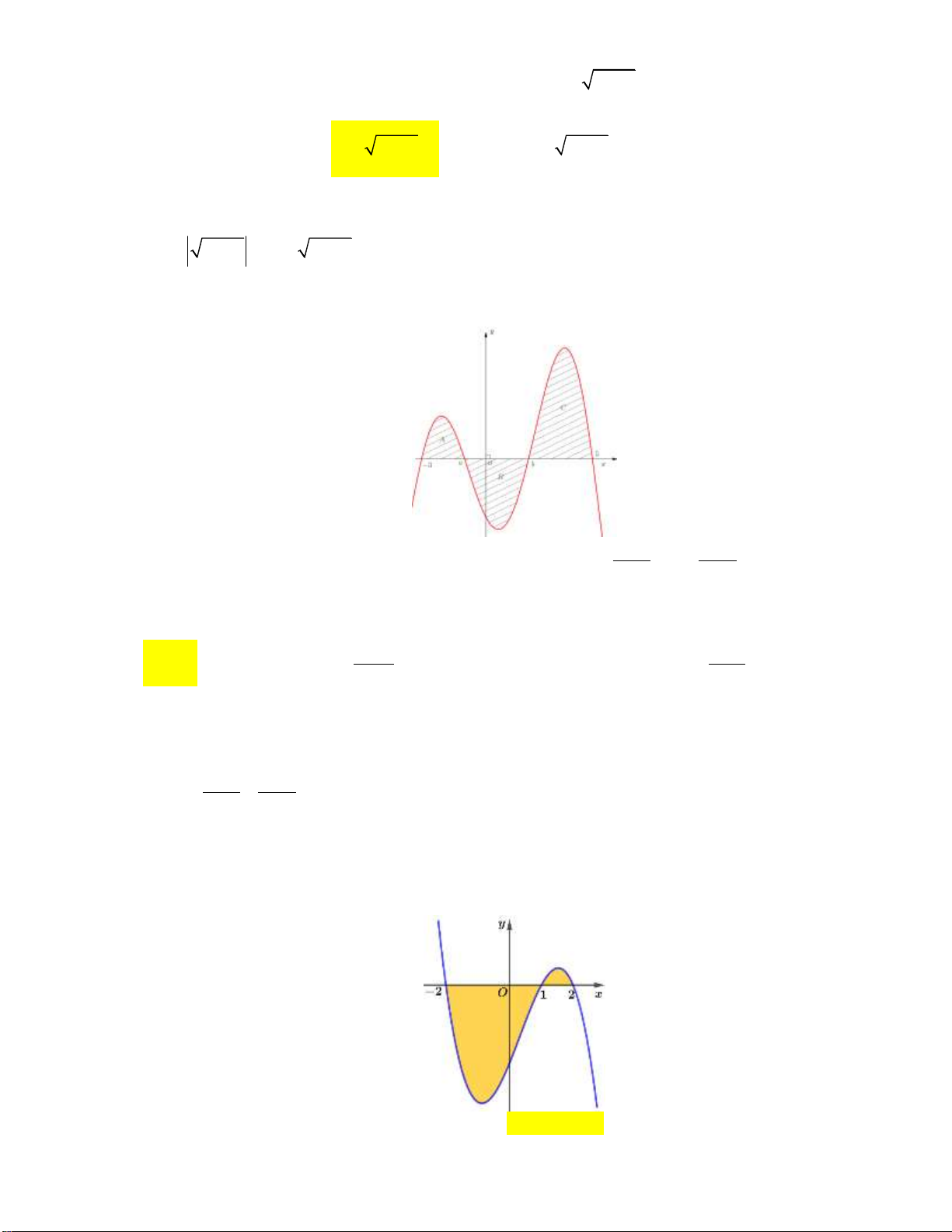
A B, C có diện tích lần lượt là S  188, S  , S  . Khi đó A B 4 C 4 5  f
  x1dx  bằng 3  2417 2401 A. 520. B. . C. -504. D. . 2 2 1 2
Câu 7: Cho đồ thị y  f  x như hình vẽ sau đây. Biết rằng f
 xdx  a và f
 xdx  b . Tính 2  1
diện tích S của phần hình phẳng được tô đậm.
A. S  a  b .
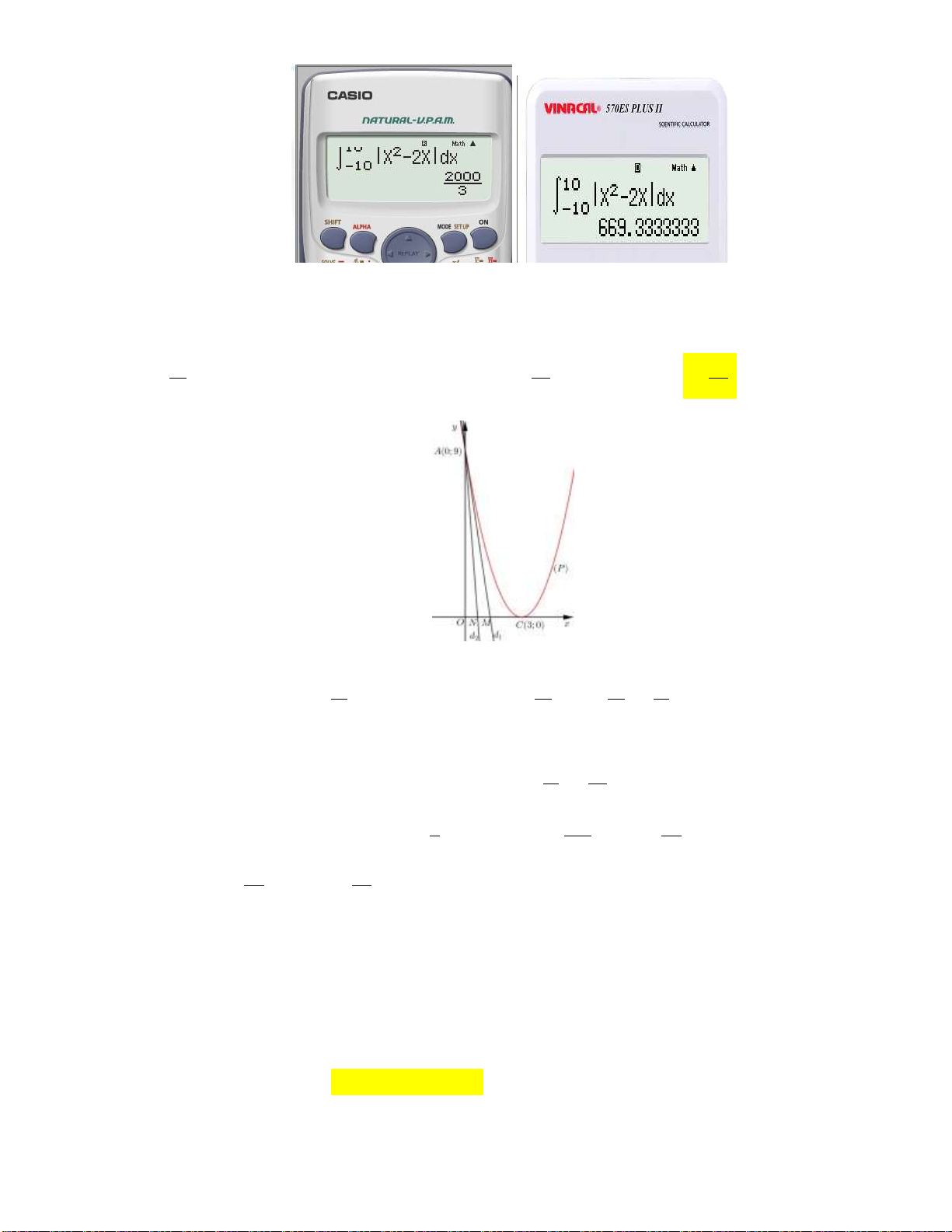
B. S  a  b .
C. S  b  a .
D. S  a  b .
Câu 8: Gọi S là diện tích hình phẳng giới hạn bởi các đường 2
y  x  2x 1; y  m m  0 và
x  0; x  1. Tìm m sao cho S  4. 5 5 3 A. m  . B. m   . C. m   . D. m  4 . 3 3 5
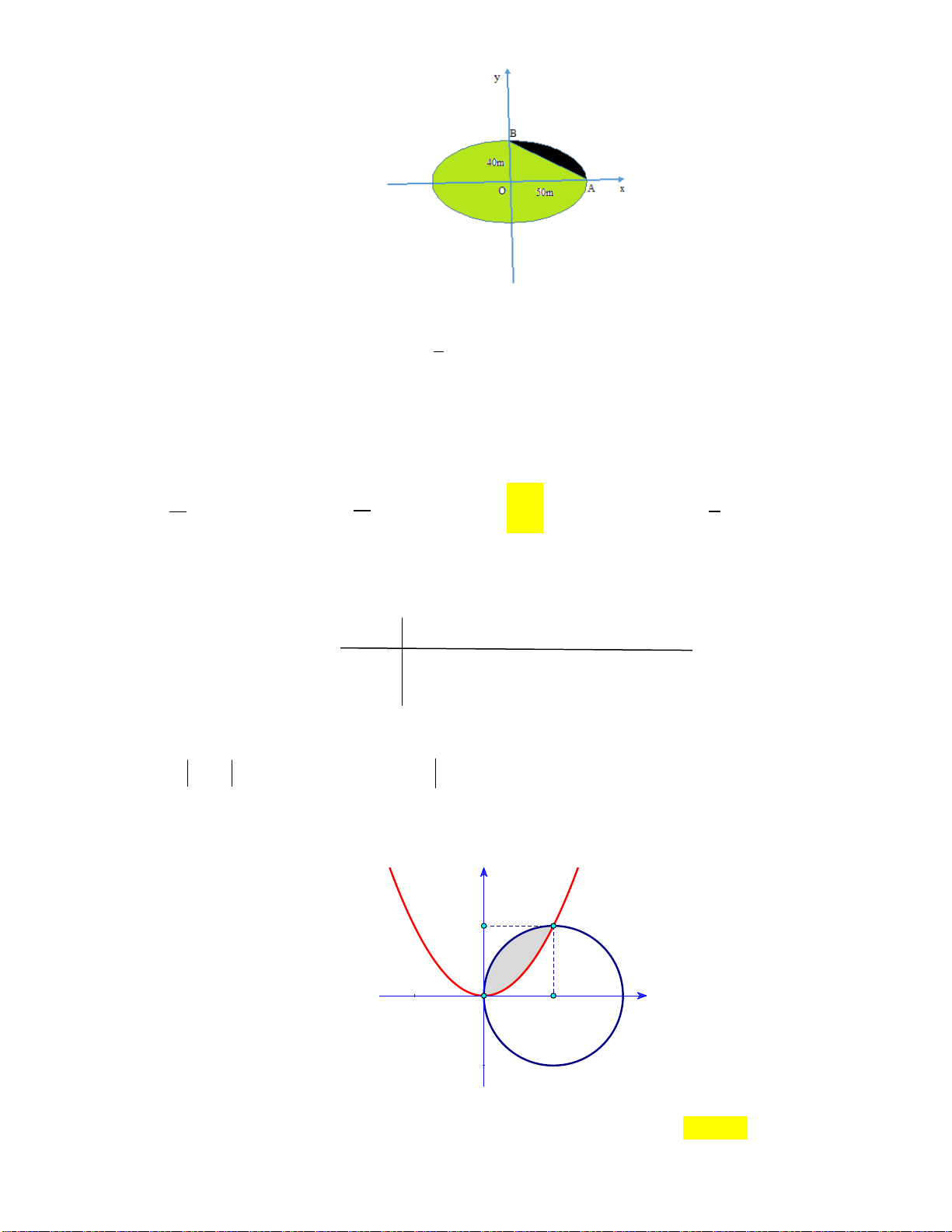
Câu 9: Ông A đã cải tạo một miếng đất thành hình elip. Elip này có độ dài trục lớn là 12 mét. Trong
elip có một đường tròn đi qua các đỉnh trên trục nhỏ và các tiêu điểm F , F .Ông A muốn 1 2
trồng cỏ May Mắn cho mảnh đất là phần bên trong Elip và bên ngoài đường tròn. Biết rằng
chi phí cho việc trồng cỏ May Mắn là 60 nghìn đồng trên một mét vuông. Hỏi tổng chi phí
trồng cỏ May Mắn gần nhất với số tiền nào sau đây? A. 2811 nghìn đồng.
B. 1405 nghìn đồng. C. 447 nghìn đồng. D. 895 nghìn đồng.
Câu 10: Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai đường 2 2
y  2x , y  4 . x 2 4 4 2 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 11: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 2
y  x  2x 1 và 2
y  x 1 là 189 27 3 A. S  . B. S  . C. S  6 . D. S  . 4 4 4
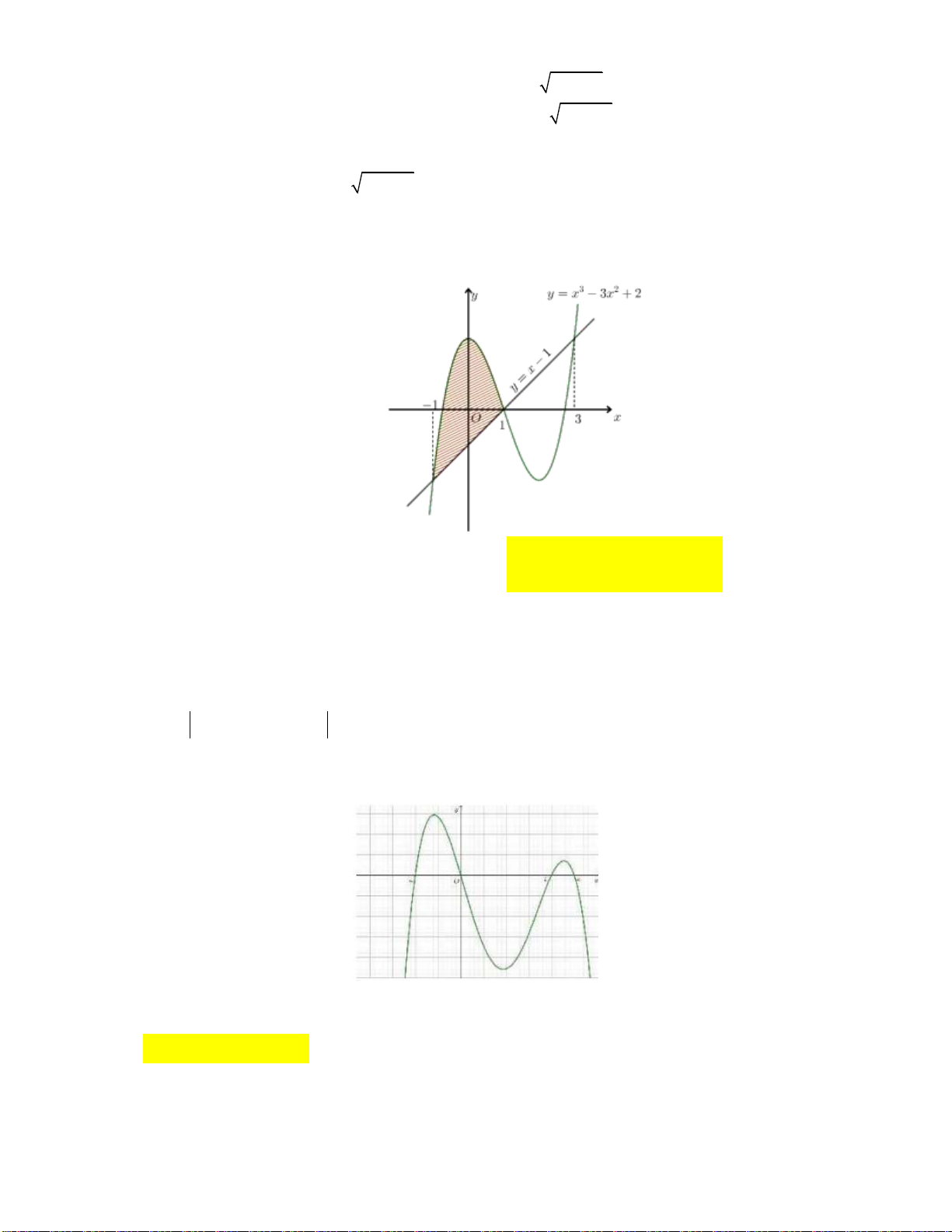
Câu 12: Cho hàm số bậc ba f  x có đồ thị như hình vẽ bên. Biết đồ thị hàm số f  x cắt trục
hoành tại ba điểm phân biệt có hoành độ x , x , x thoả mãn x  x  2 3 và x , x , x theo 1 2 3 3 1 1 2 3
thứ tự lập thành một cấp số cộng. Diện tích hình phẳng gạch sọc trong hình vẽ bằng A. 6 3 . B. 4 6 . C. 4 3 . D. 6 .
Câu 13: Cho hai hàm số y  f  x , y  g  x có đạo hàm liên tục trên
. Biết rằng đồ thị của hai hàm
số này cắt nhau tại hai điểm có hoành độ lần lượt là 1 và 2 , phần hình phẳng gạch sọc giới
hạn bởi hai đồ thị đã cho và hai đường thẳng x  1 , x  2 có diện tích bằng 4 và 2 g
 xdx  7. 1
Mệnh đề nào sau đây đúng? 2 2 2 2 A. f
 xdx 15. B. f
 xdx 11. C. f
 xdx  22. D. f
 xdx  3. 1 1 1 1
Câu 14: Hình giới hạn bởi một đường parabol và một nửa đường tròn tâm O bán kính bằng 2
(phần gạch sọc) trong hình vẽ bên có diện tích bằng 5  7  4  2  A.  . B.  . C.  . D.  3 2 3 2 3 2 3 2
Câu 15: Cho đường cong C y  3 :
x . Xét điểm A có hoành độ dương thuộc C , tiếp tuyến của C
tại A tạo với C một hình phẳng có diện tích bằng 27 . Hoành độ điểm A thuộc khoảng nào dưới đây?  1   1   3   3  A.  0;  . B.  ;1 . C. 1;  . D.  ; 2.  2   2   2   2 
Câu 16: Diện tích hình phẳng giới hạn vởi đồ thị hai hàm số 2
y  x  4x  3 và y  3  x bằng 7 9 13 A. . B. . C. . D. 2. 3 2 6
Câu 17: Cho hai hàm số 3 3
f (x)  ax  bx  c, g(x)  bx  ax  c, (a  0) có đồ thị như hình vẽ bên dưới: 1 Gọi S , S S  S  3 f (x)dx  1
2 là diện tích hình phẳng được gạch trong hình vẽ. Khi 1 2 thì 0 bằng A. 3 . B. 3  . C. 6 . D. 6  . Câu 18: Cho hàm số 4 2
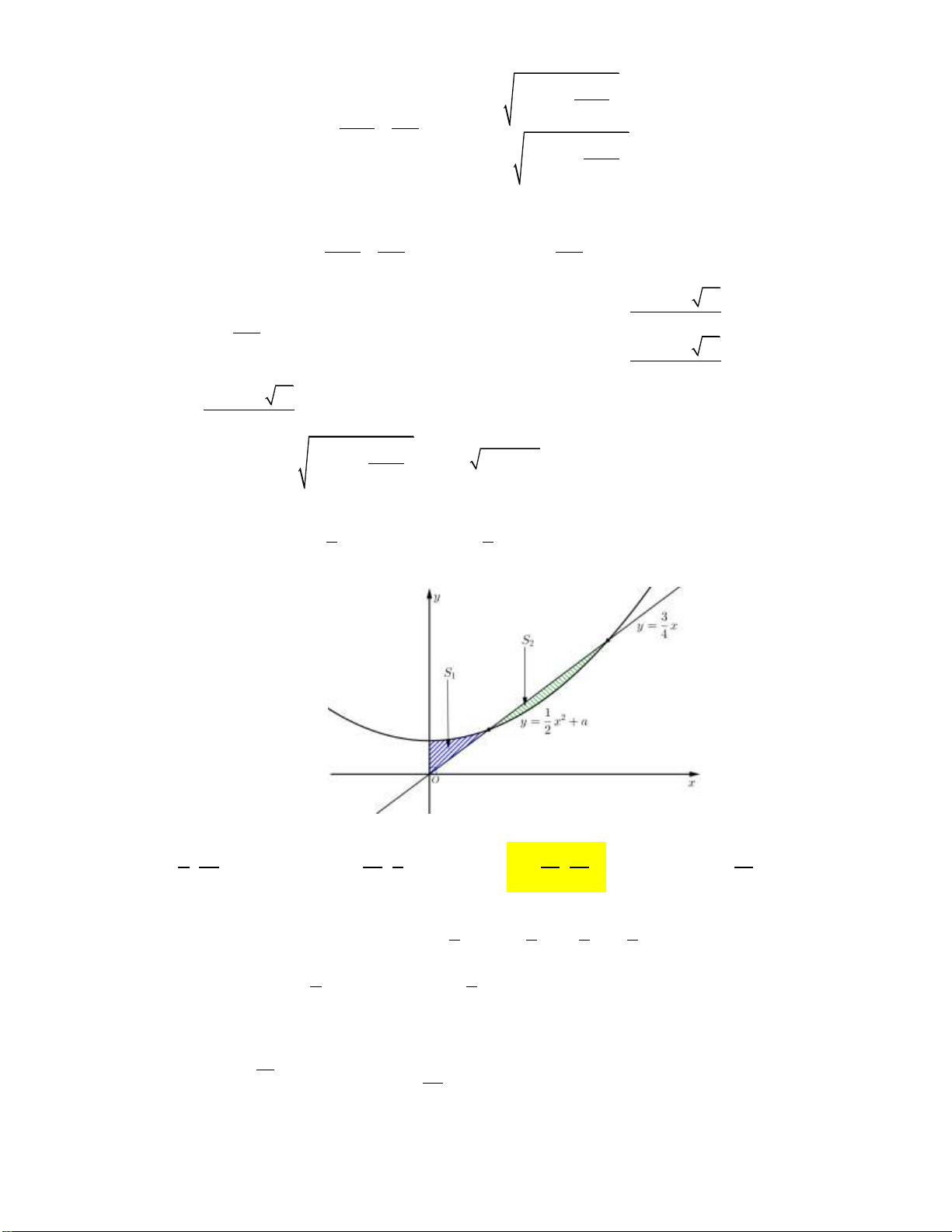
y  ax  bx  c, (a  0) có đồ thị (C) và tiếp tuyến d của đồ thị (C) tại điểm có
hoành độ x  1, cắt (C) tại hai giao điểm còn lại có hoành bằng x  0, x  2 (tham khảo hình vẽ).
Biết rằng hình phẳng giới hạn bởi (C), d và đường thẳng x  0, x  2 có diện tích bằng 28/5.
Tính diện tích hình phẳng giới hạn bởi đồ thị (C), đường thẳng d và x  0, x  1. 27 29 1 5 A.  B.  C.  D.  5 5 5 12
Câu 19: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của
một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường
kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và
cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không tô màu) dành để
trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản
tương ứng là 150.000 đồng/ 2 m và 100.000 đồng/ 2
m . Hỏi số tiền cần để trồng hoa và trồng cỏ
Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây? A. 3.739.000 (đồng).
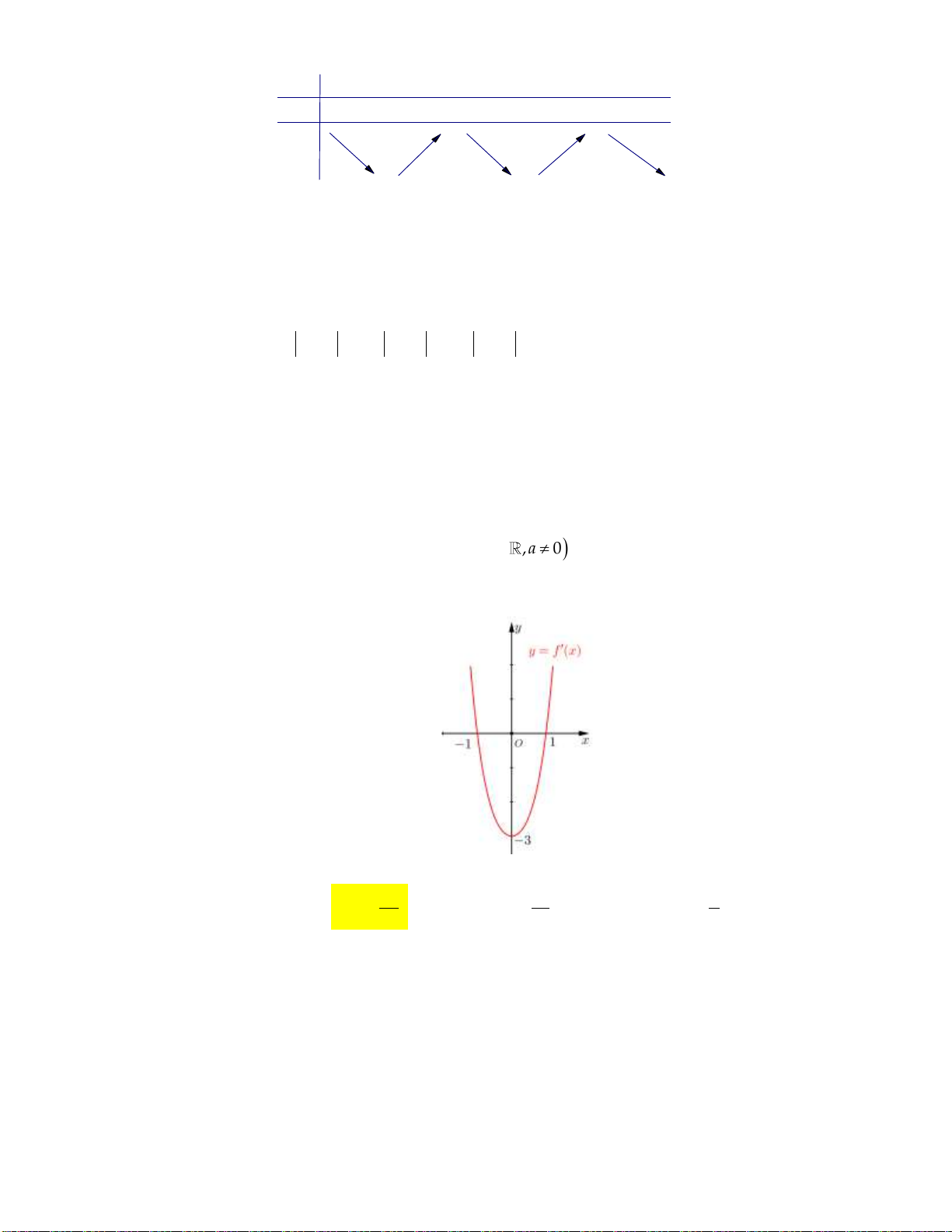
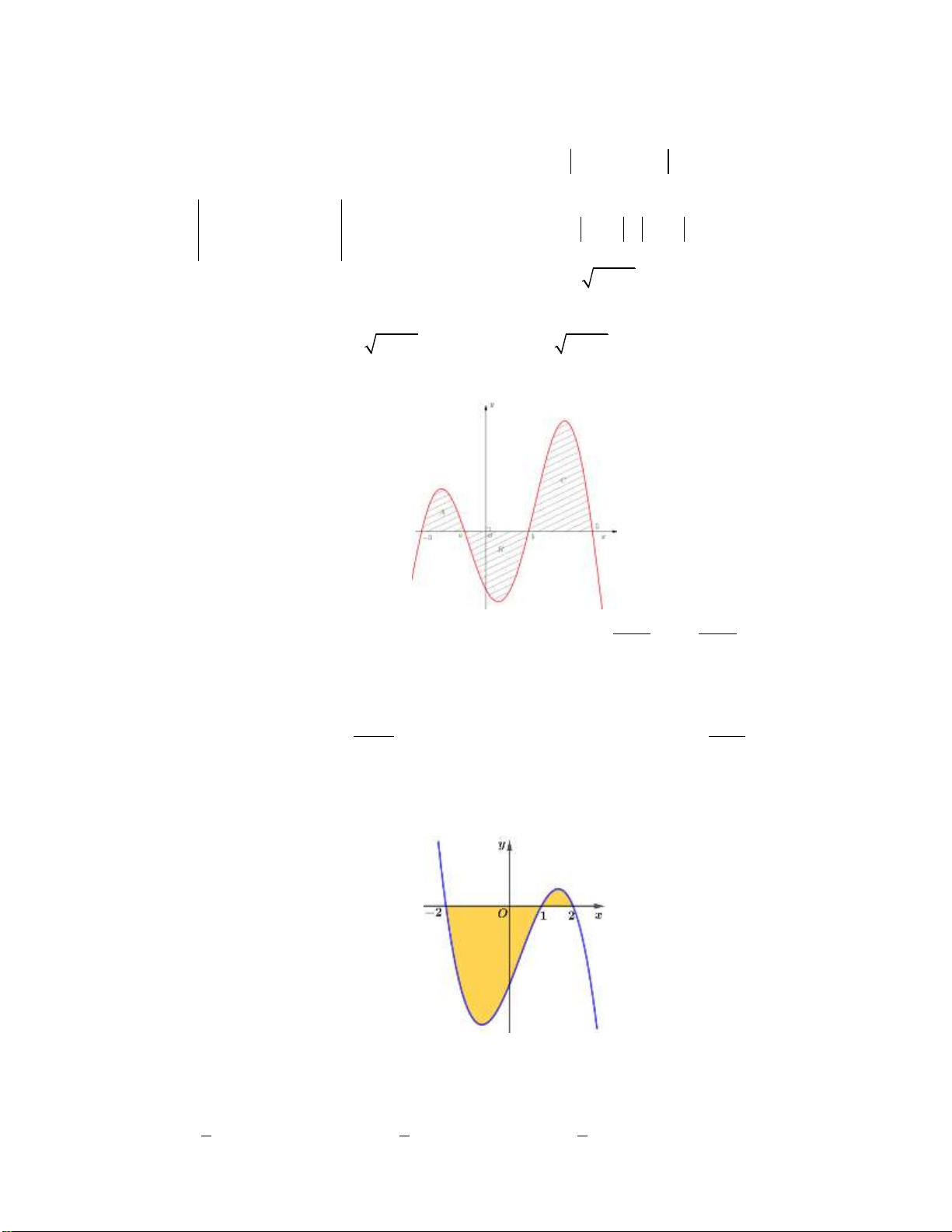
B. 1.948.000 (đồng). C. 3.926.000 (đồng). D. 4.115.000 (đồng). Câu 20: Cho hàm số 4 2
y  x  mx có đồ thị C
với tham số m  0 được cho như hình vẽ. Giả sử m 
C cắt trục Ox tại ba điểm phân biệt như hình vẽ bên dưới: m 
Gọi S và S là diện tích các miền được giới hạn bởi đồ thị C
và trục Ox . Biết m là giá trị m  1 2 0 10 5
để S  S 
, hỏi m thuộc khoảng nào sau đây? 1 2 0 3 A. 15;30 . B. 5;10 . C. 0;3 . D. 2;6 .
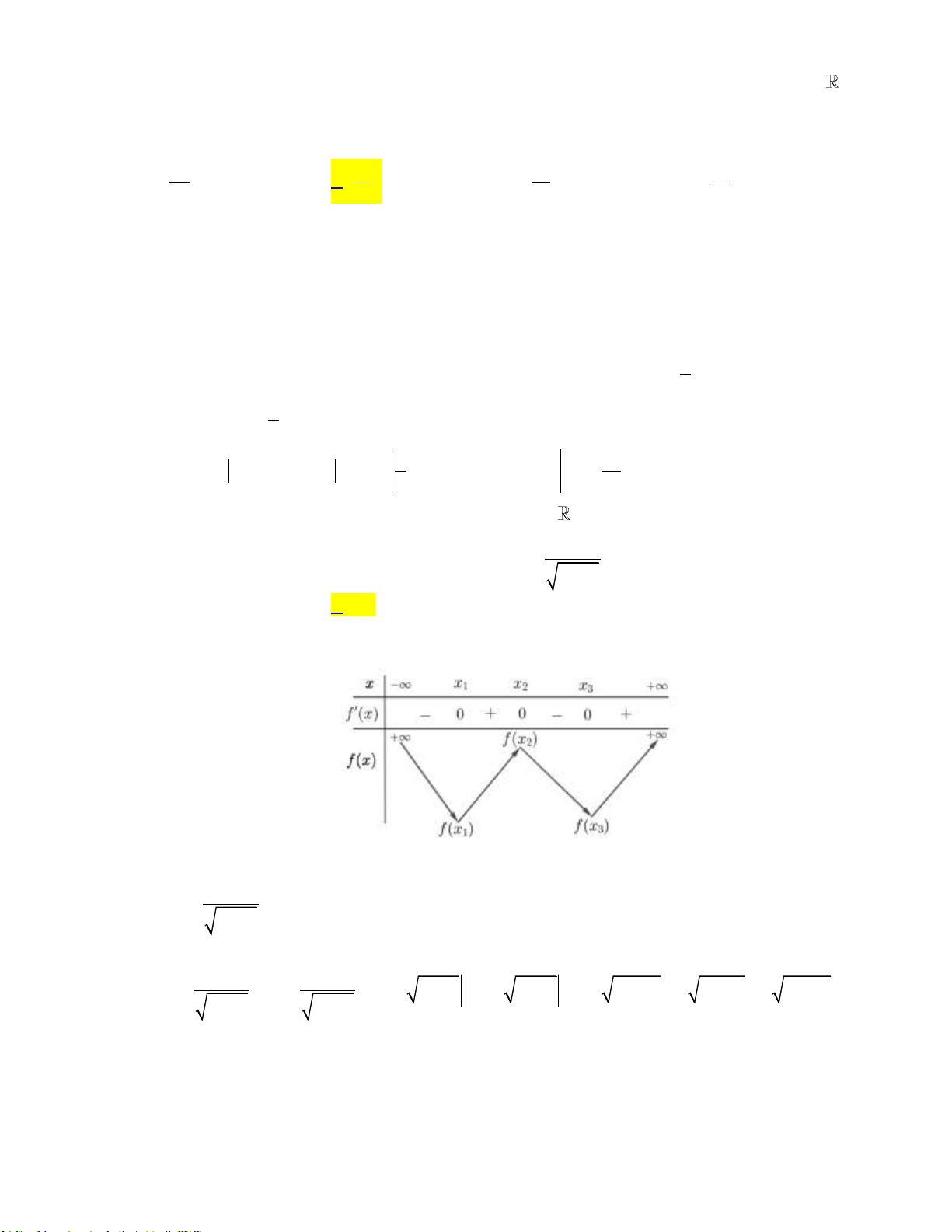
____________________________HẾT____________________________
Huế, 11h00’ Ngày 14 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 5_TrNg 2022
LỜI GIẢI CHI TIẾT
Câu 1: Cho đồ thị y  f (x) như hình vẽ sau đây:
Diện tích của hình phẳng được gạch chéo trong hình vẽ là 2 1 2 A. S  f (x)dx  . B. S 
f (x)dx  f (x)dx   . 1  1  1 1 2 1 2
C. S   f (x)dx  f (x)dx   . D. S 
f (x)dx  f (x)dx   . 1  1 1  1 Lời giải: 2 1 2 1 2
 Có S 
f (x) dx 
f (x) dx 
f (x) dx 
f (x)dx  ( f (x))d . x      1  1  1 1  1
 Chọn đáp án D.
Câu 2: Cho hàm số y  f  x liên tục trên đoạn 5;6có đồ thị như hình vẽ bên dưới: y 6 4 -1 O 1 2 x -5 -2 -1 6 -2 0 Giá trị của f
 xdx bằng 5  25 19 11 13 A. . B. . C. . D. . 2 2 2 2 Lời giải: y A 6 4 B C -1 D O 1 2 F x -5 -2 -1 6 G E -2 Ta có 1 1 S
 BC.AB  .6.3  1 1 9; S
 DF.EF  .1.2 1. ABC 2 2 DEE 2 2 1 S  GO  EF DO   FEGO   1 3 .3.1 . 2 2 2 0 2  1  0 3 13 Khi đó: f
 xdx  f
 xdx  f
 xdx  f
 xdx  S S  S  9 1  . ABC DEE FEGO 2 2 5  5  2  1 
 Chọn đáp án D.
Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 2 x y
e , trục hoành và hai đường thẳng x 0 , x 3 là 6 e 1 6 e 1 6 e 1 6 e 1 A. . B. . C. . D. . 2 2 3 3 2 2 3 3 Lời giải:
Xét phương trình hoành độ giao điểm của đồ thị hàm số 2 x y
e , trục hoành Ox : 2 x e 0 x 0 . 3 3 6 e x x 1 3 x 1 1
Diện tích hình phẳng cần tính là 2 2 2 S 
e dx  e dx  e   
 6e  1   . 2 0 2 2 2 0 0
 Chọn đáp án C.
Câu 4: Cho hàm số y  f  x, y  g  x liên tục trên đoạn a;b . Diện tích hình phẳng giới hạn bởi
đồ thị hàm số y  f  x, y  g  x và các đường thẳng x  a, x  b là b b
A. S   f x  g xdx . B. S  f
 x gxdx . a a b b
C. S   f x  g xdx .
D. S   f x  g x dx . a a Lời giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x, y  g  x và các đường thẳng b
x  a, x  b được tính theo công thức S  f
 x gxd .x a
 Chọn đáp án B.
Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  1 3x , trục Ox và hai đường thẳng
x  0, x  1 bằng 1 1 1 1
A. 1 3xdx B. 1 3xdx  . C.  1 3xdx  .
D.  1 3xdx . 0 0 0 0 Lời giải: 1 1 S  1 3x dx  1 3xdx   . 0 0
 Chọn đáp án B.
Câu 6: Cho hàm số y  f (x) liên tục và có đồ thị trên [3;5] như hình bên. 1377 2673 Biết các miền ,
A B, C có diện tích lần lượt là S  188, S  , S  . Khi đó A B 4 C 4 5  f
  x1dx  bằng 3  2417 2401 A. 520. B. . C. -504. D. . 2 2 Lời giải: 5 5 5 a b 5  f
  x1 dx  f 
 xdx dx  f 
 xdx f
 xdx f
 xdx8 S
  S  S  8 A B C 3  3  3  3  a b 1377 2673 188    8  520. 4 4
 Chọn đáp án A. 1 2
Câu 7: Cho đồ thị y  f  x như hình vẽ sau đây. Biết rằng f
 xdx  a và f
 xdx  b . Tính 2  1
diện tích S của phần hình phẳng được tô đậm.
A. S  a  b .
B. S  a  b .
C. S  b  a .
D. S  a  b . Lời giải: 1 2
Ta có S   f
 xdx f
 xdx  a b. 2  1
 Chọn đáp án C.
Câu 8: Gọi S là diện tích hình phẳng giới hạn bởi các đường 2
y  x  2x 1; y  m m  0 và
x  0; x  1. Tìm m sao cho S  4. 5 5 3 A. m  . B. m   . C. m   . D. m  4 . 3 3 5 Lời giải:
Diện tích hình phẳng giới hạn bởi các đường 2
y  x  2x 1; y  m m  0 và x  0; x  1 là 1 1 2 S 
x  2x 1 m dx  
 2x 2x1mdx do m  0. 0 0 1 1 3  x 
Suy ra S  4   2
x  2x 1 m 2 dx  4  
 x  x  mx   4  3  0 0 1 5 2
 1 1 m  4  m   . 3 3
 Chọn đáp án B.
Câu 9: Ông A đã cải tạo một miếng đất thành hình elip. Elip này có độ dài trục lớn là 12 mét. Trong
elip có một đường tròn đi qua các đỉnh trên trục nhỏ và các tiêu điểm F , F .Ông A muốn 1 2
trồng cỏ May Mắn cho mảnh đất là phần bên trong Elip và bên ngoài đường tròn. Biết rằng
chi phí cho việc trồng cỏ May Mắn là 60 nghìn đồng trên một mét vuông. Hỏi tổng chi phí
trồng cỏ May Mắn gần nhất với số tiền nào sau đây? A. 2811 nghìn đồng.
B. 1405 nghìn đồng. C. 447 nghìn đồng. D. 895 nghìn đồng. Lời giải:
Gắn hệ trục tọa độ Oxy như hình vẽ. 2 2 x y Phương trình elip 
1 với a b  0 và phương trình đường tròn 2 2 2
x  y  R . 2 2 a b
Độ dài trục lớn là 12 mét, suy ra a  6 .
Vì đường tròn đi qua các đỉnh trên trục nhỏ và tiêu điểm của elip nên b  c  R . Do đó 2 2 2 2 2 2
c  a  b  2c  a  2c  36  c  3 2
Tổng chi phí để trồng cỏ May Mắn là 6 2 3 2  x  2 T  4. 3 2 1 dx 
18  x dx .60000  1405    nghìn đồng. 36  0 0  
 Chọn đáp án B.
Câu 10: Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai đường 2 2
y  2x , y  4 . x 2 4 4 2 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải:
Theo hình vẽ ta có 2
y  4x  y  2 x .
Xét phương trình hoành độ giao điểm của hai đường 2
y  2x , y  2 x  x  0 x  0 2
2x  2 x     .   x  1 x 1
Dựa vào đồ thị, diện tích của hình phẳng cần tính là  
S  2 x  2x  1 1 4 2 2 2 3 dx  x x  x    .  3 3  3 0 0
 Chọn đáp án D.
Câu 11: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 2
y  x  2x 1 và 2
y  x 1 là 189 27 3 A. S  . B. S  . C. S  6 . D. S  . 4 4 4 Lời giải: Phương trình hoành độ giao điểm của hai đồ thị đã cho là x  0 3 2 2 3 2
x  2x 1  x 1  x  3x  0  
. Vậy diên tích hình phẳng cần tìm là: x  3  
S    x  x     x   x
d    x  x  3 3 3 3 2 2 3 2 1 4 3 27 2 1 1 3 x d   x  x    .  4  4 0 0 0
 Chọn đáp án B.
Câu 12: Cho hàm số bậc ba f  x có đồ thị như hình vẽ bên. Biết đồ thị hàm số f  x cắt trục
hoành tại ba điểm phân biệt có hoành độ x , x , x thoả mãn x  x  2 3 và x , x , x theo 1 2 3 3 1 1 2 3
thứ tự lập thành một cấp số cộng. Diện tích hình phẳng gạch sọc trong hình vẽ bằng A. 6 3 . B. 4 6 . C. 4 3 . D. 6 . Lời giải:
Diện tích phần gạch sọc trên hình là hình phẳng giới hạn bởi các đường
y  3, y  f  x, x  x , x  x . Do đó, 1 3 3 x x x x x
S   3  f x 3 3 dx  3dx 
f  x dx  3  x  x  f x dx  6       f x dx 3 1  3   3   1 x 1 x 1 x 1 x 1 x Xét f  x 3 2
 ax  bx  cx  d. Theo viet có     b x x x 1 2 3 a
Mặt khác x , x , x theo thứ tự lập thành cấp số cộng nên 1 2 3       b b x x x x x x
2x  x  3x    x  
 U x ;0 là điểm uốn của đồ thị 1 2 3  1 3 2 2 2 2 2  2  a 3a
hàm số đã cho. Vì vậy, trục hoành cùng với đồ thị hàm số f  x tạo thành hai hình có x x x 2 3 3
diện tích bằng nhau tức  f xdx   f xdx   f xdx  0. Vậy S  6 . 1 x 2 x 1 x
 Chọn đáp án D.
Câu 13: Cho hai hàm số y  f  x , y  g  x có đạo hàm liên tục trên
. Biết rằng đồ thị của hai hàm
số này cắt nhau tại hai điểm có hoành độ lần lượt là 1 và 2 , phần hình phẳng gạch sọc giới
hạn bởi hai đồ thị đã cho và hai đường thẳng x  1 , x  2 có diện tích bằng 4 và 2 g
 xdx  7. 1
Mệnh đề nào sau đây đúng? 2 2 2 2 A. f
 xdx 15. B. f
 xdx 11. C. f
 xdx  22. D. f
 xdx  3. 1 1 1 1 Lời giải:
Từ hình vẽ suy ra 2 2 2 2 f
 x gx dx   f
 x gxdx  4  f 
 xdx g
 xdx  4 1 1 1 1 2 2  f
 xdx  4 g
 xdx  47 11. 1 1
 Chọn đáp án B.
Câu 14: Hình giới hạn bởi một đường parabol và một nửa đường tròn tâm O bán kính bằng 2
(phần gạch sọc) trong hình vẽ bên có diện tích bằng 5  7  4  2  A.  . B.  . C.  . D.  3 2 3 2 3 2 3 2 Lời giải:
Phương trình nhánh trên đường tròn 2 y 
2  x . x  1  y  1.
Parabol có đỉnh 0;  
1 và đi qua hai điểm 1;  1 , 1;  1 có phương trình : 2 y  2x 1. 1 5  2 S  2 x   2 2x 1     dx     . 3 2 1 
 Chọn đáp án A.
Câu 15: Cho đường cong C y  3 :
x . Xét điểm A có hoành độ dương thuộc C , tiếp tuyến của C
tại A tạo với C một hình phẳng có diện tích bằng 27 . Hoành độ điểm A thuộc khoảng nào dưới đây?  1   1   3   3  A.  0;  . B.  ;1 . C. 1;  . D.  ; 2.  2   2   2   2  Lời giải: Ta có y  2 3x .
Do A C  A 3
a ; a , a  0 .
Phương trình tiếp tuyến d của C tại A là d y  2
a x  a  3 : 3 a hay d y  2
a x  a  3 : 3 a .
Ta có phương trình hoành độ giao điểm của d và C là x  a
x  a x  a  a  x  a2 3 2 3 3
x2a  0   . x    2a
Gọi S là diện tích của hình phẳng giới hạn bởi tiếp tuyến d và C . a Ta có S  27 
x  3a x  a  a dx   3 2 3 27 2a a a  4 2 2 x 3a x  
x 3a x2a dx   3 2 3 27     3 2a x   27   4 2  2a 2a  27 a   2 4 a  27   . 4
a   2 (ktma   0) Vậy a  2 .
 Chọn đáp án C.
Câu 16: Diện tích hình phẳng giới hạn vởi đồ thị hai hàm số 2
y  x  4x  3 và y  3  x bằng 7 9 13 A. . B. . C. . D. 2. 3 2 6 Lời giải: x  0 
Xét phương trình hoành độ giao điểm: 2
x  4x  3  3  x  x  2  . x  3 
Khi đó diện tích hình phẳng giới hạn bởi hai đồ thị là: 2 3 S  3 x 1 13 2 2
 x  4x  3 dx  x  4x  3  3 x dx  2     . 6 6 0 2
 Chọn đáp án C.
Câu 17: Cho hai hàm số 3 3
f (x)  ax  bx  c, g(x)  bx  ax  c, (a  0) có đồ thị như hình vẽ bên dưới: 1 Gọi S , S S  S  3 f (x)dx  1
2 là diện tích hình phẳng được gạch trong hình vẽ. Khi 1 2 thì 0 bằng A. 3 . B. 3  . C. 6 . D. 6  . Lời giải: x  1 
Phương trình hoành độ giao điểm: 3
(a  b)x  (b  a)x  0  (a  b)  3
x  x  0   x  0
Ký hiệu S3 là diện tích hình phẳng như hình vẽ dưới. 0 0
 S  ( f (x) g(x))dx  (a b)     1 3 x  x dx  (a  b) 1  1  1   4
Cách 1: Ta có:   S  S .
S  (g(x)  f (x))dx  (a b)  
 x  x 1 3 1 1 1 3 dx  (a  b) 3  0 0  4 1 1 1
Vậy S  S  3  S  S  3 
(g(x)  f (x))dx  g
 (x)dx  3 
f (x)dx  3  .    1 2 3 2 0 0 0 0 0 1
Cách 2: S 
( f (x)  g(x))dx  (a  b) 
  3x  x dx  (a b); 1  1  1  4 1 1  b a  S  
g(x)dx      3
bx  ax  c dx     c 2    0 0  4 2  1 b a
Vi vậy S  S  3  (a  b) 
  c  3  a  2b  4c  1  2 . 1 2 4 4 2 1 1 a b
a  2b  4c Suy ra
f (x)dx     3
ax  bx  cdx    c   3  . 0 0 4 2 4
 Chọn đáp án B. Câu 18: Cho hàm số 4 2
y  ax  bx  c, (a  0) có đồ thị (C) và tiếp tuyến d của đồ thị (C) tại điểm có
hoành độ x  1, cắt (C) tại hai giao điểm còn lại có hoành bằng x  0, x  2 (tham khảo hình vẽ).
Biết rằng hình phẳng giới hạn bởi (C), d và đường thẳng x  0, x  2 có diện tích bằng 28/5.
Tính diện tích hình phẳng giới hạn bởi đồ thị (C), đường thẳng d và x  0, x  1. 27 29 1 5 A.  B.  C.  D.  5 5 5 12 Lời giải:
Phương trình tiếp tuyến có dạng d : y  mx  n
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là 4 2
ax  bx  c  mx  n  f  x 4 2
 ax  bx  mx  c  n  0   1
Theo bài ra phương trình  
1 có 3 nghiệm x  1
 , x  0, x  2 trong đó x  1 là nghiệm 2 2
kép, suy ra f  x 4 2
 ax  bx  mx  c  n  a x  
1  x  0 x  2  ax  x   1  x  2
Gọi S là diện tích hình phẳng giới hạn bởi (C), d và đường thẳng x  0, x  2 ta có 1 2 2 28      2 a S
ax x 1  x  2dx  a x  x 2 28 1 x  2 dx   a 1. 1   5 5 0 0 0 1 2 1
Vậy diện tích S cần tìm là S 
f  xdx  x  x  2 x   1 dx    . 5 1  0
 Chọn đáp án C.
Câu 19: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của
một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường
kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và
cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không tô màu) dành để
trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản
tương ứng là 150.000 đồng/ 2 m và 100.000 đồng/ 2
m . Hỏi số tiền cần để trồng hoa và trồng cỏ
Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây? A. 3.739.000 (đồng).
B. 1.948.000 (đồng). C. 3.926.000 (đồng). D. 4.115.000 (đồng). Lời giải:
Kết hợp vào hệ trục tọa độ, ta được:
Gọi parabol là  P 2
: y  ax . Do F 2; 4  P nên  P 2 : y  x .
Gọi đường tròn có tâm ở gốc tọa độ là C  2 2 2
: x  y  R . Do F 2; 4 C  nên nửa đường tròn trên là 2
y  20  x .   2 5 8
Đặt S là diện tích phần tô đậm. Khi đó: S  2.  2 2 20  x  x dx  20 arcsin    . 1   0  1 5 3   1  5  8
Đặt S là diện tích phần không tô đậm. Khi đó: 2 S 
. .R  S  10  20 arcsin    . 2 2 1   2 5 3  
Vậy: Số tiền cần để trồng hoa và cỏ Nhật Bản là: T  150000.S 100000.S  3738574 (đồng). 1 2
 Chọn đáp án A. Câu 20: Cho hàm số 4 2
y  x  mx có đồ thị C
với tham số m  0 được cho như hình vẽ. Giả sử m 
C cắt trục Ox tại ba điểm phân biệt như hình vẽ bên dưới: m 
Gọi S và S là diện tích các miền được giới hạn bởi đồ thị C
và trục Ox . Biết m là giá trị m  1 2 0 10 5
để S  S 
, hỏi m thuộc khoảng nào sau đây? 1 2 0 3 A. 15;30 . B. 5;10 . C. 0;3 . D. 2;6 . Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là 2 x  0 x  0 4 2
x  mx  0     . 2 x  m x   m
Do đồ thị hàm số nhận trục tung làm trục đối xứng nên S  S . 1 2 10 5 10 5 5 5
Ta có S  S   2S   S  . 1 2 2 2 3 3 3 m m 5 5  x mx  5 5
Mà S   x  mx  5 3 4 2 dx       2 3  5 3  3 0 0
 m5 m m3 5 5 5 25 5 5 2      m   m   3,78 . 5 5 3 3 2 4
 Chọn đáp án D.
____________________________HẾT____________________________
Huế, 11h00’ Ngày 14 tháng 02 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 6_TrNg 2024 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI Câu 1:
Cho hàm số y  f  x và y  g  x có đồ thị như hình vẽ bên dưới:
Diện tích S của phần gạch chéo trong hình vẽ trên được tính bằng công thức nào dưới đây? c c
A. S  g
 x f xdx  . B. S  f
 x gx dx. a a c c C. S   f
 x gxdx  .
D. S   f
 x gxdx  . a a Câu 2:
Cho hình phẳng D giới hạn bởi đồ thị của ba hàm số y  f (x) , y  g(x) , y  ( h x) như hình bên dưới.
Diện tích hình phẳng D là S . Mệnh đề nào sau đây đúng? b c b c
A. S   f (x)  g(x)dx  g(x)  h(x)dx . B. S   f (x)  g(x)dx  g(x)  h(x)dx . a b a b c b c
C. S   f (x)  g(x)dx .
D. S   f (x)  h(x)dx  g(x)  h(x)dx . a a b Câu 3:
Cho hàm số f  x liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
y  f  x, y  0, x  1
 , x  2 (như hình vẽ).
Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S  f
 x dx  f
 x dx .
B. S   f
 x dx f
 x dx . 1  1 1  1 1 2 1 2
C. S   f
 x dx f
 x dx . D. S  f
 x dx f
 x dx . 1  1 1  1 Câu 4:
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? y
y=x2-2x -1 O x y= -x2+3 2 2 A.   2
 x  2dx .
B.  2x  2dx . 1  1  2 2 C.   2
2x  2x  4dx . D.   2 2
 x  2x  4dx . 1  1  Câu 5:
Gọi S là diện tích hình phẳng  H  giới hạn bởi đồ thị của hai hàm số 2
y  x và y  x . Mệnh đề nào sau đây đúng? 1 1 1 1
A. S    2
x  x dx . B. S   2
x  xdx . C. S   2 4
x  x dx . D. S   2
x  x dx . 0 0 0 0 Câu 6:
Cho hàm số y  f  x liên tục trên đoạn 0;8 và có đồ thị như hình vẽ bên dưới:
Trong các giá trị sau, giá trị nào lớn nhất? 3 8 8 5 A.  d  f x x . B.  d  f x x . C.  d  f x x . D.  d  f x x . 0 3 0 0 Câu 7:
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x 1 , trục hoành và hai đường
thẳng x  0, x  2 là
A. S  11 .
B. S  12 .
C. S  10 . D. S  9 . Câu 8:
Cho hàm số y  f x  liên tục trên
và có đồ thị như hình vẽ, diện tích hai phần S ,S lần 1 2 lượt bằng 12 và 3. 3 Giá trị của I  f  xdx bằng 2  A. 15. B. 9. C. 36. D. 27. x 1 Câu 9:
Gọi S là hình phẳng giới hạn bởi đồ thị hàm số (H ) : y 
và các trục tọa độ. Khi đó, giá x 1 trị của S bằng A. ln 2 1. B. 2 ln 2 1 . C. ln 2 1. D. 2 ln 2 1 .
Câu 10: Cho  H  là hình phẳng giới hạn bởi các đường y  x , y  x  2 và trục hoành. Diện tích của  H  bằng y 2 y  x 2  x  y O 2 4 x 7 8 10 16 A. . B. . C. . D. . 3 3 3 3
Câu 11: Diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số 4 y  x và 4
y  32  x được xác
định bởi công thức nào sau đây? 2 2 2 2
A. S  2   4
x 16dx . B. S    4
16  x dx . C. S  4 4
16  x dx . D. S  2 4 16  x dx 2  2  0 0 3
Câu 12: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: y  x  3x , y  x . Tính S . A. S  4 . B. S  8 .
C. S  2 . D. S  0 .
Câu 13: Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B như hình vẽ bên dưới. Biết 1 2 1 2
chi phí để sơn phần tô đậm là 2 200.000 n
v đ / m và phần còn lại 2 100.000 n v đ / m . Hỏi số tiền
để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết A A  8m , B B  6m và tứ giác 1 2 1 2
MNPQ là hình chữ nhật có MQ  3m ? B2 M N A1 A2 Q P B1
A. 5.526.000 đồng.
B. 5.782.000 đồng
C. 7.322.000 đồng. D. 7.213.000 đồng. 1
Câu 14: Cho đường thẳng y 
x  a và parabol 2
y  x ( a là tham số thực). Gọi S , S 1 2 lần lượt là 2
diện tích của hai hình phẳng được tô đậm và gạch chéo trong hình vẽ bên dưới: Khi S  S 1
2 thì a thuộc khoảng nào dưới đây?  7   1 5   5   7  A. ; 4   . B.  ;   . C. ;3   . D. 3;   .  2   16 2   2   2 
Câu 15: Cho hàm số bậc bốn f  x có đồ thị f  x; f ' x như hình vẽ bên dưới: Gọi S ; S S  1 S 1
2 là diện tích hai hình phẳng được gạch trong hình vẽ, khi 1 thì 2 bằng 70 57 84 A. 104 . B. . C. . D. . 23 23 23 23
Câu 16: Cho hàm số y  f  x có đồ thị như hình vẽ và diện tích hai phần ,
A B lần lượt bằng 11 và 2. 0 Giá trị của I  f 3x   1dx bằng 1  13 A. . B. 3. C. 9. D. 13. 3
Câu 17: Cho parabol  P 2
: y  x và một đường thẳng d thay đổi cắt  P tại hai điểm A , B sao cho
AB  2018 . Gọi S là diện tích hình phẳng giới hạn bởi  P và đường thẳng d . Tìm giá trị lớn nhất S của S. max 3 2018 1 3 2018 3 2018 1 3 2018 A. S  . B. S  . C. S  . D. S  . max 6 max 3 max 6 max 6
Câu 18: Trong mặt phẳng Oxy cho là hình phẳng  H  giới hạn bởi parabol 2
y  4  x và trục hoành.
Đường thẳng x  k, 2
  k  2 chia H  thành hai phần H , H như hình vẽ bên dưới: 1   2  20
Biết rằng diện tích  H gấp
lần diện tích  H
, hỏi giá trị k thuộc khoảng nào sau đây? 2  1  7 A. 2;   1 . B. 0;  1 .
C. 1;0 . D. 1; 2 .
Câu 19: Cho hai hàm số f  x 4 3 2
 ax  bx  cx  2x và g x 3 2
 mx  nx  2x với a, , b c, , m n  . Biết
hàm số y  f  x  g  x có ba điểm cực trị là 1; 2 và 3 . Diện tích hình phẳng giới hạn bởi
hai đường y  f  x và y  g x bằng 32 71 71 64 A. . B. . C. . D. . 3 9 6 9 Câu 20: Cho hàm số   4 3 2
f x  x  bx  cx  dx  e ( b, c, d, e 
) có các giá trị cực trị là 1, 4 và 9 . Diện f  x
tích hình phẳng giới hạn bởi đồ thị hàm số g  x   
và trục hoành bằng f  x A. 4. B. 6. C. 2. D. 8.
____________________________HẾT____________________________
Huế, 11h00’ Ngày 13 tháng 01 năm 2024
Page: CLB GIÁO VIÊN TRẺ TP HUẾ §Ò KIÓM TRA §ÞNH Kú M«n: To¸n 12
Chñ ®Ò: Ứng dụng tích phân
DIỆN TÍCH HÌNH PHẲNG
ĐỀ ÔN TẬP SỐ 6_TrNg 2024
LỜI GIẢI CHI TIẾT Câu 1:
Cho hàm số y  f  x và y  g  x có đồ thị như hình vẽ bên dưới:
Diện tích S của phần gạch chéo trong hình vẽ trên được tính bằng công thức nào dưới đây? c c
A. S  g
 x f xdx  . B. S  f
 x gx dx. a a c c C. S   f
 x gxdx  .
D. S   f
 x gxdx  . a a Lời giải:
Áp dụng công thức tính diện tích hình phẳng giới hạn bởi hai đường cong y  f  x , c
y  g  x và hai dường thẳng x  a , x  c ta có S  f
 x gx dx. a Câu 2:
Cho hình phẳng D giới hạn bởi đồ thị của ba hàm số y  f (x) , y  g(x) , y  ( h x) như hình bên dưới.
Diện tích hình phẳng D là S . Mệnh đề nào sau đây đúng? b c b c
A. S   f (x)  g(x)dx  g(x)  h(x)dx . B. S   f (x)  g(x)dx  g(x)  h(x)dx . a b a b c b c
C. S   f (x)  g(x)dx .
D. S   f (x)  h(x)dx  g(x)  h(x)dx . a a b Lời giải:
Dựa vào hình trên, ta thấy b c S 
f (x)  g(x) dx 
g(x)  h(x) dx   a b b b
Trên đoạn a;b , f (x) g(x) nên
f (x)  g(x) dx  
 f (x) g(x)dx . a a c c Trên đoạn ;
b c , g(x)
h(x) nên g(x)  h(x) dx   
g(x)h(x)dx. b b b c
Vậy S   f (x)  g(x)dx  g(x)  ( h x)dx . a b Câu 3:
Cho hàm số f  x liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
y  f  x, y  0, x  1
 , x  2 (như hình vẽ).
Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S  f
 x dx  f
 x dx .
B. S   f
 x dx f
 x dx . 1  1 1  1 1 2 1 2
C. S   f
 x dx f
 x dx . D. S  f
 x dx f
 x dx . 1  1 1  1 Lời giải: 1 2
Dựa vào đồ thị, ta có S  f
 x dx  f
 x dx . 1  1 Câu 4:
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? y
y=x2-2x -1 O x y= -x2+3 2 2 A.   2
 x  2dx .
B.  2x  2dx . 1  1  2 2 C.   2
2x  2x  4dx . D.   2 2
 x  2x  4dx . 1  1  Lời giải: x  1 
Phương trình hoành độ giao điểm: 2 2 2
x  2x 1  x  3  2x  2x  4  0   . x  2 2 2
Diện tích hình phẳng cần tìm là S     2 x  3 2 x  2x   1  dx    2 2
 x  2x  4dx . 1  1  Câu 5:
Gọi S là diện tích hình phẳng  H  giới hạn bởi đồ thị của hai hàm số 2
y  x và y  x . Mệnh đề nào sau đây đúng? 1 1 1 1
A. S    2
x  x dx . B. S   2
x  xdx . C. S   2 4
x  x dx . D. S   2
x  x dx . 0 0 0 0 Lời giải: x  0
Xét phương trình hoành độ giao điểm: 2
x  x  0   . x 1 1 1 Suy ra: 2 S 
x  x dx    2
x  x dx . 0 0 Câu 6:
Cho hàm số y  f  x liên tục trên đoạn 0;8 và có đồ thị như hình vẽ bên dưới:
Trong các giá trị sau, giá trị nào lớn nhất? 3 8 8 5 A.  d  f x x . B.  d  f x x . C.  d  f x x . D.  d  f x x . 0 3 0 0 Lời giải: 8 Ta có: f
 xdx  S S  S . 1 2 3 0 8 8 3
S  S  S  S  0 
f x dx  S  S  S  S   f
 xdx  f
 xdx (1) 3 2 2 3   1 2 3 1 0 0 0 8 8 8
S  S  S  S  0 
f x dx  S  S  S  S   f
 xdx  f
 xdx (2) 1 2 2 1   1 2 3 3 0 0 5 5 3 5 Ta có f
 xdx  S S  S  f x dx  f x dx   (2) 1 2 1     0 0 0 8
Từ (1), (2) và (3) suy ra trong các giá trị trên, giá trị nào lớn nhất là f  xdx  . 0 Câu 7:
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x 1 , trục hoành và hai đường
thẳng x  0, x  2 là
A. S  11 .
B. S  12 .
C. S  10 . D. S  9 . Lời giải: 2 Ta có S    2 3x   1 dx   3
x  x 2  8  2  10 . 0 0 Câu 8:
Cho hàm số y  f x  liên tục trên
và có đồ thị như hình vẽ, diện tích hai phần S ,S lần 1 2 lượt bằng 12 và 3. 3 Giá trị của I  f  xdx bằng 2  A. 15. B. 9. C. 36. D. 27. Lời giải: 3 I  f
 xdx S S  9 . 1 2 2  x 1 Câu 9:
Gọi S là hình phẳng giới hạn bởi đồ thị hàm số (H ) : y 
và các trục tọa độ. Khi đó, giá x 1 trị của S bằng A. ln 2 1. B. 2 ln 2 1 . C. ln 2 1. D. 2 ln 2 1 . Lời giải:
Phương trình trục (Ox) và (Oy) lần lượt là y  0 và x  0 . x 1
Phương trình hoành độ giao điểm của hàm số (H ) và trục Ox:  0  x 1. x 1 1 x 1 x 1 Ta có: S  dx  . Vì  0, x  0 
;1 nên diện tích cần tìm là: x 1 x 1 0 1 1 x 1  2  S   dx  1   dx    
x 2ln x1 1  2ln21. x 1  x 1 0 0 0
Câu 10: Cho  H  là hình phẳng giới hạn bởi các đường y  x , y  x  2 và trục hoành. Diện tích của  H  bằng y 2 y  x 2  x  y O 2 4 x 7 8 10 16 A. . B. . C. . D. . 3 3 3 3 Lời giải: y  x y  x  2  
Xét các hình phẳng  H :  y  0
và  H :  y  0 . 2  1    x  0, x  4  x  2, x  4 
H   H \ H 1   2  Ta có  .
H  H  H 2   1 4 4 2 2 4  x  4 16 10
Do đó S  H   S H  S H  xdx  x  2 dx  x x    
 2x    2  1   2   3 0  2 2  3 3 0 2 2 x  y  2 10
Cách khác: Ta có  H  : x  y  2
. Suy ra S  H  2
 y   y  2dy   .  3 y  0, y  2  0
Câu 11: Diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số 4 y  x và 4
y  32  x được xác
định bởi công thức nào sau đây? 2 2 2 2
A. S  2   4
x 16dx . B. S    4
16  x dx . C. S  4 4
16  x dx . D. S  2 4 16  x dx 2  2  0 0 Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị hàm số 4 y  x và 4
y  32  x : x  2 4 4 4
x  32  x  x  16   . x  2 
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số là: 2 2 2 S 
x  32  x dx  2x  32dx     322x  2 4 4 4 4 dx  2   4 16  x dx 2  2  2  2  2 2 Mặt khác vì hàm số 4
y  16  x là hàm số chẵn nên   4
16  x dx  2 4
16  x dx . 2  0 2 Vậy S  4 4
16  x dx . 0 3
Câu 12: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: y  x  3x , y  x . Tính S . A. S  4 . B. S  8 .
C. S  2 . D. S  0 . Lời giải: x  2   Ta có 3
x  3x  x 3
 x  4x  0  x  0  . x  2  2 0 2 Vậy 3 S 
x  4x dx  
  3x 4xdx   3x 4xdx  4 4  8. 2  2  0
Câu 13: Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B như hình vẽ bên dưới. Biết 1 2 1 2
chi phí để sơn phần tô đậm là 2 200.000 n
v đ / m và phần còn lại 2 100.000 n v đ / m . Hỏi số tiền
để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết A A  8m , B B  6m và tứ giác 1 2 1 2
MNPQ là hình chữ nhật có MQ  3m ? B2 M N A1 A2 Q P B1
A. 5.526.000 đồng.
B. 5.782.000 đồng
C. 7.322.000 đồng. D. 7.213.000 đồng. Lời giải: y B2 3 M N 4 A1 O 1
A2 x Q P B1 2 2 x y
Gọi phương trình chính tắc của elip  E  có dạng:  1 2 2 a b
A A  8  2a a  4 x y 3 Với 1 2     E 2 2 2 :  1  y   16  x . B B  6  2b b    3 16 9 4 1 2
Suy ra diên tích của hình elip là S
  a b    2 . 12 m . E     3 
Vì MNPQ là hình chữ nhật và MQ  3  M ; x    E  2  2 x 1  3   3  2 
 1 x 12  M 2  3; ; N 2 3;     16 4  2   2 
Gọi S ; S lần lượt là diện tích phần bị tô màu và không bị tô màu 1 2 4 4 3 Ta có: 2 2 x4sin  4. 16  d  3 16  d t S x x x
x  S  4  6 3    2 m 2 2  4 2 3 2 3 Suy ra: S  S
 S  8  6 3 . Gọi T là tổng chi phí. Khi đó ta có 1 E 2
T  4  6 3.100  8  6 3.200 7.322.000 (đồng). 1
Câu 14: Cho đường thẳng y 
x  a và parabol 2
y  x ( a là tham số thực). Gọi S , S 1 2 lần lượt là 2
diện tích của hai hình phẳng được tô đậm và gạch chéo trong hình vẽ bên dưới: Khi S  S 1
2 thì a thuộc khoảng nào dưới đây?  7   1 5   5   7  A. ; 4   . B.  ;   . C. ;3   . D. 3;   .  2   16 2   2   2  Lời giải: 1
Phương trình hoành độ giao điểm của của hai đồ thị: 2 2
x  a  x  2x  x  2a  0 2 1
Theo giả thiết, phương trình có hai nghiệm phân biệt    1 16a  0  a   16  1
S  x  x 
Khi đó, phương trình có hai nghiệm x , x x  x thỏa: 1 2  2 1 2  1 2 
P  x .x    a 1 2 2 2 1
Lưu ý: x  x  x  x  x  x  4x x   4a. 2 1  2 1  1 2 1 2 4 1 x 0 2 3     1 x 0 x x x Diện tích hình phẳng: 2 S   a dx  x dx       ax   1 2  a  2  1 x 4 3   2  a 1 x 1 2 1 2 2 1 3 1 3 1 2 2
 x  ax  .4a  2a  x   x  x  ax  a 1 1 1 1 1 1 4 4 3 3 4 3    2 x 1 x x 2  2 1
Diện tích hình phẳng S 
x  a  x dx   2   1 x  2  6 1 x x  x
Theo giả thiết, S  S  x  4a
 a x  2a   1 2  2 2 1   1   3 3 1 2 1 4 3 6 1    1 x x  x
 x .x x  x   . a x  a  0 1 2  2 3 3 1 2  2 1  1 2 1 6 2 4   1 116 1 1 3 1 a a a 2 1 116a 2      4a   . a  a  0    a 3,684 . 6  8 2  2 4 64 4
Câu 15: Cho hàm số bậc bốn f  x có đồ thị f  x; f ' x như hình vẽ bên dưới: Gọi S ; S S  1 S 1
2 là diện tích hai hình phẳng được gạch trong hình vẽ, khi 1 thì 2 bằng 70 57 84 A. 104 . B. . C. . D. . 23 23 23 23 Lời giải: 2 2
Đặt f  x  k  x  5  x  2 , k  0 . 2 2
Khi đó f  x  2k  x  5 x  2  2k  x  5  x  2  k  x  5 x  24x 14
Xét hàm g  x  f  x  f  x  k  x   x   2 5 2
x  3x  4 x  5 x  2
Suy ra g  x  0   x  4  x  1 2  4  4 
Từ đó ta suy ra: S  g
 x dx   g
 xdx  k  x5x 2 2x 3x4 dx 1  5  5  5  23 10 
k  1  k  10 23 2  2  10 104 Vậy S 
g  x dx 
x 5x  2 2x 3x  4 dx    2  23 23 4  4 
Câu 16: Cho hàm số y  f  x có đồ thị như hình vẽ và diện tích hai phần ,
A B lần lượt bằng 11 và 2. 0 Giá trị của I  f 3x   1dx bằng 1  13 A. . B. 3. C. 9. D. 13. 3 Lời giải: 0 dt +) Xét I  f 3x  
1dx, đặt 3x  1  t  dt  3dx  dx  3 1  x  1   t  2  +) Đổi cận 
x  0  t 1 1 0 1 1    I  f
 t 1  f  t f  t 1
  S  S    A B  1 dt= dt + dt 11 2 3. 3 3 3 3 2   2  0 
Câu 17: Cho parabol  P 2
: y  x và một đường thẳng d thay đổi cắt  P tại hai điểm A , B sao cho
AB  2018 . Gọi S là diện tích hình phẳng giới hạn bởi  P và đường thẳng d . Tìm giá trị lớn nhất S của S. max 3 2018 1 3 2018 3 2018 1 3 2018 A. S  . B. S  . C. S  . D. S  . max 6 max 3 max 6 max 6 Lời giải: Giả sử 2 ( A a; a ) ; 2 B( ;
b b ) (b  a) sao cho AB  2018 .
Phương trình đường thẳng d là: y  (a  b)x  ab . b b 1
Khi đó: S  (a  b)x  ab  x dx  
 abxab x dx  ba3 2 2 . 6 a a 2 2 2 2 Vì AB 
 b  a   2 2 b  a  2 
 b  a  b  a  2 2018 2018 1  2018 . 3   2018 b  a2 2
 2018  b  a  b  a  2018  S  . 6 3 2018 Vậy S 
khi a  1009 và b  1009 . max 6
Câu 18: Trong mặt phẳng Oxy cho là hình phẳng  H  giới hạn bởi parabol 2
y  4  x và trục hoành.
Đường thẳng x  k, 2
  k  2 chia H  thành hai phần H , H như hình vẽ bên dưới: 1   2  20
Biết rằng diện tích  H gấp
lần diện tích  H
, hỏi giá trị k thuộc khoảng nào sau đây? 2  1  7 A. 2;   1 . B. 0;  1 .
C. 1;0 . D. 1; 2 . Lời giải:
Gọi S, S , S lần lượt là diện tích của hình phẳng  H , H và  H . 2  1  1 2 20 27
Ta có S  S  S , S  S  S  S . 1 2 1 2 2 7 7 2 32 7 32 224 Mặt khác S   2
4  x dx   S  .   . 2 3 27 3 81 2   1  16 k 3 16 k 224
Mà S  4  x  2 2 3 2 3 dx  4x  x  
 4k nên ta được   4k  2    3  3 3 3 3 81 k k 3 k 208   4k   0 3
 27k  324k  208  0 3 81  3k  2 2 2
9k  6k 104  0  k  (do k  2  ;2 ). 3
Câu 19: Cho hai hàm số f  x 4 3 2
 ax  bx  cx  2x và g x 3 2
 mx  nx  2x với a, , b c, , m n  . Biết
hàm số y  f  x  g  x có ba điểm cực trị là 1; 2 và 3 . Diện tích hình phẳng giới hạn bởi
hai đường y  f  x và y  g x bằng 32 71 71 64 A. . B. . C. . D. . 3 9 6 9 Lời giải:
Ta có: y  h  x  f  x  g  x
 hx  f x  gx 3 2 2
 4ax  3bx  2cx  2  3mx  2nx  2 .  hx 3
 ax   b  m 2 4 3 3
x  2c  2n x  4
Do hàm số h  x  f  x  g  x có ba cực trị là 1; 2 và 3 nên h x có dạng
h x  4a  x  
1  x  2 x  3 ; h    a    1 0 4 4 .1. 2 3  4  a  6
f  x  g x 2  x  
1  x  2 x  3 3 3 3 2 71 Vậy S 
f  x  g x dx  x  
1  x  2 x  3 dx    . 3 9 1  1  Câu 20: Cho hàm số   4 3 2
f x  x  bx  cx  dx  e ( b, c, d, e 
) có các giá trị cực trị là 1, 4 và 9 . Diện f  x
tích hình phẳng giới hạn bởi đồ thị hàm số g  x   
và trục hoành bằng f  x A. 4. B. 6. C. 2. D. 8. Lời giải:
+) Gọi x  x  x là ba điểm cực trị của hàm số f  x . Ta có bảng biến thiên: 1 2 3
+) Phương trình hoành độ giao điểm của đồ thị hàm số g  x và trục hoành là: f  x  f    x      g  x   0 x x (i 1, 2, 3) i       f  x 0  f   x  0  f   x  i  0 (TM)
+) Diện tích cần tìm là: x x 2 f  x 3 f  x x x 2 3 S  dx  dx  2 f  
x  2 f x  4 f x  2 f x  2 f x  6. 2   1  3 f  x f  x 1 x 2 x x x 1 2
____________________________HẾT____________________________
Huế, 11h00’ Ngày 13 tháng 01 năm 2024

Bài tập trắc nghiệm ứng dụng tích phân để tính diện tích hình phẳng Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề nguyên hàm – tích phân Toán 12

Gắn hệ tọa độ Oxyz để giải các bài toán hình học không gian – Phương Nguyễn Toán 12

20 kĩ thuật chinh phục vận dụng cao số phức – Hoàng Xuân Nhàn Toán 12

Phân dạng bài tập và lời giải chi tiết chuyên đề Tích phân – Lưu Huy Thưởng Toán 12

Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12