17 trang 61 lượt tải

Bài tập tự luận và trắc nghiệm tích phân – Đặng Ngọc Hiền Toán 12

122

Bài tập tự luận và trắc nghiệm tích phân – Đặng Ngọc Hiền Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 200 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/17
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 1 ĐT: 0977802424
TÍCHPHÂN
1.Kháiniệmtíchphân
Cho
Fxlàmộtnguyênhàmcủa
fxvà
fxliêntụctrênđoạn 

;ab thì


d() () () ()
b
b
a
a
fx x Fx Fb Fa
Đốivớibiếnsốlấytíchphân,tacóthểchọnbấtkìmộtchữkhácthaychox,tứclà:



ddtd( ) ( ) ( ) ... ( ) ( )
bbb
aaa
fx x ft fu u Fb Fa
2.Tínhchấtcủatíchphân
Giảsửcáchàm ,fgliêntụctrên K và ,,abclà3sốbấtkìthuộc K .Tacó:
d() 0
a
a
fx x


dd() ()
ba
ab
fx x fx x


dd() () ,
bb
aa
kfxx kfxxk



ddd() () () ()
bbb
aaa
f x gx x f x x gx x


ddd() () ()
bcb
aac
fx x fx x fx x
Chúý:

ddd()() () . ()
bbb
aaa
fxgx x fx x gx x
,
d
d
d
()
()
.
()
()
b
b
a
b
a
a
fx x
fx
x
gx
gx x
A. BÀITẬP TỰLUẬN
LOẠI1.DÙNGBẢNGNGUYÊNHÀM,ĐỊNHNGHĨAVÀTÍNHCHẤT

d() () () ()
b
b
a
a
fx x Fx Fb Fa
Bài 1: Tínhcáctíchphânsau:
a)

d
2
3
1
(21)xx x
. b)

d
1
2
0
()(21)xxx x
. c).
d
2
3
2
1
xx
x
x
d)

d
1
2
0
1
231
x
x
xx
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 2 ĐT: 0977802424
Bài 2: Tínhcáctíchphânsau:
a)
d
2
2
0
xxx. b).


d
2
2
0
max 3 1, 1xxx x
c)
d
0
1cos2xx
d)


d
2
2
0
min 2 1, 1xx x x
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
LOẠI2.DÙNGPHƯƠNGPHÁPĐỔIBIẾNSỐ
. Dạng1:Giảsửtacầntính
 


d
b
a
Ifuxuxx
.
Đặt
tux

ddtuxx
Đổicận:
 ;xa tuaxb tub
Tacó:







d
ub
ub
ua
ua
IftxFt
MỘT SỐ DẠNG HAY GẶP
d(sin )cos .fxxx
Đặt
sintx
d(cos )sin .fxxx
Đặt
costx
d
1
(ln ) .fx x
x
Đặt
lntx
fx
chỉ chứa 1 lượng căn
n
ax b
Đặt

n
taxb
d
2
1
(tan ) .
cos
fx x
x
Đặt
tantx
d
2
1
(cot ) .
sin
fx x
x
Đặt
cottx
d() .
xx
fe e x Đặt
x
te
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 3 ĐT: 0977802424
. Dạng2:Giảsửtacầntính


d 0Ifxx.
Bài 3: Tínhcáctíchphânsau:
a)
d
1
3
23
0
(1 )
xx
x
. b).
d
1
2
0
2.xxx
c).
d
1
32
0
1xxx
d)
d
1
1 3ln ln
e
xx
x
x
e)

d
2
5
0
1sin .cosxxx
f)
d
ln2
0
1
x
x
e
x
e
g)
d
1
2
2
0
1
x
x
 h)
d
3
2
0
3
x
x
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
f(
x
)
có chứa Cách đổi biến
22
ax
sin ,
22
xa t t
22
ax
tan ,
22
xa t t
22
xa






,;\0
sin 2 2
a
xt
t
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 4 ĐT: 0977802424
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
LOẠI3.PHƯƠNGPHÁPTÍCHPHÂNTỪNGPHẦN


dd.
bb
b
a
aa
uv uv vu
Dạng:
d().()
b
a
Px Qx x
Nhưngchưatìmđượcnguyênhàm
Đểlàmdạngnàytatạmđịnhnghĩacácnhómhàmnhưsau:
Nhómhàmlôgarit
ln ( ),log ( )
nn
a
fx fx
.(Chưacónguyênhàmtrongbảng)
Nhómhàmđathức: 
2
01 2
( ) ...
n
n
fx a ax ax ax.(Cónguyênhàmyếu)
Nhómhàmlượnggiác:
sin( ),cos( )ax b ax b .(Cónguyênhàmtrongbảng)
Nhómhàmmũ:

,
mx n mx n
ea
.(Cónguyênhàmtrongbảng)
Phươngpháp:
Nhậndạng:Hàmsốdướidấunguyênhàmcó2trong4nhómhàmtrênnhânvớinhau.
Cáchgiải:Ưutiênnhómhàmchưacónguyênhàmđặtlàu,cònlạilàdv.Từđótacó
cáchđặtucủacácdạngnguyênhàmtừngphầnthườnggặptuântheocâuthầnchúsau:
Nhấtlô–Nhìđa–Tamlượng–Tứmũ.
Bài 4: Tínhcáctíchphân
a)
d
2
0
(3)sinxxx. b)
d
1
0
(3)
x
xex
. c)
d
1
(2)ln
e
xxx
. d)
d
1
2
0
()
xx
exex
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
.................................................. .......................................................................................................................
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 5 ĐT: 0977802424
B. PHẦNBÀITẬPTRẮCNGHIỆM
Loại1.Địnhnghĩavàtínhchấtc ủatíchphân
Câu 1. Nếu
()
Fx
làmộtnguyênhàmcủa

,fx

d
7
2
(7 ) 9, ( ) 2Ffxxthìgiátrị
(2)F
bằng?
A.11 . B. 7. C.7. D. 20 .
Câu 2. Nếu
(1) 2, (6) 21ff
,
()fx
liêntụcthìgiátrị
d
6
1
()fxxbằng?
A. 23 . B. 19 . C. 5 . D.19 .
Câu 3. Nếu 

d d
25
11
() 3, () 10fx x fx x thìgiátrị
d
5
2
()fx xbằng?
A.7 . B.13 . C. 7 . D.3.
Câu 4. Nếu
d
6
0
() 20fx x
thìgiátrị
d
3
0
(2 )fxx
bằng?
A. 40 . B.10 . C. 20.. D. 24.
Câu 5. Nếu 

dd
33
11
() 4, () 3fx x gx x thìgiátrị 

d
3
1
3() 2()fx gx xbằng?
A.6 . B.7 . C.18 D. 22 .
Câu 6. Cho
()fx
làhàmsốliêntụctrên


;ab
.Đẳngthứcnàosauđây
SAI?
A.
 


dd.
ba
ab
fx x fx x
B.


d; .
b
a
kx kb a k
C.
  




ddd;;.
bcb
aac
fx x fx x fx xc ab
D.
 

dd.
ba
ab
fx x fx x
Câu 7. Giảsử
  


d d d
144
010
2; 3; 4fx x fx x gx x
.KhẳngđịnhnàosauđâylàSAI?
A.
 

dd
44
00
fx x gxx
. B.
 



d
4
0
1.fx gx x
C.
 



d
4
0
9fx gx x
. D.
 

dd
44
00
.fx x gxx
Câu 8. Trongcáckhẳngđịnhsau,khẳngđịnhnàoSAI?
A.Nếu 

() 0, ;fx x abthì
d() 0
b
a
fx x
.
B.Nếu


,
;fx fx x aathì

d 0
a
a
fx x .
C.
   



ddgd..
bbb
aaa
fxgx x fxx xx
,vớimọihàmsố
,fx gxliêntụctrên 

;ab .
D.Nếu

d ,fx x Fx CC
thì
 



d
2
1
21
1
,0
x
x
fax b x Fax b Fax b a
a
.
Câu 9. Nếuhàmsố
yfxxácđịnh,liêntụcvàkhôngđổidấutrên 

;ab thìđẳngthứcnào
sauđâylàđúng?
A.
 

dd
ba
ab
fx x fx x
. B.
 


dd.
ba
ab
fx x fx x
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 6 ĐT: 0977802424
C.
 


dd
ba
ab
fx x fx x
. D.
 

dd.
ba
ab
fx x fx x
Câu 10. Nếucáchàmsố
fxvà
gxđềuxácđịnh,liêntụcvàcócùngmộtdấutrên 

;ab
thìđẳngthứcnàosauđâylàđúng?
A.
   







.d d d..
baa
abb
fxgx x fx x gx x B.




d
d
d
.
a
b
b
a
a
b
fx x
fx
x
gx
gx x
C.
   


ddd.
baa
abb
f x gx x f x x gx x D.
  




dd.
ba
ab
fx gx x fx gx x
Câu 11. Giảsử
 


d d
56
00
5, 8.fx x fx x
Khiđó

d
6
5
fx x
bằng
A. 3 . B. 3 . C.13 . D.13.
Câu 12. Nếu
 


dd
55
14
,fx x a fx x bthì

d
4
1
fx xbằng
A.
ab
. B.
ba
. C.
ab
. D.
4ab
.
Câu 13. Cho

d
0
5
a
fx x
và
fxlàhàmsốchẵn.Khiđó

d
0
a
fx x
bằng
A.0. B.5. C.5 . D.10.
Câu 14. Cho

d
8
1
15fx x .Khiđó

d
3
0
31fx x
bằng
A.
45
. B.
9
. C.
5
. D. 24 .
Câu 15. Cho


d
1
0
25 15fx x
.Khiđó

d
7
5
fx x
bằng
A.
15
2
. B.17 . C. 21. D.30 .
Loại2.Dùngbảngnguyênhàm


,dx x c kdx kx C

d
1
,( 1)
1
x
xx C

d
1
1( )
() . ,(1)
1
ax b
ax b x C
a

d
2
1
,( 0)
x
Cx
x
x
 
d
2
11
.,(/)
()
x
Cx ba
aax b
ax b
Câu 16. Tính 
d
3
2
1
(2 4 1)Ixxx
A.
7
3
I . B.
9
4
I . C.
10
3
I . D.
3
5
I .
Câu 17. Giátrịcủatíchphân


d
1
32
0
32yy y
là
A.4. B.
3
4
. C.6. D.3.
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 7 ĐT: 0977802424
Câu 18. Tìma,biết 
d
2
1
(3 2 1) 5
a
xx x.
A.
2a
. B.
3a
. C.
4a
. D.
5a
.
Câu 19. Tậphợpcácgiátrịcủa b saocho


d
0
24 5
b
xx
là
A.
5 . B.
5; 1 . C.
4 . D.
4; 1 .
Câu 20. Biết


d
0
25 6
m
xx
,tấtcảgiátrị
m
là
A. 1, 6mm . B. 1, 6mm. C.  1, 6mm. D. 
d
2
1
,( 0)
x
Cx
x
x
.
Câu 21. Đẳngthứcnàosauđâylàđúng?
A.
d
3
2
3
0xx
. B.


d
3
2
3
10xx
. C.
d
3
3
3
0xx
. D.


d
3
2
3
0.xxx
Câu 22. Tíchphân
d
2
4
1
x
I
x
bằng
A.
31
5
. B.
31
5
. C.
7
24
. D.
7
24
.
Câu 23. Tìma,biết

d
2
3
1
2
100
31
a
x
x
.
A.
6a
.
B.
7a
. C.
4a
. D.
8a
.
Câu 24. Cho


d
2
3
1
8
a
xx c
b
với
,,abc ;
a
b
làphânsốtốigiản.Tính

5
Tabc.
A. 8T . B. 6T . C. 6T . D. 8T .
Câu 25. Cho

d
3
1
5
21
ab
xx
c
với
,;ab c .Tính
Tabc
A.
8T
. B.
5T
. C. 7T . D.
6T
.
Câu 26. Tìma,biết
*
aNvà
d
2
4
2
42 25
3
a
x
x
x
.
A. 1a . B. 2a . C. 3a . D. 4a .
Câu 27. Cho

d
2
3
3
1
22xx x a b c
x
xd
với
,, ;abc d .Tính Tabcd
A. 5T . B. 5T . C. 10T . D. 10T
Câu 28. Tìma,biết
d
1
2
0
22ln
3
(2 1)
a
x
x
.
A. 1a . B. 2a . C. ea . D.
2
3
a .
Câu 29. Giátrịcủatíchphân

d
3
2
0
2xx x
là
A.4. B.5. C.3. D.
31
.
6
Câu 30. Tíchphân

d
4
2
1
32
a
xx x
b
với
,ab ;
a
b
làphânsốtốigiản.Tính 2Ta b.
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 8 ĐT: 0977802424
A. 22T . B. 17T . C. 23T . D. 67T .
Loại2.Dùngbảngnguyênhàm(tt)

d
ln ,( 0)
x
xCx
x

d 1
ln ,( / )
x
ax b C x b a
ax b a
Câu 31. Tìma,biết
0a
và


d
3
2
1
221 1
22ln
a
xx
xa
a
x
A.
2a
. B.
3a
. C.
4a
. D.
1a
.
Câu 32. Giảsử
d
5
1
1
ln
21
xA
x
,giátrịcủa
A
là
A.3. B.9. C.81. D.8.
Câu 33. Giảsử
d
5
3
ln .
1
x
a
x
Khiđógiátrịcủa a là
A.
2
. B. 3 . C.5 . D.15.
Câu 34. Tìm
a
,biết
1a
và


d
2
1
231 1
ln( 2 1)
21 2
a
xx
xa
x
.
A. 1a . B. 2a . C. 3a . D.
1
2
a .
Câu 35. Tính

d
1
2
0
43
x
I
xx
.
A.
3
ln
2
I
. B.
13
ln
32
I
. C.

13
ln
22
I
. D.
13
ln
22
I
.
Câu 36. Cho

d
1
2
0
ln
56
xa
b
xx
với
,ab ;
a
b
làphânsốtốigiản.Tính
2Tab.
A. 3T . B. 10T . C. 11T . D. 4T .
Câu 37. Biết
0a
và
d
1
2
3
0
32
(1)
xx a
x
.Tìma.
A. 2a . B. 4a . C. 2a . D. 3a .
Câu 38. Tính

d
2
2
0
(2 4)
43
xx
J
xx
.
A.
ln 2J
. B.
ln 3J
. C.
ln5J
. D.
ln 5J
.
Câu 39. Cho


d
2
2
0
(1)
ln 5 ln 3
43
x
xa b
xx
với
,
ab
.Tính
2Ta b
.
A. 8T . B. 7T . C. 9T . D. 9T .
Câu 40. Cho
d
3
2
2
ln
1
xac
x
bd
x
với
,,,abcd ;
a
b
,
c
d
là các phân số tối giản. Tính
Tabcd.
A. 5T . B. 4T  C. 12T . D. 14T .
Câu 41. Biết

d
3
2
2
ln( 1)
2
21
xa
xx
.
Tìm a .
A. 1a . B. ae. C. 1ae. D. 1ae.
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 9 ĐT: 0977802424
Loại2.Dùngbảngnguyênhàm(tt)

d
xx
exe C


d
1
ax b ax b
exe C
a

d ,(0 1)
x
x
a
ax C a
lna

d
1
.
mx n
mx n
a
ax C
m Lna
Câu 42. Giátrị
d
2
2
0
2
x
ex
bằng
A.
4
.e
B.
4
1e
. C.
4
4e
. D.
4
3e
.
Câu 43. Cho

d
1
4
22 2
0
(1 )
x
eb
exe
ac
với
b
;
b
c
làphânsốtốigiản.Trongkhônggianvới
hệtrụctọađộ
Oxyz gọiđiểm
;;Mabc.Khoảngcáchtừđiểm M đếnmặtphẳngOxy bằng
A.1. B. 4. C. 17 . D. 3 .
Câu 44. Cho

d
1
2
2
0
11
(1 )
x
a
ex
ec
be
với ,,abc .Tính Tabc
A. 2T . B. 4T . C. 6T . D. 8T .
Câu 45. Nếu




d
0
2
2
42
x
IexKethìgiátrịcủa
K
là
A.11. B.9. C.
25
.
2
. D.10.
Câu 46. Tính


d
1
2
0
23
xx
Ix.
A. 
4129
ln 4 ln 6 ln 9
I . B. 
3108
ln 4 ln 6 ln 9
I .
C.

3108
ln 4 ln 6 ln9
I
. D.
ln 2 2ln 3I
.
Loại2.Dùngbảngnguyênhàm(tt)

dsin cosxx x C

d
1
sin( ) cos( )ax b x ax b C
a

dcos sinxx x C 
d
1
cos( ) sin( )ax b x ax b C
a

d
2
tan
cos
x
xC
x

d
2
1
tan( )
cos ( )
x
ax b C
a
ax b

d
2
cot
sin
x
xC
x

d
2
1
cot( )
sin ( )
x
ax b C
a
ax b

dtan ln cosxx x C 
d
1
tan( ) ln cos( )ax b x ax b C
a

dcot ln sinxx x C

d
1
cot( ) ln sin( )ax b x ax b C
a
Câu 47. Tính

d
2
0
(1 cos 2 )Ixx.
A.

1
22
I
.
B.
2
I
.
C. 0I . D.
4
I
.
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 10 ĐT: 0977802424
Câu 48. Cho

d
2
0
(1 sin 3 )
b
xx
ac
với
,ac ;
b
c
làphânsốtốigiản.Tính 2Tabc.
A.
4T
. B.
2T
. C. 6T . D. 8T .
Câu 49. Cho


d
2
0
sin cos 1xxx b
a
với
,ab
.Tronghệtrụctọađộ
Oxyz
gọi

;;3Mab
.
Tínhđộdàiđoạn
OM
.
A. 17OM . B. 7OM . C. 17OM . D. 8OM .
Câu 50. Cho

d
4
2
0
()
cos
x
xx
e
ee x a
b
x
với
,ab
.Tính
2Ta b
.
A.
9T
.
B.
6T
. C. 2T . D. 7T
Câu 51. Cho
d
4
22
6
1
sin .cos
ac
x
b
xx
với
,bc ;
a
b
làphânsốtốigiản.Tính  2Ta bc.
A. 11T . B.
5T
. C.
10T
. D. 11T.
Câu 52. Cho

d
4
22
6
cos2
3
sin .cos
xb
xa
c
xx
với với
,;bc a ;
b
c
là phân số tối giản. Tính
Tabc.
A. 9T . B. 5T . C. 5T . D. 9T .
Câu 53. Để




d0,
2
0
1
sin
2
x
ttvới
k
thì
x
thỏa:
A.
2xk . B.
xk. C.
2
k
x
. D.
2xk
Câu 54. Nếu


d
0
sin cos 0, 0 2
a
xxx athìgiátrịabằng:
A.
4
. B.
2
. C.
3
2
. D.
Câu 55. Vớigiátrịnàocủathamsốm thìtíchphân


d
2
0
sin
m
Ix xx
bằng


2
48
32
?
A.
1m
. B.
6
m . C.
3
m . D.
4
m .
Câu 56. Đẳngthứcnàosauđâylàđúng?
A.


dd
22
00
sin cosxx xx
. B.


dd
22
00
sin tan .xx xx
C.



dd
22
00
sin cosxx xx
. D.



dd
22
00
sin tan .xx xx
Câu 57. Tính
d
3
4
tanIxx
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 11 ĐT: 0977802424
A.
6
ln
2
I . B. ln 2I . C.
ln2I
. D. ln 2I
Câu 58. Cho
d
3
4
cot ln
ac
xx
bd
với
,bd
;
,
ac
bd
làcácphânsốtốigiản.Trongmặtphẳngtọa
độ
Oxy gọi
;, ;Mab Ncd.Tínhđộdàiđoạnthẳng MN
A. 2MN . B. 42MN . C. 22MN . D. 4MN .
Câu 59. Tính
d
4
2
0
sinIxx
A.

1
84
I . B.

1
82
I . C.

1
82
I . D.

1
84
I
Câu 60. Cho

d
4
2
0
cos
a
xx
bc
với
,ac ;
a
b
làphânsốtốigiản.Tính
Tabc.
A. 11T . B. 13T . C. 8T . D. 9T
Câu 61. Nếu

d
0
sin cos 0,0 2
a
xxx a
thìabằng
A.
a . B.
2
a
. C.
3
2
a
. D.
4
a
Câu 62. Giảiphươngtrìnhẩn m sauđây
d
0
cos 0.
m
xx
A.
.
3
m
. B.
 2, .
3
mkk
C.
 2, .
6
mkk
. D.

,
.mk k
Câu 63. Tính
d
4
0
sin 3 cosIxxx.
A. 0I . B. 1I . C.
1
2
I . D.
1
4
I .
Câu 64. Cho
d
4
0
cos3 cos
a
xxx
b
với
b ;
a
b
làphânsốtốigiản.Tính Tab
A.
1T
. B. 5T . C. 3T . D. 3T
Câu 65. Cho
d
4
0
sin 3 sin
a
xxx
b
với
b ;
a
b
là phân số tối giản. Trong mặt phẳng tọađộ
Oxy ,điểm
;Mablàtâmđốixứngcủađồthịhàmsốnàosauđây?
A.
4
1
x
y
x
.
B.
14
1
x
I
x
.
C.
41
1
x
y
x
.
D.
2
4
x
y
x
Câu 66. Cho
d
4
0
1
1sin2
a
x
xb
với
b ;
a
b
làphânsốtốigiản.TrongmặtphẳngtọađộOxy ,
điểm
;Iablàđỉnhcủaparabolcóphươngtrìnhnàosauđây?
A. 
2
23yx x . B. 
2
45yx x . C. 
2
67yx x. D. 
2
23yx x .
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 12 ĐT: 0977802424
Câu 67. Cho
d
4
0
1
1cos2
a
x
xb
vớivới
b ;
a
b
làphânsốtốigiản.Tính Tab
A.
1T
. B.
1T
. C. 3T . D.
2I
Câu 68. Cho

d
2
3
1
1cos
xab
x
với
,ab
.Tính
2Tab
.
A.
11T
.
B.
5T
. C.
6T
. D.
7T
Câu 69. Tìmkhẳngđịnhđúngtrongcáckhẳngđịnhsau:
A.






dd
4
00
sin sin
44
xx xx
.
B.


 

 
 

dd
00
sin cos
44
xx xx.
C.


  

  
  

ddd
3
4
3
00
4
sin sin sin
444
xx xx xx
.
D.

 

 
 

dd
4
00
sin 2 sin
44
xx xx
.
Loại3.Đổibiếnsố
Câu 70. Tíchphân

d
1
2
0
1
25
x
Ix
xx
bằng
A.
8
ln
5
. B.
18
ln
25
. C.
8
2ln
5
. D.
8
2ln
5
.
Câu 71.
Tíchphân:
d
1
3
0
(1)
xx
J
x
bằng
A.
1
8
J . B.
1
4
J . C. 2
J
. D. 1
J
.
Câu 72. Cho
d
3
2
2
ln
1
xac
x
bd
x
với
,;,bd ac
;
,
ac
bd
là các phân số tối giản. Tính
Sabcd.
A. 5S . B. 11S . C. 13S . D. 16S .
Câu 73. Gọi
d
1
2
0
1
xx
I
x
thì
A.
.
2
I B.
.
4
I C.
ln 2
2
I . D. ln 2.I
Câu 74. Cho 
d
3
2
1
12
ac
xxx
bd
với
,bd ; ,ac ;
,
ac
bd
làcácphânsốtốigiản.Trong
mặtphẳngtọađộ
Oxy ,gọi
;, ;Mab Ncd.Tọađộtrungđiểmcủađoạn MN là
A.



3
;3
2
.
B.
3; 3 . C.



5
;3
2
.
D.
5; 3 .
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 13 ĐT: 0977802424
Câu 75. Tíchphân


d
1
19
0
1Ix xxbằng
A.
1
420
.
B.
1
380
.
C.
1
342
.
D.
1
462
.
Câu 76. Tíchphân

d
1
2
0
1Lx xx
bằng
A. 1L . B.
1
4
L
.
C. 1L . D.
1
3
L
.
Câu 77. Cho 
d
2
2
1
21Ixxxvà

2
1ux x
.Chọnkhẳngđịnh
saitrongcáckhẳngđịnhsau:
A.
d
3
0
Iuu
. B.
2
27
3
I
. C.
d
2
0
Iuu
. D.
3
3
2
0
2
.
3
Iu
Câu 78. Biếttíchphân

d
1
0
1
M
xxx
N
,với
M
N
làphânsốtốigiản.Giátrị MNbằng:
A.18 . B.19 . C.20 . D. 21
Câu 79. Tíchphân

d
7
3
0
1
11
Ix
x
cógiátrịlà:
A.
33
3ln
22
. B.
93
3ln
22
. C.
92
3ln
23
. D.
92
3ln
23
.
Câu 80. Cho

d
2
1
cos ln
e
x
Ix
x
,tatínhđược:
A.
cos1I
. B. 1I . C.
sin1I
. D.
sin 2 sin1I
.
Câu 81. Cho

d
3
2
2
0
sin .cos 1
ln 2
cos 1
xxa
x
bc
x
với
b ; ,ac ;
a
b
là phân số tối giản. Tính
Tabc.
A. 2T . B.
6T
. C.
3T
. D. 1T .
Câu 82.
Chotíchphân
d
1
0
3
x
Ix
x
và
d
2
0
cos
3sin 12
x
J
x
x
,phátbiểunàosauđâyđúng:
A. IJ. B. 2I . C.
1
ln 5
3
J
. D. 2IJ.
Câu 83.
Tíchphân
d
0
2
cos
2sin
x
Ix
x
cógiátrịlà:
A.ln 3 . B.0 . C.
ln 2
. D.
ln 2
.
Câu 84.
Cho

d
6
0
1
sin cos
64
m
Ixxx.Khiđó m bằng
A.6. B.5. C.4. D.3.
Câu 85. Tíchphân
d
6
3
0
sin .cosIxxx
bằng:
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 14 ĐT: 0977802424
A.6 . B. 5 . C.4 . D.
1
64
.
Câu 86.
Tính

d
2
0
1cos sin
n
xxx
tađược
A.


d
2
0
1
1cos sin
2
n
xxx
n
. B.


d
2
0
1
1cos sin .
1
n
xxx
n
C.


d
2
0
1
1cos sin
1
n
xxx
n
. D.


d
2
0
1
1cos sin .
21
n
xxx
n
Câu 87.
Tíchphân


d
4
44
0
cos2 cos sinIxxxx
bằng
A.
5
6
. B.
5
24
. C.
7
12
. D.
5
12
.
Câu 88. Tíchphân
d
2
1
1ln
e
x
Ix
x
cógiátrịlà:
A.
1
3
. B.
2
3
. C.1 . D.
4
3
.
Câu 89. Tíchphân
d
2
1
1
0
.
x
Ixe x
cógiátrịlà:
A.
2
2
ee
.
B.
2
3
ee
.
C.
2
2
ee
.
D.
2
3
ee
.
Câu 90. Tíchphân

d
2
sin
0
cos
x
Ixexm
thì
m
thỏamãnphươngtrình
A. ln 1x . B.
ln 1 0x
. C.

ln 1 0x
. D.
ln 1 1x
.
Câu 91. Tíchphân
d
23
2
2
3
3
Ix
xx
bằng:
A.
6
. B.
. C.
3
. D.
2
.
Câu 92. Đặt
d
6
2
32
9
x
I
xx
và
3
.
cos
x
t
Trongcáckhẳngđịnhsau,khẳngđịnhnàoSAI?
A.
dd
2
3sin
cos
t
xt
t
. B.
.
36
I
C.
d
3
4
sin
3cos tan
tt
I
tt
. D.
dd
2
sin
.
3cos tan
9
xtt
tt
xx
Câu 93.
Tíchphân


d
22 2
0
0
a
xa xxa
bằng
A.
4
.
8
a
.
B.
4
.
16
a
.
C.
3
.
16
a
.
D.
3
.
8
a
.
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 15 ĐT: 0977802424
Câu 94. Cho


d
3
1
16xf x x .Tính

d
2
23
0
11Ixf x x.
A.
9I
. B.
6I
. C. 4I . D. 2I .
Câu 95. Cho


d
4
1
1 2000
x
xf e x
.Tính


d
2
3
1
1
x
Ixf ex
.
A. 2000I . B. 4000I . C. 1000I . D. 3000I .
Câu 96. Cho

d
2
2
0
15xf x x
.Tính

d
5
1
Ixfxx.
A.
5
2
I
. B.
10I
. C.
55I
. D.
5I
.
Câu 97. Đổibiến 2sinxttíchphân
d
1
2
0
4
x
x
trởthành:
A.
d
6
0
tt
. B.
d
6
0
t
. C.
d
6
0
1
t
t
. D.
d
3
0
t
Loại4.Phươngpháptíchphântừngphần


dd.
bb
b
a
aa
uv uv vu
Câu 98. Tíchphân
d
0
sinLxxx
bằng:
A.
L . B.
L . C. 2L . D. 0L .
Câu 99. Cho

d
3
0
13
cos
xxx
ab
với ,ab .Tính

2
2Tab
.
A. 5T . B. 9T . C. 14T . D. 16T .
Câu 100. Tíchphân
d
2
0
sinIx xx
bằng:
A.
2
4 . B.
2
4 . C.
2
23. D.
2
23
Câu 101. Cho

d
4
0
22
.cosxxx c
ab
với
,,abc .Tính
Tabc
.
A. 15T . B. 13T . C.
11T
. D. 9T .
Câu 102.
Cho 
d
2
1
(2 1)ln ln 2
b
xxxa
c
với
;, ;
b
cab
c
là phân số tối giản. Tính
Tabc.
A. 6T . B. 3T . C. 5T . D. 1T .
Câu 103. Cho


d
ln2
0
ln 2
x
a
xe x c d
b
với
;,,bacd;
a
b
là phân số tối giản. Tính
Tabcd
A.
3T
. B.
5T
. C. 4T . D. 7T .
Câu 104. Giátrị
d
1
1
0
x
xe x
bằng
A. 1 e . B. 2e . C.1. D. 1 .
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 16 ĐT: 0977802424
Câu 105. Tíchphân
d
2
2
1
ln x
Ix
x
bằng:
A.

1
1ln2
2
. B.

1
1ln2
2
. C.

1
ln 2 1
2
. D.

1
1ln2
4
.
Câu 106. Cho


d
1
0
1.
x
xe x ae b
với ,ab .TrongmặtphẳngtọađộOxy , khoảngcáchtừ
điểm

;Mabđếnđườngthẳng :20xy bằng
A.
52
2
. B.
32
2
. C.
2
2
. D.3 .
Câu 107. Cho 
d
3
2
2
ln( ) ln 3xxxab với ,ab .Tính
Tab
.
A.
3T
. B.
3T
. C.
5T
. D.
5T
.
Câu 108. Tìm
0a
saocho
d
2
0
.4
a
x
xe x
A. 4. B.
1
4
. C.
1
2
. D.2 .
Câu 109. Cho

d
1
23 3
0
.
x
ac
xe x e
bd
với
,bd
;
,ac
;
,
ac
bd
là các phân số tối giản. Tính
Sabcd
.
A.
75S
. B.
57S
. C.
61S
. D.
67S
.
Loại5.Mộtsốdạngđặcbiệt
Câu 110. Đẳngthứcnàosauđâylàđúng?
A.
d
3
2
3
0xx
. B.


d
3
2
3
10xx
. C.
d
3
3
3
0xx
. D.


d
3
2
3
0xxx
.
Câu 111. Đẳngthứcnàosauđâylàđúng?
A.
dsin 0xx
. B.
dcos 0xx
.
C.

d
2
sin 0xx
. D.

d
2
cos 0xx
.
Câu 112. Giátrịcủatíchphân
d
1
2
0
3
1 2016
x
x
Ix
A. 3 . B. 2 . C.1 . D.0 .
Câu 113. Đẳngthứcnàosauđâyđúng
A.
d
5
2017
3
5
sin
0
2cos
x
x
x
.B.
d
5
2
5
3
0.
15
x
x
x
C.
d
3
2
2
3
3
0
1
x
x
x
. D.


d
2
sin cos 0.xxx
Câu 114. Tíchphân

d
2
0
cos
cos sin
x
Ixm
xx
thì m lànghiệmphươngtrìnhnàosauđây?
A.
sin 2 0x
. B.
cos 0x
. C.
sin 1x
. D.
cos 2 0x
.
Câu 115. Tíchphân


d
4
2
0
max 2 1, 1Ixxxx
.
A.
83
6
. B.
7
6
. C.
7
6
. D.
83
6
.
Câu 116. Tíchphân


d
3
2
0
min ,Ixxxx
.
NGUYÊNHÀM–TÍCHPHÂN–ỨNGDỤNG
Biên tập: ĐẶNG NGỌC HIỀN Page 17 ĐT: 0977802424
A.
11
6
. B.
19
6
. C.
11
6
. D.
19
6
.
ĐÁPÁN
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
ĐA C D A B A D A C D D A A C C D C B
Câu 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
ĐA A B A C C B B C A B C D C A A A B
Câu 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
ĐA D C A C A D C B B A D B B C A A A
Câu 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
ĐA B C C D A B A A B A D C B B A A D
Câu 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85
ĐA C B A D C B A D C B A B D A D D D
Câu 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102
ĐA B D D C D A D B C C D B A C A D A
Câu 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
ĐA A B A C C D B C A C A D A B

Tài liệu khác của Toán 12

Preview text:

NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG TÍCH PHÂN
1. Khái niệm tích phân
 Cho F x là một nguyên hàm của f x và f x liên tục trên đoạn a;b   thì b b
f (x) x F(x)  F(b)   d F(a) a a
 Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác thay cho x, tức là: b b b f (x d
) x f (t d ) t  f (u d
) u  ...  F(b)     F(a) a a a
2. Tính chất của tích phân
Giả sử các hàm f , g liên tục trên K và a,b,c là 3 số bất kì thuộc K . Ta có: a b a b b
f (x) x   d 0  f (x d ) x   
f(x d)xkf (x d
) x k f (x d ) x, k     a a b a a b b b b c b
  f (x)  (
g x) dx f (x d ) x      (gx d)xf (x d
) x f (x d ) x   
f(x d)x a a a a a c b f x x b  ( d) b b b f (x)
Chú ý: f (x) ( g x d ) x  
f(x d) .xg(x d)x, dx   a . ( g x) b a a a a  (gx d)x a
A. BÀI TẬP TỰ LUẬN
LOẠI 1. DÙNG BẢNG NGUYÊN HÀM, ĐỊNH NGHĨA VÀ TÍNH CHẤT b b
f (x) x F(x)  F(b)   d F(a) a a Bài 1: Tính các tích phân sau: 2 1 2 3 x x 1 x  1 a) 3 (x  2x   1 d ) x . b) 2
(x x)(2x   1 d ) x . c).  dx d)  dx 2 x 2 2x  3x  1 1 0 1 0
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
Biên tập: ĐẶNG NGỌC HIỀN Page 1 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG Bài 2: Tính các tích phân sau: 2 2 a) 2 x   x dx . b). max 2
x  3x  1, x   1dx 0 0  2 c) 1   cos 2xdx d) min 2
2x x  1, x   1dx 0 0
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
LOẠI 2. DÙNG PHƯƠNG PHÁP ĐỔI BIẾN SỐ b .
Dạng 1: Giả sử ta cần tính I f
 ux 
u xdx . a
Đặt t ux dt  
u xdx
Đổi cận: x a t ua; x b t ub ubub Ta có: I
f tx   d F t uaua
MỘT SỐ DẠNG HAY GẶP f(sinx)cos d x . x
Đặt t  sin x f(cosx)sin d x . x
Đặt t  cos x  1
Đặt t  ln x f (ln x) d . x x
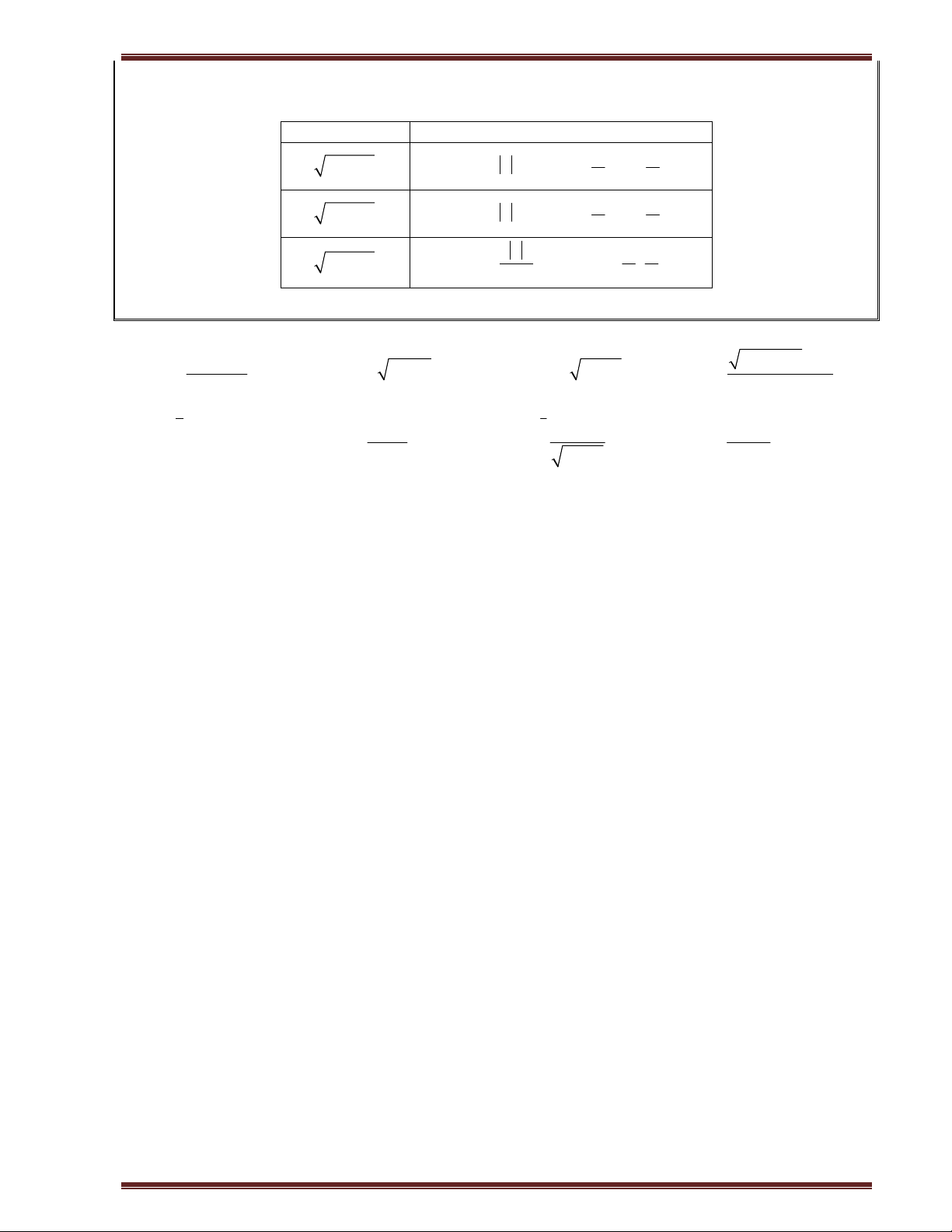
f x chỉ chứa 1 lượng căn n ax b Đặt  n t ax b  1
Đặt t  tan x f (tan x) d . x 2 cos x  1
Đặt t  cot x f (cot x) d . x 2 sin x  ( x) x f e e d . x Đặt  x t e
Biên tập: ĐẶNG NGỌC HIỀN Page 2 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG .
Dạng 2: Giả sử ta cần tính I f xx   d 0 . f(x) có chứa Cách đổi biến   2  2 a x
x a sin t,   t 2 2   2  2 a x
x a tan t,   t 2 2 a     2  2 x a x  , t   ;  \    t   0 sin 2 2 Bài 3: Tính các tích phân sau: 1 3 x x 1 1 e
1  3 ln x ln x a)  d . b). x 2   2 x d . x c). 3 x 1   2 x dx d)  dx (1  2 3 x ) x 0 0 0 1  1 2 ln 2 x e 2 x 3 x e) 1  5 sin x.cos d x x f)  dx g)  d h)  d 1  x e 2 x  3 0 1  2 0 0 x 0
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
Biên tập: ĐẶNG NGỌC HIỀN Page 3 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
LOẠI 3. PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN b b d u v b . u v   v u a  d a a b Dạng :  ( P x). ( Q x d
) x Nhưng chưa tìm được nguyên hàm a
Để làm dạng này ta tạm định nghĩa các nhóm hàm như sau:
Nhóm hàm lôgarit lnn f (x),logn f (x .(Chưa có nguyên hàm trong bảng) a )
Nhóm hàm đa thức: f (x)  a a x  2 a x  ...  n
a x .(Có nguyên hàm yếu) 0 1 2 n
Nhóm hàm lượng giác: sin(ax b),cos(ax b
) .(Có nguyên hàm trong bảng)
Nhóm hàm mũ: mxn mx , n e a
. (Có nguyên hàm trong bảng) Phương pháp:
Nhận dạng: Hàm số dưới dấu nguyên hàm có 2 trong 4 nhóm hàm trên nhân với nhau.
Cách giải: Ưu tiên nhóm hàm chưa có nguyên hàm đặt là u, còn lại là dv. Từ đó ta có
cách đặt u của các dạng nguyên hàm từng phần thường gặp tuân theo câu thần chú sau:
Nhất lô – Nhì đa – Tam lượng – Tứ mũ. Bài 4: Tính các tích phân  2 1 e 1 a) (x   3) sin d x x . b)  (   3) x x e dx . c) (x   2) ln d x x . d) 2 ( x   ) x e x e dx 0 0 1 0
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
.........................................................................................................................................................................
Biên tập: ĐẶNG NGỌC HIỀN Page 4 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG
B. PHẦN BÀI TẬP TRẮC NGHIỆM
Loại 1. Định nghĩa và tính chất của tích phân 7
Câu 1. Nếu F(x) là một nguyên hàm của f x , F(7)  9, f (x) x   d
2 thì giá trị F(2) bằng? 2 A. 11 . B. 7 . C. 7 . D. 20 . 6
Câu 2. Nếu f (1)  2
, f (6)  21, f (x) liên tục thì giá trị f
 (x d)x bằng ? 1 A. 23 . B. 19 . C. 5 . D. 19 . 2 5 5
Câu 3. Nếu f (x d
) x  3, f (x d ) x   
10 thì giá trị  f(x d ) x bằng ? 1 1 2 A. 7 . B. 13 . C. 7 . D. 3. 6 3
Câu 4. Nếu f (x) x   d
20 thì giá trị  f (2x d ) x bằng ? 0 0 A. 40 . B. 10 . C. 20.. D. 24. 3 3 3
Câu 5. Nếu f (x d ) x  4, ( g x d ) x   
3 thì giá trị 3 f (x)  2 ( g x)   dx bằng ? 1 1 1 A. 6 . B. 7 . C. 18 D. 22 .
Câu 6. Cho f (x) là hàm số liên tục trên a; b 
 . Đẳng thức nào sau đây SAI? b a b
A. f xdx   
f xd .x
B. kdx k b a;  k   . a b a b c b b a
C.f xdx   f xdx   f xdx;c a;b 
. D. f xdx  
f xd .x a a c a b 1 4 4
Câu 7. Giả sử f xdx  2; f xdx  3; gxdx    
4 . Khẳng định nào sau đây là SAI? 0 1 0 4 4 4
A. f xdx  
gxdx . B.
f x gxdx    1. 0 0 0 4 4 4 C.
f x gxdx    9 .
D. f xdx  
gxd .x 0 0 0
Câu 8. Trong các khẳng định sau, khẳng định nào SAI? b
A. Nếu f (x)  0, x  a; b 
 thì f (x) x   d 0 . a a
B. Nếu f x   f x , x  a; a 
 thì f xx   d 0 . a b b b C.
f x.gxdx   
f xdx.gxdx, với mọi hàm số f x, gx liên tục trên a;b   . a a a x2 1
D. Nếu f xdx F x  C, C  
 thì  f ax bdx  Fax b F ax b , a 0 . 2    1     a x1
Câu 9. Nếu hàm số y f x xác định, liên tục và không đổi dấu trên a;b   thì đẳng thức nào sau đây là đúng? b a b a
A. f xdx  
f x dx .
B. f xdx   
f x d .x a b a b
Biên tập: ĐẶNG NGỌC HIỀN Page 5 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG b a b a
C. f xdx   
f x dx. D.
f x dx  
f xdx . a b a b
Câu 10. Nếu các hàm số f x và gx đều xác định, liên tục và có cùng một dấu trên a;b  
thì đẳng thức nào sau đây là đúng? a f x x b   d ba   af xA.
f x.gxdx   f xdx. gxdx   b    . B.x g x a   d  . a ab   b
gxdx b b a a b a C.
f x  g x dx f xdx   
gxdx . D.f x gx dx    f x 
g x dx . a b b a b 5 6 6
Câu 11. Giả sử f xdx  5, f xdx   
8. Khi đó  f xdx bằng 0 0 5 A. 3 . B. 3 . C. 13 . D. 13. 5 5 4
Câu 12. Nếu f xdx a, f xdx   
b thì  f xdx bằng 1 4 1
A. a b .
B. b a .
C. a b .
D. a  4b . aa
Câu 13. Cho f xx   d
5 và f x là hàm số chẵn. Khi đó  f xdx bằng 0 0 A. 0. B. 5. C. 5 . D. 10. 8 3
Câu 14. Cho f xx   d
15 . Khi đó f 3x   1dx bằng 1 0 A. 45 . B. 9 . C. 5 . D. 24 . 1 7
Câu 15. Cho f 2x  5 x   d
15 . Khi đó  f xdx bằng 0 5 15 A. . B. 17 . C. 21. D. 30 . 2
Loại 2. Dùng bảng nguyên hàm
dx x c, kdx kx    C  1 x   ax  1 1 ( b)   x x   C  ,(    d  (ax b) x  .  C,  (    1)   d 1)  1 a   1 x 1 x 1 1 
   C,(x   d 0)    .  C,(x    d
b / a) 2 x x (ax  2 b) a ax b 3
Câu 16. Tính I  2 (2x  4x   1 d ) x 1
A. I  7 .
B. I  9 .
C. I  10 . D. I  3 . 3 4 3 5 1
Câu 17. Giá trị của tích phân  3 y  2 3y   2dy là 0 A. 4. B.  3 . C. 6. D. 3. 4
Biên tập: ĐẶNG NGỌC HIỀN Page 6 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG a
Câu 18. Tìm a, biết 2
(3x  2x  1) x   d 5 . 1
A. a  2 .
B. a  3 .
C. a  4 . D. a  5 . b
Câu 19. Tập hợp các giá trị của b sao cho 2x  4 x   d 5 là 0 A.   5 . B. 5;   1 . C.   4 . D. 4;   1 . m
Câu 20. Biết 2x  5 x   d
6 , tất cả giá trị m là 0 x 1
A. m  1, m  6 .
B. m  1, m  6 .
C. m  1, m  6 . D.
   C,(x   d 0) . 2 x x
Câu 21. Đẳng thức nào sau đây là đúng? 3 3 3 3 A. 2 x x   d 0 . B.  2 x  1 x   d 0 . C. 3 x x   d 0 . D.  2
x xx   d 0. 3 3 3 3 2 Câu 22. x
Tích phân I   d bằng 4 x 1 31 7 A. . B.  31 . C. . D.  7 . 5 5 24 24 2 Câu 23. 2 a Tìm a, biết dx    . 3x  13 100 1
A. a  6 .
B. a  7 .
C. a  4 . D. a  8 . 2 Câu 24. a a Cho 3 x x   8   d c với 
a,b,c   ; là phân số tối giản. Tính    5 T a b c . b b 1
A. T  8 .
B. T  6 .
C. T  6 . D. T  8 . 3 a 5  Câu 25. b Cho 2x  1 x   d với 
a,b  ; c   . Tính T a b c c 1
A.T  8 .
B. T  5 .
C. T  7 . D. T  6 . 2 4 4x Câu 26. 2 25
Tìm a, biết  * a N và x   d . 2 x 3 a
A. a  1.
B. a  2 .
C. a  3 . D. a  4 . 2 x x  3 x a 2  3 b 2  Câu 27. c Cho x   d với 
a,b,c  ; d   . Tính T a b c d x d 1
A.T  5 .
B. T  5 .
C. T  10 . D. T  10 1 Câu 28. 2 2 ln a Tìm a, biết x   d . (2x  2 1) 3 0
A. a  1.
B. a  2 .
C. a  e.
D. a  2 . 3 3
Câu 29. Giá trị của tích phân 2 x x   2 dx là 0 31 A. 4. B. 5. C. 3. D. . 6 4 Câu 30. a a Tích phân 2
x  3x  2 x   d với 
a,b   ; là phân số tối giản. Tính T a  2b .  b b 1
Biên tập: ĐẶNG NGỌC HIỀN Page 7 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG
A. T  22 .
B. T  17 .
C. T  23 . D. T  67 .
Loại 2. Dùng bảng nguyên hàm(tt) x x   x C x   d ln ,( 0)  
ax b C x    d 1 ln ,(
b / a) x ax b a a 3 2x  2x Câu 31. 1 1
Tìm a, biết a  0 và x  2    d 2 ln a 2 x a 1
A. a  2 .
B. a  3 .
C. a  4 . D. a  1 . 5 Câu 32. 1 Giả sử x   d
ln A , giá trị của A là 2x  1 1 A. 3. B. 9. C. 81. D. 8. 5 Câu 33. x Giả sử 
 d ln .a Khi đó giá trị của a là x 1 3 A. 2 . B. 3 . C. 5 . D. 15. a 2 2x  3x Câu 34. 1 1
Tìm a , biết a  1 và
dx   ln(2a   1) . 2x  1 2 1
A. a  1 .
B. a  2 .
C. a  3 . D. a  1 . 2 1 Câu 35. x Tính I   d . 2 x  4x  3 0 A. I  3 ln . B. I  1 3 ln . C. I   1 3 ln . D. I  1 3 ln . 2 3 2 2 2 2 2 1 Câu 36. x a a Cho   d ln với 
a,b   ; là phân số tối giản. Tính T  2a b . 2 x  5x  6 b b 0
A. T  3 .
B. T  10 .
C. T  11. D. T  4 . 1 2 Câu 37. x x a Biết a  0 và   d . Tìm a. (x  3 1) 32 0
A. a  2 .
B. a  4 .
C. a  2 . D. a  3 . 2 (2x Câu 38. 4) x Tính J   d . 2 x  4x  3 0
A. J  ln 2 .
B. J  ln 3 .
C. J  ln 5 .
D. J  ln 5 . 2 (x Câu 39. 1) Cho x a ln 5   d
b ln 3 với a,b   . Tính T a  2b . 2 x  4x  3 0
A. T  8 .
B. T  7 .
C. T  9 . D. T  9 . 3 Câu 40. x a c a c Cho x   d ln với 
a,b,c,d   ; ,
là các phân số tối giản. Tính 2 x  1 b d b d 2
T a b c d .
A.T  5 .
B.T  4
C. T  12 . D. T  14 . 3 x ln(a Câu 41. 1) Biết   d
. Tìm a . 2 x  2x  1 2 2
A. a  1 .
B. a e .
C. a  1  e .
D. a  1  e .
Biên tập: ĐẶNG NGỌC HIỀN Page 8 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG
Loại 2. Dùng bảng nguyên hàm(tt) xx e x e   d C axb ax  b e x e   d 1 C a x a mxn ax a x   Ca   d ,(0 1)  mxn a x    d 1 . C lna m Lna 2
Câu 42. Giá trị  2 2 x e dx bằng 0 A. 4 e . B. 4 e  1. C. 4 4e . D. 4 3e . 1 4 Câu 43. e b b Cho (1  2x 2 e ) x  2 e    d với 
b   ; là phân số tối giản. Trong không gian với a c c 0
hệ trục tọa độ Oxyz gọi điểm M a; b; c . Khoảng cách từ điểm M đến mặt phẳng Oxy bằng A. 1 . B. 4 . C. 17 . D. 3 . 1 Câu 44. x a 1 1 Cho  (1  2 e ) x     d
với a,b,c   . Tính T a b c 2 e be c 0
A.T  2 .
B. T  4 .
C. T  6 . D. T  8 . 0   x
Câu 45. Nếu I   4  2
e  dx K  2e thì giá trị của K là 2   25 A. 11. B. 9. C. . . D. 10. 2 1 2
Câu 46. Tính  2x   3x I  dx. 0 4 12 9 3 10 8 A. I    . B. I    . ln 4 ln 6 ln 9 ln 4 ln 6 ln 9 3 10 8 C. I    .
D. I  ln 2  2 ln 3 . ln 4 ln 6 ln 9
Loại 2. Dùng bảng nguyên hàm(tt)
 sin x x  cos x   d C
ax b x   ax b   d 1 sin( ) cos( ) C a
 cos x x  sin x   d C ax b x ax b   d 1 cos( ) sin( ) C a x x 1   tan x   d C
 tan(ax b)   d C 2 cos x 2 cos (ax b) a x x 1    cot x   d C
  cot(ax b)   d C 2 sin x 2 sin (ax b) a
 tan x x  ln cos x   d C
ax b x   ax b   d 1 tan( ) ln cos( ) C a
 cot x x  ln sin x   d C ax b x ax b   d 1 cot( ) ln sin( ) C a  2
Câu 47. Tính I  (1  cos2x d)x. 0    A. I   1 . B. I  .
C. I  0 . D. I  . 2 2 2 4
Biên tập: ĐẶNG NGỌC HIỀN Page 9 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG  2  Câu 48. b b
Cho (1  sin 3x) x    d với 
a,c   ; là phân số tối giản. Tính T  2a b c . a c c 0
A.T  4 .
B. T  2 .
C. T  6 . D. T  8 .  2 
Câu 49. Cho sin x  cos x  1 x    d
b với a,b   . Trong hệ trục tọa độ Oxyz gọi M a; b; 3 . a 0
Tính độ dài đoạn OM .
A. OM  17 .
B. OM  7 .
C. OM  17 . D. OM  8 .  4 x xx e
Câu 50. Cho e (e  ) x a   d
với a,b   . Tính T a  2b . 2 cos x b 0
A. T  9 .
B. T  6 .
C. T  2 . D. T  7  4 Câu 51. 1 a c a Cho x   d với 
b,c   ; là phân số tối giản. Tính T a  2b c . 2 2  sin . x cos x b b 6
A. T  11.
B. T  5 .
C. T  10 .
D. T  11 .  4 Câu 52. cos 2x b b Cho x a   d 3 với với 
b,c   ; a   ;
là phân số tối giản. Tính 2 2  sin . x cos x c c 6
T a b c .
A.T  9 .
B. T  5 .
C. T  5 .
D. T  9 . x  1  Câu 53. Để 2 sin t  dt   
0, với k  thì x thỏa: 2 0    k
A. x k  2 . B. x   k . C. x  .
D. x    k  2 2 a
Câu 54. Nếu sin x  cosxdx  0, 0  a  
2 thì giá trị a bằng: 0    3 A. . B. . C. . D.  4 2 2 m  2   4  Câu 55. 8
Với giá trị nào của tham số m thì tích phân I  x   2
sin xdx bằng ? 32 0   
A. m  1 . B. m  . C. m  . D. m  . 6 3 4
Câu 56. Đẳng thức nào sau đây là đúng?     2 2 2 2 A. sin d x x   cos d x x . B. sin d x x   tan d x . x 0 0 0 0     2 2 2 2 C. sin d x x    cos d x x . D. sin d x x    tan d x . x 0 0 0 0  3
Câu 57. Tính I   tan d x x  4
Biên tập: ĐẶNG NGỌC HIỀN Page 10 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG A. I  6 ln .
B. I  ln 2 .
C. I  ln 2 .
D. I   ln 2 2  3 Câu 58. a c a c Cho cot x x   d ln với 
b,d   ; , là các phân số tối giản. Trong mặt phẳng tọa  b d b d 4
độ Oxy gọi M a; b , N c; d . Tính độ dài đoạn thẳng MN
A. MN  2 .
B. MN  4 2 .
C. MN  2 2 . D. MN  4 .  4
Câu 59. Tính I   2 sin d x x 0     A. I   1 . B. I   1 . C. I   1 . D. I   1 8 4 8 2 8 2 8 4  4 2 a Câu 60. a Cho cos x x    d với 
a,c   ; là phân số tối giản. Tính T a b c . b c b 0
A.T  11.
B. T  13 .
C. T  8 . D. T  9 a
Câu 61. Nếu sin x cos x x  0,0  a    d 2 thì a bằng 0   
A. a   . B. a  .
C. a  3 . D. a  2 2 4 m
Câu 62. Giải phương trình ẩn m sau đây cos x x   d 0. 0    A. m  . . B. m   k
2 , k  . C. m   k
2 , k  . . D. m   k , k  . 3 3 6  4
Câu 63. Tính I   sin3xcos d x x . 0
A. I  0 .
B. I  1 .
C. I  1 .
D. I  1 . 2 4  4 Câu 64. a a
Cho cos 3x cos x x   d với 
b   ; là phân số tối giản. Tính T a b b b 0
A.T  1.
B. T  5 .
C. T  3 . D. T  3  4 Câu 65. a a
Cho sin 3x sin x x   d với  b   ;
là phân số tối giản. Trong mặt phẳng tọa độ b b 0
Oxy , điểm M a; b là tâm đối xứng của đồ thị hàm số nào sau đây? x  4 1  4x 4x  1 x  2 A. y  . B. I  . C. y  . D. y x  1 1  x x  1 x  4  4 Câu 66. 1 a a Cho x   d với 
b   ; là phân số tối giản. Trong mặt phẳng tọa độ Oxy , 1  sin 2x b b 0
điểm I a; b là đỉnh của parabol có phương trình nào sau đây? A. y  2
x  2x  3 . B. y  2
x  4x  5 . C. y   2
x  6x  7 . D. y  2
x  2x  3 .
Biên tập: ĐẶNG NGỌC HIỀN Page 11 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG  4 Câu 67. 1 a a Cho x   d với với 
b   ; là phân số tối giản. Tính T a b 1  cos 2x b b 0
A.T  1.
B. T  1 .
C. T  3 . D. I  2  2 Câu 68. 1 Cho x a   d b với 
a   ,b   . Tính T  2a b . 1   cos x 3
A.T  11. B. T  5 .
C. T  6 . D. T  7
Câu 69. Tìm khẳng định đúng trong các khẳng định sau:      4    A. sin x  dx  sin x        dx . 4 4 0   0           B. sin x  dx  cos x       dx . 4 4 0   0   3  4           C. sin x  dx  sin x  dx  sin x          dx . 4 4 4 0   0   3   4      4    D. sin x
dx  2 sin x       dx . 4 4 0   0  
Loại 3. Đổi biến số 1 x Câu 70. 1 Tích phân I   dx bằng 2 x  2x  5 0 8 1 8 8 A. ln . B. ln . C. 2 ln . D.  8 2 ln . 5 2 5 5 5 1 Câu 71. x x Tích phân: J   d bằng (x  3 1) 0
A. J  1 .
B. J  1 .
C. J  2 . D. J  1 . 8 4 3 Câu 72. x a c a c Cho x   d ln với 
b,d   ; a,c   ;
, là các phân số tối giản. Tính 2 x  1 b d b d 2
S a b c d .
A. S  5 .
B. S  11 .
C. S  13 . D. S  16 . 1 Câu 73. x x Gọi I   d thì 2 x  1 0   A. I  . B. I  .
C. I  ln 2 . D. I  ln 2. 2 4 2 3 Câu 74. a c a c Cho x 1  2 x x    d 2 với 
b,d   ; a,c   ; , là các phân số tối giản. Trong b d b d 1
mặt phẳng tọa độ Oxy , gọi M a; b , N c; d . Tọa độ trung điểm của đoạn MN là  3   5  A.  ; 3 . B. 3; 3 . C.  ; 3 . D. 5; 3 .  2   2 
Biên tập: ĐẶNG NGỌC HIỀN Page 12 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG 1 Câu 75. 19
Tích phân I x 1  x dx bằng 0 1 1 1 1 A. . B. . C. . D. . 420 380 342 462 1
Câu 76. Tích phân L x 1  2 x dx bằng 0
A. L  1 .
B. L  1 .
C. L  1 . D. L  1 . 4 3 2
Câu 77. Cho I  2 2x x   d
1 x và ux  2
x  1 . Chọn khẳng định sai trong các khẳng định sau: 1 3 3 2 3 2 A. I   d u u .
B. I  2 27 . C. I   d u u . D. I  2 u . 3 3 0 0 0 1 Câu 78. M M
Biết tích phân x 1  x x   d , với
là phân số tối giản. Giá trị M N bằng: N N 0 A. 18 . B. 19 . C. 20 . D. 21 7 Câu 79. 1 Tích phân I  
dx có giá trị là: 1  3 0 x  1 3 3 9 3 9 2 9 2 A.  3 ln . B.  3 ln . C.  3 ln . D.  3 ln . 2 2 2 2 2 3 2 3  2 e cos ln x
Câu 80. Cho I  
dx , ta tính được: x 1
A. I  cos1.
B. I  1 .
C. I  sin 1 .
D. I  sin 2  sin 1 .  2 3 Câu 81. sin . x cos x a 1 a Cho x    d ln 2 với 
b   ; a,c   ;
là phân số tối giản. Tính 2 cos x  1 b c b 0
T a b c .
A. T  2 .
B. T  6 .
C. T  3 .
D. T  1 .  1 2 Câu 82. x cos x
Cho tích phân I  
dx và J  
dx , phát biểu nào sau đây đúng: 3 sin x  12 0 x  3 0
A. I J .
B. I  2 .
C. J  1 ln 5 .
D. I  2J . 3 0 Câu 83. cos x Tích phân I  
dx có giá trị là: 2   sin x  2 A. ln 3 . B. 0 . C.  ln 2 . D. ln 2 .  6 Câu 84. m 1
Cho I  sin x cos x x   d . Khi đó m bằng 64 0 A. 6. B. 5. C. 4. D. 3.  6
Câu 85. Tích phân I   3 sin . x cos d x x bằng: 0
Biên tập: ĐẶNG NGỌC HIỀN Page 13 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG 1 A. 6 . B. 5 . C. 4 . D. . 64  2 Câu 86. n Tính 1  cosx sin d x x ta được 0   2 2 n 1 n 1
A. 1 cos x sin x x   d .
B. 1 cos x sin d x x  . 2n n  1 0 0   2 2 n 1 n 1
C. 1 cos x sin d x x .
D. 1 cos x sin d x x  . n  1 2n  1 0 0  4
Câu 87. Tích phân I  cos 2x 4 cos x   4
sin xdx bằng 0 5 5 7 5 A. . B. . C. . D. . 6 24 12 12 e 1 2 Câu 88. ln x Tích phân I  
dx có giá trị là: x 1 1 2 4 A. . B. . C. 1 . D. . 3 3 3 1 Câu 89. 2 Tích phân    1 . x I x e
dx có giá trị là: 0 2 e e 2 e e 2 e e 2 e e A. . B. . C. . D. . 2 3 2 3  2
Câu 90. Tích phân  sin cos x I xe x   d
m thì m thỏa mãn phương trình 0
A. ln x  1.
B. ln x  1  0 .
C. ln x  1  0 .
D. ln x  1  1 . 2 3 Câu 91. 3 Tích phân I   dx bằng: 2 2 x x  3    A. . B.  . C. . D. . 6 3 2 6 Câu 92. x Đặt I   d
và x  3 . Trong các khẳng định sau, khẳng định nào SAI? 2 cos t 3 2 x x  9 3 sin tA. dx  dt . B. I  . 2 cos t 36  3 sin t t dx sin tdt C. I   d . D.  .
 3 cos t tan t 2  3 cos t tan 9 t x x 4 a Câu 93. Tích phân 2 2 x a  2 x x a   d 0 bằng 0  4 .a  4 .a  3 .a  3 .a A. . B. . C. . D. . 8 16 16 8
Biên tập: ĐẶNG NGỌC HIỀN Page 14 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG 3 2
Câu 94. Cho xf 1 xx   d 6 . Tính I  2 x f 1 3 x   1dx . 1 0
A. I  9 . B. I  6 .
C. I  4 . D. I  2 . 4 2 Câu 95. Cho 1 x xf e x   d 2000 . Tính  3 1  x I x f e dx . 1 1
A. I  2000 .
B. I  4000 .
C. I  1000 . D. I  3000 . 2 5
Câu 96. Cho xf  2x 1 x   d
5 . Tính I   xf xdx. 0 1
A. I  5 .
B. I  10 .
C. I  5 5 .
D. I  5 . 2 1 Câu 97. x
Đổi biến x  2 sin t tích phân  d trở thành:  2 0 4 x     6 6 6 1 3
A. tdt .
B.  dt .
C.  dt .
D.  dt t 0 0 0 0
Loại 4. Phương pháp tích phân từng phần b b d u v b . u v   v u a  d a a
Câu 98. Tích phân L   xsin d x x bằng: 0
A. L   . B. L    .
C. L  2 .
D. L  0 .  3 1  Câu 99. 3
Cho x cos x x    d
với a,b   . Tính T  2 2a b . a b 0
A. T  5 .
B. T  9 .
C. T  14 .
D. T  16 .
Câu 100. Tích phân I   2 x sin d x x bằng : 0 A. 2  4 . B. 2  4 . C.  2 2  3 . D.  2 2  3  4  Câu 101. 2 2 Cho .c x os x x     d
c với a,b,c   . Tính T a b c . a b 0
A. T  15 .
B. T  13 .
C. T  11 .
D. T  9 . 2 Câu 102. b b Cho
(2x  1) ln x x a ln 2   d với 
c   ; a,b  ; là phân số tối giản. Tính c c 1
T a b c .
A. T  6 .
B.T  3 .
C.T  5 . D.T  1 . ln 2 Câu 103. a a Cho x xe x  c   d d ln 2 với 
b   ; a,c,d   ;
là phân số tối giản. Tính b b 0
T a b c d
A.T  3 .
B.T  5 .
C.T  4 . D.T  7 . 1 Câu 104. Giá trị   1 x xe dx bằng 0
A. 1  e .
B. e  2 . C. 1. D. 1 .
Biên tập: ĐẶNG NGỌC HIỀN Page 15 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG 2 Câu 105. ln x Tích phân I   dx bằng: 2 x 1 1 1 1 1
A. 1 ln 2 .
B. 1 ln 2 .
C. ln 2  1 . D. 1 ln 2 . 2 2 2 4 1
Câu 106. Cho 1  x x e x  . a e   d
b với a,b   . Trong mặt phẳng tọa độ Oxy , khoảng cách từ 0
điểm M a; b đến đường thẳng  : x y  2  0 bằng 5 2 3 2 2 A. . B. . C. . D. 3 . 2 2 2 3 Câu 107. Cho 2
ln(x x) x a   d
b ln 3 với a,b   . Tính T a b . 2
A. T  3 .
B. T  3 .
C. T  5 . D. T  5 . a x
Câu 108. Tìm a  0 sao cho 2 . x e x   d 4 0 1 1 A. 4 . B. . C. . D. 2 . 4 2 1 Câu 109. a c a c Cho 2 3x x e x    d 3 .e với 
b,d   ; a,c   ;
, là các phân số tối giản. Tính b d b d 0
S a b c d .
A. S  75 .
B. S  57 .
C. S  61. D. S  67 .
Loại 5. Một số dạng đặc biệt
Câu 110. Đẳng thức nào sau đây là đúng? 3 3 3 3 A. 2 x x   d 0 . B.  2 x  1 x   d 0 . C. 3 x x   d 0 . D.  2
x xx   d 0 . 3 3 3 3
Câu 111. Đẳng thức nào sau đây là đúng?     2 2 A. sin x x   d 0 . B. cos x x   d 0 .
C. sin xx   d 0 .
D. cos xx   d 0 .     1 2 Câu 112. 3x
Giá trị của tích phân I   dx 1  2016x 0 A. 3 . B. 2 . C.1 . D. 0 .
Câu 113. Đẳng thức nào sau đây đúng 5 2017  sin x 5 2 3x 3 2 3x 2 A. x   d 0 . B. x   d 0. C. x   d 0 .
D. sin x  cos xx   d 0. 2  3 1  2 x   cos x 5x 1 5 5 3   2 Câu 114. cos x Tích phân I x   d
m thì m là nghiệm phương trình nào sau đây? cos x  sin x 0
A. sin 2x  0 .
B. cos x  0 .
C. sin x  1.
D. cos 2x  0 . 4
Câu 115. Tích phân I  max 2
x  2x  1, x   1dx. 0 83 7 A. . B. . C.  7 . D.  83 . 6 6 6 6 3
Câu 116. Tích phân I  min 2 x   x,  x dx . 0
Biên tập: ĐẶNG NGỌC HIỀN Page 16 ĐT: 0977802424
NGUYÊN HÀM – TÍCH PHÂN – ỨNG DỤNG 19 11 A.  11 . B. . C. . D.  19 . 6 6 6 6 ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ĐA C D A B A D A C D D A A C C D C B Câu 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 ĐA A B A C C B B C A B C D C A A A B Câu 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 ĐA D C A C A D C B B A D B B C A A A Câu 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 ĐA B C C D A B A A B A D C B B A A D Câu 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 ĐA C B A D C B A D C B A B D A D D D Câu 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 ĐA B D D C D A D B C C D B A C A D A
Câu 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 ĐA A B A C C D B C A C A D A B
Biên tập: ĐẶNG NGỌC HIỀN Page 17 ĐT: 0977802424

Tài liệu liên quan: