lOMoAR cPSD| 40551442
Dạng 1: Tìm tập xác định, tập giá trị của hàm số
Tìm miền xác định của các hàm số sau:
z = p ( x 2 + y 2 − 1)(4 − x 2 − y 2 ) √
z = x sin y
1. Hàm số z = p(x2 + y2 − 1)(4 − x2 − y2) xác định khi (x2 + y2 − 1)(4 − x2 − y2) ≥ 0.
Miền xác định của hàm số là tập hợp D = {(x,y) ∈ R2|1 ≤ x2 + y2 ≤ 4}.
2. Hàm số z = √x siny xác định khi
Miền xác định của tập hợp này là D = D1 ∪ D2 với D1 =
{(x,y) ∈ R2|x ≥ 0,2kπ ≤ y ≤ π + 2kπ(k ∈ Z)}
D2 = {(x,y) ∈ R2|x ≤ 0,−π + 2kπ ≤ y ≤ 2kπ(k ∈ Z)}
Dạng 2: Giới hạn hàm số a) Ta có: Ta có: ( Theo nguyên lý kẹp ) lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Tương tự:
Do đó: lnI = 0 ⇒ I = e0 = 1 b)
+) Cho (x,y) → (0,0) theo phương y = x3, ta có:
+) Cho (x,y) → (0,0) theo phương y = 2x3, ta có: Từ (1) và (2) không tồn tại c) Ta có: Mà có:
Theo nguyên lý kẹp ta có: d) Ta có: (theo nguyên lý kẹp). 1 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
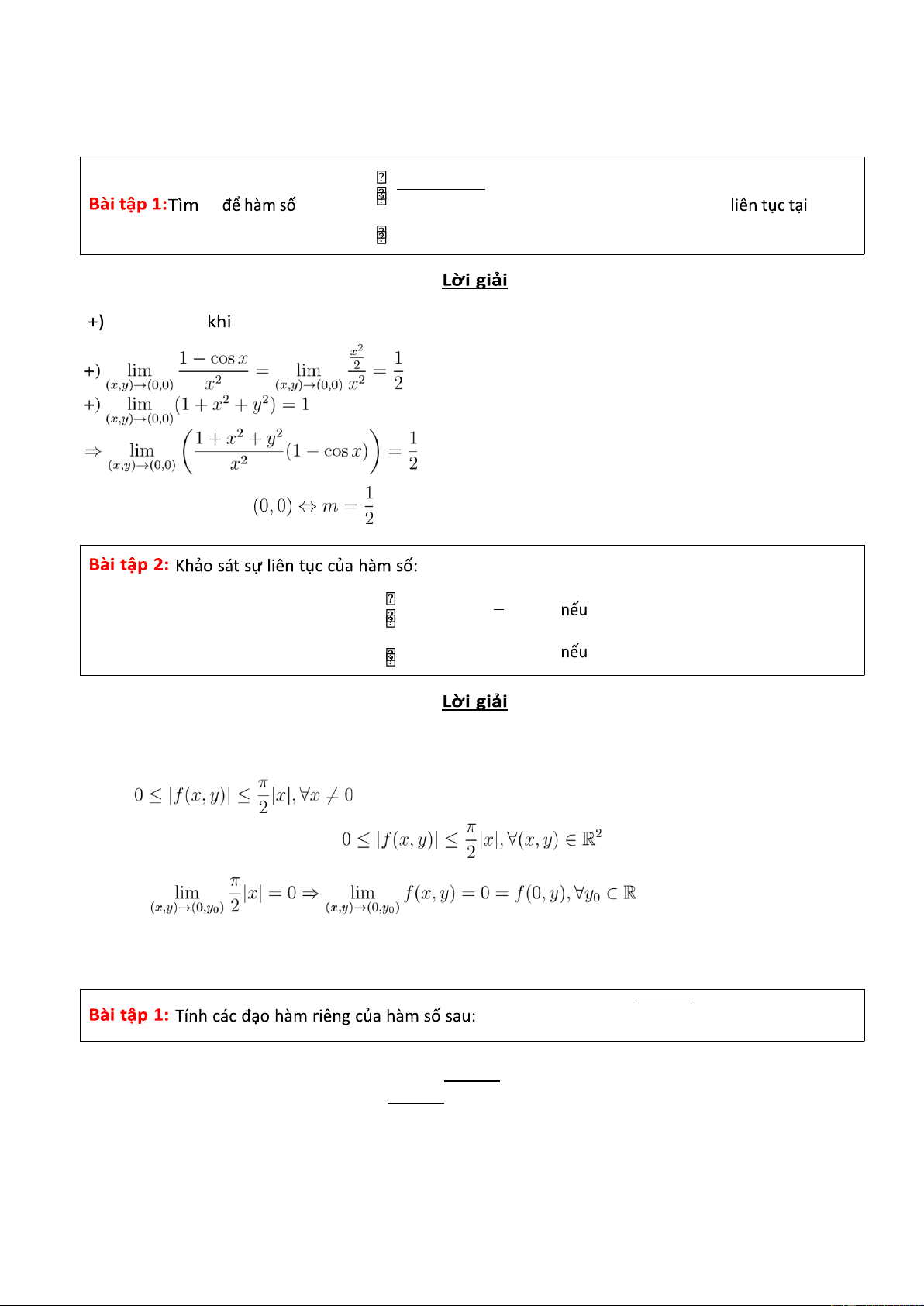
Dạng 3: Tính liên tục của hàm số 1+ x 2 + y 2 m f ( x,y )= x 2
(1 − cos x ) , ( x,y ) = (0 , 0) (0 , 0) . m , (
x,y ) = (0 , 0)
f ( x,y )= m
( x,y )=(0 , 0)
Để hàm số liên tục tại 2 y x arctan , x =0 f ( x,y )= x 0 , x =0
Hàm số f(x,y) liên tục với mọi (x,y) ∈ R2, x = 0̸ Ta có:
. Lại có f(0,y) = 0, nên ta có đánh giá tổng quát sau: Ta lại có .
⇒ f(x,y) liên tục trên R2
Dạng 4: Đạo hàm, đạo hàm riêng
f ( x,y )= ln x + p x 2 + y 2 Lời giải
Tập xác định: D = n(x,y) ∈ R2|x + px2 + y2 > 0o.
Các đạo hàm riêng của hàm số: 2 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập . 3 lOMoAR cPSD| 40551442
Bài tập 2: Tìm đạo hàm riêng của hàm số: z = p3 x4 + y4
Hỗ trợ sinh viên Bách Khoa Lời giải
CLB Hỗ Trợ Học Tập -
Khi (x,y) = (0̸ ,0) ta có các đạo hàm riêng: -
Khi (x,y) = (0,0) Ta có: . Chứng minh rằng
Bài tập 3: Cho hàm số: Lời giải +) Xét tại x = 0: +) Xét tại x ̸= 0: + ∆y
Từ (1),(2) ⇒ fy′(x,0) = x,∀x ∈ R
Dạng 5: Vi phân, tính khả vi
Bài tập 1: Cho hàm số f(x;y) = x4 + 2x2y + y3. Tính df(1;1). Lời giải Ta có: . 4 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Xét tính khả vi của các hàm số sau tại (0 , 0) xy f ( x,y )= x 2 + y 2
( x,y ) =(0 , 0) 0
( x,y )=(0 , 0) x 3 f ( x,y )= x 2 + y 2
( x,y ) = (0 , 0)
0 ( x,y ) = (0 , 0) 1. Xét
Cho (x,y) → (0,0) theo
phương x = y ta có:
Cho (x,y) → (0,0) theo
phương x = 2y ta có: Từ
không tồn tại. Do đó hàm số f(x,y) không liên tục tại (0,0)
Do đó f(x,y) không khả vi tại (0,0)
khi (x,y) = (0̸ ,0) 2.
0 khi (x,y) = (0,0)
- Xét tính liên tục tại (0,0) Xét Ta có: Lại có: 5 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Do đó: (theo nguyên lý kẹp) x3
⇒ (x,ylim)→(0,0) f(x,y) = (x,ylim)→(0,0) x 2 + y2 = 0 =
f(0,0) Vậy f(x,y) liên tục tại (0,0)
- Tính đạo hàm riêng tại (0,0) Ta có: − − −
- Xét tính khả vi tại (0,0) ′ ′ Xét
Cho (∆x,∆y) → (0,0) theo phương ∆y = ∆x ta có: Khi Khi Do đó: không tồn tại Do đó không tồn tại
Do đó hàm số không khả vi tại (0,0) 6 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập y
a) z = sin( x 2 + y 2 ) z = ln tan x x z + y = arctan u x
= x y 2 z − y a. b. . c. d.
Dạng 6: Ứng dụng vi phân tính gần đúng
Tính gần đúng nhờ vi phân:
A = p 2 , 02 2 +3 , 04 2 +3 B = 3
p (1 , 02) 2 +(0 , 05) 2
C =(1 , 02) 1 ,01
1. A = p2,022 + 3,042 + 32 2
Xét hàm số f(x,y) = px + y + 3 Ta có
x = 2,∆x = 0,02 7 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Chọn 0
, Áp dụng công thức tính gần đúng :
Vậy A ≈ 4,04
2. B = p3 (1,02)2 + (0,05) 2 3 Xét
hàm số f(x,y) = px2 + y2
∀(x,y) = (0̸ ,0) ta có: Ta có:
Với x0 = 1,∆x = 0,02,y0 = 0,∆y = 0,05. Áp dụng công thức tính gần đúng ta có:
3. C = (1,02)1,01 Xét hàm số f(x,y) = xy
∀x > 0,y > 0 ta có: Ta có:
Với x0 = 1,∆x = 0,02,y0 = 1,∆y = 0,01. Áp dụng công thức tính gần đúng ta có:
f(x0 + ∆x,y0 + ∆y) ≈ f(x0,y0) + fx′ (x0,y0)∆x + fy′(x0,y0)∆y
= f(1,1) + fx′ (1,1).0,02 + fy′(1,1).0,01
= 1 + 1.0,02 + 0.0,01 = 1,02 8 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Dạng 7: Đạo hàm hàm hợp, hàm ẩn
Bài tập 1: Tính các đạo hàm riêng của hàm số hợp sau:
TXĐ: D = {(x,y) ∈ R2|xy > Lời giải
0,x + 2y > 2} Ta có: +) Bài tập 2:
trong đó z là hàm ẩn x,y xác định bởi phương trình: zez = xex + yey. Cho Tính . Lời giải
Đặt F(x,y,z) = −zez + yey + xex = 0 Ta có:
Bài tập 3: Phương trình x3 + 3x2y + y5 − 5 = 0 xác định hàm ẩn y = y(x). Tính y′(1). 9 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Lời giải
Đặt F(x,y) = x3 + 3x2y + y5 − 5. . 2 z 2 + = p y x 2 − z 2
z = f ( x ; y ) . Chứng minh rằng: 1 1 x2
z ′ x + z y ′ y = z Đặt . . Khi (đpcm).
Dạng 8: Đạo hàm, vi phân cấp cao 2 xy f ( x,y )=
x 2 + y 2 ,x 2 + y 2 =0 .
f ′ x ( x,y ) ,f ” xy (0 , 0) . 0 , x 2 + y 2 =0
x 2 + y 2 =0 , .
+) Tại x2 + y2 = 0, có: 10 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập .
Do đó không tồn tại f”xy(0,0).
Bài tập 2: Cho z(x,y) = exy2. Tính d2z. Lời giải
+) zx′ = y2exy2,zy′ = 2xyexy2.
+) z”xx = y4exy2,z”xy = 2yexy2 + 2y3exy2,z”yy = 2xexy2 + 4x2y2exy2. +) .
Dạng 9: Khai triển Taylor, Maclaurin
Bài tập 1: Tìm khai triển Taylor của hàm số f(x,y) = ex siny đến bậc 3 tại điểm (2,0) Lời giải
Bài tập 2: Tìm khai triển Taylor của hàm số f(x,y) = x2 ln(1 + y) đến bậc 2 tại điểm (1,0) Lời giải Ta có: Ta lại có:
⇒ d2f(1,0) = 4dxdy − dy2
Có f(1,0) = 0. Ta có khai triển Taylor của hàm số đến cấp 2 là: 11 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Bài tập 3: Tìm khai triển Maclaurin của các hàm số sau đến bậc 3:
a) f(x,y) = ln(1 + x + y) b) Lời giải
1. f(x,y) = ln(1 + x + y) Từ khai triển Maclaurin: 2. Từ khai triển Maclaurin:
Dạng 10: Cực trị tự do của hàm số
Bài tập 1: Tìm cực trị của hàm số: z = 3x2y2 − 2x3 − 6y4 Lời giải Xét hệ phương trình: Xét
- Tại M1 (4,−2):
Ta có: B2 − AC = (−96)2 − (−24)(−192) = 4608 > 0 nên M1 không là cực trị của hàm số
- Tại M2 (4,2):
Ta có: B2 − AC = 962 − (−24)(−192) = 4608 > 0 nên M2 không là cực trị của hàm số - Tại M3(0,0)
Ta có: B2 − AC = 02 − 0.0 = 0 12 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Xét hiệu ∆ = z(x,y) − z(0,0) = 3x2y2 − 2x3 − 6y4 Với y =
−x ta có: ∆ = −3x4 − 2x3 = x3(−3x − 2)
Khi x → 0+,∆ → 0− (1)
Khi x → 0−,∆ → 0+ (2)
Từ (1)(2) ⇒ Hàm số không đạt cực trị tại (0,0) Kết
luận: Hàm số không có cực trị. y
Tìm cực trị của hàm số: z =( x 2 + y ) e 2 Lời giải Suy ra hàm
số đạt cực tiểu tại .
Bài tập 3: Tìm cực trị của hàm số
z(x,y) = 4(x − y) − x2 − y2. Lời giải
Tập xác định: D = R2. Giải hệ
⇒ M(2,−2) là điểm dừng. Ta có:
⇒ Hàm số đã cho đạt cực trị tại duy nhất 1 điểm là M(2,−2) và là điểm cực đại, zCĐ = z(2,−2) = 8.
Dạng 11: Cực trị có điều kiện
Bài tập 1: Tìm cực trị của hàm số: z = (2x + 4)2 + 2(y + 1)2 với 2x2 + y2 = 4. Lời giải
Xét hàm: L(x,y,λ) = (2x + 4)2 + 2(y + 1)2 − λ(2x2 + y2 − 4) Ta có: Ly′x = 0
4(22x + 4)2 − 4λx = 0
2x2+ 4 =2 λx(1) 13 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập L′ = 0 ⇔
4(y + 1) − 2λy = 0 ⇔
2y + 2 = λy (2) L′λ = 0
2x + y − 4 = 0
2x + y − 4 = 0 (3) +) Với
+)Thay vàoVới λ ̸= 2(3):ta được:Từ (1),(2) ⇒ x = λ − 2,y = λ − 2 Ta có: • Tại
là cực đại của hàm số • Tại
là cực tiểu của hàm số 1 1 1 1 1
Tìm cực trị của hàm số: z = + với điều kiện x y
x 2 + y 2 = a 2 Lời giải Đặt Khi đó: Ta có: Với
Điểm (|a|√2;|a|√2) là điểm cực đại, . Với
Điểm (−|a|√2 ;−|a|√2) là điểm cực tiểu, . 14 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Dạng 12: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài tập 1: Tính giá trị lớn nhất, giá trị bé nhất của hàm số z = 3x2 −4y2 trong miền đóng: .
Lời giải Với điều kiện Ta có: Đẳng thức xảy ra Ta có: Đẳng thức xảy ra
Vậy trên miền đã cho thì:
- Giá trị nhỏ nhất của z là −12 đạt được tại (x,y) = (0,±√3)
- Giá trị lớn nhất của z là 12 đạt được tại (x,y) = (±2,0)
Bài tập 2: Tìm giá trị lớn nhất và nhỏ nhất trong miền D là hình tam giác với các đỉnh (2,0),(0,2) và
(0,−2) của hàm số f(x,y) = x2 + y2 − 2x. Lời giải
Miền D được xác định bởi: x − 2 y 2 − x
f(x,y) = x2 + y2 − 2x = (x − 1)2 + y2 − 1 ≥ 0 + 0 − 1 = −1
Đẳng thức xảy ra ⇔ (x,y) = (1,0) điểm này thuộc miền D 15 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Ta có: |y| ≤ |2 − x| ⇔ y2 ≤ (2 − x)2
⇒ f(x,y) ≤ x2 + (2 − x)2 − 2x = 2x2 − 6x + 4 ≤ x(2x − 6) + 4 ≤ 0 + 4 Đẳng thức xảy ra
, 2 điểm này thuộc miền D Vậy
- GTNN của f(x,y) trên miền D là −1 đạt được tại (x,y) = (1,0)
- GTLN của f(x,y) trên miền D là 4 đạt được tại (x,y) = (0,2) hoặc (x,y) = (0,−2)
Bài tập 3: Giả sử bạn có một nhà máy sản suất mè rang. Chi phí nhân công mỗi giờ là 20 $ và giá 1 tấn
mè là 80 $. Lợi nhuận R được mô hình hoá như sau:
trong đó h là số giờ làm việc, s là số tấn mè.
Hãy tính lợi nhuận lớn nhất có thể thu được nếu kinh phí của bạn là 20000 $ và để đạt được lợi nhuận
đó, ta cần sản xuất bao nhiêu tấn mè ? Lời giải
Nhận xét: Thực chất bài toán là tìm cực trị của hàm
với điều kiện h,s > 0 và 20h +
80s = 20000 hay h + 4s = 1000. Cách 1: Ta có: (AM-GM) Dấu ” = ” xảy ra khi
Vậy lợi nhuận lớn nhất có thể thu được nếu kinh phí của bạn là 20000 $ là
và để đạt được lợi
nhuận đó, ta cần sản xuất tấn mè. Cách 2: Ta xét hàm Lagrange . Từ hệ phương trình: 16 lOMoAR cPSD| 40551442
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Ta thu được điểm tới hạn ứng với . Lúc đó ta có:
Do đó: d2R(M) < 0, M là điểm cực đại có điều kiện và
Vậy lợi nhuận lớn nhất có thể thu được nếu kinh phí của bạn là 20000 $ là
và để đạt được lợi
nhuận đó, ta cần sản xuất tấn mè. 17