Bài tập VD – VDC đường tiệm cận của đồ thị hàm số có đáp án và lời giải Toán 12

Bài tập VD – VDC đường tiệm cận của đồ thị hàm số có đáp án và lời giải Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

35 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 1
BÀI TẬP VD - VDC
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
- Strong Team Toán VD - VDC -
I. ĐỀ BÀI
Câu 1: Đồ thị hàm số
2
31 21
x
x
y
xx

có bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C. 3. D. 0 .
Câu 2: Tìm
m
để đồ thị hàm số
2
2
31mx x
y
xx

có
2
đường tiệm cận đứng và
2
đường tiệm
cận ngang tạo thành hình chữ nhật có diện tích bằng
2
.
A.
1m  . B. 0m . C. 2m . D. 1m .
Câu 3: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số

42
2
xxm
y
x

có
đúng ba đường tiệm cận?
A.
17
. B. 11. C.
0
. D.
18
.
Câu 4: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
2020 1
2
x
y
x
mx m


có đúng hai
tiệm cận đứng?
A. 1. B. 2. C. 3. D. 4.
Câu 5: Gọi
,mn
lần lượt là số đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
2
2
31
4
xx x
y
x

. Khi đó mn bằng:
A.
4 . B.
3
. C. 2 . D. 1.
Câu 6: Có bao nhiêu giá trị nguyên của tham để
m
đồ thị hàm số
2
2019 2020 4038xx
y
xm

có tiệm cận đứng?
A.
1. B. 2 . C.
2019
. D.
2020
.
Câu 7: Cho hàm số
32
yf
xaxbxcxd
0a
có đồ thị như hình vẽ bên dưới:
Tìm m để đồ thị hàm số


2
1
3
gx
f
xm

có đúng 6 tiệm cận đứng?
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 2
A.
0m
. B.
20m
. C.
31m
. D.
04m
.
Câu 8: Cho hàm số


2
2018
gx
hx m m

với

43 2
h x mx nx px qx

,, ,mn pq
. Hàm số

yhx
có đồ thị như hình vẽ bên dưới:
Tìm các giá trị
m
nguyên để số tiệm cận đứng của đồ thị hàm số

ygx
là
2
.
A.
11
. B.
10
. C.
9
. D.
20
.
Câu 9: Cho hàm số

yfx
liên tục trên
, có đồ thị như hình vẽ:
Tìm số tiệm cận đứng của đồ thị hàm số


2
6
4
yhx
fx

.
A.
2
. B.
4
. C.
6
. D.
5
.
Câu 10: Cho hàm số

yfx
liên tục trên

;1
và

1; 
, có bảng biến thiên như hình:
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

 
2
8
65
yhx
fx fx


.
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 11: Cho

fx
là hàm bậc 4 và có bảng biến thiên như hình vẽ sau:
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 3
Đồ thị hàm số

 
2
2
2
34
x
gx
fx fx

có mấy đường tiệm cận đứng?
.
A.
2
. B. 3. C.
4
. D. 5.
Câu 12: Cho

f
x
là hàm bậc 4 và có bảng biến thiên như hình vẽ sau:
Đồ thị hàm số

 
42
2
2
23
xx
gx
fx fx

có mấy đường tiệm cận?
.
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 13: Cho hàm số
32
f
xaxbxcxd
có đồ thị như sau:
Đặt

 
2
2
.
xx
gx
xfx
Đồ thị hàm số
y
gx
có bao nhiêu tiệm cận đứng?
A.
4
. B.
2
. C.
5
. D.
3
.
Câu 14: Cho hàm số
y
fx
xác định và liên tục trên và có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:

3
14
312
3
gx
x
fx




là:
A.
2 . B. 4 . C. 1. D.
3
.
Câu 15: Cho hàm số có bảng biến thiên dưới đây:
f
x
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 4
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số

2020
2020 2021
y
fx
.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 16: Cho hàm số


322
3
321
x
yC
xmx m xm

.Có tất cả bao nhiêu giá trị nguyên thuộc
khoảng
10;10
của tham số để đồ thị hàm số có tổng số đường tiệm cận là nhiều nhất?
A.
20
. B.
15
. C.
16
. D.
18
.
Câu 17: Cho hàm số
32
2
3(2)
x
y
x
xm xm

. Tìm điều kiện của tham số
m
để đồ thị hàm số có 4
đường tiệm cận?
A.
1m
. B.
1
0
m
m
. C.
1m
. D.
1
0
m
m
.
Câu 18: Cho hàm số
2
3
21
x
y
x
mx

. Tìm số các giá trị của tham số
m
để đồ thị hàm số có 1 đường
tiệm cận đứng?
A.
0
. B. 1. C. 2 . D.
3
.
Câu 19: Đồ thị của hàm số
3
2
2
32
mx
y
xx

có hai tiệm cận đứng khi và chỉ khi?
A.
0m
và
2m
. B.
1m
và
2m
. C.
0m
. D.
2m
và
1
4
m .
Câu 20: Cho hàm số
2
1
24
x
y
x
mx

có đồ thị là

C
. Tìm tất cả các giá trị thực của tham số m để đồ
thị
C
có đúng
3
đường tiệm cận?
A.
2
2
5
2
m
m
m



. B.
2
2
m
m

. C.
2m
. D.
2
5
2
m
m


.
Câu 21: Cho hàm số
2
2
12 4
62
x
x
y
x
xm


có đồ thị
m
C
. Tìm tập
S
tất cả các giá trị của tham số thực
m để
m
C
có đúng hai tiệm cận đứng.
A.
8; 9S
. B.
9
4;
2
S


. C.
9
4;
2
S



. D.
0;9S
.
Câu 22: Với giá trị nào của
m
, đồ thị hàm số

2
2
13
12
x
xx
y
xmxm


có đúng hai đường tiệm cận?
m
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 5
A.
m
. B.
1
2
3
m
m
m


. C.
1
2
m
m

. D.
2
3
m
m


.
Câu 23: Cho hàm số

2
2
32
xm
yfx
xx



có đồ thị

C
. Gọi
S
là tập chứa tất cả các giá trị n guyên
của tham số
m
để đồ thị

C
có đúng một tiệm cận đứng và một đường tiệm cận ngang. Số phần tử của
tập
S là:
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 24: Cho hàm số
2
213
2
mx x m x
y
x

có đồ thị

C
. Gọi
S
là tập chứa tất cả các giá trị
thực của tham số
m để đồ thị

C
có đúng hai đường tiệm cận. Tổng giá trị tất cả các phần tử của
S
bằng?
A.
31
7
.
B. 25 . C.
5
9
.
D.
86
5
.
Câu 25: Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
1
42 1
x
y
x
xm x

có đúng bốn
đường tiệm cận.
A.

7
;6 \ 2
3
m




. B.
7
;6
3
m




.
C.

7
;6 \ 2
3
m




. D.

7
;6 \ 2
3
m



.
Câu 26: Cho hàm số
y
fx
có bảng biến thiên như hình vẽ bên. Hỏi đồ thị của hàm số

1
23
y
fx
có bao nhiêu đường tiệm cận?
A. 1. B.
3
. C. 2. D.
0
.
Câu 27: Cho hàm số
yf
x
có bảng biến thiên như hình dưới đây:
Gọi tập
S
là tập chứa tất cả các giá trị nguyên của tham số

10;10m
để đồ thị hàm số
 
2
2x
y
f
xm
f
x
có đúng hai đường tiệm cận đứng. Số phần tử của tập
S
là:
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 6
A. 9. B. 12. C. 13. D. 8.
Câu 28: Cho hàm số

yfx
có đồ thị như hình dưới đây:
Gọi tập
S
là tập chứa tất cả các giá trị tham số
m
để đồ thị hàm số

2
3
24
xx
y
fx f x m



có đúng ba
đường tiệm cận đứng. Khẳng định nào sau đây là đúng:
A.

;3 S
. B.

;2 S
.
C.
S 
. D.

6;8 S
.
Câu 29: Cho hàm số bậc ba
32
()f x ax bx cx d
có đồ thị như hình vẽ. Với giá trị nào của
m
thì
hàm số
2
()
() 2()
mx
gx
fx fx
có 5 tiệm cận đứng?
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Câu 30: Cho hàm số bậc ba
32
()f x ax bx cx d
có đồ thị như hình vẽ. có bao nhiêu giá trị của
m
để hàm số
22 2
2
(2 1) 3
()
(x-4)[ ( ) 4 ( )]
xmxmm xx
gx
fx fx

có 3 tiệm cận đứng?
A.
1
. B.
2
. C.
3
. D.
4
Câu 31: Cho hàm số
3
23 2
xm
ym
x




có đồ thị

.C
Giả sử

;
MM
Mx y
là 1 điểm bất kỳ thuộc

.C
Gọi
,AB
lần lượt là khoảng cách từ
M
tới các đường tiệm cận ngang và tiệm cận đứng của

.C
Biết diện tích
MAB
bằng
1.
Khẳng định nào sau đây là đúng?
A.
511
;.
22
m




B.
511
;.
22
m




C.
511
;.
22
m




D.
511
;.
22
m



O
x
y
2
4
1
3
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 7
Câu 32: Cho hàm số
22
1
x
y
x
có đồ thị
.C
Giả sử
;
MM
M
x
y
là điểm thuộc

C
thỏa mãn tổng
khoảng cách từ
M
tới trục hoành và đường tiệm cận đứng của

C
đạt giá trị nhỏ nhất. Giá trị của
M
M
x
y
bằng:
A. 2. B. 2. C. 1. D. 1.
Câu 33: Cho hàm số
23mx
y
xm
+
=
-
có đồ thị
()
C
và
I
là giao điểm của hai đường tiệm cận của
()
C
.Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho tiếp tuyến tại điểm
M
trên đồ thị
()
C cắt hai
đường tiệm cận tại hai điểm
,AB
và tam giác
IAB
có diện tích bằng
64
.Tổng các phần tử của tập hợp
S
là:
A.
58
. B.
258
. C.
258-
. D. 0 .
Câu 34: Cho hàm số
21
1
x
y
x
-
=
+
có đồ thị
()
C và
I
là giao điểm của hai đường tiệm cận. Giả sử
()
00
;Mx y
là điểm trên đồ thị
()
C
có hoành độ dương sao cho tiếp tuyến tại
M
với
()
C
cắt tiệm cận
đứng và tiệm cận ngang lần lượt tại hai điểm
,AB
thỏa mãn
22
40IA IB+=
. Giá trị của biểu thức
22
0000
Px y xy=++ bằng:
A.
8
. B.
3
. C.
5
. D.
7
.
Câu 35: Cho hàm số
2
1
x
y
x
có đồ thị là

C
. Gọi
I
là giao điểm hai đường tiệm cận và
00
;
M
x
y
là điểm nằm trên

C
với
0
0x
. Biết tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng và tiệm cận
ngang lần lượt tại hai điểm
P
và
Q
sao cho bán kính đường tròn nội tiếp tam giác
IPQ
lớn nhất. Tính
tổng
00
x
y
.
A.
00
0xy
. B.
00
223xy
. C.
00
2xy
. D.
00
23xy
.
Câu 36: Cho hàm số
21
22
x
y
x
có đồ thị là

C
. Gọi
I
là giao điểm hai đường tiệm cận và
M
là điểm
nằm trên

C
có hoành độ lớn hơn
1
. Tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng và tiệm cận
ngang lần lượt tại hai điểm
A
và
B
. Hoành độ của điểm
M
thuộc khoảng nào sau đây để
PIAIB
đạt giá trị nhỏ nhất?
A.
4;1
. B.

;4
. C.
4; 
. D.
1; 4
.
Câu 37: Cho hàm số
2
3
x
y
x
có đồ thị

C
. Gọi
00
;
M
x
y
là một điểm thuộc

C
sao cho tổng
khoảng cách từ
M
đến hai đường tiệm cận của

C
là nhỏ nhất. Tính
00
2
x
y
biết
0
0y
.
A.
00
24xy
. B.
00
22xy
. C.
00
26xy
. D.
00
210xy
.
Câu 38: Cho hàm số
1
3
x
y
x
có đồ thị là

C
. Gọi
I
là giao điểm của hai đường tiệm cận và
00
;
M
x
y
là một điểm thuộc

C
. Phương trình tiếp tuyến của

C
tại
M
cắt tiệm cận đứng và tiệm
cận ngang của

C
lần lượt tại hai điểm
A
,
B
sao cho
22
32IA IB
. Tìm tọa độ điểm
M
biết
0
0y
.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 8
A.
5;3
. B.
1
2;
5



. C.
1
3;
3



. D.
1; 1
.
Câu 39: Cho hàm số
21
1
x
y
x
có đồ thị

C
. Có bao nhiêu điểm
M
thuộc

C
sao cho tổng khoảng
cách từ
M
đến hai đường tiệm gấp
2
lần tích khoảng cách từ
M
đến hai đường tiệm cận của

C
?
A. 0 . B.
1
. C.
4
. D.
2
.
Câu 40: Cho hàm số
1
2
x
y
x
có đồ thị

C
. Gọi
I
là giao điểm hai đường tiệm cận của

C
. Có bao
nhiêu điểm trên

C
có hoành độ âm sao cho tam giác OMI có diện tích bằng
1
2
biết O là gốc tọa độ?
A. 0 . B.
1
. C.
4
. D.
2
.
II. BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
B A A A D D A B D B
11 12 13 14 15 16 17 18 19 20
C C C A C B D D D A
21 22 23 24 25 26 27 28 29 30
B C C D B C B D D B
31 32 33 34 35 36 37 38 39 40
A D D D A D D C C B
III. LỜI GIẢI CHI TIẾT
Câu 1: Đồ thị hàm số
2
31 21
x
x
y
xx

có bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Tập xác định của hàm số là:

1
,\0;1
2



22
2
31 21
31 21
lim lim lim 0
1
1
xx x
xx
xx xx
y
xx
x
  



.
Đường thẳng
0y
là tiệm cận ngang của đồ thị hàm số.
Ta lại có:
2
11
31 21
lim lim
xx
xx
y
xx




2
11
31 21
lim lim
xx
xx
y
xx




Đường thẳng
1
x
là tiệm cận đứng của đồ thị hàm số.
2
00
31 21
lim lim 2




xx
xx
y
xx
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 9
Đường thẳng
0x
không là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có
2
đường tiệm cận.
Câu 2: Tìm m để đồ thị hàm số
2
2
31mx x
y
xx

có
2
đường tiệm cận đứng và
2
đường tiệm
cận ngang tạo thành hình chữ nhật có diện tích bằng
2
.
A.
1m 
. B.
0m
. C.
2m
. D.
1m
.
Lời giải
Tập xác định:
;1 0;D 
Ta có
2
2
2
31
1
lim lim 1
1
1
xx
m
xx
ym
x
 



2
2
2
31
1
lim lim 1
1
1
xx
m
xx
ym
x
 


Suy ra để đồ thị hàm số có
2
đường tiệm cận ngang thì
11 0mmm
2
2
00
31
lim lim
xx
mx x
y
xx




2
2
11
31
1
lim lim
1
xx
mx x
khi m
y
khi m
xx

 




Vậy khi
0, 1mm
thì đồ thị hàm số có
2
đường tiệm cận ngang là
1; 1ym y m
và
2
đường tiệm cận đứng là
0; 1xx
. Để
2
đường tiệm cận đứng và
2
đường tiệm cận ngang
tạo thành hình chữ nhật có diện tích bằng
2
thì
1.2 2 1mm
Đối chiếu điều kiện
1m 
.
Câu 3: Có bao nhiêu giá trị m nguyên thuộc khoảng
10;10
để đồ thị hàm số

42
2
xxm
y
x

có
đúng ba đường tiệm cận?
A.
17
. B.
11
. C.
0
. D.
18
.
Lời giải
Điều kiện:
40
2
xxm
x

.
+) Ta có
2
4
lim lim 2
2
1
xx
m
xx
y
x
 





và
2
4
lim lim 2
2
1
xx
m
xx
y
x
 


.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 10
Suy ra,
m
, đồ thị hàm số luôn có
2
đường tiệm cận ngang là
2y 
.
+) Mà



2
42
42
2
24 2
xxm
xmx
y
x
xxxm




, đặt

2
42
g
xxmx
.
Yêu cầu bài toán
đồ thị hàm số

41
2
xxm
y
x

có duy nhất
1
đường tiệm cận đứng là đường thẳng
2x

24.2 0
20
m
g

8
7
m
m
9; 8;...;6;8m
.
Câu 4: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
2
2020 1
2
x
y
x
mx m


có đúng hai
tiệm cận đứng?
A. 1. B. 2. C. 3. D. 4.
Lời giải
Đồ thị hàm số có đúng hai tiệm cận đứng khi và chỉ khi phương trình

2
20*xmxm
có 2 nghiệm
phân biệt lớn hơn hoặc bằng
1
.
Ta có
2
2
20
2
x
x
mx m m
x

.
Xét hàm số

2
2
x
yfx
x

với
1; .x
Có

2
2
4
4
0.
0
2
x
xx
y
x
x


Dựa vào bảng biến thiên ta thấy phương trình
*
có 2 nghiệm phân biệt biệt lớn hơn hoặc bằng
1
khi
và chỉ khi
0;1 1.mm
Câu 5: Gọi
,mn
lần lượt là số đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
2
2
31
4
xx x
y
x

. Khi đó mn bằng:
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Điều kiện:
3
2
x
x
+ Tiệm cận ngang:
∞
+
1
0
x
y'
y
0
+
+
1
∞
0
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 11
2
2
31
4
xx x
x

22
2
311
1
4
1
xx
x
xx
x
x







2
22
2
311
1
4
1
x
x
xx
x
x







(do 3x )
22
311
1
4
1
x
xx
x

22
311
1
lim lim 1
4
1
xx
xxx
y
x
 


Suy ra đồ thị hàm số có
1
tiệm cận ngang
1y
+ Tiệm cận đứng:
Điều kiện cần: Xét phương trình
2
40 2xx
Điều kiện đủ: Đặt
2
() ( 3 1)fx x x x
Xét
2x
, ta có
20f
nên ta sẽ đi tìm bậc của
2x
của

f
x
2
31
x
x
22
2
(3 1)(3 1)
31
xxxx
xx
 

2
2
()
xx
g
x

( 2)()
x
hx
Suy ra
(2)() ()
(2)(2) 2
x
hx hx
y
xx x


, suy ra 2x không phải là tiệm cận đứng
Xét
2x 
, ta có
2f
không tồn tại hay
2x 
không phải là tiệm cận đứng.
Vậy
1, 0mn
1mn
.
Câu 6: Có bao nhiêu giá trị nguyên của tham để m đồ thị hàm số
2
2019 2020 4038xx
y
xm

có tiệm cận đứng?
A. 1. B. 2 . C.
2019
. D.
2020
.
Lời giải
2
2019 2020xx
xác định khi
2
2019 2020 0 1 2020xx x
Đặt

2
2019 2020 4038 fx x x
Xét
0
x
mxm
.
Đồ thị nếu có tiệm cận đứng chỉ có thể là
x
m , khi đó điều kiện là:



2
1; 2019 1
1 2019
0
201
920
2
0247*
m
x
fm
mm





Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 12
Ta có

2
1
* 2019 2018 0 2
2018
m
mm
m

Từ



1 , 2 1; 2020 \ 1; 2019m
Vậy có
2022 2 2020
số nguyên
m
thỏa mãn bài toán.
Câu 7:
Cho hàm số

32
yfx axbxcxd

0a
có đồ thị như hình vẽ bên dưới:
Tìm m để đồ thị hàm số


2
1
3
gx
fx m

có đúng 6 tiệm cận đứng?
A.
0m
.
B.
20m
.
C.
31m
.
D.
04m
.
Lời giải
Xét hàm số


2
3hx f x


2
2. 3hx xf x




2
2
2
0
0
0
0312
30
2
31
x
x
x
hx x x
fx
x
x




-
Ta có bảng biến thiên
Từ bảng biến thiên ta có đồ thị hàm số


2
1
3
gx
fx m

có đúng 6 tiệm cận đứng

hx m
có 6
nghiệm phân biệt
04m
.
Câu 8:
Cho hàm số


2
2018
gx
hx m m

với

43 2
h x mx nx px qx

,, ,mn pq
. Hàm số

yhx
có đồ thị như hình vẽ bên dưới:
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 13
Tìm các giá trị
m
nguyên để số tiệm cận đứng của đồ thị hàm số

ygx
là 2 .
A.
11
.
B.
10
.
C.
9
.
D.
20
.
Lời giải
Ta có

32
432h x mx nx px q

. Từ đồ thị ta có

1
5
0
4
3
x
hx x
x


và

0m
.
Suy ra
 
32
5
41 3413215
4
h x m x x x mx mx mx m




.
Suy ra

432
13
15
3
h x mx mx mx mx C
. Từ đề bài ta có
0C
.
Vậy

432
13
15
3
h x mx mx mx mx
.
Xét

2432
13
0151
3
hx m m m x x x x
.
Xét hàm số

432
13
15 1
3
fx x x x x

32
4132150fx x x x

1
5
4
3
x
x
x


.
Bảng biến thiên
Để đồ thị hàm số

gx
có 2 đường tiệm cận đứng
phương trình

2
0hx m m
có 2 nghiệm phân
biệt
phương trình
432
13
15 1
3
mx x x x
có 2 nghiệm phân biệt.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 14
Từ bảng biến thiên kết hợp thêm điều kiện 0m ta có
35
1
3
m.
Do
m nguyên nên
11; 10;...; 2m
. Vậy có
10
số nguyên m thỏa mãn yêu cầu bài toán.
Câu 9: Cho hàm số
yf
x
liên tục trên , có đồ thị như hình vẽ:
Tìm số tiệm cận đứng của đồ thị hàm số


2
6
4
yhx
fx

.
A.
2
. B.
4
. C.
6
. D.
5
.
Lời giải
Xét hàm số


2
6
4
yhx
fx

.







2
2
3;
2
40 ;2
2
1; 1
1; 3
x
xa
fx
fx xb
fx
xc
xd






.
Có




2
22
6
lim lim
4
xx
hx
fx

 

;


2
6
lim lim
4
xa xa
hx
fx



;


2
6
lim lim
4
xb xb
hx
fx



;


2
6
lim lim
4
xc xc
hx
fx



;


2
6
lim lim
4
xd xd
hx
fx



.
Suy ra đồ thị hàm số
y
hx
có tất cả
5
tiệm cận đứng
2; ; ; ;
x
xaxbxcxd
.
Câu 10: Cho hàm số
yf
x
liên tục trên
;1
và
1; 
, có bảng biến thiên như hình:
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

 
2
8
65
yhx
fx fx


.
A.
3
. B. 4 . C.
5
. D.
6
.
Lời giải
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 15
Xét hàm số

 
2
8
65
yhx
fx fx


.
a/ Tìm tiệm cận đứng:
 

2
5
650
1
fx
fx fx
fx

.
Có
50fx x
.


0;1
1
1;
xa
fx
xb



.

 
2
00
8
lim lim
65
xx
hx
fx fx




;

 
2
8
lim lim
65
xa xa
hx
fx fx




;

 
2
8
lim lim
65
xb xb
hx
fx fx




0; ;
x
xaxb
là các tiệm cận đứng của đồ thị hàm số
y
hx
.
b/ Tìm tiệm cận ngang:

 
2
8
lim lim
65
xx
hx
fx fx
 


;

 
2
8
lim lim 2
65
xx
hx
fx fx
 


2y
là tiệm cận ngang của đồ thị hàm số
y
hx
.
Vậy đồ thị hàm số
y
hx
có tất cả 4 tiệm cận.
Câu 11: Cho

f
x
là hàm bậc 4 và có bảng biến thiên như hình vẽ sau:
Đồ thị hàm số

 
2
2
2
34
x
gx
fx fx

có mấy đường tiệm cận đứng?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Dễ dàng chứng minh được nếu
0
x
x
với
0
2x 
là nghiệm đơn của mẫu hoặc
0
x
x
là nghiệm kép
của mẫu thì đường thẳng
0
x
x
là đường TCĐ của đồ thị hàm số
g
x
.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 16
Ta có
 


2
1
340
4
fx
fx fx
fx


Dựa vào BBT ta được PT

1fx
có hai nghiệm kép là
2x 
và
2x
và PT
4fx
có hai nghiệm đơn là
2xa
và
2xb
.
Vậy đồ thị hàm số
g
x
có 4 đường TCĐ là
,, 2xaxbx
và
2x 
.
Câu 12: Cho

f
x
là hàm bậc 4 và có bảng biến thiên như hình vẽ sau:
Đồ thị hàm số

 
42
2
2
23
xx
gx
fx fx

có mấy đường tiệm cận?
A. 3. B.
4
. C. 5. D. 6 .
Lời giải
Ta có
42
0
20
2
x
xx
x


, trong đó 0x là nghiệm kép.
Dễ dàng chứng minh được nếu
0
x
x
với
0
0; 2x 
là nghiệm đơn của mẫu hoặc
0
x
x
là nghiệm
kép khác
0
của mẫu thì đường thẳng
0
x
x
là đường TCĐ của đồ thị hàm số
g
x
. Nếu
0x
là nghiệm
kép bội hai của mẫu thì đường thẳng
0x
không là TCĐ của đồ thị hàm số
g
x
.
Ta có
 


2
1
230
3
fx
fx fx
fx


Dựa vào BBT ta được PT

1fx
có hai nghiệm kép là
2x 
và
2x
và PT
3fx
có hai nghiệm đơn là
2xa
và
2xb
và một nghiệm kép
0x
.
Khi đó đồ thị hàm số
g
x
có 4 đường TCĐ là
,, 2xaxbx
và
2x 
.
Mặt khác, bậc của tử là bậc 4 và bậc của mẫu là bậc 8 nên dễ tính được
lim 0
x
gx

. Khi đó đồ thị hàm
số
g
x
có đường TCN là
0y
.
Vậy đồ thị hàm số
g
x
có 5 đường tiệm cận.
Câu 13: Cho hàm số
32
f
xaxbxcxd
có đồ thị như sau:
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 17
Đặt

 
2
2
.
xx
gx
xfx
Đồ thị hàm số
y
gx
có bao nhiêu tiệm cận đứng?
A.
4
. B.
2
. C. 5. D. 3.
Lời giải
Điều kiện:
 

2
0
0
1
fx
fx fx
fx

Xét
 


2
0
0
1
fx
fx fx
fx

Dựa vào đồ thị ta có
0fx
có hai nghiệm phân biệt
1
0xx
và
1
x
(nghiệm kép).



21 2
33
44
1
101
1
xxx x
fx x x x
xxx



Vậy
   
2
22
1 234
11
f
xfx fxfx axxx xxxxxx 

.
Khi đó ta có:

 



2
2
2
2
1234
2
1 234
1
1
1
xx
gx
fx fx
xx
axx x xx xx xx
x
axx x xx xx xx


Vậy đồ thị hàm số có 5 tiệm cận đứng.
Câu 14: Cho hàm số
y
fx
xác định và liên tục trên
và có bảng biến thiên như sau:
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 18
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:

3
14
312
3
gx
x
fx




là:
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Đặt
3
3,
3
x
ux
ta có
33
lim 3 , lim 3
33
xx
xx
xx
 
 
 
 
 
.
Mặt khác ta xét:
3
3
3
x
yx
có
2
30,yx x

nên với mọi
u
thì phương trình
3
3
3
x
x
u
có duy nhất một nghiệm
x
.
Xét
33
3120 3 12
33
xx
fx fx
 

 
 
.
Từ bảng biến thiên ta thấy phương trình có duy nhất một nghiệm nên đồ thị hàm số

3
14
312
3
gx
x
fx




có một tiệm cận đứng.
Ta có:




3
3
14 14
lim lim lim 0
12
312
3
14 14
lim lim lim 0
12
312
3
xx u
xx u
gx
fu
x
fx
gx
fu
x
fx
  
  




























Vậy đồ thị hàm số

3
14
312
3
gx
x
fx




có duy nhất một tiệm cận ngang.
Vậy đồ thị hàm số có một tiệm cận đứng và một tiệm cận ngang.
Câu 15: Cho hàm số có bảng biến thiên dưới đây:
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số

2020
2020 2021
y
fx
.
f
x
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 19
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Từ bảng biến thiên ta có .
Do đó

2020 2020
lim .
2020 2021 4041
x
fx

Vậy đồ thị hàm số

2020
2020 2021
y
fx
có 1 đường tiệm cận
ngang là đường thẳng
2020
4041
y .
Ta có
 
2021
2020 2021 0
2020
fx fx có hai nghiệm nghiệm vì đường thẳng
2021
:
2020
dy cắt
đồ thị hàm số
yf
x
tại hai điểm phân biêt. Suy ra đồ thị hàm số

2020
2020 2021
y
fx
có hai tiệm cận
đứng.
tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số

2020
2020 2021
y
fx
là
3
.
Câu 16: Cho hàm số


322
3
321
x
yC
xmx m xm

.Có tất cả bao nhiêu giá trị nguyên thuộc
khoảng
10;10
của tham số để đồ thị hàm số có tổng số đường tiệm cận là nhiều nhất?
A.
20
. B.
15
. C.
16
. D.
18
.
Lời giải
Ta có:

322
3
lim 0
321
x
x
xmx m xm


và

322
3
lim 0
321
x
x
xmx m xm


nên đồ thị hàm số có 1
đường tiệm cận ngang là
Do đó có tổng số đường tiệm cận là nhiều nhất khi có 3 đường tiệm cận đứng nên phương trình
322
321 01xmx m xm
có 3 nghiệm phân biệt
3x
.
Ta có:



2
2
1210
2102
xm
xmx mx
gx x mx


Suy ra
3m
và phương trình (2) có 2 nghiệm phân biệt khác 3

2
3
3
3
1
010
1
10 6 0
30
5
3
m
m
m
m
m
m
m
g
m





Mà nguyên thuộc khoảng
10;10
nên
9;8;7;6 5;4;3;2;2;4;5;6;7;8;9m
.
Câu 17: Cho hàm số
32
2
3(2)
x
y
x
xm xm

. Tìm điều kiện của tham số
m
để đồ thị hàm số có 4
đường tiệm cận?
lim lim 1
xx
fx fx
 

m
0.y

C

C
m
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 20
A.
1m
. B.
1
0
m
m
. C.
1m
. D.
1
0
m
m
.
Lời giải
Gọi

C
là đồ thị hàm số
32
2
3(2)
x
y
x
xm xm

.
Ta có


32
2
22
3(2)
12
xx
y
xxmxm
x
xxm




Vì
23
32
23
12
2
lim lim 0
32
3(2)
1
xx
x
xx
mm
xxmxm
xx x
 



nên đồ thị hàm số có 1 đường tiệm cận ngang
là
0.y
Do đó

C
có 4 đường tiệm cận khi và chỉ khi

C
có 3 đường tiệm cận đứng
2
12 0xxxm
có 3 nghiệm phân biệt khác
2
2
20xxm
có 2 nghiệm phân biệt khác
1
;
2
.
2
2
'1 0
1
1
12.1 0 1
0.
0
22.2 0
m
m
m
mm
m
m
m





Câu 18: Cho hàm số
2
3
21
x
y
x
mx

. Tìm số các giá trị của tham số
m
để đồ thị hàm số có 1 đường
tiệm cận đứng?
A.
0
. B. 1. C. 2 . D.
3
.
Lời giải
Gọi

C
là đồ thị hàm số
2
3
21
x
y
x
mx

.

C
có 1 đường tiệm cận đứng:
Phương trình
2
210xmx
có nghiệm kép hoặc có hai nghiệm phân biệt (trong đó có một nghiệm
bằng
3
)
 
2
2
2
1
'10
11
'10
15
3
32.310
5
3
m
m
mm
m
m
m
m
m











Câu 19: Đồ thị của hàm số
3
2
2
32
mx
y
xx

có hai tiệm cận đứng khi và chỉ khi?
A.
0m
và
2m
. B.
1m
và
2m
. C.
0m
. D.
2m
và
1
4
m .
Lời giải
Điều kiện xác định:
1; 2xx
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 21
Để đồ thị hàm số
3
2
2
32
mx
y
xx

có hai tiệm cận đứng thì
1
x
và
2x
không phải là nghiệm của
phương trình
3
20mx
.
Đặt
3
2gx mx
Khi đó: YCBT


2
10
20
1
20
820
4
m
g
m
g
m
m





.
Câu 20: Cho hàm số
2
1
24
x
y
x
mx

có đồ thị là

C
. Tìm tất cả các giá trị thực của tham số m để đồ
thị
C
có đúng 3 đường tiệm cận?
A.
2
2
5
2
m
m
m



. B.
2
2
m
m

. C.
2m
. D.
2
5
2
m
m


.
Lời giải
Điều kiện xác định:
2
240xmx
Do
lim 0
x
y

nên đồ thị hàm số luôn có tiệm cận ngang
0y
Để đồ thị hàm số có đủ 3 tiệm cận thì

2
24gx x mx có hai nghiệm phân biệt khác 1 .
 
2
2
2
40
2
12 140
5
2
m
m
m
m
m









Câu 21: Cho hàm số
2
2
12 4
62
x
x
y
x
xm


có đồ thị
m
C
. Tìm tập
S
tất cả các giá trị của tham số thực
m để
m
C
có đúng hai tiệm cận đứng.
A.
8; 9S
. B.
9
4;
2
S


. C.
9
4;
2
S



. D.
0;9S
.
Lời giải
ĐKXĐ:
2
04
62 0
x
xxm


.
Ta có
2
12 4 0
x
xx
nên để
m
C
có hai tiệm cận đứng thì phương trình

22
62 0 62 0*xxm xxm 
có hai nghiệm phân biệt thuộc
0; 4 .
Cách 1.
Đế phương trình có 2 nghiệm phân biệt thì
9
92 0
2
mm

Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 22
Gọi 2 nghiệm phân biệt của (*) là
12
x
x
ta có
12
04xx
.
Theo định lí Vi-et ta có
12
12
6
.2
xx
x
xm

Khi đó


12
12
12
12
0
0
440
440
xx
xx
xx
xx





12
12
12 1 2
12
0
0
4160
80
xx
xx
xx x x
xx



20
60
224160
68 0
m
m


0
280
m
m

4m. Kết
hợp nghiệm ta có
9
4
2
m
.
Cách 2.
2
62 0xxm
2
26mx x
Xét hàm số

2
6
f
xxx
trên đoạn
0; 4

26
f
xx

Cho
03fx x

.
Bảng biến thiên
x
0
3
4

f
x
0

f
x
0
9
8
Phương trình có hai nghiệm phân biệt thuộc
0; 4
9
82 9 4
2
mm

Câu 22: Với giá trị nào của
m
, đồ thị hàm số

2
2
13
12
x
xx
y
xmxm


có đúng hai đường tiệm cận?
A.
m
. B.
1
2
3
m
m
m


. C.
1
2
m
m

. D.
2
3
m
m


.
Lời giải

2
2
13
12
x
xx
y
xmxm


. Hàm số xác định khi:
3
0
1
2
x
x
x
xm


.
Ta có



2
2
22
13 1 1
12
1213 213
xxx x
y
xmxm
x
xm x x x xm x x x




.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 23
lim 0 0
x
yy


là tiệm cận ngang.
Hàm số có hai tiệm cận khi có một tiệm cận đứng
23 1
20 2
mm
mm






.
Câu 23: Cho hàm số

2
2
32
xm
yfx
xx



có đồ thị

C
. Gọi S là tập chứa tất cả các giá trị nguyên
của tham số
m để đồ thị

C
có đúng một tiệm cận đứng và một đường tiệm cận ngang. Số
phần tử của tập
S
là
A.
4
. B.
1
. C. 3. D.
2
.
Lời giải



2
24
32
12 4
xm xm
yfx
xx
xx xm




Điều kiện:
1
2
x
m
x
x
Đồ thị hàm số có một tiệm cận ngang
0y
do
lim 0
x
y

Đồ thị hàm số có một tiệm cận đứng khi và chỉ khi
140
2
240
1
2
1
240
m
m
m
m
m
m
m



3
2
12
m
m
m



mà m
3
2
2
m
m
m


.
Câu 24: Cho hàm số
2
213
2
mx x m x
y
x

có đồ thị

C
. Gọi
S
là tập chứa tất cả các giá trị
thực của tham số
m để đồ thị

C
có đúng hai đường tiệm cận. Tổng giá trị tất cả các phần tử
của
S
bằng
A.
31
7
.
B.
25
. C.
5
9
.
D.
86
5
.
Lời giải
Xét 0m thì đồ thị hàm số không có tiệm cận ngang nên tối đa chỉ có một đường TCĐ.
Xét
0m
thì đồ thị hàm số chỉ có duy nhất một tiệm cận ngang
3y
.
Xét
0m
, ta có
2
213
lim lim 3
2
xx
mx x m x
ym
x
 


,
2
213
lim lim 3
2
xx
mx x m x
ym
x
 


Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 24
Đồ thị hàm số không có đường tiệm cận đứng thì
2
41
.2 2.2 1 3. 2 0
5
mm m .
Đồ thị hàm số có một đường tiệm cận ngang thì
339mmm .
Vậy với
41
5
m
thì đồ thị hàm số có hai đường tiệm cận ngang và với
9m thì đồ thị hàm số đường
tiệm cận ngang và một đường tiệm cận đứng.
Nên
41
;9
5
S



suy ra tổng các phần tử của tập
S
bằng
86
5
.
Câu 25: Tìm tất cả các giá trị của tham số m để đồ thị hàm số
2
1
42 1
x
y
x
xm x

có đúng bốn
đường tiệm cận.
A.

7
;6 \ 2
3
m




. B.
7
;6
3
m




.
C.

7
;6 \ 2
3
m




. D.

7
;6 \ 2
3
m



.
Lời giải
Ta có
lim 1
x
y

và
1
lim
3
x
y

 suy ra đồ thị hàm số có đường hai tiệm cận ngang là
1y
và
1
3
y  .
Để đồ thị có đúng bốn đường tiệm cận thì phương trình
2
42 10xxmx
có hai nghiệm phân biệt
khác 1.
Ta có
2
42 10xxmx
2
42 1xxmx

2
1
341 1
x
xx m


Yêu cầu bài toán tương đương phương trình
1
có hai nghiệm phân biệt
1x 
và
1
x
.
Xét hàm số
2
341yx x
với
1x 
và
1
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên phương trình
2
341
x
xm
với
1x 
và
1
x
có hai nghiệm thì

7
;6 \ 2
3
m



.
Câu 26: Cho hàm số
y
fx
có bảng biến thiên như hình vẽ bên. Hỏi đồ thị của hàm số

1
23
y
fx
có bao nhiêu đường tiệm cận?
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 25
A.
1
. B. 3. C. 2. D. 0 .
Lời giải
Từ bảng biến thiên ta có

11 1
lim 0 lim
2333
xx
yy
fx
 

là một tiệm cận ngang.
Ta có:
 
3
230
2
fx fx

. Căn cứ vào bảng biến thiên đồ thị

3
,
2
yfxy

cắt nhau tại
một điểm nên đồ thị có một tiệm cận đứng.
Câu 27: Cho hàm số
yf
x
có bảng biến thiên như hình dưới đây
Gọi tập
S
là tập chứa tất cả các giá trị nguyên của tham số

10;10m
để đồ thị hàm số
 
2
2x
y
f
xmfx
có đúng hai đường tiệm cận đứng. Số phần tử của tập
S
là:
A. 9. B. 12. C. 13. D. 8.
Lời giải
Xét hàm

 
2
2x
ygx
f
xmfx

với
2x
(1).
Khi đó
 

2
0
0
f
xm
fxmfx
fx

Phương trình




1
012
2,
xa a
fx x b b
x
cc cn

 

Với
x
a ,
x
b
loại vì không thõa điều kiện (1).
Với
,lim
xc
xc gx

nên đường
x
c là một tiệm cận đứng của đồ thị
g
x
.
Đồ thị
g
x
có hai đường tiệm cận đứng

f
xm
có một nghiệm
2x
và
x
c
Dựa vào BTT của
yf
x
,

f
xm
có một nghiệm
2x
và
x
c
2
0
m
m

.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 26
Câu 28: Cho hàm số
yf
x
có đồ thị như hình dưới đây
Gọi tập
S
là tập chứa tất cả các giá trị tham số m để đồ thị hàm số

2
3
24
xx
y
fx f x m



có đúng ba
đường tiệm cận đứng. Khẳng định nào sau đây là đúng:
A.
;3 S
. B.

;2 S
.
C.
S 
. D.
6;8 S
.
Lời giải
Xét hàm




2
3
3
24 24
xx
xx
ygx
fx f x m fx f x m


 

Khi đó


0
240
240
fx
fx f xm
fxm




Xét

1
2
0
0
3
x
fx
x

Với
1
0x
là nghiệm đơn nên 0x không là tiệm cận đứng của đồ thị
yg
x
.
Với
2
3x
là nghiệm kép nên
3x
là tiệm cận đứng của đồ thị.
yg
x
.
Xét
 

3
4
1
21
2
2402 4
23
2
m
x
xm
fxm fxm
xmcc
cm
x



Với
3
1
2
m
x
là nghiệm kép nên
1
2
m
x
là tiệm cận đứng của đồ thị
yg
x
.
Đồ thị
yg
x
có ba đường tiệm cận đứng
2
cm
x
 là tiệm cận đứng của đồ thị
yg
x
0
2
3
2
cm
cm

3
6
mc
c
mc



.
Câu 29: Cho hàm số bậc ba
32
()
f
xaxbxcxd
có đồ thị như hình vẽ. Với giá trị nào của m thì
hàm số
2
()
() 2()
mx
gx
f
xfx
có 5 tiệm cận đứng?
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 27
A.
2m
.
B.
2m
.
C.
2m
.
D.
2m
.
Lời giải
Chọn D
Xét hàm số
2
()
() 2()
mx
gx
fx fx
Biểu thức
mx
xác định khi
0(1)mx xm
Ta có
2
1
2
() 2() 0(2)
(2;1)
0
() 0
(1; 2)
)2
1
2
fx fx
xx
x
fx
xx
fx
x
x




Hàm số có 5 tiệm cận đứng khi phương trình
(2)
có 5 nghiệm thỏa mãn điều kiện của
(1)
2m
Câu 30:
Cho hàm số bậc ba
32
()f x ax bx cx d
có đồ thị như hình vẽ. có bao nhiêu giá trị của
m
để hàm số
22 2
2
(2 1) 3
()
(x-4)[ ( ) 4 ( )]
xmxmm xx
gx
fx fx

có 3 tiệm cận đứng?
A.
1
.
B.
2
.
C.
3
.
D.
4
Lời giải
Chọn B
Xét hàm số
22 2
2
(2 1) 3
()
(x-4)[ ( ) 4 ( )]
xmxmm xx
gx
fx fx

Biểu thức
2
3xx
có điều kiện là:
2
30 (;0][3;)xx x
Ta có
O
x
y
2
4
1
3
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 28
2
2
(x-4)[ ( ) 4 ( )]=0(1)
4
4
40
40
3
() 0 3
1
() 4()
() 4 1
0
2( )
fx fx
x
x
xx
x
x
fx x
x
fx fx
fx x
x
x Loaïi





Đặt
22
() 3 1hx x mx m m
. Nếu
()hx
không có nghiệm thuộc
1; 0; 3; 4
thì
()gx
có 4 tiệm cận
đứng. Xét các trường hợp sau
Thường hợp 1:
4
x
là nghiệm của
()hx
2
7170mm
(vô nghiệm)
Thường hợp 2:
3
x
là nghiệm của
()hx
2
5100mm
(vô nghiệm)
Thường hợp 3:
1
x

là nghiệm của
()hx
2
320mm
1
2
m
m


Thường hợp 4:
0
x
là nghiệm của
()hx
2
10mm
(vô nghiệm)
Như vậy khi
1
2
m
m


thì hàm số đã cho có 3 tiệm cận đứng.
Câu 31: Cho hàm số
3
23 2
xm
ym
x




có đồ thị
.C
Giả sử
;
MM
M
x
y
là 1 điểm bất kỳ thuộc
.C
Gọi
,
A
B
lần lượt là khoảng cách từ
M
tới các đường tiệm cận ngang và tiệm cận đứng
của
.C
Biết diện tích
M
AB
bằng
1.
Khẳng định nào sau đây là đúng?
A.
511
;.
22
m




B.
511
;.
22
m




C.
511
;.
22
m




D.
511
;.
22
m



Lời giải
Với
3
,
2
m  đồ thị

C
có đường tiệm cận đứng là
3
2
x  và tiệm cận ngang
1
.
2
y
Khoảng cách từ
M
tới đường tiệm cận đứng:
1
3
.
2
M
dx
Khoảng cách từ
M
tới đường tiệm cận ngang:

2
23
123
.
232223223
M
MMM
m
xm m
d
xxx



Từ giả thiết,
M
AB vuông tại
M
nên
12 12
11
..12
22
MAB
SMAMBdddd

Do đó
5
238
23
3
2
.2238
238 11
222 3
2
M
M
m
m
m
xm
m
x
m




Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 29
Câu 32: Cho hàm số
22
1
x
y
x
có đồ thị
.C
Giả sử
;
MM
M
x
y
là điểm thuộc

C
thỏa mãn tổng
khoảng cách từ
M
tới trục hoành và đường tiệm cận đứng của

C
đạt giá trị nhỏ nhất. Giá trị
của
M
M
x
y
bằng
A. 2. B. 2. C. 1. D. 1.
Lời giải
Đồ thị

C
có đường tiệm cận đứng
1.x
Ta có
M
C
nên
22
.
1
M
M
M
x
y
x
Khoảng cách từ
M
tới đường tiệm cận đứng:
1
1.
M
dx
Khoảng cách từ
M
tới trục hoành:
2
22
.
1
M
M
M
x
dy
x

Tổng khoảng cách từ
M
tới tiệm cận đứng và trục hoành:
12
22
1
1
M
M
M
x
ddd x
x

Nếu
1,
M
x
ta có
21
122122.24
1
M
MM
M
x
dx x
x

Nếu
11,
M
x
ta có

 
2
2
22 22
121
11
11 22 1
12 2
2222.
111
MM
MM
MM
MMM M
MM
MMM
xx
dx x
xx
xxx x
xx
xxx





  

Dấu bằng xảy ra khi và chỉ khi
1.
M
x 
Nếu
1,
M
x 
ta có
22
112
1
M
MM
M
x
dx x
x

Vậy
2,d
dấu bằng chỉ xảy ra khi
1,
M
x 
do đó

1;0 .M
Câu 33: Cho hàm số
23mx
y
xm
+
=
-
có đồ thị
()
C và
I
là giao điểm của hai đường tiệm cận của
()
C
.Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho tiếp tuyến tại điểm
M
trên đồ thị
()
C cắt hai đường tiệm cận tại hai điểm
,AB
và tam giác
IAB
có diện tích bằng
64
.Tổng các
phần tử của tập hợp
S
là
A. 58 . B. 258. C. 258- . D.
0
.
Lời giải
Đồ thị
(
)
:C
23mx
y
xm
+
=
-
có tiệm cận đứng
xm=
và tiệm cận ngang
2ym=
nên giao điểm của hai
tiệm cận là
(
)
2;Im m.
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 30
Giả sử
()
0
0
0
23
;
mx
Mx C
xm
æö
+
÷
ç
÷
çÎ
÷
ç
÷
÷
ç
-
èø
Phương trình tiếp tuyến
D
với
()
C tại
M
là
()
()
2
0
0
2
0
0
23
23
mx
m
yxx
xm
xm
+
+
=- - +
-
-
.
Tiếp tuyến cắt TCĐ
xm=
tại
2
0
0
226
;
mx m
Am
xm
æö
++
÷
ç
÷
ç
÷
ç
÷
ç
÷
-
èø
, cắt tiệm cận ngang tại
()
0
22;Bx mm-
Ta có
2
0
46m
IA
xm
+
=
-
và
0
2IB x m=-
.
Diện tích tam giác
IAB
là
2
2
0
0
1146 58
64 64 2 64 4 6 64
22 2
..
IAB
m
SIAIB xmm m
xm
+
= = -= +==
-
Vậy
58 58
0
22
S
æö
÷
ç
÷
ç
=+- =
÷
ç
÷
ç
÷
ç
èø
.
Câu 34: Cho hàm số
21
1
x
y
x
-
=
+
có đồ thị
()
C
và
I
là giao điểm của hai đường tiệm cận. Giả sử
()
00
;Mx y là điểm trên đồ thị
()
C có hoành độ dương sao cho tiếp tuyến tại
M
với
()
C cắt
tiệm cận đứng và tiệm cận ngang lần lượt tại hai điểm
,AB
thỏa mãn
22
40IA IB+=
. Giá trị
của biểu thức
22
0000
Px y xy=++
bằng:
A. 8 . B. 3 . C.
5
. D.
7
.
Lời giải
Đồ thị
(
)
:C
21
1
x
y
x
-
=
+
có tiệm cận đứng
1x =-
và tiệm cận ngang
2y =
nên
(
)
12;I -
.
Vì
(
)
MCÎ nên
()
0
00
0
21
0
1
;,
x
Mx x
x
æö
-
÷
ç
÷
ç
>
÷
ç
÷
÷
ç
+
èø
Phương trình tiếp tuyến với
()
C
tại
M
là
(
)
()
0
0
2
0
0
21
3
1
1
x
yxx
x
x
-
=-+
+
+
.
()
0
0
0
24
1212
1
;, ;
x
ABx
x
æö
-
÷
ç
÷
ç
- +
÷
ç
÷
÷
ç
+
èø
Ta có
0
6
1
IA
x
=
+
và
0
21IB x=+.
Khi đó
22
40IA IB+=
()
()
2
00
2
0
36
4140 0
1
,xx
x
++=>
+
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 31
(
)
(
)
()
(
)
42
00
2
0
2
0
110 190
11
19
xx
x
x
+- ++=
é
+=
ê
ê
ê
+=
ê
ë
0
0
00
0
0
0
2
21
2
4
()
()
()
()
xl
xl
xy
xn
xl
é
=
ê
ê
=-
ê
==
ê
=
ê
ê
=-
ê
ë
.
Suy ra
()
21;M
Giá trị của biểu thức
7.P =
Câu 35:
Cho hàm số
2
1
x
y
x
có đồ thị là

C
. Gọi
I
là giao điểm hai đường tiệm cận và
00
;
M
x
y
là điểm nằm trên

C
với
0
0x
. Biết tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng và
tiệm cận ngang lần lượt tại hai điểm
P
và
Q
sao cho bán kính đường tròn nội tiếp tam giác
IPQ
lớn nhất. Tính tổng
00
x
y
.
A.
00
0xy
. B.
00
223xy
. C.
00
2xy
. D.
00
23xy
.
Lời giải
Đồ thị

C
có đường tiệm đứng
1x 
và đường tiệm cận ngang
1y
.
Giao điểm hai đường tiệm cận

1;1I
.
Gọi

0
0
0
2
;
1
x
M
xC
x



với
0
0x
. Ta có

2
3
1
y
x
.
Phương trình tiếp tuyến của

C
tại điểm
M
là


0
0
2
0
0
2
3
1
1
x
yxx
x
x

.
Tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng tại điểm
0
0
5
1;
1
x
P
x



và cắt tiệm cận ngang tại
điểm

0
21;1Qx
.
Ta có
0
0
116
..216
221
IPQ
SIPIQ x
x

.
Mặt khác
6
IPQ
IPQ
S
Sprr
pp

nên
r
đạt giá trị lớn nhất khi và chỉ khi
p
đạt giá trị nhỏ nhất hay
chu vi tam giác
IPQ
đạt giá trị nhỏ nhất.
Mà chu vi tam giác
IPQ
:
22
22 . 2212C IPIQPQ IPIQ IP IQ IPIQ 
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 32
Nên chu vi tam giác
IPQ
nhỏ nhất khi
0
0
0
0
13
6
21
1
13
x
IP IQ x
x
x



.
Do
0
0x
nên
0
13 13;13xM
.
Vậy
00
0xy
.
Câu 36: Cho hàm số
21
22
x
y
x
có đồ thị là

C
. Gọi I là giao điểm hai đường tiệm cận và
M
là điểm
nằm trên

C
có hoành độ lớn hơn
1
. Tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng và
tiệm cận ngang lần lượt tại hai điểm
A
và
B
. Hoành độ của điểm
M
thuộc khoảng nào sau
đây để
PIAIB
đạt giá trị nhỏ nhất?
A.
4;1
. B.

;4
. C.
4; 
. D.
1; 4
.
Lời giải
Đồ thị

C
có đường tiệm đứng 1
x
và đường tiệm cận ngang
1y
.
Giao điểm hai đường tiệm cận

1;1I
.
Gọi

0
0
0
21
;
22
x
M
xC
x



với
0
1x
. Ta có

2
2
22
y
x

.
Phương trình tiếp tuyến của

C
tại điểm
M
là


0
0
2
0
0
21
2
22
22
x
yxx
x
x

.
Tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng tại
0
0
1;
1
x
A
x



và cắt tiệm cận ngang tại điểm
0
21;1Bx
.
Ta có

0
0
1
2122
1
IA IB x
x

Suy ra
22Min IA IB
khi

0
0
0
0
22
1
2
21
1
22
2
x
x
x
x

.
Do
0
1x
nên
0
22
2
x
.
Vậy
0
22
2
x
.
Câu 37: Cho hàm số
2
3
x
y
x
có đồ thị

C
. Gọi
00
;
M
x
y
là một điểm thuộc

C
sao cho tổng
khoảng cách từ
M
đến hai đường tiệm cận của

C
là nhỏ nhất. Tính
00
2
x
y
biết
0
0y
.
A.
00
24xy
. B.
00
22xy
. C.
00
26xy
. D.
00
210xy
.
Lời giải
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 33
Gọi

00
;
M
x
y
C
0
0
0
2
;
3
x
Mx
x



.
Đồ thị

C
có tiệm cận đứng
3x
và tiệm cận ngang
1y 
.
Khoảng cách từ
M
đến tiệm cận đứng là
10
3dx
.
Khoảng cách từ
M
đến tiệm cận ngang là
2
0
1
3
d
x
.
Ta có
12 0
0
1
32
3
dd x
x

. Dấu
'' ''
xảy ra khi và chỉ khi
0
0
1
3
3
x
x

00
00
20
42
xy
xy


.
Mà
0
0y
nên
0
2y 
. Vậy
00
22.4210xy
.
Câu 38: Cho hàm số
1
3
x
y
x
có đồ thị là

C
. Gọi
I
là giao điểm của hai đường tiệm cận và
00
;
M
x
y
là một điểm thuộc

C
. Phương trình tiếp tuyến của

C
tại
M
cắt tiệm cận đứng
và tiệm cận ngang của

C
lần lượt tại hai điểm
A
,
B
sao cho
22
32IA IB
. Tìm tọa độ
điểm
M
biết
0
0y
.
A.
5;3
. B.
1
2;
5



. C.
1
3;
3



. D.
1; 1
.
Lời giải
Đồ thị

C
có tiệm cận đứng
3x 
và tiệm cận ngang
1y
.
Giao điểm của hai đường tiệm cận
3;1I
.
Ta có điểm

0
00 0
0
1
;;
3
x
Mx y C M x
x




và

2
4
3
y
x
,
3x
.
Phương trình tiếp tuyến của

C
tại
M
có dạng


0
0
2
0
0
1
4
3
3
x
yxx
x
x

.
Cho
1y
 
2
0000
344 1 3xxxxx
0
23xx
.
Cho
3x 


00
0
2
00
0
15
4
3
33
3
xx
yx
xx
x



.
Suy ra tiếp tuyến của

C
tại điểm
M
cắt tiệm cận đứng tại
0
0
5
3;
3
x
A
x



và cắt tiệm cận ngang tại
điểm

0
23;1Bx
.
Ta có
22
32IA IB


2
0
2
0
64
4332
3
x
x

00
00
32 1
32 5
xx
xx






Với
00
11xy 
(loại vì
0
0y
).
Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 34
Với
00
53xy
(nhận).
Vậy

5;3M
.
Câu 39: Cho hàm số
21
1
x
y
x
có đồ thị

C
. Có bao nhiêu điểm
M
thuộc

C
sao cho tổng khoảng
cách từ
M
đến hai đường tiệm gấp
2
lần tích khoảng cách từ
M
đến hai đường tiệm cận của

C
?
A. 0 . B.
1
. C.
4
. D.
2
.
Lời giải
Đồ thị hàm số có tiệm cận đứng
1
:1dx
và tiệm cận ngang
2
:2dy
.
Giả sử

0
0
0
21
;
1
x
M
xC
x



với
0
1x
.
Ta có:
10
;1dMd x
;

0
2
00
21
1
;2
11
x
dMd
xx


Theo đề bài:
00
00
11
121.2
11
xx
xx


0
0
0
2
11
0
x
x
x

.
Vậy có
2 điểm
M
thỏa mãn đề bài.
Câu 40: Cho hàm số
1
2
x
y
x
có đồ thị

C
. Gọi
I
là giao điểm hai đường tiệm cận của

C
. Có bao
nhiêu điểm trên

C
có hoành độ âm sao cho tam giác
OMI
có diện tích bằng
1
2
biết
O
là
gốc tọa độ?
A.
0
. B.
1
. C.
4
. D.
2
.
Lời giải
Đồ thị hàm số có tiệm cận đứng
2x
và tiệm cận ngang
1y
.
Do đó
2;1I
.
Suy ra
5OI
và đường thẳng
OI
có phương trình:
:20xy
.
Giả sử

1
;
2
m
M
mC
m



với
0m
.
Ta có:

2
1
2.
42
2
;
552
m
m
mm
m
dM h
m


Theo đề bài:
2
1
2.
42
11
2
.1
22
55
OMI
mm
SOIhh
m


Strong Team Toán VD – VDC TOANMATH.com
TOANMATH.com Trang 35
2
42 2mm m
2
2
0 (L)
42 2 5 (L)
1
422
4 (L)
m
mm m m
m
mm m
m




.
Vậy có
1
điểm thỏa mãn đề bài.
____________________ HẾT ____________________
| 1/35
| | Tải xuống

Có thể bạn quan tâm:

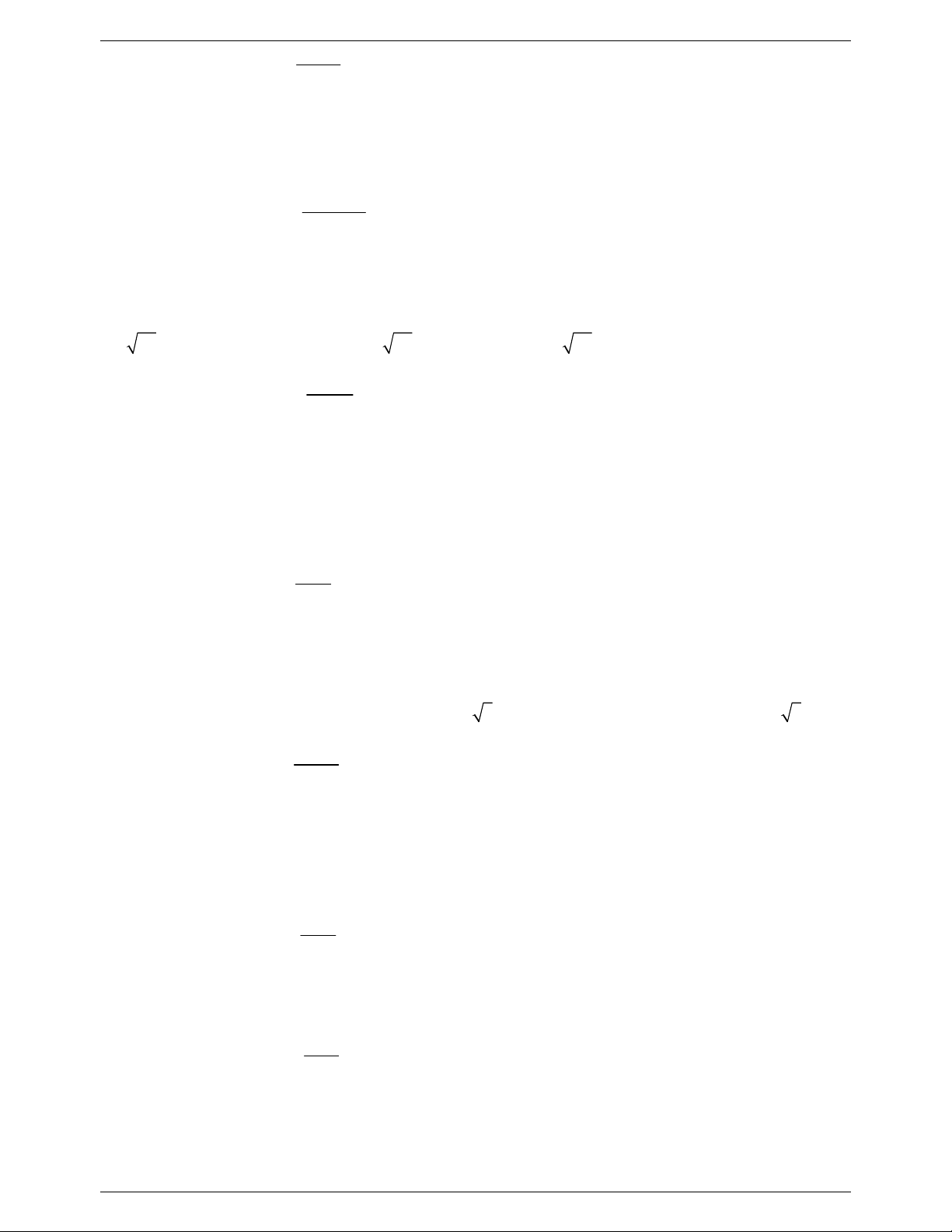
Preview text:

Strong Team Toán VD – VDC TOANMATH.com BÀI TẬP VD - VDC
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
- Strong Team Toán VD - VDC - I. ĐỀ BÀI
3x 1 2x 1
Câu 1: Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 x x A. 1. B. 2 . C. 3. D. 0 . 2
mx x  3 1
Câu 2: Tìm m để đồ thị hàm số y
có 2 đường tiệm cận đứng và 2 đường tiệm 2 x x
cận ngang tạo thành hình chữ nhật có diện tích bằng 2 . A. m  1. B. m  0 . C. m  2 . D. m 1.
x 4x m  2 Câu 3:
Có bao nhiêu giá trị m nguyên thuộc khoảng  10
 ;10 để đồ thị hàm số y  có x  2
đúng ba đường tiệm cận? A. 17 . B. 11. C. 0 . D. 18 . 2020  x 1
Câu 4: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y  có đúng hai 2
x mx  2m tiệm cận đứng? A. 1. B. 2. C. 3. D. 4.
Câu 5: Gọi m, n lần lượt là số đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
x  2x 3  x 1 y
. Khi đó m n bằng: 2 x  4 A. 4 . B. 3. C. 2 . D. 1. 2
x  2019x  2020  4038
Câu 6: Có bao nhiêu giá trị nguyên của tham để m đồ thị hàm số y x m có tiệm cận đứng? A. 1. B. 2 . C. 2019 . D. 2020 .
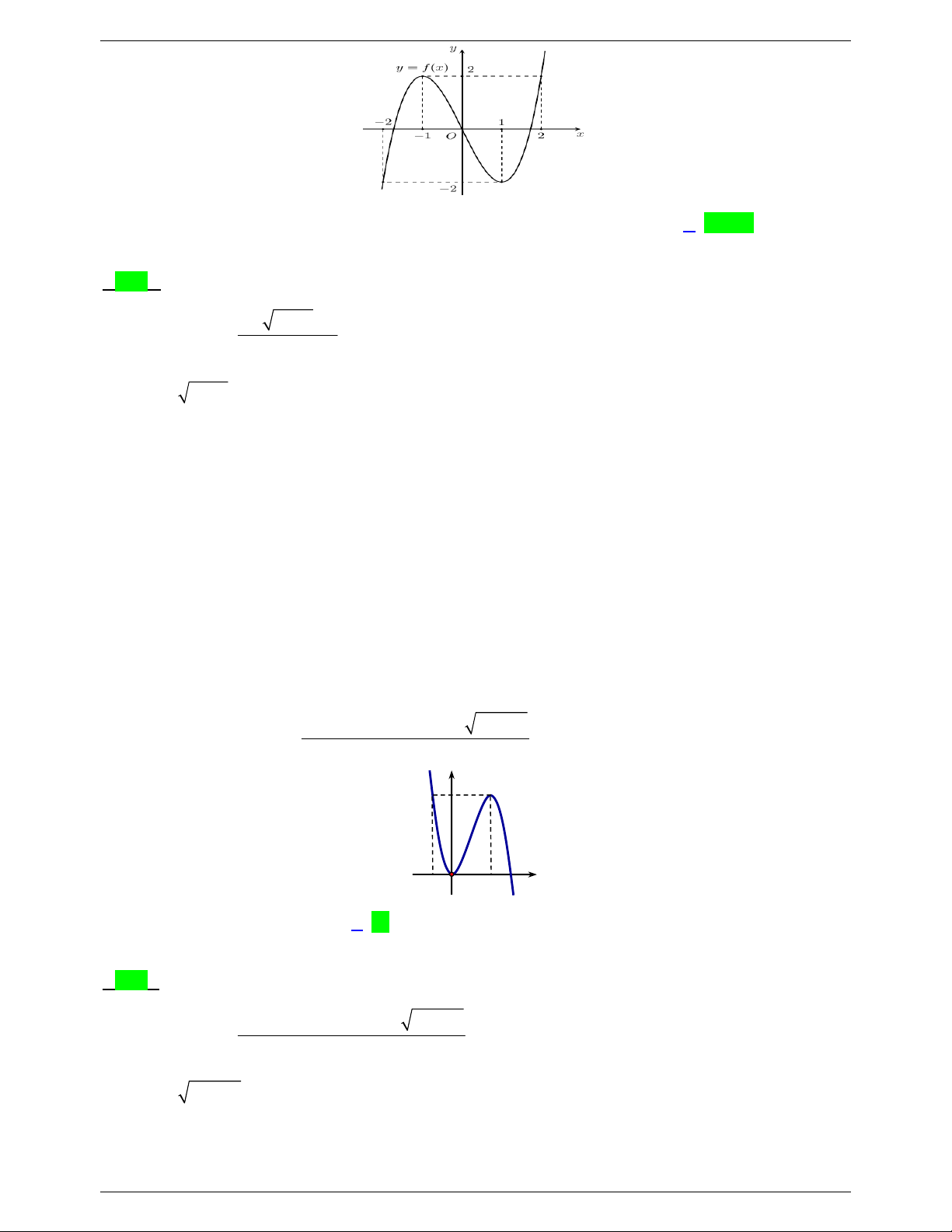
Câu 7: Cho hàm số    3 2 y
f x ax bx cx d a  0 có đồ thị như hình vẽ bên dưới: 1
Tìm m để đồ thị hàm số g x 
có đúng 6 tiệm cận đứng? f  2 x  3  m TOANMATH.com Trang 1 Strong Team Toán VD – VDC TOANMATH.com
A. m  0 . B. 2
  m  0 . C. 3   m  1  .
D. 0  m  4 . 2018
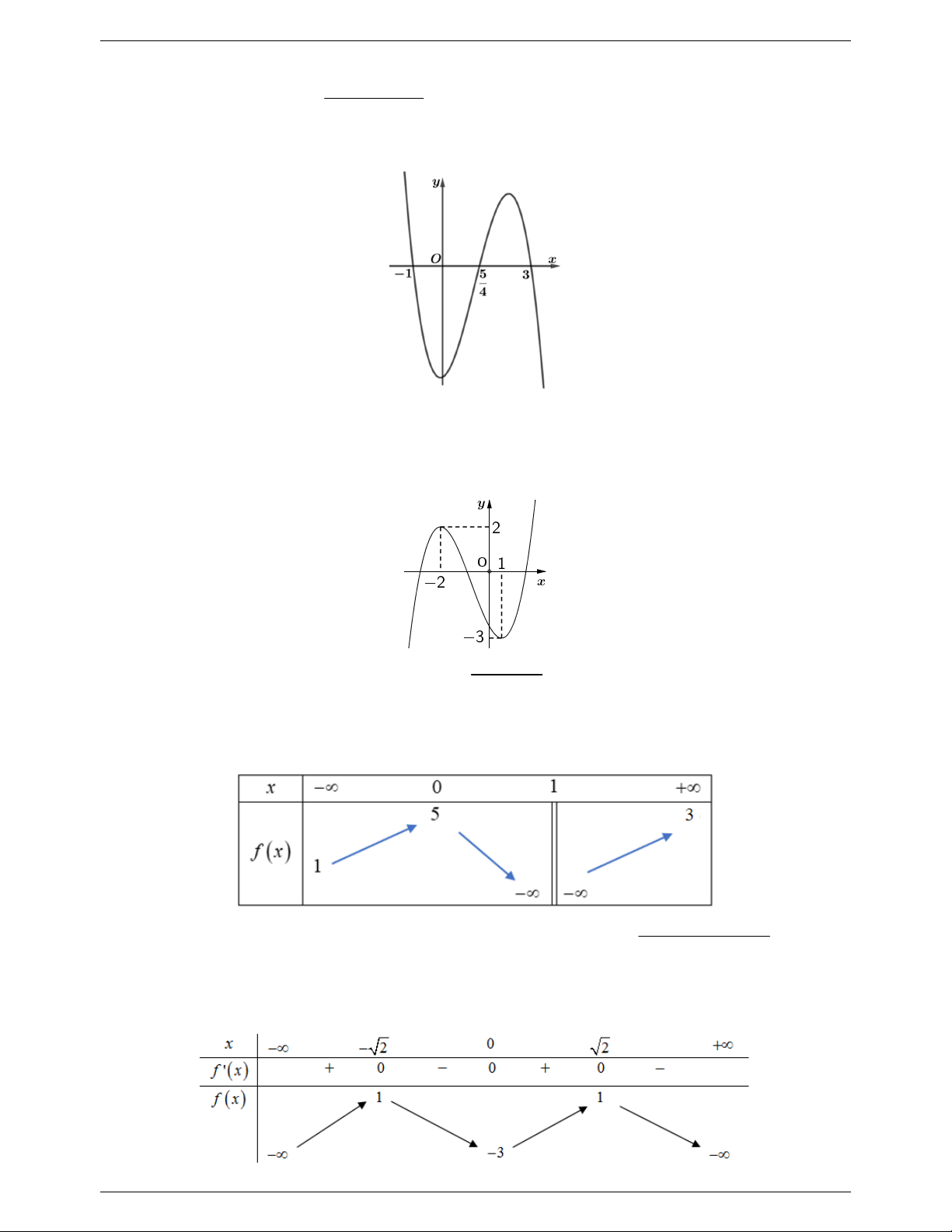
Câu 8: Cho hàm số g x  với   4 3 2
h x mx nx px qx m,n, p,q. Hàm số hx 2  m m
y h x có đồ thị như hình vẽ bên dưới:
Tìm các giá trị m nguyên để số tiệm cận đứng của đồ thị hàm số y g x là 2 . A. 11. B. 10 . C. 9. D. 20 .
Câu 9: Cho hàm số y f x liên tục trên  , có đồ thị như hình vẽ: 6
Tìm số tiệm cận đứng của đồ thị hàm số y hx  . 2 f x  4 A. 2 . B. 4 . C. 6 . D. 5.
Câu 10: Cho hàm số y f x liên tục trên   ;1
 và 1;, có bảng biến thiên như hình: 8
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y hx  . 2
f x  6 f x  5 A. 3. B. 4 . C. 5. D. 6 .
Câu 11: Cho f x là hàm bậc 4 và có bảng biến thiên như hình vẽ sau: TOANMATH.com Trang 2 Strong Team Toán VD – VDC TOANMATH.com 2 x  2
Đồ thị hàm số g x 
có mấy đường tiệm cận đứng? 2
f x  3 f x  4 . A. 2. B. 3. C. 4 . D. 5.
Câu 12: Cho f x là hàm bậc 4 và có bảng biến thiên như hình vẽ sau: 4 2 x  2x
Đồ thị hàm số g x 
có mấy đường tiệm cận? 2
f x  2 f x  3 . A. 3. B. 4. C. 5. D. 6 .
Câu 13: Cho hàm số   3 2
f x ax bx cx d có đồ thị như sau: 2 x x
Đặt g x 
. Đồ thị hàm số y g x có bao nhiêu tiệm cận đứng? 2
f x  f xA. 4 . B. 2 . C. 5. D. 3.
Câu 14: Cho hàm số y f x xác định và liên tục trên  và có bảng biến thiên như sau: 14
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số: g x  là: 3  xf  3x 12    3  A. 2 . B. 4 . C. 1. D. 3.
Câu 15: Cho hàm số f x có bảng biến thiên dưới đây: TOANMATH.com Trang 3 Strong Team Toán VD – VDC TOANMATH.com 2020
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  .
2020 f x  2021 A. 1. B. 2 . C. 3 . D. 0 . x  3
Câu 16: Cho hàm số y
C .Có tất cả bao nhiêu giá trị nguyên thuộc
x  3mx  2m     3 2 2 1 x m khoảng  10
 ;10 của tham số m để đồ thị hàm số có tổng số đường tiệm cận là nhiều nhất? A. 20 . B. 15. C. 16 . D. 18 . x  2
Câu 17: Cho hàm số y
. Tìm điều kiện của tham số m để đồ thị hàm số có 4 3 2
x  3x  (m  2)x m
đường tiệm cận? m  1 m  1 A. m 1. B.  . C. m 1. D.  . m  0 m  0 x  3
Câu 18: Cho hàm số y
. Tìm số các giá trị của tham số m để đồ thị hàm số có 1 đường 2 x  2mx 1 tiệm cận đứng? A. 0 . B. 1. C. 2 . D. 3. 3 mx  2
Câu 19: Đồ thị của hàm số y
có hai tiệm cận đứng khi và chỉ khi? 2 x  3x  2 1
A. m  0 và m  2 .
B. m  1 và m  2 . C. m  0 .
D. m  2 và m  . 4 x 1
Câu 20: Cho hàm số y
có đồ thị là C . Tìm tất cả các giá trị thực của tham số m để đồ 2 x  2mx  4
thị C có đúng 3 đường tiệm cận? m  2  m  2  m  2  m  2   A.  . B.  . C. m  2 . D.  5 .  5 m  2 m    m     2  2 2 Câu 21: Cho hàm số 12  4x x y
có đồ thị C . Tìm tập S tất cả các giá trị của tham số thực m  2
x  6x  2m
m để C có đúng hai tiệm cận đứng. m   9   9 
A. S  8;9 . B. S  4;  . C. S  4;  .
D. S  0;9.  2  2 2
x 1 x  3x
Câu 22: Với giá trị nào của m, đồ thị hàm số y
có đúng hai đường tiệm cận? 2
x  m   1 x m  2 TOANMATH.com Trang 4 Strong Team Toán VD – VDC TOANMATH.com m  1  m  1 m  2  A. m . B.  m  2  . C.  . D.  .  m  2  m  3  m  3  x m  2
Câu 23: Cho hàm số y f x 
có đồ thị C . Gọi S là tập chứa tất cả các giá trị n guyên 2 x  3x  2
của tham số m để đồ thị C có đúng một tiệm cận đứng và một đường tiệm cận ngang. Số phần tử của
tập S là: A. 4 . B. 1. C. 3. D. 2 . 2
mx  2x m 1  3 x
Câu 24: Cho hàm số y
có đồ thị C . Gọi S là tập chứa tất cả các giá trị x  2
thực của tham số m để đồ thị C có đúng hai đường tiệm cận. Tổng giá trị tất cả các phần tử của S bằng? 31 5 86 A. . B. 25 . C. . D. . 7 9 5 x 1
Câu 25: Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  có đúng bốn 2
4x  2x m x 1
đường tiệm cận.  7   7 
A. m   ;6 \   2  .
B. m   ;6 . 3     3     7   7 
C. m   ;6 \     2 .
D. m   ;6 \    2 .  3  3   
Câu 26: Cho hàm số y f x có bảng biến thiên như hình vẽ bên. Hỏi đồ thị của hàm số 1 y
có bao nhiêu đường tiệm cận?
2 f x  3 A. 1. B. 3. C. 2. D. 0 .
Câu 27: Cho hàm số y f x có bảng biến thiên như hình dưới đây:
Gọi tập S là tập chứa tất cả các giá trị nguyên của tham số m 10
 ;10 để đồ thị hàm số x  2 y
có đúng hai đường tiệm cận đứng. Số phần tử của tập S là: 2
f x  mf x TOANMATH.com Trang 5 Strong Team Toán VD – VDC TOANMATH.com A. 9. B. 12. C. 13. D. 8.
Câu 28: Cho hàm số y f x có đồ thị như hình dưới đây: 2 x  3x
Gọi tập S là tập chứa tất cả các giá trị tham số m để đồ thị hàm số y  có đúng ba
f x  f
 2x m  4
đường tiệm cận đứng. Khẳng định nào sau đây là đúng: A.  ;3    S . B.  ;2    S . C. S   .
D. 6;8  S .
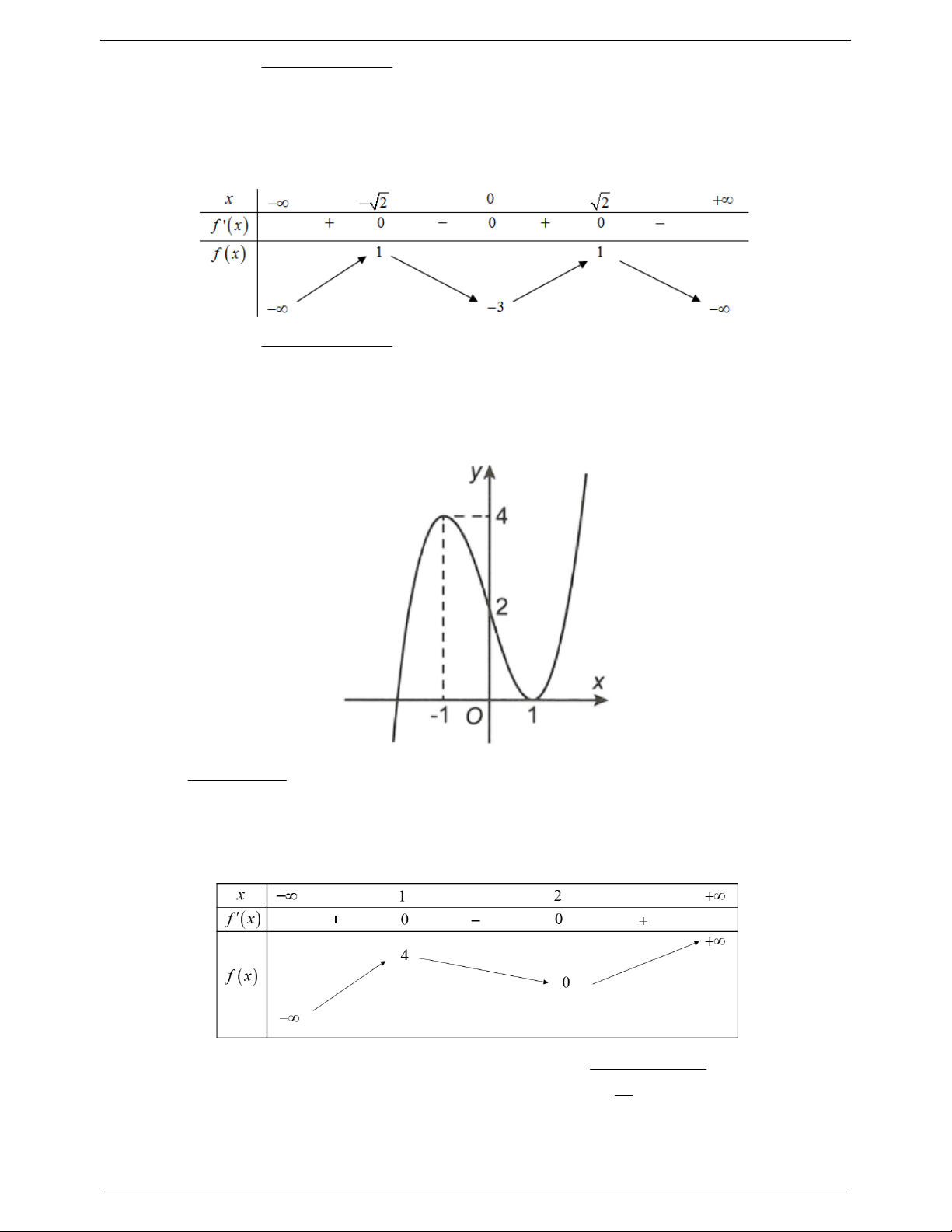
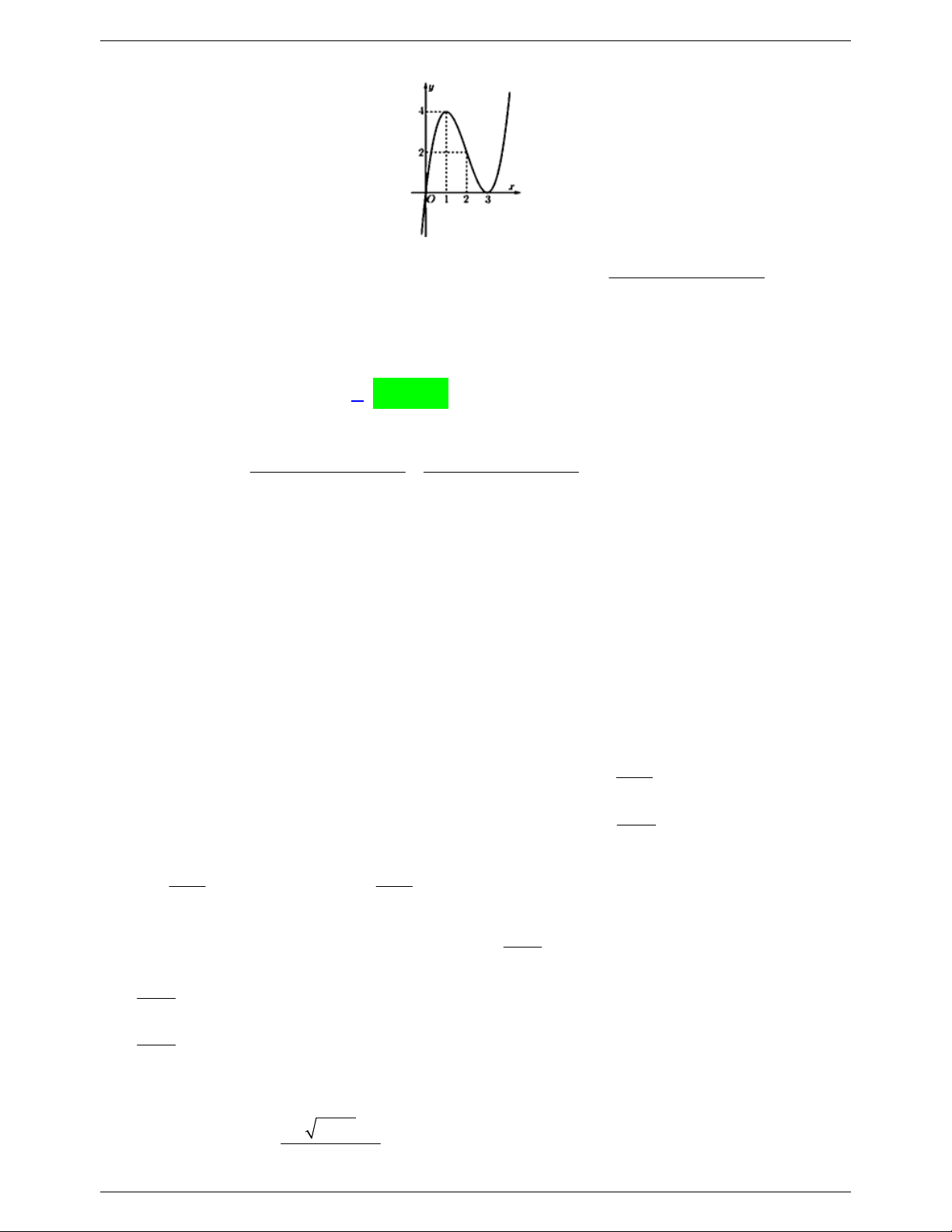
Câu 29: Cho hàm số bậc ba 3 2
f (x)  ax bx cx d có đồ thị như hình vẽ. Với giá trị nào của m thì m x hàm số ( g x)  có 5 tiệm cận đứng? 2
f (x)  2 f (x) A. m  2 . B. m  2 . C. m  2 . D. m  2 .
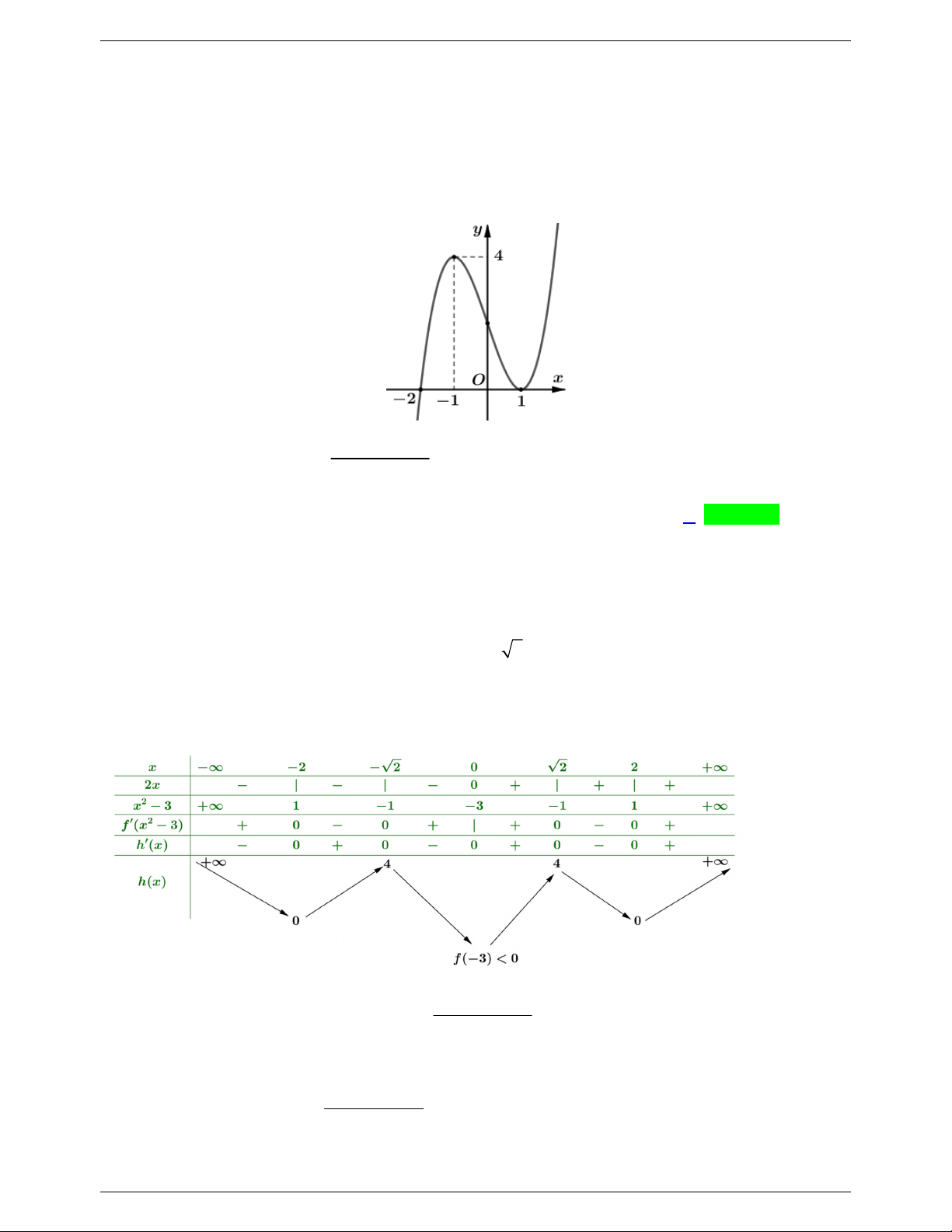
Câu 30: Cho hàm số bậc ba 3 2
f (x)  ax bx cx d có đồ thị như hình vẽ. có bao nhiêu giá trị của m 2 2 2
(x  2mx m m 1) x  3x
để hàm số g(x)  có 3 tiệm cận đứng? 2
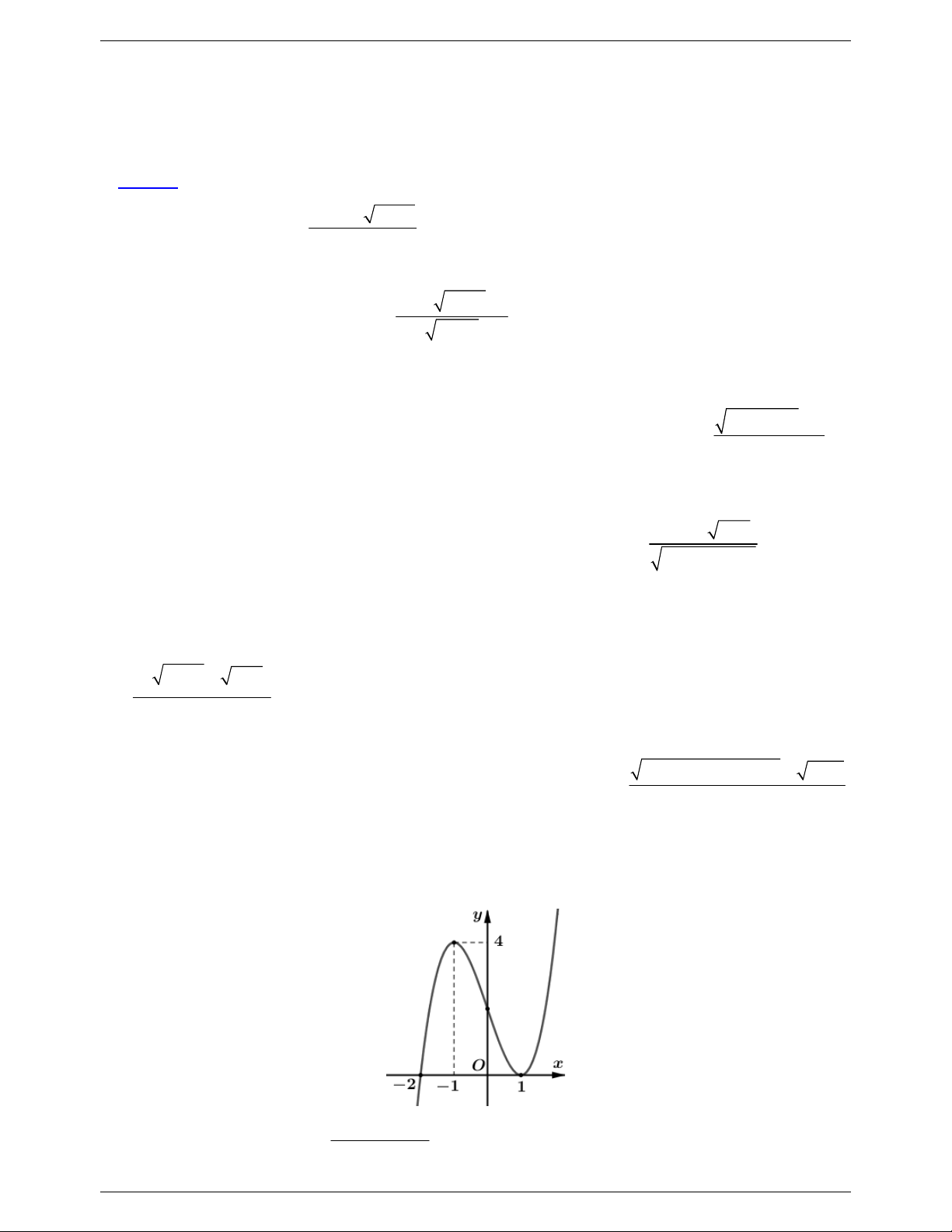
(x-4)[f (x)  4 f (x)] y 4 1  O 2 3 x A. 1 . B. 2 . C. 3. D. 4 x m  3 
Câu 31: Cho hàm số y m   
 có đồ thị C. Giả sử M x ; y là 1 điểm bất kỳ thuộc M M  2x  3  2 
C. Gọi ,A B lần lượt là khoảng cách từ M tới các đường tiệm cận ngang và tiệm cận đứng của C.
Biết diện tích MAB bằng 1. Khẳng định nào sau đây là đúng? 5 11  5 11  5 11 5 11
A. m   ; .
B. m   ; . C. m ; .
D. m  ; . 2 2   2 2   2 2  2 2  TOANMATH.com Trang 6 Strong Team Toán VD – VDC TOANMATH.com 2x  2
Câu 32: Cho hàm số y
có đồ thị C. Giả sử M x ; y là điểm thuộc C thỏa mãn tổng M M x 1
khoảng cách từ M tới trục hoành và đường tiệm cận đứng của C đạt giá trị nhỏ nhất. Giá trị của
x y bằng: M M A. 2. B. 2.  C. 1. D. 1.  2mx + 3
Câu 33: Cho hàm số y =
có đồ thị (C ) và I là giao điểm của hai đường tiệm cận của (C ) x - m
.Gọi S là tập hợp tất cả các giá trị của tham số m sao cho tiếp tuyến tại điểm M trên đồ thị (C ) cắt hai
đường tiệm cận tại hai điểm ,
A B và tam giác IAB có diện tích bằng 64 .Tổng các phần tử của tập hợp S là: A. 58 . B. 2 58 . C. 2 - 58 . D. 0 . 2x - 1
Câu 34: Cho hàm số y =
có đồ thị (C ) và I là giao điểm của hai đường tiệm cận. Giả sử x + 1
M (x ;y là điểm trên đồ thị (C ) có hoành độ dương sao cho tiếp tuyến tại M với (C ) cắt tiệm cận 0 0 )
đứng và tiệm cận ngang lần lượt tại hai điểm , A B thỏa mãn 2 2
IA + IB = 40 . Giá trị của biểu thức 2 2
P = x + y + x y bằng: 0 0 0 0 A. 8 . B. 3 . C. 5. D. 7 . x  2
Câu 35: Cho hàm số y
có đồ thị là C . Gọi I là giao điểm hai đường tiệm cận và M x ; y 0 0  x 1
là điểm nằm trên C với x  0 . Biết tiếp tuyến của C tại điểm M cắt tiệm cận đứng và tiệm cận 0
ngang lần lượt tại hai điểm P và Q sao cho bán kính đường tròn nội tiếp tam giác IPQ lớn nhất. Tính
tổng x y . 0 0
A. x y  0 .
B. x y  2  2 3 . C. x y  2 .
D. x y  2 3 . 0 0 0 0 0 0 0 0 2x 1
Câu 36: Cho hàm số y
có đồ thị là C . Gọi I là giao điểm hai đường tiệm cận và M là điểm 2x  2
nằm trên C có hoành độ lớn hơn 1. Tiếp tuyến của C tại điểm M cắt tiệm cận đứng và tiệm cận
ngang lần lượt tại hai điểm A và B . Hoành độ của điểm M thuộc khoảng nào sau đây để P IA IB
đạt giá trị nhỏ nhất? A.  4;   1 . B.  ;  4   . C. 4; . D. 1;4 . x  2
Câu 37: Cho hàm số y
có đồ thị C . Gọi M x ; y là một điểm thuộc C sao cho tổng 0 0  3  x
khoảng cách từ M đến hai đường tiệm cận của C là nhỏ nhất. Tính 2x y biết y  0 . 0 0 0
A. 2x y  4 .
B. 2x y  2 .
C. 2x y  6 .
D. 2x y 10 . 0 0 0 0 0 0 0 0 x 1
Câu 38: Cho hàm số y
có đồ thị là C . Gọi I là giao điểm của hai đường tiệm cận và x  3
M x ; y là một điểm thuộc C . Phương trình tiếp tuyến của C tại M cắt tiệm cận đứng và tiệm 0 0 
cận ngang của C lần lượt tại hai điểm A , B sao cho 2 2
IA IB  32 . Tìm tọa độ điểm M biết y  0 . 0 TOANMATH.com Trang 7 Strong Team Toán VD – VDC TOANMATH.com  1   1  A.  5;   3 . B. 2;  . C. 3;  . D.  1;    1 .  5   3  2x 1
Câu 39: Cho hàm số y
có đồ thị C . Có bao nhiêu điểm M thuộc C sao cho tổng khoảng x 1
cách từ M đến hai đường tiệm gấp 2 lần tích khoảng cách từ M đến hai đường tiệm cận của C ? A. 0 . B. 1. C. 4 . D. 2. x 1
Câu 40: Cho hàm số y
có đồ thị C . Gọi I là giao điểm hai đường tiệm cận của C . Có bao x  2 1
nhiêu điểm trên C có hoành độ âm sao cho tam giác OMI có diện tích bằng biết O là gốc tọa độ? 2 A. 0 . B. 1. C. 4 . D. 2. II. BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 B A A A D D A B D B 11 12 13 14 15 16 17 18 19 20 C C C A C B D D D A 21 22 23 24 25 26 27 28 29 30 B C C D B C B D D B 31 32 33 34 35 36 37 38 39 40 A D D D A D D C C B
III. LỜI GIẢI CHI TIẾT
3x 1 2x 1
Câu 1: Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 x x A. 1. B. 2 . C. 3. D. 0 . Lời giải  1 
Tập xác định của hàm số là:  ,   \   0;  1  2  3 1 2 1    2 2
3x 1 2x 1 lim  lim  lim x x x x y  0 . 2 x x x x x  1 1 x
Đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số.
3x 1 2x 1
Ta lại có: lim y  lim     2 x 1  x 1  x x
3x 1 2x 1 lim y  lim     2 x 1  x 1  x x
Đường thẳng x  1 là tiệm cận đứng của đồ thị hàm số.
3x 1 2x 1 lim y  lim  2    2 x0 x0 x x TOANMATH.com Trang 8 Strong Team Toán VD – VDC TOANMATH.com
Đường thẳng x  0 không là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận. 2
mx x  3 1
Câu 2: Tìm m để đồ thị hàm số y
có 2 đường tiệm cận đứng và 2 đường tiệm 2 x x
cận ngang tạo thành hình chữ nhật có diện tích bằng 2 . A. m  1. B. m  0 . C. m  2 . D. m 1. Lời giải
Tập xác định: D   ;    1 0;  2 3 1 m  1   2 Ta có lim  lim x x y  1 m x x 2 1  1  x 2 3 1 m  1   2 lim  lim x x ym 1 x x 2 1 1  x
Suy ra để đồ thị hàm số có 2 đường tiệm cận ngang thì m 1  1 m m  0 2
mx x  3 1 lim y  lim   x 0 x 0   2 x x 2
mx x  3 1  khi m 1 lim y  lim    x 1 x 1   2  khi m 1 x x
Vậy khi m  0, m  1 thì đồ thị hàm số có 2 đường tiệm cận ngang là y m  1; y  1  m và
2 đường tiệm cận đứng là x  0; x  1. Để 2 đường tiệm cận đứng và 2 đường tiệm cận ngang
tạo thành hình chữ nhật có diện tích bằng 2 thì 1.2 m  2  m  1 
Đối chiếu điều kiện m  1.
x 4x m  2
Câu 3: Có bao nhiêu giá trị m nguyên thuộc khoảng  10
 ;10 để đồ thị hàm số y  có x  2
đúng ba đường tiệm cận? A. 17 . B. 11. C. 0 . D. 18 . Lời giải
x4x m  0 Điều kiện:  . x  2  m 2   4    m 2 x x 4   +) Ta có lim y lim     2  và lim  lim x x y  2 . x x 2 x x 2 1 1 x x TOANMATH.com Trang 9 Strong Team Toán VD – VDC TOANMATH.com Suy ra, m
  , đồ thị hàm số luôn có 2 đường tiệm cận ngang là y  2 .
x x m 2 4  2 4x mx  2 +) Mà y  
, đặt g x 2
 4x mx  2 . x  2
x  2 x4xm 2
x 4x m 1
Yêu cầu bài toán  đồ thị hàm số y
có duy nhất 1 đường tiệm cận đứng là đường thẳng x  2 2
 4.2  m  0 m  8 x  2      m 9  ; 8  ;...;6;  8 . g  2  0 m  7 2020  x 1
Câu 4: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y  có đúng hai 2
x mx  2m tiệm cận đứng? A. 1. B. 2. C. 3. D. 4. Lời giải
Đồ thị hàm số có đúng hai tiệm cận đứng khi và chỉ khi phương trình 2
x mx  2m  0   * có 2 nghiệm
phân biệt lớn hơn hoặc bằng 1. 2 x Ta có 2
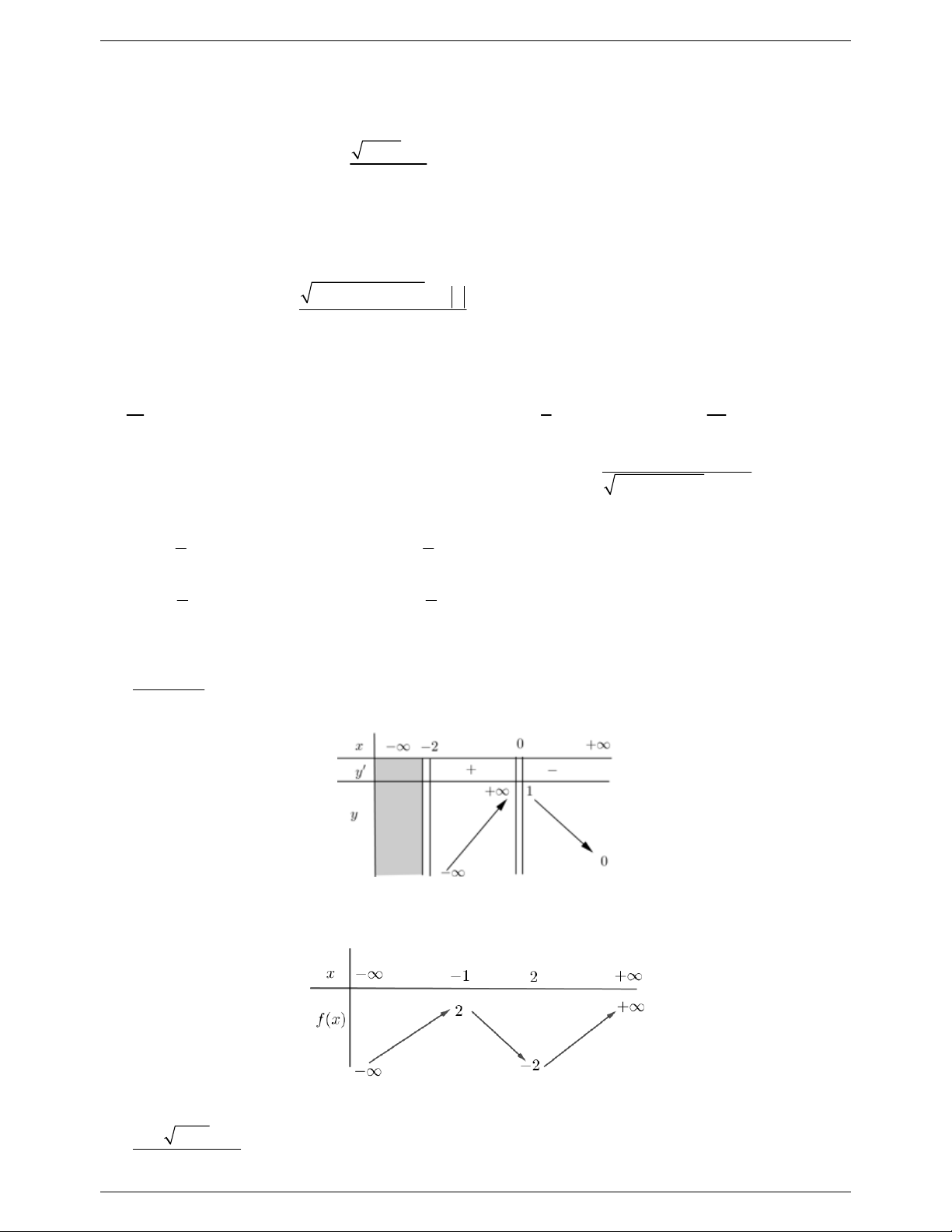
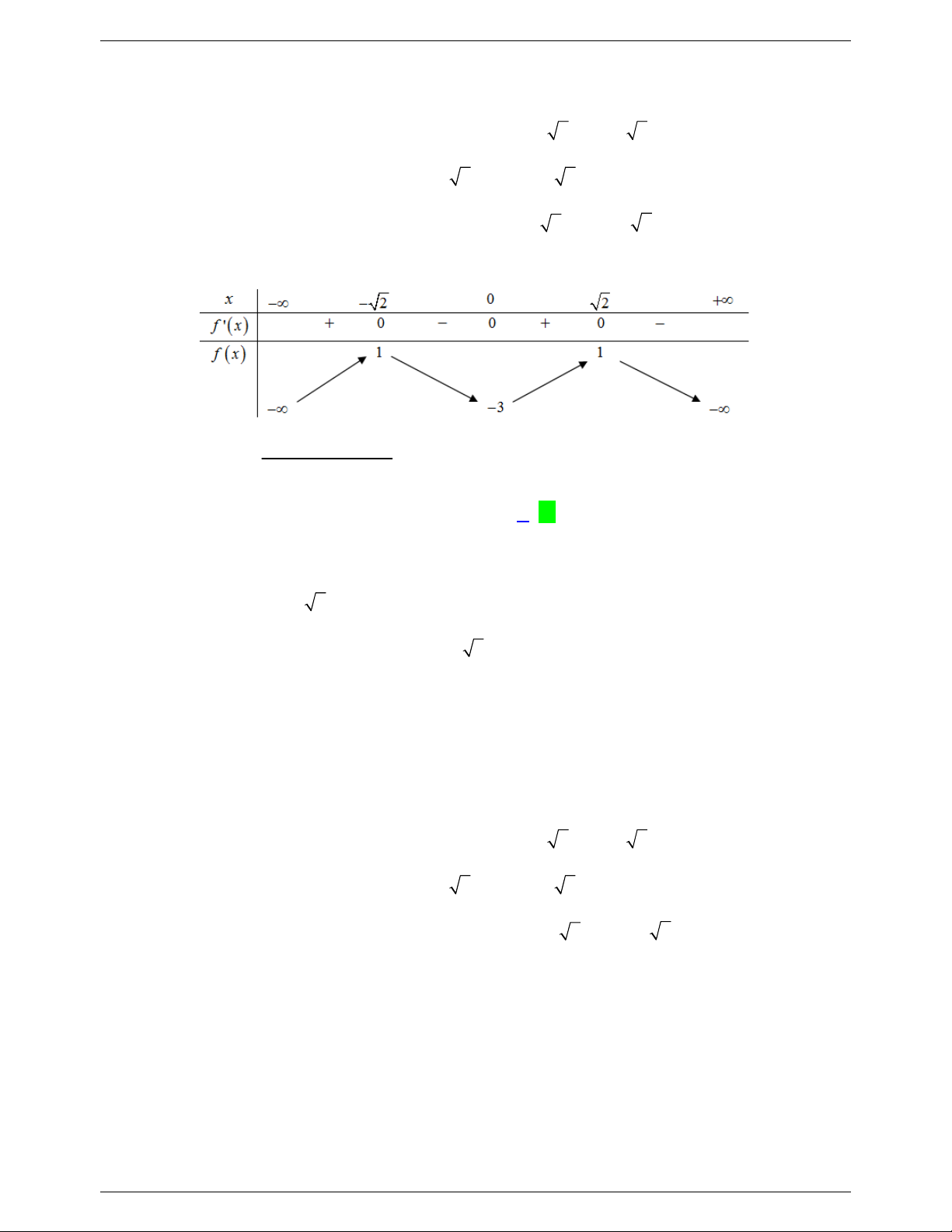
x mx  2m  0   m . x  2 2 x 2 x  4xx  4
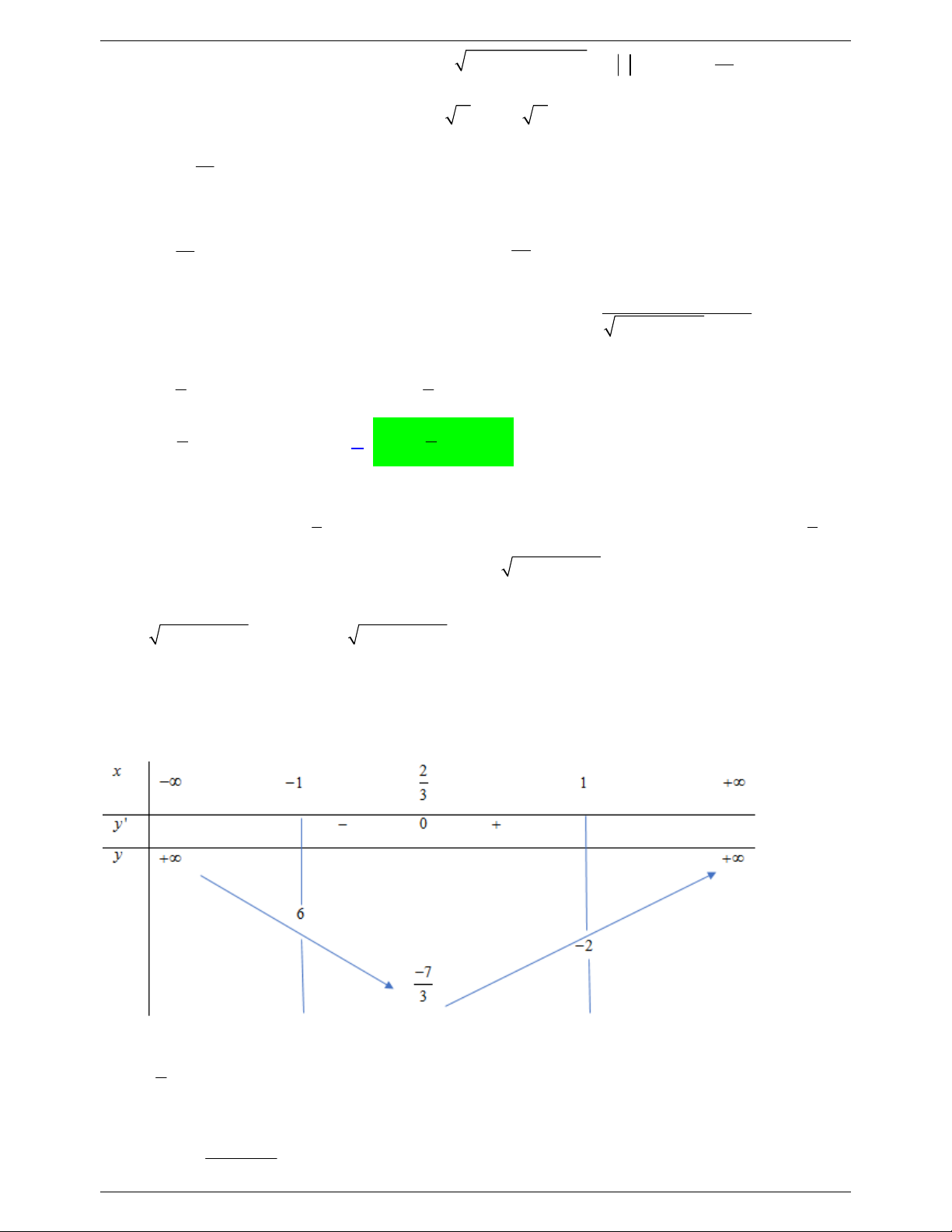
Xét hàm số y f x  với x  1
 ;. Có y   0  . x  2   x  2 x  0 2 x 1 0 + ∞ y' 0 + + ∞ 1 y 0
Dựa vào bảng biến thiên ta thấy phương trình  
* có 2 nghiệm phân biệt biệt lớn hơn hoặc bằng 1 khi
và chỉ khi m0;  1  m 1.
Câu 5: Gọi m, n lần lượt là số đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
x  2x 3  x 1 y
. Khi đó m n bằng: 2 x  4 A. 4 . B. 3. C. 2 . D. 1. Lời giải x  3 Điều kiện:  x  2 + Tiệm cận ngang: TOANMATH.com Trang 10 Strong Team Toán VD – VDC TOANMATH.com  3 1 1   3 1 1      2    
x  2x 3  x 1 x x 1  x 1  2 2 x x x   2 2 x x x     (do x  3 ) 2 x  4 2  4   4  x 1   2 x 1    x   x  3 1 1 1   2 2 x x x  4 1 x 3 1 1 1   2 2  lim  lim x x x y  1 x x 4 1 x
Suy ra đồ thị hàm số có 1 tiệm cận ngang y  1 + Tiệm cận đứng:
Điều kiện cần: Xét phương trình 2
x  4  0  x  2 Điều kiện đủ: Đặt 2
f (x)  x( x  3  x 1)
Xét x  2 , ta có f 2  0 nên ta sẽ đi tìm bậc của  x  2 của f x 2 2       2 x x  2 2 ( x 3 x 1)( x 3 x 1)
x  3  x 1  
 (x  2)h(x) 2
x  3  x 1 g(x)
(x  2)h(x) h(x) Suy ra y  
, suy ra x  2 không phải là tiệm cận đứng
(x  2)(x  2) x  2 Xét x  2  , ta có f  2
  không tồn tại hay x  2
 không phải là tiệm cận đứng.
Vậy m  1, n  0  m n 1. 2
x  2019x  2020  4038
Câu 6: Có bao nhiêu giá trị nguyên của tham để m đồ thị hàm số y x m có tiệm cận đứng? A. 1. B. 2 . C. 2019 . D. 2020 . Lời giải 2
x  2019x  2020 xác định khi 2
x  2019x  2020  0  1  x  2020
Đặt f x 2
 x  2019x  2020  4038
Xét x m  0  x m .
Đồ thị nếu có tiệm cận đứng chỉ có thể là x m , khi đó điều kiện là:  1   x  2019 m    1  ;2019   1     f  m 2  0
 m  2019m  2020  24 7  * TOANMATH.com Trang 11 Strong Team Toán VD – VDC TOANMATH.com m  1 Ta có * 2
 m  2019m  2018  0   2 m  2018 Từ  
1 ,2  m 1  ;2020\1;201  9
Vậy có 2022  2  2020 số nguyên m thỏa mãn bài toán.
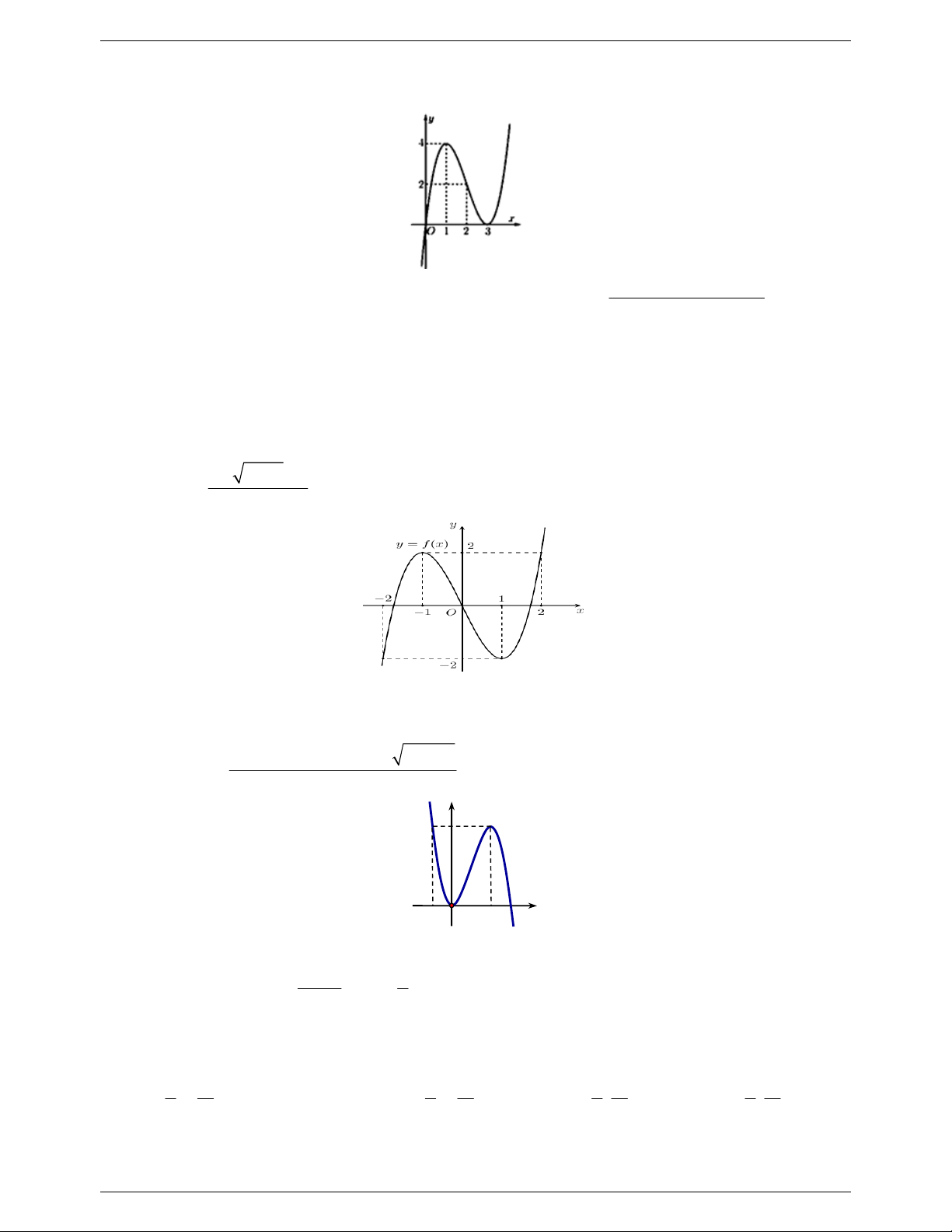
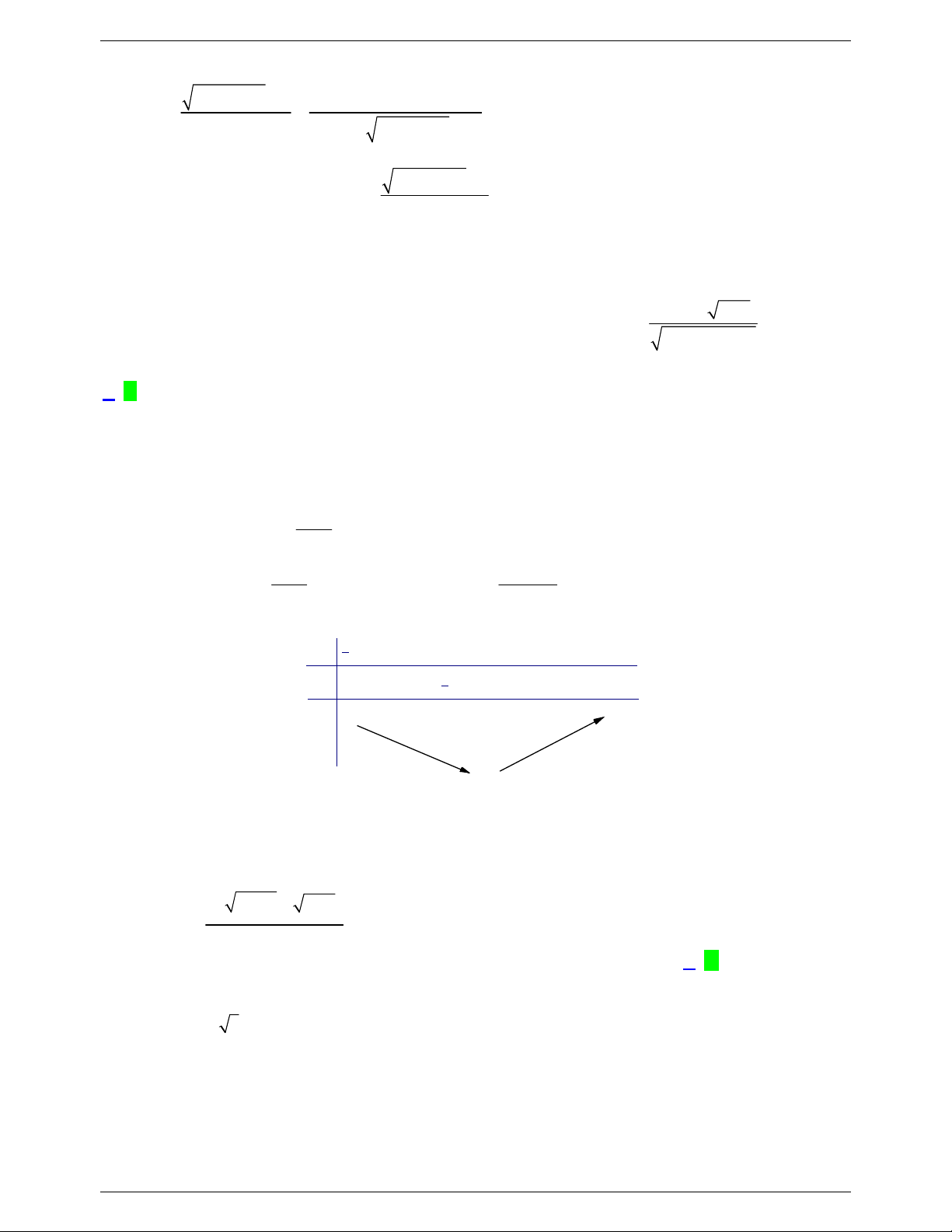
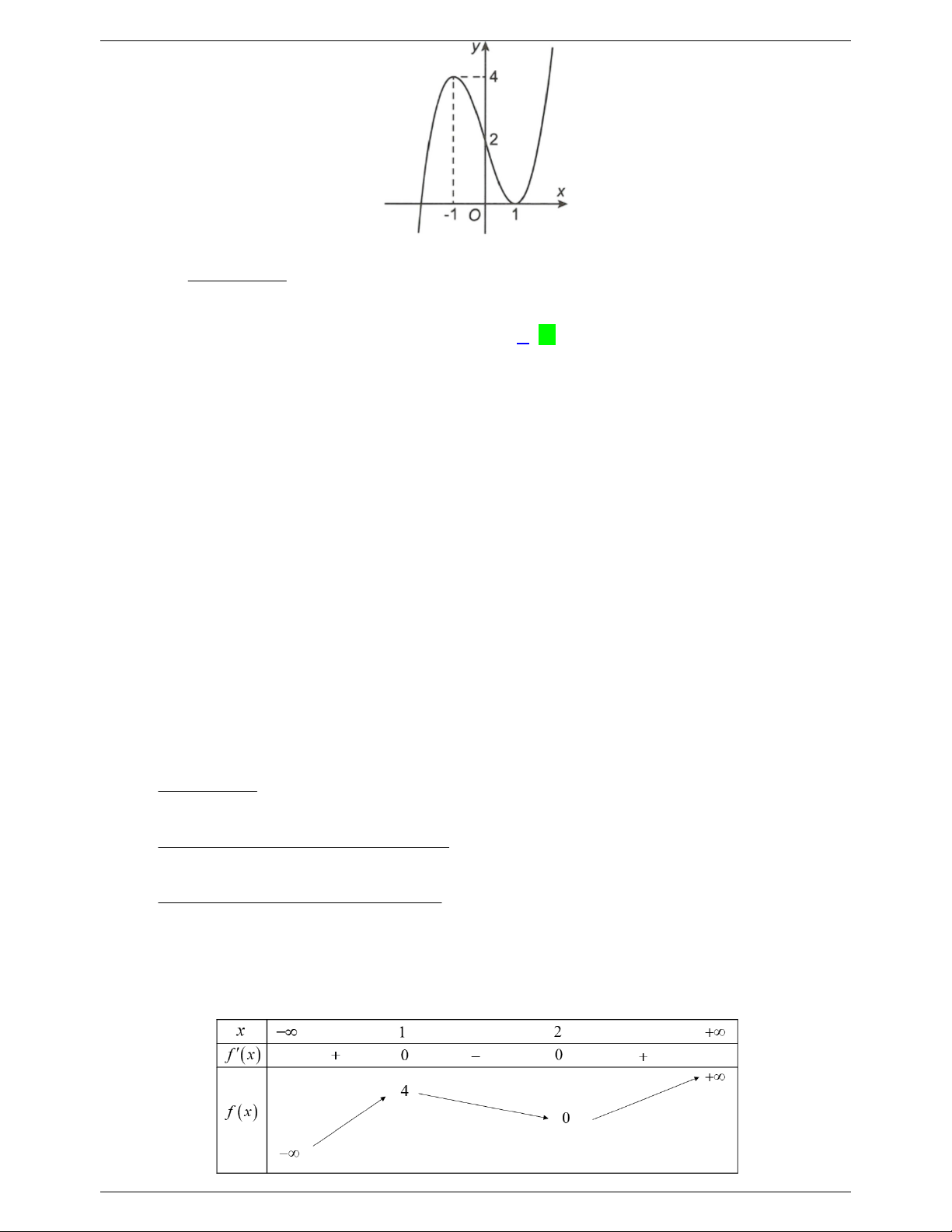
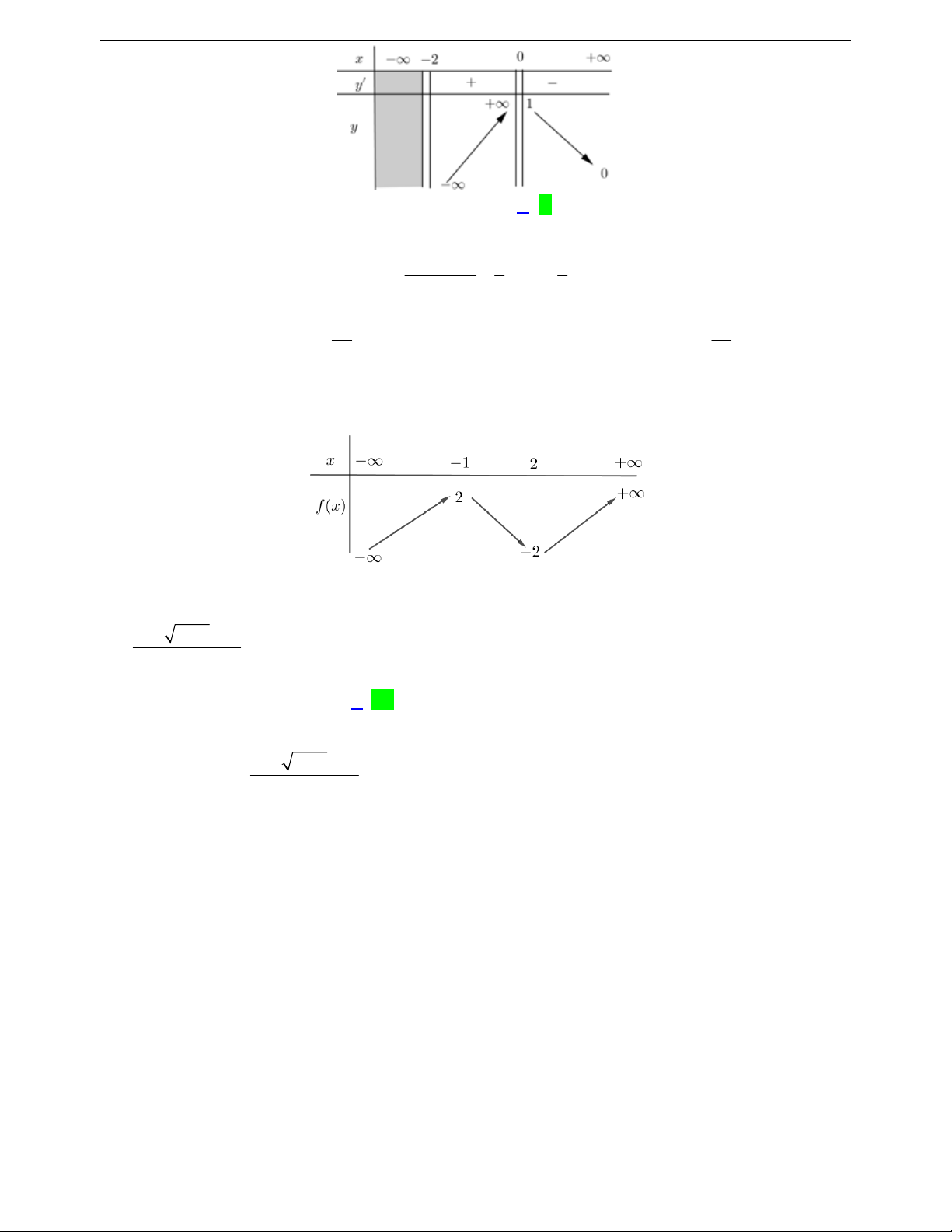
Câu 7: Cho hàm số    3 2 y
f x ax bx cx d a  0 có đồ thị như hình vẽ bên dưới: 1
Tìm m để đồ thị hàm số g x 
có đúng 6 tiệm cận đứng? f  2 x  3  m
A. m  0 . B. 2
  m  0 . C. 3   m  1  .
D. 0  m  4 . Lời giải
Xét hàm số h x  f  2
x  3  h x  x f  2 2 . x  3 x  0 x  0 x  0  
hx  0     -  
x     x   f x  3 2 3 1 2 2  0   2 x 3 1 x  2   Ta có bảng biến thiên 1
Từ bảng biến thiên ta có đồ thị hàm số g x 
có đúng 6 tiệm cận đứng  hx  m có 6 f  2
x  3  m
nghiệm phân biệt  0  m  4 . 2018
Câu 8: Cho hàm số g x  với   4 3 2
h x mx nx px qx m,n, p,q. Hàm số hx 2  m m
y h x có đồ thị như hình vẽ bên dưới: TOANMATH.com Trang 12 Strong Team Toán VD – VDC TOANMATH.com
Tìm các giá trị m nguyên để số tiệm cận đứng của đồ thị hàm số y g x là 2 . A. 11. B. 10 . C. 9. D. 20 . Lời giải x  1  5
Ta có h x 3 2
 4mx  3nx  2px q . Từ đồ thị ta có hx  0  x  và m  0 .  4 x  3   5 
Suy ra h x  4mx   1 x    x  3 3 2
 4mx 13mx  2mx 15m .  4  13 Suy ra hx 4 3 2  mx
mx mx 15mx C . Từ đề bài ta có C  0 . 3 13 Vậy hx 4 3 2  mx
mx mx 15mx . 3 13 Xét h x 2 4 3 2
m m  0  m x
x x 15x 1. 3 x  1  13  5
Xét hàm số f x 4 3 2  x
x x 15x 1  f  x 3 2
 4x 13x  2x 15  0  x  . 3  4 x  3  Bảng biến thiên
Để đồ thị hàm số g x có 2 đường tiệm cận đứng  phương trình hx 2
m m  0 có 2 nghiệm phân 13 biệt  phương trình 4 3 2 m x
x x 15x 1 có 2 nghiệm phân biệt. 3 TOANMATH.com Trang 13 Strong Team Toán VD – VDC TOANMATH.com 35
Từ bảng biến thiên kết hợp thêm điều kiện m  0 ta có   m  1  . 3
Do m nguyên nên m 1  1;10;...; 
2 . Vậy có 10 số nguyên m thỏa mãn yêu cầu bài toán.
Câu 9: Cho hàm số y f x liên tục trên  , có đồ thị như hình vẽ: 6
Tìm số tiệm cận đứng của đồ thị hàm số y hx  . 2 f x  4 A. 2 . B. 4 . C. 6 . D. 5. Lời giải 6
Xét hàm số y hx  . 2 f x  4 x  2  
x a 3;
f x  2 2 f x 4 0     
x b ;  2   .  f   x 2   
x c 1  ;  1  x d   1;3 6 6
Có lim hx  lim
  ; lim hx  lim   ;   2 x     x     2 2 2 f x  4 xa xa f x  4 6 6 hx 6 lim  lim
  ; lim hx  lim
  ; lim hx  lim   .   2 x bx bf x  4   2 xc xc f x  4   2 xd xd f x  4
Suy ra đồ thị hàm số y hx có tất cả 5 tiệm cận đứng x  2; x a; x b; x c; x d .
Câu 10: Cho hàm số y f x liên tục trên   ;1
 và 1;, có bảng biến thiên như hình: 8
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y hx  . 2
f x  6 f x  5 A. 3. B. 4 . C. 5. D. 6 . Lời giải TOANMATH.com Trang 14 Strong Team Toán VD – VDC TOANMATH.com 8
Xét hàm số y hx  . 2
f x  6 f x  5 a/ Tìm tiệm cận đứng:
f x  5 2
f x  6 f x  5  0   .  f   x 1
Có f x  5  x  0 .
x a 0;  f x 1  1   . x b  1; hx 8 lim  lim   ;   2 x0 x0
f x  6 f x  5 hx 8 lim  lim   ;   2 xa xa
f x  6 f x  5 hx 8 lim  lim     2 x bx b
f x  6 f x  5
x  0; x a; x b là các tiệm cận đứng của đồ thị hàm số y hx . b/ Tìm tiệm cận ngang: hx 8 lim  lim   ; 2 x
x f x  6 f x  5 hx 8 lim  lim  2
  y  2 là tiệm cận ngang của đồ thị hàm số y hx . 2 x
x f x  6 f x  5
Vậy đồ thị hàm số y hx có tất cả 4 tiệm cận.
Câu 11: Cho f x là hàm bậc 4 và có bảng biến thiên như hình vẽ sau: 2 x  2
Đồ thị hàm số g x 
có mấy đường tiệm cận đứng? 2
f x  3 f x  4 A. 2. B. 3. C. 4 . D. 5. Lời giải
Dễ dàng chứng minh được nếu x x với x   2 là nghiệm đơn của mẫu hoặc x x là nghiệm kép 0 0 0
của mẫu thì đường thẳng x x là đường TCĐ của đồ thị hàm số g x . 0 TOANMATH.com Trang 15 Strong Team Toán VD – VDC TOANMATH.com
f x 1 Ta có 2
f x  3 f x  4  0    f   x  4 
Dựa vào BBT ta được PT f x 1 có hai nghiệm kép là x   2 và x  2
và PT f x  4
 có hai nghiệm đơn là x a   2 và x b  2 .
Vậy đồ thị hàm số g x có 4 đường TCĐ là x a, x b, x  2 và x   2 .
Câu 12: Cho f x là hàm bậc 4 và có bảng biến thiên như hình vẽ sau: 4 2 x  2x
Đồ thị hàm số g x 
có mấy đường tiệm cận? 2
f x  2 f x  3 A. 3. B. 4. C. 5. D. 6 . Lời giải x  0 Ta có 4 2
x  2x  0  
, trong đó x  0 là nghiệm kép. x   2
Dễ dàng chứng minh được nếu x x với x  0;  2 là nghiệm đơn của mẫu hoặc x x là nghiệm 0   0 0
kép khác 0 của mẫu thì đường thẳng x x là đường TCĐ của đồ thị hàm số g x . Nếu x  0 là nghiệm 0
kép bội hai của mẫu thì đường thẳng x  0 không là TCĐ của đồ thị hàm số g x .
f x 1 Ta có 2
f x  2 f x  3  0    f   x  3 
Dựa vào BBT ta được PT f x 1 có hai nghiệm kép là x   2 và x  2
và PT f x  3
 có hai nghiệm đơn là x a   2 và x b  2 và một nghiệm kép x  0 .
Khi đó đồ thị hàm số g x có 4 đường TCĐ là x a, x b, x  2 và x   2 .
Mặt khác, bậc của tử là bậc 4 và bậc của mẫu là bậc 8 nên dễ tính được lim g x  0 . Khi đó đồ thị hàm x
số g x có đường TCN là y  0 .
Vậy đồ thị hàm số g x có 5 đường tiệm cận.
Câu 13: Cho hàm số   3 2
f x ax bx cx d có đồ thị như sau: TOANMATH.com Trang 16 Strong Team Toán VD – VDC TOANMATH.com 2 x x
Đặt g x 
. Đồ thị hàm số y g x có bao nhiêu tiệm cận đứng? 2
f x  f xA. 4 . B. 2 . C. 5. D. 3. Lời giải f   x  0 Điều kiện: 2
f x  f x  0    f   x  1
f x  0 Xét 2
f x  f x  0    f   x 1
Dựa vào đồ thị ta có f x  0 có hai nghiệm phân biệt x x  0 và x 1(nghiệm kép). 1
x x x x  1  2  1 2  
f x 1  x x 0  x 1 3  3 
x x x 1  4  4 
Vậy f x  f x  f x  f
  x 1  a
x x x  2 2 2 1 x x x x x x . 1  2   3   4  Khi đó ta có: 2   x x g x  2
f x  f xx x   1 
a x x  x  2 2 1 x x x x x x 1  2   3   4  x  2
a x x x 1 x x x x x x 1    2   3   4 
Vậy đồ thị hàm số có 5 tiệm cận đứng.
Câu 14: Cho hàm số y f x xác định và liên tục trên  và có bảng biến thiên như sau: TOANMATH.com Trang 17 Strong Team Toán VD – VDC TOANMATH.com 14
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số: g x  là: 3  xf  3x 12    3  A. 2 . B. 4 . C. 1. D. 3. Lời giải 3 x 3 3  x   x  Đặt u
 3x, ta có lim   3x  , lim   3x   . 3 x  3 x   3  3 x 3 x
Mặt khác ta xét: y   3x có 2
y  x  3  0, x
  nên với mọi u  thì phương trình  3x u 3 3
có duy nhất một nghiệm x . 3 3  x   x
Xét f   3x 12  0  f   3x 12 .  3   3 
Từ bảng biến thiên ta thấy phương trình có duy nhất một nghiệm nên đồ thị hàm số g x 14 
có một tiệm cận đứng. 3  xf  3x 12    3  Ta có:       g x 14 14 lim lim     lim    0 3 x x     u x  f  u 12  f 3x 12         3         g x 14 14 lim lim     lim    0 3 x x     u x  f  u 12  f 3x 12         3   14
Vậy đồ thị hàm số g x 
có duy nhất một tiệm cận ngang. 3  xf  3x 12    3 
Vậy đồ thị hàm số có một tiệm cận đứng và một tiệm cận ngang.
Câu 15: Cho hàm số f x có bảng biến thiên dưới đây: 2020
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  .
2020 f x  2021 TOANMATH.com Trang 18 Strong Team Toán VD – VDC TOANMATH.com A. 1. B. 2 . C. 3 . D. 0 . Lời giải
Từ bảng biến thiên ta có lim f x  lim f x  1 . x x 2020 2020 2020 Do đó lim 
Vậy đồ thị hàm số y  có 1 đường tiệm cận x f x . 2020  2021 4041
2020 f x  2021 2020
ngang là đường thẳng y  . 4041 2021 Ta có f x 
  f x 2021 2020 2021 0  
có hai nghiệm nghiệm vì đường thẳng d : y   cắt 2020 2020 2020
đồ thị hàm số y f x tại hai điểm phân biêt. Suy ra đồ thị hàm số y  có hai tiệm cận
2020 f x  2021 đứng.  2020
tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  là 3 .
2020 f x  2021 x  3
Câu 16: Cho hàm số y
C .Có tất cả bao nhiêu giá trị nguyên thuộc
x  3mx  2m     3 2 2 1 x m khoảng  10
 ;10 của tham số m để đồ thị hàm số có tổng số đường tiệm cận là nhiều nhất? A. 20 . B. 15. C. 16 . D. 18 . Lời giải x  3 x  3 Ta có: lim  0 và lim
 0 nên đồ thị hàm số có 1 3 2
x x  3mx   2 2m   1 x m 3 2
x x  3mx   2 2m   1 x m
đường tiệm cận ngang là y  0.
Do đó C có tổng số đường tiệm cận là nhiều nhất khi C có 3 đường tiệm cận đứng nên phương trình 3 2 x mx   2 3 2m  
1 x m  0 
1 có 3 nghiệm phân biệt x  3. x m Ta có:  
1   x m 2
x  2mx   1  0   g   x 2
x  2mx 1  02
Suy ra m  3 và phương trình (2) có 2 nghiệm phân biệt khác 3  m  3 m  3 m  3    m  1 2    0
 m 1  0        g   m 3 1  0 10  6m  0   5 m   3 Mà nguyên m thuộc khoảng  10
 ;10 nên m 9  ; 8  ; 7  ; 6  5; 4  ; 3  ; 2  ;2;4;5;6;7;8;  9 . x  2
Câu 17: Cho hàm số y
. Tìm điều kiện của tham số m để đồ thị hàm số có 4 3 2
x  3x  (m  2)x m
đường tiệm cận? TOANMATH.com Trang 19 Strong Team Toán VD – VDC TOANMATH.com m  1 m  1 A. m 1. B.  . C. m 1. D.  . m  0 m  0 Lời giải x  2
Gọi C là đồ thị hàm số y  . 3 2
x  3x  (m  2)x m x  2 x  2 Ta có y   3 2
x  3x  (m  2)x m x   1  2
x  2x m 1 2  2 3 x  2 Vì lim  lim x x
 0 nên đồ thị hàm số có 1 đường tiệm cận ngang 3 2
x x  3x  (m  2) x x m  3 m  2 m 1   2 3 x x x là y  0.
Do đó C có 4 đường tiệm cận khi và chỉ khi C có 3 đường tiệm cận đứng   x   2
1 x  2x m  0 có 3 nghiệm phân biệt khác 2 2
x  2x m  0 có 2 nghiệm phân biệt khác 1; 2 .
 '  1 m  0 m  1   m  1 2  1
  2.1 m  0  m  1     m  0. 2 2  2.2  m  0 m  0   x  3
Câu 18: Cho hàm số y
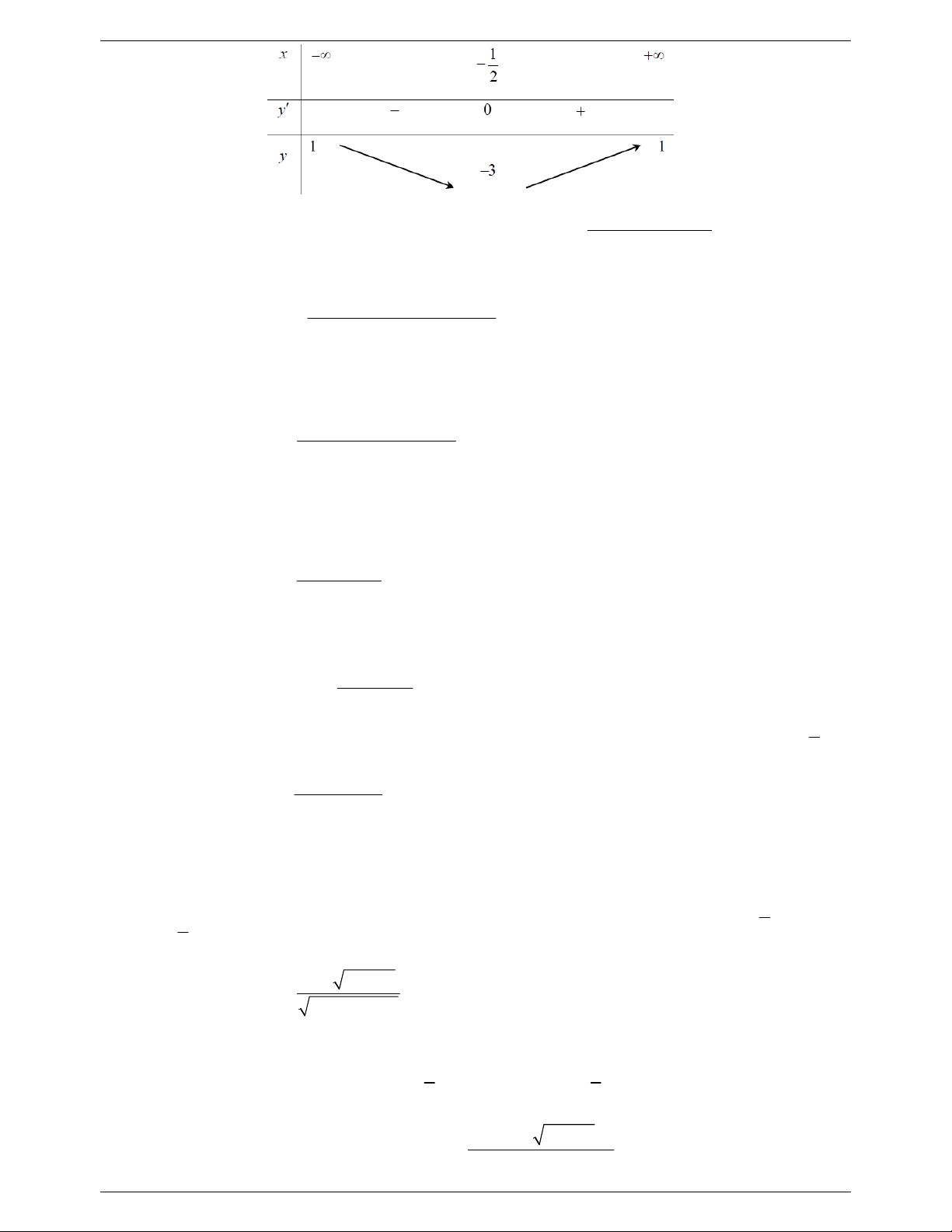
. Tìm số các giá trị của tham số m để đồ thị hàm số có 1 đường 2 x  2mx 1 tiệm cận đứng? A. 0 . B. 1. C. 2 . D. 3. Lời giải x  3
Gọi C là đồ thị hàm số y
. C có 1 đường tiệm cận đứng: 2 x  2mx 1  Phương trình 2
x  2mx 1  0 có nghiệm kép hoặc có hai nghiệm phân biệt (trong đó có một nghiệm bằng 3  ) m  1  2
 '  m 1  0 m 1 m  1    2
 '  m 1  0  
 m  1    5    m      3   2  2 . m  3   1 0  5  3 m     3 3 mx  2
Câu 19: Đồ thị của hàm số y
có hai tiệm cận đứng khi và chỉ khi? 2 x  3x  2 1
A. m  0 và m  2 .
B. m  1 và m  2 . C. m  0 .
D. m  2 và m  . 4 Lời giải
Điều kiện xác định: x  1; x  2 TOANMATH.com Trang 20 Strong Team Toán VD – VDC TOANMATH.com 3 mx  2
Để đồ thị hàm số y
có hai tiệm cận đứng thì x  1 và x  2 không phải là nghiệm của 2 x  3x  2 phương trình 3 mx  2  0 .
Đặt g x 3  mx  2    g   m 2 1  0  m  2  0  Khi đó: YCBT       . g    1 2  0 8  m  2  0 m   4 x 1
Câu 20: Cho hàm số y
có đồ thị là C . Tìm tất cả các giá trị thực của tham số m để đồ 2 x  2mx  4
thị C có đúng 3 đường tiệm cận? m  2  m  2  m  2  m  2   A.  . B.  . C. m  2 . D.  5 .  5 m  2 m    m     2  2 Lời giải Điều kiện xác định: 2
x  2mx  4  0
Do lim y  0 nên đồ thị hàm số luôn có tiệm cận ngang y  0 x
Để đồ thị hàm số có đủ 3 tiệm cận thì g x 2
x  2mx  4 có hai nghiệm phân biệt khác 1  . m  2 2
  m  4  0    m  2         1   2 2m 1    4  0  5 m    2 2 Câu 21: Cho hàm số 12  4x x y
có đồ thị C . Tìm tập S tất cả các giá trị của tham số thực m  2
x  6x  2m
m để C có đúng hai tiệm cận đứng. m   9   9 
A. S  8;9 . B. S  4;  . C. S  4;  .
D. S  0;9.  2  2 Lời giải 0  x  4 ĐKXĐ:  . 2
x  6x  2m  0 Ta có 2
12  4x x  0 x
 nên để C có hai tiệm cận đứng thì phương trình m  2 2
x  6x  2m  0  x  6x  2m  0 * có hai nghiệm phân biệt thuộc 0;  4 . Cách 1. 9
Đế phương trình có 2 nghiệm phân biệt thì   9  2m  0  m  2 TOANMATH.com Trang 21 Strong Team Toán VD – VDC TOANMATH.com
Gọi 2 nghiệm phân biệt của (*) là x x ta có 0  x x  4 . 1 2 1 2 x x  6 Theo định lí Vi-et ta có 1 2 
x .x  2m  1 2 Khi đó x x  0   1 2 x x 0 2m  0  1 2 x x  0   x x  0  1 2  1 2 6  0 m  0       m  4 . Kết
x  4 x  4  0   
x x  4 x x 16  0 2m  24 16  0 2m 8  0 1 2  1 2  1  2     
x  4  x  4  0  
x x 8  0   6  8  0 1 2  1   2  9
hợp nghiệm ta có 4  m  . 2 Cách 2. 2
x  6x  2m  0 2
 2m  x  6x
Xét hàm số f x 2
 x  6x trên đoạn 0;  4
f x  2  x  6
Cho f  x  0  x  3. Bảng biến thiên x 0 3 4 f x  0  f x 9 0 8 9
Phương trình có hai nghiệm phân biệt thuộc 0; 
4  8  2m  9  4  m  2 2
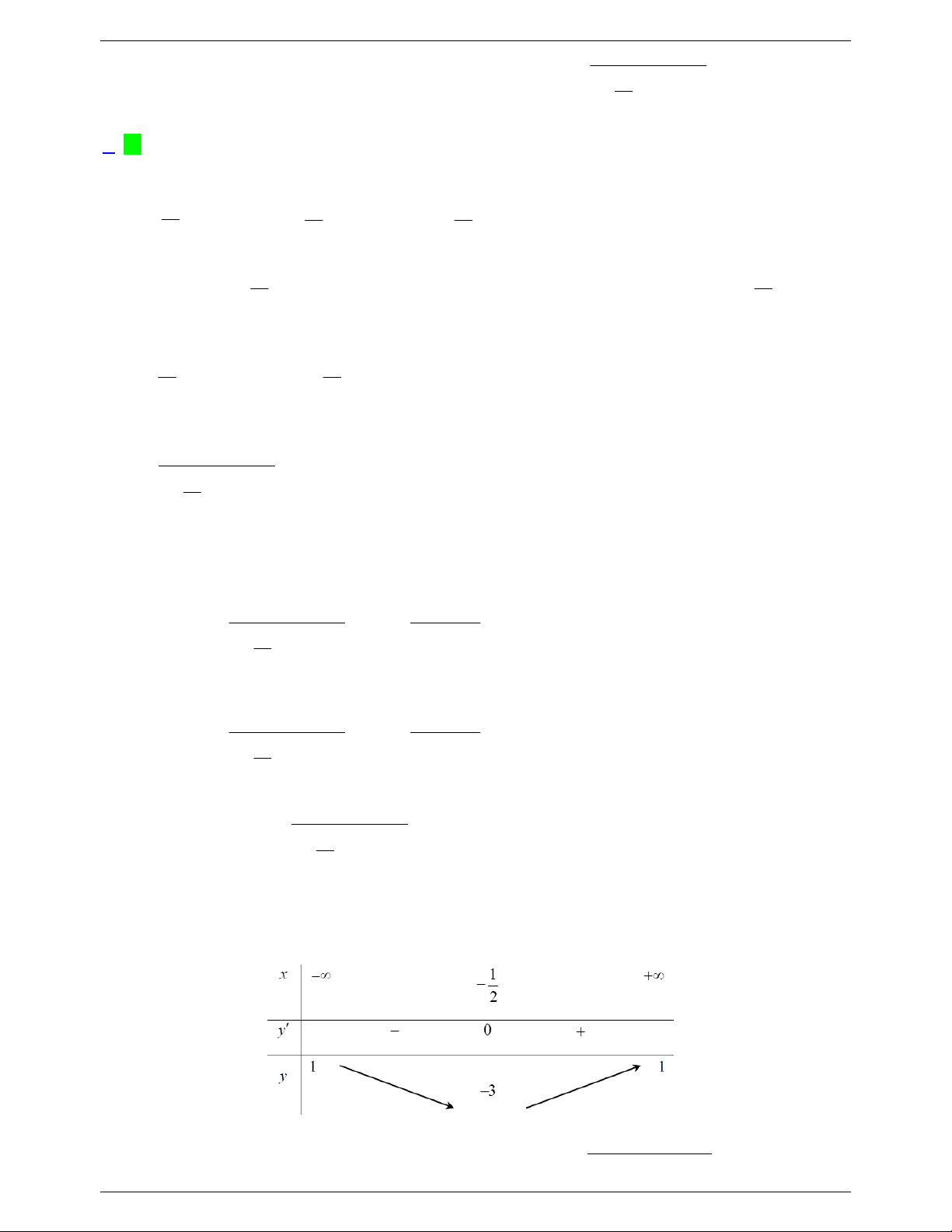
x 1 x  3x
Câu 22: Với giá trị nào của m, đồ thị hàm số y
có đúng hai đường tiệm cận? 2
x  m   1 x m  2 m  1  m  1 m  2 A. m . B.  m  2  . C.  . D.  .  m  2  m  3 m  3  Lời giải x  3   x  0 2
x 1 x  3xy
. Hàm số xác định khi: x 1 . 2
x  m   1 x m  2
x  m 2   2
x 1 x  3xx 1 1 Ta có y    . 2
x  m   1 x m  2 x  
1  x m  2 2
x 1 x  3x  x m  2 2
x 1 x  3x  TOANMATH.com Trang 22 Strong Team Toán VD – VDC TOANMATH.com
lim y  0  y  0 là tiệm cận ngang. x m  2  3  m 1
Hàm số có hai tiệm cận khi có một tiệm cận đứng    .  m 2 0     m  2  x m  2
Câu 23: Cho hàm số y f x 
có đồ thị C . Gọi S là tập chứa tất cả các giá trị nguyên 2 x  3x  2
của tham số m để đồ thị C có đúng một tiệm cận đứng và một đường tiệm cận ngang. Số
phần tử của tập S là A. 4 . B. 1. C. 3. D. 2 . Lời giải    
y f xx m 2 x m 4   2 x  3x  2 x  
1  x  2 x m  4 x m
Điều kiện: x 1 x  2 
Đồ thị hàm số có một tiệm cận ngang y  0 do lim y  0 x
Đồ thị hàm số có một tiệm cận đứng khi và chỉ khi   1   m  4  0  2  m  m  3  m  3 
2  m  4  0     m  2 
mà m  m  2  . 1   m    1   m  2 m  2    2  m   1   m
2 m  4  0  2
mx  2x m 1  3 x
Câu 24: Cho hàm số y
có đồ thị C . Gọi S là tập chứa tất cả các giá trị x  2
thực của tham số m để đồ thị C có đúng hai đường tiệm cận. Tổng giá trị tất cả các phần tử của S bằng 31 5 86 A. . B. 25 . C. . D. . 7 9 5 Lời giải
Xét m  0 thì đồ thị hàm số không có tiệm cận ngang nên tối đa chỉ có một đường TCĐ.
Xét m  0 thì đồ thị hàm số chỉ có duy nhất một tiệm cận ngang y  3 . Xét m  0 , ta có 2
mx  2x m 1  3x 2
mx  2x m 1  3x lim y  lim
m 3 , lim y  lim   m  3 x x x  2 x x x  2 TOANMATH.com Trang 23 Strong Team Toán VD – VDC TOANMATH.com 41
Đồ thị hàm số không có đường tiệm cận đứng thì 2 .2 m
 2.2  m 1  3. 2  0  m  . 5
Đồ thị hàm số có một đường tiệm cận ngang thì m  3   m  3  m  9 . 41 Vậy với m
thì đồ thị hàm số có hai đường tiệm cận ngang và với m  9 thì đồ thị hàm số đường 5
tiệm cận ngang và một đường tiệm cận đứng. 41  86
Nên S   ;9 suy ra tổng các phần tử của tập S bằng .  5  5 x 1
Câu 25: Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  có đúng bốn 2
4x  2x m x 1
đường tiệm cận.  7   7 
A. m   ;6 \   2  .
B. m   ;6 . 3     3     7   7 
C. m   ;6 \     2 .
D. m   ;6 \    2 .  3  3    Lời giải 1 1
Ta có lim y 1và lim y   suy ra đồ thị hàm số có đường hai tiệm cận ngang là y  1 và y   . x x 3 3
Để đồ thị có đúng bốn đường tiệm cận thì phương trình 2
4x  2x m x 1  0 có hai nghiệm phân biệt khác 1. x  1   Ta có 2
4x  2x m x 1  0 2
 4x  2x m x 1   2 3
x  4x 1  m   1
Yêu cầu bài toán tương đương phương trình  
1 có hai nghiệm phân biệt x  1  và x 1. Xét hàm số 2
y  3x  4x 1 với x  1  và x 1. Bảng biến thiên:
Dựa vào bảng biến thiên phương trình 2
3x  4x 1  m với x  1
 và x 1 có hai nghiệm thì  7  m   ;6 \    2 . 3   
Câu 26: Cho hàm số y f x có bảng biến thiên như hình vẽ bên. Hỏi đồ thị của hàm số 1 y
có bao nhiêu đường tiệm cận?
2 f x  3 TOANMATH.com Trang 24 Strong Team Toán VD – VDC TOANMATH.com A. 1. B. 3. C. 2. D. 0 . Lời giải 1 1 1
Từ bảng biến thiên ta có lim y  0  lim
  y  là một tiệm cận ngang. x
x 2 f x  3 3 3  
Ta có: f x    f x 3 2 3 0 
. Căn cứ vào bảng biến thiên đồ thị y f x 3 , y  cắt nhau tại 2 2
một điểm nên đồ thị có một tiệm cận đứng.
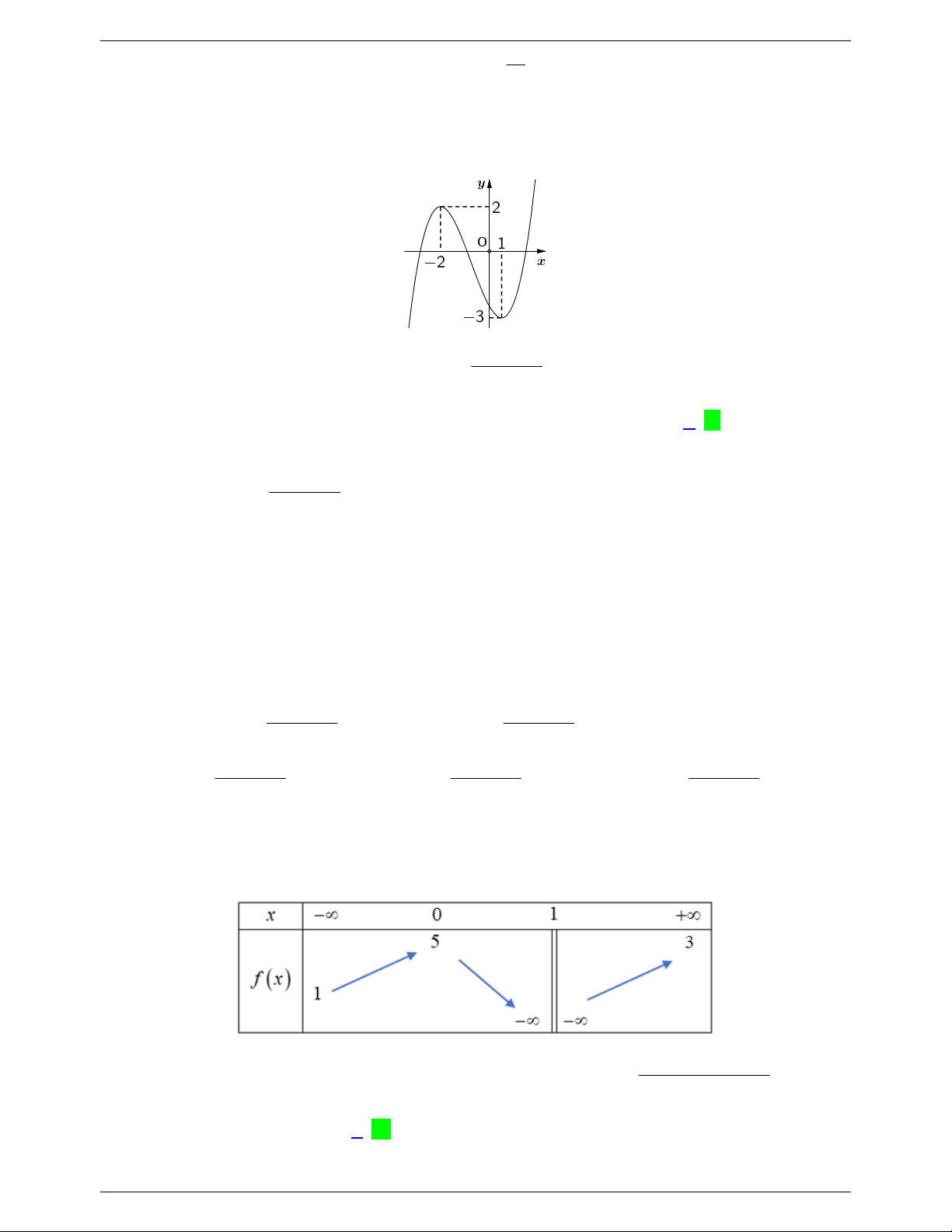
Câu 27: Cho hàm số y f x có bảng biến thiên như hình dưới đây
Gọi tập S là tập chứa tất cả các giá trị nguyên của tham số m 10
 ;10 để đồ thị hàm số x  2 y
có đúng hai đường tiệm cận đứng. Số phần tử của tập S là: 2
f x  mf xA. 9. B. 12. C. 13. D. 8. Lời giải x  2
Xét hàm y g x  với x  2 (1). 2
f x  mf x
f x  m Khi đó 2
f x  mf x  0    f   x  0
x a a    1 
Phương trình f x  0  x b  1   b  2 x c
c  2, c n
Với x a , x b loại vì không thõa điều kiện (1).
Với x c, lim g x   nên đường x c là một tiệm cận đứng của đồ thị g x . x c 
Đồ thị g x có hai đường tiệm cận đứng  f x  m có một nghiệm x  2 và x c m  2 
Dựa vào BTT của y f x , f x  m có một nghiệm x  2 và x c   . m  0 TOANMATH.com Trang 25 Strong Team Toán VD – VDC TOANMATH.com
Câu 28: Cho hàm số y f x có đồ thị như hình dưới đây 2 x  3x
Gọi tập S là tập chứa tất cả các giá trị tham số m để đồ thị hàm số y  có đúng ba
f x  f
 2x m  4
đường tiệm cận đứng. Khẳng định nào sau đây là đúng: A.  ;3    S . B.  ;2    S . C. S   .
D. 6;8  S . Lời giải 2 x  3x x x  3
Xét hàm y g x  
f x  f
 2x m  4 f  x f
 2x m  4
f x  0
Khi đó f x  f 2x m  4  0      f
 2x m  4  0 x  0 Xét f x 1  0   x  3  2
Với x  0 là nghiệm đơn nên x  0 không là tiệm cận đứng của đồ thị y g x . 1
Với x  3 là nghiệm kép nên x  3 là tiệm cận đứng của đồ thị. y g x . 2  1 m x      3 2x m 1
Xét f x m    f x m 2 2 4 0 2  4    
2x m c  c  3 c mx  4  2 1 m 1 m Với x
là nghiệm kép nên x
là tiệm cận đứng của đồ thị y g x . 3 2 2 c m
Đồ thị y g x có ba đường tiệm cận đứng  x
là tiệm cận đứng của đồ thị y g x 2 c m  0  2 m  c     c  3. c m      m 6 c 3  2
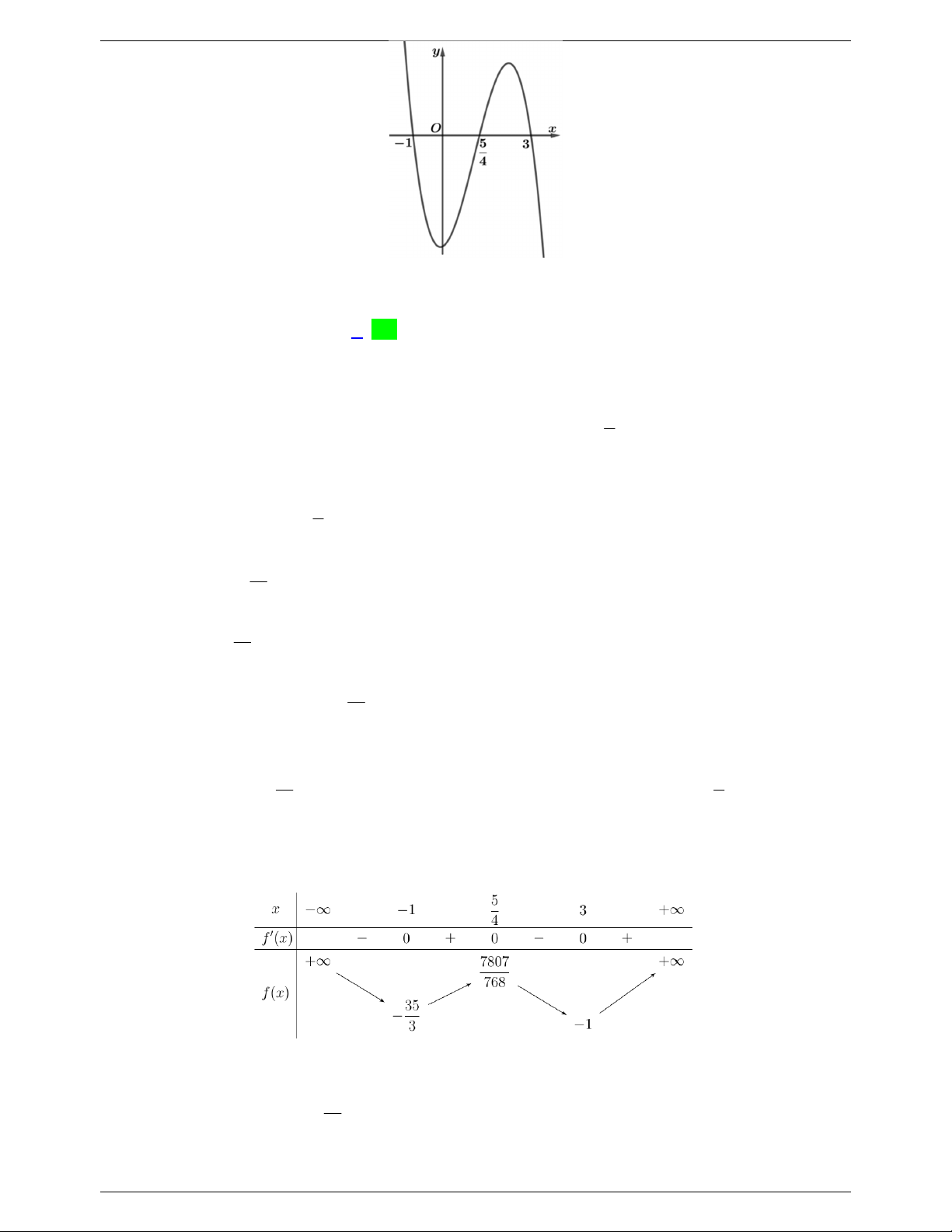
Câu 29: Cho hàm số bậc ba 3 2
f (x)  ax bx cx d có đồ thị như hình vẽ. Với giá trị nào của m thì m x hàm số ( g x)  có 5 tiệm cận đứng? 2
f (x)  2 f (x) TOANMATH.com Trang 26 Strong Team Toán VD – VDC TOANMATH.com A. m  2 . B. m  2 . C. m  2 . D. m  2 . Lời giải Chọn D m x Xét hàm số ( g x)  2
f (x)  2 f (x)
Biểu thức m x xác định khi m x  0  x m (1) Ta có 2
f (x)  2 f (x)  0(2)
x x (2; 1  ) 1 x  0 f (x) 0   
 x x   (1;2) 2  fx)  2  x  1  x  2 
Hàm số có 5 tiệm cận đứng khi phương trình (2) có 5 nghiệm thỏa mãn điều kiện của (1)  m  2
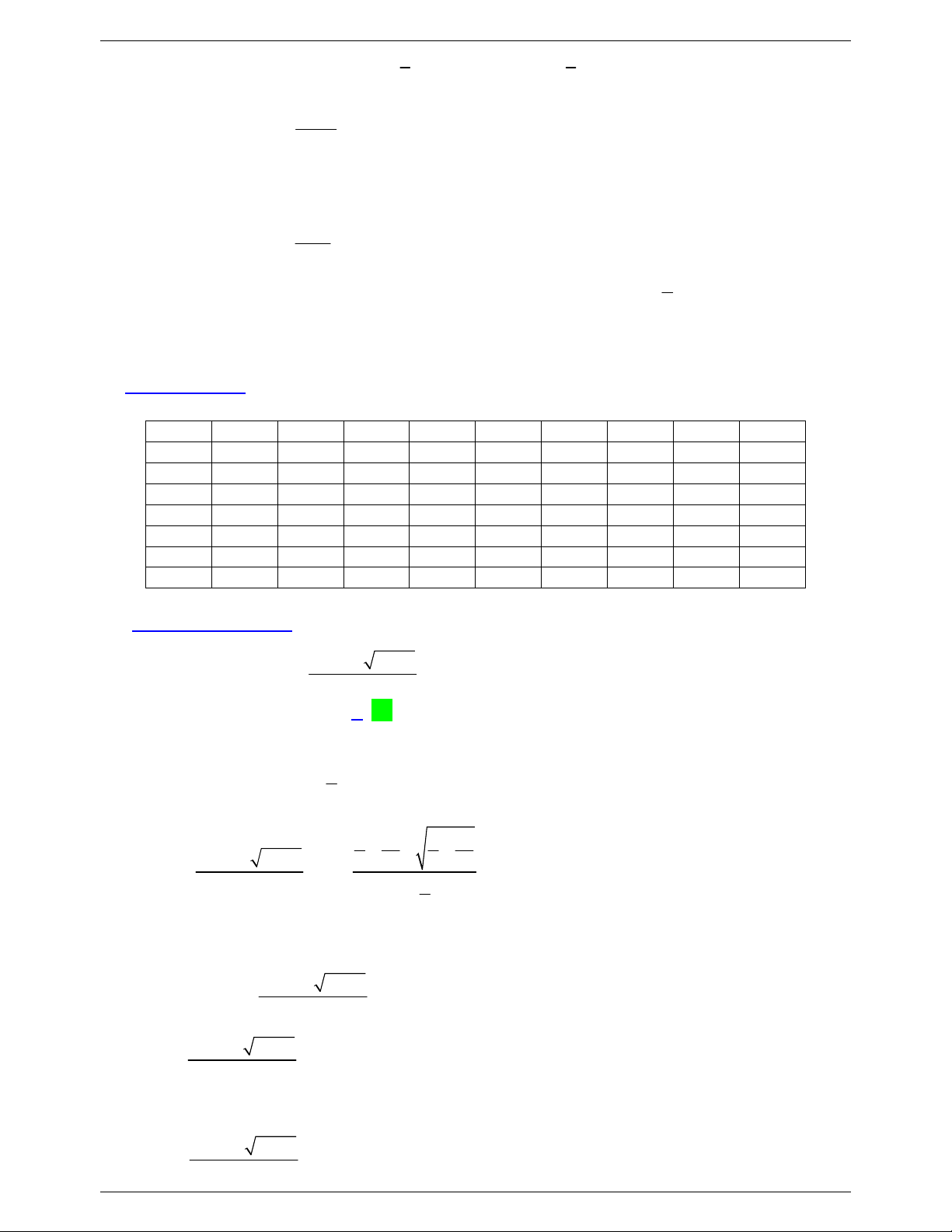
Câu 30: Cho hàm số bậc ba 3 2
f (x)  ax bx cx d có đồ thị như hình vẽ. có bao nhiêu giá trị của m 2 2 2
(x  2mx m m 1) x  3x
để hàm số g(x)  có 3 tiệm cận đứng? 2
(x-4)[f (x)  4 f (x)] y 4 1  O 2 3 x A. 1 . B. 2 . C. 3. D. 4 Lời giải Chọn B 2 2 2
(x  2mx m m 1) x  3x
Xét hàm số g(x)  2
(x-4)[f (x)  4 f (x)] Biểu thức 2
x  3x có điều kiện là: 2
x  3x  0  x  (;0][3;) Ta có TOANMATH.com Trang 27 Strong Team Toán VD – VDC TOANMATH.com 2
(x-4)[f (x)  4 f (x)]=0(1) x  4  x  4 x  4 x  0 x  4  0    x  3  
f (x)  0  x  3   2
f (x)  4 f (x)   x  1  f (x)  4 x  1     x  0 x  2(Loaïi)  Đặt 2 2
h(x)  x  3mx m m 1. Nếu h(x) không có nghiệm thuộc 1;0;3; 
4 thì g(x) có 4 tiệm cận
đứng. Xét các trường hợp sau
Thường hợp 1: x  4 là nghiệm của h(x) 2
m  7m 17  0 (vô nghiệm)
Thường hợp 2: x  3 là nghiệm của h(x) 2
m  5m 10  0 (vô nghiệm)
Thường hợp 3: x  1
 là nghiệm của h(x) 2
m  3m  2  0 m  1   m  2 
Thường hợp 4: x  0 là nghiệm của h(x) 2
m m 1  0 (vô nghiệm) m  1  Như vậy khi 
thì hàm số đã cho có 3 tiệm cận đứng. m  2  x m  3 
Câu 31: Cho hàm số y m   
 có đồ thị C. Giả sử M x ; y là 1 điểm bất kỳ thuộc M M  2x  3  2 
C. Gọi ,A B lần lượt là khoảng cách từ M tới các đường tiệm cận ngang và tiệm cận đứng
của C. Biết diện tích MAB bằng 1. Khẳng định nào sau đây là đúng? 5 11  5 11  5 11 5 11
A. m   ; .
B. m   ; . C. m  ; .
D. m  ; . 2 2   2 2   2 2  2 2  Lời giải 3 3 1
Với m   , đồ thị C có đường tiệm cận đứng là x   và tiệm cận ngang y  . 2 2 2 3
Khoảng cách từ M tới đường tiệm cận đứng: d x  . 1 M 2 x m 1 2  m  3 2m  3
Khoảng cách từ M tới đường tiệm cận ngang: M d     . 2 2x  3 2 2 x x M 2 3 M  2 2 3 M 1 1
Từ giả thiết, MAB vuông tại M nên SM .
A MB d .d  1 d d  2 MAB  1 2 1 2 2 2  5 m  3 2m  3 2m  3  8  Do đó 2 x  .
 2  2m  3  8     M 2 2 2x  3 2m  3  8  11 Mm    2 TOANMATH.com Trang 28 Strong Team Toán VD – VDC TOANMATH.com 2x  2
Câu 32: Cho hàm số y
có đồ thị C. Giả sử M x ; y là điểm thuộc C thỏa mãn tổng M M x 1
khoảng cách từ M tới trục hoành và đường tiệm cận đứng của C đạt giá trị nhỏ nhất. Giá trị
của x y bằng M M A. 2. B. 2.  C. 1. D. 1.  Lời giải 2x  2
Đồ thị C có đường tiệm cận đứng x 1. Ta có M C nên M y  . M x 1 M
Khoảng cách từ M tới đường tiệm cận đứng: d x 1 . 1 M 2x  2
Khoảng cách từ M tới trục hoành: M d y  . 2 M x 1 M 2x  2
Tổng khoảng cách từ M tới tiệm cận đứng và trục hoành: d d d x 1 M  1 2 M x 1 M 2 x 1
Nếu x  1, ta có d x 1 M
 2 2 x 1  2 2.2  4 M M x 1 M M Nếu 1   x 1, ta có M 2x  2 x M d   x
    x M  2 2 1 2 1 M M 1 x 1 x M M  1   xx x x   x x M  1 M  2 2 M 1 2 2 M MM 2 2 1  2   2   2   2. 1 x 1 x 1 x M M M
Dấu bằng xảy ra khi và chỉ khi x  1.  M 2x  2 Nếu x  1,  ta có d 1 Mx  1 x  2 M M x 1 M M
Vậy d  2, dấu bằng chỉ xảy ra khi x  1,  do đó M  1;  0. M 2mx + 3
Câu 33: Cho hàm số y =
có đồ thị (C ) và I là giao điểm của hai đường tiệm cận của (C ) x - m
.Gọi S là tập hợp tất cả các giá trị của tham số m sao cho tiếp tuyến tại điểm M trên đồ thị
(C ) cắt hai đường tiệm cận tại hai điểm ,
A B và tam giác IAB có diện tích bằng 64 .Tổng các
phần tử của tập hợp S là A. 58 . B. 2 58 . C. 2 - 58 . D. 0 . Lời giải 2mx + 3
Đồ thị (C ) : y =
có tiệm cận đứng x = m và tiệm cận ngang y = 2m nên giao điểm của hai x - m
tiệm cận là I ( ; m 2m). TOANMATH.com Trang 29 Strong Team Toán VD – VDC TOANMATH.com æ 2mx 3ö + Giả sử ç 0 M x ç ; ÷÷ Î C ç 0 ÷ ( ) çè x - m ÷ø 0 2 2m + 3 2mx + 3
Phương trình tiếp tuyến D với (C ) tại M là y = - x - x + . 2 ( 0 ) 0 ( - ) x - m x m 0 0 æ 2 2mx 2m 6ö + + ç ÷
Tiếp tuyến cắt TCĐ x = m tại 0 Aç ; m ÷ ç
÷ , cắt tiệm cận ngang tại B (2x - ; m 2m 0 ) ç x - m ÷÷ è 0 ø 2 4m + 6 Ta có IA =
và IB = 2 x - m . x - m 0 0
Diện tích tam giác IAB là 2 1 1 4m + 6 58 2 S = 64  I . A IB = 64 
.2 x - m = 64  4m + 6 = 64  m =  IAB 0 2 2 x - m 2 0 58 æç 58ö÷ Vậy S = + ç ÷ - ç ÷ = 0 . 2 ç 2 ÷÷ è ø 2x - 1
Câu 34: Cho hàm số y =
có đồ thị (C ) và I là giao điểm của hai đường tiệm cận. Giả sử x + 1
M (x ;y là điểm trên đồ thị (C ) có hoành độ dương sao cho tiếp tuyến tại M với (C ) cắt 0 0 )
tiệm cận đứng và tiệm cận ngang lần lượt tại hai điểm , A B thỏa mãn 2 2
IA + IB = 40 . Giá trị của biểu thức 2 2
P = x + y + x y bằng: 0 0 0 0 A. 8 . B. 3 . C. 5. D. 7 . Lời giải 2x - 1
Đồ thị (C ) : y =
có tiệm cận đứng x = -1 và tiệm cận ngang y = 2 nên I (-1; 2). x + 1 æ 2x 1ö -
Vì M Î (C ) nên ç 0 M x ç ; ÷÷, x > 0 ç 0 ÷ ( 0 ) çè x + 1 ÷ø 0 3 2x - 1
Phương trình tiếp tuyến với (C ) tại M là y = x - x + . 2 ( 0 ) 0 (x + ) x + 1 1 0 0 æ 2x 4ö - ç 0  Aç-1; ÷÷ ç
÷, B (2x + 1; 2 0 ) çè x + 1 ÷ø 0 6 Ta có IA =
và IB = 2 x + 1 . x + 1 0 0 36 Khi đó 2 2 IA + IB = 40 
+ 4 x + 1 = 40 , x > 0 2 ( 0 )2 (x +1 0 ) 0 TOANMATH.com Trang 30 Strong Team Toán VD – VDC TOANMATH.com  (x + )4 1 - 10(x + )2 1 + 9 = 0 0 0 (éêx + )2 1 = 1 0  ê(êx + ê )2 1 = 9 0 ë x é = 0 (l) ê 0 x ê = -2 (l) ê 0 
x = 2  y = 1 ê . 0 0
x = 2 (n) ê 0 x ê ê = -4 (l) 0 ë Suy ra M (2; ) 1
Giá trị của biểu thức P = 7. x  2
Câu 35: Cho hàm số y
có đồ thị là C . Gọi I là giao điểm hai đường tiệm cận và M x ; y 0 0  x 1
là điểm nằm trên C với x  0 . Biết tiếp tuyến của C tại điểm M cắt tiệm cận đứng và 0
tiệm cận ngang lần lượt tại hai điểm P và Q sao cho bán kính đường tròn nội tiếp tam giác
IPQ lớn nhất. Tính tổng x y . 0 0
A. x y  0 .
B. x y  2  2 3 . C. x y  2 .
D. x y  2 3 . 0 0 0 0 0 0 0 0 Lời giải
Đồ thị C có đường tiệm đứng x  1
 và đường tiệm cận ngang y  1.
Giao điểm hai đường tiệm cận I  1;   1 .  x  2  3 Gọi 0 M x ;
 C với x  0 . Ta có y  . 0   x 1  0 x  2 0  1 3 x  2
Phương trình tiếp tuyến của C tại điểm M là y x x  . 2  0  0 x   1 x 1 0 0  x  5 
Tiếp tuyến của C tại điểm M cắt tiệm cận đứng tại điểm 0 P 1; 
 và cắt tiệm cận ngang tại x 1  0 
điểm Q2x 1;1 . 0  1 1 6 Ta có SI . P IQ  .2 x 1  6 . IPQ 0 2 2 x 1 0 S IPQ  6 Mặt khác Spr r
 nên r đạt giá trị lớn nhất khi và chỉ khi p đạt giá trị nhỏ nhất hay IPQ p p
chu vi tam giác IPQ đạt giá trị nhỏ nhất.
Mà chu vi tam giác IPQ : 2 2
C IP IQ PQ IP IQ IP IQ  2  2 I .
P IQ  2  2 12 TOANMATH.com Trang 31 Strong Team Toán VD – VDC TOANMATH.com 6 x  1   3
Nên chu vi tam giác IPQ nhỏ nhất khi 0 IP IQ   2 x 1   . 0 x 1 0 x  1   3  0
Do x  0 nên x  1 3  M 1 3 ;1 3 . 0   0
Vậy x y  0 . 0 0 2x 1
Câu 36: Cho hàm số y
có đồ thị là C . Gọi I là giao điểm hai đường tiệm cận và M là điểm 2x  2
nằm trên C có hoành độ lớn hơn 1. Tiếp tuyến của C tại điểm M cắt tiệm cận đứng và
tiệm cận ngang lần lượt tại hai điểm A và B . Hoành độ của điểm M thuộc khoảng nào sau
đây để P IA IB đạt giá trị nhỏ nhất? A.  4;   1 . B.  ;  4   . C. 4; . D. 1;4 . Lời giải
Đồ thị C có đường tiệm đứng x 1 và đường tiệm cận ngang y  1.
Giao điểm hai đường tiệm cận I 1;  1 .  2x 1  2 Gọi 0 M x ;
 C với x 1. Ta có y   . 0   2x  2  0 2x  22 0  2 2x 1
Phương trình tiếp tuyến của C tại điểm M là y   x x  . 2  0  0 2x  2 2x  2 0 0  x
Tiếp tuyến của C tại điểm M cắt tiệm cận đứng tại 0 A1;
 và cắt tiệm cận ngang tại điểm x 1  0  B2x 1;1 . 0  1
Ta có IA IB   2x 1  2 2 0  x 1 0  2  2 x  1
Suy ra MinIA IB  2 2 khi  x   0 2 2 1   . 0 x 1  0 2  2 x  0  2 2  2
Do x 1 nên x  . 0 0 2 2  2 Vậy x  . 0 2 x  2
Câu 37: Cho hàm số y
có đồ thị C . Gọi M x ; y là một điểm thuộc C sao cho tổng 0 0  3  x
khoảng cách từ M đến hai đường tiệm cận của C là nhỏ nhất. Tính 2x y biết y  0 . 0 0 0
A. 2x y  4 .
B. 2x y  2 .
C. 2x y  6 .
D. 2x y 10 . 0 0 0 0 0 0 0 0 Lời giải TOANMATH.com Trang 32 Strong Team Toán VD – VDC TOANMATH.com  x  2 
Gọi M x ; y C 0  M x ; . 0 0    0  3  x  0 
Đồ thị C có tiệm cận đứng x  3 và tiệm cận ngang y  1.
Khoảng cách từ M đến tiệm cận đứng là d x  3 . 1 0 1
Khoảng cách từ M đến tiệm cận ngang là d  . 2 3  x0 1 1
x  2  y  0
Ta có d d x  3 
 2. Dấu ''  ' xảy ra khi và chỉ khi x 3  0 0  . 1 2 0 3 x 0 3  x
x  4  y  2 0 0  0 0
Mà y  0 nên y  2
 . Vậy 2x y  2.4  2  10 . 0 0   0 0 x 1
Câu 38: Cho hàm số y
có đồ thị là C . Gọi I là giao điểm của hai đường tiệm cận và x  3
M x ; y là một điểm thuộc C . Phương trình tiếp tuyến của C tại M cắt tiệm cận đứng 0 0 
và tiệm cận ngang của C lần lượt tại hai điểm A , B sao cho 2 2
IA IB  32 . Tìm tọa độ
điểm M biết y  0 . 0  1   1  A.  5;   3 . B. 2;  . C. 3;  . D.  1;    1 .  5   3  Lời giải
Đồ thị C có tiệm cận đứng x  3
 và tiệm cận ngang y  1.
Giao điểm của hai đường tiệm cận I  3;  1 .  x 1  4
Ta có điểm M x ; y C  0  M x ; và y  , x   3  . 0 0 0  x  3  x  32 0  4 x 1
Phương trình tiếp tuyến của C tại M có dạng y x x  . 2  0  0 x  3 x  3 0 0
Cho y  1   x  32  4x  4x x 1 x  3  x  2x  3. 0 0  0  0  0 4 x 1 x  5 Cho x  3   y  3  x   . 2  0  0 0 x  3 x  3 x  3 0 0 0  x  5 
Suy ra tiếp tuyến của C tại điểm M cắt tiệm cận đứng tại 0 A 3;
 và cắt tiệm cận ngang tại x  3  0 
điểm B2x  3;1 . 0  64  x  3  2  x  1 Ta có 2 2
IA IB  32   4 x  3  32 0 0   2  0 2    x  3 x  3  2 x  5   0  0 0 Với x  1   y  1
 (loại vì y  0 ). 0 0 0 TOANMATH.com Trang 33 Strong Team Toán VD – VDC TOANMATH.com Với x  5
  y  3 (nhận). 0 0 Vậy M  5;  3 . 2x 1
Câu 39: Cho hàm số y
có đồ thị C . Có bao nhiêu điểm M thuộc C sao cho tổng khoảng x 1
cách từ M đến hai đường tiệm gấp 2 lần tích khoảng cách từ M đến hai đường tiệm cận của C? A. 0 . B. 1. C. 4 . D. 2. Lời giải
Đồ thị hàm số có tiệm cận đứng d : x 1 và tiệm cận ngang d : y  2 . 1 2  2x 1 Giả sử 0 M x ;
 C với x 1. 0   x 1  0 0  2x 1 1
Ta có: d M;d x 1 ; d M;d   2  2  0 1  0 x 1 x 1 0 0 1 1
Theo đề bài: x 1   2 x 1 .  2 0 0 x 1 x 1 0 0 x  2 0  x 1 1 . 0 x  0  0
Vậy có 2 điểm M thỏa mãn đề bài. x 1
Câu 40: Cho hàm số y
có đồ thị C . Gọi I là giao điểm hai đường tiệm cận của C . Có bao x  2 1
nhiêu điểm trên C có hoành độ âm sao cho tam giác OMI có diện tích bằng biết O là 2 gốc tọa độ? A. 0 . B. 1. C. 4 . D. 2 . Lời giải
Đồ thị hàm số có tiệm cận đứng x  2 và tiệm cận ngang y  1. Do đó I 2;  1 .
Suy ra OI  5 và đường thẳng OI có phương trình:  : x  2 y  0 .  m 1  Giả sử M ; m  
 C với m  0.  m  2  m 1 m  2. 2 m  4m  2 m  2
Ta có: d M ;    h 5 5 m  2 1 2 2. 1 1 m  4m  2 Theo đề bài: 2 S
OI.h h     1 OMI  2 5 5 m  2 TOANMATH.com Trang 34 Strong Team Toán VD – VDC TOANMATH.com 2
m  4m  2  m  2 m  0 (L) 2 m 4m 2 m 2       m  5 (L)     . 2
m  4m  2  2  mm  1  m  4 (L)
Vậy có 1 điểm thỏa mãn đề bài.
____________________ HẾT ____________________ TOANMATH.com Trang 35