Bài tập VD – VDC Toán 11 trong các đề thi thử THPT 2020 môn Toán

Tài liệu gồm 89 trang, được tổng hợp bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn 101 câu hỏi và bài tập trắc nghiệm chuyên đề Toán 11

89 45 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

89 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. XÁC SUẤT
Câu 1. (Chuyên Biên Hòa - Hà Nam - 2020) Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các
chữ số của số đó bằng 7?
A.
165
. B.
1296
. C.
343
. D.
84
.
Câu 2. (Chuyên ĐH Vinh - Nghệ An -2020) Ban chỉ đạo phòng chống dịch Covid-19 của sở Y tế Nghệ
An có 9 người, trong đó có đúng 4 bác sĩ. Chia ngẫu nhiên Ban đó thành ba tổ, mỗi tổ 3 người để
đi kiểm tra công tác phòng dịch ở địa phương. Trong mỗi tổ, chọn ngẫu nhiên một người làm tổ
trưởng. Xác suất để ba tổ trưởng đều là bác sĩ là
A.
1
42
. B.
1
21
. C.
1
14
. D.
1
7
.
Câu 3. (Chuyên Hưng Yên - 2020) Cho tập
1;2;...;19;20S
gồm 20 số tự nhiên từ 1 đến 20. Lấy
ngẫu nhiên ba số thuộc
S
. Xác suất để ba số lấy được lập thành cấp số cộng là
A.
5
38
. B.
7
38
. C.
3
38
. D.
1
114
.
Câu 4. (Chuyên KHTN - 2020) Xếp
4
bạn nam và
2
bạn nữ thành một hàng ngang. Xác suất để
2
bạn
nữ không ngồi cạnh nhau bằng
A.
1
6
. B.
2
3
. C.
1
4
. D.
1
3
.
Câu 5. (Chuyên KHTN - 2020) Một công ty may mặc có hai hệ thống máy chạy song song. Xác suất để
hệ thống máy thứ nhất hoạt động tốt là 90%, xác suất để hệ thống máy thứ hai hoạt động tốt là
80%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy
hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là
A. 98%. B. 2%. C. 80%. D. 72%.
Câu 6. (Chuyên Lam Sơn - 2020) Giải bóng chuyền VTV cup gồm 12 đội tham gia, trong đó có 9 đội
nước ngoài và 3 đội Việt Nam. Ban tổ chức bốc cho thăm ngẫu nhiên và chia thành 3 bảng đấu
, ,A B C
mỗi bảng 4 đội. Xác suất để ba đội Việt Nam nằm ở 3 bảng gần nhất với số nào dưới đây?
A.
11
25
. B.
3
20
. C.
39
100
. D.
29
100
.
Câu 7. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Xếp ngẫu nhiên 5 học sinh
, , , ,A B C D E
ngồi
vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi một ghế). Tính xác suất để hai bạn
A
và
B
không
ngồi cạnh nhau.
A.
1
5
. B.
3
5
. C.
2
5
. D.
4
5
.
Câu 8. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Hai bạn A và B mỗi bạn viết ngẫu nhiên một số tự
nhiên gồm ba chữ số đôi một khác nhau. Xác suất để các chữ số có mặt ở hai số bạn A và B viết
giống nhau bằng
A.
31
2916
. B.
1
648
. C.
1
108
. D.
25
2916
Câu 9. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Một nhóm gồm 10 học sinh trong đó có 7
học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động.
Tinh xác suất để trong 3 học sinh được chọn có ít nhất 1 học sinh nữ.
A.
4
9
. B.
17
24
. C.
17
48
. D.
2
3
.
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
44 CÂU HỎI VD - VDC CHƯƠNG 7. ĐẠI SỐ 11
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 10. (Chuyên Thái Bình - 2020) Có tất cả bao nhiêu số tự nhiên gồm
6
chữ số đôi một khác nhau
trong đó có đúng
3
chữ số chẵn
A.
72000
. B.
64800
. C.
. D.
60000
.
Câu 11. (Chuyên Bắc Ninh - 2020) Cho
S
là tập các số tự nhiên có
8
chữ số. Lấy một số bất kì của tập
S
. Tính xác suất để lấy được số lẻ và chia hết cho
9
.
A.
3
8
. B.
1
9
. C.
2
9
. D.
1
18
.
Câu 12. (Chuyên Bến Tre - 2020) Đội học sinh giỏi trường trung học phổ thông chuyên bến tre gồm có 8
học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 8 học sinh. Xác suất
để trong 8 học sinh được chọn có đủ 3 khối là
A.
71131
75582
. B.
35582
3791
. C.
143
153
. D.
71128
75582
.
Câu 13. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho tập
1,2,3,4,5,6
A
. Gọi
S
là tập hợp các tam
giác có độ dài ba cạnh là các phần tử của
A
. Chọn ngẫu nhiên một phần tử thuộc
S
. Xác suất để
phần tử được chọn là một tam giác cân bằng.
A.
6
34
. B.
19
34
. C.
27
34
. D.
7
34
.
Câu 14. (Chuyên Hùng Vương - Gia Lai - 2020) Cho một đa giác đều 18 đỉnh nội tiếp trong một đường
tròn tâm
O
. Gọi
X
là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính
xác suất
P
để chọn được một tam giác từ tập
X
là tam giác cân nhưng không phải tam giác đều.
A.
144
136
P
. B.
7
816
P
. C.
23
136
P
. D.
21
136
P
.
Câu 15. (Chuyên Lào Cai - 2020) Chọn ngẫu nhiên bốn số tự nhiên khác nhau từ
70
số nguyên dương
đầu tiên. Tính xác suất để bốn số được chọn lập thành một cấp số nhân có công bội nguyên.
A.
12
916895
. B.
11
916895
. C.
10
916895
. D.
9
916895
.
Câu 16. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có 6 học sinh gồm 2 học sinh lớp A, 2 học sinh
lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm bất kì 3
học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C.
A.
1
120
. B.
1
3
. C.
1
30
. D.
1
15
.
Câu 17. (Chuyên Sơn La - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6
học sinh gồm 3 nam 3 nữ
ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học
sinh nam đều ngồi đối diện với một học sinh nữ bằng
A.
1
10
. B.
3
5
. C.
1
20
D.
2
5
.
Câu 18. (Sở Phú Thọ - 2020) Cho đa giác đều
H
có 30 đỉnh. Lấy tùy ý 3 đỉnh của
H
. Xác suất để 3
đỉnh lấy được tạo thành một tam giác tù bằng
A.
39
140
. B.
39
58
. C.
45
58
. D.
39
280
.
Câu 19. (Sở Hà Tĩnh - 2020) Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10
, lấy ngẫu
nhiên
5
quả cầu. Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho
3
bằng
A.
5
12
. B.
7
12
. C.
1
12
. D.
11
12
.
Câu 20. (Sở Bắc Ninh - 2020) Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một
khác nhau. Chọn ngẫu nhiên một số thuộc A. Xác suất để số tự nhiên được chọn chia hết cho 25
bằng
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
43
.
324
B.
1
.
27
C.
11
.
324
D.
17
.
81
Câu 21. (Sở Yên Bái - 2020) Gọi S là tập tất cả các số tự nhiên có ba chữ số đôi một khác nhau được lập
từ các chữ số
0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia hết
cho 6.
A.
13
60
. B.
2
9
. C.
17
45
. D.
11
45
.
Câu 22. (Bỉm Sơn - Thanh Hóa - 2020) Trường trung học phổ thông Bỉm Sơn có 23 lớp, trong đó khối
10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có một em
làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường chọn ngẫu
nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thị xã. Tính xác suất để 9 em được chọn có đủ cả ba
khối?
A. . B. . C. . D. .
Câu 23. (Đặng Thúc Hứa - Nghệ An - 2020) Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp mặt
10
em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp số
cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có
5
ghế và mỗi ghế chỉ
được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng
nhau.
A.
1
954
. B.
1
252
. C.
1
945
. D.
1
126
.
Câu 24. (Đô Lương 4 - Nghệ An - 2020) Người ta muốn chia tập hợp 16 học sinh gồm 3 học sinh lớp
12A, 5 học sinh lớp 12B và 8 học sinh lớp 12C thành hai nhóm, mỗi nhóm có 8 học sinh. Xác suất
sao cho ở mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B là
A.
42
143
. B.
84
143
. C.
356
1287
. D.
56
143
.
Câu 25. (Hậu Lộc 2 - Thanh Hóa - 2020) Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15. Chọn
ngẫu nhiên 6 tấm thẻ trong hộp. Xác suất để tổng các số ghi trên 6 tấm thẻ được chọn là một số lẻ
bằng.
A.
71
143
. B.
56
715
. C.
72
143
. D.
56
143
.
Câu 26. (Kim Liên - Hà Nội - 2020) Một số điện thoại có bảy chữ số, trong đó chữ số đầu tiên là
8
. Số
điện thoại này được gọi là
may mắn nếu bốn chữ số đầu là chữ số chẵn phân biệt và ba chữ số còn lại là lẻ, đồng thời hai
chữ số
0
và
9
không đứng liền nhau. Tính xác suất để một người khi lắp điện thoại ngẫu nhiên
được số điện thoại may mắn.
A.
7
5100
( )
10
P A
. B.
7
2850
( )
10
P A
. C.
6
5100
( )
10
P A
. D.
6
2850
( )
10
P A
.
Câu 27. (Lê Lai - Thanh Hóa - 2020) Cho tập hợp . Gọi là tập hợp tất cả các số tự
nhiên có ít nhất chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập
. Chọn ngẫu nhiên một số từ tập , tính xác xuất để số được chọn có tổng các chữ số bằng .
A. B. C. D.
Câu 28. (Liên trường Nghệ An - 2020) Gọi
S
là tập hợp các số tự nhiên có
4
chữ số đôi một khác nhau
lập thành từ các chữ số
0,1,2,3,4,5,6,7
. Chọn ngẫu nhiên một số từ tập
S
. Tính xác suất để số
được chọn có đúng
2
chữ số chẵn.
7345
7429
7012
7429
7234
7429
7123
7429
1; 2; 3; 4; 5
A
S
3
A
S
10
1
.
30
3
.
25
22
.
25
2
.
25
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
24
35
. B.
144
245
. C.
72
245
. D.
18
35
.
Câu 29. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tập
1;2;3;...;19;20S
gồm 20 số tự nhiên từ 1 đến
20. Lấy ngẫu nhiên ba số thuộc
.S
Xác suất để ba số lấy được lập thành một cấp số cộng là
A.
7
38
. B.
5
38
. C.
3
38
. D.
1
114
.
Câu 30. (Nguyễn Huệ - Phú Yên - 2020) Một bàn cờ vua gồm
8 8
ô vuông, mỗi ô có cạnh bằng 1 đơn
vị. Một ô vừa là hình vuông hay hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên một
hình chữ nhật trên bàn cờ. Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn
vị bằng
A.
5
216
. B.
17
108
. C.
51
196
. D.
29
216
.
Câu 31. (Tiên Du - Bắc Ninh - 2020) Gọi
M
là tập hợp các số tự nhiên có ba chữ số lập được từ các chữ
số 0, 1, 2, 3, 4, 5, 6, 7. Lấy ngẫu nhiên đồng thời 2 số từ tập
.M
Xác suất để cả 2 số lấy được đều
có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là
A.
8
21
. B.
5
16
. C.
296
2051
. D.
695
7152
.
Câu 32. (Hải Hậu - Nam Định - 2020) Một hộp có chứa
5
viên bi đỏ,
3
viên bi xanh và
n
viên bi vàng (
các viên bi kích thước như nhau,
n
là số nguyên dương). Lấy ngẫu nhiên
3
viên bi từ hộp. Biết
xác suất để trong ba viên vi lấy được có đủ
3
màu là
45
182
. Tính xác suất
P
để trong
3
viên bi lấy
được có nhiều nhất hai viên bi đỏ.
A.
135
364
P
. B.
177
182
P
. C.
45
182
P
. D.
31
56
P
.
Câu 33. (Kìm Thành - Hải Dương - 2020) Gọi
S
là tập hợp tất cả các số tự nhiên gồm
9
chữ số đôi một
khác nhau. Chọn ngẫu nhiên một số từ
S
. Tính xác suất để được chọn có đúng
4
chữ số lẻ và
chữ số
0
đứng giữa hai chữ số lẻ. (Các chữ số liền trước và liền sau của chữ số
0
là các chữ số
lẻ).
A.
5
648
. B.
5
27
. C.
5
54
. D.
20
189
.
Câu 34. (Trường VINSCHOOL - 2020) Có
6
học sinh nam và
4
học sinh nữ xếp thành hàng ngang.
Xác suất để có đúng hai bạn nữ đứng cạnh nhau bằng
A.
1
24
. B.
1
2
. C.
14
17
. D.
7
13
.
Câu 35. (Thanh Chương 1 - Nghệ An - 2020) Gọi
S
là tập hợp tất cả các số tự nhiên có 5 chữ số mà các
chữ số đều khác 0. Lấy ngẫu nhiên một số từ
S
. Xác suất để lấy được số chỉ có mặt 3 chữ số gần
với số nào nhất trong các số sau?
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
0,34
. B.
0,36
. C.
0,21
. D.
0,13
.
Câu 36. (Tiên Lãng - Hải Phòng - 2020) Một xưởng sản xuất thực phẩm gồm 4 kỹ sư chế biến thực
phẩm, 3 kĩ thuật viên và 13 công nhân. Để đảm bảo sản xuất thực phẩm chống dịch Covid 19,
xưởng cần chia thành 3 ca sản xuất theo thời gian liên tiếp nhau sao cho ca I có 6 người và 2 ca
còn lại mỗi ca có 7 người. Tính xác suất sao cho mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế
biến thực phẩm.
A.
440
3320
. B.
441
3230
. C.
41
230
. D.
401
3320
.
Câu 37. (Trần Phú - Quảng Ninh - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu
nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học
sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A.
1
3
. B.
1
30
. C.
8
63
. D.
8
37
.
Câu 38. (Đại Học Hà Tĩnh - 2020) Cho đa giác đều 12 đỉnh nội tiếp đường tròn tâm A.
Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác
không có cạnh nào là cạnh của đa giác đã cho.
A.
2
5
. B.
31
55
. C.
28
55
. D.
52
55
.
Câu 39. (ĐHQG Hà Nội - 2020) Có
12
học sinh gồm
6
nam và
6
nữ ngồi vào hai hàng ghế đối diện nhau
tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là?
A.
1
924
. B.
4
165
. C.
8
165
. D.
16
231
.
Câu 40. (Sở Hưng Yên - 2020) Có 50 tấm thẻ đánh số từ 1 đến 50. Rút ngẫu nhiên 3 thẻ. Xác suất để
tổng các số ghi trên thẻ chia hết cho 3 bằng
A.
8
89
. B.
11
171
. C.
769
2450
. D.
409
1225
.
PHẦN 2. MỘT SỐ BÀI TOÁN KHÁC
Câu 41. (Chuyên Bắc Ninh - 2020) Cho
0, 1
x x
. Tìm số hạng không chứa
x
trong khai triển Niu-tơn
của
20
2
3
3
1 1
1
x x
P
x x
x x
.
A.
. B.
167960
. C.
1600
. D.
125970
.
Câu 42. (Sở Phú Thọ - 2020) Giả sử
n
là một số nguyên dương thoả mãn
2 3
3 24
n n
C C
. Hệ số của số
hạng chứa
12
x
trong khai triển
2
2
n
x x
x
bằng
A.
12
672x
. B.
12
672x
. C.
672
. D.
672
.
Câu 43. (Sở Bình Phước - 2020) Trên một cái bảng đã ghi sẵn các số tự nhiên từ
1
đến
2020
. Ta thực
hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số
vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn
lại trên bảng là
A.
4040
. B.
2041210
. C.
4082420
. D.
2020
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
44. (Yên Lạc 2 - Vĩnh Phúc - 2020) Xác định
n
biế
t rằng hệ số của
n
x
trong
khai triển
2
2
1 2 ...
n
x x nx
bằng
6n
.
A.
8
n
. B.
6
n
. C.
n
. D.
5
n
.
-------------------- HẾT --------------------
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. XÁC SUẤT
Câu 1. (Chuyên Biên Hòa - Hà Nam - 2020) Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các
chữ số của số đó bằng 7?
A.
165
. B.
1296
. C.
343
. D.
84
.
Lời giải
Chọn D
7 có thể phân tích thành 11 nhóm sau:
7 = (7+0+0+0)
= (6+1+0+0)
= (5+2+0+0) = (5+1+1+0)
= (4+3+0+0) = (4+2+1+0) = (4+1+1+1)
= (3+3+1+0) = (3+2+2+0) = (3+2+1+1)
= (2+2+2+1)
+) Với nhóm (7+0+0+0) viết được 1 số, đó là số: 7000.
+) Với các nhóm (6+1+0+0); (2+2+0+0) và (4+3+0+0): mỗi nhóm viết được 6 số
(chẳng hạn: với nhóm (6+1+0+0) ta có các số 6100, 6010, 6001 và hoán vị của số 6 và số 1).
+) Với nhóm (3+3+1+0); (5+1+1+0) và (3+2+2+0): mỗi nhóm viết được
4! 3!
9
2
số
(
3!
là các số có số 0 đứng đầu, chia 2 vì có 1 số xuất hiện 2 lần).
+) Với nhóm (4+2+1+0) viết được:
4! 3! 18
số (
3!
là các số có số 0 đứng đầu).
+) Với nhóm (3+2+1+1) viết được:
4!
12
2
số (vì xuất hiện 2 số 1).
+) Với các nhóm (4+1+1+1) và (2+2+2+1): mỗi nhóm viết được 4 số
(chẳng hạn: với nhóm (4+1+1+1) ta có các số: 4111; 1411; 1141; 1114).
Tổng số các số viết được là:
1 6.3 9.3 18 12 4.2 84
(số).
Câu 2. (Chuyên ĐH Vinh - Nghệ An -2020) Ban chỉ đạo phòng chống dịch Covid-19 của sở Y tế
Nghệ An có 9 người, trong đó có đúng 4 bác sĩ. Chia ngẫu nhiên Ban đó thành ba tổ, mỗi tổ 3
người để đi kiểm tra công tác phòng dịch ở địa phương. Trong mỗi tổ, chọn ngẫu nhiên một
người làm tổ trưởng. Xác suất để ba tổ trưởng đều là bác sĩ là
A.
1
42
. B.
1
21
. C.
1
14
. D.
1
7
.
Lời giải
Chọn B
Chọn 3 người vào nhóm A và có một tổ trưởng ta có:
3
9
.3C
cách.
Chọn 3 người vào nhóm B và có một tổ trưởng ta có:
3
6
.3C
cách.
3 người còn lại vào nhóm C và có một tổ trưởng ta có:
3
3
.3C
cách.
Từ đó ta có số phần tử của không gian mẫu là:
3 3 3
9 6 3
.3. .3. .3 45360.n C C C
Gọi
M
là biến cố thỏa mãn bài toán.
Vì có 4 bác sĩ nên phải có một nhóm có 2 bác sĩ.
Chọn nhóm có 2 bác sĩ mà có 1 tổ trưởng là bác sĩ có
2 1
4 5
. .2C C
Chọn nhóm có 1 bác sĩ và bác sí là tổ trưởng có:
1 2
2 4
.C C
.
1 bác sĩ còn lại và 2 người còn lại vào nhóm có 1 cách.
Chọn một trong 3 nhóm
, ,A B C
có 2 bác sĩ có
1
3
C
cách.
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
CHƯƠNG 7. ĐẠI SỐ 11
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 1 1 2 1
4 5 2 4 3
, .2. . . 2160
n M C C C C C
.
2160 1
45360 21
P M
.
Câu 3. (Chuyên Hưng Yên - 2020) Cho tập
1;2;...;19;20
S
gồm 20 số tự nhiên từ 1 đến 20. Lấy
ngẫu nhiên ba số thuộc
S
. Xác suất để ba số lấy được lập thành cấp số cộng là
A.
5
38
. B.
7
38
. C.
3
38
. D.
1
114
.
Lời giải
Chọn C
Ta có:
3
20
( )
n C
.
Gọi A là biến cố: “ba số lấy được lập thành cấp số cộng “.
Giả sử ba số
, b, c
a
theo thứ tự đó lập thành cấp số cộng, khi đó ta có
2a c b
. Hay
a c
là
một số chẵn và mỗi cách chọn 2 số a và c thỏa mãn
a c
là số chẵn sẽ có duy nhất cách chọn
b. Số cách chọn hai số có tổng chẵn sẽ là số cách chọn ba số tạo thành cấp số cộng.
TH1: Hai số lấy được đều là số chẵn, có:
2
10
C
cách lấy.
TH2: Hai số lấy được đều là số lẻ, có:
2
10
C
cách lấy.
2 2
10 10
( )
n A C C
2 2
10 10
3
10
( ) 3
( )
( ) 38
C C
n A
P A
n C
.
Câu 4. (Chuyên KHTN - 2020) Xếp
4
bạn nam và
2
bạn nữ thành một hàng ngang. Xác suất để
2
bạn nữ không ngồi cạnh nhau bằng
A.
1
6
. B.
2
3
. C.
1
4
. D.
1
3
.
Lời giải
Chọn B
Số phần tử không gian mẫu là
6! 720
n .
Gọi
A
là biến cố: “xếp
4
bạn nam và
2
bạn nữ thành một hàng ngang mà
2
bạn nữ không
ngồi cạnh nhau”.
Khi đó
A
là biến cố: “xếp
4
bạn nam và
2
bạn nữ thành một hàng ngang mà
2
bạn nữ ngồi
cạnh nhau”.
Xếp
4
bạn nam và 1 bạn nữ thành một hàng ngang, có
5! 120
cách.
Xếp bạn nữ còn lại ngồi cạnh bạn nữ đã xếp ở trên, có
2
cách.
Khi đó
120.2 240
A
n
.
Xác suất cần tìm bằng
240 2
1 1 1
720 3
A
n
P A P A
n
.
Câu 5. (Chuyên KHTN - 2020) Một công ty may mặc có hai hệ thống máy chạy song song. Xác suất
để hệ thống máy thứ nhất hoạt động tốt là 90%, xác suất để hệ thống máy thứ hai hoạt động tốt
là 80%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống
máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là
A. 98%. B. 2%. C. 80%. D. 72%.
Lời giải
Chọn A
Goi A là biến cố : « Hệ thống máy thứ nhất hoạt động tốt »
B là biến cố : « Hệ thống máy thứ hai hoạt động tốt »
C là biến cố : « Công ty hoàn thành đúng hạn »
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Ta có
A
là biến cố : « Hệ thống máy thứ nhất hoạt động không tốt »
B
là biến cố : « Hệ thống máy thứ hai hoạt động không tốt »
( ) 0,9
P A
;
( ) 0,8
P B
;
( ) 0,1
P A
;
( ) 0,2
P B
.
( ) ( . ) ( ). ( ) 0,02
P C P A B P A P B
( ) 1 ( ) 0,98
P C P C
.
Câu 6. (Chuyên Lam Sơn - 2020) Giải bóng chuyền VTV cup gồm 12 đội tham gia, trong đó có 9
đội nước ngoài và 3 đội Việt Nam. Ban tổ chức bốc cho thăm ngẫu nhiên và chia thành 3 bảng
đấu
, ,A B C
mỗi bảng 4 đội. Xác suất để ba đội Việt Nam nằm ở 3 bảng gần nhất với số nào
dưới đây?
A.
11
25
. B.
3
20
. C.
39
100
. D.
29
100
.
Lời giải
Chọn D
Số cách chọn 4 đội cho bảng
A
là
4
12
C
. Khi đó sẽ có
4
8
C
số cách chọn 4 đội cho bảng
B
và số
cách chọn 4 đội cho bảng
C
là
4
4
C
.
Vậy số phần tử của không gian mẫu là:
4 4 4
12 8 4
. .n C C C
.
Đặt
T
là biến cố: “3 đội Việt Nam nằm ở 3 bảng khác nhau”.
Số cách chọn 1 đội Việt Nam và 2 đội nước ngoại cho bảng
A
là
1 3
3 9
.C C
. Với mỗi cách chọn
cho bảng
A
ta có
1 3
2 6
.C C
số cách chọn 1 đội Việt Nam và 2 đội nước ngoại cho bảng
B
. Khi
đó, số cách chọn 1 đội Việt Nam và 2 đội nước ngoại cho bảng
C
là
1 3
1 3
.C C
.
Số phần tử của biến cố
T
là:
1 3 1 3 1 3
3 9 2 6 1 3
. . . .
T
n C C C C C C
.
Xác suất cần tính là
1 3 1 3 1 3
3 9 2 6 1 3
4 4 4
12 8 4
. . . .
16
. . 55
T
T
n
C C C C C C
P
n C C C
.
Câu 7. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Xếp ngẫu nhiên 5 học sinh
, , , ,A B C D E
ngồi
vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi một ghế). Tính xác suất để hai bạn
A
và
B
không
ngồi cạnh nhau.
A.
1
5
. B.
3
5
. C.
2
5
. D.
4
5
.
Lời giải
Chọn B
Số phần tử của không gian mẫu:
5! 120
n
.
Gọi
X
là biến cố “Hai bạn
A
và
B
không ngồi cạnh nhau”.
X
“Hai bạn
A
và
B
ngồi cạnh nhau”
Có 4 vị trí để hai bạn
A
và
B
ngồi cạnh nhau, hai bạn đổi chỗ được một cách xếp mới.
Nên số cách xếp để hai bạn
A
và
B
ngồi cạnh nhau là
4.2!.3! 48
Xác suất của biến cố
X
là:
48 2
120 5
n X
P X
n
Vây xác suất của biến cố
X
là:
3
1
5
P X P X
Câu 8. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Hai bạn A và B mỗi bạn viết ngẫu nhiên một số
tự nhiên gồm ba chữ số đôi một khác nhau. Xác suất để các chữ số có mặt ở hai số bạn A và B
viết giống nhau bằng
A.
31
2916
. B.
1
648
. C.
1
108
. D.
25
2916
Lời giải
Chọn D
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mỗi bạn có
2
9
9.A
cách viết nên số phần tử của không gian mẫu là
2
2
9
9.
n A
.
Ta tìm cách viết mà các chữ số các chữ số có mặt trong hai số mà bạn A và B viết giống nhau
Bạn A có tất cả
2
9
9.A
cách viết, trong đó
3
9
A
cách viết mà số không gồm chữ số
0
và có
2 3
9 9
9.
A A
cách viết mà số có chữ số 0.
TH1: Nếu A viết số không gồm chữ số
0
có
3
9
A
cách, lúc này B có
3!
cách viết.
TH2: Nếu A viết số có chữ số
0
có
2 3
9 9
9.
A A
cách, lúc này B có
4
cách viết.
Vậy có
3 2 3
9 9 9
.3! 9. .4
A A A
cách viết thỏa mãn.
Xác suất cần tính bằng
3 2 3
9 9 9
2
2
9
.3! 9. .4
25
2916
A A A
A
.
Câu 9. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Một nhóm gồm 10 học sinh trong đó có
7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao
động. Tinh xác suất để trong 3 học sinh được chọn có ít nhất 1 học sinh nữ.
A.
4
9
. B.
17
24
. C.
17
48
. D.
2
3
.
Lời giải
Chọn B
Ta có
3
10
120.
n C
Đặt
A
”3 học sinh được chọn có ít nhất 1 nữ”
A
”3 học sinh được chọn không có nữ”
Khi đó
3
7
35
n A C
7
24
n A
p A
n
Vậy
17
1 .
24
p A p A
Câu 10. (Chuyên Thái Bình - 2020) Có tất cả bao nhiêu số tự nhiên gồm
6
chữ số đôi một khác nhau
trong đó có đúng
3
chữ số chẵn
A.
72000
. B.
64800
. C.
. D.
60000
.
Lời giải
Chọn B
TH1:
3
chữ số chẵn được chọn khác chữ số
0
Chọn
3
chữ số chẵn khác chữ số
0
là
3
4
C
Chọn
3
chữ số lẻ là
3
5
C
Số tự nhiên gồm
6
chữ số đôi một khác nhau lập từ các số đã chọn là
3 3
4 5
. .6! 28800
C C
.
TH3:
3
chữ số chẵn được chọn có
1
chữ số là chữ số
0
Chọn
2
chữ số chẵn khác chữ số
0
là
2
4
C
Chọn
3
chữ số lẻ là
3
5
C
Số tự nhiên gồm
6
chữ số đôi một khác nhau lập từ các số đã chọn là
2 3
4 5
. . 6! 5! 36000
C C
.
Số các số tự nhiên thỏa mãn là
28800 36000 64800
.
Câu 11. (Chuyên Bắc Ninh - 2020) Cho
S
là tập các số tự nhiên có
8
chữ số. Lấy một số bất kì của
tập
S
. Tính xác suất để lấy được số lẻ và chia hết cho
9
.
A.
3
8
. B.
1
9
. C.
2
9
. D.
1
18
.
Lời giải
Chọn D
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Số phần tử của không gian mẫu là
7
9.10
n
.
Gọi
A
là biến cố: “lấy được số lẻ và chia hết cho
9
”.
+ Dãy các số lẻ có 8 chữ số và chia hết cho 9 là 10000017; 10000035; 10000053;.; 99999999.
+ Dãy số trên là 1 cấp số cộng với số hạng đầu
1
10000017
u
, số hạng cuối
99999999
n
u
và
công sai
18
d
, suy ra số phần tử của dãy số là
6
99999999 10000017
1 5000000 5.10
18
Do đó
6
5.10
n A
.
Vậy xác suất của biến cố
A
là
6
7
5.10 1
9.10 18
n A
P A
n
.
Câu 12. (Chuyên Bến Tre - 2020) Đội học sinh giỏi trường trung học phổ thông chuyên bến tre gồm
có 8 học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 8 học sinh.
Xác suất để trong 8 học sinh được chọn có đủ 3 khối là
A.
71131
75582
. B.
35582
3791
. C.
143
153
. D.
71128
75582
.
Lời giải
Chọn D
Số phần tử không gian mẫu:
8
19
75582
n C
.
Gọi
A
là biến cố:” trong 8 học sinh được chọn có đủ 3 khối”.
Ta có:
8 8 8 8 8
19 14 13 11 8
21128
n C C C C C
.
71128
75582
P A
.
Câu 13. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho tập
1,2,3,4,5,6
A
. Gọi
S
là tập hợp các
tam giác có độ dài ba cạnh là các phần tử của
A
. Chọn ngẫu nhiên một phần tử thuộc
S
. Xác
suất để phần tử được chọn là một tam giác cân bằng.
A.
6
34
. B.
19
34
. C.
27
34
. D.
7
34
.
Lời giải
Chọn C
Tập các bộ ba số khác nhau có giá trị bằng số đo 3 cạnh là:
2;3;4 , 2;4;5 , 2;5;6 , 3;4;5 , 3;4;6 , 3;5;6 , 4;5;6
có 7 tam giác không cân.
Xét các tam giác cân có cạnh đáy bằng
a
, cạnh bên bằng
b
2
b a
. Ta xét các trường hợp
1 1b a
: 1 tam giác cân.
2 1;2;3
b a
: 3 tam giác cân.
3 1;2;3;4;5
b a
: 5 tam giác cân.
4;5;6 1;2;3;4;5;6
b a
: có 18 tam giác cân.
Vậy ta có
7 1 3 5 18 34
n
. Gọi
A
là biến cố:” để phần tử được chọn là một tam
giác cân”, suy ra
1 3 5 18 27
n A
.
Suy ra
27
34
n A
p A
n
.
Câu 14. (Chuyên Hùng Vương - Gia Lai - 2020) Cho một đa giác đều 18 đỉnh nội tiếp trong một
đường tròn tâm
O
. Gọi
X
là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác
trên. Tính xác suất
P
để chọn được một tam giác từ tập
X
là tam giác cân nhưng không phải
tam giác đều.
A.
144
136
P
. B.
7
816
P
. C.
23
136
P
. D.
21
136
P
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Số phần tử của không gian mẫu là
3
18
( )
n X C
.
Ký hiệu đa giác là
1 2 18
...A A A
nội tiếp đường tròn
( )O
, xét đường kính
1 10
A A
khi đó số tam giác
cân có đỉnh cân là
1
A
hoặc
10
A
là
2x8 16
(tam giác cân); Mà có tất cả là 9 đường kính do vậy
số tam giác cân có các đỉnh là đỉnh của đa giác là
9x16 144
(tam giác cân).
Ta lại có số tam giác đều có các đỉnh là đỉnh của đa giác đều 18 đỉnh là
6
.
Vậy xác suất
P
để chọn được một tam giác từ tập
X
là tam giác cân nhưng không phải tam
giác đều là
3
18
144 6 23
136
P
C
.
Câu 15. (Chuyên Lào Cai - 2020) Chọn ngẫu nhiên bốn số tự nhiên khác nhau từ
70
số nguyên dương
đầu tiên. Tính xác suất để bốn số được chọn lập thành một cấp số nhân có công bội nguyên.
A.
12
916895
. B.
11
916895
. C.
10
916895
. D.
9
916895
.
Lời giải
Chọn B
Xét phép thử “Chọn ngẫu nhiên bốn số tự nhiên khác nhau từ
70
số nguyên dương đầu tiên”.
Khi đó
4
70
916895
n C
.
Xét biến cố
A
: “Bốn số được chọn lập thành một cấp số nhân có công bội nguyên”.
Ta gọi bốn số đó lần lượt là
2 3
, , ,a aq aq aq
. Theo giả thiết
3 3
70 70 4
aq q q
.
Vì bốn số khác nhau và đều dương nên ta có
0 1 2;3;4
q q
.
TH1.
2 8 70 8q a a
. Khi đó có 8 bộ số thỏa mãn.
TH2.
3 27 70 2q a a
. Khi đó có 2 bộ số thỏa mãn.
TH3.
4 64 70 1q a a
. Khi đó có 1 bộ số thỏa mãn.
Vậy
11
11
916895
n A P A
.
Câu 16. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có 6 học sinh gồm 2 học sinh lớp A, 2 học
sinh lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm
bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C.
A.
1
120
. B.
1
3
. C.
1
30
. D.
1
15
.
Lời giải
Chọn D
Xét phép thử: Xếp ngẫu nhiên 6 học sinh của 3 lớp thành một hàng ngang, ta có:
6!
n
Gọi D là biến cố: nhóm bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3
lớp A, B, C.
Ta thấy rằng để 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C
thì các học sinh của cùng 1 lớp phải đc xếp vào các vị trí
1;4 , 2;5 , 3;6
.
Xếp 2 học sinh lớp A vào vị trí (1; 4) có 2 cách, xếp 2 học sinh lớp B vào vị trí (2; 5) có 2 cách,
xếp 2 học sinh lớp C vào vị trí (3; 6) có 2 cách và có 3! cách để hoán vị vị trí của các nhóm học
sinh theo lớp.
Suy ra
3!.2.2.2 48
n D
.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Vậy xác suất cần tìm là:
48 1
720 15
n D
P D
n
.
Câu 17. (Chuyên Sơn La - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6
học sinh gồm 3 nam 3 nữ
ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học
sinh nam đều ngồi đối diện với một học sinh nữ bằng
A.
1
10
. B.
3
5
. C.
1
20
D.
2
5
.
Lời giải
Chọn D
Sắp 6 học sinh vào 6 cái ghế có
6!
cách.
Suy ra
6!n
.
Đánh số thự tự 6 cái ghế như hình bên dưới
Gọi
A
là biến cố: “Nam nữ ngồi đối diện”.
Học sinh nam thứ nhất có 6 cách chọn một vị trí ngồi.
Học sinh nam thứ hai có 4 cách chọn một vị trị ngồi (trừ vị trí đối diện với người nam thứ
nhất).
Học sinh nam thứ ba có hai cách chọn một vị trí ngồi (trừ hai vị trí đối diện với hai nam thứ
nhất và thứ hai).
Xếp ba học sinh nữ vào ba vị trí còn lại có
3!
cách.
6.4.2.3!n A
6.4.2.3! 2
6! 5
P A
.
Câu 18. (Sở Phú Thọ - 2020) Cho đa giác đều
H
có 30 đỉnh. Lấy tùy ý 3 đỉnh của
H
. Xác suất
để 3 đỉnh lấy được tạo thành một tam giác tù bằng
A.
39
140
. B.
39
58
. C.
45
58
. D.
39
280
.
Lời giải
Chọn B
Chọn ngẫu nhiên 3 đỉnh có
3
30
C
.
Gọi
T
là đường tròn ngoại tiếp đa giác
H
.
Giả sử chọn được một tam giác tù
ABC
với góc
A
nhọn,
B
tù,
C
nhọn.
Chọn 1 đỉnh bất kì làm đỉnh
A
có 30 cách. Kẻ đường kính của đường tròn
T
đi qua đỉnh vừa
chọn chia đường tròn
T
thành hai phần.(Bên trái và bên phải).
Để tạo thành một tam giác tù thì hai đỉnh còn lại cùng nằm bên trái hoặc cùng nằm bên phải.
Hai đỉnh cùng nằm bên trái có
2
14
C
cách.
Hai đỉnh cùng nằm bên phải có
2
14
C
cách.
Vì trong mỗi tam giác vai trò của đỉnh
A
và
C
như nhau nên số tam giác tù tạo thành là:
2 2
14 14
30
2730
2
C C
.
Xác suất cần tìm là
3
30
2730 39
58
P
C
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. (Sở Hà Tĩnh - 2020) Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10
, lấy
ngẫu nhiên
5
quả cầu. Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho
3
bằng
A.
5
12
. B.
7
12
. C.
1
12
. D.
11
12
.
Lời giải
Chọn D
Không gian mẫu của phép thử là
5
10
252
n C
.
Gọi
A
là biến cố để “tích các số ghi trên
5
quả cầu đó chia hết cho
3
”.
Các quả cầu có số thứ tự chia hết cho
3
gồm các quả có số thứ tự
3
,
6
,
9
.
Do vậy để tích các số ghi trên
5
quả cầu đó chia hết cho
3
thì 5 quả đó phải chứa ít nhất một
quả có số thứ tự
3
,
6
,
9
.
Suy ra
A
là biến cố để “tích các số ghi trên
5
quả cầu đó không chia hết cho
3
”.
Số phần tử của
A
là cách lấy
5
quả từ tập hợp gồm các phần tử
1;2;4;5;7;8;10
.
Vậy ta có
5
7
21 1
21
252 12
n A
n A C P A
n
.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho
3
là
1 11
1 1
12 12
P A P A
.
Câu 20. (Sở Bắc Ninh - 2020) Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau.
Chọn ngẫu nhiên một số thuộc A. Xác suất để số tự nhiên được chọn chia hết cho 25 bằng
A.
43
.
324
B.
1
.
27
C.
11
.
324
D.
17
.
81
Lời giải
Chọn C
Ta có
7
9
( ) 9.A .
n
Gọi a là số tự nhiên thuộc tập A.
Ta có
7 6 5 4 3 2
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
.10 .10 .10 .10 .10 .10 .10
a a a a a a a a a a a a a a a a a
.
Do đó,
7 8
25 (10 ) 25
a a a
trong đó
8
a
hoặc
8
a
. Suy ra
7 8
a a
là một trong các số
sau:
50;25;75
.
Th1: Nếu
7 8
50
a a
thì có
6
8
A
cách chọn các chữ số còn lại.
Th2: Nếu
7 8
25
a a
hoặc
7 8
75
a a
thì có
5
7
7.A
cách chọn các chữ số còn lại.
Vậy xác suất cần tìm là
6 5
8 7
7
9
2.7.
11
324
9.
A A
A
.
Câu 21. (Sở Yên Bái - 2020) Gọi S là tập tất cả các số tự nhiên có ba chữ số đôi một khác nhau được
lập từ các chữ số
0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia
hết cho 6.
A.
13
60
. B.
2
9
. C.
17
45
. D.
11
45
.
Lời giải
Chọn A
Gọi số tự nhiên có ba chữ số đôi một khác nhau thỏa mãn bài toán có dạng
abc
(
0
a
)
Theo bài ra: Vì
abc
chia hết cho 6 nên
abc
phải là số chẵn.
Như vậy, c có 4 cách chọn.
Trường hợp 1: c = 0
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Khi đó, (a;b) là hoán vị của bộ số (1;2), (1;5), (2;4), (3;6), (4;5)
Mỗi trường hợp có 2 cách sắp xếp
Như vậy có 5.2 = 10 số tự nhiên thỏa mãn bài toán trong trường hợp 1.
Trường hợp 2: c = 2
Khi đó, (a;b) là hoán vị của bộ số (0;1), (0;4), (1;3), (1;6), (3;4), (4;6)
Mỗi trường hợp có chữ số 0 có 1 cách sắp xếp
Mỗi trường hợp không có chữ số 0 có 2 cách sắp xếp
Như vậy, có 2 + 4.2 = 10 số tự nhiên thỏa mãn bài toán trong trường hợp 2.
Trường hợp 3: c = 4
Khi đó, (a;b) là hoán vị của bộ số (0;2), (0;5), (2;3), (2;6), (3;5), (5;6)
Làm tương tự trường hợp 2, có 2 + 4.2 = 10 số tự nhiên thỏa mãn bài toán trong trường hợp 3.
Trường hợp 4: c = 6
Khi đó, (a;b) là hoán vị của bộ số (0;3), (1;2), (1;5), (2;4), (4;5)
Làm tương tự trường hợp 2, trường hợp này có 1 + 4.2 = 9 số tự nhiên thỏa mãn bài toán.
Số phần tử của không gian mẫu:
( ) 6.6.5 180n
Xác suất để chọn được số chia hết cho 6:
10 10 10 9 39 13
180 180 60
P
Câu 22. (Bỉm Sơn - Thanh Hóa - 2020) Trường trung học phổ thông Bỉm Sơn có 23 lớp, trong đó
khối 10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có
một em làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường
chọn ngẫu nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thị xã. Tính xác suất để 9 em được
chọn có đủ cả ba khối?
A. . B. . C. . D. .
Lời giải
Chọn C
Số phần tử của không gian mẫu là: .
Gọi là biến cố “9 em được chọn có đủ cả ba khối”
“9 em được chọn không có đủ ba khối”
Vì mỗi khối số bí thư đều nhỏ hơn 9 nên có các khả năng sau:
TH1: Chỉ có học sinh ở khối 10 và 11. Có cách.
TH2: Chỉ có học sinh ở khối 11 và 12. Có cách.
TH3: Chỉ có học sinh ở khối 10 và 12. Có cách.
Số phần tử của biến cố là:
Xác suất của biến cố là: .
Xác suất của biến cố là: .
Câu 23. (Đặng Thúc Hứa - Nghệ An - 2020) Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp
mặt
10
em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp
số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có
5
ghế và mỗi ghế
chỉ được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau
là bằng nhau.
A.
1
954
. B.
1
252
. C.
1
945
. D.
1
126
.
Lời giải
Chọn C
7345
7429
7012
7429
7234
7429
7123
7429
9
23
817190
n C
X
X
9
16
C
9
15
C
9
15
C
X
9 9 9
16 15 15
21450
n X C C C
X
21450 195
817190 7429
P X
X
7234
1
7429
P X P X
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số phần tử của không gian mẫu là số cách sắp xếp 10 học sinh vào hai dãy bàn đối diện
10!n
.
Gọi
A
là biến cố “tổng các số thứ tự của hai e ngồi đối diện là bằng nhau”.
Đánh số thứ tự của các em từ 1 đến 10.
Để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau phải chia thành 5 cặp đối
diện
1;10 , 2;9 , 3;8 , 4;7 , 5;6
.
Ta xếp dãy 1, dãy 2 chỉ có một cách chọn.
Vị trí
1
A có
10
cách chọn 1 học sinh,
1
B có 1 cách chọn.
Vị trí
2
A có
8
cách chọn 1 học sinh,
2
B có 1 cách chọn.
Vị trí
3
A có
6
cách chọn 1 học sinh,
3
B có 1 cách chọn.
Vị trí
4
A có
4
cách chọn 1 học sinh,
4
B có 1 cách chọn.
Vị trí
5
A có
2
cách chọn 1 học sinh,
5
B có 1 cách chọn.
Suy ra số phần tử của biến cố
A
là
10.8.6.4.2n A
Vậy xác suất để biến cố
A
xảy ra là:
10.8.6.4.2 1
10! 945
n A
P A
n
.
Câu 24. (Đô Lương 4 - Nghệ An - 2020) Người ta muốn chia tập hợp 16 học sinh gồm 3 học sinh lớp
12A, 5 học sinh lớp 12B và 8 học sinh lớp 12C thành hai nhóm, mỗi nhóm có 8 học sinh. Xác
suất sao cho ở mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B
là
A.
42
143
. B.
84
143
. C.
356
1287
. D.
56
143
.
Lời giải
Chọn B
Gọi
A
là biến cố mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp
12B.
Chọn ra 8 học sinh từ 16 học sinh được 1 nhóm, 8 học sinh còn lại tạo thành nhóm thứ 2. Vì ở
đây không phân biệt thứ tự các nhóm nên ta có
8
16
2!
C
n
.
Mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B nên 1 nhóm
có 1 hoặc 2 học sinh lớp 12A và có 2 hoặc 3 học sinh lớp 12B. Do đó
1 2 5 1 3 4
3 5 8 3 5 8
. . . .
2!
C C C C C C
n A
.
Vậy
84
143
n A
P A
n
.
Câu 25. (Hậu Lộc 2 - Thanh Hóa - 2020) Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15. Chọn
ngẫu nhiên 6 tấm thẻ trong hộp. Xác suất để tổng các số ghi trên 6 tấm thẻ được chọn là một số
lẻ bằng.
A.
71
143
. B.
56
715
. C.
72
143
. D.
56
143
.
Lời giải
Chọn C
Số phần tử của không gian mẫu của phép thử:
6
15
5005n C
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Chia 15 tấm thẻ thành 2 tập hợp nhỏ gồm:
+ Tập các tấm ghi số lẻ:
1;3;5;7;9;11;13;15 8
số
+ Tập các tấm ghi số chẵn:
2;4;6;8;10;12;14 7
số
Các trường hợp thuận lợi cho biến cố:
TH1. 1 tấm số lẻ: 5 tấm số chẵn
- Số phần tử:
1 5
8 7
. 168C C
TH2. 3 tấm số lẻ: 3 tấm số chẵn
- Số phần tử:
3 3
8 7
. 1960C C
TH3. 5 tấm số lẻ: 1 tấm số chẵn
- Số phần tử:
5 1
8 7
. 392C C
Tổng số phần tử thuận lợi của biến cố là:
168 1960 392 2520
Vậy xác suất của biến cố là:
2520 72
5005 143
P
.
Câu 26. (Kim Liên - Hà Nội - 2020) Một số điện thoại có bảy chữ số, trong đó chữ số đầu tiên là
8
. Số
điện thoại này được gọi là
may mắn nếu bốn chữ số đầu là chữ số chẵn phân biệt và ba chữ số còn lại là lẻ, đồng thời hai
chữ số
0
và
9
không đứng liền nhau. Tính xác suất để một người khi lắp điện thoại ngẫu nhiên
được số điện thoại may mắn.
A.
7
5100
( )
10
P A
. B.
7
2850
( )
10
P A
. C.
6
5100
( )
10
P A
. D.
6
2850
( )
10
P A
.
Lời giải
Chọn D
Số phần tử của không gian mẫu:
6
( ) 10n .
Gọi
A
là biến cố: “Số điện thoại may mắn”. Có
2
trường hợp xảy ra:
TH1: Số điện thoại may mắn dạng:
2 3 5 6 7
8 0a a a a a
Chọn
2 3
,a a từ
2;4;6
có
2
3
6A
cách.
Chọn
5
a từ
1;3;5;7
có
4
cách.
Chọn
6 7
,a a từ
1;3;5;7;9
có
5.5 25
cách.
Các số may mắn
6.4.125 600
số.
TH2: Số điện thoại may mắn dạng:
2 3 4 5 6 7
8a a a a a a
trong đó
4
0a .
Chọn
4
a từ
2;4;6
có 3 cách.
Chọn
2 3
,a a từ
0;2;4;6
có
2
3
6A
cách (do phải khác
4
a ).
Chọn
5 6 7
, ,a a a từ có
3
5 125
cách.
Các số may mắn
3.6.125 2250
số.
( ) 600 2250 2850n A
.
6
2850
( )
10
P A
.
Câu 27. (Lê Lai - Thanh Hóa - 2020) Cho tập hợp . Gọi là tập hợp tất cả các số
tự nhiên có ít nhất chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc
tập . Chọn ngẫu nhiên một số từ tập , tính xác xuất để số được chọn có tổng các chữ số
bằng .
A. B. C. D.
Lời giải
1; 2; 3; 4; 5
A
S
3
A
S
10
1
.
30
3
.
25
22
.
25
2
.
25
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Vì S là tập hợp tất cả các số tự nhiên có ít nhất
3
chữ số, các chữ số đôi một khác nhau được
lập thành từ các chữ số thuộc tập
A
nên ta tính số phần tử thuộc tập
S
như sau:
Số các số thuộc
S
có
3
chữ số là
3
5
A
.
Số các số thuộc
S
có
4
chữ số là
4
5
A
.
Số các số thuộc
S
có
5
chữ số là
5
5
A
.
Suy ra số phần tử của tập
S
là
3 4 5
5 5 5
300
A A A
.
Số phần tử của không gian mẫu là
1
300
300
n C
Gọi
X
là biến cố
''
Số được chọn có tổng các chữ số bằng
10
''
. Các tập con của
A
có tổng số
phần tử bằng
10
là
1
1; 2; 3; 4
A
,
2
2; 3; 5
A
,
3
1; 4; 5
A
.
● Từ
1
A
lập được các số thuộc
S
là
4!
.
● Từ
2
A
lập được các số thuộc
S
là
3!
.
● Từ
3
A
lập được các số thuộc
S
là
3!
.
Suy ra số phần tử của biến cố
X
là
4! 3! 3! 36.
X
n
Vậy xác suất cần tính
36 3
.
300 25
X
n
P X
n
Câu 28. (Liên trường Nghệ An - 2020) Gọi
S
là tập hợp các số tự nhiên có
4
chữ số đôi một khác
nhau lập thành từ các chữ số
0,1,2,3,4,5,6,7
. Chọn ngẫu nhiên một số từ tập
S
. Tính xác
suất để số được chọn có đúng
2
chữ số chẵn.
A.
24
35
. B.
144
245
. C.
72
245
. D.
18
35
.
Lời giải
Chọn D
Có
3
7
7.A
số có
4
chữ số khác nhau được lập từ tập
S
.
Xét các số có đúng hai chữ số chẵn, hai chữ số lẻ.
+ TH1: Số đó có chữ số
0
Có
1
3
C
cách chọn thêm chữ số chẵn khác và
2
4
C
cách chọn
2
chữ số lẻ; có
3.3!
cách sắp xếp
4
chữ số được chọn, suy ra có
1 2
3 4
. .3.3! 324
C C
số thỏa mãn.
+ TH2: Số đó không có chữ số
0
Có
2
3
C
cách chọn
2
chữ số chẵn,
2
4
C
cách chọn
2
chữ số lẻ; có
4!
cách sắp xếp
4
chữ số đã
chọn, suy ra có
2 2
3 4
. .4! 432
C C
số thỏa mãn.
Vậy có
324 432 756
số có đúng hai chữ số chẵn thỏa mãn.
Xác suất cần tìm là
3
7
756 18
7. 35
P
A
.
Câu 29. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tập
1;2;3;...;19;20
S
gồm 20 số tự nhiên từ 1 đến
20. Lấy ngẫu nhiên ba số thuộc
.S
Xác suất để ba số lấy được lập thành một cấp số cộng là
A.
7
38
. B.
5
38
. C.
3
38
. D.
1
114
.
Lời giải
Chọn C
Số phần tử không gian mẫu
3
20
n C
.
Gọi
, ,a b c
là ba số lấy ra theo thứ tự đó lập thành cấp số cộng, nên
2
a c
b
. Do đó
a
và
c
cùng chẵn hoặc cùng lẻ và hơn kém nhau ít nhất 2 đơn vị.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Số cách chọn bộ
; ;a b c
theo thứ tự đó lập thành cấp số cộng bằng số cặp
;a c
cùng chẵn
hoặc cùng lẻ, số cách chọn là
2
10
2.C
. Vậy xác suất cần tính là
2
10
3
20
2
3
38
C
P
C
.
Câu 30. (Nguyễn Huệ - Phú Yên - 2020) Một bàn cờ vua gồm
8 8
ô vuông, mỗi ô có cạnh bằng 1
đơn vị. Một ô vừa là hình vuông hay hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên
một hình chữ nhật trên bàn cờ. Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn
4 đơn vị bằng
A.
5
216
. B.
17
108
. C.
51
196
. D.
29
216
.
Lời giải
Chọn A
Bàn cờ
8 8
cần 9 đoạn thẳng nằm ngang và 9 đoạn thẳng dọc. Ta coi bàn cờ vua được xác
định bởi các đường thẳng
0, 1,..., 8x x x
và
0, 1,..., 8y y y
.
Mỗi hình chữ nhật được tạo thành từ hai đường thẳng
x
và hai đường thẳng
y
nên có
2 2
8 8
.C C
hình chữ nhật hay không gian mẫu là
2 2
9 9
. 1296n C C
.
Gọi
A
là biến cố hình được chọn là hình vuông có cạnh
a
lớn hơn 4.
Trường hợp 1:
5a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 5 đơn vị và
hai đường thẳng
y
cách nhau 5 đơn vị có
4.4 16
cách chọn.
Trường hợp 2:
6a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 6 đơn vị và
hai đường thẳng
y
cách nhau 6 đơn vị có
3.3 9
cách chọn.
Trường hợp 3:
7a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 7 đơn vị và
hai đường thẳng
y
cách nhau 7 đơn vị có
2.2 4
cách chọn.
Trường hợp 3:
8a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 8 đơn vị và
hai đường thẳng
y
cách nhau 8 đơn vị có
1.1 1
cách chọn.
Suy ra
16 9 4 1 30n A
.
Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị là
30 5
1296 216
n A
P A
n
.
Câu 31. (Tiên Du - Bắc Ninh - 2020) Gọi
M
là tập hợp các số tự nhiên có ba chữ số lập được từ các
chữ số 0, 1, 2, 3, 4, 5, 6, 7. Lấy ngẫu nhiên đồng thời 2 số từ tập
.M
Xác suất để cả 2 số lấy
được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là
A.
8
21
. B.
5
16
. C.
296
2051
. D.
695
7152
.
Lời giải
Chọn D
Số tự nhiên có ba chữ số có dạng
.abc
Số các số tự nhiên có ba chữ số được lập từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là
7.8.8 448
số.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số phần tử không gian mẫu
2
448
.C
Gọi
A
là biến cố: “ 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và
hàng đơn vị”.
Trường hợp
0
b
có
7.7 49
số.
Trường hợp
1b
có
6.6 36
số.
Trường hợp
2
b
có
5.5. 25
số.
Trường hợp
3
b
có
4.4 16
số.
Trường hợp
4
b
có
3.3 9
số.
Trường hợp
5
b
có
2.2 4
số.
Trường hợp
6
b
có
1.1 1
số.
Vậy có
49 36 25 16 9 4 1 140
số thỏa mãn chữ số hàng chục nhỏ hơn chữ số hàng
đơn vị và hàng trăm.
2
140
.
A
C
Vậy
695
.
7152
A
P A
Câu 32. (Hải Hậu - Nam Định - 2020) Một hộp có chứa
5
viên bi đỏ,
3
viên bi xanh và
n
viên bi vàng
( các viên bi kích thước như nhau,
n
là số nguyên dương). Lấy ngẫu nhiên
3
viên bi từ hộp.
Biết xác suất để trong ba viên vi lấy được có đủ
3
màu là
45
182
. Tính xác suất
P
để trong
3
viên bi lấy được có nhiều nhất hai viên bi đỏ.
A.
135
364
P
. B.
177
182
P
. C.
45
182
P
. D.
31
56
P
.
Lời giải
Chọn B
Số cách lấy 3 viên bi bất kì từ hộp là:
3
8 n
C
.
Số cách lấy 3 viên đủ 3 màu là:
1 1 1
5 3
. . 15
n
C C C n
.
Vì xác suất để trong ba viên vi lấy được có đủ
3
màu là
45
182
3
8
15 45
182
n
n
C
6
n
.
có 5 viên bi đỏ, 3 viên bi xanh và
6
viên bi vàng.
Số cách lấy 3 bi bất kì là
3
14
C
.
Trường hợp 1: 3 bi lấy ra không có bi đỏ, khi đó số cách lấy là
3
9
C
.
Trường hợp 2: 3 bi lấy ra có 1 bi đỏ, khi đó số cách lấy là
1 2
5 9
.C C
Trường hợp 2: 3 bi lấy ra có 2 bi đỏ, khi đó số cách lấy là
2 1
5 9
.C C
.
Vậy xác suất để trong
3
viên bi lấy được có nhiều nhất hai viên bi đỏ là
177
182
P
Câu 33. (Kìm Thành - Hải Dương - 2020) Gọi
S
là tập hợp tất cả các số tự nhiên gồm
9
chữ số đôi
một khác nhau. Chọn ngẫu nhiên một số từ
S
. Tính xác suất để được chọn có đúng
4
chữ số
lẻ và chữ số
0
đứng giữa hai chữ số lẻ. (Các chữ số liền trước và liền sau của chữ số
0
là các
chữ số lẻ).
A.
5
648
. B.
5
27
. C.
5
54
. D.
20
189
.
Lời giải
Chọn C
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Xem nhóm 3 chữ số gồm số 0 ở giữa 2 chữ số lẻ là một
Chọn 2 chữ số lẻ và sắp xếp có
2
5
A
cách.
Chọn thêm 2 chữ số lẻ có
2
3
C
cách.
Chọn 4 chữ số chẵn có
4
4
C
cách.
Sắp xếp có 7! cách.
Như vậy có
2 2 4
5 3 4
. . .7! 302400
A C C
số thỏa mãn yêu cầu bài toán.
Xác suất cần tìm
8
9
302400 5
9. 54
A
.
Câu 34. (Trường VINSCHOOL - 2020) Có
6
học sinh nam và
4
học sinh nữ xếp thành hàng ngang.
Xác suất để có đúng hai bạn nữ đứng cạnh nhau bằng
A.
1
24
. B.
1
2
. C.
14
17
. D.
7
13
.
Lời giải
Chọn B
Chọn 2 trong 4 bạn nữ và xếp vào 2 vị trí cạnh nhau có
2
4
A
(cách).
Hai bạn nữ được chọn và đã được xếp chỗ đứng cạnh nhau kết hợp với 2 bạn nữ còn lại xem là
,A
,B
C
.
Lấy 6 bạn nam làm vách ngăn, số cách tạo vách ngăn là
6!
(cách).
Có 6 vách ngăn sẽ có 7 khoảng trống, sắp xếp
,A
,B
C
vào 7 khoảng trống có
3
7
A
(cách).
Từ đó suy ra số cách xếp
6
học sinh nam và
4
học sinh nữ thành hàng ngang mà có đúng hai
bạn nữ đứng cạnh nhau là:
2
4
A
.
6!
.
3
7
A
Số cách xếp
6
học sinh nam và
4
học sinh nữ xếp thành hàng ngang tùy ý là:
10!
.
Vậy xác suất để xếp
6
học sinh nam và
4
học sinh nữ thành hàng ngang mà có đúng hai bạn
nữ đứng cạnh nhau là:
2 3
4 7
.6!.
1
10! 2
A A
.
Câu 35. (Thanh Chương 1 - Nghệ An - 2020) Gọi
S
là tập hợp tất cả các số tự nhiên có 5 chữ số mà
các chữ số đều khác 0. Lấy ngẫu nhiên một số từ
S
. Xác suất để lấy được số chỉ có mặt 3 chữ
số gần với số nào nhất trong các số sau?
A.
0,34
. B.
0,36
. C.
0,21
. D.
0,13
.
Lời giải
Chọn C
Số phần tử của không gian mẫu là
5
9
n
.
Gọi
A
là biến cố số được chọn chỉ có mặt 3 chữ số:
Chọn 3 chữ số khác nhau ta có
3
9
C
cách
Trường hợp 1: Có 1 chữ số bị lặp 3 lần, 2 chữ số khác xuất hiện 1 lần
1
3
5!
.
3!
C
cách
Trường hợp 2: Có 2 chữ số xuất hiện 2 lần, 1 chữ số xuất hiện 1 lần
2
3
5!
.
2!2!
C
cách
3 1 2
9 3 3
5! 5!
12600
3! 2!2!
n A C C C
0,213
P A
.
Câu 36. (Tiên Lãng - Hải Phòng - 2020) Một xưởng sản xuất thực phẩm gồm 4 kỹ sư chế biến thực
phẩm, 3 kĩ thuật viên và 13 công nhân. Để đảm bảo sản xuất thực phẩm chống dịch Covid 19,
xưởng cần chia thành 3 ca sản xuất theo thời gian liên tiếp nhau sao cho ca I có 6 người và 2 ca
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
còn lại mỗi ca có 7 người. Tính xác suất sao cho mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế
biến thực phẩm.
A.
440
3320
. B.
441
3230
. C.
41
230
. D.
401
3320
.
Lời giải
Chọn B
Ca I có 6 người, ca II có 6 người và ca III có 6 người nên số phần tử của không gian mẫu là:
6 7 7
20 14 7
. . 133024320
n C C C
Gọi biến cố
X
“mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm”.
Để mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm, ta có các trường hợp:
TH1: Ca I có 1 kĩ thuật viên, 2 kĩ sư và 3 công nhân.
Ca II có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Ca III có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Số cách chọn cho trường hợp này là:
1 2 3 1 1 5 1 1 5
3 4 13 2 2 10 1 1 5
. . . . . . . . 5189184
C C C C C C C C C
.
TH2: Ca I có 1 kĩ thuật viên, 1 kĩ sư và 4 công nhân.
Ca II có 1 kĩ thuật viên, 2 kĩ sư và 4 công nhân.
Ca III có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Số cách chọn cho trường hợp này là:
1 1 4 1 2 4 1 1 5
3 4 13 2 3 9 1 1 5
. . . . . . . . 6486480
C C C C C C C C C
.
TH2: Ca I có 1 kĩ thuật viên, 1 kĩ sư và 4 công nhân.
Ca II có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Ca III có 1 kĩ thuật viên, 2 kĩ sư và 4 công nhân.
Số cách chọn cho trường hợp này là:
1 1 4 1 1 5 1 2 4
3 4 13 2 3 9 1 2 4
. . . . . . . . 6486480
C C C C C C C C C
.
Số phần tử của biến cố
X
là:
5189184 6486480 6486480 18162144
n X
.
Xác suất của biến cố
X
là:
18162144 441
133024320 3230
P X
.
Câu 37. (Trần Phú - Quảng Ninh - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp
ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một
học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A.
1
3
. B.
1
30
. C.
8
63
. D.
8
37
.
Lời giải
Chọn C
Số cách xếp 10 học sinh vào 10 ghế là
10!
.
Ta có
10!
n
.
Để xếp chỗ ngồi cho 10 học sinh mà mỗi học sinh nam đều ngồi đối diện với một học sinh nữ
ta làm như sau:
Xếp chỗ ngồi cho bạn nam thứ nhất có 10 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ hai có 8 cách xếp vì trừ đi ghế ngồi đối diện với bạn nam đầu
tiên.
Tương tự:
Xếp chỗ ngồi cho bạn nam thứ ba có 6 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ tư có 4 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ năm có 2 cách xếp.
Xếp chỗ ngồi cho 5 bạn nữ vào 5 ghế còn lại có
5!
.
Theo quy tắc nhân, ta có
10.8.6.4.2.5!
n A
460800
.
Do vậy xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ là:
460800
10!
p
8
63
.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 38. (Đại Học Hà Tĩnh - 2020) Cho đa giác đều 12 đỉnh nội tiếp đường tròn tâm A. Chọn ngẫu
nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không
có cạnh nào là cạnh của đa giác đã cho.
A.
2
5
. B.
31
55
. C.
28
55
. D.
52
55
.
Lời giải
Chọn C
Số tam giác được tạo thành là
3
12
C
.
Số tam giác có chung 1 cạnh với đa giác là
1
8
12C
.
Số tam giác có chung 2 cạnh với đa giác là
12
.
Vậy xác suất để được tam giác không có chung cạnh với đa giác là
2
8
3
12
12 12
28
1
55
C
C
.
Câu 39. (ĐHQG Hà Nội - 2020) Có
12
học sinh gồm
6
nam và
6
nữ ngồi vào hai hàng ghế đối diện
nhau tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là?
A.
1
924
. B.
4
165
. C.
8
165
. D.
16
231
.
Lời giải
Chọn D
Số cách xếp
12
học sinh vào
12
chỗ là
12! 12!
n
Gọi
A
là biến cố “Xếp mỗi một em nam ngồi đối diện với một em nữ”.
Ta có vị trí
1
có
12
cách chọn; vị trí
2
có
6
cách chọn; vị trí
3
có
10
cách chọn;; vị trí
4
có
5
cách chọn.
Nên
16
12.6.10.5.8.4.6.3.4.2.2.1
231
n A
n A P A
n
Câu 40. (Sở Hưng Yên - 2020) Có 50 tấm thẻ đánh số từ 1 đến 50. Rút ngẫu nhiên 3 thẻ. Xác suất để
tổng các số ghi trên thẻ chia hết cho 3 bằng
A.
8
89
. B.
11
171
. C.
769
2450
. D.
409
1225
.
Lời giải
Chọn D
Gọi
là không gian mẫu của phép thử rút ngẫu nhiên 3 thẻ.
Ta có:
3
50
19600
n C
.
Gọi
A
là biến cố “tổng các số ghi trên thẻ chia hết cho 3”.
50 thẻ được chia thành 3 loại gồm:
+ 16 thẻ có số chia hết cho 3 là
{3;6;...; 48}
.
+ 17 thẻ có số chia cho 3 dư 1 là
{1; 4;7;...; 49}
.
+ 17 thẻ có số chia cho 3 dư 2 là
{2;5;8;...;50}
.
Ta xét các trường hợp sau:
TH1: 3 thẻ được chọn cùng một loại có
3 3 3
16 17 17
C C C
cách.
TH2: 3 thẻ được chọn mỗi loại 1 thẻ có
1 1 1
16 17 17
. .C C C
cách.
Do đó
3 3 3 1 1 1
16 17 17 16 17 17
. . 6544
n A C C C C C C
.
1
2
3
4
5
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xác suất để tổng các số ghi trên thẻ chia hết cho 3 bằng:
6544 409
19600 1225
n
P A
n A
.
PHẦN 2. MỘT SỐ BÀI TOÁN KHÁC
Câu 41. (Chuyên Bắc Ninh - 2020) Cho
0, 1
x x
. Tìm số hạng không chứa
x
trong khai triển Niu-
tơn của
20
2
3
3
1 1
1
x x
P
x x
x x
.
A.
. B.
167960
. C.
1600
. D.
125970
.
Lời giải
Chọn D
+) Ta có:
2
3
3 3
3 3
2 2
3 3
3 3
1 1
1 1 1
1 1 1
1
1
1 1
x x x
x x x
x x
x x
x x x x
x x
x x x x
+)
20
20
20
3 3
20
0
1 1
. .
k
k
k
k
P x C x
x x
.
20
20
3
2
20
0
. 1 . .
k
k
k
k
k
C x x
40 5
20
6
20
0
. 1 .
k
k
k
k
C x
+) Số hạng không chứa
x
trong khai triển ứng với
40 5
0 8
6
k
k
.
Vậy số hạng không chứa
x
trong khai triển là
8
8
20
. 1 125970
C
.
Câu 42. (Sở Phú Thọ - 2020) Giả sử
n
là một số nguyên dương thoả mãn
2 3
3 24
n n
C C
. Hệ số của số
hạng chứa
12
x
trong khai triển
2
2
n
x x
x
bằng
A.
12
672x
. B.
12
672x
. C.
672
. D.
672
.
Lời giải
Chọn D
Điều kiện xác định:
*
; 3
n N n
.
Khi đó:
2 3
3 1 1 2
3 ! !
3 24 24 24
2 !2! 3 !3! 2 6
n n
n n n n n
n n
C C
n n
3 2
9
12 11 144 0
3 73
2
n
n n n
n
.
Kết hợp với điều kiện xác định suy ra
9
n
.
Ta có:
9
45 7
9 9
9
2 2
2
9 9
0 0
2 2
. . . 2 .
k
k
k
k
k k
k k
x x C x x C x
x x
.
Số hạng chứa
12
x
trong khai triển ứng với
k
thỏa mãn:
45 7
12 3
2
k
k
.
TÀI
LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Vậy hệ số của
số hạng chứa
12
x
l
à
3
3
9
.
2 672
C
.
C
âu 43. (Sở Bình Phước - 2020) Trên một cái bảng đã ghi sẵn các số tự nhiên từ
1
đế
n
2
020
.
Ta thực
hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai
số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng
còn lại trên bảng là
A
.
4040
. B.
2
041210
. C.
4
082420
. D.
2
020
.
Lờ
i giải
Chọn
B
Với
cách thực hiện công việc như vậy, số cuối cùng còn lại trên bảng sẽ là tổng của tất cả các
số tự nhiên ban đầu đã ghi, tức là tổng các số tự nhiên từ
1
đến
2
020
.
Dễ dàng nhận thấy đây là tổng
20
20
số hạng đầu
tiên của cấp số cộng có số hạng đầu bằng
1
và
công sai bằng
1
.
Vậy, số cuối
cùng còn lại trên bảng là:
2020
1 2020
2041210
2
.
Câu 44. (Yên Lạc 2 - Vĩnh Phúc - 2020) Xác định
n
biế
t rằng hệ số của
n
x
trong
khai triển
2
2
1
2 ...
n
x
x nx
bằng
6n
.
A
.
8
n
. B.
6
n
. C.
n
. D.
5
n
.
Lờ
i giải
Chọn
D
Ta
có:
2
2
2 1 1 2
1
2 ... 1 2 ... 1 1 ... 1
n
n n n n
x
x nx x x n x nx nx n x x x
Suy ra hệ số của
n
x
là:
1
. 1 2. 2 ... 2 .2 1 .1n n n n n n
1
. 1 2. 2 ... 2 . 2 1 . 1
n
n n n n n n n n n
2
2
2 2
2
1. 2. ... 1 . . 1 2 ... 1
n
n n n n n n n n
2
2
2 2
2
1 2 .. 1 2 ... 1
n
n n n n
3
1
(
1)(2 1) 11
2
.
2
6 6
n
n
n
n n n n
n
n
Vậy
3
3
11
6 11 36 5
6
n
n
n n n n n
(Vì
*
n
).
-------------------- HẾT --------------------
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. GÓC
Câu 1. (Chuyên Biên Hòa - Hà Nam - 2020) Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
.
Khi đó
cos ,AB DM
bằng
A.
2
2
. B.
3
6
. C.
1
2
. D.
3
2
.
Câu 2. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp
.S ABCD
có
SA
vuông góc với
mặt phẳng đáy, 3SA a , tứ giác
ABCD
là hình vuông,
2BD a
(minh họa như hình bên).
Góc giữa đường thẳng
SB
và mặt phẳng
SAD
bằng
A.
0
. B.
30
. C.
45
. D.
60
.
Câu 3. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hình chóp
.S ABC
có
SA
vuông góc với mặt
phẳng
3
,
2
a
ABC SA
, tam giác
ABC
đều cạnh bằng
a
(minh họa như hình dưới). Góc tạo
bởi giữa mặt phẳng
SBC
và
ABC
bằng
A.
0
90
. B.
0
30
. C.
0
45
. D.
0
60
.
Câu 4. (Chuyên Thái Bình - 2020) Cho hình chóp tứ giác đều
.S ABCD
có đáy là hình vuông tâm
O
,
cạnh
a
. Gọi
,M N
lần lượt là trung điểm của
SA
và
BC
. Góc giữa đường thẳng
MN
và mặt
phẳng
ABCD
bằng
60
. Tính cos của góc giữa đường thẳng
MN
và mặt phẳng
SBD
.
A.
41
4
. B.
5
5
. C.
2 5
5
. D.
2 41
4
.
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
57 CÂU VD - VDC CHƯƠNG 6. HÌNH HỌC 11
C
B
A
S
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Chuyên Vĩnh Phúc - 2020) Cho hình lăng trụ đứng
.
ABC A B C
có
1
AA AB AC
và
0
120
BAC
. Gọi
I
là trung điểm cạnh
CC
. Côsin góc giữa hai mặt phẳng
ABC
và
AB I
bằng
A.
370
20
. B.
70
10
. C.
30
20
. D.
30
10
.
Câu 6. (ĐHQG Hà Nội - 2020) Cho hình chóp
.
S ABCD
có đáy hình vuông. Cho tam giác
SAB
vuông
tại
S
và góc
SBA
bằng
0
30
. Mặt phẳng
SAB
vuông góc mặt phẳng đáy. Gọi
,M N
là trung
điểm
,AB BC
. Tìm cosin góc tạo bởi hai đường thẳng
,
SM DN
.
A.
2
5
. B.
1
5
. C.
1
3
. D.
2
3
.
Câu 7. (Sở Ninh Bình) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
, độ dài cạnh
2AC a
, các tam giác
,
SAB SCB
lần lượt vuông tại
A
và
C
. Khoảng cách từ
S
đến mặt
phẳng
( )ABC
bằng
a
. Giá trị cosin của góc giữa hai mặt phẳng
( )SAB
và
( )SCB
bằng
A.
2 2
3
. B.
1
3
. C.
2
3
. D.
5
3
.
Câu 8. (Sở Bắc Ninh - 2020) Cho hình chóp
.
S ABCD
có đáy là hình thoi cạnh
0
, 120 ,
a ABC SA
vuông góc với mặt phẳng
.ABCD
Biết góc giữa hai mặt phẳng
SBC
và
SCD
bằng
0
60 ,
khi đó
A.
6
.
4
a
SA
B.
6.
SA a
C.
6
2
a
SA
. D.
3
2
a
SA
.
Câu 9. (Sở Bình Phước - 2020) Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác cân đỉnh
A
.
Biết
3BC a
và
30
o
ABC
, cạnh bên
AA a
. Gọi
M
là điểm thỏa mãn
2 3
CM CC
. Gọi
là góc tạo bởi hai mặt phẳng
ABC
và
AB M
, khi đó
sin
có giá trị bằng
A.
66
22
. B.
. C.
3
22
. D.
418
22
.
Câu 10. (Đô Lương 4 - Nghệ An - 2020) Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, tâm
O
. Gọi
M
và
N
lần lượt là trung điểm của
SA
và
BC
. Biết rằng góc giữa
MN
và
ABCD
bằng
60
, côsin của góc giữa đường thẳng
MN
và mặt phẳng
SBD
bằng:
A.
5
5
. B.
41
41
. C.
2 5
5
. D.
2 41
41
.
Câu 11. (Kim Liên - Hà Nội - 2020) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam
giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
I
là trung điểm của đoạn
AB
.
Khẳng định nào sau đây là sai?
A. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
45
.
B.
SBC
là tam giác vuông.
C.
SI ABCD
.
D. Khoảng cách giữa đường thẳng
DC
và mặt phẳng
SAB
bằng
a
.
Câu 12. (THPT Nguyễn Viết Xuân - 2020) Cho hình lăng trụ đứng
.
ABC A B C
có
, 120
AB AC a BAC
. Gọi
lần lượt là trung điểm của
B C
và
CC
. Biết thể tích
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
khối lăng trụ
.
ABC A B C
bằng
3
3
4
a
. Gọi
là góc giữa mặt phẳng
AMN
và mặt phẳng
ABC
. Khi đó
A.
3
cos
2
. B.
1
cos
2
. C.
13
cos
4
. D.
3
cos
4
.
Câu 13. (Tiên Du - Bắc Ninh - 2020) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
,a
SA
vuông góc với mặt phẳng
ABC
và
.
2
a
SA
Góc giữa mặt phẳng
SBC
và mặt phẳng
ABC
bằng
A.
45
. B.
90
. C.
30
. D.
60
.
Câu 14. (Kìm Thành - Hải Dương - 2020) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
2AB a
,
SA
vuông góc với mặt đáy và góc giữa
SB
và mặt đáy bằng
60
. Gọi
là góc
giữa hai mặt phẳng
SBC
và
ABC
. Giá trị
cos
bằng
A.
15
5
. B.
2
5
. C.
1
7
. D.
2
7
.
PHẦN 2. KHOẢNG CÁCH
Câu 15. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang
vuông tại
A
và
;D
2 ;AB AD a
DC a
. Điểm
I
là trung điểm đoạn
,AD
hai mặt phẳng
SIB
và
SIC
cùng vuông góc với mặt phẳng
ABCD
. Mặt phẳng
SBC
tạo với mặt phẳng
ABCD
một góc
60
. Tính khoảng cách từ
D
đến
SBC
theo
a
.
A.
15
5
a
. B.
9 15
10
a
. C.
2 15
5
a
. D.
9 15
20
a
.
Câu 16. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
, ,A AC a I
là trung điểm
SC
. Hình chiếu vuông góc của
S
lên
ABC
là trung điểm
H
của
BC
. Mặt phẳng
SAB
tạo với
ABC
một góc
60
. Tính khoảng cách từ
I
đến mặt phẳng
SAB
.
A.
3
4
a
. B.
3
5
a
. C.
5
4
a
. D.
2
3
a
.
Câu 17. (Chuyên Hưng Yên - 2020) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác cân,
BA BC a
và
30
BAC
. Cạnh bên
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
D
là điểm đối xứng
với
B
qua
AC
. Khoảng cách từ
B
đến mặt phẳng
SCD
bằng
A.
2 21
.
7
a
B.
2
.
2
a
C.
21
.
14
a
D.
21
7
a
.
Câu 18. (Chuyên KHTN - 2020) Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật
, 2 AB a AD a
,
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
M
là trung điểm của
AD
. Tính khoảng cách giữa
hai đường thẳng
BM
và
SD
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
6
3
a
. B.
2
2
a
. C.
2 5
5
a
. D.
6
6
a
.
Câu 19. (Chuyên Lam Sơn - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
. Tam
giác
ABC
là tam giác đều, hình chiếu vuông góc của đỉnh
S
lên mặt phẳng
ABCD
trùng với
trọng tâm tam giác
ABC
. Góc giữa đường thẳng
SD
và mặt phẳng
ABCD
bằng
30
. Tính
khoảng cách từ điểm
B
đến mặt phẳng
SCD
theo
a
.
A.
21
7
a
. B.
3a
C.
a
. D.
2 21
3
a
.
Câu 20. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp
.S ABCD
có đáy là hình
vuông,
,AB a
SA
vuông góc với mặt phẳng đáy và
2SA a
(minh họa như hình vẽ bên dưới ).
Gọi
M
là trung điểm của
CD
, khoảng cách giữa điểm
M
và mặt phẳng
( )SBD
bằng
A.
2
3
a
. B.
2
a
. C.
2
a
. D.
3
a
.
Câu 21. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hình chóp
.S ABC
có đáy ABC là tam giác
vuông cân tại
,A
mặt bên
( )SBC
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông góc với
mặt phẳng đáy. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
A.
3
4
a
. B.
2
4
a
. C.
5
4
a
. D.
3
3
a
Câu 22. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp
.S ABCD
có đáy là hình
thoi tâm
O
cạnh
a
và có góc
0
60BAD . Đường thẳng
SO
vuông góc với mặt đáy
ABCD
và
3
4
a
SO
. Khoảng cách từ
O
đến mặt phẳng
SBC
bằng
A.
3
4
a
. B.
3
a
. C.
3
4
a
. D.
3
8
a
.
M
D
B
C
A
S
B
C
S
D
A
M
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 23. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là
hình thang vuông tại
A
và
D
,
3 ,AB a
AD DC a
. Gọi
I
là trung điểm của
AD
, biết hai
mặt phảng
SBI
và
SCI
cùng vuông góc với đáy và mặt phẳng
SBC
tạo với đáy một góc
0
60
. Tính theo
a
khoảng cách từ trung điểm cạnh
SD
đến mặt phẳng
SBC
.
A.
17
5
a
. B.
6
19
a
. C.
3
15
a
. D.
15
20
a
.
Câu 24. (Chuyên Thái Bình - 2020) Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
2 ,AB a BC a
, tam giác đều
SAB
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa
BC
và
SD
là
A.
3a
. B.
3
2
a
. C.
2 5
5
a
. D.
5
5
a
.
Câu 25. (Chuyên Bắc Ninh - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a
và
SA
vuông góc với mặt đáy.
M
là trung điểm
SD
. Tính khoảng cách giữa
SB
và
CM
.
A.
3
6
a
. B.
2
3
a
. C.
3
2
a
. D.
3
3
a
.
Câu 26. (Chuyên Bến Tre - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
2SA a
và vuông góc với
ABCD
. Gọi
M
là trung điểm của
SD
. Tính khoảng cách d giữa hai
đường thẳng SB và CM.
A.
3
a
d
. B.
2
2
a
d
. C.
2
3
a
d
. D.
6
a
d
.
Câu 27. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho hình chóp
.S ABCD
có
SA ABCD
,
6SA a
,
ABCD
là nửa lục giác đều nội tiếp đường tròn đường kính
2AD a
. Khoảng cách từ
điểm B đến mặt phẳng
SCD
bằng
A.
6
2
a
. B.
3
2
a
. C.
2
2
a
. D.
3
4
a
.
Câu 28. (Chuyên Hùng Vương - Gia Lai - 2020) Cho lăng trụ đứng tam giác
.ABC A B C
có đáy là một
tam giác vuông cân tại
B
,
2 ,AB AA a
M
là trung điểm
BC
(minh họa như hình dưới).
Khoảng cách giữa hai đường thẳng
AM
và
B C
bằng
A.
2
a
. B.
2
3
a
. C.
7
7
a
. D.
3a
Câu 29. (Chuyên Lào Cai - 2020) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh 2a
và
0
90 .SBA SCA
Biết góc giữa đường thẳng SA và mặt đáy bằng 45
0
. Tính khoảng cách từ
điểm B đến mặt phẳng (SAC).
A.
15
5
a
. B.
2 15
5
a
. C.
2 15
3
a
. D.
2 51
5
a
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 30. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
M
là trung điểm của cạnh
AD
. Tính khoảng cách giữa hai đường thẳng
AB
và
CM
.
A.
33
11
a
. B.
33
a
. C.
22
a
. D.
22
11
a
.
Câu 31. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hình lăng trụ đều
. ’ ’ ’ABC A B C
có tất cả các
cạnh có độ dài bằng 2 (tham khảo hình vẽ). Tính khoảng cách giữa hai đường thẳng AC’ và A’B.
A.
2
5
. B.
3
2
. C.
1
2
. D.
3
5
.
Câu 32. (Chuyên Vĩnh Phúc - 2020) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt phẳng
ABC
; góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
60
. Gọi
M
là trung điểm cạnh
AB
. Khoảng cách từ
B
đến
SMC
bằng
A.
39
13
a
. B. 3a . C.
a
. D.
2
a
.
Câu 33. (Đại Học Hà Tĩnh - 2020) Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2AA a
,
M
là trung điểm của
BC
. Tính khoảng cách
d
của hai đường thẳng
AM
và
B C
.
A.
6
6
a
d
. B.
2
2
a
d
. C.
7
7
a
d
. D.
3
3
a
d
.
Câu 34. (ĐHQG Hà Nội - 2020) Cho lăng trụ đứng
/ / /
ABCA B C
có tất cả các cạnh bằng a. Gọi
M
là
trung điểm của
/
AA . Tính khoảng cách giữa hai đường thẳng
BM
và
/
B C
.
A.
3
5
a . B.
3
10
a . C.
3
2 2
a . D.
3
7
a
Câu 35. (Sở Phú Thọ - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
, cạnh
, 2AB a AD a
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
là trung điểm của
đoạn
OA
. Góc giữa
SC
và mặt phẳng
ABCD
bằng
30
. Khoảng cách từ
C
đến mặt phẳng
SAB
bằng
A.
9 22
44
a
. B.
3 22
11
a
. C.
22
11
a
. D.
3 22
44
a
.
Câu 36. (Sở Phú Thọ - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Hình chiếu
vuông góc của
S
trên mặt phẳng
ABCD
là trung điểm của cạnh
AB
, góc giữa mặt phẳng
SAC
và đáy bằng
45
. Gọi
M
là trung điểm của cạnh
SD
. Khoảng cách giữa hai đường
AM
và
SC
bằng
A.
a
. B.
2
4
a
. C.
5
10
a
. D.
5
5
a
.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 37. (Sở Hà Tĩnh - 2020) Cho tứ diện
ABCD
có
, ,AB AC AD
đôi một vuông góc với nhau và
2, 1AD AB AC
. Gọi
I
là trung điểm của đoạn thẳng
BC
, khoảng cách giữa hai đường
thẳng
AI
và
BD
bằng
A.
3
.
2
B.
2
.
5
C.
5
.
2
D.
2
.
3
Câu 38. (Sở Ninh Bình) Cho hình chóp
.S ABC
có
SA a
, tam giác
ABC
đều, tam giác
SAB
vuông cân
tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
SAC
bằng
A.
42
7
a
. B.
42
14
a
. C.
42
12
a
. D.
42
6
a
.
Câu 39. (Sở Yên Bái - 2020) Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại
B
,
biết , , là trung điểm của . Tính khoảng cách giữa hai đường
thẳng và .
A.
7
7
a
. B.
2 5
5
a
. C.
6
2
a
. D.
15
5
a
.
Câu 40. (Bỉm Sơn - Thanh Hóa - 2020) Cho hình chóp có đáy là hình chữ nhật,
. Tam giác cân tại và nằm trong mặt phẳng vuông góc với đáy. Góc
giữa đường thẳng và mặt phẳng bằng . Gọi là trung điểm của , hãy tính
theo khoảng cách từ đến mặt phẳng .
A. B. C. D.
Câu 41. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
,
cạnh
SA
tạo với mặt phẳng đáy một góc
o
30
. Khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
A.
2 15
5
a
. B.
3 14
5
a
. C.
2 10
5
a
. D.
4 5
5
a
.
Câu 42. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông
tại
A
và
B
,
2 2 2AD AB BC a
,
SA
vuông góc với đáy, góc giữa
SB
và mặt phẳng đáy bằng
0
60
. Gọi
H
là hình chiếu vuông góc của
A
lên
SB
. Khoảng cách từ
H
đến mặt phẳng
SCD
bằng
A.
3a
. B.
3 30
20
a
. C.
3 30
10
a
. D.
3 30
40
a
.
Câu 43. (Kim Liên - Hà Nội - 2020) Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA
vuông
góc với mặt phẳng đáy, góc giữa mặt phẳng
SBC
và mặt phẳng đáy là
60
(minh họa như hình
dưới đây). Gọi
,M N
lần lượt là trung điểm của
,AB AC
.
Khoảng cách giữa hai đường thẳng
SB
và
MN
bằng
A.
3
8
a
. B.
6
2
a
. C.
3
4
a
. D.
6a
.
.
ABC A B C
AB BC a
2AA a
M
BC
AM
B C
.
S ABCD
ABCD
, 2AB a AD a
SAB
S
SC
ABCD
45
M
SD
a
M
SAC
2 1513
.
89
a
d
1315
.
89
a
d
2 1315
.
89
a
d
1513
.
89
a
d
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 44. (Lê Lai - Thanh Hóa - 2020) Cho hình chóp có đáy là hình thang vuông tại
và , , , , vuông góc với mặt phẳng đáy và (minh
họa như hình bên dưới). Khoảng cách từ đến mặt phẳng bằng
A. . B. . C. . D. .
Câu 45. (Liên trường Nghệ An - 2020) Cho tứ diện
ABCD
có
0
90 , 2 ,ABC ADC ACD BC a CD a
, góc giữa đường thẳng
AB
và mặt phẳng
BCD
bằng
0
60
. Tính khoảng cách giữa hai đường thẳng
AC
và
BD
.
A.
6
31
a
. B.
2 6
31
a
. C.
2 3
31
a
. D.
3
31
a
.
Câu 46. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tứ diện
OABC
có
, ,OA OB OC
đôi một vuông góc với
nhau và
OA OB a
,
2OC a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa hai đường
thẳng
OM
và
AC
bằng
A.
2
3
a
. B.
2 5
5
a
. C.
2
2
a
. D.
2
3
a
.
Câu 47. (Nguyễn Huệ - Phú Yên - 2020) Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
A
,
, 2 ,AB a AC a SA
vuông góc với mặt phẳng đáy và
2SA a
. Gọi
G
là trọng tâm của
ABC
.
Khoảng cách giữa hai đường thẳng
SG
và
BC
bằng
A.
2
7
a
. B.
6
3
a
. C.
2 6
9
a
. D.
4
7
a
.
Câu 48. (Nguyễn Trãi - Thái Bình - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và
11, SA SB SC
góc
30 , SAB
góc
60 , SBC
góc
45 SCA
. Tính khoảng cách
d
giữa hai đường thẳng
AB
và
SD
.
A.
2 22
. B.
22
. C.
22
2
. D.
4 11
.
Câu 49. (THPT Nguyễn Viết Xuân - 2020) Cho hình hộp
.
ABCD A B C D
có đáy
ABCD
là hình vuông
cạnh
a
, tâm
O
. Hình chiếu vuông góc của
A
lên mặt phẳng
ABCD
trùng với
O
. Biết tam
giác
AA C
vuông cân tại
A
. Tính khoảng cách
h
từ điểm
D
đến mặt phẳng
ABB A
.
A.
6
6
a
h
. B.
2
6
a
h
. C.
2
3
a
h
. D.
6
3
a
h
.
Câu 50. (Tiên Du - Bắc Ninh - 2020) Cho hình lăng trụ tam giác
.ABC A B C
có cạnh bên bằng
2a
,
đáy
ABC
là tam giác vuông tại
, 3,B BC a AB a
. Biết hình chiếu vuông góc của đỉnh
A
lên
mặt đáy là điểm
M
thoả mãn
3AM AC
. Khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
A.
210
15
a
. B.
210
45
a
. C.
714
17
a
. D.
714
51
a
.
Câu 51. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2 2AD AB a
. Cạnh bên
2SA a
và vuông góc với đáy. Gọi
,M N
lần lượt là trung điểm của
SB
và
SD
. Tính khoảng cách
d
từ điểm
S
đến mặt phẳng
AMN
.
A.
2d a
. B.
3
2
a
d
. C.
6
3
a
d
. D. 5d a .
.
S ABCD
ABCD
B
C
2
CD AB
AD a
30
ADC
SA
2SA a
D
SBC
2 57
19
a
57
19
a
4 57
19
a
3a
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 52. (Hải Hậu - Nam Định - 2020) Cho hình chóp đều
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
. Biết rằng bán kính mặt cầu ngoại tiếp hình chóp bằng
9 2
8
a
, độ dài cạnh bên lớn hơn độ
dài cạnh đáy. Khoảng cách giữa hai đường thẳng
AB
và
SD
bằng
A.
2 17
17
a
. B.
4 17
17
a
. C.
4 34
17
a
. D.
2 34
17
a
.
Câu 53. (Kìm Thành - Hải Dương - 2020) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
, biết
SA ABC
và
2AB a
,
3AC a
,
4SA a
. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng
A.
2
11
a
d . B.
6 29
29
a
d
. C.
12 61
61
a
d
. D.
43
12
a
.
Câu 54. (Lương Thế Vinh - Hà Nội - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2AB a
,
3AD a
(tham khảo hình vẽ). Tam giác
SAB
cân tại
S
và nằm trong mặt phẳng vuông
góc với mặt đáy; góc giữa mặt phẳng
SCD
và mặt đáy là
45
. Gọi
H
là trung điểm cạnh
AB
.
Tính theo
a
khoảng cách giữa hai đoạn thẳng
SD
và
CH
.
A.
3 11
11
a
. B.
3 14
7
a
. C.
3 10
109
a
. D.
3 85
17
a
.
Câu 55. (Trường VINSCHOOL - 2020) Cho hình chóp
.S ABCD
có đáy là hình chữ nhật, cạnh
2AB AD a
. Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy
ABCD
.
Khoảng cách từ điểm
A
đến mặt phẳng
SBD
bằng
A.
3
4
a
. B.
3
2
a
. C.
2
a
. D.
2a
.
Câu 56. (Thanh Chương 1 - Nghệ An - 2020) Cho hình chóp
SABC
, có đáy là tam giác vuông tại
A
,
4AB a
,
3AC a
. Biết 2 3SA a ,
30SAB
và
SAB ABC
. Khoảng cách từ
A
đến
mặt phẳng
SBC
bằng
A.
3 7
14
a
. B.
8 7
3
a
. C.
6 7
7
a
. D.
3 7
2
a
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
57. (Tiên Lãng - Hải Phòng - 2020) Cho hình lăng trụ đứng
.
A
BC A B C
có
A
B a
,
2A
C a
,
0
120
BAC
.
Gọi
M
là
trung điểm cạnh
CC
t
hì
0
90
B
MA
. Tính khoảng cách từ điểm
A
đến
mặ
t phẳng
BMA
.
A.
7
7
a
. B.
5
3
a
. C.
5
7
a
. D.
5
5
a
.
-------------------- HẾT --------------------
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. GÓC
Câu 1. (Chuyên Biên Hòa - Hà Nam - 2020) Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Khi đó
cos ,AB DM
bằng
A.
2
2
. B.
3
6
. C.
1
2
. D.
3
2
.
Lời giải
Chọn B
Gọi
N
là trung điểm của
.AC
Suy ra
//MN AB
Do đó:
cos , cos ,AB DM MN DM
Gọi
a
là độ dài cạnh của tứ diện đều
ABCD
, suy ra
2
a
MN
;
3
2
a
ND MD
Trong tam giác
MND
ta có:
2 2 2
3
cos
2. . 6
MN MD ND
NMD
MN MD
3
cos , cos
6
AB DM NMD
.
Câu 2. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp
.S ABCD
có
SA
vuông góc
với mặt phẳng đáy, 3SA a , tứ giác
ABCD
là hình vuông,
2BD a
(minh họa như hình
bên). Góc giữa đường thẳng
SB
và mặt phẳng
SAD
bằng
A.
0
. B.
30
. C.
45
. D.
60
.
Lời giải
Chọn B
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
57 CÂU VD - VDC CHƯƠNG 6. HÌNH HỌC 11
N
M
B
D
C
A
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đáy
ABCD
là hình vuông có đường chéo
2BD a
nên cạnh
AB a
.
Ta có:
AB AD
AB SAD
AB SA
SA
là hình chiếu của
SB
trên mặt phẳng
SAD
, ,SB SAD SB SA BSA
.
Trong tam giác vuông
BSA
, ta có:
3
tan
3
3
AB a
BSA
AS
a
30BSA .
Vậy,
, 30SB SAD
.
Câu 3. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hình chóp
.S ABC
có
SA
vuông góc với mặt
phẳng
3
,
2
a
ABC SA
, tam giác
ABC
đều cạnh bằng
a
(minh họa như hình dưới). Góc tạo
bởi giữa mặt phẳng
SBC
và
ABC
bằng
A.
0
90
. B.
0
30
. C.
0
45
. D.
0
60
.
Lời giải
Chọn C
Gọi
M
là trung điểm
BC
.
C
B
A
S
M
C
B
A
S
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
ABC
đều cạnh
a
nên
AM BC
và
3
2
a
AM
.
Ta có
SA ABC
Hình chiếu của
SM
trên mặt phẳng
ABC
là
AM
.
Suy ra
SM BC
(theo định lí ba đường vuông góc).
Có
,
,
SBC ABC BC
AM ABC AM BC
SM SBC SM BC
. Do đó góc giữa mặt phẳng
SBC
và
ABC
là góc giữa
SM
và
AM
, hay là góc
SMA (do
SA ABC SA AM SAM
vuông).
Xét tam giác
SAM
vuông tại
A
có
0
3
2
tan 1 45
3
2
a
SA
SMA SMA
AM
a
.
Vậy góc cần tìm là
0
45
.
Câu 4. (Chuyên Thái Bình - 2020) Cho hình chóp tứ giác đều
.S ABCD
có đáy là hình vuông tâm
O
, cạnh
a
. Gọi
,M N
lần lượt là trung điểm của
SA
và
BC
. Góc giữa đường thẳng
MN
và
mặt phẳng
ABCD
bằng
60
. Tính cos của góc giữa đường thẳng
MN
và mặt phẳng
SBD
.
A.
41
4
. B.
5
5
. C.
2 5
5
. D.
2 41
4
.
Lời giải
Chọn C
Từ giả thiết ta có
SO ABCD
.
Gọi
I
là trung điểm
OA
thì
MI
là đường trung bình của
SOA
//MI SO
MI ABCD
I
là hình chiếu của
M
trên mặt phẳng
ABCD
IN
là hình chiếu của
MN
trên mặt
phẳng
ABCD
. Suy ra
, , 60 MN ABCD MN IN MNI
.
Ta có
1
2 2
a
NC BC
;
3 3 2
4 4
a
IC AC
.
Áp dụng định lý cosin trong
INC
ta có
2 2 2
2 . .cosIN CI CN CI CN NCI
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
2
3 2 3 2 5
2. . .cos45
4 2 4 2 8
a a a a a
IN
10
4
a
IN
.
Do
MIN
vuông tại
I
nên
cos
IN
MNI
MN
10 1 10
:
cos60 4 2 2
IN a a
MN
.
Lại có
,AC BD AC SO AC SBD
.
Gọi
E
là trung điểm
OB EN
là đường trung bình của
BOC
//EN OC
hay
//EN AC
NE SBD
hay
E
là hình chiếu của
N
trên mặt phẳng
SBD
.
Gọi
F
là trung điểm của
SO MF
là đường trung bình của
SAO
//MF AO
hay
//MF AC
MF SBD
hay
F
là hình chiếu của
M
trên mặt phẳng
SBD
.
Ta có
//MF NE
nên bốn điểm
, , ,E N F M
cùng nằm trên một mặt phẳng.
Trong mặt phẳng
ENFM
gọi
J MN EF J MN SBD
(do
EF SBD
).
Suy ra
, ,MN SBD MN EF EJN
(do
90 EJN ).
Ta có
1 1 2
2 4 4
a
EN OC AC
;
1 1 2
2 4 4
a
MF AO AC
EN MF
, mà
//EN MF
Tứ giác
ENFM
là hình bình hành
J
là trung điểm
1 10
2 4
a
MN JN MN
.
Vậy
2 2
cos , cos
JE JN EN
MN SBD EJN
JN JN
2 2
10 2
4 4
10
4
a a
a
2 5
5
.
Câu 5. (Chuyên Vĩnh Phúc - 2020) Cho hình lăng trụ đứng
.ABC A B C
có
1AA AB AC
và
0
120BAC
. Gọi
I
là trung điểm cạnh
CC
. Côsin góc giữa hai mặt phẳng
ABC
và
AB I
bằng
A.
370
20
. B.
70
10
. C.
30
20
. D.
30
10
.
Lời giải
Chọn D
Gọi
là góc giữa hai mặt phẳng
ABC
và
AB I
.
5
2 , .
2
AB AI
2 2 2
2 . .cos 3 3BC AB AC AB AC A BC B C
.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
2 2
13
2
B I B C C I
.
Vì
2 2 2
AB AI B I AB I
vuông tại điểm
A
.
1 3
. .sin
2 4
ABC
S AB AC A
và
1 10
.
2 4
AB I
S AI AB
.
Hình chiếu vuông góc của
AB I
lên mặt phẳng
ABC
là
ABC
.
Ta có
30
.cos cos
10
ABC
ABC AB I
AB I
S
S S
S
.
Câu 6. (ĐHQG Hà Nội - 2020) Cho hình chóp
.S ABCD
có đáy hình vuông. Cho tam giác
SAB
vuông tại
S
và góc
SBA
bằng
0
30
. Mặt phẳng
SAB
vuông góc mặt phẳng đáy. Gọi
,M N
là
trung điểm
,AB BC
. Tìm cosin góc tạo bởi hai đường thẳng
,SM DN
.
A.
2
5
. B.
1
5
. C.
1
3
. D.
2
3
.
Lời giải
Chọn B
Trong
SAB
, kẻ
SH AB
tại
H
. Ta có:
,
ABCD
SAB ABCD AB ABCD
SH S
SAB
SH
AB SH AB
.
Kẻ tia
Az
//
SH
và chọn hệ trục tọa độ
Axyz
như hình vẽ sau đây.
Trong tam giác
SAB
vuông tại
S
,
0
3
.cos .cos30
2
a
SB AB SBA a
.
Trong tam giác
SBH
vuông tại
H
,
3
.cos
4
a
BH SB SBH
và
3
.sin
4
a
SH BH SBA
.
3
4 4
a a
AH AB BH a
3
0; ;0 0; ;
4 4 4
a a a
H S
.
0; ;0
2
a
M
,
;0;0D a
,
; ;0
2
a
N a
.
Ta có:
3
0; ;
4 4
a a
SM
,
; ;0
2
a
DN a
2
.
1
4
cos ,
.
5 5
.
2 2
a
SM DN
SM DN
SN DN
a a

.
Câu 7. (Sở Ninh Bình) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
, độ dài cạnh
2AC a
, các tam giác
, SAB SCB
lần lượt vuông tại
A
và
C
. Khoảng cách từ
S
đến mặt
phẳng
( )ABC
bằng
a
. Giá trị cosin của góc giữa hai mặt phẳng
( )SAB
và
( )SCB
bằng
z
x
y
N
M
C
B
A
D
S
H
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 2
3
. B.
1
3
. C.
2
3
. D.
5
3
.
Lời giải
Chọn C
+ Gọi
,O I
lần lượt là trung điểm của
,AC SB
chúng ta có
O
là tâm của đường tròn ngoại tiếp
tam giác
ABC
và vì các tam giác
, SAB SCB
lần lượt vuông tại
A
và
C
nên
I
là tâm mặt
cầu ngoại tiếp tứ diện
SABC
do đó
( )OI ABC
.
+ Gọi
D
là hình chiếu của
S
lên mặt phẳng
( )ABC
ta có
/ /SD OI
và
2SD OI
suy ra
O
là
trung điểm của
BD
. Từ đây ta có
ABCD
là hình vuông cạnh bằng
2
2
2
a
a
và
SD a
.
+ Gọi
,H K
lần lượt là hình chiếu của
D
lên
,SC SA
ta có
( ) SD ABCD SD BC
đồng thời
ABCD
là hình vuông nên
BC DC
từ hai ý này ta có
( ) BC SCD BC DH
, từ đó suy ra
( )DH SCB
.
Chứng minh tương tự ta có
( )DK SAB
+ Vì vậy góc giữa hai mặt phẳng
( )SCB
và
( )SAB
bằng góc giữa hai đường thẳng
DK
và
DH
.
+ Xét 2 tam giác vuông
, SAD SCD
bằng nhau ta có hai đường cao
6
3
a
DK DH
+ Trong tam giác
SAC
ta có
2
2
1 2
3 3
HK SH SD a
HK
AC SC SC
, trong tam giác
DHK
có
2 2 2
2
cos
2 . 3
DH KD KH
HDK
DH KD
Câu 8. (Sở Bắc Ninh - 2020) Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
0
, 120 ,a ABC SA
vuông góc với mặt phẳng
.ABCD
Biết góc giữa hai mặt phẳng
SBC
và
SCD
bằng
0
60 ,
khi đó
A.
6
.
4
a
SA
B.
6.SA a
C.
6
2
a
SA
. D.
3
2
a
SA
.
Lời giải
Chọn A
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Gọi
O
là giao điểm của
, .AC BD
Gọi
H
là hình chiếu vuông góc của
O
trên
.SC
Khi đó
DSC HB
vì
, .SC BD SC OH
Vậy góc giữa hai mặt phẳng
SBC
và
SCD
là góc giữa hai đường thẳng
, .HB HD
Vì
.SCD SBC HB HD
Đặt
0 .SA x x
Ta có
2 2
2 2 2
0 2 2 2
2
2
60 2
2 .
3
HB BD
HB HD BD
cos HB HB BD
BD
HB HD
HB
Ta có
. . 1CHO CSA OH CS CO SA
Trong tam giác
ABC
ta có
3,
2
a
AC a OB BD a
TH1 :
2 2
3
2
a
HB BD a OH HB OB
. Thay vào (1) ta có
2 2
3 .x x a (vô
nghiệm).
TH2 :
2 2
3 3 3
3 3 6
BD a a
HB OH HB OB
.
Thay vào (1) ta có
2 2
2 2 2
3 6
3
12 4 4
a a a
x a x x
.
Câu 9. (Sở Bình Phước - 2020) Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác cân đỉnh
A
.
Biết
3BC a
và
30
o
ABC
, cạnh bên
AA a
. Gọi
M
là điểm thỏa mãn
2 3CM CC
.
Gọi
là góc tạo bởi hai mặt phẳng
ABC
và
AB M
, khi đó
sin
có giá trị bằng
A.
66
22
. B.
481
22
. C.
3
22
. D.
418
22
.
Lời giải
Chọn D
O
A
B
D
C
S
H
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Cách 1: Gọi
O
là trung điểm
BC
.
Ta có:
3
.cos30
cos30
3
2.
2
o
o
BO a
BO AB AB a AC
và
.sin30
2
o
a
AO AB
.
Theo đề bài:
3 3 1
2 3
2 2 2 2
a
CM CC CM CC CC C M CC C M CC C M
.
Gọi
là góc giữa hai mặt phẳng
ABC
và
AB M
.
Theo công thức diện tích hình chiếu ta có:
.cos cos
ABC
ABC AB C
AB C
S
S S
S
.
Ta có
2
1 1 3
. . . . 3
2 2 2 4
ABC
a a
S AH BC a
;
2 2 2 2
2AB AB BB a a a
;
2
2
2 2
13
3
2 2
a a
B M C M B C a
;
2
2 2 2
3 13
2 2
a a
AM AC CM a
.
Khi đó
13 13
2
2 13
2 2
2 2 2
a a
a
AB B M AM a a
p
.
Áp dụng công thức Hê-rông vào
AB M
ta có:
2
22
4
AB M
a
S p p AB p B M p AM
.
Vậy
2
2
2
3
3 19 418
4
cos sin 1 cos
22 22 22
22
4
ABC
AB C
a
S
S
a
.
Cách 2:
Gọi
O
là trung điểm
BC
.
Ta có:
3
.cos30
cos30
3
2.
2
o
o
BO a
BO AB AB a AC
và
.sin30
2
o
a
AO AB
.
Theo đề bài:
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
3 3 1
2 3
2 2 2 2
a
CM CC CM CC CC C M CC C M CC C M
.
Coi
1a
.
Gắn hệ trục tọa độ
Oxyz
như hình vẽ với
0;0;0O
,
1
0; ;0
2
A
,
3
;0;0
2
B
,
3
;0;0
2
C
,
3
;0;1
2
B
,
3 3
;0;
2 2
M
.
Khi đó
: 0ABC Oxy z ABC
có một véc-tơ pháp tuyến là
0;0;1k
.
Ta có:
3 1
; ;1
2 2
AB
,
3 1 3
; ;
2 2 2
AM
4 , 1;5 3;2 3
AB M
n AB AM
.
Gọi
là góc giữa hai mặt phẳng
ABC
và
AB M
.
Vậy
2
.
2 3
3 19 418
cos sin 1 cos
22 22 22
1.2 22
.
AB M
AB M
k n
k n
.
Câu 10. (Đô Lương 4 - Nghệ An - 2020) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
,
tâm
O
. Gọi
M
và
N
lần lượt là trung điểm của
SA
và
BC
. Biết rằng góc giữa
MN
và
ABCD
bằng
60
, côsin của góc giữa đường thẳng
MN
và mặt phẳng
SBD
bằng:
A.
5
5
. B.
41
41
. C.
2 5
5
. D.
2 41
41
.
Lời giải
Chọn C
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn hệ trục tọa độ
Oxyz
như hình vẽ. Đặt
, 0SO m m
.
2 2 2
;0;0 ; 0;0; ; ; ;0
2 4 4
a a a
A S m N
2
;0;
4 2
a m
M
.
2 2
; ;
2 4 2
a a m
MN
. Mặt phẳng
ABCD
có véc tơ pháp tuyến
0;0;1k
.
2 2
2
2 2
.
3 15 3
2
sin ,
2 8 4
5
8 4
m
MN k
a m
MN ABCD m
MN k
a m
.
2 2
30
2 15
2
a
m a m
2 2 30
; ;
2 4 4
a a a
MN
, mặt phẳng
SBD
có véc tơ pháp tuyến là
1;0;0i
.
2 2 2
2
.
5 2 5
2
sin , os ,
5 5
30
2 8 16
a
MN i
MN SBD c MN SBD
MN i
a a a


.
Câu 11. (Kim Liên - Hà Nội - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
.
Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
I
là trung điểm của đoạn
AB
. Khẳng định nào sau đây là sai?
A. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
45
.
B.
SBC
là tam giác vuông.
C.
SI ABCD
.
D. Khoảng cách giữa đường thẳng
DC
và mặt phẳng
SAB
bằng
a
.
Lời giải
Chọn A
z
y
x
H
N
M
O
D
C
B
S
A
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
+) Vì
SAB
đều và
I
là trung điểm của đoạn
AB
nên
SI AB
Mà
,SAB ABCD SAB ABCD AB
, suy ra
SI ABCD
.
+)
SI ABCD SI BC
, mà
BC AB BC SAB BC SB
.
Do đó
SBC
là tam giác vuông.
+)
, ,SC ABCD SC IC SCI
.
SAB
đều, cạnh
a
nên
3
2
a
SI
và
5
2
a
IC
nên
3
tan
5
SI
SCI
IC
.
+)
//DC SAB
nên
, ,d DC SAB d G SAB
(với
G
là trung điểm của
DC
).
GI AB
và
GI SI
nên
,GI SAB d G SAB GI a
.
Đối chiếu các đáp án ta thấy đáp án A sai.
Câu 12. (THPT Nguyễn Viết Xuân - 2020) Cho hình lăng trụ đứng
.ABC A B C
có
, 120AB AC a BAC
. Gọi
, M N
lần lượt là trung điểm của
B C
và
CC
. Biết thể tích
khối lăng trụ
.ABC A B C
bằng
3
3
4
a
. Gọi
là góc giữa mặt phẳng
AMN
và mặt phẳng
ABC
. Khi đó
A.
3
cos
2
. B.
1
cos
2
. C.
13
cos
4
. D.
3
cos
4
.
Lời giải
G
I
C
B
A
D
S
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Lấy
H
là trung điểm của
BC
.
Ta có:
3
. ' '
3
.
4
ABC A BC ABC
a
V CC S CC a
vì
2
3
4
ABC
a
S
.
Chọn hệ trục tọa độ
Oxyz
như hình vẽ. Ta có
M O
.
3 3 3
0;0;0 , ;0;0 , 0; ;0 , C 0; ;0 ; ;0; ; 0; ;
2 2 2 2 2 2
a a a a a a
M A B A a N
.
Ta có:
ABC Oz
nên
ABC
có một vectơ pháp tuyến là
0;0;1k
.
Ta có
;0;
2
a
MA a
,
3
0; ;
2 2
a a
MN
.
Gọi
1 1
1;0;2
2
a
v MA v
,
2 2
0; 3;1
2
a
v MN v
.
Khi đó mặt phẳng
AMN
song song hoặc chứa giá của hai vectơ không cùng phương là
1
v
và
2
v
nên có một vectơ pháp tuyến là
1 2
, 2 3; 1; 3n v v
.
Vậy
.
3
cos cos ,
4
.
k n
k n
k n
.
Câu 13. (Tiên Du - Bắc Ninh - 2020) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a
SA
vuông góc với mặt phẳng
ABC
và
.
2
a
SA
Góc giữa mặt phẳng
SBC
và mặt phẳng
ABC
bằng
A.
45
. B.
90
. C.
30
. D.
60
.
Lời giải
Chọn C
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Gọi
I
là trung điểm
.BC
Ta có
AI BC
(tam giác
ABC
đều) (1).
Lại có
SA BC
SA ABC
.
Suy ra
BC SAI BC SI
(2).
BC SBC ABC
(3).
Từ (1), (2) và (3) suy ra
, , .SBC ABC SI AI SIA
Xét tam giác
SAI
vuông tại
A
ta có
1
2
tan .
3 3
2
a
SA
SIA
AI
a
Suy ra
30 .SIA
Vậy
, 30 .SBC ABC
Câu 14. (Kìm Thành - Hải Dương - 2020) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân
tại
A
,
2AB a
,
SA
vuông góc với mặt đáy và góc giữa
SB
và mặt đáy bằng
60
. Gọi
là
góc giữa hai mặt phẳng
SBC và
ABC . Giá trị
cos
bằng
A.
15
5
. B.
2
5
. C.
1
7
. D.
2
7
.
Lời giải
Chọn C
Gọi
M
là trung điểm
BC AM BC
(1)
Có
BC SA
BC SM
BC AM
(2)
Từ (1) và (2) suy ra
,SBC ABC SMA
.
Do
SA ABC SA AB và
AB
là hình chiếu vuông góc của
SB
lên
ABC
60SBA
.
SAB
có
.tan 2 .tan60 2 3SA AB SBA a a
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ABC
có
2 2
2 2
1 1 1
2 2 2
2 2 2
AM BC AB AC a a a
.
SAM
vuông tại
A
có
2 2 2 2
2 1
cos
7
2 3 2
AM AM a
SM
SA AM
a a
.
PHẦN 2. KHOẢNG CÁCH
Câu 15. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang
vuông tại
A
và
;D 2 ;AB AD a
DC a
. Điểm
I
là trung điểm đoạn
,AD
hai mặt phẳng
SIB
và
SIC
cùng vuông góc với mặt phẳng
ABCD
. Mặt phẳng
SBC
tạo với mặt
phẳng
ABCD
một góc
60
. Tính khoảng cách từ
D
đến
SBC
theo
a
.
A.
15
5
a
. B.
9 15
10
a
. C.
2 15
5
a
. D.
9 15
20
a
.
Lời giải
Chọn A
Theo đề ta có
.SI ABCD
Gọi
K
là hình chiếu vuông góc của
I
trên
BC
.
Suy ra: Góc giữa hai mặt phẳng
, 60SBC ABCD SKI
Gọi
E
là trung điểm của
,AB
.M IK DE
Do
BCDE
là hình bình hành nên
//DE SBC
, , ,d D SBC d DE SBC d M SBC
Gọi
H
là hình chiếu vuông góc của
M
trên
SK
. Suy ra
,d M SCD MH
Dễ thấy:
1 1 1
2 2 2
IM AU KN MK
1 5
2 2
IN IM MK KN MK MK MK MK
Suy ra:
2 2
2 2 2 5
5 5 5
a
MK IN ID DN
.
Trong tam giác
,MHK
ta có:
15
.sin 60
5
a
MH MK
Câu 16. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
, ,A AC a I
là trung điểm
SC
. Hình chiếu vuông góc của
S
lên
ABC
là trung điểm
H
của
M
I
E
A
D
C
B
S
K
H
V
U
J
M
K
C
E
I
A
D
B
N
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
BC
. Mặt phẳng
SAB
tạo với
ABC
một góc
60
. Tính khoảng cách từ
I
đến mặt phẳng
SAB
.
A.
3
4
a
. B.
3
5
a
. C.
5
4
a
. D.
2
3
a
.
Lời giải.
Chọn A
Gọi
M
là trung điểm cạnh
AB
thì
MH
là đường trung bình của tam giác
ABC
nên
,
2
//AC
a
MH MH
MH AB
.
Mặt khác, do
SH ABC
nên
SMH BC
. Suy ra góc giữa
SAB
và
ABC
là góc giữa
SM
và
MH
; lại có
SH MH
nên góc này bằng góc
SMH . Từ giả thiết suy ra
60SMH .
Gọi
K
là hình chiếu của
H
lên
SM
thì
HK SAB
.
Xét tam giác vuông
3 3
, .tan 60 ,
2 2 4
a a a
SMH SH MH MH HK
.
Gọi khoảng cách từ
, ,I C H
đến mặt phẳng
SAB
lần lượt là
, , , , ,I SAB C SAB H SABd d d
.
Cách 1:
Ta có
1
, ,
2
1
, ,
2
I SAB C SAB
H SAB C SAB
d = d
d d
3
, ,
4
a
I SAB H SAB d d
.
Cách 2:
IH
là đường trung bình của tam giác
SBC
nên
// //IH SB IH SAB
3
, ,
4
a
I SAB H SAB d d
Câu 17. (Chuyên Hưng Yên - 2020) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân,
BA BC a
và
30BAC . Cạnh bên
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
D
là điểm đối
xứng với
B
qua
AC
. Khoảng cách từ
B
đến mặt phẳng
SCD
bằng
A.
2 21
.
7
a
B.
2
.
2
a
C.
21
.
14
a
D.
21
7
a
.
Lời giải
Chọn D
K
M
I
H
B
C
A
S
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tam giác
ABC
cân tại
B
có
30BAC và
D
đối xứng với
B
qua
AC
nên tứ giác
ABCD
là
hình thoi có
120ADC ABC .
Trong mặt phẳng
ABC
, kẻ
AH
vuông góc với đường thẳng
CD
tại
H
. Khi đó
CD AH
và
CD SA
nên
CD SAH
. Do đó
SCD SAH
.
Trong mặt phẳng
SAH
, kẻ
AK SH
tại
K
. Khi đó,
AK SCD
và
,AK d A SCD
.
Ta có
3
.sin 60
2
a
AH AD
.
Áp dụng hệ thức lượng trong tam giác vuông
SAH
, ta có
2 2 2 2
1 1 1 7
3AK AH SA a
. Từ đó,
21
7
a
AK
.
Vì
//AB SCD
nên
21
, ,
7
a
d B SCD d A SCD AK
.
Câu 18. (Chuyên KHTN - 2020) Cho hình chóp
.S ABCD
có đáy là hình chữ nhật
, 2 AB a AD a
,
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
M
là trung điểm của
AD
. Tính khoảng cách
giữa hai đường thẳng
BM
và
SD
.
M
D
B
C
A
S
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
6
3
a
. B.
2
2
a
. C.
2 5
5
a
. D.
6
6
a
.
Lời giải
Chọn D
Gọi
I
là trung điểm của
BC
.
Vì
//BM DI
nên
//BM SDI
.
Do đó
, , , d BM SD d BM SDI d M SDI
.
Vì
AD SDI D
và
M
là trung điểm của
AD
nên
1
, ,
2
d M SDI d A SDI
.
Trong
ABCD
, kẻ
AK DI K DI
,
AK BM J
.
Trong
SAK
, kẻ
AH SK H SK
.
Vì
DI AK
DI SAK
DI SA
mà
AH SAK DI AH
.
Suy ra
, AH SDI d A SDI AH
.
Ta có
// //BM DI JM DK
và
M
là trung điểm của
AD
nên
2AK AJ
.
Lại có
2 2 2 2 2 2
1 1 1 1 1 2
AJ AB AM a a a
.
Suy ra
2
2
2
a
AJ AK a
.
Mặt khác
2 2 2 2 2 2
1 1 1 1 1 3 6
2 2 3
a
AH
AH AK SA a a a
.
J
K
I
M
D
B
C
A
S
H
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó
1 6
, .
2 6
a
d M SDI AH
.
Cách khác:
Gọi
E DI AB
thì
2 2 AE AB a
.
1
, , ,
2
d BM SD d B SDI d A SDE
.
Vì
.S ADE
là tứ diện vuông tại
A
nên đặt
,h d A SDE
thì ta có
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 3 6
4 4 2 3
a
h
h SA AD AE a a a a
.
Suy ra
6
,
2 6
h a
d BM SD
.
Câu 19. (Chuyên Lam Sơn - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
. Tam
giác
ABC
là tam giác đều, hình chiếu vuông góc của đỉnh
S
lên mặt phẳng
ABCD
trùng với
trọng tâm tam giác
ABC
. Góc giữa đường thẳng
SD
và mặt phẳng
ABCD
bằng
30
. Tính
khoảng cách từ điểm
B
đến mặt phẳng
SCD
theo
a
.
A.
21
7
a
. B.
3a
C.
a
. D.
2 21
3
a
.
Lời giải
E
I
M
D
B
C
A
S
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Chọn A
Gọi
H
là trọng tâm tam giác
ABC
,
O
là tâm của hình thoi
ABCD
.
Do
SH ABCD
:
, 30 SD ABCD SDH
.
Xét tam giác
SDH
vuông tại
H
có:
30 SDH ;
2 4 4 3 2 3
.
3 3 3 2 3
a a
HD BD BO
.
2 3 2
tan .tan .tan 30 .
3 3
SH a a
SDH SH HD SDH
HD
Từ
H
hạ
HI SC
tại
I
.
Ta có:
,
HI SC
HI CD CD SHC
HI SCD
SC CD SCD
SC CD C
Từ đó, khoảng cách từ điểm
H
đến mặt phẳng
SCD
:
, d H SCD HI
.
Xét tam giác
SHC
vuông tại
H
, đường cao
HI
:
2 2 2
2
2 3
.
. 2 21
3 3
21
2 3
3 3
a a
HS HC a
HI
HS HC
a a
.
Mặt khác:
,
3
2
,
d B SCD
DB
DH
d H SCD
.
Vậy khoảng cách từ điểm
B
đến mặt phẳng
SCD
:
3 3 3 2 21 21
, , .
2 2 2 21 7
a a
d B SCD d H SCD HI
.
Cách khác:
Thể tích khối chóp
.S BCD
:
3
.
1 1 1 1 2 1 3 3
. . . . .sin . . . . .
3 3 2 3 3 2 2 18
S BCD BCD
a a
V SH S SH CB CD BCD a a
(đvtt).
Xét tam giác
SCD
có:
2 2
4 7
; ;
sin30 3 3
SH a a
SD CD a SC SH HC
.
Diện tích tam giác
SCD
:
2
7
6
SCD
a
S p p SC p SD p CD
(đvdt).
30
O
A
D
B
C
S
H
I
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
(
2
SC SD CD
p
là nửa chu vi tam giác
SCD
).
Vậy khoảng cách từ điểm
B
đến mặt phẳng
SCD
:
3
. .
2
3
3.
3. 3.
21
18
, .
7
7
6
B SCD S BCD
SCD SCD
a
V V
a
d B SCD
S S
a
Câu 20. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp
.S ABCD
có đáy là hình
vuông,
,AB a
SA
vuông góc với mặt phẳng đáy và
2SA a
(minh họa như hình vẽ bên dưới
). Gọi
M
là trung điểm của
CD
, khoảng cách giữa điểm
M
và mặt phẳng
( )SBD
bằng
A.
2
3
a
. B.
2
a
. C.
2
a
. D.
3
a
.
Lời giải
Chọn D
Gọi
I
là giao điểm của
AM
và
BD
,
O
là tâm hình vuông
ABCD
.
Ta có
1
( ,( ) ( ,( ))
2
d M SBD d A SBD
.
Dựng
AH
vuông góc với
SO
tại
.H
Ta có
( )
BD SA
BD SAO BD AH
BD AO
.
( )
AH SO
AH SBD
AH BD
nên
( ,( ))d A SBD AH
.
B
C
S
D
A
M
O
I
B
C
S
D
A
M
H
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 9 2
4 4 3
a
AH
AH AS AB AD a a a a
.
Vậy,
( ,( )
3
a
d M SBD
.
Câu 21. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hình chóp
.S ABC
có đáy ABC là tam
giác vuông cân tại
,A
mặt bên
( )SBC
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông
góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
A.
3
4
a
. B.
2
4
a
. C.
5
4
a
. D.
3
3
a
Lời giải
Chọn A
Gọi H là trung điểm của BC. Khi đó
SH ABCD
. Do tam giác ABC vuông cân tại A nên
AH BC
và
2
a
AH
.
Dựng điểm D sao cho ABCD là hình bình hành.
Khi đó
, , ,d SA BC s BC SAD d H SAD
Kẻ
3
.
3
2 2
,
4
a a
a
HI SA d H SAD HI
a
.
Câu 22. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp
.S ABCD
có đáy là hình
thoi tâm
O
cạnh
a
và có góc
0
60BAD . Đường thẳng
SO
vuông góc với mặt đáy
ABCD
và
3
4
a
SO
. Khoảng cách từ
O
đến mặt phẳng
SBC
bằng
A.
3
4
a
. B.
3
a
. C.
3
4
a
. D.
3
8
a
.
Lời giải
Chọn D
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có: tứ giác
ABCD
là hình thoi cạnh
a
có
0
60BAD suy ra tam giác
BCD
là tam giác đều
cạnh
a
.
Gọi
M
là trung điểm cạnh
BC
. Suy ra
DM BC
và
3
2
a
DM
.
Kẻ
/ / ,OK DM K BC OK BC
và
1 3
2 4
a
OK DM
.
Vì
SO ABCD
BC SO
BC SOK
.
Kẻ
,OH SK H SK
OH SBC
.
Từ đó ta có:
2 2 2
2
3 3
.
. 3
4 4
,
8
3 3
4 4
a a
OK SO a
d O SBC OH
OK SO
a a
.
Câu 23. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
3 ,AB a
AD DC a
. Gọi
I
là trung điểm của
AD
, biết hai mặt phảng
SBI
và
SCI
cùng vuông góc với đáy và mặt phẳng
SBC
tạo
với đáy một góc
0
60
. Tính theo
a
khoảng cách từ trung điểm cạnh
SD
đến mặt phẳng
SBC
.
A.
17
5
a
. B.
6
19
a
. C.
3
15
a
. D.
15
20
a
.
Lời giải
Chọn B
H
K
O
M
D
C
B
A
S
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Kẻ
0
; S 60IK BC K BC SBC ABCD KI
Gọi
M AD BC
. Ta có
1
3 2
MD a
MD
MA
Ta có
MIK
đồng dạng với
MBA
nên suy ra
2
2
2 5
15
3
3
2
IK MI a
BA MB
a
a
2 5 2 5
.3
15 5
a
IK a
Gọi
N
là trung điểm của
SD
.
Ta có
1 1
, , ,
2 4
d N SBC d D SBC d I SBC
Từ
I
kẻ
IH SK
suy ra
0
15 15
, .sin 60 ,
5 20
a a
IH d I SBC IK d N SBC
Câu 24. (Chuyên Thái Bình - 2020) Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
2 ,AB a BC a
, tam giác đều
SAB
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách
giữa
BC
và
SD
là
A.
3a
. B.
3
2
a
. C.
2 5
5
a
. D.
5
5
a
.
Lời giải
Chọn A
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
//
//
BC AD
AD SAD BC SAD
BC SAD
, do đó
, , ,d BC SD d BC SAD d B SAD
.
Tam giác
SAB
đều, gọi
H
là trung điểm
SA
thì
BH SA
(1).
Ta có
SAB ABCD
AD SAB SAB SAD
AD AB
(2).
Từ (1) và (2) suy ra
BH SAD
, do đó
2 3
, 3
2
a
d B SAD BH a
.
Câu 25. (Chuyên Bắc Ninh - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a
và
SA
vuông góc với mặt đáy.
M
là trung điểm
SD
. Tính khoảng cách giữa
SB
và
CM
.
A.
3
6
a
. B.
2
3
a
. C.
3
2
a
. D.
3
3
a
.
Lời giải
Chọn D
Cách 1
Gọi
E
là điểm đối xứng với
D
qua
A
,
N
là trung điểm của
SE
và
K
là trung điểm của
BE
Ta có các tứ giác
NMCB
và
ACBE
là các hình bình hành.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Có
//CM SBE
nên
, , , , d CM SB d CM SBE d C SBE d A SBE
.
ABE
vuông cân tại
A
có
AB a
nên
AK BE
và
2
2
a
AK
.
Kẻ
AH SK
,
H SK
.
Có
BE AK
BE SAK
BE SA
BE AH
.
Có
AH BE
AH SK
,AH SBE d A SBE AH
.
Ta có
2
2
a
AK
,
2 2
3
2
a
SK SA AK
;
.SA AK
AH
SK
2
.
3
2
3
3
2
a
a
a
a
.
Vậy
3
,
3
a
d CM SB
.
Cách 2:
Chọn hệ trục tọa độ
Oxyz
sao cho:
0;0;0 , ;0;0 , 0; ;0 , 0;0;A B a D a S a
; ;0C a a
,
0; ;
2 2
a a
M
.
Ta có
; ;SC a a a
,
;0; , a; ;
2 2
a a
SB a a MC
2 2 2
, ; ;
2 2 2
a a a
SB MC
.
Khoảng cách giữa hai đường thẳng
SB
và
CM
là:
, .
,
,
SB MC SC
d SB CM
SB MC
3 3 3
4 4 4
2 2 2
3
3
4 4 4
a a a
a
a a a
.
Vậy
3
,
3
a
d CM SB
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 26. (Chuyên Bến Tre - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
2SA a
và vuông góc với
ABCD
. Gọi
M
là trung điểm của
SD
. Tính khoảng cách d giữa
hai đường thẳng SB và CM.
A.
3
a
d
. B.
2
2
a
d
. C.
2
3
a
d
. D.
6
a
d
.
Lời giải
Chọn C
Gọi
O AC BD
.
Vì ABCD là hình vuông cạnh a nên O là trung điểm của BD mà M là trung điểm của SD nên
/ /OM SB
suy ra
/ /SB ACM
.
Do đó
, , , ,d SB CM d SB ACM d B ACM d D ACM
.
Gọi H là trung điểm của AD nên
/ /MH SA MH ABCD
.
, , 2 ,d SB CM d D ACM d H ACM
.
Kẻ
HI AC MHI MAC
theo giao tuyến
MI
, kẻ
HK MI HK ACM
hay
,d H ACM HK
.
Có
2 2
1 1 1 2
2 4 4 4
a
HI OD BD AB AD
,
1
2
MH SA a
.
Suy ra
2
2 2 2 2 2 2 2
1 1 1 1 1 1 1 9
3
2
4
a
HK
HK HM HI HK a HK a
a
.
Vậy
2
, 2 , 2
3
a
d SB CM d H ACM HK
.
Câu 27. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho hình chóp
.S ABCD
có
SA ABCD
,
6SA a
,
ABCD
là nửa lục giác đều nội tiếp đường tròn đường kính
2AD a
. Khoảng cách
từ điểm
B
đến mặt phẳng
SCD
bằng
A.
6
2
a
. B.
3
2
a
. C.
2
2
a
. D.
3
4
a
.
Lời giải
Chọn C
O
K
I
H
M
S
D
C
B
A
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Gọi I là trung điểm AD và H là trung điểm
SD
suy ra
//HI SA HI ABCD
.
Do
ABCD
là nửa lục giác đều và I là trung điểm AD nên
//BI CD
.
Suy ra
, ,d B SCD d I SCD
.
Do
ABCD
là nửa lục giác đểu nên dễ thấy
ICD
là tam giác đều.
Gọi
M
là trung điểm
CD
suy ra
CD HIM
.
Trong
IHM
kẻ
IK HM
.
Ta có:
IK HM
IK SCD
IK CD CD HIM
.
,d I SCD IK
.
Xét
IHM
có:
2 2 2 2 2 2
1 1 1 1 1 2
6 3
2 2
IK IH IM a
a a
.
2
2
a
IK
. Vậy
2
,
2
a
d B SCD
.
Câu 28. (Chuyên Hùng Vương - Gia Lai - 2020) Cho lăng trụ đứng tam giác
.ABC A B C
có đáy là
một tam giác vuông cân tại
B
,
2 ,AB AA a
M
là trung điểm
BC
(minh họa như hình
dưới). Khoảng cách giữa hai đường thẳng
AM
và
B C
bằng
A.
2
a
. B.
2
3
a
. C.
7
7
a
. D. 3a
M
I
S
C
B
D
A
H
K
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
Gọi
N
là trung điểm
BB
/ / / /MN B C B C AMN
.
Khi đó
, , ,d AM B C d B C AMN d C AMN
.
Ta có
BC AMN M
và
MB MC
nên
, ,d C ABM d B ABM
.
Gọi
h
là khoảng cách từ
B
đến mặt phẳng
ABM
. Tứ diện
BAMN
có
, ,BA BM BN
đôi một
vuông góc nên:
2 2 2 2 2
1 1 1 1 1
h BH BA BM BN
2AB a BC
.
1 1 2
2 2 2
a
BN BB AA a
.
1
2
BM BC a
.
Suy ra
2
2
2 2 2 2 2
1 1 1 1 9 4 2
4 4 9 3
a a
h h
h a a a a
.
Vậy khoảng cách giũa hai đường thẳng
AM
và
B C
bằng
2
3
a
.
Câu 29. (Chuyên Lào Cai - 2020) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh
2a và
0
90 .SBA SCA
Biết góc giữa đường thẳng SA và mặt đáy bằng 45
0
. Tính khoảng
cách từ điểm B đến mặt phẳng (SAC).
A.
15
5
a
. B.
2 15
5
a
. C.
2 15
3
a
. D.
2 51
5
a
.
Lời giải
Chọn B
2a
2a
N
A'
M
B'
A
B
C
C'
H
B
N
M
A
I
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Gọi I là trung điểm của SA.
Tam giác SAB và SAC là các tam giác vuông tại
,B C IS IA IB IC
.
Gọi G là trọng tâm tam giác đều
ABC IG ABC
Trong SAG kẻ
/ /SH IG H CG SH ABC
Dễ thấy khi đó IG là đường trung bình của tam giác
2SAH SH IG
Tam giác ABC đều cạnh =
2 2 3 2 3
2 .
3 2 3
a a
a AG
Ta có:
0
, , 45SA ABC SA AH SAH AIG
vuông cân tại G
2 3 4 3
2
3 3
a a
IG AG SH IG
2
3
.
2 3
1 1 4 3 4
. . .
3 3 3 4 3
S ABC ABC
a
a a
V SH S
Ta có:
,GA GB GC GA GH
( IG là đường trung bình của tam giác SAH)
GA GB GC GH G
là tâm đường tròn ngoại tiếp tứ giác ABHC.
AH là đường kính đường tròn ngoại tiếp tứ giác ABHC
0
90ACH
(góc nội tiếp chắn
nửa đường tròn)
Ta có:
2 2
4 3 2
2
3
3
a a
AH AG CH AH AC
2
2
2 2
4 3 2 2 15
3 3
3
a a a
SC SH HC
2
1 1 2 15 2 15
. . .2
2 2 3 3
SAC
a a
S SC AC a
Vậy
3
.
2
4
3.
3 2 15
3
,
5
2 15
3
S ABC
SAC
a
V a
d B SAC
S
a
Câu 30. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
M
là trung điểm của cạnh
AD
. Tính khoảng cách giữa hai đường thẳng
AB
và
CM
.
A.
33
11
a
. B.
33
a
. C.
22
a
. D.
22
11
a
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Ta có:
3
3
12
ABCD
a
V
;
3
1 2
2 24
ABCD
ABCM
ABCM
V
a
V
V
1
. . ( , ).sin( , )
6
ABCM
V AB CM d AB CM AB CM
2 2
.
.
4 2
3
os( , )
. . 6
3
.
2
a a
AB AM AC
AB CM
c AB CM
AB CM AB CM
a a

1 11
sin( , ) 1
12 12
AB CM
.Vậy
6
22
( , )
. .sin( , ) 11
ABCM
V
a
d AB CM
AB CM AB CM
.
Câu 31. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hình lăng trụ đều
. ’ ’ ’ABC A B C
có tất cả các
cạnh có độ dài bằng 2 (tham khảo hình vẽ). Tính khoảng cách giữa hai đường thẳng AC’ và
A’B.
A.
2
5
. B.
3
2
. C.
1
2
. D.
3
5
.
M
B
D
A
C
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Lời giải
Chọn A
Gọi
D
là điểm đối xứng của
C
qua
A
ta có tứ giác
ADA C
là hình bình hành do đó
//
A D AC
, suy ra khoảng cách
( , ) ( ,( )) ( ,( ))
d AC BA d AC A BD d A A BD
.
Theo giả thiết
.
ABC A B C
là lăng trụ đều nên
( )
AA ABC
hay
( )
AA ABCD
suy ra
(1)
A A BD
.
Ta có
ABD
có
AB AD
nên là tam giác cân tại
A
, gọi
I
là trung điểm
BD
ta có
(2)AI BD
.
Xét tam giác
BCD
có
,A I
lần lượt là trung điểm của
,DC DB
nên
1
1
2
AI BC
.
Trong mặt phẳng
( ' )A AI
dựng
; (3)
AH A I H A I
.
Từ (1) và (2) suy ra
( ' ) (4) BD A AI BD AH
.
Từ (3) và (4) suy ra
( ' )AH A BD
do đó khoảng cách
( ,( )) d A SBD AH
.
Trong tam giác
'A AI
vuông tại
A
ta có
2 2
. ' 2
5
( ')
AI AA
AH
AI AA
.
Từ đây chọn đáp án A.
Câu 32. (Chuyên Vĩnh Phúc - 2020) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt phẳng
ABC
; góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
60
.
Gọi
M
là trung điểm cạnh
AB
. Khoảng cách từ
B
đến
SMC
bằng
A.
39
13
a
. B. 3a . C.
a
. D.
2
a
.
Lời giải
Chọn A
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
SB ABC SBA SA a a, 60 tan 60 . 3
.
Vì M là trung điểm của
AB
d B SMC d A SMC, ,
.
Dựng
AH
vuông góc với
SM
tại
H
d A SMC AH,
mà
1
2 2
a
AM AB
.
Xét tam giác vuông
SAM
ta có:
2 2 2 2 2 2
1 1 1 1 4 13 39
3 3 13
a
AH
AH SA AM a a a
.
Câu 33. (Đại Học Hà Tĩnh - 2020) Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông và
AB BC a
,
2AA a
,
M
là trung điểm của
BC
. Tính khoảng cách
d
của hai đường
thẳng
AM
và
B C
.
A.
6
6
a
d
. B.
2
2
a
d
. C.
7
7
a
d
. D.
3
3
a
d
.
Lời giải
Chọn C
Cách 1:
A
B
C
A
B
C
M
N
K
H
Do
ABC
vuông và có
AB BC
nên
ABC
vuông cân tại
B
.
Gọi
N
là trung điểm của
BB
, ta có:
//B C AMN
.
Khi đó:
, , , ,d AM B C d B C AMN d C AMN d B AMN
.
Kẻ
BH AM
tại
H
và kẻ
BK NH
tại
K
.
Ta có:
,BH AM BN AM AM NBH BK AM
.
Do
BK NH
,
BK AM
nên
BK AMN
.
H
M
C
B
A
S
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Suy ra:
,
d B AMN BK
.
Mặt khác:
2 2
. 5
5
BM BA a
BH
BM BA
;
2 2
. 7
7
BH BN a
BK
BH BN
.
Vậy
7
, ,
7
a
d AM B C d B AMN BK
.
Cách 2:
A
O B
C
A
B
C
M
x
y
z
Do
ABC
vuông và có
AB BC
nên
ABC
vuông cân tại
B
.
Chọn hệ trục tọa độ
Oxyz
như hình vẽ. Không mất tính tổng quát, ta giả sử
1
a
.
Ta có:
1
1;0;0 , 0; ;0 , 0;0; 2 , 0;1;0
2
A M B C
.
1
1; ;0 , 0;1; 2 , 1;1;0
2
AM B C AC
 
;
2
, ; 2; 1
2
AM B C
.
Khi đó:
2
2 0
, .
2
7
,
7
1
,
2 1
2
AM B C AC
d AM B C
AM B C
.
Trong trường hợp tổng quát, ta có:
7
,
7
a
d AM B C
.
Câu 34. (ĐHQG Hà Nội - 2020) Cho lăng trụ đứng
/ / /
ABCA B C
có tất cả các cạnh bằng a. Gọi
M
là
trung điểm của
/
AA
. Tính khoảng cách giữa hai đường thẳng
BM
và
/
B C
.
A.
3
5
a
. B.
. C.
3
2 2
a
. D.
3
7
a
Lời giải
Chọn B
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
O và I lần lượt là trung điểm của B
/
C
/
, BC. Chọn hệ trục tọa độ
Oxyz
sao cho:
/ / / /
3 1
(0;0;0); Ox ( ;0;0); (0; ;0); (0;0;1)
2 2
O A A C Oy C I Oz I
/
1 1 1 3 3 1
(0; ;0); (0; ;1); (0; ;1); ( ;0;1); ( ;0; )
2 2 2 2 2 2
B C B A M
/ /
3 1 1 3 3
(0;1;1); ( ; ; ) , (1; ; )
2 2 2 2 2
B C BM BM B C
(0;1;0)BC
Vậy khoảng cách giữa hai đường thẳng
BM
và
/
B C
là:
/
/
/
3
. ,
3
2
( ; )
3 3 10
,
1
4 4
BC BM B C
d BM B C
BM B C
nên chọn đáp án B
Câu 35. (Sở Phú Thọ - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
, cạnh
, 2AB a AD a
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
là trung điểm của
đoạn
OA
. Góc giữa
SC
và mặt phẳng
ABCD
bằng
30
. Khoảng cách từ
C
đến mặt phẳng
SAB
bằng
A.
9 22
44
a
. B.
3 22
11
a
. C.
22
11
a
. D.
3 22
44
a
.
Lời giải
Chọn B
Gọi
H
là trung điểm
AO
, ta có
SH ABCD
.
a
a
B
/
x
y
a
B
A
C
A
/
C/
z
O
I
M
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Góc giữa
SC
và
ABCD
bằng
SCH bằng
30
.
Ta có
4CA HA
, suy ra
, 4 ,
d C SAB d H SAB
.
Kẻ
,HI AB HK SI
, ta suy ra
HK SAB
.
,d H SAB HK
.
1 2
4 4
a
HI AD
.
3 3 3
4 4
a
CH AC
Suy ra
3
.tan30
4
a
SH CH
.
Xét tam giác
SHI
vuông tại
H
có
HK
là đường cao.
Suy ra
2 2 2 2 2
1 1 1 16 16
9 2HK HS HI a a
3
2 22
a
HK .
3 3 22
, 4 , 4.
11
2 22
a a
d C SAB d H SAB .
Câu 36. (Sở Phú Thọ - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Hình
chiếu vuông góc của
S
trên mặt phẳng
ABCD
là trung điểm của cạnh
AB
, góc giữa mặt
phẳng
SAC
và đáy bằng
45
. Gọi
M
là trung điểm của cạnh
SD
. Khoảng cách giữa hai
đường
AM
và
SC
bằng
A.
a
. B.
2
4
a
. C.
5
10
a
. D.
5
5
a
.
Lời giải
Chọn D
Gọi
H
là trung điểm cạnh
AB
,
I
là trung điểm cạnh
AO
. Suy ra
SH ABCD
,
, 45SAC ABCD SIH
. Do đó
1 2
2 4
a
SH IH BO
.
Gọi
N
là trung điểm cạnh
CD
, khi đó
HN AB
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn hệ trục tọa độ trong không gian như hình vẽ, ta có tọa độ các điểm
0;0;0H
,
2 2
0; ;0 ; 0;0; ; ; ;0 ; ; ; ; ; ;0
2 4 2 2 4 8 2
a a a a a a a
A S D a M C a
.
Nên
2 2
; ; ; ; ; ; ; ;0
2 4 8 2 4
a a a a a
AM SC a AC a a
.
Khoảng cách giữa hai đường
AM
và
SC
là
, .
5
,
5
,
AM SC AC
a
d AM SC
AM SC
.
Câu 37. (Sở Hà Tĩnh - 2020) Cho tứ diện
ABCD
có
, ,AB AC AD
đôi một vuông góc với nhau và
2, 1AD AB AC
. Gọi
I
là trung điểm của đoạn thẳng
BC
, khoảng cách giữa hai đường
thẳng
AI
và
BD
bằng
A.
3
.
2
B.
2
.
5
C.
5
.
2
D.
2
.
3
Lời giải
Chọn D
Vì tứ diện
ABCD
có
, ,AB AC AD
đôi một vuông góc với nhau, nên ta chọn hệ trục tọa độ
Axyz
như hình vẽ (với
A
là gốc tọa độ, đường thằng
AC
nằm trên trục
Ax
,
AD
nằm trên
trục
Ay
và
AB
nằm trên trục
Az
).
Từ đó suy ra:
0;0;0A
,
0;0;1B
vì
B Az
,
1;0;0C
vì
C Ax
,
0;2;0D
vì
D Ay
.
Vì
I
là trung điểm của
BC
nên
1 1
;0;
2 2
I
.
Từ đó, ta quay về bài toán tính khoảng cách giữa hai đường thẳng chéo nhau trong hệ tọa độ
không gian
Axyz
.
Ta có
1 1 1
;0; , 0;2; 1 , 1; ;1
2 2 2
AI BD AI BD
và
0;0;1AB
.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Ta có
2
2
2
1
1 .0 .0 1.1
, .
2
2
,
3
,
1
1 1
2
AI BD AB
d AI BD
AI BD

.
Câu 38. (Sở Ninh Bình) Cho hình chóp
.S ABC
có
SA a
, tam giác
ABC
đều, tam giác
SAB
vuông
cân tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ
B
đến mặt
phẳng
SAC
bằng
A.
42
7
a
. B.
42
14
a
. C.
42
12
a
. D.
42
6
a
.
Lời giải
Chọn A
Gọi
, ,H M N
lần lượt là trung điểm của các cạnh
, ,AB AC AM
.
Do tam giác
SAB
vuông cân tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy
SH ABC
.
Kẻ
1HK SN
.
Ta có:
AC HN
AC SHN
AC SH
2AC HK
.
Từ
1
và
2
HK SAC
;d H SAC HK
.
Ta có
; 2 ;d B SAC d H SAC
.
Do tam giác
SAB
vuông cân tại
S
và
SA a
2
2
2
AB a
a
SH
.
Do tam giác
ABC
đều
6
2
6
4
a
BM
a
HN
.
Xét tam giác vuông
SHN
, ta có
2 2
. 42
14
SH HN
HK a
SH HN
.
Vậy
42
; 2 ; 2
7
d B SAC d H SAC HK a
.
Câu 39. (Sở Yên Bái - 2020) Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại
B
,
biết , , là trung điểm của . Tính khoảng cách giữa hai đường
thẳng và .
.
ABC A B C
AB BC a
2AA a
M
BC
AM
B C
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
7
7
a
. B.
2 5
5
a
. C.
6
2
a
. D.
15
5
a
.
Lời giải
Chọn A
Kẻ
.
Ta có tứ diện là tứ diện vuông
Câu 40. (Bỉm Sơn - Thanh Hóa - 2020) Cho hình chóp có đáy là hình chữ nhật,
. Tam giác cân tại và nằm trong mặt phẳng vuông góc với đáy. Góc
giữa đường thẳng và mặt phẳng bằng . Gọi là trung điểm của , hãy
tính theo khoảng cách từ đến mặt phẳng .
A. B. C. D.
Lời giải
Chọn D
Gọi là trung điểm của ( cân tại ).
Ta có .
C
B
A
C'
B'
A'
M
A
B
B'
C
N
M
// //
MN B C B C AMN
, , , ,
d d B C MN d B C AMN d C AMN d B AMN
BAMN
2 2
2 2 2 2 2 2
1 1 1 1 1 1 1 7 7
.
7
2
2
2
a
d
d BA BM BN a a
a
a
.
S ABCD
ABCD
, 2AB a AD a
SAB
S
SC
ABCD
45
M
SD
a
M
SAC
2 1513
.
89
a
d
1315
.
89
a
d
2 1315
.
89
a
d
1513
.
89
a
d
H
AB SH AB
SAB
S
SAB ABCD AB
SAB ABCD SH ABCD
SH AB cmt
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Vì , nên hình chiếu vuông góc của đường thẳng lên mặt phẳng là
, suy ra
vuông tại , có
vuông cân tại , suy ra
Ta có
Mặt khác .
Từ đó
Trong mặt phẳng , kẻ và kẻ .
Ta có .
Ta có
vuông tại , có
AI IH AH
AIH ABC
AB BC AC
. . 2 . 5
2 5
2. 5
BC AH BC AB a a a
IH
AC AC
a
.
vuông tại , có
Câu 41. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, cạnh
SA
tạo với mặt phẳng đáy một góc
o
30
. Khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
A.
2 15
5
a
. B.
3 14
5
a
. C.
2 10
5
a
. D.
4 5
5
a
.
Lời giải
Chọn C
Gọi
O
là tâm của mặt đáy,
M
là trung điểm của
AB
,
H
là hình chiếu của
O
trên
SM
.
Ta có
o o
2
, , 30 tan 30
3
a
SA ABCD SA OA SAO SAO SO AO .
Ta có
,AB OM AB SO AB SOM AB OH
, mà
SM OH OH SAB
.
SH ABCD
SC
ABCD
HC
, , 45 .
SC ABCD SC HC SCH
HBC
B
2 2
2
2 2 2
17
2 .
2 2 2
AB a a
HC HB BC BC a
SHC
H
17
.
2
a
SH HC
,
1 1 1
, , , .
2 2 2
,
d M SAC
MS
d M SAC d D SAC d B SAC
DS
d D SAC
,
2 , 2 ,
,
d B SAC
BA
d B SAC d H SAC
HA
d H SAC
, , .d M SAC d H SAC
SAC
HI AC
HK SI
AC HI gt
AC SHI AC HK
AC SH SH ABCD
, .
HK SI gt
HK SAC d H SAC HK
HK AC cmt
ABC
B
2
2 2 2
2 5.
AC AB BC a a a
SHI
H
2 2 2 2
17 5
.
. 1513
2 5
.
89
17 5
2 5
a a
SH HI a
HK
SH HI
a a
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tam giác
SOM
vuông tại
O
và có đường cao
OH
nên
2 2 2 2 2 2
1 1 1 3 1 5 10
2 2 5
a
OH
OH SO OM a a a
.
Vì
2 10
// , , , 2 , 2
5
a
CD AB d CD SA d CD SAB d C SAB d O SAB OH
.
Câu 42. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông
tại
A
và
B
,
2 2 2AD AB BC a
,
SA
vuông góc với đáy, góc giữa
SB
và mặt phẳng đáy
bằng
0
60
. Gọi
H
là hình chiếu vuông góc của
A
lên
SB
. Khoảng cách từ
H
đến mặt phẳng
SCD
bằng
A.
3a
. B.
3 30
20
a
. C.
3 30
10
a
. D.
3 30
40
a
.
Lời giải
Chọn D
Kẽ
/ / / /HK SC HK SCD
. Khi đó
, ,d H SCD d K SCD
.
Ta có
0
.tan .tan ; .tan 60 3SA AB SBA a SB ABCD a a .
2 2
2SB SA AB a
.
Mà
2
2
2
1
.
4
BH AB
AB BH SB
SB SB
. Vì
/ /HK SC
nên
1 3
4 4 4
BK a a
BK KC
BC
.
Vì
/ /KC AD
nên
;
3 3
; ;
8 8
;
d K SCD
KC
d K SCD d A SCD
AD
d A SCD
.
Gọi
F
là hình chiếu vuông góc của
A
lên
SC
.
Do
AC DC
DC SAC DC AF
SA DC
.
Vì
AF SC
AF SCD
AF DC
nên
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
2 2
. 30
;
5
SA AC a
d A SCD AF
SA AC
, với
2 2
2AC AB BC a
.
Vậy
3 3 30
; ; ;
8 40
a
d H SCD d K SCD d A SCD
.
Câu 43. (Kim Liên - Hà Nội - 2020) Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA
vuông
góc với mặt phẳng đáy, góc giữa mặt phẳng
SBC
và mặt phẳng đáy là
60
(minh họa như
hình dưới đây). Gọi
,M N
lần lượt là trung điểm của
,AB AC
.
Khoảng cách giữa hai đường thẳng
SB
và
MN
bằng
A.
3
8
a
. B.
6
2
a
. C.
3
4
a
. D.
6a
.
Lời giải
Chọn A
Gọi
E
là trung điểm của
,BC
vì tam giác
ABC
đều
AE BC
, lại có
SA BC BC SE
Mặt khác
, 60SBC ABC BC SBC ABC SEA
.
Gọi
P
là trung điểm của
// , //SA SB MP MP MNP SB MNP
, , , ,d SB MN d SB MNP d B MNP d A MNP
Gọi
60AE MN I PIA SEA và
AI MN
Ta có
,MN AI MN PI MN API PMN API
Mà
PMN API PI
, kẻ
,AH PI AH PMN d A PMN AH
.
Xét
API
có
1 3 3 3 3
60 , .sin .
2 4 4 2 8
a a a
AIP AI AE AH AI AIP
.
Vậy
3
,
8
a
d SB MN
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 44. (Lê Lai - Thanh Hóa - 2020) Cho hình chóp
có đáy là hình thang vuông
tại và , , ,
, vuông góc với mặt phẳng
đáy và (minh họa như hình bên
dưới). Khoảng cách từ đến mặt phẳng
bằng
A. . B. .
C. . D. .
Lời giải
Chọn C
+) Gọi
E
là giao điểm của
AD
và
BC DA
cắt mặt phẳng
SBC
tại
E
.
,
,
d D SBC
DE
AE
d A SBC
(1).
+) Theo giả thiết
//
1
2
AB CD
AB CD
AB
là đường trung bình của tam giác
ECD
(2).
Từ (1) và (2)
,
2
,
d D SBC
DE
AE
d A SBC
, 2 ,d D SBC d A SBC
.
+) Ta có
BC AB
BC SAB SBC SAB
BC SA
, do đó nếu gọi
H
là hình chiếu vuông
góc của
A
lên
SB
thì
AH SBC
,d A SBC AH
.
+) Tam giác
ECD
vuông tại
C
, có:
CA
là đường trung tuyến
CA AE AD a
tam giác
AEC
là tam giác cân tại
A
.
30 60EDC CEA ;
tam giác
EAC
là tam giác đều cạnh
a
đường cao
3
2
a
AB
.
+) Tam giác
SAB
vuông tại
A
có
AH
là đường cao
.
S ABCD
ABCD
B
C
2
CD AB
AD a
30
ADC
SA
2SA a
D
SBC
2 57
19
a
57
19
a
4 57
19
a
3a
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
2
2 2 2
2
3
2 .
. 3 2 57
2
19
19
3
4
2
4
a
a
SA AB a a
AH
a
SA AB a
a
.
Vậy
4 57
, 2 , 2
19
a
d D SBC d A SBC AH
.
Câu 45. (Liên trường Nghệ An - 2020) Cho tứ diện
ABCD
có
0
90 , 2 ,ABC ADC ACD BC a CD a
, góc giữa đường thẳng
AB
và mặt phẳng
BCD
bằng
0
60
. Tính khoảng cách giữa hai đường thẳng
AC
và
BD
.
A.
6
31
a
. B.
2 6
31
a
. C.
2 3
31
a
. D.
3
31
a
.
Lời giải
Chọn C
Gọi
H
là chân đường cao của tứ diện
ABCD
.
Ta có:
BC AB
BC HB
BC AH
1
.
Lại có:
CD AD
CD HD
CD AH
2
.
Mà
90BCD .
Từ đây ta suy ra
HBCD
là hình chữ nhật.
Mặt khác:
, 60AB BCD ABH
. Suy ra: .tan 60 3AH HB a .
Chọn hệ trục
.Oxyz H DBA
như hình vẽ.
Ta có:
0;0;0H
,
0;0; 3A a ,
0; ;0B a
,
2 ; ;0C a a
,
2 ;0;0D a
.
2 ; ; 3AC a a a

,
2 ; ;0BD a a

,
0; ; 3AB a a

.
Vậy
3
2 2
2
2 2 2
, .
2 3 2 93
,
31
,
3 2 3 4
AC BD AB
a a
d AC BC
AC BD
a a a
.
Câu 46. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tứ diện
OABC
có
, ,OA OB OC
đôi một vuông góc
với nhau và
OA OB a
,
2OC a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa hai
đường thẳng
OM
và
AC
bằng
z
y
x
2a
a
60
0
A
B
C
D
H
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
3
a
. B.
2 5
5
a
. C.
2
2
a
. D.
2
3
a
.
Lời giải
Chọn D
Dựng
//AE OM
, khi đó
//OM CAE
. Do đó
, ,( ) ,( )d OM AC d OM CAE d O CAE
Dựng
OK AE
, ta có:
AE OK
AE COK
AE OC CO A CVì B
Mà
AE CAE
nên
CAE COK
.
Ta có
CAE COK CK
. Kẻ
OH CK
, khi đó
OH COK
. Suy ra
,( )d O CAE OH
Xét tam giác
OAB
ta có :
2 2
2AB OA OB a
.
Dễ thấy
OKAM
là hình chữ nhật nên
2
2 2
AB a
OK AM
.
Xét tam giác
COK
ta có :
2 2
2 2 2 2
1 1 1 1 1 1 2
3
2
2
2
OH a
OH OK OC OH
a
a
.
Câu 47. (Nguyễn Huệ - Phú Yên - 2020) Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
A
,
, 2 ,AB a AC a SA
vuông góc với mặt phẳng đáy và
2SA a
. Gọi
G
là trọng tâm của
ABC
. Khoảng cách giữa hai đường thẳng
SG
và
BC
bằng
A.
2
7
a
. B.
6
3
a
. C.
2 6
9
a
. D.
4
7
a
.
Lời giải
Chọn A
E
M
A
C
O
B
K
H
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Gọi
M
là trung điểm của
BC
. Trong mp
SAM
dựng
/ /S M SG
. Suy ra
3
3
2
S A SA a
Do đó
, , ,d SG BC d SG S BC d G S BC
.
Vì
3AM GM
nên
1
, ,
3
d G S BC d A S BC
.
Kẻ
AH BC
ta có
BC S AH
.
Kẻ
,AK S H AK d A S BC
.
Ta có
2 2 2
1 1 1 2
5
a
AH
AH AB AC
. Suy ra
2 2 2
1 1 1 6
7
a
AK
AK S A AH
.
Do đó
1 2
,
3 7
a
d G S BC AK
.
Câu 48. (Nguyễn Trãi - Thái Bình - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành
và
11, SA SB SC
góc
30 , SAB
góc
60 , SBC
góc
45 SCA
. Tính khoảng
cách
d
giữa hai đường thẳng
AB
và
SD
.
A.
2 22
. B.
22
. C.
22
2
. D.
4 11
.
Lời giải
Chọn B
Trong tam giác
SAB
ta có
2 2 2
2 . .cos30 11 3 SB SA AB SA AB AB .
Trong tam giác
SBC
ta có
11, 60 SB SC SBC
nên
SBC
đều suy ra
11BC
.
Trong tam giác
SCA
ta có
11, 45 SC SA SCA
nên
SCA
vuông cân tại
S
suy ra
11 2AC
.
Xét tam giác
ABC
có
2 2 2
BC AC AB
do vậy
ABC
vuông tại
C
.
Gọi
I
là hình chiếu của
S
lên mặt phẳng
( )ABCD
vì
SA SB SC
nên
I
là tâm của đường
tròn ngoại tiếp tam giác
ABC
, vì
ABC
vuông tại
C
nên
I
là trung điểm của
AB
và
( ) (1) SI ABCD SI CD
. Vẽ
(2), (3) IK CD IH SK
.
Từ (1) và (2) suy ra
( ) (4) CD SIK CD IH
.
Từ (3) và (4) suy ra
( )IH SCD
do đó khoảng cách
( ,( )) d I SCD IH
.
Ta lại có
//AB CD
suy ra khoảng cách
( , ) ( ,( )) ( ,( )) d AB SD d AB SCD d I SCD IH
.
Trong mặt phẳng đáy vẽ
CJ AB
ta suy ra
. 11 6
3
CACB
IK CJ
AB
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Trong tam giác
SAB
cân tại
S
có
2
2
11
4 2
AB
SI SA
.
Trong tam giác
SIK
vuông tại
I
ta có
2 2
.
22
IK SI
IH
IK SI
.
Câu 49. (THPT Nguyễn Viết Xuân - 2020) Cho hình hộp
.
ABCD A B C D
có đáy
ABCD
là hình
vuông cạnh
a
, tâm
O
. Hình chiếu vuông góc của
A
lên mặt phẳng
ABCD
trùng với
O
.
Biết tam giác
AA C
vuông cân tại
A
. Tính khoảng cách
h
từ điểm
D
đến mặt phẳng
ABB A
.
A.
6
6
a
h
. B.
2
6
a
h
. C.
2
3
a
h
. D.
6
3
a
h
.
Lời giải
Chọn D
Ta có:
2 2 2 2
2 AC AB BC a a a
.
Vì tam giác
AA C
vuông cân tại
A
nên ta có:
2
2 2
AC a
A O
.
Gọi
M
là trung điểm của
AB
. Suy ra
OM AB
.
Trong mặt phẳng
A OM
: kẻ
OH A M
.
Ta có:
AB A OM
(vì
AB OM
và
AB A O
). Suy ra
AB OH
.
Vì
OH A M
OH ABB A
OH AB
. Do đó:
;
d O ABB A OH
.
Do
, ,D O B
thẳng hàng và
2DB OB
nên
; 2 ; 2
d D ABB A d O ABB A OH
.
Ta có:
2 2 2
2
2
.
. 6
2 2
6
2
2 2
a a
A O OM a
OH
A O OM
a a
.
Vậy
6
; 2
3
a
d D ABB A h OH
.
Câu 50. (Tiên Du - Bắc Ninh - 2020) Cho hình lăng trụ tam giác
.ABC A B C
có cạnh bên bằng
2a
,
đáy
ABC
là tam giác vuông tại
, 3,B BC a AB a
. Biết hình chiếu vuông góc của đỉnh
A
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
lên mặt đáy là điểm
M
thoả mãn
3AM AC
. Khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
A.
210
15
a
. B.
210
45
a
. C.
714
17
a
. D.
714
51
a
.
Lời giải
Chọn A
Dựng hình bình hành
ABCD
, vì tam giác
ABC
là tam giác vuông tại B nên
ABCD
là hình
chữ nhật.
Suy ra
/ / / /BC AD BC A AD
.
Do đó
, , ,d BC AA d BC A AD d C A AD
.
Mà
3AM AC
nên
, 3 ,d C A AD d M A AD
.
Kẻ
MH AD A MH A AD A H
.
Kẻ
,MK A H MK A AD MK d M A AD
.
Mặt khác ta có
2 2 2 2
1 2 14
2
3 3 3
a a
AC AB BC a AM AC A M A A AM
.
Và
1 1 1
/ /
3 3 3 3
MH AM a
MH CD MH CD AB
CD AC
.
Suy ra
2 2
2 2 2 2 2 2
1 1 1 1 1 1 1 135 210
14 45
14
3
3
a
MK
MK A M MH MK MK a
a
a
.
Vậy
210 210
, , 3 , 3 3
45 15
a a
d BC AA d C A AD d M A AD MK
.
Câu 51. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2 2AD AB a
. Cạnh bên
2SA a
và vuông góc với đáy. Gọi
,M N
lần lượt là trung điểm
của
SB
và
SD
. Tính khoảng cách
d
từ điểm
S
đến mặt phẳng
AMN
.
A.
2d a
. B.
3
2
a
d
. C.
6
3
a
d
. D.
5d a
.
Lời giải
Chọn C
K
H
D
M
a
a 3
a 2
A'
B'
C'
C
B
A
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ
A
kẻ đường thẳng vuông góc với
BD
tại
H
, ta có:
/ /
BD SAH
MN SAH AMN SAH
MN BD
Mặt khác
AMN SAH SE
, suy ra:
; ;d S AMN d S AE
.
Xét tam giác vuông
SAH
có:
2 2
. .2 2 5
5
4
AB AD a a a
AH
BD
a a
.
2
2 2 2
20 2 30
4
25 5
a a
SH SA AH a .
Vì
MN
là đường trung bình của tam giác
SBD
nên
E
là trung điểm của
SH
, suy ra:
1 30
2 5
a
AE SH
.
2
. 2 .2 5 6
;
2. 3
30
2.5.
5
SAE SAH
S S
AS AH a a a
d S AE
AE AE AE
a
.
Câu 52. (Hải Hậu - Nam Định - 2020) Cho hình chóp đều
.S ABCD
có đáy
ABCD
là hình vuông
cạnh
2a
. Biết rằng bán kính mặt cầu ngoại tiếp hình chóp bằng
9 2
8
a
, độ dài cạnh bên lớn
hơn độ dài cạnh đáy. Khoảng cách giữa hai đường thẳng
AB
và
SD
bằng
A.
2 17
17
a
. B.
4 17
17
a
. C.
4 34
17
a
. D.
2 34
17
a
.
Lời giải
Chọn D
Gọi
O AC BD
,
M
là trung điểm
SC
.
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Trong tam giác
SAC
, dựng đường trung trực của đoạn thẳng
SC
cắt
SO
tại
I
,
I
là tâm mặt
cầu ngoại tiếp hình chóp
.
S ABCD
, bán kính
9 2
8
a
R SI
.
Vì độ dài cạnh bên lớn hơn độ dài cạnh đáy nên tâm
I
của mặt cầu ngoại tiếp hình chóp thuộc
đoạn
SO
.
Gọi
x
là độ dài cạnh bên của hình chóp.
Ta có
SOC
đồng dạng với
SMI
.
Suy ra
2 2
9 2
8
2
a
x
SI SM
SC SO x
x a
2
2 2 2 2 2 2 2 2 4
9 2
9 2 2 81 8
8 2
a x
x a a x a x a x a x
2
2
2
4 2 2 4
2
2
9
8 81 81 0 8 81 81 0
9
8
x
a
x x
x a x a
a a
x
a
2
9
8
x
a
không thỏa vì
2x a
.
2
9 3
x
x a
a
.
Suy ra
2
2 2 2
3 8SO a a a
; , ; 2 ;
d AB SD d AB SDC d A SCD d O SCD
.
Gọi
E
là trung điểm
CD
, kẻ
OH SE
, khi đó
,
d O SCD OH
.
2 2 2 2 2
1 1 1 1 2 2 2
8 17
a
OH
OH SO OE a a
.
4 34
; 2
17
a
d AB SD OH
.
Câu 53. (Kìm Thành - Hải Dương - 2020) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
, biết
SA ABC
và
2AB a
,
3AC a
,
4SA a
. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng
A.
2
11
a
d
. B.
6 29
29
a
d
. C.
12 61
61
a
d
. D.
a
.
Lời giải
Chọn C
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
SA ABC
SA BC
BC ABC
.
Trong
ABC
, kẻ
AH BC
, mà
BC SA BC SAH BC SH
.
Trong
SAH
, kẻ
AK SH
, mà
SH BC
AK SBC
hay
;d A SBC AK
.
Vì
ABC
vuông tại
A
nên
2 2
13BC AB AC a
.
Mặt khác có
AH
là đường cao nên
. 6 13
13
AB AC a
AH
BC
.
Vì
SAH
vuông tại
A
nên
2 2
2 793
13
a
SH SA AH
.
Vậy có
AK
là đường cao
. 12 61
61
SA AH a
AK
SH
.
Câu 54. (Lương Thế Vinh - Hà Nội - 2020) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
với
2AB a
,
3AD a
(tham khảo hình vẽ). Tam giác
SAB
cân tại
S
và nằm trong mặt phẳng
vuông góc với mặt đáy; góc giữa mặt phẳng
SCD
và mặt đáy là
45
. Gọi
H
là trung điểm
cạnh
AB
. Tính theo
a
khoảng cách giữa hai đoạn thẳng
SD
và
CH
.
A.
3 11
11
a
. B.
3 14
7
a
. C.
3 10
109
a
. D.
3 85
17
a
.
Lời giải
Chọn B
Cách 1:
A
C
B
S
H
K
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Ta có:
;
SAB ABCD
SAB ABCD
SH AB SH SAB
SH ABCD
.
Kẻ
HK CD
(
K
là trung điểm của
CD
)
CD SHK
CD SK
.
; ;SCD ABCD SK HK
45SKH
SHK
vuông cân tại
H
3SH HK a
.
Kẻ
d
qua
D
song song với
HC
cắt
AB
tại
E
10ED HC a .
; ;d CH SD d CH SED
;d H SED
.
Kẻ
HF ED
ED SHF
.
Kẻ
HG SF
HG SED
;d H SED HG
.
Ta có:
1 1
. .
2 2
HED
S AD EH HF ED
.AD EH
HF
ED
3 .2 3 10
5
10
a a a
a
.
Xét tam giác
SHF
vuông tại
H
ta có:
2 2 2
1 1 1
HG SH HF
2 2
.SH HF
HG
SH HF
2
2
3 10
3 .
5
18
9
5
a
a
a
a
3 14
7
a
.
3 14
;
7
a
d CH SD
.
Cách 2:
Ta có:
;
SAB ABCD
SAB ABCD
SH AB SH SAB
SH ABCD
.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Kẻ
HK CD
(
K
là trung điểm của
CD
)
CD SHK
CD SK
.
; ;SCD ABCD SK HK
45SKH
SHK
vuông cân tại
H
3SH HK a
.
Chọn hệ trục tọa độ như hình vẽ
H O
, tia
Ox
chứa
HK
, tia
Oy
chứa
HA
, tia
Oz
chứa
HS
Khi đó:
0;0;0H
;
3 ; ;0C a a
;
3 ; ;0D a a
;
0;0;3S a
.
Ta có:
3 ; ;0HC a a

,
3 ; ; 3SD a a a
,
0;0; 3SH a
.
2 2 2
; 3 ;9 ;6HC SD a a a
. ;
;
;
SH HC SD
d CH SD
HC SD


2
2 2 2
2 2 2
6 . 3
3 9 6
a a
a a a
3 14
7
a
.
Câu 55. (Trường VINSCHOOL - 2020) Cho hình chóp
.S ABCD
có đáy là hình chữ nhật, cạnh
2AB AD a
. Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy
ABCD
.
Khoảng cách từ điểm
A
đến mặt phẳng
SBD
bằng
A.
3
4
a
. B.
3
2
a
. C.
2
a
. D.
2a
.
Lời giải
Chọn A
Gọi
H
là trung điểm của
AB
. Từ giả thiết suy ra
SH ABCD
.
Từ
H
kẻ
HG BD
tại
G
, kẻ
HI SG
tại
I
.
Suy ra
HI SBD
,d H SBD HI
.
Ta có
2
2 2 2
5
4 2
a a
BD AB AD a ,
3
2
a
SH
.
Lại có
BGH
đồng dạng với
BAD
nên
.
. 5
2 2
10
5
2
a a
HG BH AD BH a
HG
AD BD BD
a
.
Khi đó
2 2
2 2 2
1 1 1 1 1
3 5
2 10
HI SH HG
a a
H
A
B
C
D
S
G
I
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Suy ra
3
8
a
HI
.
Lại có
3 3
, 2 , 2. 2.
8 4
a a
d A SBD d H SBD HI
.
Câu 56. (Thanh Chương 1 - Nghệ An - 2020) Cho hình chóp
SABC
, có đáy là tam giác vuông tại
A
,
4AB a
,
3AC a
. Biết 2 3SA a ,
30SAB
và
SAB ABC
. Khoảng cách từ
A
đến
mặt phẳng
SBC
bằng
A.
3 7
14
a
. B.
8 7
3
a
. C.
6 7
7
a
. D.
3 7
2
a
.
Lời giải
Chọn C
Gọi
SH
là đường cao của khối chóp
SH
là đường cao của tam giác
SAB
.
SAH
có
30 , 90 .cos30 3 3SAH SHA AH SA a SH a
; 4 ;d A SBC d H SBC
.
Tính khoảng cách từ
H
đến mặt phẳng
SBC
:
Từ
H
kẻ
HK BC
tại
K
, kẻ
HI SK
tại
I
;d H SBC HI
Mà
HBK CBA
. 3
5
BH HK BH CA
HK a
BC CA BC
TỔ
NG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2 2
1
1 1 28 3 7
9 14
a
HI
HI SH HK a
6 7
; .
7
a
d A SBC
Câu 57. (Tiên Lãng - Hải Phòng - 2020) Cho hình lăng trụ đứng
.A
BC A B C
có
A
B a
,
2A
C a
,
0
120BAC . Gọi
M
là trung điểm cạnh
C
C
thì
0
90BMA
. Tính khoảng cách từ điểm
A
đến mặt phẳng
B
MA
.
A.
7
7
a
. B.
5
3
a
. C.
5
7
a
. D.
5
5
a
.
Lời
giải
Chọn B
Ta có:
2
2 2
2. . .cosBC AB AC AB AC BAC
2
2
0 2
2
2. .2 .cos120 7a a a a a
.
Đặt
2C
C x CM MC x
.
Vì
.A
BC A B C
là
hình lăng trụ đứng nên ta có tam giác
B
CM
vuôn
g tại
C
và
tam giác
A C M
vuôn
g tại
C
.
Ta
có:
2
2 2 2 2
7BM BC CM a x
;
2
2
2 2 2 2 2
2 4A M A C C M a x a x
;
2
2 2 2 2
4A B A A AB x a
.
Vì
0
90BMA
nên
tam giác
BMA
vuôn
g tại
M
,
do đó:
2
2 2
A
B BM A M
2 2 2 2 2 2
4 7 4x a a x a x
2
2
5 5x a x a .
Ta có:
1
.
.sin
2
AB
C
S AB AC BAC
1
.
. ,
2
AB d C AB
,
3d C AB a .
Lại có:
, , ,d M ABA d C ABA d C AB
( vì
/ /CC ABA
và
ABC ABA
).
Suy ra.
Ta có:
2
1
.
5
2
ABA
S
AB AA a
;
2
1
.
3 3
2
M
BA
S
MB MA a
.`
1
1
. . , . . ,
3 3
AA BM ABA MBA
V
S d M ABA S d A BMA
5
,
3
a
d
A BMA
.
A
'
B'
C'
M
C
B
A
-------------------- HẾT --------------------
| 1/89
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
44 CÂU HỎI VD - VDC CHƯƠNG 7. ĐẠI SỐ 11 PHẦN 1. XÁC SUẤT Câu 1.
(Chuyên Biên Hòa - Hà Nam - 2020) Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các
chữ số của số đó bằng 7? A. 165 . B. 1296 . C. 343 . D. 84 . Câu 2.
(Chuyên ĐH Vinh - Nghệ An -2020) Ban chỉ đạo phòng chống dịch Covid-19 của sở Y tế Nghệ
An có 9 người, trong đó có đúng 4 bác sĩ. Chia ngẫu nhiên Ban đó thành ba tổ, mỗi tổ 3 người để
đi kiểm tra công tác phòng dịch ở địa phương. Trong mỗi tổ, chọn ngẫu nhiên một người làm tổ
trưởng. Xác suất để ba tổ trưởng đều là bác sĩ là 1 1 1 1 A. . B. . C. . D. . 42 21 14 7 Câu 3.
(Chuyên Hưng Yên - 2020) Cho tập S  1;2;...;19; 
20 gồm 20 số tự nhiên từ 1 đến 20. Lấy
ngẫu nhiên ba số thuộc S . Xác suất để ba số lấy được lập thành cấp số cộng là 5 7 3 1 A. . B. . C. . D. . 38 38 38 114 Câu 4.
(Chuyên KHTN - 2020) Xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang. Xác suất để 2 bạn
nữ không ngồi cạnh nhau bằng 1 2 1 1 A. . B. . C. . D. . 6 3 4 3 Câu 5.
(Chuyên KHTN - 2020) Một công ty may mặc có hai hệ thống máy chạy song song. Xác suất để
hệ thống máy thứ nhất hoạt động tốt là 90%, xác suất để hệ thống máy thứ hai hoạt động tốt là
80%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy
hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là A. 98%. B. 2%. C. 80%. D. 72%. Câu 6.
(Chuyên Lam Sơn - 2020) Giải bóng chuyền VTV cup gồm 12 đội tham gia, trong đó có 9 đội
nước ngoài và 3 đội Việt Nam. Ban tổ chức bốc cho thăm ngẫu nhiên và chia thành 3 bảng đấu , A ,
B C mỗi bảng 4 đội. Xác suất để ba đội Việt Nam nằm ở 3 bảng gần nhất với số nào dưới đây? 11 3 39 29 A. . B. . C. . D. . 25 20 100 100 Câu 7.
(Chuyên Lương Văn Chánh - Phú Yên - 2020) Xếp ngẫu nhiên 5 học sinh ,
A B, C, D, E ngồi
vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi một ghế). Tính xác suất để hai bạn A và B không ngồi cạnh nhau. 1 3 2 4 A. . B. . C. . D. . 5 5 5 5 Câu 8.
(Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Hai bạn A và B mỗi bạn viết ngẫu nhiên một số tự
nhiên gồm ba chữ số đôi một khác nhau. Xác suất để các chữ số có mặt ở hai số bạn A và B viết giống nhau bằng 31 1 1 25 A. . B. . C. . D. 2916 648 108 2916 Câu 9.
(Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Một nhóm gồm 10 học sinh trong đó có 7
học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động.
Tinh xác suất để trong 3 học sinh được chọn có ít nhất 1 học sinh nữ. 4 17 17 2 A. . B. . C. . D. . 9 24 48 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 10. (Chuyên Thái Bình - 2020) Có tất cả bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau
trong đó có đúng 3 chữ số chẵn A. 72000 . B. 64800 . C. 36000 . D. 60000 .
Câu 11. (Chuyên Bắc Ninh - 2020) Cho S là tập các số tự nhiên có 8 chữ số. Lấy một số bất kì của tập
S . Tính xác suất để lấy được số lẻ và chia hết cho 9 . 3 1 2 1 A. . B. . C. . D. . 8 9 9 18
Câu 12. (Chuyên Bến Tre - 2020) Đội học sinh giỏi trường trung học phổ thông chuyên bến tre gồm có 8
học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 8 học sinh. Xác suất
để trong 8 học sinh được chọn có đủ 3 khối là 71131 35582 143 71128 A. . B. . C. . D. . 75582 3791 153 75582
Câu 13. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho tập A  1, 2,3, 4,5, 
6 . Gọi S là tập hợp các tam
giác có độ dài ba cạnh là các phần tử của A . Chọn ngẫu nhiên một phần tử thuộc S . Xác suất để
phần tử được chọn là một tam giác cân bằng. 6 19 27 7 A. . B. . C. . D. . 34 34 34 34
Câu 14. (Chuyên Hùng Vương - Gia Lai - 2020) Cho một đa giác đều 18 đỉnh nội tiếp trong một đường
tròn tâm O . Gọi X là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính
xác suất P để chọn được một tam giác từ tập X là tam giác cân nhưng không phải tam giác đều. 144 7 23 21 A. P  . B. P  . C. P  . D. P  . 136 816 136 136
Câu 15. (Chuyên Lào Cai - 2020) Chọn ngẫu nhiên bốn số tự nhiên khác nhau từ 70số nguyên dương
đầu tiên. Tính xác suất để bốn số được chọn lập thành một cấp số nhân có công bội nguyên. 12 11 10 9 A. . B. . C. . D. . 916895 916895 916895 916895
Câu 16. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có 6 học sinh gồm 2 học sinh lớp A, 2 học sinh
lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm bất kì 3
học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C. 1 1 1 1 A. . B. . C. . D. . 120 3 30 15
Câu 17. (Chuyên Sơn La - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh gồm 3 nam 3 nữ
ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học
sinh nam đều ngồi đối diện với một học sinh nữ bằng 1 3 1 2 A. . B. . C. D. . 10 5 20 5
Câu 18. (Sở Phú Thọ - 2020) Cho đa giác đều  H  có 30 đỉnh. Lấy tùy ý 3 đỉnh của  H  . Xác suất để 3
đỉnh lấy được tạo thành một tam giác tù bằng 39 39 45 39 A. . B. . C. . D. . 140 58 58 280
Câu 19. (Sở Hà Tĩnh - 2020) Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10 , lấy ngẫu
nhiên 5 quả cầu. Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng 5 7 1 11 A. . B. . C. . D. . 12 12 12 12 Câu 20.
(Sở Bắc Ninh - 2020) Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một
khác nhau. Chọn ngẫu nhiên một số thuộc A. Xác suất để số tự nhiên được chọn chia hết cho 25 bằng
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 43 1 11 17 A. . B. . C. . D. . 324 27 324 81
Câu 21. (Sở Yên Bái - 2020) Gọi S là tập tất cả các số tự nhiên có ba chữ số đôi một khác nhau được lập từ các chữ số
0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia hết cho 6. 13 2 17 11 A. . B. . C. . D. . 60 9 45 45
Câu 22. (Bỉm Sơn - Thanh Hóa - 2020) Trường trung học phổ thông Bỉm Sơn có 23 lớp, trong đó khối
10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có một em
làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường chọn ngẫu
nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thị xã. Tính xác suất để 9 em được chọn có đủ cả ba khối? 7345 7012 7234 7123 A. . B. . C. . D. . 7429 7429 7429 7429
Câu 23. (Đặng Thúc Hứa - Nghệ An - 2020) Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp mặt
10 em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp số
cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ
được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau. 1 1 1 1 A. . B. . C. . D. . 954 252 945 126
Câu 24. (Đô Lương 4 - Nghệ An - 2020) Người ta muốn chia tập hợp 16 học sinh gồm 3 học sinh lớp
12A, 5 học sinh lớp 12B và 8 học sinh lớp 12C thành hai nhóm, mỗi nhóm có 8 học sinh. Xác suất
sao cho ở mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B là 42 84 356 56 A. . B. . C. . D. . 143 143 1287 143
Câu 25. (Hậu Lộc 2 - Thanh Hóa - 2020) Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15. Chọn
ngẫu nhiên 6 tấm thẻ trong hộp. Xác suất để tổng các số ghi trên 6 tấm thẻ được chọn là một số lẻ bằng. 71 56 72 56 A. . B. . C. . D. . 143 715 143 143
Câu 26. (Kim Liên - Hà Nội - 2020) Một số điện thoại có bảy chữ số, trong đó chữ số đầu tiên là 8. Số
điện thoại này được gọi là
may mắn nếu bốn chữ số đầu là chữ số chẵn phân biệt và ba chữ số còn lại là lẻ, đồng thời hai
chữ số 0 và 9 không đứng liền nhau. Tính xác suất để một người khi lắp điện thoại ngẫu nhiên
được số điện thoại may mắn. 5100 2850 5100 2850 A. P( ) A  . B. P( ) A  . C. P( ) A  . D. P( ) A  . 7 10 7 10 6 10 6 10
Câu 27. (Lê Lai - Thanh Hóa - 2020) Cho tập hợp A  1; 2; 3; 4; 
5 . Gọi S là tập hợp tất cả các số tự
nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập
A . Chọn ngẫu nhiên một số từ tập S , tính xác xuất để số được chọn có tổng các chữ số bằng 10 . 1 3 22 2 A. . B. . C. . D. . 30 25 25 25
Câu 28. (Liên trường Nghệ An - 2020) Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau
lập thành từ các chữ số 0,1, 2, 3, 4, 5, 6, 7 . Chọn ngẫu nhiên một số từ tập S . Tính xác suất để số
được chọn có đúng 2 chữ số chẵn.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 24 144 72 18 A. . B. . C. . D. . 35 245 245 35
Câu 29. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tập S  1; 2;3;...;19; 2 
0 gồm 20 số tự nhiên từ 1 đến
20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là 7 5 3 1 A. . B. . C. . D. . 38 38 38 114
Câu 30. (Nguyễn Huệ - Phú Yên - 2020) Một bàn cờ vua gồm 8 8
 ô vuông, mỗi ô có cạnh bằng 1 đơn
vị. Một ô vừa là hình vuông hay hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên một
hình chữ nhật trên bàn cờ. Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng 5 17 51 29 A. . B. . C. . D. . 216 108 196 216
Câu 31. (Tiên Du - Bắc Ninh - 2020) Gọi M là tập hợp các số tự nhiên có ba chữ số lập được từ các chữ
số 0, 1, 2, 3, 4, 5, 6, 7. Lấy ngẫu nhiên đồng thời 2 số từ tập M. Xác suất để cả 2 số lấy được đều
có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là 8 5 296 695 A. . B. . C. . D. . 21 16 2051 7152
Câu 32. (Hải Hậu - Nam Định - 2020) Một hộp có chứa 5 viên bi đỏ, 3 viên bi xanh và n viên bi vàng (
các viên bi kích thước như nhau, n là số nguyên dương). Lấy ngẫu nhiên 3 viên bi từ hộp. Biết 45
xác suất để trong ba viên vi lấy được có đủ 3 màu là
. Tính xác suất P để trong 3 viên bi lấy 182
được có nhiều nhất hai viên bi đỏ. 135 177 45 31 A. P  . B. P  . C. P  . D. P  . 364 182 182 56
Câu 33. (Kìm Thành - Hải Dương - 2020) Gọi S là tập hợp tất cả các số tự nhiên gồm 9 chữ số đôi một
khác nhau. Chọn ngẫu nhiên một số từ S . Tính xác suất để được chọn có đúng 4 chữ số lẻ và
chữ số 0 đứng giữa hai chữ số lẻ. (Các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ). 5 5 5 20 A. . B. . C. . D. . 648 27 54 189
Câu 34. (Trường VINSCHOOL - 2020) Có 6 học sinh nam và 4 học sinh nữ xếp thành hàng ngang.
Xác suất để có đúng hai bạn nữ đứng cạnh nhau bằng 1 1 14 7 A. . B. . C. . D. . 24 2 17 13
Câu 35. (Thanh Chương 1 - Nghệ An - 2020) Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số mà các
chữ số đều khác 0. Lấy ngẫu nhiên một số từ S . Xác suất để lấy được số chỉ có mặt 3 chữ số gần
với số nào nhất trong các số sau?
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 A. 0,34 . B. 0,36 . C. 0, 21. D. 0,13 .
Câu 36. (Tiên Lãng - Hải Phòng - 2020) Một xưởng sản xuất thực phẩm gồm 4 kỹ sư chế biến thực
phẩm, 3 kĩ thuật viên và 13 công nhân. Để đảm bảo sản xuất thực phẩm chống dịch Covid 19,
xưởng cần chia thành 3 ca sản xuất theo thời gian liên tiếp nhau sao cho ca I có 6 người và 2 ca
còn lại mỗi ca có 7 người. Tính xác suất sao cho mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm. 440 441 41 401 A. . B. . C. . D. . 3320 3230 230 3320
Câu 37. (Trần Phú - Quảng Ninh - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu
nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học
sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng 1 1 8 8 A. . B. . C. . D. . 3 30 63 37 Câu 38.
(Đại Học Hà Tĩnh - 2020) Cho đa giác đều 12 đỉnh nội tiếp đường tròn tâm
A.
Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác
không có cạnh nào là cạnh của đa giác đã cho. 2 31 28 52 A. . B. . C. . D. . 5 55 55 55
Câu 39. (ĐHQG Hà Nội - 2020) Có 12 học sinh gồm 6 nam và 6 nữ ngồi vào hai hàng ghế đối diện nhau
tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là? 1 4 8 16 A. . B. . C. . D. . 924 165 165 231
Câu 40. (Sở Hưng Yên - 2020) Có 50 tấm thẻ đánh số từ 1 đến 50. Rút ngẫu nhiên 3 thẻ. Xác suất để
tổng các số ghi trên thẻ chia hết cho 3 bằng 8 11 769 409 A. . B. . C. . D. . 89 171 2450 1225
PHẦN 2. MỘT SỐ BÀI TOÁN KHÁC
Câu 41. (Chuyên Bắc Ninh - 2020) Cho x  0, x  1 . Tìm số hạng không chứa x trong khai triển Niu-tơn của 20  x  1 x  1  P     3 2 3  x x  1 x x  . A. 38760 . B. 167960 . C. 1600 . D. 125970 .
Câu 42. (Sở Phú Thọ - 2020) Giả sử n là một số nguyên dương thoả mãn 2 3
3C C  24 . Hệ số của số n n n  2  hạng chứa 12 x trong khai triển 2 x x    bằng  x A. 12 672x . B. 12 672  x . C. 672 . D. 6  72 .
Câu 43. (Sở Bình Phước - 2020) Trên một cái bảng đã ghi sẵn các số tự nhiên từ 1 đến 2020 . Ta thực
hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số
vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng là A. 4040 . B. 2041210 . C. 4082420 . D. 2020 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 44. (Yên Lạc 2 - Vĩnh Phúc - 2020) Xác định n biết rằng hệ số của n x trong khai triển      2 2 1 2 ... n x x nx bằng 6n . A. n  8 . B. n  6 . C. n  10 . D. n  5 .
-------------------- HẾT --------------------
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020 CHƯƠNG 7. ĐẠI SỐ 11 PHẦN 1. XÁC SUẤT Câu 1.
(Chuyên Biên Hòa - Hà Nam - 2020) Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các
chữ số của số đó bằng 7? A. 165 . B. 1296 . C. 343 . D. 84 . Lời giải Chọn D
7 có thể phân tích thành 11 nhóm sau: 7 = (7+0+0+0) = (6+1+0+0) = (5+2+0+0) = (5+1+1+0)
= (4+3+0+0) = (4+2+1+0) = (4+1+1+1)
= (3+3+1+0) = (3+2+2+0) = (3+2+1+1) = (2+2+2+1)
+) Với nhóm (7+0+0+0) viết được 1 số, đó là số: 7000.
+) Với các nhóm (6+1+0+0); (2+2+0+0) và (4+3+0+0): mỗi nhóm viết được 6 số
(chẳng hạn: với nhóm (6+1+0+0) ta có các số 6100, 6010, 6001 và hoán vị của số 6 và số 1). 4! 3!
+) Với nhóm (3+3+1+0); (5+1+1+0) và (3+2+2+0): mỗi nhóm viết được  9 số 2
( 3! là các số có số 0 đứng đầu, chia 2 vì có 1 số xuất hiện 2 lần).
+) Với nhóm (4+2+1+0) viết được: 4! 3!  18 số ( 3! là các số có số 0 đứng đầu). 4!
+) Với nhóm (3+2+1+1) viết được:
 12 số (vì xuất hiện 2 số 1). 2
+) Với các nhóm (4+1+1+1) và (2+2+2+1): mỗi nhóm viết được 4 số
(chẳng hạn: với nhóm (4+1+1+1) ta có các số: 4111; 1411; 1141; 1114).
Tổng số các số viết được là: 1  6.3  9.3 18 12  4.2  84 (số). Câu 2.
(Chuyên ĐH Vinh - Nghệ An -2020) Ban chỉ đạo phòng chống dịch Covid-19 của sở Y tế
Nghệ An có 9 người, trong đó có đúng 4 bác sĩ. Chia ngẫu nhiên Ban đó thành ba tổ, mỗi tổ 3
người để đi kiểm tra công tác phòng dịch ở địa phương. Trong mỗi tổ, chọn ngẫu nhiên một
người làm tổ trưởng. Xác suất để ba tổ trưởng đều là bác sĩ là 1 1 1 1 A. . B. . C. . D. . 42 21 14 7 Lời giải Chọn B
Chọn 3 người vào nhóm A và có một tổ trưởng ta có: 3 C .3 cách. 9
Chọn 3 người vào nhóm B và có một tổ trưởng ta có: 3 C .3 cách. 6
3 người còn lại vào nhóm C và có một tổ trưởng ta có: 3 C .3 cách. 3
Từ đó ta có số phần tử của không gian mẫu là: n  3 3 3
C .3.C .3.C .3  45360. 9 6 3
Gọi M là biến cố thỏa mãn bài toán.
Vì có 4 bác sĩ nên phải có một nhóm có 2 bác sĩ.
Chọn nhóm có 2 bác sĩ mà có 1 tổ trưởng là bác sĩ có 2 1 C .C .2 4 5
Chọn nhóm có 1 bác sĩ và bác sí là tổ trưởng có: 1 2 C .C . 2 4
1 bác sĩ còn lại và 2 người còn lại vào nhóm có 1 cách. Chọn một trong 3 nhóm ,
A B, C có 2 bác sĩ có 1 C cách. 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2160 1  n M  2 1 1 2 1
C ,C .2.C .C .C  2160 .  P M    . 4 5 2 4 3 45360 21 Câu 3.
(Chuyên Hưng Yên - 2020) Cho tập S  1;2;...;19; 
20 gồm 20 số tự nhiên từ 1 đến 20. Lấy
ngẫu nhiên ba số thuộc S . Xác suất để ba số lấy được lập thành cấp số cộng là 5 7 3 1 A. . B. . C. . D. . 38 38 38 114 Lời giải Chọn C Ta có: 3 n()  C . 20
Gọi A là biến cố: “ba số lấy được lập thành cấp số cộng “.
Giả sử ba số a, b, c theo thứ tự đó lập thành cấp số cộng, khi đó ta có a c  2b . Hay a c là
một số chẵn và mỗi cách chọn 2 số a và c thỏa mãn a c là số chẵn sẽ có duy nhất cách chọn
b. Số cách chọn hai số có tổng chẵn sẽ là số cách chọn ba số tạo thành cấp số cộng.
TH1: Hai số lấy được đều là số chẵn, có: 2 C cách lấy. 10
TH2: Hai số lấy được đều là số lẻ, có: 2 C cách lấy. 10 2 2
n(A)  C C 10 10 2 2 n( A) C C 3 10 10 P (A)    . 3 n() C 38 10 Câu 4.
(Chuyên KHTN - 2020) Xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang. Xác suất để 2
bạn nữ không ngồi cạnh nhau bằng 1 2 1 1 A. . B. . C. . D. . 6 3 4 3 Lời giải Chọn B
Số phần tử không gian mẫu là n  6!  720 . 
Gọi A là biến cố: “xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang mà 2 bạn nữ không ngồi cạnh nhau”.
Khi đó A là biến cố: “xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang mà 2 bạn nữ ngồi cạnh nhau”.
Xếp 4 bạn nam và 1 bạn nữ thành một hàng ngang, có 5!  120 cách.
Xếp bạn nữ còn lại ngồi cạnh bạn nữ đã xếp ở trên, có 2 cách.
Khi đó n  120.2  240 . A n
Xác suất cần tìm bằng P A   P A 240 2 1  1 A  1  . n 720 3  Câu 5.
(Chuyên KHTN - 2020) Một công ty may mặc có hai hệ thống máy chạy song song. Xác suất
để hệ thống máy thứ nhất hoạt động tốt là 90%, xác suất để hệ thống máy thứ hai hoạt động tốt
là 80%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống
máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là A. 98%. B. 2%. C. 80%. D. 72%. Lời giải Chọn A
Goi A là biến cố : « Hệ thống máy thứ nhất hoạt động tốt »
B là biến cố : « Hệ thống máy thứ hai hoạt động tốt »
C là biến cố : « Công ty hoàn thành đúng hạn »
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Ta có A là biến cố : « Hệ thống máy thứ nhất hoạt động không tốt »
B là biến cố : « Hệ thống máy thứ hai hoạt động không tốt » P( )
A  0, 9 ; P(B)  0,8 ; P( )
A  0,1 ; P(B)  0, 2 .
P(C)  P( . A B)  P( )
A .P(B)  0, 02  P(C)  1 P(C)  0,98 . Câu 6.
(Chuyên Lam Sơn - 2020) Giải bóng chuyền VTV cup gồm 12 đội tham gia, trong đó có 9
đội nước ngoài và 3 đội Việt Nam. Ban tổ chức bốc cho thăm ngẫu nhiên và chia thành 3 bảng đấu , A ,
B C mỗi bảng 4 đội. Xác suất để ba đội Việt Nam nằm ở 3 bảng gần nhất với số nào dưới đây? 11 3 39 29 A. . B. . C. . D. . 25 20 100 100 Lời giải Chọn D
Số cách chọn 4 đội cho bảng A là 4 C . Khi đó sẽ có 4
C số cách chọn 4 đội cho bảng B và số 12 8
cách chọn 4 đội cho bảng C là 4 C . 4
Vậy số phần tử của không gian mẫu là: 4 4 4 n
C .C .C .  12 8 4
Đặt T là biến cố: “3 đội Việt Nam nằm ở 3 bảng khác nhau”.
Số cách chọn 1 đội Việt Nam và 2 đội nước ngoại cho bảng A là 1 3
C .C . Với mỗi cách chọn 3 9 cho bảng A ta có 1 3
C .C số cách chọn 1 đội Việt Nam và 2 đội nước ngoại cho bảng B . Khi 2 6
đó, số cách chọn 1 đội Việt Nam và 2 đội nước ngoại cho bảng C là 1 3 C .C . 1 3
Số phần tử của biến cố T là: 1 3 1 3 1 3 n
C .C C .C .C .C . T  3 9 2 6 1 3 1 3 1 3 1 3 nT
C .C C .C .C .C 16 Xác suất cần tính là 3 9 2 6 1 3 P    . T  4 4 4 n C .C .C 55  12 8 4 Câu 7.
(Chuyên Lương Văn Chánh - Phú Yên - 2020) Xếp ngẫu nhiên 5 học sinh ,
A B, C, D, E ngồi
vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi một ghế). Tính xác suất để hai bạn A và B không ngồi cạnh nhau. 1 3 2 4 A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn B
Số phần tử của không gian mẫu: n   5!  120 .
Gọi X là biến cố “Hai bạn A và B không ngồi cạnh nhau”.
X “Hai bạn A và B ngồi cạnh nhau”
Có 4 vị trí để hai bạn A và B ngồi cạnh nhau, hai bạn đổi chỗ được một cách xếp mới.
Nên số cách xếp để hai bạn A và B ngồi cạnh nhau là 4.2!.3!  48 n X  48 2
Xác suất của biến cố X là: P X     n  120 5
Vây xác suất của biến cố X là: P X    P X  3 1  5 Câu 8.
(Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Hai bạn A và B mỗi bạn viết ngẫu nhiên một số
tự nhiên gồm ba chữ số đôi một khác nhau. Xác suất để các chữ số có mặt ở hai số bạn A và B
viết giống nhau bằng 31 1 1 25 A. . B. . C. . D. 2916 648 108 2916 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Mỗi bạn có 2
9.A cách viết nên số phần tử của không gian mẫu là n   9.A . 9 2 2 9
Ta tìm cách viết mà các chữ số các chữ số có mặt trong hai số mà bạn A và B viết giống nhau Bạn A có tất cả 2
9.A cách viết, trong đó 3
A cách viết mà số không gồm chữ số 0 và có 9 9  2 3
9.A A cách viết mà số có chữ số 0. 9 9 
TH1: Nếu A viết số không gồm chữ số 0 có 3
A cách, lúc này B có 3! cách viết. 9
TH2: Nếu A viết số có chữ số 0 có  2 3
9.A A cách, lúc này B có 4 cách viết. 9 9  Vậy có 3 A .3!  2 3
9.A A .4 cách viết thỏa mãn. 9 9 9  3 A .3!  2 3 9.A A .4 9 9 9  25
Xác suất cần tính bằng  .  A 2 2 2916 9 Câu 9.
(Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Một nhóm gồm 10 học sinh trong đó có
7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao
động. Tinh xác suất để trong 3 học sinh được chọn có ít nhất 1 học sinh nữ. 4 17 17 2 A. . B. . C. . D. . 9 24 48 3 Lời giải Chọn B Ta có n  3  C  120. 10
Đặt A  ”3 học sinh được chọn có ít nhất 1 nữ”
A  ”3 học sinh được chọn không có nữ” n A 7
Khi đó n A 3
C  35  p A   7 n  24
Vậy p A   p A 17 1  . 24
Câu 10. (Chuyên Thái Bình - 2020) Có tất cả bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau
trong đó có đúng 3 chữ số chẵn A. 72000 . B. 64800 . C. 36000 . D. 60000 . Lời giải Chọn B
TH1: 3 chữ số chẵn được chọn khác chữ số 0
Chọn 3 chữ số chẵn khác chữ số 0 là 3 C 4 Chọn 3 chữ số lẻ là 3 C 5
Số tự nhiên gồm 6 chữ số đôi một khác nhau lập từ các số đã chọn là 3 3
C .C .6!  28800 . 4 5
TH3: 3 chữ số chẵn được chọn có 1 chữ số là chữ số 0
Chọn 2 chữ số chẵn khác chữ số 0 là 2 C 4 Chọn 3 chữ số lẻ là 3 C 5
Số tự nhiên gồm 6 chữ số đôi một khác nhau lập từ các số đã chọn là 2 3
C .C . 6! 5!  36000 . 4 5  
Số các số tự nhiên thỏa mãn là 28800  36000  64800 .
Câu 11. (Chuyên Bắc Ninh - 2020) Cho S là tập các số tự nhiên có 8 chữ số. Lấy một số bất kì của
tập S . Tính xác suất để lấy được số lẻ và chia hết cho 9 . 3 1 2 1 A. . B. . C. . D. . 8 9 9 18 Lời giải Chọn D
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Số phần tử của không gian mẫu là n  7  9.10 .
Gọi A là biến cố: “lấy được số lẻ và chia hết cho 9 ”.
+ Dãy các số lẻ có 8 chữ số và chia hết cho 9 là 10000017; 10000035; 10000053;.; 99999999.
+ Dãy số trên là 1 cấp số cộng với số hạng đầu u  10000017 , số hạng cuối u  99999999 và 1 n 99999999 10000017
công sai d  18 , suy ra số phần tử của dãy số là 6 1  5000000  5.10 18
Do đó n A 6  5.10 . n A 6 5.10 1
Vậy xác suất của biến cố A là P A    . n  7 9.10 18
Câu 12. (Chuyên Bến Tre - 2020) Đội học sinh giỏi trường trung học phổ thông chuyên bến tre gồm
có 8 học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 8 học sinh.
Xác suất để trong 8 học sinh được chọn có đủ 3 khối là 71131 35582 143 71128 A. . B. . C. . D. . 75582 3791 153 75582 Lời giải Chọn D
Số phần tử không gian mẫu: n  8   C  75582 . 19
Gọi A là biến cố:” trong 8 học sinh được chọn có đủ 3 khối”. Ta có: n  8   C  8 8 8 8
C C C C  21128 . 19 14 13 11 8  P  71128 A  . 75582
Câu 13. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho tập A  1, 2,3, 4,5, 
6 . Gọi S là tập hợp các
tam giác có độ dài ba cạnh là các phần tử của A . Chọn ngẫu nhiên một phần tử thuộc S . Xác
suất để phần tử được chọn là một tam giác cân bằng. 6 19 27 7 A. . B. . C. . D. . 34 34 34 34 Lời giải Chọn C
Tập các bộ ba số khác nhau có giá trị bằng số đo 3 cạnh là:
2;3;4,2;4;5,2;5;6,3;4;5,3;4;6,3;5;6,4;5;6 có 7 tam giác không cân.
Xét các tam giác cân có cạnh đáy bằng a , cạnh bên bằng b  2b a . Ta xét các trường hợp
b  1 a  1: 1 tam giác cân.
b  2  a  1; 2;  3 : 3 tam giác cân.
b  3  a  1;2;3;4;  5 : 5 tam giác cân.
b  4;5;6  a  1; 2;3; 4;5;  6 : có 18 tam giác cân.
Vậy ta có n   7 1 3  5 18  34 . Gọi A là biến cố:” để phần tử được chọn là một tam
giác cân”, suy ra n A  1 3  5 18  27 . n A 27
Suy ra p A   . n  34
Câu 14. (Chuyên Hùng Vương - Gia Lai - 2020) Cho một đa giác đều 18 đỉnh nội tiếp trong một
đường tròn tâm O . Gọi X là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác
trên. Tính xác suất P để chọn được một tam giác từ tập X là tam giác cân nhưng không phải tam giác đều. 144 7 23 21 A. P  . B. P  . C. P  . D. P  . 136 816 136 136
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C
Số phần tử của không gian mẫu là 3
n( X )  C . 18
Ký hiệu đa giác là A A ...A nội tiếp đường tròn (O) , xét đường kính A A khi đó số tam giác 1 2 18 1 10
cân có đỉnh cân là A hoặc A là 2x8  16 (tam giác cân); Mà có tất cả là 9 đường kính do vậy 1 10
số tam giác cân có các đỉnh là đỉnh của đa giác là 9x16  144 (tam giác cân).
Ta lại có số tam giác đều có các đỉnh là đỉnh của đa giác đều 18 đỉnh là 6 .
Vậy xác suất P để chọn được một tam giác từ tập X là tam giác cân nhưng không phải tam 144  6 23 giác đều là P   . 3 C 136 18
Câu 15. (Chuyên Lào Cai - 2020) Chọn ngẫu nhiên bốn số tự nhiên khác nhau từ 70số nguyên dương
đầu tiên. Tính xác suất để bốn số được chọn lập thành một cấp số nhân có công bội nguyên. 12 11 10 9 A. . B. . C. . D. . 916895 916895 916895 916895 Lời giải Chọn B
Xét phép thử “Chọn ngẫu nhiên bốn số tự nhiên khác nhau từ 70 số nguyên dương đầu tiên”. Khi đó n  4  C  916895 . 70
Xét biến cố A : “Bốn số được chọn lập thành một cấp số nhân có công bội nguyên”.
Ta gọi bốn số đó lần lượt là 2 3
a, aq, aq , aq . Theo giả thiết 3 3
aq  70  q  70  q  4 .
Vì bốn số khác nhau và đều dương nên ta có 0  q  1  q 2;3;  4 .
TH1. q  2  8a  70  a  8 . Khi đó có 8 bộ số thỏa mãn.
TH2. q  3  27a  70  a  2 . Khi đó có 2 bộ số thỏa mãn.
TH3. q  4  64a  70  a  1. Khi đó có 1 bộ số thỏa mãn. 11
Vậy n A  11  P A  . 916895
Câu 16. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có 6 học sinh gồm 2 học sinh lớp A, 2 học
sinh lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm
bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C. 1 1 1 1 A. . B. . C. . D. . 120 3 30 15 Lời giải Chọn D
Xét phép thử: Xếp ngẫu nhiên 6 học sinh của 3 lớp thành một hàng ngang, ta có: n   6!
Gọi D là biến cố: nhóm bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C.
Ta thấy rằng để 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của cả 3 lớp A, B, C
thì các học sinh của cùng 1 lớp phải đc xếp vào các vị trí 1; 4, 2;5, 3;6 .
Xếp 2 học sinh lớp A vào vị trí (1; 4) có 2 cách, xếp 2 học sinh lớp B vào vị trí (2; 5) có 2 cách,
xếp 2 học sinh lớp C vào vị trí (3; 6) có 2 cách và có 3! cách để hoán vị vị trí của các nhóm học sinh theo lớp.
Suy ra n D  3!.2.2.2  48 .
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 n D 48 1
Vậy xác suất cần tìm là: P D    . n  720 15
Câu 17. (Chuyên Sơn La - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh gồm 3 nam 3 nữ
ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học
sinh nam đều ngồi đối diện với một học sinh nữ bằng 1 3 1 2 A. . B. . C. D. . 10 5 20 5 Lời giải Chọn D
Sắp 6 học sinh vào 6 cái ghế có 6! cách.
Suy ra n   6!.
Đánh số thự tự 6 cái ghế như hình bên dưới
Gọi A là biến cố: “Nam nữ ngồi đối diện”.
Học sinh nam thứ nhất có 6 cách chọn một vị trí ngồi.
Học sinh nam thứ hai có 4 cách chọn một vị trị ngồi (trừ vị trí đối diện với người nam thứ nhất).
Học sinh nam thứ ba có hai cách chọn một vị trí ngồi (trừ hai vị trí đối diện với hai nam thứ nhất và thứ hai).
Xếp ba học sinh nữ vào ba vị trí còn lại có 3! cách.
n A  6.4.2.3! 6.4.2.3! 2 P A   . 6! 5
Câu 18. (Sở Phú Thọ - 2020) Cho đa giác đều  H  có 30 đỉnh. Lấy tùy ý 3 đỉnh của  H  . Xác suất
để 3 đỉnh lấy được tạo thành một tam giác tù bằng 39 39 45 39 A. . B. . C. . D. . 140 58 58 280 Lời giải Chọn B
Chọn ngẫu nhiên 3 đỉnh có 3 C . 30
Gọi T  là đường tròn ngoại tiếp đa giác  H  .
Giả sử chọn được một tam giác tù ABC với góc A nhọn, B tù, C nhọn.
Chọn 1 đỉnh bất kì làm đỉnh A có 30 cách. Kẻ đường kính của đường tròn T  đi qua đỉnh vừa
chọn chia đường tròn T  thành hai phần.(Bên trái và bên phải).
Để tạo thành một tam giác tù thì hai đỉnh còn lại cùng nằm bên trái hoặc cùng nằm bên phải.
Hai đỉnh cùng nằm bên trái có 2 C cách. 14
Hai đỉnh cùng nằm bên phải có 2 C cách. 14
Vì trong mỗi tam giác vai trò của đỉnh A và C như nhau nên số tam giác tù tạo thành là: 30  2 2 C C 14 14   2730 . 2 2730 39
Xác suất cần tìm là P   . 3 C 58 30
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 19. (Sở Hà Tĩnh - 2020) Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10 , lấy
ngẫu nhiên 5 quả cầu. Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng 5 7 1 11 A. . B. . C. . D. . 12 12 12 12 Lời giải Chọn D
Không gian mẫu của phép thử là n  5  C  252 . 10
Gọi A là biến cố để “tích các số ghi trên 5 quả cầu đó chia hết cho 3 ”.
Các quả cầu có số thứ tự chia hết cho 3 gồm các quả có số thứ tự 3 , 6 , 9 .
Do vậy để tích các số ghi trên 5 quả cầu đó chia hết cho 3 thì 5 quả đó phải chứa ít nhất một
quả có số thứ tự 3 , 6 , 9 .
Suy ra A là biến cố để “tích các số ghi trên 5 quả cầu đó không chia hết cho 3 ”.
Số phần tử của A là cách lấy 5 quả từ tập hợp gồm các phần tử 1; 2; 4;5;7;8;1  0 . n A 21 1 5  
Vậy ta có n A  C  21 P A    . 7
  n 252 12
Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 là
P A   P A 1 11 1  1  . 12 12
Câu 20. (Sở Bắc Ninh - 2020) Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau.
Chọn ngẫu nhiên một số thuộc A. Xác suất để số tự nhiên được chọn chia hết cho 25 bằng 43 1 11 17 A. . B. . C. . D. . 324 27 324 81 Lời giải Chọn C Ta có 7 n()  9.A . 9
Gọi a là số tự nhiên thuộc tập A. Ta có 7 6 5 4 3 2
a a a a a a a a a a .10  a .10  a .10  a .10  a .10  a .10  a .10  a . 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
Do đó, a25  (10a a )25 trong đó a  5 hoặc a  0 . Suy ra a a là một trong các số 7 8 8 8 7 8 sau: 50; 25; 75 .
Th1: Nếu a a  50 thì có 6
A cách chọn các chữ số còn lại. 7 8 8
Th2: Nếu a a  25 hoặc a a  75 thì có 5
7.A cách chọn các chữ số còn lại. 7 8 7 8 7 6 5 A  2.7.A 11
Vậy xác suất cần tìm là 8 7  . 7 9.A 324 9
Câu 21. (Sở Yên Bái - 2020) Gọi S là tập tất cả các số tự nhiên có ba chữ số đôi một khác nhau được lập từ các chữ số
0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia hết cho 6. 13 2 17 11 A. . B. . C. . D. . 60 9 45 45 Lời giải Chọn A
Gọi số tự nhiên có ba chữ số đôi một khác nhau thỏa mãn bài toán có dạng abc ( a  0 )
Theo bài ra: Vì abc chia hết cho 6 nên abc phải là số chẵn.
Như vậy, c có 4 cách chọn.
Trường hợp 1: c = 0
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Khi đó, (a;b) là hoán vị của bộ số (1;2), (1;5), (2;4), (3;6), (4;5)
Mỗi trường hợp có 2 cách sắp xếp
Như vậy có 5.2 = 10 số tự nhiên thỏa mãn bài toán trong trường hợp 1.
Trường hợp 2: c = 2
Khi đó, (a;b) là hoán vị của bộ số (0;1), (0;4), (1;3), (1;6), (3;4), (4;6)
Mỗi trường hợp có chữ số 0 có 1 cách sắp xếp
Mỗi trường hợp không có chữ số 0 có 2 cách sắp xếp
Như vậy, có 2 + 4.2 = 10 số tự nhiên thỏa mãn bài toán trong trường hợp 2.
Trường hợp 3: c = 4
Khi đó, (a;b) là hoán vị của bộ số (0;2), (0;5), (2;3), (2;6), (3;5), (5;6)
Làm tương tự trường hợp 2, có 2 + 4.2 = 10 số tự nhiên thỏa mãn bài toán trong trường hợp 3.
Trường hợp 4: c = 6
Khi đó, (a;b) là hoán vị của bộ số (0;3), (1;2), (1;5), (2;4), (4;5)
Làm tương tự trường hợp 2, trường hợp này có 1 + 4.2 = 9 số tự nhiên thỏa mãn bài toán.
Số phần tử của không gian mẫu: n()  6.6.5  180
Xác suất để chọn được số chia hết cho 6: 10  10  10  9 39 13 P    180 180 60
Câu 22. (Bỉm Sơn - Thanh Hóa - 2020) Trường trung học phổ thông Bỉm Sơn có 23 lớp, trong đó
khối 10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có
một em làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường
chọn ngẫu nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thị xã. Tính xác suất để 9 em được
chọn có đủ cả ba khối? 7345 7012 7234 7123 A. . B. . C. . D. . 7429 7429 7429 7429 Lời giải Chọn C
Số phần tử của không gian mẫu là: n  9 C  817190 . 23
Gọi X là biến cố “9 em được chọn có đủ cả ba khối”
X “9 em được chọn không có đủ ba khối”
Vì mỗi khối số bí thư đều nhỏ hơn 9 nên có các khả năng sau:
TH1: Chỉ có học sinh ở khối 10 và 11. Có 9 C cách. 16
TH2: Chỉ có học sinh ở khối 11 và 12. Có 9 C cách. 15
TH3: Chỉ có học sinh ở khối 10 và 12. Có 9 C cách. 15
Số phần tử của biến cố X là: n X C C C  21450   9 9 9 16 15 15
Xác suất của biến cố X là: P X   .   21450 195 817190 7429
Xác suất của biến cố X là: P X    P X  .   7234 1 7429
Câu 23. (Đặng Thúc Hứa - Nghệ An - 2020) Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp
mặt 10 em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp
số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế
chỉ được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau. 1 1 1 1 A. . B. . C. . D. . 954 252 945 126 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Số phần tử của không gian mẫu là số cách sắp xếp 10 học sinh vào hai dãy bàn đối diện n 10!.
Gọi A là biến cố “tổng các số thứ tự của hai e ngồi đối diện là bằng nhau”.
Đánh số thứ tự của các em từ 1 đến 10.
Để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau phải chia thành 5 cặp đối diện
1;10,2;9,3;8,4;7,5;6 .
Ta xếp dãy 1, dãy 2 chỉ có một cách chọn.
Vị trí A có 10 cách chọn 1 học sinh, B có 1 cách chọn. 1 1
Vị trí A có 8 cách chọn 1 học sinh, B có 1 cách chọn. 2 2
Vị trí A có 6 cách chọn 1 học sinh, B có 1 cách chọn. 3 3
Vị trí A có 4 cách chọn 1 học sinh, B có 1 cách chọn. 4 4
Vị trí A có 2 cách chọn 1 học sinh, B có 1 cách chọn. 5 5
Suy ra số phần tử của biến cố A là nA 10.8.6.4.2 n A 10.8.6.4.2 1
Vậy xác suất để biến cố A xảy ra là: P A    . n  10! 945
Câu 24. (Đô Lương 4 - Nghệ An - 2020) Người ta muốn chia tập hợp 16 học sinh gồm 3 học sinh lớp
12A, 5 học sinh lớp 12B và 8 học sinh lớp 12C thành hai nhóm, mỗi nhóm có 8 học sinh. Xác
suất sao cho ở mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B là 42 84 356 56 A. . B. . C. . D. . 143 143 1287 143 Lời giải Chọn B
Gọi A là biến cố mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B.
Chọn ra 8 học sinh từ 16 học sinh được 1 nhóm, 8 học sinh còn lại tạo thành nhóm thứ 2. Vì ở 8 C
đây không phân biệt thứ tự các nhóm nên ta có n  16  . 2!
Mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B nên 1 nhóm
có 1 hoặc 2 học sinh lớp 12A và có 2 hoặc 3 học sinh lớp 12B. Do đó 1 2 5 1 3 4
C .C .C C .C .C n A 3 5 8 3 5 8  . 2! n A 84
Vậy P A   . n  143
Câu 25. (Hậu Lộc 2 - Thanh Hóa - 2020) Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15. Chọn
ngẫu nhiên 6 tấm thẻ trong hộp. Xác suất để tổng các số ghi trên 6 tấm thẻ được chọn là một số lẻ bằng. 71 56 72 56 A. . B. . C. . D. . 143 715 143 143 Lời giải Chọn C
Số phần tử của không gian mẫu của phép thử: n  6  C  5005 15
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Chia 15 tấm thẻ thành 2 tập hợp nhỏ gồm:
+ Tập các tấm ghi số lẻ: 1;3;5;7;9;11;13;1  5  8 số
+ Tập các tấm ghi số chẵn: 2; 4;6;8;10;12;1  4  7 số
Các trường hợp thuận lợi cho biến cố:
TH1. 1 tấm số lẻ: 5 tấm số chẵn - Số phần tử: 1 5 C .C  168 8 7
TH2. 3 tấm số lẻ: 3 tấm số chẵn - Số phần tử: 3 3 C .C  1960 8 7
TH3. 5 tấm số lẻ: 1 tấm số chẵn - Số phần tử: 5 1 C .C  392 8 7
Tổng số phần tử thuận lợi của biến cố là: 168 1960  392  2520 2520 72
Vậy xác suất của biến cố là: P   . 5005 143
Câu 26. (Kim Liên - Hà Nội - 2020) Một số điện thoại có bảy chữ số, trong đó chữ số đầu tiên là 8. Số
điện thoại này được gọi là
may mắn nếu bốn chữ số đầu là chữ số chẵn phân biệt và ba chữ số còn lại là lẻ, đồng thời hai
chữ số 0 và 9 không đứng liền nhau. Tính xác suất để một người khi lắp điện thoại ngẫu nhiên
được số điện thoại may mắn. 5100 2850 5100 2850 A. P( ) A  . B. P( ) A  . C. P( ) A  . D. P( ) A  . 7 10 7 10 6 10 6 10 Lời giải Chọn D
Số phần tử của không gian mẫu: 6 n()  10 .
Gọi A là biến cố: “Số điện thoại may mắn”. Có 2 trường hợp xảy ra:
TH1: Số điện thoại may mắn dạng: 8a a 0a a a 2 3 5 6 7
Chọn a , a từ 2;4;  6 có 2 A  6 cách. 2 3 3
Chọn a từ 1;3;5;  7 có 4 cách. 5
Chọn a , a từ 1;3;5;7;  9 có 5.5  25 cách. 6 7
Các số may mắn 6.4.125  600 số.
TH2: Số điện thoại may mắn dạng: 8a a a a a a trong đó a  0 . 2 3 4 5 6 7 4
Chọn a từ 2; 4;  6 có 3 cách. 4
Chọn a , a từ 0; 2; 4;  6 có 2
A  6 cách (do phải khác a ). 2 3 3 4
Chọn a , a , a từ có 3 5 125cách. 5 6 7
Các số may mắn 3.6.125  2250 số. ( n )
A  600  2250  2850 . 2850 P( ) A  . 6 10
Câu 27. (Lê Lai - Thanh Hóa - 2020) Cho tập hợp A  1; 2; 3; 4; 
5 . Gọi S là tập hợp tất cả các số
tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc
tập A . Chọn ngẫu nhiên một số từ tập S , tính xác xuất để số được chọn có tổng các chữ số bằng 10 . 1 3 22 2 A. . B. . C. . D. . 30 25 25 25 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Chọn B
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được
lập thành từ các chữ số thuộc tập A nên ta tính số phần tử thuộc tập S như sau:
 Số các số thuộc S có 3 chữ số là 3 A . 5
 Số các số thuộc S có 4 chữ số là 4 A . 5
 Số các số thuộc S có 5 chữ số là 5 A . 5
Suy ra số phần tử của tập S là 3 4 5
A A A  300 . 5 5 5
Số phần tử của không gian mẫu là 1 n C  300  300
Gọi X là biến cố ' Số được chọn có tổng các chữ số bằng 10 ' . Các tập con của A có tổng số
phần tử bằng 10 là A  1; 2; 3; 4 , A  2; 3; 5 , A  1; 4; 5 . 3   2   1  
● Từ A lập được các số thuộc S là 4!. 1
● Từ A lập được các số thuộc S là 3!. 2
● Từ A lập được các số thuộc S là 3!. 3
Suy ra số phần tử của biến cố X là n  4! 3! 3!  36. X n 36 3
Vậy xác suất cần tính P X X    . n 300 25 
Câu 28. (Liên trường Nghệ An - 2020) Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác
nhau lập thành từ các chữ số 0,1, 2, 3, 4, 5, 6, 7 . Chọn ngẫu nhiên một số từ tập S . Tính xác
suất để số được chọn có đúng 2 chữ số chẵn. 24 144 72 18 A. . B. . C. . D. . 35 245 245 35 Lời giải Chọn D Có 3
7.A số có 4 chữ số khác nhau được lập từ tập S . 7
Xét các số có đúng hai chữ số chẵn, hai chữ số lẻ.
+ TH1: Số đó có chữ số 0 Có 1
C cách chọn thêm chữ số chẵn khác và 2
C cách chọn 2 chữ số lẻ; có 3.3! cách sắp xếp 4 3 4
chữ số được chọn, suy ra có 1 2
C .C .3.3!  324 số thỏa mãn. 3 4
+ TH2: Số đó không có chữ số 0 Có 2
C cách chọn 2 chữ số chẵn, 2
C cách chọn 2 chữ số lẻ; có 4! cách sắp xếp 4 chữ số đã 3 4 chọn, suy ra có 2 2
C .C .4!  432 số thỏa mãn. 3 4
Vậy có 324  432  756 số có đúng hai chữ số chẵn thỏa mãn. 756 18
Xác suất cần tìm là P   . 3 7.A 35 7
Câu 29. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tập S  1; 2;3;...;19; 2 
0 gồm 20 số tự nhiên từ 1 đến
20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là 7 5 3 1 A. . B. . C. . D. . 38 38 38 114 Lời giải Chọn C
Số phần tử không gian mẫu n  3  C . 20 a c Gọi a, ,
b c là ba số lấy ra theo thứ tự đó lập thành cấp số cộng, nên b
  . Do đó a và 2
c cùng chẵn hoặc cùng lẻ và hơn kém nhau ít nhất 2 đơn vị.
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 Số cách chọn bộ  ; a ;
b c theo thứ tự đó lập thành cấp số cộng bằng số cặp  ; a c cùng chẵn 2 2C 3
hoặc cùng lẻ, số cách chọn là 2
2.C . Vậy xác suất cần tính là 10 P   . 10 3 C 38 20
Câu 30. (Nguyễn Huệ - Phú Yên - 2020) Một bàn cờ vua gồm 8 8
 ô vuông, mỗi ô có cạnh bằng 1
đơn vị. Một ô vừa là hình vuông hay hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên
một hình chữ nhật trên bàn cờ. Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng 5 17 51 29 A. . B. . C. . D. . 216 108 196 216 Lời giải Chọn A Bàn cờ 8 8
 cần 9 đoạn thẳng nằm ngang và 9 đoạn thẳng dọc. Ta coi bàn cờ vua được xác
định bởi các đường thẳng x  0, x  1,..., x  8 và y  0, y  1,..., y  8 .
Mỗi hình chữ nhật được tạo thành từ hai đường thẳng x và hai đường thẳng y nên có 2 2 C .C 8 8
hình chữ nhật hay không gian mẫu là n  2 2
  C .C 1296 . 9 9
Gọi A là biến cố hình được chọn là hình vuông có cạnh a lớn hơn 4.
Trường hợp 1: a  5 . Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 5 đơn vị và
hai đường thẳng y cách nhau 5 đơn vị có 4.4 16 cách chọn.
Trường hợp 2: a  6 . Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 6 đơn vị và
hai đường thẳng y cách nhau 6 đơn vị có 3.3  9 cách chọn.
Trường hợp 3: a  7 . Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 7 đơn vị và
hai đường thẳng y cách nhau 7 đơn vị có 2.2  4 cách chọn.
Trường hợp 3: a  8 . Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 8 đơn vị và
hai đường thẳng y cách nhau 8 đơn vị có 1.11 cách chọn. Suy ra n 
A 16  9  4 1 30 .
Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị là n  PAA 30 5    . n   1296 216
Câu 31. (Tiên Du - Bắc Ninh - 2020) Gọi M là tập hợp các số tự nhiên có ba chữ số lập được từ các
chữ số 0, 1, 2, 3, 4, 5, 6, 7. Lấy ngẫu nhiên đồng thời 2 số từ tập M. Xác suất để cả 2 số lấy
được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là 8 5 296 695 A. . B. . C. . D. . 21 16 2051 7152 Lời giải Chọn D
Số tự nhiên có ba chữ số có dạng a . bc
Số các số tự nhiên có ba chữ số được lập từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là 7.8.8  448 số.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Số phần tử không gian mẫu 2   C . 448
Gọi A là biến cố: “ 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị”.
Trường hợp b  0 có 7.7  49 số.
Trường hợp b  1 có 6.6  36 số.
Trường hợp b  2 có 5.5.  25 số.
Trường hợp b  3 có 4.4  16 số.
Trường hợp b  4 có 3.3  9 số.
Trường hợp b  5 có 2.2  4 số.
Trường hợp b  6 có 1.1  1 số.
Vậy có 49  36  25 16  9  4 1  140 số thỏa mãn chữ số hàng chục nhỏ hơn chữ số hàng đơn vị và hàng trăm. 2   C . A 140 A 695
Vậy P A   .  7152
Câu 32. (Hải Hậu - Nam Định - 2020) Một hộp có chứa 5 viên bi đỏ, 3 viên bi xanh và n viên bi vàng
( các viên bi kích thước như nhau, n là số nguyên dương). Lấy ngẫu nhiên 3 viên bi từ hộp. 45
Biết xác suất để trong ba viên vi lấy được có đủ 3 màu là
. Tính xác suất P để trong 3 182
viên bi lấy được có nhiều nhất hai viên bi đỏ. 135 177 45 31 A. P  . B. P  . C. P  . D. P  . 364 182 182 56 Lời giải Chọn B
Số cách lấy 3 viên bi bất kì từ hộp là: 3 C . 8 n
Số cách lấy 3 viên đủ 3 màu là: 1 1 1
C .C .C  15n . 5 3 n 45 15n 45
Vì xác suất để trong ba viên vi lấy được có đủ 3 màu là    n  6 . 182 3 C 182 8n
 có 5 viên bi đỏ, 3 viên bi xanh và 6 viên bi vàng.
Số cách lấy 3 bi bất kì là 3 C . 14
Trường hợp 1: 3 bi lấy ra không có bi đỏ, khi đó số cách lấy là 3 C . 9
Trường hợp 2: 3 bi lấy ra có 1 bi đỏ, khi đó số cách lấy là 1 2 C .C 5 9
Trường hợp 2: 3 bi lấy ra có 2 bi đỏ, khi đó số cách lấy là 2 1 C .C . 5 9 177
Vậy xác suất để trong 3 viên bi lấy được có nhiều nhất hai viên bi đỏ là P  182
Câu 33. (Kìm Thành - Hải Dương - 2020) Gọi S là tập hợp tất cả các số tự nhiên gồm 9 chữ số đôi
một khác nhau. Chọn ngẫu nhiên một số từ S . Tính xác suất để được chọn có đúng 4 chữ số
lẻ và chữ số 0 đứng giữa hai chữ số lẻ. (Các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ). 5 5 5 20 A. . B. . C. . D. . 648 27 54 189 Lời giải Chọn C
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Xem nhóm 3 chữ số gồm số 0 ở giữa 2 chữ số lẻ là một
Chọn 2 chữ số lẻ và sắp xếp có 2 A cách. 5
Chọn thêm 2 chữ số lẻ có 2 C cách. 3
Chọn 4 chữ số chẵn có 4 C cách. 4 Sắp xếp có 7! cách. Như vậy có 2 2 4
A .C .C .7!  302400 số thỏa mãn yêu cầu bài toán. 5 3 4 302400 5 Xác suất cần tìm  . 8 9.A 54 9
Câu 34. (Trường VINSCHOOL - 2020) Có 6 học sinh nam và 4 học sinh nữ xếp thành hàng ngang.
Xác suất để có đúng hai bạn nữ đứng cạnh nhau bằng 1 1 14 7 A. . B. . C. . D. . 24 2 17 13 Lời giải Chọn B
Chọn 2 trong 4 bạn nữ và xếp vào 2 vị trí cạnh nhau có 2 A (cách). 4
Hai bạn nữ được chọn và đã được xếp chỗ đứng cạnh nhau kết hợp với 2 bạn nữ còn lại xem là ,
A B, C .
Lấy 6 bạn nam làm vách ngăn, số cách tạo vách ngăn là 6! (cách).
Có 6 vách ngăn sẽ có 7 khoảng trống, sắp xếp ,
A B, C vào 7 khoảng trống có 3 A (cách). 7
Từ đó suy ra số cách xếp 6 học sinh nam và 4 học sinh nữ thành hàng ngang mà có đúng hai
bạn nữ đứng cạnh nhau là: 2 A . 6!. 3 A 4 7
Số cách xếp 6 học sinh nam và 4 học sinh nữ xếp thành hàng ngang tùy ý là: 10!.
Vậy xác suất để xếp 6 học sinh nam và 4 học sinh nữ thành hàng ngang mà có đúng hai bạn 2 3 A .6!.A 1
nữ đứng cạnh nhau là: 4 7  . 10! 2
Câu 35. (Thanh Chương 1 - Nghệ An - 2020) Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số mà
các chữ số đều khác 0. Lấy ngẫu nhiên một số từ S . Xác suất để lấy được số chỉ có mặt 3 chữ
số gần với số nào nhất trong các số sau? A. 0, 34 . B. 0, 36 . C. 0, 21. D. 0,13 . Lời giải Chọn C
Số phần tử của không gian mẫu là n  5  9 .
Gọi A là biến cố số được chọn chỉ có mặt 3 chữ số:
Chọn 3 chữ số khác nhau ta có 3 C cách 9 5!
Trường hợp 1: Có 1 chữ số bị lặp 3 lần, 2 chữ số khác xuất hiện 1 lần 1 C . cách 3 3! 5!
Trường hợp 2: Có 2 chữ số xuất hiện 2 lần, 1 chữ số xuất hiện 1 lần 2 C . cách 3 2!2!  5! 5!   n A 3 1 2  C CC  12600 9 3 3  3! 2!2!  
P A  0, 213 .
Câu 36. (Tiên Lãng - Hải Phòng - 2020) Một xưởng sản xuất thực phẩm gồm 4 kỹ sư chế biến thực
phẩm, 3 kĩ thuật viên và 13 công nhân. Để đảm bảo sản xuất thực phẩm chống dịch Covid 19,
xưởng cần chia thành 3 ca sản xuất theo thời gian liên tiếp nhau sao cho ca I có 6 người và 2 ca
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
còn lại mỗi ca có 7 người. Tính xác suất sao cho mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm. 440 441 41 401 A. . B. . C. . D. . 3320 3230 230 3320 Lời giải Chọn B
Ca I có 6 người, ca II có 6 người và ca III có 6 người nên số phần tử của không gian mẫu là: n  6 7 7
C .C .C  133024320 20 14 7
Gọi biến cố X “mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm”.
Để mỗi ca có 1 kĩ thuật viên, ít nhất một kĩ sư chế biến thực phẩm, ta có các trường hợp:
TH1: Ca I có 1 kĩ thuật viên, 2 kĩ sư và 3 công nhân.
Ca II có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Ca III có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Số cách chọn cho trường hợp này là:  1 2 3
C .C .C . 1 1 5
C .C .C . 1 1 5 C .C .C  5189184 . 3 4 13 2 2 10 1 1 5 
TH2: Ca I có 1 kĩ thuật viên, 1 kĩ sư và 4 công nhân.
Ca II có 1 kĩ thuật viên, 2 kĩ sư và 4 công nhân.
Ca III có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Số cách chọn cho trường hợp này là:  1 1 4
C .C .C . 1 2 4
C .C .C . 1 1 5 C .C .C  6486480 . 3 4 13 2 3 9 1 1 5 
TH2: Ca I có 1 kĩ thuật viên, 1 kĩ sư và 4 công nhân.
Ca II có 1 kĩ thuật viên, 1 kĩ sư và 5 công nhân.
Ca III có 1 kĩ thuật viên, 2 kĩ sư và 4 công nhân.
Số cách chọn cho trường hợp này là:  1 1 4
C .C .C . 1 1 5
C .C .C . 1 2 4 C .C .C  6486480 . 3 4 13 2 3 9 1 2 4 
Số phần tử của biến cố X là: n X   5189184  6486480  6486480  18162144 . 18162144 441
Xác suất của biến cố X là: P X    . 133024320 3230
Câu 37. (Trần Phú - Quảng Ninh - 2020) Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp
ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một
học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng 1 1 8 8 A. . B. . C. . D. . 3 30 63 37 Lời giải Chọn C
Số cách xếp 10 học sinh vào 10 ghế là 10! .
Ta có n   10!.
Để xếp chỗ ngồi cho 10 học sinh mà mỗi học sinh nam đều ngồi đối diện với một học sinh nữ ta làm như sau:
Xếp chỗ ngồi cho bạn nam thứ nhất có 10 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ hai có 8 cách xếp vì trừ đi ghế ngồi đối diện với bạn nam đầu tiên. Tương tự:
Xếp chỗ ngồi cho bạn nam thứ ba có 6 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ tư có 4 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ năm có 2 cách xếp.
Xếp chỗ ngồi cho 5 bạn nữ vào 5 ghế còn lại có 5!.
Theo quy tắc nhân, ta có n A  10.8.6.4.2.5!  460800 .
Do vậy xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ là: 460800 8 p   . 10! 63
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Câu 38. (Đại Học Hà Tĩnh - 2020) Cho đa giác đều 12 đỉnh nội tiếp đường tròn tâm
A. Chọn ngẫu
nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không
có cạnh nào là cạnh của đa giác đã cho. 2 31 28 52 A. . B. . C. . D. . 5 55 55 55 Lời giải Chọn C
Số tam giác được tạo thành là 3 C . 12
Số tam giác có chung 1 cạnh với đa giác là 1 12C . 8
Số tam giác có chung 2 cạnh với đa giác là 12. 2 12C 12 28
Vậy xác suất để được tam giác không có chung cạnh với đa giác là 8 1  . 3 C 55 12
Câu 39. (ĐHQG Hà Nội - 2020) Có 12 học sinh gồm 6 nam và 6 nữ ngồi vào hai hàng ghế đối diện
nhau tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là? 1 4 8 16 A. . B. . C. . D. . 924 165 165 231 Lời giải Chọn D
Số cách xếp 12 học sinh vào 12 chỗ là 12!  n   12!
Gọi A là biến cố “Xếp mỗi một em nam ngồi đối diện với một em nữ”. 1 3 5 2 4
Ta có vị trí 1 có 12 cách chọn; vị trí 2 có 6 cách chọn; vị trí 3 có 10 cách chọn;; vị trí 4 có 5 cách chọn. n A 16
Nên n A  12.6.10.5.8.4.6.3.4.2.2.1  P A   n  231
Câu 40. (Sở Hưng Yên - 2020) Có 50 tấm thẻ đánh số từ 1 đến 50. Rút ngẫu nhiên 3 thẻ. Xác suất để
tổng các số ghi trên thẻ chia hết cho 3 bằng 8 11 769 409 A. . B. . C. . D. . 89 171 2450 1225 Lời giải Chọn D
Gọi  là không gian mẫu của phép thử rút ngẫu nhiên 3 thẻ. Ta có: n  3  C  19600 . 50
Gọi A là biến cố “tổng các số ghi trên thẻ chia hết cho 3”.
50 thẻ được chia thành 3 loại gồm:
+ 16 thẻ có số chia hết cho 3 là {3; 6;...; 48} .
+ 17 thẻ có số chia cho 3 dư 1 là {1; 4; 7;...; 49} .
+ 17 thẻ có số chia cho 3 dư 2 là {2;5;8;...;50} .
Ta xét các trường hợp sau:
TH1: 3 thẻ được chọn cùng một loại có  3 3 3
C C C cách. 16 17 17 
TH2: 3 thẻ được chọn mỗi loại 1 thẻ có 1 1 1
C .C .C cách. 16 17 17
Do đó n A   3 3 3
C C C  1 1 1
C .C .C  6544 . 16 17 17 16 17 17
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 n  6544 409
Xác suất để tổng các số ghi trên thẻ chia hết cho 3 bằng: P A    . n A 19600 1225
PHẦN 2. MỘT SỐ BÀI TOÁN KHÁC
Câu 41. (Chuyên Bắc Ninh - 2020) Cho x  0, x  1 . Tìm số hạng không chứa x trong khai triển Niu- tơn của 20  x  1 x  1  P     3 2 3  x x  1 x x  . A. 38760 . B. 167960 . C. 1600 . D. 125970 . Lời giải Chọn D +) Ta có: x x
 3 x  13 2 3 x x   1  x   1  x   1 x  1 1 1 1 3       x  1   x  3 3 3   3 2 2 3 x x  1 x x x x  1 x x   1 x x 20 20 k 20  1 kk  1  +) 3 P x   C .   3 x .    . 20     x k 0  x  20 20k k 20 405k kk kC .    3 2 1 .x .x kC . 1 .x  20   6 20 k 0 k 0 40  5k
+) Số hạng không chứa x trong khai triển ứng với  0  k  8 . 6
Vậy số hạng không chứa x trong khai triển là C .  8 8 1  125970 . 20
Câu 42. (Sở Phú Thọ - 2020) Giả sử n là một số nguyên dương thoả mãn 2 3
3C C  24 . Hệ số của số n n n  2  hạng chứa 12 x trong khai triển 2 x x    bằng  x A. 12 672x . B. 12 672  x . C. 672 . D. 6  72 . Lời giải Chọn D
Điều kiện xác định: *
n N ; n  3. Khi đó: 3n! n! 3n n 1 n n 1 n  2 2 3     
3C C  24    24    24 n n
n  2!2! n  3!3! 2 6 n  9 3 2 n 12n 11n 144 0        3  73 . n   2
Kết hợp với điều kiện xác định suy ra n  9 . 9 9 k 9 457 k 9  2 kk  2  k Ta có: 2 x x   C .     2x x  . k   C .    2 2 .x . 9 9  x    x k 0  k 0 45  7k Số hạng chứa 12
x trong khai triển ứng với k thỏa mãn:  12  k  3 . 2
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Vậy hệ số của số hạng chứa 12
x là C .23 3  672 . 9
Câu 43. (Sở Bình Phước - 2020) Trên một cái bảng đã ghi sẵn các số tự nhiên từ 1 đến 2020 . Ta thực
hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai
số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng là A. 4040 . B. 2041210 . C. 4082420 . D. 2020 . Lời giải Chọn B
Với cách thực hiện công việc như vậy, số cuối cùng còn lại trên bảng sẽ là tổng của tất cả các
số tự nhiên ban đầu đã ghi, tức là tổng các số tự nhiên từ 1 đến 2020 .
Dễ dàng nhận thấy đây là tổng 2020 số hạng đầu tiên của cấp số cộng có số hạng đầu bằng 1 và công sai bằng 1. 2020 1 2020
Vậy, số cuối cùng còn lại trên bảng là:  2041210 . 2
Câu 44. (Yên Lạc 2 - Vĩnh Phúc - 2020) Xác định n biết rằng hệ số của n x trong khai triển      2 2 1 2 ... n x x nx bằng 6n . A. n  8 . B. n  6 . C. n  10 . D. n  5 . Lời giải Chọn D Ta có:  nx x   nx 2 2   2  x x
 n   n 1  n xnx  n
nx  n   n 1  2 1 2 ... 1 2 ... 1 1 x
 ...  x x   1
Suy ra hệ số của n x là:
n 1.n  
1  2.n  2  ... n  2.2  n   1 .1 n
n  1.n  
1  2.n  2  ...  n  2.n  n  2  n  
1 . n  n   1   n      n n n
 n   n n n      n  2 2 2 2 2 1. 2. ... 1 . . 1 2 ... 1  n
n n     n      n  2 2 2 2 2 1 2 .. 1 2 ... 1  n n n   3 1
n(n 1)(2n 1) n 11n  2n  . n   2 6 6 3 n 11n Vậy 3
 6n n 11n  36n n  5 (Vì * n   ). 6
-------------------- HẾT --------------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
57 CÂU VD - VDC CHƯƠNG 6. HÌNH HỌC 11 PHẦN 1. GÓC Câu 1.
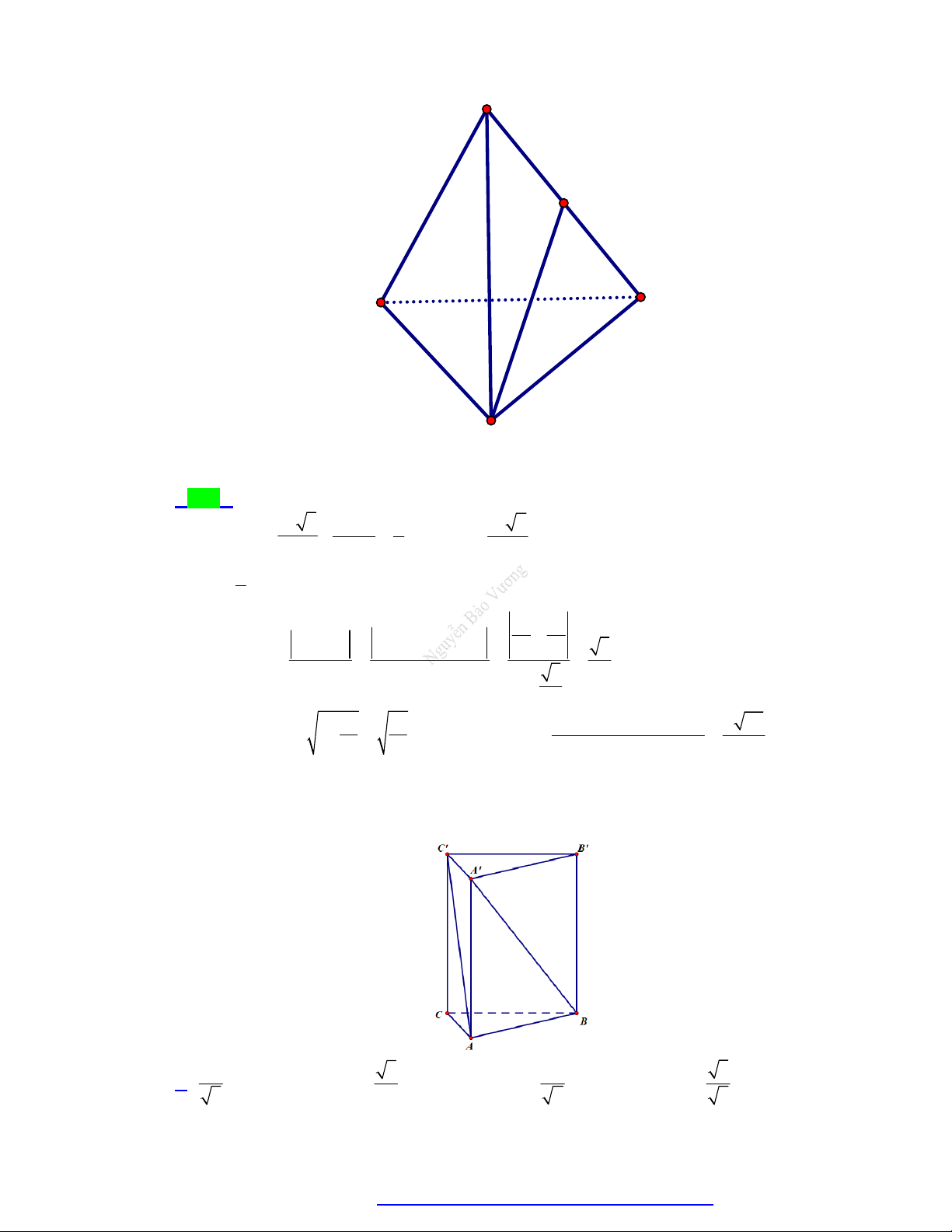
(Chuyên Biên Hòa - Hà Nam - 2020) Cho tứ diện đều ABCD , M là trung điểm của cạnh BC .
Khi đó cos  AB, DM  bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2 Câu 2.
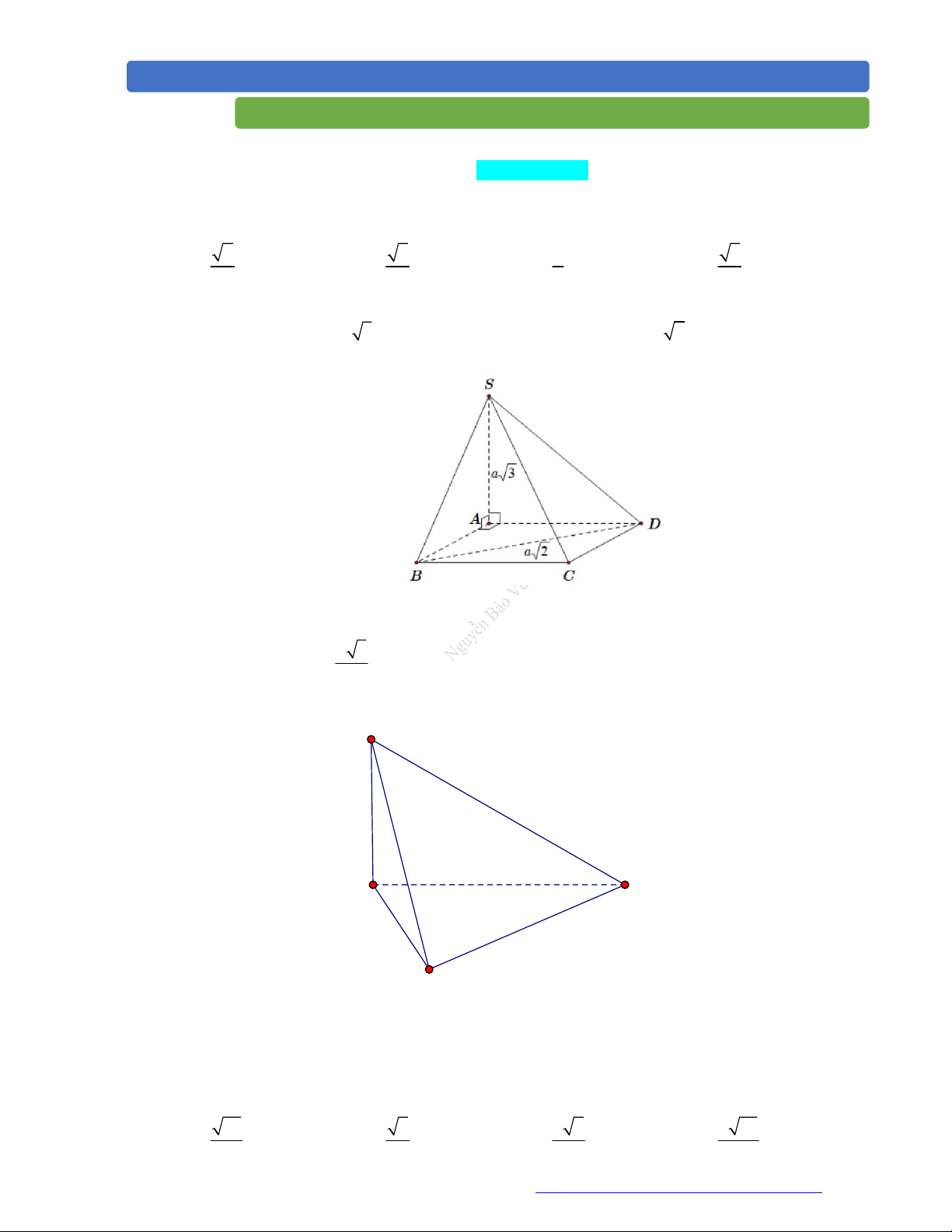
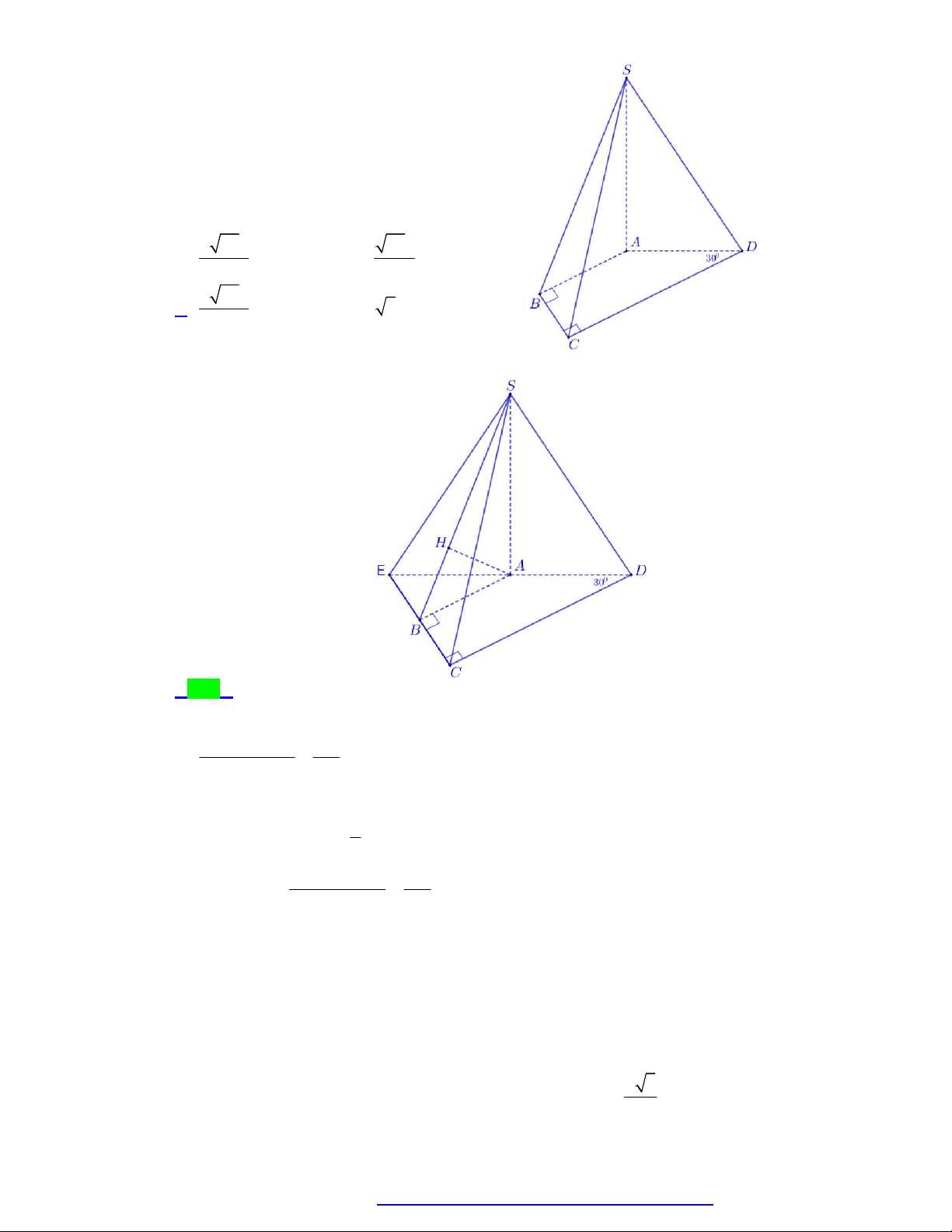
(Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp S.ABCD có SA vuông góc với
mặt phẳng đáy, SA a 3 , tứ giác ABCD là hình vuông, BD a 2 (minh họa như hình bên).
Góc giữa đường thẳng SB và mặt phẳng SAD bằng A. 0 . B. 30 . C. 45 . D. 60 . Câu 3.
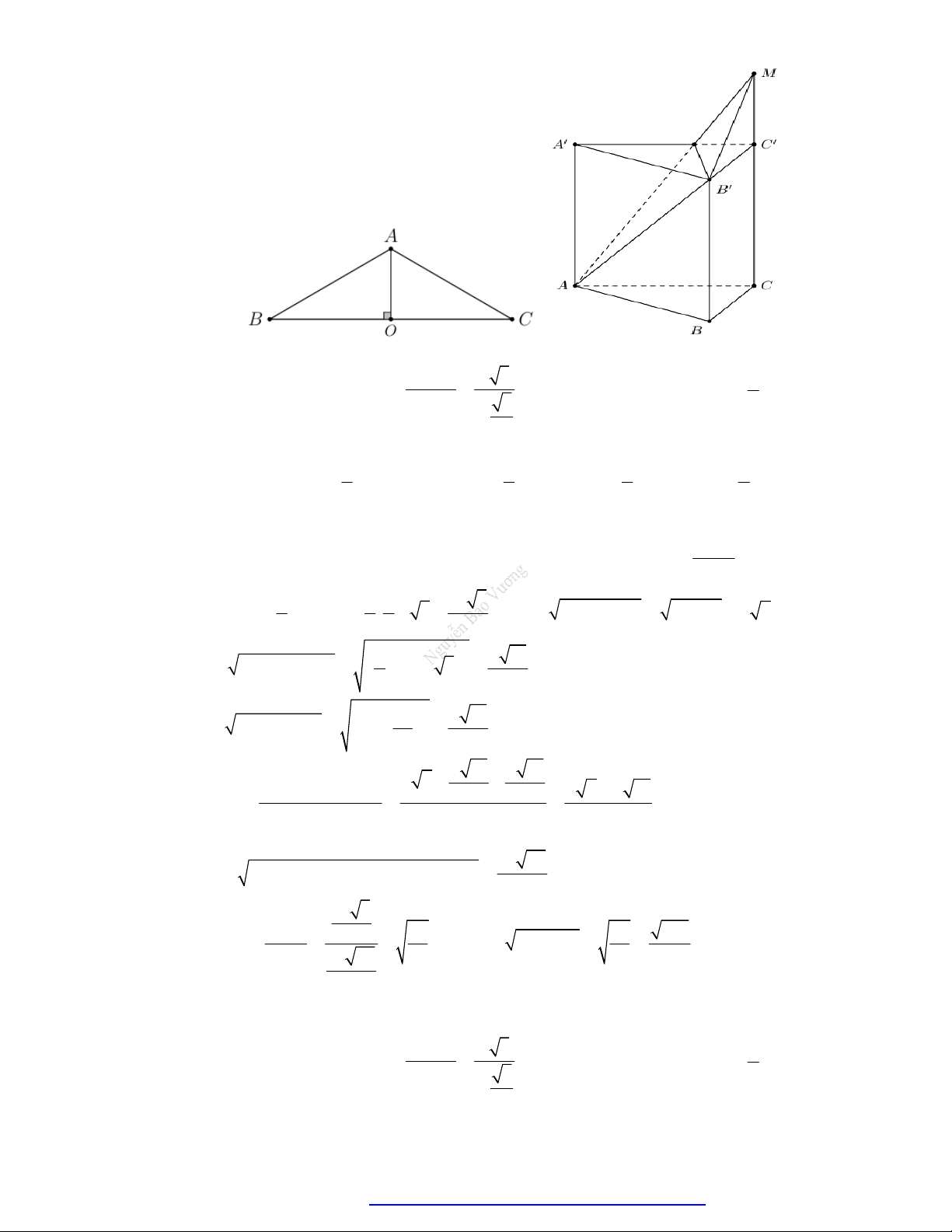
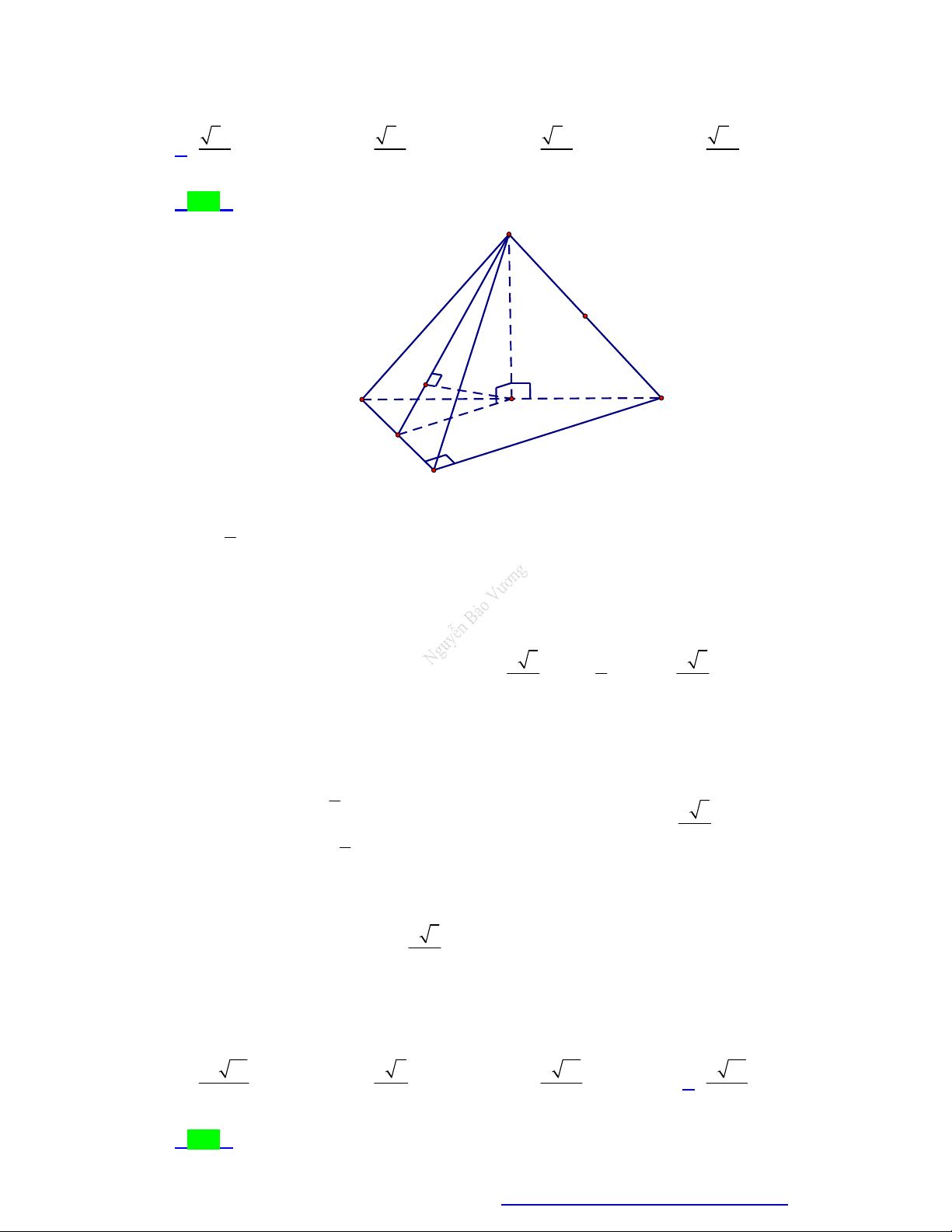
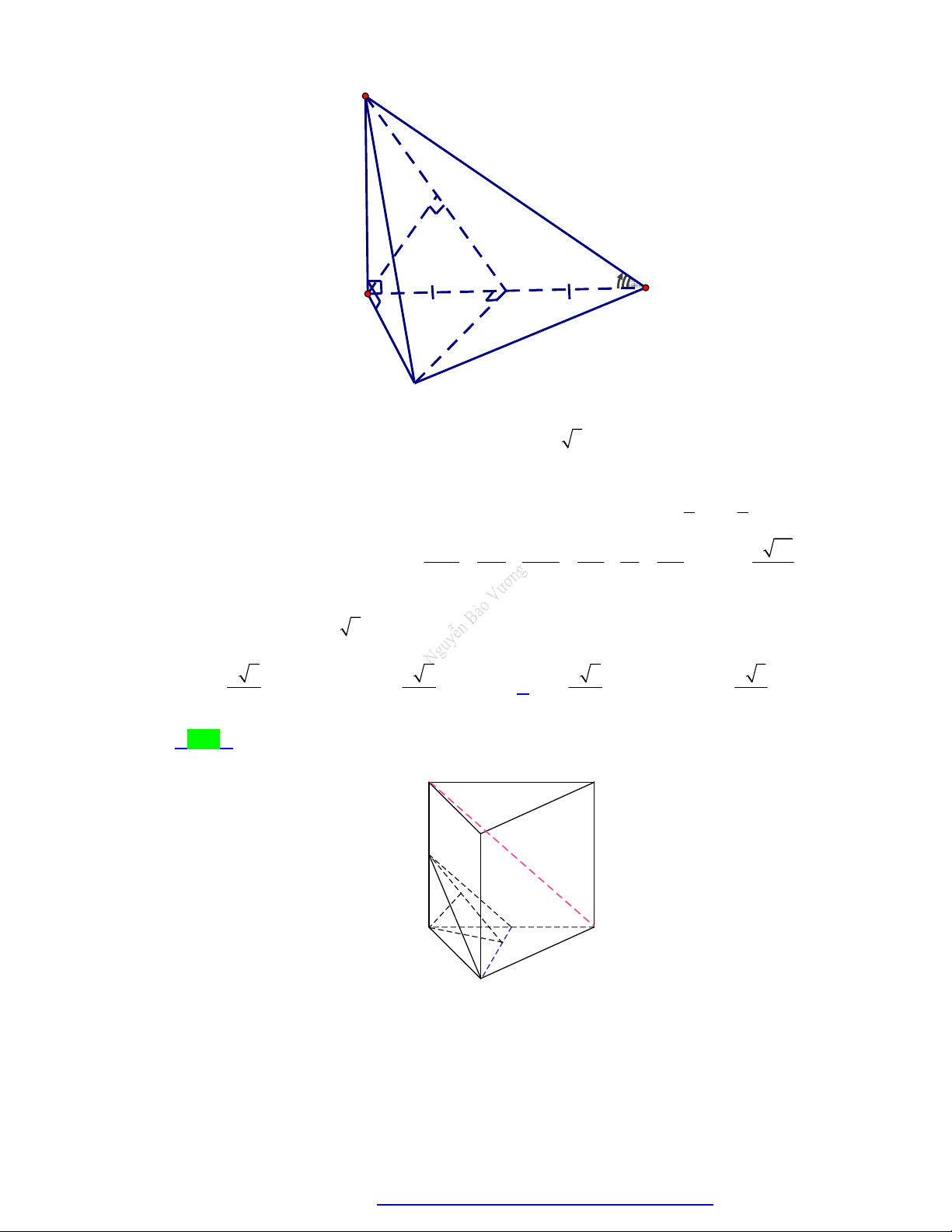
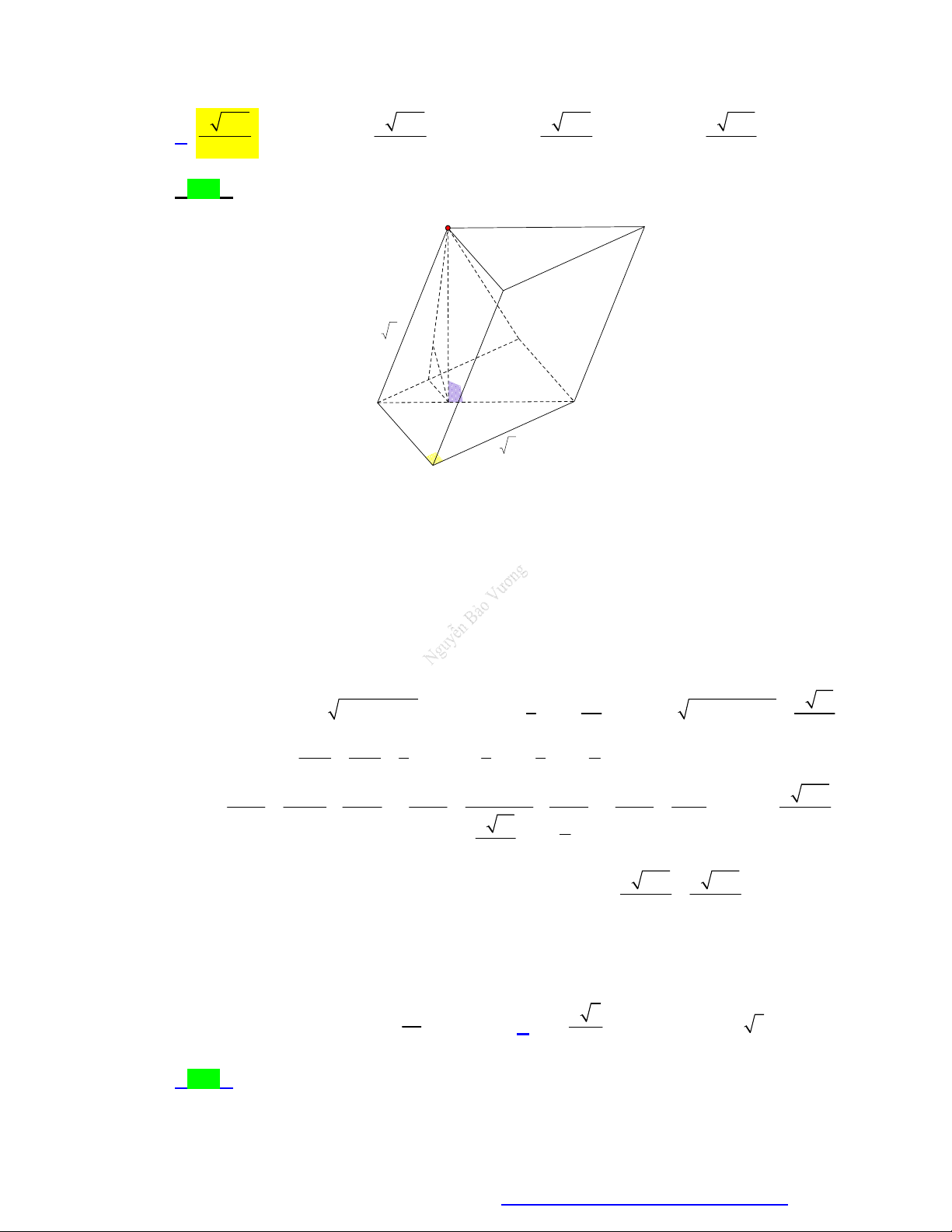
(Chuyên Hùng Vương - Gia Lai - 2020) Cho hình chóp S.ABC có SA vuông góc với mặt a 3
phẳng  ABC , SA
, tam giác ABC đều cạnh bằng a (minh họa như hình dưới). Góc tạo 2
bởi giữa mặt phẳng SBC  và  ABC bằng S A C B A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 . Câu 4.
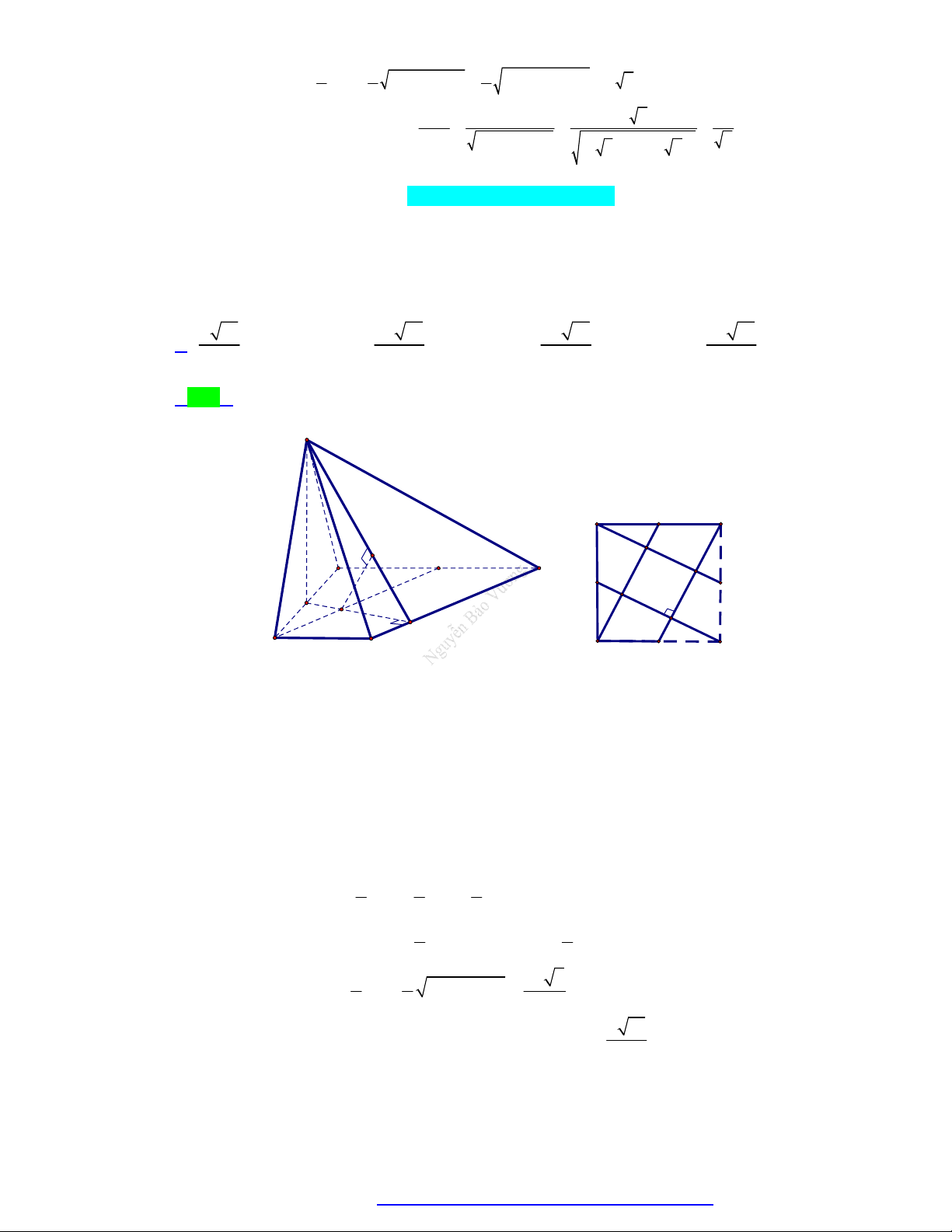
(Chuyên Thái Bình - 2020) Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O ,
cạnh a . Gọi M , N lần lượt là trung điểm của SA và BC . Góc giữa đường thẳng MN và mặt
phẳng  ABCD bằng 60 . Tính cos của góc giữa đường thẳng MN và mặt phẳng SBD . 41 5 2 5 2 41 A. . B. . C. . D. . 4 5 5 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Câu 5.
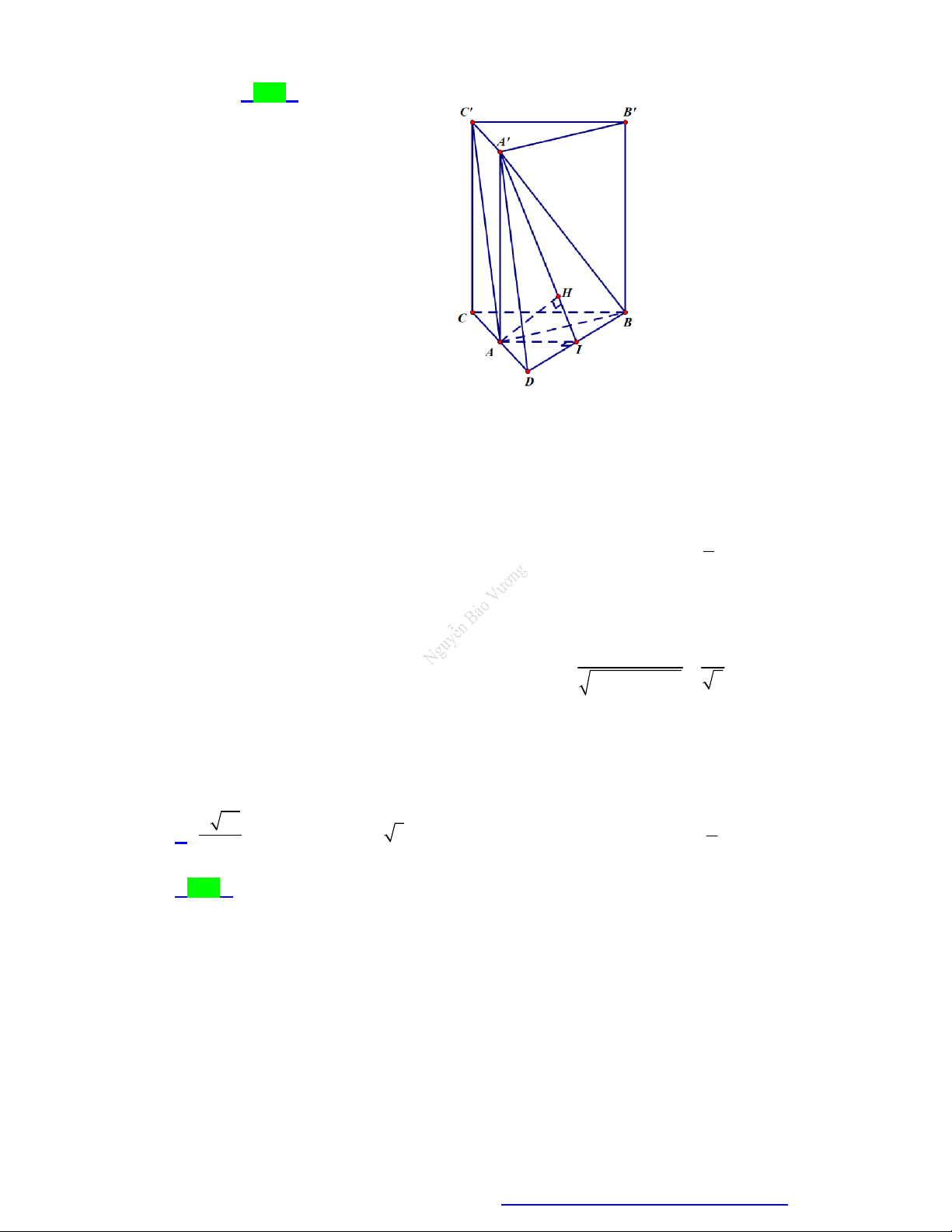
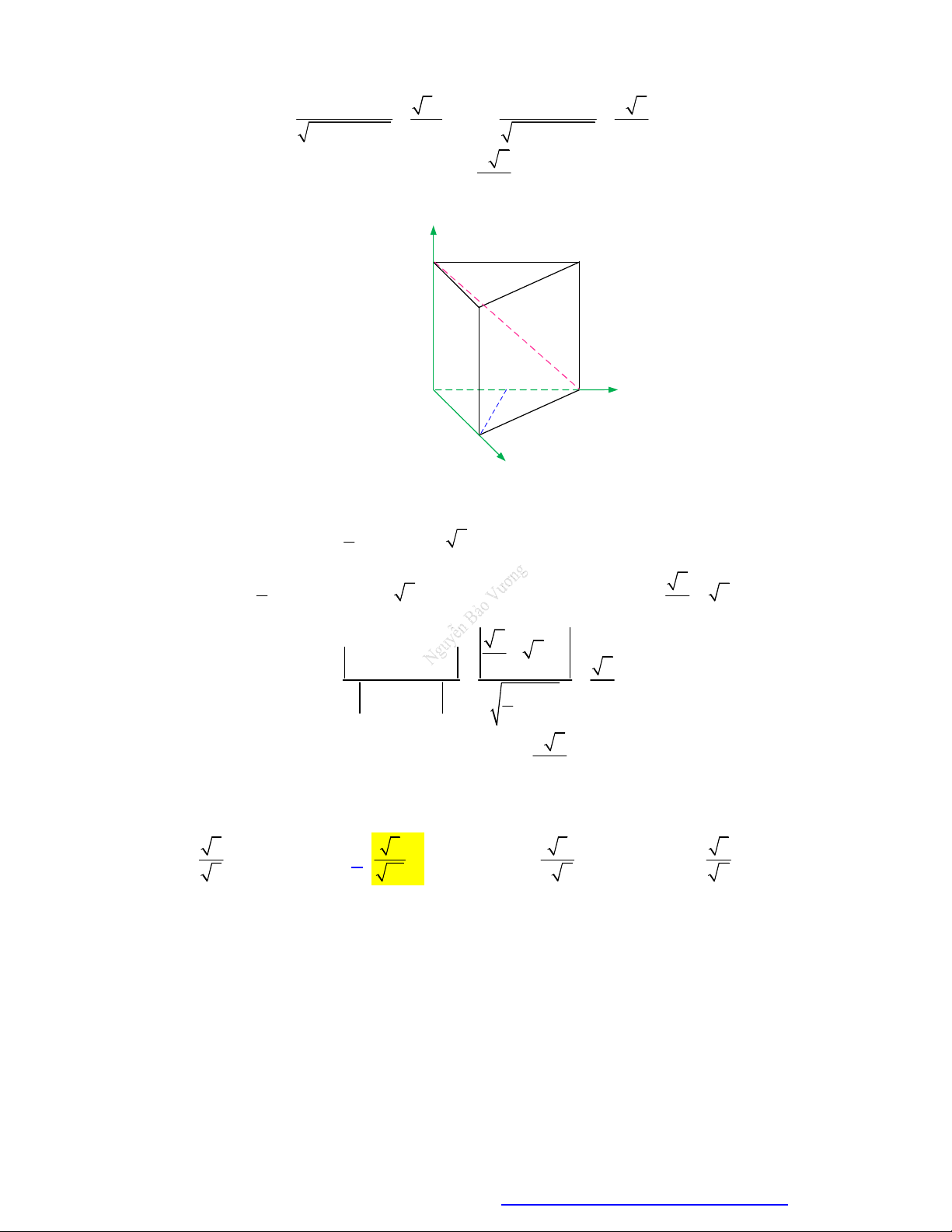
(Chuyên Vĩnh Phúc - 2020) Cho hình lăng trụ đứng ABC.AB C
  có AA  AB AC  1 và  0
BAC  120 . Gọi I là trung điểm cạnh CC . Côsin góc giữa hai mặt phẳng  ABC  và  AB I   bằng 370 70 30 30 A. . B. . C. . D. . 20 10 20 10 Câu 6.
(ĐHQG Hà Nội - 2020) Cho hình chóp S.ABCD có đáy hình vuông. Cho tam giác SAB vuông
tại S và góc SBA bằng 0
30 . Mặt phẳng  SAB vuông góc mặt phẳng đáy. Gọi M , N là trung
điểm AB, BC . Tìm cosin góc tạo bởi hai đường thẳng SM , DN  . 2 1 1 2 A. . B. . C. . D. . 5 5 3 3 Câu 7.
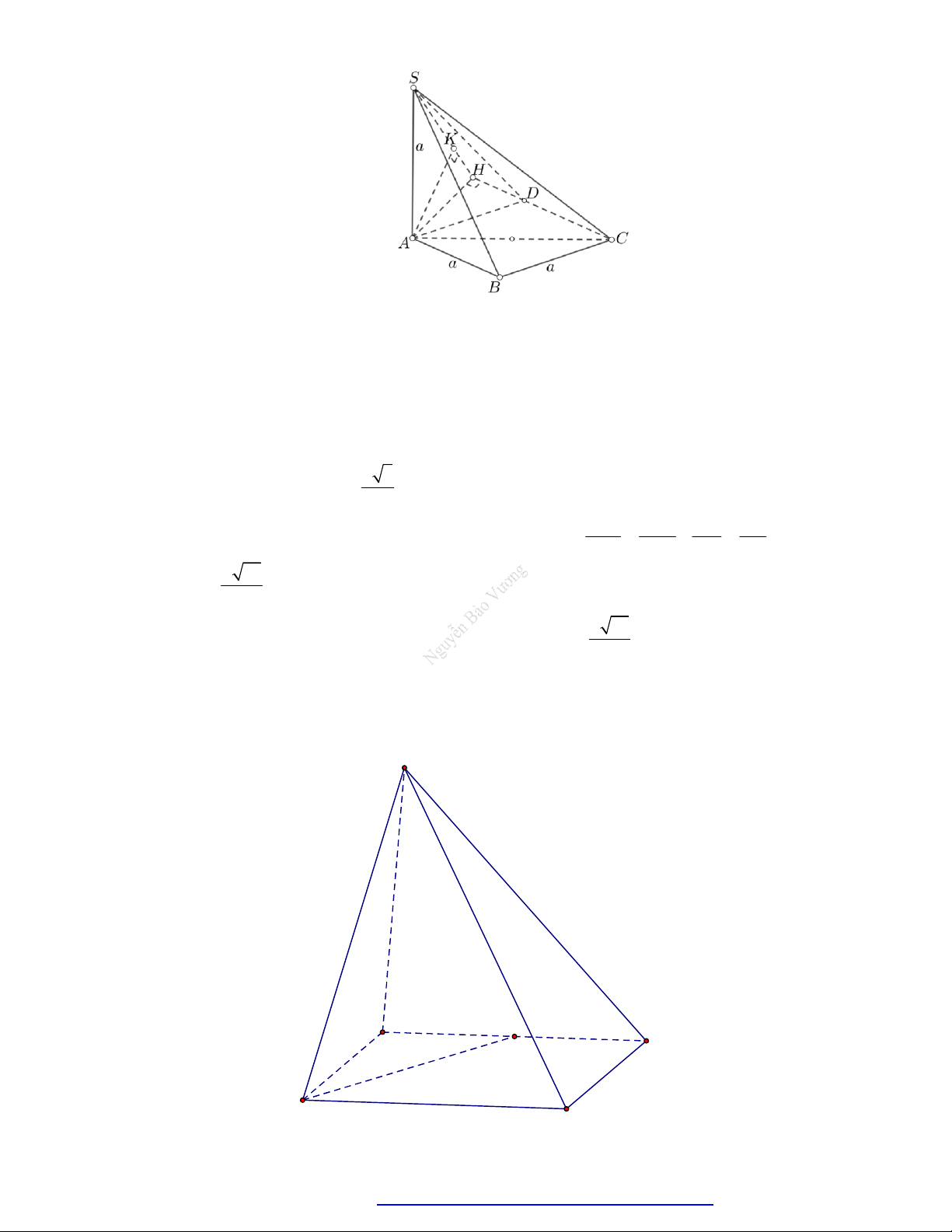
(Sở Ninh Bình) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , độ dài cạnh
AC  2a , các tam giác SA ,
B SCB lần lượt vuông tại A và C . Khoảng cách từ S đến mặt
phẳng ( ABC) bằng a . Giá trị cosin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng 2 2 1 2 5 A. . B. . C. . D. . 3 3 3 3 Câu 8.
(Sở Bắc Ninh - 2020) Cho hình chóp
S.ABCD có đáy là hình thoi cạnh  0
a, ABC  120 , SA vuông góc với mặt phẳng  ABCD. Biết góc giữa hai mặt phẳng SBC  và SCD bằng 0 60 , khi đó a 6 a 6 a 3 A. SA  .
B. SA a 6. C. SA  . D. SA  . 4 2 2 Câu 9.
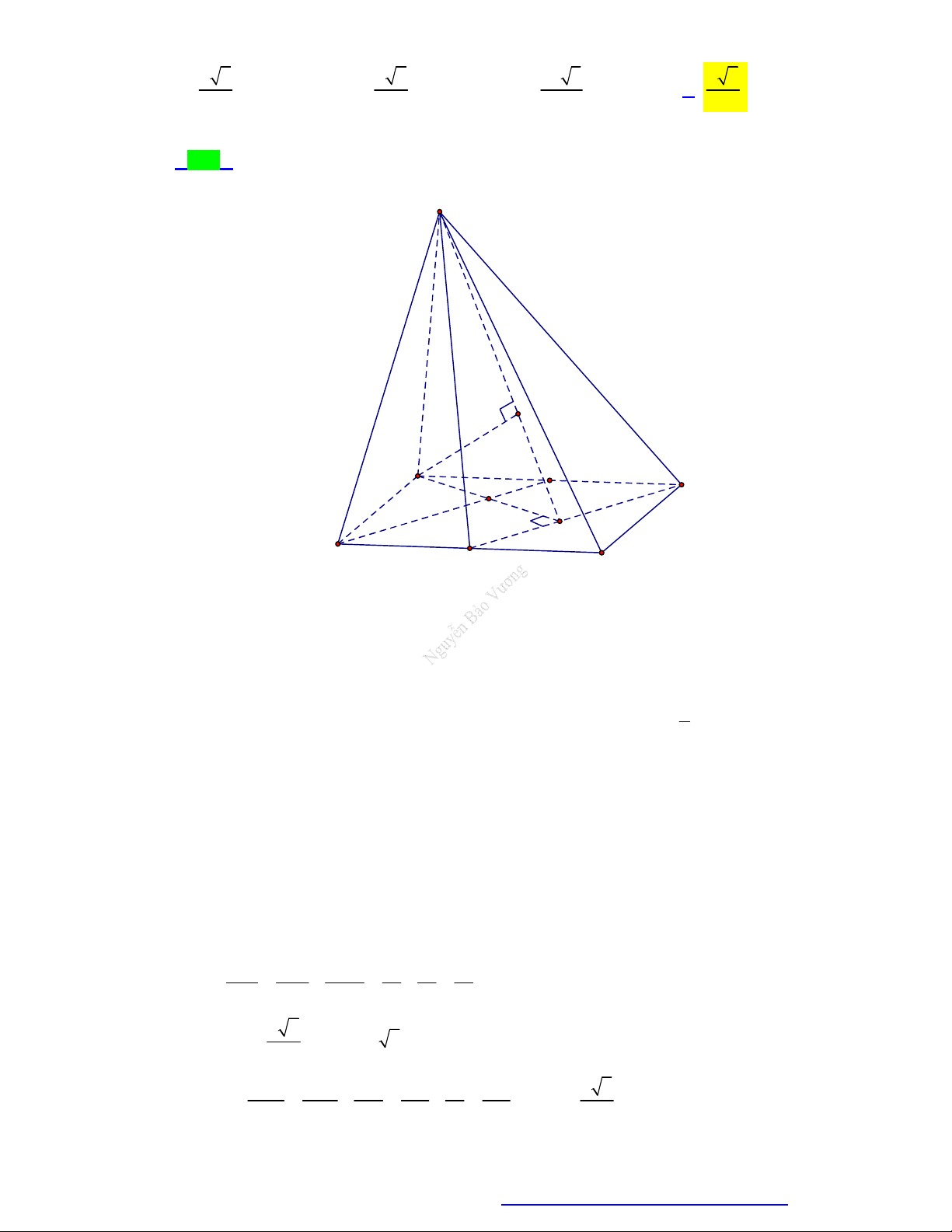
(Sở Bình Phước - 2020) Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác cân đỉnh A .   
Biết BC a 3 và 30o ABC
, cạnh bên AA  a . Gọi M là điểm thỏa mãn 2CM  3CC . Gọi
 là góc tạo bởi hai mặt phẳng  ABC và  AB M
 , khi đó sin có giá trị bằng 66 481 3 418 A. . B. . C. . D. . 22 22 22 22
Câu 10. (Đô Lương 4 - Nghệ An - 2020) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , tâm
O . Gọi M và N lần lượt là trung điểm của SA và BC . Biết rằng góc giữa MN và  ABCD
bằng 60 , côsin của góc giữa đường thẳng MN và mặt phẳng SBD bằng: 5 41 2 5 2 41 A. . B. . C. . D. . 5 41 5 41
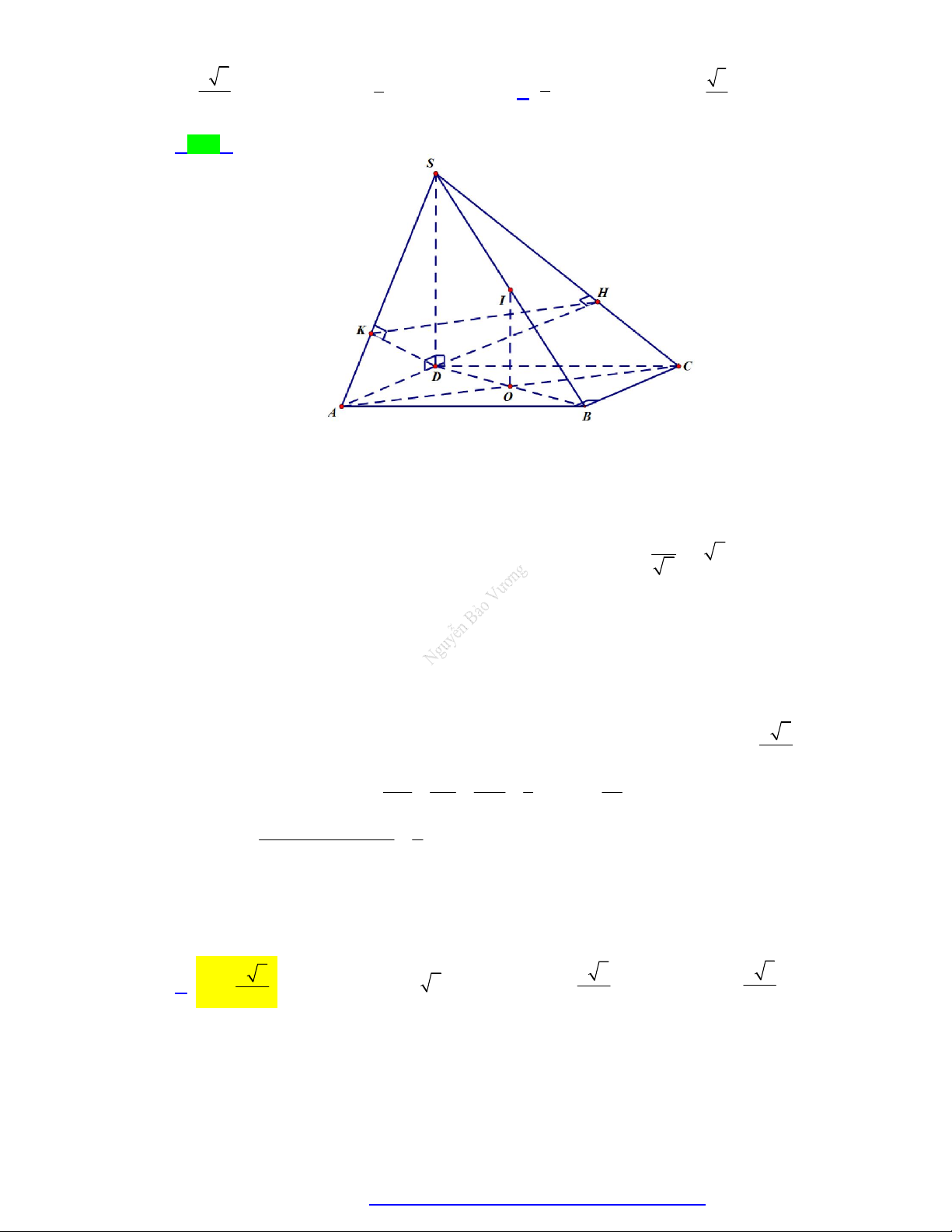
Câu 11. (Kim Liên - Hà Nội - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam
giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của đoạn AB .
Khẳng định nào sau đây là sai?
A. Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 45 .
B. SBC là tam giác vuông.
C. SI   ABCD .
D. Khoảng cách giữa đường thẳng DC và mặt phẳng  SAB bằng a .
Câu 12. (THPT Nguyễn Viết Xuân - 2020) Cho hình lăng trụ đứng
ABC.AB C   có
AB AC a, BAC  120 . Gọi M , N lần lượt là trung điểm của B C
  và CC . Biết thể tích
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 3 3a
khối lăng trụ ABC.AB C   bằng
. Gọi  là góc giữa mặt phẳng  AMN  và mặt phẳng 4  ABC  . Khi đó 3 1 13 3 A. cos  . B. cos  . C. cos  . D. cos  . 2 2 4 4
Câu 13. (Tiên Du - Bắc Ninh - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA a
vuông góc với mặt phẳng  ABC  và SA  . Góc giữa mặt phẳng  SBC  và mặt phẳng  ABC 2 bằng A. 45 . B. 90 . C. 30 . D. 60 .
Câu 14. (Kìm Thành - Hải Dương - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại
A , AB  2a , SA vuông góc với mặt đáy và góc giữa SB và mặt đáy bằng 60 . Gọi  là góc
giữa hai mặt phẳng SBC và  ABC . Giá trị cos bằng 15 2 1 2 A. . B. . C. . D. . 5 5 7 7
PHẦN 2. KHOẢNG CÁCH
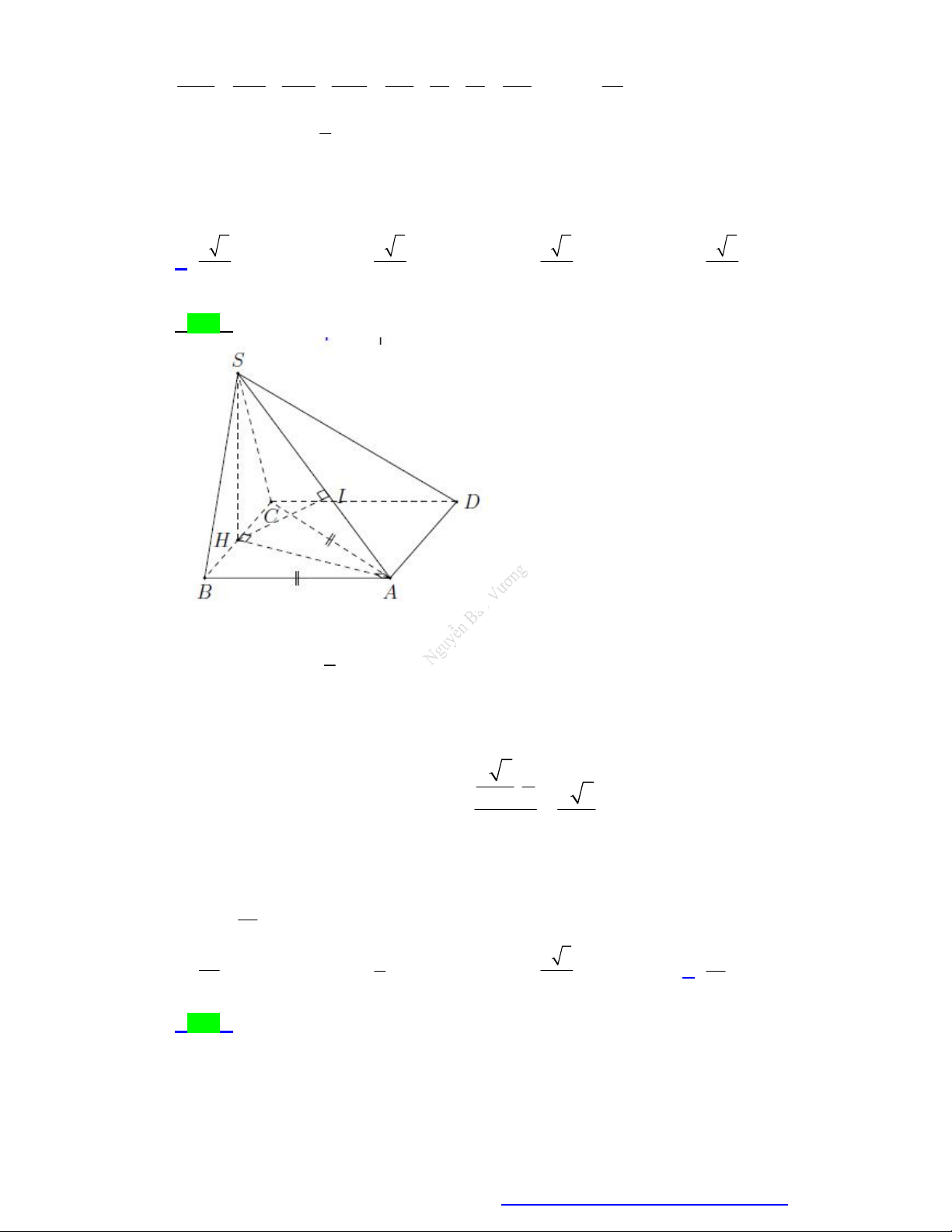
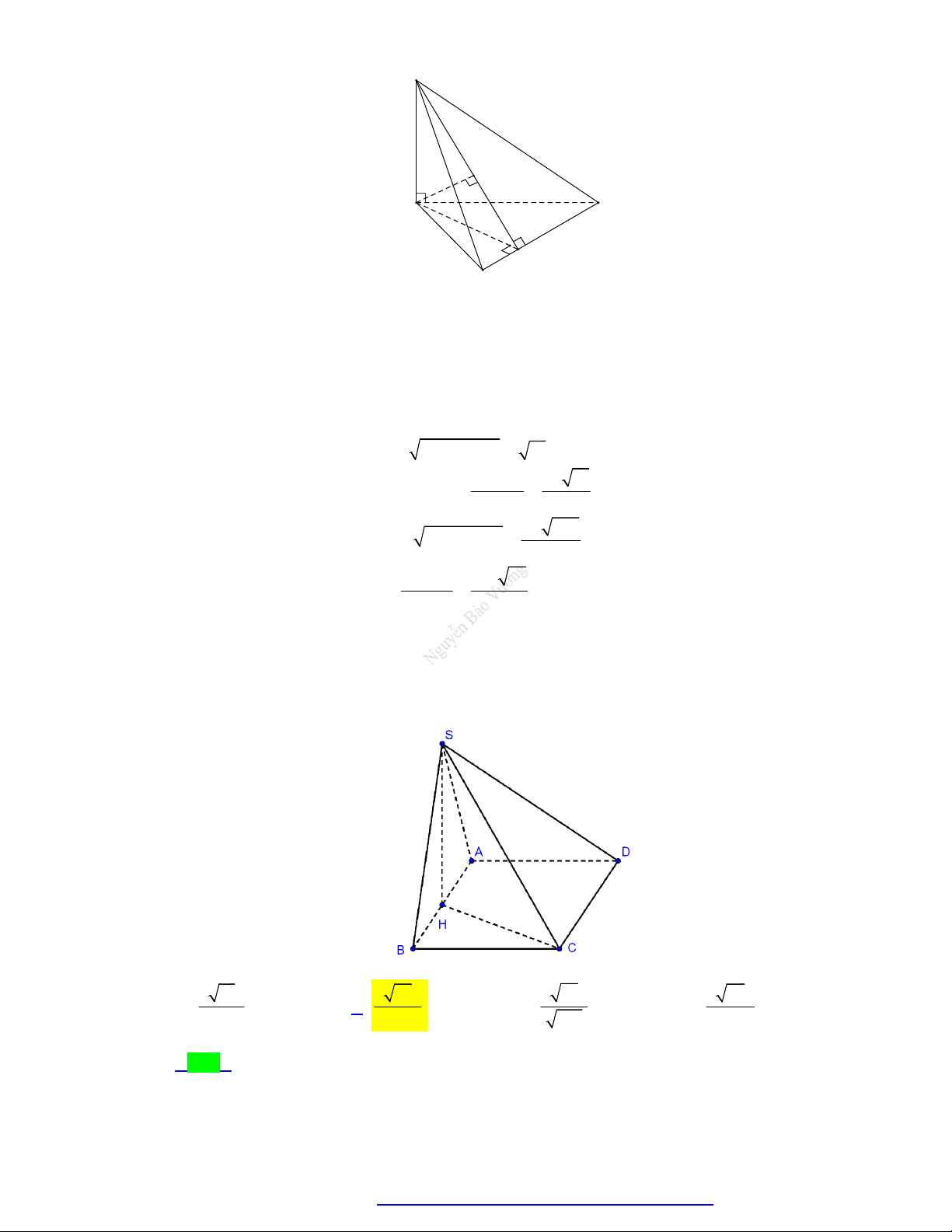
Câu 15. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và ;
D AB AD  2a; DC a . Điểm I là trung điểm đoạn AD, hai mặt phẳng
SIB và SIC  cùng vuông góc với mặt phẳng  ABCD . Mặt phẳng SBC  tạo với mặt phẳng
ABCD một góc 60. Tính khoảng cách từ D đến SBC  theo a . a 15 9a 15 2a 15 9a 15 A. . B. . C. . D. . 5 10 5 20
Câu 16. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hình chóp S.ABC có đáy là tam giác vuông tại , A AC  ,
a I là trung điểm SC . Hình chiếu vuông góc của S lên  ABC  là trung điểm H của
BC . Mặt phẳng SAB tạo với  ABC  một góc 60 . Tính khoảng cách từ I đến mặt phẳng SAB . 3a 3a 5a 2a A. . B. . C. . D. . 4 5 4 3
Câu 17. (Chuyên Hưng Yên - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác cân, BA BC a và 
BAC  30 . Cạnh bên SA vuông góc với mặt phẳng đáy và SA a . Gọi D là điểm đối xứng
với B qua AC . Khoảng cách từ B đến mặt phẳng  SCD bằng 2a 21 a 2 a 21 a 21 A. . B. . C. . D. . 7 2 14 7
Câu 18. (Chuyên KHTN - 2020) Cho hình chóp S.ABCD có đáy là hình chữ nhật AB a, AD  2a , SA
vuông góc với mặt phẳng đáy và SA a . Gọi M là trung điểm của AD . Tính khoảng cách giữa
hai đường thẳng BM và SD .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 S D A M B C a 6 a 2 2a 5 a 6 A. . B. . C. . D. . 3 2 5 6
Câu 19. (Chuyên Lam Sơn - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Tam
giác ABC là tam giác đều, hình chiếu vuông góc của đỉnh S lên mặt phẳng  ABCD  trùng với
trọng tâm tam giác ABC . Góc giữa đường thẳng SD và mặt phẳng  ABCD  bằng 30 . Tính
khoảng cách từ điểm B đến mặt phẳng SCD  theo a . a 21 2a 21 A. . B. a 3 C. a . D. . 7 3
Câu 20. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp S.ABCD có đáy là hình vuông, AB  ,
a SA vuông góc với mặt phẳng đáy và SA  2a (minh họa như hình vẽ bên dưới ).
Gọi M là trung điểm của CD , khoảng cách giữa điểm M và mặt phẳng (SB ) D bằng S D A M B C 2a a a a A. . B. . C. . D. . 3 2 2 3
Câu 21. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A mặt bên (SBC) là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với
mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 3 a 2 a 5 a 3 A. . B. . C. . D. 4 4 4 3
Câu 22. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp S.ABCD có đáy là hình 
thoi tâm O cạnh a và có góc 0
BAD  60 . Đường thẳng SO vuông góc với mặt đáy  ABCD và 3a SO
. Khoảng cách từ O đến mặt phẳng  SBC  bằng 4 3a a a 3 3a A. . B. . C. . D. . 4 3 4 8
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Câu 23. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp S.ABCD có đáy ABCD là
hình thang vuông tại A và D , AB  3a, AD DC a . Gọi I là trung điểm của AD , biết hai
mặt phảng  SBI  và  SCI  cùng vuông góc với đáy và mặt phẳng  SBC  tạo với đáy một góc 0
60 . Tính theo a khoảng cách từ trung điểm cạnh SD đến mặt phẳng  SBC  . a 17 a 6 a 3 a 15 A. . B. . C. . D. . 5 19 15 20
Câu 24. (Chuyên Thái Bình - 2020) Cho hình chóp S.ABCD có đáy là hình chữ nhật với
AB  2a, BC a , tam giác đều SAB nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa
BC và SD là 3 2 5 5 A. 3a . B. a . C. a . D. a . 2 5 5
Câu 25. (Chuyên Bắc Ninh - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,
SA a và SA vuông góc với mặt đáy. M là trung điểm SD . Tính khoảng cách giữa SB và CM . a 3 a 2 a 3 a 3 A. . B. . C. . D. . 6 3 2 3
Câu 26. (Chuyên Bến Tre - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,
SA  2a và vuông góc với  ABCD . Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM. a a 2 2a a A. d  . B. d  . C. d  . D. d  . 3 2 3 6
Câu 27. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho hình chóp S.ABCD có SA   ABCD ,
SA a 6 , ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD  2a . Khoảng cách từ
điểm B đến mặt phẳng SCD bằng a 6 a 3 a 2 a 3 A. . B. . C. . D. . 2 2 2 4
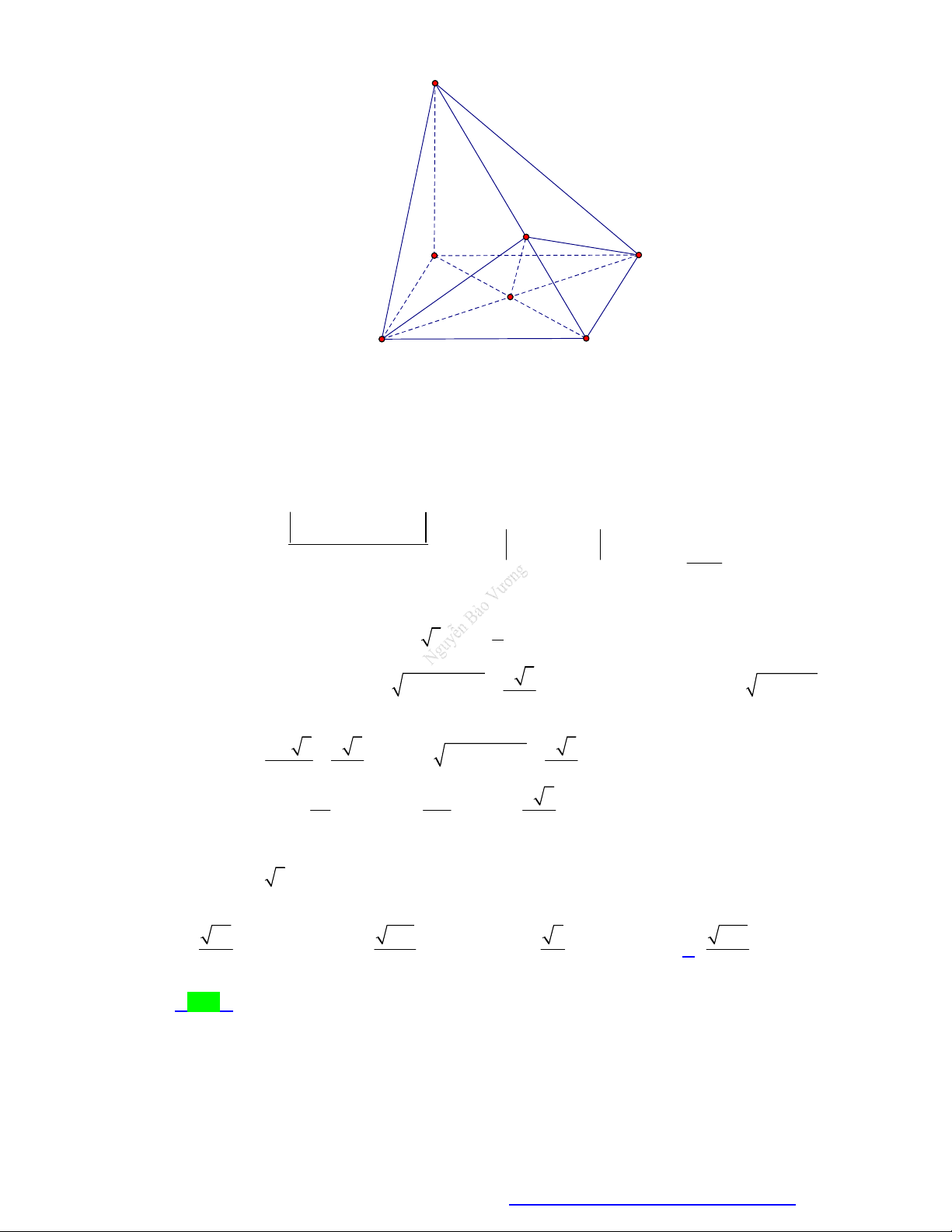
Câu 28. (Chuyên Hùng Vương - Gia Lai - 2020) Cho lăng trụ đứng tam giác ABC.AB C   có đáy là một
tam giác vuông cân tại B , AB AA  2a, M là trung điểm BC (minh họa như hình dưới).
Khoảng cách giữa hai đường thẳng AM và B C  bằng a 2a a 7 A. . B. . C. . D. a 3 2 3 7
Câu 29. (Chuyên Lào Cai - 2020) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh 2a   và 0
SBA SCA  90 . Biết góc giữa đường thẳng SA và mặt đáy bằng 450. Tính khoảng cách từ
điểm B đến mặt phẳng (SAC). 15 2 15 2 15 2 51 A. a . B. a . C. a . D. a . 5 5 3 5
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 30. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho tứ diện đều ABCD có cạnh bằng a . Gọi
M là trung điểm của cạnh AD . Tính khoảng cách giữa hai đường thẳng AB và CM . a 33 a a a 22 A. . B. . C. . D. . 11 33 22 11
Câu 31. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hình lăng trụ đều ABC. ’ A ’
B C’ có tất cả các
cạnh có độ dài bằng 2 (tham khảo hình vẽ). Tính khoảng cách giữa hai đường thẳng AC’ và A’B. 2 3 1 3 A. . B. . C. . D. . 5 2 2 5
Câu 32. (Chuyên Vĩnh Phúc - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA
vuông góc với mặt phẳng  ABC; góc giữa đường thẳng SB và mặt phẳng ABC bằng 60 . Gọi
M là trung điểm cạnh AB . Khoảng cách từ B đến SMC bằng a 39 a A. . B. a 3 . C. a . D. . 13 2
Câu 33. (Đại Học Hà Tĩnh - 2020) Cho lăng trụ đứng AB . C AB C
  có đáy là tam giác vuông và
AB BC a , AA  a 2 , M là trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và B C  . a 6 a 2 a 7 a 3 A. d  . B. d  . C. d  . D. d  . 6 2 7 3
Câu 34. (ĐHQG Hà Nội - 2020) Cho lăng trụ đứng / / /
ABCA B C có tất cả các cạnh bằng a. Gọi M là trung điểm của /
AA . Tính khoảng cách giữa hai đường thẳng BM và / B C . 3 3 3 3 A. a . B. a . C. a . D. a 5 10 2 2 7
Câu 35. (Sở Phú Thọ - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , cạnh
AB a, AD a 2 . Hình chiếu vuông góc của S trên mặt phẳng  ABCD là trung điểm của
đoạn OA . Góc giữa SC và mặt phẳng  ABCD bằng 30 . Khoảng cách từ C đến mặt phẳng SAB bằng 9 22a 3 22a 22a 3 22a A. . B. . C. . D. . 44 11 11 44
Câu 36. (Sở Phú Thọ - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hình chiếu
vuông góc của S trên mặt phẳng  ABCD là trung điểm của cạnh AB , góc giữa mặt phẳng
SAC và đáy bằng 45. Gọi M là trung điểm của cạnh SD . Khoảng cách giữa hai đường AM và SC bằng a 2 a 5 a 5 A. a . B. . C. . D. . 4 10 5
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
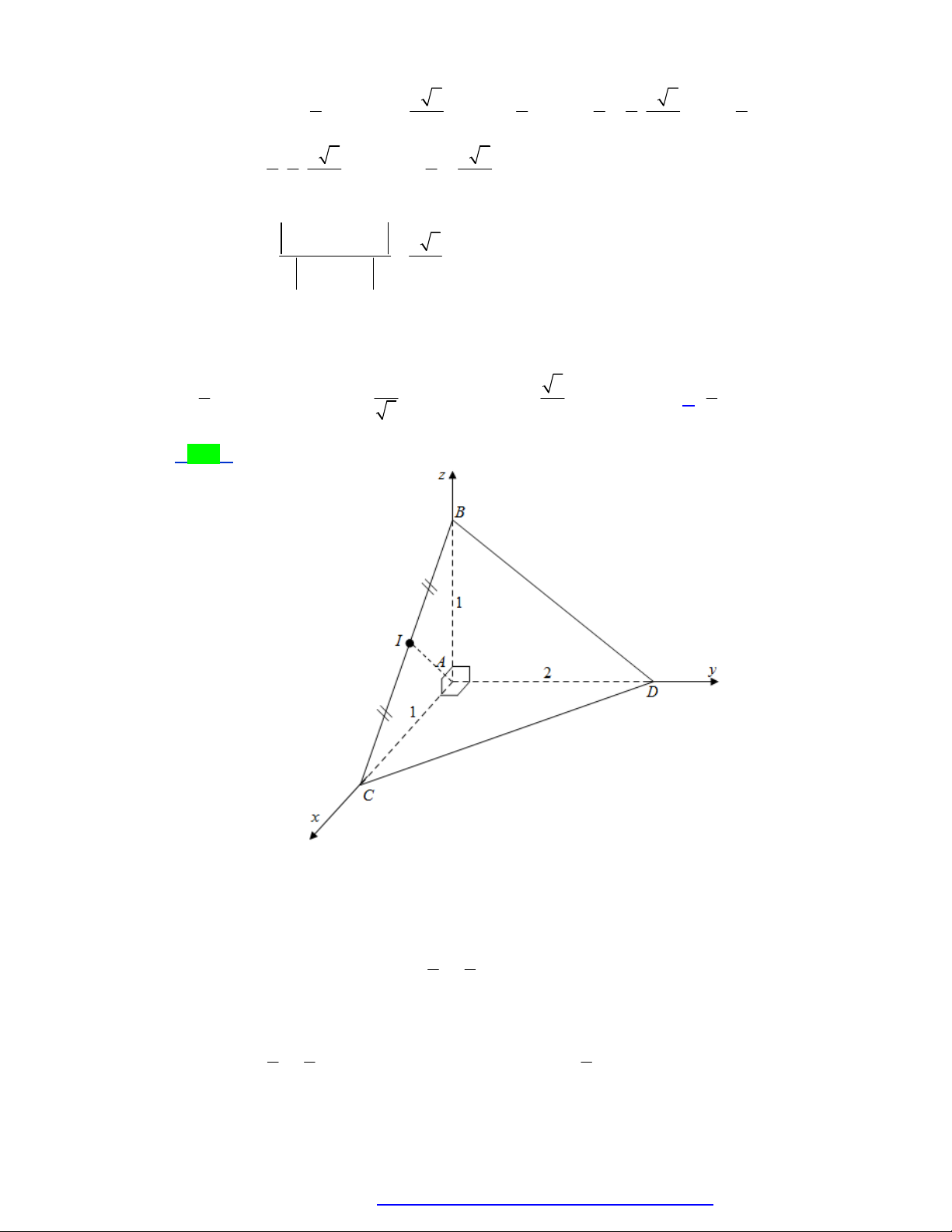
Câu 37. (Sở Hà Tĩnh - 2020) Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc với nhau và
AD  2 , AB AC  1. Gọi I là trung điểm của đoạn thẳng BC , khoảng cách giữa hai đường
thẳng AI và BD bằng 3 2 5 2 A. . B. . C. . D. . 2 5 2 3
Câu 38. (Sở Ninh Bình) Cho hình chóp S . ABC có SA a , tam giác ABC đều, tam giác SAB vuông cân
tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng
SAC bằng a 42 a 42 a 42 a 42 A. . B. . C. . D. . 7 14 12 6
Câu 39. (Sở Yên Bái - 2020) Cho hình lăng trụ đứng ABC.A BC
  có đáy là tam giác vuông cân tại B ,
biết AB BC a , AA  a 2 , M là trung điểm của BC . Tính khoảng cách giữa hai đường
thẳng AM và B C  . a 7 2a 5 a 6 a 15 A. . B. . C. . D. . 7 5 2 5
Câu 40. (Bỉm Sơn - Thanh Hóa - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a , AD  2a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc
giữa đường thẳng SC và mặt phẳng  ABCD bằng 45 . Gọi M là trung điểm của SD , hãy tính
theo a khoảng cách từ M đến mặt phẳng  SAC  . 2a 1513 a 1315 2a 1315 a 1513 A. d  . B. d  . C. d  . D. d  . 89 89 89 89
Câu 41. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a ,
cạnh SA tạo với mặt phẳng đáy một góc o
30 . Khoảng cách giữa hai đường thẳng SA và CD bằng 2 15a 3 14a 2 10a 4 5a A. . B. . C. . D. . 5 5 5 5
Câu 42. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông
tại A và B , AD  2AB  2BC  2a , SA vuông góc với đáy, góc giữa SB và mặt phẳng đáy bằng 0
60 . Gọi H là hình chiếu vuông góc của A lên SB . Khoảng cách từ H đến mặt phẳng SCD bằng 3a 30 3a 30 3a 30 A. a 3 . B. . C. . D. . 20 10 40
Câu 43. (Kim Liên - Hà Nội - 2020) Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA vuông
góc với mặt phẳng đáy, góc giữa mặt phẳng  SBC  và mặt phẳng đáy là 60 (minh họa như hình
dưới đây). Gọi M , N lần lượt là trung điểm của AB, AC .
Khoảng cách giữa hai đường thẳng SB và MN bằng 3a a 6 3a A. . B. . C. . D. a 6 . 8 2 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 44. (Lê Lai - Thanh Hóa - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B C CD  2 AB AD a ADC  30 SA SA  2a và , , , ,
vuông góc với mặt phẳng đáy và (minh DSBC
họa như hình bên dưới). Khoảng cách từ đến mặt phẳng bằng 2 57a 57a 4 57a A. . B. . C. . D. 3a . 19 19 19 Câu 45. (Liên trường Nghệ An - 2020) Cho tứ diện ABCD có    0
ABC ADC ACD  90 , BC  2a, CD a , góc giữa đường thẳng AB và mặt phẳng  BCD bằng 0
60 . Tính khoảng cách giữa hai đường thẳng AC và BD . a 6 2a 6 2a 3 a 3 A. . B. . C. . D. . 31 31 31 31
Câu 46. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với
nhau và OA OB a , OC  2a . Gọi M là trung điểm của AB . Khoảng cách giữa hai đường
thẳng OM và AC bằng 2a 2 5a 2a 2a A. . B. . C. . D. . 3 5 2 3
Câu 47. (Nguyễn Huệ - Phú Yên - 2020) Cho hình chóp S.ABC có đáy là tam giác vuông tại A ,
AB a, AC  2a, SA vuông góc với mặt phẳng đáy và SA  2a . Gọi G là trọng tâm của ABC .
Khoảng cách giữa hai đường thẳng SG và BC bằng 2a a 6 2a 6 4a A. . B. . C. . D. . 7 3 9 7
Câu 48. (Nguyễn Trãi - Thái Bình - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và
SA SB SC  11, góc SAB  30 ,
 góc SBC  60 ,
 góc SCA  45 . Tính khoảng cách d
giữa hai đường thẳng AB và SD . 22 A. 2 22 . B. 22 . C. . D. 4 11 . 2
Câu 49. (THPT Nguyễn Viết Xuân - 2020) Cho hình hộp ABC . D A B C 
D có đáy ABCD là hình vuông
cạnh a , tâm O . Hình chiếu vuông góc của A lên mặt phẳng  ABCD trùng với O . Biết tam giác 
AA C vuông cân tại A . Tính khoảng cách h từ điểm D đến mặt phẳng  ABB  A  . a 6 a 2 a 2 a 6 A. h  . B. h  . C. h  . D. h  . 6 6 3 3
Câu 50. (Tiên Du - Bắc Ninh - 2020) Cho hình lăng trụ tam giác ABC.AB C
  có cạnh bên bằng a 2 ,
đáy ABC là tam giác vuông tại B, BC a 3, AB a . Biết hình chiếu vuông góc của đỉnh A lên  
mặt đáy là điểm M thoả mãn 3AM AC . Khoảng cách giữa hai đường thẳng AA và BC bằng a 210 a 210 a 714 a 714 A. . B. . C. . D. . 15 45 17 51
Câu 51. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
AD  2 AB  2a . Cạnh bên SA  2a và vuông góc với đáy. Gọi M , N lần lượt là trung điểm của
SB và SD . Tính khoảng cách d từ điểm S đến mặt phẳng  AMN  . 3a a 6
A. d  2a . B. d  . C. d  .
D. d a 5 . 2 3
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Câu 52. (Hải Hậu - Nam Định - 2020) Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh 9a 2
a 2 . Biết rằng bán kính mặt cầu ngoại tiếp hình chóp bằng
, độ dài cạnh bên lớn hơn độ 8
dài cạnh đáy. Khoảng cách giữa hai đường thẳng AB và SD bằng 2a 17 4a 17 4a 34 2a 34 A. . B. . C. . D. . 17 17 17 17
Câu 53. (Kìm Thành - Hải Dương - 2020) Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại
A , biết SA   ABC  và AB  2a , AC  3a , SA  4a . Khoảng cách từ điểm A đến mặt phẳng SBC bằng 2a 6a 29 12a 61 a 43 A. d  . B. d  . C. d  . D. . 11 29 61 12
Câu 54. (Lương Thế Vinh - Hà Nội - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
AB  2a , AD  3a (tham khảo hình vẽ). Tam giác SAB cân tại S và nằm trong mặt phẳng vuông
góc với mặt đáy; góc giữa mặt phẳng  SCD và mặt đáy là 45 . Gọi H là trung điểm cạnh AB .
Tính theo a khoảng cách giữa hai đoạn thẳng SD và CH . 3 11a 3 14a 3 10a 3 85a A. . B. . C. . D. . 11 7 109 17
Câu 55. (Trường VINSCHOOL - 2020) Cho hình chóp S.ABCD có đáy là hình chữ nhật, cạnh
AB  2 AD a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy  ABCD .
Khoảng cách từ điểm A đến mặt phẳng SBD bằng a 3 a 3 a A. . B. . C. . D. 2a . 4 2 2
Câu 56. (Thanh Chương 1 - Nghệ An - 2020) Cho hình chóp SABC , có đáy là tam giác vuông tại A ,
AB  4a , AC  3a . Biết SA  2a 3 , 
SAB  30 và  SAB   ABC . Khoảng cách từ A đến
mặt phẳng  SBC  bằng 3 7a 8 7a 6 7a 3 7a A. . B. . C. . D. . 14 3 7 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 57. (Tiên Lãng - Hải Phòng - 2020) Cho hình lăng trụ đứng ABC.AB C
  có AB a , AC  2a ,  0
BAC  120 . Gọi M là trung điểm cạnh CC thì  0
BMA  90 . Tính khoảng cách từ điểm A đến
mặt phẳng  BMA . a 7 a 5 a 5 a 5 A. . B. . C. . D. . 7 3 7 5
-------------------- HẾT --------------------
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
TUYỂN CHỌN CÂU HỎI VẬN DỤNG - VẬN DỤNG CAO TỪ CÁC ĐỀ THI THỬ TRÊN CẢ NƯỚC NĂM 2020
57 CÂU VD - VDC CHƯƠNG 6. HÌNH HỌC 11 PHẦN 1. GÓC Câu 1.
(Chuyên Biên Hòa - Hà Nam - 2020) Cho tứ diện đều ABCD , M là trung điểm của cạnh
BC . Khi đó cos  AB, DM  bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2 Lời giải Chọn B A N B D M C
Gọi N là trung điểm của AC. Suy ra MN // AB
Do đó: cos  AB, DM   cos MN , DM a a 3
Gọi a là độ dài cạnh của tứ diện đều ABCD , suy ra MN  ; ND MD  2 2
MN MD ND
Trong tam giác MND ta có:  2 2 2 3 cos NMD   2.MN.MD 6  AB DM   3 cos ,  cos NMD  . 6 Câu 2.
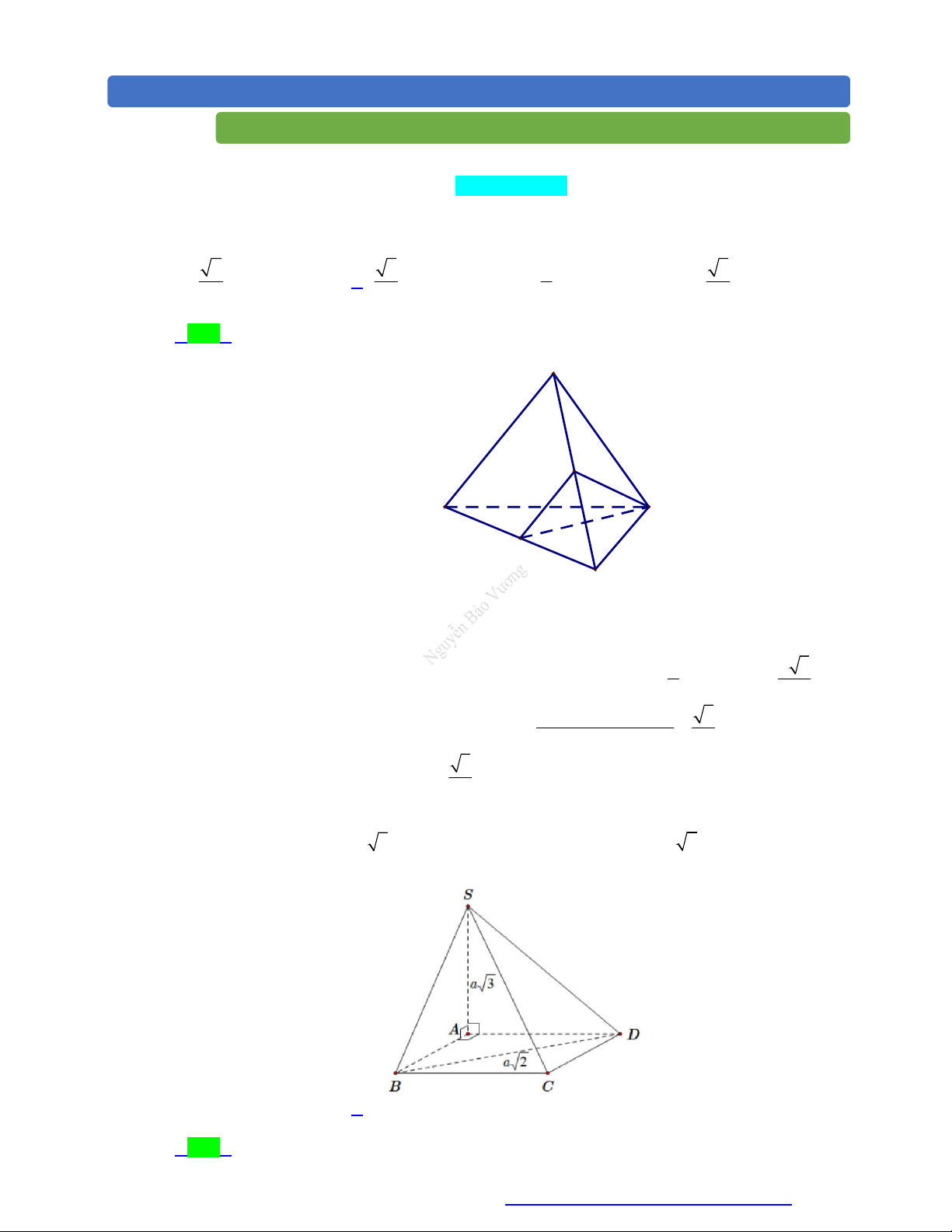
(Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp S.ABCD có SA vuông góc
với mặt phẳng đáy, SA a 3 , tứ giác ABCD là hình vuông, BD a 2 (minh họa như hình
bên). Góc giữa đường thẳng SB và mặt phẳng SAD bằng A. 0 . B. 30 . C. 45 . D. 60 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Đáy ABCD là hình vuông có đường chéo BD a 2 nên cạnh AB a . AB AD Ta có:
  AB   SAD  SA là hình chiếu của SB trên mặt phẳng  SADAB SA   SB SAD      SB SA  , ,  BSA . AB a
Trong tam giác vuông BSA , ta có:  3 tan BSA      BSA  30 . AS a 3 3
Vậy, SB , SAD     30. Câu 3.
(Chuyên Hùng Vương - Gia Lai - 2020) Cho hình chóp S.ABC có SA vuông góc với mặt a 3
phẳng  ABC , SA
, tam giác ABC đều cạnh bằng a (minh họa như hình dưới). Góc tạo 2
bởi giữa mặt phẳng SBC  và  ABC bằng S A C B A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 . Lời giải Chọn C S A C M B
Gọi M là trung điểm BC .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 a 3
ABC đều cạnh a nên AM BC và AM  . 2
Ta có SA ABC   Hình chiếu của SM trên mặt phẳng  ABC là AM .
Suy ra SM BC (theo định lí ba đường vuông góc). 
SBC   ABC   BC
Có AM  ABC , AM BC . Do đó góc giữa mặt phẳng SBC  và  ABC là góc giữa SM
SM SBC, SM BC  
và AM , hay là góc SMA (do SA   ABC   SAAM SAM vuông). a 3 SA
Xét tam giác SAM vuông tại A có  2  0 tan SMA    1  SMA  45 . AM a 3 2 Vậy góc cần tìm là 0 45 . Câu 4.
(Chuyên Thái Bình - 2020) Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm
O , cạnh a . Gọi M , N lần lượt là trung điểm của SA và BC . Góc giữa đường thẳng MN và
mặt phẳng  ABCD bằng 60 . Tính cos của góc giữa đường thẳng MN và mặt phẳng  SBD . 41 5 2 5 2 41 A. . B. . C. . D. . 4 5 5 4 Lời giải Chọn C
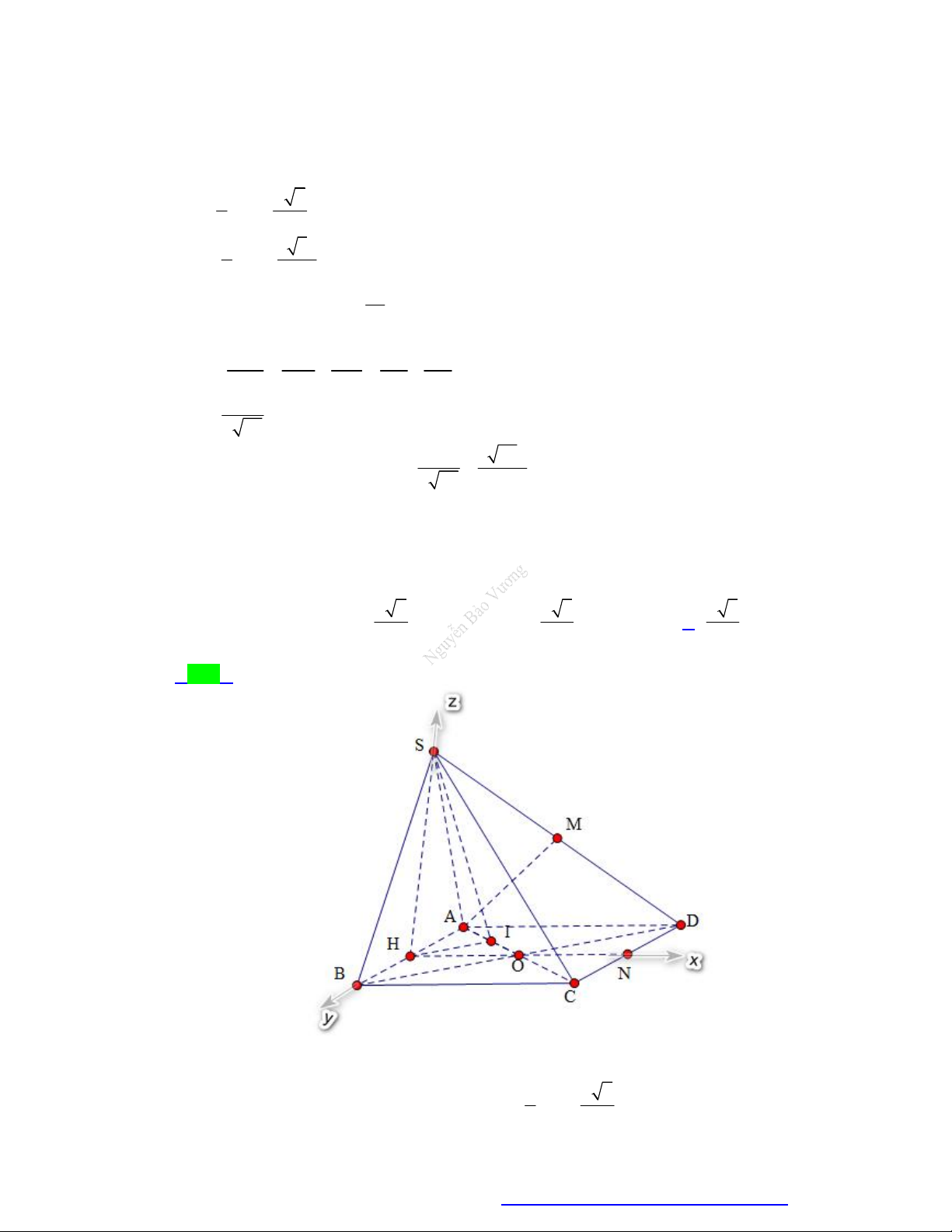
Từ giả thiết ta có SO   ABCD .
Gọi I là trung điểm OA thì MI là đường trung bình của S
OA MI // SO MI   ABCD
I là hình chiếu của M trên mặt phẳng  ABCD  IN là hình chiếu của MN trên mặt
phẳng  ABCD . Suy ra MN ABCD      MN IN   , ,  MNI  60 . 1 a 3 3a 2 Ta có NC BC  ; IC AC  . 2 2 4 4
Áp dụng định lý cosin trong INC ta có 2 2 2 
IN CI CN  2CI.CN.cos NCI
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2 2 2  3a 2   a  3a 2 a 5a a 10 2  IN      2. . .cos 45     IN  .  4   2  4 2 8   4 IN IN a 10 1 a 10 Do M
IN vuông tại I nên  cos MNI   MN   :  . MN cos 60 4 2 2
Lại có AC B ,
D AC SO AC  SBD .
Gọi E là trung điểm OB EN là đường trung bình của B
OC EN // OC hay EN // AC
NE  SBD hay E là hình chiếu của N trên mặt phẳng SBD .
Gọi F là trung điểm của SO MF là đường trung bình của S
AO MF // AO hay MF // AC
MF   SBD hay F là hình chiếu của M trên mặt phẳng SBD .
Ta có MF // NE nên bốn điểm E, N , F , M cùng nằm trên một mặt phẳng.
Trong mặt phẳng  ENFM  gọi J MN EF J MN   SBD (do EF   SBD ).
Suy ra MN SBD      MN EF   , ,  EJN (do  EJN  90 ). 1 1 a 2 1 1 a 2 Ta có EN OC AC  ; MF AO AC
EN MF , mà EN // MF 2 4 4 2 4 4 1 a 10
 Tứ giác ENFM là hình bình hành  J là trung điểm MN JN MN  . 2 4 2 2  a 10   a 2       JE JN EN 4 4     2 5 Vậy MN SBD     2 2 cos ,  cos EJN     . JN JN a 10 5 4 Câu 5.
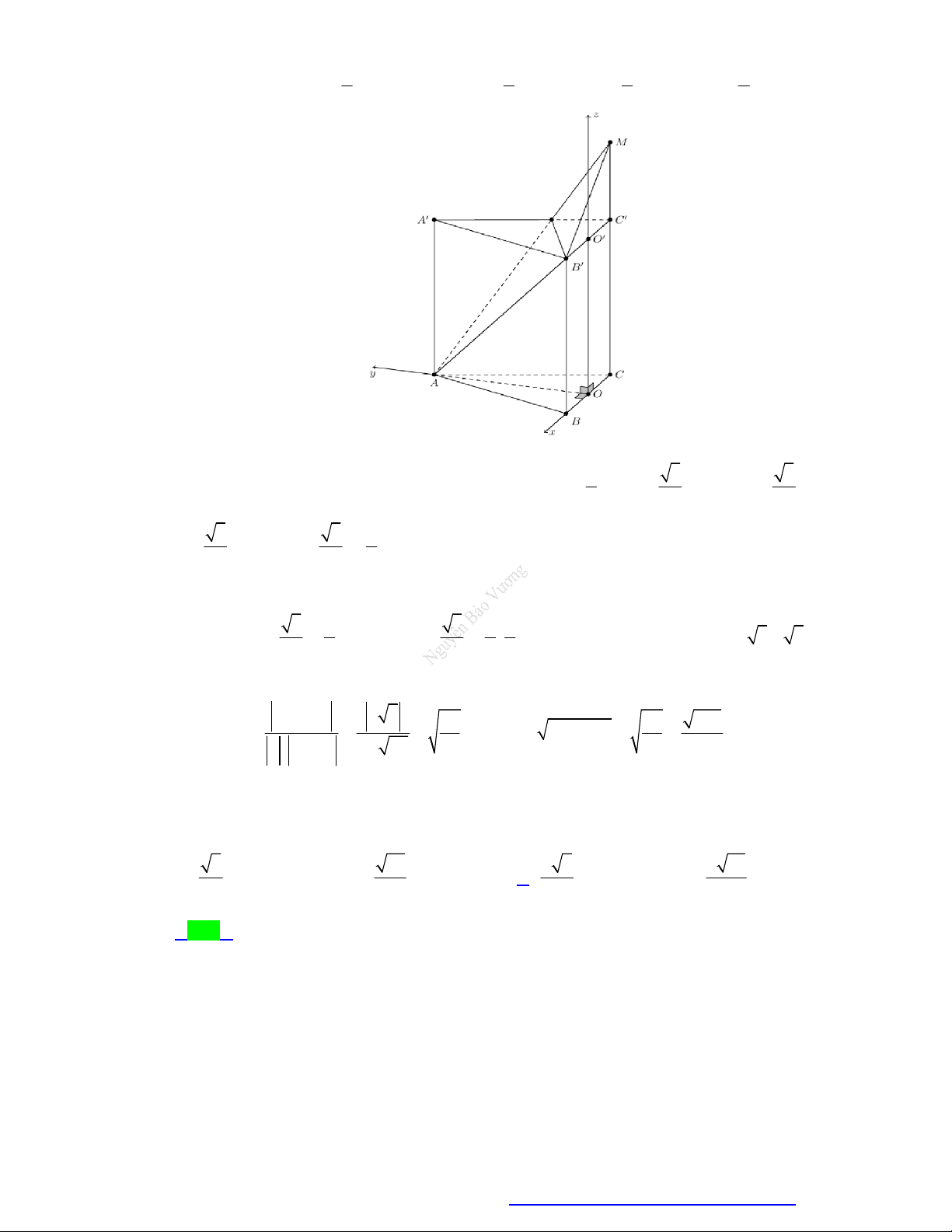
(Chuyên Vĩnh Phúc - 2020) Cho hình lăng trụ đứng ABC.AB C
  có AA  AB AC  1 và  0
BAC  120 . Gọi I là trung điểm cạnh CC . Côsin góc giữa hai mặt phẳng  ABC và  AB I   bằng 370 70 30 30 A. . B. . C. . D. . 20 10 20 10 Lời giải Chọn D
Gọi  là góc giữa hai mặt phẳng  ABC và  AB I   . 5 AB  2 , AI  . 2 2 2 2
BC AB AC  2 A .
B AC.cos A  3  BC B C    3 .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 13 2 2 B I   B C    C I   . 2 Vì 2 2 2
AB  AI B I   AB I
 vuông tại điểm A . 1 3 1 10 S  . AB AC.sin A  và SAI.AB  . ABC  2 4 AB I 2 4
Hình chiếu vuông góc của AB I
 lên mặt phẳng  ABC là ABC . S 30 Ta có SS .cos  cos ABC    . ABC AB IS 10 AB ICâu 6.
(ĐHQG Hà Nội - 2020) Cho hình chóp S.ABCD có đáy hình vuông. Cho tam giác SAB
vuông tại S và góc SBA bằng 0
30 . Mặt phẳng SAB vuông góc mặt phẳng đáy. Gọi M , N là
trung điểm AB, BC . Tìm cosin góc tạo bởi hai đường thẳng SM , DN  . 2 1 1 2 A. . B. . C. . D. . 5 5 3 3 Lời giải Chọn B
SAB   ABCD 
Trong  SAB , kẻ SH AB tại H . Ta có: SAB   ABCD  AB SH   ABCD .
SH  SAB,SH AB
Kẻ tia Az // SH và chọn hệ trục tọa độ Axyz như hình vẽ sau đây. z S D A x M B H y N Ca 3
Trong tam giác SAB vuông tại S , 0 SB A . B cos SBA  . a cos 30  . 2  3aa 3
Trong tam giác SBH vuông tại H , BH  . SB cos SBH
và SH BH.sin SBA  . 4 4 3a a aa a 3   
AH AB BH a  
H 0; ; 0  S    0; ;  . 4 4 4  4 4       a   aM 0; ; 0 
 , D a; 0; 0 , N ; ; a 0   .  2   2  2   a
  a a 3    aSM .DN 1 Ta có: SM  4  0; ;   , DN   ; ;
a 0  cos  SM , DN     .    4 4     2  SN.DN a a 5 5 . 2 2 Câu 7.
(Sở Ninh Bình) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , độ dài cạnh
AC  2a , các tam giác SA ,
B SCB lần lượt vuông tại A và C . Khoảng cách từ S đến mặt
phẳng ( ABC) bằng a . Giá trị cosin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2 2 1 2 5 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C + Gọi ,
O I lần lượt là trung điểm của AC, SB chúng ta có O là tâm của đường tròn ngoại tiếp
tam giác ABC và vì các tam giác SA ,
B SCB lần lượt vuông tại A và C nên I là tâm mặt
cầu ngoại tiếp tứ diện SABC do đó OI  ( ABC) .
+ Gọi D là hình chiếu của S lên mặt phẳng ( ABC) ta có SD / /OI và SD  2OI suy ra O là 2a
trung điểm của BD . Từ đây ta có ABCD là hình vuông cạnh bằng
a 2 và SD a . 2
+ Gọi H , K lần lượt là hình chiếu của D lên SC, SA ta có
SD  ( ABCD)  SD BC đồng thời ABCD là hình vuông nên BC DC từ hai ý này ta có
BC  (SCD)  BC DH , từ đó suy ra DH  (SCB) .
Chứng minh tương tự ta có DK  (SAB)
+ Vì vậy góc giữa hai mặt phẳng (SCB) và (SAB) bằng góc giữa hai đường thẳng DK và DH . a 6
+ Xét 2 tam giác vuông SAD, SCD bằng nhau ta có hai đường cao DK DH  3 2 HK SH SD 1 2a
+ Trong tam giác SAC ta có     HK
, trong tam giác DHK có 2 AC SC SC 3 3  2 2 2
DH KD KH 2 cos HDK   2DH .KD 3 Câu 8.
(Sở Bắc Ninh - 2020) Cho hình chóp
S.ABCD có đáy là hình thoi cạnh  0
a, ABC  120 , SA vuông góc với mặt phẳng  ABCD. Biết góc giữa hai mặt phẳng SBC  và SCD bằng 0 60 , khi đó a 6 a 6 a 3 A. SA  .
B. SA a 6. C. SA  . D. SA  . 4 2 2 Lời giải Chọn A
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 S H A B O D C
Gọi O là giao điểm của AC, B .
D Gọi H là hình chiếu vuông góc của O trên SC. Khi đó SC   H D B  vì SC  , BD SC OH.
Vậy góc giữa hai mặt phẳng  SBC  và  SCD là góc giữa hai đường thẳng HB, H . D
Vì SCD  SBC HB  . HD
Đặt SA x x  0. 2 2 2 2 2 HB BD
HB HD BD  Ta có 0 2 2 2 cos60 
HB  2HB BD  2  2 2 . BD HB HD HB    3 Ta có CHO CS
A OH.CS C . O SA   1 a
Trong tam giác ABC ta có AC a 3, OB   BD a 2 a TH1 : 2 2 3
HB BD a OH HB OB  . Thay vào (1) ta có 2 2 x x  3a . (vô 2 nghiệm). BD 3 a 3 a 3 TH2 : 2 2 HB    OH HB OB  . 3 3 6 2 2 a 3a a 6 Thay vào (1) ta có  2 2 x  3a  2  x x  . 12 4 4 Câu 9.
(Sở Bình Phước - 2020) Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác cân đỉnh A .   
Biết BC a 3 và 30o ABC
, cạnh bên AA  a . Gọi M là điểm thỏa mãn 2CM  3CC .
Gọi  là góc tạo bởi hai mặt phẳng  ABC và  AB M
 , khi đó sin có giá trị bằng 66 481 3 418 A. . B. . C. . D. . 22 22 22 22 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Cách 1: Gọi O là trung điểm BC . BO a o 3 a
Ta có: BO A .
B cos30  AB  
a AC và AO A . B sin30o  . cos30o 3 2 2. 2 Theo đề bài:  
 3 
  3 
 1  a
2CM  3CC  CM
CC  CC  C M   CC  C M   CC  C M   . 2 2 2 2
Gọi  là góc giữa hai mặt phẳng  ABC và  AB M   . S
Theo công thức diện tích hình chiếu ta có: SS .cos  cos ABC    . ABC ABCS AB C  2 1 1 a a 3 Ta có S  .AH.BC  . .a 3  ; 2 2 2 2 AB 
AB BB  a a a 2 ; ABC 2 2 2 4 2  a           a B M C M B C a 32 13 2 2    ;  2  2 2  3a a 13 2 2 2 AM
AC CM a     .  2  2 a 13 a 13 a 2   AB  B M   AM a 2  a 13 Khi đó 2 2 p    . 2 2 2
Áp dụng công thức Hê-rông vào AB M  ta có: 2 a 22 Sp p ABp B Mp AM  . AB M      4 2 a 3 S 3 19 418 Vậy ABC 4 2 cos   
 sin  1 cos    . 2 S  a AB C 22 22 22 22 4 Cách 2:
Gọi O là trung điểm BC . BO a o 3 a
Ta có: BO A .
B cos30  AB  
a AC và AO A . B sin30o  . cos30o 3 2 2. 2 Theo đề bài:
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020  
 3 
  3 
 1  a
2CM  3CC  CM
CC  CC  C M   CC  C M   CC  C M   . 2 2 2 2 Coi a  1.  1   3   3 
Gắn hệ trục tọa độ Oxyz như hình vẽ với O 0;0;0 , A 0; ;0   , B  ; 0;0 , C   ; 0; 0 ,  2   2      2    3   3 3  B ;0;1 M   ;0;  ,  . 2      2 2   
Khi đó  ABC  Oxy : z  0   ABC có một véc-tơ pháp tuyến là k  0;0  ;1 .
  3 1    3 1 3     Ta có: AB  
;  ;1 AM    ;  ;  n  4  AB ,  AM   .    1;5 3;2 3 AB M   ,  2 2        2 2 2  
Gọi  là góc giữa hai mặt phẳng  ABC và  AB M   .   k.n 2 3  AB M   3 19 418 Vậy 2
cos     
 sin  1 cos    . k . n 1.2 22 22 22 22  AB M  
Câu 10. (Đô Lương 4 - Nghệ An - 2020) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
tâm O . Gọi M và N lần lượt là trung điểm của SA và BC . Biết rằng góc giữa MN và
ABCD bằng 60 , côsin của góc giữa đường thẳng MN và mặt phẳng SBD bằng: 5 41 2 5 2 41 A. . B. . C. . D. . 5 41 5 41 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 z S M D C O N A H x B y
Chọn hệ trục tọa độ Oxyz như hình vẽ. Đặt SO m, m  0 .  a 2   a 2 a 2   a 2 m A
; 0; 0 ; S 0;0;m; N   ; ; 0   M  ; 0; .   2   4 4        4 2  
  a 2 a 2 m    MN    ; ; 
 . Mặt phẳng  ABCD có véc tơ pháp tuyến k  0; 0  ;1 .  2 4 2      m 2 2 MN.k a m  sin  3 15 3
MN ,  ABCD 2 2       m   . 2 2 2 8 4 MN k 5a m  8 4 a 30 2 2
 2m  15a m  2
  a 2 a 2 a 30    MN    ; ; 
 , mặt phẳng  SBD có véc tơ pháp tuyến là i  1; 0; 0 .  2 4 4      a 2 MN.i   5 2 5 MN SBD 2 sin ,       os c
MN,SBD  . 2 2 2 MN i 5 5 a a 30a   2 8 16
Câu 11. (Kim Liên - Hà Nội - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a .
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của đoạn
AB . Khẳng định nào sau đây là sai?
A. Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 45 . B. S
BC là tam giác vuông.
C. SI   ABCD .
D. Khoảng cách giữa đường thẳng DC và mặt phẳng  SAB bằng a . Lời giải Chọn A
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 S A D G I B C +) Vì SA
B đều và I là trung điểm của đoạn AB nên SI AB
Mà  SAB   ABCD,  SAB  ABCD  AB , suy ra SI   ABCD .
+) SI   ABCD  SI BC , mà BC AB BC  SAB  BC SB . Do đó S
BC là tam giác vuông.
+) SC ABCD  SC IC   , ,  SCI . a 3 a 5  SI 3 S
AB đều, cạnh a nên SI  và IC  nên tan SCI   . 2 2 IC 5
+) DC //  SAB nên d DC,SAB  d G,SAB (với G là trung điểm của DC ).
GI AB và GI SI nên GI   SAB  d G,SAB  GI a .
Đối chiếu các đáp án ta thấy đáp án A sai.
Câu 12. (THPT Nguyễn Viết Xuân - 2020) Cho hình lăng trụ đứng
ABC.AB C   có
AB AC a, BAC  120 . Gọi M , N lần lượt là trung điểm của B C
  và CC . Biết thể tích 3 3a
khối lăng trụ ABC.A BC   bằng
. Gọi  là góc giữa mặt phẳng  AMN  và mặt phẳng 4  ABC  . Khi đó 3 1 13 3 A. cos  . B. cos  . C. cos  . D. cos  . 2 2 4 4 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Chọn D
Lấy H là trung điểm của BC . 3 3a 2 3a Ta có: VCC .S
CC a vì S  .
ABC.A ' BC ' ABC 4 ABC 4
Chọn hệ trục tọa độ Oxyz như hình vẽ. Ta có M O . a  3a   3aa  3a a     
M 0;0;0, A ; 0;0 , B    0; ;0, C 0; ; 0; A ;0; a ; N    0;  ;  . 2  2   2  2  2 2            
Ta có:  ABC  Oz nên  ABC  có một vectơ pháp tuyến là k  0;0;  1 .   a    3a a  Ta có MA  ;0; a   , MN   0;  ;  .  2   2 2     a    a   Gọi 1 v MA  1
v  1;0;2 , v2  MN v2  0; 3;  1 . 2 2 
Khi đó mặt phẳng  AMN  song song hoặc chứa giá của hai vectơ không cùng phương là 1 v và     v   
2 nên có một vectơ pháp tuyến là n 1 v , v2    2 3; 1  ;  3  .     k.n 3
Vậy cos  cos k,n     . k . n 4
Câu 13. (Tiên Du - Bắc Ninh - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA a
vuông góc với mặt phẳng  ABC và SA  . Góc giữa mặt phẳng  SBC  và mặt phẳng 2
ABC bằng A. 45 . B. 90 . C. 30 . D. 60 . Lời giải Chọn C
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Gọi I là trung điểm B . C
Ta có AI BC (tam giác ABC đều) (1).
Lại có SA BC SA   ABC .
Suy ra BC  SAI   BC SI (2).
BC  SBC   ABC (3).
Từ (1), (2) và (3) suy ra SBC   ABC   SI AI   , ,  S . IA a SA
Xét tam giác SAI vuông tại A ta có  1 2 tan SIA    . AI a 3 3 2  Suy ra SIA  30 . 
Vậy SBC, ABC  30 . 
Câu 14. (Kìm Thành - Hải Dương - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân
tại A , AB  2a , SA vuông góc với mặt đáy và góc giữa SB và mặt đáy bằng 60 . Gọi  là
góc giữa hai mặt phẳng SBC và  ABC . Giá trị cos bằng 15 2 1 2 A. . B. . C. . D. . 5 5 7 7 Lời giải Chọn C
Gọi M là trung điểm BC AM BC (1) 
Có BC SA BC SM (2) BC AM
Từ (1) và (2) suy ra SBC  ABC   ,  SMA  .
Do SA   ABC  SA AB và AB là hình chiếu vuông góc của SB lên  
ABC  SBA  60 . SAB  có SA A .
B tan SBA  2 .
a tan60  2 3a .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 1 1 1 ABC 2 2 có 2 2 AM BC AB AC
2a  2a  a 2 . 2 2 2 AM AM a 2 1 S
AM vuông tại A có cos     . 2 2 SM SA AM
a2  a 2 7 2 3 2
PHẦN 2. KHOẢNG CÁCH
Câu 15. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và ;
D AB AD  2a; DC a . Điểm I là trung điểm đoạn AD, hai mặt phẳng
SIB và SIC  cùng vuông góc với mặt phẳng  ABCD . Mặt phẳng SBC  tạo với mặt
phẳng  ABCD một góc 60 . Tính khoảng cách từ D đến  SBC  theo a . a 15 9a 15 2a 15 9a 15 A. . B. . C. . D. . 5 10 5 20 Lời giải Chọn A S E A B H E A B U I V J I M K M K D C D C N
Theo đề ta có SI   ABCD.
Gọi K là hình chiếu vuông góc của I trên BC .
Suy ra: Góc giữa hai mặt phẳng SBC   ABCD     ,  SKI  60
Gọi E là trung điểm của A ,
B M IK D . E
Do BCDE là hình bình hành nên DE //  SBC
d D,SBC   d DE,SBC   d M ,SBC 
Gọi H là hình chiếu vuông góc của M trên SK . Suy ra d M ,SCD  MH 1 1 1 Dễ thấy: IM AU KN MK 2 2 2 1 5
IN IM MK KN
MK MK MK MK 2 2 2 2 2a 5 Suy ra: 2 2 MK IN ID DN  . 5 5 5 a 15
Trong tam giác MHK , ta có: MH MK.sin 60  5
Câu 16. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hình chóp S.ABC có đáy là tam giác vuông tại , A AC  ,
a I là trung điểm SC . Hình chiếu vuông góc của S lên  ABC là trung điểm H của
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
BC . Mặt phẳng SAB tạo với  ABC một góc 60 . Tính khoảng cách từ I đến mặt phẳng SAB . 3a 3a 5a 2a A. . B. . C. . D. . 4 5 4 3 Lời giải. Chọn A S I K B C H M A
Gọi M là trung điểm cạnh AB thì MH là đường trung bình của tam giác ABC nên a MH
, MH //AC MH AB . 2
Mặt khác, do SH   ABC  nên SMH   BC . Suy ra góc giữa SAB và  ABC là góc giữa
SM và MH ; lại có SH MH nên góc này bằng góc 
SMH . Từ giả thiết suy ra  SMH  60 .
Gọi K là hình chiếu của H lên SM thì HK   SAB . a 3 a a 3
Xét tam giác vuông SMH , SH MH . tan 60  , MH   HK  . 2 2 4
Gọi khoảng cách từ I,C, H đến mặt phẳng SAB lần lượt là
d I,SAB,d C,SAB,d H,SAB . Cách 1: d 1
I , SAB = d C,SAB   2 a Ta có 
 d  I SAB  d  H SAB 3 , ,  .  4 d  1
H , SAB  d C,SAB   2 Cách 2:
IH là đường trung bình của tam giác SBC nên IH //SB IH // SAB  d  a
I SAB  d H SAB 3 , ,  4
Câu 17. (Chuyên Hưng Yên - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác cân, BA BC a và 
BAC  30 . Cạnh bên SA vuông góc với mặt phẳng đáy và SA a . Gọi D là điểm đối
xứng với B qua AC . Khoảng cách từ B đến mặt phẳng  SCD bằng 2a 21 a 2 a 21 a 21 A. . B. . C. . D. . 7 2 14 7 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Tam giác ABC cân tại B có 
BAC  30 và D đối xứng với B qua AC nên tứ giác ABCD là hình thoi có  
ADC ABC  120 .
Trong mặt phẳng  ABC , kẻ AH vuông góc với đường thẳng CD tại H . Khi đó CD AH
và CD SA nên CD   SAH  . Do đó SCD  SAH  .
Trong mặt phẳng SAH  , kẻ AK SH tại K . Khi đó, AK  SCD và AK d  , A SCD   . a 3 Ta có AH  . AD sin 60  . 2 1 1 1 7
Áp dụng hệ thức lượng trong tam giác vuông SAH , ta có    . Từ đó, 2 2 2 2 AK AH SA 3a a 21 AK  . 7 a 21
Vì AB//  SCD nên d B, SCD  d  ,
A SCD  AK      . 7
Câu 18. (Chuyên KHTN - 2020) Cho hình chóp S.ABCD có đáy là hình chữ nhật AB a, AD  2a ,
SA vuông góc với mặt phẳng đáy và SA a . Gọi M là trung điểm của AD . Tính khoảng cách
giữa hai đường thẳng BM và SD . S D A M B C
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 a 6 a 2 2a 5 a 6 A. . B. . C. . D. . 3 2 5 6 Lời giải Chọn D S H A M D J K B I C
Gọi I là trung điểm của BC .
Vì BM // DI nên BM // SDI  .
Do đó d BM , SD  d BM ,SDI   d M ,SDI  . 1
Vì AD  SDI   D và M là trung điểm của AD nên d M ,SDI   d  ,
A SDI  . 2
Trong  ABCD , kẻ AK DI K DI  , AK BM J .
Trong  SAK  , kẻ AH SK H SK  . DI AK Vì 
DI  SAK  mà AH  SAK   DI AH . DI   SA
Suy ra AH  SDI   d  ,
A SDI   AH .
Ta có BM // DI JM // DK và M là trung điểm của AD nên AK  2 AJ . 1 1 1 1 1 2 Lại có      . 2 2 2 2 2 2 AJ AB AM a a a a 2 Suy ra AJ
AK a 2 . 2 1 1 1 1 1 3 a 6 Mặt khác       AH  . 2 2 2 2 2 2 AH AK SA 2a a 2a 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 a
Do đó d M SDI  1 6 ,  .AH  . 2 6 Cách khác: S A M D B I C E
Gọi E DI AB thì AE  2 AB  2a . 1
d BM , SD  d B,SDI   d  ,
A SDE  . 2
Vì S.ADE là tứ diện vuông tại A nên đặt h d  ,
A SDE  thì ta có 1 1 1 1 1 1 1 3 a 6         h  . 2 2 2 2 2 2 2 2 h SA AD AE a 4a 4a 2a 3 h a 6
Suy ra d BM , SD   . 2 6
Câu 19. (Chuyên Lam Sơn - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Tam
giác ABC là tam giác đều, hình chiếu vuông góc của đỉnh S lên mặt phẳng  ABCD  trùng với
trọng tâm tam giác ABC . Góc giữa đường thẳng SD và mặt phẳng  ABCD  bằng 30 . Tính
khoảng cách từ điểm B đến mặt phẳng SCD  theo a . a 21 2a 21 A. . B. a 3 C. a . D. . 7 3 Lời giải
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 S I A 30 D O H B C Chọn A
Gọi H là trọng tâm tam giác ABC , O là tâm của hình thoi ABCD .
Do SH   ABCD  : SD ABCD     ,  SDH  30 . 2 4 4 a 3 2a 3
Xét tam giác SDH vuông tại H có: 
SDH  30 ; HD BD BO  .  . 3 3 3 2 3 SH   2a 3 2a
 tan SDH SH H . D tan SDH  . tan 30  . HD 3 3
Từ H hạ HI SC tại I . HI SCHI CD   
CD  SHC  Ta có: 
  HI   SCD
SC, CD   SCD   SC CDC   
Từ đó, khoảng cách từ điểm H đến mặt phẳng SCD  : d H ,SCD  HI .
Xét tam giác SHC vuông tại H , đường cao HI : 2a a 3 . HS.HC 2a 21 3 3 HI    . 2 2 2 2 21 HS HC 2aa 3          3  3  
d B,SCD DB 3 Mặt khác:   .
d H ,SCD DH 2
Vậy khoảng cách từ điểm B đến mặt phẳng SCD : d  3 3 3 2a 21 a 21
B,SCD  d H,SCD  HI  .  . 2 2 2 21 7 Cách khác:
Thể tích khối chóp S.BCD : 1 1 1  3 1 2a 1 3 a 3 VSH.SSH. .C . B C . D sin BCD  . . . . a . a  (đvtt). S .BCD 3 BCD 3 2 3 3 2 2 18 SH 4a a 7
Xét tam giác SCD có: 2 2 SD   ;CD  ;
a SC SH HC  . sin 30 3 3 2 a 7
Diện tích tam giác SCD : Sp p SC p SD p CD  (đvdt). SCD     6
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
SC SD CD ( p
là nửa chu vi tam giác SCD ). 2
Vậy khoảng cách từ điểm B đến mặt phẳng SCD : 3 a 3 3. d  3.V 3.V a 21 B SCD B.SCD S .BCD 18 ,     . 2 S S aSCDSCD 7 7 6
Câu 20. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp S.ABCD có đáy là hình vuông, AB  ,
a SA vuông góc với mặt phẳng đáy và SA  2a (minh họa như hình vẽ bên dưới
). Gọi M là trung điểm của CD , khoảng cách giữa điểm M và mặt phẳng (SB ) D bằng S D A M B C 2a a a a A. . B. . C. . D. . 3 2 2 3 Lời giải Chọn D S H D A I O M B C
Gọi I là giao điểm của AM và BD , O là tâm hình vuông ABCD . 1
Ta có d (M , (SBD)  d( , A (SBD)) . 2
Dựng AH vuông góc với SO tại H. Ta có
BD SA  BD  (SAO)  BD AH . BD AOAH SO
  AH  (SBD) nên d( , A (SB ) D )  AH . AH BD
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 1 1 1 1 1 1 1 9 2a         AH  . 2 2 2 2 2 2 2 2 AH AS AB AD 4a a a 4a 3 a
Vậy, d (M , (SBD)  . 3
Câu 21. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A mặt bên (SBC) là tam giác đều cạnh a và nằm trong mặt phẳng vuông
góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 3 a 2 a 5 a 3 A. . B. . C. . D. 4 4 4 3 Lời giải Chọn A
Gọi H là trung điểm của BC. Khi đó SH   ABCD . Do tam giác ABC vuông cân tại A nên a
AH BC và AH  . 2
Dựng điểm D sao cho ABCD là hình bình hành.
Khi đó d S ,
A BC   sBC,SAD  d H,SAD a 3 a . a 3 2 2
Kẻ HI SA d H ,SAD  HI   . a 4
Câu 22. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp S.ABCD có đáy là hình
thoi tâm O cạnh a và có góc  0
BAD  60 . Đường thẳng SO vuông góc với mặt đáy  ABCD 3a và SO
. Khoảng cách từ O đến mặt phẳng  SBC  bằng 4 3a a a 3 3a A. . B. . C. . D. . 4 3 4 8 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 S H C D M O K A B
Ta có: tứ giác ABCD là hình thoi cạnh a có  0
BAD  60 suy ra tam giác BCD là tam giác đều cạnh a . a 3
Gọi M là trung điểm cạnh BC . Suy ra DM BC và DM  . 2 1 a 3
Kẻ OK / / DM ,  K BC   OK BC và OK DM  . 2 4
Vì SO   ABCD  BC SO BC   SOK  .
Kẻ OH SK,  H SK   OH   SBC  . a 3 3a . OK.SO 3a
Từ đó ta có: d O SBC  4 4 ,  OH    . 2 2 2 2 8 OK SOa 3   3a       4  4   
Câu 23. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hình chóp S.ABCD có đáy
ABCD là hình thang vuông tại A và D , AB  3a, AD DC a . Gọi I là trung điểm của
AD , biết hai mặt phảng  SBI  và SCI  cùng vuông góc với đáy và mặt phẳng  SBC  tạo với đáy một góc 0
60 . Tính theo a khoảng cách từ trung điểm cạnh SD đến mặt phẳng  SBC  . a 17 a 6 a 3 a 15 A. . B. . C. . D. . 5 19 15 20 Lời giải Chọn B
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Kẻ IK BC K BC   SBC   ABCD  0 ;  SKI  60 MD 1 a
Gọi M AD BC . Ta có   MD MA 3 2 IK MI a 2 5
Ta có MIK đồng dạng với MBA nên suy ra    2 BA MB 15  3a   3a2     2  2 5 2a 5  IK  .3a  15 5
Gọi N là trung điểm của SD . 1 1
Ta có d N,SBC   d D,SBC   d I ,SBC  2 4 a 15 a 15
Từ I kẻ IH SK suy ra IH d I,SBC  0  IK.sin 60 
d N,SBC   5 20
Câu 24. (Chuyên Thái Bình - 2020) Cho hình chóp S.ABCD có đáy là hình chữ nhật với
AB  2a, BC a , tam giác đều SAB nằm trong mặt phẳng vuông góc với đáy. Khoảng cách
giữa BC và SD là 3 2 5 5 A. 3a . B. a . C. a . D. a . 2 5 5 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 BC//AD
Ta có  AD   SAD  BC// SAD , do đó d BC, SD  d BC,SAD  d B,SAD .
BC  SAD 
Tam giác SAB đều, gọi H là trung điểm SA thì BH SA (1).  
SAB   ABCD Ta có 
AD  SAB  SAB  SAD (2).  AD ABa
Từ (1) và (2) suy ra BH  SAD , do đó d B SAD 2 3 ,  BH   a 3 . 2
Câu 25. (Chuyên Bắc Ninh - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,
SA a và SA vuông góc với mặt đáy. M là trung điểm SD . Tính khoảng cách giữa SB và CM . a 3 a 2 a 3 a 3 A. . B. . C. . D. . 6 3 2 3 Lời giải Chọn D Cách 1
Gọi E là điểm đối xứng với D qua A , N là trung điểm của SE và K là trung điểm của BE
Ta có các tứ giác NMCB và ACBE là các hình bình hành.
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Có CM //  SBE nên d CM , SB  d CM ,SBE  d C,SBE  d  ,
A SBE . a 2 A
BE vuông cân tại A có AB a nên AK BE và AK  . 2
Kẻ AH SK , H S K . BE AK Có 
BE  SAK   BE AH . BE SA  AH BE Có 
AH  SBE  d  ,
A SBE  AH . AH SKa 2 a 2 . a a 3 . SA AK a 3 Ta có AK  , 2 2
SK SA AK  ; AH  2   . 2 2 SK a 3 3 2 a 3
Vậy d CM , SB  . 3 Cách 2:
Chọn hệ trục tọa độ Oxyz sao cho:  a a
A0;0;0, B  ;
a 0; 0, D0; ;
a 0, S 0;0;a  C  ; a ; a 0 , M 0; ;   .  2 2   
  a a  2 2 2    a a a  Ta có SC   ;
a a;  a , SB   ;
a 0;  a, MC  a; ;  
  SB, MC   ;  ;   .  2 2    2 2 2  
Khoảng cách giữa hai đường thẳng SB và CM là:
   3 3 3 a a aS , B MC  .SC     2 2 2 a 3
d SB,CM       . S , B MC  4 4 4 3 a a a     4 4 4 a 3
Vậy d CM , SB  . 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 26. (Chuyên Bến Tre - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,
SA  2a và vuông góc với  ABCD . Gọi M là trung điểm của SD . Tính khoảng cách d giữa
hai đường thẳng SB và CM. a a 2 2a a A. d  . B. d  . C. d  . D. d  . 3 2 3 6 Lời giải Chọn C S M K A D H I O B C
Gọi O AC BD .
Vì ABCD là hình vuông cạnh a nên O là trung điểm của BD mà M là trung điểm của SD nên
OM / /SB suy ra SB / /  ACM  .
Do đó d S ,
B CM   d SB, ACM   d B, ACM   d  ,
D ACM  .
Gọi H là trung điểm của AD nên MH / /SA MH   ABCD .
d SB,CM   d  ,
D ACM   2d H, ACM  .
Kẻ HI AC  MHI    MAC  theo giao tuyến MI , kẻ HK MI HK   ACM  hay
d H, ACM   HK . 1 1 1 a 2 1 Có 2 2 HI OD BD AB AD  , MH SA a . 2 4 4 4 2 1 1 1 1 1 1 1 9 a Suy ra         HK  . 2 2 2 2 2 2 2 2 HK HM HI HK a HK a 3  a 2    4   a
Vậy d SB CM   d H ACM  2 , 2 ,  2HK  . 3
Câu 27. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho hình chóp S.ABCD có SA   ABCD ,
SA a 6 , ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD  2a . Khoảng cách
từ điểm B đến mặt phẳng SCD bằng a 6 a 3 a 2 a 3 A. . B. . C. . D. . 2 2 2 4 Lời giải Chọn C
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 S H I K A D M B C
Gọi I là trung điểm AD và H là trung điểm SD suy ra HI //SA HI   ABCD .
Do ABCD là nửa lục giác đều và I là trung điểm AD nên BI //CD . Suy ra d  ,
B SCD  d I,SCD.
Do ABCD là nửa lục giác đểu nên dễ thấy IC
D là tam giác đều.
Gọi M là trung điểm CD suy ra CD  HIM  .
Trong IHM  kẻ IK HM . IK HM  Ta có: 
IK SCD . IK CDCD   HIM   
d I,SCD  IK . 1 1 1 1 1 2 Xét IHM có:      . 2 2 2 2 2 2 IK IH IM  6   3 a a a       2   2      a 2 aIK
. Vậy d B SCD 2 ,  . 2 2
Câu 28. (Chuyên Hùng Vương - Gia Lai - 2020) Cho lăng trụ đứng tam giác ABC.AB C   có đáy là
một tam giác vuông cân tại B , AB AA  2a, M là trung điểm BC (minh họa như hình
dưới). Khoảng cách giữa hai đường thẳng AM và B C  bằng a 2a a 7 A. . B. . C. . D. a 3 2 3 7
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B A C M A 2a B 2a H N B M A' C' I B' N
Gọi N là trung điểm BB  MN / /B C   B C  / /  AMN  .
Khi đó d AM , B C
   d B C
 , AMN   d C, AMN  .
Ta có BC   AMN   M và MB MC nên d C, ABM   d B, ABM  .
Gọi h là khoảng cách từ B đến mặt phẳng  ABM  . Tứ diện BAMN có B ,
A BM , BN đôi một 1 1 1 1 1 vuông góc nên:     2 2 2 2 2 h BH BA BM BN
AB  2a BC . 1 1 2a BN BB  AA   a . 2 2 2 1 BM BC a . 2 2 1 1 1 1 9 4a 2a Suy ra 2      h   h  . 2 2 2 2 2 h 4a a a 4a 9 3 2a
Vậy khoảng cách giũa hai đường thẳng AM và B C  bằng . 3
Câu 29. (Chuyên Lào Cai - 2020) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh   2a và 0
SBA SCA  90 . Biết góc giữa đường thẳng SA và mặt đáy bằng 450. Tính khoảng
cách từ điểm B đến mặt phẳng (SAC). 15 2 15 2 15 2 51 A. a . B. a . C. a . D. a . 5 5 3 5 Lời giải Chọn B
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Gọi I là trung điểm của SA.
Tam giác SAB và SAC là các tam giác vuông tại B, C IS IA IB IC .
Gọi G là trọng tâm tam giác đều ABC IG   ABC
Trong SAG kẻ SH / / IG H CG  SH   ABC
Dễ thấy khi đó IG là đường trung bình của tam giác SAH SH  2IG 2 2a 3 2a 3
Tam giác ABC đều cạnh = 2a AG  .  3 2 3
Ta có: SA ABC    SA AH    0 , ,
SAH  45  A
IG vuông cân tại G 2a 3 4a 3
IG AG
SH  2IG  3 3 1 1 4a 3 2a2 3 3 4aVSH.S  . .  S . ABC 3 ABC 3 3 4 3
Ta có: GA GB GC, GA GH ( IG là đường trung bình của tam giác SAH)
GA GB GC GH G là tâm đường tròn ngoại tiếp tứ giác ABHC.
 AH là đường kính đường tròn ngoại tiếp tứ giác ABHC 0
ACH  90 (góc nội tiếp chắn nửa đường tròn) 4a 3 2a Ta có: 2 2 AH  2 AG   CH AH AC  3 3 2 2  4a 3   2a  2 15a 2 2  SC
SH HC        3    3  3 2 1 1 2 15a 2 15a SSC.AC  . .2a SAC 2 2 3 3 3 4a 3. 3V 2a 15
Vậy d B SAC  S . ABC 3 ,    2 S a SAC 2 15 5 3
Câu 30. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho tứ diện đều ABCD có cạnh bằng a . Gọi
M là trung điểm của cạnh AD . Tính khoảng cách giữa hai đường thẳng AB và CM . a 33 a a a 22 A. . B. . C. . D. . 11 33 22 11
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 A M B D C Lời giải Chọn C 3 a 3 3 V 1 a 2 Ta có:V  ; ABCD   VABCD 12 V 2 ABCM 24 ABCM 1 VA .
B CM .d ( AB,CM ).sin( AB,CM ) ABCM 6 2 2  
   a a  . AB CM A .
B AM AC 4 2 3 os
c ( AB, CM )     . AB CM . AB CM 3 6 . a a 2 1 11 6V a 22
 sin( AB,CM )  1 
.Vậy d ( AB, CM ) ABCM   . 12 12 .
AB CM .sin( AB,CM ) 11
Câu 31. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hình lăng trụ đều ABC. ’ A ’
B C’ có tất cả các
cạnh có độ dài bằng 2 (tham khảo hình vẽ). Tính khoảng cách giữa hai đường thẳng AC’ và A’B. 2 3 1 3 A. . B. . C. . D. . 5 2 2 5
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 Lời giải Chọn A
Gọi D là điểm đối xứng của C qua A ta có tứ giác AD
A C là hình bình hành do đó 
A D//AC , suy ra khoảng cách d ( AC ,  BA )
  d ( AC , (  A BD))  d ( , A (  A BD)) .
Theo giả thiết ABC. 
A BC là lăng trụ đều nên 
AA  ( ABC) hay A
A  ( ABCD) suy ra 
A A BD (1) .
Ta có ABD có AB AD nên là tam giác cân tại A , gọi I là trung điểm BD ta có AI BD (2) . 1
Xét tam giác BCD có ,
A I lần lượt là trung điểm của DC, DB nên AI BC  1. 2
Trong mặt phẳng ( A ' AI ) dựng AH   A I ; H   A I (3) .
Từ (1) và (2) suy ra BD  ( A' AI )  BD AH (4) .
Từ (3) và (4) suy ra AH  ( A ' BD) do đó khoảng cách d ( ,
A (SBD))  AH . AI.AA' 2
Trong tam giác A' AI vuông tại A ta có AH   . 2 2 AI  ( AA') 5 Từ đây chọn đáp án A.
Câu 32. (Chuyên Vĩnh Phúc - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA
vuông góc với mặt phẳng  ABC; góc giữa đường thẳng SB và mặt phẳng ABC bằng 60 .
Gọi M là trung điểm cạnh AB . Khoảng cách từ B đến SMC bằng a 39 a A. . B. a 3 . C. a . D. . 13 2 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 S H M B A C Ta có  ,  
SB ABC SBA  60  SA  tan 60 a .  a 3 .
Vì M là trung điểm của AB d B,SMC  d A,SMC. 1 a
Dựng AH vuông góc với SM tại H d A,SMC  AH mà AM AB  . 2 2 1 1 1 1 4 13 a 39 Xét tam giác vuông SAM ta có:       AH  . 2 2 2 2 2 2 AH SA AM 3a a 3a 13
Câu 33. (Đại Học Hà Tĩnh - 2020) Cho lăng trụ đứng ABC.A BC
  có đáy là tam giác vuông và
AB BC a , AA  a 2 , M là trung điểm của BC . Tính khoảng cách d của hai đường
thẳng AM và B C  . a 6 a 2 a 7 a 3 A. d  . B. d  . C. d  . D. d  . 6 2 7 3 Lời giải Chọn C Cách 1: BC AN K M B C H A Do A
BC vuông và có AB BC nên A
BC vuông cân tại B .
Gọi N là trung điểm của BB , ta có: B C  //  AMN  .
Khi đó: d AM , B C
   d B C
 , AMN   d C, AMN   d B, AMN  .
Kẻ BH AM tại H và kẻ BK NH tại K .
Ta có: BH AM , BN AM AM   NBH   BK AM .
Do BK NH , BK AM nên BK   AMN  .
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Suy ra: d B, AMN   BK . BM .BA 5a BH .BN a 7 Mặt khác: BH   ; BK   . 2 2 5 BM BA 2 2 7 BH BN a
Vậy d AM B C
   d B AMN  7 , ,  BK  . 7 Cách 2: z BC AM C y O B A x Do A
BC vuông và có AB BC nên A
BC vuông cân tại B .
Chọn hệ trục tọa độ Oxyz như hình vẽ. Không mất tính tổng quát, ta giả sử a  1.  1 
Ta có: A1; 0;0, M 0; ;0 , B  
0;0; 2, C 0;1;0 .  2    1   
   2 
AM  1; ; 0 , B C    
0;1; 2, AC  1;1;0; AM, B C      ;  2; 1   .  2     2    2
    2  0  AM , B C   .AC 2   7
Khi đó: d AM , B C   
    .  AM , B C   1 7    2 1 2 a 7
Trong trường hợp tổng quát, ta có: d AM , B C    . 7
Câu 34. (ĐHQG Hà Nội - 2020) Cho lăng trụ đứng / / /
ABCA B C có tất cả các cạnh bằng a. Gọi M là trung điểm của /
AA . Tính khoảng cách giữa hai đường thẳng BM và / B C . 3 3 3 3 A. a . B. a . C. a . D. a 5 10 2 2 7 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 z B a I A C B/ x M a O C/ A/ a y
Gọi O và I lần lượt là trung điểm của B/C/, BC. Chọn hệ trục tọa độ Oxyz sao cho:  3 1 / / / /
O(0; 0; 0); A  Ox  A (
; 0; 0);C Oy C (0; ; 0); I Oz I (0; 0;1) 2 2 1 1 1   3  3 1 /  B (0;
; 0);C(0; ;1); B(0; ;1); ( A ; 0;1); M ( ; 0; ) 2 2 2 2 2 2  
   3 1 1 3  3 / / B C (0;1;1); BM ( ; ; ) BM , B C       (1; ; ) 2 2 2   2 2   BC  (0;1;0)
Vậy khoảng cách giữa hai đường thẳng BM và / B C là:
   / 3
BC. BM , B C    3 / 2
d (BM ; B C) 
    nên chọn đáp án B /   3 3 10 BM , B C 1    4 4
Câu 35. (Sở Phú Thọ - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , cạnh
AB a, AD a 2 . Hình chiếu vuông góc của S trên mặt phẳng  ABCD là trung điểm của
đoạn OA . Góc giữa SC và mặt phẳng  ABCD bằng 30 . Khoảng cách từ C đến mặt phẳng SAB bằng 9 22a 3 22a 22a 3 22a A. . B. . C. . D. . 44 11 11 44 Lời giải Chọn B
Gọi H là trung điểm AO , ta có SH   ABCD .
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Góc giữa SC và  ABCD bằng  SCH bằng 30 .
Ta có CA  4HA , suy ra d C,SAB  4d H,SAB .
Kẻ HI AB, HK SI , ta suy ra HK   SAB .
d H,SAB  HK . 1 a 2 HI AD  . 4 4 3 3 3a CH AC  4 4 3a
Suy ra SH CH . tan 30  . 4
Xét tam giác SHI vuông tại H có HK là đường cao. 1 1 1 16 16 Suy ra     2 2 2 2 2 HK HS HI 9a 2a 3a HK  . 2 22  a a
d C SAB  d H SAB 3 3 22 , 4 ,  4.  . 2 22 11
Câu 36. (Sở Phú Thọ - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hình
chiếu vuông góc của S trên mặt phẳng  ABCD là trung điểm của cạnh AB , góc giữa mặt
phẳng  SAC  và đáy bằng 45 . Gọi M là trung điểm của cạnh SD . Khoảng cách giữa hai
đường AM và SC bằng a 2 a 5 a 5 A. a . B. . C. . D. . 4 10 5 Lời giải Chọn D
Gọi H là trung điểm cạnh AB , I là trung điểm cạnh AO . Suy ra SH   ABCD ,  1 a 2
SAC   ABCD   ,
SIH  45 . Do đó SH IH BO  . 2 4
Gọi N là trung điểm cạnh CD , khi đó HN AB .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Chọn hệ trục tọa độ trong không gian như hình vẽ, ta có tọa độ các điểm aa 2  aa a a 2       a
H 0;0;0 , A 0;  ;0 ; S    0; 0; ; D a;  ; 0 ; M    ;  ; ;C a; ; 0   . 2  4  2  2 4 8       2     
  a a a 2    a a 2   Nên AM   ; ;
; SC   a; ; 
; AC  a; a; 0 .  2 4 8   2 4     
Khoảng cách giữa hai đường AM và SC là
  
AM , SC.AC   a 5
d AM , SC      .   5 AM , SC  
Câu 37. (Sở Hà Tĩnh - 2020) Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc với nhau và
AD  2 , AB AC  1. Gọi I là trung điểm của đoạn thẳng BC , khoảng cách giữa hai đường
thẳng AI và BD bằng 3 2 5 2 A. . B. . C. . D. . 2 5 2 3 Lời giải Chọn D
Vì tứ diện ABCD có AB , AC , AD đôi một vuông góc với nhau, nên ta chọn hệ trục tọa độ
Axyz như hình vẽ (với A là gốc tọa độ, đường thằng AC nằm trên trục Ax , AD nằm trên
trục Ay và AB nằm trên trục Az ).
Từ đó suy ra: A0;0;0 , B 0;0; 
1 vì B Az , C 1;0;0 vì C Ax , D0; 2;0 vì D Ay .  1 1 
Vì I là trung điểm của BC nên I ; 0;   .  2 2 
Từ đó, ta quay về bài toán tính khoảng cách giữa hai đường thẳng chéo nhau trong hệ tọa độ không gian Axyz .    1 1      1  Ta có AI  ; 0; , BD    0;2; 
1   AI , BD  1; ;1 
 và AB  0; 0  ;1 . 2 2      2 
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
   1     1 .0  .0 1.1
AI , BD .AB   2 2
Ta có d AI , BD      . 2   3 AI , BD  1    2  2 1  1    2 
Câu 38. (Sở Ninh Bình) Cho hình chóp S . ABC có SA a , tam giác ABC đều, tam giác SAB vuông
cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt
phẳng  SAC  bằng a 42 a 42 a 42 a 42 A. . B. . C. . D. . 7 14 12 6 Lời giải Chọn A
Gọi H , M , N lần lượt là trung điểm của các cạnh AB , AC , AM .
Do tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy
SH   ABC  .
Kẻ HK SN   1 .  AC HN Ta có: 
AC  SHN   AC HK 2 . AC SH  Từ  
1 và 2  HK  SAC   d H ;SAC  HK .
Ta có d B;SAC  2d H ;SAC .  AB a 2 
Do tam giác SAB vuông cân tại S và SA a   a 2 . SH   2  a 6 BM    2
Do tam giác ABC đều   .  a 6 HN    4 SH . HN 42
Xét tam giác vuông SHN , ta có HK   a . 2 2 14 SH HN
Vậy d B SAC   d H SAC  42 ; 2 ;  2HK a . 7
Câu 39. (Sở Yên Bái - 2020) Cho hình lăng trụ đứng AB . C A BC
  có đáy là tam giác vuông cân tại B ,
biết AB BC a , AA  a 2 , M là trung điểm của BC . Tính khoảng cách giữa hai đường
thẳng AM và B C  .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 a 7 2a 5 a 6 a 15 A. . B. . C. . D. . 7 5 2 5 Lời giải Chọn A C' A A' B' M B C A C M N B B' Kẻ MN // B C   B C  //  AMN
d d B C
 , MN   d B C
 , AMN   d C, AMN   d  ,
B AMN  .
Ta có tứ diện BAMN là tứ diện vuông 1 1 1 1 1 1 1 7 a 7          d  . 2 2 2 2 2 2 2 2 d BA BM BN aa a 7   a 2    2     2  
Câu 40. (Bỉm Sơn - Thanh Hóa - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a , AD  2a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc
giữa đường thẳng SC và mặt phẳng  ABCD bằng 45. Gọi M là trung điểm của SD , hãy
tính theo a khoảng cách từ M đến mặt phẳng  SAC  . 2a 1513 a 1315 2a 1315 a 1513 A. d  . B. d  . C. d  . D. d  . 89 89 89 89 Lời giải Chọn D
Gọi H là trung điểm của AB SH AB ( SA
B cân tại S ). 
SAB   ABCD  AB  Ta có 
SAB   ABCD
SH   ABCD .
SH ABcmt 
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Vì SH   ABCD , nên hình chiếu vuông góc của đường thẳng SC lên mặt phẳng  ABCD là
HC , suy ra SC ABCD  SC HC  , ,  SCH  45 .  2 2  AB   a  2 a 17 H
BC vuông tại B , có 2 2 2 HC HB BC   BC       2a  .  2   2  2 a 17 S
HC vuông cân tại H , suy ra SH HC  . 2
d M ,SAC  MS 1 1 1 Ta có  
d M ,SAC   d D ,SAC   d B ,SAC .
d D ,SAC  DS 2 2 2
d B ,SAC  BA Mặt khác 
 2  d B ,SAC   2d H ,SAC  .
d H ,SAC HA
Từ đó d M ,SAC   d H ,SAC .
Trong mặt phẳng  SAC  , kẻ HI AC và kẻ HK SI .
AC HI gt   Ta có 
AC  SHI   AC HK .
AC SH SH    ABCD  HK SI   gt  Ta có 
HK  SAC   d H ,SAC   HK. HK AC  cmt  A
BC vuông tại B , có AC
AB BC a   a2 2 2 2 2  a 5. AI IH AH BC AH BC AB a a aAIH  . . 2 . 5 ABC     IH     . AB BC AC AC 2 AC 2.a 5 5 a 17 a 5 . SH.HI a 1513 S
HI vuông tại H , có 2 5 HK    . 2 2 2 2 89 SH HIa 17   a 5       2 5    
Câu 41. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
2a , cạnh SA tạo với mặt phẳng đáy một góc o
30 . Khoảng cách giữa hai đường thẳng SA và CD bằng 2 15a 3 14a 2 10a 4 5a A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn C
Gọi O là tâm của mặt đáy, M là trung điểm của AB , H là hình chiếu của O trên SM . a 2 Ta có  ,
SA ABCD   , SA OA   o o
SAO SAO  30  SO AO tan 30  . 3
Ta có AB OM , AB SO AB  SOM   AB OH , mà SM OH OH  SAB .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Tam giác SOM vuông tại O và có đường cao OH nên 1 1 1 3 1 5 10a       OH  . 2 2 2 2 2 2 OH SO OM 2a a 2a 5 a
Vì CD AB d CD SA  d CD SAB  d C SAB  d O SAB 2 10 // , , , 2 ,  2OH  . 5
Câu 42. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông
tại A và B , AD  2AB  2BC  2a , SA vuông góc với đáy, góc giữa SB và mặt phẳng đáy bằng 0
60 . Gọi H là hình chiếu vuông góc của A lên SB . Khoảng cách từ H đến mặt phẳng SCD bằng 3a 30 3a 30 3a 30 A. a 3 . B. . C. . D. . 20 10 40 Lời giải Chọn D
Kẽ HK / /SC HK / /  SCD . Khi đó d H ,SCD  d K,SCD .  Ta có SA AB SBA a
SB ABCD  0 .tan . tan ;  .
a tan 60  a 3 . 2 2
SB SA AB  2a . 2 BH AB 1 BK 1 a 3a Mà 2
AB BH.SB   
. Vì HK / /SC nên   BK   KC  . 2 SB SB 4 BC 4 4 4
d K;SCD KC 3 3
Vì KC / / AD nên  
d K;SCD  d  ;
A SCD . d  ; A SCD AD 8 8
Gọi F là hình chiếu vuông góc của A lên SC . AC DC Do 
DC   SAC   DC AF . SA DC   AF SC Vì 
AF  SCD nên AF DC
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 d  . SA AC a 30 ;
A SCD  AF   , với 2 2 AC
AB BC a 2 . 2 2 5 SA AC 3 3a 30
Vậy d H;SCD  d K;SCD  d  ;
A SCD  . 8 40
Câu 43. (Kim Liên - Hà Nội - 2020) Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA vuông
góc với mặt phẳng đáy, góc giữa mặt phẳng  SBC  và mặt phẳng đáy là 60 (minh họa như
hình dưới đây). Gọi M , N lần lượt là trung điểm của AB, AC .
Khoảng cách giữa hai đường thẳng SB và MN bằng 3a a 6 3a A. . B. . C. . D. a 6 . 8 2 4 Lời giải Chọn A
Gọi E là trung điểm của BC, vì tam giác ABC đều  AE BC , lại có
SA BC BC SE
Mặt khác  SBC    ABC   BC  SBC   ABC   ,  SEA  60 .
Gọi P là trung điểm của SA SB // M ,
P MP   MNP  SB // MNP
d SB, MN   d SB,MNP  d B,MNP  d  , A MNP Gọi  
AE MN I PIA SEA  60 và AI MN
Ta có MN AI , MN PI MN   API    PMN    API
Mà  PMN    API   PI , kẻ AH PI AH   PMN   d  ,
A PMN   AH .  1 a 3  a 3 3 3a Xét A
PI có AIP  60 ,  AI AE
AH AI.sin AIP  .  . 2 4 4 2 8 3a
Vậy d SB, MN   . 8
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Câu 44. (Lê Lai - Thanh Hóa - 2020) Cho hình chóp
S.ABCD có đáy ABCD là hình thang vuông tại B và C , CD  2 AB , AD a , 
ADC  30 , SA vuông góc với mặt phẳng
đáy và SA  2a (minh họa như hình bên
dưới). Khoảng cách từ D đến mặt phẳng SBC  bằng 2 57a 57a A. . B. . 19 19 4 57a C. . D. 3a . 19 Lời giải Chọn C
+) Gọi E là giao điểm của AD và BC DA cắt mặt phẳng  SBC  tại E .
d D,SBC DE   (1).
d A,SBC AEAB // CD  +) Theo giả thiết  1
AB là đường trung bình của tam giác ECD (2). AB CD   2
d D,SBC DE Từ (1) và (2)  
 2  d D ,SBC   2d A,SBC  .
d A,SBC AEBC AB +) Ta có 
BC  SAB  SBC   SAB , do đó nếu gọi H là hình chiếu vuông BC SA
góc của A lên SB thì AH   SBC   d A,SBC   AH .
+) Tam giác ECD vuông tại C , có:
CA là đường trung tuyến  CA AE AD a  tam giác AEC là tam giác cân tại A .   
EDC  30  CEA  60 ; a 3
 tam giác EAC là tam giác đều cạnh a  đường cao AB  . 2
+) Tam giác SAB vuông tại A có AH là đường cao
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 a 3 2 . a 2 . SA AB a 3 2a 57 2  AH     . 2 2 2 SA AB 3a a 19 19 2 4a  4 2 a
Vậy d D SBC  d A SBC 4 57 , 2 ,  2AH  . 19 Câu 45. (Liên trường Nghệ An - 2020) Cho tứ diện ABCD có    0
ABC ADC ACD  90 , BC  2 ,
a CD a , góc giữa đường thẳng AB và mặt phẳng  BCD bằng 0
60 . Tính khoảng cách giữa hai đường thẳng AC và BD . a 6 2a 6 2a 3 a 3 A. . B. . C. . D. . 31 31 31 31 Lời giải Chọn C z A 600 H B y 2a D a C x
Gọi H là chân đường cao của tứ diện ABCD . BC AB Ta có: 
BC HB   1 . BC AHCD   AD Lại có: 
CD HD 2 . CD AH  Mà  BCD  90 .
Từ đây ta suy ra HBCD là hình chữ nhật.
Mặt khác: AB BCD     ,
ABH  60 . Suy ra: AH H .
B tan 60  a 3 .
Chọn hệ trục Oxyz H .DBA như hình vẽ.
Ta có: H 0;0;0 , A0;0;a 3 , B0; ;
a 0 , C 2 ; a ;
a 0 , D 2 ; a 0; 0 .   
AC  2a;a; a 3 , BD  2 ; a  ;
a 0 , AB  0; ; a a 3  .
  
AC, BD .AB 3   2a 3 2a 93
Vậy d AC, BC       .  AC BD   a 2   a 2   a 2 2 2 2 31 , 3 2 3 4
Câu 46. (Lý Nhân Tông - Bắc Ninh - 2020) Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc
với nhau và OA OB a , OC  2a . Gọi M là trung điểm của AB . Khoảng cách giữa hai
đường thẳng OM và AC bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2a 2 5a 2a 2a A. . B. . C. . D. . 3 5 2 3 Lời giải Chọn D C H O B E K M A
Dựng AE //OM , khi đó OM // CAE  . Do đó d OM , AC  d OM , (CAE)  d  , O (CAE)
Dựng OK AE , ta có:  AE OK      AE COK AE
OC Vì CO    ABC    
Mà AE  CAE nên CAE  COK  .
Ta có CAE  COK   CK . Kẻ OH CK , khi đó OH  COK  . Suy ra d  ,
O (CAE)  OH
Xét tam giác OAB ta có : 2 2
AB OA OB a 2 . AB a 2
Dễ thấy OKAM là hình chữ nhật nên OK AM   . 2 2
Xét tam giác COK ta có : 1 1 1 1 1 1 2       OH a . 2 2 2 2 2 OH OK OC OH   2 2 a a 2 3   2  
Câu 47. (Nguyễn Huệ - Phú Yên - 2020) Cho hình chóp S.ABC có đáy là tam giác vuông tại A ,
AB a, AC  2a, SA vuông góc với mặt phẳng đáy và SA  2a . Gọi G là trọng tâm của A
BC . Khoảng cách giữa hai đường thẳng SG và BC bằng 2a a 6 2a 6 4a A. . B. . C. . D. . 7 3 9 7 Lời giải Chọn A
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 3
Gọi M là trung điểm của BC . Trong mp SAM  dựng S M
/ /SG . Suy ra S A   SA  3a 2
Do đó d SG, BC   d SG,S B
C  d G,S BC  . 1
Vì AM  3GM nên d G,S BC    d  , A S BC   . 3
Kẻ AH BC ta có BC   S AH  . Kẻ AK S H
AK d  , A S BC  . 1 1 1 2a 1 1 1 6a Ta có    AH  . Suy ra    AK  . 2 2 2 AH AB AC 5 2 2 2 AK S AAH 7 a
Do đó d G S BC   1 2 ,  AK  . 3 7
Câu 48. (Nguyễn Trãi - Thái Bình - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành
và SA SB SC  11, góc SAB  30 ,
 góc SBC  60 ,
 góc SCA  45 . Tính khoảng
cách d giữa hai đường thẳng AB và SD . 22 A. 2 22 . B. 22 . C. . D. 4 11 . 2 Lời giải Chọn B
Trong tam giác SAB ta có 2 2 2
SB SA AB  2 . SA A .
B cos 30  AB  11 3 .
Trong tam giác SBC ta có SB SC  11, SBC  60 nên SBC đều suy ra BC  11.
Trong tam giác SCA ta có SC SA  11, SCA  45 nên SCA vuông cân tại S suy ra AC  11 2 .
Xét tam giác ABC có 2 2 2
BC AC AB do vậy ABC vuông tại C .
Gọi I là hình chiếu của S lên mặt phẳng ( ABCD) vì SA SB SC nên I là tâm của đường
tròn ngoại tiếp tam giác ABC , vì ABC vuông tại C nên I là trung điểm của AB và
SI  ( ABCD)  SI CD (1) . Vẽ IK CD (2), IH SK (3) .
Từ (1) và (2) suy ra CD  (SIK )  CD IH (4) .
Từ (3) và (4) suy ra IH  (SCD) do đó khoảng cách d (I , (SCD))  IH .
Ta lại có AB//CD suy ra khoảng cách d ( AB, SD)  d ( AB, (SCD))  d (I , (SCD))  IH . C . A CB 11 6
Trong mặt phẳng đáy vẽ CJ AB ta suy ra IK CJ   . AB 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2 AB 11
Trong tam giác SAB cân tại S có 2 SI SA   . 4 2 IK.SI
Trong tam giác SIK vuông tại I ta có IH   22 . 2 2 IK SI
Câu 49. (THPT Nguyễn Viết Xuân - 2020) Cho hình hộp ABC . D A B C 
D có đáy ABCD là hình
vuông cạnh a , tâm O . Hình chiếu vuông góc của A lên mặt phẳng  ABCD trùng với O . Biết tam giác 
AA C vuông cân tại A . Tính khoảng cách h từ điểm D đến mặt phẳng  ABB  A  . a 6 a 2 a 2 a 6 A. h  . B. h  . C. h  . D. h  . 6 6 3 3 Lời giải Chọn D Ta có: 2 2 2 2 AC
AB BC a a a 2 . AC a 2 Vì tam giác 
AA C vuông cân tại A nên ta có:  A O   . 2 2
Gọi M là trung điểm của AB . Suy ra OM AB . Trong mặt phẳng  
A OM  : kẻ OH   A M . Ta có: AB   
A OM  (vì AB OM và AB  
A O ). Suy ra AB OH . OH   A M Vì 
OH   ABB 
A  . Do đó: d  ; O ABB 
A   OH . OH   AB
Do D, O, B thẳng hàng và DB  2OB nên d  ; D AB B
A   2d  ; O ABB 
A   2OH . a 2 a .  A . O OM a 6 Ta có: 2 2 OH    . 2 2 2 2  6 A O OMa 2   a       2  2    a
Vậy d D ABB  A  6 ;
h  2OH  . 3
Câu 50. (Tiên Du - Bắc Ninh - 2020) Cho hình lăng trụ tam giác ABC.AB C
  có cạnh bên bằng a 2 ,
đáy ABC là tam giác vuông tại B, BC a 3, AB a . Biết hình chiếu vuông góc của đỉnh A
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020  
lên mặt đáy là điểm M thoả mãn 3AM AC . Khoảng cách giữa hai đường thẳng AA và BC bằng a 210 a 210 a 714 a 714 A. . B. . C. . D. . 15 45 17 51 Lời giải Chọn A A' C' B' a 2 K D H A C M a a 3 B
Dựng hình bình hành ABCD , vì tam giác ABC là tam giác vuông tại B nên ABCD là hình chữ nhật.
Suy ra BC / / AD BC / /  AAD .
Do đó d BC, AA  d BC, AAD  d C, A AD .  
Mà 3AM AC nên d C, AAD  3d M , AAD .
Kẻ MH AD   AMH    AAD  AH .
Kẻ MK AH MK   AAD  MK d M , AAD . 1 2a a 14 Mặt khác ta có 2 2 2 2 AC
AB BC  2a AM AC   AM A A   AM  . 3 3 3 MH AM 1 1 1 a Và MH / /CD     MH CD AB  . CD AC 3 3 3 3 1 1 1 1 1 1 1 135 a 210 Suy ra         MK  . 2 2 2 2 2 2 2 2 MK A MMH MK    a MK 14a 45 a 14       3 3    a a
Vậy d BC AA  d C A A
D  d M A AD 210 210 , , 3 ,  3MK  3  . 45 15
Câu 51. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
AD  2 AB  2a . Cạnh bên SA  2a và vuông góc với đáy. Gọi M , N lần lượt là trung điểm
của SB và SD . Tính khoảng cách d từ điểm S đến mặt phẳng  AMN  . 3a a 6
A. d  2a . B. d  . C. d  .
D. d a 5 . 2 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Từ A kẻ đường thẳng vuông góc với BD tại H , ta có: 
BD   SAH  
MN  SAH    AMN    SAH  MN / / BD
Mặt khác  AMN   SAH   SE , suy ra: d S; AMN   d S; AE . . AB AD .2 a a 2a 5
Xét tam giác vuông SAH có: AH    . 2 2 BD 5 a  4a 2 20a 2a 30 2 2 2 SH
SA AH  4a   . 25 5
Vì MN là đường trung bình của tam giác SBD nên E là trung điểm của SH , suy ra: 1 a 30 AE SH  . 2 5 2S S AS.AH 2 .2 a a 5 a 6
d S; AE SAESAH       . AE AE 2.AE a 30 3 2.5. 5
Câu 52. (Hải Hậu - Nam Định - 2020) Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông 9a 2
cạnh a 2 . Biết rằng bán kính mặt cầu ngoại tiếp hình chóp bằng
, độ dài cạnh bên lớn 8
hơn độ dài cạnh đáy. Khoảng cách giữa hai đường thẳng AB và SD bằng 2a 17 4a 17 4a 34 2a 34 A. . B. . C. . D. . 17 17 17 17 Lời giải Chọn D
Gọi O AC BD , M là trung điểm SC .
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
Trong tam giác SAC , dựng đường trung trực của đoạn thẳng SC cắt SO tại I , I là tâm mặt 9a 2
cầu ngoại tiếp hình chóp S.ABCD , bán kính R SI  . 8
Vì độ dài cạnh bên lớn hơn độ dài cạnh đáy nên tâm I của mặt cầu ngoại tiếp hình chóp thuộc đoạn SO .
Gọi x là độ dài cạnh bên của hình chóp. Ta có S
OC đồng dạng với SMI . 9a 2 x SI SM Suy ra 8 2    2 2 SC SO x x a 2 9a 2 x 2 2 2 2 2 2  x a
 9a x a  2 2x  81a  2 2 x a  4  8x 8 2 2  x  2   9 2    x   x   a 4 2 2 4  8x 81a x 81a 0 8 81 81 0            2    2 a a       x  9      a  8 2  x  9   
không thỏa vì x a 2 .  a  8 2
x   9  x  3a   .  a
Suy ra SO   a2 2 2 2 3  a  8a d A ;
B SD  d AB,SDC  d  ;
A SCD  2d  ;
O SCD .
Gọi E là trung điểm CD , kẻ OH SE , khi đó d O,SCD  OH . 1 1 1 1 2 2 2a      OH  2 2 2 2 2 OH SO OE 8a a 17 . 4 34a
d AB; SD  2OH  . 17
Câu 53. (Kìm Thành - Hải Dương - 2020) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại
A , biết SA   ABC  và AB  2a , AC  3a , SA  4a . Khoảng cách từ điểm A đến mặt phẳng SBC bằng 2a 6a 29 12a 61 a 43 A. d  . B. d  . C. d  . D. . 11 29 61 12 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 S K A C H B Ta có
SA   ABC    SA BC .
BC   ABC 
Trong  ABC  , kẻ AH BC , mà BC SA BC  SAH   BC SH .
Trong SAH  , kẻ AK SH , mà SH BC AK  SBC hay d  ;
A SBC  AK .
Vì ABC vuông tại A nên 2 2 BC
AB AC  13a . . AB AC 6a 13
Mặt khác có AH là đường cao nên AH   . BC 13 2a 793
Vì SAH vuông tại A nên 2 2 SH SA AH  . 13 S . A AH 12a 61
Vậy có AK là đường cao AK   . SH 61
Câu 54. (Lương Thế Vinh - Hà Nội - 2020) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
với AB  2a , AD  3a (tham khảo hình vẽ). Tam giác SAB cân tại S và nằm trong mặt phẳng
vuông góc với mặt đáy; góc giữa mặt phẳng  SCD và mặt đáy là 45 . Gọi H là trung điểm
cạnh AB . Tính theo a khoảng cách giữa hai đoạn thẳng SD và CH . 3 11a 3 14a 3 10a 3 85a A. . B. . C. . D. . 11 7 109 17 Lời giải Chọn B Cách 1:
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020
SAB   ABCD  Ta có: 
SAB   ABCD
SH   ABCD . SH  ;
AB SH  SAB 
Kẻ HK CD ( K là trung điểm của CD )
CD  SHK   CD SK .
 SCD  ABCD   SK HK  ; ;   SKH  45  S
HK vuông cân tại H SH HK  3a .
Kẻ d qua D song song với HC cắt AB tại E ED HC a 10 .
d CH ; SD  d CH ;SED  d H;SED .
Kẻ HF ED ED   SHF  .
Kẻ HG SF HG   SED  d H ;SED  HG . 1 1 A . D EH 3 . a 2a 3 10a Ta có: S  . AD EH
HF.ED HF    . HED 2 2 ED a 10 5
Xét tam giác SHF vuông tại H ta có: 3 10a 3 . a 1 1 1 SH .HF 3 14a    HG  5   . 2 2 2 HG SH HF 2 2 SH HF 2 18a 7 2 9a  5 3 14a
d CH ; SD  . 7 Cách 2:
SAB   ABCD  Ta có: 
SAB   ABCD
SH   ABCD . SH  ;
AB SH  SAB 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
Kẻ HK CD ( K là trung điểm của CD )
CD  SHK   CD SK .
 SCD  ABCD   SK HK  ; ;   SKH  45  S
HK vuông cân tại H SH HK  3a .
Chọn hệ trục tọa độ như hình vẽ H O , tia Ox chứa HK , tia Oy chứa HA , tia Oz chứa HS
Khi đó: H 0;0;0 ; C 3a;  a ;0 ; D 3a; a;0 ; S 0;0;3a .   
Ta có: HC  3a;  a ; 0 , SD  3a; a;  3a , SH  0; 0;  3a .  
 HC SD   2 2 2 ;
3a ;9a ; 6a   
  
SH. HC; SD 2   6a . 3  a 3 14a
d CH ; SD      . HC; SD 2 2 2 2 2 2 7  
3a   9a   6a
Câu 55. (Trường VINSCHOOL - 2020) Cho hình chóp S.ABCD có đáy là hình chữ nhật, cạnh
AB  2 AD a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy  ABCD .
Khoảng cách từ điểm A đến mặt phẳng SBD bằng a 3 a 3 a A. . B. . C. . D. 2a . 4 2 2 Lời giải Chọn A S I A D H G B C
Gọi H là trung điểm của AB . Từ giả thiết suy ra SH   ABCD .
Từ H kẻ HG BD tại G , kẻ HI SG tại I .
Suy ra HI  SBD  d H ,SBD  HI . 2 a a 5 a 3 Ta có 2 2 2 BD AB AD a   , SH  . 4 2 2 a a . HG BH . AD BH a 5 Lại có BGH  đồng dạng với BAD nên 2 2   HG    . AD BD BD a 5 10 2 1 1 1 1 1 Khi đó     2 2 2 2 2 HI SH HGa 3   a 5      2 10    
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU VD-VDC TRÍCH TỪ CÁC ĐỀ THI THỬ TNTHPT 2020 a 3 Suy ra HI  . 8 a a
Lại có d A SBD  d H SBD 3 3 , 2 ,  2.HI  2.  . 8 4
Câu 56. (Thanh Chương 1 - Nghệ An - 2020) Cho hình chóp SABC , có đáy là tam giác vuông tại A ,
AB  4a , AC  3a . Biết SA  2a 3 , 
SAB  30 và SAB   ABC . Khoảng cách từ A đến
mặt phẳng  SBC  bằng 3 7a 8 7a 6 7a 3 7a A. . B. . C. . D. . 14 3 7 2 Lời giải Chọn C
Gọi SH là đường cao của khối chóp  SH là đường cao của tam giác SAB . SAH   
có SAH  30 , SHA  90  AH S .
A cos 30  3a SH a 3
d A;SBC   4d H ;SBC  .
Tính khoảng cách từ H đến mặt phẳng  SBC  :
Từ H kẻ HK BC tại K , kẻ HI SK tại I
d H ;SBC   HI BH HK BH CA Mà HBK  . 3 CBA    HK   a BC CA BC 5
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 1 1 1 28 3a 7      HI  2 2 2 2 HI SH HK 9a 14   a
d A SBC  6 7 ;  . 7
Câu 57. (Tiên Lãng - Hải Phòng - 2020) Cho hình lăng trụ đứng ABC.AB C
  có AB a , AC  2a ,  0 
BAC  120 . Gọi M là trung điểm cạnh CC thì 0
BMA  90 . Tính khoảng cách từ điểm A
đến mặt phẳng  BMA . a 7 a 5 a 5 a 5 A. . B. . C. . D. . 7 3 7 5 Lời giải Chọn B A C B M A' C' B' Ta có: 2 2 2 
BC AB AC  2.A .
B AC.cos BAC a   a2 2 0 2 2  2. .2 a .
a cos120  7a .
Đặt CC  2x CM MC  x . Vì ABC.A BC
  là hình lăng trụ đứng nên ta có tam giác BCM vuông tại C và tam giác A CM  vuông tại C . Ta có: 2 2 2 2 2
BM BC CM  7a x ; AM AC  C M    a2 2 2 2 2 2 2 2
x  4a x ; 2 2 2 2 2
AB AA AB  4x a .  Vì 0
BMA  90 nên tam giác BMA vuông tại M , do đó: 2 2 2
AB BM AM 2 2 2 2 2 2
 4x a  7a x  4a x 2 2
x  5a x a 5 . 1 1 Ta có:  SA . B AC.sin BAC  . .
AB d C, AB  d C, AB  a 3 . ABC 2 2
Lại có: d M , ABA  d C, ABA  d C, AB ( vì CC / /  ABA và  ABC   ABA ). Suy ra. 1 1 Ta có: 2 S  . AB AA  a 5 ; 2 SM .
B MA  3 3a .` ABA 2 MBA 2 1 a VS d M ABA  S d A BMA
d A BMA 5 ,  . AABM ABA  1 . . ,   . . MBA  ,  3 3 3
-------------------- HẾT --------------------
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • [NBV]-44 CÂU HỎI VD-VDC ĐẠI SỐ & GIẢI TÍCH 11 (FULL ĐÁP ÁN CHI TIẾT)
  • [NBV]-57 CÂU HỎI VD-VDC HÌNH HỌC 11 (FULL ĐÁP ÁN CHI TIẾT)