










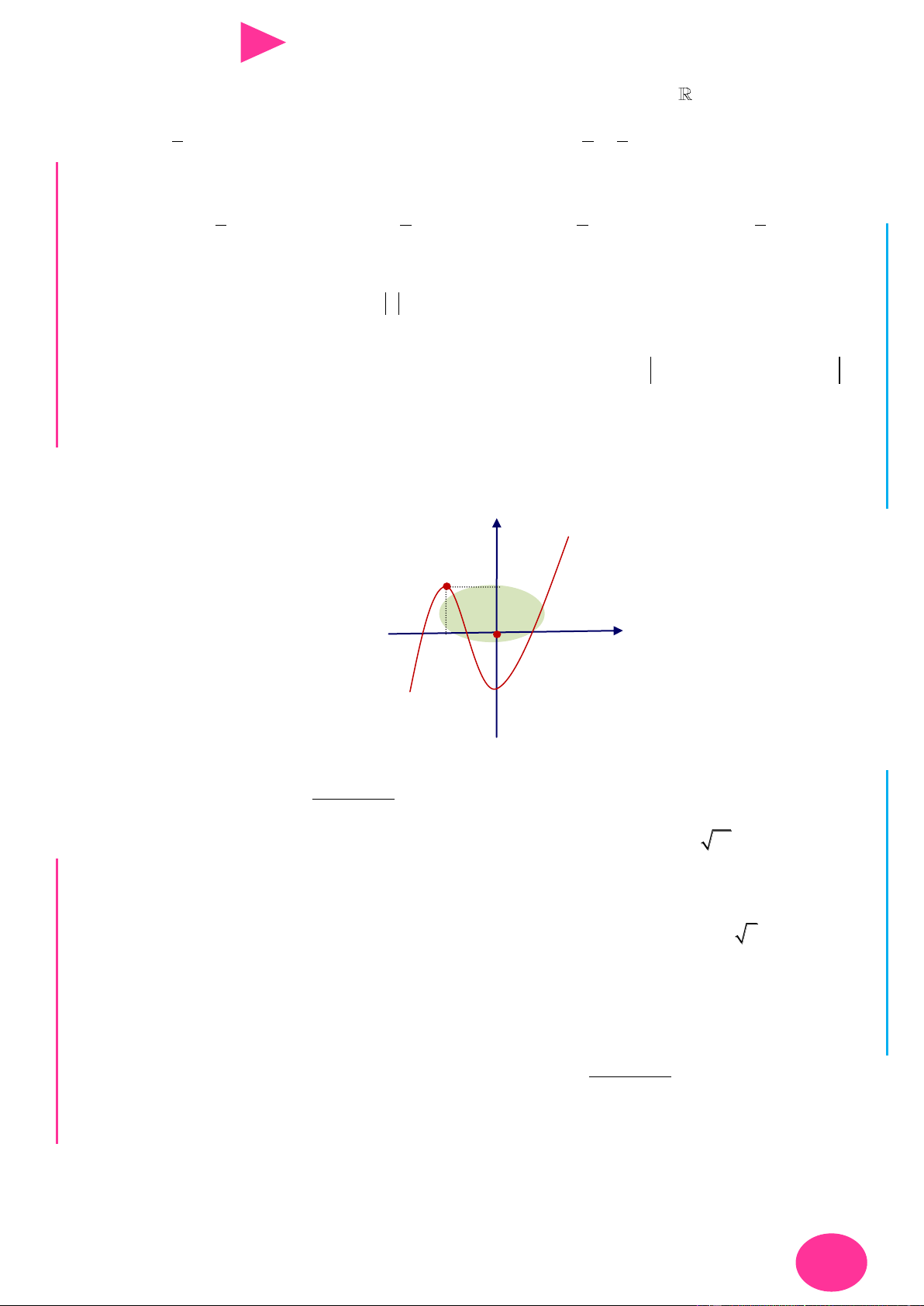





Preview text:
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHỦ ĐỀ: CỰC TRỊ
VẬN DỤNG – VẬN DỤNG CAO DẠNG 1
TÌM CỰC TRỊ CỦA HÀM SỐ Câu 1.
Biết M (0; 2) , N(2; 2
) là các điểm cực trị của đồ thị hàm số 3 2
y ax bx cx d . Tính
giá trị của hàm số tại x 3
A. y(3) 2 .
B. y(3) 11.
C. y(3) 0 . D. y(3) 3 Câu 2. Đồ thị hàm số 3 2
y x 3x 9x 1 có hai điểm cực trị A và B . Điểm nào dƣới đây I
thuộc đƣờng thẳng AB ? Ơ
A. M 0; 1 . B. Q 1 ;10 .
C. P 1;0 .
D. N 1;10 .
M D Câu 3. Hàm số f x 0 1 2 2 2019 2019 C
C x C x ... C x
có bao nhiêu điểm cực trị? Ầ 2019 2019 2019 2019 Đ A. 0 . B. 2018 . C. 1. D. 2019 . NHỊĐ Câu 4. Cho hàm số 1 2 2 10 10
f (x) 1 C x C x ... C x . Số điểm cực trị của hàm số đã cho bằng 10 10 10 G THPT N.C.Đ A.10 . B. 0 . C. 9 . D.1 . N
NG Câu 5. Giá trị cực đại của hàm số y x sin 2x trên 0; là: CÔ Ờ N 3 3 2 3 2 3 A. . B. . C. . D. . YỄ TRƢ 3 2 6 2 3 2 3 2 GU
N Câu 6. Gọi A , B , C là các điểm cực trị của đồ thị hàm số 4 2
y x 2x 4 . Bán kính đƣờng N
tròn nội tiếp tam giác ABC bằng A. 2 1. B. 2 . C. . D. 1. ÁO VIÊ 2 1
GI Câu 7. Cho hàm số 4 2
y x 2x 1 có đồ thị C . Biết rằng đồ thị C có ba điểm cực trị tạo
thành ba đỉnh của một tam giác, gọi là . ABC Tính diện tích . ABC 1 A. S 2 .
B. S 1. C. S . D. S 4 . 2 Câu 8.
Cho hàm số y f (x) có đúng ba điểm cực trị là 2
; 1; 0 và có đạo hàm liên tục trên . Khi đó hàm số 2
y f (x 2x) có bao nhiêu điểm cực trị? A. 6. B. 4. C. 5. D. 3. Câu 9. Cho hàm số 2 3 ( ) ( 1) x f x x x
e có một nguyên hàm là hàm số F(x) . Số điểm cực trị của
hàm số F(x) là A. 1. B. 2 . C. 3 . D. 0 . x
Câu 10. Số điểm cực trị của hàm số y sin x , x ; là 4 A. 2 . B. 4 . C. 3 . D. 5 .
TÌM CỰC TRỊ CỦA HÀM SỐ 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 11. Biết phƣơng trình 3 2
ax bx cx d 0 a 0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số 3 2
y ax bx cx d có bao nhiêu điểm cực trị? A. 4 . B. 5 . C. 2 . D. 3 . Câu 12. Cho hàm số 3 2
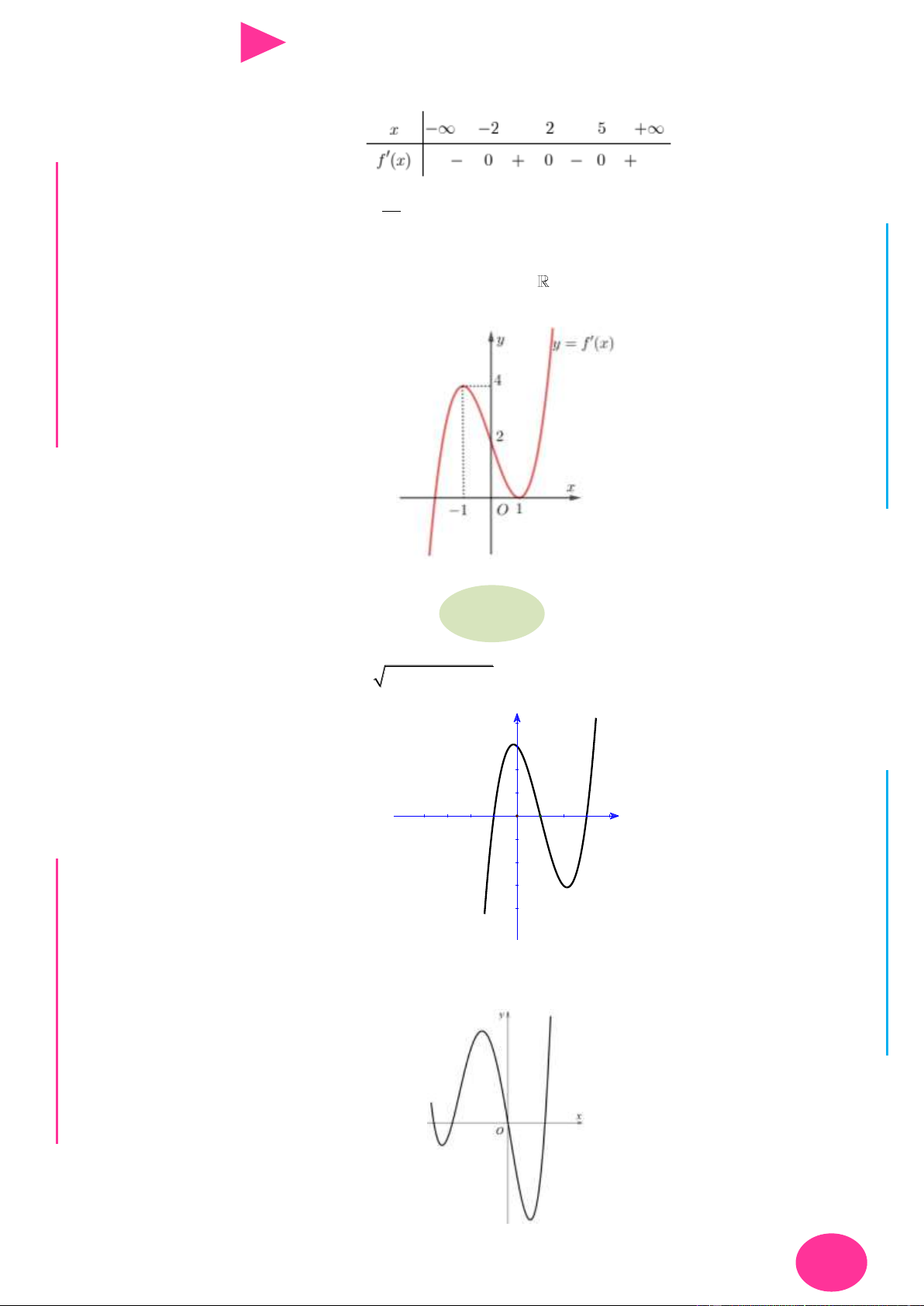
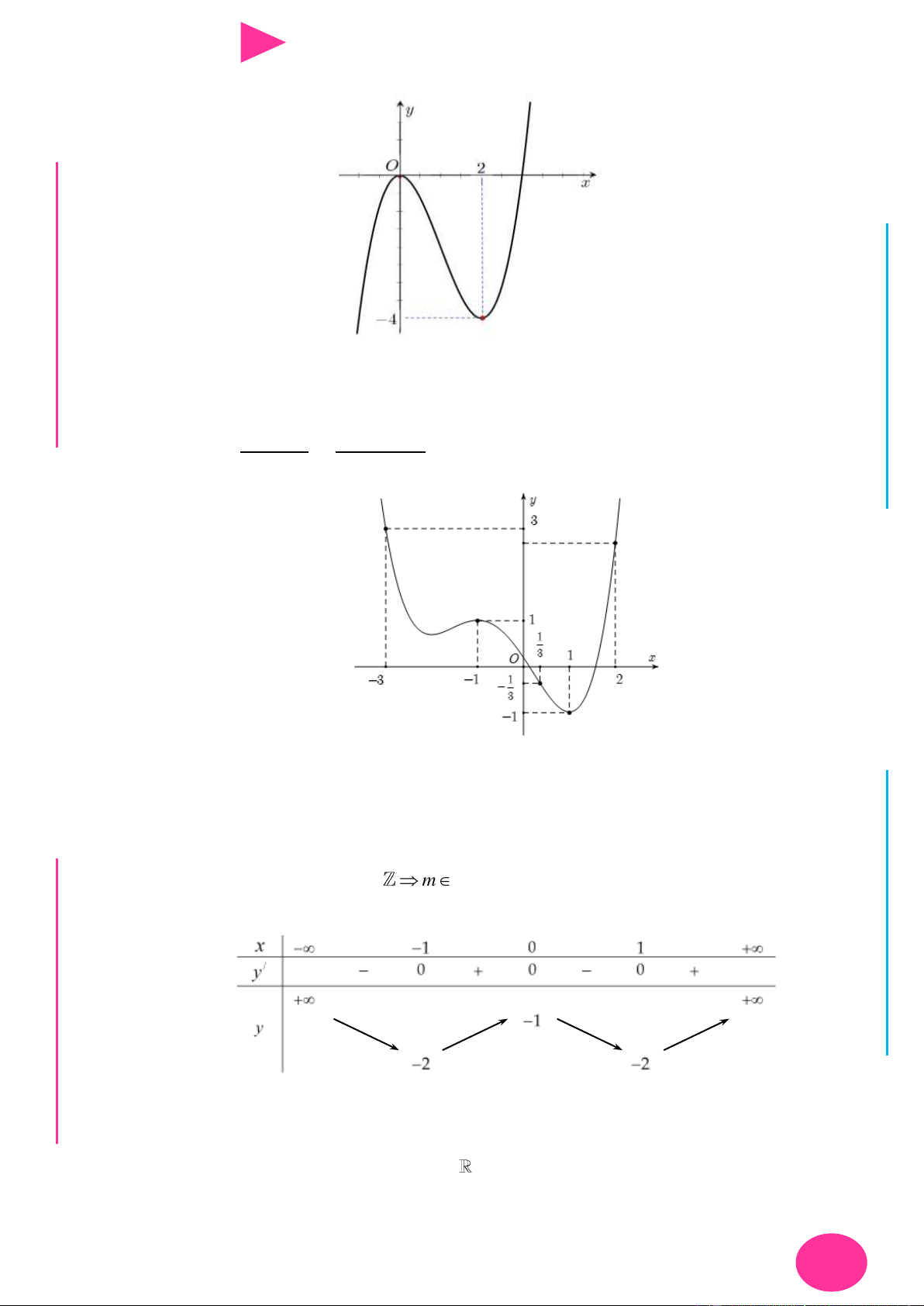
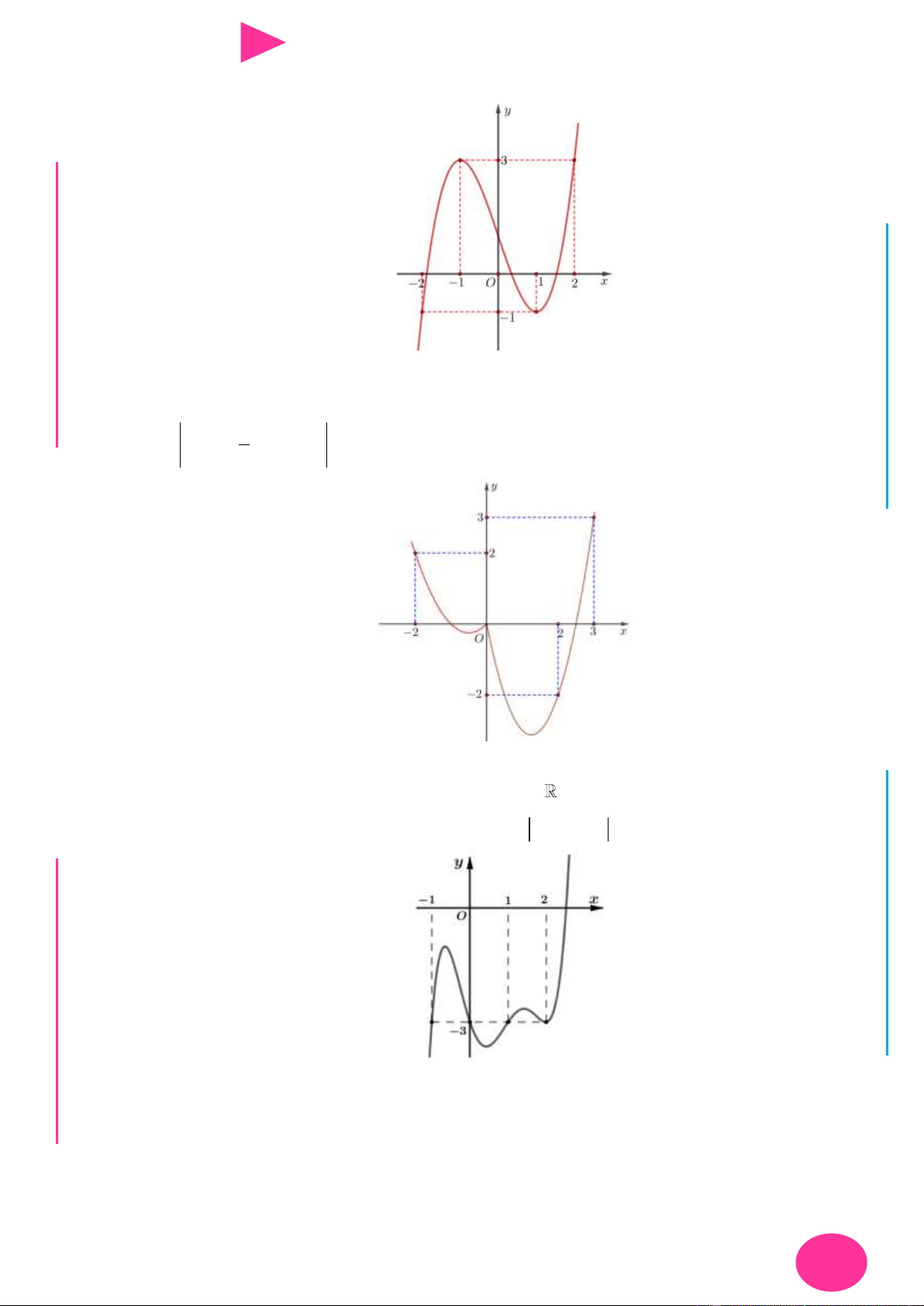
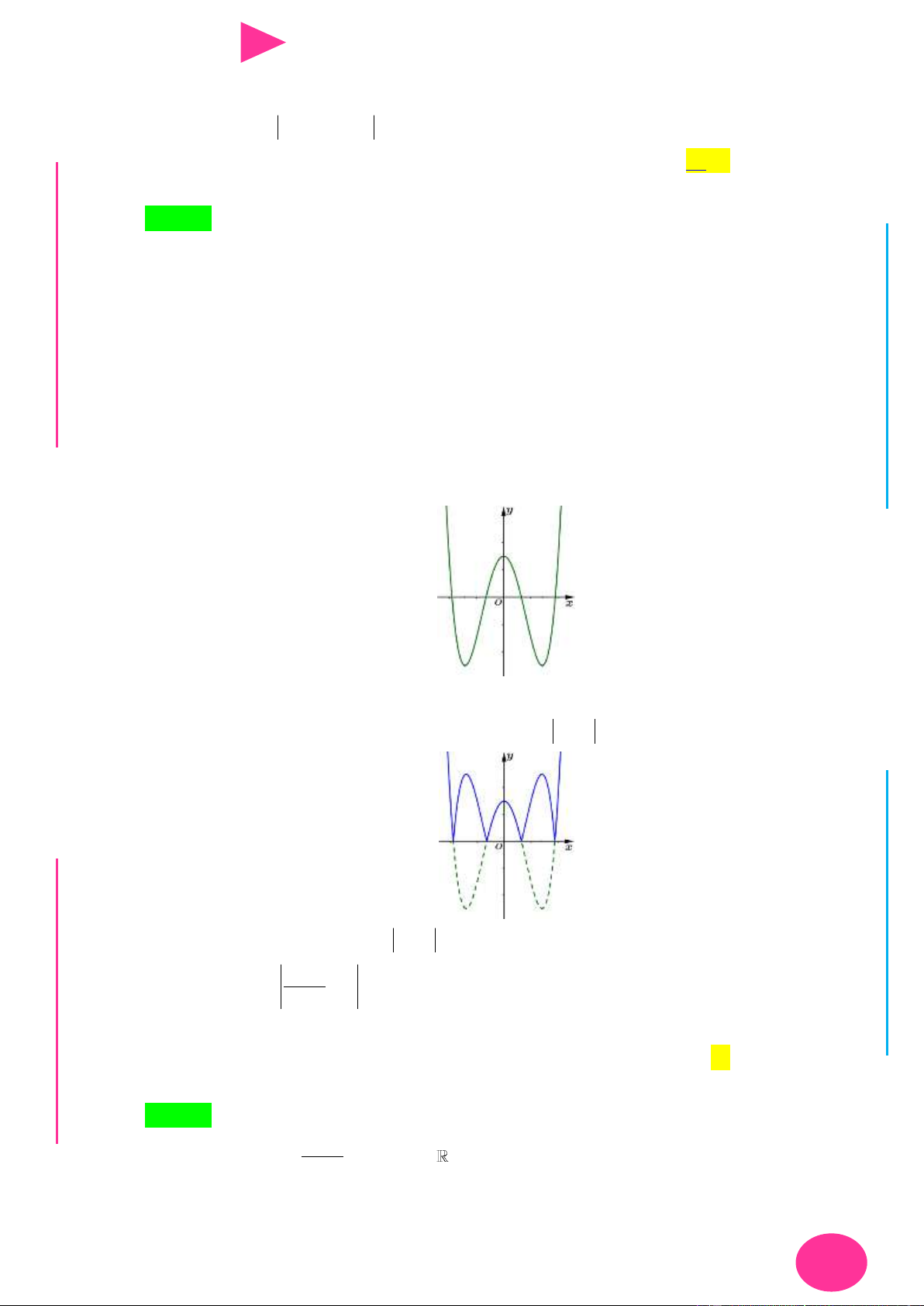
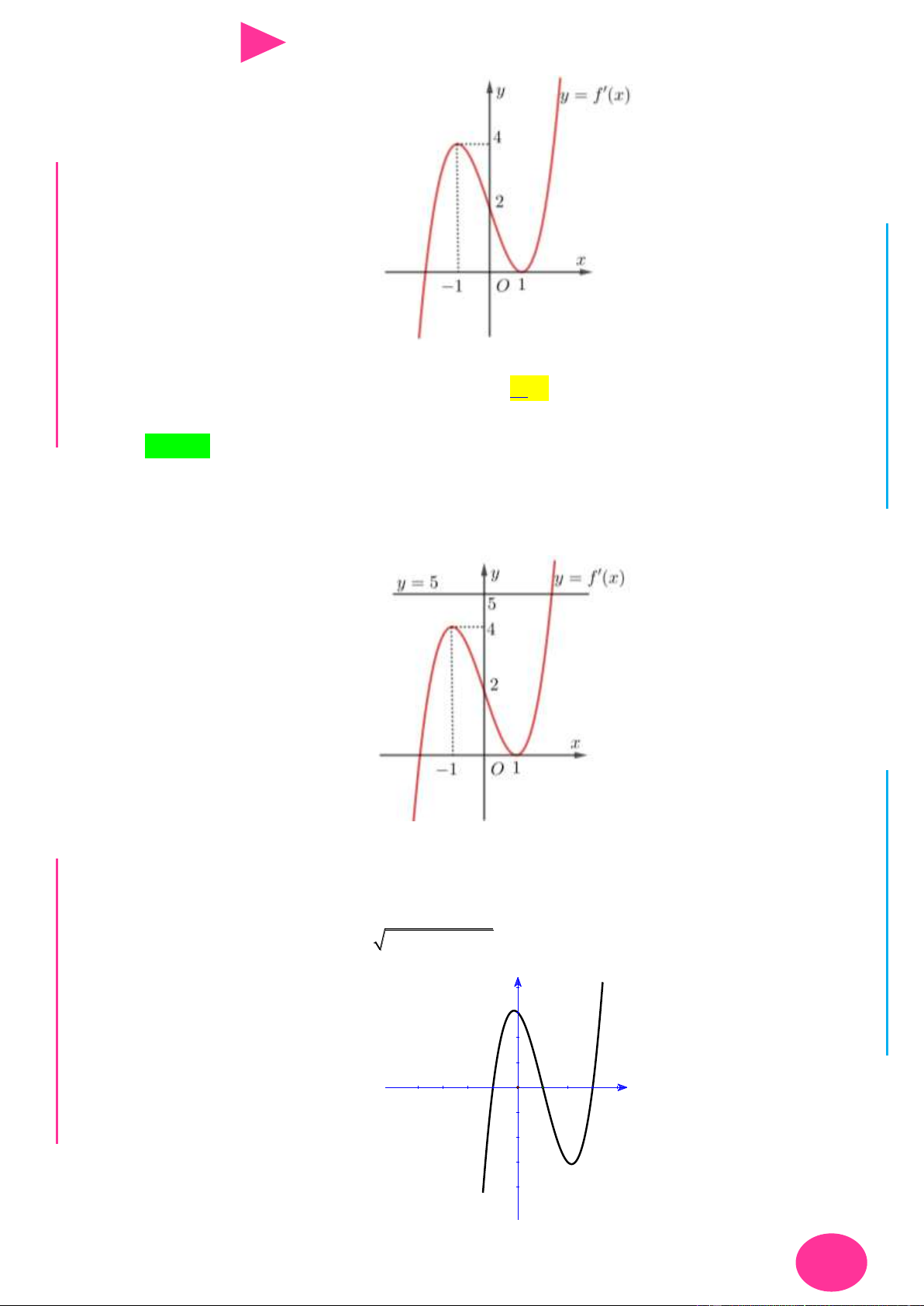
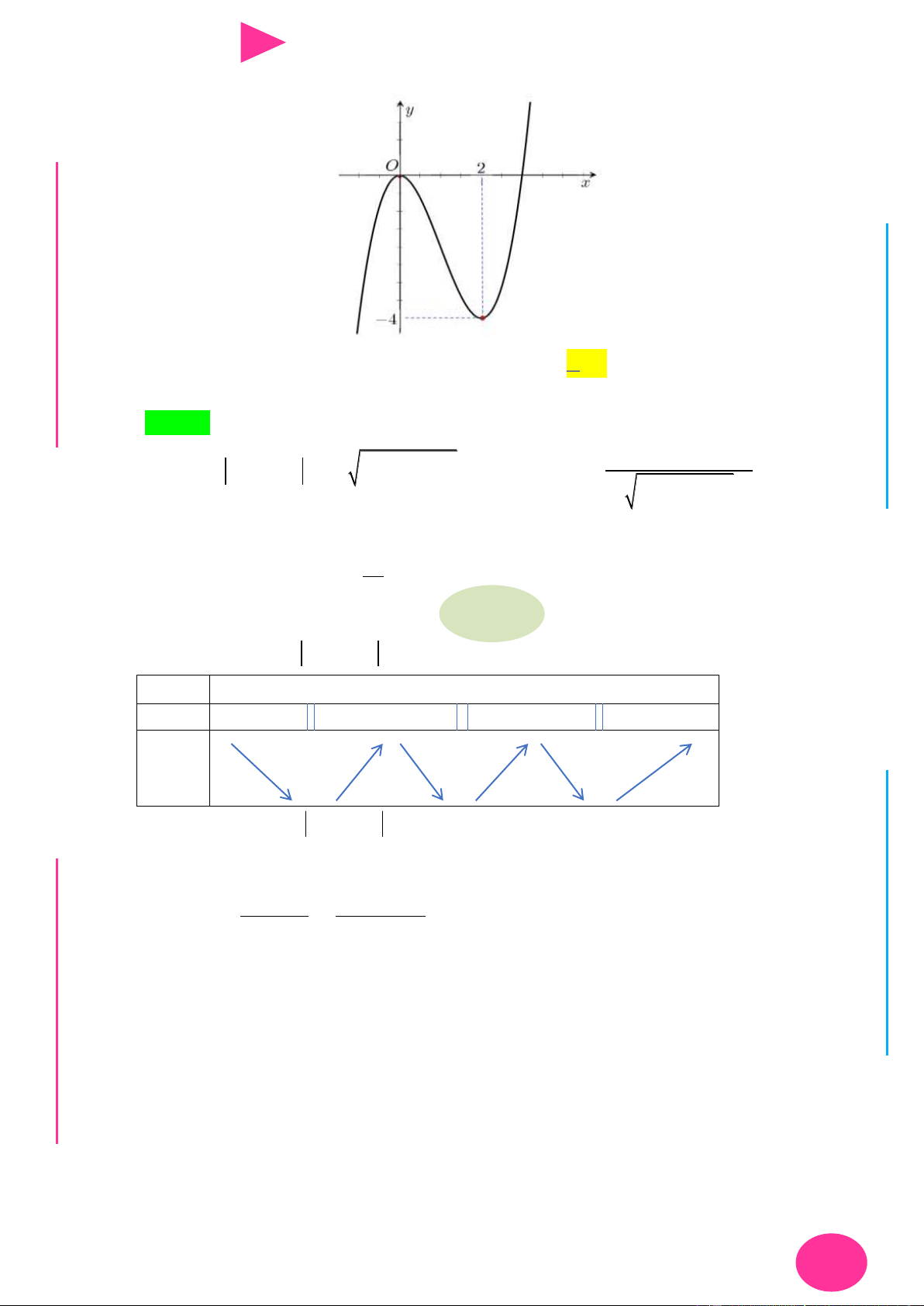
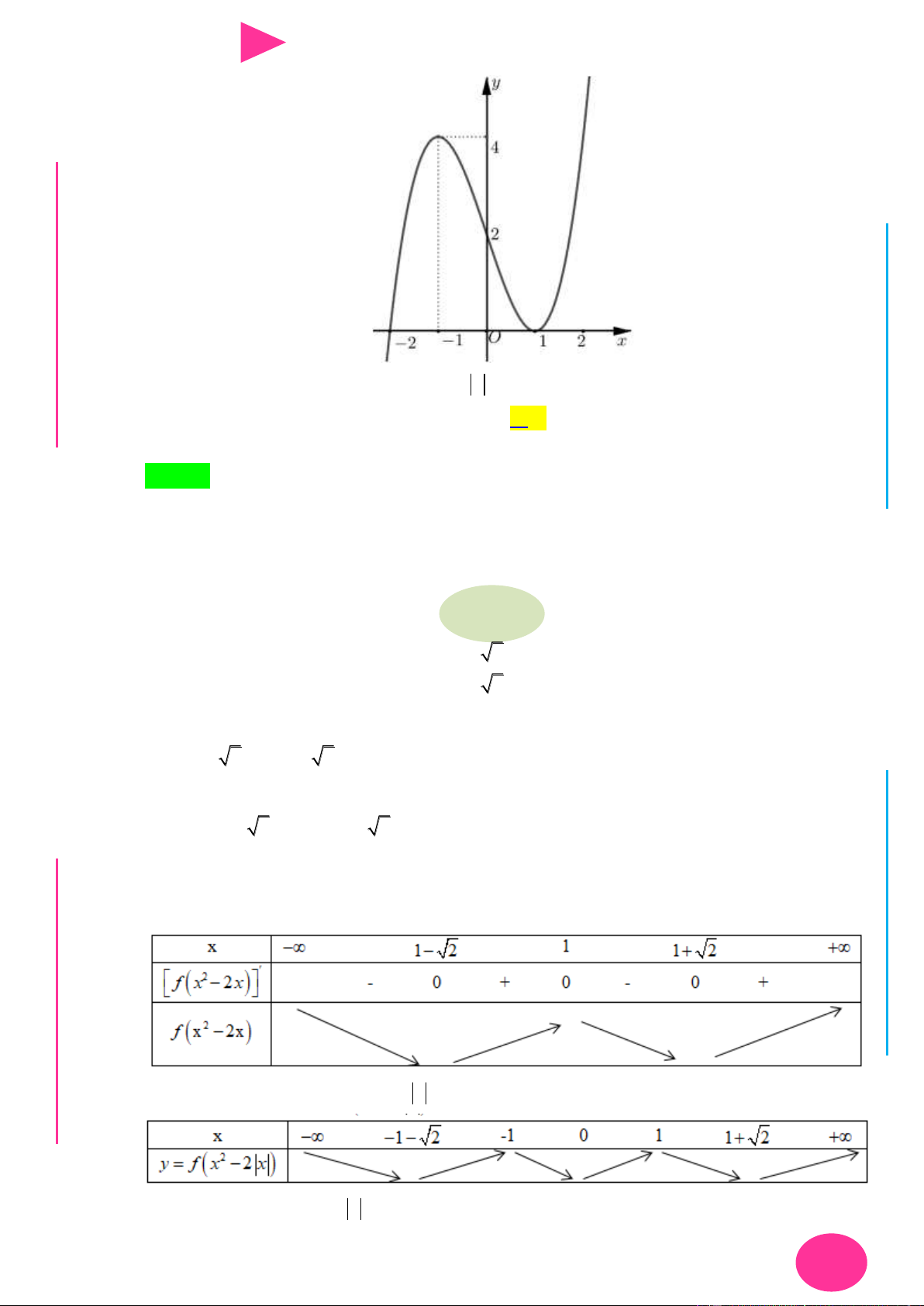
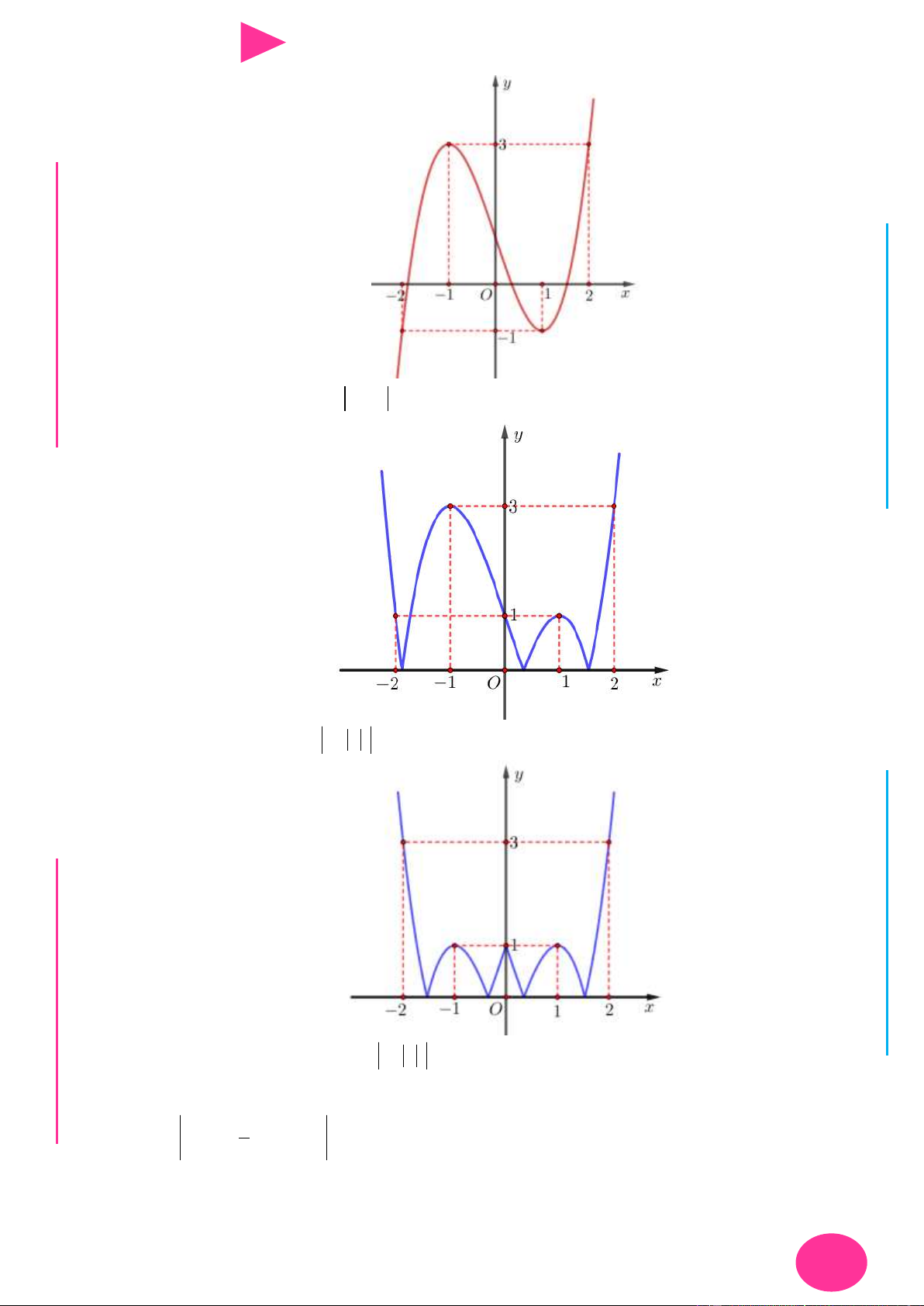
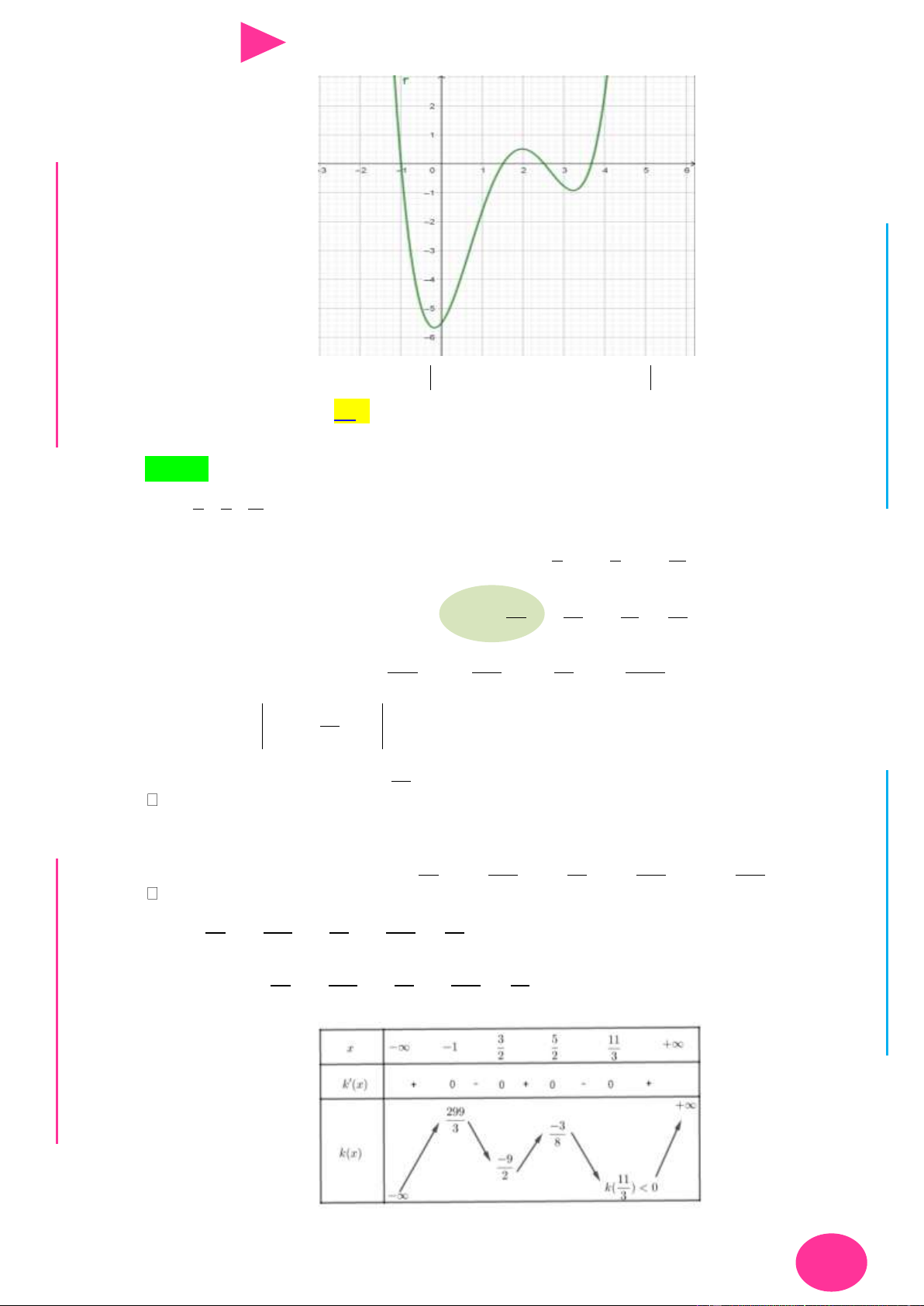
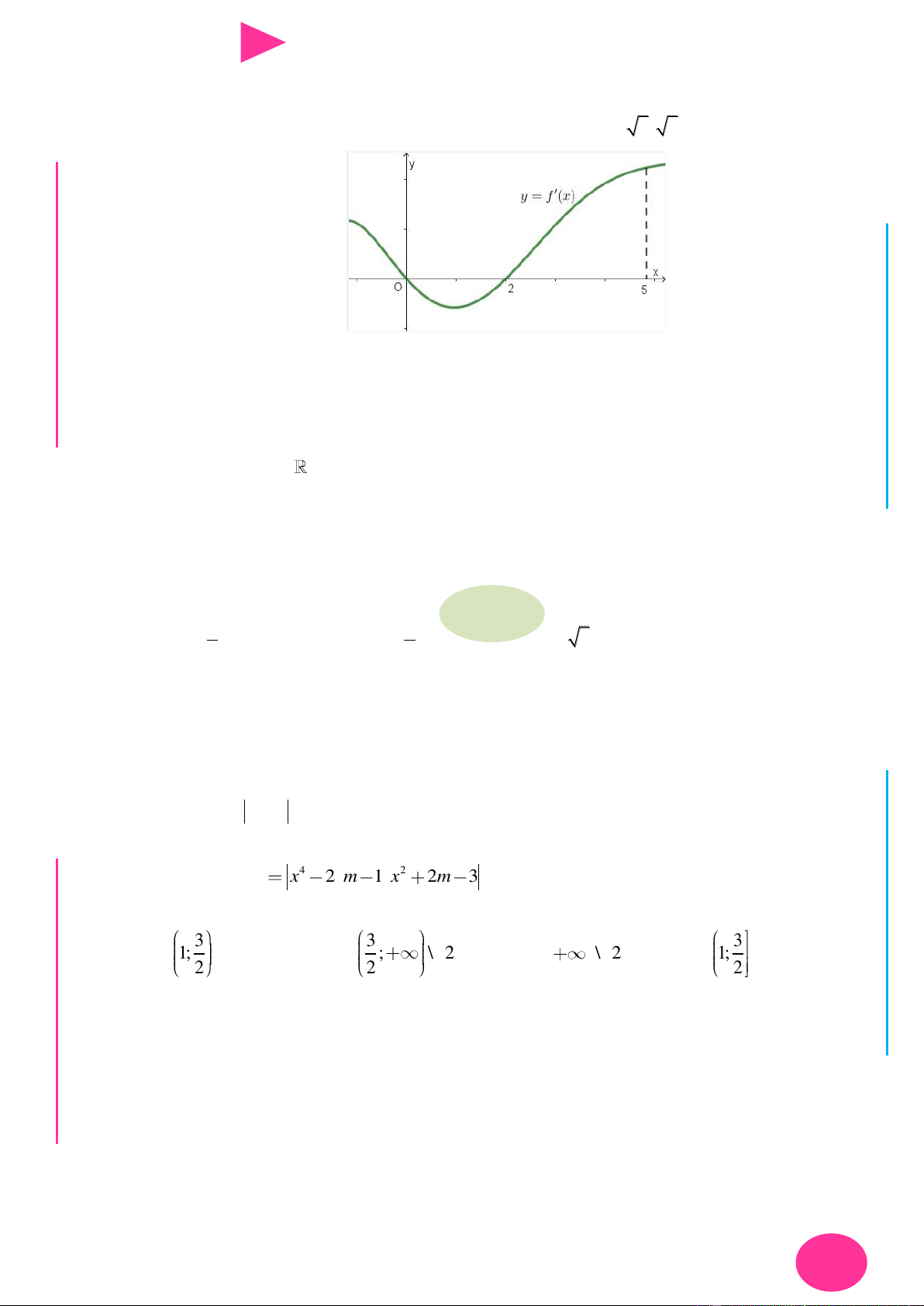
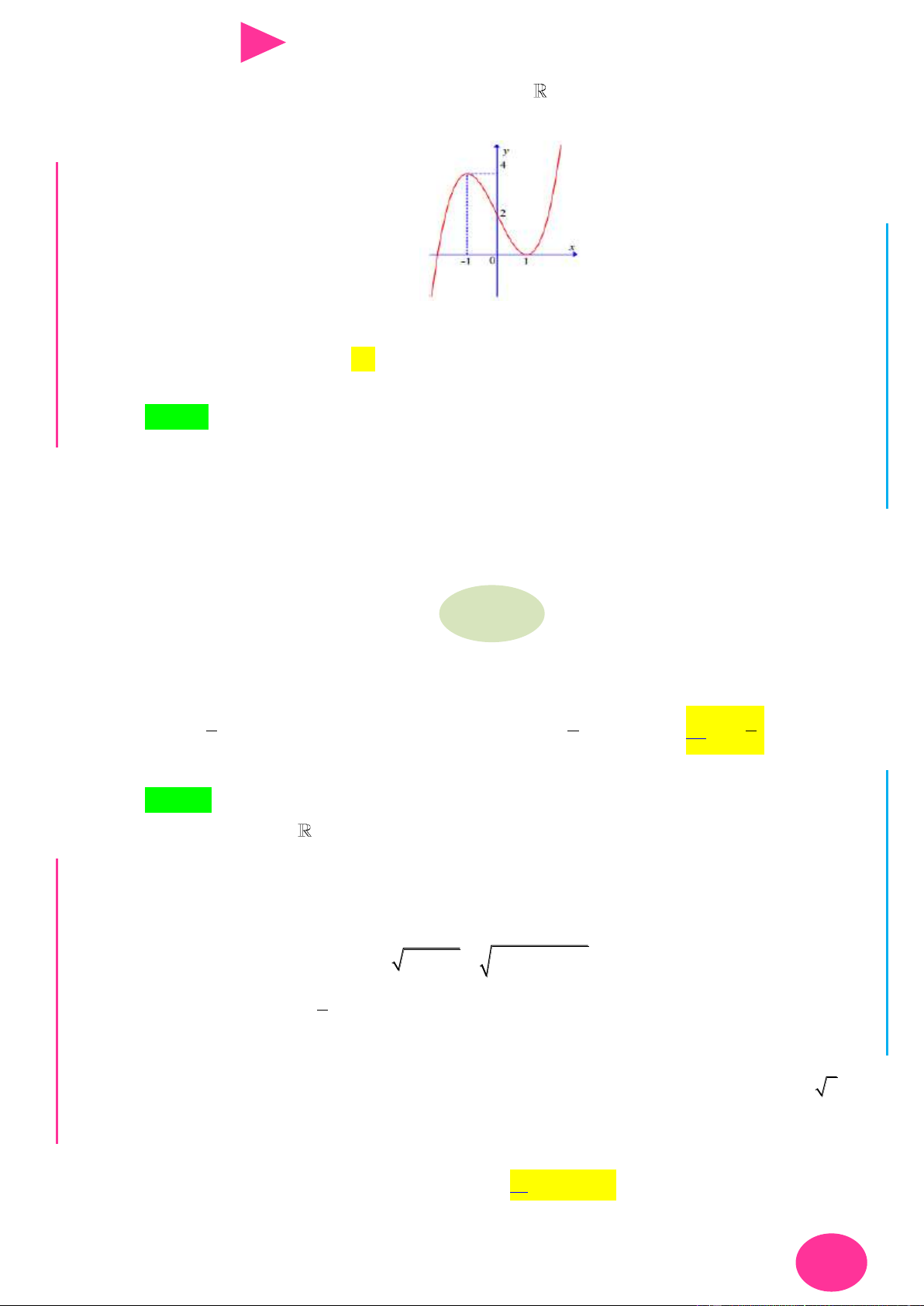
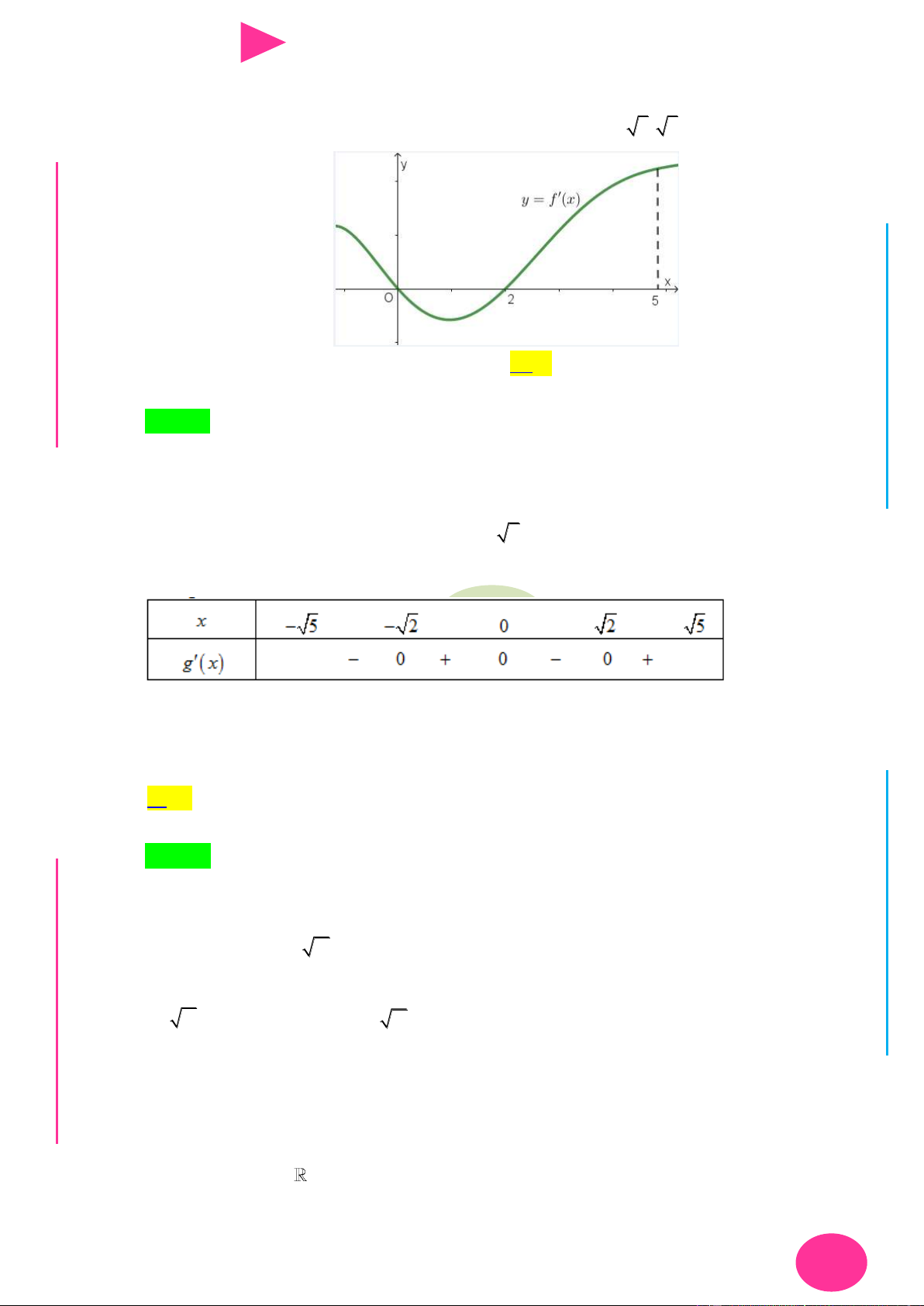
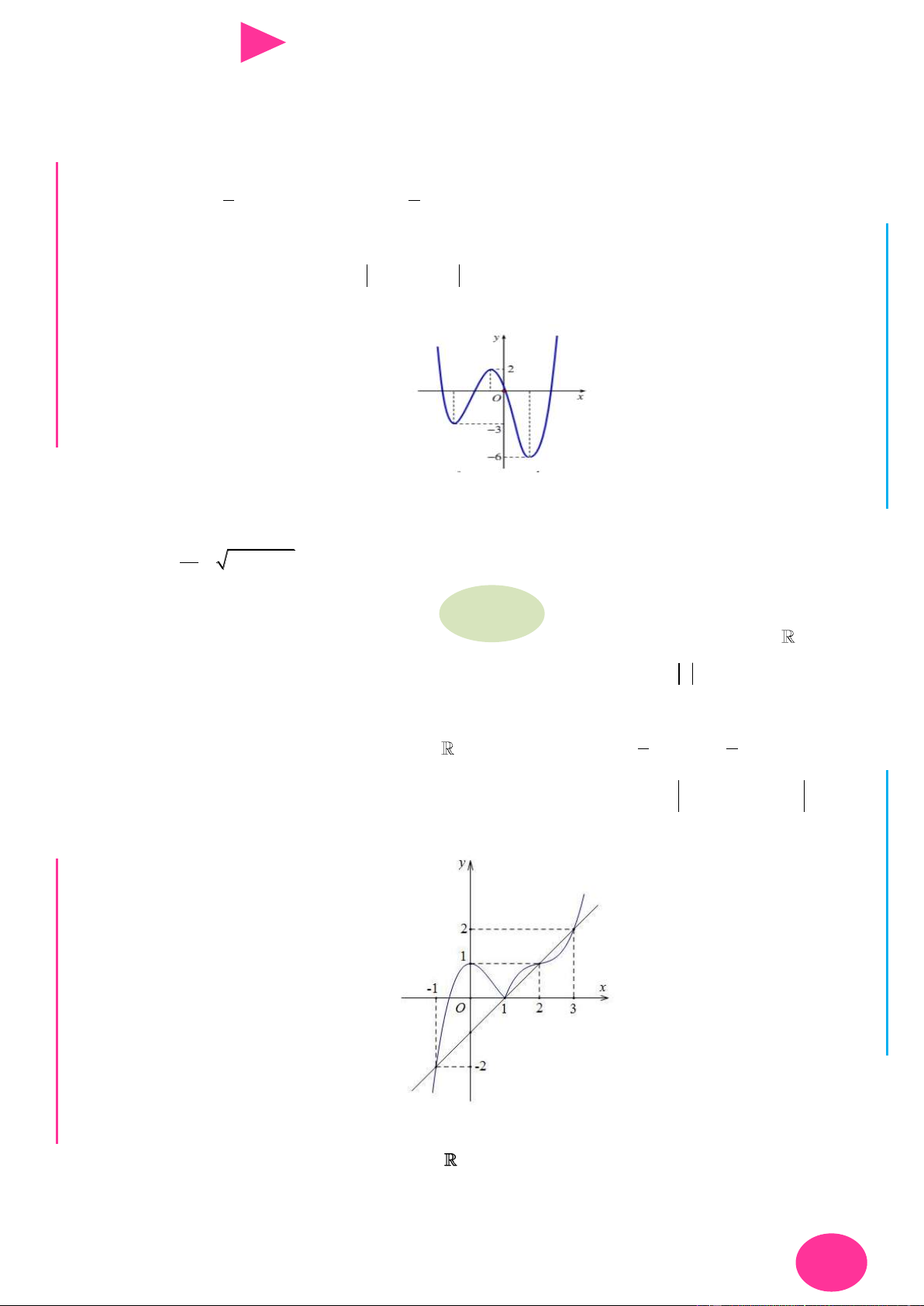
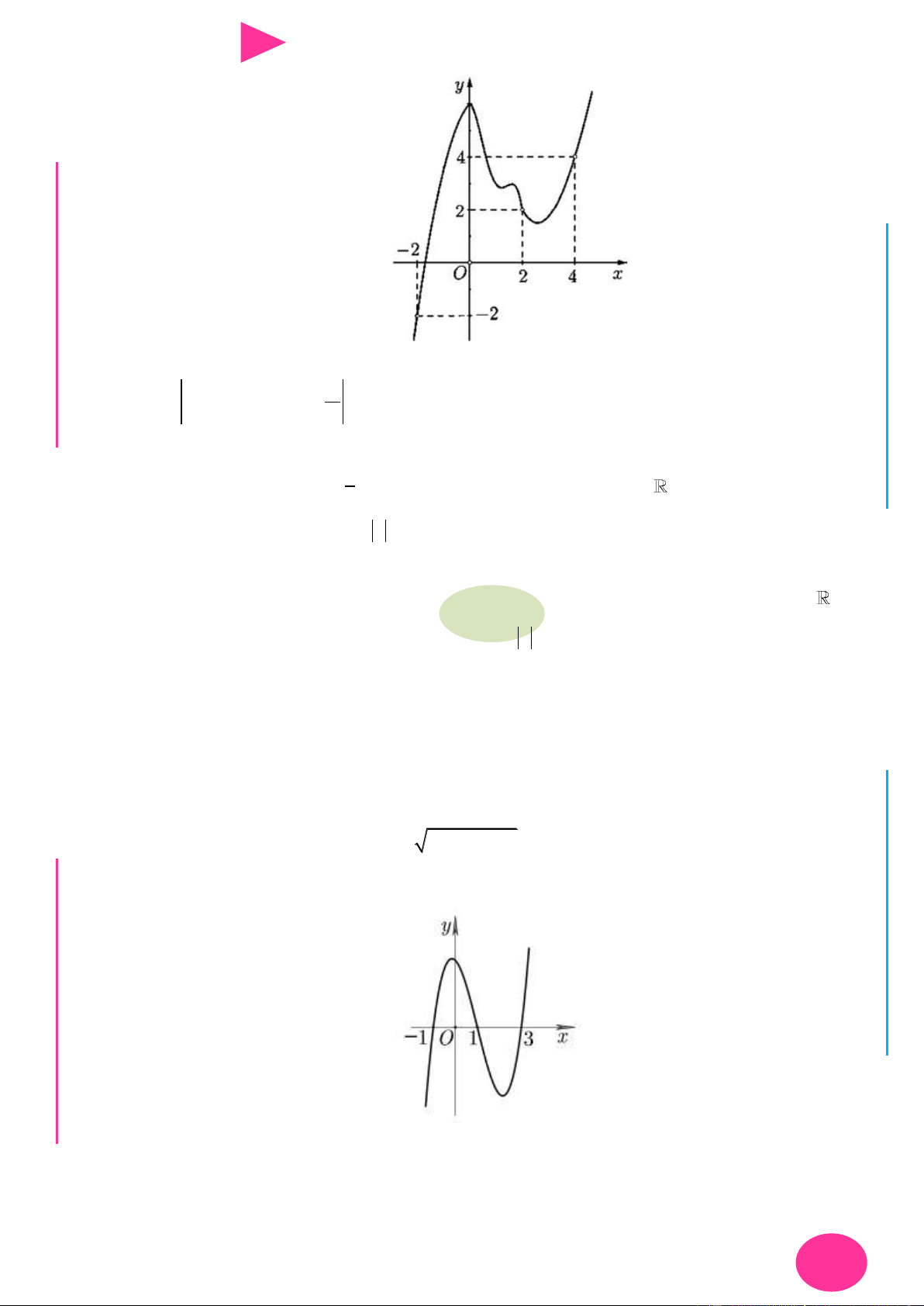
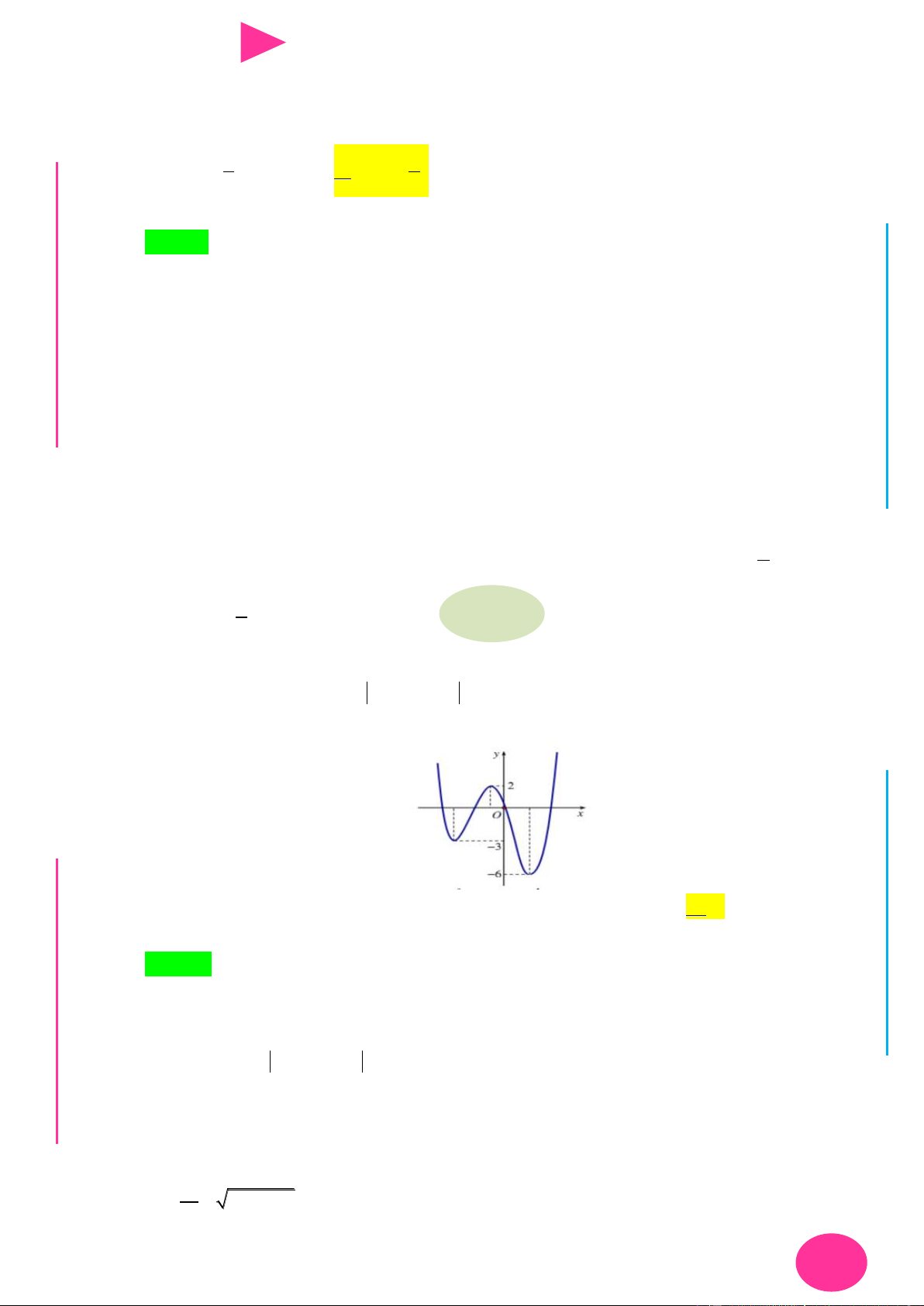
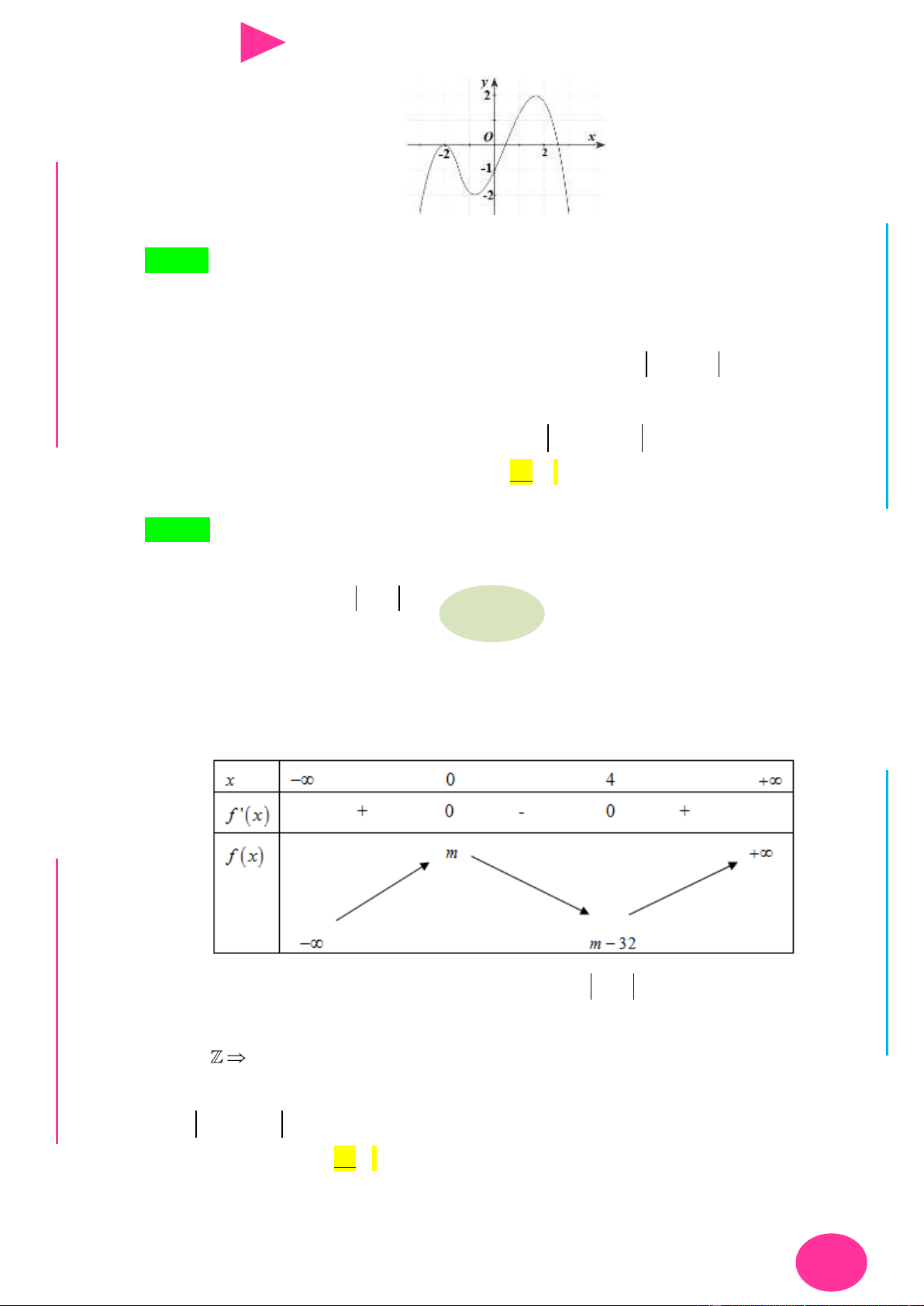
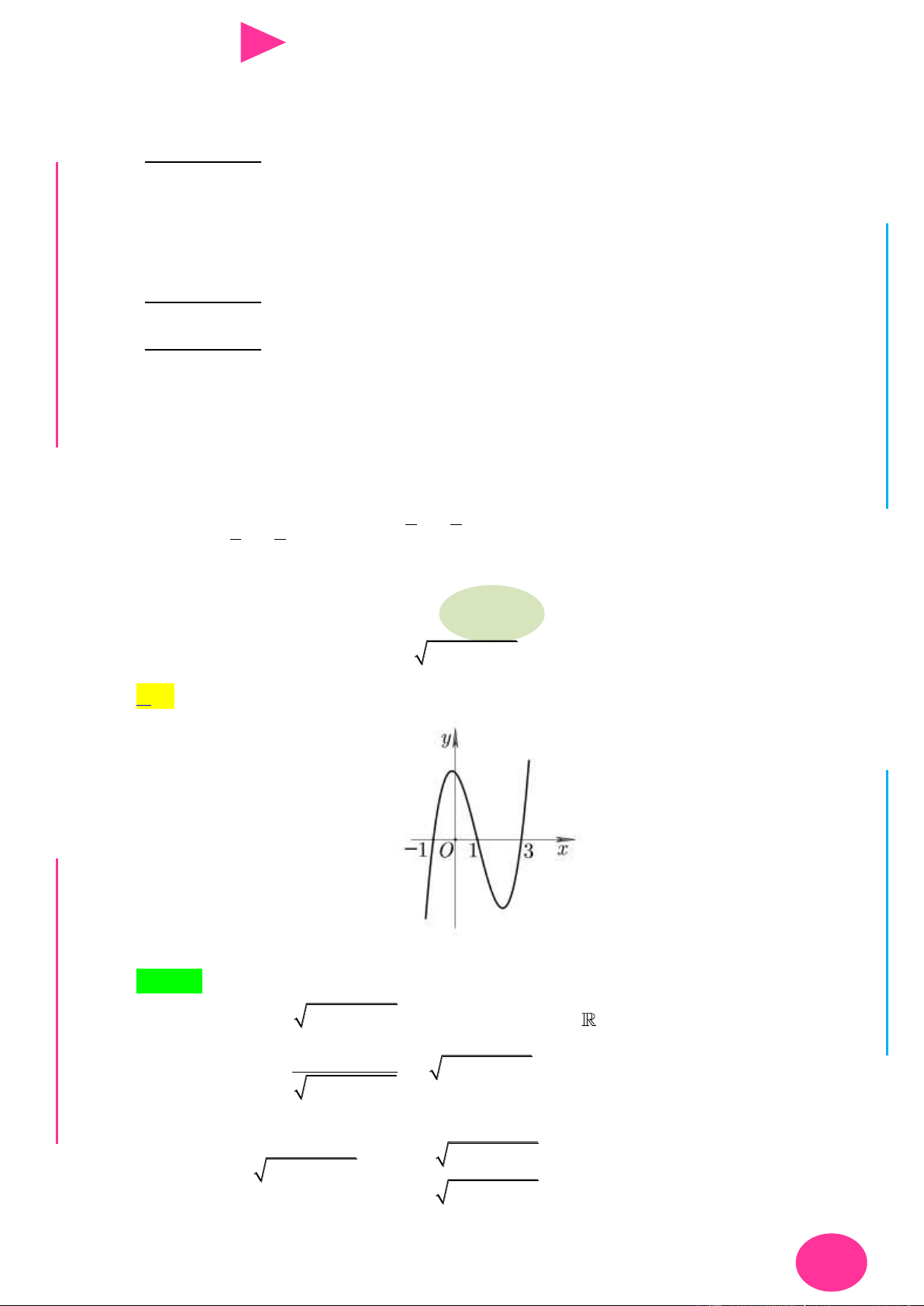
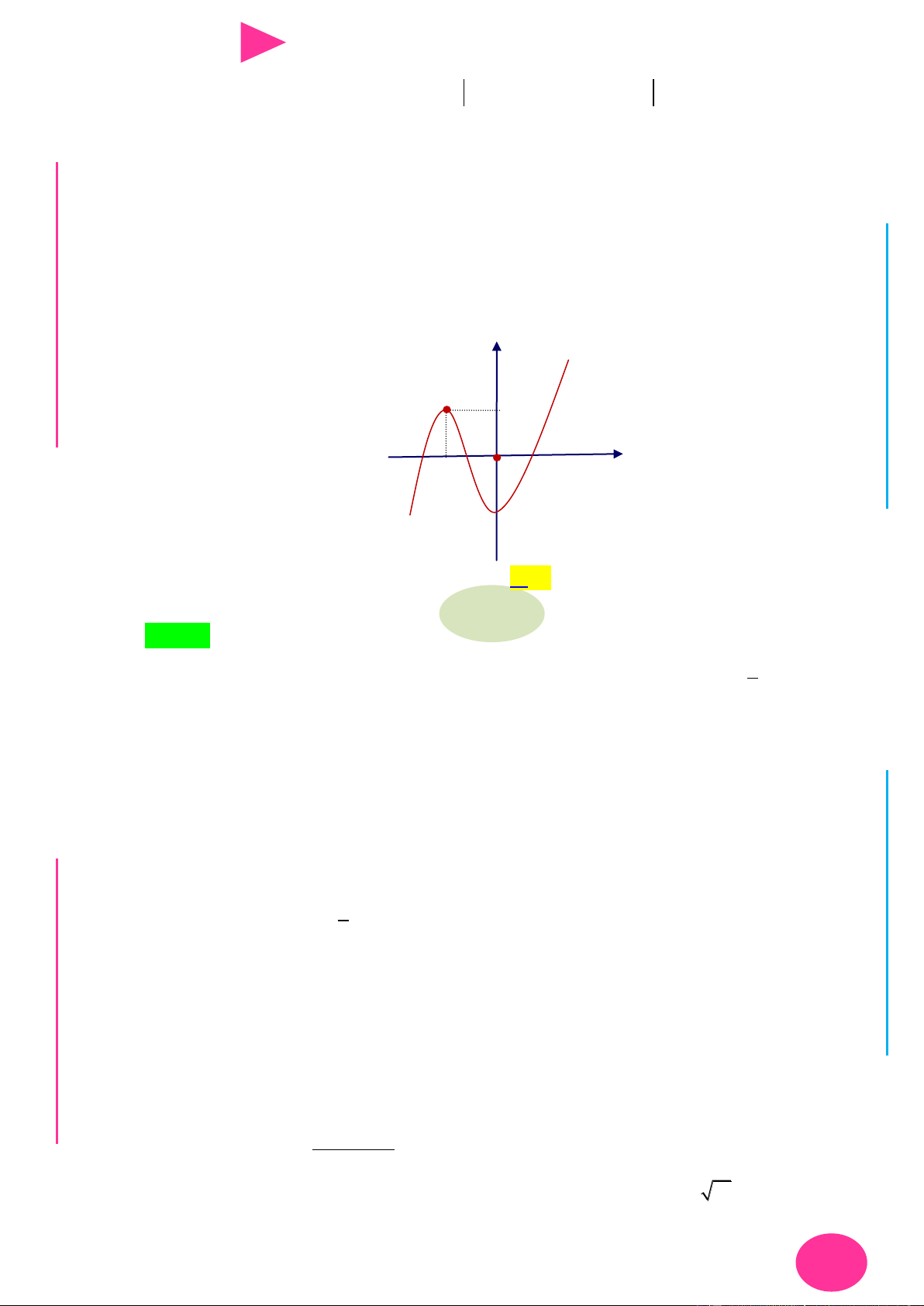
f (x) ax bx cx d có đồ thị nhƣ hình vẽ bên. Số điểm cực trị của hàm số 2 y f ( 2
x 4x) là. A. 3 . B. 4 . C. 2 . D. 5 . 1 1
Câu 13. Biết rằng đồ thị hàm số 2 y x 3x
có ba điểm cực trị thuộc một đƣờng tròn C . 2 x
Bán kính của C gần đúng với giá trị nào dƣới đây? A. 12, 4 . B. 6, 4 . C. 4, 4 . D. 27 .
Câu 14. Cho hàm số y f x có đạo hàm f x x 2 3 x 1 2x, x . Hỏi hàm số
y f x 2
x 1 có bao nhiêu điểm cực tiểu. I Ơ A. 2. B. 3. C. 4. D. 1. Câu 15. Cho hàm số 4 2
f x ax bx c với a 0 , c 2018 và a b c 2018. Số điểm cực trị M D Ầ
của hàm số y f x là Đ 2018 NHỊ A. 1. B. 3 . C. 5 . D. 7 . Đ x G THPT N.C.Đ
Câu 16. Hàm số f x
m (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực 2 N x 1 NG CÔ trị? Ờ N A. 2 . B. 3 . C. 5 . D. 4 . YỄ
TRƢ Câu 17. Cho hàm số y f x có đạo hàm f x 2 x
1 x 4 với mọi x . Hàm số GU N N
g x f 3 x có bao nhiêu điểm cực đại? A. 0. B. 1. C. 2. D. 3.
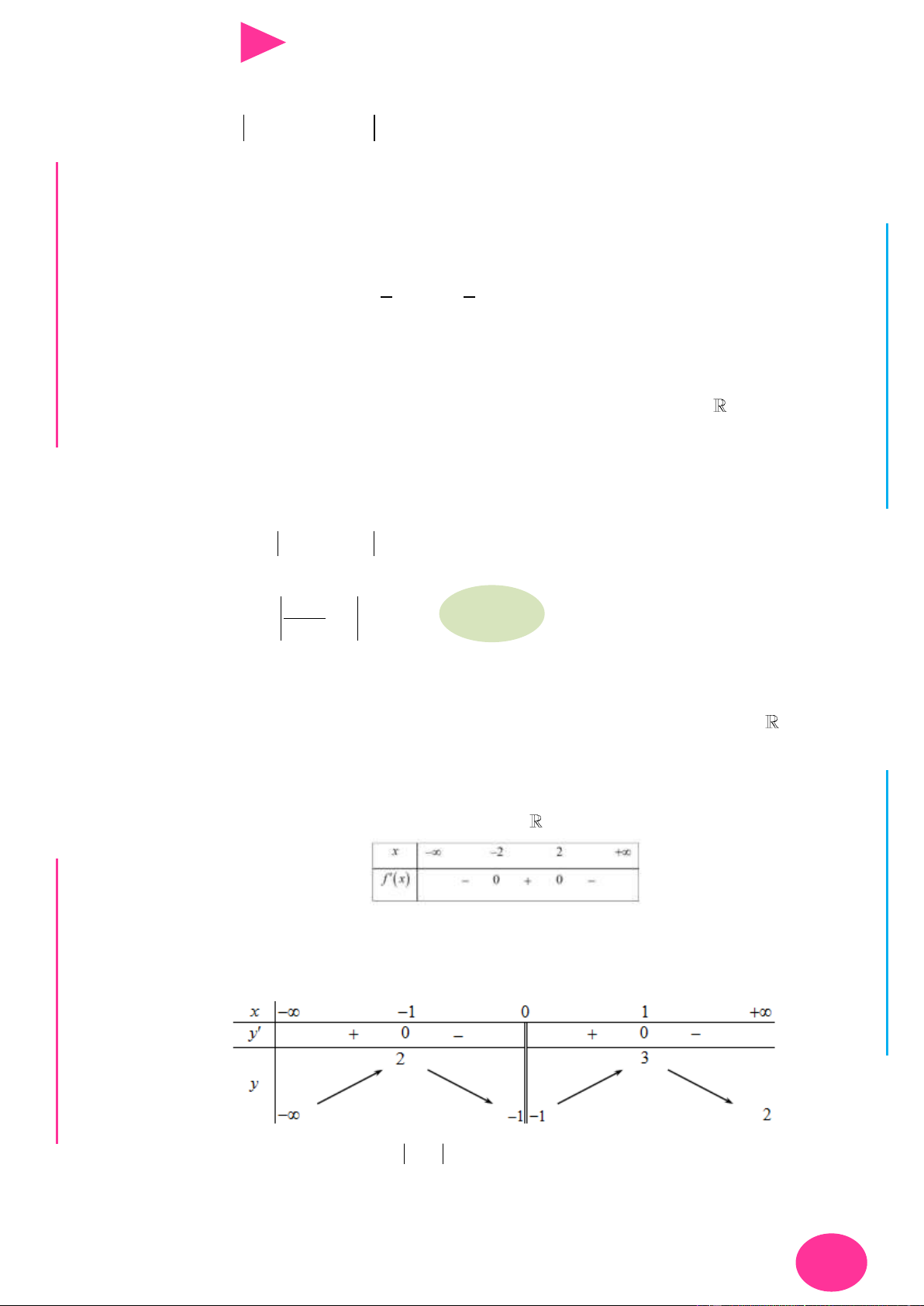
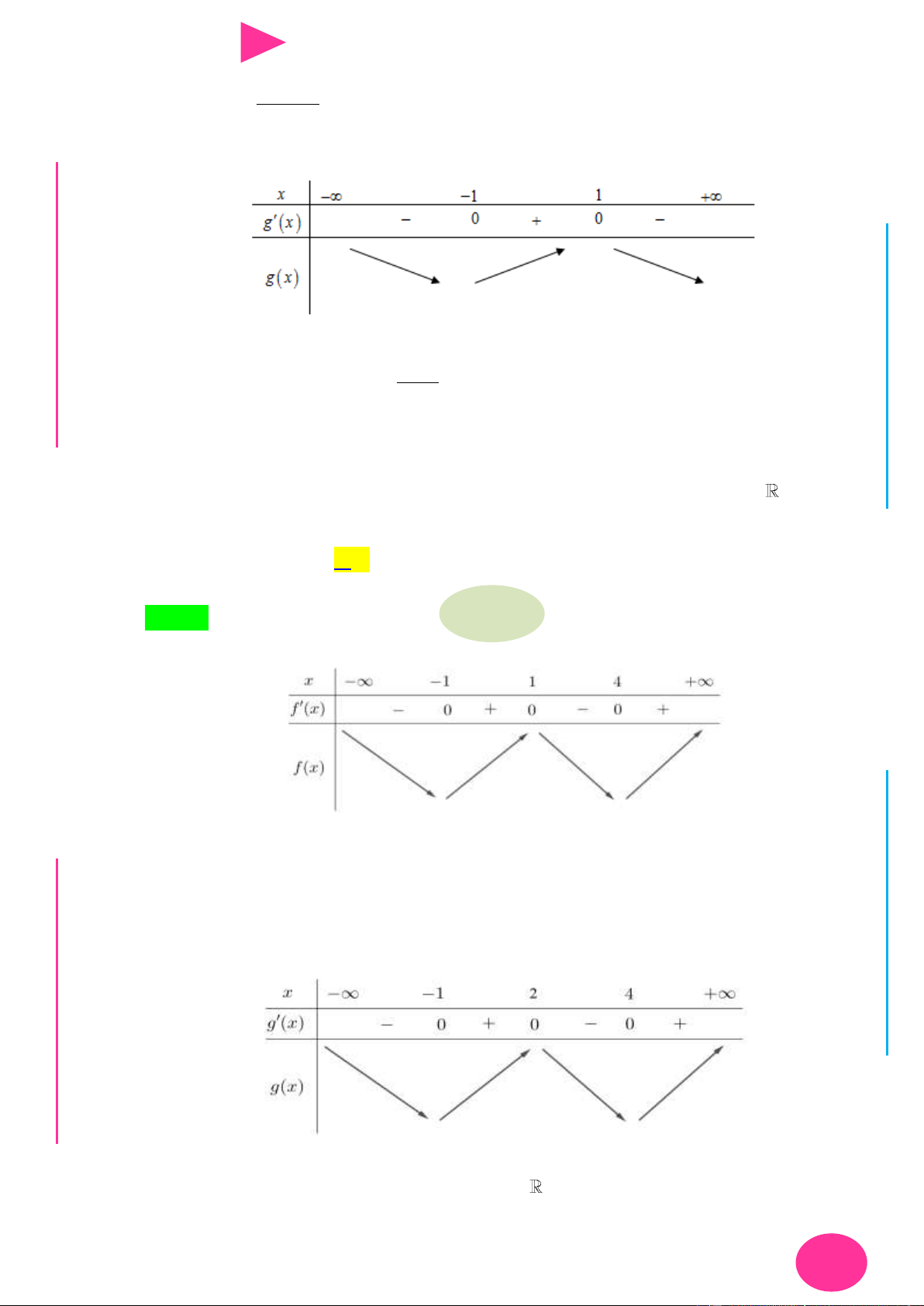
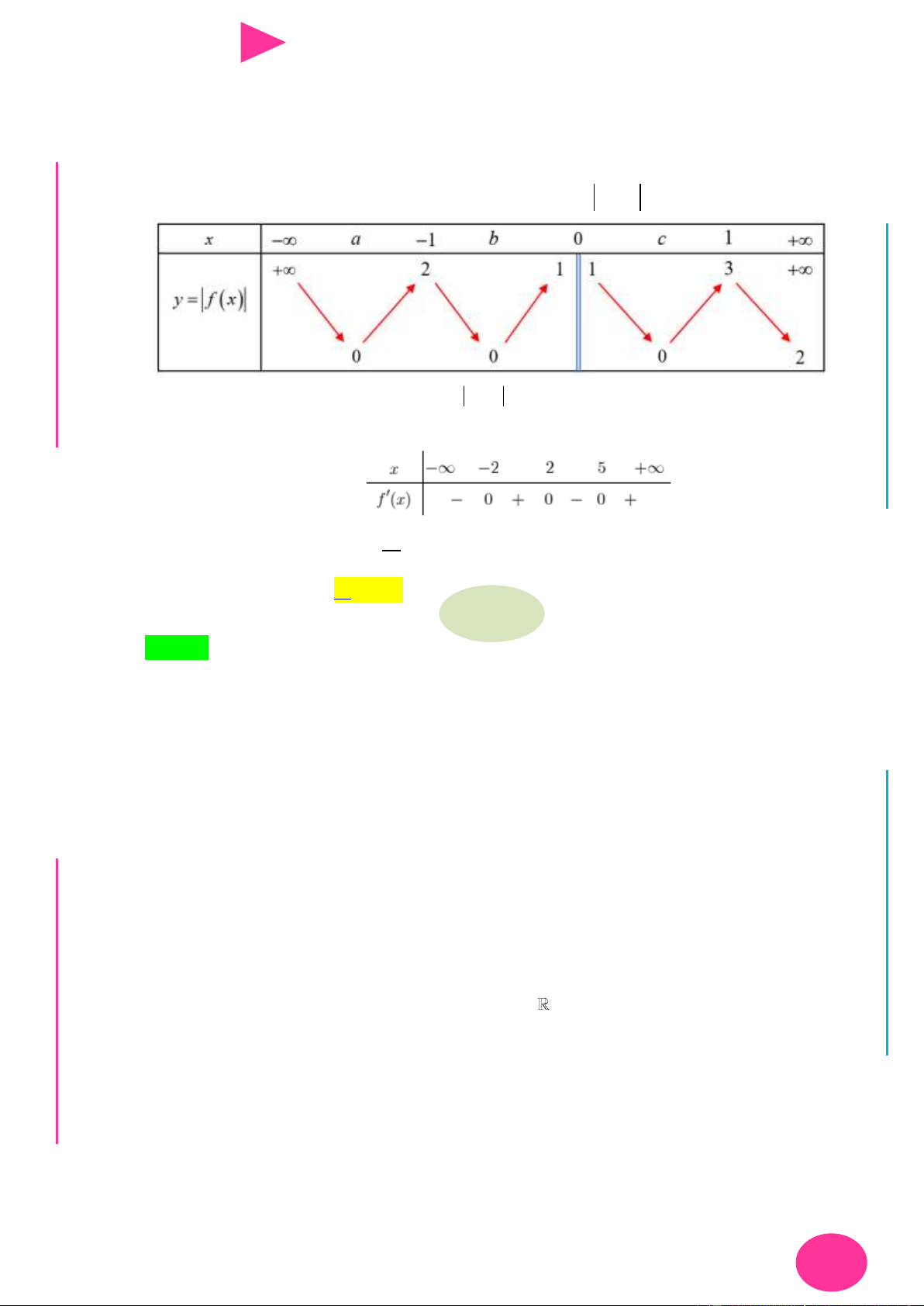
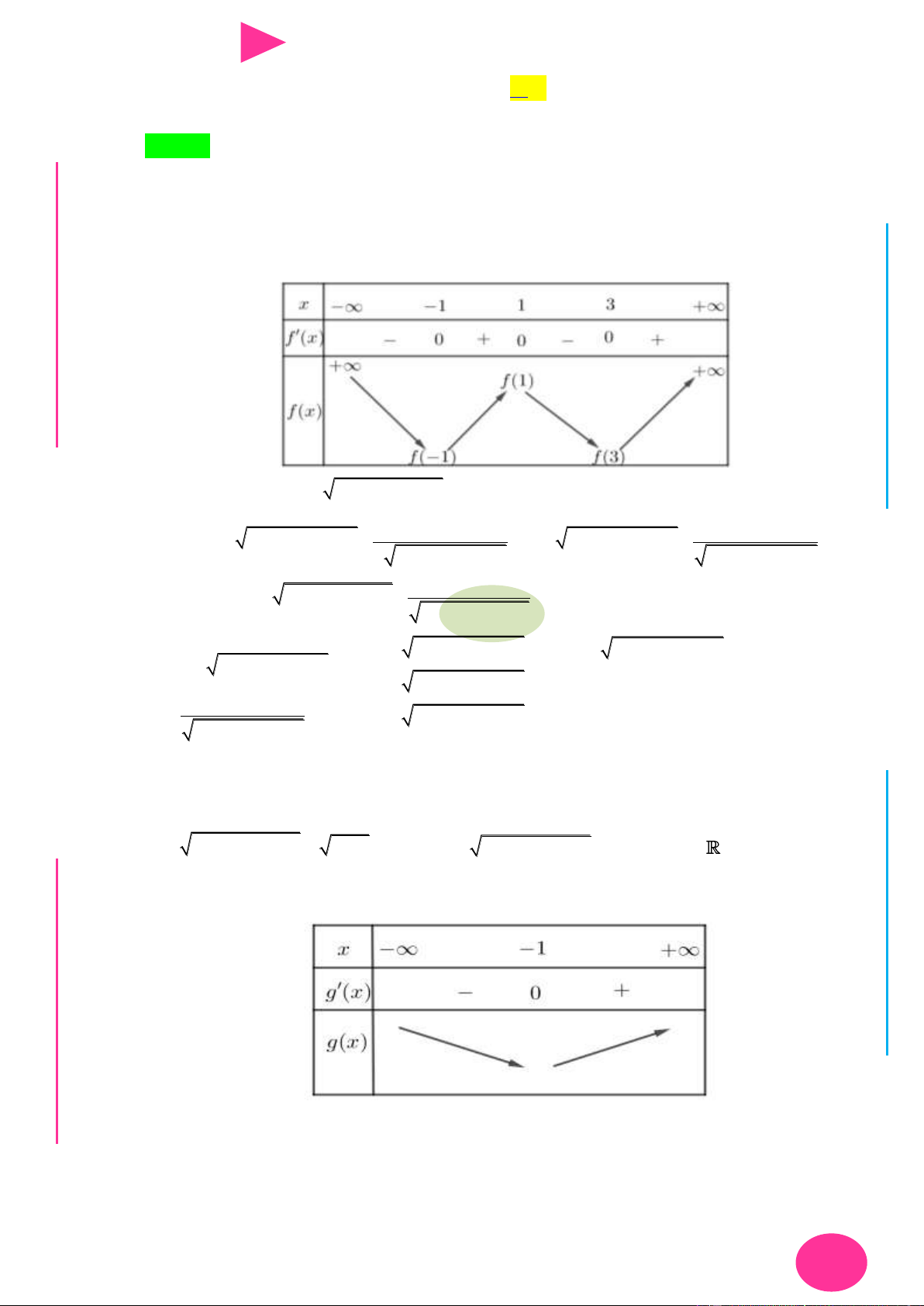
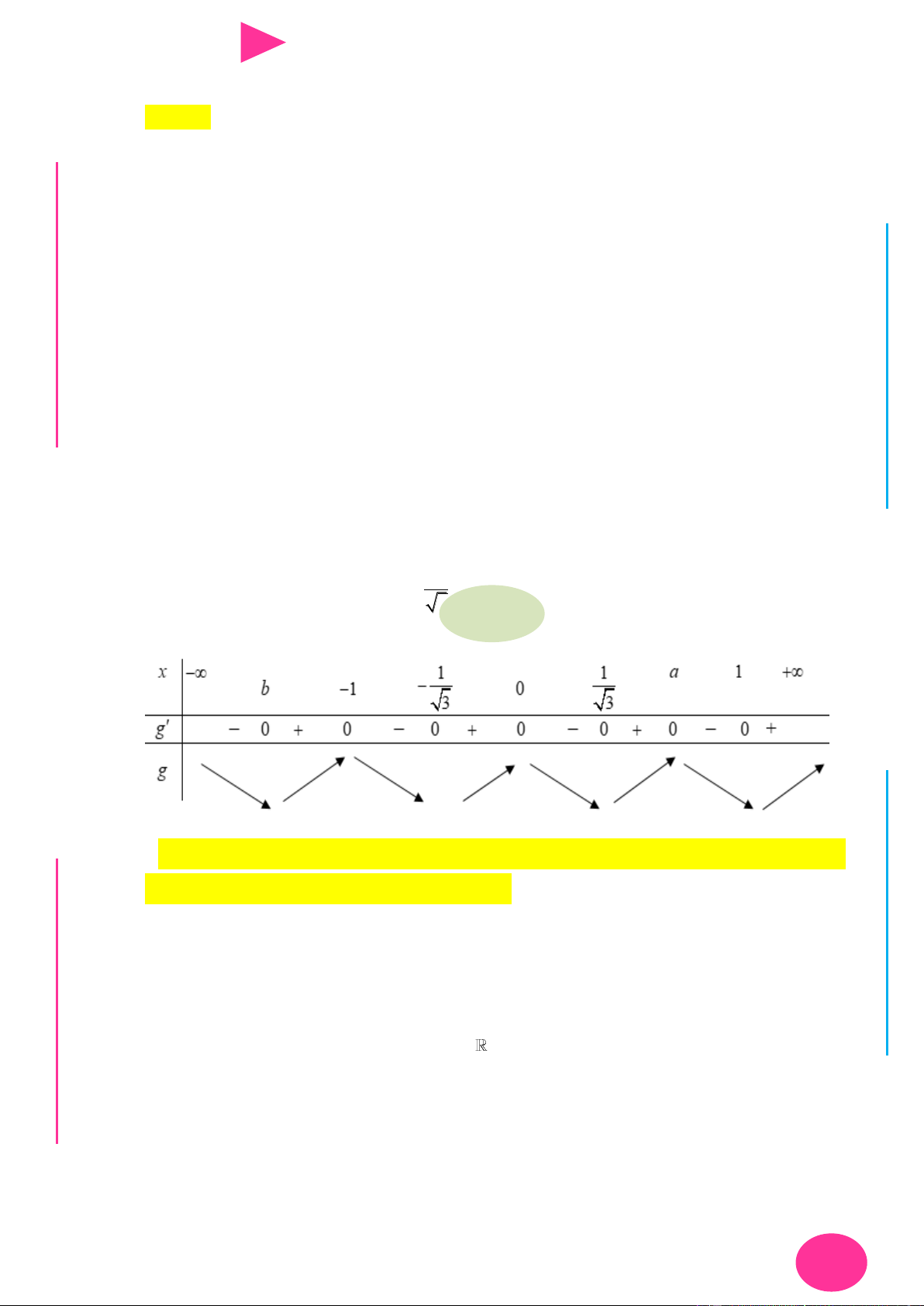
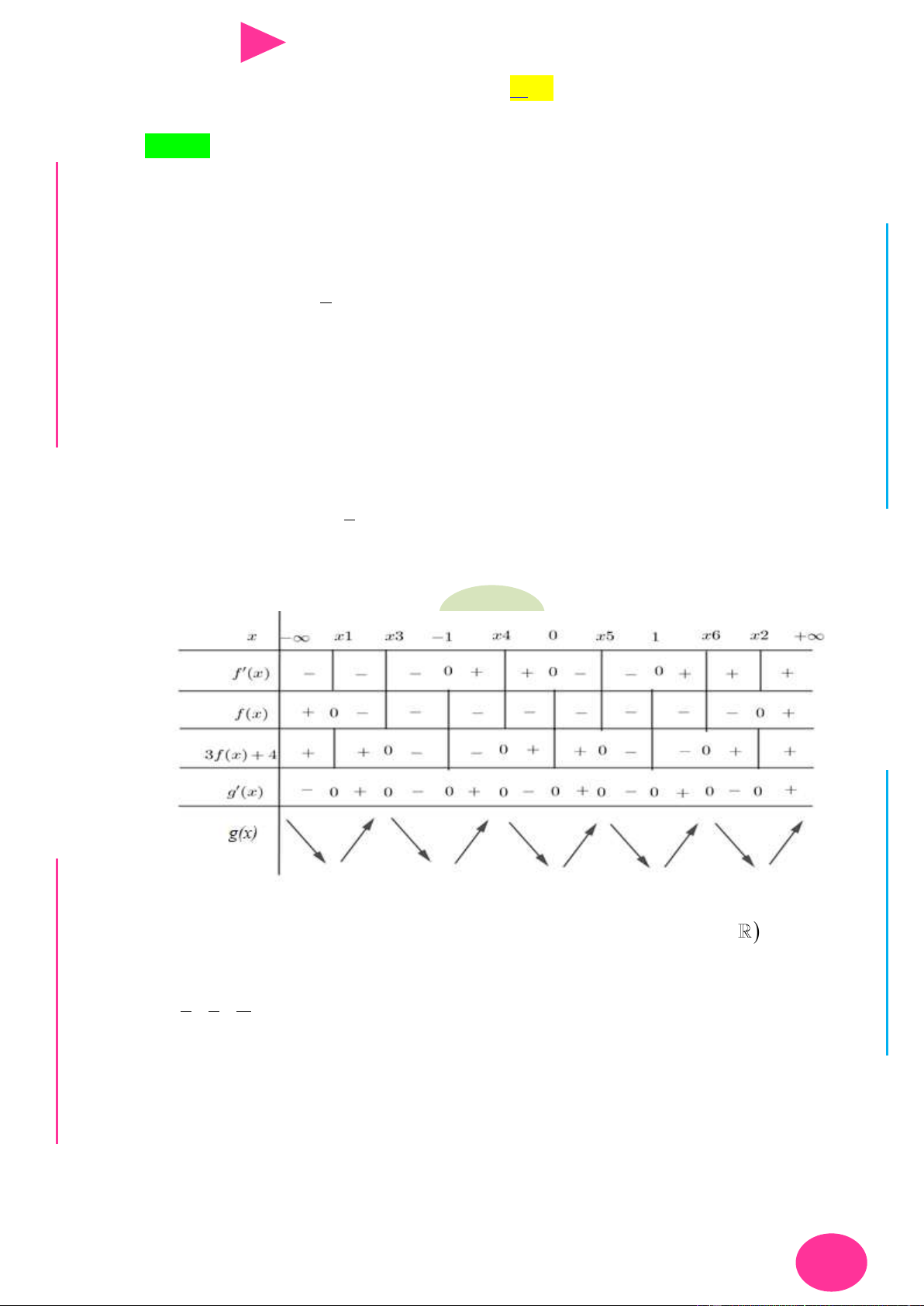
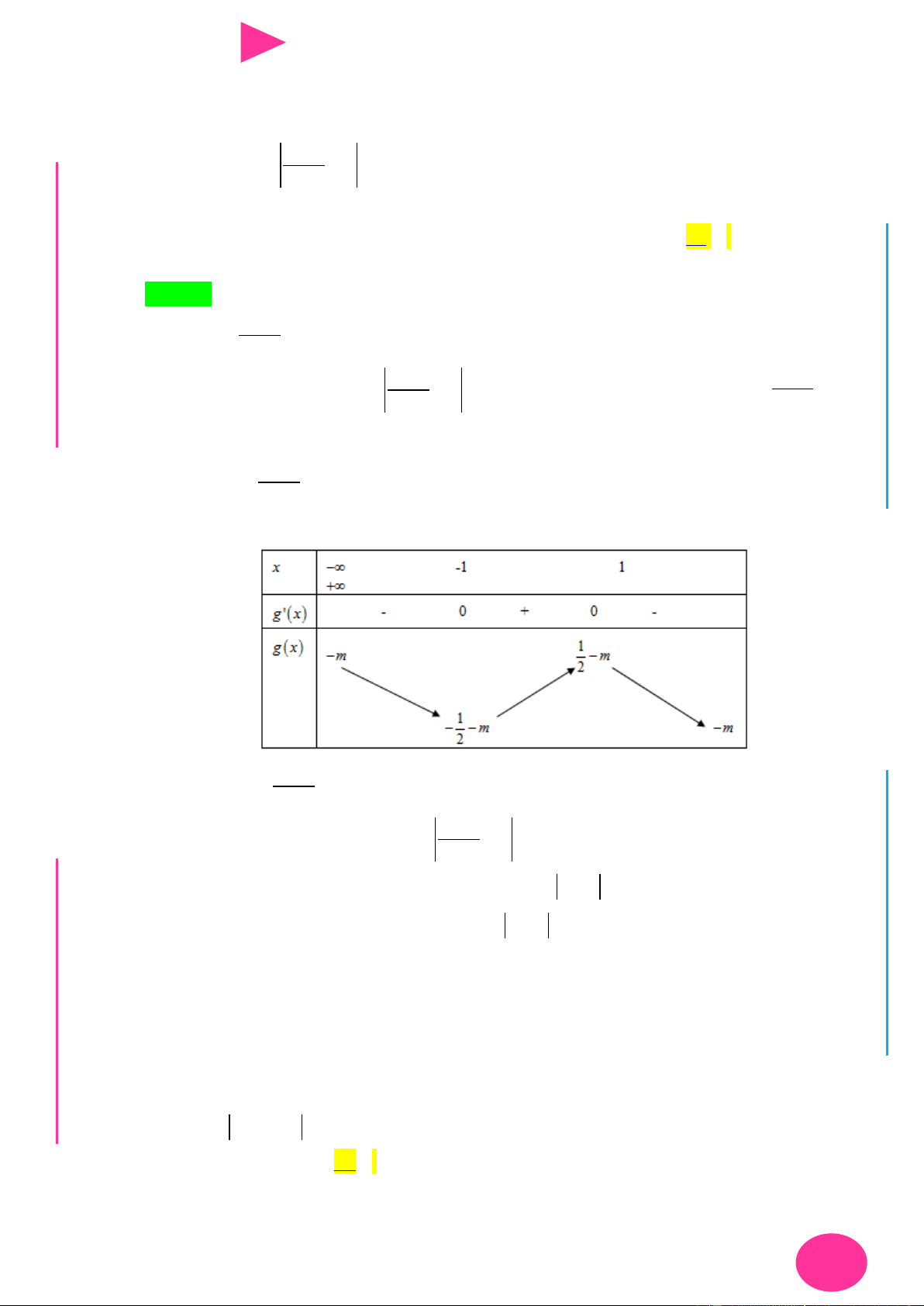
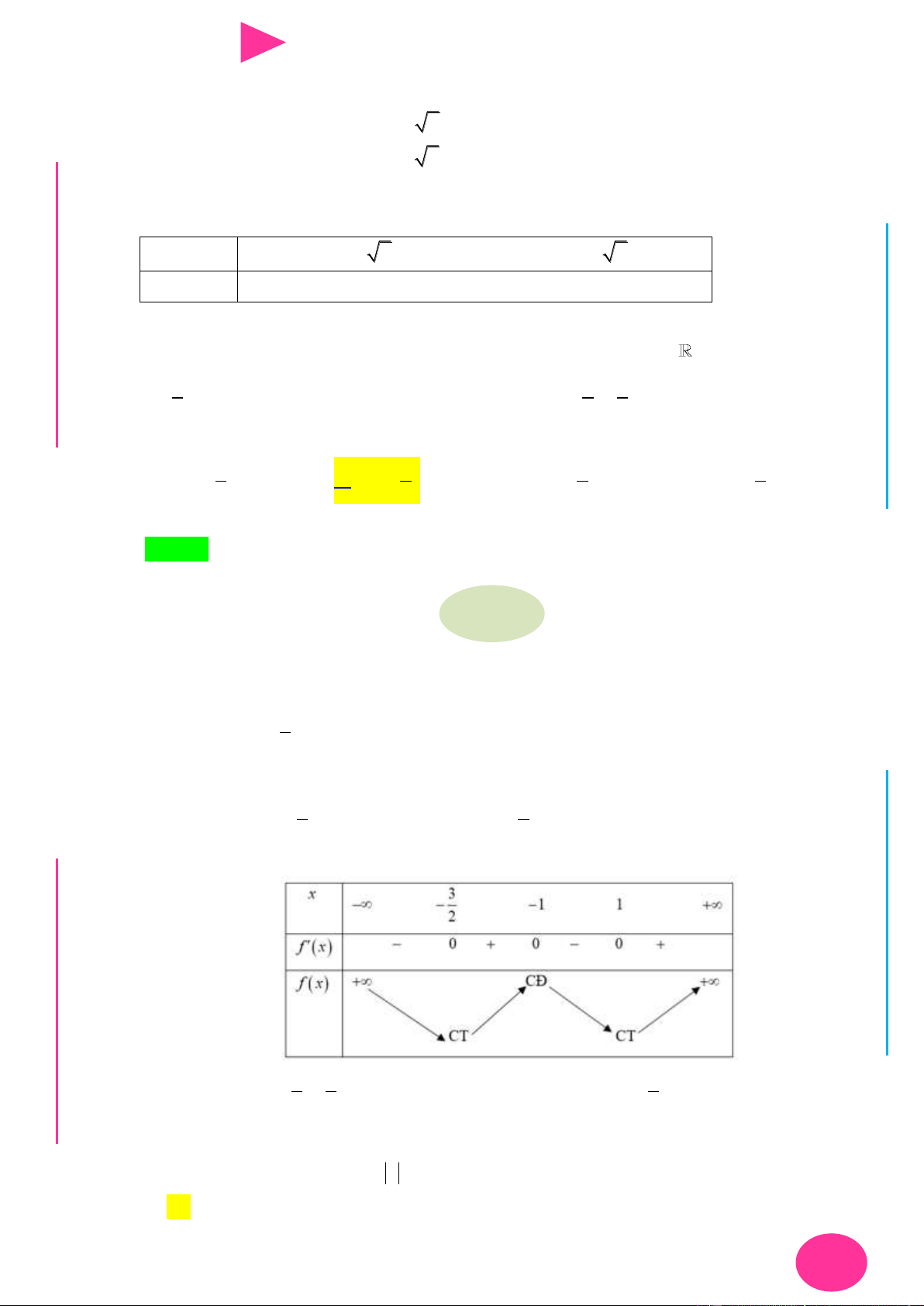
ÁO VIÊ Câu 18. Cho hàm số y f (x) có đạo hàm liên tục trên và bảng xét dấu đạo hàm GI Hàm số 4 2 6 4 2
y 3 f (x 4x 6) 2x 3x 12x có tất cả bao nhiêu điểm cực tiểu? A. 3. B. 0. C. 1. D. 2.
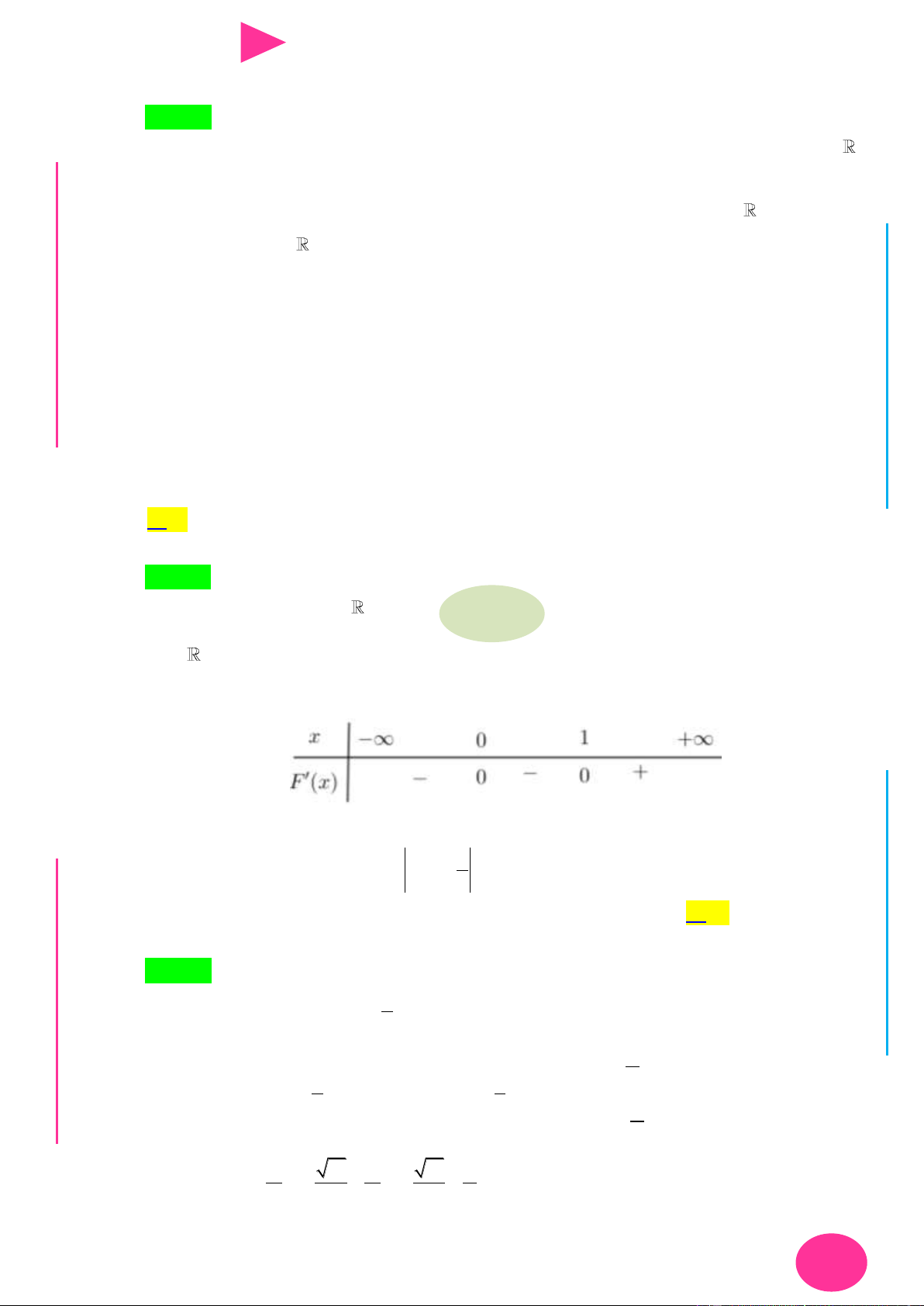
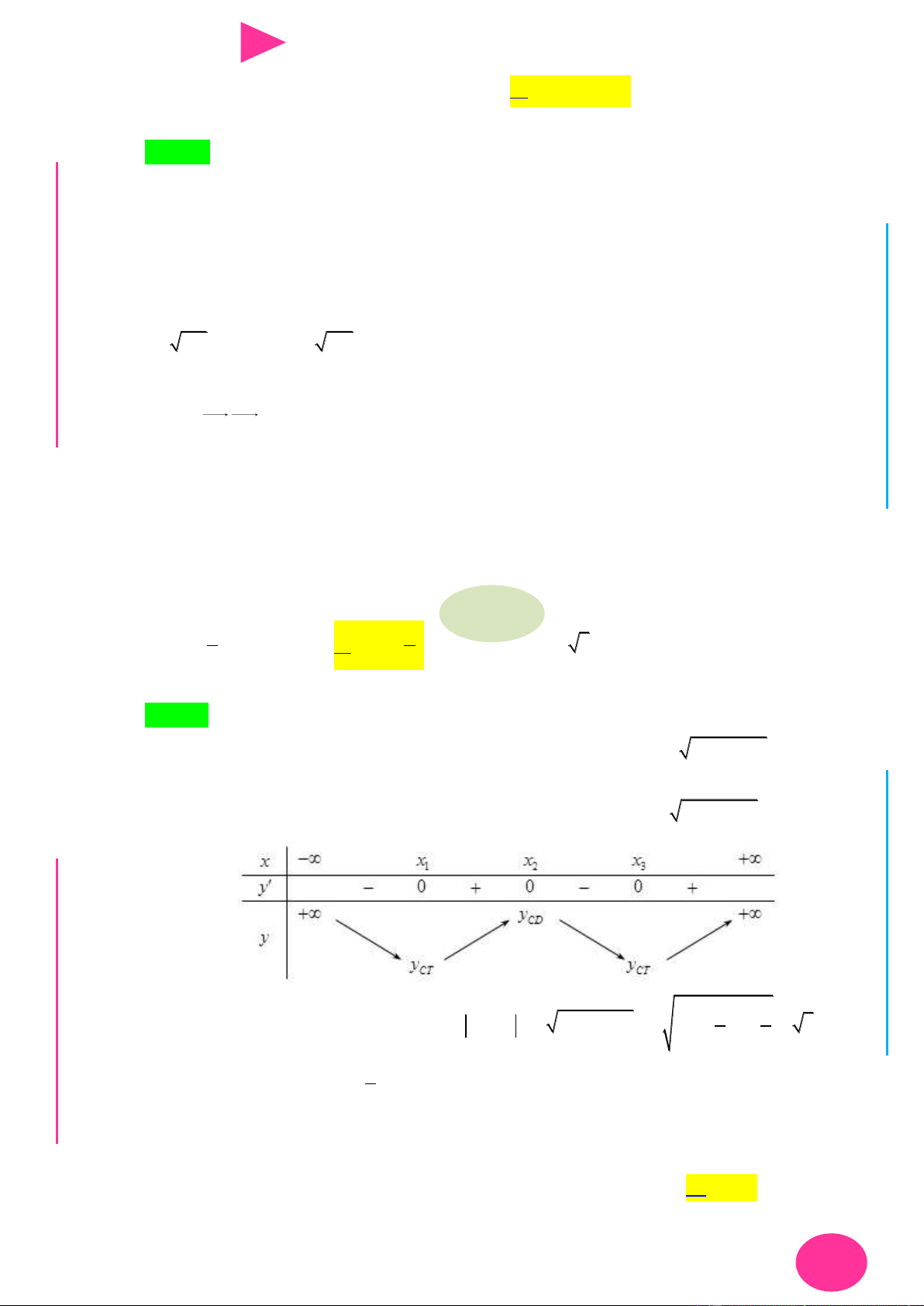
Câu 19. Cho hàm số y f (x) có bảng biến thiên nhƣ sau
Số điểm cực trị của hàm số y f (x) là A. 7 . B. 5 . C. 6 . D. 8 .
TÌM CỰC TRỊ CỦA HÀM SỐ 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 20. Cho hàm số y f x có bảng xét dấu của f x x
Hỏi hàm số g x f x 3 2 1
x 3x đạt cực tiểu tại điểm nào dƣới đây? 3 A. x 1 .
B. x 3.
C. x 2 . D. x 3 .
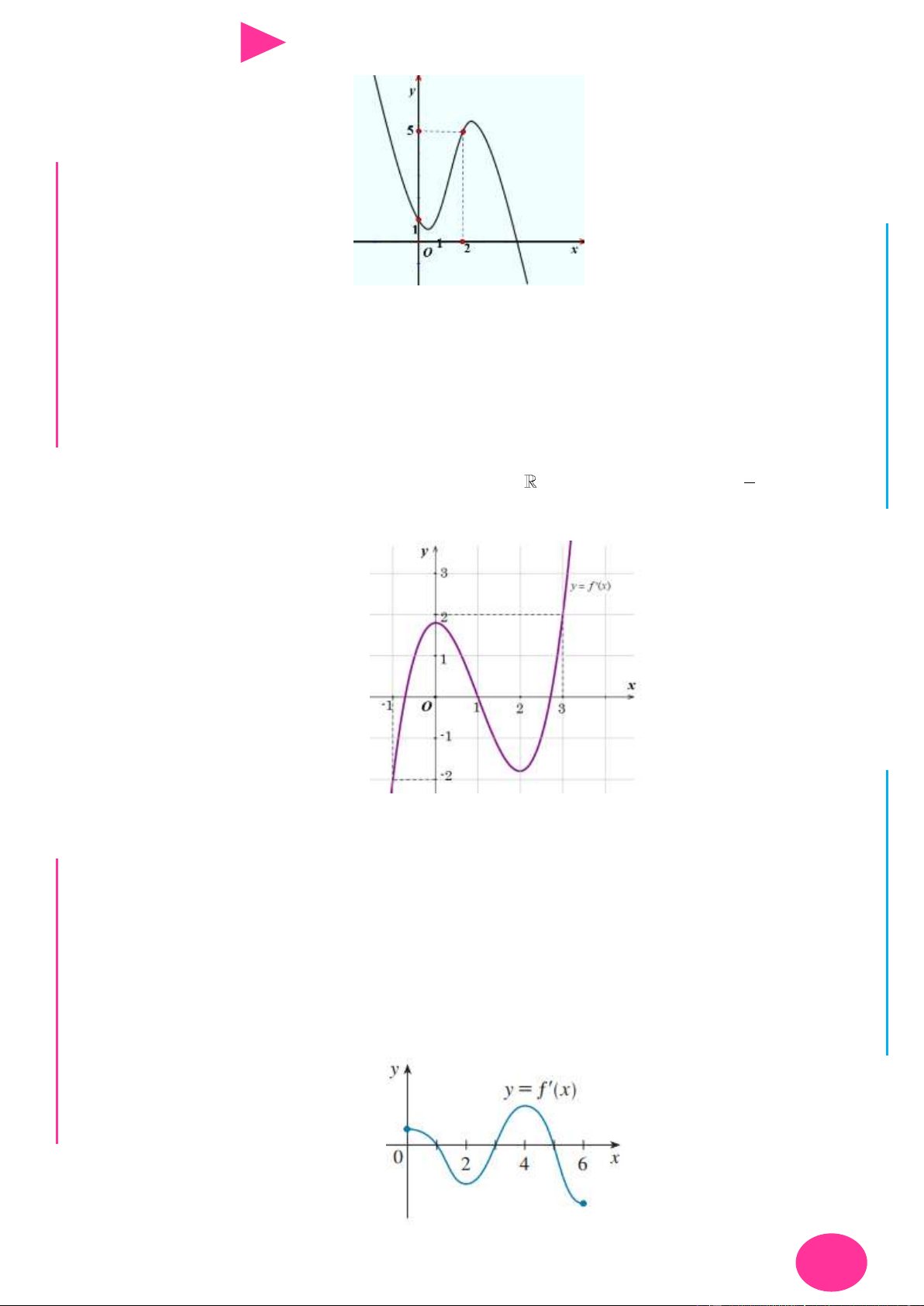
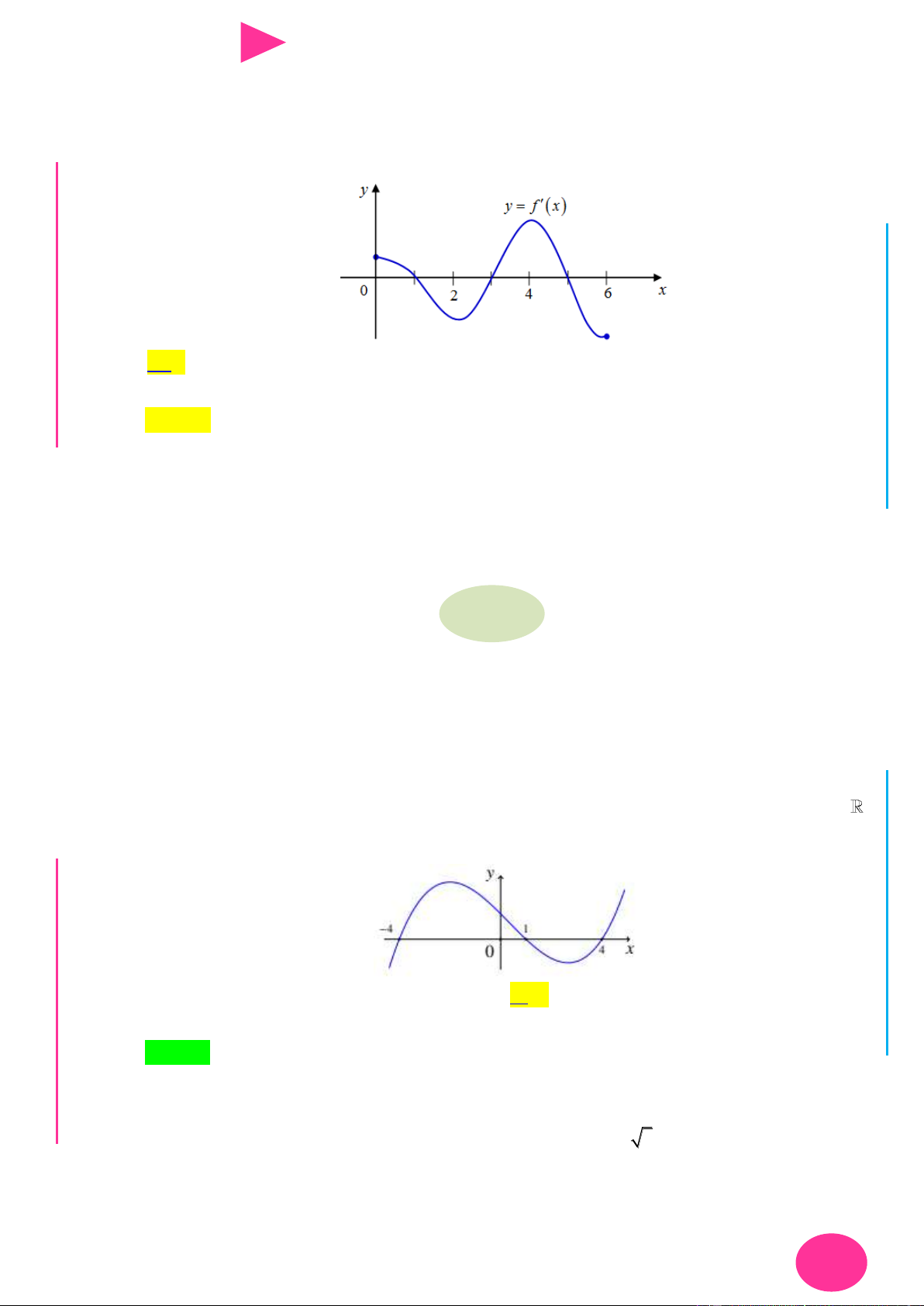
Câu 21. Cho hàm số y f (x) có đạo hàm liên tục trên
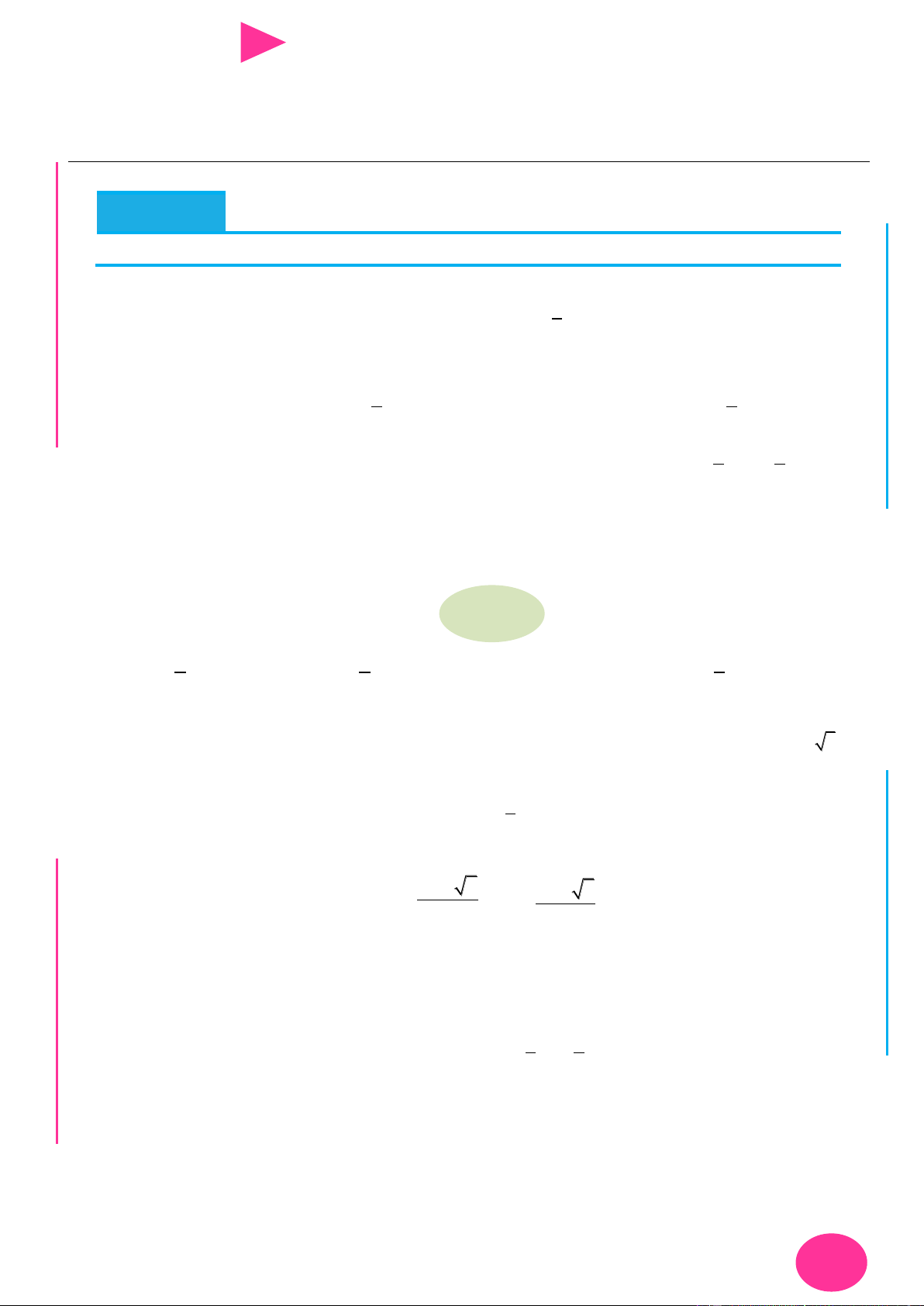
. Đồ thị hàm số y f ( x) nhƣ hình vẽ sau: I Ơ M D Ầ Đ NHỊ
Số điểm cực trị của hàm số y f (x) 5x là Đ G A. 3 . B. 4 . C. 1. D. 2 . THPT N.C.Đ N
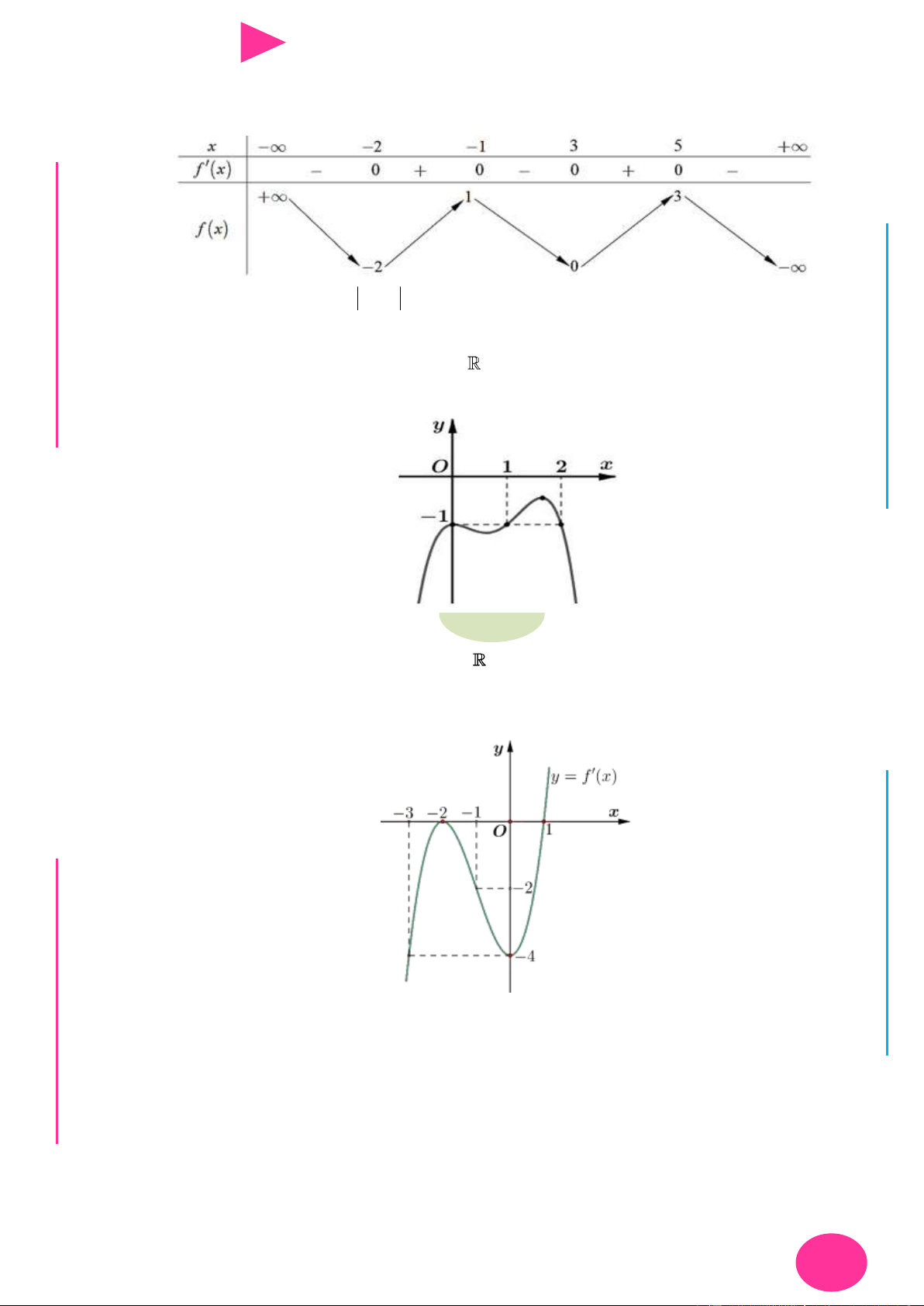
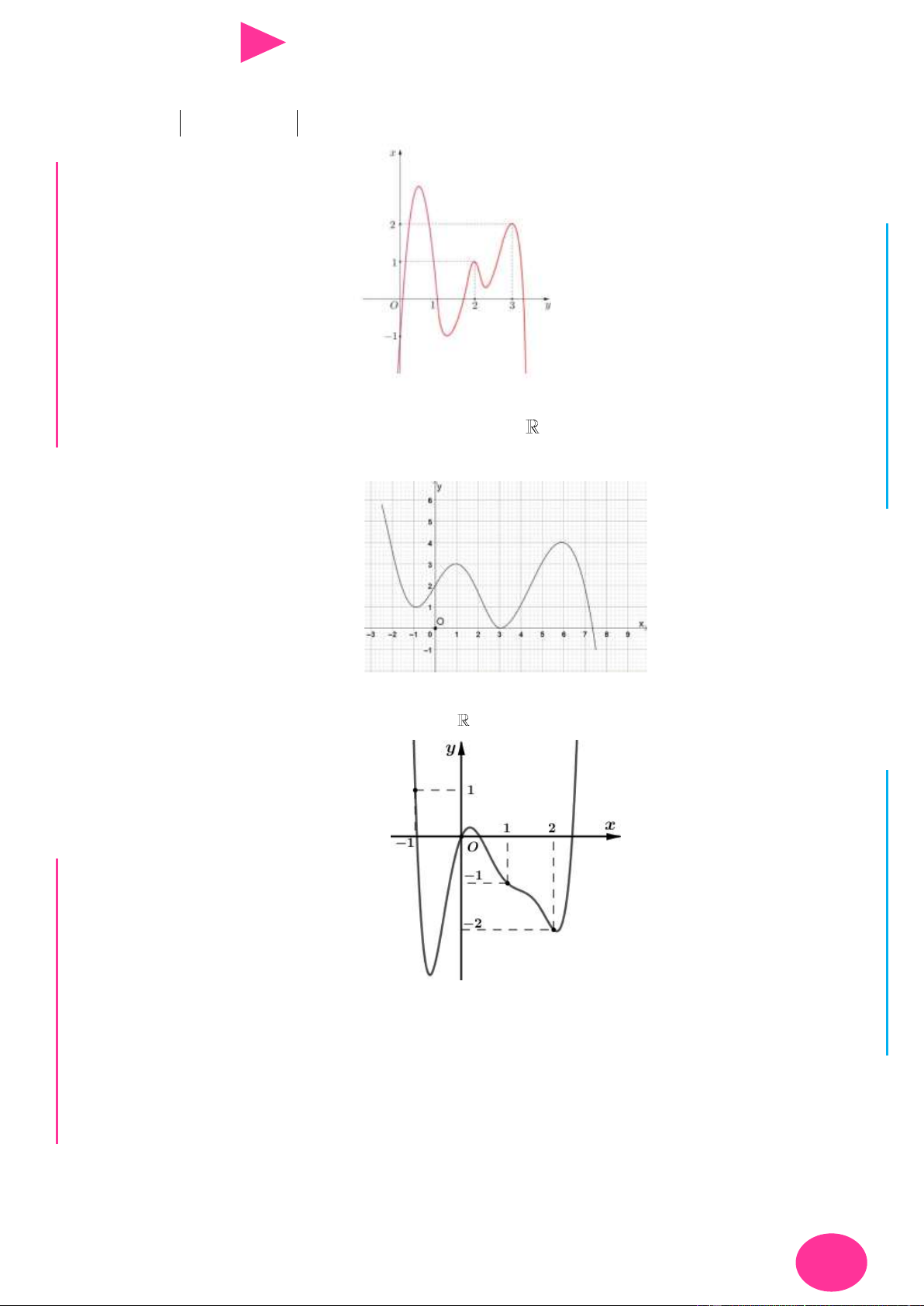
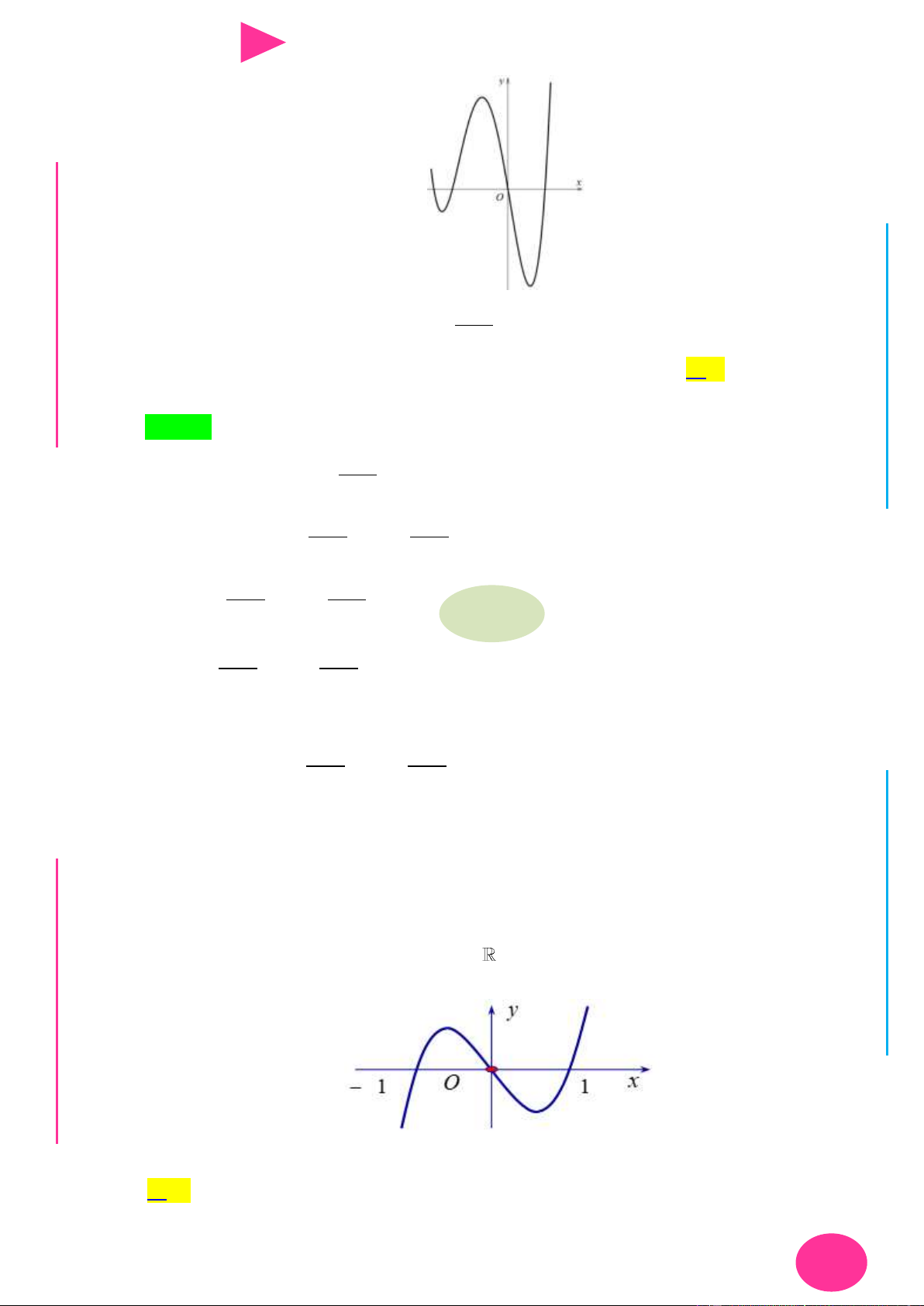
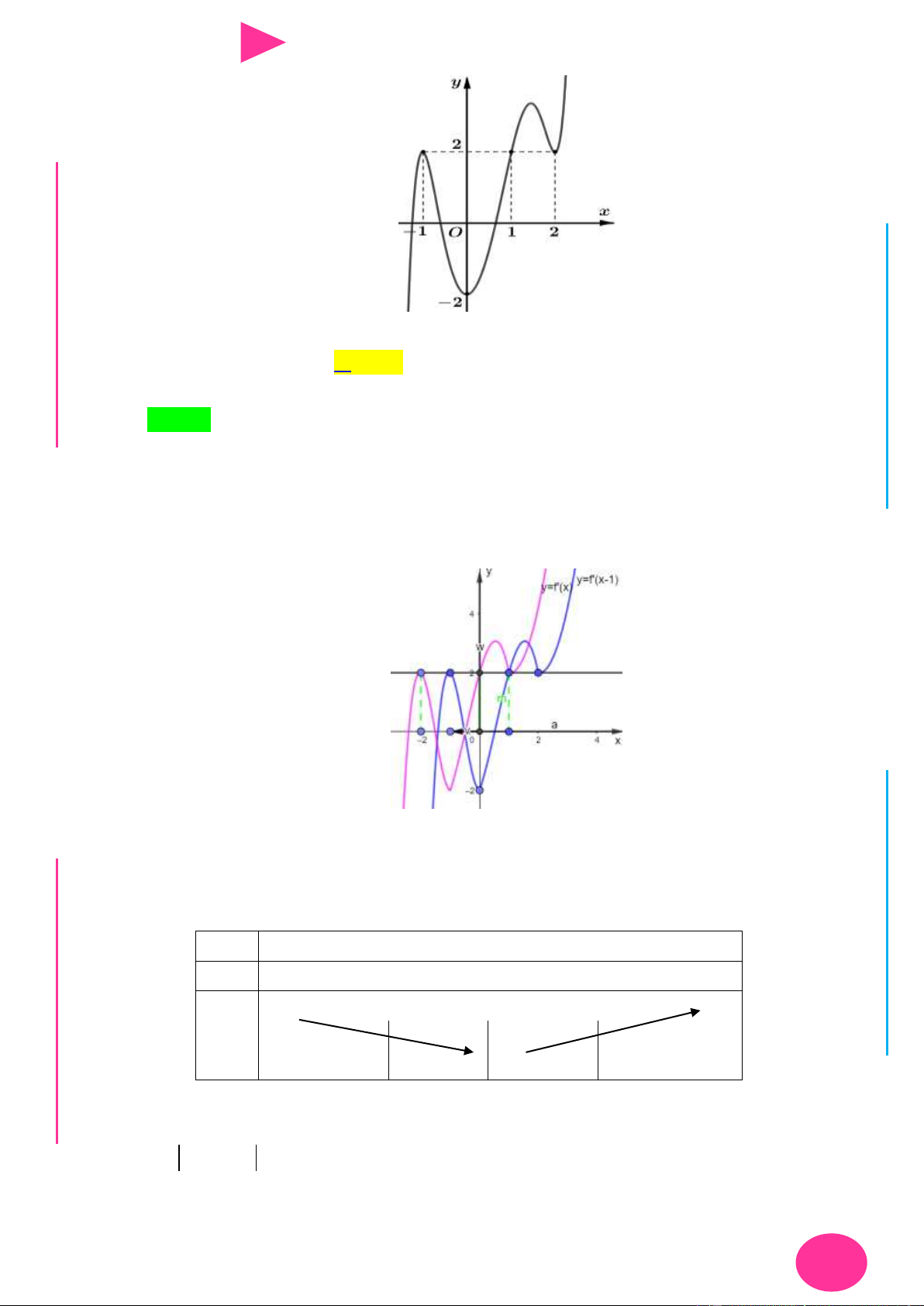
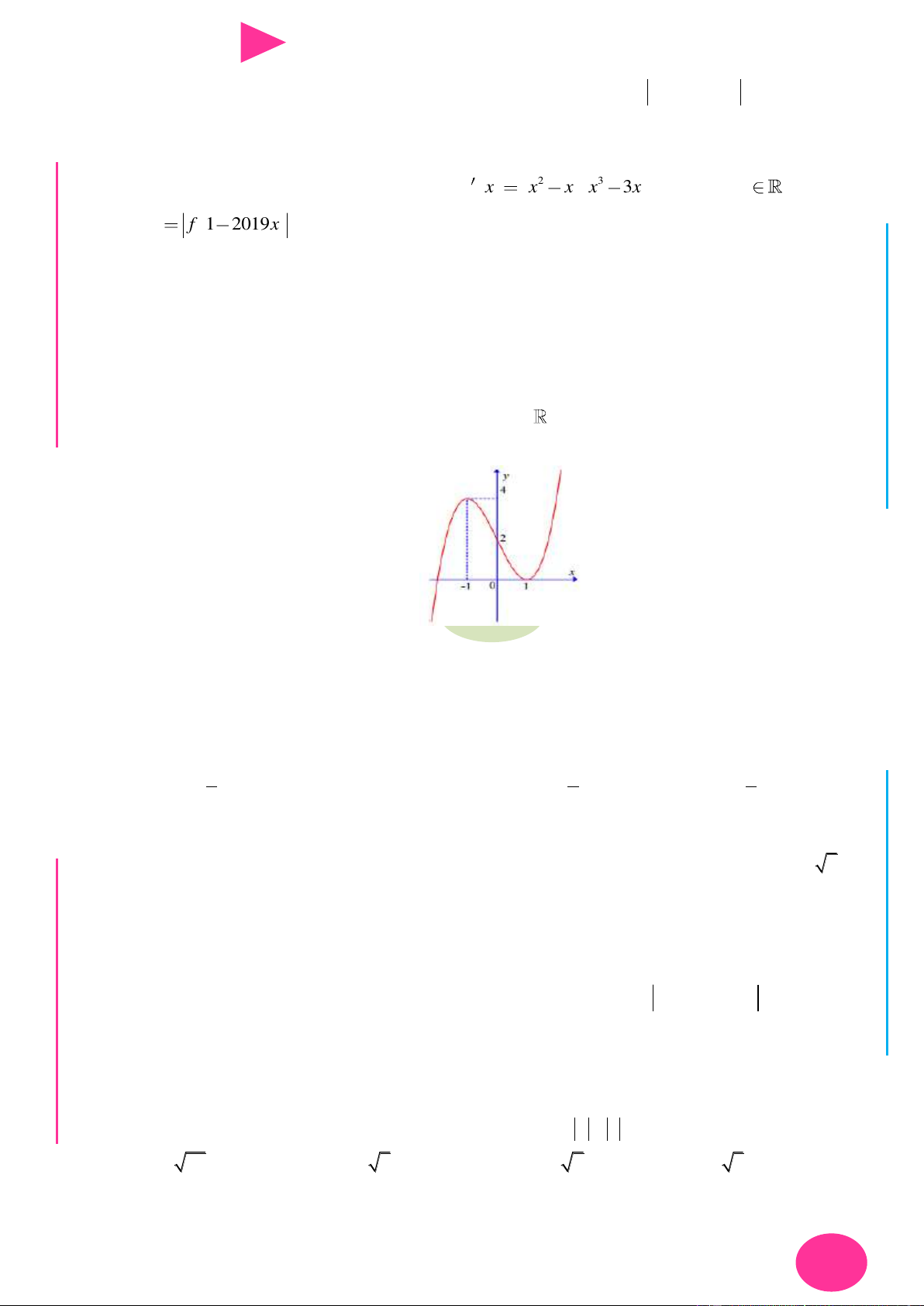
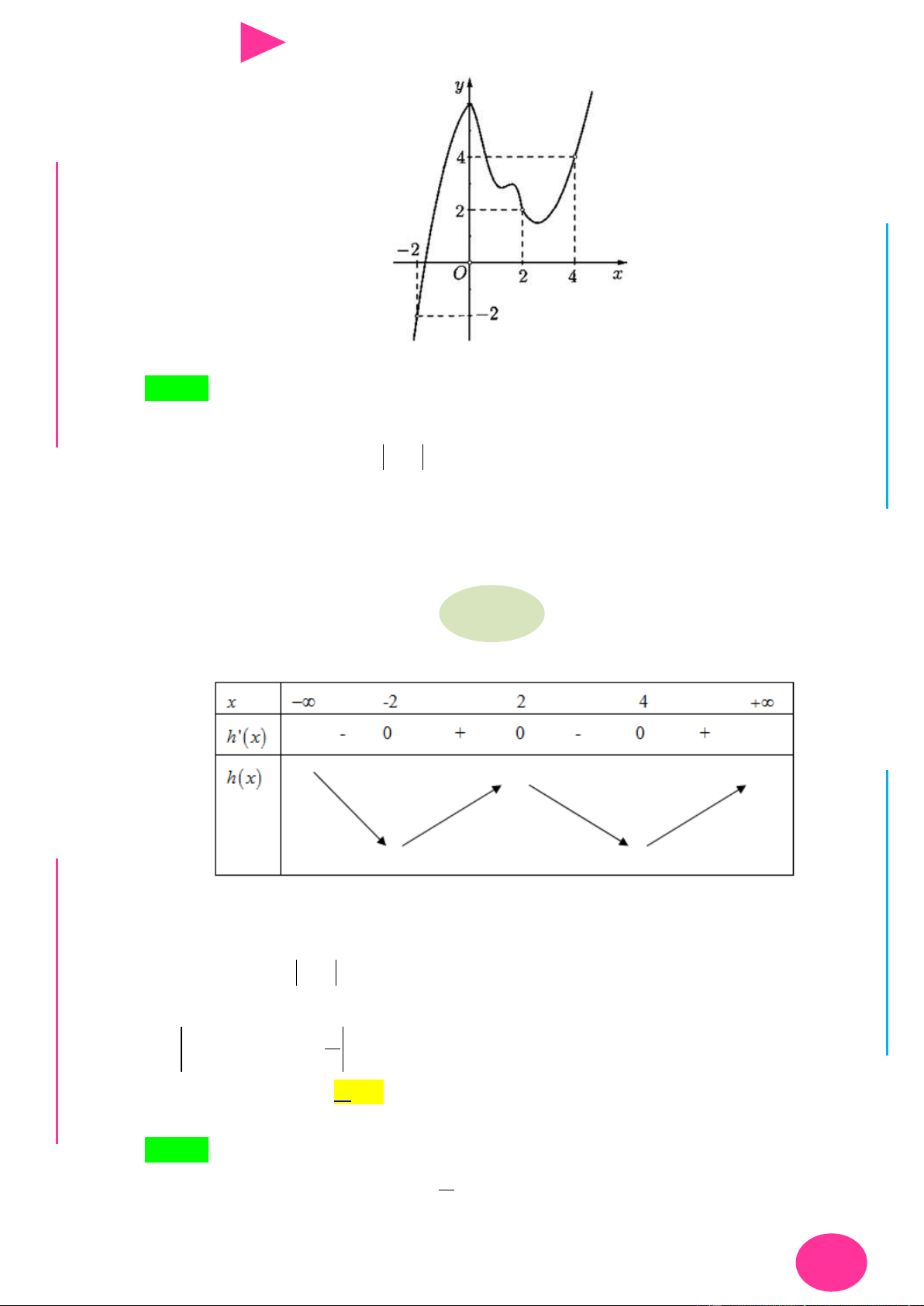
Câu 22. Cho hàm số y f x là hàm số bậc bốn. Hàm số y f x có đồ thị nhƣ hình bên. Số NG CÔ Ờ 2 N
điểm cực trị của hàm số f x 2x 2019 là YỄ TRƢ y GU N N ÁO VIÊ -1 O 1 3 x GI A. 3. B. 2. C. 1. D. 4.
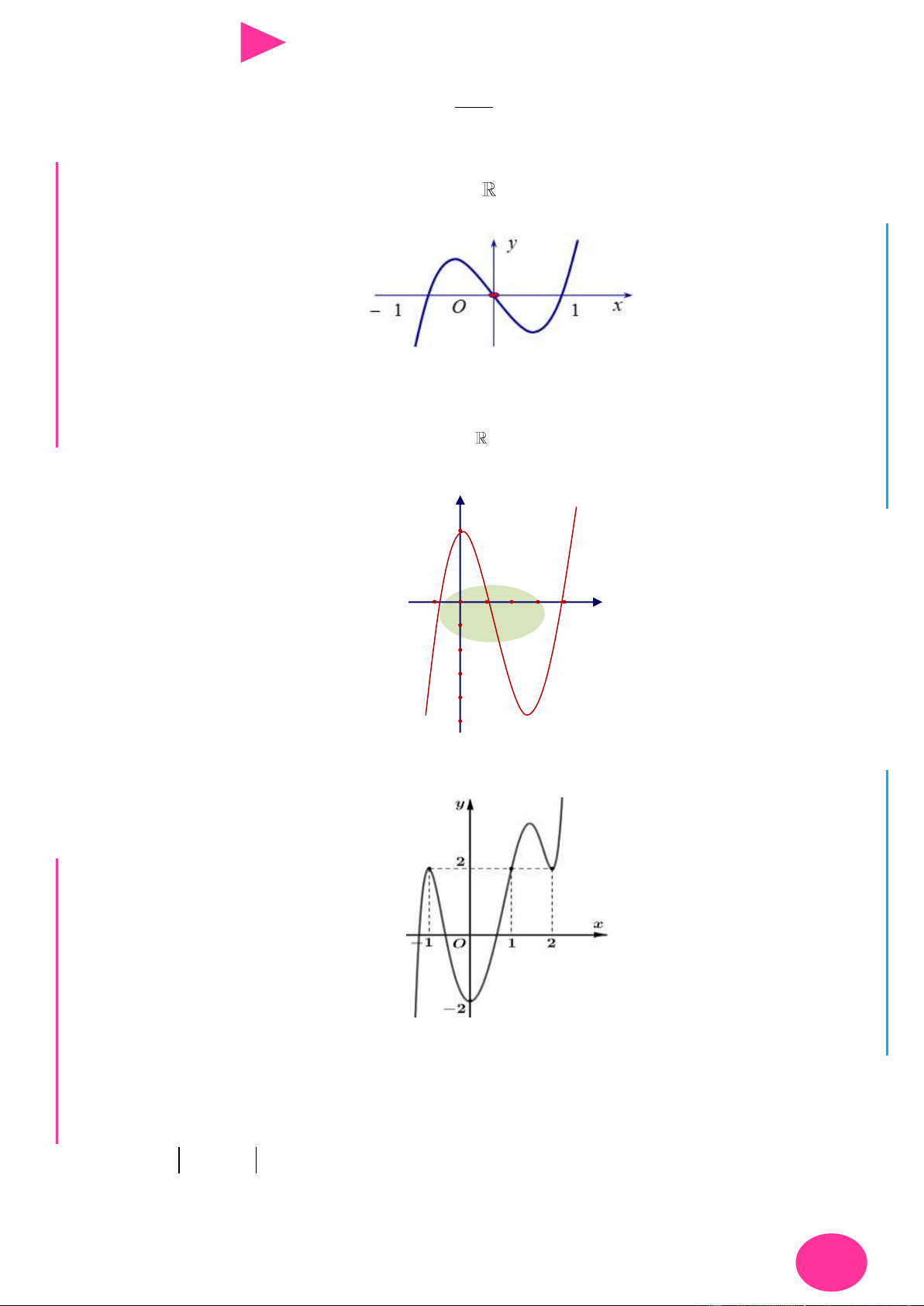
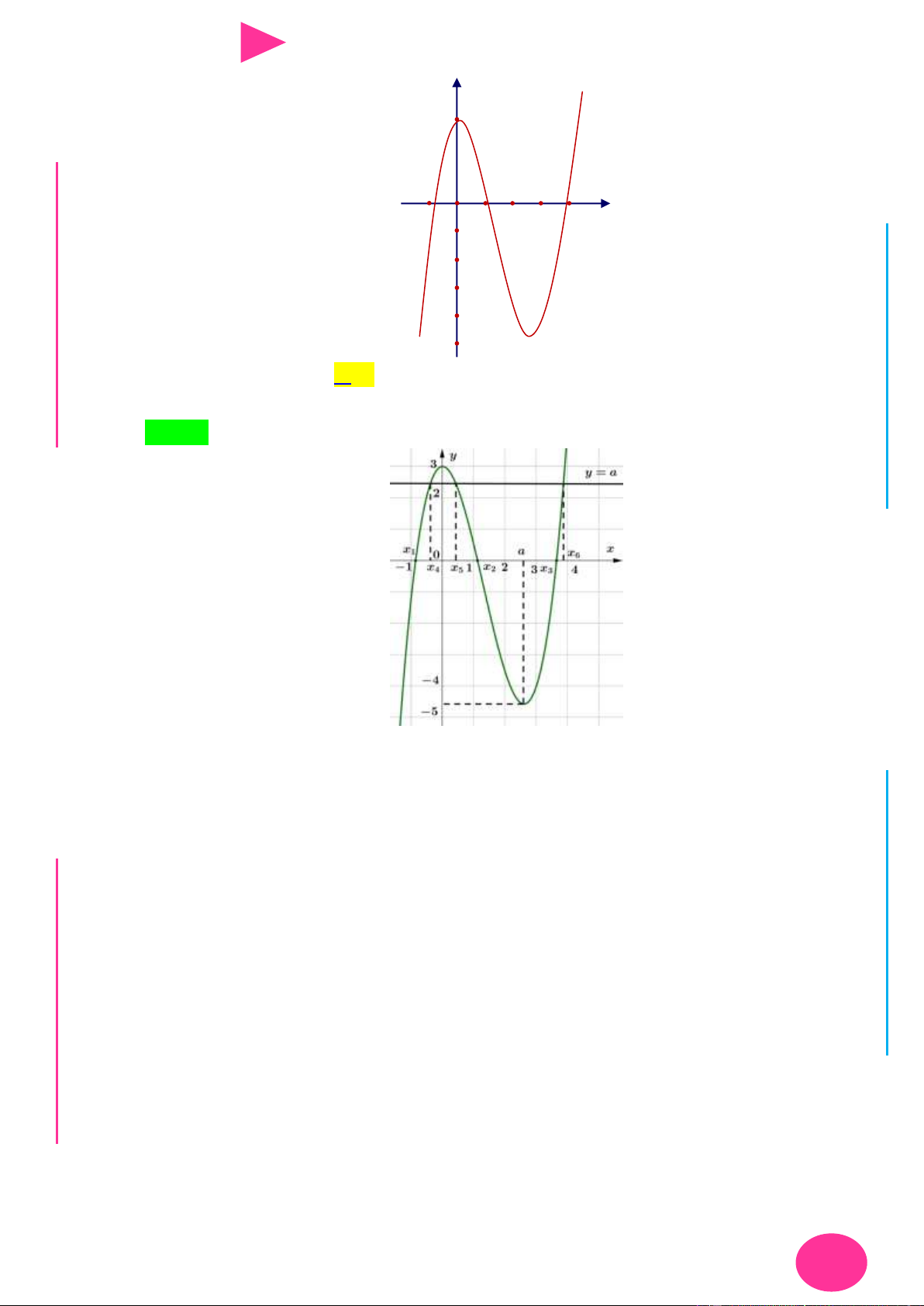
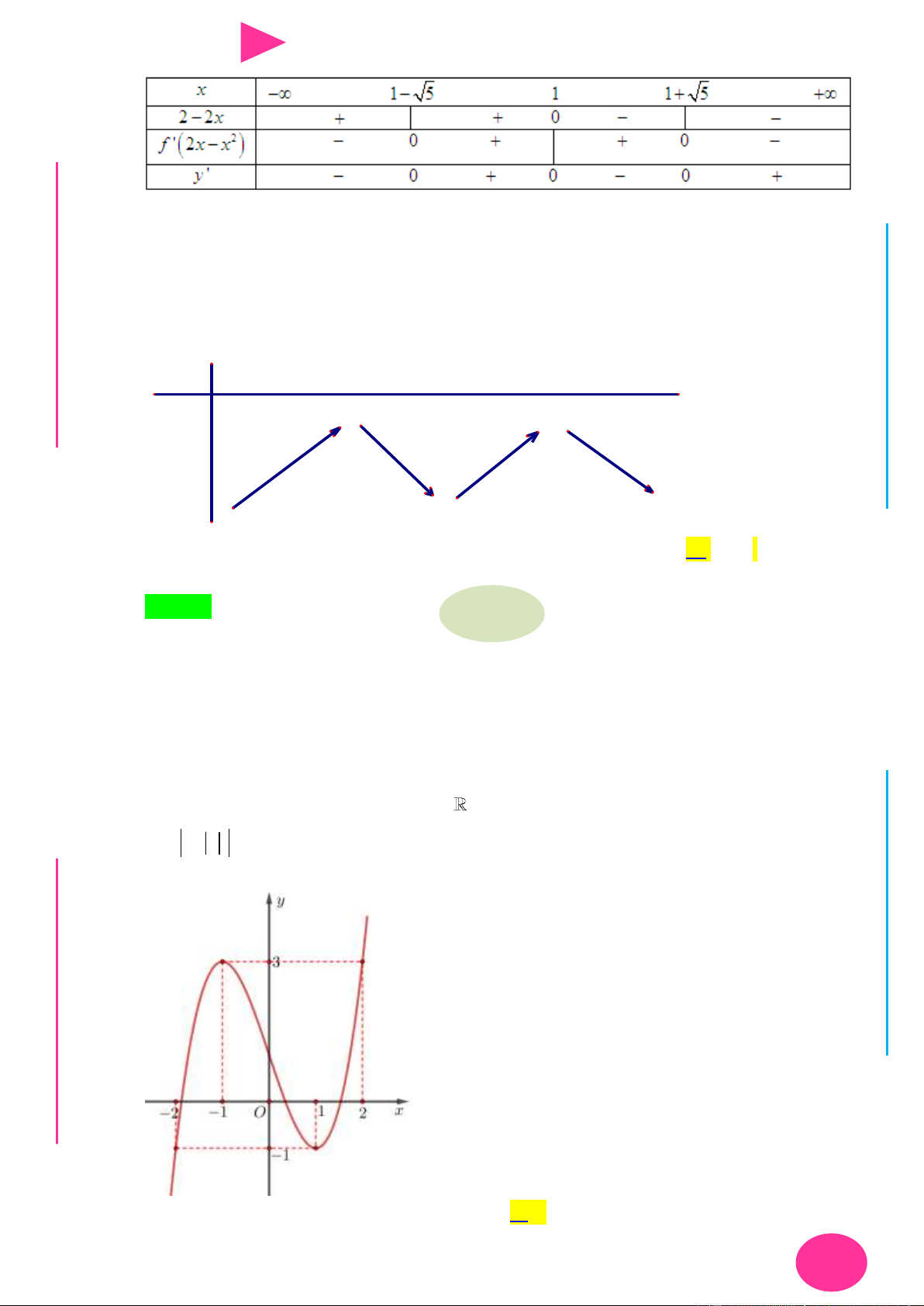
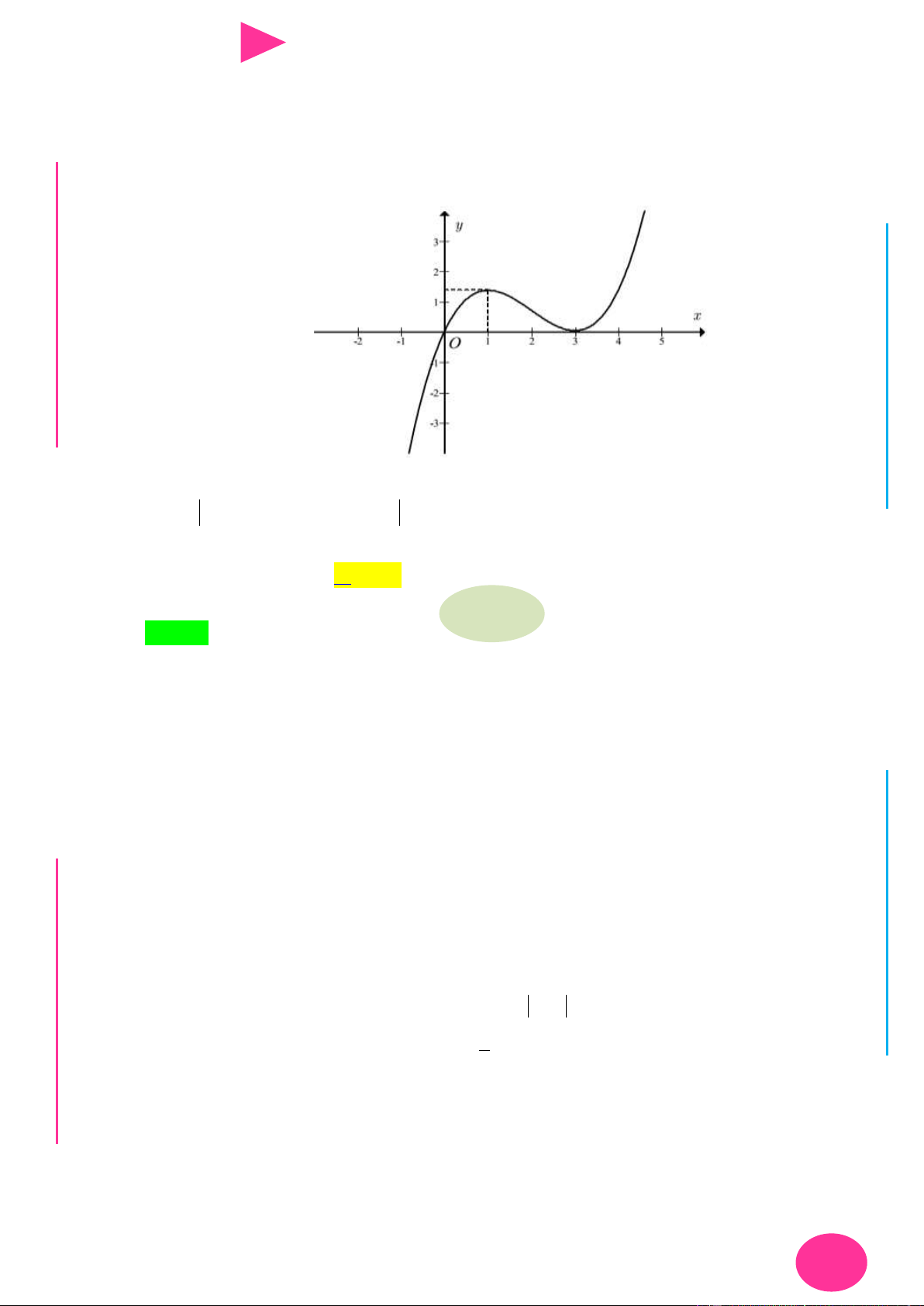
Câu 23. Cho hàm số y f (x) có đồ thị nhƣ hình vẽ dƣới đây:
TÌM CỰC TRỊ CỦA HÀM SỐ 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 f x 1 f x
Tìm số điểm cực đại của hàm số y 2019 2018 A. 1. B. 3. C. 0. D. 2. 3 2
Câu 24. Cho hàm số y
f (x) có đạo hàm tại x
, hàm số f (x) x ax bx c
Có đồ thị ( nhƣ hình vẽ )
Số điểm cực trị của hàm số y f f x là A. 7 . B. 11. C. 9 . D. 8 .
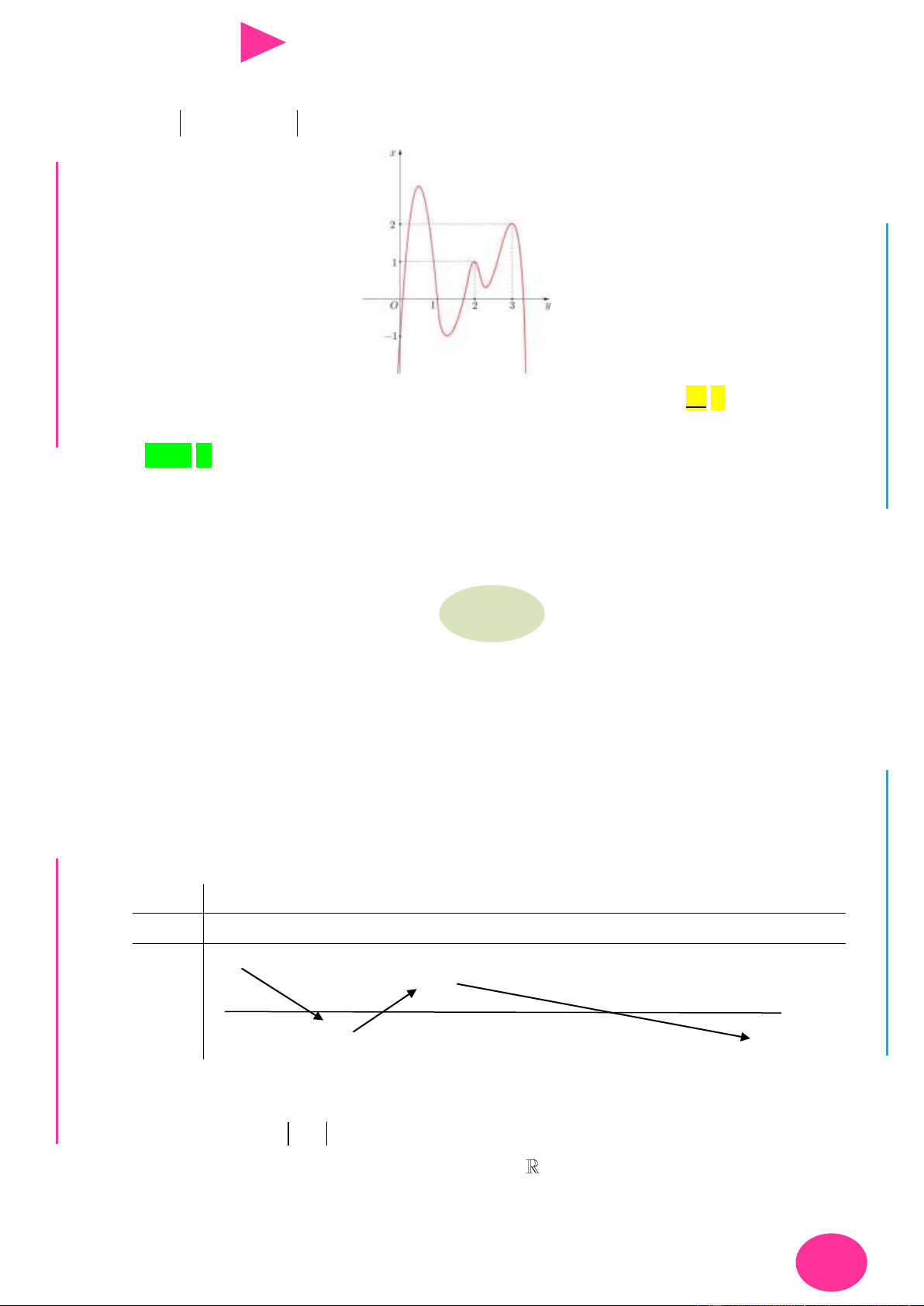
Câu 25. Cho hàm số y f x có đạo hàm trên và có đồ thị là đƣờng cong nhƣ hình vẽ. Đặt I Ơ
g x 3 f f x 4 . Tìm số điểm cực trị của hàm số g x? y M D Ầ 3 Đ NHỊĐ 1 1 2 3 4 G THPT N O .C.Đ x N NG CÔ Ờ N YỄ TRƢ GU N A. 2 . B. 8 . C. 10 . D. 6 . N
Câu 26. Cho hàm số y f (
x 1) có đồ thị nhƣ hình vẽ. ÁO VIÊ GI 2 f x Hàm số 4 x y
đạt cực tiểu tại điểm nào? A. x 1. B. x 0 . C. x 2 . D. x 1 .
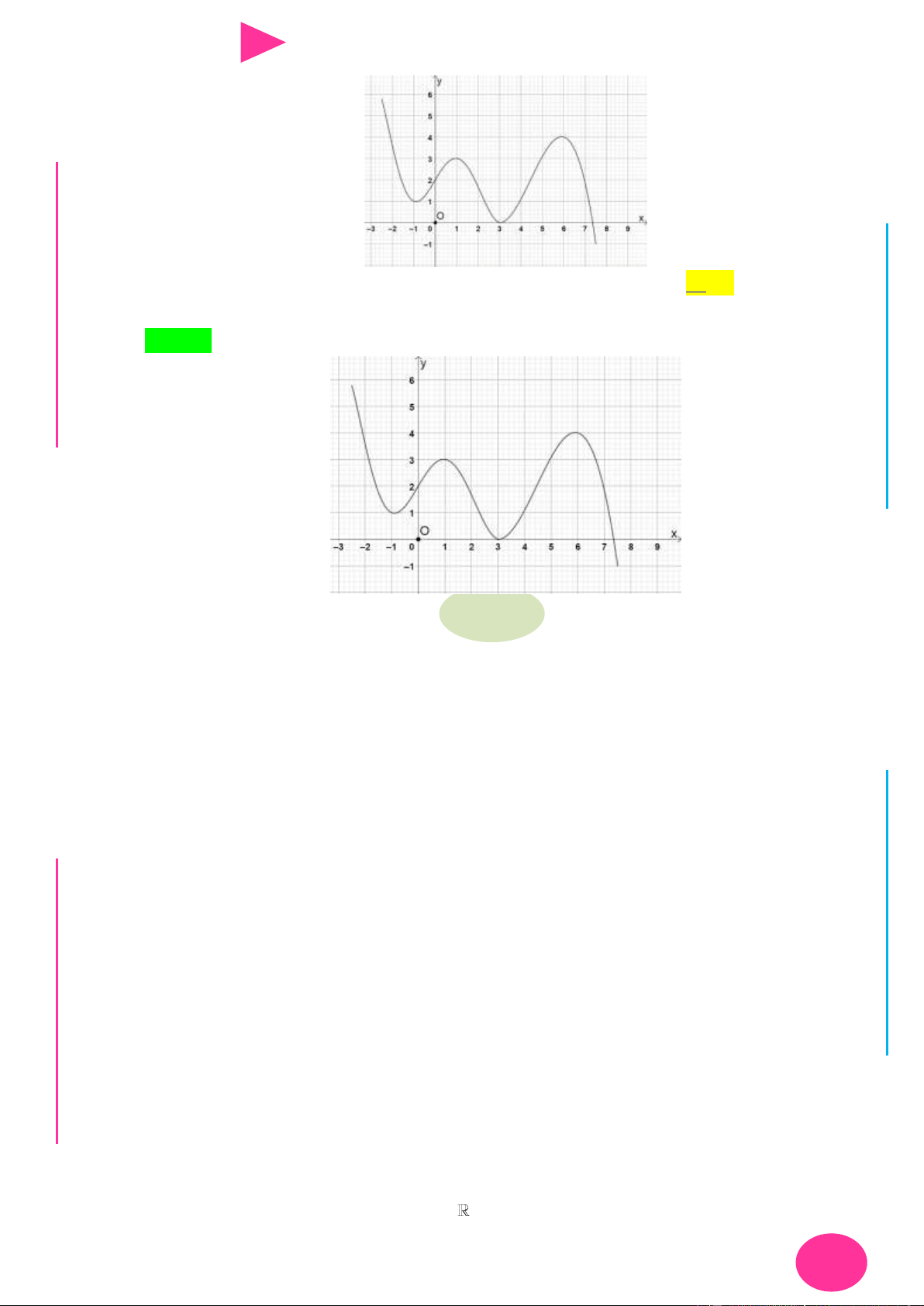
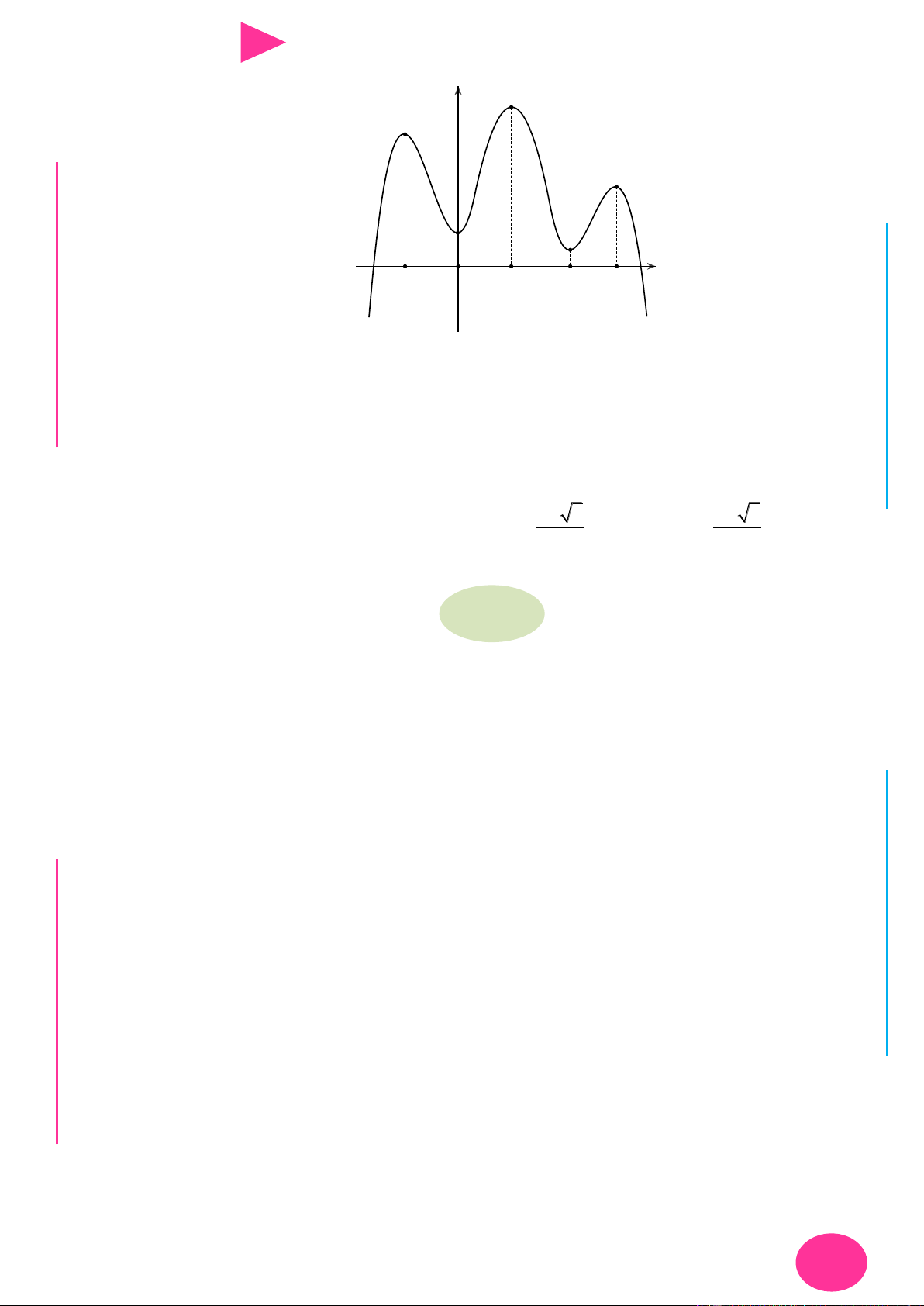
Câu 27. Cho hàm số y f x có đồ thị nhƣ hình vẽ. Số điểm cực trị của hàm số
y 2 f x 5 3 là
TÌM CỰC TRỊ CỦA HÀM SỐ 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 2 . B. 3 . C. 5 . D. 7 .
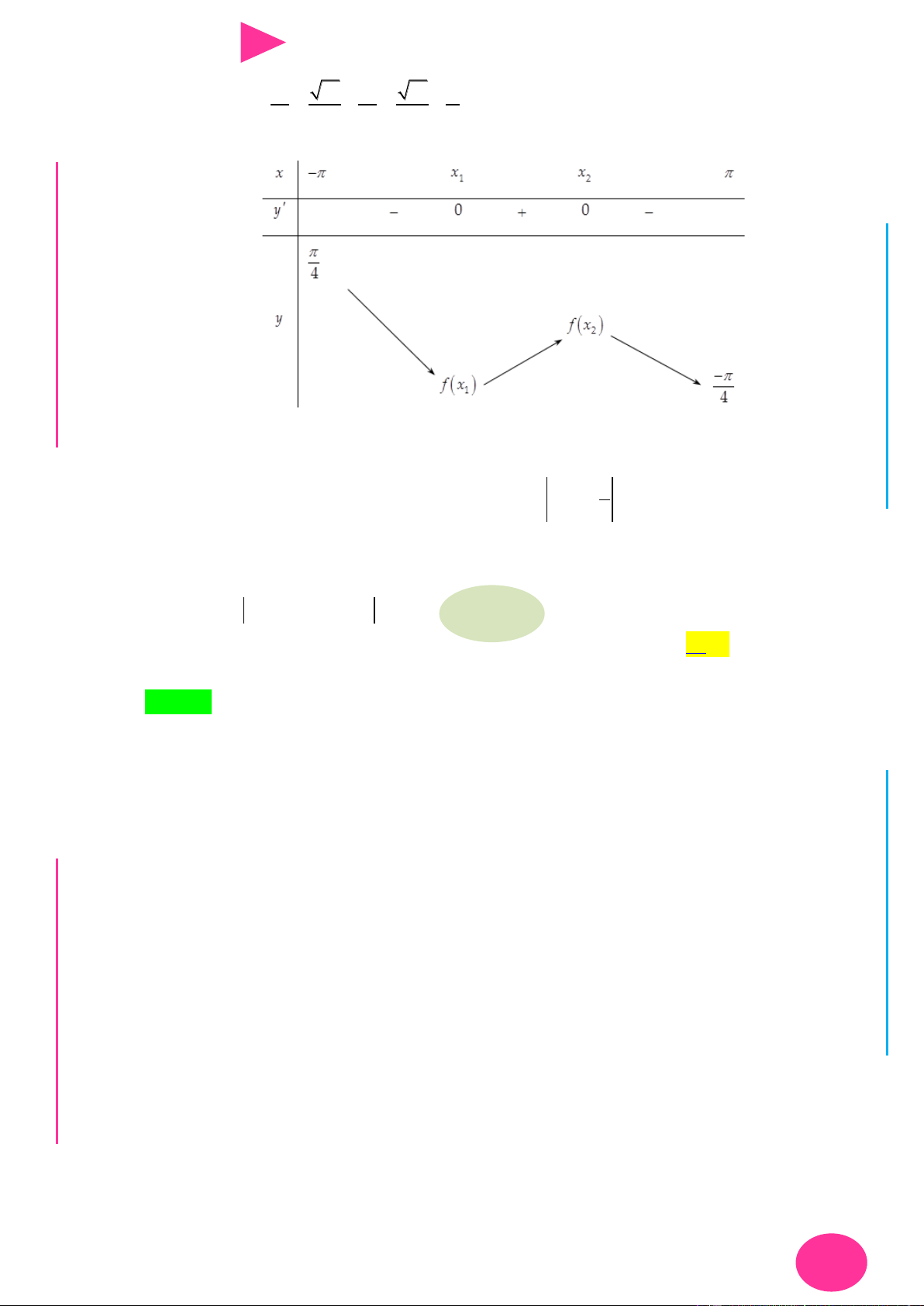
Câu 28. Cho hàm số y f x , hàm số y f x có đồ thị nhƣ hình vẽ. Hàm số g x 5sin x 1 x 2 5sin 1 I 2 f 3
có bao nhiêu điểm cực trị trên khoảng 0; 2 ? Ơ 2 4 M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N A. 9 . B. 7 . C. 6 . D. 8 . N 3
Câu 29. Cho hàm số y f x biết f x 2
x x 2 1
x 2mx m 6 . Số giá trị nguyên của tham ÁO VIÊ
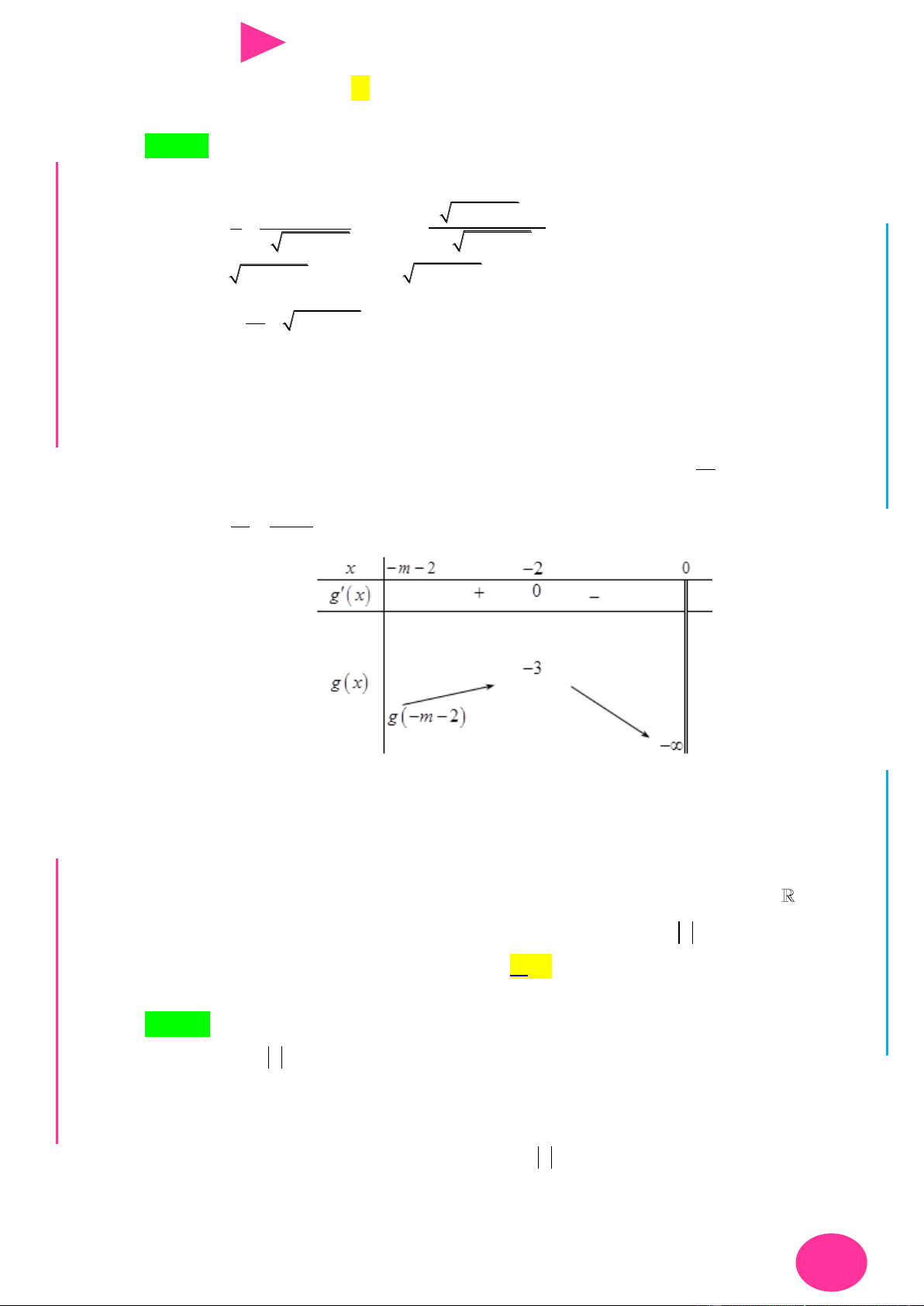
số m để hàm số đã cho có đúng một điểm cực trị là GI A. 7 . B. 5 . C. 6 . D. 4 . Vậy m 2 ; 3
7 , mà m m 2 ; 1 ;0;1;2;3; 7 .
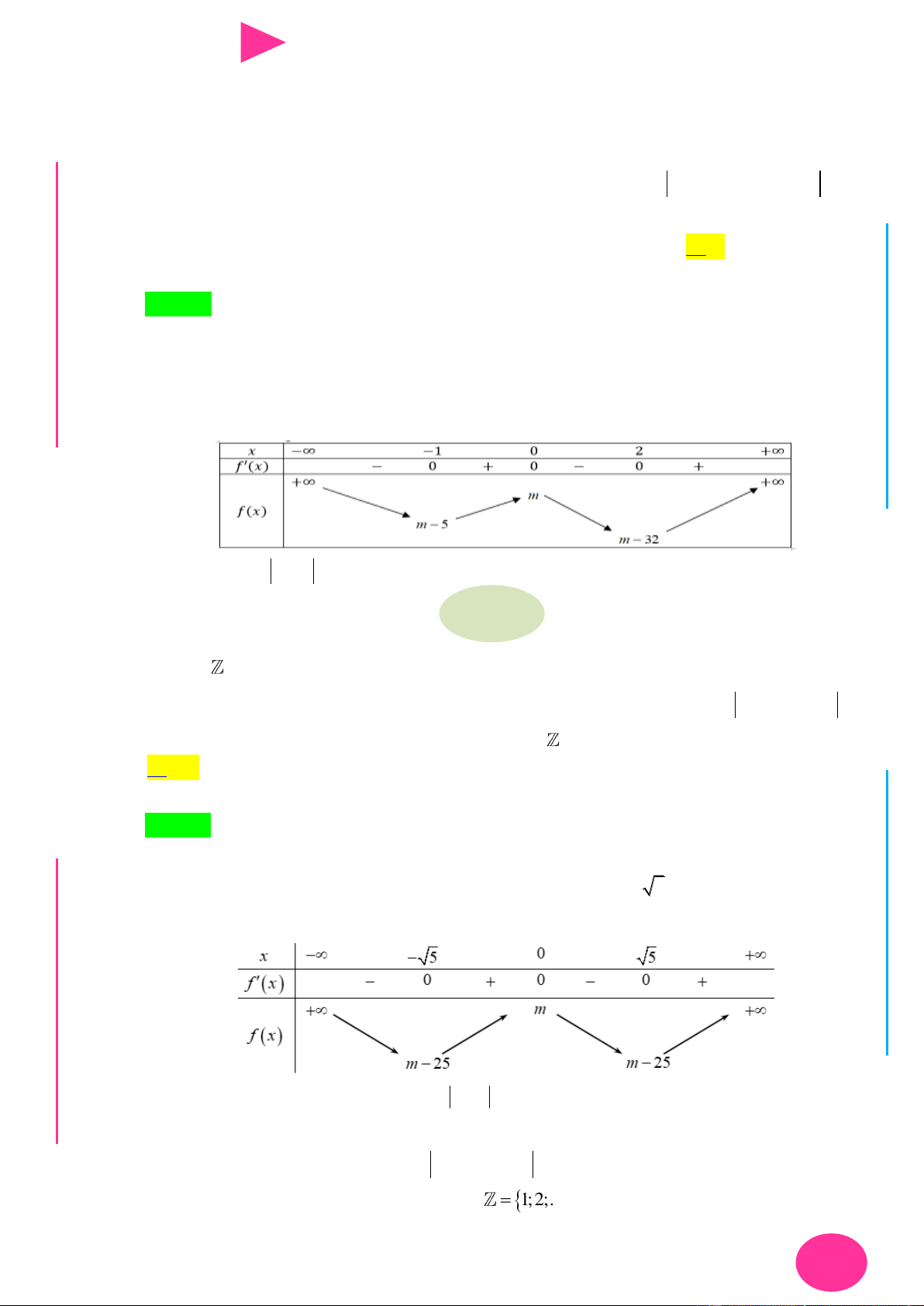
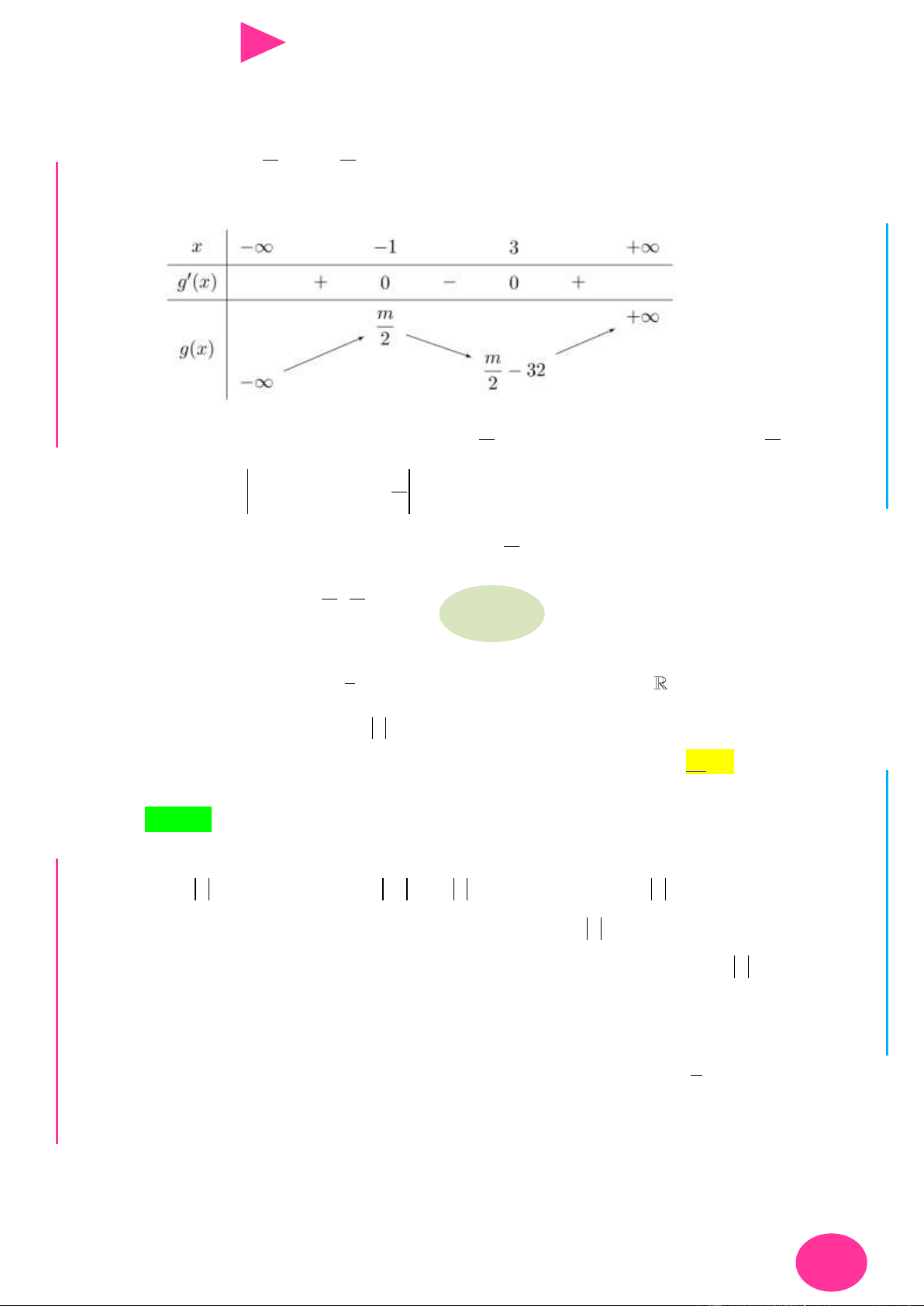
Câu 30. Cho hàm số y f x có bảng biến thiên nhƣ sau: 3 2
Số điểm cực tiểu của hàm số g x 2 f x 4 f x 1 là A. 4 . B. 9 . C. 5 . D. 3
Câu 31. Cho hàm số y f x có đạo hàm trên và đồ thị của hàm số y f x nhƣ hình bên.
TÌM CỰC TRỊ CỦA HÀM SỐ 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Khẳng định nào dƣới đây đúng ?
A. Hàm số y f x 2
x x 2019 đạt cực đại tại x 0 .
B. Hàm số y f x 2
x x 2019 đạt cực tiểu tại x 0 .
C. Hàm số y f x 2
x x 2019 không có cực trị.
D. Hàm số y f x 2
x x 2019 không có cực trị tại x 0 . I Ơ 1
Câu 32. Cho hàm số y f (x) liên tục trên tập số thực và hàm số 2
g(x) f (x)
x x 1. Biết 2 M D
đồ thị của hàm số y f (
x) nhƣ hình vẽ dƣới đây Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ
Khẳng định nào sau đây đúng ? GI
A. Đồ thị hàm số y
g(x) có 2 điểm cực tiểu và 1 điểm cực đại.
B. Đồ thị hàm số y g(x) có 2 điểm cực tiểu và không có điểm cực đại.
C. Đồ thị hàm số y g(x) có 1 điểm cực tiểu và 2 điểm cực đại.
D. Đồ thị hàm số y g(x) có 3 điểm cực tiểu và 1 điểm cực đại.
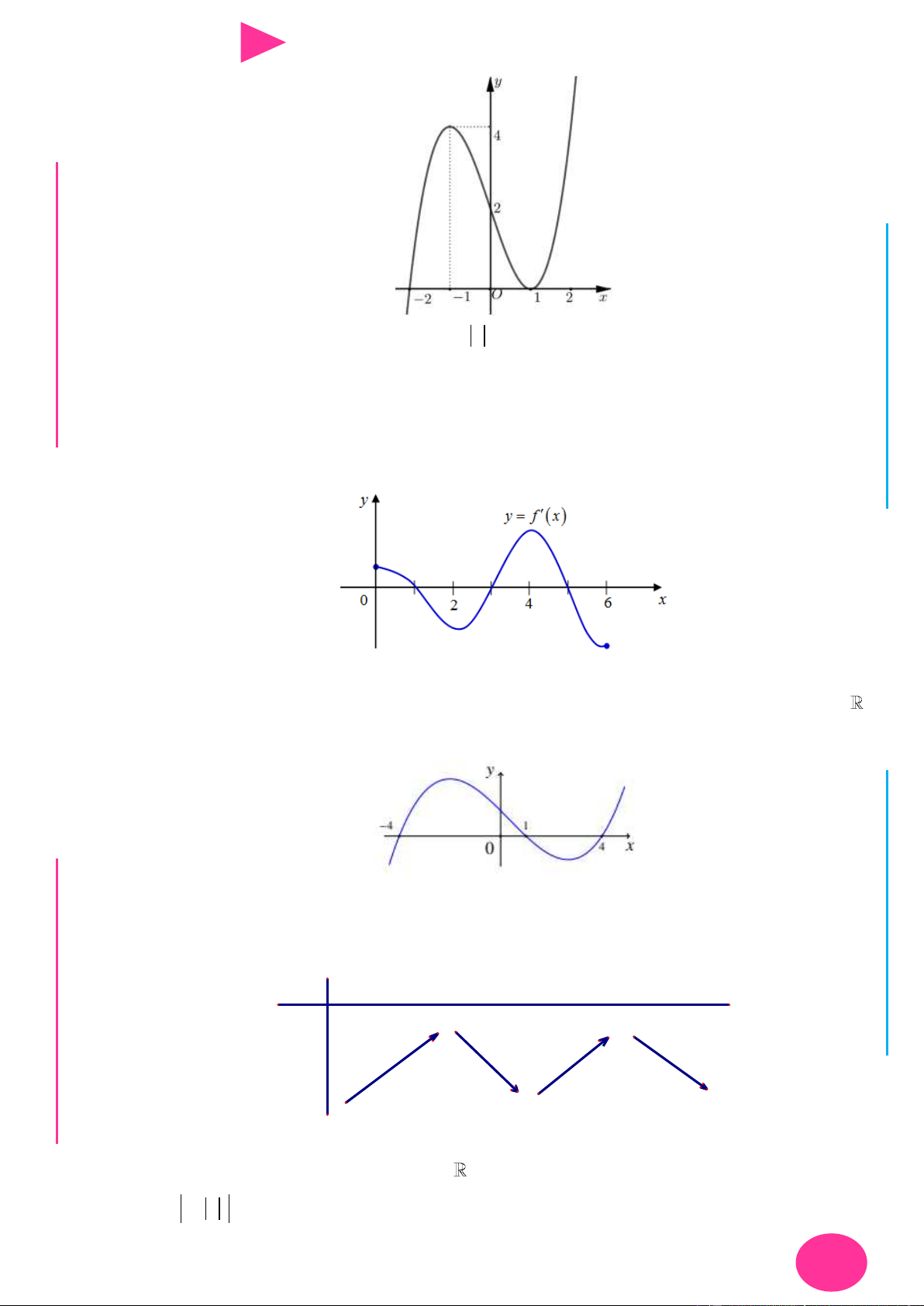
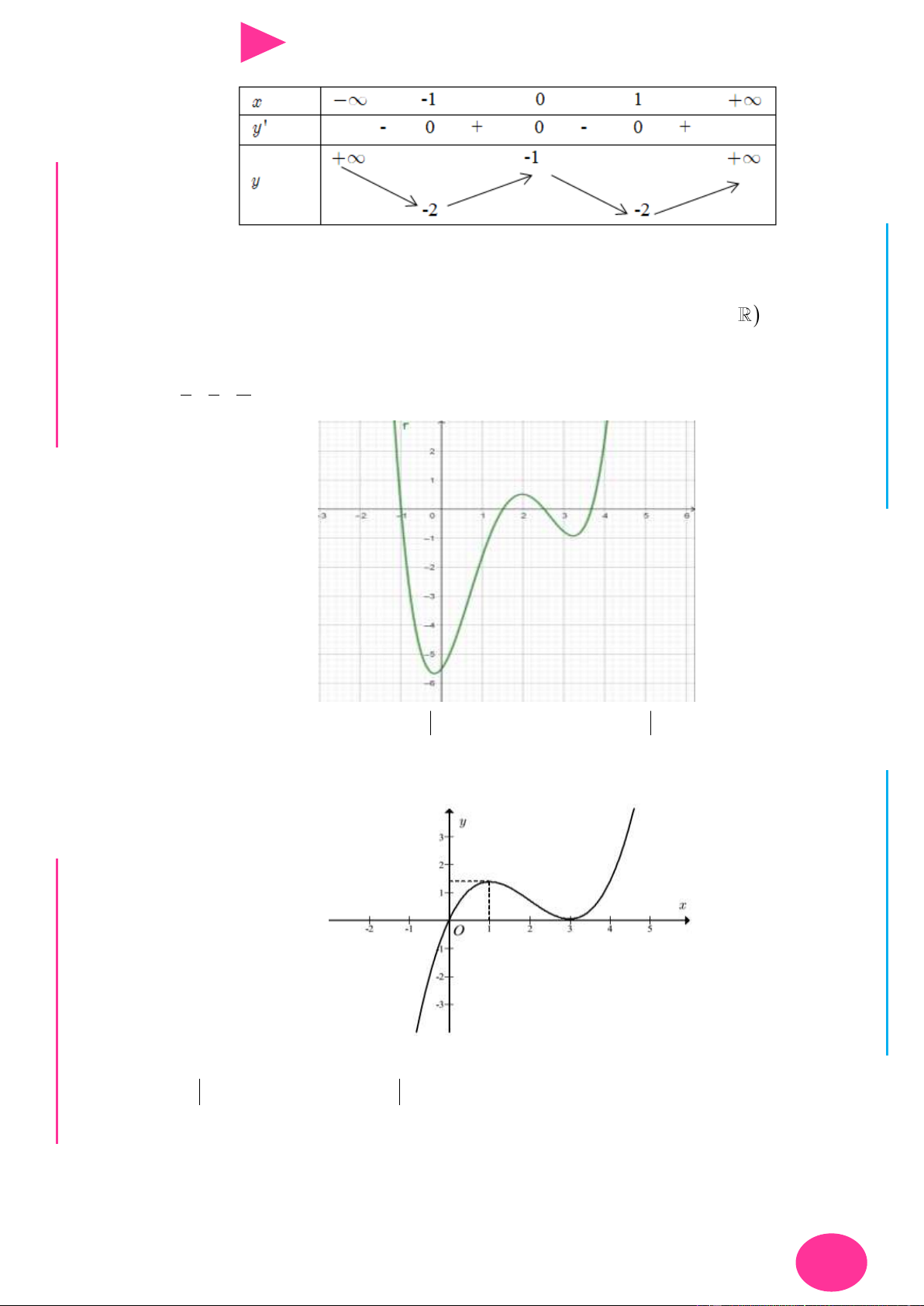
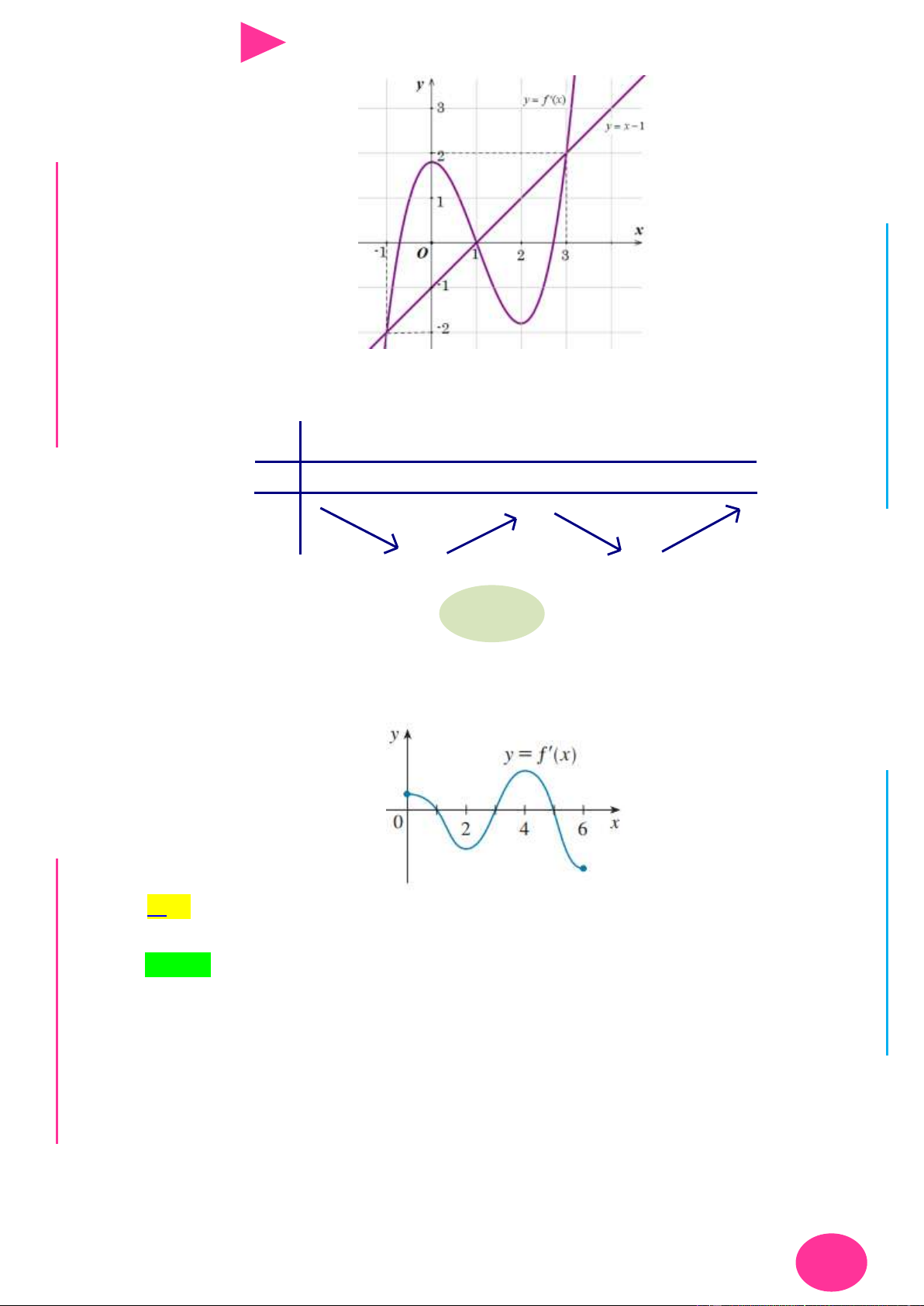
Câu 33. Cho hàm số y f x liên tục và có đạo hàm trên 0;6 . Đồ thị của hàm số y f x
trên đoạn 0;6 đƣợc cho bởi hình bên dƣới. Hỏi hàm số y f x 2 2019 có tối đa
bao nhiêu điểm cực trị trên đoạn 0;6 .
TÌM CỰC TRỊ CỦA HÀM SỐ 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 7 . B. 6 . C. 4 . D. 3 .
Câu 34. Cho hàm số y f (x) có bảng biến thiên nhƣ hình vẽ
Xét hàm số y g x f x 2019 ( ) 4 2018
. Số điểm cực trị của hàm số g(x) bằng A. 5 . B. 1. C. 9 . D. 2 .
Câu 35. Cho hàm số y f x có đạo hàm trên . Biết hàm số có đồ thị y f ' x nhƣ hình vẽ.
Hàm số g x f x x đạt cực tiểu tại điểm. I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N
A. x 1.
B. x 2.
C. không có điểm cực tiểu. D. x 0. NG
y f x
y f x CÔ Câu 36. Cho hàm số có đạo hàm trên và hàm số
có đồ thị là đƣờng cong Ờ N trong YỄ TRƢ hình vẽ dƣới đây GU N N ÁO VIÊ GI
Số điểm cực đại của hàm số g x f 3
x 3x là A. 5. B. 2. C. 3. D. 4.
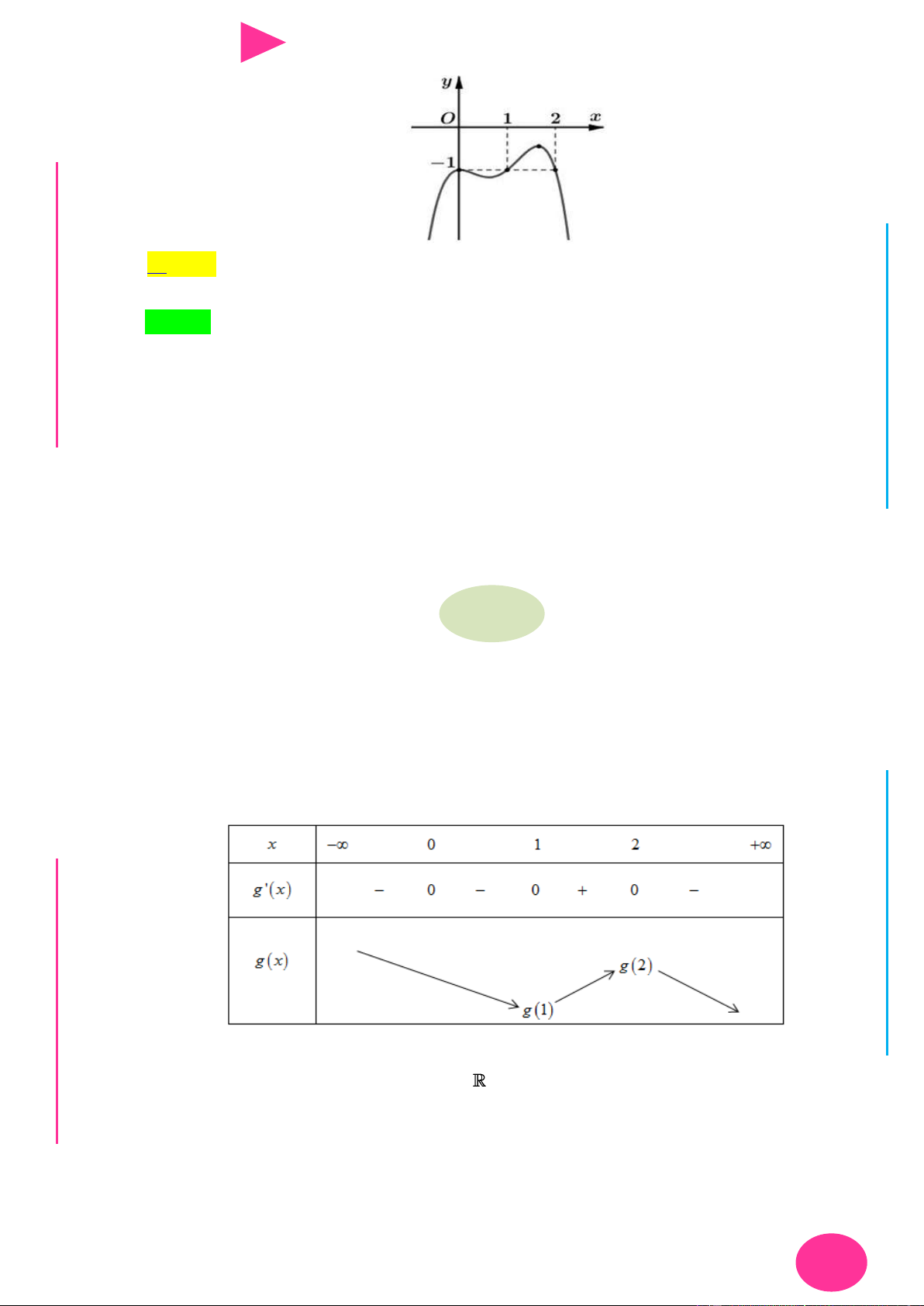
Câu 37. Cho hàm số y f (x) là một hàm đa thức có đồ thị nhƣ hình vẽ
TÌM CỰC TRỊ CỦA HÀM SỐ 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực trị của hàm số y f 2
x 2 x là A. 3. B. 4. C. 5. D. 6.
Câu 38. Cho hàm số y f x liên tục và có đạo hàm trên 0;6. Đồ thị của hàm số y f x
trên đoạn 0;6 đƣợc cho bởi hình bên dƣới. Hỏi hàm số 2 y f x có tối đa bao I Ơ nhiêu cực trị? M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ A. 7. B. 5. C. 4. D. 6. N
Câu 39. Cho hàm số 4 3 2 y
f x ax bx cx dx e . Biết rằng hàm số y f x liên tục trên YỄ TRƢ 2 GU N
và có đồ thị nhƣ hình vẽ bên. Hỏi hàm số y f 2x x có bao nhiêu điểm cực đại? N ÁO VIÊ GI A. 5 . B. 3 . C. 1. D. 2 .
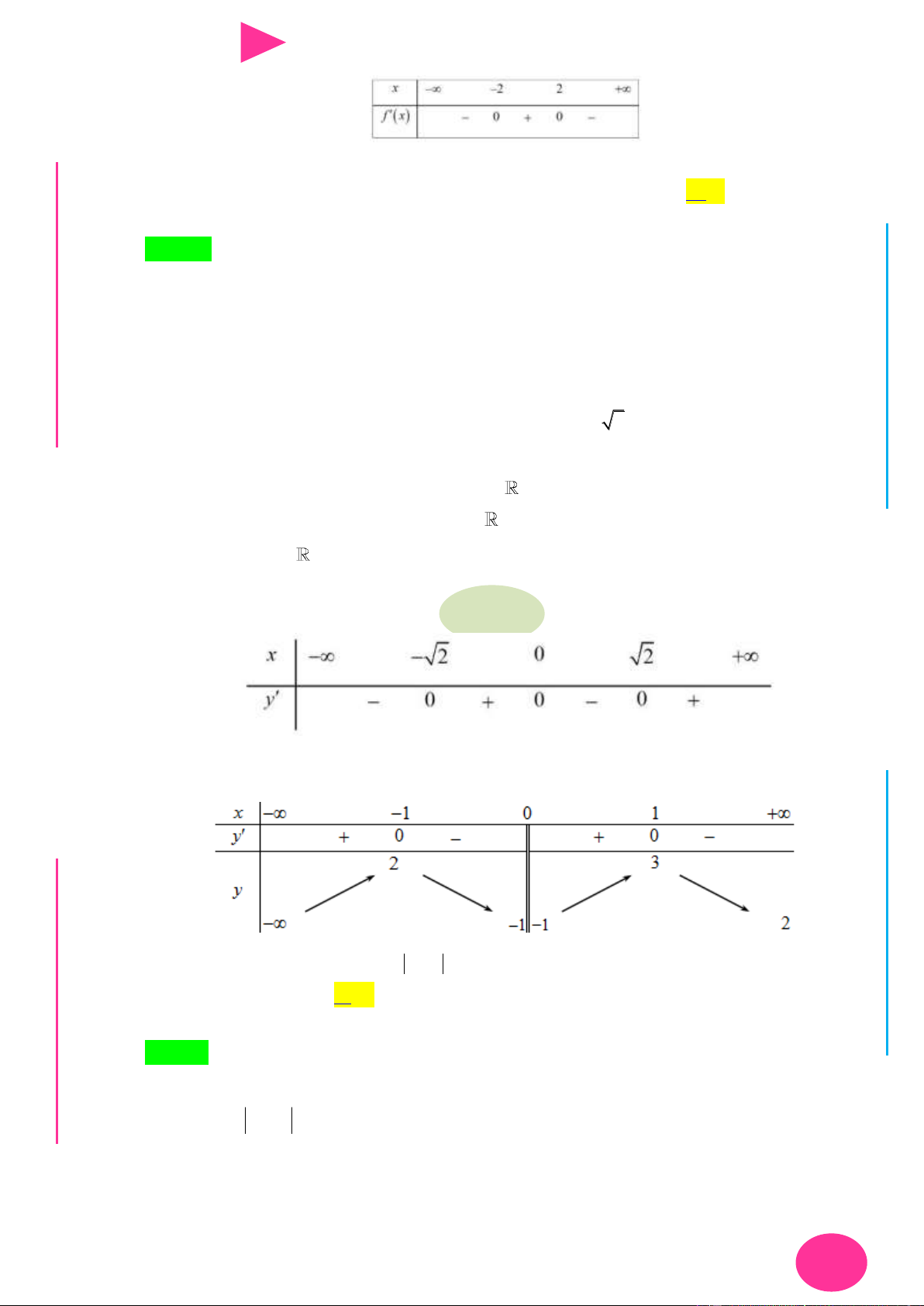
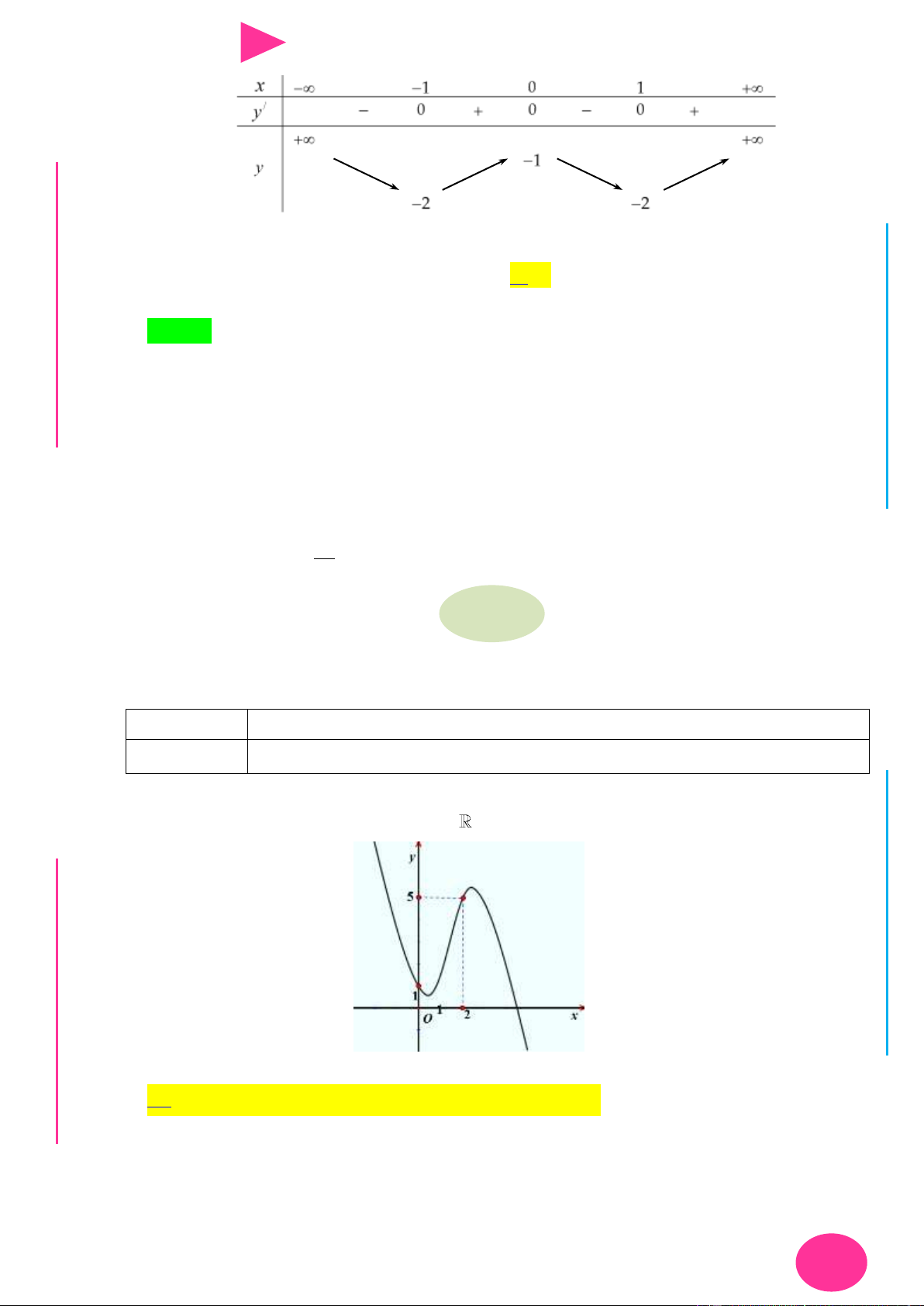
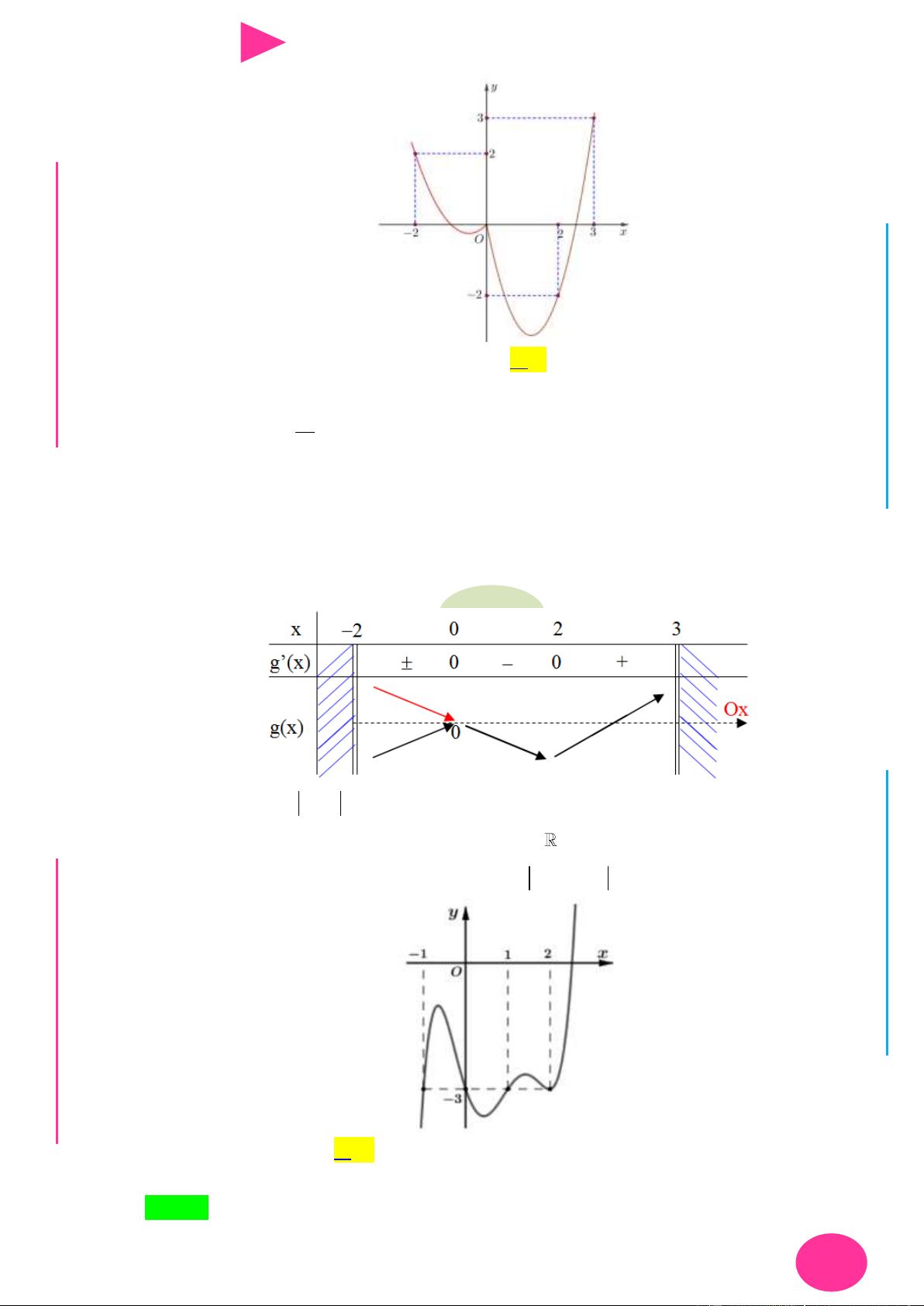
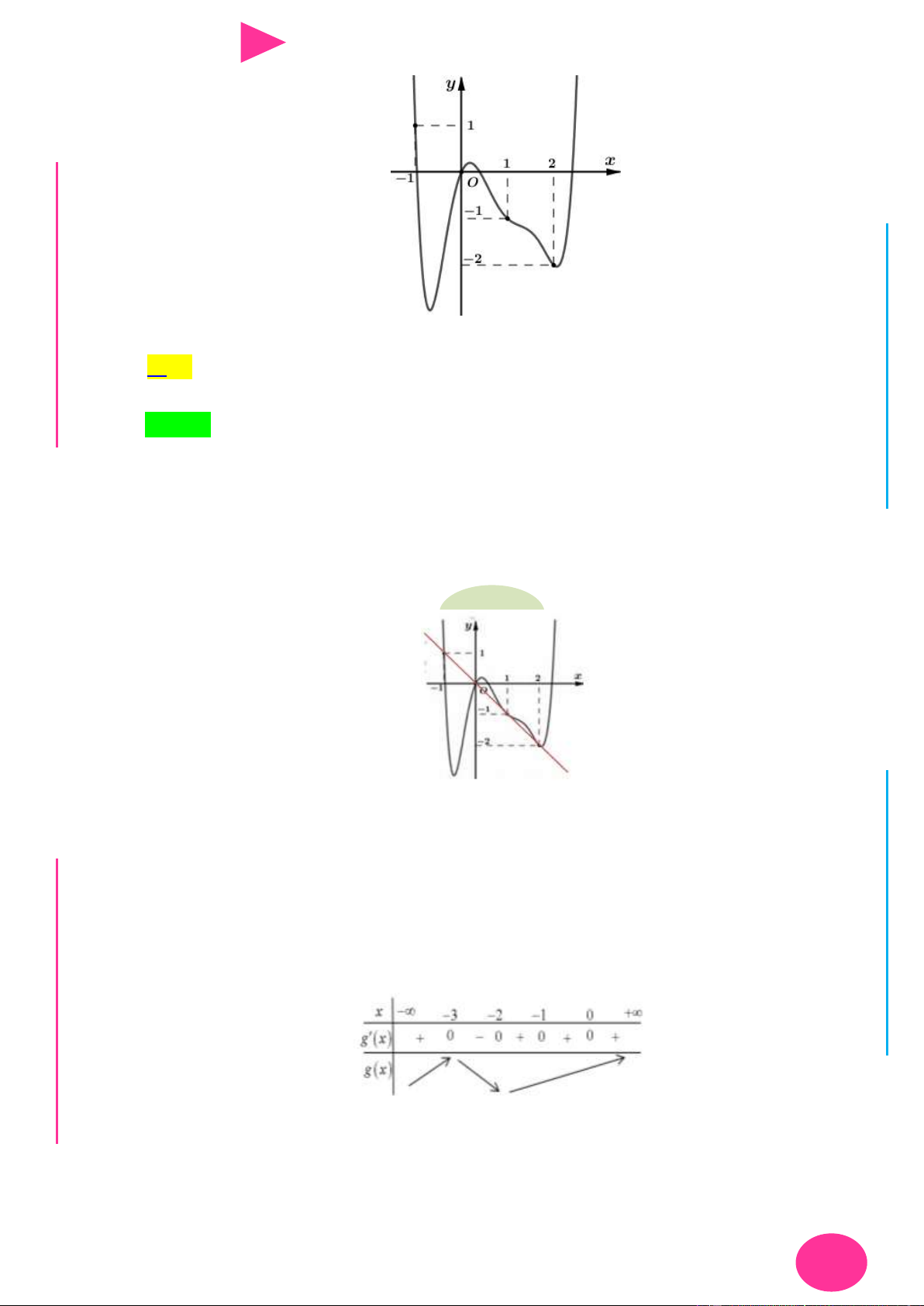
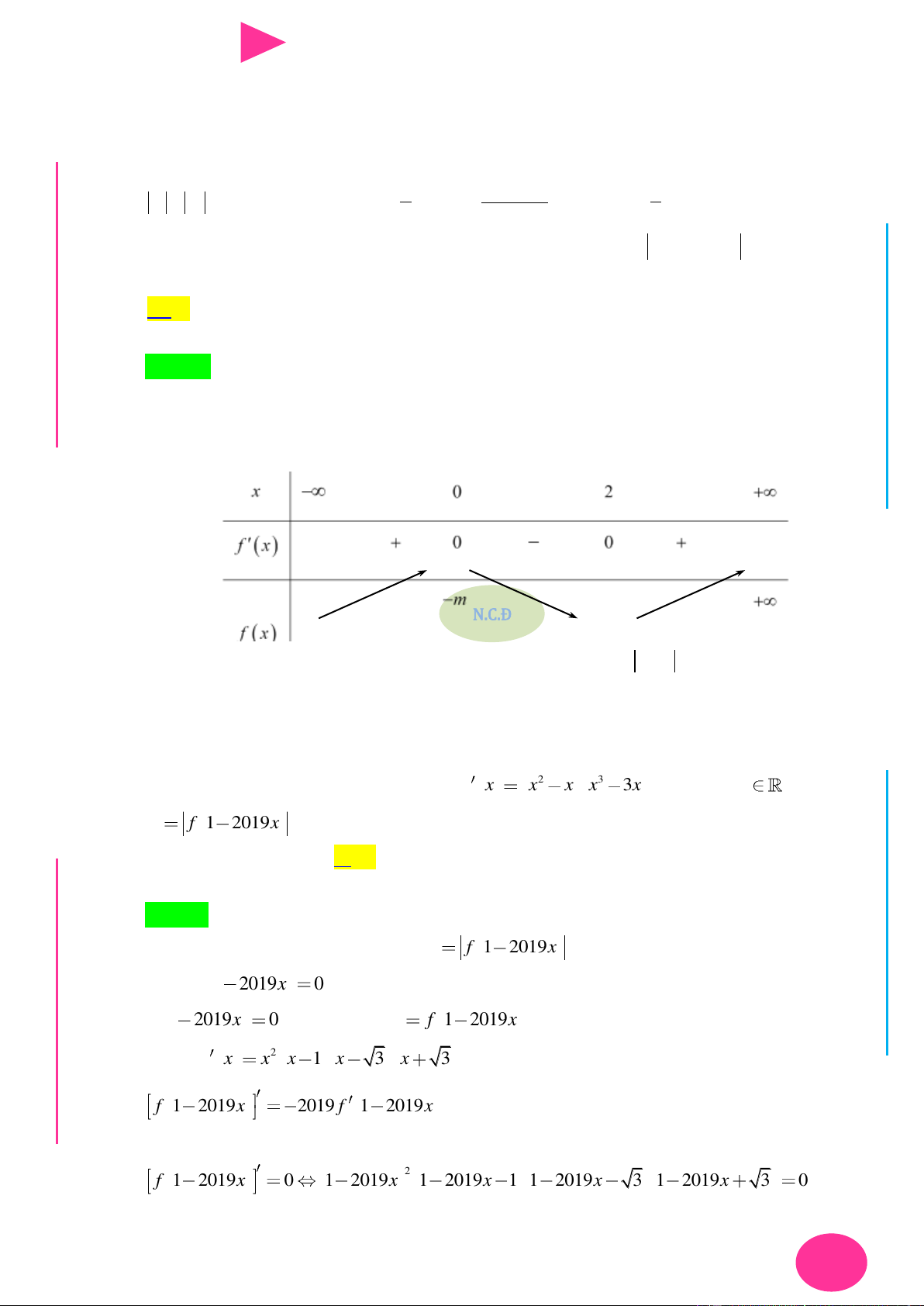
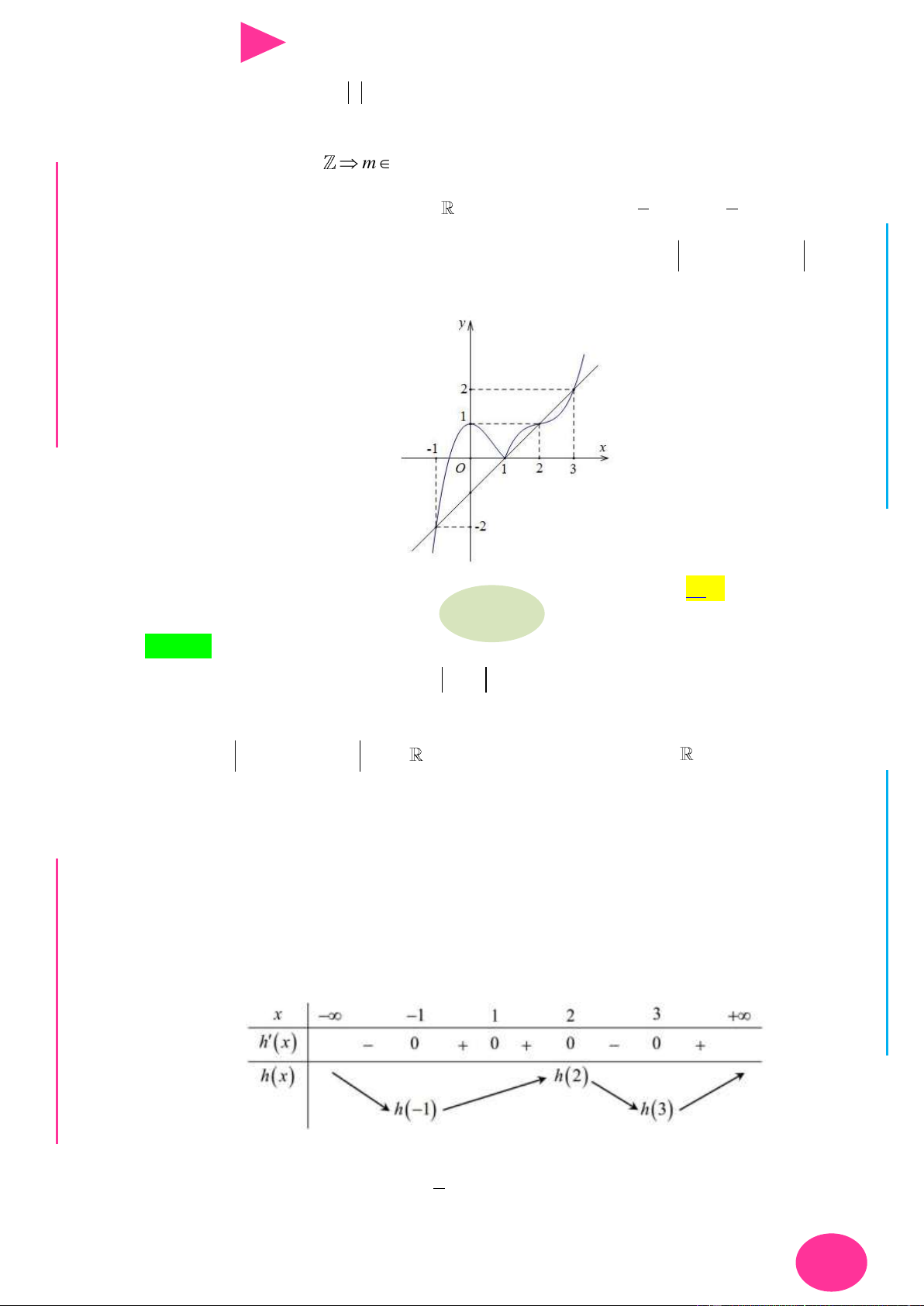
Câu 40. Cho hàm số y f (x) có bảng biến thiên nhƣ hình vẽ bên. Hàm số y f (x 3) đạt cực đại tại x -∞ -1 0 2 +∞ 1 1 f(x) -2 A. x 1
B. x 2 . C. x 0 . D. x 3 .
Câu 41. Cho hàm số y f x liên tục trên
và có đồ thị nhƣ hình vẽ. Hỏi đồ thị hàm số
y f x
TÌM CỰC TRỊ CỦA HÀM SỐ 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
có tất cả bao nhiêu điểm cực trị? A. 6 . B. 8 . C. 7. D. 9.
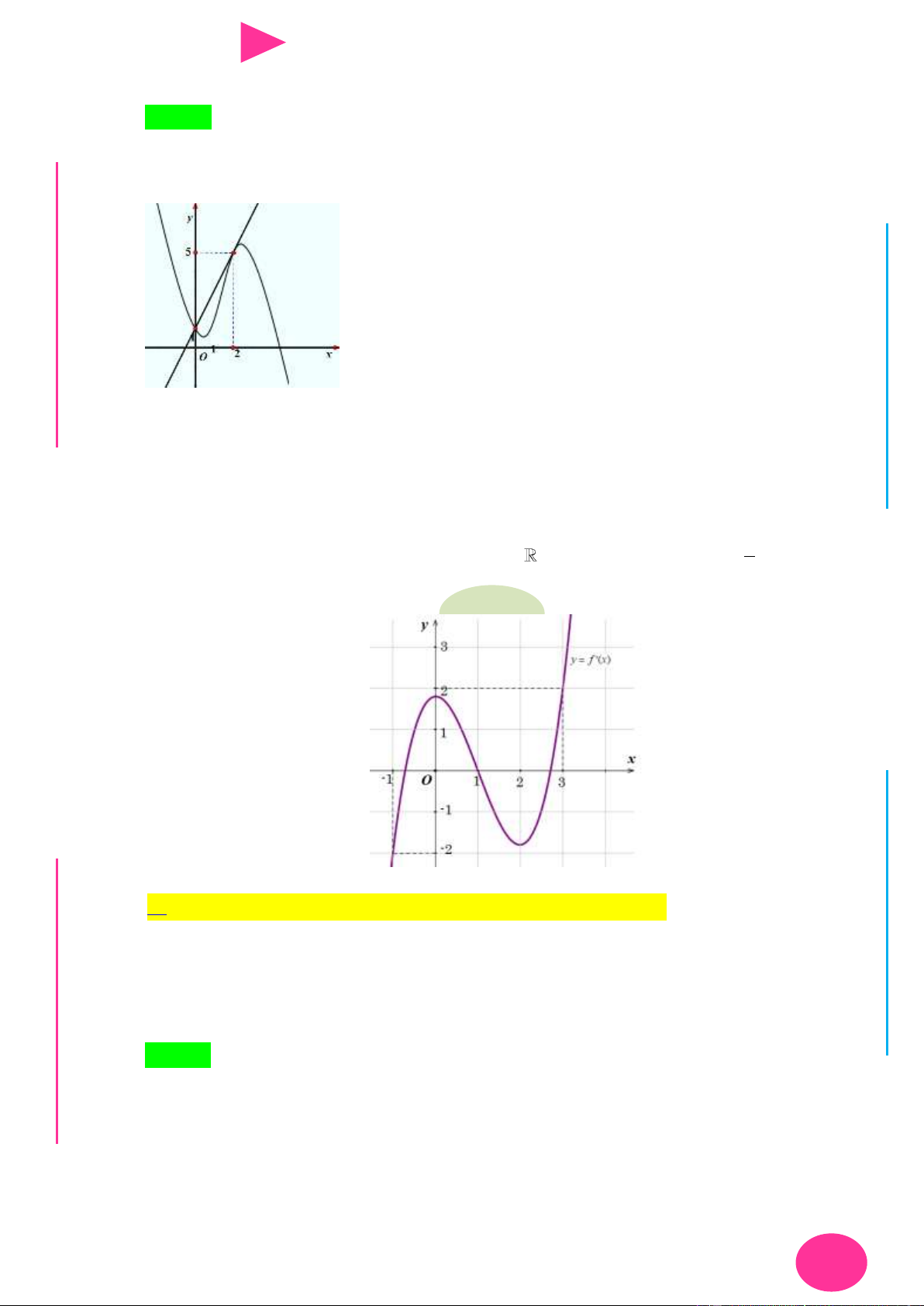
Câu 42. Cho hàm số f x có đồ thị hàm số y f ' x đƣợc cho nhƣ hình vẽ bên. Hàm số
y f x 1 2
x f 0 có nhiều nhất bao nhiêu điểm cực trị trong khoảng 2 ;3? I 2 Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N A. 6 . B. 8 . C. 3. D. 5.
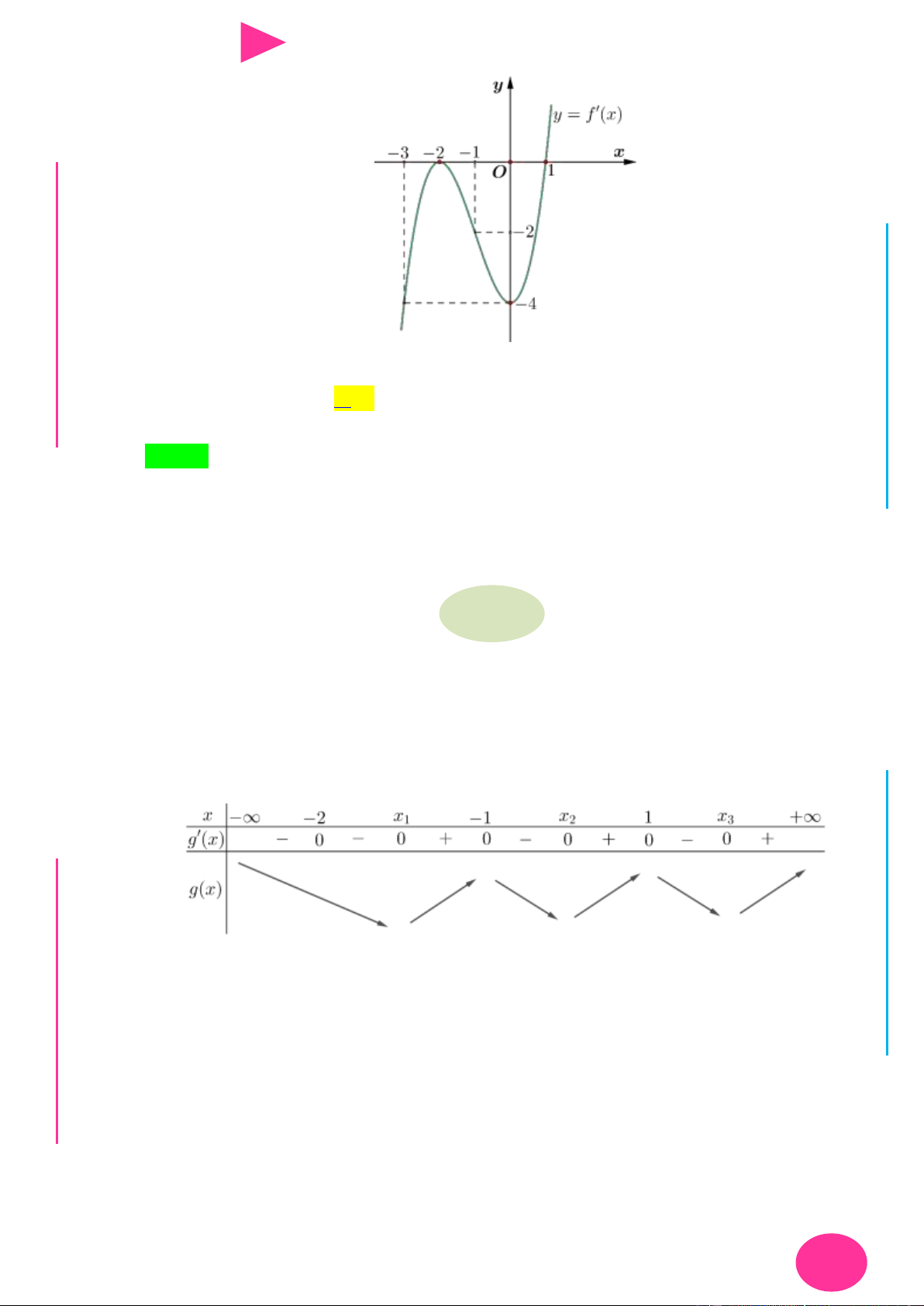
Câu 43. Cho hàm số đa thức y f x có đạo hàm trên
, f 0 0 và đồ thị hình bên dƣới là ÁO VIÊ
đồ thị của đạo hàm f x . Hỏi hàm số g x f x 3x có bao nhiêu điểm cực trị ? GI A. 4 . B. 5 . C. 3 . D. 6 .
Câu 44. Cho hàm số y f (x) có bảng biến thiên nhƣ sau:
TÌM CỰC TRỊ CỦA HÀM SỐ 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực tiểu của hàm số 3 2
g(x) 2 f (x) 4 f ( ) x 1 là A. 4 . B. 9 . C. 5 . D. 3 .
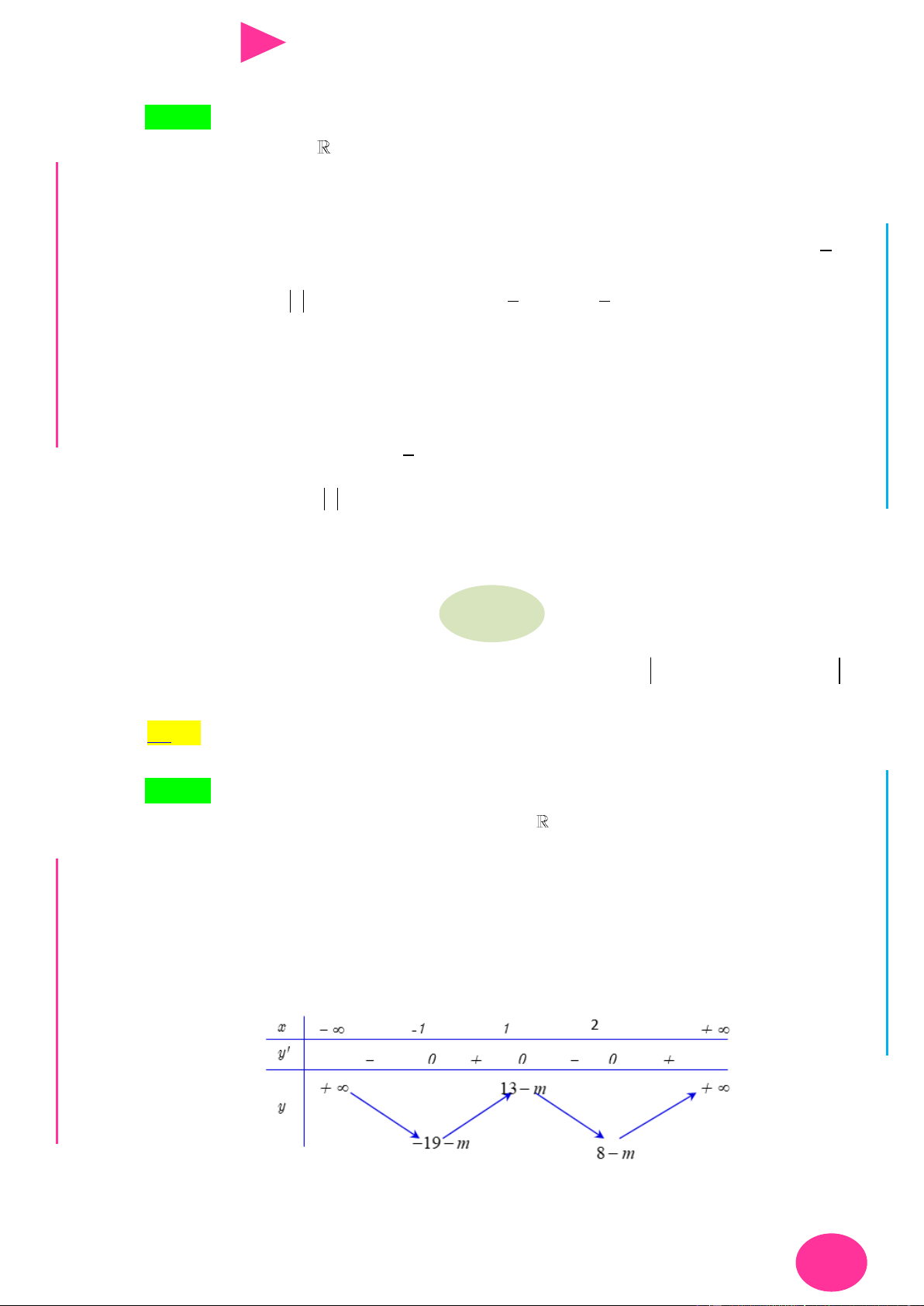
Câu 45. Cho hàm số đa thức 5 4 3 2
f x mx nx px qx hx r , , m , n , p , q ,
h r . Đồ thị hàm
số y f x (nhƣ hình vẽ bên dƣới) cắt trục hoành tại các điểm có hoành độ lần lƣợt là 3 5 11 1 ; ; ; . 2 2 3 I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ
Số điểm cực trị của hàm số g x f x m n p q h r là GU N N A. 6. B. 7. C. 8. D. 9.
Câu 46. Cho hàm số y f (x) có đồ thị nhƣ hình bên dƣới ÁO VIÊ GI
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m 1 00;100 để hàm số 2 (
h x) f (x 2) 4 f (x 2) 3m có đúng 3 điểm cực trị. Tổng giá trị của tất cả các phần
tử thuộc S bằng A. 5047 . B. 5049 . C. 5050 . D. 5043 .
TÌM CỰC TRỊ CỦA HÀM SỐ 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 47. Cho f (x) là một hàm đa thức và có đồ thị của hàm số f '(x) nhƣ hình vẽ bên. Hàm số 2
y 2 f (x) (x 1) có tối đa bao nhiêu điểm cực trị ? A. 9. B. 3. C. 7. D. 5.
Câu 48. Cho hàm số y f (x) có đạo hàm liên tục trên
và đồ thị hàm số y f (x) nhƣ hình vẽ I
bên. Tìm số điểm cực trị của hàm số 1 2019f f x y . Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N A. 13. B. 11. C. 10. D. 12. YỄ
TRƢ Câu 49. Cho hàm số y f x có đạo hàm trên . Đồ thị hàm số nhƣ hình vẽ bên dƣới. GU N N ÁO VIÊ GI
Số điểm cực tiểu của hàm số g x 2 f x 2 x 1 x 3 là A. 2 . B. 1. C. 3 . D. 4 .
TÌM CỰC TRỊ CỦA HÀM SỐ 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI Câu 1.
Biết M (0; 2) , N(2; 2
) là các điểm cực trị của đồ thị hàm số 3 2
y ax bx cx d . Tính
giá trị của hàm số tại x 3
A. y(3) 2 .
B. y(3) 11.
C. y(3) 0 . D. y(3) 3 Lời giải Chọn A Đạo hàm 2
y ' 3ax 2bx c y(0) 2 d 2 a 1 y(2) 2 8
a 4b 2c d 2 b 3
Từ giả thiết ta có y '(0) 0 c 0 c 0 y'(2) 0 1
2a 4b c 0 d 2 3 2
y x 3x 2 y(3) 2 I
Ơ Câu 2. Đồ thị hàm số 3 2
y x 3x 9x 1 có hai điểm cực trị A và B . Điểm nào dƣới đây
thuộc đƣờng thẳng AB ? M D Ầ
A. M 0; 1 . B. Q 1 ;10 .
C. P 1;0 .
D. N 1;10 . Đ NHỊ Lời giải Đ Chọn D G THPT N.C.Đ N
Cách 1: Xét hàm số y f x 3 2
x 3x 9x 1, f x 2
3x 6x 9. NG CÔ Ờ 1 1
Ta có f x x . f
x8x 2. N 3 3 YỄ TRƢ
Đồ thị hàm số f x có hai điểm cực trị A và B nên f x f x 0 . A B GU N N
y f x x A A 8 2 Suy ra A
y f x x B B 8 2 B ÁO VIÊ
Do đó phƣơng trình đƣờng thẳng AB là y 8 x 2 . GI
Khi đó ta có N 1;10 thuộc đƣờng thẳng AB . Chọn D
Cách 2: Xét hàm số y f x 3 2
x 3x 9x 1, f x 2
3x 6x 9. x f x 2
0 3x 6x 9 3 0 . x 1
Suy ra tọa độ hai điểm cực trị của đồ thị hàm số là A3; 26 và B 1 ;6 . Ta có AB 4
;32 cùng phƣơng với u 1 ;8 .
Phƣơng trình đƣờng thẳng AB đi qua B 1
;6 và nhận u 1
;8 làm vecto chỉ phƣơng x 1 t là t
y 6 8t
Khi đó ta có N 1;10 thuộc đƣờng thẳng AB . Chọn D
Câu 3. Hàm số f x 0 1 2 2 2019 2019 C
C x C x ... C x
có bao nhiêu điểm cực trị? 2019 2019 2019 2019
TÌM CỰC TRỊ CỦA HÀM SỐ 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 0 . B. 2018 . C. 1. D. 2019 . Lời giải Chọn A
Ta có: f x C C x C x ... C x 1 x2019 0 1 2 2 2019 2019 2019 2019 2019 2019 f x 2018 ' 2019.(1 x)
f 'x 0 x 1 Vì x 1
là nghiệm bội chẵn nên x 1
không phải là điểm cực trị của hàm số. Câu 4. Cho hàm số 1 2 2 10 10
f (x) 1 C x C x ... C x . Số điểm cực trị của hàm số đã cho bằng 10 10 10 A.10 . B. 0 . C. 9 . D.1 . Lời giải Chọn D
Áp dụng khai triển nhị thức Niu tơn, ta có: I 1 2 2 10 10 10
f (x) 1 C x C x ... C x (1 x) Ơ 10 10 10
f '(x) 101 x9 M D Ầ Bảng biến thiên Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N
Vậy hàm số đã cho có duy nhất một điểm cực trị x 1 . YỄ
TRƢ Câu 5. Giá trị cực đại của hàm số y x sin2x trên 0; là: GU N N 3 3 2 3 2 3 A. . B. . C. . D. . 3 2 6 2 3 2 3 2 ÁO VIÊ Lời giải GI Chọn A Ta có: y 1 1
2cos2x y 0 cos2x 2 2x
k2 x k . 2 3 3 2
Xét trên 0; ta có x và x . 3 3 Ta có y 4 sin 2x . y 2 3 0 nên x là điểm cực đại. 3 3 2 2 y 2 3 0 nên x là điểm cực tiểu. 3 3 3
Vậy giá trị cực đại là y . 3 3 2
Câu 6. Gọi A , B , C là các điểm cực trị của đồ thị hàm số 4 2
y x 2x 4 . Bán kính đƣờng
tròn nội tiếp tam giác ABC bằng
TÌM CỰC TRỊ CỦA HÀM SỐ 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 2 1. B. 2 . C. 2 1. D. 1. Lời giải Chọn C Cách 1: x 0 Ta có 3
y ' 4x 4x . Khi đó y 0 . x 1 Suy ra đồ thị hàm số 4 2
y x 2x 4 có ba điểm cực trị là A0;4 , B 1;3 và C 1 ; 3 .
Gọi I là tâm đƣờng tròn nội tiếp tam giác ABC , ta có BC.IA A . C IB A . B IC 0 . 4 3 2
Mà AB AC 2 và BC 2 nên suy ra I 0; . 1 2
Phƣơng trình đƣờng thẳng BC là y 3 .
Bán kính đƣờng tròn nội tiếp tam giác ABC là r d(I , BC) 2 1. I Cách 2: Ơ
Áp dụng công thức tính bán kính đƣờng tròn nội tiếp tam giác ABC ta có: M D S
( p a)( p b)( p c) ABC Ầ r 2 1 Đ p p NHỊ
a b c Đ
trong đó a BC 2; b c AB AC 2 ; p G 2 THPT N.C.Đ N Cách 3: NG CÔ Ờ
Áp dụng công thức tính bán kính đƣờng tròn nội tiếp tam giác ABC ta có: N A 3 ( 2 ) 8.1
r ( p a) tan 2 1 0 cosA 0 A 90 YỄ với . TRƢ 2 3 ( 2 ) 8 1 GU
N Câu 7. Cho hàm số 4 2
y x 2x 1 có đồ thị C . Biết rằng đồ thị C có ba điểm cực trị tạo N
thành ba đỉnh của một tam giác, gọi là . ABC Tính diện tích . ABC ÁO VIÊ 1 A. S 2 .
B. S 1. C. S . D. S 4 . GI 2 Lời giải Chọn B x 0 Ta có 3
y 4x 4 ; x y 0 x 1
Tọa độ các điểm cực trị của đồ thị hàm số là: A0; 1 , B 1
;0 , C 1;0 A . B AC 0 AB 1 ; 1 ; AC 1; 1 .
AB AC 2 1 Suy ra ABC
vuông cân tại A do đó S A . B AC 1. 2 Câu 8.
Cho hàm số y f (x) có đúng ba điểm cực trị là 2
; 1; 0 và có đạo hàm liên tục trên . Khi đó hàm số 2
y f (x 2x) có bao nhiêu điểm cực trị? A. 6. B. 4. C. 5. D. 3.
TÌM CỰC TRỊ CỦA HÀM SỐ 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn D
Do hàm số y f (x) có đúng ba điểm cực trị là 2
; 1; 0 và có đạo hàm liên tục trên nên f (
x) 0có ba nghiệm ( đơn hoặc bội lẻ) là x 2
; x 1; x 0.
Đặt g x 2
f x x gx x 2 ( 2 ) 2 2 . f (
x 2x) . Vì f (x) liên tục trên nên g (x) cũng liên tục trên
. Do đó những điểm g (
x) có thể đổi dấu thuộc tập các điểm thỏa mãn 2x 2 0 x 1 2 x 2x 2
x 0 . Ba nghiệm trên đều là nghiệm đơn hoặc bội lẻ nên hàm số g(x) 2 x 2x 1 x 2 2
x 2x 0 có ba điểm cực trị.
I Câu 9. Cho hàm số 2 3 ( ) ( 1) x f x x x
e có một nguyên hàm là hàm số F(x) . Số điểm cực trị của Ơ
hàm số F(x) là M D A. 1. B. 2 . C. 3 . D. 0 . Ầ Đ Lời giải NHỊ Chọn A Đ f x F x F x f x G
Hàm số có TXĐ là , có một nguyên hàm là hàm số '( ) ( ) , THPT N.C.Đ N x NG x nên 2 3 (
) 0 ( ) 0 ( 1) x F x f x x x e 0 0 . CÔ Ờ x 1 N
Ta có bảng xét dấu F ( x) nhƣ sau YỄ TRƢ GU N N ÁO VIÊ
Dựa vào bảng trên, ta thấy hàm số F(x) có một điểm cực trị. GI x
Câu 10. Số điểm cực trị của hàm số y sin x , x ; là 4 A. 2 . B. 4 . C. 3 . D. 5 . Lời giải Chọn D x
Xét hàm số y f x sin x với x ; . 4 x x ; 0 1 1 2
Ta có f x 1
cos x . f x 0 cos x . 4 4 x x 0; 2 2 f x x 15 x 15 1 1 sin x 0 . 1 1 4 4 4 4 8
TÌM CỰC TRỊ CỦA HÀM SỐ 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 f x x 15 x 15 2 2 sin x 0. 2 2 4 4 4 4 8 BBT
Dựa vào bảng biến thiên, ta thấy hàm số có hai điểm cực trị và đồ thị hàm số cắt trục I hoành tại Ơ x
ba điểm phân biệt khác x , x . Suy ra hàm số y sin x , với x
; có 5 điểm cực 1 2 M D 4 Ầ Đ trị. NHỊ
Câu 11. Biết phƣơng trình 3 2
ax bx cx d 0 a 0 có đúng hai nghiệm thực. Hỏi đồ thị ĐG hàm số 3 2
y ax bx cx d có bao nhiêu điểm cực trị? THPT N.C.Đ N A. NG 4 . B. 5 . C. 2 . D. 3 . CÔ Ờ Lời giải N Chọn D YỄ TRƢ Phƣơng trình 3 2
ax bx cx d 0 , a 0 là sự tƣơng giao của đồ thị hàm số GU N N 3 2
ax bx cx d 0 , a 0 và trục hoành. Do phƣơng trình 3 2
ax bx cx d 0 , a 0 có đúng hai nghiệm thực nên phƣơng ÁO VIÊ trình 3 2 2
ax bx cx d 0 có thể viết dƣới dạng a x x x x
0 với x , x là hai 1 2 GI 1 2
nghiệm thực của phƣơng trình (giả sử x x ). Khi đó đồ thị hàm số 1 2 3 2
y ax bx cx d a 0 tiếp xúc trục hoành tại điểm có hoành độ x và cắt trục 1
hoành tại điểm có hoành độ x . 2 Đồ thị hàm số 3 2
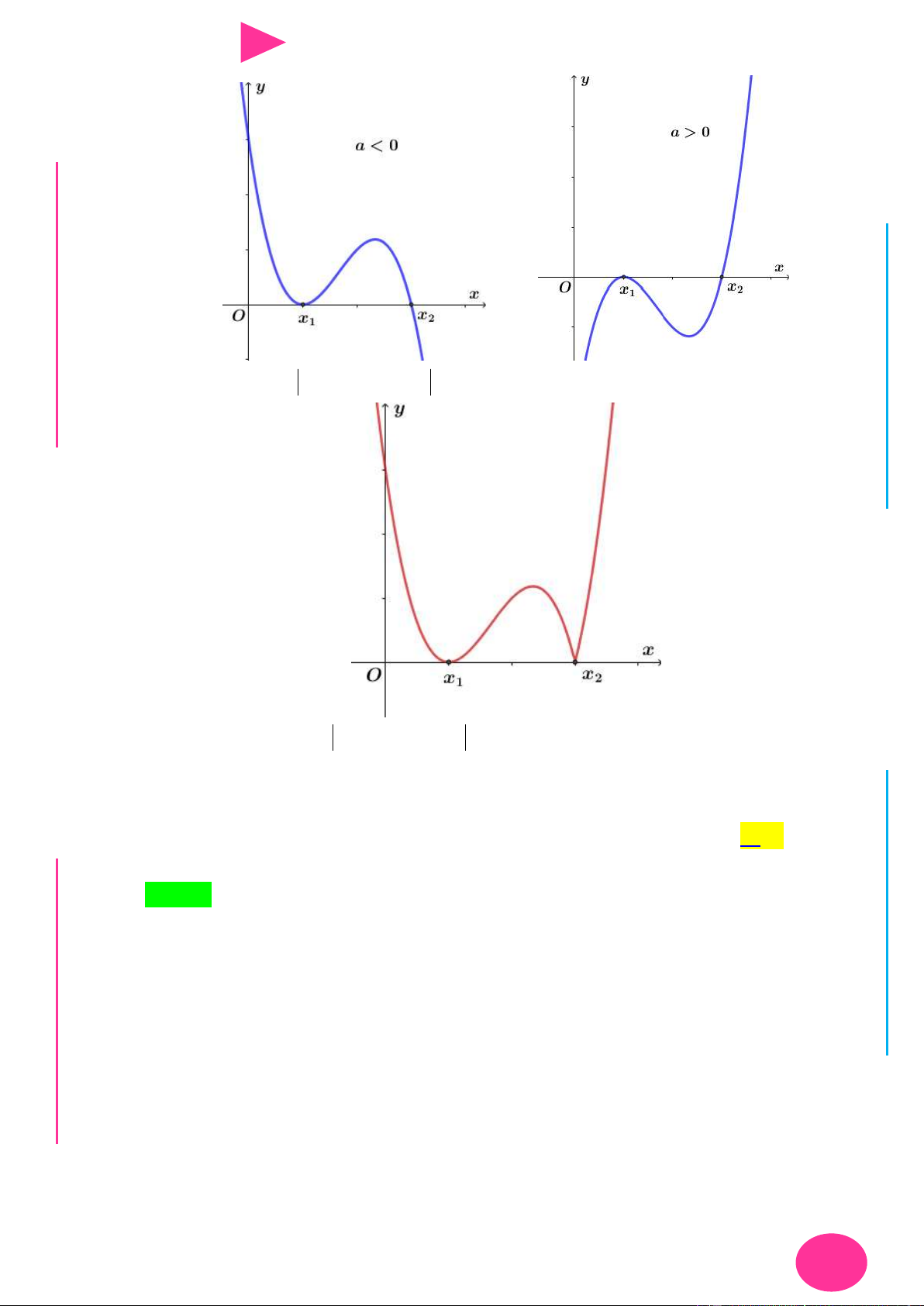
y ax bx cx d a 0 ứng với từng trƣờng hợp a 0 và a 0 :
TÌM CỰC TRỊ CỦA HÀM SỐ 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Đồ thị hàm số 3 2
y ax bx cx d a 0 tƣơng ứng là I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ 3 2
y ax bx cx d a 0 GU N Vậy đồ thị hàm số
có tất cả 3 điểm cực trị. N Câu 12. Cho hàm số 3 2
f (x) ax bx cx d có đồ thị nhƣ hình vẽ bên. Số điểm cực trị của hàm số 2 y f ( 2
x 4x) là. ÁO VIÊ GI A. 3 . B. 4 . C. 2 . D. 5 . Lời giải Chọn D
Quan sát đồ thị f (x) , ta thấy hàm số có hai điểm cực trị x 2
; x 0 vì vậy 2
f '(x) 3ax 2bx c có hai nghiệm x 2
; x 0 nên f '(x) 3a(x 2)x . Ta có : 2 2 2
y ' f ( 2
x 4x) ' ( 4
x 4) f '( 2
x 2x) ( 4 x 4)( 2 x 4x) . 2 2 3a( 4 x 4)( 2 x 4x)( 2
x 4x 2) 2 y ' 4
8ax(x 2)(x 1)(x 2x 1) .
TÌM CỰC TRỊ CỦA HÀM SỐ 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 0 x 1
y ' 0 x 2
và dấu của y ' đổi khi x qua mỗi nghiệm trên. Vậy hàm số đã cho có x 1 2 x 1 2 5 điểm cực trị. 1 1
Câu 13. Biết rằng đồ thị hàm số 2 y x 3x
có ba điểm cực trị thuộc một đƣờng tròn C . 2 x
Bán kính của C gần đúng với giá trị nào dƣới đây? A. 12, 4 . B. 6, 4 . C. 4, 4 . D. 27 . Lời giải Chọn B I
TXĐ: D ;0 0; Ơ 3 2 1 x 3x 1
y x 3 2 2 M D x x Ầ x 2,8794 Đ 1 3 2 NH Ị y 0 x 3x 1 0 x 0, 6527 . 2 Đ x 0 ,5321 3 G THPT N.C.Đ N
Tọa độ các điểm cực trị: A 2,879; 4,84, B 0,653;3,277,C 0 ,532;3,617 . NG CÔ Ờ Gọi C 2 2
: x y 2ax 2by c 0
1 là đƣờng tròn đi qua ba điểm cực trị . N Thay tọa độ ba điểm , A , B C vào
1 ta đƣợc hệ phƣơng trình 3 ẩn sau: YỄ TRƢ GU N 5
,758a 9,68b c 31,71 a 5,374 N 1
,306a 6,554b c 11,17 b 1,0833 1
,064a 7,234b c 13,37 c 11 , 25 ÁO VIÊ 2 2 GI
R a b c 41,3 6,4 Chọn B
Câu 14. Cho hàm số y f x có đạo hàm f x x 2 3 x 1 2x, x . Hỏi hàm số
y f x 2
x 1 có bao nhiêu điểm cực tiểu. A. 2. B. 3. C. 4. D. 1. Lời giải Chọn D
Ta có f x 3 2
x 3x 3x 3 y f x 2 2x 3
x 4x 3 . 2 13
y 0 x ; 3 2 13 2 13 y 6
x 4 ; y 2 13 0 ; y 2 13 0 3 3
Suy ra hàm số có 1 điểm cực tiểu.
TÌM CỰC TRỊ CỦA HÀM SỐ 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 15. Cho hàm số 4 2
f x ax bx c với a 0 , c 2018 và a b c 2018. Số điểm cực trị
của hàm số y f x 2018 là A. 1. B. 3 . C. 5 . D. 7 . Lời giải Chọn D
Xét hàm số g x f x 4 2
2018 ax bx c 2018 . a 0 a 0 Ta có c 2018 b 0 .
a b 0 hàm số y g x là hàm trùng phƣơng
a b c 2018 c 2018 có 3 điểm cực trị.
Mà g 0 c 2018 g 0 0 , g
1 a b c 2018 0 g x g 1 0 đồ thị CT I hàm số y
g x cắt trục hoành tại 4 điểm phân biệt. Ơ
Đồ thị hàm số y g x có dáng điệu nhƣ sau M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N
Từ đồ thị y g x , ta giữ nguyên phần phía trên trục Ox , phần dƣới trục Ox ta lấy YỄ TRƢ
đối xứng qua trục Ox , ta đƣợc đồ thị hàm số y g x . GU N N ÁO VIÊ GI
Từ đó ta nhận thấy đồ thị y g x có 7 điểm cực trị. x
Câu 16. Hàm số f x
m (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực 2 x 1 trị? A. 2 . B. 3 . C. 5 . D. 4 . Lời giải Chọn D x
Xét hàm số g x m 2 x , TXĐ: . 1
TÌM CỰC TRỊ CỦA HÀM SỐ 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 1 x x
Ta có g x ; g x 1 0 . 1 x 2 2 x 1 Bảng biến thiên
Từ bảng biến thiên ta có hàm số y g x luôn có hai điểm cực trị. x
Xét phƣơng trình g x 0 2
m 0 mx x m 0 2 x , phƣơng trình này có 1 nhiều nhất hai nghiệm. I
Vậy hàm số f x có nhiều nhất bốn điểm cực trị.
Ơ Câu 17. Cho hàm số y f x có đạo hàm f x 2x 1x4 với mọi x . Hàm số M D
g x f 3 x có bao nhiêu điểm cực đại? Ầ Đ A. 0. B. 1. C. 2. D. 3. NHỊĐ Lời giải G THPT N.C.Đ Chọn B N NG
Từ giả thiết, ta có bảng biến thiên của hàm số f x CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ
Ta có g x f 3 x g x f 3 x . GI
Từ bảng biến thiên của hàm số f x ta có 3 x 1 x 4
g x 0 f 3 x 0 . 1 3 x 4 1 x 2
Nhƣ thế ta có bảng biến thiên của hàm số g x
Từ bảng biến thiên, ta nhận thấy hàm số g x có một điểm cực đại.
Câu 18. Cho hàm số y f (x) có đạo hàm liên tục trên
và bảng xét dấu đạo hàm
TÌM CỰC TRỊ CỦA HÀM SỐ 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Hàm số 4 2 6 4 2
y 3 f (x 4x 6) 2x 3x 12x có tất cả bao nhiêu điểm cực tiểu? A. 3. B. 0. C. 1. D. 2. Lời giải Chọn D Có 3 4 2 5 3 y (
12x 24x). f (x 4x 6) 12x 12x 24x 2 4 2 x x
f x x x 4 2 12 ( 2). ( 4 6) 12
x x 2 2 x x 4 2
f x x 2 12 ( 2). ( 4 6) x 1 . x 0 x 0 Khi đó 4 2 2
y ' 0 f (
x 4x 6) (x 1) 0 x 2 . 2 I x 2 0 4 2 2 f (
x 4x 6) x 1 Ơ Ta có 4 2 2 2
x 4x 6 (
x 2) 2 2 , x . M D Do đó 4 2 f (
x 4x 6) f 2 0, x . Ầ Đ Mà 2 x 1 1, x . NHỊ Do đó phƣơng trình 4 2 2
f '(x 4x 6) x 1vô nghiệm. Đ 2 G THPT Hàm số 4 2 6 4
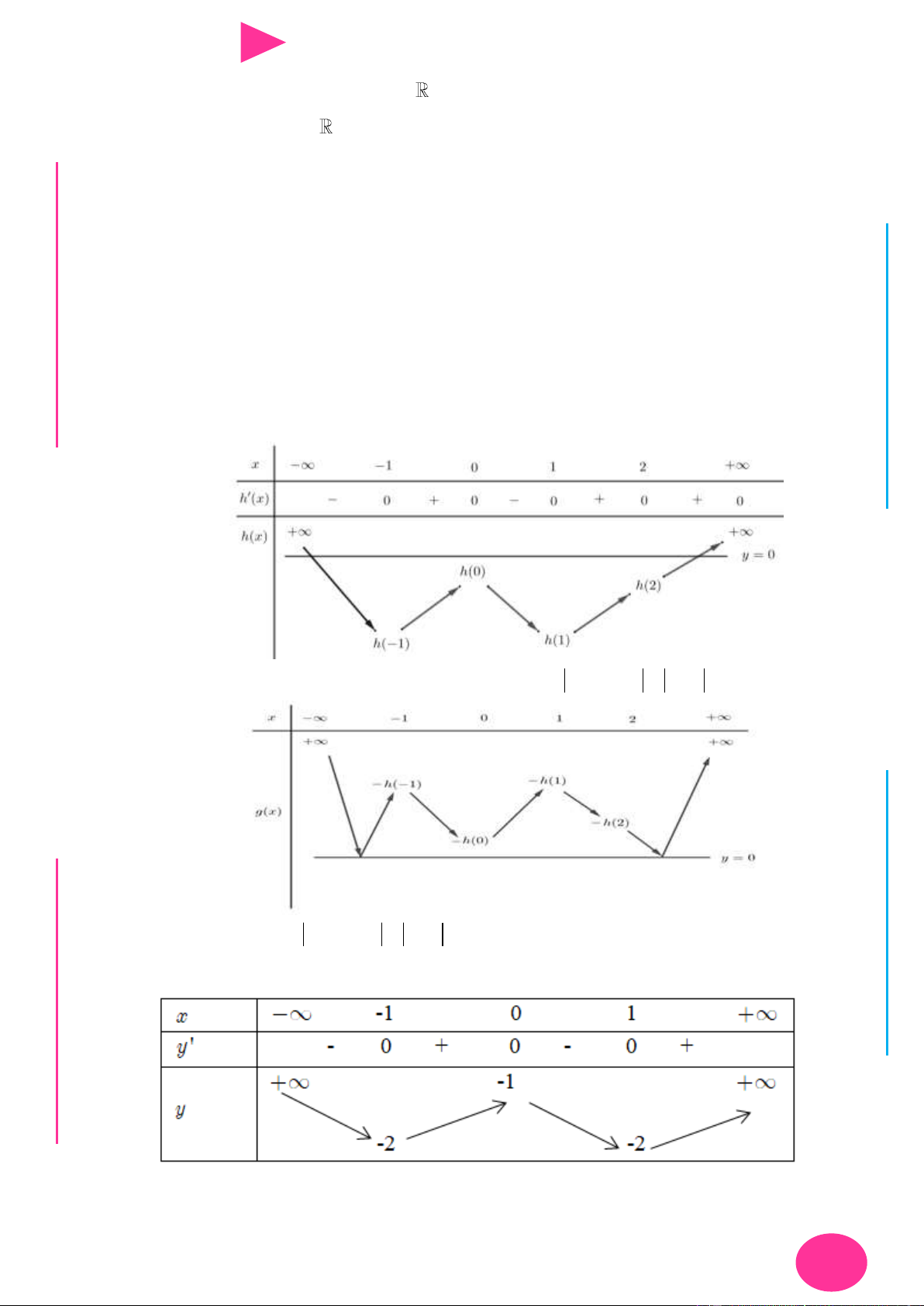
y 3 f (x 4x 6) 2x 3x N .C 1 .Đ
2x có bảng xét dấu đạo hàm nhƣ sau N NG CÔ Ờ N YỄ TRƢ GU N N Vậy hàm số 4 2 6 4 2 y 3 f ( x 4x 6) 2x 3x
12x có 2 điểm cực tiểu.
Câu 19. Cho hàm số y f (x) có bảng biến thiên nhƣ sau ÁO VIÊ GI
Số điểm cực trị của hàm số y f (x) là A. 7 . B. 5 . C. 6 . D. 8 . Lời giải Chọn B
Gọi đồ thị của hàm số y f x là C .
Đặt g x f x và gọi C là đồ thị của hàm số y g x . Đồ thị C đƣợc suy ra
từ đồ thị C nhƣ sau:
+) Giữ nguyên phần đồ thị của C phía trên Ox ta đƣợc phần I.
TÌM CỰC TRỊ CỦA HÀM SỐ 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
+) Với phần đồ thị của C phía dƣới Ox ta lấy đối xứng qua Ox , ta đƣợc phần II.
Hợp của phần I và phần II ta đƣợc C .
Từ cách suy ra đồ thị của C từ C , kết hợp với bảng biến thiên của hàm số
y f x ta có bảng biến thiên của hàm số y g x f x nhƣ sau:
Từ bảng biến thiên ta thấy hàm số y f (x) có 5 điểm cực trị.
Câu 20. Cho hàm số y f x có bảng xét dấu của f x I Ơ M D Ầ x Đ
Hỏi hàm số g x f x 3 2 1
x 3x đạt cực tiểu tại điểm nào dƣới đây? NH 3 Ị Đ A. x 1 .
B. x 3.
C. x 2 . D. x 3 . G THPT N.C.Đ Lời giải N NG Chọn B CÔ Ờ N f 2 0 YỄ y f x x x x f 2 TRƢ Ta có:
đạt cực tiểu tại 2,
5 và đạt cực đại tại 2 , nên : 0 . GU N f 5 0 N g
1 f 2 0 0 g3 ÁO VIÊ 0
+ g x f x 2 1
x 2x 3 . GI g
2 f 1 3 0 g 3
f 4 12 0 g '
1 f ' 2 4 0
Mặt khác: g ' x f ' 1 x 2x 2 g
f . ' 3 ' 2 4 0
Vậy hàm số đã cho đạt cực tiểu tại x 3.
Câu 21. Cho hàm số y f (x) có đạo hàm liên tục trên
. Đồ thị hàm số y f ( x) nhƣ hình vẽ sau:
TÌM CỰC TRỊ CỦA HÀM SỐ 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực trị của hàm số y f (x) 5x là A. 3 . B. 4 . C. 1. D. 2 . Lời giải Chọn C I Ơ
Ta có y f (x) 5x . Suy ra y f ( x) 5 .
Số điểm cực trị của hàm số y f (x) 5x là số nghiệm bội lẻ của phƣơng trình y 0 . M D Ầ
Ta có y f (
x) 5 0 f (x) 5. Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
Dựa vào đồ thị ta có y f (
x) cắt đƣờng thẳng y 5 tại duy nhất một điểm. Suy ra số
điểm cực trị của hàm số y f (x) 5x là 1.
Câu 22. Cho hàm số y f x là hàm số bậc bốn. Hàm số y f x có đồ thị nhƣ hình bên. Số
điểm cực trị của hàm số f 2
x 2x 2019 là y -1 O 1 3 x
TÌM CỰC TRỊ CỦA HÀM SỐ 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 3. B. 2. C. 1. D. 4. Lời giải Chọn C x 1
Từ đồ thị hàm số y f x ta thấy f x 0 x 1 . x 3 Bảng biến thiên I Ơ
Xét hàm số g x f 2
x 2x 2019 . M D Ầ x 1
g x f 2x 2 2
x 2x 2019 .
f 2x 2x 2019. . Đ 2
2 x 2x 2019 2
x 2x 2019 NHỊ x 1 Đ
g x 0 f 2
x 2x 2019 . 0 2 G THPT x 2 N x .C .Đ 20 19 N 2 2 NG
x 2x 2019 1vn x 2x 2019 1 2 CÔ f
x 2x 2019 Ờ 0 2 2 N
x 2x 2018 0vn x 2x 2019 1 x 1 YỄ TRƢ 0 2 2
x 2x 2019 3
x 2x 2010 0vn 2
x 2x 2019 GU N x 1 x 1 N x 1 .
Từ đồ thị hàm số y f x ta có: x 3 thì f x 0. ÁO VIÊ GI Mà 2
x 2x 2019 2018 3 nên f 2
x 2x 2019 0 với x . Bảng biến thiên
Vậy g x chỉ đổi dấu qua nghiệm x 1
. Số điểm cực trị của hàm số là 1.
Câu 23. Cho hàm số y f (x) có đồ thị nhƣ hình vẽ dƣới đây:
TÌM CỰC TRỊ CỦA HÀM SỐ 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 f x 1 f x
Tìm số điểm cực đại của hàm số y 2019 2018 A. 1. B. 3. C. 0. D. 2. Lời giải Chọn D I f x 1 f x Ơ
Xét hàm số y g x 2019 . 2018 M D f x 1 1 f x Ầ
Ta có: g' x f ' x ln f ' x 2019 ln 2019 Đ 2018 2018 NHỊ f x 1 1 Đ f 'x f x ln 2019 ln 2019 1 G THPT 2018 2018 N.C.Đ N f x NG 1 1 f x CÔ Ờ Ta có: ln 2019 ln 2019 0; x 2 . N 2018 2018 YỄ TRƢ Xét phƣơng trình: GU N f x 1 1 N
g' x 0 f ' x f x ln 2019 ln 2019
0 f 'x 0 . 2018 2018 ÁO VIÊ
Dựa vào đồ thị hàm số y f (x) ta thấy hàm số có một điểm cực đại và hai điểm cực GI tiểu. Mà từ
1 và 2 ta thấy g ' x trái dấu với f ' x .
Vậy hàm số y g x có hai điểm cực đại và một điểm cực tiểu. 3 2
Câu 24. Cho hàm số y
f (x) có đạo hàm tại x
, hàm số f (x) x ax bx c
Có đồ thị ( nhƣ hình vẽ )
Số điểm cực trị của hàm số y f f x là A. 7 . B. 11. C. 9 . D. 8 .
TÌM CỰC TRỊ CỦA HÀM SỐ 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn A
Quan sát đồ thị, nhận thấy đồ thị hàm số 3 2 f (
x) x ax bx c đi qua các điểm
O 0;0; A 1
;0; B1;0. Khi đó ta có hệ phƣơng trình: c 0 a 0 a b 1 b 1
f x 3
x x f x 2 3x 1. a b 1 c 0
Đặt: g x f f x 3
Ta có: g x f f x f f x f x 3
x x 3 x x 2 . 3x 1
xx x 3
x x 3
x x 2 1 1 1 1 3x 1 x 0 x 0 I x 1 Ơ x 1 x 1 x 1 M D
g x 0
x a ( 0,76) 3 Ầ
x x 1 0 Đ x b b 1 ,32 3
x x 1 0 NH Ị 1 2 Đ 3x 1 0 x 3 G THPT N.C.Đ N Ta có bảng biến thiên: NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
* Cách xét dấu g x : chọn x 21; ta có: g2 0 g x 0 x
1; , từ đó
suy ra dấu của g x trên các khoảng còn lại.
Dựa vào BBT suy ra hàm số có 7 điểm cực trị.
* Trắc nghiệm: Số điểm cực trị bằng số nghiệm đơn ( nghiệm bội lẻ) của phƣơng trình
đa thức g x 0. PT g x 0 có 7 nghiệm phân biệt nên hàm số đã cho có 7 điểm cực trị.
Câu 25. Cho hàm số y f x có đạo hàm trên và có đồ thị là đƣờng cong nhƣ hình vẽ. Đặt
g x 3 f f x 4 . Tìm số điểm cực trị của hàm số g x?
TÌM CỰC TRỊ CỦA HÀM SỐ 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 y 3 1 1 2 3 4 O x A. 2 . B. 8 . C. 10 . D. 6 . Lời giải Chọn B I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N
g x 3 f f x. f x . N
f x 0
f f x ÁO VIÊ 0
f x a
g x 0 3 f f x. f x 0
, 2 a 3 . GI f x 0 x 0 x a
f x 0 có 3 nghiệm đơn phân biệt x , x , x khác 0 và a . 1 2 3
Vì 2 a 3 nên f x a có 3 nghiệm đơn phân biệt x , x , x khác x , x , x , 0 , a . 4 5 6 1 2 3
Suy ra g x 0 có 8 nghiệm đơn phân biệt. Do đó hàm số g x 3 f f x 4 có 8 điểm cực trị.
Câu 26. Cho hàm số y f (
x 1) có đồ thị nhƣ hình vẽ.
TÌM CỰC TRỊ CỦA HÀM SỐ 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Hàm số
2 f x 4x y
đạt cực tiểu tại điểm nào? A. x 1. B. x 0 . C. x 2 . D. x 1 . Lời giải: Chọn B 2 f x 4 x I Ta có: y 2 f x 4 ln . Ơ
y 0 2 f x 4 0 f x 2 . M D
Đồ thị hàm số y f x nhận đƣợc từ việc tịnh tiến đồ thị hàm số y f x 1 sang Ầ Đ trái 1 đơn vị NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ x 2 GI
nên f x 2 x 0 . x 1 Do x 2
và x 1 là nghiệm bội chẵn nên ta có bảng biến thiên sau: x 2 0 1 y 0 0 0 y
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại x 0 .
Câu 27. Cho hàm số y f x có đồ thị nhƣ hình vẽ. Số điểm cực trị của hàm số
y 2 f x 5 3 là
TÌM CỰC TRỊ CỦA HÀM SỐ 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 2 . B. 3 . C. 5 . D. 7 . Lời giải Chọn C I
2 2 f x 5 f ' x
y 2 f x 5 3 2 f x 52 Ơ Ta có 3. Khi đó y' .
2 f x 52 M D Ầ
Xét f ' x 0 dựa vào đồ thị có hai nghiệm x 0; x 2 . Đ NHỊ Xét f x f x 5 2 5 0 ( )
dựa vào đồ thị có ba nghiệm x , x , x thỏa mãn 1 2 3 Đ 2 G THPT x x x N.C.Đ 0 2 . 1 2 3 N NG
Khi đó hàm số y 2 f x 5 3 có bảng biến thiên: CÔ Ờ N x x x x 1 0 2 2 3 YỄ TRƢ y ' - + 0 - + 0 - + GU N N y ÁO VIÊ
Do đó hàm số y 2 f x 5 3 có 5 điểm cực trị. GI
Câu 28. Cho hàm số y f x , hàm số y f x có đồ thị nhƣ hình vẽ. Hàm số g x 5sin x 1 x 2 5sin 1 2 f 3
có bao nhiêu điểm cực trị trên khoảng 0; 2 ? 2 4
TÌM CỰC TRỊ CỦA HÀM SỐ 29
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 9 . B. 7 . C. 6 . D. 8 . I Lời giải Ơ Chọn B M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI 2
5sin x 1 5sin x 1
Ta có g x 2 f 3 2 2 cos x 0
g x 5cos x 5sin x 1 5sin x 1 2 f 2. 0 5sin x 1 5sin x 1 2 2 2 2 f 2. 0 2 2 5sin x 1 Đặt t
vì x 0;2 t 3 ;2 2 t 1 1 5sin x 1 5sin x 1 t Khi đó : 2 f 2. 0
thành f t t 3 2 2 t 1 t 3
TÌM CỰC TRỊ CỦA HÀM SỐ 30
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 5sin x 1 3
x 0;2 1 t 1
1 sin x 2 5 x 0; 2 2 Với . 1 5sin x 1 1 1 x 0;2 3 t
sin x 3 2 3 3 x 0; 2 4 Với . 5sin x 1 1 x 0;2 5 t 1 1
sin x 2 5 x 0; 2 6 Với . 5sin x 1 3 t 3 3 sin x 1 x 0;2 Với 2 2 . x 0;2 2 cos x 0 3 x 0;2 2 . I Ơ 3 Vì x
là nghiệm kép nên không là điểm cực trị của hàm số y g x . 2 M D
Vậy hàm số y g x có 7 điểm cực trị trên khoảng 0; 2 . Ầ Đ 3 2 2 NH
Câu 29. Cho hàm số y f x biết f x x x
1 x 2mx m 6 . Số giá trị nguyên của tham ỊĐ
số m để hàm số đã cho có đúng một điểm cực trị là G THPT N.C.Đ N A. 7 . B. 5 . C. 6 . D. 4 . NG Lời giải CÔ Ờ N Chọn A YỄ TRƢ x 0 GU N
Cho f x 0 x 1 . N g x 2
x 2mx m 6 0 ÁO VIÊ
Trong đó x 0 là nghiệm bội chẵn và x 1 là nghiệm bội lẻ. GI
Hàm số đã có một cực trị khi và chỉ khi f x đổi dấu một lần khi và chỉ khi f x 0
có một nghiệm bội lẻ.
+ Trƣờng hợp 1: Phƣơng trình g x 0 vô nghiệm hoặc có nghiệm kép: Khi đó: 2
0 m m6 0 2 m 3.
+ Trƣờng hợp 2: g x 0 có hai nghiệm phân biệt, trong đó có 1 nghiệm x 1 1
Với x 1, ta có: g
1 1 2m m 6 0 m 7 . 1 x 1
Với m 7 g x 2
x 14x 13 0 (thỏa mãn) x 13 Vậy m 2 ; 3
7 , mà m m 2 ; 1 ;0;1;2;3; 7 .
Câu 30. Cho hàm số y f x có bảng biến thiên nhƣ sau:
TÌM CỰC TRỊ CỦA HÀM SỐ 31
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 3 2
Số điểm cực tiểu của hàm số g x 2 f x 4 f x 1 là A. 4 . B. 9 . C. 5 . D. 3 Lời giải Chọn C 2
Đạo hàm: g x 6 f x f x 8 f x f x . x 1 x 0 I x 1 Ơ
f x 0 x x 1 1 M D
g x 0 f x 0 x x 1 . 2 Ầ Đ f x 4 x x ( 1 x x ) 3 3 1 NHỊ 3 x x 1 x 0 4 4 Đ
x x 0 x 1 5 5 G THPT N.C.Đ N
x x 1 x x 6 6 2 NG CÔ Ờ Bảng biến thiên: N YỄ TRƢ x x x 1
x 0 x 1 x x 1 3 4 5 6 2 GU N / N g x
0 0 0 0 0 0 0 0 0
Dựa vào bảng biến thiên, hàm số g x có 5 điểm cực tiểu.
ÁO VIÊ Câu 31. Cho hàm số y f x có đạo hàm trên và đồ thị của hàm số y f x nhƣ hình bên. GI
Khẳng định nào dƣới đây đúng ?
A. Hàm số y f x 2
x x 2019 đạt cực đại tại x 0 .
B. Hàm số y f x 2
x x 2019 đạt cực tiểu tại x 0 .
C. Hàm số y f x 2
x x 2019 không có cực trị.
D. Hàm số y f x 2
x x 2019 không có cực trị tại x 0 .
TÌM CỰC TRỊ CỦA HÀM SỐ 32
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn D
Ta có y f x 2x 1.
Cho y 0 f x 2x 1 1 .
Dựa vào đồ thị của hàm số y f x và đƣờng thẳng y 2x 1 ta có thể nhận thấy phƣơng trình
1 có ít nhất 2 nghiệm là x 0 và x 2 . I Ơ
Xét dấu x 10;2 , ta có y 1 f
1 5 0 từ đó ta nhận định hàm số
y f x 2 M D x
x 2019 đạt cực đại tại x 0 . Ta chọn đáp án A. Ầ Đ 1
Câu 32. Cho hàm số y f (x) liên tục trên tập số thực và hàm số 2
g(x) f (x)
x x 1. Biết NH 2 Ị Đ
đồ thị của hàm số y f (
x) nhƣ hình vẽ dƣới đây G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
Khẳng định nào sau đây đúng ?
A. Đồ thị hàm số y g(x) có 2 điểm cực tiểu và 1 điểm cực đại.
B. Đồ thị hàm số y g(x) có 2 điểm cực tiểu và không có điểm cực đại.
C. Đồ thị hàm số y g(x) có 1 điểm cực tiểu và 2 điểm cực đại.
D. Đồ thị hàm số y g(x) có 3 điểm cực tiểu và 1 điểm cực đại. Lời giải Chọn A Ta có g (
x) f (x) x 1 . g (
x) 0 f (x) x 1 đây là phƣơng trình hoành độ giao điểm của đồ thị hàm số y f (
x) và đƣờng thẳng y x 1.
TÌM CỰC TRỊ CỦA HÀM SỐ 33
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Từ đồ thị hàm số y f (
x) và đƣờng thẳng y x 1 ta có g ( )
x 0 x 1
, x 1, x 3 Bảng biến thiên - ∞ x -1 1 3 +∞ I Ơ g'(x) - 0 + 0 - 0 + M D g(1) g(x) Ầ Đ g(-1) g(3) NH Ị Đ
Từ bảng biến thiên suy ra đồ thị hàm số y g(x) có 2 điểm cực tiểu và 1 điểm cực đại. G THPT N.C.Đ y f x 0;6
y f x N Câu 33. Cho hàm số
liên tục và có đạo hàm trên . Đồ thị của hàm số NG CÔ Ờ
trên đoạn 0;6 đƣợc cho bởi hình bên dƣới. Hỏi hàm số y f x 2 2019 có tối đa N
bao nhiêu điểm cực trị trên đoạn 0;6 . YỄ TRƢ GU N N ÁO VIÊ GI A. 7 . B. 6 . C. 4 . D. 3 . Lời giải Chọn A
f x 0
Ta có y 2 f x f x ; y 0 . f x 0 x 1
Từ đồ thị của hàm số y f x trên đoạn 0;6 suy ra f x 0 x 3 . x 5
Bảng biến thiên của hàm số y f x trên đoạn 0;6 :
TÌM CỰC TRỊ CỦA HÀM SỐ 34
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Từ bảng biến thiên suy ra phƣơng trình f x 0 có tối đa 4 nghiệm phân biệt trong
0;6 là x 0;1 , x 1;3 , x 3;5 , x 5;6 . 4 3 2 1
Vậy hàm số y f x 2 2019
có tối đa 7 điểm cực trị trên đoạn 0; 6 .
Câu 34. Cho hàm số y f (x) có bảng biến thiên nhƣ hình vẽ I Ơ M D
Xét hàm số y g x f x 2019 ( ) 4 2018
. Số điểm cực trị của hàm số g(x) bằng Ầ Đ A. 5 . B. 1. C. 9 . D. 2 . NHỊĐ Lời giải G THPT N.C.Đ Chọn A N C y f x NG
Gọi ( ) là đồ thị của hàm số ( ) . CÔ Ờ N Khi đó hàm số y
f x 4 có đồ thị (C ') với (C ') là ảnh của (C) qua phép tịnh tiến YỄ TRƢ sang phải 4 đơn vị. GU N
Từ bảng biến thiên của hàm y f (x) suy ra bảng biến thiên của hàm số y f x 4 N là : ÁO VIÊ GI
Từ đó suy ra bảng biến thiên của hàm số y f x 4 là
Vậy hàm số y f x 4 cho có 5 cực trị.
Do đó hàm số y g x f x 2019 ( ) 4 2018 có 5 cực trị.
Câu 35. Cho hàm số y f x có đạo hàm trên . Biết hàm số có đồ thị y f ' x nhƣ hình vẽ.
Hàm số g x f x x đạt cực tiểu tại điểm.
TÌM CỰC TRỊ CỦA HÀM SỐ 35
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
A. x 1.
B. x 2.
C. không có điểm cực tiểu. D. x 0. Lời giải Chọn A
Ta có g ' x f ' x 1. Khi đó g ' x 0 f ' x 1 (1).
Nghiệm của (1) là hoành độ giao điểm của đồ thị hàm số y f ' x và đƣờng thẳng y 1 . I
Dựa vào đồ thị hàm số y f ' x , ta thấy đồ thị hàm số y f ' x và đƣờng thẳng Ơ y 1 có M D x 0 Ầ Đ
ba điểm chung có hoành độ là 0;1; 2 . Do đó f ' x 1 x 1 . NHỊ x 2 Đ G THPT x 0 N.C.Đ N
Suy ra g ' x 0 x 1 . NG CÔ Ờ x 2 N Trên ;1
đƣờng thẳng y 1
tiếp xúc hoặc nằm trên đồ thị hàm số y f 'x . YỄ TRƢ GU N
Trên 1;2 đƣờng thẳng y 1 nằm dƣới đồ thị hàm số y f ' x . N
Trên 2; đƣờng thẳng y 1
nằm trên đồ thị hàm số y f 'x. Ta có bảng biến thiên ÁO VIÊ GI
Từ bảng biến thiên suy ra hàm số g x đạt cực tiểu tại điểm x 1.
Câu 36. Cho hàm số y f x có đạo hàm trên
và hàm số y f x có đồ thị là đƣờng cong trong hình vẽ dƣới đây
TÌM CỰC TRỊ CỦA HÀM SỐ 36
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực đại của hàm số g x f 3
x 3x là A. 5. B. 2. C. 3. D. 4. Lời giải I Chọn B Ơ 3 3x 3 0 (1)
Ta có: g x 2
x f 3 3 3
x 3x, g x 0 M D f ' 3
x 3x 0 (2) Ầ Đ (1) x 1 . NHỊ 3 Đ
x 3x 2
Dựa vào đồ thị đã cho thì (2) G THPT 3 N.C.Đ x 3x 1 N NG x 1 CÔ Ờ Trong đó phƣơng trình 3 x 3x 2 . N x 2 YỄ TRƢ Còn phƣơng trình: 3
x 3x 1 có 3 nghiệm phân biệt: 2 x 1 , 1 x 0 và 1 2 GU N 1 x 2 N 3
Ta có bảng biến thiên của hàm số g x ÁO VIÊ GI
Vậy hàm số g x có 2 điểm cực đại
Câu 37. Cho hàm số y f (x) là một hàm đa thức có đồ thị nhƣ hình vẽ
TÌM CỰC TRỊ CỦA HÀM SỐ 37
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực trị của hàm số y f 2
x 2 x là A. 3. B. 4. C. 5. D. 6. Lời giải I Ơ Chọn C ' 2 2 ' 2 f M D
Xét hàm số f x 2x có x 2x 2x 1 f x 2x Ầ Đ ' x 1 2 NH
Cho f x 2x 0 Ị ' f 2 x 2x 0 Đ G THPT N.C.Đ
Dựa theo đồ thị hàm số f (x) , ta thấy f (x) có 2 cực trị tại x 1 ;x 1. Do đó N NG x 1 2 CÔ Ờ x 2x 1 ' N f x 2x 2 2 0 x 1 2 2 x 2x 1 YỄ TRƢ x 1 GU N ' 2 N
+ Với 1 2 x 1 2 thì 2 2 0 x 1 2 1
x 2x 1. Khi đó, f x 2 x 0
(theo đồ thị hàm số f (x) ) ÁO VIÊ
+ Với x 1 2 hay x 1 2 thì 2 2 x 1
2 x 2x 1. Khi đó, 'f 2
x 2 x 0 (theo GI
đồ thị hàm số f (x) ) '
Từ đó, ta có bảng xét dấu của f 2
x 2 x
Bảng biến thiên của y f 2
x 2 x nhƣ sau
Vậy hàm số y f 2
x 2 x có 5 cực trị.
TÌM CỰC TRỊ CỦA HÀM SỐ 38
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 38. Cho hàm số y f x liên tục và có đạo hàm trên 0;6. Đồ thị của hàm số y f x
trên đoạn 0;6 đƣợc cho bởi hình bên dƣới. Hỏi hàm số 2 y f x có tối đa bao nhiêu cực trị? A. 7. B. 5. C. 4. D. 6. Lời giải Chọn A I Ta có 2 y f x
y 2 f x. f x. Ơ
f x 0 y 0 M D f x 0 Ầ Đ
f x 0 x 1;3; 5 . NHỊĐ
Dựa vào đồ thị hàm số của y f x ta có bảng biến thiên của hàm số y f x trên G THPT N.C.Đ N đoạn 0;6 là NG CÔ Ờ
Từ bảng biến thiên, ta thấy phƣơng trình f x 0 có tối đa bốn nghiệm phân biệt với N
0 x 1 x 3 x 5 x 6 . 1 2 3 4 YỄ TRƢ
Do đó, phƣơng trình y 0 có tối đa 7 nghiệm phân biệt và đều là nghiệm đơn. GU N N
Vậy hàm số 2 y f x
có tối đa 7 cực trị.
Câu 39. Cho hàm số 4 3 2 y
f x ax bx cx dx e . Biết rằng hàm số y f x liên tục trên ÁO VIÊ GI
và có đồ thị nhƣ hình vẽ bên. Hỏi hàm số y f 2
2x x có bao nhiêu điểm cực đại? A. 5 . B. 3 . C. 1. D. 2 . Lời giải Chọn C x 1 2 2x x 4 x 1
Ta có: y x f 2 2 2 .
2x x 0 . 2
2x x 1 x 1 5 2
2x x 4
TÌM CỰC TRỊ CỦA HÀM SỐ 39
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Suy ra hàm số có 1 cực đại.
Lưu ý: Ở bài toán này, vấn đề mấu chốt là chúng ta phải xét dấu đƣợc lƣợng f 2 2x x .
Câu 40. Cho hàm số y f (x) có bảng biến thiên nhƣ hình vẽ bên. Hàm số y f (x 3) đạt cực đại tại x -∞ -1 0 2 +∞ 1 1 I f(x) Ơ M D -2 Ầ Đ A. x 1
B. x 2 . C. x 0 . D. x 3 . NHỊ Lời giải Đ G Chọn D THPT N.C.Đ N
Đặt x 3 t . NG CÔ Ờ Ta thấy f
x 3 f (x 3) f (t) nên để hàm số y f x đạt cực đại thì N ( 3) YỄ TRƢ hàm số y
f (t) phải đạt cực tiểu GU N
Theo bảng biến thiên thì hàm số y f (t) đạt cực tiểu tại t 0 N
Suy ra hàm số y f (x 3) đạt cực đại tại x 3 0 hay x 3
Câu 41. Cho hàm số y f x liên tục trên
và có đồ thị nhƣ hình vẽ. Hỏi đồ thị hàm số ÁO VIÊ GI
y f x
có tất cả bao nhiêu điểm cực trị? A. 6 . B. 8 . C. 7. D. 9.
TÌM CỰC TRỊ CỦA HÀM SỐ 40
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn C
Gọi các nghiệm của phƣơng trình f x 0 lần lƣợt là x ; x ; x trong đó 1 2 3
x 0 x 1 x . 1 2 3
f x, x
0; x x ; 2 3 f
x khi f x 0
f x, x x ; x 2 3 y . f
x khi f x 0 f
x, x ;
x x ;0 3 2 f x, x
x ;x 3 2
f x, x
0; x x ; 2 3
f x, x x ; x 2 3 y f x, x ;
x x ;0 3 2 f
x, x
x ;x 3 2 I Ơ
y 0 x 1 x 0 M D Ầ
y không xác định tại x x 2 Đ x x NH 3 Ị Đ
Khi đó ta có bảng biến thiên của hàm số y f x nhƣ sau: G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N
Nên hàm số có 7 cực trị. Cách 2: ÁO VIÊ
Hàm số y f x có một cực trị dƣơng là x 1và phƣơng trình f x 0 có 2 nghiệm GI
dƣơng nên hàm số y f x có 3 cực trị và phƣơng trình f x 0 có 4 nghiệm nên
hàm số y f x có 7 cực trị.
Cách khác: Từ đồ thị của hàm số y f x
TÌM CỰC TRỊ CỦA HÀM SỐ 41
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Ta có đồ thị hàm số y f x là: I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N
Và đồ thị hàm số y f x là: N ÁO VIÊ GI
Từ đồ thị suy ra hàm số y f x có 7 điểm cực trị.
Câu 42. Cho hàm số f x có đồ thị hàm số y f ' x đƣợc cho nhƣ hình vẽ bên. Hàm số
y f x 1 2
x f 0 có nhiều nhất bao nhiêu điểm cực trị trong khoảng 2 ;3? 2
TÌM CỰC TRỊ CỦA HÀM SỐ 42
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 6 . B. 8 . C. 3. D. 5. Bài giải 2 x
Đặt g x f x f 0 2 I Ơ x 2 (L)
Ta có: g ' x f ' x x , g ' x 0 x 0 M D Ầ x 2 Đ NH
( Nhận xét: x 2 là nghiệm bội lẻ, x 0 có thể nghiệm bội lẻ hoặc nghiệm bội chẳn tuy nhiên ỊĐ
không ảnh hưởng đáp số bài toán) G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N
Suy ra hàm số y g x có nhiều nhất 3 điểm cực trị trong khoảng 2 ;3 ÁO VIÊ
GI Câu 43. Cho hàm số đa thức y f x có đạo hàm trên , f 0 0 và đồ thị hình bên dƣới là
đồ thị của đạo hàm f x . Hỏi hàm số g x f x 3x có bao nhiêu điểm cực trị ? A. 4 . B. 5 . C. 3 . D. 6 . Lời giải Chọn B
TÌM CỰC TRỊ CỦA HÀM SỐ 43
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Xét hàm số h x f x 3x , x .
h x f x 3 , x . x 1
h x f x x 0 0 3 . x 1 x 2
Với x 2 là nghiệm kép vì qua nghiệm x 2 thì h x không đổi dấu. f x 3 x ; 1 0 ;1
Dựa vào đồ thị hàm số của f x , ta có: . f x 3 x 1
;0 1;2 2;
Mặt khác h0 f 0 3.0 0 .
Bảng biến thiên của hàm h x f x 3x : I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N
Từ đó ta suy ra bảng biến thiên của hàm số g x f x 3x h x : YỄ TRƢ GU N N ÁO VIÊ GI
Hàm số g x f x 3x hx có 5 điểm cực trị.
Câu 44. Cho hàm số y f (x) có bảng biến thiên nhƣ sau:
Số điểm cực tiểu của hàm số 3 2
g(x) 2 f (x) 4 f ( ) x 1 là
TÌM CỰC TRỊ CỦA HÀM SỐ 44
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 4 . B. 9 . C. 5 . D. 3 . Lời giải Chọn C 2
g '(x) 6 f '( ) x f ( ) x 8 f '( ) x f ( ) x 2 f '( ) x f ( ) x 3 f ( ) x 4 . f '(x) 0 g '(x) 0 f (x) 0 . 4
f (x) 3
Từ bảng biến thiên của hàm số y f (x) ta có: x 1
+ f '(x) 0 x 1 . x 0 I Ơ
+ Phƣơng trình f (x) 0 có 2 nghiệm x và x (giả sử x < x ). Suy ra x < 1 và 1< x . 1 2 1 2 1 2 . 4 M D
+ Phƣơng trình f (x) có 4 nghiệm x , x , x x (giả sử x < x < x < x ). Và 4 giá 3 4 5 6 3 4 5 6 Ầ 3 Đ
trị thỏa mãn yêu cầu sau: x x 1 ; 1
x 0; 0 x 1;1 x x . NH 1 3 4 5 6 2 Ị Đ
Bảng biến thiên của hàm số y g(x) G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
Suy ra hàm số y g(x) có 5 điểm cực tiểu.
Câu 45. Cho hàm số đa thức 5 4 3 2
f x mx nx px qx hx r , , m , n , p , q ,
h r . Đồ thị hàm
số y f x (nhƣ hình vẽ bên dƣới) cắt trục hoành tại các điểm có hoành độ lần lƣợt là 3 5 11 1 ; ; ; . 2 2 3
TÌM CỰC TRỊ CỦA HÀM SỐ 45
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực trị của hàm số g x f x m n p q h r là A. 6. B. 7. C. 8. D. 9. Lời giải I Ơ Chọn B 3 5 11 Vì 1, , ,
là nghiệm của phƣơng trình f x 0 nên: M D 2 2 3 Ầ Đ f x 3 5 11 4 4 2
5mx 4nx 3px 2qx h 5mx 1 x x x . NH Ị 2 2 3 Đ 20 43 14 55 G 4 3 2 THPT Suy ra 4 4 2
5mx 4nx 3 px 2qx h 5m N x .C.Đ x x x . N 3 4 3 4 NG 2 5 215 35 2 75 CÔ Ờ
Đồng nhất hệ số, ta đƣợc n ; m p ; m q ; m h m . N 3 12 3 4 YỄ TRƢ
Suy ra g x f x 93 m r GU N 2 N
h x f x 93 m r Xét 2 . ÁO VIÊ
hx f x 0 có bốn nghiệm phân biệt, nên hx có bốn cực trị. GI h x 25 215 35 274 93 5 4 3 2 0 mx mx mx mx mx r m r Xét 4 12 3 4 2 25 215 35 274 93 5 4 3 2 x x x x x 0. 4 12 3 4 2 25 215 35 274 93
Đặt k x 5 4 3 2 x x x x x . 4 12 3 4 2
TÌM CỰC TRỊ CỦA HÀM SỐ 46
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Từ bảng biến thiên, suy ra phƣơng trình h x 0 k x 0 có 3 nghiệm đơn phân biệt.
Vậy hàm số g x có 7 cực trị.
Câu 46. Cho hàm số y f (x) có đồ thị nhƣ hình bên dƣới I Ơ
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m 1 00;100 để hàm số 2 M D (
h x) f (x 2) 4 f (x 2) 3m có đúng 3 điểm cực trị. Tổng giá trị của tất cả các phần Ầ Đ
tử thuộc S bằng NHỊ A. 5047 . B. 5049 . C. 5050 . D. 5043 . Đ Lời giải G THPT N.C.Đ N Chọn B NG CÔ Đặt 2 ' ' ' Ờ g(x) f (x 2) 4 f (x 2) 3m g (x) 2 f (x 2). f (x 2) 4 f (x 2) N x 2 1 YỄ TRƢ f x
g (x) 2 f (x 2). f (x 2) 2 ' ( 2) 0 ' ' 0 x 2 3 GU N
f (x 2) 2
x 2 a ( 1 ;0) N x 1 ÁO VIÊ x 1 là 3 nghiệm đơn của ' g (x) 0 . GI
x a 2 3 ; 2
Suy ra hàm số y g(x) có 3 điểm cực trị.
Đặt t f (x 2) t R và mỗi giá trị t R thì phƣơng trình t f (x 2) luôn có nghiệm. 2 2
g(x) f (x 2) 4 f (x 2) 3m (
h t) t 4t 3m
Vì hàm số g(x) có 3 cực trị nên để hàm số y g(x) có 3 điểm cực trị thì. 4 2
t 4t 3m 0,t R 4 3m 0 m .( Vì hàm y (
h t) là hàm bậc hai có hệ số 3 a 0 ) Do m 1 00;10
0 ; m Z m2,3, 4,...,10 0 .
Vậy tổng các giá trị của m là 2 3 4 ...100 5049 .
TÌM CỰC TRỊ CỦA HÀM SỐ 47
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 47. Cho f (x) là một hàm đa thức và có đồ thị của hàm số f '(x) nhƣ hình vẽ bên. Hàm số 2
y 2 f (x) (x 1) có tối đa bao nhiêu điểm cực trị ? A. 9. B. 3. C. 7. D. 5. Lời giải I Chọn D Ơ Xét hàm số 2
g(x) 2 f ( )
x (x 1) . M D
Tìm số điểm cực trị của g x Ầ Đ x 0 NHỊ x 1 Đ
Ta có : g '(x) 0 2 f '(x) 2(x 1) 0 f '(x) x 1 . G x 2 THPT N.C.Đ N x 3 NG CÔ Ờ
Kẻ đƣờng thẳng y x 1cắt đồ thị f x tại bốn điểm phân biệt có hoành độ N
x 0; x 1; x 2; x 3 x x YỄ
trong đó tại các điểm có hoành độ 2; 3 là các điểm tiếp TRƢ g GU N xúc, do đó
x chỉ đổi dấu khi qua các điểm x 0; x 1. Vì vậy hàm số gxcó hai N
điểm cực trị x 0; x 1
Ta tìm số nghiệm của phƣơng trình g x 0. ÁO VIÊ GI Bảng biến thiên: x 0 1 2 3
g '(x) - 0 + 0 - 0 - 0 - g(x) g(1) y = 0 g(0)
Suy ra phƣơng trình có tối đa ba nghiệm phân biệt.
Vậy hàm số y g(x) có tối đa 2 + 3 = 5 điểm cực trị.
Câu 48. Cho hàm số y f (x) có đạo hàm liên tục trên
và đồ thị hàm số y f (x) nhƣ hình vẽ
bên. Tìm số điểm cực trị của hàm số 1 2019f f x y .
TÌM CỰC TRỊ CỦA HÀM SỐ 48
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 13. B. 11. C. 10. D. 12. Lời giải Chọn D I Ơ M D Ầ Đ NHỊĐ
f f x 1 G
y ' f ' x f ' f x THPT Ta có 1 2019 lN n .C 2 .Đ 01 9 N NG
f 'x 0 (1) CÔ Ờ y ' 0 N f '
f x 1 0 (2) YỄ TRƢ x 1 1 GU N x 1 2 N Giải (1) :
f ' x 0 x 3 3 x 6 ÁO VIÊ 4 GI
f (x) 1 1 f (x) 0 f (x) 1 1 f (x) 2
Giải (2) : f ' f (x) 1 0 f (x) 1 3 f (x) 4
f (x) 1 6 f (x) 7 Dựa vào đồ thị ta có
+) f (x) 0 có 1 nghiệm x 6 là nghiệm bội l, 5
+) f (x) 2 có 5 nghiệm x 1 ; 1
x 1;1 x 3;3 x 6;6 x x là các nghiệm bội 6 7 8 9 10 5 1,
+) f (x) 4 có 1 nghiệm x x là nghiệm bội 1, 11 6
+) f (x) 7 có 1 nghiệm x x là nghiệm bội 1, 12 11
Suy ra y ' 0 có 12 nghiệm phân biệt mà qua đó y ' đổi dấu. Vậy hàm số 1 2019f f x y có 12 điểm cực trị.
Câu 49. Cho hàm số y f x có đạo hàm trên . Đồ thị hàm số nhƣ hình vẽ bên dƣới.
TÌM CỰC TRỊ CỦA HÀM SỐ 49
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Số điểm cực tiểu của hàm số g x 2 f x 2 x 1 x 3 là A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn A I
Ta có g x 2 f x 2 2x 4 . Ơ
g x 0 f x 2 x 2. M D
Đặt t x 2 ta đƣợc f t t . 1 Ầ Đ
1 là phƣơng trình hoành độ giao điểm của đồ thị f t và đƣờng thẳng d : y t NHỊĐ (hình vẽ) G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ
Dựa vào đồ thị của f t và đƣờng thẳng y t ta có GI t 1 x 3 t 0 x 2
ta có f t t hay . t 1 x 1 t 2 x 0
Bảng biến thiên của hàm số g x .
Vậy đồ thị hàm số có một điểm cực tiểu.
TÌM CỰC TRỊ CỦA HÀM SỐ 50
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
TÌM CỰC TRỊ CỦA HÀM SỐ 51
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHỦ ĐỀ: CỰC TRỊ HÀM SỐ
VẬN DỤNG – VẬN DỤNG CAO DẠNG 2
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 1 Câu 1.
Tìm tất cả các giá trị của tham số m để hàm 3 y
x m 3 2
x 4m 3 3
x m m đạt 3
cực trị tại x ,x thỏa mãn 1
x x . 1 2 1 2 7 m 3 7 A. 3 m 1 .
B. m 3 . C. .
D. m 2 . 2 m 1 2 I 3 1
Câu 2. Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số 3 2 3 y x mx m có hai Ơ 2 2
điểm cực trị đối xứng nhau qua đƣờng thẳng y x ? M D Ầ A. 1 . B. 3 . C. 2 . D. 0 . Đ NH
Câu 3. Tập hợp tất cả các giá trị tham số thực m để đồ thị hàm số ỊĐ 3 2
y x mx 2 m 3 3 3
1 x m có hai điểm cực trị nằm về hai phía trục hoành là a ;b . G THPT N.C.Đ N
Khi đó giá trị a 2b bằng NG 3 4 2 CÔ Ờ A. . B. . C. 1. D. . N 2 3 3 YỄ
TRƢ Câu 4. Có bao nhiêu giá trị nguyên dƣơng của m để khoảng cách từ gốc tọa độ O đến đƣờng GU N
thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3
y x 3x m nhỏ hơn hoặc bằng 5 . N A. 5 . B. 2 . C. 11. D. 4 . 1
ÁO VIÊ Câu 5. Tìm tất cả các giá trị của m để hàm số 3 2 y
x mx (m 2)x có cực trị và giá trị của 3 GI
hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dƣơng. 2 2 7 2 2 7 A. m 2 . B. m 2; . C. m 1 . D. m 1 . 3 3
Câu 6. Tìm tất cả giá trị thực của tham số m để hàm số 3 2
y x 3(m 1)x 12mx 2019 có 2
điểm cực trị x , x thỏa mãn x x 2x x 8 . 1 2 1 2 1 2 A. m 1.
B. m 2.
C. m 1. D. m 2. 1 1 Câu 7.
Gọi x , x là hai điểm cực trị của hàm số 3 2 y x
mx 4x 10 . Tìm giá trị lớn nhất 1 2 3 2
của biểu thức S 2 x 1 2 x 1 . 1 2 A. 9 . B. 4 . C. 0 . D. 8 .
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 8. Cho hàm số 3 2 2 3
y x 3mx 3(m 1)x m với m là tham số, gọi C là đồ thị của hàm
số đã cho. Biết rằng, khi m thay đổi, điểm cực đại của đồ thị C luôn nằm trên một
đƣờng thẳng d cố định. Xác định hệ số góc k của đƣờng thẳng d . 1 1 A. k 3 .
B. k .
C. k 3. D. k . 3 3 Câu 9. Cho hàm số 3
y x m 2 2
1 x m
1 x m 1. Có bao nhiêu giá trị của số tự nhiên
m 20 để đồ thị hàm số có hai điểm cực trị nằm về hai phía trục hoành? A. 18. B. 19 . C. 21 . D. 20 .
Câu 10. Tìm tất các giá trị thực của tham số m để đồ thị hàm số 3 2 2
y x 3mx 3m có hai điểm
cực trị là A, B mà OAB có diện tích bằng 24 ( O là gốc tọa độ ).
A. m 2 . B. m 1. C. m 2 . D. m 1 .
Câu 11. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2 2 2 I
y x (m 1)x (m 2)x m 3 có hai điểm cực trị và hai điểm cực trị đó nằm về Ơ
cùng một phía đối với trục hoành? M D A. 4 . B. 1. C. 3 . D. 2 . Ầ 3 5 3
Đ Câu 12. Cho hàm số f x xác định trên , có đạo hàm f x x
1 x 2 x 3 . Số điểm NHỊ
cực trị của hàm số f x là Đ G THPT N.C.Đ A. 3 . B. 5 . C. 1. D. 2 . N
NG Câu 13. Có bao nhiêu số nguyên m để hàm số 3 2 y x 3x mx
4 có hai điểm cực trị thuộc CÔ Ờ N khoảng 3;3 ? YỄ TRƢ A. 12 . B. 11. C. 13 . D. 10 . GU N 1 Câu 14. Cho hàm số 3 2 y
x 2mx m 2
1 x 2m 1 ( m là tham số). Xác định khoảng cách lớn N 3
nhất từ gốc tọa độ O 0;0 đến đƣờng thẳng đi qua hai điểm cực trị của đồ thị hàm số ÁO VIÊ trên. GI 2 10 A. . B. 3 . C. 2 3 . D. . 9 3
Câu 15. Xét các số thực với a 0,b 0 sao cho phƣơng trình 3 2 ax x b 0 có ít nhất hai
nghiệm thực. Giá trị lớn nhất của biểu thức 2 a b bằng: 15 27 4 4 A. . B. . C. . D. . 4 4 27 15 1 3
Câu 16. Các giá trị của m để đồ thị hàm số 2 y
x mx m 6 x 2019 có 5 điểm cực trị là 3 A. m 2 . B. 2
m 0 . C. 0 m 3. D. m 3 . Câu 17. Cho hàm số 3
y x m 2 2
2 x 5x 1. Tìm tất cả các giá trị thực của tham số m sao cho
hàm số có hai điểm cực trị x , x x x thỏa mãn x x 2 . 1 2 1 2 1 2 7 1 A. . B. 1 . C. . D. 5 . 2 2
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 18. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2
y x 3x m có 5 điểm cực trị? A. 3 . B. 6 . C. 4 . D. 5 .
Câu 19. Xét các hàm số f x có đạo hàm 2 3 f x x x x
3x với mọi x . Hàm số y f 1
2019x có nhiều nhất bao nhiêu điểm cực trị? A. 9 . B. 7 . C. 8 . D. 6 . Câu 20. Cho hàm số 3 2
y x 3mx 3m 1 với m là tham số thực. Giá trị của m thuộc tập hợp
nào để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đƣờng thẳng
d : x 8y 74 0 . A. m 1 ; 1 . B. m 3 ; 1 . C. m3; 5 . D. m1; 3 .
Câu 21. Cho hàm số y f x có đạo hàm liên tục trên
. Đồ thị hàm số y f ' x nhƣ hình vẽ I sau: Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ . N NG
Số điểm cực trị của hàm số y f x 2018 2019x 1 là CÔ Ờ N A. 2. B. 1. C. 3. D. 4. YỄ
TRƢ Câu 22. Với giá trị nào của tham số m để đồ thị hàm số 3 2
y x 3x m có hai điểm cực trị A , GU N
B thỏa mãn OA OB ( O là gốc tọa độ)? N 3 1 5
A. m .
B. m 3 . C. m . D. m . 2 2 2
ÁO VIÊ Câu 23. Cho hàm số 3
y x 6mx 4 có đồ thị C
. Gọi m là giá trị của m để đƣờng thẳng đi m GI 0
qua điểm cực đại, điểm cực tiểu của C cắt đƣờng tròn tâm I 1;0 , bán kính 2 tại m hai điểm phân biệt ,
A B sao cho tam giác IAB có diện tích lớn nhất. Chọn khẳng định đúng
A. m 3; 4 . B. m 1; 2 .
C. m 0;1 . D. m 2;3 . 0 0 0 0
Câu 24. Có bao nhiêu số nguyên m 7
;7 để đồ thị hàm số 4 2
y x 3mx 4 có đúng ba điểm cực trị , A ,
B C và diện tích tam giác ABC lớn hơn 4. A. 4. B. 2. C. 1. D. 3
Câu 25. Biết hai hàm số f x 3 2
x ax 2x 1 và g x 3 2
x bx 3x 1 có chung ít nhất một
điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P a b A. 30 . B. 2 6 . C. 3 6 . D. 3 3 .
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 26. Tìm tất cả các giá trị của m để đƣờng thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số 3
y x 3mx 2 cắt đƣờng tròn tâm I 1
;1 , bán kính R 1 tại hai điểm phân biệt ,
A B sao cho diện tích tam giác IAB đạt giá trị lớn nhất? 1 3 2 3 2 5 2 3 A. m . B. m . C. m . D. m . 2 2 2 3
Câu 27. Các giá trị của m để đƣờng thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số 3
y x 3mx 2 cắt đƣờng tròn C x 2 2 :
1 y 2 có tâm I tại hai điểm phân biệt ,
A B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. 1 3 3 m m 3 8 A. m . B. 2 . C. m . D. 2 . 8 1 3 3 1 m m 2 2 3 2
I Câu 28. Cho hàm số f x m 1 x 5x
m 3x 3. Có tất cả bao nhiêu giá trị nguyên của Ơ
tham số m để hàm số y f x có đúng 3 điểm cực trị ? M D A. 1. B. 4 . C. 5 . D. 3 . Ầ
Đ Câu 29. Gọi S là tập giá trị nguyên m0 1
; 00 để hàm số 3 2 3
y x 3mx 4m 12m 8 có 5 NHỊĐ
cực trị. Tính tổng các phần tử của S. G THPT N.C.Đ A.10096. B.10094. C. 4048 . D. 5047 . N 4 2
NG Câu 30. Cho hàm số y x 2mx 1
1 . Tổng lập phƣơng các giá trị của tham số m để đồ thị CÔ Ờ N hàm số
1 có ba điểm cực trị và đƣờng tròn đi qua 3 điểm này có bán kính R 1 bằng YỄ TRƢ 5 5 1 5 GU N A. . B . . C. 2 5 . D. 1 5 . 2 2 N
Câu 31. Tìm số thực k để đồ thị hàm số 4 2
y x 2kx k có ba điểm cực trị tạo thành một tam ÁO VIÊ 1
giác nhận điểm G 0; làm trọng tâm. GI 3 A. 1 k 1 ;k . B. 1 k 1; k . 2 3 C. 1 k 1; k . D. 1 1 k ; k . 2 3 2
Câu 32. Cho hàm số 4
y x 2
m m 2 2
1 x m 1. Tìm m để hàm số có ba điểm cực trị và
khoảng cách gi a hai điểm cực tiểu là nhỏ nhất. 1
A. m 1.
B. m 1. C. m=1.
D. m = 2 Câu 33. Cho hàm số 4 2 4
y x 2mx m 2 .
m Tìm tất cả các giá trị của m để các điểm cực trị của
đồ thị hàm số lập thành một tam giác đều.
A. m 2 2. B. m 1. C. 3 m 3. D. 3 m 4.
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 34. Cho hàm số f x có đạo hàm là f x . Đồ thị của hàm số y f x nhƣ hình vẽ bên.
Tính số điểm cực trị của hàm số 2 y
f x trên khoảng 5; 5 . A. 2 . B. 4 . C. 3 . D. 5 . Câu 35. Cho hàm số 4 2
y x 2mx 3m 2 (với m là tham số). Có bao nhiêu giá trị của tham số
m để đồ thị hàm số có ba điểm cực trị đều nằm trên các trục tọa độ? A. 2 . B. 0 . C. 3 . D. 1. I
Ơ Câu 36. Biết m m ; m là giá trị của tham số m để đồ thị hàm số 4 2 y x 2mx 1 có ba 0 0
điểm cực trị tạo thành một tam giác vuông. Khẳng định nào sau đây đúng? M D Ầ
A. m 0;3 . B. m 5; 3 . C. m 3;0 . D. m 3;7 . 0 0 0 0 Đ NH Câu 37. Cho hàm số 4 2 2
y x 2(m m 1)x m có đồ thị C . Tìm m để đồ thị hàm số C có 3 ỊĐ
điểm cực trị và khoảng cách gi a hai điểm cực tiểu nhỏ nhất. G THPT N.C.Đ N 1 1
A. m .
B. m .
C. m 3.
D. m 0. NG 2 2 CÔ Ờ N
Câu 38. Để đồ thị hàm số 4 2
y x 2mx m 1 có ba điểm cực trị tạo thành một tam giác có YỄ TRƢ
diện tích bằng 2, giá trị của tham số m thuộc khoảng nào sau đây? GU N A. (2;3). B. ( 1 ;0). C. (0;1). D. (1;2). N
Câu 39. Cho hàm số f x 4 2 2
x 2mx 4 2m . Có tất cả bao nhiêu số nguyên m 1 0;10 để ÁO VIÊ hàm số y
f x có đúng 3 điểm cực trị? GI A. 6 . B. 8 . C. 9 . D. 7 . Câu 40. Cho hàm số 4 2 y x 2 m 1 x 2m
3 . Tập hợp tất cả các giá trị thực của tham số m
để hàm số đã cho có đúng 5 điểm cực trị là 3 3 3 A. 1; . B. ; \ 2 . C. 1; \ 2 . D. 1; . 2 2 2
Câu 41. Cho hàm số y f x có đồ thị nhƣ hình vẽ. Biết tất cả các điểm cực trị của hàm số
y f x là 2 ; 0; 2; ;
a 6 với 4 a 6 .
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 y -2 O 2 a 6 x y = f(x)
Số điểm cực trị của hàm số y f 6 2
x 3x là: A. 8 .
B.11 .C.9. D. 7 . Câu 42. Cho hàm số 4 2
y x 2mx m , với m là tham số thực. Gọi S là tập hợp tất cả các giá trị I
của m để đồ thị hàm số đã cho có 3 điểm cực trị và đƣờng tròn đi qua 3 điểm cực trị Ơ
này có bán kính bằng 1. Tổng giá trị của các phần tử của S bằng M D 1 5 1 5 A. 1. B. 0 . C. . D. . Ầ 2 2 Đ NH Ị Đ G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI 1 Câu 1.
Tìm tất cả các giá trị của tham số m để hàm 3 y
x m 3 2
x 4m 3 3
x m m đạt 3
cực trị tại x ,x thỏa mãn 1
x x . 1 2 1 2 7 m 3 7 A. 3 m 1 .
B. m 3 . C. .
D. m 2 . 2 m 1 2 Lời giải Chọn B Ta có 2
y x 2m 3 x 4m 3
Đặt t x 1 x t 1. Khi đó 2
y t 2m 2t 2m 7
Hàm số đạt cực trị tại x ,x thỏa mãn 1 x x 2
x 2m 3 x 4m 3 0 có hai 1 2 1 2
nghiệm phân biệt x ,x thỏa mãn 1 x x 2
t 2m 2t 2m 7 0 có hai nghiệm 1 2 1 2 I
phân biệt dƣơng. Điều này tƣơng đƣơng với Ơ m 3 M D 2
m 2m 3 0 m 1 Ầ S 2 m 2 7 Đ 0 m 2
m 3 . 2 NH Ị
P 2m 7 0 7 m Đ 2 G THPT N.C.Đ N Cách 2 NG 2 CÔ Ờ
Ta có y f (x) x 2m 3 x 4m 3 N
Hàm số đạt cực trị tại x ,x thỏa mãn 1 x x 2
x 2m 3 x 4m 3 0 có hai YỄ TRƢ 1 2 1 2 x , x 1 x x GU N nghiệm phân biệt thỏa mãn
. Điều này tƣơng đƣơng với 1 2 1 2 N m 3 m 1 2 ÁO VIÊ 0
m 2m 3 0 7 7 GI . a f ( 1 ) 0 1
2(m 3) 4(m 3) 0 m m 3 . 2 2 S 2(m 3) 1 1 m 3 2 2 3 1
Câu 2. Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số 3 2 3 y x mx m có hai 2 2
điểm cực trị đối xứng nhau qua đƣờng thẳng y x ? A. 1 . B. 3 . C. 2 . D. 0 . Lời giải Chọn C x 0 Ta có 2
y' 3x 3mx ; y ' 0 x m
Hàm số có hai điểm cực trị khi và chỉ khi y' 0 có hai nghiệm phân biệt m 0 .
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1
Với điều kiện m 0 , giả sử hai điểm cực trị của đồ thị hàm số là 3 A 0; m , B ;0 m . 2 1 3 m m 3 AB ; m m và I ;
là trung điểm của đoạn thẳng AB . 2 2 4 1 3 m m 0 A . B u 0 m d 2 2 Yêu cầu bài toán 3 I d m m m 0 2 4
Đối chiếu điều kiện ta đƣợc m 2 .
Câu 3. Tập hợp tất cả các giá trị tham số thực m để đồ thị hàm số 3 2
y x mx 2 m 3 3 3
1 x m có hai điểm cực trị nằm về hai phía trục hoành là a ;b .
Khi đó giá trị a 2b bằng 3 4 2 I A. . B. . C. 1. D. . 2 3 3 Ơ Lời giải M D Chọn D Ầ Đ Ta có 2 2
y ' 3x 6mx 3(m 1) . NHỊ
x m 1 Đ Xét 2 2
3x 6mx 3(m 1) 0 . G
x m 1 THPT N.C.Đ N
Hai nghiệm trên phân biệt với mọi m . NG CÔ Ờ
Đƣờng thẳng qua 2 điểm cực trị của đồ thị là y 2 x m . N
Vậy nên các giá trị cực trị y(m 1) 3m 2 , y(m 1) 3m 2 . YỄ TRƢ GU N
Theo yêu cầu bài toán ta phải có m m 2 2 3 2 3 2 0 m . N 3 3 2
Vậy a 2b . ÁO VIÊ 3
GI Câu 4. Có bao nhiêu giá trị nguyên dƣơng của m để khoảng cách từ gốc tọa độ O đến đƣờng
thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3
y x 3x m nhỏ hơn hoặc bằng 5 . A. 5 . B. 2 . C. 11. D. 4 . Lời giải Chọn A Ta có 2
y 3x 3 x 1 2
y 0 3x 3 0 x 1
Hai điểm cực trị của đồ thị hàm số là A1;m 2 , B 1 ;m 2
Phƣơng trình đƣờng thẳng đi qua 2 điểm cực trị của đồ thị hàm số là y 2 x m
hay 2x y m 0 m
Theo giả thiết d ; O AB 5
5 m 5 5 m 5 . 5
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Mà m nguyên dƣơng nên có 5 giá trị. 1
Câu 5. Tìm tất cả các giá trị của m để hàm số 3 2 y
x mx (m 2)x có cực trị và giá trị của 3
hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dƣơng. 2 2 7 A. m 2 . B. m 2;
. C. 2 2 7 m 1 . D. m 1 . 3 3 Lời giải Chọn B Cách 1: Ta có: 2
y x 2mx m 2 . 2
y 0 x 2mx m 2 0 1 .
Để hàm số có hai điểm cực trị thì phƣơng trình
1 có hai nghiệm phân biệt. m 1 2
0 m m 2 0 * I m 2 Ơ
Phƣơng trình đƣờng thẳng đi qua điểm CĐ, CT của hàm số là: M D 2 2 4 1 2 y m m x m m 2 Ầ . 3 3 3 3 Đ NHỊ
Gọi Ax ; y , B x ; y là hai điểm cực đại, cực tiểu của đồ thị hàm số, khi đó để hàm số 1 1 2 2 Đ G
có giá trị cực đại, và giá trị cực tiểu dƣơng thì y y 0 và đồ thị hàm số THPT N.C.Đ 1 2 N 1 3 2 NG y
x mx (m 2)x cắt trục hoành tại 1 điểm duy nhất. CÔ Ờ 3 N
Theo định lý vi-et ta có x x 2m 1 2 YỄ TRƢ 2 2 4 2 2 GU N Nên y y 0 m m x x m m 2 0 1 2 1 2 3 3 3 3 N 2 2 4 2 2
m m
2m mm 2 0 ÁO VIÊ 3 3 3 3 GI m 2 2 2
m 3m 6 0 3 57 3 57 m ; 0; * * . 4 4 1 Để đồ thị hàm số 3 2 y
x mx (m 2)x cắt trục hoành tại 1 điểm duy nhất thì phƣơng 3 1 trình y 0 có 3 2
1 nghiệm đơn duy nhất, khi đó
x mx (m 2)x 02 có 1 nghiệm 3 đơn duy nhất. 1 x 0 Ta có: 3 2
x mx (m 2)x 0 x 2
x 3mx 3m 6 0 . 3 2
x 3mx 3m 6 0 3 Để phƣơng trình
1 có 1 nghiệm đơn duy nhất thì phƣơng trình 3 vô nghiệm, khi 2 2 7 2 2 7 đó điều kiện là 2
9m 12m 24 0 m *** . 3 3
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 2 7 Kết hợp * ,* * ,**
* ta đƣợc tập các giá trị của m thỏa mãn là 2 m . 3 Cách 2: Ta có: 2
y x 2mx m 2 . 2
y 0 x 2mx m 2 0 1 .
Để hàm số có hai điểm cực trị thì phƣơng trình
1 có hai nghiệm phân biệt, khi đó m 1 2
0 m m 2 0 * m 2 1
Để hàm số có giá trị cực đại, cực tiểu dƣơng thì đồ thị hàm số 3 2 y
x mx (m 2)x 3
cắt trục hoành tại 1 điểm duy nhất và giá trị của hàm số tại điểm uốn luôn dƣơng. 1 Để đồ thị hàm số 3 2 y
x mx (m 2)x cắt trục hoành tại 1 điểm duy nhất thì phƣơng 3 1 3 2 I
trình y 0 có nghiệm duy nhất, khi đó x mx (m 2)x 02 có 1 nghiệm đơn duy Ơ 3 nhất. M D 1 3 2 2 Ầ
Ta có: x mx (m 2)x 0 x x 3mx 3m 6 0 Đ 3 NHỊ x 0 Đ . 2
x 3mx 3m 6 0 3 G THPT N.C.Đ N Để phƣơng trình
1 có nghiệm đơn duy nhất thì phƣơng trình 3 vô nghiệm, khi đó NG CÔ Ờ N 2 2 7 2 2 7 điều kiện : 2
9m 12m 24 0 m ** . YỄ 3 3 TRƢ
Để giá trị của hàm số tại điểm uốn luôn dƣơng: GU N N 2
y x 2mx m 2, y 2x 2m
y 0 2x 2m 0 x m ÁO VIÊ 3 m 3 GI
Ta có: y m 0
m mm 2 0 3 m 2 2
m 3m 6 0 3 57 3 57 m ; 0; ** * 4 4 2 2 7 Kết hợp * ,* * ,**
* ta đƣợc tập các giá trị của m thỏa mãn là 2 m 3
Câu 6. Tìm tất cả giá trị thực của tham số m để hàm số 3 2
y x 3(m 1)x 12mx 2019 có 2
điểm cực trị x , x thỏa mãn x x 2x x 8 . 1 2 1 2 1 2 A. m 1.
B. m 2.
C. m 1. D. m 2. Lời giải Chọn A
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2
y ' 3x 6(m 1)x 12m ; 2 2
y ' 0 3x 6(m 1)x 12m 0 x 2(m 1)x 4m 0 (1) .
Để hàm số có 2 cực trị x , x Phƣơng trình (1) có 2 nghiệm phân biệt. 1 2 2
' 0 (m 1) 0 m 1.
x x 2(m 1)
Với điều kiện m 1 ta có 1 2 . x x 4m 1 2
Do đó x x 2x x 8
2m 2 8m 8 m 1 . 1 2 1 2 Vậy m 1
thỏa mãn yêu cầu của bài toán. 1 1 Câu 7.
Gọi x , x là hai điểm cực trị của hàm số 3 2 y x
mx 4x 10 . Tìm giá trị lớn nhất 1 2 3 2
của biểu thức S 2 x 1 2 x 1 . 1 2 A. 9 . B. 4 . C. 0 . D. 8 . I Lời giải Ơ Chọn A M D 1 1 y x
mx 4x 10 y ' x mx 4 Ầ Ta có: 3 2 2 . Đ 3 2 2 NH Ị y ' 0 x mx 4 0 . Đ 2
m 16 0, m
nên phƣơng trình y ' 0 luôn có hai nghiệm phân biệt x , x . 1 2 G THPT N.C.Đ N b NG x x m 1 2 CÔ a Ờ
Áp dụng định lí viet: . N c
x .x 4 1 2 YỄ TRƢ a 2 2 2 2 2 2 GU N
S (x 1)(x 1) (x x ) [(x x ) 2x .x ] 1 16 (m 8) 1 9 m 9 . 1 2 1 2 1 2 1 2 N Câu 8. Cho hàm số 3 2 2 3
y x 3mx 3(m 1)x m với m là tham số, gọi C là đồ thị của hàm ÁO VIÊ
số đã cho. Biết rằng, khi m thay đổi, điểm cực đại của đồ thị C luôn nằm trên một GI
đƣờng thẳng d cố định. Xác định hệ số góc k của đƣờng thẳng d . 1 1 A. k 3 .
B. k .
C. k 3. D. k . 3 3 Lời giải Chọn A Ta có: 2 2 2 2
y 3x 6mx 3(m 1) 3(x 2mx m 1) x m 1 2 2
y 0 x 2mx m 1 x m 1 Bảng biến thiên:
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Dựa vào bảng biến thiên ta thấy điểm cực đại của đồ thị C là điểm M m 1; 3 m 2 . Nhận xét: y 3 m 2 3 (m 1) 1 3
x 1 M d : y 3 x 1, . m M M
Vậy: khi m thay đổi, điểm cực đại của đồ thị C luôn nằm trên một đƣờng thẳng d cố
định có phƣơng trình: y 3 x 1.
Vậy đƣờng thẳng d có hệ số góc k 3 . Câu 9. Cho hàm số 3
y x m 2 2
1 x m
1 x m 1. Có bao nhiêu giá trị của số tự nhiên
m 20 để đồ thị hàm số có hai điểm cực trị nằm về hai phía trục hoành? I A. 18. B. 19 . C. 21 . D. 20 . Ơ Lời giải M D Chọn B Ầ Đ
+ Ta có: y x 2
1 x 2mx 1 m . NHỊĐ
+ Hàm số có hai điểm cực trị nằm về hai phía trục hoành khi và chỉ khi đồ thị y cắt trục G THPT N.C.Đ2
hoành tại ba điểm phân biệt. y x
1 x 2mx 1 m 0 có ba nghiệm phân biệt. N NG 2
x 2mx 1 m 0 có hai nghiệm phân biệt khác 1. CÔ Ờ N 1 5 YỄ m TRƢ 2 2 GU N
m m 1 0 1 5 N m . 2 3m 0 2 2 ÁO VIÊ m 3 GI
+ Do m N,m 20 nên 1 m 20 . Vậy có 19 số tự nhiên thỏa mãn bài toán.
Câu 10. Tìm tất các giá trị thực của tham số m để đồ thị hàm số 3 2 2
y x 3mx 3m có hai điểm
cực trị là A, B mà OAB có diện tích bằng 24 ( O là gốc tọa độ ).
A. m 2 . B. m 1. C. m 2 . D. m 1 . Lời giải Chọn C Xét 2
y 3x 6mx 3x x 2m .
y x x m x 0 0 3 2 0 . x 2m
Đồ thị hàm số có hai điểm cực trị m 0 .
Tọa độ hai điểm cực trị là A 2 m B 2 3 0;3 ,
2m;3m 4m .
Phƣơng trình đƣờng thẳng OA : x 0 .
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 1 Ta có: S O . A d B OA m m 2
m m 8 m 2 . OAB ; 2 3 . 2 24 2 2
Câu 11. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2 2 2
y x (m 1)x (m 2)x m 3 có hai điểm cực trị và hai điểm cực trị đó nằm về
cùng một phía đối với trục hoành? A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn C
Tập xác định của hàm số đã cho là . 2
y x m 2 3 2
1 x m 2 có 2 2
m 2m 7 . Để đồ thị hàm số 3 2 2 2
y x (m 1)x (m 2)x m 3 có hai điểm cực trị thì y đổi dấu
hai lần, tức là y có hai nghiệm phân biệt, tƣơng đƣơng 1 15 1 15 I 2 0 2
m 2m 7 0 m , Ơ 2 2
Vì m nên đƣợc m 1 ; 0;1; 2 . M D Ầ
Lúc này, hai nghiệm x , x của y lần lƣợt là hoành độ các điểm cực trị của hàm số. 1 2 Đ NH
Hai điểm cực trị đó nằm về cùng một phía đối với trục hoành khi và chỉ khi ỊĐ
f x . f x 0 , tƣơng đƣơng đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm 1 2 G THPT N.C.Đ N
(hình vẽ minh họa bên dƣới), tức là, phƣơng trình 3 2 2 2
x (m 1)x (m 2)x m 3 0 (*) NG CÔ Ờ
có duy nhất một nghiệm thực. N YỄ TRƢ GU N N ÁO VIÊ GI Xét m 1
thì phƣơng trình (*) là 3
x x 2 0 : phƣơng trình này có đúng một nghiệm
thực (dùng MTCT) nên chọn m 1 .
Xét m 0 thì phƣơng trình (*) là 3 2
x x 2x 3 0 : phƣơng trình này có đúng một
nghiệm thực (dùng MTCT) nên chọn m 0 .
Xét m 1 thì phƣơng trình (*) là 3 2
x 2x x 2 0 : phƣơng trình này có ba nghiệm
thực phân biệt (dùng MTCT) nên không chọn m 1.
Xét m 2 thì phƣơng trình (*) là 3 2
x 3x 2x 1 0 : phƣơng trình này có đúng một
nghiệm thực (dùng MTCT) nên chọn m 2 . Đáp số: m 1 ; 0; 2 . Câu 12. Cho hàm số 3 5 3
f x xác định trên
, có đạo hàm f x x
1 x 2 x 3 . Số điểm
cực trị của hàm số f x là
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 3 . B. 5 . C. 1. D. 2 . Lời giải Chọn A
+ Hàm số y f x là hàm chẵn nên đồ thị của hàm số nhận trục tung làm trục đối xứng.
+ Gọi n là số điểm cực trị của hàm số y f x trên miền x 0 . Khi đó số điểm cực trị
của hàm số y f x là 2n 1. x 1
+ Ta có f x x 3 x 5 x 3 0 1 2 3 0 x 2 ( nghiệm bội lẻ ) x 3
Số điểm cực trị của hàm số y f x trên miền x 0 là 1.
Số điểm cực trị của hàm số y f x là 2.11 3. I
Ơ Câu 13. Có bao nhiêu số nguyên m để hàm số 3 2
y x 3x mx 4 có hai điểm cực trị thuộc M D khoảng 3;3 ? Ầ Đ A. 12 . B. 11. C. 13 . D. 10 . NHỊ Lời giải Đ Chọn B G THPT N.C.Đ N Ta có: 2
y ' 3x 6x m NG CÔ Ờ Để hàm số 3 2 y x 3x mx
4 có hai điểm cực trị thuộc khoảng 3;3 thì phƣơng N trình y ' 0 hay 2
3x 6x m 0 có hai nghiệm phân biệt thuộc khoảng 3 ;3 . YỄ TRƢ Cách 1: GU N N
Khi đó, đặt f x 2
3x 6x m thì ' 0 ÁO VIÊ a f 9 3m 0 . 3 0 GI a f 45 m 0 3 m 9 . 3 0 9 m 0 S 3 1 3 3 3 2
Do đó có 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Cách 2:
Khi đó, đặt f x 2
3x 6x m thì 9 3m 0 ' 0 3 m 9 3 9 3m 3 9 3m 3
x x 3 1 2 3 3 3 3
Do đó có 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Cách 3: Ta có: 2
y 3x 6x m
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Hàm số 3 2
y x 3x mx 4 có hai điểm cực trị thuộc khoảng 3 ;3 Phƣơng trình y 0 hay 2
3x 6x m có hai nghiệm phân biệt thuộc khoảng 3 ;3 .
Đặt f x 2 3x 6 , x x 3 ; 3 . Ta có:
f x 6x 6 ; f x 0 x 1. Bảng biến thiên: Yêu cầu bài toán 3 m 9 .
Vậy có 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán. I Ơ 1 Câu 14. Cho hàm số 3 2 y
x 2mx m 2
1 x 2m 1 ( m là tham số). Xác định khoảng cách lớn 3 M D
nhất từ gốc tọa độ O 0;0 đến đƣờng thẳng đi qua hai điểm cực trị của đồ thị hàm số Ầ Đ trên. NHỊĐ 2 10 A. . B. 3 . C. 2 3 . D. . G THPT N.C.Đ 9 3 N NG Lời giải CÔ Ờ Chọn D N
y x mx m y YỄ Ta có 2 4
1. Để đồ thị hàm số có hai điểm cực trị thì phƣơng trình 0 TRƢ GU N có hai nghiệm phân biệt 2 4m m 1 0 m . N 1 2m 8 2 2 8 2
Mà y x y x 2 2 . x m m x m m 1 . 3 3 3 3 3 3 3 ÁO VIÊ
Suy ra đƣờng thẳng đi qua hai điểm cực trị của đồ thị hàm số là đƣờng thẳng : GI 8 2 2 8 2 2 2 y m m x m m 1 . 3 3 3 3 3 1
Ta thấy đƣờng thẳng luôn qua điểm cố định A 1; . 3
Gọi H là hình chiếu vuông góc của O lên . Khi đó ta có d ;
O OH OA (Hình vẽ) O A H
Do đó khoảng cách lớn nhất khi H A hay OA . 10
Vậy khoảng cách lớn nhất là OA . 3
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 15. Xét các số thực với a 0,b 0 sao cho phƣơng trình 3 2 ax x b 0 có ít nhất hai
nghiệm thực. Giá trị lớn nhất của biểu thức 2 a b bằng: 15 27 4 4 A. . B. . C. . D. . 4 4 27 15 Lời giải Chọn C Xét hàm số 3 2
f x ax x b x .
x 0 y b f x 2
3ax 2x 0 2 4 . x y b 2 3a 27a Để phƣơng trình 3 2
ax x b 0 có ít nhất 2 nghiệm thực khi và chỉ khi 4 4 4 4 2 2 y .y 0 b b 0 b 0 a b 0 a b . CD CT 2 2 27a 27a 27 27 I Ơ 4
Vậy giá trị lớn nhất của biểu thức 2 a b bằng . 27 M D 1 3 2
Ầ Câu 16. Các giá trị của m để đồ thị hàm số y x mx
m 6 x 2019 có 5 điểm cực trị là Đ 3 NH Ị
A. m 2 . B. 2 m 0 . C. 0 m 3. D. m 3 . Đ Lời giải G THPT N.C.Đ N Chọn D NG 1 3 2 CÔ Ờ
Xét hàm số : y x mx m 6 x 2019 . N 3 YỄ TRƢ TXĐ : D . 2 GU N
Ta có : y x 2mx m 6 . N 1 3 Để đồ thị hàm số 2 y
x mx m 6 x 2019 có 5 điểm cực trị thì đồ thị hàm số 3 ÁO VIÊ 1 3 2 y
x mx m 6 GI
x 2019 có 2 điểm cực trị nằm bên phải trục tung 3 phƣơng trình 2
y x 2mx m 6 0 có hai nghiệm dƣơng phân biệt 2 0
m m 6 0
S 0 2m 0 m 3. P 0 m 6 0 Câu 17. Cho hàm số 3
y x m 2 2
2 x 5x 1. Tìm tất cả các giá trị thực của tham số m sao cho
hàm số có hai điểm cực trị x , x x x thỏa mãn x x 2 . 1 2 1 2 1 2 7 1 A. . B. 1 . C. . D. 5 . 2 2 Lời giải Chọn C Tính đƣợc: 2
y 3x 4m 2 x 5.
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Khi đó m 2 4 2
15 0 nên hàm số luôn có hai điểm cực trị x , x x x . 1 2 1 2 Nhận xét .
a c 0 nên x 0 x 1 2 Suy ra: b 4m 2 x x 2
x x 2 2 2 1 m . 1 2 1 2 a 3 2
Câu 18. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2
y x 3x m có 5 điểm cực trị? A. 3 . B. 6 . C. 4 . D. 5 . Lời giải Chọn A x 0 Đặt 3 2
f (x) x 3x m . Ta có 2
f '(x) 3x 6x ;
f '(x) 0 x 2 I Bảng biến thiên: Ơ M D Ầ Đ NHỊĐ G THPT N.C.Đ N NG y f x CÔ Suy ra hàm số y
f (x) có 2 điểm cực trị. Do đó hàm số ( ) Ờ
có 5 điểm cực trị khi N
và chỉ khi đồ thị hàm số y f (x) cắt trục hoành tại 3 điểm phân biệt. YỄ TRƢ
Từ bảng biến thiên ta có điều kiện cần tìm là m 4 0 m 4 m 0. GU N N
Vậy có 3 giá trị nguyên của tham số m thỏa mãn yêu cầu.
Câu 19. Xét các hàm số f x có đạo hàm 2 3 f x x x x
3x với mọi x . Hàm số ÁO VIÊ y f 1
2019x có nhiều nhất bao nhiêu điểm cực trị? GI A. 9 . B. 7 . C. 8 . D. 6 . Lời giải Chọn B
● Nhận xét: Số cực trị của hàm số y f 1
2019x bằng tổng số nghiệm của phƣơng trình f 1 2019x
0 và số cực trị (không phải là nghiệm phƣơng trình f 1 2019x 0 ) của hàm số y f 1 2019x . Ta có 2 f x x x 1 x 3 x 3 . f 1 2019x
2019 f 1 2019x . Do đó 2 f 1 2019x 0 1 2019x
1 2019x 1 1 2019x 3 1 2019x 3 0
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 17
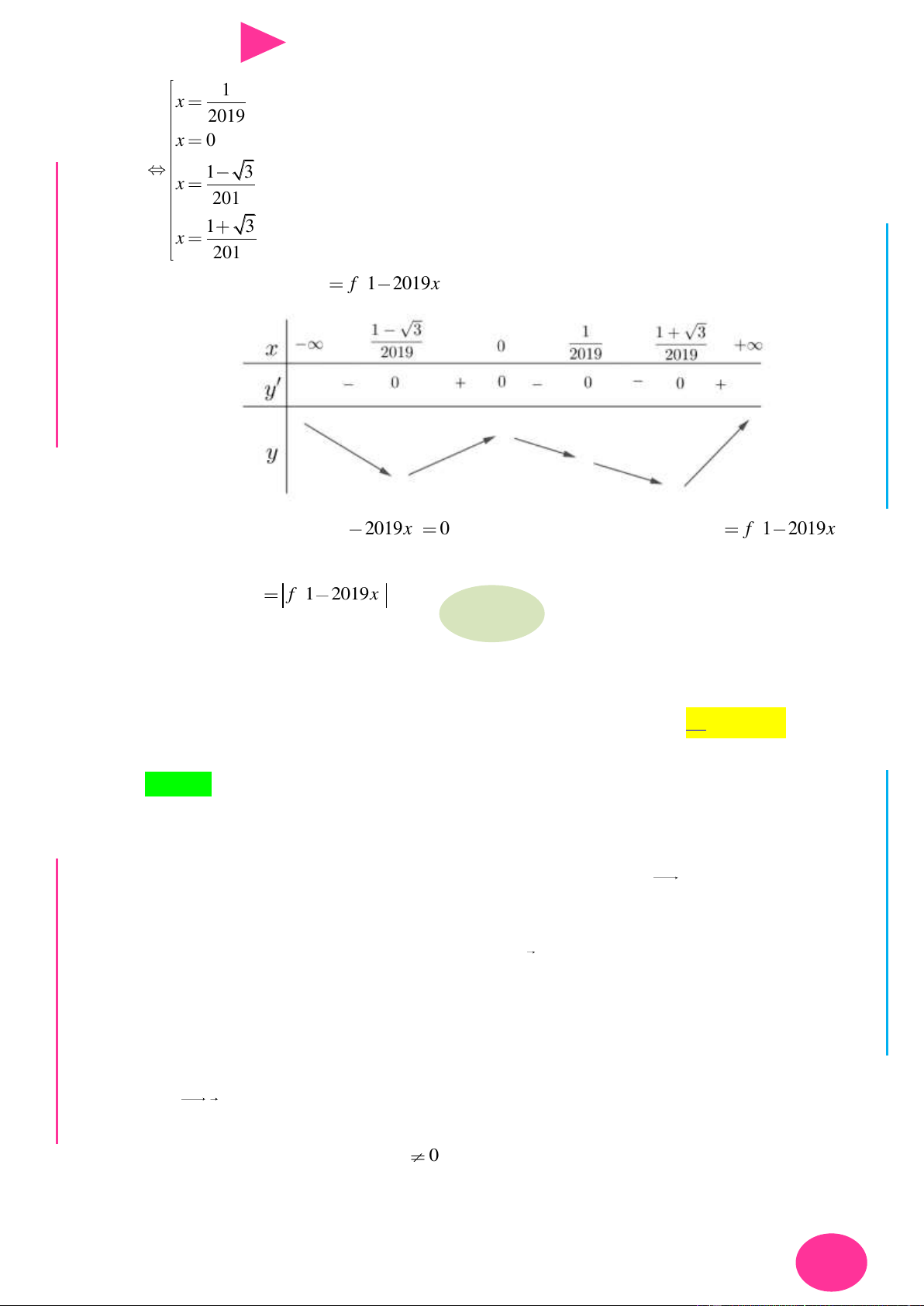
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 x 2019 x 0 1 3 . x 2019 1 3 x 2019
Bảng biến thiên của y f 1 2019x I Ơ M D Ầ
Do đó phƣơng trình f 1 2019x
0 có tối đa 4 nghiệm và hàm số y f 1 2019x có Đ NH ba điểm cực trị. Ị Đ Vậy hàm số y f 1
2019x có tối đa 7 điểm cực trị. G THPT N.C.Đ N Câu 20. Cho hàm số 3 2
y x 3mx 3m 1 với m là tham số thực. Giá trị của m thuộc tập hợp NG CÔ
nào để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đƣờng thẳng Ờ N
d : x 8y 74 0 . YỄ TRƢ A. m 1 ; 1 . B. m 3 ; 1 . C. m3; 5 . D. m1; 3 . GU N N Lời giải Chọn D ÁO VIÊ 2 y 3
x 6mx ; y 0 x 0 x 2m. GI
Hàm số có CĐ, CT khi và chỉ khi PT y 0 có 2 nghiệm phân biệt m 0 .
Khi đó 2 điểm cực trị là: A0; 3 m 1 ; B 3 2 ;
m 4m 3m 1 AB 3 2 ; m 4m .
Trung điểm I của AB có toạ độ: I 3 ;
m 2m 3m 1 .
Đƣờng thẳng d : x 8y 74 0 có một VTCP u 8; 1 . I d
và B đối xứng với nhau qua d AB d m m m 8
2m 3m 3 16 23 82 0 3 3 1 74 0 1
6m 23m 82 0 m 0 3 1
6m 4m 0 A . B u 0 m 2
m 2( thỏa mãn điều kiện m 0). Suy ra m1; 3 .
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 21. Cho hàm số y f x có đạo hàm liên tục trên
. Đồ thị hàm số y f ' x nhƣ hình vẽ sau: .
Số điểm cực trị của hàm số y f x 2018 2019x 1 là A. 2. B. 1. C. 3. D. 4. Lời giải Chọn B
y f x 2018 2019x 1 y ' f ' x 2018 2019 I . Ơ
Do đó y ' 0 f ' x 2018 2019 (1). M D
Số nghiệm của phƣơng trình (1) bằng số giao điểm của đồ thị hàm số y f ' x với Ầ Đ
đƣờng thẳng y 2019 . NHỊ y Đ Từ đồ thị hàm số
f ' x ta thấy (1) chỉ có 1 nghiệm đơn. Vậy hàm số G THPT N.C.Đ
y f x 2018 2019x 1 N
chỉ có 1 điểm cực trị.
NG Câu 22. Với giá trị nào của tham số m để đồ thị hàm số 3 2
y x 3x m có hai điểm cực trị A , CÔ Ờ N
B thỏa mãn OA OB ( O là gốc tọa độ)? YỄ TRƢ 3 1 5
A. m .
B. m 3 . C. m . D. m . GU N 2 2 2 N Lời giải Chọn D ÁO VIÊ
Tập xác định: D . GI x 0 2
y 3x 6x , 2
y 0 3x 6x 0 . x 2
Do đó đồ thị hàm số đã cho luôn có hai điểm cực trị lần lƣợt có tọa độ là A0;m và 2 2 B 2; 4 m Ta có 2 2 2 OA OB m m 2 0 2 4
m 4 4 m 5
20 8m 0 m . 2 Câu 23. Cho hàm số 3
y x 6mx 4 có đồ thị C
. Gọi m là giá trị của m để đƣờng thẳng đi m 0
qua điểm cực đại, điểm cực tiểu của C cắt đƣờng tròn tâm I 1;0 , bán kính 2 tại m hai điểm phân biệt ,
A B sao cho tam giác IAB có diện tích lớn nhất. Chọn khẳng định đúng
A. m 3; 4 . B. m 1; 2 .
C. m 0;1 . D. m 2;3 . 0 0 0 0 Lời giải.
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Chọn C Xét hàm số 3
y x 6mx 4 có tập xác định . 2 2
y 3x 6m; y ' 0 x 2m .
Đồ thị hàm số có 2 điểm cực trị y đổi dấu 2 lần
y 0 có hai nghiệm phân biệt m 0 . 1 Ta có y
y '.x 4mx 4 . 3
Gọi M x ; y , N x ; y là hai điểm cực trị của đồ thị hàm số. 1 1 2 2
yx y x 0 1 2 1 y 4 mx 4
Ta có y y x y x 1 1
.x 4mx 4 . 1 1 1 1 1 3 y 4 mx 4 2 2 1 y y x
y x .x 4mx 4 2 2 2 2 2 I 3 Ơ
Suy ra M , N thuộc đƣờng thẳng d có phƣơng trình y 4 mx 4. M D
Vậy phƣơng trình đƣờng thẳng qua hai điểm cực trị của C là: y 4 mx 4. m Ầ Đ
Gọi T là đƣờng tròn có tâm I 1;0 và bán kính R 2 . NHỊ
Đƣờng thẳng d cắt đƣờng tròn tại hai điểm phân biệt ,
A B và tạo thành tam giác IAB Đ G THPT N .C m .Đ 1 N
0 d I,d R 0 d I,d 2 4 m 4 (*). NG 2 CÔ Ờ 2 N 16m 1 YỄ Cách 1: TRƢ GU N
Do đƣờng thẳng d luôn đi qua điểm K 0;4 , IK 17 R K nằm ngoài đƣờng N
tròn nên tồn tại hai điểm ,
A B là giao điểm của d với đƣờng tròn để tam giác IAB vuông tại I . ÁO VIÊ 1 1 GI Do đó: S I . A I . B sin AIB I . A IB . IAB 2 2 R
Dấu bằng xảy ra IA IB d I, d 1 (thỏa mãn (*)). 2 4 m 4 15 1 m . 2 32 16m 1 R
Bình luận: Nếu đƣờng thẳng d luôn đi qua điểm K cố định mà IK thì sẽ không 2
có vị trí của đƣờng thẳng d để tam giác IAB vuông tại I . Khi đó, nếu làm nhƣ trên sẽ
bị sai. Trong trƣờng hợp đó thì ta phải đặt d I, d t 0 t l , với l là độ dài đoạn
thẳng IK , rồi tính S
f t và tìm giá trị lớn nhất của f t trên nửa khoảng 0;l. I AB
Cách 2: Phƣơng trình đƣờng tròn là: x 2 2
1 y 2 C
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 2 2 1 y 2 Xét hệ 2 16m 2
1 x 216m 1 x 15 0 1 . y 4 mx 4
d cắt C tại hai điểm phân biệt , A B
1 có 2 nghiệm phân biệt a,b m 2 16 1 1516m 1 0 .
IA a 1; 4 ma 4 Khi đó A ; a 4
ma 4, B ; b 4 mb 4 IB b 1; 4 mb 4
IA IB ab a b 2 .
16m ab ma b 1 1 0
ab a b 2
16m ab 16ma b 17 0 2 16m
1 ab 16m
1 a b 17 0 216m 2 1 16m 2 1 15 15 17 0 16 m 2 2 16m 1 16m . 1 32
Câu 24. Có bao nhiêu số nguyên m 7
;7 để đồ thị hàm số 4 2
y x 3mx 4 có đúng ba I Ơ điểm cực trị , A ,
B C và diện tích tam giác ABC lớn hơn 4. A. 4. B. 2. C. 1. D. 3 M D Ầ Lời giải Đ Chọn D NHỊĐ Xét 4 2
y x 3mx 4 . G THPT N.C.Đ x 0 N 3 NG y 4x 6mx 0 3m 2 CÔ x Ờ 2 N 3m YỄ TRƢ Trƣờng hợp 1: 0 m 0 . 2 GU N N m m m m Hàm số 4 2
y x 3mx 4 có 3 cực trị: A 2 2 3 9 3 9 0; 4 , B ; 4,C ; 4 2 4 2 4 ÁO VIÊ Suy ra 4 2
y x 3mx 4 có 5 cực trị. GI 3m Trƣờng hợp 2:
0 m 0 (1) suy ra hàm số 4 2
y x 3mx 4 có 1 cực tiểu là: 2 A0; 4 Suy ra hàm số 4 2
y x 3mx 4 có 3 điểm cực trị là: A0; 4, B x ;0 ,C x ;0 , trong 1 1
đó x là nghiệm của phƣơng trình 4 2
x 3mx 4 0 . x 0 (do ac 4 nên phƣơng 1 1 trình 4 2
x 3mx 4 0 luôn có nghiệm) (2) 1 1
Diện tích tam giác ABC bằng: S .d ;
A BC .BC .4.2 x 4 x . 1 1 2 2 4 2 x 4 x 4
Do S 4 x 1. Từ phƣơng trình (2) suy ra 1 1 m với x 1. 1 2 2 3x 3 3x 1 1 1
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 x 4 Do 2 1
x 1 x 1 m 1
kết hợp với (1) suy ra 1
m 0 suy ra chỉ có 1 1 2 3 3x1
m 0 thỏa mãn đề bài.
Câu 25. Biết hai hàm số f x 3 2
x ax 2x 1 và g x 3 2
x bx 3x 1 có chung ít nhất một
điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P a b A. 30 . B. 2 6 . C. 3 6 . D. 3 3 . Lời giải Chọn A
Ta có f x 2
3x 2ax 2 . Hàm số y f x có cực trị khi: 2
a 6 0 a 6 a 6 1 . g x 2 3
x 2bx 3. Hàm số y g x có cực trị khi 2
b 9 0 b 3
b 3 2 .
Giả sử x là điểm cực trị của cả hai hàm số y f x và y g x I 0 Ơ 1 1 3 a b a x 0 2 3
x 2ax 2 0 2x x 2 M D 0 0 0 0 Ầ 2 3
x 2bx 3 0 3 1 3 1 Đ 0 0 b x b x 0 0 NH 2 x 2 x Ị 0 0 Đ G 1 3 3 1 5 THPT N.C.Đ
P a b
x x 3x 0 0 0 N x 2 2 x 2x 0 0 0 NG CÔ Ờ 25 25 2 2 2 N P 9x 15 2
.9x 15 30 P 30 2 0 2 0 4x 4x 0 0 YỄ TRƢ Dấu “=” xảy ra khi: GU N N 1 3 1 1 3 1
x x 0
x x 0 0 0 0 0 x 2 x x 2 x 5 0 0 0 0 x . ÁO VIÊ 0 25 6 2 5 GI 9x 2 0 x 0 4x 0 6
Với hai giá trị x , ta tìm đƣợc hai cặp giá trị a,b thoả (1) và (2). Vậy min P 30 . 0
Câu 26. Tìm tất cả các giá trị của m để đƣờng thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số 3
y x 3mx 2 cắt đƣờng tròn tâm I 1
;1 , bán kính R 1 tại hai điểm phân biệt ,
A B sao cho diện tích tam giác IAB đạt giá trị lớn nhất? 1 3 2 3 2 5 2 3 A. m . B. m . C. m . D. m . 2 2 2 3 Lời giải Chọn B Ta có 3 2
y x 3mx 2 y 3x 3m Hàm số 3
y x 3mx 2 có 2 điểm cực trị phƣơng trình 2
y 3x 3m 0 có hai nghiệm phân biệt m 0 1
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 Ta có y .
x y 2mx 2 . 3
Suy ra phƣơng trình đƣờng thẳng đi qua hai điểm cực đại và cực tiểu là y 2
mx 2 2mx y 2 0
Đƣờng thẳng cắt đƣờng tròn tâm I 1
;1 , bán kính R 1 tại hai điểm phân biệt , A B I Ơ
d I 2m 1 ; R 1 2
2m 1 4m 1 4
m 0 luôn đúng do m 0 2 4m 1 M D 1 1 1 Ầ Ta có S .I . A IB.sin AIB .sin AIB Đ IAB 2 2 2 NHỊ
Dấu bằng xảy ra sin AIB 1 AIB 90. Đ G THPT
Khi đó tam giác IAB vuông cân tại I c N ó .C.Đ IA 1 nên N 2m 1 2 2 3 NG d I 2 ; 2
4m 8m 1 0 m thỏa mãn đk 1 CÔ Ờ 2 2 2 4m 1 2 N 2 3 YỄ TRƢ
Vậy diện tích tam giác IAB đạt giá trị lớn nhất khi m . 2 GU N N
Câu 27. Các giá trị của m để đƣờng thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số 3
y x 3mx 2 cắt đƣờng tròn C x 2 2 :
1 y 2 có tâm I tại hai điểm phân biệt ÁO VIÊ ,
A B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. GI 1 3 3 m m 3 8 A. m . B. 2 . C. m . D. 2 . 8 1 3 3 1 m m 2 2 Lời giải Chọn A
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Ta có 2
y x m 2 3 3 3 x m , 2
y 0 x m .
Suy ra hàm số có hai điểm cực trị khi và chỉ khi m 0. 1
Ta có y y . x 2mx 2
nên đƣờng thẳng đi qua hai điểm cựa trị của đồ thị hàm số 3 là : y 2
mx 2 hay : 2mx y 2 0.
Đƣờng tròn C có tâm I (1;0) , bán kính R 2 .
Đƣờng thẳng d cắt đƣờng tròn C tại hai điểm phân biệt , A B khi I 2m 2 d , 2 2 2
4m 8m 4 8m 2 2
4m 8m 2 0. 2 4m 1 1
Khi đó, diện tích tam giác IAB là S I . A I . B sin AIB . IAB 2 1 1 1 Mà I . A I . B sin AIB I . A IB 2 R 1. I 2 2 2 Ơ
Nhƣ thế diện tích tam giác
IAB đạt giá trị lớn nhất khi sin AIB 1 AIB 90 . M D 1 2m 2
Từ đó d I, 1 AB .R 2 1 1 2 2
4m 8m 4 4m 3 1 m . Ầ 2 2 2 8 Đ 4m 1 NHỊ 3
Vậy giá trị m cần tìm là m . Đ 8 G THPT N.C.Đ 3 2 N
Câu 28. Cho hàm số f x m
1 x 5x m 3 x 3. Có tất cả bao nhiêu giá trị nguyên của NG CÔ Ờ
tham số m để hàm số y
f x có đúng 3 điểm cực trị ? N A. 1. B. 4 . C. 5 . D. 3 . YỄ TRƢ Lời giải GU N N Chọn B
Tập xác định D . ÁO VIÊ
f x m 2 3
1 x 10x m 3 . GI
* Trƣờng hợp 1: m 1.
Lúc đó f x 1
0x 4. Ta có f x 2
0 x . Suy ra hàm số y f x có một điểm 5
cực trị dƣơng. Suy ra hàm số y f x có đúng 3 điểm cực trị.
* Trƣờng hợp 2: m 1.
Lúc này hàm số y f x là hàm bậc ba. Hàm số y f x có đúng ba điểm cực trị khi
và chỉ khi phƣơng trình f x 0 có hai nghiệm phân biệt x , x thoả mãn x 0 x 1 2 1 2
hoặc x 0 x . 1 2
Phƣơng trình f x 0 có hai nghiệm trái dấu m
1 .m 3 0 3 m 1.
Phƣơng trình f x 0 có nghiệm x 0 x 1 2
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 m 3 0 P 0 m 3 10
. Hệ phƣơng trình này vô nghiệm. S 0 m 0 m 1 3 1
Kết hợp các trƣờng hợp, ta có 3
m 1. Vì m nên m 2 ; 1 ;0; 1 .
Vậy có 4 giá trị nguyên của m để hàm số y f x có đúng 3 điểm cực trị.
Câu 29. Gọi S là tập giá trị nguyên m0 1
; 00 để hàm số 3 2 3
y x 3mx 4m 12m 8 có 5
cực trị. Tính tổng các phần tử của S. A.10096. B.10094. C. 4048 . D. 5047 . Lời giải Chọn D Để hàm số 3 2 3
y x 3mx 4m 12m 8 có 5 cực trị khi và chỉ khi hàm số 3 2 3 I y x 3mx 4m
12m 8 có 2 cực trị nằm về hai phía đối với trục Ox Ơ
Xét hàm số: y f x 3 2 3
x 3mx 4m 12m 8 M D 3 2 x 0 y 4m 12m 8 Ầ
Có: y' 3x 6mx 0 Đ
x 2m y 1 2m 8 NHỊ 3 Đ
Hai cực trị của hàm số y
f x là: A0;4m 12m 8,B2m; 1 2m 8 G THPT N.C.Đ N
Để hai cực trị nằm về hai phía đối với trục Ox khi và chỉ khi NG 3 2 CÔ
4m 12m8 12m80 m; 1 1; 2; Ờ N 3 YỄ TRƢ Mà: m0 1
; 00 m3;4;5;6;... 1 ; 0 0 GU N 310098 N
Vậy tổng các giá trị của m là: 5047 . 2 Câu 30. Cho hàm số 4 2
y x 2mx 1
1 . Tổng lập phƣơng các giá trị của tham số m để đồ thị ÁO VIÊ GI hàm số
1 có ba điểm cực trị và đƣờng tròn đi qua 3 điểm này có bán kính R 1 bằng 5 5 1 5 A. . B . . C. 2 5 . D. 1 5 . 2 2 Lời giải Chọn D 3
y x mx x 2 ' 4 4 4
x m; y ' 0 x 0; x m với m 0 Gọi A B 2
m m C 2 0;1 , ; 1 ,
m;m
1 là 3 điểm cực trị của hàm số (1); khi đó tam giác ABC cân tại ,
A I là tâm đƣờng tròn đi qua , A ,
B C nên I Oy , gọi I 0;b
Ta có: IA R 1 1 b 1 b 0
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 4 2 4 2
IB R 1 m m 2m 1 1 m 2m m 0
mm 1 1 5 2 m m
1 0 m 0; m 1; m 1 2 3,4 2
Kết hợp điều kiện m 0 nên loại m và m 4 1 Ta có 3 3 m m 1
5 . Vậy chọn đáp án D. 2 3
Câu 31. Tìm số thực k để đồ thị hàm số 4 2
y x 2kx k có ba điểm cực trị tạo thành một tam 1
giác nhận điểm G 0; làm trọng tâm. 3 A. 1 k 1 ;k . B. 1 k 1; k . 2 3 C. 1 k 1; k . D. 1 1 k ; k . 2 3 2 Lời giải I Chọn C Ơ Ta có: 3
y x kx x 2 4 4 4 x k . M D Ầ x 0 Đ y ' 0 . 2 NH x k 1 Ị Đ
Đồ thị hàm số có ba điểm cực trị y 0 có ba nghiệm phân biệt và y đổi dấu khi x G THPT N.C.Đ N
đi qua 3 nghiệm đó PT
1 có hai nghiệm phân biệt khác không k 0. Khi đó ba NG CÔ Ờ
điểm cực trị của đồ thị hàm số là N
A0; k , B 2
k ;k k , C 2
k ; k k . YỄ TRƢ 2 2 GU N 1
k k k k k y y y A B C N
Từ yêu cầu bài toán ta có: y G 3 3 3 k 1 ÁO VIÊ 2 2k 3k 1 0 1 . GI k 2
Câu 32. Cho hàm số 4
y x 2
m m 2 2
1 x m 1. Tìm m để hàm số có ba điểm cực trị và
khoảng cách gi a hai điểm cực tiểu là nhỏ nhất. 1
A. m 1.
B. m 1. C. m=1.
D. m = 2 Lời giải Chọn D 3
y' x 2
m m x = x 2 2 4 4 1 4
x m + m 1 . x
y ' 0 4x 0 2 2
x m + m 1 0 2 2
x m m+1
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Hàm số có ba điểm cực trị khi và chỉ khi phƣơng trình y' 0 có ba nghiệm phân biệt hay phƣơng trình 2 2
x m +m 1 0 có hai nghiệm phân biệt khác không 2 1 3 2
m m+1 0 m 0 luôn đúng m . 2 4
Khi đó phƣơng trình y' 0 có ba nghiệm phân biệt 2 2
x m m 1, x m m 1, x 0. 1 2 3 Bảng biến thiên. x x 0 x 1 2 y' 0 0 0 I y 2 Ơ y y y 1 1 M D Ầ Đ
Khi đó đồ thị hàm số có hai điểm cực tiểu là B 2
m m 1; y và C 2
m m 1; y . 1 1 NHỊĐ 2 1 3 2 G THPT
Khoảng cách gi a hai điểm cực tiểu là N B .C C .Đ
= 2 m m 1 2 m 3. N 2 4 NG 1 CÔ Ờ
Dấu " " xảy ra khi m = N 2 YỄ
TRƢ Câu 33. Cho hàm số 4 2 4
y x 2mx m 2 .
m Tìm tất cả các giá trị của m để các điểm cực trị của GU N
đồ thị hàm số lập thành một tam giác đều. N
A. m 2 2. B. m 1. C. 3 m 3. D. 3 m 4. Lời giải ÁO VIÊ GI Chọn C x 0
Tập xác định của hàm số: D . Ta có 3
y 4x 4mx 4x 2
x m y ' 0 2 x . m
Hàm số trùng phƣơng có 3 cực trị y ' 0 có 3 nghiệm phân biệt m 0 1 .
Gọi ba điểm cực trị của đồ thị hàm số là , A ,
B C với A là điểm thuộc trục tung. Khi đó, 4 4 2 4 2 ( A 0; m 2 ) m , ( B
m; m m 2 )
m , C( m; m m 2 ) m .
Vì đồ thị hàm số trùng phƣơng nhận trục tung làm trục đối xứng. Ở bài này, hai điểm
cực tiểu đối xứng nhau qua trục tung và điểm cực đại nằm trên trục tung nên ABC
cân tại A . Do đó, các điểm cực trị của đồ thị hàm số lập thành một tam giác đều m 0 ABC có AB BC 4 4 4
m m 4m m m 4m m 3m 0 . 3 m 3 3
Từ điều kiện (1) kết luận m 3 thỏa mãn yêu cầu bài toán.
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 34. Cho hàm số f x có đạo hàm là f x . Đồ thị của hàm số y f x nhƣ hình vẽ bên.
Tính số điểm cực trị của hàm số 2 y
f x trên khoảng 5; 5 . A. 2 . B. 4 . C. 3 . D. 5 . Lời giải Chọn C 2 2 I
Xét hàm số g x f x gx 2xf x . Ơ x 0 x 0 x 0 M D
g x 0 2 x 0 . 2 Ầ f x 0 x 2 Đ 2 x 2 NHỊ Ta có bảng xét dấu : Đ G THPT N.C.Đ N NG CÔ Ờ N Từ đó suy ra hàm số 2 y
f x có 3 điểm cực trị. YỄ TRƢ GU
N Câu 35. Cho hàm số 4 2
y x 2mx 3m 2 (với m là tham số). Có bao nhiêu giá trị của tham số N
m để đồ thị hàm số có ba điểm cực trị đều nằm trên các trục tọa độ? A. 2 . B. 0 . C. 3 . D. 1. ÁO VIÊ Lời giải GI Chọn A Ta có 4 2 3
y x 2mx 3m 2 y 4x 4mx . x 0 Khi y 0 . x m
Với m 0 thì đồ thị hàm số có 3 điểm cực trị và các điểm cực trị là A0;3m 2 , B 2
m ; m 3m 2 và C 2
m ; m 3m 2.
Điểm A đã nằm trên trục tung, vậy để các điểm cực trị đều nằm trên các trục tọa độ thì m 2
hai điểm B và C phải nằm trên trục hoành, suy ra 2
m 3m 2 0 . m 1
Vậy có 2 giá trị của tham số m thỏa mãn yêu cầu bài toán.
Câu 36. Biết m m ; m là giá trị của tham số m để đồ thị hàm số 4 2
y x 2mx 1 có ba 0 0
điểm cực trị tạo thành một tam giác vuông. Khẳng định nào sau đây đúng?
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
A. m 0;3 . B. m 5 ;3 . C. m 3 ;0 . D. m 3;7 . 0 0 0 0 Lời giải Chọn C
Cách 1. Ta có 3
y 4x 4mx . x 0 Xét phƣơng trình 3
y 0 4x 4mx 0 . 2 x m
Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi m 0 . Khi đó 3 điểm cực trị là A0 ; 1 , B 2
m ;1 m , C 2
m ;1 m .
Ta thấy ABC cân tại A . Nên ABC vuông khi và chỉ khi ABC vuông cân tại A . m 0 Do đó 4 A .
B AC 0 m m 0 m 3
1 m 0
. Kết hợp m 0 ta có m 1 . m 1 I Ơ
Cách 2. ( Dùng công thức tính nhanh ). Gọi , A ,
B C là ba điểm cực trị của đồ thị hàm số. M D Ầ
ABC vuông cân b a m3 3 3 8 2 8 m 1 m 1 . Đ NH Ị Câu 37. Cho hàm số 4 2 2 y x 2(m m 1)x
m có đồ thị C . Tìm m để đồ thị hàm số C có 3 Đ
điểm cực trị và khoảng cách gi a hai điểm cực tiểu nhỏ nhất. G THPT N.C.Đ N 1 1
A. m .
B. m .
C. m 3.
D. m 0. NG 2 2 CÔ Ờ N Lời giải YỄ TRƢ Chọn B GU N 2
x m m 1 N 1 Ta có: 3
y x 2 4
4 m m 1 x 2 x x 2 4 m m 1 0 x 0 . 2 2 ÁO VIÊ
x m m 1 3 GI 2 1 3
Khoảng cách gi a 2 điểm cực tiểu: 2
d x x 2 m m 1 2 m 3 . 3 1 2 4 1
Dấu bằng xảy ra khi m . 2
Câu 38. Để đồ thị hàm số 4 2
y x 2mx m 1 có ba điểm cực trị tạo thành một tam giác có
diện tích bằng 2, giá trị của tham số m thuộc khoảng nào sau đây? A. (2;3). B. ( 1 ;0). C. (0;1). D. (1;2).
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 29
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn D 3
y x mx x 2 ' 4 4 4 x m x 0 Xét y ' 0
x m,(m 0)
Tọa độ ba điểm cực trị là: A m B 2
m m m C 2 (0; 1), ; 1 ,
m; m m 1 2 AH m
Gọi H là trung điểm của cạnh BC , ta có BC 2 m 1 2 5 S
AH BC m m 2 m 4. ABC 2
Câu 39. Cho hàm số f x 4 2 2
x 2mx 4 2m . Có tất cả bao nhiêu số nguyên m 1 0;10 để I
hàm số y f x có đúng 3 điểm cực trị? Ơ A. 6 . B. 8 . C. 9 . D. 7 . M D Ầ Lời giải Đ Chọn C NHỊ Đ m 0 G m 2 THPT N.C.Đ 2 4 2m 0 N
Để hàm số y f x có đúng ba điểm cực trị thì: 2 3 . NG m 0 0 m CÔ Ờ 3 2 N 4 3m 0 YỄ TRƢ
Vậy các số nguyên m thỏa mãn bài toán là 9
;8; 7; 6;5; 4;3; 2; 1 . GU
N Câu 40. Cho hàm số 4 2 y x 2 m 1 x 2m
3 . Tập hợp tất cả các giá trị thực của tham số m N
để hàm số đã cho có đúng 5 điểm cực trị là ÁO VIÊ 3 3 3 A. 1; . B. ; \ 2 . C. 1; \ 2 . D. 1; . GI 2 2 2 Lời giải Chọn D Đặt: 4 2 f (x) x 2 m 1 x 2m 3 3 f ' x 4x 4 m 1 x x 0 f ' x 0 2 x m 1
Vì hàm số f (x) có a 1 0 nên hàm số y
f x có đúng 5 cực trị Hàm số f (x) m 1 0 m 1 3
phải có 3 cực trị thỏa y 0 m 1; cd f 0 0 2m 3 0 2 Vậy chọn D
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 30
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 41. Cho hàm số y f x có đồ thị nhƣ hình vẽ. Biết tất cả các điểm cực trị của hàm số
y f x là 2 ; 0; 2; ;
a 6 với 4 a 6 . y -2 O 2 a 6 x y = f(x)
Số điểm cực trị của hàm số y f 6 2
x 3x là: I Ơ A. 8 .
B.11 .C.9. D. 7 . Lời giải M D Ầ Chọn C Đ 6 2 NH
g(x) f x 3x . Ị Đ g ' x 6 2 6 2 6 2 5 6 2 f x 3x ' x 3x
'. f ' x 3x
6x 6x f ' x 3x . G THPT N.C.Đ N NG x 0 CÔ Ờ N x 1 6 2 YỄ x 3x 2 TRƢ 1 5
6x 6x 0 5 6 2 6 2 GU N
y ' 0 6x 6x f ' x 3x 0
x 3x 0 2 . 6 2 N f '
x 3x 0 6 2
x 3x 2 3 6 2
x 3x a 4 ÁO VIÊ GI 6 2
x 3x 6 5 6 2
x x 6 2 2 3
2 1 x 3x 2 0 x 1 x 1 . 2 x 0 * x 0 6 2
x 3x 02 . 4 4 x 3 x 3 6 2
x x 6 2 2 3
2 3 x 3x 2 0 x 2 x 2 .
Ta xét bảng biến thiên của hàm số:
y h x 6 2 x 3x
x 0 h0 0
y ' h ' x 5
6x 6x 0 x 1 h 1 2 x 1 h 1 2
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 31
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Từ bảng biến thiên ta suy ra phƣơng trình 6 2
x 3x a
4 có một nghiệm biệt khác 0; 1 ;
1 và khác nghiệm của phƣơng trình 2;3 Phƣơng trình 6 2 x 3x 6
5 có hai nghiệm phân biệt khác 0; 1 ; 1 và khác nghiệm
của phƣơng trình 2;3;4 . Ta có thể lấy nghiệm gần đúng nhƣ sau: x m x 2,355 6 2
x 3x 65 6 2 2
x 3x 6 0 x ,
m m 5,547, m 5;6 x 2 ,355 x m I 2 Ơ
n x m 6 2
x 3x a4 4
m x n 6 2
4 x 3x 6 n 2,195 M D 4 4 a 6
n x m m 2, 355 Ầ Đ NH Ị Đ
Vậy y ' g ' x 0 có: G THPT N.C.Đ
+) 2 nghiệm bằng x 1 x 1 không là điểm cực trị. N NG
+) 2 nghiệm bằng x 1 x 1
không là điểm cực trị. CÔ Ờ N
+) 3 nghiệm bằng x 0 x 0 là 1 điểm cực trị. YỄ TRƢ +) 1 nghiệm bằng 4 4 x 3 x 3 là 1 điểm cực trị. GU N +) 1 nghiệm bằng 4 4
x 3 x 3 là 1 điểm cực trị. N
+) 1 nghiệm bằng x m x m là 1 điểm cực trị.
+) 1 nghiệm bằng x m x m là 1 điểm cực trị. ÁO VIÊ GI
+) 1 nghiệm bằng x 2 x 2 là 1 điểm cực trị.
+) 1 nghiệm bằng x 2 x 2 là 1 điểm cực trị.
+) 1 nghiệm x và x m; n x là 1 điểm cực trị. 1 1 1
+) 1 nghiệm x và x
n; m x là 1 điểm cực trị. 2 2 2
Vậy có tất cả 9 điểm cực trị . Câu 42. Cho hàm số 4 2
y x 2mx m , với m là tham số thực. Gọi S là tập hợp tất cả các giá trị
của m để đồ thị hàm số đã cho có 3 điểm cực trị và đƣờng tròn đi qua 3 điểm cực trị
này có bán kính bằng 1. Tổng giá trị của các phần tử của S bằng 1 5 1 5 A. 1. B. 0 . C. . D. . 2 2 Lời giải Chọn C
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 32
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 3
y x mx x 2 4 4 4 x m
Hàm số có 3 cực trị khi y 0 có 3 nghiệm phân biệt m 0 x 0 Xét y 0 m 0 x m
Tọa độ ba điểm cực trị: A0;m, B 2
m ; m m, C 2
m ; m m .
Gọi H là trung điểm của cạnh BC . Ta có H 2
0; m m 1 A . B AC.BC S AH.BC (do ABC cân tại A ) ABC 2 4R 2 AH m 2
AB 2AH.R trong đó 4
AB m m Suy ra 4 2
m m 2m m 3
m m mm 2 2 1 0
1 m m 1 0 I m 0 Ơ m 1 M D 1 5 1 5
. Đối chiếu điều kiện ta đƣợc S 1; . Ầ m 2 Đ 2 NH Ị 1 5 m Đ 2 G THPT N.C.Đ N 1 5
Do đó tổng giá trị các phần tử thuộc S bằng . NG 2 CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
CỰC TRỊ HÀM BẬC BA, HÀM TRÙNG PHƯƠNG 33
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHUÛ ÑEÀ: CÖÏC TRÒ HAØM SOÁ
VẬN DỤNG – VẬN DỤNG CAO DẠNG 3
CỰC TRỊ CÁC HÀM SỐ KHÁC Câu 1.
Cho S là tập hợp tất cả các giá trị thực của tham số m để điểm cực trị của đồ thị hàm số 2
y x 2mx 8 cũng là điểm cực trị của đồ thị hàm số 1 m y x
m 1 x m m 2 3 3 2 x
. Tính tổng bình phƣơng tất cả các phần tử của tập 3 3 hợp S . A. 8 . B. 10 . C. 18 . D. 16 .
I Câu 2. Cho hàm số 2
y f x liên tục trên
và có f x x 2 2
x 3x 4 . Gọi S là tập các Ơ số nguyên m 1 0;1
0 để hàm số y f 2
x 4x m có đúng 3 điểm cực trị. Số phần tử M D Ầ của S bằng: Đ NHỊ A. 10. B. 5. C. 14. D. 4. Đ
Câu 3. Cho hàm số f x có đạo hàm f x 2
x x 2
1 x 2mx 5 . Gọi S là tập hợp tất cả các G THPT N.C.Đ N
giá trị nguyên của m để hàm số f x có đúng một điểm cực trị, tìm số tập con khác NG CÔ Ờ
rỗng của S ? N A. 127 . B. 15 . C. 63 . D. 31. YỄ
TRƢ Câu 4. Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số GU N 3 N
y x m 2 2
1 x 3m x 5 có 3 điểm cực trị. 1 1
A. 1;. B. ; . C. ; 0. D. 0; 1; . ÁO VIÊ 4 4
GI Câu 5. Cho hàm số f x x 2 2 ' 2 x 4x
3 với mọi x . Có bao nhiêu giá trị nguyên
dƣơng của tham số m để hàm số y f 2
x 10x m 9 có 5 điểm cực trị? A. 18 . B. 17 . C. 16 . D. 15 . Câu 6.
Cho hàm số f x 4 mx 2 m 2 2001
4 x 2019 , với m là tham số. Có bao nhiêu giá trị
nguyên của tham số m để hàm số y f x có 2 điểm cực đại và 1 điểm cực tiểu? A. 0 . B.vô số. C. 2 . D. 1 . Câu 7.
Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y 3x 4x 12x m có 7 điểm cực trị? A. 3. B. 6. C. 5. D. 4. Câu 8.
Gọi S là tập hợp tất cả các số thực m thỏa mãn đồ thị hàm số 4 2
y x 10x m có
đúng 7 điểm cực trị. Số phần tử của tập hợp S là
CỰC TRỊ CÁC HÀM SỐ KHÁC 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 24. B. 23. C. 26. D. 25. 3 Câu 9.
Tìm các giá trị thực của tham số m để đồ thị hàm số y x 2
1 3m x 1 2 có
hai điểm cực trị cách đều gốc tọa độ. 1 1 A. m . B. m . C. m 5 . D. m 5. 3 2
Câu 10. vẽ bên là đồ thị của hàm số y f (x) . Gọi S là tập hợp các giá trị nguyên dƣơng của
tham số m để hàm số y f (x 1) m có 7 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng I Ơ A. 6. B. 9. C. 12. D. 3.
M D Câu 11. Có bao nhiêu giá trị nguyên dƣơng của tham số m không vƣợt quá 2019 để hàm số Ầ Đ 2 x y
x m 2 không có điểm cực trị? NHỊ 8 Đ A. 0. B. 1. C. 2018. D. 2019. G THPT N.C.Đ N 4 5 3
Câu 12. ho hàm số y f x có đạo hàm f ' x x
1 x m x 3 với mọi x . ó bao NG CÔ Ờ
nhiêu giá trị nguyên của tham số m 5 ;
5 để hàm số g x f x có 3 điểm cực trị N YỄ A. TRƢ 3. B. 6. C. 5. D. 4. GU
N Câu 13. Cho hàm số y f x xác định trên có f 3 8 ; f 9 4 ; f 1 2 . Biết rằng hàm N 2 2
số y f x có đồ thị nhƣ hình vẽ bên. Hỏi đồ thị hàm số y
f x x 2 2 1 có bao ÁO VIÊ GI nhiêu điểm cực trị? A. 2. B. 3. C. 6. D. 5.
Câu 14. Cho hàm số y f x xác định trên và hàm số y f x có đồ thị nhƣ hình bên dƣới.
CỰC TRỊ CÁC HÀM SỐ KHÁC 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 y 2 1 O x -3 -1 2 5 - 1 - 2 - 3
Đặt g x f x m . Có bao nhiêu giá trị nguyên của tham số m để hàm số g x có đúng 7 điểm cực trị? A. 2 . B. 3 . C. 1. D. vô số.
Câu 15. Cho hàm số f x có đạo hàm 2 f (
x) (x 1) 2
x 4x .Có bao nhiêu giá trị nguyên
dƣơng của tham số m để hàm số g x f 2 ( )
2x 12x m có đúng 5 điểm cực trị ? I A. 18. B. 17. C. 16. D. 19. Ơ 3
Câu 16. Có bao nhiêu giá trị nguyên của tham số m để hàm số y x m 2 2
1 x 3m x 5 có M D ba điểm cực trị? Ầ Đ A. Vô số. B. 3. C. 2. D. 1. NHỊ x Đ
Câu 17. Hàm số f x
m (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực 2 x 1 G THPT N.C.Đ N trị? NG CÔ Ờ A. 2 . B.. C. 5 . D. 4 . N
Câu 18. Cho hàm số y f x có đồ thị nhƣ hình vẽ dƣới. Tập các giá trị của tham số m để hàm YỄ
TRƢ số gx f xm có 7 điểm cực trị là ;ab. Tính T 2b .a GU N N A. 2 . B. 2 . C. 0 . D. 6 . ÁO VIÊ GI
Câu 19. Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y x 6x m có 5 điểm cực trị. A. 32 . B. 31. C. 31. D. 34 .
Câu 20. Cho hàm số y f x có đồ thị y f ' x nhƣ hình vẽ sau. Đồ thị hàm số
g x f x 2 2
x có tối đa bao nhiêu điểm cực trị? A. 3 . B. 7 . C. 5 . D. 6 .
CỰC TRỊ CÁC HÀM SỐ KHÁC 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 21. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số m 3 2
y x 3x 9x 5
có 5 điểm cực trị? 2 A. 62 . B. 63 . C. 64 . D. 65 . I Ơ 1
Câu 22. Cho hàm số y f x 3
x 2m 2
1 x 8 m x 2 với m . Tập hợp tất cả các giá 3 M D Ầ
trị của m để hàm số y f x có 5 cực trị là khoảng ; a b . Tích . a b bằng Đ NH A. 12. B. 16. C. 10. D. 14. Ị 3 Đ
Câu 23. Cho hàm số y f x có đạo hàm f x x 2
x m 2 1 4
5 x m 7m 6, x . Có G THPT N.C.Đ N
bao nhiêu số nguyên m để hàm số g x f x có 5 điểm cực trị? NG CÔ Ờ A. 2 . B. 3 . C. 4 . D. 5 . N 4 3 f x 2 2
f x x x 2
x 4 x 2 m 3 x 6m 18. YỄ
Câu 24. Cho hàm số có đạo hàm TRƢ Có tất GU N
cả bao nhiêu giá trị nguyên của m để hàm số f x có đúng một điểm cực trị? N A. 7 . B. 5 . C. 8 . D. 6 .
Câu 25. Cho hàm số bậc bốn y f (x) . Hàm số y f (
x) có đồ thị nhƣ hình vẽ dƣới đây. Số ÁO VIÊ GI
điểm cực đại của hàm số y f 2
x 2x 2 là: A. 1. B. 2. C. 4. D. 3.
CỰC TRỊ CÁC HÀM SỐ KHÁC 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2
Câu 26. Cho hàm số f x x 2 1
mx 4mx m n 2 với , m n . Biết trên khoảng 7 7 5 ; 0
hàm số đạt cực đại tại x 1 . Trên đoạn ;
hàm số đã cho đạt cực tiểu 6 2 4 tại 7 3 5 5 A. x .
B. x .
C. x . D. x . 2 2 2 4
Câu 27. Cho hàm số f x m 3 2
1 x 5x m 3 x 3. Có tất cả bao nhiêu giá trị nguyên của
tham số m để hàm số y f x có đúng 3 điểm cực trị? A. 4 . B. 3 . C. 5 . D. 1.
Câu 28. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số 4 3 2
y 3x 8x 6x 24x m có
7 điểm cực trị. Tính tổng các phần tử của S . A. 42 . B. 50 . C. 30 . D. 63 .
I Câu 29. Cho hàm số bậc ba y f x có đồ thị nhƣ hình vẽ. Hỏi hàm số 2 g x
f x x có bao Ơ nhiêu điểm cực trị? M D Ầ y Đ NHỊĐ 2 G THPT N.C.Đ N NG 2 O x CÔ Ờ N 2 YỄ TRƢ GU N N A. 2 . B. 3 . C. 5 . D. 4 . 2
x px q
Câu 30. Cho hàm số f (x) p
p q . Có bao nhiêu cặp p; q sao 2 ÁO VIÊ x , trong đó 2 2 0, 1 1 GI
cho khoảng cách giữa hai điểm cực trị của đồ thị hàm số trên bằng 10 ? A. 2. B. 1. C. 3. D. 0.
Câu 31. Gọi m0 là giá trị của tham số m để đƣờng thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số 3
y x 6mx 4 cắt đƣờng tròn tâm I 1;0 , bán kính bằng 2 tại hai điểm
phân biệt A , B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
A. m 2;3 . B. m 3; 4 .
C. m 0;1 . D. m 1; 2 . 0 0 0 0 2 x mx 5
Câu 32. Gọi m là giá trị của m thỏa mãn đồ thị hàm số y
có hai điểm cực trị A , 0 2 x 1
B sao cho đƣờng thẳng AB đi qua điểm I 1; 3
. Khẳng định nào sau đây là đúng
A. 0 m 3 . B. 5 m 3 . C. 3
m 0.
D. 3 m 5 . 0 0 0 0
Câu 33. ó bao nhiêu giá trị nguyên của tham số m để hàm số 9 7 2 6
y x (m 2)x (m 4)x 7
đạt cực tiểu tại x 0 ?
CỰC TRỊ CÁC HÀM SỐ KHÁC 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 3 . B. 4 . C. Vô số. D. 5 . 5 x m Câu 34. Cho hàm số 4 3 y 2m 1 x x
2019 . Có bao nhiêu giá trị của tham số m để 5 3
hàm số đạt cực tiểu tại x 0 ? A.Vô số . B.1 . C.2 . D.0 .
Câu 35. Có bao nhiêu giá trị nguyên của m thuộc khoảng 2019; 2019 để hàm số m 1 m 2 5 4 y x
x m 5 đạt cực đại tại x 0? 5 4 A. 110 . B. 2016 . C. 100 . D. 10 .
Câu 36. Cho hàm số f x có đạo hàm trên thỏa mãn 2 f x h f x h h , 2019 29m x , h
0 . Đặt g x x f
x x f x 4 2 m m 2 29
100 sin x 1, m
là tham số nguyên và m 27 . Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho I
hàm số g x đạt cực tiểu tại x 0 . Tính tổng bình phƣơng các phần tử của S . Ơ A. 100 . B. 50 . C. 108 . D. 58 . M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
CỰC TRỊ CÁC HÀM SỐ KHÁC 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI Câu 1.
Cho S là tập hợp tất cả các giá trị thực của tham số m để điểm cực trị của đồ thị hàm số 2
y x 2mx 8 cũng là điểm cực trị của đồ thị hàm số 1 m y x
m 1 x m m 2 3 3 2 x
. Tính tổng bình phƣơng tất cả các phần tử của tập 3 3 hợp S . A. 8 . B. 10 . C. 18 . D. 16 . Lời giải Chọn A b Vì 2
y x 2mx 8 là một parabol nên có đỉnh là I 2 ; ;
m m 8 là một 2a 4a
cực trị của đồ thị hàm số. 1 m
Xét hàm số y x m
1 x m m 2 3 3 2 x . I 3 3 Ơ 2
y x 2m
1 x mm 2 . M D
Để thỏa mãn yêu cầu bài toán thì điểm I là cực trị của đồ thị hàm số Ầ Đ 1 m NH y
x m
1 x m m 2 3 3 2 x . Ị 3 3 Đ 2 G m
1 m m 2 THPT 0 N.C.Đ 0 y N m 2 2
m 2mm
1 m m 2 NG y m 0 0 . CÔ m 2 Ờ 2 N y m 2 m 8 2m 8 YỄ TRƢ S 2 ; 2 . GU N N
Vậy tổng bình phƣơng các phần tử của tập hợp S là : 2 2 2 2 8 . Câu 2. Cho hàm số 2
y f x liên tục trên
và có f x x 2 2
x 3x 4 . Gọi S là tập các ÁO VIÊ 2 GI số nguyên m 1 0;1
0 để hàm số y f x 4x m có đúng 3 điểm cực trị. Số phần tử của S bằng: A. 10. B. 5. C. 14. D. 4. Lời giải Chọn B x 22 0 Ta có: f ( x) 0 2
x 3x 4 0
Đặt y g x f 2 ( )
x 4x m
g x x 2 ( ) 2 4 f (
x 4x m)
CỰC TRỊ CÁC HÀM SỐ KHÁC 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 2 2x 4 0
x 4x m 22 2 0 g ( x) 0 2
f (x 4x m) 0 h x 2 1 x 4x m 1 0(1) 2 2 h (x) x 4x m 4 0(2)
Hàm số có 3 cực trị khi một trong 2 phƣơng trình (1) và (2) có 2 nghiêm phân biệt khác
2 và phƣơng trình có lại có 1 nghiệm hoặc vô nghiệm. 1 h (2) 0 1 0 0 m 5 2 0
m 3 0 m 5 2 h (2) 0 m 0 1 0 2 0 I Ơ mà m 1 0;1
0 do đó m 0;1;2;3; 4 có 5 phần tử. 2 2
M D Câu 3. Cho hàm số f x có đạo hàm f x x x 1 x
2mx 5 . Gọi S là tập hợp tất cả các Ầ Đ
giá trị nguyên của m để hàm số f x có đúng một điểm cực trị, tìm số tập con khác NHỊ
rỗng của S ? Đ G THPT A. 127 . B. 15 . N.C.Đ C. 63 . D. 31. N Lời giải NG CÔ Ờ Chọn C N
Hàm số f x có đúng một điểm cực trị khi và chỉ khi: YỄ TRƢ
Trường hợp 1: Phƣơng trình 2
x 2mx 5 0 vô nghiệm hoặc có nghiệm kép. GU N N
Điều đó xảy ra khi và chỉ khi 2
m 5 0 5 m 5 * .
Trường hợp 2: Phƣơng trình 2
x 2mx 5 0 có hai nghiệm phân biệt trong đó có một ÁO VIÊ nghiệm là 1
. Điều đó xảy ra khi và chỉ khi: GI m 5 2 m 5 0
m 3 ** . 2 m 5 1 2m 5 0 m 3 Từ * ,*
* suy ra m 5; 5 3 .
Do m m 2 ; 1 ;0;1;2; 3 hay S 2 ; 1 ;0;1;2; 3 .
Suy ra số tập con khác rỗng của S bằng 1 2 3 4 5 6
C C C C C C 63 . 6 6 6 6 6 6 Câu 4.
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số 3
y x m 2 2
1 x 3m x 5 có 3 điểm cực trị. 1 1
A. 1;. B. ; . C. ; 0. D. 0; 1; . 4 4 Lời giải Chọn C
CỰC TRỊ CÁC HÀM SỐ KHÁC 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Xét hàm số f x 3
x m 2 2
1 x 3mx 5 , có f x 2
3x 22m 1 x 3m . 3
Hàm số y f x x m 2 2
1 x 3m x 5 có 3 điểm cực trị khi và chỉ khi hàm số
y f x có hai điểm cực trị x , x thỏa mãn x 0 x
phƣơng trình f x 0 có hai 1 2 1 2
nghiệm x , x sao cho x 0 x . 1 2 1 2
Ta có phƣơng trình f x 0 có hai nghiệm x , x thoả mãn x 0 x thì 1 2 1 2 1 2 0
4m 5m 1 0
m 1 m 4 m 0 . P 0 m 0 m 0 Thử lại: +) với m
0 thì phƣơng trình f x 2
3x 22m
1 x 3m có hai nghiệm x 0 x (thỏa mãn). 1 2 x 0
+) với m 0 thì f x 2
3x 6x 0 (thỏa mãn). x 2 I Ơ Vậy m ;0
thỏa mãn yêu cầu bài toán. 2 2
M D Câu 5. Cho hàm số f 'x x 2 x 4x
3 với mọi x . Có bao nhiêu giá trị nguyên Ầ Đ
dƣơng của tham số m để hàm số y f 2
x 10x m 9 có 5 điểm cực trị? NHỊĐ A. 18 . B. 17 . C. 16 . D. 15 . G THPT N.C.Đ Lời giải N NG Chọn C CÔ Ờ Dấu của: N YỄ TRƢ GU N N
Vì y x f 2 ' 2
10 . ' x 10x m 9 . ÁO VIÊ x 5 GI 2
x 10x m 9 1 y ' 0 . 2
x 10x m 9 2(L) 2
x 10x m 9 3 x 5
Vậy hàm số đã cho có 5 cực trị 2
x 10x m 9 1 (1)
có 5 nghiệm phân biệt khác 5. 2
x 10x m 9 3 (2)
Mỗi pt (1) và (2) có 2 nghiệm phân biệt khác 5.
25 m 8 0 25 m 6 0 m 17 . m 17 m 19
Vậy các giá trị m nguyên dƣơng thõa mãn: m 1; 2; 3....; 1 6 .
CỰC TRỊ CÁC HÀM SỐ KHÁC 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 6.
Cho hàm số f x 4 mx 2 m 2 2001
4 x 2019 , với m là tham số. Có bao nhiêu giá trị
nguyên của tham số m để hàm số y f x có 2 điểm cực đại và 1 điểm cực tiểu? A. 0 . B.vô số. C. 2 . D. 1 . Lời giải Chọn B f x 3 mx 2
m x x 2 2 ' 8004 2 4 2
4002mx m 4
+ TH1: m 0 thì f ' x 8
x 0 x 0 , f "0 8
0 . Hàm số chỉ có một cực đại tại
x 0 nên không thỏa mãn đề bài. x 0 + TH2: m 0 thì f ' x 2 0 4 m 2 x 4002m
Để hàm số có 3 cực trị thì f ' x 0 có 3 nghiệm phân biệt , khi đó I 2 Ơ 4 m m 2 0 4002m 0 m 2 M D 2 Ầ 4 m Đ
Phƣơng trình f ' x 0 có 3 nghiệm phân biệt x 0; x . 1,2 4002m NHỊ Đ
Nếu 0 m 2 ta có bảng biến thiên G THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N
Hàm số có 2 điểm cực tiểu và 1 điểm cực đại nên 0 m 2 không thỏa mãn đề bài. Nếu m 2
ta có bảng biến thiên ÁO VIÊ GI
Hàm số có 2 điểm cực đại và 1 điểm cực tiểu nên m 2 thỏa mãn đề bài.
Chú ý: Khi làm trắc nghiệm ta làm nhƣ sau f x 3 mx 2
m x x 2 2 ' 8004 2 4 2
4002mx m 4
+ Xét m 0 thì f ' x 8
x 0 x 0 , f "0 8
0 . Hàm số chỉ có một cực đại tại
x 0 nên không thỏa mãn đề bài. 2001m 0
+ Để hàm số y f x có 2 điểm cực đại và 1 điểm cực tiểu thì 2 2001 ( m m 4) 0
CỰC TRỊ CÁC HÀM SỐ KHÁC 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 m 0 m 0 m 0 m 2 m 2 . 2 2
m(m 4) 0 m 4 0 m 2 Câu 7.
Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y 3x 4x 12x m có 7 điểm cực trị? A. 3. B. 6. C. 5. D. 4. Lời giải Chọn D x 0
Xét hàm số f x 4 3 2
3x 4x 12x m . Ta có f x 3 2
12x 12x 24x 0 x 1 . x 2 Bảng biến thiên: I Ơ M D Ầ Đ NH y f x y f x Ị Để hàm số
có 7 điểm cực trị thì đồ thị hàm số
phải cắt trục Ox tại 4 Đ m 0 G THPT N.C.Đ điểm phân biệt 0 m 5 . N m 5 0 NG CÔ Ờ Mà m m1;2;3;
4 . Vậy có 4 giá trị nguyên của m thỏa mãn bài toán. N Câu 8.
Gọi S là tập hợp tất cả các số thực m thỏa mãn đồ thị hàm số 4 2
y x 10x m có YỄ TRƢ GU N
đúng 7 điểm cực trị. Số phần tử của tập hợp S là N A. 24. B. 23. C. 26. D. 25. Lời giải ÁO VIÊ Chọn A GI x 0 Gọi f x 4 2
x 10x m . Ta có f x 3
4x 20x 0 x 5
Bảng biến thiên của hàm số f x 4 2
x 10x m:
Ta có số điểm cực trị của hàm số y f (x) bằng tổng số điểm cực trị của hàm số
y f (x) và số nghiệm của phƣơng trình f (x) 0 (không trùng với các điểm cực trị
của hàm số). Do đó để hàm số 4 2
y x 10x m có đúng 7 điểm cực trị thì f (x) 0 có 4
nghiệm phân biệt 0 m 25 . Vậy S 1;2;...;2 4 .
CỰC TRỊ CÁC HÀM SỐ KHÁC 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 3 Câu 9.
Tìm các giá trị thực của tham số m để đồ thị hàm số y x 2
1 3m x 1 2 có
hai điểm cực trị cách đều gốc tọa độ. 1 1 A. m . B. m . C. m 5 . D. m 5. 3 2 Lời giải Chọn B
Ta có y x 2 2 ' 3 1 3m . x m x m y 0 3 x 2
1 3m 0 x 2 1 1 2 2 1 m .
x 1 m x 1 m
Để hàm số có 2 cực trị thì m 0 .
Gọi A, B là hai điểm cực trị của đồ thị hàm số có hoành độ lần lƣợt là
x 1 m; x 1 m . Khi đó A 3
m m B 3 1 ;2 2 ;
1 m; 2m 2 . I A B Ơ
Hai điểm cực trị cách đều gốc tọa độ nên 2 2
OA OB OA OB M D
m 0ktm 2 2 Ầ
m2 m m2 3 3 1 2 2 1 2 m 2 3
4m m 0 . Đ 1
m tm NHỊ 2 Đ 1 G THPT Vậy m . N.C.Đ N 2 NG y f x CÔ
Câu 10. vẽ bên là đồ thị của hàm số
( ) . Gọi S là tập hợp các giá trị nguyên dƣơng của Ờ N
tham số m để hàm số y f (x 1) m có 7 điểm cực trị. Tổng giá trị tất cả các phần tử YỄ TRƢ của S bằng GU N N ÁO VIÊ GI A. 6. B. 9. C. 12. D. 3. Lời giải Chọn D
Xét hàm số g(x) f (x 1) m . Ta có g (
x) f (x 1) .
Vì hàm số f x có 3 điểm cực trị do đó hàm số g(x) f (x 1) m có 3 điểm cực trị.
Để hàm số y f (x 1) m có 7 điểm cực trị thì phƣơng trình f (x 1) m phải có có 4
nghiệm đơn phân biệt hay 3 m 2 2 m 3.
Vì m nguyên dƣơng nên m1, 2 , chọn D.
Câu 11. Có bao nhiêu giá trị nguyên dƣơng của tham số m không vƣợt quá 2019 để hàm số 2 x y
x m 2 không có điểm cực trị? 8
CỰC TRỊ CÁC HÀM SỐ KHÁC 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 0. B. 1. C. 2018. D. 2019. Lời giải Chọn B
Tập xác định: D m 2; x 1
x x m 2 2 Ta có y y 4 2 x m 2 4 x m 2
y 0 x x m 2 2 0 x x m 2 2 1 2 x Hàm số y
x m 2 không có điểm cực trị phƣơng trình y 0 vô nghiệm 8
hoặc có nghiệm kép
1 vô nghiệm hoặc có nghiệm kép
Vì m nguyên dƣơng nên m 2 0
m 2 x 0
m 2 x 0
m 2 x 0 I Ta có: 1 2 4 x
x m 2 3 x m 2 2
m 2 x g x 2 Ơ 4 x 4 x M D g x 3 8 x 8 1 0 x 2 Ầ 3 3 x x Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N
Từ bảng biến thiên của g x suy ra ÁO VIÊ
1 vô nghiệm hoặc có nghiệm kép m 2 3 m 1 GI
Kết hợp với điều kiện m nguyên dƣơng nên suy ra m 1. 4 5 3
Câu 12. ho hàm số y f x có đạo hàm f ' x x
1 x m x 3 với mọi x . ó bao
nhiêu giá trị nguyên của tham số m 5 ;
5 để hàm số g x f x có 3 điểm cực trị A. 3. B. 6. C. 5. D. 4. Lời giải Chọn C
Đồ thị hàm f x đƣợc suy ra từ đồ thị hàm số f x bằng cách.
- ỏ phần bên trái trục . Oy
- Giữ và lấy đối x ng phần đồ thị nằm bên phải trục Oy qua trục . Oy
Ta thấy x 0 là một điểm cực trị của hàm số f x .
CỰC TRỊ CÁC HÀM SỐ KHÁC 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Do đó hàm số g x f x có 3 điểm cực trị khi phần đồ thị bên phải trục Oy có một
điểm cực trị f ' x đổi dấu 1 lần với x 0 m 0 . Mà m 5 ;
5 và m m1;2;3;4; 5 .
Câu 13. Cho hàm số y f x xác định trên có f 3 8 ; f 9 4 ; f 1 2 . Biết rằng hàm 2 2
số y f x có đồ thị nhƣ hình vẽ bên. Hỏi đồ thị hàm số y
f x x 2 2 1 có bao nhiêu điểm cực trị? I Ơ M D Ầ Đ NH Ị Đ A. 2. B. 3. C. 6. D. 5. G THPT N.C.Đ Lời giải N NG Chọn D CÔ Ờ N
Nhận xét: Số cực trị của hàm số y f x bằng số cực trị của hàm số y
f x cộng YỄ TRƢ
với số giao điểm của đồ thị hàm số y f x với trục hoành. GU N N Đặt g x
f x x 2 ( ) 2 1 , x và h x
f x x 2 2 1 , x .
Ta có: h ' x 2 f ' x 2 x
1 h ' x 0 f ' x x 1 (*) ÁO VIÊ
Dự vào đồ thị, nghiệm của phƣơng trình (*) là hoành độ giao điểm của đồ thị y f x GI x 1 x 1
và đƣờng thẳng y x 1, ta có: * x 2 x 3
Ta có bảng biến thiên của hàm số h x nhƣ sau: Ta có: 1
h f 2 2 2 2 2 1 0 vì f (2) 2
CỰC TRỊ CÁC HÀM SỐ KHÁC 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
h f 2 3 2 3 3 1 0 vì f 3 8
h f 2 4 2 4 4 1 0 vì f 9 4 2
Suy ra h x 0 có đúng hai nghiệm phân biệt x 3
;1 và x 3;4 . 2 1
Suy ra g x h x có đúng 5 điểm cực trị.
Câu 14. Cho hàm số y f x xác định trên và hàm số y f x có đồ thị nhƣ hình bên dƣới. y 2 1 O x -3 -1 2 5 - 1 - 2 I Ơ - 3 M D
Đặt g x f x m . Có bao nhiêu giá trị nguyên của tham số m để hàm số g x có Ầ Đ đúng 7 điểm cực trị? NHỊ A. 2 . B. 3 . C. 1. D. vô số. Đ G Lời giải THPT N.C.Đ N Chọn A NG CÔ Ờ
Từ đồ thị của hàm số y
f x ta có bảng biến thiên của hàm số y
f x nhƣ sau: N YỄ TRƢ x ∞ 3 1 2 5 + ∞ GU N N f'(x) + 0 0 + 0 0 + ÁO VIÊ f(x) GI
Hàm số y f x xác định trên
Hàm số g x f x m là hàm số chẵn trên
Đồ thị của hàm số y g x nhận trục tung làm trục đối x ng.
Để g x có đúng 7 điểm cực trị thì hàm số y f x m phải có đúng 3 điểm cực trị m 3
phía bên phải trục tung 3 m 1
, do m nguyên nên . m 2
Câu 15. Cho hàm số f x có đạo hàm 2 f (
x) (x 1) 2
x 4x .Có bao nhiêu giá trị nguyên
dƣơng của tham số m để hàm số g x f 2 ( )
2x 12x m có đúng 5 điểm cực trị ? A. 18. B. 17. C. 16. D. 19. Lời giải.
CỰC TRỊ CÁC HÀM SỐ KHÁC 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Chọn B Ta có : x 1 2 f (
x) 0 (x 1) 2
x 4x 0 x 0 , trong đó x 1 là nghiệm kép. x 4 g x f 2 x
x m gx x f 2 ( ) 2 12 4 12
2x 12x m
Xét g x 0 x f 2 4 12
2x 12x m 0 (*) x 3 x 3 2 2
2x 12x m 1
2x 12x m 1 (l) 2 2
2x 12x m 0
2x 12x m 1 2 2
2x 12x m 4
2x 12x 4 m 2
( Điểm cực trị của hàm số g x là nghiệm bội lẻ của phƣơng trình (*) nên ta loại I Ơ phƣơng trình 2
2x 12x m 1 ) Xét hàm số 2
y 2x 12x có đồ thị (C): y ' 4x 12 M D Ầ Ta có bảng biến thiên Đ NHỊ Đ G THPT N.C.Đ – N NG CÔ Ờ N YỄ TRƢ GU N N
Để g x có đúng 5 điểm cực trị thì mỗi phƣơng trình
1 ;2 đều có hai nghiệm phân ÁO VIÊ biệt khác 3 . GI
Do đó, mỗi đƣờng thẳng y 4 m và y m phải cắt đồ thị (C) tại 2 điểm phân biệt có
hoành độ khác 3. Nhận xét: đƣờng thẳng y 4 m luôn nằm trên đƣờng thẳng y m . Ta có: 18
m m 18. Vậy có 17 giá trị m nguyên dƣơng . 3
Câu 16. Có bao nhiêu giá trị nguyên của tham số m để hàm số y x m 2 2
1 x 3m x 5 có ba điểm cực trị? A. Vô số. B. 3. C. 2. D. 1. Lời giải Chọn A 3
Hàm số y x m 2 2
1 x 3m x 5 có 3 điểm cực trị khi và chỉ khi hàm số 3
y x m 2 2
1 x 3mx 5 có hai điểm cực trị x , x thỏa mãn x 0 x . 1 2 1 2 Ta có 2
y 3x 22m 1 x 3m .
CỰC TRỊ CÁC HÀM SỐ KHÁC 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2
Δ 4m 5m 1 0
m 0. Vậy có vô số m thỏa mãn đề bài. P m 0 x
Câu 17. Hàm số f x
m (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực 2 x 1 trị? A. 2 . B.. C. 5 . D. 4 . Lời giải Chọn D x
Đặt g x m 2 x 1 x x
Số cực trị của hàm số f x
m bằng tổng số cực trị của hàm g x m 2 x 1 2 x 1
và số nghiệm đơn hoặc nghiệm bội lẻ của phƣơng trình g x 0 . I Ơ 1 x
Ta có g ' x 2 0 x 1 2 x 1 M D Bảng biến thiên Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N x
Hàm số g x
m có 2 cực trị và phƣơng trình g x 0 có tối đa 2 nghiệm đơn 2 x 1 ÁO VIÊ x GI
(hoặc bội lẻ). Do đó hàm số f x
m có nhiều nhất 4 điểm cực trị. 2 x 1
Bài toán tổng quát: Tìm số cực trị của hàm số y f x
+ ơ sở lý thuyết: Số cực trị của hàm số y f x bằng tổng số cực trị của hàm
y f x và số nghiệm đơn hoặc nghiệm bội lẻ của phƣơng trình f x 0 .
+ Khi giải bài toán học sinh đƣa về hai bài toán cơ bản: tìm số cực trị của hàm số
y f x và số nghiệm của phƣơng trình f x 0 . Do đó học sinh có thể lập bảng biến
thiên để xét đồng thời 2 bài toán đơn đó.
Câu 18. Cho hàm số y f x có đồ thị nhƣ hình vẽ dƣới. Tập các giá trị của tham số m để hàm
số g x f x m có 7 điểm cực trị là ;
a b . Tính T 2b . a A. 2 . B. 2 . C. 0 . D. 6 .
CỰC TRỊ CÁC HÀM SỐ KHÁC 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn B
Số cực trị của hàm số g x bằng tổng số cực trị của hàm y f x m và số nghiệm
đơn hoặc nghiệm bội lẻ của phƣơng trình f x 0 .
Hàm số y f x m có 3 điểm cực trị. Do đó hàm số g x f x m có 7 điểm cực trị
khi và chỉ khi phƣơng trình f x m có 4 nghiệm phân biệt 2
m 0 T 2.
Câu 19. Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y x 6x m có 5 điểm cực trị. I Ơ A. 32 . B. 31. C. 31. D. 34 . Lời giải M D Ầ Chọn C Đ
Đặt f x 3 2
x 6x m NHỊĐ
Số cực trị của hàm số y f x bằng tổng số cực trị của hàm y f x và số nghiệm G THPT N.C.Đ N
đơn hoặc nghiệm bội lẻ của phƣơng trình f x 0 . NG CÔ Ờ x 0 N
Ta có f ' x 2
3x 12x 0 x 4 YỄ TRƢ Bảng biến thiên GU N N ÁO VIÊ GI
Hàm số y f x có 3 điểm cực trị. Do đó hàm số y f x có 5 điểm cực trị khi và chỉ
khi phƣơng trình f x 0 có 3 nghiệm phân biệt m 32 0 m 0 m 32
Mà m có 31 giá trị nguyên của m thỏa mãn.
Câu 20. Cho hàm số y f x có đồ thị y f ' x nhƣ hình vẽ sau. Đồ thị hàm số
g x f x 2 2
x có tối đa bao nhiêu điểm cực trị? A. 3 . B. 7 . C. 5 . D. 6 .
CỰC TRỊ CÁC HÀM SỐ KHÁC 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn B
Đặt h x f x 2 2 x I
Số cực trị của hàm số g x h x bằng tổng số cực trị của hàm y h x và số nghiệm Ơ
đơn hoặc nghiệm bội lẻ của phƣơng trình h x 0 . M D
h ' x 2 f ' x 2x 0 f ' x x Ầ Ta có Đ NH
Nghiệm của phƣơng trình h ' x 0 là hoành độ giao điểm của hai đồ thị y f ' x và Ị Đ y x . G THPT N.C.Đ N
Do đó phƣơng trình có nghiệm 2 ; 2; 4. NG CÔ Ta có bảng biến thiên Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
Dựa vào bảng biến thiên ta có hàm số y h x có 3 điểm cực trị và phƣơng trình
h x 0 có tối đa 4 nghiệm phân biệt
hàm số g x hx có tối đa 7 điểm cực trị.
Câu 21. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số m 3 2
y x 3x 9x 5
có 5 điểm cực trị? 2 A. 62 . B. 63 . C. 64 . D. 65 . Lời giải Chọn B m Xét hàm số 3 2
g(x) x 3x 9x 5 . 2
CỰC TRỊ CÁC HÀM SỐ KHÁC 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 1 Ta có: 2 g (
x) 3x 6x 9; g (x) 0 . x 3 m m Ta có: g( 1 ) ; g(3) 32 . 2 2
Bảng biến thiên của hàm số g(x) : m m Hàm số g(x)
có giá trị cực tiểu là g(3)
32 và giá trị cực đại là g( 1) . I 2 2 Ơ m Hàm số 3 2
y x 3x 9x 5 có 5 điểm cực trị 2 M D Ầ m Đ Đồ thị hàm số 3 2 g(x) x 3x 9x 5
cắt trục hoành tại ba điểm phân biệt 2 NHỊ m m Đ g( 1 ).g(3) 0
32 0 0 m 64 . G THPT 2 2 N.C.Đ N
Vì m là số nguyên nên có NG
63 giá trị m thỏa mãn bài toán. CÔ Ờ 1 3 2 N
Câu 22. Cho hàm số y f x x 2m
1 x 8 m x 2 với m . Tập hợp tất cả các giá 3 YỄ TRƢ
trị của m để hàm số y f x có 5 cực trị là khoảng ; a b . Tích . a b bằng GU N N A. 12. B. 16. C. 10. D. 14. Lời giải ÁO VIÊ Chọn D GI Ta có 2
y x 22m
1 x 8 m .
Vì f x là hàm chẵn do f x f x , nên đồ thị hàm f x đối x ng qua trục Oy .
Do đó, khi hàm f x có hai cực trị dƣơng thì hàm f x sẽ có thêm hai cực trị đối x ng
qua trục Oy và một cực trị còn lại chính là giao điểm của đồ thị hàm f x và trục Oy .
Yêu cầu bài toán tƣơng đƣơng với phƣơng trình y 0 có 2 nghiệm dƣơng phân biệt.
m m 0
m m 2 2 4 3 7 0 2 1 8 0 1
Điều kiện tƣơng đƣơng là S 0 2m 1 0 m 2 P 0 8 m 0 m 8
CỰC TRỊ CÁC HÀM SỐ KHÁC 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 7 m 1 m 4 1 7 m m ;8 . 2 4 m 8 7 Vậy a , b 8 và . a b 14 . 4 3
Câu 23. Cho hàm số y f x có đạo hàm f x x 2
x m 2 1 4
5 x m 7m 6, x . Có
bao nhiêu số nguyên m để hàm số g x f x có 5 điểm cực trị? A. 2 . B. 3 . C. 4 . D. 5 . Lời giải Chọn B I Nhận xét: Ơ
+) x 1 là nghiệm bội ba của phƣơng trình x 3 1 0 . M D Ầ
+) Hàm g x f x là hàm chẵn nên đồ thị nhận trục Oy làm trục đối x ng. Đ NH g x f x y f x Ị Do đó hàm
có 5 điểm cực trị Hàm số
chỉ có hai điểm cực trị Đ 2
x m x 2 4 5
m 7m 6 0 G dƣơng Phƣơng trình
có nghiệm kép dƣơng khác 1 * THPT N.C.Đ N 2
x m x 2 4 5
m 7m 6 0 NG hoặc phƣơng trình
có hai nghiệm trái dấu khác 1 ** . CÔ Ờ 2 N
m 2 4 5
4 m 7m 6 0 3 6 YỄ TRƢ Giải * 4 5 m m (loại). 6 0 1 GU N 2 N m1;6 2
m 7m 6 0 ÁO VIÊ Giải ** m 1 . 1 4m 5 2
m 7m 6 0 GI m 2
Mà m nên m3;4; 5 .
Vậy có 3 giá trị m nguyên thỏa mãn yêu cầu bài toán. 4 3
Câu 24. Cho hàm số f x có đạo hàm f x 2
x x x 2 2
4 x 2m 3 x 6m 18. Có tất
cả bao nhiêu giá trị nguyên của m để hàm số f x có đúng một điểm cực trị? A. 7 . B. 5 . C. 8 . D. 6 . Lời giải Chọn C 2 x 0 x 0 x 24 0 x 2
Ta có f x 0 x 3 x 4 4 0
x m x m x 2 m3 2 2 2 3 6 18 0 * x 6m 18 0
CỰC TRỊ CÁC HÀM SỐ KHÁC 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Để hàm số f x có đúng một điểm cực trị Phƣơng trình * vô nghiệm, có nghiệm
kép hoặc có hai nghiệm phân biệt trong đó có nghiệm là 4.
Trường hợp 1. Phƣơng trình * vô nghiệm 2 2
4m 24m 36 24m 72 4m 36 0 3 m 3 m 2 ; 1 ; 0 ; 1 ; 2 m 3
Trường hợp 2. Phƣơng trình * có nghiệm kép 2
4m 36 0 . m 3
Trường hợp 3. Phƣơng trình * có hai nghiệm phân biệt x , x . Trong đó x 4. 1 2 1 m 3
Phƣơng trình có hai nghiệm phân biệt 2
x , x 4m 36 0 . 1 2 m 3
S x x 4 x 2 m 6 I
Theo định lí Viète ta có 1 2 2
P x .x 4
.x 6m 18 Ơ 1 2 2 x 2 m 2 2 M D 3 9 2
m 2 m m 5 3 9 . Ầ x m 2 2 Đ 2 2 2 NHỊ Vậy m 3
; 2 ; 1 ; 0 ; 1 ; 2 ; 3 ;
5 thỏa mãn yêu cầu đề bài. Đ G THPT y f x N.C.Đ y
Câu 25. Cho hàm số bậc bốn ( ) . Hàm số
f (x) có đồ thị nhƣ hình vẽ dƣới đây. Số N NG
điểm cực đại của hàm số y f 2
x 2x 2 là: CÔ Ờ N A. 1. B. 2. C. 4. D. 3. YỄ TRƢ GU N N ÁO VIÊ GI Lời giải: Chọn A
Đặt y g x f 2 ( )
x 2x 2 có tập xác định D . x 1
Ta có: y g ( x) f 2
x 2x 2 . 2 x 2x 2 x 1 x 1 y 0 2
x 2x 2 1 f 2
x 2x 2 0 2
x 2x 2 3
CỰC TRỊ CÁC HÀM SỐ KHÁC 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 1 x 1 x 1 2 2 . 2
x 2x 7 0 x 1 2 2 Bảng xét dấu: x 1 2 2 -1 1 2 2 g ( x) - 0 + 0 - 0 +
Vậy hàm số có 3 điểm cực trị, trong đó có 1 điểm cực đại. 2
Câu 26. Cho hàm số f x x 2 1
mx 4mx m n 2 với , m n . Biết trên khoảng 7 7 5 ; 0
hàm số đạt cực đại tại x 1 . Trên đoạn ;
hàm số đã cho đạt cực tiểu 6 2 4 tại I Ơ 7 3 5 5 A. x .
B. x .
C. x . D. x . 2 2 2 4 M D Lời giải Ầ Đ Chọn B NHỊ
Ta có f x x 2
1 4mx 10mx 6m 2n 4 . Đ G THPT 2 N.C.Đ
Cho f x 0 x
1 4mx 10mx 6m 2n 4 0 N NG x 1 CÔ Ờ . 2 N
4mx 10mx 6m 2n 4 0 1 YỄ TRƢ 7 Trên khoảng ;0
hàm số đạt cực đại tại x 1
nên phƣơng trình 1 có hai nghiệm GU N 6 N
phân biệt trong đó có một nghiệm x 1 . 1 3 5 ÁO VIÊ
m 0 và x (vì theo Vi – ét x x và x 1 ). 2 1 2 1 GI 2 2 Bảng biến thiên: 7 5 3 Vậy trên đoạn ;
hàm số đã cho đạt cực tiểu tại x . 2 4 2
Câu 27. Cho hàm số f x m 3 2
1 x 5x m 3 x 3. Có tất cả bao nhiêu giá trị nguyên của
tham số m để hàm số y f x có đúng 3 điểm cực trị? A. 4 . B. 3 . C. 5 . D. 1.
CỰC TRỊ CÁC HÀM SỐ KHÁC 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn A
+) Tập xác định: D .
+) f x m 2 3
1 x 10x m 3 .
+) Trƣờng hợp 1: a 0 m 1 2
Khi đó hàm số trở thành f x 2 5
x 4x 3. Hàm số có một điểm cực đại là x 5 khi 2 2
đó hàm số y f x có 3 điểm cực trị: x ; x 0; x nên nhận m 1. 5 5
+) Trƣờng hợp 2: a 0 m 1. Hàm số y f x m 3 2
1 x 5x m 3 x 3 có 2 cực
trị thỏa 0 x x . 1 2
Khi đó x 0 là nghiệm của phƣơng trình: f x 0 m 3 khi m 3 đồ thị hàm số 5 I
y f x có 2 cực trị: x 0; x . Ơ 6
Khi đó hàm số y f x có 1 điểm cực trị: x 0 . Loại m 3 . M D 3 2 Ầ
+) Trƣờng hợp 3: a 0 m 1 Hàm số y f x m
1 x 5x m 3 x 3 có 2 cực Đ NH
trị thỏa x 0 x . Khi đó phƣơng trình f x 0 có 2 nghiệm trái dấu Ị 1 2 Đ m
1 m 3 0 3 m 1. G THPT N.C.Đ N
Vậy có 4 giá trị nguyên của tham số m . NG CÔ
Ờ Câu 28. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số 4 3 2
y 3x 8x 6x 24x m có N 7 YỄ
điểm cực trị. Tính tổng các phần tử của S . TRƢ A. 42 . B. 50 . C. 30 . D. 63 . GU N N Lời giải Chọn A ÁO VIÊ
Xét hàm số f x 4 3 2
3x 8x 6x 24x m trên . GI
Ta có f x 3 2
12x 24x 12x 24 . x 1
f x 0 x 2 . x 1
Bảng biến thiên của hàm số
CỰC TRỊ CÁC HÀM SỐ KHÁC 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Dựa vào T suy ra đồ thị hàm số 4 3 2
y 3x 8x 6x 24x m có 7 điểm cực trị khi và
chỉ khi đồ thị của hàm số f x 4 3 2
3x 8x 6x 24x m cắt trục hoành tại 4 điểm phân biệt 1 3 m 0 8 m 13. 8 m 0
Mà m nguyên nên m9;10;11;1
2 S . Suy ra tổng tất cả các phần tử của tập S là 42 .
Câu 29. Cho hàm số bậc ba y f x có đồ thị nhƣ hình vẽ. Hỏi hàm số 2 g x
f x x có bao nhiêu điểm cực trị? y 2 I Ơ 2 O x M D 2 Ầ Đ NHỊ A. 2 . B. 3 . C. 5 . D. 4 . Đ G Lời giải THPT N.C.Đ N Chọn C NG CÔ Ờ 1 2 x 1 0 x N
Ta có: g x x f 2 2 1
x x gx 0 2 . 2 YỄ f
x x 0 TRƢ f 2
x x 0 1 GU N N
Mà y f x có các điểm cực trị là x 2
và x 0 suy ra f 2
0 , f 0 0 2. x 1 ÁO VIÊ 2
x x 2 2
x x 2 0 x 2 GI Từ 1 , 2 có: . 2
x x 0 2
x x 0 x 0 x 1 1 x 2 x 1 Nên g0 0 x 2 . x 0 x 1
g x 0 có 5 nghiệm đơn nên 2 g x
f x x có 5 điểm cực trị. 2
x px q
Câu 30. Cho hàm số f (x) p
p q . Có bao nhiêu cặp p; q sao 2 x , trong đó 2 2 0, 1 1
cho khoảng cách giữa hai điểm cực trị của đồ thị hàm số trên bằng 10 ?
CỰC TRỊ CÁC HÀM SỐ KHÁC 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 2. B. 1. C. 3. D. 0. Lời giải Chọn A D .
2x p. 2x 12 .x 2x px q 2
px 2.1 q x p y . 2 x 2 2 1 2x 1 2
y 0 px 2.1 q x p 0 1 .
Đồ thị hàm số có 2 điểm cực trị phƣơng trình (1) có 2 nghiệm phân biệt. Do p 0 nên 2
ac p 0 phƣơng trình (1) luôn có 2 nghiệm phân biệt. p
Ta có phƣơng trình đƣờng đi qua 2 điểm cực trị của đồ thị hàm số là: y 1 . 2x
Gọi 2 nghiệm của phƣơng trình 1 là x , x . 1 2 I p p Ơ
Khi đó hai điểm cực trị là A x ;1
, B x ;1 . 2 1 2x 2x 2 1 M D 2 Ầ p p x x 10 . 1 2 2 Đ Theo bài ra: 2
AB 10 AB 10 2x 2x NH 1 2 Ị 2 Đ 2 2 p x x p 2 1 G x x
10 x x .1 10. 1 2 2 2 1 2 THPT N.C.Đ 2 2 N 4 x x 4x x 1 2 1 2 NG 2 CÔ p Ờ
x x 2 4x x 1 10 2 . 1 2 1 2 2 2 N 4x x 1 2 YỄ TRƢ 2 1 q GU N x x Theo định lý Viet ta có: 1 2 p . N x x 1 1 2 ÁO VIÊ
Thay vào phƣơng trình (2) ta có GI 2 2 1 q p 1 q2 2 p 4 4 1 10 4 11 10 . p 4 2 p 4 2 2 (1 q) p 4 11 10 (do 2 2 p 1 q ). 2 1 q 4 2 1 q 1 q 2 2 5 q 4 1 1 10 4 10. 1 q 4 1 q 4 q 2
q q 2 5 5 1 q 5q 5 0 . q 0 Với 2 q 5 p 2 4 ( vô nghiệm ). Với 2
q 0 p 1 p 1.
Vậy có 2 cặp số p;q thỏa mãn là 1
;0 ;1;0 . Chọn A
CỰC TRỊ CÁC HÀM SỐ KHÁC 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 31. Gọi m0 là giá trị của tham số m để đƣờng thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số 3
y x 6mx 4 cắt đƣờng tròn tâm I 1;0 , bán kính bằng 2 tại hai điểm
phân biệt A , B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
A. m 2;3 . B. m 3; 4 .
C. m 0;1 . D. m 1; 2 . 0 0 0 0 Lời giải Chọn C Ta có 2
y 3x 6m , 2
y 0 x 2m . Đồ thị hàm số có điểm cực đại, điểm cực tiểu khi
và chỉ khi y 0 có hai nghiệm phân biệt. Do đó m 0 . x Ta có y 2
. 3x 6m 4mx 4 phƣơng trình đƣờng thẳng đi qua điểm cực đại 3 I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ
và cực tiểu của đồ thị hàm số đã cho là: y 4
mx 4 4mx y 4 0. Ờ N YỄ TRƢ
Đƣờng thẳng cắt đƣờng tròn đã cho tại hai điểm phân biệt A , B sao cho I , A , B GU N N 4m 4
là ba đỉnh của một tam giác 0 d I; 2 0 2 . 2 16m 1 ÁO VIÊ 1
Gọi H là trung điểm đoạn AB S
IH.AB IH.AH 2 2
IH. R IH 2
IH. 2 IH GI IAB 2 IH IH
IH .2 IH 2 2 2 2 2 1 S 1. 2 IAB
Vậy diện tích tam giác IAB đạt giá trị lớn nhất bằng 1 2 2
IH 2 IH IH 1 15 2
4m 4 16m 1 m 2 2 4 4
16m 1 m
(thỏa mãn điều kiện ). 32 15 Vậy m nên m 0;1 . 0 0 32 2 x mx 5
Câu 32. Gọi m là giá trị của m thỏa mãn đồ thị hàm số y
có hai điểm cực trị A , 0 2 x 1
B sao cho đƣờng thẳng AB đi qua điểm I 1; 3
. Khẳng định nào sau đây là đúng
A. 0 m 3 . B. 5 m 3 . C. 3
m 0.
D. 3 m 5 . 0 0 0 0 Lời giải Chọn D
CỰC TRỊ CÁC HÀM SỐ KHÁC 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2
mx 12x m TXĐ: D ; y . x 2 2 1
Hàm số có hai điểm cực trị y 0 có hai nghiệm phân biệt m 0 2
mx 12x m 0 có hai nghiệm phân biệt m 0 1 . 2
36 m 0
Gọi x ; y là điểm cực trị của đồ thị hàm số 2
mx 12x m 0. 0 0 0 0 u x
u x .v x u x .v x
Với y f x f x
v x vx 2 u x u x 0 0
Ta có f x 0 u x .v x u x .v x 0 v x
0, vx 0 ). 0 0 0 0 0 0 v x v ( 0 x 0 0 u x 2x m x m 2 mx 12 2 x m 0 0 0 m 0 0 y x 5 . 0 v x 2x 2x 2 0 0 I 0 0 Ơ m
Do đó đƣờng thẳng qua hai điểm cực trị A , B có phƣơng trình y x 5 . 2 M D Ầ m I 1; 3
AB 3
.1 5 m 4 (thỏa ĐK 1 ). Đ 2 NHỊ
Vậy m 4 . Chọn D Đ 0 G THPT N.C.Đ
Câu 33. ó bao nhiêu giá trị nguyên của tham số m để hàm số 9 7 2 6
y x (m 2)x (m 4)x 7 N NG
đạt cực tiểu tại x 0 ? CÔ Ờ N A. 3 . B. 4 . C. Vô số. D. 5 . YỄ Lời giải TRƢ Chọn A GU N N 8
y x m 6 x 2 m 5 9 7 2 6
4 x y0 0, m . 7 y x
m 5x 2 m 4 9.8 7.6 2 6.5
4 x y 0 0, m . ÁO VIÊ GI
Ta nhận thấy y0 4 y 0 5
y 0 0, m Ta có (6) 3 y x m x 2 9.8.7.6.5.4 7.6.5.4.3.2 2 6.5.4.3.2.1 m 4 (6) y 2 0
6.5.4.3.2.1 m 4 . m 2 *TH1: (6) y 0 0 thì: m 2 + 8
m 2 y 9x 0, x
nên hàm số đồng biến trên nên không đạt cực trị tại x 0 . + 6
m y x 2 2
9x 28 không đổi dấu khi qua x 0 nên không đạt cực trị tại x 0 . *TH2: (6) y
0 0 m 2
Khi đó để hàm số đạt cực tiểu tại x 0 thì cần thêm (6) y 2 m 2 0 0 6.5.4.3.2.1
4 0 m 4 0 2
m 2 m 1 ;0; 1 .
Vậy có 3 giá trị nguyên của tham số m .
CỰC TRỊ CÁC HÀM SỐ KHÁC 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 5 x m Câu 34. Cho hàm số 4 3 y 2m 1 x x
2019 . Có bao nhiêu giá trị của tham số m để 5 3
hàm số đạt cực tiểu tại x 0 ? A.Vô số . B.1 . C.2 . D.0 . Lời giải Chọn B Ta có 4 3 2 y x 4 2m 1 x mx 2 2 x x 4 2m 1 x m . Dễ thấy x
0 là một nghiệm của đạo hàm y . Do đó hàm số đạt cực tiểu tại x 0 khi
và chỉ khi y đổi dấu từ âm sang dƣơng khi đi qua nghiệm x
0 . Ta thấy dấu của y là dấu của hàm số 2 g x x 4 2m 1 x
m . Hàm số g x đổi dấu khi đi qua giá trị x 0 khi x
0 là nghiệm của g x . Khi đó g 0 0 m 0 . Thử lại, với m 0 thì 2 g x x
4x đổi dấu từ âm sang dƣơng khi đi qua giá trị x 0 I Ơ .
Vậy có 1 giá trị m thỏa mãn yêu cầu bài toán.
M D Câu 35. Có bao nhiêu giá trị nguyên của m thuộc khoảng 2019; 2019 để hàm số Ầ Đ m 1 m 2 5 4 NH Ị y x x
m 5 đạt cực đại tại x 0? 5 4 Đ G THPT A. 110 . B. 2016 . N.C.Đ C. 100. D. 10 . N Lời giải NG CÔ Ờ Chọn B N Ta có 4
y m x m 3 ( 1) 2 x . YỄ TRƢ 3 GU N
+ TH1: m 1. Khi đó 4 3 y
x 6 y 3x . Suy ra hàm số đạt cực tiểu tại x 0 (loại). N 4 x 0 1 ÁO VIÊ
+ TH2: m 1. Khi đó y 0 m 2 . x GI 2 m 1 Nhận thấy nếu 4
x x 0 m 2 y 3 x 0 x
Hàm số luôn nghịch biến 2 1 trên
nên hàm số không có cực trị ( loại) m 1 m 1 0 2 m 1 x x 1 2
Vì vậy yêu cầu bài toán tƣơng đƣơng với m 1 m 2 . m 1 0 m 2 x x 1 2 m 1
Suy ra số giá trị m nguyên thuộc khoảng 2019; 2019 là 2016.
Câu 36. Cho hàm số f x có đạo hàm trên thỏa mãn 2 f x h f x h h , 2019 29m x , h
0 . Đặt g x x f
x x f x 4 2 m m 2 29
100 sin x 1, m
CỰC TRỊ CÁC HÀM SỐ KHÁC 29
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
là tham số nguyên và m 27 . Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho
hàm số g x đạt cực tiểu tại x 0 . Tính tổng bình phƣơng các phần tử của S . A. 100 . B. 50 . C. 108 . D. 58 . Lời giải. Chọn A Từ giả thiết ta có
f x 2h f x h
f x h f x 2 2 h , h 0 . x h , h 0 2 x 2
f x 2h f x h 0 lim
lim 0 f x 0, x
f x C , với C là hằng h 0 x 2h h 0 x 2 số. Ta có m
g x 2019 x f x 2018
1 f x29mx f x 28
1 f x I 4 2
m 29m 100sin 2x Ơ 2018 28m x m x 4 2 2019 29
m 29m 100sin 2x . M D Ầ 2017
27m g x x m m x 4 2 2019.2018 29 28
2 m 29m 100 Đ cos 2x . NHỊ
Khi đó g0 0 ; g 4 2 0
2 m 29m 100 . Đ G THPT 4 2 N 2 .C .Đ g 0 0 m 29m 100 0 4 m 25 m 5 ; 2 2; 5 . N NG
Trƣờng hợp m 2 , ta có g x 2018 26 26 x x x 1992 2019 27 2019x 27. CÔ Ờ N
Vì x 0 là nghiệm bội chẵn của phƣơng trình g x 0 nên trƣờng hợp này loại. YỄ TRƢ
Trƣờng hợp m 5, ta có g x 2018 23 23 x x x 1995 2019 24 2019x 24. GU N N Trƣờng hợp m 2
, ta có gx 2018 30 30 x x x 1988 2019 31 2019x 3 1 .
Vì x 0 là nghiệm bội chẵn của phƣơng trình g x 0 nên trƣờng hợp này loại. ÁO VIÊ GI
Trƣờng hợp m 5, ta có g x 2018 23 23 x x x 1995 2019 24 2019x 24.
Dễ thấy g x đổi dấu từ âm sang dƣơng khi qua x 0 nên hàm số g x đạt cực tiểu tại x 0 . Trƣờng hợp m 5
, ta có gx 2018 33 33 x x x 1985 2019 34 2019x 34 .
Dễ thấy g x đổi dấu từ âm sang dƣơng khi qua x 0 nên hàm số g x đạt cực tiểu tại x 0 .
Vậy m S 5 ; 4; 3;3;4;
5 nên tổng các bình phƣơng của các phần tử của S là 100 .
CỰC TRỊ CÁC HÀM SỐ KHÁC 30
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ N NG CÔ Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
CỰC TRỊ CÁC HÀM SỐ KHÁC 31




