



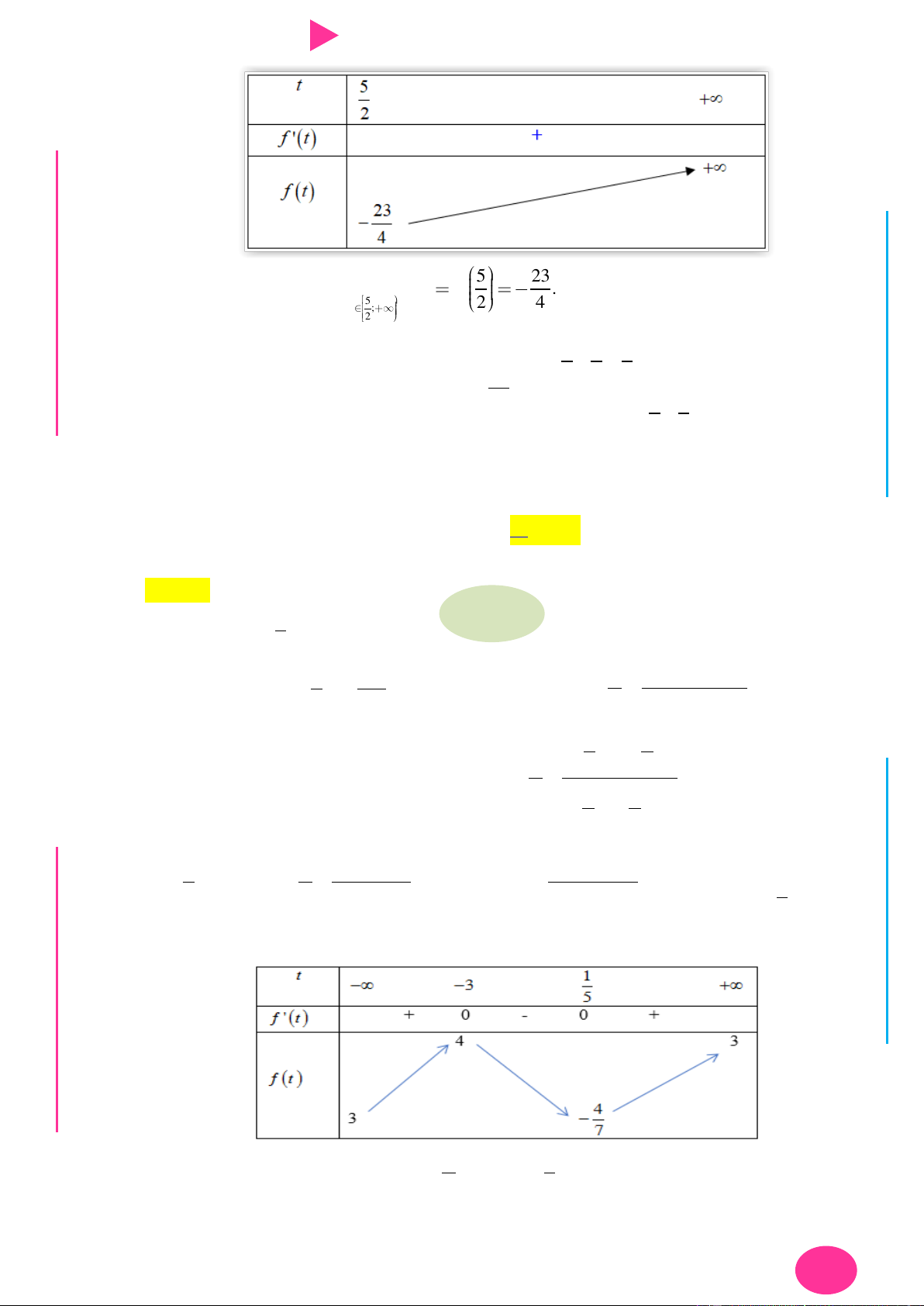
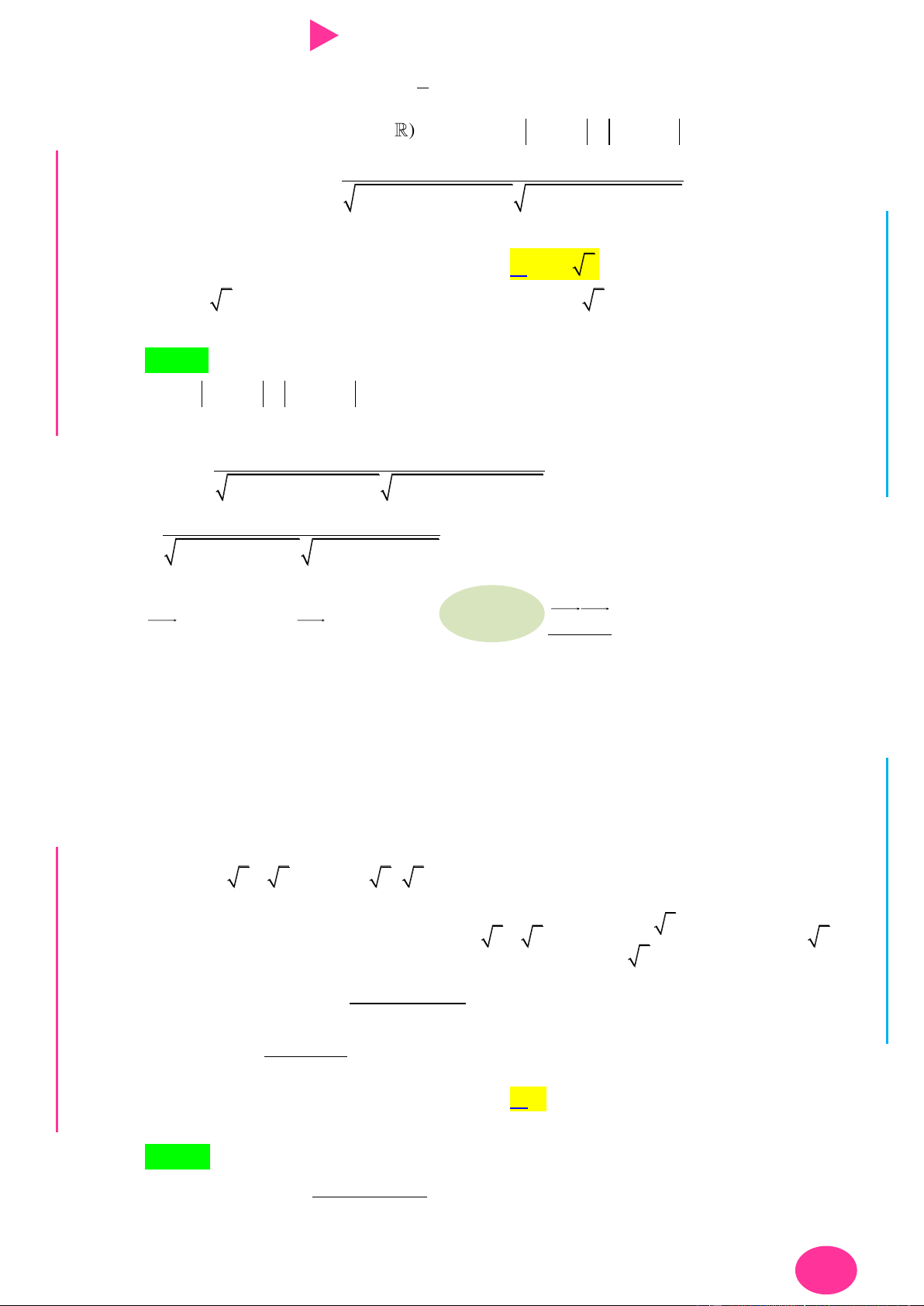

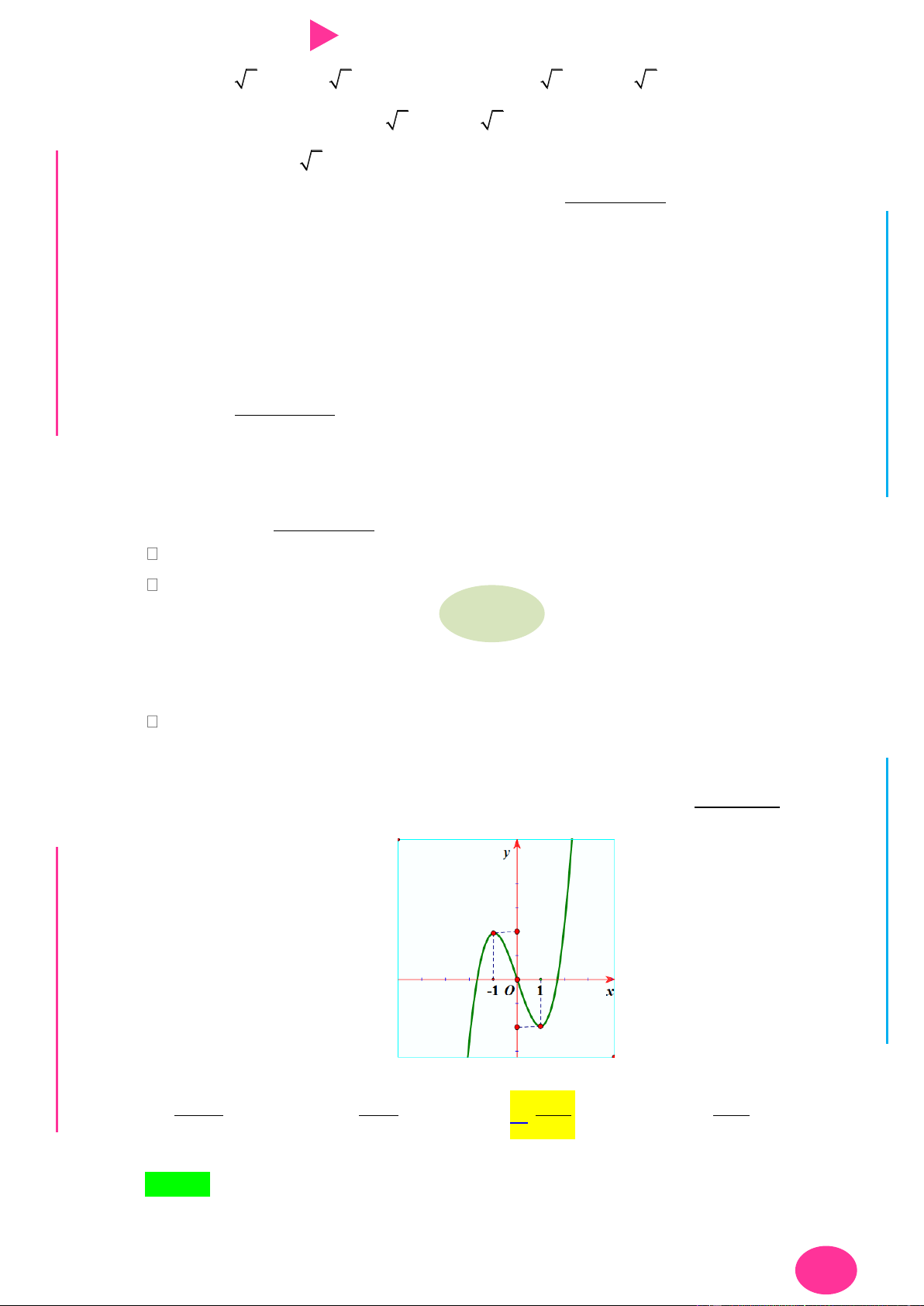
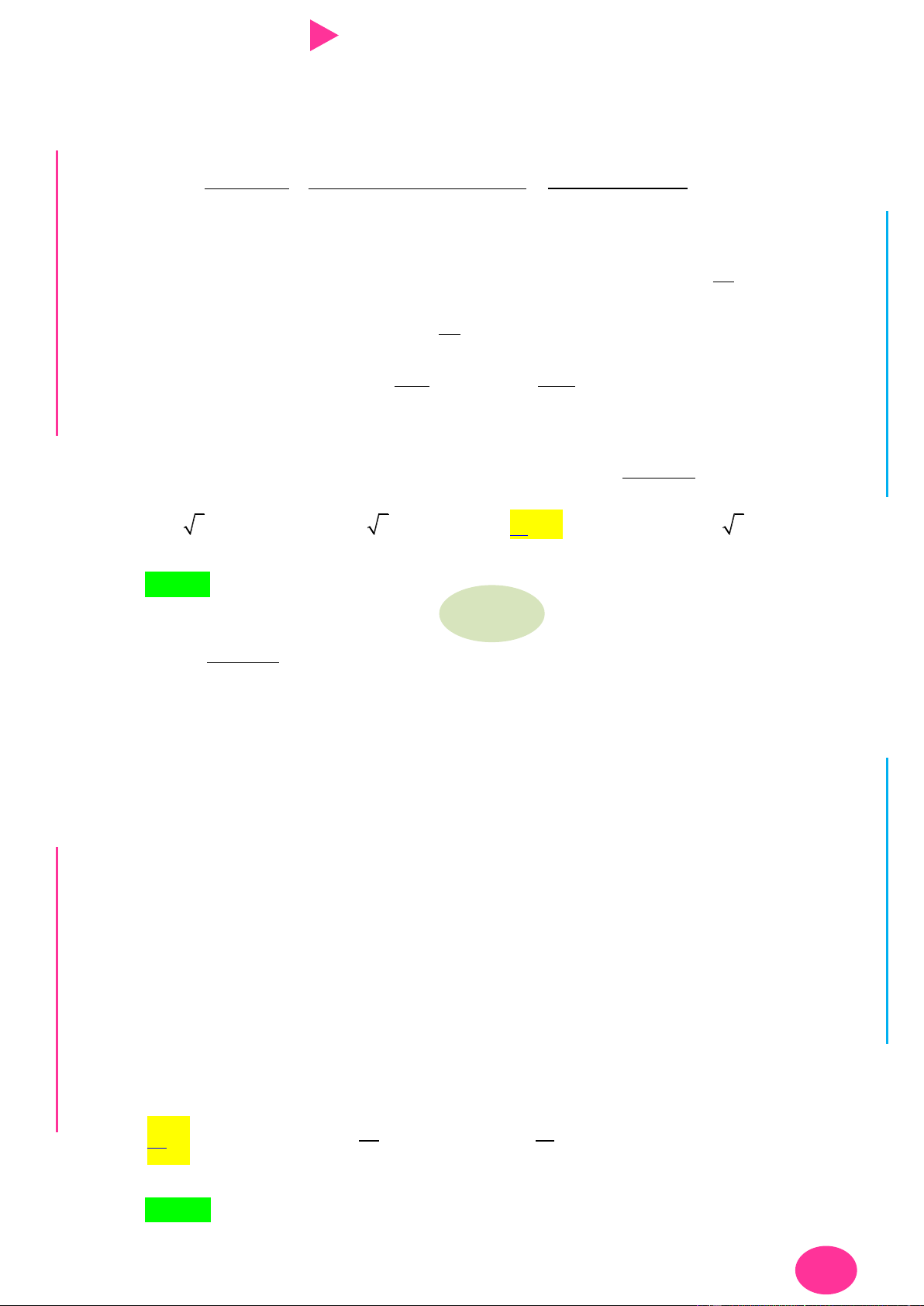

















Preview text:
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHỦ ĐỀ: GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
VẬN DỤNG – VẬN DỤNG CAO DẠNG 1
TÌM GTLN – GTNN CỦA HÀM SỐ THEO CÔNG THỨC x m
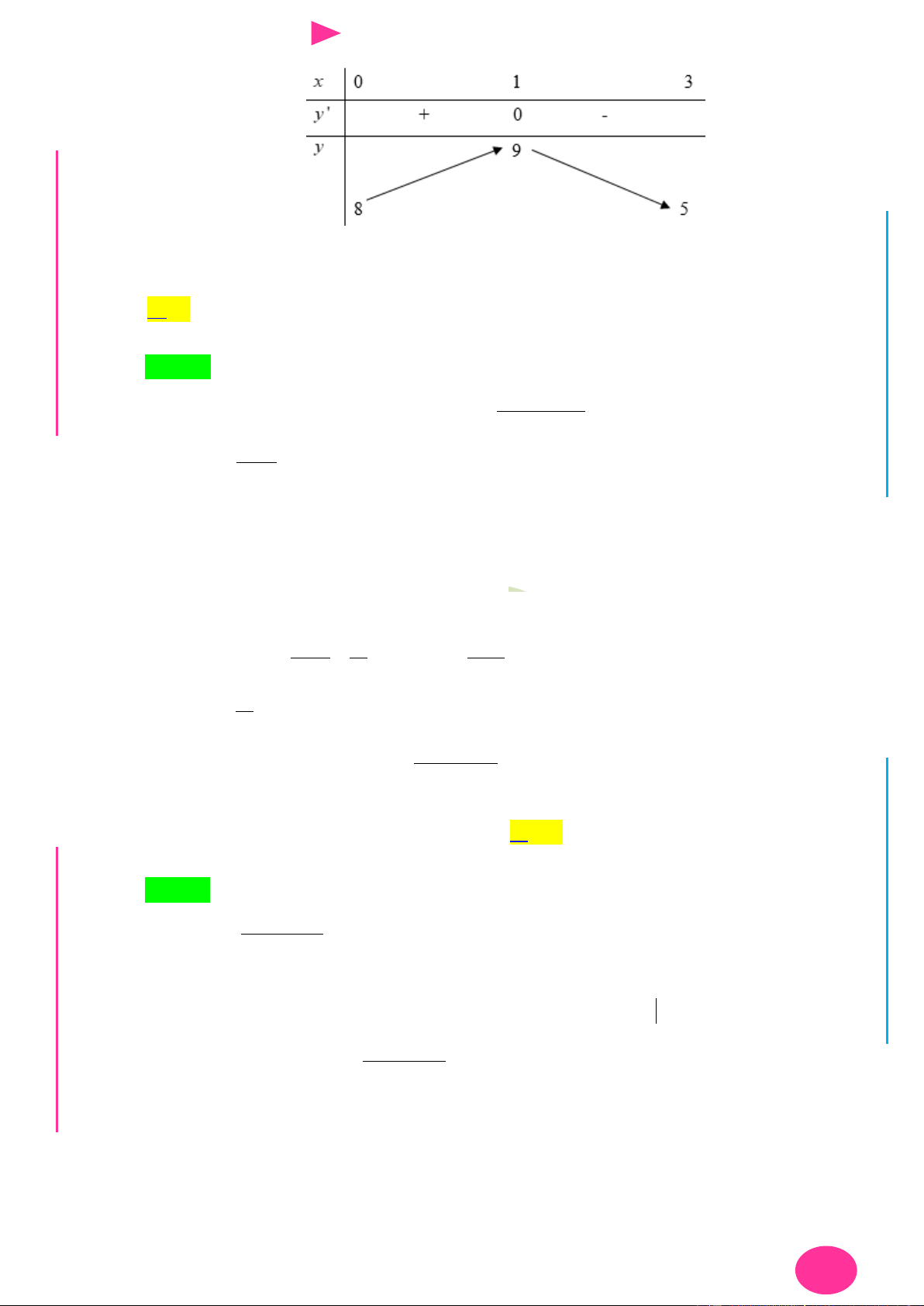
Câu 1. Cho hàm số y f x 2
. Tính tổng các giá trị của tham số m để x 1
max f x min f x 2 . 2; 3 2; 3 A. 4 . B. 2 . C. 1 . D. 3 . Câu 2. Gọi ,
A a lần lƣợt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số: 3
y x 3x m trên
đoạn0; 2 . Gọi S là tập các giá trị thực của tham số m để Aa 12 . Tổng các phần tử I của S bằng Ơ A. 0 . B. 2 . C. 2 . D. 1 M D mx 1
Ầ Câu 3. Gọi T là tập hợp tất cả giá trị của tham số m để hàm số y có giá trị lớn nhất 2 Đ x m NH 5 Ị trên đoạn 2;
3 bằng . Tính tổng của các phần tử trong T . Đ 6 G THPT 17 16 N.C.Đ A. . B. . C. 2 . D. 6 . NG 5 5 CÔN Ờ 2 2 4 N Câu 4.
Cho hàm số f x x
1 ax 4ax a b 2, với a , b . Biết trên khoảng ;0 3 YỄ TRƢ 5 GU N
hàm số đạt giá trị lớn nhất tại x 1 . Hỏi trên đoạn 2;
hàm số đạt giá trị nhỏ N 4
nhất tại giá trị nào của x ? ÁO VIÊ 5 4 3
A. x . B. x .
C. x . D. x 2 . GI 4 3 2
Câu 5. Cho hàm số y x x m2 3 3
. Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ
nhất của hàm số trên đoạn 1 ;1 bằng 1 là A. 1. B. 4 . C. 0 . D. 4 . Câu 6.
Có bao nhiêu giá trị nguyên dƣơng của tham số m để giá trị nhỏ nhất của hàm số 2 x m y trên đoạn 2; 3 bằng 14. x 1 A. 2 . B. 1. C. 0 . D. 4. 2 x m 2 Câu 7.
Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y trên x m đoạn 0;4 bằng 1 . A. 0 . B. 2 . C. 3 . D. 1.
TÌM GTLN, GTNN THEO CÔNG THỨC 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 8. Cho hàm số 3
y ax cx d, a 0 có min f x f 2
. Giá trị lớn nhất của hàm số x ;0
y f x trên đoạn 1; 3 bằng
A. d 11a .
B. d 16a .
C. d 2a .
D. d 8a .
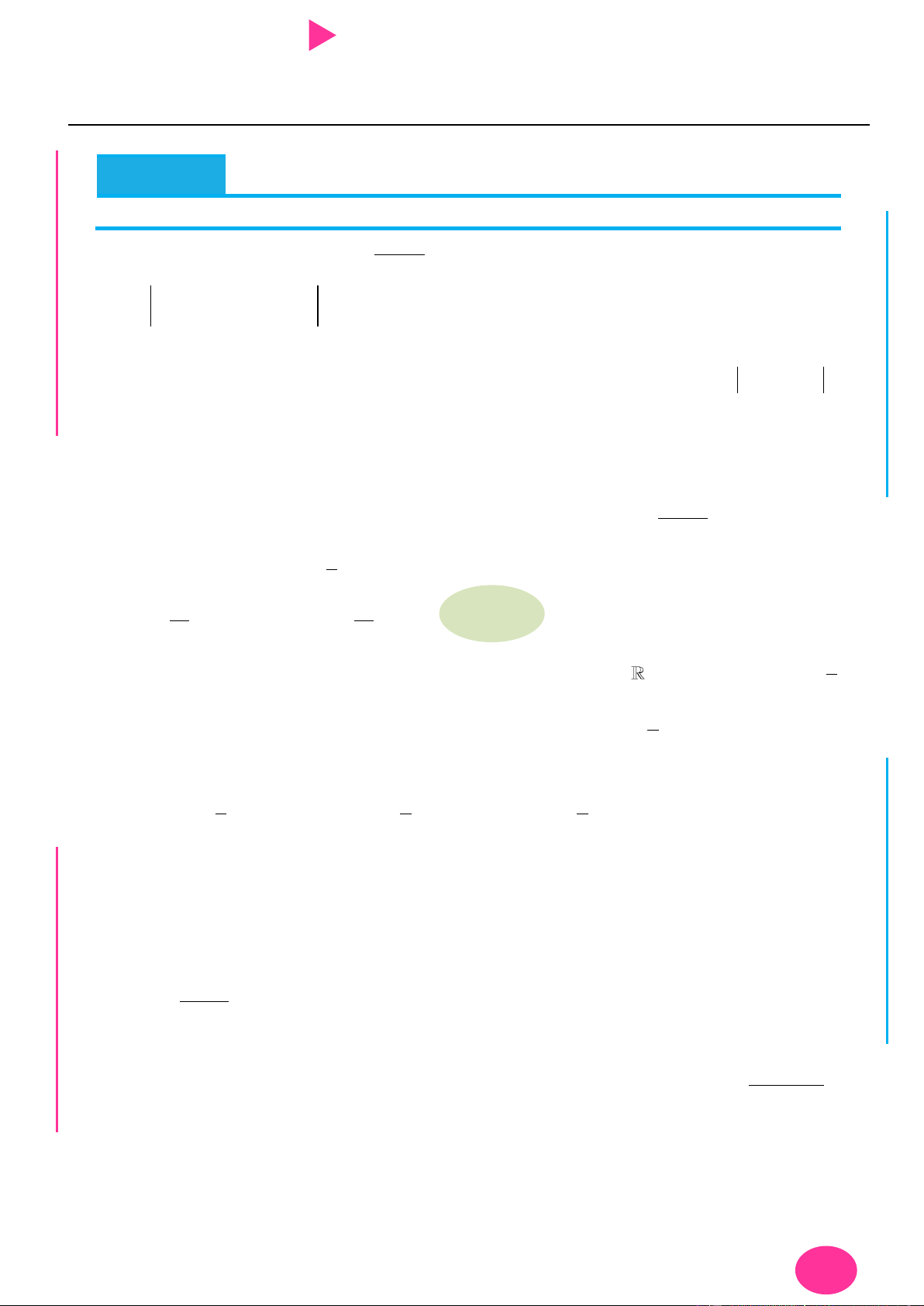
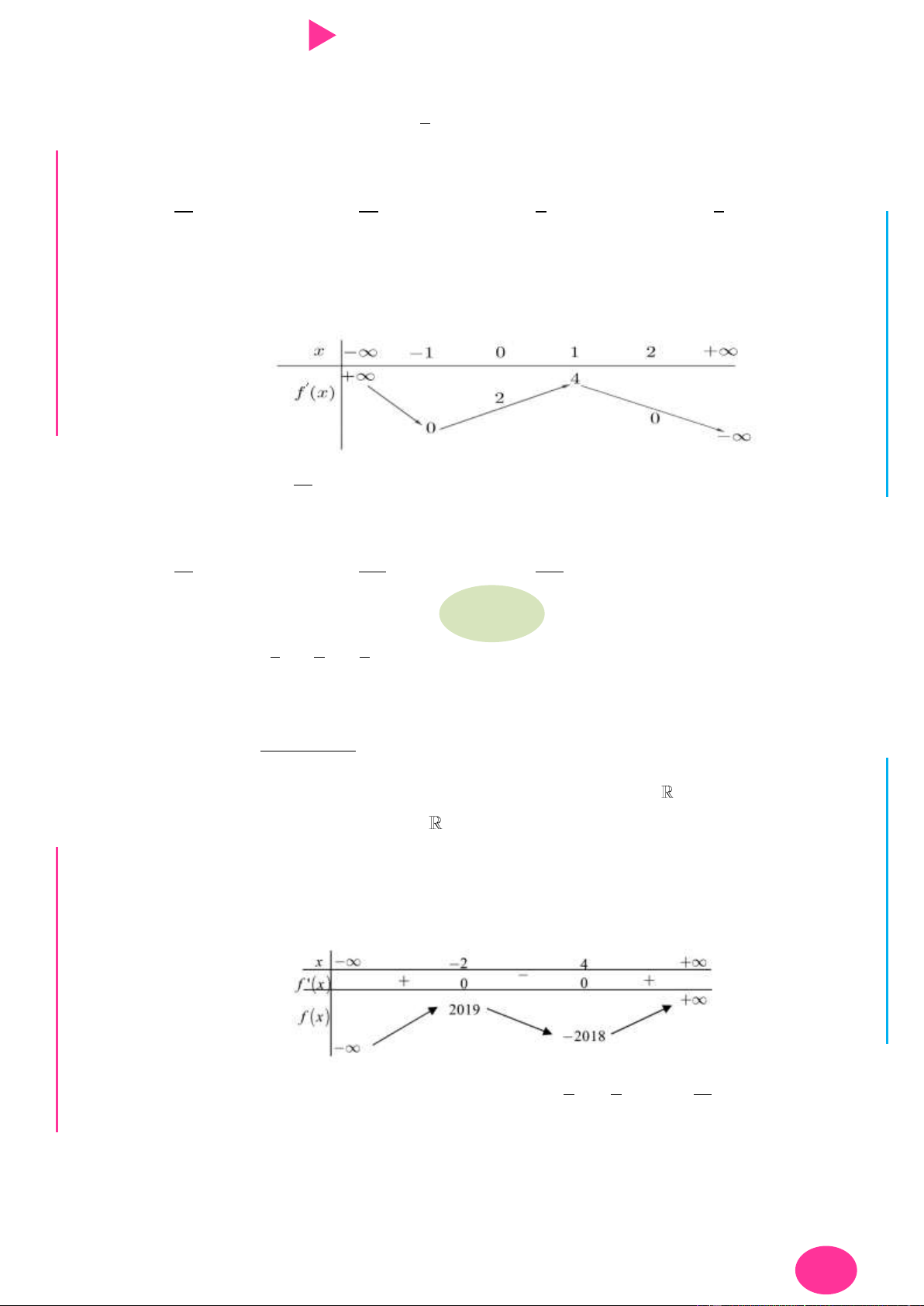
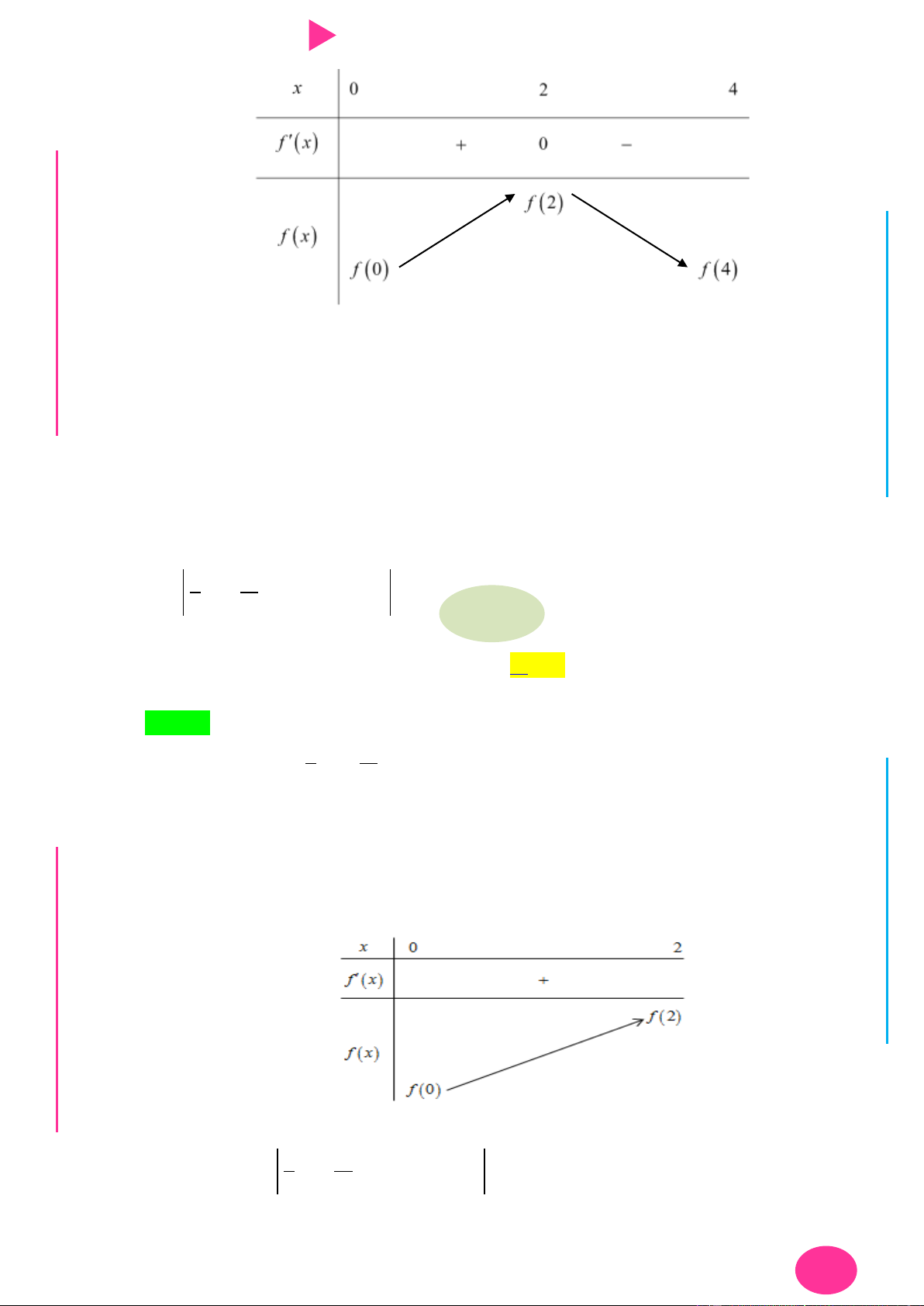
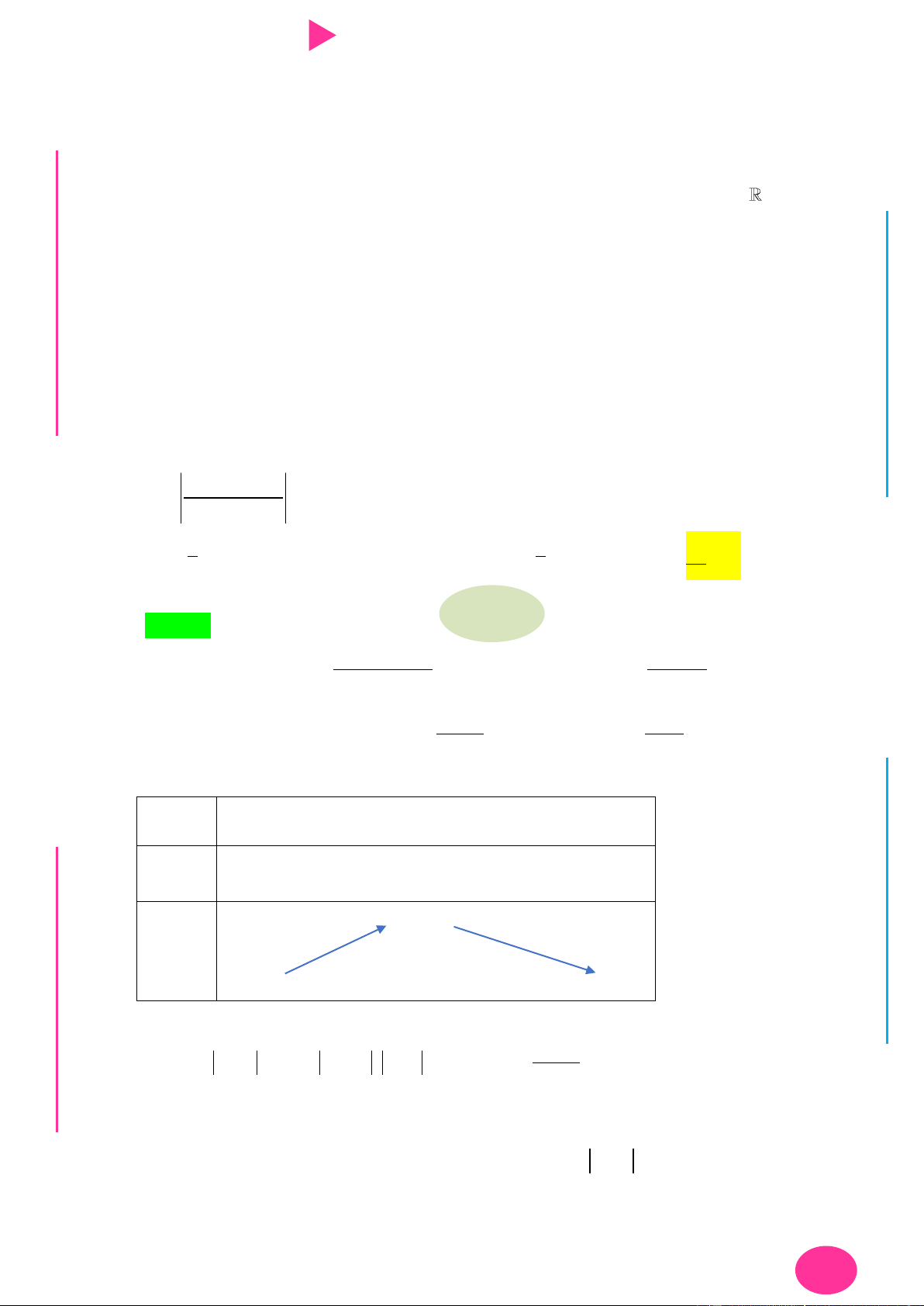
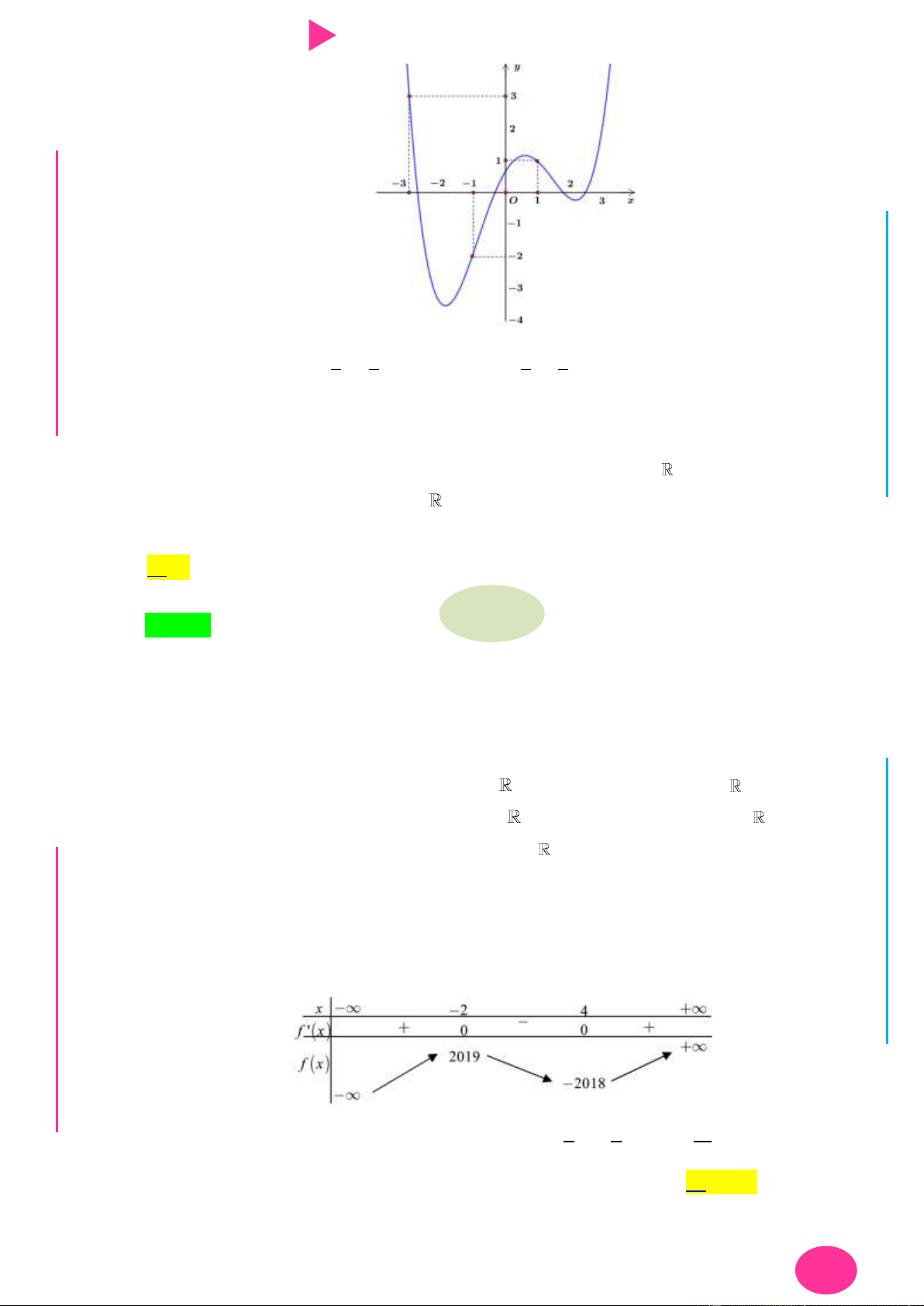
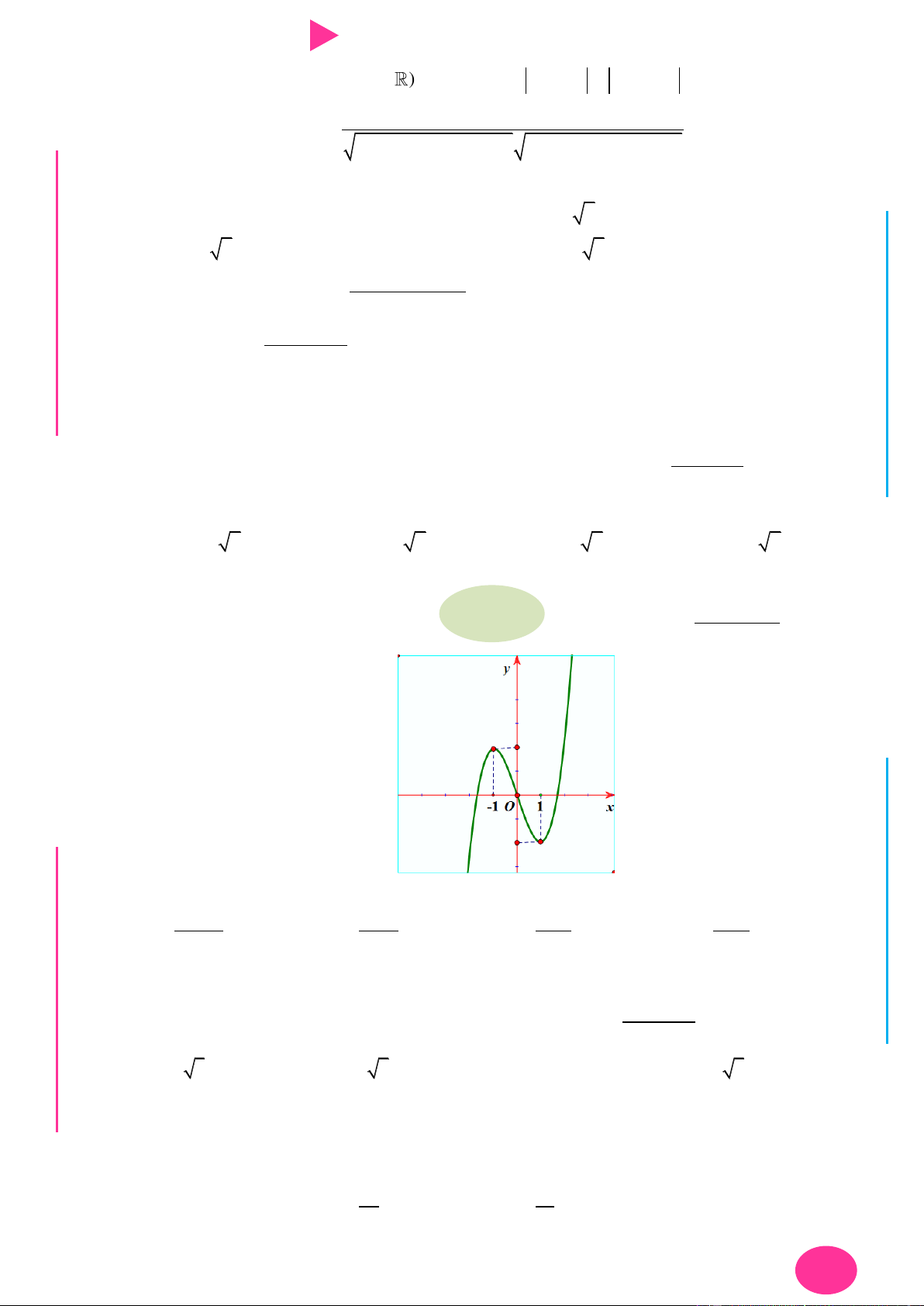
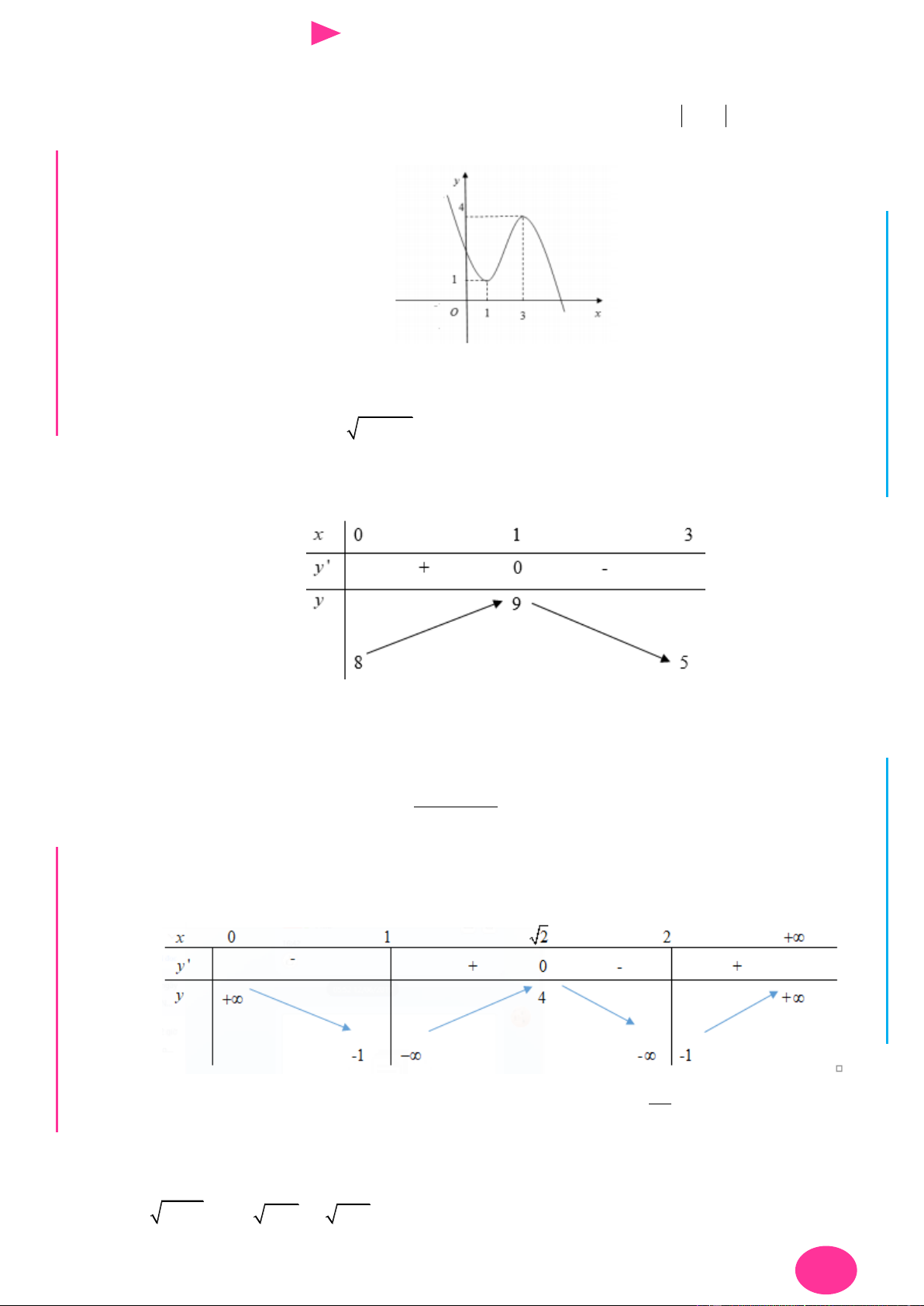
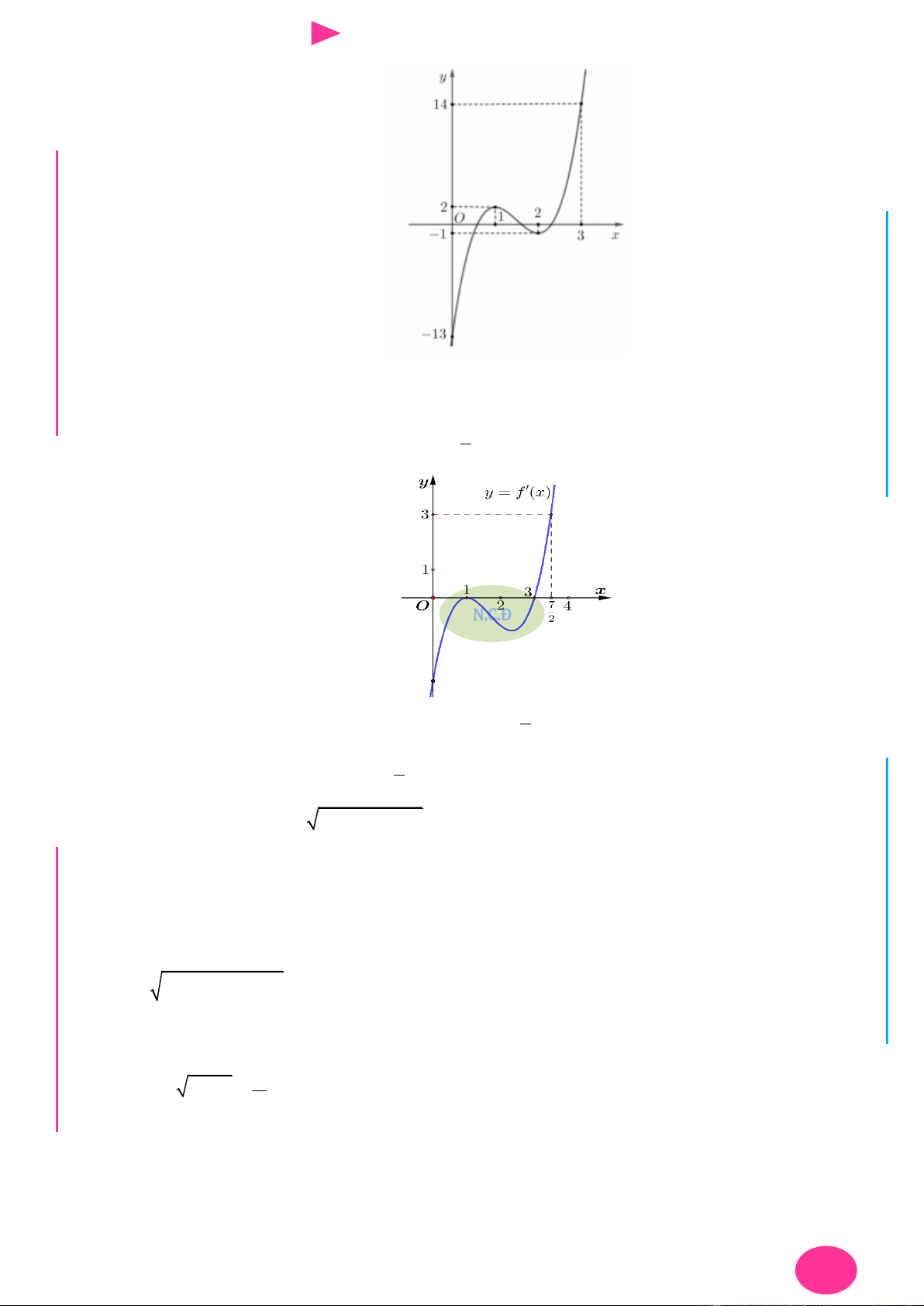
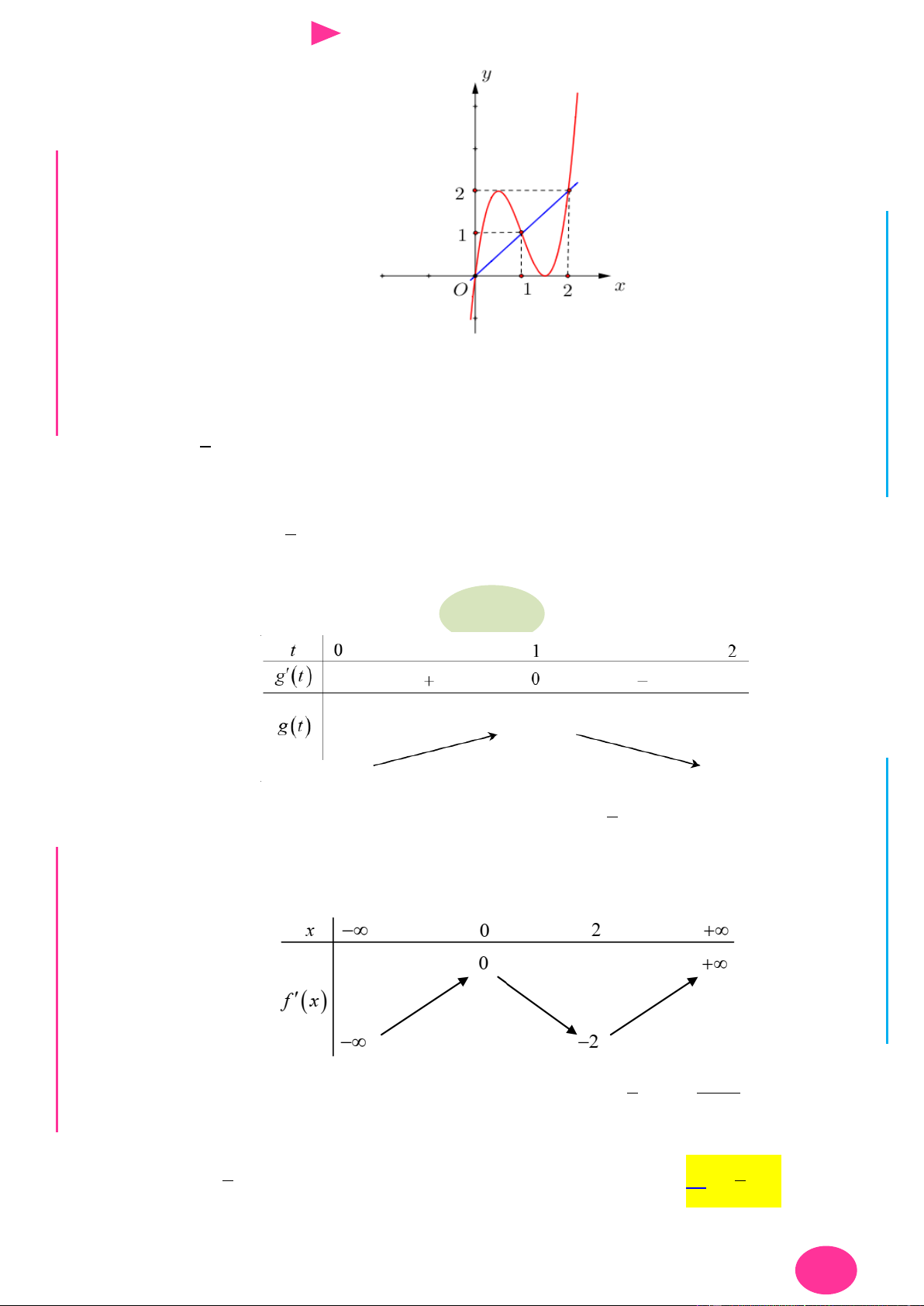
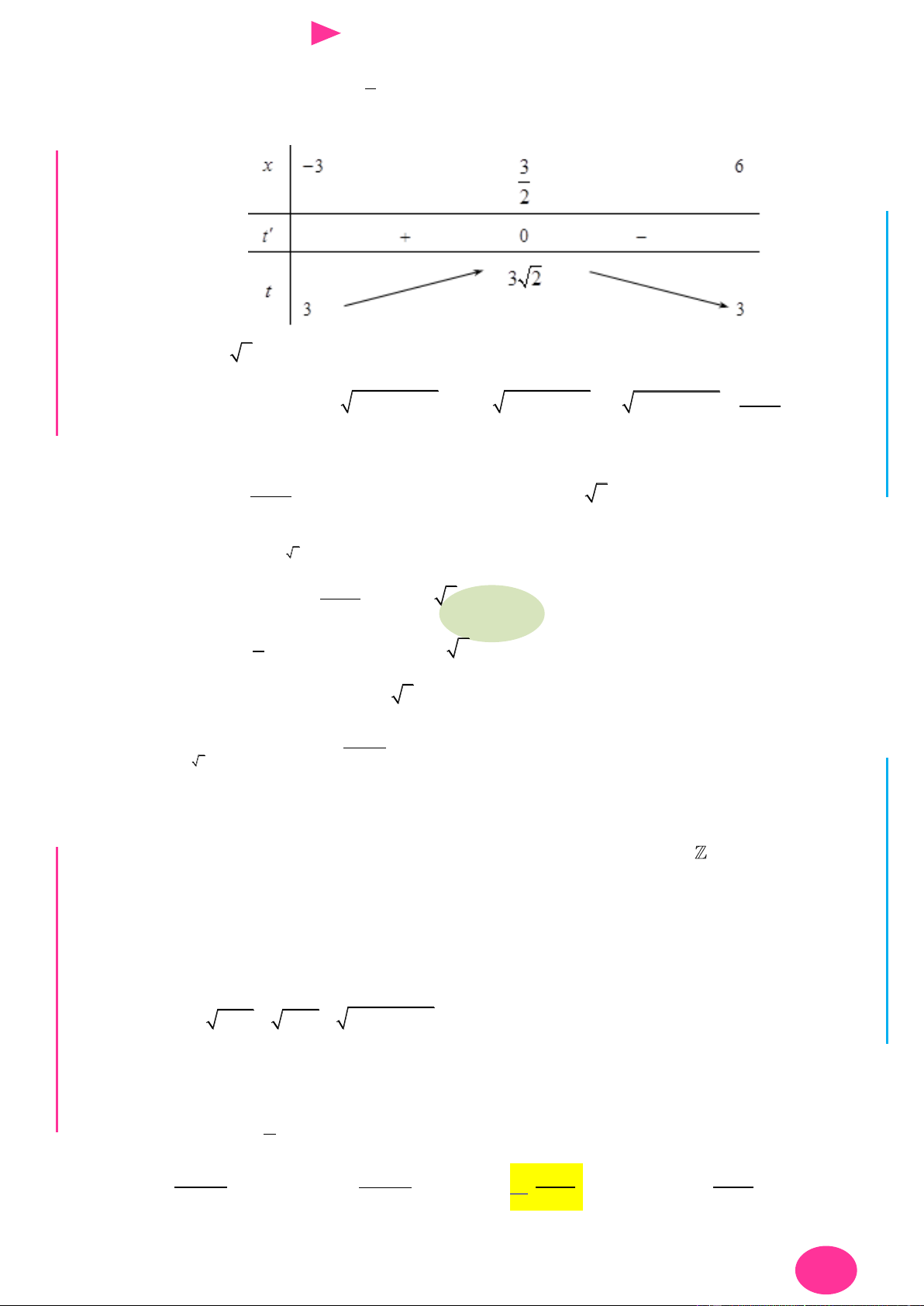
Câu 9. Cho hàm số có f x có đạo hàm là hàm f ' x . Đồ thị hàm số f ' x nhƣ hình vẽ bên.
Biết rằng f 0 f
1 2 f 2 f 4 f 3 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất
M của f x trên đoạn 0; 4 . y x 2 4 O I Ơ
A. m f 4, M f 2 .
B. m f
1 , M f 2 M D Ầ
C. m f 4, M f 1 .
D. m f 0, M f 2 . Đ NHỊ
Câu 10. Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số Đ 1 19 4 2 G THPT y x x
30x m 20 trên đoạn 0; 2 không vƣợt quá 20 . Tổng các phần tử 4 2 N.C.Đ NG của S bằng CÔN Ờ N A. 210. B. 195 . C. 105. D. 300. YỄ
TRƢ Câu 11. Cho hàm số y f x 4 3 2
x 4x 4x a . Gọi M ,m lần lƣợt là giá trị lớn nhất, giá trị GU N N
nhỏ nhất của hàm số đã cho trên đoạn 0;2 . Số giá trị nguyên a thuộc đoạn 3 ; 3 sao
cho M 2m là ÁO VIÊ A. 3 . B. 5 . C. 6 . D. 7 .
GI Câu 12. Gọi S là tập hợp các giá trị của m để hàm số 3 2
y x 3x m đạt giá trị lớn nhất bằng
50 trên [ 2; 4]. Tổng các phần tử thuộc S là A. 4 . B. 36 . C. 140 . D. 0 .
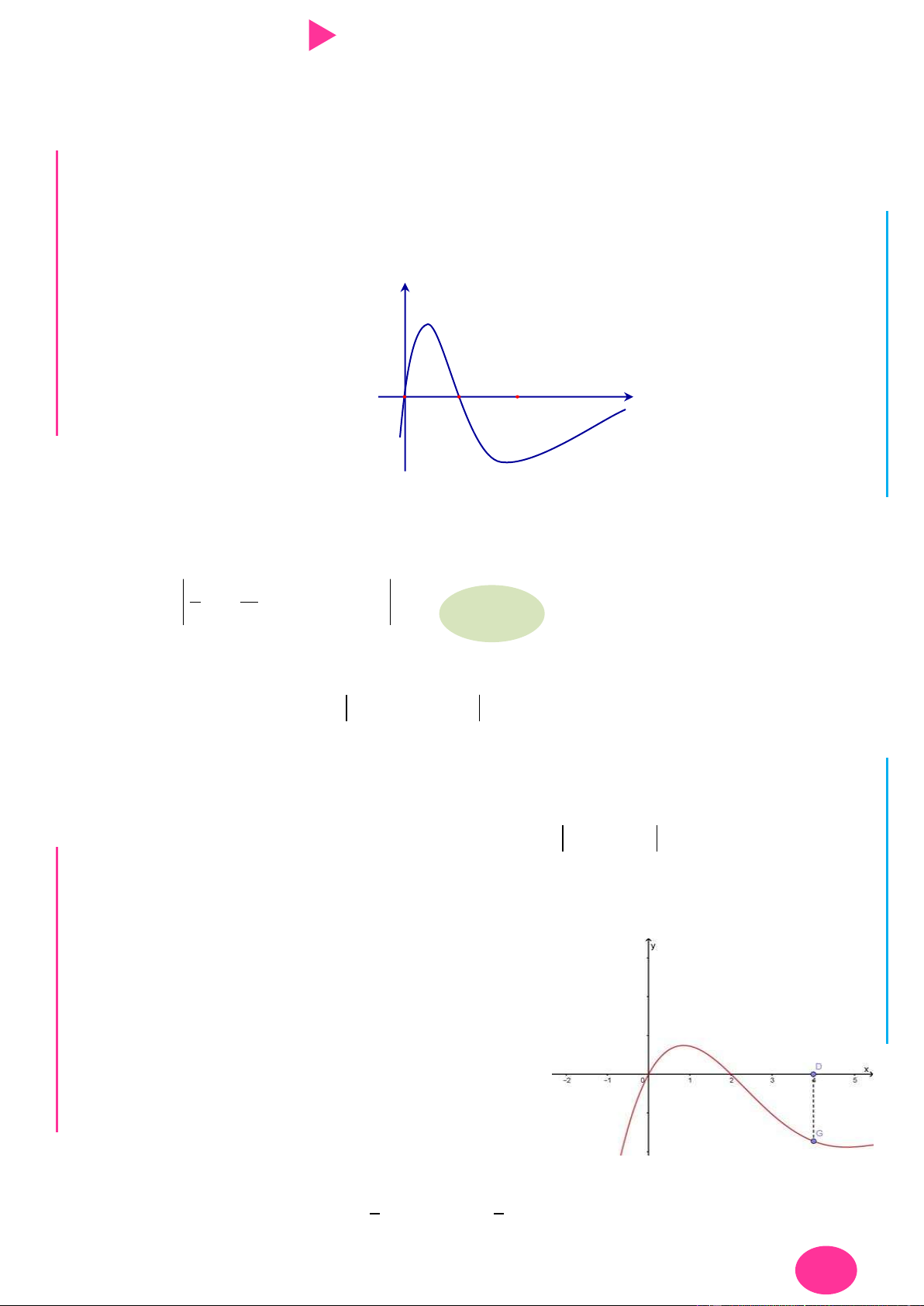
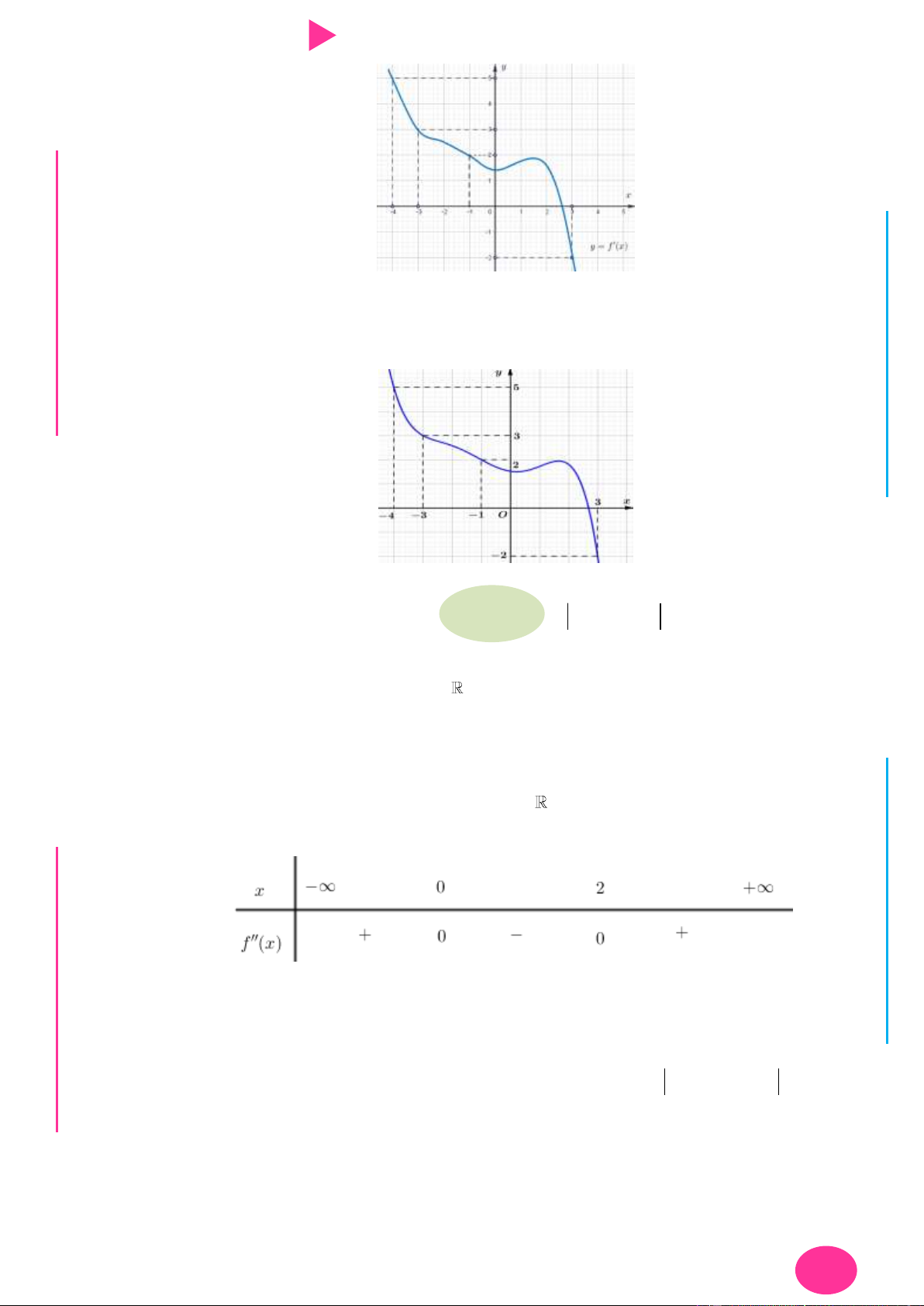
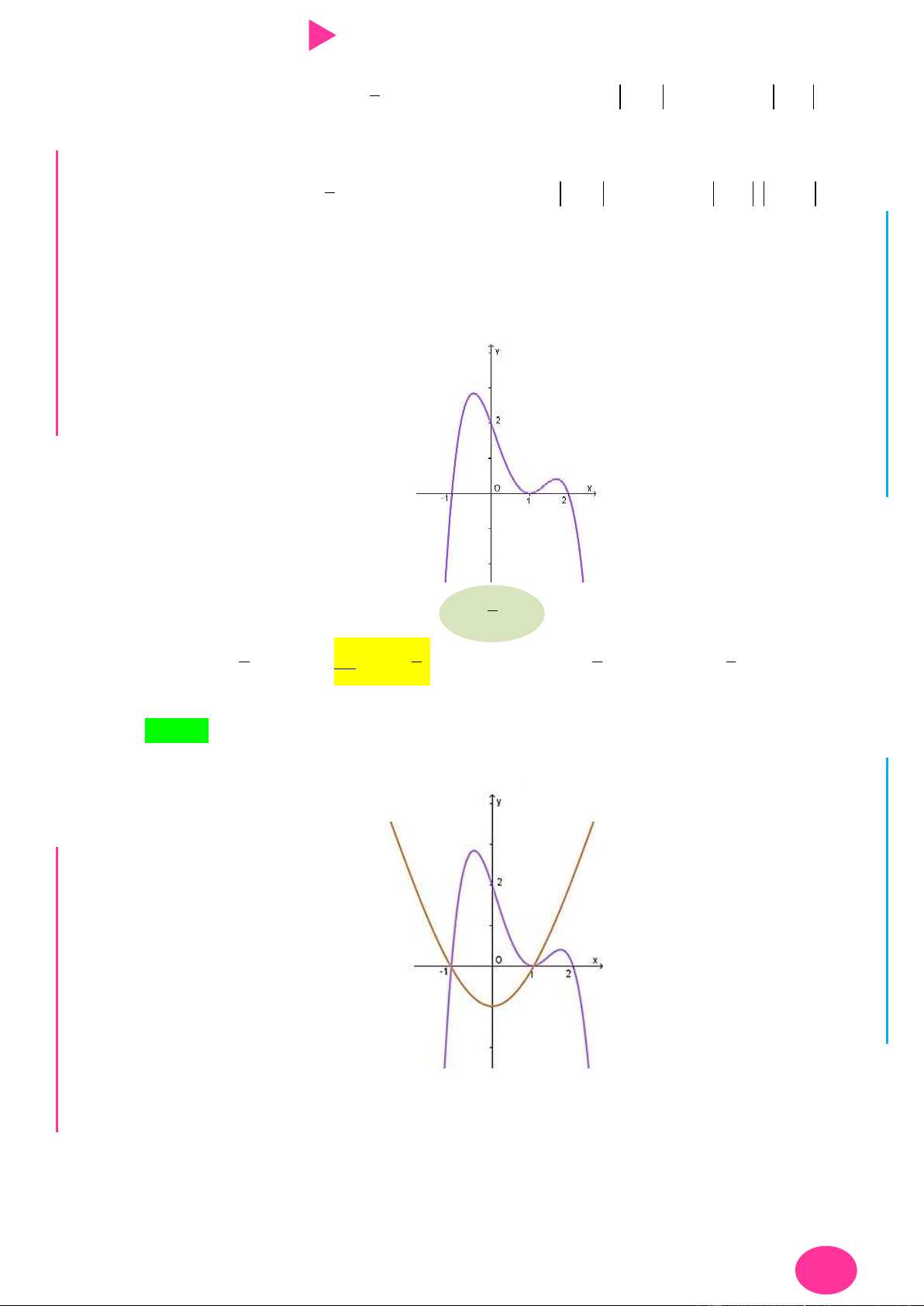
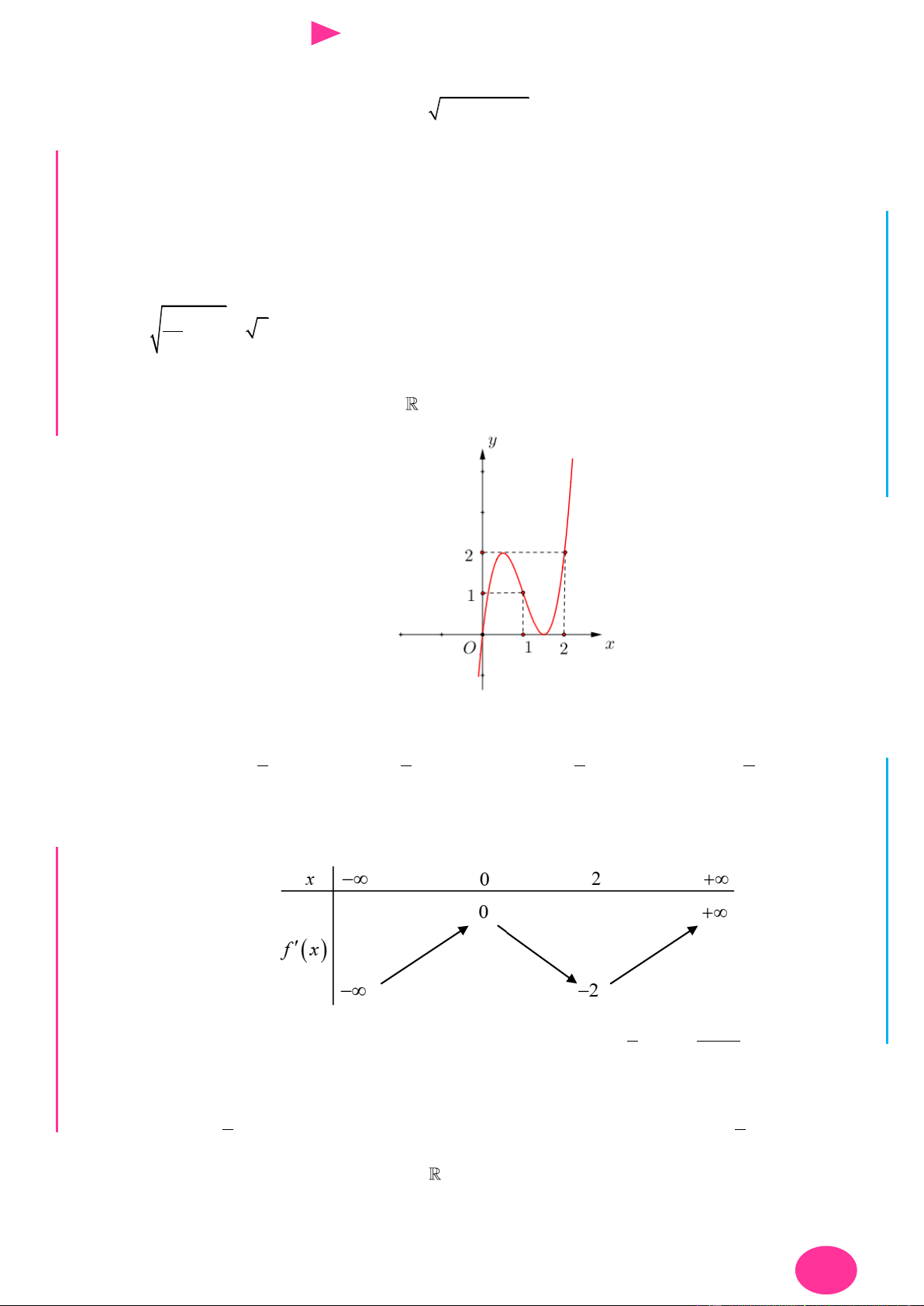
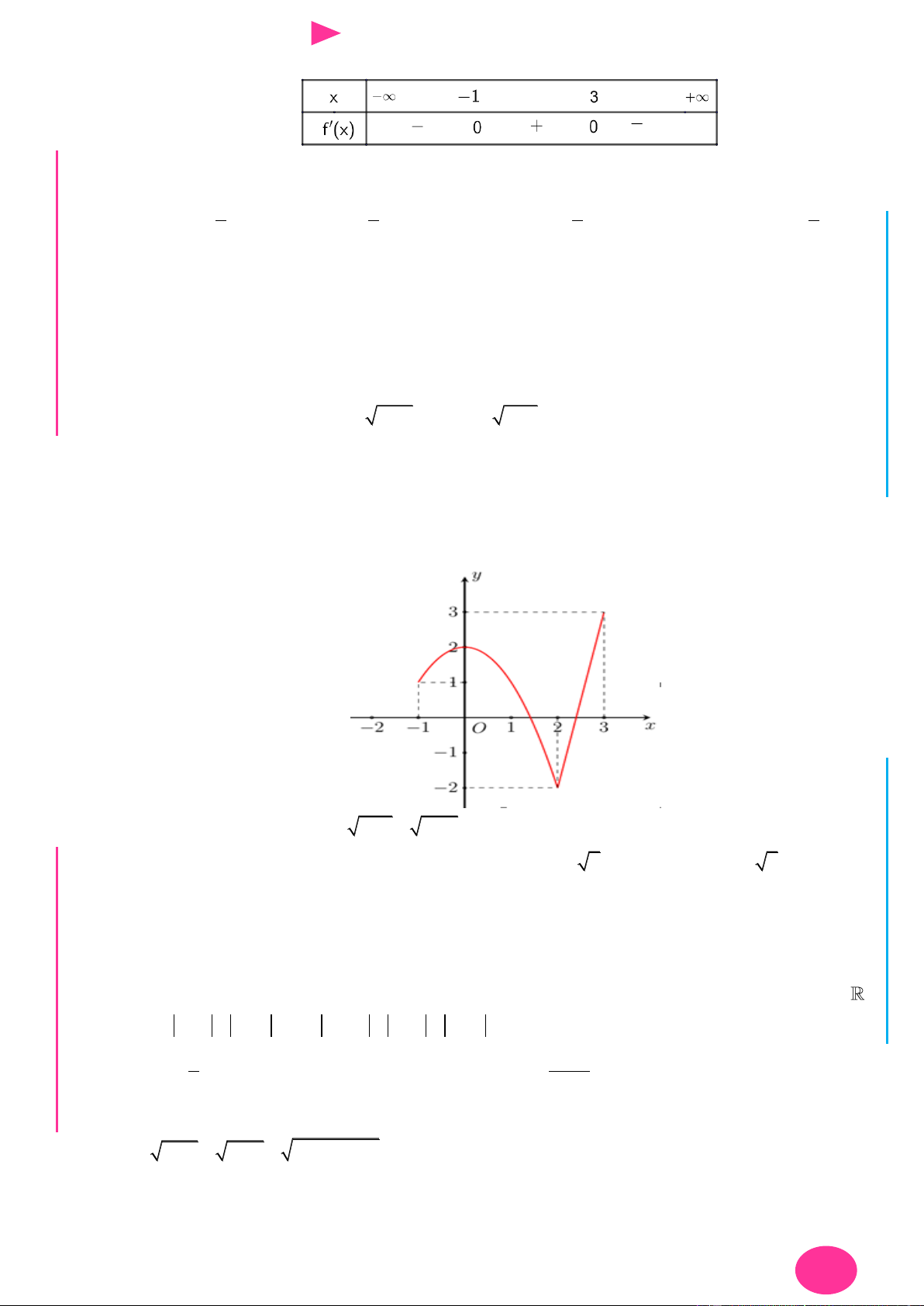
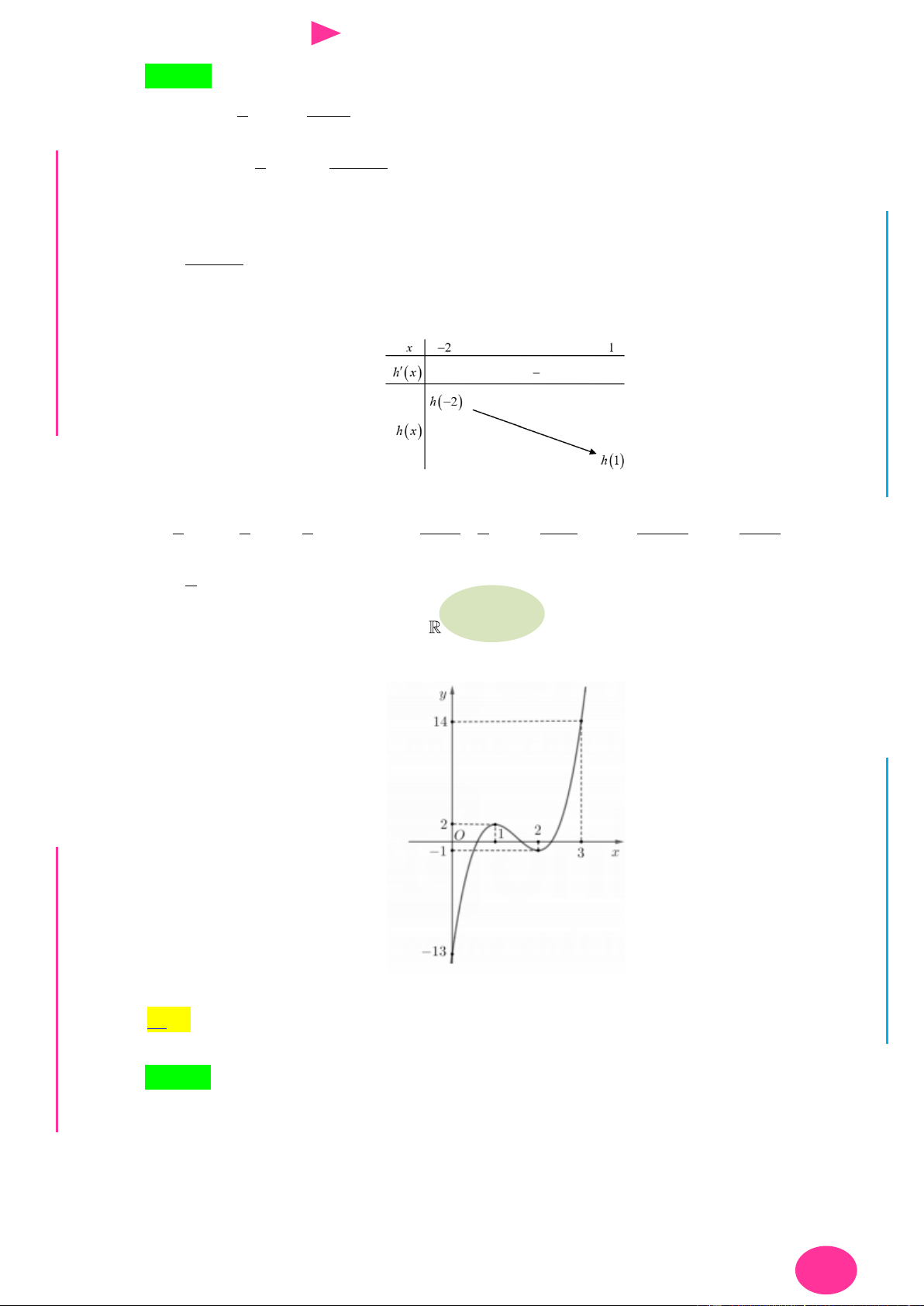
Câu 13. Cho hàm số f x có đạo hàm là f x . Đồ thị
của hàm số y f x cho nhƣ hình vẽ.
Biết rằng f 2 f 4 f 3 f 0 . Giá trị nhỏ
nhất và lớn nhất của f x trên đoạn 0; 4 lần lƣợt là
A. f 2, f 0.
B. f 4, f 2 .
C. f 0, f 2.
D. f 2, f 4 .
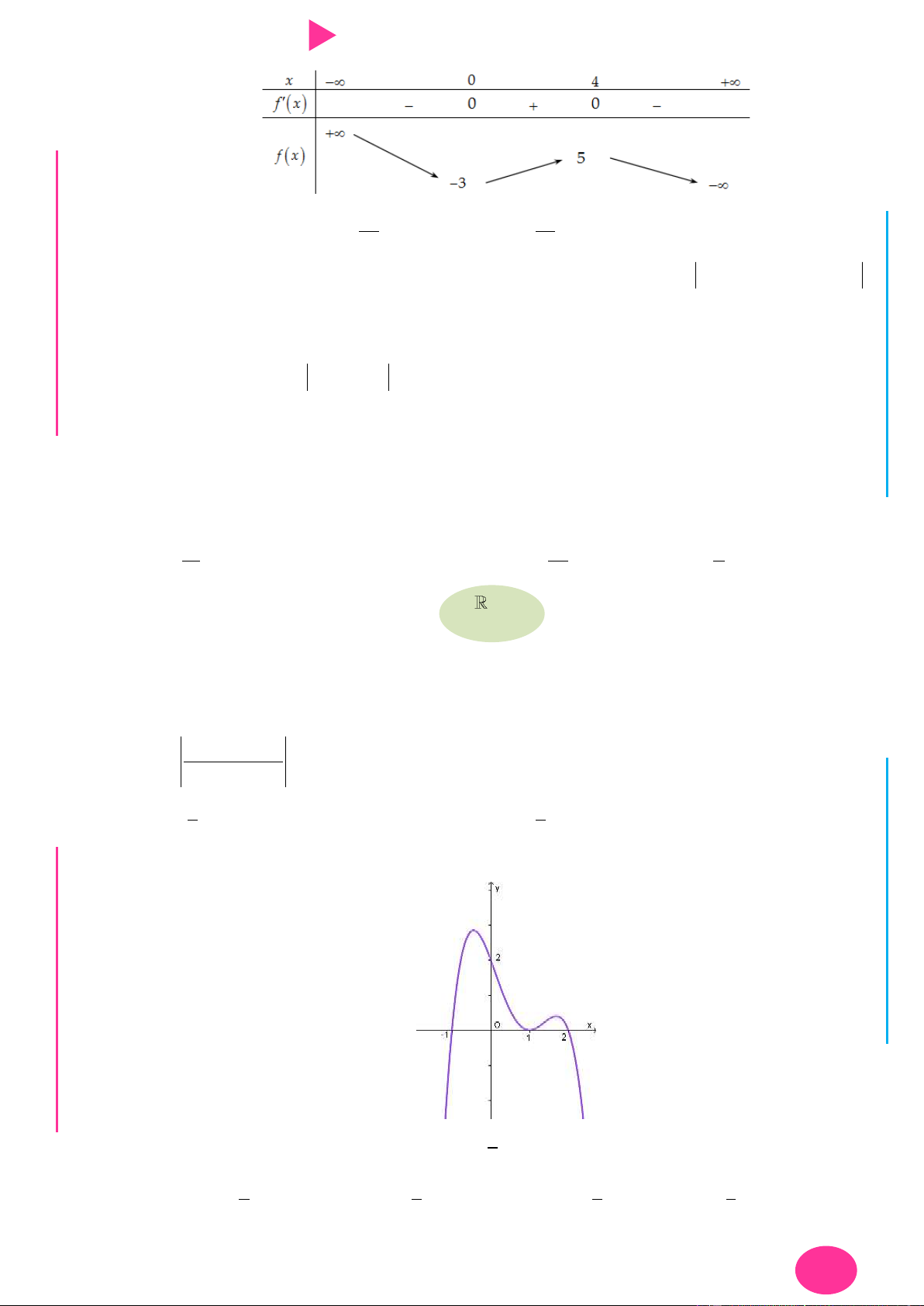
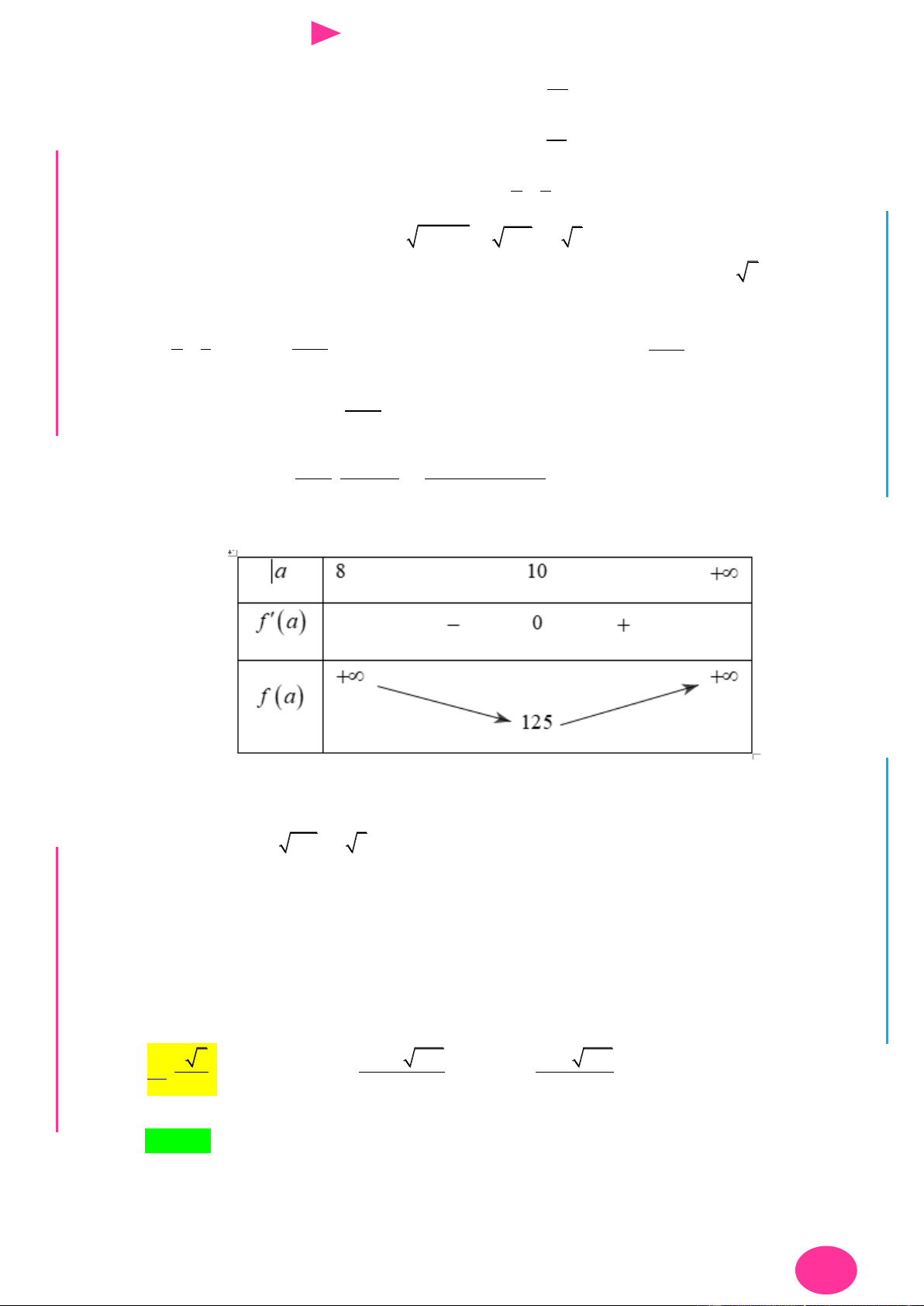
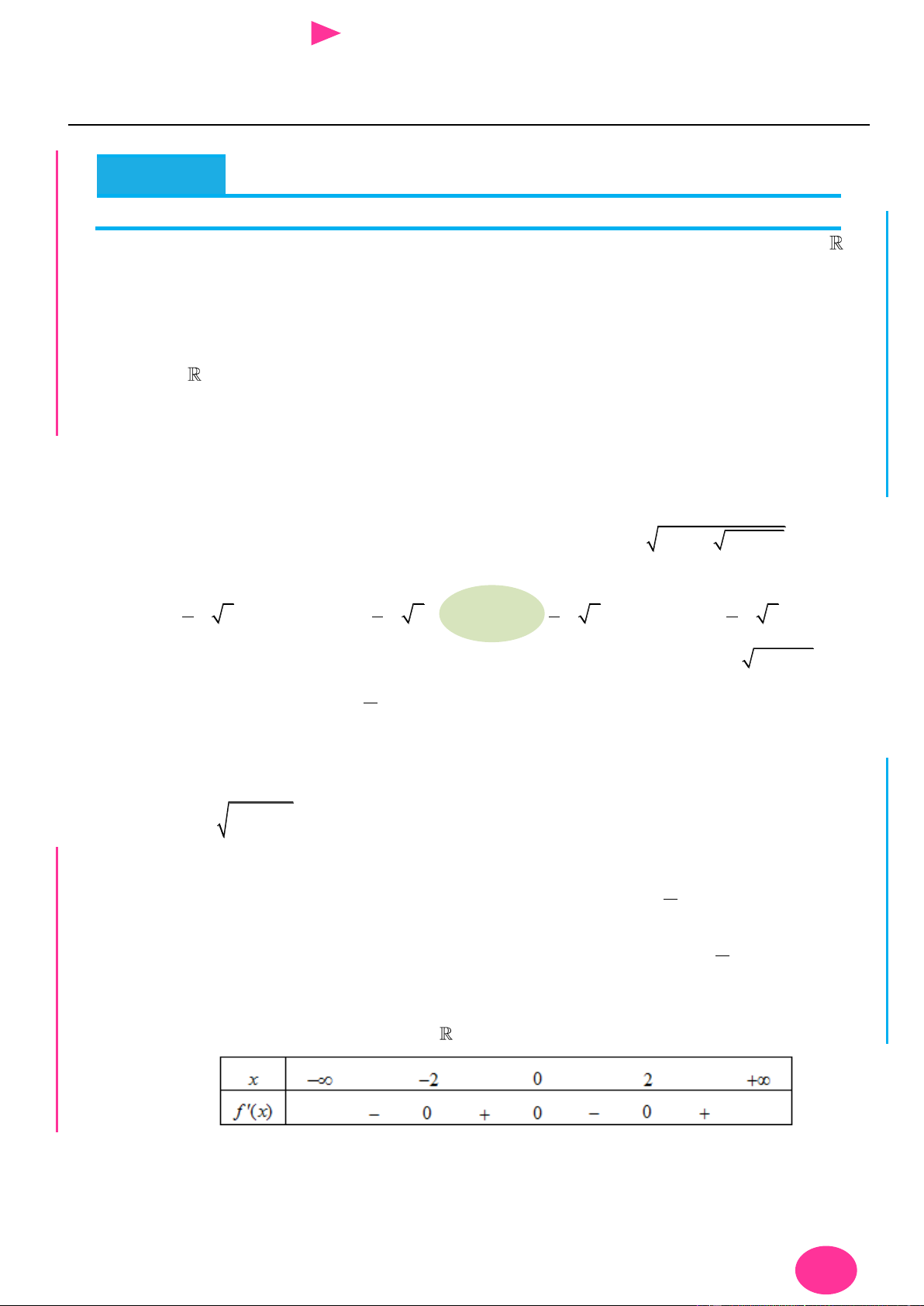
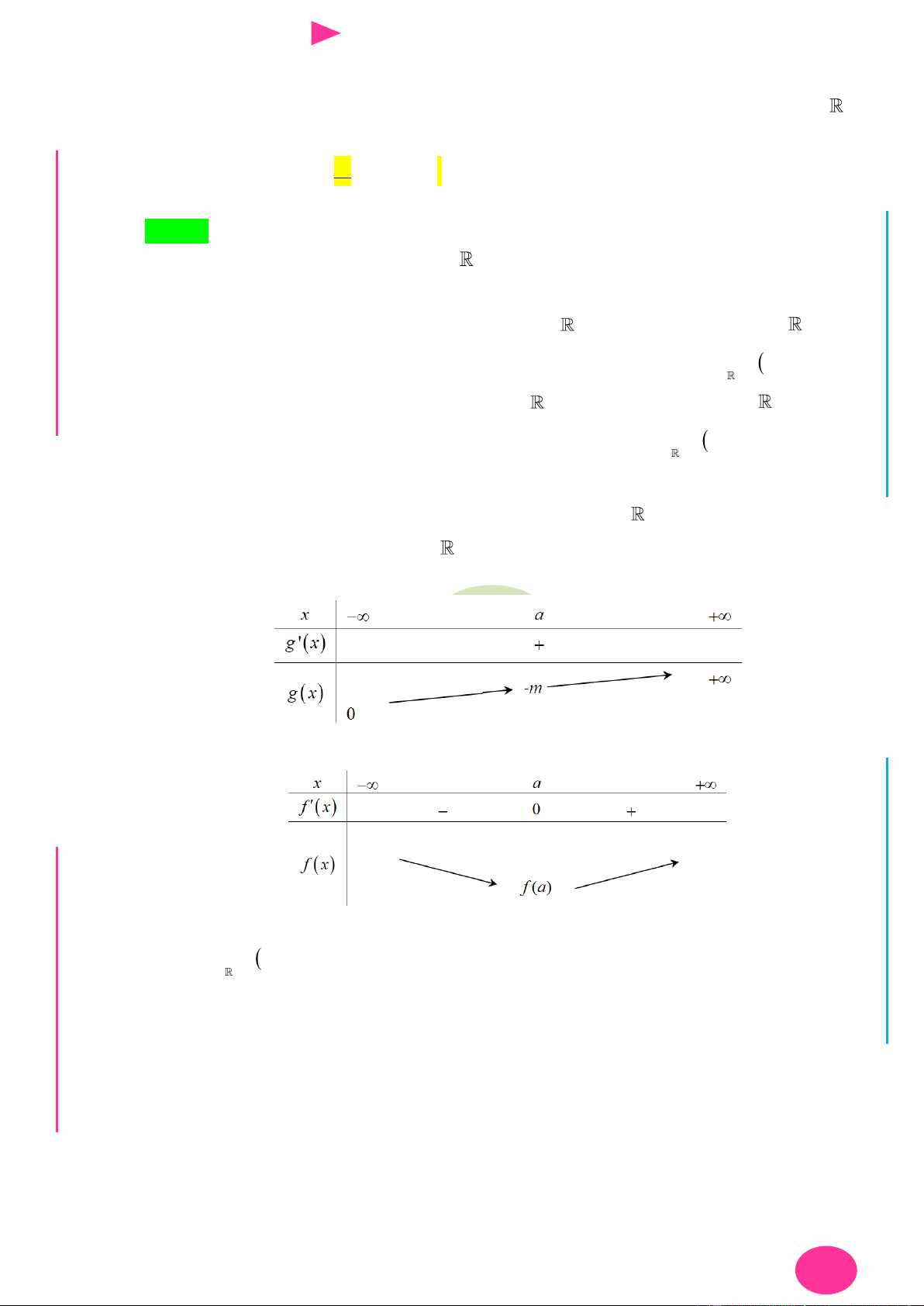
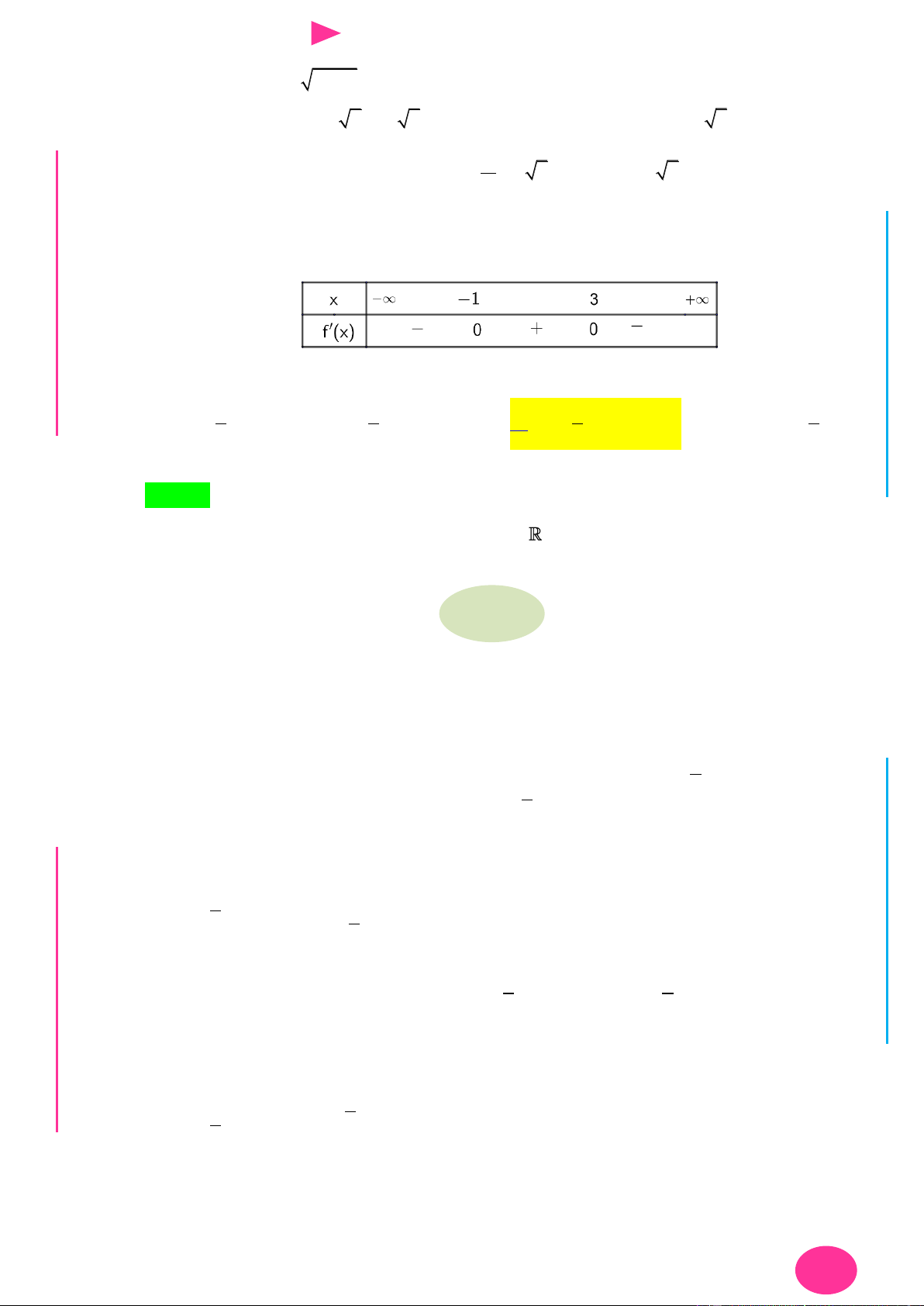
Câu 14. Cho hàm số y f x có bảng biến thiên nhƣ hình dƣới đây. Tìm giá trị lớn nhất của 1 1
hàm số g x f 2 4x x 3 2
x 3x 8x trên đoạn 1; 3 . 3 3
TÌM GTLN, GTNN THEO CÔNG THỨC 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 25 19 A. 15. B. . C. . D. 12. 3 3
Câu 15. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số 4 2
y x 38x 120x 4m
trên đoạn0;2 đạt giá trị nhỏ nhất. A. 26 . B. 13 . C. 14 . D. 27 .
Câu 16. Xét hàm số 2
f x x ax b , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên 1 ;
3 . Khi M nhận giá trị nhỏ nhất có thể đƣợc, tính a 2b . I A. 2 . B. 4 . C. 4 . D. 3 .
Ơ Câu 17. Cho hàm số y x xm2 2
. Tổng tất cả các giá trị thực tham số m sao cho min y 4 [ 2 ;2] M D Ầ bằng Đ 31 23 9 NHỊ A. . B. 8 . C. . D. . 4 4 4 Đ G
max f x f 2
THPT Câu 18. Cho hàm số y
f x liên tục trên N.C .Đs ao cho 4 . Xét hàm số x 0;10 NG
g x f 3 x x 2
x 2x m . Giá trị của tham số m để max g x 8 là CÔN Ờ x 0;2 N A. 5 . B. 4 . C. 1 . D. 3 . YỄ
TRƢ Câu 19. Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số GU N 2 N
x mx 2m y 1;
1 bằng 3 . Tính tổng tất cả các phần tử của S . x trên đoạn 2 ÁO VIÊ 8 5 A. . B. 5 . C. . D. 1 . GI 3 3
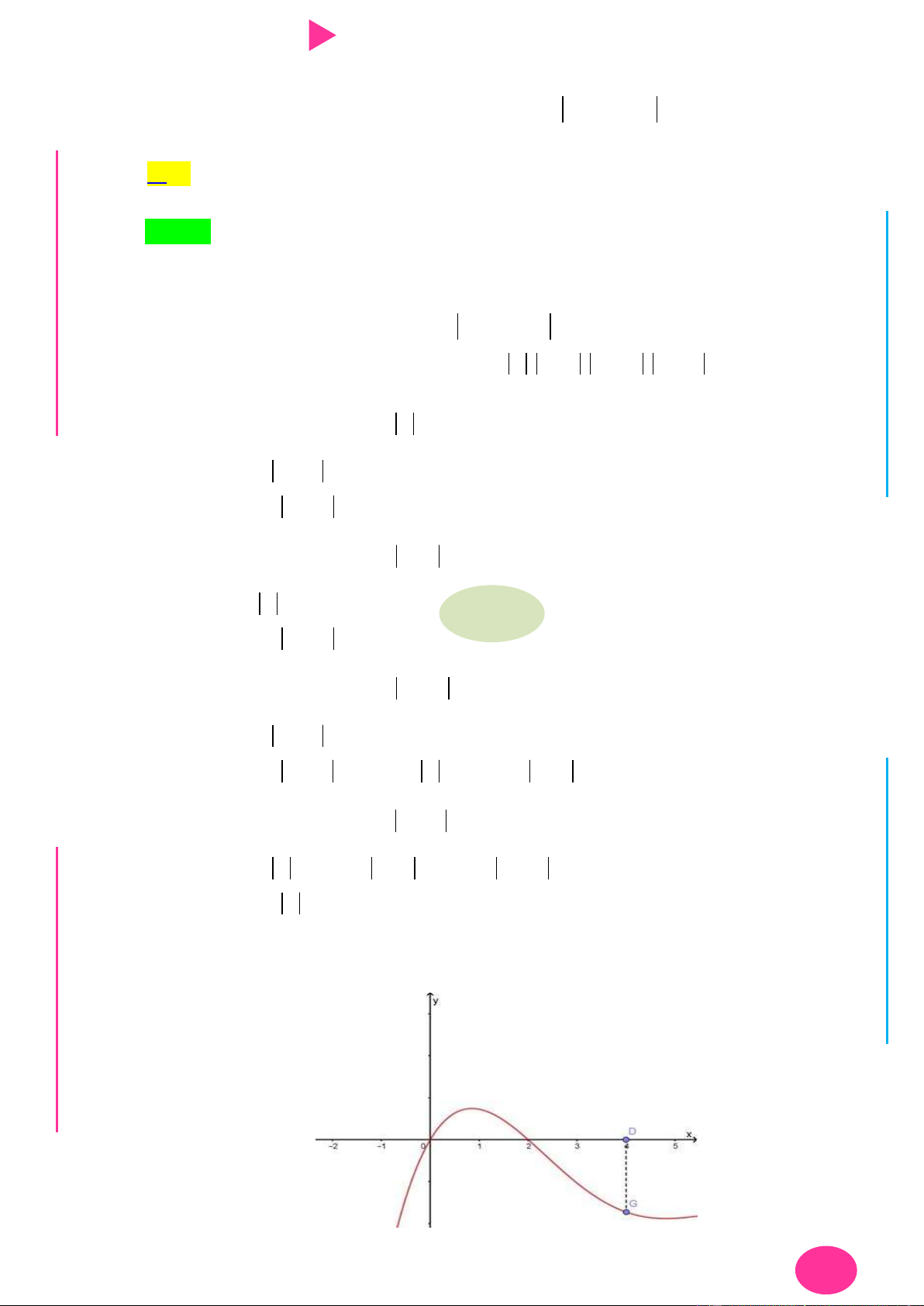
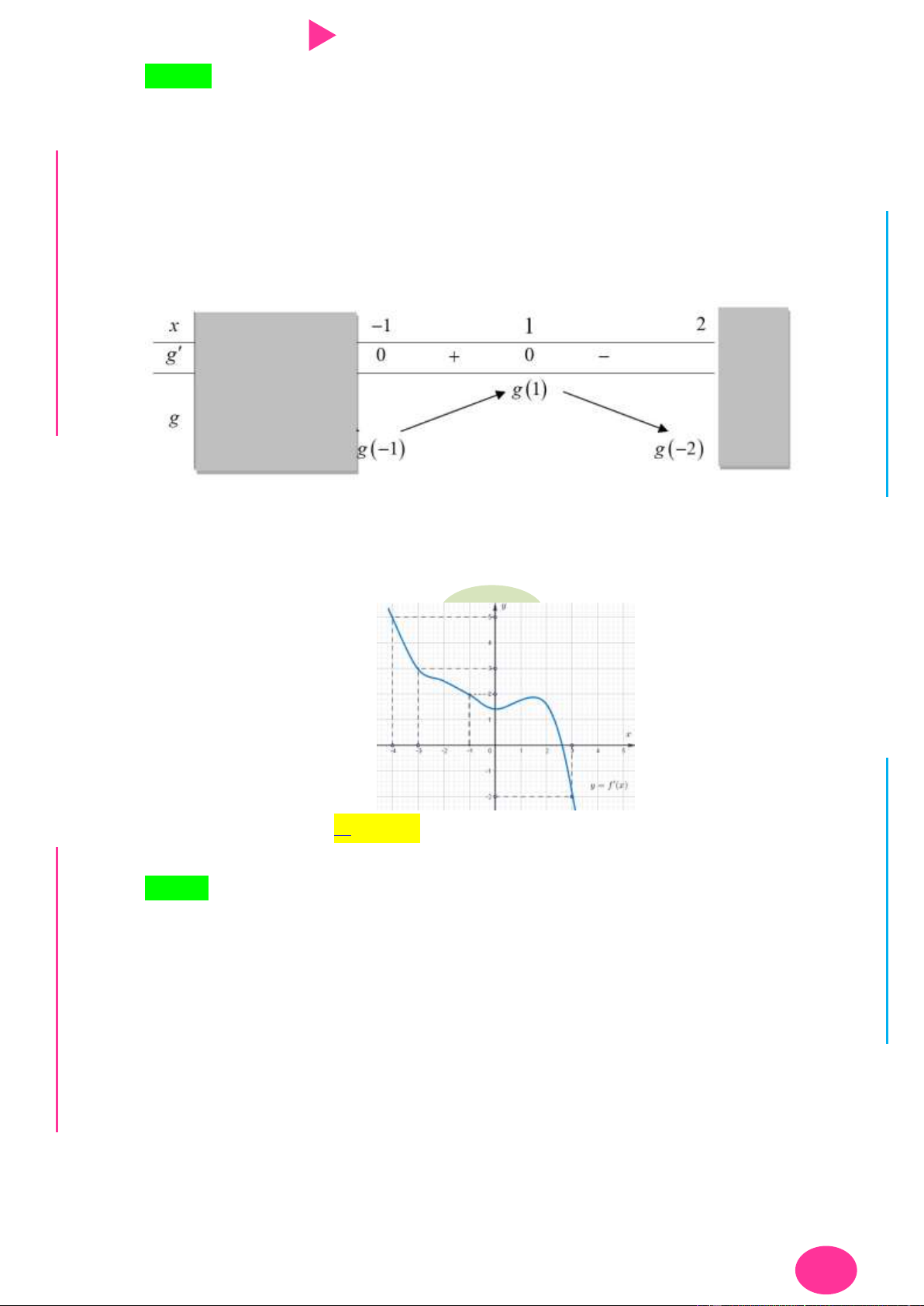
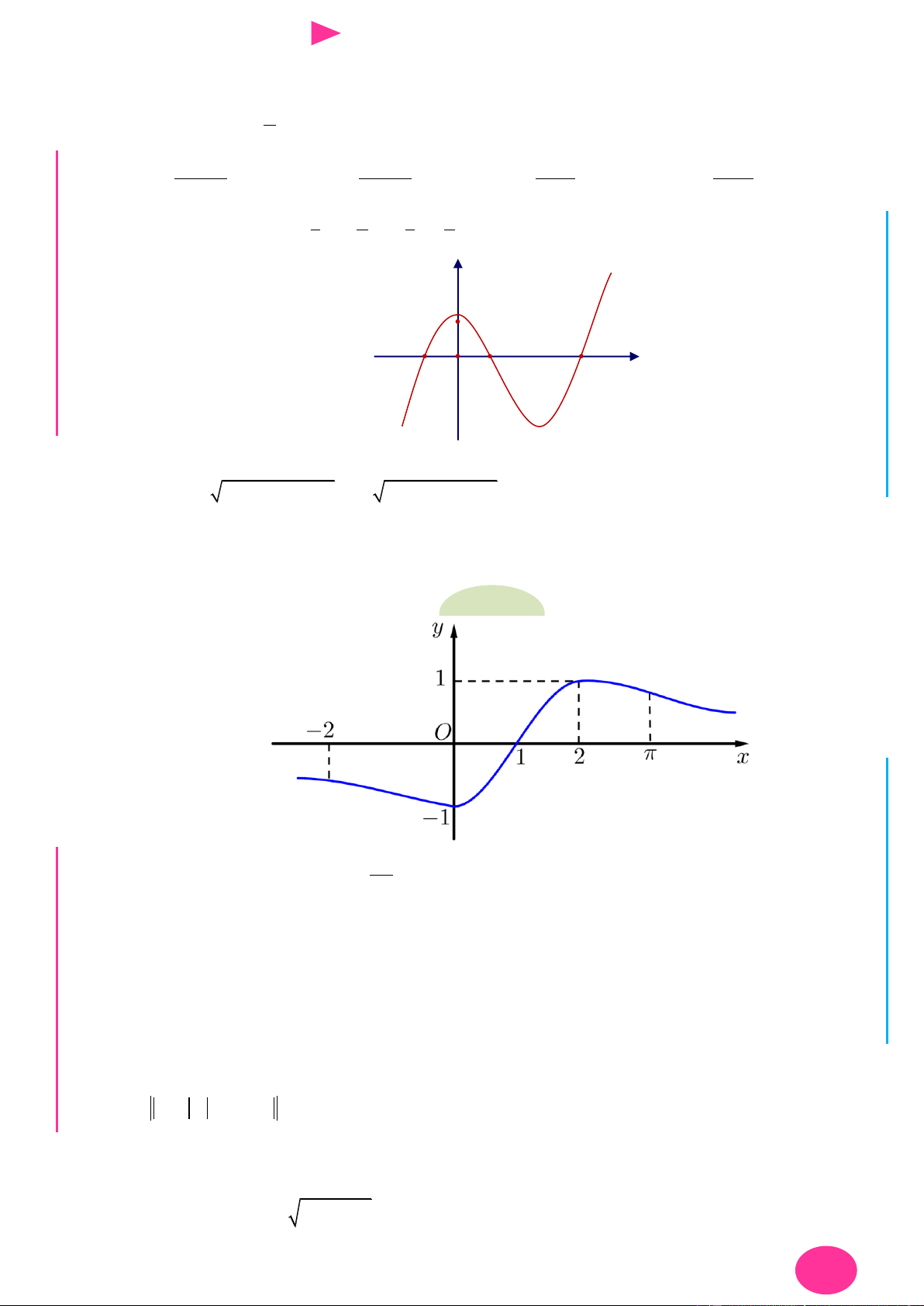
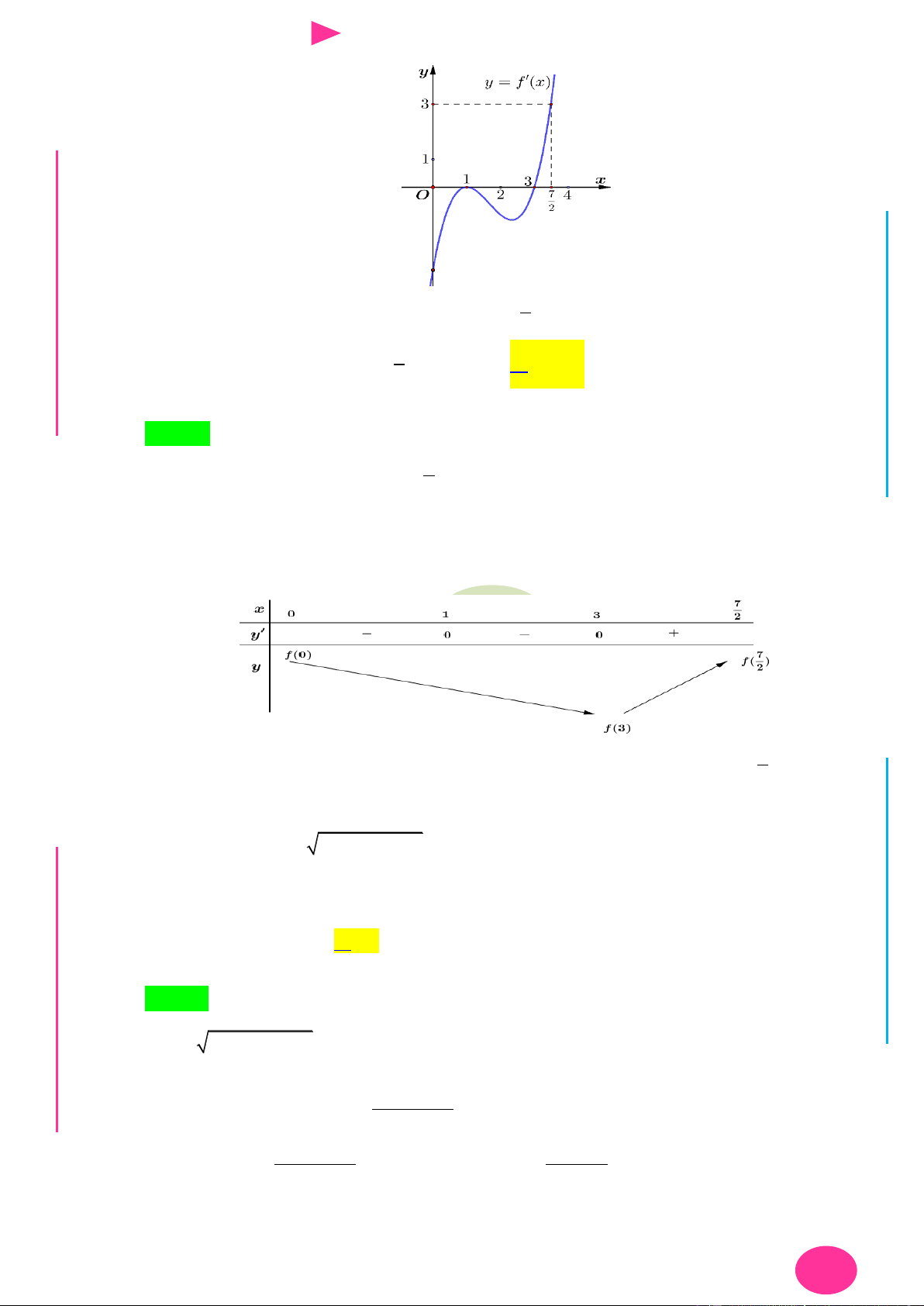
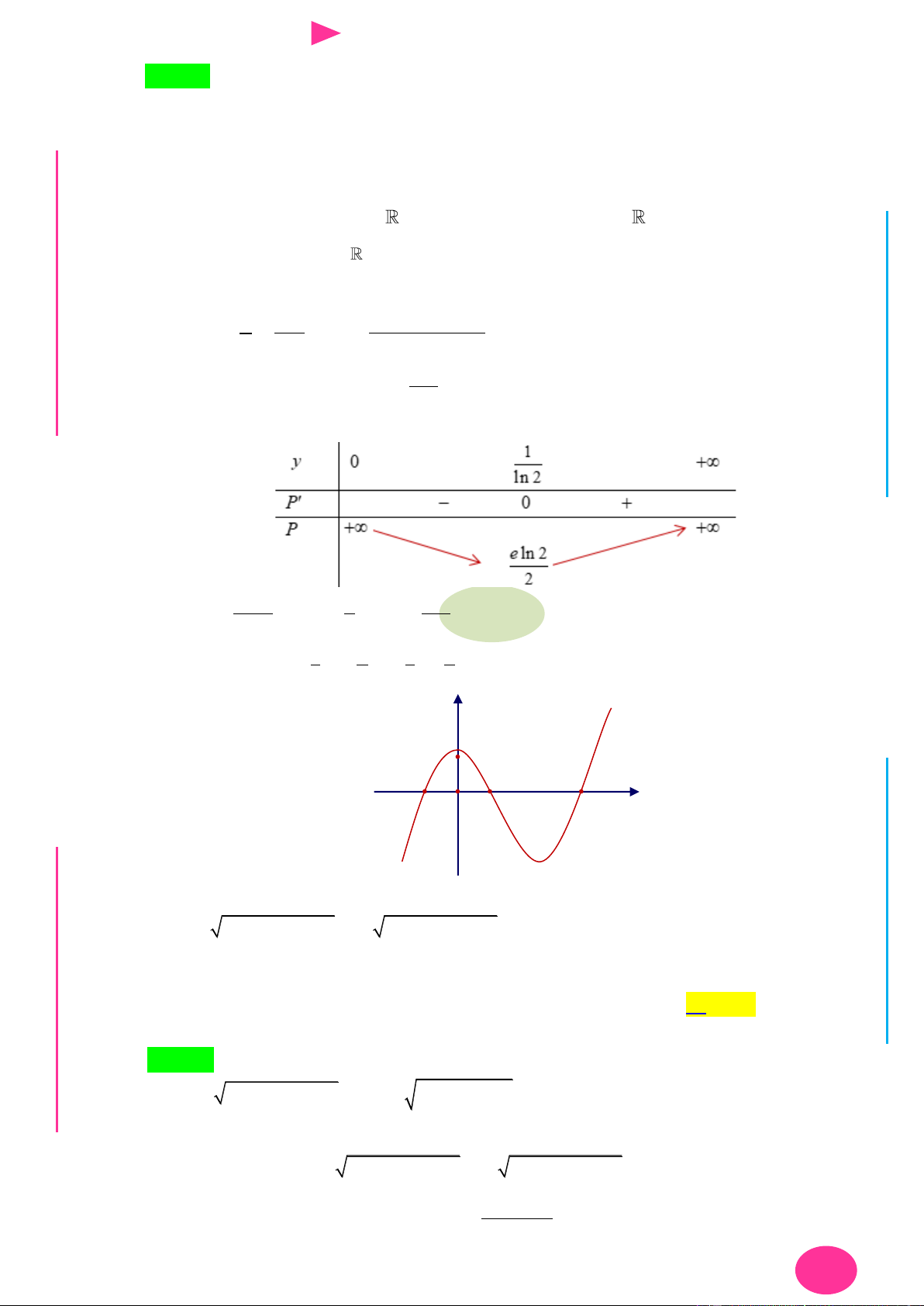
Câu 20. Cho hàm số y f x có đồ thị f x nhƣ hình vẽ 1
Giá trị lớn nhất của hàm số g x f x 3
x x 1 trên đoạn 1 ;2 bằng 3 1
A. f 5 1 . B. f 1 1 . C. f 5 2 . D. . 3 3 3 3
TÌM GTLN, GTNN THEO CÔNG THỨC 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 21. Cho hàm số f x liên tục trên 0; thỏa mãn x f x 2
x f x 2 3 .
2 f x, với
f x 0 , x
0; và f 1 1
. Gọi M , m lần lƣợt là giá trị lớn nhất và giá trị nhỏ 3
nhất của hàm số y f x trên đoạn 1;2 . Tính M m. 9 21 7 5 A. . B. . C. . D. . 10 10 3 3
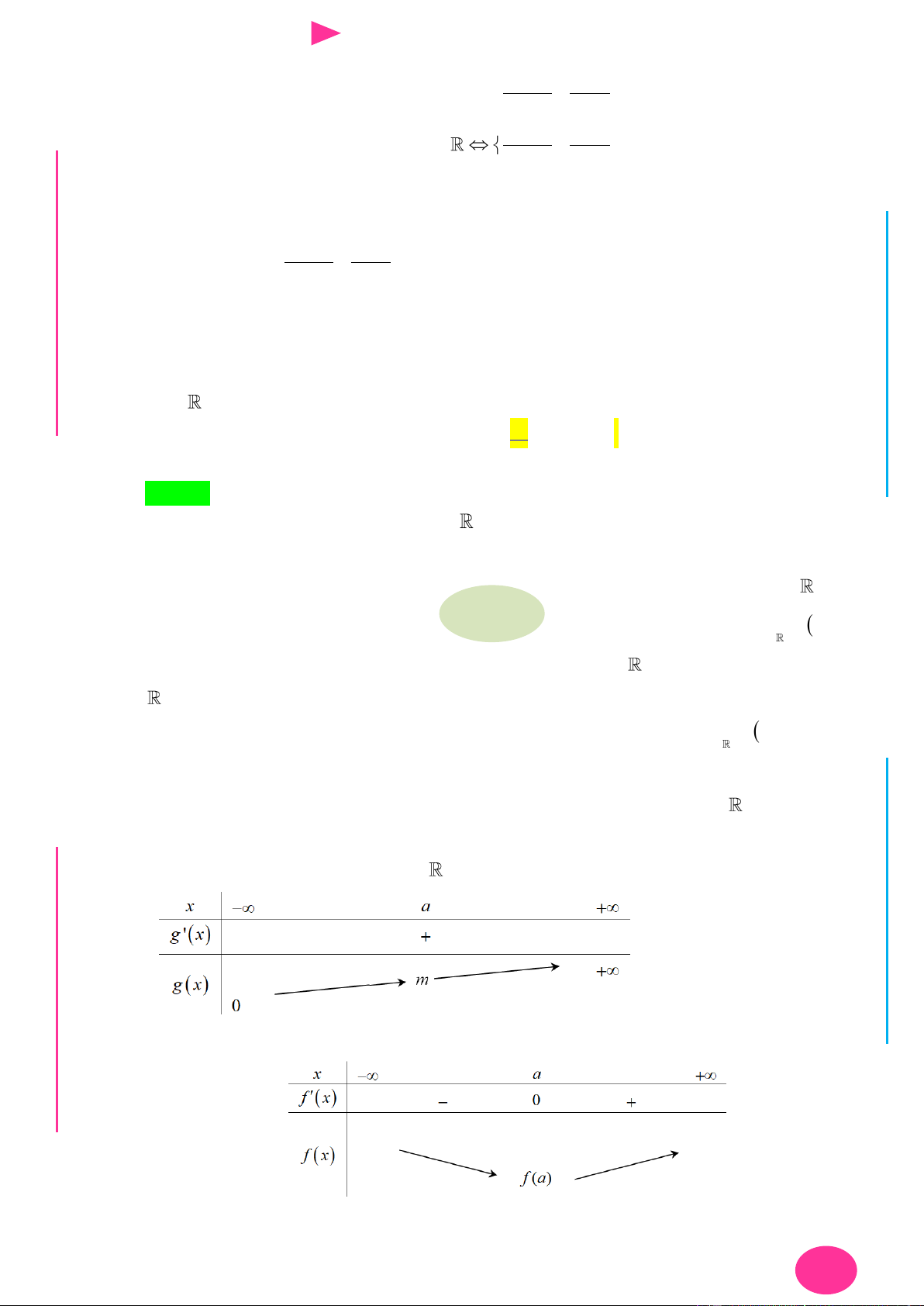
Câu 22. Cho hàm số y f x có đạo hàm f x . Hàm số y f x liên tục trên tập số thực và
có bảng biến thiên nhƣ sau: I Ơ
Biết rằng f 10 1
, f 2 6 . Giá trị nhỏ nhất của hàm số g x 3
f x 3 f x trên M D 3 Ầ đoạn 1 ;2 bằng Đ NHỊ 10 820 730 A. . B. . C. . D. 198 . Đ 3 27 27 G
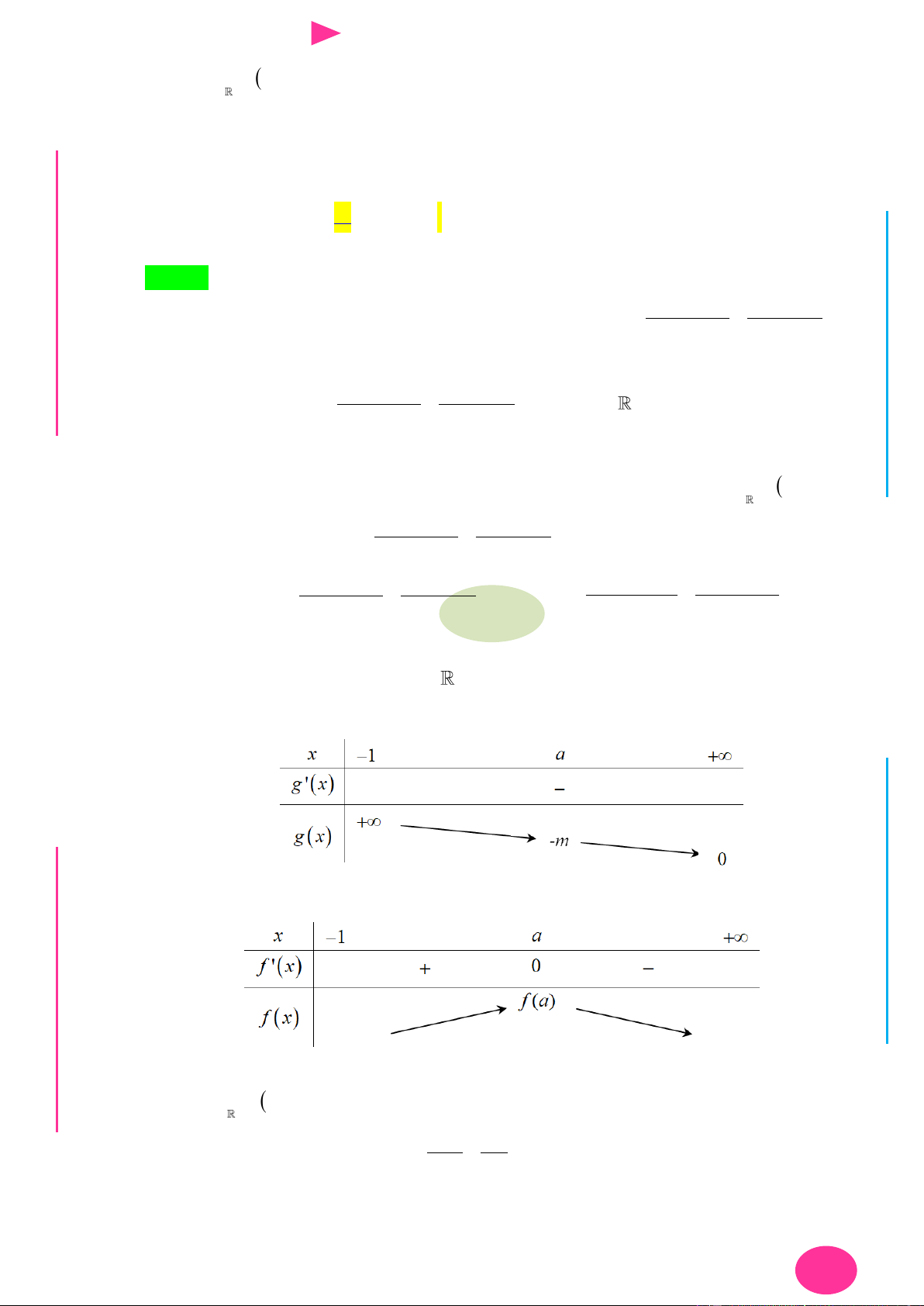
THPT Câu 23. Cho hàm số y f x. Đồ thị hàm số N. đạo C.Đ
hàm y f 'x nhƣ hình vẽ dƣới đây. Xét hàm NG 1 3 3 CÔN Ờ
số g x f x 3 2
x x x 2018 . Mệnh đề nào dƣới đây đúng? N 3 4 2 YỄ
A. min g x g 1 .
B. min g x g 3 . TRƢ 3 ; 1 3 ; 1 GU N g 3 g 1 N C. min g x .
D. min g x g 1 . 3 ; 1 2 3 ; 1 Câu 24. Cho hàm số
y f (x) nghịch biến trên và thỏa mãn ÁO VIÊ
f (x) x 6 4 2 GI
f (x) x 3x 2x , x
. Gọi M và m lần lƣợt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số y f (x) trên đoạn 1;2. Giá trị của 3M m bằng A. 4. B. 28. C. 3. D. 33.
Câu 25. Cho hàm số y f x có bảng biến thiên nhƣ sau 1 2 2
Tìm giá trị lớn nhất của hàm số g x f 3 x 3x 5 3
x x 3x trên đoạn 1 ;2 ? 5 3 15 A. 2022 . B. 2019 . C. 2020 . D. 2021.
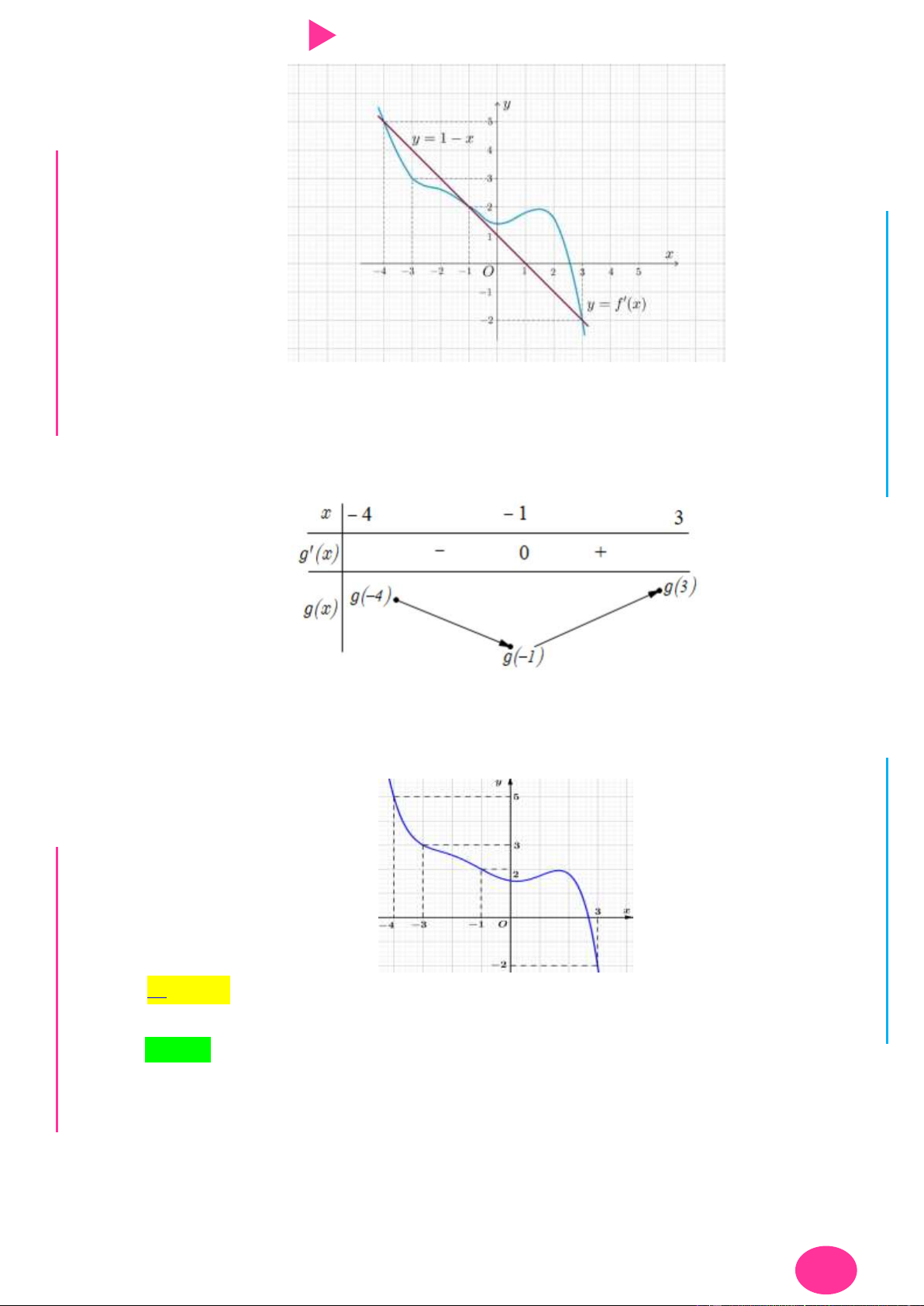
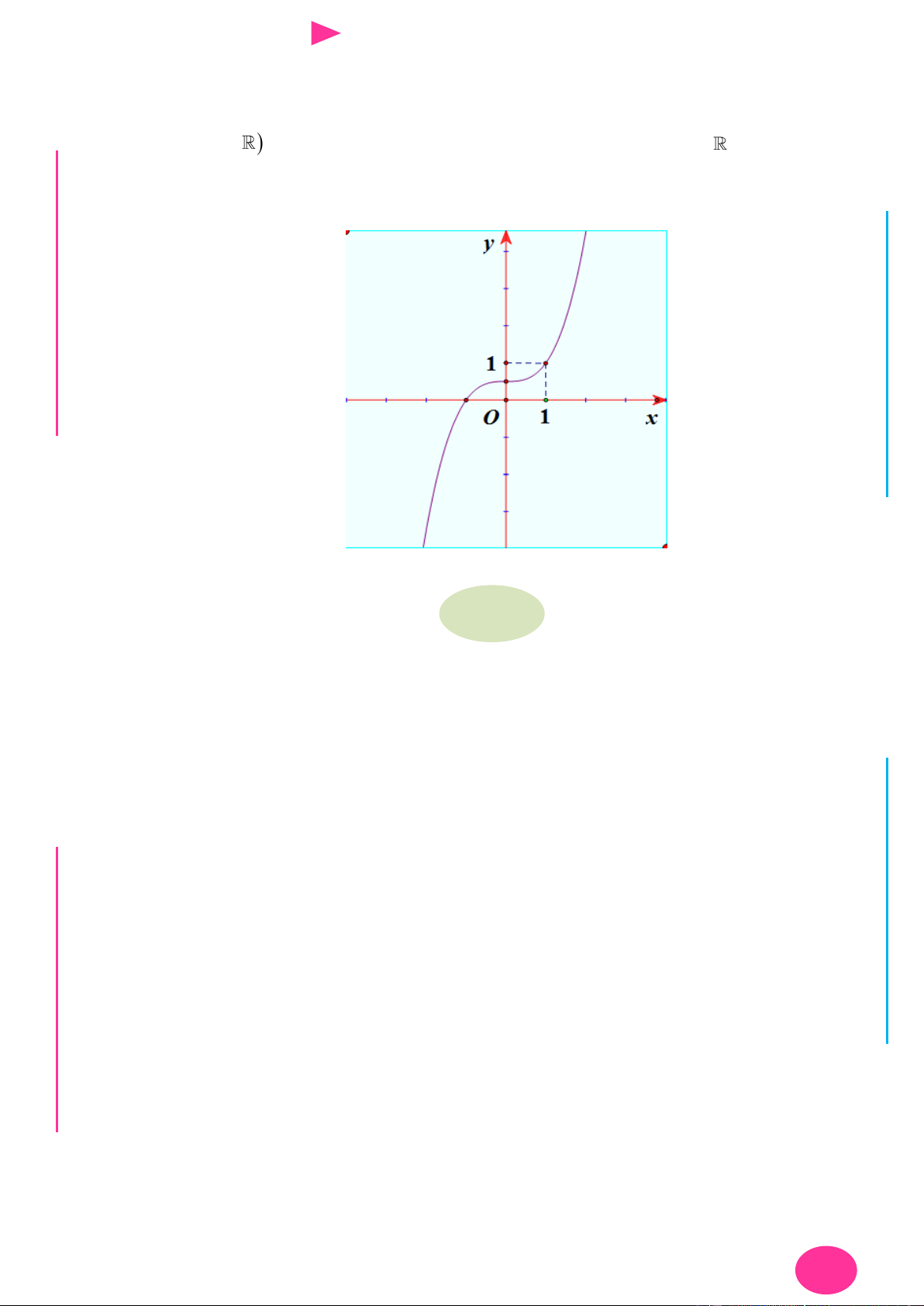
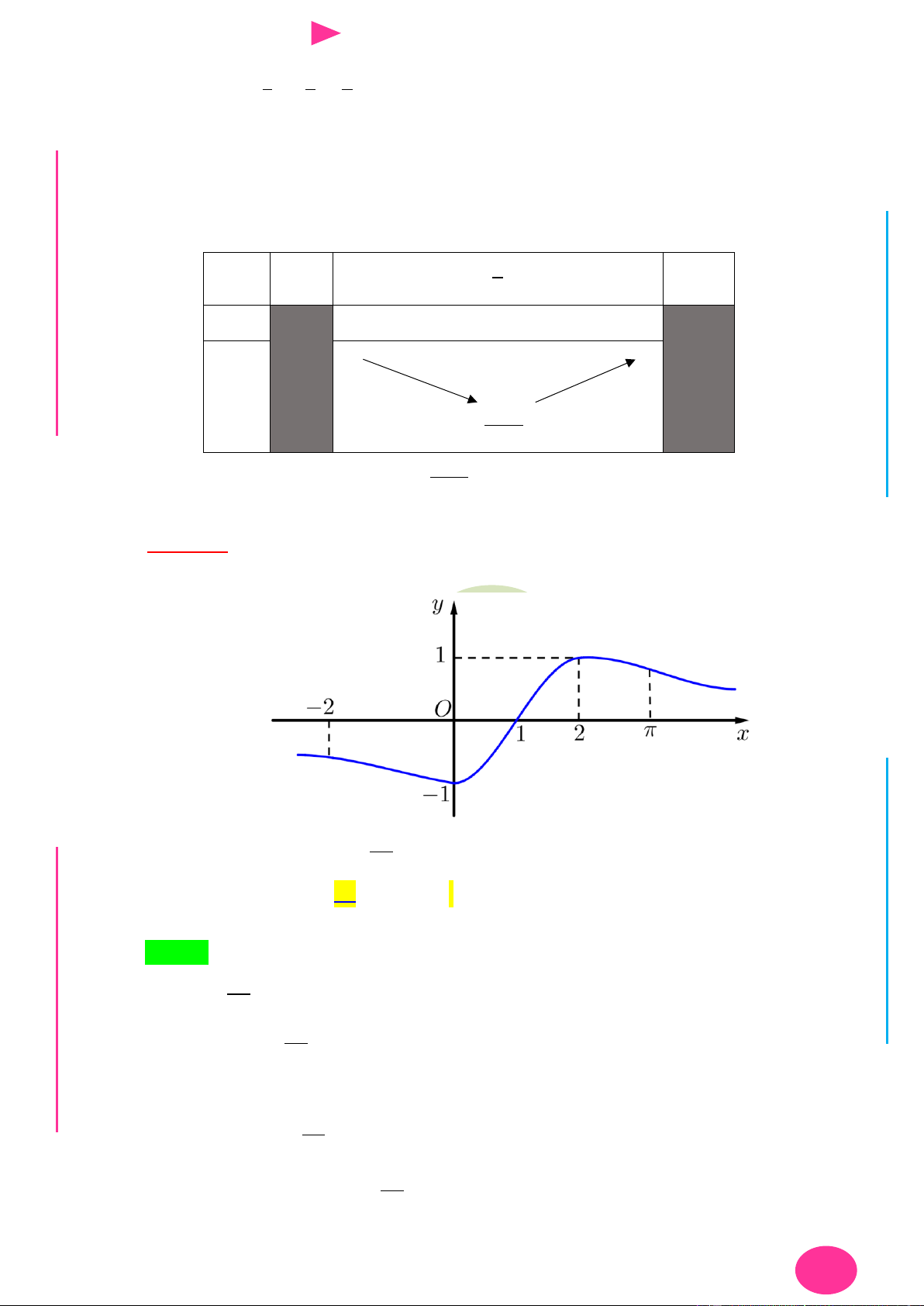
Câu 26. Cho hàm số f x . Biết hàm số y f x có đồ thị nhƣ hình bên. Trên đoạn 4 ; 3 , hàm
số g x f x x2 2 1
đạt giá trị nhỏ nhất tại điểm
TÌM GTLN, GTNN THEO CÔNG THỨC 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. x 4 . B. x 1 .
C. x 3. D. x 3 . 0 0 0 0
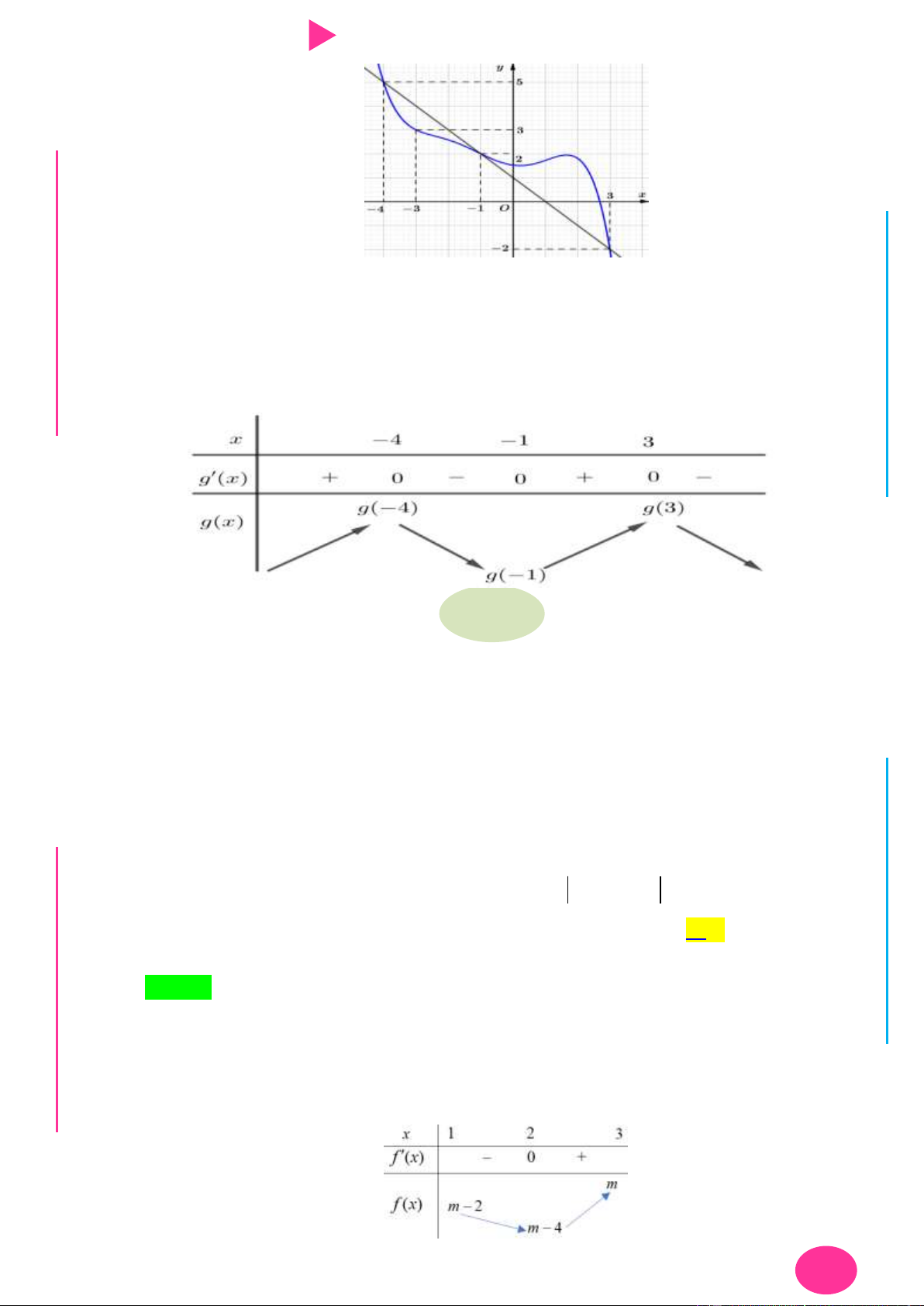
Câu 27. Cho hàm số f (x) . Biết hàm số y f (
x) có đồ thị nhƣ hình bên. Trên đoạn [ 4;3] , hàm số 2
g(x) 2 f (x) (1 x) đạt giá trị nhỏ nhất tại điểm. I Ơ M D Ầ Đ NH Ị Đ A. x 1 .
B. x 3. C. x 4 . D. x 3 . 0 0 0 0 G
THPT Câu 28. Có bao nhiêu giá trị nguyên của tham sN ố . C.Đ m để 3 2
max x 3x m 4? 1; 3 NG CÔN Ờ A. Vô số. B. 4. C. 6. D. 5. N
Câu 29. Cho hàm số y f x liên tục trên
sao cho max f x 3 . Xét g x f 3x 1 m . YỄ TRƢ 1 ; 2 GU N
Tìm tất cả các giá trị của tham số m để max g x 1 0 . 0; 1 N A. 13 . B. 7 . C. 13 . D. 1 .
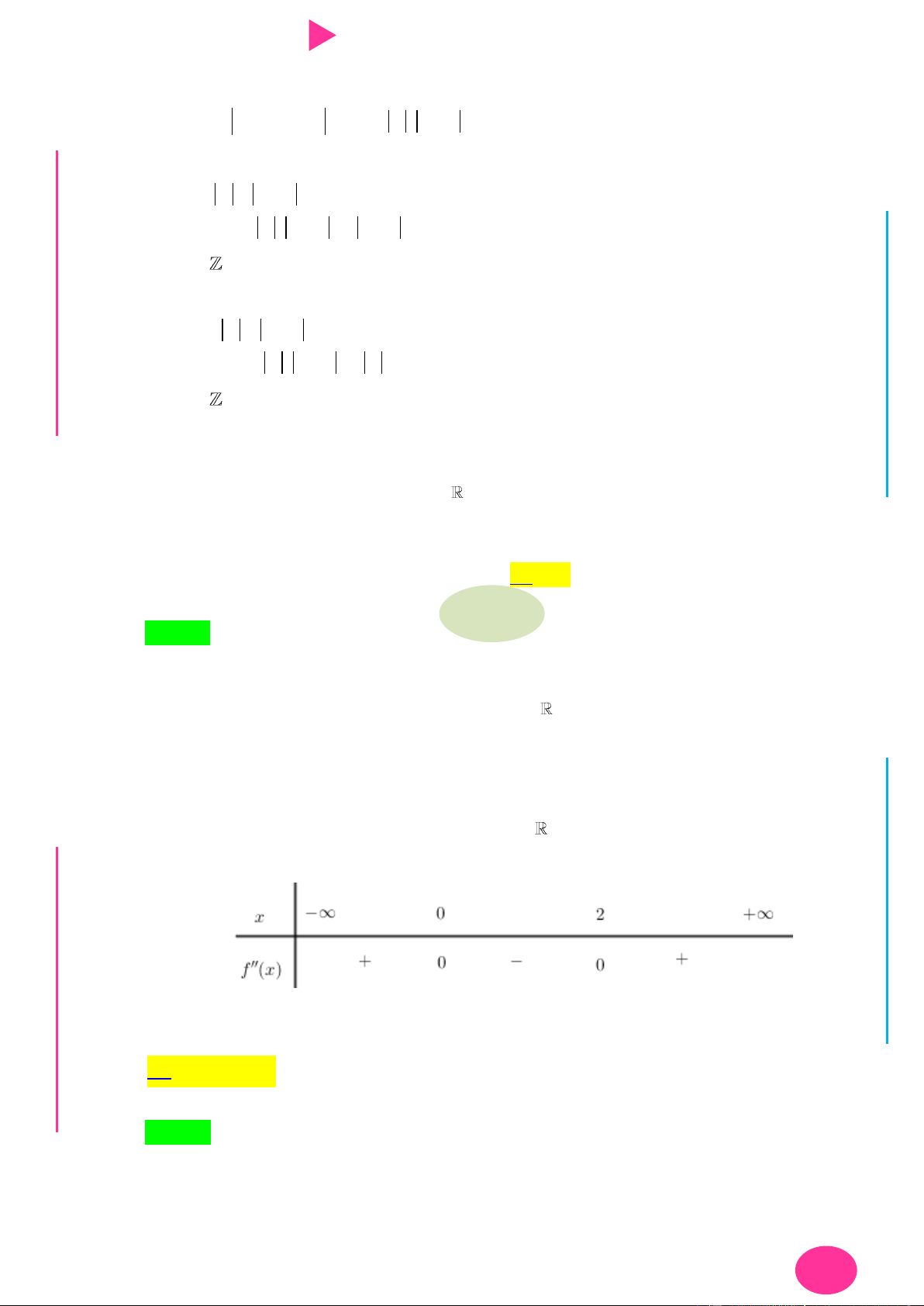
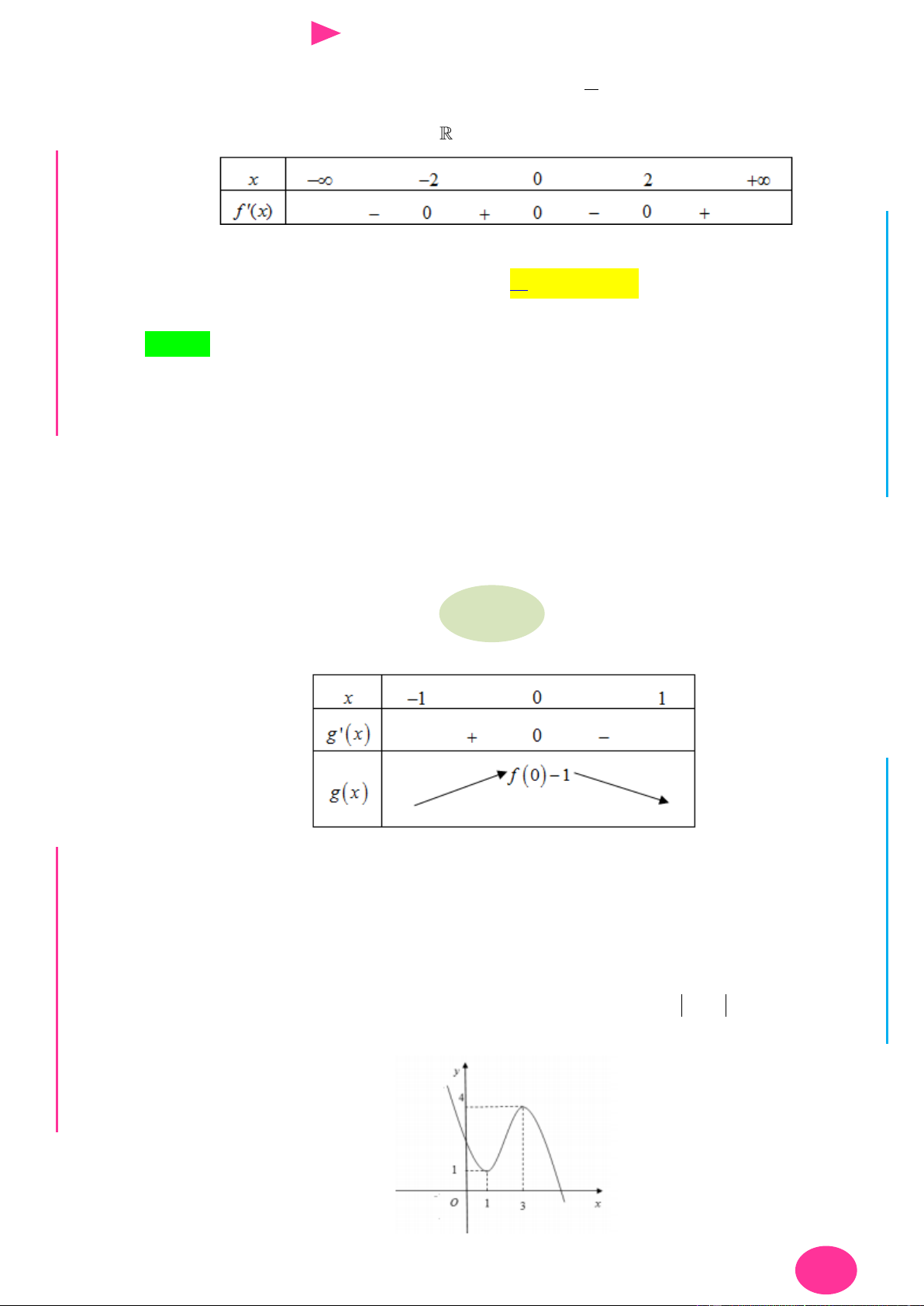
ÁO VIÊ Câu 30. Cho hàm số y f x có đạo hàm cấp hai trên . Biết f 0 3 , f 2 2 018 và bảng GI
xét dấu của f x nhƣ sau:
Hàm số y f x 2017 2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau 0 đây? A. ; 2017 .
B. 2017; . C. 0; 2 . D. 2 017;0 .
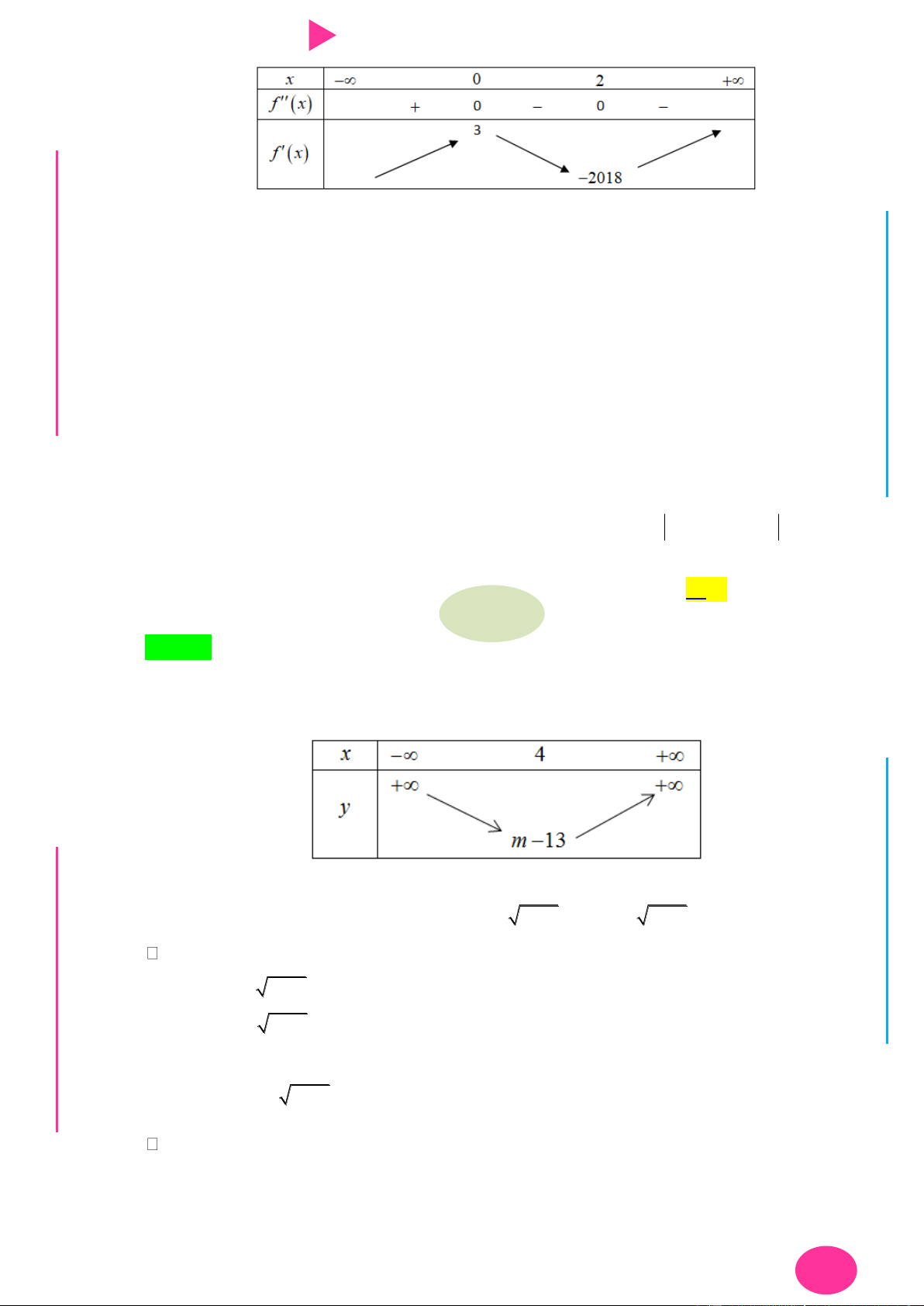
Câu 31. Có bao nhiêu số thực m để giá trị nhỏ nhất của hàm số 2
y x 4x m 3 4x bằng 5 . A. 2 . B. 3 . C. 0 . D. 1 .
TÌM GTLN, GTNN THEO CÔNG THỨC 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 I Ơ M D Ầ Đ NHỊĐG THPT N.C.Đ NG CÔN Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
TÌM GTLN, GTNN THEO CÔNG THỨC 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI x m
Câu 1. Cho hàm số y f x 2
. Tính tổng các giá trị của tham số m để x 1
max f x min f x 2 . 2; 3 2; 3 A. 4 . B. 2 . C. 1 . D. 3 . Lời giải Chọn A x m
Hàm số y f x 2
xác định và liên tục trên 2; 3 . x 1 Với m 2
, hàm số trở thành y 2 max f x min f x 2 (không thỏa). 2; 3 2; 3 2 m Với m 2
, ta có y x . 2 1 I
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên 2; 3 . Ơ
max f x f 2; min f x f 3 M D 2 ;3 2 ;3 Suy ra . Ầ
max f x f 3; min f x f 2 Đ 2 ;3 2 ;3 NHỊ 6 m 2 m Đ
Do đó: max f x min f x f 3 f 2 4 m . 2; 3 2; 3 G 2 2 THPT N.C.Đ 2 m m 2 NG
Theo giả thiết max f x min f x 2 2 . CÔN Ờ 2; 3 2; 3 2 m 6 N
Vậy tổng các giá trị của tham số m thỏa mãn yêu cầu bài toán là: 4 . YỄ TRƢ
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức GU N N
max f x min f x 2 là không cần thiết. 2; 3 2; 3
ÁO VIÊ Câu 2. Gọi ,
A a lần lƣợt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số: 3
y x 3x m trên GI
đoạn0; 2 . Gọi S là tập các giá trị thực của tham số m để Aa 12 . Tổng các phần tử của S bằng A. 0 . B. 2 . C. 2 . D. 1 Lời giải Chọn A
Đặt: u x 3
x x m ux 2 3 3x 3 x 10;2 u x 2
0 3x 3 0 x 1 0;2
Ta có: u 0 m;u
1 m 2;u 2 m 2
Suy ra: Max u x m 2; Min u x m 2 Max y Max m 2 ; m 2 . 0;2 0;2 0;2
TH1: m 2.m 2 0 2
m 2 a Min y 0( loại ) 0;2
(vì ko thỏa mãn giả thiết Aa 12 )
TÌM GTLN, GTNN THEO CÔNG THỨC 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
TH 2 : m 2 0 m 2 Min y m 2; A Max y m 2 . 0;2 0;2 m 4(TM )
Từ giả thiết: Aa 12 m 2m 2 2
12 m 16 m 4 (koTM )
TH 3 : m 2 0 m 2
Min y m 2 ;Max y m 2. 0;2 0;2
m 4(koTM )
Từ giả thiết: Aa 12 m 2m 2 2
12 m 16 m 4 ( TM )
Kết hợp các trƣờng hợp suy ra: S 4 ; 4
Vậy tổng các phần tử của S bằng: 4 4 0 . mx 1 Câu 3.
Gọi T là tập hợp tất cả giá trị của tham số m để hàm số y có giá trị lớn nhất 2 x m 5 trên đoạn 2;
3 bằng . Tính tổng của các phần tử trong T . I 6 Ơ 17 16 A. . B. . C. 2 . D. 6 . M D 5 5 Ầ Lời giải Đ NH Chọn A Ị Đ mx 1 Ta có y . G THPT 2 x m N.C.Đ NG Điều kiện 2 x m . CÔN Ờ 3 N mx 1 m 1 y y . 2 2 2 x m YỄ xm TRƢ GU N x 1 N
- Nếu m 1 thì y
. Khi đó max y 1, suy ra m 1 không thỏa mãn. x 1 [2;3] mx 1 - Nếu 3
m 1 0 m 1 thì y 0 . Suy ra hàm số y
đồng biến trên đoạn [2;3] . ÁO VIÊ 2 x m GI m 3 3m 1 5 Khi đó
max y y 3 2
5m 18m 9 0 . 2 3 [2;3] 3 m 6 m 5
Đối chiếu với điều kiện m 1, ta có m 3 thỏa mãn yêu cầu bài toán. mx 1 - Nếu 3
m 1 0 m 1 thì y 0 . Suy ra hàm số y
nghịch biến trên đoạn [2;3] . 2 x m m 2 2m 1 5 Khi đó
max y y 2 2
5m 12m 4 0 . 2 2 [2;3] 2 m 6 m 5 2
Đối chiếu với điều kiện m 1, ta có m
thỏa mãn yêu cầu bài toán. 5 2 2 17 Vậy T 3;
. Do đó tổng các phần tử của T là 3 . 5 5 5
TÌM GTLN, GTNN THEO CÔNG THỨC 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 4 Câu 4.
Cho hàm số f x x 2 1
ax 4ax a b 2, với a , b . Biết trên khoảng ;0 3 5
hàm số đạt giá trị lớn nhất tại x 1 . Hỏi trên đoạn 2;
hàm số đạt giá trị nhỏ 4
nhất tại giá trị nào của x ? 5 4 3
A. x . B. x .
C. x . D. x 2 . 4 3 2 Lời giải Chọn C
Tập xác định của hàm số là .
Ta có: f x x 2 2
1 2ax 5ax 3a b 2 . 4 Vì trên khoảng ;0
hàm số đạt giá trị lớn nhất tại x 1
nên hàm số đạt cực trị tại 3 I x 1
( cũng là điểm cực đại của hàm số) và a 0 . Ơ f 1 0 4 ( 6
a b 2) 0 b 6a 2. M D
f x ax 2 2
1 2x 5x 3 . Ầ Đ NH 3 Ị x Đ 2 G THPT
Khi đó f x 0 x 1
. ( đều là các nghiệm đơn) N.C.Đ x 1 NG CÔN Ờ N
Hàm số đạt cực đại tại x 1
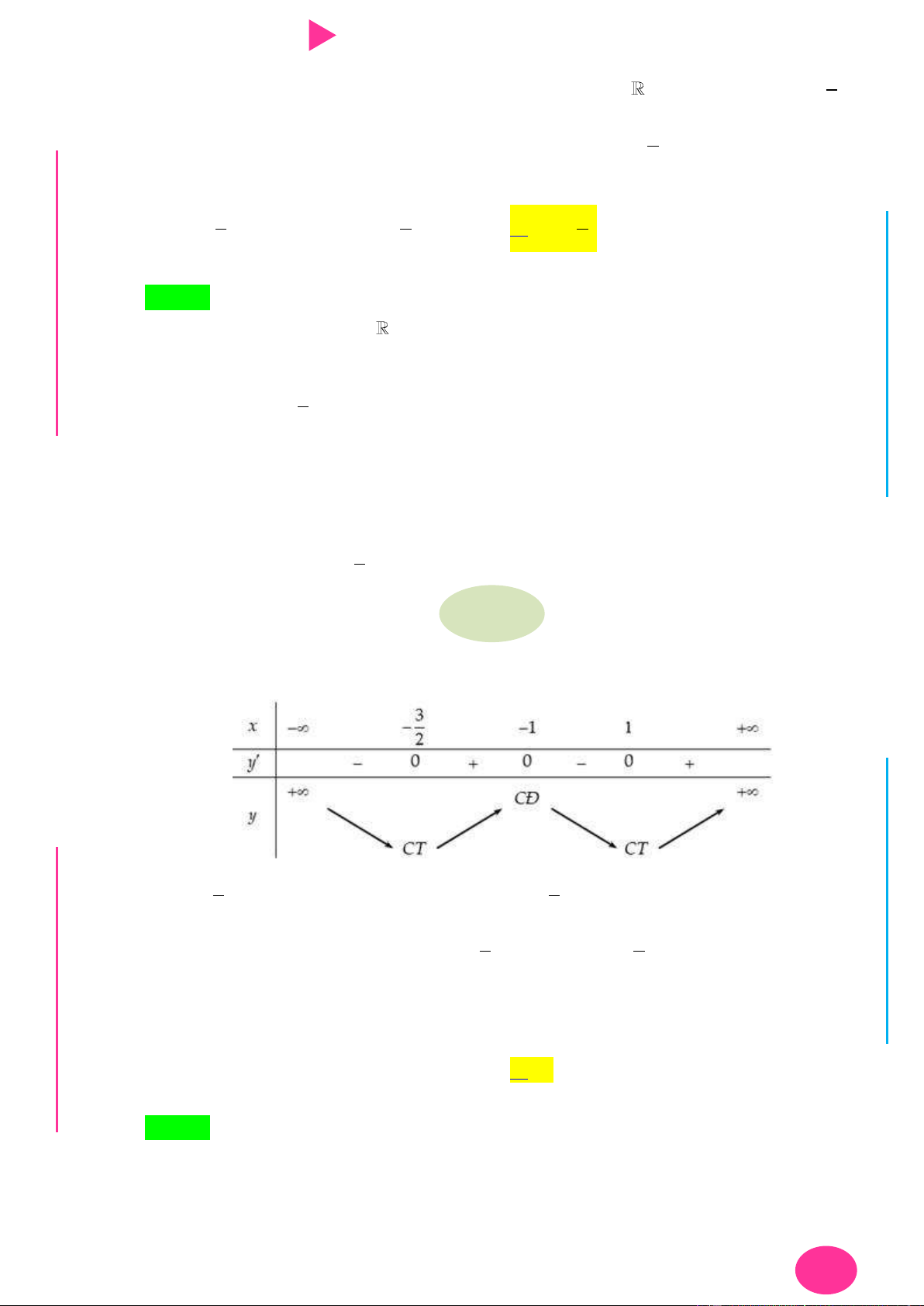
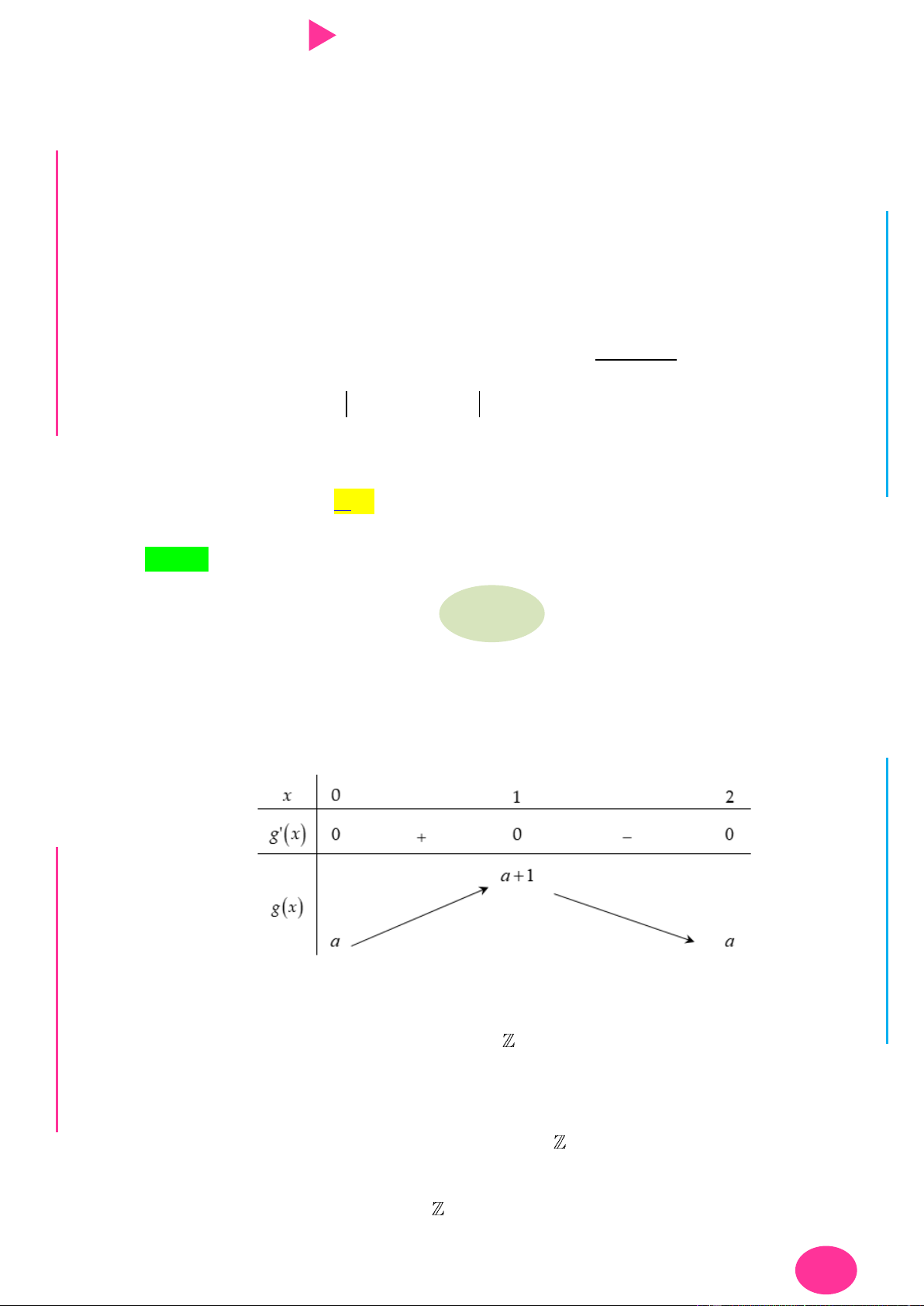
nên có bảng biến thiên: YỄ TRƢ GU N N ÁO VIÊ GI 3 5 x
là điểm cực tiểu duy nhất thuộc 2; . 2 4 3 5
Vậy hàm số đạt giá trị nhỏ nhất tại x trên đoạn 2; . 2 4
Câu 5. Cho hàm số y x x m2 3 3
. Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ
nhất của hàm số trên đoạn 1 ;1 bằng 1 là A. 1. B. 4 . C. 0 . D. 4 . Lời giải Chọn C
TÌM GTLN, GTNN THEO CÔNG THỨC 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Xét hàm số f x 3
x 3x m .
Để GTNN của hàm số y x x m2 3 3 trên đoạn 1
;1 bằng 1 thì min f x 1 hoặc 1 ; 1
max f x 1 . 1 ; 1 x
Ta có f x 2
3x 3; f x 1 0
f x nghịch biến trên 1 ;1 . x 1
Suy ra max f x f
1 2 m và min f x f 1 2 m . 1 ; 1 1 ; 1
Trƣờng hợp 1: min f x 1 2
m 1 m 3 . 1 ; 1
Trƣờng hợp 2: max f x 1 2 m 1 m 3 . 1 ; 1
Vậy tổng các giá trị của tham số m là 0 . Câu 6.
Có bao nhiêu giá trị nguyên dƣơng của tham số m để giá trị nhỏ nhất của hàm số I 2 x m Ơ y trên đoạn 2; 3 bằng 14. x 1 M D A. 2 . B. 1. C. 0 . D. 4. Ầ Lời giải Đ NH Chọn B Ị Đ
Tập xác định D \ 1 . G THPT 2 N.C.Đ 1 m NG Ta có y 0 , x D . 2 CÔN x Ờ 1 N
Do đó hàm số nghịch biến trên đoạn 2; 3 . YỄ TRƢ 2 3 m GU N
Suy ra min y y 3 14 m 5
. Vậy có 1 giá trị nguyên dƣơng của m . N 2; 3 3 1 2 x m 2 Câu 7.
Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y trên ÁO VIÊ x m GI đoạn 0;4 bằng 1 . A. 0 . B. 2 . C. 3 . D. 1. Lời giải Chọn D
Điều kiện: x m .
Hàm số đã cho xác định trên 0; 4 khi m0;4 (*). 2 1 7 m 2 m m 2 2 4 Ta có y x với 0;4. x m 0 2 x m2 2 m
Hàm số đồng biến trên đoạn 0;4 nên max y y 4 2 . 0;4 4 m 2 2 m m 2 max y 1 1 2
m m 6 0 . 0;4 4 m m 3
TÌM GTLN, GTNN THEO CÔNG THỨC 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Kết hợp với điều kiện (*) ta đƣợc m 3
. Do đó có một giá trị của m thỏa yêu cầu bài toán. Câu 8. Cho hàm số 3
y ax cx d, a 0 có min f x f 2
. Giá trị lớn nhất của hàm số x ;0
y f x trên đoạn 1; 3 bằng
A. d 11a .
B. d 16a .
C. d 2a .
D. d 8a . Lời giải
Tác giả: Đinh Thị Thúy Nhung; Fb: Thúy Nhung Đinh Chọn B Vì 3
y ax cx d, a 0 là hàm số bậc ba và có min f x f 2
nên a 0 và y ' 0 có x ;0 hai nghiệm phân biệt. Ta có 2
y ' 3ax c 0 có hai nghiệm phân biệt ac 0 . I c Ơ
Vậy với a 0, c 0 thì y ' 0 có hai nghiệm đối nhau x 3a M D c c c
Từ đó suy ra min f x f 2 2 c 1 2a Ầ x ;0 3a 3a 3a Đ NHỊ Ta có bảng biến thiên Đ G THPT N.C.Đ NG CÔN Ờ N YỄ TRƢ GU N N
Ta suy ra max f x f 2 8a 2c d 1 6a d . x 1; 3
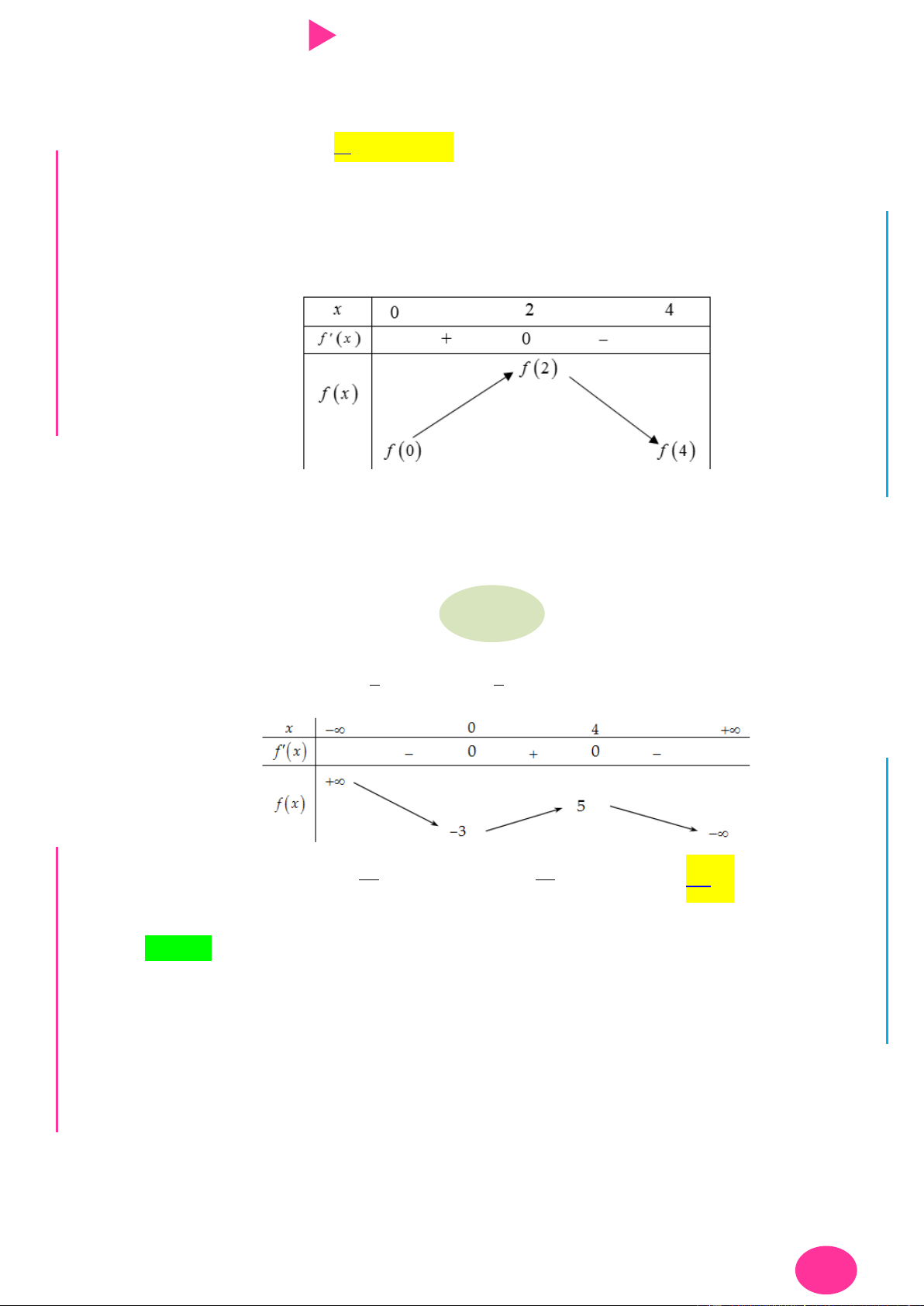
Câu 9. Cho hàm số có f x có đạo hàm là hàm f ' x . Đồ thị hàm số f ' x nhƣ hình vẽ bên. ÁO VIÊ GI
Biết rằng f 0 f
1 2 f 2 f 4 f 3 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất
M của f x trên đoạn 0; 4 . y x 2 4 O
A. m f 4, M f 2 .
B. m f
1 , M f 2
C. m f 4, M f 1 .
D. m f 0, M f 2 . Lời giải Chọn A
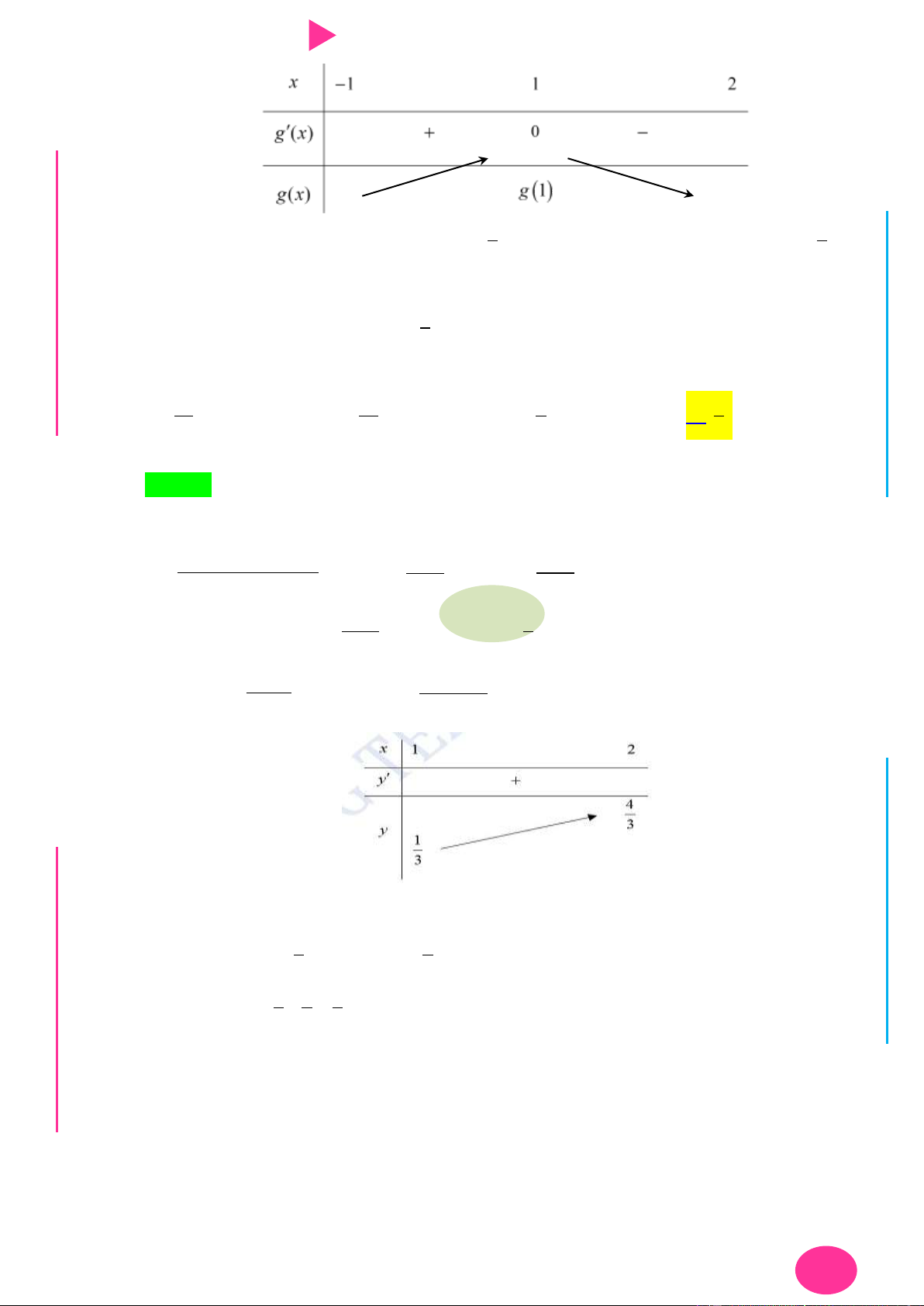
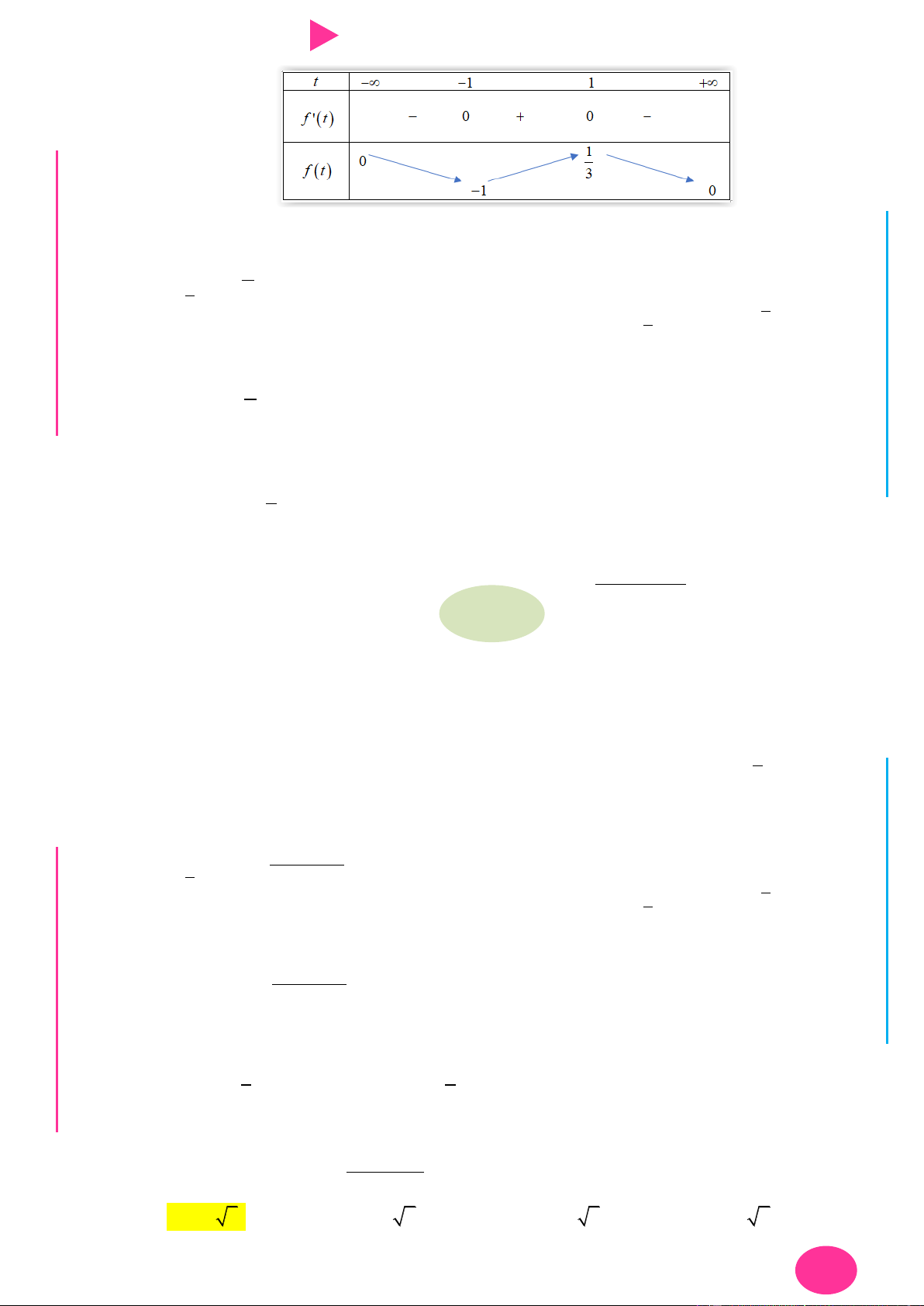
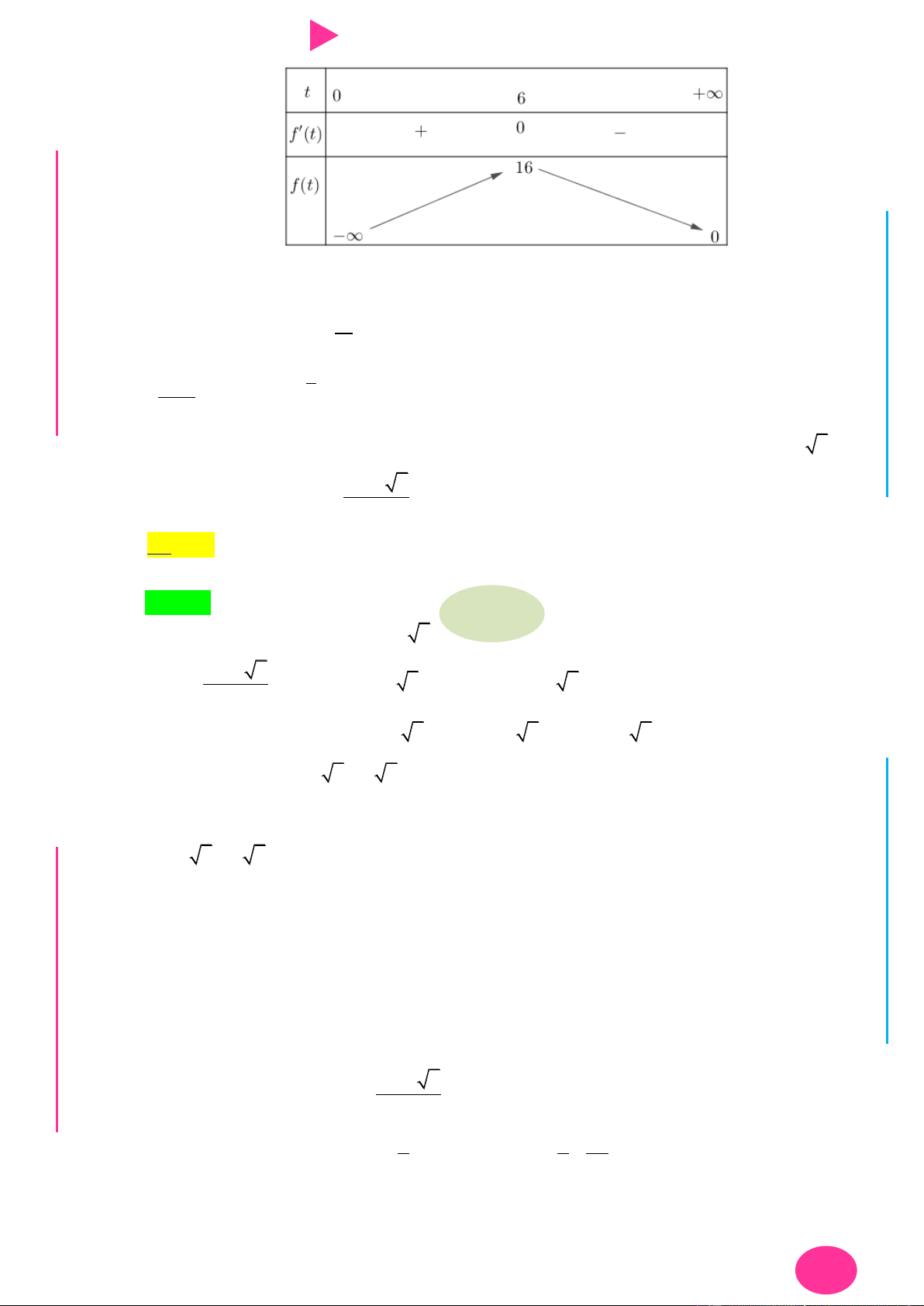
Dựa vào đồ thị của hàm f ' x ta có bảng biến thiên.
TÌM GTLN, GTNN THEO CÔNG THỨC 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Vậy giá trị lớn nhất M f 2 .
Hàm số đồng biến trên khoảng 0; 2 nên f 2 f
1 f 2 f 1 0 .
Hàm số nghịch biến trên khoảng 2; 4 nên f 2 f 3 f 2 f 3 0 . I
Theo giả thuyết: f 0 f
1 2 f 2 f 4 f 3 Ơ
f 0 f 4 f 2 f
1 f 2 f
3 0 f 0 f 4 M D m f 4 Ầ Vậy giá trị nhỏ nhất . Đ NH
Câu 10. Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số ỊĐ 1 19 4 2 y x
x 30x m 20 trên đoạn 0; 2 không vƣợt quá 20 . Tổng các phần tử G THPT 4 2 N.C.Đ NG của S bằng CÔN Ờ N A. 210. B. 195 . C. 105. D. 300. YỄ Lời giải TRƢ Chọn C GU N N 1 19
Xét hàm số f x 4 2 x
x 30x m 20 trên đoạn 0; 2 . 4 2 ÁO VIÊ
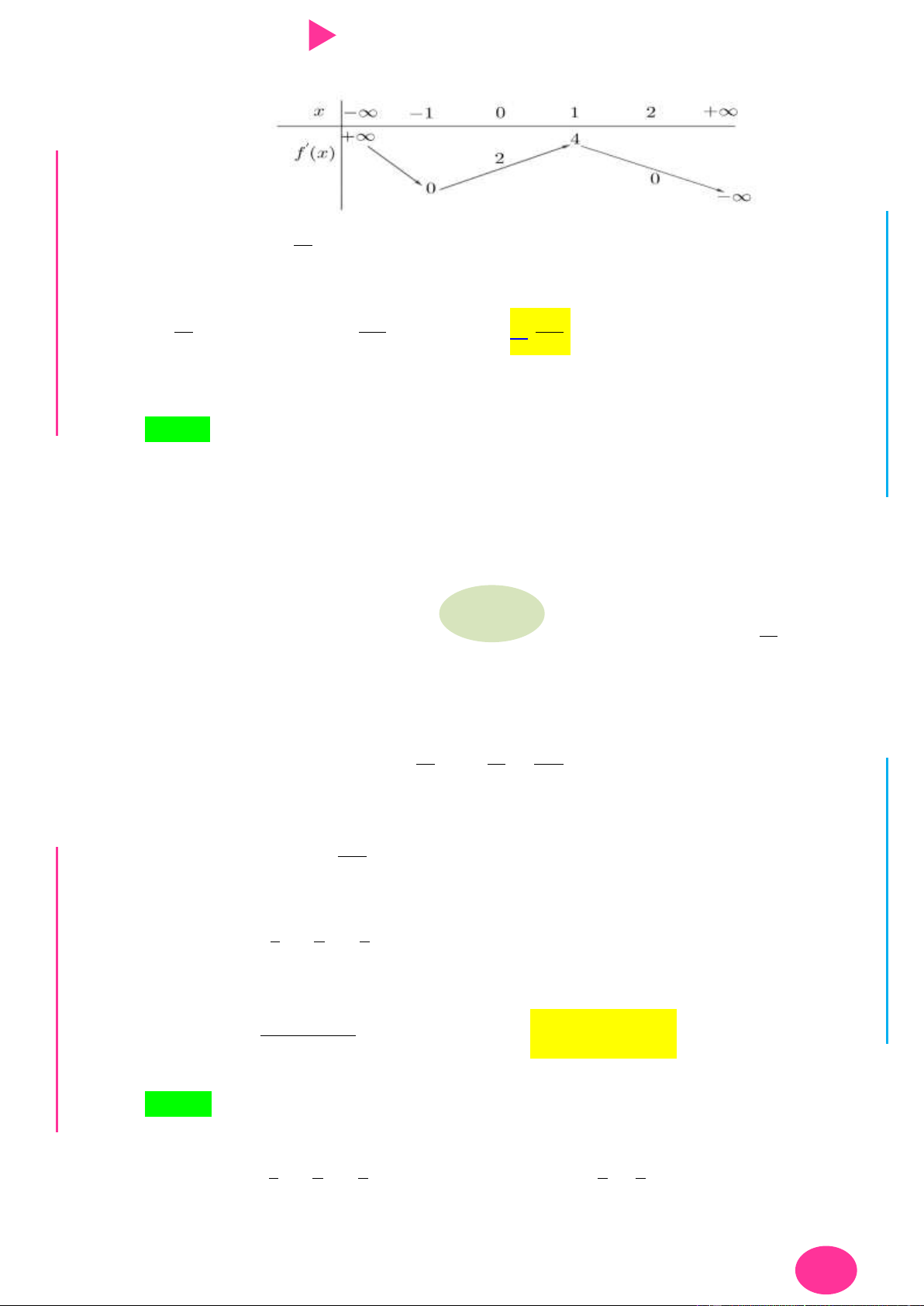
x 5 0;2 GI f x 3
x 19x 300 x 2 0;2 x3 0;2 Bảng biến thiên:
với f 0 m 20 ; f 2 m 6. 1 19 Xét hàm số 4 2 y x
x 30x m 20 trên đoạn 0; 2 . 4 2
+ Trƣờng hợp 1: m 20 0 m 20. Ta có
TÌM GTLN, GTNN THEO CÔNG THỨC 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Max y = m 6 20 m 14. Kết hợp m 20 suy ra không có giá trị m. 0;2
+ Trƣờng hợp 2: m 6 20 m m 7. Ta có:
Max y = m 6 20 m 14. Kết hợp m 7 suy ra 7 m 14 . 0;2
Vì m nguyên nên m 7; 8;9;10;11;12;13;1 4 .
+ Trƣờng hợp 3: 20 m m 6 m 7. Ta có:
Max y = 20 m 20 m 0. Kết hợp m 7 suy ra 0 m 7 . 0;2
Vì m nguyên nên m 0; 1;2;3;4;5;6; 7 . 140.15
Vậy S 0; 1;2;...;14 . Tổng các phần tử của S bằng 105. 2
Câu 11. Cho hàm số y f x 4 3 2
x 4x 4x a . Gọi M ,m lần lƣợt là giá trị lớn nhất, giá trị I
nhỏ nhất của hàm số đã cho trên đoạn 0;2 . Số giá trị nguyên a thuộc đoạn 3; 3 sao Ơ
cho M 2m là M D A. 3 . B. 5 . C. 6 . D. 7 . Ầ Đ Lời giải NHỊ Chọn B Đ Xét g x 4 3 2
x 4x 4x a với x0;2. G THPT N.C.Đ x 0 NG 3 2 2 CÔN
g x 4x 12x 8x 4x x 3x 2 Ờ ; g x 0 x 1 . N x 2 YỄ TRƢ
g 0 a ; g
1 1 a ; g 2 a . GU N N
Bảng biến thiên g x ÁO VIÊ GI
Trƣờng hợp 1: a 0 . Khi đó M a 1; m a . a 3 ;3
Ta có M 2m 1 a 2a a 1. Với a 1;2; 3 . a
Trƣờng hợp 2: a 1 0 a 1
. Khi đó M a ; m a 1 . a 3 ;3
Ta có M 2m a 2 a 1 a 2 . Với a 3 ; 2 . a a 3 ;3 Trƣờng hợp 3: 1
a 0 . Với a . a
TÌM GTLN, GTNN THEO CÔNG THỨC 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Vậy có 5 giá trị a cần tìm.
Câu 12. Gọi S là tập hợp các giá trị của m để hàm số 3 2
y x 3x m đạt giá trị lớn nhất bằng
50 trên [ 2; 4]. Tổng các phần tử thuộc S là A. 4 . B. 36 . C. 140 . D. 0 . Lời giải Chọn A x Xét hàm số 3 2
g(x) x 3 x m có g x 2
3x 6 x . Xét gx 0 0 . x 2
Khi đó giá trị lớn nhất của hàm số 3 2
y x 3x m trên [ 2;4] là:
max y maxy 0; y 2
; y2; y4 maxm ; m4 ; m20 ; m16. x 2 ;4 m 50
Trường hợp 1: Giả sử max y m 50 . I m 50 Ơ
Với m 50 thì m 16 66 50 ( loại). M D Với m 50
thì m 20 70 50 (loại). Ầ Đ m 54 NH
Trường hợp 2: Giả sử max y m 4 50 . Ị m 46 Đ G THPT
Với m 54 m 54 50 (loại). N.C.Đ NG Với m 46
thì m 20 66 50 ( loại). CÔN Ờ N m 70
Trường hợp 3: Giả sử max y m 20 50 YỄ TRƢ m 30 GU N
Với m 70 thì m 16 86 50 (loại). N Với m 30
thì m 16 14 50 , m 30 50 ; m 4 34 50 (thỏa mãn). ÁO VIÊ m 34 y m GI
Trường hợp 4: Giả sử max 16 50 . m 66
Với m 34 thì m 34 50, m 4 30 50, m 20 14 50 (thỏa mãn). Với m 66
thì m 66 50 (loại). Vậy S 3 0;3
4 . Do đó tổng các phẩn tử của S là: 3 0 34 4 .
Câu 13. Cho hàm số f x có đạo hàm là f x . Đồ thị của hàm số y f x cho nhƣ hình vẽ.
TÌM GTLN, GTNN THEO CÔNG THỨC 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Biết rằng f 2 f 4 f 3 f 0 . Giá trị nhỏ nhất và lớn nhất của f x trên đoạn
0;4 lần lƣợt là
A. f 2, f 0.
B. f 4, f 2 .
C. f 0, f 2.
D. f 2, f 4 . Lời giải x
Ta có: f x 0 0 x 2 .
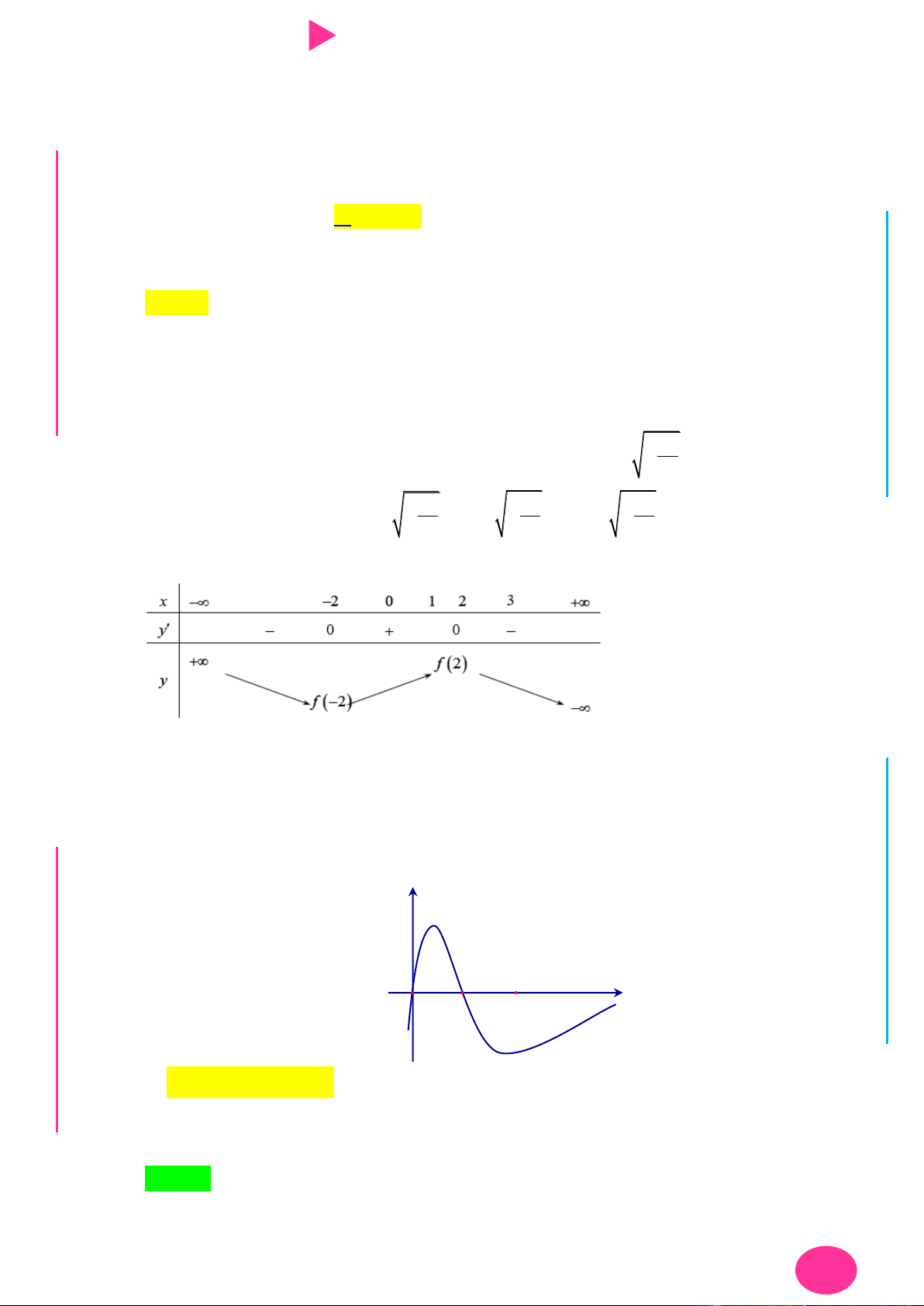
Bảng biến thiên của hàm số f x trên đoạn 0;4 . I Ơ
Nhìn vào bảng biến thiên ta thấy max f (x) f (2). M D 0; 4 Ầ
Ta có f 2 f 4 f 3 f 0 f 0 f 4 f 2 f 3 0 . Đ NHỊ
Suy ra: f 4 f (0) . Do đó min f (x) f (4). 0;4 Đ G THPT
Vậy giá trị nhỏ nhất và lớn nhất của f x N.C .Đ
tr ên đoạn 0;4 lần lƣợt là: f 4, f 2 .
NG Câu 14. Cho hàm số y f x có bảng biến thiên nhƣ hình dƣới đây. Tìm giá trị lớn nhất của CÔN Ờ N 1 1
hàm số g x f 2 4x x 3 2
x 3x 8x trên đoạn 1; 3 . YỄ TRƢ 3 3 GU N N ÁO VIÊ GI 25 19 A. 15. B. . C. . D. 12. 3 3 Lời giải Chọn D
g x x f 2 x x 2 4 2 4
x 6x 8 x f 2 2 2
4x x 4 x .
Với x 1;3 thì 4 x 0 ; 2
3 4x x 4 nên f 2
4x x 0 . Suy ra f 2 2
4x x 4 x 0 , x 1; 3 . Bảng biến thiên
TÌM GTLN, GTNN THEO CÔNG THỨC 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Suy ra max g x g 2 f 4 7 12 . 1; 3
Câu 15. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số 4 2
y x 38x 120x 4m
trên đoạn0;2 đạt giá trị nhỏ nhất. A. 26 . B. 13 . C. 14 . D. 27 . Lời giải Chọn D I Xét u x 4 2 x 38x
120x 4m trên đoạn 0;2 ta có Ơ x 5 0;2 M D 3
u 0 4x 76x 120 0 x 20;2 . Ầ Đ x 3 0;2 NHỊ
max u x maxu(0),u(2
) max4m , 4m 10 4 4m 104 Đ [0;2] G Vậy . THPT min
u x minu(0),u(2 ) min4 N m.C , .Đ 4 m 10 4 4 m [0;2] NG CÔN Ờ Cách 1: N
Nếu 4m 0 thì min f x 4m 0 YỄ [0;2] TRƢ m m min f x 4 m 104 0 GU N Nếu 4 104 0 26 thì [0;2] N
Nếu 4m 0 4m 104 2
6 m 0 thì min f x 0. Vậy có 27 số nguyên thỏa mãn. [0;2] ÁO VIÊ Cách 2: GI
Khi đó minmin y 0 4 (
m 4m 104) 0 2
6 m 0. Có 27 số nguyên thoả mãn. [0;2]
Câu 16. Xét hàm số 2
f x x ax b , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên 1 ;
3 . Khi M nhận giá trị nhỏ nhất có thể đƣợc, tính a 2b . A. 2 . B. 4 . C. 4 . D. 3 . Lời giải Chọn C Xét hàm số 2
f x x ax b . Theo đề bài, M là giá trị lớn nhất của hàm số trên 1 ; 3 .
M f 1
M 1 a b
Suy ra M f 3 M 9 3a b 4M 1 a b 9 3a b 2 1
a b M f 1
M 1 a b
1 a b 9 3a b 2( 1 a )
b 4M 8 M 2 .
TÌM GTLN, GTNN THEO CÔNG THỨC 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Nếu M 2 thì điều kiện cần là 1 a b 9 3a b 1
a b 2 và 1 a b , 9 3a b
1 a b 9 3a b 1
a b 2 a 2 , 1
a b cùng dấu . 1
a b 9 3a b 1
a b 2 b 1 a 2 Ngƣợc lại, khi
ta có, hàm số f x 2
x 2x 1 trên 1 ; 3 . b 1
Xét hàm số g x 2
x 2x 1 xác định và liên tục trên 1 ; 3 .
g x 2x 2 ; g x 0 x 1 1 ; 3
M là giá trị lớn nhất của hàm số f x trên 1 ;
3 M max g
1 ; g 3 ; g 1 =2 . a 2 Vậy
. Ta có: a 2b 4 . b 1
Câu 17. Cho hàm số y x x m2 2
. Tổng tất cả các giá trị thực tham số m sao cho min y 4 [ 2 ;2] I bằng Ơ 31 23 9 A. . B. 8 . C. . D. . M D 4 4 4 Ầ Lời giải Đ NHỊ Chọn C Đ 1 G Xét 2
u x x m trên đoạn [-2;2] ta có u ' 0 2x 1 0 x . THPT N.C.Đ 2 NG 1 1 CÔN u 2 Ờ
Ta tính đƣợc u 2 m 2; u m ; m 6. N 2 4 YỄ 1 1 TRƢ
Nhận xét m m 2 m 6, m
nên A maxu m 6 ; a minu m 4 2 ;2 2 ;2 4 GU N N 2 1 1 9 7
Nếu a 0 m
min y m
4 m (t / )
m ; m (l). [ 2 ;2] 4 4 4 4 ÁO VIÊ
Nếu A 0 m 6
min y m 62 4 m 8 (t / ) m ; m 4 (l). GI [ 2 ;2] 1 Nếu . A a 0 6
m min y 0(l). [ 2 ;2] 4 9 23
Vậy tổng các giá trị thực của tham số là 8 . 4 4
Câu 18. Cho hàm số y f x liên tục trên
sao cho max f x f 2 4 . Xét hàm số x 0;10
g x f 3 x x 2
x 2x m . Giá trị của tham số m để max g x 8 là x 0;2 A. 5 . B. 4 . C. 1 . D. 3 . Lời giải Chọn D
Xét hàm số 3 h x
f x x trên 0;2 . Đặt 3 t x , x x 0; 2 . Ta có 2
t 3x 1 0 x
nên t 0;10. Vì vậy max f 3
x x max f t 4 khi t 2 x 1. x 0; 2 t 0;1 0
TÌM GTLN, GTNN THEO CÔNG THỨC 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Mặt khác p x x x m x 2 2 2
1 m 1 m 1. Suy ra max p x m 1 khi x 1. x 0;2
Vậy max g x 4 m 1 m 5 8 m 3 . x 0; 2
Cách 2: Phương pháp trắc nghiệm
Chọn hàm y f x 4 thỏa mãn giả thiết: hàm số y f x liên tục trên có
max f x f 2 4 . x 0;10
Ta có g x f 3 x x 2 2
x 2x m 4 x 2x m .
g x 2
x 2; gx 0 x 1.
Xét hàm số g x liên tục trên đoạn 0;2 , g x 0 x 1. Ta có g 0 4 m , g
1 5 m , g 2 4 m .
Rõ ràng g 0 g 2 g
1 nên max g x g
1 . Vậy 5 m 8 m 3. x 0;2
I Câu 19. Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số Ơ 2
x mx 2m M D y
1;1 bằng 3 . Tính tổng tất cả các phần tử của S . x trên đoạn 2 Ầ Đ 8 5 NH A. . B. 5 . C. . D. 1 . Ị 3 3 Đ G Lời giải THPT N.C.Đ Chọn A NG CÔN Ờ
x mx m 4 N
Xét hàm số y f x 2 2 1;
1 có f x 1 ; x trên 2 x 22 YỄ TRƢ x 0 3m 1 m 1 GU N
f x 0 ; f 1 ; f 0 ; m f 1 N x 4 1 ;1 3 1 . Bảng biến thiên ÁO VIÊ x 1 0 1 GI f x 0 f x f 0 f 1 f 1
Trƣờng hợp 1. f 0 0 m 0. Khi đó m
3 max f x max f 1 ; f 1 3 1 3 max
;m 1 m 1 3 m 2 . 1 ; 1 3
Trƣờng hợp 2. f 0 0 m 0 . f 1 0 Khả năng 1.
. Khi đó 3 max f x f 0 m 3 . f m 1 1 0 1 ; 1
TÌM GTLN, GTNN THEO CÔNG THỨC 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 f 1 0 Khả năng 2. 1
m . Khi đó
. 3 max f x max f 0; f 1 3 f 1 0 1 ; 1 3 max ; m m
1 : Trƣờng hợp này vô nghiệm. 1
Khả năng 3. m 0 . Khi đó 3 max f x max f 0; f 1 ; f 1 : Vô 3 1 ; 1 nghiệm.
Vậy có hai giá trị thỏa mãn là m 3
, m 2 . Do đó tổng tất cả các phần tử của S là 1 2 1 .
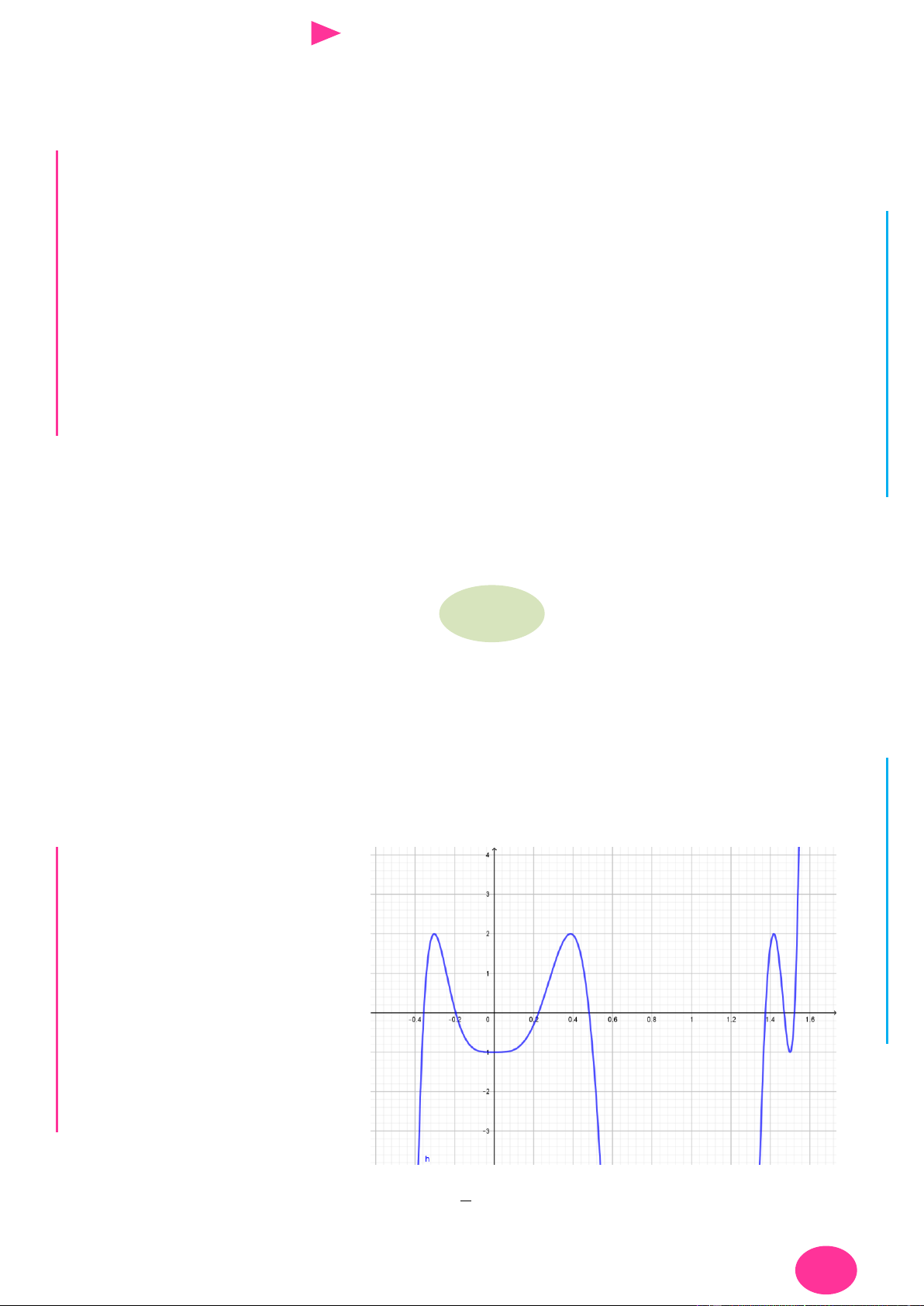
Câu 20. Cho hàm số y f x có đồ thị f x nhƣ hình vẽ I Ơ M D Ầ Đ NHỊĐ G 1 THPT
Giá trị lớn nhất của hàm số g x f xN.
C.Đx 3 x 1 trên đoạn 1 ;2 bằng 3 NG CÔN 1 Ờ
A. f 5 1 . B. f 1 1 . C. f 5 2 . D. . N 3 3 3 3 YỄ TRƢ Lời giải GU N Chọn B N
Ta có: g x f x 2
x f x 2
x f x 2 1 1 0 x 1 (*) ÁO VIÊ GI
Từ đồ thị ta cáo bảng xét dấu
TÌM GTLN, GTNN THEO CÔNG THỨC 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1
Giá trị lớn nhất của hàm số g x f x 3
x x 1 trên đoạn 1
;2 bằng f 1 1 3 3
Câu 21. Cho hàm số f x liên tục trên 0; thỏa mãn x f x 2
x f x 2 3 .
2 f x, với
f x 0 , x
0; và f 1 1
. Gọi M , m lần lƣợt là giá trị lớn nhất và giá trị nhỏ 3
nhất của hàm số y f x trên đoạn 1;2 . Tính M m. 9 21 7 5 A. . B. . C. . D. . 10 10 3 3 I Ơ Lời giải Chọn D M D 2 2 3 .
x f x x f x 2 f x 2 3 2
3x f x x f x 2xf x Ầ Ta có Đ 2 3 NH
3x f x x f x 3 3 Ị x x 2x 2x 2 x C . Đ 2 f x f (x) f (x) G THPT N.C.Đ 1
Thay x 1 vào ta đƣợc
1 C , vì f 1 1 nên suy ra C 2 . NG f 1 3 CÔN Ờ N x 4 2 x 6x Nên f x 3
. Ta có f x
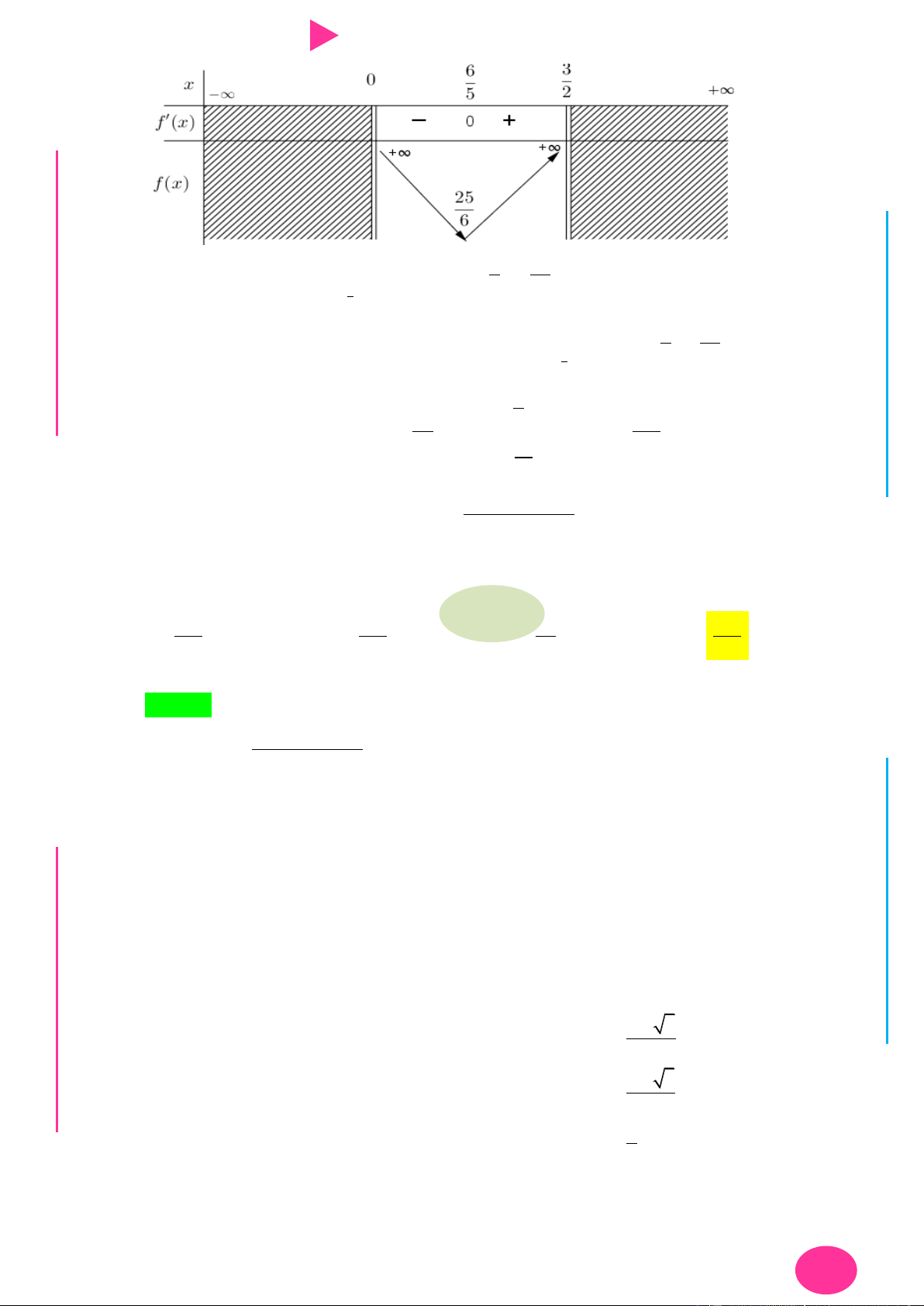
; f x 0 x 0. YỄ TRƢ 2 x 2 x 22 2 GU N N ÁO VIÊ GI
Khi đó, f x đồng biến trên 1;2 .
Suy ra m f 1 1
; M f 4 2 . 3 3 1 4 5
Suy ra M m . 3 3 3
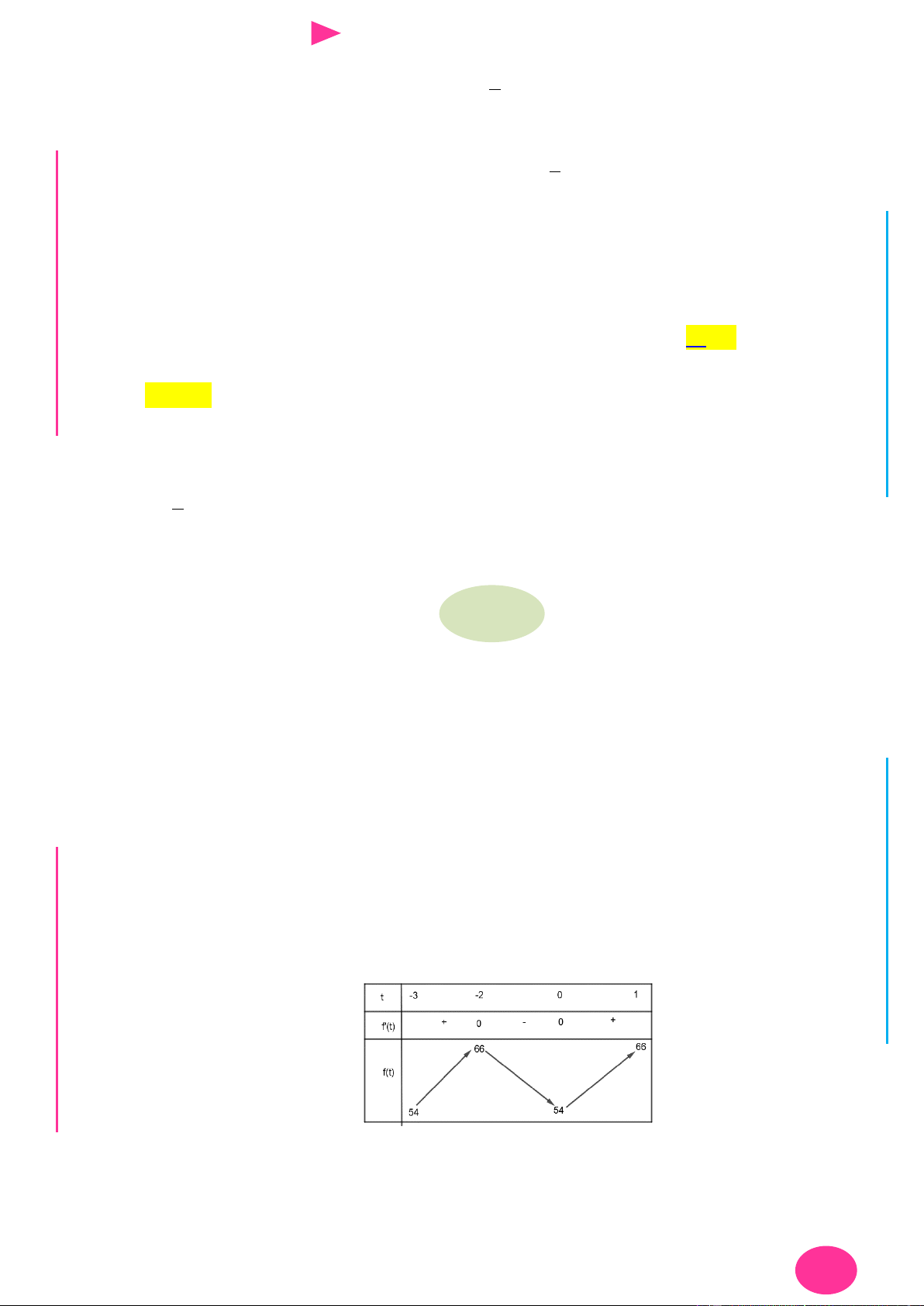
Câu 22. Cho hàm số y f x có đạo hàm f x . Hàm số y f x liên tục trên tập số thực và
có bảng biến thiên nhƣ sau:
TÌM GTLN, GTNN THEO CÔNG THỨC 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Biết rằng f 10 1
, f 2 6 . Giá trị nhỏ nhất của hàm số g x 3
f x 3 f x trên 3 đoạn 1 ;2 bằng 10 820 730 A. . B. . C. . D. 198 . 3 27 27 Lời giải
Tác giả:Trần Phương; Fb: Trần Phương Chọn C I 3 Ơ
Xét hàm số g x f x 3 f x trên đoạn 1 ;2
f x 0 1 M D g x 2
3 f x 1 f x
, g x 0 . 2 Ầ f x 1 2 Đ NHỊ x 1 1 ;2 Đ
Từ bảng biến thiên, ta có: 1 x 2 1 ;2 G THPT N.C.Đ
f x f 10 NG
Và f x 0 , x
1;2 nên f x đồng biến trên 1;2 1 CÔN 3 Ờ N
f x 1 2
f x 1, x 1
;2 nên 2 vô nghiệm. YỄ TRƢ
Do đó, g x 0 chỉ có 2 nghiệm là x 1 và x 2 . GU N 3 N 10 10 730 Ta có g 3 1 f 1 3 f 1 3 . 3 3 27 ÁO VIÊ 3 g 3
2 f 2 3 f 2 6 36 198 . GI 730
Vậy min g x g 1 . 1 ; 2 27
Câu 23. Cho hàm số y f x . Đồ thị hàm số đạo hàm y f 'x nhƣ hình vẽ dƣới đây. Xét hàm 1 3 3
số g x f x 3 2
x x x 2018 . Mệnh đề nào dƣới đây đúng? 3 4 2
A. min g x g 1 .
B. min g x g 3 . 3 ; 1 3 ; 1 g 3 g 1 C. min g x .
D. min g x g 1 . 3 ; 1 2 3 ; 1 Lời giải Chọn D
Cho hàm số y f x . Đồ thị hàm số đạo hàm y f 'x nhƣ hình vẽ dƣới đây. Xét hàm 1 3 3 3 3
số g x f x 3 2
x x x 2018 g 'x f 'x 2 x x 3 4 2 2 2
TÌM GTLN, GTNN THEO CÔNG THỨC 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 3 3 3 3 3
Cho g ' x f ' x 2
x x 0 f 'x 2
x x x 1 2 2 2 2 x 1
Dựa vào đồ thị ta so sánh đƣợc min g x g 1 . I 3 ; 1 Ơ Câu 24. Cho hàm số
y f (x) nghịch biến trên và thỏa mãn
f (x) x 6 4 2 M D
f (x) x 3x 2x , x
. Gọi M và m lần lƣợt là giá trị lớn nhất và giá trị Ầ Đ
nhỏ nhất của hàm số y f (x) trên đoạn 1;2. Giá trị của 3M m bằng NHỊ A. 4. B. 28. C. 3. D. 33. Đ G Lời giải THPT N.C.Đ Chọn A NG 2 6 4 2 CÔN Ờ
Ta có: f x x 6 4 2 ( )
f (x) x 3x 2x f (x) xf (x) x 3x 2x N 2 6 4 2
4 f (x) 4xf (x) 4x 12x 8x 2 2 6 4 2
4 f (x) 4xf (x) x 4x 12x 9x YỄ TRƢ 3
2 f (x) x 2x 3x 3
f (x) x 2x GU N
f x x2 3 2 2 ( )
(2x 3x) N 3
2 f (x) x 2 x 3x 3
f (x) x x Với 3 ' 2
f (x) x 2x f (x) 3x 2 0, x
nên f (x) đồng biến trên . ÁO VIÊ Với 3 ' 2
f (x) x x f (x) 3
x 1 0, x
nên f (x) nghịch biến trên . GI Suy ra: 3
f (x) x .
x Vì f (x) nghịch biến trên
nên M max f (x) f (1) 2 1; 2
và m min f (x) f (2) 1 0. 1; 2
Từ đây ,ta suy ra: 3M m 3. 2
10 4 chọn đáp án A
Câu 25. Cho hàm số y f x có bảng biến thiên nhƣ sau 1 2 2
Tìm giá trị lớn nhất của hàm số g x f 3 x 3x 5 3
x x 3x trên đoạn 1 ;2 ? 5 3 15 A. 2022 . B. 2019 . C. 2020 . D. 2021. Lời giải
TÌM GTLN, GTNN THEO CÔNG THỨC 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Chọn D
g x 2
x f 3 x x 4 2
x x 2
x f
3x x 2 3 3 3 2 3 1 3 3 x 3
3 f 3x 3x 2 g x x 3 0 0 2 x 1 0 Mà x 3
x x f 3
x x f 3 x x 2 1; 2 3 2; 2 3 0 3 3
x 3 0 , do đó g x 2
0 x 1 0 x 1 . Ta có I Ơ M D
Vậy max y g 1 f 2 2 2021. 1 ; 2 Ầ
Đ Câu 26. Cho hàm số f x . Biết hàm số y f x có đồ thị nhƣ hình bên. Trên đoạn 4 ; 3 , hàm NHỊĐ
số g x f x x2 2 1
đạt giá trị nhỏ nhất tại điểm G THPT N.C.Đ NG CÔN Ờ N YỄ TRƢ GU N N ÁO VIÊ GI A. x 4 . B. x 1 .
C. x 3. D. x 3 . 0 0 0 0 Lời giải Chọn B
Ta có g x 2 f x 21 x 2 f x 1 x
Vẽ đƣờng thẳng y 1 x trên cùng hệ trục chứa đồ thị y f x .
TÌM GTLN, GTNN THEO CÔNG THỨC 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 4
Dựa vào hình vẽ ta có g x 0 f x 1 x x 1 . x 3 I Ơ Ta có bảng biến thiên M D Ầ Đ NHỊĐG THPT N.C.Đ NG CÔN Ờ N YỄ
Vậy hàm số g x f x x2 2 1
đạt giá trị nhỏ nhất tại x 1 TRƢ 0 GU
N Câu 27. Cho hàm số f (x) . Biết hàm số y f (x) có đồ thị nhƣ hình bên. Trên đoạn [ 4;3] , N hàm số 2
g(x) 2 f (x) (1 x) đạt giá trị nhỏ nhất tại điểm. ÁO VIÊ GI A. x 1 .
B. x 3. C. x 4 . D. x 3 . 0 0 0 0 Lời giải Chọn A
TÌM GTLN, GTNN THEO CÔNG THỨC 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Ta có 2
g(x) 2 f (x) (1 x) g '(x) 2 f (
x) 2(1 x) 2[ f ( ) x (1 x)] x 4
g '(x) 0 f '(x) 1 x x 1 . x 3 Ta có bảng biến thiên: I Ơ M D Ầ Đ NHỊĐ G THPT
Từ bảng biến thiên, suy ra g(x) đạt gi N á t .rCị .Đ
nhỏ nhất trên đoạn [ 4;3] tại x 1 0 NG Ta có: 2
g(x) 2 f (x) (1 x) g '(x) 2 f (
x) 2(1 x) 2[ f ( ) x (1 x)] CÔN Ờ N Vì trong đoạn [ 4; 1
] đồ thị hàm số y f '(x) nằm phía dƣới đồ thị hàm số y 1 x YỄ TRƢ f '( ) x 1 x x [ 4; 1 ] g '( ) x 0x [ 4 ; 1 ] g( )
x nghịch biến trên (-4;-1) GU N g( 4 ) g( 3 ) g( 1 ) (*) N
Vì trong đoạn [-1;3] đồ thị hàm số y f '(x) nằm phía trên đồ thị hàm số y 1 x f '( ) x 1 x x
[-1;3] g '( ) x 0x [ 1 ;3] g( )
x đồng biến trên (-1;3) ÁO VIÊ GI g(3) g( 1) (**)
Từ (*) và (**) suy ra g(x) đạt giá trị nhỏ nhất trên đoạn [ 4;3] tại x 1 0
Câu 28. Có bao nhiêu giá trị nguyên của tham số m để 3 2
max x 3x m 4? 1; 3 A. Vô số. B. 4. C. 6. D. 5. Lời giải Chọn D Đặt 3 2 2
f (x) x 3x m f ( ) x 3x 6 . x x 0 f ( x) 0 . x 2 Bảng biến thiên
TÌM GTLN, GTNN THEO CÔNG THỨC 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Ta thấy max f (x) f (3) m và min f (x) f (2) m 4. [1;3] [1;3] Ta có 3 2
max x 3x m max m ; m 4. 1; 3 Trường hợp 1: 2 2
m m 4
m m 8m 16 m 2 m max m ; m4 0 2, m 4 4 4 m 4 4 0 m 8
mà m nên m0;1; 2 . Trường hợp 2: 2 2
m m 4
m m 8m 16 m 2 m max m ; m4 2 4, m 4 4 m 4 4 m 4
mà m nên m3; 4 .
Vậy, có 5 giá trị nguyên của tham số m. I Ơ
Vậy chọn đáp án D.
Câu 29. Cho hàm số y f x liên tục trên
sao cho max f x 3 . Xét g x f 3x 1 m . M D 1 ; 2 Ầ Đ
Tìm tất cả các giá trị của tham số m để max g x 1 0 . 0; 1 NHỊĐ A. 13 . B. 7 . C. 13 . D. 1 . G THPT N. L Cờ.Đ i giải NG Chọn C CÔN Ờ
max g x max f 3x
1 m m max f 3x 1 N Ta có: . 0; 1 0; 1 0; 1 YỄ TRƢ
Đặt t 3x 1. Ta có hàm số t x đồng biến trên . Mà x 0; 1 t 1 ;2. GU N N
Suy ra: max f 3x 1
max f t 3. Suy ra max g x m 3. 0; 1 1 ; 2 0; 1
Do đó max g x 1 0 m 3 1 0 m 1 3. 0; ÁO VIÊ 1
GI Câu 30. Cho hàm số y f x có đạo hàm cấp hai trên . Biết f 0 3 , f 2 2 018 và bảng
xét dấu của f x nhƣ sau:
Hàm số y f x 2017 2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau 0 đây? A. ; 2017 .
B. 2017; . C. 0; 2 . D. 2 017;0 . Lời giải. Chọn A
Dựa vào bảng xét dấu của f x ta có bảng biến thiên của hàm sồ f x
TÌM GTLN, GTNN THEO CÔNG THỨC 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Đặt t x 2017 .
Ta có y f x 2017 2018x f t 2018t 2017.2018 g t .
gt f t 2018 .
Dựa vào bảng biến thiên của hàm số f x suy ra phƣơng trình gt có một nghiệm đơn ;0
và một nghiệm kép t 2 .
Ta có bảng biến thiên g t
Hàm số g t đạt giá trị nhỏ nhất tại t ;0 . 0 I Ơ Suy ra hàm số y
f x 2017 2018x đạt giá trị nhỏ nhất tại x mà 0 x 2017 ; 0 x ; 2 017 . 0 0 M D
Ầ Câu 31. Có bao nhiêu số thực m để giá trị nhỏ nhất của hàm số 2
y x 4x m 3 4x bằng Đ NHỊ 5 . Đ A. 2 . B. 3 . C. 0 . D. 1 . G THPT N.C.Đ Lời giải NG CÔN Chọn D Ờ N Xét f x 2
x 4x m 3 có 1 m . YỄ TRƢ
TH1. m 1: f x 2 0 x
y x 8x m 3. GU N N ÁO VIÊ GI min y 5
m 8 (TM).
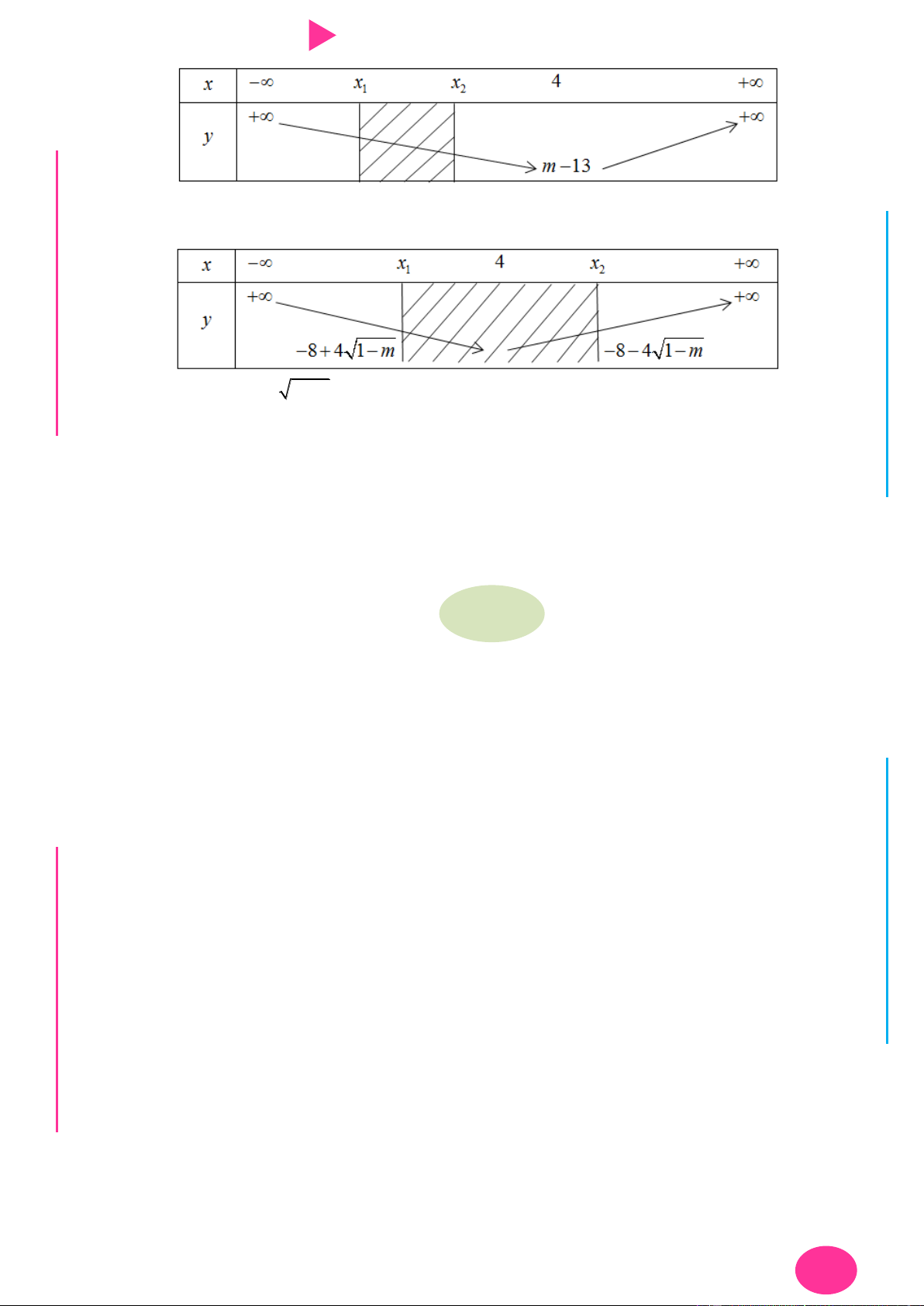
TH2. m 1: f x 0 có hai nghiệm x 2 1 m ; x 2 1 m . 1 2
Nếu x x ; x : 2
y x 3 m . 1 2 y x 8 4 1 m . 1 y x 8 4 1 m . 2
y x y x 1 2 min y 8 4 1 m 8 (Không TM). 1x; 2x
Nếu x x ; x : 2
y x 8x 3 m . 1 2
) x 4 1 m 3 : 2
TÌM GTLN, GTNN THEO CÔNG THỨC 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
min y m 13 5
m 8 (Loại).
) x 4 m 3 : 2 min y 8 4 1 m 8
(Không TM). Vậy có 1 giá trị của m . I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N YỄ TRƢ GU N N ÁO VIÊ GI
TÌM GTLN, GTNN THEO CÔNG THỨC 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHỦ ĐỀ: GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
VẬN DỤNG – VẬN DỤNG CAO DẠNG 2
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 3 9x x Câu 1.
Cho hai số thực dương x, y thỏa mãn
3y 2 . Giá trị lớn nhất của biểu thức y 1
S 6x y là: 89 11 17 82 A. . B. . C. . D. . 12 3 12 3 Câu 2. Cho x, y
thỏa mãn x y 1 và 2 2
x y xy x y 1. Gọi M , m lần lượt là giá trị I xy Ơ
lớn nhất và giá trị nhỏ nhất của biểu thức P . Tính M m. x y 1 M D 1 2 1 1 A. . B. . C. . D. . Ầ 3 3 2 3 Đ NH Câu 3. Cho ,
x y là các số thực thỏa mãn 2 2
x xy y 1 . Gọi M , m lần lượt là giá trị lớn nhất , Ị Đ 4 4 x y 1 G
giá trị nhỏ nhất của P . Giá trị của là: THPT A M 15m 2 2 x y 1 N.C.Đ NG A. 17 2 6 . B. 17 6 C. 17 2 6 D. 17 6 . CÔN Ờ N
x y x y y y x Ễ
Câu 4. Cho hai số thực x , y thỏa mãn 2 2 2 2 4 6 4 6 10 6 4 x . Gọi M Y TRƯ
, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2 T
x y a . Có bao GU N N
nhiêu giá trị nguyên thuộc đoạn 1
0;10 của tham số a để M 2m? A. 17. B. 15. C. 18. D. 16. ÁO VIÊ 2 2
GI Câu 5. Cho x, y là các số thực thỏa mãn x 3 y 1
5 . Tìm giá trị nhỏ nhất của biểu 2
3y 4xy 7x 4 y 1 thức P . x 2 y 1 114 A. 3 . B. 3 . C. . D. 2 3 . 11
Câu 6. Cho các số thực dương a,b thỏa mãn 2 2
2 a b ab (a )
b (ab 2) . Giá trị nhỏ nhất 3 3 2 2 a b a b
của biểu thức P 4 9 thuộc khoảng nào? 3 3 2 2 b a b a A. (-6 ;-5) . B. (-10 ;-9) . C. (-11 ;-9) . D. (-5 ;-4) .
Câu 7. Cho các số thực x, y thay đổi nhưng luôn thỏa mãn 2 2
3x 2xy y 5 . Giá trị nhỏ nhất của biểu thức 2 2
P x xy 2y thuộc khoảng nào sau đây. A. 4;7 . B. 2 ;1. C. 1;4 . D. 7;10 .
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 8. Cho số phức z x yi (x, y ) . Thỏa mãn z 2 i z 2 5i và biểu thức sau đạt 2 2
x y 3y 1
giá trị nhỏ nhất: H
. Giá trị của 2x y 2 2 2 2
x y 2x 2y 2 x y 2x 4y 5 bằng: A. 6 B. 6 5 C. 3 5 D. 6 5 x y Câu 9. Cho , x y thỏa mãn log
x(x 9) y( y 9) xy Tìm giá trị lớn nhất của 3 2 2
x y xy 2 3x 2 y 9 biểu thức P khi ,
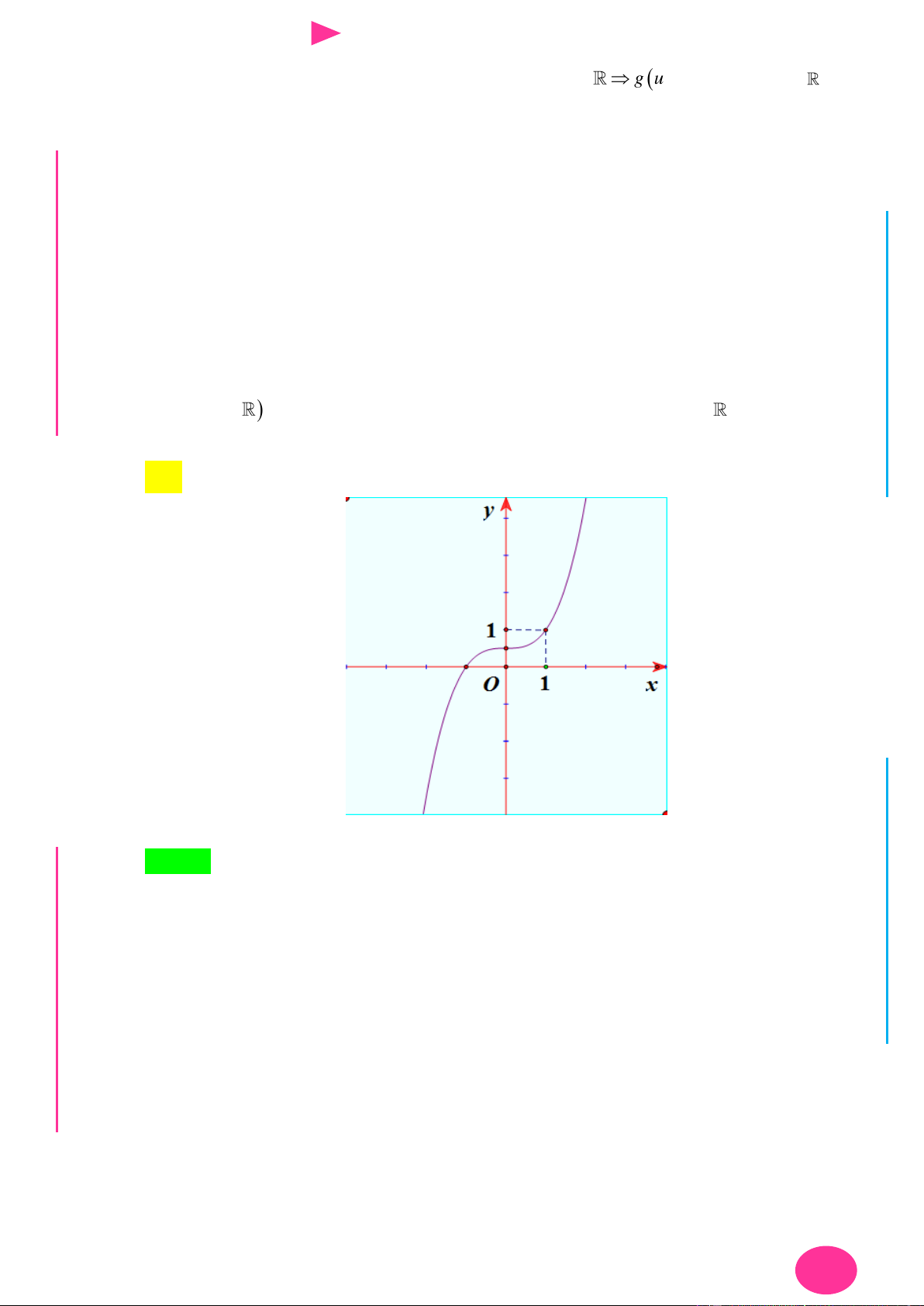
x y thay đổi. x y 10 A. 2. B. 3. C. 1. D. 0.
Câu 10. Cho các số thực x , y thay đổi thỏa mãn 2 2
x y xy 1 và hàm số f t 3 2
2t 3t 1. I
5x y 2 Ơ
Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của Q f
. Tổng M m
x y 4 M D bằng Ầ Đ A. 4 3 2 . B. 4 5 2 . C. 4 4 2 . D. 4 2 2 . NHỊ
x y xy y f x Đ
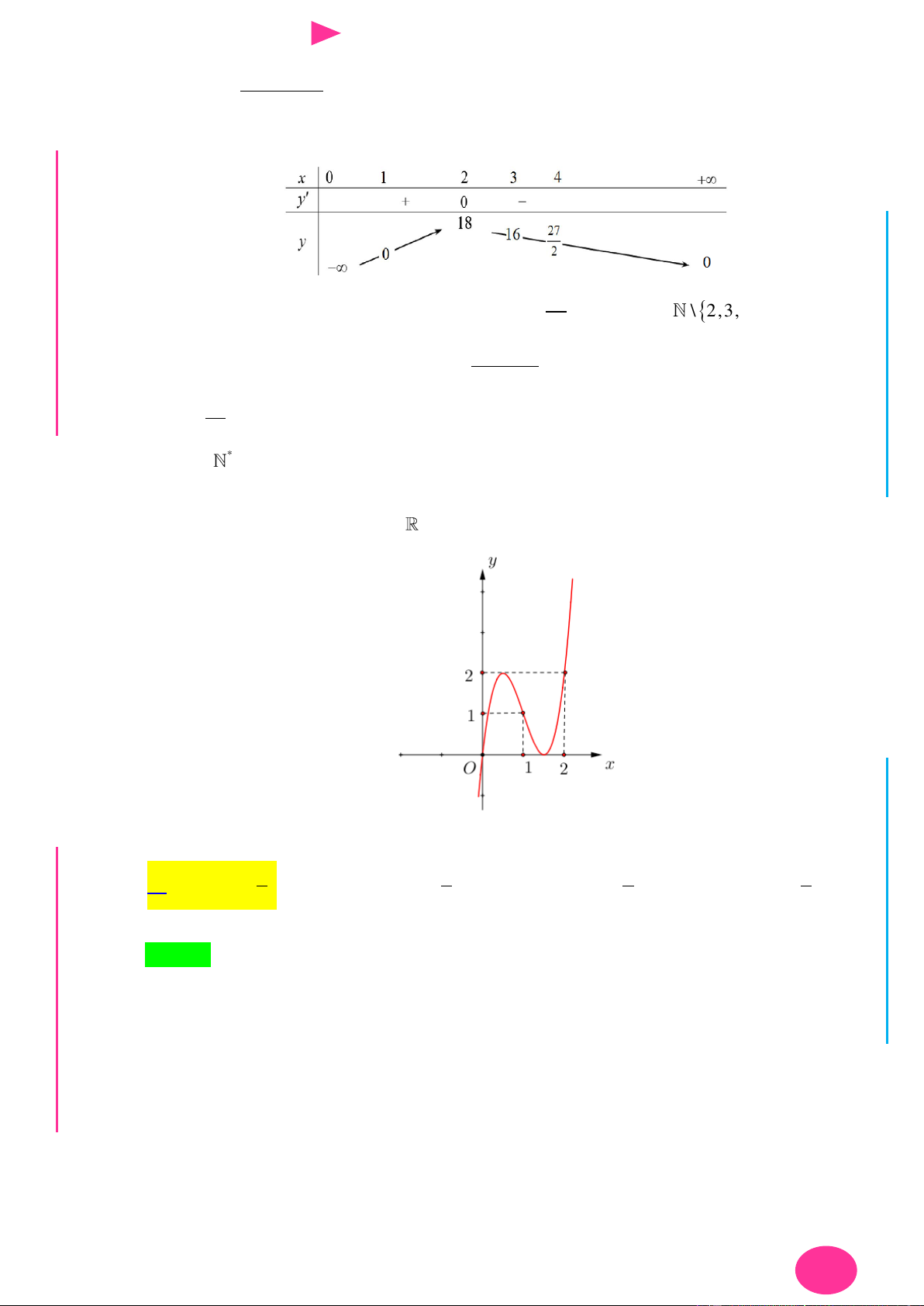
Câu 12. Cho 2 số x , y thỏa mãn 2 2 5 1 4 và hàm số bậc ba
có đồ thị như hình G THPT N.C.Đ
2x 3y 3
vẽ. Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của P f . NG x 4 y 4 CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
Tích M.m bằng 1436 3380 1436 1944 A. B. C. D. 1331 1331 1331 1331
Câu 13. Cho các số thực ,
x y thay đổi thỏa mãn 2 2
x 5y 2xy 1 và hàm số f t 4 2
t 2t 2
x y 1
Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của Q f
. Tổng M m
x 3y 2 A. 4 3 2 . B. 8 3 2 . C. 66 . D. 9 3 17
xy yz zx 8
Câu 14. Cho các số thực ,
x y, z thỏa mãn
và hàm số f x 2
x 4x 5
x y z 5
Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của f x . Tổng M m 28 19 A. 3 . B. . C. . D. 2 9 9
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 15. Cho các số thực dương ,
x y, z thay đổi và thỏa mãn: 2 2 2
5 x y z 9xy 2yz zx . x 1
Tìm giá trị lớn nhất của biểu thức: P bằng 2 2 y z
x y z3 A. 18. B. 12 . C. 16. D. 24 .
Câu 16. Cho hàm số f x 3 2
2x 6x 1 và các số thực m , n thỏa mãn 2 2
m 4mn 5n 2 2n 1 . m 2 2
Giá trị nhỏ nhất của f bằng n A. 99 . B. 100 . C. 5 . D. 4 . 3 4 1
Câu 17. Cho x , y 0 thỏa mãn x y và biểu thức P
đạt giá trị nhỏ nhất. 2 x 4 y Tính 2 2
x y . 25 5 2313 153 A. . B. . C. . D. . I 16 4 1156 100 Ơ 2 x x y 2018
Câu 18. Cho 0 x, y 1 thỏa mãn 1 2017
. Gọi M , m lần lượt là giá trị lớn 2 M D
y 2 y 2019 Ầ 2 2 Đ
nhất, giá trị nhỏ nhất của biểu thức S 4x 3y4y 3x 25x .
y Khi đó M m bằng NHỊ bao nhiêu? Đ G 383 136 25 391 THPT A. . B. . N.C.Đ C. . D. . 16 3 2 16 NG CÔN
Ờ Câu 19. Biết đồ thị của hàm số 3 y x 3x 2 tiếp xúc với parabol 2 y ax
b tại điểm có hoành N Ễ
độ x 0;2 . Giá trị lớn nhất của S a b là. Y TRƯ A . S 1 . B . S 0 . C . S 1. D . S 3 . max max max max GU N N 2 2 2
Câu 20. Hàm số f x x
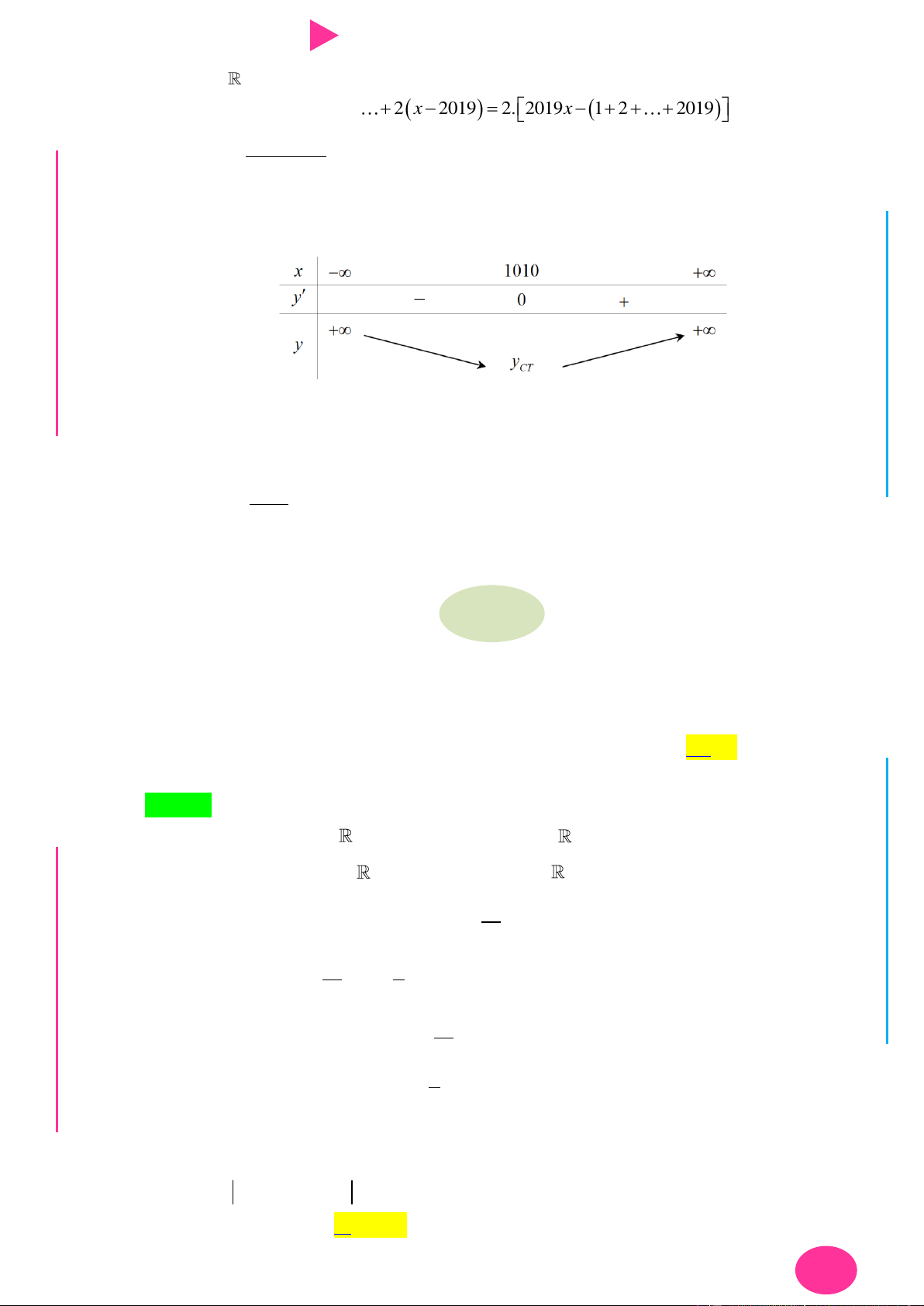
1 x 2 ... x 2019 (x ) đạt giá trị nhỏ nhất khi x bằng A. 2020 . B. 1010 . C. 2019 . D. 0 . ÁO VIÊ GI Câu 21. Hàm số 4 3 2 y x ax bx
1 đạt giá trị nhỏ nhất tại x 0 . Giá trị nhỏ nhất của biểu thức
S a b là A. 2 . B. 0 . C. 2 . D. 1.
Câu 22. Cho các số thực a, , b c thỏa mãn 2 2 2
a b c 2a 4b 4 . Tính P a 2b 3c khi
biểu thức 2a b 2c 7 đạt giá trị lớn nhất. A. P 7 .
B. P 3. C. P 3 . D. P 7 .
Câu 23. Cho ba số thực dương a, , b c thỏa mãn 2 2 2
a b c 2a 4b 6c 10 và a c 2 .
Tính giá trị biểu thức P 3a 2b c khi 2 2 2
Q a b c 14a 8b 18c đạt giá trị lớn nhất. A. 10. B. 10 . C. 12. D. 12 .
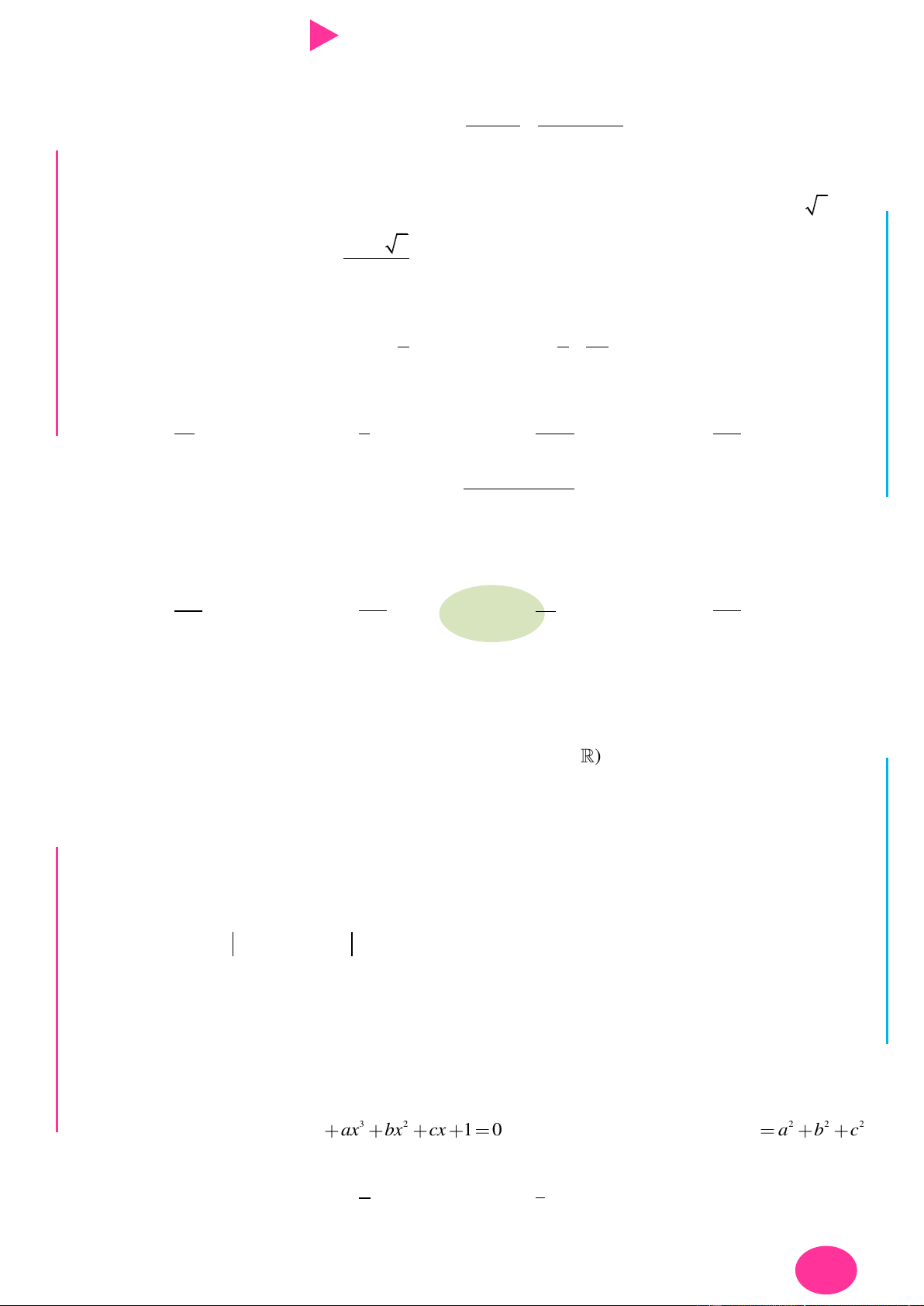
Câu 24. Cho phương trình 4 3 2 x ax bx cx 1
0 có nghiệm. Giá trị nhỏ nhất 2 2 2 P a b c bằng 4 8 A. 2 . B. . C. . D. 4 . 3 3
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 25. Biết hai hàm số f x 3 2
x ax 4x 2 và g x 3 2
x bx 2x 3 có chung ít nhất một
điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P a b . A. 3 2 . B. 6 2 . C. 6. D. 3.
BỔ SUNG BÀI TẬP TỰ LUẬN HÀM NHIỀU BIẾN Bài 1.
Cho các số thực a, b, c thuộc đoạn 3 ; 1
và thỏa mãn điều kiện a b c 6. Tìm giá trị
a2b2 b2c2 c2a2 abc 12 72 1
lớn nhất của biểu thức P abc
ab bc ca 2 Bài 2: Cho , x y, z 2 ; 1
. Tìm giá trị lớn nhất của biểu thức
2 xy yz zx 8 y z 4 A xyz
2 2x y z
2xy z yz 4 yz 1 Bài 3:
Cho các số thực không âm a, b, c thỏa mãn a , 1 b ,
2 c 3 . Tìm giá trị lớn nhất của I biểu thức Ơ
2 2ab ac bc 8 B b b
1 2a b 3c
b c ba c M D 8 12 2 a 3 2 b 27 2 c 8
Ầ Bài 4: Cho x, y, z là các số thực dương thỏa mãn y z x 2 2
y z . Tìm giá trị nhỏ nhất của Đ NH 1 1 1 4 Ị biểu thức P 2 2 2 Đ
1 x 1 y 1 z 1 x1 y1 z G
THPT Bài 5: Cho a b c 0. Tìm giá trị nhỏ nhất cN ủ.C.Đ a b iểu thức 1 1 1 NG P 2 a 2 b 2
c ab bc ca CÔN Ờ
a b2 b c2 c a2 N Ễ 2 Y Bài 6: Cho , x y, z ; 0 xy
z x y z 20 . Tìm giá trị nhỏ nhất của P
x yx z 2 y z TRƯ 1 a b b c c a GU
N Bài 7: Cho a,b,c 1 ;
. Tìm giá trị lớn nhất của biểu thức P N 2 c a b c c Bài 8: Cho 2 2 2 2 a, , b c ,
0 a 2b a b . Tìm giá trị lớn nhất của P c 2 1 ÁO VIÊ b a
GI Bài 9: Cho a, b, c là các số thực thỏa mãn a,c ;
1 b 2 . Tìm giá trị nhỏ nhất của biểu thức
ab c
ca b
3a c2 b 2 2 8 P b c 2 b 2a 4 3 ac
Bài 10: Cho các số thực , x y, z 1 ; 0 và z mi n x, y,
z . Tìm giá trị nhỏ nhất của biểu thức y z2 yz 1 2 P x z
yy z
xy xz yz
Bài 11: Cho các số , a , b c 1 ; 0
. Tìm giá trị lớn nhất của biểu thức a b c P abc 1 bc 1 ac 1 ab
Có nhiều bài toán tìm cực trị của biểu thức ta chỉ cần sử dụng các biến đổi cơ bản đã làm giảm
được số biến. Tuy nhiên bài toán cực trị có dạng phân thức ta phải sử dụng các bất đẳng thức
để đánh giá mới làm giảm được số biến của bài toán.
Các bất đẳng thức thường dùng 1. Cho 2
a, b R ta có a b 4ab a b 3 3 3
2. Cho a,b 0 ta có 2 2 a b a b ab 4
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 1 4
3. Cho a,b 0 ta có a b a b 2 2 2
a b c2
4. Cho a,b,c R ta có a b c
ab bc ca 3 5. Cho 2
a,b, c R ta có ab bc ca 3
abc a b c 1 1 1 9
6. Cho a,b,c 0 ta có a b c
a b c 1 1 2
7. Cho a,b 0 và ab 1 ta có 1 a 1 b 1 ab 1 1 2
8.Cho a,b 0 và ab 1 ta có 1 a 1 b 1 ab
Nhận xét: Trên đây chỉ là một số BĐT tiêu biểu thường sử dụng để tìm cực trị bằng cách dồn
biến, ngoài ra ta có thể sử dụng các hệ quả khác hoặc các bất đẳng thức khác. Ứng dụng các
BĐT trên để giải các bài toán sau đây.
a2 b2 2ab
I Bài 12: Cho các số thực , a , b c 2 ; 1
. Tìm giá trị nhỏ nhất của biểu thức: P Ơ c2
4 ab bc ca
Bài 13: Cho các số không âm a, b, c thỏa mãn c 0 và 3 3
a b cc
1 . Tìm giá trị nhỏ nhất của M D 2 2 2 Ầ a b c biểu thức: P Đ
a b c2 NHỊ
Bài 14: Cho x, y, z 0 thoả mãn x y z 0 . Tìm giá trị nhỏ nhất của biểu thức Đ 3 3 3 G THPT x y 16z P N.C.Đ
x y z3 NG CÔN
Ờ Bài 15: Cho x, y, zlà ba số thực thuộc đoạn 2 ;
1 . Tìm giá trị nhỏ nhất của biểu thức N 2 Ễ x y Y TRƯ P
2 x y z2 2 2 2 x y 2 z GU N N 1 2 2
Bài 16: Cho các số thực a, , b c 0 thỏa mãn
. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 c a b a b c ÁO VIÊ P 2 2 2 b c a c
a b c
GI Bài 17: Cho các số thực dương x, y, z thay đổi thỏa mãn điều kiện x 2y z 0. Tìm giá trị nhỏ x y x 2 y
nhất của biểu thức: P 10y z
x y z 2x 3y
Bài 18: Cho các số thực dương a, b, c thay đổi thỏa mãn điều kiện a b, a c . Tìm giá trị lớn a b c
nhất của biểu thức: P
5 a b c a 5 c 2 a 5 b 2
Bài 19: Cho ba số thực dương x, y, z thỏa mãn 0 x y z . Tìm giá trị nhỏ nhất của biểu thức: x3z y4 z3 15x3 P
y2 xz y2
z2 xz y2 x2z ab
Bài 20: Cho a, b, c là các số thực dương thỏa mãn a c b c
. Tìm giá trị nhỏ nhất của c 2 a b c c biểu thức: P 2 2 b c c a a b a b
Bài 21: Cho a, b, c là các số thực dương thỏa mãn: a b c . Tìm giá trị nhỏ nhất của biểu thức:
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
a2 c2 abbc ca T
abc a b c
Bài 22: Cho x, y, z là các số thực dương thỏa mãn: 2 2 2
x y z 1 . Tìm giá trị lớn nhất của biểu 3 3 3 3 xy yz x y y z thức: P 2 2 3 3 1 z 1 x 24x z 4 4 x y z x
Bài 23: Cho x, y, z là các số thực dương thỏa mãn 2 y z x z 2 y2 2z2 3z
Tìm giá trị lớn nhất của biểu thức: P x2 y2 y2 z2 2x z I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI 3 9x x Câu 1.
Cho hai số thực dương x, y thỏa mãn
3y 2 . Giá trị lớn nhất của biểu thức y 1
S 6x y là: 89 11 17 82 A. . B. . C. . D. . 12 3 12 3 Lời giải Chọn B
Theo giả thiết y 0 nên ta có : 3 9x x 3y 2 9x x 3y 2 y 1
3x3 3x 3y 23 3 3y 2 y 1
f 3x f 3y 2 với 3
f t t t . I
Ta có f t 2 3t 1 0, t
nên hàm số f t đồng biến trên , suy ra 3x 3y 2 Ơ 2 2 hay 2 y 3x
. Do y 0 và 3x 3y 2 nên x . M D 3 3 Ầ 2 2 11 11 Đ
Khi đó S 6x y 6x 3x 3
x 6x 3x 2 2 2 1 . NH 3 3 3 3 Ị Đ 11 Do đó max S khi x 1. G THPT 3 N.C.Đ
NG Câu 2. Cho x, y thỏa mãn x y 1 và 2 2 x y xy x
y 1. Gọi M , m lần lượt là giá trị CÔN Ờ N xy
lớn nhất và giá trị nhỏ nhất của biểu thức P
. Tính M m. Ễ x y 1 Y TRƯ 1 2 1 1 GU N A. . B. . C. . D. . N 3 3 2 3 Lời giải ÁO VIÊ Chọn B GI Cách 1: xy Với điều kiện 2 2 x y 1
; x y xy x y 1 ta có P . 2 2
x y xy x 1 1 5 Nếu y 0 thì x . Khi đó P 0 . 2
x x 1 0 2 x y x t
Nếu y 0 thì P . Đặt t . Ta có P 2 2 x x y
t t , t . 1 1 y y t 2 t 1
Xét f t f t
; f t 0 t 1 2
t t , t . 1
t t 2 2 1
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Từ bảng biến thiên: x y x x y 1 1 1 x y x 1 M tại y 1 . 3 2 3
x 2x 1 0
x y 2 2 1
x y xy x y 1 x 3 3 x 1 x x y 1 x y y 1 m 1 tại y x 1 2 x 1 0 x 1 2 2 I
x y xy x y 1 x 1 Ơ y 1 2 M D
Vậy M m . Ầ 3 Đ Cách 2: NHỊ xy Đ Với điều kiện 2 2 x y 1
; x y xy x y 1 ta có P . 2 2 G
x y xy THPT N.C.Đ 2
Px xyP 2
1 Py 0 (*) NG CÔN Ờ
+) Nếu P 0 thì x 0 hoặc y 0 . N Ễ Y x 0 TRƯ
+) Nếu P 0 thì . y 0 GU N N 1
Để phương trình (*) có nghiệm x thì 2 y P P
P . x 1 3 1 0 1 3 ÁO VIÊ Ta có: GI x y y P 1 x y 1 1 x y x y x 1 M tại 2P 1 . 3 2 3
x 2x 1 0
x y 2 2 1
x y xy x y 1 x 3 3
y P x 1 1 x y x y x y y 1 m 1 tại 2P x 1 2 x 1 0 x 1 2 2
x y xy x y 1 x 1 y 1 1 2
Do đó M ; m 1. Vậy M m . 3 3 Câu 3. Cho ,
x y là các số thực thỏa mãn 2 2
x xy y 1 . Gọi M , m lần lượt là giá trị lớn nhất , 4 4 x y 1
giá trị nhỏ nhất của P A M m là: 2 2
x y . Giá trị của 15 1 A. 17 2 6 . B. 17 6 C. 17 2 6 D. 17 6 .
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn A 2 3 2 Ta có 2 2
x xy y 1 x y 1 3xy 1 x y 2 x y 2 4 2 2 1 2 Mặt khác: 2 2
x y x y 2xy x y _ 2 2 3 3 2 2 t 4t 1 Đặt 2 2
t x y t 2 . Vậy P g t 3 t 1 t t
Xét hàm số g t 2 4 1 2 t ; 2 t 1 3 g t 2 t 2t 5 2 ' t ; 2 ;
g t 2 '
0 t 1 6 ; 2 . t 1 3 3 11
Vậy min g t
; max g t 6 2 6 I 15 2 2 t ;2 Ơ t ;2 3 3 M D
Vậy A M 15m 17 2 6 Ầ
Nhận xét: đây là bài toán thường gặp trong các đề thi TSĐH những năm trước đây. Tư Đ NHỊ
tưởng của các bài toán này là sử dụng ứng dụng đạo hàm tìm GTNN, GTLN của hàm Đ
số sau khi áp dụng phương pháp dồn biến. G THPT N.C.Đ
Câu 4. Cho hai số thực x , y thỏa mãn 2 2 2 2
x y 4x 6y 4
y 6y 10 6 4x x . Gọi M NG CÔN Ờ
, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2 T
x y a . Có bao N Ễ Y TRƯ
nhiêu giá trị nguyên thuộc đoạn 1
0;10 của tham số a để M 2m? GU N A. 17. B. 15. C. 18. D. 16. N Lời giải Chọn D ÁO VIÊ GI Ta có 2 2 2 2
x y 4x 6y 4
y 6y 10 6 4x x 2 2 2 2
y 6y 10
y 6y 10 6 4x x 6 4x x . *
Xét hàm f t 2
t t , có f (t) 2t 10 , t 0.
Ta có hàm y f t đồng biến trên 0; , 2
y 6 y 10 0; , 2
6 4x x 0; . Nên * f 2 y y f 2 x x 2 2 6 10 6 4
y 6y 10 6 4x x y y
x x x 2 y 2 2 2 6 10 6 4 2 3 9 . Xét điểm 2 2
A x; y thuộc đường tròn (C) có phương trình x 2 y 3 9 . Ta có 2 2 OA x y .
Đường tròn (C) có tâm I 2; 3 , bán kính R 3 nên điểm O 0;0 nằm ngoài (C) .
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Gọi A , A là giao điểm của đường thẳng OI với đường tròn (C) . 1 2 A ;
x y(C) : OA OA
OA OI R
OA OI R OA , với 13 3 và 13 3 . 1 2 1 2 Tức là ta có 2 2 13 3
x y 13 3 2 2
13 3 a x y a 13 3 a .
a a I Th1 : 13 3 0 13 3 , 1 Ơ
Khi đó M 13 3 a và m 13 3 a . M D
M 2m 13 3 a 2 13 3 a a 13 9 . Ầ Đ
Kết hợp với điều kiện
1 và a nguyên thuộc đoạn 1 0;10 ta có NHỊ Đ a 5
; 4; 3; 2;1; 0 . G THPT N.C.Đ
Th2: 13 3 a 0 a 13 3 , ** NG CÔN Ờ
Khi đó M a 13 3 và m a 13 3 . N Ễ
M 2m a 13 3 2 a 13 3 a 13 9 . Y TRƯ GU N
Kết hợp với điều kiện ** và a nguyên thuộc đoạn 1
0;10 ta có a 7;8;9;1 0 . N
13 3 a 0 Th3:
13 3 a 13 3 , *** a ÁO VIÊ 13 3 0 GI
Khi đó M 0 và m 0 nên ta luôn có M 2m Kết hợp điều kiện
*** và a nguyên thuộc đoạn 1
0;10 ta có a1;2;3;4;5; 6 . Vậy a 5
; 4;3; 2;1;0;1;2;3;4;5;6;7;8;9;1 0 . Câu 5. Cho 2 2
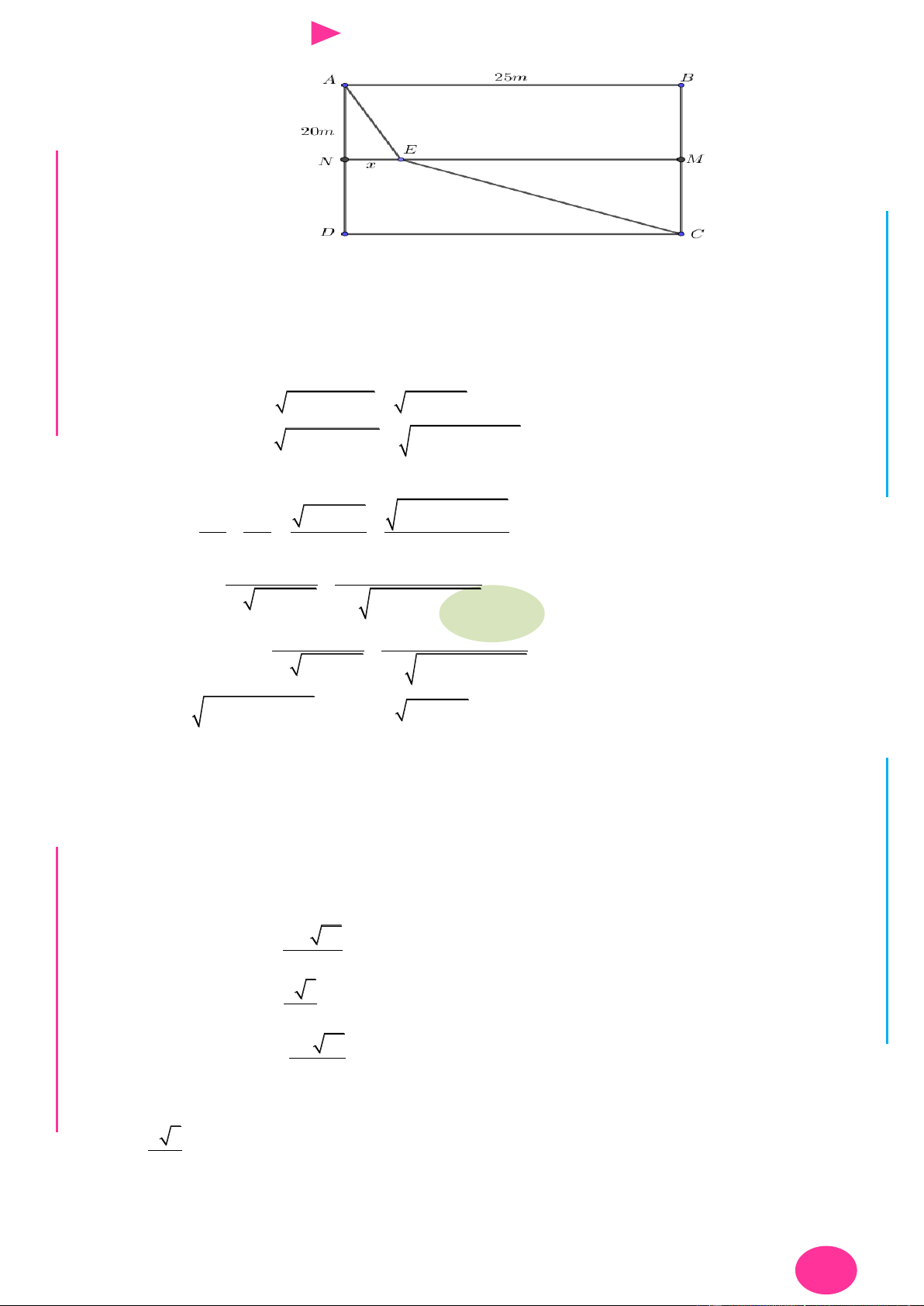
x, y là các số thực thỏa mãn x 3 y 1
5 . Tìm giá trị nhỏ nhất của biểu 2
3y 4xy 7x 4 y 1 thức P . x 2 y 1 114 A. 3 . B. 3 . C. . D. 2 3 . 11 Lời giải Chọn A
x 2 y 2 2 2 3 1
5 x y 6x 2y 5 0 .
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2
3y 4xy 7x 4 y 1 2 2
x y 6x 2 y 5 P x 2 y 1
4 y 4xy x x 2 y 4 2y x2 2 2
x 2y 4 . x 2 y 1 x 2 y 1
Đặt t x 2 y .
x 2 y 2 2 2 1 2 3
1 x 3 2 y 2 2
x y 2 2 5
25 0 x 2y 10 . 2 t t 4 4 P t , 0 t 10 . t 1 t 1
Sử dụng MTCT min P 3 khi t 1.
Câu 6. Cho các số thực dương a,b thỏa mãn 2 2
2 a b ab (a )
b (ab 2) . Giá trị nhỏ nhất 3 3 2 2 a b a b
của biểu thức P 4 9 thuộc khoảng nào? 3 3 2 2 b a b a I Ơ A. (-6 ;-5) . B. (-10 ;-9) . C. (-11 ;-9) . D. (-5 ;-4) . Lời giải M D Ầ Chọn A Đ 2 2 NH
Vì a,b dương nên từ giả thiết 2a
b ab (a )
b (ab 2) , ta chia hai vế cho ab Ị Đ a b 1 1 2 2 G
2 a b ab (a b)(ab 2) 2
1 (a b) 2 THPT . b aN.C.Đ a b NG 1 1 CÔN Ờ
Áp dụng bất đẳng thức Cô – Si cho hai số dương (a b) và 2 : N a b Ễ Y TRƯ 1 1 1 1 a b (a b) 2
2 (a b).2 2 2 2 . GU N a b a b b a N 1 1
Dấu " " xảy ra khi (a b) 2 . a b ÁO VIÊ GI a b a b a b Suy ra 2 1 2 2 2
. Đặt t ,(t 0). b a b a b a 5 t 5 Khi đó: 2 2
2t 1 2 2(t 2) 4t 4t 15 0
. Do đó, ta có điều kiện t . 3 2 t 2 3 2 3 3 2 2 a b a b a b a b a b Mặt khác: P 4 9 4 3 9 2 3 3 2 2 b a b a b a b a b a 3 2 3 2
4t 3t9t 2 4t 9t 12t 18. 5
Đặt f t 3 2
4t 9t 12t 18 f '(t) 12t 2 18t 12 0, t . 2 Bảng biến thiên
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 5 23
Từ bảng biến thiên ta có, Min f (t) f . 5 t ; 2 4 2 a 2 a b 5 23 b a 2 b 1
Vậy giá trị nhỏ nhất của biểu thức P là khi . 4 1 1 a 1 (a b) 2 a b b 2 I
Ơ Câu 7. Cho các số thực x, y thay đổi nhưng luôn thỏa mãn 2 2
3x 2xy y 5 . Giá trị nhỏ nhất M D của biểu thức 2 2 P x xy
2y thuộc khoảng nào sau đây. Ầ A. 4;7 . B. 2 ;1. C. 1;4 . D. 7;10 . Đ NHỊ Lời giải Đ Chọn C G THPT N.C.Đ 5
Xét y 0 P loại phương án A và D. NG 3 CÔN Ờ 2 N 2 y 7y 2 2 5
3x 2xy y Ễ
Xét y 0 P x 0
khi đó ta có biểu thức 2 2 Y TRƯ 2 4 P
x xy 2y GU N 2 x x N 3 2 1 5 y y
Chia cả tử và mẫu của vế phải cho 2 y tâ được . 2 P x x ÁO VIÊ 2 GI y y t 3 2 2 x 5 3t 2t 1 5t 14t 3 Đặt
t (t R)
f t f ' t
, f ' t 0 2 2 2 1 y P t t 2 (t t 2) t 5
Bảng Biến thiên hàm số f t .
Từ bảng biến thiên ta có f t 5 5 4 4 P . P 4
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 5
Vậy P đạt giá trị nhỏ nhất bằng , dấu bằng xảy ra khi t 3 x 3 y . 4
Câu 8. Cho số phức z x yi (x, y ) . Thỏa mãn z 2 i z 2 5i và biểu thức sau đạt 2 2
x y 3y 1
giá trị nhỏ nhất: H
. Giá trị của 2x y 2 2 2 2
x y 2x 2y 2 x y 2x 4y 5 bằng: A. 6 B. 6 5 C. 3 5 D. 6 5 Lời giải Chọn B
Ta có: z 2 i z 2 5i x y 3 0 (1). Gọi M là điểm biểu diễn của số phức z thì
M thuộc đường thẳng d có phương trình (1). I 2 2 Ơ
x y 3y 1 Mà H 2 x 2
y 2x 2y 2 2 x 2
y 2x 4y 5 M D Ầ
(x 1)(x 1) (y 1)(y 2) Đ (2) 2 2 2 2 NH
(x 1) (y 1) (x 1) (y 2) Ị Đ Đặt ( A 1
;1), B(1;2), M( ; x y) thì G THPT N.C.Đ AMBM AM
x 1; y
1 , MB (x 1; y 2) cos AMB H NG AM.BM CÔN Ờ N Ễ
Mà A, B cùng thuộc một nửa mặt phẳng bờ là đường thẳng d, M thuộc d nên cos AMB Y TRƯ
nhỏ nhất khi góc AMB lớn nhất. GU N N
Gọi (C) là đường tròn đi qua A, B và tiếp xúc với đường thẳng d tại C.
Phương trình đường thẳng AB là: x 2y 3 0 . ÁO VIÊ
Gọi E là giao điểm của AB và d thì E 3 ;0 GI Vậy C thỏa mãn: 2 EC E . A EB 10 C( 3
5; 5), C 3 5; 5 a
Chọ C để góc CEA nhọn ta được C 3 5 3 5; 5
2a b 6 5 b 5 x y Câu 9. Cho , x y thỏa mãn log
x(x 9) y( y 9) xy Tìm giá trị lớn nhất của 3 2 2
x y xy 2 3x 2 y 9 biểu thức P khi ,
x y thay đổi. x y 10 A. 2. B. 3. C. 1. D. 0. Lời giải Chọn C x y Điều kiện xác định;
0 (x y) 0. 2 2
x y xy 2
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 y 3 Vì 2 2 2 2
x y xy 2 (x )
y 2 0 với x, y . 2 4 x y Ta có log
x(x 9) y( y 9) xy . 3 2 2
x y xy 2 2 2 2 2
log (x y) log (x y xy 2) x y xy 9(x y) . 3 3 2 2 2 2
2 log (x y) 9(x y) log (x y xy 2) x y xy 2 . 3 3 2 2 2 2
log 9(x y) 9(x y) log (x y xy 2) x y xy 2 (1) . 3 3
Đặt f (t) log t t ( t 0) . 3 1 Có f '(t) 1 0 với ( t
0) f là hàm đồng biến với ( t 0) . Khi đó: t.ln 3 2 2 2 2
f (9(x y)) f (x y xy 2) 9(x y) x y xy 2 . 2 2
x y xy 2 9x 9y 0 . 2 2
4x 4y 4xy 8 36x 36y 0 . I 2 2 Ơ (2x y) 18(2x y) 3( y 3) 19 0 . Mà 2 2
3(y 3) 0 (2x y) 18(2x y) 19 0 1
2x y 19 . M D Ầ 2x y 19 2x y 19 x 8 Mặt khác
Dấu bằng xảy ra khi . Đ P 1 0 P 1 x y 10 y 3 0 y 3 NHỊ Đ
Câu 10. Cho các số thực x , y thay đổi thỏa mãn 2 2
x y xy 1 và hàm số f t 3 2
2t 3t 1. G THPT N.C.Đ
5x y 2
Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của Q f
. Tổng M m NG
x y 4 CÔN Ờ N bằng Ễ Y TRƯ A. 4 3 2 . B. 4 5 2 . C. 4 4 2 . D. 4 2 2 . GU N Lời giải N Chọn C 2 2 y 3y 5x y 2 ÁO VIÊ Ta có: 2 2
x y xy 1 x 1 . Ta đặt: t GI 2 4 x y 4
t x y 4 5x y 2 t 5 x t
1 y 4t 2 0 . y x t 3y t 5 3 3 2 4t . 2 2
Áp dụng bất đẳng thức Bunhiacopxki, ta có: 2 2
t t y x t
3y t t 2 2 2 2 y 3y 2 4 5 3 3 5 3 3 x 2 2 2 4
t t t 2 2 2 2 4 5 3 3 .1 2
12t 24t 0 2 t 2 .
Xét hàm số f t 3 2
2t 3t 1 với 2 t 2 . t 0
Có: f t 2
6t 6 nên f t 2
0 6t 6t 0 . t 1
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Ta có: f 2 5 4 2 , f 0 1, f
1 0 , f 2 5 4 2
Do đó M f 0 1, m f 2 5 4 2 .
Vậy M m 4 4 2 .
a x b y c Bài toán gốc: Cho 2 2
ax by cxy d . Tìm MGT 1 1 1
t a x b y c 2 2 2 Phương pháp giải: Cách 1. Lượng giác hóa 2 2 Ta có: 2 2
ax by cxy d a ' x b ' y c ' x d ' y 1
a ' x b ' y sin x msin Đặt
c ' x d ' y cos
y n cos
a x b y c Suy ra: 1 1 1 t
Asin B cos C a x b y c 2 2 2 I Ơ Ta có: 2 2 2
A B C suy ra MGT của t . Cách 2: M D Ầ
a x b y c 1 1 1 t
Amx ny Bkx qy C Đ
a x b y c 2 2 2 NH Ị 2 2 Đ
Chọn m, n, k, q sao cho 2 2 mx ny kx qy
ax by cxy G THPT 2 2 N.C.Đ
m k a NG 2 2 CÔN Ờ n q b N Ễ
2mn 2kq c Y TRƯ
Áp dụng BĐT Bunhiacoxki ta có: 2 2 2 C
A B d suy ra MGT của t . GU N N
Câu 12. Cho 2 số x , y thỏa mãn 2 2
x 5y 1 4xy và hàm số bậc ba y f x có đồ thị như hình
2x 3y 3 ÁO VIÊ
vẽ. Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của P f . GI x 4 y 4
Tích M.m bằng 1436 3380 1436 1944 A. B. C. D. 1331 1331 1331 1331 Lời giải Chọn C
Dễ thấy f x 3 x 3x
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Từ x y xy x y2 2 2 2 5 1 4 2 y 1
x 2y sin
x sin 2cos Đặt . Khi đó y cos y cos 2x 3y 3
2sin 2cos 3cos 3
2 sin cos 3 Xét t
x 4y 4 sin 2cos 4cos 4 sin 2cos 4
Ta có: t sin 2cos 4 2sin cos 3 t 2sin 1 2t cos 4t 3 * 2 Phương trình 2 2 2
* có nghiệm t 2 2t 1
4t 3 2 t 11 2
Khi đó P f t 3
t 3t với 2 t 11 718 1436
Dễ dàng tìm được M 2 , m . Vậy M .m 1331 1331
Câu 13. Cho các số thực ,
x y thay đổi thỏa mãn 2 2
x 5y 2xy 1 và hàm số f t 4 2
t 2t 2 I Ơ
x y 1
Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của Q f
. Tổng M m
x 3y 2 M D Ầ A. 4 3 2 . B. 8 3 2 . C. 66 . D. 9 3 17 Đ NH Lời giải Ị Đ Chọn C G THPT N .C.Đ Ta có: 2 2 x 5y 2xy 1 x y2 2 4y 1 NG CÔN x y 1 Ờ Đặt t
t x 3y 2 x y 1 2t 1 t
1 x y 2ty N x 3y 2 Ễ Y TRƯ
Áp dụng bất đẳng thức Bunhiacopxki, ta có: GU N 2 2
t 2 t x y 2 ty t 2 2 2 2 2 1 1 2 1 t x y
4y t t 2 2 1 1 t N 2
2t 6t 0 3 t 0 ÁO VIÊ
Xét hàm số f t 4 2
t 2t 2 với 3 t 0 GI t 0
Có: f t 3
4t 4t , nên f t 0 t 1 t 1
f 0 2, f 1 1, f 3 65
Do đó M f 3
65;m f 1 1
Vậy: M m 66
xy yz zx 8
Câu 14. Cho các số thực ,
x y, z thỏa mãn
và hàm số f x 2
x 4x 5
x y z 5
Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của f x . Tổng M m 28 19 A. 3 . B. . C. . D. 2 9 9 Lời giải Chọn A
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
xy yz zx 8
zy 8 x y z
yz 8 x5 x
Viết lại điều kiện: *
x y z 5
y z 5 x
y z 5 x Vì ,
x y, z thỏa mãn
* nên y, z là hai nghiệm của phương trình 2
T x 2 5
T 8 5x x 0 **
Điều kiện có nghiệm của phương trình ** là: 7 x2 2 x x 2 5 4 8 5
0 3x 10x 7 0 1 x 3 7
Xét hàm số f x 2
x 4x 5 với 1 x 3
Có f x 2x 4 nên f x 0 x 2 f f 7 10 1 2; 2 1; f 3 9 I
Do đó M f
1 2, m f 2 1. Ơ
Vậy M m 3 .
M D Câu 15. Cho các số thực dương ,
x y, z thay đổi và thỏa mãn: 2 2 2
5 x y z 9xy 2yz zx . Ầ Đ x 1 NH
Tìm giá trị lớn nhất của biểu thức: P bằng Ị 2 2 y z
x y z3 Đ G THPT A. 18. B. 12 . N.C.Đ C. 16 . D. 24 . NG Lời giải CÔN Ờ Chọn C N Ễ 2 2 2 2 2 2 Y
Ta có: 5x y z 9xy 2yz zx 5x 9 y z x 5y 5z 18yz 0 TRƯ 2 2 GU N 2
5x 9 y z x 2 y z 7
y z . N
Vì y z2 7
0 x y z x y z2 2 5 9 2
0 x 2y 2z5x y z 0 ÁO VIÊ
x 2y 2z 0 x 2 y z 0 x 2 y z . GI x 1
2 y z 1 2 Ta có: P
Do y z 2 2 2 y z 2 2 y z
x y z3 2 2 y z
2y 2z y z3 2 y z 1 4 1 P 1 y z 27 y z3 y z 27 y z3 2 2 1 3 t 3 2 t t Đặt t
0 P 4t
. Đặt f t 4t
f t 4 y z 27 27 9 f t 2
0 t 36 t 6 ( vì t 0 ).
Ta có bảng biến thiên của f t là:
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Từ bảng biến thiên ta thấy f t 16 P
16 . Dấu bằng xảy ra khi Max 1 y z y z 12
x 2y 2z 1 1 x 6 3 y z
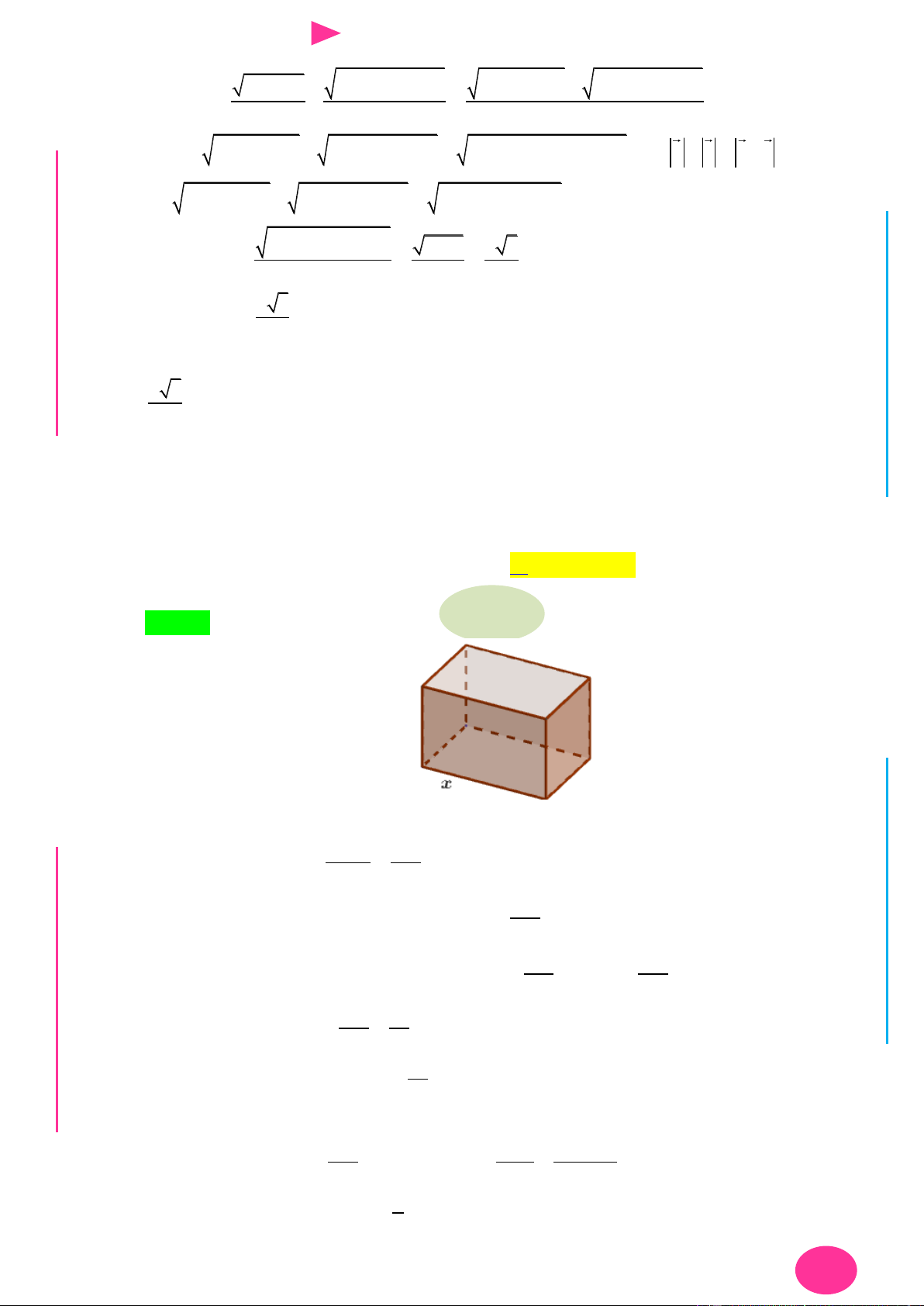
I Câu 16. Cho hàm số f x 3 2
2x 6x 1 và các số thực m , n thỏa mãn 2 2
m 4mn 5n 2 2n 1 . Ơ m 2 2
Giá trị nhỏ nhất của f bằng M D n Ầ Đ A. 99 . B. 100 . C. 5 . D. 4 . NHỊ Đ Lời giải G THPT Chọn A N.C.Đ NG +) Xét hệ thức 2 2 m 4mn 5n 2 2n 1, 1 . CÔN Ờ N m 2 2 Ễ +) Đặt
t . Ta có m 2 2 nt m nt 2 2 . Y TRƯ n 2 GU N +) Thay vào
1 ta được: nt nt 2 2 2 4
2 2 n 5n 2 2n 1 N
2t t 2 4
5 n 2 2 2t 5 2 n 9 0 2 . ÁO VIÊ
+) Có các số thực m , n thỏa mãn
1 phương trình 2 có nghiệm 0 GI t 2 2 2 2 5 2
9 t 4t 5 0 2
t 4t 5 0 t 5 ; 1 .
+) Xét hàm số f t 3 2
2t 6t 1 trên đoạn 5 ;1 . t 0 5 ; 1 f t 2
6t 12t ; f t 0 . t 2 5 ; 1 Ta có f 5 9 9 , f 2
9 , f 0 1, f 1 9 .
Suy ra min f t 9 9 khi t 5 . 5; 1 m 2 2
Vậy giá trị nhỏ nhất của f bằng 99 . n 3 4 1
Câu 17. Cho x , y 0 thỏa mãn x y và biểu thức P
đạt giá trị nhỏ nhất. 2 x 4 y Tính 2 2
x y .
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 25 5 2313 153 A. . B. . C. . D. . 16 4 1156 100 Lời giải Chọn D
Cách 1: Áp dụng bất đẳng thức Cauchy – Schwarz ta có: 4 1 4 1 2 2 2 4 1 25 25 P . x 4 y 4x 4 y 4x 4 y 3 6 4. 2 6 x 4 1 3
Dấu “ =” xảy ra khi và chỉ khi 5
x 4 y mà x y nên . 4x 4 y 2 3 y 10 6 x 25 5 153 2 2 I
Suy ra giá trị nhỏ nhất của P là khi x y . 6 3 100 Ơ y 10 M D Cách 2: Ầ Đ 4 1 4 25 1 25 25 Ta có P x y x y. NHỊ x 4 y x 9 4y 9 9 Đ G
Áp dụng bất đẳng thức Cauchy ta có: THPT N.C.Đ 4 25 4 25x 20 1 25 1 25y 5 NG x 2 . ; y 2 . 20 5 25 3 25 P . . CÔN Ờ x 9 x 9 3 4 y 9 4 y 9 3 3 3 9 2 6 N Ễ 4 25 6 Y x
x 0; y 0 TRƯ x x 9
Dấu “ =” xảy ra khi và chỉ khi mà 5 3 . GU N 1 25 x y 3 N y y 2 4 y 9 10 6 ÁO VIÊ x 25 5 153 GI
Suy ra giá trị nhỏ nhất của P là khi 2 2 x y . 6 3 100 y 10 Cách 3: 3 3
Do x 0 và x y nên x 0; . 2 2 3
Xét hàm số f x 4 1 trên 0; . x 6 4x 2 4 4
Ta có f x ; 2 x 64x2 6 3 x 0; x x 5 2 f
x 0 6 4x2 6 4 2 x .
6 4x x 3 x 2 0; 2 Bảng biến thiên
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 6 25
Ta có lim f x ; lim f x ; f . x0 3 5 6 x 2 6 25
Dựa vào bảng biến thiên của hàm số f x ta có min f x f . 3 0; 5 6 2 6 x 25 153
Suy ra giá trị nhỏ nhất của 5 P là khi 2 2 x y . I 6 3 100 Ơ y 10 2 M D x x y 2018
Câu 18. Cho 0 x, y 1 thỏa mãn 1 2017
. Gọi M , m lần lượt là giá trị lớn Ầ 2
y 2 y 2019 Đ NH 2 2 Ị
nhất, giá trị nhỏ nhất của biểu thức S 4x 3y4y 3x 25x .
y Khi đó M m bằng Đ G bao nhiêu? THPT N.C.Đ 383 136 25 391 NG A. . B. . C. . D. . CÔN 16 3 2 16 Ờ N Lời giải Ễ Y TRƯ Chọn D GU N 2 x x y 2018 2 1 1 y 2 x N +) 2017
1 y 2018 .2017
x 2018 .2017 (1). 2
y 2 y 2019 +) Xét hàm số 2 ( ) 2018.2017t f t t , t 0 , ta có: ÁO VIÊ GI t f t 2 ( )
2017 t ln 2017 2t 2018.ln 2017 0, t
0 suy ra f (t) đồng biến trên 0; .
Từ đó ta có (1) f x f 1 y 1 y x y 1 x .
+) Xét biểu thức: S 2 x y 2 4 3
4y 3x 25xy
x x x2 2
x x x 4 3 2 4 3 1 4 1 3 25 1
16x 32x 18x 2x 12 .
+) Tìm GTLN, GTNN của hàm số g x 4 3 2
16x 32x 18x 2x 12 trên 0 ;1 . 2 3 x 0 ;1 4 2 3
Ta có: g x 3 2
64x 96x 36x 2. Suy ra gx 0 x 0 ;1 . 4 1 x 0 ;1 2
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 3 191 2 3 191 1 25 Ta có g ; g ; g ; g 012; g 1 12 . 4 16 4 16 2 2 25 191 391 Khi đó M ; m M m . 2 16 16 1
Cách khác: đặt t xy với 0 t thì 2
S 16t 2t 12 . Khảo sát hàm số 2
y 16t 2t 12 4 1 trên 0; để tìm max, min. 4
Câu 19. Biết đồ thị của hàm số 3
y x 3x 2 tiếp xúc với parabol 2
y ax b tại điểm có hoành
độ x 0;2 . Giá trị lớn nhất của S a b là. A . S 1 . B . S 0 . C . S 1. D . S 3 . max max max max Lời giải Chọn B I Ơ Đồ thị của hàm số 3
y x 3x 2 tiếp xúc với parabol 2
y ax b tại điểm có hoành độ 3 2
x 3x 2 ax b 1 M D
x 0;2 khi và chỉ khi hệ phương trình
có nghiệm x 0;2 . 2 Ầ 3
x 3 2ax 2 Đ NH 2 Ị 3x 3
Vì x 0;2 nên từ 2 suy ra: 2a thay vào 1 ta được: 3
2b x 3x 4 . Đ x G THPT 3 N.C.Đ Suy ra: 3
2S 2a 2b x 4 . NG x CÔN Ờ 3 N Xét f x 3
x 4 trên khoảng 0;2. Ễ x Y TRƯ 3 GU N
Ta có: f x 2 3 x . 2 N x f x 3 2 4 0 3 x
0 x 1 x 1. 2 x ÁO VIÊ GI Bảng biên thiên:
Dựa vào BBT, ta có GTLN của 2S 0 nên GTLN của S 0 . Vậy đáp án B. 2 2 2
Câu 20. Hàm số f x x
1 x 2 ... x 2019 (x ) đạt giá trị nhỏ nhất khi x bằng A. 2020 . B. 1010 . C. 2019 . D. 0 . Lời giải Chọn B Cách 1:
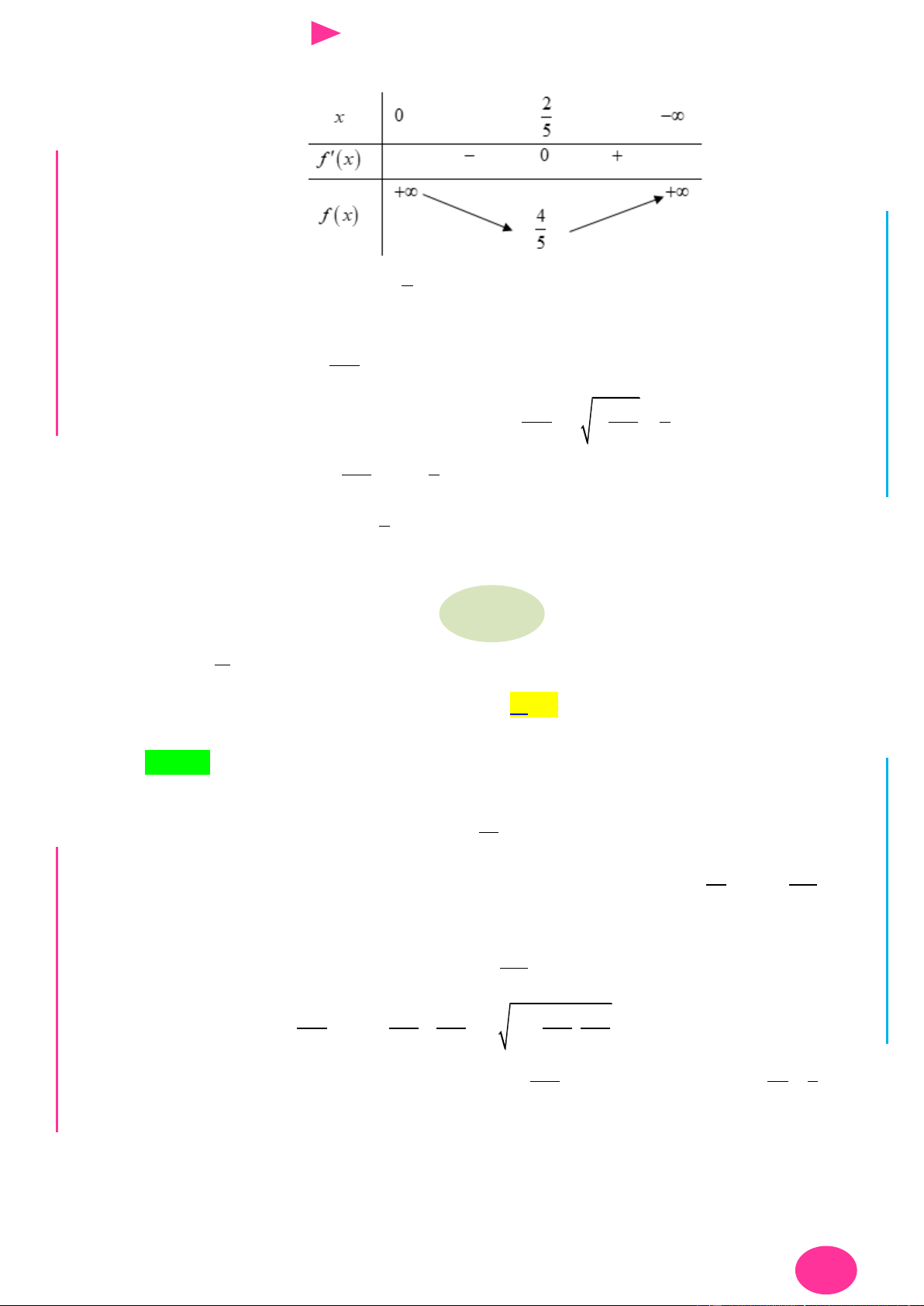
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 TXĐ: D
f x 2 x
1 2 x 2
2x 2019 2.2019x 1 2 2019 2019.2020 2 2019x
20192x 2020 . 2
f x 0 20192x 2020 0 x 1010 . Ta có BBT:
Vậy hàm số đạt giá trị nhỏ nhất tại x 1010 . Cách 2: I 2 2 2 2 Ơ
Ta có f x 2019x 21 2 3..... 2019 x 1 2 ..... 2019 2019 M D 2 2019x 2.
1 2019 x 2 2 2
1 2 ..... 2019 Ầ 2 Đ 2 2 x x 2 2 2 2 2019 2020. 1010
1 2 ..... 2019 2019.1010 NHỊ 2 2 2 2 2 Đ
2019x 1010 1 2 ..... 2019 2019.1010 G THPT 2 2 2 2 N.C.Đ
1 2 ..... 2019 2019.1010 , x . NG CÔN Ờ
Do đó f x đạt giá trị nhỏ nhất khi x 1010 . N Ễ Câu 21. Hàm số 4 3 2
y x ax bx 1 đạt giá trị nhỏ nhất tại x 0 . Giá trị nhỏ nhất của biểu thức Y TRƯ
S a b là GU N N A. 2 . B. 0 . C. 2 . D. 1. Lời giải ÁO VIÊ Chọn D GI
Ta có f x f 0, x 4 3 2
x ax bx 0, x . 2 x 2
x ax b 0, x 2
x ax b 0, x . 2 a 0 2
a 4b 0 b . 4 2 2 a a
Khi đó: S a b a 1 1 1 , a . 4 2 2 a b b 1
Dấu “ ” xảy ra khi và chỉ khi 4 . a a 2 1 0 2 Vậy min S 1 , khi a 2 , b 1.
Câu 22. Cho các số thực a, , b c thỏa mãn 2 2 2
a b c 2a 4b 4 . Tính P a 2b 3c khi
biểu thức 2a b 2c 7 đạt giá trị lớn nhất. A. P 7 .
B. P 3. C. P 3 . D. P 7 .
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải Chọn B
Cách 1: phương pháp đại số. 2 2 Ta có: 2 2 2
a b c a b
a b 2 2 4 4 1 2 c 9 .
Áp dụng bất đẳng thức giá trị tuyệt đối và bất đẳng thức BCS, ta có kết quả sau:
2a b 2c 7 2a
1 b 2 2c 11 2a
1 b 2 2c 11 BCS a 2
1 b 22 c 2 1 2 2 2 2 2 11 20. 2a
1 b 2 2c 0 a 3
a 1 b 2 c
Đẳng thức xảy ra khi: b 3 2 1 2 a c 2 2 1 b 22 2 c 9 I Ơ Khi đó: P a 2b 3c 3 2.3 3. 2 3.
Cách 2: phương pháp hình học. M D Ầ
Trong không gian Oxyz , gọi mặt cầu S có tâm I 1;2;0 , bán kính R 3. Khi đó: Đ 2 2 2 2 2 2 NH
S:x 1
y 2 z 9 x y z 2x 4y 4. Ị Đ
và mặt phẳng P : 2x y 2z 7 0. G THPT N.C.Đ
a b c NG Gọi M ; a ;
b c , ta có: d M P 2 2 7 ; . CÔN Ờ 3 N 2 2 2 Ễ
Vì a b c 2a 4b 4 M S . Y TRƯ GU
d M ; P N
Bài toán đã cho trở thành: Tìm M S sao cho lớn nhất. N x 1 2t
Gọi là đường thẳng qua I và vuông góc P : y 2 t . ÁO VIÊ GI z 2t
Điểm M cần tìm chính là 1 trong 2 giao điểm của với S : M 3;3; 2 ,M 1 ;1;2 . 1 2 20 2 20
Ta có: d M ; P
d M ; P Maxd M ; P M M . 1 2 1 3 3 3
Vậy P a 2b 3c 3 2.3 3. 2 3.
Phân tích: Khi quan sát 2 cách giải, đối với giáo viên ta sẽ dễ chọn Cách 1 vì ngắn gọn và tiết
kiệm thời gian. Tuy nhiên học sinh không nhiều em đã từng được tiếp cận bất đẳng thức BCS.
Đối với Cách 2, về mặt trình bày có thể dài hơi, nhiều tính toán hơn nhưng đó chỉ là những
bước tính toán khá cơ bản, một học sinh khá nếu nhận ra ý đồ tác giả thì việc giải bài toán cũng
không mất quá nhiều thời gian. Bài toán sẽ dễ hơn nếu đề bài chỉ yêu cầu tìm Min hoặc Max của
biểu thức 2a b 2c 7 .
Câu 23. Cho ba số thực dương a, , b c thỏa mãn 2 2 2
a b c 2a 4b 6c 10 và a c 2 .
Tính giá trị biểu thức P 3a 2b c khi 2 2 2
Q a b c 14a 8b 18c đạt giá trị lớn nhất.
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 10. B. 10 . C. 12. D. 12 . Lời giải Chọn D
Gọi S là mặt cầu tâm I 1; 2
;3 , bán kính R 24 . Khi đó: S 2 2 2
: x y z 2x 4 y 6z 10.
Gọi P là mặt phẳng có phương trình x z 2 và điểm K 7;4; 9 . Với M ; a ;
b c . Theo giả thiết ta có: M S và M P M S P . Hơn nữa:
Q a b c a b
c a 2 b 2 c 2 2 2 2 2 14 8 18 7 4 9 146 KM 146 .
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu S và mặt
phẳng P sao cho KM lớn nhất. I Ơ M D Ầ Đ I NHỊ Đ B G THPT H A J N.C.Đ M NG CÔN Ờ P N Ễ Y TRƯ K GU N
P có VTPT n 1;0; 1. N x 7 t ÁO VIÊ
Gọi là đường thẳng qua K và vuông góc P : y 4 . GI z 9 t
Gọi H là hình chiếu của K lên mặt phẳng P H P H 9;4; 7 . Ta có: 2 2 2
KM KH HM , mà KH không đổi nên KM lớn nhất khi HM lớn nhất. x 1 t
Gọi d là đường thẳng qua I và vuông góc P d : y 2 . z 3 t
Gọi J là tâm đường tròn giao tuyến của S và P J là hình chiếu của I lên P
J d P J 0; 2 ;2 . x 3t
Phương trình đường thẳng HJ : y 2 2t. z 2 3t
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Gọi ,
A B là các giao điểm của HJ và S A 3 ; 4
;5,B3;0; 1 .
Ta có: HA 4 22 HB 2 22 .
Vậy MaxHM 4 22 M A 3 ; 4
;5 . Khi đó: P 3a 2b c 1 2.
Câu 24. Cho phương trình 4 3 2 x ax bx cx 1
0 có nghiệm. Giá trị nhỏ nhất 2 2 2 P a b c bằng 4 8 A. 2 . B. . C. . D. 4 . 3 3 Lời giải Chọn B Gọi x 4 3 2 x ax bx cx 1 0
0 là một nghiệm của phương trình (*). 4 3 2 3 2 4 x ax bx cx 1 0 ax bx cx x 1 0 0 0 0 0 0 0 0 .
Theo bất đẳng thức Bunhiacopxki ta có: I 2 2 4 3 2 2 2 2 6 4 2 x 1 ax bx cx a b c x x x 0 0 0 0 0 0 0 Ơ 2 4 x 1 2 2 2 0 M D a b c ( x
0 không là nghiệm của phương trình (*) ). 6 4 2 Ầ x x x 0 0 0 0 Đ 2 2 NH t 1 Ị Đặt 2 t x (t 0) 2 2 2 a b c 0 ta có 3 2 . Đ t t t G THPT 2 2 N.C.Đ t 1 NG Đặt f t (t 0) 3 2 CÔN t t t Ờ N 2 3 3 3 2 4 2 2 4 2 Ễ 4t 4t t t t t 2t 1 3t 2t 1 t 1 (t 1) t 1 t 1 t 1 / Y f t TRƯ 2 2 2 3 2 3 2 3 2 t t t t t t t t t GU N N Bảng biến thiên: ÁO VIÊ GI 4 4
Từ bảng biến thiên ta có min f t khi t 1 2 2 2 a b c . 0 3 3 2 4 Khi a b c thì 2 2 2 a b c và phương trình 4 3 2 x ax bx cx 1 0 có 3 3 nghiệm x 1 0 . 4 Vậy giá trị nhỏ nhất 2 2 2 P a b c bằng . 3
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 25. Biết hai hàm số f x 3 2
x ax 4x 2 và g x 3 2
x bx 2x 3 có chung ít nhất một
điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P a b . A. 3 2 . B. 6 2 . C. 6. D. 3. Lời giải Chọn C
Ta có f x 2
3x 2ax 4 và gx 2 3
x 2bx 2 .
Vì f x và g x có chung ít nhất một điểm cực trị nên f x 0 và g x 0 có chung 2 3 t 4 2 a 3
t 2at 4 0 2t
nghiệm là t . Suy ra . 2 2 3
t 2bt 2 0 3t 2 b 2t 2 2 2 3 t 4 3t 2 3t 3 1
Ta có P a b
3 t 6. (bất đẳng thức Cauchy) I 2t 2t t t Ơ 1
Dấu bằng xảy ra khi và chỉ khi t t 1 . M D t Ầ Đ Vậy min P 6. NHỊ Đ G BÀI TẬP BỔ SUNG THPT N.C.Đ
NG Bài 1 : Cho các số thực a, b, c thuộc đoạn 3 ; 1
và thỏa mãn điều kiện a b c 6. Tìm giá trị CÔN Ờ N
a2b2 b2c2 c2a2 abc 12 72 1 Ễ
lớn nhất của biểu thức P abc Y TRƯ
ab bc ca 2 GU N Lời giải N
Ta có: ab bc ca2 a2b2 b2c2 c2a2 2
abc a b c a2b2 b2c2 c2a2 abc 12
a b c2
Đặt x ab bc ca 12 ÁO VIÊ 3 GI Ta có: , a , b c 3 ; 1 a 1 b 1 c
1 0 abc ab bc
ac a b c 1 0
abc x 5 0 abc x 5 Lại có: a 3 b 3 c 3 0 abc
3 ab bc ca
9 a b c 27 0
abc 3x 27. Do đó: 3x 27 abc x 5 2x 22 x 11. 2 x 72 1 2 x 72 1 x 72 5 Ta có: P abc
x 5 x 2 x 2 2 x 2 x 72 5
Xét hàm số f (x) , x 12 ; 11 2 x 2 1 72 160
Ta có: f '(x) 0 x 12 ; 11
nên P f (x) f ) 11 ( 2 2 x 11 160 Vậy max P khi a ; 1 b ; 2 c 3 11
Nhận xét: Đây là bài toán rất hay. Ta phải dùng hai lần giả thiết của các biến ; a ; b c 3 ; 1
để tìm ra miền giá trị của x ab bc ca và đánh giá được P thông qua biến x.
Cũng từ bài toán trên phải chăng bằng việc đánh giá điều kiện ban đầu chúng ta sẽ giải quyết
được một lớp các bài toán dạng này bằng cách đưa về hàm số một biến, chính vì vậy qua chuyên
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
đề này tác giả muốn rèn luyện cho học sinh kỹ năng giải toán cực trị bằng phương pháp dồn biến. Bài 2: Cho , x y, z 2 ; 1
. Tìm giá trị lớn nhất của biểu thức
2 xy yz zx 8 y z 4 A xyz
2 2x y z
2xy z yz 4 yz 1 Lời giải Vì , x y, z 2 ; 1 , nên ta có x
1 y 2z 2 0 xyz
2 2x y z
2 y zx yz 4
Dấu bằng xảy ra khi x 1 hoặc y 2 hoặc z 2 . Do đó
2 xy yz zx 8 y z 4
2xy z yz 4 yz 4 y z 4 A
2xy z yz 4
2xy z yz 4 yz 4
2xy z yz 4 yz 1 yz 4 y z 4 yz 4 y z 4 A 1
2xy z 1 yz 4 yz 1
2 y z yz 4 yz 1 I yz 4 2 yz 4 Ơ A 1
yz 4 yz 4 yz 1 M D
Đặt t yz ; t 2 ; 1 Ầ Đ 2 t 4 2t 4
Xét hàm số: f (t) 1 với t 2 ; 1 NH 2 Ị t 2 t 1 Đ 4t 8 2 4 2 G f t THPT Ta có ( )
, nên f(t) đồng biến trên 2 ; 1 . t 23 t 0 1 2 27 9 N.C.Đ NG 7 CÔN Ờ
Suy ra A f (t) f (2) N 6 Ễ 7 Y TRƯ
Vậy max A khi x ; 1 y z 2 6 GU N a , 1 b , 2 c N Bài 3:
Cho các số thực không âm a, b, c thỏa mãn
3 . Tìm giá trị lớn nhất của biểu thức
2 2ab ac bc 8 b b ÁO VIÊ B
1 2a b 3c
b c ba c 8 2 2 2 a b c GI 12 3 27 8 Lời giải Ta có a 12 2 b 3 2 c 27 2 3 a 4 2 b2 c 9 2 a 2 b c 3 (1)
Mặt khác 2a b 3c b c
b a c a c2 b 0 a 2 b c
3 b c
b a c (2)
Lại có 2ab ac bc b c
b a c b ca 1 0 ab 2
ac bc b c
b a c (3)
Từ (1), (2), (3) ta được
2b c ba c 8 B b b
1 b c b(a c)
b c b(a c) 8
b c b(a c) 8
2b c ba c 8 B
1 b c b(a c)
b c b(a c) 8
Đặt t b c b(a c) 0 t 13 2t 8
Xét hàm số f (t) với t 13 ; 0 t 1 t 8
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 8 2 3t 10 6 t f ( t) t t 1 2 t 82
t 12t 8 0 6 2 16 47 f (0) , 1 f ( ) 6 , f ) 13 ( 7 21 16 16 2
Từ đó suy ra B f (t) max B
đạt được khi a , 1 b , 2 c 7 7 3 Bài 4:
Cho x, y, z là các số thực dương thỏa mãn y z x 2 2
y z . Tìm giá trị nhỏ nhất của 1 1 1 4 biểu thức P 1 x2
1 y2 1 z2 1 x1 y1 z Lời giải 2 2 2 2
Từ giả thiết ta có: xy z 2xy z
2 y z y z x 2 2 1 1 2 1 x
Do đó: 1 y1 z 2 y z2 2 2 4 4 x x I 1 2 4
Áp dụng bất đẳng thức Cauchy ta có: P Ơ
1 x2 1 y1 z 1 x1 y1 z 2 2 3 2 2x 1 4x
2x 6x x 1 M D P 2 3 Ầ
1 x 1 x 1 x3 Đ 3 2
2x 6x x 1 NH Ị
Xét hàm số: f (x) 1 x3 Đ G 25x THPT 1 1
Ta có: f '(x) 0 x . 4 N.C.Đ 1 x 5 NG CÔN Ờ 1 91
P f x f N
Lập bảng biến thiên ta được: ( ) Ễ 5 108 Y TRƯ 91 1
Vậy giá trị nhỏ nhất của P bằng
. Khi x , y z 5 . GU N 108 5 N Bài 5:
Cho a b c 0. Tìm giá trị nhỏ nhất của biểu thức P 1 1 1 2 a 2 b 2
c ab bc ca ÁO VIÊ
a b2 b c2 c a2 GI Lời giải
Nhận xét: Giả thiết đã cho chính là gợi ý của bài toán. Cách làm giảm biến số quen thuộc là đặt
a c x, b c y x y 0 Khi đó:
a2 b2 c2 ab bc ca c x2 c y2 c2 c xc y c yc cc x
x2 y2 xy 1 1 1
Do đó ta viết lại P dưới dạng P 2 x xy 2 y
x y2 2 2 y x
Như vậy với cách đặt ẩn phụ này, ta đã làm giảm số biến của P thành hai biến.
Thậm chí là P là đồng bậc giữa x và y. Ta chỉ việc đặt ẩn phụ quen thuộc x 2 1 1 Đặt t
1 ta được P t t 1 1 f (t y t ); 1 2 2 t
Xét hàm f(t) trên ; 1 ta có:
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
f '(t) 2t 1 1 1 1 2 2 t t 1 2 2 2 t 1 t t 3 3 1 t
2t 1 3tt 1tt 3 3
1 t t 3 1 2
2 t t 1 3
t t 3 1 f '(t) 3 t t 3 1
Cách đặt này khá phức tạp. Ta có thể đặt theo cách khác sau đây x y Đặt t
t 2 . Khi đó ta có y x x y xy xy xy x y 1 x y
P 1 1 y
x x y2 2 2 y x y x x y y x 2 y x
P t 1 t 13 1 t f (t) t 2 t 2
Xét hàm f(t) trên ; 2
ta được:ln f (t) 3ln(t )1 ln(t ) 2 I Ơ f ' (t) 3 1 2t 5 f (t) t 1 t 2
t 1t 2 M D 2t 5 t 1 2 5 Ầ f '(t)
f '(t) 0 t Đ t 22 2 NHỊ 5 27 Đ
Lập bảng biến thiên ta được P f (t) f 2 4 G THPT N.C.Đ x y 5
Đẳng thức xảy ra khi và chỉ khi
t x 2y a b d c 2d,d 0 NG y x 2 CÔN Ờ N 27 Ễ
Vậy giá trị nhỏ nhất của biểu thức P là Y 4
TRƯ Bài 6: Cho ,x y,z ;0xy zx y z 20. Tìm giá trị nhỏ nhất của P x yx z 2 2 y z GU N N Lời giải
Nhận xét:Có một chú ý quan trọng của bài 6 là một phép biến đổi nhỏ ÁO VIÊ x 2 20
yx z x xy xz yz xx y z yz yz GI yz
Như vậy biến mới được hình thành. 20 2 20
Đặt t yz 0 suy ra 2 P
t t f (t) . Xét f t() t t trên ; 0 t t 20 2 3 2 t t 20
t 22 2t 5t 10 Ta có: f (
t) 2t 1 0 t 2 2 2 2 t t t
Lập bảng biến thiên ta suy ra f (t) f (2) 16
xyz x y z 10 x y 2
Do đó P 16 . Đẳng thức xảy ra khi và chỉ khi yz 2 z 1 x y 2
Kết luận: min P 16 z 1 1 a b b c c a Bài 7:
Cho a, b, c 1 ;
. Tìm giá trị lớn nhất của biểu thức P 2 c a b Lời giải
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 29
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Nhận xét:Khi gặp bài toán trên, ta chưa thể tìm cách phá giá dấu giá trị tuyệt đối. Do vậy cứ
thử quy đồng và tách tung ra xem có gì đặc biệt không. Bởi vì lưu ý rằng: khi cho a ,
b b c, c a P 0 . Nên sau khi biến đổi chắc chắn sẽ chứa nhân tử a bb cc a
ab a b
bc b c cac a
ab a b
bc a b
bc a c caa c Do đó: P abc abc
a bb cc a P abc 1 Đến đây ta giả sử
c b a 1 để mục tiêu làm mất dấu giá trị tuyệt đối. 2
a bb cc a P abc
Nhận xét rằng có một phép biến đổi làm giảm biến số một cách đơn giản là x a c Đặt:
1 y x 2 b I y Ơ
c x yy 1x 1 x1 x P .x 1 y
f x; y M D Ta có: xy x y Ầ Đ
Mục tiêu viết như trên là đạo hàm theo biến y (hoặc biến x). NHỊ x 1 x Đ f ; . 1 ; 0 ; 1 y x y f 2 y x y y x x x y G THPT N.C.Đ
Lập bảng biến thiên ta thu được NG 2 2 CÔN x x x x t t t t Ờ P f ;
x y f ; x x
1 1 1 1 ,t x 3 ;1 2 N x x t Ễ Y TRƯ
t 13t 1 hay P g(t) 2 GU N t N ;1 2 Xét hàm g(t) trên ta có: ln g t ( ) . 3 ln t 1 ln t 1 . 2 ln t g ( t) 3 1 2 3 2 t 3 2
t t t 2 2 t 2 2 2 t 2t 2 ; 0 t ; 1 2 ÁO VIÊ g(t) t 1 t 1 t
t 1t 1t
t 1t 1t GI 3 2 2 1 2 1 2 1
Từ đó ta có g(t) g 2 . 2 2 2 2 1
Như vậy P g(t) 2 y x x 2 a 2c 2 1
Đẳng thức xảy ra khi ; a ; b c ;1 ;
t x 2 y 2 b c 2 2 2 2 2 1 2 1 Vậy max P ; a ; b c ;1 ; 2 2 2 c c Bài 8: Cho 2 2 2 2 a, , b c ,
0 a 2b a b . Tìm giá trị lớn nhất của P c 2 1 b a Lời giải
Nhận xét: Giả thiết chỉ cho dữ liệu liên quan tới a, b dù không dự đoán được đẳng thức xảy ra
nhưng ta vẫn có thể khai thác được giả thiết bằng bất đẳng thức Cauchy-Schwarz với mục tiêu là chỉ còn biến c.
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 30
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 c x c y 2 2 2 c c 2 2 x y Ta có: . . 2 2 2 2 x b y a x y b a 2 2 2 2 1 2
Từ thiết a 2b a b 1 2 2 b a Như vậy ta phải chọn 2 x , 1 2 y 2 2 2 c c c c 2 1 2 2 3 Do đó ta có: P c 1 c 1 2 c
c 2c 1 b a 1 2 2 2 b a 2 2 6
P c 2
c 1 f (c) 2 6 6
Xét hàm số f(c) trên ; 0
ta có: f (c) 2 c 2
f (c) 0 c 1 2 4 2 6 6 3 6
Lập bảng biến thiên ta suy ra: P f (c) f 1 1 1 I 4 4 8 2 Ơ 3 6 6 6 Vậy max P
a 6,b , c 1 8 2 2 4 M D
Ầ Bài 9: Cho a, b, c là các số thực thỏa mãn a,c ;
1 b 2 . Tìm giá trị nhỏ nhất của biểu thức Đ
ab c
ca b
3a c2 2 2 NH b 8 Ị P b c 2 b 2a 4 3 ac Đ G THPT Lời giải N.C.Đ
Ta có 1 a2 b 0 2 2a b ab 0 2a b ab 2 NG CÔN 1 1
ca b
ca b Ờ N b a ab b a ab Ễ 2 2 2 2 Y TRƯ
ab c
ab c Tương tự ta có GU N b 2c bc 2 N Lại có
3a c2 2 2 b 8 2 ac2 2
b a c2 8
4 a cb 4ac 8
4 ab ac bc 2 ÁO VIÊ
ca b
ab c
4 ab bc ca 2 P GI ab 2 bc 2 4 ac 3 ac bc
ab bc
ab bc ca 2 1 1 2 ab 2 bc 2 ac 3
ab bc ca
ab bc ca 2 1 1 1 9 3 2 2
ab 2 bc 2 ac 3
ab bc ca 7 9 t 2 45 45 13
Xét hàm số f (t) 2 7
mà t ab bc ca 5 P 7 t 7 t 7 5 7 4 13 Vậy min P ; a ; b c ; 1 1 ; 2 4
Bài 10: Cho các số thực , x y, z 1 ; 0 và z mi n x, y,
z . Tìm giá trị nhỏ nhất của biểu thức y z2 yz 1 2 P x z
yy z
xy xz yz Lời giải
Với những bài toán có điều kiện ban đầu , x y, z 1 ; 0
chúng ta sẽ tìm cách khai thác nó,
dự đoán điểm rơi là z y ; 1 z 0
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 31
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 Hơn nữa với
có chứa xy xz yz ở mẫu, đây là hạng tử có thể gợi ý cho
xy xz yz
chúng ta dồn biến về xy xz yz. y z2 2
x y z2
x2 y z2 Ta có x 1 ; 0
suy ra x x ; x z x x z x x z 1
Áp dụng bất đẳng thức Cauchy ta được 2
. Dấu bằng xảy ra khi và chỉ khi A B . A B
A B 0 . Vì dự đoán điểm rơi z y ;
1 z 0 nên khả năng x x z và y y z là
hoàn toàn có thể xảy ra.
x2 y z2 yz 12 2 2 2 2 2 Ta có:
x y z . và yz 1 .
xx z 2x z
yy z 2 y z
2x2 y z2 2 yz 1 2 2
xy yz xz 12 2 Do đó P 2x z 2 y z
xy xz yz
x y z
xy xz yz Với điều kiện , x y, z 1 ; 0 ta luôn có I
1 x1 y1 z Ơ
0 xy yz xz 1 xyz x y z x y z Suy ra P 2
x y z M D
xy xz yz Ầ Đ
Áp dụng bất đẳng thức Cauchyta có NH 2 2 2 2 2 Ị
x y z 2
x y z x y z
2 xy xz yz Đ
Mà x, y, z 1 ; 0
x y z x2 y2 z2
2 xy xz yz G THPT 2 N.C.Đ P
2 xy xz yz 4 NG
xy xz yz CÔN Ờ N x y 1 Ễ
Dấu bằng xảy ra khi và chỉ khi Y z TRƯ 0 x y GU N
Vậy min P 4 đạt được khi ; 1 x 0 N
Bài 11: Cho các số , a , b c 1 ; 0
. Tìm giá trị lớn nhất của biểu thức a b c P abc ÁO VIÊ 1 bc 1 ac 1 ab GI Lời giải
Không mất tính tổng quát của bài toán, ta có thể giả sử 0 c b a 1 a b c 1 b c 1 b c Ta có P abc
bc bc 1 bc 1 ac 1 ab 1 bc 1 bc 1 bc 1 bc 1 bc b c
Từ giả thiết ta được 1 b1 c 0 1 bc b c 0 1 1 bc 1 1
Suy ra A bc 1
. Đặt t 1 bc 1 t 2 . Xét hàm số f (t) t ;t ; 1 2 1 bc t 1 5
Ta có f '(t) 1 0t ;
1 2 suy ra f(t) đồng biến trên ;
1 2 f (t) f (2) . 2 t 2 5
Vậy giá trị lớn nhất của biểu thức P là khi a b c 1 2
a2 b2 2ab
Bài 12: Cho các số thực , a , b c 2 ; 1
. Tìm giá trị nhỏ nhất của biểu thức: P c2
4 ab bc ca Lời giải
Áp dụng hệ quả 1 a b2 4ab
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 32
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
a2 b2 2ab a b2 Ta có P c2
4 ab bc ca c2 c
4 a b a M b 2 Do , a , b c 2 ; 1
nên a b 0 , chia tử và mẫu của M cho a 2 b ta được: 1 1 c M với t . 2 2 c c t 4t 1 a b 4 1 a b a b c 1 1 1 Với , a , b c 2 ; 1 và t t 1 ;
. Xét hàm số f (t) trên 1 ; a b 4 2 t 4t 1 4 2 t 2 1 1
Ta có f '(t) , t 1 ;
f (t) nghịch biến trên 1 ; 2 2 t 4t 0 1 4 4 1 1 1
f (t) f ) 1 ( ;t 1 ; hay P 6 4 6 1 Vậy MinP
, giá trị nhỏ nhất đạt được khi a b 1và c 2 6 I c 3 3
a b c c
Ơ Bài 13: Cho các số không âm a, b, c thỏa mãn 0 và
1. Tìm giá trị nhỏ nhất của 2 2 2
a b c biểu thức: P M D
a b c2 Ầ Đ Lời giải NHỊ
Nhận xét: từ giả thiết ta nhận thấy các biến a và b có tính chất đối xứng, do đó để giải bài toán Đ a b 2 2 2 G THPT ta sử dụng a b 2 N.C.Đ NG a b 2 2 a b CÔN Ờ 2 c 2 N 2 c Ễ Ta có: P
vì c 0 2 Y
a b c 2 a b TRƯ 2 1 c GU N N 1 3 1
Với hai số thực x, y tùy ý, ta có 2 2
x xy y
x y2 x y2 x y2 . 4 4 4 3 3
a b cc ÁO VIÊ
Từ giả thiết c 0và
1 sử dụng đánh giá trên ta thu được GI a b a b a b 2 3 3
c c a b c a b 2
a ab b 3 2 3 c 2 . c 0 1. 4 4 c a b 2 t 2 Đặt t
0 t 1 (vì a,b 0 và c 0). Khi đó P c 2t 2 1 2 t 2 t 2
Xét hàm số f (t) trên 1 ; 0
, ta có f '(t) , t 1 ; 0 2 t 2 1 t 0 1 3 3
Do đó f (t) là hàm số nghịch biến trên 1 ; 0
f (t) f ) 1 ( , t 1 ; 0 8 3 Hay P , a, ,
b c 0 thỏa mãn c 0 và 3 3
a b cc 1 . 8 3
Vậy MinP , giá trị nhỏ nhất đạt được khi a b ; 1 c 2 8
Bài 14: Cho x, y, z 0 thoả mãn x y z 0 . Tìm giá trị nhỏ nhất của biểu thức 3 3 3
x y 16z P
x y z3 Lời giải
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 33
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 3 3 3 x y z Ta có P 16
x y z
x y z
x y z 3 3 3 3 x y 1 x y 1 z
Áp dụng hệ quả 2 ta có 1
x y z
x y z
4 x y z 4
x y z 3 3 1 z z z Do đó P 1 16 . Đặt t t 1 ; 0 . 4
x y z
x y z
x y z 1 1 Khi đó P 1 t3 3
16t . Xét hàm số f (t) 1 t3 3 16t trên 1 ; 0 4 4 t 1 2 189t 6t 1 ; 0 3 9
Ta có f '(t)
f '(t) 0 4
t 1 1 ; 0 7 1 16 16
Lập bảng biến thiên suy ra f (t) f , t 1 ; 0
P f (t) I 9 81 81 Ơ 16 Vậy MinP
, giá trị nhỏ nhất đạt được khi x y 4z 81 M D Ầ
Đ Bài 15: Cho x, y, zlà ba số thực thuộc đoạn 2 ;
1 . Tìm giá trị nhỏ nhất của biểu thức NHỊ x y2 Đ P 2 2 2 G
2 x y z 2 x y 2 THPT z N.C.Đ Lời giải NG 2 2 2 2 2 CÔN Ờ
Nhận xét: Ta chỉ cần biến đổi
2 x y z
2 x y z z
4 x yz 4xy N 2 2 Ễ x y x y Y TRƯ Ta có P
2 x y z2
2 x2 y2 z2 z2
4 x yz 4xy GU N 2 N x y x y 2 z z
Ta có xy x 2 4 y .Do đó P 2 z
4 x yz x y2 2 ÁO VIÊ x y x y 1 4 GI z z z z x y 2 t Đặt t
, vì x, y, z thuộc đoạn ; 1 2 t 4 ; 1 . Khi đó ta có P z z 2 1 4t t 2 t
Xét hàm f (t) trên ; 1 4 2 1 4t t 4 2 t 2t
Ta có f '(t) f '(t) t 4 ; 1 f (t) 2 , . Suy ra
là hàm số đồng biến trên 1 4 2 t t 0 1 1 ;
1 4.Do đó f (t) f ) 1 ( , t 4 ; 1 hay P , , x y, z 2 ; 1 6 6 1 Vậy MinP
, giá trị nhỏ nhất đạt được khi x y 1 và z 2 6 1 2 2
Bài 16: Cho các số thực a, , b c 0 thỏa mãn
. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 c a b a b c P 2 2 2 b c a c
a b c
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 34
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Lời giải a b 1
Vì c 0do đó ta có P c c 2 2 b a 1 1 a b 1 c c c c a b Đặt x , y
x, y 0 (vì a, ,
b c 0 ) khi đó biểu thức P trở thành c c x y 1 P y 1 x 1 2 2 x y 1 1 2 2 Biến đổi giả thiết ta thu được 2 2 2 c a b 2 2 1 2 2 1 c c 1 1 1 2 2 x y 2 2 2 x y 2 2 2 2 2 2 2 c a b 2 a b 2 x y
Ta có x2 y2
2 x2 y2 x y2 xy x y I và 2 2
x y 1 x y2 2xy 1 x y2
2 x y1 x y 2 1 (1) Ơ
Ta lại có x y2 4xy
4 x y x y 4 (2) (vì x, y 0 ) M D 2 2
x y 1 x y 1 Ầ Từ (1) và (2) Đ
Biến đổi biểu thức P, ta thu được NHỊ x y 1 1 1 1 Đ P 2 1 1
x y 1 2 2 2 2 G y 1 x 1 x y
x 1 y 1 x y THPT 1 1 N.C.Đ 4 1 4 1 NG
Từ hệ quả 3, ta có: P 2 x y 1 P 2 CÔN Ờ x y 2 x y 1 x y 2 x y 1 N Ễ 4 1
t x y t P 2 Y Đặt 4 . Do đó TRƯ t 2 t 1 GU N 4 1 f t N Xét hàm số ( ) 2 trên ; 4 t 2 t 1 3tt 4
Ta có f '(t)
, t ; 4
và f '(t) 0 t 4 (vì t ; 4 ) ÁO VIÊ
t 12t 0 2 2 GI
Suy ra f (t) là hàm số đồng biến trên ; 4 5 5
f (t) f (4) , t ; 4
hay P f (t) 3 3 5 Vậy MinP
giá trị nhỏ nhất đạt được khi a b c 2 3
Bài 17: Cho các số thực dương x, y, z thay đổi thỏa mãn điều kiện x 2 y z 0 . Tìm giá trị nhỏ x y x 2 y
nhất của biểu thức: P 10y z
x y z 2x 3y Lời giải
x y z 2x 3y
Ta có x 2 y z 0 z x 2 y
10y z x 12y x y x 2 y x y x 2 y Do đó P 10y z
x y z 2x 3y x 12y 2x 3y 2x 3y
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 35
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x x 3 x x 3 P
y y y x 12y 2x 3y x x 12 2 3 y y x t t 3 Đặt t
t 0 . Khi đó P . y t 12 2t 3 t t 3
Xét hàm số f (t) trên ; 0 t 12 2t 3 t 2 ; 0 12t 3
Ta có f '(t)
f '(t) 0 t 12 2 4 2t 2 3 2 2 18 t 12 2t 3
t ; 0 5 6 6
Lập bảng biến thiên suy ra f (t) f (2) , t ; 0 . Suy ra P . 7 7 6 Vậy MinP
, giá trị nhỏ nhất đạt được khi x 2 y, z 4 y . 7 I Ơ
Nhận xét ta có thể coi P là hàm của z và x, y là tham số và xét hàm P(z) trên ;
0 x 2y
M D Bài 18: Cho các số thực dương a, b, c thay đổi thỏa mãn điều kiện a b,a c . Tìm giá trị lớn Ầ Đ a b c
nhất của biểu thức: P NHỊ
5 a b c a 5 c 2 a 5 b 2 Đ Lời giải G THPT b N.C.Đ c NG 1 Vì a 0 do đó a a P CÔN Ờ b c c b N 51 5 . 2 5 . 2 Ễ a a a a Y TRƯ b x GU N a N Đặt
x, y 1 ; 0 vì a, ,
b c 0 và a b, a c . c y a ÁO VIÊ 1 x y GI
Khi đó biểu thức P được viết lại như sau: P
5 1 x y 5 2 y 5 2x 2 1 1 2P 2
2x 2y 5
5 1 x y
5 2y 5 2x 1 1 4 Ta có
và 2x 2y 5 , 0 , x y 1 ; 0 5 2x 5 2 y
10 2x 2 y 2 4 Do đó 2P 2
2x 2y 5
5 1 x y 102x2y 2 5 hay P
5 1 x y 1 5 x y
Đặt t x y t 2 ; 0 vì , x y 1 ; 0 . 2 5 Khi đó ta có P 5 t 1 1 5 t 2 5
Xét hàm số f (t) trên 2 ; 0 5 t 1 1 5 t
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 36
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 25 t 1 2 t 52 24 2 t 60t
Ta có f '(t) , 0 t 2 ; 0
5t 12t 52
5t 12t 5 2 11
Do đó f (t) là hàm số đồng biến trên ;
0 2 f (t) f (2) , t ; 0 2 15 11 hay P , với mọi a, ,
b c 0 thỏa mãn điều kiện a b, a c . 15 11 Vậy MaxP
, giá trị lớn nhất đạt được khi a b c 15
Bài 19: Cho ba số thực dương x, y, z thỏa mãn 0 x y z . Tìm giá trị nhỏ nhất của biểu thức: x3z y4 z3 15x3 P
y2 xz y2
z2 xz y2 x2z Lời giải 3 x 3 y
a,b,c 0 2 I y z z 15 x y z P a ;b ;c abc Ơ Ta có . Đặt 1 x y x y x z y z x c 1 y z y z x M D 3 3 Ầ a b 2 15 Đ Do đó: P c a b a b c NHỊ ab a b 2 15 2 16 Đ
Áp dụng hệ quả2, ta có P c c G a b c c THPT N.C.Đ 16 2 16
Xét hàm số f (c) c trên ; 1
. Ta có f '(c) 2c f '(c) 0 c 2 NG c 2 c CÔN Ờ N
Lập bảng biến thiên suy ra f ( ) c f ( ) 2 , 12 c ; 1 Ễ Y TRƯ 1 a b
Vậy MinP 12giá trị nhỏ nhất đạt được khi
2 hay 2x y 2 z GU N N c 2 ab
Bài 20: Cho a, b, c là các số thực dương thỏa mãn a c b c
. Tìm giá trị nhỏ nhất ÁO VIÊ c GI 2 a b c c
của biểu thức: P 2 2 b c c a a b a b Lời giải Đặt a . x ; c b . y ; c , x y 1
Thay x 1 vào giả thiết ta có: b c b c 0 (không thỏa mãn giả thiết)
Tương tự y 1 cũng không thỏa mãn . x ;
1 y 1 thay vào giả thiết ta có: x 1 y 1
xy x y 2 2 x 1 y 1 xy 2
x x y 1 2 x 1 y
1 1 0 x 1 y 1 1 0 x 1 y
1 1 xy x y 2 xy xy 4 Mặt khác x y 1 1 x2 y2 1 1 P y 1 x 1 x y x2 y2 xy x xy y x y
x y2 2xy
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 37
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x y2 1 1 P
2xy x y x y
x y2 2xy xy 1 1 xy3
2 xy2 3xy 3 Hay P 3 xy
x2 y2 2xy 3 xy2 2 xy t3 t 2 2 t 3 3 Đặt t ;
xy t 4 , khi đó ta có P 3 t 2 t 2 t3 t 2 2 t 3 3 Xét hàm số f t ( ) trên ; 4 3 t2 t 2 4 t 4 3 2
t t 6t 6 3 t t 4 2 t 6 t 4 18
Ta có f '(t) t 2 2 3 2 t 2t 3 2t 2t , 0 4 41
Suy ra hàm số f (t) đồng biến trên ; 4
. Do đó: min f (t) f (4) 4; 24 41 Vậy min P
khi x y 2 hay a b c 2 24 I
Ơ Bài 21: Cho a,b, c là các số thực dương thỏa mãn: a b c. Tìm giá trị nhỏ nhất của biểu thức:
a2 c2 abbc ca M D T
abc a b c Ầ Đ Lời giải NHỊ Đặt a x b . ; c y b
. 0 y 1 x Đ 2 2
x y x y xy
x y2 x y xy G THPT Khi đó T N.C.Đ
xy x y 1 2
xy x y 1 NG S 1 CÔN Ờ
Đặt S x y; P xy vì 0 y 1 x
0 P S N x 1 y 1 1 0 Ễ Y TRƯ 4
S S P 4
S 2S P Đặt f (P)
ta có f '(P) , 0 P ; 0 S 1 2 3 2 GU N 4P S 2 1 4P S 1 N
Do đó f P là hàm số nghịch biến trên 0; S 1 4 4 S 2S 1 S 2S 1 ÁO VIÊ
f (P) f (S ) 1 , P ; 0 S S 1 2
. Xét hàm số g(S) 4 2S 1 1 với 4 S 2 2 GI 1 S 2 2 S 2S 1 3 S Ta có g'(S)
g'(S) 0 S S 1 3 (vì ). 2 2S 2 1 4
Từ bảng biến thiên suy ra g(S) g( ) 2 , S ; 1 3 2 Do đó ta có T f (P) g(S) g( ) 2 . 3 2 Vậy MinT
, giá trị nhỏ nhất đạt được khi x y 1 hay a b c 3
Bài 22: Cho x, y, z là các số thực dương thỏa mãn: 2 2 2
x y z 1 . Tìm giá trị lớn nhất của biểu 3 3 3 3 xy yz x y y z thức: P 2 2 3 3 1 z 1 x 24x z Lời giải
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 38
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Nhận xét: Bài 22 khi ta thay giả thiết 2 2 2
x y z 1 vào biểu thức P thì P là một biểu thức
đồng bậc. Tuy nhiên nếu chỉ sử dụng các biến đổi đại số thì ta vẫn chưa làm giảm số biến của biểu
thức. Ta cần sử dụng các hệ quả để đánh giá biểu thức xy yz xy yz Ta có 2 2 1 z 1 x 2 2
x z 2 2
y z 2 2
x y 2 2 x z xy yz xy yz 2 2 1 z 1 x 2 2 2 x z 2 2 y z 2 2 2 x y 2 2 x z xy yz 1 2 2 x y 1 2 2 y z 2 2 2 2 2 2 2 2 2 2 1 z 1 x 4 x z
z y 4 x y x z xy yz 1 y2 y2 1 y2 y2 1 2 2 2 2 2 2 1 1 z 1 x 4 z y
x y 4 2 yz 2xy xy yz 1 1 y y 1 z 2 1 x2 4 8 z x 3 3 3 3 3 I 1 x y y z 1 xy yz 1 y y 3 3 3 3 x y y z xy yz3 3 Ơ Ta lại có . 3 3 3 3 4 x z 4 x z 4 z x 3 M D 1 1 y y 1 y y y y Vậy P
. Đặt t t 0 (vì x, y, z 0 ) Ầ 4 8 z x 96 z x z x Đ NH 1 1 1 3 Ị Khi đó P t t Đ 4 8 96 G THPT 1 1 1 Xét hàm số 3 f (t) t t trên N.C ; 0 .Đ 4 8 96 NG CÔN 1 1 Ờ Ta có f '(t) 2
t f ' (t) 0 t 2 (vì t 0 ) N 8 32 Ễ Y TRƯ 5 5
Lập bảng biến thiên suy ra f (t) f ( ) 2 , t ;
0 hay P f (t) GU N 12 12 N 5 1 Vậy MaxP
, giá trị lớn nhất đạt được khi x y z 12 3 ÁO VIÊ GI 4 4 x y z x
Bài 23: Cho x, y, z là các số thực dương thỏa mãn 2 y z x z 2 y2 2z2 3z
Tìm giá trị lớn nhất của biểu thức: P x2 y2 y2 z2 2x z Lời giải Từ giả thiết ta có 4 4 4 4 2 2 x x y z
x y z x z x x z 2 2 . 2 2 2 2 y z x
y z x z x z z x x Đặt t
t 0 (vì x, z 0 ). z 2 1 3 2 1
Do đó t 2 2t 2t t 2t 1 0 t 1 t 1 2t 1 0 t 1 t 2 2 2 3 Ta có P 2 2 x y x 2 1 1 1 y z z
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 39
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x y x x x y x y Nhận xét: .
vì 1 . 1. Mặt khác x, y, z 0 , 0 y z z z y z y z 1 1 2 2 Do đó 2 2 x y x x y 1 . 1 1 1 y z z y z 4 3 4 3 4 3 1 Vậy P
. Xét hàm số f (t) trên 1 ; x x 1 t 2t 1 1 t 2t 1 2 1 2 1 z z 10 2 t 4t 2 1
Ta có f '(t) , 0 t 1 ;
t 122t 2 1 2 1 1 7 1
Suy ra f (t) là hàm số nghịch biến trên 1 ;
f (t) f ,t 1 ; 2 2 6 2 4 4 7 x y z x Hay P
với mọi x, y, z 0 thỏa mãn 2 6 y z x z I 7 z Ơ 2x Vậy MaxP
, giá trị lớn nhất đạt được khi 6 y x 2 M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
TÌM GTLN, GTNN CỦA HÀM NHIỀU BIẾN 40
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHỦ ĐỀ: GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
VẬN DỤNG – VẬN DỤNG CAO DẠNG 3 BÀI TOÁN TỐI ƯU Câu 1.
Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B 1 2 1 2 như hình vẽ bên.
Người ta chia elip bởi parabol có đỉnh B B B M , N 1 , trục đối xứng 1 2 và đi qua các điểm
. Sau đó sơn phần tô đậm với giá 200.000 đồng/ 2
m và trang trí đèn led phần còn lại với giá 500.000 đồng/ 2
m . Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng A A 4 , m B B 2 , m MN 2m 1 2 1 2 . B M 2 N I Ơ A1 A2 M D Ầ Đ NHỊ B1 Đ G THPT
A. 2.341.000 đồng. B. 2.057.000 đồ N.C
ng. .Đ C. 2.760.000 đồng. D. 1.664.000 đồng.
NG Câu 2. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy CÔN Ờ N
luật s t 3 2
t 4t 12 (m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển ỄY TRƯ
động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu? GU N 8 4 N A. 2 (s). B. (s). C. 0 (s). D. (s). 3 3 Câu 3.
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán ÁO VIÊ
kính 10cm (hình vẽ). GI A. 2 160cm . B. 2 100cm . C. 2 80cm . D. 2 200cm . D C x A O B 10cm Câu 4.
Người ta muốn xây một cái bể hình hộp đứng có thể tích V 3
18 m , biết đáy bể là hình
chữ nhật có chiều dài gấp 3 lần chiều rộng và bể không có nắp. Hỏi cần xây bể có
chiều cao h bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất (biết nguyên
vật liệu xây dựng các mặt là như nhau)? 5 3
A. 2m .
B. m . C. 1 m . D. m . 2 2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 5.
Một cốc hình trụ có bán kính đáy là 2cm , chiều cao 20cm . Trong cốc đang có một ít
nước, khoảng cách giữa đáy cốc và mặt nước là 12cm (hình vẽ). Một con quạ muốn
uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6cm . Con quạ
thông minh mổ những viên đá hình cầu có bán kính 0, 6cm thả vào cốc để mực nước
dâng lên. Để uống được nước thì con quạ cần thả vào cốc ít nhất bao nhiêu viên đá? A. 30. B. 27 . C. 28 . D. 29 . Câu 6.
Một sợi dây có chiều dài 28m được cắt thành hai đoạn để làm thành một hình vuông I Ơ
và một hình tròn. Tính chiều dài (theo đợn vị mét) của đoạn dây làm thành hình vuông
được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất? M D Ầ 56 112 84 92 Đ A. . B. . C. . D. . 4 4 4 4 NHỊ Câu 7.
Để chuẩn bị cho đợt phát hành sách giáo khoa mới, một nhà xuất bản yêu cầu xưởng in ĐG THPT
phải đảm bảo các yêu cầu sau: Mỗi cuốn sách giáo khoa cần một trang chữ có diện tích N.C.Đ là 2
384cm , lề trên và lề dưới là 3 cm , lề trái và lề phải là 2 cm . Muốn chi phí sản xuất là NG CÔN Ờ
thấp nhất thì xưởng in phải in trang sách có kích thước tối ưu nhất, với yêu cầu chất NỄY
lượng giấy và mực in vẫn đảm bảo. Tìm chu vi của trang sách. TRƯ A. 82 cm .
B. 100 cm .
C. 90 cm . D. 84 cm . GU N N Câu 8.
Với tấm nhôm hình chữ nhật có kích thước 30c ;
m 40cm . Người ta phân chia tấm nhôm
như hình vẽ và cắt bỏ một phần để được gấp lên một cái hộp có nắp. Tìm x để thể tích ÁO VIÊ hộp lớn nhất. GI 35 5 13 35 4 13 35 5 13 35 4 13 A. cm . B. cm . C. cm . D. cm . 3 3 3 3 2 Câu 9.
Ông A dự định sử dụng hết 6,5 m kính để làm một bể cá bằng kính có dạng khối hình
hộp chữ nhật chữ nhật không nắp, chiều dài gấp đôi chiều rộng( các mối ghép có kích
thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu ( kết quả làm tròn
đến hàng phần trăm)?
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 3 2, 26 m . B. 3 1,01m . C. 3 1,33m . D. 3 1,50 m . 1
Câu 10. Một vật chuyển động theo quy luật 3 2
s t 6t với t là khoảng thời gian tính từ khi 3
vật bắt đầu chuyển động và s là quãng đường vật di chuyển được trong khoảng thời
gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn
nhất của vật đạt được bằng bao nhiêu? A. 243 . B. 144 . C. 27 . D. 36 .
Câu 11. Một bác nông dân cần xây dựng một hố ga không có nắp dạng hình hộp chữ nhật có thể tích 2
3200 cm , tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng 2 . Hãy xác
định diện tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất? A. 2 1200 cm . B. 2 120 cm . C. 2 160 cm . D. 2 1600 cm .
Câu 12. Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông
An muốn chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp I Ơ
elip dùng để xây bể cá cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là 1000000 đồng trên 2
1m và chi phí trồng hoa là 1200000 đồng trên 2 1m . Hỏi ông An có M D Ầ
thể thiết kế xây dựng như trên với tổng chi phí thấp nhất gần nhất với số nào sau đây? Đ
A. 67398224 đồng.
B. 67593346 đồng. C. 63389223 đồng. D. 67398228 đồng. NHỊ
Câu 13. Một cái hồ rộng có hình chữ nhật. Tại một góc nhỏ của hồ người ta đóng một cái cọc ở ĐG THPT
vị trí K cách bờ AB là 1 m và cách bờ AC là 8 m , rồi dùng một cây sào ngăn một góc N.C.Đ
nhỏ của hồ để thả bèo (như hình vẽ). Tính chiều dài ngắn nhất của cây sào để cây sào NG CÔN Ờ
có thể chạm vào 2 bờ AB , AC và cây cọc K (bỏ qua đường kính của sào). N Ễ 5 65 5 71 Y TRƯ A. . B. 5 5 . C. 9 2 . D. . 4 4 GU N N
Câu 14. Một mảnh đất hình chữ nhật ABCD có chiều dài AB 25 m , chiều rộng AD 20 m
được chia thành hai phần bằng nhau bởi vạch chắn MN ( M , N lần lượt là trung điểm ÁO VIÊ
BC và AD ). Một đội xây dựng làm một con đường đi từ A đến C qua vạch chắn MN , GI
biết khi làm đường trên miền ABMN mỗi giờ làm được 15 m và khi làm trong miền
CDNM mỗi giờ làm được 30 m . Tính thời gian ngắn nhất mà đội xây dựng làm được
con đường đi từ A đến C . 2 5 10 2 725 20 725 A. . B. . C. . D. 5 . 3 30 30
Câu 15. Để thiết kế một chiếc bể cá không có nắp đậy hình hộp chữ nhật có chiều cao 60 cm , thể tích là 3
96.000 cm , người thợ dùng loại kính để sử dụng làm mặt bên có giá thành là 70.000 đồng/ 2
m và loại kính để làm mặt đáy có giá thành là 100.000 đồng/ 2 m . Chi phí
thấp nhất để làm bể cá là
A. 283.000 đổng. B. 382.000đồng.
C. 83.200 đồng. D. 832.000đồng.
Câu 16. Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều
rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
chất liệu làm nắp hộp. Gọi h là chiều cao của hộp để giá thành của hộp là thấp nhất. m Biết h
với m , n là các số nguyên dương nguyên tố cùng nhau. Tổng m n là n A. 12 . B. 13. C. 11. D. 10 .
Câu 17. Một chiếc cổng có hình dạng là một Parabol P có kích thước như hình vẽ, biết chiều
cao cổng bằng 4 m, AB 4 m. Người ta thiết kế cửa đi là một hình chữ nhật CDEF
(với C, F AB ; ,
D E P ), phần còn lại (phần tô đậm) dùng để trang trí. Biết chi phí để
trang trí phần tô đậm là 1.000.000 đồng/ 2
m . Hỏi số tiền ít nhất dùng để trang trí phần
tô đậm gần với số tiền nào dưới đây? I Ơ M D Ầ Đ NHỊ
A. 4.450.000 đồng.
B. 4.605.000 đồng.
C. 4.505.000 đồng. D. 4.509.000 đồng. Đ
Câu 18. Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều G THPT N.C.Đ
rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của NG CÔN
chất liệu làm nắp hộp. Gọi h là chiều cao của hộp để giá thành của hộp là thấp nhất. Ờ N m Ễ Biết h
với m , n là các số nguyên dương nguyên tố cùng nhau. Tổng m n là Y TRƯ n GU N A. 12 . B. 13 . C. 11. D. 10 . N
Câu 19. Một trang trại rau sạch mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau
với giá 30000đồng/kg thì hết rau sạch, nếu giá bán rau tăng 1000 đồng/kg thì số rau ÁO VIÊ
thừa tăng thêm 20 kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá GI
2000 đồng/kg. Hỏi tiền bán rau nhiều nhất trang trại có thể thu được mỗi ngày là bao nhiêu ?
A. 32400000 đồng. B. 34400000 đồng.
C. 32420000 đồng. D. 34240000 đồng.
Câu 20. Hình vẽ bên dưới mô tả đoạn đường đi vào GARA Ô TÔ nhà cô Hiền. Đoạn đường
đầu tiên có chiều rộng bằng x (m) , đoạn đường thẳng vào cổng GARA có chiều rộng
2, 6 (m) . Biết kích thước xe ô tô là 5m 1,9m (chiều dài chiều rộng). Để tính toán và
thiết kế đường đi cho ô tô người ta coi ô tô như một khối hộp chữ nhật có kích thước
chiều dài 5 (m) , chiều rộng 1,9 (m) . Hỏi chiều rộng nhỏ nhất của đoạn đường đầu tiên
gần nhất với giá trị nào trong các giá trị bên dưới để ô tô có thể đi vào GARA được ?
(giả thiết ô tô không đi ra ngoài đường, không đi nghiêng và ô tô không bị biến dạng)
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
A. x 3, 7 (m) .
B. x 2, 6 (m) .
C. x 3,55 (m) .
D. x 4, 27 (m) . I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI Câu 1.
Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B 1 2 1 2 như hình vẽ bên.
Người ta chia elip bởi parabol có đỉnh B B B M , N 1 , trục đối xứng 1 2 và đi qua các điểm
. Sau đó sơn phần tô đậm với giá 200.000 đồng/ 2
m và trang trí đèn led phần còn lại với giá 500.000 đồng/ 2
m . Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng A A 4 , m B B 2 , m MN 2m 1 2 1 2 . B M 2 N A1 A2 B1 I Ơ
A. 2.341.000 đồng.
B. 2.057.000 đồng. C. 2.760.000 đồng. D. 1.664.000 đồng. M D Lời giải Ầ Đ Chọn A NHỊ y Đ G THPT M 1 N.C.Đ N NG CÔN Ờ x N Ễ -2 -1 O 2 Y 1 TRƯ GU N N B1 -1 ÁO VIÊ 2 2 x y
Phương trình đường Elip là:
1. Diện tích hình Elip là S a b 2 2 m GI E . 4 1 x 1 x 1
Tọa độ giao điểm M , N là nghiệm hệ: 2 2 x y . 3 1 y 4 1 2 3 3 Vậy M 1 ; , N1; . 2 2
Parabol P đối xứng qua Oy có dạng 2
y ax c a 0 . c 1 3 3
Vì B 0; 1 , N 1; P P 2 : y 1 x 1 1 . 3 2 a 1 2 2 1 2 x 3
Diện tích phần tô đậm là: 2 S 2 1
1 x 1 dx 1 4 2 0
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 x 0 t 0 2 x x dx • Tính I 1 dx sin t cost . dx . 1 . Đặt Đổi cận 4 2 2
x 1 t 0 6 6 6 6 1 3 Suy ra 2 2 I
1 sin t .2 cos tdt 2 cos tdt 1 cos 2t dt 6 t sin 2t 1 . 0 2 6 4 0 0 0 1 1 3 3 3 x 3 2 • Tính 2 I
1 x 1 dx 1 x . 2 2 2 3 6 3 0 0 3 3 2 3 4 Vậy S 2 2 m 1 . 6 4 6 3 3 6 3
Tổng số tiền sử dụng là: S .200000 S
S .500000 2.341.000 1 E 1 đồng Câu 2.
Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy I Ơ
luật s t 3 2 t 4t
12 (m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển
động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu? M D 8 4 Ầ A. 2 (s). B. (s). C. 0 (s). D. (s). Đ 3 3 NHỊ Lời giải Đ G THPT Chọn D N.C.Đ
v t st 2 3t 8t . NG CÔN Ờ N
vt 6t 8 . Có vt 4 0 t . Ễ 3 Y TRƯ GU N N ÁO VIÊ GI 4 16
Dựa vào bảng biến thiên ta có min v v . 0; 3 3 4
Vậy vận tốc của chất điểm đó đạt giá trị bé nhất khi t . 3 Câu 3.
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán
kính 10cm (hình vẽ). A. 2 160cm . B. 2 100cm . C. 2 80cm . D. 2 200cm .
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 D C x A O B 10cm Lời giải Chọn B
Đặt OA x 0 x 10 . Suy ra: AB 2x; 2 2 2
AD OD OA 100 x . Khi đó: 2 2 4 S S A . B AD 2 .
x 100 x 2 100x x ABCD 3 200x 4x Suy ra: S ' I 2 4 100x x Ơ x 0 M D 3
S ' 0 200x 4x 0 x 5 2 x 5 2 (do 0 x 10 ) Ầ Đ x 5 2 NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ
Dựa vào bảng biến thiên, ta thấy diện tích lớn nhất của hình chữ nhật ABCD bằng Y TRƯ 2
100 cm khi x 5 2 cm . GU N N Câu 4.
Người ta muốn xây một cái bể hình hộp đứng có thể tích V 3
18 m , biết đáy bể là hình
chữ nhật có chiều dài gấp 3 lần chiều rộng và bể không có nắp. Hỏi cần xây bể có ÁO VIÊ
chiều cao h bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất (biết nguyên GI
vật liệu xây dựng các mặt là như nhau)? 5 3
A. 2m .
B. m . C. 1 m . D. m . 2 2 Lời giải Chọn D
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Gọi x x 0 là chiều rộng hình chữ nhật đáy bể, suy ra chiều dài hình chữ nhật đáy bể là 3 . x 2 V . h .3 x x .3
h x 18 x 0 . 18 6 h , 2 2 3x x
Gọi P là diện tích xung quanh cộng với diện tích một đáy bể của hình hộp chữ nhật.
Nguyên vật liệu ít nhất khi P nhỏ nhất. 6 6 48 2 2 2
P 2hx 2. .3
h x 3x 2. .x 2. .3x 3x 3x . 2 2 x x x 48
Đặt f x 2
3x , x 0 . x 48 48
Ta có f x
6x , f x 3 0
6x 0 x 8 x 2 . 2 x 2 x I Bảng biến thiên: Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ 6 6 3 N
Suy ra vật liệu ít nhất khi h m. 2 Ễ x 4 2 Y
TRƯ Câu 5. Một cốc hình trụ có bán kính đáy là 2cm , chiều cao 20cm . Trong cốc đang có một ít GU N
nước, khoảng cách giữa đáy cốc và mặt nước là 12cm (hình vẽ). Một con quạ muốn N
uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6cm . Con quạ
thông minh mổ những viên đá hình cầu có bán kính 0, 6cm thả vào cốc để mực nước ÁO VIÊ GI
dâng lên. Để uống được nước thì con quạ cần thả vào cốc ít nhất bao nhiêu viên đá? A. 30. B. 27 . C. 28 . D. 29 . Lời giải Chọn C
Gọi bán kính hình trụ là r , bán kính viên đá hình cầu là R . 4 4
Thể tích một viên đá là R .0, 63 3 . 3 3
Gọi n là số viên đá con quạ thả vào cốc, n nguyên dương.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Thể tích nước cần đổ thêm vào cốc để mực nước cách miệng cốc 6cm là 2 .r .2 8 .
Để con quạ uống được nước thì lượng đá bỏ vào cốc phải làm mực nước dâng lên cách 4 24
miệng cốc không quá 6cm nên ta phải có: . n
. .0, 63 8 n 250 n . 3 4.0, 63 9
Do n nguyên dương nên suy ra n 28 .
Vậy con quạ cần thả vào cốc ít nhất 28 viên đá. Câu 6.
Một sợi dây có chiều dài 28m được cắt thành hai đoạn để làm thành một hình vuông
và một hình tròn. Tính chiều dài (theo đợn vị mét) của đoạn dây làm thành hình vuông
được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất? 56 112 84 92 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B I Ơ
Gọi l , l m lần lượt là chu vi hình vuông và hình tròn. 0 l ,l 28 1 2 1 2
Gọi a , R m lần lượt là cạnh của hình vuông và bán kính của hình tròn. Khi đó ta có: M D Ầ l l 28 1 2 Đ NH l Ị 1
l 4a a 1 Đ 4 G THPT l 28 l 2 1
l 2 R R N.C.Đ 2 2 2 NG CÔN Ờ
Tổng diện tích của hình vuông và hình tròn là: N Ễ 2 2 l 28 l Y TRƯ 2 2 1 1
S a .R . , 0 l 28 1 16 2 GU N N
Yêu cầu bài toán tương đương với tìm l 0, 28 để S đạt giá trị nhỏ nhất. Ta có: 1 l 28 l 112 1 1 S ' 0 l ÁO VIÊ 1 8 2 4 GI 112
Lập bảng biến thiên ta được S đạt giá trị nhỏ nhất tại l 1 . 4 Câu 7.
Để chuẩn bị cho đợt phát hành sách giáo khoa mới, một nhà xuất bản yêu cầu xưởng in
phải đảm bảo các yêu cầu sau: Mỗi cuốn sách giáo khoa cần một trang chữ có diện tích là 2
384cm , lề trên và lề dưới là 3 cm , lề trái và lề phải là 2 cm . Muốn chi phí sản xuất là
thấp nhất thì xưởng in phải in trang sách có kích thước tối ưu nhất, với yêu cầu chất
lượng giấy và mực in vẫn đảm bảo. Tìm chu vi của trang sách. A. 82 cm .
B. 100 cm .
C. 90 cm . D. 84 cm . Lời giải Chọn B
Ta thấy muốn chi phí sản xuất nhỏ nhất thì kích thước tối ưu là khi diện tích mỗi trang
sách phải nhỏ nhất đồng thời vẫn bảo đảm yêu cầu đề ra.
Gọi x, y thứ tự là chiều dài và chiều rộng của trang sách, đơn vị cm , điều kiện:
x 6; y 4 .
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Diện tích phần chữ trên mỗi trang là:
x 6 y 4 384 xy 4x 6y 360 2 4 .6 x y 360 .
Khi đó xy 4 6xy 360 0 xy 10 6 xy 600 , dấu “=” xảy ra khi xy 600 x 30 ( thỏa mãn). 4x 6y y 20
Vậy chu vi trang sách khi sản xuất theo kích thước tối ưu là 2 x y 100 cm. Câu 8.
Với tấm nhôm hình chữ nhật có kích thước 30c ;
m 40cm . Người ta phân chia tấm nhôm
như hình vẽ và cắt bỏ một phần để được gấp lên một cái hộp có nắp. Tìm x để thể tích hộp lớn nhất. I Ơ M D Ầ Đ NHỊ Đ G 35 5 13 35 4 13 35 5 13 35 4 13 THPT A. cm . B. cm . N.C.Đ C. cm . D. cm . 3 3 3 3 NG CÔN Ờ Lời giải N Ễ Chọn C Y TRƯ
Khối hộp chữ nhật thu được có kích thước là 30 2x ; 20 x ; x với x 0;1 5 . GU N N 355 13
Khi đó V x 30 2x20 x f x max f x f . 0;15 3 ÁO VIÊ 35 5 13 GI
Dấu " " đạt tại x . 3 2 Câu 9.
Ông A dự định sử dụng hết 6,5 m kính để làm một bể cá bằng kính có dạng khối hình
hộp chữ nhật chữ nhật không nắp, chiều dài gấp đôi chiều rộng( các mối ghép có kích
thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu ( kết quả làm tròn
đến hàng phần trăm)? A. 3 2, 26 m . B. 3 1,01m . C. 3 1,33m . D. 3 1,50 m . Lời giải Chọn D
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 y x 2x
Gọi chiều rông của bể cá là x m , chiều cao là y m ,
x y 0 , khi đó chiều dài bể cá là
2x m . Diên tích kính sử dụng là 2
S x xy xy 2 2 2 4 m . 2 2 6.5 2x 13 4x Theo bài ra ta có: 2
2x 2xy 4xy 6,5 y . 6x 12x 13 4x x 2 13 4x
Thể tích bể cá là V x 2 2 2x . 3 m . 12x 6 I Ơ x 2 13 4x 13
Ta xét hàm số V x với x 0; . 6 2 M D Ầ Đ x
Suy ra V x 2 13 12 ' V x 39 0 x . NHỊ 6 6 Đ 39 G THPT Ta có V (
x) đổi dấu từ dương sang âm khi đi qua x
nên hàm số đạt cực đại tại N.C.Đ 6 NG CÔN 39 Ờ điểm x . N 6 Ễ Y TRƯ 13 Trên khoảng 0;
hàm số V x chỉ có một điểm cực đại nên hàm số đạt giá trị lớn GU N 2 N 39 nhất tại x . ÁO VIÊ 6 GI 39 13 39
Thể tích của bể cá có giá trị lớn nhất là max V x V 1,50 3 m . 13 6 54 0; 2
Vậy bể cá có dung tích lớn nhất bằng 1,50 3 m .
Cách 2: Xử lý tìm giá trị lớn nhất của V (x) bằng bất đẳng thức Cauchy. x 2 13 4x 13
Theo cách 1, ta tính được V x với x 0; . 6 2 x 2 x 2 2 2 13 4 1
8x (13 4x )(13 4x )
Ta có V x 6 6 8
Áp dụng bất đẳng thức Cauchy ta có 3 2 2 2 3 8x 13 4x 13 4x 26 2 2 2
8x (13 4x )(13 4x ) . 3 27 3 1 26 13 39 Suy ra V (x)
1, 50 ( kết quả làm tròn đến hàng phần trăm) 6 8.27 54
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 13 39 Dấu “
” xảy ra khi và chỉ khi 2 2 8x 13 4x x . 12 6
Vậy bể cá có dung tích lớn nhất bằng 1,50 3 m . 1
Câu 10. Một vật chuyển động theo quy luật 3 2
s t 6t với t là khoảng thời gian tính từ khi 3
vật bắt đầu chuyển động và s là quãng đường vật di chuyển được trong khoảng thời
gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn
nhất của vật đạt được bằng bao nhiêu? A. 243 . B. 144 . C. 27 . D. 36 . Lời giải Chọn D 1
Ta có v t st 3 2 2 t 6t t 12t . 3 I Ơ Tập xác định D . Vì t
t t 2 2 12 6
36 36 với mọi t 0 . M D Ầ
Suy ra max vt 36 . Dấu bằng xảy ra khi và chỉ khi t 2 6 0 t 6 . Đ t 0 NHỊ
Vậy trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của Đ
vật đạt được bằng 36 . G THPT N.C.Đ
Câu 11. Một bác nông dân cần xây dựng một hố ga không có nắp dạng hình hộp chữ nhật có NG CÔN thể tích 2
3200 cm , tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng 2 . Hãy xác Ờ N Ễ
định diện tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất? Y TRƯ A. 2 1200 cm . B. 2 120 cm . C. 2 160 cm . D. 2 1600 cm . GU N Lời giải N Chọn C ÁO VIÊ Gọi ,
x y lần lượt là chiều rộng và chiều dài của đáy hố ga; h là chiều cao của hố ga GI
x, y,h 0 Ta có: h 2x 1600 2
V xyh 2x y 3200 y 2 x Diện tích bề mặt sử dụng của hố ga không nắp là 8000 2 2
S xy 2xh 2 yh 4x 5xy 4x x 8000 8000
Đặt f x 2 4x
. Ta có f x 8x x 2 x
f x 0 x 10 Bảng biến thiên
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Vậy S nhỏ nhất khi x 10 y 16 .
Diện tích đáy hố ga khi đó là 2 160 cm .
Câu 12. Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông
An muốn chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp
elip dùng để xây bể cá cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là I Ơ 1000000 đồng trên 2
1m và chi phí trồng hoa là 1200000 đồng trên 2 1m . Hỏi ông An có
thể thiết kế xây dựng như trên với tổng chi phí thấp nhất gần nhất với số nào sau đây? M D Ầ
A. 67398224 đồng.
B. 67593346 đồng. C. 63389223 đồng. D. 67398228 đồng. Đ Lời giải NHỊ Đ Chọn A G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
Gắn mảnh vườn hình elip của ông An vào hệ trục tọa độ như hình vẽ. Độ dài trục lớn
10m và độ dài trục bé bằng 8m nên ta có a 5 và b 4 . x y
Phương trình của elip là: E 2 2 : 1. 25 16 Diện tích của elip là: S ab 20 . E 2 x
Hình chữ nhật ABCD nội tiếp elip. Đặt AB 2x 0 x 5 AD 8 1 . 25 2 x
Diện tích hình chữ nhật ABCD là: S 16x 1 . ABCD 25
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 x
Diện tích phần còn lại trồng hoa là: S 20 16x 1 . hoa 25
Tổng chi phí xây dựng là: 2 2 x x
T 16000000.x 1
1200000. 20 16x 1 25 25 2 x
24000000 3200000x 1 . 25 2 2 x x 2 1 x x Mặt khác ta có: 25 25 16000000. 1 16000000. 8000000 . 5 25 2 2 x
T 24000000 3200000x 1
24000000 8000000 67398223.69. 25 2 x x 5 2 I Dấu " " xảy ra khi 1 x (thỏa mãn). Ơ 5 25 2
Vậy tổng chi phí thiết kế xây dựng thấp nhất gần với số 67398224 . M D
Ầ Câu 13. Một cái hồ rộng có hình chữ nhật. Tại một góc nhỏ của hồ người ta đóng một cái cọc ở Đ
vị trí K cách bờ AB là 1 m và cách bờ AC là 8 m , rồi dùng một cây sào ngăn một góc NHỊĐ
nhỏ của hồ để thả bèo (như hình vẽ). Tính chiều dài ngắn nhất của cây sào để cây sào G THPT
có thể chạm vào 2 bờ AB , AC và cây N cọ.C
c .ĐK (bỏ qua đường kính của sào). NG 5 65 5 71 CÔN A. . B. 5 5 . C. 9 2 . D. . Ờ 4 4 N Ễ Lời giải Y TRƯ Chọn B GU N N B P K E ÁO VIÊ GI F Q A C
Đặt AP a , AQ b a,b 0 . Gọi E và F lần lượt là hình chiếu vuông góc của K
xuống AB và AC . Suy ra KE 1, KF 8 . KE PK KF QK KF KE 8 1 Ta có: ; 1 hay 1. AQ PQ AP PQ AP AQ a b
(Hoặc có thể dùng phép tọa độ hóa: Gán A 0;0 , P 0; a, Q ;
b 0. Khi đó K 1;8 . x y 1 8
Phương trình đường thẳng PQ :
1 . Vì PQ đi qua K nên 1.) b a b a Cách 1: 8 1 Ta có: 2 2 2
PQ a b . Vì 8k k 1 k k 0 . a b a b 8k k 4k 4k k k 2 k 2 2 2 2
a b k a b 2 2 a b 3 2 3 3 16k 3 . a b a a 2b 2b 4
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 4k 2 a a k 250 k Suy ra PQ nhỏ nhất 2 2
a b nhỏ nhất 2 b a 10 . 2b b 5 8 1 1 a b
Vậy giá trị nhỏ nhất của PQ là 2 2
a b 125 5 5 . Từ đó suy ra chiều dài ngắn nhất
của cây sào để cây sào có thể chạm vào 2 bờ AB , AC và cây cọc K là 5 5 . Cách 2: 2 8 1 a a Vì 1 b a . Khi đó 2 2 2
PQ a b 2 a với a 8. a b a với 8 8 a 8 2 a
Xét hàm số f a 2 a với a 8. a 8 I 3 Ơ 2a a 8 2a 8 8
Ta có f a 2a .
; f a 0 a 10 . a 8 3 a 82 a 8 M D Ầ
BBT của f a : Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N
Vậy GTNN của f a là 125 khi a 10 . ÁO VIÊ
Từ đó suy ra chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2 bờ AB , AC GI
và cây cọc K là 125 5 5 .
Câu 14. Một mảnh đất hình chữ nhật ABCD có chiều dài AB 25 m , chiều rộng AD 20 m
được chia thành hai phần bằng nhau bởi vạch chắn MN ( M , N lần lượt là trung điểm
BC và AD ). Một đội xây dựng làm một con đường đi từ A đến C qua vạch chắn MN ,
biết khi làm đường trên miền ABMN mỗi giờ làm được 15 m và khi làm trong miền
CDNM mỗi giờ làm được 30 m . Tính thời gian ngắn nhất mà đội xây dựng làm được
con đường đi từ A đến C . 2 5 10 2 725 20 725 A. . B. . C. . D. 5 . 3 30 30 Lời giải Chọn A
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Do cần thời gian xây là ngắn nhất nên con đường làm trên mỗi miền phải là những đường thẳng.
Gọi AE và EC lần lượt là đoạn đường cần làm. Với NE x m (với 0 x 25 ).
EM 25 xm. 2 2 2
AE AN EN 100 x Ta được . 2 2 2 I
EC MC EM 100 25 x Ơ
Thời gian để làm đoạn đường từ A đến C là: M D 2 2 AE EC 100 x 25 x 100 Ầ t x h Đ (Với 0 x 25 ) 15 30 15 30 NHỊ x 25 x Đ
tx . 2 2 G THPT 15 100 x
30. 25 x 100N.C.Đ NG x 25 x CÔN
Xét t x 0 0 Ờ 2 2 N 15 100 x
30. 25 x 100 Ễ Y TRƯ
2x 25 x2 100 25 x 2 100 x GU N 2 2 N 2
4x 25 x 100 25 x 2 100 x
4x 25 x2 400x 10025 x2 25 x2 2 2 2 x 0 ÁO VIÊ 2 2 GI
425 x 2 x 25 2 x 2
20 25 x 0 .
x 5425 x2 x 5 2
x 45 x 0 x 5 t 4 29 0 6 2 5
Ta được t 5 . 3 t 1 29 25 3
Vậy thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ A đến C là 2 5 h . 3 Cách 2:
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 2 2 2 2 2 2 2 10 x 25 x 10 20 2x 25 x 10 Xét t x
(Với 0 x 25 ). 15 30 30 2 2 2 2 Lại có 2 x x 2 20 2 25
10 45 x 2x 10 do u v u v .
x2 x2 x 2 2 2 20 2 25 10 5 5 2000 . x
Do đó t x 2 5 5 2000 2000 2 5 . 30 30 3 2 5 Vậy t x
h khi và chỉ khi x 5 m . min 3
Vậy thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ A đến C là 2 5 h . 3
I Câu 15. Để thiết kế một chiếc bể cá không có nắp đậy hình hộp chữ nhật có chiều cao 60cm , Ơ thể tích là 3
96.000 cm , người thợ dùng loại kính để sử dụng làm mặt bên có giá thành là M D 70.000 đồng/ 2
m và loại kính để làm mặt đáy có giá thành là 100.000 đồng/ 2 m . Chi phí Ầ Đ
thấp nhất để làm bể cá là NHỊ
A. 283.000 đổng. B. 382.000đồng.
C. 83.200 đồng. D. 832.000đồng. Đ Lời giải G THPT N.C.Đ Chọn C NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ
Gọi x m là chiều dài của hình chữ nhật đáy x 0 . GI 0, 096 4 Khi đó chiều rộng là: . 0, 6x 25x 4
Khi đó diện tích mặt xung quanh là: 1, 2 x . 25x 4 4
Chi phí để làm mặt xung quanh là: 70.1, 2 x 84 x (nghìn đồng). 25x 25x 4 4
Diện tích mặt đáy là: . x . 25x 25 4
Cho phí để làm mặt đáy là: 100. 16 (nghìn đồng) . 25
Chi phí để làm bể cá thấp nhất khi và chỉ khi chi phí làm mặt bên thấp nhất 4 4 25x 4
Xét hàm số f x x
, x 0; f x 2 1 . 2 2 25x 25x 25x f x 2 2
0 25x 4 0 x . 5
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Bảng biến thiên 4
Khi đó chi phí thấp nhất là: 84. 16 83.200 đồng. 5 Bổ sung cách 2
Xét hàm số f x 4 x với x 0 . 25x
Áp dụng bất đẳng thức Cô-Si ta có f x 4 4 4 x 2 . x . 25x 25x 5 I Ơ 4 2
Dấu " " xẩy ra khi x x . 25x 5 M D 4 Ầ
Vậy chi phí thấp nhất là: 84. 16 83.200 đồng. Đ 5 NHỊ
Câu 16. Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều ĐG
rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của THPT N.C.Đ
chất liệu làm nắp hộp. Gọi h là chiều cao của hộp để giá thành của hộp là thấp nhất. NG CÔN Ờ m Biết h
với m , n là các số nguyên dương nguyên tố cùng nhau. Tổng m n là N n Ễ Y TRƯ A. 12 . B. 13. C. 11. D. 10 . GU N Lời giải N Chọn C
Gọi chiều rộng của hộp là x ( x 0 ) Chiều dài của hình hộp là 2x . ÁO VIÊ 24 GI
Thể tích của hộp là V . x 2 .
x h 48 h . 2 x 24 144
Tổng diện tích mặt đáy và 4 mặt bên của hộp là 2 2 2
2x 6xh 2x 6 . x 2x . 2 x x Diện tích nắp hộp là 2 2x . 144
Giá thành hộp thấp nhất f x 2 2 3 2x 2x
đạt giá trị nhỏ nhất với x 0 . x 432 216 216 216 216
Ta có f x 2 2 2 3 8x 8x 3. 8x . . 216 . x x x x x 216
Vậy min f x 216 xảy ra khi và chỉ khi 2 8x 3
x 27 x 24 8 3 h . 0; x 9 3
Vậy m 8 ; n 3 m n 8 3 11.
Câu 17. Một chiếc cổng có hình dạng là một Parabol P có kích thước như hình vẽ, biết chiều
cao cổng bằng 4 m, AB 4 m. Người ta thiết kế cửa đi là một hình chữ nhật CDEF
(với C, F AB ; ,
D E P ), phần còn lại (phần tô đậm) dùng để trang trí. Biết chi phí để
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
trang trí phần tô đậm là 1.000.000 đồng/ 2
m . Hỏi số tiền ít nhất dùng để trang trí phần
tô đậm gần với số tiền nào dưới đây?
A. 4.450.000 đồng.
B. 4.605.000 đồng.
C. 4.505.000 đồng. D. 4.509.000 đồng. Lời giải Chọn D I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ * Xét P 2
: y ax bx c a 0 có toạ độ đỉnh 0; 4 và qua điểm có toạ độ 2;0 . GI b Ta có hoành độ đỉnh:
0 b 0 ; P qua điểm 0;4 c 4 và P qua điểm 2a 2;0 a 1 Suy ra: P 2
: y x 4
* Xét đường thẳng qua E, D : y m (với 0 m 4 ). Khi đó E 4 m;m và
D 4 m;m là giao điểm của P và đường thẳng y m . Suy ra: ED 2 4 m , EF m .
* Yêu cầu của bài toán đạt được khi diện tích hình chữ nhật CDEF phải lớn nhất. Ta có: S E .
D EF 2 4 m.m CDEF
Đặt t 4 m 2 2
t 4 m m 4 t (với 0 t 2 ) Khi đó: S
f t t 2 t 3 2 4 2 t 8t CDEF
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 f t 2 6 t 8 2 0 t 3 32 3 2 8 Suy ra: MaxS khi t m CDEF 9 3 3 2 32
* Mặt khác diện tích của chiếc cổng: 2 S x 4 ( m2) 3 2 I
Suy ra diện tích nhỏ nhất của phần dùng để trang trí là: S MaxS CDEF Ơ 32 32 3 4,5083 ( m2) M D 3 9 Ầ Đ
* Vậy số tiền ít nhất dùng để trang trí phần tô đậm: 4,5083 1.000.000 4.508.300 NHỊ (đồng). Đ
(Lưu ý: Có thể dùng MTBT để tìm GTLN của S
trên khoảng 0 m 4 ). G THPT CDEF N.C.Đ
Câu 18. Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều NG CÔN Ờ
rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của NỄ
chất liệu làm nắp hộp. Gọi h là chiều cao của hộp để giá thành của hộp là thấp nhất. Y TRƯ m Biết h
với m , n là các số nguyên dương nguyên tố cùng nhau. Tổng m n là GU N n N A. 12 . B. 13 . C. 11. D. 10 . Lời giải ÁO VIÊ GI Chọn C
Gọi chiều dài, chiều rộng của hộp là 2x và x (x 0) . Khi đó, ta có thể tích của cái hộp là 2 2 2
V 2x .h 2x .h 48 x .h 24
Do giá thành làm đáy và mặt bên hộp là 3, giá thành làm nắp hộp là 1 nên giá thành làm hộp là L 2
x xh xh 2 3 2 2 4 2x
Áp dụng bất đẳng thức côsi cho ba số không âm, ta được
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2
L 8x 9xh 9xh 3 2 3 8x .9x . h 9xh x h2 2 3 3 648 216 9h 2 x x 3 8x 9xh 8
Dấu bằng xảy ra khi và chỉ khi 8 2 x h 24 2 9 h 3 .h 24 3 2 8
Vậy m 8 , n 3 và m n 11.
Câu 19. Một trang trại rau sạch mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau
với giá 30000đồng/kg thì hết rau sạch, nếu giá bán rau tăng 1000 đồng/kg thì số rau
thừa tăng thêm 20 kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá
2000 đồng/kg. Hỏi tiền bán rau nhiều nhất trang trại có thể thu được mỗi ngày là bao nhiêu ?
A. 32400000 đồng. B. 34400000 đồng.
C. 32420000 đồng. D. 34240000 đồng. Lời giải I Ơ Chọn C
Gọi số lần tăng giá là y y 0 M D Ầ
Giá bán rau sau mỗi lần tăng giá là 30000 1000 y đồng/kg. Đ NH
Số rau thừa được thu mua cho chăn nuôi là 20 y y 50 kg Ị . Đ
Số rau bán được trước khi thu mua cho chăn nuôi là 1000 20 y kg. G THPT N.C.Đ
Tổng số tiền bán rau thu được mỗi ngày là: NG CÔN P
1000 20y .(30000 1000y) 20 .y2000. Ờ N 2 Ễ P 2
0000y 440000y 30000000. Y TRƯ
P 32420000 20000 y 112 . GU N N Ta có: y 2 32420000 20000 11 32420000. ÁO VIÊ P 32420000. GI P
324200000 khi y 11 N . max
Câu 20. Hình vẽ bên dưới mô tả đoạn đường đi vào GARA Ô TÔ nhà cô Hiền. Đoạn đường
đầu tiên có chiều rộng bằng x (m) , đoạn đường thẳng vào cổng GARA có chiều rộng
2, 6 (m) . Biết kích thước xe ô tô là 5m 1,9m (chiều dài chiều rộng). Để tính toán và
thiết kế đường đi cho ô tô người ta coi ô tô như một khối hộp chữ nhật có kích thước
chiều dài 5 (m) , chiều rộng 1,9 (m) . Hỏi chiều rộng nhỏ nhất của đoạn đường đầu tiên
gần nhất với giá trị nào trong các giá trị bên dưới để ô tô có thể đi vào GARA được ?
(giả thiết ô tô không đi ra ngoài đường, không đi nghiêng và ô tô không bị biến dạng)
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
A. x 3, 7 (m) .
B. x 2, 6 (m) .
C. x 3,55 (m) .
D. x 4, 27 (m) . Lờigiải Chọn A I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
Chọn hệ trục Oxy như hình vẽ. Khi đó M 2 ,6 ; x. x y
Gọi B a ; 0suy ra A 2
0 ; 25 a . Phương trình AB : 1 0 . a 2 25 a x y
Do CD // AB nên phương trình CD : T 0 . a 2 25 a
Mà khoảng cách giữa AB và CD bằng 1,9(m) nên T 1 9,5 1,9 T 1 . 2 2 2 a 25 1 1 a a 2 25 a
Điều kiện để ô tô đi qua được là M ,O nằm khác phía đối với bờ là đường thẳng CD . Suy ra: 2 ,6 x 9, 5 1 0 a 2 2 25 a a 25 a
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 2 9,5 2, 6 25 a
x 25 a
(đúng với mọi a 0 ; 5 ) a a
Để cho nhanh, chúng ta dùng chức năng TABLE trong máy tính Casio570ES PLUS. 2 2 9,5 2, 6 25 X 5
f (X) 25 X với STEP = ; START = 0; END = 5. X X 29 2 X
Thấy GTLN của f X 2 9,5 2, 6 25 25 X xấp xỉ 3,698 . X X
Vậy chiều rộng nhỏ nhất của đoạn đường đầu tiên gần nhất với giá trị ở câu A. I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
CHỦ ĐỀ: GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
VẬN DỤNG – VẬN DỤNG CAO DẠNG 4
ỨNG DỤNG GTLN, GTNN VÀO TÌM SỐ NGHIỆM PT VÀ BPT Câu 1.
Giả sử m là số thực thỏa mãn giá trị nhỏ nhất của hàm số 31x 3x f x mx trên là 2 A. m 1 0; 5 . B. m 5 ;0.
C. m 0;5 .
D. m5;10 . Câu 2.
Giả sử m là số thực thỏa mãn giá trị nhỏ nhất của hàm số
2018x 2019x f x mx trên là 2. Khi đó: A. m 3 0; 2 0 . B. m 2 0;0 .
C. m 0;20 .
D. m20;30 .
I Câu 3. Giả sử m là số thực thỏa mãn giá trị lớn nhất của hàm số Ơ
f x log x 1 log x 1 mx 1 ; 0 31 3 trên
là . Khi đó: M D A. m 3 ; 2 . B. m 2 ;0 .
C. m 0;2 .
D. m 2;3 . Ầ
Đ Câu 4. Tập tất cả các giá trị của tham số m để phương trình m m 1 1 sin x sin x có NHỊ
nghiệm là a,b . Giá trị a b bằng Đ G THPT 1 1 1 1 A. 2. B. 2 .
N.C.Đ C. 2 . D. 2 . 4 4 2 2 NG CÔN
Ờ Câu 5. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
cos 2x m 1 tan x.cos x N Ễ Y TRƯ
có nghiệm thuộc đoạn 0; ? 3 GU N N A. 4 . B. 3 . C. 2 . D. 1. Câu 6.
Gọi S là tập hợp các giá trị nguyên của tham số m 0;2019 để bất phương trình: ÁO VIÊ
x m 1 x 3 2 2 GI
0 đúng với mọi x 1;
1 . Số phần tử của tập S bằng: A. 1 . B. 2020 . C. 2019 . D. 2. Câu 7.
Cho hàm số y f x liên tục và đồng biến trên 0; , bất phương trình 2 ln cos x f x x e
m (với m là tham số) thỏa mãn với mọi x 0; khi và chỉ khi 2
A. m f 0 1.
B. m f 0 1.
C. m f 0 1.
D. m f 0 1.
Câu 8. Cho hàm số y f x liên tục trên và có bảng xét dấu đạo hàm như sau Bất phương trình 2 x
f x e m đúng với mọi x 1 ; 1 khi và chỉ khi
A. m f 0 1.
B. m f 1 . e
C. m f 0 1.
D. m f 1 . e
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 9. Cho hàm số 3 2
f x ax bx cx d với a,b, c, d là các số thực, có đồ thị như hình bên.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x m 1 m có đúng 4 nghiệm phân biệt. A. 3. B. Vô số. C. 1. D. 2.
Câu 10. Số các giá trị nguyên của tham số m thuộc đoạn 2
019;2019 để phương trình 2
x m x m 3 2 4 1
x 4x có nghiệm là I Ơ A. 2011. B. 2012 . C. 2013. D. 2014 . f x 0;3
M D Câu 11. Cho hàm số liên tục trên đoạn
và có bảng biến thiên như sau: Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ 4 2 Y TRƯ
Có bao nhiêu số nguyên m để phương trình f x mx 2x 2 có nghiệm thuộc GU N đoạn 0; 3 . N A. 9 . B. 5 . C. 4 . D. 7 . 3 2
x x m
ÁO VIÊ Câu 12. Giá trị lớn nhất của hàm số y 0; 2 trên
bằng 5. Tham số m nhận giá trị GI x 1 là A. 5 . B. 1. C. 3 . D. 8 .
Câu 13. Cho hàm số f (x) có bảng biến thiên như hình vẽ sau 5
Phương trình f sinx 2
3 có bao nhiêu nghiệm trên đoạn 0; . 6 A. 3 . B. 2 . C. 4 . D. 5 .
Câu 14. Có bao nhiêu giá trị nguyên của tham số m 9
;9 để phương trình: 2
1 x m2 1 x 2 1 x 3 1 0 có nghiệm?
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 2
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 14 . B. 8 . C. 10. D. 12 .
Câu 15. Cho phương trình 2 3 3 2
16m x 16x 8x 2x 2 2m 10 ( m là tham số). Khẳng định nào sau đây là đúng?
A. Phương trình đã cho vô nghiệm.
B. Phương trình đã cho có đúng một nghiệm thực.
C. Phương trình đã cho có hai nghiệm thực phân biệt.
D. Số nghiệm của phương trình phụ thuộc vào giá trị của tham số m.
Câu 16. Tổng các giá trị nguyên dương của m để tập nghiệm của bất phương trình m 2 x 1
x có chứa đúng hai số nguyên là 72 A. 27 . B. 29 . C. 28 . D. 30 .
Câu 17. Cho hàm số f x liên tục trên . Hàm số y f x có đồ thị như hình vẽ I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ
Bất phương trình f x 2 2sin
2sin x m đúng với mọi x0; khi và chỉ khi GU N N
A. m f 1 1
. B. m f 1 1 .
C. m f 1 0 .
D. m f 1 0 . 2 2 2 2
ÁO VIÊ Câu 18. Cho hàm số y f x có f 2
m 1, f
1 m 2 . Hàm số y f x có bảng biến GI thiên như hình vẽ bên. 1 2x 1
Tập hợp tất cả các giá trị của tham số m để phương trình f x m có nghiệm 2 x 3 x 2 ; 1 là 7 7 A. 5; . B. 2 ;0 . C. 2 ;7 . D. ;7 . 2 2
Câu 19. Cho hàm số f x liên tục trên
và có đồ thị như hình vẽ bên. Có bao nhiêu số
nguyên m để phương trình f f x
1 m có ít nhất 6 nghiệm thực phân biệt?
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 2 . B. 3 . C. 5 . D. 4 . 7
I Câu 20. Cho hàm số y f x liên tục trên 0;
có đồ thị hàm số y f x như hình vẽ sau: Ơ 2 M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ 7
Hàm số y f x đạt giá trị nhỏ nhất trên 0;
tại điểm x nào dưới đây ? GU N 2 0 N 7
A. x 0 . B. x .
C. x 3. D. x 1. 0 0 2 0 0 ÁO VIÊ
GI Câu 21. Cho phương trình 2 2x 2mx 4
x 1 ( m là tham số). Gọi p, q lần lượt là các giá trị
m nguyên nhỏ nhất và giá trị lớn nhất thuộc 10
; 10 để phương trình có nghiệm. Khi
đó giá trị T p 2q là A. 10. B. 19. C. 20. D. 8.
Câu 22. Cho hàm số f x 3 2
x 3x 3x 4 . Số nghiệm thực phân biệt của phương trình
f f x 2 2 3 f x là A. 7 . B. 4 . C. 6 . D. 9 .
Câu 23. Gọi S là tập tất cả các giá trị nguyên âm của tham số m để phương trình m 2
x 4 x 2 có nghiệm. Tập S có bao nhiêu phần tử? A. 10. B. 6 . C. 4 . D. 2 .
Câu 24. Cho hàm số y f (x) có bảng xét dấu của f '(x) như sau:
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 2 Xét hàm số (1 ) ( ) f x x g x e
, tập nghiệm của bất phương trình g '(x) 0 là 1 1 1 A. ; . B. ; . C. 1; 2;
. D. 1 ; 1 ; 2 . 2 2 2 2 2 2 2
x y z 6
Câu 25. Cho hệ phương trình xy yz xz 3
với x, y, z là ẩn số thực, m là tham số. Số giá trị 6 6 6
x y z m
nguyên của m để hệ phương trình có nghiệm là A. 25 . B. 24 . C. 12 . D. 13 .
Câu 26. Cho phương trình m 2 x 3 2m 1
1 x m 1. Biết rằng tập hợp tất cả các giá I
trị của tham số thực m để phương trình có nghiệm là đoạn ;
a b . Giá trị của biểu thức Ơ
5a 3b bằng M D Ầ A. 13 . B. 7 . C. 19 . D. 8 .
Đ Câu 28. Cho hàm số y f x liên tục trên 1 ;
3 và có đồ thị như hình vẽ sau: NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
Bất phương trình f ( )
x x 1 7 x m có nghiệm thuộc 1 ; 3 khi và chỉ khi
A. m 7.
B. m 7 .
C. m 2 2 2 .
D. m 2 2 2 .
Câu 29. Cho hàm số f x 3 m 3 2 1
x 3x 4 m x 2 với m là tham số. Có bao nhiêu số nguyên m 2 018;201
8 sao cho f x 0 với mọi giá trị x 2;4 . A. 2021. B. 2019 . C. 2020. D. 4037 .
Câu 30. Tìm số thực m lớn nhất để bất phương trình sau có nghiệm đúng với mọi x
m sin x cos x
1 sin 2x sin x cos x 2018. 1 2017 A. . B. 2018 . C. . D. 2017 . 3 2 Câu 31. Số giá trị nguyên của tham số m 1
0;10 để bất phương 2 2
3 x 6 x 18 3x x m m 1 nghiệm đúng x 3 ;6. A. 28. B. 20. C. 4. D. 19.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 32. Cho hai số thực dương
x , y thỏa mãn 2y y 2x log y 1 x 2
. Giá trị nhỏ nhất của 2 x biểu thức P bằng y e ln 2 e ln 2 e ln 2 e A. . B. . C. . D. . 2 2 2 2 ln 2 1 4 1 4
Câu 33. Cho hàm số f x 3 2
x x x có đồ thị như hình vẽ bên. 3 3 3 3 y 1 x 1 1 4 O I Ơ
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f 2 x x 2 2019 15 30
16 m 15x 30x 16 m 0 có 4 nghiệm phân biệt thuộc đoạn M D Ầ Đ 0;2 NHỊ A. 1513. B. 1512 . C. 1515 . D. 1514 . Đ G
THPT Câu 34. Cho f (x) mà đồ thị hàm số y
f '(x) như hình vẽ bên N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI x
Bất phương trình f (x) sin
m nghiệm đúng với mọi x 1 ; 3 khi và chỉ khi 2
A. m f (0) .
B. m f (1) 1 .
C. m f ( 1 ) 1.
D. m f (2) .
Câu 35. Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình sau 6 4 3 3 2
x 3x m x 4x mx 2 0 nghiệm đúng với mọi x 1;
3 . Tổng tất cả các phần tử của S bằng: A. 3 . B. 2 . C. 1. D. 4 .
Câu 36. Số giá trị nguyên của tham số m nằm trong khoảng 0;2020 để phương trình
x 1 2019 x 2020 m có nghiệm là A. 2020 . B. 2021. C. 2019 . D. 2018 .
Câu 37. Cho hàm số f x 5 3
x 3x 4m. Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3 f f x
m x m có nghiệm thuộc đoạn 1;2 ?
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 15. B. 16 . C. 17 . D. 18 .
Câu 38. Cho hàm số 3 2
f x ax bx cx d có đồ thị như hình vẽ. gọi S là tập hợp các giá trị
của m m sao cho x 3
1 m f 2x
1 mf x f x 1 0, x . Số phần tử của tập S là? A 2 . B. 0 . C. 3 D. 1. I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 HƯỚNG DẪN GIẢI Câu 1.
Giả sử m là số thực thỏa mãn giá trị nhỏ nhất của hàm số 31x 3x f x mx trên là 2 A. m 1 0; 5 . B. m 5 ;0.
C. m 0;5 .
D. m5;10 . Lời giải Chọn B
Tập xác định của hàm số f x là D
. Ta có ' 31x ln 31 3x f x ln 3 m . Ta xét các trường hợp:
+ Khi m 0 thì ' 31x ln 31 3x f x
ln 3 m 0,x
tức f x đồng biến trên .
Mà lim f x lim 31x 3x mx nên không thỏa mãn yêu cầu Min f x 2 . x x x
+ Khi m 0 thì ' 31x ln 31 3x f x ln 3 0, x
tức f x đồng biến trên .
lim f x lim 31x 3x Min f x I Mà
0 nên không thỏa mãn yêu cầu 2 x x x Ơ
+ Khi m 0 thì ' 0 31x ln 31 3x f x ln 3 m . M D
Đặt hàm số ( ) 31x ln 31 3x g x
ln 3 thì g(x) đồng biến trên
và có tập giá trị là 0; Ầ Đ
Mà m 0 nên tồn tại duy nhất a
sao cho g(a) m ta có bảng biến thiên của NHỊ Đ g(x) G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N
Suy ra bảng biến thiên của f x là: ÁO VIÊ GI
Ta có f x đạt giá trị nhỏ nhất là f a tại duy nhất giá trị x a
Do đó, Min f x 2 f (a) f (0) a 0 x
Suy ra g(0) m m ln 31 ln 3 ln 93 5 ;0 . CÁCH 2
Nhận xét: Ta có f 0 2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
31x 1 3x 1 , m x 0 x x
31x 1 3x 1
Giả thiết bài toán ta có: f (x) 2, x , m x 0 x x f 0 2
31x 1 3x 1 Suy ra m lim
ln 31 ln 3 ln 93 m ln 93 x0 x x
Nhận xét: Để giải tốt dạng toán này học sinh cần vận dụng linh hoạt ứng dụng đạo
hàm vào khảo sát hàm số chứa tham số. Câu 2.
Giả sử m là số thực thỏa mãn giá trị nhỏ nhất của hàm số
2018x 2019x f x mx trên là 2. Khi đó: A. m 3 0; 2 0 . B. m 2 0;0 .
C. m 0;20 .
D. m20;30 . I Ơ Lời giải Chọn C M D x x Ầ
Tập xác định của hàm số f x là D
. Ta có f ' x 2018 ln 2018 2019 ln 2019 m . Đ NHỊ Ta xét các trường hợp: Đ
+ Khi m 0 thì ' 2018x ln 2018 2019x f x
ln 2019 m tức f x đồng biến trên . G THPT x x N.C.Đ
Mà lim f x lim 2018 2019 mx nên không thỏa mãn yêu cầu Min f x 2 . NG x x x CÔN Ờ m 0
' 2018x ln 2018 2019x f x ln 2019 0, x f x N + Khi thì tức đồng biến trên Ễ Y TRƯ . x x GU N
Mà lim f x lim 2018 2019 0 nên không thỏa mãn yêu cầu Min f x 2 x x x N
+ Khi m 0 thì ' 0 2018x ln 2018 2019x f x ln 2019 m . ÁO VIÊ
Đặt hàm số ( ) 2018x ln 2018 2019x g x
ln 2019 thì g(x) đồng biến trên và có tập giá GI trị là 0;
Mà m 0 nên tồn tại duy nhất a
sao cho g(a) m ta có bảng biến thiên của g(x)
Suy ra bảng biến thiên của f x là:
Ta có f x đạt giá trị nhỏ nhất là f a tại duy nhất giá trị x a
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Do đó, Min f x 2 f (a) f (0) a 0 x
Suy ra m g(0) m ln 2018 ln 2019 15, 2 nên m 0;20 . Câu 3. Giả sử
m là số thực thỏa mãn giá trị lớn nhất của hàm số
f x log x 1 log x 1 mx 1 ; 0 31 3 trên
là . Khi đó: A. m 3 ; 2 . B. m 2 ;0 .
C. m 0;2 .
D. m 2;3 . Lời giải Chọn B 1 1
Tập xác định của hàm số f x là D 1
; .Ta có f 'x m . x 1 ln 31 x 1 ln 3 Ta xét các trường hợp: 1 1
+ Khi m 0 thì f ' x
m 0,x tức f x đồng biến trên x 1 ln 31 x 1 ln 3 I 1 ;. Ơ
Mà lim f x lim log x 1 log
x 1 mx
Min f x 2 31 3 nên không thỏa . M D x 1 x 1 x Ầ 1 1 Đ
+ Khi m 0 thì f ' x 0 m . x 1 ln 31 x 1 ln 3 NHỊ Đ 1 1 1 1
Đặt hàm số g(x)
thì g '(x) nên g(x) G THPT x 1 ln 31 x 1 ln 3 2 2 N.C.Đ
x 1 ln31 x 1 ln 3 NG nghịch biến trên 1 ; 0; CÔN và có tập giá trị là Ờ N m 0 a
g(a) m Ễ Mà nên tồn tại duy nhất sao cho
ta có bảng biến thiên của Y TRƯ g(x) GU N N ÁO VIÊ GI
Suy ra bảng biến thiên của f x là:
Ta có f x đạt giá trị lớn nhất là f a tại duy nhất giá trị x a
Do đó, Max f x 0 f (a) f (0) a 0 x 1 1
Suy ra g(0) m m g(0) 1, 2 . ln 31 ln 3
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Câu 4.
Tập tất cả các giá trị của tham số m để phương trình m m 1 1 sin x sin x có
nghiệm là a,b . Giá trị a b bằng 1 1 1 1 A. 2. B. 2 . C. 2 . D. 2 . 4 4 2 2 Lời giải Chọn A
m m 1 1 sin x sin x (m 1) m 1 1 sin x (sin x 1) . 2
(m 1) c d
c m 1 1 sin x , d 1 sin x . 2
(m 1) d c
(c d)(1 c d) 0 c d m 1 1 sin x 1 sin x .
m 1 1 sin x 1 sin x . 2
m 1 t t f (t),t 1 sin x 0, 2 I . Ơ 1
Ta có max f (t) 2 2, min f (t) . 0, 2 0, 2 4 M D Ầ 1 5 Đ
Vậy phương trình đã cho có nghiệm m 1 2 2 m 1 2 . NH 4 4 Ị Đ 1
a b 2 . G THPT 4 N.C.Đ
NG Câu 5. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 cos 2x
m 1 tan x.cos x CÔN Ờ N
có nghiệm thuộc đoạn 0; ? Ễ 3 Y TRƯ A. 4 . B. 3 . C. 2 . D. 1. GU N N Lời giải Chọn B ÁO VIÊ Ta có 2
cos 2x m 1 tan x.cos x 2 2
2cos x 1 m 1 tan x.cos x GI 1 2
m 1 tan x vì x 0; cos x 0 2 cos x 3 2
1 tan x m 1 tan x . 2 1 tan x Vì x 0;
tan x 0; 3 1 tan x 0 m . 3 1 tan x 4 2 t 2t
Đặt t 1 tan x t 1; 1 3 3 m
t 2t 1 . t
Phương trình đã cho có nghiệm thuộc đoạn x 0;
khi và chỉ phương trình 1 có 3
nghiệm t 1; 1 3 .
Xét hàm số f t 3 t
2t với t 1; 1 3 .
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 11
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Có f t 2 3
t 2 . Suy ra f t 0 2 t 1; 1 3 3 . f
1 1, f 3 2 1
3 1 3 2 1 3 1 .
Do m nên phương trình
1 có nghiệm khi m 1 ; 0; 1 .
Vậy có 3 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Câu 6.
Gọi S là tập hợp các giá trị nguyên của tham số m 0;2019 để bất phương trình:
x m x 3 2 2 1
0 đúng với mọi x 1 ;
1 . Số phần tử của tập S bằng: A. 1 . B. 2020 . C. 2019 . D. 2. Lời giải Chọn C Đặt 2
t 1 x . Khi đó, 0 t 1, x [1;1] . I Ơ
Ta có, bất phương trình: 2 3 1 t m t 0, t [0;1] 3 2
m t t 1, t [0;1] M D Ầ
m f (t), t [0;1] , với 3 2
f (t) t t 1 Đ
m max f (t) NH Ị [0;1] Đ Ta có, 2 f (
t) 3t 2t G THPT N.C.Đ t 0 NG f (t) 0 CÔN 2 Ờ t N 3 Ễ Y TRƯ
Lập bảng biến thiên ta được: max f (t) 1 . [0;1] GU N N
Do đó, m 1, mà m 0;2019 m [1; 2019]
có 2019 giá trị nguyên của m . ÁO VIÊ
GI Câu 7. Cho hàm số y
f x liên tục và đồng biến trên 0; , bất phương trình 2 ln cos x f x x e
m (với m là tham số) thỏa mãn với mọi x 0; khi và chỉ khi 2
A. m f 0 1.
B. m f 0 1.
C. m f 0 1.
D. m f 0 1. Lời giải Chọn A Ta có: lncos x f x x e m ln cos x m f x x e
(*) , trong đó f x đồng x biến trên 0;
. Xét hàm số g x
x g x sin ln cos ' đồng biến trên 0; . 2 cos x 2 Xét hàm số x ' . x h x e h x
e đồng biến trên 0; . 2 ln cos x f x x e đồng biến trên 0; nên đạt GTNN trên 0; là 2 2
f 0 g 0 h0 f 0 1.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Suy ra: Bất phương trình (*) thỏa mãn với mọi x 0;
khi và chỉ khi m f 0 1. 2 Câu 8.
Cho hàm số y f x liên tục trên và có bảng xét dấu đạo hàm như sau Bất phương trình 2 x
f x e m đúng với mọi x 1 ; 1 khi và chỉ khi
A. m f 0 1.
B. m f 1 . e
C. m f 0 1.
D. m f 1 . e Lời giải Chọn C 2 2 x x f x e m
f x e m 2 2
Xét hàm số: x ;
2 x g x f x e g x f x xe . I
f x 0 Ơ Trên khoảng 1 ;0 ta có
gx 0, x 1 ;0. 2 x 0 M D Ầ f x 0
gx 0, x 0 Đ Trên khoảng 0 ;1 ta có ;1 . 2 x 0 NHỊ Đ f x 0 G
Tại điểm x 0 ta có
g x 0 . 2 THPT x N.C.Đ 2xe 0 NG CÔN
Suy ra bảng biến thiên của g x : Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
Từ bảng biến thiên ta có: max g x f 0 1. 1 ; 1
Do đó bất phương trình m g x đúng với mọi x 1 ; 1 khi và chỉ khi
m max g x f 0 1. 1 ; 1 Câu 9. Cho hàm số 3 2
f x ax bx cx d với a,b, c, d là các số thực, có đồ thị như hình bên.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x m 1 m có đúng 4 nghiệm phân biệt.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 A. 3. B. Vô số. C. 1. D. 2. Lời giải Chọn D
Đặt t x m 1 t
1 , phương trình trở thành: f t m *
+ Với t 1 x m .
+ Với t 1 x m t 1 x m t
1 . Khi đó với mỗi t 1 cho ta hai giá trị x .
Vậy phương trình có đúng 4 nghiệm thực phân biệt khi và chỉ khi * có đúng 2
nghiệm lớn hơn 1 1 m 4 m 2; 3 .
Câu 10. Số các giá trị nguyên của tham số m thuộc đoạn 2
019;2019 để phương trình 2
x m x m 3 2 4 1
x 4x có nghiệm là A. 2011. B. 2012 . C. 2013. D. 2014 . I Lời giải Ơ Chọn C Điều kiện : 3
x 4x 0 x 0 . M D Ầ
*) Nhận thấy x 0 không là nghiệm của phương trình. Đ NH Ị
*) Với x 0 chia cả hai vế của phương trình cho 3 x 4x ta được: Đ 2 x 4 x G THPT m 2 m 1. 1 2 N.C.Đ x x 4 NG 2 CÔN Ờ x 4 4 4 Đặt t x 2. . x
2 . Vậy t 2 với x 0. N x x x Ễ Y TRƯ Phương trình 1 trở thành: GU N 2 N t t 2 4 2
t m
1 t m 2 0 m
m t 2 ( t 2) 2 t 1 t . 1 ÁO VIÊ
Xét hàm số f t 4 t 2 2; . GI t trên 1 2 t 3 t t 2; 4 2 3
f t 1
; f t 0 2 2 t 1 t 1 t 1 2;
Bảng biến thiên của hàm số f t :
Phương trình đã cho có nghiệm khi và chỉ khi phương trình 2 có nghiệm t 2; .
Từ bảng biến thiên ta thấy m 7 . Kết hợp m là số nguyên và m 2 019;2019 suy ra
có 2013 giá trị m .
Câu 11. Cho hàm số f x liên tục trên đoạn 0;
3 và có bảng biến thiên như sau:
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Có bao nhiêu số nguyên m để phương trình f x m 4 2
x 2x 2 có nghiệm thuộc đoạn 0; 3 . A. 9 . B. 5 . C. 4 . D. 7 . Lời giải Chọn A f x
Theo đề ta có f x m 4 2
x 2x 2 m
có nghiệm thuộc đoạn 0; 3 (*). 4 2 x 2x 2 I f x Ơ Đặt h x
, trong đó g x 4 2
x 2x 2 . g x M D x 0 0;3 Ầ g x 3
4x 4x ; gx 0
, g 0 2 ; g
1 1; g 3 65 Đ x 1 0; 3 NHỊ
Nên min g x g
1 1; max g x g 3 65 Đ 0; 3 0; 3 G THPT
Từ bảng biến thiên ta có: max f x f
1 9; min f x f 3 5 . [0;3] N.C.Đ 0; 3 NG f 3 1 f 1 CÔN Ờ
Do đó min h x ; max h x 9. N 0; 3 g 3 0; 3 13 g 1 Ễ Y TRƯ 1 Vậy (*)
m 9 m1,...., 9 . GU N 13 N 3 2
x x m
Câu 12. Giá trị lớn nhất của hàm số y
0; 2 bằng 5 . Tham số m nhận giá trị x trên 1 ÁO VIÊ là GI A. 5 . B. 1. C. 3 . D. 8 . Lời giải Chọn C
x x m
Đặt f x 3 2 x . 1
f x 5, x 0; 2
Giá trị lớn nhất của y f x trên 0; 2 bằng 5 . x 0;2 f x 5 0 0 3 2
x x m
* f x 5, x 0; 2 5, x 0; 2 x 1 3 2
m x x 5x 5, x 0; 2
m max hx, với hx 3 2
x x 5x 5 . 0;2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x 1
+ Ta có: h x 2
3x 2x 5, hx 0 2
3x 2x 5 0 5 . x L 3 Ta có: h0 5 , h2 3 , h 1 8 .
Suy ra max h x 3
, min hx 8 . 0;2 0;2 Vậy m 3 . 1 3 2
x x m * x
0;2 f x 5
5 có nghiệm trên 0;2 . 0 0 x 1 3 2
m x x 5x 5 có nghiệm trên 0;2 . Theo phần trên, ta suy ra 8 m 3 . 2 Từ
1 và 2 suy ra m 3 . Cách dùng casio: I Ơ
Kiểm tra từng giá tri của m từ các đáp án A, B, C, D như sau x x M D
Trường hợp 1: m 5
thì f x 3 2 5 . Ầ x 1 Đ
Trước khi làm thì tắt hàm g x bằng lệnh “ SHIFT + MODE + + 5 + 1”. NHỊ Đ
Bước 1: Vào môi trường TABLE bằng lệnh “Mode + 7”. G THPT x x N.C.Đ
Bước 2: Nhập hàm f x 3 2 5 . NG x 1 CÔN Ờ 2 0 N
Bước 3: Nhập Start 0 ; End 2 ; Step . Ễ 29 Y TRƯ GU N N ÁO VIÊ GI
Quan sát bên cột f x có giá trị f x 5,67 nên loại m 5 .
Ba trường hợp còn lại làm tương tự như trên chỉ có m 3
thỏa mãn giá trị lớn nhất
của f x là 5 .
Câu 13. Cho hàm số f (x) có bảng biến thiên như hình vẽ sau
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 5
Phương trình f sinx 2
3 có bao nhiêu nghiệm trên đoạn 0; . 6 A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Chọn A 5 Với 0; sin 0; sin 1 2 x x x t 1;2. 6
Phương trình trở thành f (t) 3. Kẻ đường thẳng y 3 cắt đồ thị hàm số f x tại bốn điểm phân biệt có hoành độ lần lượt là
x a 1; x b 1; 2 ; x c 2 ;2; x d 2;.
Vậy phương trình f (t) 3 có bốn nghiệm là:
t a 1;t b 1; 2 ;t c 2 ;2;t d 2;. I Ơ
Đối chiếu điều kiện t 1;2 nhận t ; b t c . x 1 sin 2 b 1; 2 M D sin x log b 0; . 2 2 Ầ Đ 5 NH
Phương trình này có một nghiệm trên đoạn 0; . Ị 6 Đ G THPT x 1 sin 2
c 2 ;2 sin x log c ;1 . 2 N.C.Đ 2 NG CÔN Ờ 5 N
Phương trình này có hai nghiệm trên đoạn 0; . Ễ 6 Y TRƯ 5 0 ; . GU N
Vậy phương trình đã cho có tất cả 3 nghiệm trên đoạn 6 N
Câu 14. Có bao nhiêu giá trị nguyên của tham số m 9
;9 để phương trình: ÁO VIÊ 2
1 x m2 1 x 2 1 x 3 1 0 có nghiệm? GI A. 14 . B. 8 . C. 10. D. 12 . Lời giải Chọn D Điều kiện: 1 x 1
Đặt: t 1 x 1 x 1
Xét hàm số t x 1 x 1 x trên 1;1 1 1
1 x 1 x t x 2 1 x 2 1 x
2 1 x1 x
t x 0 x 0 Ta có bảng biến thiên
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Suy ra t 2; 2 t Từ 2 2 2 2 2
1 suy ra t 2 2 1 x 1 x . Khi đó PT trở thành: 2 2
t 2 m2t 3 2
1 0 t 4mt 6m 0 2 2 I
Bài toán trở thành: Tìm giá trị nguyên của tham số m để phương trình: Ơ 2
t 4mt 6m 0 có ít nhất 1 nghiệm thuộc đoạn 2 ; 2 . M D Ta có: 2 2
t 4mt 6m 0 t 2 (
m 2t 3) 0 Ầ Đ 3 9 NH
TH1: Nếu 2t 3 0 t
thay vào 2 ta được: 0 ( vô lý) Ị 2 4 Đ 2 t G 3 THPT
TH 2 : Nếu t
PT 2 2m *N .C.Đ 2 2t 3 NG CÔN t 2t t 3 Ờ
Xét hàm số: g t 2
trên 2; 2 g t N 2t 3 Ễ 2t 32 Y TRƯ t 0 2;2 GU N gt 2t t 3 0 0 N 2t 32 t 3 2 ; 2 ÁO VIÊ BBT GI 2m 4 m 2
Dựa vào BBT suy ra: để PT có nghiệm 2m 2
2 23 m 2 23
Với m 2 , m 9
;9 m 2;3;4;5;6;7;8;9 ( 8 giá trị thỏa mãn ).
Với m 2 2 3 , m 9
;9 m 6; 7 ; 8 ; 9
( 4 giá trị thỏa mãn ).
Vậy có tất cả 12 giá trị nguyên của tham số m 9
;9 thỏa mãn yêu cầu bài toán.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Câu 15. Cho phương trình 2 3 3 2
16m x 16x 8x 2x 2 2m 10 ( m là tham số). Khẳng định nào sau đây là đúng?
A. Phương trình đã cho vô nghiệm.
B. Phương trình đã cho có đúng một nghiệm thực.
C. Phương trình đã cho có hai nghiệm thực phân biệt.
D. Số nghiệm của phương trình phụ thuộc vào giá trị của tham số m. Lời giải Chọn B Ta có 2 3 3 2
16m x 16x 8x 2x 2 2m 10 2 3 3 2
16m x 16x 8x 2x 2 2m 10 0. 1 1 1 Điều kiện: 3
8x 2x 2 0 x 2
8x 4x 4 0 x 0 x . 2 2 2 1 I
Đặt: f x 2 3 3 2
16m x 16x 8x 2x 2 2m 10 với x . Ơ 2 12x 1 1
Khi đó: f x 2 2 2 48m x 16 0, x . M D 3 2 8x 2x 2 Ầ Đ Bảng biến thiên: NHỊ 1 Đ x 2 G THPT N.C.Đ f x + NG CÔN Ờ N f x Ễ Y TRƯ 18 GU N
Dựa vào bảng biến thiên ta có phương trình f x 0 có duy nhất một nghiệm với mọi N x .
Câu 16. Tổng các giá trị nguyên dương của m để tập nghiệm của bất phương trình ÁO VIÊ GI m 2 x 1
x có chứa đúng hai số nguyên là 72 A. 27 . B. 29 . C. 28 . D. 30 . Lời giải Chọn B ĐK: x 0 . m Do m dương nên 2 x 1 0, x . 72 m m Ta có, 2 x 1 x 2 x 1 x 2
mx 72x 1 1 72 72 72 x 1
Nhận thấy x 0 không là nghiệm của 1 nên 1 m 2 x 72 x 1
Xét hàm số y f (x) với x 0 . 2 x
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 72x 2 y f ( x) 0 x 2. 3 x
Bảng biến thiên của f x với x 0 : 27
Từ bảng biến thiên ta có f 2 f 3 f 4
f x, x \2,3, 4 , nên để tập 2 72 x 1
nghiệm của bất phương trình m
có chứa đúng hai số nguyên thì 2 x f 27 4
m f 3 16. (tập nghiệm chứa x 2, x 3 ) 2 I Ơ Với * m thì m 14,1 5
Do vậy, tổng các giá trị nguyên dương của m là 14 15 29 . M D
Ầ Câu 17. Cho hàm số f x liên tục trên . Hàm số y f x có đồ thị như hình vẽ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
Bất phương trình f x 2 2sin
2sin x m đúng với mọi x0; khi và chỉ khi
A. m f 1 1 .
B. m f 1 1 .
C. m f 1 0 .
D. m f 1 0 . 2 2 2 2 Lời giải Chọn A
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 f x 2 2sin
2sin x m 1
Ta có: x 0; sin x 0;
1 . Đặt 2sin x t t 0;2 ta được bất phương trình: 1 I f t 2
t m 2. Ơ 2
1 đúng với mọi x 0; khi và chỉ khi 2 đúng với mọi t 0;2. M D Ầ 1 Đ
Xét g t f t 2
t với t 0;2. 2 NHỊ Đ g t
f t t . G THPT
Từ đồ thị của hàm số y f x và y N x .C.Đ (hì
nh vẽ) ta có BBT của g t như sau: NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ
Vậy yêu cầu bài toán tương đương với m g f 1 1 1 . GI 2
Câu 18. Cho hàm số y f x có f 2
m 1, f
1 m 2 . Hàm số y f x có bảng biến thiên như hình vẽ bên. 1 2x 1
Tập hợp tất cả các giá trị của tham số m để phương trình f x m có nghiệm 2 x 3 x 2 ; 1 là 7 7 A. 5; . B. 2 ;0 . C. 2 ;7 . D. ;7 . 2 2 Lời giải
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Chọn D 1 2x 1
Đặt h x f x , với x 2 ; 1 . 2 x 3 1 5
Ta có h x
f x . 2 x 32
Dựa vào bảng biến thiên của hàm số y f x ta có f x 0, x 2 ; 1 5 và 0, x 2
;1 . Do đó hx 0, x 2 ; 1 . 2 x 3
Bảng biến thiên của hàm số y h x trên khoảng 2 ;1 . I Ơ
Khi đó, phương trình h x m có nghiệm x 2 ;
1 khi và chỉ khi h
1 m h 2 M D Ầ 1 m m 2m 7 m 7 f 3 1 1 m f 2 2 3 1 Đ 3 m 3 m 2 4 2 2 4 2 4 2 NHỊ 7 Đ m 7 . G 2 THPT N.C.Đ
Câu 19. Cho hàm số f x liên tục trên
và có đồ thị như hình vẽ bên. Có bao nhiêu số NG CÔN Ờ
nguyên m để phương trình f f x
1 m có ít nhất 6 nghiệm thực phân biệt? N Ễ Y TRƯ GU N N ÁO VIÊ GI A. 2 . B. 3 . C. 5 . D. 4 . Lời giải Chọn A
Nhận xét: Số nghiệm của phương trình f x b a cũng chính là số nghiệm của
phương trình f x a .
Xét phương trình f f x 1 m 1 .
Đặt t f x
1 Khi đó ta có phương trình f t m * .
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
+ Trường hợp 1: Với m ; 1 2; .
Khi đó phương trình
* có đúng 1 nghiệm. Suy ra phương trình 1 có tối đa 3 nghiệm (không thỏa mãn).
+ Trường hợp 2: Với m 1 . Khi đó * trở thành t 2
f x f t 1 2 1 . t t 0;1
f x 1 t , t 0;1 1
1 1
Phương trình f x
1 2 có 2 nghiệm, phương trình f x
1 t , t 0;1 có 3 nghiệm. 1 1 Suy ra phương trình
1 có 5 nghiệm (không thỏa mãn).
+ Trường hợp 3: Với m 2. Khi đó * trở thành t 1
f x f t 1 1 2 . t t 2;3
f x 1 t , t 2;3 2
2 2 I Ơ
Phương trình f x 1
1 có 3 nghiệm, phương trình f x 1 t , t 2;3 có 1 2 2
nghiệm. Suy ra phương trình
1 có 4 nghiệm (không thỏa mãn). M D Ầ
+ Trường hợp 4: Với m 1 ;2 . Khi đó Đ NHỊ
t t 0;1
f x 1 t , t 0;1 3 3 3 Đ
* t t 1;2 f x 1 t , t 1;2 . 4 4 4 G THPT N.C.Đ t t 2;3
f x 1 t , t 2;3 5 5 5 NG CÔN Ờ
Phương trình f x
1 t , t 0;1 có 3 nghiệm, phương trình f x
1 t , t 1; 2 có 4 4 3 3 N Ễ Y
3 nghiệm, phương trình f x
1 t , t 2;3 có 1 nghiệm. Dựa vào đồ thị ta thấy các 5 5 TRƯ GU N
nghiệm trên là các nghiệm phân biệt. Suy ra phương trình 1 có 7 nghiệm phân biệt N (thỏa mãn).
Vậy, phương trình f f x
1 m có ít nhất 6 nghiệm thực phân biệt 1 m 2. ÁO VIÊ GI
Vì m nguyên nên m 0 ;1 .
Minh họa bằng đồ thị: 7
Câu 20. Cho hàm số y f x liên tục trên 0;
có đồ thị hàm số y f x như hình vẽ sau: 2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 7
Hàm số y f x đạt giá trị nhỏ nhất trên 0;
tại điểm x nào dưới đây ? 2 0 7
A. x 0 . B. x .
C. x 3. D. x 1. 0 0 2 0 0 Lời giải Chọn C I Ơ 7
Xét hàm số y f x trên đoạn 0; . 2 M D Ầ x Đ
Dựa vào đồ thị ta có f x 1 0 x 3 NHỊ Đ Bảng biến thiên: G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N 7
Nhìn bảng biến thiên ta thấy hàm số y f x đạt giá trị nhỏ nhất trên 0; tại điểm 2 ÁO VIÊ x 3. 0
GI Câu 21. Cho phương trình 2
2x 2mx 4 x 1 ( m là tham số). Gọi p, q lần lượt là các giá trị
m nguyên nhỏ nhất và giá trị lớn nhất thuộc 10
; 10 để phương trình có nghiệm. Khi
đó giá trị T p 2q là A. 10. B. 19. C. 20. D. 8. Lời giải Chọn B x 1 Ta có 2
2x 2mx 4 x 1 . 2 x
2m 2 x 5 0 1 x x x 2m 2 2 2 5 2
x 5 0 m 2x 2 x 2x 5 2 2x 10 Xét hàm số y
trên 1; . Ta có y' . 2x 2 4x Bảng biến thiên sau
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Phương trình đã cho có nghiệm khi và chỉ khi phương trình (1) có nghiệm lớn hơn bằng 1 m 1
. Kết hợp điều kiện m 1
0; 10 m 1 ; 10.
Do đó p -1, q 10 p 2q 19 .
Câu 22. Cho hàm số f x 3 2
x 3x 3x 4 . Số nghiệm thực phân biệt của phương trình
f f x 2 2 3 f x là A. 7 . B. 4 . C. 6 . D. 9 . Lời giải I Chọn C Ơ
Đặt f x 2 t f x t 2 phương trình trở thành: M D
f t t f t 3 2 2 3 2
2 1 t t 3t 3t 2 1 t Ầ Đ 1 t 0 1 t 0 t 0 ,58836 NHỊ . 3 2 Đ t 3t 3t 2 1 t2 3 2 t 4t t 1 0 t 0, 40642 G THPT N.C.Đ x 1 , 21627 NG Với t 0 ,58836 , ta có: 3 2
x 3x 3x 2 0
,58836 x 0,586256. CÔN Ờ N x 3,63001 Ễ Y TRƯ x 1 ,1951 GU N Với t 0 ,40642 , ta có: 3 2
x 3x 3x 2 0
, 40642 x 0,552834. N x 3,64227
Vậy phương trình đã cho có 6 nghiệm thực phân biệt. ÁO VIÊ
GI Câu 23. Gọi S là tập tất cả các giá trị nguyên âm của tham số m để phương trình m 2
x 4 x 2 có nghiệm. Tập S có bao nhiêu phần tử? A. 10. B. 6 . C. 4 . D. 2 . Lời giải Chọn C m Ta có: 2
x 4 x
(*) điều kiện xác định: 2 x 2. 2
Xét hàm số f x 2
x 4 x , x 2 ;2 . x
Có f ' x 1 . 2 4 x x 0 x f ' x 2 0 1
0 4 x x
x 2 x 2 2 ;2 2 4 x x 2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Hàm số f x 2
x 4 x liên tục trên 2
;2; có đạo hàm trên 2 ;2 .
f 2 2; f 2 2; f 2 2 2 .Suy ra min f x 2
;max f x 2 2 . 2 ;2 2 ;2 m
Vậy phương trình (*) có nghiệm 2 2 2 4 m 4 2 . 2
Mặt khác m nguyên âm nên S 4 ; 3 ; 2 ; 1 .
Câu 24. Cho hàm số y f (x) có bảng xét dấu của f '(x) như sau: 2 Xét hàm số (1 ) ( ) f x x g x e
, tập nghiệm của bất phương trình g '(x) 0 là 1 1 1 A. ; . B. ; . C. 1; 2;
. D. 1 ; 1 ; 2 . I 2 2 2 2 Ơ Lời giải Chọn C M D Ầ 2 f 1 2 x x Đ
Ta có g '(x) 1 2x. f '1 x x .e , x NHỊ 2 f 1 2 x x Đ
Yêu cầu của bài toán g '(x) 0 1 2x f '1 x x e 0 . G THPT N.C.Đ 1 2x 0 NG (1) 2 CÔN f '
1 x x Ờ 0 N Ễ 1 2x 0 Y TRƯ f ' (2) 2
1 x x 0 GU N N 1 x 1 1 2x 0 2 ÁO VIÊ x Xét trường hợp 1: 2 2
x x 2 0 GI f ' 2
1 x x 0 2 1
1 x x 3 2
x x 2 0 1 x 1 2 1 x . 2 1 x 2 1 1 x x 1 2x 0 2 2 Xét trường hợp 2: 2 2 f '
x x
x x 2
1 x x 0 1 1 2 0 2 2
x x 1 3
x x 2 0 1 1 x x 2 2 x 2 x 1 2
x x 2 0 x 2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 1 x
Kết hợp hai trường hợp ta được 2 . x 2 1
Vậy tập nghiệm của bất phương trình là T 1; 2; . 2 2 2 2
x y z 6
Câu 25. Cho hệ phương trình xy yz xz 3
với x, y, z là ẩn số thực, m là tham số. Số giá trị 6 6 6
x y z m
nguyên của m để hệ phương trình có nghiệm là A. 25 . B. 24 . C. 12 . D. 13 . Lời giải Chọn D
Ta có: x y z2 2 2 2
x y z 2xy yz xz 6 2. 3 0 . I Ơ
Vây x y z 0 . Suy ra: z x y 2 2 2
z x 2xy y 2 2 2 2 2
x y z 2(x y xy) 1 M D 2 2 2
x y z 2 2
x y xy (1). Thay 2 2 2
x y z 6 vào (1) ta được 2 2
x y xy 3 . Ầ 2 Đ 2 NH x y 3 xy 0 Ị . Vậy 3 xy 1. Đ x y 2 33xy 0 G THPT N.C.Đ Ta có: 6 6 6 6 6 6 m x y z x y x
y ( thay z x y ) NG CÔN Ờ 2 6 2 3 3 3 3 6 2 2 3 3 N
x y 2x y x y x y.
x xy y 2x y x y Ễ Y TRƯ 2
= x y2 x y xy xy xy3 x y6 2 2 . 2 2 (2) GU N N
x y2 3 xy Thay
vào (2) ta được: x y z xy xy2 xy3 xy3 6 6 6 3 . 3 2 2 3 2 2
x y xy 3 ÁO VIÊ 2 3 6 6 6 3 3 2 GI Đặt t xy 3 t
1 . Khi đó x y z 3 t.3 2t 2t 3 t 3t 9t 54
Xét hàm số f t 3 2
3t 9t 54 trên 3
;1 . Ta có: f t 2 9t 18t . t 0 3 ; f t 1 0 t 2 3 ; 1 Bảng biến thiên:
Từ bảng biến thiên ta thấy: 54 f t 66 với t 3 ; 1 .
Hệ phương trình đã cho có nghiệm khi và chỉ khi phương trình f t m có nghiệm t 3 ; 1
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
54 m 66. Vậy có 13 giá trị nguyên của m để hệ phương trình có nghiệm.
Câu 26. Cho phương trình m 2 x 3 2m 1
1 x m 1. Biết rằng tập hợp tất cả các giá
trị của tham số thực m để phương trình có nghiệm là đoạn ;
a b . Giá trị của biểu thức
5a 3b bằng A. 13 . B. 7 . C. 19 . D. 8 . Lời giải Chọn D Cách 1:
Tập xác định : D 3 ; 1 .
2 x 3 1 x 1
Từ phương trình suy ra : m .
x 3 2 1 x 1
2 x 3 1 x 1
Xét hàm số g(x) trên đoạn 3 ;1 . I
x 3 2 1 x 1 Ơ 3 1 x x 3 1 1 1 M D 2 x 3 1 x 2 x 3 1 x Ầ
Ta có : g '(x) 0, x 3;1 . 2 Đ
x32 1x 1 NHỊ Đ
Suy ra hàm số y g(x) đồng biến trên 3 ;1 . G THPT 3 5 N.C.Đ
Do đó, min g(x) ; maxg(x) . NG 3 ; 1 3 ; 1 5 3 CÔN Ờ N 3 5
Suy ra phương trình có nghiệm m ; . Ễ 5 3 Y TRƯ
Vậy 5a 3b 8 . Đáp án D. GU N N Cách 2:
Tập xác định : D 3 ; 1 . ÁO VIÊ
2 x 3 1 x 1 GI
Từ phương trình suy ra : m .
x 3 2 1 x 1
2 x 3 1 x 1
Xét hàm số g(x) trên đoạn 3 ;1 .
x 3 2 1 x 1 3 5
Dùng máy tính ta dự đoán g(x) . 5 3
2 x 3 1 x 1 3 Ta chứng minh: . (1)
x 3 2 1 x 1 5
Ta có: (1) 10 x 3 5 1 x 5 3 x 3 6 1 x 3
7 x 3 2 1 x 0. Xét trên đoạn 3
;1 thì 7 x 3 0;2 1 x 0. Suy ra (1) luôn đúng. Dấu " " xáy ra khi x 3 .
2 x 3 1 x 1 5 Ta lại chứng minh: . (2)
x 3 2 1 x 1 3
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Ta có: (2) 6 x 3 3 1 x 3 5 x 3 10 1 x 5
x 3 7 1 x 2. Xét trên đoạn 3
;1 thì x 3 2;7 1 x 2 2. Suy ra (2) luôn đúng. Dấu " " xáy ra khi x 1. 3 5 Do đó, m . 5 3 3 5
Suy ra phương trình có nghiệm m ; . 5 3
Vậy 5a 3b 8 . Đáp án D.
Câu 28. Cho hàm số y f x liên tục trên 1 ;
3 và có đồ thị như hình vẽ sau: I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ
Bất phương trình f ( )
x x 1 7 x m có nghiệm thuộc 1 ; 3 khi và chỉ khi NG CÔN Ờ
A. m 7.
B. m 7 .
C. m 2 2 2 .
D. m 2 2 2 . N Ễ Chọn A Y TRƯ
Xét hàm số g x x 1 7 x liên tục trên 1 ; 3 ta có: GU N N g x 1 1 ' , x 1 ; 3 2 x 1 2 7 x ÁO VIÊ
g ' x 0 x 1 7 x x 1 7 x x 3 (nhận) GI g
1 2, g 3 4 max g x maxg
1 , g 3 g 3 4. 1 1 ; 3
Từ đồ thị hàm số y f x ta có: max f x f 3 3. 2 1 ; 3
Đặt h x f (x) g x trên 1 ; 3 , kết hợp với 1 và 2 ta suy ra:
h x max f x max g x f 3 g 3 7 , đẳng thức xảy ra khi x 3. 1 ; 3 1 ; 3
Vậy bất phương trình m h x có nghiệm thuộc 1 ;
3 khi và chỉ khi m max h x 7. 1 ; 3
Câu 29. Cho hàm số f x 3 m 3 2 1
x 3x 4 m x 2 với m là tham số. Có bao nhiêu số nguyên m 2 018;201
8 sao cho f x 0 với mọi giá trị x 2;4 . A. 2021. B. 2019 . C. 2020 . D. 4037 . Lời giải Chọn C Ta có:
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 29
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
f x 3 m 3 2
x x m 3 2 3 3 1 3 4
x 2 x 3x 4x 2 m x mx f x 3 2 3 3 3 3 3
0 x 3x 4x 2 m x mx (x1) x 1 m x mx (1). Xét hàm số 3
g(t) t t; t , ' 2
g (t) 3t 1 0 t .
Vậy hàm g(t) đồng biến trên .
Bất phương trình (1) g(x 1) g(mx) x 1 mx x 1
Xét x 2;4 bất phương trình m (2) x x 1 Đặt h(x) . x
Bất phương trình (2) luôn đúng với mọi x 2;4 suy ra: m min h(x). 2;4 1 5
Ta có: h '(x)
0 x 2;4 min h(x) h(4) . 2 x 2;4 4 I 5 Do đó: m . Ơ 4 Mà m 2 018;201
8 và m nguyên nên có 2020 giá trị của m thỏa mãn. M D
Ầ Câu 30. Tìm số thực m lớn nhất để bất phương trình sau có nghiệm đúng với mọi x Đ NH
m sin x cos x
1 sin 2x sin x cos x 2018. Ị Đ 1 2017 G THPT A. . B. 2018 . C. . D. 2017 . 3 N.C.Đ 2 NG Lời giải CÔN Ờ N Chọn C Ễ Y TRƯ
Đặt t sin x cos x 2
t 1 sin 2x 2 1 t 2 GU N
Khi đó bất phương trình đã cho trở thành: N 2 t t 2019 mt 2
1 t t 2019 m
f t với mọi t 1 ; 2 . t 1 ÁO VIÊ 2 GI t 2t 2020
Ta có f t . t 0, t 1; 2 2 1 2 t t 2019 2017 Vậy m
f t với mọi t 1 ; 2
m min f t f 1 . t 1 t 1 ; 2 2 Câu 31. Số giá trị nguyên của tham số m 1
0;10 để bất phương 2 2
3 x 6 x 18 3x x m m 1 nghiệm đúng x 3 ;6. A. 28. B. 20. C. 4. D. 19. Lời giải Chọn D 2 2
3 x 6 x 18 3x x m m 1 (1) nghiệm đúng x 3 ;6.
Đặt t 3 x 6 x , x 3 ;6 . 1 1 6 x 3 x t . 2 3 x 2 6 x
2 3 x. 6 x
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 30
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
t 0 6 x 3 x 3 x . 2 Bảng biến thiên: t 3;3 2 . 2 t 9 Ta có 2 2 2
t 3 x 6 x 2 18 3x x 9 2 18 3x x 2
18 3x x . 2 I
Bất phương trình (1) nghiệm đúng x 3 ;6 Ơ f t 2 t 9 2 t
m m 1 nghiệm đúng t 3;3 2 M D 2 Ầ Đ 2
m m 1 max f t . (2) NH 3;3 2 Ị Đ t G
Xét hàm số f t 2 9 t , t 3;3 2 THPT 2 N.C.Đ NG CÔN f t 1 1 2t 1 t 0 t 3;3 2 Ờ 2 N Ễ Y
f t nghịch biến trên 3;3 2 TRƯ . GU N 3 9 N
max f (t) f 3 2 3 3 . 3;3 2 2 m ÁO VIÊ Khi đó (2) 2
m m 1 3 2 . GI m 1 m
Kết hợp với điều kiện bài toán: m nguyên và m 1 0;10 . m 10 ; 1 2;10
Vậy có 19 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Nhận xét: Trên tinh thần thi trắc nghiệm, học sinh hoàn toàn có thể sử dụng tính năng
TABLE của máy tính cầm tay để tìm max f x 3 với 3 ;6 f x 2
3 x 6 x 18 3x x . Từ đó đưa bài toán về dạng giải bất phương trình bậc hai cơ bản: 2
m m 1 3 một cách dễ dàng.
Câu 32. Cho hai số thực dương
x , y thỏa mãn 2y y 2x log y 1 x 2
. Giá trị nhỏ nhất của 2 x biểu thức P bằng y e ln 2 e ln 2 e ln 2 e A. . B. . C. . D. . 2 2 2 2 ln 2 Lời giải
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 31
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Chọn C Có 2y y 2x log y 1 x 2
2y 2 log 2 2y y x x 1. 1 2 2 Đặt log 2 2y t x
2 2y 2t x
2 2t 2y x . 2
1 trở thành : 2y 2t 2y y t 1 y 1 2 1 2t y t . 2 Xét hàm số 2x f x
x, x 2x f x ln 2 1 0, x
nên hàm số 2x f x x luôn đồng biến trên
. Kết hợp với 2 ta có: t y 1 log 2 2y x y 1 2 y y 1 2x 2 2 1 2y x . x 1 2y y 1 y 1 2 y ln 2 2 Khi đó P P . y y 2 y
Cho P 0 y ln 2 1 1 0 y . ln 2 Bảng biến thiên: I Ơ M D Ầ Đ NHỊ Đ G THPT e ln 2 e 1 Vậy P khi x và y . min N.C.Đ 2 2 ln 2 NG CÔN Ờ 1 4 1 4
Câu 33. Cho hàm số f x 3 2
x x x có đồ thị như hình vẽ bên. N 3 3 3 3 Ễ Y TRƯ y GU N N 1 x 1 1 4 ÁO VIÊ O GI
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f 2 x x 2 2019 15 30
16 m 15x 30x 16 m 0 có 4 nghiệm phân biệt thuộc đoạn 0;2 A. 1513. B. 1512 . C. 1515 . D. 1514 . Lời giải Chọn D Đặt 2
t 15x 30x 16 t x 2 15
1 1 do x 0;2 nên t 1;4 .
Nhận xét : Ứng với mỗi t 1;4 thì có 2 nghiệm phân biệt x 0;2 . Phương trình: f 2 x x 2 2019 15 30
16 m 15x 30x 16 m 0 (1) 2019 f (t)
trở thành : 2019 f t mt m 0 m với t 1;4 . t 1
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 32
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 1 5 4 2 m 2019 t t m 2
673 t 5t 4 với t 1;4 . (2 ) 3 3 3
Phương trình (1) có 4 nghiệm x phân biệt thuộc đoạn 0;2 tương đương phương trình
(2) có 2 nghiệm t phân biệt thuộc nửa khoảng 1;4 .
Xét ht 2
673 t 5t 4 với t 1;4 .
Bảng biến thiên h t 5 t 1 4 2 ht 0 0 0 h t 6057 I 4 Ơ 6057
Dựa vào bảng biến thiên suy ra:
m 0 và m nguyên suy ra 1 514 m 1 . 4 M D Ầ
Vậy có 1514 giá trị m nguyên thỏa mãn. Đ
Nhận xét: Đề bài cho thừa giả thiết đồ thị y f x . NHỊ Đ
Câu 34. Cho f (x) mà đồ thị hàm số y
f '(x) như hình vẽ bên G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI x
Bất phương trình f (x) sin
m nghiệm đúng với mọi x 1 ; 3 khi và chỉ khi 2
A. m f (0) .
B. m f (1) 1 .
C. m f ( 1 ) 1.
D. m f (2) . Lời giải Chọn B x f (x) sin m 2 x m f x sin 2
Để bất phương trình nghiệm đúng với mọi x 1 ; 3 thì x m Min f x sin 1; 3 2 x
Xét hàm số g x f x sin 2
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 33
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 x
Có g x f x cos 2 2
Nhận xét : Đến đây ta khó có thể giải được phương trình g x 0 để lập bảng xét dấu.
Nhận thấy f x đổi dấu khi qua x 1 gợi ý cho ta xét dấu của hàm g x trên 2 khoảng 1 ; 1 và 1;3 Xét khoảng 1 ; 1 x 1 ;
1 f x 0 ( đồ thị hàm số f x nằm dưới trục hoành ) x x x 1; 1 ; cos 0,x 1; 1 2 2 2 2 2 x
Vậy g x f x cos 0, x 1; 1 2 2 Xét x 1 I Ơ
g f .1 1 1 cos 0 2 2 M D Xét khoảng 1;3 Ầ Đ x
1;3 f x 0 f x NH ( đồ thị hàm số nằm trên trục hoành ) Ị Đ x 3 x G x 1;3 ; cos 0, x 1;3 THPT 2 2 2 2 2 N.C.Đ NG x CÔN
g x f x cos 0, x 1;3 Ờ Vậy N 2 2 Ễ Y g x TRƯ
Ta có bảng biến thiên của hàm số như sau GU N N ÁO VIÊ GI x Vậy Min f x sin f 1 1 1 ; 3 2
Vậy m f 1 1
Câu 35. Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình sau 6 4 3 3 2
x 3x m x 4x mx 2 0 nghiệm đúng với mọi x 1;
3 . Tổng tất cả các phần tử của S bằng: A. 3 . B. 2 . C. 1. D. 4 . Lời giải
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 34
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Chọn A Ta có: 6 4 3 3 2 6 4 2 3 3
x 3x m x 4x mx 2 0 x 3x 4x 2 m x mx
x 3 x mx3 2 2 1 1 mx 1
Xét hàm đặc trưng f t 3
t t f t 2 ' 3t 1 0
f 2x f mx 2 1 1
x 1 mx
Bài toán trở thành tìm m để bất phương trình 2
x 1 mx nghiệm đúng với mọi x 1; 3 2 x 1 2
x 1 mx m
g x , x 1; 3 x g x 1 ' 1 0 x 1;
3 Min g x g 1 2 2 x 1; 3 x x 1;
Vậy để bất phương trình đã cho nghiệm đúng với mọi 3 thì m 2 S 1; 2 I
Vì m nguyên dương nên
có 2 phần tử. Tổng các phần tử bằng 3 .
Ơ Câu 36. Số giá trị nguyên của tham số m nằm trong khoảng 0;2020 để phương trình M D
x 1 2019 x 2020 m có nghiệm là Ầ Đ A. 2020 . B. 2021. C. 2019 . D. 2018 . NHỊ Lời giải Đ G Chọn D THPT N.C.Đ 2018, x 1;2019 NG
Ta có f x x 1 2019 x . CÔN Ờ
2x 2020 , x 1;2019 N Ễ Y
Vì hàm số h(x) 2x 2020 là hàm số đồng biến trên đoạn [1; 2019] nên ta có TRƯ GU N
max h(x) max h(1), h(2019
) 2018, min h( x) min ( h 1), ( h 2019 ) 2018 [1;2019] [1;2019] N
Suy ra min f x 0 và max f x 2018 . 1;2019 1;2019 ÁO VIÊ
Do đó, ta có: min f x 0 và max f x 2018. GI
Vì vậy, phương trình đã cho có nghiệm khi và chỉ khi:
0 2020 m 2018 2 m 2020.
Suy ra có 2018 giá trị nguyên của m nằm trong khoảng 0;2020 .
Câu 37. Cho hàm số f x 5 3
x 3x 4m. Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3 f f x
m x m có nghiệm thuộc đoạn 1;2 ? A. 15. B. 16 . C. 17 . D. 18 . Lời giải Chọn B Đặt 3
3 3 t f x m t f x m
f x t m 1 . Ta có 3 3 f f x
m x m , suy ra 3
f t x m 2 . Từ
1 và 2 ta có f x f t 3 3
t x f x 3
x f t 3 5 3 5 3
t x 4x t 4t 3 .
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 35
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Xét hàm số g u 5 3
u u gu 4 2 4
5u 12u 0 u
g u đồng biến trên .
Do đó 3 g x g t x t . Thay vào
1 ta được f x 3 5 3
x m x 2x 3m 4.
Xét hàm số h x 5 3
x 2x trên đoạn 1;2 .
Ta có h x 4 2
5x 6x 0 x
1;2 hx đồng biến trên đoạn 1;2.
Vậy ta có min h x h
1 3 và max h x h2 48 . 1;2 1;2
Phương trình đã cho có nghiệm thuộc 1;2 Phương trình 4 có nghiệm trên 1; 2 .
min hx 3m max hx 3 3m 48 1 m 16 . Vậy có 16 giá trị nguyên của m . 1; 2 1;2
Câu 38. Cho hàm số 3 2
f x ax bx cx d có đồ thị như hình vẽ. gọi S là tập hợp các giá trị
của m m sao cho x 3
1 m f 2x
1 mf x f x 1 0, x . Số phần tử của I tập S là? Ơ A 2 . B. 0 . C. 3 D. 1. M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI Lời giải Chọn A Cách 1
Xét g x x
1 h x 0 với x
, với hx 3
m f 2x 1 .
m f x f x 1.
x 1 0 x 1 h x 0 x 1 Do
hx 0 tại x 1 x x h x * 1 0 1 0 x 1 m 0 3 m f 1 mf 1 f 3
1 1 0 m m 0 m 1
+ Với m 0 h x f 1 1 thỏa mãn
* do hàm f x đồng biến và f 1 1.
+ Với m 1 h x f 2x 1 1 thỏa mãn *
Do x 1 thì 2x 1 1 f 2x
1 1 0 và x 1 thì 2x 1 1 f 2x 1 1 0 . + Với m 1
hx f 2x
1 2 f x 1.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 36
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019
Khi đó h x là hàm số bậc ba có hệ số a 0 nên lim h x 0 không thỏa mãn * . x
Vậy m 0 và m 1. Cách 2 f 1 1 1 a f 2 1 0 b 0 1 1
Từ đồ thị hàm số ta suy ra 0 f x 3 0 x f c 0 2 2 f 1 1 0 d 2 2 m 0
Theo đề bài f 3
1 1 m m 0 m 1 m 1
x 1 f x 1 x 1 1 3 I
Với m 0, ta có: 1 x 1 2 2 Ơ 1
x x 1 1 1 x 2 3 1 2 x x 1 0 x (Nhận) M D 2 2 Ầ Đ 1 1
Với m 1, ta có: x 1 f 2x
1 f x f x 1 x 1 2x 3 1 1 NH Ị 2 2 Đ 1 3 2 3 2 G THPT x
1 8x 12x 6x 1 1 x
1 4x 6x 3x 1 N.C.Đ 2 NG 2 2 CÔN x 1 4x 2x 1 0 x (Nhận) Ờ N Ễ 1 1 Y Với m 1
, ta có: x 1 f 2x
1 f x f x 1 x 1 2x 3 3 1 x TRƯ 2 2 GU N x 1 N x 1 3 2
x 6x 3x 0 (Loại) x 0 ÁO VIÊ
Vậy m 0 và m 1. GI Cách 3 Để x 3
1 m f 2x
1 mf x f x 1 0, x thì 3
m f 2x
1 mf x f x 1
nhận x 1 là nghiệm bội lẻ duy nhất và khi qua x 1 ( 3
m f 2x
1 mf x f x 1 m 0
đổi dấu từ sang ). Khi đó: 3
m m 0 . m 1
+ Thử lại, ta thấy với m 0 thỏa.
+ Với m 1, ta có: 3
m f 2x
1 mf x f x 1 f 2x 1 1
là một hàm số bậc ba có
hệ số bậc cao nhất dương. Ta có: lim f 2x
1 1 , lim f 2x 1 1
nên khi qua x 1 hàm số sẽ đổi x x
dấu từ sang thỏa mãn. + Với m 1 , ta có: 3
m f 2x
1 mf x f x 1 f 2x
1 2 f x 1 là một hàm
số bậc ba có hệ số bậc cao nhất âm.
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 37
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2019 Ta có: lim f 2x
1 1 , lim f 2x 1 1
nên khi qua x 1 hàm số sẽ đổi x x
dấu từ sang không thỏa mãn. I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƯ GU N N ÁO VIÊ GI
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT 38