Thông tin
Quiz

Bất đẳng thức tích phân và một số bài toán liên quan Toán 12

Bất đẳng thức tích phân và một số bài toán liên quan Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

19 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bất đẳng thức tích phân và một số bài toán liên quan Toán 12

69 35 lượt tải Tải xuống

A. KIẾN THỨC CƠ BẢN

Cho các hàm số

 

y f x



và

 

y g x



có đạo hàm liên tục trên

 

;a b

. Khi đó:

 Nếu

   

f x g x



với mọi

 

;x a b



thì

   

b b

a a

f x dx g x dx



 

 Nếu

 

f x



với mọi

 

;x a b

 thì

 

f x dx





. Hệ quả:

   

0 0

f x dx f x

  



 Bất đẳng thức Holder (Cauchy – Schwarz):

       

2 2

b b b

a a a

f x g x dx f x dx g x dx

 



 

 

  

Đẳng thức xảy ra khi và chỉ khi

   

f x kg x



với



B. BÀI TẬP

Câu 1: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;2

đồng thời thỏa mãn điều kiện

 

2 2



 

xf x dx





, và

 

' 10

f x dx



 

 



. Hãy tính tích phân

 

I x f x dx





Lời giải

Ta có:

       

2 2 2

2 2 2 2

0 0 0

1 1 1

0 ' ' 8

2 2 2

f x dx x f x x f x dx x f x dx

    

  

Cách 1: Kết hợp

 

' 10

f x dx



 

 



 

' 8

x f x dx





và

x dx 



ta được:

       

1 1

2 4 2 2

0 0

5 25 5.8 25 32 5 5

' ' 10 . 0 ' 0 '

2 16 2 16 5 4 4

f x x f x x dx f x x dx f x x

   

           

 

 

 

   

 

Cách 2:

   

2 2 2

2 4

0 0 0

64 ' ' 10 64

x f x dx x dx f x dx

 

   

 

 

 

 

  

. Đẳng thức xảy ra khi:

 

f x kx



Vì

   

2 2

2 4 2

0 0

32 5 5

8 ' '

5 4 4

x f x dx k x dx k k f x x

      

 

Khi đó:

 

5 4

12 3

f x

 

vì

 

1 2



. Khi đó thay vào tích phân

 

I x f x dx

 



CHUYÊN ĐỀ

BẤT ĐẲNG THỨC TÍCH PHÂN

VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN

Câu 2: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn điều kiện

 

1 2



 

f x dx





 

f x dx  

 



. Hãy tính tích phân

 

I xf x dx





Lời giải

Ta có:

         

1 1 1 1

0 0 0 0

1 5

' 2 ' '

3 3

f x dx xf x xf x dx xf x dx xf x dx

      

   

Cách 1: Kết hợp

 

f x dx  

 



 

xf x dx





và

x dx





ta được:

   

 

   

1 1

2 2

0 0

25 50 25

' 10 ' 25 0 ' 5 0 ' 5

3 3 3

f x xf x x dx f x x dx f x x

             

   

 

Cách 2:

   

1 1 1

0 0 0

25 1 25 25

' '

9 3 3 9

xf x dx x dx f x dx

 

    

 

 

 

  

. Đẳng thức xảy ra khi:

 

f x kx

Vì

   

1 1

0 0

5 1

' 5 ' 5

3 3

xf x dx k x dx k k f x x

      

 

Khi đó

   

1 1

2 3

0 0

5 1 5 3

2 2 2 2 8

x x x

f x I xf x dx dx

      

 

Câu 3: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

 

 

đồng thời thỏa mãn

 

f x dx

π



 

sin 6

x x f dx

 



 

 

 



, và

 



 

 

. Hãy tính tích phân

 

I f x dx



  

 



Lời giải

Ta có

         

2 2

0 0 0

3 sin sin 2 2 sin 2 2

2 2

π π

x x

π x x f d x x f x dx x x df x

   

 

     

   

   

  

           

2 2 2

2 2

0 0 0

3 sin 2 2 2 1 cos2 4 sin sin

π π π

π x x f x x f x dx xf x dx xf x dx       

  

Cách 1: Kết hợp

 

f x dx

π



 

sin

xf x dx 



và

sin

xdx 



ta được:

   

 

   

1 1

2 2 4 2 2

0 0

8sin 16sin 0 4sin 0 4sinf x xf x x dx f x x dx f x x

 

       

 

 

Cách 2:

   

2 2

2 2 2

2 4 2

0 0 0

9 3 9

sin sin 3

16 16 16

π π π

xf x dx xdx f x dx π

 

 

   

 

 

  

Đẳng thức xảy ra

 

sinf x k x

 

. Vậy

   

2 2

2 4 2

0 0

3 3

sin sin 4sin

4 16

π π

xf x dx k xdx k f x x

    

 

Khi đó:

       

4sin 2 1 cos 2 4sin 2 8cos 2f x x x f x x f x x

 

      

Thay vào ta được:

 

2 2

0 0

512 cos 2 0

π π

I f x dx xdx



  

 

 

 

Câu 4: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;2

đồng thời thỏa mãn điều kiện

 

2 1



 

x f x dx





 

f x dx  

 



. Hãy tính tích phân

 

I f x dx





Lời giải

Ta có

       

2 2 2

3 3

0 0 0

8 1 32

15 3 3 3 5

x x

f x d f x x f x dx x f x dx

 

    

  

Cách 1: Như vậy:

 

f x dx  

 



 

x f x dx







và

x dx 



Mặt khác áp dụng bất đẳng thức AM – GM ta có:

   

4 4 4 3

' 4 'f x x x x x f x

   

 

 

Do vậy:

   

2 2 2

4 3

0 0 0

' 3 4

f x dx x dx x f x dx



  

 

  

. Mà giá trị của hai vế bằng nhau.

Như vậy tồn tại dấu bằng xảy ra tức là:

   

2 2

f x x f x

   

do đó

 

I f x dx

 



Cách 2: Ta áp dụng hai lần liên tiếp bất đẳng thức Holder:

     

4 2 2 3

2 2 2 2 2

2 4

3 4 2 4

0 0 0 0 0

1048576 1048576

' '

625 625

x f x dx x dx x f x dx x dx f x dx

       



      

       

   

       

    

Dấu bằng xảy ra khi và chỉ khi:

 

f x kx

Câu 5: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

1;2

đồng thời thỏa mãn

 

x f x dx





Tìm giá trị nhỏ nhất của tích phân

 

?I f x dx





Lời giải

Ta có áp dụng hai lần liên tiếp bất đẳng thức Holder ta được:

       

4 2 2 3

2 2 2 2 2 2

4 3 4 2 2 4 4 4

1 1 1 1 1 1

31 3875

x f x dx x dx x f x dx x dx f x dx f x dx

       

    

       

       

     

Đẳng thức xảy ra khi

 

f x kx

nên

 

4 2

31 5 5k x dx k f x x

    



Câu 6: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn các điều kiện sau:

   

' 1f x f x dx 

 

 



;

   

0 1; 1 3

f f  . Tính giá trị của

 



 

 

Lời giải

Ta áp dụng bất đẳng thức AM – GM ta được:

   

 

         

1 1

2 2 2

0 0

2 ' 1 2 ' 1 0 2

f x f x dx f x f x dx f x f f

      

 

 

 

Như vậy đẳng thức phải xảy ra tức là:

         

' 1 ' 1 2 2f x f x f x f x dx dx f x x C

     

 

Mà

   

0 1; 1 3

f f  nên ta suy ra

 

2 1

f x x

 

. Vậy

 



 

 

Câu 7: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

1;2

đồng thời thỏa mãn các điều kiện sau:

 

2 4

f x

x f x

 

 





;

   

1 ; 2 1

f f

 

. Tính giá trị của

 



 

 

Lời giải

Ta áp dụng bất đẳng thức AM – GM ta được:

 

     

2 2

2 4 2

1 1

6 1 1

42 9 6 6 42

1 2

f x

x dx dx

x f x f x f x f f

 

 

 

 

 

       

 

 

 

  

 

 

Như vậy đẳng thức phải xảy ra tức là:

 

2 2

2 2 3

' '

3 3

f x f x

x dx x dx f x

f x f x C x

    



 

Mà

   

1 ; 2 1

f f

 

nên ta suy ra

 

f x





. Vậy

3 8

2 45

 



 

 

Câu 8: Cho hàm số

 

y f x



. Đồ thị của hàm số

 

y f x





như hình

vẽ bên. Đặt

     

2 1

g x f x x

  

. Mệnh đề nào dưới đây

đúng sao cho sao cho tồn tại số thực m thỏa mãn

 

g x dx



 

 

 

 



   

6 1 3

g m g

  

   

6 1 6 3

g m g

  

   

3 1 3 3

g m g

  

   

3 1 3 3

g m g

   

Lời giải

       

2 2 2 0 1 1

g x f x x g x f x x x

 





   

          







Lập BBT của hàm số

 

y g x



như hình vẽ bên.

Dựa vào bảng biến thiên

 



nhỏ nhất trong các giá trị

 



 

Ta có:

       

1 3 1 3

1 2

3 1 3 1

2 1 2 1

S S x f x dx f x x dx g x dx g x dx

 

   

          

   

   

   

           

3 1 3 1 3 3g g g g g g

        

min, max của

 

g x

trên

 

3;3



lần lượt là

 



     

6 1 6 3

g g x dx g



   



. Mà

   

3 3

0 2

g x dx m g x dx

 

 

   

 

 

 



Để phương trình đã cho có nghiệm

   

3 1 3 3

g m g

   

Câu 9: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn các điều kiện sau:

 

xf x

f x





;

   

0 1; 1

f f e 

. Tính giá trị của

 



 

 

Lời giải

Cách 1: Áp dụng Holder:

 

1 1 1

0 0 0

' ' 1

1 ln 1

2 0

xf x f x f

dx xdx dx

f x f x f

 

 

   

 

 

  

Vậy đẳng thức xảy ra khi và chỉ khi:

 

'f x

f x



. Thay vào

 

xf x

f x





ta được



Vì

 

4 ln 2

f x

x f x x C

f x

   

mà

   

0 1; 1

f f e 

nên



vậy

 

f x e f e

 

  

 

 

Cách 2: Áp dụng AM – GM:

 

1 1 1

0 0 0

' ' 1

1 1

2 4 4 1 ln 2

2 2 0

f x f x f

x dx xdx dx

f x f x f

 

     

 

 

  

Đẳng thức xảy ra khi và chỉ khi

 

4 ln 2

f x

x f x x C

f x

   

mà

   

0 1; 1

f f e 

nên



vậy

 

f x e f e

 

  

 

 

Câu 10: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;2

đồng thời thỏa mãn điều kiện

 

2 16



 

xf x dx 



và

 

1152

f x dx





 

 



. Hãy tính tích phân

 

I f x dx





Lời giải

Cách 1:

         

2 2 2 2

2 2 2

2 2

0 0 0 0

64 1 192

5 2 2 2 2 5

x x x

f x d f x f x dx x f x dx x f x dx

 

  

      

 

 

   

Kết hợp

 

1152

f x dx





 

 



;

 

192

x f x dx







và

x dx 



ta được

       

2 2

2 4 2 2

0 0

1152 192 32

12. 36 12. 36. 0 6 0 6

5 5 5

f x x f x x dx f x x f x x

 

   

 

          

 

 

 

Cách 2:

   

2 2 2

2 4

0 0 0

36864 32 1152 36864

. .

25 5 5 25

x f x dx x dx f x dx

 

 

   

 

 

 

 

  

Dấu

" "

xảy ra

 

f x kx



 

. Mà

   

2 2

2 4 2

0 0

192 32

6 6

5 5

x f x dx k x dx k k f x x

 

      

 

Câu 11: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn điều kiện

 

1 1



 

x f x dx 



và

   

 

f x d f x







. Hãy tính

 

Lời giải

Cách 1:

         

1 1 1 1

6 6 6

5 6

0 0 0 0

11 2

78 6 6 6 13

x x x

x f x dx f x d f x f x dx x f x dx

 

 

     

 

 

   

Lại có:

   

 

1 1

0 0

4 4

13 13

f x d f x f x dx

 

  

 

 

 

. Kết hợp với

x dx





ta được

       

1 1

6 12 6 6

0 0

4 2 1

4 4 4. 4. 0 2 0 2

13 13 13

f x x f x x dx f x x dx f x x

 

   

 

          

 

 

 

Cách 2:

   

1 1 1

6 12

0 0 0

4 1 4 4

. .

169 13 13 169

x f x dx x dx f x dx

 

 

   

 

 

 

 

  

Dấu

" "

xảy ra

 

f x kx



 

. Mà

   

1 1

6 12 6

0 0

2 2

13 13

x f x dx k x dx k f x x

 

      

 

Câu 12: Cho hàm số

 

y f x



xác định và liên tục trên

 

0;2

và có bảng biến thiên như hình bên. Hỏi

có bao nhiêu giá trị nguyên của m để thỏa mãn

điều kiện

 

f x m dx

 

 

 



Lời giải

Dựa vào bảng biến thiên ta có:

 

 

 

 

   

2 2 2

0;2

0 0 0

0;2

max 7

5 7

min 5

f x

dx f x dx dx

f x







   









  

Hay:

 

10 14

f x dx

  



. Mặt khác

   

2 2

0 0

0 2 .f x m dx m f x dx

   

 

 

 

Như vậy để phương trình có nghiệm

10 2 14 5 7

m m

       

. Vậy có 13 giá trị m nguyên thỏa

mãn yêu cầu đề bài.

Câu 13: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn điều kiện

 

1 2



 

x f x dx





 

f x dx  

 



. Hãy tính tích phân

 

I f x dx





Lời giải

         

1 1 1 1

5 5 5 5 5

0 0 0 0

3 1 1 1 1 7 7

' ' '

11 5 5 5 5 55 11

f x dx x f x x f x dx x f x dx x f x dx      

   

Cách 1: Kết hợp

 

f x dx  

 



 

x f x dx





và

x dx





ta được:

   

 

   

1 1

5 10 5 5

0 0

49 98 49

' 14 ' 49 0 ' 7 0 ' 7

11 11 11

f x x f x x dx f x x dx f x x

 

           

 

 

Cách 2: Ta có:

   

1 1 1

5 10

0 0 0

49 1 49 49

' '

121 11 11 121

x f x dx x dx f x dx

 

    

 

 

 

  

Đẳng thức xảy ra khi:

 

f x kx



. Vì

   

1 1

5 10 5

0 0

7 1

' 7 ' 7

11 11

x f x dx k x dx k k f x x

      

 

Khi đó:

 

7 5

6 6

f x

 

vì

 

1 2



. Khi đó thay vào tích phân

 

1 1

0 0

7 5

6 6

I f x dx dx   

 

Câu 14: Tính giới hạn:

 

lim ?

x n









Lời giải

Ta có với

 

0;1

x 

thì

   

1 1

2 1 2 2 1 2

x n x n

x x nx

x x

e e ne ne ne

e e

 



    

 

Do đó:

     

 

1 1 1 1

1 1 1

0 0 0 0

lim lim lim lim lim

2 1 2 2 1 2 1

x n x n x n

nx n

x x

n e

ne ne ne e ne

dx dx dx dx

e e n



  

 



    

  

   

Vậy

 

1 1

lim

2 1 2

x n



 





cho nên ta suy ra

 

lim

1 2

x n









Câu 15: Tính giới hạn:

 

lim 1 ...

x x x dx

   



với

0 1a b  

Lời giải

Ta có

 

1 1

1 ... ln

1 1 1 1

b b b b

n n

a a a a

x a x

x x x dx dx dx dx

x x b x

 



       

   

   

Mà

  

1 1

0 0

1 1 1 2

dx x dx

x b b n



   

   

 

. Vậy

 

lim 1 ... ln

x x x dx



    





Câu 16: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

1;2

đồng thời thỏa mãn các điều kiện sau:

 

f x

xf x

 

 





;

   

1 1; 2 16

f f

 

. Tính giá trị của

 

2 ?



Lời giải

Ta áp dụng bất đẳng thức AM – GM ta được:

 

     

 

2 2

1 1

48 16 8 16 16 2 1 48

f x

x dx dx f x f f

xf x

f x

 

 

 

 

      

 

 

 

 

Như vậy đẳng thức phải xảy ra tức là:

 

   

 

2 2

' '

4 2

f x f x

x dx xdx f x x C f x x C

f x f x

        

 

Mà

   

1 1; 2 16

f f

 

nên ta suy ra

 

f x x



. Vậy

 

2 4



Câu 17: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

1;1



đồng thời thỏa mãn điều kiện

 

f x



với mọi

 

1;1

x  

và

 

f x dx







. Tìm giá trị nhỏ nhất của

 

x f x dx







1

Lời giải

Ta đặt

 

   

1 1 1 1

2 2 2 2

1 1 1 1

I x f x dx I x a f x dx x a f x dx x a dx a

   

         

   



Do đó ta suy ra

min

I x a dx





 





. Đến đây ta chia bài toán thành 3 trường hợp như sau:

Trường hợp 1: Nếu



thì

 

1 1

2 2

0 0

1 1

2 2

min min min 2

3 3

a a a

x a dx x a dx a

  

 

 

     

 

 

 



Trường hợp 2: Nếu



thì

 

1 1

2 2

1 1

2 4

min min min 2

3 3

a a a

x a dx a x dx a

  

 

 

     

 

 

 



Trường hợp 3: Nếu

 

0;1

a 

thì

 

     

1 1

2 2 2 2

0;1

1 1

min min

a a

x a dx x a dx a x dx x a dx



 

 



 

      

 

 

   



 

3 3 3

0;1

min min

3 3 3

a a

x x x

x a dx ax ax ax

 



 

     



       

 

     



 



     

 





 

0;1

8 2 1

min min 2

3 3 2

a a

x a dx a

 



 

     

 

 





khi và chỉ khi



Kết luận: Như vậy

min

x a dx





 





do đó

1 1

min

2 2

I I

   

Câu 18: Cho hàm số

 

y f x



có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn

 

 

8;8

f x  

với

mọi

 

0;1

x 

và

 

xf x dx





. Tìm giá trị lớn nhất của

 

?x f x dx



Lời giải

Ta đặt

 

I x f x dx





khi đó:

 

   

1 1

3 3

0 0

I a x ax f x dx x ax f x dx

    

 

1 1 1

3 3 3

0 0 0

3 8 3 8 min 3 8

I a x ax dx a I a x ax dx a I a x ax dx



 

               

 

 

  



 

Trường hợp 1: Nếu



khi đó

 

1 1

3 3

0 0

min 3 8 min 3 8 min 2 2

a a a

a x ax dx a x ax dx a

  

   

       

   

   

 



Trường hợp 2: Nếu



khi đó

 

1 1

3 3

1 1

0 0

min 3 8 min 3 8 min 7 2 5

a a a

a x ax dx a ax x dx a

  

   

       

   

   

 



Trường hợp 3: Nếu

 

0;1

a 

khi đó ta có đánh giá sau:

 

   

 

 

1 1

3 3 3 2

0;1 0;1

0 0

min 3 8 min 3 8 8 min 4 2

a a a

a x ax dx a ax x dx x ax dx a a

  

 

          

 

 

  



Kết luận: Vậy

31 31

min 3 8

16 16

a x ax dx I



 

    

 

 





. Đẳng thức xảy ra khi

1 31 3

; 3

8 12 8

a I a

   

Câu 19: Cho hàm số

 

y f x



liên tục trên

 

0;1

đồng thời thỏa mãn các điều kiện sau:

 

 

0;1

max 6

f x



và

 

x f x dx





. Giá trị lớn nhất của tích phân

 

x f x dx



bằng bao nhiêu?

 

3 2 4



2 4



Lời giải

Ta có với mọi số thực



thì

 

ax f x dx





do đó:

 

   

1 1 1 1

3 3 2 3 2 3 2

0 0 0 0

6x f x dx x ax f x dx x ax f x dx x ax dx a

       

   



Do đó:

   

1 1

3 3 2

0 0

min 6 min

a a

x f x dx x ax dx g a

 

  

 

 

. Tới đây ta chia các trường hợp sau:

Trường hợp 1: Nếu



thì

 

 

3 2 2

0 0;1

x ax x x a x     

. Khi đó:

   

1 1

3 2 3 2

0 0

1 3

6 6 6 min

4 3 2

g a x ax dx x ax dx g a



 

       

 

 

 

Trường hợp 2: Nếu



thì

 

 

3 2 2

0 0;1

x ax x x a x     

. Khi đó:

   

1 1

3 2 2 3

0 0

1 1

6 6 6 min

3 4 2

g a x ax dx ax x dx g a



 

       

 

 

 

Trường hợp 3: Nếu

 

0;1

a 

thì

 

1 1

3 2 2 3 3 2

0 0

2 4 3

6 6

a a

f a x ax dx ax x dx x ax dx

 

      

  

Ta tìm được

 

 

 

 

0;1 0;1

3 2 4

2 4 3 1 3

min min

2 4 2 2

a a

g a

 



 

 

   

 

 

vậy

 

3 2 4

min

g a









Do vậy:

     

 

 

 

3 3

1 1 1

3 3 3

0;1

0 0 0

3 2 4 3 2 4

min max

4 4

x f x dx g a x f x dx x f x dx



 

    

  



Câu 20: Cho hàm số

 

y f x



có đạo hàm liên tục trên đoạn

 

0;1

thỏa mãn

   

2018

3 '

f x xf x x

 

với

mọi

 

0;1

x 

. Giá trị nhỏ nhất của tích phân

 

f x dx



bằng:

2021 2022



2018 2021



2018 2019



2019 2021



Lời giải

Ta có:

   

2018

3 . '

f x x f x x

 

   

2 3 2020

3 '

x f x x f x x

  

   

 

 

2018

3 2020 3 2020

0 0

0;1

2021

t t

x f x x x f x dx x dx t f t

 

   

       

   

 

Khi đó

 

1 1

2018

0 0

2021 2019.2021

f x dx dx  

 

Giá trị nhỏ nhất của tích phân

 

f x dx



là

2019.2021

Câu 21: Cho hàm số

 

f x

có đạo hàm liên tục trên

 

0;1

thỏa mãn

   

1 0,



 

 

 



f f x dx

và

 

 



x f x dx

. Tích phân

 



f x dx

bằng



Lời giải

     

1 1

5 5

0 0

5 5

 



 

 

 

 

x x

x f x dx f x f x dx

. Suy ra

 







x f x dx

. Hơn nữa ta dễ dàng tính được

 





x dx

. Do đó

   

 

1 1 1

5 5

0 0 0

2 0

 

  

 

 

  

f x dx x f x dx x dx

 



 

  

 



f x x dx

Suy ra

 



f x x

, do đó

 

 f x x C

. Vì

 

1 0

nên

 

. Vậy

 

1 1

0 0

1 1

6 7

 

 

 

f x dx dx

Câu 22: Cho hàm số

 

f x

có đạo hàm liên tục trên

 

0;1

thỏa mãn

   

1 0, 2ln 2



   

 



f f x dx

và

 

2ln 2

 





f x

. Tích phân

 



f x dx

bằng

1 2ln 2



3 2ln 2



3 4ln 2



1 ln 2



Lời giải

Ta có:

 

     

1 1 1

0 0 0

1 1 1

 

     



     

     

 

  

     



 

  

f x

dx f x d f x f x dx

x x x

Suy ra

 

1 3

1 2ln 2

1 2

 



  

 



 



f x dx

. Hơn nữa ta tính được:

 

1 1

0 0

1 1 1 1 3

1 1 2 2ln 1 2 ln 2

1 1 1 2

 

 

 

          

 

 

  

 



 

 

 

dx dx x x

x x x

Do đó

     

2 2

1 1 1 3

0 0 0 0

1 1 1

2 1 1 0 1 0

1 1 1

     

  

        

 

   

 

 

  

     

   

f x dx f x dx dx f x dx

x x x

Suy ra

 



 



f x

, do đó

   

ln 1

   f x x x C

. Vì

 

1 0

nên

ln 2 1 

Ta được

   

1 1

0 0

ln 1 ln 2 1 ln 2

       

 

 

f x dx x x dx

Câu 23: Cho hàm số

 

y f x



nhận giá trị không âm và liên tục trên đoạn

 

0;1

đồng thời ta đặt

   

g x f t dt

 



. Biết

   

g x f x



với mọi

 

0;1

x 

. Tích phân

 

g x



có giá trị lớn

nhất bằng:

Lời giải

Đặt

         

 

 

 

1 0;1 1 0 0;1

F x

F x f t dt g x F x f x x x

F x



           





 

1 1

F x

h t dx t

F t

F x

 



 

     

 



 



là hàm số đồng biến trên

 

0;1

do vậy ta có đánh giá:

   

 

   

 

 

1 1 1 1

0 0;1 1 0 1 0;1

1 1 2

h x h x x x x dx

F x F x g x

             

 



Câu 24: Cho hàm số

 

y f x



nhận giá trị không âm và liên tục trên đoạn

 

0;1

đồng thời ta đặt

   

1 3

g x f t dt

 



. Biết

   

g x f x



với mọi

 

0;1

x 

. Tích phân

 

g x dx



có giá trị

lớn nhất bằng:

Lời giải

Đặt

         

 

 

 

1 3 0;1 1 0 0;1

3 1

F x

F x f t dt g x F x f x x x

F x



           





 

2 2

1 3 1

3 3

3 1

F x

h t dx F t t

F x

 



 

      

 



 



là hàm số nghịch biến trên

 

0;1

do vậy ta có:

   

 

   

 

 

2 2 3 7

0 0;1 3 1 0 3 1 1 0;1

3 3 2 4

h x h x F x t F x x x g x dx

               



Câu 25: Cho hàm số

 

y f x



nhận giá trị không âm và liên tục trên đoạn

 

0;1

đồng thời ta đặt

   

g x f t dt

 



. Biết

 

g x xf x



với mọi

 

0;1

x 

. Tích phân

 

g x dx



có giá trị

lớn nhất bằng:

Lời giải

Đặt

 

   

 

 

 

2 2 2

1 2 0;1 1 0 0;1

xf x

F x f t dt g x F x xf x x x

F x

           





 

1 ln 1

xf x

h t dx F t t

F x

 

 

     

 



 



là hàm số nghịch biến trên

 

0;1

do vậy ta có:

   

 

 

 

 

0 0;1 ln 1 0 1 0;1 2

h x h x F x x F x e x g x dx

             



Câu 26: Cho hàm số

 

y f x



nhận giá trị không âm và liên tục trên đoạn

 

0;1

đồng thời ta đặt

   

1 2

g x f t dt

 



. Biết

   

g x f x



 

 

với mọi

 

0;1

x 

. Tích phân

 

g x dx 

 



có giá

trị lớn nhất bằng:

Lời giải

Ta đặt

   

F x f t dt





khi đó

     

 

1 2 0;1

g x F x f x x    

 

 

Do vậy

 

 

 

 

3 3

1 0 0;1 1 0 0;1

1 2 1 2

f x F x

x x

F x F x



        

 

Xét hàm số:

 

 

3 3

1 1 2 0;1

4 4

1 2

F x

h t dx F t t t

F x

 



 

       

 



 



là hàm nghịch biến trên

 

0;1

cho nên

   

 

 

 

2 2

3 3

3 3 4

0 0;1 1 2 0 1 2 1 0;1

4 4 3

h t h t F t t F t t t             

Do đó:

 

 

   

1 1 1

2 2

3 3

0 0 0

4 4 5

1 0;1 1

3 3 3

g x x x g x dx x dx g x dx

 

        

   

 

   

 

  

. Chọn A.

Câu 27: Cho hàm số

có đạo hàm liên tục trên

 

1;8

đồng thời thỏa mãn điều kiện:

   

 

2 2 8 2

3 3 2

1 1 1 1

2 1

f x dx f x dx f x dx x dx

 

   

 

   

Tính tích phân

 

f x dx



 

 



bằng:

8ln 2

ln 2

Lời giải

Đặt

3 2

t x dt x dx

  

. Khi đó:

   

 

2 2 8 2

3 3 2

1 1 1 1

2 1

f x dx f x dx f x dx x dx

 

   

 

   

   









8 8 8

3 32 2

3 3 32 2 2

1 1 1

1 1 2 1

2 1 1 0

f t dt f t t dt t dt

t t t

     

 

 

  

 

   

3 2

8 2

1 1

8ln 2

0 1

f t t

dt f t t f x dx

 

 



 

       

 

 

 

 

. Chọn A.

Câu 28: Cho hàm số

 

f x

có đạo hàm dương, liên tục trên

 

0;1

đồng thời thỏa mãn các điều kiện

 

0 1



và

       

1 1

0 0

3 2

f x f x dx f x f x dx

 

 

 

 

 

 

. Tính tích phân

 

f x dx



Lời giải

Theo bất đẳng thức Holder ta có:

       

1 1 1

0 0 0

1f x f x dx f x f x dx dx

 

 



 

 

  

Như vậy:

           

2 2

1 1 1

2 2 2

0 0 0

1 1

9 4 9 0

9 9

f x f x dx f x f x dx f x f x dx

   

   

  

    

   

   

   

   

  

Do đó:

       

2 3 3

1 1 7

9 3 6

f x f x f x x f x dx



     



Câu 29: Cho hàm số

 

f x

có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn các điều kiện

 



;

 

f x dx





và

   

 

1 1

2 3

x f x dx



   





. Tính tích phân

 

f x dx





203

Lời giải

Sử dụng tích phân từng phần ta có:

       

1 1 1

0 0 0

5 2

6 3

f x dx f xf x dx xf x dx

 

    

  

Mặt khác:

   

 

   

 

2 2

2 1 1 1 1

2 2

x x

x f x x f x

x x

 

     

 

Tích phân hai vế ta

 

1 1

2 2

0 0

2 4 2

3 3 2 2 3

x x

f x dx f x dx

x x

 

    

 

 

Áp dụng Holder:

         

 

1 1 1 1

0 0 0 0

2 2

9 2 2

x x

xf x dx x x f x dx x x dx f x dx

x x

 

  

    

 

 

 

   

Do vậy

 

2 3

f x dx



 





nên dấu bằng

     

2 2

2 60

f x x f x x f x dx



       



Câu 30: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn điều kiện

 

0 2



và

 

     

 

21 1 12 1 12 ' 0;1

x x xf x f x x        

 

. Tính

 

f x dx





2



Lời giải

Ta có

 

     

21 1 12 1 12 '

x x xf x f x      

 

 

1 1

0 0

6 1 '

f x d x f x dx

     

 

 

 

   

1 1

0 0

6 1 ' '

x f x dx f x dx

      

 

 

   

2 3

' 3 3 0 3 2

f x x dx f x x x

 

       

 



. Chọn đáp án A.

Câu 31: Cho hàm số

 

f x

có đạo hàm liên tục trên

 

0;1

thỏa mãn

 

   

1 1

0 0

' 1 . .

f x dx x e f x dx



  

 

và

 

1 0



. Tính

 

f x dx





2 e

2 e

1 e

Lời giải

Ta có:

     

 

1 1

0 0

1 . . .

x x

x e f x dx f x d x e



  

 

 

. . '

x e f x dx

 



 

1 1 1

2 2

0 0 0

' . . ' .

x x

f x dx x e f x dx x e dx



    

  

 

1 1 1

2 2

0 0 0

' . 2 . . ' 0

x x

f x dx x e dx x e f x dx

   

  

 

' . 0

f x x e dx

  



     

' . 1

x x

f x x e f x e x

     

 

f x dx e  



. Chọn đáp án B.

Câu 32: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

đồng thời thỏa mãn điều kiện

   

0 0, 1 1

f f

 

và

 

f x

e e

 

 







. Tính tích phân

 

I f x dx

 





  

1 2

e e

 

Lời giải

Theo bất đẳng thức Holder ta có:

 

   

1 1 1

0 0 0

. ' . 1 1

f x

dx e dx f x dx e

e e

 

 

   

 



 

  

Đẳng thức xảy ra khi và chỉ khi:

 

. ' .

x x

f x

k e f x k e

  

. Vì

 

' 1

f x dx k

  





Vậy

 

e C

f x







. Mà

   

0 0, 1 1

f f

 

và

 

f x







. Vậy







. Chọn đáp án A.

Câu 33: Cho hàm số

 

y f x



dương và liên tục trên

 

1;3

thỏa mãn

 

 

 

 

1;3

max 2;min

f x f x

 

và

biểu thức

 

3 3

1 1

S f x dx dx

f x



 

đạt giá trị lớn nhất. Khi đó tính

 

f x dx



Lời giải

Ta có:

 

f x

 

 

2 1 2 0

f x f x

   

 

1 5

f x

  

 

1 5

f x

  

   

3 3

1 1

S f x dx f x dx

 

  

 

 

 

. Ta tìm được

max

S 

khi

 

f x dx





Câu 34: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

đồng thời

   

0 0, 1 1

f f

 

và

 

' 1

ln 1 2

f x x dx   

 





. Tính tích phân

 

f x

x



bằng?

 

ln 1 2



 

2 1

ln 1 2





 

ln 1 2



   

2 1 ln 1 2

 

Lời giải

Theo bất đẳng thức Holder ta có:

   

1 1 1

0 0 0

' 1 . ' 1

f x x dx dx f x dx

 

    

 

 



 

  

Mặt khác

 

ln 1 ln 1 2

dx x x

    





Vậy đẳng thức xảy ra khi

   

2 2

' . 1 '

1 1

k k

f x x f x

x x

   

 

Vì

 

' 1f x dx 



nên

 

ln 1 2

k 



. Vậy

 

.ln 1

ln 1 2

f x x x C   



Vì

 

0 0

1 1















nên

0C 

. Do đó

 

ln 1 2

f x

 





. Chọn đáp án C.

Câu 35: Tìm giá trị nhỏ nhất của

 



S x ax dx

với

 

0 1



a ,

2 2



. B.

2 1



. C.

2 2



. D.

2 1



Lời giải

Phá dấu trị tuyệt đối ta có

   

1 1

3 2 3 2 3

2 2 2

0 0

2 3 2

3 3 3 3 6

x ax x ax a a

S x ax dx x ax dx x ax dx

   

  

           

   

   

  

1 2 2



 

 

 

 

min

S f

Câu 36: Cho hàm số

 



y f x

nhận giá trị dương và có đạo hàm liên tục trên đoạn

 

0 1;

và thỏa mãn

   

 

1 0 1

 

  

 

 



f x

f e. f e; dx

f x

. Tìm mệnh đề đung

 



 

 

f e

. B.

 



 

 

f e

. C.

 



 

 

f e

. D.

1 1

2 2

 



 

 

Lời giải

Ta có

 

     

 

1 0 1

    



f x f

dx=ln f x lnf ln f ln lne

f x f

Nên

 

2 2

1 1

0 0

1 1 0

 

   

 

   

   

 

   

 

 

' '

f x f x

dx dx

f x f x

 

2 2

1 1

0 0

2 1 0 1 0 1 0

 

   

 

        

 

 

 

 

   

 

 

' ' ' '

f x f x f x f x

. dx dx

f x f x f x f x

Vậy:

 



f x A.e

. Mà

   

1 0

 f e. f e

Nên

 

 

  

 

 

f x e f e

Câu 37: Cho

a b ab

  

và

a b

. Tìm giá trị nhỏ nhất của biểu thức

 

I x a b x ab dx

   



4 3

. B.

. C.

2 3

. D.

Lời giải

Ta có

 

3 3 3

2 2 2

3 3

4 4 4 2 12

36 36 36 36 36

4 3

a b ab ab ab ab



     

     

 

Câu 38: Tìm giá trị nhỏ nhất của

 

2 2

I x m x dx

   



trong đó

a b

là hai nghiệm cảu phương

trình

 

2 2 0

x m x

   

128

. B.

8 2

. C.

. D.

2 2

Lời giải

 

2 8

128 8 2

36 36 9 3

I I



 

    

Câu 39: Tìm giá trị nhỏ nhất của

S x ax dx

 



với

 

0 1



a ,

2 2



. B.

. C.

. D.

2 2



Lời giải

   

2 4 4 2

3 3

2 2 2 2

2 4 4 2

1 1 1 1 1

2 4 4 2 4 2 2 2 8 8

a.x x x a.x

S a.x x dx x a.x dx

a a a a a

S a

   

       

   

   

   

 

         

   

 

 

   

 

Câu 40: Gọi a,b lần lượt là giá trị lớn nhất và nhỏ nhất của

3 2 2 3

4 5 2

S x mx m x m dx

   



với

 

1 3m ;



. Mệnh đề nào dưới đây đúng

a b 

. B.

1a b 

. C.

a b 

. D.

a b

 

Lời giải

           

 

2 2 2

2 2

m m m

S x m x m dx x m x m dx x m x m m dx

           

  

   

 

4 3

2 2

3 2

4 3 12

m m

x m m x m

S x m dx+m x m dx=

 

  

     

 

 

 

Thay

 

1 3m ;



vào ta có

a b 

Câu 41: Cho

là tập các hàm số

lien tục trên đoạn

 

0 1;

và nhận giá trị không âm trên đoạn

 

0 1;

Tìm m nhỏ nhất sao cho

 

1 1

2018

0 0

f x dx m. f x dx f A  

 

2018

. B.

. C.

2018

. D.

2018

Lời giải

Đặt

2018 2017

2018

t x dx .t dt

  

nên

 

   

1 1 1

2017

2018

0 0 0

2018

f x dx=2018. t . f t .dt f t .dt



  

Tìm m nhỏ nhất nên

2018



. Ta sẽ Cm

2018



là số cần tìm. Xét

 

f x x

ta có

 

1 1

2018

0 0

2018 1

2018

2018 1 2018

n / n

x dx m x dx m

n n n



    

  

 

Cho

n  

ta có

2018



. Vậy

2018



là hằng số nhỏ nhất cần tìm.

Câu 42: Cho hàm số

 

y f x



nhận giá trị dương và có đạo hàm

 

f x

liên tục trên đoạn

 

0 1;

thỏa

mãn

   

1 2018 0

f . f

. Tìm giá trị nhỏ nhất biểu thức

 

1 1

0 0

M dx f x dx

f x

 

 

 

 

 

 

2018

. B.

2 2018

. C.

. D.

2018e

Lời giải

 

1 1 1

0 0 0

2 2 2 2 2018

' '

f x f x

M= f x dx dx dx ln f x ln

f x f x f x

 

    

 

 

  

Câu 43: Cho

a b ab

  

và

a b

. Tìm giá trị nhỏ nhất của biểu thức

   

I x a x b dx

  



A. 12. B. 0. C.

. D.

Lời giải

             

2 2 2

b b b

a a a

S x a x a a b dx x a x a dx a b x a dx

             

 

  

   

 

2 2 2

4 2 2 2

1 1 1 1

4 4 4 2 12 12

12 12 12 12

S a b a b ab ab ab ab

           

Câu 44: Cho

 

2 2

a b a b

   

và

a b

. Tìm giá trị lớn nhất của biểu thức

 

I x a b x ab dx

   



. B.

. C.

. D.

Lời giải

 

   

 

2 2 2 2

2 2

3 3

2 2

4 1

4 4

36 36 36 36 3

a b a b a b a b a b

a b a b



         

  

    

Khi đó

 

2 2

a b

 



 







 



 



 



Câu 45: Cho hàm số

 

y f x



nhận giá trị dương và có đạo hàm

 

f x

liên tục trên đoạn

 

0 1;

thỏa

mãn

   

1 0

f e. f

. Biểu thức

 

1 1

0 0

dx f x dx

f x

 

 

 

 

 

 

. Mệnh đề nào đúng

 





. B.

 





. C.

 

2 2







. D.

 

2 2







Lời giải

Viết lại biểu thức cho dưới dạng

 

f x dx

f x

 

 

 

 



. Dấu bằng xảy ra khi

 

     

 

   

1 1

0 1

' '

f x f x dx f x .d f x

f x f x

f x

x c f x x c

     

     

 

Thay



vào ta có

 

0 2

2 2 1

0 1

1 2 2

f c

e c

f e

f c









    





 





   

2 2

1 2

2 1

1 1

f x x f

e e

    

 

Câu 46: Cho

là tập các hàm số

lien tục trên đoạn

 

0 1;

Tìm



   

201

f A

x x .m min x. f x

f x dx





 



 

 



2019



. B.

16144



. C.

2017

2018



. D.

16140



Lời giải

Biểu thức đã cho là tam thức bậc 2 ẩn là

 

f x

có hệ số

2018

a x;b x ;c

   

Nên biểu thức Min tại

 

2017

1 1

4036 4035

0 0

2 2

4 4 4 4036 16144

min

b x

f x

x x

m dx dx

a .x x







 





   



   





 

Câu 47: Cho m là tham số thuộc đoạn

 

1 3;

. Gọi

a,b

lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của

   

2 2

P x m x m dx

  



. Tính

a b 

. B.

. C.

122

. D.

121

Lời giải

5 5 5

1 3 3 1 122

30 30 30 30 15

P ; T

 



    

 

 

Câu 48: Giá trị nhỏ nhất của

   

2 2

2 2 3

2 1 4

P x m m x m m dx



     



là

S ;a,b



nguyên dương

và

tối giản. Tính

T a b 

A. 7. B. 337. C. 25. D. 91

Lời giải

Ta có :

 

4 1

4 3 9

9 16 25

3 3 4 16

m m

P . T

 

 

      

 

 

_______________ TOANMATH.com _______________

Bấm Tải xuống để xem toàn bộ.

| 1/19

| | Tải xuống

Preview text:

CHUYÊN ĐỀ
BẤT ĐẲNG THỨC TÍCH PHÂN
VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
A. KIẾN THỨC CƠ BẢN
Cho các hàm số y  f  x và y  g  x có đạo hàm liên tục trên  ; a b . Khi đó: b b 
Nếu f  x  g  x với mọi x  ;
a b thì f  x dx  g  x dx   . a a b b 
Nếu f  x  0 với mọi x  ;
a b thì f  x dx  0  . Hệ quả: 2
f  x dx  0  f  x  0  . a a 2 b b b   
Bất đẳng thức Holder (Cauchy – Schwarz):  f  x g  x 2
dx   f  x 2
dx g  x dx    .  a  a a
Đẳng thức xảy ra khi và chỉ khi f  x  kg  x với k   . B. BÀI TẬP Câu 1:
Cho hàm số y  f  x có đạo hàm liên tục trên 0; 2 đồng thời thỏa mãn điều kiện f 2  2 , 2 2 2 2
xf  x dx  0  , và
 f ' x dx  10  2  
. Hãy tính tích phân I  x f  x dx  ? 0 0 0 Lời giải 2 2 2 1 1 2 1 Ta có: 0  f  x 2 2 dx  x f  x 2  x f ' x 2 dx 
x f ' x dx  8    . 2 2 0 2 0 0 0 2 2 2 2 32
Cách 1: Kết hợp  f ' x dx  10  2 4   ,
x f ' x dx  8  và x dx   ta được: 5 0 0 0 1 1 2  5 25  5.8 25 32  5  5
 f ' x 2 2   x f ' x 4  x     dx  10   .  0  f ' x 2  x
dx  0  f ' x 2  x  . 2 16 2 16 5  4      4 0 0 2 2 2 2   2 32 Cách 2: 2
64   x f ' x 4
dx   x dx  f ' x dx  10  64     
. Đẳng thức xảy ra khi: f  x 2 '  kx . 5  0  0 0 2 2 32 5 5 Vì 2
8  x f ' x 4
dx  k x dx  k  k   f ' x 2  x   . 5 4 4 0 0 3 5x 4 2 8
Khi đó: f  x   vì f  
1  2 . Khi đó thay vào tích phân 2
I  x f  x dx   . 12 3 9 0 Câu 2:
Cho hàm số y  f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn điều kiện f   1  2 , 1 1 1 1 2 25
f  x dx   ,
 f ' x dx  
. Hãy tính tích phân I  xf  x dx  ? 3   3 0 0 0 Lời giải 1 1 1 1 1 1 5 Ta có: 
f  x dx  xf  x  xf ' x dx  2  xf ' x dx 
xf ' x dx      . 3 0 3 0 0 0 0 1 1 1 2 25 5 1
Cách 1: Kết hợp  f ' x dx   2   ,
xf ' x dx   và x dx   ta được: 3 3 3 0 0 0 1 1  25 50 25
 f ' x 2
 10xf ' x  25x  
dx     0   f 'x 2 2
 5x dx  0  f ' x  5x  . 3 3 3   0 0 2 1 1 1 25   2 1 25 25 Cách 2:
  xf ' x 2
dx   x dx  f ' x dx     
. Đẳng thức xảy ra khi: f ' x  kx . 9   3 3 9  0  0 0 1 1 5 1 Vì  xf ' x 2
dx  k x dx 
k  k  5  f ' x  5x   . 3 3 0 0 2 1 1 3 5x 1 5x x 3
Khi đó f  x  
 I  xf  x dx   dx    . 2 2 2 2 8 0 0 π  π  2 Câu 3:
Cho hàm số y  f  x có đạo hàm liên tục trên 0; 2  đồng thời thỏa mãn
f  x dx  3π  , 2    0 π π  x  π 2    3
sin x  x f  dx  6π    , và f  0  
. Hãy tính tích phân I   f  x dx    ?  2   2  0 0 Lời giải π π π 2 2
 x   x 
Ta có 3π  sin x  x f  d      
sin 2x  2x f  x dx  sin 2x  2x df  x    2   2  0 0 0 π π π π 2 2 2 3π
 3π  sin 2x  2x f  x 2  2 1 cos 2x f  x 2
dx  4 sin xf  x 2 dx 
sin xf  x dx     . 4 0 0 0 0 π π π 2 2 3π 2 3π Cách 1: Kết hợp 2
f  x dx  3π  , 2
sin xf  x dx   và 4 sin xdx   ta được: 4 16 0 0 0 1 1  2 2 f  x 2
 8sin xf  x 4 16 sin 
x dx  0   f  x 2
 4sin x dx  0  f  x 2  4sin x    0 0 2 π π π   2 2 2 2 2 9π   3π 9π Cách 2: 2  sin xf  x 4 2 dx
 sin xdx f  x dx  3π     . 16   16 16 0 0 0     π π 2 2 3π 3π
Đẳng thức xảy ra  f  x 2
 k sin x . Vậy 2
 sin xf  x 4
dx  k sin xdx 
k  f  x 2  4sin x   . 4 16 0 0
Khi đó: f  x 2
 4sin x  21 cos 2x  f  x  4sin 2x  f  x  8cos 2x . π π 2 2 3
Thay vào ta được: I   f  x 3
 dx  512 cos 2xdx  0     . 0 0 Câu 4:
Cho hàm số y  f  x có đạo hàm liên tục trên 0; 2 đồng thời thỏa mãn điều kiện f 2  1 , 2 8 2 32 2 2 4
x f  x dx   ,
 f ' x dx  
. Hãy tính tích phân I 
f  x dx  ? 15   5 0 0 0 Lời giải 2 3 3 2 2 8 x x 2 1 32 Ta có 
f  x d  f  x 3  x f  x 3 dx 
x f  x dx     . 15 3 3 0 3 5 0 0 0 2 2 2 4 32 32 32
Cách 1: Như vậy:  f ' x dx   3 4   ,
x f  x dx   và x dx   . 5 5 5 0 0 0 4
Mặt khác áp dụng bất đẳng thức AM – GM ta có:  f  x 4 4 4 3 '
  x  x  x  4x f ' x   . 2 2 2 4
Do vậy:  f ' x 4 3
 dx  3 x dx  4 x f  x dx     
. Mà giá trị của hai vế bằng nhau. 0 0 0 2 x 1 2 7
Như vậy tồn tại dấu bằng xảy ra tức là: f ' x  x  f  x   do đó I 
f  x dx   . 2 2 3 0
Cách 2: Ta áp dụng hai lần liên tiếp bất đẳng thức Holder: 4 2 2 3 2 2 2 2 2 1048576         1048576
  x f  x dx    x dx   x  f ' x 2  dx         x dx 
 f ' x 4 3 4 2 4  dx    625   625  0   0   0   0  0
Dấu bằng xảy ra khi và chỉ khi: f ' x  kx . 2 Câu 5:
Cho hàm số y  f  x có đạo hàm liên tục trên 1; 2 đồng thời thỏa mãn 3
x f  x dx  31  . 1 2
Tìm giá trị nhỏ nhất của tích phân 4 I 
f  x dx ? 1 Lời giải
Ta có áp dụng hai lần liên tiếp bất đẳng thức Holder ta được: 4 2 2 3 2 2 2 2 2 2         4 3
31   x f  x 4 2 2
dx    x dx   x f  x 4 4
dx    x dx  f  x 4 dx 
f  x dx  3875       .  1   1   1   1  1 1 2
Đẳng thức xảy ra khi f  x  kx nên 4
k x dx  31  k  5  f  x 2  5x  . 1 Câu 6:
Cho hàm số y  f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn các điều kiện sau: 1  1 
 f  x f ' x 2  dx  1   
; f 0  1; f  
1  3 . Tính giá trị của f  ?    2  0 Lời giải
Ta áp dụng bất đẳng thức AM – GM ta được: 1 1   1 2
 f  x f ' x 2    
1dx  2 f x f 'x 2
dx  f  x 2  f   2 1  f 0  2  0 0 0
Như vậy đẳng thức phải xảy ra tức là: f  x f ' x  1  f  x f ' x dx  1dx  f  x  2x  2C   .  1 
Mà f 0  1; f  
1  3 nên ta suy ra f  x  2x 1 . Vậy f  2   .  2  Câu 7:
Cho hàm số y  f  x có đạo hàm liên tục trên 1; 2 đồng thời thỏa mãn các điều kiện sau:
 f ' x 2 2    1  3  dx  21  ; f  
1  ; f 2  1. Tính giá trị của f  ? 2 4   x f x 8  2  1   Lời giải
Ta áp dụng bất đẳng thức AM – GM ta được:
  f ' x 2 2  2     f ' x 6 2  1 1   2   42  
 9x  dx  6 dx    6     42  2 4  x f  x 2 f x f x 1  f 1 f 2  1   1             f ' x f ' x 1 2  
Như vậy đẳng thức phải xảy ra tức là: 2  3x 
dx  3x dx  f x  2  2    . f  x f  x 3 C  x 1 1  3  8 Mà f  
1  ; f 2  1 nên ta suy ra f  x  . Vậy f    . 8 3 9  x  2  45 Câu 8:
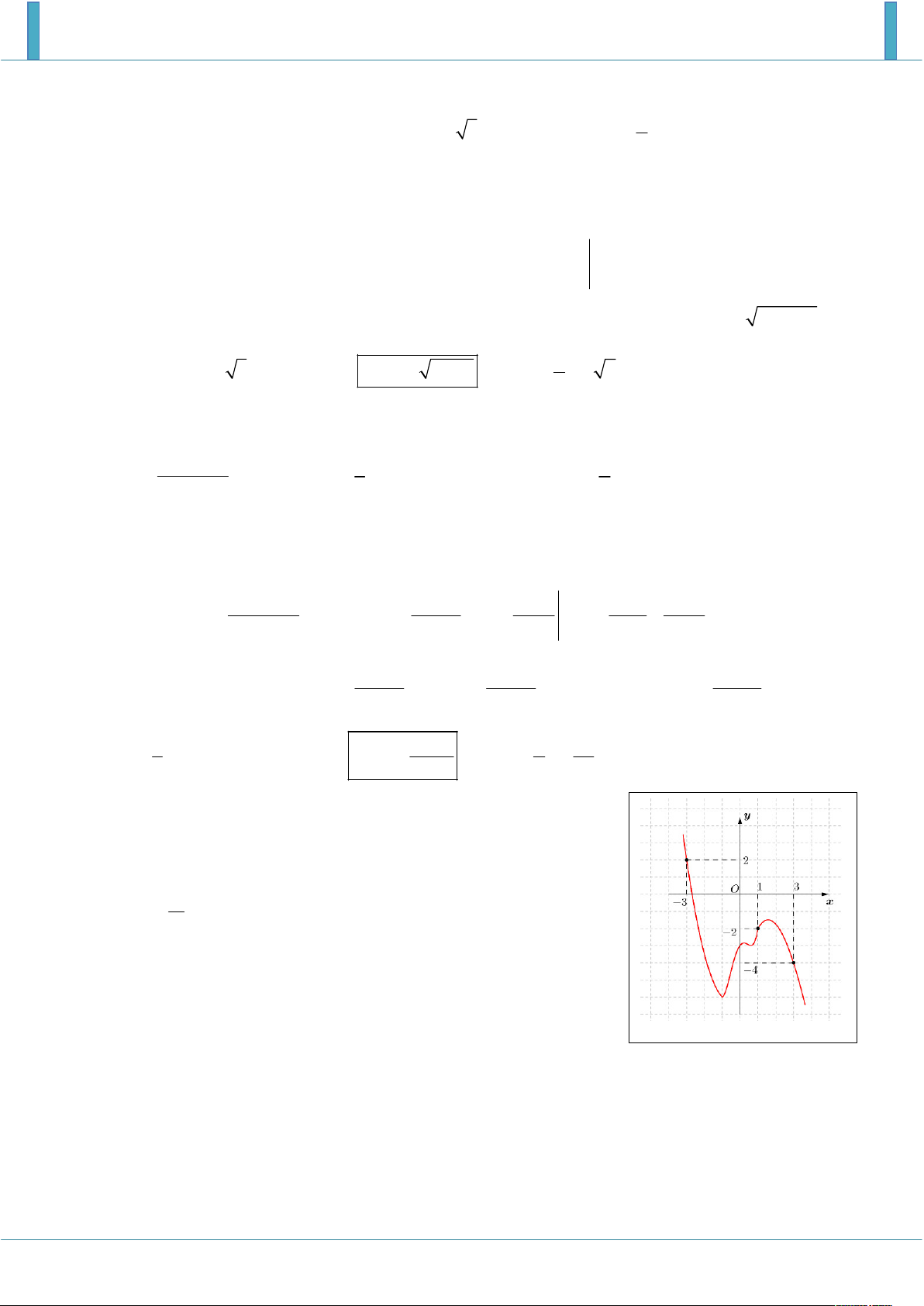
Cho hàm số y  f  x . Đồ thị của hàm số y  f  x như hình
vẽ bên. Đặt g  x  f  x   x  2 2
1 . Mệnh đề nào dưới đây
đúng sao cho sao cho tồn tại số thực m thỏa mãn 3  m 
 g  x dx  0   . 3    3  A. 6g  
1  m  g  3   B. 6g  
1  m  6g  3   C. 3g  
1  m  3g  3
  D. 3g  
1  m  3g  3   Lời giải x  3 
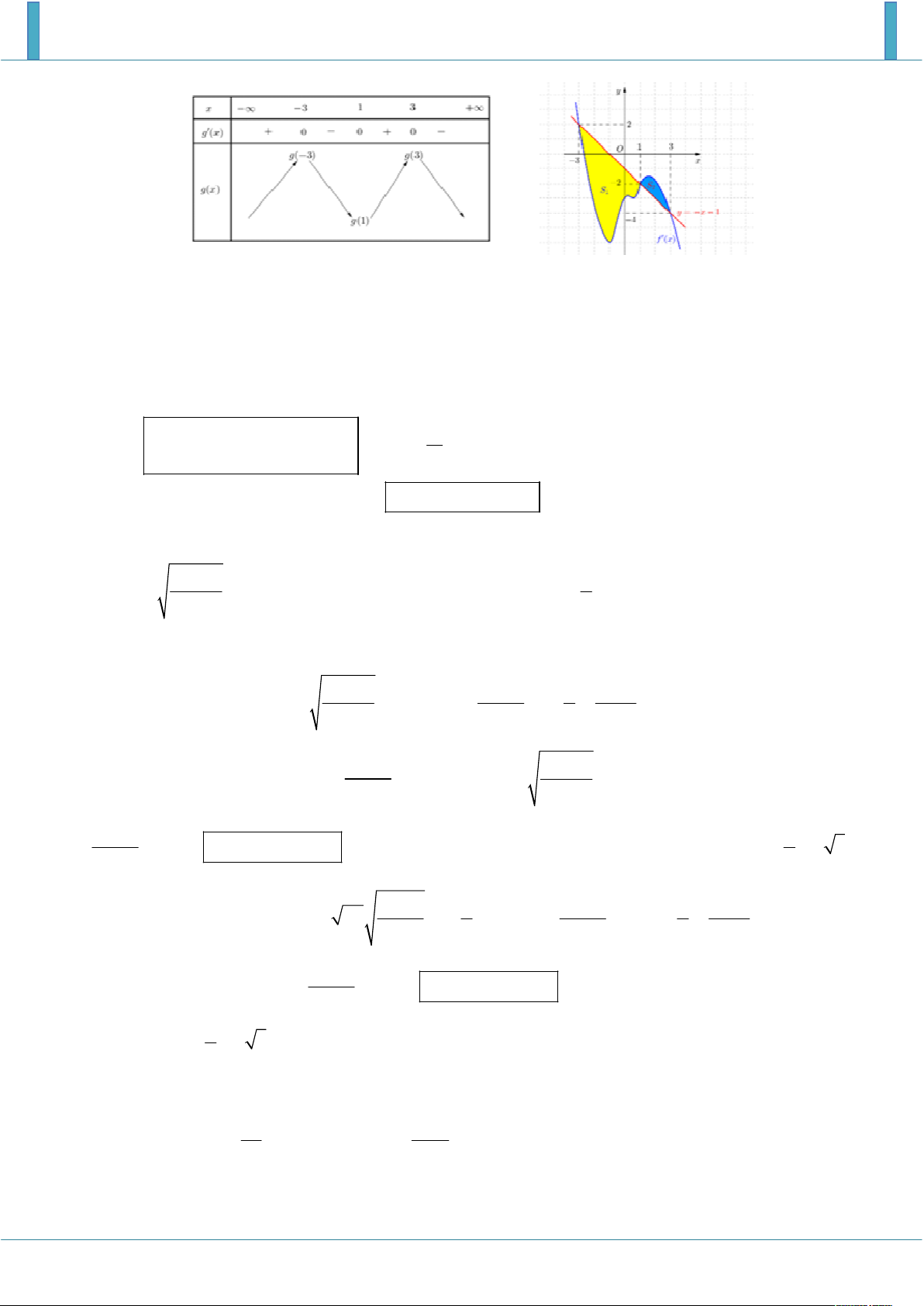
g x  2 f  x  2x  2  g x  0  f  x  x 1  x  1  x  3 
Lập BBT của hàm số y  g  x như hình vẽ bên.
Dựa vào bảng biến thiên  g  
1 nhỏ nhất trong các giá trị g  3   , g   1 , g 3 . Ta có: 1 3 1 3
S  S  2 x 1 f  x  dx  2  f  x  x 1 dx   g x dx  g x dx 1 2                 3  1 3 1  g  3    g  
1  g 3  g   1  g  3
   g 3  min, max của g  x trên  3  ; 
3 lần lượt là g   1 , 3 3 3  m  g  3    6g   1 
g  x dx  6g 3  . Mà
 g  x dx  0  2m  g  x dx    . 3    3  3  3 
 Để phương trình đã cho có nghiệm  3g  
1  m  3g  3   Câu 9:
Cho hàm số y  f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn các điều kiện sau: 1 xf ' x  1  dx  1  ; f    f   2 0 1;
1  e . Tính giá trị của f  ?   f x  2  0   Lời giải 2 1  xf ' x 1 1  f ' x 1 f   1
Cách 1: Áp dụng Holder: 1   dx   xdx dx  ln  1     f x  f x 2 f 0 0   0 0       f ' x 1 xf ' x
Vậy đẳng thức xảy ra khi và chỉ khi:  kx . Thay vào dx  1  ta được k  4 . f  x f x 0   f ' x x  1  Vì
 4x  ln f  x 2
 2x  C mà f    f   2 0 1;
1  e nên C  0 vậy f  x 2 2  e  f  e   f  x  2  1 f ' x 1 1 1  f ' x  1 f   1
Cách 2: Áp dụng AM – GM: 2  4x dx   4xdx  dx   1 ln  2    . f x 2  f x  2 f 0 0    0 0      f ' x
Đẳng thức xảy ra khi và chỉ khi
 4x  ln f  x 2
 2x  C mà f    f   2 0 1;
1  e nên C  0 vậy f  x x  1  f  x 2 2  e  f  e   .  2 
Câu 10: Cho hàm số y  f  x có đạo hàm liên tục trên 0;2 đồng thời thỏa mãn điều kiện f 2  16 , 2 64 2 2 2 1152
xf  x dx   và
 f  x dx  
. Hãy tính tích phân I 
f  x dx  5   5 0 0 0 Lời giải 2 2 2 2 2 2 2 2 64  x  x x 1 192 Cách 1: 
f  x d  f  x  f  x 2 dx  32  x f  x 2 dx 
x f  x dx        5 2 2 2 2 5 0   0 0 0 0 2 2 2 2 1152 192 32
Kết hợp  f  x dx   2 4  
; x f  x dx   và x dx   ta được 5 5 5 0 0 0 2 2 2 2 1152 192 32
 f  x 2
 12.x f  x 4  36x    dx  12.  36.
 0   f  x 2
 6x   0  f  x 2  6x     5 5 5     0 0 2 2 2 2 36864   2 32 1152 36864 Cách 2: 2
  x f  x 4 dx   x .
dx  f  x dx  .     . 25   5 5 25  0  0 0 2 2 192 32 Dấu "  " xảy ra    2 f x  kx . Mà 2
 x f  x 4
dx  k x dx 
k  k  6  f  x 2  6x   5 5 0 0
Câu 11: Cho hàm số y  f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn điều kiện f   1  1, 1 11 1 4 5
x f  x dx   và
f  x d  f  x  
. Hãy tính f 2 ? 78 13 0 0 Lời giải 1 1 1 6 6 1 6 1 11  x  x x 2 Cách 1: 5
 x f  x dx  f  x d  f  x  f  x 6 dx 
x f  x dx        78 6 6 6 13 0 0   0 0 0 1 1 4 1 2 4 1 Lại có:
f  x d 
 f x 
  f  x dx   . Kết hợp với 12 x dx   ta được 13   13 13 0 0 0 1 1 2 2 4 2 1
 f  x 6
  4x f  x 12  4x    dx   4.  4.
 0   f  x 6
 2x  dx  0  f  x 6  2x     13 13 13     0 0 2 1 1 1 4   2 1 4 4 Cách 2: 6
  x f  x 12 dx   x .
dx  f  x dx  .     169   13 13 169  0  0 0 1 1 2 2 Dấu "  " xảy ra    6 f x  kx . Mà 6
 x f  x 12
dx  k x dx 
 k  2  f  x 6  2x   13 13 0 0
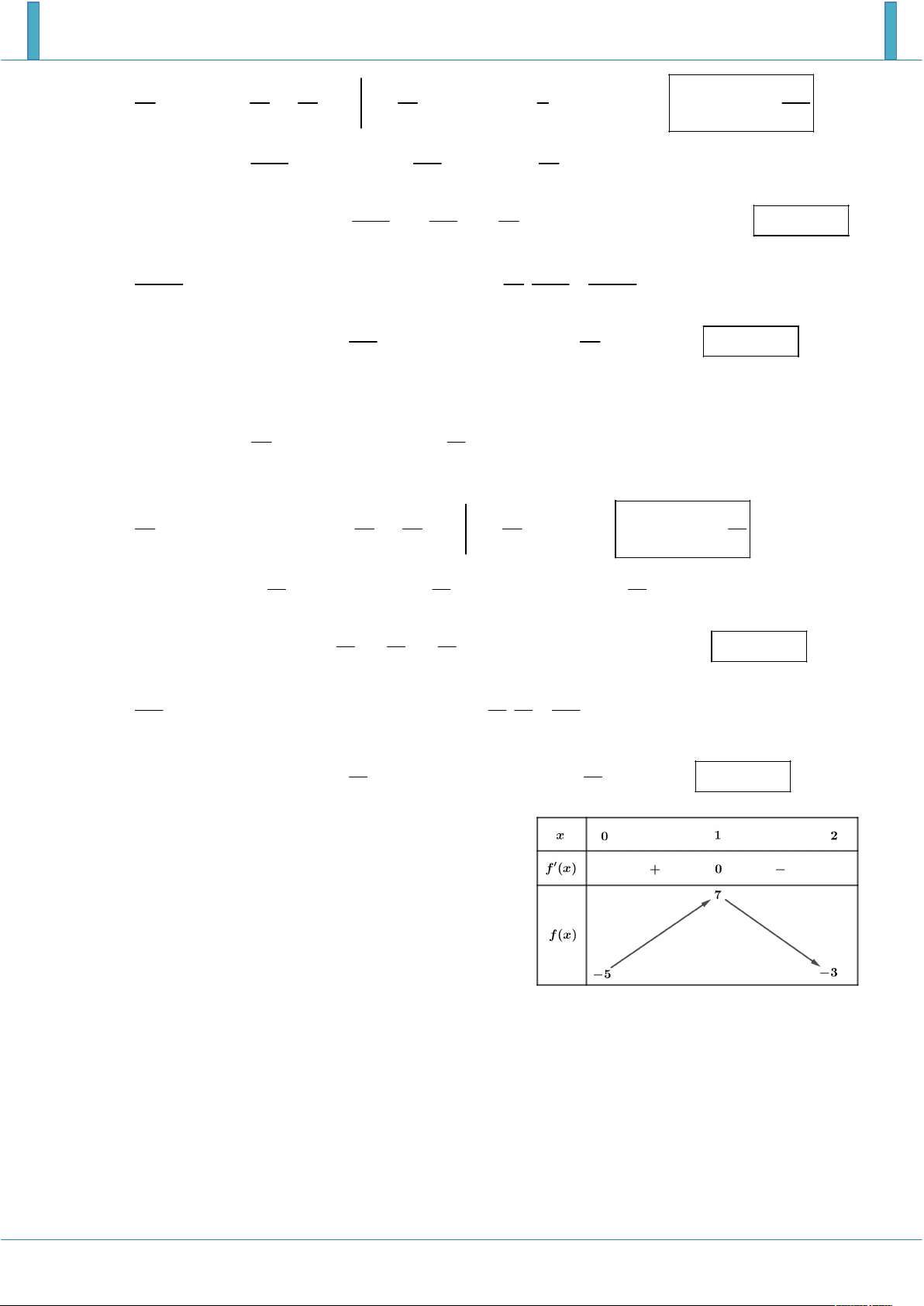
Câu 12: Cho hàm số y  f  x xác định và liên tục trên
0;2 và có bảng biến thiên như hình bên. Hỏi
có bao nhiêu giá trị nguyên của m để thỏa mãn 2
điều kiện  f  x  m dx  0    . 0 Lời giải
Dựa vào bảng biến thiên ta có:
max f  x  7 2 2 2  x   0;2    5
  dx  f  x dx  7dx    . min f   x  5 0 0 0 x   0;2  2 2 2 Hay: 10 
f  x dx  14 
. Mặt khác  f  x  m dx  0  2m  f  x . dx     0 0 0
Như vậy để phương trình có nghiệm  10 
 2m  14  5  m  7 . Vậy có 13 giá trị m nguyên thỏa mãn yêu cầu đề bài.
Câu 13: Cho hàm số y  f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn điều kiện f   1  2 , 1 3 1 49 1 4 2
x f  x dx   ,
 f ' x dx  
. Hãy tính tích phân I 
f  x dx  ? 11   11 0 0 0 Lời giải 1 1 1 1 3 1 1 1 1 1 7 7  f  x 5 5 dx  x f  x 5  x f ' x 5 dx  x f ' x 5 dx  
x f ' x dx      . 11 5 5 0 5 5 55 11 0 0 0 0 1 1 1 2 49 7 1
Cách 1: Kết hợp  f ' x dx   5 10   ,
x f ' x dx   và x dx   ta được: 11 11 11 0 0 0 1 1  2 49 98 49 2  f ' x 5
 14x f ' x 10  49x  
dx     0   f 'x 5
 7x  dx  0  f ' x 5  7x  . 11 11 11   0 0 2 1 1 1 49   2 1 49 49 Cách 2: Ta có: 5
  x f ' x 10
dx   x dx  f ' x dx      . 121   11 11 121  0  0 0 1 1 7 1
Đẳng thức xảy ra khi: f  x 5 '  kx . Vì 5
 x f ' x 10
dx  k x dx 
k  k  7  f ' x 5  7x   . 11 11 0 0 6 7x 5 1 1 6 7x 5
Khi đó: f  x   vì f  
1  2 . Khi đó thay vào tích phân I 
f  x dx   dx  1   . 6 6 6 6 0 0 1 x1n ne
Câu 14: Tính giới hạn: lim dx  ?  1 x  e 0 Lời giải x x nx x1n x1n 1 e e ne ne ne
Ta có với x 0  ;1 thì      . 2 1 x  e 2 2 1 x  e 2  nx 1  1   n x1n n   1 1 1 1 1 1 n x n x n 1  e ne ne ne e ne  Do đó: lim dx  lim dx  lim dx  lim  lim dx      . 2 1 x  e 2 2 1 x  e 2 n 1 0 0 0 0   1 x1n 1 ne 1 1 x1n ne 1 Vậy  lim dx   cho nên ta suy ra lim dx   . 2 1 x  e 2 1 x  e 2 0 0 b
Câu 15: Tính giới hạn:  2 lim
1 x  x  ... n
 x  dx với 0  a  b  1. a Lời giải b b b n 1  b n 1 x a x   n 1 1 Ta có  2
1 x  x  ...  x  dx  dx  dx  ln  dx    . 1 x 1 x 1 b 1 x a a a a b n 1  1 x 1 b  a n 1 n 1 Mà 1 0  dx  x dx   0   . Vậy lim  2
1 x  x  ...  x  dx  ln . 1 x 1 b 1 b n  2 1 b a 0    a
Câu 16: Cho hàm số y  f  x có đạo hàm liên tục trên 1; 2 đồng thời thỏa mãn các điều kiện sau:
 f ' x 2 2    dx  24  ; f  
1  1; f 2  16 . Tính giá trị của f  2   ? xf x 1   Lời giải
Ta áp dụng bất đẳng thức AM – GM ta được:
  f 'x 2 2  2      f ' x 2 48  
16x dx  8
dx  16 f  x  16  
 f 2  f  1  48 xf x f x 1 1     1    
Như vậy đẳng thức phải xảy ra tức là: f ' x f ' x  4x  dx  2xdx 
f  x  x  C  f  x    x  C2 2 2 . f  x 2 f  x Mà f  
1  1; f 2  16 nên ta suy ra   4
f x  x . Vậy f  2   4 .
Câu 17: Cho hàm số y  f  x có đạo hàm liên tục trên 1 
;1 đồng thời thỏa mãn điều kiện 2 f  x  1 1 1 với mọi x  1   ;1 và
f  x dx  0 
. Tìm giá trị nhỏ nhất của 2
x f  x dx  ? 1  1  1 1 2 A.  B.  C.  D. 1 2 4 3 Lời giải 1 1 1 1 Ta đặt 2 I 
x f  x dx  I   2
x  a f  x 2 dx 
x  a f  x 2 dx  x  a dx a        . 1 1  1  1 1 Do đó ta suy ra 2 I  min
x  a dx . Đến đây ta chia bài toán thành 3 trường hợp như sau:   a 1  1 1  2  2
Trường hợp 1: Nếu a  0 thì 2 min
x  a dx  min .     2
x  a dx  min  2a    a a0 a0  3  3 1  1  1 1  2  4
Trường hợp 2: Nếu a  1 thì 2 min
x  a dx  min .     2
a  x  dx  min 2a     a a 1  a 1   3  3 1  1  1  a a 1  
Trường hợp 3: Nếu a 0  ;1 thì 2 min
x  a dx  min      2
x  a dx    2
a  x  dx    2
x  a dx  a a   0;  1   1  1    a a  1 3 3 3  x  a x a 1 x        2  min
x  a dx  min   ax  ax    ax          a a   0;  1  3   1 3 3     a   a 1    1  8a a 2  1 1 2  min
x  a dx  min   2a   
khi và chỉ khi a  .   a a   0;  1  3 3  2 4 1   1 1 1 1
Kết luận: Như vậy 2 min x  a dx  do đó I   min I   .   a 2 2 2 1 
Câu 18: Cho hàm số y  f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn f  x 8;8 với 1 1 mọi x 0 
;1 và xf  x dx  3 
. Tìm giá trị lớn nhất của 3
x f  x dx ?  0 0 31 4 17 A. 2 B. C. D. 16 3 8 Lời giải 1 1 1 Ta đặt 3
I  x f  x dx 
khi đó: I  3a   3
x  ax f  x 3 dx 
x  ax f  x dx  0 0 0 1 1 1   3 3 3
 I  3a  8 x  ax dx a
    I  3a  8 x  ax dx a
    I  min 3a  8 x  ax dx    .   a 0 0  0  1 1    
Trường hợp 1: Nếu a  0 khi đó 3
min 3a  8 x  ax dx   min 3a  8    3
x  ax dx   min 2  a  2 a a0 a0  0   0  1 1    
Trường hợp 2: Nếu a  1 khi đó 3
min 3a  8 x  ax dx   min 3a  8    3
ax  x  dx  min 7a  2  5 a a 1  a 1   0   0 
Trường hợp 3: Nếu a 0 
;1 khi đó ta có đánh giá sau: 1 a 1     31 3
min 3a  8 x  ax dx   min 3a  8     3
ax  x  dx  8   3
x  ax dx   min  2
4a  a  2  a a   0;  1   a   0;  1 16  0  0  a  1   31 31 1 31 3 Kết luận: Vậy 3
min 3a  8 x  ax dx    I 
. Đẳng thức xảy ra khi a  ; I   3a  .   a 16 16  8 12 8 0 
Câu 19: Cho hàm số y  f  x liên tục trên 0 
;1 đồng thời thỏa mãn các điều kiện sau: max f  x  6 0;  1 1 1 và 2
x f  x dx  0 
. Giá trị lớn nhất của tích phân 3
x f  x dx  bằng bao nhiêu? 0 0 3 1 32  4  3 2  4 1 A. B. C. D. 8 4 16 24 Lời giải 1
Ta có với mọi số thực a   thì 2
ax f  x dx  0  do đó: 0 1 1 1 1 3
x f  x dx   3 2
x  ax  f  x 3 2 dx  x  ax f  x 3 2
dx  6 x  ax dx a        0 0 0 0 1 1 Do đó: 3 x f  x 3 2
dx  min 6 x  ax dx  min g a 
. Tới đây ta chia các trường hợp sau:   a a 0 0
Trường hợp 1: Nếu a  0 thì 3 2 2
x  ax  x  x  a  0 x  0  ;1 . Khi đó: 1 1  1 a  3 g a 3 2 3 2
 6 x  ax dx  6 x  ax dx  6 
 min g a      a0  4 3  2 0 0
Trường hợp 2: Nếu a  1 thì 3 2 2
x  ax  x  x  a  0 x  0  ;1 . Khi đó: 1 1  a 1  1 g a 3 2 2 3
 6 x  ax dx  6 ax  x dx  6 
 min g a      a 1  3 4   2 0 0 1 a 1 4 2a  4a  3
Trường hợp 3: Nếu a 0 
;1 thì f a 3 2 2 3 3 2
 6 x  ax dx  6 ax  x dx  x  ax dx     . 2 0 0 a 3 3
 a  a    3 4 2  4 2 4 3  1 3 32  4 
Ta tìm được min g a  min     
vậy min g a  . a   0;  1 a   0;  1 2 4 2 2   a 4 3 3 2  4  3 3 1 1 1 2  4 3 3 3  Do vậy:
x f  x dx  min g a  x f  x dx 
 max x f  x dx   .    a 0;  1 4 4 0 0 0
Câu 20: Cho hàm số y  f  x có đạo hàm liên tục trên đoạn 0 
;1 thỏa mãn f  x  xf  x 2018 3 '  x với 1 mọi x 0 
;1 . Giá trị nhỏ nhất của tích phân
f  x dx  bằng: 0 1 1 1 1 A. B. C. D. 2021 2022 2018 2021 2018 2019 2019  2021 Lời giải
Ta có: f  x  x f  x 2018 3 . '  x 2  x f  x 3  x f  x 2020 3 '  x t t 2018   t 3
  x f  x 2020 3   x
 x f  x 2020  dx  x dx t  0 
;1  f t         2021 0 0 1 1 2018 x 1 1 1 Khi đó 
f  x dx  dx  .  
Giá trị nhỏ nhất của tích phân
f  x dx  là . 2021 2019.2021 2019.2021 0 0 0 1 2 1
Câu 21: Cho hàm số f  x có đạo hàm liên tục trên 0;  1 thỏa mãn f  
1  0,  f  x dx     và 11 0 1 1 1 4      x f x dx . Tích phân    f x dx bằng 55 0 0 1 1 1 1 A. B. C. D. 7 7 55 11 Lời giải 1 1 5 1 5  x  x 1 4 1
x f  x dx   5  f  x  f    x  dx . Suy ra     x f x dx
. Hơn nữa ta dễ dàng tính được 5 5 11 0   0 0 0 1 1 1 1 1  2 1 2 2 2 5   x dx . Do đó
 f  x 5
 dx  2 x f  x dx   5     5
x  dx  0        0  f x x dx . 11   0 0 0 0 0 1 1 1 1 6 x 1 1 
Suy ra f  x 5 
 x , do đó f  x 6 
x  C . Vì f   1  0 nên C   . Vậy
f  x dx  dx    . 6 6 6 7 0 0 1 2 3
Câu 22: Cho hàm số f  x có đạo hàm liên tục trên 0;  1 thỏa mãn f  
1  0,  f  x dx   2ln 2    2 0 1 f  x 1 3 và dx  2ln 2   . Tích phân    f x dx bằng  x  2 1 2 0 0 1 2 ln 2 3  2 ln 2 3  4ln 2 1 ln 2 A. B. C. D. 2 2 2 2 Lời giải f  x 1 1 1 1  1   1    1  Ta có:
dx  f x d 1  1 f x  1 f   x dx . 2               x 1  x 1  x 1     x 1 0   0 0 0 1  1  3 Suy ra 1 f   
 x dx   2ln 2 . Hơn nữa ta tính được:  x 1  2 0 1 1 2 1 1  1 1   1    3 1 dx  1 2  dx   
 x  2 ln x 1     2 ln 2  .  x 1   x 1  x  2 1  x 1 2 0 0       0 1 1 1 2 3 2 2  1   1   1 
Do đó  f  x dx  2 1 f      
 x dx  1 dx  0  f     x  1 dx  0  .  x 1  x 1    x 1      0 0 0 0 1
Suy ra f  x  1
, do đó f  x  x  ln  x  
1  C . Vì f  
1  0 nên C  ln 2 1. x 1 1 1 1 Ta được
f  x dx  x  ln  x  
1  ln 2 1 dx   ln 2     . 2 0 0
Câu 23: Cho hàm số y  f  x nhận giá trị không âm và liên tục trên đoạn 0  ;1 đồng thời ta đặt x 1 1
g  x  1 f t  dt 
. Biết g  x 
f  x với mọi x 0  ;1 . Tích phân dx  có giá trị lớn g x 0   0 nhất bằng: 1 2 1 A. B. 1 C. D. 3 2 2 Lời giải x F  x
Đặt F  x  f t  dt  g  x  1 F  x  f  x x  0  ;1  1  0 x  0;1  2   0
F  x   1 t  F  x   1
 h t   
1 dx  1 t  
là hàm số đồng biến trên 0 
;1 do vậy ta có đánh giá:
 F  x  2  F t 1 0 1     1 1 1 1 1
h  x  h 0 x  0  ;1  1 x   0   1 x x  0  ;1  dx   . F  x 1 F  x 1 g x 2 0  
Câu 24: Cho hàm số y  f  x nhận giá trị không âm và liên tục trên đoạn 0  ;1 đồng thời ta đặt x 1
g  x  1 3 f t  dt  . Biết   2
g x  f  x với mọi x 0  ;1 . Tích phân
g  xdx  có giá trị 0 0 lớn nhất bằng: 5 4 7 9 A. B. C. D. 2 3 4 5 Lời giải x F  x 2  
Đặt F  x  f t  dt  g  x  1 3F  x  f  x x  0;  1  1  0 x  0  ;1  0 3F  x 1 t  F  x   2 2
 h t    1 dx 
3F t  1  t  
là hàm số nghịch biến trên 0  ;1 do vậy ta có:  3F x 1   3 3 0     1 2 2 3 7
h  x  h0 x  0  ;1 
3F  x 1  t   0  3F  x 1  x 1 x  0  ;1 
g  xdx   . 3 3 2 4 0
Câu 25: Cho hàm số y  f  x nhận giá trị không âm và liên tục trên đoạn 0  ;1 đồng thời ta đặt 2 x 1
g  x  1
f t  dt 
. Biết g  x  xf  2 2
x  với mọi x 0 
;1 . Tích phân g  xdx  có giá trị 0 0 lớn nhất bằng: A. 2 B. 3 C. 4 D. 1 Lời giải 2 x 2xf  2 x 2 2 2 
Đặt F  x   f t  dt  g  x  1 F 
x   2xf x  x  0  ;1  1  0 x  0  ;1 1 F  2 x 0  t  2xf  2 x  
 h t   
1 dx  ln 1 F t  t 
là hàm số nghịch biến trên 0  ;1 do vậy ta có: 2     1 F x  0     1
   0  0 
;1  ln 1     0  1   x h x h x F x x F x  e x  0  ;1 
g  xdx  2  . 0
Câu 26: Cho hàm số y  f  x nhận giá trị không âm và liên tục trên đoạn 0  ;1 đồng thời ta đặt x 1 2
g  x  1 2 f t  dt 
. Biết       3 g x f x  3 
 với mọi x 0  ;1 . Tích phân
 g  x dx    có giá 0 0 trị lớn nhất bằng: 5 4 A. B. 4 C. D. 5 3 3 Lời giải x 3
Ta đặt F  x  f t  dt 
khi đó g  x  1 2F  x   f  x x  0  ;1   . 0 f  x F  x Do vậy 1  0 x  0  ;1  1  0 x  0  ;1 .
3 1 2F  x
3 1 2F  x t  F  x  2 3 3
Xét hàm số: h t    1 dx  
3 1 2F t t  t  0 
;1 là hàm nghịch biến trên  3 1 2F x   4 4 0     2 2 3 3 4 0 
;1 cho nên h t   h 0 t  0  ;1 
3 1 2F t t   0  3 1 2F t  t 1 t  0  ;1 . 4 4 3 1 1 1 2 4 2  4 2  5
Do đó:  3 g x  x 1 x  0  3 ;1  g  x 3  dx  x 1 dx  g     
 x dx   . Chọn A. 3 3     3 0 0 0
Câu 27: Cho hàm số f có đạo hàm liên tục trên 1;8 đồng thời thỏa mãn điều kiện: 2 2 8 2  f  x  2  dx  2 f  x  2 2 3 3 dx 
f  x dx    2 x   1 dx   3 1 1 1 1 2 3
Tính tích phân  f  x dx    bằng: 1 8 ln 2 ln 2 4 5 A. B. C. D. 27 27 3 4 Lời giải 2 2 8 2 2 2 2 Đặt 3 2
t  x  dt  3x dx . Khi đó:  f   3
x  dx  2 f   3 x  dx 
f  x dx    2 x   1 dx   3 1 1 1 1 8 8 8 2 1 1 2 1   f t  2  dt  2
f t  1 t dt  1 t dt  0      2 2  3 2  2  3 2 3 3 3  3 1 t 1 t 1 t 2 8  f t 3 2 2 1 t    8 ln 2  
 dt  0  f t   t 1   f  x 3 3 2  dx    . Chọn A. 3    t  27 1 1  
Câu 28: Cho hàm số f  x có đạo hàm dương, liên tục trên 0 
;1 đồng thời thỏa mãn các điều kiện 1 1 1  1  f 0  1 và 3 f  x 2 f  x  dx  2
f  x f  x dx  3   . Tính tích phân
f  x dx  ? 9    0 0 0 3 5 5 7 A. B. C. D. 2 4 6 6 Lời giải 2 1 1 1  
Theo bất đẳng thức Holder ta có: 
f  x f  x dx   f  x 2
f  x dx 1dx    .  0  0 0 2 2 1 1 1  1   1      Như vậy: 9 f  x 2 f  x 
dx   4 f  x 2
f  x dx  9 f  x 2 f  x  dx   0     . 9   9       0  0  0  1 1 1 7
Do đó: f  x 2 f  x 3   f  x 3  x 1 
f  x dx   . 9 3 6 0 3
Câu 29: Cho hàm số f  x có đạo hàm liên tục trên 0 
;1 đồng thời thỏa mãn các điều kiện f   1  ; 2 1 5 1 x 1 2 1
f  x dx   và  x   1 1 
 f x dx   . Tính tích phân 2
f  x dx  ?  6 x  2 3 0 0 0 7 8 53 203 A. B. C. D. 3 15 60 60 Lời giải 1 1 1 5 2
Sử dụng tích phân từng phần ta có:
f  x dx   f  
1  xf  x dx  xf  x dx     . 6 3 0 0 0 x 2 2 x 2
Mặt khác: 2 1 x 1
 f x  1 x 1
 f x . x  2 x  2 1 1 2 4 x 2 x 2 2 Tích phân hai vế ta    
 f x dx  
 f x dx  . 3 3 x  2 2  x 3 0 0 2 2 1 1 1 1   4  x  x 2
Áp dụng Holder:  xf  x dx     x 2  x
f  x dx   x 2  x dx    
 f  x dx . 9  2 x   2  x  0   0  0 0 1 x 2 1 2 2 x 53 Do vậy  
 f x dx  nên dấu bằng  f x  2  x  f x 2  2x  
f  x dx   . 2  x 3 2 60 0 0
Câu 30: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
1 đồng thời thỏa mãn điều kiện f 0  2 1 2 2 2 và  2 21 x   1 12  x  
1 12xf  x   f ' x x     0; 
1 . Tính f  x dx  ? 0 3 4 5 A. B. C. 2  D.  4 3 4 Lời giải 2 2 2 Ta có  2 21 x   1 12  x  
1 12xf  x   f ' x   1 1 36 1 1 24 2 
 6 f  x d  x  
1   f ' x 2 2  dx     6  2 x  
1 f ' x dx   f ' x dx  5   5   0 0 0 0 1
  f ' x 2 2
 3x  3 dx  0  f  x 3
 x  3x  2    . Chọn đáp án A. 0 Câu 31: Cho hàm số f  x có đạo hàm liên tục trên 0;  1 thỏa mãn 1 1 2 1  e 1
f ' x2 dx   x   1 . x
e . f  x dx    và f  
1  0 . Tính f  x dx  ?  4 0 0 0 A. 2  e B. 2  e C. e D. 1  e Lời giải 2 1 1 e 1 1 Ta có:   x   1 . x
e . f  x dx  f  x d    . x
x e    . x
x e . f ' x dx  4 0 0 0 1 1 2 1    e  x 1
f ' x2 dx   .
x e . f ' x 2 2 dx   x . x e dx   4 0 0 0 1 1 1 1 2    ' 2 2 2  . x  2 . x f x dx x e dx
x e . f ' x dx  0  
   '   . x f x x e  dx  0 0 0 0 0 1 
'    . x    x f x x e
f x  e  x   1 
f  x dx  2  e  . Chọn đáp án B. 0
Câu 32: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
1 đồng thời thỏa mãn điều kiện
 f ' x 2 1  1   1
f 0  0, f   1  1 và dx  
. Tính tích phân I 
f  x dx  ? x  e e 1 0 0 e  2 e 1 1 A. B. C. 1 D. e 1 e  2 e   1 e  2 Lời giải
 f ' x 2 2 1 1 1      x 1
Theo bất đẳng thức Holder ta có: . dx e dx  f '     x dx  .   e   1  1 x e e 1 0 0  0  f ' x 1 1
Đẳng thức xảy ra khi và chỉ khi:  k. x
e  f ' x  k. x e . Vì
f ' x dx  1 k   x e e 1 0 x e  C x e 1 e  2
Vậy f  x 
. Mà f 0  0, f  
1  1 và f  x  . Vậy I  . Chọn đáp án A. e 1 e 1 e 1 1
Câu 33: Cho hàm số y  f  x dương và liên tục trên 1; 
3 thỏa mãn max f  x  2; min f  x  và 1;  3 1  ;3 2 3 3 1 3 biểu thức S 
f  x dx dx  
đạt giá trị lớn nhất. Khi đó tính
f  x dx  ? f x 1 1   1 7 5 7 3 A. B. C. D. 2 2 5 5 Lời giải 1 1 5 Ta có:
 f  x  2  2 f  x  
1  f  x  2  0  f  x   2 f  x 2 1 5 3 3  5  25 3 5  
 f  x  S  f  x dx 
 f  x dx   
. Ta tìm được max S  khi
f  x dx   . f  x 2 2 4 2 1  1  1
Câu 34: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
1 đồng thời f 0  0, f   1  1 và 1 1 1 f  x
 f ' x 2 2  1  x dx     . Tính tích phân dx  bằng? 2 0 ln 1 2  0 1  x 1 2 1 A. 2 ln 1 2  B. 2 ln 1 2  2 2 1 C. ln 1 2  D.  2   1 ln 1 2 2 Lời giải 2 1 1 1 2 1  
Theo bất đẳng thức Holder ta có:  f ' x 2  1 x . dx dx  f '       x dx 1   2 0 0 1 x  0  1 1 1 Mặt khác dx  ln   2 x  1  x  ln 1  2 2    0 0 1  x k k
Vậy đẳng thức xảy ra khi f ' x 4 2 . 1  x 
 f ' x  4 2 2 1  x 1  x 1 1 1 Vì
f ' x dx  1  nên k 
. Vậy f  x  .ln  2
x  1  x   C 0 ln 1 2  ln 1 2  f  0  0 1 f  x 1 Vì 
nên C  0 . Do đó dx  ln 1  2  . Chọn đáp án C. 2   f    1  1  2 0 1  x 1
Câu 35: Tìm giá trị nhỏ nhất của 2 S  x  
ax dx với a 0,  1 0 2  2 2 1 2  2 2 1 A. . B. . C. . D. 6 3 3 6 Lời giải
Phá dấu trị tuyệt đối ta có a 1 1 a 1 3 2 3 2 3  x ax   x ax  2a  3a  2 2 S 
x  ax dx     2
x  ax dx   2
x  ax dx          3 3 3 3 6 0 0 a     0 a  1  2  2 S  f  . min    2  6
Câu 36: Cho hàm số y  f  x nhận giá trị dương và có đạo hàm liên tục trên đoạn 0  1 ; và thỏa mãn 2 1  ' f  x  f  
1  e. f 0  e;   dx  1  . Tìm mệnh đề đung   f x 0      1   1   1   1  1 A. 2 f    e . B. f    e . C. f    e . D. f     2   2   2   2  2e Lời giải 1 ' f  x 1 f   1 Ta có
dx=ln f  x  lnf  
1  ln f 0  ln  ln e  1  f  x 0 f 0 0   2 2 1 '   1  ' f x f  x      Nên   dx  1    1dx  0       f x  f x  0     0       2 2 1  '    '    1  '    ' f x f x f x f  x    2. 1dx  0   1 dx  0  1  0      f x f x  f x f x 0       0         x  1  Vậy:    x f x
A.e . Mà f  
1  e. f 0  e Nên f  x  e  f    e .  2  b
Câu 37: Cho a  b  ab  4 và a  b . Tìm giá trị nhỏ nhất của biểu thức 2 I 
x  a  b x  ab dx a A. 4 3 . B. 12 . C. 2 3 . D. 48 Lời giải Ta có   3 3 3
a  b2  4ab
ab  42  4ab ab  22 3 12 3 12 2 I       48 4 36.a 36 36 36 36  I  4 3 b
Câu 38: Tìm giá trị nhỏ nhất của 2 I 
x  2  m x  2 dx 
trong đó a  b là hai nghiệm cảu phương a trình 2
x  2  m x  2  0 128 8 2 A. . B. . C. 8 . D. 2 2 9 3 Lời giải  2m 83 2 3 128 8 2 I     I  . 4 36a 36 9 3 1
Câu 39: Tìm giá trị nhỏ nhất của 3 S  x  ax dx 
với a 0,  1 0 2  2 1 1 2  2 A. . B. . C. . D. 6 8 4 8 Lời giải a 1 a 1 2 4 4 2     S    a.x x x a.x 3
a.x  x  dx    3
x  a.x dx         2 4 4 2 0 a     0 a 2 2 2 2 2  a a   1 a a a  1  1  1 1 S        a          2 4 4 2 4 2 2      2  8 8 2m
Câu 40: Gọi a,b lần lượt là giá trị lớn nhất và nhỏ nhất của 3 2 2 3 S 
x  4mx  5m x  2m dx  với m m 1; 
3 . Mệnh đề nào dưới đây đúng 41 21
A. a  b  .
B. a  b  1.
C. a  b  .
D. a  b  2 6 4 Lời giải 2m 2m 2m S 
 x  m2  x  m dx    x  m2  x  m dx    x  m2 2 2   
x  m  mdx m m m 2m m m   3 2
  x  m4
m  x  m3 2 2 4 m
S    x  m dx+m  x  m dx=       4 3  12 m m   m 41
Thay m 1; 
3 vào ta có a  b  . 6
Câu 41: Cho A là tập các hàm số f lien tục trên đoạn 0  1
; và nhận giá trị không âm trên đoạn 0  1 ; . 1 1 Tìm m nhỏ nhất sao cho f
 2018 x dx  m. f xdx f   A  0 0 1 A. 2018 . B. 1. C. . D. 2018 2018 Lời giải 1 1 1 Đặt 2018 2017 t
 x  dx  2018.t dt nên f  2018 x  2017 dx=2018. t
. f t  .dt  2018 f t  .dt   0 0 0
Tìm m nhỏ nhất nên m  2018 . Ta sẽ Cm m  2018 là số cần tìm. Xét   n
f x  x ta có 1 1 m n  n / n 2018 2018 1 2018   x
dx  m x dx    m    n  2018 n 1 n  2018 0 0
Cho n   ta có m  2018 . Vậy m  2018 là hằng số nhỏ nhất cần tìm.
Câu 42: Cho hàm số y  f  x nhận giá trị dương và có đạo hàm '
f  x liên tục trên đoạn 0  1 ; thỏa 1 1 2 1 mãn f  
1  2018. f 0 . Tìm giá trị nhỏ nhất biểu thức ' M  dx   f x  dx  2     
0  f  x  0   A. ln 2018 . B. 2 ln 2018 . C. 2e . D. 2018e Lời giải 2 1 1  1  f x f x '   1   1 M= 
 f  x dx  2 dx  2 dx  2 ln f x  ln   '  . '   2 2018 f  x f  x f  x 0 0   0 0 b 2
Câu 43: Cho a  b  ab  4 và a  b . Tìm giá trị nhỏ nhất của biểu thức I 
 x  a  x  b dx a 64 49 A. 12. B. 0. C. . D. 3 3 Lời giải b b b
S    x  a2  x  a  a  b dx    x  a2  x  a dx  a  b  x  a2 dx      a a a 2 2 2 1 1 1 1 S 
a  b4 
a b2 4ab  ab 42 4ab  ab 22 12 12. 12 12 12 12 Câu 44: Cho
a  b  a  b 2 2 2 2  4 và
a  b . Tìm giá trị lớn nhất của biểu thức b 2 I 
x  a  b x  ab dx a 16 9 4 3 A. . B. . C. . D. 9 16 3 4 Lời giải 2
4  a  b2  a  b   a  b2 1 a  b2   a  b2 2 2   3 3
a  b2  4ab a b2 3  3 4 4 2 I      4 36a 36 36 36 3 a  b  0  a  1  Khi đó    . a b 
   a  b 2 2 2 2  4 b  1  
Câu 45: Cho hàm số y  f  x nhận giá trị dương và có đạo hàm '
f  x liên tục trên đoạn 0  1 ; thỏa 1 1 2 1 mãn f  
1  e. f 0 . Biểu thức ' dx   f x  dx  2  . Mệnh đề nào đúng 2     
0  f  x  0   2e 2 2e 2 e  2 2 e  2 A. f   1  . B. f   1  . C. f   1  . D. f   1  e 1 2 e 1 e 1 2 e 1 Lời giải 2 1  1 
Viết lại biểu thức cho dưới dạng ' 
 f  x dx  0  . Dấu bằng xảy ra khi f x 0     1 ' 1     0 ' f x 
 f  x  1dx  f  x .d    f x f  x f  x 2 f  x  x  c 
 f  x  2 x  c 2  f  0  2c f   1 2  2c 1
Thay x  0 vào ta có    e   c   f   1  2  2 f c 0 2 2c e 1  2 1 2e
 f  x  2x   f   1  . 2 2 e 1 e 1
Câu 46: Cho A là tập các hàm số f lien tục trên đoạn 0  1 ; . 1 1   Tìm m   2
min  x. f  x 2018 x d  x
. f  x dx   f A  0 0  1  1  2017  1  A. . B. . C. . D. 2019 16144 2018 16140 Lời giải
Biểu thức đã cho là tam thức bậc 2 ẩn là f  x có hệ số 2018
a  x;b  x ;c  0 2017  b  x f  x    2a 2 
Nên biểu thức Min tại  1 . 1 1 4036 4035  x x 1 m  dx  dx   min    4a 4.x 4x4036 16144  0 0 0
Câu 47: Cho m là tham số thuộc đoạn 1; 
3 . Gọi a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của 2m P 
 x  m2  x  m2 2 dx 
. Tính a  b  m 122 121 A. 31. B. 36 . C. . D. 15 4 Lời giải 5 5 5 m  1 3  3 1 122 P   ;  T     . 30 30 30 30 15   2 2m 2 a
Câu 48: Giá trị nhỏ nhất của 2 P  x    2
m  m   x   3 2 1
4 m  m dx là S  ;a,b nguyên dương b m a và
tối giản. Tính T  a  b b A. 7. B. 337. C. 25. D. 91 Lời giải
m  m  3 2 3 4 1 4  3  9 Ta có : P   . 
 T  9 16  25   3 3  4  16
_______________ TOANMATH.com _______________