Biện luận nghiệm của bất phương trình dựa vào bảng biến thiên hoặc đồ thị hàm số Toán 12

Biện luận nghiệm của bất phương trình dựa vào bảng biến thiên hoặc đồ thị hàm số Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 1

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU HỌC TẬP SỐ 07_TrNg 2021

CHUY£N §Ò TR¾C NGHIÖM

M«n:

To¸n 12

Chuyªn ®Ò: Kh¶O S¸T HµM Sè

MỘT SỐ BÀI TOÁN VỀ BẤT PHƯƠNG TRÌNH

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

I. MỘT SỐ KẾT QUẢ

Trong thực tế, chúng ta gặp rất nhiều các dạng bài tập khác nhau, trong phần trình bày lý thuyết,

chúng tôi xin giới thiệu 2 bài toán thường gặp sau:

1. Bài toán 1

Xét hàm số

 

y g x

liên tục trên

 

;ab

và

 

có bảng biến thiên như sau:

 





 

Dựa vào BBT trên, các bài toán có kết quả tương ứng như sau:

 

m g x

nghiệm đúng

   

;.x a b m g b   

 

m g x

nghiệm đúng

   

;.x a b m g a   

 

m g x

có nghiệm trên

   

;.a b m g a

 

m g x

có nghiệm trên

   

;.a b m g b

2. Bài toán 2

Xét hàm số

 

y g x

liên tục trên

;ab





và

 

có bảng biến thiên như sau:

 





 

Dựa vào BBT trên, các bài toán có kết quả tương ứng như sau:

 

m g x

nghiệm đúng

 

;.x a b m g b



   



 

m g x

nghiệm đúng

 

;.x a b m g a



   



 

m g x

có nghiệm trên

 

;.a b m g a







 

m g x

có nghiệm trên

 

;.a b m g b







Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 2

II. BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Tìm tất cả các giá trị của

để bất phương trình

 

11f x m  

có nghiệm.

4.m

1.m

2.m

5.m

Câu 2: Cho hàm số

 

y f x

liên tục trên đoạn

1;4 .







Hàm số

 



có đồ thị trên đoạn

1;4







như

hình vẽ dưới đây:

Tất cả các các trị của tham số

để bất phương trình

 

0f x m

nghiệm đúng với mọi

3 10

;









là

 

4.mf









 

3.mf









Câu 3: Cho hàm số

 

y f x

liên tục trên và có đồ thị như hình vẽ dưới đây:

Tập hợp tất cả các giá trị thực của tham số

để phương trình

 

cosf f x m

nghiệm đúng

với mọi giá trị

0;x









là



; 1 .



 



1;1







. C.

1;3







. D.





 



Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 3

Câu 4: Cho hàm số

 

xác định và nghịch biến trên khoảng

 

;. 

Biết bất phương trình

 

f x x x m  

có nghiệm thuộc đoạn

 

2;4 ,

trong đó

là tham số thực. Khẳng định nào

dưới đây đúng?

 

4 12.mf

 

2 2.mf

 

2 2.mf

 

4 12.mf

Câu 5: Cho hàm số

 

có đạo hàm

 

y f x





liên tục trên và có bảng biến thiên như sau:



1



 





Bất phương trình

 

f x x x x m    

(

là tham số thực) nghiệm đúng

 

1;1x  

khi và

chỉ khi

 

1 1.mf

 

1 3.mf  

 

1 1.mf

 

1 3.mf  

Câu 6: Cho hàm số

 

.fx

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ dưới đây:

Bất phương trình

 

f x x m

(

là tham số) nghiệm đúng với mọi

 

0; 2x

khi và chỉ khi

 

22mf

. B.

 

0mf

. C.

 

22mf

. D.

 

0mf

Câu 7: Cho hàm số

 

y f x

có hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

2f x x m

(

là tham số thực) nghiệm đúng với mọi

 

0;2x

khi và

chỉ khi

 

0mf

. B.

 

0mf

. C.

 

24mf

. D.

 

24mf

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 4

Câu 8: Cho hàm số

 

.y f x

Biết hàm số

 



liên tục trên và có đồ thị như hình vẽ sau:

Bất phương trình

 

f x x m

có nghiệm





0;2x

khi và chỉ khi

 

2 2.mf

 

0.mf

 

2 2.mf

 

0.mf

Câu 9: Cho hàm số

 

y f x

. Hàm số

 



y f x

có bảng biến thiên như sau:

Bất phương trình

 



f x x m

đúng với mọi

 

1;1x

khi và chỉ khi

 

11mf

. B.

 

11mf

. C.

 

  13mf

. D.

 

13mf

Câu 10: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình vẽ sau:

Bất phương trình

 

36 1







nghiệm đúng với mọi

 

0;1x

khi và chỉ khi

 

m 



 





 

m 



 

1 36





Câu 11: Cho hàm số

 

y f x

. Hàm số

 

y f x





có bảng biến thiên như sau:

Bất phương trình

 

2f x m x x  

có nghiệm đúng với mọi

 

2;2x

khi chỉ khi

 

2 8.mf  

 

2mf

 

28mf  

 

2mf

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 5

Câu 12: Cho hàm số

 

y f x

có đạo hàm trên . Bảng biến thiên của hàm số

 

'y f x

như sau:

Tìm tất cả giá trị của tham số

để bất phương trình

 

m x f x x  

nghiệm đúng với

mọi

 

0;3x

(0)mf

. B.

(0)mf

. C.

(3)mf

. D.

(1)

mf

Câu 13: Cho hàm số

 

.y f x

Hàm số

 

y f x





có bảng biến thiên như sau:



1



 





2



Bất phương trình

 

cosf x x m  

nghiệm đúng với mọi

 

0;x





khi và chỉ khi

 

0 1.mf

 

0.mf











 

0 1.mf

Câu 14: Cho hàm số

 

y f x

có đạo hàm trên . Bảng biến thiên của hàm số

 

'y f x

như sau:

Tìm

để bất phương trình

 

2sinm x f x

nghiệm đúng với mọi

 

0;x 

(0)mf

. B.

(1) 2sin1mf

. C.

(0)mf

. D.

(1) 2sin1mf

Câu 15: Cho đồ thị hàm số

 

y f x

như hình vẽ sau:

Hỏi có tất cả bao nhiêu giá trị nguyên của tham số

để bất phương trình

 

  

2 10f x x f mx

nghiệm đúng với mọi

?x 

. B.

. C.

. D.

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 6

Câu 16: Cho hàm số

 

y f x

liên tục trên và có đồ thị hàm số

 



y f x

như hình vẽ sau:

Bất phương trình

 

  

3f x x m

có nghiệm đúng

 

  1;1x

khi và chỉ khi

 

03mf

. B.

 

03mf

. C.

 

13mf

. D.

 

13mf

Câu 17: Cho hàm số

 

.fx

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ dưới đây:

Bất phương trình

 

f x x m  

(

là tham số thực) nghiệm đúng với mọi

 

0; 2x

khi và

chỉ khi

 

22mf

. B.

 

0mf

. C.

 

22mf

. D.

 

0mf

Câu 18: Cho hàm số

 

y f x

liên tục trên . Hàm số

 

y f x





có đồ thị như hình dưới đây:

Bất phương trình

 

33f x x x m  

nghiệm đúng với mọi

 

1;3x

khi và chỉ khi

 

33mf

. B.

 

33mf

. C.

 

3 1 4mf  

. D.

 

3 1 4mf  

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 7

Câu 19: Cho hàm số

 

.y f x

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

38f x m x x x   

(

là tham số thực) nghiệm đúng với mọi

 

0;3x

khi và chỉ khi

 

3 24mf

. B.

 

3 24mf

. C.

 

0mf

. D.

 

0mf

Câu 20: Cho hàm số

 

liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

2 2 3f x x m x  

nghiệm đúng với mọi

 

1;3x

khi và chỉ khi

10.m 

5.m 

3.m 

2.m 

Câu 21: Cho hàm số

 

y f x

, hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

38f x m x x x   

(

là tham số thực) nghiệm đúng với mọi

 

0;3x

khi và chỉ khi

 

0mf

. B.

 

3 24mf

. C.

 

0mf

. D.

 

3 24mf

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 8

Câu 22: Cho hàm số

 

y fx

liên tục trên

 

1;3

và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

17f x x x m    

có nghiệm thuộc

 

1;3

khi và chỉ khi

7m 

. B.

7m 

. C.

2 2 2m 

. D.

2 2 2m 

Câu 23: Cho hàm số

 

.y f x

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên

dưới:

Bất phương trình

 

11f x x m   

(

là tham số thực) nghiệm đúng với mọi

 

1;3x

khi và chỉ

 

22mf

. B.

 

0mf

. C.

 

22mf

. D.

 

0mf

Câu 24: Cho hàm số

 

y f x

. Hàm số

'( )fx

liên tục trên và có đồ thị như hình vẽ sau:

-4

-1

-2

Bất phương trình

(sin ) 4f x x m  

nghiệm đúng với mọi

;













khi và chỉ khi

(1) 2mf





. B.

( 1) 2mf



  

. C.

 

12mf



  

. D.

(1) 2mf





Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 9

Câu 25: Cho hàm số đa thức

 

có đồ thị hàm số

 

y f x





như hình vẽ sau:

Bất phương trình

 

2sin 2sinf x x m

nghiệm đúng với mọi

 

0;x





khi và chỉ khi

 

mf

. B.

 

22mf

. C.

 

mf

. D.

 

22mf

Câu 26: Cho

()fx

mà đồ thị hàm số

'( )y f x

như hình vẽ bên dưới:

Bất phương trình

( ) sin

f x m





nghiệm đúng với mọi

1;3x







khi và chỉ khi

(0)mf

. B.

(1) 1mf

. C.

( 1) 1  mf

. D.

(2)mf

Câu 27: Cho hàm số

 

y f x

có đạo hàm trên . Đồ thị hàm số

 

'y f x

như hình vẽ bên dưới:

Tìm

để bất phương trình

 

2 2 4 3m x f x x    

nghiệm đúng với mọi

 

3;x  

2 (0) 1mf

. B.

2 (0) 1mf

. C.

2 ( 1)mf

. D.

2 ( 1)mf

Câu 28: Cho hàm số

 

y f x

có đạo hàm trên . Đồ thị của hàm số

 

y f x





như hình dưới

Tìm

để bất phương trình

 

4 2 1 2m x f x x    

nghiệm đúng với mọi

 

4;2x

2 (0) 1mf

. B.

2 ( 3) 4mf  

. C.

2 (3) 16mf

. D.

2 (1) 4mf



2

1

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 10

Câu 29: Cho hàm số

 

y f x

liên tục trên đoạn

 

1;4

và có đồ thị như hình vẽ bên dưới:

Có tất cả bao nhiêu giá trị nguyên của

thuộc đoạn

 

10;10

để bất phương trình

 

2f x m m

đúng với mọi

thuộc đoạn

 

1;4

. B.

. C.

. D.

Câu 30: Cho hai hàm số đa thức bậc bốn

 

y f x

và

 

y g x

có đồ

thị như hình vẽ, trong đó đường đậm hơn là đồ thị hàm số

 

y f x

. Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm

có hoành độ là

3

và cắt nhau tại hai điểm nữa có hoành độ

lần lượt là

1

và

. Có bao nhiêu giá trị nguyên của tham số







12;12m

để bất phương trình

   

f x g x m

nghiệm

đúng với mọi







3;3x

. B.

. D.

Câu 31: Tìm tất cả các giá trị tham số

để bất phương trình

  

6 2 8 1x x x x m     

nghiệm

đúng với mọi

 

2;8 .x

16.m

15.m

8.m

2 16.  m

Câu 32: Gọi

là tập hợp tất cả các giá trị nguyên dương của tham số

để bất phương trình sau

6 4 3 3 2

3 4 2 0x x m x x mx     

nghiệm đúng với mọi

 

1;3x

. Tổng tất cả các phần tử của

bằng

. B.

. C.

. D.

_______________HẾT_______________

Huế, 15h00 ngày 23 tháng 7 năm 2021

III. LỜI GIẢI CHI TIẾT BÀI

Câu 1: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 11

Tìm tất cả các giá trị của

để bất phương trình

 

11f x m  

có nghiệm.

4.m

1.m

2.m

5.m

Lời giải:

Đặt

1 1 1t x t    

. Khi đó BPT

 

11f x m  

trở thành

   

1f t m

Khi đó BPT

 

11f x m  

có nghiệm khi và chỉ khi BPT

   

1f t m

có nghiệm

1t 

 

min 4

m f t m



    



Chọn đáp án A.

Câu 2: Cho hàm số

 

y f x

liên tục trên đoạn

1;4 .







Hàm số

 



có đồ thị trên đoạn

1;4







như

hình vẽ dưới đây:

Tất cả các các trị của tham số

để bất phương trình

 

0f x m

nghiệm đúng với mọi

3 10

;









là

 

4.mf









 

3.mf









Lời giải:

Ta có

   

0, ,f x m x m f x x       

(1).

Xét bảng biến thiên:

1

 







 



 



Vậy từ (1) suy ra

 

3.mf



Chọn đáp án C.

Câu 3: Cho hàm số

 

y f x

liên tục trên và có đồ thị như hình vẽ dưới đây:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 12

Tập hợp tất cả các giá trị thực của tham số

để phương trình

 

cosf f x m

nghiệm đúng

với mọi giá trị

0;x









là



; 1 .



 



1;1







. C.

1;3







. D.





 



Lời giải:

Đặt

costx

. Với

0;x









thì

   

 

1;1 1;3 1.t f t f f t

   

       

   

Do đó bất phương trình

 

cosf f x m

nghiệm đúng với mọi giá trị

 

0; min cos 1.

x m f f x



 





    





Chọn đáp án C.

Câu 4: Cho hàm số

 

xác định và nghịch biến trên khoảng

 

;. 

Biết bất phương trình

 

f x x x m  

có nghiệm thuộc đoạn

 

2;4 ,

trong đó

là tham số thực. Khẳng định nào

dưới đây đúng?

 

4 12.mf

 

2 2.mf

 

2 2.mf

 

4 12.mf

Lời giải:

Ta có:

     

1      f x x x m m f x x x

Đặt

   

g x f x x x  

. Vì

 

có nghiệm thuộc đoạn

 

2;4

nên

 

 

2;4

m > min

x

   

' ' 2 1;  g x f x x

Ta có:

 

 

   

 

' 0 2;4 .

' ' 2 1 0 2;4 .

2 1 0 2;4 .



  



      



    





f x x

g x f x x x

Suy ra

 

 

   

2;4

min 4 4 12



  

g x g f

. Do đó

 

4 12.mf



Chọn đáp án A.

Câu 5: Cho hàm số

 

có đạo hàm

 

y f x





liên tục trên và có bảng biến thiên như sau:



1



 





Bất phương trình

 

f x x x x m    

(

là tham số thực) nghiệm đúng

 

1;1x  

khi và

chỉ khi

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 13

 

1 1.mf

 

1 3.mf  

 

1 1.mf

 

1 3.mf  

Lời giải:

Ta có

   

3 2 3 2

f x x x x m m f x x x x         

 

Xét hàm số

   

g x f x x x x   

trên

 

1;1

Ta có

   

3 2 1 0g x f x x x



    

 

1;1x  

nên hàm số

 

đồng biến trên

 

1;1 .

1

 





 

1g 

 

Do đó

 

nghiệm đúng

 

1;1x  

khi

   

1 1 3.m g f    



Chọn đáp án B.

Câu 6: Cho hàm số

 

.fx

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ dưới đây:

Bất phương trình

 

f x x m

(

là tham số) nghiệm đúng với mọi

 

0; 2x

khi và chỉ khi

 

22mf

. B.

 

0mf

. C.

 

22mf

. D.

 

0mf

Lời giải:

Ta có:

     

f x x m g x f x x m     

Từ đồ thị hàm số

 

y f x





ta thấy:

   

 

     

0;2

1 0 max 0 0g x f x g x g f



     

Do đó: bất phương trình

 

f x x m

nghiệm đúng với mọi

 

0; 2x

khi và chỉ khi

 

   

0;2

max 0g x m f m  



Chọn đáp án C.

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 14

Câu 7: Cho hàm số

 

y f x

có hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

2f x x m

(

là tham số thực) nghiệm đúng với mọi

 

0;2x

khi và

chỉ khi

 

0mf

. B.

 

0mf

. C.

 

24mf

. D.

 

24mf

Lời giải:

Ta có

 

2f x x m

đúng với mọi

 

0;2x

       

2 , 0;2 , 0;2m f x x x m g x x        

trong đó

   

2g x f x x

Xét

   

2g x f x x

;

   

2g x f x





Từ đồ thị suy ra

   

2 0,g x f x



  

 

0;2x

Suy ra bảng biến thiên của hàm số

 

Do đó bài toán thỏa mãn khi và chỉ khi

   

2 2 4m g m f   



Chọn đáp án C.

Câu 8: Cho hàm số

 

.y f x

Biết hàm số

 



liên tục trên và có đồ thị như hình vẽ sau:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 15

Bất phương trình

 

f x x m

có nghiệm





0;2x

khi và chỉ khi

 

2 2.mf

 

0.mf

 

2 2.mf

 

0.mf

Lời giải:

Có

   

.f x x m m f x x    

Xét hàm số

   

g x f x x

trên





0;2 .

Có

    



1 0, 0;2 .g x f x x



    

Khi đó hàm số

 

có bảng biến thiên sau

Dựa vào bảng biến thiên ta có

      



2 2 0 , 0;2 .f g x f x    

Khi đó

 

m g x

có nghiệm









   

0;2

0;2 min 2 2.x m g x m f     



Chọn đáp án C.

Câu 9: Cho hàm số

 

y f x

. Hàm số

 



y f x

có bảng biến thiên như sau:

Bất phương trình

 



f x x m

đúng với mọi

 

1;1x

khi và chỉ khi

 

11mf

. B.

 

11mf

. C.

 

  13mf

. D.

 

13mf

Lời giải:

Bất phương trình

   

    

f x x m m f x x

Xét hàm số

   



g x f x x

. Ta có:

   



' ' 3g x f x x

Với

 

  1;1x

, ta có

 

















Bảng biến thiên:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 16

Từ bảng biến thiên, ta có:

 

         

, ( 1;1) ( ), ( 1;1)f x x m x m g x x

   

    1 1 1m g m f



Chọn đáp án B .

Câu 10: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình vẽ sau:

Bất phương trình

 

36 1







nghiệm đúng với mọi

 

0;1x

khi và chỉ khi

 

m 



 





 

m 



 

1 36





Lời giải:

Xét hàm số

 

36 1







Hàm số

 

y g x

  



có:

 

' 0, 0;1

2 3 3 2

g x x

    

  

(Vì

   

' 0, 0;1f x x  

)

Suy ra hàm số

 

đồng biến trên

 

0;1

       

 

0 , 0;1 , 0;1 .

g x g x g x x        



Do đó

   

 

, 0;1 .

g x m x m     





Chọn đáp án C.

Câu 11: Cho hàm số

 

y f x

. Hàm số

 

y f x





có bảng biến thiên như sau:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 17

Bất phương trình

 

2f x m x x  

có nghiệm đúng với mọi

 

2;2x

khi chỉ khi

 

2 8.mf  

 

2mf

 

28mf  

 

2mf

Lời giải:

Ta có:

 

2f x m x x  

với

 

2; 2x  

với

 

2; 2x  

Xét

   

2g x f x x x  

với

 

2; 2x

, có

   

22g x f x x



  

Dựa vào bảng biến thiên

 



ta thấy

 

2; 2x  

thì

 

3fx





và

 

2; 2x  

thì

2 2 2x   

. Do đó

   

2 2 1 0g x f x x



    

với

 

2; 2x  

 Hàm số

 

đồng biến trên

 

2;2

và liên tục trên

 

2;2

Suy ra:

 

     

-2;2

max 2 2g x g f

. Vậy

 

2mf



Chọn đáp án D.

Câu 12: Cho hàm số

 

y f x

có đạo hàm trên . Bảng biến thiên của hàm số

 

'y f x

như hình

dưới:

Tìm tất cả giá trị của tham số

để bất phương trình

 

m x f x x  

nghiệm đúng với

mọi

 

0;3x

(0)mf

. B.

(0)mf

. C.

(3)mf

. D.

(1)

mf

Lời giải:

Ta có

   

2 3 3 2

m x f x x m f x x x      

Đặt

   

g x f x x x  

Ta có

     

 

22g x f x x x f x x x

  

      

   

02g x f x x x



    

Mà

   

1, 0;3f x x



  

và

   

2 1 1 1, 0;3x x x x       

nên

   

0, 0;3g x x



  

Từ đó ta có bảng biến thiên của

()gx

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 18

Bất phương trình

 

m f x x x  

nghiệm đúng với mọi

 

0;3x



 

0 (0)m g m f  



Chọn đáp án B.

Câu 13: Cho hàm số

 

.y f x

Hàm số

 

y f x





có bảng biến thiên như sau:



1



 





2



Bất phương trình

 

cosf x x m  

nghiệm đúng với mọi

 

0;x





khi và chỉ khi

 

0 1.mf

 

0.mf











 

0 1.mf

Lời giải:

Ta có:

   

cos cosf x x m m f x x     

(1)

Xét hàm số

         

cos , 0; sin .g x f x x x g x f x x





     

Ta có:

 

           

0; : sin 0, 0; cos 0 0 1.

0 sin 1

x g x f x x x f x x g f













            









Yêu cầu bài toán

 

0 1.mf  



Chọn đáp án A.

Câu 14: Cho hàm số

 

y f x

có đạo hàm trên . Bảng biến thiên của hàm số

 

'y f x

như sau:

Tìm

để bất phương trình

 

2sinm x f x

nghiệm đúng với mọi

 

0;x 

(0)mf

. B.

(1) 2sin1mf

. C.

(0)mf

. D.

(1) 2sin1mf

Lời giải:

Ta có

   

2sin 2sinm x f x m f x x    

Đặt

   

2sing x f x x

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 19

Ta có

   

2cosg x f x x





;

   

0 2cosg x f x x



  

Mà

   

2, 0;f x x



   

và

 

2cosx 2, 0;x   

nên

   

0, 0;g x x



   

 

'( ) 2

2cos 2

g x x







   







Từ đó ta có bảng biến thiên của

()gx

Bất phương trình

    

2 2 1 3m f x x x    

nghiệm đúng với mọi

 

3;x  



 

0 (0)m g m f  



Chọn đáp án C.

Câu 15: Cho đồ thị hàm số

 

y f x

như hình vẽ sau:

Hỏi có tất cả bao nhiêu giá trị nguyên của tham số

để bất phương trình

 

  

2 10f x x f mx

nghiệm đúng với mọi

?x 

. B.

. C.

. D.

Lời giải:

Quan sát đồ thị ta nhận thấy hàm số

 

nghịch biến trên .

Bất phương trình:

 

   

           

2 2 2

2 10 2 10 2 10 0f x x f mx x x mx x m x

với

x

 

          

2 40 0 2 2 10 2 2 10mm

Vì

m

nên ta có

  48m

Vậy có tất cả

giá trị

nguyên thỏa mãn bài toán.



Chọn đáp án D.

Câu 16: Cho hàm số

 

y f x

liên tục trên và có đồ thị hàm số

 



y f x

như hình vẽ sau:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 20

Bất phương trình

 

  

3f x x m

có nghiệm đúng

 

  1;1x

khi và chỉ khi

 

03mf

. B.

 

03mf

. C.

 

13mf

. D.

 

13mf

Lời giải:

Đặt

   

  

3g x f x x

. Ta có

   



2g x f x x

;

   



  02g x f x x

Đường thẳng

 2yx

đi qua hai điểm

   

0;0 , 1;2

Ta có đồ thị hàm số như sau:

Xét bảng biến thiên:

Dựa vào BBT, ta có:

       

        , 1; 1 0 0 3m g x x m g m f



Chọn đáp án B.

Câu 17: Cho hàm số

 

.fx

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ dưới đây:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 21

Bất phương trình

 

f x x m  

(

là tham số thực) nghiệm đúng với mọi

 

0; 2x

khi và

chỉ khi

 

22mf

. B.

 

0mf

. C.

 

22mf

. D.

 

0mf

Lời giải:

Ta có:

     

f x x m g x f x x m



       





Từ đồ thị hàm số

 

y f x





ta thấy:

               

0;2 : 1 0 0;2 : 0 0 0 0

x g x f x x g x g f f





            





Do đó, bất phương trình

 

f x x m

nghiệm đúng với mọi

 

0; 2x

khi và chỉ khi

 

0.mf



Chọn đáp án B.

Câu 18: Cho hàm số

 

y f x

liên tục trên . Hàm số

 

y f x





có đồ thị như hình dưới đây:

Bất phương trình

 

33f x x x m  

nghiệm đúng với mọi

 

1;3x

khi và chỉ khi

 

33mf

. B.

 

33mf

. C.

 

3 1 4mf  

. D.

 

3 1 4mf  

Lời giải:

Ta có:

 

3 2 3 2

3 3 3 ( ) 3f x x x m f x x x m      

nghiệm đúng với mọi

 

1;3x

Xét

( ) 3 ( ) 3g x f x x x  

với

 

1;3x

Khi đó:

( ) 3 ( ) 3 6 3 ( ) 2g x f x x x f x x x



  

     



Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 22

Nghiệm của phương trình

( ) 0gx





là hoành độ giao điểm của đồthị

()y f x





và parabol

2y x x

Phương trình

( ) 0gx





có ba nghiệm

1; 3; 1x x x   

trên đoạn

1;3







     

lim lim 3 3 3 1 4

g x f x x x f



 



     



;

     

lim lim 3 3 3 3

g x f x x x f







   



Ta có bảng biến thiên sau:

1

()gx



()gx

 

3 1 4f 

 

33f

Bất phương trình

 

33f x x x m  

nghiệm đúng với mọi

 

1;3x

khi và chỉ khi

   

, 1;3m g x x   

3 ( 1) 4mf   



Chọn đáp án D.

Câu 19: Cho hàm số

 

.y f x

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

38f x m x x x   

(

là tham số thực) nghiệm đúng với mọi

 

0;3x

khi và chỉ khi

 

3 24mf

. B.

 

3 24mf

. C.

 

0mf

. D.

 

0mf

Lời giải:

Ta có :

       

3 2 3 2

3 8 , 0;3 3 8 , 0;3f x m x x x x f x x x x m x            

Xét hàm số

     

3 8 , 0;3g x f x x x x x     

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 23

Ta có :

     

 

3 6 8 3 6 8 , 0;3g x f x x x f x x x x

  

         

Ta có trên khoảng

 

0;3

 

5fx





và

5 3 6 8 17xx   

nên

   

0, 0;3g x x



  

Do đó hàm số

 

nghịch biến trên

 

0;3

hay

       

3 0 , 0;3g g x g x   

Vậy

       

, 0;3 3 3 24g x m x m g f      



Chọn đáp án B.

Câu 20: Cho hàm số

 

liên tục trên và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

2 2 3f x x m x  

nghiệm đúng với mọi

 

1;3x

khi và chỉ khi

10.m 

5.m 

3.m 

2.m 

Lời giải:

Ta có

   

3 2 3 2

2 2 3 2 3 2f x x m x f x x x m       

Nhận xét

 

   

1;3

minf 2 3xf



  

Đặt

   

3 2m, 1;3g x x x x      

   

3 6 , 0

g x x x g x







    







     

0 2 ; 1 4 2 ; 3 2g m g m g m    

và

 

2 4 2gm

 

   

1;3

max 2 4 2g x g m



   

Yêu cầu bài toán

 

1;3

2min max 6 2 4 5.



        f x g x m m



Chọn đáp án B.

Câu 21: Cho hàm số

 

y f x

, hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ.

Bất phương trình

 

38f x m x x x   

(

là tham số thực) nghiệm đúng với mọi

 

0;3x

khi và chỉ khi

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 24

 

0mf

. B.

 

3 24mf

. C.

 

0mf

. D.

 

3 24mf

Lời giải:

 

38f x m x x x    

 

38f x x x x m   

Đặt

   

38h x f x x x x   

     

 

3 6 8 3 6 8 .h x f x x x f x x x

  

        

Đặt

 

3 6 8g x x x  

và vẽ đồ thị của

 

lên hệ trục Oxy.

Từ hình vẽ, ta thấy

     

, 0;3 .f x g x x



  

Do đó

   

0, 0;3 .h x x



  

Vì vậy ta có bảng biến thiên:

Từ bảng biến thiên, yêu cầu bài toán

   

3 3 24.m h m f    



Chọn đáp án D.

Câu 22: Cho hàm số

 

y fx

liên tục trên

 

1;3

và có đồ thị như hình vẽ bên dưới:

Bất phương trình

 

17f x x x m    

có nghiệm thuộc

 

1;3

khi và chỉ khi

7m 

. B.

7m 

. C.

2 2 2m 

. D.

2 2 2m 

Lời giải:

Bất phương trình

 

17f x x x m    

có nghiệm thuộc

 

1;3

khi và chỉ khi

 

 

1;3

max 17    f x xm x

Xét hàm số

 

17g x x x   

trên đoạn

 

1;3

Ta có

 

1 1 7 1

2 1 2 7 2 7 . 1

x x x x

  



  

   

 

0gx





7 1 0xx    

3x

 

1 8 2 2g   

 

3 2 2 4g   

Suy ra

 

 

1;3

max 4



gx

tại

3x 

. (1)

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 25

Mặt khác, dựa vào đồ thị của

 

ta có

 

 

1;3

max 3



fx

tại

3x 

.(2)

Từ (1) và (2) suy ra

 

 

1;3

max 717 f x x x

tại

3x 

Vậy bất phương trình đã cho có nghiệm thuộc

 

1;3

khi và chỉ khi

7m 



Chọn đáp án A.

Câu 23: Cho hàm số

 

.y f x

Biết hàm số

 

y f x





liên tục trên và có đồ thị như hình vẽ bên

dưới:

Bất phương trình

 

11f x x m   

(

là tham số thực) nghiệm đúng với mọi

 

1;3x

khi và chỉ

 

22mf

. B.

 

0mf

. C.

 

22mf

. D.

 

0mf

Lời giải:

Đặt

1ux

. Vì

   

1;3 0;2xu   

   

f u u m f u u m     

Xét hàm số

   

g u f u u

với

0; 2u







. Ta có

   

1g u f u





Dựa vào độ thì ta thấy

0; 2u







thì

 

1, 0;2f u u





  



 

gu

nghịch biến trên

 

0;2

Vậy để

 

11f x x m   

(

là tham số thực ) nghiệm đúng với mọi

 

1;3x

thì

   

, 0;2f u u m u   

     

0;2

max 0 0

m g u g f

 



   



Chọn đáp án D.

Câu 24: Cho hàm số

 

y f x

. Hàm số

'( )fx

liên tục trên và có đồ thị như hình vẽ sau:

-4

-1

-2

Bất phương trình

(sin ) 4f x x m  

nghiệm đúng với mọi

;













khi và chỉ khi

(1) 2mf





. B.

( 1) 2mf



  

. C.

 

12mf



  

. D.

(1) 2mf





Lời giải:

Ta có

 

sin 4 , ;

f x x m x







    





   

4 sin , ;

m g x x f x x







     





Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 26

   

4 cos . sing x x f x





;













nên

1 sin 1x  

, kết hợp với đồ thị của

 



ta có

 

4 sin 0fx



  

Ta lại có

0 cos 1x

;





  





nên

 

4 cos . sin 0x f x



  

Suy ra

   

4 cos . sin 0 ;

g x x f x x







     





Do đó hàm

 

đồng biến trên khoảng

;











   

g x g f





   





Bất phương trình

(sin ) 4f x x m  

nghiệm đúng với mọi

;













   

4 sin , ;

m g x x f x x







     





 

m g f





   







Chọn đáp án A.

Câu 25: Cho hàm số đa thức

 

có đồ thị hàm số

 

y f x





như hình vẽ sau:

Bất phương trình

 

2sin 2sinf x x m

nghiệm đúng với mọi

 

0;x





khi và chỉ khi

 

mf

. B.

 

22mf

. C.

 

mf

. D.

 

22mf

Lời giải:

Bất phương trình

 

2sin 2sinf x x m

nghiệm đúng với mọi

 

0;x





khi và chỉ

khi

 

maxg







với

   

2sin 2sing x f x x

Ta đặt

2sintx

, khi

 

0;x





thì



0; 2t







Khi đó

   

2sin 2sing x f x x

trở thành

   

g t f t

Ta có

   

g t f t t t









    







Dựa vào đồ thị ta thấy rằng

 

0; t 1;2f t t





   



nên

   

12gg

Khi đó



     

 

0;1 0;

maxg 1 1 maxg .

t g f x



  



   

Vậy

 

mf

thỏa yêu cầu bài toán.



Chọn đáp án A.

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 27

Câu 26: Cho

()fx

mà đồ thị hàm số

'( )y f x

như hình vẽ bên dưới:

Bất phương trình

( ) sin

f x m





nghiệm đúng với mọi

1;3x







khi và chỉ khi

(0)mf

. B.

(1) 1mf

. C.

( 1) 1mf  

. D.

(2)mf

Lời giải:

Xét

   

sin

g x f x





   

' ' cos

g x f x



  

• Với



1;1 ; cos 0

2 2 2 2

   





      









(1)

Đồng thời dựa vào đồ thị

 

'fx

ta thấy

  

' 0, 1;1f x x



   



(2)

Từ (1), (2) ta suy ra

  

' 0, 1;1g x x



   



• Với



1;3x







; cos 0

2 2 2 2

   



   







(3)

Đồng thời dựa vào đồ thị ta thấy

  

' 0, 1;3f x x



  



(4)

Từ (3), (4) ta suy ra

 

'0gx



1;3x







Tại

 

' 1 0

1: ' 1 0

cos 0









  









. Ta có bảng biến thiên của

 

như sau:

Để bất phương trình

 

sin

f x m





nghiệm đúng với mọi

1;3x







     

1;3

min 1 1 1m g x m g f

 



     



Chọn đáp án B.

Câu 27: Cho hàm số

 

y f x

có đạo hàm trên . Đồ thị hàm số

 

'y f x

như hình vẽ bên dưới:

Tìm

để bất phương trình

 

2 2 4 3m x f x x    

nghiệm đúng với mọi

 

3;x  



2

1

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 28

2 (0) 1mf

. B.

2 (0) 1mf

. C.

2 ( 1)mf

. D.

2 ( 1)mf

Lời giải:

Ta có

   

2 2 4 3 2 2 4 3m x f x x m f x x x          

Đặt

   

2 2 4 3g x f x x x    

. Ta có

   

2 2 2 4g x f x x



   

     

0 2 2g x f x x



     

Đặt

2tx

ta được

 

f t t





 

là phương trình hoành độ giao điểm của đồ thị

 



và đường thẳng

yt

(hình

vẽ)

Dựa vào đồ thị của

 



và đường thẳng

yt

ta có

 

f t t

























hay



















Bảng biến thiên của hàm số

 

Bất phương trình

    

2 2 1 3m f x x x    

nghiệm đúng với mọi

 

3;x  



 

2 2 (0) 1m g m f    



Chọn đáp án B.

Câu 28: Cho hàm số

 

y f x

có đạo hàm trên . Đồ thị của hàm số

 

y f x





như hình dưới

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 29

Tìm

để bất phương trình

 

4 2 1 2m x f x x    

nghiệm đúng với mọi

 

4;2x

2 (0) 1mf

. B.

2 ( 3) 4mf  

. C.

2 (3) 16mf

. D.

2 (1) 4mf

Lời giải:

 

   

4 2 1 2 2 1 2m x f x x m f x x         

Đặt

     

2 1 2g x f x x   

Ta có

         

 

2 1 2 2 2 1 2g x f x x f x x

  

       

   

0 1 2g x f x x



    

Đặt

1tx

ta được

 

1f t t





 

là phương trình hoành độ giao điểm của đồ thị

 



và đường thẳng

1yt

(hình

vẽ)

Dựa vào đồ thị của

 



và đường thẳng

1yt

ta có:

 















hay















Xét hàm

( ) 1t t x x  

đồng biến trên suy ra bảng biến thiên của hàm số

 

Bất phương trình

 

4 2 1 2m x f x x    

nghiệm đúng với mọi

 

4;2x



 

0 2 (1) 4m g m f   



Chọn đáp án D.

Câu 29: Cho hàm số

 

y f x

liên tục trên đoạn

 

1;4

và có đồ thị như hình vẽ bên dưới:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 30

Có tất cả bao nhiêu giá trị nguyên của

thuộc đoạn

 

10;10

để bất phương trình

 

2f x m m

đúng với mọi

thuộc đoạn

 

1;4

. B.

. C.

. D.

Lời giải:

Vì

 

2f x m m

nên suy ra

0m 

Do đó

     

2 2 2 3f x m m m f x m m m f x m          

Ta có

 

 

 

 

1;4

max 3;min 2f x f x



  

Để bất phương trình

 

2f x m m

đúng với mọi

thuộc đoạn

 

1;4

thì ta phải có

 

 

 

 

1;4

3 min maxm f x f x m



   

3 2 3 3m m m       

Do đó trong đoạn

 

10;10

có 7 giá trị nguyên của

thỏa mãn yêu cầu bài toán.



Chọn đáp án C.

Câu 30: Cho hai hàm số đa thức bậc bốn

 

y f x

và

 

y g x

có đồ

thị như hình vẽ, trong đó đường đậm hơn là đồ thị hàm số

 

y f x

. Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm

có hoành độ là

3

và cắt nhau tại hai điểm nữa có hoành độ

lần lượt là

1

và

. Có bao nhiêu giá trị nguyên của tham số







12;12m

để bất phương trình

   

f x g x m

nghiệm

đúng với mọi







3;3x

. B.

. D.

Lời giải:

Phương trình hoành độ giao điểm có dạng:

        

. 3 1 3 , .f x g x a x x x a     

Ta có :

   

       

0 0 1 27 1

f g a a

Hay

        

     

3 1 3

f x g x x x x

Đặt

     

h x f x g x

       

 

  

      

h x f x g x x x

;

 









   







h x x

Bảng xét dấu

 

* Bất phương trình:

   

    ( ) ( )f x g x m m f x g x

nghiệm đúng



  



3;3x

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia

Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 31

 

3;3

12 8 3

min .

m h x

 





  

Vậy





 











12 8 3

;



Chọn đáp án D.

Câu 31: Tìm tất cả các giá trị tham số

để bất phương trình

  

6 2 8 1x x x x m     

nghiệm

đúng với mọi

2;8 .x







16.m 

15.m 

8.m 

2 16.m  

Lời giải:

Xét bất phương trình:

    

6 2 8 1 1x x x x m     

, điều kiện

2;8 .x







Đặt

  

28t x x  

2;8 .x







Ta có:

  







' 0 3tx  

Bảng biến thiên:

Suy ra

0; 5t







. Khi đó

 

trở thành:

 

15 2t t m  

Xét hàm số

 

15f t t t  

 

' 2 1 0, 0; 5f t t t



    



Bất phương trình

 

nghiệm đúng với mọi

2;8x







khi và chỉ khi

 

nghiệm đúng với

mọi

0;5t







0;5

max







 

15f t m m  



Chọn đáp án B.

Câu 32: Gọi

là tập hợp tất cả các giá trị nguyên dương của tham số

để bất phương trình

6 4 3 3 2

3 4 2 0x x m x x mx     

nghiệm đúng với mọi

1;3x







. Tổng tất cả các phần tử của

bằng

. B.

. C.

. D.

Lời giải:

Ta có:

6 4 3 3 2 6 4 2 3 3

3 4 2 0 3 4 2x x m x x mx x x x m x mx           

   

1 1 1x x mx mx     

Xét hàm đặc trưng

   

' 3 1 0f t t t f t t     

 

1 1 1f x f mx x mx     

Bài toán trở thành tìm

để bất phương trình

1x mx

nghiệm đúng với mọi

1;3x







 

1 , 1;3 ;

x mx m g x x





      



     

1;3

' 1 0 1;3 min 1 2

g x x g x g

 





       



Vậy để bất phương trình đã cho nghiệm đúng với mọi

1;3x







thì

2m 

Vì

nguyên dương nên

 

1;2S 

có

phần tử. Tổng các phần tử bằng



Chọn đáp án A.

_______________HẾT_______________

Huế, 15h00 ngày 23 tháng 7 năm 2021

Bấm Tải xuống để xem toàn bộ.

| 1/31

| | Tải xuống

Preview text:

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12
Chuyªn ®Ò: Kh¶O S¸T HµM Sè
MỘT SỐ BÀI TOÁN VỀ BẤT PHƯƠNG TRÌNH
PHIẾU HỌC TẬP SỐ 07_TrNg 2021 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ, HuÕ.
I. MỘT SỐ KẾT QUẢ
Trong thực tế, chúng ta gặp rất nhiều các dạng bài tập khác nhau, trong phần trình bày lý thuyết,
chúng tôi xin giới thiệu 2 bài toán thường gặp sau: 1. Bài toán 1
Xét hàm số y  g x liên tục trên a;b và gx có bảng biến thiên như sau: x a b gx  g x g b g a
Dựa vào BBT trên, các bài toán có kết quả tương ứng như sau:
1) m  g x nghiệm đúng x
 a;b  m  gb.
2) m  g x nghiệm đúng x
 a;b  m  ga.
3) m  g x có nghiệm trên a;b  m  ga.
4) m  g x có nghiệm trên a;b  m  gb. 2. Bài toán 2
Xét hàm số y  g x liên tục trên a;b 
 và gx có bảng biến thiên như sau: x a b gx  g x g b g a
Dựa vào BBT trên, các bài toán có kết quả tương ứng như sau:
1) m  g x nghiệm đúng x
  a;b  m  g   b.
2) m  g x nghiệm đúng x
  a;b  m  g   a.
3) m  g x có nghiệm trên a;b  m  g   a.
4) m  g x có nghiệm trên a;b  m  g   b.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 1
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
II. BÀI TẬP TRẮC NGHIỆM Câu 1:
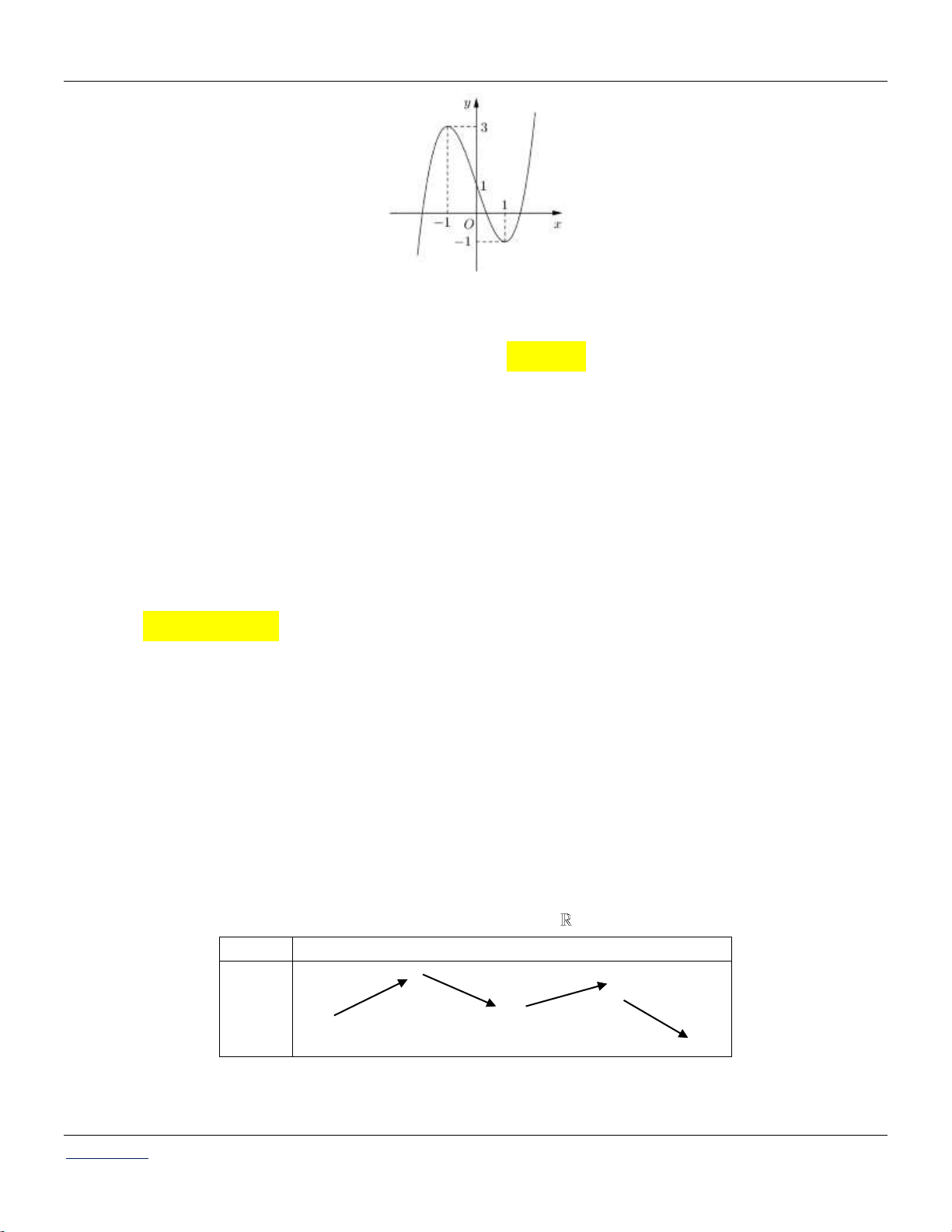
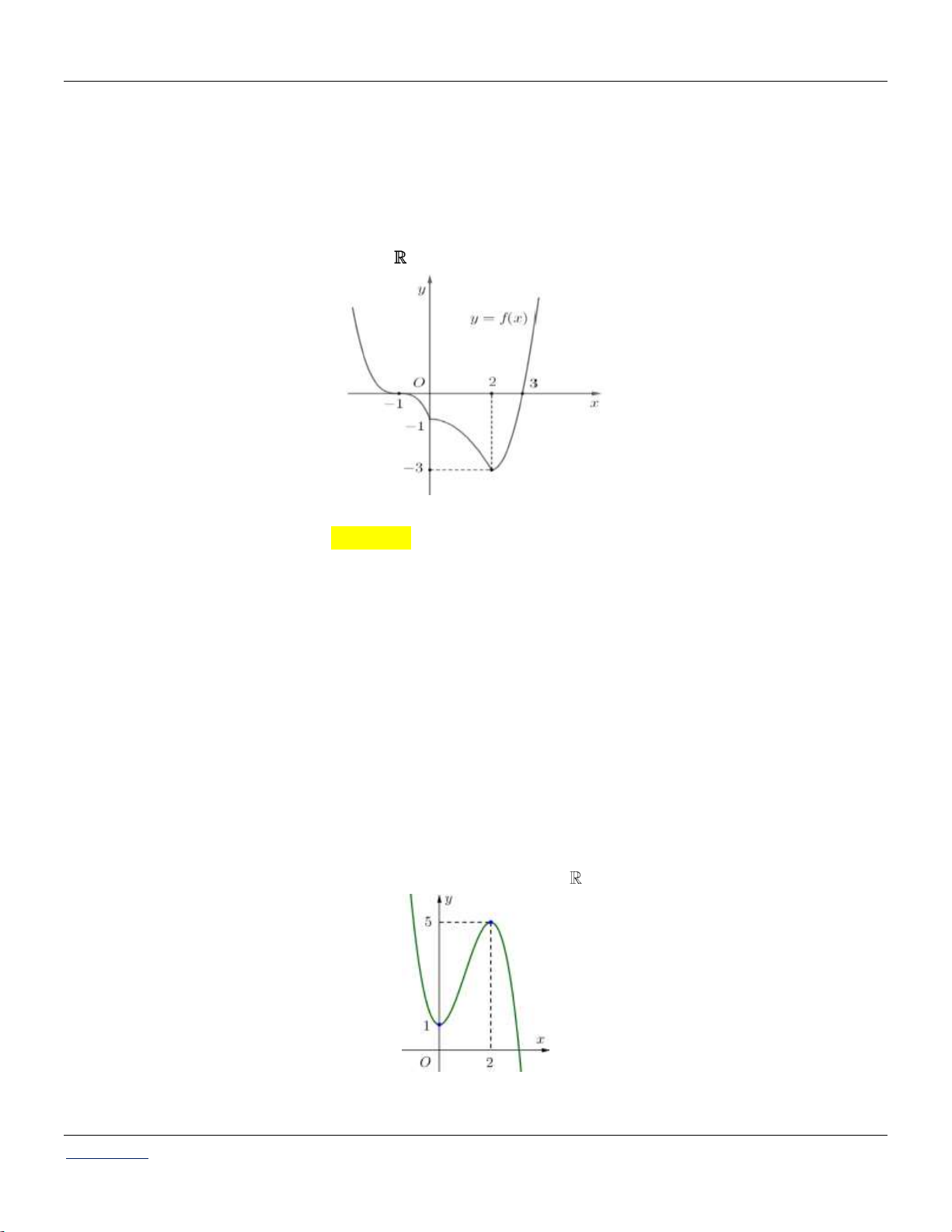
Cho hàm số y  f  x có bảng biến thiên như sau:
Tìm tất cả các giá trị của m để bất phương trình f  x 1   1  m có nghiệm. A. m  4. B. m  1. C. m  2. D. m  5. Câu 2:
Cho hàm số y  f x liên tục trên đoạn 1; 4. 
 Hàm số f x có đồ thị trên đoạn 1; 4   như hình vẽ dưới đây:
Tất cả các các trị của tham số m để bất phương trình f x  m  0 nghiệm đúng với mọi  3 10 x  ;   là 2 3   10   3 
A. m  f 4. B. m  f  .
C. m  f 3.
D. m  f  .  3   2  Câu 3:
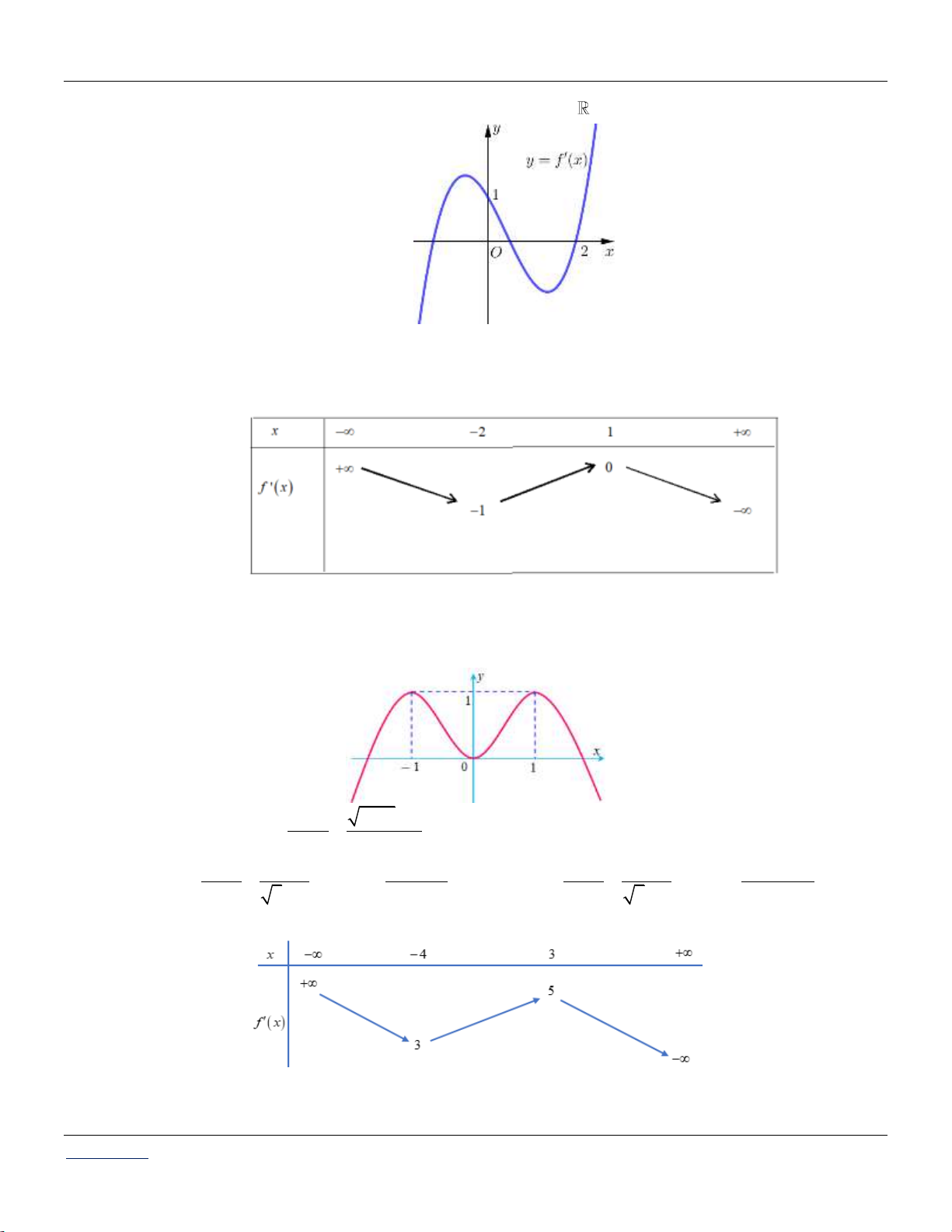
Cho hàm số y  f x liên tục trên và có đồ thị như hình vẽ dưới đây:
Tập hợp tất cả các giá trị thực của tham số m để phương trình f  f cos x  m nghiệm đúng
với mọi giá trị x  0;    là A. ; 1.  B. 1;1   . C. 1; 3   . D. 1;   .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 2
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 4:
Cho hàm số f  x xác định và nghịch biến trên khoảng  ;
 . Biết bất phương trình   2
f x  x  x  m có nghiệm thuộc đoạn 2;4, trong đó m là tham số thực. Khẳng định nào dưới đây đúng?
A. m  f 4 12.
B. m  f 2  2.
C. m  f 2  2.
D. m  f 4 12. Câu 5:
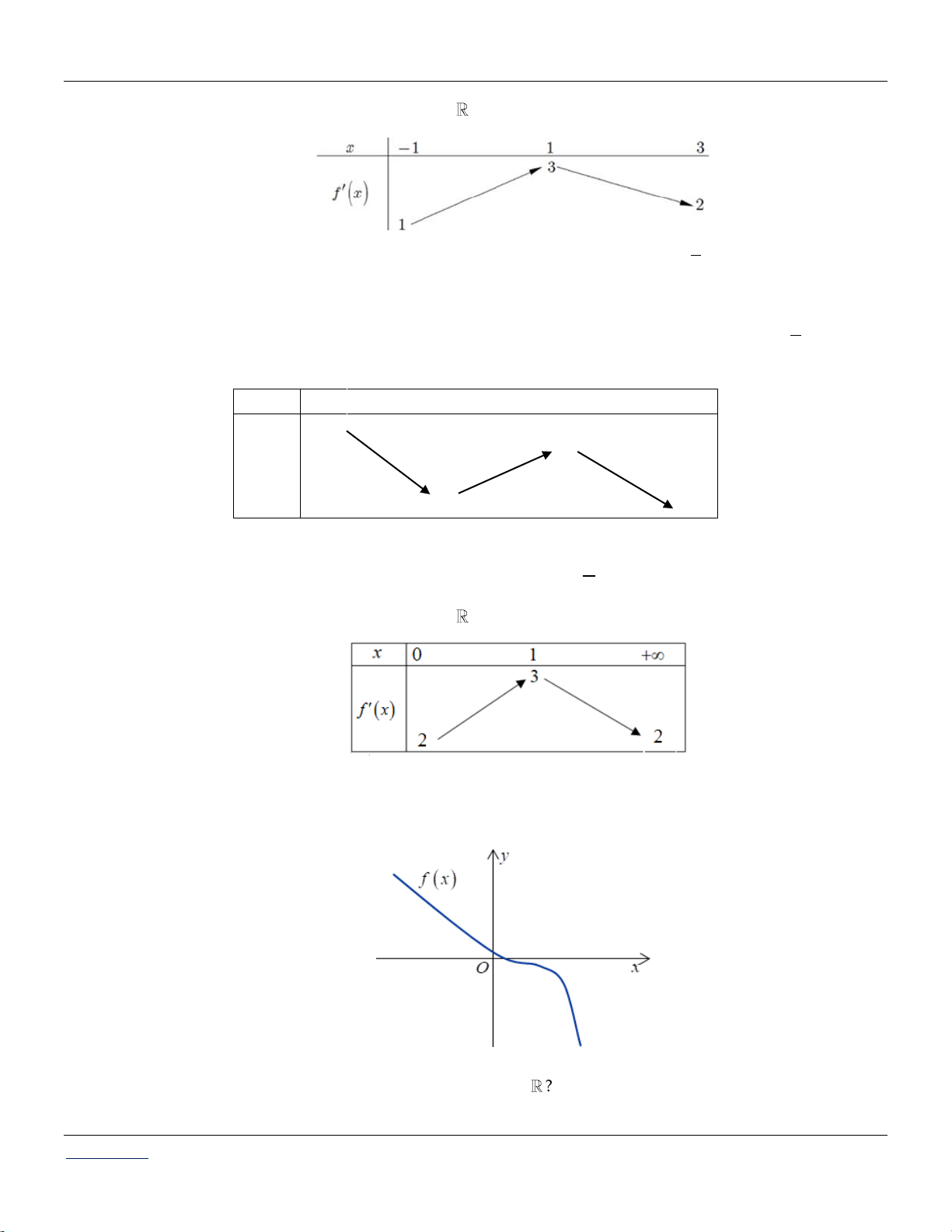
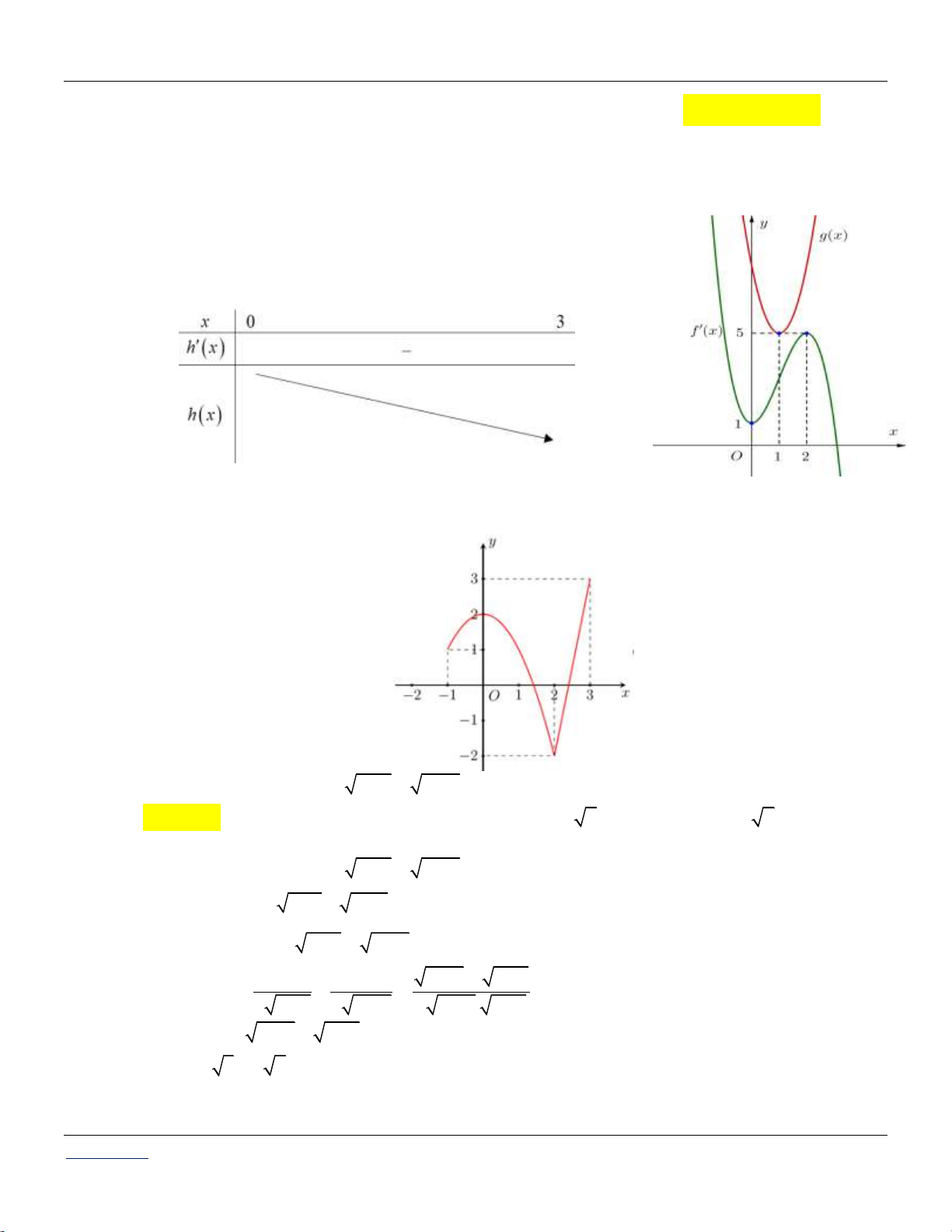
Cho hàm số f x có đạo hàm y  f x liên tục trên và có bảng biến thiên như sau: x  1  0 1  5 f x 3 0   Bất phương trình   3 2
f x  x  x  x  m ( m là tham số thực) nghiệm đúng x   1  ;1 khi và chỉ khi
A. m  f 1  1. B. m  f  1    3.
C. m  f 1  1. D. m  f  1    3. Câu 6:
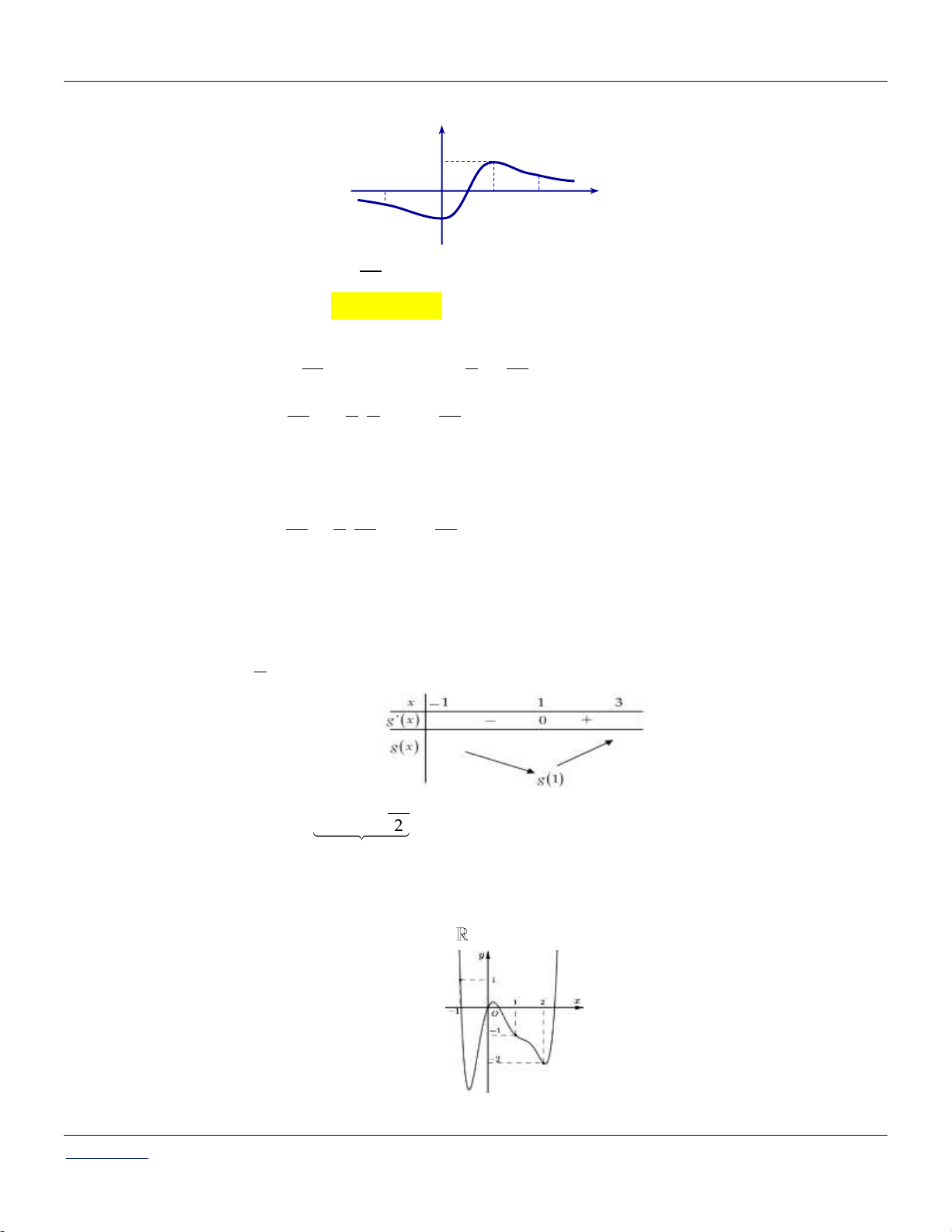
Cho hàm số f x. Biết hàm số y  f x liên tục trên và có đồ thị như hình vẽ dưới đây:
Bất phương trình f x  x  m ( m là tham số) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m  f 2  2 .
B. m  f 0 .
C. m  f 2  2 .
D. m  f 0 . Câu 7:
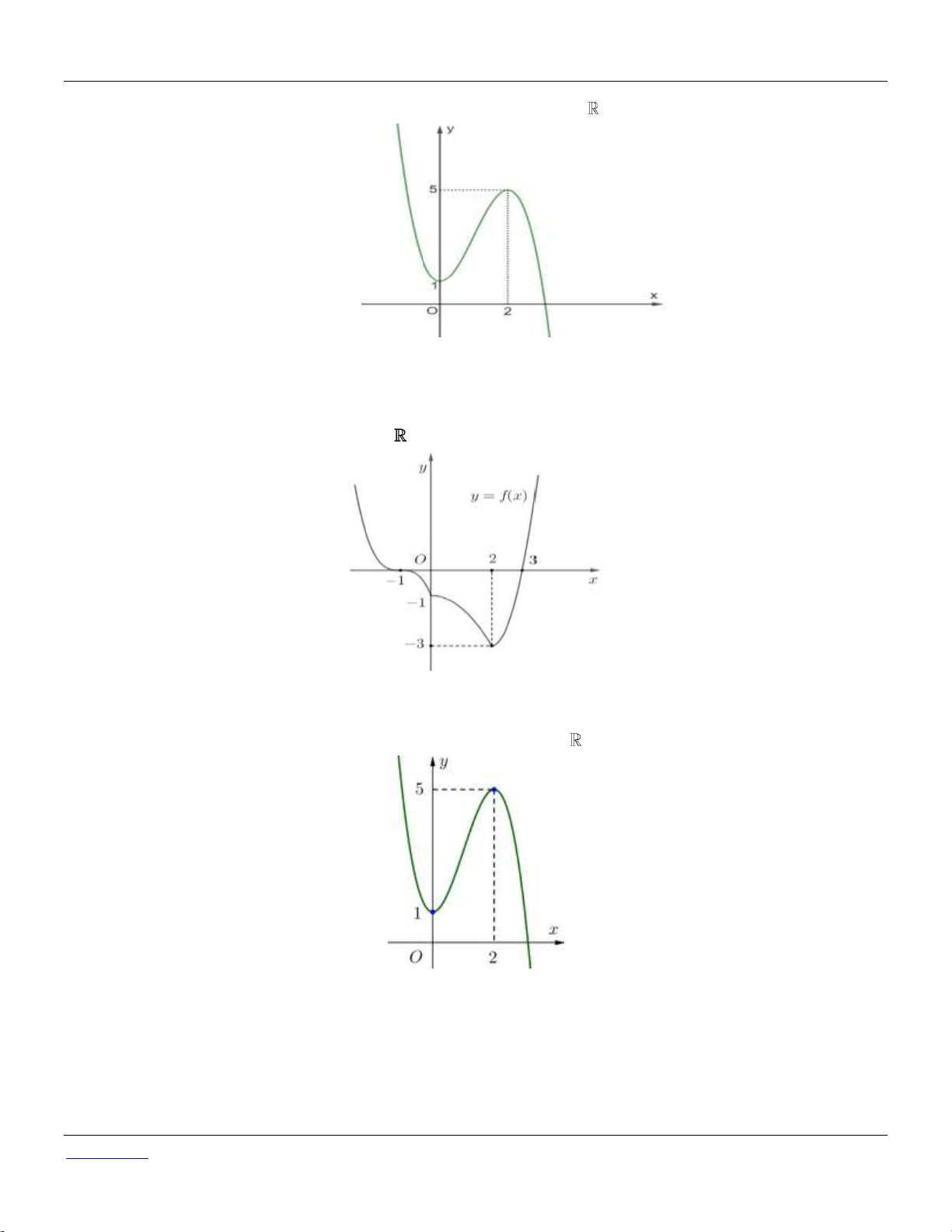
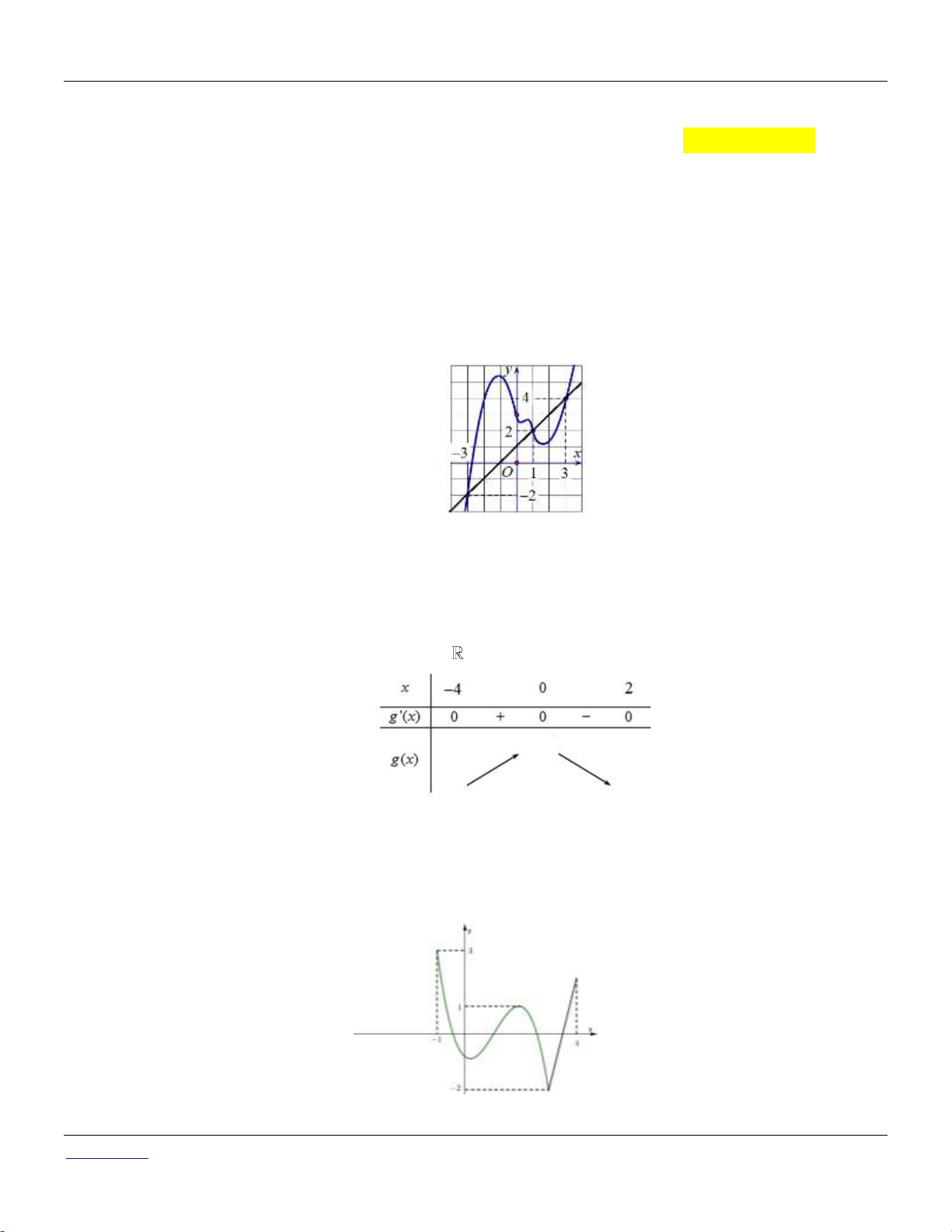
Cho hàm số y  f  x có hàm số y  f  x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x  2x  m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m  f 0 .
B. m  f 0 .
C. m  f 2  4 .
D. m  f 2  4 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 3
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 8:
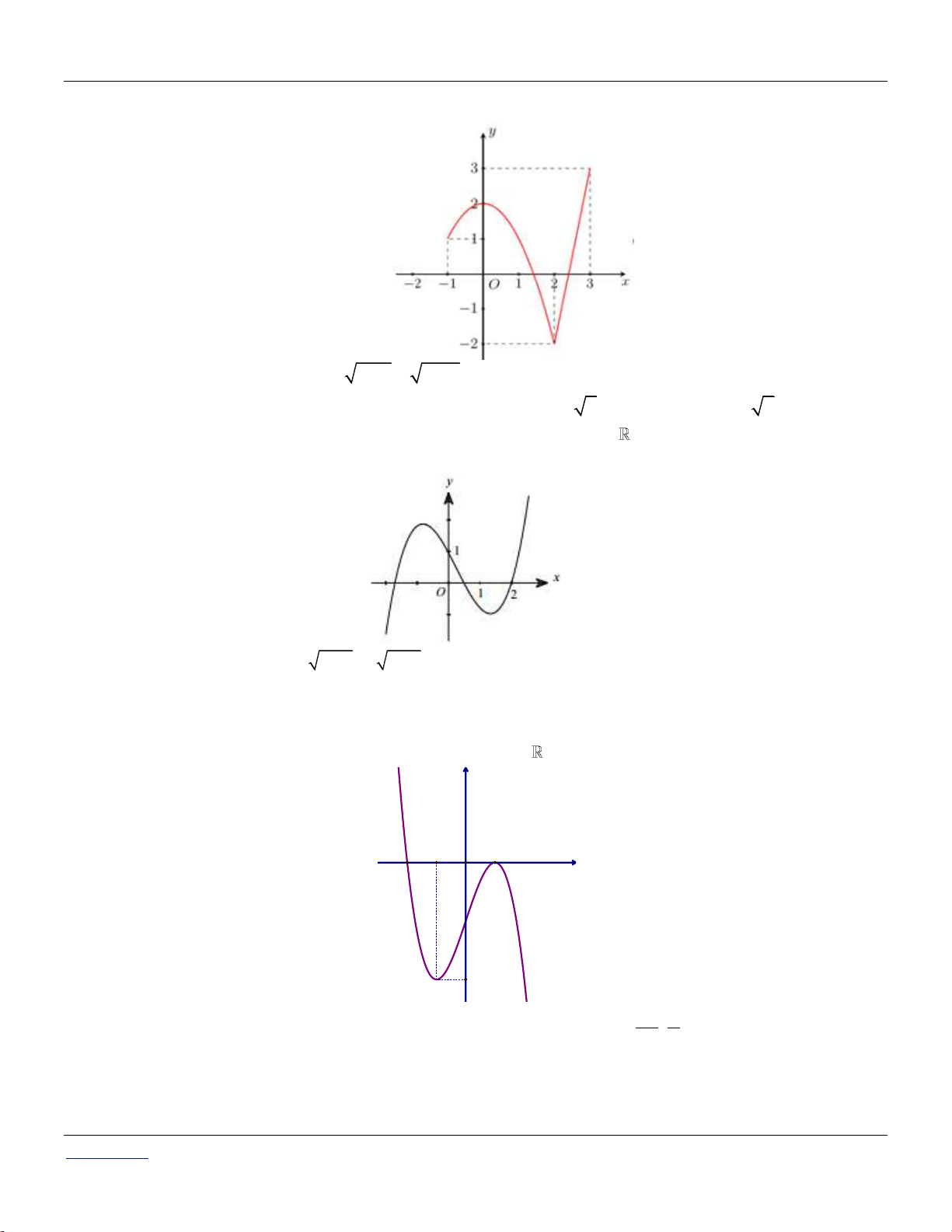
Cho hàm số y  f  x. Biết hàm số f  x liên tục trên
và có đồ thị như hình vẽ sau:
Bất phương trình f  x  x  m có nghiệm x  0; 2 khi và chỉ khi
A. m  f 2  2.
B. m  f 0.
C. m  f 2  2.
D. m  f 0. Câu 9:
Cho hàm số y  f x . Hàm số y  f x có bảng biến thiên như sau:
Bất phương trình    3 f x
x  m đúng với mọi x 1;  1 khi và chỉ khi
A. m  f 1  1 .
B. m  f 1  1.
C. m  f 1  3 .
D. m  f 1  3 .
Câu 10: Cho hàm số y  f  x . Hàm số y  f ' x có đồ thị như hình vẽ sau: f  x x  3  2 Bất phương trình   m
x  0;1 khi và chỉ khi 36 x  nghiệm đúng với mọi   1 f 0 1 f   1  9 f 0 1 f   1  36 A. m   . B. m  . C. m   . D. m  . 36 3  2 36 36 3  2 9
Câu 11: Cho hàm số y  f  x . Hàm số y  f  x có bảng biến thiên như sau:
Bất phương trình f  x 2
 m  x  2x có nghiệm đúng với mọi x  2
 ;2 khi chỉ khi
A. m  f 2  8.
B. m  f 2 C. m  f  2   8
D. m  f 2 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 4
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 12: Cho hàm số y  f  x có đạo hàm trên
. Bảng biến thiên của hàm số y  f ' x như sau: 1
Tìm tất cả giá trị của tham số m để bất phương trình 2
m  x  f  x 3
 x nghiệm đúng với 3
mọi x  0;3 . 2
A. m  f (0) .
B. m  f (0) .
C. m  f (3) .
D. m  f (1)  . 3
Câu 13: Cho hàm số y  f x. Hàm số y  f x có bảng biến thiên như sau: x  1  5   f x 0 2  
Bất phương trình f x  cos x  m nghiệm đúng với mọi x 0;  khi và chỉ khi   
A. m  f 0  1.
B. m  f 0.
C. m  f  .
D. m  f 0  1.  2 
Câu 14: Cho hàm số y  f  x có đạo hàm trên
. Bảng biến thiên của hàm số y  f ' x như sau:
Tìm m để bất phương trình m  2sin x  f  x nghiệm đúng với mọi x 0;  .
A. m  f (0) .
B. m  f (1)  2sin1.
C. m  f (0) .
D. m  f (1)  2sin1.
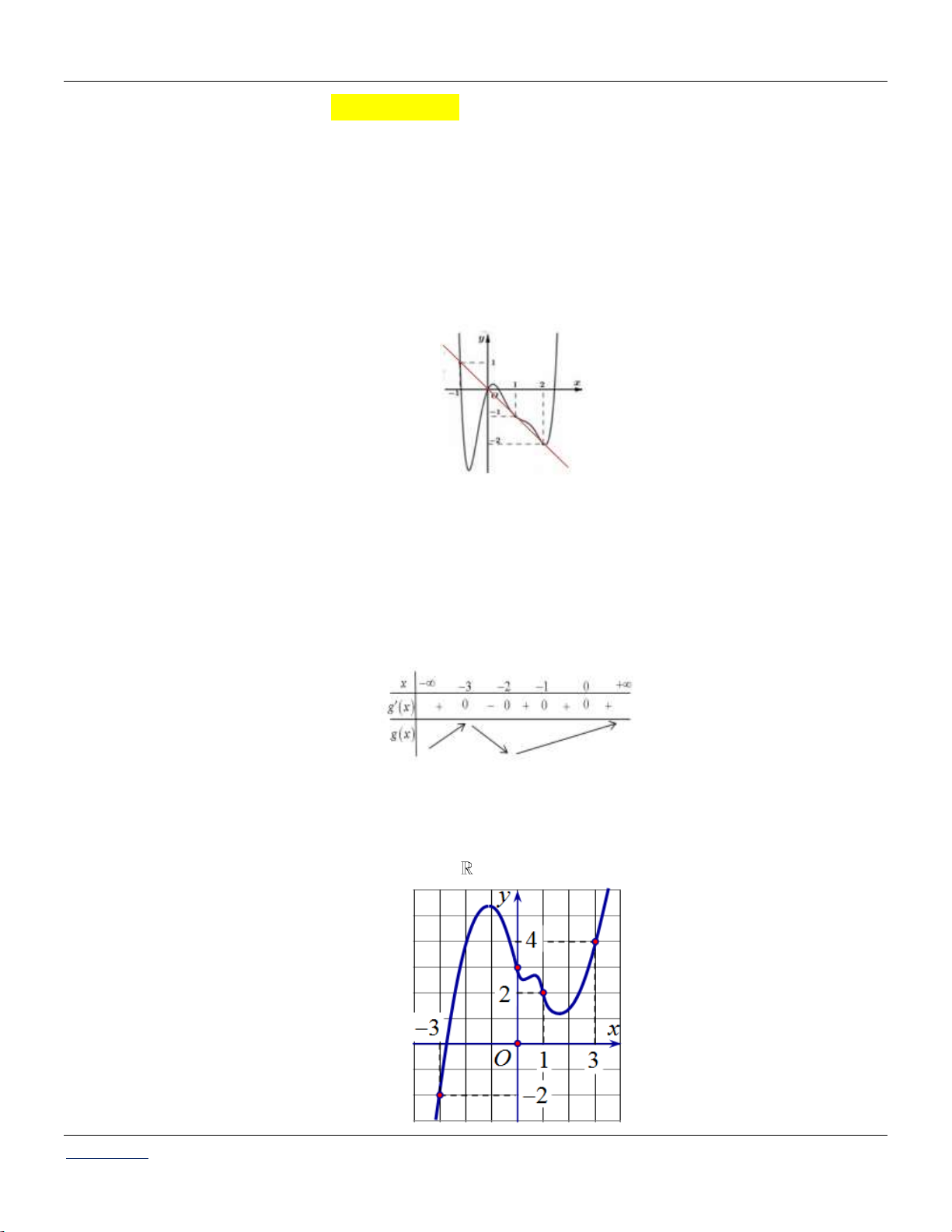
Câu 15: Cho đồ thị hàm số y  f x như hình vẽ sau:
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình f  2
x  2x  f mx  10 nghiệm đúng với mọi x  ? A. 10 . B. 11 . C. 12 . D. 13 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 5
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 16: Cho hàm số y  f x liên tục trên và có đồ thị hàm số y  f x như hình vẽ sau:
Bất phương trình f x  2
x  3  m có nghiệm đúng x 1;1 khi và chỉ khi
A. m  f 0  3 .
B. m  f 0  3 .
C. m  f 1  3 .
D. m  f 1  3 .
Câu 17: Cho hàm số f x. Biết hàm số y  f x liên tục trên và có đồ thị như hình vẽ dưới đây: x
Bất phương trình f x 2 
 x  m ( m là tham số thực) nghiệm đúng với mọi x0;2 khi và 4 chỉ khi
A. m  f 2  2 .
B. m  f 0 .
C. m  f 2  2 .
D. m  f 0 .
Câu 18: Cho hàm số y  f x liên tục trên . Hàm số y  f x có đồ thị như hình dưới đây:
Bất phương trình f x 3 2 3
 x  3x  m nghiệm đúng với mọi x 1  ;3 khi và chỉ khi
A. m  3 f 3 .
B. m  3 f 3 .
C. m  3 f  1    4 .
D. m  3 f  1    4 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 6
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 19: Cho hàm số y  f x. Biết hàm số y  f x liên tục trên và có đồ thị như hình vẽ bên dưới:
Bất phương trình f x 3 2
 m  x  3x  8x ( mlà tham số thực) nghiệm đúng với mọi x0;3 khi và chỉ khi
A. m  f 3  24 .
B. m  f 3  24 . C. m  f 0 .
D. m  f 0 .
Câu 20: Cho hàm số f  x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x 3 2 2
 x  2m  3x nghiệm đúng với mọi x 1
 ;3 khi và chỉ khi A. m  10. B. m  5. C. m  3. D. m  2.
Câu 21: Cho hàm số y  f  x , hàm số y  f  x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x 3 2
 m  x  3x  8x ( m
là tham số thực) nghiệm đúng với mọi
x  0;3 khi và chỉ khi
A. m  f 0 .
B. m  f 3  24 .
C. m  f 0 .
D. m  f 3  24 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 7
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 22: Cho hàm số y  f  x liên tục trên 1; 
3 và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x  x  1  7  x  m có nghiệm thuộc 1;  3 khi và chỉ khi A. m  7 . B. m  7 . C. m  2 2  2 . D. m  2 2  2 .
Câu 23: Cho hàm số y  f x. Biết hàm số y  f x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x  1  x  1  m ( m là tham số thực) nghiệm đúng với mọi x 1  ;3 khi và chỉ
A. m  f 2  2 .
B. m  f 0 .
C. m  f 2  2 .
D. m  f 0 .
Câu 24: Cho hàm số y  f x . Hàm số f '(x) liên tục trên và có đồ thị như hình vẽ sau: y -2 -1 x O 1 -4     
Bất phương trình f (sin x)  4
 x  m nghiệm đúng với mọi x ;  khi và chỉ khi  2 2 
A. m  f (1)  2 . B. m  f ( 1  )  2 . C. m  f  1    2 .
D. m  f (1)  2 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 8
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 25: Cho hàm số đa thức f x có đồ thị hàm số y  f x như hình vẽ sau:
Bất phương trình f  x 2 2 sin
 2sin x  m nghiệm đúng với mọi x0;  khi và chỉ khi
A. m  f   1 1  .
B. m  f 2  2 .
C. m  f   1 1  .
D. m  f 2  2 . 2 2
Câu 26: Cho f (x) mà đồ thị hàm số y  f '(x) như hình vẽ bên dưới: y 1 2  O 1 2  x 1   x
Bất phương trình f (x)  sin  m x    2 nghiệm đúng với mọi 1;3   khi và chỉ khi
A. m  f (0) .
B. m  f (1) 1.
C. m  f (1) 1.
D. m  f (2) .
Câu 27: Cho hàm số y  f  x có đạo hàm trên
. Đồ thị hàm số y  f ' x như hình vẽ bên dưới:
Tìm m để bất phương trình 2
m  x  2 f  x  2  4x  3 nghiệm đúng với mọi x  3;  .
A. m  2 f (0) 1.
B. m  2 f (0) 1. C. m  2 f ( 1  ) . D. m  2 f ( 1  ) .
Câu 28: Cho hàm số y  f  x có đạo hàm trên
. Đồ thị của hàm số y  f  x như hình dưới
Tìm m để bất phương trình 2
m  x  4  2  f  x  
1  2x nghiệm đúng với mọi x  4  ;2 .
A. m  2 f (0) 1.
B. m  2 f (3)  4 .
C. m  2 f (3) 16 .
D. m  2 f (1)  4 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 9
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 29: Cho hàm số y  f  x liên tục trên đoạn 1; 4 và có đồ thị như hình vẽ bên dưới:
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn 10;10 để bất phương trình
f  x  m  2m đúng với mọi x thuộc đoạn 1; 4? A. 6 . B. 5 . C. 7 . D. 8 .
Câu 30: Cho hai hàm số đa thức bậc bốn y  f x và y  gx có đồ
thị như hình vẽ, trong đó đường đậm hơn là đồ thị hàm số
y  f x . Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm
có hoành độ là 3 và cắt nhau tại hai điểm nữa có hoành độ
lần lượt là 1 và 3 . Có bao nhiêu giá trị nguyên của tham số m  12;12 
 để bất phương trình f x  gx  m nghiệm
đúng với mọi x  3; 3   ? A. 7 . B. 6 . C. 13 . D. 12 .
Câu 31: Tìm tất cả các giá trị tham số m để bất phương trình x    x  x 2 6 2 8
 x  m 1 nghiệm
đúng với mọi x  2  ;8. A. m  16. B. m  15. C. m  8. D. 2  m  16.
Câu 32: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình sau 6 4 3 3 2
x  3x  m x  4x  mx  2  0 nghiệm đúng với mọi x 1; 
3 . Tổng tất cả các phần tử của S bằng A. 3 . B. 2 . C. 1. D. 4 .
_______________HẾT_______________
Huế, 15h00 ngày 23 tháng 7 năm 2021
III. LỜI GIẢI CHI TIẾT BÀI Câu 1:
Cho hàm số y  f  x có bảng biến thiên như sau:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 10
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tìm tất cả các giá trị của m để bất phương trình f  x 1   1  m có nghiệm. A. m  4. B. m  1. C. m  2. D. m  5. Lời giải:
Đặt t  x 1 1  t  1. Khi đó BPT f  x 1  
1  m trở thành f t   m   1
Khi đó BPT f  x 1  
1  m có nghiệm khi và chỉ khi BPT f t   m   1 có nghiệm
t  1  m  min f t   m  4  . t 1 
Chọn đáp án A. Câu 2:
Cho hàm số y  f x liên tục trên đoạn 1; 4. 
 Hàm số f x có đồ thị trên đoạn 1; 4   như hình vẽ dưới đây:
Tất cả các các trị của tham số m để bất phương trình f x  m  0 nghiệm đúng với mọi  3 10 x  ;   là 2 3   10   3 
A. m  f 4. B. m  f  .
C. m  f 3.
D. m  f  .  3   2  Lời giải:
Ta có f x  m  0, x
   m  f x, x   (1). Xét bảng biến thiên: x 1  3 4 f x  0    f x f 3
Vậy từ (1) suy ra m  f 3.
 Chọn đáp án C. Câu 3:
Cho hàm số y  f x liên tục trên và có đồ thị như hình vẽ dưới đây:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 11
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tập hợp tất cả các giá trị thực của tham số m để phương trình f  f cos x  m nghiệm đúng
với mọi giá trị x  0;    là A. ; 1.  B. 1;1   . C. 1; 3   . D. 1;   . Lời giải:
Đặt t  cos x . Với x  0;    thì t   1  ;1  f   t 1  ;3  f  
 f t 1  . Do đó bất phương trình
f  f cos x  m nghiệm đúng với mọi giá trị
x  0;   m  min f  
 f cosx  1  . x0;   
Chọn đáp án C. Câu 4:
Cho hàm số f  x xác định và nghịch biến trên khoảng  ;
 . Biết bất phương trình   2
f x  x  x  m có nghiệm thuộc đoạn 2;4, trong đó m là tham số thực. Khẳng định nào dưới đây đúng?
A. m  f 4 12.
B. m  f 2  2.
C. m  f 2  2.
D. m  f 4 12. Lời giải:
Ta có: f  x 2
 x  x  m    m  f x 2 1
 x  x Đặt      2 g x
f x  x  x . Vì  
1 có nghiệm thuộc đoạn 2; 4 nên m > min g  x .   x 2;4
g ' x  f ' x  2x 1;
 f 'x  0 x  2;4. Ta có: 
 g 'x  f 'x  2x 1 0 x2;4
 x   x     . 2 1 0 2; 4 .
Suy ra min g  x  g 4  f 4 12 . Do đó m  f 4 12. x   2;4
Chọn đáp án A. Câu 5:
Cho hàm số f x có đạo hàm y  f x liên tục trên và có bảng biến thiên như sau: x  1  0 1  5 f x 3 0   Bất phương trình   3 2
f x  x  x  x  m ( m là tham số thực) nghiệm đúng x   1  ;1 khi và chỉ khi
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 12
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. m  f 1  1. B. m  f  1    3.
C. m  f 1  1. D. m  f  1    3. Lời giải: Ta có   3 2          3 2 f x x x x m m
f x  x  x  x * .
Xét hàm số      3 2 g x
f x  x  x  x trên  1  ;1 .
Ta có gx  f x 2
 3x  2x  1  0 x   1
 ;1 nên hàm số gx đồng biến trên 1;1. x 1 1 gx  g 1
g x g 1
Do đó * nghiệm đúng x   1
 ;1 khi m  g 1    f  1    3.
Chọn đáp án B. Câu 6:
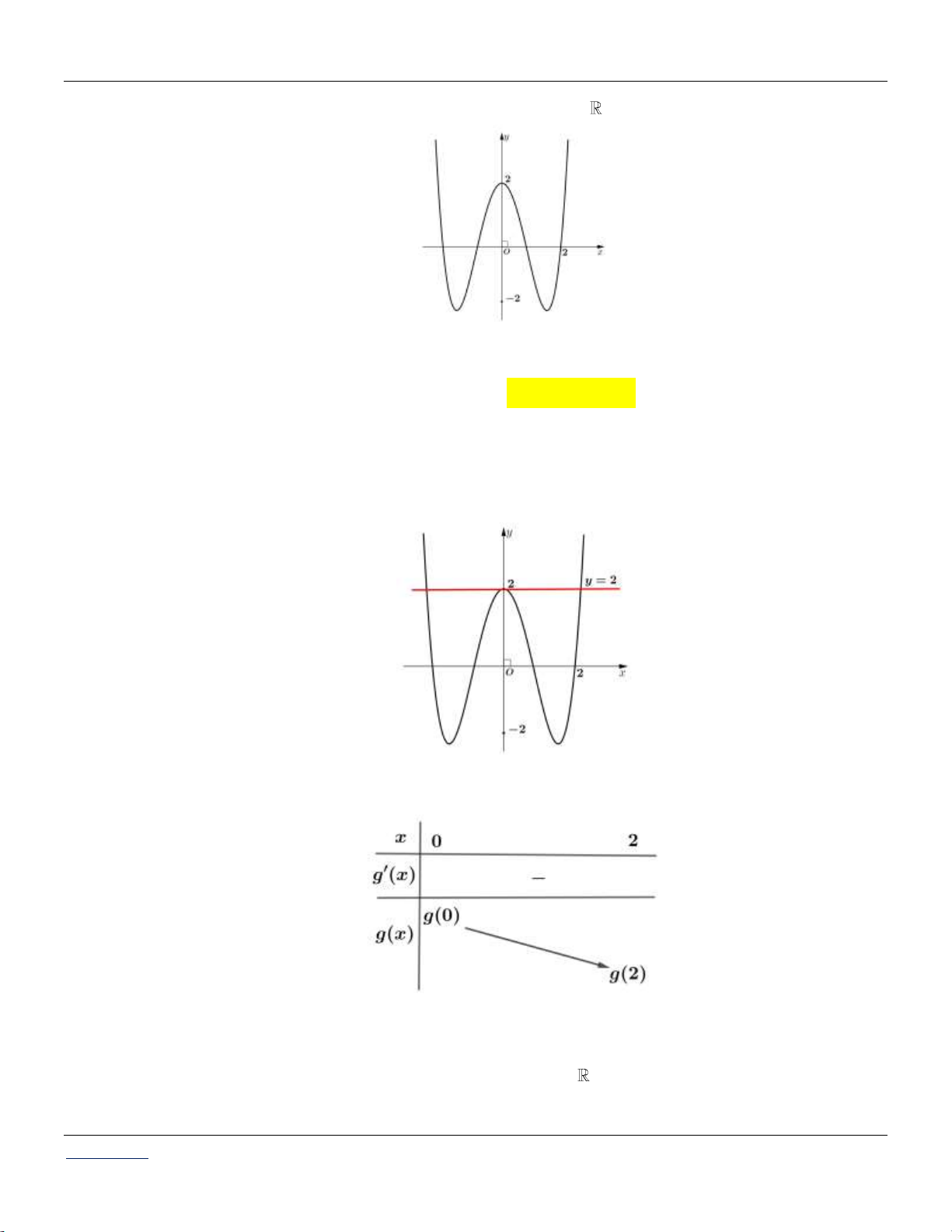
Cho hàm số f x. Biết hàm số y  f x liên tục trên và có đồ thị như hình vẽ dưới đây:
Bất phương trình f x  x  m ( m là tham số) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m  f 2  2 .
B. m  f 0 .
C. m  f 2  2 .
D. m  f 0 . Lời giải:
Ta có: f x  x  m  gx  f x  x  m .
Từ đồ thị hàm số y  f x ta thấy: gx  f x  1  0  max gx  g0  f 0 . 0;2
Do đó: bất phương trình f x  x  m nghiệm đúng với mọi x 0; 2 khi và chỉ khi
max g x  m  f 0  m . 0;2
Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 13
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 7:
Cho hàm số y  f  x có hàm số y  f  x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x  2x  m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m  f 0 .
B. m  f 0 .
C. m  f 2  4 .
D. m  f 2  4 . Lời giải:
Ta có f  x  2x  m đúng với mọi x 0; 2
 m  f x  2x, x
 0;2  m  g x, x
 0;2 trong đó g x  f x  2x .
Xét g  x  f  x  2x ; g x  f  x  2 .
Từ đồ thị suy ra g x  f  x  2  0, x  0;2 .
Suy ra bảng biến thiên của hàm số g  x :
Do đó bài toán thỏa mãn khi và chỉ khi m  g 2  m  f 2  4 .
Chọn đáp án C. Câu 8:
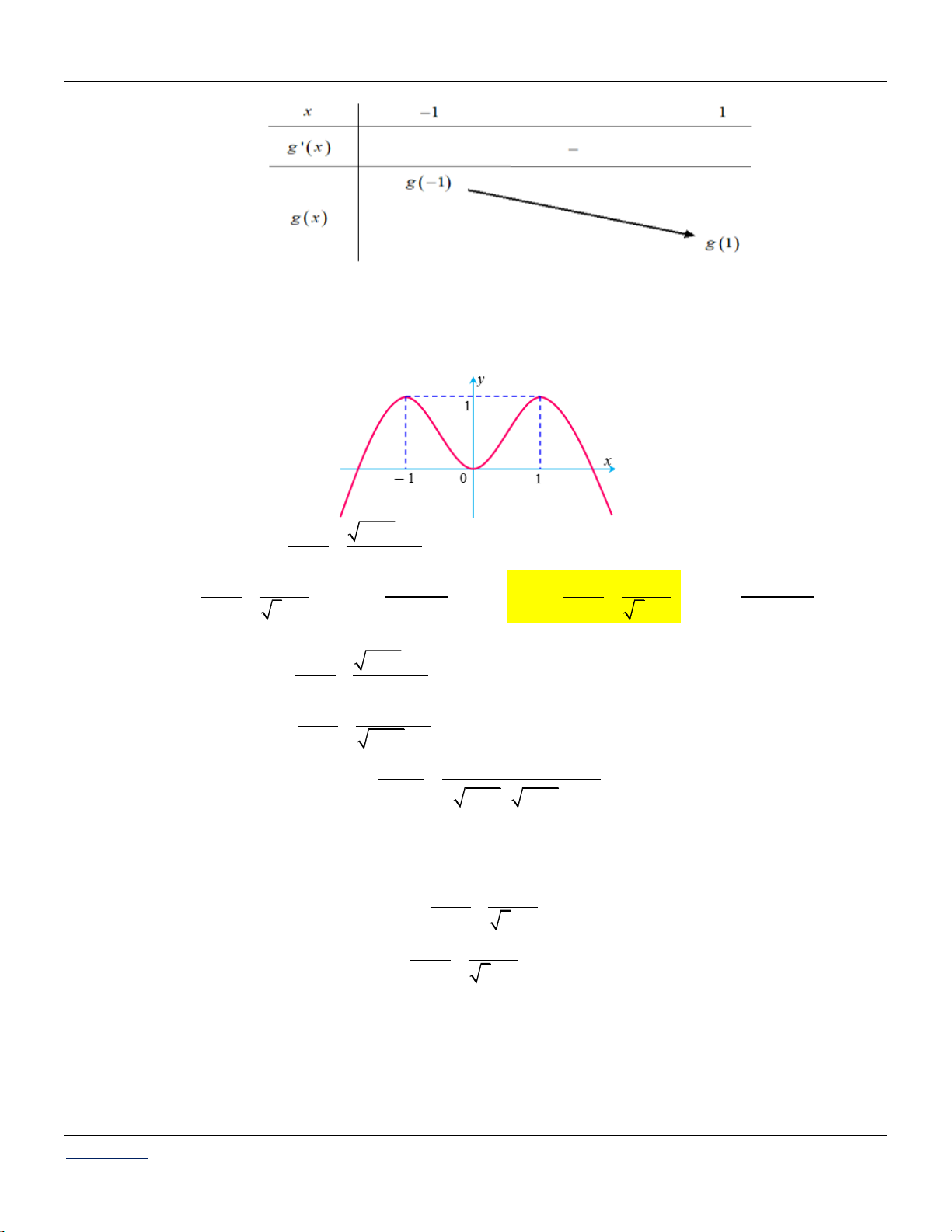
Cho hàm số y  f  x. Biết hàm số f  x liên tục trên
và có đồ thị như hình vẽ sau:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 14
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Bất phương trình f  x  x  m có nghiệm x  0; 2 khi và chỉ khi
A. m  f 2  2.
B. m  f 0.
C. m  f 2  2.
D. m  f 0. Lời giải:
Có f  x  x  m  m  f  x  .
x Xét hàm số g  x  f  x  x trên 0; 2.
Có g x  f  x 1  0, x
 0;2. Khi đó hàm số g x có bảng biến thiên sau
Dựa vào bảng biến thiên ta có f 2  2  g  x  f 0, x  0;2.
Khi đó m  g  x có nghiệm x 0; 2  m  min g  x  m  f 2  2. 0;2
Chọn đáp án C. Câu 9:
Cho hàm số y  f x . Hàm số y  f x có bảng biến thiên như sau:
Bất phương trình    3 f x
x  m đúng với mọi x 1;  1 khi và chỉ khi
A. m  f 1  1 .
B. m  f 1  1.
C. m  f 1  3 .
D. m  f 1  3 . Lời giải:
Bất phương trình    3       3 f x x m m f x x .
Xét hàm số       3 g x f x
x . Ta có: g x  f x  2 ' ' 3x .
 f 'x  0
Với x 1;1 , ta có 
 g'x  0 . 3x   2 0 Bảng biến thiên:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 15
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Từ bảng biến thiên, ta có: f x  3
x  m,x (1;1)  m  (
g x),x (1;1)  m  g 1  m  f 1  1 .
Chọn đáp án B .
Câu 10: Cho hàm số y  f  x . Hàm số y  f ' x có đồ thị như hình vẽ sau: f  x x  3  2 Bất phương trình 
 m nghiệm đúng với mọi x 0;  1 khi và chỉ khi 36 x 1 f 0 1 f   1  9 f 0 1 f   1  36 A. m   . B. m  . C. m   . D. m  . 36 3  2 36 36 3  2 9 Lời giải: f x x  
Xét hàm số g  x   3 2   . 36 x  1 f x
Hàm số y  g  x   1   có: 36 x  3  2 g  x f ' x 1 '    x   36
2 x  3  x  3  2 0, 0;1 2  
(Vì f ' x  0, x  0;  1 )
Suy ra hàm số g  x đồng biến trên 0;  1 .
 g x  g   x
    g x f 0 1 0 , 0;1   , x  0  ;1 . 36 3  2 f 0 1
Do đó g  x  , m x  0    ;1  m   . 36 3  2
Chọn đáp án C.
Câu 11: Cho hàm số y  f  x . Hàm số y  f  x có bảng biến thiên như sau:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 16
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Bất phương trình f  x 2
 m  x  2x có nghiệm đúng với mọi x  2
 ;2 khi chỉ khi
A. m  f 2  8.
B. m  f 2 C. m  f  2   8
D. m  f 2 . Lời giải:
Ta có: f  x 2
 m  x  2x với x   2  ; 2 với x   2  ; 2
Xét g  x  f  x 2
 x  2x với x  2
 ; 2 , có gx  f x  2x  2
Dựa vào bảng biến thiên f  x ta thấy x
 2; 2 thì f x  3 và x   2  ; 2 thì
2x  2  2 . Do đó gx  f x  2x  2 1  0 với x   2  ; 2 .
 Hàm số g  x đồng biến trên 2;2 và liên tục trên 2;2
Suy ra: max g  x  g 2  f 2 . Vậy m  f 2 . -2;2
Chọn đáp án D.
Câu 12: Cho hàm số y  f  x có đạo hàm trên
. Bảng biến thiên của hàm số y  f ' x như hình dưới: 1
Tìm tất cả giá trị của tham số m để bất phương trình 2
m  x  f  x 3
 x nghiệm đúng với 3
mọi x  0;3 . 2
A. m  f (0) .
B. m  f (0) .
C. m  f (3) .
D. m  f (1)  . 3 Lời giải: 1 1 Ta có 2
m  x  f  x 3
 x  m  f x 3 2  x  x . 3 3 1
Đặt g  x  f  x 3 2  x  x . 3
Ta có g x  f  x 2
 x  x  f x   2 2
x  2x .
g x   f  x 2 0
 x  2x . 2
Mà f  x  1, x  0;3 và 2
x  2x  1 x   1  1, x
 0;3 nên gx  0, x  0;3.
Từ đó ta có bảng biến thiên của g(x) :
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 17
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1
Bất phương trình m  f  x 3 2
 x  x nghiệm đúng với mọi x 0;3 3
 m  g 0  m  f (0) .
Chọn đáp án B.
Câu 13: Cho hàm số y  f x. Hàm số y  f x có bảng biến thiên như sau: x  1  5   f x 0 2  
Bất phương trình f x  cos x  m nghiệm đúng với mọi x 0;  khi và chỉ khi   
A. m  f 0  1.
B. m  f 0.
C. m  f  .
D. m  f 0  1.  2  Lời giải:
Ta có: f x  cos x  m  m  f x  cos x (1)
Xét hàm số gx  f x  cos x, x0;   gx  f x  sin . x
 f  x  0 Ta có: x  0;    : 
 gx  f x  sinx  0, x
 0;   f x  cosx  g0  f 0  1. 0  sin x  1
Yêu cầu bài toán  m  f 0  1.
Chọn đáp án A.
Câu 14: Cho hàm số y  f  x có đạo hàm trên
. Bảng biến thiên của hàm số y  f ' x như sau:
Tìm m để bất phương trình m  2sin x  f  x nghiệm đúng với mọi x 0;  .
A. m  f (0) .
B. m  f (1)  2sin1.
C. m  f (0) .
D. m  f (1)  2sin1. Lời giải:
Ta có m  2sin x  f  x  m  f  x  2sin x .
Đặt g  x  f  x  2sin x .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 18
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Ta có g x  f  x  2 cos x ; g x  0  f  x  2 cos x .
Mà f  x  2, x
 0; và 2cosx  2, x
 0; nên gx  0, x  0;.   g x f '(x) 2  0    x  0 . 2cos x  2
Từ đó ta có bảng biến thiên của g(x) :
Bất phương trình m  2 f  x  2   x  
1  x  3 nghiệm đúng với mọi x  3;  
 m  g 0  m  f (0) .
Chọn đáp án C.
Câu 15: Cho đồ thị hàm số y  f x như hình vẽ sau:
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình f  2
x  2x  f mx  10 nghiệm đúng với mọi x  ? A. 10 . B. 11 . C. 12 . D. 13 . Lời giải:
Quan sát đồ thị ta nhận thấy hàm số f x nghịch biến trên .
Bất phương trình: f  2
x  x  f mx    2
x  x  mx   2 2 10 2 10
x  2  mx  10  0 với  2 x 
   2  m  40  0  2  2 10  m  2  2 10 .
Vì m  nên ta có 4  m  8 .
Vậy có tất cả 13 giá trị m nguyên thỏa mãn bài toán.
Chọn đáp án D.
Câu 16: Cho hàm số y  f x liên tục trên và có đồ thị hàm số y  f x như hình vẽ sau:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 19
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Bất phương trình f x  2
x  3  m có nghiệm đúng x 1;1 khi và chỉ khi
A. m  f 0  3 .
B. m  f 0  3 .
C. m  f 1  3 .
D. m  f 1  3 . Lời giải:
Đặt gx  f x  2
x  3 . Ta có gx  f x  2x ; gx  0  f x  2x .
Đường thẳng y  2x đi qua hai điểm 0;0 , 1; 2 .
Ta có đồ thị hàm số như sau: Xét bảng biến thiên:
Dựa vào BBT, ta có: m  g x , x1; 1  m  g0  m  f 0  3 .
 Chọn đáp án B.
Câu 17: Cho hàm số f x. Biết hàm số y  f x liên tục trên và có đồ thị như hình vẽ dưới đây:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 20
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x
Bất phương trình f x 2 
 x  m ( m là tham số thực) nghiệm đúng với mọi x0;2 khi và 4 chỉ khi
A. m  f 2  2 .
B. m  f 0 .
C. m  f 2  2 .
D. m  f 0 . Lời giải: 2 2 x  x 
Ta có: f x 
 x  m  gx  f x  
 x  m . 4  4 
Từ đồ thị hàm số y  f x ta thấy:    x  x
0; 2 : gx  f x   1  0  x
 0;2 : gx  g0  f 0  0    f 0 .  2 
Do đó, bất phương trình f x  x  m nghiệm đúng với mọi x 0; 2 khi và chỉ khi m  f 0.
Chọn đáp án B.
Câu 18: Cho hàm số y  f x liên tục trên . Hàm số y  f x có đồ thị như hình dưới đây:
Bất phương trình f x 3 2 3
 x  3x  m nghiệm đúng với mọi x 1  ;3 khi và chỉ khi
A. m  3 f 3 .
B. m  3 f 3 .
C. m  3 f  1    4 .
D. m  3 f  1    4 . Lời giải:
Ta có: f x 3 2 3 2 3
 x  3x  m  3 f (x)  x  3x  m nghiệm đúng với mọi x 1  ;3 . Xét 3 2
g(x)  3 f (x)  x  3x với x  1  ;3 . Khi đó: 2 2 g (
 x)  3 f (x)  3x  6x  3 f (x)  x  2x   .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 21
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Nghiệm của phương trình g (
 x)  0 là hoành độ giao điểm của đồthị y  f (x) và parabol 2
y  x  2x . Phương trình g (
 x)  0 có ba nghiệm x  1
 ; x  3; x  1 trên đoạn 1;3   .
lim g x  lim 3 f 3 2  x 3 2
 x  3x   3 f   ; lim gx  lim 3 f 
x x  3x   3f .    3     1 4 x 1  x 1  x3 x3
Ta có bảng biến thiên sau: x 1  1 3 g (  x) 0 - 0 - 0 3 f  1    4 g(x) 3 f 3 Bất phương trình f x 3 2 3
 x  3x  m nghiệm đúng với mọi x 1  ;3 khi và chỉ khi
m  g x , x   1
 ;3  m  3 f ( 1  )  4 .
 Chọn đáp án D.
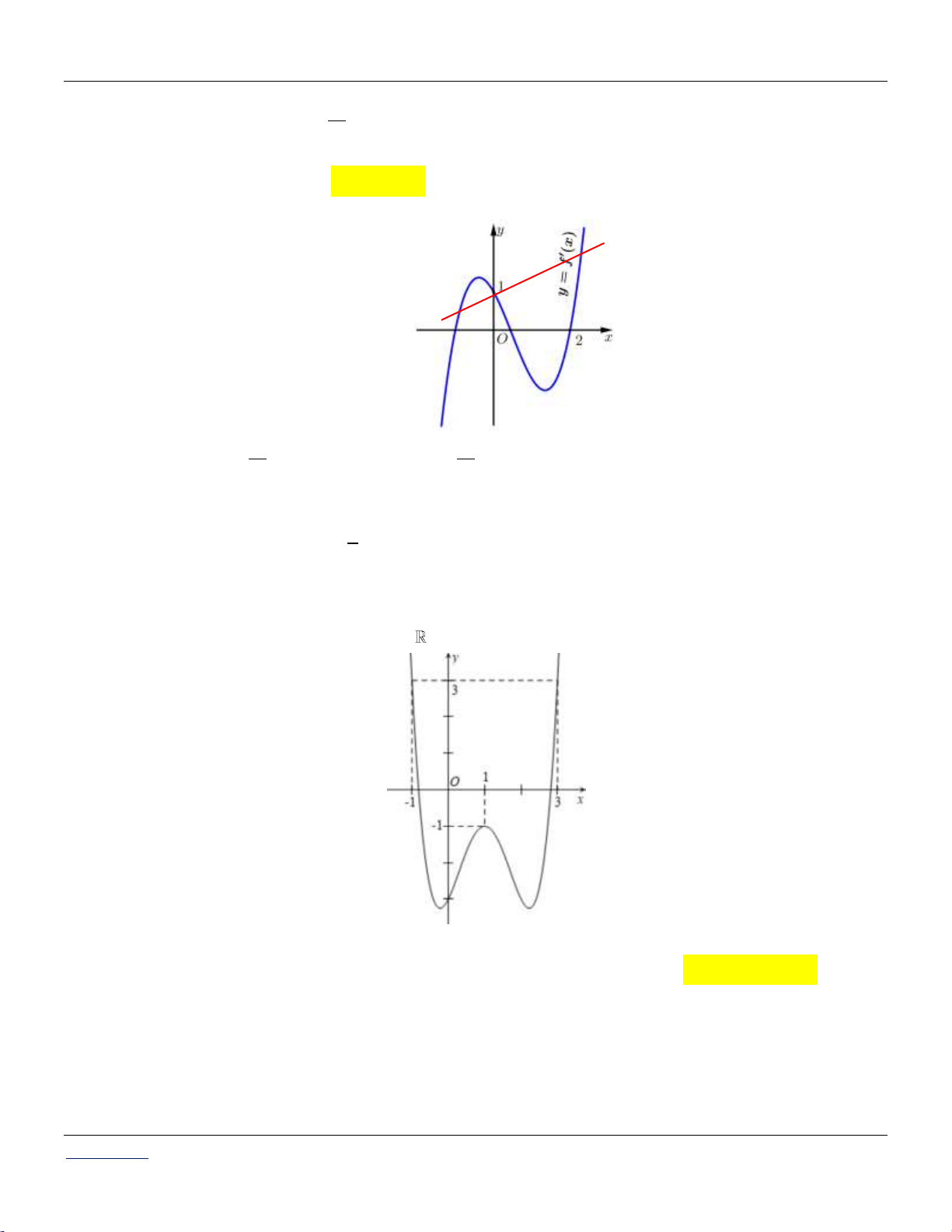
Câu 19: Cho hàm số y  f x. Biết hàm số y  f x liên tục trên và có đồ thị như hình vẽ bên dưới:
Bất phương trình f x 3 2
 m  x  3x  8x ( mlà tham số thực) nghiệm đúng với mọi x0;3 khi và chỉ khi
A. m  f 3  24 .
B. m  f 3  24 . C. m  f 0 .
D. m  f 0 . Lời giải:
Ta có : f x 3 2
 m  x  x  x x  
  f x 3 2 3 8 , 0; 3
 x  3x  8x  m, x  0;3 .
Xét hàm số gx  f x 3 2
 x  3x  8x, x  0;3 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 22
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Ta có : gx  f x 2
 x  x   f x   2 3 6 8
3x  6x  8, x  0;3 .
Ta có trên khoảng 0; 3 : f x  5 và 2
5  3x  6x  8  17 nên gx  0, x  0;3 .
Do đó hàm số g x nghịch biến trên 0; 3 hay g3  gx  g0 , x  0;3 .
Vậy gx  m, x
 0;3  m  g3  f 3  24 .
 Chọn đáp án B.
Câu 20: Cho hàm số f  x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x 3 2 2
 x  2m  3x nghiệm đúng với mọi x 1
 ;3 khi và chỉ khi A. m  10. B. m  5. C. m  3. D. m  2. Lời giải:
Ta có f  x 3 2
 x  m  x  f x 3 2 2 2 3 2
 x  3x  2m
Nhận xét minf  x  f 2  3   1  ;3
Đặt g  x 3 2
 x  3x  2m, x  1;3 x  0 g x 2  3
 x  6x, gx  0   x  2 g 0  2 ; m g   1  4  2 ;
m g 3  2m và g 2  4  2m
 max g x  g 2  4  2m  1  ;3
Yêu cầu bài toán  2 min f  x  max g  x  6
  2m  4  m  5  .  1  ;3  1  ;3
 Chọn đáp án B.
Câu 21: Cho hàm số y  f  x , hàm số y  f  x liên tục trên
và có đồ thị như hình vẽ.
Bất phương trình f  x 3 2
 m  x  3x  8x ( m
là tham số thực) nghiệm đúng với mọi
x  0;3 khi và chỉ khi
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 23
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. m  f 0 .
B. m  f 3  24 .
C. m  f 0 .
D. m  f 3  24 . Lời giải: f  x 3 2
 m  x  3x  8x  f x 3 2
 x  3x  8x  m .
Đặt h  x  f  x 3 2
 x  3x  8x  hx  f x 2
 x  x   f x   2 3 6 8
3x  6x  8.
Đặt g  x 2
 3x  6x  8 và vẽ đồ thị của g x lên hệ trục Oxy.
Từ hình vẽ, ta thấy f  x  g  x, x  0;3.
Do đó h x  0, x
 0;3. Vì vậy ta có bảng biến thiên:
Từ bảng biến thiên, yêu cầu bài toán  m  h 3  m  f 3  24.
 Chọn đáp án D.
Câu 22: Cho hàm số y  f  x liên tục trên 1; 
3 và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x  x  1  7  x  m có nghiệm thuộc 1;  3 khi và chỉ khi A. m  7 . B. m  7 . C. m  2 2  2 . D. m  2 2  2 . Lời giải:
Bất phương trình f  x  x  1  7  x  m có nghiệm thuộc 1;  3 khi và chỉ khi
m  max  f  x  x 1  7  x  . 1;  3
Xét hàm số g  x  x 1  7  x trên đoạn 1;  3 .  x  x 
Ta có g x 1 1 7 1    . 2 x  1 2 7  x
2 7  x. x 1
g x  0  7  x  x  1  0  x  3 . g  
1  8  2 2 , g 3  2  2  4 .
Suy ra max g  x  4 tại x  3 . (1)  1   ;3
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 24
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Mặt khác, dựa vào đồ thị của f  x ta có max f  x  3 tại x  3 .(2)  1   ;3
Từ (1) và (2) suy ra max  f  x  x 1  7  x   7 tại x  3. 1;  3
Vậy bất phương trình đã cho có nghiệm thuộc 1; 
3 khi và chỉ khi m  7 .
 Chọn đáp án A.
Câu 23: Cho hàm số y  f x. Biết hàm số y  f x liên tục trên
và có đồ thị như hình vẽ bên dưới:
Bất phương trình f  x  1  x  1  m ( m là tham số thực) nghiệm đúng với mọi x 1  ;3 khi và chỉ
A. m  f 2  2 .
B. m  f 0 .
C. m  f 2  2 .
D. m  f 0 . Lời giải:
Đặt u  x  1 . Vì x  1
 ;3  u0;2  f u  u  m  f u  u  m .
Xét hàm số g u  f u  u với u 0; 2 
 . Ta có gu  f u  1
Dựa vào độ thì ta thấy u 0; 2 
 thì f u  1, u   0;2 
  gu nghịch biến trên 0; 2 .
Vậy để f  x  1  x  1  m ( m là tham số thực ) nghiệm đúng với mọi x 1  ;3 thì
f u  u  m, u
 0;2  m  max gu  g0  f 0 . u0;2  
Chọn đáp án D.
Câu 24: Cho hàm số y  f x . Hàm số f '(x) liên tục trên và có đồ thị như hình vẽ sau: y -2 -1 x O 1 -4     
Bất phương trình f (sin x)  4
 x  m nghiệm đúng với mọi x ;  khi và chỉ khi  2 2 
A. m  f (1)  2 . B. m  f ( 1  )  2 . C. m  f  1    2 .
D. m  f (1)  2 . Lời giải:          
Ta có f sin x  4
 x  m, x   ;
  m  gx  4x  f sin x, x   ;  .  2 2   2 2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 25
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
gx  4  cos .
x f sin x .      Do x  ;
 nên 1  sin x  1 , kết hợp với đồ thị của f x ta có 4
  f sin x  0 .  2 2     
Ta lại có 0  cos x  1 x     ;  nên 4   cos .
x f sin x  0 .  2 2     
Suy ra gx  4  cos .
x f sin x  0 x     ;   2 2         
Do đó hàm g x đồng biến trên khoảng  ;
  gx  g  f   1    2 .  2 2   2      
Bất phương trình f (sin x)  4
 x  m nghiệm đúng với mọi x ;   2 2         
 m  gx  4x  f sinx, x   ;   m  g  f   1    2 .  2 2   2 
Chọn đáp án A.
Câu 25: Cho hàm số đa thức f x có đồ thị hàm số y  f x như hình vẽ sau:
Bất phương trình f  x 2 2 sin
 2sin x  m nghiệm đúng với mọi x0;  khi và chỉ khi
A. m  f   1 1  .
B. m  f 2  2 .
C. m  f   1 1  .
D. m  f 2  2 . 2 2 Lời giải:
Bất phương trình f  x 2 2 sin
 2sin x  m nghiệm đúng với mọi x0;  khi và chỉ
khi m  max g x với gx  f  x 2 2 sin  2sin x . x   0; 
Ta đặt t  2 sin x , khi x 0;  thì t 0; 2 . t
Khi đó gx  f  x 2 2 sin
 2sin x trở thành gt  f t 2  . 2 t  0 
Ta có gt  f t  t  0  t  1  t  2 
Dựa vào đồ thị ta thấy rằng f t  t  0;t  1  ;2 
 nên g1  g2 . 1
Khi đó maxgt  g 
1  f 1   max gx. Vậy m  f   1 1 
thỏa yêu cầu bài toán. t   0;1 x    0;  2 2
Chọn đáp án A.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 26
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 26: Cho f (x) mà đồ thị hàm số y  f '(x) như hình vẽ bên dưới: y 1 2  O 1 2  x 1   x
Bất phương trình f (x)  sin
 m nghiệm đúng với mọi x  1  ;3   khi và chỉ khi 2
A. m  f (0) .
B. m  f (1)  1 . C. m  f ( 1  )  1 .
D. m  f (2) . Lời giải:  x   x
Xét gx  f x  sin
 g'x  f 'x  cos 2 2 2  x      x • Với x   1  ;  1   ;  cos    0 (1) 2  2 2  2
Đồng thời dựa vào đồ thị f 'x ta thấy f 'x  0, x    1  ;1   (2)
Từ (1), (2) ta suy ra g'x  0, x    1  ;1   .  x   3   x
• Với x 1; 3   ;  cos   0  (3) 2  2 2  2
Đồng thời dựa vào đồ thị ta thấy f 'x  0, x  1;3 (4)
Từ (3), (4) ta suy ra g'x  0 , x  1;3 .  f '1  0  Tại x  1 :   g' 
1  0 . Ta có bảng biến thiên của gx như sau: cos  0  2  x
Để bất phương trình f x  sin
 m nghiệm đúng với mọi x  1  ;3   2 gx
 m  min gx  m  g  1  f   1  1.  1  ;3  
Chọn đáp án B.
Câu 27: Cho hàm số y  f  x có đạo hàm trên
. Đồ thị hàm số y  f ' x như hình vẽ bên dưới:
Tìm m để bất phương trình 2
m  x  2 f  x  2  4x  3 nghiệm đúng với mọi x  3;  .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 27
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. m  2 f (0) 1.
B. m  2 f (0) 1. C. m  2 f ( 1  ) . D. m  2 f ( 1  ) . Lời giải: Ta có 2 m  x 
f  x    x   m  f  x   2 2 2 4 3 2
2  x  4x  3 .
Đặt g  x  f  x   2 2
2  x  4x  3 . Ta có g x  2 f  x  2  2x  4 .
g x  0  f  x  2    x  2 .
Đặt t  x  2 ta được f t   t  .   1
 1 là phương trình hoành độ giao điểm của đồ thị f t và đường thẳng d : y  t (hình vẽ)
Dựa vào đồ thị của f t  và đường thẳng y  t ta có t  1  x  3   t  0 x  2
ta có f t   t      hay . t  1 x  1   t  2 x  0
Bảng biến thiên của hàm số g  x :
Bất phương trình m  2 f  x  2   x  
1  x  3 nghiệm đúng với mọi x  3;  
 m  g  2
   m  2 f (0) 1.
Chọn đáp án B.
Câu 28: Cho hàm số y  f  x có đạo hàm trên
. Đồ thị của hàm số y  f  x như hình dưới
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 28
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tìm m để bất phương trình 2
m  x  4  2  f  x  
1  2x nghiệm đúng với mọi x  4  ;2 .
A. m  2 f (0) 1.
B. m  2 f (3)  4 .
C. m  2 f (3) 16 .
D. m  2 f (1)  4 . Lời giải:
m  x    f  x    x  m  f  x     x  2 2 4 2 1 2 2 1 2
Đặt g  x  f  x     x  2 2 1 2
Ta có g x  2 f  x  
1  2  x  2  2 f  x  
1   x  2 . g x  0  f  x   1  x  2
Đặt t  x 1 ta được f t   t 1   1
 1 là phương trình hoành độ giao điểm của đồ thị f t và đường thẳng d : y  t 1 (hình vẽ)
Dựa vào đồ thị của f t  và đường thẳng y  t 1 ta có: t  3  x  4     1  t  1  hay x  0  . t  3  x  2 
Xét hàm t  t(x)  x 1 đồng biến trên suy ra bảng biến thiên của hàm số g  x : Bất phương trình 2
m  x  4  2  f  x  
1  2x nghiệm đúng với mọi x  4  ;2 .
 m  g 0  m  2 f (1)  4.
Chọn đáp án D.
Câu 29: Cho hàm số y  f  x liên tục trên đoạn 1; 4 và có đồ thị như hình vẽ bên dưới:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 29
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn 10;10 để bất phương trình
f  x  m  2m đúng với mọi x thuộc đoạn 1; 4? A. 6 . B. 5 . C. 7 . D. 8 . Lời giải:
Vì f  x  m  2m nên suy ra m  0 .
Do đó f  x  m  2m  2
 m  f x  m  2m  3m  f x  m .
Ta có max f  x  3; min f  x  2  .  1  ;4  1  ;4
Để bất phương trình f  x  m  2m đúng với mọi x thuộc đoạn 1; 4 thì ta phải có 3
 m  min f x  max f x  m  3m  2  3  m  m  3 .  1  ;4  1  ;4
Do đó trong đoạn 10;10 có 7 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn đáp án C.
Câu 30: Cho hai hàm số đa thức bậc bốn y  f x và y  gx có đồ
thị như hình vẽ, trong đó đường đậm hơn là đồ thị hàm số
y  f x . Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm
có hoành độ là 3 và cắt nhau tại hai điểm nữa có hoành độ
lần lượt là 1 và 3 . Có bao nhiêu giá trị nguyên của tham số m  12;12 
 để bất phương trình f x  gx  m nghiệm
đúng với mọi x  3; 3   ? A. 7 . B. 6 . C. 13 . D. 12 . Lời giải: 2
Phương trình hoành độ giao điểm có dạng: f x  gx  .
a x  3 x  1x  3 ,a .
Ta có : f    g     a   a   1 0 0 1 27 1 27 1 2
Hay f x  gx  
x  3 x 1x  3 27 x  3 4 
Đặt hx  f x  gx  hx  f x  gx  
x 3 2x 3 ; hx  0  x   3 27 x   3
Bảng xét dấu hx
* Bất phương trình: f (x)  (
g x)  m  m  f x  gx nghiệm đúng x 3; 3  
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 30
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia   12    8 3 m  hx 12 8 3 min  . Vậy m ;  .   3  ;3   9  9 
Chọn đáp án D.
Câu 31: Tìm tất cả các giá trị tham số m để bất phương trình x    x  x 2 6 2 8
 x  m  1 nghiệm
đúng với mọi x   2  ;8.   A. m  16. B. m  15. C. m  8. D. 2  m  16. Lời giải:
Xét bất phương trình: x    x  x 2 6 2 8
 x  m  1 1 , điều kiện x 2  ;8.   3  x
Đặt t  2  x8  x , x  2  ;8.   Ta có: t'      , t' 0 x 3
2  x8  x Bảng biến thiên: Suy ra t  0; 5 
 . Khi đó 1 trở thành: 2
t  t  15  m 2 .
Xét hàm số f t 2
 t  t  15 , f 't  2t  1  0, t   0; 5  
Bất phương trình 1 nghiệm đúng với mọi x  2  ;8 
 khi và chỉ khi 2 nghiệm đúng với mọi t  0 ; 5 
  max f t  m  m  15 . 0;5  
Chọn đáp án B.
Câu 32: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình 6 4 3 3 2
x  3x  m x  4x  mx  2  0 nghiệm đúng với mọi x  1; 3 
 . Tổng tất cả các phần tử của S bằng A. 3 . B. 2 . C. 1 . D. 4 . Lời giải: Ta có: 6 4 3 3 2 6 4 2 3 3
x  3x  m x  4x  mx  2  0  x  3x  4x  2  m x  mx
 x  3  x    mx3 2 2 1 1  mx 1
Xét hàm đặc trưng f t 3
 t  t  f t 2 '  3t  1  0
   f  2x    f mx 2 1 1
 x  1  mx
Bài toán trở thành tìm m để bất phương trình 2
x  1  mx nghiệm đúng với mọi x  1; 3   2  2 x 1 1
x  1  mx  m 
 gx , x   1  ;3; 
 g'x  1   0 x   1
 ;3  min g x  g 1  2 2       x x 1; 3 x    
Vậy để bất phương trình đã cho nghiệm đúng với mọi x  1; 3   thì m  2
Vì m nguyên dương nên S  1; 
2 có 2 phần tử. Tổng các phần tử bằng 3 .
Chọn đáp án A.
_______________HẾT_______________
Huế, 15h00 ngày 23 tháng 7 năm 2021
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 31

Biện luận nghiệm của bất phương trình dựa vào bảng biến thiên hoặc đồ thị hàm số Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số