Bộ câu hỏi tích phân chống Casio có lời giải chi tiết – Đặng Việt Hùng Toán 12

Bộ câu hỏi tích phân chống Casio có lời giải chi tiết – Đặng Việt Hùng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

12 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
VIDEO BÀI GIẢNG và LỜI GIẢI CHI TIẾT CÁC BÀI TẬP chỉ có tại website MOON.VN
Group trao ñổi bài : www.facebook.com/groups/Thayhungdz
Câu 1: Cho tích phân
ln
1
ln
e
x
a
x e
I dx e b
x
+
= = −
∫
, giá trị của
2
a b
+
bằng
A.
2
B.
3
2
C.
5
2
D.
.
Câu 2:
Cho
đẳ
ng th
ứ
c
( )
1
3
2
4
0
4
2 3. 0
2
x
m dx
x
− =
+
∫
. Khi
đ
ó
2
144 1
m
−
bằng
A.
2
3
−
B.
1
3
−
C.
1
3
D.
2
3
.
Câu 3: Cho tích phân
(
)
0
2 1 2
1
1 ln
1 2
x
a
x
x e x
e
dx
e
+ +
+
= +
+
∫
, giá trị của số thực dương
a
bằng
A.
3
2
a
=
B.
1
2
a
=
C.
1
a
=
D.
2
a
=
.
Câu 4: Cho đẳng thức tích phân
1
2
1
ln3
3 . 6 0
m
x
dx
x
+ =
∫
và tham số thực
m
, giá trị của
m
bằng
A.
3
2
m
=
B.
1
2
m
=
C.
1
m
=
D.
2
m
=
.
Câu 5: Cho tích phân
( )
2
cos ln
1
a
e
e
x
I dx
x
π
= =
∫
với
[
]
1;1
a∈ − , giá trị của
a
bằng
A.
1
a
= −
B.
1
a
=
C.
1
2
a
=
D.
0
a
=
.
Câu 6: Biết rằng
1
2
0
ln3 ln2 ln4
5 6
dx
a b c
x x
= − −
+ +
∫
với
, ,
a b c
là các số thực. Tính
2 2
2
P a b c
= + +
A.
2.
B.
4.
C.
6.
D.
8.
Câu 7: Biết rằng
2
2
1
8 5
ln2 ln3 ln5
6 7 2
x
dx a b c
x x
+
= + +
+ +
∫
với
, ,
a b c
là các số thực. Tính
2 3
3
P a b c
= + +
A.
1.
B.
2.
C.
3.
D.
4.
Câu 8: Biết rằng
1
2
2
0
3
1 x dx
a b
π
− = +
∫
với
,
a b
là các số nguyên. Tính
P a b
= +
A.
10.
B.
12.
C.
15.
D.
20.
Câu 9: Biết rằng
2
0
sin 2 cos
ln2
1 cos
x x
dx a b
x
π
= +
+
∫
với
,
a b
là các số nguyên. Tính
2 3
2 3
P a b
= +
A.
5.
B.
7.
C.
8.
D.
11.
Tài liệu bài giảng (Chinh phục Tích phân – Số phức)
BỘ CÂU HỎI TÍCH PHÂN CHỐNG CASIO
Thầy Đặng Việt Hùng – Moon.vn
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Câu 10: Biết rằng
1
2
0
x
x e dx ae b
= +
∫
với
,
a b
là các số nguyên. Tính
3
2
P a b
= +
A.
0.
B.
2.
C.
2.
−
D.
1.
Câu 11: Cho hàm số
(
)
f x
có đạo hàm trên đoạn
[
]
1;4
và
(
)
(
)
1 2; 4 10.
f f= = Tính
( )
4
1
' .
I f x dx
=
∫
A.
48.
I
=
B.
3.
I
=
C.
8.
I
=
D.
12.
I
=
Câu 12: Biết
(
)
F x
là một nguyên hàm của hàm số
( )
1
5
f x
x
=
−
và
(
)
6 4.
F
=
Tính
(
)
10 .
F
A.
(
)
10 4 ln5.
F = + B.
(
)
10 5 ln5.
F = + C.
( )
21
10 .
5
F =
D.
( )
1
10 .
5
F
=
Câu 13:
Cho
( )
6
0
20.
f x dx =
∫
Tính
( )
3
0
2 .
I f x dx
=
∫
A.
40.
I
=
B.
10.
I
=
C.
20.
I
=
D.
5.
I
=
Câu 14: Cho hàm số
(
)
f x
liên tục trên đoạn
[
]
0;6
thỏa mãn
( )
6
0
10
f x dx
=
∫
và
( )
4
2
6.
f x dx
=
∫
Tính giá trị
của biểu thức
( ) ( )
2 6
0 4
.
P f x dx f x dx
= +
∫ ∫
A.
4.
P
=
B.
16.
P
=
C.
8.
P
=
D.
10.
P
=
Câu 15: Biết
5
2
2
ln2 ln5,
dx
a b
x x
= +
−
∫
với
,
a b
là hai số nguyên. Tính
2 2
2 3 .
P a ab b
= + +
A.
18.
P
=
B.
6.
P
=
C.
2.
P
=
D.
11.
P
=
Câu 16: Biết
4
2
2
2 1
ln3 ln2
x
I dx a b
x x
−
= = +
−
∫
, với
;
a b
là các số nguyên. Giá trị của biểu thức
2 2
A a b
= +
là:
A.
2
A
=
B.
A
=
C.
10
A
=
D.
20
A
=
Câu 17: Biết rằng
( )
2
1
2ln 1
ln2
ln 1
e
x b
I dx a
c
x x
+
= = −
+
∫
, với
, ,
a b c
là các số nguyên dương và
b
c
là phân số tối
giản. Tính
S a b c
= + +
A.
3
S
=
B.
5
S
=
C.
7
S
=
D.
10
S
=
Câu 18: Biết rằng
( )
4
0
ln 2 1 .ln3
a
I x x dx c
b
= + = −
∫
; với
, ,
a b c
là các số nguyên dương và
a
b
là phân số tối
giản. Tính
S a b c
= + +
.
A.
60
S
=
B.
68
S
=
C.
70
S
=
D.
64
S
=
Câu 19: Biết rằng
( )
2
0
cos . sin 8
I x f x dx
π
= =
∫
. Tính
( )
2
0
sin . cos
K x f x dx
π
=
∫
.
A.
8
K
= −
B.
4
K
=
C.
8
K
=
D.
16
K
=
Câu 20: Cho hàm số
(
)
.
x
f x a e b
= +
có đạo hàm trên đoạn
[
]
0;
a
,
(
)
0 3
f a
=
và
( )
0
' 1
a
f x e
= −
∫
. Tính giá trị
của biểu thức
2 2
P a b
= +
.
A.
25
P
=
B.
20
P
=
C.
P
=
D.
10
P
=
Câu 21:
Biết rằng
(
)
f x
là hàm liên tục trên
ℝ
và
( )
9
0
T f x dx
= =
∫
. Tính
( )
3
0
3
D f x T dx
= +
∫
.
A.
30
D
=
B.
3
D
=
C.
12
D
=
D.
27
D
=
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Câu 22: Kết quả của tích phân
( )
3
2
2
ln
I x x dx
= −
∫
được viết ở dạng
.ln3
I a b
= −
với
,
a b
là các số nguyên.
Khi đó
a b
−
nhận giá trị nào sau đây ?
A.
2
−
B.
C.
1
D.
Câu 23: Cho
( ) ( )
0
2 3 .ln 1
a
I x x dx
= − −
∫
biết rằng
1
0
. 4
a dx
=
∫
và
(
)
(
)
.ln 1
I a b a
= + −
, giá trị của
b
bằng :
A.
1
b
=
B.
4
b
=
C.
2
b
=
D.
3
b
=
.
Câu 24: Cho
a
là một số thực khác
0
, ký hiệu
2
a
x
a
e
b dx
x a
−
=
+
∫
. Tính
( )
2
0
3
a
x
dx
I
a x e
=
−
∫
theo
a
và
b
.
A.
a
B.
a
b
e
C.
b
D.
.
a
e b
Câu 25: Cho hình cong
(
)
H
giới hạn bởi các đường
2
1; 0; 0
y x x y x
= + = =
và
3
x
= . Đường thẳng
x k
=
với
1 3
k
< < chia
(
)
H
thành 2 phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Để
1 2
6
S S
= thì
k
gần bằng
A.
1,37
B.
1,63
C.
0,97
D.
1,24
Câu 26: Biết rằng hàm số
( )
y f x
=
liên tục trên
ℝ
và
9
0
( ) 9.
f x dx
=
∫
Khi đó, giá trị của
3
0
(3 )
f x dx
∫
là:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 27: Tích phân
2017
6
sin
xdx
π
π
∫
bằng:
A.
2.
B.
1.
−
C.
0.
D.
1.
Câu 28: Có bao nhiêu số thực
a
thỏa mãn
2
3
2?
a
x dx
=
∫
A.
0.
B.
1.
C.
2.
D.
3.
Câu 29: Có bao nhiêu số thực
(
)
0;2017
a∈ sao cho
0
sin 0?
a
xdx
=
∫
A.
301.
B.
311.
C.
321.
D.
331.
Câu 30: Biết rằng
1
2
0
3 1 5
3ln
6 9 6
x a
dx
x x b
−
= −
+ +
∫
trong đó
,
a b
là hai số nguyên dương và
a
b
là phân số tối
giản. Khi đó
ab
bằng:
A.
5.
B.
12.
C.
6.
D.
8.
Câu 31: Biết rằng
1
0
1 1 1
ln
2 1 3 1 6
a
dx
x x b
− =
+ +
∫
trong đó
,
a b
là hai số nguyên dương và
a
b
là phân số tối
giản. Khẳng định nào sau đây là sai?
A.
3
7.
a b
+ =
B.
22.
a b
+ <
C.
4 9 251.
a b
+ >
C.
10.
a b
− >
Câu 32: Số nào sau đây gần bằng nghiệm của phương trình
2017
0
2 1
x
t
e dt
= −
∫
(ẩn
)?
x
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
A.
1395.
B.
1401.
C.
1398.
D.
1404.
Câu 33: Biết rằng hàm số
( )
y f x
=
có đạo hàm liên tục trên
ℝ
và có
(
)
0 1.
f
=
Khi đó
( )
0
'
x
f t dt
∫
bằng:
A.
(
)
1.
f x
+
B.
(
)
1 .
f x
+
C.
(
)
.
f x
D.
(
)
1.
f x
−
Câu 34: Xét tích phân
3
5 2
0
1
a
I x x dx
b
= + =
= + == + =
= + =
∫
∫∫
∫
là một số phân số tối giản. Tính hiệu
a b
−
−−
−
.
A. 743 B. – 64 C. 27 D. – 207
Câu 35: Khẳng định nào sau đây đúng về kết quả
3
1
3 1
ln
e
a
e
x xdx
b
+
=
∫
?
A.
. 64
a b
=
B.
. 46
a b
=
C.
12
a b
− =
D.
4
a b
− =
WWW.TOANMATH.COM
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
VIDEO BÀI GIẢNG và LỜI GIẢI CHI TIẾT CÁC BÀI TẬP chỉ có tại website MOON.VN
Group trao ñổi bài : www.facebook.com/groups/Thayhungdz
Câu 1: Cho tích phân
ln
1
ln
e
x
a
x e
I dx e b
x
+
= = −
∫
, giá trị của
2
a b
+
bằng
A.
2
B.
3
2
C.
5
2
D.
.
HD:
Ta có
( )
( )
ln 2
ln ln
1 1
1
ln ln 1 1
ln ln 1
2 2 2
e
e e
x
x x
x e x
I dx x e d x e e e
x
+
= = + = + = + − = −
∫ ∫
.
Mà
1 1
1; 2 1 1 2
2 2
a
I e b e a b a b
= − = − → = = ⇒ + = + =
.
Chọn A.
Câu 2:
Cho
đẳ
ng th
ứ
c
( )
1
3
2
4
0
4
2 3. 0
2
x
m dx
x
− =
+
∫
. Khi
đ
ó
2
144 1
m
−
bằng
A.
2
3
−
B.
1
3
−
C.
1
3
D.
2
3
.
HD: Ta có
( )
(
)
( )
1
4
1 1
3
2 2
4
4 4
0 0
0
4 1 1 1 1
2 3 2 6
2 2
d x
x
dx
x
x x
= = − = − − − =
+
+ +
∫ ∫
.
Khi
đó
( )
1
3
2
2
4
0
4 1 3 2
2 3. 0 2 3. 0 144 1
6 36 3
2
x
m dx m m m
x
− = ⇔ − = ⇔ = ⇒ − = −
+
∫
. Chọn A.
Câu 3: Cho tích phân
(
)
0
2 1 2
1
1 ln
1 2
x
a
x
x e x
e
dx
e
+ +
+
= +
+
∫
, giá trị của số thực dương
a
bằng
A.
3
2
a
=
B.
1
2
a
=
C.
1
a
=
D.
2
a
=
.
HD: Ta có
( )
(
)
0 0 0
2 1
2 1 2
2
1 1 1
x x
x
a a a
x
x x x
x e e
x e x
e
dx dx x dx
e e e
+ +
+ +
= = +
+ + +
∫ ∫ ∫
.
(
)
( ) ( )
2 2
0
0 0
1
2 ln 1 ln 1 ln2
1
x
a a
a
x a
x
d e
x dx dx x e a e
e
+
= + = + + = + + −
+
∫ ∫
.
( )
( )
( )
2
1
1 ln 1 ln 1 ln2 ln 1 1 ln 1 1
2
a
e
e a e e a
+
= + = + + − ⇔ + + = + + ⇔ =
. Chọn C.
C
âu 4:
Cho đẳng thức tích phân
1
2
1
ln3
3 . 6 0
m
x
dx
x
+ =
∫
và tham số thực
m
, giá trị của
m
bằng
Tài liệu bài giảng (Chinh phục Tích phân – Số phức)
BỘ CÂU HỎI TÍCH PHÂN CHỐNG CASIO
Thầy Đặng Việt Hùng – Moon.vn
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
A.
3
2
m
=
B.
1
2
m
=
C.
1
m
=
D.
2
m
=
.
HD: Ta xét
1 1 1 1
2
1 1
1
ln3 1
3 . 3 .ln3 3 3 3
m
m m
x x x m
I dx d
x x
= = − = − = − +
∫ ∫
.
Mà
1
2
1
ln3
3 . 6 0
m
x
dx
x
+ =
∫
nên suy ra
1 1
2
1 1
3 3 6 0 3 9 3 2
2
m m
m
m
− + + = ⇔ = = ⇔ = ⇔ =
. Chọn B.
Câu 5: Cho tích phân
( )
2
cos ln
1
a
e
e
x
I dx
x
π
= =
∫
với
[
]
1;1
a∈ − , giá trị của
a
bằng
A.
1
a
= −
B.
1
a
=
C.
1
2
a
=
D.
0
a
=
.
HD: Ta có
( )
( ) ( ) ( )
( )
2 2
2
2
1
cos ln
cos ln ln sin ln sin ln sin ln 1 sin
a a
e e
e
a
e e
x
I dx x d x x e e a
x
π π
π
π
= = = = − = −
∫ ∫
.
Mà
( )
2
cos ln
1 1 sin 1 sin 0 0
a
e
e
x
I dx a a a
x
π
= = → − = ⇔ = ⇔ =
∫
vì
[
]
1;1
a∈ − . Chọn D.
Câu 6: Biết rằng
1
2
0
ln3 ln2 ln 4
5 6
dx
a b c
x x
= − −
+ +
∫
với
, ,
a b c
là các số thực. Tính
2 2
2
P a b c
= + +
A.
2.
B.
4.
C.
6.
D.
8.
HD: Ta có
(
)
(
)
( )( )
1 1
1
2
00 0
3 2
2
ln 2ln3 ln2 ln4
2 3 3
5 6
x x
dx x
dx
x x x
x x
+ − +
+
= = = − −
+ + +
+ +
∫ ∫
Do đó
2 2
2; 1; 1 2 6
a b c P a b c
= = − = − ⇒ = + + =
. Chọn C.
Câu 7:
Biết rằng
2
2
1
8 5
ln2 ln3 ln5
6 7 2
x
dx a b c
x x
+
= + +
+ +
∫
với
, ,
a b c
là các số thực. Tính
2 3
3
P a b c
= + +
A.
1.
B.
2.
C.
3.
D.
4.
HD: Ta có
(
)
(
)
( )( )
2 2
2
2
11 1
2 3 2 2 1
9 5 1 2
ln 2 1 ln 3 2 ln 2 ln3 ln5
2 1 3 2 3 3
6 7 2
x x
x
dx dx x x
x x
x x
+ + +
+
= = + + + = − +
+ +
+ +
∫ ∫
Do đó
2 3
2
1; 1; 3 4
3
a b c P a b c
= = − =
⇒
= + + =
. Chọn D.
Câu 8: Biết rằng
1
2
2
0
3
1 x dx
a b
π
− = +
∫
với
,
a b
là các số nguyên. Tính
P a b
= +
A.
10.
B.
12.
C.
15.
D.
20.
HD : Đặt
sin cos
x t dx tdt
= ⇒ =
. Đỗi cận
1
0 0;
2 6
x t x t
π
= ⇒ = = ⇒ =
( )
1
6 6 6
2
6
2 2 2
0 0 0 0
0
1 1 1 3
1 1 sin cos cos 1 cos2 sin 2
2 2 4 12 8
x dx t tdt tdt t dt x t
π π π
π
π
⇒ − = − = = + = + = +
∫ ∫ ∫ ∫
Do
đó
12; 8 20
a b P a b
= = ⇒ = + =
. Chọn D.
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Câu 9: Biết rằng
2
0
sin 2 cos
ln2
1 cos
x x
dx a b
x
π
= +
+
∫
với
,
a b
là các số nguyên. Tính
2 3
2 3
P a b
= +
A.
5.
B.
7.
C.
8.
D.
11.
HD: Ta có
( )
2 2
2 2 2
0 0 0
sin 2 cos sin cos cos
2 2 cos
1 cos 1 cos 1 cos
x x x xdx x
dx d x
x x x
π π π
= = −
+ + +
∫ ∫ ∫
( )
( )
2
2
2
0
0
1
2 cos 1 cos cos 2 2ln 1 cos 2ln 2 1
1 cos
x d x x x x
x
π
π
= − − + = − + − + = −
+
∫
Do
đó
2 3
2; 1 2 3 11
a b P a b
= = − ⇒ = + =
. Chọn D.
Câu 10: Biết rằng
1
2
0
x
x e dx ae b
= +
∫
với
,
a b
là các số nguyên. Tính
3
2
P a b
= +
A.
0.
B.
2.
C.
2.
−
D.
1.
HD: Ta có
( ) ( ) ( )
1 1 1 1 1
1
2 2 2 2
00 0 0 0 0
2 2
x x x x x x
x e dx x d e x e e d x e xe dx e xd e
= = − = − = −
∫ ∫ ∫ ∫ ∫
1
1 1
0 00
2 2 2 2 2 2 2
x x x
e xe e dx e e e e e e
− + = − + = − + − = −
∫
Do đó
3
1; 2 2 0
a b P a b
= = − ⇒ = + =
. Chọn A.
Câu 11: Cho hàm số
(
)
f x
có đạo hàm trên đoạn
[
]
1;4
và
(
)
(
)
1 2; 4 10.
f f= = Tính
( )
4
1
' .
I f x dx
=
∫
A.
48.
I
=
B.
3.
I
=
C.
8.
I
=
D.
12.
I
=
HD: Ta có
( ) ( ) ( )
4
1
4 1 8.
I f x f f
= = − =
Chọn C
Câu 12: Biết
(
)
F x
là một nguyên hàm của hàm số
( )
1
5
f x
x
=
−
và
(
)
6 4.
F
=
Tính
(
)
10 .
F
A.
(
)
10 4 ln5.
F = + B.
(
)
10 5 ln5.
F = + C.
( )
21
10 .
5
F =
D.
( )
1
10 .
5
F
=
HD:
Ta có
( )
1
ln 5 .
5
F x dx x C
x
= = − +
−
∫
Mà
(
)
(
)
6 4 ln1 4 4 10 ln5 4.
F C C F
= ⇒ + = ⇒ = ⇒ = +
Chọn A
Câu 13:
Cho
( )
6
0
20.
f x dx =
∫
Tính
( )
3
0
2 .
I f x dx
=
∫
A.
40.
I
=
B.
10.
I
=
C.
20.
I
=
D.
5.
I
=
HD: Đặt
( ) ( ) ( )
6 6 6
0 0 0
1 1 1
2 .20 10.
2 2 2 2
t
x t I f t d f t dt f x dx
=
⇒
= = = = =
∫ ∫ ∫
Chọn B
Câu 14: Cho hàm số
(
)
f x
liên tục trên đoạn
[
]
0;6
thỏa mãn
( )
6
0
10
f x dx
=
∫
và
( )
4
2
6.
f x dx
=
∫
Tính giá trị
của biểu thức
( ) ( )
2 6
0 4
.
P f x dx f x dx
= +
∫ ∫
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
A.
4.
P
=
B.
16.
P
=
C.
8.
P
=
D.
10.
P
=
HD: Ta có
( ) ( ) ( ) ( ) ( ) ( )
2 4 6 4 6 6
0 2 4 0 4 0
6 10 4.
P f x dx f x dx f x dx f x dx f x dx f x dx P
+ = + + = + = = ⇒ =
∫ ∫ ∫ ∫ ∫ ∫
Chọn A
Câu 15: Biết
5
2
2
ln2 ln5,
dx
a b
x x
= +
−
∫
với
,
a b
là hai số nguyên. Tính
2 2
2 3 .
P a ab b
= + +
A.
18.
P
=
B.
6.
P
=
C.
2.
P
=
D.
11.
P
=
HD: Ta có
( )
5 5 5
5 5
2
2 2
2 2 2
1 1 1
ln 1 ln
1 1
dx
dx dx x x
x x x x x x
= = − = − −
− − −
∫ ∫ ∫
( )
3
ln4 ln5 ln 2 3ln2 ln5 6.
1
a
P
b
=
= − − = − ⇒ ⇒ =
= −
Chọn B
Câu 16: Biết
4
2
2
2 1
ln3 ln2
x
I dx a b
x x
−
= = +
−
∫
, với
;
a b
là các số nguyên. Giá trị của biểu thức
2 2
A a b
= +
là:
A.
2
A
=
B.
A
=
C.
10
A
=
D.
20
A
=
HD: Ta có:
(
)
2
4
4
2
2
2
2
ln ln12 ln 2 ln6 ln3 ln 2 1 2
d x x
I x x a b A
x x
−
= = − = − = = + ⇒ = = ⇒ =
−
∫
. Chọn A.
Câu 17: Biết rằng
( )
2
1
2ln 1
ln2
ln 1
e
x b
I dx a
c
x x
+
= = −
+
∫
, với
, ,
a b c
là các số nguyên dương và
b
c
là phân số tối
giản. Tính
S a b c
= + +
A.
3
S
=
B.
5
S
=
C.
7
S
=
D.
10
S
=
HD : Đặt
( ) ( )
1 1
2 2
0 0
2 1 2 1
ln
1
1 1
dx t
t x dt I dt dt
x t
t t
+
= ⇒ = ⇒ = = −
+
+ +
∫ ∫
1
0
2; 1
1 1
2ln 1 2ln2 5
2
1 2
a b
t S
c
t
= =
= + + = − ⇒ ⇒ =
=
+
. Chọn B.
Câu 18: Biết rằng
( )
4
0
ln 2 1 .ln3
a
I x x dx c
b
= + = −
∫
; với
, ,
a b c
là các số nguyên dương và
a
b
là phân số tối
giản. Tính
S a b c
= + +
.
A.
60
S
=
B.
68
S
=
C.
70
S
=
D.
64
S
=
HD: Đặt
( )
2 2
2
ln 2 1
2 1
1 4 1
2 8 8
du
u x
x
x x
dv xdx
v
=
= +
+
⇒
−
=
= − =
Khi đó
( )
4
4 4
2 2
0 00
63; 4
4 1 2 1 63 63
ln 2 1 ln9 ln3 3
3
8 4 8 4 4 4
a b
x x x x
I x dx
c
= =
− −
= + − = − − = − ⇒
=
∫
D
o
đó
70
S
=
. Chọn C.
Câu 19:
Biết rằng
( )
2
0
cos . sin 8
I x f x dx
π
= =
∫
. Tính
( )
2
0
sin . cos
K x f x dx
π
=
∫
.
A.
8
K
= −
B.
4
K
=
C.
8
K
=
D.
16
K
=
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
HD: Đặt
2
t x dx dt
π
= − ⇒ = −
. Đổ
i c
ậ
n
0
2
0
2
x t
x t
π
π
= ⇒ =
= ⇒ =
.
( ) ( ) ( )
0
2 2
0 0
2
cos sin sin . cos sin . cos 8
2 2
I t f t dt t f t dt x f x dx
π π
π
π π
⇒ = − − − = = =
∫ ∫ ∫
.
Chọn C.
Câu 20:
Cho hàm s
ố
(
)
.
x
f x a e b
= +
có
đạ
o hàm trên
đ
o
ạ
n
[
]
0;
a
,
(
)
0 3
f a
=
và
( )
0
' 1
a
f x e
= −
∫
. Tính giá trị
của biểu thức
2 2
P a b
= +
.
A.
25
P
=
B.
20
P
=
C.
P
=
D.
10
P
=
HD: Ta có
(
)
0
0 3 . 3 2
f a a e b a b a
= ⇒ + = ⇔ =
. Mặt khác
( ) ( ) ( )
0
' 2 0 2
a
f x e f a f e
= + ⇒ − = +
∫
.
(
)
. 3 1 . 1 . 1 1 0 1 2 5
a a a
a e b a e a e a e a e e a b P
⇔ + − = − ⇔ − = − ⇔ − − + = ⇒ = ⇒ = ⇒ =
. Chọn C.
Câu 21: Biết rằng
(
)
f x
là hàm liên tục trên
ℝ
và
( )
9
0
T f x dx
= =
∫
. Tính
( )
3
0
3
D f x T dx
= +
∫
.
A.
30
D
=
B.
3
D
=
C.
12
D
=
D.
27
D
=
HD: Xét
( ) ( ) ( ) ( )
3 3 3 3 3 3
0 0 0 0 0 0
3 3 3 9 3 27
D f x T dx f x dx T dx f x dx dx f x dx
= + = + = + = +
∫ ∫ ∫ ∫ ∫ ∫
.
Đặt
( ) ( ) ( )
3 9 9
0 0 0
1
3 3 . . 3
3 3 3 3
dt dt T
t x dx f x dx f t f t dt
= ⇒ = ⇒ = = = =
∫ ∫ ∫
. Do đó
30
D
=
. Chọn A.
Câu 22:
Kết quả của tích phân
( )
3
2
2
ln
I x x dx
= −
∫
được viết ở dạng
.ln3
I a b
= −
với
,
a b
là các số nguyên.
Khi đó
a b
−
nhận giá trị nào sau đây ?
A.
2
−
B.
C.
1
D.
HD: Đặt
( )
( )
2
3
3
2
2
2
2
2 1
ln
2 1
.ln 3.ln6 2.ln2
1
x
u x x
du dx
x
I x x x dx D
x x
x
dv dx
v x
−
= −
=
−
⇔ ⇒ = − − = − −
−
−
=
=
∫
.
Xét
( )
3 3
3
2
2 2
3
2 1 1
2 2 ln 1 2 ln2 3.ln3 2
2
1 1
a
x
D dx dx x x I
b
x x
=
−
= = + = + − = + ⇒ = − ⇒
= −
− −
∫ ∫
. Chọn D.
Câu 23: Cho
( ) ( )
0
2 3 .ln 1
a
I x x dx
= − −
∫
biết rằng
1
0
. 4
a dx
=
∫
và
(
)
(
)
.ln 1
I a b a
= + −
, giá trị của
b
bằng :
A.
1
b
=
B.
4
b
=
C.
2
b
=
D.
3
b
=
.
HD: Ta có
( ) ( ) ( )
1 4
1
0
0 0
. 4 4 4 2 3 ln 1
a dx ax a I x x dx
= ⇔ = ⇔ = ⇒ = − −
∫ ∫
.
Đặt
( )
( )
2
ln 1
1
2 3
3 2
dx
u x
du
x
dv x dx
v x x
= −
=
⇔
−
= −
= − +
. Khi đó
( )
( ) ( )
4
4
2
0
0
3 2 ln 1 2 6.ln3
I x x x x dx= − + − − − =
∫
.
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Do đó
(
)
(
)
.ln 1 6.ln3 6 2
I a b a a b b
= + − = ⇔ + = ⇔ =
. Chọn C.
Câu 24: Cho
a
là một số thực khác
0
, ký hiệu
2
a
x
a
e
b dx
x a
−
=
+
∫
. Tính
( )
2
0
3
a
x
dx
I
a x e
=
−
∫
theo
a
và
b
.
A.
a
B.
a
b
e
C.
b
D.
.
a
e b
HD: Đặt
3 2
a x t a
t a x
dx dt
− = +
= − ⇔
= −
và đổi cận
0
2
x t a
x a t a
= → =
= → = −
. Khi đó
( )
2
a
a t
a
dt
I
t a e
−
−
= −
+
∫
.
( ) ( )
2 2
a a
t x
a a
a a
e e
I dt dx
t a e x a e
− −
⇒ = =
+ +
∫ ∫
mà
2
a
x
a
a
e b
b dx I
x a e
−
= ⇒ =
+
∫
. Chọn B.
Câu 25: Cho hình cong
(
)
H
giới hạn bởi các đường
2
1; 0; 0
y x x y x
= + = =
và
3
x = . Đường thẳng
x k
=
với
1 3
k< < chia
(
)
H
thành 2 phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Để
1 2
6
S S
= thì k gần bằng
A.
1,37
B.
1,63
C.
0,97
D.
1,24
HD: Ta có:
( )
( )
3
2
3 3
3
2 2 2
1
1 2 1 1
0 0
0
1
1 7 7
1 1 1 2
2 3 3 6 3
x
S
S S S x x dx x d x S S
+
= + = + = + + = = ⇒ + = ⇒ =
∫ ∫
.
L
ại có
( ) ( )
3 3
2 2
3
1
1
1 1 1
2 49 1 1,63
3 3
k
x k
S k
+ + −
= = = ⇒ = − ≈ . Chọn B.
Câu 26: Biết rằng hàm số
( )
y f x
=
liên tục trên
ℝ
và
9
0
( ) 9.
f x dx
=
∫
Khi đó, giá trị của
3
0
(3 )
f x dx
∫
là:
A.
1.
B.
2.
C.
3.
D.
4.
HD:
( )
3 3 9
0 0 0
1 1
(3 ) (3 ) 3 ( ) 3
3 3
f x dx f x d x f x dx
= = =
∫ ∫ ∫
. Chọn C.
Câu 27: Tích phân
2017
6
sin
xdx
π
π
∫
bằng:
A.
2.
B.
1.
−
C.
0.
D.
1.
HD:
2017
2017
6
6
sin cos 2
xdx x
π
π
π
π
= − =
∫
. Chọn A.
Câu 28:
Có bao nhiêu số thực
a
thỏa mãn
2
3
2?
a
x dx
=
∫
A.
0.
B.
1.
C.
2.
D.
3.
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
HD:
2
2
4 4
3 4
4
2 4 8 8
4 4
a
a
x a
x dx a a
= = = − ⇔ = ⇔ = ±
∫
. Chọn C.
Câu 29: Có bao nhiêu số thực
(
)
0;2017
a∈ sao cho
0
sin 0?
a
xdx
=
∫
A.
301.
B.
311.
C.
321.
D.
331.
HD:
0
0
sin cos cos 1 0 cos 1 2
a
a
xdx x a a a k
π
= − = − + = ⇔ = ⇔ =
∫
với k
∈
ℤ
Vì
(
)
2 0;2017 0 321
a k k
π
= ∈ ⇔ < ≤ . Có tất cả 321 giá trị
k
ứng với 321 giá trị
a
thỏa mãn. Chọn C.
Câu 30:
Biết rằng
1
2
0
3 1 5
3ln
6 9 6
x a
dx
x x b
−
= −
+ +
∫
trong đó
,
a b
là hai số nguyên dương và
a
b
là phân số tối
giản. Khi đó
ab
bằng:
A.
5.
B.
12.
C.
6.
D.
8.
HD: Ta có
(
)
( ) ( )
1
1 1 1 1
2 2
2
0 0 0 0
0
3 3 10
5 3 1 10
3ln 3 10 3ln 3
6 6 9 3 3
3 3
x
a x dx dx
dx dx x
b x x x x
x x
+ −
−
− = = = − = + +
+ + + +
+ +
∫ ∫ ∫ ∫
( ) ( )
4
5 10 4 5
3ln 4 3ln 3 3ln 12
3
2 3 3 6
a
ab
b
=
= + − − = − ⇒ ⇒ =
=
. Chọn B.
Câu 31: Biết rằng
1
0
1 1 1
ln
2 1 3 1 6
a
dx
x x b
− =
+ +
∫
trong đó
,
a b
là hai số nguyên dương và
a
b
là phân số tối
giản. Khẳng định nào sau đây là sai?
A.
3
7.
a b
+ =
B.
22.
a b
+ <
C.
4 9 251.
a b
+ >
C.
10.
a b
− >
HD: Ta có
( ) ( )
1
1 1 1
0 0 0
0
ln 2 1 ln 3 1
2 1 3 1
1 1 1 1
2 1 3 1 2 2 1 3 3 1 2 3
x x
d x d x
dx
x x x x
+ +
+ +
− = − = −
+ + + +
∫ ∫ ∫
(
)
(
)
3
3
2
2
3
ln 3 ln 4
1 3 1
ln ln
2 3 6 4 6
4
a
a
b
b
=
= − = = ⇔
=
Chọn B.
Câu 32: Số nào sau đây gần bằng nghiệm của phương trình
2017
0
2 1
x
t
e dt
= −
∫
(ẩn
)?
x
A.
1395.
B.
1401.
C.
1398.
D.
1404.
HD:
( )
2017 2017 2017
0
0
2 1 1 2 ln 2 2017ln 2 1398
x
x
t t x x
e dt e e e x− = = = − ⇔ = ⇔ = = ≈
∫
. Chọn C.
Câu 33: Biết rằng hàm số
( )
y f x
=
có đạo hàm liên tục trên
ℝ
và có
(
)
0 1.
f
=
Khi đó
( )
0
'
x
f t dt
∫
bằng:
A.
(
)
1.
f x
+
B.
(
)
1 .
f x
+
C.
(
)
.
f x
D.
(
)
1.
f x
−
HD:
( ) ( ) ( ) ( ) ( )
0
0
' 0 1
x
x
f t dt f t f x f f x
= = − = −
∫
. Chọn D.
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Câu 34: Xét tích phân
3
5 2
0
1
a
I x x dx
b
= + =
= + == + =
= + =
∫
∫∫
∫
là một số phân số tối giản. Tính hiệu
a b
−
−−
−
.
A. 743 B. – 64 C. 27 D. – 207
HD: Đặt
2 2 2
1 1
t x t x tdt xdx
= + ⇒ = + ⇒ = . Đổi cận
0 1
3 2
x t
x t
= ⇒ =
= ⇒ =
Khi đó
( ) ( )
2 2
2
7 5 3
2
2 2 6 4 2
11 1
848
1 . 2 2
7 5 3 105
t t t a
I t t dt t t t dt
b
= − = − + = − + = =
∫ ∫
Suy ra
743
a b
− =
. Chọn A.
Câu 35:
Khẳng định nào sau đây đúng về kết quả
3
1
3 1
ln
e
a
e
x xdx
b
+
=
∫
?
A.
. 64
a b
=
B.
. 46
a b
=
C.
12
a b
− =
D.
4
a b
− =
HD: Đặt
4 3 4 4 4
3
4
1
1
ln
ln 1 3 1
4 4 4 16 16
4
e
e
dx
du
u x
x x x e e e
x
I dx
dv x dx
x
v
=
=
− +
⇒ ⇒ = − = − =
=
=
∫
Do đó
4; 16 64
a b ab
= = ⇒ =
. Chọn A.
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tài liệu bài giảng (Chinh phục Tích phân – Số phức)
BỘ CÂU HỎI TÍCH PHÂN CHỐNG CASIO
Thầy Đặng Việt Hùng – Moon.vn
VIDEO BÀI GIẢNG và LỜI GIẢI CHI TIẾT CÁC BÀI TẬP chỉ có tại website MOON.VN
Group trao ñổi bài : www.facebook.com/groups/Thayhungdz e ln ln x x + e
Câu 1: Cho tích phân a I = ∫
dx = e − b , giá trị của a + 2b bằng x 1 3 5 A. 2 B. C. D. 3 . 2 2 1 3 4x
Câu 2: Cho đẳng thức 2 3.m − ∫ ( dx = . Khi đó 2 144m −1 bằng x + 2) 0 2 4 0 2 1 1 2 A. − B. − C. D. . 3 3 3 3 a (2x + ) 1 x e + 2x e +1
Câu 3: Cho tích phân ∫ dx = 1+ ln
, giá trị của số thực dương a bằng x e +1 2 0 3 1 A. a = B. a = C. a = 1 D. a = 2 . 2 2 m 1 ln 3
Câu 4: Cho đẳng thức tích phân ∫ 3x.
dx + 6 = 0 và tham số thực m , giá trị của m bằng 2 x 1 3 1 A. m = B. m = C. m = 1 D. m = 2 . 2 2 π 2 e cos (ln x)
Câu 5: Cho tích phân I = ∫
dx = 1 với a ∈[−1; ]
1 , giá trị của a bằng x a e 1 A. a = −1 B. a = 1 C. a = D. a = 0 . 2 1 dx
Câu 6: Biết rằng ∫
= a ln 3 − bln 2 − c ln 4 với a,b,c là các số thực. Tính 2 2
P = 2a + b + c 2 x + 5x + 6 0 A. 2. B. 4. C. 6. D. 8. 2 8x + 5
Câu 7: Biết rằng ∫
dx = a ln 2 + b ln 3 + c ln 5 với a,b, c là các số thực. Tính 2 3
P = a + b + 3c 2 6x + 7x + 2 1 A. 1. B. 2. C. 3. D. 4. 1 2 π 3 Câu 8: Biết rằng 2 ∫ 1− x dx = +
với a, b là các số nguyên. Tính P = a + b a b 0 A. 10. B. 12. C. 15. D. 20. π 2 sin 2x cos x
Câu 9: Biết rằng ∫
dx = a ln 2 + b với a,b là các số nguyên. Tính 2 3
P = 2a + 3b 1 + cos x 0 A. 5. B. 7. C. 8. D. 11.
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 1 Câu 10: Biết rằng 2 x
∫ x e dx = ae + b với a,b là các số nguyên. Tính 3
P = 2a + b 0 A. 0. B. 2. C. −2. D. 1. 4
Câu 11: Cho hàm số f ( x) có đạo hàm trên đoạn [1;4] và f ( )
1 = 2; f (4) = 10. Tính I = ∫ f '( x) . dx 1 A. I = 48. B. I = 3. C. I = 8. D. I = 12.
Câu 12: Biết F ( x) là một nguyên hàm của hàm số f ( x) 1 =
và F (6) = 4. Tính F (10). x − 5
A. F (10) = 4 + ln 5.
B. F (10) = 5 + ln 5. C. F ( ) 21 10 = . D. F ( ) 1 10 = . 5 5 6 3
Câu 13: Cho ∫ f ( x) dx = 20. Tính I = ∫ f (2x) d . x 0 0 A. I = 40. B. I = 10. C. I = 20. D. I = 5. 6 4
Câu 14: Cho hàm số f ( x) liên tục trên đoạn [0;6] thỏa mãn ∫ f ( x) dx = 10 và ∫ f ( x) dx = 6. Tính giá trị 0 2 2 6
của biểu thức P = ∫ f ( x) dx + ∫ f ( x) d . x 0 4 A. P = 4. B. P = 16. C. P = 8. D. P = 10. 5 dx Câu 15: Biết ∫
= a ln 2 + bln 5, với a, b là hai số nguyên. Tính 2 2
P = a + 2ab + 3b . 2 x − x 2 A. P = 18. B. P = 6. C. P = 2. D. P = 11. 4 2x −1
Câu 16: Biết I = ∫
dx = a ln 3 + b ln 2 , với a;b là các số nguyên. Giá trị của biểu thức 2 2
A = a + b là: 2 x − x 2 A. A = 2 B. A = 5 C. A = 10 D. A = 20 e 2 ln x +1 b b
Câu 17: Biết rằng I = ∫ =
− , với a,b,c là các số nguyên dương và là phân số tối x ( dx a ln x + ) ln 2 2 1 c c 1
giản. Tính S = a + b + c A. S = 3 B. S = 5 C. S = 7 D. S = 10 4 a a
Câu 18: Biết rằng I = ∫ x ln (2x + ) 1 dx =
.ln 3 − c ; với a,b, c là các số nguyên dương và là phân số tối b b 0
giản. Tính S = a + b + c . A. S = 60 B. S = 68 C. S = 70 D. S = 64 π π 2 2
Câu 19: Biết rằng I = ∫ cos .
x f (sin x) dx = 8 . Tính K = ∫ sin .
x f (cos x) dx . 0 0 A. K = 8 − B. K = 4 C. K = 8 D. K = 16 a Câu 20: Cho hàm số ( ) = . x f x
a e + b có đạo hàm trên đoạn [0;a] , f (0) = 3a và ∫ f '( x) = e −1. Tính giá trị 0 của biểu thức 2 2
P = a + b .
A. P = 25 B. P = 20 C. P = 5 D. P = 10 9 3
Câu 21: Biết rằng f ( x) là hàm liên tục trên ℝ và T = ∫ f ( x) dx = 9 . Tính D =  ∫ f
 (3x) + T dx  . 0 0 A. D = 30 B. D = 3 C. D = 12 D. D = 27
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 3
Câu 22: Kết quả của tích phân I = ∫ ln ( 2
x − x)dx được viết ở dạng I = .
a ln 3 − b với a,b là các số nguyên. 2
Khi đó a − b nhận giá trị nào sau đây ? A. −2 B. 3 C. 1 D. 5 a 1
Câu 23: Cho I = ∫ (2x − 3).ln ( x − ) 1 dx biết rằng .
a ∫ dx = 4 và I = (a + b).ln (a − )
1 , giá trị của b bằng : 0 0 A. b = 1 B. b = 4 C. b = 2 D. b = 3 . a x e 2a dx
Câu 24: Cho a là một số thực khác 0 , ký hiệu b = ∫
dx . Tính I = ∫
theo a và b . x + 2a 3 x a − x e 0 ( ) −a b A. a B. C. b D. a e .b a e
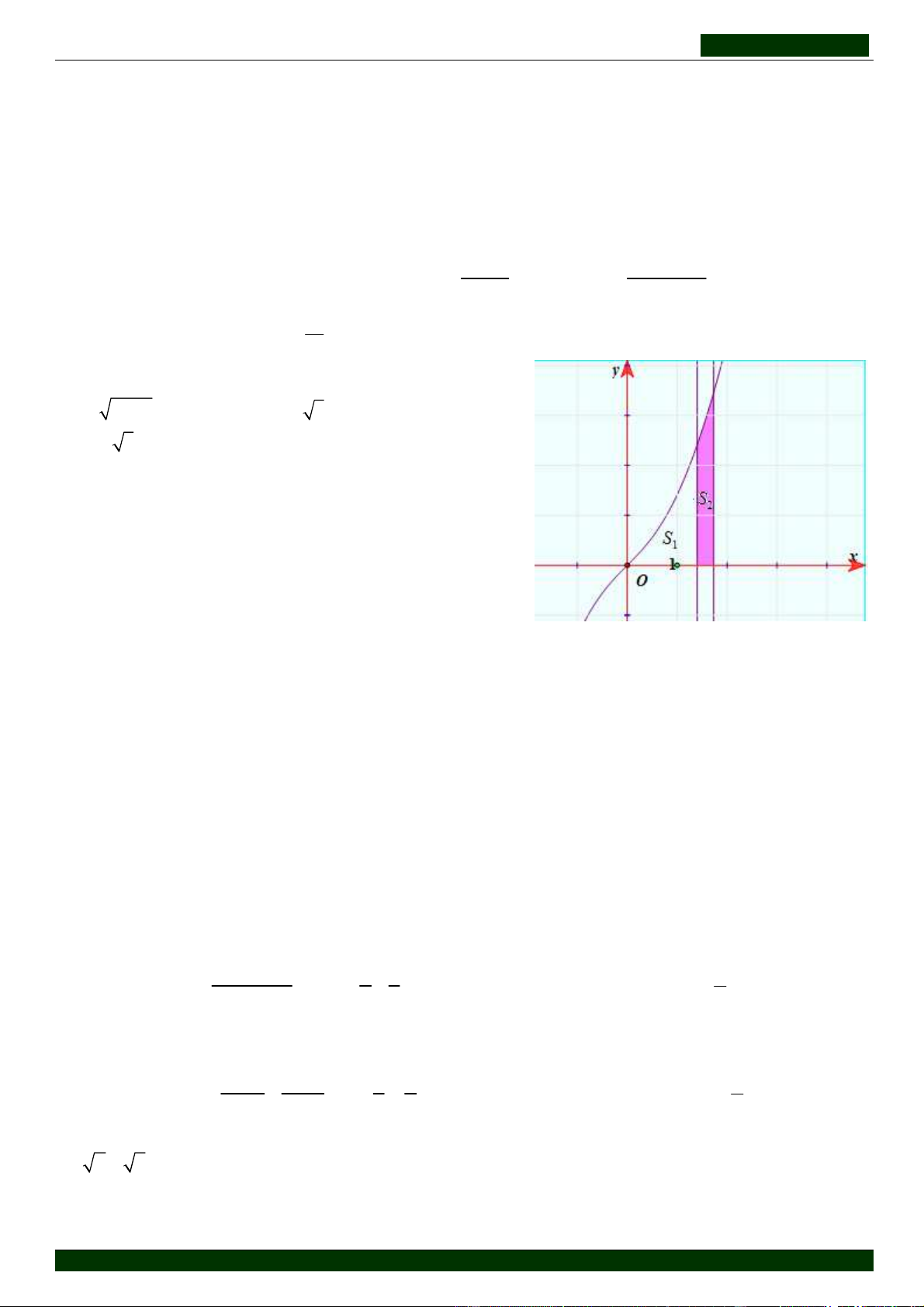
Câu 25: Cho hình cong ( H ) giới hạn bởi các đường 2
y = x x +1; y = 0; x = 0 và x = 3 . Đường thẳng x = k với
1 < k < 3 chia ( H ) thành 2 phần có diện tích là S và S 1 2
như hình vẽ bên. Để S = 6S thì k gần bằng 1 2 A. 1, 37 B. 1, 63 C. 0, 97 D. 1, 24 9 3
Câu 26: Biết rằng hàm số y = f (x) liên tục trên ℝ và ∫ f (x)dx = 9. Khi đó, giá trị của ∫ f (3x)dx là: 0 0 A. 1. B. 2. C. 3. D. 4. 2017π
Câu 27: Tích phân ∫ sin xdx bằng: 6π A. 2. B. −1. C. 0. D. 1. 2
Câu 28: Có bao nhiêu số thực a thỏa mãn 3 ∫ x dx = 2? a A. 0. B. 1. C. 2. D. 3. a
Câu 29: Có bao nhiêu số thực a ∈ (0;2017) sao cho ∫ sin xdx = 0? 0 A. 301. B. 311. C. 321. D. 331. 1 3x −1 a 5 a
Câu 30: Biết rằng ∫ dx = 3ln
− trong đó a,b là hai số nguyên dương và là phân số tối 2 x + 6x + 9 b 6 b 0
giản. Khi đó ab bằng: A. 5. B. 12. C. 6. D. 8. 1  1 1  1 a a
Câu 31: Biết rằng ∫  −
dx = ln trong đó a,b là hai số nguyên dương và là phân số tối
 2x +1 3x +1 6 b b 0
giản. Khẳng định nào sau đây là sai?
A. 3 a + b = 7.
B. a + b < 22.
C. 4a + 9b > 251.
C. a − b > 10. x
Câu 32: Số nào sau đây gần bằng nghiệm của phương trình t 2017
∫e dt = 2 −1 (ẩn x)? 0
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 A. 1395. B. 1401. C. 1398. D. 1404. x
Câu 33: Biết rằng hàm số y = f (x) có đạo hàm liên tục trên ℝ và có f (0) = 1. Khi đó ∫ f '(t ) dt bằng: 0
A. f ( x) +1.
B. f ( x + ) 1 .
C. f ( x).
D. f ( x) −1. 3 a
Câu 34: Xét tích phân 5 2
I = ∫ x x +1dx = là một số phân số tối giản. Tính hiệu a − b . b 0 A. 743 B. – 64 C. 27 D. – 207 e 3 a e + 1
Câu 35: Khẳng định nào sau đây đúng về kết quả 3 ∫ x ln xdx = ? b 1 A. . a b = 64 B. . a b = 46
C. a − b = 12
D. a − b = 4 WWW.TOANMATH.COM
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Tài liệu bài giảng (Chinh phục Tích phân – Số phức)
BỘ CÂU HỎI TÍCH PHÂN CHỐNG CASIO
Thầy Đặng Việt Hùng – Moon.vn
VIDEO BÀI GIẢNG và LỜI GIẢI CHI TIẾT CÁC BÀI TẬP chỉ có tại website MOON.VN
Group trao ñổi bài : www.facebook.com/groups/Thayhungdz e ln ln x x + e
Câu 1: Cho tích phân a I = ∫
dx = e − b , giá trị của a + 2b bằng x 1 3 5 A. 2 B. C. D. 3 . 2 2 e e ln x e 2 ln x + exx ln x 1 1
HD: Ta có I = ∫ dx = ∫ ( ln ln x + e ) d (ln x) ln = 
+ e  = e + −1 = e − . x  2  2 2 1 1 1 a 1 1
Mà I = e − b = e −
→ a =1; b = ⇒ a + 2b =1+1 = 2. Chọn A. 2 2 1 3 4x
Câu 2: Cho đẳng thức 2 3.m − ∫ ( dx = . Khi đó 2 144m −1 bằng x + 2) 0 2 4 0 2 1 1 2 A. − B. − C. D. . 3 3 3 3 3 4 d ( 4 1 1 x x ) 1  1  1  1  1 HD: Ta có ∫ ( dx = ∫ = −  = − −  −  = . x + 2)2 (x +2)2 4 4 4  x + 2  3  2  6 0 0 0 1 3 4x 1 3 2 Khi đó 2 2 3.m − ∫ ( dx = ⇔ m − = ⇔ m = ⇒ m − = − . Chọn A. x + 2) 0 2 3. 0 144 1 2 4 6 36 3 0 a (2x + ) 1 x e + 2x e +1
Câu 3: Cho tích phân ∫ dx = 1+ ln
, giá trị của số thực dương a bằng x e +1 2 0 3 1 A. a = B. a = C. a = 1 D. a = 2 . 2 2 a ( x x 2x + ) 1 x e + 2 a x 2x (e + ) 1 a x + eeHD: Ta có ∫ dx = ∫
dx = ∫  2x +  dx . x e +1 x e +1 xe +1  0 0 0 d ( x a a e + ) 1 a 2 ∫ 2x dx ∫ dxx ln  ( xe ) 2 1  = + = + + = a + ln  ( ae + − . x )1 ln2 0 e +1 0 0 e +1 =1+ ln =1+ ln (e + ) 2
1 − ln 2 ⇔ a + ln ( a e + ) 1 = 1+ ln (e + )
1 ⇔ a = 1. Chọn C. 2 m 1 ln 3
Câu 4: Cho đẳng thức tích phân ∫ 3x.
dx + 6 = 0 và tham số thực m , giá trị của m bằng 2 x 1
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 3 1 A. m = B. m = C. m = 1 D. m = 2 . 2 2 m m 1 m 1 1 1 ln 3  1   
HD: Ta xét = ∫ 3x.
= −∫3x.ln3   = −3x  = −3m I dx d + 3. 2 xx    1 1 1 m 1 ln 3 1 1 1 1 Mà ∫ 3x. dx + 6 = 0 nên suy ra 2
−3m + 3+ 6 = 0 ⇔ 3m = 9 = 3 ⇔
= 2 ⇔ m = . Chọn B. 2 x m 2 1 π 2 e cos (ln x)
Câu 5: Cho tích phân I = ∫
dx = 1 với a ∈[−1; ]
1 , giá trị của a bằng x a e 1 A. a = −1 B. a = 1 C. a = D. a = 0 . 2 π π π 2 e cos (ln x) 2 e π   2 e
HD: Ta có I = ∫
dx = ∫ cos(ln x) d (ln x) = sin (ln x) 2
= sin ln e  − sin ln a e =1− sin a . 1 ( ) x a a   e e π 2 e cos (ln x) Mà I = ∫
dx = 1 → 1− sin a = 1 ⇔ sin a = 0 ⇔ a = 0 vì a ∈[−1; ] 1 . Chọn D. x a e 1 dx
Câu 6: Biết rằng ∫
= a ln 3 − bln 2 − c ln 4 với a,b,c là các số thực. Tính 2 2
P = 2a + b + c 2 x + 5x + 6 0 A. 2. B. 4. C. 6. D. 8. 1 1 dx
(x + 3) −(x + 2) 1 x + 2 HD: Ta có ∫ = ∫ dx = ln = 2ln 3 − ln 2 − ln 4 2 x + 5x + 6 x + 2 x + 3 x + 3 0 0 ( )( ) 0 Do đó 2 2
a = 2;b = −1;c = −1 ⇒ P = 2a + b + c = 6 . Chọn C. 2 8x + 5
Câu 7: Biết rằng ∫
dx = a ln 2 + b ln 3 + c ln 5 với a,b, c là các số thực. Tính 2 3
P = a + b + 3c 2 6x + 7x + 2 1 A. 1. B. 2. C. 3. D. 4. 2 2 9x + 5
2(3x + 2) + (2x + ) 2 1  1  2 HD: Ta có ∫ dx = ∫
dx =  ln 2x + 1 + ln 3x + 2  = ln 2 − ln 3 + ln 5 2 6x + 7x + 2 2x + 1 3x + 2  3  3 1 1 ( )( ) 1 2 Do đó 2 3
a = 1;b = −1; c =
⇒ P = a + b + 3c = 4 . Chọn D. 3 1 2 π 3 Câu 8: Biết rằng 2 ∫ 1− x dx = +
với a, b là các số nguyên. Tính P = a + b a b 0 A. 10. B. 12. C. 15. D. 20. 1 π
HD : Đặt x = sin t ⇒ dx = cos tdt . Đỗi cận x = 0 ⇒ t = 0; x = ⇒ t = 2 6 1 π π π π 2 6 6 6 1   π
⇒ ∫ 1− x dx = ∫ 1− sin t costdt = ∫ cos tdt = ∫(1+ cos2t) 1 1 6 3 2 2 2
dt =  x + sin 2t  = + 2  2 4  12 8 0 0 0 0 0
Do đó a = 12;b = 8 ⇒ P = a + b = 20 . Chọn D.
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 π 2 sin 2x cos x
Câu 9: Biết rằng ∫
dx = a ln 2 + b với a,b là các số nguyên. Tính 2 3
P = 2a + 3b 1 + cos x 0 A. 5. B. 7. C. 8. D. 11. π π π 2 2 2 2 2 sin 2x cos x sin x cos xdx cos x HD: Ta có ∫ dx = 2∫ = −2∫ d (cos x) 1 + cos x 1 + cos x 1 + cos x 0 0 0 π π 2  1  = −2∫cos x −1+
d (cos x) = (− cos x + 2x − 2ln 1+ cos x ) 2 2 = 2ln 2 −1  1 + cos x  0 0 Do đó 2 3
a = 2;b = −1 ⇒ P = 2a + 3b = 11. Chọn D. 1 Câu 10: Biết rằng 2 x
∫ x e dx = ae + b với a,b là các số nguyên. Tính 3
P = 2a + b 0 A. 0. B. 2. C. −2. D. 1. 1 1 1 1 1 1 HD: Ta có 2 x 2 ∫ = ∫ ( x) 2 x x = − ∫ ( 2) = −2 x ∫ = − 2∫ ( x x e dx x d e x e e d x e xe dx e xd e ) 0 0 0 0 0 0 1 1 1 − 2 x + 2 x ∫ = − 2 + 2 x e xe e dx e e e
= −e + 2e − 2 = e − 2 0 0 0 Do đó 3
a = 1;b = −2 ⇒ P = 2a + b = 0 . Chọn A. 4
Câu 11: Cho hàm số f ( x) có đạo hàm trên đoạn [1;4] và f ( )
1 = 2; f (4) = 10. Tính I = ∫ f '( x) d . x 1 A. I = 48. B. I = 3. C. I = 8. D. I = 12. 4
HD: Ta có I = f ( x) = f (4) − f ( ) 1 = 8. Chọn C 1
Câu 12: Biết F ( x) là một nguyên hàm của hàm số f ( x) 1 =
và F (6) = 4. Tính F (10). x − 5
A. F (10) = 4 + ln 5.
B. F (10) = 5 + ln 5. C. F ( ) 21 10 = . D. F ( ) 1 10 = . 5 5
HD: Ta có F ( x) 1 = ∫
dx = ln x − 5 + C. x − 5
Mà F (6) = 4 ⇒ ln1+ C = 4 ⇒ C = 4 ⇒ F (10) = ln 5 + 4. Chọn A 6 3
Câu 13: Cho ∫ f ( x) dx = 20. Tính I = ∫ f (2x) d . x 0 0 A. I = 40. B. I = 10. C. I = 20. D. I = 5. 6 6 6  t  1 1 1
HD: Đặt 2x = t ⇒ I = ∫ f (t ) d   = ∫ f (t ) dt = ∫ f ( x) dx = .20 = 10. Chọn B  2  2 2 2 0 0 0 6 4
Câu 14: Cho hàm số f ( x) liên tục trên đoạn [0;6] thỏa mãn ∫ f ( x) dx = 10 và ∫ f ( x) dx = 6. Tính giá trị 0 2 2 6
của biểu thức P = ∫ f ( x) dx + ∫ f ( x) d . x 0 4
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 A. P = 4. B. P = 16. C. P = 8. D. P = 10. 2 4 6 4 6 6
HD: Ta có P + 6 = ∫ f ( x) dx + ∫ f ( x) dx + ∫ f ( x) dx = ∫ f ( x) dx + ∫ f ( x) dx = ∫ f ( x) dx = 10 ⇒ P = 4. 0 2 4 0 4 0 Chọn A 5 dx Câu 15: Biết ∫
= a ln 2 + bln 5, với a, b là hai số nguyên. Tính 2 2
P = a + 2ab + 3b . 2 x − x 2 A. P = 18. B. P = 6. C. P = 2. D. P = 11. 5 5 5 5 5 dx 1  1 1  HD: Ta có ∫ = ∫ dx = ∫
− dx = ln x −1 − ln x 2 x − x x x −1  x −1 x  2 2 ( ) 2 2 2 = − ( − ) a = 3 ln 4
ln 5 ln 2 = 3ln 2 − ln 5 ⇒ 
⇒ P = 6. Chọn B b  = 1 − 4 2x −1
Câu 16: Biết I = ∫
dx = a ln 3 + b ln 2 , với a;b là các số nguyên. Giá trị của biểu thức 2 2
A = a + b là: 2 x − x 2 A. A = 2 B. A = 5 C. A = 10 D. A = 20 d ( 2 4 x − x) 4 HD: Ta có: 2 I = ∫
= ln x − x = ln12 − ln 2 = ln 6 = ln 3+ ln 2 ⇒ a = b =1⇒ A = 2 . Chọn A. 2 x − x 2 2 e 2 ln x +1 b b
Câu 17: Biết rằng I = ∫ =
− , với a,b,c là các số nguyên dương và là phân số tối x ( dx a ln x + ) ln 2 2 1 c c 1
giản. Tính S = a + b + c A. S = 3 B. S = 5 C. S = 7 D. S = 10 1 1   dx 2t +1 2 1
HD : Đặt t = ln x ⇒ dt = ⇒ I = ∫ =  ∫ −  x (   t + ) dt dt 2 1 t +1  (t + )2 1 0 0  1  1  1 a = 2;b = 1 = 2ln t +1 + = 2ln 2 − ⇒  ⇒ S = 5   . Chọn B. t +1 2 c = 2 0 4 a a
Câu 18: Biết rằng I = ∫ x ln (2x + ) 1 dx =
.ln 3 − c ; với a,b, c là các số nguyên dương và là phân số tối b b 0
giản. Tính S = a + b + c . A. S = 60 B. S = 68 C. S = 70 D. S = 64  2 du = u  ln (2x )1  = +  2x +1 HD: Đặt  ⇒  2 2 dv = xdxx 1 4x −1 v = − =  2 8 8 2 4 4 2 4 4x −1 2x −1 63  x x  63 a = 63;b = 4 Khi đó I = ln (2x + ) 1 − ∫ dx = ln 9 −  −  = ln 3 − 3 ⇒  8 4 8  4 4  4 c = 3 0 0 0
Do đó S = 70 . Chọn C. π π 2 2
Câu 19: Biết rằng I = ∫ cos .
x f (sin x) dx = 8 . Tính K = ∫ sin .
x f (cos x) dx . 0 0 A. K = 8 − B. K = 4 C. K = 8 D. K = 16
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 π π x = 0 ⇒ t = 2 HD: Đặt t =
− x ⇒ dx = −dt . Đổi cận . 2 π x = ⇒ t = 0 2 π π 0  π    π 
⇒ I = ∫ cos −t f sin  
− t (−dt) 2
= ∫sint. f (cost) 2 dt = ∫ sin .
x f (cos x) dx = 8 . Chọn C.  2    2 π  0 0 2 a Câu 20: Cho hàm số ( ) = . x f x
a e + b có đạo hàm trên đoạn [0;a] , f (0) = 3a và ∫ f '( x) = e −1. Tính giá trị 0 của biểu thức 2 2
P = a + b . A. P = 25 B. P = 20 C. P = 5 D. P = 10 a HD: Ta có f ( ) 0 0 = 3a ⇒ .
a e + b = 3a ⇔ b = 2a . Mặt khác ∫ f '( x) = e + 2 ⇒ f (a) − f (0) = e + 2 . 0
⇔ . a + − 3 = −1 ⇔ . a − = −1 ⇔ .( a a e b a e a e a e a e − )
1 − e +1 = 0 ⇒ a = 1 ⇒ b = 2 ⇒ P = 5 . Chọn C. 9 3
Câu 21: Biết rằng f ( x) là hàm liên tục trên ℝ và T = ∫ f ( x) dx = 9 . Tính D =  ∫ f
 (3x) + T dx  . 0 0 A. D = 30 B. D = 3 C. D = 12 D. D = 27 3 3 3 3 3 3 HD: Xét D =  ∫ f
 (3x) + T dx
= ∫ f (3x)dx + ∫T dx = ∫ f (3x)dx +9∫ dx = ∫ f (3x)dx + 27 . 0 0 0 0 0 0 3 9 9 dt dt 1 T
Đặt t = 3x ⇒ dx =
⇒ ∫ f (3x)dx = ∫ f (t). = .∫ f (t)dt = = 3 . Do đó D = 30 . Chọn A. 3 3 3 3 0 0 0 3
Câu 22: Kết quả của tích phân I = ∫ ln ( 2
x − x)dx được viết ở dạng I = .
a ln 3 − b với a,b là các số nguyên. 2
Khi đó a − b nhận giá trị nào sau đây ? A. −2 B. 3 C. 1 D. 5  x − u
 = ln ( 2x − x) 2 1 3 3 du = dx 2x −1 HD: Đặt 2  ⇔  x − x ⇒ I = . x ln ( 2 x − x) − ∫
dx = 3.ln 6 − 2.ln 2 − D . 2  x  =  −1 dv dx 2 v = x 3 3   3 2x −1 1 a = 3 Xét D = ∫ dx = ∫  2 +
dx = (2x + ln x −1 ) = 2 + ln 2 ⇒ I = 3.ln 3 − 2 ⇒  . Chọn D. 2 x −1  x −1  b  = −2 2 2 a 1
Câu 23: Cho I = ∫ (2x − 3).ln ( x − ) 1 dx biết rằng .
a ∫ dx = 4 và I = (a + b).ln (a − )
1 , giá trị của b bằng : 0 0 A. b = 1 B. b = 4 C. b = 2 D. b = 3 . 1 4 1 HD: Ta có .
a ∫ dx = 4 ⇔ (ax) = 4 ⇔ a = 4 ⇒ I = ∫ (2x − 3)ln ( x − ) 1 dx . 0 0 0  dx u  = ln (x − ) 1 du = 4 4 Đặt  ⇔  − . Khi đó I = ( 2
x − 3x + 2)ln ( x − ) 1
− ∫(x − 2)dx = 6.ln3 . dv  = ( x − ) x 1 2 3 dx  0 2
v = x − 3x + 2 0
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95
Do đó I = (a + b).ln (a − )
1 = 6.ln 3 ⇔ a + b = 6 ⇔ b = 2 . Chọn C. a x e 2a dx
Câu 24: Cho a là một số thực khác 0 , ký hiệu b = ∫
dx . Tính I = ∫
theo a và b . x + 2a 3 x a − x e 0 ( ) −a b A. a B. C. b D. a e .b a e 3
a − x = t + 2a
x = 0 → t = a −a dt
HD: Đặt t = a − x ⇔  và đổi cận  . Khi đó I = − ∫ . dx = − dt
x = 2a → t = −a
(t + 2a) a−t e a a t a x e e a x ⇒ e b I = ∫ ( dt = ∫ dx mà b = ∫ dx ⇒ I = . Chọn B. t + 2a) a e + a + − ( x 2a ) a e − x 2a e a a −a
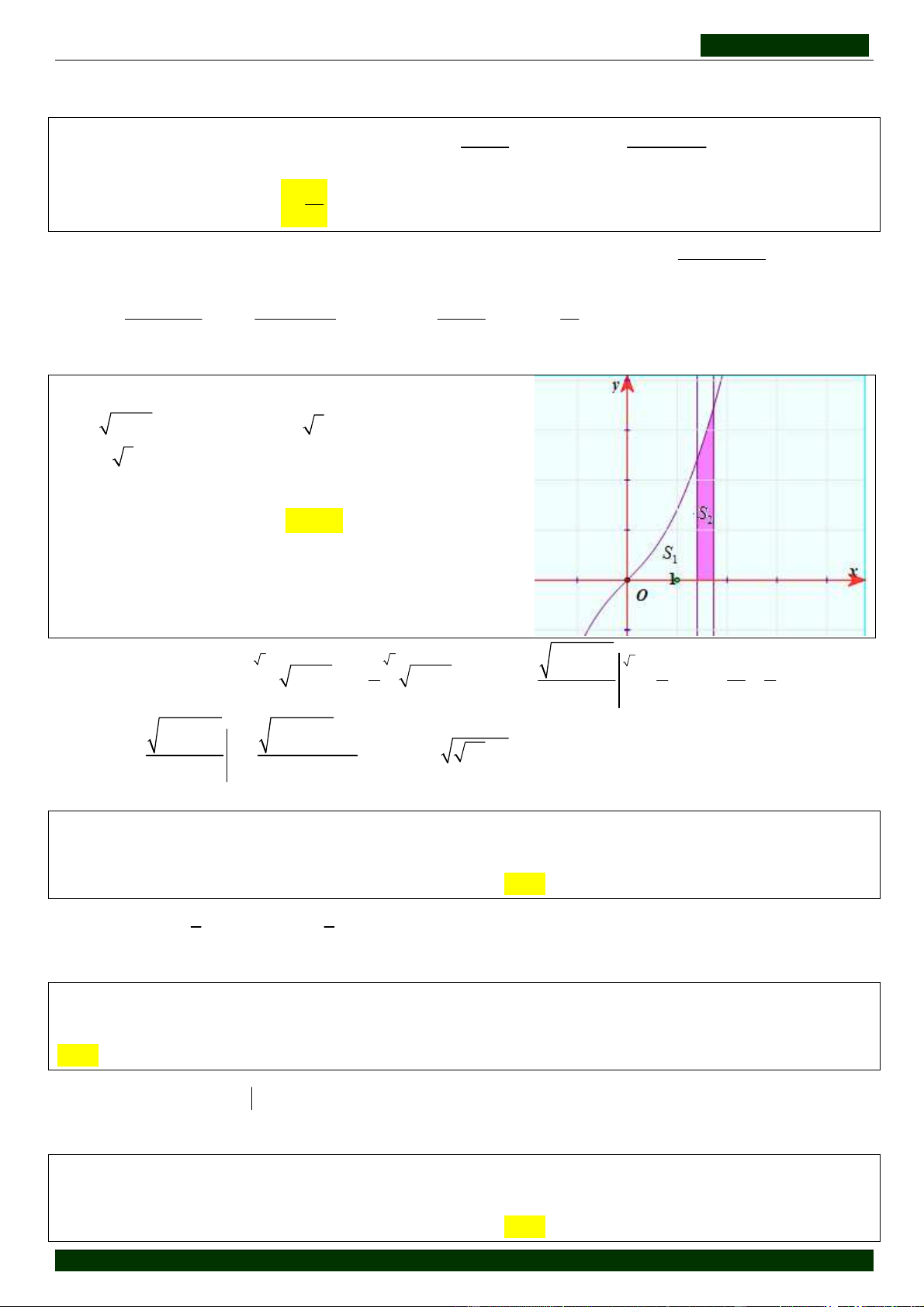
Câu 25: Cho hình cong ( H ) giới hạn bởi các đường 2
y = x x +1; y = 0; x = 0 và x = 3 . Đường thẳng x = k với
1 < k < 3 chia ( H ) thành 2 phần có diện tích là S và S 1 2
như hình vẽ bên. Để S = 6S thì k gần bằng 1 2 A. 1, 37 B. 1, 63 C. 0, 97 D. 1, 24 x +1 1 7 S 7
HD: Ta có: S = S + S = ∫ x x +1dx = ∫ x +1d (x + ) ( )3 2 3 3 3 2 2 2 1 1 = = ⇒ S + = ⇒ S = 2 . 1 2 1 1 2 3 3 6 3 0 0 0 ( + )3 1 k x (k + )3 2 2 1 −1 Lại có 3 S = = = 2 ⇒ k =
49 −1 ≈ 1, 63 . Chọn B. 1 3 3 1 9 3
Câu 26: Biết rằng hàm số y = f (x) liên tục trên ℝ và ∫ f (x)dx = 9. Khi đó, giá trị của ∫ f (3x)dx là: 0 0 A. 1. B. 2. C. 3. D. 4. 3 3 9 1 1
HD: ∫ f (3x)dx = ∫ f (3x)d (3x) = ∫ f (x)dx = 3 . Chọn C. 3 3 0 0 0 2017π
Câu 27: Tích phân ∫ sin xdx bằng: 6π A. 2. B. −1. C. 0. D. 1. 2017π 2017π
HD: ∫ sin xdx = − cos x = 2 . Chọn A. 6π 6π 2
Câu 28: Có bao nhiêu số thực a thỏa mãn 3 ∫ x dx = 2? a A. 0. B. 1. C. 2. D. 3.
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 2 2 4 4 x a HD: 3 4 4 2 = ∫ x dx = = 4 −
⇔ a = 8 ⇔ a = ± 8 . Chọn C. 4 4 a a a
Câu 29: Có bao nhiêu số thực a ∈ (0;2017) sao cho ∫ sin xdx = 0? 0 A. 301. B. 311. C. 321. D. 331. a a
HD: ∫ sin xdx = − cos x = − cos a +1 = 0 ⇔ cos a = 1 ⇔ a = k2π với k ∈ ℤ 0 0
Vì a = k 2π ∈(0; 2017) ⇔ 0 < k ≤ 321. Có tất cả 321 giá trị k ứng với 321 giá trị a thỏa mãn. Chọn C. 1 3x −1 a 5 a
Câu 30: Biết rằng ∫ dx = 3ln
− trong đó a,b là hai số nguyên dương và là phân số tối 2 x + 6x + 9 b 6 b 0
giản. Khi đó ab bằng: A. 5. B. 12. C. 6. D. 8. a 5 3x −1 3( x + 3) 1 1 1 1 1 −10 dx dx  10  HD: Ta có 3ln − = ∫ dx = ∫ dx =3∫ −10∫ = 3ln x + 3 +  2 b 6 x + 6x + 9 x + 3 x + 3 x + 3  x + 3  0 0 ( )2 0 0 ( )2 0 a = = 3ln (4) 5 + − 3ln (3) 10 4 5 4 − = 3ln − ⇒ 
⇒ ab =12 . Chọn B. 2 3 3 6 b  = 3 1  1 1  1 a a
Câu 31: Biết rằng ∫  −
dx = ln trong đó a,b là hai số nguyên dương và là phân số tối
 2x +1 3x +1 6 b b 0
giản. Khẳng định nào sau đây là sai?
A. 3 a + b = 7.
B. a + b < 22.
C. 4a + 9b > 251.
C. a − b > 10.  1 1  1 d (2x + ) 1 1 d (3x + ) 1 1 1 1 1
 ln 2x +1 ln 3x +1  HD: Ta có ∫  −  dx = ∫ − ∫ =  − 
 2x +1 3x +1 2 2x +1 3 3x +1  2 3  0 0 0 0 ln (3) ln (4) 3 3 1 3 1 a a = 3 = − = ln = ln ⇔  Chọn B. 2 2 2 3 6 4 6 b b  = 4 x
Câu 32: Số nào sau đây gần bằng nghiệm của phương trình t 2017
∫e dt = 2 −1 (ẩn x)? 0 A. 1395. B. 1401. C. 1398. D. 1404. x x HD: 2017 t t x x 2017 2
−1 = ∫e dt = e = e −1⇔ e = 2 ⇔ x = ln( 2017 2
= 2017 ln 2 ≈ 1398. Chọn C. 0 ) 0 x
Câu 33: Biết rằng hàm số y = f (x) có đạo hàm liên tục trên ℝ và có f (0) = 1. Khi đó ∫ f '(t ) dt bằng: 0
A. f ( x) +1.
B. f ( x + ) 1 .
C. f ( x).
D. f ( x) −1. x x
HD: ∫ f '(t ) dt = f (t) = f ( x) − f (0) = f ( x) −1. Chọn D. 0 0
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!
Chinh phục NGUYÊN HÀM – TÍCH PHÂN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 3 a
Câu 34: Xét tích phân 5 2
I = ∫ x x +1dx = là một số phân số tối giản. Tính hiệu a − b . b 0 A. 743 B. – 64 C. 27 D. – 207 x = 0 ⇒ t = 1 HD: Đặt 2 2 2
t = x +1 ⇒ t = x +1 ⇒ tdt = xdx . Đổi cận x = 3 ⇒ t = 2 2 2 7 5 3 2 2  t t t  848 a Khi đó I = ∫ ( 2 t − ) 2 1 .t dt = ∫ ( 6 4 2
t − 2t + t ) dt =  − 2 +  = =  7 5 3  105 b 1 1 1
Suy ra a − b = 743 . Chọn A. e 3 a e + 1
Câu 35: Khẳng định nào sau đây đúng về kết quả 3 ∫ x ln xdx = ? b 1 A. . a b = 64 B. . a b = 46
C. a − b = 12
D. a − b = 4  dx du =  4 e e 3 4 4 4 u  = ln xx x ln x x e
e −1 3e +1 HD: Đặt  ⇒  ⇒ I = − ∫ dx = −  = 3 4 dv = x dxx 4 4 4  16  16 1 1 v =  4
Do đó a = 4;b = 16 ⇒ ab = 64 . Chọn A.
Tham gia các khóa Chinh phục; Luyện đề; Về đích Toán tại MOON.VN : Tự tin hướng đến kì thi THPT Quốc Gia 2017!