Bộ đề kiểm tra giữa học kỳ 2 Toán 11 Kết nối tri thức (có đáp án)

Bộ đề kiểm tra giữa học kỳ 2 Toán 11 Kết nối tri thức có đáp án được soạn dưới dạng file word và PDF gồm 11 trang với 38 câu hỏi giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

50 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

11 trang 8 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
ĐỀ ÔN TẬP GIỮA HỌC KỲ II-ĐỀ 1
MÔN TOÁN - KHỐI LỚP 11
A. CÂU HỎI TRẮC NGHIỆM (7,0 điểm):
Câu 1 (NB): Cho là hai số thực dương và là hai số thực tùy ý. Đẳng thức nào sau đây sai?
A. B. C. D.
Câu 2 (NB): Cho các số thực . Khẳng định nào sau đây là đúng?
A. . B. . C. . D. .
Câu 3 (TH): Với là số thực dương tùy ý, bằng
A. . B. . C. . D. .
Câu 4 (NB): Với mọi số thực dương , , , và , mệnh đề nào sau đây sai?
A. . B. .
C. . D. .
Câu 5 (NB): Với a là số thực dương tùy ý, bằng
A. 7 B. 2 C. D. +
Câu 6 (TH): Với là số thực dương tùy ý, bằng
A. . B. . C. . D. .
Câu 7 (NB): Trong các hàm số sau, hàm số nào không phải là hàm số mũ?
A. B. C. D.
Câu 8 (NB): Trong các hàm số sau, hàm số nào không phải là hàm số logarit?
A. B. C.
D.
Câu 9 (TH): Cho hàm số có đồ thị như hình vẽ:
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên
D. Hàm số đồng biến trên
Câu 10 (TH): Cho hàm số có đồ thị như hình vẽ:
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên
D. Hàm số đồng biến trên
,xy
,mn
mn
m
n
xx
yy
-
æö
=
ç÷
èø
( )
n
nn
xy x y=
( )
.
m
nnm
xx=
( )
,, , , 0abmn ab>
.
mn mn
aa a
+
=
( )
n
mmn
aa
+
=
( )
m
mm
ab a b+=+
m
n
m
n
a
a
a
=
a
1
4
2
.aa
8
a
2
a
7
2
a
9
2
a
a
b
x
y
,1ab¹
( ) ( ) ( )
log log log
aaa
xy x y=
( )
log log log
aaa
xy x y=+
log
a
b
ab=
log log log
aaa
x
xy
y
=-
2
7
log a
2
log a
7
log a
1
2
7
log a
1
2
2
log a
a
( )
3
log 3 a
3
3loga-
3
1loga-
3
3loga+
3
1loga+
2
8.
x
y =
2.
x
y
-
=
2
.yx
-
=
lg .yx=
3
log .yx=
ln .yx=
(3)ln2.yx=+
x
ya=
( )
01a<¹
( )
0; .+¥
( )
0; .+¥
( )
01a<¹
( )
0; .+¥
( )
0; .+¥
x
y
1
2
2
O
Trang 2
Câu 11 (NB): Nghiệm của phương trình là
A. . B. . C. . D.
.
Câu 12 (NB): Nghiệm của phương trình là
A. B. C. D.
Câu 13 (TH): Phương trình có nghiệm là
A. . B. . C. . D. .
Câu 14 (TH): Nghiệm phương trình .
A. . B. . C. . D. .
Câu 15 (NB): Góc giữa hai đường thẳng bất kỳ trong không gian là góc giữa:
A. Hai đường thẳng cùng đi qua một điểm và tương ứng song song với hai đường thẳng đó.
B. Hai đường thẳng lần lượt vuông góc với hai đường thẳng đó.
C. Hai đường thẳng cắt nhau và không song song với hai đường thẳng đó.
.
D. Hai đường thẳng cắt nhau và tương ứng vuông góc với hai đường thẳng đó.
Câu 16 (NB): Cho hình hộp có các mặt là hình chữ nhật ( như hình vẽ)
. Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 17 (NB): Trong không gian cho đường thẳng d và điểm . Qua có bao nhiêu đường thẳng vuông
góc với d ?
A.
3.
B.
Vô số.
C.
1.
D.
2.
Câu 18 (NB): Cho hình chóp có đáy ABCD là hình chữ nhật và . Tìm hình
chiếu vuông góc của điểm S trên mặt phẳng ( ABCD) ?
A.C. B.D. C.A. D. B.
Câu 19 (TH): Cho hình chóp có đáy ABCD là hình chữ nhật và .
. Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 20 (TH): Cho hình chóp có đáy là hình vuông, vuông góc với đáy .
Tìm hình chiếu vuông góc của lên mặt phẳng (SAD).
A. . B. . C. . D. .
Câu 21 (TH): Cho hai đường thẳng phân biệt a, b và mặt phẳng (α). Mệnh đề nào sau đây đúng ?
A.Nếu a // (α) và thì . B.Nếu a // (α) và thì .
C.Nếu a // (α) và b // (α) thì b // a. D.Nếu a (α) và thì b // (α).
Câu 22 (NB): Gọi là góc giữa hai mặt phẳng và . Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 23 (NB): Cho phát biểu sau?
(1) Hai mặt phẳng (P) và (Q) có giao tuyến là đường thẳng a và cùng vuông góc với mặt phẳng
(R) thì .
(2) Hai mặt phẳng (P) và (Q) vuông góc với nhau và có giao tuyến là đường thẳng a một đường
thẳng b nằm trong mặt phẳng (P) và vuông góc với đường thẳng a thì .
(4) Mặt phẳng (P) chứa đường thẳng a và a vuông góc với (Q) thì .
72
x
=
2
7
x =
7x =
9x =
5x =
6x =
8x =
21
33
x-
=
1x =
0x =
1
2
x =
2x =
( )
3
log 1 2x -=
7x =
9x =
8x =
10x =
.ABCD A B C D
¢¢¢¢
C'
B'
C
D
B
D'
A'
A
AC B D
¢¢
^
AA CD
¢¢
^
AB CD
¢¢
^
CD A D
¢¢
^
O
O
.S ABCD
()SA ABCD^
.S ABCD
()SA ABCD^
()AC SAB^
()SC SAB^
()AB SAD^
()BD SAB^
.S ABCD
SA
( )
ABCD
SC
SD
SA
AD
AC
()b
a
^
ab^
ba^
b
a
^
^
ba^
j
()P
()Q
090
j
°£ £ °
090
j
°< < °
0180
j
°£ £ °
0180
j
°< < °
().aR^
().bQ^
() ().PQ^
Trang 3
(5) Đường thẳng a nằm trong mặt phẳng (P) và mặt phẳng (P) vuông góc với mặt phẳng (Q) thì
Số phát biểu đúng trong các phát biểu trên.
A.1. B.2. C.3. D.4.
Câu 24 (TH): Cho hình chóp S.ABCD có đáy ABCD là hìn bình hành, SA ^ (ABCD). Mệnh đề nào sau đây đúng?
A. (SAC) ^ (ABCD) B. (SBC) ^ (ABCD) C. (SCD) ^ (ABCD). D. (SBD) ^ (ABCD).
Câu 25 (TH): Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.
B. Hình lăng trụ đứng có các mặt bên là hình chữ nhật và vuông góc với mặt đáy.
C. Hình lăng trụ đứng có các mặt là hình chữ nhật gọi là hình lập phương.
D. Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ đều.
Câu 26 (NB):Cho hình chóp tam giác có đáy ABC là tam giác vuông tại B, SA ^ (ABC) . Đường
thẳng nào sau đây là đường vuông góc chung của hai đường thẳng SA và ?
A. AC. B. BC. C. SC. D. AB.
Câu 27 (TH):Cho hình hộp chữ nhật . Khoảng cách giữa hai mặt phẳng và
bằng
A. . B. . C. . D. .
Câu 28 (NB):Gọi là góc giữa đường thẳng a và mặt phẳng . Khẳng định nào sau đây đúng?
A. B. . C. . D. .
Câu 29 (NB):Cho hai nửa mặt phẳng và có chung bờ . Gọi là góc phẳng nhị diện
. Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 30 (NB): Cho hình chóp có đáy là hình vuông và . Góc nào sau đây là
góc giữa đường thẳng và mặt phẳng ?
A. . B. . C. . D.
Câu 31 (TH): Cho hình chóp tứ giác đều .Phát biểu nào sau đây đúng?
A.Số đo của góc nhị diện [S,AB,B] bằng . B. Số đo của góc nhị diện [D,SA,B] bằng .
C. Số đo của góc nhị diện [S,AC,B] bằng . D. Số đo của góc nhị diện [D,SA,B] bằng .
Câu 32 (TH): Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, cạnh bên SA vuông góc với đáy. Biết
, . Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng?
A. . B. . C. . D. .
Câu 33 (NB): Thể tích của khối lăng trụ có diện tích đáy S và chiều cao là
A. . B. . C. . D. .
Câu 34 (NB): Cho hình chóp cụt đều. Khẳng định nào sau đây đúng SAI?
A. Mỗi mặt bên là một hình thang cân. B. Đáy lớn và đáy nhỏ nằm trên hai mặt phẳng song song..
C. Có các cạnh bên bằng nhau . D. Mỗi mặt bên là một hình thang.
Câu 35 (TH): Thể tích của khối hình hộp chữ nhật có chiều dài ba cạnh 2,3,4 là.
A.8. B. 24. C.12. D.6.
B. CÂU HỎI TỰ LUẬN (3,0 điểm):
Câu 1: (1,0 điểm) Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và có cạnh SA
vuông góc với mặt phẳng (ABC).
a/ Chứng minh
b/ Gọi AH là đường cao của tam giác SAB. Chứng minh
().aQ^
.S ABC
BC
.ABCD A B C D
¢¢¢¢
( )
ABCD
( )
ABCD
¢¢¢¢
AC
¢
AB
¢
AD
¢
AA
¢
j
()P
090
j
°£ £ °
090
j
°< < °
0180
j
°£ £ °
0180
j
°< < °
()P
()Q
a
j
[,, ]PaQ
0180
j
°£ £ °
090
j
°< < °
090
j
°£ £ °
0180
j
°< < °
.S ABCD
()SA ABCD^
SB
()SAB
∑
ASD
∑
ASC
∑
ASB
∑
ABS
.S ABCD
∑
SBC
0
90
0
90
∑
BSD
3
3
a
SA =
AB a=
0
30
0
45
0
60
0
90
h
3Sh
Sh
4
3
Sh
1
3
Sh
()BC SAB^
Trang 4
Câu 2: (1,0 điểm): Cho hình chóp có đáy ABCD là hình vuông cạnh a. SA vuông góc với
mặt phẳng đáy, Tính thể tích của khối chóp theo a.
.
Câu 3: (1,0 điểm): Giả sử sự tăng trưởng của một loại vi khuẩn trong quá trình nuôi cấy tuân theo
công thức N(t)= , trong đó là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là
thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 500 con và sau 2 giờ có 1500 con. Hỏi
sau bao lâu thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi?
……………………………………………Hết……………………………………………………..
HƯỚNG DẪN CHẤM
Câu hỏi
Lời giải
Điểm
Câu 1
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và có
cạnh SA vuông góc với mặt phẳng (ABC).
a/ Chứng minh
b/ Gọi AH là đường cao của tam giác SAB. Chứng minh
1,0 đ
a/ Vì nên
ta có
từ đó suy ra
0,25 đ
0,25 đ
b/ Vì và AH nằm trong (SAB) nên .
Ta lại có nên
Từ đó suy ra
0,25 đ
0,25đ
Câu 2
Cho hình chóp có đáy ABCD là hình vuông cạnh a. SA vuông
.SABCD
3.SA a=
0
.
rt
Ne
0
N
()BC SAB^
H
C
B
A
S
()SA ABC^
SA BC^
,.BC SA BC AB^^
(SAB)BC ^
(SAB)BC ^
,AH BC AH SB^^
(SBC).AH ^
SC.AH ^
.SABCD
Trang 5
góc với mặt phẳng đáy, Tính thể tích của khối chóp theo a.
Diện tích mặt đáy hình vuông:
Thể tích khối chóp:V= (đvtt)
1,0 đ
Câu 3
Giả sử sự tăng trưởng của một loại vi khuẩn trong quá trình nuôi cấy
tuân theo công thức N(t)= , trong đó là số lượng vi khuẩn ban
đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng
số lượng vi khuẩn ban đầu là 500 con và sau 2 giờ có 1500 con. Hỏi sau
bao lâu thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi?
1,0 đ
Tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này là:
Ta có:
0,5đ
Thời gian để số lượng vi khuẩn ban đầu tăng gấp đôi là:
(giờ)
0,5đ
ĐỀ ÔN TẬP GIỮA HỌC KỲ II-ĐỀ 2
MÔN TOÁN - KHỐI LỚP 11
A. CÂU HỎI TRẮC NGHIỆM (7,0 điểm):
Câu 1 (NB): Cho số nguyên m, số dương a và số tự nhiên n . Trong các tính chất sau, tính
chất nào đúng ?
A. B. C. D.
Câu 2 (NB): Cho là hai số thực dương và là hai số thực tùy ý. Đẳng thức nào sau đây là
sai?
A.
.
B.
C. D.
.
Câu 3 (TH): Với là số thực dương tùy ý, bằng
A. B. C. D.
3.SA a=
2
.
ABCD
Saaa==
3
3
3
a
0
.
rt
Ne
0
N
22
ln 3
1500 500. 3 2 l n 3
2
rr
ee r r=Û=Û=Û=
00
2 . 2 ln 2 1,16
rt rt
N N e e rt t=Û=Þ=Þ»
(2)n ³
.
m
m
n
n
aa=
.
n
m
n
m
aa=
.
.
mmn
n
aa=
.
mmn
n
aa
-
=
,xy
,mn
.
mn mn
xx x
+
=
( )
...
n
nn
xy x y=
( )
.
m
nnm
xx=
( )
.
mn
mn
xy xy
+
=
a
1
2
3
.aa
2
3
.a
7
3
.a
5
3
.a
4
3
.a
Trang 6
Câu 4 (TH): Rút gọn biểu thức với b > 0.
A. B. C.
D.
Câu 5 (NB): Trong các mệnh đề sau, mệnh đề nào đúng?
A. với mọi số thực dương và .
B. với mọi số thực dương .
C. với mọi số thực .
D. với mọi số thực và .
Câu 6 (TH): Với mọi số thực dương bằng
A. . B. . C. . D. .
Câu 7 (TH): Cho và , khi đó bằng
A. . B. . C. . D. .
Câu 8 (NB): Trong các hàm số sau, hàm số nào là hàm số logarit?
A. B. C.
D.
Câu 9 (NB): Trong các hàm số sau, hàm số nào không phải là hàm số mũ?
A. B. C. D.
Câu 10 (NB): Hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. . B. . C. . D. .
Câu 11 (TH): Cho hàm số có đồ thị như hình vẽ:
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R. B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên D. Hàm số đồng biến trên
Câu 12 (TH): Nghiệm của phương trình là
( )
2
31
23
b:b
-
-
.b
2
.b
3
.b
4
.b
log log
aa
bb
a
a
=
,ab
1a ¹
log log
aa
bb
a
a
=
,ab
log log
aa
bb
a
a
=
,ab
log log
aa
bb
a
a
=
,ab
1a ¹
( )
4
,log 4aa
4
1loga+
4
1loga-
4
log a
4
4log a
0a >
1a ¹
4
log
a
a
4
1
4
1
4
-
4-
lg
2.
x
y =
3
log .yx=
ln 3
.yx=
(3)ln2.yx=+
2.
x
y =
2
2
.
3
x
y
æö
=-
ç÷
èø
2.
x
y
-
=
2
.yx
-
=
1
2
x
y
æö
=
ç÷
èø
2
x
y =
1
2
logyx=
( )
01a<¹
x
y
1
2
2
O
( )
0; .+¥
( )
0; .+¥
( )
2
log 4 3x +=
O
x
y
1
Trang 7
A. . B. . C. . D. .
Câu 13 (TH): Nghiệm của phương trình là
A. . B. . C. . D. .
Câu 14 (NB): Góc giữa hai đường thẳng bất kỳ trong không gian là góc giữa:
A. Hai đường thẳng cắt nhau và không song song với chúng
.
B. Hai đường thẳng lần lượt vuông góc với chúng.
C. Hai đường thẳng cùng đi qua một điểm và lần lượt song song với chúng.
D. Hai đường thẳng cắt nhau và lần lượt vuông góc với chúng.
Câu 15 (NB): Cho hình hộp có các mặt là hình chữ nhật. Khẳng định nào sau đây
đúng?
A. . B. . C. . D. .
Câu 16 (NB): Cho hình chóp có đáy ABCD là hình chữ nhật và . Khẳng định
nào sau đây đúng?
A. . B. . C. . D. .
Câu 17 (NB): Thể tích của khối chóp có diện tích đáy B và chiều cao h là
A. . B. . C. . D. .
Câu 18 (NB): Thể tích của khối lăng trụ có diện tích đáy và chiều cao là
A. . B. . C. . D. .
Câu 19 (TH): Cho đường thẳng vuông góc với mặt phẳng và đường thẳng khác . Chọn
khẳng định sai trong các khẳng định sau:
A. Đường thẳng thì . B. Đường thẳng thì .
C. Đường thẳng thì . D. Đường thẳng thì .
Câu 20 (TH): Cho tứ diện có cạnh , , đôi một vuông góc. Gọi là chân
đường vuông góc hạ từ tới thì:
A. là trọng tâm tam giác . B. là tâm đường tròn ngoại tiếp tam giác
.
C. là tâm đường tròn nội tiếp tam giác . D.
là trực tâm tam giác .
Câu 21 (NB): Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng vuông góc thì chúng cắt nhau.
B. Hai mặt phẳng cắt nhau thì không vuông góc.
C. Hai mặt phẳng vuông góc thì góc của chúng bằng .
D. Hai mặt phẳng có góc bằng thì chúng vuông góc.
Câu 22 (NB): Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc
với mặt phẳng kia.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Cả ba mệnh đề trên đều sai.
Câu 23 (NB): Gọi là góc giữa hai mặt phẳng và . Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 24 (TH): Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy.
B. Hình lăng trụ đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.
5x =
4x =
2x =
12x =
3x =
2x =
1x =
1x =-
.ABCD A B C D
¢¢¢¢
AC B D
¢¢
^
AA CD
¢¢
^
AB CD
¢¢
^
CD A D
¢¢
^
.S ABCD
()SA ABCD^
()AC SAB^
()SC SAB^
()AD SAB^
()BD SAB^
1
3
VBh=
3VBh=
VBh=
B
h
3Bh
Bh
4
3
Bh
1
3
Bh
d
( )
a
D
d
// dD
( )
a
D^
// dD
( )
//
a
D
( )
//
a
D
dD^
( )
a
D^
// dD
OABC
3
OA
OB
OC
H
O
()ABC
H
ABC
H
ABC
H
ABC
H
ABC
90°
90°
j
()P
()Q
090
j
°£ £ °
090
j
°< < °
0180
j
°£ £ °
0180
j
°< < °
Trang 8
C. Hình hộp có các cạnh bằng nhau gọi là hình lập phương.
D. Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ đều.
Câu 25 (TH): Cho hình lập phương . Góc giữa hai mặt phẳng và
bằng?
A. . B. . C. . D. .
Câu 26 (TH): Cho hình chóp có đáy là hình vuông cạnh bằng ,
. Gọi là góc giữa mặt phẳng và . Mệnh đề nào dưới đây là
đúng?
A. . B. . C. . D. .
Câu 27 (NB): Cho hình lập phương cạnh a. Đường thẳng nào sau đây là đường
vuông góc chung của hai đường thẳng và ?
A. . B. . C. . D. .
Câu 28 (NB): Cho hình chóp có đáy ABCD là hình chữ nhật và . Đường
thẳng nào sau đây là đường vuông góc chung của hai đường thẳng và ?
A. . B. . C. . D. .
Câu 29 (TH): Cho hình lập phương cạnh a. Khoảng cách giữa hai đường thẳng
và bằng
A. . B. . C. . D. .
Câu 30 (TH): Cho hình lập phương có cạnh bằng . Tính khoảng từ điểm đến
mặt phẳng .
A. . B. . C. . D. .
Câu 31 (NB): Cho hình chóp có đáy là hình vuông và . Góc nào sau đây là
góc giữa đường thẳng và mặt phẳng ?
A. . B. . C. . D. .
Câu 32 (NB): Cho hai nửa mặt phẳng và có chung bờ . Gọi là góc phẳng nhị diện
. Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 33 (TH): Cho hình chóp có đáy là tam giác cân tại , , mặt bên
là tam giác đều cạnh và nằm trong mặt phẳng vuông góc với đáy. Tính góc giữa đường
thẳng và mặt phẳng .
A. . B. . C. . D. .
Câu 34 (NB): Cho hình chóp cụt đều. Khẳng định nào sau đây đúng?
A. Mỗi mặt bên là một hình tam giác cân. B. Mỗi mặt bên là một hình thang cân.
C. Mỗi mặt bên là một hình chữ nhật. D. Mỗi mặt bên là một hình vuông.
Câu 35 (NB): Cho hình chóp cụt đều. Khẳng định nào sau đây sai?
A. Các cạnh bên đồng quy tại một điểm. B. Hai mặt đáy luôn song song nhau.
C. Các cạnh bên bằng nhau. D. Hai mặt đáy là các đa giác đều bằng nhau.
B. CÂU HỎI TỰ LUẬN (3,0 điểm):
Câu 1 (0,5 điểm): Ông A gửi tiết kiệm 50 triệu đồng ở ngân hàng X với lãi suất không đổi 5,5% một
năm. Bà B gửi tiết kiệm 95
triệu đồng ở ngân hàng Y với lãi suất không đổi 6,0% một năm. Hỏi sau
.ABCD A B C D
¢¢¢¢
()ACC A
¢¢
()BDD B
¢¢
45°
60°
30°
90°
.S ABCD
ABCD
2a
2SA SB SC SD a== = =
j
( )
SCD
( )
ABCD
2
tan
2
j
=
tan 3
j
=
tan 2
j
=
tan 2
j
=
.ABCD A B C D
¢¢¢¢
AB
BD
¢¢
AC
BB
¢
BD
AB
¢
.S ABCD
()SA ABCD^
SD
BC
SB
SC
CD
BD
.ABCD A B C D
¢¢¢¢
AC
BD
¢¢
2a
a
2a
3a
.ABCD A B C D
¢¢¢¢
a
B
( )
AB C
¢
2
3
a
3
2
a
3
3
a
6
3
a
.S ABCD
()SA ABCD^
SB
()SAD
∑
ASD
∑
ASC
∑
ASB
∑
ABS
()P
()Q
a
j
[,, ]PaQ
0180
j
°£ £ °
090
j
°< < °
090
j
°£ £ °
0180
j
°< < °
.S ABC
ABC
C
10AC BC a==
SAB
2a
SC
( )
ABC
30°
45°
90°
60°
Trang 9
ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn
lãi của ông
Câu 2 (2,0 điểm): Cho hình chóp có đáy ABCD là hình vuông cạnh a. SA vuông góc với
mặt phẳng đáy,
a) Tính góc giữa và mặt phẳng
.
b) Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM.
Câu 3 (0,5 điểm): Sự tăng trưởng của một loại vi khuẩn tuân theo công thức S= A.e
rt
, trong đó A là
số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số
lượng vi khuẩn ban đầu là 1000 con và sau 5 giờ có 3000 con. Hỏi sau bao nhiêu phút thì số lượng
vi khuẩn ban đầu sẽ tăng gấp đôi?
…Hết…
HƯỚNG DẪN CHẤM
Câu hỏi
Lời giải
Điểm
Câu 1
Ông A gửi tiết kiệm 50 triệu đồng ở ngân hàng X với lãi suất không đổi
5,5% một năm. Bà B gửi tiết kiệm 95
triệu đồng ở ngân hàng Y với lãi
suất không đổi 6,0% một năm. Hỏi sau ít nhất bao nhiêu năm thì tổng
số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn
lãi của ông
0,5 đ
Giả sử là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là: (triệu
đồng) và của bà B là: (triệu đồng)
0,25 đ
Để tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn
lẫn lãi của ông thì
Hay
Vậy sau 11 năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần
tổng số tiền cả vốn lẫn lãi của ông .
0,25 đ
Câu 2
Cho hình chóp có đáy ABCD là hình vuông cạnh a. SA
vuông góc với mặt phẳng đáy,
c) Tính góc giữa và mặt phẳng
.
d) Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường
thẳng AB và CM.
2đ
?A
.SABCD
3.SA a=
AC
( )
SB C
?A
( )
0nn>Î!
( )
1
50 1 0,055
n
n
S =+
( )
2
95 1 0, 06
n
n
S =+
A
( ) ( )
2.50 1 0,055 95 1 0, 06
nn
+<+
1, 055 95
1, 06 100
n
æö
Û<
ç÷
èø
1,055
1,06
95
log 11.
100
nn
æö
Û> Þ³
ç÷
èø
A
.SABCD
3.SA a=
AC
( )
SB C
Trang 10
Trong mặt phẳng kẻ
(1)
Mà (2)
Từ (1) và (2) suy ra
0,25đ
0,25đ
Suy ra hình chiếu của AC lên (SBC) là HC
0,25 đ
Xét tam giác vuông SAB ta có
0,25 đ
Xét vuông góc H có:
Vậy góc giữa đường thẳng AC và mặt phẳng (SBC) là
0,25 đ
Câu 2b
Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng
AB và CM.
Trong , kẻ đường cao AK (1)
(2)
Từ (1) và (2)
0,25đ
A
B
D
C
S
H
K
M
( )
SAB
( )
.AH SB H SB^Œ
( )
.
BC AB
BC SAB
BC SA
Ï
Ô
^
Ô
fi^
Ì
Ô
^
Ô
Ó
()BCAHAH SABÌÞ^
( )
AH SBC^
( )
( )
( )
∑
,,AC SBC AC HC ACHfi==
2222
1114 3
2
3
a
AH
AH AB SA a
=+=fi=
ACHD
∑
6
sin .
4
AH
ACH
AC
==
Þ
∑
0
37ACH ª
0
37
SADD
AK SDÞ^
()CDAK
CD AD
CD SAD
CD SA
^
ü
Þ^ Þ^
ý
^
þ
()AK SCDÞ^
Trang 11
Có AB//CD
Mà
0.5đ
Xét vuông tại A có:
Vậy khoảng cách giữa hai đường thẳng AB và CM là
0.25đ
Câu 3
Sự tăng trưởng của một loại vi khuẩn tuân theo công thức
S= A.e
rt
, trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng
trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn
ban đầu là 1000 con và sau 5 giờ có 3000 con. Hỏi sau bao nhiêu phút
thì số lượng vi khuẩn ban đầu sẽ tăng gấp đôi?
0,5 đ
Tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này là:
Ta có:
0,25đ
Thời gian để số lượng vi khuẩn ban đầu tăng gấp đôi là:
(giờ)
Vậy để số lượng vi khuẩn ban đầu tăng gấp đôi thì cần thời gian là
3,15(giờ)=189 phút.
0,25đ
/ /(SCD)ABÞ
()d(AB,CM)(,())(,())AKCM SCD d AB SCD d A SCDÌÞ = = =
SADD
22 2222
111114 3
33 2
a
AK
AK SA AD a a a
=+ =+=Þ=
3
2
a
55
ln 3
3000 1000. 3 5 l n 3
5
rr
ee r r=Û=Û=Þ=
ln 2 ln 2
2000 1000. 2 ln 2 3,15
ln 3
5
rt rt
ee rt t
r
=Û=Þ=Þ==»
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ ÔN TẬP GIỮA HỌC KỲ II-ĐỀ 1
MÔN TOÁN - KHỐI LỚP 11
A. CÂU HỎI TRẮC NGHIỆM (7,0 điểm):
Câu 1 (NB): Cho x, y là hai số thực dương và ,
m n là hai số thực tùy ý. Đẳng thức nào sau đây sai? m-n m x æ x ö m m x A. = B. ( )n n n
xy = x y C. ( n ) n.m x = x D. m-n = x n ç ÷ y è y ø n x
Câu 2 (NB): Cho các số thực , a , b , m n ( ,
a b > 0). Khẳng định nào sau đây là đúng? m a A. m. n m n a a a + = . B. ( )n m m n a a + =
. C. ( + )m m m a b
= a +b . D. n m = a . n a 1
Câu 3 (TH): Với a là số thực dương tùy ý, 4 2
a .a bằng 7 9 A. 8 a . B. 2 a . C. 2 a . D. 2 a .
Câu 4 (NB): Với mọi số thực dương a , b , x , y và a,b ¹ , m 1
ệnh đề nào sau đây sai?
A. log (xy) = log (x)log y log xy = x + y a ( ) log log a a a ( ). B. . a a x
C. loga b a
= b. D. log
= log x - log y . a a a y
Câu 5 (NB): Với a là số thực dương tùy ý, 2 log a bằng 7 1 1
A. 7 log a B. 2 log a C. log a D. + log a 2 7 2 7 2 2
Câu 6 (TH): Với a là số thực dương tùy ý, log 3a 3 ( ) bằng A. 3 - log a . B. 1- log a . C. 3 + log a . D. 1+ log a. 3 3 3 3
Câu 7 (NB): Trong các hàm số sau, hàm số nào không phải là hàm số mũ? x A. ( 2)x y = . B. 2 y = 8 . C. 2 .x y - = D. 2 y x- = .
Câu 8 (NB): Trong các hàm số sau, hàm số nào không phải là hàm số logarit? A. y = lg .
x B. y = log .
x C. y = ln . x y = (x + 3)ln 2. 3 D.
Câu 9 (TH): Cho hàm số x
y = a (0 < a ¹ )
1 có đồ thị như hình vẽ:
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên (0;+¥).
D. Hàm số đồng biến trên (0;+¥).
Câu 10 (TH): Cho hàm số y = log x (0 < a ¹ )
1 có đồ thị như hình vẽ: a
Khẳng định nào sau đây là đúng? y
A. Hàm số nghịch biến trên R. 2
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên (0;+¥). O x 1 2
D. Hàm số đồng biến trên (0;+¥). Trang 1
Câu 11 (NB): Nghiệm của phương trình 7x = 2 là 2
A. x = log 2 .
B. x = log 7 . C. x = . D. 7 2 7 x = 7 .
Câu 12 (NB): Nghiệm của phương trình log x = 2 là 3
A. x = 9
B. x = 5
C. x = 6 D. x = 8
Câu 13 (TH): Phương trình 2x 1 3 - = 3 có nghiệm là 1 A. x = 1 .
B. x = 0 .
C. x = . D. x = 2 . 2
Câu 14 (TH): Nghiệm phương trình log x -1 = 2 3 ( ) .
A. x = 7 .
B. x = 9 .
C. x = 8 . D. x = 10 .
Câu 15 (NB): Góc giữa hai đường thẳng bất kỳ trong không gian là góc giữa:
A. Hai đường thẳng cùng đi qua một điểm và tương ứng song song với hai đường thẳng đó.
B. Hai đường thẳng lần lượt vuông góc với hai đường thẳng đó.
C. Hai đường thẳng cắt nhau và không song song với hai đường thẳng đó..
D. Hai đường thẳng cắt nhau và tương ứng vuông góc với hai đường thẳng đó.
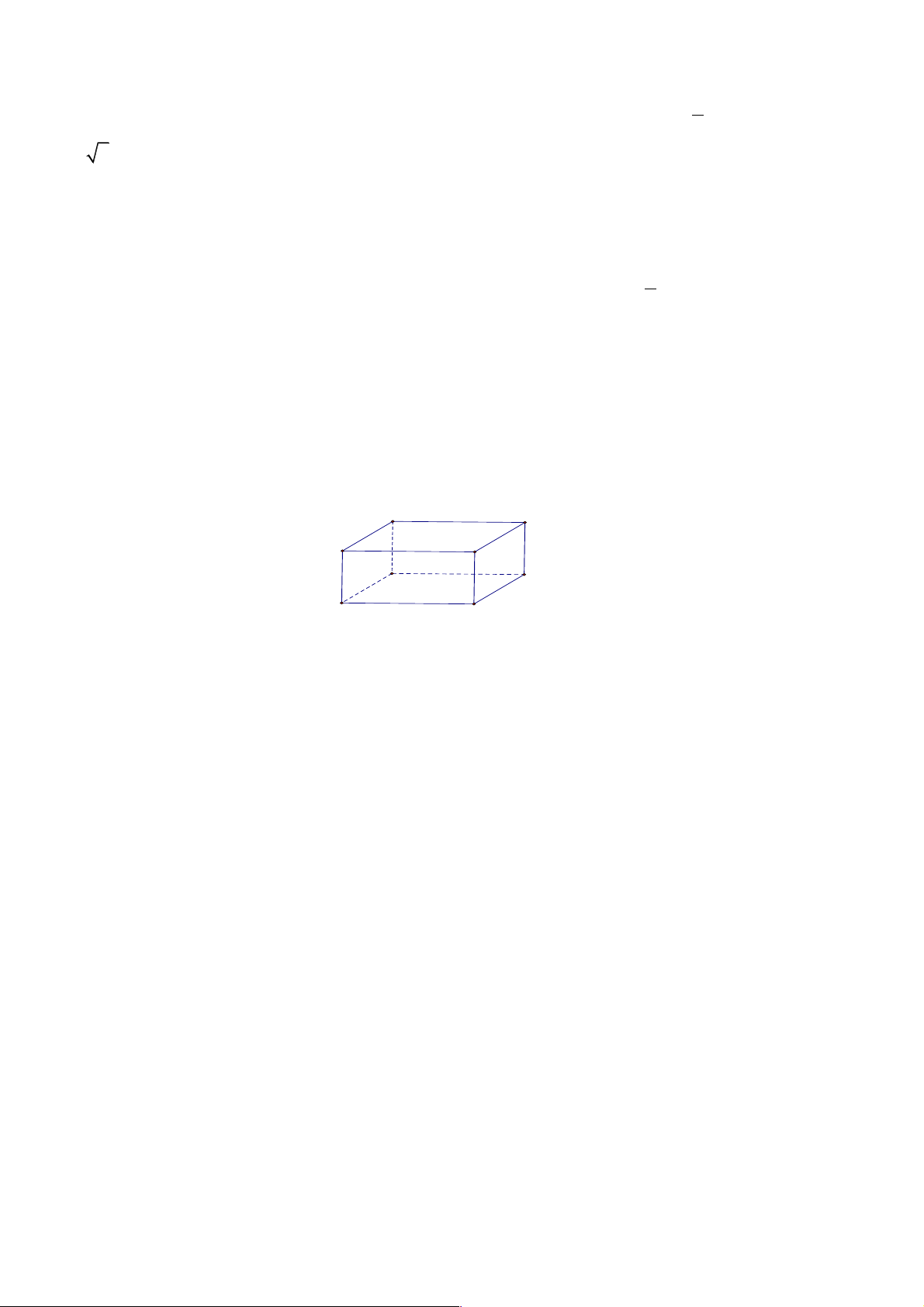
Câu 16 (NB): Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có các mặt là hình chữ nhật ( như hình vẽ) B C A D B' C'
. Khẳng định nào sau đây đúng? A' D'
A. AC ^ B D
¢ ¢ . B. AA¢ ^ CD¢.
C. AB¢ ^ CD¢ .
D. CD ^ A D ¢ ¢ .
Câu 17 (NB): Trong không gian cho đường thẳng d và điểm O . Qua O có bao nhiêu đường thẳng vuông góc với d ? A. 3. B. Vô số. C. 1. D. 2.
Câu 18 (NB): Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ^ (ABCD). Tìm hình
chiếu vuông góc của điểm S trên mặt phẳng ( ABCD) ? A.C. B.D.
C.A. D. B.
Câu 19 (TH): Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ^ (ABCD).
. Khẳng định nào sau đây đúng?
A. AC ^ (SAB) . B. SC ^ (SAB). C. AB ^ (SAD). D. BD ^ (SAB).
Câu 20 (TH): Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy ( ABCD).
Tìm hình chiếu vuông góc của SC lên mặt phẳng (SAD). A. SD .
B. SA . C. AD . D. AC .
Câu 21 (TH): Cho hai đường thẳng phân biệt a, b và mặt phẳng (α). Mệnh đề nào sau đây đúng ?
A.Nếu a // (α) và b ^ (a ) thì a ^ b . B.Nếu a // (α) và b ^ a thì b ^ a .
C.Nếu a // (α) và b // (α) thì b // a. D.Nếu a ^ (α) và b ^ a thì b // (α).
Câu 22 (NB): Gọi j là góc giữa hai mặt phẳng (P) và (Q) . Khẳng định nào sau đây đúng?
A. 0° £ j £ 90°. B. 0° < j < 90°. C. 0° £ j £180° .
D. 0° < j <180° .
Câu 23 (NB): Cho phát biểu sau?
(1) Hai mặt phẳng (P) và (Q) có giao tuyến là đường thẳng a và cùng vuông góc với mặt phẳng
(R) thì a ^ (R)..
(2) Hai mặt phẳng (P) và (Q) vuông góc với nhau và có giao tuyến là đường thẳng a một đường
thẳng b nằm trong mặt phẳng (P) và vuông góc với đường thẳng a thì b ^ (Q)..
(4) Mặt phẳng (P) chứa đường thẳng a và a vuông góc với (Q) thì (P) ^ (Q).. Trang 2
(5) Đường thẳng a nằm trong mặt phẳng (P) và mặt phẳng (P) vuông góc với mặt phẳng (Q) thì a ^ (Q).
Số phát biểu đúng trong các phát biểu trên. A.1. B.2. C.3. D.4.
Câu 24 (TH): Cho hình chóp S.ABCD có đáy ABCD là hìn bình hành, SA ^ (ABCD). Mệnh đề nào sau đây đúng?
A. (SAC) ^ (ABCD) B. (SBC) ^ (ABCD) C. (SCD) ^ (ABCD). D. (SBD) ^ (ABCD).
Câu 25 (TH): Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.
B. Hình lăng trụ đứng có các mặt bên là hình chữ nhật và vuông góc với mặt đáy.
C. Hình lăng trụ đứng có các mặt là hình chữ nhật gọi là hình lập phương.
D. Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ đều.
Câu 26 (NB):Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B, SA ^ (ABC) . Đường
thẳng nào sau đây là đường vuông góc chung của hai đường thẳng SA và BC ? A. AC.
B. BC. C. SC. D. AB.
Câu 27 (TH):Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ . Khoảng cách giữa hai mặt phẳng ( ABCD) và (A B ¢ C ¢ D ¢ ¢)bằng A. AC¢. B. AB¢. C. AD¢ . D. AA¢ .
Câu 28 (NB):Gọi j là góc giữa đường thẳng a và mặt phẳng (P) . Khẳng định nào sau đây đúng?
A. 0° £ j £ 90° B. 0° < j < 90°. C. 0° £ j £180° . D. 0° < j <180° .
Câu 29 (NB):Cho hai nửa mặt phẳng (P) và (Q) có chung bờ a . Gọi j là góc phẳng nhị diện
[P, a,Q]. Khẳng định nào sau đây đúng?
A. 0° £ j £180° . B. 0° < j < 90°. C. 0° £ j £ 90°.
D. 0° < j <180° .
Câu 30 (NB): Cho hình chóp S.ABCD có đáy là hình vuông và SA ^ (ABCD). Góc nào sau đây là
góc giữa đường thẳng SB và mặt phẳng (SAB)? A. ∑ ASD . B. ∑ ASC . C. ∑ ASB . D. ∑ ABS
Câu 31 (TH): Cho hình chóp tứ giác đều S.ABCD .Phát biểu nào sau đây đúng?
A.Số đo của góc nhị diện [S,AB,B] bằng ∑
SBC . B. Số đo của góc nhị diện [D,SA,B] bằng 0 90 .
C. Số đo của góc nhị diện [S,AC,B] bằng 0
90 . D. Số đo của góc nhị diện [D,SA,B] bằng ∑ BSD.
Câu 32 (TH): Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, cạnh bên SA vuông góc với đáy. Biết a 3 SA =
, AB = a . Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng? 3 A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 33 (NB): Thể tích của khối lăng trụ có diện tích đáy S và chiều cao h là 4 1 A. 3Sh.
B. Sh . C. Sh . D. Sh . 3 3
Câu 34 (NB): Cho hình chóp cụt đều. Khẳng định nào sau đây đúng SAI?
A. Mỗi mặt bên là một hình thang cân. B. Đáy lớn và đáy nhỏ nằm trên hai mặt phẳng song song..
C. Có các cạnh bên bằng nhau . D. Mỗi mặt bên là một hình thang.
Câu 35 (TH): Thể tích của khối hình hộp chữ nhật có chiều dài ba cạnh 2,3,4 là. A.8. B. 24. C.12. D.6.
B. CÂU HỎI TỰ LUẬN (3,0 điểm):
Câu 1: (1,0 điểm) Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và có cạnh SA
vuông góc với mặt phẳng (ABC).
a/ Chứng minh BC ^ (SAB)
b/ Gọi AH là đường cao của tam giác SAB. Chứng minh AH ^ SC Trang 3
Câu 2: (1,0 điểm): Cho hình chóp S .A BCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với
mặt phẳng đáy, SA = a 3.Tính thể tích của khối chóp theo a. .
Câu 3: (1,0 điểm): Giả sử sự tăng trưởng của một loại vi khuẩn trong quá trình nuôi cấy tuân theo công thức N(t)= . rt
N e , trong đó N là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là 0 0
thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 500 con và sau 2 giờ có 1500 con. Hỏi
sau bao lâu thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi?
……………………………………………Hết……………………………………………………..
HƯỚNG DẪN CHẤM Câu hỏi Lời giải Điểm
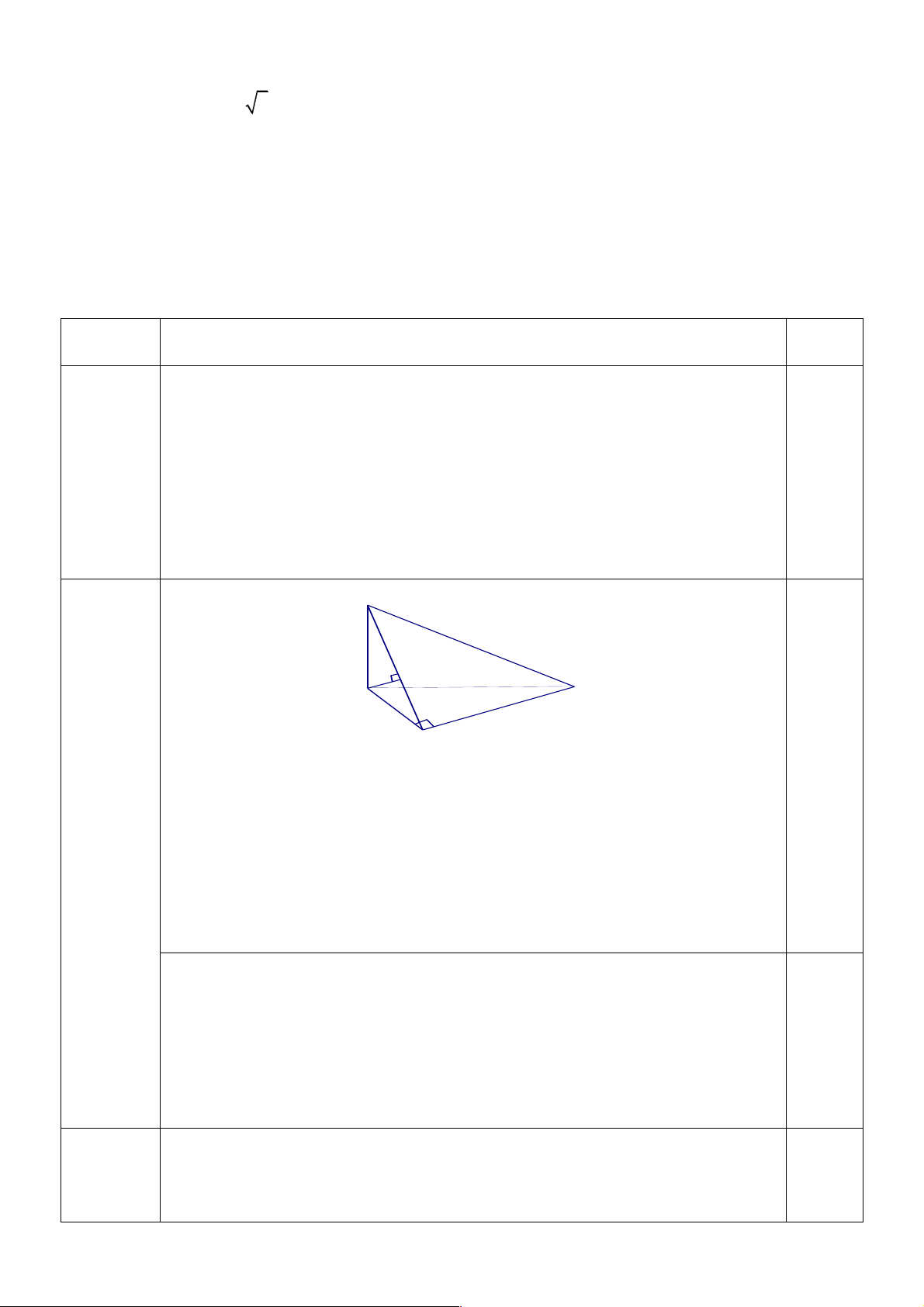
Câu 1 Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và có 1,0 đ
cạnh SA vuông góc với mặt phẳng (ABC).
a/ Chứng minh BC ^ (SAB)
b/ Gọi AH là đường cao của tam giác SAB. Chứng minh AH ^ SC S H A C B 0,25 đ
a/ Vì SA ^ (ABC) nên SA ^ BC ta có BC ^ S , A BC ^ . AB 0,25 đ
từ đó suy ra BC ^ (SAB)
b/ Vì BC ^ (SAB) và AH nằm trong (SAB) nên BC ^ AH . 0,25 đ
Ta lại có AH ^ BC, AH ^ SB nên AH ^ (SBC). 0,25đ
Từ đó suy ra AH ^ SC. Câu 2
Cho hình chóp S .A BCD có đáy ABCD là hình vuông cạnh a. SA vuông Trang 4
góc với mặt phẳng đáy, SA = a 3.Tính thể tích của khối chóp theo a. 2
Diện tích mặt đáy hình vuông: S = . a a = a ABCD 1,0 đ 3
Thể tích khối chóp:V= a 3 (đvtt) 3 Câu 3 1,0 đ
Giả sử sự tăng trưởng của một loại vi khuẩn trong quá trình nuôi cấy
tuân theo công thức N(t)= . rt
N e , trong đó N là số lượng vi khuẩn ban 0 0
đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng
số lượng vi khuẩn ban đầu là 500 con và sau 2 giờ có 1500 con. Hỏi sau
bao lâu thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi?
Tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này là: 0,5đ Ta có: r r ln 3 2 2
1500 = 500.e Û e = 3 Û 2r = ln 3 Û r = 2
Thời gian để số lượng vi khuẩn ban đầu tăng gấp đôi là: 0,5đ 2 = . rt rt N
N e Û e = 2 Þ rt = ln 2 Þ t » 1,16(giờ) 0 0
ĐỀ ÔN TẬP GIỮA HỌC KỲ II-ĐỀ 2
MÔN TOÁN - KHỐI LỚP 11
A. CÂU HỎI TRẮC NGHIỆM (7,0 điểm):
Câu 1 (NB): Cho số nguyên m, số dương a và số tự nhiên n (n ³ 2). Trong các tính chất sau, tính chất nào đúng ? m n A. n m n
a = a . B. n m m
a = a . C. n m m.n a = a . D. n m m n a a - = .
Câu 2 (NB): Cho x, y là hai số thực dương và ,
m n là hai số thực tùy ý. Đẳng thức nào sau đây là sai? A. m. n m n x x x + = n m m+n . B.( . ) n = . n x y x y . ( nx) nm = m. n x y = (xy) C. x . D. . 1
Câu 3 (TH): Với a là số thực dương tùy ý, 2 3 a .a bằng 2 7 5 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . Trang 5
Câu 4 (TH): Rút gọn biểu thức ( - )2 3 1 2 - 3 b : b với b > 0. A. . b B. 2 b . C. 3 b . D. 4 b .
Câu 5 (NB): Trong các mệnh đề sau, mệnh đề nào đúng?
A. log ba = a log b với mọi số thực dương a,b và a ¹ 1 . a a
B. log ba = a log b với mọi số thực dương a,b. a a
C. log ba = a log b với mọi số thực a,b. a a
D. log ba = a log b với mọi số thực a,b và a ¹ 1 . a a
Câu 6 (TH): Với mọi số thực dương , a log 4a 4 ( ) bằng A. 1+ log a .
B. 1- log a. C. log a . D. 4log a . 4 4 4 4
Câu 7 (TH): Cho a > 0 và a ¹ 1, khi đó 4 log a bằng a 1 1
A. 4 . B. . C. - . D. -4 . 4 4
Câu 8 (NB): Trong các hàm số sau, hàm số nào là hàm số logarit? A. lg 2 .x y = B. y = log . x C. ln3 y = x . y = (x + 3)ln 2. 3 D.
Câu 9 (NB): Trong các hàm số sau, hàm số nào không phải là hàm số mũ? 2 æ 2 x ö A. 2x y = . B. y = - . C. 2 .x y - = D. 2 y x- = . ç ÷ è 3 ø
Câu 10 (NB): Hình vẽ bên là đồ thị của hàm số nào dưới đây? y 1 O x æ 1 x A. ö y = . B. 2x y = .
C. y = log x .
D. y = log x . ç ÷ è 2 ø 2 1 2
Câu 11 (TH): Cho hàm số y = log x (0 < a ¹ )
1 có đồ thị như hình vẽ: a y 2 O x 1 2
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên (0;+¥).
D. Hàm số đồng biến trên (0;+¥).
Câu 12 (TH): Nghiệm của phương trình log x + 4 = 3 2 ( ) là Trang 6
A. x = 5 . B. x = 4 . C. x = 2 . D. x = 12 .
Câu 13 (TH): Nghiệm của phương trình 2x-4 5 = 25 là
A. x = 3. B. x = 2 . C. x =1. D. x = 1 - .
Câu 14 (NB): Góc giữa hai đường thẳng bất kỳ trong không gian là góc giữa:
A. Hai đường thẳng cắt nhau và không song song với chúng.
B. Hai đường thẳng lần lượt vuông góc với chúng.
C. Hai đường thẳng cùng đi qua một điểm và lần lượt song song với chúng.
D. Hai đường thẳng cắt nhau và lần lượt vuông góc với chúng.
Câu 15 (NB): Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có các mặt là hình chữ nhật. Khẳng định nào sau đây đúng?
A. AC ^ B D ¢ ¢ .
B. AA¢ ^ CD¢.
C. AB¢ ^ CD¢ .
D. CD ^ A D ¢ ¢ .
Câu 16 (NB): Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ^ (ABCD). Khẳng định nào sau đây đúng?
A. AC ^ (SAB) .
B. SC ^ (SAB).
C. AD ^ (SAB).
D. BD ^ (SAB).
Câu 17 (NB): Thể tích của khối chóp có diện tích đáy B và chiều cao h là 1 A. V = 4 Bh .
B. V = Bh .
C. V = 3Bh .
D. V = Bh. 3 3
Câu 18 (NB): Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 4 1 A. 3Bh . B. Bh. C. Bh . D. Bh . 3 3
Câu 19 (TH): Cho đường thẳng d vuông góc với mặt phẳng (a ) và đường thẳng D khác d . Chọn
khẳng định sai trong các khẳng định sau:
A. Đường thẳng D // d thì D ^ (a ) .
B. Đường thẳng D // d thì D // (a ).
C. Đường thẳng D // (a ) thì D ^ d .
D. Đường thẳng D ^ (a ) thì D // d .
Câu 20 (TH): Cho tứ diện OABC có 3 cạnh OA , OB , OC đôi một vuông góc. Gọi H là chân
đường vuông góc hạ từ O tới (ABC) thì:
A. H là trọng tâm tam giác ABC .
B. H là tâm đường tròn ngoại tiếp tam giác ABC .
C. H là tâm đường tròn nội tiếp tam giác ABC . D. H là trực tâm tam giác ABC .
Câu 21 (NB): Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng vuông góc thì chúng cắt nhau.
B. Hai mặt phẳng cắt nhau thì không vuông góc.
C. Hai mặt phẳng vuông góc thì góc của chúng bằng 90° .
D. Hai mặt phẳng có góc bằng 90° thì chúng vuông góc.
Câu 22 (NB): Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Cả ba mệnh đề trên đều sai.
Câu 23 (NB): Gọi j là góc giữa hai mặt phẳng (P) và (Q) . Khẳng định nào sau đây đúng? A. 0° £ j £ 90°.
B. 0° < j < 90°. C. 0° £ j £180° .
D. 0° < j <180° .
Câu 24 (TH): Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy.
B. Hình lăng trụ đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật. Trang 7
C. Hình hộp có các cạnh bằng nhau gọi là hình lập phương.
D. Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ đều.
Câu 25 (TH): Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Góc giữa hai mặt phẳng (ACC A ¢ )¢ và (BDD B ¢ )¢ bằng? A. 45°. B. 60° . C. 30° . D. 90° .
Câu 26 (TH): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a ,
SA = SB = SC = SD = 2a . Gọi j là góc giữa mặt phẳng (SCD) và ( ABCD). Mệnh đề nào dưới đây là đúng? A. 2 tanj = . B. tanj = 3 . C. tanj = 2. D. tanj = 2 . 2
Câu 27 (NB): Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a. Đường thẳng nào sau đây là đường
vuông góc chung của hai đường thẳng AB và B D ¢ ¢ ? A. AC . B. BB¢ . C. BD . D. AB¢ .
Câu 28 (NB): Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ^ (ABCD). Đường
thẳng nào sau đây là đường vuông góc chung của hai đường thẳng SD và BC ? A. SB . B. SC . C. CD . D. BD .
Câu 29 (TH): Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a. Khoảng cách giữa hai đường thẳng AC và B D ¢ ¢ bằng A. a 2 . B. a . C. 2a . D. a 3 .
Câu 30 (TH): Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng a . Tính khoảng từ điểm B đến mặt phẳng ( AB C ¢ ). A. a 2 . B. a 3 . C. a 3 . D. a 6 . 3 2 3 3
Câu 31 (NB): Cho hình chóp S.ABCD có đáy là hình vuông và SA ^ (ABCD). Góc nào sau đây là
góc giữa đường thẳng SB và mặt phẳng (SAD)? A. ∑ ASD . B. ∑ ASC . C. ∑ ASB . D. ∑ ABS .
Câu 32 (NB): Cho hai nửa mặt phẳng (P) và (Q) có chung bờ a . Gọi j là góc phẳng nhị diện
[P, a,Q]. Khẳng định nào sau đây đúng? A. 0° £ j £180° .
B. 0° < j < 90°. C. 0° £ j £ 90°.
D. 0° < j <180° .
Câu 33 (TH): Cho hình chóp S.ABC có đáy ABC là tam giác cân tại C , AC = BC = a 10 , mặt bên
SAB là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Tính góc giữa đường
thẳng SC và mặt phẳng ( ABC). A. 30° . B. 45°. C. 90° . D. 60° .
Câu 34 (NB): Cho hình chóp cụt đều. Khẳng định nào sau đây đúng?
A. Mỗi mặt bên là một hình tam giác cân.
B. Mỗi mặt bên là một hình thang cân.
C. Mỗi mặt bên là một hình chữ nhật.
D. Mỗi mặt bên là một hình vuông.
Câu 35 (NB): Cho hình chóp cụt đều. Khẳng định nào sau đây sai?
A. Các cạnh bên đồng quy tại một điểm.
B. Hai mặt đáy luôn song song nhau.
C. Các cạnh bên bằng nhau.
D. Hai mặt đáy là các đa giác đều bằng nhau.
B. CÂU HỎI TỰ LUẬN (3,0 điểm):
Câu 1 (0,5 điểm): Ông A gửi tiết kiệm 50 triệu đồng ở ngân hàng X với lãi suất không đổi 5,5% một
năm. Bà B gửi tiết kiệm 95 triệu đồng ở ngân hàng Y với lãi suất không đổi 6,0% một năm. Hỏi sau Trang 8
ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông A?
Câu 2 (2,0 điểm): Cho hình chóp S .A BCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với
mặt phẳng đáy, SA = a 3.
a) Tính góc giữa A C và mặt phẳng (SBC ) .
b) Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM.
Câu 3 (0,5 điểm): Sự tăng trưởng của một loại vi khuẩn tuân theo công thức S= A.ert, trong đó A là
số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số
lượng vi khuẩn ban đầu là 1000 con và sau 5 giờ có 3000 con. Hỏi sau bao nhiêu phút thì số lượng
vi khuẩn ban đầu sẽ tăng gấp đôi? …Hết… HƯỚNG DẪN CHẤM Câu hỏi Lời giải Điểm Câu 1
Ông A gửi tiết kiệm 50 triệu đồng ở ngân hàng X với lãi suất không đổi 0,5 đ
5,5% một năm. Bà B gửi tiết kiệm 95 triệu đồng ở ngân hàng Y với lãi
suất không đổi 6,0% một năm. Hỏi sau ít nhất bao nhiêu năm thì tổng
số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông A?
Giả sử n> 0 (nÎ!) là số năm gửi tiền trong ngân hàng của ông A và bà B. 0,25 đ
Sau n năm, số tiền cả gốc lẫn lãi của ông A là: S = 50 1+ 0,055 n 1 n ( ) (triệu
đồng) và của bà B là: S =95 1+0,06 n n2 ( ) (triệu đồng)
Để tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn 0,25 đ
lẫn lãi của ông A thì 2S < S 1 n n2 n æ ö
Hay 2.50(1 0,055)n 95(1 0,06)n + < + 1,055 95 Û < ç 1,06 ÷ è ø 100 æ 95 ö Û n > log Þ n ³11. 1,055 ç ÷ è100 ø 1,06
Vậy sau 11 năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần
tổng số tiền cả vốn lẫn lãi của ông A .
Cho hình chóp S .A BCD có đáy ABCD là hình vuông cạnh a. SA Câu 2
vuông góc với mặt phẳng đáy, SA = a 3.
c) Tính góc giữa A C và mặt phẳng (SBC ) 2đ .
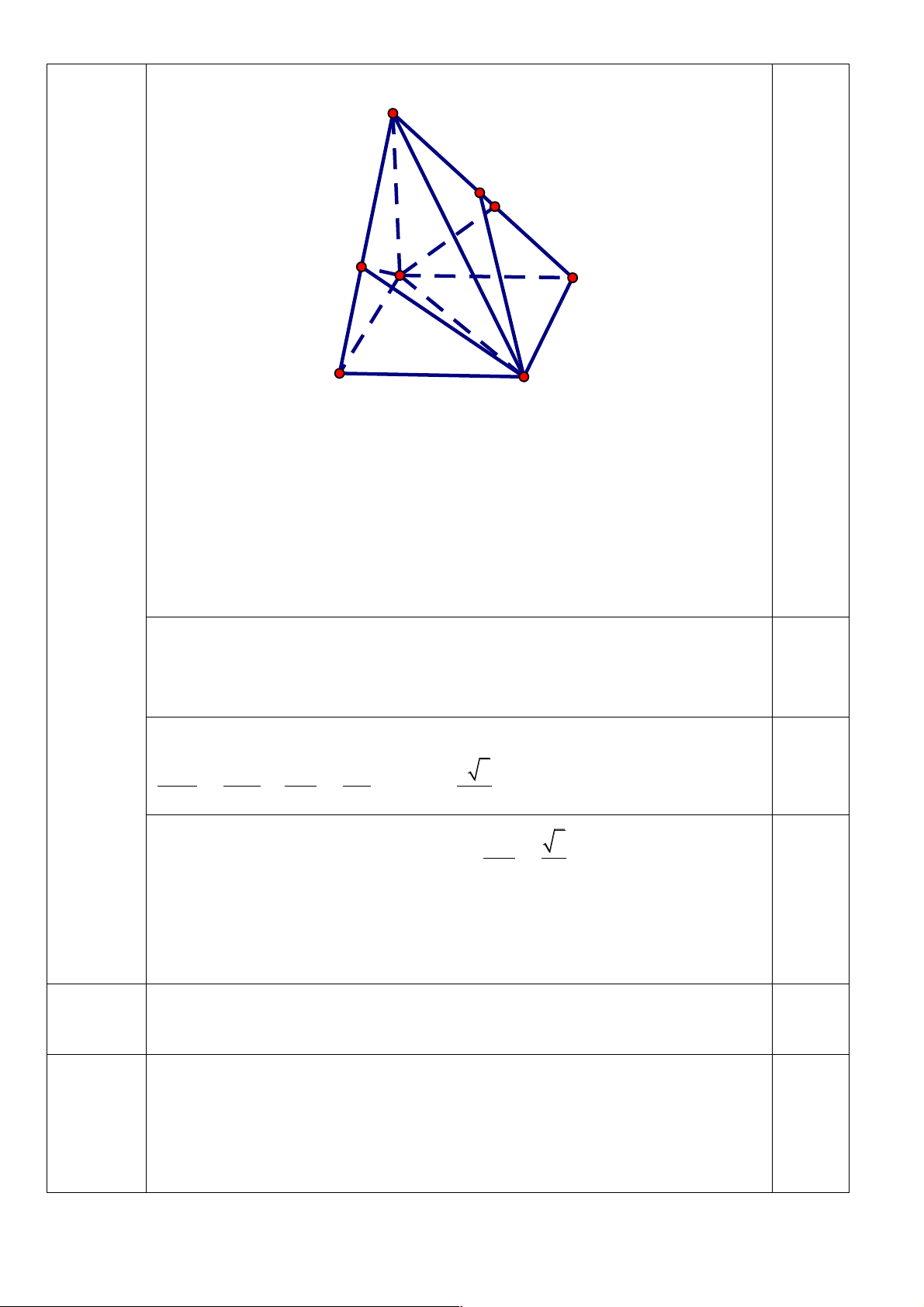
d) Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM. Trang 9 S K M H A D 0,25đ B C
Trong mặt phẳng (SAB )kẻ AH ^ SB (H S Œ B ). (1) Ï BC Ô ^ A B Ô Ì
fi BC ^ (SA B ). BC Ô ^ SA Ô Ó
Mà AH Ì (SAB) Þ BC ^ AH (2)
Từ (1) và (2) suy raAH ^ (SBC ) 0,25đ
Suy ra hình chiếu của AC lên (SBC) là HC 0,25 đ
fi (AC (SBC ) = (AC HC ) ∑ , , = A CH
Xét tam giác vuông SAB ta có 0,25 đ 1 1 1 4 a 3 = + = fi A H = 2 2 2 2 A H A B SA 3a 2 0,25 đ A H Xét ACH D vuông góc H có: ∑ 6 sin A CH = = . A C 4 Þ ∑ 0 A CH ª 37 0 37
Vậy góc giữa đường thẳng AC và mặt phẳng (SBC) là Câu 2b
Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM. Trong SA
D D , kẻ đường cao AK Þ AK ^ SD (1) 0,25đ
CD ^ ADüýÞCD ^(SAD)ÞCD ^ AK (2) CD ^ SA þ
Từ (1) và (2) Þ AK ^ (SCD) Trang 10
Có AB//CD Þ AB / /(SCD) 0.5đ
Mà CM Ì (SCD) Þ d(AB,CM) = d(A ,
B (SCD)) = d( , A (SCD)) = AK Xét SA
D D vuông tại A có: 0.25đ 1 1 1 1 1 4 a 3 = + = + = Þ AK = 2 2 2 2 2 2 AK SA AD 3a a 3a 2 a 3
Vậy khoảng cách giữa hai đường thẳng AB và CM là 2 Câu 3
Sự tăng trưởng của một loại vi khuẩn tuân theo công thức 0,5 đ
S= A.ert, trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng
trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn
ban đầu là 1000 con và sau 5 giờ có 3000 con. Hỏi sau bao nhiêu phút
thì số lượng vi khuẩn ban đầu sẽ tăng gấp đôi?
Tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này là: 0,25đ r r ln 3 Ta có: 5 5
3000 =1000.e Û e = 3 Û 5r = ln 3 Þ r = 5
Thời gian để số lượng vi khuẩn ban đầu tăng gấp đôi là: 0,25đ rt rt ln 2 ln 2
2000 =1000.e Û e = 2 Þ rt = ln 2 Þ t = = » 3,15 (giờ) r ln 3 5
Vậy để số lượng vi khuẩn ban đầu tăng gấp đôi thì cần thời gian là 3,15(giờ)=189 phút. Trang 11