Thông tin
Quiz

Bộ đề ôn tập giữa kì 2 Toán 11 năm 2024 – 2025 trường Trần Cao Vân – TP HCM

Bộ đề ôn tập giữa kì 2 Toán 11 năm 2024 – 2025 trường Trần Cao Vân – TP HCM. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 57 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem.

Chủ đề:

Đề giữa HK2 Toán 11 233 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:

57 trang 1 tuần trước

Tác giả:

Kim Ngân Lê

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bộ đề ôn tập giữa kì 2 Toán 11 năm 2024 – 2025 trường Trần Cao Vân – TP HCM

11 6 lượt tải Tải xuống

TRƯỜNG THCS-THPT TRẦN CAO VÂN

TOÁN

BỘ ĐỀ ÔN TẬP GKII - GIÁO VIÊN

LƯU HÀNH NỘI BỘ

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 1 -

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2

NĂM HỌC 2024 – 2025

---------------------

Thầy Đỗ Minh Tiến

ĐỀ ÔN TẬP SỐ 01

Môn: TOÁN 11

Thời gian: 90 phút

ĐỀ SỐ 01

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi

câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Cho biểu thức

.P x x

, với

0x 

. Mệnh đề nào dưới đây đúng?

P x

. B.

P x

. C.

P x

. D.

P x

Câu 2: Cho số thực dương

thỏa mãn

24 23

1 1

a a

   

 

 

 



 

 

 

 

 

   

. Khẳng định nào sau đây là đúng?

0 1a 

. B.

a 

. C.

a 

. D.

1a 

Câu 3: Biết

2 5.



Khi đó:

log 5a 

. B.

log 2a 

. C.

log 2a 

. D.

log 2a 

Câu 4: Biết

log 3

b 

. Tính

log



9

. B.

. C.

. D.

6

Câu 5: Hàm số nào sau đây đồng biến trên

 

; 

 

5 2

y  

. B.



 



















 

. C.

 

0,7

y 

. D.

 



















 

Câu 6: Tập xác định của hàm số

 

ln 2y x 

là











. B.

 

2;

. C.



. D.

 

\ 2

Câu 7: Nghiệm của phương trình

3 27

x



là

4x 

. B.

3x 

. C.

2x 

. D.

1x 

Câu 8: Tập nghiệm

của bất phương trình

   

1 1

2 2

log 1 log 2 1x x  

là

 

2;S  

. B.

 

;2S  

. C.

 



















 

. D.

 

1;2S  

Câu 9: Chọn mệnh đề đúng?

A. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó cắt nhau.

B. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó chéo nhau.

C. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó song song với nhau.

D. Nếu hai đường thẳng vuông góc với nhau thì chúng hoặc chéo nhau hoặc cắt nhau.

Câu 10: Cho hình chóp

.S ABC

có

 

,SA ABC

tam giác

ABC

vuông tại

, kết luận nào sau đây sai?

   

SAC SBC

. B.

   

SAB ABC

. C.

   

SAB SBC

   

SAC ABC

Câu 11: Cho hình chóp

.S ABC

có

vuông góc với mặt đáy

 

ABC

. Mệnh đề

nào sau đây là đúng?

SA SB

SA SC

SA BC

SB SC

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 2 -

Câu 12: Cho hình lăng trụ đều

ABC A B C

  

có



và





Góc tạo bởi giữa hai mặt phẳng

( )

A BC



và

( )

ABC

bằng

45 .



60 .



30 .



75 .



PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 13: Cho hàm số

( ) log ( 2).

y f x x

  

Khi đó các mệnh đề sau đúng hay sai?

a) Tập xác định của hàm số là

( 2; ).

  

b) Đồ thị hàm số đi qua điểm

( 1;0).



c) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ

 

d) Bất phương trình

( ) 1

f x



có tập nghiệm

( ; 3).

 

Câu 14: Cho hình chóp

S ABC

có đáy

ABC

là tam giác vuông cân tại

, .

B AB a



Cạnh bên

vuông góc với đáy và

SA a



là

trung điểm của

SA BC



( ).

BM SAC



c) Mặt phẳng

( )

SAB

vuông góc với mặt phẳng

( ).

SAC

d) Mặt phẳng

( )

SBC

tạo với mặt phẳng đáy một góc có số đo là

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15

đến câu 18.

Câu 15: Cho

log 2, log 3.

a a

b c

 

Khi đó:

2 3

log ( )

P a bc



bằng

Đáp số:

13.

Câu 16: Tổng các nghiệm của phương trình





bằng

Đáp số:



Lời giải tham khảo

Ta có:

2 2

8 2 2

2 2 2 8 2

x x x

x x





 



      









Câu 17: Để dự báo dân số của một quốc gia, người ta sử dụng công thức

;

S Ae



trong đó

là dân số

của năm lấy làm mốc tính,

là dân số sau

năm,

là tỉ lệ tăng dân số hàng năm. Năm

2020

(lấy làm mốc tính), dân số một nước là

100

triệu người. Giả sử tỉ lệ tăng dân số hàng năm không

đổi là

0, 8%,

dự báo dân số nước đó năm 2035 là bao nhiêu triệu người?(kết quả làm tròn đến chữ

số hàng đơn vị)?

Đáp số:

113.

Lời giải tham khảo

Lấy năm

2020

làm mốc, ta có

100; 2035 2020 15

A n

   

Suy ra: dân số nước đó vào năm 2035 là

100. 113

S e

 

triệu người.

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 3 -

Câu 18: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

 

SA ABCD

và

6SA a

Gọi



là góc giữa

và mặt phẳng

( ).SAB

Khi đó

cos 

bằng

Đáp số:

PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 24.

Câu 19: Biết rằng

2 2 14

x x

 

. Tính giá trị biểu thức

4 4 10

x x



  

Câu 20: Cho

3 3

log 5 , log 2 .a b 

Tính giá trị biểu thức

log 30P 

theo

, .a b

Câu 21: Giải phương trình:

2 2

log log ( 3) 2.x x  

Câu 22: Giải bất phương trình

 

0,2

x 

 



















 

Câu 23: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

Cạnh bên

vuông góc với đáy

và

3.SA a

Gọi

là hình chiếu của

trên cạnh

a) Chứng minh

( ).CD SAD

b) Tính số đo góc tạo bởi hai mặt phẳng

( )SCD

và

( ).ABCD

---- HẾT ----

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2

NĂM HỌC 2024 – 2025

---------------------

Cô Hồ Thị Mỹ Ly

ĐỀ ÔN TẬP SỐ 02

Môn: TOÁN 11

Thời gian: 90 phút

ĐỀ SỐ 02

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi

câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Biểu thức rút gọn của

2 3

x x x

là:

. B.

. C.

. D.

Câu 2: Cho số thực dương

và số nguyên dương

tùy ý. Mệnh đề nào sau đây là đúng?

2n n

a a





. B.

2n n

a a

. C.

a a

. D.

a a

Câu 3: Biết

3 2

log 2, log 5a b 

. Tính

log 5

theo

,a b

log 5



. B.

log 5 ab

. C.

log 5

b a





. D.

log 5



Câu 4: Cho

log 16x 

. Tính

8 4

A = log (log ).x

. B.

. C.

. D.

Câu 5: Tập nghiệm của phương trình

4 2

2 3

3 2

x x 

 



















 

là:

 

2 2;2 2 .S   

 

2 3; 2 3 .S   

 

2 5; 2 5 .S   

 

1; 3 .S 

Câu 6: Nghiệm của phương trình

log ( 1) 3x  

là:

10.

Câu 7: Nghiệm của bất phương trình

2 3

x

 



















 

là:

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 4 -

x 





x 

Câu 8: Nghiệm của bất phương trình

0,5 0,5

log ( 3) log (6 2 )

x x

  

là:





1 3.

 

3 1

  

Câu 9: Cho hình chóp

S ABC

có

vuông góc với đáy. Mệnh đề nào sau đây là đúng?

SA BC.



SA SC.



SA SB.



SC BC.



Câu 10: Đường thẳng

gọi là vuông góc với mặt phẳng

( )



nếu:

A. Đường thẳng

vuông góc với một đường thẳng bất kỳ nằm trong mặt phẳng

( )



B. Đường thẳng

vuông góc với hai đường thẳng bất kỳ nằm trong mặt phẳng

( )



C. Đường thẳng

vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng

( )



D. Đường thẳng

vuông góc với hai đường thẳng phân biệt nằm trong mặt phẳng

( )



Câu 11: Cho hình chóp

S ABCD

có đáy

ABCD

là hình chữ nhật,

vuông góc với đáy. Mặt phẳng

(SCD)

vuông góc với mặt phẳng nào sau đây?

(ABCD)

. B.

(SAD)

. C.

(SBD)

. D.

(SAC)

Câu 12: Mặt phẳng

( )



gọi là vuông góc với mặt phẳng

( )



nếu:

A. Một đường thẳng trong mặt phẳng

( )



vuông góc với một đường thẳng trong mặt phẳng

( )



B. Hai đường thẳng trong mặt phẳng

( )



vuông góc với hai đường thẳng trong mặt phẳng

( )



C. Một đường thẳng trong mặt phẳng

( )



vuông góc với hai đường thẳng cắt nhau trong mặt

phẳng

( )



D. Một đường thẳng trong mặt phẳng

( )



vuông góc với hai đường thẳng phân biệt trong mặt

phẳng

( )



PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 13: Cho

, ,

a b c

là các số thực dương tùy ý,



. Khi đó:

log ( ) 1 log

a a

ab b

 

. b)

log .

2 log

 



















 

log ( ) log .log .

a a a

bc b c



log 2 log log log ( 2).

a a a

b c a b c

    

Lời giải

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 5 -

log ( ) log log 1 log .

a a a a

ab a b b

   

Đúng

3 2

log log log 3 log 2 log .

a a a a a

a b a b

 







   











 

Sai

log ( ) log log .

a a a

bc b c

 

Sai

2 2

log 2 log log log log log og ( ).

a a a a a

b c a b c a l b c a

       

Sai

Câu 14: Cho hình chóp

S ABCD

có đáy

ABCD

là hình chữ nhật và

( )

SA ABCD



. Phát biểu nào sau

đây là đúng?

( , ) 90 .

SA CD



( ).

CD SAD



( ).

BD SAC



(( ),( )) 60 .

SCD SAD



Lời giải

( ) ( , ) 90 .

SA ABCD SA CD SA CD

    

Đúng

( ).

CD AD

CD SAD

CD SA









 











Đúng

BD SA



nhưng

không vuông góc với

nên

không vuông góc với

( ).

SAC

Sai

( )

( ) ( ) (( ),( )) 90 .

( )

CD SAD

SAD SCD SAD SCD

CD SCD









   











Sai

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.

Câu 15: Cho biểu thức

a a a



. Hỏi

m n

 

Lời giải

Đáp số: 11

3 5 5 5

3 3

2 2 2 6

. 11.

a a a a a a a m n

        

Câu 16: Tập xác định của hàm số

log ( 1)

y x

 

là

( ; ) ( ; )

D b a

   

. Hỏi

a b

 

Lời giải

Đáp số: 2

Điều kiện:

1 0 ( ; 1) (1; ) 1, 1 1 ( 1) 2.

x D a b a b



 



                  









Câu 17: Phương trình

2 2

9 3

x x x x

  



có hai nghiệm

1 2

x x

. Tính

1 2

| |

x x



Lời giải

Đáp số: 3

2 2 2 2

2 2 2 2 2 2

1 2

9 3 (3 ) 3 2( ) 2 2 0

| | | 1 2 | 3

x x x x x x x x

x x x x x x

x x

     

           



 



      









TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 6 -

Câu 18: Cho chóp

S ABC

có đáy

ABC

là tam giác vuông cân tại A,

AB a



SC a



( ).

SA ABC



Tính góc giữa

và đáy.

Lời giải

Đáp số: 45

  

2 2

( ,( )) ( , ) , cos 45 .

2 2

AC a

SC ABC SC AC SCA SCA SCA

SC a

      

PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 23.

Câu 19: Rút gọn biểu thức

9 3

log 4 log 5





Lời giải

Ta có:

9 3 9 3 9 3

log 4 log 5 log 4 log 5 log 3 log 3

3 3 .3 4 .5 4 .5 2.5 10.



     

Câu 20: Rút gọn biểu thức

3 4

log .log .

B b a



Lời giải

Ta có:

3 4 3 4

3 3 3

log .log log .log .log .4 log 24 log log 24 log .

b b b b

B b a b a b a b a a

    

Câu 21: Giải phương trình

(7 4 3) 3(2 3) 2 0.

x x

    

Lời giải









(7 4 3) 3(2 3) 2 0 2 3 3 2 3 2 0

x x

          

Đặt





2 3 , 0.

t t

  

3 2 0

t t

   









2 3

2 ( ) 2 3 2 log 2

1 ( ) 2 3 1 log 1 0

t n x







     







      





Câu 22: Giải phương trình

log 0.

4 2

x x

 























 

Lời giải

Điều kiện:

0 2

4 2

x x



 





 



 







. PT

4 2

x x



 



2 2

1( )

1 4 2 3 4 0

4( )

4 2

x n

x x

x x x x x

x n









          



 







Câu 23: Cho hình chóp

S ABCD

có đáy

ABCD

là hình vuông tâm

cạnh bằng

vuông góc với

đáy,

SA a



. Gọi

là trung điểm của cạnh

a) Chứng minh:

( )

CD SAD



b) Tính góc giữa

và mặt phẳng đáy (làm tròn đến đơn vị độ).

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 7 -

Lời giải

a) Ta có: ( )

CD SA

CD SAD

CD AD









 











b) Ta có:

là hình chiếu của

lên

( )ABCD

là hình chiếu của

lên

( )ABCD



là hình chiếu của

lên

( )ABCD



( ,( )) ( , )SM ABCD SM AM SMA  

Ta có:

2 2 2

2 2

a a

AM AB BM a

 







    











 

Xét

SAM

vuông tại

ta có:



2 2 10

tan

SA a

SAM

  

 

0 0

54 ( ,( )) 54 .SAM SM ABCD SAM    

---- HẾT ----

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2

NĂM HỌC 2024 – 2025

---------------------

Thầy Lê Kinh Huỳnh

ĐỀ ÔN TẬP SỐ 03

Môn: TOÁN 11

Thời gian: 90 phút

ĐỀ SỐ 03

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi

câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Cho  là số thực dương tùy ý, biểu thức .

√





bằng

A. 





. B. 





. C. 





. D. 





Câu 2: Tính giá trị biểu thức  =





√











√











√







A.  = −2



B. −1. C. −2



. D. 2



Câu 3: Nếu2



= 9 thì 











có giá trị bằng





. B. 3. C.



√



. D.





Câu 4: Cho  = 4







. Khi đó giá trị của  bằng

A. 9. B. 6. C.

√

3. D. 81.

Câu 5: Nếu 



 = 2 và 



 = 3. Tính  = 



(









)

A.  = 31. B.  = 13. C.  = 30. D.  = 108.

Câu 6: Hàm số nào sau đây không là hàm số mũ?

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 8 -

A.  = 









. B.  = 









. C.  = 



. D.  =

√



Câu 7: Giá trị của biểu thức M = log



2 + log



4 + log



8 + ⋯+ log



2048 bằng

A. 11. B. 66. C. 4096. D. 11



2048.

Câu 8: Tìm tập xác định của hàm số  = 



(

 − 3

)

A.  =

(

3;+∞

)

. B.  = (−3;+∞

)

. C.  =

(

0;+∞

)

. D.  = ℝ\

{

}

Câu 9: Tập nghiệm của bất phương trình 3







> 27 là

(

;+∞

)

(

−;

)

(

−∞;−

)

∪

(

;+∞

)

(

−∞;−

)

Câu 10: Cho hình lập phương .















. Tính góc giữa hai đường thẳng 







và CC’.

A. 90°. B. 45°. C. 60°. D. °.

Câu 11: Cho hình chóp tứ giác đều

S ABCD

có cạnh đáy là

và tam giác

SAC

đều. Tính độ dài

cạnh bên của hình chóp.

. B.

. C.

. D.

Câu 12: Cho hình chóp .có đáy là hình thoi tâm ,  = , = . Trong các khẳng định sau

khẳng định nào đúng?

A.  ⊥

(



)

. B.  ⊥

(



)

. C.  ⊥

(



)

. D.  ⊥

(



)

PHẦN II. Thí sinh trả lời từ câu 13 đến câu 15. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 13: Cho hàm số





log 2 2

y x x m

   

a) Với



thì hàm số có tập xác định là





b) Với



, đồ thị hàm số không cắt trục hoành.

c) Đồ thị hàm số đi qua điểm





2;7

khi

 

d) Có 2022 giá trị nguyên của

thuộc đoạn

2021;2021

 



 

 

để hàm số có tập xác định là



Câu 14: Cho hình chóp

S ABCD

, có đáy là hình vuông

ABCD

cạnh bằng

, tâm

. Cạnh bên

vuông góc với đáy và

SA 

. Điểm

là trung điểm cạnh

. Khi đó:





BD SAC



. b)

BD SC



. c)





CD SBC



. d)

AM SB



Lời giải

Câu1. a) Đúng.

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 9 -

Với

0m 

thì hàm số

 

log 2 2y x x  

xác định

 

2 2 0 1 1 0,x x x x          

Vậy hàm số có tập xác định là

D  

b) Sai. Đồ thị hàm số

 

log 2 2y x x  

cắt trục hoành tại điểm có hoành độ thỏa mãn

phương trình

 

2 2 2

log 2 2 0 2 2 1 2 1 0 1x x x x x x x            

Vậy đồ thị hàm số cắt trục hoành tại 1 điểm.

c) Sai. Với

5m  

thì hàm số

 

log 2 7y x x  

Khi đó

2x 

thì

log 7y 

Vậy đồ thị hàm số qua điểm

 

2;log 7

mà không đi qua điểm

d) Đúng. Điều kiện:

2 2 0

x x m

   

Hàm số có tập xác định



2 2 0,x x m x       

1 2 0 1m m



        .

nguyên thuộc đoạn

2021;2021

 



 

 

nên có 2022 giá trị

thỏa yêu cầu bài toán.

Câu 15:

a) Đúng. Ta có

   

( ( ))

( )

BD AC

BD SA do SA ABCD

BD SAC

SA SAC AC SAC









 

 





 





b) Đúng. Do

( )

BD SAC

BD SC

SC SAC









 











c) Sai. Ta có

   

( )

CD AD

CD SA

CD SAD

SA SAD AD SAD











 





 





 

( ) 1SD SAD CD SD  

Nếu

 

( ), ( ) 2CD SBC CD SC SBC CD SC    

Từ

 

và

 

SCD 

có hai góc vuông ( vô lí).

d) Đúng. Đáy

ABCD

, cạnh bằng

.Ta có

2 2

AC a

AO AO SA SAO     

vuông

cân tại

. Suy ra  ⊥ 

(

)

 

( )

BD SAC

BD AM

AM SAC









 











. Từ (3) và (4) suy ra

( )AM SBD AM SB  

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 16 đến câu 19.

Câu 16: Cho số dương và số thực

, biết

a a a

. Tính

Đáp án: 0,5

Ta có

1 1

1 1 3 1 1

3 3

1 .

0,5

2 2 2 3 2

.a a a a a a a a



   

 

 

 

 

    

 

 

 

 

   

Câu 17: Cho

   

log 4, log 5

x y

yz zx 

. Khi đó

 

log



, trong đó

0 , , 1;x y z 

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 10 -

,a b

 

và

là phân số tối giản. Tính

2 2

P a b 

Đáp án:

482

Ta có:

 

log

1 log

log

log log

x x

z z



 

(1)

Từ giả thiết:

 

log log 4

log

log 4

log 1

log 5

log

x x

y z









 















  

 



  

  



  







 







Thay vào (1) ta được:

 

log 11; 19.

19 19

xy a b



    

2 2 2 2

11 19 482

P a b

     

Câu 18: Bất phương trình

 

3 3

log 2 1 log 5x  

có bao nhiêu nghiệm nguyên?

Đáp án: 3

Ta có:

 

3 3

log 2 1 log 5 0 2 1 5 3

x x x        

Vậy bất phương trình trên có 3 nghiệm nguyên.

Câu 19: Cho tứ diện

ABCD

có

12,AC 

16BD 

. Gọi

,M N

lần lượt

là trung điểm của

và

.BC

Biết

vuông góc với

.BD

Tính

.MN

Đáp án:

Gọi

là trung điểm của

.AB

Ta có:

;PM PN

lần lượt là đường trung bình của

; .ABD ABC 

/ / ; 8

/ / ; 6

PM BD PM BD

PN AC PN AC





 









 





BD AC

nên

PM PN

hay tam giác

PMN

vuông tại

2 2 2 2

8 6 10.MN PM PN     

PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 20 đến câu 24.

Câu 20: Rút gọn biểu thức

.P x x

với

0x 

Lời giải: Ta có:

1 1 1 1 1 1

3 3 6 3 6 2

. .P x x x x x x x



    

Câu 21: Tính giá trị của biểu thức

log

P a

với

0 1a 

Lời giải: Ta có:

log log 2 log 2

P a a a   

Câu 22: Giải phương trình sau:

 

2 2

log log 1 1x x  

Lời giải

Điều kiện xác định:

1 0









 





 





   

2 1 2

2 2 2

log log 1 2 log 1 1 2 2 0x x x x x x x x

 

            

 

 











 





Dựa vào điều kiện ta thấy phương trình có nghiệm duy nhất là

2x 

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 11 -

Câu 23: Giải bất phương trình

 

0,5

log 3 1x  

Lời giải

Ta có:

 

0,5

3 0

log 3 1 1 3

3 2

3 0, 5

x x





 

 







       

 

 

 

 







Câu 24: Cho hình chóp . có đáy  là hình vuông cạnh bằng . Gọi  là trung điểm của ,

 vuông góc với mặt đáy, SH = a. Gọi  là trung điểm của .

a) Chứng minh  vuông góc với mặt phẳng

(



)

b) Chứng minh

(



)

vuông góc với

(



)

c) Tính giá trị tang của góc giữa hai mặt phẳng

(



)

và

(



)

a) Ta có:  ⊥

(



)

⇒  ⊥ 

 ⊥ 

 ⊥ 

, ⊂

(



)

⟹ AB ⊥ (SAD)

b) SH ⊥ (ABCD) ⇒ SH ⊥ BC

BC ⊥ HM

BC ⊥ SH

AH, HM ⊂ (SHM)⟹ BC ⊥ (SHM)

Mà BC ⊂ (SBC) nên (SBC) ⊥ (SHM)

c) Trong mặt phẳng (SAM), kẻ AI ⊥ SM, ta có: DI ⊥ SM

(Vì SM ⊥ (AID))

(SDM) ∩ (SAM) = SM

AI ⊥ SM

DI ⊥ SM

⟹∠((SDM)(SAM)) = ∠(AID)

Ta có: SH = a (gt)

△SDM = △SAM (c-c-c)

⇒ ID = IA (2 đường cao tương ứng bằng nhau)

⇒ △AID cân tại I ⇒  ⊥ AD

Xét △SHM, ta có:

SM² = SH² + HM² = 2a² ⇒ SM = a√2

Vì △SHM vuông cân tại H nên:

HI =





SM =

√



Xét △AIH, ta có: tan∠(AIH)=

√



Từ đó ta suy ra:

tan∠(AID) =

∠()

²∠()

√

/

= 2√2

---- HẾT ----

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2

NĂM HỌC 2024 – 2025

---------------------

Thầy Nguyễn Hoàng Phúc

ĐỀ ÔN TẬP SỐ 04

Môn: TOÁN 11

Thời gian: 90 phút

ĐỀ SỐ 04

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi

câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Cho

là số thực dương. Biểu thức

.a a

viêt dưới dạng luỹ thừa với số mũ hữu tỉ là?

Câu 2: Nếu

3 6

a a

và

3 5

b b

thì:

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 12 -

1;0 1a b  

. B.

1; 1a b 

. C.

0 1; 1a b  

1;0 1a b  

Câu 3: Cho

là số thực dương khác 1. Tính

log

I a

3I  

0I 

3I 

I 

Câu 4: Với các số thực dương

,a b

bất kì. Mệnh đề nào dưới đây đúng.

3 3 3

log 1 3log log

a b

 

  

 

 

. B.

3 3 3

9 1

log 1 log log

a b

 

  

 

 

3 3 3

9 1

log 2 log log

a b

 

  

 

 

. D.

3 3 3

log 2 3log log

a b

 

  

 

 

Câu 5: Hàm số

 

log 2 3y x 

có tập xác định là?

;

 



 

 

;

 



 

 

;

 







 



Câu 6: Cho ba số thực dương , , khác . Đồ thị các hàm số , , được cho trong

hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?

A. . B. . C. . D. .

Câu 7: Phương trình

 

log 3 2 2x  

có nghiệm là?

x 

. B.

x 

. C.

1x 

. D.

2x 

Câu 8: Tập nghiệm của bất phương trình

2 1

3 27

x



là?

 

3;

. B.

;

 



 

 

. C.

;

 



 

 

. D.

 

2; 

Câu 9: Xét các phát biểu sau:

(I) Trong không gian hai đường thẳng vuông góc với nhau thì cắt nhau.

(II) Trong không gian cho hai đường thẳng

và

song song với nhau. Nếu đường thẳng

vuông góc với

thì

cũng vuông góc với

(III) Trong không gian nếu hai đường thẳng

và b cùng vuông góc với đường thẳng

thì

và

song song với nhau.

Số phát biểu đúng là:

. B.

. C.

. D.

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông và

 

SA ABCD

. Mệnh đề nào sau đây

đúng?

 

BC SCD

. B.

 

AC SBD

. C.

 

BD SAC

. D.

 

CD SBC

Câu 11: Cho hình chóp .S ABC có

 

,SA ABC

tam giác ABC vuông tại

, kết luận nào sau đây sai?

   

SAC SBC

. B.

   

SAB ABC

. C.

   

SAB SBC

   

SAC ABC

Câu 12: Cho hình chóp tứ giác đều

.S ABCD

đáy là hình vuông tâm

, gọi

là trung điểm cạnh

Góc giữa mặt bên và mặt đáy là:

y a



y b



y c



b c a

 

a b c

 

c a b

 

a c b

 

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 13 -



SCO

. B.



SDO

. C.



SMO

. D.



SMA

PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 13: Cho hàm số

 

f x 

và

 

log 3g x x  

. Khi đó:

Các mệnh đề sau đúng hay sai?

a) Đồ thị của hàm số

 

f x

là hình dưới đây:

b) Hàm số

 

g x

có tập xác định:

 

3; 3D  

2x 

là nghiệm của phương trình

 

f x





d) Bất phương trình

 

log 2g x x

có tập nghiệm

 

3;1S  

Lời giải

Từ hình



a) Đúng.

ĐK:

3 0 3 3x x      



b) Đúng.

 

2 3 6

8 2 2 3

x x x

f x x

 

    



c) Sai.

 

3 3 3

log 2 log 3 log 2 0 1

3 1

2 3 0

g x x x x x

x x





         

 

  

   





d) Sai.

Câu 14: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật, biết

 

SA ABCD

. Gọi

là hình chiếu

của

lên các cạnh

. Khi đó?

a) SA CD . b) Tam giác SBC vuông tại

 

AH SBC

. d)

   

SAC SBD

Lời giải

 

SA ABCD

SA CD

CD ABCD





 











a) Đúng.





 

BC AB gt

BC SAB

BC SA SA ABCD







 



 





mà

 

SB SAB

BC SB 



b) Đúng.

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 14 -

 

AH SB

AH SBC

AH BC BC SAB cmt







 



 







c) Đúng.

ABCD

là hình chữ nhậtd) Sai.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.

Câu 15: Cho

log 2

b 

và

log 3

c 

. Tính

 

2 3

log

P b c

Lời giải

Ta có:

 

2 3 2 3

log log log 2 log 3log 2.2 3.3 13

a a a a a

P b c b c b c       

Câu 16: Cường độ một trận động đất

(độ Richter) được cho bởi công thức

log log

M A A

 

, với

là biên độ rung chấn tối đa và

là một biên độ chuẩn ( hằng số). Đầu thế kỉ

, một trận động

đất ở San Francisco có cường độ

độ Richter. Trong cùng năm đó, một trận động đất khác ở

Nam Mỹ có biên độ rung chấn mạnh gấp

lần. Hỏi cường độ của trận động đất ở Nam Mỹ là

bao nhiêu (kết quả làm tròn đến hàng phần chục)?

Lời giải

Gọi

1 2

,M M

lần lượt là cường độ của trận động đất ở San Francisco và Nam Mỹ. Trận động đất

ở San Francisco có cường độ là

độ Richter nên:

1 0 0

log log 8 log logM A A A A    

Trận động đất ở Nam Mỹ có biên độ là

, khi đó cường độ của trận động đất ở Nam Mỹ là:

   

2 0 0

log 4 log 8 log 4 log log log 4 8 8,6M A A A A        

(độ Richter).

Câu 17: Ông Phúc gửi

100

triệu đồng vào ngân hàng theo hình thức lãi kép với lãi suất không đổi là

/ năm. Hỏi sau

năm ông Phúc nhận được tiền lãi là bao nhiêu (làm tròn đơn vị triệu đồng)?

Lời giải

Số tiền lãi sau

năm:

 

100. 1 8% 100 116A    

(triệu đồng)

Câu 18: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông tâm

cạnh

 

, 3SA ABCD SA a 

Gọi



là góc giữa mặt phẳng

 

SBD

và

 

ABCD

. Biết

tan x y





. Tính

2 3

16 9P x y  ?

Lời giải

Ta có:

   

SBC ABCD BD 

 

BD AO

BD SAO

BD SA SA ABCD







 



 





   

 



,SBC ABCD SOA 

Ta có:

2 2

AC a

AO  

Xét

SOA

vuông tại

có:



tan 3 2

SOA

 

2 3 2 3

3; 2 16 9 16.3 9.2 216

x y P x y        

PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 22.

Câu 19: Rút gọn biểu thức

 

10 2

log log

M a b



 

với

, 0; , 1a b a b 

Lời giải

   

 

2 1

10 2 2

log log 5 log 5 6 1

M a b b

 

        

Câu 20: Biết rằng

81 81 23

x x

 

. Tính giá trị biểu thức

15 4.9 4.9

x x



  

Lời giải

Ta có:

81 81 23

x x

 

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 15 -

     

 

2 2 2

9 9 5

9 9 2.9 .9 23 2.9 .9 9 9 25

9 9 5

x x

x x x x x x x x

x x



   





 

        



  





 

15 4.9 4.9 15 4 9 9 15 4.5 5

x x x x

 

         

Câu 21: Giải phương trình sau:

   

2 2

log 5 log 2 3x x   

Lời giải

Điều kiện:

5 0 5

2 0 2

x x

  

 

  

 

   

 

Phương trình:

  

log 5 2 3x x   

 

2 2

3 10 8 3 18 0

x x x x

x l





        



 



Vậy tập nghiệm:

 

6S 

Câu 22: Giải bất phương trình sau:

2 1

4 8

x x





Lời giải

2 1 4 3 3

4 8 2 2 4 3 3 3

x x x x

x x x

 

       

. Vậy tập nghiệm:





3;S  

Câu 23: Cho hình chóp tam giác

.S ABC

, có đáy là tam giác vuông tại

 

SA ABC

a) Chứng minh

 

BC SAB

b) Vẽ

vuông góc với

tại

. Chứng minh:

   

SHB SAC

Lời giải

a) Chứng minh

 

BC SAB

Ta có:

 

BC AB gt

BC SA SA ABC

SAB SA AB A





 





 





 

BC SAB 

b) Vẽ

vuông góc với

tại

. Chứng minh:

   

SHB SAC

Ta có:

 

BH AC gt

BH SA SA ABC

SAC SA AC A





 





 





 

BH SAC 

. Mà

 

BC SHB

   

SHB SAC 

---- HẾT ----

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2

NĂM HỌC 2024 – 2025

---------------------

Thầy Phan Duy Thành

ĐỀ ÔN TẬP SỐ 05

Môn: TOÁN 11

Thời gian: 90 phút

ĐỀ SỐ 05

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi

câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Biểu thức

P x x x x



 

(với

0x 

), giá trị của



là

. B.

. C.

. D.

Câu 2: Cho các số thực

 

, , , , 0a b m n a b 

. Khẳng định nào sau đây là đúng?

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 16 -



. B.





m m n

a a





. C.





m m

a b a b

  

. D.

m n m n

a a a





Câu 3: Với mọi

a b

thỏa mãn

2 2

log 3log 2

a b

 

, khẳng định nào dưới đây đúng?

a b



. B.

3 4

a b

 

. C.

3 2

a b

 

. D.



Câu 4: Tính giá trị biểu thức

   

10 2 2

log log log

a b

P a b b



 







  











 

(với

0 1;0 1

a b

   

. B.

. C.

. D.

Câu 5: Tập xác định của hàm số





log 4

y x

 

là.







. B.







. C.







. D.





;

 

Câu 6: Tìm hàm số đồng biến trên







f x



. B.





f x





. C.

 

f x

 



















 

. D.

 

f x 

Câu 7: Nghiệm của phương trình





log 7 5

 

là



. B.



. C.



. D.



Câu 8: Giải phương trình

2 3 4

4 8

x x

 



. B.



. C.



. D.



Câu 9: Cho hình lập phương

ABCD A B C D

   

. Góc giữa hai đường thẳng

và

A D



bằng



. B.



. C.



. D.



Câu 10: Cho hình chóp

S ABCD

có đáy

ABCD

là hình vuông và

vuông góc đáy. Mệnh đề nào sau

đây sai?





BC SAB



. B.





AC SBD



. C.





BD SAC



. D.





CD SAD



Câu 11: Cho hình chóp

S ABCD

có





SA ABCD



, đáy

ABCD

là hình thang vuông tại

và

. Biết

SA AD DC a

  

AB a



. Khẳng định nào sau đây sai?









SBD SAC



. B.









SAB SAD



. C.









SAC SBC



. D.









SAD SCD



Câu 12: Cho hình chóp

S ABC

có đáy là tam giác vuông tại





SA ABC



3 cm



1 cm



2 cm



. Mặt bên





SBC

hợp với đáy một góc bằng:



. B.



. C.



. D.



PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 13: Các mệnh đề sau đúng hay sai?

a) Hàm số

log (2 1)

y x

 

có tập xác định của hàm số là:

;

 







 











 

b) Hàm số

log

y x



nghịch biến trên tập xác định của nó.

x

 



















 

có nghiệm lớn nhất là



1 1

9 9

log ( 2 1) log ( 1)

x x

   

tập nghiệm của bất phương này là:

2 1

;

3 2

 







  











 

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 17 -

Câu 14: Cho hình chóp

S ABCD

có

vuông góc với mặt phẳng

( ), 2

ABCD SA a



ABCD

là hình

thang vuông tại

và

với

2 ,

AB a AD DC a

  

. Khi đó:

AB SD



( )

CD SAD



( ) ( )

SBC SAC



(( ),( )) 60

SBC ABC





Lời giải

Gọi

là trung điểm

, khi đó

AMCD

là hình vuông, đường chéo

AC a



Tam giác

ACB

có trung tuyến

thoả mãn

CM 

nên

ACB

là tam giác vuông tại

Ta có: ( )

( do ( ))

AC BC

BC SAC BC SC

SA BC SA ABCD









   





 





Khi đó:



( ) ( )

, (( ),( )) ( , )

( ), ( )

SBC ABC BC

AC BC SC BC SBC ABC SC AC SCA

AC ABC SC SBC





 



    





 





Tam giác

SAC

vuông tại

có:

 

tan 1 45

SA a

SCA SCA



    

Vậy



(( ),( )) 45

SBC ABC SCA



 

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18. Ở mỗi câu thí sinh

điền đáp án của câu đó.

Câu 15: Rút gọn biểu thức sau:





3 1 2 3

2 2

( 0)

a a

Q a

 







  . Biết

Q a



khi đó giá trị của m là bao nhiê?

Lời giải

Đáp án: 5.

Ta có:





3 1 2 3 3 1 2 3 3

2 2

2 2 ( 2 2)( 2 2) 2

a a a a

Q a

a a a

    





   





  



  





 





Câu 16: Cho

log 3



và

log 4



với

; ; 0; 1

a b c a

 

. Tính giá trị của

log

a b

 

 





















 

Lời giải

Đáp án: - 8,5.

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 18 -

2 3

log log log log 2 log 3 log

Ta có:

1 3 17

2 log 3 log 2 12 .

2 2 2

a a a a a a

a a

a b

P a b c b c

b c

 

 







      













 



      

Câu 17: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức

( ) (0) 2

s t s

 

, trong đó

(0)

là số lượng vi khuẩn

lúc ban đầu,

( )

s t

là số lượng vi khuẩn

có sau

phút.

Biết sau 3 phút thì số lượng vi khuẩn

là 625 con. Hỏi sau phút, kể từ lúc ban đầu, số lượng vi

khuẩn A là 10 triệu con?

Lời giải

Đáp án: 7

Ta có:

(3)

(3) (0) 2 (0) 78,125

s s s    

nghìn con.

Do đó

( ) 10

s t



triệu con

10000



nghìn con khi:

10000

10000 (0) 2 2 128 2 7 phút.

78,125

t t

s t       

Câu 18: Trong không gian cho tam giác đều

SAB

và hình vuông

ABCD

cạnh

nằm trên hai mặt phẳng

vuông góc. Góc giữa hai mặt phẳng





SAB

và





SCD

là bao nhiêu độ (làm tròn đến hàng phần

chục).

Lời giải

Đáp số: 54,6

Gọi

là trung điểm của



là trung tuyến đồng thời là đường cao của tam giác

SAB

Ta có:









   





SAB ABCD

AB SAB ABCD

SH SAB SH AB









 





 









SH ABCD

 

Gọi

là trung điểm của



là đường trung bình của hình vuông

ABCD

HI a HI CD

  

CD SH

CD HI























CD SHI

 

CD SI

 

TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11

BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025

Trang

- 19 -

Lại có









   

;

/ /

S SAB SCD

AB SAB CD SCD

AB CD





 



 















Sx SAB SCD

  

với

/ / / /

Sx AB CD

Ta có:

/ /

Sx AB

AB SH















SH Sx

 

. Chứng minh tương tự:

Sx SI



Khi đó:









 





Sx SCD SAB

SH SAB SH AB

SI SCD SI CD





 



 





 





















, ,SAB SCD SH SI HSI



 

   

 

 

Xét

SHI



có:

2 3

tan

   .

PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 24.

Câu 19: Rút gọn các biểu thức sau:

( 0,,

A a b a b



 









  













 

Lời giải

6 1 6 1

3 2

3 3 3 3

a b a b ab

   



 









  













 

Câu 20: Cho

là một số thực dương. Rút gọn biểu thức sau:

1 9

log log log .

A a a

  

Lời giải

Áp dụng công thức đổi cơ số, ta đưa các biểu thức lôgarit về lôgarit cơ số 3 như sau:

3 3 3

1 3

3 3 3

3 3

log log log

log log ;

1 1

log 3

log

log log log

log 2 log 2 2 2 4 log ;

log 3

1 1

log log

log

log .

log 9 2

log 3

a a a

a a

a a a

a a



    



       

   

Thay các kết quả trên vào biểu thức

, ta được:

3 3 3

log

log 4 log log .

2 2

A a a a

     

Vậy

log

A a

  .

Câu 21: Giải phương trình sau:

2 1

9 243

x x

 



Lời giải

2 1 2( 2) 5( 1)

9 243 3 3 2( 2) 5( 1) 3

x x x x

x x x

   

         

Vậy phương trình có nghiệm là

 

Câu 22: Giải bất phương trình sau:

0,5 0,5

log ( 3) log ( 2) 1

x x

    

Lời giải

0,5 0,5

log ( 3) log ( 2) 1

x x

    

Bấm Tải xuống để xem toàn bộ.

| 1/57

| | Tải xuống

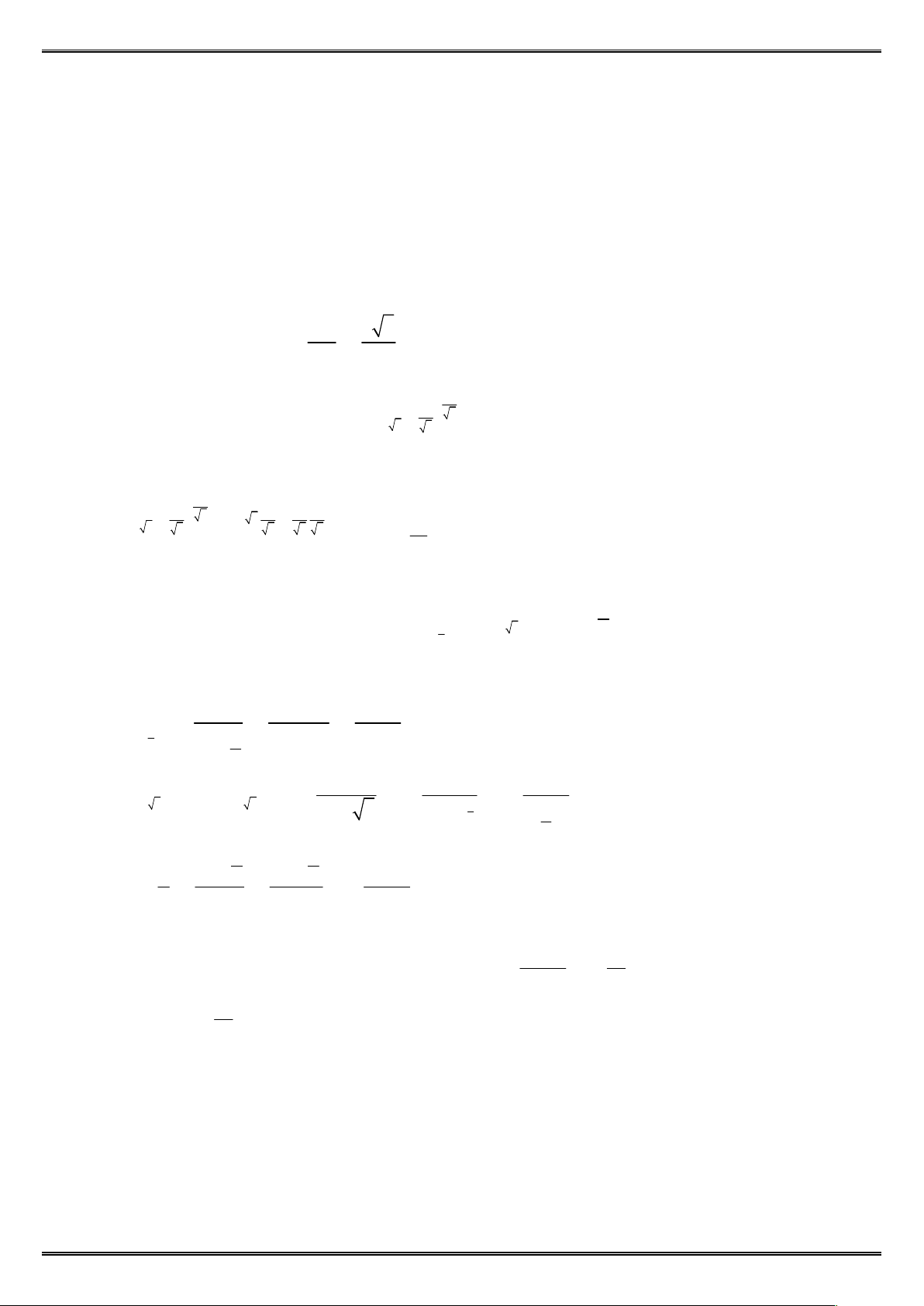
Preview text:

TRƯỜNG THCS-THPT TRẦN CAO VÂN TO T ÁN O 11
BỘ ĐỀ ÔN TẬP GKII - GIÁO VIÊN π π π π π π π π π π π π π π LƯU π HÀNH NỘI BỘ π π π π π
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2
ĐỀ ÔN TẬP SỐ 01
NĂM HỌC 2024 – 2025 Môn: TOÁN 11 --------------------- Thời gian: 90 phút
Thầy Đỗ Minh Tiến ĐỀ SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn 1 phương án.
Câu 1: Cho biểu thức 3 2
P  x .x , với x  0 . Mệnh đề nào dưới đây đúng? 7 8 2 A. 3
P  x .
B. P  x . C. 3 P  x . D. 3 P  x . 24 23 1 1    
Câu 2: Cho số thực dương a thỏa mãn      
. Khẳng định nào sau đây là đúng? a  a       1 1
A. 0  a  1 . B. a  . C.  a  1 . D. a  1 . 2 2
Câu 3: Biết 2a  5. Khi đó:
A. a  log 5 .
B. a  log 2 .
C. a  log 2 .
D. a  log 2 . 2 5
Câu 4: Biết log b  3 . Tính 2 log b . a a 1 A. 9 . B. 6 . C. . D. 6 . 9
Câu 5: Hàm số nào sau đây đồng biến trên  ;    ? x x x  3     x e  
A. y   5  2 . B. y     y  0, 7 y     . C.   . D. .  2
Câu 6: Tập xác định của hàm số y  ln x  2 là A. 2;     . B. 2;. C.  . D.  \   2 .
Câu 7: Nghiệm của phương trình x 1 3   27 là A. x  4 . B. x  3 . C. x  2 . D. x  1 .
Câu 8: Tập nghiệm S của bất phương trình log
x  1  log 2x  1 là 1   1   2 2 1   
A. S  2; .
B. S   ;  2 .
C. S   ;2  S  1  ;2  . D.  . 2 
Câu 9: Chọn mệnh đề đúng?
A. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó cắt nhau.
B. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó chéo nhau.
C. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó song song với nhau.
D. Nếu hai đường thẳng vuông góc với nhau thì chúng hoặc chéo nhau hoặc cắt nhau.
Câu 10: Cho hình chóp S.ABC có SA  ABC , tam giác ABC vuông tại B , kết luận nào sau đây sai?
A. SAC   SBC . B. SAB  ABC  . C. SAB  SBC  D. SAC   ABC .
Câu 11: Cho hình chóp S.ABC có SA vuông góc với mặt đáy ABC . Mệnh đề S nào sau đây là đúng?
A. SA  SB .
B. SA  SC .
C. SA  BC .
D. SB  SC . C A B
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 1 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
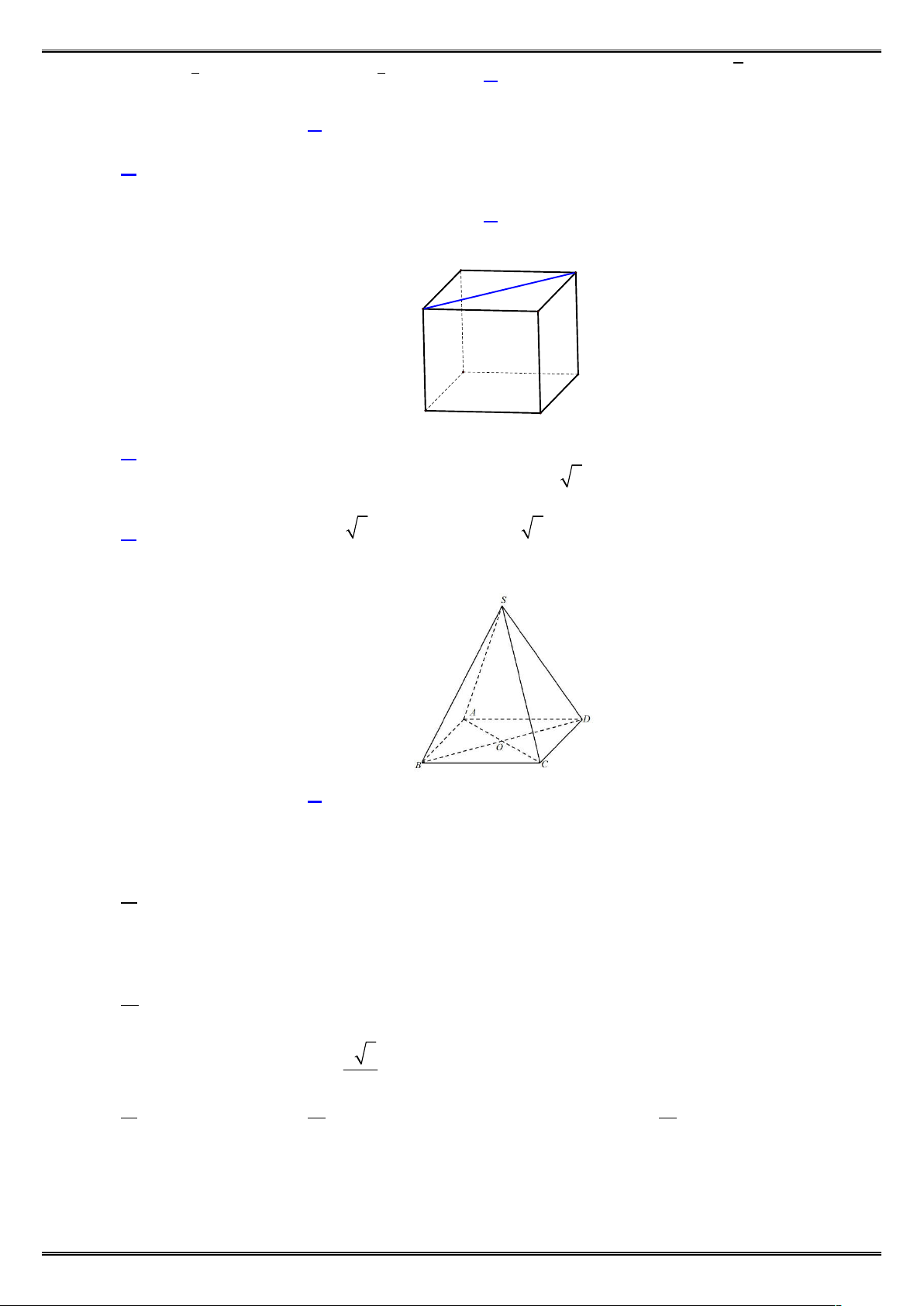
Câu 12: Cho hình lăng trụ đều ABC .AB C
  có AB  2 và AA  1. Góc tạo bởi giữa hai mặt phẳng (A B
 C ) và (ABC ) bằng A' C' B' A C B A. 45. B. 60. C. 30. D. 75 . 
PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13: Cho hàm số y  f (x)  log (x  2). Khi đó các mệnh đề sau đúng hay sai? 5
a) Tập xác định của hàm số là D  (2;  )  .
b) Đồ thị hàm số đi qua điểm M (1; 0).
c) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ x  1.
d) Bất phương trình f (x )  1 có tập nghiệm S  ( ;  3).
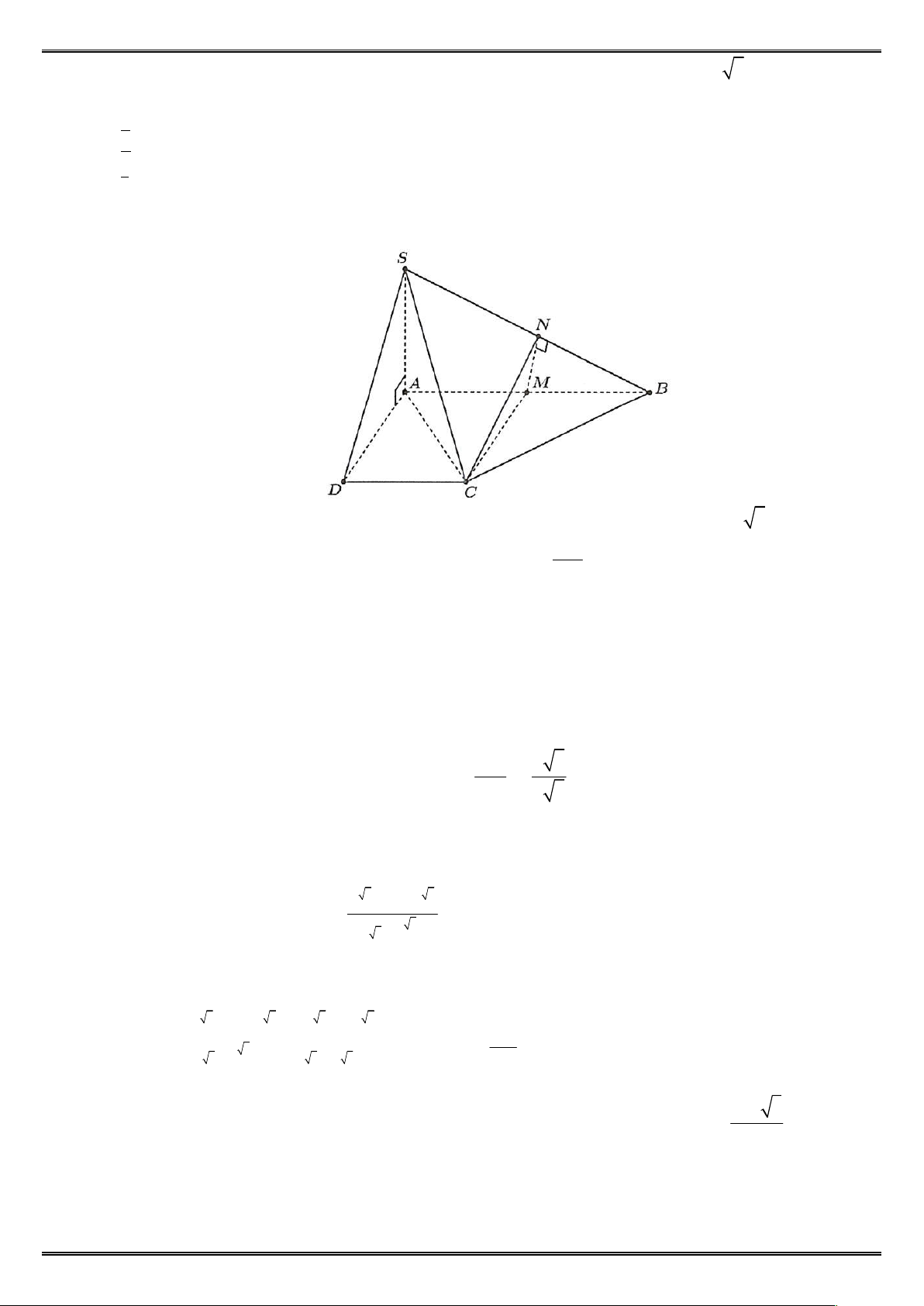
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại
B,AB  a. Cạnh bên SA vuông góc với đáy và SA  a 3 . M là S
trung điểm của AC . a) SA  BC .
b) BM  (SAC ).
c) Mặt phẳng (SAB) vuông góc với mặt phẳng(SAC ).
d) Mặt phẳng (SBC ) tạo với mặt phẳng đáy một góc có số đo là C A 0 30 . B
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15: Cho log b  2, log c  3. Khi đó: 2 3
P  log (a bc ) bằng a a a Đáp số: 13. 2 x 1
Câu 16: Tổng các nghiệm của phương trình 2  bằng x 4 4  Đáp số: 2.
Lời giải tham khảo x   x 1 4 2 2  Ta có: x 8 2  x 2 2   2  2
 x  8  2x  . x 4 4  x  2 
Câu 17: Để dự báo dân số của một quốc gia, người ta sử dụng công thức nr
S  Ae ; trong đó A là dân số
của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2020
(lấy làm mốc tính), dân số một nước là 100 triệu người. Giả sử tỉ lệ tăng dân số hàng năm không
đổi là 0, 8%, dự báo dân số nước đó năm 2035 là bao nhiêu triệu người?(kết quả làm tròn đến chữ số hàng đơn vị)? Đáp số: 113.
Lời giải tham khảo
Lấy năm 2020 làm mốc, ta có A  100;n  2035  2020  15 0,8 15.
Suy ra: dân số nước đó vào năm 2035 là 0 10 S  100.e  113 triệu người.
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 2 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
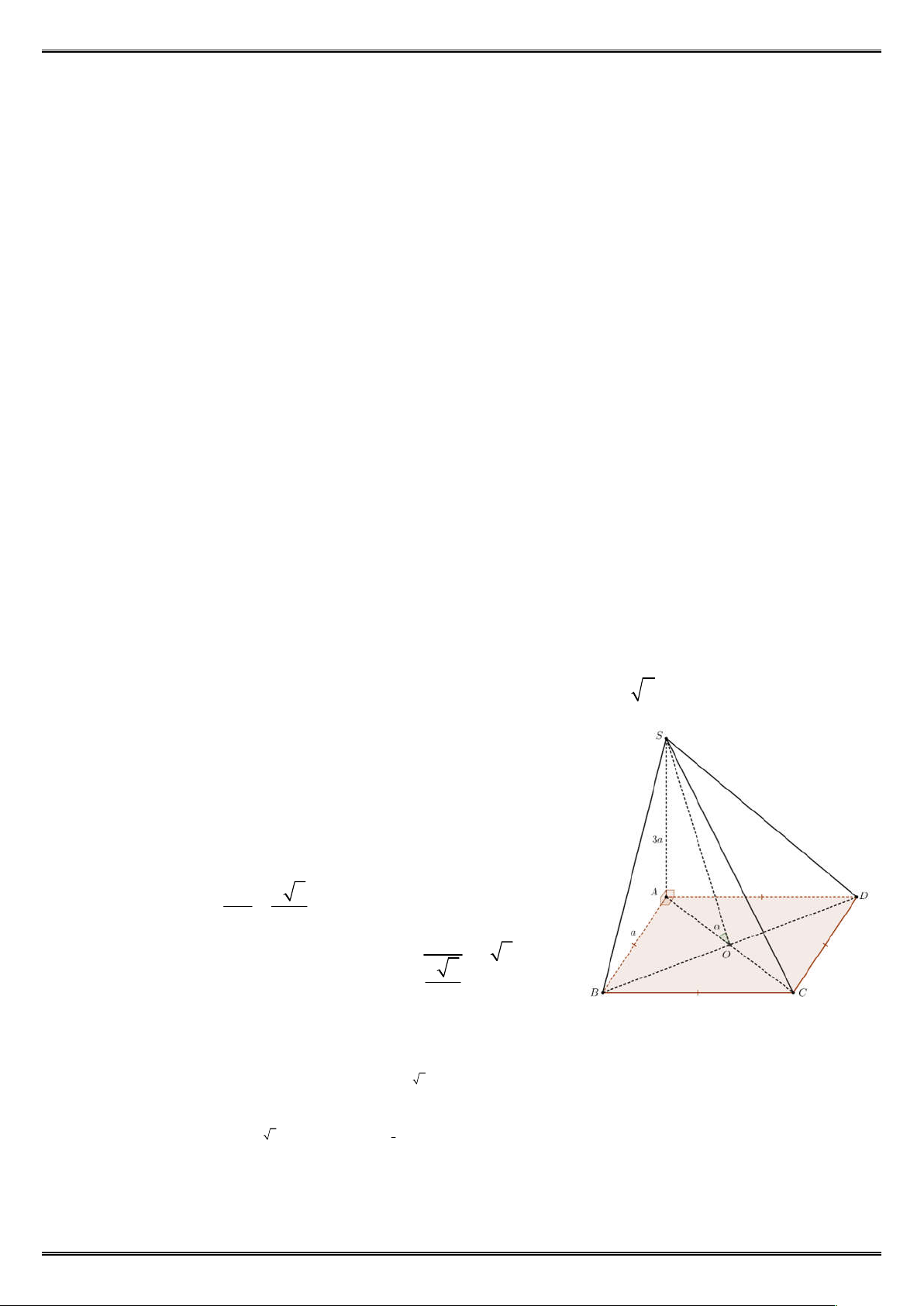
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA  ABCD và SA  a 6 .
Gọi  là góc giữa BC và mặt phẳng (SAB). Khi đó cos  bằng Đáp số: 0.
PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 24.
Câu 19: Biết rằng 2x 2 x  
 14 . Tính giá trị biểu thức 4x 4 x P     10 ?
Câu 20: Cho log 5  a, log 2  .
b Tính giá trị biểu thức P  log 30 theo , a . b 3 3 2
Câu 21: Giải phương trình: log x  log (x  3)  2. 2 2 4x x 3 1  
Câu 22: Giải bất phương trình 0,2 2     . 5
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy
và SA  a 3. Gọi H là hình chiếu của A trên cạnh SD .
a) Chứng minh CD  (SAD).
b) Tính số đo góc tạo bởi hai mặt phẳng (SCD) và (ABCD). ---- HẾT ----
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2
ĐỀ ÔN TẬP SỐ 02
NĂM HỌC 2024 – 2025 Môn: TOÁN 11 --------------------- Thời gian: 90 phút Cô Hồ Thị Mỹ Ly ĐỀ SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn 1 phương án. 3 2 4
Câu 1: Biểu thức rút gọn của 3 A= x x x là: 23 23 3 A. 24 x . B. 12 x . C. 11 x . D. 4 x .
Câu 2: Cho số thực dương a và số nguyên dương n tùy ý. Mệnh đề nào sau đây là đúng? n 2 A. n n 2 a a   . B. n 2n a  a . C. n 2 a  a . D. n n a  a
Câu 3: Biết a  log 2,b  log 5 . Tính log 5 theo a,b . 3 2 3 a b b A. log 5  .
B. log 5  ab . C. log 5  . D. log 5  . 3 b 3 3 b  a 3 a
Câu 4: Cho log x  16 . Tính 2 A = log (log x ). 2 8 4 3 1 4 A. . B. . C. . D. 3 . 4 3 3 2 x 4  x 2  2   3
Câu 5: Tập nghiệm của phương trình     là: 3 2
A. S  2  2;2  2.
B. S  2  3; 2  3.
C. S  2  5; 2  5.
D. S  1;  3 .
Câu 6: Nghiệm của phương trình log (x  1)  3 là: 2 A. 7 B. 6. C. 10. D. 9. 2x 3  1  
Câu 7: Nghiệm của bất phương trình    9  là: 3
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 3 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 1 1 A. x  . B. x  2. C. x  2. D. x  . 2 2
Câu 8: Nghiệm của bất phương trình log (x  3)  log (6  2x) là: 0,5 0,5 A. x  3. B. x  1.
C. 1  x  3.
D. 3  x  1 .
Câu 9: Cho hình chóp S.ABC có SA vuông góc với đáy. Mệnh đề nào sau đây là đúng? A. SA  BC. B. SA  SC. C. SA  SB. D. SC  BC.
Câu 10: Đường thẳng a gọi là vuông góc với mặt phẳng () nếu:
A. Đường thẳng a vuông góc với một đường thẳng bất kỳ nằm trong mặt phẳng () .
B. Đường thẳng a vuông góc với hai đường thẳng bất kỳ nằm trong mặt phẳng () .
C. Đường thẳng a vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng () .
D. Đường thẳng a vuông góc với hai đường thẳng phân biệt nằm trong mặt phẳng () .
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy. Mặt phẳng
(SCD) vuông góc với mặt phẳng nào sau đây? A. (ABCD) . B. (SAD) . C. (SBD) . D. (SAC) .
Câu 12: Mặt phẳng () gọi là vuông góc với mặt phẳng () nếu:
A. Một đường thẳng trong mặt phẳng () vuông góc với một đường thẳng trong mặt phẳng ()
B. Hai đường thẳng trong mặt phẳng () vuông góc với hai đường thẳng trong mặt phẳng ()
C. Một đường thẳng trong mặt phẳng () vuông góc với hai đường thẳng cắt nhau trong mặt phẳng () .
D. Một đường thẳng trong mặt phẳng () vuông góc với hai đường thẳng phân biệt trong mặt phẳng () .
PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13: Cho a, ,
b c là các số thực dương tùy ý, a  1. Khi đó:  3 a    3
a) log (ab)  1  log b . b) log    . a a a   2
b  2 log b a c) log (bc)  log . b log . c d) 2
log b  2 log c  log a  log (b  c  2). a a a a a 2 a Lời giải
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 4 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
a) log (ab)  log a  log b  1  log b. Đúng a a a a  3 a    b) 3 2
log    log a  log b  3 log a  2 log . b Sai a   2 a a a a b 
c) log (bc)  log b  log . c Sai a a a d) 2 2
log b  2 log c  log a  log b  log c  log a  l og (b  c  a). Sai a a 2 a a 2 a
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA  (ABCD) . Phát biểu nào sau đây là đúng? a) 0 ( , SA CD)  90 .
b) CD  (SAD).
c) BD  (SAC ). d) 0
((SCD),(SAD))  60 . Lời giải a) 0
SA  (ABCD)  SA  CD  (S ,
A CD)  90 . Đúng C  D  AD  b) 
 CD  (SAD). Đúng C  D  SA 
c) BD  SA nhưng BD không vuông góc với AC nên BD không vuông góc với (SAC ). Sai C
 D  (SAD)  d) 0 
 (SAD)  (SCD)  ((SAD),(SCD))  90 . Sai C  D  (SCD) 
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18. m 3
Câu 15: Cho biểu thức 3 n
a a  a . Hỏi m  n  ? Lời giải Đáp số: 11 3 5 5 5 3 3 :3 3 m 5 3 2 2 2 6
a a  a.a  a  a  a  
m  n  11. n 6
Câu 16: Tập xác định của hàm số 2
y  log (x  1) là D  ( ;
 b)  (a; )
 . Hỏi a b  ? 2 Lời giải Đáp số: 2 Điều kiện: x  1 2 x 1 0     D  ( ;  1)  (1; )
 a  1, b  1  a b  1  (1)  2.  x  1  2 2
Câu 17: Phương trình x x  x x  2 9 3  
có hai nghiệm x , x . Tính | x  x |. 1 2 1 2 Lời giải Đáp số: 3 2 2 2 2 x x  x x  2  2 x x  x x  2  2 2 2 9  3  (3 )  3
 2(x  x)  x  x  2  x  x  2  0 x  1   |  x  x | |  1  2 | 3  1 2 x  2 
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 5 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
Câu 18: Cho chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB  a 2 , SC  2a ,
SA  (ABC ). Tính góc giữa SC và đáy. Lời giải Đáp số: 45   AC 2a 2  0
(SC,(ABC ))  (SC,AC )  S , CA cosSCA     SCA  45 . SC 2a 2
PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 23. log 4 l  og 5
Câu 19: Rút gọn biểu thức 9 3 A  3 . Lời giải 1 log 4log 5 log 4 log 5 log 3 log 3 Ta có: 9 3 9 3 9 3 1 2 A  3  3 .3  4 .5  4 .5  2.5  10.
Câu 20: Rút gọn biểu thức 3 4
B  log b .log a . 3 b Lời giải 3 Ta có: 3 4 3 4
B  log b .log a  log b .log a  .log .4
b log a  24 log b log a  24 log a. 1 b b 3 b 3 b 3 3 2 3 1 2
Câu 21: Giải phương trình (7 4 3)x 3(2 3)x     2  0. Lời giải x x   
     2x x (7 4 3) 3(2 3) 2 0 2 3
 32  3  2  0 x
Đặt t  2  3 , t  0. PT 2
 t  3t  2  0  x
t  2 (n)  
2 3  2x  log 2 2 3   x
t  1 (n)  
2 3 1x  log 1 0 2 3   2 x x    
Câu 22: Giải phương trình log    0. 2   4  2x  Lời giải 2 x  x x   1 2  x  x Điều kiện:  0  . PT 0   2 4  2x 0  x  2  4  2x 2 x  x x  1(n) 2 2 1 x x 4 2x x 3x 4 0             4  2x x  4(n) 
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a , SA vuông góc với
đáy, SA  a 2 . Gọi M là trung điểm của cạnh BC .
a) Chứng minh: CD  (SAD).
b) Tính góc giữa SM và mặt phẳng đáy (làm tròn đến đơn vị độ).
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 6 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 Lời giải C  D  SA  a) Ta có: 
 CD  (SAD) C  D  AD  b) Ta có:
M là hình chiếu của M lên (ABCD)
A là hình chiếu của S lên (ABCD)
 AM là hình chiếu của SM lên (ABCD) 
 (SM,(ABCD))  (SM,AM )  SMA 2 a    a 5 Ta có: 2 2 2
AM  AB  BM  a      2 2
Xét SAM vuông tại A ta có:  SA a 2 2 10 tan SAM     0  0
 SAM  54  (SM,(ABCD))  SAM  54 . AM 5 a 5 2 ---- HẾT ----
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2
ĐỀ ÔN TẬP SỐ 03
NĂM HỌC 2024 – 2025 Môn: TOÁN 11 --------------------- Thời gian: 90 phút
Thầy Lê Kinh Huỳnh ĐỀ SỐ 03
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn 1 phương án.
Câu 1: Cho là số thực dương tùy ý, biểu thức . √ bằng A. . B. . C. . D. .
Câu 2: Tính giá trị biểu thức = √ . √ . √ A. = −2 B. −1. C. −2 . D. 2 .
Câu 3: Nếu2 = 9 thì có giá trị bằng A. . B. 3. C. . D. . √ Câu 4: Cho = 4
. Khi đó giá trị của bằng A. 9. B. 6. C. √3. D. 81. Câu 5: Nếu = 2 và = 3. Tính = ( ). A. = 31. B. = 13. C. = 30. D. = 108.
Câu 6: Hàm số nào sau đây không là hàm số mũ?
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 7 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 A. = . B. = . C. = . D. = √2 .
Câu 7: Giá trị của biểu thức M = log 2 + log 4 + log 8 + ⋯ + log 2 048 bằng A. 11. B. 66. C. 4096. D. 11 2 048.
Câu 8: Tìm tập xác định của hàm số = ( − 3). A. = (3; +∞). B. = (−3; +∞). C. = (0; +∞). D. = ℝ\{3}.
Câu 9: Tập nghiệm của bất phương trình 3 > 27 là A. ( ; +∞) B. (− ; )
C. (−∞; − ) ∪ ( ; +∞) D. (−∞; − )
Câu 10: Cho hình lập phương .
. Tính góc giữa hai đường thẳng và CC’. A' D' B' C' A D B C A. 90°. B. 45°. C. 60°. D. °.
Câu 11: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a 2 và tam giác SAC đều. Tính độ dài
cạnh bên của hình chóp. A. 2a . B. a 2 . C. a 3 . D. a .
Câu 12: Cho hình chóp .
có đáy là hình thoi tâm , = , =
. Trong các khẳng định sau khẳng định nào đúng? A. ⊥ ( ). B. ⊥ ( ). C. ⊥ ( ). D. ⊥ ( ).
PHẦN II. Thí sinh trả lời từ câu 13 đến câu 15. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13: Cho hàm số y   2
log x  2x  m   2 .
a) Với m  0 thì hàm số có tập xác định là D   .
b) Với m  0 , đồ thị hàm số không cắt trục hoành.
c) Đồ thị hàm số đi qua điểm M 2;7 khi m  5  .
d) Có 2022 giá trị nguyên của m thuộc đoạn  2021;2021  
 để hàm số có tập xác định là  .
Câu 14: Cho hình chóp S.ABCD , có đáy là hình vuông ABCD cạnh bằng a , tâm O . Cạnh bên SA a 2
vuông góc với đáy và SA 
. Điểm M là trung điểm cạnh SO . Khi đó: 2
a) BD  SAC . b) BD  SC .
c) CD  SBC  . d) AM  SB . Lời giải Câu1. a) Đúng.
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 8 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
Với m  0 thì hàm số y   2
log x  2x   2 xác định
 x  x   x  2 2 2 2 0
1  10, x   .
Vậy hàm số có tập xác định là D   .
b) Sai. Đồ thị hàm số y   2
log x  2x  
2 cắt trục hoành tại điểm có hoành độ thỏa mãn phương trình
 2x  x   2 2 log 2
2  0  x  2x  2  1  x  2x  1  0  x  1
Vậy đồ thị hàm số cắt trục hoành tại 1 điểm. c) Sai. Với m  5
 thì hàm số y   2
log x  2x  7.
Khi đó x  2 thì y  log 7 .
Vậy đồ thị hàm số qua điểm 2;log 7 mà không đi qua điểm M . d) Đúng. Điều kiện: 2
x  2x  m  2  0 .
Hàm số có tập xác định  2
 x  2x  m  2  0, x
      1  m  2  0  m  1.
Do m nguyên thuộc đoạn  2021;2021  
 nên có 2022 giá trị m thỏa yêu cầu bài toán. Câu 15: a) Đúng. Ta có B  D  AC B
 D  SA (doSA  (ABCD))  BD  (SAC)  . S
 A  SAC,AC  SAC  BD   (SAC )  b) Đúng. Do  BD  SC . S  C  (SAC )  CD   AD 
c) Sai. Ta có CD   SA  CD  (SAD)  SA
  SAD,AD  SAD 
Do SD  (SAD)  CD  SD   1
Nếu CD  (SBC ), CD  SC  (SBC )  CD  SC 2 Từ   1 và 2  S
 CD có hai góc vuông ( vô lí). AC a 2
d) Đúng. Đáy ABCD , cạnh bằng a .Ta có AO  
 AO  SA  S  AO vuông 2 2 cân tại A . Suy ra ⊥ (3) BD   (SAC )  Do
 BD  AM 4. Từ (3) và (4) suy ra AM  (SBD)  AM  SB . A  M  (SAC ) 
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 16 đến câu 19. 3
Câu 16: Cho số dương và số thực r , biết r
a a  a . Tính r .
Đáp án: 0, 5 1 1  1 3  1 3 3 1 1 1 .     Ta có 3 0,5 2 2 2 3 2 a a  a  .a     a   .      a  a  a        a
Câu 17: Cho log yz   4, log zx   5 . Khi đó log xy 
, trong đó 0  x,y, z  1; z   x y b
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 9 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 a a,b *   và
là phân số tối giản. Tính 2 2
P  a  b . b Đáp án: 482 . log xy  y x   1 log Ta có: log xy x   (1) z log z log z x x  y  z        y yz     x   5 log log 4 x x log log 4 x   Từ giả thiết: 6    z    log  zx      y   log 1 5 x 5 19    log y log  z  x  x  6 5 1  11 6
Thay vào (1) ta được: log xy    a  b  z   11; 19. 19 19 6 2 2 2 2
 P  a b  11  19  482 .
Câu 18: Bất phương trình log 2x  1  log 5 có bao nhiêu nghiệm nguyên? 3   3 Đáp án: 3 1
Ta có: log 2x  1  log 5  0  2x  1  5   x  3 . 3   3 2
Vậy bất phương trình trên có 3 nghiệm nguyên.
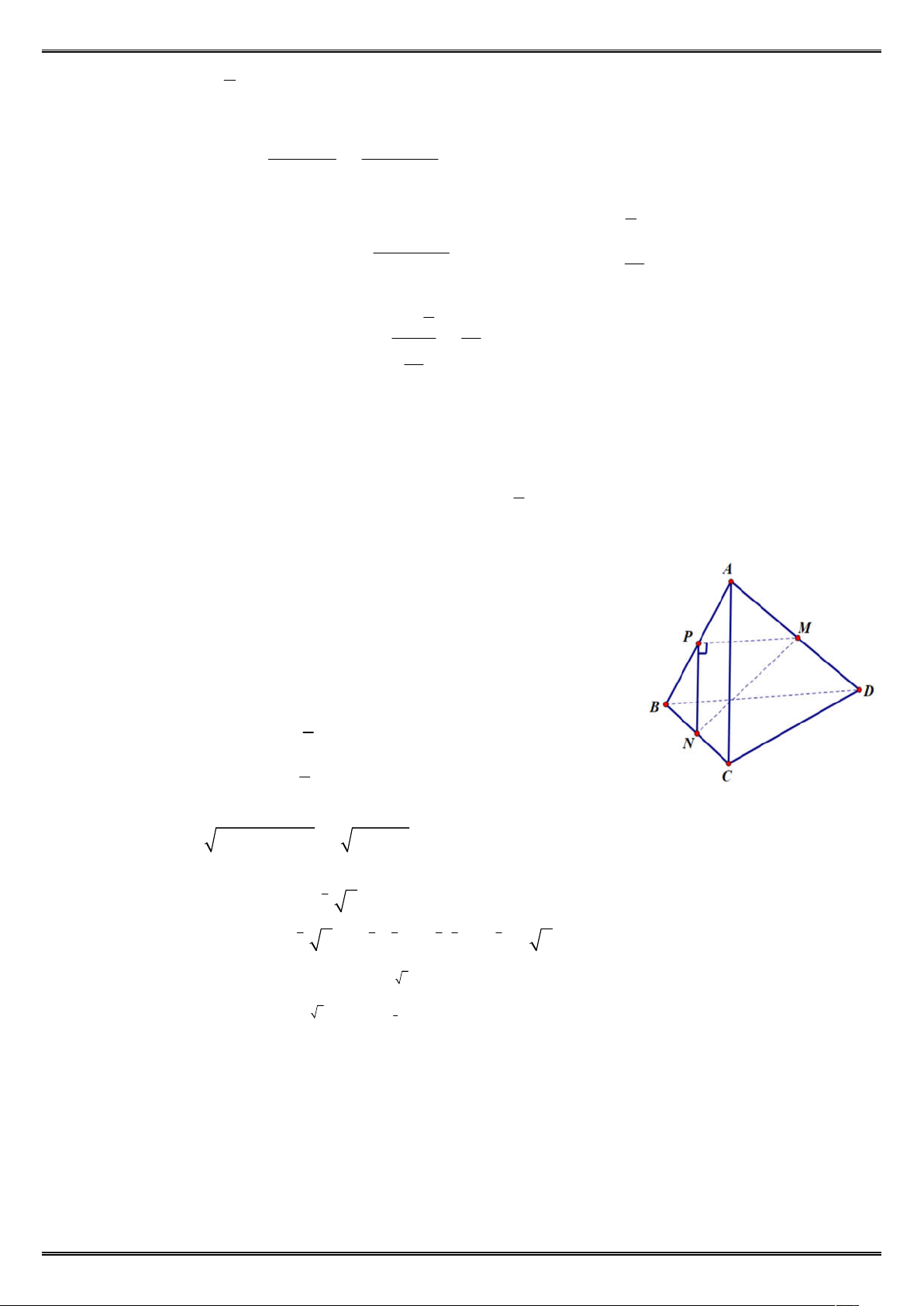
Câu 19: Cho tứ diện ABCD có AC  12, BD  16 . Gọi M , N lần lượt
là trung điểm của AD và BC . Biết AC vuông góc với BD. Tính MN . Đáp án: 10 .
Gọi P là trung điểm của AB.
Ta có: PM ;PN lần lượt là đường trung bình của ABD;ABC.  1 P
 M / /BD;PM  BD  8  2   . 1 P
 N / /AC;PN  AC  6  2
Do BD  AC nên PM  PN hay tam giác PMN vuông tại P . 2 2 2 2
 MN  PM  PN  8  6  10.
PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 20 đến câu 24. 1
Câu 20: Rút gọn biểu thức 6 3
P  x . x với x  0 . 1 1 1 1 1 1  Lời giải: Ta có: 6 3 3 6 3 6 2
P  x . x  x .x  x  x  x .
Câu 21: Tính giá trị của biểu thức P  log
a với 0  a  1 . a
Lời giải: Ta có: P  log
a  log a  2 log a  2 . 1 a a 2 a
Câu 22: Giải phương trình sau: log x  log x  1  1 2 2   Lời giải x   0 
Điều kiện xác định:   x  1 . x   1  0  x  2
log x  log x   1  2  log x    x   2 1 2
1  1  x  x  2  x  x  2  0  . 2 2 2   x  1  
Dựa vào điều kiện ta thấy phương trình có nghiệm duy nhất là x  2 .
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 10 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
Câu 23: Giải bất phương trình log 3  x  1  0,5   Lời giải 3   x  0  x   3   Ta có: log 3 x  1         x  3
 x  0,5 1 1 3 0,5 3   x  2   
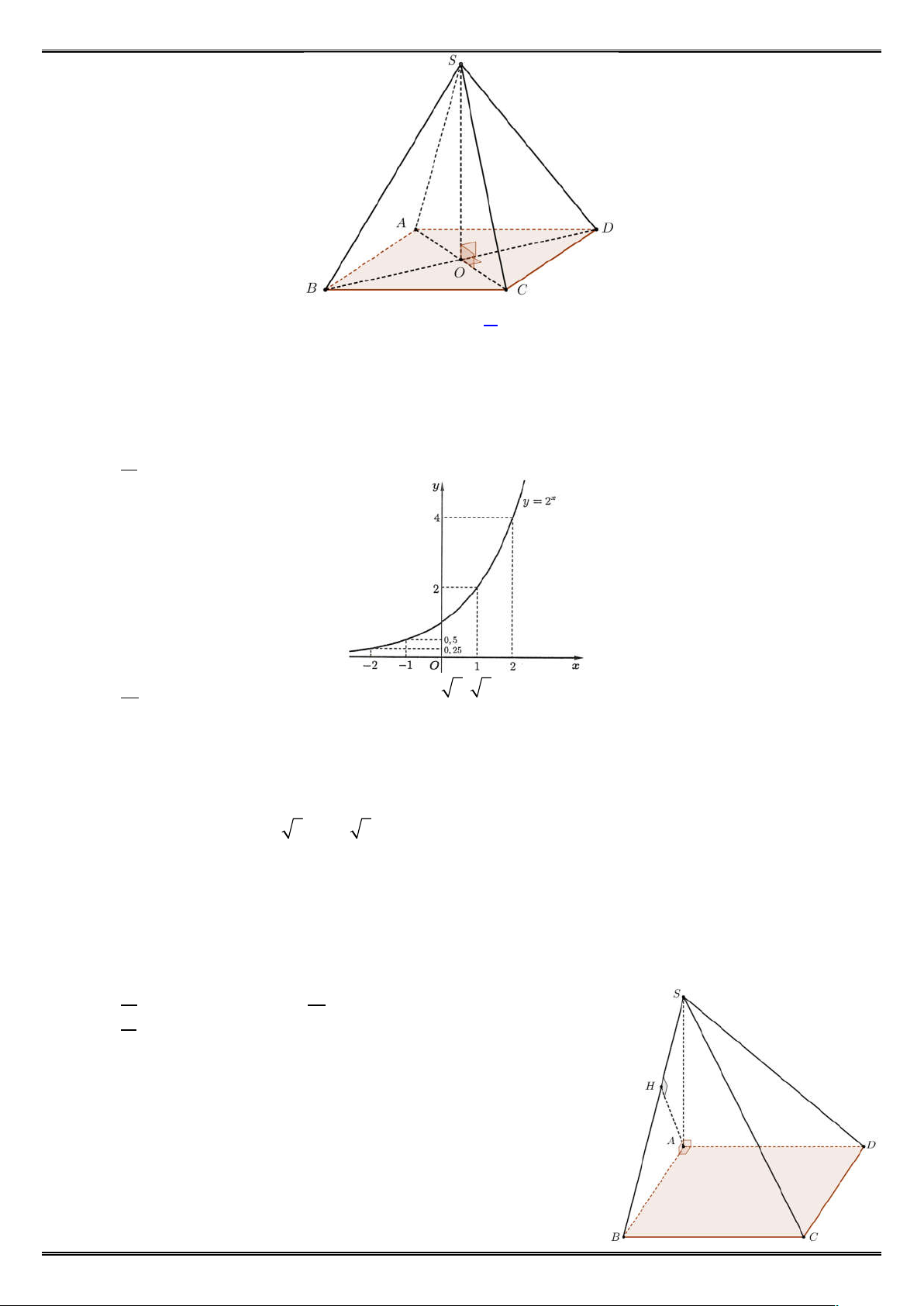
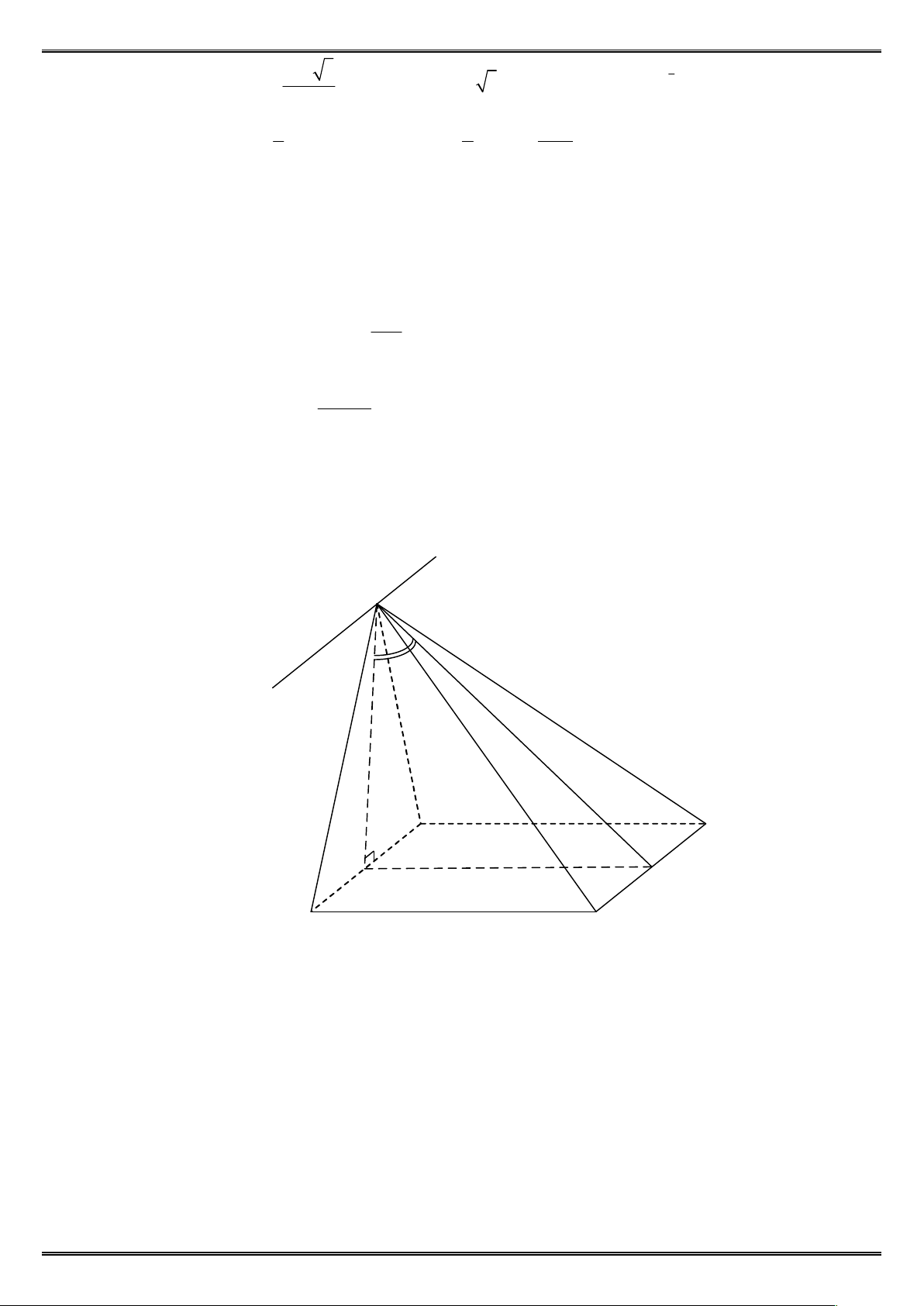
Câu 24: Cho hình chóp . có đáy
là hình vuông cạnh bằng . Gọi là trung điểm của ,
vuông góc với mặt đáy, SH = a. Gọi là trung điểm của . a) Chứng minh
vuông góc với mặt phẳng ( ). b) Chứng minh ( ) vuông góc với ( ).
c) Tính giá trị tang của góc giữa hai mặt phẳng ( )và ( ). 5 a) Ta có: ⊥ ( ) ⇒ ⊥ ⊥ ⊥ , ⊂ ( )⟹ AB ⊥ (SAD)
b) SH ⊥ (ABCD) ⇒ SH ⊥ BC BC ⊥ HM BC ⊥ SH
AH, HM ⊂ (SHM)⟹ BC ⊥ (SHM)
Mà BC ⊂ (SBC) nên (SBC) ⊥ (SHM)
c) Trong mặt phẳng (SAM), kẻ AI ⊥ SM, ta có: DI ⊥ SM (Vì SM ⊥ (AID)) (SDM) ∩ (SAM) = SM AI ⊥ SM DI ⊥ SM ⟹∠((SDM)(SAM)) = ∠(AID) Ta có: SH = a (gt) △SDM = △SAM (c-c-c)
⇒ ID = IA (2 đường cao tương ứng bằng nhau) ⇒ △AID cân tại I ⇒ ⊥ AD Xét △SHM, ta có:
SM² = SH² + HM² = 2a² ⇒ SM = a√2
Vì △SHM vuông cân tại H nên: √ HI = SM = √
Xét △AIH, ta có: tan∠(AIH)= Từ đó ta suy ra: ∠( ) √ tan∠(AID) = = = 2√2 ²∠( ) / ---- HẾT ----
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2
ĐỀ ÔN TẬP SỐ 04
NĂM HỌC 2024 – 2025 Môn: TOÁN 11 --------------------- Thời gian: 90 phút
Thầy Nguyễn Hoàng Phúc ĐỀ SỐ 04
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn 1 phương án. 2
Câu 1: Cho a là số thực dương. Biểu thức 3
a . a viêt dưới dạng luỹ thừa với số mũ hữu tỉ là? 6 7 5 11 A. 5 a B. 6 a C. 6 a D. 6 a 1 1 3 6 3 5
Câu 2: Nếu a  a và b  b thì:
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 11 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
A. a  1; 0  b  1.
B. a  1;b  1 .
C. 0  a  1;b  1
D. a  1; 0  b  1.
Câu 3: Cho a là số thực dương khác 1. Tính 3 I  log a ? a 1
A. I  3
B. I  0
C. I  3 D. I  3
Câu 4: Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng. 3  9a  3  9a  1 A. log
 1 3log a  log b . B. log
 1 log a  log b . 3   3 3   b 3 3 3   b 3   3  9a  1 3  9a  C. log
 2  log a  log b . D. log
 2  3log a  log b . 3   3 3   b 3 3 3 3   b  
Câu 5: Hàm số y  log
2x  3 có tập xác định là? 3    3   3   3  A. ;    B. ;    C. ;    D.   2   2   2 
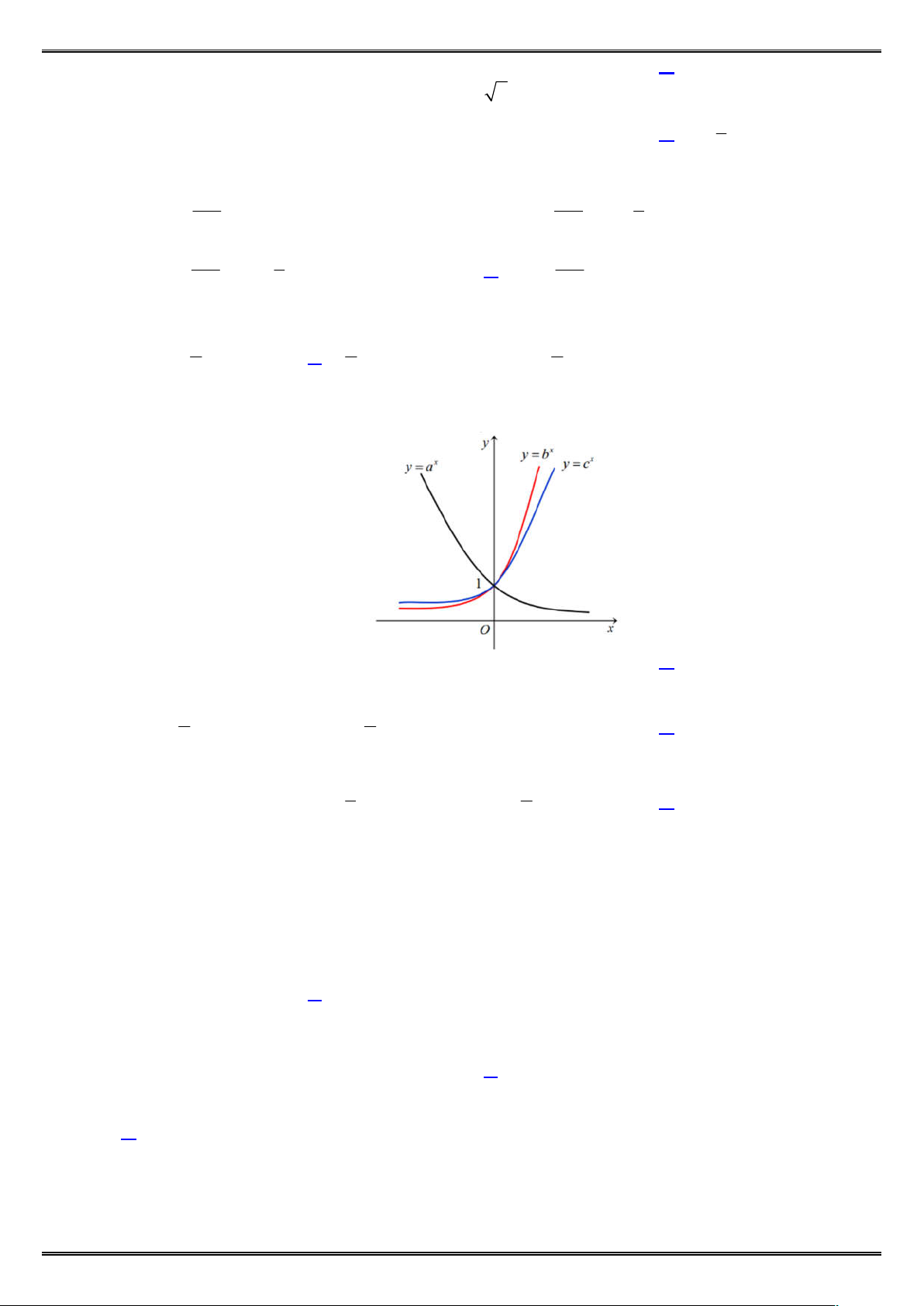
Câu 6: Cho ba số thực dương a , b , c khác 1. Đồ thị các hàm số x y  a , x y  b , x
y  c được cho trong
hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A. b  c  a .
B. a  b  c .
C. c  a  b .
D. a  c  b .
Câu 7: Phương trình log
3x  2  2 có nghiệm là? 2   4 2 A. x  . B. x  . C. x  1 . D. x  2 . 3 3
Câu 8: Tập nghiệm của bất phương trình 2x 1 3   27 là?  1   1  A. 3;  . B. ;    . C. ;    . D. 2;  .  3   2 
Câu 9: Xét các phát biểu sau:
(I) Trong không gian hai đường thẳng vuông góc với nhau thì cắt nhau.
(II) Trong không gian cho hai đường thẳng a và b song song với nhau. Nếu đường thẳng c
vuông góc với a thì c cũng vuông góc với b .
(III) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì a
và b song song với nhau.
Số phát biểu đúng là: A. 0 . B. 1. C. 2 . D. 3 .
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA   ABCD . Mệnh đề nào sau đây đúng?
A. BC  SCD .
B. AC  SBD .
C. BD   SAC  .
D. CD   SBC  .
Câu 11: Cho hình chóp S.ABC có SA   ABC  , tam giác ABC vuông tại B , kết luận nào sau đây sai?
A.  SAC    SBC  .
B.  SAB   ABC  . C. SAB  SBC 
D. SAC    ABC  .
Câu 12: Cho hình chóp tứ giác đều S.ABCD đáy là hình vuông tâm O , gọi M là trung điểm cạnh CD .
Góc giữa mặt bên và mặt đáy là:
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 12 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11     A. SCO . B. SDO . C. SMO . D. SMA .
PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 13: Cho hàm số   2x f x 
và g  x  log  2 x  3 . Khi đó: 3 
Các mệnh đề sau đúng hay sai?
a) Đồ thị của hàm số f  x là hình dưới đây:
b) Hàm số g  x có tập xác định: D   3; 3 .
c) x  2 là nghiệm của phương trình   2 8x f x   .
d) Bất phương trình g  x  log 2x có tập nghiệm S   3   ;1 . 3 Lời giải Từ hình  a) Đúng. ĐK: 2
x  3  0   3  x  3  b) Đúng. f  x x2 x 3 x6  8  2  2
 x  3  c) Sai. x  0 x  0
g  x  log 2x  log  2
x  3  log 2x    
 0  x  1  d) Sai. 3 3  3 2
x  2x  3  0 3   x  1  
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết SA   ABCD . Gọi H là hình chiếu
của A lên các cạnh SB . Khi đó? a) SA  CD .
b) Tam giác SBC vuông tại B .
c) AH  SBC  .
d) SAC   SBD . Lời giải SA    ABCD 
 SA  CD  a) Đúng. CD    ABCD 
BC  AB  gt   
 BC  SAB mà SB  SAB
BC  SASA    ABCD 
 BC  SB  b) Đúng.
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 13 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11  AH  SB  
 AH  SBC   c) Đúng.
AH  BC  BC  
SABcmt 
ABCD là hình chữ nhật  d) Sai.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15: Cho log b  2 và log c  3 . Tính P   2 3 log b c ? a  a a Lời giải Ta có: P   2 3 b c  2 3 log
 log b  log c  2 log b  3log c  2.2  3.3  13 a a a a a
Câu 16: Cường độ một trận động đất M (độ Richter) được cho bởi công thức M  log A  log A , với A 0
là biên độ rung chấn tối đa và A là một biên độ chuẩn ( hằng số). Đầu thế kỉ 20 , một trận động 0
đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, một trận động đất khác ở
Nam Mỹ có biên độ rung chấn mạnh gấp 4 lần. Hỏi cường độ của trận động đất ở Nam Mỹ là
bao nhiêu (kết quả làm tròn đến hàng phần chục)? Lời giải
Gọi M , M lần lượt là cường độ của trận động đất ở San Francisco và Nam Mỹ. Trận động đất 1 2
ở San Francisco có cường độ là 8 độ Richter nên:
M  log A  log A  8  log A  log A . 1 0 0
Trận động đất ở Nam Mỹ có biên độ là 4 A , khi đó cường độ của trận động đất ở Nam Mỹ là:
M  log 4 A  log A  8  log 4  log A  log A
 log 4  8  8, 6 (độ Richter). 2   0  0 
Câu 17: Ông Phúc gửi 100 triệu đồng vào ngân hàng theo hình thức lãi kép với lãi suất không đổi là 8%
/ năm. Hỏi sau 10 năm ông Phúc nhận được tiền lãi là bao nhiêu (làm tròn đơn vị triệu đồng)? Lời giải
Số tiền lãi sau 10 năm: A  100.1 8%10 100  116 (triệu đồng) 10
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a , SA   ABCD, SA  3a .
Gọi  là góc giữa mặt phẳng SBD và  ABCD . Biết tan  x y . Tính 2 3
P  16x  9 y ? Lời giải Ta có:
SBC    ABCD  BD BD  AO  
 BD  SAO
BD  SASA    ABCD 
 SBC  ABCD  ,  SOA . AC a 2 Ta có: AO   2 2  3a
Xét SOA vuông tại A có: tan SOA   3 2 a 2 2 2 3 2 3
 x  3; y  2  P  16x  9 y  16.3  9.2  216
PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 22.
Câu 19: Rút gọn biểu thức 10 2 M log a log b  
với a,b  0; a,b  1 ? 2 3 a b   Lời giải 10 2 2
M  log a  log b  5  log b  5  6   1  2 3 a b   1     3 b
Câu 20: Biết rằng 81x  81x  23 . Tính giá trị biểu thức 15 4.9x 4.9 x A     ? Lời giải
Ta có: 81x  81x  23
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 14 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 x  x   
  x 2   x 2 x  x x  x      x  x  2 9 9 5 9 9 2.9 .9 23 2.9 .9 9 9  25  
9x  9x  5l   15 4.9x 4.9 x 15 4 9x 9 x A          15 4.5  5 
Câu 21: Giải phương trình sau: log x  5  log x  2  3 ? 2   2   Lời giải x  5  0 x  5 Điều kiện:     x  5 x  2  0 x  2   x  6 Phương trình:  log x  5 x  2  3 2 2
 x  3x 10  8  x  3x 18  0  2   
x  3l 
Vậy tập nghiệm: S    6
Câu 22: Giải bất phương trình sau: 2x x 1 4 8   . Lời giải 2 x x 1  4 x 3x3 4  8  2  2
 4x  3x  3  x  3 . Vậy tập nghiệm: S  3; 
Câu 23: Cho hình chóp tam giác S.ABC , có đáy là tam giác vuông tại B , SA   ABC  .
a) Chứng minh BC  SAB
b) Vẽ BH vuông góc với AC tại H . Chứng minh:  SHB   SAC  . Lời giải
a) Chứng minh BC  SAB
BC  AB  gt   
Ta có: BC  SASA   ABC   BC  SAB . SAB 
 : SA AB  A 
b) Vẽ BH vuông góc với AC tại H . Chứng minh:
SHB  SAC  .
BH  AC  gt   
Ta có: BH  SASA   ABC  SAC 
 : SA  AC  A 
 BH  SAC  . Mà BC  SHB  SHB  SAC  ---- HẾT ----
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 2
ĐỀ ÔN TẬP SỐ 05
NĂM HỌC 2024 – 2025 Môn: TOÁN 11 --------------------- Thời gian: 90 phút Thầy Phan Duy Thành ĐỀ SỐ 05
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn 1 phương án. 3 5 Câu 1: Biểu thức 2 P x x x x   
(với x  0 ), giá trị của  là 1 5 9 3 A. . B. . C. . D. . 2 2 2 2
Câu 2: Cho các số thực , a , b ,
m n a,b  
0 . Khẳng định nào sau đây là đúng?
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 15 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 m a n A. m  a . B.  n m m n a a   . C.   m m m a b
 a  b . D. m . n m n a a a   . n a Câu 3: Với mọi ,
a b thỏa mãn log a  3log b  2 , khẳng định nào dưới đây đúng? 2 2 4 A. 3
a  4b .
B. a  3b  4 .
C. a  3b  2 . D. a  . 3 b  a    
Câu 4: Tính giá trị biểu thức 10 2 2
P  log a b  log    log b 2   a   3 a b    b 
(với 0  a  1; 0  b  1 ). A. 3 . B. 1. C. 2 . D. 2 .
Câu 5: Tập xác định của hàm số y  log x  4 là. 3   A.  ;  4. B. 4;   . C. 5;   . D.  ;    .
Câu 6: Tìm hàm số đồng biến trên  . x     A.   3x f x  . B.   3 x f x   .
C. f x  1      f x   . D.   3 .  3  3x
Câu 7: Nghiệm của phương trình log x  7  5 là 2   A. x  18 . B. x  25 . C. x  39 . D. x  3 .
Câu 8: Giải phương trình 2x3 4 4 8 x   . 6 2 4 A. x  . B. x  . C. x  2 . D. x  . 7 3 5
Câu 9: Cho hình lập phương ABCD.AB C  D
  . Góc giữa hai đường thẳng AC và AD bằng A. 45 . B. 30 . C. 60 . D. 90 .
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai?
A. BC  SAB .
B. AC  SBD.
C. BD  SAC .
D. CD  SAD .
Câu 11: Cho hình chóp S.ABCD có SA  ABCD, đáy ABCD là hình thang vuông tại A và D . Biết
SA  AD  DC  a , AB  2a . Khẳng định nào sau đây sai?
A. SBD  SAC . B. SAB  SAD. C. SAC   SBC . D. SAD  SCD .
Câu 12: Cho hình chóp S.ABC có đáy là tam giác vuông tại B , SA  ABC , SA  3 cm ,
AB  1 cm , BC  2 cm . Mặt bên SBC  hợp với đáy một góc bằng: A. 30 . B. 90 . C. 60 . D. 45 .
PHẦN II. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13: Các mệnh đề sau đúng hay sai? 1   
a) Hàm số y  log (2x  1) có tập xác định của hàm số là: D   ;   . 2 2 
b) Hàm số y  log x nghịch biến trên tập xác định của nó. 1 2 x   1 x 1   c) 1 5     x  
có nghiệm lớn nhất là 25 3  2 1  
d) log (2x  1)  log (x  1) tập nghiệm của bất phương này là: S    ;  1 1  3 2 9 9
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 16 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11
Câu 14: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD),SA  a 2 , ABCD là hình
thang vuông tại A và D với AB  2a, AD  DC  a . Khi đó: a) AB  SD b) CD  (SAD)
c) (SBC )  (SAC )
d) ((SBC ),(ABC )) 60  Lời giải
Gọi M là trung điểm AB , khi đó AMCD là hình vuông, đường chéo AC  a 2 . AB
Tam giác ACB có trung tuyến CM thoả mãn CM 
nên ACB là tam giác vuông tại C . 2 A  C  BC  Ta có: 
 BC  (SAC )  BC  SC . SA 
 BC( do SA  (ABCD))  (
 SBC)  (ABC)  BC   Khi đó: A
 C  BC,SC  BC
 ((SBC ),(ABC ))  (SC,AC )  SCA  . A
 C  (ABC),SC  (SBC)   SA a 2 
Tam giác SAC vuông tại A có: tan SCA 1 SCA 45      . AC a 2 
Vậy ((SBC ),(ABC )) SCA 45   .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18. Ở mỗi câu thí sinh
điền đáp án của câu đó. 3 1  2 3 a a
Câu 15: Rút gọn biểu thức sau: Q  (a  0) . Biết m
Q  a khi đó giá trị của m là bao nhiê?   a   2 2 2 2 Lời giải Đáp án: 5.  3 1  2 3 3 1  2   3 3 a a  a  a 3  a  Ta có: 5       .  a   2 2 Q a 2 2 2 ( 2 2)( 2 2) 2  a  a a       2 a b   
Câu 16: Cho log b  3 và log c  4 với a; ;
b c  0;a  1. Tính giá trị của P  log     a a a 3  c    Lời giải Đáp án: - 8,5.
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 17 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11  2  1 a  b  2 3    2 P log    log a  log
b  log c  2  log b  3 log c a 3   a a a a a Ta có:  c    1 3 17
 2  log b  3 log c  2   12  . 2 a a 2 2
Câu 17: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức ( )  (0)  2t s t s
, trong đó s(0) là số lượng vi khuẩn A lúc ban đầu, s(t) là số lượng vi khuẩn A có sau t phút.
Biết sau 3 phút thì số lượng vi khuẩn A là 625 con. Hỏi sau phút, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con? Lời giải Đáp án: 7 s(3) Ta có: 3
s(3)  s(0) 2  s(0)   78,125 nghìn con. 8
Do đó s(t)  10 triệu con  10000 nghìn con khi: t t 10000 7
10000  s(0)  2  2 
 128  2  t  7 phút. 78,125
Câu 18: Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng
vuông góc. Góc giữa hai mặt phẳng SAB và SCD là bao nhiêu độ (làm tròn đến hàng phần chục). Lời giải
Đáp số: 54,6 S x A D H I B C
Gọi H là trung điểm của AB  SH là trung tuyến đồng thời là đường cao của tam giác SAB SAB   ABCD 
Ta có: AB  SAB  ABCD  SH  ABCD    SH  
SAB,SH  AB 
Gọi I là trung điểm của CD  HI là đường trung bình của hình vuông ABCD
 HI  a, HI  CD C  D  SH  Do 
 CD  SHI   CD  SI C  D  HI 
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 18 -
TỔ TOÁN TRƯỜNG THCS-THPT TRẦN CAO VÂN NHÓM GV TOÁN 11 S   SAB  SCD 
Lại có AB  SAB; CD  SCD  Sx  SAB  SCD Sx AB CD      với / / / / AB / /CD  Sx / /AB  Ta có: 
 SH  Sx . Chứng minh tương tự: Sx  SI . AB   SH  Sx   SCD   SAB   
Khi đó: SH  SAB,SH  AB  SAB
SCD  SH SI  HSI               , ,   SI  
SCD,SI CD  HI 2 3
Xét SHI có: tan    . SH 3
PHẦN IV. Tự luận. Thí sinh trình bày lời giải từ câu 19 đến câu 24. 1 6    3     
Câu 19: Rút gọn các biểu thức sau: 3 3 A a  b
 ,(a  0,b  0)   .     Lời giải 1 6 1 6 1    3 3        a 3 3 3 3 3 2 a  b   a b  ab    . 2   b  
Câu 20: Cho a là một số thực dương. Rút gọn biểu thức sau: 1 2
A  log a  log a  log . 1 3 9 a 3 Lời giải
Áp dụng công thức đổi cơ số, ta đưa các biểu thức lôgarit về lôgarit cơ số 3 như sau: log a log a log a 3 3 3 log a     log a; 1 1 3 1 log 3 1 3 3 log3 3 log a log a log a 2 3 3 3
log a  2 log a  2   2   2   4 log a; 3 3 1 3 1 log 3 2 3 log 3 3 2 1 1 log log 3 3 1 log a a a 3 log     . 9 2 a log 9 log 3 2 3 3
Thay các kết quả trên vào biểu thức A , ta được: log a 11 3
A  log a  4 log a    log a. 3 3 3 2 2 11 Vậy A   log a . 3 2
Câu 21: Giải phương trình sau: x 2  x 1 9 243   Lời giải x 2  x 1  2(x 2  ) 5(x 1  ) 9  243  3  3
 2(x  2)  5(x  1)  x  3 .
Vậy phương trình có nghiệm là x  3 .
Câu 22: Giải bất phương trình sau: log (x  3)  log (x  2)  1 . 0,5 0,5 Lời giải
log (x  3)  log (x  2)  1 . 0,5 0,5
BỘ ĐỀ ÔN TẬP TOÁN 11 GK2-2025 Trang - 19 -