









Preview text:
TRƯỜNG THPT CHU VĂN AN GV: PHẠM LÊ DUY BỘ ĐỀ ÔN TẬP T HỌC KÌ 1 LỚP 11 Toán T THEO CẤU TRÚC MỚI CD-KNTT&CS-CT CD-KNT ST T&CS-CT
TÀI LIỆU LƯU HÀNH NỘI BỘ
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 GV: PHẠM LÊ DUY / Trang 2/87 MỤC LỤC PHẦN I Sách Cánh Diều 5 A Đề 1 7 B Đề 2 11 C Đề 3 15 D Đề 4 20 E Đề 5 24 F Đề 6 29 PHẦN II
Sách Chân Trời Sáng Tạo 33 G Đề 1 35 H Đề 2 39 I Đề 3 43 J Đề 4 47 K Đề 5 51 L Đề 6 55 PHẦN III
Sách Kết Nối Tri Thức & Cuộc Sống 61 M Đề 1 63 3
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 N Đề 2 67 O Đề 3 71 P Đề 4 75 Q Đề 5 79 R Đề 6 83 GV: PHẠM LÊ DUY / Trang 4/87 Phần I Sách Cánh Diều 5
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 A. ĐỀ 1
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Phương trình tan 2x = 1 có họ nghiệm là π kπ π A. x = + , k ∈ Z. B. x = + kπ, k ∈ Z. 8 2 4 π π C. x = + k2π, k ∈ Z. D. x = + k2π, k ∈ Z. 4 4
Câu 2. Cho cấp số cộng có u1 = 1, u2 = 3. Hãy tìm công sai d của cấp số cộng đó. A. d = 2. B. d = −2. C. d = 3. D. d = 4.
Câu 3. Trong các dãy số sau, dãy số nào là cấp số nhân? A. 1, 2, 4, 6. B. 1, 3, 12, 60. C. −1, 4, −16, 64. D. −1, −5, −25, 125.
Câu 4. Cho cấp số nhân (un) có u7 = −5 và u10 = 135. Công bội của cấp số nhân là 1 A. q = −3. B. q = − . C. q = 3. D. q = 9. 3 2n + 1 Câu 5. Tính L = lim . n2 + n + 32 1 A. L = 2. B. L = . C. L = 0. D. L = . 3 3 x2 + 3x − 4 Câu 6. Giá trị của lim bằng x→−4 x2 + 4x 5 5 A. 1 . B. −1 . C. . D. − . 4 4 (2x nếu x ≥ 1 Câu 7. Cho hàm số f (x) =
. Mệnh đề nào dưới đây sai? 2 nếu x < 1 A. f (1) = 2. B. f (0) = f (1).
C. f không liên tục tại x = 1. D. f liên tục tại x = 1.
Câu 8. Cho hai mặt phẳng song song (α) và (β). Đường thẳng a nằm trong mặt phẳng
(α) và đường thẳng b nằm trong mặt phẳng (β). Khẳng định nào sau đây sai? A. a k (β). B. b k (α). C. a k b.
D. Nếu tồn tại mặt phẳng γ chứa cả hai đường thẳng a và b thì a k b.
Câu 9. Hình lăng trụ có các mặt bên là hình gì? A. Hình thoi. B. Hình vuông. C. Hình chữ nhật. D. Hình bình hành.
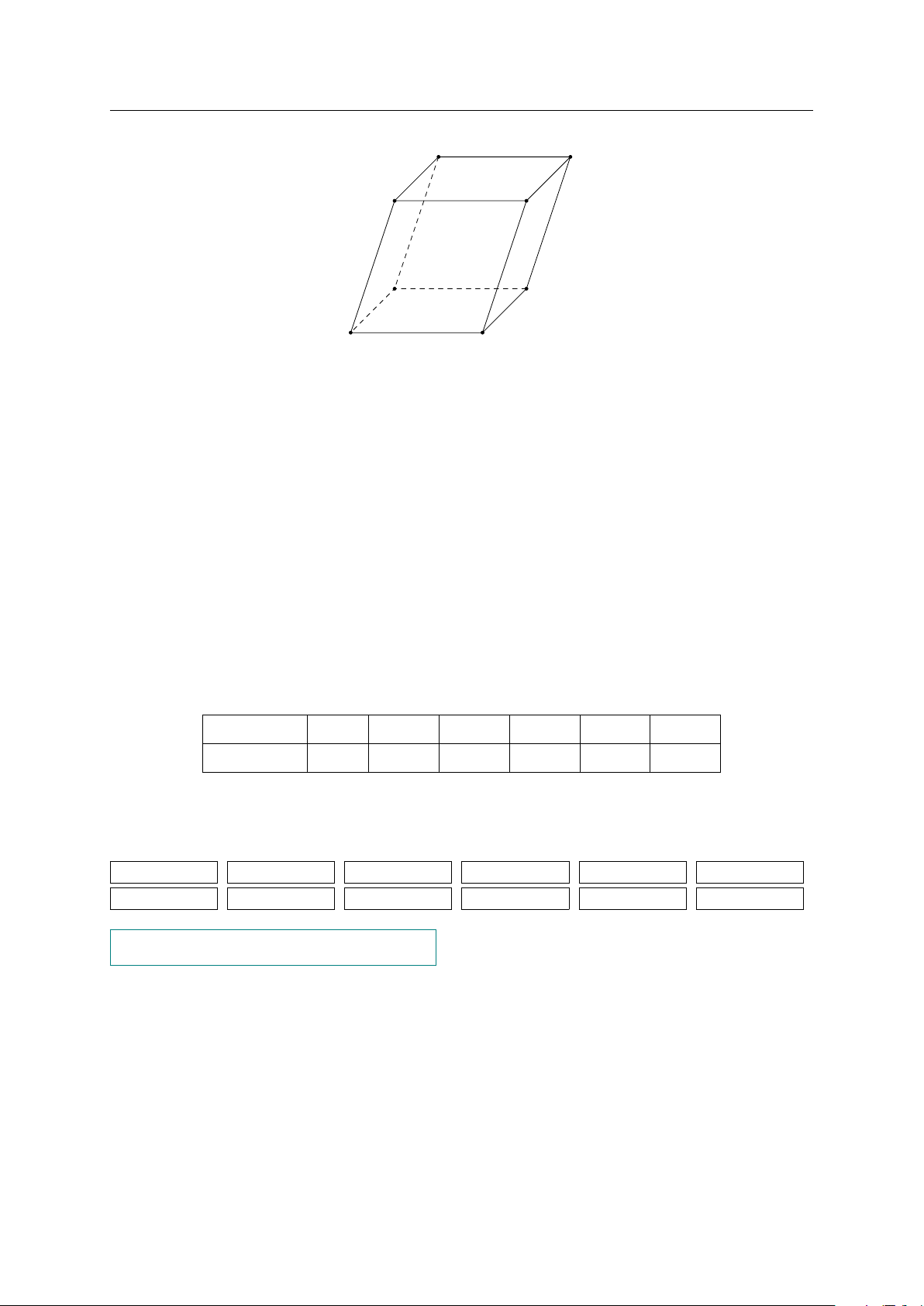
Câu 10. Cho hình hộp ABCD.AB0CD0 có hình vẽ dưới đây. GV: PHẠM LÊ DUY / Trang 7/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 A0 B0 C0 D0 A B D C
Mặt phẳng (AB0D0) song song với mặt phẳng nào trong các mặt phẳng sau đây? A. (BC0D). B. (BCA). C. (ACC). D. (BDA).
Câu 11. Xét phép chiếu song song lên mặt phẳng (P ) theo phương l. Trong các sau mệnh đề nào đúng?
A. Hình chiếu song song của hai đường thẳng cắt nhau có thể song song với nhau.
B. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
C. Hình chiếu song song của hai đường thẳng chéo nhau thì song song với nhau.
D. Hình chiếu song song của hai đường thẳng chéo nhau thì không thể song song với nhau.
Câu 12. Cho mẫu số liệu ghép nhóm về thống kê điểm số của học sinh tham dự kỳ thi
học sinh giỏi toán, ta có bảng số liệu sau Điểm
[8; 10) [10; 12) [12; 14) [14; 16) [16; 18) [18; 20) Số học sinh 6 21 30 25 14 4
Tìm nhóm chứa trung vị của mẫu số liệu ghép nhóm trên. A. [10; 12). B. [14; 16). C. [12; 14). D. [16; 18). 1. A 2. A 3. C 4. A 5. C 6. C 7. C 8. C 9. D 10. A 11. B 12. C
PHẦN 2. Câu trắc nghiệm đúng sai
Câu 1. Cho mặt phẳng (P ) và hai đường thẳng song song a và b. Khi đó
a) Có vô số mặt phẳng chứa đường thẳng a mà không chứa đường thẳng b.
b) Nếu mặt phẳng (P ) song song với đường thẳng a thì mặt phẳng (P ) cũng song song với đường thẳng b.
c) Nếu mặt phẳng (P ) cắt đường thẳng a thì mặt phẳng (P ) cũng cắt đường thẳng b.
d) Nếu mặt phẳng (P ) chứa đường thẳng a thì mặt phẳng (P ) cũng chứa đường thẳng b. GV: PHẠM LÊ DUY / Trang 8/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919
Câu 2. Cho phương trình lượng giác tan(2x − 15◦) = 1 (∗). Khi đó
a) Phương trình (∗) có nghiệm x = 30◦ + k90◦, (k ∈ Z).
b) Phương trình có nghiệm âm lớn nhất bằng −30◦.
c) Tổng các nghiệm của phương trình trong khoảng (−180◦; 90◦) bằng 180◦.
d) Trong khoảng (−180◦; 90◦) phương trình có nghiệm lớn nhất bằng 60◦. 2n + 1
Câu 3. Cho dãy số (un) có số hạng tổng quát un = . Khi đó n + 2
a) Số hạng đầu tiên của dãy số là 1. 5 7 b) Số hạng u2 = ; u3 = . 4 5 c) Dãy số (un) tăng. 167 d) Số
là số hạng thứ 252 của dãy số (un). 84 x − khi x ≤ 1 2
Câu 4. Cho các hàm số sau: f (x) = , g(x) = x2 − 3x + 1 và x2 − 3x + 2 khi x > 1 x2 − 1 πx h(x) = sin . 4
a) Hàm số f (x) liên tục tại điểm x0 = 1.
b) Hàm số g(x) liên tục tại điểm x0 = 1.
c) Hàm số h(x) không liên tục tại điểm x0 = 2.
d) Hàm số y = f (x) · g(x) không liên tục tại điểm x0 = 1. 1. a Đ b S c Đ d S 2. a Đ b S c S d S 3. a Đ b Đ c Đ d S 4. a Đ b Đ c S d S
PHẦN 3. Câu trắc nghiệm trả lời ngắn.
Câu 1. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét)
của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bời công thức Å πt π ã h = 3 cos +
+ 12. Mực nước của kênh cao nhất khi nào? KQ: 8 4
Câu 2. Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây an
toàn có tính đàn hồi kéo nảy ngược lên 60% chiều sâu của cú nhảy. Một người chơi bungee
thực hiện cú nhảy đầu tiên có độ cao nảy ngược lên là 9 (m). Tính tổng các độ cao nảy
ngược lên của người đó trong 5 lần nảy đầu (kết quả làm tròn hàng phần chục). KQ:
Câu 3. Người ta tiến hành phỏng vấn 40 người về một mẫu áo khoác. Người điều tra
yêu cầu cho điểm mẫu áo đó theo thang điểm là 100. Kết quả được trình bày trong bảng ghép nhóm sau GV: PHẠM LÊ DUY / Trang 9/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 Nhóm
[50; 60) [60; 70) [70; 80) [80; 90) [90; 100) Tần số 4 5 23 6 2
Hãy tìm trung vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng đơn vị). KQ: √ x + 2 − 2 khi x 6= 2 Câu 4. Cho hàm số f (x) = x − 2 a khi x = 2.
Tìm giá trị của tham số a để hàm số y = f (x) liên tục tại x = 2 (kết quả viết dưới dạng số thập phân). KQ:
Câu 5. Một công ty dược phẩm đang thử nghiệm một loại thuốc mới. Một thí nghiệm
bắt đầu với 1,0 · 109 vi khuẩn. Một liều thuốc được sử dụng sau mỗi bốn giờ có thể tiêu
diệt 4,0 · 108 vi khuẩn. Giữa các liều thuốc, số lượng vi khuẩn tăng lên 25%. Tìm số vi
khuẩn còn sống trước lần sử dụng thuốc thứ năm (đơn vị triệu con) (kết quả làm tròn đến hàng đơn vị). KQ:
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có tâm O, AB = 8,
SA = SB = 6. Gọi (P ) là mặt phẳng qua O và song song vơi (SAB). Mặt phẳng (P ) cắt
hình chóp S.ABCD theo các giao tuyến và các giao tuyến này tạo với nhau thành một
tứ giác. Tính diện tích tứ giác này (kết quả làm tròn đến hàng phần chục). KQ: 1. 14 2. 11,5 3. 75 4. 0,25 5. 135 6. 13,4 GV: PHẠM LÊ DUY / Trang 10/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 B. ĐỀ 2
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Cho cấp số cộng (un) có số hạng đầu u1 = −4 và công sai d = 10. Tìm số hạng
thứ 37 của cấp số cộng đã cho. A. u37 = 366. B. u37 = 352. C. u37 = 376. D. u37 = 356.
Câu 2. Cho cấp số nhân (un) có u7 = 6 và u8 = 12. Tìm công bội q cấp số nhân đã cho. 1 A. q = −6. B. q = 6. C. q = . D. q = 2. 2 1
Câu 3. Cho cấp số nhân (un) có số hạng đầu u1 = 6 và công bội q = . Tính tổng của 2
8 số hạng đầu tiên của cấp số nhân đã cho. 765 3 19 A. −12. B. . C. − . D. . 64 64 2 √
Câu 4. Nghiệm của phương trình 2 cos 2x + 3 = 0 là 5 5 A. x = π + kπ, x = − π + kπ(k ∈ Z). 12 12 1 1 B. x = − π + kπ, x = π + kπ(k ∈ Z). 6 6 5 1 C. x =
π + kπ, x = − π + kπ(k ∈ Z). 12 6 5 5 D. x =
π + kπ, x = − π + kπ(k ∈ Z). 6 6
Câu 5. Cho hai dãy số (un) và (vn) có lim un = 6 và lim vn = −10. Tính giới hạn lim(un + vn). A. 16. B. −60. C. −16. D. −4. 6 − 2x Câu 6. Giới hạn lim bằng x→0 9x − 4 3 3 2 2 A. − . B. . C. . D. − . 2 2 3 9
( − x2 + 2x − 3 khi x ≥ −5 Câu 7. Cho hàm số f (x) =
. Khẳng định nào sau đây − 2x − 53 khi x < −5 đúng?
A. Hàm số liên tục tại mọi x ∈ R.
B. Hàm số không liên tục tại x = −3.
C. Hàm số liên tục tại x = −5.
D. Hàm số không liên tục tại x = −5.
Câu 8. Cho hình lăng trụ ABC.A0B0C0. Gọi F , I và N lần lượt là trung điểm của các
cạnh AA0, BB0 và CC0. Tìm khẳng định đúng. A. (F IN ) k (A0B0C0). B. (F IN ) k (A0BC). C. (F IN ) k (BCC0B0). D. (F IN ) k (AB0C0). GV: PHẠM LÊ DUY / Trang 11/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919
Câu 9. Tìm khẳng định sai về hình lăng trụ.
A. Hình lăng trụ tứ giác có mặt bên là hình tứ giác.
B. Hình lăng trụ có các cạnh bên song song.
C. Hình hộp là hình lăng trụ có đáy là hình bình hành.
D. Hình lăng trụ tam giác có đáy là tam giác.
Câu 10. Cho hình hộp ABCD.A0B0C0D0. Cặp điểm nào sau đây là hai đỉnh đối diện của hình hộp? A. A0 và C0. B. A và C0. C. A và B0. D. A và C.
Câu 11. Cho bảng số liệu ghép nhóm về độ tuổi và số lượng khách hàng của một cửa hàng như sau
Khoảng tuổi [23; 32) [32; 41) [41; 50) [50; 59) [59; 68) Số người 15 12 7 11 12
Tính giá trị đại diện của nhóm [59; 68). A. 68. B. 31,75. C. 63,5. D. 59.
Câu 12. Cho các đoạn thẳng và đường thẳng không song song hoặc không trùng với
phương chiếu. Mệnh đề nào dưới đây là mệnh đề sai?
A. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng.
C. Hình chiếu của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau.
D. Hình chiếu song song của một đường thẳng là một đường thẳng. 1. D 2. D 3. B 4. A 5. D 6. A 7. D 8. A 9. A 10. B 11. C 12. B
PHẦN 2. Câu trắc nghiệm đúng sai 1
Câu 1. Cho phương trình lượng giác sin 2x = − (∗). Khi đó 2 π
a) Phương trình (*) tương đương sin 2x = sin . 6
b) Trong khoảng (0; π) phương trình có 3 nghiệm. 3π
c) Tổng các nghiệm của phương trình trong khoảng (0; π) bằng . 2 11π
d) Trong khoảng (0; π) phương trình có nghiệm lớn nhất bằng . 12 (u1 = −1
Câu 2. Cho dãy số (un), biết với n ≥ 1. Khi đó un+1 = un + 3 GV: PHẠM LÊ DUY / Trang 12/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919
a) Bốn số hạng đầu tiên của dãy số lần lượt là −1; 2; 5; 8.
b) Số hạng thứ năm của dãy là 13.
c) Công thức số hạng tổng quát của dãy số là un = 2n − 3.
d) 101 là số hạng thứ 35 của dãy số đã cho. x2 − 1 khi x 6= 1 Câu 3. Cho hàm số f (x) = x − 1
và g(x) = 4x2 − x + 1. Khi đó x + 1 khi x = 1 a) Ta có f (1) = 2.
b) Hàm số f (x) liên tục tại điểm x0 = 1.
c) Hàm số g(x) liên tục tại điểm x0 = 1.
d) Hàm số y = f (x) − g(x) không liên tục tại điểm x0 = 1.
Câu 4. Cho hai mặt phẳng (P ) và (Q) phân biệt, hai đường thẳng song song a và b. Khi đó
a) Chỉ có một mặt phẳng chứa đường thẳng a và đường thẳng b.
b) Nếu mặt phẳng (P ) chứa đường thẳng a và mặt phẳng (Q) chứa đường thẳng b thì
giao tuyến của (P ) và (Q) song song với đường thẳng a.
c) Nếu a ⊂ (P ) và b ⊂ (Q) thì a k (Q).
d) Nếu (P ) chứa đường thẳng a thì (P ) cũng chứa đường thẳng b. 1. a S b S c Đ d Đ 2. a Đ b S c S d Đ 3. a Đ b Đ c Đ d S 4. a Đ b Đ c Đ d S
PHẦN 3. Câu trắc nghiệm trả lời ngắn.
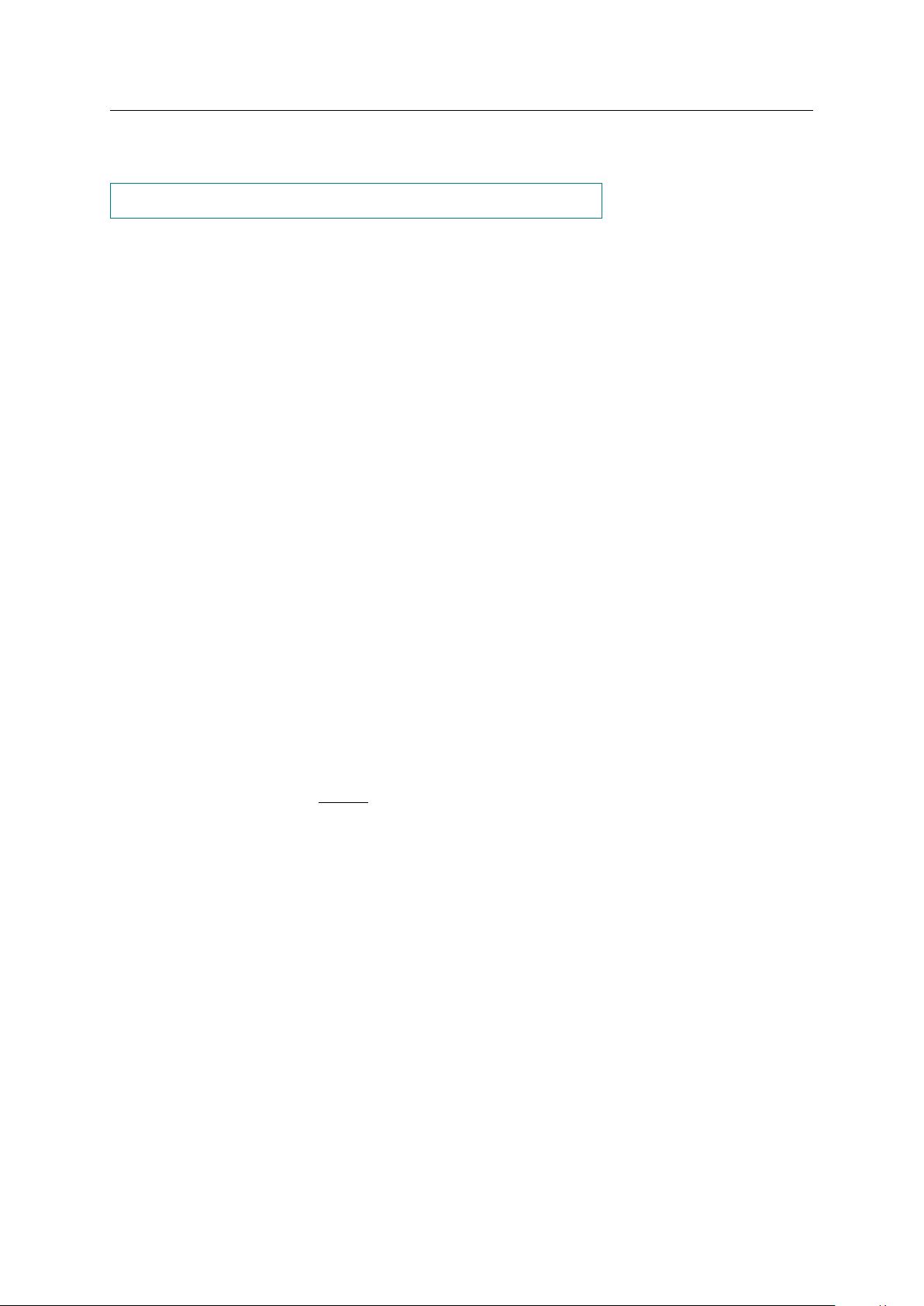
Câu 1. Hội Lim (tỉnh Bắc Ninh) vào mùa xuân
thường có trò chơi đánh đu. Khi người chơi đu nhún
đều, cây đu sẽ đưa người chơi đu dao động qua lại
vị trí cân bằng (tham khảo hình vẽ bên). Nghiên
cứu trò chơi này, người ta thấy khoảng cách h (m) bằng cân
từ người chơi đu đến vị trí cân bằng được biểu diễn rí t Vị
qua thời gian t (s) (với t ≥ 0) bởi hệ thức h = |d| h π i với d = 3 cos
(2t − 1) , trong đó quy ước d > 0 3 h
khi vị trí cân bằng ở phía sau lưng người chơi đu và
d < 0 trong trường hợp ngược lại (Nguồn: R.Larson
and B.Edwards, Calculus 10e Cengage). Tìm thời
điểm đầu tiên mà khoảng cách h lớn nhất. (Viết
kết quả dưới dạng số thập phân). GV: PHẠM LÊ DUY / Trang 13/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 KQ:
Câu 2. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên
là 100 nghìn đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30 nghìn
đồng so với giá của mét khoan ngay trước đó. Một người cần khoan một giếng sâu 20 m
để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng,
gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng? KQ:
Câu 3. Theo báo cáo của Chính phủ, dân số của nước ta tính đến tháng 12 năm 2018
là 95,93 triệu người, nếu tỉ lệ tăng trưởng dân số trung bình hằng năm là 1,33% thì dân
số nước ta vào tháng 12 năm 2025 là bao nhiêu? (Tính theo đơn vị triệu người, làm tròn đến hàng đơn vị) KQ: 3 − x √ khi x 6= 3
Câu 4. Tìm m để hàm số liên tục tại x = 3 biết f (x) = x + 1 − 2 m khi x = 3. KQ:
Câu 5. Thời gian (phút) truy cập internet mỗi buổi tối của một số học sinh được cho trong bảng sau Nhóm
[9,5; 12,5) [12,5; 15,5) [15,5; 18,5) [18,5; 21,5) [21,5; 24,5) Số học sinh 3 12 15 24 2
Tìm trung vị của mẫu số liệu ghép nhóm trên. KQ:
Câu 6. Cho tứ diện ABCD. Gọi M , P lần lượt là trung điểm các cạnh AD, BC còn 1
N là điểm trên cạnh AB sao cho AN =
AB. Gọi Q là giao điểm của DC với (M N P ). 3 DQ Tính tỉ số
. (Kết quả làm tròn đến hàng phần mười) KQ: DC 1. 0,5 2. 7 700 3. 105 4. −4 5. 18,1 6. 0,33 GV: PHẠM LÊ DUY / Trang 14/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 C. ĐỀ 3
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Số nghiệm của phương trình sin 3x = 0 với 0 < x < 180◦ là A. 1. B. 3. C. 2. D. 4.
Câu 2. Cho cấp số cộng (un) với u1 = 2 và u6 = 27. Công sai d của cấp số cộng đã cho là A. d = −4. B. d = 4. C. d = 8. D. d = 3.
Câu 3. Cho cấp số nhân (un) có số hạng đầu là u1 6= 0 và công bội q 6= 0. Số hạng tổng
quát của cấp số nhân bằng A. un = u1 + (n − 1) q. B. un = u1 · qn−1. C. un = u1 · qn. D. un = u1 · qn+1.
Câu 4. Mệnh đề nào dưới đây sai?
A. Dãy số có tất cả số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số nhân có công bội q > 1 là một dãy tăng.
Câu 5. Cho hai dãy (un) và (vn) thỏa mãn lim un = 6 và lim vn = −2. Giá trị của lim (un − vn) bằng A. 8. B. 4. C. −6. D. 6. x2 − 9 Câu 6. Giới hạn của lim là x→3 x − 3 A. 3. B. 0. C. 6. D. −6.
Câu 7. Cho hàm số y = f (x) xác định trên khoảng K và x0 ∈ K. Hàm số y = f (x) liên
tục tại x0 khi và chỉ khi A. lim f (x) = +∞. B. lim f (x) = −∞. x→x0 x→x0 C. lim f (x) = f (x0). D. lim f (x) = f (x0). x→x0 x→x+ 0
Câu 8. Cho các mệnh đề sau
1. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì chúng song song với nhau.
2. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì chúng song song với nhau. GV: PHẠM LÊ DUY / Trang 15/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919
3. Bất kì đường thẳng nào cắt một trong hai mặt phẳng song song thì nó cũng cắt mặt phẳng còn lại. Số mệnh đề sai là A. 0. B. 3. C. 1. D. 2.
Câu 9. Cho hình lăng trụ ABC.A0B0C0. Trong các khẳng định sau, khẳng định nào là khẳng định sai? A. (ABC) k (A1B1C1). B. AA1 k (BCC1). C. AB k (A1B1C1).
D. AA1B1B là hình chữ nhật.
Câu 10. Nếu thiết diện của một hình hộp và một mặt phẳng là một đa giác thì đa giác
đó có nhiều nhất mấy cạnh? A. 4 cạnh. B. 5 cạnh. C. 6 cạnh. D. 7 cạnh.
Câu 11. Hình vẽ nào sau đây không phải hình biểu diễn của hình chóp tứ giác S.ABCD? S Hình I Hình II A D A D S B B A. C . B. C . S Hình III Hình IV A D S C B A D C. C . D. B .
Câu 12. Một vườn thú ghi lại tuổi thọ (đơn vị năm) của 20 con hổ và thu được mẫu số
liệu ghép nhóm được cho ở bảng sau Nhóm
[14; 15) [15; 16) [16; 17) [17; 18) [18; 19) Tần số 1 2 7 5 5 GV: PHẠM LÊ DUY / Trang 16/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919
Giá trị đại diện của nhóm [16; 17) là A. 16. B. 17. C. 16,5. D. 1. 1. D 2. D 3. B 4. A 5. D 6. A 7. D 8. A 9. A 10. B 11. C 12. B
PHẦN 2. Câu trắc nghiệm đúng sai
Câu 1. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của
hai đường chéo. Cho M là trung điểm của SC. Xét tính đúng sai của các khẳng định sau
a) Đường thẳng OM là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Đường thẳng BC song song với mặt phẳng (AM D).
c) Đường thẳng OM song song với mặt phẳng (SAD).
d) Giao tuyến của hai mặt phẳng (OM D) và (SAD) là đường thẳng qua D và song song với SA. √3
Câu 2. Cho phương trình lượng giác cos x =
. Xét tính đúng sai của các khẳng định 2 sau π
a) Phương trình có nghiệm x = ± + k2π (k ∈ Z). 3 π
b) Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất bằng . 3 ï 5π ò c) Trong đoạn 0;
phương trình có 4 nghiệm. 2 ï 5π ò 25π
d) Tổng các nghiệm của phương trình trong đoạn 0; bằng . 2 6 3n − 1
Câu 3. Cho dãy số (un) cho bởi công thức un =
. Xét tính đúng sai của các khẳng n + 1 định sau 5 12 7 3n + 2
a) Năm số hạng đầu là 1; ; 2; ; . b) Số hạng un+1 = . 3 5 3 n + 2
c) Dãy số (un) là dãy giảm. d) Dãy số (un) bị chặn. a − 2 khi x < 2 Câu 4. Cho hàm số f (x) = π
. Xét tính đúng, sai của các khẳng định sin khi x ≥ 2 x sau
a) Tập xác định của hàm số f (x) là D = R. b) f (0) = −2, f (2) = 1. c) lim f (x) = a − 2. x→2−
d) Hàm số liên tục tại x = 2 khi a = 1. GV: PHẠM LÊ DUY / Trang 17/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 1. a S b S c Đ d Đ 2. a Đ b S c S d Đ 3. a Đ b Đ c Đ d S 4. a Đ b Đ c Đ d S
PHẦN 3. Câu trắc nghiệm trả lời ngắn. x
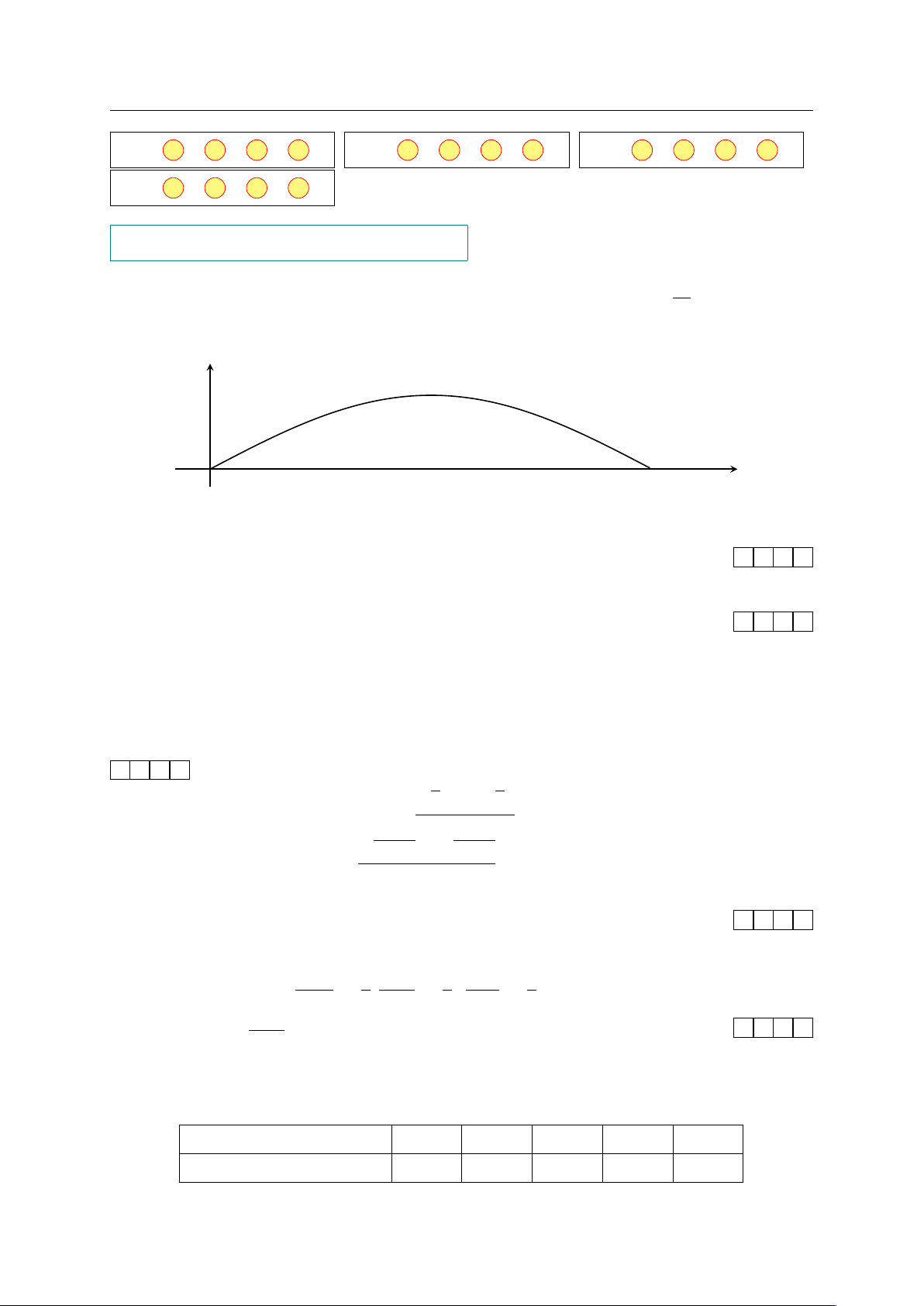
Câu 1. Một cây cầu có dạng cung OM của đồ thị hàm số y = 2,1 sin và được mô tả 10
trong hệ trục tọa độ với đơn vị trục là mét như hình vẽ dưới đây y O x M
Giả sử chiều rộng của con sông là độ dài đoạn thẳng OM . Tìm chiều rộng đó (làm tròn
kết quả đến hàng phần mười). KQ:
Câu 2. Cho phương trình 1 + 6 + 11 + 16 + · · · + x = 970. Biết rằng 1,6,11, · · · x là một cấp số cộng, Tìm x? KQ:
Câu 3. Một quả bóng được thả thẳng đứng từ độ cao 10m rơi xuống đất và nảy lên.
Giả sử sau mối một lần rơi xuống, nó nảy lên được một độ cao bằng 75% độ cao vừa rơi
xuống. Tính tổng quãng đường quả bóng di chuyển được kể từ lúc thả xuống đến khi quả
bóng chạm đất lần thứ 10 (làm tròn kết quả đến hàng phần mười của mét). KQ: √ √ 2x2 + 2x 2mx + khi x 6= 1 Câu 4. Cho hàm số f (x) = 1 + x √ √ 1 − x − 1 + x khi x = −1 x
Tìm tất cả giá trị thực của tham số m để hàm số liên tục tại x = −1 (làm tròn kết quả đến hàng phần trăm). KQ:
Câu 5. Cho hình hộp ABCD.A0B0C0D0. Trên các cạnh AA0, BB0, CC0 lần lượt lấy ba A0M 1 B0N 2 C0P 1 điểm M , N , P sao cho = ; = ; =
. Biết mặt phẳng (M N P ) cắt DD0 AA0 3 BB0 3 CC0 2 DD0 tại Q. Tính tỉ số . KQ: D0Q
Câu 6. Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức
giá nào. Kết quả được khảo sát được ghi lại ở bảng sau
Mức giá (triệu đồng/m2) [10; 14) [14; 18) [18; 22) [22; 26) [26; 30) Số khách hàng 54 78 120 45 12 GV: PHẠM LÊ DUY / Trang 18/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919
Tìm mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần chục). KQ: 1. 31,4 2. 96 3. 65,5 4. 0,29 5. 6 6. 19,4 GV: PHẠM LÊ DUY / Trang 19/87
p Bộ Đề Ôn Tập Thi HK1 Ô 0704.963.919 D. ĐỀ 4
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Cấp số cộng với số hạng đầu là u1, công sai d có số hạng tổng quát là
A. un = u1 − (n − 1)d, (n ≥ 2).
B. un = u1 + (n − 1)d, (n ≥ 2). C. un = u1 + d, (n ≥ 2).
D. un = u1 + (n + 1)d, (n ≥ 2).
Câu 2. Dãy số nào sau đây không phải là một cấp số nhân? A. 1; −3; 9; −27; 54. B. 1; 2; 4; 8; 16. C. 1; 3; 5; 7; 9. D. 1; −2; 4; −8; 16.
Câu 3. Cho cấp số nhân (un) với u1 = 3; u2 = 9. Công bội của cấp số nhân đã cho bằng A. 6. B. 3. C. 12. D. −6.
Câu 4. Đặt lim un = a, lim vn = b. Mệnh đề nào dưới đây là sai?
A. lim(un · vn) = lim un + lim vn.
B. lim(un + vn) = lim un + lim vn.
C. lim(un − vn) = lim un − lim vn.
D. lim(un · vn) = lim un · lim vn.
Câu 5. Giới hạn lim (2x + 1) có giá trị bằng x→−2 A. 5. B. −3. C. +∞. D. −∞.
Câu 6. Phương trình sin 2x = 1 có nghiệm là π π π π A. + k4π, k ∈ Z. B. + kπ, k ∈ Z. C. + k2π, k ∈ Z. D. + kπ, k ∈ Z. 2 2 4 4 2x − 1 Câu 7. Cho hàm số f (x) =
. Khẳng định nào sau đây là đúng? x3 − x
A. Hàm số liên tục tại x = −1.
B. Hàm số liên tục tại x = 0. 1
C. Hàm số liên tục tại x = 1.
D. Hàm số liên tục tại x = . 2
Câu 8. Mệnh đề nào dưới đây là đúng?
A. Qua một điểm nằm ngoài mặt phẳng cho trước, ta vẽ được một và chỉ một đường
thẳng song song với mặt phẳng cho trước đó.
B. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong
mặt phẳng (α) đều song song với mọi đường thẳng nằm trong mặt phẳng (β).
C. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân
biệt (α) và (β) thì (α) và (β) song song với nhau.
D. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong
mặt phẳng (α) đều song song với mặt phẳng (β).
Câu 9. Cho hình lăng trụ ABCD.A0B0C0D0. Mệnh đề nào dưới đây là sai?
A. mp(AA0B0B) song song với mp(CC0D0D). GV: PHẠM LÊ DUY / Trang 20/87





