Bộ đề thi giữa HK2 Toán 11 năm 2022-2023 (có đáp án)

Bộ đề thi giữa HK2 Toán 11 năm 2022-2023 có đáp án được soạn dưới dạng file PDF gồm 34 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

74 37 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

34 trang 6 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 1
MÔN TOÁN 11
A.PHẦN TRẮC NGHIỆM (7.0 điểm)
Câu 1. Cho dãy số có . Tính giới hạn .
A. B. C. D.
Câu 2. bằng:
A. . B. . C. . D. .
Câu 3. Tính giới hạn
A. B. C. D.
Câu 4. Giá trị của bằng:
A. . B. . C. . D.
Câu 5. Giá trị của bằng:
A. . B. . C. . D. .
Câu 6. Tính
A.2 B.-5 C.3 D.1
Câu 7.Tính
A. B. C. D.
Câu 8. Tính
A. B. C. D.
Câu 9. Tính
A. B. C. D.
Câu 10. Tính
A. B. C. 0 D.
Câu 11. bằng
A. B. C. D.
( )
n
u
lim 2
n
u =
31
lim
25
n
n
u
u
-
+
1
5
-
3
2
+¥
52
lim(200 3 2 )nn-+
0
1
+¥
-¥
2
2
23
lim
2
n
J
n
+
=
+
2J =
1J =
4J =
0J =
2
2
lim
31
n
nn
+
-+
+
1
13
-¥
0
1
13-
++
-
=
+
11
3.2 3
lim
23
nn
nn
C
+¥
-¥
1
3
-
1
2
1
lim(2 1)
x
x
®-
-
2023
lim (2 3 5 )
x
xx
®-¥
--
5I =-
2023I =-
.I =+•
.I =-•
2
3
2
26
lim
32
x
xx
x
®
+-
-
7
2
7
2
-
5
.
6
P =
3
4
P =-
59
7
23
lim
32
x
xx
N
x
®+¥
--
=
-
3
2
N =
.N =+•
.N =-•
0.N =
22
lim ( 4 1 4 3 )
x
Nxxx
Æ- •
=--+
3
4
3
4
-
1
2
2
x3
x6
lim
93x
-
®-
-
+
-¥
+¥
Trang 2
Câu 12 .
Cho hàm số . Chọn câu đúng trong các câu sau:
(I) liên tục tại .
(II) gián đoạn tại .
(III) liên tục trên đoạn .
A. Chỉ (I) và (III). B. Chỉ (I). C. Chỉ (II). D. Chỉ (II) và (III).
Câu 13. Cho hàm số . Giá trị của để liên tục trên là:
A. và . B. và . C. và . D. và .
Câu 14. Cho hàm số . Tính tổng tất cả các giá trị của m để hàm số liên
tục tại x = 2
A.2 B. 5 C.1 D.-1
Câu 15. Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì vuông góc với đường
thẳng còn lại.
B. Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường
thẳng còn lại.
D. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Câu 16. Trong các mệnh đề sau. Mệnh đề sai là
A. Hai mặt phẳng song song thì không có điểm chung.
B. Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song
song với mặt phẳng kia.
D. Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến
song song với nhau.
Câu 17. Trong không gian cho hai đường thẳng và vuông góc với nhau. Gọi hai vectơ và lần
lượt là hai vectơ chỉ phương của và Tìm khẳng định sai trong các khẳng định sau:
A.
B. Góc giữa hai đường thẳng và bằng
C. Hai đường thẳng và cắt nhau và trong các góc tạo thành có một góc vuông.
D.
Câu 18. Cho lăng trụ tam giác . Đặt , , . Biểu diễn vectơ qua các
vectơ . Chọn đáp án đúng.
A. . B. . C. . D. .
( )
2
4=-fx x
( )
fx
2=x
( )
fx
2=x
( )
fx
[ ]
2; 2-
( )
( )
22
2
khi 2
2 khi 2
ax x
fx
ax x
ì
£
ï
=
í
->
ï
î
a Î !
( )
fx
!
1
2
1
–1
–1
2
1
–2
2
2
26
,2
()
2
1, 2
xx
khix
yfx
x
m m khix
ì
--
¹
ï
==
-
í
ï
-+ =
î
1
d
2
d
1
u
!
2
u
!
1
d
2
.d
( )
12
,90.uu =°
!!
1
d
2
d
90 .°
1
d
2
d
12
.0.uu =
!!
.' ' 'ABC A B C
'AA u=
!!!" "
AB v=
!!!" "
wAC =
!!!" !!"
'BC
!!!!"
,,uvw
!!"!
'wBC u v=++
!!!!" " " !!"
'wBC u v=-+
!!!!" " " !!"
'wBC u v=--
!!!!" " " !!"
'wBC u v=+-
!!!!" " " !!"
Trang 3
Câu 19. Cho tứ diện có là trọng tâm tam giác . Đặt ; ; . Khẳng định
nào sau đây đúng?
A. B. C. D.
Câu 20. Trong không gian cho đường thẳng và điểm . Qua có mấy đường thẳng vuông góc với
đường thẳng
A. Vô số. B. . C. . D. .
Câu 21.Cho hình lập phương . Góc giữa 2 vec tơ và bằng
A. B. C. D.
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1 (1,0 điểm). Tính giới hạn
Câu 2 (1,0 điểm). Chứng minh rằng phương trình có nghiệm thuộc
với mọi m.
Câu 3 (1,0 điểm). Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. . Gọi M,N là lần lượt là trung
điểm của AD và SD. Tính góc giữa hai đường thẳng MN và AB.
ĐÁP ÁN
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Đ.án
C
D
A
D
C
D
C
B
B
A
B
B
D
C
C
B
C
B
A
A
D
Câu 1
Đáp án
Thang
điểm
Biến đổi về
0,25
=
0,25
=
0,25+0,25
Câu 2
Đặt
Ta có hàm số f(x) là hàm đa thức. Suy ra hàm số f(x) liên tục trên
0,25
0,25
=
0,25
Suy ra
0,25
ABCD
G
BCD
x AB=
!!!"
"
yAC=
!!!"
"
zAD=
!!!"
"
( )
1
3
AG x y z=++
!!!"
""
"
( )
2
3
AG x y z=- + +
!!!"
""
"
( )
1
3
AG x y z=- + +
!!!"
""
"
( )
2
3
AG x y z=++
!!!"
""
"
D
O
O
D
3
1
2
DCBAABCD
¢¢¢¢
.
''AC
!!!!!"
BA
!! !"
0
45
0
90
0
60
0
135
2
2
233
lim
2
x
xx
x
®
-+-
-
220222023
(35) 10mmx x-+ - -=
(2; 2)-
2
2
2
26
lim
(2)(2 33)
x
xx
xxx
®
--
--++
2
2
(2)(23)
lim
(2)(2 33)
x
xx
xxx
®
-+
--++
2
2
23 7
lim
6
233
x
x
xx
®
+
=
-++
220222023
() ( 3 5) 1fx m m x x=-+ - -
2; 2
éù
-
ëû
(0) 1f =-
2
(1) 3 5fmm-= - +
2
311
() 0,
24
mm
éù
-+>"Î
êú
ëû
!
(1).(0) 0,ff m-<"Î!
Trang 4
Suy ra phương trình f(x) =0 có ít nhất 1 nghiệm thuộc
Câu 3
Gọi
AB // OM suy ra góc giữa MN và AB bằng góc giữa MN và OM bằng hoặc bù với góc
0,5
Tính được MN= MO= ON = . Suy ra tam giác MNO đều suy ra =
0,5
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 2
MÔN TOÁN 11
A/ PHẦN TRẮC NGHIỆM (7 điểm)
Câu 1: Tính bằng:
A. B.
!"
#
. C. D.
"
#
Câu 2: Cho hình lập phương . Hãy tính góc giữa cặp vectơ và ?
A. B. C. D.
Câu 3: Gọi . Giá trị của S bằng
A. B.
C.
D.
.
Câu 4: Cho hai dãy và thỏa mãn và Giá trị của
lim$(𝑢
$
− 𝑣
$
)
bằng
A. B. C. D.
Câu 5: Chọn khẳng định đúng?
( )
( )
1; 0 2; 2-Ì-
N
M
O
D
C
B
A
S
O AC BD=Ç
∑
NMO
2
a
∑
NMO
0
60
2
2
4
34
lim
4
x
xx
xx
®-
+-
+
1-
1
.ABCD EFGH
AB
!!!"
EG
!!!"
B
C
A
D
E
G
F
H
90°
60°
45°
120°
( )
1
1
11
...
39 3
n
n
S
+
-
=-++
1
( )
n
u
( )
n
v
lim 2
n
u =
lim 3.
n
v =
1.-
6.
5.
Trang 5
A. Nếu hàm số liên tục trên và thì phương trình
!
"
#
$
%&
có ít nhất
một nghiệm thuộc
"
'()
$
B. Nếu hàm số liên tục trên và thì phương trình
!
"
#
$
%&
có ít nhất
một nghiệm thuộc
"
'()
$
C. Nếu hàm số liên tục trên và thì phương trình
!
"
#
$
%&
có ít nhất
một nghiệm thuộc
"
'()
$
D. Nếu hàm số liên tục trên và thì phương trình
𝑓
(
𝑥
)
= 0
có ít nhất
một nghiệm thuộc
(
𝑎;𝑏
)
Câu 6: Tính giới hạn . A.
−∞.
B. . C.
.
D.
.
Câu 7: Cho hình hộp ABCD.EFGH. Mệnh đề nào sau đây đúng?
A.
*+
,
,
,
,
,
-
.*/0
,
,
,
,
,
,
,
-
.*1
,
,
,
,
,
-
%*2
,
,
,
,
,
-
. B.
*+
,
,
,
,
,
-
.*3
,
,
,
,
,
-
.*/0
,
,
,
,
,
,
,
-
%*4
,
,
,
,
,
-
.
C.
𝐴𝐵
5
5
5
5
5
6
+ 𝐴𝐷$
5
5
5
5
5
5
5
6
+ 𝐴𝐸
5
5
5
5
5
6
= 𝐴𝐻
5
5
5
5
5
5
6
. D.
𝐴𝐵
5
5
5
5
5
6
+ 𝐴𝐶
5
5
5
5
5
6
+ 𝐴𝐷$
5
5
5
5
5
5
5
6
= 𝐴𝐸
5
5
5
5
5
6
.
Câu 8: Giá trị của
𝐷 = 𝑙𝑖𝑚
$
!
!%$
"
&'
$
#
&#$
!
&(
bằng:
A. . B. . C. 0 D. .
Câu 9: Chọn khẳng định sai?
A. (nếu k
56
∗
chẵn). B. (nếu k
56
∗
lẻ).
C. D. (với k nguyên dương).
Câu 10: Cho hình chóp có tất cả các cạnh đều bằng . Gọi và lần lượt là trung điểm
của
và . Số đo của góc bằng
A. . B. . C. . D. .
Câu 11: Chọn khẳng định đúng.
A. . nếu . B nếu C. nếu . D. .
nếu
Câu 12: Cho hai véctơ . Tích vô hướng được tính bởi công thức nào dưới đây?
A. . B. . C. . D.
.
Câu 13: Tính
𝐷 =
có giá trị là:
A. 0 B. C. D.
Câu 14: Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức
nào đúng ? A. B.
C. D.
Câu 15: Chọn khẳng định sai?
A. Hàm số được gọi là liên tục trên đoạn nếu nó liên tục trên khoảng .
B.Hàm số không liên tục tại được gọi là gián đoạn tại điểm đó.
C. Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
D. Cho hàm số xác định trên khoảng và Hàm số được gọi là liên
()yfx=
[a; b]
f(a).f(b) 0>
()yfx=
[a; b]
f(a).f(b) 0<
()yfx=
[a; b]
f(a).f(b) 0£
()yfx=
[a; b]
f(a).f(b) 0³
2
1
1
lim
1
x
x
x
-
®
+
-
+¥
1
0
-¥
+¥
1
lim
k
x
x
®-¥
=+¥
lim
k
x
x
®-¥
=-¥
lim
k
x
x
®-¥
=+¥
lim
k
x
x
®+¥
=+¥
.S ABCD
a
I
J
SC
BC
( )
,IJ CD
90°
60°
45°
30°
lim
n
q =+¥
1q >
lim
n
q =+¥
1q <
lim
n
q =+¥
1q >
lim
n
q =+¥
1q <
;ab
!!
.ab
!!
..ab a b=
!! ! !
( )
. . .sin ,ab a b a b=
!! ! ! ! !
( )
...cos,ab ab a b=
!! !! ! !
( )
. . .cos ,ab a b a b=
!! ! ! ! !
2
1
253
lim
23
x
xx
x
®
-+
-
+¥
-¥
1
5
-
SB SD SA SC+=+
!! " !! !" !!" !! !"
AB AC AD+=
!!!" !!!" !!!"
SA SD SB SC+=+
!!" !! !" !! " !!!"
0AB BC CD DA+++=
!!!" !!!" !!!" !!!"
()yfx=
[ ]
;ab
( )
;ab
()yfx=
0
x
()yfx=
K
0
.xKÎ
()yfx=
Trang 6
tục tại nếu
Câu 16: Trong không gian cho ba đường thẳng phân biệt , , . Khẳng định nào sau đây đúng?
A.Nếu và cùng nằm trong mp thì góc giữa và bằng góc giữa và .
B.Nếu và cùng vuông góc với thì .
C.Nếu góc giữa và bằng góc giữa và thì .
D.Nếu và thì .
Câu 17: Dãy số nào sau đây có giới hạn bằng ?
A. ?
!#
%
@
$
B. ?
'
%
@
$
. C.?
!"
#
@
$
. D.?
%
'
@
$
.
Câu 18: Cho hàm số
𝑓
(
𝑥
)
=
)
"
!)
)
"
!")&*
. Khi đó hàm số liên tục trên khoảng nào sau đây?
A.
(
−3;2
)
. B.
(
−∞;3
)
. C
(
2;+∞
)
. D.(-2;3).
Câu 19: Tìm
𝑎
để hàm số liên tục tại
𝑥 = 0.
A.
(
#
. B.
(
'
. C. . D. .
Câu 20: Cho hình lập phương ABCD.EFGH như hình vẽ bên. Véctơ nào sau đây cùng phương với
véctơ
𝐴𝐵
5
5
5
5
5
6
.
𝐴.𝐴𝐹.
5
5
5
5
5
5
6
$$$$$$$$$$$$$$$$$$$$$𝐵.$$𝐴𝐷
5
5
5
5
5
6
.$$$$$$$$$$$$$$$$$$$$$$$$$𝐶.𝐴𝐸
5
5
5
5
5
6
.$$$$$$$$$$$$$$$$$$$$$$$$$$$$$𝐷.𝐵𝐴
5
5
5
5
5
6
Câu 21: Giá trị đúng của là: A.
+∞.
B. 1. C. 7. D. -1.
B/ PHẦN TỰ LUẬN (3 điểm)
Câu 1. Tính giới hạn sau
Câu 2. Cho hàm số
7
"
8
$
%
9
√
𝟒𝒙%𝟗'
√
𝟑𝒙'𝟒
𝟑
'𝟑
𝒙'𝟒
000000000:;<=>
?8
𝟐
.@ABB0000000000:;<C>
. Tìm m để hàm số liên tục tại x=4?
Câu 3: Cho tứ diện ABCD có
DE%FG
HI%F
J
B
. Lấy E, F lần lượt trên cạnh BC, AD sao cho
EK%
𝟏
𝟑
EHGDL%
𝟏
𝟐
LI0MN0KL0
vuông góc với CD. Tính góc giữa hai đường thẳng AB và CD?
------ HẾT ------
ĐÁP ÁN
PHẦN ĐÁP ÁN CÂU TRẮC NGHIỆM:
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
TL
D
C
A
A
B
A
A
C
C
B
C
D
A
A
A
D
B
A
B
D
B
ĐÁP ÁN TỰ LUẬN
Bài
Nội dung
Điểm
Câu 1
1đ
Tính giới hạn sau
! "#$
!→#$
%&'(
)
*'
%
+,'(-.%&'+
)
*'
%
+,'(-.
&'+
)
*'
%
+,'(-
0.25đ
0.25đ
0
x
0
0
lim ( ) ( ).
xx
fx fx
®
=
a
b
c
a
b
( )
// c
a
a
c
b
c
a
b
c
//ab
a
c
b
c
//ab
//ab
ca^
cb^
0
( )
=yfx
( )
2
2 khi 0
1khi 0
+<
ì
=
í
++ ³
î
xa x
fx
xx x
1
0
B
C
A
D
E
G
F
H
4
4
7
lim
1
®+¥
+
+
x
x
x
2
lim (2 4 5 1)
x
xxx
®-¥
+-+
2
lim (2 4 5 1)
x
xxx
®-¥
+-+
Trang 7
! "#$
!→#$
*'
%
+*'
%
(,'+-
&'('
/
*+
,
'
(
-
'
%
! "#$
!→#$
&#
!
"
%'
(
)#
#
"
'
!
"
$
0=
&
)
Vậy =
&
)
0.25đ
0.25đ
Câu 2
1đ
Cho hàm số 𝒇
(
𝒙
)
=&
√
𝟒𝒙$𝟗&
√
𝟑𝒙&𝟒
𝟑
&𝟑
𝒙&𝟒
'''''''''𝒌𝒉𝒊>𝟒
𝟐𝒙
𝟐
+𝒎−𝟑𝟑''''''''''𝒌𝒉𝒊≤𝟒
. Tìm m
để hàm số liên tục tại x=4?
Tìm 1
%
*
.
! 2+-
("#$
!→)
%
1
%
'
.
! 2+-
("#$
!→)
&
1
%
'
.
!
3
&4
Để hàm số liện tục tại x=4 : 2+-!
*
%+
Vậy : 2 !
%*
%+
0.25đ
0.25đ
0.25đ
0.25đ
Câu 3
1đ
Cho tứ diện ABCD có 𝑨𝑩=𝒂, 𝑪𝑫=𝒂
√
𝟑. Lấy E, F lần lượt
trên cạnh BC, AD sao cho 𝑩𝑬=
𝟏
𝟑
𝑩𝑪,𝑨𝑭=
𝟏
𝟐
𝑭𝑫'𝒗à'𝑬𝑭' vuông
góc với CD. Tính góc giữa hai đường thẳng AB và CD?
-Dựng EM//AB, tính EM=
%,
*
.
-Lý luận MF//CD, tính MF=
,
√
*
*
- Tính cos 567
8
!
√
*
%
Vậy (AB, CD)=34
+
HS xác định được góc (AB,CD)=(ME,MF) mà không tính được
cos 9:;
8
( vẫn cho 0,25đ)
0.25đ
0.25đ
0.25đ
0.25đ
Lưu ý:
+ Học sinh giải cách khác dựa theo đáp án trên cho điểm tối đa
.+ Học sinh lý luận để hàm số liện tục tại x=4
ó
("#$
!→)
%
1
%
'
.
!("#$
!→)
&
1
%
'
.
!1
%
*
.
<
0,25 điểm
2
lim (2 4 5 1)
x
xxx
®-¥
+-+
Trang 8
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 3
MÔN TOÁN 11
Câu 1: Tính .
A. . B. . C. . D. .
Câu 2: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng
A. . B. . C. . D. .
Câu 3: Cho , trong đó là phân số tối giản. Tính .
A. . B. . C. . D. .
Câu 4: Cho hình hộp , tìm vectơ chỉ phương của đường thẳng .
A. . B. . C. . D. .
Câu 5: Trong không gian cho hình lập phương có cạnh bằng . Khẳng định nào sau đây
đúng?
A. . B. . C. . D. .
Câu 6: Hàm số nào sau đây liên tục trên ?
A. . B. . C. . D. .
Câu 7: Trong các mệnh đề sau mệnh đề nào sai?
A. Nếu thì bốn điểm đồng phẳng.
B. Tam giác có là trung điểm cạnh thì ta có đẳng thức: .
C. Vì nên suy ra là trung điểm của .
D. Vì nên 4 điểm đồng phẳng.
Câu 8: Cho , trong đó là phân số tối giản. Tính .
A. . B. . C. . D. .
Câu 9: Biết hàm số liên tục tại . Mệnh đề nào dưới đây đúng?
A. . B. . C. . D. .
Câu 10: Tổng , trong đó là phân số tối giản. Tính .
A. . B. . C. . D. .
Câu 11: Trong các giới hạn sau, giới hạn nào có giá trị bằng ?
A. . B. . C. . D. .
Câu 12: Cho hàm số liên tục trên và khi đó phương trình có
A. Có ít nhất một nghiệm thuộc . B. Có ít nhất hai nghiệm thuộc .
3
2
1
lim
1
x
x
L
x
Æ
-
=
-
7=-L
1L =-
7=L
1L =
lim 0, 1
n
n
qq
®+¥
=>
lim 0, 1
n
n
qq
®+¥
=<
lim 1 0
n
n®+¥
=
1
lim 1
n
n
®+¥
=
2
2
21
lim
13
x
xa
xx b
Æ- •
-
=
-+
a
b
22
+ab
10
6
5
13
.' ' ' 'ABCD A B C D
'AD
'AB
!!!!"
'CB
!!!"
'BC
!!!!"
''AC
!!!!!"
.' ' ' 'ABCD A B C D
a
.'0AC DD =
uuur uuu ur
2
.'
2
=
uuur uuu ur
a
AC DD
2
.'AC DD a=-
uuur uuu ur
2
.'AC DD a=
uuur uuu ur
°
( )
2
1
1
fx
x
=
-
( )
2
1
1
fx
x
=
+
( )
1
1
fx
x
=
+
( )
1
1
fx
x
=
-
0AB BC CD DA+++=
!!!" !!!" !!!" !!!" "
,,,ABCD
ABC
I
BC
2AI AB AC=+
!! " !!!" !!!"
0BA BC+=
!! !" !!!" "
B
AC
23AB AC AD=- +
!!!" !!!" !!!"
,,,ABCD
3
3
1
lim
23 2
na
nn b
-
=
+-
a
b
.ab
2-
1
1-
2
( )
31
1
xbkhix
fx
xakhix
Ï
+£-
Ô
Ô
=
Ì
Ô
+>-
Ô
Ó
1x =-
2ab=- -
2ab=- +
2ab=-
2ab=+
11 1
...
3612
a
S
b
=++ +=
a
b
ab+
11
6
7
5
1-
1
lim
1
n
n
-
+
2
lim 1
n
ʈ
˜
Á
+
˜
Á
˜
Á
˯
1
lim 2
n
ʈ
˜
Á
-+
˜
Á
˜
Á
˯
2
lim 1
n
ʈ
˜
Á
-
˜
Á
˜
Á
˯
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
0fx=
( )
;ab
( )
;ab
Trang 9
C. Có ít nhất hai nghiệm thuộc . D. Có ít nhất một nghiệm thuộc .
Câu 13: Tính .
A. . B. . C. . D. .
Câu 14: Tính .
A. . B. . C. . D. .
Câu 15: Trong không gian cho hình hộp . Khẳng định nào sau đây đúng?
A. . B. .
C. . D. .
Câu 16: Cho tứ diện . lần lượt là trung điểm của và . Mệnh đề nào đúng?
A. . B. .
C. . D. .
Câu 17: Dãy số nào sau đây có giới hạn bằng ?
A. . B. . C. . D. .
Câu 18: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa hai đường thẳng là góc nhọn.
B. Góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và thì song song với .
C. Góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và khi song song với (hoặc
trùng với ).
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.
Câu 19: Trong không gian cho hình lập phương
,
xác định góc giữa và .
A. . B. . C. . D. .
Câu 20: Cho hàm số , gián đoạn tại điểm nào sau đây?
A. . B. . C. . D. .
Câu 21: Cho hai hàm số thỏa mãn và . Giá trị của
bằng bao nhiêu?
A. . B. . C. . D. .
II. Tự luận. (3 điểm)
Bài 1. (1đ)
Tính .
Bài 2. (1đ)
Cho hàm số , xác định để hàm số liên tục tại .
Bài 3. (1đ)
[ ]
;ab
[ ]
;ab
2
5
lim
2
x
x
x
-
Æ
-
-
+•
1
-•
1-
( )
2
lim 1 2
Æ+•
-
x
x
2
2-
-•
+•
.' ' ' 'ABCD A B C D
'++ =
uur uuur uuur uur
CB CD CC CA
''CB CD CC CB++ =
uur uuur uuur uuur
''CB CD CC CD++ =
uur uuur uuur uuur
''CB CD CC CA++ =
uur uuur uuur uuur
ABCD
,MN
AB
CD
( )
2MN AB DC=+
uuur uuur uuur
( )
2MN AD BC=+
uuur uuur uu ur
( )
1
2
MN AB DC=+
uuu r uuur uuur
( )
1
2
MN AD BC=+
uuu r uuur uuur
0
2
5
n
ʈ
˜
Á
-
˜
Á
˜
Á
˯
6
5
n
ʈ
˜
Á
-
˜
Á
˜
Á
˯
7
5
n
ʈ
˜
Á
˜
Á
˜
Á
˯
7
5
n
ʈ
˜
Á
-
˜
Á
˜
Á
˯
a
b
a
c
b
c
a
b
a
c
b
c
b
c
.' ' ' 'ABCD A B C D
uu r
CA
'
uuur
CD
0
45
0
120
0
60
0
90
( )
2
1
2
x
fx
x
+
=
-
( )
fx
1x =
1x =-
2x =-
2x =
( ) ( )
,fx gx
( )
1
lim 3
x
fx
®
=
( )
1
lim 2
x
gx
®
=-
( ) ( )
1
lim .
x
fxgx
®
éù
ëû
1
6-
6
1-
( )
2
lim 2 3
Æ+ •
--+
x
xx x
( )
2
2
3
253
1
1
xx
khi x
fx
xx
mkhix
Ï
Ô
++
Ô
π-
Ô
Ô
=
+
Ì
Ô
Ô
=-
Ô
Ô
Ó
m
1x =-
Trang 10
Cho tứ diện đều . Gọi lần lượt là trung điểm của các cạnh và là trọng tâm ,
là góc giữa 2 vectơ và . Tính .
------ HẾT ------
ĐÁP ÁN
A. Phần trắc nghiệm: (7,0 điểm)
Mã đề
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
104
A
B
D
B
A
B
A
A
C
D
A
A
A
C
D
D
A
C
C
D
B
B. Phần tự luận: (3,0 điểm)
Câu
Nội dung
Điểm
1
Tính .
1.0 đ
0.5
0.25
0.25
2
Cho hàm số , xác định để hàm số liên tục tại
.
1.0 đ
0.25
0.25
Để hàm số liên tục tại thì
0.25
0.25
3
Cho tứ diện đều . Gọi lần lượt là trung điểm của các cạnh
và là trọng tâm , là góc giữa 2 vectơ và . Tính
.
1.0 đ
0.25
ABCD
,,MNP
,,AB CB AD
G
BCDD
a
MG
!!! !"
PN
!!!"
cos
a
( )
2
lim 2 3
Æ+ •
--+
x
xx x
2
23
lim
23
Æ+ •
-
=
-++
x
x
xx x
22
3
2
23
lim lim
23 23
111
Æ+ • Æ+ •
-
-
==
-+ + -+ +
xx
x
x
xx
xx xx
1=
( )
2
2
3
253
1
1
xx
khi x
fx
xx
mkhix
Ï
Ô
++
Ô
π-
Ô
Ô
=
+
Ì
Ô
Ô
=-
Ô
Ô
Ó
m
1x =-
2
2
1
253
lim 1
Æ-
++
=-
+
x
xx
xx
( )
3
1-=fm
1x =-
( ) ( )
3
1
lim 1 1
Æ-
=-€ =-
x
fx f m
1€=-m
ABCD
,,MNP
,,AB CB AD
G
BCDD
a
MG
!!! !"
PN
!!!"
cos
a
Trang 11
Đặt
Không mất tính tổng quát, giả sử độ dài các cạnh của tứ diện đều bằng 1
và
Ta có:
0.5
Thay vào (*) .
0.25
---------------------------------Hết--------------------------------
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 4
MÔN TOÁN 11
;;AB a AC b AD c===
!!!" " !!!" " !!!" "
( ) ( )
11
22
36
AG a b c MG AG AM a b cÞ= ++Þ =- =-++
!!!" " " " !!! !" !!!" !!!!" " " "
( )
1
2
PN AN AP a b c=-= +-
!!!" !!!" !!!" " " "
1abcÞ===
!!!
0
1
...1.1.cos60
2
ab bc ca=== =
!! !! !!
.
cos cos ( , ) (*)
.
MG PN
MG PN
MG PN
a
Þ= =
!!! !" !!!"
!!! !" !!!"
!!! !" !!!"
( )( )
1
.22
12
MG PN a b c a b cÞ=-+++-
!!! !" !!!" " " " " " "
(
)
22 2
11
222222
12 12
aabac abb bc ac bcc=--+++-++- =
!!!!!""!!! !!!!!!!
( ) ( )
22
1112
22 ;
6222
MG a b c PN a b c=-++ = = +-=
!!! !" " " " !!!" " " "
1
12
12
cos
6
1232
.
22
a
Þ= ==
Trang 12
I. PHẦN TRẮC NGHIỆM(7 điểm).
Câu 1: Tính .
A. . B. . C. . D. .
Câu 2: Cho các giới hạn: ; .Tính .
A.
.
B. . C.
.
D. .
Câu 3: Hàm số nào sau đây liên tục trên ?
A. . B. .
C. . D. .
Câu 4: Tính .
A. . B. . C. . D. .
Câu 5: Tính .
A. . B. . C. . D. .
Câu 6: Tính .
A. . B. . C. . D. .
Câu 7: Tính .
A. . B. . C. . D. .
Câu 8: Cho tứ diện có tất cả các cạnh đều bằng .Tính .
A. . B. . C. . D. .
Câu 9: Cho hình chóp có là hình bình hành tâm . Khẳng định nào sau đây sai?
A. . B. . C. . D. .
Câu 10: Biết . Tìm a.
A. . B. . C. . D. .
Câu 11: Cho . Tính .
A. B. . C. . D. .
Câu 12: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình hộp có các cạnh bên song song và bằng nhau.
B. Hai mặt đáy của hình hộp là hai hình bình hành.
C. Các mặt bên của hình hộp là các hình bình hành.
D. Hai đáy của hình hộp là hai đa giác đều.
Câu 13: Cho hình chóp S.ABCD .Khẳng định nào sau đây đúng?
3
3
23
Lim
32
x
x
x
®+¥
-
+
0
3
2
-
2
3
3
( )
0
lim 5
xx
fx
®
=-
( )
0
lim 4
xx
gx
®
=
( ) ( )
0
lim 2 3
xx
fx gx
®
-
éù
ëû
22-
2
9-
23
2
() 3fx x x=-+
() tanfx x=
() xfx cot=
2
21
()
2
xx
fx
x
++
=
+
x2
2x 1
lim
x2
-
®
+
-
+¥
-¥
1
2
2.3 4
lim
3.4 1
nn
n
-
-
1
3
-
1
3
0
2
3
5
lim ( 4 3 2)
x
xx
®-¥
---
-¥
2-
+¥
2
2
2
32
lim
2
x
xx
x
®
-+
-
+¥
1
3
-¥
ABCD
a
.AB AD
!!!" !!!"
2
3
2
a
-
2
3
2
a
2
2
a
-
2
2
a
.S ABCD
ABCD
0OA OB+=
!! !" !" "
2SO SB SD=+
!!!!" !! " !! !"
AC DC DA=-
!!!" !!!" !!!! "
DB DA DC=+
!!!" !!!" !!!"
2
2
52
lim 4
25
an n
n
-+
=
+
4a =-
4a =
8a =
2a =
lim( ) 5
n
u =
lim(2 3 )
n
u-
15-
17
15
13-
Trang 13
A. . B. .
C. . D. .
Câu 14: Cho hình hộp .Khẳng định nào sau đây đúng?
A. . B. .
C. . D. .
Câu 15: Hàm số nào sau đây có nghiệm trong khoảng ?
A. .
B. .
C. .
D. .
Câu 16: Tính .
A. . B. . C. . D. .
Câu 17: Trong không gian, cho 2 đường thẳng a và b vuông góc.Gọi lần lượt là véc tơ chỉ
phương của đường thẳng a và b.Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 18: Cho hình hộp . Khẳng định nào sau đây sai?
A. . B. .
C. . D. .
Câu 19: Tính tổng : .
A. . B. . C. . D. .
Câu 20: Hàm số nào sau đây không liên tục tại ?
A. . B. .
C. . D. .
Câu 21: Cho . Tính .
A. . B. . C. . D. .
II. PHẦN TỰ LUẬN ( 3 điểm).
Câu 1(1 điểm): Tính
Câu 2(1 điểm): Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc, .Tính
Câu 3(1 điểm): Chứng minh phương trình : có nghiệm
------ HẾT ------
∑
∑
(, )SA BC SAC=
∑
∑
(, )SA BC DSA=
∑
∑
(, )SA BC SDA=
∑
∑
(, )SA BC SAD=
''' '
.ABCD A B C D
''AC AA AB AD=++
!!!!" !!!" !!!" !!!"
'AC AC AB AD=++
!!!!" !!!" !!!" !!!"
''AC AA AB AD=++
!!!!"
!!!!" !!! " !!!"
'AC AA AB AD=++
!!!" !!! " !!!" !!!"
(1;0)-
5
() 2fx x x=++
5
() 2 2fx x x=-+
5
() 2fx x x=-+
5
() 3 2fx x x=++
( )
2
2
lim 3 2 1
x
xx
®
-+
17
+¥
-¥
9
,
ab
uu
!!" !!"
.1
ab
uu=-
!!" !!"
.0
ab
uu=
!!" !!"
.90
ab
uu=°
!!" !!"
cos( , ) 1
ab
uu =
!!" !!"
.ABCD A B C D
¢¢¢¢
()//('''')ABCD A B C D
()//('')ABCD ABC D
('')//('')AD D A BCC B
('')//('')DCC D ABB A
1
11 1
1... ...
39 3
n
S
-
=+ + + +
2
3
S =
3
2
S =
3
4
S =
4
3
S =
1x =
()
1
x
fx
x
=
-
()
1
x
fx
x
=
+
() cosfx x=
() sinfx x=
2
3
lim
5
x
x
a
x
®-¥
-
=
-
2a -
1-
3
3-
1
2
2
3
3103
lim
6
x
xx
xx
®-
++
+-
AB AC AD a===
.BC BD
!!!" !!!"
32 2
(2 3 1) 1 0mx m m x m+-+--=
mR"Î
Trang 14
ĐÁP ÁN
I. Phần đáp án câu trắc nghiệm:
1
C
6
C
11
D
16
D
21
C
2
A
7
B
12
D
17
B
3
A
8
D
13
D
18
B
4
B
9
A
14
C
19
B
5
A
10
C
15
D
20
A
II. PHẦN TỰ LUẬN
ĐÁP ÁN
Câu
Nội dung
Điểm
1
Câu 1: Tính:
(đúng mỗi dòng 0.25đ)
(không có hệ số 3,trừ 0.5 đ)
0.5
0.25
0.25
2
Câu 2 Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc,
.Tính
Tính
0.25
0.25
0.25
0.25
3
Câu 3: Chứng minh phương trình : có
nghiệm
Đặt
liên tục trên R liên tục trên
Chứng minh được
Suy ra PT có ít nhất một nghiệm thuộc
KL:PT có nghiệm
0.25
0.25
0.25
0.25
2
2
3
3103
lim
6
x
xx
xx
®-
++
+-
3
1
3( 3)( )
3
lim
( 3)( 2)
x
xx
xx
®-
++
=
+-
3
1
3( )
3
lim
2
x
x
x
®-
+
=
-
8
5
=
AB AC AD a===
.BC BD
!!!" !!!"
2BC BD CD a===
∑
...cosBC BD BC BD CBD=
!!!" !!!"
2. 2.cos 60aa=°
2
a=
32 2
(2 3 1) 1 0mx m m x m+-+--=
mR"Î
32 2
() (2 3 1) 1fx mx m m x m=+ -+--
()fxÞ
()fxÞ
[ ]
0; 2
2
(0) 1 0,fm mR=- - < " Î
2
(2) 3 2 1fmm=++
(2) 0,fmR>"Î
(0). (2) 0,ff R<"ÎÞ
(0;2)
mR"Î
Trang 15
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 5
MÔN TOÁN 11
PHẦN TRẮC NGHIỆM: (7 điểm)
Câu 1: Cho hai dãy số , thỏa và . Giá trị của bằng
A. . B. . C. . D. .
Câu 2: Hàm số nào sau đây liên tục trên ?
A. . B. . C. . D. .
Câu 3: Cho hai hàm số , thỏa mãn và . Giá trị của
bằng
A. . B. . C. . D. .
Câu 4: Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của AB và CD. Khẳng định nào sau đây
đúng?
A. . B. .
C. . D. .
Câu 5: bằng
A. . B. . C. . D. .
Câu 6: Cho hàm số . Giá trị của tham số để hàm số liên tục tại
bằng
A. . B. . C. . D. .
Câu 7: Hàm số liên tục trên khoảng nào sau đây?
A. . B. . C. . D. .
Câu 8: Cho hình lập phương ABCD.EFGH. Góc giữa hai đường thẳng AB và EG bằng
A. . B. . C. . D. .
Câu 9: bằng
A. . B. . C. . D. .
Câu 10: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và . Góc giữa
hai đường thẳng AB, BC bằng
A. . B. . C. . D. .
Câu 11: Cho mặt phẳng (P) song song mặt phẳng (Q). Mặt phẳng (R) cắt (P) và (Q) theo hai giao
tuyến a và b. Khẳng định nào sau đây đúng?
A. a và b trùng nhau.
B. a và b song song.
C. a và b song song hoặc trùng nhau.
()
n
u
()
n
v
lim 3
n
u =
lim 4
n
v =
lim( )
nn
uv+
7
12
1
1-
!
1
2
y
x
=
54
51yx x=+ +
32yx=-
tan 1yx=+
()fx
()gx
1
lim ( ) 2
x
fx
®
=-
1
lim ( )
x
gx
®
=+¥
1
lim[ ( ). ( )]
x
fxgx
®
2
2-
+¥
-¥
1
()
2
MN AB CD=+
!!! !" !!!" !!!"
1
()
2
MN AB CD=-
!!! !" !!!" !!!"
1
()
2
MN AD BC=-
!!! !" !!!" !!!"
1
()
2
MN AD BC=+
!!! !" !!!" !!!"
lim( 2)n +
2
+¥
-¥
1
1, khi 3
()
, khi 3
xx
fx
mx
+¹
ì
=
í
=
î
m
()fx
3x =
4
1
2
0
2
2
43
x
y
xx
=
-+
(2;0)-
(;)-¥ +¥
(2;4)
(0;2)
90°
45°
30°
60°
2
3
lim( 3 5)
x
xx
®
+-
3
13
5-
1
OA OB OC==
45°
120°
90°
60°
Trang 16
D. a và b cắt nhau.
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là
trung điểm SA, SB, SC, SD. Khẳng định nào sau đây sai?
A. (MNP) // (OCD). B. (MQO) // (SBC). C. (NQO) // (PCD). D. (MNO) // (SCD).
Câu 13: bằng
A. . B. . C. . D. .
Câu 14: bằng
A. . B. . C. . D. .
Câu 15: Cho hàm số thỏa mãn và . Giá trị của bằng
A. . B. . C. . D. .
Câu 16: bằng
A. . B. . C. . D. .
Câu 17: bằng
A. . B. . C. . D. .
Câu 18: Cho dãy số thỏa mãn . Giá trị của bằng
A. . B. . C. . D. .
Câu 19: Tính tổng
A. . B. . C. . D. .
Câu 20: Cho tứ diện ABCD, gọi G là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng?
A. . B. .
C. . D. .
Câu 21: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây đúng?
A. (ABC) // (A'B'D'). B. (ABD') // (A'B'C).
C. (ABC) // (B'C'D'). D. (ACD) // (A'D'B).
PHẦN TỰ LUẬN: (3 điểm)
Câu 1 (1 điểm): Tìm các giới hạn sau:
a) ; b)
Câu 2 (1 điểm): Chứng minh rằng phương trình luôn có ít nhất
một nghiệm âm với mọi giá trị của tham số ?
Câu 3 (1 điểm): Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. , ,
1
25
lim
1
x
x
x
+
®
+
-
5-
2
-¥
+¥
21
lim
3
n
n
-
+
2
+¥
1
3
-
2
3
()fx
1
lim ( ) 2
x
fx
+
®
=-
1
lim ( ) 2
x
fx
-
®
=-
1
lim ( )
x
fx
®
1
4
2-
4-
2
2
56
lim
2
x
xx
x
®
-+
-
1-
5-
1
5
3
lim ( 1)
x
x
®+¥
-
1
1-
+¥
-¥
()
n
u
lim( 5) 0
n
u -=
lim
n
u
10
0
5-
5
11 1
1...
3927
S =+ + + +
1
3
2
2
3
1
()
3
AG AB AC AD=+-
!!!" !!!" !!!" !!!"
1
()
2
AG AB AC AD=++
!!!" !!!" !!!" !!!"
1
()
3
AG AB AC=+
!!!" !!!" !!!"
1
()
3
AG AB AC AD=++
!!!" !!!" !!!" !!!"
2
2
25
lim
1
nn
n
+-
+
3
12
lim
3
x
x
x
®
+-
-
22
(3)240,
n
mm x x n
*
-+ - -="Ε
m
SA a=
2SB SD a==
Trang 17
. Tính góc giữa hai đường thẳng SD và AC?
------ HẾT ------
ĐÁP ÁN
1
A
6
A
11
B
16
A
21
C
2
B
7
A
12
C
17
C
3
D
8
B
13
D
18
D
4
D
9
B
14
A
19
C
5
B
10
D
15
C
20
D
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 6
MÔN TOÁN 11
PHẦN TRẮC NGHIỆM ( 7 điểm)
Câu 1. Chọn khẳng định đúng.
A. nếu có thể bé hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
B. nếu
có thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đó trở đi.
C. nếu có thể bé hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
D. nếu có thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đó trở đi.
Câu 2. Chọn khẳng định đúng:
A. nếu B. nếu .
C. nếu D. nếu .
Câu 3. Cho hai dãy số và . Biết và . Chọn khẳng định đúng.
A. B. C. D.
Câu 4. Tính .
A. B. C. D.
Câu 5. Tổng của cấp số nhân lùi vô hạn là:
A. B. C. D.
Câu 6. Tìm
A. 6 B. 8 C. 10 D. 12
Câu 7. Với k là số nguyên dương chẵn. Kết quả của giới hạn là:
A. B. 0 C. D.
Câu 8. Cho các giới hạn: ; , khi đó bằng:
3SC a=
lim
n
ua=
n
ua-
lim
n
ua=
n
ua-
lim
n
ua=
n
ua-
lim
n
ua=
n
ua-
lim 0
n
q =
1q >
lim 0
n
q =
1q <
lim 0
n
q =
1q >
lim 0
n
q =
1q <
( )
n
u
( )
n
v
lim 3
n
u =
lim
n
v =+¥
lim
n
n
u
v
= +¥
lim 0
n
n
v
u
=
lim .
nn
uv=+¥
1
lim
n
n
u
v
+
= +¥
3.2 1
lim
25
n
n
-
+
3.
.+¥
1
.
5
-
11 1
51 ...
525125
S =++ + + +
6
25
25
6
4
25
25
4
2
2
lim( 3 )
x
xx
®
+
k
x
lim x
®-¥
k
0
x
+¥
-¥
( )
®
=-
0
lim 1
xx
fx
( )
®
=
0
lim 5
xx
gx
( ) ( )
®
éù
-
ëû
0
lim 2
xx
fx gx
Trang 18
A. . B. . C. . D. .
Câu 9. Cho . Tính
A. . B. C. D.
Câu 10. Tính .
A. B. C. D.
Câu 11. Tính
A. B. C. D.
Câu 12. Mệnh đề nào sau đây sai?
A. Hàm số liên tục trên đoạn nếu nó liên tục tại mọi điểm thuộc đoạn .
B. Các hàm số đa thức, phân thức hữu tỉ, lượng giác liên tục trên các khoảng mà nó xác định.
C. Tổng, hiệu, tích của hai hàm số liên tục tại một điểm là những hàm số liên tục tại điểm đó.
D. Cho hàm số có miền xác định và . Ta nói là hàm liên tục tại khi
.
Câu 13. Cho hàm số . Chọn khẳng định đúng trong các khẳng định sau:
A. liên tục trên
B. liên tục trên các khoảng và
C. liên tục trên các khoảng
D. liên tục trên các khoảng và
Câu 14. Hàm số . Khẳng định nào sau đây đúng:
A. liên tục tại
B. liên tục tại và gián đoạn tại
C. liên tục trên
D. liên tục trên khoảng
Câu 15. Trong các khẳng định sau, khẳng định nào đúng?
A. Ba vectơ được gọi là đồng phẳng nếu giá của chúng cắt nhau từng đôi một .
B. Ba vectơ được gọi là đồng phẳng nếu giá của chúng vuông góc từng đôi một .
C. Ba vectơ được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng.
D. Ba vectơ được gọi là đồng phẳng nếu giá của chúng cắt nhau từng đôi một hoặc vuông góc từng đôi một.
Câu 16. Cho hình chóp có đáy là hình bình hành. Đặt ; ; ; .
Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 17. Cho hình hộp , tham khảo hình vẽ bên dưới .
4
3
-7
-3
lim ( ) 2, lim ( )
xx
fx gx
®-¥ ®-¥
==-¥
[ ]
lim ( ). ( )
x
Lfxgx
®-¥
=
= -¥L
.= +¥L
2.=L
0.=L
2
2
2
lim
4
x
x
x
®-
+
-
1
4
1
4
-
4-
4
3
2
lim
3
x
x
x
-
®
+
-
0
.+¥
-¥
1
( )
yfx=
[ ]
;ab
[ ]
;ab
( )
fx
aDÎ
()fx
xa=
( ) ( )
lim
xa
fx fa
®
=
32
()
1
x
fx
x
+
=
-
( )
fx
.R
( )
fx
( )
;1-¥
( )
1; +¥
( )
fx
( ) ( )
;1 1;-¥ È +¥
( )
fx
( )
;2-¥
( )
2; +¥
3, 4
()
6, 4
xkhix
fx
khi x
+¹
ì
=
í
=
î
( )
fx
4x =
( )
fx
10x =
4x =
( )
fx
( )
0; +¥
( )
fx
R
,,abc
!!!
,,abc
!!!
,,abc
!!!
,,abc
!!!
.S ABCD
ABCD
SA a=
!!"
"
SB b=
!!"
"
SC c=
!!!"
"
SD d=
!!!"
"
ad bc+=+
!!
!!
ab cd+=+
!!
!!
ac db+= +
!!
!!
0abcd+++ =
!!
!
!!
.ABCD EFGH
Trang 19
Khi đó
bằng:
A. . B. . C. . D. .
Câu 18. Trong không gian cho ba đường thẳng phân biệt , , . Khẳng định nào sau đây đúng?
A. Nếu thì B. Nếu và thì .
C. Nếu thì . D. Nếu thì
Câu 19. Cho ba đường thẳng . Mệnh đề nào sau đây sai?
A. Nếu thì B. Nếu thì
C. Nếu thì D. Nếu thì
Câu 20. Trong không gian cho ba đường thẳng . Trong các mệnh đề sau, mệnh đề nào đúng?
A. (I) và (II)
. B. (II) và (III)
.
C. Chỉ (I) . D. Chỉ (II).
Câu 21. Cho tứ diện đều (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng và
bằng
A. . B. . C. . D. .
PHẦN TỰ LUẬN ( 3 điểm)
Bài 1. Tính giới hạn sau:
Bài 2. Tìm tất cả các giá trị thực của tham số để hàm số liên tục tại
Bài 3. Cho tứ diện
có
và
Chứng minh rằng
------ HẾT ------
ĐÁP ÁN
Nội dung
Điểm
Bài 1
Tính giới hạn sau:
1,0
G
H
C
F
A
D
B
E
GF GH GC++
!!!" !!!" !!!"
GE
!!!"
GA
!!!"
GB
!!!"
GD
!!!"
a
b
c
ac
bc
^
ì
í
^
î
//ab
//ab
ca^
cb^
ac
bc
^
ì
í
^
î
ab^
ac
bc
^
ì
í
^
î
abº
,,abc
//ab
( )
∑
( )
∑
,,ac cb=
//cb
( )
∑
( )
∑
,,ab ac=
//ac
( )
∑
,0ac =°
ab^
( )
∑
( )
∑
,,ac cb=
,,abc
//
(): ( ): //
ab c a
IcbIIab
ca cb
^
ìì
Þ^ Þ
íí
^^
îî
( )
∑
(): , 0 //III a b a b=°Þ
ABCD
AB
CD
30°
45°
60°
90°
2
4
294
lim
4
x
xx
x
®
-+
-
()fx
3x =
,3
()
352
,3
3
xm x
fx
x
x
x
+£
ì
ï
=
í
--
>
ï
-
î
ABCD
2AB AC AD cm===
∑ ∑
150CAD BAD==°
.AD BC^
2
4
294
lim
4
x
xx
x
®
-+
-
Trang 20
0,5
0,25-0,25
Bài 2
Tìm tất cả các giá trị thực của tham số để hàm số liên tục tại
1,0
TXĐ:
0,25
0,25
0,25
liên tục tại
0,25
Bài 3
Cho tứ diện
có
và
Chứng minh rằng
1,0
0,25
0,25
0,25
Kết luận
0,25
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 7
MÔN TOÁN 11
I. PHẦN TRẮC NGHIỆM: ( 7 điểm)
Câu 1: Trong các khẳng định sau, khẳng định nào Đúng?
A. B. C. D.
Câu 2: Cho hàm số thỏa mãn và Giá trị của bằng:
A. B. C. D. Không tồn tại.
Câu 3: Cho hàm số y = f (x) xác định trên khoảng K và . Hàm số f(x) được gọi là liên tục tại nếu:
A. B.
C. D.
Câu 4: Biết với là tham số. Khi đó bằng:
2
44
294 (4)(21)
lim lim
44
xx
xx x x
xx
®®
-+ - -
=
--
( )
4
lim 2 1 7
x
x
®
-=
()fx
3x =
,3
()
352
,3
3
xm x
fx
x
x
x
+£
ì
ï
=
í
--
>
ï
-
î
,3DR x D==Î
(3 ) 3fm=+
33
lim ( ) lim ( ) 3
xx
fx x m m
--
®®
=+=+
33 3 3
352 3(3) 3 3
lim ( ) lim lim lim
34
( 3)( 3 5 2) 3 5 2
xx x x
xx
fx
x
xx x
++ + +
®® ® ®
-- -
== ==
-
--+ -+
()fx
3x =
Û
33
9
lim ( ) lim ( ) (3)
4
xx
fx fx f m
-+
®®
==Û=-
ABCD
2AB AC AD cm===
∑ ∑
150CAD BAD==°
.AD BC^
( )
.. ..AD BC AD AC AB AD AC AD AB=-=-
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
∑ ∑
.. ..AD AC cosCAD AD AB cosBAD=-
00
2.2. 150 2.2. 150cos cos=-
0=
AD BC^
( )
2
lim 4-=+¥n
4
1
lim = +¥
n
5
lim 0
8
æö
=
ç÷
èø
n
3
lim
4
æö
= +¥
ç÷
èø
n
( )
fx
1
lim ( ) 21
+
®
=
x
fx
1
lim ( ) 21.
-
®
=
x
fx
1
lim ( )
®x
fx
21.
2
0
0
xKÎ
0
x
( ) ( )
00
lim lim
+-
®®
=
xx xx
fx fx
( )
( )
0
0
lim
®
=
xx
fx fx
( )
0
0
lim
®
=
xx
fx x
( )
( )
0
0
lim
®
¹
xx
fx fx
2
2
311
lim
94 2
-+
=
-
an n
n
a
2
aa-
Trang 21
A. -12 B. -2 C. 0 D. -6
Câu 5: Cho dãy số thỏa mãn Giá trị của bằng:
A. B. C. D.
Câu 6: Cho hình lập phương . Vectơ nào cùng hướng với ?
A. B. C. D.
Câu 7: Cho hai dãy số thỏa mãn và . Giá trị của bằng: A.
B. C. D.
Câu 8: Cho hàm số . Gọi là giá trị của tham số để hàm số liên
tục tại . Khi đó thuộc khoảng nào sau đây?
A. B. C. D.
Câu 9: Tính bằng: A. B. C. D.
Câu 10: Giả sử ta có và . Trong các mệnh đề sau, mệnh đề nào Sai?
A. . B. .
C. D. .
Câu 11: Hàm số nào dưới đây liên tục trên
ℝ?
A.
B.
C.
D.
Câu 12: Tính bằng:A. B. C. D.
Câu 13: Tính tổng bằng:
A. B. C. D.
Câu 14: Cho hình hộp có tâm là I. Phân tích vectơ theo hai vectơ và
A. B. C. D.
Câu 15: Nếu k là số nguyên dương chẵn thì kết quả của giới hạn bằng:
A. B. C. D.
Câu 16: Cho giới hạn , trong đó là phân số tối giản. Tính
A. . B. . C. . D. .
Câu 17:Mệnh đề nào sau đây là Đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
( )
n
u
( )
lim 7 0.+=
n
u
lim
n
u
7
7-
5.
0.
.' ' ' 'ABCD A B C D
'
!!!!"
AD
'
!!!!"
AB
'
!!!!"
DC
!!!"
AB
'
!!!!"
BC
( ) ( )
,
nn
uv
lim 3=
n
u
( )
lim 0 0=>
nn
vv
lim
æö
ç÷
èø
n
n
u
v
4.
0.
.-¥
.+¥
2
45khi 2
()
3khi2
ì
-+ ¹
=
í
-=
î
xx x
fx
xm x
0
m
m
()fx
2=x
0
m
( )
0;3
( )
3; 6
( )
9; 2--
( )
5;8
( )
52
lim 4 3 1
®-¥
-+
x
xx
0.
.+¥
5.
.-¥
( )
lim
®+¥
=
x
fx a
( )
lim
®+¥
=
x
gx b
( ) ( )
lim . .
®+¥
éù=
ëû
x
fxgx ab
( ) ( )
lim
®+¥
é-ù=-
ëû
x
fx gx ab
( ) ( )
lim
®+¥
é+ù=+
ëû
x
fx gx a b
( )
( )
lim
®+¥
=
x
fx
a
gx b
( )
5
4
+
=
+
x
fx
x
cot .=yx
( )
2
3=+fx x
( )
2
4
1
+
=
-
x
fx
x
1
4
lim
2
®
-
-
x
x
x
3.
.-¥
.+¥
5.-
111 1
2 ... ...
248 2
=+ + ++ + +
n
S
3.
3
.
2
-
12
.
5
5
.
2
.
¢¢¢¢
ABCD A B C D
!!"
DI
!!!"
DA
'
!!!!"
DC
2'3=+
!!" !!!!" !!!"
DI DC DA
2'=+
!!" !!!!" !!!"
DI DC DA
'2=-
!!" !!!!" !!!"
DI DC DA
'=+
!!" !!!!" !!!"
DI DC DA
lim
k
x
x
®-¥
0.
.+¥
.-¥
1.
2
2
1
352
lim
54
®
-+
=
-+
x
xx a
xx b
a
b
22
.=+Sa b
20=S
17=S
10=S
25=S
Trang 22
D. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
Câu 18: Cho tứ diện . Gọi , lần lượt là trung điểm của các cạnh và , là trung điểm của
đoạn thẳng . Tính bằng:
A. . B. . C. . D. .
Câu 19: Cho tứ diện đều có cạnh bằng a. Tính tích vô hướng bằng:
A.
B.
C.
D.
Câu 20: Cho hình lập phương . Tính góc giữa hai vectơ và
A. B. C. D.
Câu 21: Cho tứ diện ABCD. Gọi I là trung điểm AB. Khẳng định nào sau đây là Đúng ?
A. B. C. D.
PHẦN TỰ LUẬN: ( 3 điểm)
Câu 1:(1điểm) Cho hàm số . Xét tính liên tục của hàm số f(x) tại
Câu 2: ( 1 điểm) Cho hình lập phương có cạnh bằng a. Trên các cạnh và lấy các
điểm M và N sao cho . Chứng minh hai đường thẳng và vuông góc với
nhau.
Câu 3: ( 1 điểm) Tính giới hạn sau:
ĐÁP ÁN
Phần đáp án câu trắc nghiệm:
1
C
6
D
11
C
16
C
21
C
2
A
7
D
12
A
17
A
3
B
8
B
13
A
18
A
4
D
9
D
14
B
19
D
5
B
10
D
15
B
20
C
Phần tự luận
Câu
hỏi
Bài giải
Thang
điểm
Câu 1:
(1điểm)
+ Tập xác định:
0.25đ
+
0.25đ
0.25đ
ABCD
I
J
AB
CD
G
IJ
++ +
!!!" !!!" !!!" !!!"
GA GB GC GD
0
!
2
!!"
IJ
4
!!"
GI
3
!! !"
GJ
ABCD
.
!!!" !!!"
BD DC
2
.a
2
.
2
a
2
3
.
2
a
2
.
2
-a
.
¢¢¢¢
ABCD A B C D
'
!!!!"
AB
'
!!!!"
AD
60°
45°
120°
90°
=+
!!" !! !" !!!"
CI CA CB
=+
!!" !!!" !!!"
DI DA DB
2 =+
!!" !!!" !!!"
DI DA DB
2 =-
!!" !! !" !!!"
CI CA CB
( )
2
633
khi 1
1
5 2 khi 1
ì
+-
¹
ï
=
í
-
ï
+=
î
x
x
fx
x
xx
0
1=x
.
¢¢¢¢
ABCD A B C D
AD
'CC
( )
0= ££= xaMA NC x
'BD
MN
3
2
1
81.6 2 5
lim
352
®
++--
-+
x
xxx
xx
{ }
0
1
D;\1,x1D
2
-
éö
= +¥ - = Î
÷
ê
ëø
f(1) 5.1 2 7=+=
( )( )
( )
2
x1 x1 x1
6x 3 3 6x 3 9
lim f (x) lim lim
x1
x1x1 6x33
®® ®
+- +-
+= =
-
-+ ++
Trang 23
Vì nên hàm số f(x) gián đoạn tại
0.25đ
Câu 2:
(1điểm)
Ta có:
0.25đ
0.25đ
Khi đó:
0.25đ
(Vì các cạnh BA, BC, BB’ đôi một vuông góc)
Vậy đường thẳng AC’ vuông góc với đường thẳng MN
0.25đ
Câu 3:
(1điểm)
Ta có:
0.25đ
0.25đ
( )
( )
x1
61
lim
2
x1 6x3 3
®
==
+++
x1
limf (x)f(1)
®
¹
0
1=x
BD ' BA BC BB '=++
!!!!" !!!" !!!" !!!"
( )
MN DN DM DC CN DM=- = + -
!!! !" !!!" !!! !" !!!" !!!" !!! !"
xax x x
BA BB ' AD BA BB' 1 BC
aa a a
-
æö æö
=- + + =- + + -
ç÷ ç÷
èø èø
!!!" !!!" !!!" !!!" !!!" !!!"
( )
22
xx
BD '.MN BA BC BB ' BA BB ' 1 BC
aa
xx xx
BA BA.BB ' 1 BA.BC BA.BC BB'.BC 1 BC
aa aa
éù
æö
=++ -+ +-
ç÷
êú
èø
ëû
æö æö
=- + + - - + + -
ç÷ ç÷
èø èø
!!! !" !!!!" !!!" !!!" !!!" !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
2
B .
a
xx
BA.BB ' B ' B 1BCB'
a
æö
-++-
ç÷
èø
!!!" !!!" !!!" !!!" !!!"
222
xx
BA 1 B CBB'
aa
æö
=- + - +
ç÷
èø
!!!" !!!" !!!"
222222
22 2 2
0
xx xx
BA 1 BC BB ' a 1 a .a
aa aa
xx
aa .a .a 0
aa
BD
'.MN
æö æö
=- + - + =- + - +
ç÷ ç÷
èø èø
=- + - + =
Þ=
!!! !" !!!!"
( )
( )
( )( )
( )
( )( )
3
3
22
11
3
1
81.6 222
81 5
81.6 2 5
lm
i lim
352 352
81.6 22
28 1 5
lim
13
21
32
®®
®
++-++--
++--
=
-+ -+
éù
++-
+- +
êú
=+
êú
-- --
ëû
xx
x
xx xx
xxx
xx xx
xx
xx
xx xx
Trang 24
0.25đ
0.25đ
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 8
MÔN TOÁN 11
I. Phần trắc nghiệm (7.0 điểm)
Câu 1: Cho là một cấp số nhân lùi vô hạn với công bội q , . Công thức tính tổng của cấp
số nhân lùi vô hạn là
A. . B. . C. . D. .
Câu 2: Trong không gian, khẳng định nào sau đây đúng?
A. Hai vectơ bằng nhau là hai vectơ có cùng độ dài. B. Vectơ là một đường thẳng.
C. Vectơ là một đoạn thẳng có hướng. D. Tổng của hai vectơ là một số thực.
Câu 3: Cho hàm số . Với giá trị nào của thì hàm số liên tục tại
A. B. C. D.
Câu 4: Cho hình lập phương , góc giữa hai đường thẳng và bằng
A. B.
C. D.
Câu 5: Tính tổng của cấp số nhân lùi vô hạn với
A. B. C. D.
Câu 6: Giả sử và là hai hàm số liên tục tại điểm Khẳng định nào sau đây sai?
A. Hàm số liên tục tại B. Hàm số liên tục tại
( )
( )( )
( )
( )
( )( ) ( )
2
2
1
33
8 1. 6 2 8 4(8 1) 5
lim
1
32281 5
13 2 6 2 26 2 4
®
éù
êú
++- +-+
=+
êú
éùéù
-- +++
êú
-- ++++
ëû
êú
ëû
ëû
x
xx x x
xx xx
xx x x
( )
( )( )
( )
( )( ) ( )
2
2
1
33
68 1. 1
22 21
lim
13 2 28 1 5
13 2 6 2 26 2 4
®
éù
êú
+-
-+ -
=+
êú
éùéù
-- +++
êú
-- ++++
ëû
êú
ëû
ëû
x
xx
xx
xx xx
xx x x
( )
( )
( )
( ) ( )
2
1
33
6
21
68 1
lim
32281 5
32 62 2624
19
®
éù
êú
--
+
=+
êú
éùéù
-+++
êú
-++++
ëû
êú
ëû
ëû
=
x
x
x
xxx
xx x
( )
n
u
1q <
q
u
S
-
=
1
1
1
1
-
=
q
u
S
q
u
S
+
=
1
1
1
1
u
q
S
-
=
2
2
( 0)
()
( 0)
xx
x
fx
x
ax
ì
-
¹
ï
=
í
ï
=
î
a
()fx
0.x =
3.a =-
1.a =
1.a =-
2.a =
.' ' ' 'ABCD A B C D
AB
''BD
0
45 .
0
30 .
0
60 .
0
90 .
S
( )
,
n
u
1
.
2
n
n
u =
3
.
2
S =
2.S =
1
.
2
S =
1.S =
()yfx=
()ygx=
0
.x
().()yfxgx=
0
.x
()
()
fx
y
gx
=
0
.x
Trang 25
C. Hàm số liên tục tại D. Hàm số liên tục tại
Câu 7: Mệnh đề nào sau đây sai?
A. B. . C. . D. (c là hằng số).
Câu 8: Nếu và lần lượt là hai vectơ chỉ phương của hai đường thẳng và thì
A. B. C. D.
Câu 9: Cho hình hộp (hình vẽ bên). bằng
A. B.
C. D.
Câu 10: Trong không gian cho tứ diện , gọi là trọng tâm tam giác . Mệnh đề nào sau
đây đúng?
A. B.
C. D.
Câu 11: Tính
A. B. C. D.
Câu 12: Nếu và thì bằng
A. B. C. D.
Câu 13: Nếu và . Mệnh đề nào sau đây đúng?
A. . B. C. . D. .
Câu 14: Trong không gian, ba vectơ được gọi là đồng phẳng nếu
A. các giá của chúng cùng song song với một mặt phẳng.
B. các giá của chúng cùng song song với nhau.
C. các giá của chúng cùng vuông góc với một mặt phẳng.
D. các giá của chúng không cùng nằm trong một mặt phẳng.
Câu 15: Cho hàm số là hàm đa thức bậc ba và thỏa mãn . Mệnh đề nào sau
đây sai?
A. Phương trình có ít nhất một nghiệm trên khoảng
B. Hàm số liên tục trên
C. Phương trình không có nghiệm trên khoảng
D. Phương trình có ít nhất hai nghiệm trên khoảng
Câu 16: bằng
A. B. C. 1. D. 0.
() ()yfxgx=-
0
.x
() ()yfxgx=+
0
.x
( )
1||,0lim <= qq
n
( )
*
,0
1
lim Nk
n
k
Î=
+¥=
n
1
lim
cc =lim
u
!
v
!
a
b
0.
u
ab
v
^Û =
!
!
.0.ab uv^Û =
!!
0.ab uv^Û-=
!!
0.ab uv^Û+=
!!
.' ' ' 'ABCD A B C D
'AB AD AA++
!!!" !!!" !!!"
'.AD
!!!!"
.AC
!!!"
'.AC
!!!!"
'.AB
!!! !"
ABCD
G
ABC
2.DA DB DC DG++ =
!!!" !!!" !!! " !!!"
3.DA DB DC DG++ =
!!!" !!!" !!!" !!!"
1
.
2
DA DB DC DG++ =
!!!" !!!" !!!" !!! "
1
.
3
DA DB DC DG++ =
!!!" !!!" !!!" !!! "
12
lim .
n
H
n
-
=
1.H =-
2.H =-
1.H =
2.H =
0
lim ( ) 0
xx
fx L
®
=<
0
lim ( )
xx
gx
®
=-¥
[ ]
0
lim ( ). ( )
xx
fxgx
®
.+¥
0.
.L
.-¥
( )
au
n
=lim
( )
±¥=
n
vlim
0lim =
÷
÷
ø
ö
ç
ç
è
æ
n
n
u
v
-¥=
÷
÷
ø
ö
ç
ç
è
æ
n
n
v
u
lim
0lim =
÷
÷
ø
ö
ç
ç
è
æ
n
n
v
u
+¥=
÷
÷
ø
ö
ç
ç
è
æ
n
n
v
u
lim
()yfx=
(0). (2) 0ff<
() 0fx=
( )
0; 2 .
()yfx=
.!
() 0fx=
( )
0; .+¥
() 0fx=
( )
0; .+¥
( )
3
lim 2 2
x
xx
®-¥
-+
.+¥
.-¥
Trang 26
Câu 17: Hàm số có giới hạn hữu hạn tại khi và chỉ khi
A. . B. . C. . D. .
Câu 18: bằng
A. 3. B. 2. C. 1. D.
Câu 19: Nếu thì bằng
A. B. C. D.
Câu 20: Trong không gian tích vô hướng của hai vectơ và đều khác vectơ – không được xác
định bởi công thức
A. B. C. D.
Câu 21: Cho hàm số xác định trên khoảng và Hàm số được gọi là liên
tục tại nếu
A. B. C. D.
II. Phần tự luận (3.0 điểm )
Câu 1. (1.0 điểm) Tính .
Câu 2. (1.0 điểm) Cho hàm số . Tìm để hàm số liên tục tại
Câu 3. ( 1.0 điểm) Cho tứ diện đều cạnh bằng Chứng minh
------ HẾT ----
ĐÁP ÁN
I. Phần đáp án câu trắc nghiệm:
1
A
6
B
11
B
16
B
21
C
2
C
7
C
12
A
17
B
3
C
8
B
13
C
18
C
4
A
9
C
14
A
19
C
5
D
10
B
15
C
20
A
II. Phần tự luận
Câu
Hướng dẫn chấm
Thang điểm
1 (1.0 điểm )
Tính
Ta có:
0.5 đ
)(xfy =
0
x
( )
+¥=
®
xf
xx
0
lim
( )
Lxf
xx
=
®
0
lim
( )
lim
x
fx L
®+¥
=
( )
0
lim
xx
fx
®
=-¥
1
1
lim
2
x
x
x
®
+
1
.
2
00
lim ( ) lim ( )
xx xx
fx avà gx
®®
==±¥
0
()
lim
()
xx
fx
gx
®
.a
.-¥
0.
.+¥
u
!
v
!
( )
. . .cos , .uv u v u v=
!! ! ! ! !
...uv u v=
!! ! !
( )
. . .sin , .uv u v u v=
!! ! ! ! !
( )
22
...cos,.uv u v u v=
!! ! ! ! !
()yfx=
K
0
.xKÎ
()yfx=
0
x
0
0
lim ( ) .
xx
fx x
®
=
0
0
lim ( ) ( ).
xx
fx fx
®
¹
0
0
lim ( ) ( ).
xx
fx fx
®
=
0
00
lim ( ) . ( ).
xx
fx xfx
®
=
2
1
1
lim
235
x
x
xx
®
-
+-
3
1
(1)
()
1
2( 1)
x
x
fx
x
axx
ì
-
¹
ï
=
-
í
ï
-=
î
a
()fx
0
1.x =
ABCD
.a
.AB CD^
2
1
1
lim
235
x
x
xx
®
-
+-
( )
2
11 1
111
lim lim lim
55
235
21 2
22
xx x
xx
xx
xx x
®® ®
--
==
+-
æö æö
-+ +
ç÷ ç÷
èø èø
Trang 27
0.5 đ
2 (1.0 điêm)
Cho hàm số . Tìm để hàm số liên
tục tại
+) Tập xác định của hàm số đã cho là
+)
0.25 đ
+)
0.25 đ
+) Hàm số liên tục tại thì
0.25 đ
+) Với thì hàm số liên tục tại
0.25 đ
3 (1.0 điểm)
Cho tứ diện đều cạnh bằng Chứng minh
+) Vẽ hình đúng
0.25 đ
+)
0.25 đ
+)
0.25 đ
+)
0.25 đ
-----------Hết----------
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 9
MÔN TOÁN 11
11
.
2.1 5 7
==
+
3
1
(1)
()
1
2( 1)
x
x
fx
x
axx
ì
-
¹
ï
=
-
í
ï
-=
î
a
()fx
0
1.x =
.!
( )
( )
( )
2
3
2
11 1 1
11
1
lim ( ) lim lim lim 1 3
11
xx x x
xxx
x
fx x x
xx
®® ® ®
-++
-
== =++=
--
(1) 2.1 2fa a=- =-
()fx
0
1x =
1
lim ( ) (1)
x
fx f
®
=
32 5aaÛ=-Û=
5a =
()fx
0
1.x =
ABCD
.a
.AB CD^
( )
( )
...
cos , .
.. .
AB AD AC
AB CD AB AD AB AC
AB CD
AB CD AB CD AB CD
-
-
== =
!!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!"
!!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!"
22
00
...cos60;...cos60
22
aa
AB AD a a AB AC a a== ==
!!!" !!!" !!!" !!!"
( ) ( )
22
0
2
22
cos , 0 , 90 .
aa
AB CD AB CD AB CD
a
-
==Þ =Þ^
!!!" !!!" !!!" !!!"
Trang 28
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho hình chóp có
và . Hình chóp có bao nhiêu mặt là tam giác
vuông?
A. . B. . C. . D. .
Câu 2. Cho hai đường thẳng phân biệt và hai mặt phẳng , . Mệnh đề nào sau đây sai?
A. Nếu
và thì . B. Nếu và thì .
C. Nếu và thì . D. Nếu và thì
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì song song với nhau.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.
D. Nếu mặt phẳng này chứa một đường thẳng song song với mặt phẳng kia thì hai mặt phẳng đó song song với
nhau.
Câu 4. Cho hàm số . Mệnh đề nào sau đây là sai?
A. Hàm số liên tục trên khoảng .
B. Hàm số liên tục trên khoảng .
C. Hàm số liên tục trên khoảng .
D. Hàm số liên tục trên khoảng .
Câu 5. Cho tứ diện đều cạnh Gọi là trung điểm của . Tính cosin của góc giữa hai đường thẳng
và .
A. B. . C. . D. .
Câu 6. Trong các phát biểu sau, phát biểu nào đúng?
A. với . B. với .
C. . D. với .
Câu 7. Cho hình hộp . Khẳng định nào sau đây sai?
A. . B. .
C. . D. .
Câu 8. bằng
A. . B. . C. . D. .
Câu 9. Nếu thì bằng bao nhiêu?
A. . B. . C. . D. .
Câu 10. Trong các giới hạn sau, giới hạn nào bằng ?
A. . B. .
C. . D. .
.S ABC
( )
SB ABC^
AB AC^
.S ABC
1
4
3
,ab
( )
P
( )
Q
//ab
( )
aP^
( )
bP^
( ) ( )
//PQ
( )
aQ^
( )
aP^
( )
a // Q
ba^
( )
bQ^
( )
a// P
( )
bP^
ba^
2
() 4fx x=-
()fx
( 2;2)-
()fx
(;3)-¥ -
()fx
(2; )+¥
()fx
(3; )+¥
ABCD
I
DC
AD
BI
2
.
2
3
6
2
3
3
2
lim 0,
n
q =
1q >
lim 0,
n
q =
10q-< <
3
lim 0n =
lim ,
n
q =+¥
1q <
.' ' ' 'ABCD A B C D
'D'BC BA BB B++ =
!!!" !!!" !!!" !!! !"
''BC DC C C A C++ =
!!!" !!!" !!!!" !!!!"
DD ' DB'ACDD++ =
!!!" !!!" !!!! " !!!!"
''AB AD AA AC++ =
!!!" !!!" !!!" !!!!"
2
lim ( 1 )
x
xx x
®-¥
+++
1
2
-
+¥
1
2
-¥
2
lim ( ) 1
x
fx
®
=-
2
lim[3 ( ) 4]
x
fx
®
-
1-
7-
2
4
+¥
( )
32
lim 2 3 4
x
xx
®-¥
-+ -
( )
43
lim 4 1
x
xx x
®-¥
-+ - +
(
)
2
lim 3 2
x
xx
®+¥
+-
(
)
32
3
lim 8 3 1
x
xx
®+¥
-+ +
Trang 29
Câu 11. Cho biết với tối giản. Tính .
A. . B. . C. . D. .
Câu 12. Trong các khẳng định sau, khẳng định nào sai?
A. . B. . C. . D. .
Câu 13. bằng
A. . B. . C. . D. .
Câu 14. Cho hình hộp . Mặt phẳng song song với mặt phẳng nào trong các mặt phẳng sau
đây?
A. . B. . C. . D. .
Câu 15. Có bao nhiêu giá trị nguyên dương của thỏa ?
A. . B. . C. . D. .
Câu 16. Trong không gian, cho ba đường thẳng phân biệt . Khẳng định nào sau đây sai?
A. Nếu và cùng vuông góc với thì .
B. Nếu và thì .
C. Nếu thì góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và .
D. Nếu và cùng song song với thì .
Câu 17. Tính giới hạn .
A. . B. . C. . D. .
Câu 18. Hàm số nào sau đây liên tục trên ?
A. . B. . C. . D.
Câu 19. Trong các giới hạn sau, giới hạn nào bằng ?
A. . B. . C. . D. .
Câu 20. Trong các giới hạn sau, giới hạn nào bằng 0?
A. . B. .
C. . D. .
Câu 21. Cho phương trình . Khẳng định nào sau đây đúng?
A. Phương trình có ít nhất một nghiệm thuộc khoảng .
B. Phương trình không có nghiệm âm.
C. Phương trình có duy nhất một nghiệm dương.
D. Phương trình có đúng một nghiệm âm lớn hơn .
PHẦN II: TỰ LUẬN
2
2
2
352
lim
4
x
xx a
xb
®-
+-
=
-
*
,,
a
ab
b
Î •
22
ab+
53
58
65
41
lim
o
o
xx
xx
®
=
4
lim
x
x
®-¥
=+¥
5
lim
x
x
®-¥
=-¥
1
lim
x
x
®+¥
=+¥
4
23
lim
4
x
x
x
+
®-
-
+
+¥
11-
0
-¥
.ABCD A B C D
¢¢¢¢
( )
AB D
¢¢
( )
BC D
¢
( )
ACC
¢¢
( )
BDA
¢
( )
BCA
¢
m
( )
32 2
1
lim 3 2 1
x
xmx mm
®-
+-+=
3
2
1
,,abc
a
b
c
//ab
//ab
ca^
cb^
//ab
c
c
a
b
c
//ab
23
53
(2 3 )( 2)
42
nnn
J
nn
--+
=
-+
2J =-
2J =
J = +¥
J = -¥
R
21
2
x
y
x
-
=
+
3yx=-
tanyx=
2
3
1
x
y
xx
-+
=
++
1
23
lim
32
n
nn
-
+
2021
lim
2020
n
æö
ç÷
èø
43.2
lim
54
nn
n
-+
-
( )
lim 5 3.7
nn
-
3
2
4
lim
43 2
nn
nn
+
-+ -
2
4
lim
23
n
nn
-
+-
32
2
lim
21
nn
n
-+
-
2
2
3
lim
21
n
n
+
-
32
320xx-+=
(0;1)
1-
Trang 30
Bài 1:(0.5đ) Tính giới hạn: .
Bài 2:(1đ) Xét tính liên tục của hàm số sau tại điểm x = 2
.
Bài 3:(1,5đ) Cho hình chóp có đáy là hình thang vuông tại và . Gọi là
trung điểm của . vuông góc với mặt phẳng . Biết .
a. Chứng minh và .
b. Gọi là góc giữa đường thẳng và mp . Tính .
------------------ HẾT ------------------
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
C
C
B
A
B
B
C
A
B
A
C
D
D
A
D
A
A
D
C
B
D
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 10
MÔN TOÁN 11
PHẦN TRẮC NGHIỆM: (7 ĐIỂM)
Câu 1: Chọn khẳng định sai.
A. (
là hằng số ). B. .
C. . D. với mọi .
Câu 2: Chọn khẳng định đúng.
A. nếu . B. nếu .
C. nếu . D. nếu .
Câu 3: Trong bốn giới hạn sau đây, giới hạn nào là ?
A. . B. . C. . D. .
Câu 4: Tính tổng
A. . B. . C. . D. .
Câu 5: Tính .
A. . B. . C. 1. D. .
2
2
37
lim
54
nn
n
-+
-+
2
32
khi 2
()
2
1 khi 2
xx
x
fx
x
x
ì
-+
¹
ï
=
-
í
ï
=
î
.S ABCD
ABCD
A
B
M
AB
SM
()ABCD
2,AB AD a BC a== =
( )
BC SAB^
BD SC^
a
CD
( )
SAB
tan
a
lim =
n
uc
=
n
uc
lim 0=
n
q
( )
1>q
1
lim 0=
n
1
lim 0=
k
n
*
Î •k
lim =+¥
n
q
1>q
lim =+¥
n
q
1<q
lim =+¥
n
q
1>q
lim =+¥
n
q
1<q
+¥
23
2
32
lim
nn
nn
++
+
2
3
23
lim
3
nn
nn
-
+
3
3
21
lim
2
nn
nn
+-
-
2
1
lim
12
nn
n
-+
-
11 1 (1)
... ...
3927 3
n
n
S
-
=- + - + + +
1
4
-
1
4
1
2
3
4
nn
nn
23.2
32
lim
21
-
+
++
9
2
1
2
2
3
Trang 31
Câu 6: Tính .
A. . B. . C. . D. .
Câu 7: Tính .
A. . B. . C. . D. .
Câu 8: Với k là số nguyên dương, c là hằng số. Kết quả của giới hạn là:
A. . B. . C. 0. D. .
Câu 9: Biết , và với mọi . Khi đó bằng:
A. . B. . C. . D. L.
Câu 10: Cho với là phân số tối giản. Tính giá trị biểu thức .
A. 3. B. 11. C. . D. 5.
Câu 11: Tính .
A. B. C. D.
Câu 12: Cho hàm số liên tục trên khoảng . Điều kiện cần và đủ để hàm số liên tục
trên đoạn là:
A. và . B. và .
C. và . D. và .
Câu 13: Cho hàm số . Chọn khẳng định đúng:
A. Hàm số liên tục trên tập số thực .
B. Hàm số liên tục tại điểm .
C. Hàm số gián đoạn tại điểm .
D. Hàm số gián đoạn tại điểm .
Câu 14: Cho hàm số . Mệnh đề nào dưới đây sai?
A. Hàm số liên tục trên .
B. Hàm số liên tục trên khoảng .
C. Hàm số không liên tục trên .
D. Hàm số liên tục trên khoảng .
Câu 15: Cho hình hộp . Biểu thức nào sau đây đúng?
A. . B. .
C. . D. .
Câu 16: Cho hình hộp . Chọn khẳng định đúng.
2
3
3
lim
21
x
x
x
®-
-
+
1
3
-
6
5
-
1
3
1
2
( )
43
lim 2 5 1
x
xxx
®-¥
-+++
-¥
0
4
+¥
lim
k
x
c
x
®-¥
0
k
x
+¥
-¥
0
lim ( ) 0
xx
fx L
®
=>
0
lim ( ) 0
xx
gx
®
=
() 0gx>
0
xx¹
0
()
lim
()
xx
fx
gx
®
0
+¥
-¥
2
3
215
lim
39
x
xx a
xb
®
+-
=
-
a
b
Pab=+
+¥
2
1
327
lim
1
x
xx
x
-
®
+-
-
0.
.+¥
.-¥
( )
=yfx
( )
;ab
[ ]
;ab
( ) ( )
lim
+
®
=
xa
fx fa
( ) ( )
lim
-
®
=
xb
fx fb
( ) ( )
lim
xa
fx fa
-
®
=
( ) ( )
lim
xb
fx fb
+
®
=
( ) ( )
lim
+
®
=
xa
fx fa
( ) ( )
lim
+
®
=
xb
fx fb
( ) ( )
lim
xa
fx fa
-
®
=
( ) ( )
lim
xb
fx fb
-
®
=
( )
2021
2022
x
fx
x
+
=
-
( )
fx
!
( )
fx
2022x =
( )
fx
2022x =
( )
fx
2021x =-
( )
2
4
2
2
42
x
khi x
fx
x
khi x
ì
-
¹
ï
=
-
í
ï
=
î
( )
fx
!
( )
fx
( )
;2-¥
( )
fx
!
( )
fx
( )
2; +¥
.ABCD A B C D
¢¢¢¢
''AB AB AA AD=+ +
!!!!" !!!" !!!" !!!"
''AC AB AA AD=+ +
!!!!" !!!" !!!" !!!"
''AD AB AD AC=+ +
!!!!" !!!" !!!" !!!!"
''''AD AB AC=+
!!!!" !!!!!" !!!!"
.ABCD A B C D
¢¢¢¢
Trang 32
A. đồng phẳng. B. đồng phẳng.
C. đồng phẳng. D. đồng phẳng.
Câu 17: Cho tứ diện ABCD. Hãy chọn khẳng định đúng.
A. . B. .
C. . D. .
Câu 18: Cho hình lập phương ABCD.EFGH. Số đo góc giữa cặp vectơ và bằng:
A. . B. . C. . D. .
Câu 19: Trong không gian cho ba đường thẳng phân biệt . Khẳng định nào sau đây đúng?
A. Nếu và cùng vuông góc với thì .
B. Nếu và thì .
C. Nếu góc giữa và bằng góc giữa và thì .
D. Nếu , cùng nằm trong mặt phẳng và thì góc giữa và bằng góc giữa
và .
Câu 20: Cho hình chóp có đáy là hình vuông cạnh bằng và các cạnh bên đều
bằng . Gọi và lần lượt là trung điểm của và . Số đo của góc giữa hai đường thẳng
MN và SC bằng:
A. . B. . C. . D. .
Câu 21. Cho tứ diện đều ABCD có cạnh . Khi đó bằng:
A. . B. . C. . D. .
PHẦN TỰ LUẬN: (3 ĐIỂM)
Câu 1: Tính .
Câu 2: Cho hàm số (m là tham số).
Tìm tất cả các giá trị của để hàm số
liên tục tại điểm .
Câu 3: Cho tứ diện có ba cạnh , , đôi một vuông góc với nhau. Biết .
Gọi là trung điểm của . Tính góc giữa hai đường thẳng và .
ĐÁP ÁN VÀ BIỂU ĐIỂM TỰ LUẬN:
Câu 1
Tính .
0,25
0,25
0,25
,,BD BD BC
¢¢
!!!" !!! !" !!!!"
,,BA BD BD
¢¢
!!!" !!!!" !!!"
,,BA BD BC
¢¢
!!!" !!!!" !!!"
,,BA BD BC
¢¢¢
!!!" !!! !" !!! !"
BC AB DA DC+=-
!!!" !!!" !!!" !!! "
AC AD BD BC-=-
!!!" !!!" !!!" !!!"
AB AC DB DC-=-
!!!" !!!" !!!" !!! "
AB AD CD BC-=+
!!!" !!!" !!!" !!!"
AB
!!!"
EG
!!!"
90°
60°
45°
120°
,,abc
a
b
c
//ab
//ab
ca^
cb^
a
c
b
c
//ab
a
b
( )
a
( )
//c
a
a
c
b
c
.S ABCD
ABCD
a
M
N
AD
SD
o
30
o
45
o
60
o
90
.AB BC
!!!" !!!"
2
2
a
2
3
2
a
2
3
2
a
-
2
2
a
-
2
2
251
lim
4
x
x
x
®-
+-
-
2021
2
2021 2020
khi x 1
()
(1)
2mx+2 khi x 1
xx
fx
x
ì
-+
¹
ï
=
-
í
ï
=
î
m
( )
fx
= 1x
SABC
SA
SB
SC
SA SB SC==
M
AC
SM
AB
2
2
251
lim
4
x
x
x
®-
+-
-
2
2
2
2
(2 51)(2 5 1)
lim
(4)(251)
24
lim
(4)(251)
x
x
xx
xx
x
xx
®-
®-
+- ++
=
-++
+
=
-++
2
2
lim
(2)(251)
x
xx
®-
=
-++
Trang 33
0,25
Câu 2
Cho hàm số
(m là tham số).
Tìm tất cả các giá trị của để hàm số
liên tục tại
điểm .
0,25
0,25
0,25
0,25
Để hàm số liên tục tại x = 1:
Câu 3
Cho tứ diện có ba cạnh , , đôi một
vuông góc với nhau. Biết . Gọi là trung
điểm của . Tính góc giữa hai đường thẳng và
.
=-
1
4
2021
2
2021 2020
khi x 1
()
(1)
2mx+2 khi x 1
xx
fx
x
ì
-+
¹
ï
=
-
í
ï
=
î
m
( )
fx
= 1x
( )
2021
2
11
2021
2
1
2020 2019 2018
1
2020 2019 2018
1
2019 2018 2017
1
2
1
2021 2020
lim lim
(1)
1 2021( 1)
lim
(1)
... 1 2021
lim
1
( 1) ( 1) ( 1) ... ( 1)
lim
1
lim( ... 1)
lim(
xx
x
x
x
x
x
xx
fx
x
xx
x
xxx x
x
xxx x
x
xxx x
x
®®
®
®
®
®
®
-+
=
-
-- -
=
-
+++++-
=
-
-+ -+ -++ -
=
-
=+++++
+
018 2017 2016
11
... 1)
... lim( 1) lim1
xx
xx x
x
®®
+++++
++ + +
2020 2019 2018 ... 2 1
2020(1 2020)
2041210
2
=+++++
+
==
( )
12 2fm=+
2 2 2041210 1020604mm+= Þ =
SABC
SA
SB
SC
SA SB SC==
M
AC
SM
AB
Trang 34
0,25
0,25
0,25
0,25
Gọi là trung điểm
.
Đặt .
Tính được: .
đều .
Vậy
N
BC
//MN ABÞ
∑
∑
(,)(, )SM AB SM MNÞ=
0SA SB SC x== =>
2
2
x
SM SN MN== =
SMNÞD
∑
60SMNÞ=°
∑
∑
∑
(,)(, ) 60SM AB SM MN SM N===°
| 1/34
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 1 MÔN TOÁN 11
A.PHẦN TRẮC NGHIỆM (7.0 điểm) u -
Câu 1. Cho dãy số (u limu = 3 1 2 lim n n ) có . Tính giới hạn . n 2u + 5 n -1 3 5 A. B. C. D. +¥ 5 2 9 Câu 2. 5 2
lim(200 -3n + 2n ) bằng: A. 0 . B. 1. C. +¥ . D. -¥ . 2 2n + 3
Câu 3. Tính giới hạn J = lim 2 n + 2 A. J = 2 B. J = 1 C. J = 4 D. J = 0 n + 2
Câu 4. Giá trị của lim bằng: 2 n - 3n +1 1 A. . B. -¥ . C. 0 1 . D. 1+ 3 1- 3 3.2n - 3n
Câu 5. Giá trị của C = lim bằng: n+1 n+ 2 + 1 3 A. +¥ . B. -¥ 1 . C. - . D. 1 . 3 Câu 6. Tính 2 lim(2x -1) x 1 ®- A.2 B.-5 C.3 D.1 Câu 7.Tính 2023 lim (2 - 3x - 5x ) x®-¥ A. I = 5 - B. I = 2023 - C. I = + • . D. I = - • . 2 2x + x - 6 Câu 8. Tính lim 3 x® 3 - 2x 2 7 7 5 3 A. B. - C. P = . D. P = - 2 2 6 4 5 9 2 - x - 3x
Câu 9. Tính N = lim 7 x®+¥ 3- 2x 3 A. N = B. N = + • .
C. N = - • . D. N = 0. 2 Câu 10. Tính 2 2
N = lim ( 4x - 1 - 4x + 3x ) xÆ- • 3 3 A. B. - 1 C. 0 D. 4 4 2 2 x - 6 Câu 11. lim bằng x 3- ®- 9 + 3x 1 A. B. -¥ 1 C. D. +¥ 6 3 Trang 1
Câu 12 . Cho hàm số f (x) 2
= x - 4 . Chọn câu đúng trong các câu sau:
(I) f (x)liên tục tại x = 2 .
(II) f (x)gián đoạn tại x = 2 .
(III) f (x)liên tục trên đoạn [ 2; - 2].
A. Chỉ (I) và (III). B. Chỉ (I). C. Chỉ (II).
D. Chỉ (II) và (III). 2 2
ìïa x khi x £ 2
Câu 13. Cho hàm số f (x) = í
. Giá trị của a Î ! để f (x) liên tục trên ! là: ( ï 2 - a î
) 2x khi x > 2 A. 1 và 2 . B. 1 và –1. C. –1 và 2 . D. 1 và –2 . 2 ì2x - x - 6 ï , khix ¹ 2
Câu 14. Cho hàm số y = f (x) = í x - 2
. Tính tổng tất cả các giá trị của m để hàm số liên ï 2
îm - m +1,khix = 2 tục tại x = 2 A.2 B. 5 C.1 D.-1
Câu 15. Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
D. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Câu 16. Trong các mệnh đề sau. Mệnh đề sai là
A. Hai mặt phẳng song song thì không có điểm chung.
B. Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
D. Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến song song với nhau. !
Câu 17. Trong không gian cho hai đường thẳng d và d vuông góc với nhau. Gọi hai vectơ u! và u lần 1 2 1 2
lượt là hai vectơ chỉ phương của d và d . Tìm khẳng định sai trong các khẳng định sau: 1 2 A. ( ! ! u ,u = 90 . ° 1 2 )
B. Góc giữa hai đường thẳng d và d bằng 90 . ° 1 2
C. Hai đường thẳng d và d cắt nhau và trong các góc tạo thành có một góc vuông. 1 2
D. u! .u! = 0. 1 2 !!!" " !!!" " !!!" !" !!!!"
Câu 18. Cho lăng trụ tam giác ABC.A' B 'C '. Đặt AA' = u, AB = v, AC = w . Biểu diễn vectơ BC ' qua các ! ! "! vectơ u, v , w
. Chọn đáp án đúng. !!!!" " " !" !!!!" " " !" !!!!" " " !" !!!!" " " !"
A. BC ' = u + v + w .
B. BC ' = u - v + w .
C. BC ' = u - v - w .
D. BC ' = u + v - w . Trang 2 !!!" !!!" " !!!"
Câu 19. Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Đặt "x = AB; y = AC ; "z = AD. Khẳng định nào sau đây đúng? !!!" 1 !!!" 2 !!!" 1 !!!" 2 A. " " " " " " " " " " " "
AG = ( x + y + z ) B. AG = - (x + y + z )
C. AG = - (x + y + z )
D. AG = (x + y + z ) 3 3 3 3
Câu 20. Trong không gian cho đường thẳng D và điểm O . Qua O có mấy đường thẳng vuông góc với đường thẳng D A. Vô số. B. 3. C. 1. D. 2 . !!!!!" !!!"
Câu 21.Cho hình lập phương ABCD.A¢B C ¢ D
¢ ¢ . Góc giữa 2 vec tơ A'C ' và BA bằng A. 0 45 B. 0 90 C. 0 60 D. 0 135
II. PHẦN TỰ LUẬN (3,0 điểm) 2 2x - x + 3 - 3
Câu 1 (1,0 điểm). Tính giới hạn lim x®2 x - 2
Câu 2 (1,0 điểm). Chứng minh rằng phương trình 2 2022 2023
(m - 3m + 5)x - x -1 = 0 có nghiệm thuộc ( 2 - ; 2) với mọi m.
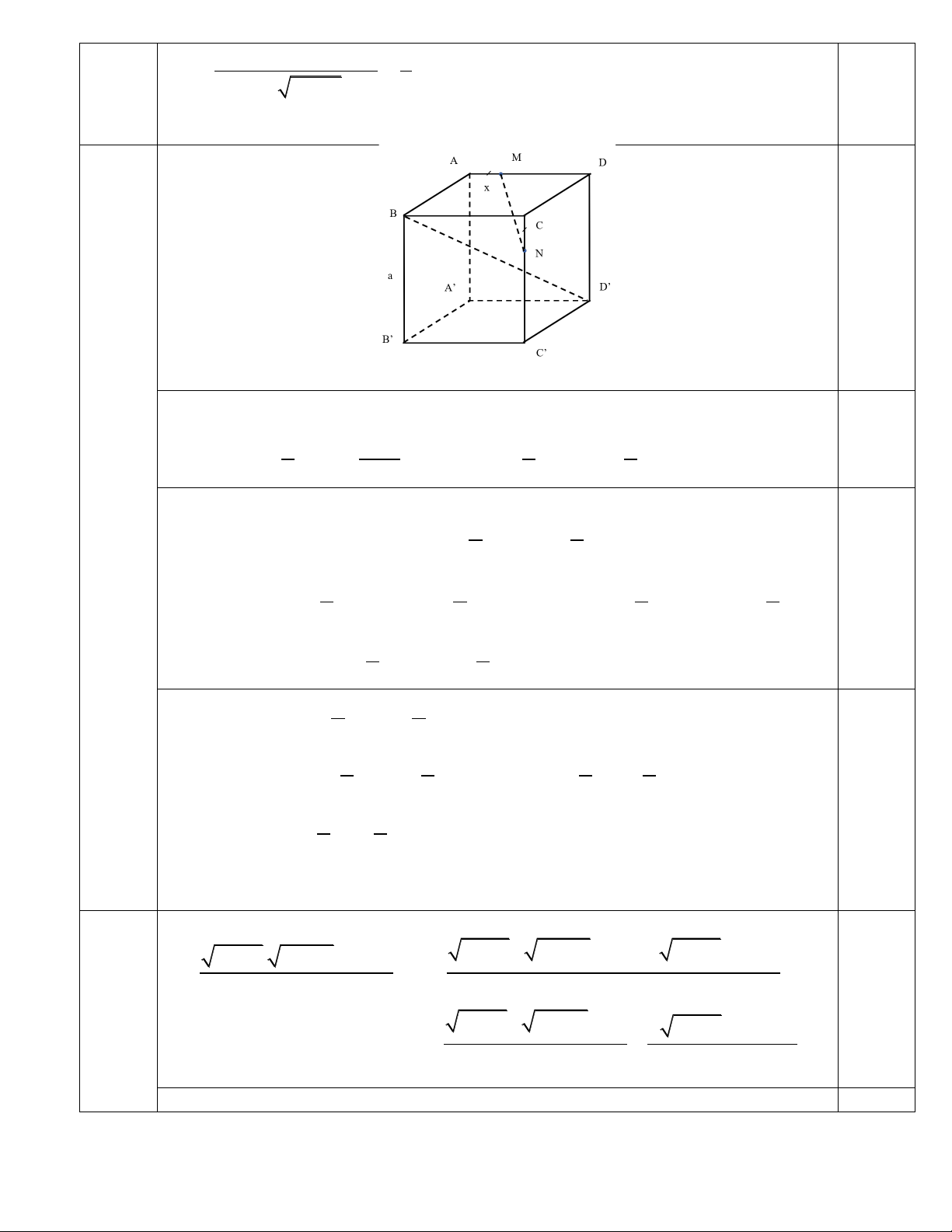
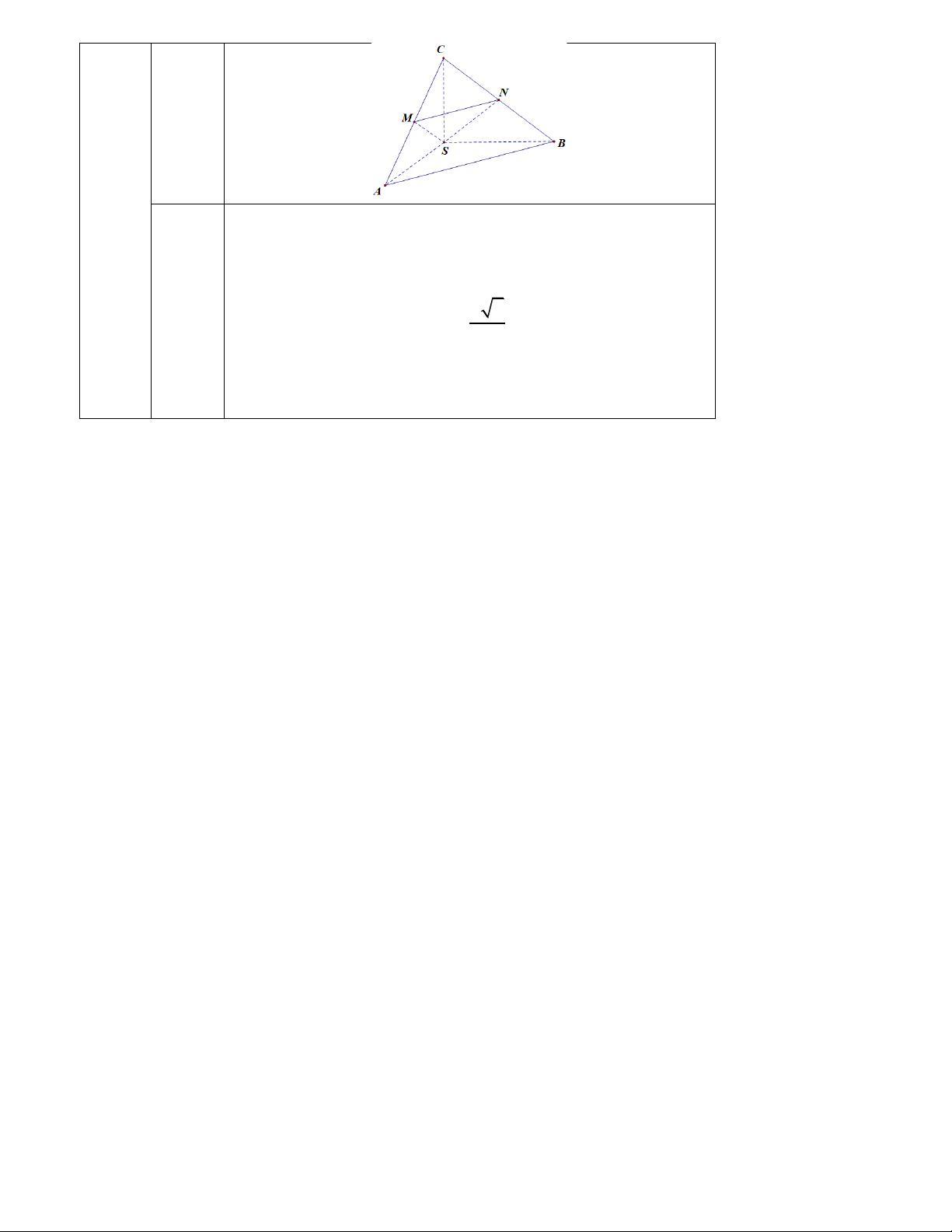
Câu 3 (1,0 điểm). Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. . Gọi M,N là lần lượt là trung
điểm của AD và SD. Tính góc giữa hai đường thẳng MN và AB. ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21
Đ.án C D A D C D C B B A B B D C C B C B A A D Câu 1 Đáp án Thang điểm 2 2x - x - 6 0,25 Biến đổi về lim x®2 2
(x - 2)( 2x - x + 3 + 3) (x - 2)(2x + 3) 0,25 = lim x®2 2
(x - 2)( 2x - x + 3 + 3) 2x + 3 7 0,25+0,25 = lim = x®2 2 2x - x + 3 + 3 6 Câu 2 Đặt 2 2022 2023
f (x) = (m - 3m + 5)x - x -1 0,25
Ta có hàm số f(x) là hàm đa thức. Suy ra hàm số f(x) liên tục trên é-2; 2 ù ë û f (0) = 1 - 0,25 2 f ( 1 - ) = m -3m + 5 é 3 11ù 0,25 = 2 (m - ) + > 0, m " Î ! ê 2 4 ú ë û Suy ra f ( 1
- ). f (0) < 0, m " Î ! 0,25 Trang 3
Suy ra phương trình f(x) =0 có ít nhất 1 nghiệm thuộc ( 1; - 0) Ì ( 2 - ; 2 ) Câu 3 S N M D A O B C
Gọi O = AC Ç BD
AB // OM suy ra góc giữa MN và AB bằng góc giữa MN và OM bằng hoặc bù với góc 0,5 ∑ NMO a 0 0,5
Tính được MN= MO= ON = . Suy ra tam giác MNO đều suy ra ∑ NMO= 60 2 Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 2 MÔN TOÁN 11
A/ PHẦN TRẮC NGHIỆM (7 điểm) 2 x + 3x - 4 lim Câu 1: Tính 2 x 4 ®- x + 4x bằng: A. 1 - B. !". C. 1 D. " # # !!!" !!!"
Câu 2: Cho hình lập phương ABC .
D EFGH . Hãy tính góc giữa cặp vectơ AB và EG ? B C A D G F E H A. 90° B. 60° C. 45° D. 120° + 1 1 (- )n 1 1
Câu 3: Gọi S = - + ...+
. Giá trị của S bằng 3 9 3n 1 3 A. B. 1 1 C. D. . 4 2 4
Câu 4: Cho hai dãy (u (v limu = 2 lim v = 3. n ) n ) và thỏa mãn và Giá trị của lim (𝑢 n n $ − 𝑣$) bằng A. 1. - B. 6. C. 5. D. 1.
Câu 5: Chọn khẳng định đúng? Trang 4
A. Nếu hàm số y = f (x)liên tục trên [a; b] và f (a).f (b) > 0thì phương trình 𝑓(𝑥) = 0 có ít nhất
một nghiệm thuộc (𝑎; 𝑏)
B. Nếu hàm số y = f (x)liên tục trên [a; b] và f (a).f (b) < 0thì phương trình 𝑓(𝑥) = 0 có ít nhất
một nghiệm thuộc (𝑎; 𝑏)
C. Nếu hàm số y = f (x)liên tục trên [a; b] và f (a).f (b) £ 0thì phương trình 𝑓(𝑥) = 0 có ít nhất
một nghiệm thuộc (𝑎; 𝑏)
D. Nếu hàm số y = f (x)liên tục trên [a;b] và f (a).f (b) ³ 0thì phương trình 𝑓(𝑥) = 0 có ít nhất
một nghiệm thuộc (𝑎; 𝑏) 2 x +1
Câu 6: Tính giới hạn lim . A.−∞. B. +¥ . C. 1 0 - . D. x 1 ® x -1 .
Câu 7: Cho hình hộp ABCD.EFGH. Mệnh đề nào sau đây đúng? A.𝐴𝐵 ,,,⃗ + 𝐴𝐷 ,,,, ⃗ + 𝐴𝐸 ,,,⃗ = 𝐴𝐺 ,,,⃗. B.𝐴𝐵 ,,,⃗ + 𝐴𝐶 ,,,⃗ + 𝐴𝐷 ,,,, ⃗ = 𝐴𝐹 ,,,⃗. C. 𝐴𝐵 555⃗ + 𝐴𝐷 5555 ⃗ + 𝐴𝐸 555⃗ = 𝐴𝐻 555⃗. D.𝐴𝐵 555⃗ + 𝐴𝐶 555⃗ + 𝐴𝐷 5555 ⃗ = 𝐴𝐸 555⃗ .
Câu 8: Giá trị của 𝐷 = 𝑙𝑖𝑚 $!!%$"&' bằng: $#$!&( A. -¥ . B. +¥ . C. 0 D.1.
Câu 9: Chọn khẳng định sai? A. lim k
x = +¥(nếu k∈ 𝑁∗ chẵn). B. lim k
x = -¥(nếu k∈ 𝑁∗ lẻ). x®-¥ x®-¥ lim k x = +¥ lim k x = +¥ C. x®-¥ D. x®+¥ (với k nguyên dương).
Câu 10: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của
SC và BC . Số đo của góc (IJ,CD) bằng A. 90° . B. 60° . C. 45°. D. 30° .
Câu 11: Chọn khẳng định đúng. A. . lim n
q = +¥nếu q > 1. B lim n
q = +¥nếu q < 1 C. lim n
q = +¥nếu q > 1. D. . lim n q = +¥ nếu q < 1 ! ! ! !
Câu 12: Cho hai véctơ a;b. Tích vô hướng .
a b được tính bởi công thức nào dưới đây? ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! .
a b = a . b .
a b = a . b .sin (a,b) . a b = . a .
b cos(a,b) A. . B. . C. . D. ! ! ! ! ! ! .
a b = a . b .cos (a,b). 2 2x - 5x + 3
Câu 13: Tính 𝐷 = lim có giá trị là: x 1 ® 2x - 3 - A. 0 B. +¥ C. -¥ 1 D. 5
Câu 14: Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức !!" !!!" !!" !!!" !!!" !!!" !!!" nào đúng ?
A. SB + SD = SA + SC B. AB + AC = AD !!" !!!" !!" !!!"
C. SA + SD = SB + SC D. !!!" !!!" !!!" !!!"
AB + BC + CD + DA = 0 Câu 15: Chọn khẳng định sai?
A. Hàm số y = f (x) được gọi là liên tục trên đoạn [ ;
a b] nếu nó liên tục trên khoảng ( ; a b).
B.Hàm số y = f (x) không liên tục tại x được gọi là gián đoạn tại điểm đó. 0
C. Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
D. Cho hàm số y = f (x) xác định trên khoảng K và x Î K. Hàm số y = f (x) được gọi là liên 0 Trang 5
tục tại x nếu lim f (x) = f (x ). 0 0 x® 0 x
Câu 16: Trong không gian cho ba đường thẳng phân biệt a , b , c . Khẳng định nào sau đây đúng?
A.Nếu a và b cùng nằm trong mp (a ) // c thì góc giữa a và c bằng góc giữa b và c.
B.Nếu a và b cùng vuông góc với c thì a // b.
C.Nếu góc giữa a và c bằng góc giữa b và c thì a // b.
D.Nếu a // b và c ^ a thì c ^ b .
Câu 17: Dãy số nào sau đây có giới hạn bằng 0 ? $ $ $ $ A. ?!#@ B. ?'@ . C.?!"@ . D.?%@ . % % # '
Câu 18: Cho hàm số 𝑓(𝑥) = )"!) . Khi đó hàm số y = f (x) liên tục trên khoảng nào sau đây? )"!")&* A.(−3; 2). B. (−∞; 3). C(2; +∞). D.(-2;3).
ì x + 2a khi x < 0
Câu 19: Tìm 𝑎 để hàm số f ( x) = í liên tục tại 𝑥 = 0. 2
îx + x +1 khi x ³ 0 A. (. B. (. C. 1. D. 0 . # '
Câu 20: Cho hình lập phương ABCD.EFGH như hình vẽ bên. Véctơ nào sau đây cùng phương với véctơ 𝐴𝐵 555⃗. B C A D G F E H 𝐴. 𝐴𝐹 555 .⃗ 𝐵. 𝐴𝐷 555⃗. 𝐶. 𝐴𝐸 555⃗. 𝐷. 𝐵𝐴 555⃗ 4 x + 7
Câu 21: Giá trị đúng của lim là: A. +∞. B. 1. C. 7. D. -1. 4 x®+¥ x +1
B/ PHẦN TỰ LUẬN (3 điểm)
Câu 1. Tính giới hạn sau 2
lim (2x + 4x - 5x +1) x®-¥ √𝟒𝒙%𝟗' √ 𝟑 𝟑𝒙'𝟒'𝟑
Câu 2. Cho hàm số 𝒇(𝒙) = 9 𝒌𝒉𝒊 > 𝟒 𝒙'𝟒
. Tìm m để hàm số liên tục tại x=4?
𝟐𝒙𝟐 + 𝒎 − 𝟑𝟑 𝒌𝒉𝒊 ≤ 𝟒
Câu 3: Cho tứ diện ABCD có 𝑨𝑩 = 𝒂, 𝑪𝑫 = 𝒂√𝟑. Lấy E, F lần lượt trên cạnh BC, AD sao cho
𝑩𝑬 = 𝟏 𝑩𝑪, 𝑨𝑭 = 𝟏 𝑭𝑫 𝒗à 𝑬𝑭 vuông góc với CD. Tính góc giữa hai đường thẳng AB và CD? 𝟑 𝟐
------ HẾT ------ ĐÁP ÁN
PHẦN ĐÁP ÁN CÂU TRẮC NGHIỆM: Câu 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 TL D C A A B A A C C B C D A A A D B A B D B ĐÁP ÁN TỰ LUẬN Bài Nội dung Điểm Câu 1 Tính giới hạn sau 2
lim (2x + 4x - 5x +1) x®-¥ 1đ
(2𝑥 + √4𝑥% − 5𝑥 + 1)(2𝑥 − √4𝑥% − 5𝑥 + 1) 0.25đ = lim !→#$
2𝑥 − √4𝑥% − 5𝑥 + 1 0.25đ Trang 6
4𝑥% − 4𝑥% + 5𝑥 − 1 = lim !→#$ 2𝑥 + 𝑥/4 − 5 0.25đ 𝑥 + 1 𝑥% 0.25đ ! = lim " =& !→#$ %'()##' ! ) " "$ Vậy 2
lim (2x + 4x - 5x +1) =& x®-¥ ) Câu 2 √𝟒𝒙$𝟗& √
𝟑 𝟑𝒙&𝟒&𝟑
Cho hàm số 𝒇(𝒙) = &
𝒌𝒉𝒊 > 𝟒 . Tìm m 1đ 𝒙&𝟒
𝟐𝒙𝟐 + 𝒎 − 𝟑𝟑 𝒌𝒉𝒊 ≤ 𝟒
để hàm số liên tục tại x=4? Tìm 𝑓(4) = 𝑚 − 1 + lim 𝑓(𝑥) = 𝑚 − 1 0.25đ !→)% 3 0.25đ + lim 𝑓(𝑥) = !→)& 20
Để hàm số liện tục tại x=4 : 𝑚 − 1 = * 0.25đ %+ 0.25đ Vậy : 𝑚 = %* %+ Câu 3
Cho tứ diện ABCD có 𝑨𝑩 = 𝒂, 𝑪𝑫 = 𝒂√𝟑. Lấy E, F lần lượt 1đ
trên cạnh BC, AD sao cho 𝑩𝑬 = 𝟏 𝑩𝑪, 𝑨𝑭 = 𝟏 𝑭𝑫 𝒗à 𝑬𝑭 vuông 𝟑 𝟐
góc với CD. Tính góc giữa hai đường thẳng AB và CD? -Dựng EM//AB, tính EM=%,. 0.25đ * 0.25đ
-Lý luận MF//CD, tính MF=,√* * - Tính cos 𝐸𝑀𝐹 8 = √* 0.25đ % Vậy (AB, CD)=30+ 0.25đ
HS xác định được góc (AB,CD)=(ME,MF) mà không tính được cos 𝑬𝑴𝑭 8 ( vẫn cho 0,25đ) Lưu ý:
+ Học sinh giải cách khác dựa theo đáp án trên cho điểm tối đa
.+ Học sinh lý luận để hàm số liện tục tại x=4 ó + lim 𝑓(𝑥) = + lim 𝑓(𝑥) = 𝑓(4). !→)% !→)& 0,25 điểm Trang 7 Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 3 MÔN TOÁN 11 3 x - 1
Câu 1: Tính L = lim . xÆ 2 1- x A. L = - 7 . B. L = - 1 . C. L = 7 . D. L = 1.
Câu 2: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng A. lim n q = 0, q > . 1 B. lim n
q = 0, q < 1. C. lim 1n = 1 0. D. lim = . 1 n®+¥ n®+¥ n®+¥ n®+¥ n 2 2x - 1 a a Câu 3: Cho lim =
, trong đó là phân số tối giản. Tính 2 2 a + b . 2
xÆ- • 1- x + 3x b b A. 10. B. 6 . C. 5 . D. 13.
Câu 4: Cho hình hộp ABC .
D A' B 'C ' D ' , tìm vectơ chỉ phương của đường thẳng A' D . !!!!" !!!" !!!!" !!!!!"
A. A' B . B. CB '. C. BC '.
D. A'C '.
Câu 5: Trong không gian cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Khẳng định nào sau đây đúng? uuur uuuur 2 uuur uuuur a uuur uuuur uuur uuuur
A. AC.DD ' = 0.
B. AC.DD ' = . C. 2 . AC DD ' = - a . D. 2
AC.DD ' = a . 2
Câu 6: Hàm số nào sau đây liên tục trên ° ? 1 1
A. f (x)= .
B. f (x)= . C. f (x) 1 = . D. f (x) 1 = . 2 x - 1 2 x + 1 x + 1 x- 1
Câu 7: Trong các mệnh đề sau mệnh đề nào sai? !!!" !!!" !!!" !!!" "
A. Nếu AB + BC + CD + DA = 0 thì bốn điểm ,
A B,C, D đồng phẳng. !!" !!!" !!!"
B. Tam giác ABC có I là trung điểm cạnh BC thì ta có đẳng thức: 2AI = AB + AC. !!!" !!!" "
C. Vì BA + BC = 0 nên suy ra B là trung điểm của AC . !!!" !!!" !!!" D. Vì AB = 2
- AC +3AD nên 4 điểm ,
A B,C, D đồng phẳng. 3 n - 1 a a Câu 8: Cho lim =
, trong đó là phân số tối giản. Tính . a b . 3 2 + 3n- 2n b b A. - 2 . B. 1. C. - 1. D. 2 . Ï 3
Ô x + b khi x £ - 1
Câu 9: Biết hàm số f (x) Ô = Ì
liên tục tại x = - 1. Mệnh đề nào dưới đây đúng? x Ô + a khi x > - 1 Ô Ó
A. a = - b - 2 .
B. a = - b + 2 .
C. a = b - 2 .
D. a = b + 2 . 1 1 1 a a
Câu 10: Tổng S = + + + ... =
, trong đó là phân số tối giản. Tính a + b . 3 6 12 b b A. 11. B. 6 . C. 7 . D. 5 .
Câu 11: Trong các giới hạn sau, giới hạn nào có giá trị bằng - 1? 1- n Ê 2ˆ Ê 1ˆ Ê 2ˆ A. lim . B. lim 1 Á ˜ + Á ˜ . C. limÁ- 2 ˜ + Á ˜ . D. lim 1 Á ˜ - Á ˜. 1+ n Á Ë n˜¯ Á Ë n˜¯ Á Ë n˜¯
Câu 12: Cho hàm số y = f (x ) liên tục trên [ ; a b
]và f (a). f (b)< 0 khi đó phương trình f (x)= 0 có
A. Có ít nhất một nghiệm thuộc (a;b . )
B. Có ít nhất hai nghiệm thuộc (a;b . ) Trang 8
C. Có ít nhất hai nghiệm thuộc [ ; a b . ]
D. Có ít nhất một nghiệm thuộc [ ; a b . ] x - 5 Câu 13: Tính lim . x 2- Æ x - 2 A. + • . B. 1. C. - • . D. - 1. Câu 14: Tính ( 2 lim 1- 2x . ) xÆ + • A. 2 . B. - 2 . C. - • . D. + • .
Câu 15: Trong không gian cho hình hộp ABC .
D A' B 'C ' D ' . Khẳng định nào sau đây đúng? uur uuur uuur uur uur uuur uuur uuur
A. CB + CD + CC ' = CA.
B. CB + CD + CC ' = CB ' . uur uuur uuur uuur uur uuur uuur uuur
C. CB + CD + CC ' = CD '.
D. CB + CD + CC ' = CA'.
Câu 16: Cho tứ diện ABCD . M , N lần lượt là trung điểm của AB và CD . Mệnh đề nào đúng? uuur uuur uuur uuur uuur uuur
A. MN = 2(AB + DC .) B. MN = 2(AD + BC .) uuur 1 uuur uuur uuur 1 uuur uuur C. MN = AB + DC . D. MN = AD + BC . ( ) ( ) 2 2
Câu 17: Dãy số nào sau đây có giới hạn bằng 0 ? 2 n Ê ˆ 6 n Ê ˆ 7 n Ê ˆ 7 n Ê ˆ A. Á ˜ - Á ˜ . B. Á ˜ - Á ˜ . C. Á ˜ Á ˜ . D. Á ˜ - Á ˜ . Á Ë 5˜¯ Á Ë 5˜¯ 5 Á ˜ Ë ¯ Á Ë 5˜¯
Câu 18: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa hai đường thẳng là góc nhọn.
B. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c .
C. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với c (hoặc b trùng với c ).
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó. uur uuur
Câu 19: Trong không gian cho hình lập phương ABC .
D A' B 'C ' D ' , xác định góc giữa CA và CD'. A. 0 45 . B. 0 120 . C. 0 60 . D. 0 90 . 2 x + 1
Câu 20: Cho hàm số f (x)= , f (x
) gián đoạn tại điểm nào sau đây? 2- x A. x = 1 . B. x = - 1. C. x = - 2 . D. x = 2 .
Câu 21: Cho hai hàm số f (x), g (x) thỏa mãn lim f (x) = 3 và lim g (x) = 2 - . Giá trị của x 1 ® x 1 ® lim é f
ë ( x).g ( x)ù bằng bao nhiêu? û x 1 ® A. 1. B. - 6 . C. 6 . D. - 1.
II. Tự luận. (3 điểm)
Bài 1. (1đ) Tính 2 lim x- x - 2x + 3 . xÆ+ • ( ) Bài 2. (1đ) 2 Ï 2 Ô x + 5x + 3 Ô Ô khi x π - 1
Cho hàm số f (x) Ô 2 = Ì x + x
, xác định m để hàm số liên tục tại x = - 1. Ô Ô 3 m Ô khi x = - 1 Ô Ó Bài 3. (1đ) Trang 9
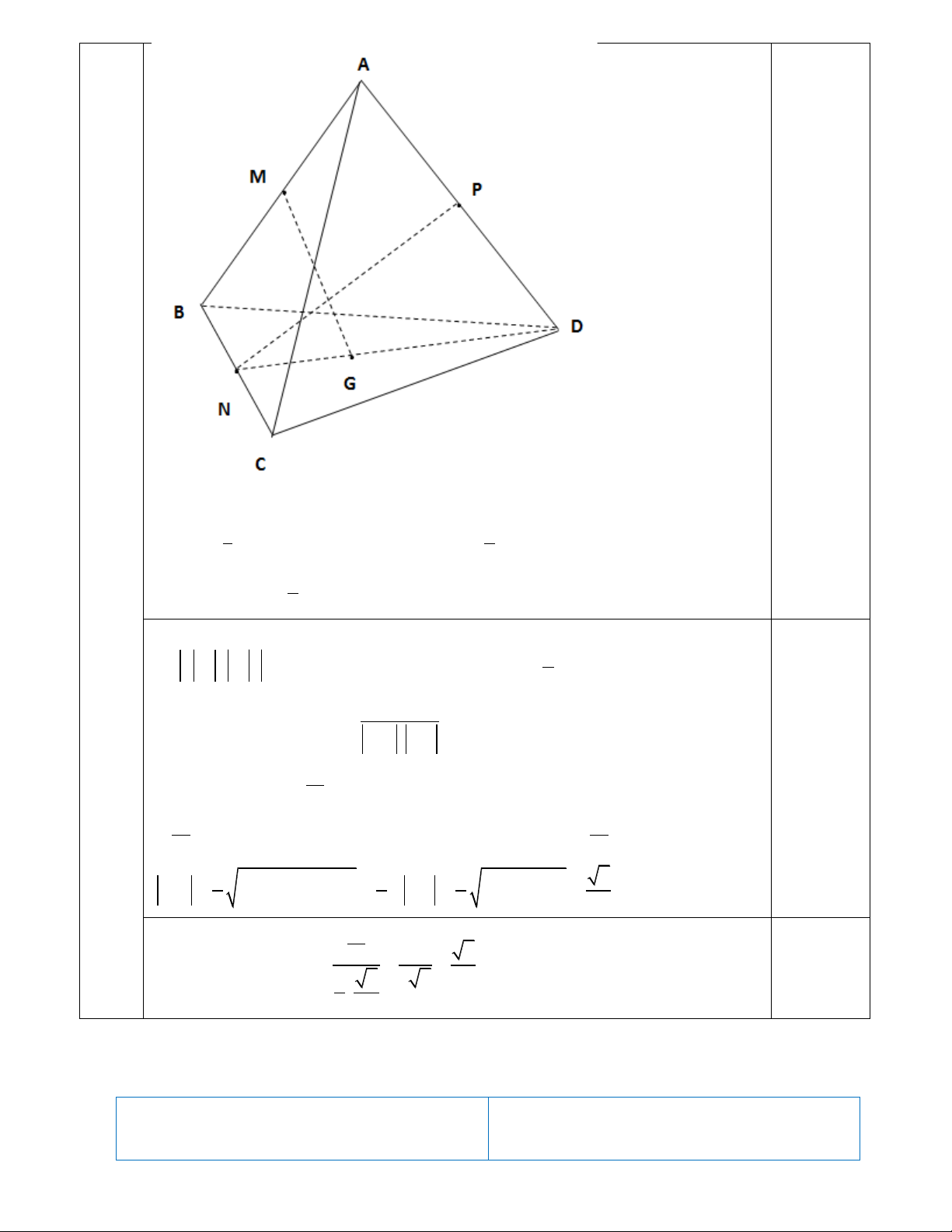
Cho tứ diện đều ABCD . Gọi M , N, P lần lượt là trung điểm của các cạnh AB,CB, AD và G là trọng tâm BCD D , !!!!" !!!"
a là góc giữa 2 vectơ MG và PN . Tính cosa .
------ HẾT ------ ĐÁP ÁN
A. Phần trắc nghiệm: (7,0 điểm) Mã đề 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 104 A B D B A B A A C D A A A C D D A C C D B
B. Phần tự luận: (3,0 điểm) Câu Nội dung Điểm 1 Tính 2 lim x- x - 2x + 3 . xÆ+ • ( ) 1.0 đ 2x- 3 0.5 = lim xÆ+ • 2
x - 2x + 3 + x 3 2 2x 3 - - = lim = lim x 0.25 xÆ + • 2 3 xÆ + • 2 3 x 1- + + x 1- + + 1 2 2 x x x x = 1 0.25 2 2 Ï 2 Ô x + 5x + 3 Ô Ô khi x π - 1
Cho hàm số f (x) Ô 2 = Ì x + x
, xác định m để hàm số liên tục tại Ô 1.0 đ Ô 3 m Ô khi x = - 1 Ô Ó x = - 1. 2 2x + 5x + 3 lim = - 1 2 0.25 xÆ- 1 x + x 0.25 f (- ) 3 1 = m
Để hàm số liên tục tại x = - 1 thì lim f (x)= f (- ) 3 1 € m = - 1 0.25 xÆ- 1 € m = - 1 0.25 3
Cho tứ diện đều ABCD . Gọi M , N, P lần lượt là trung điểm của các cạnh !!!!" !!!"
AB,CB, AD và G là trọng tâm BCD D
, a là góc giữa 2 vectơ MG và PN . Tính 1.0 đ cosa . 0.25 Trang 10 !!!" " !!!" " !!!" " Đặt AB = ; a AC = ; b AD = c !!!" 1 " " " !!!!" !!!" !!!!" 1 " " " Þ AG =
a + b + c Þ MG = AG - AM =
-a + 2b + 2c ( ) ( ) 3 6 !!!" !!!" !!!" 1 " " "
PN = AN - AP = (a +b-c) 2
Không mất tính tổng quát, giả sử độ dài các cạnh của tứ diện đều bằng 1 ! ! ! ! ! ! ! ! !
Þ a = b = c =1 1 và 0 . a b = . b c = . c a = 1.1.cos 60 = 2 !!!!" !!!" !!!!" !!!" M . G PN
Þ cosa = cos (MG, PN) = !!!!" !!!" (*) MG . PN !!!!" !!!" " " " " " " 0.5 1 Ta có: Þ . MG PN =
-a + 2b + 2c a +b -c ( )( ) 12 1 !2 !! !! ""!! !2 !! !! !! !2 1 =
-a - ab + ac + 2ab + 2b - 2bc + 2ac + 2bc - 2c = ( ) 12 12 !!!!" " " " !!!" " " " MG =
(-a + b+ c)2 = PN = (a +b-c)2 1 1 1 2 2 2 ; = 6 2 2 2 1 1 2 Thay vào (*) 12 Þ cosa = = = . 0.25 1 2 3 2 6 . 2 2
---------------------------------Hết-------------------------------- Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 4 MÔN TOÁN 11 Trang 11
I. PHẦN TRẮC NGHIỆM(7 điểm). 3 - Câu 1: Tính 2x 3 Lim . 3 x®+¥ 3x + 2 - A. 3 2 0 . B. . C. . D. 3. 2 3
Câu 2: Cho các giới hạn: lim f (x) = 5
- ; lim g ( x) = 4.Tính lim é2 f ë
(x)-3g (x)ù. û x® ® ® 0 x x 0 x x 0 x A. 22 - . B. 2 . C. 9 - . D. 23.
Câu 3: Hàm số nào sau đây liên tục trên R ? A. 2
f (x) = x - x + 3.
B. f (x) = tan x . 2 + + C. x 2x 1
f (x) = co x t .
D. f (x) = . x + 2 Câu 4: Tính 2x +1 lim . x 2- ® x - 2 A. +¥ . B. -¥ . C. 1. D. 2 . n n - Câu 5: Tính 2.3 4 lim . 3.4n -1 - A. 1. B. 1 . C. 2 0 . D. . 3 3 3 Câu 6: Tính 5 lim ( 4 - x - 3x - 2) . x®-¥ A. -¥ . B. 2 - . C. +¥ . D. 2 . 2 - + Câu 7: Tính x 3x 2 lim . x®2 x - 2 A. +¥ . B. 1. C. 3. D. -¥ . !!!" !!!"
Câu 8: Cho tứ diện ABCD có tất cả các cạnh đều bằng a .Tính . AB AD. 2 a 3 2 a 3 2 a 2 a A. - . B. . C. - . D. . 2 2 2 2
Câu 9: Cho hình chóp S.ABCD có ABCD là hình bình hành tâm O . Khẳng định nào sau đây sai? !!!" !" " !!!!" !!" !!!" !!!" !!!"!!!!" !!!" !!!" !!!"
A. OA + OB = 0.
B. 2SO = SB + SD.
C. AC = DC-DA.
D. DB = DA + DC . 2 - + Câu 10: Biết an 5n 2 lim = 4. Tìm a. 2 2n + 5 A. a = 4 - . B. a = 4 . C. a = 8. D. a = 2 .
Câu 11: Cho lim(u ) = 5. Tính lim(2 -3u ). n n A. 15 - B. 17 . C. 15. D. 13 - .
Câu 12: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình hộp có các cạnh bên song song và bằng nhau.
B. Hai mặt đáy của hình hộp là hai hình bình hành.
C. Các mặt bên của hình hộp là các hình bình hành.
D. Hai đáy của hình hộp là hai đa giác đều.
Câu 13: Cho hình chóp S.ABCD .Khẳng định nào sau đây đúng? Trang 12 A. ∑ ∑ ( , SA BC) = SAC . B. ∑ ∑ ( , SA BC) = DSA. C. ∑ ∑ ( , SA BC) = SDA. D. ∑ ∑ ( , SA BC) = SAD .
Câu 14: Cho hình hộp ' ' ' ' ABC .
D A B C D .Khẳng định nào sau đây đúng? !!!!" !!!" !!!" !!!" !!!!" !!!" !!!" !!!"
A. A'C = AA' + AB + AD.
B. AC ' = AC + AB + AD. !!!!" !!!" !!!" !!!!" !!!" !!!" !!!" !!!"
C. AC ' = AA' + AB + AD .
D. AC = AA' + AB + AD.
Câu 15: Hàm số nào sau đây có nghiệm trong khoảng ( 1 - ;0)? A. 5
f (x) = x + x + 2. B. 5
f (x) = x - 2x + 2. C. 5
f (x) = x - x + 2. D. 5
f (x) = x + 3x + 2 . Câu 16: Tính lim( 2 3x - 2x + ) 1 . x®2 A. 17 . B. +¥ . C. -¥ . D. 9. !!" !!"
Câu 17: Trong không gian, cho 2 đường thẳng a và b vuông góc.Gọi u ,u lần lượt là véc tơ chỉ a b
phương của đường thẳng a và b.Khẳng định nào sau đây đúng? !!" !!" !!" !!" !!" !!" !!" !!"
A. u .u = 1 - .
B. u .u = 0.
C. u .u = 90°.
D. cos(u ,u ) =1. a b a b a b a b
Câu 18: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Khẳng định nào sau đây sai? A. (ABC )
D / /(A' B'C ' D').
B. (ABCD) / /(ABC ' D').
C. (ADD' A') / /(BCC ' B').
D. (DCC ' D') / /(ABB' A'). Câu 19: Tính tổng : 1 1 1 S = 1+ + ...+ +.... 1 3 9 3n- 2 4 A. S = 3 . B. S = . C. 3 S = . D. S = . 3 2 4 3
Câu 20: Hàm số nào sau đây không liên tục tại x = 1 ? A. x x f (x) = .
B. f (x) = . x -1 x +1
C. f (x) = cos x.
D. f (x) = sin x . x - 3 Câu 21: Cho lim
= a. Tính a - 2 . x®-¥ 2 x - 5 A. 1 - . B. 3. C. 3 - . D. 1.
II. PHẦN TỰ LUẬN ( 3 điểm). 2 3x +10x + 3
Câu 1(1 điểm): Tính lim 2 x 3 ®- x + x - 6
Câu 2(1 điểm): Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc, AB = AC = AD = a .Tính !!!" !!!" . BC BD
Câu 3(1 điểm): Chứng minh phương trình : 3 2 2
mx + (2m - 3m +1)x - m -1 = 0 có nghiệm m " Î R
------ HẾT ------ Trang 13 ĐÁP ÁN
I. Phần đáp án câu trắc nghiệm: 1 C 6 C 11 D 16 D 21 C 2 A 7 B 12 D 17 B 3 A 8 D 13 D 18 B 4 B 9 A 14 C 19 B 5 A 10 C 15 D 20 A
II. PHẦN TỰ LUẬN ĐÁP ÁN Câu Nội dung Điểm 1 2 3x +10x + 3 Câu 1: Tính: lim 2 x 3 ®- x + x - 6 1 3(x + 3)(x + ) 3 = lim (đúng mỗi dòng 0.25đ) 0.5 x 3 ®- (x + 3)(x - 2) 1 0.25 3(x + ) 3 = lim x 3 ®- x - 2 0.25 8 = 5
(không có hệ số 3,trừ 0.5 đ) 2
Câu 2 Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc, !!!" !!!"
AB = AC = AD = a .Tính . BC BD
Tính BC = BD = CD = a 2 0.25 0.25 !!!" !!!" 0.25 ∑ . BC BD = BC. . BD cosCBD 0.25
= a 2.a 2.cos60° 2 = a 3
Câu 3: Chứng minh phương trình : 3 2 2
mx + (2m - 3m +1)x - m -1 = 0 có nghiệm m " Î R 3 Đặt 2 2
f (x) = mx + (2m - 3m +1)x - m -1 0.25
Þ f (x) liên tục trên R Þ f (x) liên tục trên[0;2] 0.25 2
f (0) = -m -1< 0, m " Î R 0.25 2
f (2) = 3m + 2m +1
Chứng minh được f (2) > 0, m " Î R 0.25
Suy ra f (0). f (2) < 0,"Î R ÞPT có ít nhất một nghiệm thuộc (0;2) KL:PT có nghiệm m " Î R Trang 14 Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 5 MÔN TOÁN 11
PHẦN TRẮC NGHIỆM: (7 điểm)
Câu 1: Cho hai dãy số (u ), (v ) thỏa limu = 3 và limv = 4. Giá trị của lim(u + v ) bằng n n n n n n A. 7 . B. 12 . C. 1. D. 1 - .
Câu 2: Hàm số nào sau đây liên tục trên ! ? 1 A. y = . B. 5 4
y = x + 5x + . 1
C. y = 3x - 2 .
D. y = tan x + . 1 2x
Câu 3: Cho hai hàm số f (x), g(x) thỏa mãn lim f (x) = 2
- và lim g(x) = +¥. Giá trị của x 1 ® x 1 ®
lim[f (x).g(x)] bằng x 1 ® A. 2 . B. 2 - . C. +¥ . D. -¥ .
Câu 4: Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của AB và CD. Khẳng định nào sau đây
đúng? !!!!" 1 !!!" !!!" !!!!" 1 !!!" !!!"
A. MN = (AB + CD).
B. MN = (AB - CD). 2 2 !!!!" 1 !!!" !!!" !!!!" 1 !!!" !!!"
C. MN = (AD - BC).
D. MN = (AD + BC). 2 2
Câu 5: lim(n + 2) bằng A. 2 . B. +¥ . C. -¥ . D. 1.
ìx +1, khi x ¹ 3
Câu 6: Cho hàm số f (x) = í
. Giá trị của tham số m để hàm số f (x) liên tục tại î , m khi x = 3 x = 3 bằng A. 4 . B. 1. C. 2 . D. 0 . 2x
Câu 7: Hàm số y =
liên tục trên khoảng nào sau đây? 2 x - 4x + 3 A. ( 2 - ;0). B. ( ; -¥ + ) ¥ . C. (2;4). D. (0;2).
Câu 8: Cho hình lập phương ABCD.EFGH. Góc giữa hai đường thẳng AB và EG bằng A. 90°. B. 45° . C. 30°. D. 60° . Câu 9: 2
lim(x + 3x - 5) bằng x®3 A. 3. B. 13 . C. 5 - . D. 1.
Câu 10: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và OA = OB = OC . Góc giữa
hai đường thẳng AB, BC bằng A. 45° . B. 120° . C. 90°. D. 60° .
Câu 11: Cho mặt phẳng (P) song song mặt phẳng (Q). Mặt phẳng (R) cắt (P) và (Q) theo hai giao
tuyến a và b. Khẳng định nào sau đây đúng?
A. a và b trùng nhau.
B. a và b song song.
C. a và b song song hoặc trùng nhau. Trang 15
D. a và b cắt nhau.
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là
trung điểm SA, SB, SC, SD. Khẳng định nào sau đây sai?
A. (MNP) // (OCD). B. (MQO) // (SBC).
C. (NQO) // (PCD).
D. (MNO) // (SCD). 2x + 5 Câu 13: lim bằng x 1+ ® x -1 A. 5 - . B. 2 . C. -¥ . D. +¥ . 2n -1 Câu 14: lim bằng n + 3 A. 2 . B. +¥ 1 . C. - 2 . D. . 3 3
Câu 15: Cho hàm số f (x) thỏa mãn lim f (x) = 2
- và lim f (x) = 2
- . Giá trị của lim f (x) bằng x 1+ ® x 1- ® x 1 ® A. 1. B. 4 . C. 2 - . D. 4 - . 2 x - 5x + 6 Câu 16: lim bằng x®2 x - 2 A. 1 - . B. 5 - . C. 1. D. 5 . Câu 17: 3
lim (x -1) bằng x®+¥ A. 1. B. 1 - . C. +¥ . D. -¥ .
Câu 18: Cho dãy số (u ) thỏa mãn lim(u - 5) = 0. Giá trị của limu bằng n n n A. 10 . B. 0 . C. 5 - . D. 5 . 1 1 1
Câu 19: Tính tổng S = 1+ + + + ... 3 9 27 1 3 2 A. . B. 1. C. . D. . 3 2 3
Câu 20: Cho tứ diện ABCD, gọi G là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng? !!!" 1 !!!" !!!" !!!" !!!" 1 !!!" !!!" !!!"
A. AG = (AB + AC - AD) .
B. AG = (AB + AC + AD) . 3 2 !!!" 1 !!!" !!!" !!!" 1 !!!" !!!" !!!"
C. AG = (AB + AC).
D. AG = (AB + AC + AD) . 3 3
Câu 21: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây đúng?
A. (ABC) // (A'B'D').
B. (ABD') // (A'B'C).
C. (ABC) // (B'C'D').
D. (ACD) // (A'D'B).
PHẦN TỰ LUẬN: (3 điểm)
Câu 1 (1 điểm): Tìm các giới hạn sau: 2 2n + n - 5 x +1 - 2 a) lim ; b) lim 2 n +1 x 3 ® x - 3
Câu 2 (1 điểm): Chứng minh rằng phương trình 2 2 ( 3) n m m x 2x 4 0, n * - + -
- = " Î • luôn có ít nhất
một nghiệm âm với mọi giá trị của tham số m ?
Câu 3 (1 điểm): Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a , SB = SD = a 2 , Trang 16
SC = a 3 . Tính góc giữa hai đường thẳng SD và AC?
------ HẾT ------ ĐÁP ÁN 1 A 6 A 11 B 16 A 21 C 2 B 7 A 12 C 17 C 3 D 8 B 13 D 18 D 4 D 9 B 14 A 19 C 5 B 10 D 15 C 20 D Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 6 MÔN TOÁN 11
PHẦN TRẮC NGHIỆM ( 7 điểm)
Câu 1. Chọn khẳng định đúng.
A. limu = a nếu u - a có thể bé hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi. n n
B. limu = a nếu u - a có thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đó trở đi. n n
C. limu = a nếu u - a có thể bé hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi. n n
D. limu = a nếu u - a có thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đó trở đi. n n
Câu 2. Chọn khẳng định đúng: A. lim n
q = 0 nếu q > 1 B. lim n
q = 0 nếu q < 1. C. lim n
q = 0 nếu q > 1 D. lim n
q = 0 nếu q < 1.
Câu 3. Cho hai dãy số (u (v limu = 3 limv = +¥ n ) n ) và . Biết và
. Chọn khẳng định đúng. n n u v u +
A. lim n = +¥
B. lim n = 0
C. limu .v = +¥ 1 D. lim n = +¥ v u n n v n n n 3.2n -1 Câu 4. Tính lim . 2n + 5 A. 0. B. 3. C. + . ¥ 1 D. - . 5 1 1 1
Câu 5. Tổng của cấp số nhân lùi vô hạn S = 5 +1+ + + +... là: 5 25 125 6 25 4 25 A. B. C. D. 25 6 25 4 Câu 6. Tìm 2 lim(x + 3x) x®2 A. 6 B. 8 C. 10 D. 12
Câu 7. Với k là số nguyên dương chẵn. Kết quả của giới hạn k lim x là: x®-¥ A. k x B. 0 C. +¥ D. -¥ 0
Câu 8. Cho các giới hạn: lim f (x) = -1; lim g(x) = 5, khi đó lim é2 f (x) - g x x x ë ( )ù bằng: x® û 0 x x® 0 x ® 0 Trang 17 A. 4 . B. 3 . C. -7 . D. -3.
Câu 9. Cho lim f ( ) x = 2, lim g( )
x = -¥. Tính L = lim [ f (x).g(x)] x®-¥ x®-¥ x®-¥
A. L = -¥ . B. L = + . ¥
C. L = 2. D. L = 0. x + 2 Câu 10. Tính lim . 2 x®-2 x - 4 1 1 A. B. - C. 4 - D. 4 4 4 x + 2 Câu 11. Tính lim x 3- ® x - 3 A. 0 B. + . ¥ C. -¥ D. 1
Câu 12. Mệnh đề nào sau đây sai?
A. Hàm số y = f (x)liên tục trên đoạn [ ;
a b]nếu nó liên tục tại mọi điểm thuộc đoạn [ ; a b].
B. Các hàm số đa thức, phân thức hữu tỉ, lượng giác liên tục trên các khoảng mà nó xác định.
C. Tổng, hiệu, tích của hai hàm số liên tục tại một điểm là những hàm số liên tục tại điểm đó.
D. Cho hàm số f (x)có miền xác định D và a Î D . Ta nói f (x) là hàm liên tục tại x = a khi lim f (x) = f (a) x®a . 3x + 2
Câu 13. Cho hàm số f (x) =
. Chọn khẳng định đúng trong các khẳng định sau: x -1
A. f (x) liên tục trên . R
B. f (x) liên tục trên các khoảng ( ) ;1 -¥ và (1;+¥)
C. f (x) liên tục trên các khoảng (-¥ ) ;1 È(1;+¥)
D. f (x) liên tục trên các khoảng ( ;2 -¥ ) và (2;+¥)
ìx + 3 , khi x ¹ 4
Câu 14. Hàm số f (x) = í
. Khẳng định nào sau đây đúng: î6 , khi x = 4
A. f (x) liên tục tại x = 4
B. f (x) liên tục tại x =10 và gián đoạn tại x = 4
C. f (x) liên tục trên (0;+¥)
D. f (x) liên tục trên khoảng R
Câu 15. Trong các khẳng định sau, khẳng định nào đúng? ! ! !
A. Ba vectơ a,b, c được gọi là đồng phẳng nếu giá của chúng cắt nhau từng đôi một . ! ! !
B. Ba vectơ a,b, c được gọi là đồng phẳng nếu giá của chúng vuông góc từng đôi một . ! ! !
C. Ba vectơ a,b, c được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng. ! ! !
D. Ba vectơ a,b, c được gọi là đồng phẳng nếu giá của chúng cắt nhau từng đôi một hoặc vuông góc từng đôi một. !!" " !!" " !!!" " !!!" "
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt SA = a ; SB = b ; SC = c ; SD = d .
Khẳng định nào sau đây đúng? ! ! ! ! ! ! ! ! ! ! ! A. ! ! ! ! ! !
a + d = b + c .
B. a + b = c + d .
C. a + c = d + b .
D. a + b + c + d = 0.
Câu 17. Cho hình hộp ABC .
D EFGH , tham khảo hình vẽ bên dưới . Trang 18 A D B C H E G F !!!" !!!" !!!"
Khi đó GF + GH + GC bằng: !!!" !!!" !!!" !!!" A. GE . B. GA. C. GB . D. GD.
Câu 18. Trong không gian cho ba đường thẳng phân biệt a , b , c . Khẳng định nào sau đây đúng? ìa ^ c A. Nếu í
thì a / /b
B. Nếu a // b và c ^ a thì c ^ b . îb ^ c ìa ^ c ìa ^ c C. Nếu í
thì a ^ b . D. Nếu í thì a º b îb ^ c îb ^ c
Câu 19. Cho ba đường thẳng a,b, c. Mệnh đề nào sau đây sai?
A. Nếu a / /b thì (∑a c) = (∑ , c,b)
B. Nếu c / /b thì (∑a b) = (∑ , a,c)
C. Nếu a / /c thì (∑a,c) = 0°
D. Nếu a ^ b thì (∑a c) = (∑ , c,b)
Câu 20. Trong không gian cho ba đường thẳng a,b, c . Trong các mệnh đề sau, mệnh đề nào đúng? ìa / /b ìc ^ a (I) : í Þ c ^ b (II) : í Þ a / /b ∑ (III ) : ( ,
a b) = 0° Þ a / /b îc ^ a îc ^ b
A. (I) và (II) .
B. (II) và (III) .
C. Chỉ (I) . D. Chỉ (II).
Câu 21. Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng AB và CD bằng A. 30° . B. 45°. C. 60° . D. 90° .
PHẦN TỰ LUẬN ( 3 điểm) 2 2x - 9x + 4
Bài 1. Tính giới hạn sau: lim x®4 x - 4
Bài 2. Tìm tất cả các giá trị thực của tham số m để hàm số f (x) liên tục tại x = 3 ìx + m , x £ 3 ï
f (x) = í 3x -5 - 2 ï , x > 3 î x - 3
Bài 3. Cho tứ diện ABCD ∑ ∑
có AB = AC = AD = 2cm và CAD = BAD = 150°
Chứng minh rằng AD ^ BC.
------ HẾT ------ ĐÁP ÁN Nội dung Điểm Bài 1 2 1,0 2x - 9x + 4 Tính giới hạn sau: lim x®4 x - 4 Trang 19 2 2x - 9x + 4 (x - 4)(2x -1) lim = lim 0,5 x®4 x®4 x - 4 x - 4 lim(2x - ) 1 = 7 x®4 0,25-0,25 Bài 2
Tìm tất cả các giá trị thực của tham số m để hàm số f (x) liên tục tại x = 3 ìx + m , x £ 3 ï 1,0
f (x) = í 3x -5 - 2 ï , x > 3 î x - 3
TXĐ: D = R , x = 3Î D 0,25 f (3) = 3 + m lim f ( ) x = lim (x + ) m = 3+ m 0,25 x 3- x 3- ® ® 3x - 5 - 2 3(x - 3) 3 3 lim f (x) = lim = lim = lim = 0,25 x 3+ x 3+ - x 3+ x 3 x 3
(x - 3)( 3x - 5 + 2) + ® ® ® ® 3x - 5 + 2 4 9
f (x) liên tục tại x = 3 Û lim f (x) = lim f (x) = f (3) Û m = - 0,25 x 3- x 3+ ® ® 4 Bài 3 Cho tứ diện ABCD ∑ ∑
có AB = AC = AD = 2cm và CAD = BAD = 150° 1,0
Chứng minh rằng AD ^ BC. !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!! " . AD BC = .
AD (AC - AB) = . AD AC - . AD AB 0,25 ∑ ∑ 0,25 = A . D A . C cosCAD - A . D A . B cosBAD 0 0 = 2.2.co 150 s - 2.2.co 150 s 0,25 = 0 0,25
Kết luận AD ^ BC Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 7 MÔN TOÁN 11
I. PHẦN TRẮC NGHIỆM: ( 7 điểm)
Câu 1: Trong các khẳng định sau, khẳng định nào Đúng? 1 æ 5 ön æ 3 ön A. ( 2 lim 4
- n ) = +¥ B. lim = +¥ C. lim = 0 D. lim = +¥ 4 ç ÷ ç ÷ n è 8 ø è 4 ø
Câu 2: Cho hàm số f ( x) thỏa mãn lim f (x) = 21 và lim f (x) = 21 .Giá trị của lim f ( ) x bằng: x 1+ ® x 1- ® x 1 ®
A. 21. B. 2 C. 0 D. Không tồn tại.
Câu 3: Cho hàm số y = f (x) xác định trên khoảng K và x Î K . Hàm số f(x) được gọi là liên tục tại x nếu: 0 0
A. lim f ( x) = lim f ( x)
B. lim f ( x) = f ( x0 ) + - x®x x® x®x 0 0 x 0
C. lim f (x) = x
D. lim f ( x) ¹ f ( x0 ) 0 x® x® 0 x 0 x 2 an - 3n +1 1 Câu 4: Biết lim
= với a là tham số. Khi đó 2 a - a bằng: 2 9 - 4n 2 Trang 20
A. -12 B. -2 C. 0 D. -6
Câu 5: Cho dãy số (u lim(u + 7 limu n ) = 0. n ) thỏa mãn Giá trị của bằng: n A. 7 B. 7 - C. 5. D. 0. !!!!"
Câu 6: Cho hình lập phương AB .
CD A' B 'C ' D '. Vectơ nào cùng hướng với A'D? !!!!" !!!!" !!!" !!!!" A. A' B B. DC ' C. AB D. B 'C æ u ö
Câu 7: Cho hai dãy số (u ), v limu = 3 limv = 0 v lim n n ( > 0 n ) n ( n) thỏa mãn và . Giá trị của bằng: A. n ç ÷ è vn ø 4. B. 0. C. . -¥ D. + . ¥ 2
ìx - 4x + 5 khi x ¹ 2
Câu 8: Cho hàm số f (x) =
. Gọi m là giá trị của tham số m để hàm số f ( ) x liên í 0
î 3x - m khi x = 2
tục tại x = 2 . Khi đó m thuộc khoảng nào sau đây? 0 A. (0;3) B. (3;6) C. ( 9; - 2 - ) D. (5;8) Câu 9: Tính ( 5 2 lim 4x - 3x + )
1 bằng: A. 0. B. + . ¥ C. 5. D. . -¥ x®-¥
Câu 10: Giả sử ta có lim f ( x) = a và lim g ( x) = b. Trong các mệnh đề sau, mệnh đề nào Sai? x®+¥ x®+¥
A. lim éë f (x).g (x)ù = . a b.
B. lim éë f (x) - g (x)ù = a - b. û û x®+¥ x®+¥ f (x) a
C. lim éë f (x) + g (x)ù = a + b D. lim = . û x®+¥
x®+¥ g ( x) b
Câu 11: Hàm số nào dưới đây liên tục trên ℝ? x + 2 4 + x A. f ( x) 5 = B. y = cot . x C. f ( x) 2
= 3 + x D. f (x) = x + 4 x -1 x - 4 Câu 12: Tính lim
bằng:A. 3. B. . -¥ C. + . ¥ D. 5. - x 1 ® x - 2 1 1 1 1
Câu 13: Tính tổng S = 2 + + + + ... + + ... bằng: 2 4 8 2n -3 12 5 A. 3. B. . C. . D. . 2 5 2 !!" !!!" !!!!"
Câu 14: Cho hình hộp ABC . D ¢ A ¢ B C¢ ¢
D có tâm là I. Phân tích vectơ DI theo hai vectơ DA và DC ' !!" !!!!" !!!" !!" !!!!" !!!" !!" !!!!" !!!" !!" !!!!" !!!"
A. DI = 2DC ' + 3DA B. 2DI = DC ' + DA C. DI = DC ' - 2DA D. DI = DC ' + DA
Câu 15: Nếu k là số nguyên dương chẵn thì kết quả của giới hạn lim k x bằng: x®-¥ A. 0. B. + . ¥ C. . -¥ D. 1. 2 3x - 5x + 2 a a
Câu 16: Cho giới hạn lim
= , trong đó là phân số tối giản. Tính 2 2
S = a + b . 2 x 1 ® x - 5x + 4 b b A. S = 20 .
B. S = 17 .
C. S = 10. D. S = 25 .
Câu 17:Mệnh đề nào sau đây là Đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau. Trang 21
D. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
Câu 18: Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của các cạnh AB và CD , G là trung điểm của !!!" !!!" !!!" !!!"
đoạn thẳng IJ . Tính GA + GB + GC + GD bằng: ! !!" !!" !!!" A. 0 .
B. 2IJ .
C. 4GI . D. 3GJ . !!!" !!!"
Câu 19: Cho tứ diện đều ABCD có cạnh bằng a. Tính tích vô hướng . BD DC bằng: A. 2 a . 2 a 2 a 3 2 -a B. . C. . D. . 2 2 2 !!!!" !!!!"
Câu 20: Cho hình lập phương ABC . D ¢ A ¢ B C¢ ¢
D . Tính góc giữa hai vectơ AB' và A'D A. 60° B. 45° C. 120° D. 90°
Câu 21: Cho tứ diện ABCD. Gọi I là trung điểm AB. Khẳng định nào sau đây là Đúng ? !!" !!!" !!!" !!" !!!" !!!" !!" !!!" !!!" !!" !!!" !!!"
A. CI = CA + CB B. DI = DA + DB C. 2DI = DA + DB D. 2CI = CA - CB
PHẦN TỰ LUẬN: ( 3 điểm) ì 6x + 3 - 3
Câu 1:(1điểm) Cho hàm số f (x) ï khi x ¹ 1 2 =
. Xét tính liên tục của hàm số f(x) tại x = í x -1 1 0 5
ïî x + 2 khi x =1
Câu 2: ( 1 điểm) Cho hình lập phương ABC . D ¢ A ¢ B C¢ ¢
D có cạnh bằng a. Trên các cạnh AD và CC ' lấy các
điểm M và N sao cho MA = NC = x (
0 £ x £ a). Chứng minh hai đường thẳng BD' và MN vuông góc với nhau. 3
8x +1. 6x + 2 - x - 5
Câu 3: ( 1 điểm) Tính giới hạn sau: lim 2 x 1 ® 3x - 5x + 2 ĐÁP ÁN
Phần đáp án câu trắc nghiệm: 1 C 6 D 11 C 16 C 21 C 2 A 7 D 12 A 17 A 3 B 8 B 13 A 18 A 4 D 9 D 14 B 19 D 5 B 10 D 15 B 20 C Phần tự luận Câu Bài giải Thang hỏi điểm é 1 - ö + Tập xác định: D = ;+¥ \ ê ÷ {- } 1 , x = 1Î D 0 0.25đ ë 2 ø
Câu 1: + f (1) = 5.1+ 2 = 7 0.25đ (1điểm) 6x + 3 - 3 6x + 3 - 9 + li mf (x) = lim = lim 2 0.25đ x 1 ® x 1 ® x 1 x -1 ® (x - ) 1 (x + ) 1 ( 6x +3 +3) Trang 22 6 1 = lim = x 1 ® (x + ) 1 ( 6x + 3 + 3) 2 0.25đ
Vì f (1) ¹ limf (x) nên hàm số f(x) gián đoạn tại x = 1 0 x 1 ® 0.25đ !!!!" !!!" !!!" !!!" Ta có: BD' = BA + BC + BB' !!!!" !!!" !!!!" !!!" !!!" !!!!" MN = DN - DM = (DC + CN) - DM !!!" !!!" !!!" !!!" !!!" !!!" 0.25đ x æ a - x ö x æ x ö = -BA + BB' + AD = -BA + BB' + 1- BC ç ÷ ç ÷ a è a ø a è a ø Khi đó: Câu 2: !!!!" !!!!"
!!!" !!!" !!!" é !!!" x !!!" æ x ö!!!"ù
(1điểm) BD'.MN = (BA + BC + BB') -BA + BB' + 1- BC ê ç ÷ ë a a ú è ø û
!!!"2 x !!!" !!!" æ x ö!!!" !!!" !!!" !!!" x !!!" !!!" æ x !!!"2 ö 0.25đ = -BA + BA.BB' + 1- BA.BC - BA.BC + BB'.BC + 1- BC ç ÷ ç ÷ a è a ø a è a ø
!!!" !!!" x !!!"2 æ x ö!!!" !!!" -BA.BB' + B B ' + 1- B . C B B ' ç ÷ a è a ø !!!"2 æ x !!!"2 ö x !!!"2 = -BA + 1-
BC + BB' (Vì các cạnh BA, BC, BB’ đôi một vuông góc) ç ÷ è a ø a æ x ö x æ x ö x 2 2 2 2 2 2 = -BA + 1- BC + BB' = -a + 1- a + .a ç ÷ ç ÷ è a ø a è a ø a 0.25đ x x 2 2 2 2 = -a + a - .a + .a = 0 a a !!!!" !!!!" Þ BD'.MN = 0
Vậy đường thẳng AC’ vuông góc với đường thẳng MN Ta có: 8x +1. x + x + - x - (3 3
6x + 2 - 2) + 2 8x +1 - x - 5 8 1. 6 2 5 lim = lim 2 2 x 1 ® x 1 3x - 5x + 2 ® 3x - 5x + 2 Câu 3: 0.25đ (1điểm)
é 8x +1.(3 6x + 2 -2) 2 8x +1-(x +5)ù = lim ê + ú x 1 ® ê (x - )1(3x - 2)
(x - )1(3x - 2) ú ë û 0.25đ Trang 23 é ù ê
8x +1.(6x + 2 - 8)
4(8x +1) - (x + 5)2 ú = lim ê + ú
x® ê(x - )( x - )é( x + )2 1 3 3 ù + x + +
(x - )1(3x - 2)é2 8x +1 + (x + 5 1 3 2 6 2 2 6 2 4 )ùú ë û ê ú ë ë û û é ù ê 6 8x +1.( x - ) 2 -x + x - ú 1 22 21 = ê + lim ú 0.25đ
x® ê(x - )( x - )é( x + )2 1 3 3 ù + x + +
(x - )1(3x - 2)é2 8x +1 + (x +5 1 3 2 6 2 2 6 2 4 )ùú ë û ê ú ë ë û û é ù ê 6 8x +1 -(x - ) 21 ú = lim ê + ú 2 x 1 ® é 3 3 ù ê x - x + + x + +
(3x - 2)é2 8x +1 + (x +5 3 2 6 2 2 6 2 4 )ùú ( )ê( ) ë û 0.25đ ú ë ë û û 19 = 6 Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 8 MÔN TOÁN 11
I. Phần trắc nghiệm (7.0 điểm) Câu 1: Cho (u q < 1
n ) là một cấp số nhân lùi vô hạn với công bội q ,
. Công thức tính tổng của cấp số nhân lùi vô hạn là - A. u u u 1 q S = 1 . B. 1 S = . C. S = 1 . D. S = . 1- q q -1 1+ q u1
Câu 2: Trong không gian, khẳng định nào sau đây đúng?
A. Hai vectơ bằng nhau là hai vectơ có cùng độ dài.
B. Vectơ là một đường thẳng.
C. Vectơ là một đoạn thẳng có hướng.
D. Tổng của hai vectơ là một số thực. 2 ì2x - x ï ¹ Câu 3: Cho hàm số (x 0) f (x) = í x
. Với giá trị nào của a thì hàm số f (x) liên tục tại x = 0. ïa (x î = 0) A. a = 3. - B. a = 1. C. a = 1. - D. a = 2.
Câu 4: Cho hình lập phương ABC .
D A' B 'C ' D ' , góc giữa hai đường thẳng AB và B ' D ' bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 . Câu 5: Tính tổng 1
S của cấp số nhân lùi vô hạn (u u = . n ) , với n 2n A. 3 S = . B. S = 1 2. C. S = . D. S = 1. 2 2
Câu 6: Giả sử y = f (x) và y = g(x) là hai hàm số liên tục tại điểm x . Khẳng định nào sau đây sai? 0 f (x)
A. Hàm số y = f (x).g(x) liên tục tại x .
B. Hàm số y = liên tục tại x . 0 g(x) 0 Trang 24
C. Hàm số y = f (x) - g(x) liên tục tại x .
D. Hàm số y = f (x) + g(x) liên tục tại x . 0 0
Câu 7: Mệnh đề nào sau đây sai? A. 1 1 limqn = , 0 (| q |< ) 1 B. lim = ( * , 0 k Î N ).
C. lim = +¥ . D. limc = c (c là hằng số). nk n ! !
Câu 8: Nếu u và v lần lượt là hai vectơ chỉ phương của hai đường thẳng a và b thì !u ! ! ! ! ! !
A. a ^ b Û ! = 0.
B. a ^ b Û . u v = 0 .
C. a ^ b Û u - v = 0.
D. a ^ b Û u + v = 0. v !!!" !!!" !!!"
Câu 9: Cho hình hộp ABC .
D A' B 'C ' D ' (hình vẽ bên). AB + AD + AA' bằng !!!!" !!!" A. AD'. B. . AC !!!!" !!!!" C. AC '. D. AB'.
Câu 10: Trong không gian cho tứ diện ABCD , gọi G là trọng tâm tam giác ABC . Mệnh đề nào sau đây đúng? !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
A. DA+ DB + DC = 2 . DG
B. DA+ DB + DC = 3 . DG !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" C. 1 1
DA + DB + DC = DG .
D. DA + DB + DC = . DG 2 3 - Câu 11: Tính 1 2n H = lim . n A. H = 1. - B. H = 2. - C. H = 1. D. H = 2.
Câu 12: Nếu lim f (x) = L < 0 và lim g(x) = -¥ thì lim [ f (x).g(x)] bằng x® ® 0 x x 0 x x® 0 x A. + . ¥ B. 0. C. . L D. . -¥
Câu 13: Nếu lim(u = lim(vn ) = ±¥ n ) a và
. Mệnh đề nào sau đây đúng? æ v ö æ u ö æ u ö æ u ö A. lim n = 0. B. n lim = -¥ C. lim n = 0. D. n lim = +¥. çç ÷÷ çç ÷÷ çç ÷÷ çç ÷÷ è u v v v n ø è n ø è n ø è n ø
Câu 14: Trong không gian, ba vectơ được gọi là đồng phẳng nếu
A. các giá của chúng cùng song song với một mặt phẳng.
B. các giá của chúng cùng song song với nhau.
C. các giá của chúng cùng vuông góc với một mặt phẳng.
D. các giá của chúng không cùng nằm trong một mặt phẳng.
Câu 15: Cho hàm số y = f (x) là hàm đa thức bậc ba và thỏa mãn f (0). f (2) < 0. Mệnh đề nào sau đây sai?
A. Phương trình f (x) = 0có ít nhất một nghiệm trên khoảng (0;2).
B. Hàm số y = f (x) liên tục trên ! .
C. Phương trình f (x) = 0không có nghiệm trên khoảng (0;+¥).
D. Phương trình f (x) = 0có ít nhất hai nghiệm trên khoảng (0;+¥). Câu 16: ( 3
lim x - 2x + 2) bằng x®-¥ A. + . ¥ B. . -¥ C. 1. D. 0. Trang 25
Câu 17: Hàm số y = f (x)có giới hạn hữu hạn tại x khi và chỉ khi 0
A. lim f (x) = +¥ .
B. lim f (x) = L.
C. lim f (x) = L.
D. lim f (x) = -¥. x®x ® ®+¥ 0 x x0 x x® 0 x + Câu 18: x 1 lim bằng x 1 ® 2x A. 3. B. 2. C. 1. D. 1 . 2 f (x)
Câu 19: Nếu lim f (x) = a và lim g(x) = ±¥ thì lim bằng x® ® 0 x x 0 x x® 0 x g(x) A. . a B. . -¥ C. 0. D. + . ¥ ! !
Câu 20: Trong không gian tích vô hướng của hai vectơ u và v đều khác vectơ – không được xác định bởi công thức ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! 2 ! 2 ! !
A. u.v = u . v .cos(u,v). B. u.v = u . v .
C. u.v = u . v .sin (u,v). D. .
u v = u . v .cos(u,v).
Câu 21: Cho hàm số y = f (x) xác định trên khoảng K và x Î K. Hàm số y = f (x) được gọi là liên 0 tục tại x nếu 0
A. lim f (x) = x .
B. lim f (x) ¹ f (x ).
C. lim f (x) = f (x ).
D. lim f (x) = x . f (x ) . 0 0 0 0 0 x® ® ® ® 0 x x 0 x x 0 x x 0 x
II. Phần tự luận (3.0 điểm )
Câu 1. (1.0 điểm) Tính x -1 lim . 2 x 1 ® 2x + 3x - 5 3 ì x -1
Câu 2. (1.0 điểm) Cho hàm số ï (x ¹ 1)
f (x) = í x -1
. Tìm a để hàm số f (x) liên tục tại x = 1. 0
ïîa -2x (x =1)
Câu 3. ( 1.0 điểm) Cho tứ diện đều ABCD cạnh bằng .
a Chứng minh AB ^ C . D
------ HẾT ---- ĐÁP ÁN
I. Phần đáp án câu trắc nghiệm: 1 A 6 B 11 B 16 B 21 C 2 C 7 C 12 A 17 B 3 C 8 B 13 C 18 C 4 A 9 C 14 A 19 C 5 D 10 B 15 C 20 A
II. Phần tự luận Câu Hướng dẫn chấm Thang điểm Tính x -1 lim 2 x 1 ® 2x + 3x - 5 x -1 x -1 1 1 (1.0 điểm ) Ta có: lim = lim = lim 2 x 1 ® x 1 ® x 1 2x + 3x - 5 æ 5 ® ö æ 5 ö 0.5 đ 2( x - ) 1 x + 2 x + ç ÷ ç ÷ è 2 ø è 2 ø Trang 26 1 1 = = . 0.5 đ 2.1+ 5 7 3 ì x -1 Cho hàm số ï (x ¹ 1)
f (x) = í x -1
. Tìm a để hàm số f (x) liên
ïîa -2x (x =1) tục tại x =1. 0
+) Tập xác định của hàm số đã cho là ! . 2 3 -
x -1 x + x +1 x 1 ( )( )
2 (1.0 điêm) +) lim f (x) = lim = lim = lim( 2 x + x + ) 1 = 3 x 1 ® x 1 ® x 1 ® x 1 ® 0.25 đ x -1 x -1
+) f (1) = a - 2.1 = a - 2 0.25 đ
+) Hàm số f (x) liên tục tại x =
1 thì lim f (x) = f (1) 0 x 1 ®
Û 3 = a - 2 Û a = 5 0.25 đ
+) Với a = 5 thì hàm số f (x) liên tục tại x = 1. 0.25 đ 0
Cho tứ diện đều ABCD cạnh bằng .
a Chứng minh AB ^ C . D +) Vẽ hình đúng 0.25 đ 3 (1.0 điểm) !!!" !!!" !!!" !!!" !!!" !!!" !!!" AB AD - AC !!!" !!!" !!!" !!!" +) ( - AB CD) . AB CD ( ) . AB AD . AB AC cos , = !!!" !!!" = !!!" !!!" = !!!" !!!" . 0.25 đ AB . CD AB . CD AB . CD 2 2 !!!" !!!" a !!!" !!!" a +) 0 0 . AB AD = . a . a cos 60 = ; . AB AC = . a . a cos 60 = 2 2 0.25 đ 2 2 a a - !!!" !!!" !!!" !!!" +) (AB CD) 2 2 cos , =
= 0 Þ AB,CD = 90 Þ AB ^ C . D 2 ( ) 0 0.25 đ a
-----------Hết---------- Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 9 MÔN TOÁN 11 Trang 27
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho hình chóp S.ABC có SB ^ ( ABC) và AB ^ AC . Hình chóp S.ABC có bao nhiêu mặt là tam giác vuông? A. 2 . B. 1. C. 4 . D. 3 .
Câu 2. Cho hai đường thẳng a, b phân biệt và hai mặt phẳng (P), (Q). Mệnh đề nào sau đây sai?
A. Nếu a//b và a ^ (P) thì b ^ (P).
B. Nếu (P) // (Q) và a ^ (Q) thì a ^ (P).
C. Nếu a // (Q) và b ^ a thì b ^ (Q).
D. Nếu a // (P) và b ^ (P) thì b ^ a
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì song song với nhau.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.
D. Nếu mặt phẳng này chứa một đường thẳng song song với mặt phẳng kia thì hai mặt phẳng đó song song với nhau. Câu 4. Cho hàm số 2
f (x) = x - 4 . Mệnh đề nào sau đây là sai?
A. Hàm số f (x) liên tục trên khoảng ( 2 - ;2).
B. Hàm số f (x) liên tục trên khoảng ( ; -¥ - 3).
C. Hàm số f (x) liên tục trên khoảng (2;+¥).
D. Hàm số f (x) liên tục trên khoảng (3;+ ) ¥ .
Câu 5. Cho tứ diện đều ABCD cạnh .
a Gọi I là trung điểm của DC . Tính cosin của góc giữa hai đường thẳng AD và BI . 2 3 2 3 A. . B. . C. . D. . 2 6 3 2
Câu 6. Trong các phát biểu sau, phát biểu nào đúng? A. lim n
q = 0,với q > . 1 B. lim n q = 0,với 1
- < q < 0. C. 3 limn = 0. D. lim n
q = +¥,với q < . 1
Câu 7. Cho hình hộp ABC .
D A'B'C'D'. Khẳng định nào sau đây sai? !!!" !!!" !!!" !!!!" !!!" !!!" !!!!" !!!!"
A. BC + BA + BB ' = D B '.
B. BC + DC + C 'C = A'C . !!!" !!!" !!!!" !!!!" !!!" !!!" !!!" !!!!" C. D A + D
C + D'D = DB'.
D. AB + AD + AA' = AC '. Câu 8. 2
lim ( x + x +1 + x) bằng x®-¥ 1 A. - . B. +¥ 1 . C. . D. -¥ . 2 2
Câu 9. Nếu lim f (x) = 1
- thì lim[3f (x) - 4] bằng bao nhiêu? x®2 x®2 A. - 1 . B. - 7 . C. 2 . D. 4 .
Câu 10. Trong các giới hạn sau, giới hạn nào bằng +¥ ? A. ( 3 2 lim 2
- x + 3x - 4). B. ( 4 3
lim -x + x - 4x + ) 1 . x®-¥ x®-¥ C. 2 lim
x + 3 - 2x . D. 3 3 2 lim 8
- x + 3x +1 . x®+¥ ( ) x®+ ¥ ( ) Trang 28 2
3x + 5x - 2 a a Câu 11. Cho biết lim = với *
a,bΕ , tối giản. Tính 2 2 a +b . 2 x®- 2 x - 4 b b A. 53 . B. 58 . C. 65 . D. 41.
Câu 12. Trong các khẳng định sau, khẳng định nào sai? 1
A. lim x = x . B. 4 lim x = +¥. C. 5 lim x = -¥. D. lim = +¥. o x® o x x®- ¥ x®-¥ x®+¥ x 2x - 3 Câu 13. lim bằng x 4+ ®- x + 4 A. +¥ . B. 11 - . C. 0 . D. -¥ .
Câu 14. Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Mặt phẳng (AB D
¢ ¢) song song với mặt phẳng nào trong các mặt phẳng sau đây? A. (BC D ¢ ). B. ( A C ¢ C ¢ ).
C. (BDA¢).
D. (BCA¢).
Câu 15. Có bao nhiêu giá trị nguyên dương của m thỏa lim ( 3 2 2
x + 3mx - 2m + m ) = ? 1 x 1 ®- A. 3 . B. 2 . C. 0 . D. 1.
Câu 16. Trong không gian, cho ba đường thẳng phân biệt a,b, c . Khẳng định nào sau đây sai?
A. Nếu a và b cùng vuông góc với c thì a//b .
B. Nếu a//b và c ^ a thì c ^ b .
C. Nếu a//b thì góc giữa hai đường thẳng a và c bằng góc giữa hai đường thẳng b và c .
D. Nếu a và b cùng song song với c thì a//b . 2 3
(2n - 3n)(-n + 2)
Câu 17. Tính giới hạn J = . 5 3 n - 4n + 2 A. J = 2 - .
B. J = 2 .
C. J = +¥ .
D. J = -¥ .
Câu 18. Hàm số nào sau đây liên tục trên R ? 2x -1 -x + 3 A. y = .
B. y = 3 - x .
C. y = tan x. D. y = x + 2 2 x + x +1
Câu 19. Trong các giới hạn sau, giới hạn nào bằng 1? 2n - 3 2021 n æ ö 4n - + 3.2n A. lim . B. lim . C. lim .
D. lim(5n 3.7n - ). ç ÷ 3n + 2n è 2020 ø 5 - 4n
Câu 20. Trong các giới hạn sau, giới hạn nào bằng 0? 3 n + 4n 4 - n A. lim . B. lim . 2 4 - + 3n - 2n 2 2n + n - 3 3 2 -n + n 2 3 + n C. lim . D. lim . 2 2n -1 2 2n -1
Câu 21. Cho phương trình 3 2
x - 3x + 2 = 0. Khẳng định nào sau đây đúng?
A. Phương trình có ít nhất một nghiệm thuộc khoảng (0;1) .
B. Phương trình không có nghiệm âm.
C. Phương trình có duy nhất một nghiệm dương.
D. Phương trình có đúng một nghiệm âm lớn hơn 1 - . PHẦN II: TỰ LUẬN Trang 29 2 n - 3n + 7
Bài 1:(0.5đ) Tính giới hạn: lim . 2 5 - n + 4
Bài 2:(1đ) Xét tính liên tục của hàm số sau tại điểm x = 2 2 ì x - 3x + 2 ï khi x ¹ 2 f (x) = í x - 2 . ïî 1 khi x = 2
Bài 3:(1,5đ) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B . Gọi M là
trung điểm của AB . SM vuông góc với mặt phẳng (ABCD) . Biết AB = AD = 2a, BC = a.
a. Chứng minh BC ^ (SAB) và BD ^ SC .
b. Gọi a là góc giữa đường thẳng CD và mp (SAB). Tính tana .
------------------ HẾT ------------------ ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 C C B A B B C A B A C D D A D A A D C B D Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 10 MÔN TOÁN 11
PHẦN TRẮC NGHIỆM: (7 ĐIỂM)
Câu 1: Chọn khẳng định sai.
A. limu = c ( u = c lim n q = 0 ( q > ) 1 n n là hằng số ). B. . C. 1 1 lim = 0. D. lim = 0 với mọi * k Î • . n k n
Câu 2: Chọn khẳng định đúng. A. lim n
q = +¥ nếu q > 1. B. lim n
q = +¥ nếu q < 1. C. lim n
q = +¥ nếu q > 1. D. lim n
q = +¥ nếu q < 1.
Câu 3: Trong bốn giới hạn sau đây, giới hạn nào là +¥ ? 2 3 + + 2 - 3 + - 2 - + A. n 3n 2 2n 3n n 2n 1 n n 1 lim . B. lim . C. lim . D. lim . 2 n + n 3 n + 3n 3 n - 2n 1- 2n n - Câu 4: Tính tổng 1 1 1 ( 1) S = - + - +...+ +... 3 9 27 3n 1 1 3 A. - 1 . B. . C. . D. . 4 4 2 4 n 1 + n 2 + + Câu 5: Tính 2 3 lim . n n 3 . 2 - 2 9 1 2 A. . B. . C. 1. D. . 2 2 3 Trang 30 2 - Câu 6: Tính x 3 lim . x 3 ®- 2x +1 1 1 A. - 6 . B. - 1 . C. . D. . 3 5 3 2 Câu 7: Tính ( 4 3 lim 2
- x + 5x + x + ) 1 . x®-¥
A. -¥ . B. 0 . C. 4 . D. +¥ .
Câu 8: Với k là số nguyên dương, c là hằng số. Kết quả của giới hạn c lim là: k x®-¥ x A. k x . B. +¥ . C. 0. D. -¥ . 0 Câu 9: Biết f (x)
lim f (x) = L > 0, lim g(x) = 0 và g(x) > 0 với mọi x ¹ x . Khi đó lim bằng: 0 x® ® 0 x x 0 x x® 0 x g(x) A. 0 . B. +¥ . C. -¥ . D. L. 2 + - Câu 10: Cho x 2x 15 a a lim
= với là phân số tối giản. Tính giá trị biểu thức P = a + b . x 3 ® 3x - 9 b b A. 3. B. 11. C. +¥ . D. 5. 2 + - Câu 11: Tính 3x 2x 7 lim . x 1- ® x -1 A. 0. B. + . ¥ C. . -¥ D. 1.
Câu 12: Cho hàm số y = f (x) liên tục trên khoảng ( ;
a b). Điều kiện cần và đủ để hàm số liên tục trên đoạn [ ; a b] là:
A. lim f (x) = f (a) và lim f (x) = f (b).
B. lim f (x) = f (a) và lim f (x) = f (b). + x®a - x®b x a- ® x b+ ®
C. lim f (x) = f (a) và lim f (x) = f (b).
D. lim f (x) = f (a) và lim f (x) = f (b). + x®a + x®b x a- ® x b- ® +
Câu 13: Cho hàm số f (x) x 2021 =
. Chọn khẳng định đúng: x - 2022
A. Hàm số f (x) liên tục trên tập số thực ! .
B. Hàm số f (x) liên tục tại điểm x = 2022 .
C. Hàm số f (x) gián đoạn tại điểm x = 2022 .
D. Hàm số f (x) gián đoạn tại điểm x = 2021 - . 2 ì x - 4 ï ¹
Câu 14: Cho hàm số f (x) khi x 2 = í x - 2
. Mệnh đề nào dưới đây sai? ïî4 khi x = 2
A. Hàm số f (x) liên tục trên ! .
B. Hàm số f (x) liên tục trên khoảng ( ;2 -¥ ).
C. Hàm số f (x) không liên tục trên ! .
D. Hàm số f (x) liên tục trên khoảng (2;+¥).
Câu 15: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Biểu thức nào sau đây đúng? !!!!" !!!" !!!" !!!" !!!!" !!!" !!!" !!!"
A. AB ' = AB + AA' + AD.
B. AC ' = AB + AA' + AD . !!!!" !!!" !!!" !!!!" !!!!" !!!!!" !!!!"
C. AD ' = AB + AD + AC '.
D. A' D = A' B ' + A'C .
Câu 16: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Chọn khẳng định đúng. Trang 31 !!!" !!!!" !!!!" !!!" !!!!" !!!"
A. BD, BD ,¢ BC¢ đồng phẳng.
B. BA ,¢ BD ,¢ BD đồng phẳng. !!!" !!!!" !!!" !!!" !!!!" !!!!"
C. BA ,¢ BD ,¢ BC đồng phẳng.
D. BA ,¢ BD ,¢ BC¢ đồng phẳng.
Câu 17: Cho tứ diện ABCD. Hãy chọn khẳng định đúng. !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
A. BC + AB = DA- DC. B. AC - AD = BD - BC . !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
C. AB - AC = DB - DC. D. AB - AD = CD + BC. !!!" !!!"
Câu 18: Cho hình lập phương ABCD.EFGH. Số đo góc giữa cặp vectơ AB và EG bằng: A. 90° . B. 60° . C. 45°. D. 120° .
Câu 19: Trong không gian cho ba đường thẳng phân biệt a,b,c. Khẳng định nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a / /b .
B. Nếu a / /b và c ^ a thì c ^ b.
C. Nếu góc giữa a và c bằng góc giữa b và c thì a / /b.
D. Nếu a , b cùng nằm trong mặt phẳng (a )và (a ) / /c thì góc giữa a và c bằng góc giữa b và c .
Câu 20: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều
bằng a . Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc giữa hai đường thẳng
MN và SC bằng: A. o 30 . B. o 45 . C. o 60 . D. o 90 . !!!" !!!"
Câu 21. Cho tứ diện đều ABCD có cạnh a . Khi đó . AB BC bằng: 2 2 2 A. a 2 . B. a 3 . C. a 3 - . D. a - . 2 2 2 2
PHẦN TỰ LUẬN: (3 ĐIỂM) + - Câu 1: Tính 2x 5 1 lim . 2 x 2 ®- x - 4 2021 ì x - 2021x + 2020 ï khi x ¹ 1 Câu 2: Cho hàm số 2 f (x) = í (x -1) (m là tham số). ï î2mx+2 khi x =1
Tìm tất cả các giá trị của m để hàm số f ( )
x liên tục tại điểm x = 1.
Câu 3: Cho tứ diện SABC có ba cạnh SA , SB , SC đôi một vuông góc với nhau. Biết SA = SB = SC .
Gọi M là trung điểm của AC . Tính góc giữa hai đường thẳng SM và AB .
ĐÁP ÁN VÀ BIỂU ĐIỂM TỰ LUẬN: + - Câu 1 Tính 2x 5 1 lim . 2 x 2 ®- x - 4 0,25
( 2x + 5 -1)( 2x + 5 +1) = lim 2 x 2 ®-
(x - 4)( 2x + 5 +1) 0,25 2x + 4 = lim 2 x 2
®- (x - 4)( 2x + 5 +1) 0,25 2 = lim x 2
®- (x - 2)( 2x + 5 +1) Trang 32 0,25 1 = - 4 2021 ì x - 2021x + 2020 ï khi x ¹ 1 Cho hàm số 2 f (x) = í (x -1) ï î2mx+2 khi x =1 Câu 2 (m là tham số).
Tìm tất cả các giá trị của m để hàm số f ( ) x liên tục tại điểm x = 1 . 2021 - + f ( x) x 2021x 2020 lim = lim 2 x 1 ® x 1 ® (x -1) 2021 x -1- 2021(x -1) = lim 2 x 1 ® (x -1) 2020 2019 2018 x + x + x + ...+ x +1- 2021 = lim x 1 ® x -1 2020 2019 2018 (x -1) + (x -1) + (x -1) + ...+ (x -1) = lim x 1 ® - x 1 2019 2018 2017 = lim(x + x + x + ...+ x +1) x 1 ® 2018 2017 2016 + lim(x + x + x + ...+ x +1) x 1 ® +...+ lim(x +1) + lim1 x 1 ® x 1 ® 0,25
= 2020 + 2019 + 2018 +...+ 2 +1 2020(1+ 2020) = = 2041210 2 f ( ) 1 = 2m + 2 0,25
Để hàm số liên tục tại x = 1:
2m + 2 = 2041210 Þ m = 1020604 0,25 0,25 Câu 3
Cho tứ diện SABC có ba cạnh SA , SB , SC đôi một
vuông góc với nhau. Biết SA = SB = SC . Gọi M là trung
điểm của AC . Tính góc giữa hai đường thẳng SM và AB . Trang 33 0,25
Gọi N là trung điểm BC 0,25 Þ MN / / AB ∑ ∑ Þ (SM, A )
B = (SM, MN).
Đặt SA = SB = SC = x > 0 . x 2
Tính được: SM = SN = MN = . 2 ∑ 0,25 Þ SM D
N đều Þ SMN = 60°. ∑ ∑ ∑ 0,25
Vậy (SM, AB) = (SM, MN) = SMN = 60° Trang 34