Các bài toán điển hình ôn thi THPTQG 2018: Chuyên đề hàm số

Các bài toán điển hình ôn thi THPTQG 2018: Chuyên đề hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

59 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
CÁCBÀITOÁNĐIỂNHÌNH2018 Page1of59
CÁC BÀI TOÁN ĐIỂN HÌNH
ÔN THI THPTQG 2018
1 Hàm số
1.1 Tìm khoảng đồng biến, nghịch biến của hàm số
Bài toán 1.1
Tìm khoảng đồng biến, nghịch biến của hàm số y =f(x).
• Tìmtậpxácđịnhcủahàmsố.
• Tínhđạohàmvàlậpbảngxétdấucủanó.
• Căncứvàobảngxétdấuđểkếtluận.
Lưu ý 1.1
Cáchtínhnhanhđạohàmcủamộtsốhàmsố
• Hàmsốphânthứcy =
ax+b
cx+d
thìcáchnhớlà“anh dũng trừ bắt cướp”
y
0
=
ad −bc
(cx +d)
2
• Hàmsốphânthứcy =
a
1
x
2
+b
1
x+c
1
a
2
x
2
+b
2
x+c
2
thìcáchnhớlà“anh bạn - ăn cháo
hai lần - bỏ cơm”
y
0
=
a
1
b
1
a
2
b
2
x
2
+2
a
1
c
1
a
2
c
2
x +
b
1
c
1
b
2
c
2
a
2
x
2
+b
2
x +c
2
2
Ví dụ 1.1
Chohàmsốy =x
3
+3x
2
−2.Khẳngđịnhnàosauđâylàkhẳngđịnhđúng?
A. Hàmsốđồngbiếntrênkhoảng
(
−∞;−2
)
và
(
0;+∞
)
.
B. Hàmsốđồngbiếntrênkhoảng
(
−∞;0
)
và
(
2;+∞
)
.
C. Hàm số nghịch biến trên
khoảng
(
−∞;−2
)
và
(
0;+∞
)
.
D. Hàm số nghịch biến trên
khoảng
(
−2;1
)
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page2of59
Cách 1. Tínhnhanhđạohàm:y
0
= 3x
2
+6x =3(x
2
+2x),vàlậpđượcbảngbiến
thiên(thựcrachỉcầnlậpbảngxétdấucủađạohàm):
x −∞ −2 0 +∞
y
0
+ 0 − 0 +
y
% & %
TừđóchọnđápánA.
Cách 2. Chúngtasửdụngtínhnăngtínhđạohàmcủahàmsốbằngmáytính
CASIO,sửdụngphímd/dx.
Riêngđốivớibaloạihàmquenthuộc(bậcba,bậcbốntrùngphươngvàphânthức
bậcnhất)chúngtacóthểcócáchlàmriêng.Chẳnghạncâunày,tabiếtđâylà
hàmsốbậcbavớihệsốa =1> 0nênđồthịcódạngdấu ngã,tứclàsẽđồngbiến
trêncáckhoảng(−∞;x
1
) và(x
2
;+∞),nghịchbiếntrênkhoảng(x
1
;x
2
) vớix
1
,x
2
là
hainghiệmcủaphươngtrìnhy
0
=0.Dođó,cóthểkhẳngđịnhđượcngayphương
ánAlàphươngánđúng.Sauđâylàmộtsốbàitậpđiểnhình.
Ví dụ 1.2
ĐH năm 2017 Mã đề 101
Hàmsốy =
2
x
2
+1
nghịchbiếntrênkhoảngnàodướiđây?
A. (0;+∞). B. (−1;1). C. (−∞;+∞). D. (−∞;0).
Hướng dẫn. TậpxácđịnhD =R. Đạohàm
y
0
=
−4x
x
2
+1
2
Dođó,y
0
< 0⇔ x > 0.ChọnphươngánA.
Ví dụ 1.3
Hàmsốnàodướiđâyđồngbiếntrênkhoảng(−∞;+∞)?
A. y =
x+1
x+3
. B. y =x
3
+x. C. y =
x−1
x−2
. D. y =−x
3
−
3x.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page3of59
1.2 Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài toán 1.2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y =f(x) trên tập
K.
Chúngtacóhaiphươngphápchủyếu:
• LậpbảngbiếnthiêncủahàmsốtrênK. NếutậpK làmộtđoạn[a;b]
thìkhôngcầnlậpbảngbiếnthiênmàchỉcần
+Giảiphươngtrìnhy
0
= 0vàtìmracácđiểmx
i
màtạiđóy
0
= 0
hoặcy
0
khôngxácđịnh.
+Tínhvàsosánhcácgiátrịf(a),f(b),f(x
i
)đểtìmragiátrịlớnnhất,
giátrịnhỏnhất.
• Sửdụng bất đẳng thứcquen thuộc hoặc điều kiện có nghiệm của
phươngtrình.
Lưu ý 1.2
Lưuýrằng,hàmsốy =f(x)muốnđạtđượcgiátrịlớnnhấthoặcgiátrị
nhỏnhấtbằngM thìtaphảitìmđượcítnhấtmộtsốx
0
hữuhạnsaocho
f(x
0
)=M.
Lưu ý 1.3
Điềukiệncónghiệmcủamộtsốphươngtrìnhquenthuộc:
• Phươngtrìnhbậchaiđiềukiệnlà∆> 0.
• Phươngtrìnhsinx =m,cosx =m điềukiệnlà|m| 6 1.
• Phươngtrìnhasinx +bcosx =c điềukiệnlà
|c|
√
a
2
+b
2
6 1hayc
2
6
a
2
+b
2
.
Cầnnhớhaicáchđểtìmgiátrịlớnnhất,giátrịnhỏnhất.Haicáchđólàgì?Đôi
khichúngtahayđổibiến(đặtẩnphụ)đểđưavềkhảosátmộthàmsốđơngiản
hơn.
Ví dụ 1.4
ĐH năm 2017 Mã đề 102
Chohàmsốy =
x+m
x+1
,vớim làthamsốthực,thỏamãnmax
[1;2]
y +min
[1;2]
y =
16
3
.
Mệnhđềnàosauđâylàđúng?
A. m 6 0. B. m > 4. C. 0< m 6 2. D. 2< m 6 4.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page4of59
Hướng dẫn. Điềukiệnxácđịnhx 6=1,nênhàmsốluônxácđịnhvàliêntụctrên
đoạn[1;2]. Có
y
0
=
1−m
(x +1)
2
Chỉcóthểxảyrahaikhảnăng,nếuy
0
> 0thìhàmsốđồngbiếntrênđoạn[1;2],
dođómax
[1;2]
y =y(2),min
[1;2]
y =y(1).Ngượclại,nếuy
0
< 0thìhàmsốnghịchbiến
trênđoạn[1;2],dođómax
[1;2]
y =y(1),min
[1;2]
y =y(2).Dùchokhảnăngnàoxảyrathì
max
[1;2]
y,min
[1;2]
y cũngchỉcóthểnhậnhaigiátrịy(1) vày(2).Dođó,yêucầubàitoán
tươngđươngvới
y(1)+y(2)=
16
3
⇔
1+m
2
+
2+m
3
=
16
3
Giảiphươngtrìnhnày,tìmđượcm =5,tứclàm > 4.
Ví dụ 1.5
Tìmm đểhàmsốf(x)=−x
4
−2x
2
+m cógiátrịlớnnhấttrênkhoảng(−2;4)
bằng2.
Hướng dẫn. Talậpđượcbảngbiếnthiêncủahàmsốf(x) nhưsau
x −2 0 3
f
0
(x) + 0 −
f(x)
m−24%
m
& m − 99
Suyra,giátrịlớnnhấtcủahàmsốtrênkhoảng(−2;3)làm.Dođó,yêucầubài
toántươngđươngvớim =2.
Ví dụ 1.6
Xéthàmsốy =
x
3
−3x +1
trênđoạn[0;3].Mệnhđềnàotrongcácmệnh
đềsaulàsai?
A. Giátrịnhỏnhấtcủahàmsốtrênđoạn[0;3] là1.
B. Giátrịlớnnhấtcủahàmsốtrênđoạn[0;3] là19.
C. Hàmsốcógiátrịlớnnhấtvàgiátrịnhỏnhấttrongđoạn[0;3].
D. Hàmsốđạtgiátrịlớnnhấtkhix =3.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page5of59
Ví dụ 1.7
ĐH Khối B năm 2003
Tìmgiátrịlớnnhất,giátrịnhỏnhấtcủahàmsốf(x)=x +
√
4−x
2
.
Hướng dẫn. TậpxácđịnhD =[−2;2].Tacóbảngbiếnthiêncủahàmsốđãcho:
x −2
√
2 2
f
0
(x) + 0 −
f(x)
−2%
2
√
2
& 2
Nhưvậymaxf(x)=f(
√
2)=2
√
2,minf(x)=f(−2)=−2.
1.3 Tìm điều kiện để hàm số đơn điệu
Bài toán 1.3
Tìm điều kiện để hàm số y =f(x) đồng biến trên tập K.
• Hàmsốy =f(x) đồngbiếntrêntậpK khivàchỉkhi
+y
0
> 0, ∀x ∈ K nếudấucủay
0
còn phụthuộcbiếnx, chẳnghạn
cáchàmđathứcbậcba,bậcbốn.
+y
0
> 0, ∀x ∈ K nếudấucủay
0
không còn phụthuộcbiếnx, chẳng
hạncáchàmy =
ax+b
cx+d
.
• Xétcáctìnhhuốngsau:
+NếutậpK làR thìsửdụngđịnhlýdấutamthứcbậchai.
+Nếucôlậpđượcthamsốm đưađiềukiệntrênvềdạngm 6
g(x), ∀x ∈ K hoặcm > g(x), ∀x ∈ K thìsửdụngnguyênlýcực
trị.
+Nếukhôngthìlậpbảngbiếnthiêncóchứacảthamsốđểbiện
luận.
Lưu ý 1.4
Định lý dấu tam thức bậc hai
Chotamthứcbậchaif(x)=ax
2
+bx +c vớia 6=0 thì
• f(x)> 0,∀x ∈ R ⇔
(
a > 0
∆6 0.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page6of59
• f(x)6 0,∀x ∈ R ⇔
(
a < 0
∆6 0.
Lưu ý 1.5 Nguyên lý cực trị
• m 6 g(x), ∀x ∈ K ⇔ m 6 min
K
g(x),
• m > g(x), ∀x ∈ K ⇔ m > max
K
g(x).
Ví dụ 1.8
Chohàmsốy =−x
3
−mx
2
+(4m+9)x +5 vớim làthamsố.Cóbaonhiêu
giátrịnguyêncủam đểhàmsốnghịchbiếntrênkhoảng(−∞;+∞)?
A. 4. B. 6. C. 5. D. 7.
Hướng dẫn. Cóy
0
=−3x
2
−2mx +4m+9.HàmsốđãchonghịchbiếntrênR khi
vàchỉkhi
y
0
6 0∀x ∈ R ⇔
(
a =−1< 0
∆
0
=m
2
+3(4m+9)6 0
Giảihệnàytìmđược−96 m 6 −3.Kếthợpđiềukiệnm nguyên,tađượctấtcả7
giátrịcủam.
Ví dụ 1.9
Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
1
3
x
3
+x
2
+mx +1
nghịchbiếntrênkhoảng(2;3).
A. m 6 −15. B. m > −15. C. m 6 −8. D. m > −8.
Hướng dẫn. Yêucầubàitoántươngđươngvớiy
0
=x
2
+2x +m 6 0∀x ∈ [2;3].
Điềunàytươngđươngvới
m 6 min
[2;3]
−x
2
−2x
=min
[2;3]
f(x)
x 2 3
f
0
(x) −
f
−8
& −15
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page7of59
Tìmgiátrịnhỏnhấtcủahàmsốf(x) = −x
2
− 2x trênđoạn[2;3]vàsuyragiátrị
cầntìmcủam làm 6 −15.
Nhận xét. Bàinàycóthểsửdụngđịnhlýđảovềdấutamthứcbậchai,xemởtrang
23,nhưsau.
• Nhậnxétrằnghệsốa > 0nênhàmsốchỉcóthểnghịchbiếnởkhoảng
(
x
1
;x
2
)
trongđóx
1
,x
2
làhainghiệmcủaphươngtrìnhy
0
=0.
• Dođó,yêucầubàitoántrởthànhtìmđiềukiệnđểphươngtrìnhy
0
=0có
hainghiệmthỏamãnx
1
6 2< 36 x
2
. Điềukiệncầnvàđủlà
(
a·y
0
(2)6 0
a·y
0
(3)6 0.
Giảihệbấtphươngtrìnhnàycũngtìmđượcđápsốnhưcáchtrên.
Ví dụ 1.10
Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
x+m
√
x
2
+1
đồngbiến
trongkhoảng(0;+∞).
A. m 6 −1. B. m 6 2. C. m 6 1. D. m 6 0.
Ví dụ 1.11
Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
x
3
3
− (m +1)x
2
+
(m
2
+2m)x +1 nghịchbiếntrên(2;3).
A. 1< m < 2. B. m > 2. C. m < 1. D. 16 m 6 2.
Hướng dẫn. Yêucầubàitoántươngđươngvớiy
0
= x
2
− 2(m +1)x +m
2
+2m 6
0, ∀x ∈ (2;3).Rõràngchúngtakhôngcôlậpđượcthamsốm nênphảiđưavềviệc
lậpbảngbiếnthiên.Phươngtrìnhy
0
=0luônluôncónghiệmx
1
=m < x
2
=m+2
nêntacóbảngbiếnthiênsau:
x −∞ m m+2 +∞
y
0
(x) + 0 − 0 +
y
−∞%
y
1
& y
2
%
+∞
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page8of59
Suyra,hàmsốđãchonghịchbiếntrênkhoảng(2;3) khivàchỉkhikhoảng(2;3) là
tậpconcủakhoảng(m,m+2).Nghĩalà
(
m 6 2
36 m+2
Từđótìmđượcđápsố16 m 6 2.
Ví dụ 1.12
Tìmtấtcảcácgiátrịcủam đểhàmsốy =
√
x
2
+4mx +4m
2
+3nghịch
biếntrênkhoảng
(
−∞;2
)
?
A. m > −1. B. m < 2. C. m < −1. D. m > 2.
Hướng dẫn. Hàmsốluônxácđịnhvàliêntụcvớimọix ∈ R. Dođó,tasẽtìmđiều
kiệnđểhàmsốluônnghịchbiếntrênnửakhoảng(−∞;2].Tacó
y
0
=
x +2m
√
x
2
+4mx +4m
2
+3
.
Hàmsốnghịchbiếntrên
(
−∞;2
)
khivàchỉkhi
y
0
6 0,∀x 6 2⇔ x +2m 6 0,∀x 6 2.
Từđótìmđượcđápsốm 6 −1.
Ví dụ 1.13
Tìmtấtcảcácgiátrịcủam đểhàmsốy =
−cosx +m
cosx +m
đồngbiếntrên
khoảng
0;
π
2
.
A. m > 0 hoặcm 6 −1.
B. m > 1.
C. m > 0.
D. m 6 −1.
Hướng dẫn. Đặtt =cosx thìtathấyhàmsốy =cosx nghịchbiếntrên
0;
π
2
,
nênhàmsốđãchođồngbiếntrên
0;
π
2
khivàchỉkhihàmsốy =
−t+m
t+m
nghịch
biếntrên
(
0;1
)
.Điềukiệncầnvàđủlà
(
y
0
=
−2m
(
t+m
)
2
< 0
−m /∈
(
0;1
)
⇔ m > 0.
Nhưvậy,tachọnđápánC.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page9of59
Nhận xét. Bàinàycóthểlàmtrựctiếpmàkhôngcầnđặtẩnphụ.Sửdụngcông
thứctínhđạohàmcủahàmsốhợp,tatìmđược
y
0
=
−2m
(cosx +m)
2
·
(
−sinx
)
.
Chúýrằngtrongkhoảng(0;
π
2
)thìsinx > 0, nênyêucầubàitoántươngđươngvới
(
2m
(cosx+m)
2
> 0
cosx +m 6=0,∀x ∈
0;
π
2
Từđócũngtìmđượcđápsốnhưtrên.
1.4 Cực trị của hàm số
Bài toán 1.4
Tìm cực trị của hàm số y =f(x).
• Đốivớimộthàmsốcụthể,talậpbảngxétdấucủađạohàmvàkết
luận.
• Đốivớihàmẩn,muốnx
0
thuộctậpxácđịnhlàmộtđiểmcựctrịcủa
hàmsốy =f(x) thìphảithỏamãnhaiđiềukiện:
+f
0
(x
0
)=0 hoặcf
0
(x) khôngxácđịnhtạix
0
.
+f
0
(x)phảiđổidấukhiđiquax
0
,nếuđổidấutừdươngsangâm
(tứclàhàmsốchuyểntừđồngbiếnsangnghịchbiến)thìx
0
là
điểmcựcđại;đổidấutừâmsangdươngthìx
0
làđiểmcựctiểu.
Cũngcóthểsửdụngđếnđạohàmcấphai,f
00
(x
0
)< 0thìx
0
là
điểmcựcđại;cònf
00
(x
0
)> 0 thìx
0
làđiểmcựctiểu.
Lưu ý 1.6
Cầnphânbiệtrõbakháiniệmđiểm cực trị của hàm số, điểm cực trị của đồ
thị hàm số vàgiá trị cực trị của hàm số.
Lưu ý 1.7
Phươngtrìnhđườngthẳngđiquahaiđiểmcựctrịcủa
• Đồthịhàmsốbậcbay =ax
3
+bx
2
+cx +d chínhlàphầndưkhichia
y choy
0
.Thựchiệnphépchia,tađượcy =y
0
·
1
3
x +
b
9a
+mx +n thì
đườngthẳngcầntìmchínhlày =mx +n.Cáchtìmnhanhnhưsau:
+Tanhậnthấymx +n =y−y
0
·
1
3
x +
b
9a
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page10of59
+Sửdụngmáytính,viếthàmy−y
0
·
1
3
x +
b
9a
rồiCALC tạix =0
tìmđượcn,CALC tiếptạix =1thuđượcm+n vàtừđótìmđược
m.
• Đồthịhàmsốphânthứcbậchaichiabậcnhấty =
ax
2
+bx+c
dx+e
=
u(x)
v(x)
chínhlày =
u
0
(x)
v
0
(x)
.
Ví dụ 1.14
Chohàmsốy = f
(
x
)
cóđồthịhàmsốy = f
0
(
x
)
nhưhìnhvẽbên.Hỏihàm
sốy =f
(
x
)
cóbaonhiêuđiểmcựctrị?
A. 1 B. 2 C. 3 D. 4.
Ví dụ 1.15
GọiA,B,C làbađiểmcựctrịcủađồthịhàmsốy =−x
4
+2x
2
+1. Tính
diệntíchS củatamgiácABC.
A. S =1. B. S =2. C. S =3. D. S =4.
Ví dụ 1.16
Viếtphươngtrìnhđườngthẳngđiquahaiđiểmcựctrịcủađồthịhàmsố
y =x
3
−3x
2
+2.
Đáp số. y =−2x +2.
Ví dụ 1.17
Viếtphươngtrìnhđườngthẳngđiquahaiđiểmcựctrịcủađồthịhàmsố
y =x
3
+3x
2
−5x +1.
Đáp số. lày =−
16
3
x +
8
3
.
Ví dụ 1.18
Phươngtrìnhđườngthẳngđiquahaiđiểmcựctrịcủađồthịhàmsốy =
x
3
−x +4 là...
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page11of59
Ví dụ 1.19
ĐH năm 2017 Mã đề 101
Đồthịhàmsốy = x
3
− 3x
2
− 9x +1 cóhaiđiểmcựctrịA vàB.Điểmnào
dướiđâythuộcđườngthẳngAB?
A. P(1;0). B. M(0;−1). C. N(1;−10). D. Q(−1;10).
Ví dụ 1.20
ĐH năm 2017 Mã đề 103
Đồthịcủahàmsốy =−x
3
+3x
2
+5 cóhaiđiểmcựctrịA vàB.Tínhdiện
tíchS củatamgiácOAB vớiO làgốctọađộ.
A. S =9. B. S =
10
3
. C. S =5. D. S =10.
Ví dụ 1.21
Hàmsốy =sinx − 2cosx cóbaonhiêucựctrịtrênđoạn[−π,π]?
Ví dụ 1.22
Hàmsốy =sinx − x cóbaonhiêucựctrịtrênđoạn[0,10]?
1.5 Tìm điều kiện để hàm số đạt cực trị tại điểm cho trước
Bài toán 1.5
Tìm điều kiện của m để hàm số y =f(x) đạt cực trị tại x
0
.
• Điều kiện cần. Hàmsốđạtcựctrịtạix
0
thìf
0
(x
0
)=0hoặcf
0
(x
0
)không
xácđịnh.Từđótìmđượcgiátrịcủam.
• Điều kiện đủ. Vớim vừatìmđược,thayvàohàmsốđãchovàtìmcực
trịcủanóđểkiểmtra.
Ví dụ 1.23
Chohàmsố:y =
1
3
x
3
−mx
2
+(m
2
−m+1)x +1.Xácđịnhm đểhàmsốđạt
cựcđạitạiđiểmx =1.
Cách 1. Tacóy
0
=x
2
−2mx +m
2
−m+1,y
00
=2x − 2m.
• Điều kiện cần: Giảsửhàmsốđạtcựcđạitạix =1.Suyraf
0
(1)=0⇔ m =
1,m =2.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page12of59
• Điều kiện đủ:
+Vớim =1hàmsốđãchotrởthànhy =
1
3
x
3
− x
2
+x +1.Tacóbảng
biếnthiênsau:
x −∞ 1 +∞
y
0
(x) + +
y
−∞%
4
3
%
+∞
Căncứvàobảngbiếnthiêntathấyhàmsốkhông đạt cực đại tạix =1.
Dođó,m =1 khôngthỏamãnyêucầu.
+Vớim =2 hàmsốđãchotrởthànhy =
1
3
x
3
−2x
2
+3x +1.Tacóbảng
biếnthiên:
x −∞ 1 3 +∞
y
0
(x) + 0 − 0 +
y
−∞%
7
3
& 1%
+∞
Tathấy,khim =2 thìhàmsốđạtcựcđạitạix =1.
Vậygiátrịcầntìmlàm =2.
Cách 2. Taxéthaitrườnghợp:
• Khiy
00
(1)=0⇔ m =1 thìhàmsốtrởthànhy =
1
3
x
3
−x
2
+x +1.Lậpbảng
biếnthiênnhưCách 1 vàkhẳngđịnhm =1 khôngthỏamãnyêucầu.
• Khiy
00
(1)6=0⇔ m 6=1 thìhàmsốđạtcựcđạitạix =1 khivàchỉkhi
(
y
0
(1)=0
y
00
(1)< 0
⇔ m =2
Kếthợphaitrườnghợpđượcđápsốm = 2. Vậyvớim = 2 thìhàmsốđãchođạt
cựcđạitạix =1.
Ví dụ 1.24
ĐH năm 2017 Mã đề 102
Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
1
3
x
3
−mx
2
+(m
2
−
4)x +3 đạtcựcđạitạix =3.
A. m =1. B. m =−1. C. m =5. D. m − 7.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page13of59
Ví dụ 1.25
Tìmm đểhàmsốy =
mx
2
+x+m
x−1
đạtcựcđạitạix =2.
Hướng dẫn. TậpxácđịnhD =R.Tacóy
0
=
mx
2
−2mx−1−m
(x−1)
2
.
• Điềukiệncần:Giảsửhàmsốđạtcựcđạitạix =2. Suyray
0
(2)=0⇔ m =
−1.
• Điềukiệnđủ:Khim =−1 hàmsốđãchotrởthànhy =
−x
2
+x−1
x−1
.Tacóbảng
biếnthiên:
x −∞ 0 1 2 +∞
y
0
(x) − 0 + + 0 −
y
+∞
& 1%
+∞
−∞%
−3
& −∞
Vậyvớim =−1 thìhàmsốđãchođạtcựcđạitạix =2.
1.6 Tìm điều kiện để hàm số có cực trị
Bài toán 1.6
Tìm điều kiện để hàm số y =f(x) có cực trị.
Tổngquát,muốnhàmsốcócựctrịthìđạohàmphảicónghiệmvàphảiđổi
dấukhiđiquanghiệmnày.Ởđâychúngtaxétbaloạihàmthườnggặp.
• Hàmsốbậcbay = ax
3
+bx
2
+cx +d,vớia 6=0,thìđạohàmy
0
là
tamthứcbậchainêncóhaikhảnăng:
+Phươngtrìnhy
0
=0vônghiệmhoặccónghiệmképthìhàmsố
khôngcótrị.
+Phươngtrìnhy
0
=0cóhainghiệmphânbiệtthìhàmsốcóhai
điểmcựctrị.
Nhưvậy,hàmsốbậcbachỉcóhaitìnhhuốngkhông có cực trị vàcó
cực trị,nếucóthìsẽcóhaiđiểmcựctrị,gồmmộtđiểmcựcđạivàmột
điểmcựctiểu.
• Hàmsốbậcbốntrùngphươngy =ax
4
+bx
2
+c,vớia 6=0, thìphương
trìnhy
0
=0 tươngđươngvới
x =0
x
2
=−
b
2a
. (∗)
Phươngtrìnhy
0
=0 nàyluôncónghiệmx =0 nêntacóhaikhảnăng:
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page14of59
+Phươngtrình(∗) vônghiệmhoặccónghiệmkép,nghiệmképnày
cũngbằng0,thìhàmsốcómộtđiểmcựctrị.
+Phươngtrình(∗)cóhainghiệmphânbiệt,thìhàmsốcóbađiểm
cựctrị.
Nhưvậy,hàmsốbậcbốntrùngphươngluônluôncócựctrị,cóthểcó
mộthoặcbađiểmcựctrị.
• Hàmsốphânthứcbậcnhấttrênbậcnhấtthìkhôngcócựctrị.
Ví dụ 1.26
Tìmđiềukiệnđểhàmsốy =
x
2
+2mx+1
x−1
cócựctrị?
Hướng dẫn. Điềukiệnxácđịnhx 6=1. Tacóy
0
=
x
2
−2x−2m−1
(x−1)
2
nên
y
0
=0⇔
x
2
−2x −2m−1
(x − 1)
2
=0⇔
(
x 6=1
x
2
−2x −2m−1=0 (∗)
Đặtg(x)=x
2
−2x − 2m−1.Hàmsốđãchocócựctrịkhivàchỉkhiphươngtrình
(∗) cóhainghiệmphânbiệtkhác1
⇔
∆
0
> 0
g(1)6=0
⇔
2m+2> 0
−2m−26=0
⇔
m > −1
m 6=−1
⇔ m > −1
Vậyvớim > −1 thìhàmsốcócựcđạivàcựctiểu.
Ví dụ 1.27
Tìmđiềukiệnđểhàmsốy =x
3
−3x
2
+mx +m−1 cócựctrị?
Hướng dẫn. Tacóy
0
=3x
2
−6x +m nên
y
0
=0⇔ 3x
2
−6x +m =0 (1)
Hàmsốcócựctrịkhivàchỉkhiphươngtrình(1) cóhainghiệmphânbiệt
⇔ ∆
0
=9− 3m > 0⇔ m < 3
Vậyvớim < 3 thìhàmsốluôncócựcđạivàcựctiểu.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page15of59
Ví dụ 1.28
Tìmđiềukiệnđểhàmsốy =x
4
−2(m+1)x
2
−m cócựcđại,cựctiểu?
Hướng dẫn. Tacóy
0
=4x
3
−4(m+1)x =4x(x
2
−m− 1) nên
y
0
=0⇔ 4x(x
2
−m− 1)=0⇔
x =0
x
2
=m +1 (∗)
Dođó,hàmsốcócựcđạivàcựctiểukhivàchỉkhiphươngtrình(∗) cóhainghiệm
phânbiệtkhác0
⇔ m +1> 0⇔ m > −1
Vậyvớim < −1 thìhàmsốluôncócựcđạivàcựctiểu.
Ví dụ 1.29
ĐH Khối B năm 2002
Tìmm đểhàmsốy =mx
4
+(m
2
−9)x
2
+10 cóbađiểmcựctrị?
Đáp số. m < −3 hoặc0< m < 3.
Ví dụ 1.30
Chohàmsốy =f
(
x
)
cóđạohàmy
0
=x
2
−
√
12x +
1
4
(
b+3a
)
, ∀x ∈ R.Biết
rằnghàmf(x)sốluôncóhaicựctrịvớia,b làcácsốnguyênkhôngâmthỏa
mãn3b−a 6 6.TìmgiátrịlớnnhấtcủabiểuthứcP =2a +b.
A. 1. B. 9. C. 8. D. 6.
Hướng dẫn. Tacóy
0
= x
2
−
√
bx −
3
4
a +3. Hàmsốluôncóhaicựctrịkhivàchỉ
khi
∆> 0⇔ 12−b− 3a > 0.
Nhưvậycácsốnguyêna vàb thỏamãncácđiềukiệnsau
a > 0
b > 0
3b−a 6 6
b+3a < 12
BiểudiễncácbấtphươngtrìnhnàylênhệtrụctọađộOab tasẽđượcmiềntứgiác
OABC vớiO
(
0;0
)
, A
(
0;2
)
, B
(
3;3
)
, C
(
4;0
)
.Trongsốcácđiểmcótọađộnguyên
thuộcmiềntứgiácOABC thìcóđiểmM
(
3;2
)
làmbiểuthứcP đạtgiátrịlớnnhất,
vàgiátrịlớnnhấtđólàP
max
=2.3+2=8.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page16of59
1.7 Tìm điều kiện để hàm số có cực trị thỏa mãn yêu cầu cho trước
Bài toán 1.7
Tìm điều kiện để hàm số y =f(x) có cực trị thỏa mãn yêu cầu cho
trước.
Đốivớibàitoánnày,trướctiêntatìmđiềukiệnđểhàmsốcócựctrịđã.Sauđó,
nếuphươngtrìnhy
0
=0cónghiệmđẹpthìtatìmcụthểcácnghiệmnày,nếukhông
thìgọicácnghiệmlàx
1
,x
2
vàsửdụngViète.
Ví dụ 1.31
CĐ năm 2009
Tìmm đểhàmsốy =x
3
−(2m −1)x
2
+(2−m)x +2 cócựcđại,cựctiểuvà
cácđiểmcựcđại,cựctiểucóhoànhđộdương?
Hướng dẫn. TậpxácđịnhD =R.
Cóy
0
=3x
2
−2(2m− 1)x +(2− m) nênphươngtrìnhy
0
=0 tươngđươngvới
3x
2
−2(2m− 1)x +(2− m) (2)
Hàmsốđãchocócựcđại,cựctiểuvàcácđiểmcựcđại,cựctiểucóhoànhđộdương
⇔ phươngtrình(2) cóhainghiệmdươngphânbiệt
⇔
∆
0
> 0
S > 0
P > 0
⇔
(2m−1)
2
−3(2− m)> 0
2m−1> 0
2−m > 0
⇔
5
4
< m < 2
Vậyđápsốcầntìmlà
5
4
< m < 2.
Ví dụ 1.32
ĐH Khối D năm 2012
Tìmm đểhàmsốy =
2
3
x
3
−mx
2
−2
3m
2
−1
x+
2
3
cóhaiđiểmcựctrịx
1
,x
2
thỏamãnx
1
x
2
+2(x
1
+x
2
)=1
Hướng dẫn. Cóy
0
=2x
2
−2mx −2(3m
2
−1)nênphươngtrìnhy
0
=0 tươngđương
với
2x
2
−2mx −2(3m
2
−1) (3)
Hàmsốđãchocóhaiđiểmcựctrị⇔ phươngtrình(3) cóhainghiệmphânbiệt
⇔ ∆
0
> 0⇔ m ∈ (−∞,−
2
√
13
)∪(
2
√
13
,+∞)
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page17of59
Khiđó,x
1
,x
2
lànghiệmcủaphươngtrình(3)vàtheoViètetacóx
1
+x
2
=m và
x
1
x
2
=1− 3m
2
Dođó,yêucầucủađềbàix
1
x
2
+2(x
1
+x
2
)=1 tươngđươngvới
1−3m
2
+2m =1⇔ m =
2
3
hoặcm =0
Kếthợpđiềukiệnđượcđápsốm =
2
3
.
Ví dụ 1.33
Tìmm đểđồthịhàmsốy =
1
3
x
3
− (m − 2)x
2
+(m − 2)x +
1
3
m
2
cóhaiđiểm
cựctrịnằmvềphíabênphảitrụctung?
1.m > 2
2.m > 3∨ m < 2
3.m > 3
4.m < 2
Hướng dẫn. TrongmặtphẳngtọađộOxy,nhữngđiểmnằmvềbênphảitrụctung
nghĩalànhữngđiểmnàycóđặcđiểmgì?Đồthịhàmsốcóhaiđiểmcựctrịnằm
vềbênphảitrụctungnghĩalàhoànhđộcủachúngdương?Hoànhđộtìmđượctừ
đâu?
Mởrộngbàitoán,haiđiểmcựctrịnằmvềbêntráitrụctung,nằmvềhaiphíađối
vớitrụctung.
Ví dụ 1.34
Chứngminhrằngvớimọim 6=0thìđồthịhàmsốy =mx
3
−3mx
2
+3
(
m−1
)
luôncóhaiđiểmcựctrị.GiảsửhaiđiểmcựctrịnàylàA,B. Tìmm để
2AB
2
−(OA
2
+OB
2
)=20 vớiO làgốctọađộ.
Hướng dẫn. ChỉraA(0,3m−3) vàB(2,−m− 3) vàtìmđượcm =1,m =−
17
11
.
Ví dụ 1.35
Chohàmsốy =x
4
−2m
2
x
2
+1.Xácđịnhm đểhàmsốcó3điểmcựctrịlà
3đỉnhcủatamgiácvuôngcân.
Hướng dẫn. Tacóy
0
=4x
3
−4m
2
x =4x(x
2
−m
2
) nên
y
0
=0⇔
x =0
x
2
−m
2
=0 (∗)
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page18of59
Hàmsốcóbađiểmcựctrị⇔ Phươngtrình(∗)cóhainghiệmphânbiệtkhác0
⇔ m 6=0
Khiđó,bađiểmcựctrịcủađồthịhàmsốlà
A(0;1),B(m;−m
4
+1),C(−m;−m
4
+1)
Tacó
−→
AB =(m;−m
4
)⇒ AB =
p
m
2
+m
8
−→
AC =(−m;−m
4
)⇒ AC =
p
m
2
+m
8
Vì∆ABC cântạiA nên3điểmcựctrịcủađồthịtạothànhmộttamgiácvuôngcân
khivàchỉkhi
−→
AB ⊥
−→
AC ⇔
−→
AB.
−→
AC =0⇔ −m
2
+m
8
=0⇔ m
2
(m
6
−1)=0⇔
m =0
m =±1
Đốichiếuvớiđiềukiện,đượcđápsốm =±1.
Ví dụ 1.36
Tìmcácgiátrịcủam đểhàmsốy =
1
3
x
3
−
1
2
mx
2
+
m
2
−3
x cócựcđạix
1
,
cựctiểux
2
vàx
1
,x
2
làđộdàicáccạnhgócvuôngcủamộttamgiácvuôngcó
độdàicạnhhuyềnbằng
q
5
2
.
Hướng dẫn. TậpxácđịnhD =R.
Cóy
0
=x
2
−mx +m
2
−3 nêny
0
=0⇔ x
2
−mx +m
2
−3=0
Vìy
0
làmộttamthứcbậchainênhàmsốcócựcđạix
1
,cựctiểux
2
thỏayêucầu
bàitoánkhivàchỉkhiphươngtrìnhy
0
=0 có2nghiệmdươngphânbiệt
⇔
∆> 0
S > 0
P > 0
⇔
4−m
2
> 0
m > 0
m
2
−3> 0
⇔
√
3< m < 2
Khiđó,ápdụngViètetađược
x
2
1
+x
2
2
=
5
2
⇔ 2(x
1
+x
2
)
2
−4x
1
x
2
=5⇔ 2m
2
−4(m
2
−3)=5⇔ m =±
√
14
2
Đốichiếuđiềukiệnởtrêntacógiátrịm =
√
14
2
thỏayêucầubàitoán
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page19of59
Ví dụ 1.37
Tìmm đểđồthịhàmsốy =−x
3
+3mx
2
−3m−1 cócựcđạivàcựctiểuđối
xứngnhauquađườngthẳngd :x +8y −74=0.
Hướng dẫn. Cóy
0
= −3x
2
+6mx =0nênđồthịhàmsốcócựctrịkhivàchỉkhi
m 6=0. Suyra,mộtđiểmcựctrịcủađồthịhàmsốlàA(0;−3m − 1).Yêucầubài
toántươngđươngvớitrungđiểmI củahaiđiểmcựctrịcủađồthịhàmsốphảinằm
trênđườngthẳngd vàIA ⊥ d.MàI cũngchínhlàđiểmuốncủađồthịhàmsố,nên
cóI(m;2m
3
−3m− 1).Dođó,điềukiệncầnvàđủlà
(
−→
AI ·
~
u
d
=0
m+8(2m
3
−3m− 1)−74=0
Từđótìmđượcm =2.
Lưu ý 1.8
Bađiểmcựctrịcủađồthịhàmsốbậcbốntrùngphươngluôntạothànhmột
tamgiáccân.
Ví dụ 1.38
ĐH Khối A năm 2012
Tìmm đểbađiểmcựctrịcủađồthịhàmsốy =x
4
− 2(m +1)x
2
+m
2
tạo
thànhbađỉnhcủamộttamgiácvuông.
Hướng dẫn. Tacóy
0
=4x
3
−4(m+1)x =4x(x
2
−m− 1).Dođó,đồthịhàmsốcó
bađiểmcựctrị⇔ m > −1. Khiđó,bađiểmcựctrịcủađồthịhàmsốlà
A(0,m
2
),B(
√
m+1,−2m− 1) vàC(−
√
m+1,−2m− 1)
Suyra
−→
AB =(−
√
m+1,−(m+1)
2
),
−→
AC =(
√
m+1,−(m+1)
2
).Nhậnthấytamgiác
ABC cântạiA nêntamgiácABC vuôngkhivàchỉkhi
−→
AB.
−→
AC =
~
0⇔ (m +1)
4
−(m+1)=0⇔ m =0 hoặcm =−1
Kếthợpđiềukiệnđượcđápsốm =0.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page20of59
Ví dụ 1.39
Tìmm đểđồthịhàmsốy = x
4
− 2(m − 2)x
2
+m
2
− 5m +5cócựcđạivà
cựctiểu,đồngthờicácđiểmnàytạothànhmộttamgiácđều.
Hướng dẫn. Cóy
0
=4x
3
−4(m−2)x =0⇔ x =0∨x
2
=m−2.Suyra,đồthịhàm
sốcócựcđạivàcựctiểu
⇔ m − 2> 0⇔ m > 2.
Khiđó,bađiểmcựctrịlàA(0,m
2
−5m+5),B(
√
m−2,1−m)vàC(−
√
m−2,1−m)
tạothànhmộttamgiáccântạiA.Dođó,yêucầubàitoántươngđươngvới
b
A =60
◦
⇔ cosA =
1
2
⇔
−→
AB ·
−→
AC
−→
AB
·
−→
AC
=
1
2
Từđótìmđượcđápsốm =2+
3
√
3.
Ví dụ 1.40
Chohàmsốy =x
4
−2mx
2
+2m
2
−4,m làthamsốthực.Xácđịnhm đểđồ
thịhàmsốđãchocó3cựctrịtạothànhmộttamgiáccódiệntíchbằng1.
Hướng dẫn. TXĐ:D =R.
Tacóy
0
=4x
3
−4mx,nêny
0
=0⇔ 4x
3
−4mx =0⇔
x =0
x
2
=m
Suyra,đồthịhàmsốcóbađiểmcựctrịkhivàchỉkhim > 0.
Khiđóbađiểmcựctrịcủađồthịhàmsốlà
A(0;2m
2
−4);B(
√
m;m
2
−4);C(−
√
m;m
2
−4).
TathấyB,C đốixứngquaOy vàA thuộcOy nên∆ABC cântạiA.Dođó,gọiH
làtrungđiểmBC thìAH ⊥ BC vàcó
S
∆ABC
=
1
2
AH.BC ⇔ 2=|y
B
−y
A
|.|2x
B
| ⇔ 2=2m
2
√
m ⇔ m =1.
Đốichiếuvớiđiềukiệnđượcm =1 làgiátrịcầntìm.
Ví dụ 1.41
Tìmm đểbađiểmcựctrịcủađồthịhàmsốy =x
4
+2mx
2
−m−1tạothành
mộttamgiáccódiệntíchbằng4
√
2.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page21of59
Hướng dẫn. Hàmsốcó3điểmcựctrịkhivàchỉkhim < 0. Khiđó,bađiểmcựctrị
là
A(0;−m − 1),B(
√
−m;−m
2
−m− 1),C(−
√
−m;−m
2
−m− 1).
GọiI làtrungđiểmBC thì
S
∆ABC
=4
√
2⇔
1
2
IA.BC =4
√
2⇔ m =−2.
Sosánhđiềukiệnđượcđápsốm =−2.
Ví dụ 1.42
Tìmtấtcảcácgiátrịthựccủathamsốm đểđồthịhàmsốy =x
4
+2mx
2
+1
cóbađiểmcựctrịtạothànhmộttamgiácvuôngcân.
A. m =
−1
3
√
9
. B. m =−1. C. m =
1
3
√
9
. D. m =1.
Hướng dẫn. Trướctiêntatìmđiềukiệnđểđồthịhàmsốcóbađiểmcựctrị,tứclà
phươngtrìnhy
0
=0 phảicóbanghiệmphânbiệt.
y
0
=0⇔ 4x(x
2
+m)=0⇔
x =0
x
2
=−m
Dođó,phươngtrìnhy
0
=0cóbanghiệmphânbiệtkhivàchỉkhi−m > 0⇔ m < 0.
Lúcnày,tađãloạiđượchaiphươngánCvàDvàđồngthờitínhđượctoạđộba
điểmcựctrịlà
A(0;1),B(−
√
−m;−m
2
+1),C(
√
−m;−m
2
+1)
Từđótìmđược
−→
AB =(−
√
−m;−m
2
),
−→
AC =(
√
−m;−m
2
).RõràngtamgiácABC chỉ
cóthểvuôngcântạiA, tứclà
−→
AB ·
−→
AC =0.
m+m
4
=0⇔ m =−1.
Sosánhđiềukiệnđượcđápsốcuốicùnglàm =−1.
BàinàysaukhiloạiđượchaiphươngánCvàD,tacũngcóthểchọnmộtphương
án(nênchọnphươngánm =−1)đểthayvàovàtìmcụthểtoạđộcácđiểmcực
trị,rồikiểmtraxemcótạothànhmộttamgiácvuônghaykhông.Cáchnàycóvẻ
sẽnhanhhơn.
Ví dụ 1.43
Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
1
3
x
3
−mx
2
+(m
2
+
m−1)x đạtcựctrịtạihaiđiểmx
1
,x
2
thỏamãn|x
1
+x
2
| =4.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page22of59
A. m =2. B. m ∈ ∅. C. m =−2. D. m =±2.
Bàinàycóthểlàmxuôi,tứclàtìmragiátrịcủam rồisosánhvớicácphươngán.
Hoặc,chủđộngthaycácgiátrịcủam trongcácphươngánvàovàkiểmtra.Chúng
tasẽcùngtìmhiểucảhaicách.
Cách 1. Tacóy
0
= x
2
− 2mx +m
2
+m − 1.Hàmsốcóhaicựctrịkhivàchỉkhi
phươngtrìnhy
0
=0 cóhainghiệmphânbiệt.Điềukiệncầnvàđủlà
∆
0
=m
2
−(m
2
+m− 1)> 0⇔ m < 1.
Khiđó,phươngtrìnhy
0
=0 cóhainghiệmphânbiệtx
1
,x
2
.TheoViètecóx
1
+x
2
=
−b/a = m,nênyêucầubàitoántrởthành|2m| = 4⇔ m =±2.Sosánhvớiđiều
kiệnđượcđápsốm =−2.
Cách 2. Tasẽlầnlượtthửvớim =2 vàm =−2. Vớim =2 hàmsốtrởthành
y =
1
3
x
3
−2x
2
+5x
Cóy
0
=x
2
−4x+5.Phươngtrìnhy
0
=0 vônghiệmnênloạim =2.Vớim =−2 thì
làmtươngtựtathấythỏamãnyêucầu.Tómlại,chúngtachọnđápánm =−2.
Ví dụ 1.44
Tìmtấtcảcácgiátrịthựccủam saochođồthịhàmsốy =x
4
− 2mx
2
+
2m+m
4
cóbađiểmcựctrịtạothànhmộttamgiácđều.
A. m =0. B. m =
3
√
3. C. m =−
3
√
3. D. m =
√
3.
Ví dụ 1.45
Chohàmsốy = x
4
− mx
2
+2m −1 cóđồthịlà(C
m
).Tìmtấtcảcácgiátrị
thựccủathamsốm để(C
m
) có3điểmcựctrịcùngvớigốctọađộtạothành
mộthìnhthoi.
A. m = ±1 +
√
2.
B. m =2±
√
2 C. m =4±
√
2. D. m ∈ ∅.
Hướng dẫn. Đồthịhàmsốđãchocó3điểmcựctrịkhivàchỉkhim > 0.Khiđó,
tacóbađiểmcựctrịcủađồthịhàmsốlà
A
(
0;2m−1
)
,B
r
m
2
;−
m
2
4
+2m− 1
,C
−
r
m
2
;−
m
2
4
+2m− 1
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page23of59
YêucầubàitoántươngđươngvớiOB =AB ⇔
m
4
16
=
−
m
2
4
+2m− 1
2
⇔ m =
2±
√
2.
Ví dụ 1.46
Tìmcácgiátrịcủathamsốmđểhàmsốy =
1
3
x
3
+(m+3)x
2
+4(m+3)x+m
2
−m
cócácđiểmcựctrịx
1
,x
2
thỏamãnđiềukiện−1< x
1
< x
2
A.
(
−∞;−2
)
B.
−
7
2
;−2
C.
(
−∞;−3
)
∪
(
1;+∞
)
D.
−
7
2
;−3
Hướng dẫn. Tacóy
0
=x
2
+2(m +3)x +4(m +3). Hàmsốcóhaiđiểmcựctrịkhi
vàchỉkhiphươngtrìnhy
0
=0cóhainghiệmphânbiệt.Điềukiệncầnvàđủlà
∆> 0⇔ m ∈ (−∞;−3)∪(1;+∞).
Khiđó,giảsửhaiđiểmcựctrịlàx
1
,x
2
thìtheoViètetacó
x
1
+x
2
=−2(m +3)
x
1
·x
2
=4(m +3)
Mặtkhác,điềukiện−1< x
1
< x
2
cóthểviếtlạithành
(x
1
+1)(x
2
+1)> 0
x
1
+x
2
> −2
Giảihệphươngtrìnhnàyđượcm ∈
−
7
2
;−2
.Kếthợpđiềukiệntađượcđápsố
m ∈
−
7
2
;−3
.
Nhận xét. Thựcra,bàinàycóthểsửdụngđịnhlýđảovềdấutamthứcbậchai.
Yêucầubàitoántươngđươngvớiphươngtrìnhy
0
=0 cóhainghiệmphânbiệtvà
số−1 nằmbêntráikhoảnghainghiệm.Điềukiệncầnvàđủlà
∆> 0
a·f(−1)> 0
−1<
S
2
Giảihệnàycũngtìmđượcđápsốnhưtrên.
Lưu ý 1.9
Định lý đảo về dấu tam thức bậc hai
Xéttamthứcf(x)=ax
2
+bx +c vớia 6=0 vàmộtsốthựcε.Khif(x) cóhai
nghiệmphânbiệtx
1
,x
2
,giảsửthêmrằngx
1
< x
2
,thì
• x
1
< ε < x
2
⇔ a · f(ε)< 0, tứclàsốε nằmtrongkhoảnghainghiệm.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page24of59
• ε < x
1
< x
2
⇔
∆> 0
a·f(ε)> 0,
ε <
S
2
tứclàsốε nằmngoài,ởbêntrái
khoảnghainghiệm.
• x
1
< x
2
< ε ⇔
∆> 0
a·f(ε)> 0,
ε <
S
2
tứclàsốε nằmngoài,ởbênphải
khoảnghainghiệm.
Tươngtự,tacũngcó
x
1
6 ε 6 x
2
⇔ a · f(ε)6 0
1.8 Tiệm cận của đồ thị hàm số
Bài toán 1.8
Tiệm cận của đồ thị hàm số
Đườngthẳngx =x
0
đượcgọilàtiệmcậnđứngcủađồthịhàmsốnếu
lim
x→x
0
y =∞
Đườngthẳngy =y
0
đượcgọilàtiệmcậnngangcủađồthịhàmsốnếu
lim
x→∞
y =y
0
6=∞
Chúýrằng,trongcáccôngthứctrênkhôngcầnphânbiệt+∞ hay−∞.
Lưu ý 1.10
Đểtínhđượccácgiớihạntrongbàitoántiệmcận,chủyếudùnghaicông
thứcsau.
• lim
1
∞
=0 vàlim
1
0
=∞.
• QuytắcL’Hospitalđểkhửcácdạngvôđịnh
lim
f(x)
g(x)
=lim
f
0
(x)
g
0
(x)
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page25of59
Lưu ý 1.11
Chúýrằngmộtđườngtiệmcậnvẫncóthểcắtđồthịhàmsố,vídụhàmsố
y =
x+3
√
x
2
+1
cótiệmcậnnganglàđườngthẳngy =1, nhưngvẫncắtđường
tiệmcậnngangnàytạix =−
4
3
.
Ví dụ 1.47
Đề thử nghiệm 2017
Đườngthẳngnàodướiđâylàtiệmcậnđứngcủađồthịhàmsốy =
2x+1
x+1
.
A. x =1. B. y =−1. C. y =2. D. x =−1.
Ví dụ 1.48
ĐH năm 2017 Mã đề 101
Tìmsốtiệmcậnđứngcủađồthịhàmsốy =
x
2
−3x−4
x
2
−16
.
A. 2. B. 3. C. 1. D. 0.
Hướng dẫn. Trướchếttacầnphảixácđịnhrõyêucầu,ởđâylàtìmsốtiệmcận
đứng,dođótasẽđitínhcácgiớihạndạng lim
x→x
0
f(x)trongđóx
0
lànghiệmcủa
mẫu.
Ví dụ 1.49
ĐH năm 2017 Mã đề 104
Đồthịhàmsốy =
x−2
x
2
−4
cóbaonhiêutiệmcận?
A. 2. B. 3. C. 1. D. 0.
Hướng dẫn. Rõràng,ởcâunày,chúngtaphảitìmcảtiệmcậnđứngvàtiệmcận
ngang.Tứclàphảiđitínhcảcácgiớihạndạng lim
x→∞
f(x) và lim
x→x
0
f(x).
Ví dụ 1.50
ĐH năm 2017 Mã đề 102
Tìmsốtiệmcậnđứngcủađồthịhàmsốy =
x
2
−5x+4
x
2
−1
.
A. 2. B. 3. C. 1. D. 0.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page26of59
Hướng dẫn. Trướchếttacầnphảixácđịnhrõyêucầu,ởđâylàtìmsốtiệmcận
đứng,dođótasẽđitínhcácgiớihạndạng lim
x→x
0
f(x)trongđóx
0
lànghiệmcủa
mẫu.
Ví dụ 1.51
ĐH năm 2017 Mã đề 103
Đồthịcủahàmsốnàotrongcáchàmsốdướiđâycótiệmcậnđứng?
A. y =
1
√
x
.
B. y =
1
x
2
+x+1
.
C. y =
1
x
4
+1
.
D. y =
1
x
2
+1
.
Hướng dẫn. Tacầnlầnlượtđitínhcácgiớihạn lim
x→x
0
f(x)trongđóf(x)lầnlượtlà
cáchàmđãchoởbốnphươngán.Nhưngmuốncógiớihạnnày,phảitìmđượccác
sốx
0
,dođó,mụctiêucủatalàđitìmxemtrongcáchàmsốđãcho,hàmsốnàocó
sốx
0
làmchomẫukhôngxácđịnh.Hiểnnhiên,ởđâychỉcóhàmsốy =
1
√
x
.
Ví dụ 1.52
Tìmtiệmcậnngangcủađồthịhàmsốy =
x+3
√
x
2
+1
.
Hướng dẫn. Chúngtathấybậccaonhấtcủacảtửvàmẫulà1,nêntachiacảtử
vàmẫuchox được
lim
x→+∞
x +3
√
x
2
+1
= lim
x→+∞
1+
1
x
q
1+
1
x
2
=1
lim
x→−∞
x +3
√
x
2
+1
= lim
x→−∞
1+
1
x
−
q
1+
1
x
2
=−1
Suyra,đồthịhàmsốcóhaiđườngtiệmcậnnganglày =1 vày =−1.
Trongvídụtrên,chúngtakhôngthểtínhchungkhix → ∞ được.Màphảiphân
biệtkhix → +∞ vàx → −∞ vìvớimỗimộttrườnghợp,tacóthểthuđượcmột
tiệmcậnngangkhácnhau.
Ví dụ 1.53
Đề minh hoạ 2017
Chohàmsốy = f(x)có lim
x→+∞
f(x) = 1và lim
x→−∞
f(x) = −1.Khẳngđịnhnào
sauđâylàkhẳngđịnhđúng?
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page27of59
A. Đồthịhàmsốđãchokhôngcótiệmcậnngang.
B. Đồthịhàmsốđãchocóđúngmộttiệmcậnngang.
C. Đồthịhàmsốđãchocóhaitiệmcậnnganglàcácđườngthẳngy =1
vày =−1.
D. Đồthịhàmsốđãchocóhaitiệmcậnnganglàcácđườngthẳngx =1
vàx =−1.
Ví dụ 1.54
Tìmtấtcảcácgiátrịthựccủathamsốm đểđồthịhàmsốy =
2x
2
−3x+m
x−m
khôngcótiệmcậnđứng.
A. m =0. B. m = 0;m =
1.
C. m =1. D. m ∈ ∅.
Hướng dẫn. Nghiệmcủamẫusốlàx =m. Yêucầubàitoántươngđươngvớitửsố
phảicónghiệmlàm. Từđótìmđượcđápsốm =0,m =1.
Ví dụ 1.55
Tìmtấtcảcácgiátrịthựccủam đểđồthịhàmsốy =
x
2
+2
√
mx
4
+3
cóhaiđường
tiệmcậnngang.
A. m =0. B. m < 0. C. m > 0. D. m > 3.
Ví dụ 1.56
Tìmtấtcảcácgiátrịthựccủathamsốm đểđườngtiệmcậnđứng,tiệmcận
ngangcủađồthịhàmsốy =
2mx+m
x−1
cùngvớihaitrụctọađộtạothànhmột
hìnhchữnhậtcódiệntíchbằng8?
A. m =2. B. m =±
1
2
. C. m =±4. D. m 6=±2.
Hướng dẫn. Đồthịhàmsốcótiệmcậnđứnglàđườngthẳngx =1, tiệmcậnngang
làđườngthẳngy = 2m. Haiđườngthẳngnàycùngvớihaitrụctoạđộtạothành
mộthìnhchữnhậtcócáccạnhbằng1 và|2m|.Dođó,diệntíchhìnhchữnhậtnày
bằng8 tươngđươngvới|2m| =8⇔ m =±4.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page28of59
Ví dụ 1.57
Tìmphươngtrìnhcácđườngtiệmcậncủađồthịhàmsốhàmsốy =f(x) =
x+1
√
x
2
−4
.
Hướng dẫn. Đồthịhàmsốcóhaitiệmcậnngangy =±1vàhaitiệmcậnđứng
x =±2.
Ví dụ 1.58
Đồthịhàmsốy =
√
x
2
+2x
x−2
cóbaonhiêuđườngtiệmcận?
Hướng dẫn. Rõràngđồthịhàmsốđãchocótiệmcậnđứnglàđườngthẳngx =2.
Đểtìmcáctiệmcậnngang,tađitínhcácgiớihạn lim
x→+∞
f(x)và lim
x→−∞
f(x),từđó
tìmđượcthêmhaitiệmcậnngangnữa.Nhưvậy,đồthịhàmsốđãchocóba đường
tiệmcận.
Ví dụ 1.59
Đề thử nghiệm 2017
Tìmtấtcảcáctiệmcậnđứngcủađồthịhàmsố
y =
2x − 1−
√
x
2
+x +3
x
2
−5x +6
A. x =−3 vàx =−2.
B. x =−3.
C. x =3 vàx =2.
D. x =3.
Ví dụ 1.60
Đề tham khảo 2017
Chohàmsốy =f(x)cóbảngbiếnthiênnhưhìnhvẽdướiđây.Hỏiđồthị
củahàmsốđãchocóbaonhiêuđườngtiệmcận?
x −∞ −2 0 +∞
y
0
(x) + −
y
−∞%
+∞ 1
& 0
A. 1. B. 2. C. 3. D. 4.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page29of59
Ví dụ 1.61
Tìmm đểđồthịhàmsốy =f(x)=
2x
2
−3x+m
x−m
khôngcótiệmcậnđứng.
Đáp số. m =0;m =1
Ví dụ 1.62
Đề minh hoạ 2017
Tìmm saochođồthịhàmsốy =
x+1
√
mx
2
+1
cóhaitiệmcậnngang.
Đáp số. m > 0.
Ví dụ 1.63
Đồthịhàmsốy =
ln
(
x−1
)
x
2
+x
cóbaonhiêuđườngtiệmcận?
Hướng dẫn. Tathấyngay,đồthịhàmsốcómộtđườngtiệmcậnđứnglàđường
thẳngx =1. ChúngtasẽsửdụngquytắcL’Hospitalđểtínhgiớihạn,từđótìm
đượctiệmcậnngang–nếucó–củađồthịhàmsố.Tacó
lim
x→+∞
ln
(
x − 1
)
x
2
+x
= lim
x→+∞
(
ln(x − 1)
)
0
(x
2
+x)
0
= lim
x→+∞
1
x−1
2x +1
= lim
x→+∞
1
(x − 1)(2x +1)
=0
Suyra,đồthịhàmsốcómộttiệmcậnnganglàđườngthẳngy =0. Vàdođó,nó
cóhaiđườngtiệmcận.
Ví dụ 1.64
Tìmtấtcảcácgiátrịcủathamsốm đểđồthịhàmsốy =
x +1
√
m
2
x
2
+m− 1
cóbốnđườngtiệmcận.
A. m ∈
(
1;+∞
)
.
B. m ∈
(
−∞;1
)
\
n
0;
−1±
√
5
2
o
.
C. m ∈
(
−∞;1
)
.
D. m ∈
(
−∞;0
)
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page30of59
Hướng dẫn. Nếum = 0 thìhàmsốkhôngxácđịnh.Dođó,điềukiệntrướctiênlà
m 6=0. Khiđócó
lim
x→+∞
y = lim
x→+∞
1+
1
x
q
m
2
+
m−1
x
2
=
1
√
m
2
; lim
x→−∞
y = lim
x→−∞
1+
1
x
−
q
m
2
+
m−1
x
2
=−
1
√
m
2
Suyrađồthịhàmsốcóhaiđườngtiệmcậnngang.
Đồthịhàmsốcóhaiđườngtiệmcậnđứngkhivàchỉkhiphươngtrìnhm
2
x
2
=1−m
có2nghiệmphânbiệtvàkhác−1.Điềukiệncầnvàđủlà
m
2
+m− 16=0
1−m > 0
m 6=0
⇔
m < 1
m 6=
−1±
√
5
2
m 6=0
Nhưvậy,tachọnphươngánB.
1.9 Tiếp tuyến của đồ thị hàm số
Bài toán 1.9
Viết phương trình tiếp tuyến ∆của đồ thị hàm số (C):y =f(x).
Chúngtaxétbatìnhhuống:
• BiếttiếpđiểmlàM(x
0
;y
0
)thìtínhf
0
(x
0
)vàthayluônvàophươngtrình
y−y
0
=f
0
(x
0
)(x − x
0
) (4)
• Biếthệsốgócbằngk.GọitiếpđiểmlàM(x
0
;y
0
)vàđigiảiphương
trình
f
0
(x
0
)=k
tìmđượcx
0
rồithayvàophươngtrình(4).
• BiếttiếptuyếnđiquađiểmA(a,b),chúýrằngđiểmnàykhôngbiếtcó
làtiếpđiểmhaykhông.Khiđótathựchiệncácbước:
+GọitiếpđiểmlàM(x
0
;y
0
), lưuýlày
0
=f(x
0
).
+Tínhđạohàmvàsuyrahệsốgóccủatiếptuyếnlàf
0
(x
0
),từđó
viếtđượcphươngtrìnhtiếptuyếncódạngy−y
0
=f
0
(x
0
)(x −x
0
).
+VìtiếptuyếnđiquaA(a,b) nêntacóphươngtrình
b−f(x
0
)=f
0
(x
0
)(a−x
0
)
Giảiphươngtrìnhtrên,tìmđượcx
0
vàtừđóviếtđượcphươngtrình
tiếptuyếncầntìm.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page31of59
Lưu ý 1.12
• Chođườngthẳng∆:y =ax +b thì
+a làhệsốgóc,đượctínhbởia =tanα -trongđóα làgóctạo
bởitiaOx vàđườngthẳng∆lấytheochiềudương;
+b làhệsốtựdo.
• Haiđườngthẳngsongsongnếuhệsốgócbằngnhauvàhệsốtựdo
khácnhau.
• Haiđườngthẳngvuônggócnếutíchcáchệsốgóccủachúngbằng−1.
Ví dụ 1.65
Tìmhệsốgóccủatiếptuyếnvớiđồthịhàmsốy = f(x)=x
3
− 1tạigiao
điểmcủađồthịhàmsốvớitrụctung.
Ví dụ 1.66
CĐ2010
Viếtphươngtrìnhtiếptuyếncủađồthịhàmsốy =x
3
+3x
2
−1 tạiđiểmcó
hoànhđộbằng−1.
Đáp số. y =−3x −2.
Ví dụ 1.67
D2005
Chohàmsốy =
1
3
x
3
−
m
2
x
2
+
1
3
cóđồthịlà(C
m
)vàđiểmM ∈ (C
m
),biếtrằng
x
M
=−1,tìmm đểtiếptuyếntạiM songsongvớiđườngthẳng5x −y =0.
Đáp số. m =4.
Ví dụ 1.68
Chohàmsốy =−x
4
+2mx
2
− 2m +1.Tìmm đểcáctiếptuyếnvớiđồthị
hàmsốtạicácđiểmA(1;0),B(−1;0) vuônggócvớinhau.
Đáp số. m =
5
4
;m =
3
4
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page32of59
Ví dụ 1.69
Tìma vàb đểđồthịhàmsốy =
ax+b
x−1
cắttrụcOy tạiđiểmM(0;−1)đồng
thờitiếptuyếnvớiđồthịhàmsốtạiM cóhệsốgóck =3.
Đáp số. a =−4;b =1.
Ví dụ 1.70
Viếtphươngtrìnhtiếptuyếncủađồthịhàmsốy =x
3
− 3x
2
+2biếttiếp
tuyếnsongsongvớiđườngthẳngcóphươngtrìnhy =2016− 3x
Hướng dẫn. GọitiếpđiểmlàM(x
0
,y
0
)thìhệsốgóccủatiếptuyếnlàf
0
(x
0
)=
3x
2
0
−6x
0
. Vìtiếptuyếnsongsongvớiđườngthẳngy =2016−3x nên
3x
2
0
−6x
0
=−3
⇔ x
0
=1
Dođóy
0
=0 vàphươngtrìnhtiếptuyếnlày =−3x +3.
Ví dụ 1.71
GiảsửM làmộtđiểmcótungđộbằng5,thuộcđồthị
(
C
)
củahàmsố
y =
2x+1
x−1
.Tiếptuyếncủa(C) tạiM cắtcáctrụctoạđộOx,Oy lầnlượttạiA
vàB.HãytínhdiệntíchtamgiácOAB.
A.
121
6
B.
119
6
C.
123
6
D.
125
6
Ví dụ 1.72
Tìmtấtcảcácgiátrịm saochotrênđồthị
(C
m
):y =
1
3
mx
3
+(m− 1)x
2
+(4− 3m)x +1
tồntạiđúnghaiđiểmcóhoànhđộdươngmàtiếptuyếntạiđóvuônggócvới
đườngthẳng(d):x +2y −3=0.
Hướng dẫn. Tacóy
0
= mx
2
+2(m − 1)x +4− 3m. GọiM(x
0
,y
0
) làtiếpđiểmcần
tìmthìtiếptuyếntạiM vuônggócvớiđườngthẳng(d):x +2y−3=0 khivàchỉ
khiphươngtrìnhy
0
(x
0
)·
−
1
2
=−1 cóđúnghainghiệmdươngphânbiệt.Nghĩalà
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page33of59
phươngtrìnhmx
2
+2(m − 1)x +2− 3m =0 cóhainghiệmdươngphânbiệt.Điều
kiệncầnvàđủlà
m 6=0
∆
0
> 0
S > 0
P > 0
⇔
m 6=0
4m
2
−4m+1> 0
m−1
m
< 0
2−3m
m
> 0
⇔
m 6=0
m 6=
1
2
0< m < 1
0< m <
2
3
⇔
0< m <
1
2
1
2
< m <
2
3
Vậym ∈
0;
1
2
∪
1
2
;
2
3
làcácgiátrịcầntìm.
Ví dụ 1.73
Viếtphươngtrìnhtiếptuyếncủađồthịhàmsốy =
2x
x−2
biếttiếptuyếncắt
Ox,Oy lầnlượttạiA,B màtamgiácOAB thỏamãnAB =OA
√
2.
Hướng dẫn. GiảsửM(x
0
;y
0
),vớix
0
6=2,làmộtđiểmthuộcđồthịhàmsố.Phương
trìnhtiếptuyếnd củađồthịhàmsốtạiđiểmM códạng:
y−
2x
0
x
0
−2
=
−4
(x
0
−2)
2
(x − x
0
).
DotiếptuyếncắtcáctrụcOx,Oy tạicácđiểmA,B vàtamgiácOAB cóAB =OA
√
2
nêntamgiácOAB vuôngcântạiO.Khiđótiếptuyếnd tạovớitiaOx mộtgóc45
◦
hoặc135
◦
.
• Tiếptuyếnd tạovớitiaOx mộtgóc45
◦
, thìhệsốgóccủatiếptuyếnlà1.Do
đó,tacóphươngtrìnhy
0
(x
0
)=1⇔
−4
(x
0
−2)
2
=1.Phươngtrìnhnàyvônghiệm.
• Tiếptuyếnd tạovớitiaOx mộtgóc135
◦
, thìhệsốgóccủatiếptuyếnlà−1.
Dođó,tacóphươngtrình
y
0
(x
0
)=1⇔
−4
(x
0
−2)
2
=−1⇔
x
0
=0
x
0
=4
Từđótìmđược,phươngtrìnhtiếptuyếnlà
d :y =−x
d :y =−x +8
Đườngthẳngy =−x điquagốctọađộnênbịloại.Nhưvậychỉcómộttiếptuyến
thỏayêucầubàitoánlàd :y =−x +8.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page34of59
Ví dụ 1.74
Chohàmsốy =
x−2
x+1
.Viếtphươngtrìnhtiếptuyếncủađồthịbiếttiếptuyến
cắtOx,Oy tạiA,B saochobánkínhđườngtrònnộitiếptamgiácOAB lớn
nhất.
Hướng dẫn. Tiệmcậnđứng:x = −1, tiệmcậnngang:y = 1,giaođiểmhaiđường
tiệmcậnlàI(−1;1).Giảsửhoànhđộtiếpđiểmlàx
0
thìphươngtrìnhtiếptuyếnlà:
y =
3
(
x
0
+1
)
2
(
x − x
0
)
+
x
0
−2
x
0
+1
TiếptuyếncắttiệmcậnđứngtạiđiểmA
−1;
x
0
−5
x
0
+1
vàcắttiệmcậnngangtạiđiểm
B
(
2x
0
+1;1
)
.Từđótínhđược
IA =
x
0
−5
x
0
+1
−1
=
6
|x
0
+1|
,IB =|2x
0
+1− (−1)| =2|x
0
+1|
SuyradiệntíchtamgiácIAB là
S =
1
2
IA · IB =
1
2
·
6
|x
0
+1|
·2|x
0
+1| =6.
Gọip lànửachuvitamgiácIAB,thìbánkínhđườngtrònnộitiếptamgiácnàylà:
r =
S
p
=
6
p
Bởivậy,bánkínhr lớnnhấtkhivàchỉkhip nhỏnhất.Mặtkhác,tamgiácIAB
vuôngtạiI nên:
2p =IA +IB +
p
IA
2
+IB
2
> 2
√
IA.IB +
√
2IA.IB =4
√
3+2
√
6.
DấuđẳngthứcxảyrakhiIA =IB ⇔
(
x
0
+1
)
2
=3⇔ x =−1±
√
3
• Vớix =−1−
√
3 tacótiếptuyến:d
1
:y =x +2
1+
√
3
.
• Vớix =−1+
√
3 tacótiếptuyến:d
1
:y =x +2
1−
√
3
.
Nhưvậy,tatìmđượchaitiếptuyếncóphươngtrìnhnhưtrên.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page35of59
Ví dụ 1.75
Viếtphươngtrìnhtiếptuyếncủađồthịhàmsốy = f(x) =x
3
− 3x +2 biết
tiếptuyếnđiquađiểmA(−1;4).
Ví dụ 1.76
ĐH Sư phạm II - Khối B năm 99
Tìmtrêntrụchoànhnhữngđiểmmàtừđókẻđượcbatiếptuyếnđếnđồthị
hàmsố
y =−x
3
+3x +2
Hướng dẫn. GọiA(a;0)bấtkìthuộctrụchoànhvàM(x
0
;y
0
)làtọađộtiếpđiểm.
PhươngtrìnhtiếptuyếntạiM là
y−y
0
=f
0
(x
0
)(x − x
0
)
⇔ y =(−3x
2
0
+3)(x −x
0
)−x
3
0
+3x
0
+2
MàtiếptuyếnđiquaA(a;0) nên
(−3x
2
0
+3)(a− x
0
)−x
3
0
+3x
0
+2=0
⇔ (x
0
+1)(2x
2
0
−(3a+2)x
0
+3a+2)=0
TừA kẻđượcbatiếptuyếnđếnđồthịhàmsốkhivàchỉkhiphươngtrình2x
2
0
−
(3a+2)x
0
+3a+2=0 cóhainghiệmphânbiệtkhác−1.
⇔
(
∆> 0
6(a+1)6=0
Tìmđượcđápsốa > 2 hoặc−16=a < −
2
3
.
Ví dụ 1.77
Chohàmsốy = −x
3
+3x
2
− 2. TìmđiểmđiểmM thuộcđồthịhàmsốsao
choquađiểmM kẻđượchaitiếptuyếnvớiđồthịhàmsốmàtíchcáchệsố
góccủahaitiếptuyếnnhỏnhất.
Hướng dẫn. Cóy
0
=−3x
2
+6x.GiảsửA(a,−a
3
+3a
2
−2)thuộcđồthịhàmsốvà
tiếpđiểmlàM(x
0
,−x
3
0
+3x
2
0
−2). Suyraphươngtrìnhtiếptuyếnlà:
y−(−x
3
0
+3x
2
0
−2)=(−3x
2
0
+6x
0
)(x − x
0
)
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page36of59
DotiếptuyếnđiquađiểmA nêntacóphươngtrình
−a
3
+3a
2
−2− (−x
3
0
+3x
2
0
−2)=(−3x
2
0
+6x
0
)(a−x
0
)
Phântíchthànhnhântử,thuđượcx
0
=a,x
0
=
3−a
2
. QuađiểmA kẻđượchaitiếp
tuyến⇔ a 6=
3−a
2
⇔ a 6=1. Khiđóhệsốgóccủahaitiếptuyếnlà
k
1
=...,k
2
=...
Suyra
k
1
·k
2
=
1
4
−3a
2
+6a+
9
2
2
−
81
16
> −
81
16
TừđótìmđượcA(
2±
√
10
2
,±
√
10
4
).
1.10 Nhận dạng đồ thị
Bài toán 1.10
Nhận dạng đồ thị
Tacầnmộtsốkếtquảquenthuộcsau:
• Hìnhdángcủađồthịcáchàmsốbậcba,bậcbốntrùngphương,phân
thứcbậcnhấttươngứngvớicáctrườnghợphệsốcủachúng.
• Xéttheochiềutăngcủabiếnx,từtráiquaphải,thìđồthịhàmsố
đồngbiếnsẽcóhướngđilên–ngàycàngcaohơn–,cònđồthịhàm
sốnghịchbiếnsẽcóhướngđixuống–ngàycàngthấpđi.
• MộtđiểmM(x
0
,y
0
) thuộc(nằmtrên)đồthịhàmsốy =f(x) khivàchỉ
khiy
0
=f(x
0
).
• Đồthịhàmsốy = f(x)nếucắttrụctungthìgiaođiểmcótọađộ
(0,f(0));cònđểtìmgiaođiểmvớitrụchoànhtađigiảiphươngtrình
hoànhđộgiaođiểmf(x)=0.
• Sốgiaođiểmcủahaiđồthịhàmsốy = f(x)vày = g(x)chínhbằng
sốnghiệmcủaphươngtrìnhf(x)=g(x).
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page37of59
Ví dụ 1.78
Chohàmsốy = ax
3
+bx
2
+cx +d
cóđồthịnhưđườngcongởhìnhvẽ
bên.Khẳngđịnhnàosauđâyđúng?
A. a,d > 0;b,c < 0.
B. a,b,c < 0;d > 0.
C. a,c,d > 0;b < 0.
D. a,b,d > 0;c < 0.
1.11 Đọc bảng biến thiên
Bài toán 1.11
Đọc bảng biến thiên
Ví dụ 1.79
ĐH năm 2017 Mã đề 102
Chohàmsốf(x) cóbảngbiếnthiênnhưhìnhvẽsau
x −∞ −2 2 +∞
y
0
(x) + 0 − 0 +
y
−∞%
3
& 0%
+∞
Tìmgiátrịcựcđạiy
CĐ
vàgiátrịcựctiểuy
CT
củahàmsốđãcho.
A. y
CĐ
=3 vày
CT
=−2.
B. y
CĐ
=2 vày
CT
=0.
C. y
CĐ
=−2 vày
CT
=2.
D. y
CĐ
=3 vày
CT
=0.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page38of59
Ví dụ 1.80
ĐH năm 2017 Mã đề 103
Chohàmsốf(x) cóbảngbiếnthiênnhưhìnhvẽsau
x −∞ −1 2 +∞
y
0
(x) + 0 − 0 +
y
2 %
4
& −5%
2
Mệnhđềnàodướiđâyđúng?
A. Hàmsốcóbốnđiểmcựctrị.
B. Hàmsốđạtcựctiểutạix =2.
C. Hàmsốkhôngcócựcđại.
D. Hàmsốđạtcựctiểutạix =−5.
Ví dụ 1.81
Đề minh hoạ 2017
Chohàmsốf(x) xácđịnh,liêntụctrênR vàcóbảngbiếnthiênnhưhìnhvẽ
sau
x −∞ 0 1 +∞
y
0
(x) + − 0 +
y
−∞%
0
& −1%
+∞
Mệnhđềnàodướiđâyđúng?
A. Hàmsốcóđúngmộtcựctrị.
B. Hàmsốcógiátrịcựctiểubằng
1.
C. Hàmsốcógiátrịlớnnhấtbằng
0 vàgiátrịnhỏnhấtbằng−1.
D. Hàmsốđạtcựcđạitạix =0và
đạtcựctiểutạix =1.
Ví dụ 1.82
ĐH năm 2017 Mã đề 101
Chohàmsốf(x) cóbảngbiếnthiênnhưhìnhvẽsau
x −∞ −1 0 1 +∞
y
0
(x) − 0 + 0 − 0 +
y
+∞
& −1%
0
& −1%
+∞
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page39of59
Mệnhđềnàodướiđâysai?
A. Hàmsốcóbađiểmcựctrị.
B. Hàmsốcógiátrịcựcđạibằng
3.
C. Hàmsốcógiátrịcựcđạibằng
0.
D. Hàmsốcóhaiđiểmcựctiểu.
1.12 Đồ thị hàm số chứa dấu giá trị tuyệt đối
Bài toán 1.12
Cho đồ thị hàm số y =f(x). Vẽ đồ thị các hàm số y =|f(x)| và
y =f
(
|x|
)
.
Tasửdụngđịnhnghĩagiátrịtuyệtđốiđểviếtlạihàmsốđãcho.
y =f(|x|)=
(
f(x) khix > 0,
f(−x) khix < 0.
y =|f(x)| =
(
f(x) khif(x)> 0,
−f(x) khif(x)< 0.
Từđó,tacócáchvẽnhưsau:
• Đốivớihàmsốy =f(|x|),taxóaphầnđồthịnằmbêntráitrụctung–
phầnđồthịứngvớix < 0 –vàlấyđốixứngphầncònlạiquatrụctung.
• Đốivớihàmsốy =|f(x)|,talấyđốixứngphầnđồthịnằmdướitrục
hoành–phầnđồthịứngvớif(x)< 0–vàxóabỏphầnđồthịnằmdưới
trụchoànhđó.
Ví dụ 1.83
Đồthịhàmsốy =
x
3
−3x
cắtđườngthẳngy =2 tạimấyđiểm?
Hướng dẫn. Lậpbảngbiếnthiên:
x −∞ −
√
3 −1 0 1
√
3 +∞
y
0
(x) − + 0 − + 0 − +
y
+∞
& 0 %
2
& 0%
2
& 0 %
+∞
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page40of59
Ví dụ 1.84
Phươngtrình
x
3
−3x +2
=log
2
10 cóbaonhiêunghiệm?
A. 2 B. 0 C. 4 D. 3
Hướng dẫn. Cầnnhớlạiđịnhnghĩagiátrịtuyệtđốivàcáchvẽđồthịhoặclập
bảngbiếnthiêncáchàmsốy =|f(x)| vày =f(|x|) nhưthếnào?
x −∞ −2 −1 1 +∞
y
0
(x) − + 0 − +
y
+∞
& 0 %
4
& 0%
+∞
Ví dụ 1.85
ĐH năm 2017 Mã đề 102
Chohàmsốy =f(x) cóbảngbiếnthiênnhưsau:
x −∞ −1 3 +∞
y
0
(x) + 0 − 0 +
y
−∞%
5
& 1%
+∞
Đồthịhàmsốy =|f(x)| cóbaonhiêuđiểmcựctrị?
A. 4. B. 2. C. 3. D. 5.
1.13 Tương giao của hai đồ thị hàm số
Bài toán 1.13
Tương giao của hai đồ thị hàm số y =f(x) và y =g(x).
• Sốgiaođiểmcủahaiđồthịhàmsốchínhbằngsốnghiệmcủaphương
trìnhhoànhđộgiaođiểm
f(x)=g(x)
• Biếnđổiphươngtrìnhtrênđưavề:
+Phương trình trùng phương. Đặtẩnphụđưavềbiệnluậnphương
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page41of59
trìnhbậchai.
+Phương trình bậc ba. Đoánnghiệmđặcbiệtrồiphântíchthành
tíchphươngtrìnhbậcnhấtvàphươngtrìnhbậchai;gọihainghiệm
củaphươngtrìnhbậchailàx
1
,x
2
rồisửdụngViète.Nếukhông
đượcthìcôlậpthamsốm vàđưavềxéttươnggiaocủađường
thẳngy =m vàmộtđồthịhàmsốmới.
+Phương trình bậc hai. Gọihainghiệmx
1
,x
2
vàsửdụngViète.
Ví dụ 1.86
Tìmsốgiaođiểmcủađồthịhàmsốy =x
3
−3x +3 vàđườngthẳngy =x.
A. Một. B. Hai. C. Ba. D. Không.
Chứng minh. Hướngdẫn]Phươngtrìnhhoànhđộgiaođiểmx
3
− 3x +3 = x.Giải
phươngtrìnhnàytìmđượcbanghiệmnênđápsốlàcóbagiaođiểm.
Ví dụ 1.87
Tìmtấtcảcácgiátrịthựccủathamsốm đểđồthịhàmsốy =x
3
−3x+2−m
cắttrụchoànhtạibađiểmphânbiệt.
A. 0< m < 4.
B. 06 m 6 4.
C. m > 4.
D. m < 0.
Ví dụ 1.88
Đề tham khảo 2017
Chohàmsốy =x
3
−3x cóđồthị(C).Tìmsốgiaođiểmcủa(C)vàtrụchoành.
Ví dụ 1.89
Đề thử nghiệm 2017
Đồthịhàmsốy =x
4
−2x
2
+2 vàđồthịhàmsốy =−x
2
+4 cótấtcảbao
nhiêuđiểmchung?
Ví dụ 1.90
ĐH 2017 Mã đề 103
Chohàmsốy =(x −2)(x
2
+1) cóđồthị(C) .Mệnhđềnàodướiđâyđúng?
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page42of59
A. (C) cắttrụchoànhtạihaiđiểm.
B. (C)cắttrụchoànhtạimộtđiểm.
C. (C) khôngcắttrụchoành.
D. (C) cắttrụchoànhtạibađiểm.
Ví dụ 1.91
Đề thử nghiệm 2017
Chohàmsốy =f(x)xácđịnhtrênR \{0},liêntụctrênmỗikhoảngxácđịnh
vàcóbảngbiếnthiênnhưsau
x −∞ 0 1 +∞
y
0
(x) − + 0 −
y
+∞
& −1 −∞%
2
& −∞
Tìmtậphợptấtcảcácgiátrịcủathamsốthựcm saochophươngtrình
f(x)=m cóbanghiệmthựcphânbiệt.
A. [−1;2]. B. (−1;2). C. (−1;2]. D. (−∞;2]
Hướng dẫn.
Ví dụ 1.92
Đề minh hoạ 2017
Biếtrằngđườngthẳngy =−2x +2cắtđồthịhàmsốy =x
3
+x +2tại
điểmduynhất;kíhiệu(x
0
;y
0
) làtọađộcủađiểmđó.Tìmy
0
.
Bài toán 1.14
Biện luận số nghiệm của phương trình h(x,m) = 0 bằng đồ thị hàm
số.
• Côlậpthamsốm, đưaphươngtrìnhđãchovềdạngf(x)=g(m).
• Lậpbảngbiếnthiênhoặcvẽđồthịcủahàmsốf(x).
• Căncứvàobảngbiếnthiênđểkếtluận.
Lưu ý 1.13
Đồthịhàmsốy =g(m) làmộtđườngthẳngsongsongvớitrụchoànhvàcắt
trụctungtạiđiểmcótungđộg(m).Chẳnghạn,đồthịhàmsốy =m
2
−2m+3
làmộtđườngthẳngchứkhôngphảilàmộtparabolnhưnhiềuhọcsinhlầm
tưởng.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page43of59
Ví dụ 1.93
Tìmcácgiátrịcủam đểphươngtrìnhx
2
(x
2
−2)+3=m cóhainghiệmphân
biệt.
Hướng dẫn. Xéthàmsốy =x
2
(x
2
−2)+3 trênR. Tacóbảngbiếnthiên
x −∞ −1 0 1 +∞
y
0
(x) − 0 + 0 − 0 +
y
+∞
& 2 %
3
& 2%
+∞
Căncứvàobảngbiếnthiêntacó,phươngtrìnhcóhainghiệmphânbiệtkhivàchỉ
khim =2 hoặcm > 3.
Ví dụ 1.94
ĐH năm 2017 Mã đề 104
Chohàmsốy =−x
4
+2x
2
cóđồthịnhưhìnhbên.Tìmtấtcảcácgiátrịthực
củathamsốm đểphươngtrình−x
4
+2x
2
=m cóbốnnghiệmthựcphân
biệt.
A. m > 0. B. o 6 m 6 1. C. 0< m < 1. D. m < 1.
Ví dụ 1.95
Tìmtấtcảcácgiátrịcủathamsốm saochophươngtrìnhlog
2
2
x−2log
2
x =m
cónghiệmtrongkhoảng(0,1)?
1.m > 0 2.m > 0 3.m > −1 4.> −1
Hướng dẫn. Đặtt =log
2
x thìt < 0vớimọix ∈ (0,1).Dođó,taxéthàmsố
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page44of59
f(t)=t
2
−2t trênkhoảng(−∞,0) cóbảngbiếnthiênnhưsau:
t −∞ 0
f
0
(t) −
f(t)
+∞
& 0
Suyra,phươngtrìnhđãchocónghiệmx ∈ (0,1) khivàchỉkhim > 0.
Ví dụ 1.96
Tìmtấtcảcácgiátrịthựccủathamsốm đểđồthịhàmsốy =
2x+3
x+2
và
đườngthẳngd :y =x +m cắtnhautạihaiđiểmphânbiệt.
A. m > 2.
B. m > 6.
C. m =2.
D. m < 2∨ m > 6.
Ví dụ 1.97
ĐH Khối D năm 2011
Chohàmsốy =
2x+1
x+1
.Tìmk đểđườngthẳngy =kx +2k +1 cắtđồthịhàm
sốđãchotạihaiđiểmphânbiệtA,B saochokhoảngcáchtừA vàB đến
trụchoànhbằngnhau.
Đáp số. k =−3.
Ví dụ 1.98
ĐH Khối B năm 2010
Chohàmsốy =
2x+1
x+1
.Tìmm đểđườngthẳngy =−2x+m cắtđồthịhàmsố
đãchotạihaiđiểmphânbiệtA,B saochotamgiácOAB códiệntíchbằng
√
3,vớiO làgốctọađộ.
Đáp số. m =±2.
Ví dụ 1.99
Tìmtấtcảcácgiátrịthựccủathamsốm đểđườngthẳngd :y =x +1 cắt
đồthịhàmsốy =x
3
− 3x
2
+mx +1tạibađiểmphânbiệtcóhoànhđộ
x
1
,x
2
,x
3
thỏamãnx
2
1
+x
2
2
+x
2
3
> 1.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page45of59
A. m <
13
4
∨m 6=1.
B. m 6 5.
C. 06 m 6 5.
D. 56 m 6 10.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểmlàx
3
− 3x
2
+mx +1 = x +1.Đặt
nhântửchungtađược
x
x
2
−3x +m−1
=0 (5)
Đườngthẳngd cắtđồthịhàmsốy =x
3
−3x
2
+mx +1 tạibađiểmphânbiệtkhi
vàchỉkhiphươngtrình(5)cóbanghiệmphânbiệt.Vìphươngtrình(5)luôncómột
nghiệmlàx =0 nênđiềukiệncầnvàđủlàphươngtrình
x
2
−3x +m−1=0 (6)
cóhainghiệmphânbiệtkhác0.Từđótìmđượcđiềukiệnm 6=1,m <
13
4
.
Khiđó,theoViète,phươngtrình(6)cóhainghiệmx
2
,x
3
thỏamãn
(
x
2
+x
3
=3,
x
2
·x
3
=m − 1.
Dođó,yêucầux
2
1
+x
2
2
+x
2
3
> 1⇔ 3
2
−2
(
m−1
)
> 1⇔ m 6 5.Nhưvậy,điềukiện
cầntìmlàm 6=1,m <
13
4
.
Ví dụ 1.100
Tìmtấtcảcácgiátrịthựccủathamsốm đểđồthịhàmsốy =
2x+3
x−1
cắt
đườngthẳng∆:y =x +m tạihaiđiểmphânbiệtA,B saochotamgiác
OAB vuôngtạiO.
A. m =6. B. m =−3. C. m =5. D. m =−1.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểmcủa(C) vàđườngthẳng∆là
2x +3
x − 1
=x +m ⇔ x
2
+(m− 3)x −m− 3=0 (x 6=1) (7)
Đườngthẳng∆ cắt(C) tạihaiđiểmphânbiệtkhivàchỉkhiphươngtrình(7) cóhai
nghiệmphânbiệtvà
1
khác1.
⇔
(
∆> 0
1
2
+(m− 3)·1−m − 36=0
⇔ m ∈ R.
1
Thựcrachỉcầnđiềukiệncóhainghiệmphânbiệtlàđủ,điềukiệnsauluônluônđúngvớimọi
bàitoándạngnày.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page46of59
Khiđó,gọihainghiệmcủaphươngtrình(7)làx
1
,x
2
thìgiaođiểmcủahaiđồthị
đãcholàA(x
1
,x
1
+m),B(x
2
,x
2
+m).TamgiácOAB vuôngtạiO khivàchỉkhi
−→
OA ·
−→
OB =0⇔ x
1
x
2
+(x
1
+m)(x
2
+m)=0.
SửdụngViètecóx
1
+x
2
=−m +3 vàx
1
x
2
=−m − 3,tatìmđượcm =6.
Ví dụ 1.101
Tìmm đểđườngthẳngd :y =x −2cắtđồthị(C) củahàmsốy =x
3
+(m−
1)x
2
−(m− 2)x −2 tạibađiểmphânbiệt.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểm:
x
3
+(m− 1)x
2
−(m− 2)x −2=x − 2
⇔ x
x
2
+(m− 1)x −m+1
=0
⇔
x =0
x
2
+(m− 1)x −m+1=0 (∗)
Đườngthẳngd cắtđồthị(C)tại3điểmphânbiệtkhivàchỉkhiphươngtrình(∗)
cóhainghiệmphânbiệtkhác0
⇔
∆=m
2
+2m− 3> 0
g(0)=−m +16=0
⇔
m < −3
m > 1
m 6=1
⇔
m < −3
m > 1
Vậy,giátrịcầntìmlàm < −3 hoặcm > 1.
Ví dụ 1.102
Tìmm đểđồthịhàmsốy =x
3
+mx +2 cắttrụchoànhtạiđúngmộtđiểm.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểm
x
3
+mx +2=0
Nhậnxétx =0khôngthểlànghiệmcủaphươngtrình,nênchiahaivếchox thì
đượcphươngtrìnhtươngđương
m =−x
2
−
2
x
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page47of59
Xéthàmsốf(x)=−x
2
−
2
x
trên(−∞;0)∪(0;+∞) tacóbảngbiếnthiênsau
x −∞ 0 1 +∞
f
0
(x) + + 0 −
f(x)
−∞%
+∞
−∞%
−3
& −∞
Suyra,giátrịcầntìmcủam làm > −3.
Ví dụ 1.103
Tìmm đểđồthịhàmsốy = x
3
− mx − m cắttrụchoànhtạibađiểmphân
biệt.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểm
x
3
−mx −m =0.
Phươngtrìnhtrênkhôngcónghiệmđặcbiệt,nhưnglạicóthểcôlậpđượcthamsố
m nênsẽchuyểnvềtìmđiềukiệnđểhaiđồthịhàmsốmới cắtnhautạibađiểm
phânbiệt.Chúýrằngx =−1khôngthỏamãnphươngtrìnhnênchiahaivếcho
x +1 tađượcphươngtrìnhmớitươngđương
m =
x
3
x +1
.
Yêucầubàitoántươngđươngvớiviệctìmđiềukiệnđểđườngthẳngy =m cắtđồ
thịhàmsốf(x)=
x
3
x+1
.Tacóbảngbiếnthiêncủaf(x) nhưsau
x −∞ −
3
2
−1 0 +∞
f
0
(x) − 0 + + 0 +
f(x) +∞
&
27
4
%
+∞
−∞%
0%
+∞
Căncứvàobảngbiếnthiên,tacóđápsốm > 27/4.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page48of59
Ví dụ 1.104
Chohàmsố:y =x
3
−mx
2
+(2m+1)x −m−2.Tìmm đểđồthịhàmsốcắt
trụcOx tại3điểmphânbiệtcóhoànhđộdương.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểm:
x
3
−mx
2
+(2m+1)x −m− 2=0⇔
x =1
x
2
−(m− 1)x +m+2=0 (∗)
ĐồthịhàmsốcắttrụcOx tại3điểmphânbiệtcóhoànhđộdươngkhivàchỉkhi
phươngtrình(∗) có2nghiệmdươngphânbiệtkhác1
⇔
∆=m
2
−6m− 7> 0
m+2> 0
m−1> 0
⇔
m < −1∨ m > 7
m > −2
m > 1
⇔ m > 7
Vậyvớim > 7thìđồthịhàmsốcắttrụcOx tại3điểmphânbiệtcóhoànhđộ
dương.
Ví dụ 1.105
Chohàmsốy =x
3
−2(m+1)x
2
+(m−2)x +m+3cóđồthị(C).Xácđịnhm
đểđồthị(C)cắttrụchoànhtại3điểmphânbiệtcóhoànhđộx
1
,x
2
,x
3
sao
choP =x
2
1
+x
2
2
+x
2
3
nhỏnhất.
Hướng dẫn. Phươngtrìnhhoànhđộgiaođiểmcủađồthị(C) vàtrụchoànhlà
x
3
−2(m+1)x
2
+(m− 2)x +m+3=0
⇔ (x −1)
x
2
−(2m+1)x −(m+3)
=0
⇔
x =1
x
2
−(2m+1)x −(m+3)=0 (∗)
Đồthị(C) cắttrụchoànhtại3điểmphânbiệtkhivàchỉkhi
∆> 0
g(1)6=0
⇔
4m
2
+8m+13> 0,∀m
−3m−36=0
⇔ m 6=−1
Vớim 6=−1,phươngtrình(∗)cóhainghiệmphânbiệtx
1
,x
2
khác1;nghĩalà,
phươngtrìnhy =0 cóbanghiệmx
1
,x
2
vàx
3
=1.Vàdođó
P =x
2
1
+x
2
2
+x
2
3
=x
2
1
+x
2
2
+1=1+(x
1
+x
2
)
2
−2x
1
x
2
=1+
(
2m+1
)
2
+2(m+3)=4m
2
+6m+8=
2m+
3
2
2
+
23
4
>
23
4
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page49of59
VậygiátrịnhỏnhấtcủaP bằng
23
4
khim =−
3
4
.
Ví dụ 1.106
ĐH năm 2017 Mã đề 101
Tìmtấtcảcácgiátrịthựccủathamsốm đểđườngthẳngy = mx − m +1
cắtđồthịcủahàmsốy =x
3
−3x
2
+x +2tạibađiểmA,B,C phânbiệtsao
choAB =BC.
A. m ∈ (−∞;0]∪ [4;+∞).
B. m ∈ R.
C. m ∈
−
5
4
;+∞
.
D. m ∈ (−2;+∞).
Hướng dẫn. Tìmđiềukiệnđểđườngthẳngd vàđồthị(C)cắtnhautạihaiđiểm
phânbiệt.Sauđósửdụngtínhchấttâmđốixứngcủa(C),tứcđiểmuốn,phảithuộc
đườngthẳngd.
Ví dụ 1.107
ĐH năm 2017 Mã đề 102
Tìmtấtcảcácgiátrịthựccủathamsốm đểđườngthẳngy =−mx cắt
đồthịhàmsốy =x
3
− 3x
2
− m +2tạibađiểmphânbiệtA,B,C saocho
AB =BC.
Ví dụ 1.108
Viếtphươngtrìnhđườngthẳngd cắtđồthị(C):y =x
3
−3x +2 tạibađiểm
phânbiệtA,B,C saochox
A
=2 vàBC =2
√
2.
Hướng dẫn. Cóx
A
=2 suyray
A
=4 vàA(2;4).Giảsửd làđườngthẳngđiquaA
vàcóhệsốgóclàk thìphươngtrìnhcủad là
d :y−y
A
=k(x −x
A
)⇔ y =kx − 2k +4
Phươngtrìnhhoànhđộgiaođiểmcủa(C) vàđườngthẳngd là
x
3
−3x+2=kx−2k+4⇔ (x−2)(x
2
+2x+1−k)=0⇔
x =2
g(x)=x
2
+2x +1−k =0
Nhưvậyd cắt(C) tại3điểmphânbiệtA,B,C khivàchỉkhiphươngtrìnhg(x)=0
cóhainghiệmphânbiệtvàkhác2.Điềukiệncầnvàđủlà
(
∆
0
=k > 0
g(2)=9− k 6=0
⇔ 0< k 6=9
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page50of59
Khiđó,phươngtrìnhcóhainghiệmx
B
,x
C
thỏamãn
(
x
B
+x
C
=−2
x
B
·x
C
=1− k
MàcácđiểmB,C thuộcđườngthẳngd nêntacó
y
B
=kx
B
−2k +4;y
C
=kx
C
−2k +4.
MặtkhácBC =2
√
2⇔ BC
2
=8 nênsuyra
(x
B
−x
C
)
2
+k
2
(x
B
−x
C
)
2
=8⇔
(x
B
+x
C
)
2
−4x
B
x
C
(1+k
2
)=8⇔ k =1.
Kiểmtrathấythỏamãnđiềukiện.Thayvàotìmđượcđườngthẳngd :y =x+2.
Ví dụ 1.109
Chohàmsốy =4x
3
− 6mx
2
+1,m làthamsố.Tìmm đểđườngthẳng
d :y = −x +1cắtđồthịhàmsốtại3điểmA(0;1),B,C màB,C đốixứng
quađườngphângiáccủagócphầntưthứnhất.
Hướng dẫn. Hoànhđộgiaođiểmcủađườngthẳngd vàđồthị(C)lànghiệmcủa
phươngtrình:
4x
3
−6mx
2
+1=−x +1
⇔ x(4x
2
−6mx +1)=0 (8)
Phươngtrìnhcóbanghiệmphânbiệtkhivàchỉkhiphươngtrình4x
2
−6mx+1=0
có2nghiệmphânbiệt
⇔ ∆
0
=9m
2
−4> 0⇔
m >
2
3
m <
−2
3
Giảsửx
1
,x
2
lànghiệmcủaphươngtrình(8)thìB(x
1
;−x
1
+1),C(x
2
;−x
2
+1).Do
đó,B vàC đốixứngquađườngphângiáccủagócphầntưthứnhất
⇔
(
x
1
=y
2
y
1
=x
2
⇔
(
x
1
=−x
2
+1
x
2
=−x
1
+1
⇔ x
1
+x
2
=1⇔
3
2
m =1⇔ m =
2
3
Sosánhvớiđiềukiện,thấykhôngtìmđượcgiátrịnàocủam thỏamãnyêucầu.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page51of59
Ví dụ 1.110
Chohàmsốy =
2x+1
x−1
cóđồthịlà(H).Gọid làđườngthẳngđiquađiểm
A(−2;2)vàcóhệsốgócm.Tìmm đểđườngthẳngd cắtđồthị(H)tạihai
điểmphânbiệt?
Hướng dẫn. Đườngthẳngd điquađiểmA(−2;2) vàcóhệsốgócm nêncóphương
trình
y =mx +2m+2
Phươngtrìnhhoànhđộgiaođiểmcủađườngthẳngd vàđồthị(H) là
2x +1
x − 1
=mx +2m+2⇔ g(x)=mx
2
+mx −(2m+3)=0.
vìx =1 luônkhôngthểlànghiệmcủaphươngtrìnhtrên.
Đườngthẳngd cắtđồthị(H)tạihaiđiểmphânbiệtkhivàchỉkhiphươngtrình
g(x)=0 cóhainghiệmphânbiệtkhác1.Điềukiệncầnvàđủlà
a 6=0
∆> 0
g(1)6=0
⇔ m < −
4
3
hoặcm > 0
Vậygiátrịcầntìmlàm < −
4
3
hoặcm > 0.
1.14 Biện luận phương trình, bất phương trình
Bài toán 1.15
Khibiệnluậnsốnghiệmcủaphươngtrình,bấtphươngtrìnhtahaysửdụng
mộtsốkếtquảsau:
• Phươngtrìnhm =f(x) cónghiệmtrênD ⇔ min
D
f(x)6 m 6 max
D
f(x),
• Bấtphươngtrìnhm 6 f(x) cótậpnghiệmlàD ⇔ m 6 min
D
f(x),
• Bấtphươngtrìnhm > f(x) cótậpnghiệmlàD ⇔ m > max
D
f(x).
Ví dụ 1.111
Tìmm đểphươngtrìnhmx
2
+2mx −3=0 cónghiệmx ∈ [1;2]
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page52of59
Hướng dẫn. Tacó
mx
2
+2mx −3=0⇔ m =
3
x
2
+2x
(vìx
2
+2x 6=0, ∀x ∈ [1;2])
Xéthàmsốf(x)=
3
x
2
+2x
trênđoạn[1;2],tacóbảngbiếnthiênsau
x 1 2
f
0
(x) −
f(x)
1
&
3
8
Phươngtrìnhđãchocónghiệmx ∈ [1;2] khivàchỉkhimin
[1;2]
f
(
x
)
6 m 6 max
[1;2]
f
(
x
)
.Từ
đótìmđượcđápsố
3
8
6 m 6 1.
Ví dụ 1.112
Tìmm đểbấtphươngtrìnhx +
√
2x
2
+1− m > 0 cótậpnghiệmlàR?
Hướng dẫn. Tacóbấtphươngtrìnhx +
√
2x
2
+1−m > 0 cótậpnghiệmlàR khi
vàchỉkhi
x +
p
2x
2
+1− m > 0, ∀x ∈ R
⇔ m < min
R
f(x)
trongđóf(x)=x +
√
2x
2
+1. Tacóbảngbiếnthiên
x −∞ −
√
2
2
+∞
f
0
(x) − 0 +
f(x)
+∞
&
√
2
2
%
+∞
Suyramin
R
f(x)=
√
2
2
vàdođó,đápsốlàm <
√
2
2
.
Ví dụ 1.113
ĐH Khối B năm 2007
Chứngminhrằngvớimọim > 0,phươngtrìnhsaucóhainghiệmphânbiệt
x
2
+2x −8=
p
m(x − 2) (9)
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page53of59
Hướng dẫn. Vìm > 0 nênđiềukiệncủaphươngtrìnhlàx > 2 vàphươngtrình(9)
tươngđươngvới
(x − 2)(x
3
+6x
2
−32− m)=0⇔
x =2
x
3
+6x
2
−32− m =0
Tachứngminhphươngtrình
x
3
+6x
2
−32=m (10)
cóđúngmộtnghiệmtrongkhoảng(2,+∞).
Xéthàmsốf(x)=x
3
+6x
2
−32 trên(2,+∞) cóbảngbiếnthiênsau
x 2 +∞
f
0
(x) +
f(x)
0%
+∞
Rõràngkhim > 0 thìđườngthẳngy =m cắtđồthịhàmsốy =f(x) tạiđúngmột
điểmcóhoànhđộlớnhơn2,tứclàphươngtrình(10)cóđúngmộtnghiệmtrong
khoảng(2,+∞).Dođó,phươngtrình(9) cóđúnghainghiệmkhim > 0.
Ví dụ 1.114
ĐH Khối A năm 2007
Tìmm đểphươngtrình
3
√
x − 1+m
√
x +1=2
4
p
x
2
−1 (11)
cónghiệm.
Hướng dẫn. Điềukiện:x > 1,phươngtrình(11)tươngđươngvới
−3
r
x − 1
x +1
+2
4
r
x − 1
x +1
=m.
Đặtu =
4
q
x−1
x+1
=
4
q
1−
2
x+1
∈ [0,1
)
tađượcphươngtrình
−3u
2
+2u =m (12)
Xéthàmsốf(t)=−3t
2
+2t trên[0;1) tacóbảngbiếnthiên
t 0
1
3
1
f
0
(t) + 0 −
f
(
t
)
0%
1
3
& −1
Dođóphươngtrình(11)cónghiệmkhivàchỉkhiphươngtrình(12)cónghiệm
u ∈ [0;1).Điềukiệncầnvàđủlà−1< m 6
1
3
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page54of59
1.15 Biến đổi hàm số
Bài toán 1.16
Tịnh tiến đồ thị hàm số y =f(x)
Ví dụ 1.115
Biếtđồthịhàmsốy = f(x)cómộttiệmcậnnganglàđườngthẳngy =3.
Khiđóđồthịhàmsốy =2f(x)− 4 cómộttiệmcậnnganglà
A. y =3. B. y =2. C. y =1. D. y =−4.
Chứng minh. Hướngdẫn]Tacó lim
x→∞
2f(x)−4
=2· 3−4=2.
1.16 Điểm thuộc đồ thị
Bài toán 1.17
Tìm điểm M thuộc đồ thị (C) của hàm số y =f(x) thỏa mãn điều
kiện cho trước.
Chúýnhữngtínhchấtcủađồthịhàmsốphânthức...
Lưu ý 1.14
ĐiểmđốixứngvớiđiểmM(a;b) quagốctọađộlàM
0
(−a;−b),đốixứngqua
trụchoànhlàM
00
(a;−b),đốixứngquatrụctunglàM
000
(−a;b).
Ví dụ 1.116
Chohàmsốy =
x+2
x−1
cóđồthịlà(C).
1.Xácđịnhphươngtrìnhtiệmcậnđứngvàtiệmcậnngangcủa(C).
2.Viếtphươngtrìnhtiếptuyến∆của(C) tạiđiểmM(2;4)
3.Giảsửtiếptuyến∆ cắttiệmcậnđứngtạiA,cắttiệmcậnngangtạiB.
ChứngminhrằngM làtrungđiểmAB.
Ví dụ 1.117
Tìmtrênđồthịhàmsốy =
x+2
x−1
nhữngđiểmcáchđềuhaitrụctọađộ.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page55of59
Hướng dẫn. GiảsửM(m,
m+2
m−1
)thuộcđồthịhàmsốđãcho.Tacó,điểmM cáchđều
haitrụctọađộkhivàchỉkhi
|m| =
m+2
m−1
Giảiphươngtrìnhtrêntìmđượcm =−1±
√
3. TừđótìmđượcđápsốM(−1±
√
3,−5∓3
√
3).
Ví dụ 1.118
TìmđiểmM trênđồthịy =
2x
x+1
saochotiếptuyếncủađồthịcùngvớihai
trụctạothànhmộttamgiáccódiệntíchlà
1
4
.
Ví dụ 1.119
ĐH Khối B năm 2003
Tìmm đểđồthịhàmsốy =x
3
−3x
2
+m cóhaiđiểmphânbiệtđốixứngvới
nhauquagốctọađộ.
Hướng dẫn. Đồthịhàmsốđãchocóhaiđiểmphânbiệtđốixứngnhauquagốc
tọađộkhivàchỉkhitồntạix
0
6=0 saochoy(x
0
)=−y(−x
0
).Điềunàyđồngnghĩa
vớiphươngtrình
x
3
0
−3x
2
0
+m =−
(−x
0
)
3
−3(−x
0
)
2
+m
⇔ 3x
2
0
=m
cónghiệmx
0
6=0. Dođó,điềukiệncầnvàđủlàm > 0.
Ví dụ 1.120
ĐH Khối D năm 2007
TìmđiểmM trênđồthịy =
2x
x+1
saochotiếptuyếnđồthịcùngvớihaitrục
tọađộtạothànhmộttamgiáccódiệntíchlà
1
4
.
Ví dụ 1.121
TìmhaiđiểmM,N thuộchainhánhcủađồthịhàmsốy =
3x−1
x−3
saochođộ
dàiđoạnthẳngMN ngắnnhất.
Hướng dẫn. Đồthịhàmsốcótiệmcậnđứnglàđườngthẳngx = 3 nên,giảsửM
nằmnhánhbêntráiđồthịthìhoànhđộcủanónhỏhơn3. Dođó,gọitọađộđiểm
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page56of59
M là(3− a,3− 8/a)và,tươngtự,tọađộcủaN(3+b,3+8/b)–vớia,b > 0.Ta
tínhđượcMN =
q
(a+b)
2
+
(
8/a +8/b
)
2
.SửdụngbấtđẳngthứcCauchy,tacó
(a+b)
2
+
8
a
+
8
b
2
>
2
√
ab
2
+64
2
r
1
a
·
1
b
!
2
> 64
Suyra,giátrịnhỏnhấtcủaMN là8.Đẳngthứcxảyra,khia = b = 2
√
2,từđó
tìmđượcM vàN.
Ví dụ 1.122
Chohàmsốy =
2x−3
x−2
cóđồthị(C).Tìmtrênđồthị(C)nhữngđiểmM saocho
tiếptuyếntạiM của(C) cắthaitiệmcậncủa(C) tạiA,B màAB ngắnnhất.
A. M(3;3),M(1;1).
B. M(3;3),M
0;
3
2
.
C. M
0;
3
2
,M
−1;
5
3
.
D. M(1;1),
(
2;4
)
.
Hướng dẫn. GiảsửM(a,
2a−3
a−2
),vớia 6=2,làmộtđiểmthuộcđồthị(C).Phương
trìnhtiếptuyến∆ của(C) tạiđiểmM là
∆:y =
−x
(a−2)
2
+
2a
2
−6a+6
(a−2)
2
Tiếptuyến∆cắttiệmcậnđứngtạiđiểmA
2;
2a−2
a−2
vàcắttiệmcậnngangtạiđiểm
B
(
2a−2;2
)
.Dođó,độdàiđoạnAB là
AB =
s
4(a−2)
2
+
4
(a−2)
2
SửdụngbấtđẳngthứcCauchycóAB > 2
√
2. VậyđoạnAB ngắnnhấtbằng2
√
2,
khia =3 hoặca =1. TừđótìmđượchaiđiểmM(3;3) hoặcM(1;1).
Ví dụ 1.123
TìmđiểmM thuộcđườngthẳng∆ :y = 3x − 2saotổngkhoảngcáchtừM
tớihaiđiểmcựctrịcủađồthịhàmsốy =x
3
−3x
2
+2 làngắnnhất.
A. M
4
5
;
2
5
. B. M
(
0;−2
)
. C. M
(
1;1
)
. D. M
1
2
;−
1
2
.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page57of59
Hướng dẫn. Tìmđượchaiđiểmcựctrịcủađồthịhàmsốy =x
3
− 3x
2
+2là
A(0;2) vàB(2;−2).NhậnxétrằngA vàB nằmvềhaiphíacủađườngthẳng∆,nên
MA+MB ngắnnhấtkhivàchỉkhibađiểmM,A,B thẳnghàng.Nóicáchkhác,M
làgiaođiểmcủađườngthẳng∆vàđườngthẳngAB.Từđótìmđượctoạđộcủa
M
4
5
;
2
5
.
Ví dụ 1.124
ChoM làmộtđiểmbấtkỳthuộcđồthịhàmsốy =
x+1
x−1
.Tìmkhoảngcách
ngắnnhấttừM đếnđườngthẳng∆:y =−
1
2
x +1.
A.
√
3.
B.
5
√
3
3
. C.
√
3
2
.
D.
1
√
3
.
Hướng dẫn. Gọid làtiếptuyếncủađồthịhàmsốy =
x+1
x−1
mànósongsongvới
đườngthẳng∆.Suyrahệsốgóccủad là−
1
2
.Từđótìmđượctoạđộcáctiếpđiểm
làE(3;2) hoặcF(−1;0).
TínhđượckhoảngcáchtừE đếnđườngthẳng∆làd(E,∆) =
5
√
3
;khoảngcáchtừ
F đếnđườngthẳng∆ làd(F,∆)=
√
3.Suyrakhoảngcáchnhỏnhấtcầntìmlà
√
3
khiM trùngvớiF.
1.17 Bài toán thực tế
Bài toán 1.18
Bài toán thực tế.
Đốivớicácbàitoánvềchuyểnđộngcầnlưuý,nếuquãngđườngs theothời
giant đượctínhbởiphươngtrìnhs =s(t) thìvậntốclàv =s
0
(t) còngiatốc
làa =v
0
(t)=s
00
(t).
Đốivớicácbàitoánvềdiệntích,thểtíchlớnnhất,nhỏnhấttacóthểđặt
mộtkíchthướclàx vàbiểudiễncáckíchthướccònlạitheox.Sauđólập
hàmsốvàkhảosátđểtìmragiátrịlớnnhất,giátrịnhỏnhất.Cóthểthay
trựctiếpcácphươngánvàovàsosánh.
Ví dụ 1.125
Đề minh hoạ 2017
Chomộttấmnhômhìnhvuôngcạnh12cm.Ngườitacắtởbốngóccủatấm
nhômđóbốnhìnhvuôngbằngnhau,mỗihìnhvuôngcócạnhbằngxcm,rồi
gậptấmnhômlạiđểđượcmộtcáihộpkhôngnắp.Tìmx đểhộpnhậnđược
cóthểtíchlớnnhất.
A. x =6. B. x =3. C. x =2. D. x =4.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page58of59
Ví dụ 1.126
Mộtvậtchuyểnđộngtheoquyluậts = −
1
2
t
3
+9t
2
,vớit (giây)làkhoảng
thờigiantínhtừlúcvậtbắtđầuchuyểnđộngvàs (mét)làquãngđườngvật
điđượctrongkhoảngthờigianđó.Hỏitrongkhoảngthờigian10giây,kểtừ
lúcbắtđầuchuyểnđộng,vậntốclớnnhấtcủavậtđạtđượcbằngbaonhiêu?
A. 216m/s. B. 30m/s. C. 400m/s. D. 54m/s.
Hướng dẫn. Chúngtacầntìmgiátrịlớnnhấtcủavậntốctrongkhoảngthờigian
t ∈ [0;10].Cóv(t) = s
0
(t)nênta xéthàm sốv(t) = −
3
2
t
2
+ 18t có đạohàm
v
0
(t)=−3t +18 trênđoạn[0;10].Tacóbảngbiếnthiênsau
t 0 6 10
v
0
(t) + 0 −
v(t)
0%
54
& 30
Suyra,giátrịlớnnhấtcủavậntốclà54m/s,đạtđượctạithờiđiểmt =6giây.
Ví dụ 1.127
Mộtvậtchuyểnđộngtheoquyluậts =−
1
2
t
3
+6t
2
vớit (tínhbằnggiây)là
khoảngthờigiantínhtừkhivậtbắtđầuchuyểnđộngvàs (tínhbằngmét)
làquãngđườngvậtdichuyểnđượctrongkhoảngthờigianđó.Hỏitrong
khoảngthờigian6 giây,kểtừlúcvậtbắtđầuchuyểnđộng,vậntốclớnnhất
đạtđượccủavậtlàbaonhiêu?
A. 24m/s. B. 108m/s. C. 64m/s. D. 18m/s.
Hướng dẫn. Vậntốcchuyểnđộngcủavậtbiếnđổitheoquyluật
v =s
0
=−
3
2
t
2
+12t
Lậpbảngbiếnthiêncủahàmsốnàytrênđoạn[0;6] tađược
t 0 4 6
v
0
(t) + 0 −
v
0%
24
& 18
Suyra,vậntốclớnnhấtcóthểđạtđượclà24m/s.
toicodongiuamotbiennguoi.wordpress.com
CÁCBÀITOÁNĐIỂNHÌNH2018 Page59of59
Ví dụ 1.128
Mộtviênđáđượcbắnthẳnglêntrênvớivậntốcbanđầulà40m/stừmột
điểmcao5msovớimặtđất.Vậntốccủaviênđásaut giâyđượcchobởi
côngthứcv(t)=40−10t m/s.Tínhđộcaolớnnhấtviênđácóthểlêntớiso
vớimặtđất.
A. 75m. B. 80m. C. 90m. D. 85m.
Ví dụ 1.129
Ngườitamuốnmạvàngchobềmặtphíangoàicủamộtcáihộpcódạnghình
hộpđứngkhôngnắp,cóđáylàmộthìnhvuông.Tìmchiềucaocủahộpđể
lượngvàngdùngđểmạlàítnhất,biếtlớpmạởmọinơilànhưnhau,giao
giữacácmặtkhôngđángkểvàthểtíchcủahộplà4dm
3
.
A. 1dm. B. 0.5dm. C. 2dm. D. 1.5dm.
Ví dụ 1.130
Mộttấmtônhìnhchữnhậtcókíchthước80cm× 50cmđượccắtđiởbốngóc
nhữnghìnhvuôngbằngnhau,đểkhigấplạithìđượcmộtcáithùngkhông
nắpdạnghìnhhộp.Thểtíchhìnhhộptạothànhlớnnhấtkhibốnhìnhvuông
bịcắtđicócạnhlàbaonhiêu?
A. 10cm. B. 25cm. C. 20cm. D. 40cm.
toicodongiuamotbiennguoi.wordpress.com
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 1 of 59
CÁC BÀI TOÁN ĐIỂN HÌNH ÔN THI THPTQG 2018 1 Hàm số 1.1
Tìm khoảng đồng biến, nghịch biến của hàm số Bài toán 1.1
Tìm khoảng đồng biến, nghịch biến của hàm số y f x . = ( )
• Tìm tập xác định của hàm số.
• Tính đạo hàm và lập bảng xét dấu của nó. •
Căn cứ vào bảng xét dấu để kết luận. Lưu ý 1.1
Cách tính nhanh đạo hàm của một số hàm số • y ax b +
anh dũng trừ bắt cướp Hàm số phân thức = cx
d thì cách nhớ là “ ” + ad − bc y0 = cx d 2 ( + ) • y a x2 b x c 1 + 1 + 1 anh bạn - ăn cháo Hàm số phân thức = a x2 b x c thì cách nhớ là “ 2 + 2 + 2
hai lần - bỏ cơm” a b a c b c 1 1 1 1 1 1 x 2 x + 2 + a b a c b c y0 2 2 2 2 2 2 = a x 2 2 b x c 2 + 2 + 2 Ví dụ 1.1 y x3 x2 − đúng Cho hàm số = + 3
2. Khẳng định nào sau đây là khẳng định ? A. C.
Hàm số đồng biến trên khoảng Hàm số nghịch biến trên −∞ − ∞ −∞ − ∞ ( ; 2) và (0; + ). khoảng ( ; 2) và (0; + ). B. D.
Hàm số đồng biến trên khoảng Hàm số nghịch biến trên −∞ ∞ − ( ; 0) và (2; + ). khoảng ( 2; 1).
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 2 of 59 Cách 1. y0 x2 x x2 x Tính nhanh đạo hàm: = 3 + 6 = 3( + 2
), và lập được bảng biến
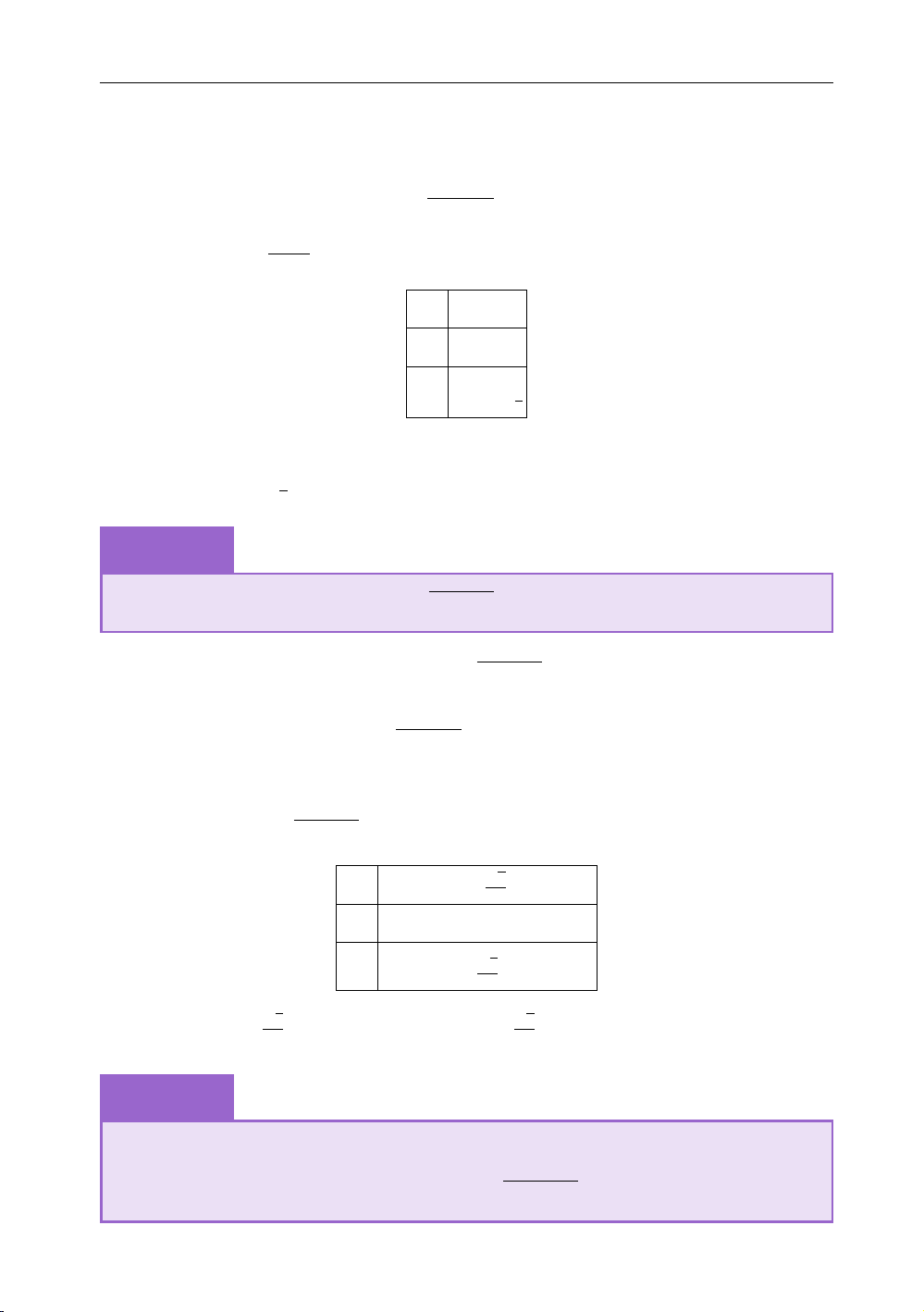
thiên (thực ra chỉ cần lập bảng xét dấu của đạo hàm): x −∞ − ∞ 2 0 + y0 − + 0 0 + y % & % Từ đó chọn đáp án A.
Cách 2. Chúng ta sử dụng tính năng tính đạo hàm của hàm số bằng máy tính CASIO, sử dụng phím d/dx.
Riêng đối với ba loại hàm quen thuộc (bậc ba, bậc bốn trùng phương và phân thức
bậc nhất) chúng ta có thể có cách làm riêng. Chẳng hạn câu này, ta biết đây là a > dấu ngã
hàm số bậc ba với hệ số = 1 0 nên đồ thị có dạng
, tức là sẽ đồng biến −∞ x x ∞ x x x , x trên các khoảng ( ; 1 ) và ( 2 ; +
), nghịch biến trên khoảng ( 1 ; 2 ) với 1 2 là y0
hai nghiệm của phương trình
= 0. Do đó, có thể khẳng định được ngay phương
án A là phương án đúng. Sau đây là một số bài tập điển hình. Ví dụ 1.2 ĐH năm 2017 Mã đề 101 y 2 Hàm số = x2
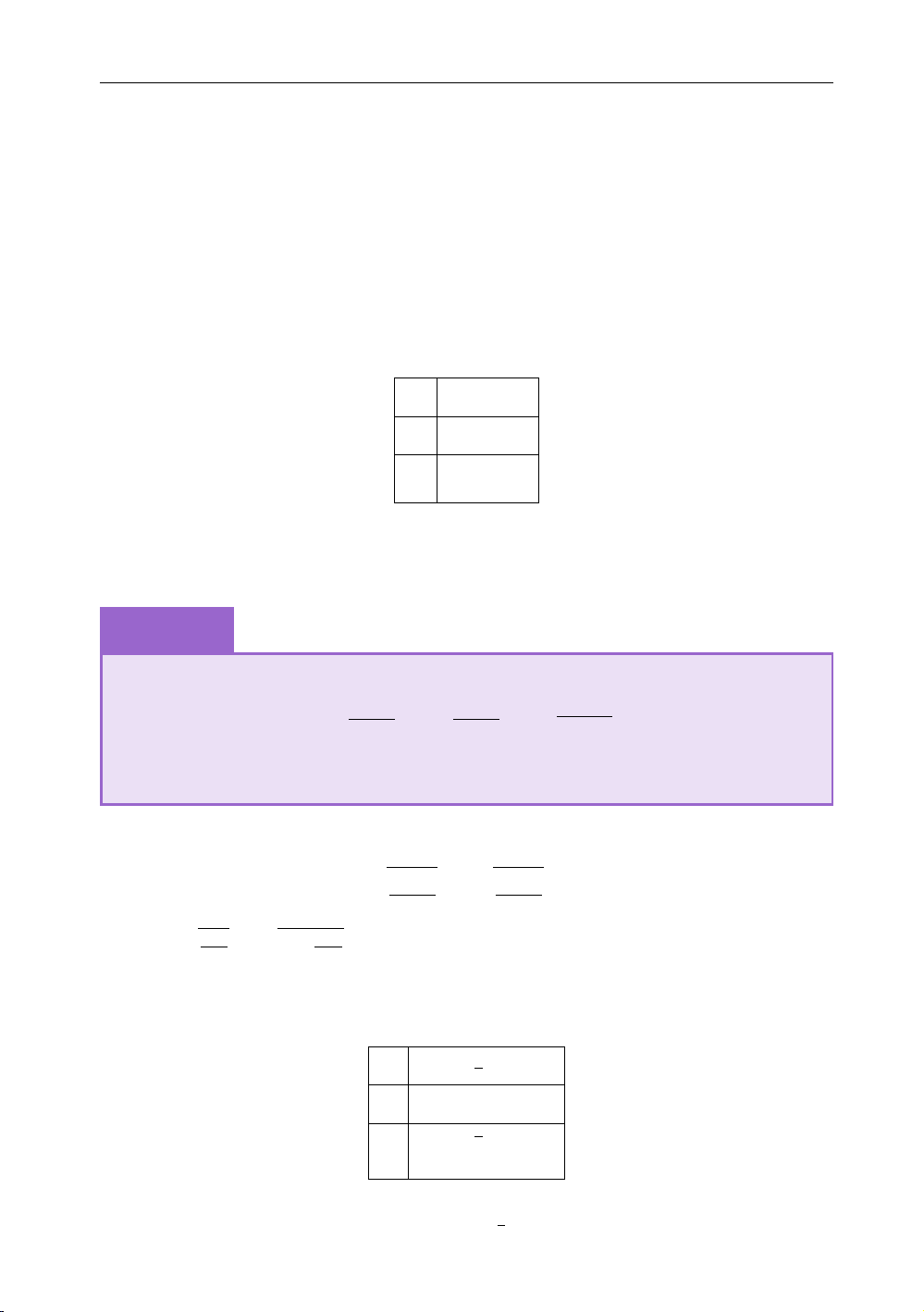
nghịch biến trên khoảng nào dưới đây? +1 A. ∞ B. − . C. −∞ ∞ . D. −∞ (0; + ). ( 1; 1) ( ; + ) ( ; 0). Hướng dẫn. D R. Tập xác định = Đạo hàm − x y0 4 = x 2 2 + 1 y0 < ⇔ x > Do đó, 0 0. Chọn phương án A. Ví dụ 1.3 −∞ ∞
Hàm số nào dưới đây đồng biến trên khoảng ( ; + )? A. y x x− +1 B. y x3 x. C. y 1 D. y −x3 − = x . = + = x− . = +3 2 x. 3
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 3 of 59 1.2
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x trên tập Bài toán 1.2 = ( ) K.
Chúng ta có hai phương pháp chủ yếu: • K. K a b
Lập bảng biến thiên của hàm số trên Nếu tập là một đoạn [ ; ]
thì không cần lập bảng biến thiên mà chỉ cần y0 x y0 + Giải phương trình = 0 và tìm ra các điểm i mà tại đó = 0 y0 hoặc không xác định. f a , f b , f x +
Tính và so sánh các giá trị ( ) ( ) (
i) để tìm ra giá trị lớn nhất, giá trị nhỏ nhất.
• Sử dụng bất đẳng thức quen thuộc hoặc điều kiện có nghiệm của phương trình. Lưu ý 1.2 y f x Lưu ý rằng, hàm số = (
) muốn đạt được giá trị lớn nhất hoặc giá trị M x nhỏ nhất bằng
thì ta phải tìm được ít nhất một số 0 hữu hạn sao cho f x M. ( 0 ) = Lưu ý 1.3
Điều kiện có nghiệm của một số phương trình quen thuộc: • > .
Phương trình bậc hai điều kiện là ∆ 0 • x m, x m |m| 6 . Phương trình sin = cos = điều kiện là 1 • a x b x c |c| √ 6 c2 6 Phương trình sin + cos = điều kiện là a 1 hay 2 b2 + a2 b2. +
Cần nhớ hai cách để tìm giá trị lớn nhất, giá trị nhỏ nhất. Hai cách đó là gì? Đôi
khi chúng ta hay đổi biến (đặt ẩn phụ) để đưa về khảo sát một hàm số đơn giản hơn. Ví dụ 1.4 ĐH năm 2017 Mã đề 102 y x m + m y y 16 . Cho hàm số = x , với
là tham số thực, thỏa mãn max + min = +1 3 [1;2] [1;2]
Mệnh đề nào sau đây là đúng? A. m 6 . B. m > . C. < m 6 . D. < m 6 . 0 4 0 2 2 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 4 of 59 Hướng dẫn. x 6 Điều kiện xác định
= 1, nên hàm số luôn xác định và liên tục trên . đoạn [1; 2] Có − m y0 1 = x 2 ( + 1) y0 >
Chỉ có thể xảy ra hai khả năng, nếu
0 thì hàm số đồng biến trên đoạn [1; 2], y y , y y y0 < do đó max = (2) min = (1). Ngược lại, nếu
0 thì hàm số nghịch biến [1;2] [1;2] y y , y y
trên đoạn [1; 2], do đó max = (1) min =
(2). Dù cho khả năng nào xảy ra thì [1;2] [1;2] y, y y y max min
cũng chỉ có thể nhận hai giá trị (1) và
(2). Do đó, yêu cầu bài toán [1;2] [1;2] tương đương với m m y y 16 ⇔ 1 + 2 + 16 (1) + (2) = + = 3 2 3 3 m m > .
Giải phương trình này, tìm được = 5, tức là 4 Ví dụ 1.5 m f x −x4 − x2 m − Tìm để hàm số ( ) = 2 +
có giá trị lớn nhất trên khoảng ( 2; 4) . bằng 2 Hướng dẫn. f x
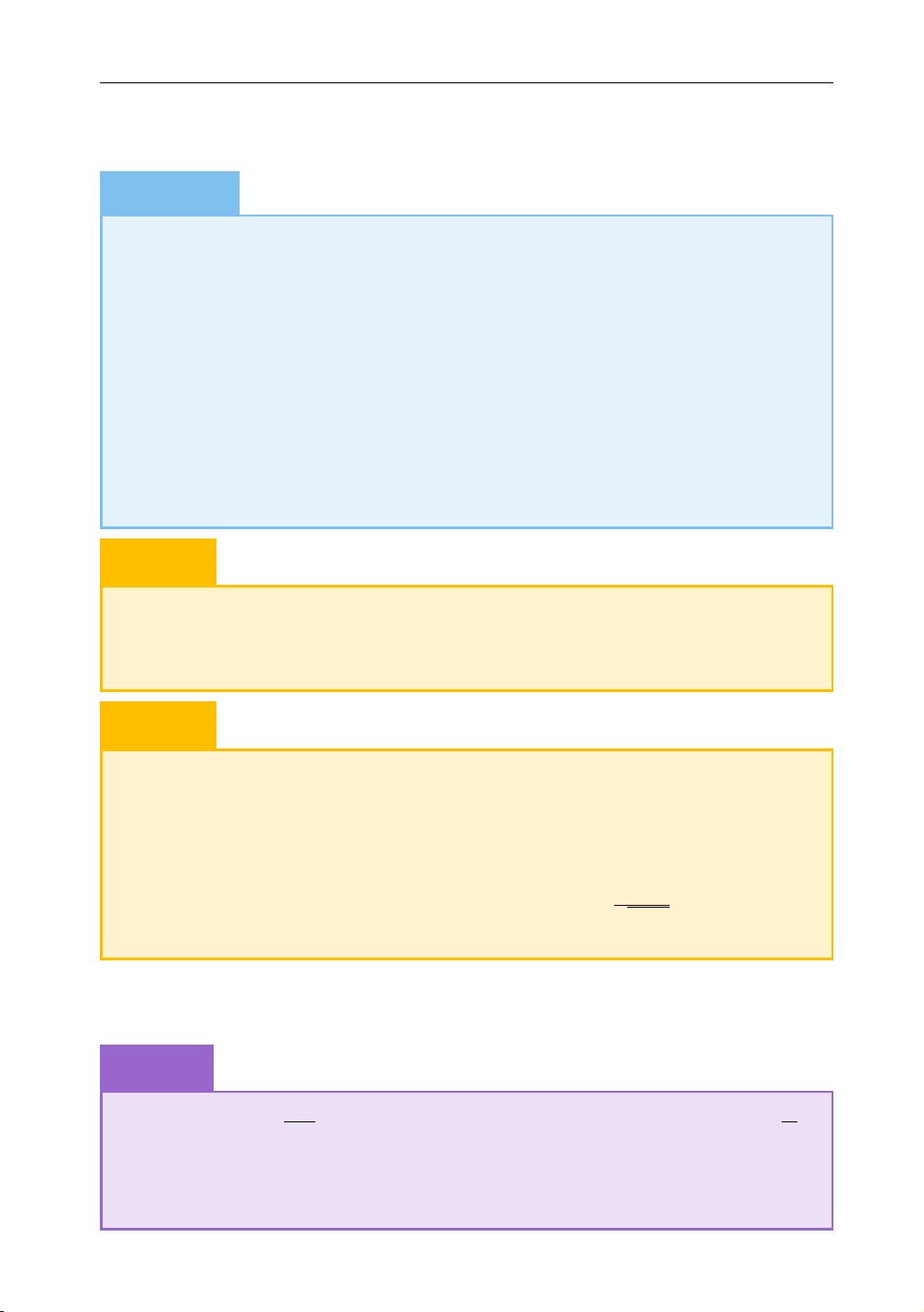
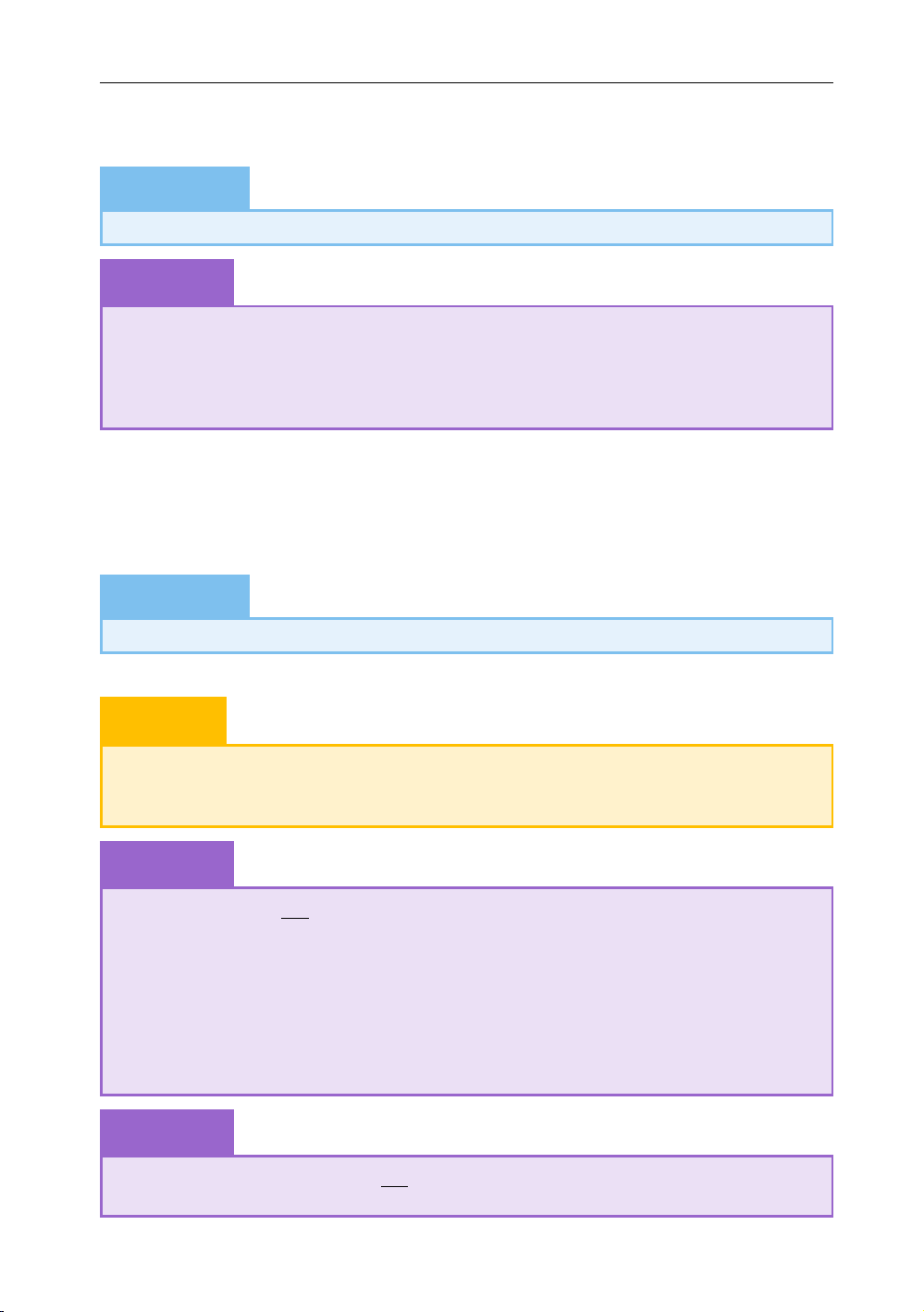
Ta lập được bảng biến thiên của hàm số ( ) như sau x −2 0 3 f 0 x − ( ) + 0 m f x ( ) m − % & m − 24 99 − m
Suy ra, giá trị lớn nhất của hàm số trên khoảng ( 2; 3) là . Do đó, yêu cầu bài m . toán tương đương với = 2 Ví dụ 1.6 y x 3 − x Xét hàm số = 3 + 1
trên đoạn [0; 3]. Mệnh đề nào trong các mệnh đề sau là sai? A. .
Giá trị nhỏ nhất của hàm số trên đoạn [0; 3] là 1 B. .
Giá trị lớn nhất của hàm số trên đoạn [0; 3] là 19 C. .
Hàm số có giá trị lớn nhất và giá trị nhỏ nhất trong đoạn [0; 3] D. x .
Hàm số đạt giá trị lớn nhất khi = 3
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 5 of 59 Ví dụ 1.7 ĐH Khối B năm 2003 √ f x x − x2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số ( ) = + 4 . Hướng dẫn. D − Tập xác định = [
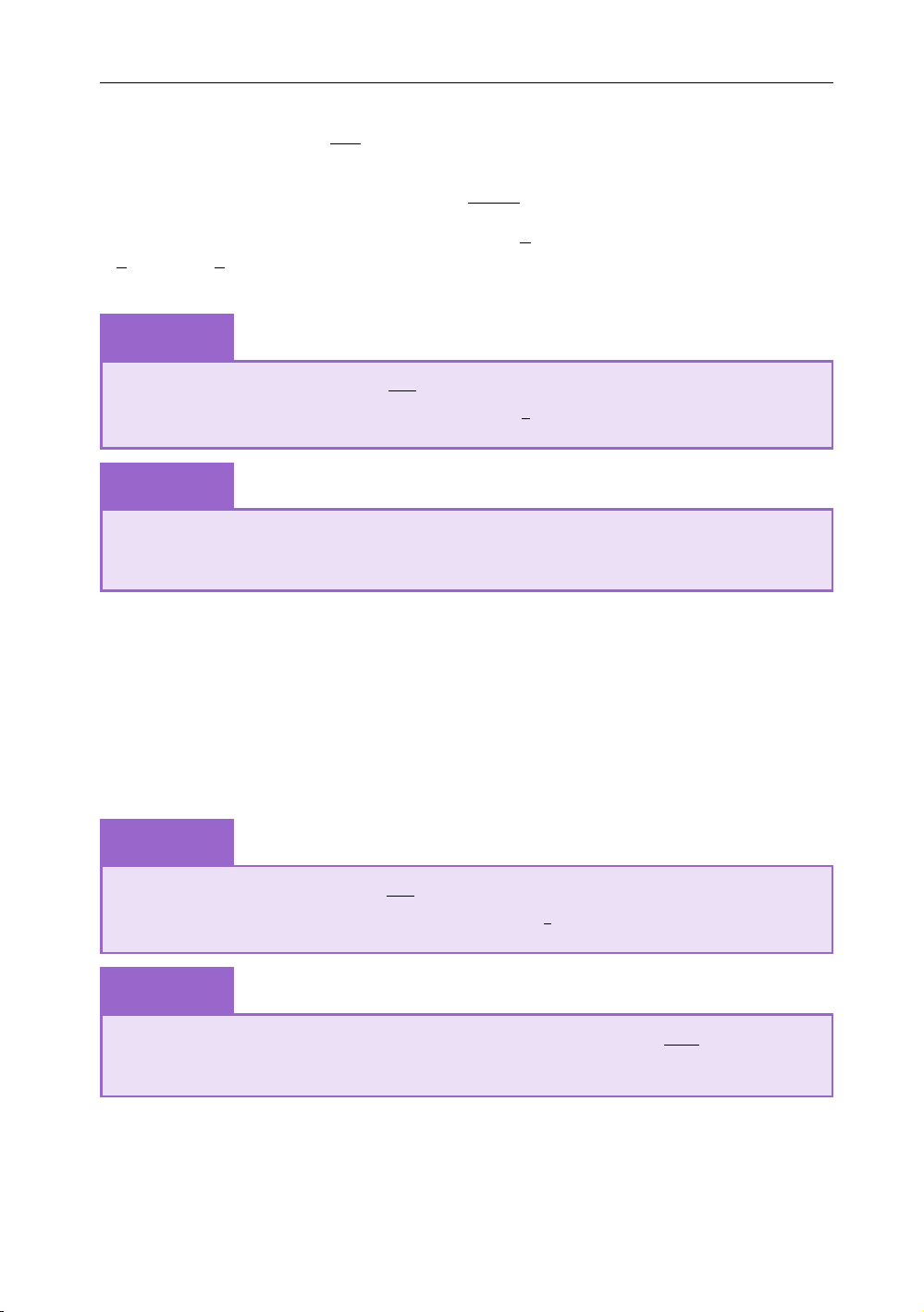
2; 2]. Ta có bảng biến thiên của hàm số đã cho: √ x −2 2 2 f 0 x − ( ) + 0 √ f x 2 2 ( ) − % & 2 2 √ √ f x f , f x f − − . Như vậy max ( ) = ( 2) = 2 2 min ( ) = ( 2) = 2 1.3
Tìm điều kiện để hàm số đơn điệu Bài toán 1.3
Tìm điều kiện để hàm số y
f x đồng biến trên tập K. = ( ) • y f x K Hàm số = ( ) đồng biến trên tập khi và chỉ khi
y0 > , ∀x ∈ K y0 còn x, + 0 nếu dấu của phụ thuộc biến chẳng hạn
các hàm đa thức bậc ba, bậc bốn. y0 > , ∀x ∈ K y0 không còn x, + 0 nếu dấu của phụ thuộc biến chẳng y ax b + hạn các hàm = cx d . +
• Xét các tình huống sau: K R + Nếu tập là
thì sử dụng định lý dấu tam thức bậc hai. m m 6 + Nếu cô lập được tham số đưa điều kiện trên về dạng g x , ∀x ∈ K
m > g x , ∀x ∈ K ( ) hoặc ( )
thì sử dụng nguyên lý cực trị. +
Nếu không thì lập bảng biến thiên có chứa cả tham số để biện luận. Lưu ý 1.4
Định lý dấu tam thức bậc hai f x ax2 bx c a 6 Cho tam thức bậc hai ( ) = + + với = 0 thì (a >
• f x > , ∀x ∈ 0 R ⇔ ( ) 0 6 . ∆ 0
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 6 of 59 (a <
• f x 6 , ∀x ∈ 0 R ⇔ ( ) 0 6 . ∆ 0 Lưu ý 1.5 Nguyên lý cực trị
• m 6 g x , ∀x ∈ K ⇔ m 6 g x , ( ) min ( ) K
• m > g x , ∀x ∈ K ⇔ m > g x . ( ) max ( ) K Ví dụ 1.8 y −x3 − mx2 m x m Cho hàm số = + (4 + 9) + 5 với là tham số. Có bao nhiêu m −∞ ∞ giá trị nguyên của
để hàm số nghịch biến trên khoảng ( ; + )? A. . B. . C. . D. . 4 6 5 7 Hướng dẫn. y0 − x2 − mx m R Có = 3 2 + 4
+ 9. Hàm số đã cho nghịch biến trên khi và chỉ khi (a − < y0 6 ∀x ∈ = 1 0 R ⇔ 0 0 m2 m 6 ∆ = + 3(4 + 9) 0
− 6 m 6 − m Giải hệ này tìm được 9 3. Kết hợp điều kiện
nguyên, ta được tất cả 7 m. giá trị của Ví dụ 1.9 m y 1 x 3 x2 mx
Tìm tất cả các giá trị thực của tham số để hàm số = + + + 1 3
nghịch biến trên khoảng (2; 3).
A. m 6 − .
B. m > − .
C. m 6 − . D. m > − . 15 15 8 8 Hướng dẫn. y0 x2 x m 6 ∀x ∈
Yêu cầu bài toán tương đương với = + 2 + 0 [2; 3].
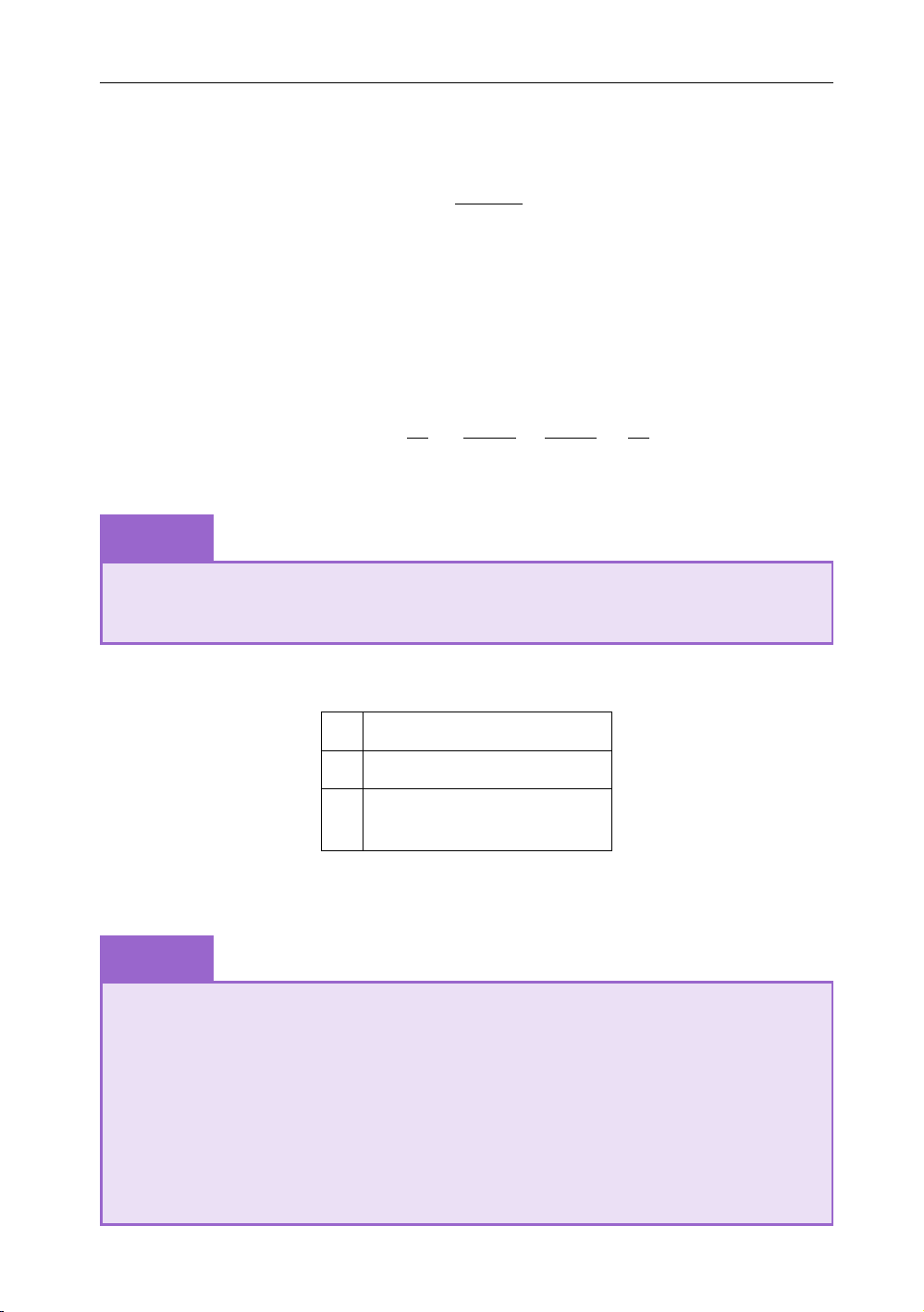
Điều này tương đương với m 6 −x2 − x f x min 2 = min ( ) [2;3] [2;3] x 2 3 f 0 x − ( ) − f 8 & −15
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 7 of 59 f x −x2 − x
Tìm giá trị nhỏ nhất của hàm số ( ) = 2
trên đoạn [2; 3] và suy ra giá trị m m 6 − . cần tìm của là 15
Nhận xét. Bài này có thể sử dụng định lý đảo về dấu tam thức bậc hai, xem ở trang 23, như sau. • a > x x Nhận xét rằng hệ số
0 nên hàm số chỉ có thể nghịch biến ở khoảng ( 1 ; 2 ) x , x y0 . trong đó 1 2
là hai nghiệm của phương trình = 0 • y0
Do đó, yêu cầu bài toán trở thành tìm điều kiện để phương trình = 0 có x 6 < 6 x . hai nghiệm thỏa mãn 1 2 3 2
Điều kiện cần và đủ là (a · y0 6 (2) 0 a · y0 6 . (3) 0
Giải hệ bất phương trình này cũng tìm được đáp số như cách trên. Ví dụ 1.10 m y x m + √
Tìm tất cả các giá trị thực của tham số để hàm số = x đồng biến 2 +1 ∞ trong khoảng (0; + ).
A. m 6 − . B. m 6 . C. m 6 . D. m 6 1 2 1 0. Ví dụ 1.11 m y x3 − m x2
Tìm tất cả các giá trị thực của tham số để hàm số = ( + 1) + 3 m2 m x ( + 2 )
+ 1 nghịch biến trên (2; 3). A. < m <
B. m > . C. m < D. 6 m 6 . 1 2. 2 1. 1 2 Hướng dẫn. y0 x2 − m x m2 m 6
Yêu cầu bài toán tương đương với = 2( + 1) + + 2 , ∀x ∈ m 0
(2; 3). Rõ ràng chúng ta không cô lập được tham số nên phải đưa về việc y0 x m < x m
lập bảng biến thiên. Phương trình = 0 luôn luôn có nghiệm 1 = 2 = + 2
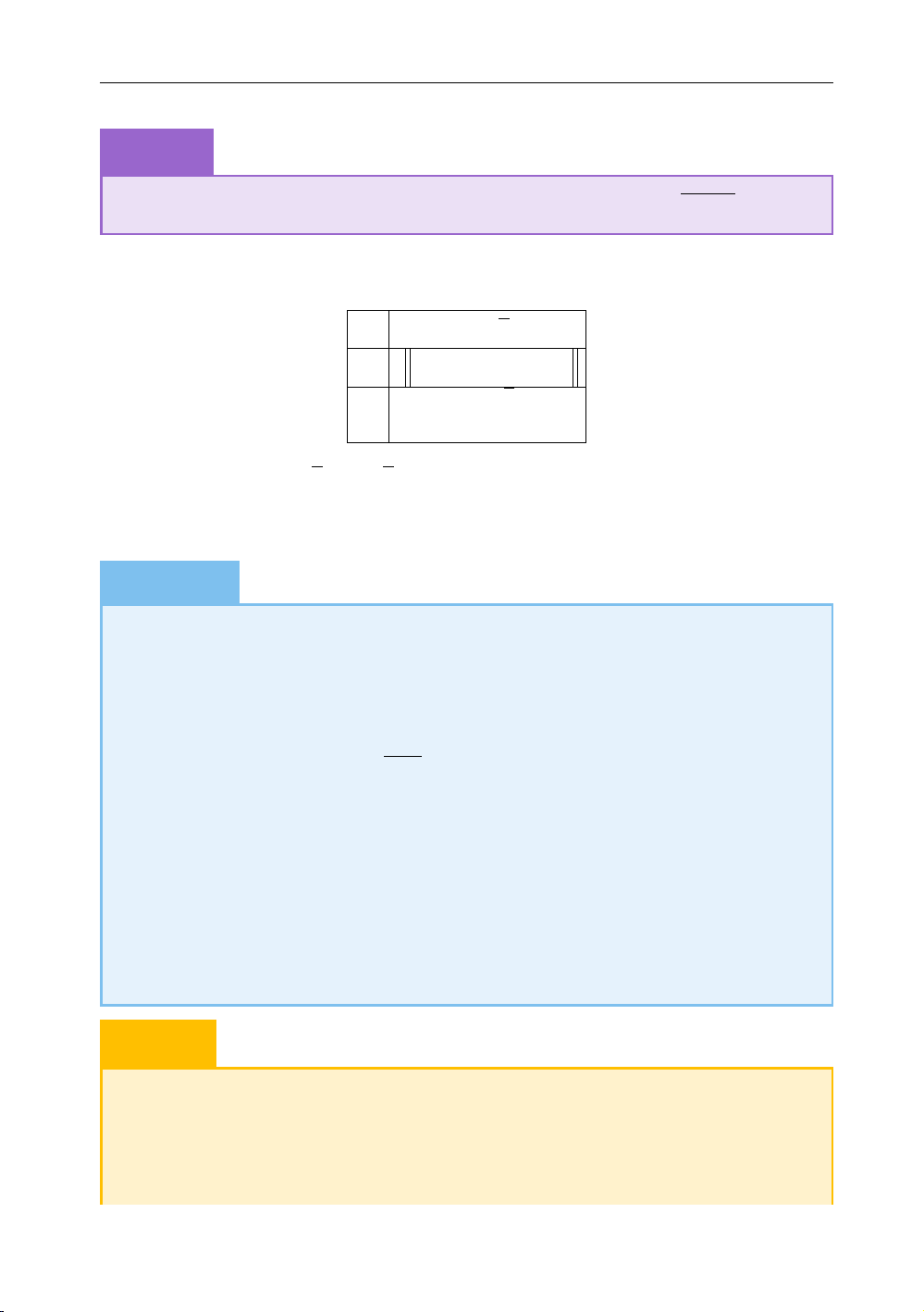
nên ta có bảng biến thiên sau: x −∞ m m ∞ + 2 + y0 x − ( ) + 0 0 + y ∞ y 1 + −∞ % & y % 2
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 8 of 59
Suy ra, hàm số đã cho nghịch biến trên khoảng (2; 3) khi và chỉ khi khoảng (2; 3) là m, m tập con của khoảng ( + 2). Nghĩa là (m 6 2 6 m 3 + 2 6 m 6 .
Từ đó tìm được đáp số 1 2 Ví dụ 1.12 √ m y x2 mx m2
Tìm tất cả các giá trị của để hàm số = + 4 + 4 + 3 nghịch −∞ biến trên khoảng ( ; 2)? A. m > − B. m < C. m < − D. m > 1. 2. 1. 2. Hướng dẫn. x ∈ R.
Hàm số luôn xác định và liên tục với mọi Do đó, ta sẽ tìm điều −∞
kiện để hàm số luôn nghịch biến trên nửa khoảng ( ; 2]. Ta có x m y0 + 2 √ . = x2 mx m2 + 4 + 4 + 3 −∞
Hàm số nghịch biến trên ( ; 2) khi và chỉ khi y0 6 , ∀x 6 ⇔ x
m 6 , ∀x 6 . 0 2 + 2 0 2 m 6 −
Từ đó tìm được đáp số 1. Ví dụ 1.13 − x m m y cos +
Tìm tất cả các giá trị của để hàm số = x m đồng biến trên cos + π khoảng 0; . 2 A. m > m 6 − C. m > 0 hoặc 1. 0. B. m >
D. m 6 − 1. 1. Hướng dẫn. t x y x π Đặt = cos thì ta thấy hàm số = cos nghịch biến trên 0; , 2 π y −t m +
nên hàm số đã cho đồng biến trên 0; khi và chỉ khi hàm số = t m nghịch 2 +
biến trên (0; 1). Điều kiện cần và đủ là ( y0 − m 2 < = t m 2 0 ( + ) ⇔ m > . −m / ∈ 0 (0; 1)
Như vậy, ta chọn đáp án C.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 9 of 59
Nhận xét. Bài này có thể làm trực tiếp mà không cần đặt ẩn phụ. Sử dụng công
thức tính đạo hàm của hàm số hợp, ta tìm được − m y0 2 · − x . = x m ( sin ) 2 (cos + ) π x > ,
Chú ý rằng trong khoảng (0; ) thì sin 0
nên yêu cầu bài toán tương đương với 2 ( m 2 > x m 2 0 (cos + ) x m 6 , ∀x ∈ π cos + = 0 0; 2
Từ đó cũng tìm được đáp số như trên. 1.4
Cực trị của hàm số Bài toán 1.4
Tìm cực trị của hàm số y f x . = ( )
• Đối với một hàm số cụ thể, ta lập bảng xét dấu của đạo hàm và kết luận. • x Đối với hàm ẩn, muốn 0
thuộc tập xác định là một điểm cực trị của y f x hàm số = (
) thì phải thỏa mãn hai điều kiện: f 0 x f 0 x x . + ( 0 ) = 0 hoặc ( ) không xác định tại 0 f 0 x x + (
) phải đổi dấu khi đi qua 0 ,
nếu đổi dấu từ dương sang âm x
(tức là hàm số chuyển từ đồng biến sang nghịch biến) thì 0 là x
điểm cực đại; đổi dấu từ âm sang dương thì 0 là điểm cực tiểu. f 00 x < x
Cũng có thể sử dụng đến đạo hàm cấp hai, ( 0 ) 0 thì 0 là f 00 x > x điểm cực đại; còn ( 0 ) 0 thì 0 là điểm cực tiểu. Lưu ý 1.6
điểm cực trị của hàm số, điểm cực trị của đồ
Cần phân biệt rõ ba khái niệm thị hàm số
giá trị cực trị của hàm số. và Lưu ý 1.7
Phương trình đường thẳng đi qua hai điểm cực trị của • y ax3 bx2 cx d Đồ thị hàm số bậc ba = + + + chính là phần dư khi chia y y0 y y0 · b 1 x mx n cho
. Thực hiện phép chia, ta được = + a + + thì 3 9 y mx n
đường thẳng cần tìm chính là = + . Cách tìm nhanh như sau: mx n y − y0 · b 1 x + Ta nhận thấy + = + a . 3 9
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 10 of 59 y − y0 · b 1 x CALC x +
Sử dụng máy tính, viết hàm + a rồi tại = 0 3 9 n CALC x m n tìm được , tiếp tại = 1 thu được + và từ đó tìm được m. • y ax2 bx c u x + + ( )
Đồ thị hàm số phân thức bậc hai chia bậc nhất = dx e = v x + ( ) y u0 x ( ) chính là = v 0 x . ( ) Ví dụ 1.14 y f x y f 0 x Cho hàm số = ( ) có đồ thị hàm số = (
) như hình vẽ bên. Hỏi hàm y f x số = (
) có bao nhiêu điểm cực trị? A. B. C. D. 1 2 3 4. Ví dụ 1.15 A, B, C y −x4 x2 . Gọi
là ba điểm cực trị của đồ thị hàm số = + 2 + 1 Tính S ABC diện tích của tam giác . A. S . B. S . C. S . D. S . = 1 = 2 = 3 = 4 Ví dụ 1.16
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y x3 − x2 = 3 + 2. Đáp số. y − x . = 2 + 2 Ví dụ 1.17
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y x3 x2 − x = + 3 5 + 1. Đáp số. y − 16 x 8 . là = + 3 3 Ví dụ 1.18 y
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số =
x3 − x + 4 là...
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 11 of 59 Ví dụ 1.19 ĐH năm 2017 Mã đề 101 y
x3 − x2 − x A B Đồ thị hàm số = 3 9
+ 1 có hai điểm cực trị và . Điểm nào AB
dưới đây thuộc đường thẳng ? A. P B. M − C. N − D. Q − (1; 0). (0; 1). (1; 10). ( 1; 10). Ví dụ 1.20 ĐH năm 2017 Mã đề 103 y −x3 x2 A B Đồ thị của hàm số = + 3
+ 5 có hai điểm cực trị và . Tính diện S OAB O tích của tam giác với là gốc tọa độ. A. S . B. S 10 . C. S . D. S . = 9 = = 5 = 10 3 Ví dụ 1.21 y x − x −π, π Hàm số = sin 2 cos
có bao nhiêu cực trị trên đoạn [ ]? Ví dụ 1.22 y x − x , Hàm số = sin
có bao nhiêu cực trị trên đoạn [0 10]? 1.5
Tìm điều kiện để hàm số đạt cực trị tại điểm cho trước Bài toán 1.5
Tìm điều kiện của m để hàm số y
f x đạt cực trị tại x . = ( ) 0
• Điều kiện cần. x f 0 x f 0 x
Hàm số đạt cực trị tại 0 thì ( 0 ) = 0 hoặc ( 0 ) không m.
xác định. Từ đó tìm được giá trị của
• Điều kiện đủ. m Với
vừa tìm được, thay vào hàm số đã cho và tìm cực
trị của nó để kiểm tra. Ví dụ 1.23 y 1 x 3 − mx 2 m2 − m x m Cho hàm số: = + ( + 1) + 1. Xác định để hàm số đạt 3 x cực đại tại điểm = 1. Cách 1. y0 x2 − mx m2 − m , y00 x − m. Ta có = 2 + + 1 = 2 2
• Điều kiện cần: x f 0 ⇔ m
Giả sử hàm số đạt cực đại tại = 1. Suy ra (1) = 0 = , m . 1 = 2
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 12 of 59
• Điều kiện đủ: m y 1 x 3 − x 2 x + Với
= 1 hàm số đã cho trở thành = + + 1. Ta có bảng 3 biến thiên sau: x −∞ ∞ 1 + y0 x ( ) + + ∞ + y 4 % 3 −∞ %
không đạt cực đại x .
Căn cứ vào bảng biến thiên ta thấy hàm số tại = 1 m Do đó,
= 1 không thỏa mãn yêu cầu. m y 1 x 3 − x2 x + Với
= 2 hàm số đã cho trở thành = 2 + 3 + 1. Ta có bảng 3 biến thiên: x −∞ ∞ 1 3 + y0 x − ( ) + 0 0 + 7 ∞ y + 3 −∞ % & % 1 m x Ta thấy, khi
= 2 thì hàm số đạt cực đại tại = 1. m .
Vậy giá trị cần tìm là = 2
Cách 2. Ta xét hai trường hợp: • y00 ⇔ m y 1 x 3 − x 2 x Khi (1) = 0
= 1 thì hàm số trở thành = + + 1. Lập bảng 3 Cách 1 m biến thiên như và khẳng định
= 1 không thỏa mãn yêu cầu. • y00 6 ⇔ m 6 x Khi (1) = 0
= 1 thì hàm số đạt cực đại tại = 1 khi và chỉ khi (y0(1) = 0 ⇔ m y00 < = 2 (1) 0 m . m
Kết hợp hai trường hợp được đáp số = 2 Vậy với
= 2 thì hàm số đã cho đạt x . cực đại tại = 1 Ví dụ 1.24 ĐH năm 2017 Mã đề 102 m y 1 x 3 − mx 2 m2 −
Tìm tất cả các giá trị thực của tham số để hàm số = + ( 3 x x . 4) + 3 đạt cực đại tại = 3 A. m . B. m − . C. m . D. m − . = 1 = 1 = 5 7
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 13 of 59 Ví dụ 1.25 m y mx2 x m + + x . Tìm để hàm số = x− đạt cực đại tại = 2 1 Hướng dẫn.
mx2− mx− −m D R y0 2 1 Tập xác định = . Ta có = x− 2 . ( 1) • x . y0 ⇔ m
Điều kiện cần: Giả sử hàm số đạt cực đại tại = 2 Suy ra (2) = 0 = − . 1 • m − y −x2 x− + 1 Điều kiện đủ: Khi =
1 hàm số đã cho trở thành = x− . Ta có bảng 1 biến thiên: x −∞ ∞ 0 1 2 + y0 x − − ( ) 0 + + 0 ∞ ∞ − y + + 3 & % −∞ % & −∞ 1 m − x . Vậy với =
1 thì hàm số đã cho đạt cực đại tại = 2 1.6
Tìm điều kiện để hàm số có cực trị Bài toán 1.6
Tìm điều kiện để hàm số y f x có cực trị. = ( )
Tổng quát, muốn hàm số có cực trị thì đạo hàm phải có nghiệm và phải đổi
dấu khi đi qua nghiệm này. Ở đây chúng ta xét ba loại hàm thường gặp. • y ax3 bx2 cx d a 6 y0 Hàm số bậc ba = + + + , với = 0, thì đạo hàm là
tam thức bậc hai nên có hai khả năng: y0 + Phương trình
= 0 vô nghiệm hoặc có nghiệm kép thì hàm số không có trị. y0 + Phương trình
= 0 có hai nghiệm phân biệt thì hàm số có hai điểm cực trị. không có cực trị có
Như vậy, hàm số bậc ba chỉ có hai tình huống và
cực trị, nếu có thì sẽ có hai điểm cực trị, gồm một điểm cực đại và một điểm cực tiểu. • y ax4 bx2 c a 6 ,
Hàm số bậc bốn trùng phương = + + , với = 0 thì phương y0 trình = 0 tương đương với x = 0 x2 − b . ∗ = a ( ) 2 y0 x Phương trình = 0 này luôn có nghiệm
= 0 nên ta có hai khả năng:
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 14 of 59 ∗ + Phương trình (
) vô nghiệm hoặc có nghiệm kép, nghiệm kép này
cũng bằng 0, thì hàm số có một điểm cực trị. ∗ + Phương trình (
) có hai nghiệm phân biệt, thì hàm số có ba điểm cực trị.
Như vậy, hàm số bậc bốn trùng phương luôn luôn có cực trị, có thể có
một hoặc ba điểm cực trị. •
Hàm số phân thức bậc nhất trên bậc nhất thì không có cực trị. Ví dụ 1.26 y x2 mx +2 +1
Tìm điều kiện để hàm số = x− có cực trị? 1 Hướng dẫn. x 6 . y0 x2− x− m− 2 2 1 Điều kiện xác định = 1 Ta có = x− 2 nên ( 1) (
x2 − x − m − x 6 y0 ⇔ 2 2 1 ⇔ = 1 = 0 x − = 0 2
x2 − x − m − ∗ ( 1) 2 2 1 = 0 ( ) g x
x2 − x − m − Đặt ( ) = 2 2
1. Hàm số đã cho có cực trị khi và chỉ khi phương trình ∗ (
) có hai nghiệm phân biệt khác 1 0 > m > m > − ⇔ ∆ 0 ⇔ 2 + 2 0 ⇔ 1 ⇔ m > − g 6 − m − 6 m 6 − 1 (1) = 0 2 2 = 0 = 1 m > − Vậy với
1 thì hàm số có cực đại và cực tiểu. Ví dụ 1.27 y x3 − x2 mx m −
Tìm điều kiện để hàm số = 3 + + 1 có cực trị? Hướng dẫn. y0 x2 − x m Ta có = 3 6 + nên y0 ⇔ x2 − x m = 0 3 6 + = 0 (1)
Hàm số có cực trị khi và chỉ khi phương trình (1) có hai nghiệm phân biệt ⇔ 0 − m > ⇔ m < ∆ = 9 3 0 3 m < Vậy với
3 thì hàm số luôn có cực đại và cực tiểu.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 15 of 59 Ví dụ 1.28 y x4 − m x2 − m
Tìm điều kiện để hàm số = 2( + 1)
có cực đại, cực tiểu? Hướng dẫn. y0 x3 − m x x x2 − m − Ta có = 4 4( + 1) = 4 ( 1) nên x y0 ⇔ x x = 0 2 − m − ⇔ = 0 4 ( 1) = 0 x2 m ∗ = + 1 ( ) ∗
Do đó, hàm số có cực đại và cực tiểu khi và chỉ khi phương trình ( ) có hai nghiệm phân biệt khác 0 ⇔ m > ⇔ m > − + 1 0 1 m < − Vậy với
1 thì hàm số luôn có cực đại và cực tiểu. Ví dụ 1.29 ĐH Khối B năm 2002 m y mx4 m2 − x2 Tìm để hàm số = + ( 9)
+ 10 có ba điểm cực trị? Đáp số. m < − < m < 3 hoặc 0 3. Ví dụ 1.30 √ y f x y0 x2 − x 1 b a , ∀x ∈ R Cho hàm số = ( ) có đạo hàm = 12 + ( + 3 ) . Biết 4 f x a, b rằng hàm (
) số luôn có hai cực trị với
là các số nguyên không âm thỏa b − a 6 P a b mãn 3
6. Tìm giá trị lớn nhất của biểu thức = 2 + . A. B. C. D. 1. 9. 8. 6. √ Hướng dẫn. y0 x2 − bx − 3 a . Ta có = + 3
Hàm số luôn có hai cực trị khi và chỉ 4 khi > ⇔ − b − a > . ∆ 0 12 3 0 a b Như vậy các số nguyên và
thỏa mãn các điều kiện sau  a >  0   b > 0 b − a 6  3 6   b a < + 3 12 Oab
Biểu diễn các bất phương trình này lên hệ trục tọa độ
ta sẽ được miền tứ giác OABC O , A , B , C với (0; 0) (0; 2) (3; 3)
(4; 0). Trong số các điểm có tọa độ nguyên OABC M P thuộc miền tứ giác thì có điểm (3; 2) làm biểu thức
đạt giá trị lớn nhất, P . .
và giá trị lớn nhất đó là max = 2 3 + 2 = 8
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 16 of 59 1.7
Tìm điều kiện để hàm số có cực trị thỏa mãn yêu cầu cho trước
Tìm điều kiện để hàm số y
f x có cực trị thỏa mãn yêu cầu cho Bài toán 1.7 = ( ) trước.
Đối với bài toán này, trước tiên ta tìm điều kiện để hàm số có cực trị đã. Sau đó, y0 nếu phương trình
= 0 có nghiệm đẹp thì ta tìm cụ thể các nghiệm này, nếu không x , x thì gọi các nghiệm là 1 2 và sử dụng Viète. Ví dụ 1.31 CĐ năm 2009 m y x3 − m − x2 − m x Tìm để hàm số = (2 1) + (2 )
+ 2 có cực đại, cực tiểu và
các điểm cực đại, cực tiểu có hoành độ dương? Hướng dẫn. D R. Tập xác định = y0 x2 − m − x − m y0 Có = 3 2(2 1) + (2 ) nên phương trình = 0 tương đương với x2 − m − x − m 3 2(2 1) + (2 ) (2)
Hàm số đã cho có cực đại, cực tiểu và các điểm cực đại, cực tiểu có hoành độ dương
⇔ phương trình (2) có hai nghiệm dương phân biệt  0> m − 2 − − m > ∆ 0 (2 1) 3(2 ) 0   ⇔ S > ⇔ m − >
⇔ 5 < m < 0 2 1 0 2   4 P >− m > 0 2 0 5 < m < .
Vậy đáp số cần tìm là 2 4 Ví dụ 1.32 ĐH Khối D năm 2012 m y
2 x 3 − mx 2 − m2 − x 2 x , x Tìm để hàm số = 2 3 1 + có hai điểm cực trị 1 2 3 3 x x x x thỏa mãn 1 2 + 2( 1 + 2 ) = 1 Hướng dẫn. y0 x2 − mx − m2 − y0 Có = 2 2 2(3 1) nên phương trình = 0 tương đương với x2 − mx − m2 − 2 2 2(3 1) (3) ⇔
Hàm số đã cho có hai điểm cực trị
phương trình (3) có hai nghiệm phân biệt ⇔
0 > ⇔ m ∈ −∞, − 2 √ ∪ 2 √ , ∞ ∆ 0 ( ) ( + ) 13 13
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 17 of 59 x , x x x m Khi đó, 1 2
là nghiệm của phương trình (3) và theo Viète ta có 1 + 2 = và x x − m2 x x x x 1 2 = 1 3
Do đó, yêu cầu của đề bài 1 2 + 2( 1 + 2 ) = 1 tương đương với − m 2 2 m ⇔ m m 1 3 + 2 = 1 = hoặc = 0 3 m 2 .
Kết hợp điều kiện được đáp số = 3 Ví dụ 1.33 m y 1 x 3 − m − x2 m − x 1 m2 Tìm để đồ thị hàm số = ( 2) + ( 2) + có hai điểm 3 3
cực trị nằm về phía bên phải trục tung? m > m > 1. 2 3. 3 m > ∨ m < m < 2. 3 2 4. 2 Hướng dẫn. Oxy
Trong mặt phẳng tọa độ
, những điểm nằm về bên phải trục tung
nghĩa là những điểm này có đặc điểm gì? Đồ thị hàm số có hai điểm cực trị nằm
về bên phải trục tung nghĩa là hoành độ của chúng dương? Hoành độ tìm được từ đâu?
Mở rộng bài toán, hai điểm cực trị nằm về bên trái trục tung, nằm về hai phía đối với trục tung. Ví dụ 1.34 m 6 y mx3 − mx2 m −
Chứng minh rằng với mọi = 0 thì đồ thị hàm số = 3 + 3 ( 1) A, B. m luôn có hai điểm cực trị. Giả sử hai điểm cực trị này là Tìm để AB2 − OA2 OB2 O 2 ( + ) = 20 với là gốc tọa độ. Hướng dẫn. A , m − B , −m − m , m − 17 . Chỉ ra (0 3 3) và (2 3) và tìm được = 1 = 11 Ví dụ 1.35 y
x4 − m2x2 m Cho hàm số = 2 + 1. Xác định
để hàm số có 3 điểm cực trị là
3 đỉnh của tam giác vuông cân. Hướng dẫn. y0
x3 − m2x x x2 − m2 Ta có = 4 4 = 4 ( ) nên x y0 ⇔ = 0 = 0 x2 − m2 ∗ = 0 ( )
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 18 of 59 ⇔ ∗
Hàm số có ba điểm cực trị Phương trình (
) có hai nghiệm phân biệt khác 0 ⇔ m 6= 0
Khi đó, ba điểm cực trị của đồ thị hàm số là A , B m −m4 , C −m −m4 (0; 1) ( ; + 1) ( ; + 1) Ta có −→ p AB m −m4 ⇒ AB m2 m8 = ( ; ) = + −→ p AC
−m −m4 ⇒ AC m2 m8 = ( ; ) = + ABC A Vì ∆ cân tại
nên 3 điểm cực trị của đồ thị tạo thành một tam giác vuông cân khi và chỉ khi −→ −→ −→ −→ m AB ⊥ AC ⇔ AB.AC ⇔ −m = 0 2 m8
⇔ m2 m6 − ⇔ = 0 + = 0 ( 1) = 0 m ± = 1 m ±
Đối chiếu với điều kiện, được đáp số = 1. Ví dụ 1.36 m y
1 x 3 − 1 mx 2 m2 − x x Tìm các giá trị của để hàm số = + 3 có cực đại 1 , 3 2 x x , x cực tiểu 2 và 1 2
là độ dài các cạnh góc vuông của một tam giác vuông có q 5
độ dài cạnh huyền bằng . 2 Hướng dẫn. D R. Tập xác định = y0 x2 − mx m2 − y0 ⇔ x2 − mx m2 − Có = + 3 nên = 0 + 3 = 0 y0 x x Vì
là một tam thức bậc hai nên hàm số có cực đại 1 , cực tiểu 2 thỏa yêu cầu y0
bài toán khi và chỉ khi phương trình
= 0 có 2 nghiệm dương phân biệt   > − m2 > ∆ 0 4 0   √ ⇔ S > ⇔ m > ⇔ < m < 0 0 3 2   P >m2 − > 0 3 0
Khi đó, áp dụng Viète ta được √ x 5 14 2 x2 ⇔ x x 2 − x x ⇔ m2 − m2 − ⇔ m ± + = 2( 4 2 4( 3) = 5 = 1 2 1 + 2 ) 1 2 = 5 2 2 √ m 14
Đối chiếu điều kiện ở trên ta có giá trị = thỏa yêu cầu bài toán 2
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 19 of 59 Ví dụ 1.37 m y −x3 mx2 − m − Tìm để đồ thị hàm số = + 3 3
1 có cực đại và cực tiểu đối d x y − .
xứng nhau qua đường thẳng : + 8 74 = 0 Hướng dẫn. y0 − x2 mx Có = 3 + 6
= 0 nên đồ thị hàm số có cực trị khi và chỉ khi m 6 . A − m − = 0
Suy ra, một điểm cực trị của đồ thị hàm số là (0; 3 1). Yêu cầu bài I
toán tương đương với trung điểm
của hai điểm cực trị của đồ thị hàm số phải nằm d IA ⊥ d I trên đường thẳng và . Mà
cũng chính là điểm uốn của đồ thị hàm số, nên I m m3 − m − có ( ; 2 3
1). Do đó, điều kiện cần và đủ là (− → AI · ~ ud = 0 m m3 − m − − + 8(2 3 1) 74 = 0 m . Từ đó tìm được = 2 Lưu ý 1.8
Ba điểm cực trị của đồ thị hàm số bậc bốn trùng phương luôn tạo thành một tam giác cân. Ví dụ 1.38 ĐH Khối A năm 2012 m y x4 − m x2 m2 Tìm
để ba điểm cực trị của đồ thị hàm số = 2( + 1) + tạo
thành ba đỉnh của một tam giác vuông. Hướng dẫn. y0 x3 − m x x x2 − m − Ta có = 4 4( + 1) = 4 (
1). Do đó, đồ thị hàm số có ⇔ m > − . ba điểm cực trị 1
Khi đó, ba điểm cực trị của đồ thị hàm số là √ √ A , m2 , B m , − m − C − m , − m − (0 ) ( + 1 2 1) và ( + 1 2 1) −→ √ −→ √ AB − m , − m 2 , AC m , − m 2 Suy ra = ( + 1 ( + 1) ) = ( + 1 (
+ 1) ). Nhận thấy tam giác ABC A ABC cân tại nên tam giác vuông khi và chỉ khi −→ −→ AB.AC ~ ⇔ m 4 − m ⇔ m m − = 0 ( + 1) ( + 1) = 0 = 0 hoặc = 1 m .
Kết hợp điều kiện được đáp số = 0
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 20 of 59 Ví dụ 1.39 m y x4 − m − x2 m2 − m Tìm để đồ thị hàm số = 2( 2) + 5 + 5 có cực đại và
cực tiểu, đồng thời các điểm này tạo thành một tam giác đều. Hướng dẫn. y0 x3 − m − x ⇔ x ∨ x2 m − Có = 4 4( 2) = 0 = 0 = 2. Suy ra, đồ thị hàm
số có cực đại và cực tiểu ⇔ m − > ⇔ m > . 2 0 2 √ √ A , m2 − m , B m − , − m C − m − , − m
Khi đó, ba điểm cực trị là (0 5 + 5) ( 2 1 ) và ( 2 1 ) A
tạo thành một tam giác cân tại
. Do đó, yêu cầu bài toán tương đương với −→ −→ ◦ AB · AC 1 1 b A ⇔ A ⇔ = 60 cos = − → −→ = 2 AB · AC 2 √ m 3
Từ đó tìm được đáp số = 2 + 3. Ví dụ 1.40 y x4 − mx2 m2 − , m m Cho hàm số = 2 + 2 4
là tham số thực. Xác định để đồ
thị hàm số đã cho có 3 cực trị tạo thành một tam giác có diện tích bằng 1. Hướng dẫn. D R. TXĐ: = x y0 x = 0 3 − mx y0 ⇔ x3 − mx ⇔ Ta có = 4 4 , nên = 0 4 4 = 0 x2 m = m >
Suy ra, đồ thị hàm số có ba điểm cực trị khi và chỉ khi 0.
Khi đó ba điểm cực trị của đồ thị hàm số là √ √ A m2 − B m m2 − C − m m2 − . (0; 2 4); ( ; 4); ( ; 4) B, C Oy A Oy ABC A H Ta thấy đối xứng qua và thuộc nên ∆ cân tại . Do đó, gọi BC AH ⊥ BC là trung điểm thì và có √ S 1 ABC AH.BC ⇔ |yB − yA| . | xB| ⇔ m2 m ⇔ m . ∆ = 2 = 2 2 = 2 = 1 2 m
Đối chiếu với điều kiện được = 1 là giá trị cần tìm. Ví dụ 1.41 m y x4 mx2 − m − Tìm
để ba điểm cực trị của đồ thị hàm số = + 2 1 tạo thành √
một tam giác có diện tích bằng 4 2.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 21 of 59 Hướng dẫn. m < .
Hàm số có 3 điểm cực trị khi và chỉ khi 0
Khi đó, ba điểm cực trị là √ √ A −m − , B
−m −m2 − m −
, C − −m −m2 − m − . (0; 1) ( ; 1) ( ; 1) I BC Gọi là trung điểm thì √ √ S ABC ⇔ 1 IA.BC ⇔ m − . ∆ = 4 2 = 4 2 = 2 2 m − .
So sánh điều kiện được đáp số = 2 Ví dụ 1.42 m y x4 mx2
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số = + 2 + 1
có ba điểm cực trị tạo thành một tam giác vuông cân. A. m −1 √ B. m − . C. m 1 √ D. m = 3 . = 1 = 3 . = 1. 9 9
Hướng dẫn. Trước tiên ta tìm điều kiện để đồ thị hàm số có ba điểm cực trị, tức là y0 phương trình
= 0 phải có ba nghiệm phân biệt. x y0 ⇔ x x = 0 2 m ⇔ = 0 4 ( + ) = 0 x2 −m = y0 −m > ⇔ m < . Do đó, phương trình
= 0 có ba nghiệm phân biệt khi và chỉ khi 0 0
Lúc này, ta đã loại được hai phương án C và D và đồng thời tính được toạ độ ba điểm cực trị là √ √ A , B − −m −m2 , C −m −m2 (0; 1) ( ; + 1) ( ; + 1) −→ √ −→ √ AB
− −m −m2 , AC −m −m2 ABC Từ đó tìm được = ( ; ) = ( ; ). Rõ ràng tam giác chỉ −→ −→ A, AB · AC . có thể vuông cân tại tức là = 0 m m4 ⇔ m − . + = 0 = 1 m − .
So sánh điều kiện được đáp số cuối cùng là = 1
Bài này sau khi loại được hai phương án C và D, ta cũng có thể chọn một phương m − án (nên chọn phương án =
1) để thay vào và tìm cụ thể toạ độ các điểm cực
trị, rồi kiểm tra xem có tạo thành một tam giác vuông hay không. Cách này có vẻ sẽ nhanh hơn. Ví dụ 1.43 m y 1 x 3 − mx 2 m2
Tìm tất cả các giá trị thực của tham số để hàm số = + ( + 3 m − x x , x |x x | . 1)
đạt cực trị tại hai điểm 1 2 thỏa mãn 1 + 2 = 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 22 of 59 A. m .
B. m ∈ ∅. C. m − . D. m ± . = 2 = 2 = 2 m
Bài này có thể làm xuôi, tức là tìm ra giá trị của
rồi so sánh với các phương án. m
Hoặc, chủ động thay các giá trị của
trong các phương án vào và kiểm tra. Chúng
ta sẽ cùng tìm hiểu cả hai cách. Cách 1. y0 x2 − mx m2 m − Ta có = 2 + +
1. Hàm số có hai cực trị khi và chỉ khi y0 phương trình
= 0 có hai nghiệm phân biệt. Điều kiện cần và đủ là 0 m2 − m2 m − > ⇔ m < . ∆ = ( + 1) 0 1 y0 x , x x x Khi đó, phương trình
= 0 có hai nghiệm phân biệt 1 2 . Theo Viète có 1 + 2 = −b/a m | m| ⇔ m ± =
, nên yêu cầu bài toán trở thành 2 = 4 = 2. So sánh với điều m − . kiện được đáp số = 2 Cách 2. m m − . m
Ta sẽ lần lượt thử với = 2 và = 2 Với = 2 hàm số trở thành y 1 x3 − x2 x = 2 + 5 3 y0 x2 − x y0 m m − Có = 4 + 5. Phương trình = 0 vô nghiệm nên loại = 2. Với = 2 thì m − .
làm tương tự ta thấy thỏa mãn yêu cầu. Tóm lại, chúng ta chọn đáp án = 2 Ví dụ 1.44 m y x4 − mx2
Tìm tất cả các giá trị thực của sao cho đồ thị hàm số = 2 + m m4 2 +
có ba điểm cực trị tạo thành một tam giác đều. √ √ √ A. m . B. m 3 C. m − 3 D. m . = 0 = 3. = 3. = 3 Ví dụ 1.45 y x4 − mx2 m − C Cho hàm số = + 2 1 có đồ thị là (
m). Tìm tất cả các giá trị m C thực của tham số để (
m) có 3 điểm cực trị cùng với gốc tọa độ tạo thành một hình thoi. √ √ A. m ± B. m ± C. m ± D. m ∈ ∅ = 1 + √ = 2 2 = 4 2. . 2. Hướng dẫn. m >
Đồ thị hàm số đã cho có 3 điểm cực trị khi và chỉ khi 0. Khi đó,
ta có ba điểm cực trị của đồ thị hàm số là r m m r 2 m m2 A m − , B − m − , C − − m − . (0; 2 1) ; + 2 1 ; + 2 1 2 4 2 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 23 of 59 2 OB AB ⇔ m4 − m2 m − ⇔ m
Yêu cầu bài toán tương đương với = = + 2 1 = 16 4 √ ± 2 2. Ví dụ 1.46 y 1 x 3 m x2 m x m2−m
Tìm các giá trị của tham số m để hàm số = +( +3) +4( +3) + 3 x , x − < x < x có các điểm cực trị 1 2 thỏa mãn điều kiện 1 1 2 A. −∞ − C. −∞ − ∪ ∞ ( ; 2) ( ; 3) (1; + ) B. − 7 − D. − 7 − ; 2 ; 3 2 2 Hướng dẫn. y0 x2 m x m . Ta có = + 2( + 3) + 4( + 3)
Hàm số có hai điểm cực trị khi y0 và chỉ khi phương trình
= 0 có hai nghiệm phân biệt. Điều kiện cần và đủ là > ⇔ m ∈ −∞ − ∪ ∞ . ∆ 0 ( ; 3) (1; + ) x , x
Khi đó, giả sử hai điểm cực trị là 1 2 thì theo Viète ta có x x − m 1 + 2 = 2( + 3) x · x m 1 2 = 4( + 3) − < x < x Mặt khác, điều kiện 1 1 2 có thể viết lại thành x x > ( 1 + 1)( 2 + 1) 0 x x > − 1 + 2 2 m ∈ − 7 −
Giải hệ phương trình này được ; 2
. Kết hợp điều kiện ta được đáp số 2 m ∈ − 7 − ; 3 . 2
Nhận xét. Thực ra, bài này có thể sử dụng định lý đảo về dấu tam thức bậc hai. y0
Yêu cầu bài toán tương đương với phương trình
= 0 có hai nghiệm phân biệt và − số
1 nằm bên trái khoảng hai nghiệm. Điều kiện cần và đủ là  > ∆ 0  a · f − > ( 1) 0  − < S 1 2
Giải hệ này cũng tìm được đáp số như trên. Lưu ý 1.9
Định lý đảo về dấu tam thức bậc hai f x ax2 bx c a 6 ε f x Xét tam thức ( ) = + + với = 0 và một số thực . Khi ( ) có hai x , x x < x nghiệm phân biệt 1 2 , giả sử thêm rằng 1 2 , thì
• x < ε < x ⇔ a · f ε < , ε 1 2 ( ) 0 tức là số
nằm trong khoảng hai nghiệm.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 24 of 59  > ∆ 0 
• ε < x < x ⇔ a · f ε > , ε 1 2 ( ) 0 tức là số nằm ngoài, ở bên trái  ε < S 2 khoảng hai nghiệm.  > ∆ 0 
• x < x < ε ⇔ a · f ε > , ε 1 2 ( ) 0 tức là số nằm ngoài, ở bên phải  ε < S 2 khoảng hai nghiệm. Tương tự, ta cũng có
x 6 ε 6 x ⇔ a · f ε 6 1 2 ( ) 0 1.8
Tiệm cận của đồ thị hàm số Bài toán 1.8
Tiệm cận của đồ thị hàm số x x Đường thẳng = 0
được gọi là tiệm cận đứng của đồ thị hàm số nếu y ∞ lim x→x = 0 y y Đường thẳng = 0
được gọi là tiệm cận ngang của đồ thị hàm số nếu y y 6 ∞ lim x→∞ = 0 = ∞ −∞
Chú ý rằng, trong các công thức trên không cần phân biệt + hay . Lưu ý 1.10
Để tính được các giới hạn trong bài toán tiệm cận, chủ yếu dùng hai công thức sau. • 1 1 ∞. lim ∞ = 0 và lim = 0
• Quy tắc L’Hospital để khử các dạng vô định f x f 0 x ( ) ( )
lim g x = lim g0 x ( ) ( )
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 25 of 59 Lưu ý 1.11
Chú ý rằng một đường tiệm cận vẫn có thể cắt đồ thị hàm số, ví dụ hàm số y x+3 √ y , = x
có tiệm cận ngang là đường thẳng = 1 nhưng vẫn cắt đường 2 +1 x − 4 . tiệm cận ngang này tại = 3 Ví dụ 1.47 Đề thử nghiệm 2017 y x 2 +1 .
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số = x+1 A. x . B. y − . C. y . D. x − . = 1 = 1 = 2 = 1 Ví dụ 1.48 ĐH năm 2017 Mã đề 101 y x2− x− 3 4 .
Tìm số tiệm cận đứng của đồ thị hàm số = x2−16 A. . B. . C. . D. . 2 3 1 0
Hướng dẫn. Trước hết ta cần phải xác định rõ yêu cầu, ở đây là tìm số tiệm cận f x x
đứng, do đó ta sẽ đi tính các giới hạn dạng lim x→x ( ) trong đó 0 là nghiệm của 0 mẫu. Ví dụ 1.49 ĐH năm 2017 Mã đề 104 y x−2 Đồ thị hàm số = x2− có bao nhiêu tiệm cận? 4 A. . B. . C. . D. . 2 3 1 0
Hướng dẫn. Rõ ràng, ở câu này, chúng ta phải tìm cả tiệm cận đứng và tiệm cận f x f x
ngang. Tức là phải đi tính cả các giới hạn dạng lim x→∞ ( ) và lim x→x ( ). 0 Ví dụ 1.50 ĐH năm 2017 Mã đề 102 y x2− x 5 +4 .
Tìm số tiệm cận đứng của đồ thị hàm số = x2−1 A. . B. . C. . D. . 2 3 1 0
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 26 of 59
Hướng dẫn. Trước hết ta cần phải xác định rõ yêu cầu, ở đây là tìm số tiệm cận f x x
đứng, do đó ta sẽ đi tính các giới hạn dạng lim x→x ( ) trong đó 0 là nghiệm của 0 mẫu. Ví dụ 1.51 ĐH năm 2017 Mã đề 103
Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? A. y 1 √ . C. y 1 . = x = x4+1 B. y 1 . D. y 1 . = x2 x = x2 + +1 +1 Hướng dẫn. f x f x
Ta cần lần lượt đi tính các giới hạn lim x→x ( ) trong đó ( ) lần lượt là 0
các hàm đã cho ở bốn phương án. Nhưng muốn có giới hạn này, phải tìm được các x số
0 , do đó, mục tiêu của ta là đi tìm xem trong các hàm số đã cho, hàm số nào có x y 1 √ . số 0
làm cho mẫu không xác định. Hiển nhiên, ở đây chỉ có hàm số = x Ví dụ 1.52 y x+3 √ .
Tìm tiệm cận ngang của đồ thị hàm số = x2+1
Hướng dẫn. Chúng ta thấy bậc cao nhất của cả tử và mẫu là 1, nên ta chia cả tử x và mẫu cho được x 1 + 3 √ 1 + x lim x→ ∞ = lim x→ ∞ q = 1 + x2 + + 1 1 1 + x2 x 1 + 3 √ 1 + x − lim x→−∞ q x = lim x→−∞ = 1 2 + 1 − 1 1 + x2 y y − .
Suy ra, đồ thị hàm số có hai đường tiệm cận ngang là = 1 và = 1 x → ∞
Trong ví dụ trên, chúng ta không thể tính chung khi được. Mà phải phân x → ∞ x → −∞ biệt khi + và
vì với mỗi một trường hợp, ta có thể thu được một tiệm cận ngang khác nhau. Ví dụ 1.53 Đề minh hoạ 2017 y f x f x f x − Cho hàm số = ( ) có lim x→ ∞ ( ) = 1 và lim x→−∞ ( ) = 1. Khẳng định nào +
sau đây là khẳng định đúng?
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 27 of 59
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. C. y
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng = 1 y − . và = 1 D. x
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng = 1 x − . và = 1 Ví dụ 1.54 m y x2− x m 2 3 +
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số = x−m
không có tiệm cận đứng. A. m . B. m m C. m . D. m ∈ ∅ = 0 = 0; = = 1 . . 1 Hướng dẫn. x m. Nghiệm của mẫu số là =
Yêu cầu bài toán tương đương với tử số m. m , m . phải có nghiệm là
Từ đó tìm được đáp số = 0 = 1 Ví dụ 1.55 m y x2+2 √
Tìm tất cả các giá trị thực của để đồ thị hàm số = mx có hai đường 4 +3 tiệm cận ngang. A. m . B. m < . C. m > . D. m > . = 0 0 0 3 Ví dụ 1.56 m
Tìm tất cả các giá trị thực của tham số
để đường tiệm cận đứng, tiệm cận y mx m 2 +
ngang của đồ thị hàm số = x−
cùng với hai trục tọa độ tạo thành một 1
hình chữ nhật có diện tích bằng 8? A. m B. m ± 1 C. m ± D. m 6 ± = 2. = . = 4. = 2. 2 Hướng dẫn. x ,
Đồ thị hàm số có tiệm cận đứng là đường thẳng = 1 tiệm cận ngang y m. là đường thẳng = 2
Hai đường thẳng này cùng với hai trục toạ độ tạo thành | m|
một hình chữ nhật có các cạnh bằng 1 và 2
. Do đó, diện tích hình chữ nhật này | m| ⇔ m ± .
bằng 8 tương đương với 2 = 8 = 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 28 of 59 Ví dụ 1.57 y f x
Tìm phương trình các đường tiệm cận của đồ thị hàm số hàm số = ( ) = x+1 √x . 2 −4 Hướng dẫn. y ±
Đồ thị hàm số có hai tiệm cận ngang = 1 và hai tiệm cận đứng x ± . = 2 Ví dụ 1.58 √ y x2 x +2 Đồ thị hàm số = x−
có bao nhiêu đường tiệm cận? 2 Hướng dẫn. x .
Rõ ràng đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng = 2 f x f x
Để tìm các tiệm cận ngang, ta đi tính các giới hạn lim x→ ∞ ( ) và lim
x→−∞ ( ), từ đó + ba
tìm được thêm hai tiệm cận ngang nữa. Như vậy, đồ thị hàm số đã cho có đường tiệm cận. Ví dụ 1.59 Đề thử nghiệm 2017
Tìm tất cả các tiệm cận đứng của đồ thị hàm số √ x − − x2 x y 2 1 + + 3 = x2 − x 5 + 6 A. x − x − . C. x x . = 3 và = 2 = 3 và = 2 B. x − . D. x . = 3 = 3 Ví dụ 1.60 Đề tham khảo 2017 y f x Cho hàm số = (
) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị
của hàm số đã cho có bao nhiêu đường tiệm cận? x −∞ − ∞ 2 0 + y0 x − ( ) + ∞ y + 1 −∞ % & 0 A. B. C. D. 1. 2. 3. 4.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 29 of 59 Ví dụ 1.61 m y f x x2− x m 2 3 + Tìm để đồ thị hàm số = ( ) = x−m
không có tiệm cận đứng. Đáp số. m m = 0; = 1 Ví dụ 1.62 Đề minh hoạ 2017 m y x+1 √ Tìm sao cho đồ thị hàm số = mx có hai tiệm cận ngang. 2 +1 Đáp số. m > . 0 Ví dụ 1.63 y x− ln( 1) Đồ thị hàm số = x2 x
có bao nhiêu đường tiệm cận? +
Hướng dẫn. Ta thấy ngay, đồ thị hàm số có một đường tiệm cận đứng là đường x . thẳng = 1
Chúng ta sẽ sử dụng quy tắc L’Hospital để tính giới hạn, từ đó tìm
được tiệm cận ngang – nếu có – của đồ thị hàm số. Ta có x − x − 0 1 ln ( 1) (ln( 1)) x− 1 1 lim x→ ∞ x 0 = lim = lim = 0 2 x = lim x→ ∞ x2 x x→ ∞ x x→ ∞ x − x + + + ( + ) + 2 + 1 + ( 1)(2 + 1) y .
Suy ra, đồ thị hàm số có một tiệm cận ngang là đường thẳng = 0 Và do đó, nó
có hai đường tiệm cận. Ví dụ 1.64 x m y + 1 √
Tìm tất cả các giá trị của tham số để đồ thị hàm số = m2x2 m − + 1
có bốn đường tiệm cận. A. m ∈ ∞ C. m ∈ −∞ (1; + ). ( ; 1). √ n o B. m ∈ −∞ \ − ± 1 5 D. m ∈ −∞ ( ; 1) 0; . ( 2 ; 0).
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 30 of 59 Hướng dẫn. m Nếu
= 0 thì hàm số không xác định. Do đó, điều kiện trước tiên là m 6 . = 0 Khi đó có 1 1 y 1 + x 1 √ y 1 + x − 1 √ lim x→ ∞ = lim x→ ∞ q = ; lim = lim q = m− x→−∞ x→−∞ m− + + m m2 m2 2 1 − m2 1 + x2 + x2
Suy ra đồ thị hàm số có hai đường tiệm cận ngang. m2x2 − m
Đồ thị hàm số có hai đường tiệm cận đứng khi và chỉ khi phương trình = 1 −
có 2 nghiệm phân biệt và khác
1. Điều kiện cần và đủ là  m  2 m − 6 m <  + 1 = 0  1 √ − m > ⇔ m 6 − ± 1 5 1 0 = 2  m 6m 6 = 0 = 0
Như vậy, ta chọn phương án B. 1.9
Tiếp tuyến của đồ thị hàm số Bài toán 1.9
Viết phương trình tiếp tuyến
của đồ thị hàm số C y f x . ∆ ( ) : = ( )
Chúng ta xét ba tình huống: • M x y f 0 x Biết tiếp điểm là ( 0 ; 0 ) thì tính (
0 ) và thay luôn vào phương trình y − y f 0 x x − x 0 = ( 0 )( 0 ) (4) • k M x y Biết hệ số góc bằng . Gọi tiếp điểm là ( 0 ; 0 ) và đi giải phương trình f 0 x k ( 0 ) = x tìm được 0
rồi thay vào phương trình (4). • A a, b
Biết tiếp tuyến đi qua điểm (
), chú ý rằng điểm này không biết có
là tiếp điểm hay không. Khi đó ta thực hiện các bước: M x y , y f x . + Gọi tiếp điểm là ( 0 ; 0 ) lưu ý là 0 = ( 0 ) f 0 x +
Tính đạo hàm và suy ra hệ số góc của tiếp tuyến là ( 0 ), từ đó y − y f 0 x x − x .
viết được phương trình tiếp tuyến có dạng 0 = ( 0 )( 0 ) A a, b + Vì tiếp tuyến đi qua ( ) nên ta có phương trình b − f x f 0 x a − x ( 0 ) = ( 0 )( 0 ) x
Giải phương trình trên, tìm được
0 và từ đó viết được phương trình tiếp tuyến cần tìm.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 31 of 59 Lưu ý 1.12 • y ax b Cho đường thẳng ∆ : = + thì a a α α +
là hệ số góc, được tính bởi = tan - trong đó là góc tạo Ox bởi tia
và đường thẳng ∆ lấy theo chiều dương; b + là hệ số tự do.
• Hai đường thẳng song song nếu hệ số góc bằng nhau và hệ số tự do khác nhau. • − .
Hai đường thẳng vuông góc nếu tích các hệ số góc của chúng bằng 1 Ví dụ 1.65 y f x x3 −
Tìm hệ số góc của tiếp tuyến với đồ thị hàm số = ( ) = 1 tại giao
điểm của đồ thị hàm số với trục tung. Ví dụ 1.66 CĐ2010 y x3 x2 −
Viết phương trình tiếp tuyến của đồ thị hàm số = + 3 1 tại điểm có − . hoành độ bằng 1 Đáp số. y − x − . = 3 2 Ví dụ 1.67 D2005 y 1 x 3 − m x 2 1 C M ∈ C Cho hàm số = + có đồ thị là ( m) và điểm ( m), biết rằng 3 2 3 xM − m M x − y . = 1, tìm để tiếp tuyến tại
song song với đường thẳng 5 = 0 Đáp số. m . = 4 Ví dụ 1.68 y −x4 mx2 − m m Cho hàm số = + 2 2 + 1.Tìm
để các tiếp tuyến với đồ thị A , B − hàm số tại các điểm (1; 0) ( 1; 0) vuông góc với nhau. Đáp số. m 5 m 3 = ; = . 4 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 32 of 59 Ví dụ 1.69 a b y ax b + Oy M − Tìm và để đồ thị hàm số = x− cắt trục tại điểm (0; 1) đồng 1 M k
thời tiếp tuyến với đồ thị hàm số tại có hệ số góc = 3. Đáp số. a − b = 4; = 1. Ví dụ 1.70 y x3 − x2
Viết phương trình tiếp tuyến của đồ thị hàm số = 3 + 2 biết tiếp y − x
tuyến song song với đường thẳng có phương trình = 2016 3 Hướng dẫn. M x , y f 0 x Gọi tiếp điểm là ( 0 0 ) thì hệ số góc của tiếp tuyến là ( 0 ) = x2 − x . y − x 3 6
Vì tiếp tuyến song song với đường thẳng = 2016 3 nên 0 0 x2 − x − 3 6 3 0 0 = ⇔ x0 = 1 y y − x . Do đó 0
= 0 và phương trình tiếp tuyến là = 3 + 3 Ví dụ 1.71 M C Giả sử là một điểm có tung độ bằng 5, thuộc đồ thị ( ) của hàm số y x 2 +1 C M Ox, Oy A = x− . Tiếp tuyến của ( ) tại cắt các trục toạ độ lần lượt tại 1 B OAB. và
. Hãy tính diện tích tam giác A. 121 B. 119 C. 123 D. 125 6 6 6 6 Ví dụ 1.72 m
Tìm tất cả các giá trị sao cho trên đồ thị C y 1 mx3 m − x2 − m x ( m) : = + ( 1) + (4 3 ) + 1 3
tồn tại đúng hai điểm có hoành độ dương mà tiếp tuyến tại đó vuông góc với d x y − đường thẳng ( ) : + 2 3 = 0. Hướng dẫn. y0 mx2 m − x − m. M x , y Ta có = + 2( 1) + 4 3 Gọi ( 0 0 ) là tiếp điểm cần M d x y − tìm thì tiếp tuyến tại
vuông góc với đường thẳng ( ) : + 2 3 = 0 khi và chỉ y0 x · − 1 − khi phương trình ( 0 ) =
1 có đúng hai nghiệm dương phân biệt. Nghĩa là 2
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 33 of 59 mx2 m − x − m phương trình + 2( 1) + 2 3
= 0 có hai nghiệm dương phân biệt. Điều kiện cần và đủ là    m 6 m 6 m 6     = 0  = 0  = 0     0    >m2 − m >m 6 1 < m < 1 ∆ 0 ⇔ 4 4 + 1 0 ⇔ = 0 2 ⇔ 2 S > m−1 < < m < 1 < m < 2     0  m 0 0 1 2 3      − m  P >  2 3 >< m < 2 0 m 0 0 3 m ∈ 1 ∪ 1 2 Vậy 0; ;
là các giá trị cần tìm. 2 2 3 Ví dụ 1.73 y x 2
Viết phương trình tiếp tuyến của đồ thị hàm số = x− biết tiếp tuyến cắt √ 2 Ox, Oy A, B OAB AB OA lần lượt tại mà tam giác thỏa mãn = 2. Hướng dẫn. M x y x 6 Giả sử ( 0 ; 0 ), với 0
= 2, là một điểm thuộc đồ thị hàm số. Phương d M trình tiếp tuyến
của đồ thị hàm số tại điểm có dạng: x − y − 2 0 4 x − x . x − = x − ( 0 ) 2 0 2 ( 0 2) √ Ox, Oy A, B OAB AB OA
Do tiếp tuyến cắt các trục tại các điểm và tam giác có = 2 OAB O d Ox ◦ nên tam giác vuông cân tại . Khi đó tiếp tuyến tạo với tia một góc 45 ◦ hoặc 135 . • d Ox ◦, Tiếp tuyến tạo với tia một góc 45
thì hệ số góc của tiếp tuyến là 1. Do y0 x ⇔ −4 đó, ta có phương trình ( 0 ) = 1
x − 2 = 1. Phương trình này vô nghiệm. ( 0 2) • d Ox ◦, − Tiếp tuyến tạo với tia một góc 135
thì hệ số góc của tiếp tuyến là 1.
Do đó, ta có phương trình − x y0 x ⇔ 4 − ⇔ 0 = 0 ( 0 ) = 1 x − = 1 2 x ( 0 2) 0 = 4 d y −x : =
Từ đó tìm được, phương trình tiếp tuyến là d y −x : = + 8 y −x Đường thẳng =
đi qua gốc tọa độ nên bị loại. Như vậy chỉ có một tiếp tuyến d y −x
thỏa yêu cầu bài toán là : = + 8.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 34 of 59 Ví dụ 1.74 y x−2 Cho hàm số = x
. Viết phương trình tiếp tuyến của đồ thị biết tiếp tuyến +1 Ox, Oy A, B OAB cắt tại
sao cho bán kính đường tròn nội tiếp tam giác lớn nhất. Hướng dẫn. x − , y Tiệm cận đứng: = 1 tiệm cận ngang:
= 1, giao điểm hai đường I − x tiệm cận là (
1; 1). Giả sử hoành độ tiếp điểm là 0
thì phương trình tiếp tuyến là: x − y 3 x − x 0 2 = x ( 0 ) + 2 x ( 0 + 1) 0 + 1 A − x − 0 5
Tiếp tuyến cắt tiệm cận đứng tại điểm 1; x
và cắt tiệm cận ngang tại điểm 0 +1 B x (2 0 + 1; 1). Từ đó tính được x − IA 0 5 6 − , IB | x − − | |x | = 1 = = 2 0 + 1 ( 1) = 2 0 + 1 x |x | 0 + 1 0 + 1 IAB Suy ra diện tích tam giác là S 1 IA · IB 1 · 6 · |x | . = = |x | 2 0 + 1 = 6 2 2 0 + 1 p IAB Gọi là nửa chu vi tam giác
, thì bán kính đường tròn nội tiếp tam giác này là: S r 6 = p = p r p IAB Bởi vậy, bán kính lớn nhất khi và chỉ khi
nhỏ nhất. Mặt khác, tam giác I vuông tại nên: √ √ √ √ p p IA IB IA2 IB2 > IA.IB IA.IB . 2 = + + + 2 + 2 = 4 3 + 2 6 √ IA IB ⇔ x 2 ⇔ x − ±
Dấu đẳng thức xảy ra khi = ( 0 + 1) = 3 = 1 3 √ √ • x − − d y x Với = 1 3 ta có tiếp tuyến: 1 : = + 2 1 + 3 . √ √ • x − d y x − Với = 1 + 3 ta có tiếp tuyến: 1 : = + 2 1 3 .
Như vậy, ta tìm được hai tiếp tuyến có phương trình như trên.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 35 of 59 Ví dụ 1.75 y f x x3 − x
Viết phương trình tiếp tuyến của đồ thị hàm số = ( ) = 3 + 2 biết A − tiếp tuyến đi qua điểm ( 1; 4). Ví dụ 1.76
ĐH Sư phạm II - Khối B năm 99
Tìm trên trục hoành những điểm mà từ đó kẻ được ba tiếp tuyến đến đồ thị hàm số y −x3 x = + 3 + 2 Hướng dẫn. A a M x y Gọi (
; 0) bất kì thuộc trục hoành và ( 0 ; 0 )
là tọa độ tiếp điểm. M
Phương trình tiếp tuyến tại là y − y f 0 x x − x 0 = ( 0 )( 0 ) ⇔ y − x2 x − x − x3 x = ( 3 + 3)( + 3 0 0 ) 0 0 + 2 A a Mà tiếp tuyến đi qua ( ; 0) nên − x2 a − x − x3 x ( 3 + 3)( + 3 0 0 ) 0 0 + 2 = 0 ⇔ x x2 − a x a ( 0 + 1)(2 (3 + 2) + 2) = 0 0 0 + 3 A x2 − Từ
kẻ được ba tiếp tuyến đến đồ thị hàm số khi và chỉ khi phương trình 2 0 a x a − . (3 + 2) 0 + 3
+ 2 = 0 có hai nghiệm phân biệt khác 1 ( > ⇔ ∆ 0 a 6 6( + 1) = 0 a > − 6 a < − 2 . Tìm được đáp số 2 hoặc 1 = 3 Ví dụ 1.77 y −x3 x2 − . M Cho hàm số = + 3 2 Tìm điểm điểm
thuộc đồ thị hàm số sao M cho qua điểm
kẻ được hai tiếp tuyến với đồ thị hàm số mà tích các hệ số
góc của hai tiếp tuyến nhỏ nhất. Hướng dẫn. y0 − x2 x A a, −a3 a2 − Có = 3 + 6 . Giả sử ( + 3
2) thuộc đồ thị hàm số và M x , −x3 x2 − . tiếp điểm là ( 0 + 3 2)
Suy ra phương trình tiếp tuyến là: 0 0 y − −x3 x2 − − x2 x x − x ( + 3 2) = ( 3 + 6 0 0 0 0 )( 0 )
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 36 of 59 A
Do tiếp tuyến đi qua điểm nên ta có phương trình −a3 a2 − − −x3 x2 − − x2 x a − x + 3 2 ( + 3 2) = ( 3 + 6 0 0 0 0 )( 0 ) x a, x −a 3 . A
Phân tích thành nhân tử, thu được 0 = 0 = Qua điểm kẻ được hai tiếp 2 ⇔ a 6 −a 3 ⇔ a 6 . tuyến = = 1
Khi đó hệ số góc của hai tiếp tuyến là 2 k ..., k ... 1 = 2 = Suy ra 2 k · k 1 − a 9 2 a
− 81 > − 81 1 2 = 3 + 6 + 4 2 16 16 √ √ A ± 2 10 , ± 10 . Từ đó tìm được ( ) 2 4 1.10
Nhận dạng đồ thị Bài toán 1.10 Nhận dạng đồ thị
Ta cần một số kết quả quen thuộc sau:
• Hình dáng của đồ thị các hàm số bậc ba, bậc bốn trùng phương, phân
thức bậc nhất tương ứng với các trường hợp hệ số của chúng. • x Xét theo chiều tăng của biến , từ trái qua phải, thì đồ thị hàm số
đồng biến sẽ có hướng đi lên – ngày càng cao hơn –, còn đồ thị hàm
số nghịch biến sẽ có hướng đi xuống – ngày càng thấp đi. • M x , y y f x Một điểm ( 0 0 )
thuộc (nằm trên) đồ thị hàm số = ( ) khi và chỉ y f x . khi 0 = ( 0 ) • y f x Đồ thị hàm số = ( ) nếu cắt trục tung thì giao điểm có tọa độ , f (0
(0)); còn để tìm giao điểm với trục hoành ta đi giải phương trình f x hoành độ giao điểm ( ) = 0. • y f x y g x
Số giao điểm của hai đồ thị hàm số = ( ) và = ( ) chính bằng f x g x .
số nghiệm của phương trình ( ) = ( )
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 37 of 59 Ví dụ 1.78 y ax3 bx2 cx d Cho hàm số = + + +
có đồ thị như đường cong ở hình vẽ
bên. Khẳng định nào sau đây đúng? A. a, d > b, c < 0; 0. B. a, b, c < d > 0; 0. C. a, c, d > b < 0; 0. D. a, b, d > c < 0; 0. 1.11
Đọc bảng biến thiên Bài toán 1.11 Đọc bảng biến thiên Ví dụ 1.79 ĐH năm 2017 Mã đề 102 f x Cho hàm số (
) có bảng biến thiên như hình vẽ sau x −∞ − ∞ 2 2 + y0 x − ( ) + 0 0 + ∞ y 3 + −∞ % & % 0 y y Tìm giá trị cực đại CĐ và giá trị cực tiểu CT của hàm số đã cho. A. y y − . C. y − y . CĐ = 3 và CT = 2 CĐ = 2 và CT = 2 B. y y . D. y y . CĐ = 2 và CT = 0 CĐ = 3 và CT = 0
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 38 of 59 Ví dụ 1.80 ĐH năm 2017 Mã đề 103 f x Cho hàm số (
) có bảng biến thiên như hình vẽ sau x −∞ − ∞ 1 2 + y0 x − ( ) + 0 0 + y 4 2 % & − % 2 5
Mệnh đề nào dưới đây đúng? A. C.
Hàm số có bốn điểm cực trị.
Hàm số không có cực đại. B. x . D. x − .
Hàm số đạt cực tiểu tại = 2
Hàm số đạt cực tiểu tại = 5 Ví dụ 1.81 Đề minh hoạ 2017 f x R Cho hàm số (
) xác định, liên tục trên
và có bảng biến thiên như hình vẽ sau x −∞ ∞ 0 1 + y0 x − ( ) + 0 + ∞ y 0 +
−∞ % & − % 1
Mệnh đề nào dưới đây đúng? A. C.
Hàm số có đúng một cực trị.
Hàm số có giá trị lớn nhất bằng − .
0 và giá trị nhỏ nhất bằng 1 B. D. x
Hàm số có giá trị cực tiểu bằng
Hàm số đạt cực đại tại = 0 và x . 1. đạt cực tiểu tại = 1 Ví dụ 1.82 ĐH năm 2017 Mã đề 101 f x Cho hàm số (
) có bảng biến thiên như hình vẽ sau x −∞ − ∞ 1 0 1 + y0 x − − ( ) 0 + 0 0 + ∞ ∞ y + 0 +
& − % & − % 1 1
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 39 of 59
Mệnh đề nào dưới đây sai? A. C.
Hàm số có ba điểm cực trị.
Hàm số có giá trị cực đại bằng . B. 0
Hàm số có giá trị cực đại bằng . D. 3
Hàm số có hai điểm cực tiểu. 1.12
Đồ thị hàm số chứa dấu giá trị tuyệt đối
Cho đồ thị hàm số y
f x . Vẽ đồ thị các hàm số y |f x | và Bài toán 1.12 = ( ) = ( ) y f |x| . = ( )
Ta sử dụng định nghĩa giá trị tuyệt đối để viết lại hàm số đã cho. ( ( f x x > , f x f x > , y f |x| ( ) khi 0 y |f x | ( ) khi ( ) 0 = ( ) = f −x x < . = ( ) = −f x f x < . ( ) khi 0 ( ) khi ( ) 0
Từ đó, ta có cách vẽ như sau: • y f |x| Đối với hàm số = (
), ta xóa phần đồ thị nằm bên trái trục tung – x < phần đồ thị ứng với
0 – và lấy đối xứng phần còn lại qua trục tung. • y |f x | Đối với hàm số = (
) , ta lấy đối xứng phần đồ thị nằm dưới trục f x <
hoành – phần đồ thị ứng với ( )
0 – và xóa bỏ phần đồ thị nằm dưới trục hoành đó. Ví dụ 1.83 y x 3 − x y Đồ thị hàm số = 3 cắt đường thẳng = 2 tại mấy điểm?
Hướng dẫn. Lập bảng biến thiên: √ √ x −∞ − − ∞ 3 1 0 1 3 + y0 x − − − ( ) + 0 + 0 + ∞ ∞ y + 2 2 + & % & % & % 0 0 0
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 40 of 59 Ví dụ 1.84 x 3 − x Phương trình 3 + 2 = log 10 có bao nhiêu nghiệm? 2 A. B. C. D. 2 0 4 3
Hướng dẫn. Cần nhớ lại định nghĩa giá trị tuyệt đối và cách vẽ đồ thị hoặc lập y |f x | y f |x|
bảng biến thiên các hàm số = ( ) và = ( ) như thế nào? x −∞ − − ∞ 2 1 1 + y0 x − − ( ) + 0 + ∞ ∞ y + 4 + & % & % 0 0 Ví dụ 1.85 ĐH năm 2017 Mã đề 102 y f x Cho hàm số = (
) có bảng biến thiên như sau: x −∞ − ∞ 1 3 + y0 x − ( ) + 0 0 + ∞ y 5 + −∞ % & % 1 y |f x | Đồ thị hàm số = ( )
có bao nhiêu điểm cực trị? A. B. C. D. 4. 2. 3. 5. 1.13
Tương giao của hai đồ thị hàm số Bài toán 1.13
Tương giao của hai đồ thị hàm số y f x và y g x . = ( ) = ( )
• Số giao điểm của hai đồ thị hàm số chính bằng số nghiệm của phương
trình hoành độ giao điểm f x g x ( ) = ( )
• Biến đổi phương trình trên đưa về:
Phương trình trùng phương. +
Đặt ẩn phụ đưa về biện luận phương
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 41 of 59 trình bậc hai.
Phương trình bậc ba. +
Đoán nghiệm đặc biệt rồi phân tích thành
tích phương trình bậc nhất và phương trình bậc hai; gọi hai nghiệm x , x
của phương trình bậc hai là 1 2
rồi sử dụng Viète. Nếu không m
được thì cô lập tham số
và đưa về xét tương giao của đường y m thẳng =
và một đồ thị hàm số mới.
Phương trình bậc hai. x , x + Gọi hai nghiệm 1 2 và sử dụng Viète. Ví dụ 1.86 y x3 − x y x
Tìm số giao điểm của đồ thị hàm số = 3 + 3 và đường thẳng = . A. B. C. D. Một. Hai. Ba. Không. Chứng minh. x3 − x x
Hướng dẫn] Phương trình hoành độ giao điểm 3 + 3 = . Giải
phương trình này tìm được ba nghiệm nên đáp số là có ba giao điểm. Ví dụ 1.87 m y x3 − x −m
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số = 3 + 2
cắt trục hoành tại ba điểm phân biệt. A. < m < . C. m > . 0 4 4 B. 6 m 6 . D. m < . 0 4 0 Ví dụ 1.88 Đề tham khảo 2017 y x3 − x C C Cho hàm số = 3 có đồ thị (
). Tìm số giao điểm của ( ) và trục hoành. Ví dụ 1.89 Đề thử nghiệm 2017 y x4 − x2 y −x2 Đồ thị hàm số = 2 + 2 và đồ thị hàm số = + 4 có tất cả bao nhiêu điểm chung? Ví dụ 1.90 ĐH 2017 Mã đề 103 y x − x2 C Cho hàm số = ( 2)( + 1) có đồ thị (
) . Mệnh đề nào dưới đây đúng?
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 42 of 59 A. C C. C (
) cắt trục hoành tại hai điểm. ( ) không cắt trục hoành. B. C D. C (
) cắt trục hoành tại một điểm. (
) cắt trục hoành tại ba điểm. Ví dụ 1.91 Đề thử nghiệm 2017 y f x R \ { } Cho hàm số = ( )xác định trên 0
, liên tục trên mỗi khoảng xác định
và có bảng biến thiên như sau x −∞ ∞ 0 1 + y0 x − − ( ) + 0 ∞ y + 2 & −
−∞ % & −∞ 1 m
Tìm tập hợp tất cả các giá trị của tham số thực sao cho phương trình f x m ( ) =
có ba nghiệm thực phân biệt. A. − B. − C. − . D. −∞ [ 1; 2]. ( 1; 2). ( 1; 2] ( ; 2] Hướng dẫn. Ví dụ 1.92 Đề minh hoạ 2017 y − x y x3 x
Biết rằng đường thẳng = 2
+ 2 cắt đồ thị hàm số = + + 2 tại x y y
điểm duy nhất; kí hiệu ( 0 ; 0 )
là tọa độ của điểm đó. Tìm 0 .
Biện luận số nghiệm của phương trình h x, m bằng đồ thị hàm Bài toán 1.14 ( ) = 0 số. • m, f x g m . Cô lập tham số
đưa phương trình đã cho về dạng ( ) = ( ) • f x
Lập bảng biến thiên hoặc vẽ đồ thị của hàm số ( ).
• Căn cứ vào bảng biến thiên để kết luận. Lưu ý 1.13 y g m Đồ thị hàm số = (
) là một đường thẳng song song với trục hoành và cắt g m y m2 − m
trục tung tại điểm có tung độ (
). Chẳng hạn, đồ thị hàm số = 2 + 3
là một đường thẳng chứ không phải là một parabol như nhiều học sinh lầm tưởng.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 43 of 59 Ví dụ 1.93 m x2 x2 − m Tìm các giá trị của để phương trình ( 2) + 3 = có hai nghiệm phân biệt. Hướng dẫn. y x2 x2 − R. Xét hàm số = ( 2) + 3 trên Ta có bảng biến thiên x −∞ − ∞ 1 0 1 + y0 x − − ( ) 0 + 0 0 + ∞ ∞ y + 3 + & % & % 2 2
Căn cứ vào bảng biến thiên ta có, phương trình có hai nghiệm phân biệt khi và chỉ m m > . khi = 2 hoặc 3 Ví dụ 1.94 ĐH năm 2017 Mã đề 104 y −x4 x2 Cho hàm số = + 2
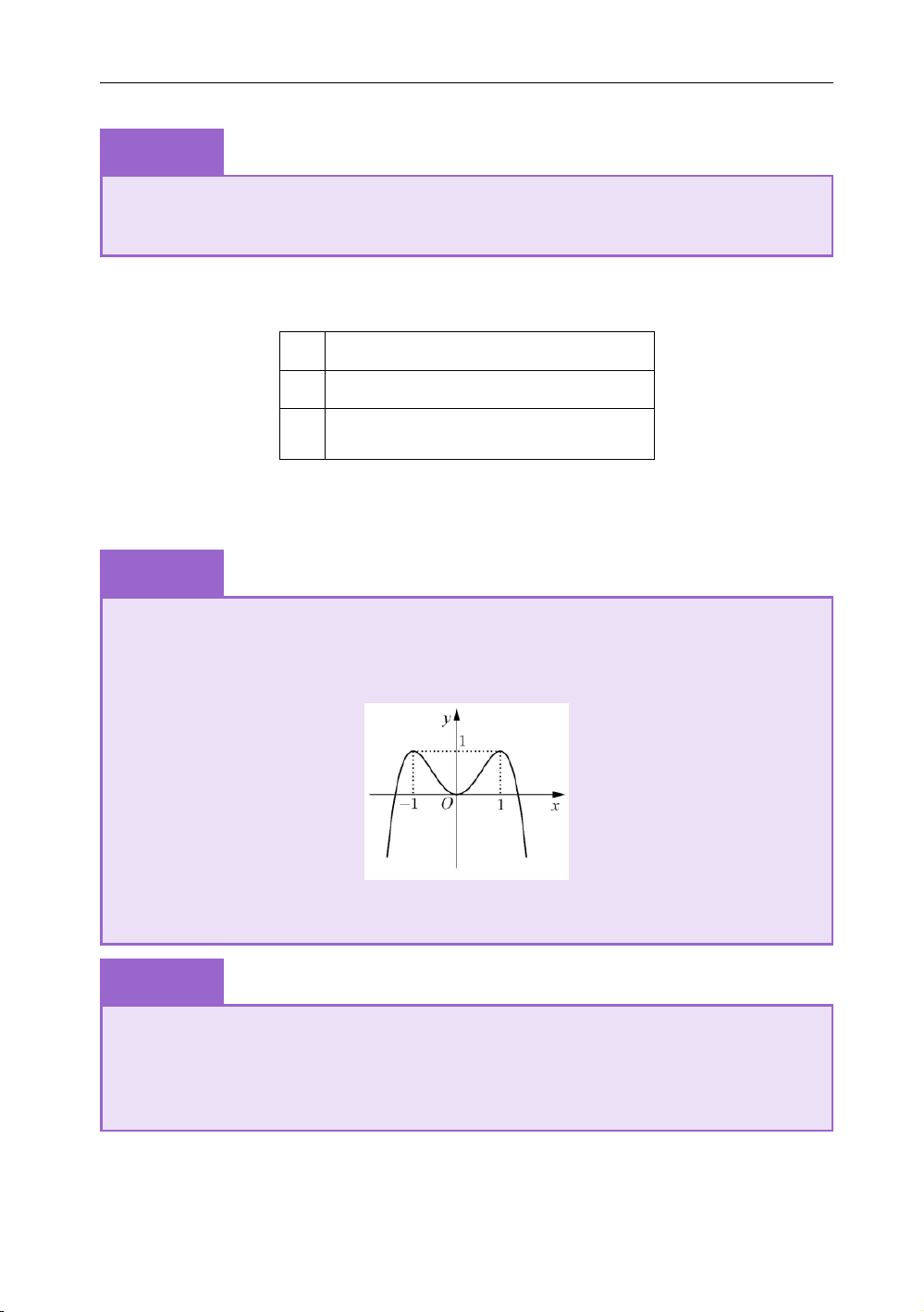
có đồ thị như hình bên. Tìm tất cả các giá trị thực m −x4 x2 m của tham số để phương trình + 2 =
có bốn nghiệm thực phân biệt. A. m > .
B. o 6 m 6 C. < m < D. m < 0 1. 0 1. 1. Ví dụ 1.95 m 2 x − x m
Tìm tất cả các giá trị của tham số sao cho phương trình log 2 log = 2 2 , có nghiệm trong khoảng (0 1)? m > m > m > − > − 1. 0 2. 0 3. 1 4. 1 Hướng dẫn. t x t < x ∈ , Đặt = log thì 0 với mọi (0 1). Do đó, ta xét hàm số 2
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 44 of 59 f t t2 − t −∞, ( ) = 2 trên khoảng (
0) có bảng biến thiên như sau: t −∞ 0 f 0 t − ( ) ∞ f t + ( ) & 0 x ∈ , m > .
Suy ra, phương trình đã cho có nghiệm (0 1) khi và chỉ khi 0 Ví dụ 1.96 m y x 2 +3
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số = x và +2 d y x m đường thẳng : = +
cắt nhau tại hai điểm phân biệt. A. m > . C. m . 2 = 2 B. m > . D. m < ∨ m > . 6 2 6 Ví dụ 1.97 ĐH Khối D năm 2011 y x 2 +1 k y kx k Cho hàm số = x . Tìm để đường thẳng = + 2 + 1 cắt đồ thị hàm +1 A, B A B
số đã cho tại hai điểm phân biệt sao cho khoảng cách từ và đến trục hoành bằng nhau. Đáp số. k − = 3. Ví dụ 1.98 ĐH Khối B năm 2010 y x 2 +1 m y − x m Cho hàm số = x . Tìm để đường thẳng = 2 + cắt đồ thị hàm số +1 A, B OAB
đã cho tại hai điểm phân biệt sao cho tam giác có diện tích bằng √ O 3, với là gốc tọa độ. Đáp số. m ± = 2. Ví dụ 1.99 m d y x
Tìm tất cả các giá trị thực của tham số để đường thẳng : = + 1 cắt y x3 − x2 mx đồ thị hàm số = 3 +
+ 1 tại ba điểm phân biệt có hoành độ x , x , x x2 x2 x2 > 1 2 3 thỏa mãn + + 1. 1 2 3
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 45 of 59
A. m < 13 ∨ m 6 . C. 6 m 6 = 1 0 5. 4 B. m 6 D. 6 m 6 5. 5 10. Hướng dẫn. x3 − x2 mx x
Phương trình hoành độ giao điểm là 3 + + 1 = + 1. Đặt nhân tử chung ta được x x2 − x m − 3 + 1 = 0 (5) d y x3 − x2 mx Đường thẳng cắt đồ thị hàm số = 3 +
+ 1 tại ba điểm phân biệt khi
và chỉ khi phương trình (5) có ba nghiệm phân biệt. Vì phương trình (5) luôn có một x nghiệm là
= 0 nên điều kiện cần và đủ là phương trình x2 − x m − 3 + 1 = 0 (6) m 6 , m < 13
có hai nghiệm phân biệt khác 0. Từ đó tìm được điều kiện = 1 . 4 x , x
Khi đó, theo Viète, phương trình (6) có hai nghiệm 2 3 thỏa mãn (x x , 2 + 3 = 3 x · x m − . 2 3 = 1 x2 x2 x2 > ⇔ 2 − m − > ⇔ m 6 Do đó, yêu cầu + + 1 3 2 ( 1) 1 5. Như vậy, điều kiện 1 2 3 m 6 , m < 13 cần tìm là = 1 . 4 Ví dụ 1.100 m y x 2 +3
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số = x− cắt 1 y x m A, B đường thẳng ∆ : = + tại hai điểm phân biệt sao cho tam giác OAB O vuông tại . A. m B. m − C. m D. m − = 6. = 3. = 5. = 1. Hướng dẫn. C
Phương trình hoành độ giao điểm của (
) và đường thẳng ∆ là x 2 + 3 x m ⇔ x2 m − x − m − x 6 x − = + + ( 3) 3 = 0 ( = 1) (7) 1 C Đường thẳng ∆ cắt (
) tại hai điểm phân biệt khi và chỉ khi phương trình (7) có hai 1 . nghiệm phân biệt và khác 1 ( > ⇔ ∆ 0 ⇔ m ∈ R. 2 m − · − m − 6 1 + ( 3) 1 3 = 0 1
Thực ra chỉ cần điều kiện có hai nghiệm phân biệt là đủ, điều kiện sau luôn luôn đúng với mọi bài toán dạng này.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 46 of 59 x , x
Khi đó, gọi hai nghiệm của phương trình (7) là 1 2
thì giao điểm của hai đồ thị A x , x m , B x , x m OAB O đã cho là ( 1 1 + ) ( 2 2 + ). Tam giác vuông tại khi và chỉ khi −→ −→ OA · OB ⇔ x x x m x m . = 0 1 2 + ( 1 + )( 2 + ) = 0 x x −m x x −m − m . Sử dụng Viète có 1 + 2 = + 3 và 1 2 = 3, ta tìm được = 6 Ví dụ 1.101 m d y x − C y x3 m − Tìm để đường thẳng : = 2 cắt đồ thị ( ) của hàm số = + ( x2 − m − x − 1) ( 2)
2 tại ba điểm phân biệt.
Hướng dẫn. Phương trình hoành độ giao điểm: x3 m − x2 − m − x − x − + ( 1) ( 2) 2 = 2 ⇔ x x2 m − x − m + ( 1) + 1 = 0 x ⇔ = 0 x2 m − x − m ∗ + ( 1) + 1 = 0 ( ) d C ∗ Đường thẳng cắt đồ thị (
) tại 3 điểm phân biệt khi và chỉ khi phương trình ( )
có hai nghiệm phân biệt khác 0  m < − m 3 2 m − >m < − ⇔ ∆ = + 2 3 0 ⇔ m > ⇔ 3 g −m 6 1 m > (0) = + 1 = 0  m 6 1 = 1 m < − m >
Vậy, giá trị cần tìm là 3 hoặc 1. Ví dụ 1.102 m y x3 mx Tìm để đồ thị hàm số = +
+ 2 cắt trục hoành tại đúng một điểm.
Hướng dẫn. Phương trình hoành độ giao điểm x3 mx + + 2 = 0 x x Nhận xét
= 0 không thể là nghiệm của phương trình, nên chia hai vế cho thì
được phương trình tương đương m −x2 − 2 = x
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 47 of 59 f x −x2 − 2 −∞ ∪ ∞ Xét hàm số ( ) = x trên ( ; 0) (0; +
) ta có bảng biến thiên sau x −∞ ∞ 0 1 + f 0 x − ( ) + + 0 ∞ − f x + 3 ( ) −∞ % −∞ % & −∞ m m > − .
Suy ra, giá trị cần tìm của là 3 Ví dụ 1.103 m y x3 − mx − m Tìm để đồ thị hàm số =
cắt trục hoành tại ba điểm phân biệt.
Hướng dẫn. Phương trình hoành độ giao điểm x3 − mx − m . = 0
Phương trình trên không có nghiệm đặc biệt, nhưng lại có thể cô lập được tham số m mới
nên sẽ chuyển về tìm điều kiện để hai đồ thị hàm số cắt nhau tại ba điểm x − phân biệt. Chú ý rằng =
1 không thỏa mãn phương trình nên chia hai vế cho
x + 1 ta được phương trình mới tương đương x3 m . = x + 1 y m
Yêu cầu bài toán tương đương với việc tìm điều kiện để đường thẳng = cắt đồ f x x3 f x thị hàm số ( ) = x
. Ta có bảng biến thiên của ( ) như sau +1 x −∞ − 3 − ∞ 1 0 + 2 f 0 x − ( ) 0 + + 0 + ∞ + f x ∞ ∞ % ( ) + + 0 & 27 % −∞ % 4 m > / .
Căn cứ vào bảng biến thiên, ta có đáp số 27 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 48 of 59 Ví dụ 1.104 y x3 − mx2 m x − m − m Cho hàm số: = + (2 + 1) 2. Tìm
để đồ thị hàm số cắt Ox trục
tại 3 điểm phân biệt có hoành độ dương.
Hướng dẫn. Phương trình hoành độ giao điểm: x x = 1 3 − mx 2 m x − m − ⇔ + (2 + 1) 2 = 0 x2 − m − x m ∗ ( 1) + + 2 = 0 ( ) Ox
Đồ thị hàm số cắt trục
tại 3 điểm phân biệt có hoành độ dương khi và chỉ khi ∗ phương trình (
) có 2 nghiệm dương phân biệt khác 1  m  2 − m − > m < − ∨ m >  ∆ = 6 7 0  1 7 ⇔ m > ⇔ m > − ⇔ m > + 2 0 2 7  m − >m > 1 0 1 m > Ox Vậy với
7 thì đồ thị hàm số cắt trục
tại 3 điểm phân biệt có hoành độ dương. Ví dụ 1.105 y x3 − m x2 m − x m C m Cho hàm số = 2( + 1) + ( 2) + + 3 có đồ thị ( ). Xác định C x , x , x để đồ thị (
) cắt trục hoành tại 3 điểm phân biệt có hoành độ 1 2 3 sao P x2 x2 x2 cho = + + nhỏ nhất. 1 2 3 Hướng dẫn. C
Phương trình hoành độ giao điểm của đồ thị ( ) và trục hoành là x3 − m x2 m − x m 2( + 1) + ( 2) + + 3 = 0 ⇔ x − x2 − m x − m ( 1) (2 + 1) ( + 3) = 0 x ⇔ = 1 x2 − m x − m ∗ (2 + 1) ( + 3) = 0 ( ) C Đồ thị (
) cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi > m2 m > , ∀m ∆ 0 ⇔ 4 + 8 + 13 0 ⇔ m 6 − g 6 − m − 6 = 1 (1) = 0 3 3 = 0 m 6 − ∗ x , x Với = 1, phương trình ( ) có hai nghiệm phân biệt 1 2 khác 1; nghĩa là, y x , x x phương trình = 0 có ba nghiệm 1 2 và 3 = 1. Và do đó P x2 x2 x2 = + + 1 2 3 x2 x2 x x 2 − x x = + + 1 = 1 + ( 2 1 2 1 + 2 ) 1 2 2 m 3 23 2 m m2 m m > 23 = 1 + (2 + 1) + 2( + 3) = 4 + 6 + 8 = 2 + + 2 4 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 49 of 59 P 23 m − 3
Vậy giá trị nhỏ nhất của bằng khi = . 4 4 Ví dụ 1.106 ĐH năm 2017 Mã đề 101 m y mx − m
Tìm tất cả các giá trị thực của tham số để đường thẳng = + 1 y x3 − x2 x A, B, C
cắt đồ thị của hàm số = 3 + + 2 tại ba điểm phân biệt sao AB BC cho = . A. m ∈ −∞ ∪ ∞ C. m ∈ − 5 ∞ ( ; 0] [4; + ). ; + . 4
B. m ∈ R. D. m ∈ − ∞ ( 2; + ). Hướng dẫn. d C
Tìm điều kiện để đường thẳng và đồ thị ( ) cắt nhau tại hai điểm C
phân biệt. Sau đó sử dụng tính chất tâm đối xứng của (
), tức điểm uốn, phải thuộc d đường thẳng . Ví dụ 1.107 ĐH năm 2017 Mã đề 102 m y −mx
Tìm tất cả các giá trị thực của tham số để đường thẳng = cắt y
x3 − x2 − m A, B, C đồ thị hàm số = 3
+ 2 tại ba điểm phân biệt sao cho AB BC . = Ví dụ 1.108 d C y x3 − x
Viết phương trình đường thẳng cắt đồ thị ( ) : = 3 + 2 tại ba điểm √ A, B, C x BC phân biệt sao cho A = 2 và = 2 2. Hướng dẫn. x y A d A Có A = 2 suy ra A = 4 và (2; 4). Giả sử là đường thẳng đi qua k d và có hệ số góc là thì phương trình của là d y − y k x − x ⇔ y kx − k : A = ( A) = 2 + 4 C d
Phương trình hoành độ giao điểm của ( ) và đường thẳng là x x = 2 3 − x kx− k ⇔ x− x2 x −k ⇔ 3 +2 = 2 +4 ( 2)( +2 +1 ) = 0 g x x2 x − k ( ) = + 2 + 1 = 0 d C A, B, C g x Như vậy cắt ( ) tại 3 điểm phân biệt
khi và chỉ khi phương trình ( ) = 0
có hai nghiệm phân biệt và khác 2. Điều kiện cần và đủ là ( 0 k > ∆ = 0 ⇔ < k 6 g − k 6 0 = 9 (2) = 9 = 0
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 50 of 59 x
Khi đó, phương trình có hai nghiệm B, xC thỏa mãn (xB x − + C = 2 xB · xC − k = 1 B, C d Mà các điểm thuộc đường thẳng nên ta có yB kx k y kx k . = B − 2 + 4; C = C − 2 + 4 √ BC ⇔ BC 2 Mặt khác = 2 2 = 8 nên suy ra x 2 k2 x 2 ⇔ x x 2 − x k2 ⇔ k . ( B − xC ) + ( B − xC ) = 8 ( B + C ) 4 BxC (1 + ) = 8 = 1 d y x
Kiểm tra thấy thỏa mãn điều kiện. Thay vào tìm được đường thẳng : = + 2. Ví dụ 1.109 y x3 − mx2 m m Cho hàm số = 4 6 + 1, là tham số. Tìm để đường thẳng d y −x A , B, C B, C : =
+ 1 cắt đồ thị hàm số tại 3 điểm (0; 1) mà đối xứng
qua đường phân giác của góc phần tư thứ nhất. Hướng dẫn. d C
Hoành độ giao điểm của đường thẳng và đồ thị ( ) là nghiệm của phương trình: x3 − mx2 −x 4 6 + 1 = + 1 ⇔ x x2 − mx (4 6 + 1) = 0 (8) x2 − mx
Phương trình có ba nghiệm phân biệt khi và chỉ khi phương trình 4 6 + 1 = 0 có 2 nghiệm phân biệt m > 2 ⇔ 0 m2 − > ⇔ 3 ∆ = 9 4 0 m < −2 3 x , x B x −x , C x −x Giả sử 1 2
là nghiệm của phương trình (8) thì ( 1 ; 1 + 1) ( 2 ; 2 + 1). Do B C đó, và
đối xứng qua đường phân giác của góc phần tư thứ nhất ( ( x y x −x ⇔ 1 = 2 ⇔ 1 = 2 + 1 ⇔ x x ⇔ 3 m ⇔ m 2 y x x −x 1 + 2 = 1 = 1 = 2 3 1 = 2 2 = 1 + 1 m
So sánh với điều kiện, thấy không tìm được giá trị nào của thỏa mãn yêu cầu.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 51 of 59 Ví dụ 1.110 y x 2 +1 H d Cho hàm số = x− có đồ thị là ( ). Gọi
là đường thẳng đi qua điểm 1 A − m m d H ( 2; 2) và có hệ số góc . Tìm để đường thẳng cắt đồ thị ( ) tại hai điểm phân biệt? Hướng dẫn. d A − m Đường thẳng đi qua điểm ( 2; 2) và có hệ số góc nên có phương trình y mx m = + 2 + 2 d H
Phương trình hoành độ giao điểm của đường thẳng và đồ thị ( ) là x 2 + 1 mx m ⇔ g x mx2 mx − m . x − = + 2 + 2 ( ) = + (2 + 3) = 0 1 x vì
= 1 luôn không thể là nghiệm của phương trình trên. d H Đường thẳng cắt đồ thị (
) tại hai điểm phân biệt khi và chỉ khi phương trình g x (
) = 0 có hai nghiệm phân biệt khác 1. Điều kiện cần và đủ là  a 6  = 0 > ⇔ m < − 4 m > ∆ 0 hoặc 0  g 6 3 (1) = 0 m < − 4 m >
Vậy giá trị cần tìm là hoặc 0. 3 1.14
Biện luận phương trình, bất phương trình Bài toán 1.15
Khi biện luận số nghiệm của phương trình, bất phương trình ta hay sử dụng một số kết quả sau: • m f x D ⇔ f x 6 m 6 f x Phương trình = ( ) có nghiệm trên min ( ) max ( ), D D • m 6 f x D ⇔ m 6 f x Bất phương trình ( ) có tập nghiệm là min ( ), D • m > f x D ⇔ m > f x Bất phương trình ( ) có tập nghiệm là max ( ). D Ví dụ 1.111 m mx2 mx − x ∈ Tìm để phương trình + 2 3 = 0 có nghiệm [1; 2]
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 52 of 59 Hướng dẫn. Ta có mx 3 2 mx − ⇔ m x2 x 6 , ∀x ∈ + 2 3 = 0 = x + 2 = 0 [1; 2]) 2 x (vì + 2 f x 3 Xét hàm số ( ) = x2
x trên đoạn [1; 2], ta có bảng biến thiên sau +2 x 1 2 f 0 x − ( ) f x 1 ( ) & 38 x ∈ f x 6 m 6 f x
Phương trình đã cho có nghiệm [1; 2] khi và chỉ khi min ( ) max ( ). Từ [1;2] [1;2] 3 6 m 6 đó tìm được đáp số 1. 8 Ví dụ 1.112 √ m x x2 − m > R Tìm để bất phương trình + 2 + 1 0 có tập nghiệm là ? √ Hướng dẫn. x x2 − m > R Ta có bất phương trình + 2 + 1 0 có tập nghiệm là khi và chỉ khi p x x2 − m > , ∀x ∈ R + 2 + 1 0 ⇔ m < f x min ( ) R √ f x x x2 . trong đó ( ) = + 2 + 1 Ta có bảng biến thiên √ x −∞ − 2 ∞ + 2 f 0 x − ( ) 0 + ∞ ∞ f x + √ + ( ) & 2 % 2 √ √ f x 2 m < 2 . Suy ra min ( ) = và do đó, đáp số là R 2 2 Ví dụ 1.113 ĐH Khối B năm 2007 m >
Chứng minh rằng với mọi
0, phương trình sau có hai nghiệm phân biệt p x2 x − m x − + 2 8 = ( 2) (9)
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 53 of 59 Hướng dẫn. m > x > Vì
0 nên điều kiện của phương trình là 2 và phương trình (9) tương đương với x x − x = 2 3 x2 − − m ⇔ ( 2)( + 6 32 ) = 0 x3 x2 − − m + 6 32 = 0
Ta chứng minh phương trình x3 x2 − m + 6 32 = (10) , ∞
có đúng một nghiệm trong khoảng (2 + ). f x x3 x2 − , ∞ Xét hàm số ( ) = + 6 32 trên (2 + ) có bảng biến thiên sau x ∞ 2 + f 0 x ( ) + ∞ f x + ( ) % 0 m > y m y f x Rõ ràng khi 0 thì đường thẳng = cắt đồ thị hàm số = ( ) tại đúng một
điểm có hoành độ lớn hơn 2, tức là phương trình (10) có đúng một nghiệm trong , ∞ m > . khoảng (2 +
). Do đó, phương trình (9) có đúng hai nghiệm khi 0 Ví dụ 1.114 ĐH Khối A năm 2007 m Tìm để phương trình √ √ p x − m x 4 x2 − 3 1 + + 1 = 2 1 (11) có nghiệm. Hướng dẫn. x > Điều kiện:
1, phương trình (11) tương đương với r r x − x − − 1 4 1 m. 3 x + 2 x = + 1 + 1 q q u x− 4 1 4 − 2 ∈ , Đặt = x = 1 x [0 1) ta được phương trình +1 +1 − u2 u m 3 + 2 = (12) f t − t2 t Xét hàm số ( ) = 3 + 2
trên [0; 1) ta có bảng biến thiên t 1 0 1 3 f 0 t − ( ) + 0 1 f t 3 ( ) % & − 0 1 Do đó phương trình (11) có nghiệm khi và chỉ khi phương trình (12) có nghiệm u ∈ − < m 6 1
[0; 1). Điều kiện cần và đủ là 1 . 3
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 54 of 59 1.15 Biến đổi hàm số Bài toán 1.16
Tịnh tiến đồ thị hàm số y f x = ( ) Ví dụ 1.115 y f x y Biết đồ thị hàm số = (
) có một tiệm cận ngang là đường thẳng = 3. y f x − Khi đó đồ thị hàm số = 2 ( )
4 có một tiệm cận ngang là A. y . B. y . C. y . D. y − . = 3 = 2 = 1 = 4 Chứng minh. f x − · − . Hướng dẫn] Ta có lim x→∞ 2 ( ) 4 = 2 3 4 = 2 1.16
Điểm thuộc đồ thị
Tìm điểm M thuộc đồ thị C của hàm số y f x thỏa mãn điều Bài toán 1.17 ( ) = ( ) kiện cho trước.
Chú ý những tính chất của đồ thị hàm số phân thức... Lưu ý 1.14 M a b M0 −a −b
Điểm đối xứng với điểm ( ; ) qua gốc tọa độ là ( ; ), đối xứng qua M00 a −b M000 −a b trục hoành là ( ;
), đối xứng qua trục tung là ( ; ). Ví dụ 1.116 y x+2 C Cho hàm số = x− có đồ thị là ( ). 1 C 1.
Xác định phương trình tiệm cận đứng và tiệm cận ngang của ( ). C M 2.
Viết phương trình tiếp tuyến ∆ của ( ) tại điểm (2; 4) A B 3.
Giả sử tiếp tuyến ∆ cắt tiệm cận đứng tại
, cắt tiệm cận ngang tại . M AB Chứng minh rằng là trung điểm . Ví dụ 1.117 y x+2
Tìm trên đồ thị hàm số = x−
những điểm cách đều hai trục tọa độ. 1
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 55 of 59 Hướng dẫn. M m, m+2 M Giả sử (
m− ) thuộc đồ thị hàm số đã cho. Ta có, điểm cách đều 1
hai trục tọa độ khi và chỉ khi m |m| + 2 = m − 1 √ m − ± . M − ±
Giải phương trình trên tìm được = 1 3
Từ đó tìm được đáp số ( 1 √ √ , − ∓ . 3 5 3 3) Ví dụ 1.118 M y x 2 Tìm điểm trên đồ thị = x
sao cho tiếp tuyến của đồ thị cùng với hai +1 1 .
trục tạo thành một tam giác có diện tích là 4 Ví dụ 1.119 ĐH Khối B năm 2003 m y x3 − x2 m Tìm để đồ thị hàm số = 3 +
có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ.
Hướng dẫn. Đồ thị hàm số đã cho có hai điểm phân biệt đối xứng nhau qua gốc x 6 y x −y −x
tọa độ khi và chỉ khi tồn tại 0 = 0 sao cho ( 0 ) = ( 0 ). Điều này đồng nghĩa với phương trình x3 − x2 m − −x 3 − −x 2 m ⇔ x2 m 3 + = ( 3( + 3 = 0 0 0 ) 0 ) 0 x 6 . m > . có nghiệm 0 = 0
Do đó, điều kiện cần và đủ là 0 Ví dụ 1.120 ĐH Khối D năm 2007 M y x 2 Tìm điểm trên đồ thị = x
sao cho tiếp tuyến đồ thị cùng với hai trục +1 1 .
tọa độ tạo thành một tam giác có diện tích là 4 Ví dụ 1.121 M, N y x− 3 1 Tìm hai điểm
thuộc hai nhánh của đồ thị hàm số = x− sao cho độ 3 MN dài đoạn thẳng ngắn nhất. Hướng dẫn. x M
Đồ thị hàm số có tiệm cận đứng là đường thẳng = 3 nên, giả sử .
nằm nhánh bên trái đồ thị thì hoành độ của nó nhỏ hơn 3
Do đó, gọi tọa độ điểm
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 56 of 59 M − a, − /a N b, /b a, b > là (3 3 8
) và, tương tự, tọa độ của (3 + 3 + 8 ) – với 0. Ta q MN a b 2 /a /b 2 tính được = ( + ) + (8 + 8
) . Sử dụng bất đẳng thức Cauchy, ta có ! r 2 2 √ 2 a b 8 8 1 2 > ab · 1 > ( + ) + a + b 2 + 64 2 a b 64 √ MN a b
Suy ra, giá trị nhỏ nhất của
là 8. Đẳng thức xảy ra, khi = = 2 2, từ đó M N tìm được và . Ví dụ 1.122 y x− 2 3 C C M Cho hàm số = x− có đồ thị ( ). Tìm trên đồ thị ( ) những điểm sao cho 2 M C C A, B AB tiếp tuyến tại của (
) cắt hai tiệm cận của ( ) tại mà ngắn nhất. A. M , M C. M 3 , M − 5 (3; 3) (1; 1). 0; 1; . 2 3 B. M , M 3 D. M , (3; 3) 0; . (1; 1) (2; 4). 2 Hướng dẫn. M a, a− 2 3 a 6 C Giả sử ( a− ), với
= 2, là một điểm thuộc đồ thị ( ). Phương 2 C M
trình tiếp tuyến ∆ của ( ) tại điểm là −x a2 − a y 2 6 + 6 ∆ : = a − + 2 a − 2 ( 2) ( 2) A a− 2 2
Tiếp tuyến ∆ cắt tiệm cận đứng tại điểm 2; a−
và cắt tiệm cận ngang tại điểm 2 B a − AB (2
2; 2). Do đó, độ dài đoạn là s AB a − 4 2 = 4( 2) + a − 2 ( 2) √ √ AB > . AB
Sử dụng bất đẳng thức Cauchy có 2 2 Vậy đoạn ngắn nhất bằng 2 2, a a . M M . khi = 3 hoặc = 1
Từ đó tìm được hai điểm (3; 3) hoặc (1; 1) Ví dụ 1.123 M y x − M Tìm điểm
thuộc đường thẳng ∆ : = 3
2 sao tổng khoảng cách từ y x3 − x2
tới hai điểm cực trị của đồ thị hàm số = 3 + 2 là ngắn nhất. A. M 4 2 B. M − C. M
D. M 1 − 1 ; . (0; 2). (1; 1). ; . 5 5 2 2
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 57 of 59 Hướng dẫn. y x3 − x2 Tìm được hai điểm cực trị của đồ thị hàm số = 3 + 2 là A B − A B (0; 2) và (2; 2). Nhận xét rằng và
nằm về hai phía của đường thẳng ∆, nên MA MB M, A, B M +
ngắn nhất khi và chỉ khi ba điểm
thẳng hàng. Nói cách khác, AB
là giao điểm của đường thẳng ∆ và đường thẳng
. Từ đó tìm được toạ độ của M 4 2 ; . 5 5 Ví dụ 1.124 M y x+1 Cho
là một điểm bất kỳ thuộc đồ thị hàm số =
x− . Tìm khoảng cách 1 M y − 1 x ngắn nhất từ đến đường thẳng ∆ : = + 1. 2 √ √ √ A. . B. 5 3 . C. 3 . D. 1 √ . 3 3 2 3 Hướng dẫn. d y x+1 Gọi
là tiếp tuyến của đồ thị hàm số = x− mà nó song song với 1 d − 1
đường thẳng ∆. Suy ra hệ số góc của là
. Từ đó tìm được toạ độ các tiếp điểm 2 E F − là (3; 2) hoặc ( 1; 0). E d E, 5 √
Tính được khoảng cách từ
đến đường thẳng ∆ là ( ∆) = ; khoảng cách từ √ 3 √ F d F ,
đến đường thẳng ∆ là ( ∆) =
3. Suy ra khoảng cách nhỏ nhất cần tìm là 3 M F . khi trùng với 1.17 Bài toán thực tế Bài toán 1.18 Bài toán thực tế. s
Đối với các bài toán về chuyển động cần lưu ý, nếu quãng đường theo thời t s s t v s0 t gian
được tính bởi phương trình = ( ) thì vận tốc là = ( ) còn gia tốc a v 0 t s00 t là = ( ) = ( ).
Đối với các bài toán về diện tích, thể tích lớn nhất, nhỏ nhất ta có thể đặt x x một kích thước là
và biểu diễn các kích thước còn lại theo . Sau đó lập
hàm số và khảo sát để tìm ra giá trị lớn nhất, giá trị nhỏ nhất. Có thể thay
trực tiếp các phương án vào và so sánh. Ví dụ 1.125 Đề minh hoạ 2017
Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm x
nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng cm, rồi x
gập tấm nhôm lại để được một cái hộp không nắp. Tìm để hộp nhận được có thể tích lớn nhất. A. x . B. x . C. x . D. x . = 6 = 3 = 2 = 4
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 58 of 59 Ví dụ 1.126 s − 1 t3 t2 t
Một vật chuyển động theo quy luật = + 9 , với (giây) là khoảng 2 s
thời gian tính từ lúc vật bắt đầu chuyển động và
(mét) là quãng đường vật
đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ
lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. / B. / C. / D. / 216 m s. 30 m s. 400 m s. 54 m s.
Hướng dẫn. Chúng ta cần tìm giá trị lớn nhất của vận tốc trong khoảng thời gian t ∈ v t s0 t v t − 3 t2 t [0; 10]. Có ( ) = ( ) nên ta xét hàm số ( ) = + 18 có đạo hàm 2 v 0 t − t ( ) = 3
+ 18 trên đoạn [0; 10]. Ta có bảng biến thiên sau t 0 6 10 v 0 t − ( ) + 0 v t 54 ( ) % & 0 30 / t
Suy ra, giá trị lớn nhất của vận tốc là 54 m s, đạt được tại thời điểm = 6 giây. Ví dụ 1.127 s − 1 t3 t2 t
Một vật chuyển động theo quy luật = + 6 với (tính bằng giây) là 2 s
khoảng thời gian tính từ khi vật bắt đầu chuyển động và (tính bằng mét)
là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian 6 giây, kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất
đạt được của vật là bao nhiêu? A. / B. / C. / D. / 24 m s. 108 m s. 64 m s. 18 m s.
Hướng dẫn. Vận tốc chuyển động của vật biến đổi theo quy luật v s0 − 3 t2 t = = + 12 2
Lập bảng biến thiên của hàm số này trên đoạn [0; 6] ta được t 0 4 6 v 0 t − ( ) + 0 v 24 % & 0 18 /
Suy ra, vận tốc lớn nhất có thể đạt được là 24 m s.
toicodongiuamotbiennguoi.wordpress.com
CÁC BÀI TOÁN ĐIỂN HÌNH 2018 Page 59 of 59 Ví dụ 1.128 /
Một viên đá được bắn thẳng lên trên với vận tốc ban đầu là 40 m s từ một t
điểm cao 5 m so với mặt đất. Vận tốc của viên đá sau giây được cho bởi v t − t / công thức ( ) = 40 10
m s. Tính độ cao lớn nhất viên đá có thể lên tới so với mặt đất. A. B. C. D. 75 m. 80 m. 90 m. 85 m. Ví dụ 1.129
Người ta muốn mạ vàng cho bề mặt phía ngoài của một cái hộp có dạng hình
hộp đứng không nắp, có đáy là một hình vuông. Tìm chiều cao của hộp để
lượng vàng dùng để mạ là ít nhất, biết lớp mạ ở mọi nơi là như nhau, giao 3
giữa các mặt không đáng kể và thể tích của hộp là 4 dm . A. B. . C. D. . 1 dm. 0 5 dm. 2 dm. 1 5 dm. Ví dụ 1.130 ×
Một tấm tôn hình chữ nhật có kích thước 80 cm
50 cm được cắt đi ở bốn góc
những hình vuông bằng nhau, để khi gấp lại thì được một cái thùng không
nắp dạng hình hộp. Thể tích hình hộp tạo thành lớn nhất khi bốn hình vuông
bị cắt đi có cạnh là bao nhiêu? A. B. C. D. 10 cm. 25 cm. 20 cm. 40 cm.
toicodongiuamotbiennguoi.wordpress.com
Document Outline

  • Hàm số
    • Tìm khoảng đồng biến, nghịch biến của hàm số
    • Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
    • Tìm điều kiện để hàm số đơn điệu
    • Cực trị của hàm số
    • Tìm điều kiện để hàm số đạt cực trị tại điểm cho trước
    • Tìm điều kiện để hàm số có cực trị
    • Tìm điều kiện để hàm số có cực trị thỏa mãn yêu cầu cho trước
    • Tiệm cận của đồ thị hàm số
    • Tiếp tuyến của đồ thị hàm số
    • Nhận dạng đồ thị
    • Đọc bảng biến thiên
    • Đồ thị hàm số chứa dấu giá trị tuyệt đối
    • Tương giao của hai đồ thị hàm số
    • Biện luận phương trình, bất phương trình
    • Biến đổi hàm số
    • Điểm thuộc đồ thị
    • Bài toán thực tế