Các bài toán liên quan đến đồ thị hàm số y = f'(x) – Nguyễn Chiến Toán 12

Các bài toán liên quan đến đồ thị hàm số y = f'(x) – Nguyễn Chiến Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

23 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Nguyễn Chiến 0973.514.674
CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ HÀM SỐ
y f x
Câu 1. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
C
tiếp xúc với đường thẳng
9y
tại điểm có hoành
độ âm và đồ thị hàm số
y f x
cho bởi hình vẽ
bên. Phần nguyên của giá trị diện tích hình phẳng
giới hạn bởi đồ thị
và trục hoành là
A.
2.
B.
27.
C.
29.
D.
35.
Câu 2. [Sở giáo dục Hà Nội]: Cho hàm số
32
, , , , 0 y f x ax bx cx d a b c a
có đồ
thị
C
. Biết rằng đồ thị
C
tiếp xúc với đường
thẳng
4y
tại điểm có hoành độ âm và đồ thị
hàm số
y f x
cho bởi hình vẽ dưới đây:
Tính diện tích
S
của hình phẳng giới hạn bởi đồ
thị
C
và trục hoành.
A.
.9S
B.
27
.
4
S
C.
21
.
4
S
D.
5
.
4
S
x
y
O
g
x
( )
=
x
2
2
∙
x
3
-1
3
1
x
y
1
-1
-3
O
4
Nguyễn Chiến 0973.514.674
Câu 3. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ
thị
C
đi qua gốc tọa độ và đồ thị hàm số
y f x
cho bởi hình vẽ bên. Giá trị của
31ff
là
A.
24.
B.
26.
C.
28.
D.
30.
Câu 4. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
C
đi qua gốc tọa độ và đồ thị hàm số
y f x
cho bởi
hình vẽ bên. Phần nguyên giá trị diện tích hình
phẳng giới hạn bởi đồ thị
C
và trục hoành là
A.
6.
B.
4.
C.
3.
D.
2.
x
y
2
O
g
x
( )
= 3
∙
x
2
+ 2
-1
5
1
x
y
2
O
6
3
6
3
Nguyễn Chiến 0973.514.674
Câu 5. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
hàm số
y f x
cho bởi hình vẽ bên. Hàm số
C
có thể là hàm số nào trong các hàm số sau:
A.
32
2 2. y x x x
B.
3
2 1. y x x
C.
32
2 2. y x x x
D.
32
2. y x x x
Câu 6. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
C
tiếp xúc với đường thẳng
13
3
y
tại điểm có
hoành độ dương và đồ thị hàm số
y f x
cho
bởi hình vẽ bên. Giá trị
32 a b c d
là
A.
0.
B.
2.
C.
3.
D.
4.
x
y
f
x
( )
=
3
∙
x
2
+ 2
∙
x
1
O
x
y
2
-2
f
x
( )
=
x
2
+ 4
O
4
Nguyễn Chiến 0973.514.674
Câu 7. Cho hàm số
4 3 2
0 y ax bx cx dx e a
có đồ thị
C
. Đồ thị hàm số
y f x
như hình
vẽ bên. Biết hàm số
y f x
đạt cực tiểu tại
2x
và 2 cực trị đều âm, hỏi đồ thị hàm số
C
cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A.
0.
B.
1.
C.
2.
D.
4.
Câu 8. Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ. Biết
0f a
, hỏi đồ thị
hàm số
y f x
cắt trục hoành tại nhiều nhất
bao nhiêu điểm?
A.
1.
B.
2.
C.
3.
D.
4.
x
y
-2
f
x
( )
=
x
3
+
x
2
2
O
x
y
c
b
a
f
x
( )
=
x
3
+ 1
∙
x
2
3
∙
x
1
O
1
1
Nguyễn Chiến 0973.514.674
Câu 9. Cho hàm số
42
0 y f x ax bx c a
có đồ thị
C
, đồ thị hàm số
y f x
như hình
vẽ bên. Biết đồ thị hàm số
y f x
đạt cực tiểu
tại điểm
3 8 3
;
39




. Đồ thị hàm số
y f x
tiếp
xúc với trục
Ox
tại 2 điểm. Diện tích
S
của hình
phẳng giới hạn bởi đồ thị
C
và trục hoành là
A.
7
.
15
B.
C.
14
.
15
D.
16
.
15
Câu 10. Cho hàm số

ax b
f
cx
y
d
x
, , , ; 0



d
a b c d
c
có đồ thị
C
, đồ thị hàm số
y f x
như hình vẽ bên. Biết đồ thị hàm số
y f x
cắt trục tung tại điểm có tung độ bằng 3.
Phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục hoành có dạng
A.
13
.
22
yx
B.
13
.
22
yx
C.
13
.
22
yx
D.
1
2.
2
yx
x
y
-1
1
f
x
( )
=
4
∙
x
3
4
∙
x
O
Nguyễn Chiến 0973.514.674
BÀI TẬP RÈN LUYỆN
Câu 1. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
hàm số
y f x
cho bởi hình vẽ bên.
Đồ thị hàm số có thể là đồ thị nào trong các
hình vẽ sau
A.
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
Nguyễn Chiến 0973.514.674
Câu 2. Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ. Biết
0f a
, hỏi đồ thị
hàm số
y f x
cắt trục hoành tại nhiều nhất
bao nhiêu điểm?
A.
0.
B.
1.
C.
2.
D.
4.
Câu 3. Cho hàm số
42
y f x y ax bx cx d
có đồ thị
C
, đồ thị hàm số
y f x
như hình vẽ
bên. Biết đồ thị hàm số
y f x
cắt trục tung tại
điểm có tung độ bằng
1
. Giá trị
a b c d
là
A.
4.
B.
7.
C.
13
.
4
D.
17
.
4
Câu 4. Cho hàm số
32
y f x y ax bx cx d
có đồ thị
C
, đồ thị hàm số
y f x
như hình vẽ
bên. Biết đồ thị hàm số
y f x
có điểm cực đại
nằm trên trục tung có tung độ bằng 2 . Giá trị
a b c d
là
A.
1.
B.
2.
C.
2.
D.
3.
x
y
a
O
x
y
2
2
-1
1
4
O
x
y
1
O
1
2
3
2
Nguyễn Chiến 0973.514.674
Câu 5. Cho hàm số
42
0 y ax bx c a
có đồ
thị hàm số
y f x
như hình vẽ. Biết đồ thị
hàm số
y f x
đạt cực tiểu tại điểm
3 8 3
;
39




. Đồ thị hàm số
y f x
đạt cực đại
tại điểm có tung độ bằng
3
. Phương trình
f x m
có 4 nghiệm phân biệt khi giá trị m là
A.
4 3. m
B.
0 4.m
C.
0 3.m
D.
3 4.m
Câu 6. Cho hàm số
fx
có đạo hàm
'fx
xác
định, liên tục trên và
'fx
có đồ thị như
hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
1; . 
B. Hàm số chỉ nghịch biến trên
3; 1 .
C. Hàm số đồng biến trên
;3
và
1; .
D. Hàm số chỉ đồng biến trên
1; .
x
y
-1
1
f
x
( )
=
4
∙
x
3
4
∙
x
O
x
y
-1
1
-3
-3
-4
O
Nguyễn Chiến 0973.514.674
Câu 7. Cho hàm số
42
y ax bxfx c
0a
có đồ thị
, đồ thị hàm số
y f x
như hình vẽ bên. Biết đường thẳng
2y
tiếp
xúc với đồ thị hàm số
y f x
tại điểm cực
đại. Giá trị
a b c
là
A.
1.
B.
0.
C.
1.
D.
2.
Câu 8. Cho hàm số

ax b
f
cx
y
d
x
, , , ; 0



d
a b c d
c
có đồ thị
C
, đồ thị hàm
số
y f x
như hình vẽ bên. Biết đồ thị hàm số
y f x
cắt trục hoành tại điểm có hoành độ
bằng
2
. Giá trị
a b c d
là
A.
1.
B.
3.
C.
5.
D.
6.
x
y
-6
1
O
Nguyễn Chiến 0973.514.674
CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ HÀM SỐ
y f x
Câu 1. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
C
tiếp xúc với đường thẳng
9y
tại điểm có hoành
độ âm và đồ thị hàm số
y f x
cho bởi hình vẽ
bên. Phần nguyên của giá trị diện tích hình phẳng
giới hạn bởi đồ thị
và trục hoành là
A.
2.
B.
27.
C.
29.
D.
35.
Lời giải:
Ta có
2
32
f x ax bx c
. Dựa vào đồ thị hàm số
y f x
ta thấy đồ thị hàm số
y f x
đi qua 3 điểm
1;0 , 3;0 , 1; 4
ta có hệ:
1
3 2 0
3
27 6 0 1
3 2 4 3


a
a b c
a b c b
a b c c
2
23
f x x x
2 3 2
1
2 3 3
3

f x f x dx x x dx x x x C
Do
C
tiếp xúc với đường thẳng
9y
tại điểm có hoành độ
0
x
nên
0
0 0 0
0
0
2
1
0 . 0 3
3
2 3 0
o
x
f x o x x
x
xxD
.
Suy ra
32
1
3 3 3.3 9
3
3 9 0 CfC
32
1
3
3
: xxCy x
x
y
O
g
x
( )
=
x
2
2
∙
x
3
-1
3
1
4
Nguyễn Chiến 0973.514.674
Xét phương trình hoành độ giao điểm của
C
và trục hoành:
32
1
3
3
0x x x
1
2,3
0
3 3 5
2
x
x
. Diện tích hình phẳng cần tìm là
3 3 5
2
3 3 5
32
2
1
3
3
29,25
dxx x xS
Chọn đáp án C.
Câu 2. [Sở giáo dục Hà Nội]: Cho hàm số
32
, , , , 0 y f x ax bx cx d a b c a
có đồ
thị
C
. Biết rằng đồ thị
C
tiếp xúc với đường
thẳng
4y
tại điểm có hoành độ âm và đồ thị
hàm số
y f x
cho bởi hình vẽ dưới đây:
Tính diện tích
S
của hình phẳng giới hạn bởi đồ
thị
C
và trục hoành.
A.
.9S
B.
27
.
4
S
C.
21
.
4
S
D.
5
.
4
S
Lời giải:
Ta có
2
32
f x ax bx c
. Đồ thị hàm
y f x
là hàm chẵn đối xứng qua trục tung
nên
1 1 0

f f b
. Mà
2
0 3 3
33
1 0 3 0 1
fc
f x x
f a c a
23
3 3 3

f x f x dx x dx x x C
.Do
C
tiếp xúc với đường thẳng
4y
tại
điểm có hoành độ
0
x
nên
2
0 0 0 0
0 3 3 0 1. 0 1
o
f x x x Do x x
.
Suy ra
1 4 2 fC
3
: 3 2 C y x x
Xét phương trình hoành độ giao điểm của
C
và trục hoành:
3
2
3 2 0
1
x
xx
x
.
Diện tích hình phẳng cần tìm là:
1
3
2
27
32
4
S x x dx
Chọn đáp án B.
x
y
1
-1
-3
O
Nguyễn Chiến 0973.514.674
Câu 3. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ
thị
C
đi qua gốc tọa độ và đồ thị hàm số
y f x
cho bởi hình vẽ bên. Giá trị của
31ff
là
A.
24.
B.
26.
C.
28.
D.
30.
Lời giải:
Ta có
2
32
f x ax bx c
. Đồ thị hàm
y f x
là hàm chẵn đối xứng qua trục tung
nên
1 1 0

f f b
. Mà
2
0 3 2
32
1 5 3 5 1
fc
f x x
f a c a
23
3 2 2

f x f x dx x dx x x C
, đồ thị
C
đi qua gốc tọa độ nên
0C
3
2 f x x x
3 1 30 ff
Chọn đáp án D.
Câu 4. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
C
đi qua gốc tọa độ và đồ thị hàm số
y f x
cho bởi hình vẽ bên. Phần nguyên giá trị diện tích
hình phẳng giới hạn bởi đồ thị
C
và trục hoành
là
A.
6.
B.
4.
C.
3.
D.
2.
x
y
2
O
g
x
( )
= 3
∙
x
2
+ 2
-1
5
1
x
y
2
O
6
3
6
3
Nguyễn Chiến 0973.514.674
Lời giải:
Ta có
2
32
f x ax bx c
. Đồ thị hàm
y f x
là hàm chẵn
0b
.
Mà
2
0 2 2
32
6
0 2 0 1
3



fc
f x x
f a c a
23
3 2 2

f x f x dx x dx x x C
.
Do đồ thị
đi qua gốc tọa độ nên
0C
3
:2 C y x x
Xét phương trình hoành độ giao điểm của
C
và trục hoành:
3
0
20
2


x
xx
x
.
Diện tích hình phẳng cần tìm là:
2
3
2
26
S x xdx
Chọn đáp án A.
Câu 5. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
hàm số
y f x
cho bởi hình vẽ bên. Hàm số
C
có thể là hàm số nào trong các hàm số sau:
A.
32
2 2. y x x x
B.
3
2 1. y x x
C.
32
2 2. y x x x
D.
32
2. y x x x
Lời giải:
Ta có
2
32
f x ax bx c
. Dựa vào đồ thị hàm số
y f x
ta thấy
0a
Mà
0 0 0
fc
, đồ thị hàm số
y f x
nằm hoàn toàn phía dưới trục Ox nên
x
y
f
x
( )
=
3
∙
x
2
+ 2
∙
x
1
O
Nguyễn Chiến 0973.514.674
hàm số
y f x
nghịch biến trên .
hàm số
y f x
không có cực trị
22
3 0 3 b ac b ac
Chọn đáp án D.
Câu 6. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
C
tiếp xúc với đường thẳng
13
3
y
tại điểm có
hoành độ dương và đồ thị hàm số
y f x
cho
bởi hình vẽ bên. Giá trị
32 a b c d
là
A.
0.
B.
2.
C.
3.
D.
4.
Lời giải:
Ta có
2
32
f x ax bx c
. Đồ thị hàm
y f x
là hàm chẵn
0b
.
Mà
2
0 4 4
4
1
2 0 12 0
3
fc
f x x
f a c a
23
1
44
3

f x f x dx x dx x x C
.
Do
C
tiếp xúc với đường thẳng
13
3
y
tại điểm có hoành độ
0
x
nên
2
0 0 0 0
0 4 0 2 2 .0
o
f x x x Do x x
.
Suy ra
13
21
3
fC
3
1
: 4 1
3
C y x x
3 2 4 a b c d
Chọn đáp án D.
x
y
2
-2
f
x
( )
=
x
2
+ 4
O
4
Nguyễn Chiến 0973.514.674
Câu 7. Cho hàm số
4 3 2
0 y ax bx cx dx e a
có đồ thị
C
. Đồ thị hàm số
y f x
như hình
vẽ bên. Biết hàm số
y f x
đạt cực tiểu tại
2x
và 2 cực trị đều âm, hỏi đồ thị hàm số
C
cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A.
0.
B.
1.
C.
2.
D.
4.
Lời giải:
Do hàm số
y f x
đạt cực tiểu tại
2x
và 2 cực trị đều âm nên từ đồ thị hàm số
y f x
ta có thể suy ra đồ thị hàm số
y f x
có dạng như hình bên
Từ đồ thị của hàm số
y f x
ta có bảng biến thiên:
x

1

fx
0
fx


1f
x
y
-2
f
x
( )
=
x
3
+
x
2
2
O
x
y
-2
f
x
( )
=
x
3
+
x
2
2
O
1
1
1
0y
Nguyễn Chiến 0973.514.674
đồ thị hàm số
y f x
cắt
Ox
tại nhiều
nhất 2 điểm
Chọn đáp án C.
Có thể minh họa rõ hơn bằng hình vẽ
Câu 8. Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ. Biết
0f a
, hỏi đồ thị
hàm số
y f x
cắt trục hoành tại nhiều nhất
bao nhiêu điểm?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Từ đồ thị của hàm số ta có bảng biến thiên:
x

a
b
c

fx
0
0
0
fx


fb
fa
fc
Để đồ thị hàm số
y f x
cắt trục hoành tại số điểm là nhiều nhất thì
0fc
đồ thị hàm số
y f x
cắt
Ox
tại nhiều nhất 2 điểm
Chọn đáp án B.
Có thể minh họa rõ hơn bằng hình vẽ
x
y
-2
f
x
( )
=
1
4
∙
x
4
+
1
3
∙
x
3
2
∙
x
2
O
x
y
c
b
a
f
x
( )
=
x
3
+ 1
∙
x
2
3
∙
x
1
O
x
y
c
b
a
O
0y
1
Nguyễn Chiến 0973.514.674
Câu 9. Cho hàm số
42
0 y f x ax bx c a
có đồ thị
C
, đồ thị hàm số
y f x
như hình
vẽ bên. Biết đồ thị hàm số
y f x
đạt cực tiểu
tại điểm
3 8 3
;
39




. Đồ thị hàm số
y f x
tiếp
xúc với trục
Ox
tại 2 điểm. Diện tích
S
của hình
phẳng giới hạn bởi đồ thị
C
và trục hoành là
A.
7
.
15
B.
C.
14
.
15
D.
16
.
15
Lời giải:
Từ đồ thị hàm số
y f x
với
0a
ta dễ dàng có được đồ
thị hàm số
y f x
như hình bên.
Ta có
3
42
f x ax bx
. Đồ thị hàm
y f x
qua
1; 0
và
3 8 3
;
39




nên ta có hệ :
10
3 8 3
39





f
f
3
4 2 0
3 3 8 3
42
3 3 9




ab
ab
3
1
44
2


a
f x x x
b
. Ta có:
34
4 4 2

f x f x dx x x dx x x C
.
Do
C
tiếp xúc với đường thẳng
Ox
tại điểm có hoành độ
0
x
nên
3
0
0 0 0
0
0
0 4 4 0 .
1


x
f x x x
x
Đồ thị hàm số
y f x
tiếp xúc với trục
Ox
tại 2
điểm nên 2 điểm đó có hoành độ là
1
. Suy ra
1 0 1 fC
42
: 2 1 C y x x
x
y
-1
1
f
x
( )
=
4
∙
x
3
4
∙
x
O
x
y
-1
1
f
x
( )
= 4
∙
x
3
4
∙
x
O
Nguyễn Chiến 0973.514.674
Xét phương trình hoành độ giao điểm của
C
và trục hoành:
42
1
2 1 0
1
x
xx
x
.
Diện tích hình phẳng cần tìm là:
1
42
1
16
21
15
S x x dx
Chọn đáp án D.
Câu 10. Cho hàm số

ax b
f
cx
y
d
x
, , , ; 0



d
a b c d
c
có đồ thị
C
, đồ thị hàm số
y f x
như hình vẽ bên. Biết đồ thị hàm số
y f x
cắt trục tung tại điểm có tung độ bằng 3.
Phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục hoành có dạng
A.
13
.
22
yx
B.
13
.
22
yx
C.
13
.
22
yx
D.
1
2.
2
yx
Ta có
2
ad bc
cx
x
d
f
. Từ đồ thị hàm số
y f x
ta thấy :
+ đồ thị
y f x
có tiệm cận đứng
1x
1
d
cd
c
1
+ đồ thị
y f x
qua điểm
2; 2
2
2
2 2 2
2

ad bc
ad bc c d
cd
2
+ đồ thị
y f x
cắt trục tung tại
2y
2
2
22
ad bc
ad bc d
d
3
Mà đồ thị
y f x
cắt trục tung tại điểm có tung độ bằng 3
33
b
bd
d
4
Nguyễn Chiến 0973.514.674
Từ
1
,
2
,
3
,
4
ta có hệ
2
2
1
3
22
1
2
1
3









cd
a
b
ad bc c d
c
ad bc d
d
bd
3
1
x
y f x
x
Đồ thị
C
giao với
Ox
tại
3;0
.
2
21
3
2
1

f x f
x
Phương trình tiếp tuyến của
C
tại điểm
3;0
là :
1 1 3
3
2 2 2
y x y x
Chọn đáp án A.
Nguyễn Chiến 0973.514.674
BÀI TẬP RÈN LUYỆN
Câu 1. Cho hàm số
32
y f x ax bx cx d
, , , 0a b c a
có đồ thị
C
. Biết rằng đồ thị
hàm số
y f x
cho bởi hình vẽ bên.
Đồ thị hàm số có thể là đồ thị nào trong các
hình vẽ sau
A.
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
Nguyễn Chiến 0973.514.674
Câu 2. Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ. Biết
0f a
, hỏi đồ thị
hàm số
y f x
cắt trục hoành tại nhiều nhất
bao nhiêu điểm?
A.
0.
B.
1.
C.
2.
D.
4.
Câu 3. Cho hàm số
42
y f x y ax bx cx d
có đồ thị
C
, đồ thị hàm số
y f x
như hình vẽ
bên. Biết đồ thị hàm số
y f x
cắt trục tung tại
điểm có tung độ bằng
1
. Giá trị
a b c d
là
A.
4.
B.
7.
C.
13
.
4
D.
17
.
4
Câu 4. Cho hàm số
32
y f x y ax bx cx d
có đồ thị
C
, đồ thị hàm số
y f x
như hình vẽ
bên. Biết đồ thị hàm số
y f x
có điểm cực đại
nằm trên trục tung có tung độ bằng 2 . Giá trị
a b c d
là
A.
1.
B.
2.
C.
2.
D.
3.
x
y
a
O
x
y
2
2
-1
1
4
O
x
y
1
O
1
2
3
2
Nguyễn Chiến 0973.514.674
Câu 5. Cho hàm số
42
0 y ax bx c a
có đồ
thị hàm số
y f x
như hình vẽ. Biết đồ thị
hàm số
y f x
đạt cực tiểu tại điểm
3 8 3
;
39




. Đồ thị hàm số
y f x
đạt cực đại
tại điểm có tung độ bằng
3
. Phương trình
f x m
có 4 nghiệm phân biệt khi giá trị m là
A.
4 3. m
B.
0 4.m
C.
0 3.m
D.
3 4.m
Câu 6. Cho hàm số
fx
có đạo hàm
'fx
xác
định, liên tục trên và
'fx
có đồ thị như
hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
1; . 
B. Hàm số chỉ nghịch biến trên
3; 1 .
C. Hàm số đồng biến trên
;3
và
1; .
D. Hàm số chỉ đồng biến trên
1; .
x
y
-1
1
f
x
( )
=
4
∙
x
3
4
∙
x
O
x
y
-1
1
-3
-3
-4
O
Nguyễn Chiến 0973.514.674
Câu 7. Cho hàm số
42
y ax bxfx c
0a
có đồ thị
, đồ thị hàm số
y f x
như hình vẽ bên. Biết đường thẳng
2y
tiếp
xúc với đồ thị hàm số
y f x
tại điểm cực
đại. Giá trị
a b c
là
A.
1.
B.
0.
C.
1.
D.
2.
Câu 8. Cho hàm số

ax b
f
cx
y
d
x
, , , ; 0



d
a b c d
c
có đồ thị
C
, đồ thị hàm
số
y f x
như hình vẽ bên. Biết đồ thị hàm số
y f x
cắt trục hoành tại điểm có hoành độ
bằng
2
. Giá trị
a b c d
là
A.
1.
B.
3.
C.
5.
D.
6.
x
y
-6
1
O
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ HÀM SỐ y f x
Câu 1. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị C
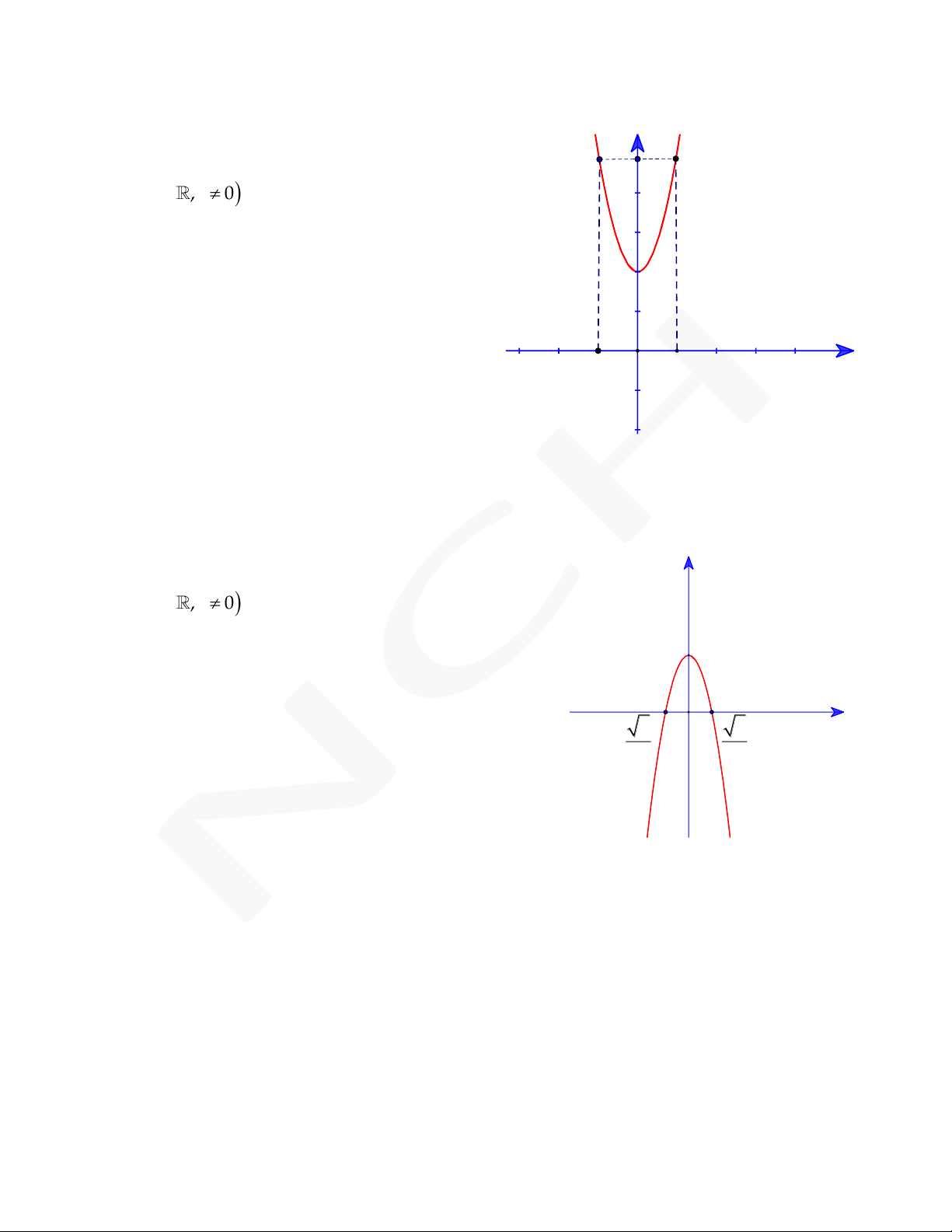
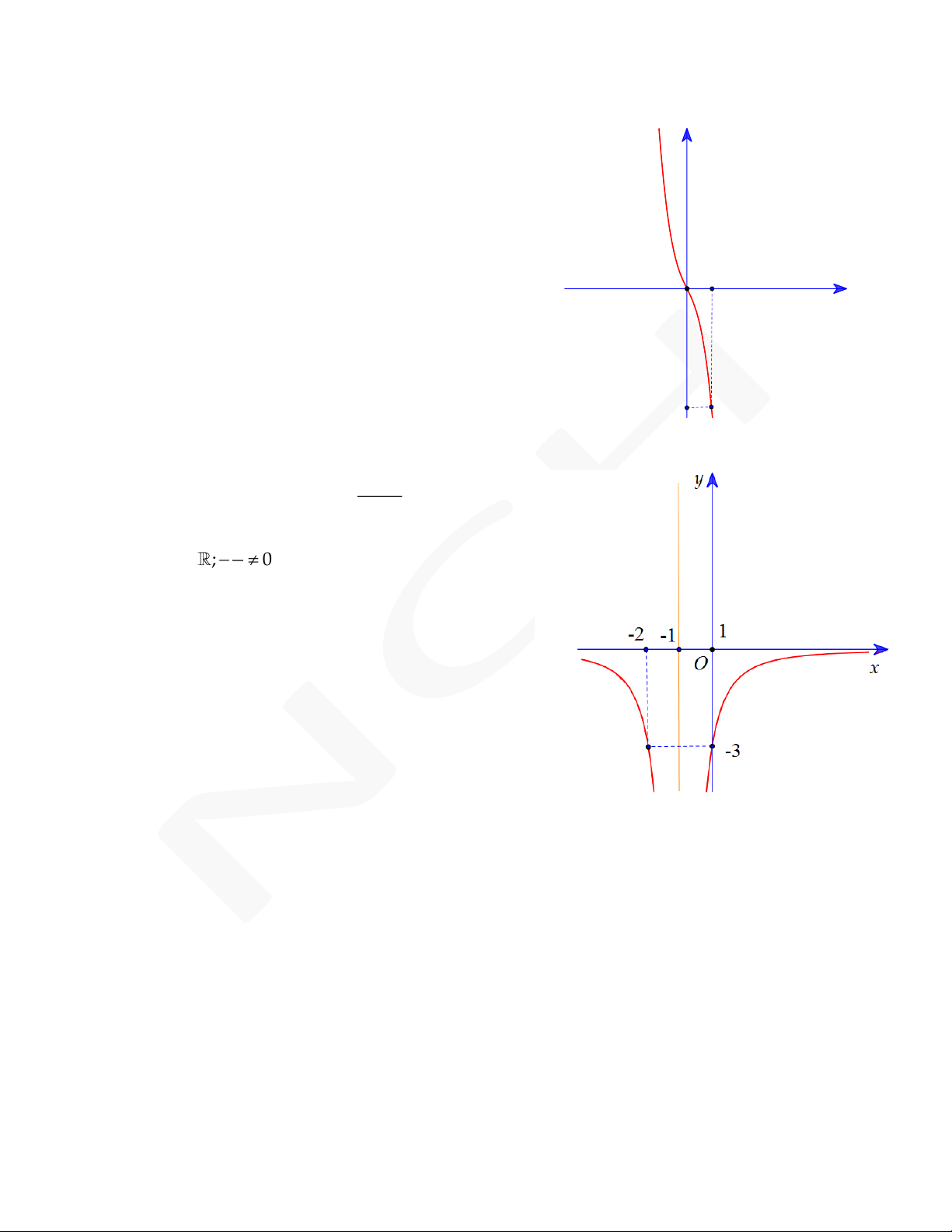
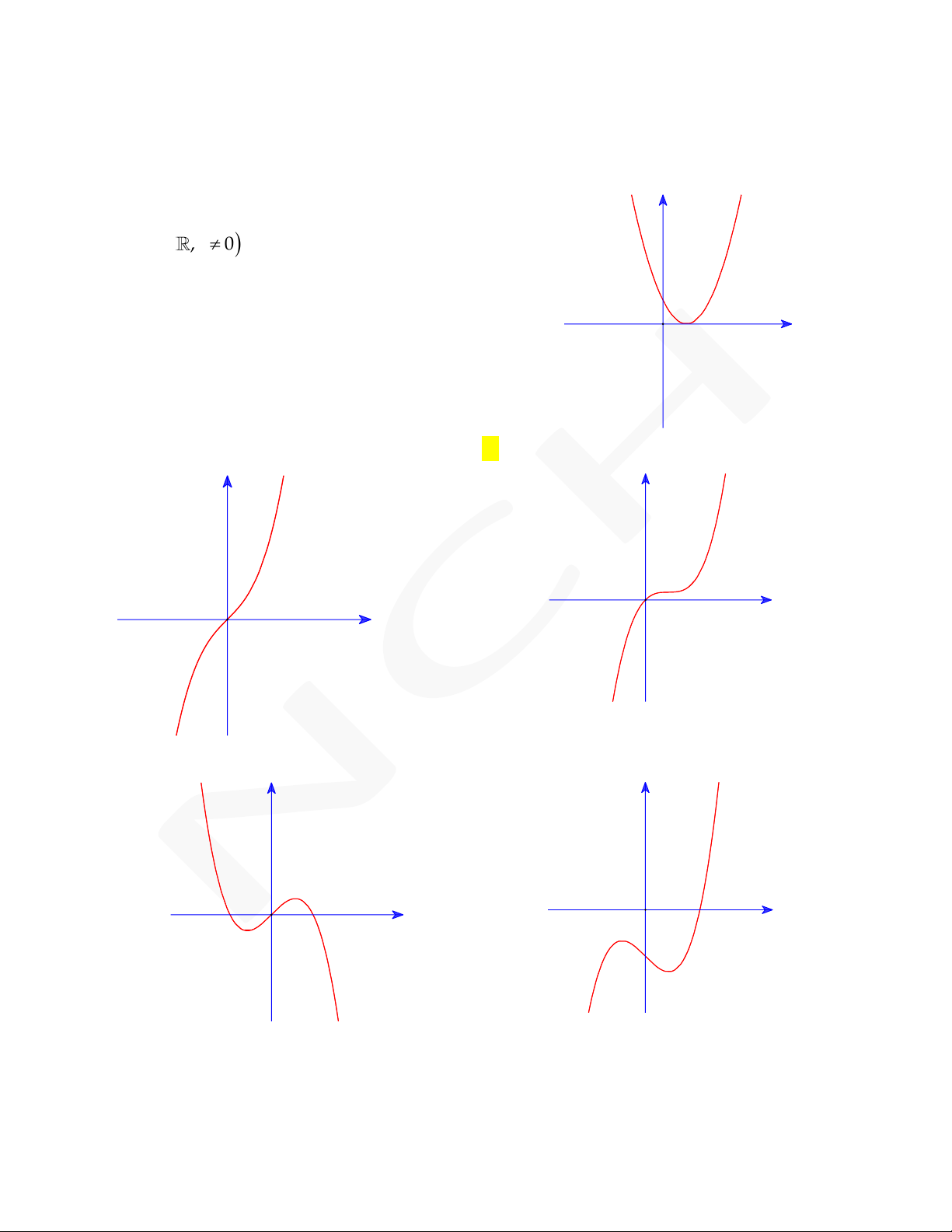
tiếp xúc với đường thẳng y  9  tại điểm có hoành O 1
độ âm và đồ thị hàm số y f x cho bởi hgì(xn ) h = x2 v 2∙ẽ x 3 -1 3 x
bên. Phần nguyên của giá trị diện tích hình phẳng
giới hạn bởi đồ thị C và trục hoành là 4  A. 2. B. 27. C. 29. D. 35.
Câu 2. [Sở giáo dục Hà Nội]: Cho hàm số y
y f x 3 2
ax bx cx d,a,b,c ,a  0 có đồ
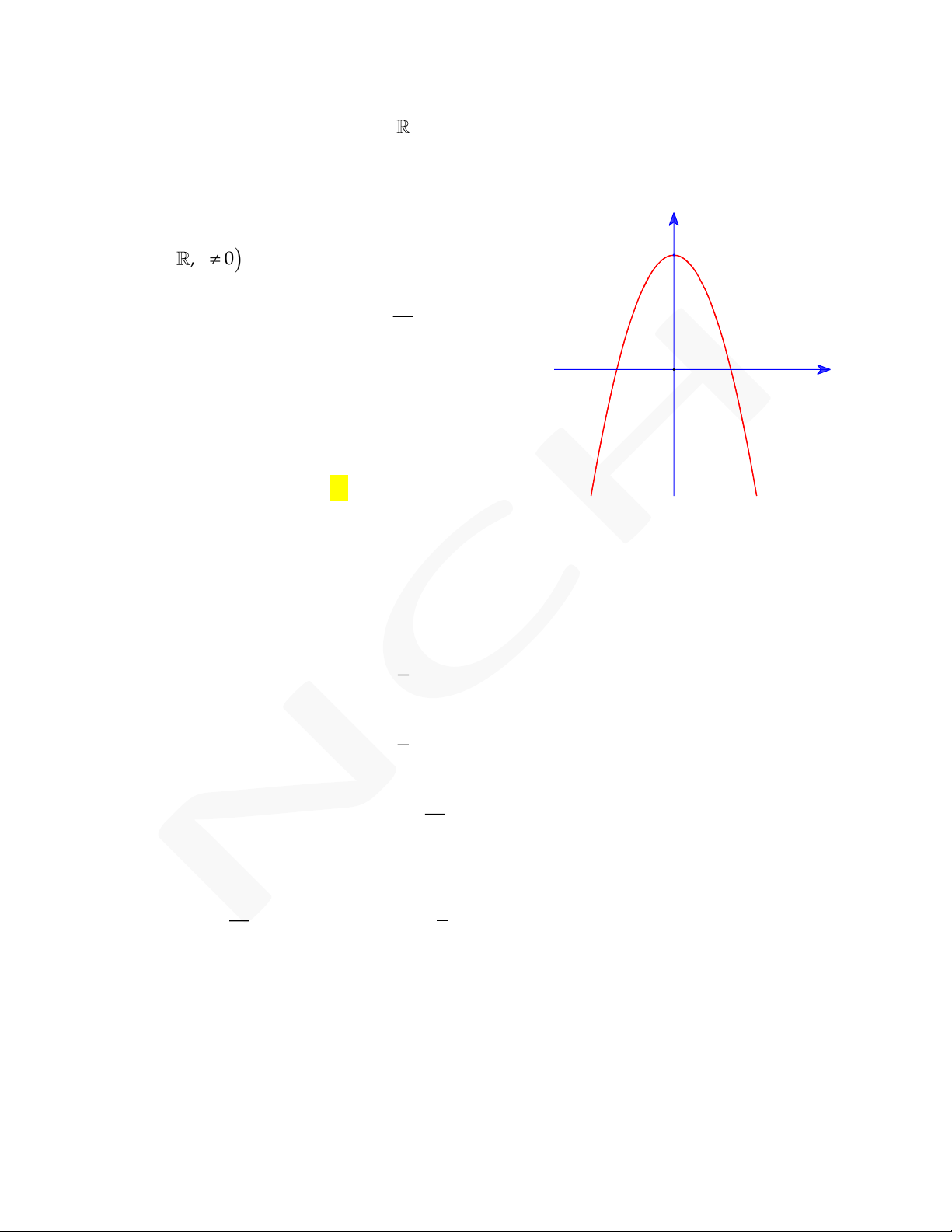
thị C . Biết rằng đồ thị C tiếp xúc với đường
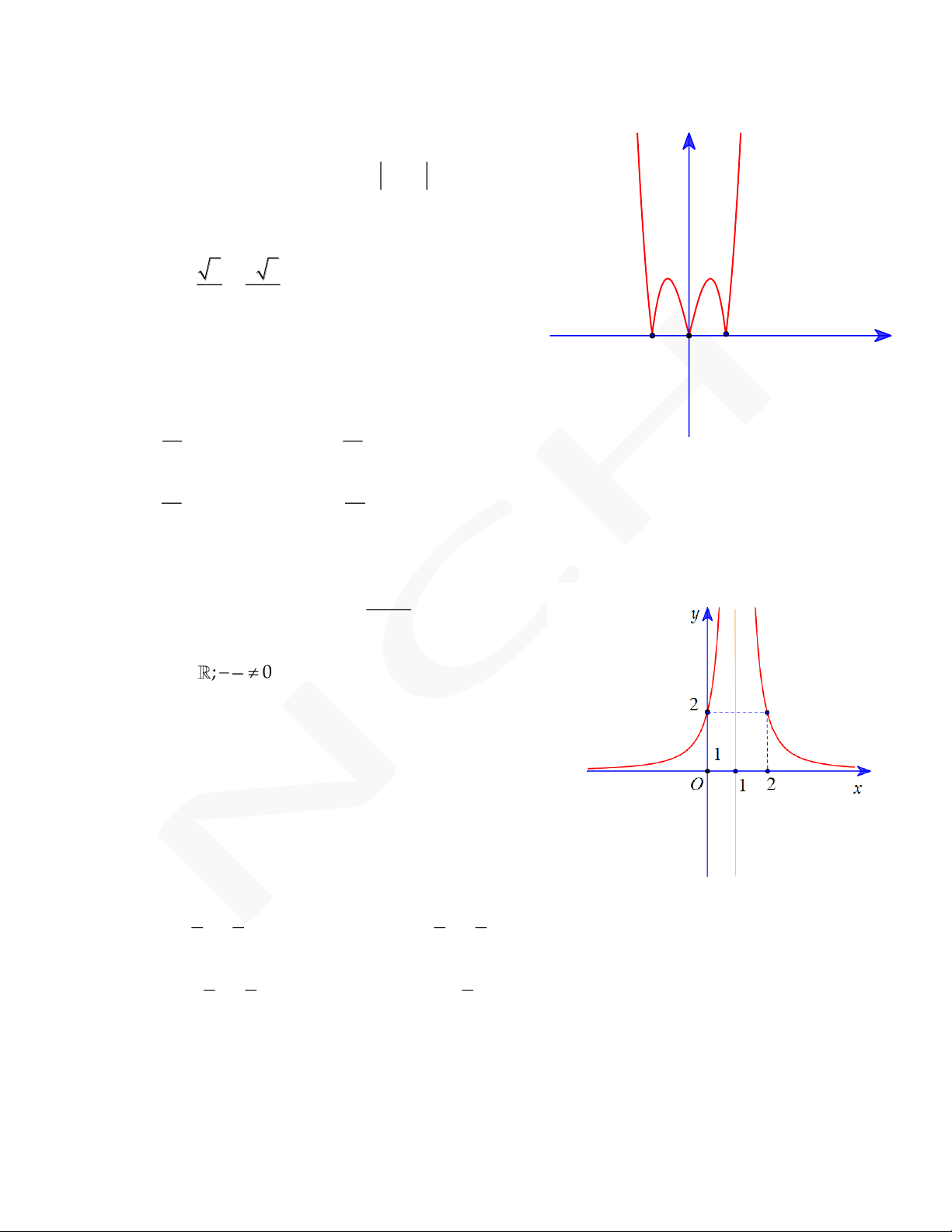
thẳng y  4 tại điểm có hoành độ âm và đồ thị
hàm số y f x cho bởi hình vẽ dưới đây: O -1 1 x
Tính diện tích S của hình phẳng giới hạn bởi đồ
thị C và trục hoành. -3 27 A. S  . 9 B. S  . 4 21 5 C. S  . D. S  . 4 4 Nguyễn Chiến 0973.514.674
Câu 3. Cho hàm số y f x 3 2 
ax bx cx d y 5
a,b,c ,a  0 có đồ thị C. Biết rằng đồ
thị C đi qua gốc tọa độ và đồ thị hàm số
y f x cho bởi hình vẽ bên. Giá trị của 2
f 3  f   1 là O g(x) = 3∙x2 + 2 -1 1 x A. 24. B. 26. C. 28. D. 30.
Câu 4. Cho hàm số y f x 3 2 
ax bx cx d y
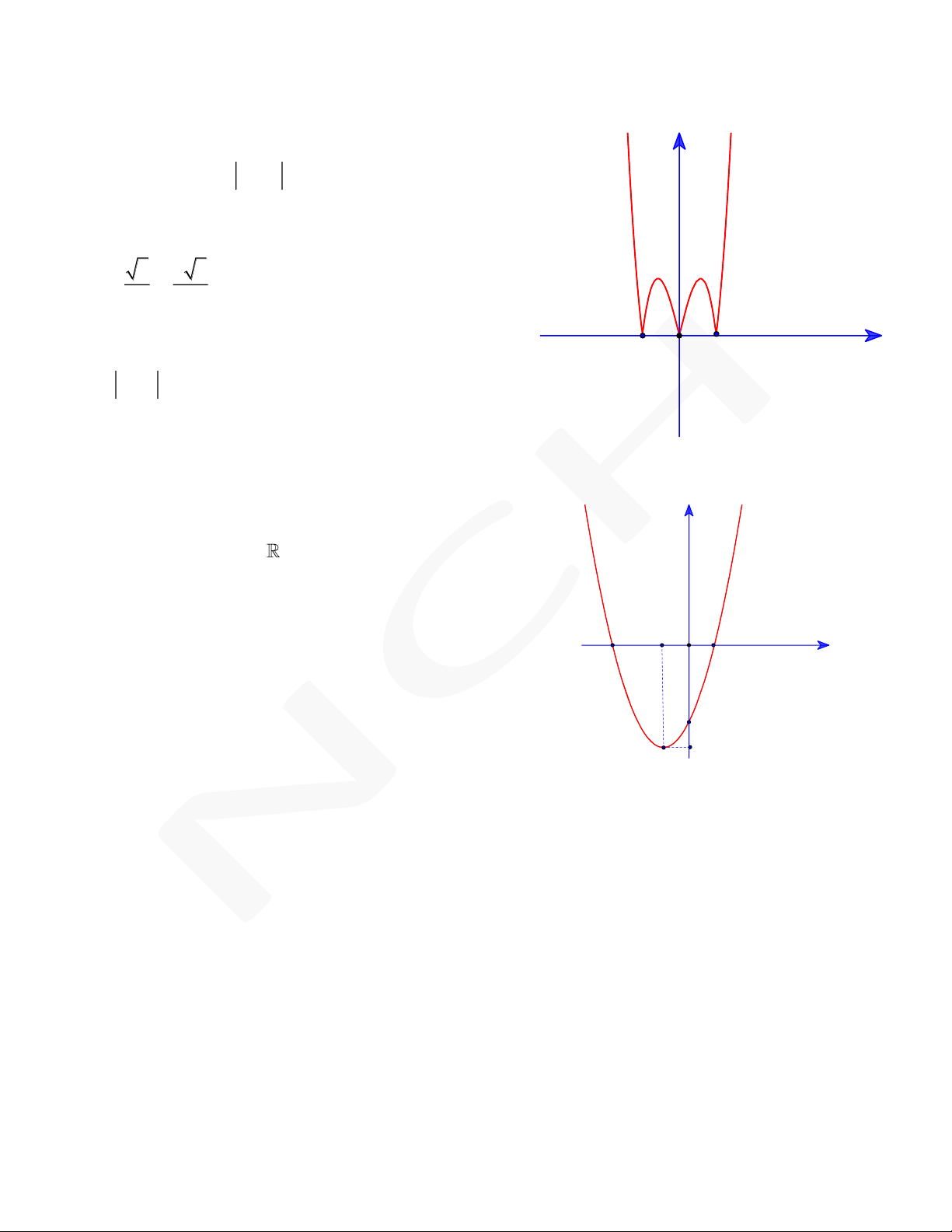
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị C
đi qua gốc tọa độ và đồ thị hàm số y f x cho bởi 2
hình vẽ bên. Phần nguyên giá trị diện tích hình O
phẳng giới hạn bởi đồ thị C và trục hoành là 6 6 x  3 3 A. 6. B. 4. C. 3. D. 2. Nguyễn Chiến 0973.514.674
Câu 5. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị
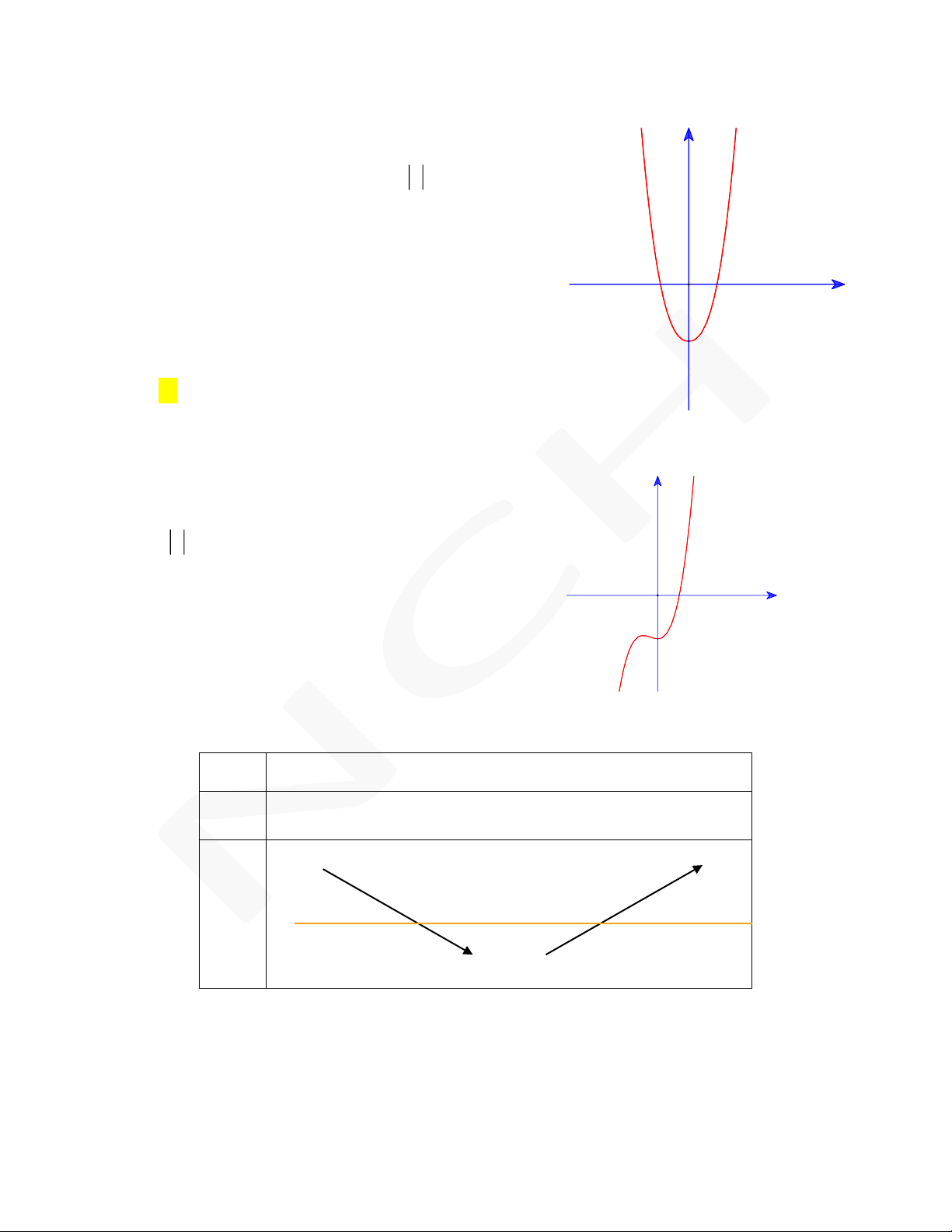
hàm số y f x cho bởi hình vẽ bên. Hàm số C f(x) = 3∙x2 + 2∙x 1
có thể là hàm số nào trong các hàm số sau: O x A. 3 2
y  x  2x x  2. B. 3
y x  2x 1. C. 3 2
y  x  2x x  2. D. 3 2
y  x x x  2.
Câu 6. Cho hàm số y f x 3 2 
ax bx cx d y  4
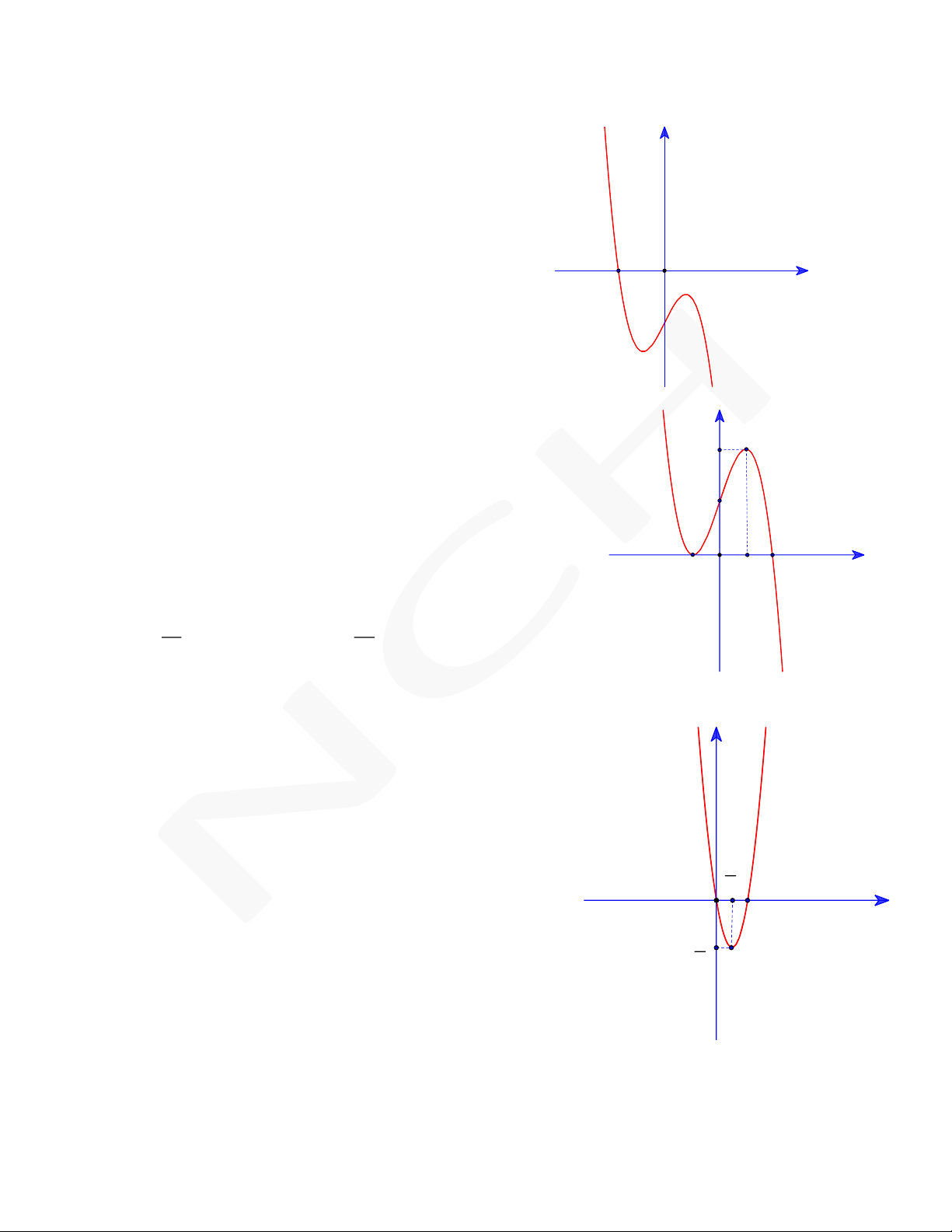
a,b,c  ,a  0 có đồ thị C . Biết rằng đồ thị  13
C  tiếp xúc với đường thẳng y  tại điểm có 3 -2 2 O
hoành độ dương và đồ thị hàm số y ff( x)x = x2 ch + 4 o x
bởi hình vẽ bên. Giá trị 3a  2b c d là A. 0. B. 2. C. 3. D. 4. Nguyễn Chiến 0973.514.674 Câu 7. Cho hàm số 4 3 2
y ax bx cx dx e a  0 y
có đồ thị C . Đồ thị hàm số y f  x  như hình
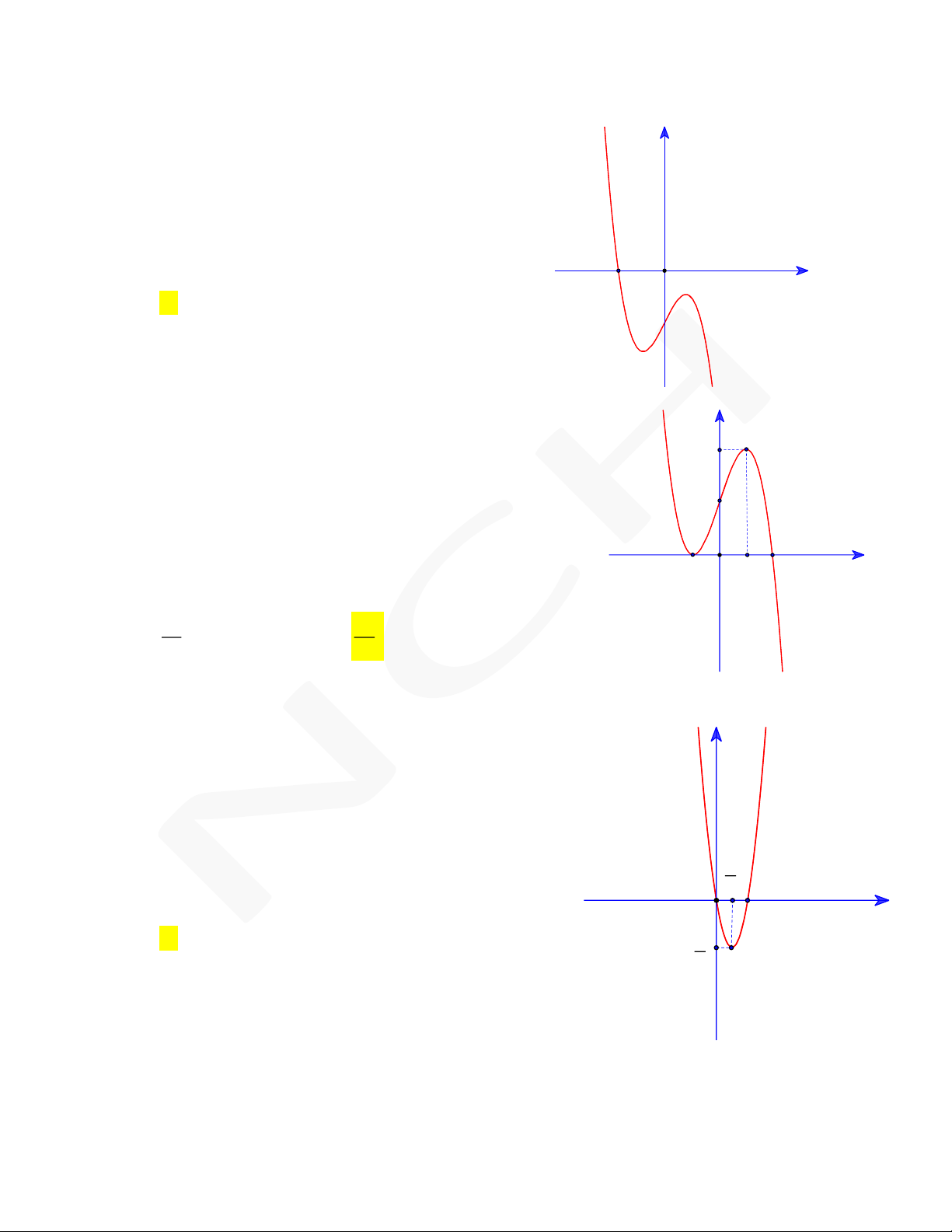
vẽ bên. Biết hàm số y f x đạt cực tiểu tại x  2
 và 2 cực trị đều âm, hỏi đồ thị hàm số CO f(x) = x3 + x2 2 x
cắt trục hoành tại nhiều nhất bao nhiêu điểm? 1  1 -2 A. 0. B. 1. C. 2. D. 4.
Câu 8. Cho hàm số y f x có đồ thị hàm số y
y f x như hình vẽ. Biết f a  0 , hỏi đồ thị
hàm số y f x cắt trục hoành tại nhiều nhất O f(x) = x3 + 1∙x2 3∙x 1 bao nhiêu điểm? a c b x A. 1. B. 2. C. 3. D. 4. Nguyễn Chiến 0973.514.674
Câu 9. Cho hàm số y f x 4 2
ax bx ca  0 y
có đồ thị C , đồ thị hàm số y f x như hình
vẽ bên. Biết đồ thị hàm số y f x đạt cực tiểu  3 8 3  tại điểm  ;   
. Đồ thị hàm số y f x tiếp 3 9 f(  x) = 4∙x3 4∙x
xúc với trục Ox tại 2 điểm. Diện tích S của hình -1 O 1 x
phẳng giới hạn bởi đồ thị C và trục hoành là 7 8 A. . B. . 15 15 14 16 C. . D. . 15 15 
Câu 10. Cho hàm số y  x  ax b f cx dd
a,b,c,d  ;   
0  có đồ thị C , đồ thị hàm số  c
y f x như hình vẽ bên. Biết đồ thị hàm số
y f x cắt trục tung tại điểm có tung độ bằng 3.
Phương trình tiếp tuyến của C tại giao điểm của
C với trục hoành có dạng 1 3 1 3 A. y
x  . B. y x  . 2 2 2 2 1 3 1
C. y   x  . D. y   x  2. 2 2 2 Nguyễn Chiến 0973.514.674
BÀI TẬP RÈN LUYỆN
Câu 1. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị
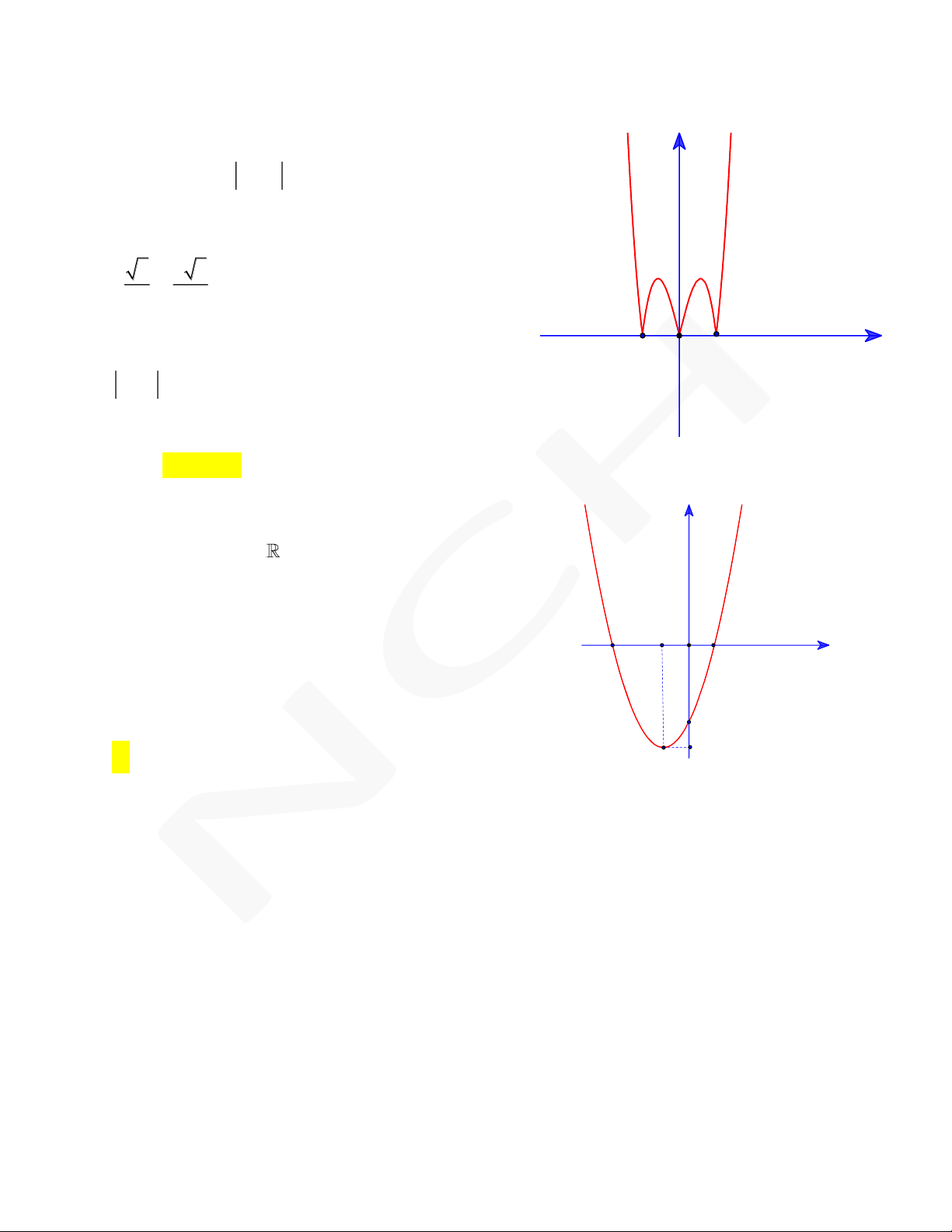
hàm số y f x cho bởi hình vẽ bên. O
Đồ thị hàm số có thể là đồ thị nào trong các x hình vẽ sau A. B. y y O O x x C. D. y y O O x x Nguyễn Chiến 0973.514.674
Câu 2. Cho hàm số y f x có đồ thị hàm số y
y f x như hình vẽ. Biết f a  0 , hỏi đồ thị
hàm số y f x cắt trục hoành tại nhiều nhất a bao nhiêu điểm? O x A. 0. B. 1. C. 2. D. 4.
Câu 3. Cho hàm số y f x 4 2
y ax bx cx d y
có đồ thị C , đồ thị hàm số y f x như hình vẽ 4 2
bên. Biết đồ thị hàm số y f x cắt trục tung tại
điểm có tung độ bằng 1 . Giá trị a b c d là O 2 -1 1 x A. 4. B. 7. 13 17 C. . D. . 4 4
Câu 4. Cho hàm số y f x 3 2
y ax bx cx d y
có đồ thị C , đồ thị hàm số y f x như hình vẽ
bên. Biết đồ thị hàm số y f x có điểm cực đại
nằm trên trục tung có tung độ bằng 2 . Giá trị 1 2
a b c d là O 1 x A. 1. B. 2.  3  2 C. 2. D. 3. Nguyễn Chiến 0973.514.674 Câu 5. Cho hàm số 4 2
y ax bx ca  0 có đồ y
thị hàm số y f x như hình vẽ. Biết đồ thị
hàm số y f x đạt cực tiểu tại điểm  3 8 3   ;   
. Đồ thị hàm số y f x đạt cực đại 3 9    f(x) = 4∙x3 4∙x
tại điểm có tung độ bằng 3  . Phương trình -1 O 1 x
f x  m có 4 nghiệm phân biệt khi giá trị m là A. 4   m  3
 . B. 0  m  4.
C. 0  m  3. D. 3  m  4.
Câu 6. Cho hàm số f x có đạo hàm f 'x xác y định, liên tục trên
và f 'x có đồ thị như
hình vẽ bên. Khẳng định nào sau đây là đúng? -1
A. Hàm số đồng biến trên  1  ; . -3 1 O x
B. Hàm số chỉ nghịch biến trên  3  ;   1 . -3
C. Hàm số đồng biến trên ; 3   và 1;. -4
D. Hàm số chỉ đồng biến trên 1; . Nguyễn Chiến 0973.514.674
Câu 7. Cho hàm số y f x 4 2 
ax bx c y
a  0 có đồ thị C, đồ thị hàm số y fx
như hình vẽ bên. Biết đường thẳng y  2 tiếp
xúc với đồ thị hàm số y f x tại điểm cực 1
đại. Giá trị a b c là O x A. 1.  B. 0. C. 1. D. 2. -6
Câu 8. Cho hàm số y  x  ax b f cx dd
a,b,c,d  ;   
0  có đồ thị C , đồ thị hàm  c
số y f x như hình vẽ bên. Biết đồ thị hàm số
y f x cắt trục hoành tại điểm có hoành độ bằng 2
 . Giá trị a b c d là A. 1.  B. 3. C. 5. D. 6. Nguyễn Chiến 0973.514.674
CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ HÀM SỐ y f x
Câu 1. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị C
tiếp xúc với đường thẳng y  9  tại điểm có hoành O 1
độ âm và đồ thị hàm số y f x cho bởi hgì(xn ) h = x2 v 2ẽ∙ x 3 -1 3 x
bên. Phần nguyên của giá trị diện tích hình phẳng
giới hạn bởi đồ thị C và trục hoành là 4  A. 2. B. 27. C. 29. D. 35. Lời giải:
Ta có f x 2
 3ax  2bx c . Dựa vào đồ thị hàm số y f x ta thấy đồ thị hàm số  1 a
3a  2b c  0  3  
y f x đi qua 3 điểm  1  ;0,3;0,1; 4
  ta có hệ: 27a  6b c  0  b  1  
3a  2b c  4 c  3      1 f x 2
x  2x  3  f x  f xdx   2
x  2x  3 3 2
dx x x  3x    C 3
Do C tiếp xúc với đường thẳng y  9
 tại điểm có hoành độ x nên 0 f x  x  1  2 0
 0  x  2x  3  0   . o
D x  0  x  3 . 0 0 0 o 0 x  3  0 1 3 2 1 Suy ra f 3  9
  3 3  3.3C  9
  C  0  C 3 2
: y x x  3x 3 3 Nguyễn Chiến 0973.514.674 1
Xét phương trình hoành độ giao điểm của C và trục hoành: 3 2
x x  3x  0 3 x  0 33 5 1  2  1 3 2 
3  3 5 . Diện tích hình phẳng cần tìm là S
x x  3x  29,25  dx x  3 2,3   2 3 3 5 2
Chọn đáp án C.
Câu 2. [Sở giáo dục Hà Nội]: Cho hàm số y
y f x 3 2
ax bx cx d,a,b,c ,a  0 có đồ
thị C . Biết rằng đồ thị C tiếp xúc với đường
thẳng y  4 tại điểm có hoành độ âm và đồ thị
hàm số y f x cho bởi hình vẽ dưới đây: O
Tính diện tích S của hình phẳng giới hạn bởi đồ -1 1 x
thị C và trục hoành. 27 -3 A. S  . 9 B. S  . 4 21 5 C. S  . D. S  . 4 4 Lời giải:
Ta có f x 2
 3ax  2bx c . Đồ thị hàm y f x là hàm chẵn đối xứng qua trục tung  f 0  3   c  3   nên f   1  f   1  b  0 . Mà  f x x f        2  3  3
1  0  3a c  0  a   1
f x  f xdx   2 x   3 3
3 dx x  3x   
C .Do C tiếp xúc với đường thẳng y  4 tại
điểm có hoành độ x nên f x  0  3x  3  0  x  1
 . Do x  0  x  1  . 0  2 0 0 0 o 0 Suy ra f  
1  4  C  2  C 3
: y x  3x  2 x  2 
Xét phương trình hoành độ giao điểm của C và trục hoành: 3
x  3x  2  0   . x   1 1 27
Diện tích hình phẳng cần tìm là: 3 S
x  3x  2dx  
Chọn đáp án B.  4 2 Nguyễn Chiến 0973.514.674
Câu 3. Cho hàm số y f x 3 2 
ax bx cx d y 5
a,b,c ,a  0 có đồ thị C. Biết rằng đồ
thị C đi qua gốc tọa độ và đồ thị hàm số
y f x cho bởi hình vẽ bên. Giá trị của 2
f 3  f   1 là O g(x) = 3∙x2 + 2 A. 24. B. 26. -1 1 x C. 28. D. 30. Lời giải:
Ta có f x 2
 3ax  2bx c . Đồ thị hàm y f x là hàm chẵn đối xứng qua trục tung  f 0  3   c   2 nên f   1  f   1  b  0 . Mà  f x x f        2  3  2
1  5  3a c  5  a   1
f x  f xdx   2 x   3 3
2 dx x  2x   
C , đồ thị C đi qua gốc tọa độ nên C  0  f x 3
x  2x f 3 f  
1  30  Chọn đáp án D.
Câu 4. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị
C đi qua gốc tọa độ và đồ thị hàm số y fx 2
cho bởi hình vẽ bên. Phần nguyên giá trị diện tích O
hình phẳng giới hạn bởi đồ thị C và trục hoành 6 6 x  3 3 là A. 6. B. 4. C. 3. D. 2. Nguyễn Chiến 0973.514.674 Lời giải:
Ta có f x 2
 3ax  2bx c . Đồ thị hàm y f x là hàm chẵn  b  0.
f 0  2  c  2  Mà     f x 2  3  x  2 6 f   
  0  2a c  0  a  1   3    
f x  f xdx   2  x   3 3
2 dx  x  2x    C .
Do đồ thị C đi qua gốc tọa độ nên C  0  C 3
: y  x  2x x  0
Xét phương trình hoành độ giao điểm của C và trục hoành: 3
x  2x  0   . x    2 2
Diện tích hình phẳng cần tìm là: 3 S x  2xdx  6 
Chọn đáp án A.  2
Câu 5. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị
hàm số y f x cho bởi hình vẽ bên. Hàm số C f(x) = 3∙x2 + 2∙x 1
có thể là hàm số nào trong các hàm số sau: O A. 3 2
y  x  2x x  2. x B. 3
y x  2x 1. C. 3 2
y  x  2x x  2. D. 3 2
y  x x x  2. Lời giải:
Ta có f x 2
 3ax  2bx c . Dựa vào đồ thị hàm số y f x ta thấy a  0
Mà f 0  0  c  0 , đồ thị hàm số y f x nằm hoàn toàn phía dưới trục Ox nên Nguyễn Chiến 0973.514.674
hàm số y f x nghịch biến trên .  hàm số y f x không có cực trị 2 2
b  3ac  0  b  3ac Chọn đáp án D.
Câu 6. Cho hàm số y f x 3 2 
ax bx cx d y  4
a,b,c  ,a  0 có đồ thị C . Biết rằng đồ thị  13
C  tiếp xúc với đường thẳng y  tại điểm có 3 -2 2
hoành độ dương và đồ thị hàm số O
y ff( x)x = x2 ch + 4 o x
bởi hình vẽ bên. Giá trị 3a  2b c d là A. 0. B. 2. C. 3. D. 4. Lời giải:
Ta có f x 2
 3ax  2bx c . Đồ thị hàm y f x là hàm chẵn  b  0.
f 0  4  c  4  Mà   f x 2 x f        4 1
2  0  12a c  0  a    3
f x  f xdx   2 x  4 1 3
dx   x  4x    C . 3 13
Do C tiếp xúc với đường thẳng y
tại điểm có hoành độ x nên 3 0 f x  2
 0  x  4  0  x  2
 . Do x  0  x  2 . 0 0 0 o 0 1 Suy ra f   13 2   C  1   C 3
: y   x  4x  1  3a  2b c d  4 3 3
Chọn đáp án D. Nguyễn Chiến 0973.514.674 Câu 7. Cho hàm số 4 3 2
y ax bx cx dx e a  0 y
có đồ thị C . Đồ thị hàm số y f  x  như hình
vẽ bên. Biết hàm số y f x đạt cực tiểu tại x  2
 và 2 cực trị đều âm, hỏi đồ thị hàm số CO f(x) = x3 + x2 2 x
cắt trục hoành tại nhiều nhất bao nhiêu điểm? 1  1 A. 0. B. 1. -2 C. 2. D. 4. Lời giải:
Do hàm số y f x đạt cực tiểu tại x  2  y
và 2 cực trị đều âm nên từ đồ thị hàm số
y f  x  ta có thể suy ra đồ thị hàm số
y f x có dạng như hình bên O f(x) = x3 + x2 2 x 1 -2
Từ đồ thị của hàm số y f x ta có bảng biến thiên: x  1  f x  0    f xy  0 f   1 Nguyễn Chiến 0973.514.674
đồ thị hàm số y f x cắt Ox tại nhiều y
nhất 2 điểm  Chọn đáp án C.
Có thể minh họa rõ hơn bằng hình vẽ O 1 1 f(x) = ∙x4 + ∙x3 2∙x 2 4 3 x 1 -2
Câu 8. Cho hàm số y f x có đồ thị hàm số y
y f x như hình vẽ. Biết f a  0 , hỏi đồ thị
hàm số y f x cắt trục hoành tại nhiều nhất O f(x) = x3 + 1∙x2 3∙x 1 bao nhiêu điểm? a c b x A. 1. B. 2. C. 3. D. 4. Lời giải:
Từ đồ thị của hàm số ta có bảng biến thiên: x
 a b c  f x  0  0  0   f xf bf ay  0 f c
Để đồ thị hàm số y f x cắt trục hoành tại số điểm là nhiều nhất thì f c  0
 đồ thị hàm số y f x cắt Ox tại nhiều nhất 2 điểm Chọn đáp án B. y
Có thể minh họa rõ hơn bằng hình vẽ O a c b x Nguyễn Chiến 0973.514.674
Câu 9. Cho hàm số y f x 4 2
ax bx ca  0 y
có đồ thị C , đồ thị hàm số y f x như hình
vẽ bên. Biết đồ thị hàm số y f x đạt cực tiểu  3 8 3  tại điểm  ;   
. Đồ thị hàm số y f x tiếp 3 9 f(  x) = 4∙x3 4∙x
xúc với trục Ox tại 2 điểm. Diện tích S của hình -1 O 1 x
phẳng giới hạn bởi đồ thị C và trục hoành là 7 8 A. . B. . 15 15 14 16 C. . D. . 15 15 Lời giải: y
Từ đồ thị hàm số y f x với a  0 ta dễ dàng có được đồ
thị hàm số y f x như hình bên.
Ta có f x 3
 4ax  2bx. Đồ thị hàm y f x qua 1;0và  f(x) = 4∙x3 4∙x 3 8 3   ;    nên ta có hệ : 3 9    -1 O 1 xf 1  0
4a  2b  0     3 3  8 3    3  3 8 3 f        4a   2b   3  9       3 3 9    a  1    f x 3  4x  4 3 4
f x f x dx
x x dx x x  
x . Ta có:      4 4  2 C . b 2  
Do C tiếp xúc với đường thẳng Ox tại điểm có hoành độ x nên 0 f x  x  0 3 0
 0  4x  4x  0  
. Đồ thị hàm số y f x tiếp xúc với trục Ox tại 2 0 0 0 x  1   0
điểm nên 2 điểm đó có hoành độ là 1  . Suy ra f  
1  0  C  1  C 4 2
: y x  2x  1 Nguyễn Chiến 0973.514.674 x  1 
Xét phương trình hoành độ giao điểm của C và trục hoành: 4 2
x  2x  1  0   . x   1 1 16
Diện tích hình phẳng cần tìm là: 4 2 S
x  2x  1dx  
Chọn đáp án D.  15 1 
Câu 10. Cho hàm số y  x  ax b f cx dd
a,b,c,d  ;   
0  có đồ thị C , đồ thị hàm số  c
y f x như hình vẽ bên. Biết đồ thị hàm số
y f x cắt trục tung tại điểm có tung độ bằng 3.
Phương trình tiếp tuyến của C tại giao điểm của
C với trục hoành có dạng 1 3 1 3 A. y
x  . B. y x  . 2 2 2 2 1 3 1
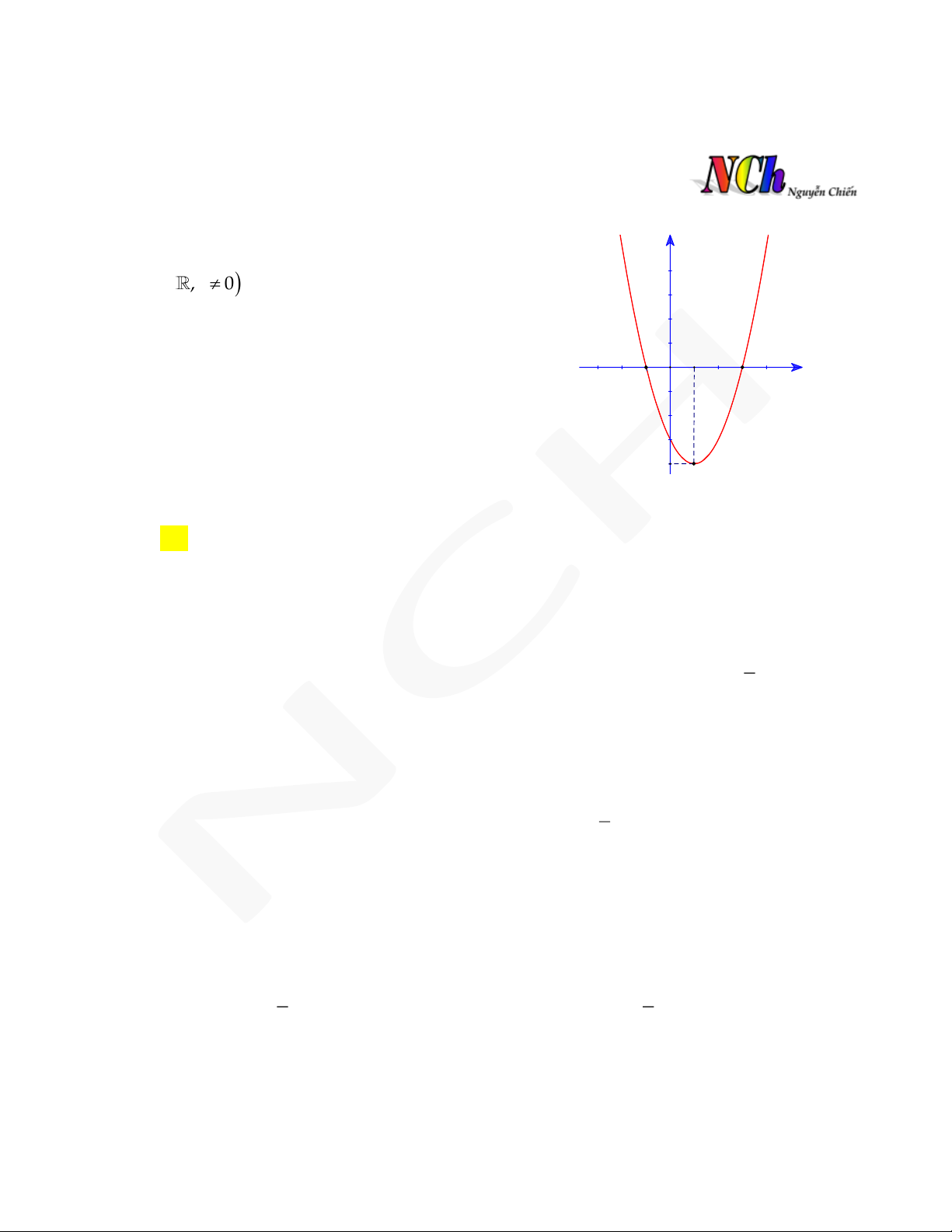
C. y   x  . D. y   x  2. 2 2 2 ad bc
Ta có f x  y f   . Từ đồ thị hàm số x ta thấy : cx d2 d
+ đồ thị y f x có tiệm cận đứng x  1    1  c  d 1 c ad bc
+ đồ thị y f x qua điểm 2; 2 
 2  ad bc  2 2c d 2 2  2 2cd 
+ đồ thị y f x cắt trục tung tại y  2 2
ad bc  2  ad bc  2d 3 2 d b
Mà đồ thị y f x cắt trục tung tại điểm có tung độ bằng 3   3  b  3d 4 d Nguyễn Chiến 0973.514.674 c  da  1  
ad bc  22c d2 b  3  x
Từ 1 , 2 , 3 , 4 ta có hệ   
y f x 3  2 c  ad bc  1 2dx  1  d  1 b 3   d   2 1
Đồ thị C giao với Ox tại 3; 0 . f x   f  3  2   x  2 1 1 1 3
Phương trình tiếp tuyến của C tại điểm 3; 0 là : y  x  3  y x  2 2 2
Chọn đáp án A. Nguyễn Chiến 0973.514.674
BÀI TẬP RÈN LUYỆN
Câu 1. Cho hàm số y f x 3 2 
ax bx cx d y
a,b,c ,a  0 có đồ thị C. Biết rằng đồ thị
hàm số y f x cho bởi hình vẽ bên. O
Đồ thị hàm số có thể là đồ thị nào trong các x hình vẽ sau A. B. y y O O x x C. D. y y O O x x Nguyễn Chiến 0973.514.674
Câu 2. Cho hàm số y f x có đồ thị hàm số y
y f x như hình vẽ. Biết f a  0 , hỏi đồ thị
hàm số y f x cắt trục hoành tại nhiều nhất a bao nhiêu điểm? O x A. 0. B. 1. C. 2. D. 4.
Câu 3. Cho hàm số y f x 4 2
y ax bx cx d y
có đồ thị C , đồ thị hàm số y f x như hình vẽ 4 2
bên. Biết đồ thị hàm số y f x cắt trục tung tại
điểm có tung độ bằng 1 . Giá trị a b c d là O 2 -1 1 x A. 4. B. 7. 13 17 C. . D. . 4 4
Câu 4. Cho hàm số y f x 3 2
y ax bx cx d y
có đồ thị C , đồ thị hàm số y f x như hình vẽ
bên. Biết đồ thị hàm số y f x có điểm cực đại
nằm trên trục tung có tung độ bằng 2 . Giá trị 1 2
a b c d là O 1 x A. 1. B. 2.  3  2 C. 2. D. 3. Nguyễn Chiến 0973.514.674 Câu 5. Cho hàm số 4 2
y ax bx ca  0 có đồ y
thị hàm số y f x như hình vẽ. Biết đồ thị
hàm số y f x đạt cực tiểu tại điểm  3 8 3   ;   
. Đồ thị hàm số y f x đạt cực đại 3 9    f(x) = 4∙x3 4∙x
tại điểm có tung độ bằng 3  . Phương trình -1 O 1 x
f x  m có 4 nghiệm phân biệt khi giá trị m là A. 4   m  3
 . B. 0  m  4.
C. 0  m  3. D. 3  m  4.
Câu 6. Cho hàm số f x có đạo hàm f 'x xác y định, liên tục trên
và f 'x có đồ thị như
hình vẽ bên. Khẳng định nào sau đây là đúng? -1
A. Hàm số đồng biến trên  1  ; . -3 1 O x
B. Hàm số chỉ nghịch biến trên  3  ;   1 . -3
C. Hàm số đồng biến trên ; 3   và 1;. -4
D. Hàm số chỉ đồng biến trên 1; . Nguyễn Chiến 0973.514.674
Câu 7. Cho hàm số y f x 4 2 
ax bx c y
a  0 có đồ thị C, đồ thị hàm số y fx
như hình vẽ bên. Biết đường thẳng y  2 tiếp
xúc với đồ thị hàm số y f x tại điểm cực 1
đại. Giá trị a b c là O x A. 1.  B. 0. C. 1. D. 2. -6
Câu 8. Cho hàm số y  x  ax b f cx dd
a,b,c,d  ;   
0  có đồ thị C , đồ thị hàm  c
số y f x như hình vẽ bên. Biết đồ thị hàm số
y f x cắt trục hoành tại điểm có hoành độ bằng 2
 . Giá trị a b c d là A. 1.  B. 3. C. 5. D. 6. Nguyễn Chiến 0973.514.674