


































Preview text:
THPT Marie Curie Chuyeân ñeà: 1 GIẢI TÍCH VẤN ĐỀ 1.
TÍNH CHẤT ĐƠN ĐIỆU CỦA HÀM SỐ 1/ Định nghĩa
Cho hàm số y f x xác định trên khoảng (đoạn hoặc nửa khoảng) K và với mọi x , x K. 1 2
Nếu x x f x f x thì hàm số y f x gọi là đồng biến trên K . 1 2 1 2
Nếu x x f x f x thì hàm số y f x gọi là nghịch biến trên K . 1 2 1 2 2/ Định lý
Cho hàm số y f x có đạo hàm trên K . Nếu f (
x) 0,x K và f '(x) 0 chỉ tại một số hữu hạn điểm thì hàm số y f x đồng biến trên K . Nếu f (
x) 0,x K và f '(x) 0 chỉ tại một số hữu hạn điểm thì hàm số y f x nghịch biến trên K . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
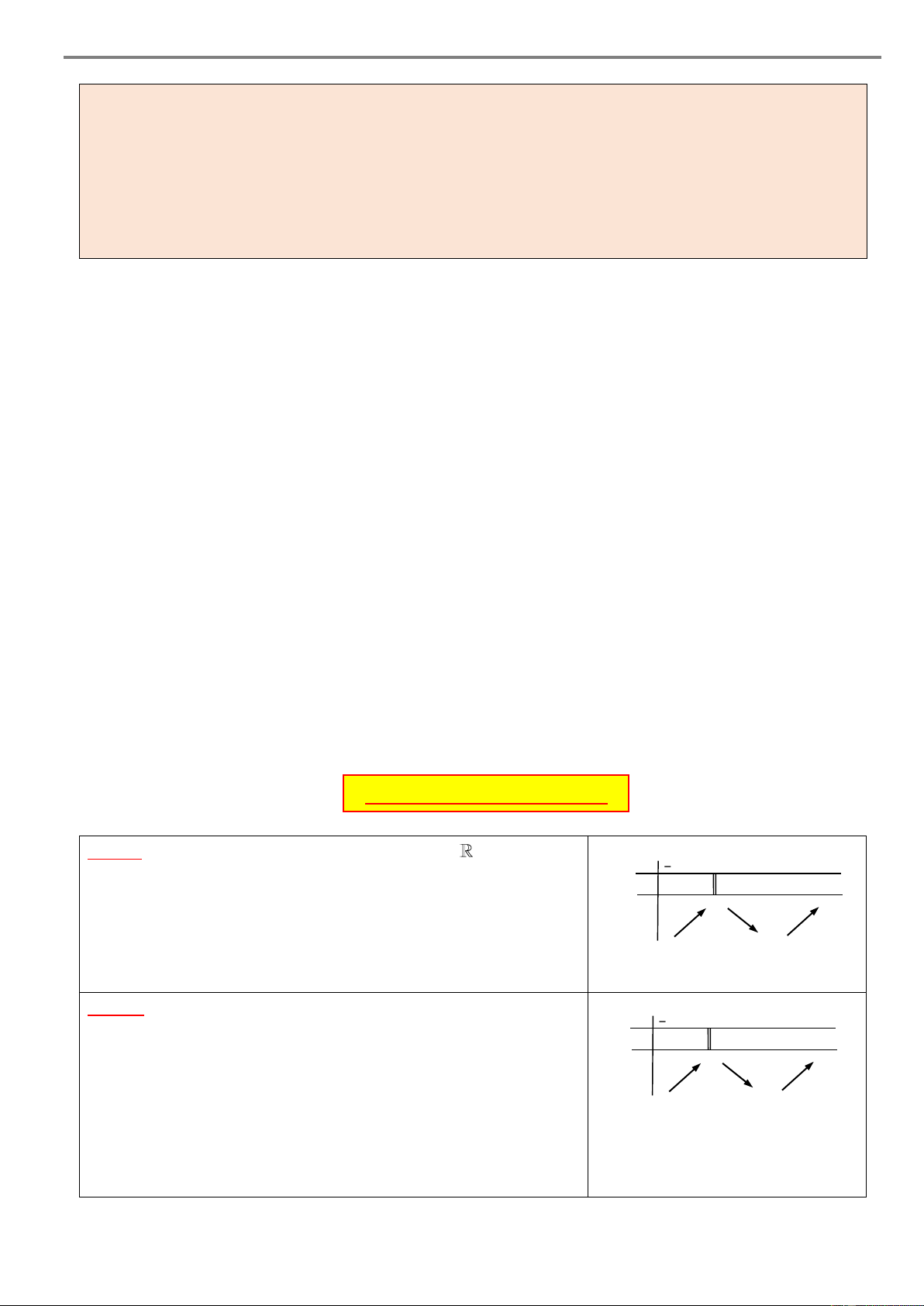
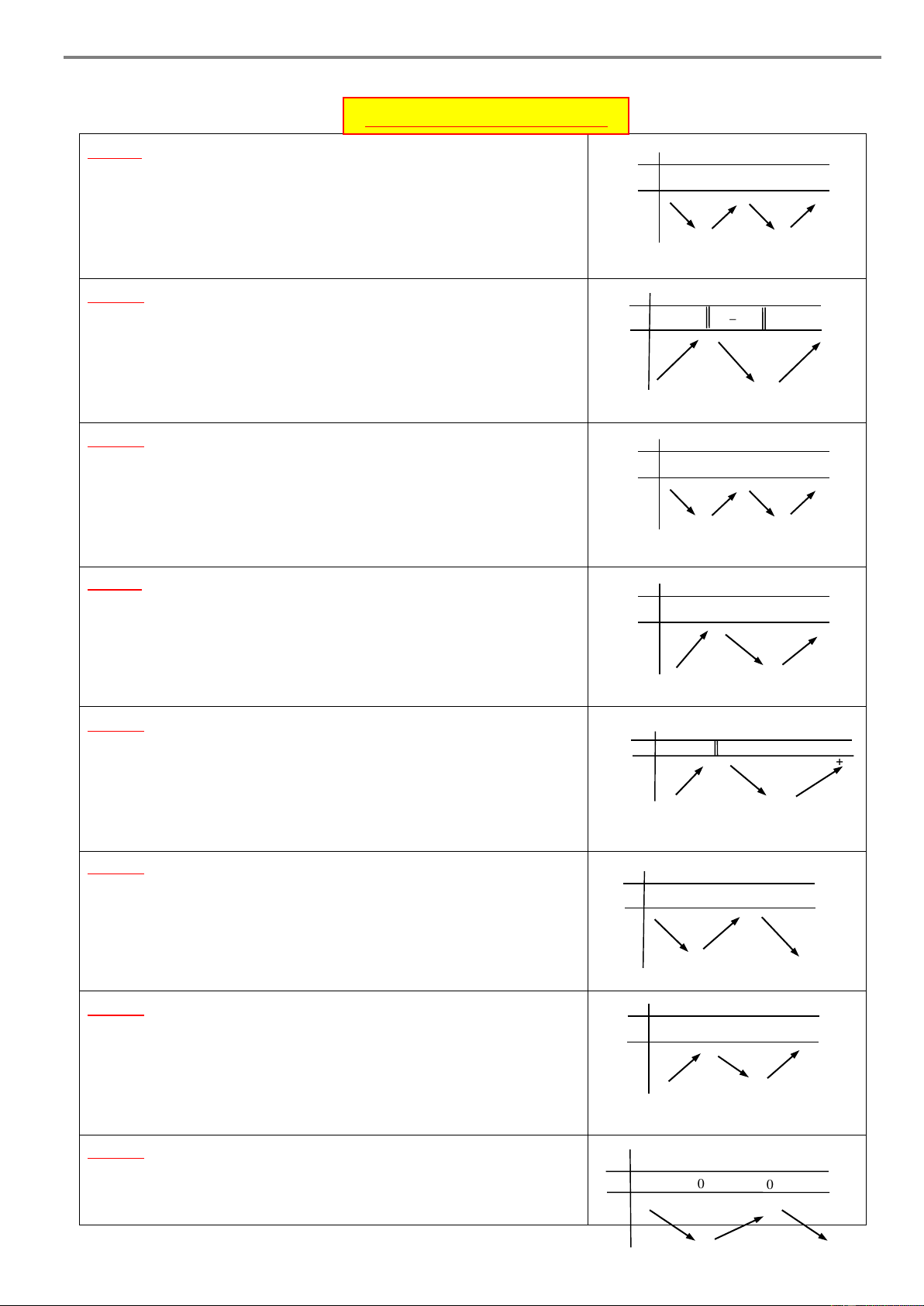
DẠNG 1. DỰA VÀO BẢNG BIẾN THIÊN A. PHƯƠNG PHÁP
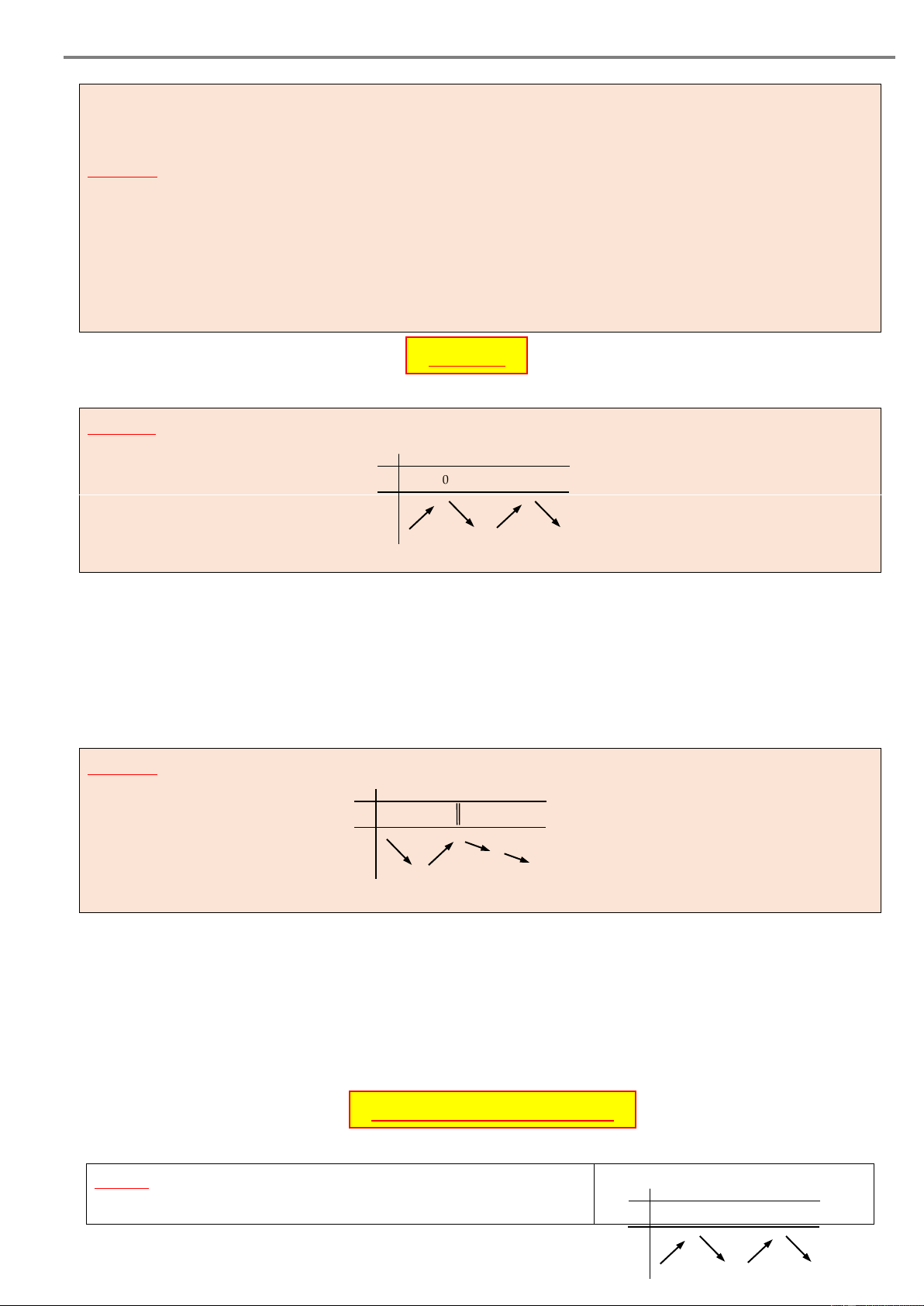
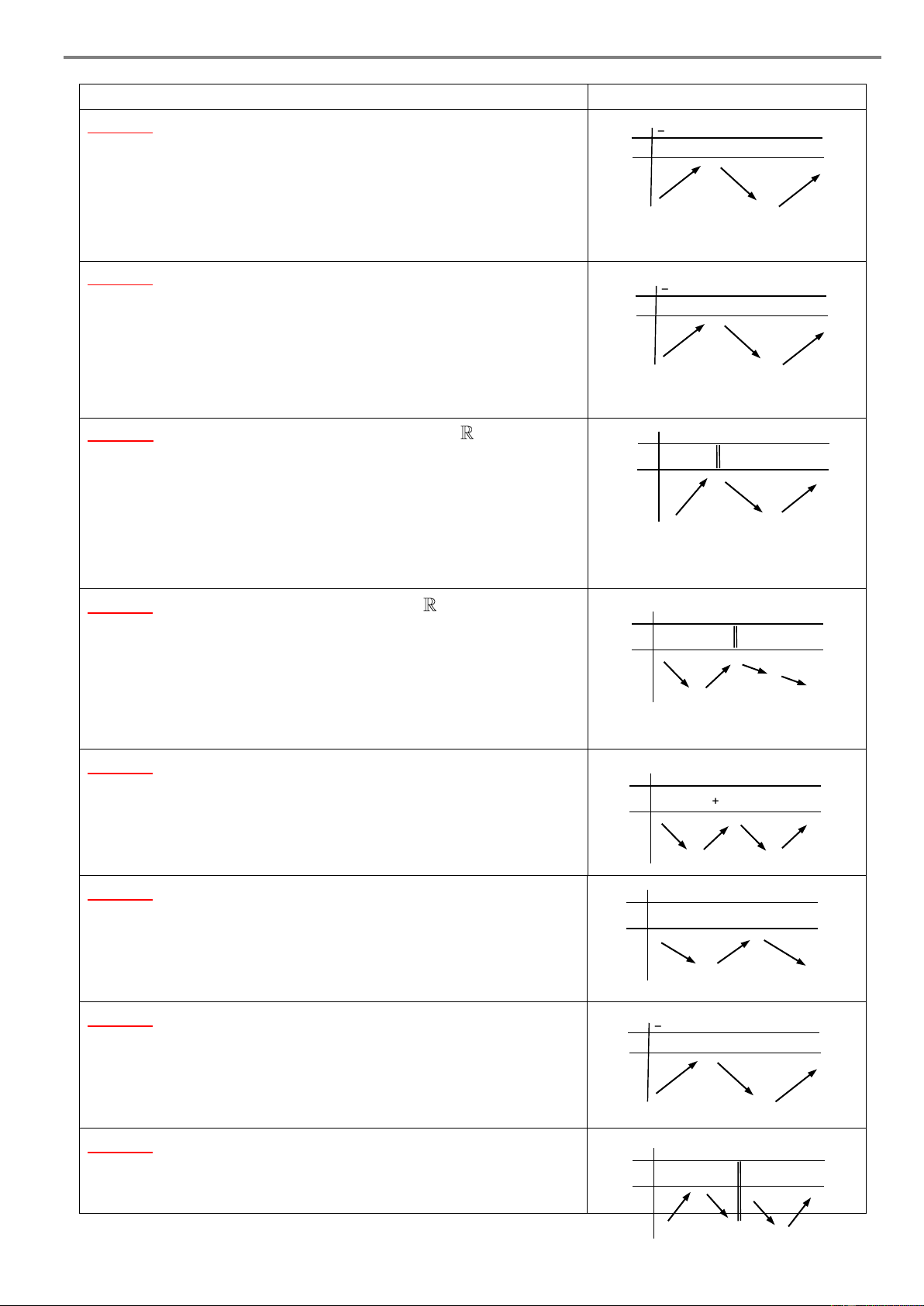
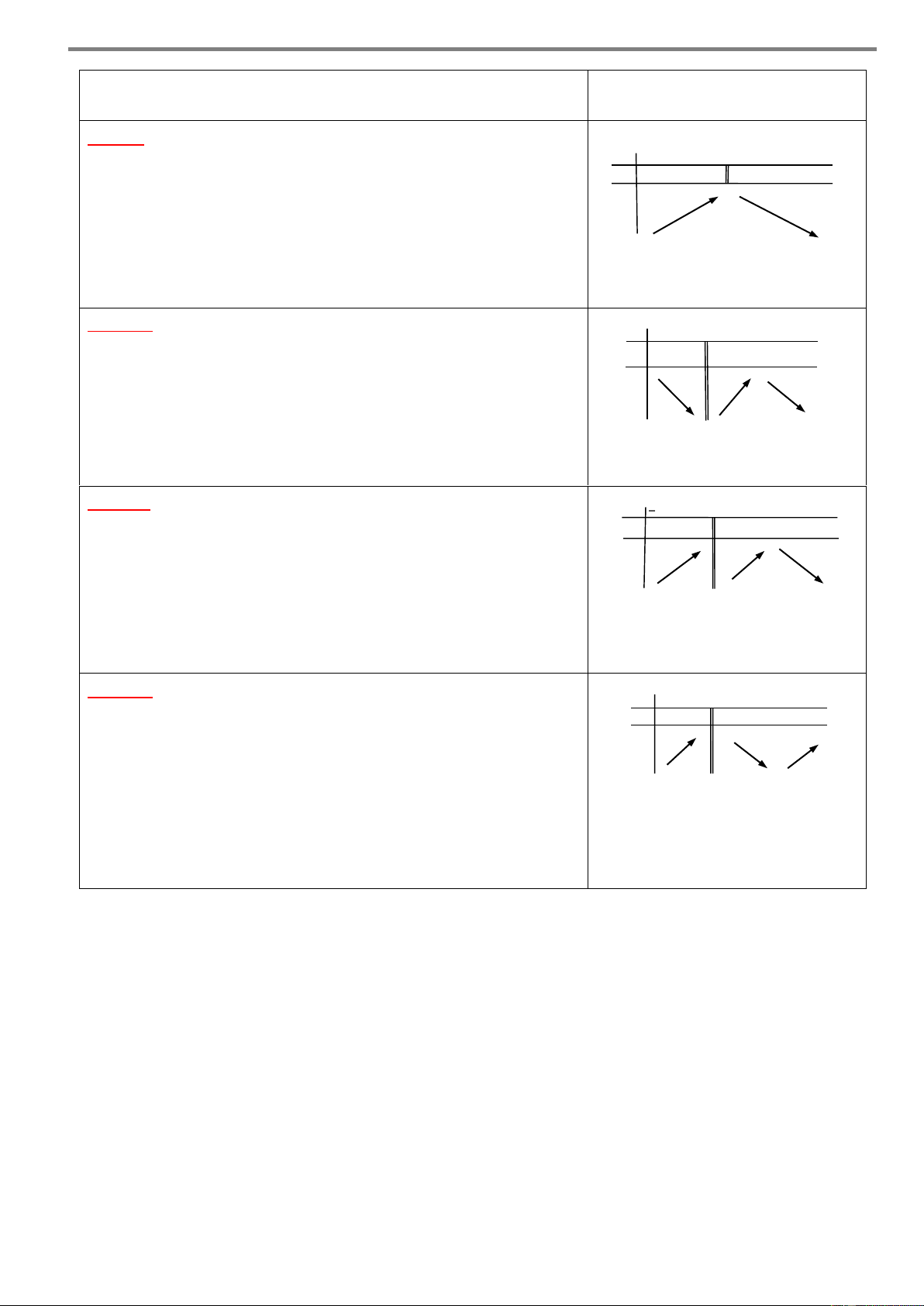
Cho hàm số y f x có bảng biến thiên như sau x – a b c d e f + 1 y’ 1 + 0 – – 0 + 0 – 0 + + r m + y q n – p – Khi đó: – 1
Tài liệu học tập Toán 12
Hàm số y f x đồng biến trên các khoảng ;
a, c;d và ; d f .
Hàm số y f x nghịch biến trên các khoảng ;
a c và d, f . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
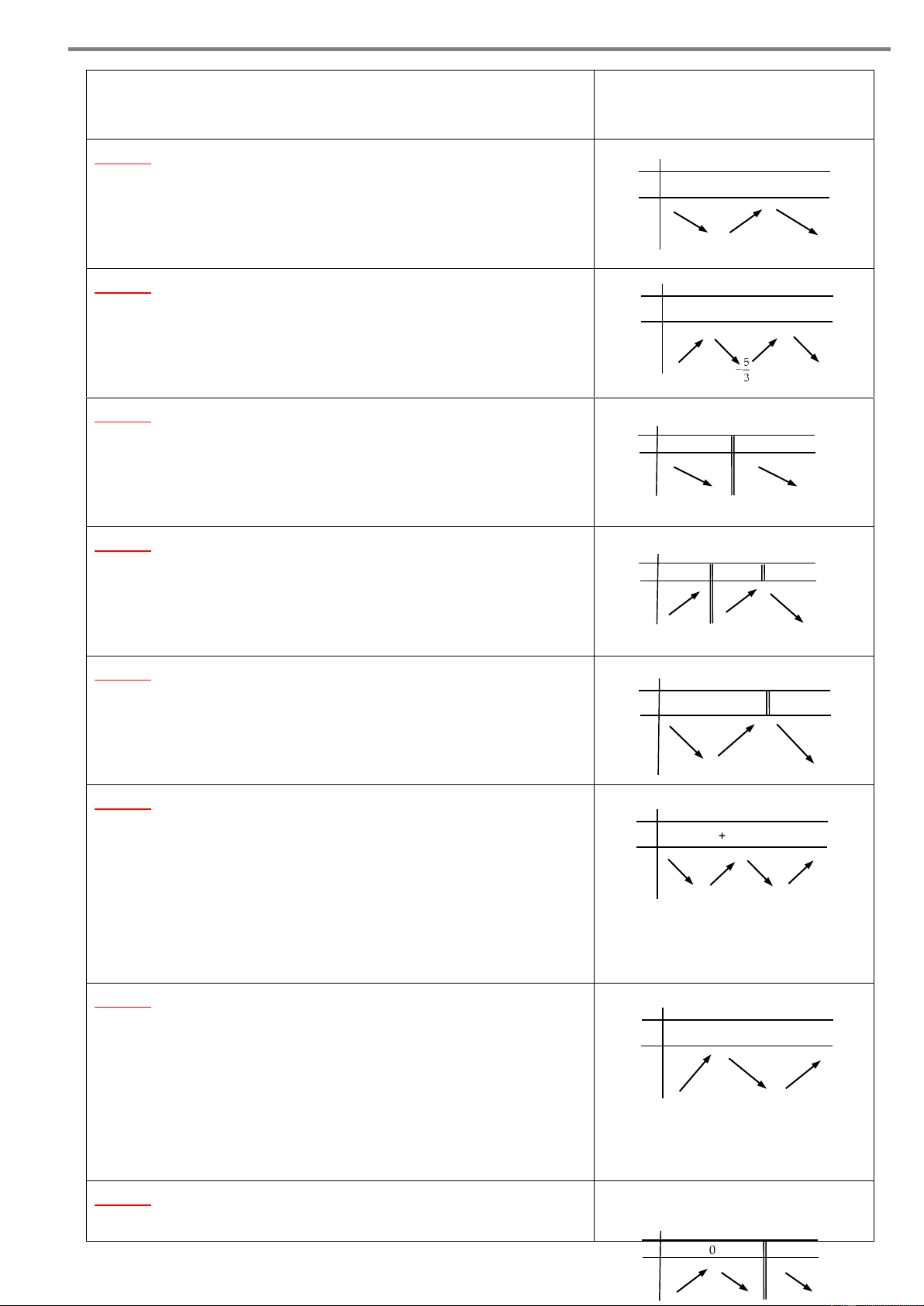
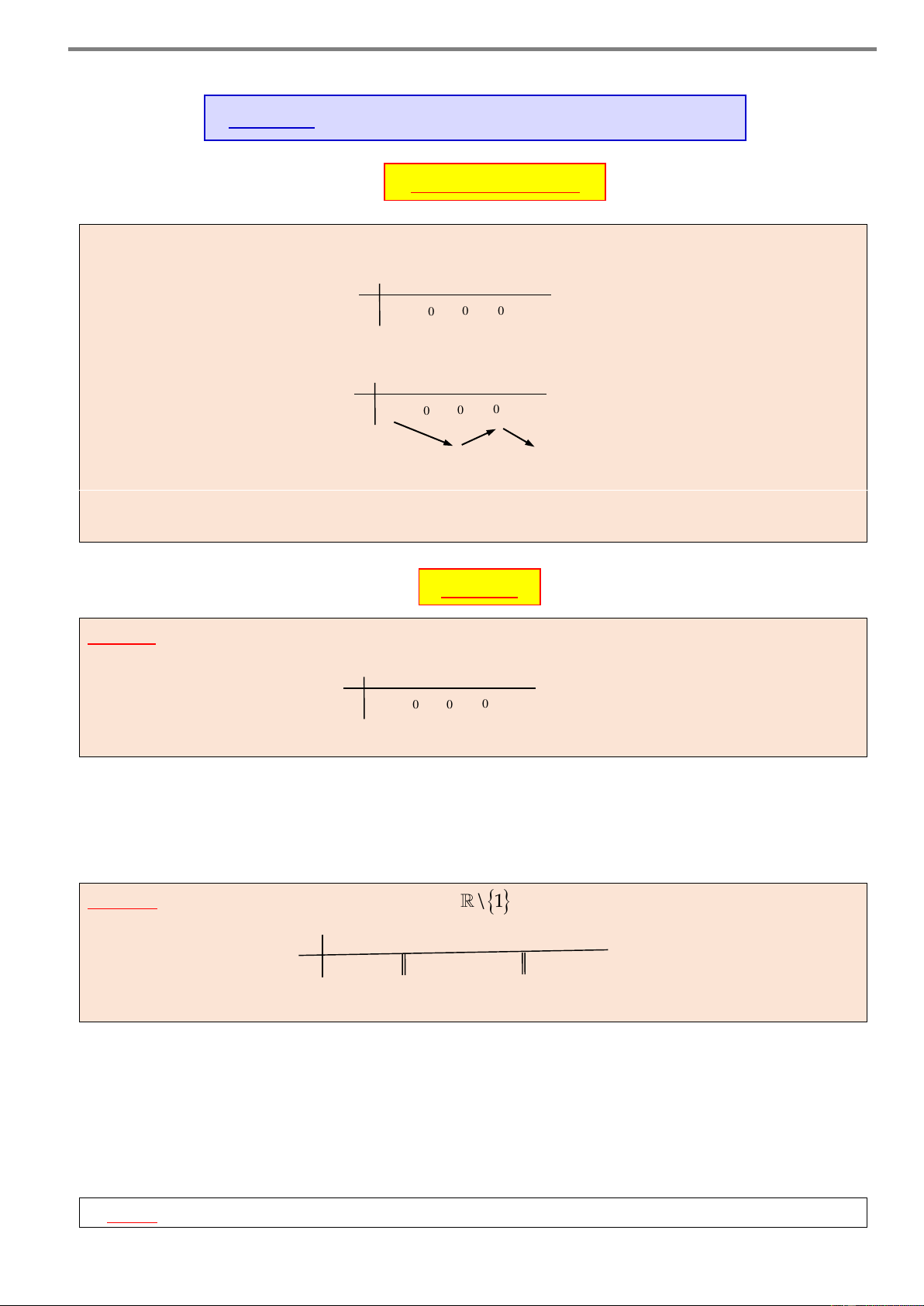
Ví dụ 1. Cho hàm số y f x có bảng biến thiên như sau x – –4 1 2 + y’ 1 + 0 – 0 + 0 – 5 3 y –1 – – 1
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
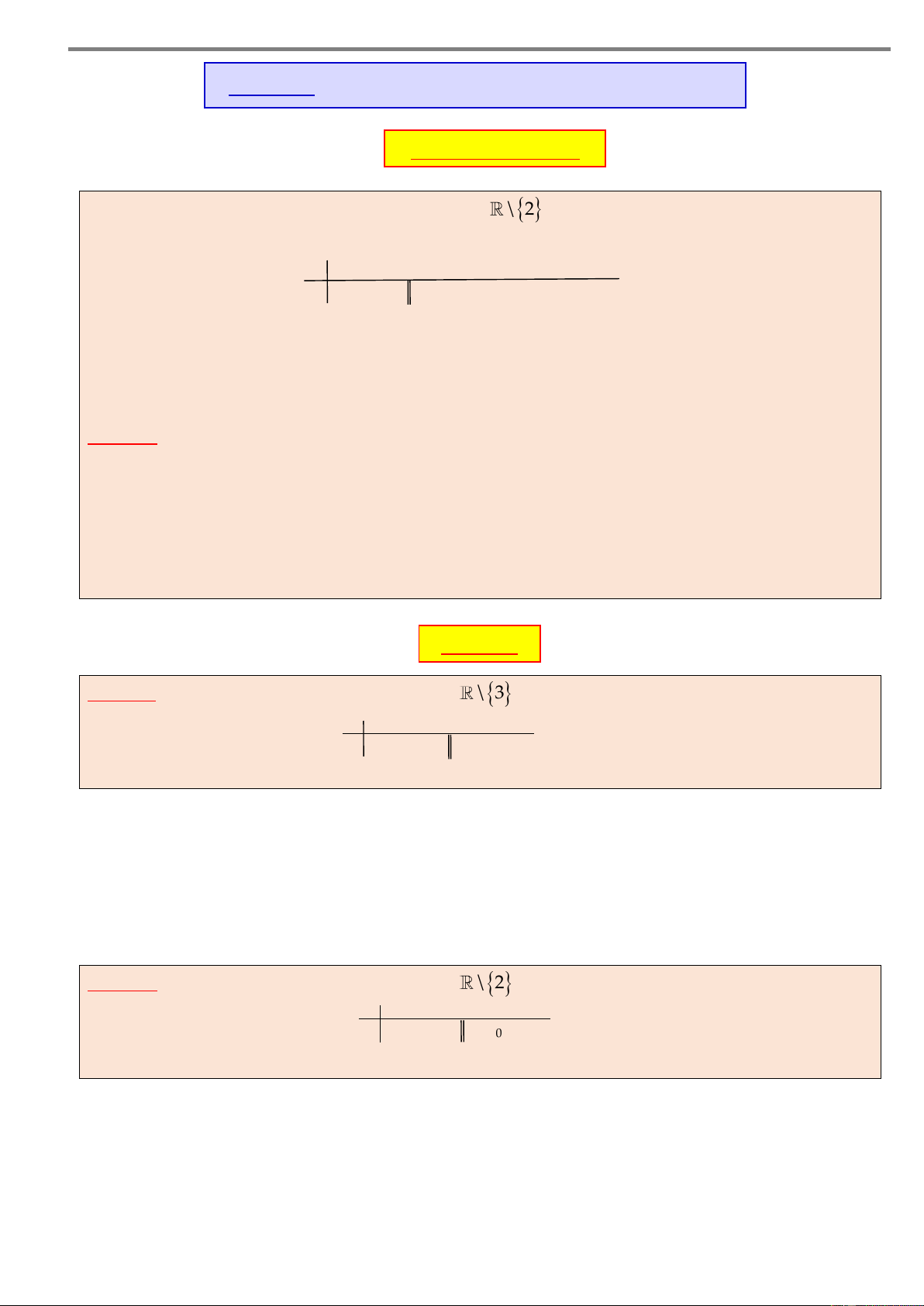
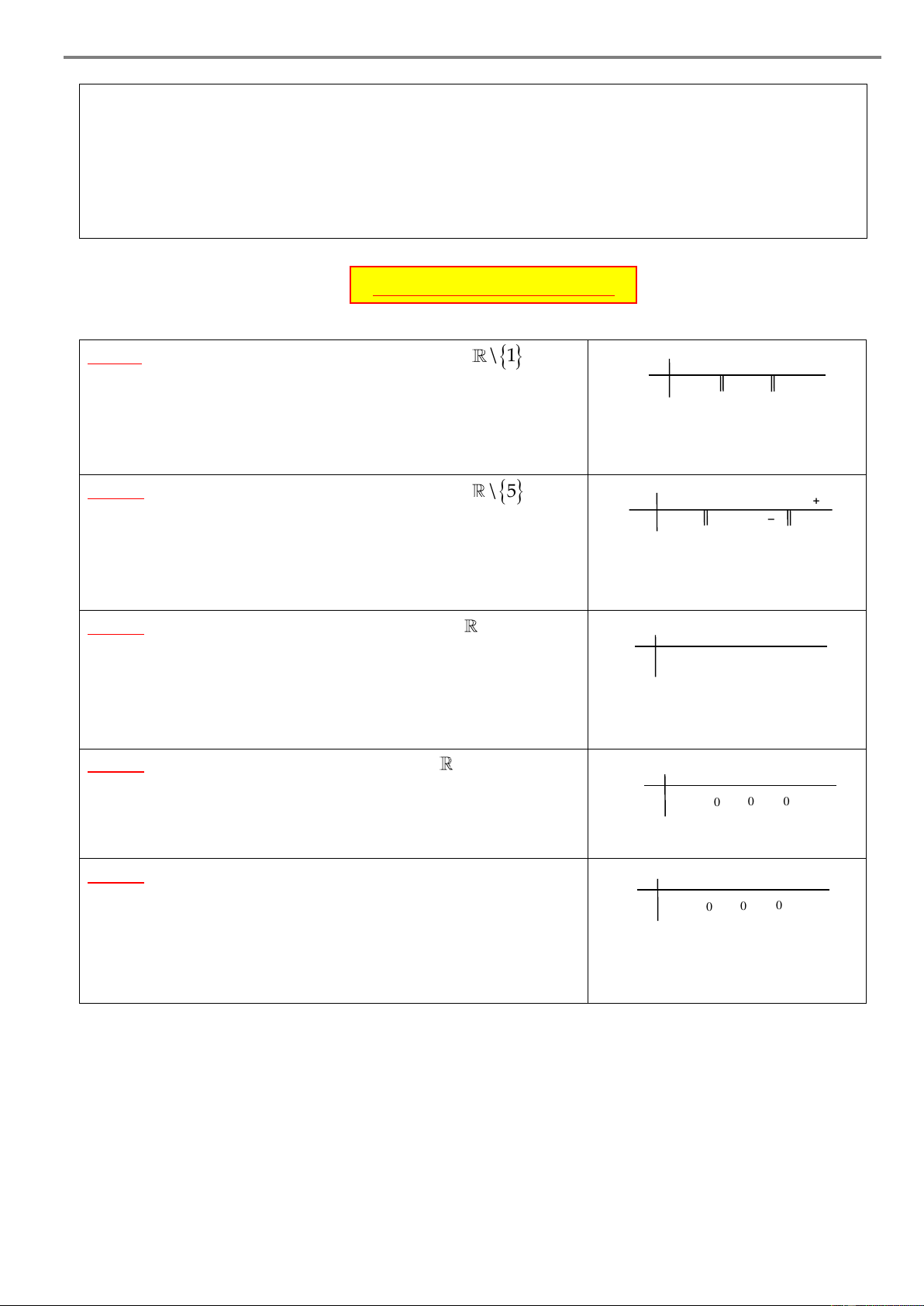
Ví dụ 2. Cho hàm số y f x có bảng biến thiên như sau x – –1 2 5 + 1 y’ – 0 + – 0 – + 3 y 1 –1 –
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
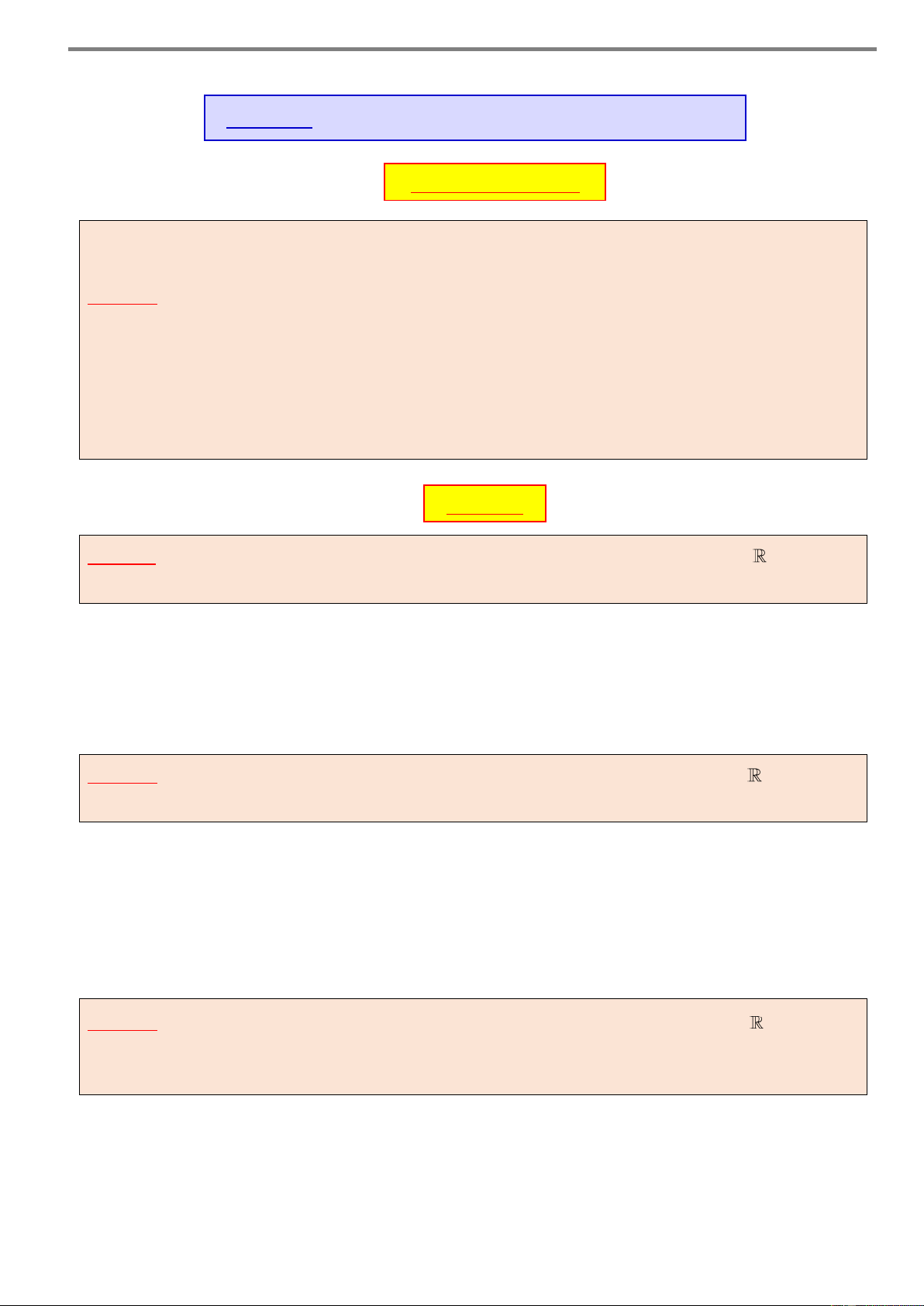
Câu 1. Cho hàm số y f x có bảng biến thiên như hình x – –2 0 2 +
bên. Hàm số đã cho nghịch biến trên khoảng y’ 1 + 0 – 0 + 0 – 3 3 y 2 –1 – – 1 THPT Marie Curie A. 2 ;0. B. ; 2 .
C. 0; 2 . D. 0; .
Câu 2. Cho hàm số y f x có bảng biến thiên như hình x – –4 6 +
bên. Hàm số đã cho đồng biến trên khoảng y’ 1 – 0 + 0 – + A. 2 ;7 . 7 B. 4 ;6. y 3 –2 – C. ; 6 . D. 6; .
Câu 3. Cho hàm số y f x có bảng biến thiên như hình x – –3 0 3 + 1
bên. Hàm số đã cho không đồng biến trên khoảng y’ + 0 – 0 + 0 – 0 0 A. ; 3 . B. 1; 2 . y – – C. 1; 4 . D. 0; 3 .
Câu 4. Cho hàm số y f x có bảng biến thiên như hình x – 1 +
bên. Hàm số đã cho nghịch biến trên khoảng y’ – – 2 +
A. ; 2. B. ; . y – 2 C. ; \ 1 . D. ;1 .
Câu 5. Cho hàm số y f x có bảng biến thiên như hình x – 1 2 +
bên. Hàm số đã cho đồng biến trên khoảng y’ + + – + 3
A. ; 2. B. ; 3 . y – –
C. 0; 2 . D. 1; . +
Câu 6. Cho hàm số y f x có bảng biến thiên như hình – x 0 3 +
bên. Hàm số đã cho nghịch biến trên khoảng y’ – 0 + – A. 1; 2 . 8 B. 2; 4 . 4 y C. ; 3 . D. 4; 6 . 1 2
Câu 7. Cho hàm số y f x có bảng biến thiên như hình x – –1 0 1 +
bên. Mệnh đề nào sau đây sai? y’ 1 – 0 + 0 – 0 +
A. Hàm số y f x đồng biến trên khoảng 2; 3 . + + 3 y
B. Hàm số y f x đồng biến trên khoảng 1 ;0 . 2 2
C. Hàm số y f x đồng biến trên khoảng 2 ;0.
D. Hàm số y f x đồng biến trên khoảng 6; .
Câu 8. Cho hàm số y f x có bảng biến thiên như hình x – –2 2 +
bên. Mệnh đề nào sau đây đúng? y’ 1 + 0 – 0 +
A. Hàm số y f x đồng biến trên khoảng 2; . + 3 y
B. Hàm số y f x nghịch biến trên khoảng 0; 1 . 0 –
C. Hàm số y f x đồng biến trên khoảng 0; .
D. Hàm số y f x nghịch biến trên khoảng 0; 3 .
Câu 9. Cho hàm số y f x có bảng biến thiên như hình
bên. Mệnh đề nào sau đây sai? x – 1 5 + y’ + 0 – – 3 + 3 y – – 4
Tài liệu học tập Toán 12
A. Hàm số y f x đồng biến trên khoảng ;1 .
B. Hàm số y f x nghịch biến trên khoảng 1; 2 .
C. Hàm số y f x đồng biến trên khoảng 2 ;0.
D. Hàm số y f x nghịch biến trên khoảng 4; 6 .
Câu 10. Cho hàm số y f x có bảng biến thiên như hình
x – –1 2 5 +
bên. Mệnh đề nào sau đây đúng? y’ 1 + 0 + + 0 –
A. Hàm số đã cho không đồng biến trên khoảng ; 2 . + 3 y 1 – –
B. Hàm số đã cho không nghịch biến trên khoảng 5; 6 . –2
C. Hàm số đã cho không đồng biến trên khoảng 1 ;5 .
D. Hàm số đã cho không nghịch biến trên 5; . 4 THPT Marie Curie
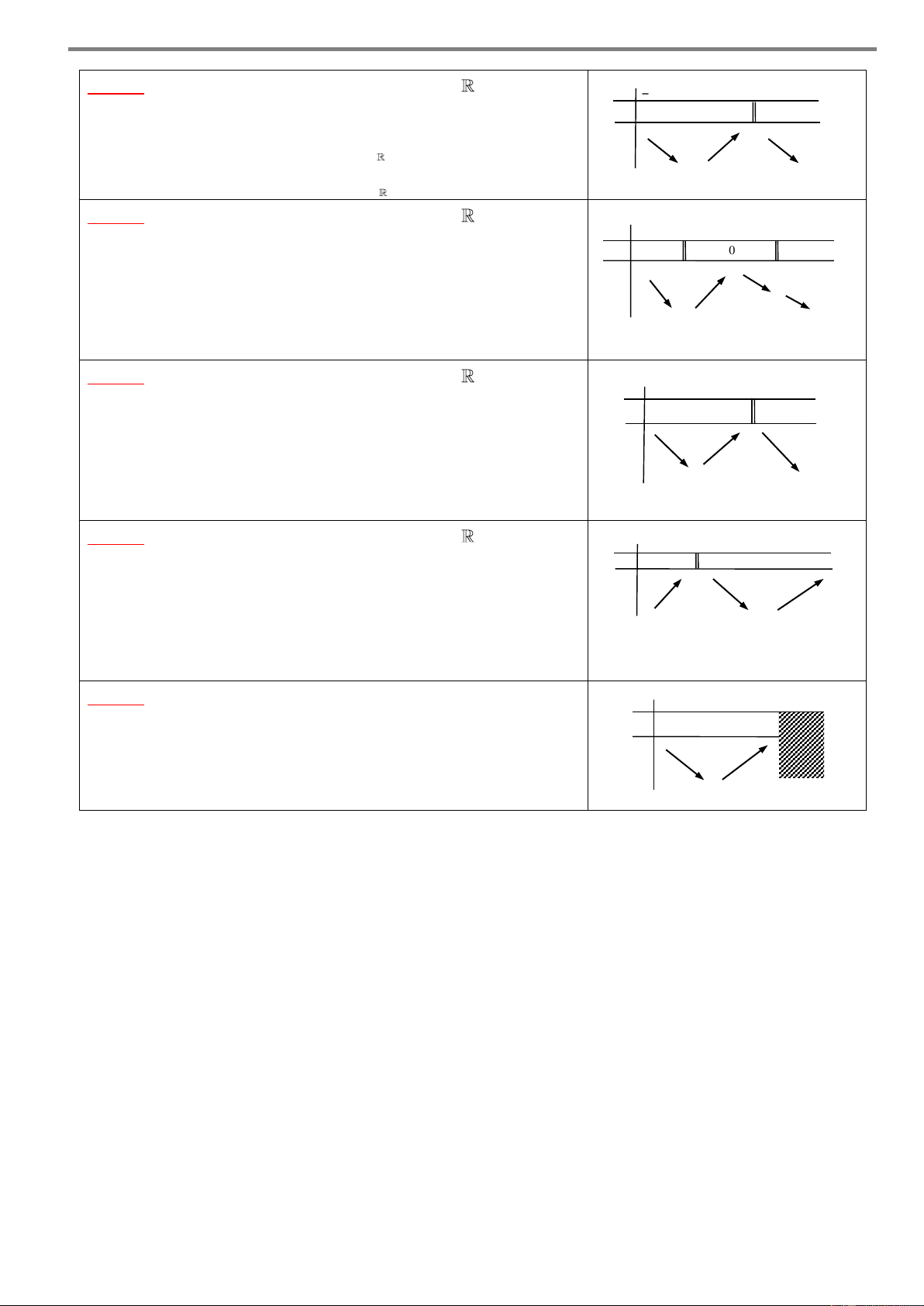
DẠNG 2. DỰA VÀO BẢNG XÉT DẤU ĐẠO HÀM A. PHƯƠNG PHÁP
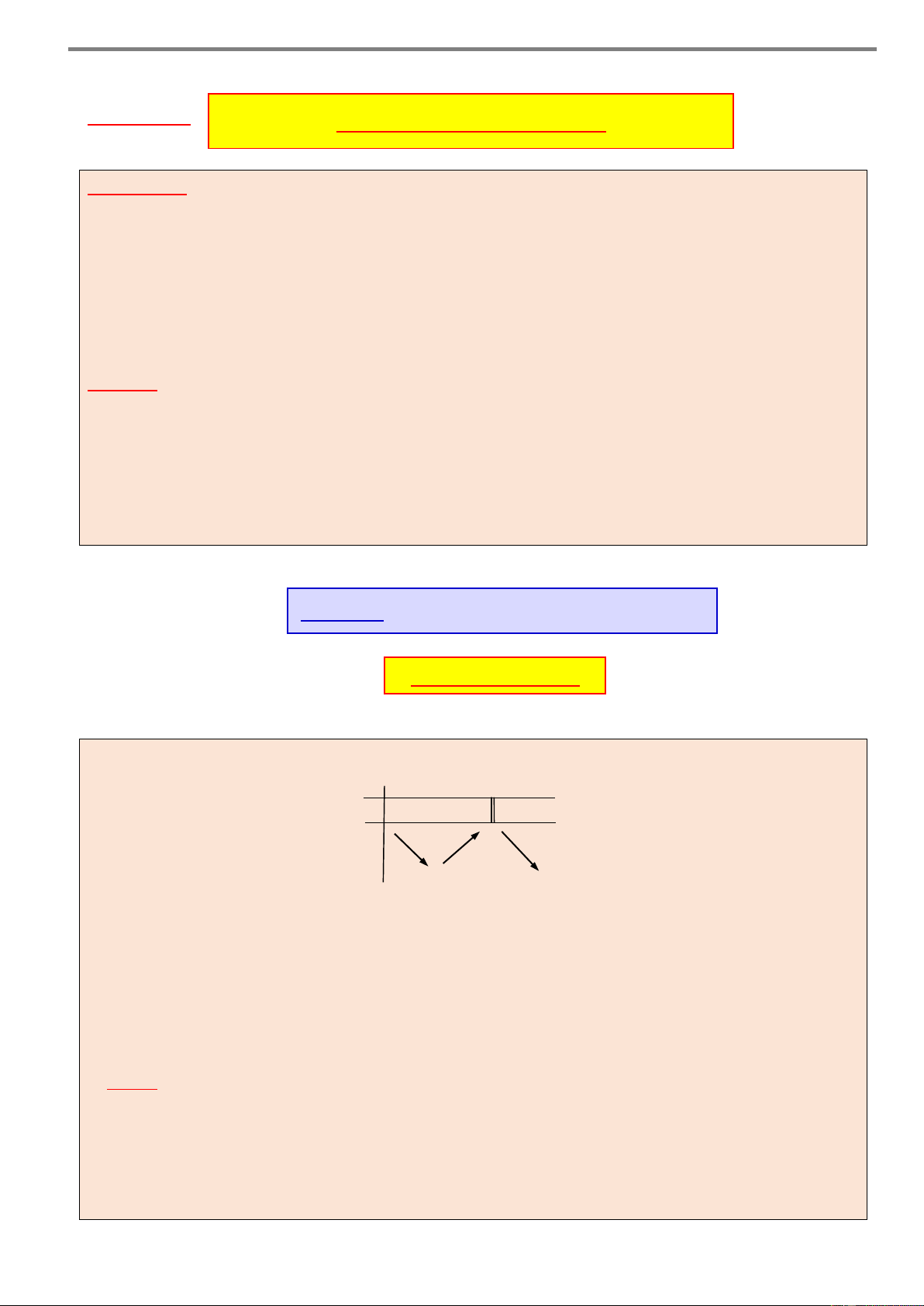
Cho hàm số y f x xác định và liên tục trên \
2 và có bảng xét dấu đạo hàm như hình sau x – 1 2 3 4 5 6 + y’ 1 + 0 – – 0 1
– 0 + 0 + 0 – Khi đó:
Hàm số y f x đồng biến trên các khoảng ;1 và 4; 6 .
Hàm số y f x nghịch biến trên các khoảng 1; 2 , 2,4 và 6; . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Cho hàm số y f x xác định trên \
3 và có bảng xét dấu đạo hàm như hình sau x – –2 3 5 + y’ 1 – 0 – – 0 +
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số y f x xác định trên \
2 và có bảng xét dấu đạo hàm như hình sau x – –1 2 3 + 1 y’ – + 0 + 0 +
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
C. CÂU HỎI TRẮC NGHIỆM
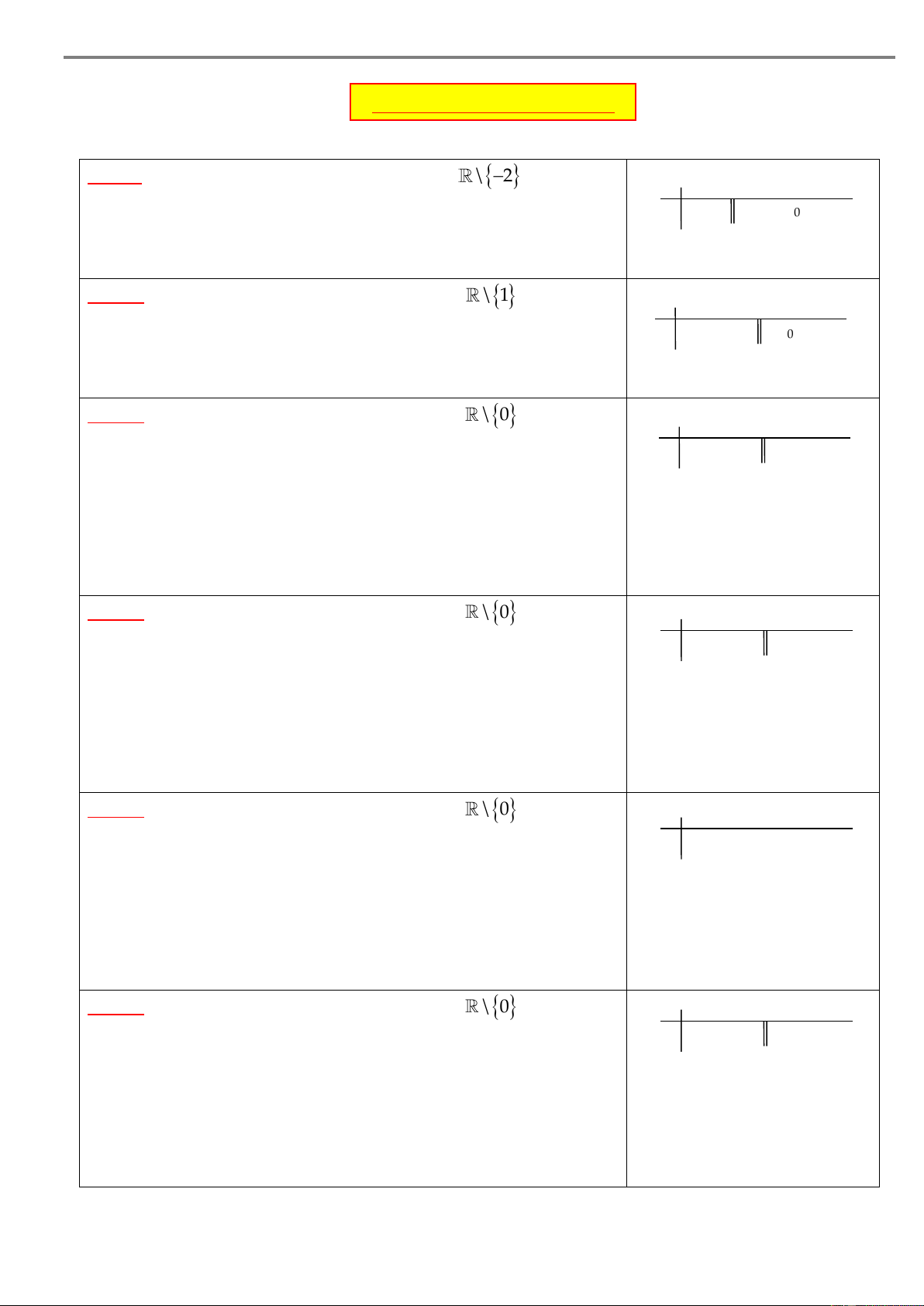
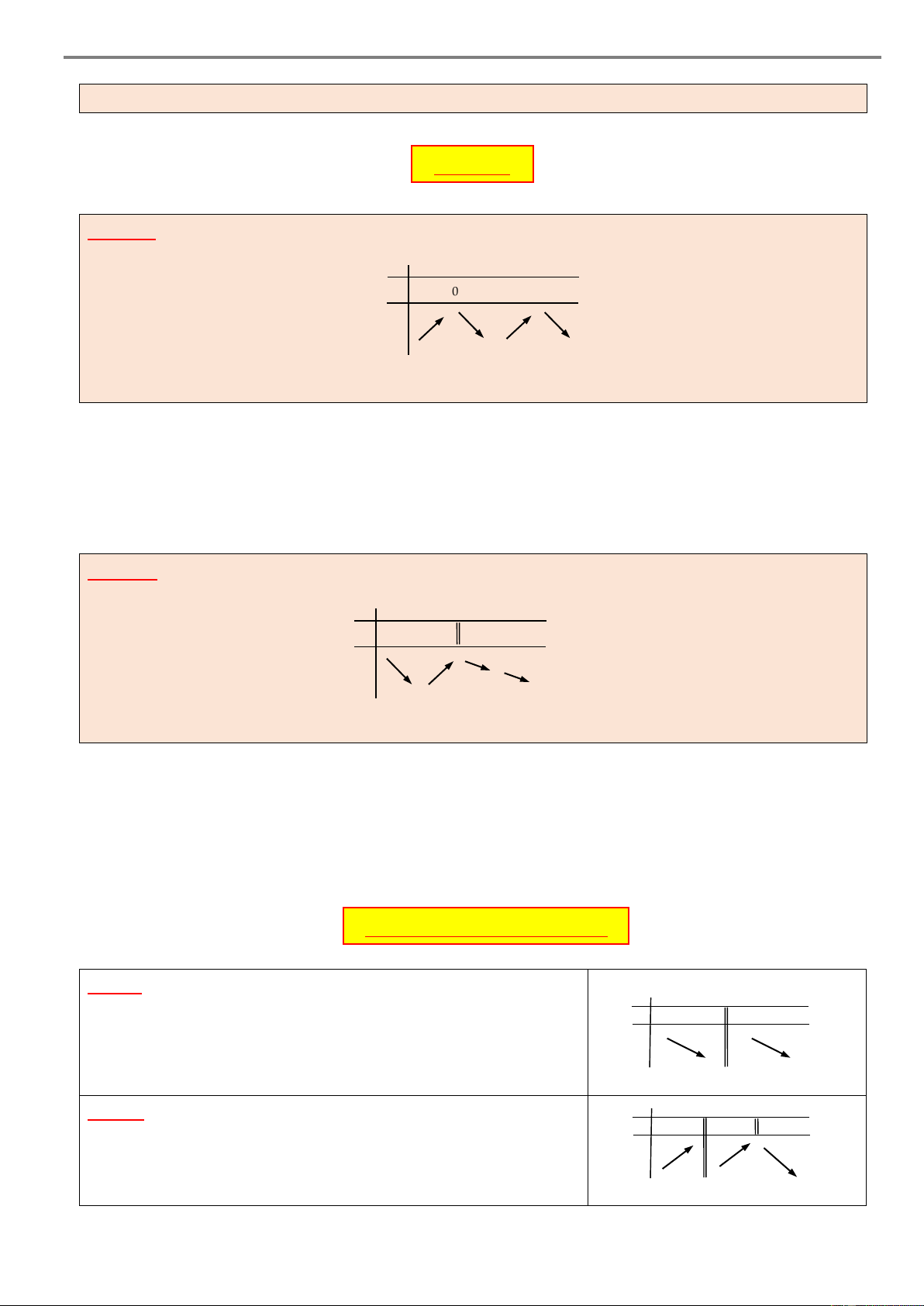
Câu 1. Cho hàm số y f x xác định trên \ 2 và có bảng x – –2 0 2 +
xét dấu đạo hàm như hình bên. Hàm số đã cho nghịch biến trên 1 y’ – – 0 + 0 – khoảng A. ; 2 .
B. ; 0 . C. 0; 2 . D. 0; .
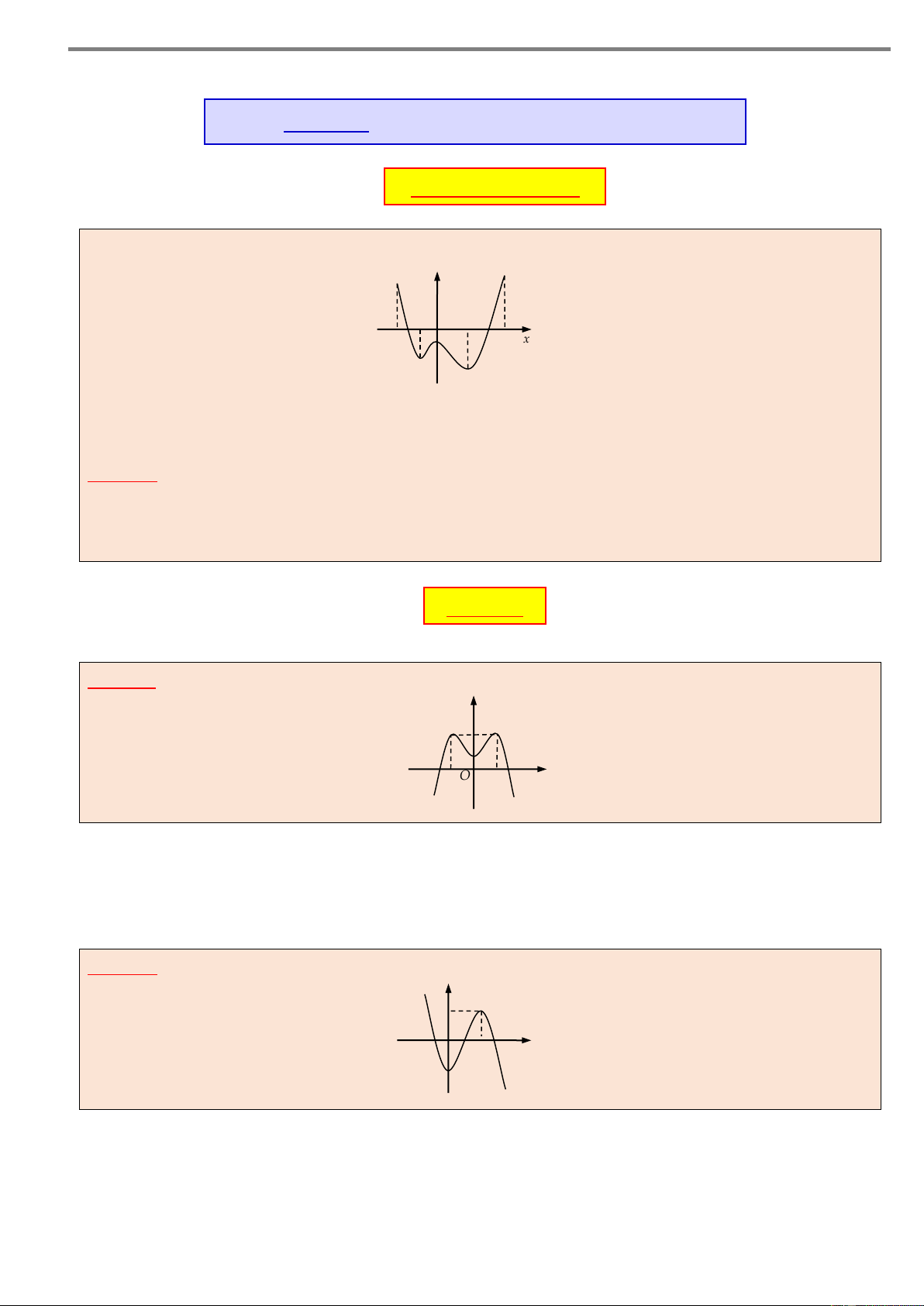
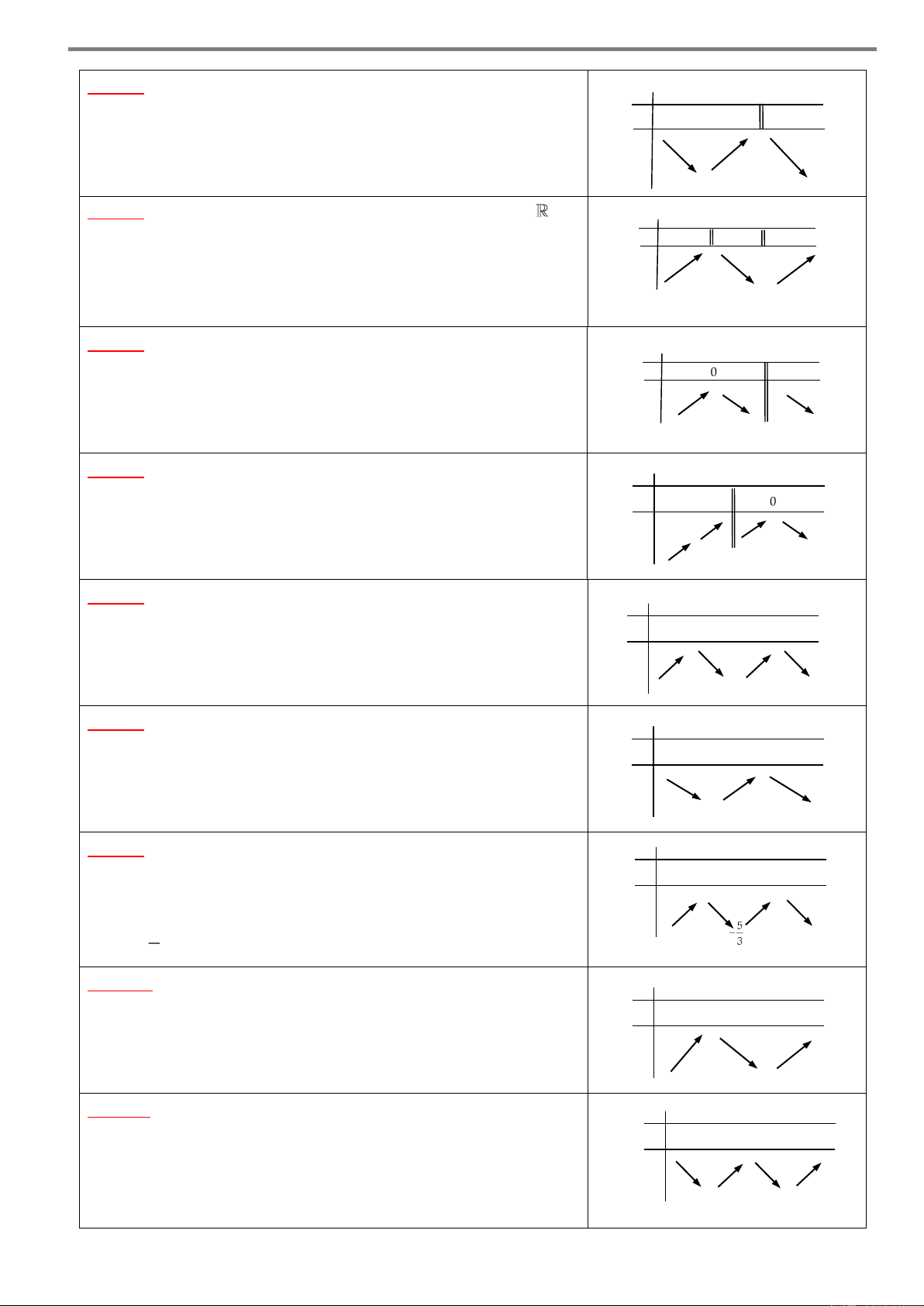
Câu 2. Cho hàm số y f x xác định trên \ 1 và có bảng x – –1 1 2 +
xét dấu đạo hàm như hình bên. Hàm số đã cho đồng biến trên 1 y’ – 0 + + 0 + khoảng A. ; 1 .
B. 1; . C. 1 ;2 . D. 1; .
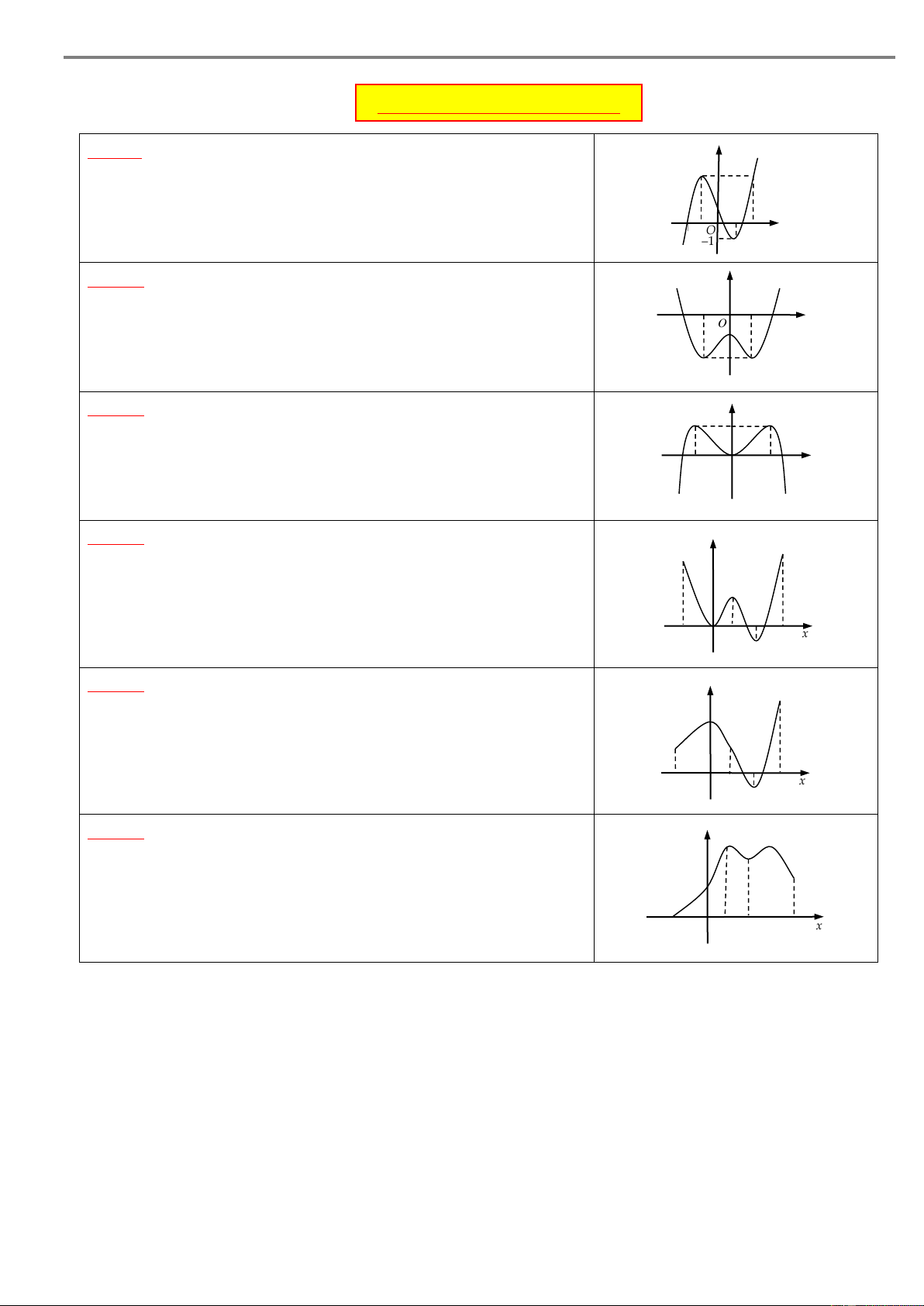
Câu 3. Cho hàm số y f x xác định trên \ 0 và có bảng x – –4 0 4 +
xét dấu đạo hàm như hình bên. Mệnh đề nào dưới đây sai? 1 y’ – 0 + + 0 +
A. Hàm số đồng biến trên khoảng 0; .
B. Hàm số đồng biến trên khoảng 0; 4 .
C. Hàm số đồng biến trên khoảng 4; .
D. Hàm số nghịch biến trên khoảng ; 4 .
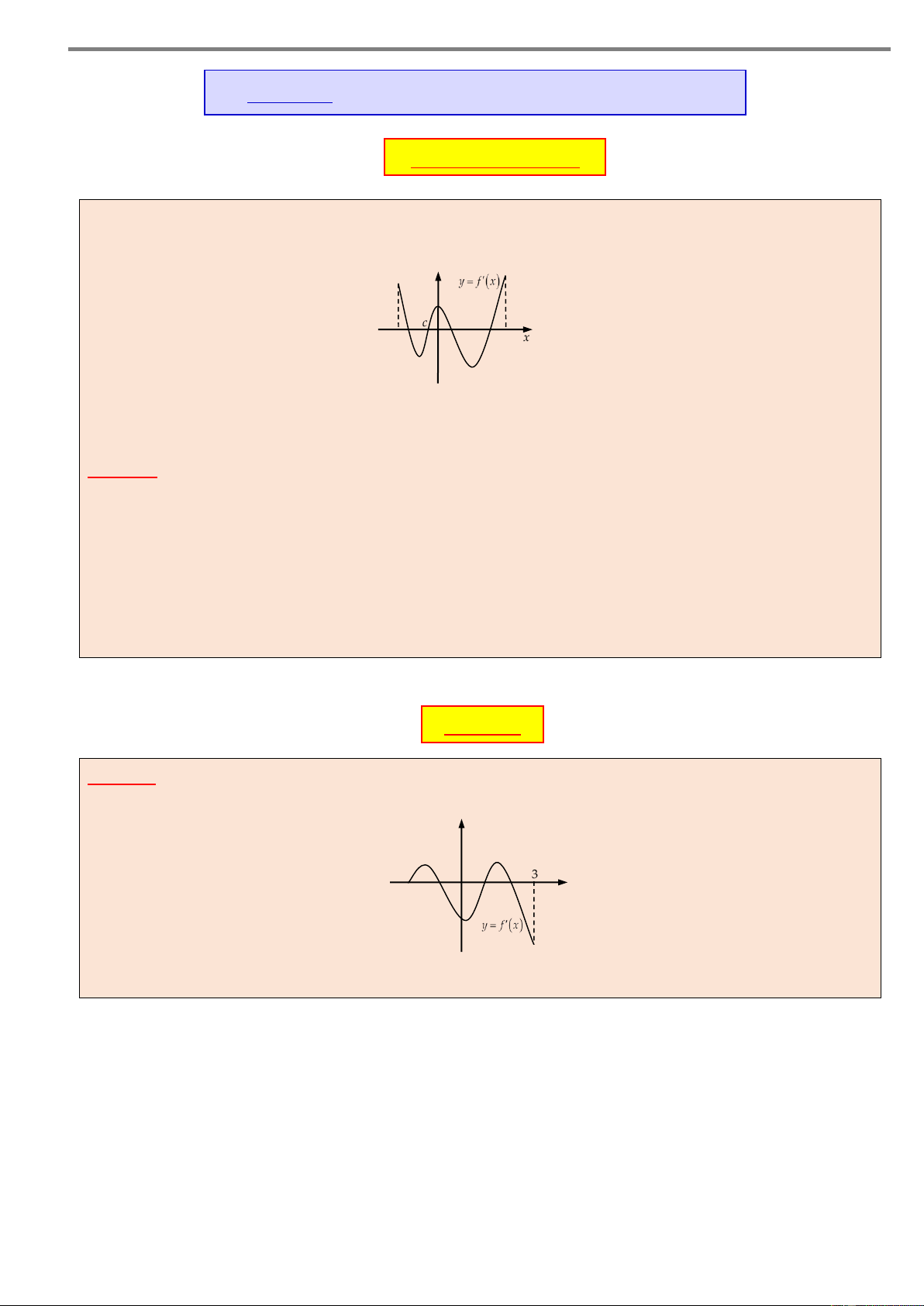
Câu 4. Cho hàm số y f x xác định trên \ 0 và có bảng x – –2 0 2 +
xét dấu đạo hàm như hình bên. Mệnh đề nào dưới đây đúng? 1 y’ + 0 – – 0 +
A. Hàm số đồng biến trên khoảng 2 ;0.
B. Hàm số đồng biến trên khoảng ; 0 .
C. Hàm số nghịch biến trên khoảng 0; 2 .
D. Hàm số nghịch biến trên khoảng ; 2 .
Câu 5. Cho hàm số y f x xác định trên \
0 và có bảng x – –4 0 5 +
xét dấu đạo hàm như hình bên. Mệnh đề nào dưới đây sai? 1 – y’ + 0 + 0 0 +
A. Hàm số đồng biến trên khoảng ; 0 .
B. Hàm số đồng biến trên khoảng ; 4 .
C. Hàm số nghịch biến trên khoảng 0; 5 .
D. Hàm số nghịch biến trên khoảng 0; .
Câu 6. Cho hàm số y f x xác định trên \ 0 và có bảng x – –1 0 3 + 1
xét dấu đạo hàm như hình bên. Mệnh đề nào dưới đây sai? y’ + 0 – – 0 +
A. Hàm số đồng biến trên khoảng ; 1 .
B. Hàm số đồng biến trên khoảng 3; .
C. Hàm số nghịch biến trên khoảng 0; 3 .
D. Hàm số nghịch biến trên khoảng 1 ;3 . 2 THPT Marie Curie
DẠNG 3. DỰA VÀO BIỂU THỨC CỦA ĐẠO HÀM A. PHƯ ƠNG PHÁP
Dựa vào biểu thức của đạo hàm để xét dấu f 'x , từ đó có kết luận về tính đơn điệu của hàm
số y f x . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Cho hàm số y f x có đạo hàm f x 2 '
x 3x 2 , x
. Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 2. 1
Cho hàm số y f x có đạo hàm f 'x 2
x 2x 2 , x
. Xét tính đơn điệu 2 của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Cho hàm số y f x có đạo hàm f x 2 '
x 2x 5, x
. Xét tính đơn điệu của hàm số đã cho. Lời giải 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số y f x có đạo hàm f x 2 ' x 1, x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 1; .
B. Hàm số đồng biến trên khoảng ; .
C. Hàm số nghịch biến trên khoảng 1 ;1.
D. Hàm số nghịch biến trên khoảng ; 0 .
Câu 2. Cho hàm số y f x có đạo hàm là fx 2 x 4 .
Mệnh đề nào dưới đây đúng?
A. Hàm số y f x đồng biến trên khoảng 2; .
B. Hàm số y f x nghịch biến trên khoảng 2 ; 2 .
C. Hàm số y f x đồng biến trên khoảng ; 2 .
D. Hàm số y f x nghịch biến trên khoảng 4 ; 4 .
Câu 3. Cho hàm số y f x có đạo hàm f x 2 '
x x, x
. Hàm số y f x nghịch biến trên khoảng A. ; 1 . B. 0; 1 . 1 C. 1 ;0 . D. ; . 2 2 THPT Marie Curie
DẠNG 4. DỰA VÀO BIỂU THỨC CỦA HÀM SỐ A. PHƯ ƠNG PHÁP
∎ Tìm tập xác định của hàm số.
∎ Tính f 'x và xét dấu f 'x , từ đó có kết luận về tính đơn điệu của hàm số y f x . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. 1
Cho hàm số y 2
x x 5 . Xét tính đơn điệu của hàm số đã cho. 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 2. 1 1 Cho hàm số 3 2
y x x 6x 5 . Xét tính đơn điệu của hàm số đã cho. 3 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Cho hàm số 3 2
y x 3x 3x 4 . Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Cho hàm số 3 2
y x x 7x 1. Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 5. 1 Cho hàm số 4 2 y
x 2x 1 . Xét tính đơn điệu của hàm số đã cho. 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Cho hàm số 4 2
y x 4x 2 . Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 7. 2x 4
Cho hàm số y
. Xét tính đơn điệu của hàm số đã cho. 3x 5 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 THPT Marie Curie
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 8. x 3
Cho hàm số y
. Xét tính đơn điệu của hàm số đã cho. 2x 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM Câu 1. Cho hàm số 3 2
y x 3x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 0; 2 .
B. Hàm số nghịch biến trên khoảng 2; .
C. Hàm số đồng biến trên khoảng 0; 2 .
D. Hàm số nghịch biến trên khoảng ; 0 . Câu 2. Cho hàm số 3 2
y x 2x x 1. Mệnh đề nào dưới đây đúng? 1
A. Hàm số đồng biến trên khoảng ;1 . 3 1
B. Hàm số nghịch biến trên khoảng ; . 3 1
C. Hàm số nghịch biến trên khoảng ;1 . 3
D. Hàm số nghịch biến trên khoảng 1; . Câu 3. Cho hàm số 3
y x 3x 2 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ; 0 và nghịch
biến trên khoảng 0; .
B. Hàm số nghịch biến trên khoảng ; .
C. Hàm số đồng biến trên khoảng ; .
D. Hàm số nghịch biến trên khoảng ; 0 và đồng
biến trên khoảng 0; . 3
Tài liệu học tập Toán 12 Câu 4. 1 1 Hàm số 3 2
y x x 1 đồng biến trên khoảng 3 2 nào dưới đây? A. . 0; 1 B. 1; . C. 1
;1. D. 0;. Câu 5. 1 1 Hàm số 3 2
y x x 2 nghịch biến trên 3 2 khoảng nào dưới đây? A. ; . B. ;1 . C. 1 ;0 . D. ; 1 . Câu 6. 1 Cho hàm số 3 2
y x x x 2 . Mệnh đề nào 3 dưới đây đúng?
A. Hàm số đồng biến trên khoảng ; .
B. Hàm số nghịch biến trên khoảng ; .
C. Hàm số nghịch biến trên khoảng ;1 và đồng biến
trên khoảng 1; .
D. Hàm số đồng biến trên khoảng ;1 và nghịch
biến trên khoảng 1; . Câu 7. Cho hàm số 3 2
y x 3x 3x 1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ; .
B. Hàm số nghịch biến trên khoảng ; .
C. Hàm số nghịch biến trên khoảng ;1 và đồng biến
trên khoảng 1; .
D. Hàm số đồng biến trên khoảng ;1 và nghịch
biến trên khoảng 1; . Câu 8. Cho hàm số 3
y x 3x 4 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 1 ;1.
B. Hàm số nghịch biến trên khoảng ; .
C. Hàm số đồng biến trên khoảng ; 1 và 1; .
D. Hàm số đồng biến trên khoảng ; . Câu 9. 1 Cho hàm số 3
y x x 3 . Mệnh đề nào dưới 3 đây đúng?
A. Hàm số đồng biến trên khoảng ; 1 và 1; . 4 THPT Marie Curie
B. Hàm số đồng biến trên khoảng ; .
C. Hàm số nghịch biến trên khoảng ; .
D. Hàm số đồng biến trên khoảng 1 ;1. Câu 10. Hàm số 4
y 2x 1 đồng biến trên khoảng 1 A. ;
. B.0; . 2 1 C. ;
. D. ; 0 . 2 Câu 11. Cho hàm số 4 2
y x 2x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ; 2 .
B. Hàm số nghịch biến trên khoảng ; 2 .
C. Hàm số đồng biến trên khoảng 1 ;1.
D. Hàm số nghịch biến trên khoảng 1 ;1. Câu 12. 1 1 Hàm số 4 2
y x x 1 nghịch biến trên khoảng 3 6 nào dưới đây? 1 1 A. ; 2
và 0;2 . B. ; 0 và ; . 2 2 1 1 C. ;
và 0; . D. 2 ;0 và 2;. 2 2 Câu 13. 1
Khoảng đồng biến của hàm số 4 2 y 9
x x 3 2
là khoảng nào dưới đây? 1 1 A. ; 6
và 0;6 . B. ; 0 và ; . 6 6 1 1 C. ;
và 0; . D. 6 ;0 và 6;. 6 6 Câu 14. Cho hàm số 4 2
y x 8x 4 . Mệnh đề nào dưới đây sai?
A. Hàm số đồng biến trên khoảng 2 ;0 và khoảng 2;.
B. Hàm số đồng biến trên khoảng 0; .
C. Hàm số nghịch biến trên khoảng ; 0 .
D. Hàm số nghịch biến trên khoảng ; 2 và khoảng 1 ;0 . Câu 15. Hàm số 4 2
y x x đồng biến trên khoảng nào dưới đây?
A. ; 0 . B. 0; . 5
Tài liệu học tập Toán 12 C. ; 1 . D. 1; .
Câu 16. Khoảng nghịch biến của hàm số 4 2 y 2
x x 1 là khoảng nào dưới đây? 1 A. ;
. B. ; 0 . 2 C. ;
. D. 0;. Câu 17. x 2
Cho hàm số y
. Mệnh đề nào dưới đây x 1 đúng?
A. Hàm số nghịch biến trên khoảng ; 1 .
B. Hàm số đồng biến trên khoảng ; 1 .
C. Hàm số đồng biến trên khoảng ; .
D. Hàm số nghịch biến trên khoảng 1; . Câu 18. 3 x
Khoảng nghịch biến của hàm số y là x khoảng nào dưới đây?
A. ; 3 và 3; . B. ; 00; . C. ;
. D. ;0 và 0;. Câu 19. 1
Hàm số y
đồng biến trên khoảng nào x 4 dưới đây? A. ;1
và 1; . B. ; 4 và 4; . C. ; 4 và 4;
. D. ; 1 và 1; . 6 THPT Marie Curie
DẠNG 5. DỰA VÀO ĐỒ THỊ HÀM SỐ A. PHƯ ƠNG PHÁP
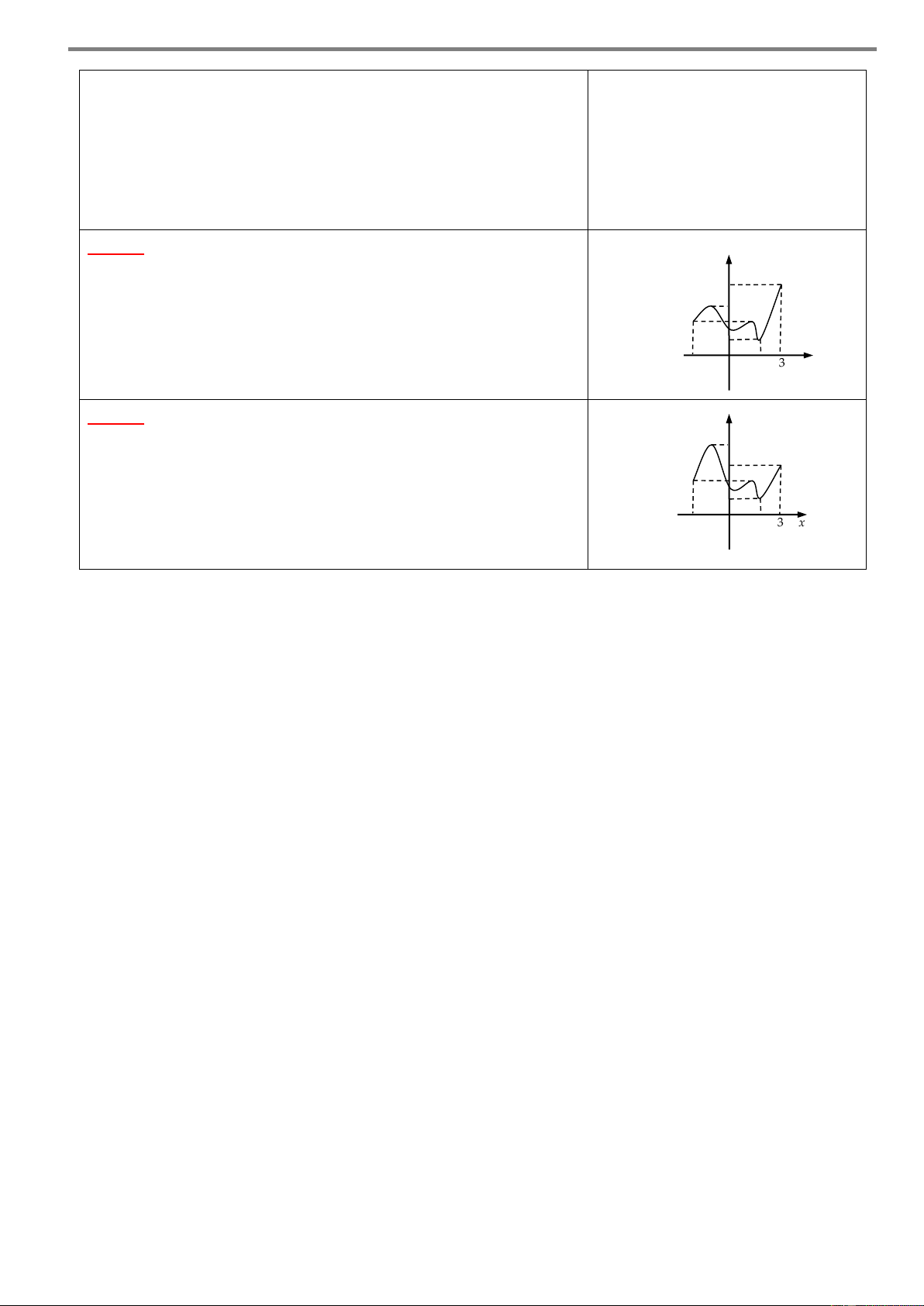
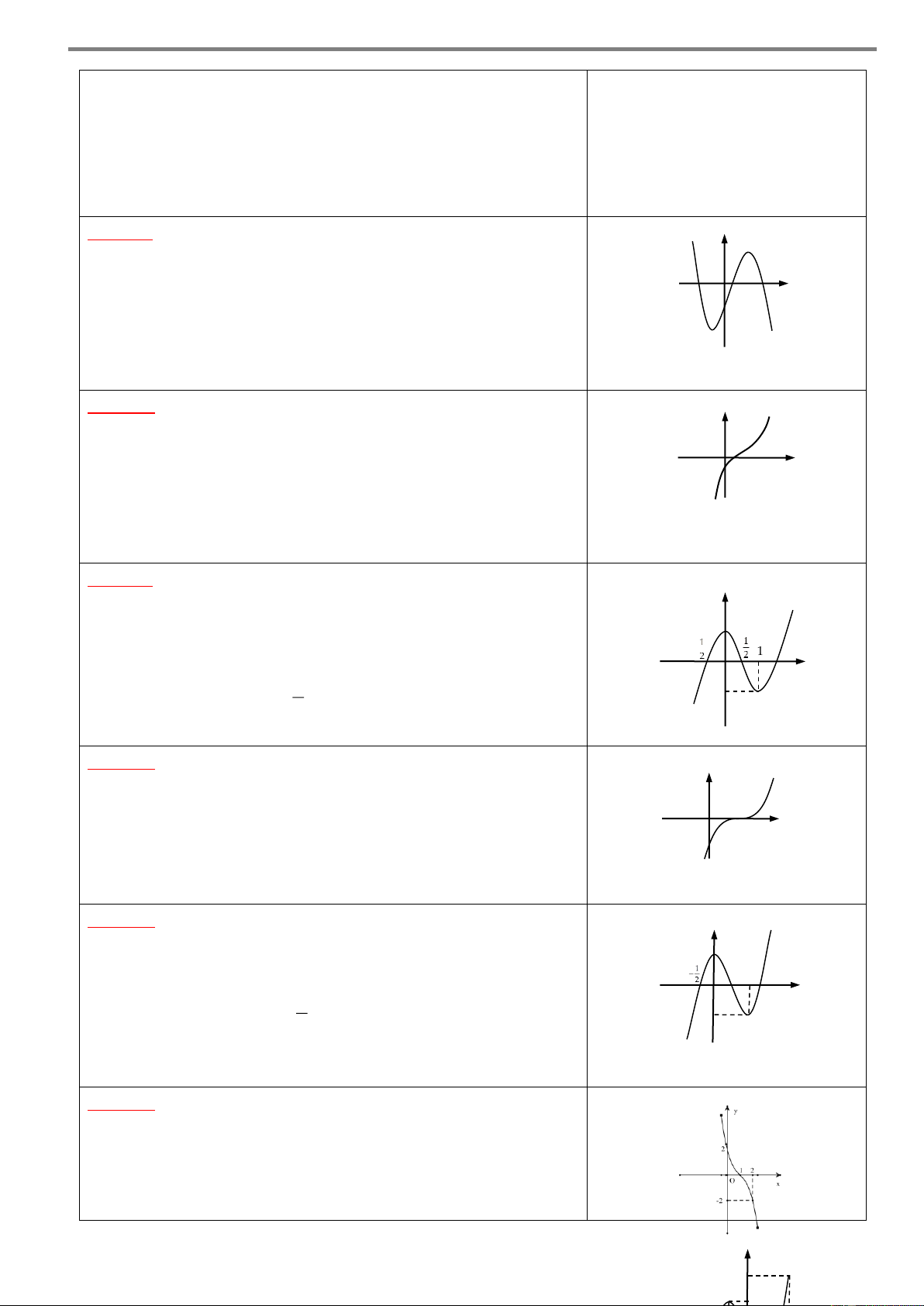
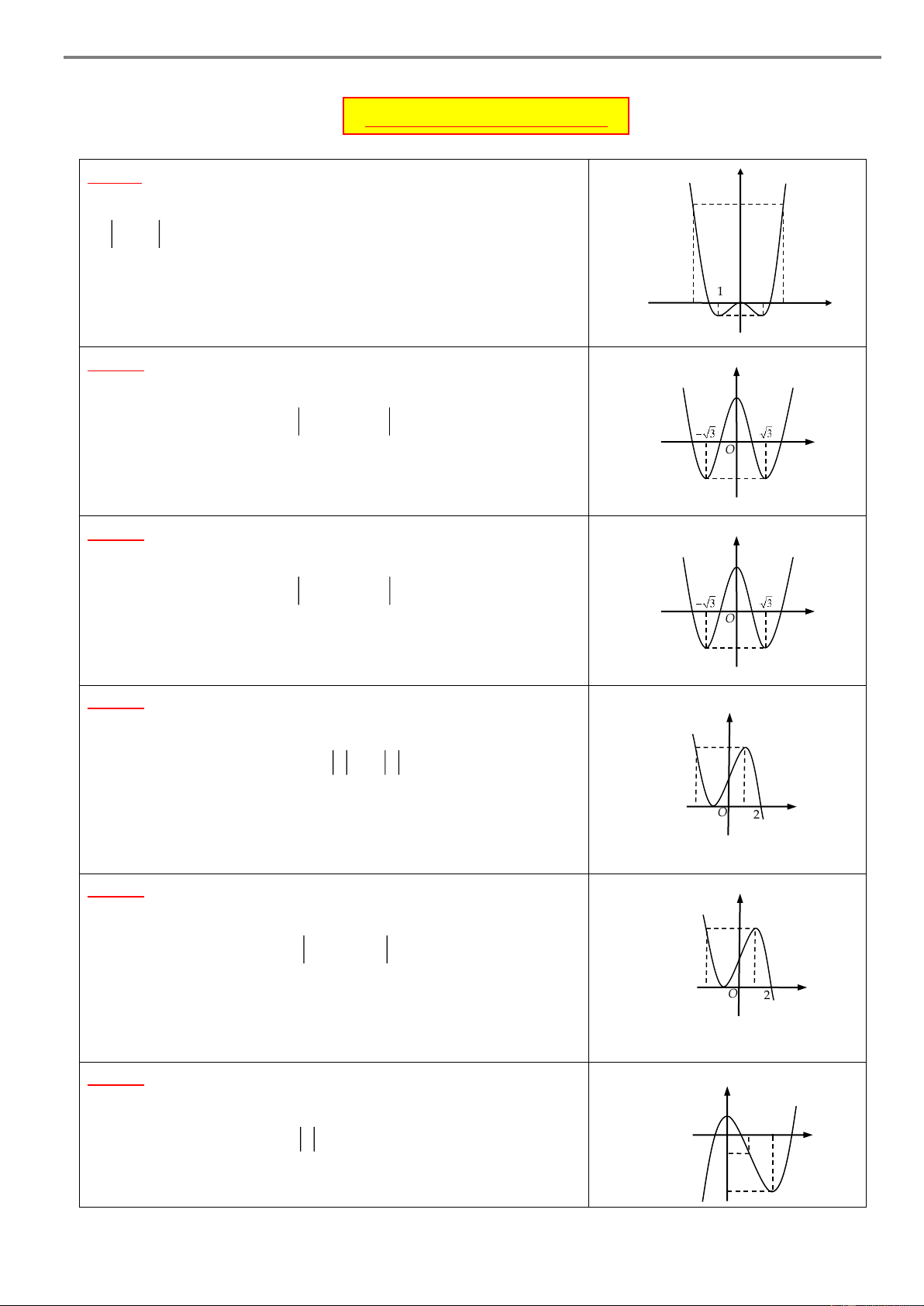
Cho hàm số y f x có đồ thị như hình vẽ sau y b c a O d x Khi đó:
Hàm số y f x đồng biến trên các khoảng b; 0 và c; d .
Hàm số y f x nghịch biến trên các khoảng ;
a b và 0,c . Chú ý
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
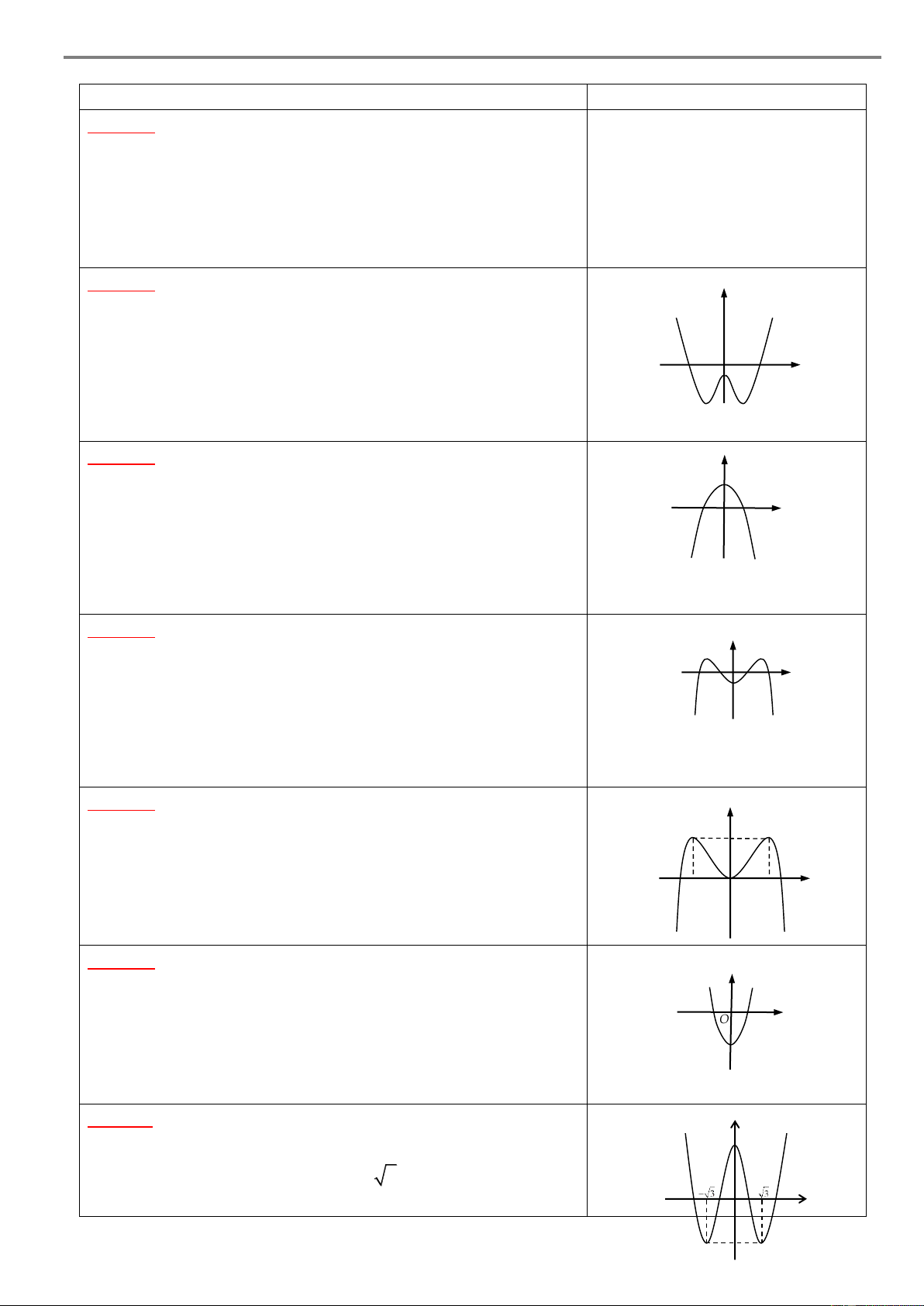
Ví dụ 1. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ sau y 2 1 x –1 O 1
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
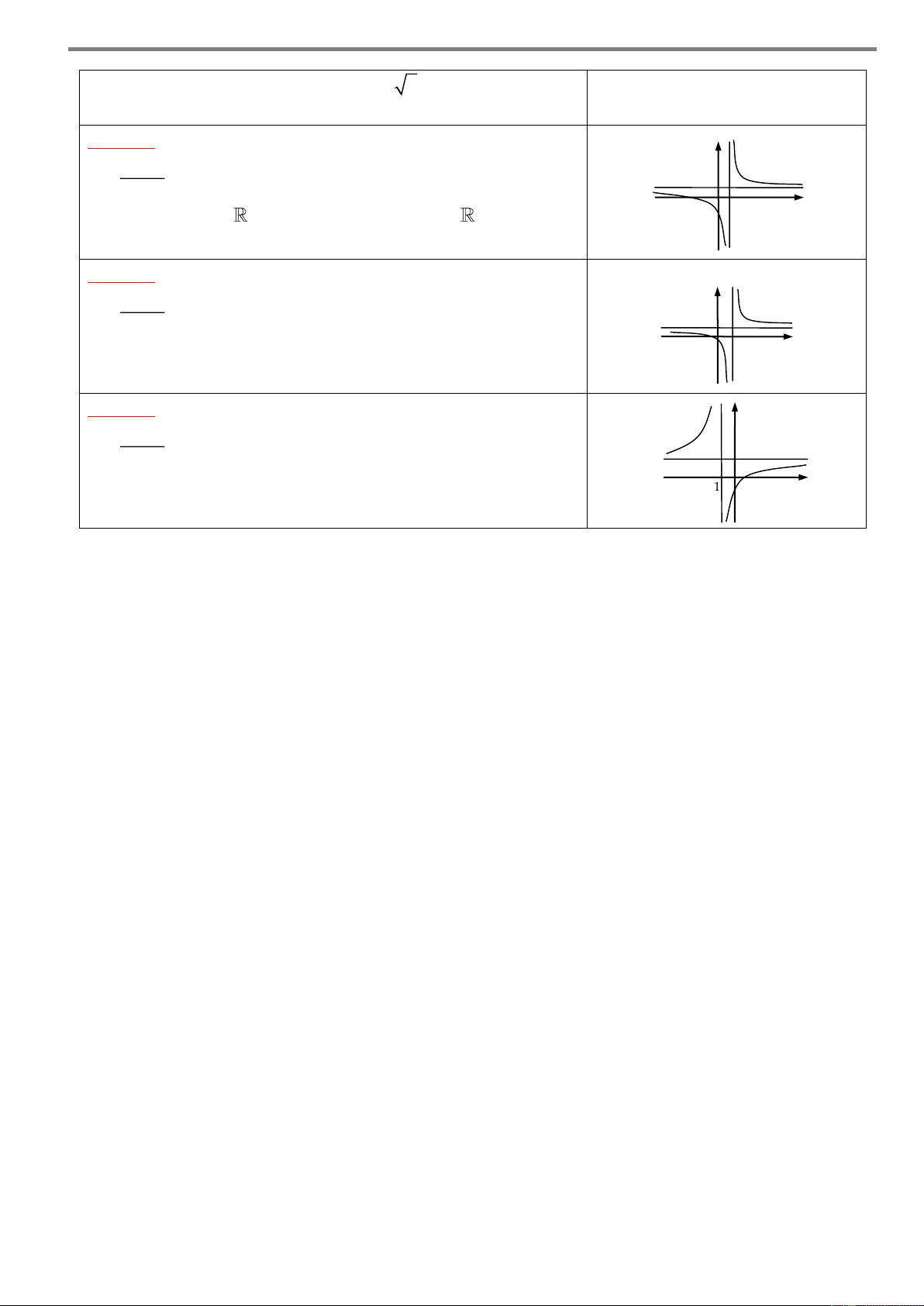
....................................................................................................................................................................... Ví dụ 2. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ sau y 2 O –1 2 x –2
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
C. CÂU HỎI TRẮC NGHIỆM
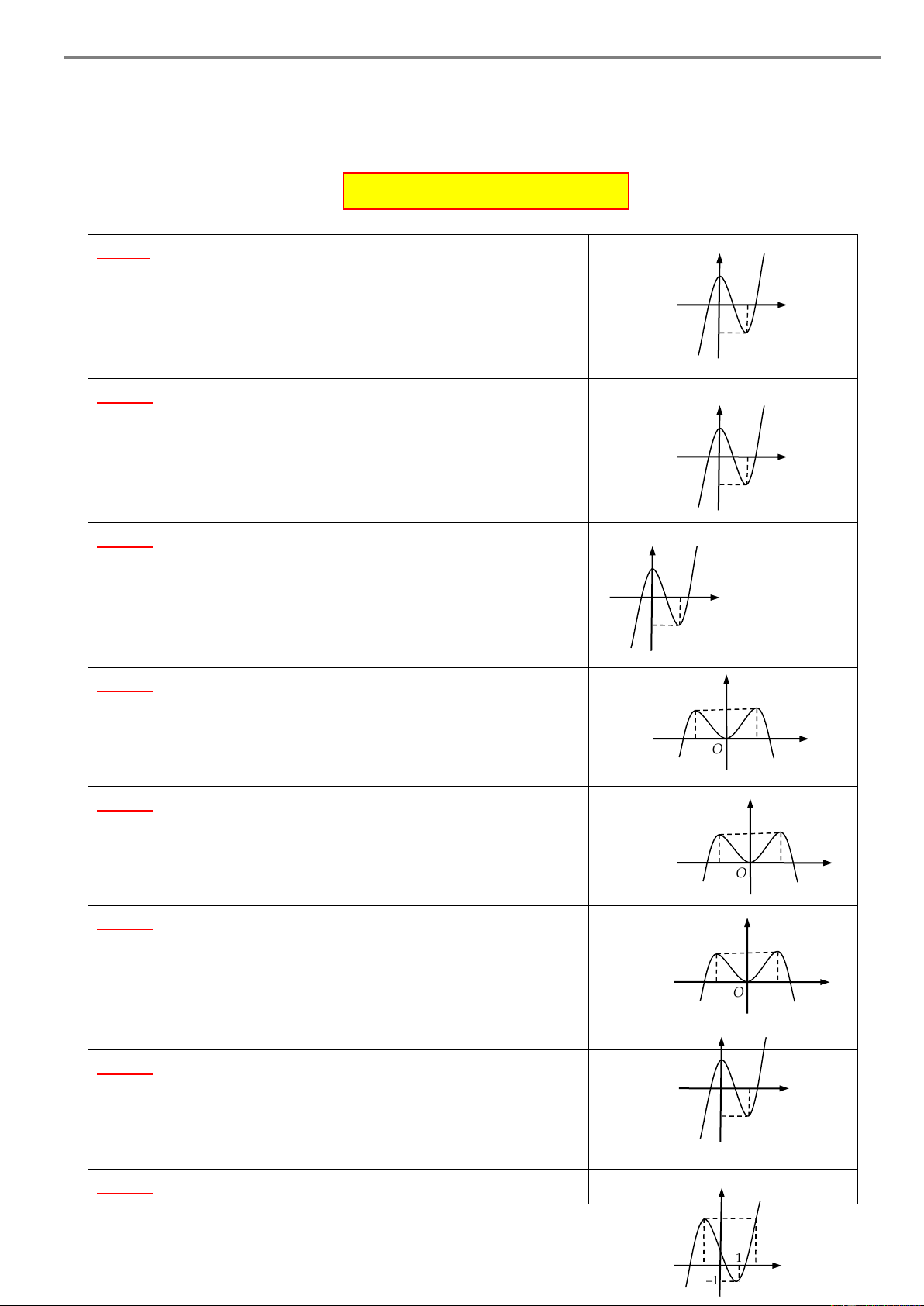
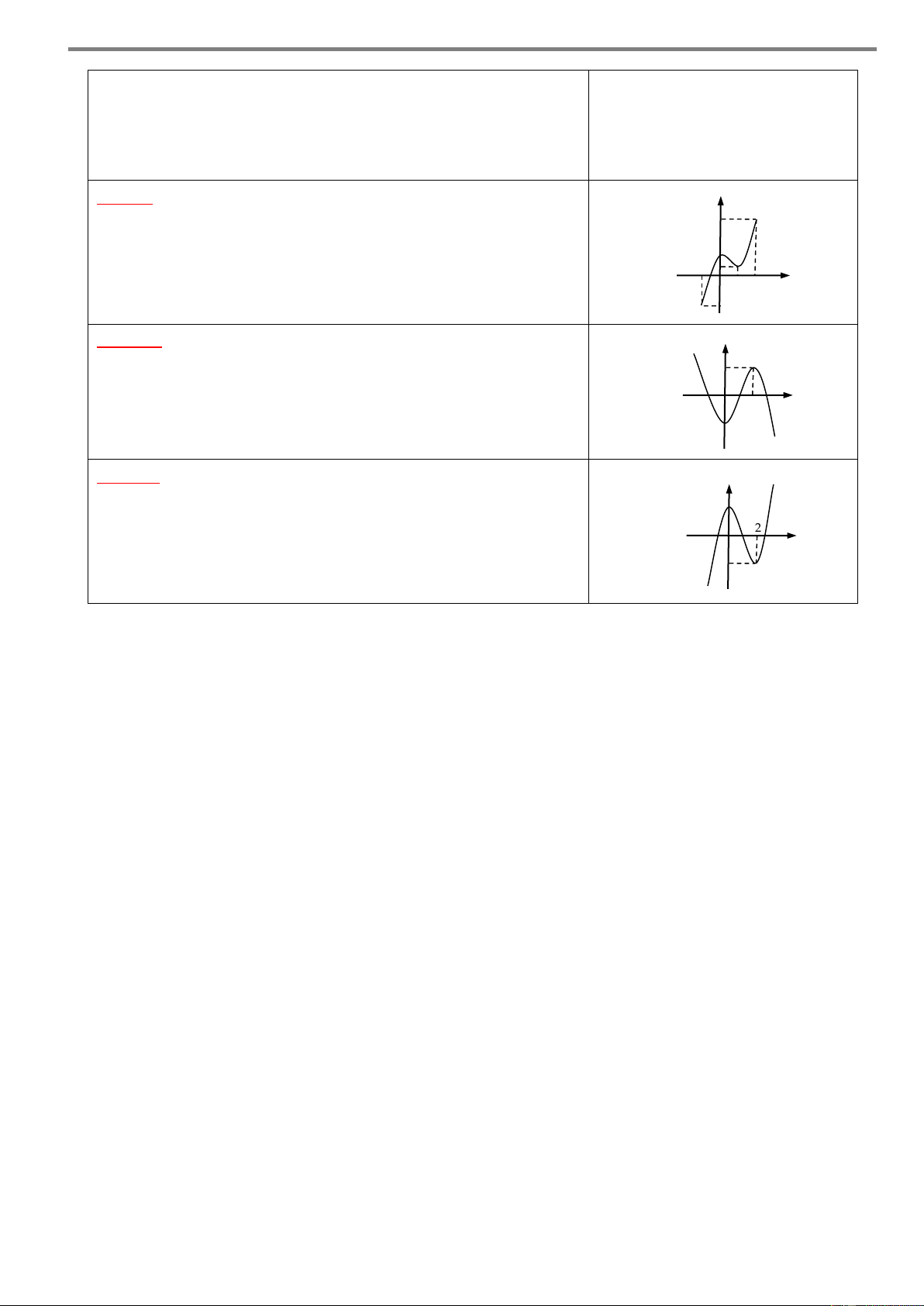
Câu 1. Cho hàm số y f x có đồ thị như hình vẽ bên. y 3
Hàm số đã cho nghịch biến trên khoảng A. 1 ;3 . B. 2; 1 . –2 1 –1 O 2 x C. 1; 2 . D. 1 ;1. –1
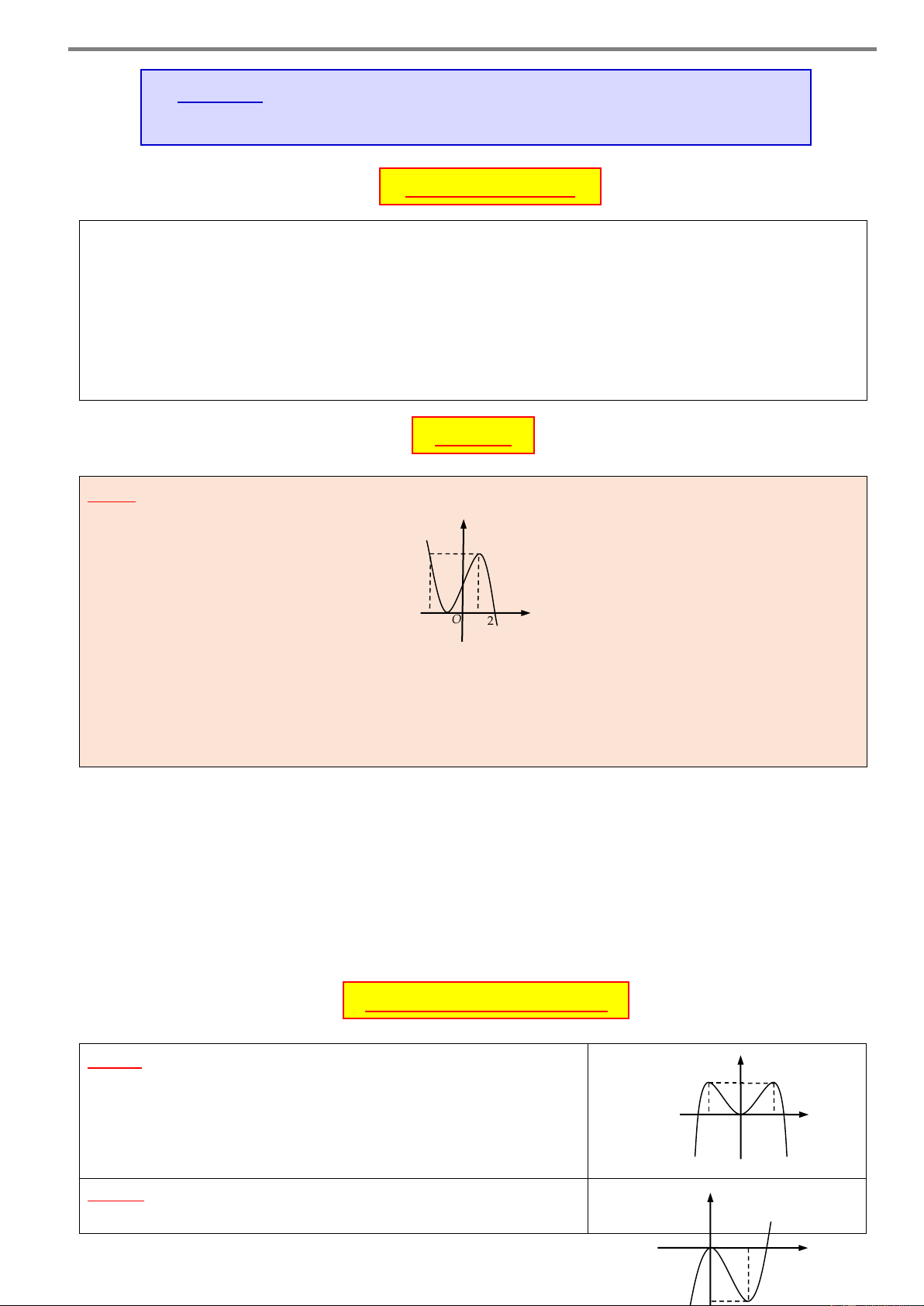
Câu 2. Cho hàm số y f x có đồ thị như hình vẽ bên. y
Hàm số đã cho đồng biến trên khoảng –1 1 O x A. 0; 1 . B. ;1 . –1 C. 1 ;1. D. 1 ;0 . –2
Câu 3. Cho hàm số y f x có đồ thị như hình vẽ bên. y 1
Hàm số đã cho nghịch biến trên khoảng A. 1 ;1. B. ; 1 . –1 O 1 x C. 1 ;0 . D. 0; 1 .
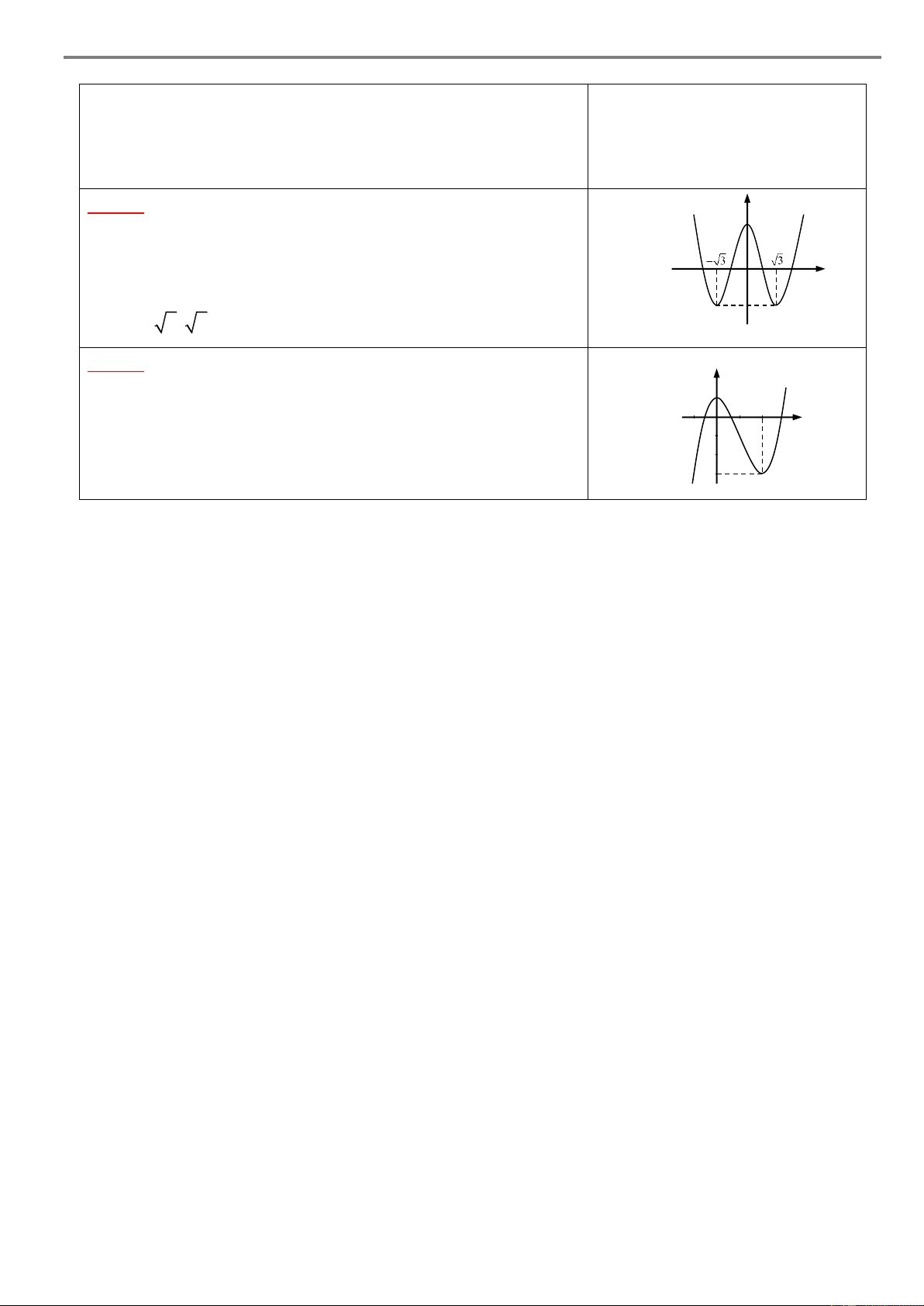
Câu 4. Cho hàm số y f x có đồ thị như hình vẽ bên. y
Hàm số đã cho đồng biến trên khoảng A. 2; 3 . B. 0; 2 . 2 C. 2; 1. D. 1; 2 . –2 O 1 3 x
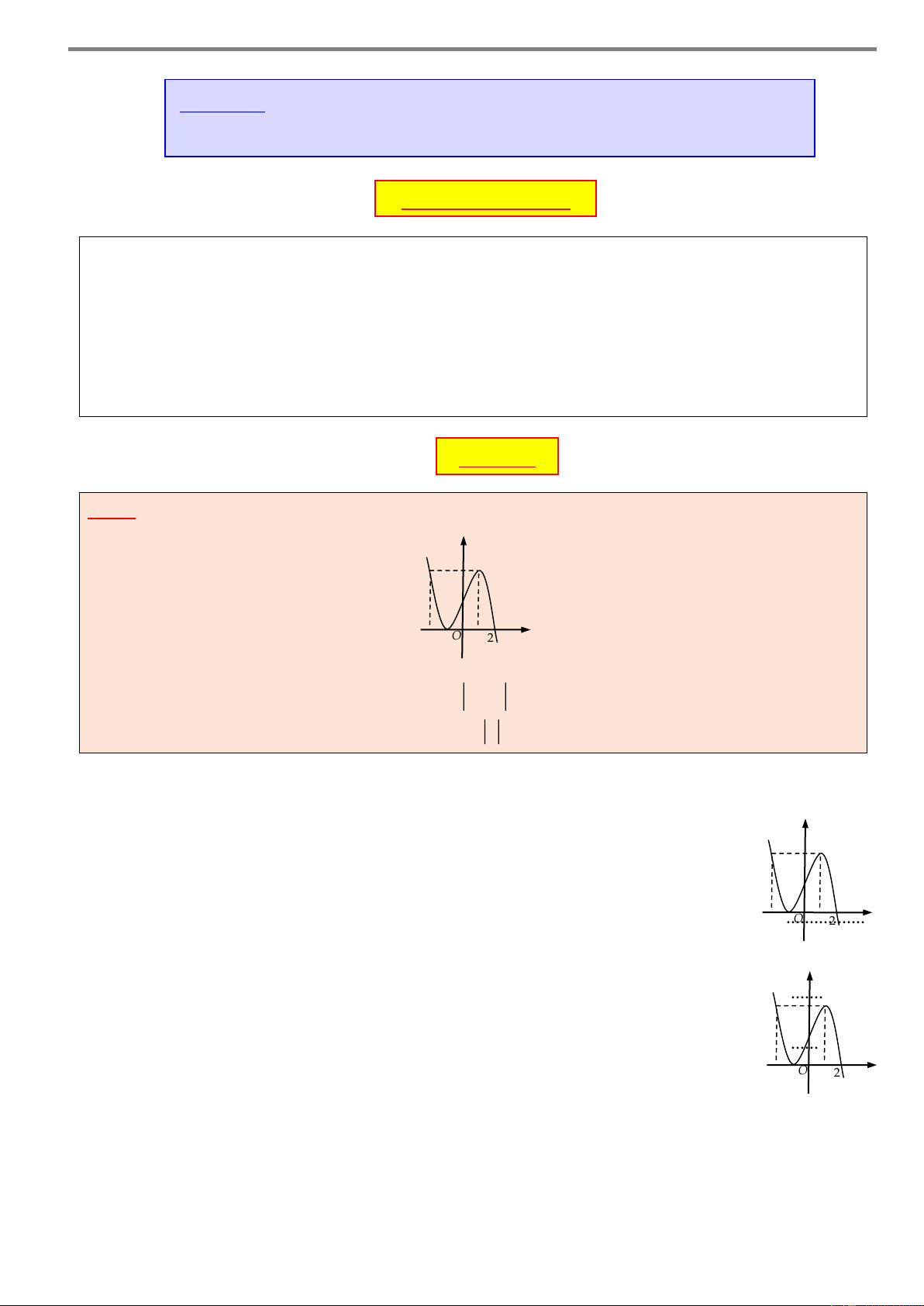
Câu 5. Cho hàm số y f x có đồ thị như hình vẽ bên. y
Hàm số đã cho nghịch biến trên khoảng A. 2; 1. B. 2 ; 2 . 2 C. 1; 3. D. 0; 2 . –2 O 1 3 x
Câu 6. Cho hàm số y f x có đồ thị như hình vẽ bên. y
Hàm số đã cho đồng biến trên khoảng A. 2 ; 4 . B. 2; 1. C. 2; 4 . D. 2 ; 2 . –2 O 1 2 4 x 2 THPT Marie Curie
DẠNG 6. DỰA VÀO ĐỒ THỊ CỦA ĐẠO HÀM A. PHƯ ƠNG PHÁP
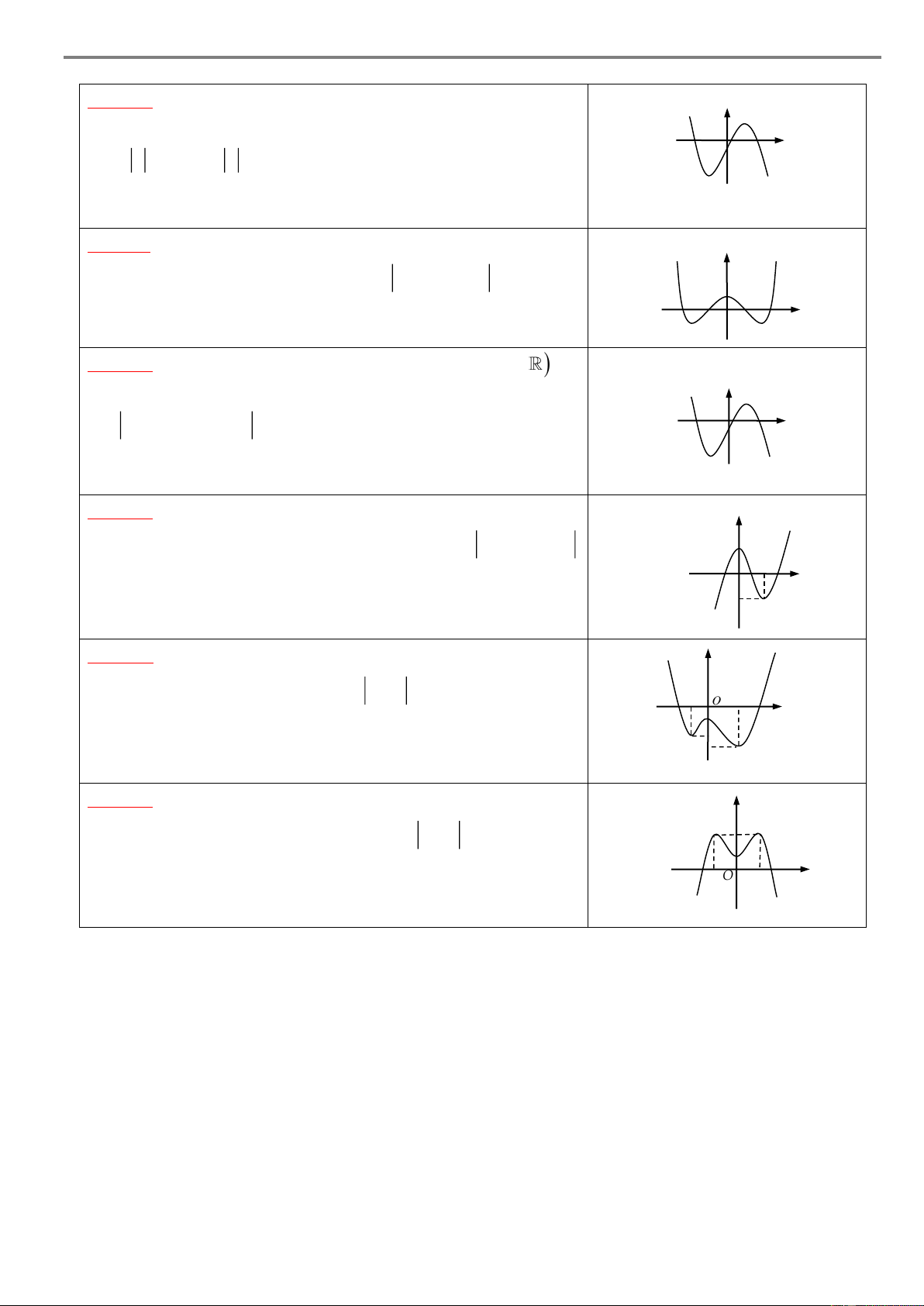
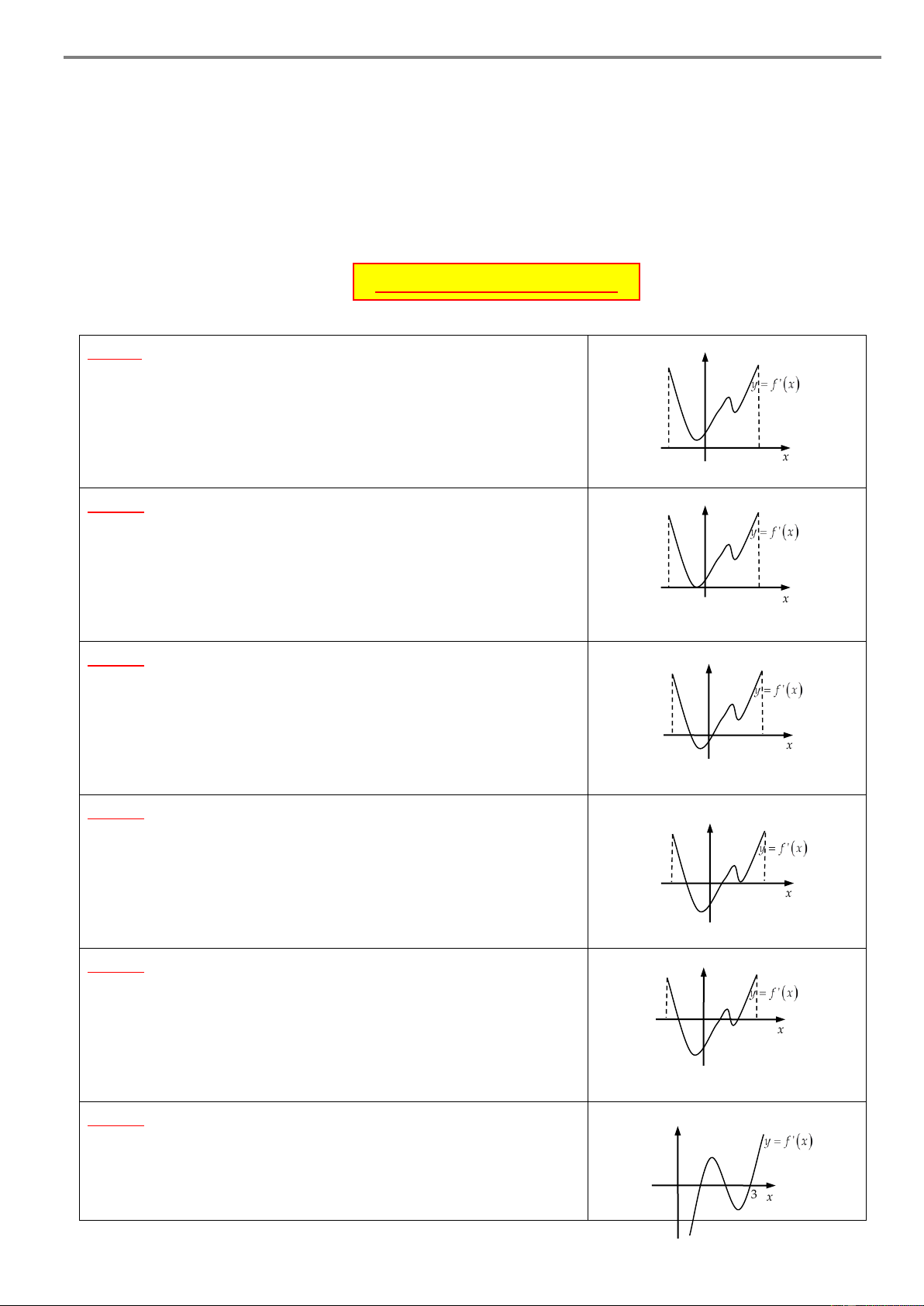
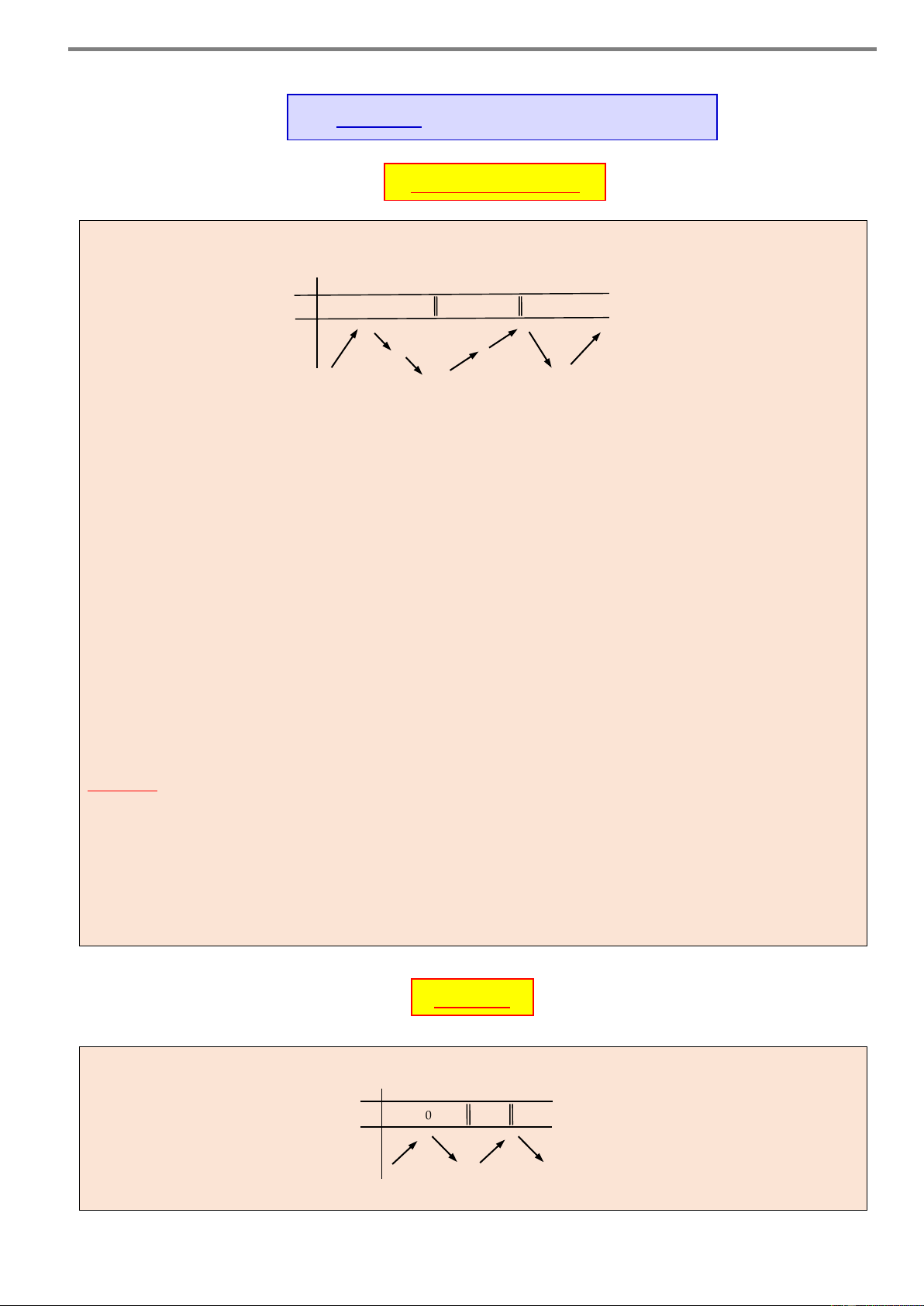
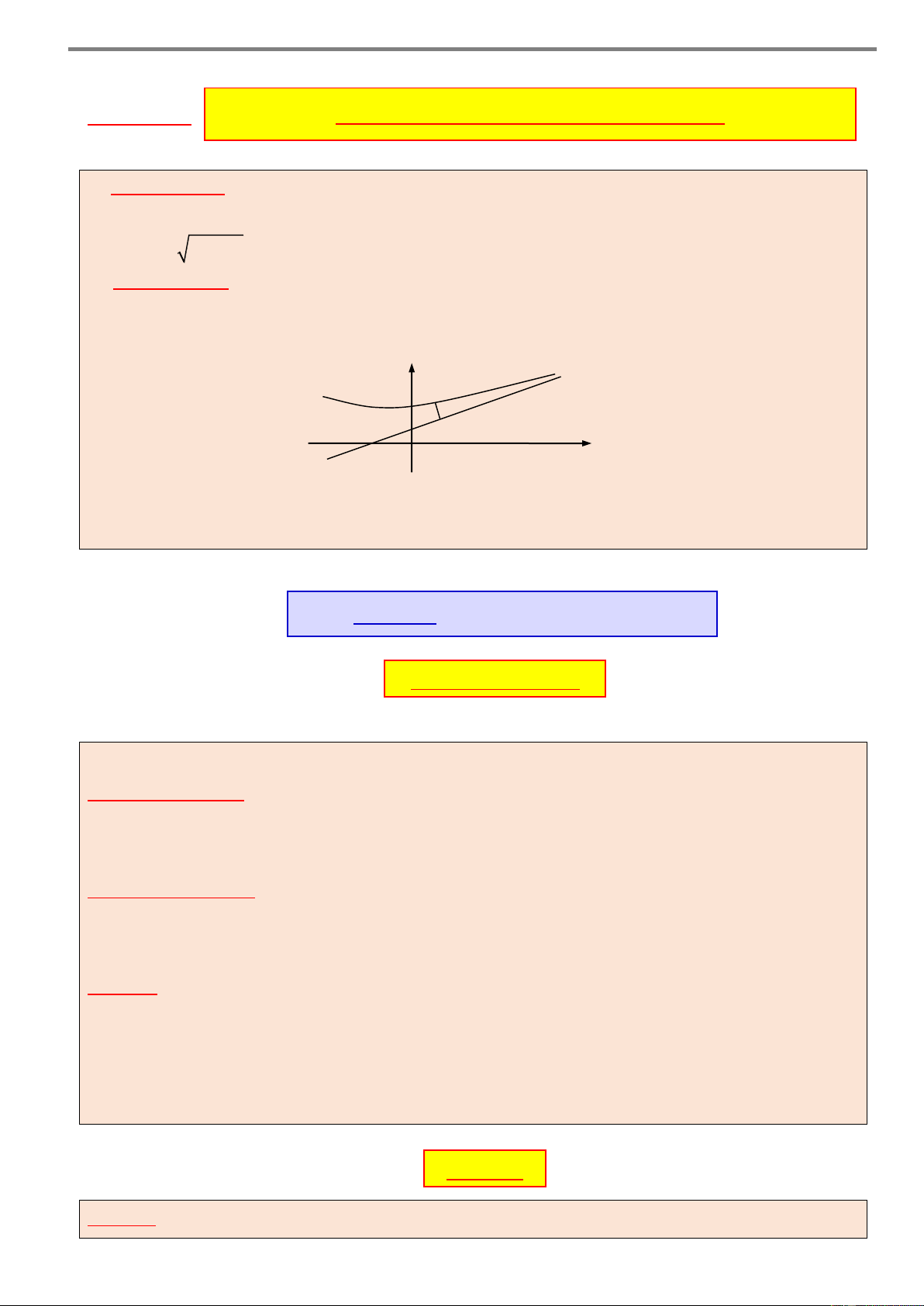
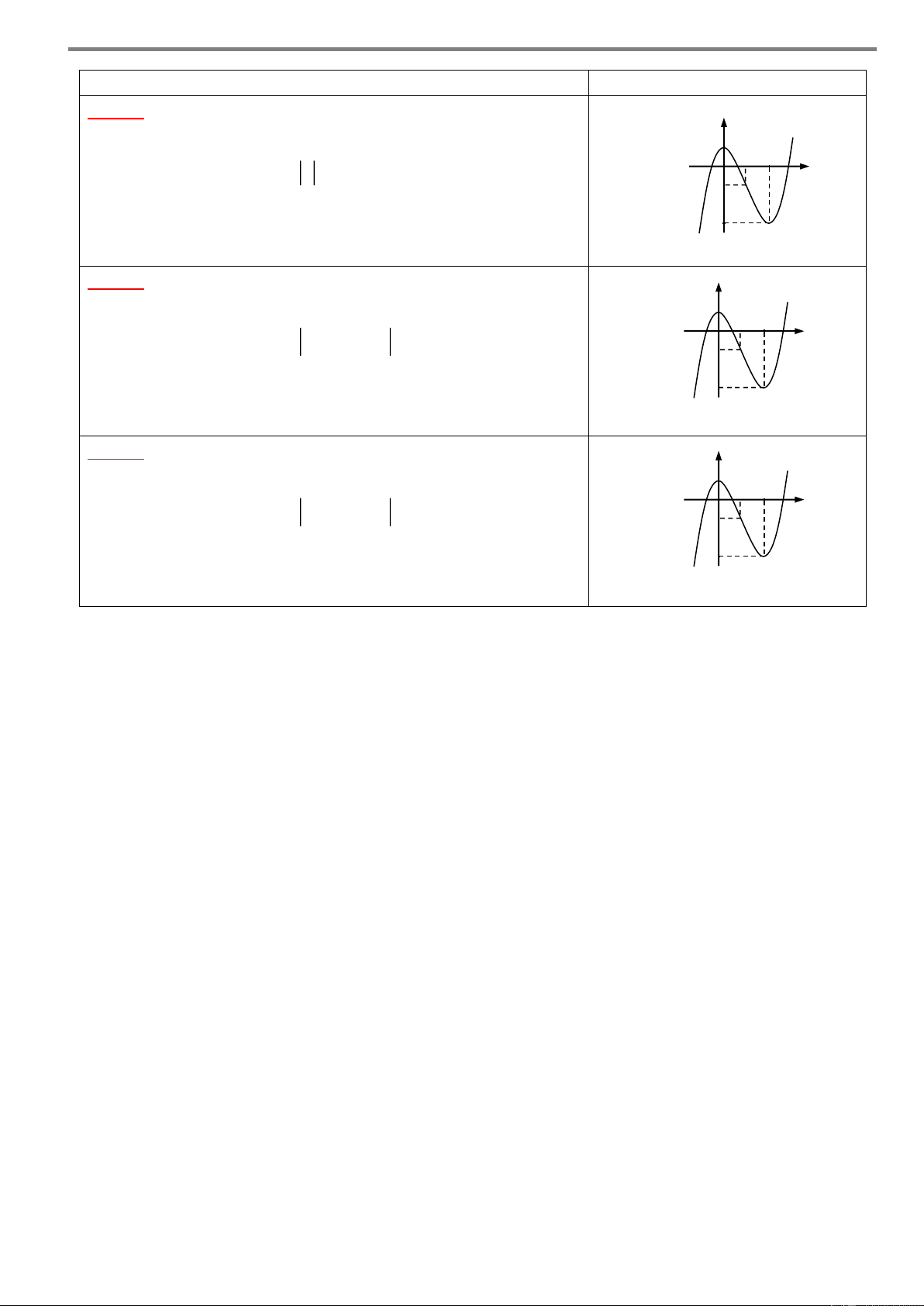
Cho hàm số y f x xác định và liên tục trên a; f
đồng thời hàm số y f 'x có đồ thị như hình vẽ sau y b c d e a O f x Khi đó:
Hàm số y f x đồng biến trên các khoảng ;
a b , c; d và e; f .
Hàm số y f x nghịch biến trên các khoảng ;
b c và d,e . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
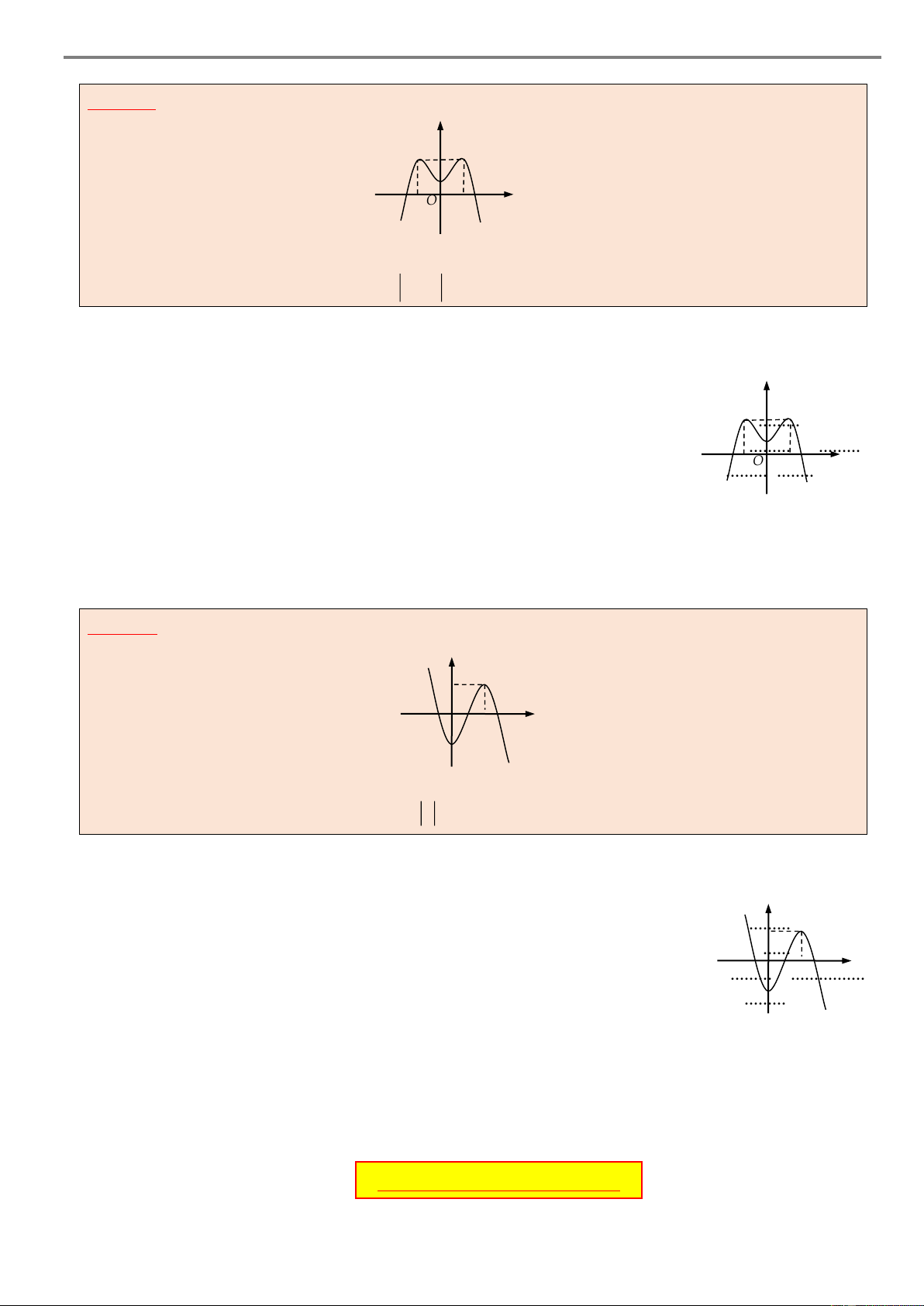
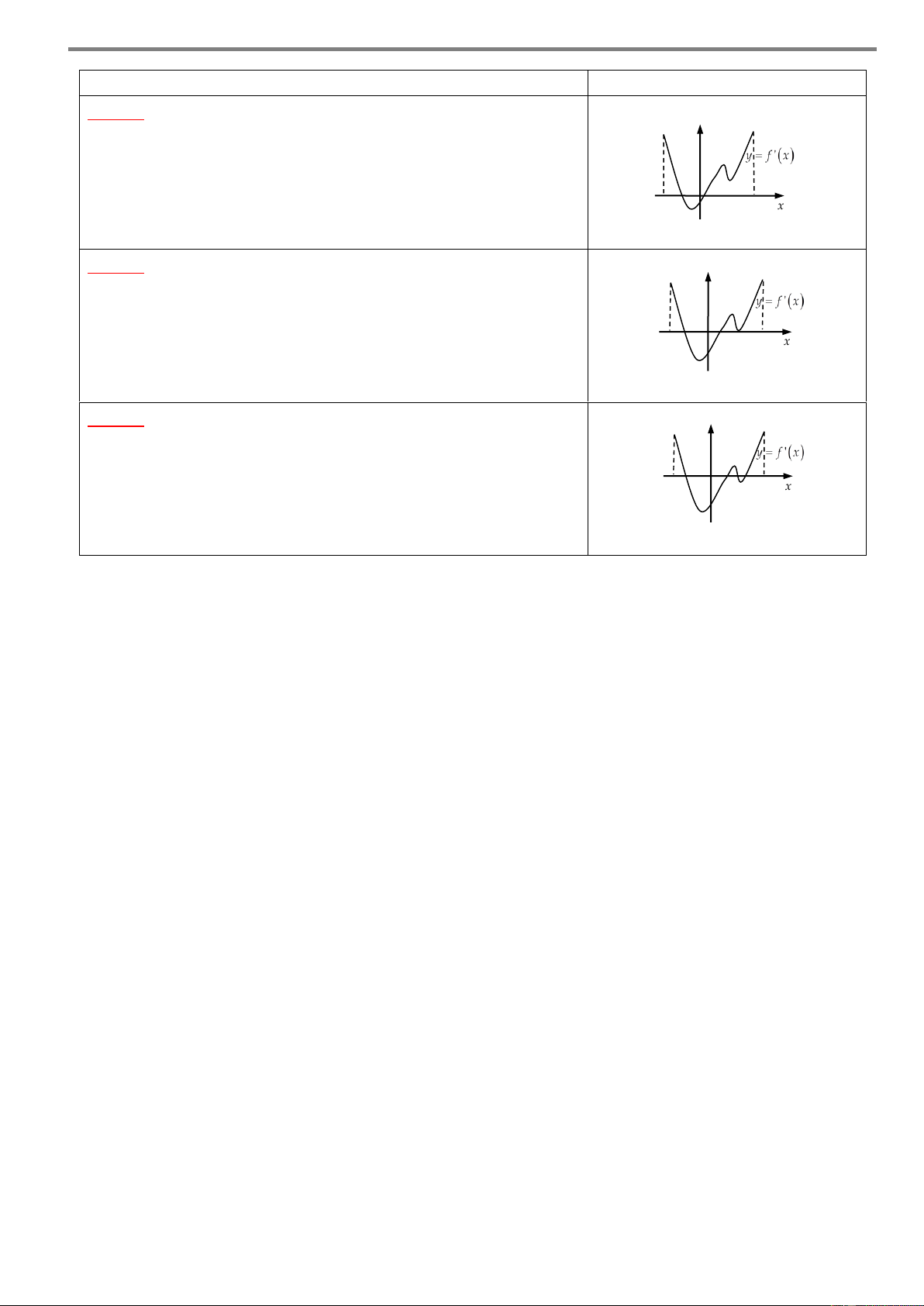
Ví dụ 1. Cho hàm số y f x xác định và liên tục trên 2; 3
đồng thời hàm số y f 'x có
đồ thị như hình vẽ sau y 1 2 3 –2 –1 O x
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
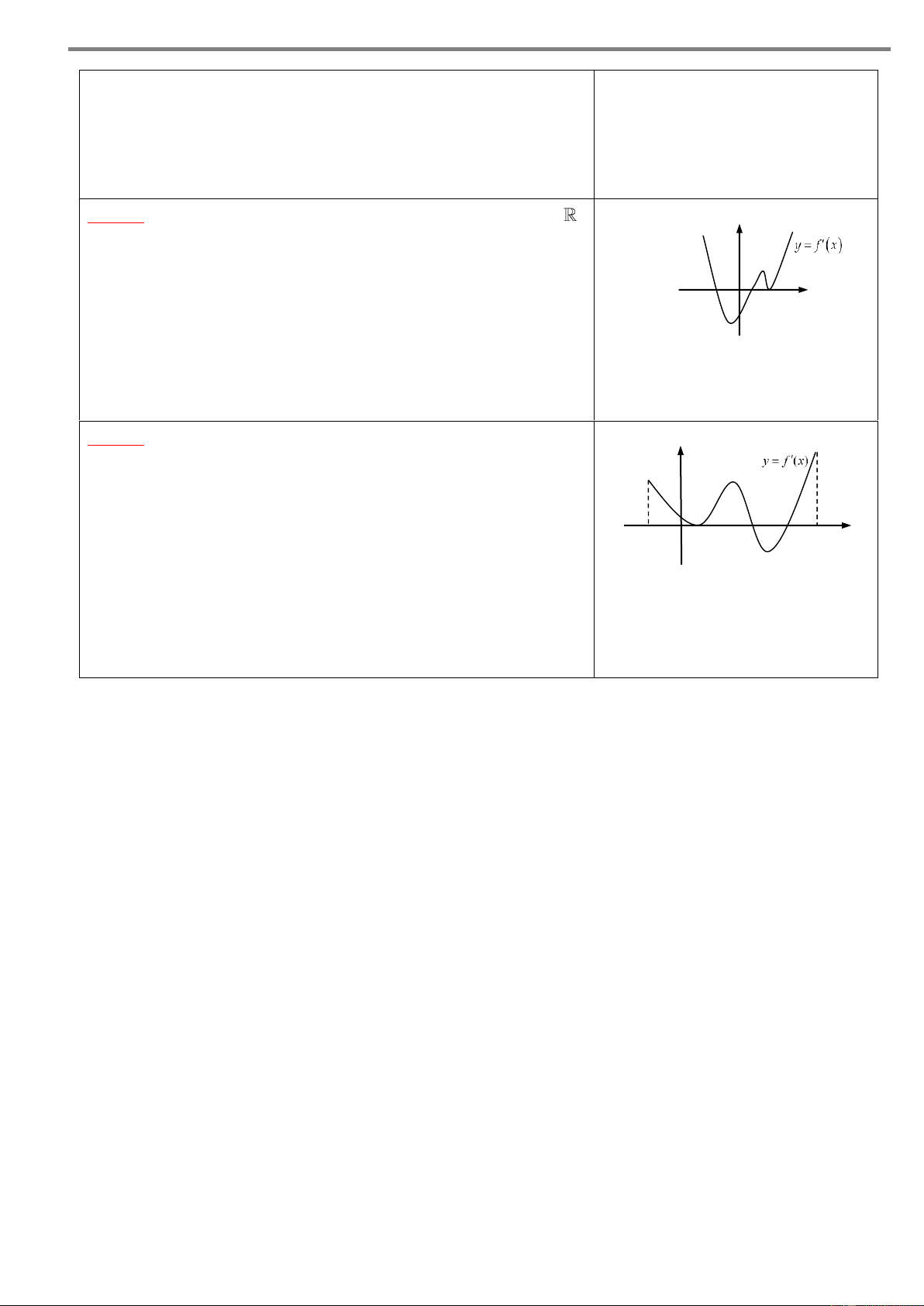
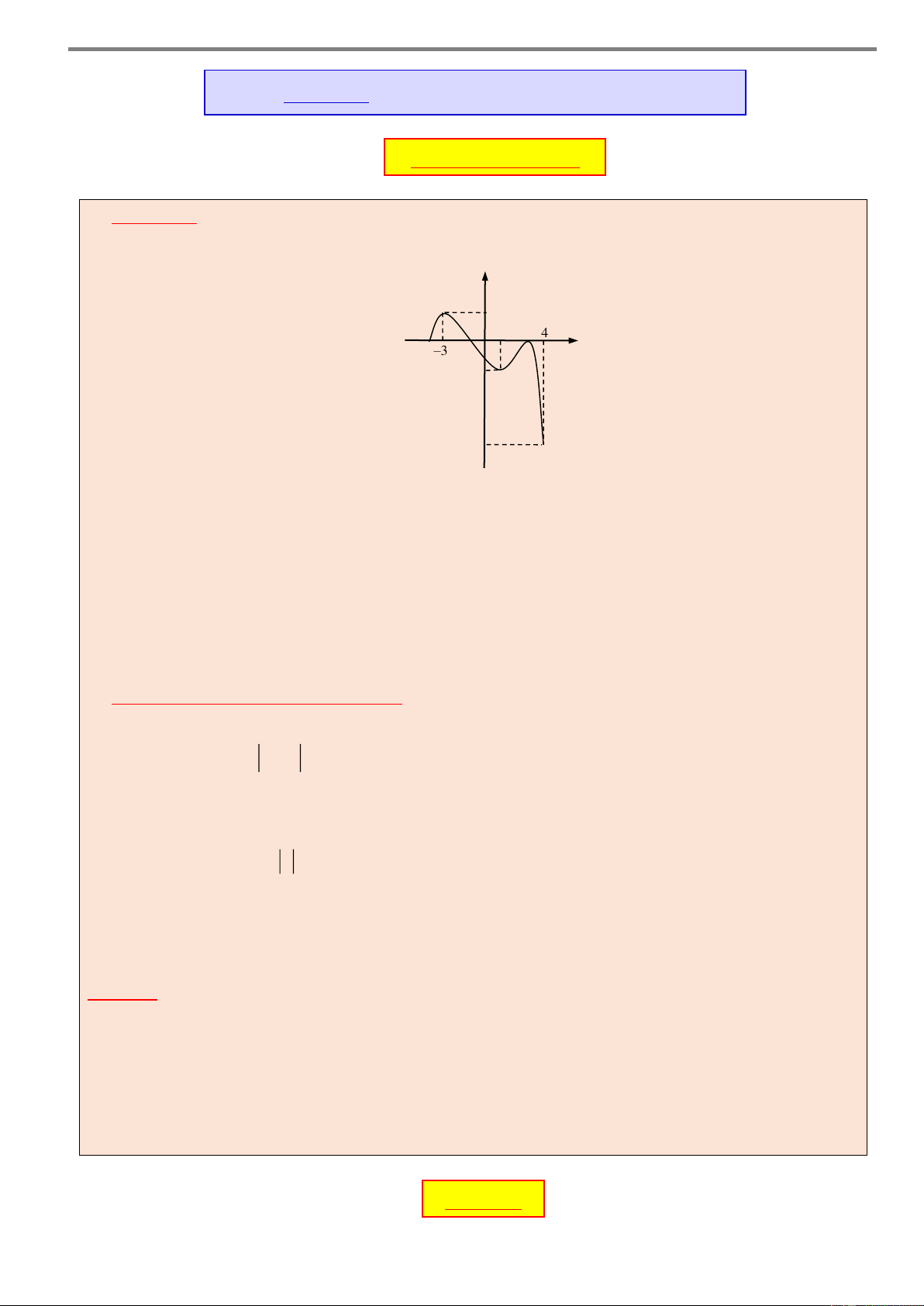
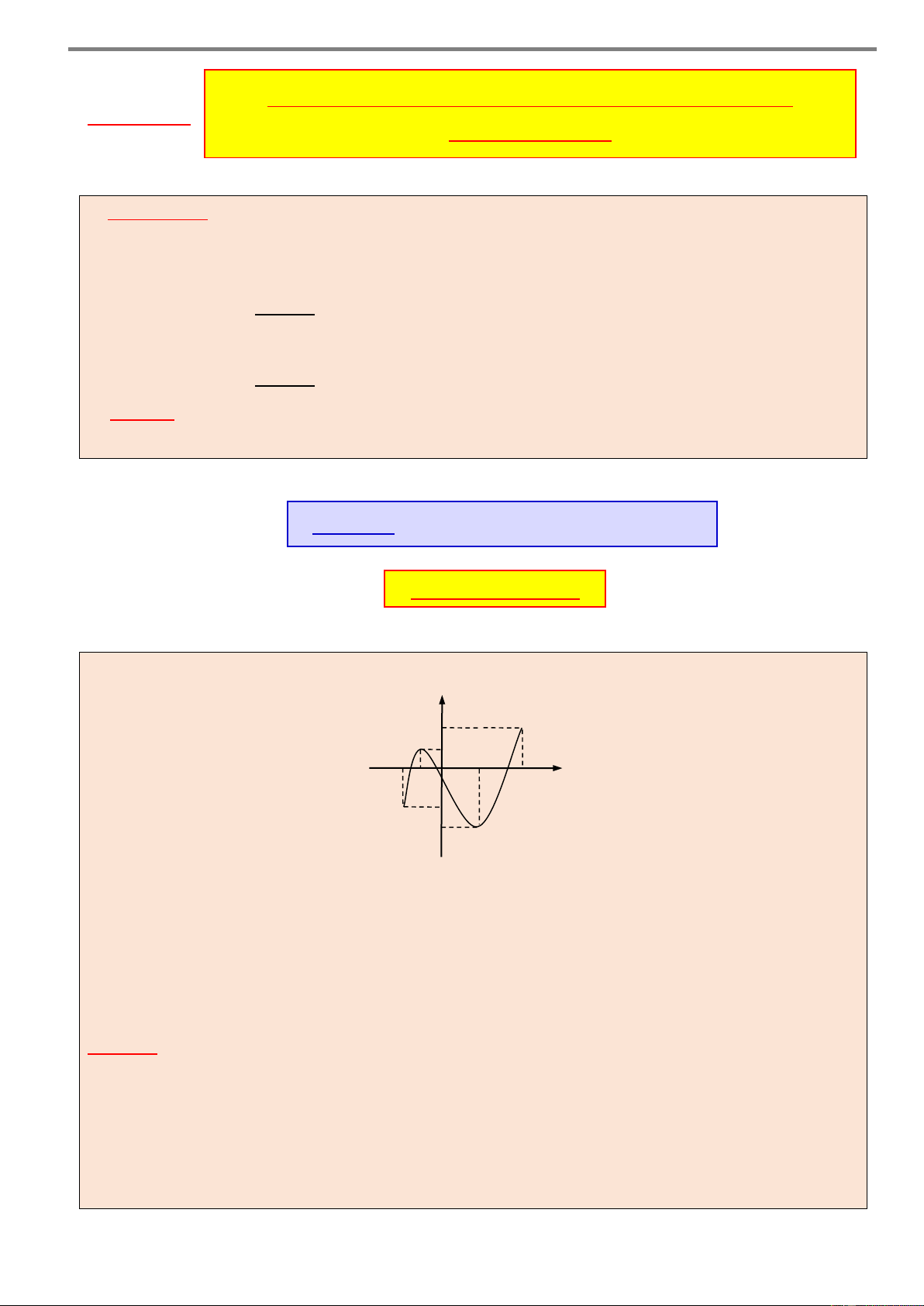
Ví dụ 2. Cho hàm số y f x xác định và liên tục trên . Biết đồ thị hàm số y f x tiếp
xúc với trục hoành tại điểm có hoành độ x 1 và cắt trục hoành tại hai điểm có hoành độ lần lượt là x 1
, x 2 như hình vẽ dưới đây y 1 2 –1 O x
Xét tính đơn điệu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
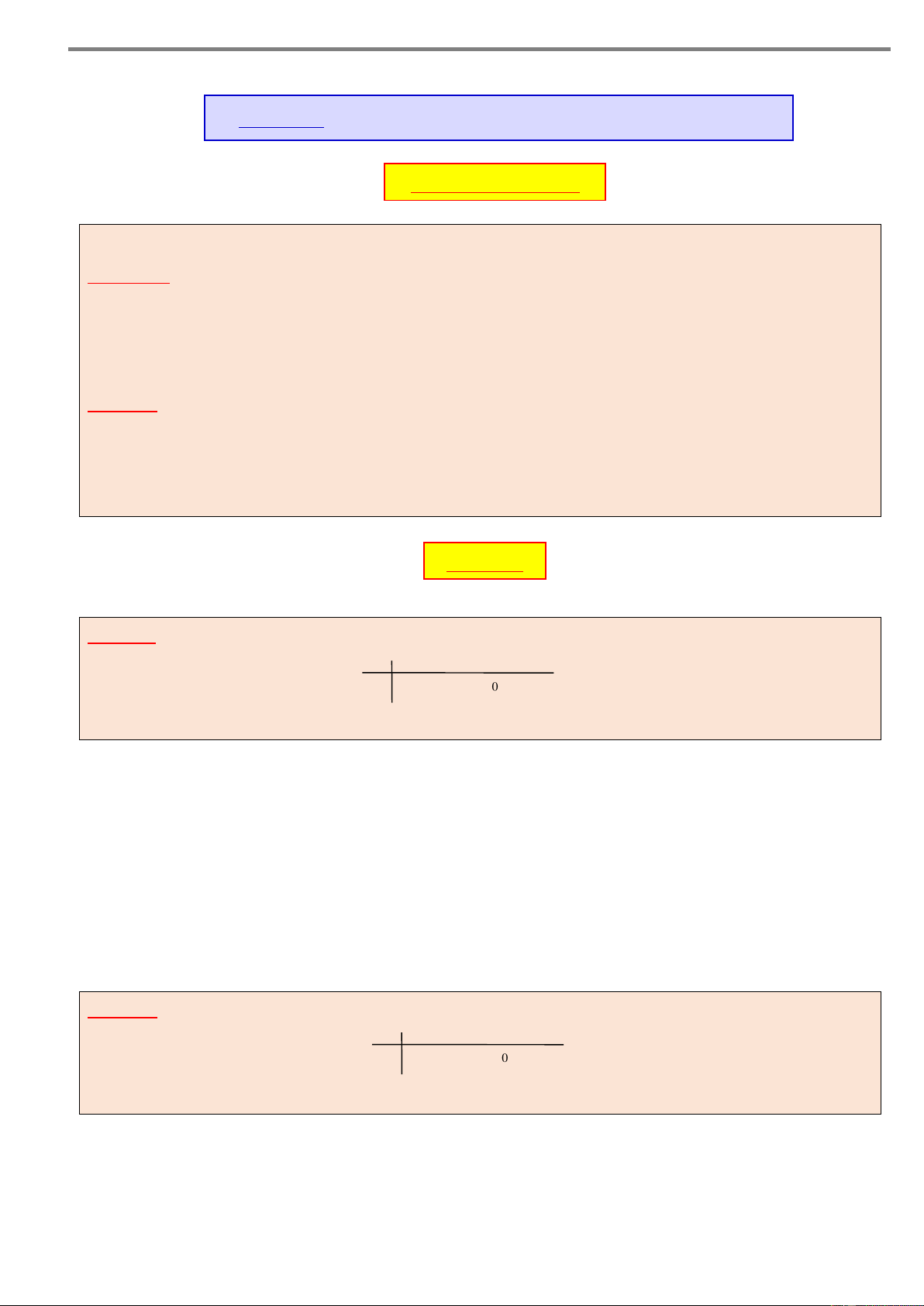
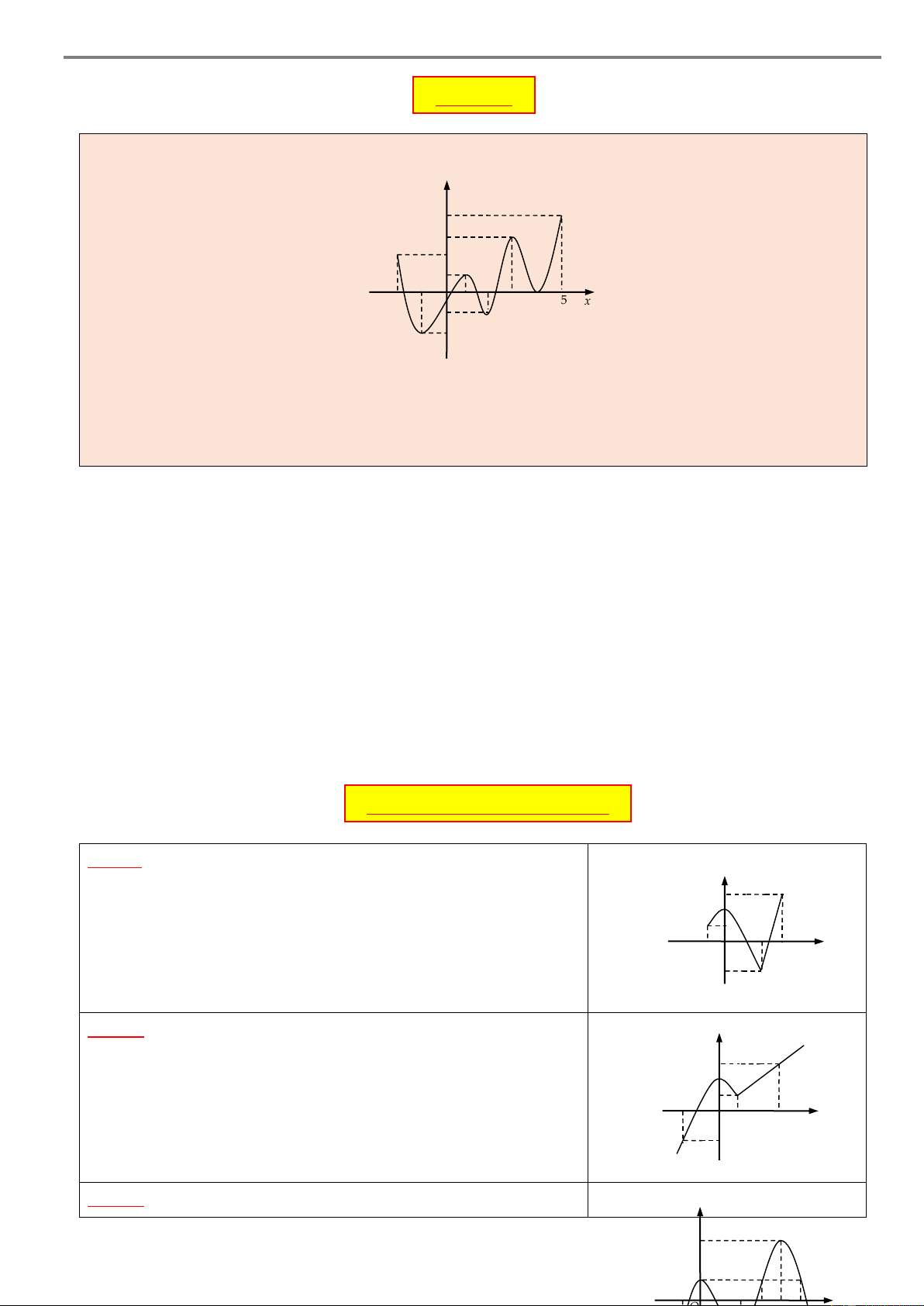
Câu 1. Cho hàm số y f x xác định và liên tục trên . y
Biết đồ thị hàm số y f x chỉ cắt trục hoành tại ba điểm 2
có hoành độ lần lượt là x 1 , x 1
và x 2 như hình vẽ 2
bên, khi đó hàm số y f x nghịch biến trên khoảng –1 1 3 O x A. 0; 2 . B. 1 ;0 . –2 C. 1; 3 . D. 1 ;1.
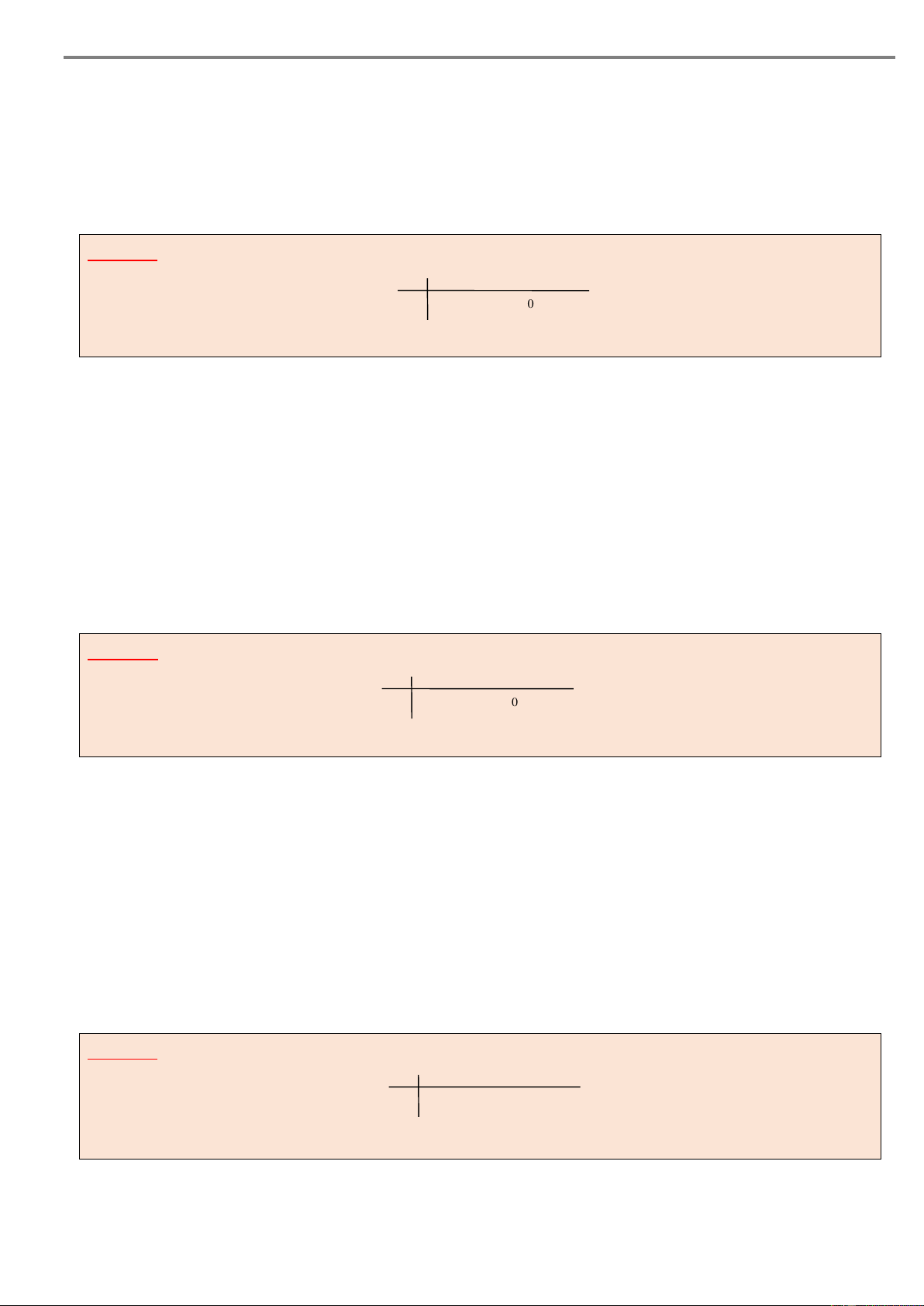
Câu 2. Cho hàm số y f x xác định và liên tục trên . y
Biết đồ thị hàm số y f x chỉ cắt trục hoành tại hai điểm –1 1
có hoành độ lần lượt là x 2
và x 2 như hình vẽ bên, khi –2 O 2 x –1
đó hàm số y f x đồng biến trên khoảng –2 A. ; 2 . B. 1; . C. 1 ;0 . D. 1 ;1.
Câu 3. Cho hàm số y f x xác định và liên tục trên . y
Biết đồ thị hàm số y f x chỉ cắt trục hoành tại bốn điểm –2 O 2 –1 1 x 2 THPT Marie Curie
như hình vẽ bên, khi đó hàm số y f x nghịch biến trên khoảng A. 2 ;0. B. 1 ;1. C. 1; 2 . D. 0; 2 .
Câu 4. Cho hàm số y f x xác định và liên tục trên . y
Biết đồ thị hàm số y f x tiếp xúc với trục hoành tại
điểm có hoành độ x 2 và cắt trục hoành tại hai điểm có –2 1
hoành độ lần lượt là x 2
, x 1 như hình vẽ bên, khi đó O 2 x
hàm số y f x đồng biến trên khoảng A. 2 ;0. B. 0; 1 . C. 1; 2 . D. 0; 2 .
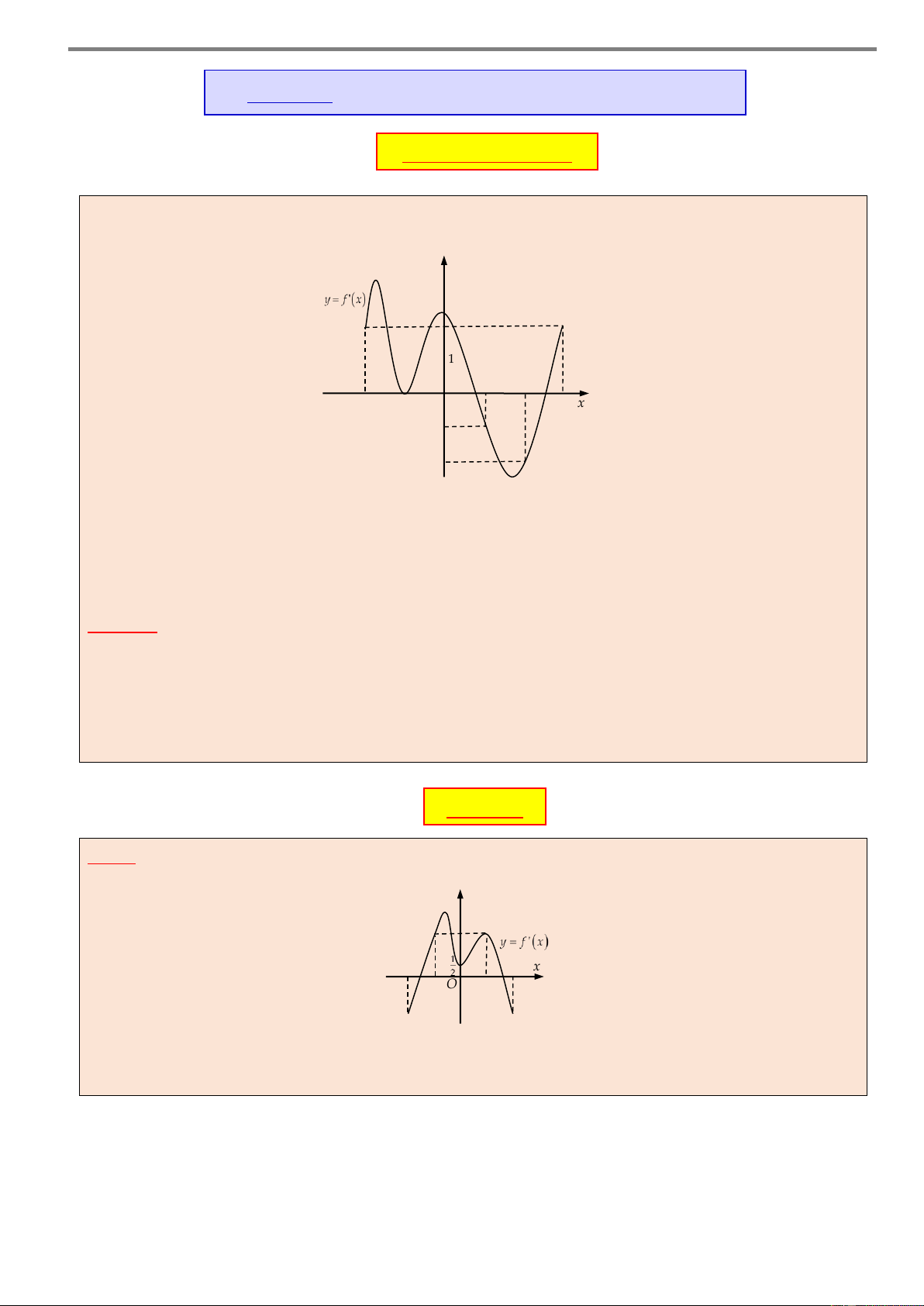
Câu 5. Cho hàm số y f x xác định và có đạo hàm liên y tục trên khoảng ;
m n . Biết đồ thị của hàm số y f x trên khoảng ;
m n tiếp xúc với trục hoành tại điểm có hoành độ
là x a và cắt trục hoành tại hai điểm có hoành độ lần lượt m O a b c n x
là x b , x c như hình vẽ bên, khi đó hàm số y f x
nghịch biến trên khoảng A. ; m a. B. ; a b . C. ; b c .
D. c; n . 3 THPT Marie Curie
DẠNG 7. XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ HỢP A. PHƯ ƠNG PHÁP
Cho hàm số y f x . Xét tính đơn điệu của hàm số gx f ( u ) x . Cách giải
Tính đạo hàm: gx u ( ) x . f ( u ) x
Dựa vào dấu của f x để xét dấu gx , từ đó tìm được các khoảng đồng biến và nghịch
biến của hàm số gx f ( u ) x . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Cho hàm số f x có bảng xét dấu của fx như hình bên dưới x – 2 4 + 1 – f’(x) 0 + 0 +
Xét tính đơn điệu của hàm số y f x 2 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới x – –1 2 + 1 + 0 – f’(x) 0 +
Xét tính đơn điệu của hàm số y f 2x 3 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Cho hàm số f x có bảng xét dấu của fx như hình bên dưới x – –4 –2 + 1 f’(x) – 0 – 0 +
Xét tính đơn điệu của hàm số y f 3 x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới x – –3 5 + 1 f’(x) – 0 + 0 –
Xét tính đơn điệu của hàm số y f 4 2x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Cho hàm số f x có bảng xét dấu của fx như hình bên dưới x – 1 + – f’(x) + 0
Xét tính đơn điệu của hàm số 2 y f x . Lời giải 2 THPT Marie Curie
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới x – 4 + f’(x) – 0 +
Xét tính đơn điệu của hàm số y f 2 x 3x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số f x liên tục và đồng biến trên 1;3,
khi đó hàm số y f 1 x nghịch biến trên khoảng A. 2 ;0. B. 1; 3 . C. 0; 2 . D. 3 ; 1 .
Câu 2. Cho hàm số f x liên tục và đồng biến trên 1 ;2 ,
khi đó hàm số y f x 2 đồng biến trên khoảng A. 1 ;2 . B. 1; 4 . C. 3 ;0 . D. 2 ; 4 .
Câu 3. Cho hàm số f x có bảng xét dấu của fx như hình bên dưới. 3
Tài liệu học tập Toán 12
Hàm số y f x 3 nghịch biến trên khoảng x – –4 0 5 + 1 f’(x)
+ 0 + 0 – 0 + A. 0; 5 . B. ; 4 . C. 1 ;3 . D. 3; 8 .
Câu 4. Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới. x – –1 6 + 1 f’(x) + 0 – 0 +
Hàm số y f 2 x đồng biến trên khoảng A. 3 ;4. B. 1 ;6 . C. 4 ;3. D. 3; .
Câu 5. Cho hàm số f x có bảng xét dấu của fx như hình bên dưới. x – 5 1 + 1 f’(x) – 0 + 0 –
Hàm số y f 1 2x 3 nghịch biến trên khoảng A. 1; 3 . B. 2 ;0. C. ;1 . D. 5; .
Câu 6. Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới. x
– –3 –1 1 + f’(x)
– 0 + 0 – 0 +
Hàm số y f 3 2x đồng biến trên khoảng A. ; 3 . B. 2; 3 . C. 3; 4 . D. 0; 2 .
Câu 7. Cho hàm số f x có bảng xét dấu của đạo hàm như hình bên dưới. x
– –1 1 4 + f’(x)
– 0 + 0 – 0 +
Hàm số g x f 2
x 1 nghịch biến trên khoảng nào sau đây? A. ; 0 . B. 0; . C. 3; . D. 0; 3 . 4 THPT Marie Curie
DẠNG 8. BÀI TOÁN MANG THAM SỐ A. PHƯ ƠNG PHÁP Xem các bài toán sau: ax b
Bài toán 1: Tìm tham số để hàm số y
đồng biến (hoặc nghịch biến) trên từng cx d khoảng xác định. Cách giải ad bc Tính y . cx d2 d
Hàm số đồng biến trên từng khoảng xác định y' 0, x
ad bc 0 . c d
Hàm số nghịch biến trên từng khoảng xác định y' 0, x
ad bc 0 . c
Chú ý: Điều kiện: y' 0 (hoặc y' 0 ) không có dấu “ = “.
Bài toán 2: Tìm tham số để hàm số 3 2
y ax bx cx d a 0 luôn đồng biến (hoặc nghịch biến) Cách giải Tính 2
y' 3ax 2bx c . 2 ' 0
b 3ac 0
Hàm số luôn đồng biến y ' 0, x . a 0 a 0 2 ' 0
b 3ac 0
Hàm số luôn nghịch biến y ' 0, x . a 0 a 0 Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. (m 1)x 2m
Tìm m để hàm số y
đồng biến trên từng khoảng xác định. x m Lời giải
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
....................................................................................................................................................................... Ví dụ 2. mx 2m 2
Tìm m để hàm số y
nghịch biến trên từng khoảng xác định. x m 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Tìm m để hàm số 3 2 2 3
y x mx (m 3m)x m 2 luôn đồng biến. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 4. 1
Tìm m để hàm số 3 2 y
x (m 2)x (m 2)x m luôn nghịch biến. 3 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Tập hợp tất cả các giá trị thực của tham số m để (m 2)x 3 hàm số y
nghịch biến trên từng khoảng xác x 1 định của nó là A. 1; . B. ;1 . C. 1; . D. ;1 . Câu 2. mx 4m
Cho hàm số y
với m là tham số. Gọi S x m
là tập hợp tất cả các giá trị nguyên của m để hàm số đã cho
nghịch biến trên các khoảng xác định. Số phần tử của S là A. 5. B. 4. C. Vô số. D. 3. Câu 3. x m
Cho hàm số y
. Có bao nhiêu giá trị nguyên x 1 2 THPT Marie Curie
của tham số m thuộc khoảng 1
0;10 để hàm số đã cho
đồng biến trên từng khoảng xác định của nó? A. 8. B. 9. C. 10. D. 11. Câu 4. Cho hàm số 3 2
y x mx 4m 9 x 5 với m là
tham số. Có bao nhiêu giá trị nguyên của m để hàm số đã
cho nghịch biến trên khoảng ; ? A. 7. B. 4. C. 6. D. 5.
Câu 5. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2
y x mx 3x 1 đồng biến trên khoảng ; ? A. 8. B. 4. C. 6. D. Vô số. Câu 6. 1 Cho hàm số 3 2
y x mx 4m 3 x 2 . Giá trị 3
lớn nhất của m để hàm số đồng biến trên ; là A. m 1. B. m 2 . C. m 0 . D. m 3 . 3 THPT Marie Curie VẤN ĐỀ 2.
CỰC TRỊ CỦA HÀM SỐ Định nghĩa
Cho hàm số y f x xác định và liên tục trên khoảng ;
a b và điểm x ; a b 0
Nếu tồn tại số h 0 sao cho f x f x , x
x h; x h \ x thì ta nói hàm số 0 0 0 0
y f x đạt cực đại tại x . 0
Nếu tồn tại số h 0 sao cho f x f x , x
x h; x h \ x thì ta nói hàm số 0 0 0 0
y f x đạt cực tiểu tại x . 0 Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
DẠNG 1. DỰA VÀO BẢNG BIẾN THIÊN A. PHƯƠNG PHÁP
Cho hàm số y f x có bảng biến thiên như sau x – a c + y’ – 0 + – d y b Khi đó:
x a là điểm cực tiểu của hàm số, hoặc hàm số đạt cực tiểu tại x a .
x b là điểm cực đại của hàm số, hoặc hàm số đạt cực đại tại x a . M ;
a b là điểm cực tiểu của đồ thị hàm số. N ;
c d là điểm cực đại của đồ thị hàm số.
y b là giá trị cực tiểu của hàm số.
y d là giá trị cực đại của hàm số. Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12 B. VÍ DỤ
Ví dụ 1. Cho hàm số y f x có bảng biến thiên như sau x – –4 1 2 + y’ 1 + 0 – 0 + 0 – 5 3 y –1 – – 1
Tìm điểm cực đại, điểm cực tiểu, giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số y f x có bảng biến thiên như sau x – –1 2 5 + y’ 1 – 0 + – 0 – + 3 y 1 –1 –
Tìm điểm cực đại, điểm cực tiểu, giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... C. CÂU HỎ I TRẮC NGHIỆM
Câu 1. Cho hàm số y f x có bảng biến thiên như hình x – 1 +
bên. Hàm số đã cho có bao nhiêu cực trị? y’ – – + A. 2 . B. 1 . 2 y C. 3 . D. 0 . – 2
Câu 2. Cho hàm số y f x có bảng biến thiên như hình x – 1 2 + y’ + + –
bên. Hàm số đã cho có bao nhiêu cực đại? + 3 y A. 2 . B. 1 . – – – C. 3 . D. 0 . 2 THPT Marie Curie
Câu 3. Cho hàm số y f x có bảng biến thiên như hình – x 0 3 +
bên. Hàm số đã cho có bao nhiêu cực trị? y’ – 0 + – A. 2 . B. 1 . 8 4 C. 3 . D. 4 . y 1 2
Câu 4. Cho hàm số y f (x) xác định, liên tục trên và x – 1 2 +
có bảng biến thiên như hình bên. Hàm số đã cho có bao y’ + – + +∞ nhiêu điểm cực trị? 3 y A. 3. B. 1. –4 –5 C. 0. D. 2.
Câu 5. Cho hàm số y f x có bảng biến thiên như hình x – 1 5 +
bên. Hàm số đã cho có bao nhiêu điểm cực tiểu? y’ + 0 – – + A. 2 . B. 1 . 3 y C. 3 . D. 0 . – – 4
Câu 6. Cho hàm số y f x có bảng biến thiên như hình
x – –1 2 5 +
bên. Hàm số đã cho có bao nhiêu cực trị? y’ 1 + 0 + + 0 – + A. 2 . B. 1 . 3 y 1 C. 3 . D. 4 . – – –2
Câu 7. Cho hàm số y f x có bảng biến thiên như hình x – –2 0 2 +
bên. Hàm số đã cho đạt cực tiểu tại điểm y’ 1 + 0 – 0 + 0 –
A. x 0 . B. x 1 . 3 3 C. x 2
. D. x 2. y –1 – – 1
Câu 8. Cho hàm số y f x có bảng biến thiên như hình x – –4 6 +
bên. Điểm cực đại của hàm số đã cho là y’ 1 + – 0 0 – A. x 4
. B. x 7 . + 7 y 3 C. x 2
. D. x 6. –2 –
Câu 9. Cho hàm số y f x có bảng biến thiên như hình x – –3 0 3 + 1
bên. Giá trị cực tiểu của hàm số đã cho bằng y’ + 0 – 0 + 0 – A. 0 . 0 0 B. 3 . y 5 – – C. . D. 3 . 3
Câu 10. Cho hàm số y f x có bảng biến thiên như hình x – –2 2 +
bên. Giá trị cực đại của hàm số đã cho bằng y’ 1 + 0 – 0 + A. 3 . B. 2 . + 3 y C. 2 . D. 0 . 0 –
Câu 11. Cho hàm số y f x có bảng biến thiên như hình x – –1 0 1 + 1
bên. Mệnh đề nào dưới đây sai? y’
– 0 + 0 – 0 + + +
A. Hàm số có ba điểm cực trị. 3 y
B. Hàm số có giá trị cực đại bằng 3. 0 0
C. Hàm số có giá trị cực đại bằng 0. 3
Tài liệu học tập Toán 12
D. Hàm số có hai điểm cực tiểu.
Câu 12. Cho hàm số có bảng biến thiên như hình bên. x – –1 2 +
Mệnh đề nào dưới đây đúng? y’ + 0 – 0 +
A. Hàm số có bốn điểm cực trị. 4 2 y
B. Hàm số đạt cực tiểu tại x 2 . 2 –5
C. Hàm số không có cực đại.
D. Hàm số đạt cực tiểu tại x 5 .
Câu 13. Hàm số y f (x) có bảng biến thiên như hình bên. x – 0 1 +
Trong các mệnh đề sau, mênh đề nào đúng? y’ + 0 – 0 +
A. Hàm số có giá trị cực đại bằng 5 . 5 + y
B. Hàm số có giá trị cực tiểu bằng 1 . – –1
C. Hàm số có giá trị cực đại bằng 1 .
D. Hàm số có giá trị cực đại bằng 0 .
Câu 14. Cho hàm số y f (x) liên tục trên và có bảng x – –1 2 +
biến thiên như hình bên. Mệnh đề nào sau đây đúng? y’ 1 + – 0 + +
A. Hàm số y f (x) đạt cực đại tại x 1. 1 y
B. Hàm số y f (x) đạt cực tiểu tại x 2. –2 –
C. Hàm số y f (x) đạt cực đại tại x 1.
D. Hàm số y f (x) không đạt cực trị tại x 1.
Câu 15. Cho hàm số f x liên tục trên và có bảng biến x – –1 2 5 +
thiên như hình bên. Khẳng định nào sau đây đúng? y’ 1 – 0 + – 0 –
A. Hàm số có 1 cực đại và 2 cực tiểu. + 3 y 1
B. Hàm số có 1 cực đại và 1 cực tiểu. –1 –
C. Hàm số có đúng 1 cực trị.
D. Hàm số có 2 cực đại và 1 cực tiểu.
Câu 16. Cho hàm số y f x có bảng biến thiên như hình x – –2 1 4 +
bên. Tổng các giá trị cực tiểu của hàm số đã cho bằng y’ 1 – 0 + 0 – 0 + A. 2 . B. 5 . + + 6 C. 11 . y D. 3 . 3 2
Câu 17. Cho hàm số y f x có bảng biến thiên như hình x – –3 4 + 1
bên. Tổng các giá trị cực đại và giá trị cực tiểu của hàm số y’ + – 0 0 – + 5 đã cho bằng y 3 A. 9. B. 1. C. 1 . D. 6. 1 –
Câu 18. Cho hàm số y f x có bảng biến thiên như hình x – 0 1 +
bên. Tổng các điểm cực đại và điểm cực tiểu của hàm số đã y’ + 0 – 0 + 5 + cho bằng y A. 5 . B. 1.
C. 4. D. 3. – –1
Câu 19. Cho hàm số y f x có bảng biến thiên như hình x – –7 –2 3 +
bên. Tổng các điểm cực trị của hàm số đã cho bằng y’ 1 + 0 – – 0 +
A. 2. B. 1. C. 4 . D. 6 . + + –4 y – – 6 4 THPT Marie Curie 5 THPT Marie Curie
DẠNG 2. DỰA VÀO BẢNG XÉT DẤU ĐẠO HÀM A. PHƯƠNG PHÁP
Cho hàm số y f x có bảng xét dấu đạo như sau x – –4 2 5 + y’
– 0 – 0 + 0 –
Từ bảng xét dấu y ' ta phát họa: x – –4 2 5 + y’
– 0 – 0 + 0 – Khi đó:
Hàm số đã cho có 2 cực trị, trong đó:
x 2 là điểm cực tiểu của hàm số.
x 5 là điểm cực đại của hàm số. B. VÍ DỤ
Ví dụ 1. Cho hàm số y f x có bảng xét dấu đạo hàm như sau x – –7 4 8 + y’
+ 0 – 0 – 0 +
Tìm điểm cực đại, điểm cực tiểu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số y f x xác định trên \
1 và có bảng xét dấu đạo hàm như sau x – –1 1 2 3 4 5 + y’ 1 – 0 +
– 0 – 0 + – 0 +
Tìm điểm cực đại, điểm cực tiểu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Chú ý 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số y f x xác định trên \ 1 và có x – 1 2 +
bảng xét dấu của đạo hàm như hình vẽ bên. Hàm số đã cho y’ – + – có bao nhiêu cực trị? A. 0. B. 1. C. 3. D. 2.
Câu 2. Cho hàm số y f x xác định trên \ 5 và có x – 1 3 5 +
bảng xét dấu của đạo hàm như hình vẽ bên. Hàm số đã cho y’ – + 0 – + có bao nhiêu cực trị? A. 4. B. 1. C. 3. D. 2.
Câu 3. Cho hàm số y f x xác định trên và có bảng x – 0 2 +
xét dấu của đạo hàm như hình vẽ bên. Hàm số đã cho đạt y’ – 0 + 0 – cực tiểu tại A. x 0. B. x 2. C. y 0. D. y 2.
Câu 4. Cho hàm số y f (x) liên tục trên và có bảng xét x – –1 2 4 +
dấu y ' như hình bên. Hàm số đã cho đạt cực đại tại y’ + 0 – 0 – 0 + A. x 2. B. x 4. C. x 1. D. x 1 và x 4.
Câu 5. Cho hàm số y f x có bảng xét dấu của đạo x – –2 1 3 +
hàm như hình bên. Hàm số y f x có bao nhiêu điểm y’
– 0 + 0 + 0 – cực đại? A. 2. B. 1. C. 3. D. 0. 2 THPT Marie Curie
DẠNG 3. DỰA VÀO BIỂU THỨC CỦA ĐẠO HÀM A. PHƯƠNG PHÁP
Phương trình f 'x 0 có bao nhiêu nghiệm bội lẻ thì hàm số y f x có bấy nhiêu điểm cực trị. Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. 2 5
Cho hàm số f x có đạo hàm f x 3
x x x 2 ' 1 6 x x 1 , x . Hỏi hàm
số đã cho có bao nhiêu điểm cực trị? Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 2. 2 3
Cho hàm số f x có đạo hàm f x x 2 ' 2
x x 6x 4 , x . Hỏi hàm
số đã cho có bao nhiêu điểm cực trị? Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 3. 3
Cho hàm số f x có đạo hàm f x x 2
x x 2 ' 1
2 x 93 , x . Hỏi hàm
số đã cho có bao nhiêu điểm cực trị, trong đó có bao nhiêu điểm cực đại và bao nhiêu điểm cực tiểu? Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM Câu 1. Cho hàm số f x có đạo hàm
f x x x x 3 1 2 , x
. Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 5 . D. 1 . Câu 2. Cho hàm số f x có đạo hàm
f x x x 4 x 3 1 2 , x
. Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 8 . D. 1 . Câu 3. Cho hàm số f x có đạo hàm
f x x x 2 x 3 5 1 2 , x
. Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 8 . D. 1 . Câu 4. Cho hàm số f x có đạo hàm
f x x x 2 x 4 ' 1 1 , x
. Số điểm cực tiểu của hàm số đã cho là A. 3. B. 2. C. 0. D. 1. Câu 5. Cho hàm số f x có đạo hàm
f x x x 2 x 3 1 2 , x
. Hàm số đã cho đạt cực đại tại A. x 2 . B. x 0 . C. x 1. D. x 2 . Câu 6. Cho hàm số f x có đạo hàm f x 3
x x
1 x 2 , x
. Điểm cực tiểu của hàm số đã cho là
A. x 0 hay x 2 . B. x 2.
C. x 1 hay x 2 . D. x 1. Câu 7. Cho hàm số
y f x có 2 THPT Marie Curie
f x x x 2 x 4 x 3 ' 2 1 2 , x
. Hàm số đã cho đạt cực đại tại A. x 2 . B. x 1. C. x 0 . D. x 2 . 3 THPT Marie Curie
DẠNG 4. DỰA VÀO BIỂU THỨC CỦA HÀM SỐ A. PHƯƠNG PHÁP
Lập bảng biến thiên cho hàm số y f x từ đó kết luận về cực trị của hàm số y f x . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. 1 Cho hàm số 3 2
y x x 3x 1. Tìm điểm cực đại, điểm cực tiểu, giá trị cực đại và 3
giá trị cực tiểu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 2. Cho hàm số 4 2
y x 4x 2 . Tìm điểm cực đại, điểm cực tiểu, giá trị cực đại và giá
trị cực tiểu của hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM 1
Tài liệu học tập Toán 12 4 Câu 1. x Cho hàm số 2 y
2x . Mệnh đề nào dưới đây 4 đúng?
A. Hàm số có giá trị cực tiểu là y 1.
B. Hàm số đạt cực đại tại điểm x 0 .
C. Hàm số đạt cực đại tại các điểm x 2 và x 2 .
D. Hàm số có giá trị cực đại là y 0 . Câu 2. 2x 3 Hàm số y có bao nhiêu cực trị? x 1 A. 3. B. 0. C.2. D.1.
Câu 3. Giá trị cực đại của hàm số 3
y x 3x 2 bằng A. 4. B. 1. C. 0. D. –1. 2 THPT Marie Curie
DẠNG 5. DỰA VÀO ĐỒ THỊ HÀM SỐ A. P HƯƠNG PHÁP Lý thuyết
Cho hàm số y f x liên tục trên khoảng ;
a b và có đồ thị như sau y 2 O 1 3 4 –4 – 3 x –2 –7 Khi đó:
Hàm số đạt cực đại tại x 3 và x 3.
Hàm số đạt cực tiểu tại x 1. A 3
;2 và B3;0 là các điểm cực đại của đồ thị hàm số. C 1; 2
là điểm cực tiểu của đồ thị hàm số.
y 2 và y 0 là các giá trị cực đại của hàm số.
y 2 là giá trị cực tiểu của hàm số.
Đồ thị hàm số chứa trị tuyệt đối
Cho hàm số y f x có đồ thị C . Khi đó:
1. Đồ thị hàm số y f x vẽ như sau:
Bên trên trục Ox : Giữ nguyên đồ thị C .
Bỏ phần đồ thị C bên dưới trục Ox và lấy phần bỏ này đối xứng qua trục Ox .
2. Đồ thị hàm số y f x vẽ như sau:
Bên phải trục Oy : Giữ nguyên đồ thị C .
Bỏ phần đồ thị C bên phải trục Oy và lấy phần C giữ nguyên ở trên đối xứng qua trục Oy . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ 1
Tài liệu học tập Toán 12
Ví dụ 1. Cho hàm số y f x có đồ thị như hình sau y 2 1 x –1 O 1
1. Tìm điểm cực đại, điểm cực tiểu, giá trị cực đại và giá trị cực tiểu của hàm số đã cho.
2. Tìm số điểm cực trị của hàm số y f x . Lời giải
....................................................................................................................................................................... y
....................................................................................................................................................................... 2
.......................................................................................................................................................................
................................................................................................................................................................ 1 ....... x –1 O 1
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số y f x có đồ thị như hình sau y 2 O –1 2 x –2
1. Tìm điểm cực đại, điểm cực tiểu, giá trị cực đại và giá trị cực tiểu của hàm số đã cho.
2. Tìm số điểm cực trị của hàm số y f x . Lời giải
....................................................................................................................................................................... y
....................................................................................................................................................................... 2
................................................................................................................................................................ O .......
................................................................................................................................................................ –1 2 ....... x
................................................................................................................................................................ –2 .......
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM 2 THPT Marie Curie
Câu 1. Cho hàm số y f x liên tục trên a;b và có đồ y
thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là a A. 4. B. 5. O b – x C. 6. D. 3.
Câu 2. Cho hàm số y f x liên tục trên a;b và có đồ y
thị như hình vẽ bên. Số điểm cực tiểu của hàm số đã cho là b a O x A. 6. B. 4. C. 3. D. 2.
Câu 3. Cho hàm số y f x liên tục trên a;b và có đồ y
thị như hình vẽ bên. Số điểm cực đại của hàm số đã cho là A. 4. B. 1. a O b x C. 2. D. 3.
Câu 4. Cho hàm số y f x liên tục trên a;b và có đồ y
thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là A. 1. B. 0. a O b x C. 2. D. 3.
Câu 5. Cho hàm số y f (x) xác định, liên tục trên đoạn y 4 2; 2
và có đồ thị là đường cong trong hình vẽ bên. Hàm 2 –2 1
số y f (x) đạt cực đại tại O 2 x –1 –2 A. x 2 . B. x 1 . –4 C. x 1. D. x 2 .
Câu 6. Cho hàm số y f x có đồ thị như hình vẽ bên. y 2
Hàm số đã cho đạt cực tiểu tại điểm A. x 1 . B. x 1. 1 x –1 O 1 C. x 0 . D. x 2 .
Câu 7. Cho hàm số y f x có đồ thị như hình bên. Hàm y
số đã cho đạt cực tiểu tại điểm A. x 2 . B. x 3 . –1 O 2 – x 1 C. x 2 . D. x 0 . –2 –3 Câu 8. Cho hàm số 3 2
y ax bx cx d có đồ thị như y
hình vẽ bên. Số điểm cực trị của hàm số 3 2
y a x bx c x d là O x A. 2. B. 3. C. 5. D. 4. Câu 9. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ y
bên. Số điểm cực trị của hàm số 4 2
y ax bx c là A. 2. B. 5. x O C. 4. D. 3. 3
Tài liệu học tập Toán 12 Câu 10. Cho hàm số 3 2
y ax bx cx d có đồ thị như y
hình vẽ bên. Số điểm cực trị của hàm số 3 2 O x
y a x bx c x d là A. 0. B. 1. C. 3. D. 2. Câu 11. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ y
bên. Số điểm cực đại của hàm số 4 2
y ax bx c là x A. 3. B. 5. O C. 6. D. 7. Câu 12. Cho hàm số 3 2
y ax bx cx d a,b,c,d có
đồ thị như hình vẽ bên. Số điểm cực tiểu của hàm số y 3 2
y ax bx cx d là O x A. 2. B. 4. C. 5. D. 3. Câu 13. Cho hàm số 3 2
y 4x – 6x 1 có đồ thị như hình vẽ y
bên. Tổng các giá trị cực đại của hàm số 3 2
y 4x – 6x 1 1 1 bằng O x A. 5. B. 2. 1 C. 3. D. 1.
Câu 14. Cho hàm số y f x có đồ thị như hình bên. Tổng y
các giá trị cực đại của hàm số y f x bằng –1 O 2 A. 5 . B. 1 . – x 1 – C. 1 . D. 6 . 2 –3
Câu 15. Cho hàm số y f x có đồ thị như hình vẽ bên. y
Tổng các giá trị cực tiểu của hàm số y f x bằng 2 A. 2 . B. 3 . 1 x –1 O 1 C. 4 . D. 1 . 4 THPT Marie Curie
DẠNG 6. DỰA VÀO ĐỒ THỊ CỦA ĐẠO HÀM A. PHƯƠNG PHÁP
Cho hàm số y f x có đạo hàm liên tục trên 2; 3
và y f 'x có đồ thị như hình vẽ sau y 2 1 1 2 –2 O 3 –1 x –1 –2
Hàm số y f x có bao nhiêu điểm cực trị?
Đồ thị hàm số y f 'x cắt trục Ox tại 2 điểm Phương trình f 'x 0 có 2 nghiệm đơn
Do đó hàm số y f x có 2 điểm cực trị. Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ: Cho hàm số y f x có đạo hàm liên tục trên 2; 2
và y f 'x có đồ thị như hình sau y 2 –2 2 x –1 O 1
1. Hàm số y f x có bao nhiêu điểm cực trị?
2. Hàm số y f x có bao nhiêu điểm cực tiểu và bao nhiêu điểm cực đại? Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số y f x có đạo hàm liên tục trên y
;ab và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực trị? A. 1. B. 2. a O b x C. 3. D. 0.
Câu 2. Cho hàm số y f x có đạo hàm liên tục trên y
;ab và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực trị? a A. 1. B. 2. O b x C. 3. D. 0.
Câu 3. Cho hàm số y f x có đạo hàm liên tục trên y
;ab và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực trị? O a b x A. 1. B. 2. C. 3. D. 4.
Câu 4. Cho hàm số y f x có đạo hàm liên tục trên y ;
a b và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực trị? a O b x A. 1. B. 2. C. 3. D. 4.
Câu 5. Cho hàm số y f x có đạo hàm liên tục trên y
;ab và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực trị? a O b x A. 1. B. 2. C. 3. D. 4.
Câu 6. Cho hàm số y f x và hàm số y' f 'x có đồ y
thị như hình bên. Khi đó hàm số y f x có bao nhiêu điểm cực tiểu? O 1 2 3 x A. 1. B. 2. 2 THPT Marie Curie C. 3. D. 0.
Câu 7. Cho hàm số y f x có đạo hàm liên tục trên y ;
a b và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực tiểu? O A. 1. B. 2. a b x C. 3. D. 0.
Câu 8. Cho hàm số y f x có đạo hàm liên tục trên y
;ab và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực đại? a O b x A. 1. B. 2. C. 3. D. 0.
Câu 9. Cho hàm số y f x có đạo hàm liên tục trên y
;ab và y f 'x có đồ thị như hình vẽ bên. Trên khoảng
;ab, hàm số y f x có bao nhiêu điểm cực đại? a O b x A. 1. B. 2. C. 3. D. 0. 3 THPT Marie Curie
GIÁ TRỊ NHỎ NHẤT VÀ GIÁ TRỊ LỚN NHẤT VẤN ĐỀ 3. CỦA HÀM SỐ 1. Định nghĩa
Cho hàm số y f x xác định trên D .
Nếu f x M, x
D và x D sao cho f x M thì M gọi là giá trị lớn nhất của hàm 0 0
số y f x trên D . Kí hiệu: max f x M . D
Nếu f x m, x D và x D 0
sao cho f x m thì m gọi là giá trị nhỏ nhất của hàm 0
số y f x trên D . Kí hiệu: min f x m . D 2. Định lý
Mọi hàm số liên tục trên a; b
đều tồn tại giá trị nhỏ nhất và giá trị lớn nhất trên đoạn a;b .
DẠNG 1. DỰA VÀO ĐỒ THỊ HÀM SỐ A. PHƯƠNG PHÁP
Cho hàm số y f x liên tục trên 2; 4
và có đồ thị như sau y 2 1 1 –2 2 1 ––1 O 1 4 x –2 –3 Khi đó:
GTNN của hàm số y f x trên 2; 4 bằng 3
và ghi min f x f 2 3 . 2 ;4
GTNN của hàm số y f x trên 2; 0 bằng 2
và ghi min f x f 2 2 . 2 ;0
GTLN của hàm số y f x trên 2; 4
bằng 2 và ghi max f x f 4 2 . 2 ;4
GTLN của hàm số y f x trên 2; 0
bằng 1 và ghi max f x f 1 1 . 2 ;0 Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12 B. VÍ DỤ
Ví dụ: Cho hàm số y f x liên tục trên 2; 5
và có đồ thị như sau y 4 3 2 1 –1 2 –2 O 1 3 4 5 x –1 –2
Tìm GTNN và GTLN của hàm số đã cho (nếu có) trên các đoạn sau: 1. 2; 0. 2. 0; 2. 3. 0; 3. 4. 2; 3. 5. 1 ;4. 6. 0; 4. 7. 2; 2. 8. 2; 5. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số y f x liên tục trên đoạn 1 ; 3 và có y
đồ thị như hình bên. Gọi M và m lần lượt là giá trị lớn 3 2
nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 ; 3 . Giá 1 2
trị của M m bằng –1 O 3 x A. 0 . B. 5 . –2 C. 4 . D. 1 .
Câu 2. Cho hàm số y f x liên tục trên đoạn 2; 3 và y
có đồ thị như hình bên. Gọi M và m lần lượt là giá trị lớn 3 2
nhất và nhỏ nhất của hàm số đã cho trên đoạn 2; 3 . Giá 1 –2
trị của M m bằng O 1 3 x A. 5 . B. 1 . –2 C. 4 . D. 2 .
Câu 3. Cho hàm số f x liên tục trên đoạn 1 ; 5 và có y 3 2 1 –1 2 O 3 4 5 x THPT Marie Curie
đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn
nhất và nhỏ nhất của hàm số đã cho trên 1 ; 5 . Giá trị của
M m bằng ? A. 4 . B. 5 . C. 6 . D. 1 .
Câu 4. Cho hàm số y f x liên tục trên đoạn 2; 3 và y
có đồ thị như hình bên. Gọi M và m lần lượt là giá trị lớn 4
nhất và nhỏ nhất của hàm số đã cho trên đoạn 2; 3 . Giá 3 2
trị của M m bằng 1 A. 4 . B. 1 . –2 O 2 3 x C. 3 . D. 2 .
Câu 5. Cho hàm số y f x liên tục trên đoạn 2; 3 và y
có đồ thị như hình bên. Gọi M và m lần lượt là giá trị lớn 4 3
nhất và nhỏ nhất của hàm số đã cho trên đoạn 2; 3 . Giá 2
trị của M m bằng 1 –2 O 2 3 x A. 2 . B. 1 . C. 4 . D. 5 . 3 THPT Marie Curie
DẠNG 2. DỰA VÀO BẢNG BIẾN THIÊN A. PHƯƠNG PHÁP
Cho hàm số y f x liên tục trên ;
và có bảng biến thiên như sau x – –4 –2 1 3 6 8 + y’ 1 1
+ 0 – 0 – + 0 + – 0 + 10 5 6 y 3 4 1 –7 –2 Khi đó:
GTNN của hàm số y f x trên ; 3 bằng 2
và ghi min f x f 1 2 ;3
GTNN của hàm số y f x trên ;
bằng 7 và ghi min f x f 8 7 . ;
GTNN của hàm số y f x trên 4; 2
bằng 3 và ghi min f x 3 . 4 ; 3
GTLN của hàm số y f x trên ; 2
bằng 10 và ghi max f x f 4 10 . ; 2
GTLN của hàm số y f x trên 2
;8 bằng 5 và ghi max f x f 6 5. 2 ;8
GTLN của hàm số y f x trên 2; 3
bằng 4 và ghi max f x 4 . 2 ;3
GTLN của hàm số y f x trên ;
bằng 10 và ghi max f x 10. ;
Hàm số y f x không tồn tại GTNN trên ; 2 .
Hàm số y f x không tồn tại GTLN trên 2; . Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ: Cho hàm số y f x liên tục trên ;
và có bảng biến thiên như sau x – –4 1 6 + 1 y’ + 0 – + – 5 7 y –1 – 2 1
Tìm GTNN và GTLN của hàm số đã cho (nếu có) trên các tập sau: 1
Tài liệu học tập Toán 12 1. ; 4 . 2. ; 4 . 3. ; 1 . 4. ;1. 5. ; 6. 6. ; 6. 7. ; . 8. 6; . 9. 4 ; 1 . 10. 4; 1. 11. 4 ; 1. 12. 4; 1. 13. 4; 6. 14. 4 ;6. 15. 4 ;6 . 16. 4; 6. 17. 4 ; . 18. 4; . 19. 1 ; . 20. 1; . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... C. CÂU HỎ I TRẮC NGHIỆM
Câu 1. Cho hàm số y f (x) liên tục trên và có bảng x – 0 1 +
biến thiên như hình bên. Khẳng định nào sau đây là đúng? y’ + – 0 +
A. Hàm số có giá trị nhỏ nhất bằng 3 . y 5 2
B. Hàm số có giá trị nhỏ nhất bằng 1 . –1 –3
C. Hàm số có giá trị lớn nhất bằng 2.
D. Hàm số có giá trị lớn nhất bằng 5.
Câu 2. Hàm số y f (x) liên tục và có bảng biến thiên x –1 0 2 3 trong đoạn [ 1
; 3] cho trong hình bên. Giá trị lớn nhất của y’ + – 0 +
hàm số y f x trên đoạn 1 ; 3 bằng y 5 4 1 A. f ( 1 ).
B. f 3 . 0
C. f (0) . D. f (2). 2 THPT Marie Curie
Câu 3. Cho hàm số y f x liên tục trên và có bảng x – 0 1 +
biến thiên như hình bên. Mệnh đề nào dưới đây sai? y’ – 0 + – + 5 A. y y CÑ 5 .
B. max y 5 . 1 2 C. y CT 1 .
D. min y 1.
Câu 4. Cho hàm số y f x liên tục trên và có bảng x – –2 1 7 +
biến thiên như hình bên. Mệnh đề nào sau đây đúng? y’ – + 0 – –
A. Hàm số có giá trị lớn nhất bằng 3 . 3 1 y
B. Hàm số có giá trị nhỏ nhất bằng 3 . –3 –4 –4
C. Hàm số có giá trị lớn nhất bằng 1 .
D. Hàm số có giá trị nhỏ nhất bằng 4 .
Câu 5. Cho hàm số y f x liên tục trên và có bảng x – 3 6 +
biến thiên như hình bên. Mệnh đề nào sau đây đúng? y’ – 0 + –
A. Giá trị nhỏ nhất của hàm số bằng 1. 8 4
B. Giá trị lớn nhất của hàm số bằng 4. y 1
C. Giá trị lớn nhất của hàm số bằng 8. 2
D. Giá trị nhỏ nhất của hàm số bằng 2.
Câu 6. Cho hàm số y f x liên tục trên và có bảng x – 0 1 +
biến thiên như hình bên. Mệnh đề nào sau đây đúng? y’ + – 0 + 2 1
A. Giá trị nhỏ nhất của hàm số bằng 2 . y –
B. Giá trị nhỏ nhất của hàm số bằng 3 . 2 –3
C. Giá trị lớn nhất của hàm số bằng 1.
D. Giá trị lớn nhất của hàm số bằng 2.
Câu 7. Cho hàm số y f x liên tục trên ; 2 và có x – –1 2 1
bảng biến thiên như hình bên. Mệnh đề nào sau đây sai? y’ – 0 + 4 5 A. y 3 . B. y . CT CÑ 5 y
C. min y 3 .
D. max y 5 . 3 ;2 ;2 3 THPT Marie Curie
DẠNG 3. DỰA VÀO BIỂU THỨC CỦA HÀM SỐ A. PHƯƠNG PHÁP
Tìm GTLN và GTNN của hàm số y f x liên tục trên a;b . Cách 1
Tính y ' , giải phương trình y' 0 và chỉ nhận những nghiệm x thuộc a; b 0 .
Tính f a , f b và f x . 0
Khi đó: min f x min f a; f b; f x . 0 a;b
max f x max f a; f b; f x . 0 a;b Cách 2 Dùng MTCT
Bước 1. Bấm: MODE 7 màn hình hiện: f(X) =
Bước 2. Nhập biểu thức f x
Bước 3. Bấm: màn hình hiện: Start? Bấm: a
Bước 4. Bấm: màn hình hiện: End? Bấm: b
Bước 5. Bấm: màn hình hiện: Step? Thông thường bấm: 0,1
Bước 6. Bấm: màn hình hiện: Bảng dữ liệu
Cột 1: Giá trị của X từ a đến b . (Mỗi giá trị của X cách nhau 0,1 đơn vị)
Cột 2: Giá trị tương ứng của biểu thức f(X). Khi cột 2 xuất hiện số nhỏ nhất thì đó là giá trị
nhỏ nhất của hàm số, xuất hiện số lớn nhất thì đó là giá trị lớn nhất của hàm số. Chú ý
Nếu hàm số y f x đồng biến trên a;b
thì min f x f a và max f x f b . a;b a;b
Nếu hàm số y f x nghịch biến trên a;b
thì min f x f b và max f x f a . a;b a;b
Nếu tìm GTLN và GTNN của hàm số y f x không phải trên a;b thì lập bảng biến thiên để kết luận.
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 3 2
x 3x 9x 4 trên 4; 4. 1
Tài liệu học tập Toán 12 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 4 2
x 8x 16 trên 1 ; 3 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 3. x
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 2 trên 3 ; 2 . x 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎ I TRẮC NGHIỆM
Câu 1. Giá trị lớn nhất của hàm số 3
f (x) x 3x trên đoạn [3; 3] bằng A. 2 . B. 18 . C. 2. D. 18.
Câu 2. Giá trị nhỏ nhất của hàm số 3
y x 3x 1 trên đoạn 1 ; 4 bằng A. 3. B. 1 . C. 1. D. 4. Câu 3. Giá trị lớn nhất của hàm số f x 3 2
2x 3x 12x 2 trên đoạn 1 ; 2 bằng A. 15. B. 66. 2 THPT Marie Curie C. 11. D. 10.
Câu 4. Giá trị nhỏ nhất của hàm số 3 2
y x 7x 11x 2 trên đoạn 0; 2 bằng A. 11 . B. 0 . C. 2 . D. 3 .
Câu 5. Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số f x 3 2
x 3x 9x 7 trên đoạn 4; 3
. Giá trị M m bằng A. 33 . B. 25 . C. 32 . D. 8 .
Câu 6. Giá trị lớn nhất của hàm số f x 4 2
x 4x 5 trên đoạn 2; 3 bằng A. 50 . B. 5 . C. 1 . D. 122 .
Câu 7. Giá trị nhỏ nhất của hàm số 4 2
y x x 13 trên đoạn 2; 3 bằng 49 51 A. . B. . 4 4 51 C. 13 . D. . 2
Câu 8. Giá trị lớn nhất của hàm số 4 2
y x x 13 trên đoạn 1 ; 2 bằng 51 A. . B. 85. 4 C. 13. D. 25.
Câu 9. Giá trị lớn nhất của hàm số 4 2
y x 2x 3 trên đoạn 0; 3 bằng A. 9 . B. 6 . C. 1 . D. 8 3 .
Câu 10. Giá trị lớn nhất của hàm số 4 2
y x 4x 9 trên đoạn 2; 3 bằng A. 201. B. 2. C. 9. D. 54. Câu 11. 2x 1
Giá trị nhỏ nhất của hàm số y trên đoạn x 1 1 ; 3 bằng 5 A. . B. 2 . 4 1 7 C. . D. . 2 2 3
Tài liệu học tập Toán 12 Câu 12. 3x 1
Cho hàm số y
. Gọi giá trị lớn nhất, giá trị x 3
nhỏ nhất của hàm số trên 0; 2
lần lượt là M và m. Khi đó
m M có giá trị là 14 A. 4. B. . 3 14 3 C. . D. . 3 5 Câu 13. x 1 Hàm số y
đạt giá trị lớn nhất trên đoạn 2x 1 0;2 tại x bằng A. 0. B. 2. 1 C. 1. D. . 2 4 THPT Marie Curie VẤN ĐỀ 4.
TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ 1/ Định nghĩa 1
Trong mặt phẳng Oxy cho điểm M x; y , ta nói điểm M dần tới vô cực, ghi là M , nếu 2 2
OM x y 2/ Định nghĩa 2
Cho hàm số y f x có đồ thị C và đường thẳng d . Gọi M x; y là điểm tùy ý thuộc
C và MH dM,d. y (C) M d H O x
Đường thẳng d gọi là tiệm cận của đồ thị C nếu lim MH 0 . M
DẠNG 1. DỰA VÀO ĐỊNH LÝ A. PHƯƠNG PHÁP
Cho hàm số y f x có đồ thị C . 1. Tiệm cận đứng
Đường thẳng x a là tiệm cận đứng của đồ thị C nếu ít nhất một trong bốn điều kiện
sau được thỏa: lim f x ; lim f x ; lim f x ; lim f x . xa xa xa xa 2. Tiệm cận ngang
Đường thẳng y b là tiệm cận ngang của đồ thị C nếu ít nhất một trong hai điều kiện
sau được thỏa: lim f x b ; lim f x b . x x Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Tìm tất cả tiệm cận đứng của đồ thị hàm số y f x biết: 1
Tài liệu học tập Toán 12
lim f (x) , lim f (x) 3 ; lim f (x) , lim f (x) 2 , lim f (x) ; lim f (x) 6 . x4 x x 7 x5 x1 x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tìm tất cả tiệm cận ngang của đồ thị hàm số y f x biết:
lim f (x) , lim f (x) 1
; lim f (x) , lim f (x) , lim f (x) ; lim f (x) 7 . x3 x x2 x 4 x x5 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số y f (x) có lim f (x) và x2
lim f (x) . Đồ thị hàm số đã cho có tiệm cận đứng là x2 đường thẳng A. y 2 .
B. y 2 và y 2 . C. x 2 .
D. x 2 và x 2 .
Câu 2. Cho hàm số y f (x) có lim f (x) và x
lim f (x) . Khẳng định nào sau đây là đúng? x
A. Đồ thị hàm số có 2 tiệm ngang.
B. Đồ thị hàm số không có tiệm ngang.
C. Đồ thị hàm số có 1 tiệm ngang.
D. Đồ thị hàm số có 1 tiệm ngang và 1 tiệm cận đứng.
Câu 3. Cho hàm số y f (x) có lim f (x) 6 và x
lim f (x) 3. Khẳng định nào sau đây là đúng? x4
A. Đồ thị hàm số có hai tiệm ngang là các đường thẳng
y 6 và y 3 .
B. Đồ thị hàm số có một tiệm ngang là đường thẳng 2 THPT Marie Curie y 6.
C. Đồ thị hàm số có một tiệm ngang là đường thẳng y 3.
D. Đồ thị hàm số không có tiệm ngang.
Câu 4. Cho hàm số y f (x) có lim f (x) và x5
lim f (x) 3 . Khẳng định nào sau đây là đúng? x5
A. Đồ thị hàm số không có tiệm đứng.
B. Đồ thị hàm số có một tiệm đứng là đường thẳng x 3.
C. Đồ thị hàm số có một tiệm đứng là đường thẳng x 5.
D. Đồ thị hàm số có hai tiệm đứng là các đường thẳng
x 3 và x 5 . Câu 5. Cho hàm số
y f (x) có
lim f (x) , x3
lim f (x) , lim f (x) 8 và lim f (x) 5 . Tổng số tiệm x x x 7
cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4. B. 2. C. 1. D. 3.
Câu 6. Cho hàm số y f (x) có lim f (x) 1 và x lim f (x) 1
. Khẳng định nào sau đây đúng? x
A. Đồ thị hàm số không có tiệm cận ngang.
B.Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là các đường
thẳng y 1 và y 1 .
D. Đồ thị hàm số có hai tiệm cận ngang là các đường
thẳng x 1 và x 1 .
Câu 7. Cho hàm số y f x có lim f x và x 1
lim f x . Mệnh đề nào sau đây đúng? 2 x 1
A. Đồ thị hàm số không có tiệm cận.
B. Đồ thị hàm số có tiệm cận đứng x 1.
C. Đồ thị hàm số có hai tiệm cận.
D. Đồ thị hàm số tiệm cận ngang y 2 .
Câu 8. Cho hàm số y f x xác định trên và
lim f x 2 , lim f x 3 . Tổng số tiệm cận đứng của đồ x x thị hàm số đã cho là A. 0 . B. 1 . C. 3 . D. 2 .
Câu 9. Biết đồ thị hàm số y f x có một tiệm cận ngang
là y 3. Khi đó đồ thị hàm số y 2 f x 4 có một tiệm
cận ngang là đường thẳng 3
Tài liệu học tập Toán 12 A. y 3. B. y 2 . C. y 1. D. y 4 .
Câu 10. Biết đồ thị hàm số y f x có một tiệm cận ngang
là y 4 . Khi đó đồ thị hàm số y 5 2 f x có một tiệm
cận ngang là đường thẳng A. y 3 . B. y 11. C. y 0 . D. y 4 . 4 THPT Marie Curie
DẠNG 2. DỰA VÀO BIỂU THỨC HÀM SỐ A. PHƯ ƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. 3x 1
Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y . 2x 5 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 2. 2 4x
Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y 3 . 7x 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 3. 5
Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y . x 3 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 4. x
Tìm giao điểm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y 2 5 . 4x Lời giải
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
....................................................................................................................................................................... 2 Ví dụ 5. 4x 3x 10
Tìm tất cả tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y . x 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 Ví dụ 6. 3x 2x 10
Tìm tất cả tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y . 2 x x 6 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 Ví dụ 7. x 4x 3
Tìm tất cả tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y . 2 x 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 8. 2x 4
Tìm tất cả tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y . 2 x x 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎ I TRẮC NGHIỆM
Câu 1. Đường thẳng nào dưới đây là tiệm cận đứng của 2x 1
đồ thị hàm số y ? x 1 A. x 1. B. y 1 . C. y 2 . D. x 1 .
Câu 2. Đường thẳng nào dưới đây là tiệm cận ngang của 2 THPT Marie Curie x 1
đồ thị hàm số y ? x 1 A. y 1. B. x 1. C. y 1. D. x 1. Câu 3. 2x 3
Đồ thị hàm số y có tiệm cận đứng là 1 2x đường thẳng A. x 3 . B. x 2 . 1 3 C. x . D. x . 2 2
Câu 4. Đường thẳng nào dưới đây là tiệm cận ngang của 3 2x
đồ thị hàm số y ? x 1 A. y 3. B. x 1 . C. y 2 . D. x 2 . Câu 5. 2 3x
Đồ thị hàm số y có tiệm cận đứng và 2x 3 ngang lần lượt là 3 3 3 A. x và y . B. x và y 1. 2 2 2 2 3 2 C. x
và y . D. x và y 1. 3 2 3
Câu 6. Giao điểm của tiệm cận đứng và tiệm cận ngang 2
của đồ thị hàm số y là điểm 3x 1 1 1 2 A. Q ; 2 . B. M ; . 3 3 3 1 1
C. N ; 2 .
D. P ; 0 . 3 3
Câu 7. Giao điểm của tiệm cận đứng và tiệm cận ngang 3x 2
của đồ thị hàm số y là điểm 1 x
A. M 1; 3. B. P 3 ; 1 . 2 C. Q1; 3 .
D. N ; 3 . 3 2 Câu 8. x 3x 4
Số tiệm cận đứng của đồ thị hàm số y 2 x 16 là A. 2. B. 3. C. 1. D. 0.
Câu 9. Số đường tiệm cận đứng và ngang của đồ thị hàm x 1 số y là 2 x x 2 A. 3. B. 1. 3
Tài liệu học tập Toán 12 C. 0. D. 2. Câu 10. x 2
Đồ thị hàm số y
có tất cả bao nhiêu tiệm 2 x 4 cận đứng và ngang? A. 0. B. 3. C. 1. D. 2.
Câu 11. Đồ thị hàm số nào dưới đây có tiệm cận đứng? 2 x 3x 2 2 x A. y . B. y . x 1 2 x 1 x C. 2 y x 1 . D. y . x 1
Câu 12. Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? 1 1 A. y . B. y . x 2 x x 1 1 1 C. y . D. y . 4 x 1 2 x 1 m Câu 13. 1 x 2
Nếu đồ thị hàm số y lần lượt nhận x n 1
trục hoành và trục tung làm đường tiệm cận ngang và
đường tiệm cận đứng thì m n bằng bao nhiêu?
A. m n 0 .
B. m n 2 .
C. m n 1 .
D. m n 1. Câu 14. 3 mx
Cho hàm số y
. Giá trị của m và n để đồ x n
thị hàm số đã cho có tiệm cận đứng x 2 và tiệm cận ngang y 2 là
A. m 2,n 2 . B. m 2 ,n 2 .
C. m 2,n 2 . D. m 2 ,n 2 .
Câu 15. Đường tiệm cận đứng và đường tiệm cận ngang mx 1
của đồ thị hàm số y
cùng với hai trục tọa độ 2m 1 x
tạo thành một hình chữ nhật có diện tích bằng 3 . Khi đó m bằng 3 3 A. 1 hay . B. 1 hay . 2 2 3 C. 1 hay . D. 1 hay 3 . 2 4 THPT Marie Curie
DẠNG 3. DỰA VÀO BẢNG BIẾN THIÊN A. PHƯƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Cho hàm số y f x có bảng biến thiên như hình bên dưới. x – –4 3 + y’ + + 0 – + 7 y 1 –2 –6
Tìm tất cả tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số y f x có bảng biến thiên như hình bên dưới. x + – 3 5 7 2 3 10 y –4 – 4
Tìm tất cả tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số y f x có bảng biến thiên như hình x – 0 1 2 + +
bên. Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng 2 + y A. x 0 . B. x 1. – – 4 C. x 2 . D. x 4 .
Câu 2. Cho hàm số y f x có bảng biến thiên như hình x – 0 1 2 + 2 + 6
bên. Đồ thị hàm số đã cho có tiệm cận ngang là đường y thẳng – – 4 A. y 2 . B. y 6 . C. y 1. D. y 4 .
Câu 3. Cho hàm số y f x có bảng biến thiên như hình x – –2 0 + –
vẽ bên. Tổng số tiệm cận đứng và tiệm cận ngang của đồ y’ + + 1 thị hàm số đã cho là y A. 1. B. 3. – 0 C. 2. D. 4.
Câu 4. Cho hàm số y f x có bảng biến thiên như hình x –8 –3 2 +
bên. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị y’ + + + + hàm số đã cho là y A. 1. B. 2. 6 5 C. 3. D. 4.
Câu 5. Cho hàm số y f x có bảng biến thiên như hình x – 1 +
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị + 5 y hàm số đã cho là A. 4 . B. 1 . 2 3 C. 3 . D. 2 .
Câu 6. Cho hàm số y f x có bảng biến thiên như hình x – 0 1 + +
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị 2 y hàm số đã cho là
– –1 –3 A. 4 . B. 1 . 1 1 C. 3 . D. 2 .
Câu 7. Cho hàm số y f x có bảng biến thiên như hình x – 0 3 +
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị y’ – 0 + – hàm số đã cho là 8 4 A. 4 . B. 1 . y C. 3 . D. 2 . 1 2
Câu 8. Cho hàm số y f x có bảng biến thiên như hình x – 0 1 8
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị 2 + hàm số đã cho là y 4 A. 4 . B. 1 . –1 –3 1 1 1 C. 3 . D. 2 .
Câu 9. Cho hàm số y f (x) có bảng biến thiên như hình x – 0 1 + y’ – 0 + + 5 +∞ 2 2 y –4 –∞ THPT Marie Curie
bên. Đồ thị hàm số y f (x) có tất cả bao nhiêu tiệm cận đứng và ngang? A. 3. B. 1. C. 2. D. 4.
Câu 10. Cho hàm số y f (x) có bảng biến thiên như hình x – 0 1 + y’ + –
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị – 0 + 2 hàm số đã cho là y A. 4 . B. 1 . –1 – – C. 3 . D. 2 .
Câu 11. Cho hàm số y f x có bảng biến thiên như hình x – 1 2 +
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị y’ + – + +∞ hàm số đã cho là 3 y A. 1. B. 2. –4 –5 C. 3. D. 0.
Câu 12. Cho hàm số y f (x) xác định, liên tục trên x – 0 1 + \ 0;
1 và có bảng biến thiên như hình bên. Đồ thị hàm y’ + + + + 3 +
số y f (x) có y
A. 2 tiệm cận đứng và 1 tiệm cận ngang.
B. 2 tiệm cận đứng và 2 tiệm cận ngang. –5 – –
C. 1 tiệm cận đứng và 1 tiệm cận ngang.
D. 1 tiệm cận đứng và 2 tiệm cận ngang.
Câu 13. Cho hàm số y f x có bảng biến thiên như hình x – –1 1 +
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị y’ + + 0 – 4 3 hàm số đã cho là y A. 4 . B. 1 . 2 – –1 C. 3 . D. 2 .
Câu 14. Cho hàm số y f (x) có bảng biến thiên như hình x – 0 3 +
bên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị y’ – 0 + – hàm số đã cho là 8 4 A. 4 . B. 1 . y 1 C. 3 . D. 2 . 2 3 THPT Marie Curie
DẠNG 4. DỰA VÀO ĐỒ THỊ HÀM SỐ A. PHƯƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Cho hàm số nhất biến y f x có đồ thị như hình vẽ bên. y b O a x
Tìm tiệm cận đứng và tiệm ngang của đồ thị hàm số đã cho Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hàm số nhất biến y f x có đồ thị như hình y
vẽ bên. Tiêm cận đứng của đồ thị hàm số đã cho là đường 1 thẳng O 2 x A. y 2 . B. x 1. C. x 2 . D. y 1.
Câu 2. Cho hàm số nhất biến y f x có đồ thị như hình
vẽ bên. Tiêm cận ngang của đồ thị hàm số đã cho là đường y thẳng 2 A. y 4 . B. x 4 . O 4 x 1
Tài liệu học tập Toán 12 C. x 2 .
D. y 2 .
Câu 3. Cho hàm số nhất biến y f x có đồ thị như hình y
vẽ bên. Tiêm cận đứng của đồ thị hàm số đã cho là đường thẳng 1 – A. x 1. B. x 3 . 3 O x C. y 3 . D. y 1.
Câu 4. Cho hàm số nhất biến y f x có đồ thị như hình y
vẽ bên. Tiêm cận ngang của đồ thị hàm số đã cho là đường 2 thẳng O A. y 1. B. x 1. –1 x C. y 2 .
D. x 2 . 2 THPT Marie Curie VẤN ĐỀ 5.
ĐỒ THỊ CỦA 3 HÀM SỐ CƠ BẢN
DẠNG 1. ĐỒ THỊ CỦA HÀM SỐ BẬC BA A. PHƯ ƠNG PHÁP 3 2
y ax bx cx d a 0
Tính y và giải phương trình y 0 .
Tính y và giải phương trình y 0 , phương trình này luôn có một nghiệm x x . Khi đó 0
điểm I x ; f (x ) gọi là điểm uốn của đồ thị. 0 0
Chọn thêm vài điểm trên đồ thị để vẽ.
Đồ thị có 6 dạng sau: Chú ý y y B A Có 2 Có 1 là trung nghiệm nghiệm I I của đoạn và O x O x B A y y Đồ thị xung Có nghiệm Có 1 I quanh điểm uốn I kép nghiệm gần như nằm O x O x ngang. y y Vô Có 1 Đồ thị xung nghiệm I I nghiệm quanh điểm uốn có độ dốc. O O x x Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12 B. VÍ DỤ
Ví dụ 1. Vẽ đồ thị hàm số 3 2
y x 3x 1 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Vẽ đồ thị hàm số 3
y x 3x 1 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Vẽ đồ thị hàm số 3 2
y x 3x 3x 1 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 4. 1
Vẽ đồ thị hàm số 3 2
y x x x 1. 3 2 THPT Marie Curie Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Vẽ đồ thị hàm số 3
y x x 1. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Vẽ đồ thị hàm số 3
y x 2x 1 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 3 THPT Marie Curie
DẠNG 2. ĐỒ THỊ CỦA HÀM SỐ BẬC BỐN A. PHƯ ƠNG PHÁP 4 x a 2 y
bx c a 0
Tính y và giải phương trình y 0 . Phương trình này luôn có ít nhất một nghiệm x 0 .
Chọn thêm vài điểm trên đồ thị để vẽ.
Đồ thị có 4 dạng sau: Chú ý y y B C Có 3 nghiệm A Tam giác ; O O x x luôn cân tại A B C y y A Có 1 nghiệm Tam giác B C B O C x O x luôn cân tại A Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Vẽ đồ thị hàm số 4 2
y x 2x 1 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Vẽ đồ thị hàm số 4 2
y x 2x 2 . 1
Tài liệu học tập Toán 12 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Vẽ đồ thị hàm số 4 2
y x x 2 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Vẽ đồ thị hàm số 4 2
y x 2x 2 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 THPT Marie Curie
DẠNG 3. ĐỒ THỊ CỦA HÀM SỐ NHẤT BIẾN A. PHƯ ƠNG PHÁP ax b
y cx d ad bc Tính y . cx d2 d
Vẽ đường thẳng đứng x (Đường thẳng này gọi là tiệm cận đứng của đồ thị) c a
Vẽ đường thẳng nằm ngang y (Đường thẳng này gọi là tiệm cận ngang của đồ thị) c
Chọn thêm vài điểm trên đồ thị để vẽ.
Đồ thị có 2 dạng sau: y y O x O x Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. 2x 1
Vẽ đồ thị hàm số y . x 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
....................................................................................................................................................................... Ví dụ 2. x 1
Vẽ đồ thị hàm số y . x 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 THPT Marie Curie
DẠNG 4. TRẮC NGHIỆM ĐỒ THỊ CỦA HÀM SỐ
Câu 1. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. y 4 x 2 x 1 . B. 3 2
y x 3x 3 . O x C. y 3 x 2 3x 3 . D. y 4 x 2 2x 1.
Câu 2. Đường cong trong hình vẽ bên là đồ thị của hàm số y nào dưới đây? x 4 x 1 1 A. y . B. y . x 1 x 1 –1 O 1 x –1 C. 4 2
y x x 1. D. 3
y x 3x 1.
Câu 3. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? x 1 O x A. 4 2
y x 2x 1 . B. y . x 1 C. 3 2
y x x 1. D. 4 2
y x x 1 .
Câu 4. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. y 3 x 1. B. 3 2
y x 3x 3x 1 . O x 1 x 1 1 C. 4 2
y x x 1 . D. y . x 3 y
Câu 5. Đường cong của hình vẽ bên là đồ thị của hàm số O x nào dưới đây? A. 4 2
y x 2x 1 . B. y 3 x 3x 1. 2x 1 C. y . D. 4 2
y x 2x 1. x 1
Câu 6. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? x 4 x 1 A. y . B. y . 1 x 3 x 3 –3 O x 3 x 2 3 x 1 C. y . D. y . x 1 x 1
Câu 7. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. y 4 x 2 x 1. B. 3
y x 3x 2 . C. 4 2
y x x 1. D. 3
y x 3x 2 . O x
Câu 8. Đường cong ở hình bên là đồ thị của một trong bốn y
hàm số dưới đây. Hàm số đó là hàm số nào? A. 4 2
y x x 1. B. 4 2
y x x 1 . O x C. 4 2
y x x 1 . D. 4 2
y x x 1 .
Câu 9. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? O x 1 1
Tài liệu học tập Toán 12 A. 4 2 y x x . B. 3 2
y x 3x 4x 8 . C. 4 2
y x x . D. y 3 x 1.
Câu 10. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? 2x 1 2x 3 2 A. y . B. y . x 1 x 1 O –1 x 2x 2 2x 1 C. y . D. y . x 1 x 1
Câu 11. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. 3
y x 3x 1 . B. 4 2
y x x 1 . O x C. 4 2
y x x 1 . D. 3
y x – 3x 1 .
Câu 12. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. 4 2
y x x 1 . B. 4 2
y x x 1. O x C. 4 2
y x x 1. D. 4 2
y x x 1 .
Câu 13. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. 4 2 y x x . B. y 4 x 2 3x . O x 1 C. 3 2
y x x . D. 3 y x . 3
Câu 14. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. 4 2
y x x 1 . B. 4 2
y x x 1. C. 4 2
y x x 1 . D. y 3 x 1 . O x
Câu 15. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? A. y 3 x x 2 . B. 4 2
y x x 2 . O x C. 3 2
y x 3x 2 . D. 3 2
y x 3x 2 .
Câu 16. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? x 2x 1 A. y . B. y . x 2 x 1 O 2 x x 1 x C. y . D. y . x 2 x 2
Câu 17. Đường cong của hình vẽ bên là đồ thị của hàm số y nào dưới đây? O x A. 4 2
y x 3x 1 . B. 4 2
y x 3x 1 . C. 4 2
y x 3x 1 . D. 4 2
y x 3x 1 .
Câu 18. Đường cong ở hình bên là đồ thị của hàm số y O x 2 THPT Marie Curie 3 2
y ax bx cx d . Mệnh đề nào sau đây đúng?
A. y 0 vô nghiệm và a 0 .
B. y 0 có 1 nghiệm và a 0 .
C. y 0 vô nghiệm và a 0 .
D. y 0 có 1 nghiệm và a 0 .
Câu 19. Đường cong ở hình bên là đồ thị của hàm số y 3 2
y ax bx cx d . Mệnh đề nào sau đây đúng?
A. y 0 có 3 nghiệm và a 0 . O x
B. y 0 có 2 nghiệm và a 0 .
C. y 0 có 3 nghiệm và a 0 .
D. y 0 có 2 nghiệm và a 0 .
Câu 20. Đường cong ở hình bên là đồ thị của hàm số y 3 2
y ax bx cx d . Mệnh đề nào sau đây đúng?
A. y 0 vô nghiệm và a 0 . O x
B. y 0 có 1 nghiệm và a 0 .
C. y 0 vô nghiệm và a 0 .
D. y 0 có 1 nghiệm và a 0 .
Câu 21. Đường cong ở hình bên là đồ thị của hàm số 3 2 y
y ax bx cx d . Khi đó phương trình y 0 1
A. có hai nghiệm x 1 hay x 1.
B. có hai nghiệm x 0 hay x 1. 1 O x 1
C. có ba nghiệm x hay x 1. 1 2
D. có đúng một nghiệm x 1.
Câu 22. Đường cong ở hình bên là đồ thị của hàm số y 3 2
y ax bx cx d . Khi đó phương trình y 0
A. có hai nghiệm x 0 hay x 1. O x 1
B. có hai nghiệm x 1 . 1 C. vô nghiệm.
D. có một nghiệm x 1.
Câu 23. Đường cong ở hình bên là đồ thị của hàm số y 3 2
y ax bx cx d . Khi đó phương trình y 0 2
A. có hai nghiệm x 2 hay x 2. 2 1 O x
B. có hai nghiệm x hay x 2 . –2 2
C. có đúng một nghiệm x 0 .
D. có hai nghiệm x 0 hay x 2 .
Câu 24. Đường cong ở hình bên là đồ thị của hàm số 3 2
y ax bx cx d . Khi đó phương trình y 0
A. có hai nghiệm x 0 hay x 2 .
B. có hai nghiệm x 2 . C. vô nghiệm. y 3 4 2
Tài liệu học tập Toán 12
D. có một nghiệm x 1.
Câu 25. Đường cong ở hình bên là đồ thị của hàm số 3 2
y ax bx cx d . Khi đó phương trình y 0
A. có hai nghiệm x 1 .
B. có một nghiệm x 0 .
C. có hai nghiệm x 2 .
D. có hai nghiệm x 4 .
Câu 26. Đường cong ở hình bên là đồ thị của hàm số y 4 2
y ax bx c . Mệnh đề nào sau đây đúng?
A. y 0 có 3 nghiệm và a 0 .
B. y 0 có 3 nghiệm và a 0 . O x
C. y 0 có 2 nghiệm và a 0 .
D. y 0 có 2 nghiệm và a 0 .
Câu 27. Đường cong ở hình bên là đồ thị của hàm số y 4 2
y ax bx c . Mệnh đề nào sau đây đúng?
A. y 0 có 2 nghiệm và a 0 . O x
B. y 0 có 3 nghiệm và a 0 .
C. y 0 có 2 nghiệm và a 0 .
D. y 0 có 1 nghiệm và a 0 .
Câu 28. Đường cong ở hình bên dưới là đồ thị của hàm số 4 2 y
y ax bx c . Mệnh đề nào sau đây đúng? O
A. y 0 có 3 nghiệm và a 0 . x
B. y 0 có 3 nghiệm và a 0 .
C. y 0 có 2 nghiệm và a 0 .
D. y 0 có 2 nghiệm và a 0 .
Câu 29. Đường cong ở hình bên là đồ thị của hàm số y 4 2
y ax bx c . Khi đó phương trình y 0 1
A. có đúng hai nghiệm x 0 hay x 1.
B. có đúng hai nghiệm x 1 . –1 O 1 x
C. có đúng ba nghiệm x 0 hay x 1 .
D. có đúng một nghiệm x 0 .
Câu 30. Đường cong ở hình bên là đồ thị của hàm số 4 2 y
y ax bx c . Khi đó phương trình y 0
A. có hai nghiệm x 1 . –1 O 1 x
B. có một nghiệm x 0 . –2
C. có ba nghiệm x 2 hay x 1 . D. vô nghiệm.
Câu 31. Đường cong ở hình bên là đồ thị của hàm số y 4 2
y ax bx c . Khi đó phương trình y 0 5
A. có ba nghiệm x 0 hay x 3 . O
B. có hai nghiệm x 1 . 1 1 x 4 4 THPT Marie Curie
C. có bốn nghiệm x 1 hay x 3 .
D. có hai nghiệm x 4 hay x 5.
Câu 32. Đường cong ở hình bên là đồ thị của hàm số y ax b y
. Mệnh đề nào dưới đây đúng? cx d O
A. y 0, x .
B. y 0, x . 1 x
C. y 0, x 1.
D. y 0, x 1.
Câu 33. Đường cong ở hình bên là đồ thị của hàm số y ax b y
. Mệnh đề nào dưới đây đúng? cx d 1
A. y 0, x 2.
B. y 0, x 1. O 2 x
C. y 0, x 2.
D. y 0, x 1.
Câu 34. Đường cong ở hình bên là đồ thị của hàm số y ax b y
. Mệnh đề nào dưới đây đúng? cx d 2
A. y 0, x 2.
B. y 0, x 1 . –1 O x
C. y 0, x 2.
D. y 0, x 1 . 5 THPT Marie Curie
BIỆN LUẬN SỐ NGHIỆM PHƯƠNG TRÌNH VẤN ĐỀ 6.
DẠNG 1. DỰA VÀO ĐỒ THỊ TÌM SỐ NGHIỆM CỦA MỘT PHƯƠNG TRÌNH A. PHƯƠNG PHÁP
Hai đồ thị C : y f x và C : y g x có bao nhiêu điểm chung thì phương trình 2 1
f x gx có bấy nhiêu nghiệm. Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ 1. Cho hàm số 4 2
f x ax bx c có đồ thị như hình bên dưới. y 1 –1 O 1 x
1. Phương trình f x 1 0 có tất cả bao nhiêu nghiệm?
2. Phương trình f x 0 có tất cả bao nhiêu nghiệm?
3. Phương trình 2 f x 1 0 có tất cả bao nhiêu nghiệm?
4. Phương trình f x 1 0 có tất cả bao nhiêu nghiệm?
5. Phương trình 3 f x 4 0 có tất cả bao nhiêu nghiệm? Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
....................................................................................................................................................................... C. CÂU HỎ I TRẮC NGHIỆM
Câu 1. Cho hàm số 3 2
f x ax bx cx d có đồ thị như y 2
hình bên. Phương trình 3 f x 4 0 có tất cả bao nhiêu 2 nghiệm? O x A. 3. B. 0. –2 C. 1. D. 2.
Câu 2. Cho hàm số 3 2
f x ax bx cx d có đồ thị như y
hình bên. Số nghiệm thực của phương trình f x 2 0 là 2 2 A. 3. B. 0. O x C. 1. D. 2. –2
Câu 3. Cho hàm số 3 2
f x ax bx cx d có đồ thị như y
hình bên. Phương trình 2 f x 5 0 có tất cả bao nhiêu 2 2 nghiệm? O x A. 3. B. 0. –2 C. 1. D. 2.
Câu 4. Cho hàm số 4 2
f x ax bx c có đồ thị như hình y 1
bên. Số nghiệm thực của phương trình 4 f x 3 0 là A. 4. B. 3. –1 O 1 x C. 2. D. 0.
Câu 5. Cho hàm số 4 2
f x ax bx c có đồ thị như hình y 1
bên. Số nghiệm thực của phương trình 2 f x 1 0 là A. 4. B. 3. –1 O 1 x C. 2. D. 0.
Câu 6. Cho hàm số 4 2
f x ax bx c có đồ thị như hình y 1
bên. Phương trình 2 f x 3 0 có tất cả bao nhiêu nghiệm? –1 O 1 x A. 4. B. 3. C. 2. D. 0. y
Câu 7. Cho hàm số 3 2
f x ax bx cx d có đồ thị như 2 2
hình bên. Số nghiệm âm của phương trình f x 1 0 là O x –2 A. 3. B. 0. C. 1. D. 2.
Câu 8. Cho hàm số 3 2
f x ax bx cx d có đồ thị như y 3 1 –2 O 1 2 –1 2 x –1 THPT Marie Curie
hình bên. Phương trình 2 f x 1 0 có tất cả bao nhiêu nghiệm dương? A. 3. B. 0. C. 1. D. 2.
Câu 9. Cho hàm số y f x liên tục trên đoạn 2; 4 và y 6
có đồ thị như hình vẽ bên. Số nghiệm thực lớn hơn 2 của
phương trình 3 f x 5 0 trên đoạn 2; 4 là 2 –2 1 A. 1. B. 0. O 2 4 x C. 2. D. 3. –3
Câu 10. Cho hàm số y f (x) có đồ thị trong hình bên. y Phương trình f ( )
x 1 0 có bao nhiêu nghiệm thực phân 2 biệt nhỏ hơn 2? O 2 x A. 1. B. 2. –2 C. 3. D. 0.
Câu 11. Cho hàm số 3 2
f x ax bx cx d có đồ thị như y
hình bên. Phương trình 3 f x 2 0 có bao nhiêu nghiệm 2 1 2 lớn hơn 1? O x A. 3. B. 0. –2 C. 1. D. 2. 3 THPT Marie Curie
DẠNG 2. DỰA VÀO ĐỒ THỊ BIỆN LUẬN SỐ NGHIỆM CỦA MỘT PHƯƠNG TRÌNH A. PHƯƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ: Cho hàm số 3 2
f x ax bx cx d có đồ thị là hình bên dưới. y 4 2 –2 O –1 1 2 x
1. Tìm m để phương trình f x m có đúng 1 nghiệm.
2. Tìm m để phương trình f x 2m 1 có đúng 2 nghiệm.
3. Tìm m để phương trình f x 1 m có đúng 3 nghiệm. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... C. CÂU HỎ I TRẮC NGHIỆM Câu 1. Cho hàm số 4 2
y x 2x có đồ thị như hình bên. y 1
Tất cả các giá trị thực của tham số m để phương trình 4 2
x 2x m có bốn nghiệm thực phân biệt là –1 O 1 x A. m 0 .
B. 0 m 1 .
C. 0 m 1 . D. m 1.
Câu 2. Cho hàm số bậc ba y f (x) có đồ thị là đường y
cong trong hình vẽ bên. Có bao nhiêu giá trị nguyên của O 2 x 1 –3
Tài liệu học tập Toán 12
tham số m để phương trình f ( )
x m có 3 nghiệm phân biệt? A. 3. B. 4. C. 2. D. 1.
Câu 3. Đồ thị của hàm số 4 2
y x 6x 5 là đường cong y 5
trong hình bên. Tập hợp các giá trị của tham số thực m để phương trình 4 2
x 6x m 0 có 4 nghiệm phân biệt là O x A. 4 ;5. B. 9 ;5. 4 C. 3; 3 . D. 9 ;0. Câu 4. Cho hàm số 3 2
y x 3x 1 có đồ thị trong hình y
bên. Tập hợp các giá trị của tham số thực m để phương 1 2 trình 3 2
x 3x m 0 có đúng 2 nghiệm phân biệt là O x A. 3 ; 1 . B. 3 ; 1 . C. 4 ;0. D. 4 ; 0 . 3 2 THPT Marie Curie
DẠNG 3. DỰA VÀO ĐỒ THỊ HÀM SỐ CHỨA TRỊ TUYỆT ĐỐI
BIỆN LUẬN SỐ NGHIỆM CỦA MỘT PHƯƠNG TRÌNH A. PHƯƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ: Cho hàm số 3 2
f x ax bx cx d có đồ thị là hình bên dưới. y 4 2 –2 O –1 1 2 x
1. Biện luận theo m số nghiệm phương trình f x m .
2. Biện luận theo m số nghiệm phương trình f x m . Lời giải
................................................................................................................................................................ y .......
................................................................................................................................................................ 4 .......
.......................................................................................................................................................................
................................................................................................................................................................ 2 .......
................................................................................................................................................................ –2 O –1 1 ....... 2 x
.......................................................................................................................................................................
................................................................................................................................................................ y .......
................................................................................................................................................................ 4 .......
.......................................................................................................................................................................
................................................................................................................................................................ 2 .......
................................................................................................................................................................ –2 O ....... –1 1 2 x
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12 C. CÂU HỎ I TRẮC NGHIỆM
Câu 1. Biết rằng hàm số 4 2
y 2x – 4x có đồ thị như hình y 16
vẽ bên. Tập hợp các giá trị của tham số m để phương trình 2 2
x x 2 m có 6 nghiệm thực phân biệt là A. 0; 1 . B. 2 ;0. 1 1 C. 2 ; 2 . D. 0; 2 . O 2 2 x 2
Câu 2. Đồ thị của hàm số 4 2
y x 6x 5 là đường cong y
trong hình bên. Có bao nhiêu giá trị nguyên của tham số 5
thực m để phương trình 4 2
x 6x 5 m có 8 nghiệm phân 1 1 biệt? O x A. 8. B. 2. 4 C. 4. D. 3.
Câu 3. Đồ thị của hàm số 4 2
y x 6x 5 là đường cong y
trong hình bên. Có bao nhiêu giá trị nguyên của tham số 5
thực m để phương trình 4 2
x 6x 5 m có 4 nghiệm phân 1 1 biệt? O x A. 0. B. 2. 4 C. 3. D. 1.
Câu 4. Biết đường cong trong hình bên là đồ thị của hàm y số 3
y x 3x 2 . Tập hợp tất cả các giá trị của tham số 4 3
thực m để phương trình x 3 x 2 m có 4 nghiệm 2 phân biệt là A. . B. 2; 4 . –2 O –1 1 2 x C. 0; 4 . D. 0; 2 .
Câu 5. Biết đường cong trong hình bên là đồ thị của hàm y số 3
y x 3x 2 . Tập hợp tất cả các giá trị của tham số 4
thực m để phương trình 3
x 3x 2 m có 4 nghiệm phân 2 biệt là –2 O –1 1 2 x A. . B. 2; 4 . C. 0; 4 . D. 0; 2 .
Câu 6. Biết đường cong trong hình bên là đồ thị của hàm y số 3 2
y x 3x 1 . Có bao nhiêu giá trị nguyên của tham số 1 3 1 2
thực m để phương trình 2
x 3x 1 m có 3 nghiệm phân O x –1 biệt? A. 0. B. 2. 3 2 THPT Marie Curie C. 3. D. 1.
Câu 7. Biết đường cong trong hình bên là đồ thị của hàm y số 3 2
y x 3x 1 . Có bao nhiêu giá trị nguyên của tham số 1 3 1 2
thực m để phương trình 2
x 3x 1 m có 2 nghiệm phân O x –1 biệt? A. Vô số. B. 2. 3 C. 3. D. 1.
Câu 8. Biết đường cong trong hình bên là đồ thị của hàm y số 3 2
y x 3x 1 . Có bao nhiêu giá trị nguyên của tham số 1 1 2
thực m để phương trình 3 2
x 3x 1 m có 6 nghiệm phân O x –1 biệt? 3 A. 0. B. 2. C. 3. D. 1.
Câu 9. Biết đường cong trong hình bên là đồ thị của hàm y số 3 2
y x 3x 1 . Có bao nhiêu giá trị nguyên của tham số 1 1 2
thực m để phương trình 3 2
x 3x 1 m có 3 nghiệm phân O x –1 biệt? 3 A. Vô số. B. 2. C. 3. D. 1. 3 THPT Marie Curie DẠNG 4. DỰA V
ÀO BẢNG BIẾN THIÊN TÌM SỐ NGHIỆM
CỦA MỘT PHƯƠNG TRÌNH A. PHƯƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ: Cho hàm số y f x có bảng biến thiên như hình bên dưới. x – 0 1 + y’ – + 0 – + 2 y
–1 – – 1
Biện luận theo m số nghiệm phương trình f x m . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12 C. CÂU HỎ I TRẮC NGHIỆM Câu 1.
Cho hàm số y f x có bảng biến thiên như hình x – –2 0 2 +
bên. Số nghiệm của phương trình 1
2 f x 3 0 là y’ – 0 + 0 – 0 + + + 1 A. 4 . B. 3 . y –2 –2 C. 2 . D. 1 . 1 1
Câu 2. Cho hàm số y f x có bảng biến thiên như hình x – –2 3 + y’ + – +
bên. Số nghiệm thực của phương trình 2 f x 3 0 là +∞ 2 A. 2. B. 1. y C. 3. D. 4. 1 –
Câu 3. Cho hàm số y f x có bảng biến thiên như hình x – –2 0 2 + y’ 1 –
bên. Số nghiệm của phương trình 2 f x 3 0 là 0 + 0 – 0 + + + 1 A. 4 . B. 3 . y –2 –2 C. 2 . D. 1 . 1 1
Câu 4. Cho hàm số y f (x) có bảng biến thiên như hình x – –1 3 + 1
bên. Phương trình f x 2 0 có bao nhiêu nghiệm? y’ + 0 – 0 + + 5 A. 1. B. 3. y C. 2. D. 0. 1 2
Câu 5. Cho hàm số y f x có bảng biến thiên như hình x – 0 1 + y’
bên. Số nghiệm của phương trình f x f 0 là + – 0 + + y 2 A. 0 . B. 3 . –2 – C. 1 . D. 2 .
Câu 6. Cho hàm số y f (x) có bảng biến thiên như hình x – 0 1 +
bên. Phương trình f x f
1 có tất cả bao nhiêu nghiệm? y’ – 0 + 0 – + 6 A. 2. B. 1. y C. 3. D. 0. 3 –
Câu 7. Cho hàm số y f x có bảng biến thiên như hình x – 1 3 + y’ + 0 – 0 +
bên. Số nghiệm của phương trình f x f 3 0 là 4 + A. 0 . B. 3 . y 2 C. 1 . D. 2 . –
Câu 8. Cho hàm số y f (x) có bảng biến thiên như hình x – –4 6 +
bên. Số nghiệm của phương trình f x f 4 0 là y’ – 0 + 0 – + A. 0 . B. 3 . y 5 –2 – 2 THPT Marie Curie C. 1 . D. 2 .
Câu 9. Cho hàm số y f x có bảng biến thiên như hình x – 2 +
bên. Tập hợp các giá trị của tham số m để phương trình y’ + –
f x m có hai nghiệm phân biệt là 1 y A. 5 ; 1 . B. 5 ; 1 . – –5 C. ;1 . D. ;1 .
Câu 10. Cho hàm số y f (x) có bảng biến thiên như hình x – 0 1 +
bên. Tập hợp các giá trị của tham số m sao cho phương y’ – + 0 – trình f ( )
x m có ba nghiệm thực phân biệt là + 2 y A. 1 ; 2 . B. 1 ;2 .
–1 – – C. 1 ; 2 . D. ; 2 . 1
Câu 11. Cho hàm số y f x có bảng biến thiên như hình x – –1 0 +
bên. Tập hợp tất cả các giá trị thực của m để phương trình y’ + + 0 – + –1
f x m có nghiệm duy nhất là y A. 0 0; 1 . B. 0; . – – C. 0; .
D. 0; 1.
Câu 12. Cho hàm số y f x có bảng biến thiên như hình x – –1 3 +
bên. Tập hợp tất cả các giá trị của tham số m sao cho y’ + – 0 + 2 + +
phương trình f x m có đúng ba nghiệm thực phân biệt y – –4 là A. 4 ; 2 . B. 4 ; 2 . C. 4; 2 .
D. ; 2 . 3 THPT Marie Curie
DẠNG 5. DỰA VÀO BIỂU THỨC C
ỦA HÀM SỐ TÌM SỐ GIAO ĐIỂM A. PHƯƠNG PHÁP
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ
Ví dụ: Tìm số giao điểm của đồ thị hàm số y 3 x 2
3x 1 với trục hoành Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Đồ thị hàm số y x 2
2 x 1 cắt trục hoành tại
tất cả bao nhiêu điểm? A. 2 . B. 3. C. 1. D. 0.
Câu 2. Đồ thị hàm số 4 2
y x x 1 cắt trục hoành tại mấy điểm phân biệt? A. 2 . B. 0 . C. 3 . D. 4 . Câu 3. Cho hàm số 3
y x 3x có đồ thị C . Số giao điểm
của C và trục hoành là A. 2 . B. 3. C. 1. D. 0.
Câu 4. Đồ thị của hàm số 4 2
y x 2x 2 và đồ thị của hàm số 2
y x 4 có tất cả bao nhiêu điểm chung? A. 0. B. 4. C. 1. D. 2. 1
Tài liệu học tập Toán 12 2
Document Outline
- van-de-1-don-dieu-dang-1-dua-vao-bang-bien-thien_39202112
- van-de-1-don-dieu-dang-2-dua-vao-bang-xet-dau-dao-ham_39202112
- van-de-1-don-dieu-dang-3-dua-vao-bieu-thuc-cua-dao-ham_39202112
- van-de-1-don-dieu-dang-4-dua-vao-bieu-thuc-cua-ham-so_39202112
- van-de-1-don-dieu-dang-5-dua-vao-do-thi-cua-ham-so_39202112
- van-de-1-don-dieu-dang-6-dua-vao-do-thi-cua-dao-ham_39202112
- van-de-1-don-dieu-dang-7-xet-don-dieu-cua-ham-so-hop_39202112
- van-de-1-don-dieu-dang-8-bai-toan-mang-tham-so_39202112
- van-de-2-cuc-tri-dang-1-dua-vao-bang-bien-thien_1592021121041
- van-de-2-cuc-tri-dang-2-dua-vao-bang-xet-dau-dao-ham_1592021121041
- van-de-2-cuc-tri-dang-3-dua-vao-bieu-thuc-cua-dao-ham_1592021121041
- van-de-2-cuc-tri-dang-4-dua-vao-bieu-thuc-cua-ham-so_1592021121041
- van-de-2-cuc-tri-dang-5-dua-vao-do-thi-cua-ham-so_1592021121041
- van-de-2-cuc-tri-dang-6-dua-vao-do-thi-cua-dao-ham_1592021121041
- van-de-3-gtnn-gtln-dang-1-dua-vao-do-thi-cua-ham-so_2492021141812
- van-de-3-gtnn-gtln-dang-2-dua-vao-bang-bien-thien_2492021141812
- van-de-3-gtnn-gtln-dang-3-dua-vao-bieu-thuc-cua-ham-so_2492021141812
- van-de-4-duong-tiem-can-dang-1-dua-vao-dinh-li_2092021225641
- van-de-4-duong-tiem-can-dang-2-dua-vao-bieu-thuc-ham-so_2092021225641
- van-de-4-duong-tiem-can-dang-3-dua-vao-bang-bien-thien_2092021225641
- van-de-4-duong-tiem-can-dang-4-dua-vao-do-thi-ham-so_2092021225641
- van-de-5-do-thi-dang-1-ham-so-bac-3_2492021141441
- van-de-5-do-thi-dang-2-ham-so-bac-4_2492021141441
- van-de-5-do-thi-dang-3-ham-so-nhat-bien_2492021141441
- van-de-5-do-thi-dang-4-trac-nghiem-do-thi_2492021141441
- van-de-6-bien-luan-so-nghiem-pt-dang-1_8102021134632
- van-de-6-bien-luan-so-nghiem-pt-dang-2_8102021134632
- van-de-6-bien-luan-so-nghiem-pt-dang-3_8102021134632
- van-de-6-bien-luan-so-nghiem-pt-dang-4_8102021134632
- van-de-6-bien-luan-so-nghiem-pt-dang-5_8102021134632




