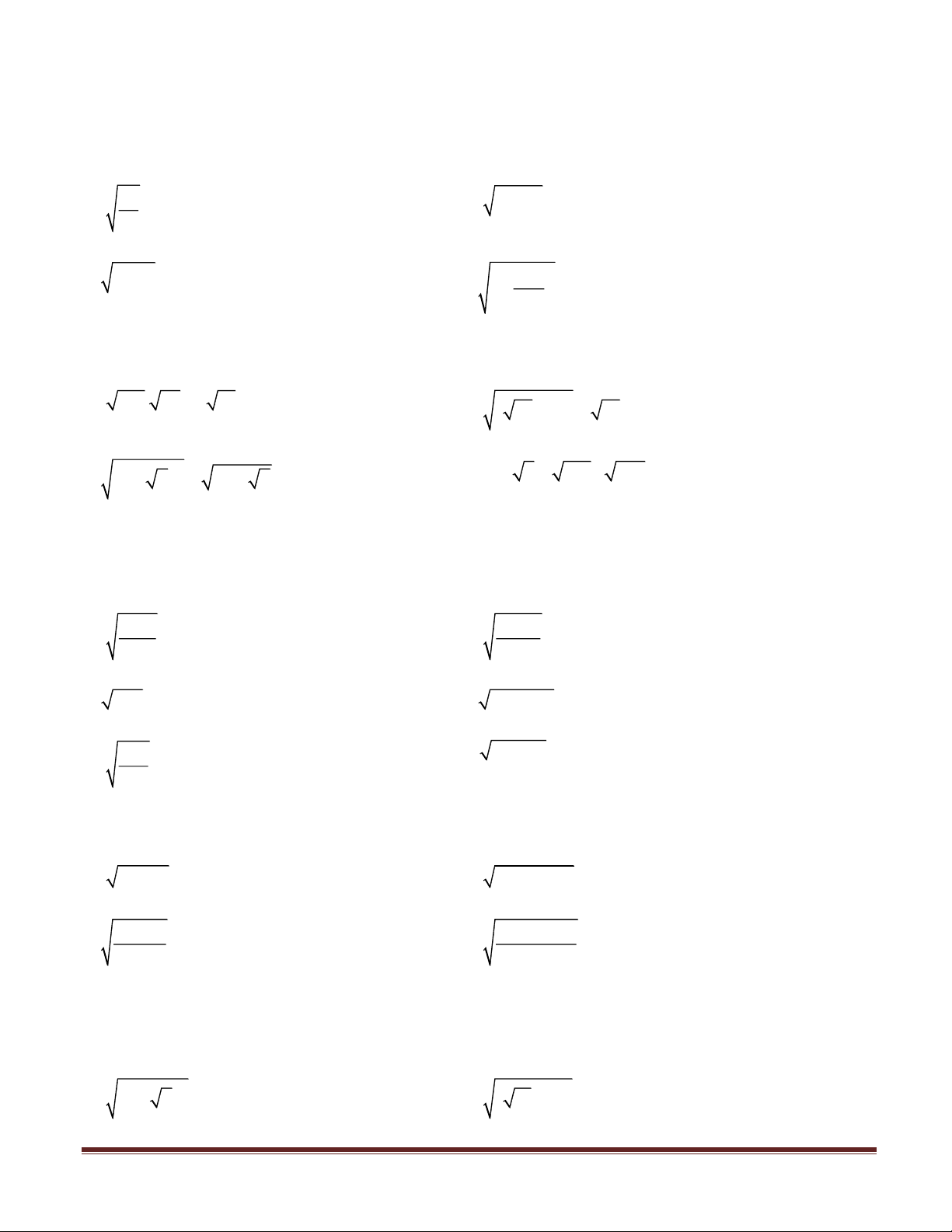
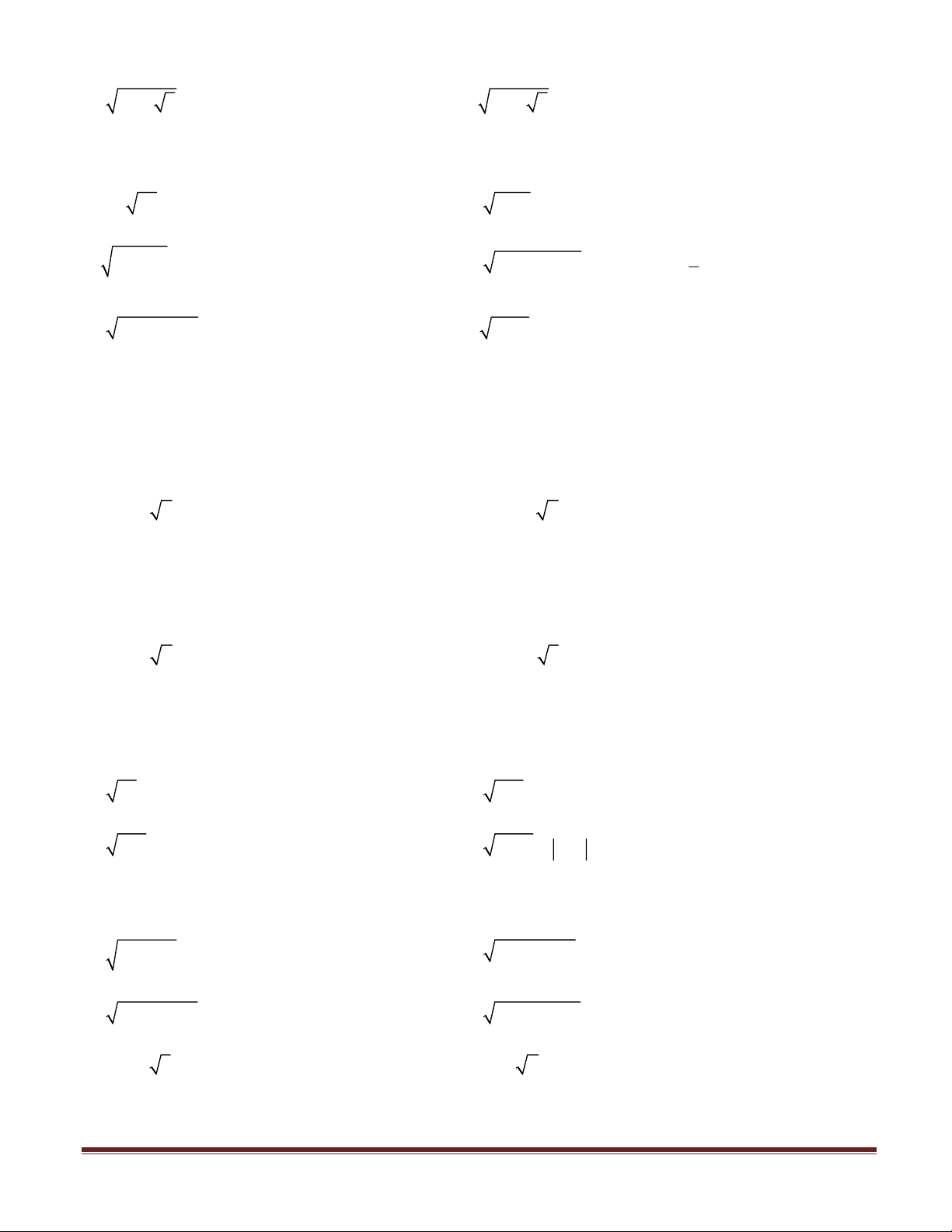
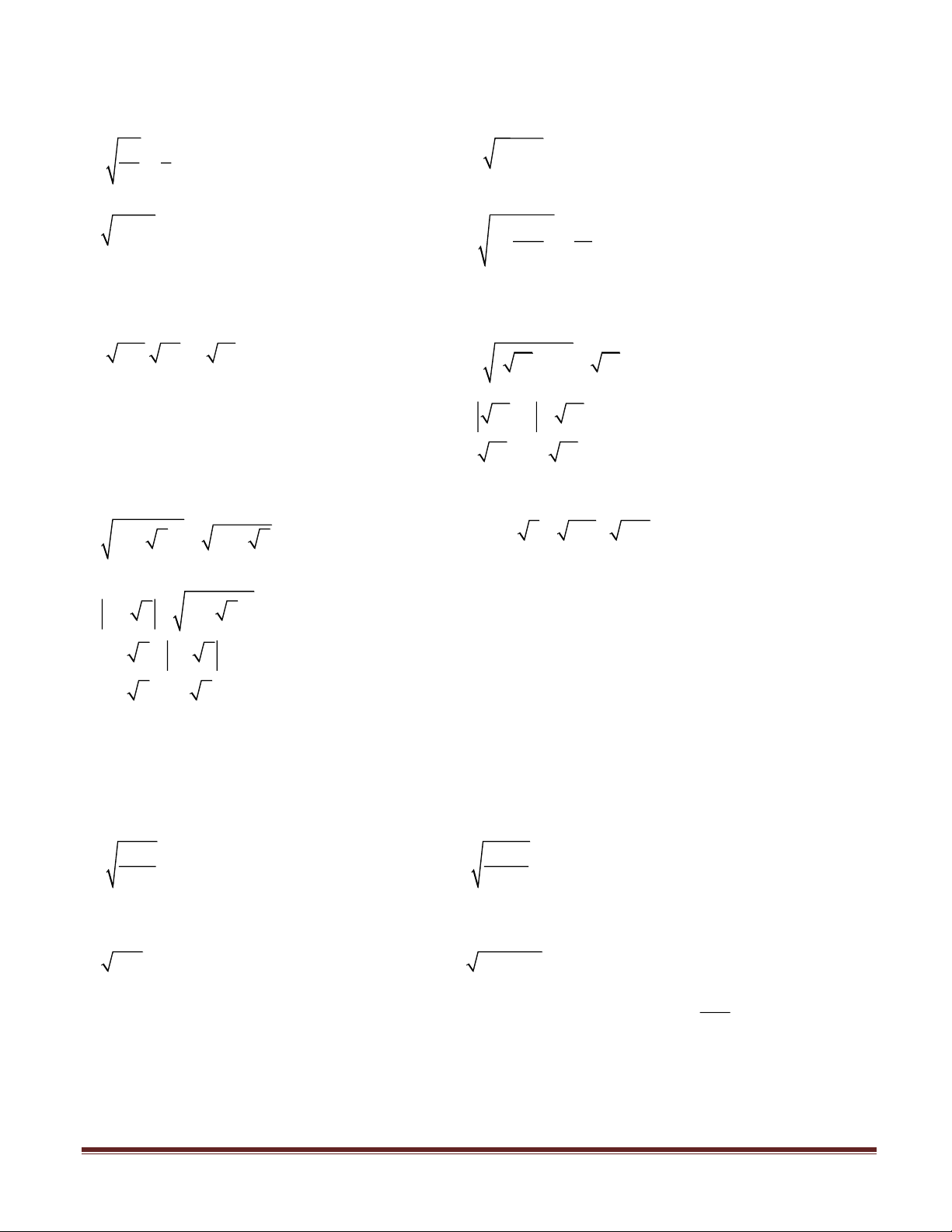
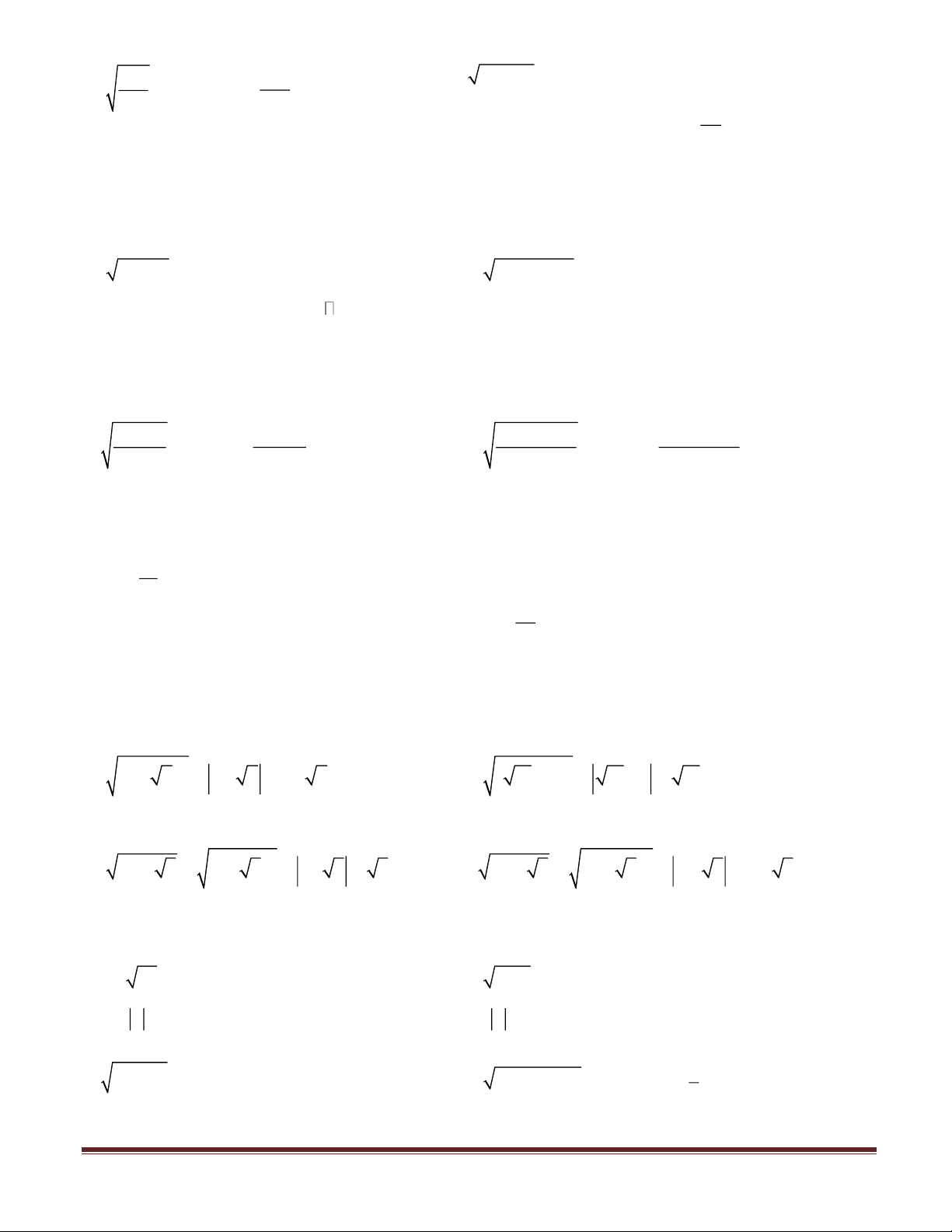



Preview text:
CÁC DẠNG TOÁN 9 BÀI : LUYỆN TẬP CĂN THỨC BẬC HAI
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai Bài 1: Tính 64 a. b. ( )2 2,5 25 c. (− )2 2 36 − d. − 169 Bài 2: Tính a. 196. 25 − 5 81 b. ( − )2 10 3 − 10 c. ( + )2 5 7 − 8 − 2 7 d. (81: 9 + 169). 225
Dạng 2: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 1: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: 15 17 − a. b. x − 2 12 − x c. 72x d. 24 +10x 13 − f. 27 − 6x e. 3x
Bài 2: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: a. 2 x +11 b. 2 x + 5x + 6 10 − 3x 4x + 2 c. d. 2 3x +1 2 x + 4x + 5
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Rút gọn các biểu thức sau: a. ( − )2 3 2 b. ( + )2 11 3 Trang 1 c. 4 − 2 3 d. 7 + 4 3
Bài 2: Rút gọn các biểu thức sau: a. 2
−2 a với a 0 b. 2
16a + 4a với a 0 c. (a − )2 1 với a 1 1 d. 2
9a − 6a +1 + 3a với a 3 e. 2
a + 6a + 9 với a −3 f. 4 2 25a − 3a
Dạng 4: Phân tích đa thức thành nhân tử
Bài 1: Phân tích đa thức thành nhân tử a. 2 x − 7 b. 2 4x − 3 c. 2 x + 2 7x + 7 d. 2 9x + 6 2x + 2
Bài 2: Phân tích đa thức thành nhân tử a. 2 x − 3 b. 2 9x − 5 c. 2 x + 2 2x + 2 d. 2 4x + 4 3x + 3
Dạng 5: Giải phương trinh
Bài 1: Giải phương trình a. 2 x = 3 b. 2 9x = 10 c. 2 4x −19 = 0 d. 2 49x = 14 −
Bài 2: Giải phương trình a. (x + )2 2 = 2 b. 2
4 − 4x + x = 3 c. 2
x − 4x + 4 = 3 + x d. 2
9x + 6x +1 = x −1 e. 2
x + 2 3x + 3 = 0
f. x − 4 x + 4 = 0 LỜI GIẢI Trang 2
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai Bài 1: Tính 64 8 a. = b. ( )2 2,5 = 2,5 25 5 c. (− )2 2 = 2 3 − 6 6 d. − = 169 13 Bài 2: Tính a. 196. 25 − 5 81 b. ( − )2 10 3 − 10 = 13.5 − 5.9 = 65 − 45 = 10 − 3 − 10 = 20 = 10 − 3− 10 = 3 − (5+ 7)2 d. (81: 9 + 169). 225 c. − 8 − 2 7 = (81:3+13).15 = + − ( − )2 5 7 1 7 = 30.15 = 450 = 5 + 7 − 1− 7 = 5 + 7 +1− 7 = 6
Dạng 2: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 1: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: 15 17 − a.
có nghĩa x − 2 0 b.
có nghĩa 12 − x 0 x − 2 12 − x x 2 x 12
c. 72x có nghĩa 72x 0
d. 24 +10x có nghĩa 24 +10x 0 x 0 12 − x 5 Trang 3 13 − 13 −
f. 27 − 6x có nghĩa 27 − 6x 0 e. có nghĩa 0 3x 3x 27 x x 0 6
Bài 2: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: a. 2 x +11 có nghĩa 2 x +11 0 b. 2
x + 5x + 6 có nghĩa 2
x + 5x + 6 0 x
(x + 2)(x + 3) 0 x 3 − x 2 − 10 − 3x 10 − 3x 4x + 2 4x + 2 c. có nghĩa 0 d. có nghĩa 0 2 3x +1 2 3x +1 2 x + 4x + 5 2 x + 4x + 5 vì 2
3x +1 1 nên 10 − 3x 0
vì x + x + = (x + )2 2 4 5 2 +1 1 10 3x nên 4x + 2 0 10 x 4x −2 3 1 − x 2
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Rút gọn các biểu thức sau: a. ( − )2 3 2 = 3− 2 = 3− 2 b. ( + )2 11 3 = 11 + 3 = 11 + 3 c. − = ( − )2 4 2 3 1 3 = 1− 3 = 3 −1 d. + = ( + )2 7 4 3 2 3 = 2 + 3 = 2 + 3
Bài 2: Rút gọn các biểu thức sau: a. 2
−2 a với a 0 b. 2
16a + 4a với a 0 = 2 − a = 2 − a = 4 a + 4 = 4 − a + 4 c. (a − )2 1 với a 1 1 d. 2
9a − 6a +1 + 3a với a 3 Trang 4
= a −1 = a −1(a ) 1 = ( a − )2 1 3
1 = 3a −1 = 1− 3a a 3 e. 2
a + 6a + 9 với a −3 f. 4 2 25a − 3a 2 2 2 = (a + )2
3 = a + 3 = a + 3
= 5a − 3a = 2a
Dạng 4: Phân tích đa thức thành nhân tử
Bài 1: Phân tích đa thức thành nhân tử a. 2
x − 7 = (x + 7 )(x − 7 ) b. 2
4x − 3 = (2x + 3)(2x − 3) c. x + x + = (x + )2 2 2 7 7 7 d. x + x + = ( x + )2 2 9 6 2 2 3 2
Bài 2: Phân tích đa thức thành nhân tử a. 2
x − 3 = (x + 3)(x − 3) b. 2
9x − 5 = (3x + 5)(3x − 5) c. x + x + = (x + )2 2 2 2 2 2 d. x + x + = ( x + )2 2 4 4 3 3 2 3
Dạng 5: Giải phương trinh
Bài 1: Giải phương trình a. 2 x = 3 b. 2 9x = 10 x = 3 ( x)2 3 =10 x = 3 3x =10 x = 3 − 3x =10 Vậy S = 3 − ; 3 3x = 1 − 0 10 x = 3 10 − x = 3 − Vậy 10 10 S = ; 3 3 c. 2 4x −19 = 0 d. 2 49x = 14 − Trang 5 2x =19 7x =14 2x =19 7x =14 2x = 1 − 9 7x = 1 − 4 19 x = 2 x = 2 x = 2 − 19 − x = − 2 Vậy S = 2; 2 − Vậy 19 19 S = ; 2 2
Bài 2: Giải phương trình a. (x + )2 2 = 2 b. 2
4 − 4x + x = 3 x + 2 = 2 ( − x)2 2 = 3 x + 2 = 2 − 2 − x = 3 x = 0 2 − x = 3 x = 4 − 2 − x = 3 − Vậy S = 0;− 4 x = 1 − x = 5 Vậy S = 5;− 1 c. 2
x − 4x + 4 = 3 + x d. 2
9x + 6x +1 = x −1 3 + x 0 x −1 0
x − 2 = 3 + x
3x +1 = x −1 x 3 − x 1
x − 2 = 3+ x
3x +1 = x −1 x − 2 = − (3+ x)
3x +1 = −( x − ) 1 0x = 5 2x = 2 − 2x = 1 − 4x = 0 1 − − 1 x = (nhận) x = 2 2 Trang 6 − − Vậy 1 S = Vậy 1 S = 2 2 e. 2
x + 2 3x + 3 = 0
f. x − 4 x + 4 = 0 (x + )2 3 = 0 (x + )2 2 = 0 = − x 2 x = − 3 Vậy S = − 2 Vậy S = − 3 Trang 7




