58 trang 4 lượt tải

Các dạng toán căn bậc hai và căn bậc ba Toán 9

8

Tài liệu gồm 58 trang, phân loại và giải chi tiết các dạng toán căn bậc hai và căn bậc ba môn Toán 9.

Chủ đề: Tài liệu chung Toán 9 129 tài liệu

Môn: Toán 9 3.4 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/58
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 1.
Chương III. CĂN BẬC HAI VÀ CĂN BẬC BA
Bài 7. CĂN BẬC HAl VÀ CĂN THỨC BẬC HAI
A. KIẾN THỨC CẦN NHỚ
1. Căn bậc hai
* Căn bậc hai của số thực không âm
a
là số thực
x
sao cho
2
=xa
.
Nhận xét:
- Số âm không có căn bậc hai;
- Số
0
có một căn bậc hai duy nhất là
0
;
- Số dương
a
có đúng hai căn bậc hai đối nhau là
a
(căn bậc hai số học của
a
) và
a
−
.
* Tính chất của căn bậc hai:
2
aa=
với mọi số thực
a
.
2. Căn thức bậc hai:
* Định nghĩa
Căn thức bậc hai là biểu thức có dạng
A
, trong đó
A
là một biểu thức đại số.
được gọi là
biểu thức lấy căn hoặc biểu thức dưới dấu căn.
A
xác định khi
A
lấy giá trị không âm, ta thường viết là
A0≥
. Ta nói
A0≥
là điều kiện xác
định (hay điều kiện có nghĩa) của
A
.
* Hằng đẳng thức
2
AA=
Tương tự như căn bậc hai của một số thực không âm, với
A
là một biểu thức, ta cũng có:
+ Với
0, ta có A ≥
2
0,( )A AA≥=
;
+
2
=AA
B. PHÂN LOẠI CÁC BÀI TẬP
I. Tìm căn bậc hai của một số
Bài toán 1. Tìm các căn bậc hai của
16
4; ;3
9
.
Lời giải
Ta có:
40>
nên
4
có hai căn bậc hai là
2
và
2−
vì
2
24=
và
2
( 2) 4−=
Ta có:
16
0
9
>
nên
16
9
có hai căn bậc hai là
4
3
và
4
3
−
vì
2
4 16
39

±=


.
Ta có
30>
nên
3
có hai căn bậc hai là
3
và
3−
. Vì
2
( 3) 3±=
.
Bài toán 2. Giải phương trình:
a)
2
4x =
; b)
2
2x =
; c)
2
2x = −
; d)
2
0x =
.
Hướng dẫn: Nghiệm của phương trình
2
xa=
(với
0
a ≥
) là các căn bậc hai của
a
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 2.
Lời giải
a) Ta có
40>
nên
4
có hai căn bậc hai là
2
và
2−
vì
2
( 2) 4
±=
.
Vậy
2
4x =
2
2
x
x
=
⇒
= −
.
Tập nghiệm của phương trình
2
4x =
là
{ }
2; 2
S = −
.
b) Ta có
20>
nên 2 có hai căn bậc hai là
2
và
2−
vì
2
( 2) 2±=
.
Vậy
2
2x =
2
2
x
x
=
⇒
= −
.
Tập nghiệm của phương trình
2
2x =
là
{
}
2; 2
S = −
.
c) Ta có:
20
−<
nên
2−
không có căn bậc hai
⇒
phương trình
2
2x = −
vô nghiệm.
Vậy
S = ∅
.
d) Ta có
2
00xx=⇒=
.
Tập nghiệm phương trình
2
0x =
là
{
}
0S =
.
(Bạn đừng nhầm với
S = ∅
và
{ }
0
S =
).
Ta có thể giải cách khác nhau sau, chẳng hạn.
*
2 22
4 20xx=⇔−=
( )( )
2 20xx⇒− +=
20
20
x
x
−=
⇒
+=
2
2
x
x
=
⇒
= −
.
*
2 2 22
2 2 0 ( 2) 0xx x=⇒−=⇒− =
( )( )
2 20xx⇒− + =
2
2
x
x
=
⇒
= −
.
Bài toán 3. Tìm căn bậc hai số học của số sau:
a) 144; b)
16
9
; c) 1,21; d)
2
( 1,69)−
.
Hướng dẫn: Gọi
x
(không âm) là căn bậc hai số học của số
a
, ta có:
2
xa=
, ta đưa về bài toán 2 .
Lời giải
a) Gọi
( )
0xx≥
là căn bậc hai số học của
144
, ta có:
144 0
>
, nên
144
có một căn số học là
12,
ta viết:
144 12=
vì
2
12 144=
.
b) Ta có:
16 4
93
=
vì
2
4
0
3
4 16
39
>

=


.
c) Ta có:
1, 21 1,1=
vì
2
1,1 0
(1,1) 1, 21
>
=
.
d) Ta có
22
( 1,69) (1,69) 1,69−= =
vì
1, 69 0>
.
II. Phương trình dạng:
AB=
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 3.
Cách giải:
2
0
B
AB
AB
≥
= ⇔
=
.
(Thực chất của vấn đề là ta đã bình phương hai vế, vì
2
()AA=
).
Bài toán 4. Giải phương trình:
a)
3x
=
; b)
21x −=
; c)
xx=
; d)
2
64 4xx x−+=+
.
Lời giải
a) Ta có:
3x
=
2
3 0 (luôn đúng)
3
x
≥
⇒
=
9x⇒=
. Tập nghiệm:
{ }
9
S =
.
b) Ta có
21x
−=
1 0 (luôn đúng)
21x
≥
⇒
−=
3x⇒=
. Tập nghiệm:
{ }
3S =
.
c) Ta có
xx=
2
0x
xx
≥
⇒
=
2
0
0
x
xx
≥
⇒
−=
( )
0
10
x
xx
≥
⇒
−=
0
1
x
x
=
⇒
=
. Tập nghiệm:
{ }
0;1S =
.
d) Ta có
2
64 4xx x−+=+
22
40
6 4 ( 4)
x
xx x
+≥
⇒
−+=+
22
4
6 4 8 16
x
xx x x
≥−
⇒
−+=++
4
12 10
x
x
≥−
⇒
= −
4
5
6
x
x
≥−
⇒
= −
5
6
x⇒=−
. Tập nghiệm:
5
6
S

= −


.
Bài toán 5. Giải phương trình:
a)
2
1 10xx−− −=
; b)
2
4 5 40x xx
+− + +=
.
Hướng dẫn: Ta đưa về dạng
AB=
Ta có
0
B
AB
≥
=
0B
AB
≥
⇔
=
.
Lời giải
a) Ta có:
22
1 10 1 1xx x x−− −=⇒ −= −
22
10 1
11 0
xx
x x xx
−≥ ≥
⇒⇒

−= − − =
(
)
1
10
x
xx
≥
⇒
−=
1
0 1 0
x
xx
≥
⇒
= ∨ −=
1
0 1
x
xx
≥
⇒
=∨=
1x⇒=
.
Tập nghiệm:
{ }
1S =
.
Chú ý: Ta có thế xét
2
0
A
AB
AB
≥
= ⇔
=
, nhưng ở bài toán này, ta không nên đặt
2
10x
−≥
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 4.
Ta xét bài toán b) sau đây:
b) Ta có:
2
4 5 40x xx+− + +=
2
4 54x xx⇒ += + +
2
40
54 4
x
xx x
+≥
⇒
+ +=+
2
4
40
x
xx
≥−
⇒
+=
( )
4
40
x
xx
≥−
⇒
+=
4
0 4 0
x
xx
≥−
⇒
=∨ +=
4
0 4
x
xx
≥−
⇒
=∨=−
0
4
x
x
=
⇒
= −
.
Tập nghiệm:
{ }
4;0S
= −
.
Ta có thể xét bài toán tương tự sau đây:
2
1 10xx−+ −=
Vì
2
10
x −≥
và
10x −≥
2
1 10xx⇒ −+ −≥
.
Vậy
2
1 10
xx−+ −=
2
10
10
x
x
−=
⇒
−=
2
10
1
10
x
x
x
−=
⇒ ⇒=
−=
.
Bạn hãy giải phương trình sau:
1)
2
9 30xx−+ −=
Đáp số:
3
x =
2)
2
3 2 10xx x− ++ −=
Đáp số:
1x =
3)
{
21 1x −<=
Đáp số:
4x =
.
III. Tìm điều kiện xác định của biểu thức
Bài toán 6. Tìm
x
để cho căn thức sau có nghĩa.
a)
21
x−+
b)
1
2x
+
c)
2
1
x
d)
2
3
1x
−
+
Hướng dẫn:
A
có nghĩa
0A⇔≥
;
1
A
có nghĩa
0A⇔≠
.
Lời giải
a)
21x−+
xác định(có nghĩa)
1
21021
2
x xx⇒ +≤
⇒⇒−≥ ≤
.
b)
1
2x +
xác định
1
0
20 2
2
20
xx
x
x
≥
⇒ +>
⇒⇒>−
+
+≠
.
c)
2
1
x
xác định
2
2
1
0
0
0
x
x
x
⇒
≥
≠
⇒ ≠
.
d)
2
3
1x
−
+
xác định
2
3
0
1x
−
≥
+
⇒
(không tồn tại).
Bài toán 7. Tìm
x
để căn thức sau có nghĩa.
a)
1xx+−
b)
( )
1xx−
c)
1
2
x
x
+
−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 5.
Hướng dẫn: Ta tìm điều kiện cho tất cả các căn bậc hai xác định.
Lời giải
a)
x
và
1 x−
xác định
00
01
10 1
xx
x
xx
≥≥

≤≤

−≥ ≤

⇒ ⇒⇒
b)
( )
1xx−
xác định
( )
10xx⇒ −≥
0
10
x
x
≥
−≥
⇒
hoặc
00
10 1
xx
xx
≤≥


−≤ ≤
⇒
hoặc
0
1
x
x
≤
≥
(vô lí)
01x⇒ ≤≤
c)
1
2
x
x
+
−
xác định
10
1
0
20
2
x
x
x
x
+≥
+
≥
−>
−
⇒⇒
hoặc
10
20
x
x
+≤
−<
12x
⇒− ≤ <
Bài toán 8. Tìm
x
để biểu thức sau xác định :
a)
( )( )
13xx−−
b)
2
1
x
−
c)
1
2
x
x
−
−
Hướng dẫn: Xem lời giải bài toán
2
.
Lời giải
a)
( )( )
13xx−−
xác định
(
)
( )
1 30
xx− −≥
⇒
10
30
x
x
−≥
−≥
⇒
hoặc
10
30
x
x
−≤
−≤
3
x⇒ ≥
hoặc
1x ≤
b)
( )
(
)
2
1 11x xx
−= − +
Vậy
2
1x −
xác định
10
10
x
x
−≥
+≥
⇒
hoặc
10
10
x
x
−≤
+≤
1x⇒ ≥
hoặc
1
x ≤−
c)
1
2
x
x
−
−
xác định
10
1
0
20
2
x
x
x
x
−≥
−
≥
−>
−
⇒⇒
hoặc
10
20
x
x
−≤
−<
2x⇒ >
hoặc
1x ≤
IV. Rút gọn biểu thức
Bài toán 9. Rút gọn:
a)
(
)
2
32A = −
b)
(
)
2
25B = −
c)
( )
2
31 3C = −−
Hướng dẫn: Áp dụng hằng đẳng thức:
2
AA=
.
Lời giải
a) Ta có :
( )
32 32A = −=− −
; vì
320−<
Vậy
23A = −
.
b) Ta có :
( )
25 25 52B =− =−− = −
;(vì
2 50−<
).
c) Ta có:
( )
31 3 31 3 1C = −−= −−=−
( vì
310−>
).
Bài toán 10. Rút gọn:
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 6.
a)
3 22 3 22A =+ −−
b)
7 43 7 43B
=− ++
c)
23 8 7 7
C =+−
d)
11 6 2 3 2D = − −+
Hướng dẫn: a) Ta có
3 2 2 1 2.1. 2 2+=+ +
(
)
(
)
22
2
1 2.1. 2 2 1 2
=+ +=+
(
)
322 1221212
⇒+ = + =+ =+
.
( Các biểu thức khác được làm tương tự ).
Lời giải
a) Ta có :
2 22 1 2 22 1A = + +− − +
( ) ( )
22
22
2 2. 2.1 1 2 2 2.1 1= + +− − +
( )
( )
22
21 21= +− −
( ) ( )
21 21 21 21 2= +− −= + − − =
b) Ta có:
4 2.2 3 3 4 2.2 3 3B = − ++ + +
( ) ( )
22
23 23=− ++
232323234= − + + =− ++ =
c) Ta có:
16 2.4. 7 7 7C = + +−
( )
2
47 747 7= + −=+−
4 7 74=+−=
d) Ta có:
9 2.3 2 2 3 2D = − +−+
( )
2
32 323232= − −+ = − −+
3 23 2 0=− −+ =
Bài toán 11. Rút gọn biểu thức: a) A =
2
12 36xx x
− +−
b) B =
122 122x xx x
−− − + −+ −
c) C =
21 21xx xx+ −+ − −
Hướng dẫn:
a) ta có:
( ) ( )
22
2
12 36 6 6 6xx x x x− +=− ⇒ − =−
b), c) Đưa các biểu thức trong một dấu căn trở thành bình phương của một tổng hoặc một hiệu.
Lời giải
a) Ta có: A =
( )
2
66x xx x− −= −−
( )
6, 6
6, 6
xxx
x xx
−− ≥
⇒
−−− <
neáu
neáu
6,
6x
−≥
⇒
<
neáu x 6
6-2x, neáu
b) Ta có: B =
( )
2 2 2.1 1 2 2 2.1 1xx x− − − ++ −+ − +
( )
( )
22
21 21 21 21x x xx
= −− + −+ = −−+ −+
Trường hợp 1:
Nếu
210 21 21x xx−−≥⇒ −≥⇒−≥
3, 2 1 2 1 2 2x xx x⇒≥ −−+ −+= −ta coù B =
Trường hợp 2:
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 7.
Nếu
210 21xx−−≤⇒−<
0 21 2 3xx⇒ ≤ − <⇒ ≤ <
Ta có:
( ) ( )
21 21 2Bx x=− −−+ −+ =
Vậy: Nếu
3
x
≥
, ta có
22Bx= −
Nếu
23x≤<
ta có
2
B =
c) Ta có
(
)
(
)
22
11 11Cx x
= −+ + −−
11 11xx= −++ −−
Trường hợp 1:
Nếu
110 2xx−−≥ ⇒ ≥
Ta có
21Cx
= −
Trường hợp 2:
Nếu
110 1 1xx−−< ⇒ −<
0 11 1 2
xx
⇒ ≤ −<⇒≤ <
Ta có:
(
)
11 11 2Cx x= −+− −− =
Vậy: Nếu
2x ≥
ta có
21Cx= −
Nếu
12x≤<
ta có
2C =
Cách giải khác: (đối với bài toán c).
Đặt
22
00
1
11
uu
ux
u x xu
>≥

= −⇒ ⇒

=−=+

Khi đó, ta có:
22
12 12Cu uu u= ++ + +−
( )
( )
22
1 1 11u u uu= + + − = ++ −
Trường hợp 1:
Nếu
10 1 11 2u ux x−≥ ⇒ ≥⇒ −≥⇒ ≥
Ta có:
( )
2 2 1 0 10Cu x u u= = − ≥⇒+>
Trường hợp 2:
Nếu
10 1 11
u ux−< ⇒ <⇒ −<
0 10
ux≥⇒ −≥
1 11 11 2xx x x⇒ ≥⇒ −<⇒ −<⇒ <
Vậy
12x≤<
Ta có:
( )
1 12Cu u= +− − =
(Bạn có thể giải lại bài toán b, theo cách này)
Bài toán 12. Tính giá trị của biểu thức
a)
2
4 2 9 6 1,A x xx=− −+ − +
với
2014x =
b)
22
44 44,Bx x x x= − ++ + +
với
2015x =
Hướng dẫn: Đưa biểu thức dưới dấu căn trở thành bình phương một tổng hoặc một hiệu và áp dụng hằng
đẳng thức
2
AA=
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 8.
Lời giải
a) Ta có:
( )
2
4 2 31 4 231Ax x x x=− −+ − =− −+ −
Thay
2014x =
vào biểu thức trên, ta được:
4.2014 2 3.2014 1
A =− −+ −
4.2014 2 3.2014 1 2014 3 2017
=− −+ −=− −=−
b) Ta có:
(
) ( )
22
2 2 22Bx x x x= − + + =−++
Thay
2015x =
vào biểu thức trên, ta được:
2015 2 2015 2 2015 2 2015 2 4030B = − + + = −+ +=
V. Giải phương trình
Bài toán 13. Giải phương trình
a)
2
5x =
b)
2
25 10
x =
c)
2
9 21xx= +
d)
2
6 93 1xx x+ += −
Hướng dẫn: Biến đổi biểu thức dưới dấu căn trở thành bình phương của một tổng hoặc một hiệu và áp
dụng hằng đẳng thức
2
AA=
.
Lời giải
a) Ta có:
( )
2
50
55 5
5
xx x
x
≥
=⇒ =⇒ ⇒=±
= ±
luoân ñuùng
Tập hợp nghiệm:
{ }
5; 5S = −
.
b) Ta có:
( )
2
2
25 10 5 10xx=⇒=
(
)
10 0
5 10 2
5 10
xx
x
≥
⇒ = ⇒ ⇒=±
= ±
luoân ñuùng
Tập hợp nghiệm:
{ }
2; 2S = −
.
c) Ta có:
2
9 21xx= +
( ) (
)
2
3 21 3 21*x x xx⇒ = +⇒ = +
Điều kiện
1
2 10
2
xx
−
+≥ ⇔ ≥
Khi đó: (*)
( )
3 21
3 21
xx
xx
= +
⇒
=−+
1
11
52
x
xx
=
⇒
−−

= ≥


thoaû maõn ñieàu kieän
Tập hợp nghiệm:
1
;1
5
S

= −


.
VI. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
Bài toán 14: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
a)
22
44x xx+ −+
b)
223 663x xx x−+ −+ ++ −
Hướng dẫn: Áp dụng hằng đẳng thức
2
AA=
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 9.
và
A B AB
+ ≥+
dấu
""=
xảy ra
0AB⇒≥
(A và B cùng dấu hoặc bằng 0).
Lời giải
a) Ta có:
( )
22 22
Axx x x x x= +−= +−≥+ − =
Vậy giá trị nhỏ nhất của A bằng 2.
Dấu
""=
xảy ra, chẳng hạn
0
x
=
(Khi đó thoả mãn điều kiện
( )
20xx−≥
)
Chú ý: Ta không cần tìm hết tất cả các giá trị của x thoả mãn
(
)
20xx
−≥
. Nếu ta có:
( )
2 00 2
xx x− ≥⇒≤≤
).
Ta có thể giải cách khác.
Ta có
2Axx= ++
Trường hợp 1:
Nếu
2 22 2x Axx x≥⇒ =+−= −
Với
224222
xxx
≥⇒ ≥⇒ −≥
Giá trị nhỏ nhất của A bằng 2.
Trường hợp 2:
Nếu
(
)
0 2 22x Ax x≤<⇒ =− − =
Trường hợp 3: Nếu
( )
0 2 22x A xx x< ⇒ =−− − =− +
Vì
020222
xxx
<⇒− >⇒− +>
Vậy kết hợp các kết quả của ba trường hợp, ta có: giá trị nhỏ nhất của A bằng 2.
Dấu
""=
xảy ra
0x
⇔=
b) Ta có:
31 33Bx x= −++ −+
Điều kiện:
30 3xx−≥⇒ ≥
khi đó biểu thức trong các dấu giá trị tuyệt đối đều dương.
Ta có:
31 33 2 34Bx x x= −++ −+= −+
Vì
32302344xx x≥⇒ −≥⇒ −+≥
Vậy giái trị nhỏ nhất của B bằng 4.
Dấu
""=
xảy ra
3x⇒=
.
Chú ý: Từ kết quả trên, ta có bài toán giải phương trình:
223 6634.x xx x−+ −+ ++ − =
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 1.
Chương III. CĂN BẬC HAI VÀ CĂN BẬC BA
BÀI 8. CĂN BẬC HAI VÀ CĂN THỨC BẬC HAI
A. KIẾN THỨC CẦN NHỚ
1. Khai căn bậc hai và phép nhân
Liên hệ giữa phép khai căn bậc hai và phép nhân:
Với A, B là các biểu thức không âm, ta có:
.A B AB=
.
Chú ý: Kết quả trên có thể mở rộng cho nhiều biểu thức không âm, chẳng hạn:
( )
. . . . 0; 0; 0vôùi A B C ABC A B C= ≥≥≥
.
2. Khai căn bậc hai và phép chia
Liên hệ giữa phép khai căn bậc hai và phép chia:
Nếu A, B là các biểu thức với
0, 0AB
≥>
thì
.
AA
B
B
=
B. PHÂN LOẠI CÁC BÀI TẬP
I. Khai căn bậc hai của một tích
Bài toán 1. Tính:
a)
90.4,9
b)
12,1.360
c)
2,5.14,4
d)
( )
2
4
2. 3−
Hướng dẫn: Áp dụng quy tắc khai căn một tích:
( )
( )
( )
2
2
. 0, 0 , 0
ab a b a b A A A A= ≥≥ = = ≥
Lời giải
a) Ta có:
90.4,9 9.49 9. 49 3.7 21= = = =
b) Ta có:
12,1.360 121.36 121. 36 11.6 66= = = =
c) Ta có:
2,5.14,4 36 6= =
Cách khác:
11
2,5.14,4 5.144. 5.12. 6
100 10
= = =
d) Ta có:
( )
( )
( )
2
22
42
2 . 3 2 . 3 4. 3 12−= −=−=
Bài toán 2. Rút gọn rồi tính:
a)
22
25 24−
b)
22
17 8
−
c)
22
117 108−
d)
22
6,8 3, 2−
e)
22
21,8 18, 2−
Hướng dẫn: Áp dụng hằng đẳng thức:
( )( )
22
a b abab−=− +
Lời giải
a) Ta có:
( )( )
22
25 24 25 24 25 24 1.49 7
−= − += =
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 2.
b) Ta có:
(
)
(
)
22
17 8 17 8 17 8 9.25 3.5 15
−= − += = =
c) Ta có:
( )
(
)
22
117 108 117 108 117 108 9.225 3.15 45−= − += ==
d) Ta có:
( )( )
22
6,8 3, 2 6,8 3, 2 6,8 3, 2 3, 6.10 36 6−= − += ==
e) Ta có:
( )( )
22
21,8 18, 2 21,8 18,2 21,8 18,2 3,6.40 36. 4 6.2 12−= − += = ==
Bài toán 3. Rút gọn:
a)
5 26A = −
b)
7 2 10 7 2 10
B =+ +−
c)
8 2 15 5C =+−
Hướng dẫn: Áp dụng quy tắc nhân các căn bậc hai
( )
. 0, 0a b ab a b= ≥≥
Lời giải
a) Ta có:
( )
( )
22
3 2. 3.2 2 3 2 3. 2 2− += − +
( )
2
32 32 32= − =−=−
b) Ta có:
5 2 5.2 2 5 2 5.2 2B = + ++ − +
2 22 2
5 2. 5. 2 2 5 2. 5. 2 2 
22
52 52

52 52

25
c) Ta có
22
5 2 5.3 3 5 5 2. 5. 3 3 5C 
2
53 5 5353  
II. Nhân các căn bậc hai
Bài toán 4. Tính:
a)
3 2. 3 2A 
b)
32 32
B 
c)
47 47C 
d)
35 35D 
Hướng dẫn: Áp dụng quy tắc nhân các căn bậc hai:
..A B AB
0; 0AB
Các bài b), c), d) ta phải bình phương hai vế, rồi sau đó khai căn bậc hai.
Lời giải
a) Ta có
22
3 2. 3 2 3 2 3 2 1A 
b) Nhận xét
3 20
3 20 
;
3 20
.
Vậy
0B
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 3.
Ta xét
2
2
32 32B 
22
32 232.32 32

32232.32 32
2 3 2.1
(xem bài toán a)
2 23
2 23B
c) Nhận xét:
0C
.
Ta xét
2
2
47 47C 
22
47 247.47 47 
47247.4747 
82167 829 
8 6 14
14C

d) Nhận xét
0D
vì
35 35 
Ta xét
2
2
35 35D 
22
35 235.35 35 
35235.3535

6 2 9 5 6 2.2 2 
2D 
(vì
0D
) .
Chú ý: Các biểu thức
AB
và
AB
được gọi là hai biểu thức liên hợp.
Bài toán 5. Tính: a)
6 10 . 4 15A 
b)
3 5 . 10 2 . 3 5B 
c)
4 15 . 10 6 . 4 15C 
Hướng dẫn: Áp dụng cả hai quy tắc khai căn một tích và nhân các căn bậc hai.
Lời giải
a) Ta có:
6 10 . 4 15A 
3.2 5.2 . 4 15
3.2 5.2.4 15 3 5.2.4 15
3 5. 24 15 3 5. 8 215 
3 5.5 25.3 3
22
3 5. 5 3 5 3 5 3 2

b) Ta có:
3 5 . 10 2 . 3 5
B 
3 5 . 5 1 . 2. 3 5
2
3 5.51. 51
3 5.51.51
2
3 5. 5 1
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 4.
3 5.6 2 5
2 3 5 3 5 2 9 5 2.4 8 
.
c) Ta có:
4 15 . 10 6 . 4 15C 
4 15 . 5 3 . 2. 4 15
4 15 . 5 3 . 8 2 15

2
4 15 . 5 3
4 15 . 8 2 15

2 4 15 4 15
2 16 15 2.1 2 
.
III. Phân tích thành nhân tử
Bài toán 6. Phân tích thành nhân tử
a)
236
A xy x y

0; 0
xy

b)
1B ab b a a
c)
32C a ab b
d)
27 5D x xy y
Hướng dẫn: Áp dụng quy tắc khai căn một tích:
.AB A B
và các phương pháp phân tích đa
thức thành nhân tử đã học ở lớp 8: Nhóm các số hạng, dùng hằng đẳng thức, thêm bớt một vài số
hạng để làm xuất hiện nhân tử chung.
Lời giải
a) Ta có:
236A xy x y
23 2
xy y

32xy

b) Ta có:
1B ab b a a
2
1a b ba a





11ba a a 

11a ba
c) Ta có:
32
C a ab b
22
. 2. 2a ab ab b

2a ba b

d) Ta có:
27 5D x xy y
22
2 2 . 5. . 5x xy xy y
25xxy yxy 
25xy x y
Bài toán 7. Phân tích thành nhân tử
a)
6Aa a
b)
33
Ba b
c)
C xx yy
Hướng dẫn: Xem cách giải bài toán 6
Lời giải
a) Ta có:
6Aa a

2
236a aa 
23 2aa a 
23
aa
;
0a
b) Ta có:
33
Ba b
33
ab
22
.a b a ab b

a b a ab b
;
0; 0ab
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 5.
c) Ta có:
C xx yy
33
xy
22
.x y x xy y

x y x xy y
;
0; 0xy
IV. Chứng minh một đẳng thức
Bài toán 8.
a) Cho
58 5xx
1
Chứng minh rằng

58 6xx 
.
58x

b) Cho
11
xx 
2
Chứng minh rằng
2
0xx
.
01x
Hướng dẫn: Bình phương hai vế đẳng thức đã cho và tính tích của hai căn thức.
Lời giải
a) Bình phương hai vế của đẳng thức
1
ta được
2
5 8 25xx
5 2 5. 8 8 25
x x xx

5 8 25 13xx 

58 6
xx

(đpcm)
Chú ý: Em có thể giải bài toán sau:
1) Cho
58 5xx
Hãy tính

58xx
và
2
3 40
xx
.
(Ta có
2
5 8 3 40
x x xx 
)
2) Cho
51xx

. Hãy tính
5xx
.
Nhân hai vế của đẳng thức
51
xx
với
5xx
(là biểu thức liên hợp của
5xx
).
Điều kiện
0 50xx

50xx 
.
Ta có:
51xx
55 5
0
xxxxxx
x
  
55
0
x xx x
x
 
0
55
x
xx

Vậy
55xx
.
Bạn hãy giải bài toán sau:
Cho
22
25 15 2
xx
. Tính
22
25 15xx
. (Đáp số
22
25 15 5
xx
).
b) Bình phương hai vế đẳng thức
2
ta được:
2
2
1 1 2 .1 1 1x x xxx x 
10xx 
2
0xx 
. (đpcm)
Chú ý: Ta có thể giải bài toán sau:
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 6.
Giải phương trình
11xx 
. (Đáp số
1x
)
Bài toán 9. Cho
22
1 11
x xy y 
*
Chứng minh rằng
0xy
.
Hướng dẫn:
Nhân hai vế của đẳng thức
*
lần lượt với các biểu thức liên hợp của
2
1xx

và
2
1yy
Sau đó nghĩ đến việc làm xuất hiện tổng
xy
bằng cách cộng hai vế.
Lời giải
Với
0x
và
0y
suy ra
0xy
.
Giải sử
0x
, nhân hai vế của đẳng thức
*
với
2
1 xx
, ta được

2 2 22
1 1 11xx xxy y xx   
22
11
y y xx
 
**
Tương tự, nhân hai vế của đẳng thức
*
với
2
1
yy
, ta được
22
11x x yy
***
Cộng
**
với
***
ta được
2222
11 11xyxyxyxy 
20 0xy xy 
. (đpcm)
V. Giải phương trình
Bài toán 10. Giải phương trình
a)
1
4 20 5 9 45 4
3
xx x 
1
b)
16 32 12 3 9 18x xx x 
2
c)
2
9 4 12 0xx
3
Hướng dẫn: a) Áp dụng quy tắc khai căn một tích
.AB A B
0; 0AB
và công thức
2
0b
ab
ab

Lời giải
a)
1
1
45 5 954
3
xx x

1
4. 5 5 9. 5 4
3
xx x 
2. 5 5 5 4xxx 
2. 5 4x 
52x 
20
9
54
x
x


b)Ta có
2 16 1 2 4.3 3 9 1 2x xx x 
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 7.
412 23 3 312
x xx x

1 2 33
xx
0
0
1
1
1 2 9.3
29
29
x
x
x
xx
x




c) Ta có
3 3 3 4 30xx x 
3 32 0 *
3 **
xx
x

Giải
*
ta được
30x

hoặc
32x 
3x
hoặc
1x
.
Kết hợp với
**
suy ra
3x
.
Bài toán 11. Giải phương trình:
a)
11
xx
−+ =
b)
51xx+− =
c)
3 85xx++ +=
Hướng dẫn:
Bình phương hai vế với điểu kiện cẩn thiết và rút gọn, ta được phương trình chứa một căn thức.
Lời giải
a) Điều kiện:
0
01
10
x
x
x
≥
⇒≤≤
−≥
Bình phương hai vế phương trình (1) ta được:
Đối chiếu điểu kiện, ta có tập hợp nghiệm:
S {0; 1}=
.
b) Ta có: (2)
51xx⇒ +=+
(*)
2
00 0
4
5 (1 ) 5 1 2 2 4
xx x
x
x x x xx x
≥≥ ≥


⇒ ⇒ ⇒ ⇒=

+= + +=+ + =


- Cách giải khác (Dùng biểu thức liên hợp)
Nhân hai vế của phương trình (2) vơi
5xx++
(Với điều kiện
0 50x xx
≥⇒ ++ >
), ta có:
22
(5 )(5) 5 (5)( ) 5 5 5(**)xxxxxxx xxxxx++ +− = ++ ⇒ + − = ++ ⇒ ++ =
Cộng vế vợi vế (*) và (**), ta được:
2 56 53 59 4x xxx+=⇒ +=⇒+=⇒=
(thỏa mãn điều kiện
0)x ≥
VI. Chứng minh đảng thức
Bài toán 12. Chứng minh rằng:
222 2
| ax by | a b x y+≤ + +
với mọi
,,,abx y R∈
10 1
1 2 1 1 2 (1 ) 0 (1 ) 0 (1 ) 0
00
xx
x x x x xx xx xx
xx
−= =
−+−⋅+=⇒ −=⇒−=⇒−=⇒ ⇒
= =
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 8.
Bất đẳng thức Bunyakovsky.
Huớng dẫn: Bình phương hai vế bất đả
ng thức cẩn chứng minh và biến đổi tương đương.
Lời giải
Ta có:
22 22
| ax by | a b x y+ ≤ +⋅ +
( )( )
2 222 2
22 22 22 22 22 22
2
()
2
( )0
ax by a b x y
a x abxy b y a x a y b x b y
ay bx
⇒+ ≤+ +
⇒+ +≤+++
⇒− ≥
Bất đẳng thức cuối cùng luôn đúng với mọi
a, b, x, y
thuộc
.
Dấu " = " xảy ra
0 , 0, 0
ab
ay bx x y
xy
⇔ − =⇔= ≠ ≠
(với
0x =
và
0y =
, bất đẳng thức luôn đúng).
Bài toán 13. Chứng minh rằng
a b 2(a b)+≤ +
với
a 0; b 0≥≥
.
Huớng dãn: Bình phương hai vế và rút gọn như bài toán 12 .
Lời giải
Ta co:
2( ) 2 2( )a b ab a a bb ab+ ≤ + ⇒+ ⋅ +≤ +
2
2 0 ( ) 0 (luôn dúng). a ab b a b
⇒− +≥⇒ − ≥
Nhận xét: Ta có thê áp dụng bất đả
ng thức Bunyakovsky ở trên như sau:
Ta có:
22
1 a1 b|1 a1 b| 1 1 ab⋅ +⋅ = ⋅ +⋅ ≤ + ⋅ +
2 2( ) (dpcm). a b ab a b ab
⇒+≤⋅+⇒+≤ +
Bài toán 14. So sánh
xy+
và
( 0, 0)x yx y+ >>
.
Huớng dẫn: Ta chứng minh
xy x y
+< +
băng cách bình phương hai vế như đã làm ở bài
toán 12 và 13 .
Lời giải
Với
0, 0xy>>
, ta co:
xy x y+< +
2
() 2xy x y xyx xyy⇒+< + ⇒+<+ +
20xy
⇒>
(luôn đúng với
0, 0)xy>>
Nhận xét: Bạn hãy để ý các kết quả đã biết sau đây:
( 0, 0)
( 0, 0)
xy x y x y
x y x yx y
⋅= ⋅ ≥ ≥
+< + > >
Bài toán 15. So sánh:
a)
32+
và
26+
b)
23+
và
10
c)
2014 2016+
và
2 2015
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 9.
Lời giải
a) Ta co:
2
( 3 2) 3 2 3 2 4+ =+⋅ ⋅+
7 4 3. = +
Lại có:
2
( 2 6) 2 2 6 6 2
+ = ⋅ ++
8212 82 4 3 843
=+ =+⋅ ⋅ =+
22
vì 7 8 7 43 8 43 (3 2) (2 6) 3 2 2 6<⇒+ <+ ⇒ + < + ⇒ +< +
b) Ta có:
2 3 10+<
22
( 2 3) 10 2 2 2 3 3 10 2 6 5 (2 6) 25 24 25 (luôn dúng). ⇒ + <⇒+ ⋅ +<⇒ <⇔ <⇒<
c) Ta có:
2014 2016 2 2015+<
2
2
( 2014 2016) 4.2015 2014 2. 2014. 2016 2016 8060 2
2014.2016 4030
2014.2016 2015 2014.2016 2015 4060224 4060225
⇒ + < ⇒+ +<⇒ <
⇒ <⇒ < ⇒ <
Ta có thể chứng minh bài toán tổng quát sau:
Vơi
n ∈
, ta luôn có:
22 1nn n+ +< +
Bài toán 16.
a) Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
1yx x
= +−
b) Tìm giá trị lớn nhất của biểu thức
24yx x
= −+ −
c) Tìm giá trị lớn nhất của biểu thức
A x 2 y 1,= −+ −
với
x y 5. +=
Huớng dãn: a) Xét giá trị lớn nhất, nhỏ nhất của
2
y
.
b) Áp dụng bất đẳng thức Bunyakovsky.
Lời giải
a) Với điều kiện:
0x
≥
và
1 00 1xx−≥⇔≤≤
Khi đó
y0>
. Ta xét
2
y
:
22
2 (1 ) 1 1 2 (1 )yx xx xy xx=+−+−⇔=+−
Vì
(1 ) 0 1 (1 ) 1xx xx−≥⇒+ −≥
Vậy
2
11yy≤⇒ ≥
Giá trị nhỏ nhất của
y
bằng 1 .
Dấu "=" xảy ra
0
1
x
x
=
⇔
=
Lại có:
2
(1 )x x xx− =−+
2
2
1 1 1 1 11
4 4 4 2 42
xx x

=− −+ + = − − ≤ =


Vậy:
2
1
12 2 2
2
yy≥+⋅ = ⇒ ≤
Giá trị lớn nhất của y bằng
2
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 10.
Dấu "=" xảy
11
ra x 0 x
22
⇔−=⇔=
Cách khác:
Theo bất đẳng thức Bunyakovsky, ta có:
22 2 2
1 |1 1 1 | 1 1 ( ) ( 1 ) 2
x xx x x x+ − = ⋅ +⋅ − ≤ + ⋅ + − =
2
y
⇒≤
(tiếp tục như cách giải trên)
b) Điều kiện:
2x4≤≤
.
Theo bất dảng thức Bunyakovsky, ta có:
1.
22 2 2
2 1 4 1 1 ( 2) ( 4 )
xx x x− +⋅ − ≤ + ⋅ − + −
2 22=⋅=
y2⇒≤
. Vậy giá trị lớn nhất của
y
bằng 2 .
Dấu “ = " xảy
x2 4x
ra x 2 4 x x 3
11
−−
⇔ = ⇔−=−⇔ =
c) Điều kiện
2
x ≥
và
1y ≥
Theo bất đå
ng thức Bunyakovsky, ta có:
1.
22
21 1 1 1 2 1 2 3x y x y xy−+⋅ −≤ + + −+−= ⋅ +−
Vì
5 2 53 2xy A+=⇒ ≤ ⋅ −=
Vậy giá trị lớn nhất của
A
bằng 2 .
Dấu "=" xảy ra
3
21
2
5
x
xy
y
xy
=
−= −
⇒⇒

=
+=
.
Bài toán 17. Tìm
x
, biết:
a)
9 36 121 8xx x
−+ <
b)
1 54 4 9 9 4x xx−+ − − − <
c)
2
4 20xx−− −>
Huớng dẩn: Áp dụng quy tắc khai căn một tích.
Lời giải
a) (1)
3 6 11 8xx x
⇒−+ <
8 8 10 1xx x⇒ <⇒ <⇒ ≤ <
.
b) (2)
x110x13x1 4⇒ −+ −− −<
1
8 14 1
2
xx⇒ −< ⇒ −<
10
5
1
1
4
1
4
x
x
x
−≥
⇒ ⇒≤ <
−<
c) (3)
2 ( 2 1) 0xx⇒ − +−>
Điểu kiện:
20( 20xx−> −=
: không thỏa mãn)
2x⇒>
.
Khi đó: (3)
210 21xx⇒+−>⇒+>
21 1xx⇒+>⇒>−
(luôn thỏa mãn với
2x >
)
Vậy
2.x >
VII. Liên hệ giữa phép khai căn bậc hai và phép chia
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Trang: 11.
Bài toán 1. Tính: a)
6, 4
8,1
b)
0, 25
1, 44
c)
2
2
49
Lời giải
a) Ta có:
6,4 64 64 8
8,1 81 9
81
= = =
.
b) Ta có:
0,25 25 25 5
1, 44 144 12
144
= = =
.
c) Ta có:
2 100 100 10 3
21
49 49 7 7
49
= = = =
.
Bài toán 2. Rút gọn biểu thức:
a)
2
4
yx
A
xy
=
, vỡi
0, 0
xy
>≠
b)
4
2
2
2 ,0
4
b
Ba a
a
= <
c)
2
6
25a
C 5ab ,a 0, b 0
b
= <>
Lời giải
a) Ta có:
2
2
4
||
y x yx
A
x xy
y
=⋅=⋅
Vî
0 ||x xx
>⇒ =
. Vậy
2
1
( 0)
yx
Ay
xy y
=⋅= ≠
b) Ta có
42
22
2
bb
B 2a 2a
4a 2 | a |
= = ⋅
c) Ta có:
2
6
3
25a 5 | a |
C 5ab 5ab
b
b
⋅
= =
Vi
33
0 || ; 0a a ab b b<⇒ =− >⇒ =
. Vâyy
2
32
5 25
5
aa
C ab
bb
−
= = −
Bài toán 3. Rút gọn
a)
2
2
4 12 9aa
A
b
++
=
với
3
2
a >−
;
0b <
b)
( )
(
)
2
.
xy
B xy
xy
= −
−
với
0xy<<
.
c)
( )
22
4
2.
44
C xy
x xy y
= −
−+
Lời giải
a) Ta có:
( )
2
2
2
2
23
23
4 12 9
a
a
aa
A
bb
b
+
+
++
= = =

Tài liệu khác của Toán 9

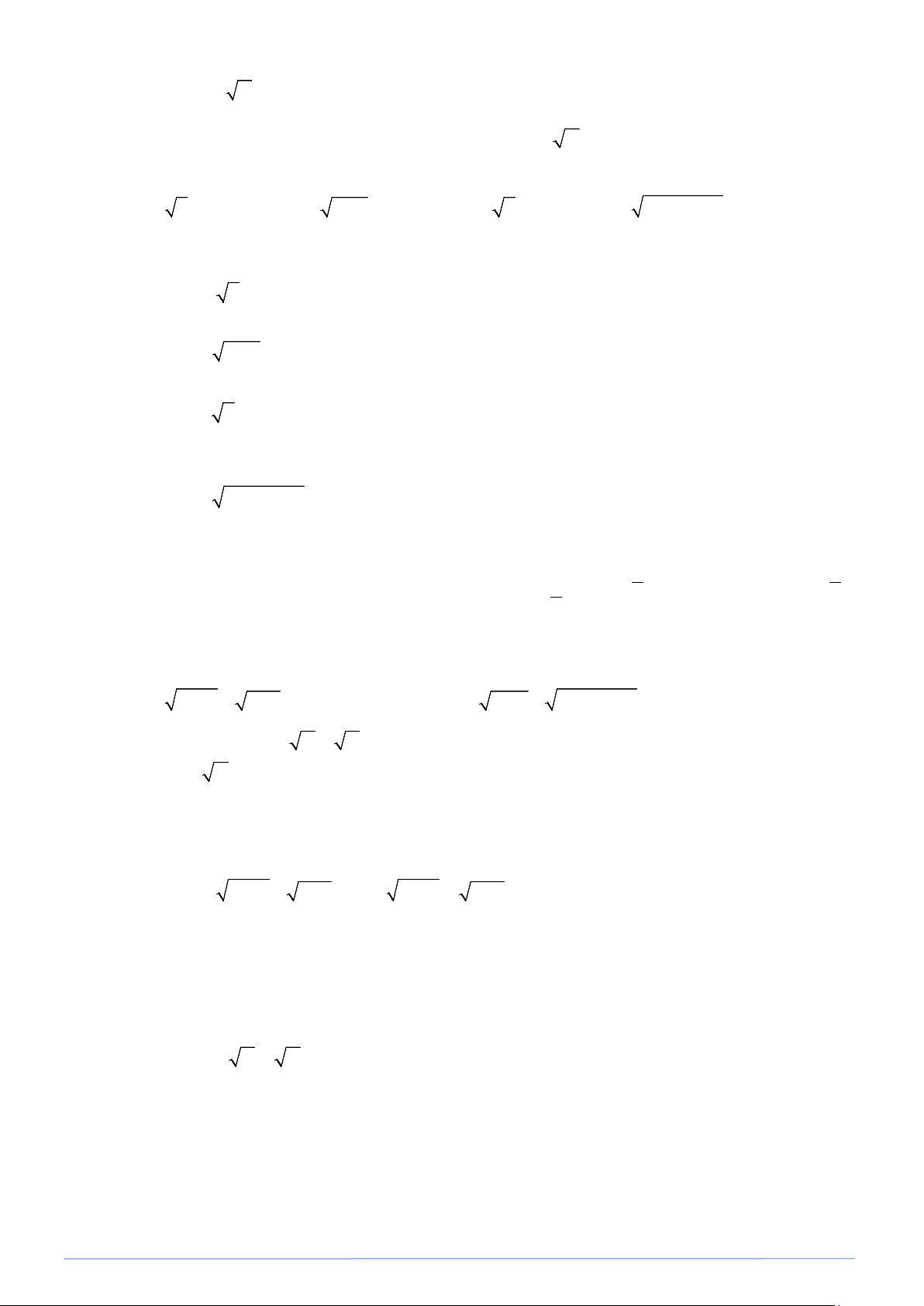
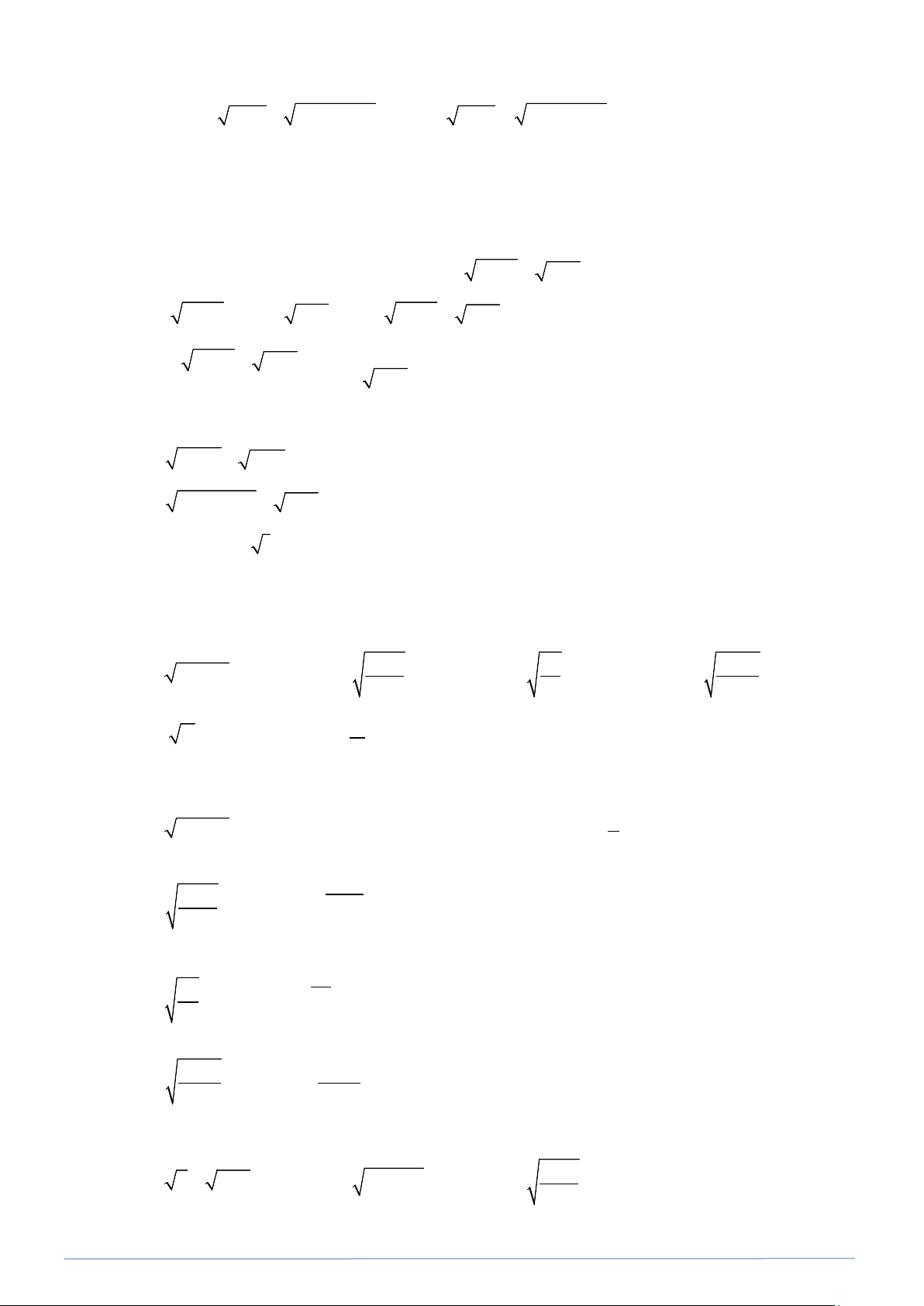
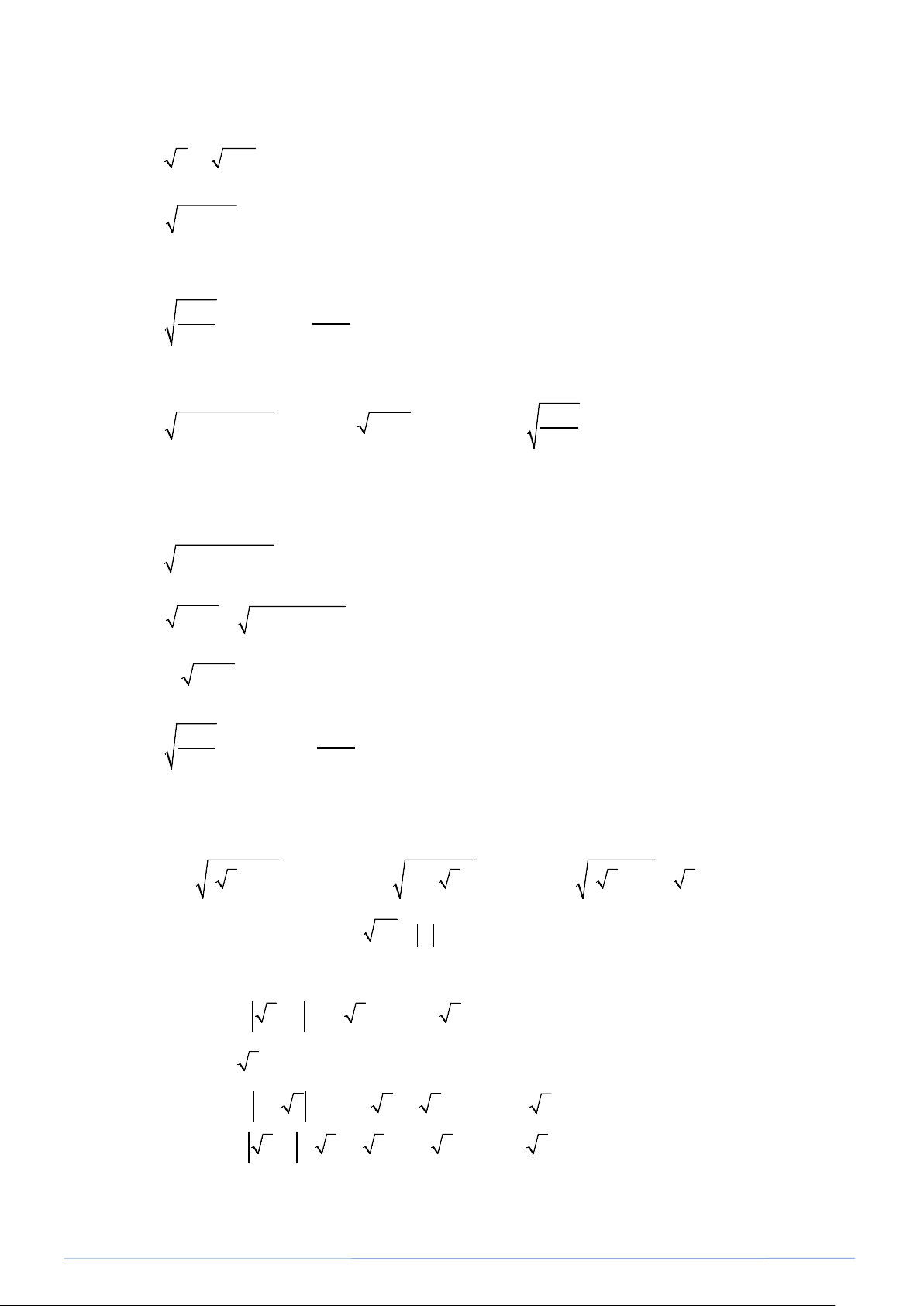
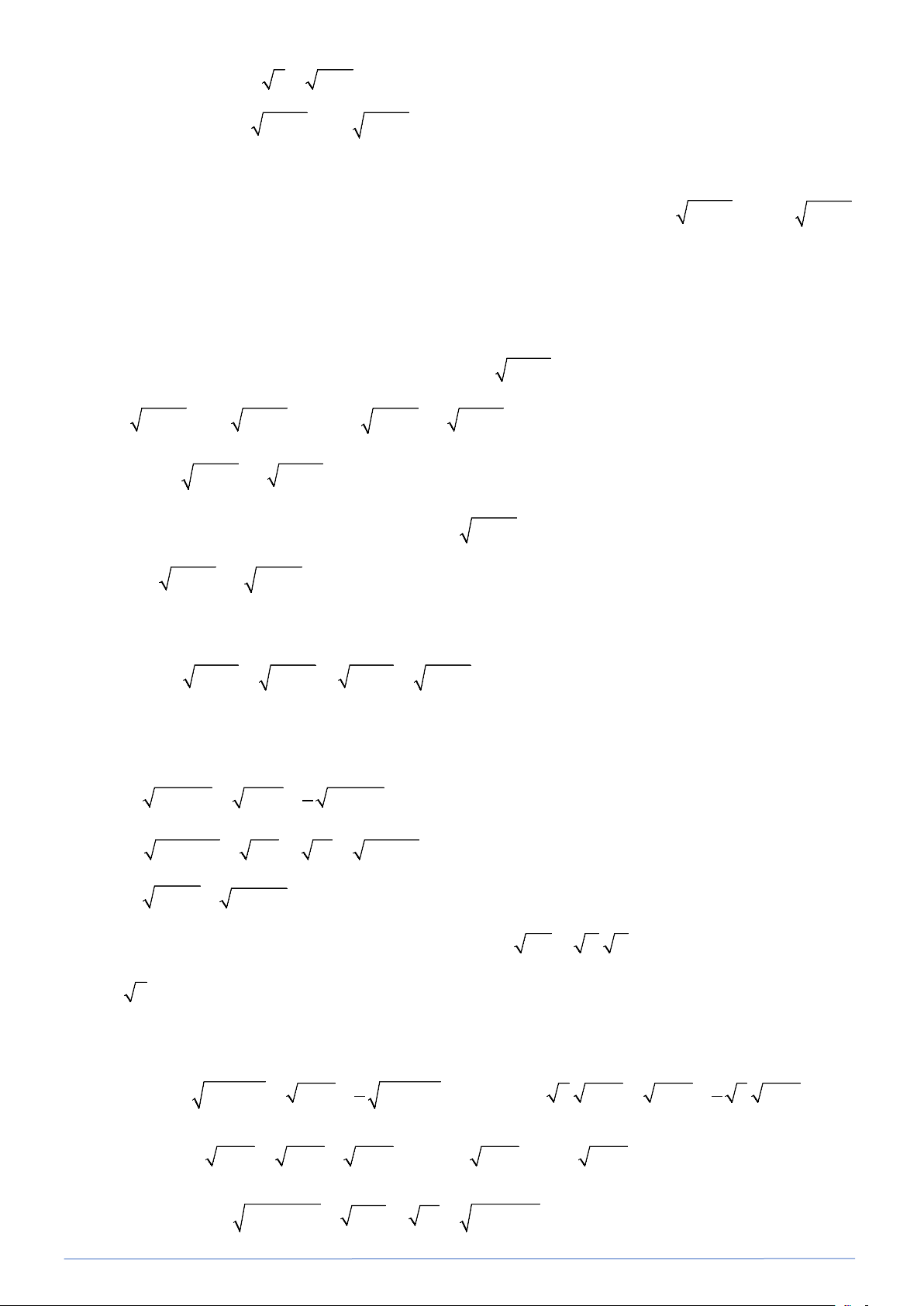
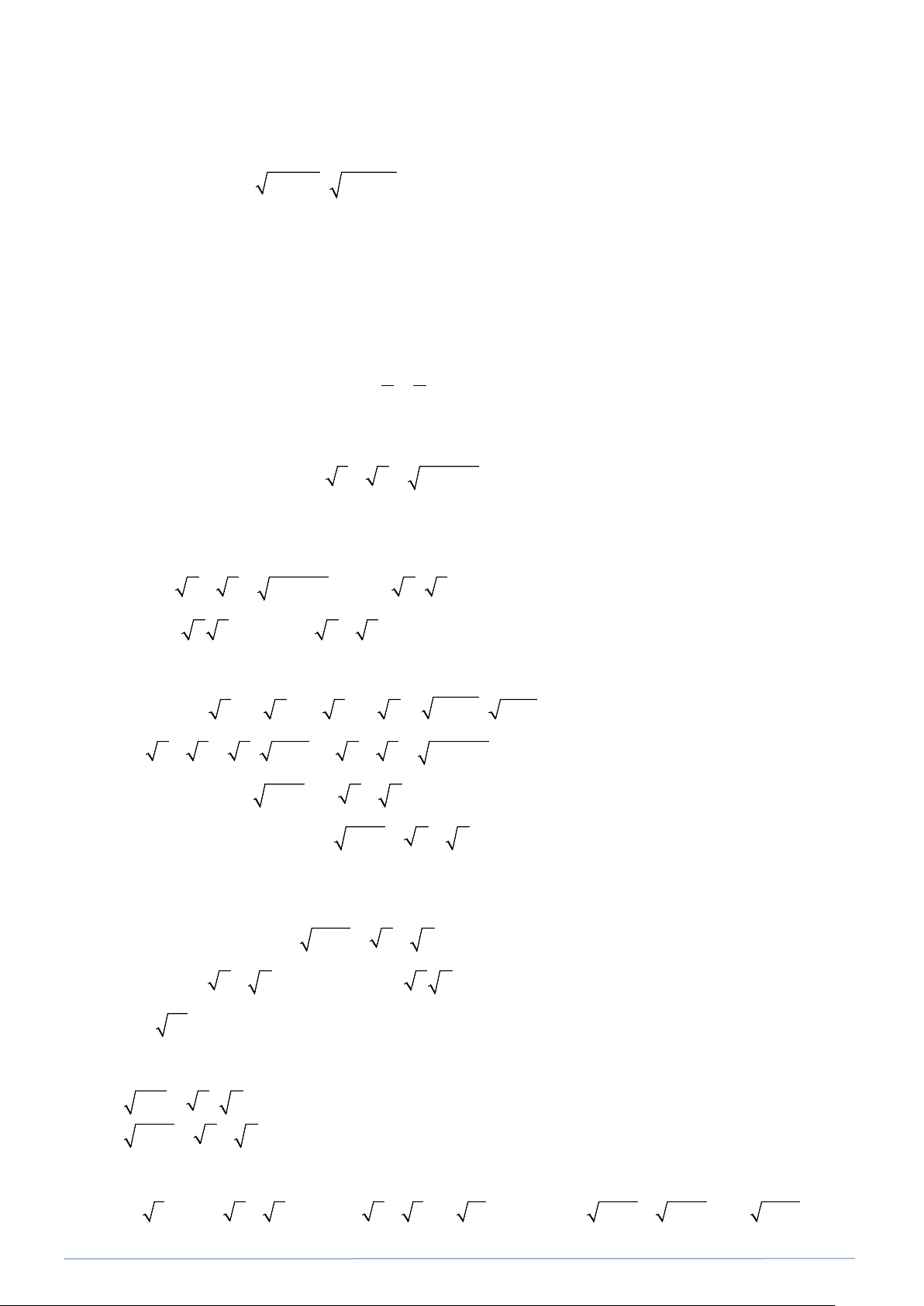
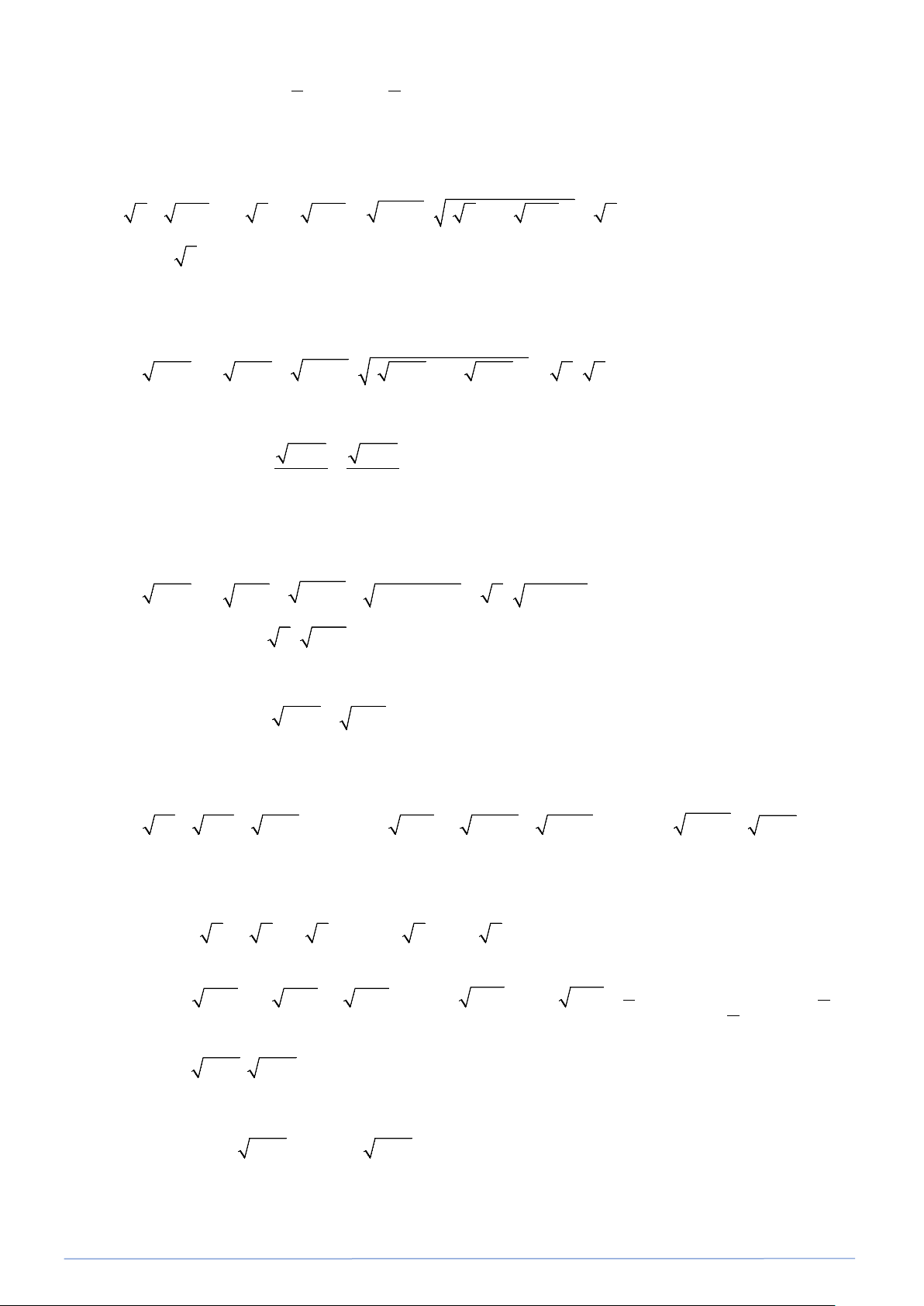
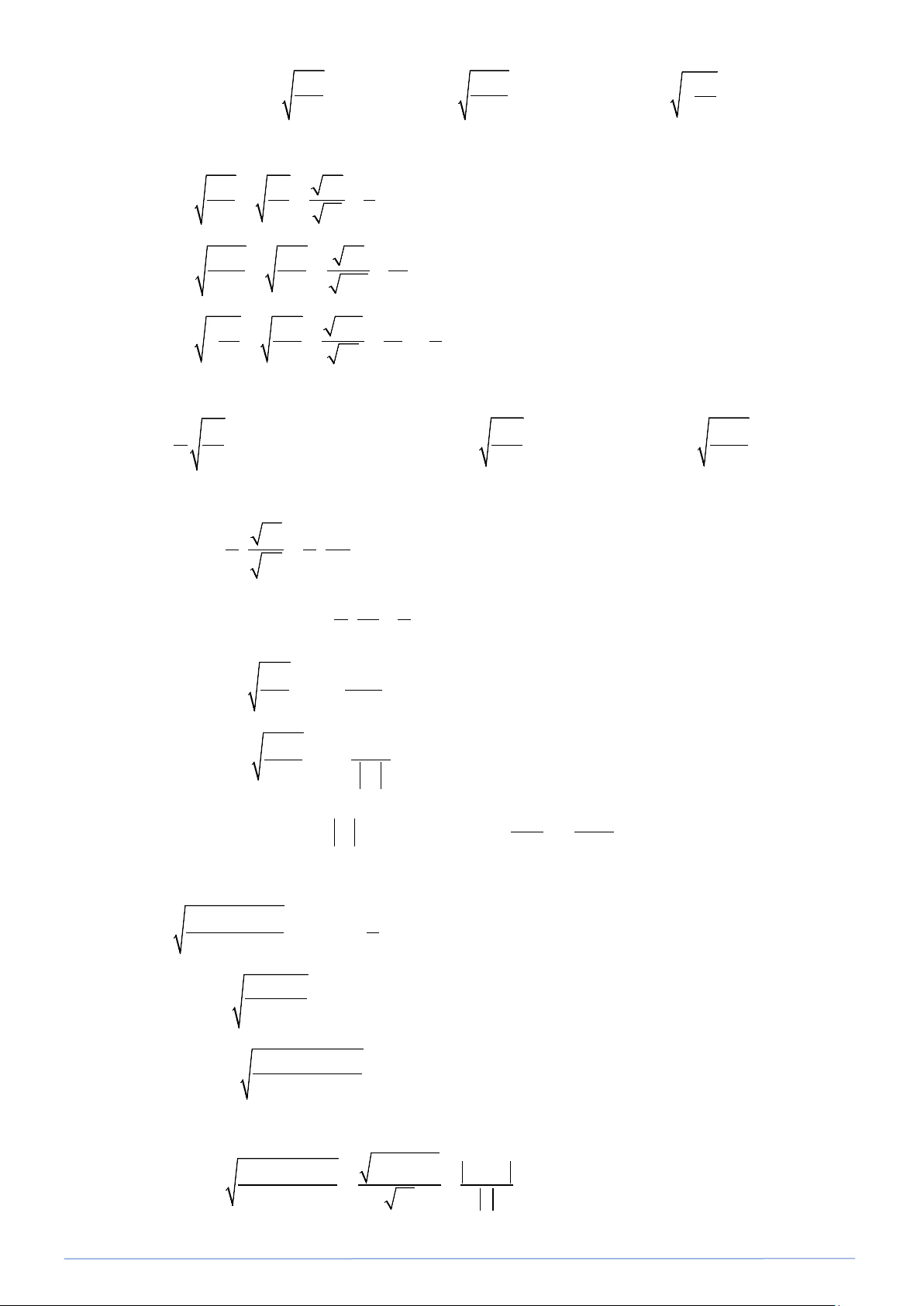
Preview text:

PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Chương III. CĂN BẬC HAI VÀ CĂN BẬC BA
Bài 7. CĂN BẬC HAl VÀ CĂN THỨC BẬC HAI
A. KIẾN THỨC CẦN NHỚ 1. Căn bậc hai
* Căn bậc hai của số thực không âm a là số thực x sao cho 2 x = a . Nhận xét:
- Số âm không có căn bậc hai;
- Số 0 có một căn bậc hai duy nhất là 0 ;
- Số dương a có đúng hai căn bậc hai đối nhau là a (căn bậc hai số học của a ) và − a .
* Tính chất của căn bậc hai: 2
a = a với mọi số thực a .
2. Căn thức bậc hai: * Định nghĩa
Căn thức bậc hai là biểu thức có dạng A , trong đó A là một biểu thức đại số. A được gọi là
biểu thức lấy căn hoặc biểu thức dưới dấu căn.
A xác định khi A lấy giá trị không âm, ta thường viết là A ≥ 0. Ta nói A ≥ 0 là điều kiện xác
định (hay điều kiện có nghĩa) của A . * Hằng đẳng thức 2 A = A
Tương tự như căn bậc hai của một số thực không âm, với A là một biểu thức, ta cũng có:
+ Với A ≥ 0, ta có 2
A ≥ 0,( A) = A; + 2 A = A
B. PHÂN LOẠI CÁC BÀI TẬP
I. Tìm căn bậc hai của một số
Bài toán 1. Tìm các căn bậc hai của 16 4; ;3 . 9 Lời giải
Ta có: 4 > 0 nên 4 có hai căn bậc hai là 2 và 2 − vì 2 2 = 4 và 2 ( 2) − = 4 2 Ta có: 16  4  16
> 0 nên 16 có hai căn bậc hai là 4 và 4 − vì ± = . 9 9 3 3  3   9
Ta có 3 > 0 nên 3 có hai căn bậc hai là 3 và − 3 . Vì 2 (± 3) = 3 .
Bài toán 2. Giải phương trình: a) 2 x = 4 ; b) 2 x = 2 ; c) 2 x = 2 − ; d) 2 x = 0 .
Hướng dẫn: Nghiệm của phương trình 2
x = a (với a ≥ 0 ) là các căn bậc hai của a .
Trang: 1.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Lời giải
a) Ta có 4 > 0 nên 4 có hai căn bậc hai là 2 và 2 − vì 2 ( 2) ± = 4 . x = 2 Vậy 2 x = 4 ⇒  . x = 2 −
Tập nghiệm của phương trình 2
x = 4 là S = { 2; − } 2 .
b) Ta có 2 > 0 nên 2 có hai căn bậc hai là 2 và − 2 vì 2 (± 2) = 2. x = 2 Vậy 2 x = 2 ⇒  . x = − 2
Tập nghiệm của phương trình 2
x = 2 là S = {− 2; 2}. c) Ta có: 2 − < 0 nên 2
− không có căn bậc hai ⇒ phương trình 2 x = 2 − vô nghiệm. Vậy S = ∅ . d) Ta có 2
x = 0 ⇒ x = 0 .
Tập nghiệm phương trình 2
x = 0 là S = { } 0 .
(Bạn đừng nhầm với S = ∅ và S = { } 0 ).
Ta có thể giải cách khác nhau sau, chẳng hạn. x − 2 = 0  x = 2 * 2 2 2
x = 4 ⇔ x − 2 = 0 ⇒ (x − 2)(x + 2) = 0 ⇒  ⇒  . x + 2 = 0 x = 2 −  x = 2 * 2 2 2 2
x = 2 ⇒ x − 2 = 0 ⇒ x − ( 2) = 0 ⇒ (x − 2)(x + 2) = 0 ⇒  . x = − 2
Bài toán 3. Tìm căn bậc hai số học của số sau: a) 144; b) 16 ; c) 1,21; d) 2 ( 1 − ,69) . 9
Hướng dẫn: Gọi x (không âm) là căn bậc hai số học của số a , ta có: 2
x = a , ta đưa về bài toán 2 . Lời giải
a) Gọi x(x ≥ 0) là căn bậc hai số học của 144, ta có: 144 > 0, nên 144 có một căn số học là 12, ta viết: 144 =12 vì 2 12 =144 . 4 > 0 3 b) Ta có: 16 4 = vì . 9 3  2   4  16 =   3    9 1,  1 > 0 c) Ta có: 1,21 =1,1 vì  . 2 (1,1) =1, 21 d) Ta có 2 2 ( 1
− ,69) = (1,69) =1,69 vì 1,69 > 0.
II. Phương trình dạng: A = B
Trang: 2.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 B ≥ 0
Cách giải: A = B ⇔  . 2  A = B
(Thực chất của vấn đề là ta đã bình phương hai vế, vì 2 ( A) = A).
Bài toán 4. Giải phương trình:
a) x = 3; b) x − 2 =1; c) x = x ; d) 2
6 − 4x + x = x + 4. Lời giải 3  ≥ 0 (luôn đúng)
a) Ta có: x = 3 ⇒ 
⇒ x = 9 . Tập nghiệm: S = { } 9 . 2 x = 3 1  ≥ 0 (luôn đúng)
b) Ta có x − 2 =1 ⇒ 
⇒ x = 3. Tập nghiệm: S = { } 3 . x − 2 = 1 x ≥ 0 x ≥ 0 x ≥ 0 x = 0
c) Ta có x = x ⇒  ⇒ ⇒ ⇒
. Tập nghiệm: S = {0; } 1 2    x = x 2 x − x = 0 x  ( x − ) 1 = 0 x = 1 . x + 4 ≥ 0 d) Ta có 2
6 − 4x + x = x + 4 ⇒  2 2
6 − 4x + x = (x + 4) x ≥ 4 − x ≥ 4 − x ≥ 4 − 5 ⇒   ⇒ ⇒
⇒ x = − . Tập nghiệm: 5 S   = − 2 2   5 
6 − 4x + x = x + 8x +16 12  x = 10 − x = −  6  6  6 .
Bài toán 5. Giải phương trình: a) 2
x −1 − x −1 = 0 ; b) 2
x + 4 − x + 5x + 4 = 0 .
Hướng dẫn: Ta đưa về dạng A = B  B ≥ 0 Ta có  B ≥ 0  ⇔  . A = BA = B Lời giải x −1≥ 0 x ≥1 a) Ta có: 2 2
x −1 − x −1 = 0 ⇒ x −1 = x −1 ⇒  ⇒ 2  2
x −1 = x −1 x − x = 0 x ≥1 x ≥1 x ≥1 ⇒  ⇒ ⇒ ⇒ x =1 x   .  ( x − ) 1 = 0 x = 0 ∨ x −1 = 0 x = 0 ∨ x =1 Tập nghiệm: S = { } 1 . A ≥ 0
Chú ý: Ta có thế xét A = B ⇔ 
, nhưng ở bài toán này, ta không nên đặt 2 x −1≥ 0 . 2  A = B
Trang: 3.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Ta xét bài toán b) sau đây:  x + 4 ≥ 0 b) Ta có: 2
x + 4 − x + 5x + 4 = 0 2
⇒ x + 4 = x + 5x + 4 ⇒  2
x + 5x + 4 = x + 4  x ≥ 4 −  x ≥ 4 −  x ≥ 4 −  x ≥ 4 −  x = 0 ⇒  ⇒ ⇒ ⇒ ⇒ . 2     x + 4x = 0 x  ( x + 4) = 0 x = 0 ∨ x + 4 = 0 x = 0 ∨ x = 4 − x = 4 −
Tập nghiệm: S = { 4; − } 0 .
Ta có thể xét bài toán tương tự sau đây: 2
x −1 + x −1 = 0 Vì 2
x −1 ≥ 0 và x −1 ≥ 0 2
⇒ x −1 + x −1 ≥ 0 . 2 x −1= 0 2 x −1 = 0 Vậy 2
x −1 + x −1 = 0 ⇒  ⇒  ⇒ x =1.  x −1 = 0 x −1 = 0
Bạn hãy giải phương trình sau: 1) 2
x − 9 + x − 3 = 0 Đáp số: x = 3 2) 2
x − 3x + 2 + x −1 = 0 Đáp số: x =1
3) {x − 2 <1= 1 Đáp số: x = 4.
III. Tìm điều kiện xác định của biểu thức
Bài toán 6. Tìm x để cho căn thức sau có nghĩa. a) 2 − x +1 b) 1 c) 1 d) 3 − x + 2 2 x 2 x +1
Hướng dẫn: A có nghĩa ⇔ A ≥ 0 ; 1 có nghĩa ⇔ A ≠ 0. A Lời giải a) 2
− x +1 xác định(có nghĩa) 1 ⇒ 2
− x +1≥ 0 ⇒ 2x ≤1⇒ x ≤ . 2  1  ≥ 0 b)
1 xác định ⇒ x+2 ⇒ x+2 > 0⇒ x > 2 − . x + 2 x + 2 ≠ 0  1  ≥ 0 c) 1 xác định 2 ⇒  x ⇒ x ≠ 0 . 2 x  2 x ≠ 0 d) 3 − xác định 3 − ⇒ ≥ 0 (không tồn tại). 2 x +1 2 x +1
Bài toán 7. Tìm x để căn thức sau có nghĩa. a) x + 1− x b) x(1− x) c) 1+ x 2 − x
Trang: 4.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Hướng dẫn: Ta tìm điều kiện cho tất cả các căn bậc hai xác định. Lời giải x ≥ 0 x ≥ 0
a) x và 1− x xác định ⇒  ⇒  ⇒ 0 ≤ x ≤1 1  − x ≥ 0 x ≤ 1 x ≥ 0 x ≤ 0 x ≥ 0 x ≤ 0
b) x(1− x) xác định ⇒ x(1− x) ≥ 0 ⇒ hoặc ⇒ hoặc (vô lí) 1      − x ≥ 0 1  − x ≤ 0 x ≤1 x ≥1 ⇒ 0 ≤ x ≤1 1+ x 1  + x ≥ 0 1  + x ≤ 0
c) 1+ x xác định⇒ ≥ 0 ⇒ hoặc ⇒ 1 − ≤ x < 2 2   − x 2 − x 2 − x > 0 2 − x < 0
Bài toán 8. Tìm x để biểu thức sau xác định : a) (x − ) 1 (x −3) b) 2 x − −1 c) x 1 x − 2
Hướng dẫn: Xem lời giải bài toán 2 . Lời giải x −1 ≥ 0 x −1 ≤ 0 a) (x − )
1 (x −3) xác định⇒ (x − )
1 (x − 3) ≥ 0 ⇒  hoặc 
⇒ x ≥ 3hoặc x ≤1 x − 3 ≥ 0 x − 3 ≤ 0 b) 2
x −1 = (x − ) 1 (x + ) 1 x −1 ≥ 0 x −1 ≤ 0 Vậy 2
x −1 xác định ⇒  hoặc 
⇒ x ≥1 hoặc x ≤ 1 − x +1 ≥ 0 x +1 ≤ 0 x −1 x −1 ≥ 0 x −1 ≤ 0
c) x −1 xác định ⇒ ≥ 0 ⇒  hoặc 
⇒ x > 2 hoặc x ≤1 x − 2 x − 2 x − 2 > 0 x − 2 < 0
IV. Rút gọn biểu thức
Bài toán 9. Rút gọn: a) A = ( − )2 3 2 b) B = ( − )2 2 5 c) C = ( − )2 3 1 − 3
Hướng dẫn: Áp dụng hằng đẳng thức: 2 A = A . Lời giải
a) Ta có : A = 3 − 2 = −( 3 − 2) ; vì 3 − 2 < 0 Vậy A = 2 − 3 .
b) Ta có : B = 2 − 5 = −(2− 5) = 5 − 2;(vì 2− 5 < 0).
c) Ta có: C = 3 −1 − 3 = ( 3 − )1− 3 = 1 − ( vì 3 −1 > 0 ).
Bài toán 10. Rút gọn:
Trang: 5.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
a) A = 3+ 2 2 − 3− 2 2
b) B = 7 − 4 3 + 7 + 4 3 c) C = 23+ 8 7 − 7
d) D = 11− 6 2 − 3+ 2 2 2
Hướng dẫn: a) Ta có 3+ 2 2 =1+ 2.1. 2 + 2 2 =1 + 2.1. 2 + ( 2) = (1+ 2)
⇒ 3+ 2 2 = (1+ 2)2 = 1+ 2 =1+ 2 .
( Các biểu thức khác được làm tương tự ). Lời giải
a) Ta có : A = 2 + 2 2 +1 − 2 − 2 2 +1 = ( )2 + + − ( )2 2 2 2 2. 2.1 1 2 − 2 2.1+1 = ( + )2 − ( − )2 2 1
2 1 = 2 +1 − 2 −1 = ( 2 + )1−( 2 − )1 = 2 b) Ta có: 2 2
B = 4 − 2.2 3 + 3 + 4 + 2.2 3 + 3 = (2− 3) + (2+ 3)
= 2 − 3 + 2 + 3 = 2 − 3 + 2 + 3 = 4
c) Ta có: C = 16 + 2.4. 7 + 7 − 7 = ( + )2 4
7 − 7 = 4 + 7 − 7 = 4 + 7 − 7 = 4
d) Ta có: D = 9 − 2.3 2 + 2 − 3+ 2 = ( − )2 3 2 − 3+ 2 = 3− 2 − 3+ 2 = 3− 2 − 3+ 2 = 0
Bài toán 11. Rút gọn biểu thức: a) A = 2
x −12x + 36 − x
b) B = x −1− 2 x − 2 + x −1+ 2 x − 2 c) C = x + 2 x −1 + x − 2 x −1 Hướng dẫn: a) ta có: 2
x −12x + 36 = (x − 6)2 ⇒ (x − 6)2 = x − 6
b), c) Đưa các biểu thức trong một dấu căn trở thành bình phương của một tổng hoặc một hiệu. Lời giải
x − 6 − x, neáu x ≥ 6  6, − neáu x ≥ 6
a) Ta có: A = (x − )2
6 − x = x − 6 − x ⇒  ⇒  −
 ( x − 6) − x, neáu x < 6 6-2x, neáu x < 6
b) Ta có: B = (x − 2) − 2 x − 2.1+1 + x − 2 + 2 2 − .1+1
= ( x − − )2 + ( x − + )2 2 1
2 1 = x − 2 −1 + x − 2 +1 Trường hợp 1:
Nếu x − 2 −1≥ 0 ⇒ x − 2 ≥1⇒ x − 2 ≥1 ⇒ x ≥ 3,ta coù B = x − 2 −1+ x − 2 +1 = 2 x − 2 Trường hợp 2:
Trang: 6.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Nếu x − 2 −1≤ 0 ⇒ x − 2 <1 ⇒ 0 ≤ x − 2 <1⇒ 2 ≤ x < 3 Ta có:
B = −( x − 2 − )1+( x − 2 + )1 = 2
Vậy: Nếu x ≥ 3, ta có B = 2 x − 2
Nếu 2 ≤ x < 3 ta có B = 2
c) Ta có C = ( x − + )2 + ( x − − )2 1 1
1 1 = x −1 +1 + x −1 −1 Trường hợp 1:
Nếu x −1 −1≥ 0 ⇒ x ≥ 2 Ta có C = 2 x −1 Trường hợp 2:
Nếu x −1 −1< 0 ⇒ x −1 < 1 ⇒ 0 ≤ x −1<1⇒1≤ x < 2
Ta có: C = x −1 +1− ( x −1− )1 = 2
Vậy: Nếu x ≥ 2 ta có C = 2 x −1
Nếu 1≤ x < 2 ta có C = 2
Cách giải khác: (đối với bài toán c). u  > 0 u  ≥ 0
Đặt u = x −1 ⇒  ⇒ 2  2 u  = x −1 x = u +1 Khi đó, ta có: 2 2
C = u +1+ 2u + u +1− 2u = (u + )2 + (u − )2 1
1 = u +1 + u −1 Trường hợp 1:
Nếu u −1≥ 0 ⇒ u ≥1⇒ x −1 ≥1⇒ x ≥ 2 Ta có: C = 2u = 2 x −1(u ≥ 0 ⇒ u +1 > 0) Trường hợp 2:
Nếu u −1< 0 ⇒ u <1⇒ x −1 <1
u ≥ 0 ⇒ x −1 ≥ 0 ⇒ x ≥1⇒ x −1 <1⇒ x −1<1⇒ x < 2 Vậy 1≤ x < 2
Ta có: C = u +1− (u − ) 1 = 2
(Bạn có thể giải lại bài toán b, theo cách này)
Bài toán 12. Tính giá trị của biểu thức a) 2 A = 4
− x − 2 + 9x − 6x +1, với x = 2014 b) 2 2
B = x − 4x + 4 + x + 4x + 4, với x = 2015
Hướng dẫn: Đưa biểu thức dưới dấu căn trở thành bình phương một tổng hoặc một hiệu và áp dụng hằng đẳng thức 2 A = A .
Trang: 7.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Lời giải
a) Ta có: A = − x − + ( x − )2 4 2 3 1 = 4
− x − 2 + 3x −1
Thay x = 2014 vào biểu thức trên, ta được: A = 4.2014 − − 2 + 3.2014 −1 = 4.2014 − − 2 + 3.2014 −1 = 2014 − − 3 = 2017 −
b) Ta có: B = (x − )2 + (x + )2 2
2 = x − 2 + x + 2
Thay x = 2015 vào biểu thức trên, ta được:
B = 2015 − 2 + 2015 + 2 = 2015 − 2 + 2015 + 2 = 4030 V. Giải phương trình
Bài toán 13. Giải phương trình a) 2 x = 5 b) 2 25x =10 c) 2 9x = 2x +1 d) 2
x + 6x + 9 = 3x −1
Hướng dẫn: Biến đổi biểu thức dưới dấu căn trở thành bình phương của một tổng hoặc một hiệu và áp dụng hằng đẳng thức 2 A = A . Lời giải 5  ≥ 0 luoân ñuùng 2 ( )
a) Ta có: x = 5 ⇒ x = 5 ⇒  ⇒ x = 5 ± x = 5 ±
Tập hợp nghiệm: S = { 5; − } 5 . 10  ≥ 0 (luoân ñuùng) b) Ta có: 2
25x =10 ⇒ (5x)2 =10 ⇒ 5x =10 ⇒  ⇒ x = 2 ± 5  x = 10 ±
Tập hợp nghiệm: S = { 2; − } 2 . c) Ta có: 2
9x = 2x +1 ⇒ ( x)2 3
= 2x +1⇒ 3x = 2x +1(*) Điều kiện 1 2x 1 0 x − + ≥ ⇔ ≥ 2 x =1 3x = 2x +1 Khi đó: (*) ⇒   ⇒ 3 −  − x = −(2x + 1 1  ) 1 x =
 thoaû maõn ñieàu kieän x ≥  5 2     1
Tập hợp nghiệm: S  ;1 = − . 5   
VI. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
Bài toán 14: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức: a) 2 2
x + x − 4x + 4
b) x − 2 + 2 x − 3 + x + 6 + 6 x − 3
Hướng dẫn: Áp dụng hằng đẳng thức 2 A = A
Trang: 8.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
và A + B ≥ A + B dấu " = "xảy ra ⇒ AB ≥ 0 (A và B cùng dấu hoặc bằng 0). Lời giải
a) Ta có: A = x + x − 2 = x + 2 − x ≥ x + (2 − x) = 2
Vậy giá trị nhỏ nhất của A bằng 2.
Dấu " = " xảy ra, chẳng hạn x = 0
(Khi đó thoả mãn điều kiện x(2 − x) ≥ 0 )
Chú ý: Ta không cần tìm hết tất cả các giá trị của x thoả mãn x(2 − x) ≥ 0 . Nếu ta có:
x(2 − x) ≥ 0 ⇒ 0 ≤ x ≤ 2).
Ta có thể giải cách khác.
Ta có A = x + x + 2 Trường hợp 1:
Nếu x ≥ 2 ⇒ A = x + x − 2 = 2x − 2
Với x ≥ 2 ⇒ 2x ≥ 4 ⇒ 2x − 2 ≥ 2
Giá trị nhỏ nhất của A bằng 2. Trường hợp 2:
Nếu 0 ≤ x < 2 ⇒ A = x − (x − 2) = 2
Trường hợp 3: Nếu x < 0 ⇒ A = −x − (x − 2) = 2 − x + 2 Vì x < 0 ⇒ 2 − x > 0 ⇒ 2 − x + 2 > 2
Vậy kết hợp các kết quả của ba trường hợp, ta có: giá trị nhỏ nhất của A bằng 2.
Dấu " = " xảy ra ⇔ x = 0
b) Ta có: B = x − 3 +1 + x − 3 + 3
Điều kiện: x − 3 ≥ 0 ⇒ x ≥ 3 khi đó biểu thức trong các dấu giá trị tuyệt đối đều dương.
Ta có: B = x − 3 +1+ x − 3 + 3 = 2 x − 3 + 4
Vì x ≥ 3 ⇒ 2 x − 3 ≥ 0 ⇒ 2 x − 3 + 4 ≥ 4
Vậy giái trị nhỏ nhất của B bằng 4.
Dấu " = "xảy ra ⇒ x = 3.
Chú ý: Từ kết quả trên, ta có bài toán giải phương trình:
x − 2 + 2 x − 3 + x + 6 + 6 x − 3 = 4.
Trang: 9.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Chương III. CĂN BẬC HAI VÀ CĂN BẬC BA
BÀI 8. CĂN BẬC HAI VÀ CĂN THỨC BẬC HAI
A. KIẾN THỨC CẦN NHỚ
1. Khai căn bậc hai và phép nhân
Liên hệ giữa phép khai căn bậc hai và phép nhân:
Với A, B là các biểu thức không âm, ta có: A. B = AB .
Chú ý: Kết quả trên có thể mở rộng cho nhiều biểu thức không âm, chẳng hạn: A. B. C = . A .
B C (vôùi A ≥ 0; B ≥ 0; C ≥ 0) .
2. Khai căn bậc hai và phép chia
Liên hệ giữa phép khai căn bậc hai và phép chia:
Nếu A, B là các biểu thức với A A A ≥ 0, B > 0 thì = . B B
B. PHÂN LOẠI CÁC BÀI TẬP
I. Khai căn bậc hai của một tích Bài toán 1. Tính: a) 90.4,9 b) 12,1.360 c) 2,5.14,4 d) 4 2 .( 3 − )2
Hướng dẫn: Áp dụng quy tắc khai căn một tích:
ab = a b (a ≥ b ≥ ) ( A)2 2 . 0, 0 ,
= A = A( A ≥ 0) Lời giải
a) Ta có: 90.4,9 = 9.49 = 9. 49 = 3.7 = 21
b) Ta có: 12,1.360 = 121.36 = 121. 36 =11.6 = 66 c) Ta có: 2,5.14,4 = 36 = 6 Cách khác: 1 1 2,5.14,4 = 5.144. = 5.12. = 6 100 10 d) Ta có: 4 (− )2 = ( 2 2 . 3 2 )2. ( 3 − )2 = 4. 3 − = 12
Bài toán 2. Rút gọn rồi tính: a) 2 2 25 − 24 b) 2 2 17 −8 c) 2 2 117 −108 d) 2 2 6,8 − 3,2 e) 2 2 21,8 −18,2
Hướng dẫn: Áp dụng hằng đẳng thức: 2 2
a − b = (a −b)(a + b) Lời giải a) Ta có: 2 2
25 − 24 = (25− 24)(25 + 24) = 1.49 = 7
Trang: 1.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 b) Ta có: 2 2
17 −8 = (17 −8)(17 +8) = 9.25 = 3.5 =15 c) Ta có: 2 2
117 −108 = (117 −108)(117 +108) = 9.225 = 3.15 = 45 d) Ta có: 2 2
6,8 − 3,2 = (6,8 −3,2)(6,8 + 3,2) = 3,6.10 = 36 = 6 e) Ta có: 2 2
21,8 −18,2 = (21,8 −18,2)(21,8 +18,2) = 3,6.40 = 36. 4 = 6.2 =12
Bài toán 3. Rút gọn:
a) A = 5 − 2 6 b) B = 7 + 2 10 + 7 − 2 10 c) C = 8 + 2 15 − 5
Hướng dẫn: Áp dụng quy tắc nhân các căn bậc hai a. b = ab (a ≥ 0, b ≥ 0) Lời giải 2 2
a) Ta có: 3− 2. 3.2 + 2 = ( 3) − 2 3. 2 +( 2) = ( − )2 3 2 = 3 − 2 = 3 − 2
b) Ta có: B = 5 + 2 5.2 + 2 + 5 − 2 5.2 + 2   2   2   2   2 5 2. 5. 2 2 5 2. 5. 2 2
   2    2 5 2 5
2  5  2  5  2  2 5 c) Ta có C       2   2 5 2 5.3 3 5 5 2. 5. 3 3  5    2 5
3  5  5  3  5  3
II. Nhân các căn bậc hai Bài toán 4. Tính: a) A  3  2 . 3  2 b) B  3  2  3  2
c) C  4 7  4 7 d) D  3 5  3 5
Hướng dẫn: Áp dụng quy tắc nhân các căn bậc hai: A. B  .
A B A  0; B  0
Các bài b), c), d) ta phải bình phương hai vế, rồi sau đó khai căn bậc hai. Lời giải a) Ta có A      2  2 3 2 . 3 2 3 2  32 1
b) Nhận xét 3  2  0  3  2  0 ; 3  2  0 . Vậy B  0 .
Trang: 2.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Ta xét B     2 2 3 2 3 2    2     2 3 2 2 3 2. 3 2 3 2
 3  2  2  3  2. 3 2  3 2   (xem bài toán a) 2 3 2.1
 2 2 3  B  2 2 3
c) Nhận xét: C  0. 2 2
Ta xét C     2 2 4 7 4 7
  4 7 2 4 7. 4 7  4 7
 4  7  2 4 7.4 7 4 7       86 14 8 2 16 7 8 2 9  C  14
d) Nhận xét D  0 vì 3 5  3 5 2 2
Ta xét D     2 2 3 5 3 5
  3 5 2 3 5. 3 5  3 5
 3 5 2 3 5.3 5 3 5       6 2 9 5 6 2.2 2
D   2 (vì D  0 ) .
Chú ý: Các biểu thức A B và A B được gọi là hai biểu thức liên hợp.
Bài toán 5. Tính: a) A  6  10. 4 15 b) B 3 5 . 10  2. 3 5
c) C 4 15. 10  6. 4 15
Hướng dẫn: Áp dụng cả hai quy tắc khai căn một tích và nhân các căn bậc hai. Lời giải
a) Ta có: A  6  10. 4 15  3.2  5.2. 4 15
  3. 2  5. 2. 4 15  3  5. 2. 4 15
  3  5. 24 15  3  5. 82 15 2 2
  3  5. 52 5. 3 3  3  5. 5  3 5  3  53 2
b) Ta có: B 3 5 . 10  2. 3 5 3 5. 5 1. 2. 3 5
         2 3 5 . 5 1 .
5 1 3 5 . 5 1 . 5 1      2 3 5 . 5 1
Trang: 3.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
3 5 .62 5
 23 53 5 29  5  2.4  8.
c) Ta có: C 4 15. 10  6. 4 15 4 15. 5 3. 2. 4 15
 4 15. 5  3. 82 15      2 4 15 . 5
3 4 15.82 15
 24 154 15  216  15  2.1 2.
III. Phân tích thành nhân tử
Bài toán 6. Phân tích thành nhân tử
a) A xy  2 x 3 y 6 x  0; y  0 b) B ab b a a 1
c) C a3 ab  2b d) D  2x7 xy 5y
Hướng dẫn: Áp dụng quy tắc khai căn một tích: AB  .
A B và các phương pháp phân tích đa
thức thành nhân tử đã học ở lớp 8: Nhóm các số hạng, dùng hằng đẳng thức, thêm bớt một vài số
hạng để làm xuất hiện nhân tử chung. Lời giải
a) Ta có: A xy  2 x 3 y 6  x y   2 3 y   2  x   3  y   2 2 b) Ta có: B  
ab b a a 1   abb a  a   1  
b a a  1 a  1  a  1b a  1 2 2
c) Ta có: C a3 ab  2b  a  a. b 2 a. b 2 b  a b a 2 b 2 2
d) Ta có: D  2x7 xy 5y  2 x 2 x. y 5. x. y 5 y
 2 x x y5 y x y  x y2 x 5 y
Bài toán 7. Phân tích thành nhân tử
a) A aa 6 b) 3 3
B a b c) C x x y y
Hướng dẫn: Xem cách giải bài toán 6 Lời giải
a) Ta có: A aa 6  a2 2 a 3 a 6
a a   2 3 a   2  a   2  a   3 ; a  0 3 3 b) Ta có: 3 3
B a b  a  b
  a b 2 2
a a. b b   a baab b; a 0; b 0
Trang: 4.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 3 3
c) Ta có: C x x y y  x  y
  x y 2 2
x x. y y   x yxxy y; x 0; y 0
IV. Chứng minh một đẳng thức Bài toán 8.
a) Cho x 5  8 x  5  
1 Chứng minh rằng x  
5 8 x  6. 5 x   8
b) Cho x  1 x 1 2 Chứng minh rằng 2
xx  0 . 0  x   1
Hướng dẫn: Bình phương hai vế đẳng thức đã cho và tính tích của hai căn thức. Lời giải
a) Bình phương hai vế của đẳng thức   1 ta được
x  x2 5 8
 25  x 5 2 x 5. 8 x 8 x  25  x  
5 8 x  2513  x  
5 8 x  6 (đpcm)
Chú ý: Em có thể giải bài toán sau:
1) Cho x 5  8 x  5 Hãy tính x   5 8 x và 2
x 3x  40 .
(Ta có x    x 2 5 8
 x 3x  40 )
2) Cho x 5  x 1. Hãy tính x 5  x .
Nhân hai vế của đẳng thức x 5  x 1với x 5  x (là biểu thức liên hợp của x 5  x ).
Điều kiện x  0  x 5 0  x 5  x  0 .
 x5 x
 x5 x x5 x
Ta có: x 5  x 1   x0 
x5 x x5   x x  0       x  0 
 x5  x  5 
Vậy x 5  x  5.
Bạn hãy giải bài toán sau: Cho 2 2
25 x  15 x  2 . Tính 2 2
25 x  15 x . (Đáp số 2 2
25 x  15 x  5).
b) Bình phương hai vế đẳng thức 2 ta được:
x  x2 2 1
1  x  2 x. 1 x 1 x 1  x1 x  0 2
xx  0 . (đpcm)
Chú ý: Ta có thể giải bài toán sau:
Trang: 5.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Giải phương trình x  1 x 1. (Đáp số x 1) Bài toán 9. Cho  2
x   x  2 1
y  1 y 1  * Chứng minh rằng xy  0. Hướng dẫn:
Nhân hai vế của đẳng thức  
* lần lượt với các biểu thức liên hợp của 2
x  1 x và 2 y  1 y
Sau đó nghĩ đến việc làm xuất hiện tổng x y bằng cách cộng hai vế. Lời giải
Với x  0 và y  0suy ra x y  0 .
Giải sử x  0 , nhân hai vế của đẳng thức   * với 2
1 x x , ta được  2
x x 2
x x 2 y   y  2 1 1 1
 1 x x   2 y   y  2 1
 1 x x   **
Tương tự, nhân hai vế của đẳng thức   * với 2
1 y y , ta được  2 x   x  2 1
 1 y y   *** Cộng   ** với   *** ta được 2 2 2 2
x y  1 x  1 y  1 x  1 y xy  2x y 0  x y  0. (đpcm) V. Giải phương trình
Bài toán 10. Giải phương trình a) 1
4x20  x 5  9x45  4   1 3
b) 1632x  12x  3x  918x 2 c) 2
x 9  4x12  0   3
Hướng dẫn: a) Áp dụng quy tắc khai căn một tích AB A. B A 0; B  0 và công thức b   0 a b     2 a   bLời giải a)   1 1  x  1 4 5  x5  9x  5  4
 4. x5  x5  9. x5  4 3 3 2  0 
 2. x5  x5  x5  4  2. x5  4  x5  2    x  9 x5   4 
b)Ta có 2 1612x 4.3x  3x  912x
Trang: 6.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
 4 12x 2 3x  3x 3 12x x  0 x  0    1
 12x  3 3x     1  x  1
 2x  9.3x x   29  29  x3 
x3 20  * c) Ta có   3  x  3 x   3  4x  3  0   x 3   **  Giải  
* ta được x3  0 hoặc x 3  2
x  3 hoặc x 1. Kết hợp với   ** suy ra x  3.
Bài toán 11. Giải phương trình:
a) 1− x + x =1 b) x + 5 − x =1 c) x + 3 + x + 8 = 5 Hướng dẫn:
Bình phương hai vế với điểu kiện cẩn thiết và rút gọn, ta được phương trình chứa một căn thức. Lời giải x ≥ 0 a) Điều kiện:  ⇒ 0 ≤ x ≤1 1  − x ≥ 0
Bình phương hai vế phương trình (1) ta được: 1  − x = 0 x =1
1− x + 2 1− x ⋅ x + x =1⇒ 2 (1− x)x = 0 ⇒ (1− x)x = 0 ⇒ (1− x)x = 0 ⇒  ⇒ x 0  = x = 0
Đối chiếu điểu kiện, ta có tập hợp nghiệm: S = {0;1}.
b) Ta có: (2) ⇒ x + 5 =1+ x (*) x ≥ 0 x ≥ 0 x ≥ 0 ⇒  ⇒  ⇒  ⇒ x = 4 2
x + 5 = (1+ x)
x + 5 =1+ 2 x + x 2 x = 4
- Cách giải khác (Dùng biểu thức liên hợp)
Nhân hai vế của phương trình (2) vơi x + 5 + x
(Với điều kiện x ≥ 0 ⇒ x + 5 + x > 0 ), ta có: 2 2
( x + 5 + x)( x + 5 − x) = x + 5 + x ⇒ ( x + 5) − (
x) = x + 5 + x ⇒ x + 5 + x = 5(**)
Cộng vế vợi vế (*) và (**), ta được:
2 x + 5 = 6 ⇒ x + 5 = 3 ⇒ x + 5 = 9 ⇒ x = 4 (thỏa mãn điều kiện x ≥ 0)
VI. Chứng minh đả̛ng thức
Bài toán 12. Chứng minh rằng: 2 2 2 2
| ax + by |≤ a + b x + y với mọi a,b, x, y ∈ R
Trang: 7.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Bất đẳng thức Bunyakovsky.
Huớng dẫn: Bình phương hai vế bất đả̉ng thức cẩn chứng minh và biến đổi tương đương. Lời giải Ta có: 2 2 2 2
| ax + by |≤ a + b ⋅ x + y 2
⇒ (ax + by) ≤ ( 2 2 a + b )( 2 2 x + y ) 2 2 2 2 2 2 2 2 2 2 2 2
⇒ a x + 2abxy + b y ≤ a x + a y + b x + b y 2
⇒ (ay − bx) ≥ 0
Bất đẳng thức cuối cùng luôn đúng với mọi a,b, x, y thuộc  . Dấu " = " xảy ra ⇔ − = 0 a b ay bx
⇔ = , x ≠ 0, y ≠ 0 x y
(với x = 0 và y = 0, bất đẳng thức luôn đúng).
Bài toán 13. Chứng minh rằng a + b ≤ 2(a + b) với a ≥ 0;b ≥ 0.
Huớng dãn: Bình phương hai vế và rút gọn như bài toán 12 . Lời giải
Ta co: a + b ≤ 2(a + b) ⇒ a + 2 a ⋅ b + b ≤ 2(a + b) 2
⇒ a − 2 a b + b ≥ 0 ⇒ ( a − b) ≥ 0 (luôn dúng).
Nhận xét: Ta có thê áp dụng bất đả̉ng thức Bunyakovsky ở trên như sau: Ta có: 2 2 1⋅ a +1⋅ b |
= 1⋅ a +1⋅ b |≤ 1 +1 ⋅ a + b
⇒ a + b ≤ 2 ⋅ a + b ⇒ a + b ≤ 2(a + b) (dpcm).
Bài toán 14. So sánh x + y và x + y(x > 0, y > 0) .
Huớng dẫn: Ta chứng minh x + y < x + y băng cách bình phương hai vế như đã làm ở bài toán 12 và 13 . Lời giải
Với x > 0, y > 0 , ta co: x + y < x + y 2
⇒ x + y < ( x + y) ⇒ x + y < x + 2 x y + y
⇒ 2 xy > 0 (luôn đúng với x > 0, y > 0)
Nhận xét: Bạn hãy để ý các kết quả đã biết sau đây:
x ⋅ y = x ⋅ y (x ≥ 0, y ≥ 0)
x + y < x + y(x > 0, y > 0)
Bài toán 15. So sánh:
a) 3 + 2 và 2 + 6 b) 2 + 3 và 10 c) 2014 + 2016 và 2 2015
Trang: 8.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Lời giải a) Ta co: 2
( 3 + 2) = 3+ 2⋅ 3 ⋅2 + 4 = 7 + 4 3. Lại có: 2
( 2 + 6) = 2 2 ⋅ 6 + 6 + 2 = 8 + 2 12 = 8 + 2⋅ 4 ⋅ 3 = 8 + 4 3 2 2
v ì 7 < 8 ⇒ 7 + 4 3 < 8 + 4 3 ⇒ ( 3 + 2) < ( 2 + 6) ⇒ 3 + 2 < 2 + 6 b) Ta có: 2 + 3 < 10 2 2
⇒ ( 2 + 3) <10 ⇒ 2 + 2 2 ⋅ 3 + 3 <10 ⇒ 2 6 < 5 ⇔ (2 6) < 25 ⇒ 24 < 25 (luôn dúng).
c) Ta có: 2014 + 2016 < 2 2015 2
⇒ ( 2014 + 2016) < 4.2015 ⇒ 2014 + 2. 2014. 2016 + 2016 < 8060 ⇒ 2 2014.2016 < 4030 2
⇒ 2014.2016 < 2015 ⇒ 2014.2016 < 2015 ⇒ 4060224 < 4060225
Ta có thể chứng minh bài toán tổng quát sau:
Vơi n∈ , ta luôn có: n + n + 2 < 2 n +1 Bài toán 16.
a) Tìm giá trị lớn nhất, nhỏ nhất của biểu thức y = x + 1− x
b) Tìm giá trị lớn nhất của biểu thức y = x − 2 + 4 − x
c) Tìm giá trị lớn nhất của biểu thức A = x − 2 + y −1, với x + y = 5.
Huớng dãn: a) Xét giá trị lớn nhất, nhỏ nhất của 2 y .
b) Áp dụng bất đẳng thức Bunyakovsky. Lời giải
a) Với điều kiện: x ≥ 0 và 1− x ≥ 0 ⇔ 0 ≤ x ≤1 Khi đó y > 0 . Ta xét 2 y : 2 2
y = x + 2 x(1− x) +1− x ⇔ y =1+ 2 x(1− x)
Vì x(1− x) ≥ 0 ⇒1+ x(1− x) ≥1 Vậy 2
y ≤1⇒ y ≥1
Giá trị nhỏ nhất của y bằng 1 . x = 0 Dấu "=" xảy ra ⇔  x = 1 2 Lại có: 2
x(1− x) = −x + x  2 1  1 1  1  1 1 = − x − x + + = −   x − ≤ =  4 4 4 2      4 2 Vậy: 2 1
y ≥1+ 2⋅ = 2 ⇒ y ≤ 2 2
Giá trị lớn nhất của y bằng 2 .
Trang: 9.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Dấu "=" xảy 1 1 ra ⇔ x − = 0 ⇔ x = 2 2 Cách khác:
Theo bất đẳng thức Bunyakovsky, ta có: 2 2 2 2 x + 1− x |1
= ⋅ x +1⋅ 1− x |≤ 1 +1 ⋅ ( x) + ( 1− x) = 2
⇒ y ≤ 2 (tiếp tục như cách giải trên)
b) Điều kiện: 2 ≤ x ≤ 4 .
Theo bất dảng thức Bunyakovsky, ta có: 1. 2 2 2 2
x − 2 +1⋅ 4 − x ≤ 1 +1 ⋅ ( x − 2) + ( 4 − x) = 2 ⋅ 2 = 2
⇒ y ≤ 2. Vậy giá trị lớn nhất của y bằng 2 . − − Dấu “ = " xảy x 2 4 x ra ⇔ =
⇔ x − 2 = 4 − x ⇔ x = 3 1 1
c) Điều kiện x ≥ 2 và y ≥1
Theo bất đå̉ng thức Bunyakovsky, ta có: 1. 2 2
x − 2 +1⋅ y −1 ≤ 1 +1 + x − 2 + y −1 = 2 ⋅ x + y − 3
Vì x + y = 5 ⇒ A ≤ 2 ⋅ 5 − 3 = 2
Vậy giá trị lớn nhất của A bằng 2 .
 x − 2 = y −1 x = 3 Dấu "=" xảy ra ⇒  ⇒  . x + y = 5 y = 2
Bài toán 17. Tìm x , biết:
a) 9x − 36x + 121x < 8 b) x −1 + 5 4x − 4 − 9x − 9 < 4 c) 2
x − 4 − x − 2 > 0
Huớng dẩn: Áp dụng quy tắc khai căn một tích. Lời giải
a) (1) ⇒ 3 x − 6 x +11 x < 8 ⇒ 8 x < 8 ⇒ x <1⇒ 0 ≤ x <1. x −1 ≥ 0 b) (2)  5
⇒ x −1 +10 x −1 − 3 x −1 < 4 1
⇒ 8 x −1 < 4 ⇒ x −1 < ⇒  1 ⇒1≤ x < 2 x −1 < 4  4
c) (3) ⇒ x − 2( x + 2 −1) > 0
Điểu kiện: x − 2 > 0(x − 2 = 0 : không thỏa mãn) ⇒ x > 2 .
Khi đó: (3) ⇒ x + 2 −1 > 0 ⇒ x + 2 >1 ⇒ x + 2 >1⇒ x > 1
− (luôn thỏa mãn với x > 2 ) Vậy x > 2.
VII. Liên hệ giữa phép khai căn bậc hai và phép chia
Trang: 10.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Bài toán 1. Tính: a) 6,4 b) 0,25 c) 2 2 8,1 1,44 49 Lời giải a) Ta có: 6,4 64 64 8 = = = . 8,1 81 81 9 b) Ta có: 0,25 25 25 5 = = = . 1,44 144 144 12 c) Ta có: 2 100 100 10 3 2 = = = =1 . 49 49 49 7 7
Bài toán 2. Rút gọn biểu thức: 2 4 2 a) y x 25a A b =
, vỡi x > 0, y ≠ 0 b) 2 B = 2a ,a < 0 c) C = 5ab ,a < 0, b > 0 4 x y 2 4a 6 b Lời giải 2 a) Ta có: y x y | x | A = ⋅ = ⋅ 2 4 x y x y Vî x > 0 |
⇒ x |= x . Vậy y x 1 A = ⋅ = (y ≠ 0) 2 x y y 4 2 b) Ta có 2 b 2 b B = 2a = 2a ⋅ 2 4a 2 | a | 2 c) Ta có: 25a 5⋅| a | C = 5ab = 5ab 6 3 b b 2 Vi 3 3 − a 5 25 < 0 | ⇒ a |= − ;
a b > 0 ⇒ b = b . Vâyy = 5 a a C ab = − 3 2 b b
Bài toán 3. Rút gọn 2 a) 4a +12a + 9 A = với 3
a > − ; b < 0 2 b 2 b) = ( − ). xy B x y
với x < y < 0. (x − y)2
c) C = ( x − y) 4 2 . 2 2
4x − 4xy + y Lời giải 4a +12a + 9 (2a +3)2 2 + a) Ta có: 2a 3 A = = = 2 2 b b b
Trang: 11.

Tài liệu liên quan: