Các dạng toán cực trị của hàm số thường gặp trong kỳ thi THPTQG

Các dạng toán cực trị của hàm số thường gặp trong kỳ thi THPTQG được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

92 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 2
CỰC TRỊ CỦA HÀM SỐ
MỤC LỤC
PHẦN A. CÂU HỎI ........................................................................................................................................ 1
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó ...................................... 1
Dạng 2. Tìm cực trị của hàm số khi biết y, y’ ............................................................................................... 5
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0 ............................................................................................ 8
Dạng 4. Tìm m để hàm số có n cực trị ......................................................................................................... 10
Dạng 5. Đường thẳng đi qua 2 điểm cực trị ................................................................................................ 11
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước ......................................................... 12
Dạng 7. Tam giác cực trị ............................................................................................................................... 14
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối ............................................................................. 14
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x) ............................................... 17
PHẦN B. LỜI GIẢI THAM KHẢO ............................................................................................................ 21
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó .................................... 21
Dạng 2. Tìm cực trị của hàm số khi biết y, y’ ............................................................................................. 27
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0 .......................................................................................... 40
Dạng 4. Tìm m để hàm số có n cực trị ......................................................................................................... 48
Dạng 5. Đường thẳng đi qua 2 điểm cực trị ................................................................................................ 53
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước ......................................................... 57
Dạng 7. Tam giác cực trị ............................................................................................................................... 64
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối ............................................................................. 68
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x) ............................................... 79
PHẦN A. CÂU HỎI
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó
Câu 1. (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số
y f x
có bảng biến thiên như sau
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại
5x
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại
2x
D. Hàm số không có cực đại
Câu 2. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên như
sau
Giá trị cực đại của hàm số đã cho bằng
A.
5
B.
2
C.
0
D.
1
Câu 3. (Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của
hàm số đã cho là:
A.
3
B.
1
C.
2
D.
0
Câu 4. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Tìm giá trị cực đại
C
và giá trị cực tiểu
của hàm số đã cho.
A.
2
CĐ
y
và
0
CT
y
B.
3
CĐ
y
và
0
CT
y
C.
3
CĐ
y
và
2
CT
y
D.
2
CĐ
y
và
2
CT
y
Câu 5. (Mã 103 - BGD - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Câu 6. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số
4 2
y ax bx c (
a
,
b
,
c
) có đồ thị như
hình vẽ bên.
Số điểm cực trị của hàm số đã cho là
A.
3
B.
0
C.
1
D.
2
Câu 7. (Mã 102 - BGD - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Câu 8. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số
( )y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây sai
A. Hàm số có giá trị cực đại bằng
3
B. Hàm số có hai điểm cực tiểu
C. Hàm số có giá trị cực đại bằng
0
D. Hàm số có ba điểm cực trị
Câu 9. (Mã đề 104 - BGD - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
A.
2
x
. B.
2
x
. C.
1x
. D.
3
x
.
Câu 10. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
có đồ thị
như hình vẽ bên. Số điểm cực trị của hàm số này là
A.
3
B.
2
C.
0
D.
1
Câu 11. (Mã đề 104 - BGD - 2019) Cho hàm số
( )y f x
có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đây?
A.
(0;1)
. B.
(1; )
. C.
( 1;0)
. D.
(0; )
Câu 12. (Mã đề 101 - BGD - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
1
x
. B.
3
x
. C.
2
x
. D.
1x
.
Câu 13. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị
như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
A.
2
B.
0
C.
3
D.
1
Câu 14. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
1x
B.
0x
C.
5x
D.
2x
Câu 15. Cho hàm số
y f x
xác định, liên tục trên đoạn
2;2
và có đồ thị là đường cong trong hình vẽ
bên. Hàm số
f x
đạt cực đại tại điểm nào dưới đây
?
A.
2x
. B.
1x
. C.
1x
. D.
2x
Dạng 2. Tìm cực trị của hàm số khi biết y, y’
Câu 16. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị cực đại
C§
y của hàm số
3
3 2y x x .
A.
C§
1y B.
C§
4y C.
C§
1y D.
C§
0y
Câu 17. (MĐ 104 BGD&DT NĂM 2017) Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
1
B.
3
C.
0
D.
2
Câu 18. Cho hàm số
2
3
1
x
y
x
. Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng
3
B. Cực tiểu của hàm số bằng
1
C. Cực tiểu của hàm số bằng
6
D. Cực tiểu của hàm số bằng
2
Câu 19. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
( )f x
có đạo hàm
3
( ) ( 1)( 2)f x x x x
,
x R
. Số điểm cực trị của hàm số đã cho là
A.
1
B.
3
C.
2
D.
5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
Câu 20. (Mã đề 101 - BGD - 2019) Cho hàm số
( )f x
có đạo hàm
2
( ) 2 , xf x x x
.
Số điểm cực
trị của hàm số đã cho là
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 21. (Mã 103 - BGD - 2019) Cho hàm số
f x
có đạo hàm
2
1 , .f x x x x R
Số điểm cực
trị của hàm số đã cho là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 22. (Mã đề 104 - BGD - 2019) Cho hàm số
f x
có đạo hàm
2
1 , f x x x x
. Số điểm
cực trị của hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 23. (Mã 102 - BGD - 2019) Cho hàm số
( )y f x
có đạo hàm
2
( ) ( 2)
f x x x
,
x
. Số điểm
cực trị của hàm số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 24. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho hàm số
f x
có đạo hàm
2 3 4
' 1 3 2
f x x x x x
với mọi
x
. Điểm cực tiểu của hàm số đã cho là
A.
2
x
. B.
3
x
. C.
0
x
. D.
1x
.
Câu 25. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm
3
1 2 ,f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
1
. B.
3
. C.
5
. D.
2
.
Câu 26. (ĐÊ 04 VTED NĂM 2018-2019) Hàm số
y f x
có đạo hàm
1 2 ... 2019
f x x x x
,
x R
. Hàm số
y f x
có tất cả bao nhiêu điểm cực tiểu?
A.
1008
B.
1010
C.
1009
D.
1011
Câu 27. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
F x
là một nguyên hàm
của hàm số
2 2
2019 4 3 2
x
f x x x x
. Khi đó số điểm cực trị của hàm số
F x
là
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 28. Đồ thị hàm số có điểm cực tiểu là:
A. . B. . C. . D. .
Câu 29. (THPT YÊN PHONG 1 BẮC NINH NĂM HỌC 2018-2019 LẦN 2) Hàm số
f x
có đạo hàm
3
2
1 2
f x x x x
,
x
. Hỏi
f x
có bao nhiêu điểm cực đại?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 30. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm
số
3 2
6 9y x x x
có tổng hoành độ và tung độ bằng
A.
5
. B.
1
. C.
3
. D.
1
.
3
3 y x x
( 1; 2)
(1;0)
(1; 2)
( 1;0)
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 31. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4
y x x
.
A.
6
CT
y
B.
1
CT
y
C.
2
CT
y
D.
1
CT
y
Câu 32. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm là
2
1 2f x x x x x
. Số điểm cực trị của hàm số là?
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 33. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Giá trị cực tiểu
CT
y
của hàm số
3 2
3 4
y x x
là:
A.
0
CT
y
. B.
3
CT
y
. C.
2
CT
y
. D.
4
CT
y
.
Câu 34. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm
2 3 4
1 2 3 4 , x .
f x x x x x
Số điểm cực trị của hàm số đã cho là
A.
3
B.
5
C.
2
D.
4
Câu 35. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Đồ thị hàm số
4 2
1
y x x
có bao nhiêu điểm cực trị có tung độ là số dương?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 36. (HSG BẮC NINH NĂM 2018-2019) Hàm số nào dưới đây không có cực trị?
A.
2
1
x
y
x
B.
2 2
1
x
y
x
C.
2
2 1y x x
D.
3
1y x x
Câu 37. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm
2
1 2 ,f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 38. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số
y f x
có đạo hàm
2 4
2 3 9
f x x x x
. Số điểm cực trị của hàm số
y f x
là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 39. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số
4 2
2 1
y x x
. Xét các mệnh đề sau
đây
1) Hàm số có 3 điểm cực trị.
2) Hàm số đồng biến trên các khoảng
1;0
;
1;

.
3) Hàm số có 1 điểm cực trị.
4) Hàm số nghịch biến trên các khoảng
; 1
;
0;1
.
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2. B. 1. C. 4. D. 3.
Câu 40. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm giá trị cực đại của hàm số
3 2
3 2
y x x
.
A.
2
. B.
0
. C.
2
. D.
1
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Câu 41. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số
f x
có đạo hàm
là
4
2 2
' 2 2 1
f x x x x x x
thì tổng các điểm cực trị của hàm số
f x
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 42. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số
4 3 2
1 1 5
3 2019
4 3 2
y x x x x m
m
đạt cực tiểu tại điểm:
A.
3
x
. B.
3
x
. C.
1x
. D.
1
x
.
Câu 43. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm
số
3
3 1y x x
là:
A.
1; 1
M
. B.
0;1
N
. C.
2; 1
P
. D.
1;3
Q
.
Câu 44. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Hàm số
3 2
1
3 1
3
y x x x
đạt cực tiểu
tại điểm
A.
1
x
. B.
1x
. C.
3
x
. D.
3
x
.
Câu 45. (THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 01) Tim sô điêm cưc tri cua ham sô
4 2
2y x x
.
A. 2. B. 4. C. 3. D. 1.
Câu 46. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Điểm cực tiểu
của đồ thị hàm số
3 2
5 5 y x x x
là
A.
1; 8
B.
0; 5
C.
5 40
;
3 27
D.
1;0
Câu 47. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đạo hàm
3
2 2
' 2 2
f x x x x x x
. Số điểm cực trị của hàm số là
A.
4
B.
1
C.
2
D.
3
Câu 48. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
2 3
2
x
y
x
. B.
4
y x
. C.
3
y x x
. D.
2
y x
.
Câu 49. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đạo hàm trên
và
2
1 2 3
f x x x x
. Số điểm cực trị của hàm số đã cho là:
A.
3
B.
1
C.
0
D.
2
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0
Câu 50. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1
m
B.
7
m
C.
5
m
D.
1
m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 51. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Tìm
m
để hàm số
3 2
2 1y x mx mx
đạt
cực tiểu tại
1
x
A. không tồn tại
m
. B.
1
m
. C.
1
m
. D.
1;2
m
.
Câu 52. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Tìm các giá trị thực của tham số m để
hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1, 5
m m
. B.
5
m
. C.
1
m
. D.
1
m
.
Câu 53. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Tìm tất cả các giá trị của tham số
m
để
hàm số
3 2
3 1y x x mx
đạt cực tiểu tại
2
x
.
A.
0
m
. B.
4
m
. C.
0 4
m
. D.
0 4
m
.
Câu 54. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại
1x
.
A.
0
B.
2
C.
1
D.
3
Câu 55. (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
( 1) ( 1) 1
y x m x m x
đạt cực tiểu tại
0?
x
A.
3
B.
2
C. Vô số D.
1
Câu 56. (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
2 4 1
y x m x m x
đạt cực tiểu tại
0
x
?
A. Vô số B.
3
C.
5
D.
4
Câu 57. (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
3 9 1
y x m x m x
đạt cực tiểu tại
0
x
?
A.
6
B. Vô số C.
4
D.
7
Câu 58. (MĐ 103 BGD&ĐT NĂM 2017-2018) Co bao nhiêu gia tri nguyên cua tham sô
m
đê ham sô
8 5 2 4
4 16 1
y x m x m x
đat cưc tiêu tai
0
x
.
A.
8
B. Vô sô C.
7
D.
9
Câu 59. (KTNL GIA BÌNH NĂM 2018-2019) Có bao nhiêu giá trị nguyên của tham số m để hàm số
12 7 2 6
( 5) ( 25) 1
y x m x m x
đạt cực đại tại
0
x
?
A.
8
B.
9
C. Vô số D.
10
Câu 60. Tìm tất cả tham số thực
m
để hàm số
4 2 2
1 2 2019
y m x m x
đạt cực tiểu tại
1
x
A.
0
m
. B.
2
m
. C.
1
m
. D.
2
m
.
Câu 61. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số
y f x
xác
định trên tập số thực
và có đạo hàm
3
2
' sin 3 9f x x x x m x m x
(
m
là
tham số). Có bao nhiêu giá trị nguyên của
m
để hàm số
y f x
đạt cực tiểu tại
0
x
?
A.
6
B.
7
C.
5
D.
4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Dạng 4. Tìm m để hàm số có n cực trị
Câu 62. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2
1 2 3 1
y m x m x
không có cực đại?
A.
1 3
m
B.
1
m
C.
1
m
D.
1 3
m
Câu 63. (MĐ 104 BGD&DT NĂM 2017) Tim tât ca cac gia tri thưc cua tham sô
m
đê đô thi cua ham sô
3 2 3
3 4y x mx m
co hai điêm cưc tri
A
va
B
sao cho tam giac
OAB
co diên tich băng
4
vơi
O
la gôc toa đô.
A.
0
m
B.
4
1
2
m ;
4
1
2
m
C.
1
m
;
1
m
D.
1
m
Câu 64. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tìm tất cả các giá trị của
tham số
m
để hàm số
3
2
2 1
3
x
y mx mx
có hai điểm cực trị.
A.
0 2
m
. B.
2
m
. C.
0
m
. D.
2
0
m
m
.
Câu 65. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm tất cả các giá trị của tham số để hàm số
có cực đại và cực tiểu?
A. . B. C. . D. .
Câu 66. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Tập hợp các giá trị của
m
để hàm
số
3 2
1
2 1
3
y x mx m x
có hai cực trị là:
A.
; 1 2;
 
B.
; 1 2;
 
C.
1;2
D.
1;2
Câu 67. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hàm số
4 2
1
y mx x
. Tập hợp
các số thực
m
để hàm số đã cho có đúng một điểm cực trị là
A.
0;
. B.
;0

. C.
0;
. D.
;0

.
Câu 68. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho hàm số
4 2
(2 1) 1
y mx m x
.
Tìm tất cả các giá trị thực của tham số
m
để hàm số có đúng một điểm cực tiểu.
A. Không tồn tại
m
. B.
0.
m
C.
1
.
2
m
D.
1
0.
2
m
Câu 69. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số
m
để hàm số
4 2 2
2 6 1
y x m m x m
có ba điểm cực trị.
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 70. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số
4 2
1 1 2y mx m x m
có một điểm cực trị khi
A.
0 1
m
. B.
0 1
m m
. C.
0
m
. D.
0 1
m m
.
m
3 2
3 2
y x x mx m
3
2
m
3
.
2
m
3
2
m
3
2
m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
Câu 71. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Có tất cả bao nhiêu giá
trị nguyên của
m
trên miền
10;10
để hàm số
4 2
2 2 1 7
y x m x
có ba điểm cực trị?
A.
20
B.
10
C. Vô số D.
11
Câu 72. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số
4 2 2
6 4
y mx m x
. Có bao nhiêu số nguyên
m
để hàm số có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và
một điểm cực đại ?
A.
4
B.
3
C.
2
D.
5
Câu 73. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Tìm tất cả các giá trị thực của
tham số
m
để hàm số
4 2
1 1 2y mx m x m
có một cực trị.
A.
1
m
B.
0
m
C.
0 1
m
D.
0 1
m m
Dạng 5. Đường thẳng đi qua 2 điểm cực trị
Câu 74. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
3
2
m
B.
3
4
m
C.
1
2
m
D.
1
4
m
Câu 75. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Đồ thị hàm số
3 2
3 9 1y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây thuộc đường thẳng
AB
?
A.
0; 1
M
B.
1; 10
N
C.
1; 0
P
D.
1;10
Q
Câu 76. (MĐ 105 BGD&ĐT NĂM 2017) Đô thi cua ham sô
3 2
3 5
y x x
co hai điêm cưc tri
A
va
B
. Tinh diên tich
S
cua tam giac
OAB
vơi
O
la gôc toa đô.
A.
5S
B.
10
3
S
C.
10S
D.
9S
Câu 77. Đồ thị của hàm số
3 2
3 9 1y x x x
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
.
A.
1;0
P
. B.
0; 1
M
. C.
1; 10
N
. D.
1;10
Q
.
Câu 78. (THPT Xuân Hòa-Vĩnh Phúc- Lần 1- 2018- BTN) Biết đồ thị hàm số
3
3 1y x x
có hai điểm
cực trị
A
,
B
. Khi đó phương trình đường thẳng
AB
là
A.
2 1y x
. B.
2 1.
y x
C.
2.
y x
D.
2y x
.
Câu 79. (Lương Văn Chánh - Phú Yên – 2017 - 2018 - BTN) Tìm giá trị thực của tham số
m
để đường
thẳng
: 3 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm
số
3 2
3 1
y x x
.
A.
1
3
. B.
1
6
. C.
1
6
m
. D.
1
3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Câu 80. (THPT CHUYÊN VĨNH PHÚC - LẦN 1 - 2017 - 2018 - BTN) Tìm tất cả các giá trị của tham
số
m
để đồ thị hàm số
3 2
2 3
y x x m x m
có hai điểm cực trị và điểm
9; 5
M
nằm trên
đường thẳng đi qua hai điểm cực trị của đồ thị.
A.
1.
m
B.
5.
m
C.
3.
m
D.
2.
m
Câu 81. (PTNK Cơ Sở 2 - TPHCM - 2017 - 2018 - BTN) Tìm giá trị thực của tham số
m
để đường thẳng
2 1 3
y m x m
song song với đường thẳng đi qua các điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
A.
3
4
m
. B.
1
2
m
. C.
3
4
m
. D.
1
2
m
.
Câu 82. (TT Tân Hồng Phong - 2018 - BTN) Tìm tổng tất cả các giá trị thực của tham số
m
sao cho
đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
2 3 1 6 1 2
y x m x m m x
song
song đường thẳng
4y x
.
A.
1
3
m
. B.
2
3
m
. C.
2
3
m
. D.
1
m
.
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước
Câu 83. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
3 2 2
1
1
3
y x mx m x
có hai điểm cực trị
A
và
B
sao cho
,A B
nằm
khác phía và cách đều đường thẳng
: 5 9
d y x
. Tính tổng tất cả các phần tử của
S
.
A.
3
B.
6
C.
6
D.
0
Câu 84. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số
3 2
1
1 3 2 2018
3
y mx m x m x
với
m
là tham số. Tổng bình phương tất cả các giá trị
của
m
để hàm số có hai điểm cực trị
1 2
;x x
thỏa mãn
1 2
2 1
x x bằng
A.
40
9
B.
22
9
C.
25
4
D.
8
3
Câu 85. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm tất cả cả các giá trị của tham
số m để
3 2
y x 3x mx 1
đạt cực trị tại
1 2
,x x
thỏa mãn
2 2
1 2
6
x x
A.
3
m
B.
3
m
C.
1
m
D.
1
m
Câu 86. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3 2 2 2
8 11 2 2
y x x m x m
có hai điểm cực trị nằm về hai phía của trục
Ox
.
A.
4.
B.
5.
C.
6.
D.
7.
Câu 87. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho hàm số
3 2
2 1 1 1
y x m x m x m
. Có bao nhiêu giá trị của số tự nhiên
20
m
để đồ thị hàm
số có hai điểm cực trị nằm về hai phía trục hoành?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
A.
18
. B.
19
. C.
21
. D.
20
.
Câu 88. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị nguyên của tham số
m
để đồ
thị của hàm số
3 2 2 2
1 2 3
y x m x m x m
có hai điểm cực trị và hai điểm cực trị đó
nằm về hai phía khác nhau đối với trục hoành?
A.
2
. B.
1
.
C.
3
. D.
4
.
Câu 89. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số
3 2
2 3 1 6 2 1
y x m x m x
với
m
là tham số thực. Tìm tất cả các giá trị của
m
để hàm
số có điểm cực đại và điểm cực tiểu nằm trong khoảng
2; 3
.
A.
1; 3 3; 4
m
. B.
1; 3
m
. C.
3; 4
m
. D.
1; 4
m
.
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Tổng tất cả các giá trị
thực của tham số m để hàm số:
3 2
3 2 1 3 5
y x m x mx m
có hai điểm cực trị
1 2
;x x
đồng
thời
1 2
. 0
y x y x
là:
A.
B.
39
C.
8
D.
3 11 13
Câu 91. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Gọi S là tập các giá trị dương của
tham số
m
sao cho hàm số
3 2
3 27 3 2
y x mx x m
đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
5
x x
. Biết
;S a b
. Tính
2
T b a
.
A.
51 6
T
B.
61 3
T
C.
61 3
T
D.
51 6
T
Câu 92. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Gọi
S
là tập hợp các giá trị nguyên của
tham số
m
để hàm số
3
2
2 3
3
x
y x mx
có hai điểm cực trị
1 2
, 4
x x
. Số phần tử của
S
bằng
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 93. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Tìm giá trị thực của tham số
m
để hàm
số
3 2
4 2 7 1y x m x x
có hai điểm cực trị
1 2
;x x
1 2
x x
thỏa mãn
1 2
4
x x
A.
5
m
. B.
1
2
m
. C.
3
m
. D.
7
2
m
.
Câu 94. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Có bao nhiêu giá trị nguyên của tham số
m
để điểm
3
(2 ; )M m m
tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số
3 2
2 3(2 1) 6 ( 1) 1 ( )y x m x m m x C
một tam giác có diện tích nhỏ nhất?
A.
0
B.
1
C.
2
D. không tồn tại
Câu 95. (HSG BẮC NINH NĂM 2018-2019) Tìm tất cả các giá trị thực của tham số thực m để đường
thẳng đi qua hai điểm cực đại, cực tiểu của đồ thị hàm số
3
3 2 y x mx
cắt đường tròn
có
tâm
1;1
I
, bán kính bằng 1 tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB đạt giá trị
lớn nhất.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
A.
2 3
3
m
B.
2 3
2
m
C.
1 3
2
m
D.
2 5
2
m
Câu 96. (ĐÊ 04 VTED NĂM 2018-2019) Biết đồ thị hàm số
3 2
y x ax bx c
có hai điểm cưc trị
1 1 2 2
; , ;M x y N x y
thỏa mãn
1 1 2 1 1 2
x y y y x x
. Giá trị nhỏ nhất của biểu thức
2 3P abc ab c
bằng
A.
49
4
B.
25
4
C.
841
36
D.
7
6
Dạng 7. Tam giác cực trị
Câu 97. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ
thị của hàm số
4 2
2 1
y x mx có ba điểm cực trị tạo thành một tam giác vuông cân
A.
3
1
9
m
. B.
1
m
. C.
3
1
9
m
. D.
1
m
.
Câu 98. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
1
.
A.
0 1m
B.
0m
C.
3
0 4m
D.
1m
Câu 99. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị của tham
số m để đồ thị hàm số
4 2 2
2 1
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam
giác vuông. Số phần tử của tập hợp S là
A.
2
. B.
0
. C.
4
. D.
1
.
Câu 100. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho hàm số
4 2
2 1 1
y x mx
. Tổng
lập phương các giá trị của tham số
m
để đồ thị hàm số
1
có ba điểm cực trị và đường tròn đi qua
3
điểm này có bán kính
1R
bằng
A.
5 5
2
. B.
1 5
2
. C.
2 5
. D.
1 5
.
Câu 101. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm tất cả các giá trị thực của tham số
m để đồ thị hàm số
4 2 2
2 4
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam giác
đều?
A.
0; 3; 3
m B.
6 6
0; 3; 3
m C.
6 6
3; 3
m D.
3; 3
m
Câu 102. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Tìm
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có 3 điểm cực trị lập thành một tam giác vuông cân.
A.
1
m
. B.
1;1
m
. C.
1;0;1
m
. D.
m
.
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
Câu 103. (ĐỀ THAM KHẢO BGD & ĐT 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
7
điểm cực trị?
A.
5
B.
6
C.
4
D.
3
Câu 104. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Biết phương trình
3 2
0ax bx cx d
0a
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
3 2
y ax bx cx d
có bao nhiêu điểm cực
trị?
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 105. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số
m
để đồ thị hàm số
4 2 2
2 2 12y x mx m m
có bảy điểm cực trị
A.
1
. B.
4
. C.
0
. D.
2
.
Câu 106. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số
2
1 2y x x
là
A.
2
B.
2
C.
3
D.
4
Câu 107. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Đồ thị của hàm số
y f x
có bao nhiêu điểm cực trị?
A.
4
B.
2
C.
5
D.
3
Câu 108. (KTNL GIA BÌNH NĂM 2018-2019) Cho hàm số
( )y f x
có bảng biến thiên như sau.
Hàm số
3 y f x
có bao nhiêu điểm cực trị
A.
5
B.
6
C.
3
D.
1
Câu 109. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số
( )y f x
xác định, liên tục
trên
và có bảng biến thiên như sau:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Đồ thị của hàm số
y f x
có bao nhiêu điểm cực trị?
A.
2
B.
3
C.
4
D.
5
Câu 110. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên
như sau
Đồ thị của hàm số
y f x
có bao nhiêu điểm cực trị?
A.
5
B.
3
C.
4
D.
2
Câu 111. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số
3 2
( , , , )f x ax bx cx d a b c d
và
0, 2019
2019 0
a d
a b c d
. Số cực trị của hàm số
y g x
( với
2019)g x f x
bằng
A.
2
. B.
5
. C.
3
. D.
1
.
Câu 112. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Có bao nhiêu giá trị
nguyên của tham số
m
để hàm số
4 3 2 2
3 4 12y x x x m
có đúng 5 điểm cực trị?
A.
5
. B.
7
. C.
6
. D.
4
.
Câu 113. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số
2
1 2y x x
là
A.
2
B.
2
C.
3
D.
4
Câu 114. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Có bao nhiêu giá trị nguyên dương
của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
5
điểm cực trị.
A.
16
B.
44
C.
26
D.
27
Câu 115. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số
4 2
2 2 1y x mx m
với
m
là tham số thực. Số giá trị nguyên trong khoảng
2;2
của
m
để
hàm số đã cho có
3
điểm cực trị là
A.
2
B.
4
C.
3
D.
1
Câu 116. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đồ
thị như hình vẽ bên dưới
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
2 2h x f x f x m
có đúng
3
điểm cực trị.
A.
1
m
B.
1
m
C.
2
m
D.
2
m
Câu 117. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Tập hợp các giá trị của
m
để hàm số
4 3 2
3 4 12 1
y x x x m
có
7
điểm cực trị là:
A.
(0;6)
B.
(6;33)
C.
(1;33)
D.
(1;6)
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x)
Câu 118. (Mã đề 101 - BGD - 2019) Cho hàm số
y f x
, bảng biến thiên của hàm số
'f x
như sau:
Số điêm cực trị của hàm số
2
2y f x x
là
A.
9.
B.
3.
C.
7.
D.
5.
Câu 119. (Mã đề 104 - BGD - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
Số điểm cực trị của hàm số
2
4 4y f x x
là
A. 5. B. 9. C. 7. D. 3.
Câu 120. (Mã 102 - BGD - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
'f x
như sau
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Số điểm cực trị của hàm số
2
2y f x x
là
A.
9
. B.
5
. C.
7
. D.
3
.
Câu 121. (Mã 103 - BGD - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
Số cực trị của hàm số
2
4 4y f x x
là
A.
3
. B.
9
. C.
5
. D.
7
.
Câu 122. Cho hàm số
y f x
xác định trên
và có đồ thị hàm số
y f x
là đường cong ở hình vẽ.
Hỏi hàm số
y f x
có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 123. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đồ thị
y f x
như hình vẽ sau
+∞10
-1
-∞
2
-1
-3
+∞
+∞
f'(x)
x
O
c
b
a
x
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Đồ thị hàm số
2
2
g x f x x
có tối đa bao nhiêu điểm cực trị?
A.
7
B.
5
C.
6
D.
3
Câu 124. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số
(x)f
xác định trên
và có
đồ thị
( )f x
như hình vẽ bên. Đặt
( ) ( )
g x f x x
. Hàm số đạt cực đại tại điểm thuộc khoảng nào
dưới đây?
A.
3
;3
2
B.
2;0
C.
0;1
D.
1
;2
2
Câu 125. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Cho hàm số
( 1)
y f x
có đồ thị như hình vẽ.
Hàm số
2 4f x x
y
đạt cực tiểu tại điểm nào?
A.
1x
. B.
0
x
. C.
2
x
. D.
1
x
.
Câu 126. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong như hình vẽ. Đặt
3 4
g x f f x
.
Tìm số điểm cực trị của hàm số
?g x
A.
2
. B.
8
. C.
10
. D.
6
.
O
1
1
2
3
4
3
y
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Câu 127. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
xác
định và liên tục trên
, đồ thị của hàm số
y f x
như hình vẽ. Điểm cực đại của hàm số
g x f x x
là
A.
0x
. B.
1x
.
C.
2x
. D. không có điểm cưc đại.
Câu 128. Cho hàm số
y f x
có đạo hàm liên tục trên
và có đồ thị hàm số
y f x
như hình vẽ. Đặt
3
g x f x . Tìm số điêm cưc tri của hàm số
y g x
.
A.
3
B.
5
C.
4
D.
2
Câu 129. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số
y f x
xác định trên
và hàm số
y f x
có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số
2
3y f x
.
A.
4
B.
2
C.
5
D.
3
Câu 130. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo
hàm là
f x
. Đồ thị của hàm số
y f x
như hình vẽ bên. Tính số điểm cực trị của hàm số
2
y f x
trên khoảng
5; 5 .
x
y
-2
2
O
1
O
x
y
a
b
c
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 131. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hàm số
y f x
có đạo hàm liên
tục trên
và đồ thị hàm số
y f ' x
như hình vẽ bên.
Số điểm cực trị của hàm số
y f x 2017 2018x 2019
là.
A.
3
B.
4
C.
1
D.
2
Câu 132. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
( )y f x
. Hàm số
( )y f x
có đồ thị như hình vẽ dưới đây.
Tìm
m
để hàm số
2
( )y f x m
có
3
điểm cực trị.
A.
3;m

. B.
0;3
m
. C.
0;3
m
. D.
;0
m

.
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó
Câu 1. (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại
5x
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại
2x
D. Hàm số không có cực đại
Lời giải
Chọn.C
x
y
3
2
0
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
Dựa vào bảng biến thiên. Hàm số có đạo hàm trên
và
2 0;y y
đổi dấu từ âm sang dương
khi đi qua
2x
nên hàm số đạt cực tiểu tại
2x
.
Câu 2. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên như
sau
Giá trị cực đại của hàm số đã cho bằng
A.
5
B.
2
C.
0
D.
1
Lời giải
Chọn A
Dựa bào BBT ta có: Giá trị cực đại của hàm số là
5
CD
y
Câu 3. (Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của
hàm số đã cho là:
A.
3
B.
1
C.
2
D.
0
Lời giải
Chọn A
Hàm số có ba điểm cực trị.
Câu 4. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Tìm giá trị cực đại
C
và giá trị cực tiểu
của hàm số đã cho.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
A.
2
CĐ
y
và
0
CT
y
B.
3
CĐ
y
và
0
CT
y
C.
3
CĐ
y
và
2
CT
y
D.
2
CĐ
y
và
2
CT
y
Lời giải
Chọn B
Dựa vào bảng biến thiên của hàm số ta có
3
CĐ
y
và
0
CT
y
.
Câu 5. (Mã 103 - BGD - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại:
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Lời giải
Chọn C
Hàm số
f x
xác định tại
1x
,
'(1) 0f
và đạo hàm đổi dấu từ
( )
sang
( )
Câu 6. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số
4 2
y ax bx c (
a
,
b
,
c
) có đồ thị như
hình vẽ bên.
Số điểm cực trị của hàm số đã cho là
A.
3
B.
0
C.
1
D.
2
Lời giải
Chọn A
Câu 7. (Mã 102 - BGD - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Hàm số đạt cực đại tại
A.
2
x
. B.
3
x
. C.
1x
. D.
2
x
.
Lời giải
Chọn B
Câu 8. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số
( )y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây sai
A. Hàm số có giá trị cực đại bằng
3
B. Hàm số có hai điểm cực tiểu
C. Hàm số có giá trị cực đại bằng
0
D. Hàm số có ba điểm cực trị
Lời giải
Chọn C
Câu 9. (Mã đề 104 - BGD - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2
x
. B.
2
x
. C.
1x
. D.
3
x
.
Lời giải
Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Từ bảng biến thiên ta có điểm cực tiểu của hàm số là
3
x
.
Câu 10. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
có đồ thị
như hình vẽ bên. Số điểm cực trị của hàm số này là
A.
3
B.
2
C.
0
D.
1
Lời giải
Chọn B
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị.
Câu 11. (Mã đề 104 - BGD - 2019) Cho hàm số
( )y f x
có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đây?
A.
(0;1)
. B.
(1; )
. C.
( 1;0)
. D.
(0; )
Lời giải
Chọn A
Vì trên
(0;1)
hàm số có đạo hàm mang dấu âm.
Câu 12. (Mã đề 101 - BGD - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
A.
1
x
. B.
3
x
. C.
2
x
. D.
1x
.
Lời giải
Chọn A
Theo bảng biến thiên thì hàm số đạt cực tiểu tại điểm
1
x
Câu 13. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị
như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
A.
2
B.
0
C.
3
D.
1
Lời giải
Chọn A
Câu 14. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
1x
B.
0
x
C.
5
x
D.
2
x
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy
y
đối dấu từ
sang
tại
2
x
.
Nên hàm số đạt cực đại tại điểm
2
x
.
Câu 15. Cho hàm số
y f x
xác định, liên tục trên đoạn
2;2
và có đồ thị là đường cong trong hình vẽ
bên. Hàm số
f x
đạt cực đại tại điểm nào dưới đây
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
?
A.
2x
. B.
1x
. C.
1x
. D.
2x
Lời giải
Chọn B
Từ đồ thị ta thấy hàm số đạt cực đại tại
1.x
Dạng 2. Tìm cực trị của hàm số khi biết y, y’
Câu 16. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị cực đại
C§
y của hàm số
3
3 2y x x .
A.
C§
1y B.
C§
4y C.
C§
1y D.
C§
0y
Lời giải
Chọn B
Ta có
2
3 3y x
0y
2
3 3 0x
1 1 0
1 1 4
x y
x y
3
lim 3 2
x
x x

3
2 3
3 2
lim 1 ,
x
x
x x


3
lim 3 2
x
x x

3
2 3
3 2
lim 1
x
x
x x


Bảng biến thiên
Từ bảng biến thiên, ta thấy giá trị cực đại của hàm số bằng
4
Câu 17. (MĐ 104 BGD&DT NĂM 2017) Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
1
B.
3
C.
0
D.
2
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
Chọn C
Có
2
1
0, 1
1
y x
x
nên hàm số không có cực trị.
Câu 18. Cho hàm số
2
3
1
x
y
x
. Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng
3
B. Cực tiểu của hàm số bằng
1
C. Cực tiểu của hàm số bằng
6
D. Cực tiểu của hàm số bằng
2
Lời giải
Chọn D
Cách 1.
Ta có:
2
2
2 3
1
x x
y
x
;
2
0 2 3 0
y x x
3
1
x
x
Lập bảng biến thiên. Vậy hàm số đạt cực tiểu tại
1x
và giá trị cực tiểu bằng
2
.
Cách 2.
Ta có
2
2
2 3
1
x x
y
x
;
2
0 2 3 0
y x x
3
1
x
x
3
8
1
y
x
. Khi đó:
1
1 0
2
y
;
1
3 0
2
y
.
Nên hàm số đạt cực tiểu tại
1x
và giá trị cực tiểu bằng
2
.
Câu 19. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
( )f x
có đạo hàm
3
( ) ( 1)( 2)
f x x x x
,
x R
. Số điểm cực trị của hàm số đã cho là
A.
1
B.
3
C.
2
D.
5
Lời giải
Chọn B
Phương trình
3
( ) 0 ( 1)( 2) 0
f x x x x
0
1
2
x
x
x
Do
( ) 0
f x
có ba nghiệm phân biệt và
( )f x
đổi dấu qua ba nghiệm này nên hàm số có ba điểm
cực trị.
Câu 20. (Mã đề 101 - BGD - 2019) Cho hàm số
( )f x
có đạo hàm
2
( ) 2 , xf x x x
.
Số điểm cực
trị của hàm số đã cho là
A.
2
. B.
1
. C.
0
. D.
3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
Lời giải
Chọn B
Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đã cho có đúng một điểm cực trị đó là điểm cực tiểu
0
x
.
Câu 21. (Mã 103 - BGD - 2019) Cho hàm số
f x
có đạo hàm
2
1 , .f x x x x R
Số điểm cực
trị của hàm số đã cho là
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn C
Xét dấu của đạo hàm:
Ta thấy đạo hàm đổi dấu đúng 1 lần nên hàm số đã cho có đúng 1 điểm cực trị
Câu 22. (Mã đề 104 - BGD - 2019) Cho hàm số
f x
có đạo hàm
2
1 , f x x x x
. Số điểm
cực trị của hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A
Ta có
2
2
0
0
0 1 0
1
1 0
x
x
f x x x
x
x
.
Vì nghiệm
0
x
là nghiệm bội lẻ và
1
x
là nghiệm bội chẵn nên số điểm cực trị của hàm số là
1.
Câu 23. (Mã 102 - BGD - 2019) Cho hàm số
( )y f x
có đạo hàm
2
( ) ( 2)
f x x x
,
x
. Số điểm
cực trị của hàm số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Ta có:
2
0 0
( ) 0 ( 2) 0
2 0 2
x x
f x x x
x x
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy hàm số có 1 điểm cực trị
0
x
.
Câu 24. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho hàm số
f x
có đạo hàm
2 3 4
' 1 3 2
f x x x x x
với mọi
x
. Điểm cực tiểu của hàm số đã cho là
A.
2
x
. B.
3
x
. C.
0
x
. D.
1x
.
Lời giải
Ta có
2 3 4
0
1
' 1 3 2 ' 0
2
3
x
x
f x x x x x f x
x
x
.
Bảng xét dấu đạo hàm.
Suy ra hàm số
f x
đạt cực tiểu tại
0
x
Câu 25. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm
3
1 2 ,f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
1
. B.
3
. C.
5
. D.
2
.
Lời giải
Ta có:
3
0
0 1 2 0 1
2
x
f x x x x x
x
.
Bảng xét dấu:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Dựa vào bảng xét dấu nhận thấy hàm số
f x
có
3
điểm cực trị.
Câu 26. (ĐÊ 04 VTED NĂM 2018-2019) Hàm số
y f x
có đạo hàm
1 2 ... 2019
f x x x x
,
x R
. Hàm số
y f x
có tất cả bao nhiêu điểm cực tiểu?
A.
1008
B.
1010
C.
1009
D.
1011
Lời giải
Chọn B
Ta có:
1
2
1 2 ... 2019 0
......
2019
x
x
f x x x x
x
0
f x
có
2019
nghiệm bội lẻ và hệ số
a
dương nên có
1010
cực tiểu
Câu 27. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
F x
là một nguyên hàm
của hàm số
2 2
2019 4 3 2
x
f x x x x
. Khi đó số điểm cực trị của hàm số
F x
là
A.
5
. B.
4
. C.
3
. D.
2
.
Lời giải
Ta có:
2 2
2019 4 3 2
x
F x f x x x x
.
0
F x
2 2
2019 4 3 2 0
x
x x x
2
2
1
x
x
x
.
Bảng biến thiên của
F x
:
Từ bảng biến thiên ta thấy hàm số
F x
có 1 cực đại và 1 cực tiểu, nghĩa là có 2 cực trị.
Câu 28. Đồ thị hàm số có điểm cực tiểu là:
A. . B. . C. . D. .
Lời giải
3
3 y x x
( 1; 2)
(1;0)
(1; 2)
( 1;0)
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
Ta có:
+)
2
3 3
y x ;
1
0
1
x
y
x
+)
6
y x
1 6 0
y
hàm số đạt cực đại tại
1x
.
1 6 0
y
hàm số đạt cực tiểu tại
1
x
và điểm cực tiểu là
1; 2
.
Câu 29. (THPT YÊN PHONG 1 BẮC NINH NĂM HỌC 2018-2019 LẦN 2) Hàm số
f x
có đạo hàm
3
2
1 2
f x x x x
,
x
. Hỏi
f x
có bao nhiêu điểm cực đại?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Ta có
2
3
0 0
0 1 0 1
2
2 0
x x
f x x x
x
x
.
Bảng biến thiên
Dựa vào bảng biến thiên suy ra hàm số có
1
điểm cực đại.
Câu 30. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm
số
3 2
6 9y x x x
có tổng hoành độ và tung độ bằng
A.
5
. B.
1
. C.
3
. D.
1
.
Lời giải
Ta có:
2
1
' 3 12 9 0
3
x
y x x
x
Bảng biến thiên
Khi đó:
1 4 5.
CD CD CD CD
x y x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
Câu 31. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4
y x x
.
A.
6
CT
y
B.
1
CT
y
C.
2
CT
y
D.
1
CT
y
Lời giải
Tập xác định:
D
;
2
3 3
y x
;
0
y
1
x
.
Bảng biến thiên
Vậy
1 2
CD
y y
;
1 6
CT
y y
.
Câu 32. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm là
2
1 2f x x x x x
. Số điểm cực trị của hàm số là?
A.
5
. B.
2
. C.
1
. D.
3
.
Lời giải
Ta có
0
0 1
2
x
f x x
x
. Do
0, 1x x
là nghiệm đơn, còn các nghiệm và
2
x
là nghiệm
bội chẵn nên
f x
chỉ đổi khi đi qua
0, 1x x
.
Hàm số
2
0
1 4 0 2 2
0
a
m m m
có
2
điểm cực trị.
Câu 33. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Giá trị cực tiểu
CT
y
của hàm số
3 2
3 4
y x x
là:
A.
0
CT
y
. B.
3
CT
y
. C.
2
CT
y
. D.
4
CT
y
.
Lời giai
Ta có
2
3 6 , 6 6y x x y x
0
0
2
0 6, 2 6
x
y
x
y y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
Do đó hàm số đạt cực tiểu tại
2
x
2 0
CT
y y
.
Câu 34. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm
2 3 4
1 2 3 4 , x .
f x x x x x
Số điểm cực trị của hàm số đã cho là
A.
3
B.
5
C.
2
D.
4
Lời giải
Chọn C
1
2
0
3
4
x
x
f x
x
x
Bảng biến thiên:
Dựa vào bảng biến thiên: Số điểm cực trị của hàm số đã cho là 2.
Câu 35. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Đồ thị hàm số
4 2
1
y x x
có bao nhiêu điểm cực trị có tung độ là số dương?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Tập xác định
D
.
3
4 2y x x
;
0 1
0
2 3
2 4
x y
y
x y
.
Suy ra đồ thị có hàm số
4 2
1
y x x
có
3
điểm cực trị có tung độ là số dương.
Câu 36. (HSG BẮC NINH NĂM 2018-2019) Hàm số nào dưới đây không có cực trị?
A.
2
1
x
y
x
B.
2 2
1
x
y
x
C.
2
2 1y x x
D.
3
1y x x
Lời giải
+ Xét hàm số
2 2
1
x
y
x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Tập xác định
\ 1
D
,
2
4
0,
1
y x D
x
.
Nên hàm số luôn đồng biến trên từng khoảng xác định.
Do đó hàm số
2 2
1
x
y
x
không có cực trị.
Câu 37. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo hàm
2
1 2 ,f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
5
. B.
2
. C.
1
. D.
3
.
Lời giải
Ta có
2
0
0 1 2 0 1
2
x
f x x x x x
x
.
Lập bảng xét dấu của
f x
như sau:
Ta thấy
f x
đổi dấu khi đi qua các điểm
0
x
và
1x
, do đó hàm số
y f x
có hai điểm
cực trị.
Câu 38. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số
y f x
có đạo hàm
2 4
2 3 9
f x x x x
. Số điểm cực trị của hàm số
y f x
là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
2 2
2
2 2 2
2 3 3 2 3 3 3
f x x x x x x x x
2 2
2
0 2 3 3 3 0
f x x x x x
3
3
2
x
x
x
.
Bảng biến thiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
Từ bảng biến thiên của hàm số
y f x
, ta thấy hàm số
y f x
có đúng 1 điểm cực trị.
Câu 39. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số
4 2
2 1
y x x
. Xét các mệnh đề sau
đây
1) Hàm số có 3 điểm cực trị.
2) Hàm số đồng biến trên các khoảng
1;0
;
1;

.
3) Hàm số có 1 điểm cực trị.
4) Hàm số nghịch biến trên các khoảng
; 1
;
0;1
.
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2. B. 1. C. 4. D. 3.
Lời giải
3
0 1
' 4 4 ' 0 1 0
1 0
x y
y x x y x y
x y
Bảng xét dấu:
Hàm số có
3
điểm cực trị, đồng biến trên khoảng
1;0
;
1;

và nghịch biến trên khoảng
; 1
;
0;1
. Vậy mệnh đề
1
,
2
,
4
đúng.
Câu 40. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm giá trị cực đại của hàm số
3 2
3 2
y x x
.
A.
2
. B.
0
. C.
2
. D.
1
.
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
Tập xác định của hàm số là
D
.
Ta có:
2
0
3 6 0
2
x
y x x y
x
.
6 6 0 6 0y x y

Giá trị cực đại của hàm số là:
0 2y
.
Câu 41. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số
f x
có đạo hàm
là
4
2 2
' 2 2 1f x x x x x x
thì tổng các điểm cực trị của hàm số
f x
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Lời giải
Có
2 5
2
' 2 1f x x x x
. Ta thấy
'f x
chỉ đổi dấu qua nghiệm
1x
nên hàm số
f x
có đúng một điểm cực trị là
1x
.
Vậy tổng các điểm cực trị của hàm số
f x
bằng
1
.
Câu 42. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số
4 3 2
1 1 5
3 2019
4 3 2
y x x x x m
m
đạt cực tiểu tại điểm:
A.
3x
. B.
3x
. C.
1x
. D.
1x
.
Lời giải
TXĐ:
D
.
3 2
5 3y x x x
;
3 2
3
0 5 3 0
1
x
y x x x
x
.
Hàm số đạt cực tiểu tại
3x
.
Câu 43. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm
số
3
3 1y x x là:
A.
1; 1M
. B.
0;1N
. C.
2; 1P
. D.
1;3Q
.
Lời giải
2
' 3 3; ' 0 1
'' 6 ; '' 1 6 0; '' 1 6 0
y x y x
y x y y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
Do đó hàm số đạt cực đại tại
1; 1 3
x y
. Vậy chọn đáp án
1;3
Q
.
Câu 44. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Hàm số
3 2
1
3 1
3
y x x x
đạt cực tiểu
tại điểm
A.
1
x
. B.
1x
. C.
3
x
. D.
3
x
.
Lời giải
Ta có hàm số
3 2
1
3 1
3
y x x x
có tập xác định
D
.
2
2 3y x x
;
1
0
3
x
y
x
.
2 2
y x

;
3 4 0
y
;
1 4 0
y
.
Suy ra hàm số đạt cực tiểu tại điểm
1x
.
Câu 45. (THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 01) Tim sô điêm cưc tri cua ham sô
4 2
2y x x
.
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn C
Tư luân
Tâp xac đinh:
D
.
3
0
4 4 0
1
x
y x x
x
.
Bang biên thiên:
Dưa vao bang biên thiên suy ra ham sô co 3 điêm cưc tri.
Trăc nghiêm
Ham sô bâc 4 trung phương
4 2
y ax bx c
co hê sô
. 0
a b
thi se co 3 điêm cưc tri.
Vây chon ngay đap an C.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
Câu 46. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Điểm cực tiểu
của đồ thị hàm số
3 2
5 5 y x x x
là
A.
1; 8
B.
0; 5
C.
5 40
;
3 27
D.
1;0
Lời giải
Chọn A
2
1
3 2 5 0
5
3
x
y x x
x
.
6 2

y x
.
Ta có:
1 8 0
y
Hàm số đạt cực tiểu tại
1
x
;
1 8
CT
y y
.
Vậy điểm cực tiểu của đồ thị hàm số là
1; 8
.
Câu 47. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đạo hàm
3
2 2
' 2 2
f x x x x x x
. Số điểm cực trị của hàm số là
A.
4
B.
1
C.
2
D.
3
Lời giải
Chọn D
Cách 1: Sử dụng MTCT chọn một số nằm giữa các khoảng suy ra bảng xét dấu
x
2
4
2
0
4
2

'f x
0
0
0
0
'f x
đổi dấu 3 lần qua
2
x
,
4
2
x
,
4
2
x
. suy ra hàm số có 3 cực trị.
Cách 2: Sử dụng nghiệm bội chẵn lẻ, nghiệm đơn.
3
2
2 2 4
4 4
' 2 2 2 2 2 2
f x x x x x x x x x x
'f x
đổi dấu qua 3 nghiệm đơn. 2 nghiệm bội chẵn không đổi dấu nên có 3 cực trị.
Câu 48. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
2 3
2
x
y
x
. B.
4
y x
. C.
3
y x x
. D.
2
y x
.
Lời giải
Chọn A.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
+ Hàm số
2 3
2
x
y
x
Tập xác định:
; 2 2;D
 
.
Có
2
7
' 0
2
y x D
x
hàm số luôn đồng biến trên từng khoảng xác định
hàm số
không có cực trị.
Các hàm số khác dễ dàng chứng minh được y’ có nghiệm và đổi dấu qua các nghiệm. Riêng hàm
số cuối y’ không xác định tại -2 nhưng hàm số xác định trên R và y’ đổi dấu qua -2 do đó có hàm
số có điểm cực trị x = -2.
Câu 49. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đạo hàm trên
và
2
1 2 3
f x x x x
. Số điểm cực trị của hàm số đã cho là:
A.
3
B.
1
C.
0
D.
2
Lời giải
Chọn D
Ta có
1
0 2
3
x
f x x
x
Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đã cho có
2
điểm cực trị.
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0
Câu 50. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1
m
B.
7
m
C.
5
m
D.
1
m
Lời giải
Chọn C
Ta có
2 2
2 4
y x mx m
;
2 2y x m

.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
Hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
khi và chỉ khi:
3 0
3 0
y
y
2 2
1
9 6 4 0 6 5 0
5
6 2 0 3
3
m L
m m m m
m TM
m m
m
.
Vậy
5
m
là giá trị cần tìm.
Câu 51. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Tìm
m
để hàm số
3 2
2 1y x mx mx
đạt
cực tiểu tại
1
x
A. không tồn tại
m
. B.
1
m
. C.
1
m
. D.
1;2
m
.
Lời giải
Để
1
x
là điểm cực tiểu của hàm số
1 0
1 0
y
y
1
3 4 0
1.
3
6 4 0
2
m
m m
m
m
m
Thử lại với
1,
m
ta có
3 2
2 1y x x x
;
2
3 4 1y x x
.
2
1
0 3 4 1 0 .
1
3
x
y x x
x
Bảng biến thiên:
x
1
1
3

y
0 0
y
Quan sát bảng biến thiên ta thấy
1
m
thỏa yêu cầu bài toán.
Câu 52. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Tìm các giá trị thực của tham số m để
hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1, 5
m m
. B.
5
m
. C.
1
m
. D.
1
m
.
Lời giải
Tập xác định
.
Ta có
2 2
2 4,
y x mx m
2 2 .y x m

Để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
thì
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
2
5
3 0
6 5 0
5.
1
6 2 0
3 0
3
m
y
m m
m
m
m
y
m
.
Câu 53. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Tìm tất cả các giá trị của tham số
m
để
hàm số
3 2
3 1y x x mx
đạt cực tiểu tại
2
x
.
A.
0
m
. B.
4
m
. C.
0 4
m
. D.
0 4
m
.
Lời giải
Chọn A
2
3 6
y x x m
;
6 6y x

.
Hàm số đạt cực tiểu tại
2 0
0
2 0
6 0
2 0
y
m
x m
y
.
Câu 54. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại
1x
.
A.
0
B.
2
C.
1
D.
3
Lời giải
Chọn D
2 2
' 2 1
y x mx m m
'' 2 2y x m
Hàm số đạt cực đại tại
1x
nên ta có
2
' 1 0
1 2
3 2 0
2
1
2 2 0
'' 1 0
y
m m
m m
m
m
m
y
Thử lại với
2
m
ta có
'' 2 4 '' 1 2 0
y x y
Do đó Hàm số đạt cực đại tại
1x
Câu 55. (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
( 1) ( 1) 1
y x m x m x
đạt cực tiểu tại
0?
x
A.
3
B.
2
C. Vô số D.
1
Lời giải
Chọn B
Ta có:
7 4 2 3
' 8 5( 1) 4( 1) 1
y x m x m x
3 4 2
8 5 1 4 1
x x m x m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
4 2
0
' 0
8 5 1 4 1 0 (1)
x
y
x m x m
*Nếu
1
m
thì
7
' 8y x
, suy ra hàm số đạt cực tiểu tại
0
x
.
*Nếu
1
m
thì
4
0
' 0
8 10 0
x
y
x x
3
0
5
4
x
x
, nhưng
0
x
là nghiệm bội chẵn nên không
phải cực trị.
*Nếu
1
m
: khi đó
0
x
là nghiệm bội lẻ. Xét
4 2
( ) 8 5 1 4 1
g x x m x m
. Để
0
x
là điểm cực tiểu thì
2
0
lim ( ) 4( 1) 0
x
g x m
2
1 0 1 1
m m
. Vì
m
nguyên nên chỉ có
giá trị
0
m
.
Vậy chỉ có hai tham số
m
nguyên để hàm số đạt cực tiểu tại
0
x
là
0
m
và
1
m
.
Câu 56. (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
2 4 1
y x m x m x
đạt cực tiểu tại
0
x
?
A. Vô số B.
3
C.
5
D.
4
Lời giải
Chọn D
Ta có
8 5 2 4
2 4 1
y x m x m x
7 4 2 3
8 5 2 4 4y x m x m x
.
0
y
3 4 2
8 5 2 4 4 0
x x m x m
4 2
0
8 5 2 4 4 0
x
g x x m x m
Xét hàm số
4 2
8 5 2 4 4
g x x m x m
có
3
32 5 2
g x x m
.
Ta thấy
0
g x
có một nghiệm nên
0
g x
có tối đa hai nghiệm
+ TH1: Nếu
0
g x
có nghiệm
0
x
2
m
hoặc
2
m
Với
2
m
thì
0
x
là nghiệm bội
4
của
g x
. Khi đó
0
x
là nghiệm bội 7 của
y
và
y
đổi
dấu từ âm sang dương khi đi qua điểm
0
x
nên
0
x
là điểm cực tiểu của hàm số. Vậy
2
m
thỏa ycbt.
Với
2
m
thì
4
3
0
8 20 0
5
2
x
g x x x
x
.
Bảng biến thiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
Dựa vào BBT
0
x
không là điểm cực tiểu của hàm số. Vậy
2
m
không thỏa ycbt.
+ TH2:
0 0
g
2
m
. Để hàm số đạt cực tiểu tại
0
x
0 0
g
2
4 0 2 2
m m
.
Do
m
nên
1;0;1
m
.
Vậy cả hai trường hợp ta được 4 giá trị nguyên của
m
thỏa ycbt.
Câu 57. (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
3 9 1
y x m x m x
đạt cực tiểu tại
0
x
?
A.
6
B. Vô số C.
4
D.
7
Lời giải
Chọn A
Ta có
8 5 2 4
3 9 1
y x m x m x
7 4 2 3
8 5 3 4 9y x m x m x
.
0
y
3 4 2
8 5 3 4 9 0
x x m x m
4 2
0
8 5 3 4 9 0
x
g x x m x m
Xét hàm số
4 2
8 5 3 4 9
g x x m x m
có
3
32 5 3
g x x m
.
Ta thấy
0
g x
có một nghiệm nên
0
g x
có tối đa hai nghiệm
+) TH1: Nếu
0
g x
có nghiệm
0
x
3
m
hoặc
3
m
Với
3
m
thì
0
x
là nghiệm bội
4
của
g x
. Khi đó
0
x
là nghiệm bội 7 của
y
và
y
đổi
dấu từ âm sang dương khi đi qua điểm
0
x
nên
0
x
là điểm cực tiểu của hàm số. Vậy
3
m
thỏa ycbt.
Với
3
m
thì
4
3
0
8 30 0
15
4
x
g x x x
x
.
Bảng biến thiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
Dựa vào BBT
0
x
không là điểm cực tiểu của hàm số. Vậy
3
m
không thỏa ycbt.
+) TH2:
0 0
g
3
m
. Để hàm số đạt cực tiểu tại
0
x
0 0
g
2
9 0 3 3
m m
.
Do
m
nên
2; 1;0;1;2
m
.
Vậy cả hai trường hợp ta được
6
giá trị nguyên của
m
thỏa ycbt.
Câu 58. (MĐ 103 BGD&ĐT NĂM 2017-2018) Co bao nhiêu gia tri nguyên cua tham sô
m
đê ham sô
8 5 2 4
4 16 1
y x m x m x
đat cưc tiêu tai
0
x
.
A.
8
B. Vô sô C.
7
D.
9
Lời giải
Chọn A
Ta co
7 4 2 3
' 8 5 5 4 16y x m x m x
3 4 2
8 5 4 4 16
x x m x m
3
.
x g x
Vơi
4 2
8 5 5 4 16
g x x m x m
.
● Trương hơp
1
:
0 0 4
g m
.
Vơi
7
4 ' 8m y x
. Suy ra
0
x
la điêm cưc tiêu cua ham sô.
Vơi
4 3
4 ' 8 5
m y x x
. Suy ra
0
x
không la điêm cưc tri cua ham sô.
● Trương hơp
2
:
0 0 4
g m
.
Đê ham sô đat cưc tiêu tai
0
x
thì qua giá trị
0
x
dấu của
'y
phải chuyển từ âm sang dương do
đó
0 0 4 4
g m
.
Kêt hơp hai trương hơp ta đươc
4 4
m
.
Do
3; 2; 1;0;1;2;3;4
m m
.
Vây co
8
gia tri nguyên cua tham sô
m
thoa man.
Câu 59. (KTNL GIA BÌNH NĂM 2018-2019) Có bao nhiêu giá trị nguyên của tham số m để hàm số
12 7 2 6
( 5) ( 25) 1
y x m x m x
đạt cực đại tại
0
x
?
A.
8
B.
9
C. Vô số D.
10
Lời giải
Chọn B
Ta có
11 6 2 5
' 12 7( 5) 6( 25)y x m x m x
TH1:
11
5 ' 12m y x
. Khi đó
' 0 0
y x
là nghiệm bội lẻ, đồng thời dấu của
’y
đổi từ
âm sang dương, nên
0
x
là điểm cực tiểu của hàm số,do đó không thỏa mãn,
5
m
loại.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
TH2:
6 5
5 ' (12 70) 0 0
m y x x x
là nghiệm bội chẵn, do đó
’y
không đổi dấu khi
đi qua
0
x
,
5
m
loại.
TH3:
5 6 2 5
5 ' 12 7( 5) 6( 25) . ( )m y x x m x m x g x
Với
6 2
( ) 12 7( 5) 6( 25)
g x x m x m , ta thấy
0
x
không là nghiệm của
g x
.
Để hàm số đạt cực đại tại
0
x
thì y’ phải đổi dấu từ dương sang âm khi đi qua
0
x
, xảy ra khi
và chỉ khi
0
2
0
lim ( ) 0
6( 25) 0 5 5
lim ( ) 0
x
x
g x
m m
g x
Vì
m
nguyên nên
4; 3;...;3;4
m
, vậy có
9
giá trị của
m
thỏa mãn bài toán.
Câu 60. Tìm tất cả tham số thực
m
để hàm số
4 2 2
1 2 2019
y m x m x
đạt cực tiểu tại
1
x
A.
0
m
. B.
2
m
. C.
1
m
. D.
2
m
.
Lời giải
Tập xác định:
.
D
Ta có:
3 2
4 1 2 2y m x m x
* Điều kiện cần:
Điều kiện cần để hàm số đạt cực tiểu tại
1
x
là
' 1 0
f
2
4 1 2 2 0
m m
2
2 4 0
m m
0
2
m
m
.
* Điều kiện đủ:
Trường hợp 1:
0
m
hàm số trở thành
4 2
2 2019
y x x
Ta có:
' 0
y
3
4 4 0
x x
1
0
1
x
x
x
Bảng biến thiên:
Từ bảng biến thiên ta có hàm số đạt cực đại tại
1
x
nên loại
0
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
Trường hợp 2:
2
m
hàm số trở thành
4 2
2 2019
y x x
.
Ta có:
' 0
y
3
4 4 0
x x
1
0
1
x
x
x
Bảng biến thiên:
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại
1
x
. Chọn
2
m
.
Vậy với
2
m
thì hàm số
4 2 2
1 2 2019
y m x m x
đạt cực tiểu tại
1
x
.
Câu 61. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số
y f x
xác
định trên tập số thực
và có đạo hàm
3
2
' sin 3 9f x x x x m x m x
(
m
là
tham số). Có bao nhiêu giá trị nguyên của
m
để hàm số
y f x
đạt cực tiểu tại
0
x
?
A.
6
B.
7
C.
5
D.
4
Lời giải
Điều kiện
2
9 0 3 3
m m
TH 1:
0 3
m
ta có BTT
TH 2:
3 0
m
ta có BTT
TH 2:
3
m
ta có BTT
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
Từ đó suy ra
3 3
m
có 6 giá trị nguyên của
m
thỏa mãn.
Dạng 4. Tìm m để hàm số có n cực trị
Câu 62. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2
1 2 3 1
y m x m x
không có cực đại?
A.
1 3
m
B.
1
m
C.
1
m
D.
1 3
m
Lời giải
Chọn D
TH1: Nếu
2
1 4 1
m y x
. Suy ra hàm số không có cực đại.
TH2: Nếu
1
m
.
Để hàm số không có cực đại thì
2 3 0 3
m m
. Suy ra
1 3
m
.
Vậy
1 3
m
.
Câu 63. (MĐ 104 BGD&DT NĂM 2017) Tim tât ca cac gia tri thưc cua tham sô
m
đê đô thi cua ham sô
3 2 3
3 4y x mx m
co hai điêm cưc tri
A
va
B
sao cho tam giac
OAB
co diên tich băng
4
vơi
O
la gôc toa đô.
A.
0
m
B.
4
1
2
m ;
4
1
2
m
C.
1
m
;
1
m
D.
1
m
Lời giải
Chọn C
2
3 6y x mx
.
2
0 3 6 0
y x mx
3
0 4
2 0
x y m
x m y
.
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi
0
m
.
Khi đó, hai điêm cưc tri của đồ là
3
0;4
A m
va
2 ;0
B m
,
0
m
.
1
. 4
2
OAB
S OA OB
3 4
1
. 4 2 4 1 1
2
m m m m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
Câu 64. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tìm tất cả các giá trị của
tham số
m
để hàm số
3
2
2 1
3
x
y mx mx
có hai điểm cực trị.
A.
0 2
m
. B.
2
m
. C.
0
m
. D.
2
0
m
m
.
Lời giải
Ta có:
2
2 2y x mx m
Hàm số
3
2
2 1
3
x
y mx mx
có hai điểm cực trị
0
y
có hai nghiệm phân biệt
2
2
2 0
0
m
m m
m
.
Câu 65. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm tất cả các giá trị của tham số để hàm số
có cực đại và cực tiểu?
A. . B. C. . D. .
Lời giải
+ TXĐ:
+
+ Hàm số có cực đại và cực tiểu có 2 nghiệm phân biệt.
Câu 66. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Tập hợp các giá trị của
m
để hàm
số
3 2
1
2 1
3
y x mx m x
có hai cực trị là:
A.
; 1 2;
 
B.
; 1 2;
 
C.
1;2
D.
1;2
Lời giải
Chọn B
Ta có
2
2 2
y x mx m
. Để hàm số có hai cực trị thì
0
y
có hai nghiệm phân biệt nên
2
1
0 0 2 0
2
m
y m m
m
Câu 67. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hàm số
4 2
1
y mx x
. Tập hợp
các số thực
m
để hàm số đã cho có đúng một điểm cực trị là
A.
0;
. B.
;0

. C.
0;
. D.
;0

.
Lời giải
m
3 2
3 2
y x x mx m
3
2
m
3
.
2
m
3
2
m
3
2
m
D
2
3 6 2y x x m
0
y
3
36 24 0 .
2
m m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
Tập xác định
D
.
TH1:
0
m
hàm số đã cho trở thành
2
1
y x
là một hàm bậc hai nên luôn có một cực trị.
TH2:
0
m
, ta có
3
4 2y mx x
.
0
y
3
4 2 0
mx x
2
2 2 1 0
x mx
2
0
2 1 0
x
mx
.
Để hàm số có đúng một cực trị thì phương trình
0
y
có đúng 1 nghiệm.
Ycbt
Phương trình
có một nghiệm
0
x
hoặc vô nghiệm suy ra
0
m
.
Vậy
0
m
.
Câu 68. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho hàm số
4 2
(2 1) 1
y mx m x
.
Tìm tất cả các giá trị thực của tham số
m
để hàm số có đúng một điểm cực tiểu.
A. Không tồn tại
m
. B.
0.
m
C.
1
.
2
m
D.
1
0.
2
m
Lời giải
Với
0
m
, ta có
2
1
y x
' 2y x
. Khi đó hàm số có 1 cực trị và cực trị đó là cực tiểu. Suy ra
0
m
thỏa mãn yêu cầu bài toán. (1)
Với
0
m
, ta có
3 2
' 4 2(2 1) 2 (2 2 1)
y mx m x x mx m
Hàm số có một cực trị là cực tiểu
2
0
2 2 1 0 vô nghiêm
m
mx m
0
2 1
0
2
m
m
m
0
1
0
2
0
m
m
m
m
(2)
Từ (1) và (2) suy ra hàm số có một cực trị là cực tiểu khi
0.
m
Câu 69. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số
m
để hàm số
4 2 2
2 6 1
y x m m x m
có ba điểm cực trị.
A.
6
. B.
5
. C.
4
. D.
3
.
Lời giải
Ta có
3 2 2 2
4 4 6 4 6
y x m m x x x m m
.
2 2
0
0
6 0(1)
x
y
x m m
Hàm số có ba điểm cực trị
(1) có hai nghiệm phân biệt khác 0
2
6 0 2 3
m m m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
Ta có:
, 2 3 1;0;1;2
m m m
.
Vậy có
4
giá trị nguyên của tham số
m
để hàm số có ba điểm cực trị.
Câu 70. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số
4 2
1 1 2y mx m x m
có một điểm cực trị khi
A.
0 1
m
. B.
0 1
m m
. C.
0
m
. D.
0 1
m m
.
Lời giải
Trường hợp 1:
0
m
thì hàm số đã cho trở thành
2
1
y x
. Hàm số này có 1 cực trị là cực đại
0
m
thỏa mãn.
Trường hợp 2:
0
m
thì hàm số đã cho trở thành
4 2
1 1 2y mx m x m
Ta có
3 2
4 2 1 2 2 1
y mx m x x mx m
;
2
2
0
2 0
0
1
*
2 1 0
2
x
x
y
m
x
mx m
m
YCBT
y
đổi dấu một lần
Phương trình
*
vô nghiệm hoặc có nghiệm
0
x
.
1
1
0
0
2
m
m
m
m
Kết hợp hai trường hợp ta được
0 1
m m
.
Giải nhanh: Với
a
khác
0
thì hàm số đã cho có 1 cực trị
1
0 1 0
0
m
ab m m
m
.
Câu 71. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Có tất cả bao nhiêu giá
trị nguyên của
m
trên miền
10;10
để hàm số
4 2
2 2 1 7
y x m x
có ba điểm cực trị?
A.
20
B.
10
C. Vô số D.
11
Lời giải
Chọn D
Ta có
2
' 4 2 1 y x x m x
.
2
0
0
2 1 *
x
y
x m
Hàm số đã cho có ba cực trị khi và chỉ khi
0
y
có ba nghiệm phân biệt, hay (*) có hai nghiệm
phân biệt khác
0
1
2 1 0
2
m m
.
Do
10;10
m
nên có
11
giá trị thỏa mãn.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
Câu 72. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số
4 2 2
6 4
y mx m x
. Có bao nhiêu số nguyên
m
để hàm số có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và
một điểm cực đại ?
A.
4
B.
3
C.
2
D.
5
Lời giải
Chọn C
Tập xác định
D
.
Ta có
3 2
4 2 6y mx m x
.
Hàm số đã cho có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại khi và
chỉ khi
2
4 0
0 6
6 0
m
m
m m
.
Do đó có hai giá trị nguyên của tham số
m
.
Câu 73. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Tìm tất cả các giá trị thực của
tham số
m
để hàm số
4 2
1 1 2y mx m x m
có một cực trị.
A.
1
m
B.
0
m
C.
0 1
m
D.
0 1
m m
Lời giải
Chọn D
Ta có:
3
4 2 1y mx m x
Trường hợp 1: Xét
0 2m y x
. Ta thấy phương trình
0
y
đổi dấu một lần nên hàm số
có một điểm cực trị. Suy ra
0
m
(thoả YCBT) (1)
Trường hợp 2: Xét
3
1 4m y x
.Ta thấy phương trình
0
y
đổi dấu một lần nên hàm số
có một điểm cực trị. Suy ra
1
m
(thoả YCBT) (2)
Trường hợp 3: Xét
0
m
,
2
0
0
1
2
x
y
m
x
m
Để hàm số có một điểm cực trị thì
0
1
0
1
2
m
m
m
m
(3)
Từ (1), (2) và (3) suy ra
0
1
m
m
Ghi chú: Dùng công thức tính nhanh
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
Hàm số có một điểm cực trị khi và chỉ khi
0
1 0 .
1
m
m m
m
Dạng 5. Đường thẳng đi qua 2 điểm cực trị
Câu 74. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
3
2
m
B.
3
4
m
C.
1
2
m
D.
1
4
m
Lời giải
Chọn B
Ta có
2
3 6y x x
. Từ đó ta có tọa độ hai điểm cực trị
0;1
A
,
2; 3
B
. Đường thẳng qua hai
điểm cực trị có phương trình
2 1y x
. Đường thẳng này vuông góc với đường thẳng
2 1 3
y m x m
khi và chỉ khi
3
2 1 2 1
4
m m
.
Câu 75. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Đồ thị hàm số
3 2
3 9 1y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây thuộc đường thẳng
AB
?
A.
0; 1
M
B.
1; 10
N
C.
1; 0
P
D.
1;10
Q
Lời giải
Chọn B
Ta có:
2
3 6 9
y x x
thực hiện phép chia
y
cho
y
ta được số dư là
8 2y x
.
Như thế điểm
1; 10
N
thuộc đường thẳng
AB
.
Câu 76. (MĐ 105 BGD&ĐT NĂM 2017) Đô thi cua ham sô
3 2
3 5
y x x
co hai điêm cưc tri
A
va
B
. Tinh diên tich
S
cua tam giac
OAB
vơi
O
la gôc toa đô.
A.
5S
B.
10
3
S
C.
10S
D.
9S
Lời giải
Chọn A
Ta co
2
3 6 0 0 2
y x x y x x
Dê dang xac đinh đươc toa đô cac điêm cưc tri la
0; 5 ; 2; 9
A B
Vây
5; 85; 2 5
OA OB AB
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
Goi
2
AB OA OB
p
Ap dung công thưc Heron tinh diên tich tam giac
OAB
ta co
5
OAB
S p p OA p OB p AB
Câu 77. Đồ thị của hàm số
3 2
3 9 1y x x x
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
.
A.
1;0
P
. B.
0; 1
M
. C.
1; 10
N
. D.
1;10
Q
.
Lời giải
TXĐ:
D
.
2
' 3 6 9y x x
.
2
1 6
' 0 3 6 9 0
3 26
x y
y x x
x y
Ta có
1;6 , 3; 26
A B
4; 32
AB
nên ) Chọn
8;1
AB
n
.
Phương trình đường thẳng
AB
là:
8 1 1 6 0 8 2 0
x y x y
.
Thay tọa độ các điểm
, , ,P M N Q
vào phương trình đường thẳng
AB
ta có điểm
1; 10
N
thuộc
đường thẳng.
Câu 78. (THPT Xuân Hòa-Vĩnh Phúc- Lần 1- 2018- BTN) Biết đồ thị hàm số
3
3 1y x x
có hai điểm
cực trị
A
,
B
. Khi đó phương trình đường thẳng
AB
là
A.
2 1y x
. B.
2 1.
y x
C.
2.
y x
D.
2y x
.
Lời giải
Chọn B
Thực hiện phép chia
y
cho
y
ta được:
1
. 2 1
3
y y x x
.
Giả sử hai điểm cực trị của đồ thị hàm số lần lượt là:
1 1
;A x y
và
2 2
;B x y
.
Ta có:
1 1 1 1 1 1
2 2 2 2 2 2
1
. 2 1 2 1
3
1
. 2 1 2 1
3
y y x y x x x x
y y x y x x x x
.
Ta thấy, toạ độ hai điểm cực trị
A
và
B
thoả mãn phương trình
2 1y x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
Vậy phương trình đường thẳng qua hai điểm cực trị là:
2 1y x
.
Câu 79. (Lương Văn Chánh - Phú Yên – 2017 - 2018 - BTN) Tìm giá trị thực của tham số
m
để đường
thẳng
: 3 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm
số
3 2
3 1
y x x
.
A.
1
3
. B.
1
6
. C.
1
6
m
. D.
1
3
.
Lời giải
Chọn B
Xét hàm số
3 2
3 1
y x x
Có :
2
3 6y x x
,
1 1
2 1
3 3
y x y x
.
Do đó, đường thẳng
qua hai điểm cực trị của đồ thị hàm số này có phương trình là
2 1y x
.
Để
d
vuông góc với
thì
3 1 . 2 1
m
1
6
m
.
Vậy giá trị cần tìm của
m
là
1
6
m
.
Câu 80. (THPT CHUYÊN VĨNH PHÚC - LẦN 1 - 2017 - 2018 - BTN) Tìm tất cả các giá trị của tham
số
m
để đồ thị hàm số
3 2
2 3
y x x m x m
có hai điểm cực trị và điểm
9; 5
M
nằm trên
đường thẳng đi qua hai điểm cực trị của đồ thị.
A.
1.
m
B.
5.
m
C.
3.
m
D.
2.
m
Lời giải
Chọn C
Ta có
2
3 4 3
y x x m
, để hàm số có hai điểm cực trị thì phương trình
0
y
có hai nghiệm
phân biệt
0
13
*
3
m
Ta có
1 2 2 26 7 2
.
3 9 3 9 9 3
m m
y y x x
nên phương trình đường thẳng đi qua hai điểm
cực trị là
2 26 7 2
.
3 9 9 3
m m
y x
Theo giả thiết, đường thẳng này đi qua
9; 5
M
nên
3
m
(thỏa mãn điều kiện
*
).
Câu 81. (PTNK Cơ Sở 2 - TPHCM - 2017 - 2018 - BTN) Tìm giá trị thực của tham số
m
để đường thẳng
2 1 3
y m x m
song song với đường thẳng đi qua các điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
A.
3
4
m
. B.
1
2
m
. C.
3
4
m
. D.
1
2
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
Lời giải
Chọn D
Hàm số
3 2
3 1
y x x
có TXĐ:
;
2
3 6y x x
;
0
' 0
2
x
y
x
Suy ra đồ thị hàm số có hai điểm cực trị là
0;1
A
,
2; 3 2; 4
B AB
.
Đường thẳng
d
đi qua hai điểm
A
,
B
có phương trình:
1
2 1
2 4
x y
y x
.
Đường thẳng
2 1 3
y m x m
song song với đường thẳng
2 1 2
1
3 1
2
m
d m
m
.
Câu 82. (TT Tân Hồng Phong - 2018 - BTN) Tìm tổng tất cả các giá trị thực của tham số
m
sao cho
đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
2 3 1 6 1 2
y x m x m m x
song
song đường thẳng
4y x
.
A.
1
3
m
. B.
2
3
m
. C.
2
3
m
. D.
1
m
.
Lời giải
Chọn A
Ta có
2
6 6 1 6 1 2y x m x m m
, 0
1 2
x m
y
x m
.
Để hàm số có hai cực trị thì
1 2m m
1
3
m
.
Hai điểm cực trị của đồ thị hàm số là
3 2
; 7 3
A m m m
,
3 2
1 2 ;20 24 9 1
B m m m m
. Do đó
3
1 3 ; 3 1
AB m m
. Do đó
AB
có vectơ pháp tuyến là
2
3 1 ;1
n m
.
Do đó
2
3 2
: 3 1 2 3 0
AB m x y m m m
2
3 2
3 1 2 3
y m x m m m
.
Để đường thẳng
AB
song song với đường thẳng
4y x
thì:
2
3 2
3 1 4
2 3 0
m
m m m
1
1
3
0
1
2
1
m
m
m
m
m
1
3
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước
Câu 83. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
3 2 2
1
1
3
y x mx m x
có hai điểm cực trị
A
và
B
sao cho
,A B
nằm
khác phía và cách đều đường thẳng
: 5 9
d y x
. Tính tổng tất cả các phần tử của
S
.
A.
3
B.
6
C.
6
D.
0
Lời giải
Chọn D
Cách 1: Ta có
2 2
' 2 1
y x mx m
3
1
3 2
' 0 1;
1
3
x m
m m
y A m
x m
và
3
3 2
1;
3
m m
B m
Dễ thấy phương trình đường thẳng
2
1
2
:
3 3
m m
AB y x
nên
AB
không thể song song hoặc
trùng với
d
,A B
cách đều đường thẳng
: 5 9
d y x
nếu trung điểm
I
của
AB
nằm trên
d
3 3
3
3 3
; 5 9 18 27 0
3 3
m m m m
I m d m m m
3
3 3 5
2
m
m
Với
3 ,m A B
thỏa điều kiện nằm khác phía so với
d
.
Với
3 3 5
,
2
m A B
thỏa điều kiện nằm khác phía so với
d
.
Tổng các phần tử của
S
bằng 0.
Câu 84. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số
3 2
1
1 3 2 2018
3
y mx m x m x
với
m
là tham số. Tổng bình phương tất cả các giá trị
của
m
để hàm số có hai điểm cực trị
1 2
;x x
thỏa mãn
1 2
2 1
x x bằng
A.
40
9
B.
22
9
C.
25
4
D.
8
3
Lời giải
Chọn A
Ta có
2
' x 2 1 3 2
y m m x m
Để hàm số có hai điểm cực trị thì phương trình
2
x 2 1 3 2 0
m m x m
phải có hai nghiệm
phân biệt.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
2
2
0
0
2 4 1 0
1 3 2 0
m
m
m m
m m m
Theo định lý Vi-ét ta có
1 2
1 2
2 1
.
3 2
.
m
x x
m
m
x x
m
Theo bài ta có hệ phương trình
1
1
2
1 2
2
2 1
1
3 4
2 1
.
2 1
2
m
x
m
x x m
m
m
m
m m
x x
x
2 /
3 2
3 4 2
. 3 2 3 4 2 0
2
/
3
m t m
m
m m
m m m m
m m m
m t m
Vậy
2 2
1 2
40
9
m m
.
Câu 85. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm tất cả cả các giá trị của tham
số m để
3 2
y x 3x mx 1
đạt cực trị tại
1 2
,x x
thỏa mãn
2 2
1 2
6
x x
A.
3
m
B.
3
m
C.
1
m
D.
1
m
Lời giải
Chọn A
2
y' 3x 6x m
. Hàm số đạt cực trị tại
1 2
,x x
.Vậy
1 2
,x x
là nghiệm của phương trình
y' 0
Theo viet ta có
1 2
1 2
2
.
3
x x
m
x x
2 2 2
1 2 1 2 1 2
( ) 2
x x x x x x
2
4
3
m
2
4 6
3
m
3
m
Câu 86. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3 2 2 2
8 11 2 2
y x x m x m
có hai điểm cực trị nằm về hai phía của trục
Ox
.
A.
4.
B.
5.
C.
6.
D.
7.
Lời giải
Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
Yêu cầu bài toán
đồ thị hàm số cắt trục hoành tại ba điểm phân biệt
3 2 2 2
8 11 2 2 0
x x m x m
có ba nghiệm phân biệt
3 2 2 2
8 11 2 2 0
x x m x m
2 2
2 6 1 0
x x x m
2 2
2
6 1 0(*)
x
x x m
Suy ra phương trình (*) có hai nghiệm phân biệt khác
2
2
2
' 10 0
8 0
m
m
2 2
10 10
m
m
Vậy có
7
giá trị nguyên của tham số thỏa mãn đề bài.
Câu 87. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho hàm số
3 2
2 1 1 1
y x m x m x m
. Có bao nhiêu giá trị của số tự nhiên
20
m
để đồ thị hàm
số có hai điểm cực trị nằm về hai phía trục hoành?
A.
18
. B.
19
. C.
21
. D.
20
.
Lời giải
+ Ta có:
2
1 2 1
y x x mx m
.
+ Hàm số có hai điểm cực trị nằm về hai phía trục hoành khi và chỉ khi đồ thị
y
cắt trục hoành tại
ba điểm phân biệt.
2
1 2 1 0
y x x mx m
có ba nghiệm phân biệt.
2
2 1 0
x mx m
có hai nghiệm phân biệt khác 1.
2
1 5
2
1 0
1 5
2 3 0
2
2
3
m
m m
m
m
m
.
+ Do
, 20
m N m
nên
1 20
m
. Vậy có 19 số tự nhiên thỏa mãn bài toán.
Câu 88. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị nguyên của tham số
m
để đồ
thị của hàm số
3 2 2 2
1 2 3
y x m x m x m
có hai điểm cực trị và hai điểm cực trị đó
nằm về hai phía khác nhau đối với trục hoành?
A.
2
. B.
1
.
C.
3
. D.
4
.
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
Ta có
2 2
0 3 2 1 2 0
y x m x m
.
Để hàm số có hai điểm cực trị
2
1 15 1 15
0 2 2 7 0 *
2 2
m m m
.
Ta lần lượt thử bốn giá trị nguyên của
m
thỏa mãn
*
là
1;0;1;2
.
Ta được bốn hàm số
3 3 2 3 2 3 2
2; 2 3; 2 2; 3 1y x x y x x x y x x x y x x x
.
Khi đó ta nhận thấy chỉ có
1
m
thỏa mãn yêu cầu bài toán.
Câu 89. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số
3 2
2 3 1 6 2 1
y x m x m x
với
m
là tham số thực. Tìm tất cả các giá trị của
m
để hàm
số có điểm cực đại và điểm cực tiểu nằm trong khoảng
2; 3
.
A.
1; 3 3; 4
m
. B.
1; 3
m
. C.
3; 4
m
. D.
1; 4
m
.
Lời giải
Chọn A
Ta có:
2
' 6 6 1 6 2
y x m x m
Để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng
2; 3
pt
' 0y
có 2 nghiệm
thuộc khoảng
2; 3
2
1 2 0
x m x m
có 2 nghiệm thuộc khoảng
2; 3

1 2 0
x x m
1 2; 3
2
x
x m
2 1 3
2 2 3 1 4
m m
YCBT
m m
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Tổng tất cả các giá trị
thực của tham số m để hàm số:
3 2
3 2 1 3 5
y x m x mx m
có hai điểm cực trị
1 2
;x x
đồng
thời
1 2
. 0
y x y x
là:
A.
B.
39
C.
8
D.
3 11 13
Lời giải
Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
+) Để hàm số có hai cực trị thì phương trình
0
y
phải có hai nghiệm phân biệt:
2
9 4 1 3y x m x m
có hai nghiệm phân biệt
2
4 1 27 0
m m
+) Xét
1 2
. 0
y x y x
nên ta có
3 2
3 2 1 3 5
y x m x mx m
phải tiếp xúc với trục hoành
3 2
3 2 1 3 5 0
x m x mx m
phải có nghiệm kép
2
1 3 2 5 5 0 1
x x m x m
phải có nghiệm kép
+) TH1: Phương trình
2
3 2 5 5 0
x m x m
có một nghiệm
1
1 13
x m
+) TH2: Phương trình
2
3 2 5 5 0
x m x m
có nghiệm kép khác
1
2
2
2 3
2 5 12 5 0 4 32 35 0 8
m m m m m m
1 2 3
21
m m m
Câu 91. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Gọi S là tập các giá trị dương của
tham số
m
sao cho hàm số
3 2
3 27 3 2
y x mx x m
đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
5
x x
. Biết
;S a b
. Tính
2
T b a
.
A.
51 6
T
B.
61 3
T
C.
61 3
T
D.
51 6
T
Lời giải
Chọn C
+) Ta có
2
3 6 27
y x mx
,
2
0 2 9 0
y x mx
(1)
+) Theo giả thiết hàm số đạt cực trị tại
1 2
,x x
phương trình
(1)
có
2
nghiệm phân biệt
0
2
3
9 0
3
m
m
m
(*)
+) Với điều kiện (*) thì phương trình
(1)
có
2
nghiệm
1 2
,x x
, theo Vi-ét ta có:
1 2
1 2
2
9
x x m
x x
+) Ta lại có
1 2
5
x x
2 2
1 2 1 2 1 2
25 4 25 0
x x x x x x
2
61 61
4 61 0
2 2
m m
(**)
+) Kết hợp (*), (**) và điều kiện
m
dương ta được:
61
3
2
m
3
2 61 3
61
2
a
T b a
b
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
Câu 92. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Gọi
S
là tập hợp các giá trị nguyên của
tham số
m
để hàm số
3
2
2 3
3
x
y x mx
có hai điểm cực trị
1 2
, 4
x x
. Số phần tử của
S
bằng
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
Ta có:
3
2 2
2 3 ' 4
3
x
y x mx y x x m
.
Hàm số có hai điểm cực trị
1 2
,x x
thì phương trình
' 0
y
có hai nghiệm phân biệt
' 0 4 0 4
m m
.
Khi đó giả sử
1 2
x x
,
1
2
2 4
' 0
2 4
x m
y
x m
Yêu cầu bài toán trở thành
2
4 2 4 4 0 4
x m m
.
Kết hợp với
4
m
ta được
0 4
m
. Do
m
nguyên nên
0;1;2;3
m
. Vậy có 4 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 93. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Tìm giá trị thực của tham số
m
để hàm
số
3 2
4 2 7 1y x m x x
có hai điểm cực trị
1 2
;x x
1 2
x x
thỏa mãn
1 2
4
x x
A.
5
m
. B.
1
2
m
. C.
3
m
. D.
7
2
m
.
Lời giải
Ta có
3 2
4 2 7 1y x m x x
(1)
2
' 3 8 2 7
y x m x
. Xét phương trình
2
3 8 2 7 0
x m x
(2)
2
' 4 2 21 0
m
, với mọi m
hàm số (1) luôn có hai điểm cực trị
1 2
;x x
với mọi
m
.
*Ta thấy
21 0
ac
phương trình (2) có 2 nghiệm trái dấu
1 2
0; 0
x x
1 1 2 2
;
x x x x
*Ta có
1 2
4
x x
1 2
4
x x
1 2
8 2
4 4
3
m
x x
1
2
m
Câu 94. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Có bao nhiêu giá trị nguyên của tham số
m
để điểm
3
(2 ; )M m m
tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số
3 2
2 3(2 1) 6 ( 1) 1 ( )y x m x m m x C
một tam giác có diện tích nhỏ nhất?
A.
0
B.
1
C.
2
D. không tồn tại
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
Chọn B
Ta có
2
' 6 6(2 1) 6 ( 1)
y x m x m m
' 0
1
x m
y m R
x m
, hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
3 2 3 2
( ;2 3 1), ( 1;2 3 )A m m m B m m m
Suy ra
2
AB
và phương trình đường thẳng
3 2
: 2 3 1 0
AB x y m m m
Do đó, tam giác
MAB
có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ
M
tới
AB
nhỏ nhất
Ta có
2
3 1 1
( , )
2 2
m
d M AB
, dấu "=" khi
0
m
Câu 95. (HSG BẮC NINH NĂM 2018-2019) Tìm tất cả các giá trị thực của tham số thực m để đường
thẳng đi qua hai điểm cực đại, cực tiểu của đồ thị hàm số
3
3 2 y x mx
cắt đường tròn
có
tâm
1;1
I
, bán kính bằng 1 tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB đạt giá trị
lớn nhất.
A.
2 3
3
m
B.
2 3
2
m
C.
1 3
2
m
D.
2 5
2
m
Lời giải
Ta có:
2
3 3
y x m
suy ra đồ thị hàm số có điểm cực đại và cực tiểu khi
0
m
. Các điểm cực
đại, cực tiểu của đồ thị hàm số là
;2 2 ; ;2 2 .
C m m m D m m m
Đường thẳng
đi qua các điểm CĐ, CT của đồ thị hàm số có phương trình là:
2 2 y mx
. Do
2
2 1
, 1
4 1
m
d I R
m
(vì m > 0)
luôn cắt đường tròn tâm
1;1
I
, bán kính
1R
tại 2
điểm
,A B
phân biệt. Dễ thấy
1
2
m
không thõa mãn do
, ,A I B
thẳng hàng.
Với
1
2
m
:
không đi qua I, ta có:
2
1 1 1
. .sin
2 2 2
ABI
S IA IB AIB R
.
Do đó
IAB
S
lớn nhất bằng
1
2
khi
sin 1
AIB hay
AIB
vuông cân tại
I
1
2 2
R
IH
2
2 1
1 2 3
2
2
4 1
m
m
m
(
H
là trung điểm của
AB
)
Câu 96. (ĐÊ 04 VTED NĂM 2018-2019) Biết đồ thị hàm số
3 2
y x ax bx c
có hai điểm cưc trị
1 1 2 2
; , ;M x y N x y
thỏa mãn
1 1 2 1 1 2
x y y y x x
. Giá trị nhỏ nhất của biểu thức
2 3P abc ab c
bằng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
A.
49
4
B.
25
4
C.
841
36
D.
7
6
Lời giải
Chọn A
Ta có
2
3 2
y x ax b
Chia
y
cho
y
ta được
2
1 1 2
3 9 9 3 9
a b ab
y y x a x c
.
Do
1 1 2 2
; , ;M x y N x y
là hai điểm cực trị nên
1 2
0, 0
y x y x
Do đó
2 2
1 1 2 2
2 2
;
9 3 9 9 3 9
a b ab a b ab
y x c y x c
Theo giả thiết
1 1 2 1 1 2 1 2 2 1
x y y y x x x y x y
2 2
1 2 2 1
2 2
9 3 9 9 3 9
a b ab a b ab
x x c x x c
1 2 1 2
0( ) 9
9 9 9
ab ab ab
x c x c c x x ab c
Ta có:
2
2
7 49 49
2 3 9 21 3
2 4 4
P abc ab c c c c
Vậy giá trị nhỏ nhất của biểu thức
2 3P abc ab c
bằng
49
4
Dạng 7. Tam giác cực trị
Câu 97. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ
thị của hàm số
4 2
2 1
y x mx có ba điểm cực trị tạo thành một tam giác vuông cân
A.
3
1
9
m . B.
1
m
. C.
3
1
9
m . D.
1
m
.
Lời giải
Chọn D
Hàm số
4 2
2 1
y x mx
có tập xác định:
D
Ta có:
3 3 2
2
0
' 4 4 ; ' 0 4 4 0 4 0
x
y x mx y x mx x x m
x m
Hàm số có 3 cực trị khi và chỉ khi phương trình
có 2 nghiệm phân biệt khác
0
0 0
m m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
Vậy tọa độ 3 điểm lần lượt là:
2 2
0;1 ; ;1 ; ;1
A B m m C m m
Ta có
2 2
; ; ;
AB m m AC m m

Vì
ABC
vuông cân tại
2 2 2 4 4
. 0 . 0 0 0
A AB AC m m m m m m m
1
m
( vì
0
m
)
Vậy với
1
m
thì hàm số có 3 cực trị tạo thành một tam giác vuông cân.
Câu 98. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
1
.
A.
0 1m
B.
0m
C.
3
0 4m
D.
1m
Lời giải
Chọn A
Tập xác định
D
Ta có
3
4 4y x mx
.
3
2
0
0 4 4 0
x
y x mx
x m
.
Hàm số có ba điểm cực trị khi và chỉ khi
0m
. Khi đó đồ thị hàm số có ba điểm cực trị là
0; 0
O
,
2
;
A m m
,
2
;
B m m
.
Do đó
2 2
1 1
. .2 1 0 1.
2 2
OAB
S OH AB m m m m m
Câu 99. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị của tham
số m để đồ thị hàm số
4 2 2
2 1
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam
giác vuông. Số phần tử của tập hợp S là
A.
2
. B.
0
. C.
4
. D.
1
.
Lời giải
•
4 2 2 3 2
2 1 ' 4 4 1 4 1
y x m x m y x m x x x m
.
x
y
A
O
H
B
m
m
2
m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
• Hàm số có 3 điểm cực trị
' 0
y
có 3 nghiệm phân biệt.
2
1 0
x m
có 2 nghiệm phân biệt khác 0.
1 0
m
.
1
m
.
Khi đó:
1
' 0 0
1
x m
y x
x m
.
• Giả sử
, ,A B C
là ba điểm cực trị của đồ thị hàm số.
2
1; 2 1 , 0; , 1; 2 1
A m m B m C m m
2 2
1; 1 , 1; 1
AB m m CB m m
ABC
vuông tại
B
. 0
AB CB
 
4
1
1 1 0 0
0
m
m m m
m
.
Câu 100. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho hàm số
4 2
2 1 1
y x mx . Tổng
lập phương các giá trị của tham số
m
để đồ thị hàm số
1
có ba điểm cực trị và đường tròn đi qua
3
điểm này có bán kính
1R
bằng
A.
5 5
2
. B.
1 5
2
. C.
2 5
. D.
1 5
.
Lời giải
TXĐ:
.
D
3 2
' 4 4 4 ( ).y x mx x x m
Để đồ thị hs (1) có 3 điểm cực trị
0.
m
Gọi
2 2
(0;1), ( ; 1), ( ; 1)
A B m m C m m
là các điểm cực trị của đồ thị hs (1),
2
(0; 1)
I m
là trung điểm
.BC
Ta có
2 4
, .AI m AB AC m m
Suy ra
1 . . 2
.
2 4 .
AB AC BC AI
AI BC R
R AB AC
2
4 2
4
0 ( )
1 ( )
2
1 5
1 2 0
( )
2
1 5
( )
2
m l
m n
m
m m m
m l
m m
m n
Câu 101. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm tất cả các giá trị thực của tham số
m để đồ thị hàm số
4 2 2
2 4
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam giác
đều?
A.
0; 3; 3
m B.
6 6
0; 3; 3
m C.
6 6
3; 3
m D.
3; 3
m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
Lời giải
Chọn C
Đồ thị hàm số có
3
điểm cực trị
0
m
.
Khi đó,
3
điểm cực trị của đồ thị hàm số là
0; 4
A m
,
4
; 4
B m m m
,
4
; 4
C m m m
.
Tam giác
ABC
có
AB AC
nên tam giác
ABC
cân tại
A
, suy ra tam giác
ABC
đều
AB BC
2 8 8 2 2
6
0
2 4
3
m
m m m m m m
m
.
Kết hợp điều kiện ta được
6 6
3; 3
m .
Câu 102. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Tìm
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có 3 điểm cực trị lập thành một tam giác vuông cân.
A.
1
m
. B.
1;1
m
. C.
1;0;1
m
. D.
m
.
Lời giải
4 2 2
2 1
y x m x
.
+ Cách 1:
Hàm số có 3 cực trị
2
0 2 0 0
ab m m
.
3 2
4 4
y x m x
3 2
2 2
1
1
4
2 2
4
3
3
0 4 4 0
4 0
1
0
1
1
y x m x
x x m
y
x
x m y m
x m
y m
Giả sử
0;1
A
,
4
; 1
B m m
,
4
; 1
C m m
là 3 điểm cực trị của đồ thị hàm số.
4
;
AB m m
2 8
AB m m
.
4
;
AC m m
2 8
AC m m
.
Yêu cầu bài toán
ABC
vuông cân tại
A
. 0
AB AC
AB AC
2 8
0
m
m m
2 6
1 0
m m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
0 ( )
1 ( )
1( )
m l
m n
m n
.
Vậy
1;1
m
.
+ Cách 2: (Áp dụng công thức tính nhanh cực trị hàm trùng phương)
Yêu cầu bài toán
2
6
3
2
3
2 0
0
0
0
8
1 ( )
8
1
1
1
1( )
2
m
m
ab
m
m n
a
m
m n
m
b
.
Vậy
1;1
m
.
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối
Câu 103. (ĐỀ THAM KHẢO BGD & ĐT 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2
3 4 12
y x x x m
có
7
điểm cực trị?
A.
B.
6
C.
4
D.
3
Lời giải.
Chọn C
4 3 2
3 4 12
y f x x x x m
Ta có:
3 2
12 12 24f x x x x
.;
0 0
f x x
hoặc
1
x
hoặc
2
x
.
Do hàm số
f x
có ba điểm cực trị nên hàm số
y f x
có
7
điểm cực trị khi
0
0 5
5 0
m
m
m
. Vậy có
4
giá trị nguyên thỏa đề bài là
1; 2; 3; 4
m m m m
.
Câu 104. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Biết phương trình
3 2
0
ax bx cx d
0
a
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
3 2
y ax bx cx d
có bao nhiêu điểm cực
trị?
A.
4
. B.
5
. C.
2
. D.
3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
Lời giải
Phương trình
3 2
0ax bx cx d
,
0a
là sự tương giao của đồ thị hàm số
3 2
0ax bx cx d
,
0a
và trục hoành.
Do phương trình
3 2
0ax bx cx d
,
0a
có đúng hai nghiệm thực nên phương trình
3 2
0ax bx cx d
có thể viết dưới dạng
2
1 2
0
a x x x x
với
1 2
, x x
là hai nghiệm thực
của phương trình (giả sử
1 2
x x
). Khi đó đồ thị hàm số
3 2
0
y ax bx cx d a
tiếp xúc
trục hoành tại điểm có hoành độ
1
x
và cắt trục hoành tại điểm có hoành độ
2
x
.
Đồ thị hàm số
3 2
0
y ax bx cx d a
ứng với từng trường hợp
0
a
và
0
a
:
Đồ thị hàm số
3 2
0
y ax bx cx d a
tương ứng là
Vậy đồ thị hàm số
3 2
0
y ax bx cx d a
có tất cả
3
điểm cực trị.
Câu 105. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số
m
để đồ thị hàm số
4 2 2
2 2 12
y x mx m m
có bảy điểm cực trị
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
A.
1
. B.
4
. C.
0
. D.
2
.
Lời giải
Đồ thị hàm số
4 2 2
2 2 12
y x mx m m
có bảy điểm cực trị khi và chỉ khi đồ thị hàm số
4 2 2
2 2 12
y x mx m m
cắt trục hoành tại bốn điểm phân biệt
4 2 2
2 2 12 0
x mx m m
có bốn nghiệm phân biệt khi và chỉ khi
2 2
2
2 12 0
2 0
2 12 0
m m m
m
m m
4 3
0
1 97 1 97
4 4
m
m
m m
1 97
3
4
m
Vậy không có giá trị nguyên của tham số
m
để đồ thị hàm số
4 2 2
2 2 12
y x mx m m
có
bảy điểm cực trị.
Câu 106. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số
2
1 2
y x x
là
A.
2
B.
2
C.
3
D.
4
Lời giải
Xét hàm số:
2
3 2
1 2 5 8 4
y x x x x x
.
2
3 10 8.
y x x
Lúc đó:
2
2
0 3 10 8 0 .
4
3
x
y x x
x
Vẽ đồ thị hàm số
2
1 2
y x x
bằng cách vẽ đồ thị
3 2
5 8 4
y x x x
, giữ nguyên phần
đồ thị nằm phía trên trục hoành, rồi lấy đối xứng qua trục hoành phần đồ thị ở dưới trục hoành,
sau đó xóa phần đồ thị nằm dưới trục hoành.
3
2.5
2
1.5
1
0.5
0.5
1
1 1 2 3 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
Dựa vào đồ thị hàm số
2
1 2y x x
ở trên, hàm số này có 3 điểm cực trị.
Cách 2:
Bảng biến thiên:
x

4
3
2

'( )f x
0
0
( )f x

4
27
0

Số điểm cực trị của hàm số
y f x
bằng tổng số điểm cực trị của hàm số
y f x
và số
nghiệm đơn, nghiệm bội lẻ của phương trình
0f x
.
Hàm số
3 2
5 8 4y x x x có 2 điểm cực trị.
Phương trình
2
1 2y x x
có hai nghiệm nhưng chỉ có 1 nghiệm đơn
1x
.
Do đó số điểm cực trị của hàm số
2
1 2y x x
là
2 1 3
.
Câu 107. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Đồ thị của hàm số
y f x
có bao nhiêu điểm cực trị?
A.
4
B.
2
C.
5
D.
3
Lời giải
Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72
Từ bảng biến thiên ta thấy đồ thị
y f x
có 2 điểm cực trị nằm phía trên trục
Ox
và cắt trục
Ox
tại 1 điểm duy nhất. Suy ra đồ thị
y f x
sẽ có 3 điểm cực trị (tham khảo hình vẽ)
Câu 108. (KTNL GIA BÌNH NĂM 2018-2019) Cho hàm số
( )y f x
có bảng biến thiên như sau.
Hàm số
3
y f x
có bao nhiêu điểm cực trị
A.
5
B.
6
C.
3
D.
1
Lời giải
Chọn C
3 1
y f x
,Đặt
| 3 |, 0 t x t
Thì (1) trở thành:
( )( 0)
y f t t
Có
2
2
3
( 3) '
( 3)
x
t x t
x
Có
( )
x x
y t f t
3 3
0
0 ( ) 0 2( ) 7
( ) 0
4 1
x
x x
x x
t
y t f t t L x
f t
t x
Lấy x=8 có
'(8) '(5) 0
t f
, đạo hàm đổi dấu qua các nghiệm đơn nên ta có bảng biến thiên:
Dựa vào BBT thì hàm số
3
y f x
có 3 cực trị.
Câu 109. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số
( )y f x
xác định, liên tục
trên
và có bảng biến thiên như sau:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 73
Đồ thị của hàm số
y f x
có bao nhiêu điểm cực trị?
A.
2
B.
3
C.
4
D.
5
Lời giải
Chọn B
Từ bảng biến thiên ta thấy đồ thị
y f x
có 2 điểm cực trị nằm phía trên trục
Ox
và cắt trục
Ox
tại 1 điểm duy nhất. Suy ra đồ thị
y f x
sẽ có 3 điểm cực trị (tham khảo hình vẽ)
Câu 110. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên
như sau
Đồ thị của hàm số
y f x
có bao nhiêu điểm cực trị?
A.
5
B.
3
C.
4
D.
2
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 74
Từ bảng biến thiên ta thấy đồ thị
y f x
có 2 điểm cực trị nằm phía trên trục
Ox
và cắt trục
Ox
tại 1 điểm duy nhất. Suy ra đồ thị
y f x
sẽ có 3 điểm cực trị (tham khảo hình vẽ)
Câu 111. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số
3 2
( , , , )f x ax bx cx d a b c d
và
0, 2019
2019 0
a d
a b c d
. Số cực trị của hàm số
y g x
( với
2019)g x f x
bằng
A.
2
. B.
5
. C.
3
. D.
1
.
Lời giải
+ Ta có
lim
0 2019 0
1 2019 0
lim
x
x
g x
g d
g a b c d
g x




0g x
có ba nghiệm phân biệt, mà
g x
là hàm số bậc
ba. Suy ra, hàm số
y g x
có hai điểm cực trị.
+ Vậy đồ thị của hàm số
y g x
là đồ thị của hàm số bậc ba, có hai điểm cực trị và cắt trục
Ox
tại ba điểm phân biệt. Do đó, số điểm cực trị của hàm số
y g x
bằng
5
số cực trị của hàm
số
y g x
bằng 2 hoặc bằng 3.
Câu 112. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Có bao nhiêu giá trị
nguyên của tham số
m
để hàm số
4 3 2 2
3 4 12y x x x m
có đúng 5 điểm cực trị?
A.
5
. B.
7
. C.
6
. D.
4
.
Lời giải
Xét hàm số
4 3 2 2
( ) 3 4 12f x x x x m ;
3 2
( ) 12 12 24f x x x x
1 2 3
( ) 0 0; 1; 2f x x x x
. Suy ra, hàm số
( )y f x
có 3 điểm cực trị.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 75
Hàm số
4 3 2 2
3 4 12
y x x x m
có 5 điểm cực trị khi đồ thị hàm số
( )y f x
cắt trục hoành
tại 2 điểm phân biệt
4 3 2 2
3 4 12 0
x x x m
có 2 nghiệm phân biệt.
Phương trình
4 3 2 2 4 3 2 2
3 4 12 0 3 4 12
x x x m x x x m
(1).
Xét hàm số
4 3 2
g( ) 3 4 12x x x x
;
3 2
g ( ) 12 12 24x x x x
.
Bảng biến thiên:
Phương trình (1) cớ 2 nghiệm phân biệt
2
2
0
5 32
5 32
m
m
m
.
Vậy
3;4;5; 3; 4; 5
m
.
Câu 113. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số
2
1 2
y x x
là
A.
2
B.
2
C.
3
D.
4
Lời giải
Xét hàm số:
2
3 2
1 2 5 8 4
y x x x x x
.
2
3 10 8.
y x x
Lúc đó:
2
2
0 3 10 8 0 .
4
3
x
y x x
x
Vẽ đồ thị hàm số
2
1 2
y x x
bằng cách vẽ đồ thị
3 2
5 8 4
y x x x
, giữ nguyên phần
đồ thị nằm phía trên trục hoành, rồi lấy đối xứng qua trục hoành phần đồ thị ở dưới trục hoành,
sau đó xóa phần đồ thị nằm dưới trục hoành.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 76
Dựa vào đồ thị hàm số
2
1 2
y x x
ở trên, hàm số này có 3 điểm cực trị.
Cách 2:
Bảng biến thiên:
x
4
3
2
'( )f x
0
0
( )f x
4
27
0
Số điểm cực trị của hàm số
y f x
bằng tổng số điểm cực trị của hàm số
y f x
và số
nghiệm đơn, nghiệm bội lẻ của phương trình
0
f x
.
Hàm số
3 2
5 8 4
y x x x
có 2 điểm cực trị.
Phương trình
2
1 2
y x x
có hai nghiệm nhưng chỉ có 1 nghiệm đơn
1x
.
Do đó số điểm cực trị của hàm số
2
1 2
y x x
là
2 1 3
.
Câu 114. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Có bao nhiêu giá trị nguyên dương
của tham số
m
để hàm số
4 3 2
3 4 12
y x x x m
có
5
điểm cực trị.
A.
16
B.
44
C.
26
D.
27
Lời giải
Chọn C
Đặt:
4 3 2
( ) 3 4 12
g x x x x m
Ta có:
3 2
2 32
'( ) 12 12 24 0 1 5
0
x y m
g x x x x x y m
x y m
3
2.5
2
1.5
1
0.5
0.5
1
1 1 2 3 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 77
Dựa vào bảng biến thiên, hàm số có
( )y g x
có
5
điểm cực trị khi
0
0
5 0
5 32
32 0
m
m
m
m
m
.
Vì m là số nguyên dương cho nên có 26 số m thỏa đề bài
Câu 115. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số
4 2
2 2 1
y x mx m
với
m
là tham số thực. Số giá trị nguyên trong khoảng
2;2
của
m
để
hàm số đã cho có
3
điểm cực trị là
A.
2
B.
4
C.
3
D.
1
Lời giải
Chọn B
Đặt
4 2
2 2 1
f x x mx m
,
3
4 4f x x mx
,
2
0
0
x
f x
x m
+ Trường hợp 1: hàm số có một cực trị
2;0
m
.
Đồ thị hàm số
y f x
có một điểm cực trị là
0;2 1
A m
.
Do
2;0
m
2 1 0
A
y m
nên đồ thị hàm số
y f x
cắt trục hoành tại
2
điểm phân biệt
nên hàm số
y f x
có
3
cực trị
có
3
giá trị nguyên của
m
thỏa ycbt.
+ Trường hợp 2: hàm số có ba cực trị
0;2
m
.
Khi đó đồ thị hàm số có
3
điểm cực trị là
0;2 1
A m
,
2
; 2 1
B m m m
,
2
; 2 1
C m m m
.
Do
1 0
a
nên hàm số
y f x
có
3
điểm cực trị khi hàm số
y f x
có
0
B C
y y
2
2 1 0
m m
1
m
.
Nếu
0
B C
y y
(trong bài toán này không xảy ra) thì hàm số có ít nhất
5
điểm cực trị.
Vậy có
4
giá trị của
m
thỏa ycbt.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 78
Câu 116. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đồ
thị như hình vẽ bên dưới
Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
2 2h x f x f x m
có đúng
3
điểm cực trị.
A.
1
m
B.
1
m
C.
2
m
D.
2
m
Lời giải
Chọn B
Số cực trị của hàm số
2
2 2h x f x f x m
bằng số cực trị của hàm số
2
2 2
y x f x f x m
cộng với số giao điểm (khác điểm cực trị) của đồ thị hàm số
2
2 2
y x f x f x m
và
0
y
.
Xét hàm số
2
2 2g x f x f x m
2 2 2 1
g x f x f x f x f x f x.
1
0
0 3
1
0
x
f x
g x x
f x
x
BBT
Hàm số
h x
có 3 điểm cực trị
1
2 0
2
m m
. Đáp án B là gần kết quả nhất
Câu 117. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Tập hợp các giá trị của
m
để hàm số
4 3 2
3 4 12 1
y x x x m
có
7
điểm cực trị là:
A.
(0;6)
B.
(6;33)
C.
(1;33)
D.
(1;6)
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 79
Lời giải
Chọn D
Xét hàm số
4 3 2
( ) 3 4 12 1
f x x x x m
,
Có


xf
x
lim
,


xf
x
lim
3 2 2
( ) 12 12 24 12 2
f x x x x x x x
0
( ) 0 1
2
x
f x x
x
.
Bảng biến thiên:
Từ bảng biến thiên, ta có hàm số
( )y f x
có
7
điểm cực trị
đồ thị hàm số
( )y f x
cắt
Ox
tại
4
điểm phân biệt
6 0 1 1 6
m m m
.
------------- HẾT -------------
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x)
Câu 118. (Mã đề 101 - BGD - 2019) Cho hàm số
y f x
, bảng biến thiên của hàm số
'f x
như sau:
Số điêm cực trị của hàm số
2
2y f x x
là
A.
9.
B.
3.
C.
7.
D.
5.
Lơi giải
Chọn C
Ta có
2
2 1 . 2y x f x x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 80
2
1
0
2 0
x
y
f x x
2 2
2 2
2 2
2 2
1 1
2 ; 1 2 0, ; 1 (1)
2 1;0 2 0, 1;0 (2)
2 0;1 2 0, 0;1 (3)
2 1; 2 0, 1; (4)
x x
x x a x x a a
x x b x x b b
x x c x x c c
x x d x x d d
 
.
Phương trình
(1)
vô nghiệm, các phương trình
(2),(3),(4)
đều có hai nghiệm phân biệt khác 1 và
do
, ,b c d
đôi một khác nhau nên các nghiệm của phương trình
(2),(3),(4)
cũng đôi một khác
nhau. Do đó
2
2 0
f x x
có 6 nghiệm phân biệt.
Vậy
0
y
có 7 nghiệm phân biệt, do đó số điêm cực trị của hàm số
2
2y f x x
là 7.
Câu 119. (Mã đề 104 - BGD - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
Số điểm cực trị của hàm số
2
4 4y f x x
là
A. 5. B. 9. C. 7. D. 3.
Lời giải
Chọn C
Có
2 2
4 4 8 4 4 4f x x x f x x
,
2
2
1
2
4 4 0
4 4 0
x
f x x
f x x
.
Từ bảng biến thiên trên ta có
2
1
2
2
2
2
3
2
4
4 4 ; 1
4 4 1;0
4 4 0
4 4 0;1
4 4 1;
x x a
x x a
f x x
x x a
x x a


. (1)
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 81
Xét
2
4 4g x x x
,
8 4
g x x
,
1
0
2
g x x
ta có bảng biến thiên
Kết hợp bảng biến thiên của
g x
và hệ (1) ta thấy:
Phương trình
2
1
4 4 ; 1
x x a

vô nghiệm.
Phương trình
2
2
4 4 1;0
x x a
tìm được hai nghiệm phân biệt khác
1
2
.
Phương trình
2
2
4 4 0;1
x x a
tìm được thêm hai nghiệm mới phân biệt khác
1
2
.
Phương trình
2
2
4 4 1;x x a
tìm được thêm hai nghiệm phân biệt khác
1
2
.
Vậy hàm số
2
4 4y f x x
có tất cả 7 điểm cực trị.
Câu 120. (Mã 102 - BGD - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
'f x
như sau
Số điểm cực trị của hàm số
2
2y f x x
là
A.
9
. B.
5
. C.
7
. D.
3
.
Lơi giải
Chọn C
Ta có
2
2 2
2
2
2 2 0
2 , 1
' 2 2 ' 2 0 2 , 1 0
2 ,0 1
2 , 1
x
x x a a
y x f x x x x b b
x x c c
x x d d
+∞10
-1
-∞
2
-1
-3
+∞
+∞
f'(x)
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 82
Dựa vào đồ thị ta được
' 0
y
có 7 nghiệm đơn nên nó có 7 cực trị
Câu 121. (Mã 103 - BGD - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
Số cực trị của hàm số
2
4 4y f x x
là
A.
3
. B.
9
. C.
5
. D.
7
.
Lời giải
Chọn D
Từ bảng biến thiên
Ta thấy
; 1
1;0
0
0;1
1;
x a
x b
f x
x c
x d


Với
2
4 4y f x x
, ta có
2
8 4 4 4y x f x x
8
6
4
2
2
4
6
8
15 10 5 5 10 15
d
c
b
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 83
2
2
2
2
2
1
2
4 4 ; 1 1
8 4 0
0 4 4 1;0 2
4 4 0
4 4 0;1 3
4 4 1; 4
x
x x a
x
y x x b
f x x
x x c
x x d


Xét hàm số
2
4 4g x x x
, ta có
1
8 4 0
2
g x x x
Bảng biến thiên
Từ bảng biến thiên của
g x
ta có:
Vì
; 1
a
nên
1
vô nghiệm.
Vì
1;0
b
nên
2
có
2
nghiệm phân biệt.
Vì
0;1
c
nên
3
có
2
nghiệm phân biệt.
Vì
1;d

nên
4
có
2
nghiệm phân biệt.
Vậy hàm số
2
4 4y f x x
có
7
điểm cực trị
Cách khác:
Ta có:
2
8 4 . 4 4y x f x x
.
2
2
8 4 0
0 8 4 . 4 4 0
4 4 0
x
y x f x x
f x x
+
1
8 4 0
2
x x
.
+
2
2
2
2
2
4 4 1 1
4 4 1 0 2
4 4 0
4 4 0 1 3
4 4 1 4
x x a a
x x b b
f x x
x x c c
x x d d
+ Phương trình
2 2
4 4 4 4 0
x x m x x m
có nghiệm khi
4 4 0
m
hay
1
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 84
Từ đó, ta có phương trình
1
;
2
;
3
luôn có hai nghiệm phân biệt.
Phương trình
4
vô nghiệm.
Do đó, hàm số đã cho có
7
cực trị.
Câu 122. Cho hàm số
y f x
xác định trên
và có đồ thị hàm số
y f x
là đường cong ở hình vẽ.
Hỏi hàm số
y f x
có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Từ đồ thị hàm số
y f x
ta có
0
x a
f x x b
x c
.
Từ bảng biến thiên ta thấy hàm số đã cho có
1
điểm cực trị.
Câu 123. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đồ thị
y f x
như hình vẽ sau
O
c
b
a
x
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 85
Đồ thị hàm số
2
2 g x f x x
có tối đa bao nhiêu điểm cực trị?
A.
7
B.
5
C.
6
D.
3
Lời giải
Chọn A
Xét hàm số
2
2 ' 2 ' 2h x f x x h x f x x
Từ đồ thị ta thấy
' 0 ' 2 2 4h x f x x x x x
2 4
2 2
2 4
2 2
2 ' 2 2 2 ' 0
2 2 4 2 4 2
f x x dx x f x dx
h x h x h h h h h h
Bảng biến thiên
Vậy
2
2 g x f x x
có tối đa 7 cực trị
Câu 124. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số
(x)f
xác định trên
và có
đồ thị
( )f x
như hình vẽ bên. Đặt
( ) ( )g x f x x
. Hàm số đạt cực đại tại điểm thuộc khoảng nào
dưới đây?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 86
A.
3
;3
2
B.
2;0
C.
0;1
D.
1
;2
2
Lời giải
Ta có
1
1; 0 1 1
2
x
g x f x g x f x x
x
Bảng xét dấu của
g x
:
Từ bảng xét dấu nhận thấy
g x
đạt cực đại tại
1 2;0
x
.
Câu 125. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Cho hàm số
( 1)
y f x
có đồ thị như hình vẽ.
Hàm số
2 4f x x
y
đạt cực tiểu tại điểm nào?
A.
1x
. B.
0
x
. C.
2
x
. D.
1
x
.
Lời giải:
Ta có:
2 4
2 4 ln
f x x
y f x
.
+
0
2
0
-1
1
+
x
g'(x) 0
-∞ +∞
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 87
0 2 4 0 2y f x f x
.
Đồ thị hàm số
y f x
nhận được từ việc tịnh tiến đồ thị hàm số
1y f x
sang trái 1 đơn
vị
nên
2f x
2
0
1
x
x
x
.
Do
2x
và
1x
là nghiệm bội chẵn nên ta có bảng biến thiên sau:
x
2
0
1

y
0
0
0
y


Từ bảng biến thiên ta có hàm số đạt cực tiểu tại
0x
.
Câu 126. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong như hình vẽ. Đặt
3 4g x f f x
.
Tìm số điểm cực trị của hàm số
?g x
A.
2
. B.
8
. C.
10
. D.
6
.
O
1
1
2
3
4
3
y
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 88
Lời giải
3 .g x f f x f x
.
0 3 . 0g x f f x f x
0
0
f f x
f x
0
0
f x
f x a
x
x a
,
2 3a
.
0f x
có 3 nghiệm đơn phân biệt
1
x
,
2
x
,
3
x
khác
0
và
a
.
Vì
2 3a
nên
f x a
có 3 nghiệm đơn phân biệt
4
x
,
5
x
,
6
x
khác
1
x
,
2
x
,
3
x
,
0
,
a
.
Suy ra
0g x
có 8 nghiệm đơn phân biệt. Do đó hàm số
3 4g x f f x
có 8 điểm cực
trị.
Câu 127. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
xác
định và liên tục trên
, đồ thị của hàm số
y f x
như hình vẽ. Điểm cực đại của hàm số
g x f x x
là
A.
0x
. B.
1x
.
C.
2x
. D. không có điểm cưc đại.
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 89
Ta có:
1g x f x
0 1 0 1g x f x f x
0
1
2
x
x
x
.
Bảng biến thiên:
Vậy hàm số
g x
đạt cực đại tại
1x
.
Câu 128. Cho hàm số
y f x
có đạo hàm liên tục trên
và có đồ thị hàm số
y f x
như hình vẽ. Đặt
3
g x f x . Tìm số điêm cưc tri của hàm số
y g x
.
A.
3
B.
5
C.
4
D.
2
Lời giải
Chọn A
Đặt
3
h x f x
3
h x f x .
2 3
3h x x f x
3 3 3
0 0; ; ;h x x a b c
Bảng biến thiên:
O
x
y
a
b
c
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 90
Vậy hàm số
y g x
có ba điểm cực trị.
Câu 129. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số
y f x
xác định trên
và hàm số
y f x
có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số
2
3
y f x
.
A.
4
B.
2
C.
5
D.
3
Lời giải
Chọn D
Quan sát đồ thị ta có đổi dấu từ âm sang dương qua nên hàm số có
một điểm cực trị là
2
x
.
Ta có
2 2
3 2 . 3
y f x x f x
2
2
0
0
0 3 2 1
2
3 1
x
x
x x
x
x
.
Mà
2
x
là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số
2
3
y f x
có ba
cực trị.
Câu 130. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hàm số
f x
có đạo
hàm là
f x
. Đồ thị của hàm số
y f x
như hình vẽ bên. Tính số điểm cực trị của hàm số
2
y f x
trên khoảng
5; 5
.
x
y
-2
2
O
1
y f x
2x
y f x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 91
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Xét hàm số
2 2
2
g x f x g x xf x
.
2
0
0
0
x
g x
f x
2
2
0
0
0
2
2
x
x
x
x
x
.
Ta có bảng xét dấu:
Từ đó suy ra hàm số
2
y f x
có 3 điểm cực trị.
Câu 131. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hàm số
y f x
có đạo hàm liên
tục trên
và đồ thị hàm số
y f ' x
như hình vẽ bên.
Số điểm cực trị của hàm số
y f x 2017 2018x 2019
là.
A.
3
B.
4
C.
1
D.
2
Lời giải
Chọn C
Ta có:
f x 2017 2018x 2019 0 f x 2017 2018 0 f x 2017 2018
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 92
Dựa vào đồ thị hàm số
y f ' x
suy ra phương trình
f x 2017 2018
có 1 nghiệm đơn duy
nhất. Suy ra hàm số
y f x 2017 2018x 2019
có 1 điểm cực trị.
Câu 132. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
( )y f x
. Hàm số
( )y f x
có đồ thị như hình vẽ dưới đây.
Tìm
m
để hàm số
2
( )y f x m
có
3
điểm cực trị.
A.
3;m

. B.
0;3
m
. C.
0;3
m
. D.
;0
m

.
Lời giải
Chọn C
Do hàm số
2
( )y f x m
là hàm chẵn nên hàm số có
3
cực trị khi và chỉ khi hàm số này có
đúng
1
điểm cực trị dương.
2 2
( ) 2
y f x m y xf x m
2 2
2
2 2
2 2
0 0
0
0
0
0
1 1
3 3
x x
x
x m x m
y
f x m
x m x m
x m x m
Đồ thị hàm số
y f x
tiếp xúc trục hoành tại điểm có hoành độ là
1x
nên các nghiệm của
pt
2
1x m
(nếu có) không làm
2
f x m
đổi dấu khi
x
đi qua, do đó các điểm cực trị của
hàm số
2
( )y f x m
là các điểm nghiệm của hệ
2
2
0
3
x
x m
x m
Hệ trên có duy nhất nghiệm dương khi và chỉ khi
0
0 3
3 0
m
m
m
.
x
y
3
2
0
1
| 1/92
| | Tải xuống

Có thể bạn quan tâm:

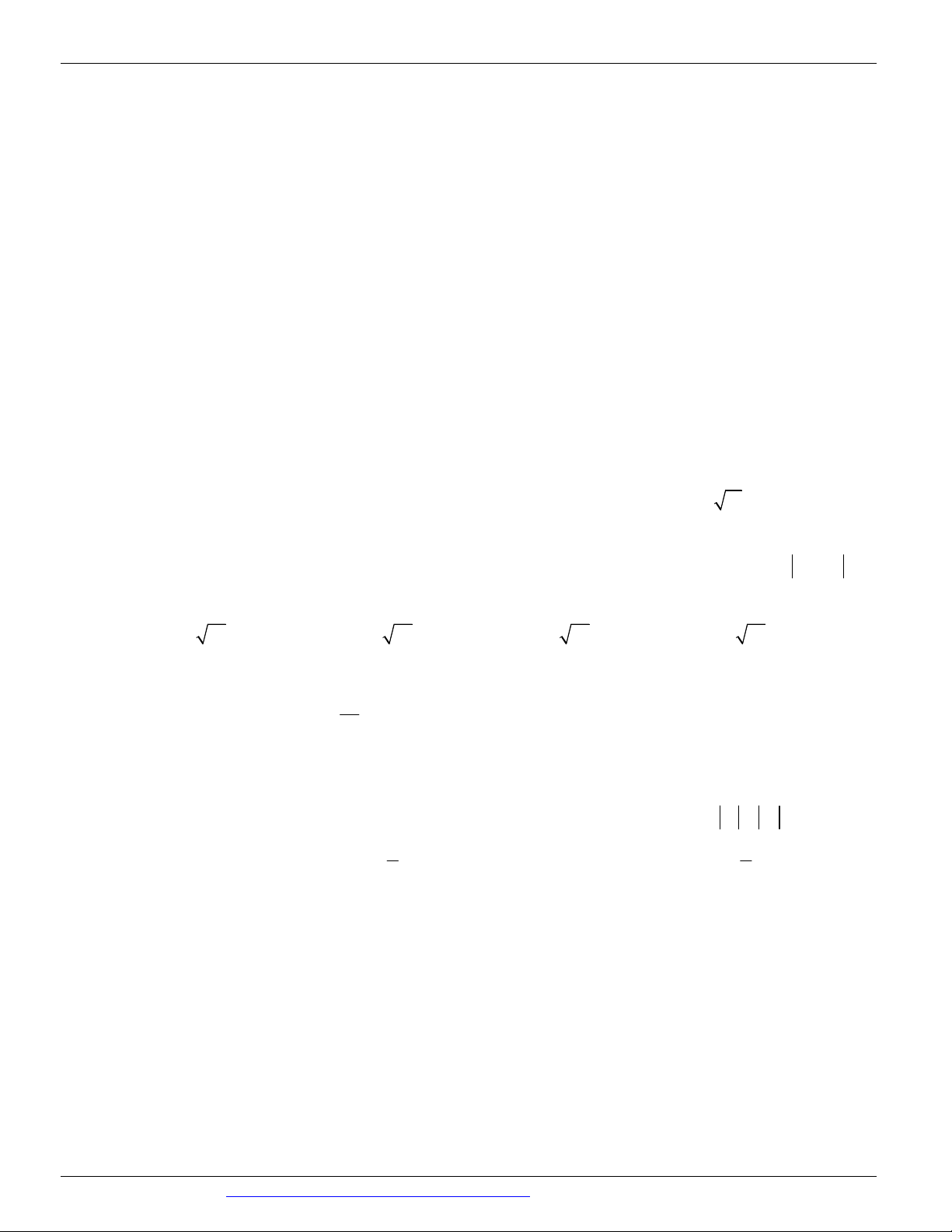
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
CỰC TRỊ CỦA HÀM SỐ ĐỀ 2 MỤC LỤC
PHẦN A. CÂU HỎI ........................................................................................................................................ 1
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó ...................................... 1
Dạng 2. Tìm cực trị của hàm số khi biết y, y’ ............................................................................................... 5
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0 ............................................................................................ 8
Dạng 4. Tìm m để hàm số có n cực trị ......................................................................................................... 10
Dạng 5. Đường thẳng đi qua 2 điểm cực trị ................................................................................................ 11
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước ......................................................... 12
Dạng 7. Tam giác cực trị ............................................................................................................................... 14
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối ............................................................................. 14
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x) ............................................... 17
PHẦN B. LỜI GIẢI THAM KHẢO ............................................................................................................ 21
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó .................................... 21
Dạng 2. Tìm cực trị của hàm số khi biết y, y’ ............................................................................................. 27
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0 .......................................................................................... 40
Dạng 4. Tìm m để hàm số có n cực trị ......................................................................................................... 48
Dạng 5. Đường thẳng đi qua 2 điểm cực trị ................................................................................................ 53
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước ......................................................... 57
Dạng 7. Tam giác cực trị ............................................................................................................................... 64
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối ............................................................................. 68
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x) ............................................... 79 PHẦN A. CÂU HỎI
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó Câu 1.
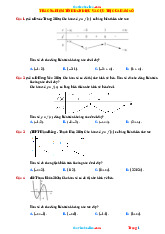
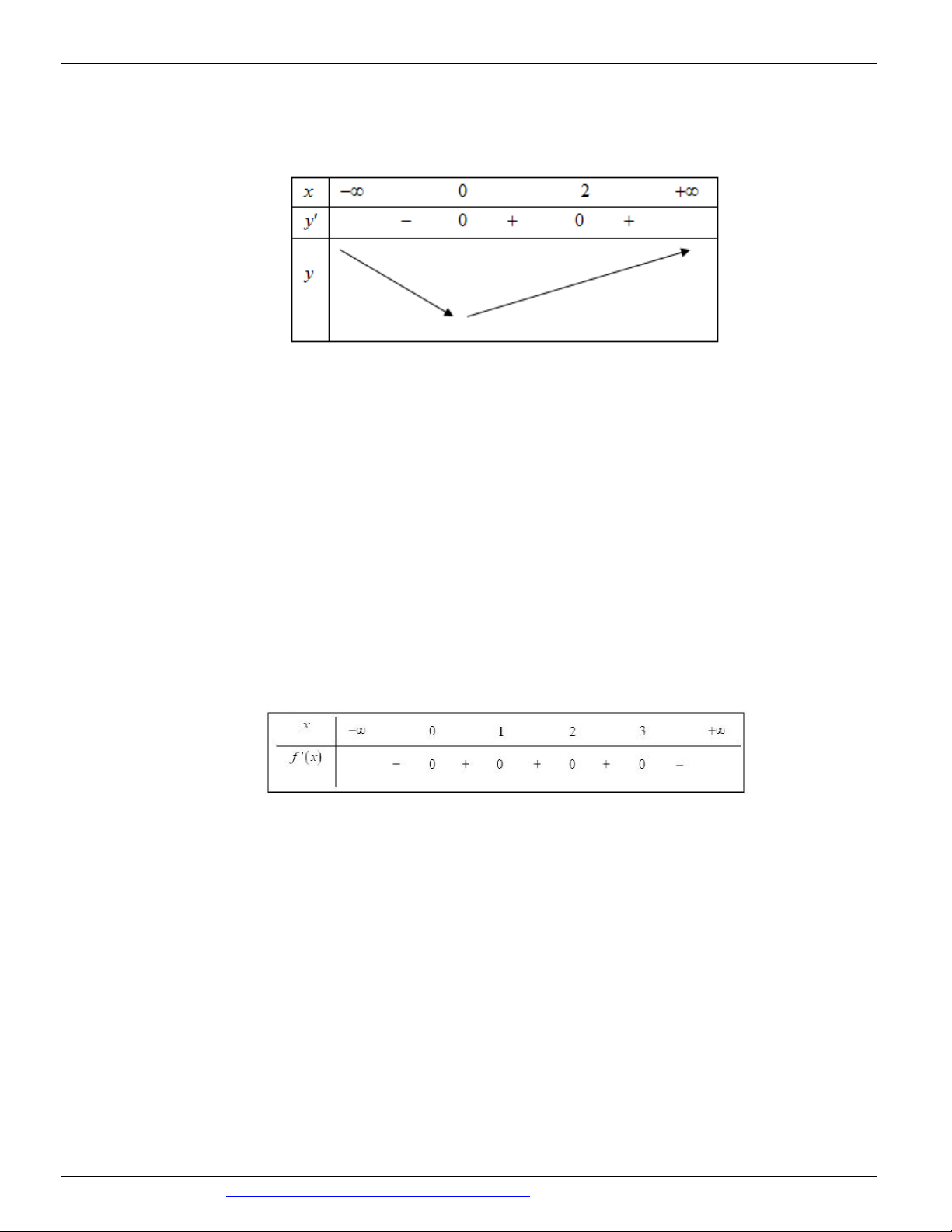
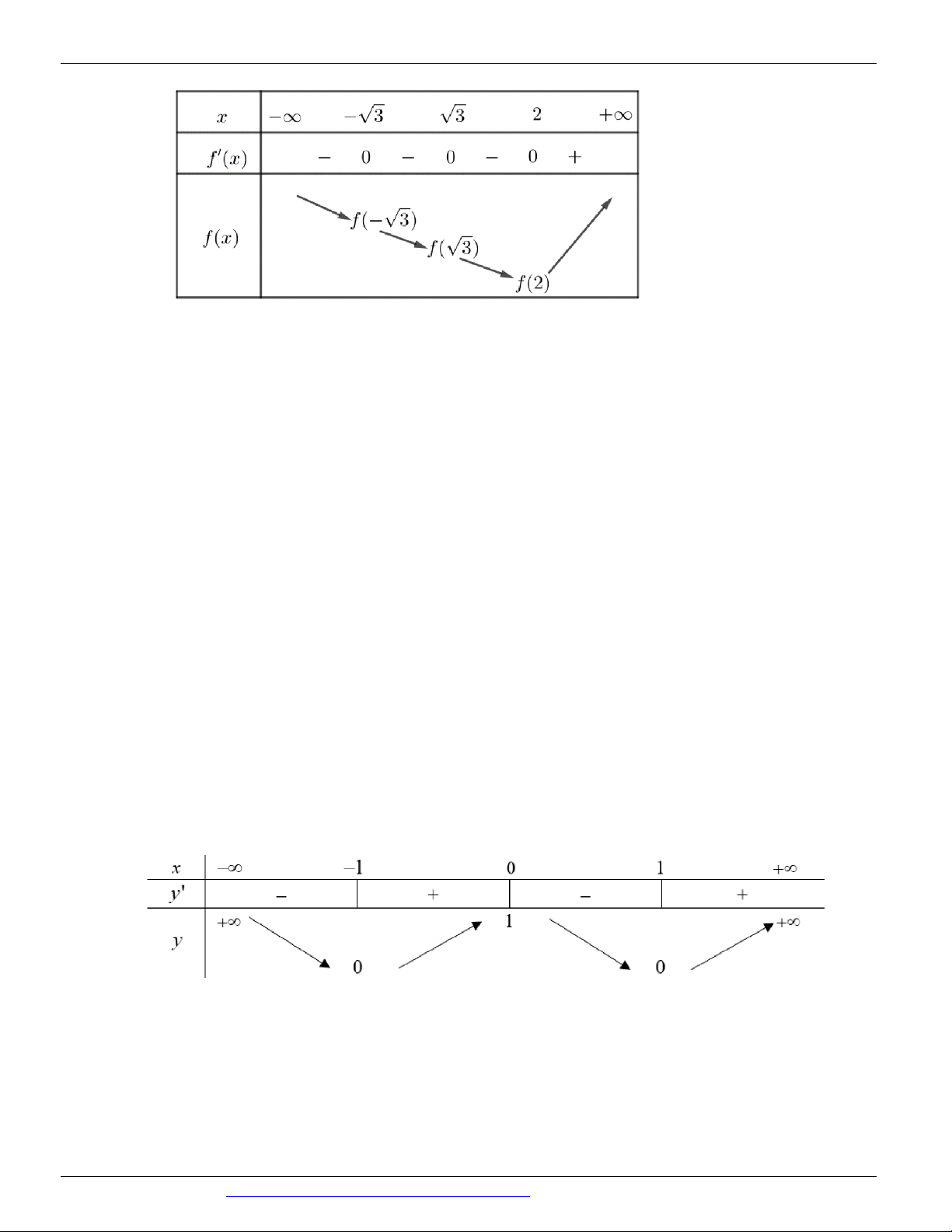
(MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y f x có bảng biến thiên như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x  5
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại x  2
D. Hàm số không có cực đại Câu 2.
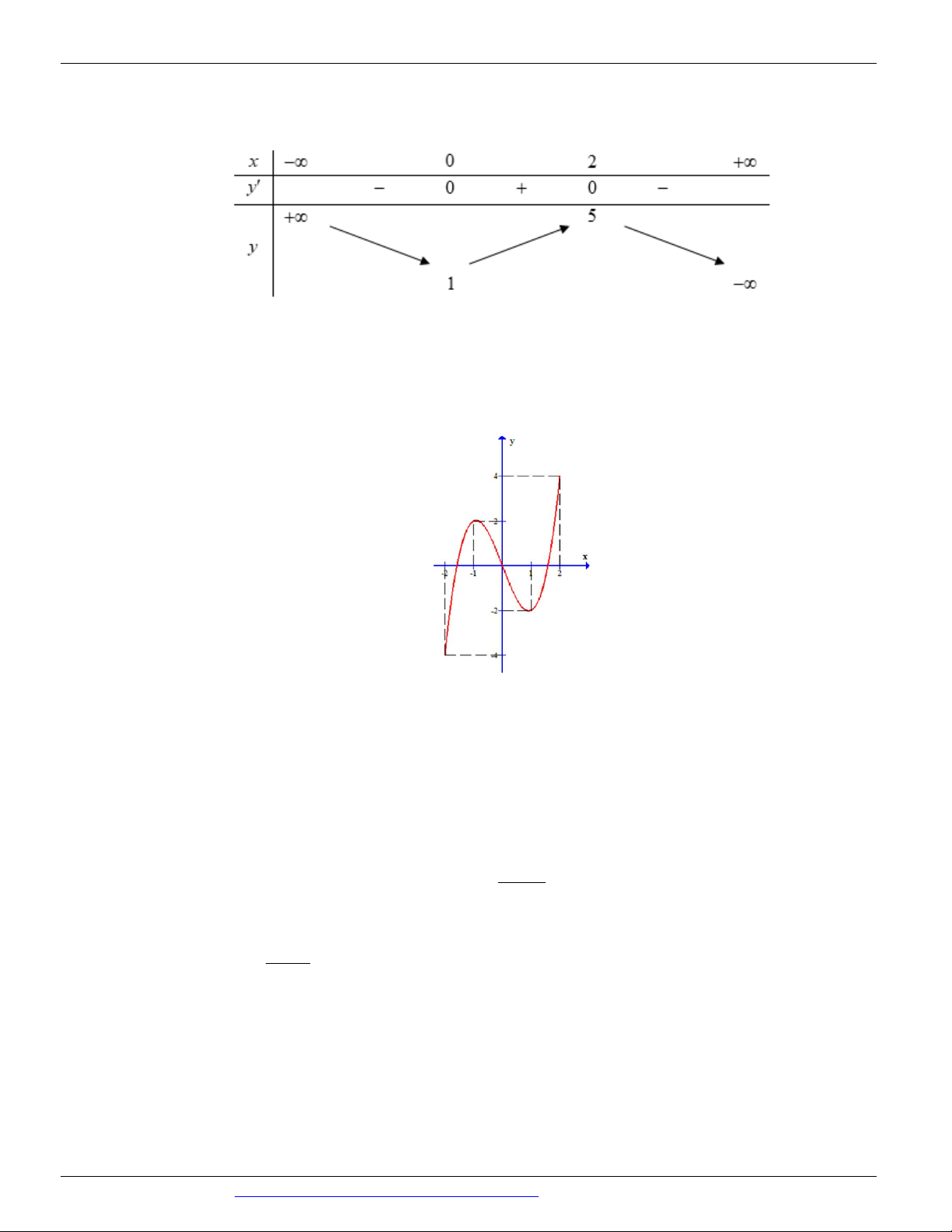
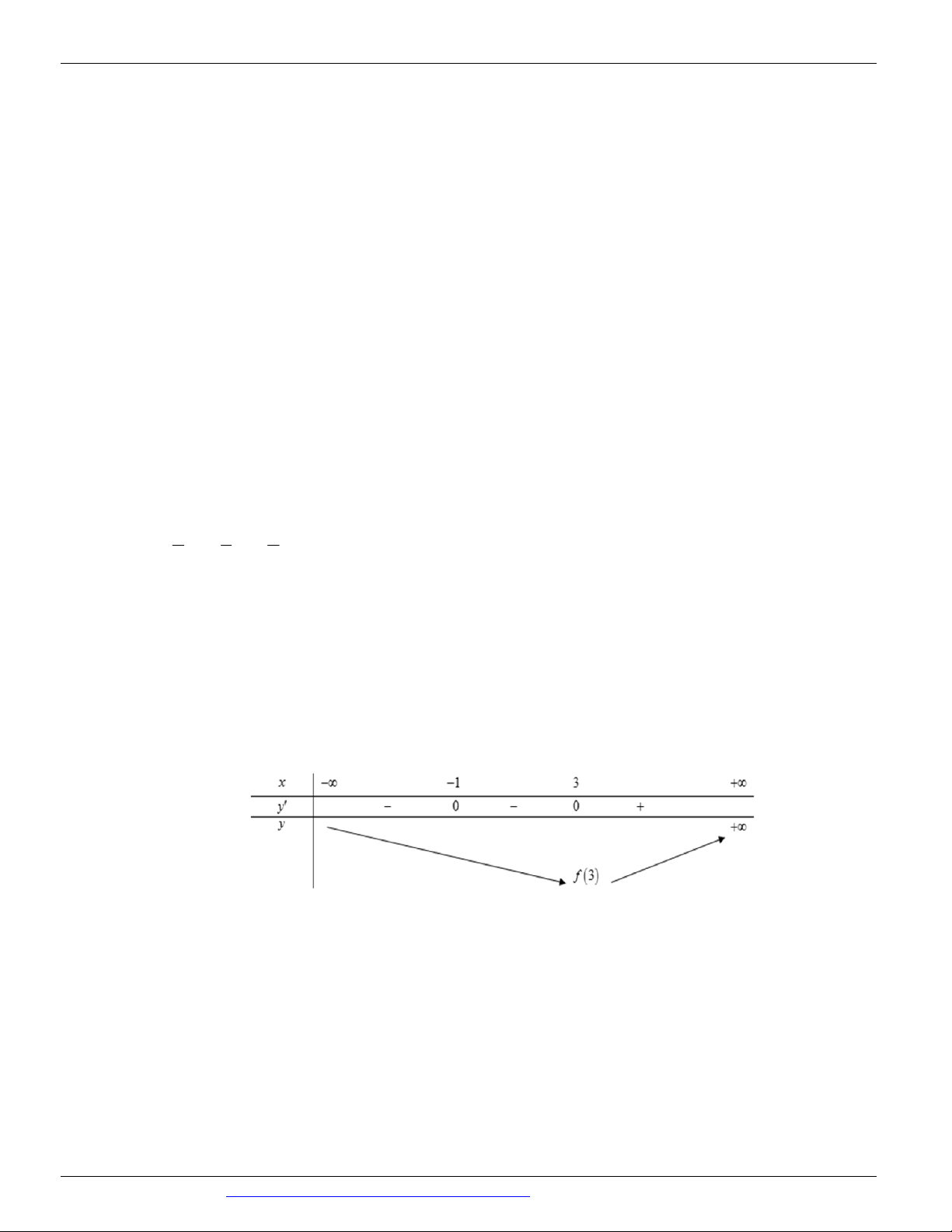
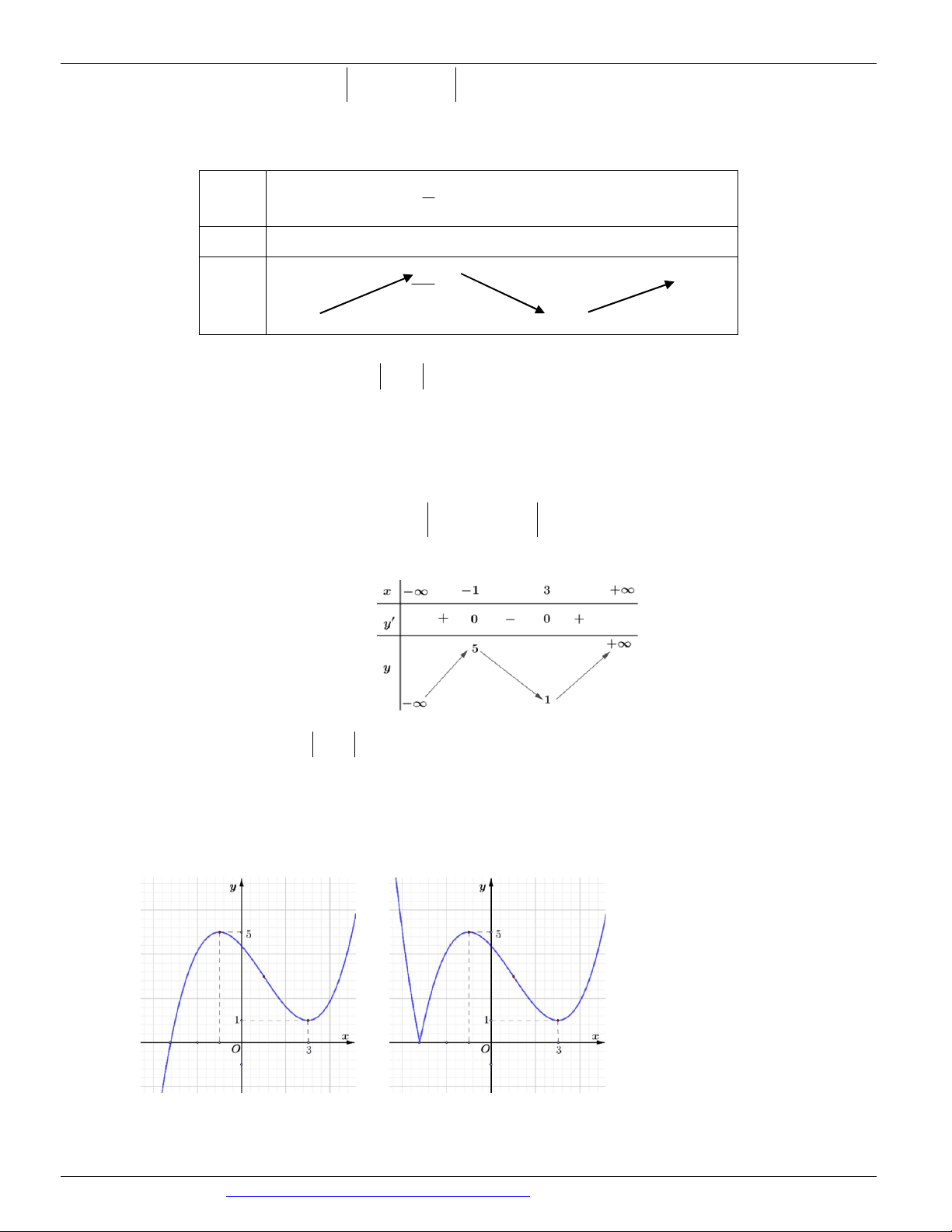
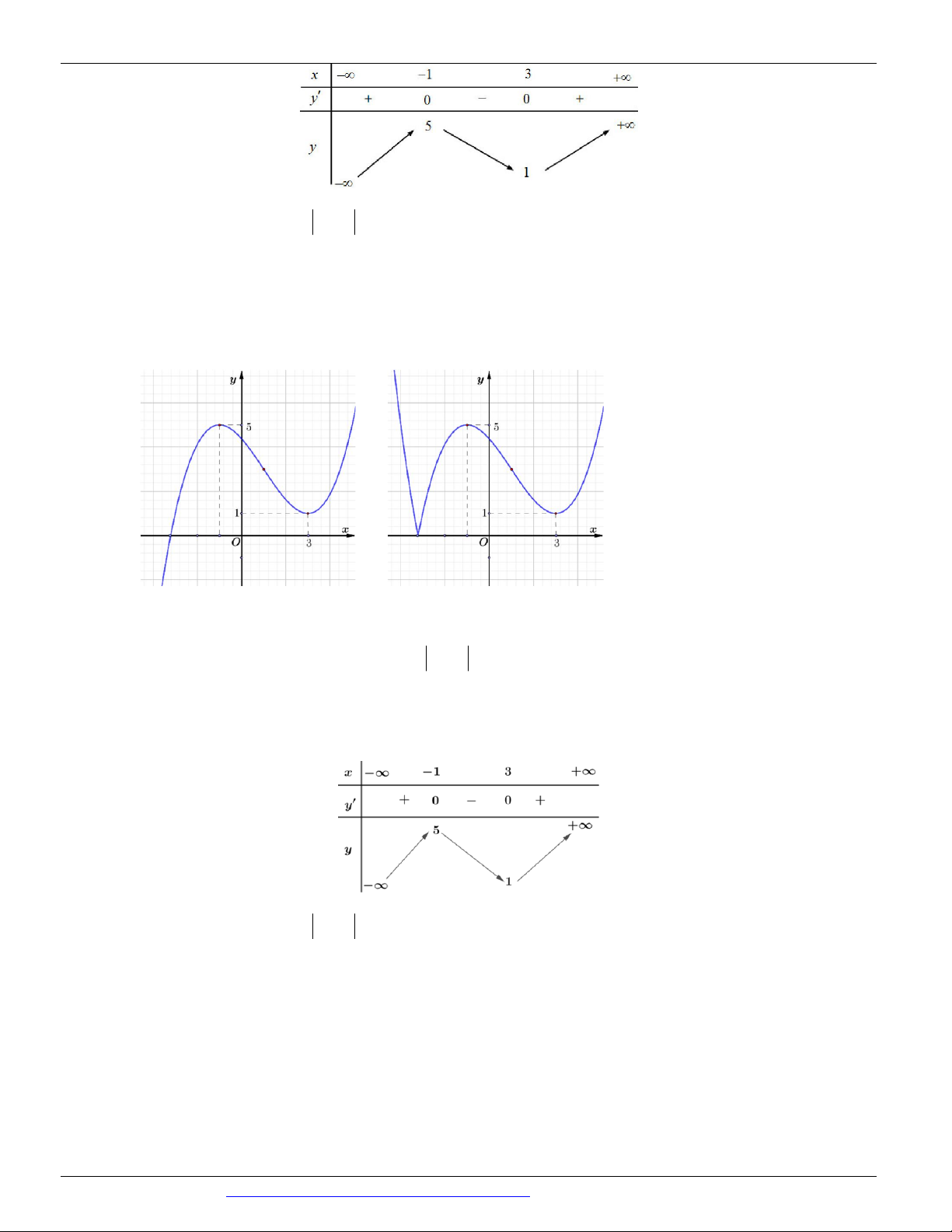
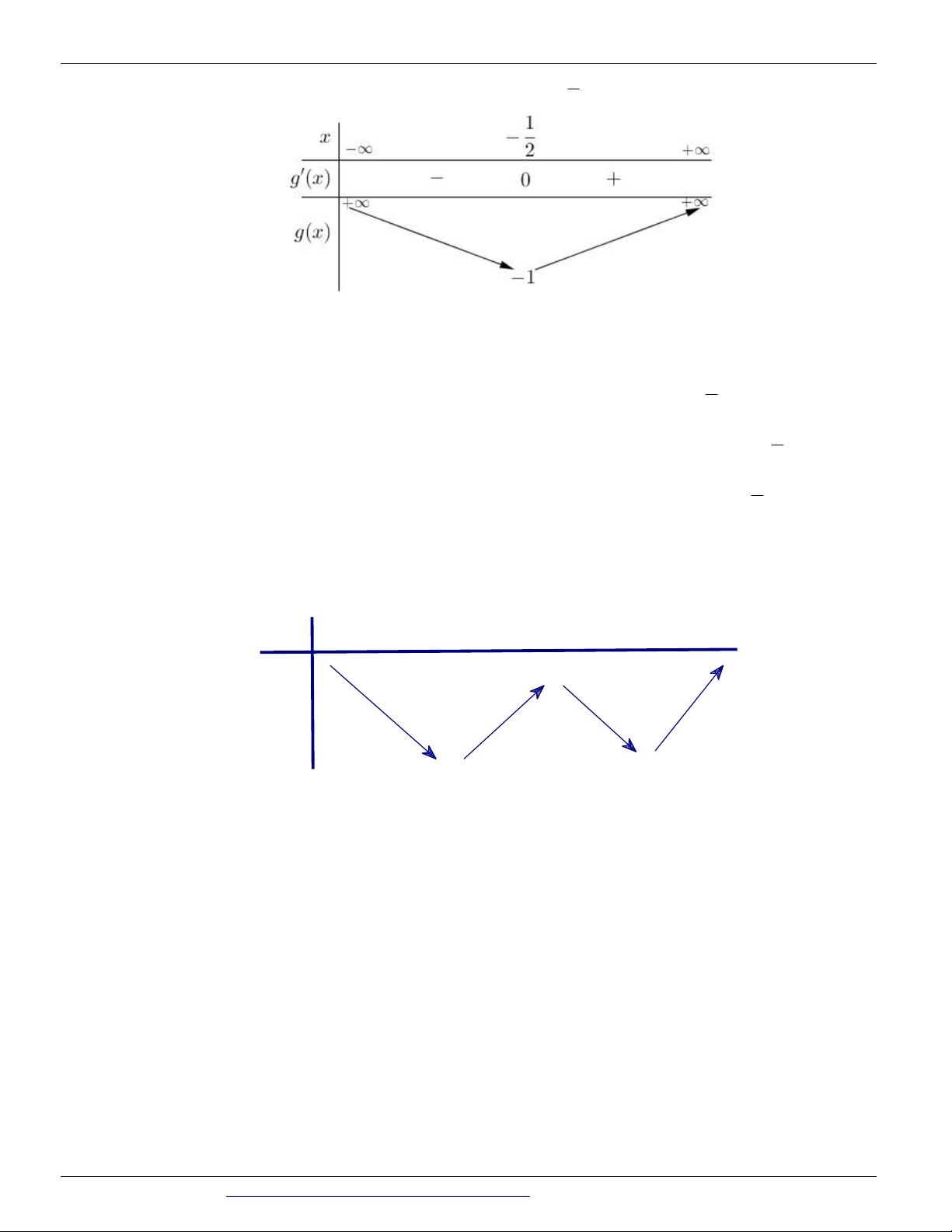
(ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Câu 3.
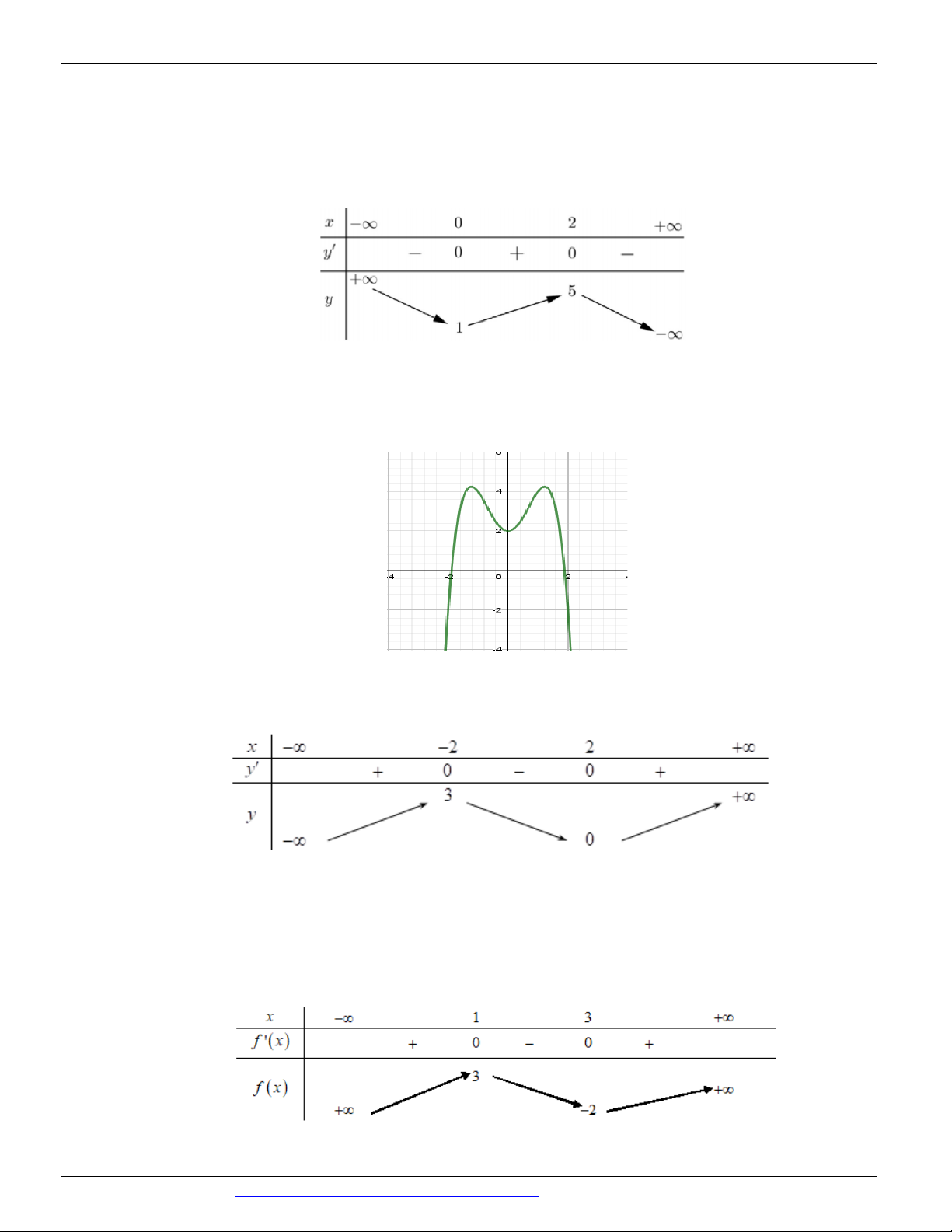
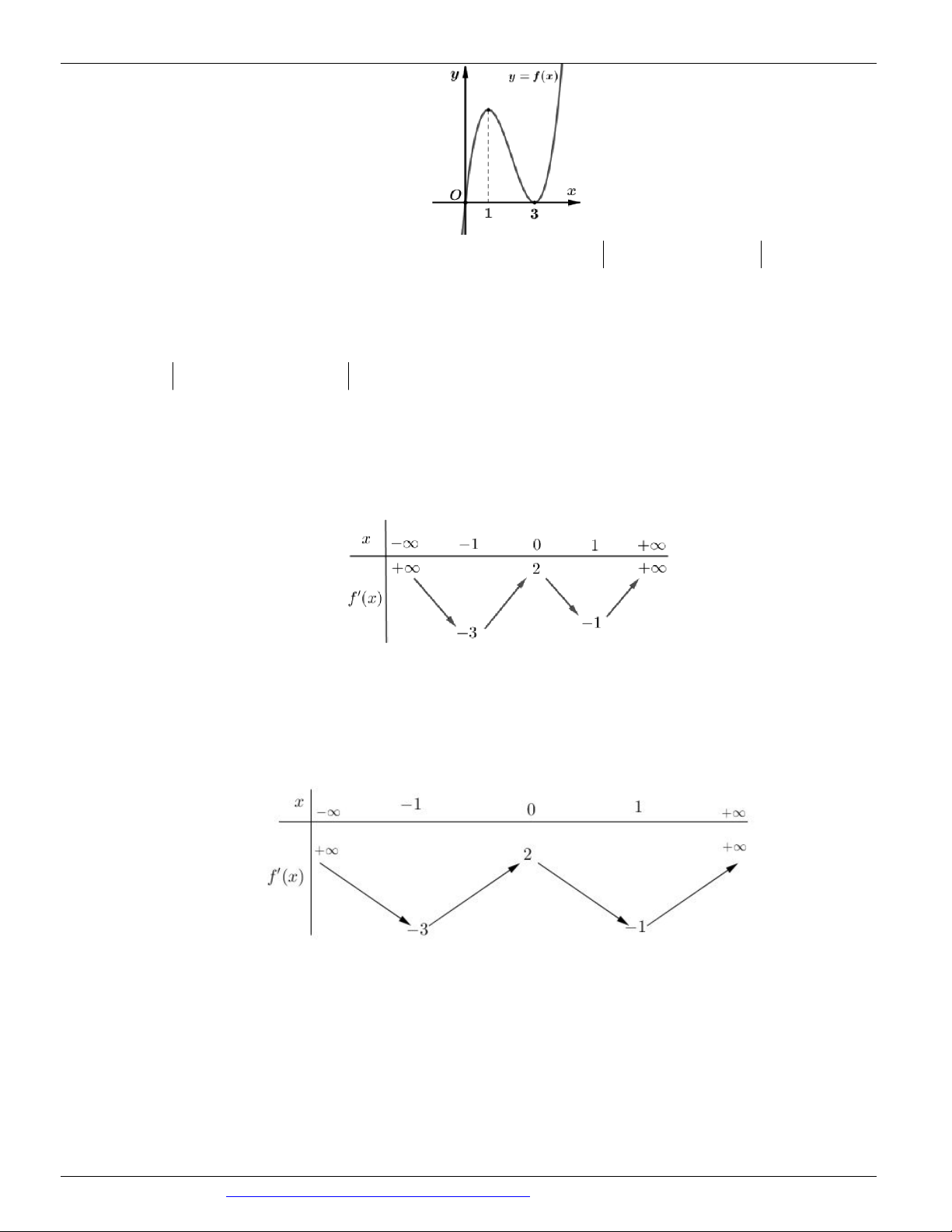
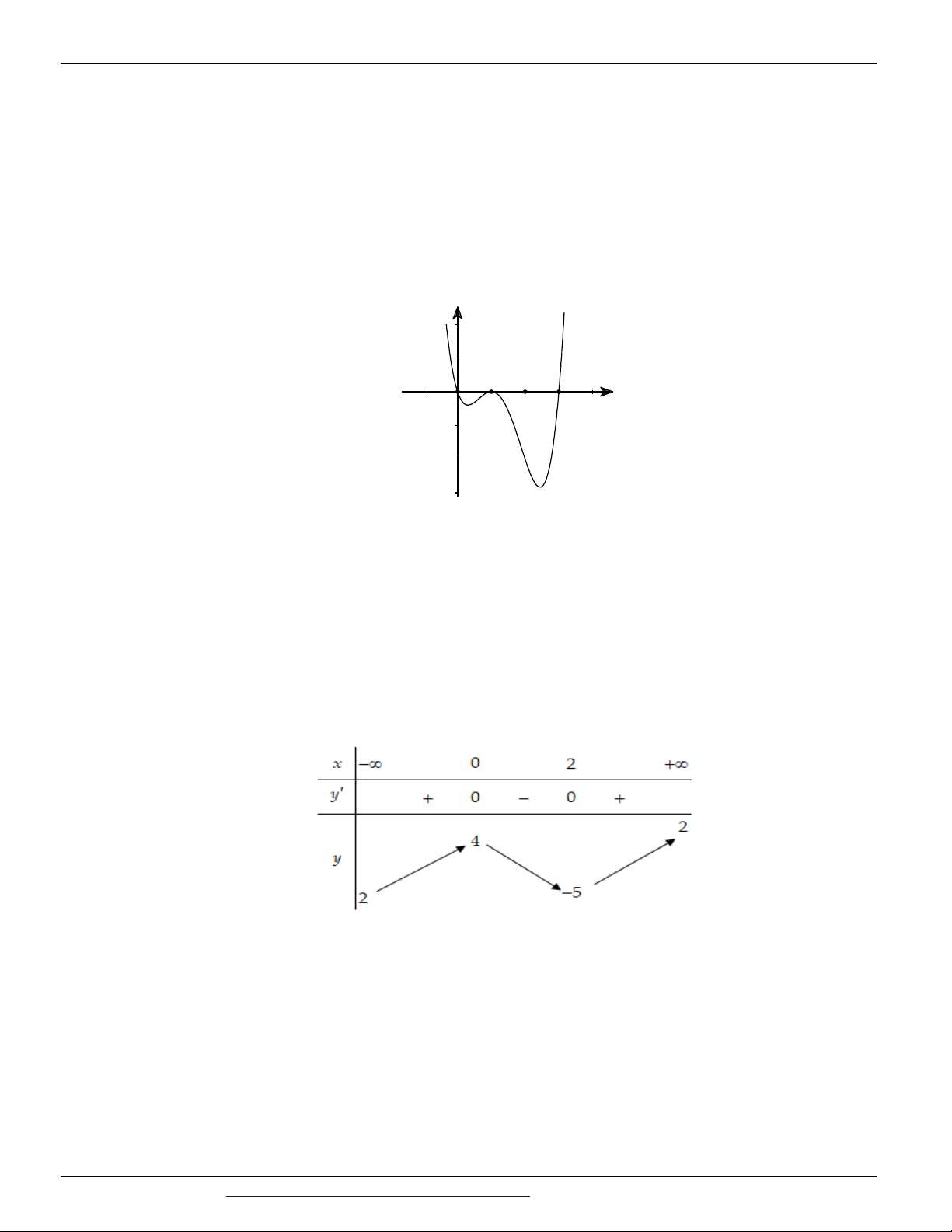
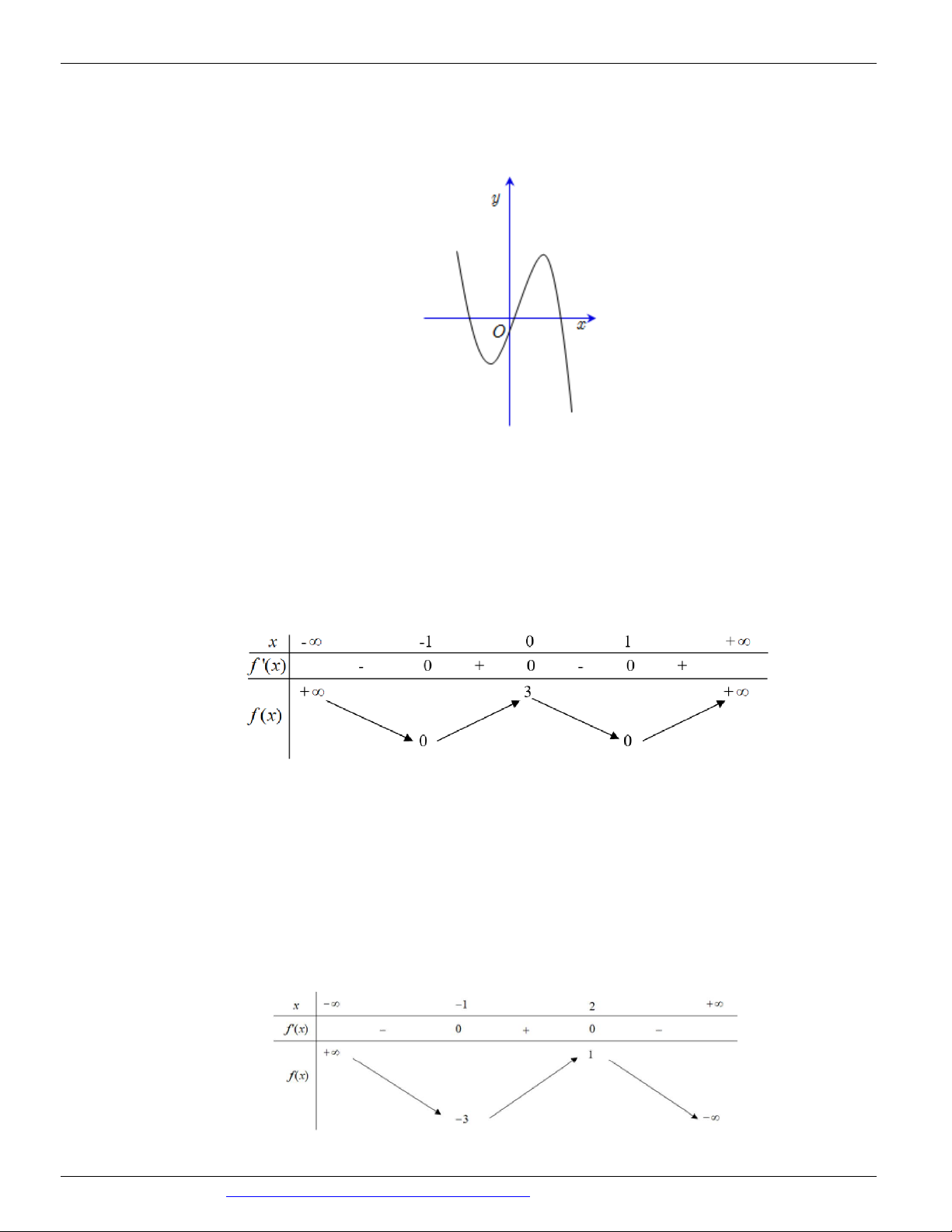
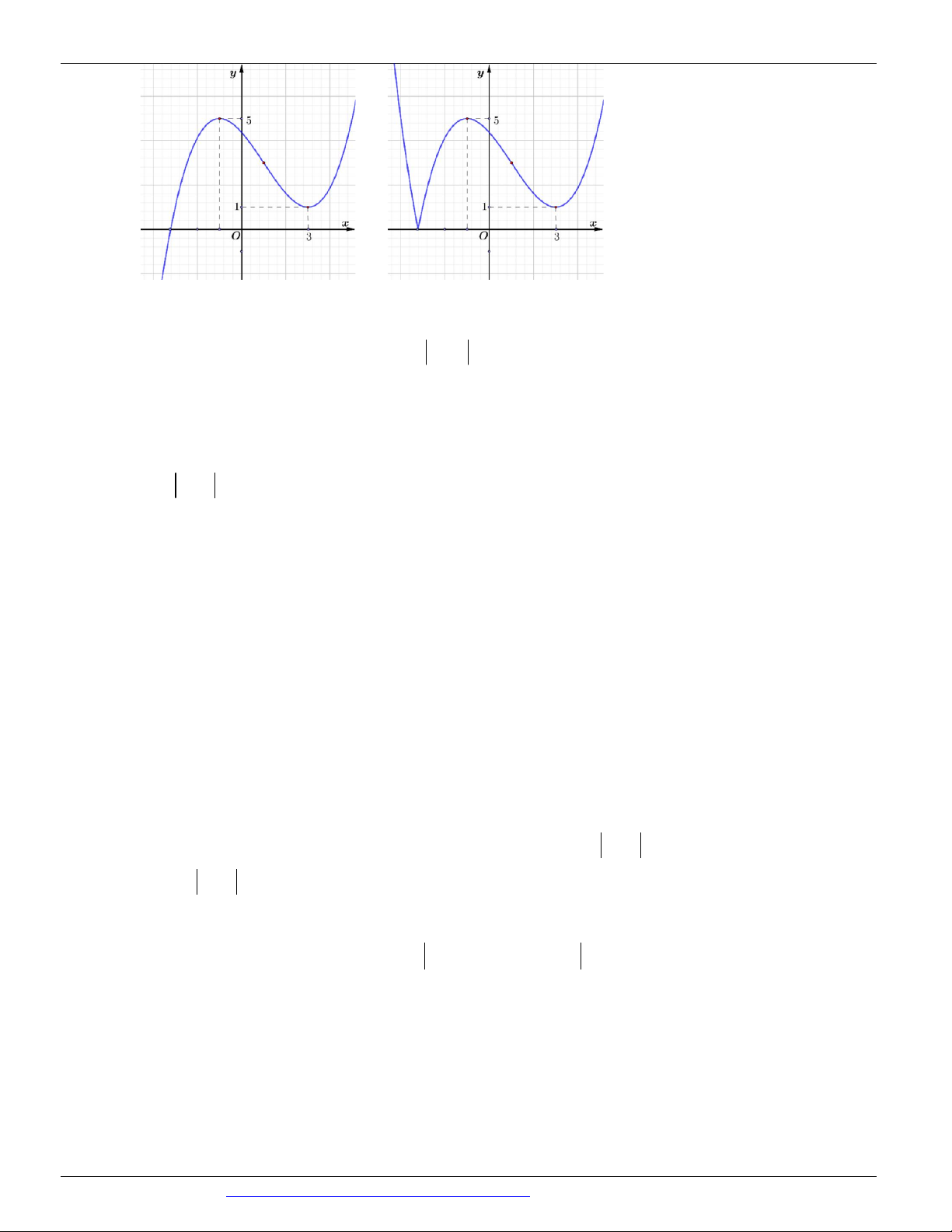
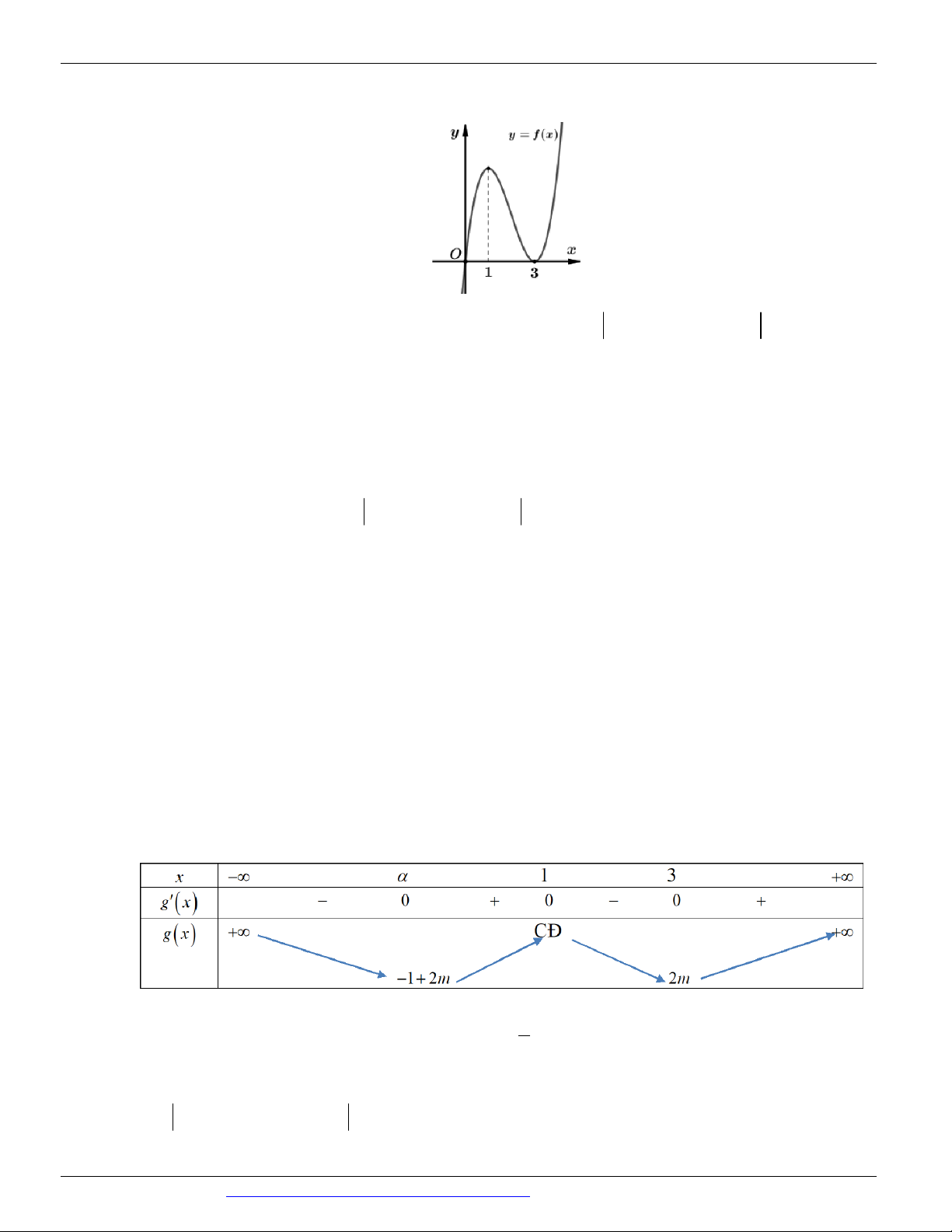
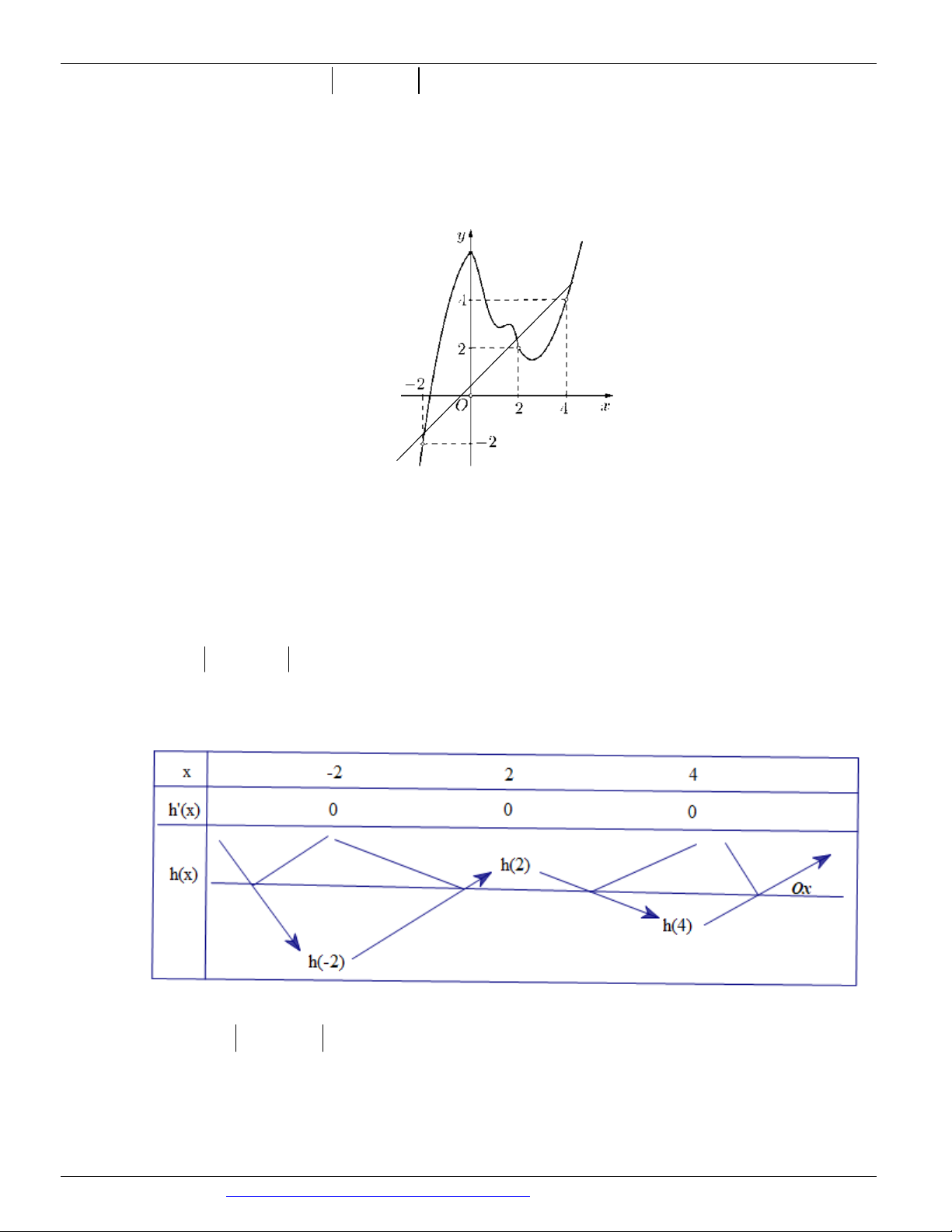
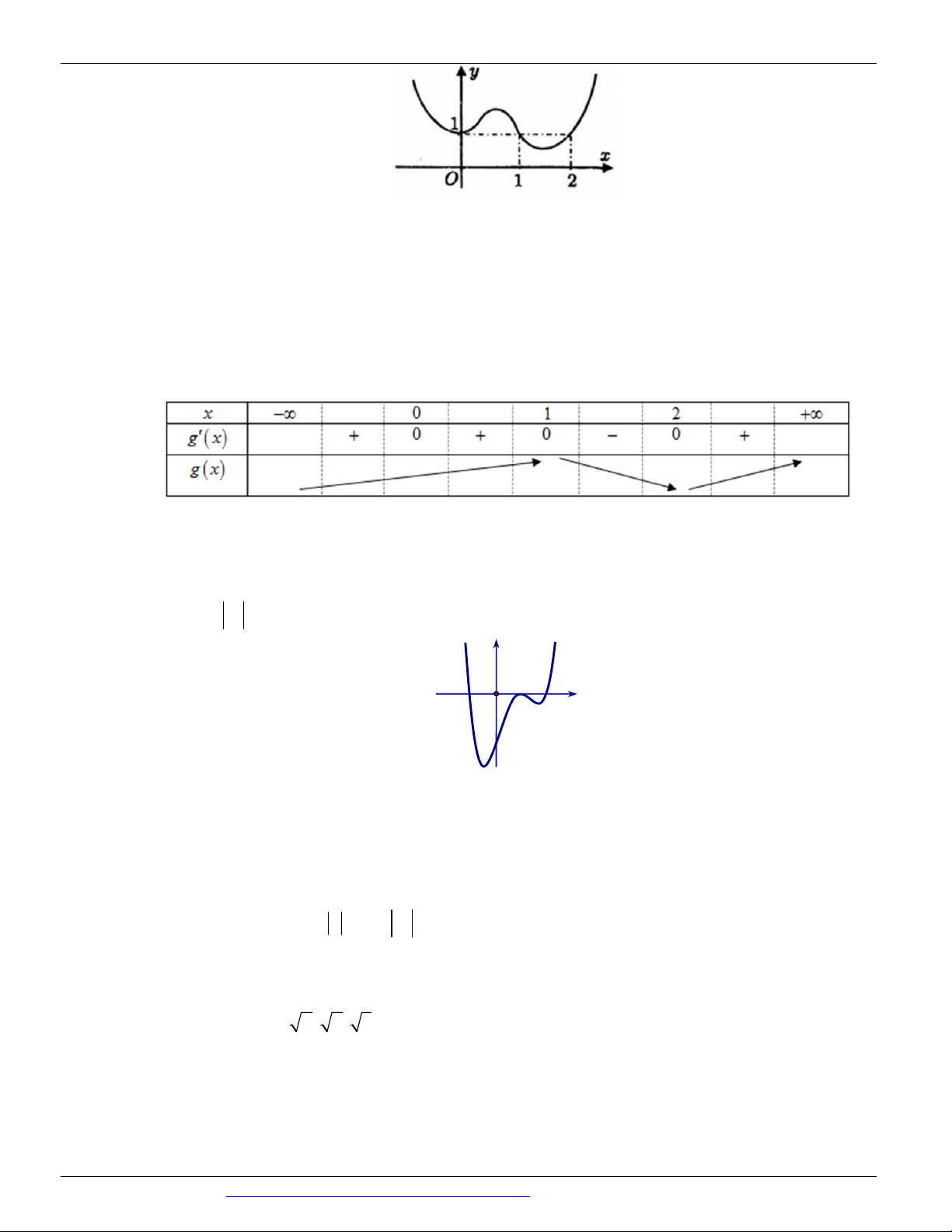
(Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 2 D. 0 Câu 4.
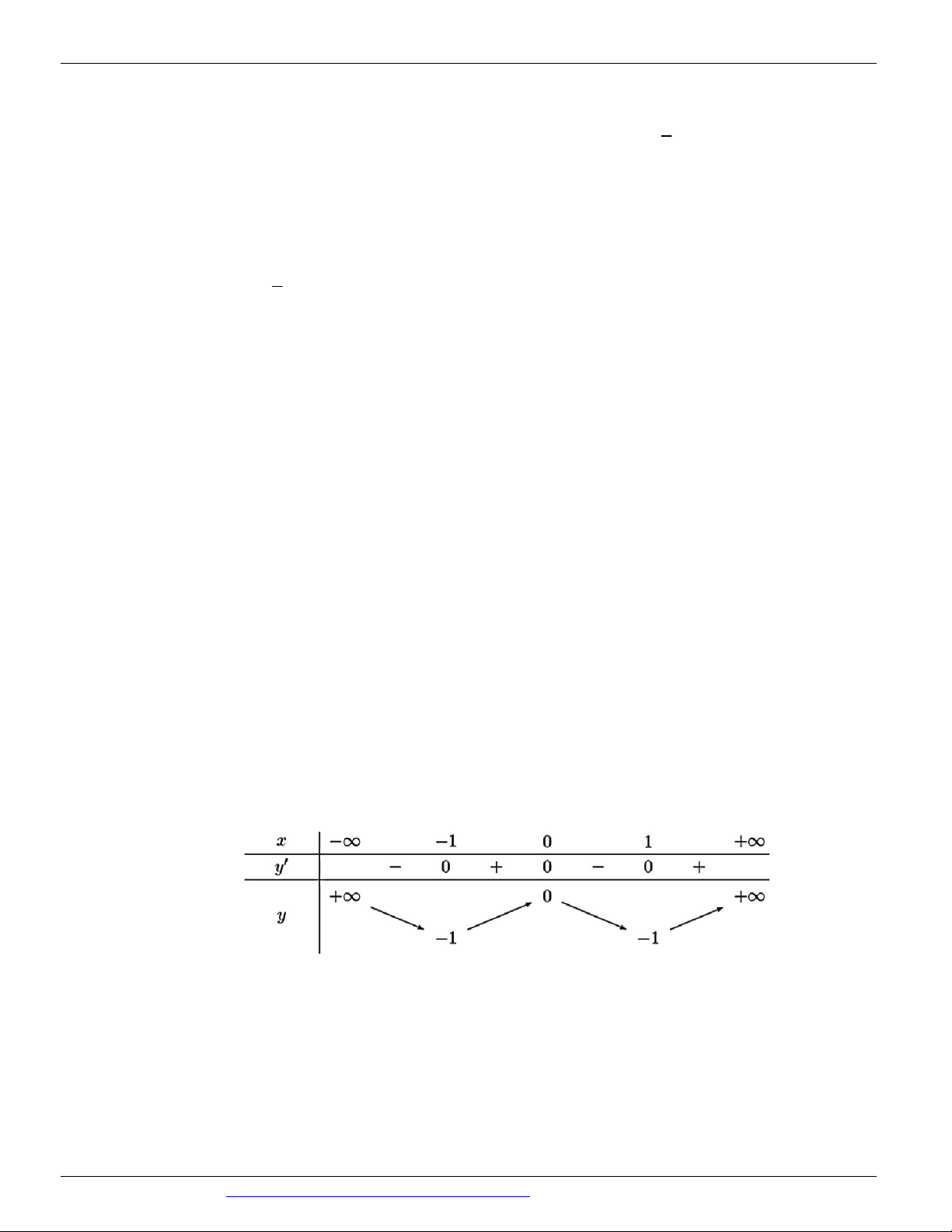
(MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y f x có bảng biến thiên như sau
Tìm giá trị cực đại y
và giá trị cực tiểu y
của hàm số đã cho. CĐ CT A. y  2 và y  0 B. y  3 và y  0 CĐ CT CĐ CT C. y  3 và y  2  D. y  2  và y  2 CĐ CT CĐ CT Câu 5.
(Mã 103 - BGD - 2019) Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số đạt cực đại tại:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. x  2  .
B. x  3 .
C. x  1 . D. x  2 . Câu 6.
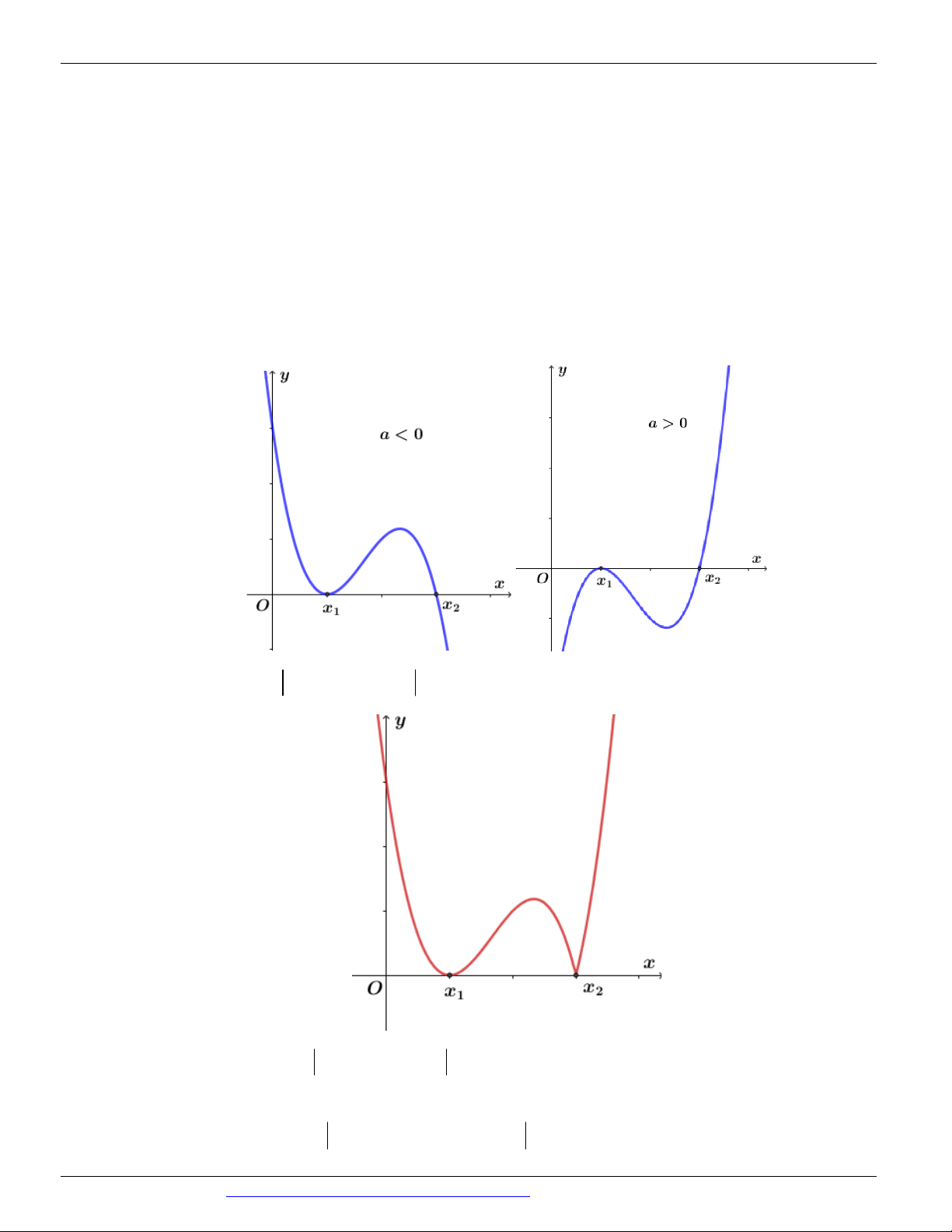
(MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số 4 2
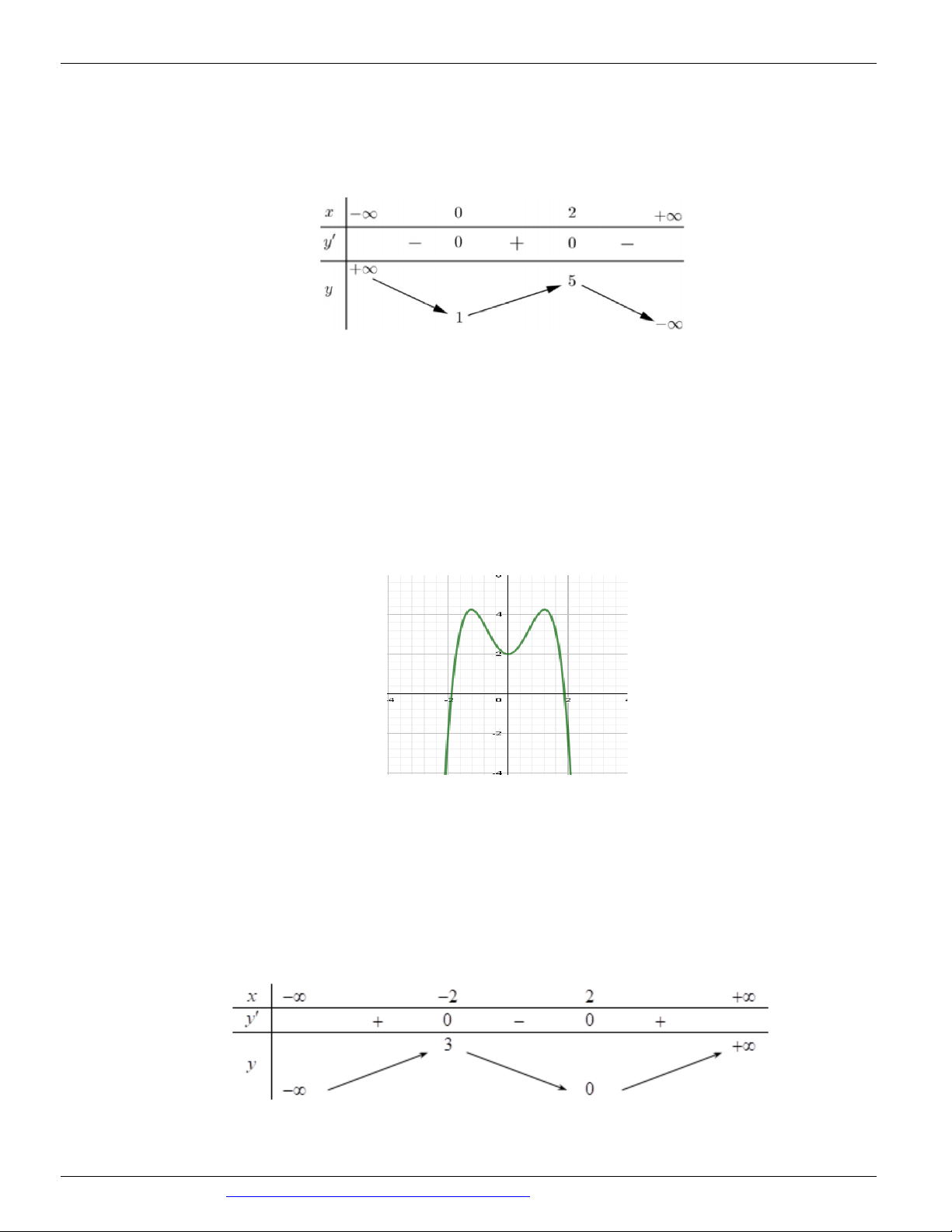
y ax bx c ( a , b , c   ) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là A. 3 B. 0 C. 1 D. 2 Câu 7.
(Mã 102 - BGD - 2019) Cho hàm số f x có bảng biến thiên như sau:
Hàm số đạt cực đại tại A. x  2  .
B. x  3 .
C. x  1 . D. x  2 . Câu 8.
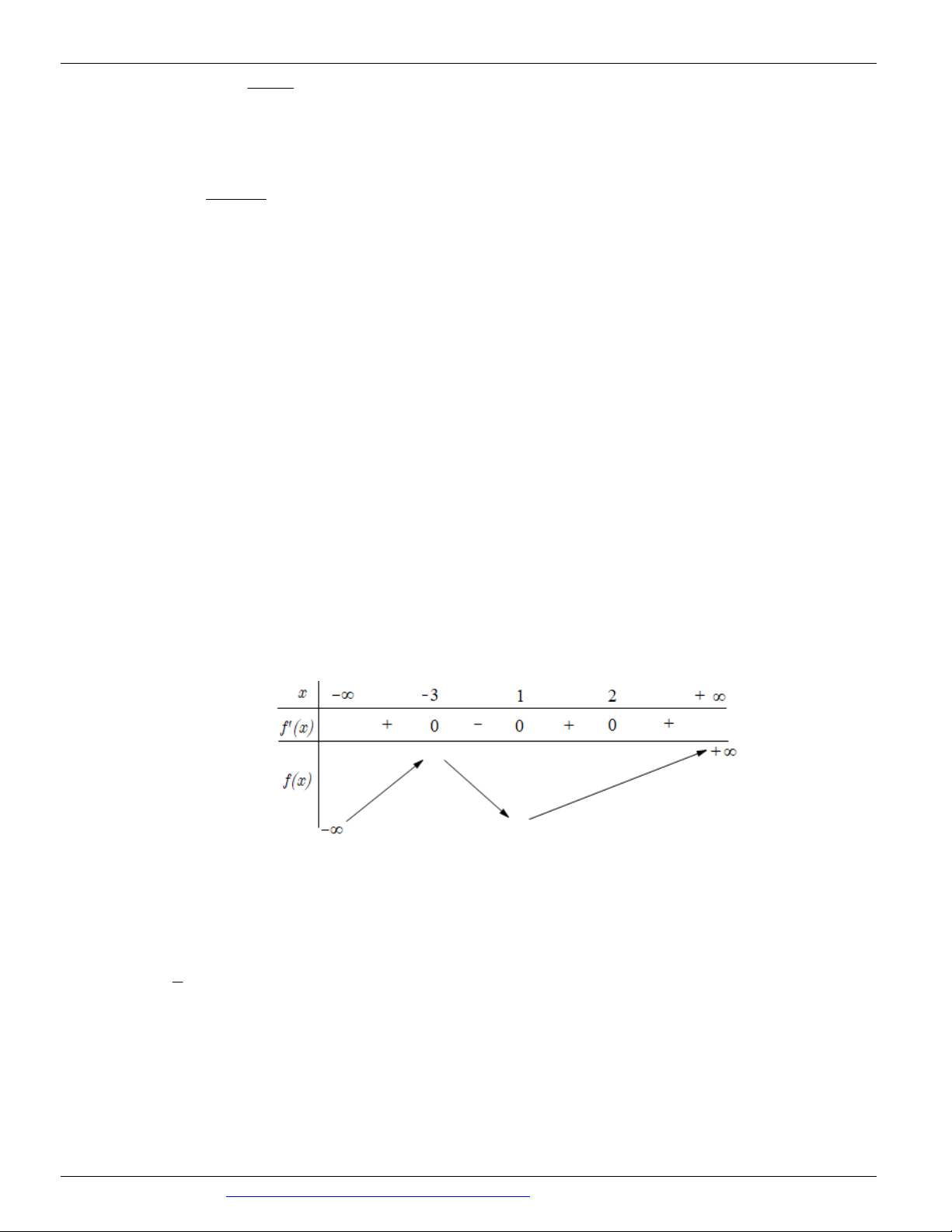
(MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y f (x) có bảng biến thiên như sau
Mệnh đề nào dưới đây sai
A. Hàm số có giá trị cực đại bằng 3
B. Hàm số có hai điểm cực tiểu
C. Hàm số có giá trị cực đại bằng 0
D. Hàm số có ba điểm cực trị Câu 9.
(Mã đề 104 - BGD - 2019) Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. x  2 . B. x  2  .
C. x  1 . D. x  3 .
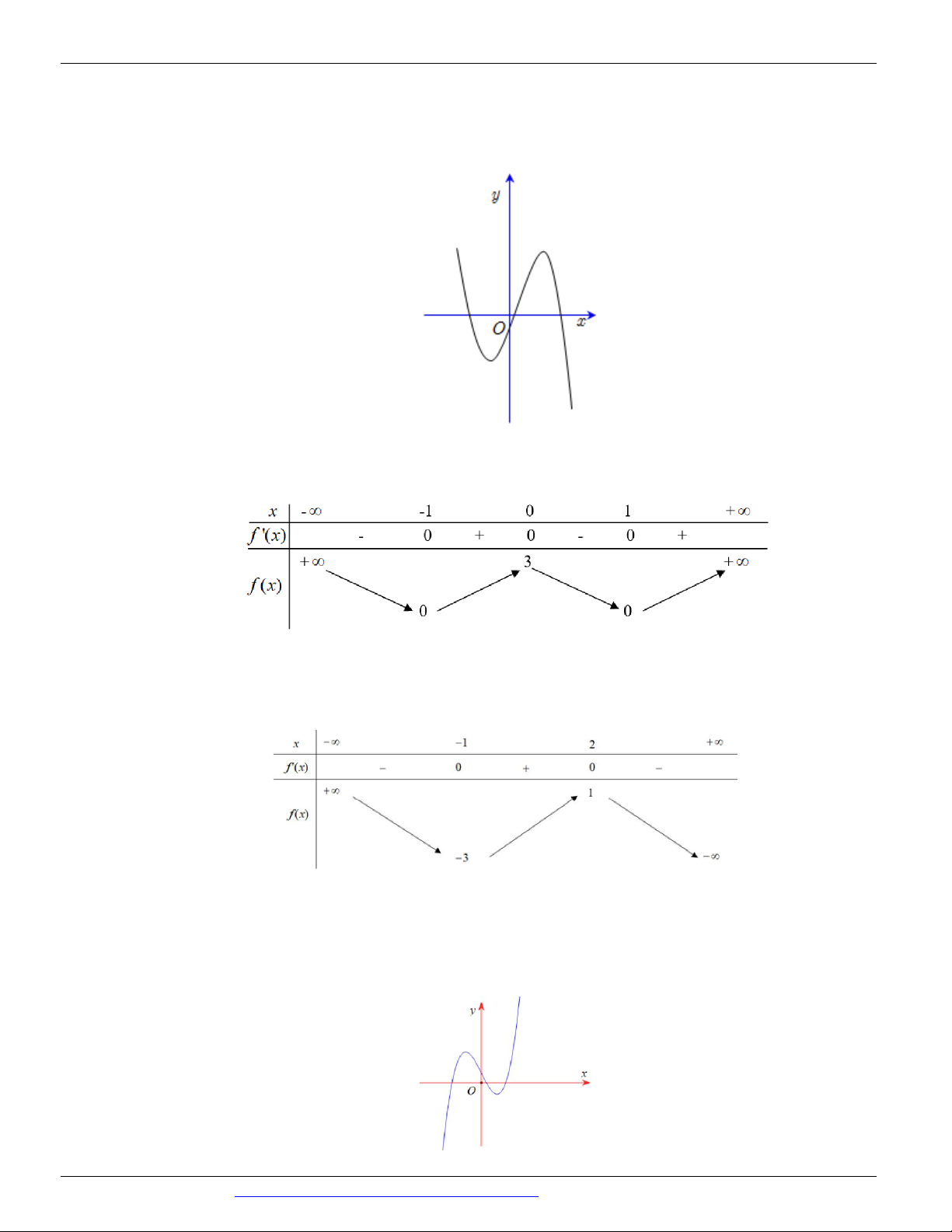
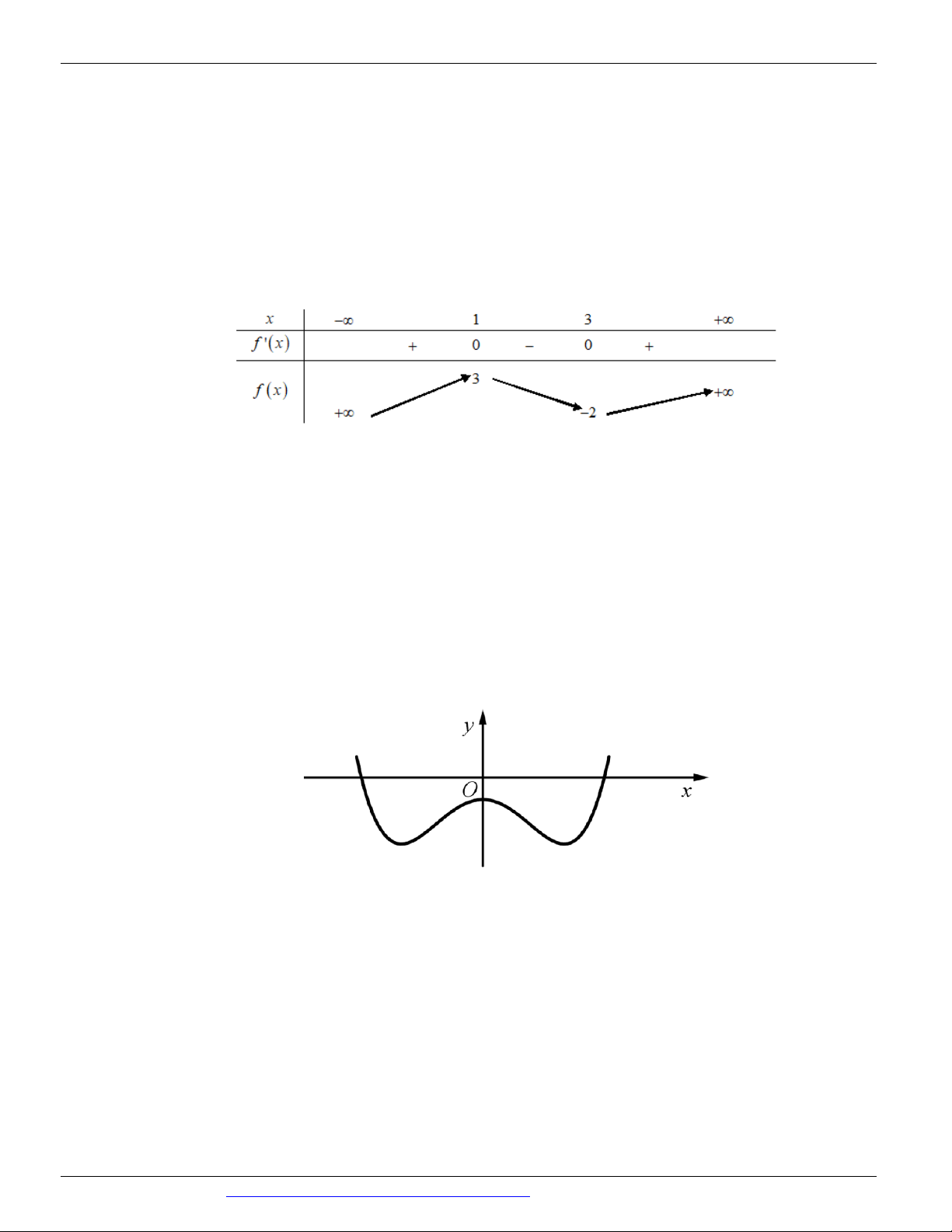
Câu 10. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số 3 2
y ax bx cx d a, , b ,
c d  có đồ thị
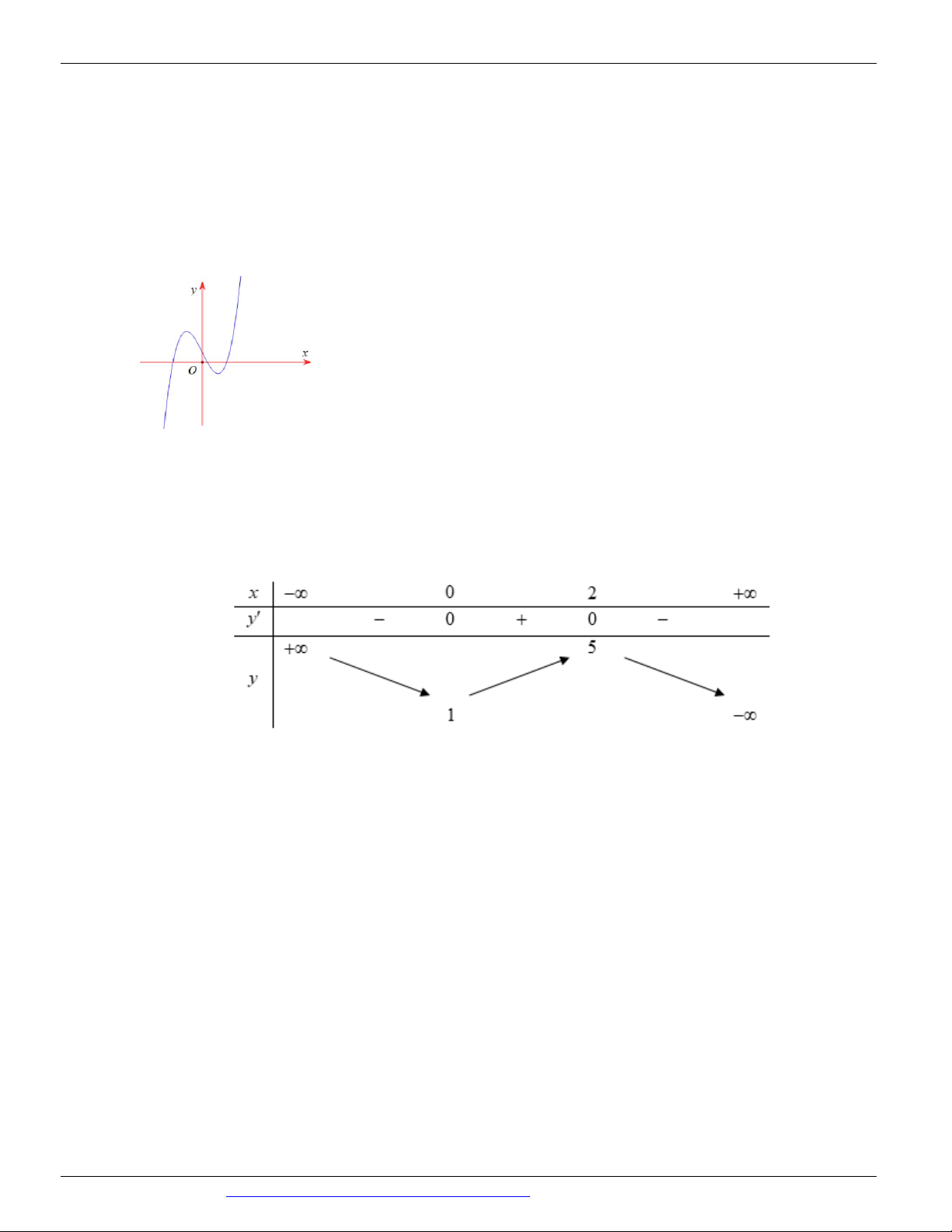
như hình vẽ bên. Số điểm cực trị của hàm số này là A. 3 B. 2 C. 0 D. 1
Câu 11. (Mã đề 104 - BGD - 2019) Cho hàm số y f (x) có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đây? A. (0;1) .
B. (1; ) . C. (1; 0) . D. (0; )
Câu 12. (Mã đề 101 - BGD - 2019) Cho hàm số f ( )
x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  1 . B. x  3  .
C. x  2 . D. x  1 .
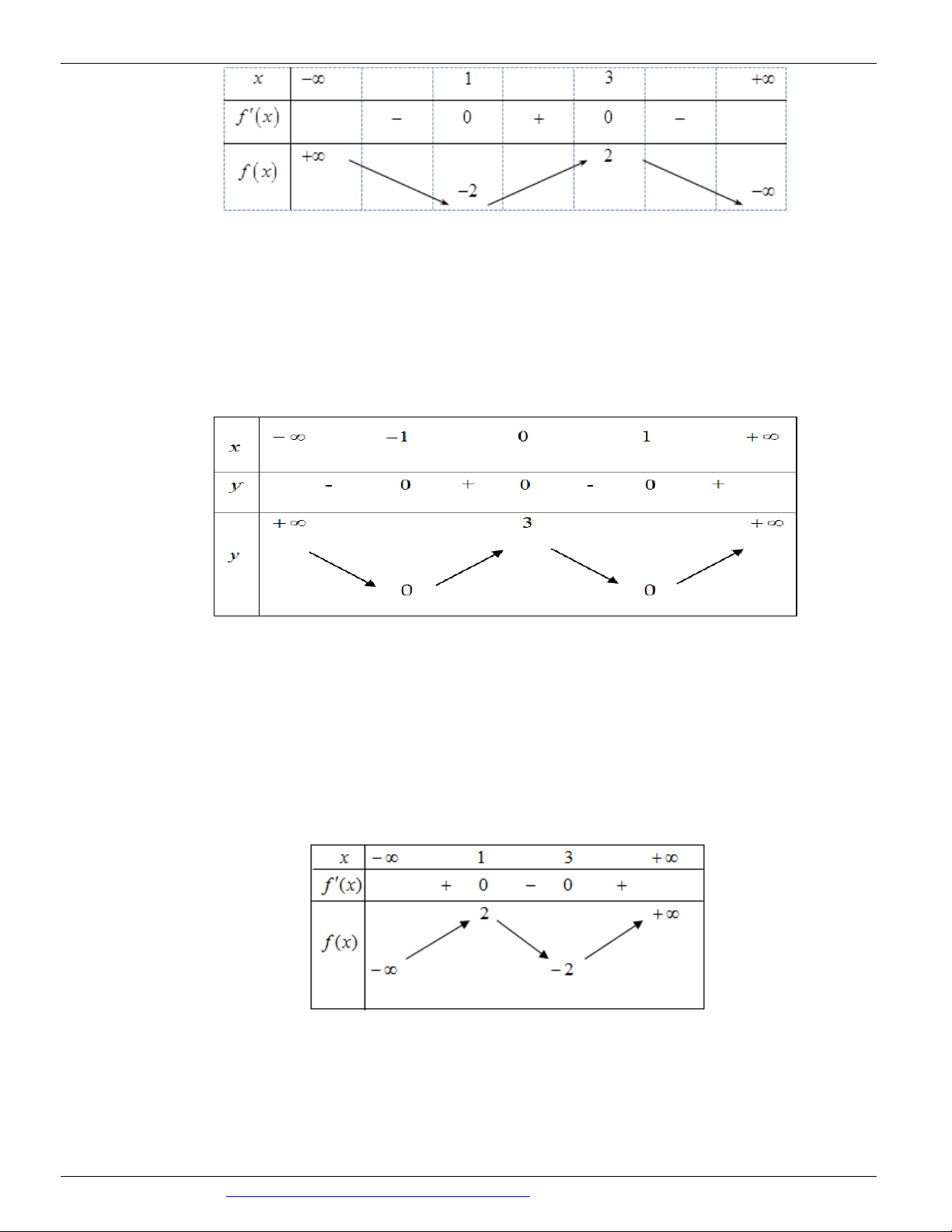
Câu 13. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số 3 2
y ax bx cx d a, , b ,
c d   có đồ thị
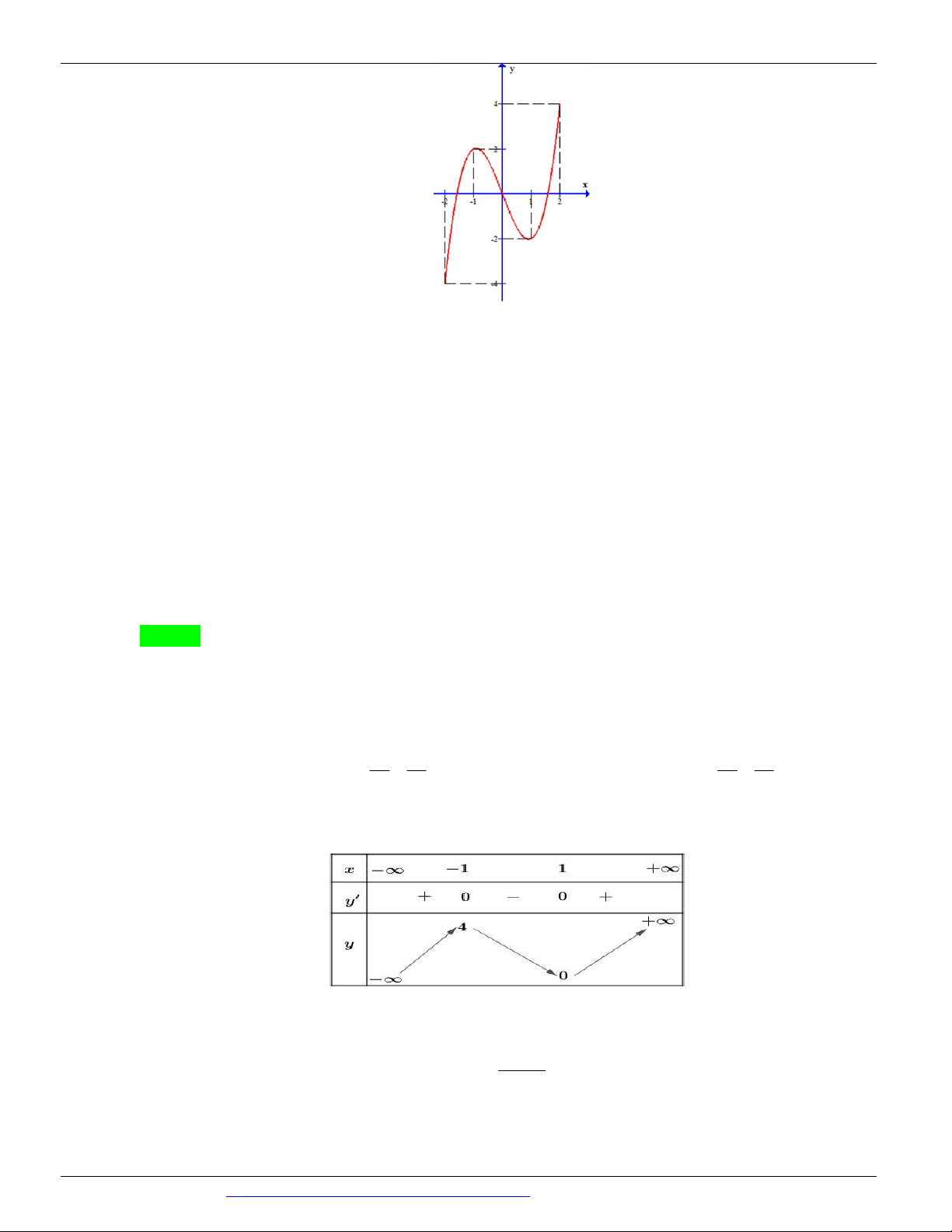
như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 2 B. 0 C. 3 D. 1
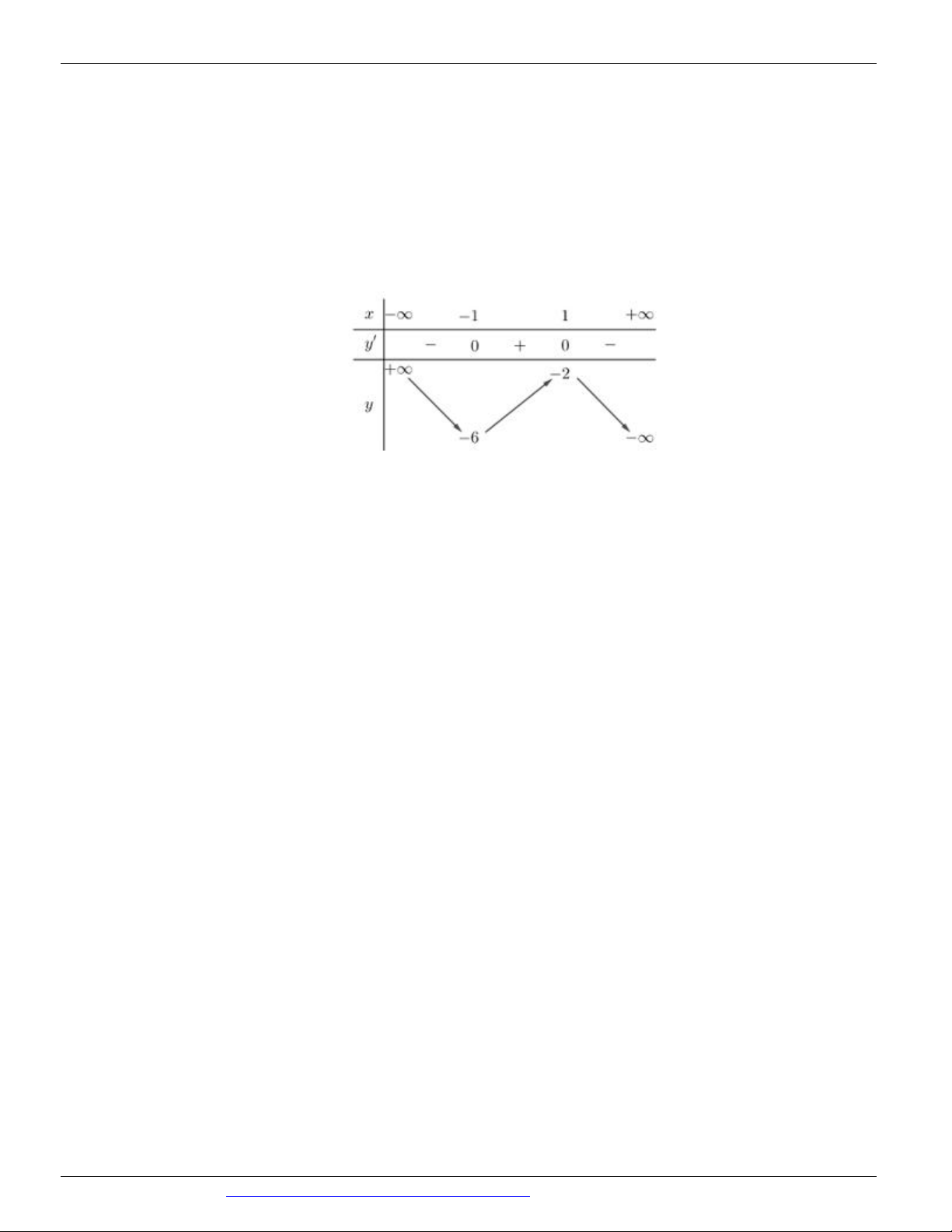
Câu 14. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y f x có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm A. x  1
B. x  0
C. x  5 D. x  2
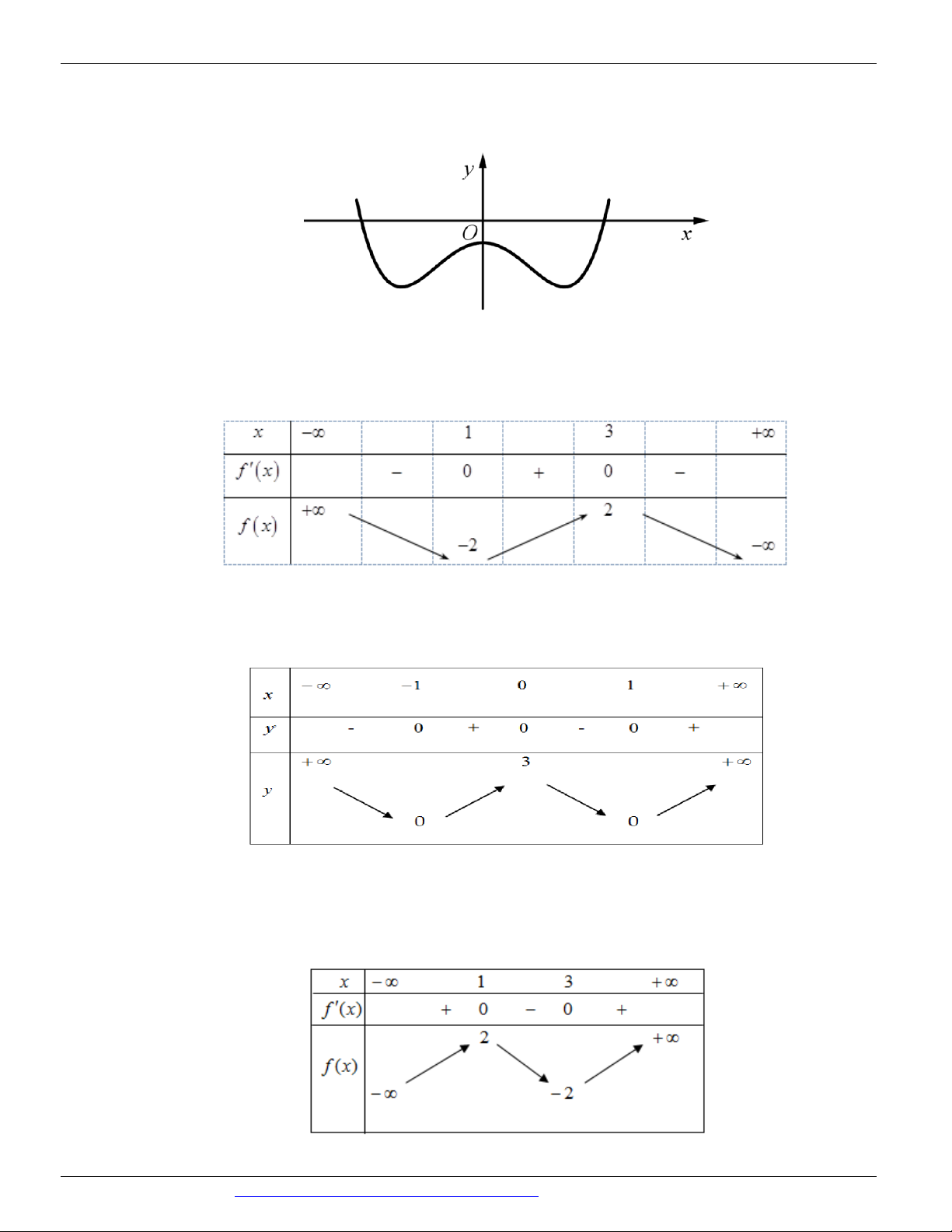
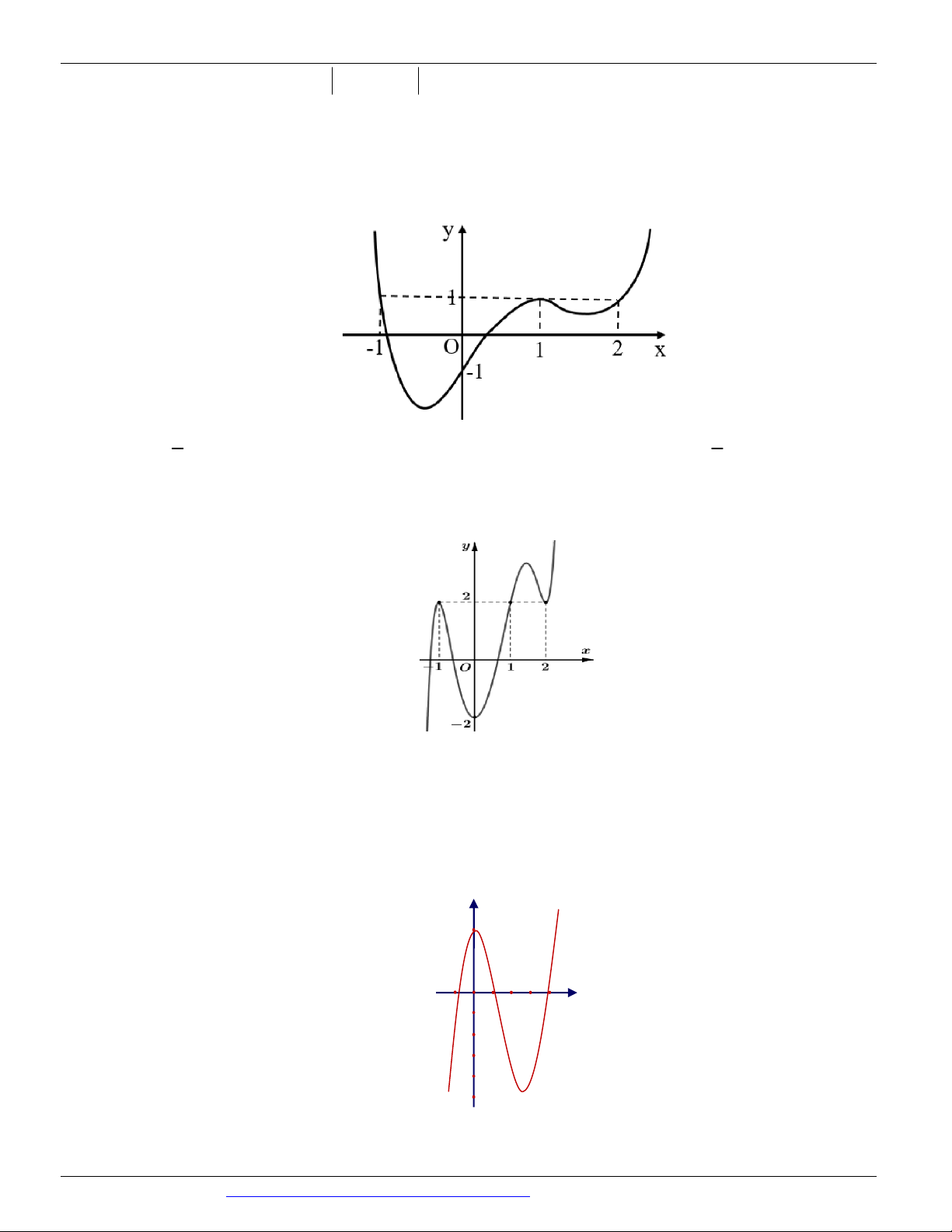
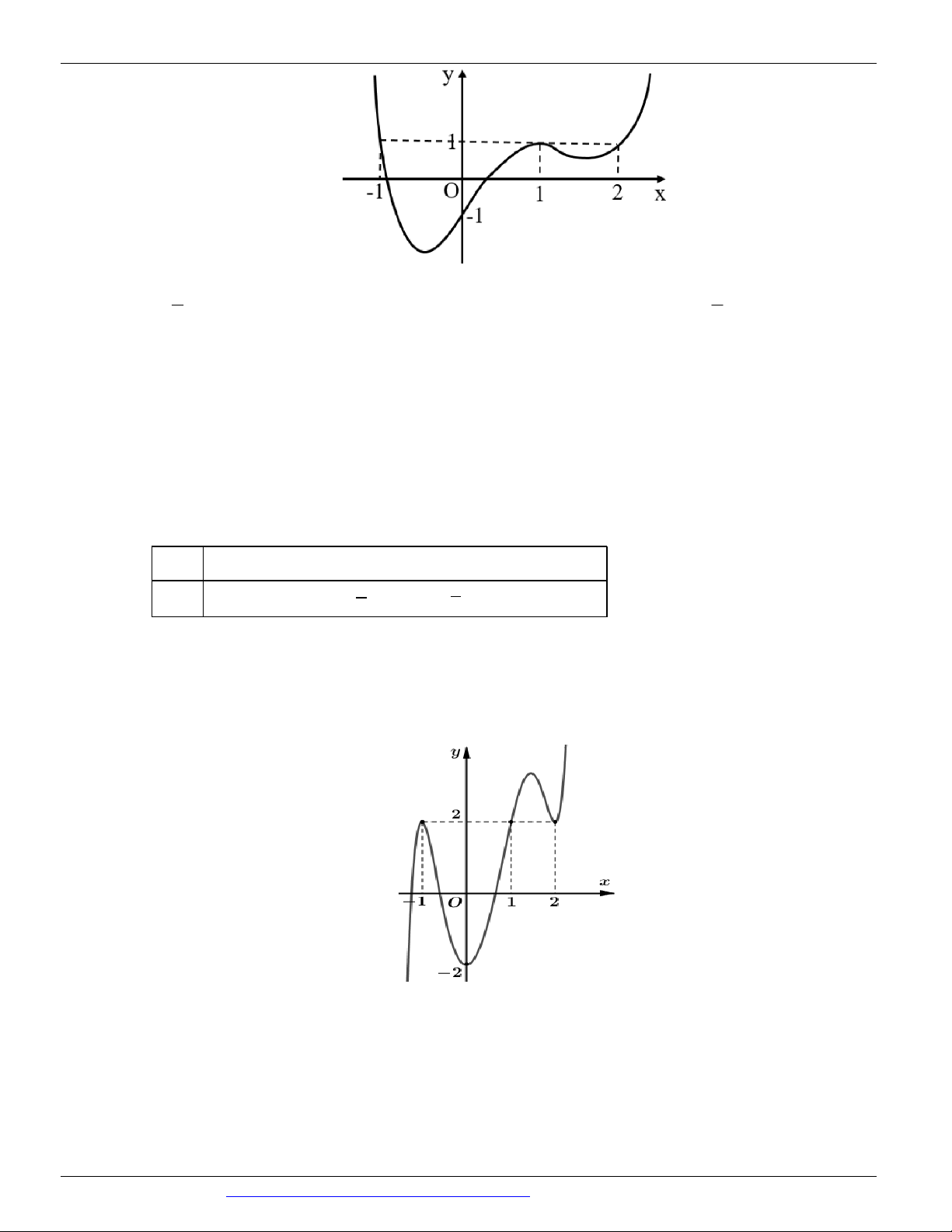
Câu 15. Cho hàm số y f x xác định, liên tục trên đoạn  2
 ; 2 và có đồ thị là đường cong trong hình vẽ
bên. Hàm số f x đạt cực đại tại điểm nào dưới đây ? A. x  2  . B. x  1  .
C. x  1. D. x  2
Dạng 2. Tìm cực trị của hàm số khi biết y, y’
Câu 16. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị cực đại y của hàm số 3
y x  3x  2 . C§ A. y  1 B. y  4 C. y  1 D. y  0 C§ C§ C§ C§ 2x  3
Câu 17. (MĐ 104 BGD&DT NĂM 2017) Hàm số y
có bao nhiêu điểm cực trị? x 1 A. 1 B. 3 C. 0 D. 2 2 x  3
Câu 18. Cho hàm số y
. Mệnh đề nào dưới đây đúng? x 1
A. Cực tiểu của hàm số bằng 3 
B. Cực tiểu của hàm số bằng 1
C. Cực tiểu của hàm số bằng 6 
D. Cực tiểu của hàm số bằng 2
Câu 19. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số f (x) có đạo hàm 3 f (
x)  x(x  1)(x  2) , x
  R. Số điểm cực trị của hàm số đã cho là A. 1 B. 3 C. 2 D. 5
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 20. (Mã đề 101 - BGD - 2019) Cho hàm số f (x) có đạo hàm f x x x  2 ( )
2 , x   . Số điểm cực
trị của hàm số đã cho là A. 2 . B. 1. C. 0 . D. 3 .
Câu 21. (Mã 103 - BGD - 2019) Cho hàm số f x có đạo hàm f  x  x x  2 1 , x   . R Số điểm cực
trị của hàm số đã cho là A. 2 . B. 0 . C. 1. D. 3 .
Câu 22. (Mã đề 104 - BGD - 2019) Cho hàm số f x có đạo hàm f  x  x x  2
1 , x   . Số điểm
cực trị của hàm số đã cho là A. 1. B. 2 . C. 3 . D. 0 .
Câu 23. (Mã 102 - BGD - 2019) Cho hàm số y f (x) có đạo hàm 2 f (
x)  x(x  2) , x   . Số điểm
cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1.
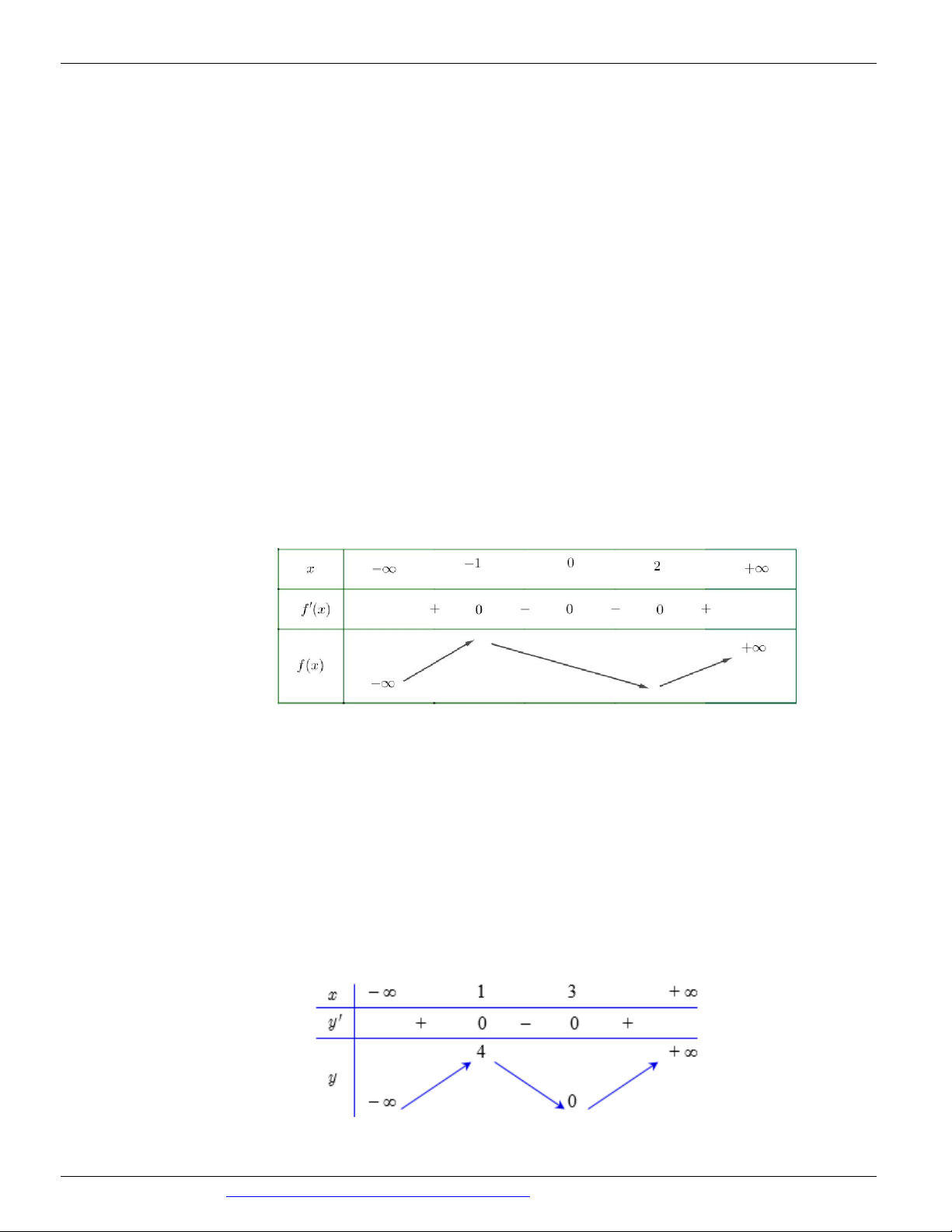
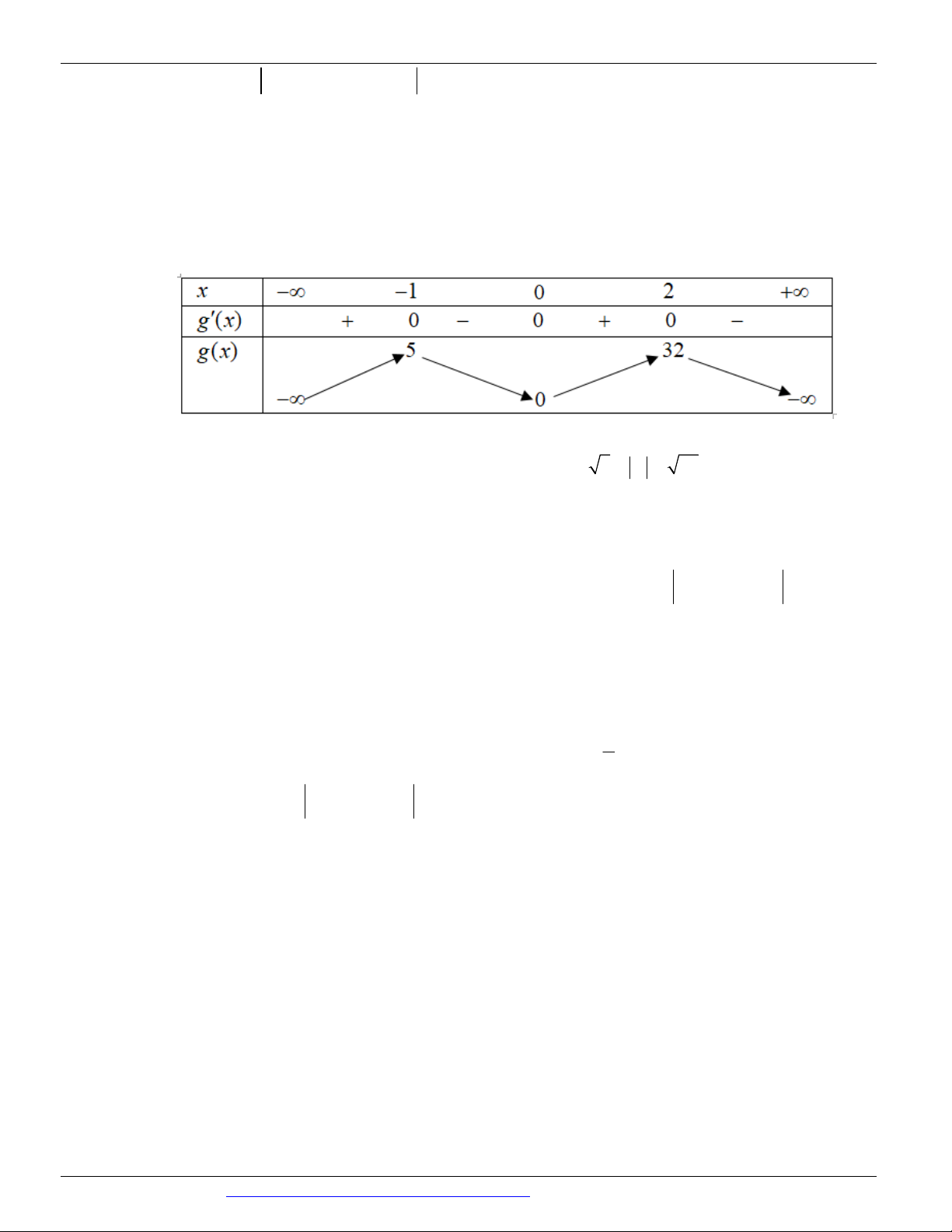
Câu 24. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho hàm số f x có đạo hàm
f x  x   x2   x3  x  4 ' 1 3
2 với mọi x   . Điểm cực tiểu của hàm số đã cho là A. x  2 . B. x  3 . C. x  0 . D. x  1 .
Câu 25. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm f  x 3
x x  
1  x  2, x
   . Số điểm cực trị của hàm số đã cho là A. 1 . B. 3 . C. 5 . D. 2 . Câu 26. (ĐỀ 04 VTED NĂM 2018-2019) Hàm số
y f x có đạo hàm
f  x   x  
1  x  2... x  2019 , x
  R . Hàm số y f x có tất cả bao nhiêu điểm cực tiểu? A. 1008 B. 1010 C. 1009 D. 1011
Câu 27. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số F x là một nguyên hàm của hàm số   x f x   2 x   2 2019 4
x  3x  2 . Khi đó số điểm cực trị của hàm số F x là A. 5 . B. 4 . C. 3 . D. 2 .
Câu 28. Đồ thị hàm số 3
y  x  3x có điểm cực tiểu là: A. ( 1  ;  2) . B. (1; 0) . C. (1;  2) . D. ( 1  ; 0) .
Câu 29. (THPT YÊN PHONG 1 BẮC NINH NĂM HỌC 2018-2019 LẦN 2) Hàm số f x có đạo hàm
f  x  x x   x  3 2 1 2 , x
   . Hỏi f x có bao nhiêu điểm cực đại? A. 2 . B. 0 . C. 1. D. 3 .
Câu 30. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm số 3 2
y x  6x  9x có tổng hoành độ và tung độ bằng A. 5 . B. 1 . C. 3 . D. 1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 31. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Tìm giá trị cực tiểu y của hàm số CT 3 y x  3x4 . A. y  6  B. y  1  C. y  2  D. y 1 CT CT CT CT
Câu 32. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm là
f  x  x x   x  2 1 2 x
   . Số điểm cực trị của hàm số là? A. 5 . B. 2 . C. 1. D. 3 .
Câu 33. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Giá trị cực tiểu y của hàm số CT 3 2
y x  3x  4 là: A. y  0 . B. y  3 . C. y  2 . D. y  4 . CT CT CT CT
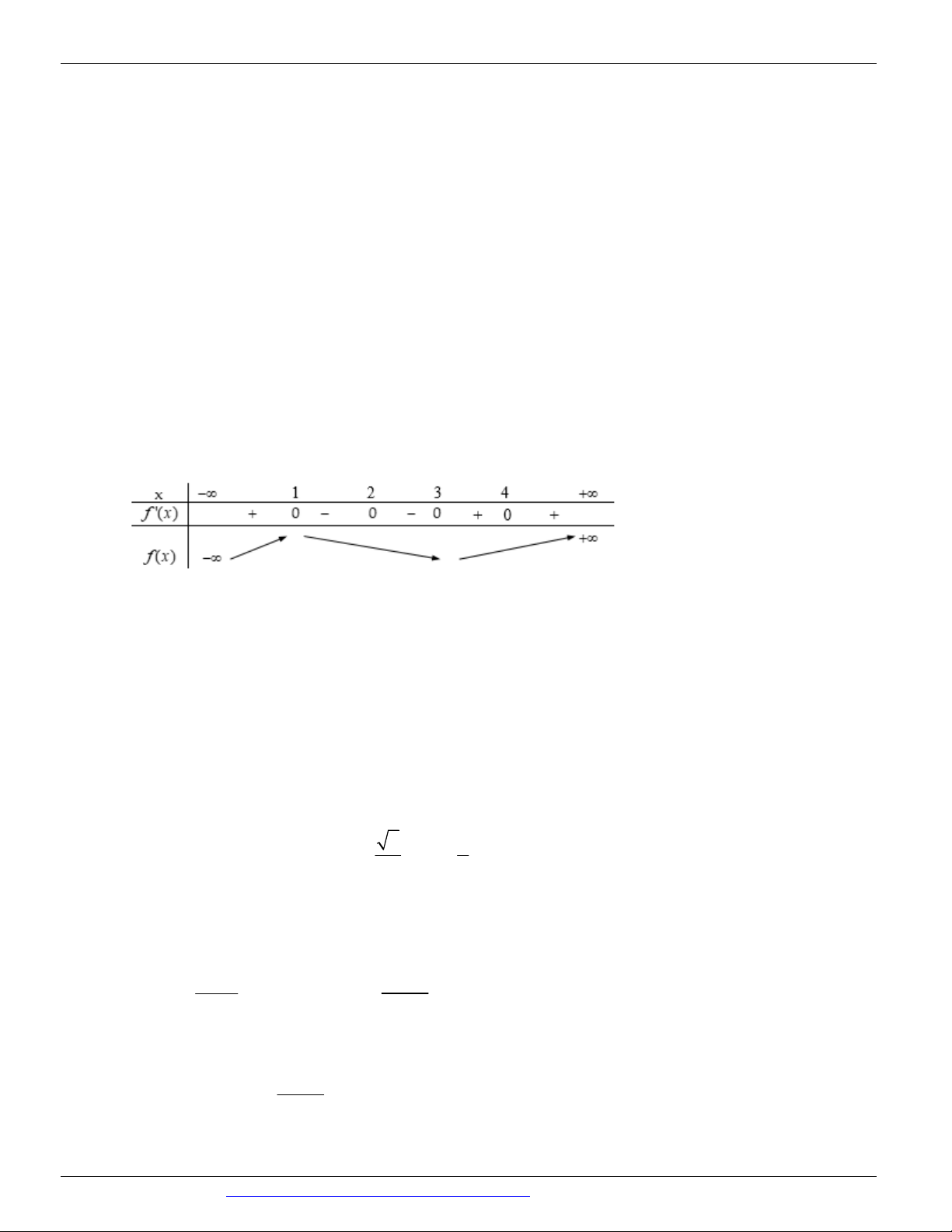
Câu 34. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm
f  x   x   x  2  x  3  x  4 1 2 3 4 , x   .
 Số điểm cực trị của hàm số đã cho là A. 3 B. 5 C. 2 D. 4
Câu 35. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Đồ thị hàm số 4 2
y x x 1
có bao nhiêu điểm cực trị có tung độ là số dương? A. 3 . B. 1. C. 2 . D. 0 .
Câu 36. (HSG BẮC NINH NĂM 2018-2019) Hàm số nào dưới đây không có cực trị? 2 x 1 2x  2 A. y B. y C. 2
y x  2x 1 D. 3
y  x x 1 x x 1
Câu 37. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm
f   x   x x    x  2 1 2
, x   . Số điểm cực trị của hàm số đã cho là A. 5 . B. 2 . C. 1. D. 3 .
Câu 38. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số y f x có đạo hàm
f  x   x   2 x   4 2 3
x  9 . Số điểm cực trị của hàm số y f x là A. 3 . B. 4 . C. 2 . D. 1.
Câu 39. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số 4 2
y x  2x 1. Xét các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị.
2) Hàm số đồng biến trên các khoảng 1;0 ; 1;  .
3) Hàm số có 1 điểm cực trị.
4) Hàm số nghịch biến trên các khoảng ;   1 ; 0  ;1 .
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên? A. 2. B. 1. C. 4. D. 3.
Câu 40. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm giá trị cực đại của hàm số 3 2
y x  3x  2 . A. 2  . B. 0 . C. 2 . D. 1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 41. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số f   x có đạo hàm
là f x  x x  x x  x  4 2 2 ' 2 2
1 thì tổng các điểm cực trị của hàm số f   x bằng A. 1. B. 2 . C. 1. D. 0 .
Câu 42. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số 1 1 5 4 3 2 y x x
x  3x  2019m m   đạt cực tiểu tại điểm: 4 3 2 A. x  3 . B. x  3  . C. x  1. D. x  1  .
Câu 43. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm số 3
y  x  3x 1 là: A. M  1  ;   1 . B. N 0;  1 .
C. P 2;   1 .
D. Q 1;3 . 1
Câu 44. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Hàm số 3 2 y
x x  3x  1 đạt cực tiểu 3 tại điểm A. x  1  . B. x  1 . C. x  3  . D. x  3 .
Câu 45. (THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 01) Tìm số điểm cực trị của hàm số 4 2
y x  2x . A. 2. B. 4. C. 3. D. 1.
Câu 46. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Điểm cực tiểu của đồ thị hàm số 3 2
y  x x  5x  5 là  5 40  A.  1  ; 8   B. 0; 5 C. ;   D. 1;0  3 27 
Câu 47. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số 3
y f x có đạo hàm f x  x  2 x x  2 ' 2
x  2 x  . Số điểm cực trị của hàm số là A. 4 B. 1 C. 2 D. 3
Câu 48. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị? 2x  3 A. y  . B. 4 y x . C. 3
y  x x .
D. y x  2 . x  2
Câu 49. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số y f x 2
có đạo hàm trên  và f  x   x  
1  x  2  x  3 . Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 0 D. 2
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0
Câu 50. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị thực của tham số m để hàm số 1 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3. 3 A. m  1  B. m  7 
C. m  5
D. m  1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 51. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Tìm m để hàm số 3 2
y x  2mx mx  1 đạt
cực tiểu tại x  1
A. không tồn tại m . B. m  1 . C. m  1.
D. m 1;  2 .
Câu 52. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Tìm các giá trị thực của tham số m để 1 hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3. 3
A. m  1, m  5 . B. m  5 . C. m  1. D. m  1  .
Câu 53. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  3x mx 1 đạt cực tiểu tại x  2 . A. m  0 . B. m  4 .
C. 0  m  4 .
D. 0  m  4 .
Câu 54. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực m để hàm số 1 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại x  1. 3 A. 0 B. 2 C. 1 D. 3
Câu 55. (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8 5 2 4
y x  (m 1)x  (m 1)x 1 đạt cực tiểu tại x  0 ? A. 3 B. 2 C. Vô số D. 1
Câu 56. (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y x  m   5 x   2 m   4 2
4 x  1 đạt cực tiểu tại x  0 ? A. Vô số B. 3 C. 5 D. 4
Câu 57. (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y x  m   5 x   2 m   4 3
9 x 1 đạt cực tiểu tại x  0 ? A. 6 B. Vô số C. 4 D. 7
Câu 58. (MĐ 103 BGD&ĐT NĂM 2017-2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y x  m   5 x   2 m   4 4
16 x  1 đạt cực tiểu tại x  0 . A. 8 B. Vô số C. 7 D. 9
Câu 59. (KTNL GIA BÌNH NĂM 2018-2019) Có bao nhiêu giá trị nguyên của tham số m để hàm số 12 7 2 6
y x  (m  5)x  (m  25)x 1 đạt cực đại tại x  0 ? A. 8 B. 9 C. Vô số D. 10
Câu 60. Tìm tất cả tham số thực m để hàm số y  m   4 x   2 m   2 1
2 x  2019 đạt cực tiểu tại x  1  A. m  0 . B. m  2  . C. m  1. D. m  2 .
Câu 61. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số y f x xác
định trên tập số thực  và có đạo hàm f x   x
x x m  x   m 3 2 ' sin 3 9 x    ( m là
tham số). Có bao nhiêu giá trị nguyên của m để hàm số y f x đạt cực tiểu tại x  0 ? A. 6 B. 7 C. 5 D. 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 4. Tìm m để hàm số có n cực trị
Câu 62. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để hàm số
y  m   4
x  m   2 1 2
3 x 1 không có cực đại?
A. 1  m  3
B. m 1
C. m  1
D. 1  m  3
Câu 63. (MĐ 104 BGD&DT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 3 2 3
y x  3mx  4m có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với
O là gốc tọa độ. 1 1
A. m  0 B. m   ; m 4 2 4 2 C. m  1  ; m 1 D. m 1
Câu 64. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tìm tất cả các giá trị của 3 x
tham số m để hàm số 2 y  
mx  2mx  1 có hai điểm cực trị. 3 m  2
A. 0  m  2. B. m  2 . C. m  0 . D.  . m  0 
Câu 65. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  3x  2mx m có cực đại và cực tiểu? 3 3 3 3 A. m  . B. m   . C. m  . D. m  . 2 2 2 2
Câu 66. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Tập hợp các giá trị của m để hàm 1 số 3 2 y
x mx  m  2 x 1 có hai cực trị là: 3 A.  ;    1  2;  B.  ;   
1  2;  C.  1  ; 2 D. 1; 2
Câu 67. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hàm số 4 2
y mx x 1. Tập hợp
các số thực m để hàm số đã cho có đúng một điểm cực trị là A. 0;   . B. ;0 . C. 0;   . D. ;0 .
Câu 68. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho hàm số 4 2
y mx  (2m 1)x 1.
Tìm tất cả các giá trị thực của tham số m để hàm số có đúng một điểm cực tiểu. 1 1
A. Không tồn tại m . B. m  0. C. m   . D.   m  0. 2 2
Câu 69. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số m để hàm số 4
y x   2
m m   2 2
6 x m 1 có ba điểm cực trị. A. 6 . B. 5 . C. 4 . D. 3 .
Câu 70. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số 4
y mx  m   2
1 x 1 2m có một điểm cực trị khi
A. 0  m  1.
B. m  0  m  1. C. m  0 .
D. m  0  m  1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 71. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Có tất cả bao nhiêu giá
trị nguyên của m trên miền  1  0;10 để hàm số 4 y x   m   2 2 2
1 x  7 có ba điểm cực trị? A. 20 B. 10 C. Vô số D. 11
Câu 72. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số 4
y mx   2 m   2 6 x  4
. Có bao nhiêu số nguyên m để hàm số có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại ? A. 4 B. 3 C. 2 D. 5
Câu 73. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Tìm tất cả các giá trị thực của
tham số m để hàm số 4
y mx  m   2
1 x 1 2m có một cực trị. A. m 1 B. m  0
C. 0  m  1
D. m  0  m  1
Dạng 5. Đường thẳng đi qua 2 điểm cực trị
Câu 74. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị thực của tham số m để đường thẳng
d : y  2m  
1 x  3  m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 3 3 1 1 A. m B. m C. m   D. m  2 4 2 4
Câu 75. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Đồ thị hàm số y  3 x  2
3x  9x  1 có hai cực trị A và B
. Điểm nào dưới đây thuộc đường thẳng AB ?
A. M 0; 1
B. N 1; 10
C. P 1; 0
D. Q 1;10
Câu 76. (MĐ 105 BGD&ĐT NĂM 2017) Đồ thị của hàm số y   3 x  2
3x  5 có hai điểm cực trị A và
B . Tính diện tích S của tam giác OAB với O là gốc tọa độ. 10
A. S  5 B. S
C. S  10 D. S  9 3
Câu 77. Đồ thị của hàm số 3 2
y x  3x  9x 1 có hai điểm cực trị A và B . Điểm nào dưới đây thuộc đường thẳng AB .
A. P 1;0 .
B. M 0;   1 . C. N 1; 1  0 . D. Q  1  ;10 .
Câu 78. (THPT Xuân Hòa-Vĩnh Phúc- Lần 1- 2018- BTN) Biết đồ thị hàm số 3
y x  3x 1 có hai điểm
cực trị A , B . Khi đó phương trình đường thẳng AB là
A. y  2x 1.
B. y  2x  1.
C. y  x  2.
D. y x  2 .
Câu 79. (Lương Văn Chánh - Phú Yên – 2017 - 2018 - BTN) Tìm giá trị thực của tham số m để đường
thẳng d : y  3m  
1 x  3  m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 1 1 1 1 A. . B.  . C. m  . D.  . 3 6 6 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 80. (THPT CHUYÊN VĨNH PHÚC - LẦN 1 - 2017 - 2018 - BTN) Tìm tất cả các giá trị của tham
số m để đồ thị hàm số 3 2
y x  2x  m  
3 x m có hai điểm cực trị và điểm M 9;  5 nằm trên
đường thẳng đi qua hai điểm cực trị của đồ thị. A. m  1  . B. m  5  .
C. m  3.
D. m  2.
Câu 81. (PTNK Cơ Sở 2 - TPHCM - 2017 - 2018 - BTN) Tìm giá trị thực của tham số m để đường thẳng
y  2m  
1 x m  3 song song với đường thẳng đi qua các điểm cực trị của đồ thị hàm số 3 2
y x  3x 1 3 1 3 1 A. m  . B. m  . C. m   . D. m   . 4 2 4 2
Câu 82. (TT Tân Hồng Phong - 2018 - BTN) Tìm tổng tất cả các giá trị thực của tham số m sao cho
đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y x  m   2 2 3
1 x  6m 1 2mx song
song đường thẳng y  4x . 1 2 2 A. m   . B. m  . C. m   . D. m  1. 3 3 3
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước
Câu 83. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Gọi S là tập hợp tất cả các giá trị thực của tham số 1
m để đồ thị của hàm số 3 2 y
x mx   2 m  
1 x có hai điểm cực trị A và B sao cho , A B nằm 3
khác phía và cách đều đường thẳng d : y  5x  9 . Tính tổng tất cả các phần tử của S . A. 3 B. 6 C. 6  D. 0
Câu 84. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số 1 3 y
mx  m   2
1 x  3m  2 x  2018 với m là tham số. Tổng bình phương tất cả các giá trị 3
của m để hàm số có hai điểm cực trị x ; x thỏa mãn x  2x  1 bằng 1 2 1 2 40 22 25 8 A. B. C. D. 9 9 4 3
Câu 85. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm tất cả cả các giá trị của tham số m để 3 2
y  x  3x  mx 1 đạt cực trị tại x , x thỏa mãn 2 2
x x  6 1 2 1 2 A. m  3  B. m  3 C. m  1  D. m 1
Câu 86. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2
y x x   2 m   2 8
11 x  2m  2
có hai điểm cực trị nằm về hai phía của trục Ox . A. 4. B. 5. C. 6. D. 7. Câu 87. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho hàm số 3
y x   m   2 2
1 x  m  
1 x m  1 . Có bao nhiêu giá trị của số tự nhiên m  20 để đồ thị hàm
số có hai điểm cực trị nằm về hai phía trục hoành?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 18 . B. 19 . C. 21. D. 20 .
Câu 88. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số 3
y x  m   2 x   2 m   2 1
2 x m  3 có hai điểm cực trị và hai điểm cực trị đó
nằm về hai phía khác nhau đối với trục hoành? A. 2 . B. 1. C. 3 . D. 4 .
Câu 89. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số 3
y x  m   2 2 3
1 x  6m  2x 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm
số có điểm cực đại và điểm cực tiểu nằm trong khoảng 2;  3 .
A. m  1; 
3 3; 4 . B. m  1;  3 .
C. m  3; 4 .
D. m  1; 4 .
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Tổng tất cả các giá trị
thực của tham số m để hàm số: 3
y x  m   2 3 2
1 x  3mx m  5 có hai điểm cực trị x ; x đồng 1 2
thời y x .y x  0 là: 1   2  A. 21 B. 3  9 C. 8  D. 3 11 13
Câu 91. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Gọi S là tập các giá trị dương của
tham số m sao cho hàm số 3 2
y x  3mx  27x  3m  2 đạt cực trị tại x , x thỏa mãn x x  5 1 2 1 2 . Biết S   ;
a b . Tính T  2b a .
A. T  51  6
B. T  61  3
C. T  61  3
D. T  51  6
Câu 92. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Gọi S là tập hợp các giá trị nguyên của 3 x
tham số m để hàm số 2 y
 2x mx  3 có hai điểm cực trị x , x  4 . Số phần tử của S bằng 3 1 2 A. 5 . B. 3 . C. 2 . D. 4 .
Câu 93. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Tìm giá trị thực của tham số m để hàm số 3
y x  m  2 4
2 x 7x 1 có hai điểm cực trị x ; x x x thỏa mãn x x  4  1 2  1 2 1 2 1 7
A. m  5 . B. m  .
C. m  3 . D. m  . 2 2
Câu 94. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Có bao nhiêu giá trị nguyên của tham số m để điểm 3
M (2m ; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số 3 2
y  2x  3(2m 1)x  6m(m 1)x 1 (C) một tam giác có diện tích nhỏ nhất? A. 0 B. 1 C. 2 D. không tồn tại
Câu 95. (HSG BẮC NINH NĂM 2018-2019) Tìm tất cả các giá trị thực của tham số thực m để đường
thẳng đi qua hai điểm cực đại, cực tiểu của đồ thị hàm số 3
y x  3mx  2 cắt đường tròn C  có tâm I 1 
;1 , bán kính bằng 1 tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB đạt giá trị lớn nhất.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2  3 2  3 1 3 2  5 A. m B. m C. m D. m  3 2 2 2
Câu 96. (ĐỀ 04 VTED NĂM 2018-2019) Biết đồ thị hàm số 3 2
y x ax bx c có hai điểm cưc trị
M x ; y , N x ; y thỏa mãn x y y y x x . Giá trị nhỏ nhất của biểu thức 1  1 2  1  1 2  1 1   2 2 
P abc  2ab  3c bằng 49 25 841 7 A. B. C. D.  4 4 36 6
Dạng 7. Tam giác cực trị
Câu 97. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 4 2
y x  2mx 1 có ba điểm cực trị tạo thành một tam giác vuông cân 1 1 A. m  .
B. m  1. C. m   . D. m  1. 3 9 3 9
Câu 98. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y  4 x  2
2mx có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1 .
A. 0  m  1
B. m  0 C. m  3 0 4
D. m  1
Câu 99. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị của tham
số m để đồ thị hàm số 4
y x  m   2 2 2
1 x m có ba điểm cực trị tạo thành ba đỉnh của một tam
giác vuông. Số phần tử của tập hợp S là A. 2 . B. 0 . C. 4 . D. 1 .
Câu 100. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho hàm số 4 2
y x  2mx 1   1 . Tổng
lập phương các giá trị của tham số m để đồ thị hàm số  
1 có ba điểm cực trị và đường tròn đi qua
3 điểm này có bán kính R  1 bằng 5  5 1 5 A. . B. . C. 2  5 . D. 1   5 . 2 2
Câu 101. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2 2
y x  2m x m  4 có ba điểm cực trị tạo thành ba đỉnh của một tam giác đều?
A. m 0; 3;  3 B. m  6 6
0; 3;  3 C. m6 6 3;   3
D. m  3;  3
Câu 102. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Tìm m để đồ thị hàm số 4 2 2
y x  2m x  1 có 3 điểm cực trị lập thành một tam giác vuông cân. A. m  1. B. m  1   ;1 . C. m  1;  0  ;1 . D. m   .
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 103. (ĐỀ THAM KHẢO BGD & ĐT 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 7 điểm cực trị? A. 5 B. 6 C. 4 D. 3
Câu 104. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Biết phương trình 3 2
ax bx cx d  0
a  0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số 3 2
y ax bx cx d có bao nhiêu điểm cực trị? A. 4 . B. 5 . C. 2 . D. 3 .
Câu 105. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số
m để đồ thị hàm số 4 2 2
y x  2mx  2m m 12 có bảy điểm cực trị A. 1. B. 4 . C. 0 . D. 2 .
Câu 106. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số y   x   x  2 1 2 là A. 2 B. 2 C. 3 D. 4
Câu 107. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y f x có bảng biến thiên như sau
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 4 B. 2 C. 5 D. 3
Câu 108. (KTNL GIA BÌNH NĂM 2018-2019) Cho hàm số y f (x) có bảng biến thiên như sau.
Hàm số y f x  3  có bao nhiêu điểm cực trị A. 5 B. 6 C. 3 D. 1
Câu 109. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y f (x) xác định, liên tục
trên  và có bảng biến thiên như sau:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5
Câu 110. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên như sau
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 5 B. 3 C. 4 D. 2 Câu 111. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số a   0,d  2019  f x 3 2
ax bx cx d (a, ,
b c, d  ) và 
. Số cực trị của hàm số a
 b c d 2019  0 
y g x ( với g x  f x 2019) bằng A. 2 . B. 5 . C. 3 . D. 1.
Câu 112. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Có bao nhiêu giá trị
nguyên của tham số m để hàm số 4 3 2 2
y  3x  4x 12x m có đúng 5 điểm cực trị? A. 5 . B. 7 . C. 6 . D. 4 .
Câu 113. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số y   x   x  2 1 2 là A. 2 B. 2 C. 3 D. 4
Câu 114. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Có bao nhiêu giá trị nguyên dương
của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 5 điểm cực trị. A. 16 B. 44 C. 26 D. 27
Câu 115. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số 4 2
y x  2mx  2m 1 với m là tham số thực. Số giá trị nguyên trong khoảng 2; 2 của m để
hàm số đã cho có 3 điểm cực trị là A. 2 B. 4 C. 3 D. 1
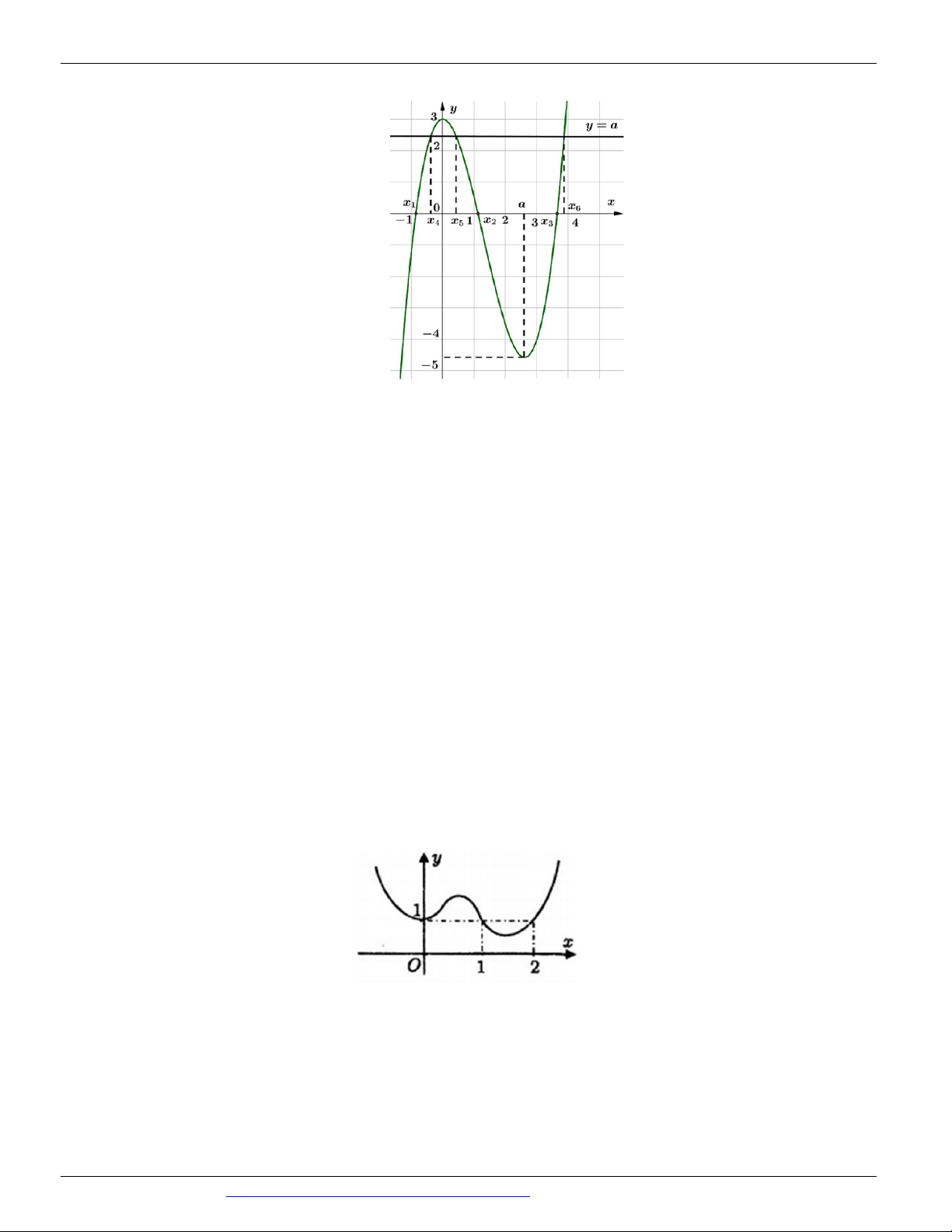
Câu 116. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số y f x có đồ
thị như hình vẽ bên dưới
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Tìm tất cả các giá trị của tham số m để đồ thị hàm số h x 2
f x  2 f x  2m có đúng 3 điểm cực trị. A. m  1 B. m  1 C. m  2
D. m  2
Câu 117. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Tập hợp các giá trị của m để hàm số 4 3 2
y  3x  4x 12x m 1 có 7 điểm cực trị là: A. (0; 6) B. (6; 33) C. (1;33) D. (1; 6)
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x)
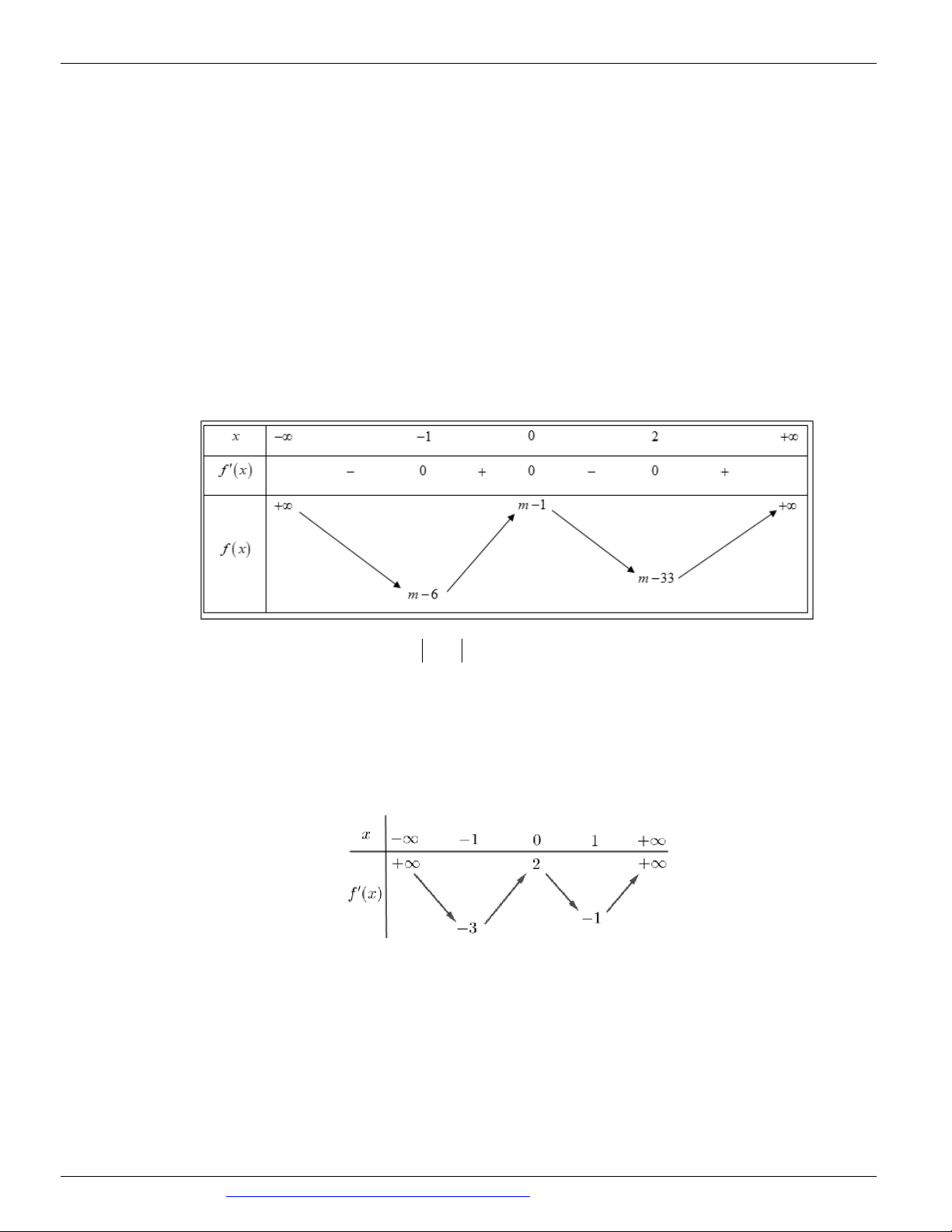
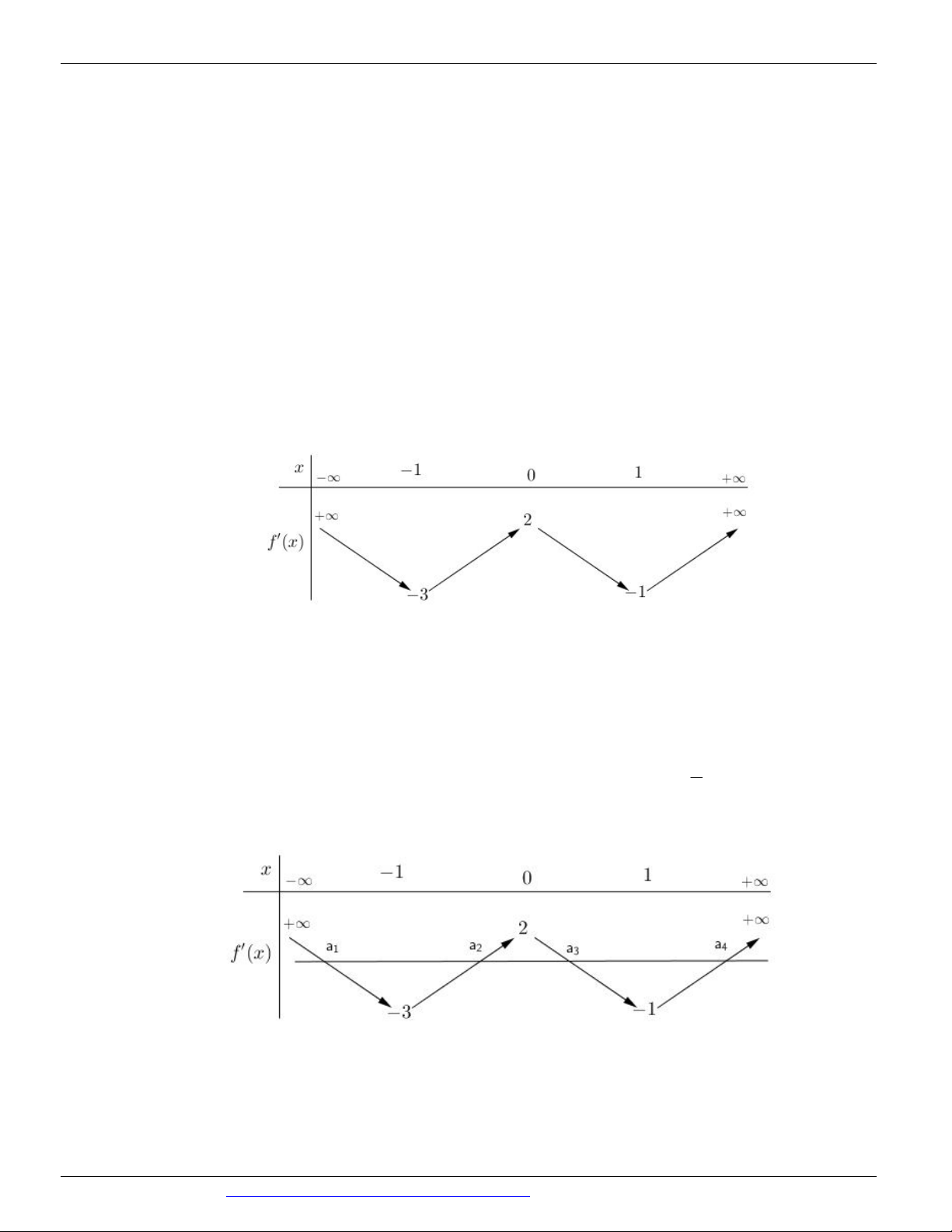
Câu 118. (Mã đề 101 - BGD - 2019) Cho hàm số y f x , bảng biến thiên của hàm số f ' x như sau:
Số điểm cực trị của hàm số y f  2
x  2x là A. 9. B. 3. C. 7. D. 5.
Câu 119. (Mã đề 104 - BGD - 2019) Cho hàm số f x , bảng biến thiên của hàm số f  x như sau:
Số điểm cực trị của hàm số y f  2
4x  4x là A. 5. B. 9. C. 7. D. 3. f x f ' x
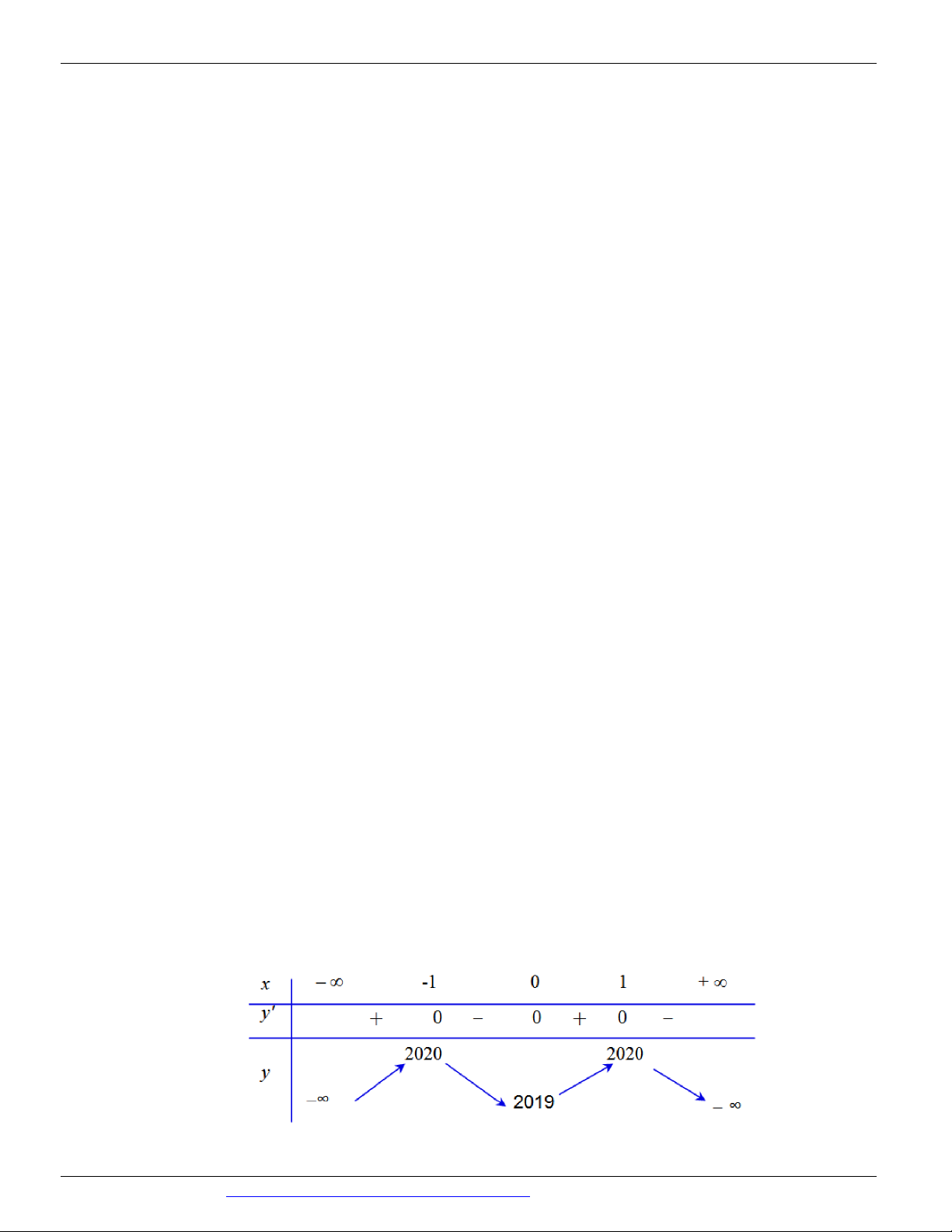
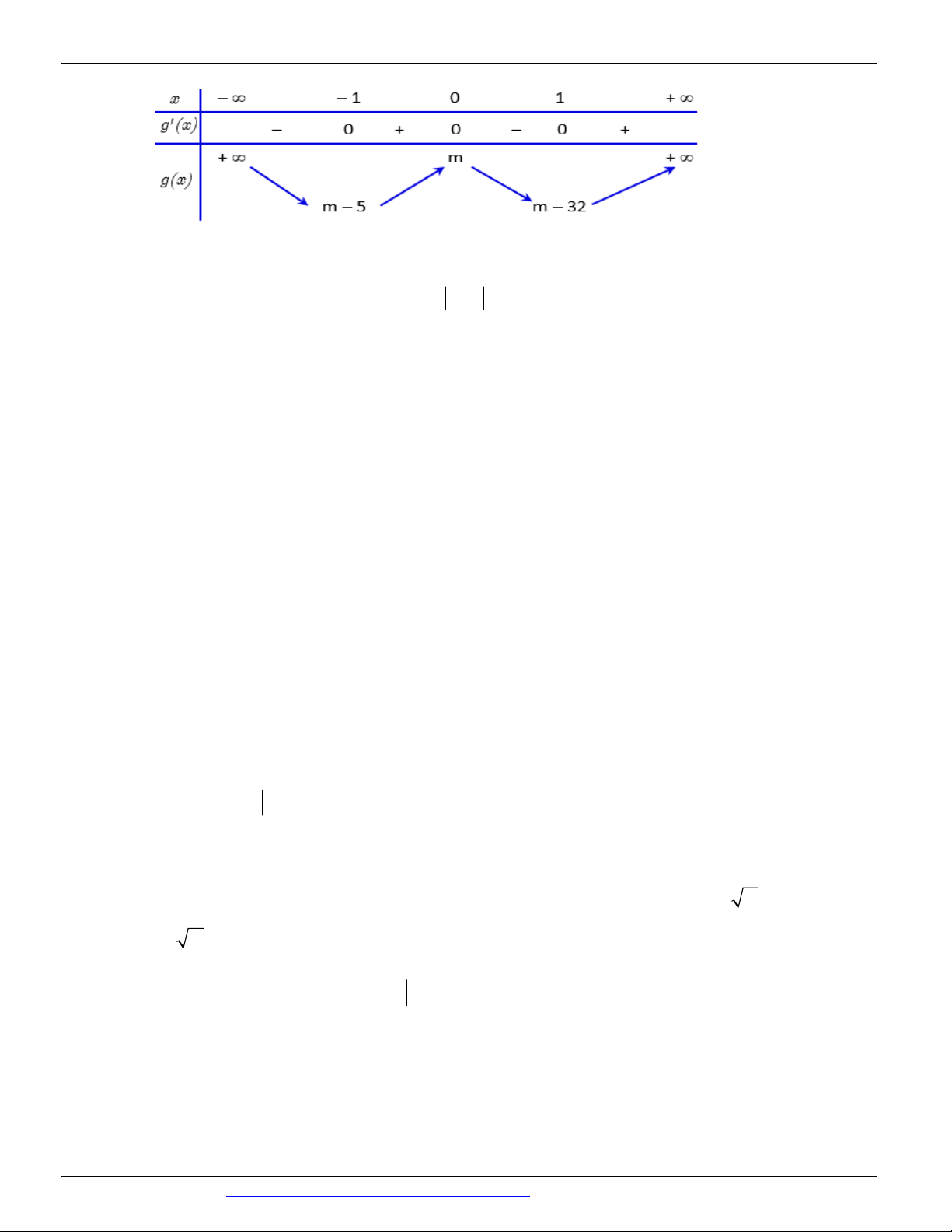
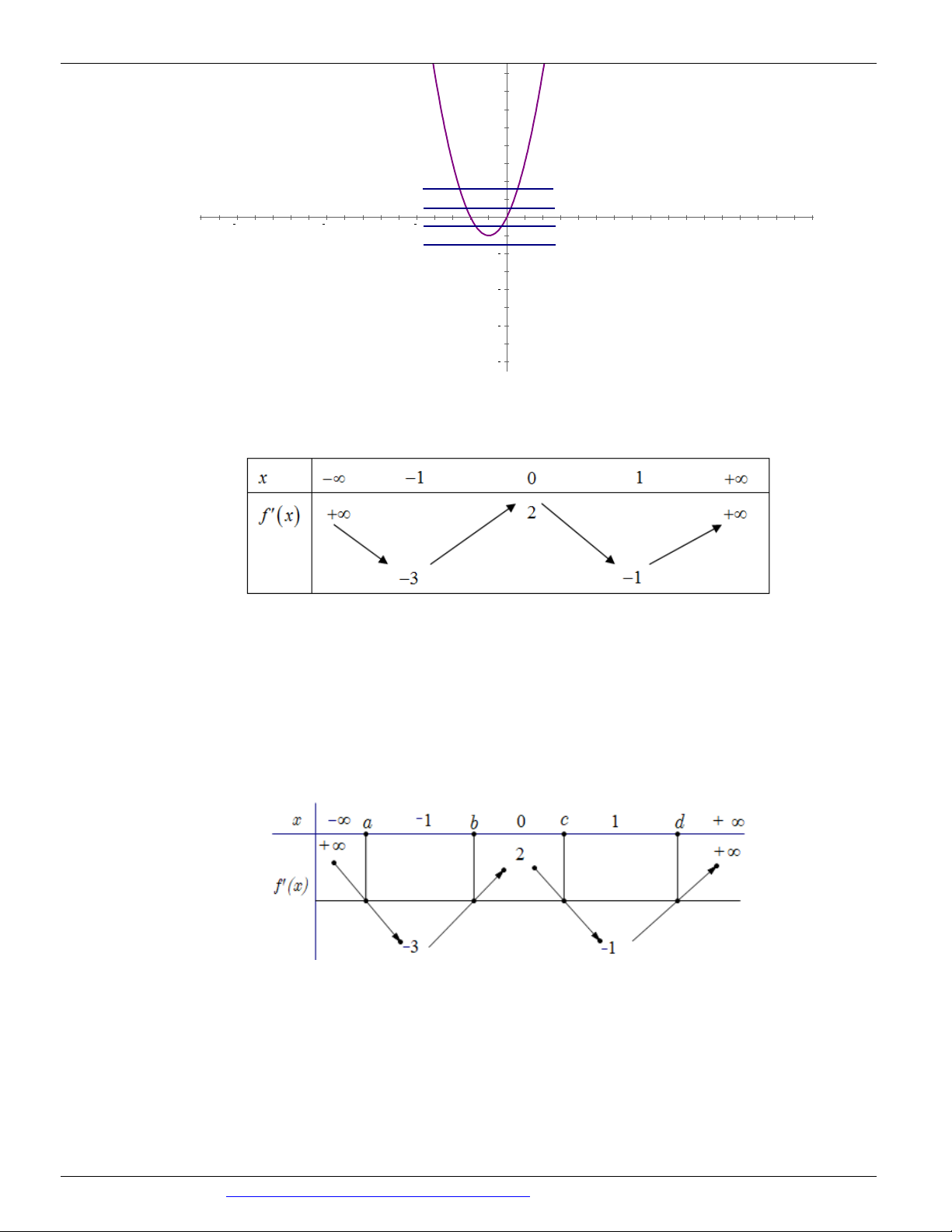
Câu 120. (Mã 102 - BGD - 2019) Cho hàm số
, bảng biến thiên của hàm số như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
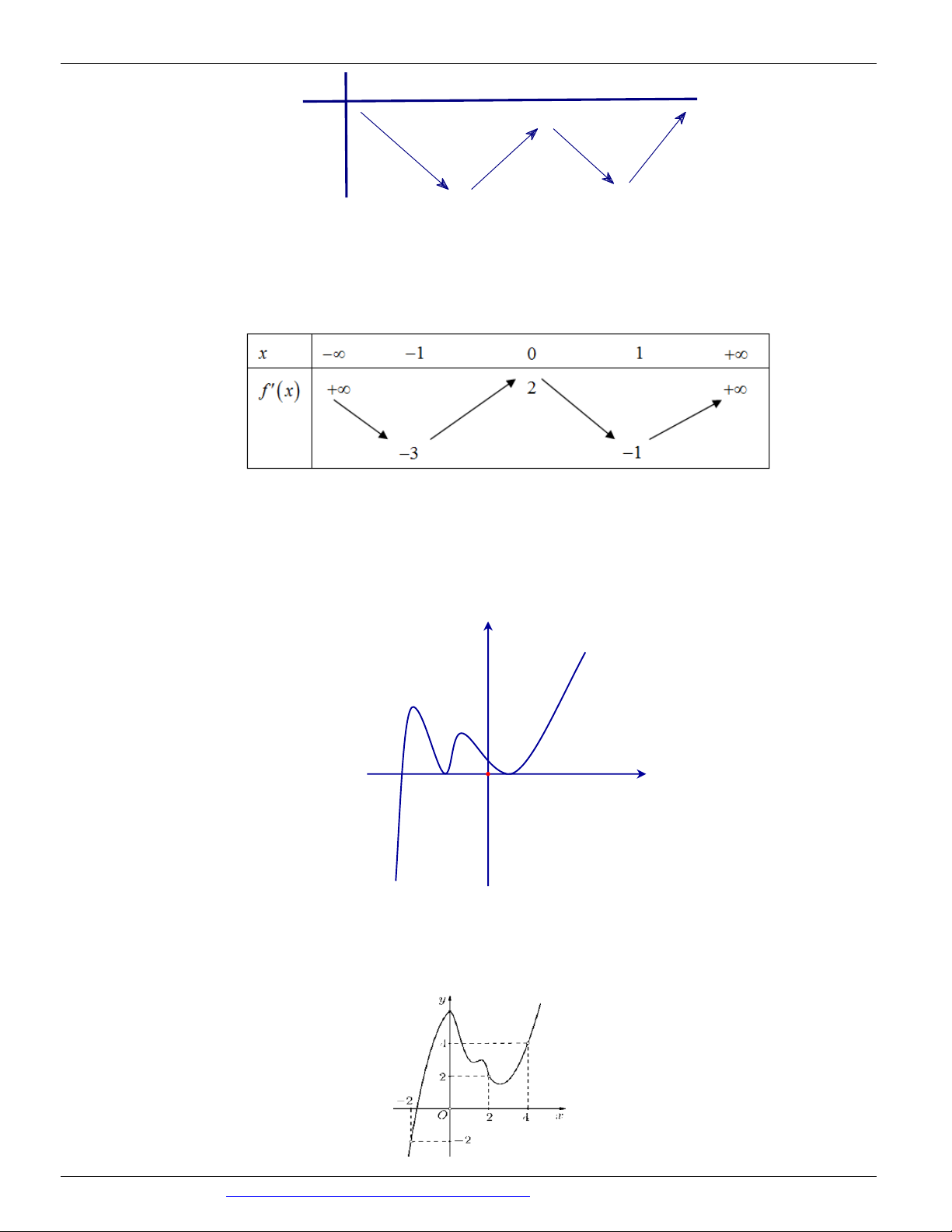
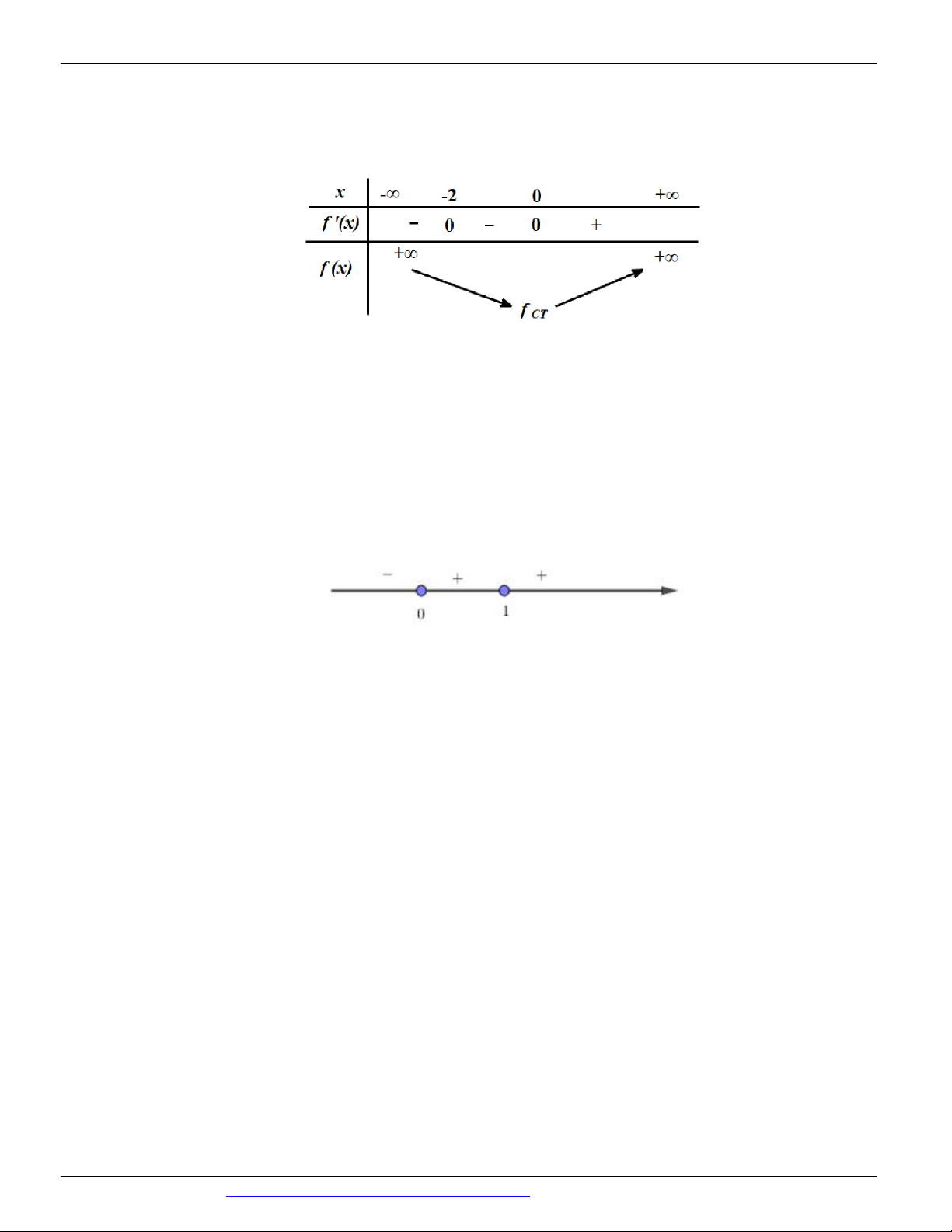
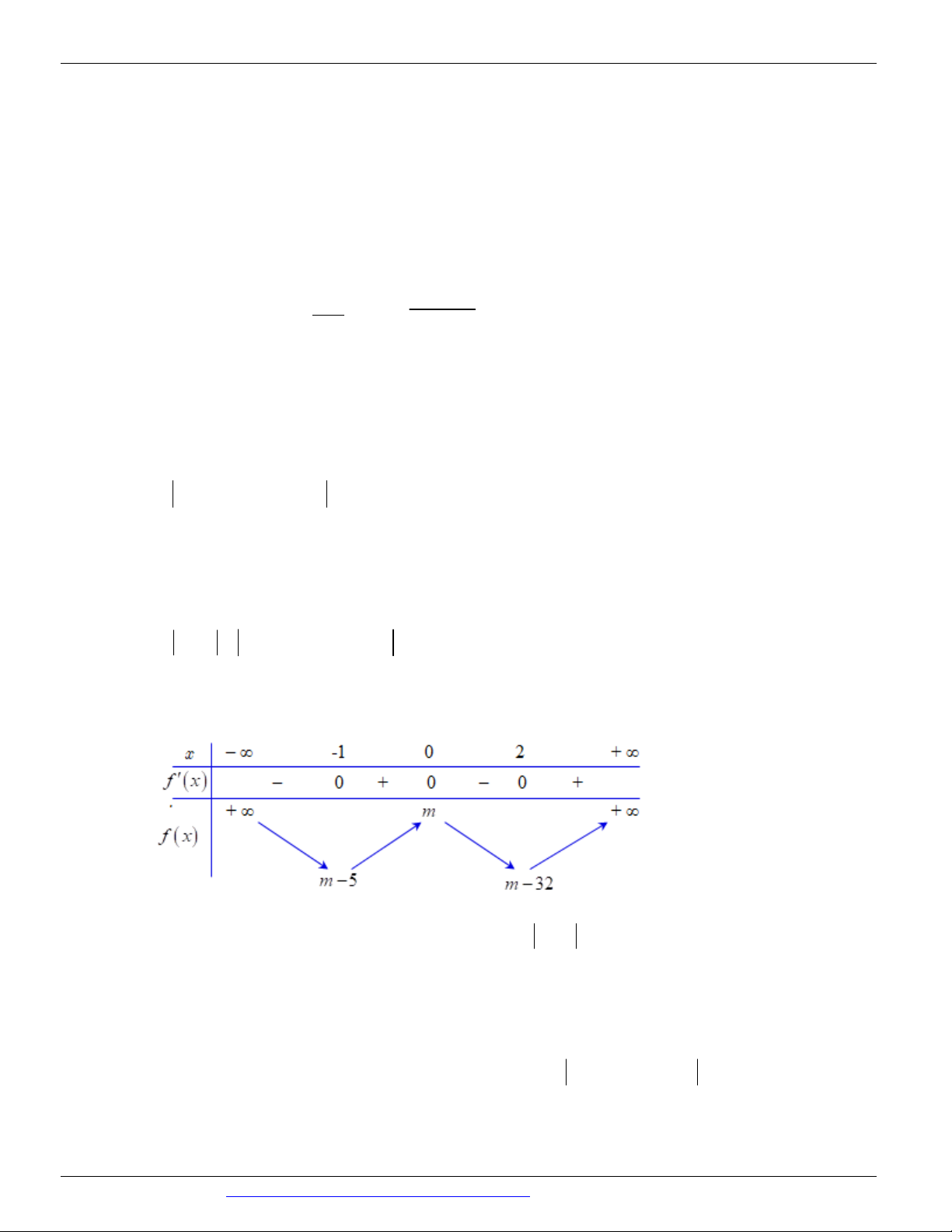
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x -∞ -1 0 1 +∞ +∞ 2 +∞ f'(x) -1 -3
Số điểm cực trị của hàm số y f  2
x  2x là A. 9. B. 5. C. 7 . D. 3.
Câu 121. (Mã 103 - BGD - 2019) Cho hàm số f x , bảng biến thiên của hàm số f  x như sau:
Số cực trị của hàm số y f  2
4x  4x là A. 3 . B. 9 . C. 5 . D. 7 .
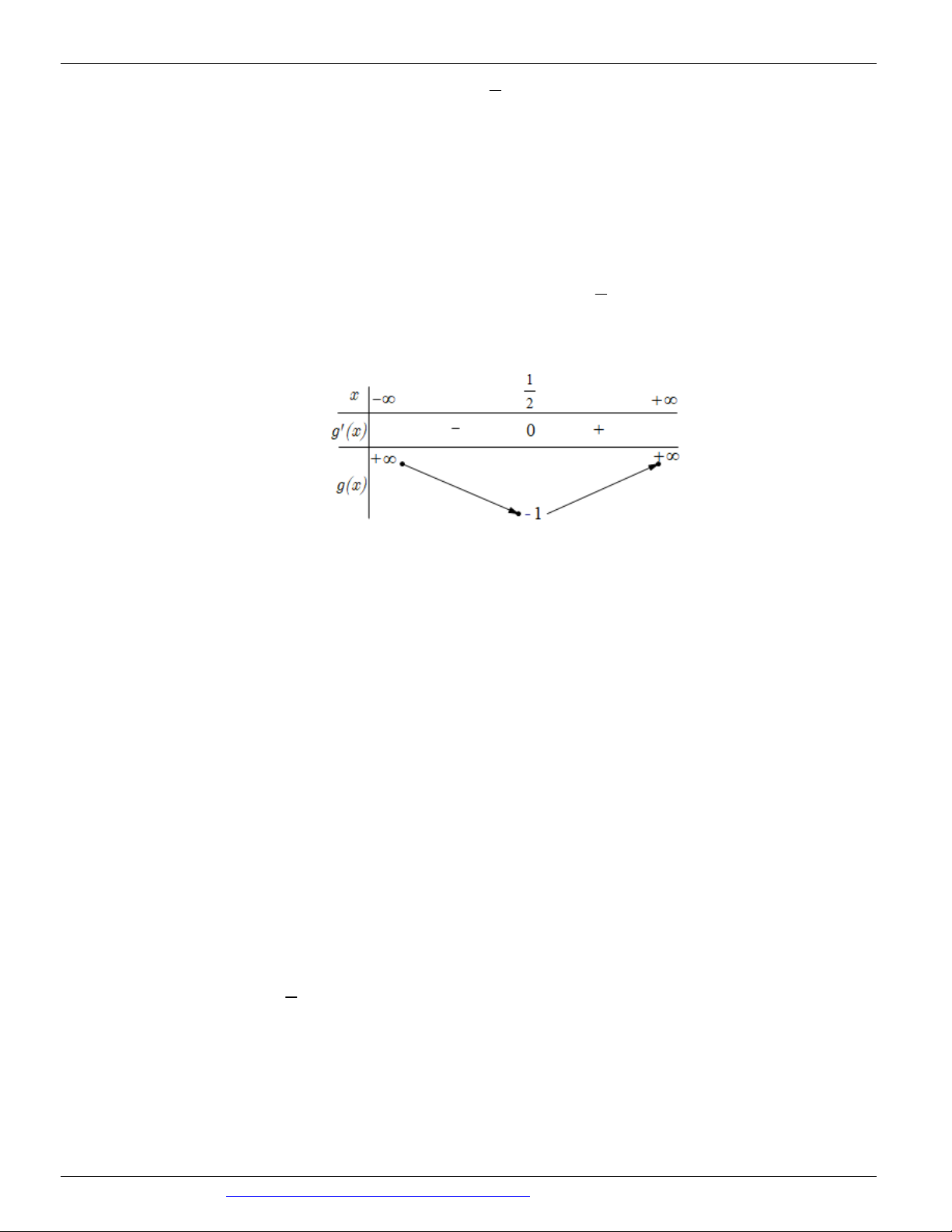
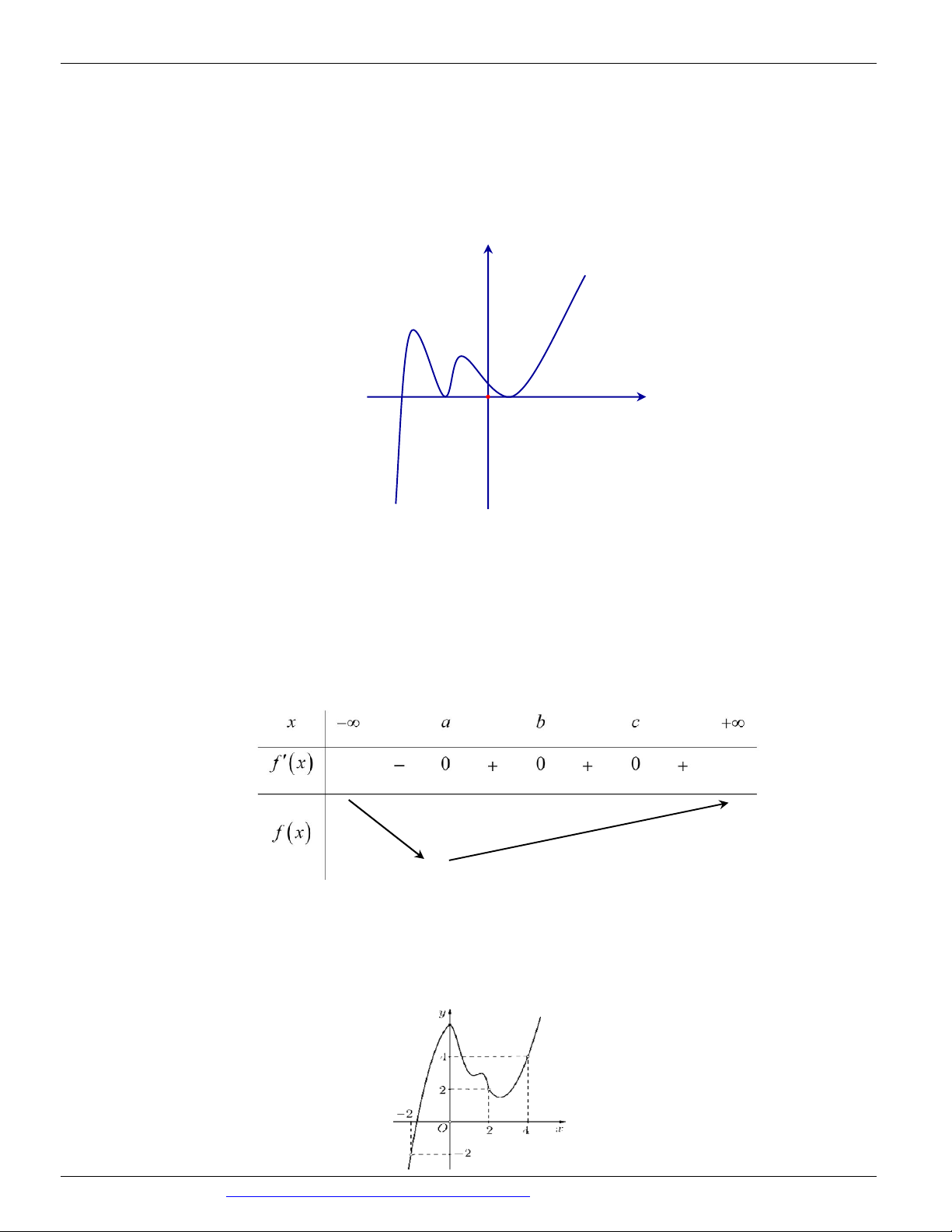
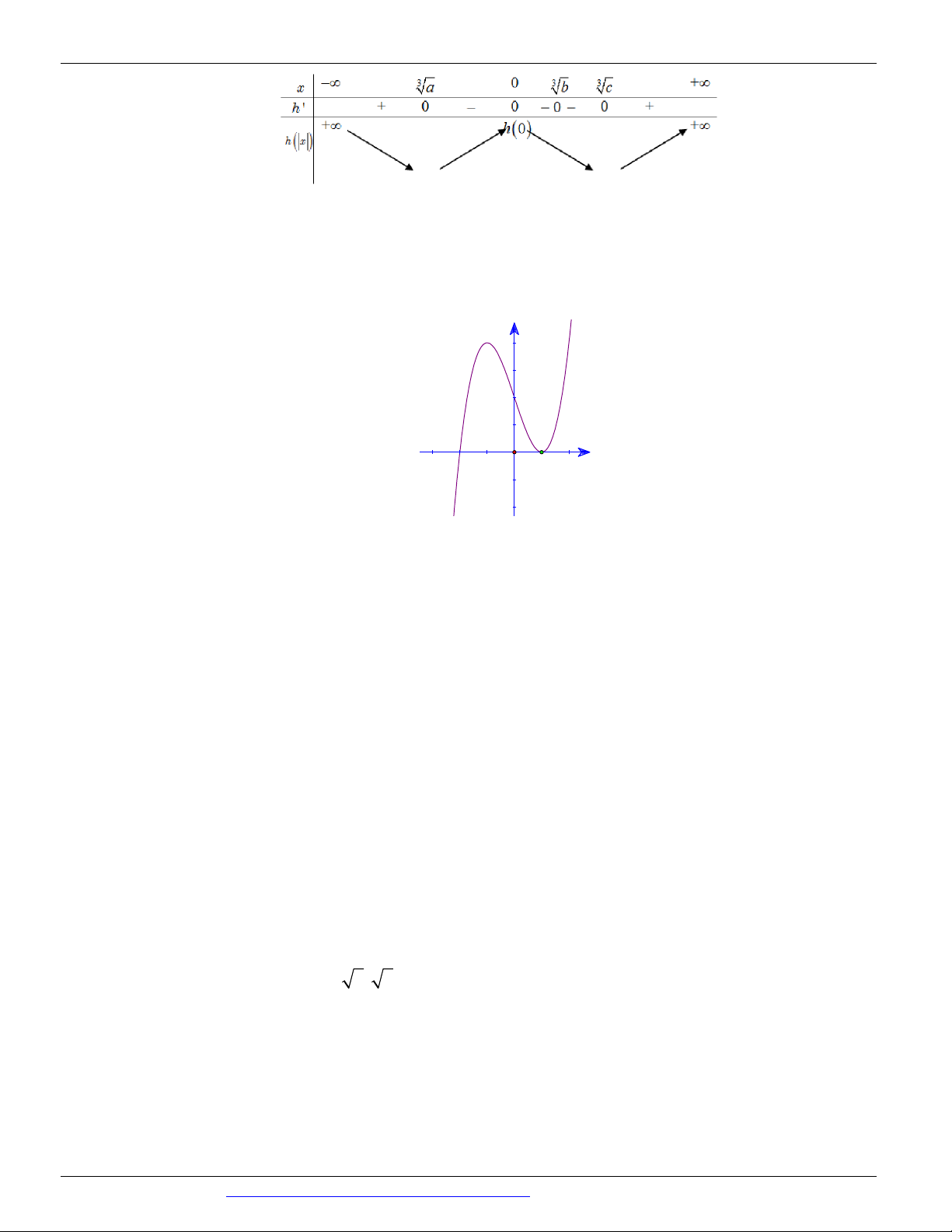
Câu 122. Cho hàm số y f x xác định trên  và có đồ thị hàm số y f  x là đường cong ở hình vẽ.
Hỏi hàm số y f x có bao nhiêu điểm cực trị? y a O c b x A. 2 . B. 3 . C. 4 . D. 1.
Câu 123. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số y f x có đồ thị
y f  x như hình vẽ sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đồ thị hàm số g x  f x 2 2
x có tối đa bao nhiêu điểm cực trị? A. 7 B. 5 C. 6 D. 3
Câu 124. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số f (x) xác định trên  và có
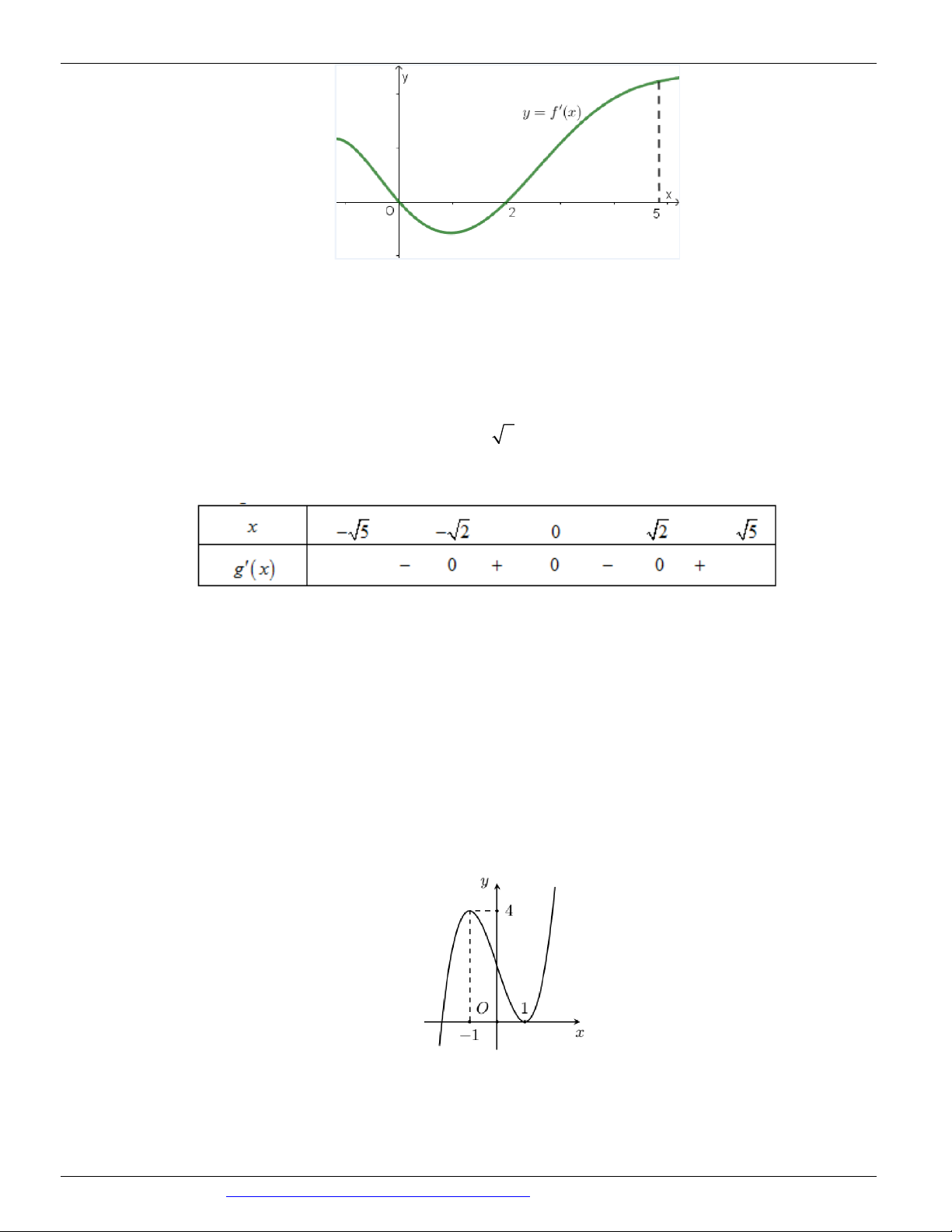
đồ thị f (x) như hình vẽ bên. Đặt g(x)  f (x)  x . Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây? 3  1  A.  ;3    B.  2  ;  0 C. 0;  1 D.  ;2 2  2 
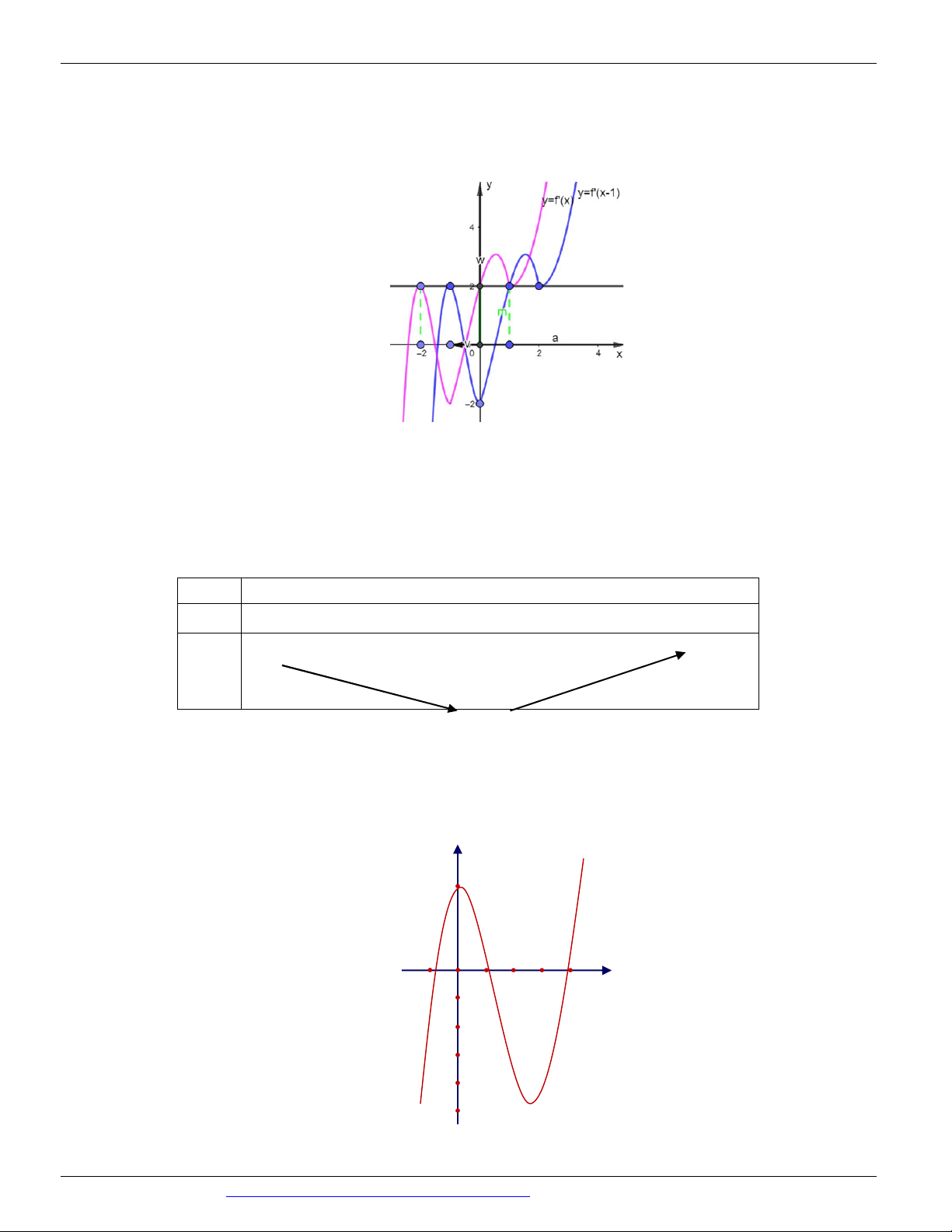
Câu 125. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số y f (
x 1) có đồ thị như hình vẽ. Hàm số
2 f x 4x y   
đạt cực tiểu tại điểm nào? A. x  1 . B. x  0 . C. x  2 . D. x  1 .
Câu 126. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số
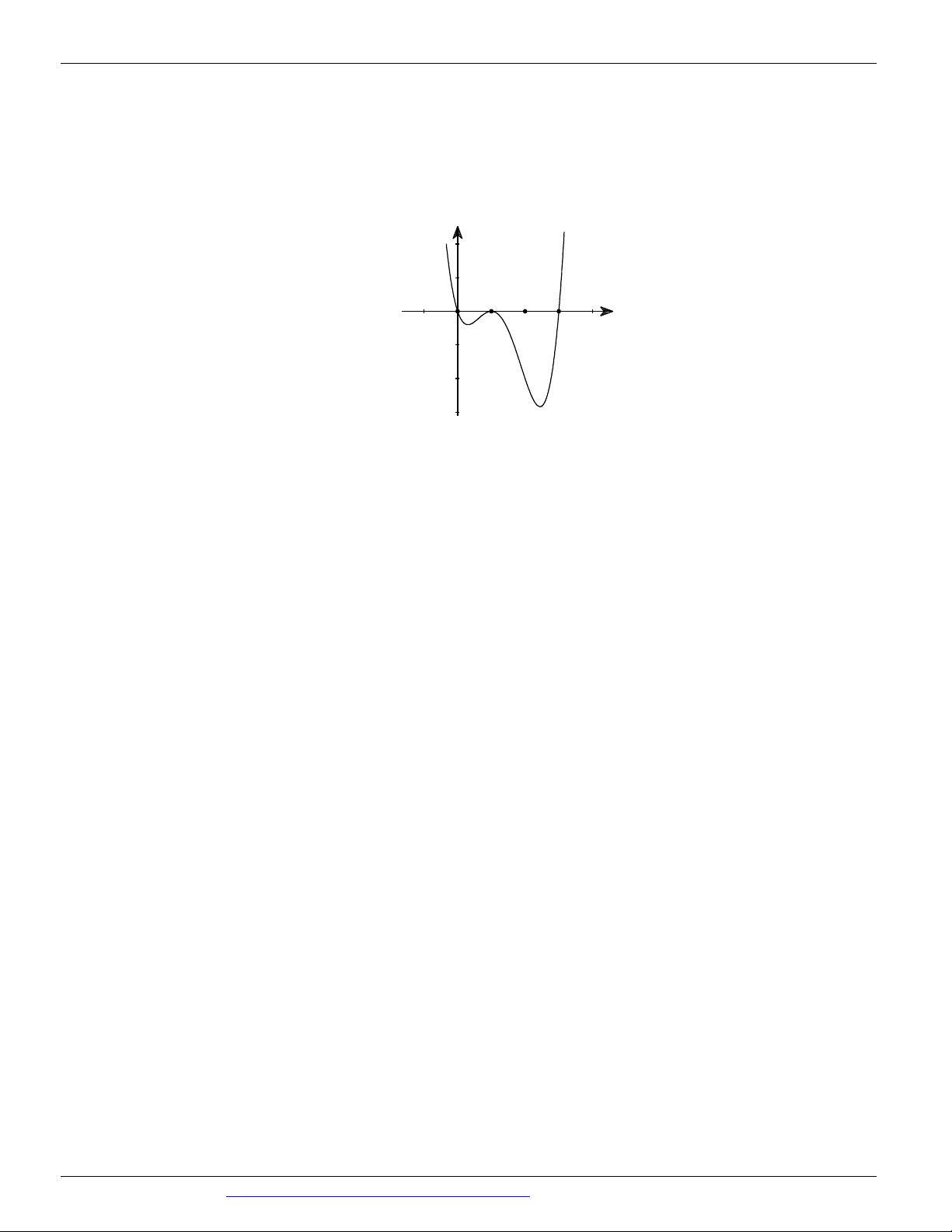
y f x có đạo hàm trên  và có đồ thị là đường cong như hình vẽ. Đặt g x  3 f f x  4 .
Tìm số điểm cực trị của hàm số g x? y 3 1  1 2 3 4 O x A. 2 . B. 8 . C. 10 . D. 6 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 127. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y f x xác
định và liên tục trên  , đồ thị của hàm số y f  x như hình vẽ. Điểm cực đại của hàm số
g x  f x  x là A. x  0 . B. x  1 . C. x  2 .
D. không có điểm cưc đại.
Câu 128. Cho hàm số y f x có đạo hàm liên tục trên  và có đồ thị hàm số y f  x như hình vẽ. Đặt     3 g x f
x  . Tìm số điểm cực trị của hàm số y g x . y a b c O x A. 3 B. 5 C. 4 D. 2
Câu 129. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số y f x xác định trên 
và hàm số y f x có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số y f  2 x   3 . y 2 1 x -2 O A. 4 B. 2 C. 5 D. 3
Câu 130. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo
hàm là f  x . Đồ thị của hàm số y f  x như hình vẽ bên. Tính số điểm cực trị của hàm số   2 y
f x  trên khoảng  5; 5 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 2 . B. 4 . C. 3 . D. 5 .
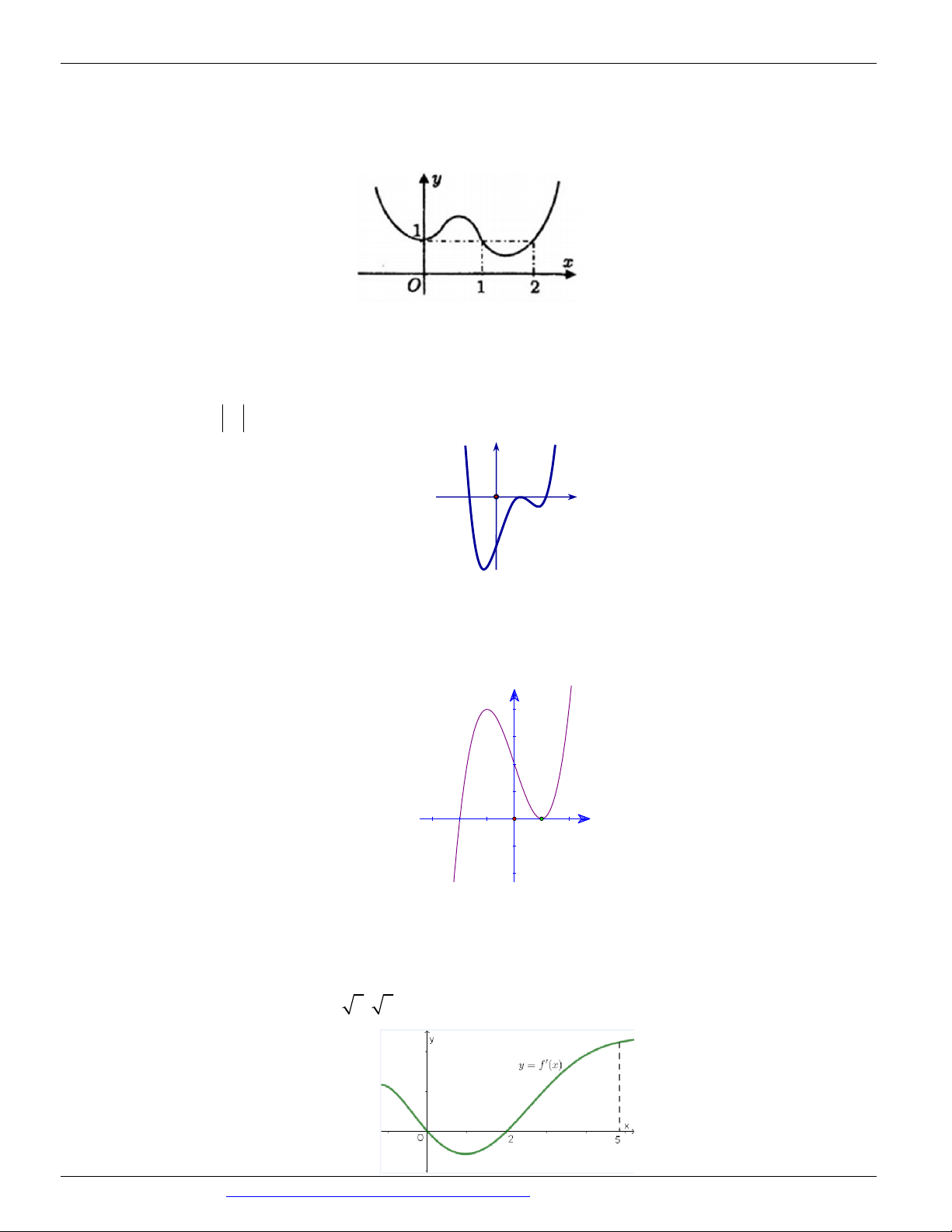
Câu 131. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hàm số y  f x  có đạo hàm liên
tục trên và đồ thị hàm số y  f 'x như hình vẽ bên.
Số điểm cực trị của hàm số y  f x  2017  2018x  2019 là. A. 3 B. 4 C. 1 D. 2
Câu 132. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số y f ( x) . Hàm số
y f (x) có đồ thị như hình vẽ dưới đây. y x 0 1 2 3
Tìm m để hàm số 2
y f (x m) có 3 điểm cực trị.
A. m  3;  .
B. m 0;  3 .
C. m 0;  3 .
D. m   ;  0 .
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó Câu 1.
(MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y f x có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x  5
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại x  2
D. Hàm số không có cực đại Lời giải Chọn.C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào bảng biến thiên. Hàm số có đạo hàm trên  và y2  0; y đổi dấu từ âm sang dương
khi đi qua x  2 nên hàm số đạt cực tiểu tại x  2 . Câu 2.
(ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Lời giải Chọn A
Dựa bào BBT ta có: Giá trị cực đại của hàm số là y  5 CD Câu 3.
(Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 2 D. 0 Lời giải Chọn A
Hàm số có ba điểm cực trị. Câu 4.
(MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y f x có bảng biến thiên như sau
Tìm giá trị cực đại y
và giá trị cực tiểu y
của hàm số đã cho. CĐ CT
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. y  2 và y  0 B. y  3 và y  0 CĐ CT CĐ CT C. y  3 và y  2  D. y  2  và y  2 CĐ CT CĐ CT Lời giải Chọn B
Dựa vào bảng biến thiên của hàm số ta có y  3 và y  0 . CĐ CT Câu 5.
(Mã 103 - BGD - 2019) Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số đạt cực đại tại: A. x  2  .
B. x  3 .
C. x  1 . D. x  2 . Lời giải Chọn C
Hàm số f x xác định tại x  1, f '(1)  0 và đạo hàm đổi dấu từ () sang () Câu 6.
(MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số 4 2
y ax bx c ( a , b , c   ) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là A. 3 B. 0 C. 1 D. 2 Lời giải Chọn A Câu 7.
(Mã 102 - BGD - 2019) Cho hàm số f x có bảng biến thiên như sau:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Hàm số đạt cực đại tại A. x  2  .
B. x  3 .
C. x  1 . D. x  2 . Lời giải Chọn B Câu 8.
(MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y f (x) có bảng biến thiên như sau
Mệnh đề nào dưới đây sai
A. Hàm số có giá trị cực đại bằng 3
B. Hàm số có hai điểm cực tiểu
C. Hàm số có giá trị cực đại bằng 0
D. Hàm số có ba điểm cực trị Lời giải Chọn C Câu 9.
(Mã đề 104 - BGD - 2019) Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  2 . B. x  2  .
C. x  1 . D. x  3 . Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ bảng biến thiên ta có điểm cực tiểu của hàm số là x  3 .
Câu 10. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số 3 2
y ax bx cx d a, , b ,
c d  có đồ thị
như hình vẽ bên. Số điểm cực trị của hàm số này là A. 3 B. 2 C. 0 D. 1 Lời giải Chọn B
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị.
Câu 11. (Mã đề 104 - BGD - 2019) Cho hàm số y f (x) có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đây? A. (0;1) .
B. (1; ) . C. (1; 0) . D. (0; ) Lời giải Chọn A
Vì trên (0;1) hàm số có đạo hàm mang dấu âm.
Câu 12. (Mã đề 101 - BGD - 2019) Cho hàm số f ( )
x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. x  1 . B. x  3  .
C. x  2 . D. x  1 . Lời giải Chọn A
Theo bảng biến thiên thì hàm số đạt cực tiểu tại điểm x  1
Câu 13. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số 3 2
y ax bx cx d a, , b ,
c d   có đồ thị
như hình vẽ bên. Số điểm cực trị của hàm số đã cho là A. 2 B. 0 C. 3 D. 1 Lời giải Chọn A
Câu 14. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y f x có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A. x  1
B. x  0
C. x  5 D. x  2 Lời giải Chọn D
Dựa vào bảng biến thiên ta thấy y đối dấu từ  sang  tại x  2 .
Nên hàm số đạt cực đại tại điểm x  2 .
Câu 15. Cho hàm số y f x xác định, liên tục trên đoạn  2
 ; 2 và có đồ thị là đường cong trong hình vẽ
bên. Hàm số f x đạt cực đại tại điểm nào dưới đây
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 ? A. x  2  . B. x  1  .
C. x  1.
D. x  2 Lời giải Chọn B
Từ đồ thị ta thấy hàm số đạt cực đại tại x  1  .
Dạng 2. Tìm cực trị của hàm số khi biết y, y’
Câu 16. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị cực đại y của hàm số 3
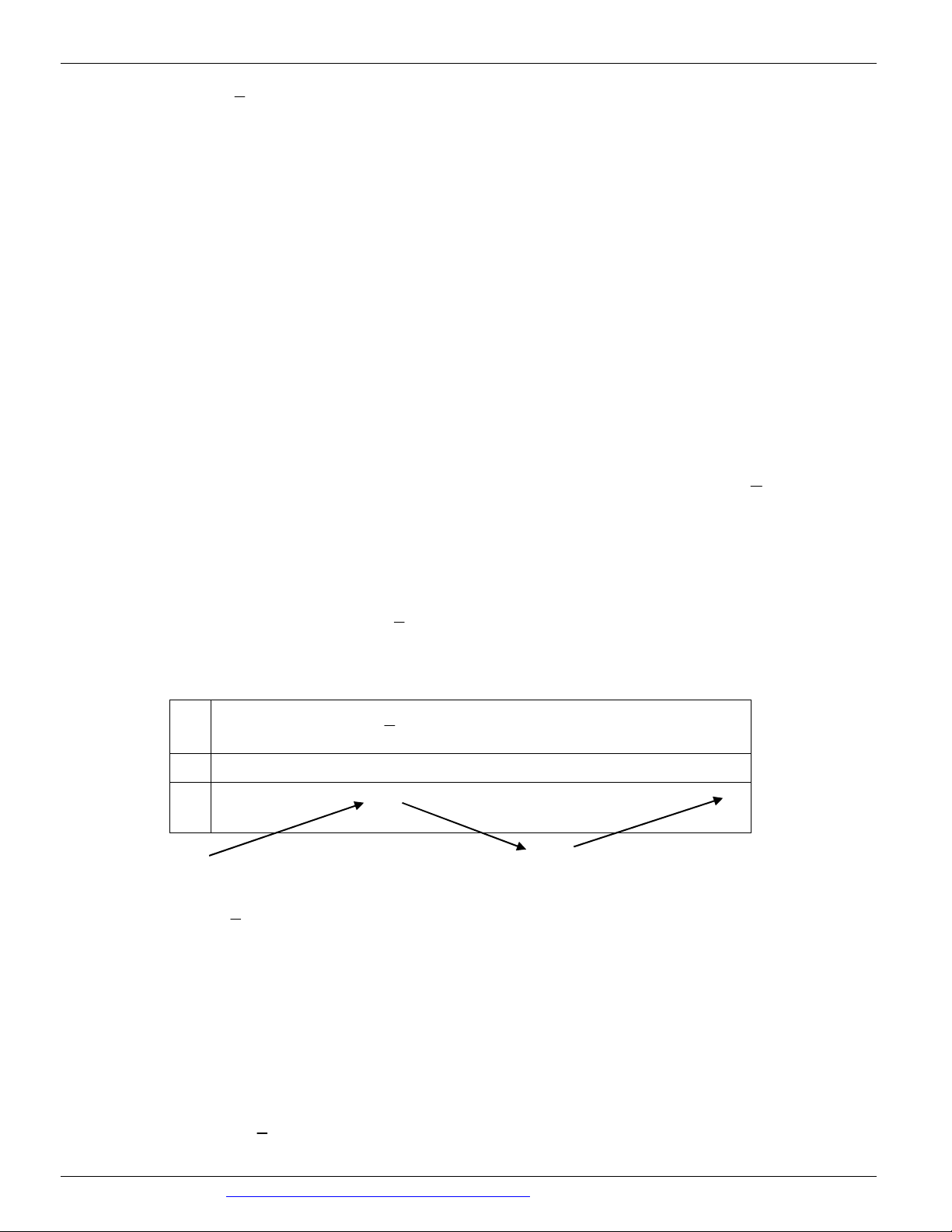
y x  3x  2 . C§ A. y  1 B. y  4 C. y  1 D. y  0 C§ C§ C§ C§ Lời giải Chọn B
x  1  y   1  0 Ta có 2
y  3x  3  y  0 2
 3x  3  0   x  1   y    1  4    3 2  3 2 3  
lim x  3x  2 3  lim x 1    ,  3 3  
lim  x  3x  2  lim x 1      x 2 3 x 2 3  x x x x  x x  Bảng biến thiên
Từ bảng biến thiên, ta thấy giá trị cực đại của hàm số bằng 4 2x  3
Câu 17. (MĐ 104 BGD&DT NĂM 2017) Hàm số y
có bao nhiêu điểm cực trị? x 1 A. 1 B. 3 C. 0 D. 2 Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn C 1 Có y   0, x  1
 nên hàm số không có cực trị. x  2 1 2 x  3
Câu 18. Cho hàm số y
. Mệnh đề nào dưới đây đúng? x 1
A. Cực tiểu của hàm số bằng 3 
B. Cực tiểu của hàm số bằng 1
C. Cực tiểu của hàm số bằng 6 
D. Cực tiểu của hàm số bằng 2 Lời giải Chọn D Cách 1. 2 x  2x  3 x  3  Ta có: y  ; 2
y  0  x  2x  3  0    x  2 1 x  1 
Lập bảng biến thiên. Vậy hàm số đạt cực tiểu tại x  1 và giá trị cực tiểu bằng 2 . Cách 2. 2 x  2x  3 x  3  Ta có y  ; 2
y  0  x  2x  3  0    x  2 1 x  1  8 1 1 y 
. Khi đó: y   1 
 0 ; y 3    0 .  x  3 1 2 2
Nên hàm số đạt cực tiểu tại x  1 và giá trị cực tiểu bằng 2 .
Câu 19. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số f (x) có đạo hàm 3 f (
x)  x(x  1)(x  2) , x
  R. Số điểm cực trị của hàm số đã cho là A. 1 B. 3 C. 2 D. 5 Lời giải Chọn B Phương trình 3 f (
x)  0  x(x  1)(x  2)  0 x  0   x  1  x  2  Do f (
x)  0 có ba nghiệm phân biệt và f (
x) đổi dấu qua ba nghiệm này nên hàm số có ba điểm cực trị.
Câu 20. (Mã đề 101 - BGD - 2019) Cho hàm số f (x) có đạo hàm f x x x  2 ( )
2 , x   . Số điểm cực
trị của hàm số đã cho là A. 2 . B. 1. C. 0 . D. 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn B Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đã cho có đúng một điểm cực trị đó là điểm cực tiểu x  0 .
Câu 21. (Mã 103 - BGD - 2019) Cho hàm số f x có đạo hàm f  x  x x  2 1 , x   . R Số điểm cực
trị của hàm số đã cho là A. 2 . B. 0 . C. 1. D. 3 . Lời giải Chọn C
Xét dấu của đạo hàm:
Ta thấy đạo hàm đổi dấu đúng 1 lần nên hàm số đã cho có đúng 1 điểm cực trị
Câu 22. (Mã đề 104 - BGD - 2019) Cho hàm số f x có đạo hàm f  x  x x  2
1 , x   . Số điểm
cực trị của hàm số đã cho là A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn A x  0 2  x  0
Ta có f  x  0  x x   1  0    .   x  2 1  0 x  1  
Vì nghiệm x  0 là nghiệm bội lẻ và x  1
 là nghiệm bội chẵn nên số điểm cực trị của hàm số là 1.
Câu 23. (Mã 102 - BGD - 2019) Cho hàm số y f (x) có đạo hàm 2 f (
x)  x(x  2) , x   . Số điểm
cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1. Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  0  x  0 Ta có: 2 f (
x)  0  x(x  2)  0     x  2  0 x  2   Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy hàm số có 1 điểm cực trị x  0 .
Câu 24. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho hàm số f x có đạo hàm
f x  x   x2   x3  x  4 ' 1 3
2 với mọi x   . Điểm cực tiểu của hàm số đã cho là A. x  2 . B. x  3 . C. x  0 . D. x  1 . Lời giải Ta có  x  0  x  1 f ' x
x 1 x2 3 x3  x 24 f ' x 0         . x  2  x  3 
Bảng xét dấu đạo hàm.
Suy ra hàm số f x đạt cực tiểu tại x  0
Câu 25. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm f  x 3
x x  
1  x  2, x
   . Số điểm cực trị của hàm số đã cho là A. 1 . B. 3 . C. 5 . D. 2 . Lời giải x  0
Ta có: f x 3 0 x x  1  x 2 0         x  1 .   x  2  Bảng xét dấu:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào bảng xét dấu nhận thấy hàm số f x có 3 điểm cực trị. Câu 26. (ĐỀ 04 VTED NĂM 2018-2019) Hàm số
y f x có đạo hàm
f  x   x  
1  x  2... x  2019 , x
  R . Hàm số y f x có tất cả bao nhiêu điểm cực tiểu? A. 1008 B. 1010 C. 1009 D. 1011 Lời giải Chọn B x  1  x  2
Ta có: f  x   x  
1  x  2... x  2019  0   .  .....  x  2019 
f  x  0 có 2019 nghiệm bội lẻ và hệ số a dương nên có 1010 cực tiểu
Câu 27. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số F x là một nguyên hàm của hàm số   x f x   2 x   2 2019 4
x  3x  2 . Khi đó số điểm cực trị của hàm số F x là A. 5 . B. 4 . C. 3 . D. 2 . Lời giải Ta có:      x F x f x   2 x   2 2019 4
x  3x  2 .  x  2  
F x  0 x   2 x   2 2019 4
x  3x  2  0  x  2 .   x  1 
Bảng biến thiên của F x :
Từ bảng biến thiên ta thấy hàm số F x có 1 cực đại và 1 cực tiểu, nghĩa là có 2 cực trị.
Câu 28. Đồ thị hàm số 3
y  x  3x có điểm cực tiểu là: A. ( 1  ;  2) . B. (1; 0) . C. (1;  2) . D. ( 1  ; 0) . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Ta có:  x  1 +) 2
y  3x  3 ; y  0   x  1  
+) y  6x y   1  6
  0  hàm số đạt cực đại tại x  1 . y  
1  6  0  hàm số đạt cực tiểu tại x  1
 và điểm cực tiểu là  1  ; 2   .
Câu 29. (THPT YÊN PHONG 1 BẮC NINH NĂM HỌC 2018-2019 LẦN 2) Hàm số f x có đạo hàm
f  x  x x   x  3 2 1 2 , x
   . Hỏi f x có bao nhiêu điểm cực đại? A. 2 . B. 0 . C. 1. D. 3 . Lời giải 2  x  0  x  0  Ta có 
f  x  0  x 1  0  x  1 .    x  3  x  2 2  0   Bảng biến thiên
Dựa vào bảng biến thiên suy ra hàm số có 1 điểm cực đại.
Câu 30. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm số 3 2
y x  6x  9x có tổng hoành độ và tung độ bằng A. 5 . B. 1 . C. 3 . D. 1. Lời giải x  1 Ta có: 2
y '  3x 12x  9  0  x  3  Bảng biến thiên Khi đó: x  1  y  4  xy  5. CD CD CD CD
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 31. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Tìm giá trị cực tiểu y của hàm số CT 3 y x  3x4 . A. y  6  B. y  1  C. y  2  D. y 1 CT CT CT CT Lời giải
Tập xác định: D   ; 2 y  3
x 3; y  0  x  1. Bảng biến thiên Vậy yy  1  2
 ; y y    . CT   1 6 CD
Câu 32. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm là
f  x  x x   x  2 1 2 x
   . Số điểm cực trị của hàm số là? A. 5 . B. 2 . C. 1. D. 3 . Lời giảix  0 
Ta có f  x  0  x  1 . Do x  0, x  1 là nghiệm đơn, còn các nghiệm và x  2  là nghiệm  x  2  
bội chẵn nên f  x chỉ đổi khi đi qua x  0, x  1 . a  0  Hàm số   2 1  
m  4  0  m  2  m  2 có 2 điểm cực trị.   0 
Câu 33. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Giá trị cực tiểu y của hàm số CT 3 2
y x  3x  4 là: A. y  0 . B. y  3 . C. y  2 . D. y  4 . CT CT CT CT Lời giải Ta có 2
y  3x  6x, y  6x  6 x  0
y  0  x  2  y 0  6
 , y 2  6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Do đó hàm số đạt cực tiểu tại x  2  yy 2  0 . CT
Câu 34. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm
f  x   x   x  2  x  3  x  4 1 2 3 4 , x   .
 Số điểm cực trị của hàm số đã cho là A. 3 B. 5 C. 2 D. 4 Lời giải Chọn C x  1 x  2
f  x  0   x  3 x  4  Bảng biến thiên:
Dựa vào bảng biến thiên: Số điểm cực trị của hàm số đã cho là 2.
Câu 35. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Đồ thị hàm số 4 2
y x x 1
có bao nhiêu điểm cực trị có tung độ là số dương? A. 3 . B. 1. C. 2 . D. 0 . Lời giải
Tập xác định D   .
x  0  y  1 3
y  4x  2x ; y 0     2 3 . x    y   2 4
Suy ra đồ thị có hàm số 4 2
y x x 1 có 3 điểm cực trị có tung độ là số dương.
Câu 36. (HSG BẮC NINH NĂM 2018-2019) Hàm số nào dưới đây không có cực trị? 2 x 1 2x  2 A. y B. y C. 2
y x  2x 1 D. 3
y  x x 1 x x 1 Lời giải 2x  2 + Xét hàm số y  . x 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 4
Tập xác định D   \   1 , y   0, x   D .  x  2 1
Nên hàm số luôn đồng biến trên từng khoảng xác định. 2x  2 Do đó hàm số y  không có cực trị. x 1
Câu 37. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm
f   x   x x    x  2 1 2
, x   . Số điểm cực trị của hàm số đã cho là A. 5 . B. 2 . C. 1. D. 3 . Lời giải x  0 
Ta có f  x  0  x x  
1  x  22  0  x  1 .   x  2 
Lập bảng xét dấu của f  x như sau:
Ta thấy f  x đổi dấu khi đi qua các điểm x  0 và x  1 , do đó hàm số y f x có hai điểm cực trị.
Câu 38. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số y f x có đạo hàm
f  x   x   2 x   4 2 3
x  9 . Số điểm cực trị của hàm số y f x là A. 3 . B. 4 . C. 2 . D. 1. Lời giải 2 2 2
f  x   x   2 x    2
x     x   x   x    2 2 3 3 2 3 3 x  3 x   3 2 2 
f  x    x   x   x    2 0 2 3 3
x  3  0  x  3 . x  2  Bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ bảng biến thiên của hàm số y f x , ta thấy hàm số y f x có đúng 1 điểm cực trị.
Câu 39. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Cho hàm số 4 2
y x  2x 1. Xét các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị.
2) Hàm số đồng biến trên các khoảng 1;0 ; 1;  .
3) Hàm số có 1 điểm cực trị.
4) Hàm số nghịch biến trên các khoảng ;   1 ; 0  ;1 .
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên? A. 2. B. 1. C. 4. D. 3. Lời giải
x  0  y  1 3
y '  4x  4x y '  0   x  1  y  0
x  1  y  0  Bảng xét dấu:
Hàm số có 3 điểm cực trị, đồng biến trên khoảng 1;0 ; 1;  và nghịch biến trên khoảng ;  1 ; 0 
;1 . Vậy mệnh đề 1, 2 , 4 đúng.
Câu 40. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm giá trị cực đại của hàm số 3 2
y x  3x  2 . A. 2  . B. 0 . C. 2 . D. 1. Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Tập xác định của hàm số là D   .  x  0 Ta có: 2
y  3x  6x y  0   . x  2 
y  6x  6  y0  6
  0  Giá trị cực đại của hàm số là: y 0  2  .
Câu 41. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số f   x có đạo hàm
là f x  x x  x x x  4 2 2 ' 2 2
1 thì tổng các điểm cực trị của hàm số f   x bằng A. 1. B. 2 . C. 1. D. 0 . Lời giải 2 5 Có f x 2 '
x x2 x  
1 . Ta thấy f ' 
x chỉ đổi dấu qua nghiệm x  1
 nên hàm số f   x
có đúng một điểm cực trị là x  1  .
Vậy tổng các điểm cực trị của hàm số f   x bằng 1.
Câu 42. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số 1 1 5 4 3 2 y x x
x  3x  2019m m   đạt cực tiểu tại điểm: 4 3 2 A. x  3 . B. x  3  . C. x  1. D. x  1  . Lời giải TXĐ: D   .  x  3 3 2
y  x x  5x  3 ; 3 2
y  0  x x  5x  3  0   . x  1  
Hàm số đạt cực tiểu tại x  3.
Câu 43. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Điểm cực đại của đồ thị hàm số 3
y  x  3x 1 là: A. M  1  ;   1 . B. N 0;  1 .
C. P 2;   1 .
D. Q 1;3 . Lời giải 2 y '  3
x  3; y '  0  x  1  y '  6  ; x y '   1  6
  0; y '   1  6  0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Do đó hàm số đạt cực đại tại x  1; y  
1  3 . Vậy chọn đáp án Q 1;3 . 1
Câu 44. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Hàm số 3 2 y
x x  3x  1 đạt cực tiểu 3 tại điểm A. x  1  . B. x  1 . C. x  3  . D. x  3 . Lời giải 1 Ta có hàm số 3 2 y
x x  3x  1 có tập xác định D   . 3  x  1 2
y  x  2x  3; y  0   . x  3  
y  2x  2 ; y 3    4
  0 ; y  1  4  0 .
Suy ra hàm số đạt cực tiểu tại điểm x  1 .
Câu 45. (THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 01) Tìm số điểm cực trị của hàm số 4 2
y x  2x . A. 2. B. 4. C. 3. D. 1. Lời giải Chọn C Tự luận
Tập xác định: D   . x  0 3
y  4x  4x  0   . x  1   Bảng biến thiên:
Dựa vào bảng biến thiên suy ra hàm số có 3 điểm cực trị.
Trắc nghiệm
Hàm số bậc 4 trùng phương 4 2
y ax bx c có hệ số .
a b  0 thì sẽ có 3 điểm cực trị.
Vậy chọn ngay đáp án C.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 46. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Điểm cực tiểu của đồ thị hàm số 3 2
y  x x  5x  5 là  5 40  A.  1  ; 8   B. 0; 5 C. ;   D. 1;0  3 27  Lời giải Chọn A x  1  2 y 3x 2x 5 0         5 . x   3
y  6x  2 .
Ta có: y 
1  8  0  Hàm số đạt cực tiểu tại x  1  ; yy   1  8  . CT
Vậy điểm cực tiểu của đồ thị hàm số là  1  ; 8   .
Câu 47. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số 3
y f x có đạo hàm f x  x  2 x x  2 ' 2
x  2 x  . Số điểm cực trị của hàm số là A. 4 B. 1 C. 2 D. 3 Lời giải Chọn D
Cách 1: Sử dụng MTCT chọn một số nằm giữa các khoảng suy ra bảng xét dấu x  2  4  2 0 4 2  f ' x  0  0  0  0 
f ' x đổi dấu 3 lần qua x  2  , 4 x   2 , 4
x  2 . suy ra hàm số có 3 cực trị.
Cách 2: Sử dụng nghiệm bội chẵn lẻ, nghiệm đơn. 3
f x  x x x  x
  x x  2 2 2 4  x   4 x   4 ' 2 2 2 2 2 x  2 
f ' x đổi dấu qua 3 nghiệm đơn. 2 nghiệm bội chẵn không đổi dấu nên có 3 cực trị.
Câu 48. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị? 2x  3 A. y  . B. 4 y x . C. 3
y  x x .
D. y x  2 . x  2 Lời giải Chọn A.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2x  3 + Hàm số y x  2
Tập xác định: D   ;  2     2  ;  . 7 Có y '   0 x
  D  hàm số luôn đồng biến trên từng khoảng xác định  hàm số  x  22 không có cực trị.
Các hàm số khác dễ dàng chứng minh được y’ có nghiệm và đổi dấu qua các nghiệm. Riêng hàm
số cuối y’ không xác định tại -2 nhưng hàm số xác định trên R và y’ đổi dấu qua -2 do đó có hàm
số có điểm cực trị x = -2.
Câu 49. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số y f x 2
có đạo hàm trên  và f  x   x  
1  x  2  x  3 . Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 0 D. 2 Lời giải Chọn D x  1 
Ta có f  x  0  x  2  x  3  Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đã cho có 2 điểm cực trị.
Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0
Câu 50. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị thực của tham số m để hàm số 1 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3. 3 A. m  1  B. m  7 
C. m  5
D. m  1 Lời giải Chọn C Ta có 2
y  x mx   2 2
m  4 ; y  2x  2m .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1  y  3  0 Hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3 khi và chỉ khi:  3 y  3  0 
m  1L 2 2 9
  6m m  4  0
m  6m  5  0     
 m  5TM  . 6 2m 0 m 3       m  3 
Vậy m  5 là giá trị cần tìm.
Câu 51. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Tìm m để hàm số 3 2
y x  2mx mx  1 đạt
cực tiểu tại x  1
A. không tồn tại m . B. m  1 . C. m  1.
D. m 1;  2 . Lời giải m  1  y    1  0
3  4m m  0 
Để x  1 là điểm cực tiểu của hàm số        m  1. 3 y    1  0  6  4m  0  m    2
Thử lại với m  1, ta có 3 2
y x  2x x  1 ; 2
y  3x  4x  1.  x  1 2 y 0 3x 4x 1 0         1 .  x   3 Bảng biến thiên: x 1  1   3 y  0  0  y
Quan sát bảng biến thiên ta thấy m  1 thỏa yêu cầu bài toán.
Câu 52. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Tìm các giá trị thực của tham số m để 1 hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3. 3
A. m  1, m  5 . B. m  5 . C. m  1. D. m  1  . Lời giải Tập xác định  . Ta có 2 2
y  x  2mx m  4, y  2x  2 . m 1 Để hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3 thì 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 m  5  y  3 2  0
m  6m  5  0    
  m  1  m  5.  . y  3  0 6  2m  0   3  m
Câu 53. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  3x mx 1 đạt cực tiểu tại x  2 . A. m  0 . B. m  4 .
C. 0  m  4 .
D. 0  m  4 . Lời giải Chọn A 2
y  3x  6x m ; y  6x  6 .  y  2  0 m  0
Hàm số đạt cực tiểu tại x  2      m  0 . y  2  0 6  0  
Câu 54. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực m để hàm số 1 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại x  1. 3 A. 0 B. 2 C. 1 D. 3 Lời giải Chọn D 2 2
y '  x  2mx m m 1
y '  2x  2m
Hàm số đạt cực đại tại x  1 nên ta có  y    2 ' 1  0
m  3m  2  0
m  1  m  2       m  2 y '    1  0 2  2m  0 m  1   
Thử lại với m  2 ta có y '  2x  4  y '   1  2   0
Do đó Hàm số đạt cực đại tại x  1
Câu 55. (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8 5 2 4
y x  (m 1)x  (m 1)x 1 đạt cực tiểu tại x  0 ? A. 3 B. 2 C. Vô số D. 1 Lời giải Chọn B Ta có: 7 4 2 3
y '  8x  5(m 1)x  4(m 1)x 1 3  x  4
x  m   x   2 8 5 1 4 m   1 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  0 y '  0   4 8x  5  m   1 x  4 2 m   1  0 (1)  *Nếu m  1 thì 7
y '  8x , suy ra hàm số đạt cực tiểu tại x  0 .  x  0  x  0 *Nếu m  1  thì y '  0    
, nhưng x  0 là nghiệm bội chẵn nên không 4 5 8x 10x  0   3 x   4 phải cực trị.
*Nếu m  1 : khi đó x  0 là nghiệm bội lẻ. Xét 4
g x x  m   x   2 ( ) 8 5 1 4 m   1 . Để x  0 là điểm cực tiểu thì 2 lim g(x)  4  (m 1)  0 2  m 1 0  1
  m  1. Vì m nguyên nên chỉ có x 0  giá trị m  0 .
Vậy chỉ có hai tham số m nguyên để hàm số đạt cực tiểu tại x  0 là m  0 và m  1.
Câu 56. (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y x  m   5 x   2 m   4 2
4 x  1 đạt cực tiểu tại x  0 ? A. Vô số B. 3 C. 5 D. 4 Lời giải Chọn D Ta có 8
y x  m   5 x   2 m   4 2 4 x  1 7
y  x  m   4 x   2 m   3 8 5 2 4 4 x . y  0 3  x  4
x  m   x   2 8 5 2 4 m  4  0  x  0   g   x 4
 8x  5m  2 x  4 2 m  4  0 
Xét hàm số g x 4
x  m   x   2 8 5 2
4 m  4 có g x 3
 32x  5m  2 .
Ta thấy g x  0 có một nghiệm nên g x  0 có tối đa hai nghiệm
+ TH1: Nếu g x  0 có nghiệm x  0  m  2 hoặc m  2 
Với m  2 thì x  0 là nghiệm bội 4 của g x . Khi đó x  0 là nghiệm bội 7 của y và y đổi
dấu từ âm sang dương khi đi qua điểm x  0 nên x  0 là điểm cực tiểu của hàm số. Vậy m  2 thỏa ycbt. x  0 Với m  2
 thì g x 4 8x 20x 0      5 .  3 x   2 Bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào BBT x  0 không là điểm cực tiểu của hàm số. Vậy m  2  không thỏa ycbt. + TH2:
g 0  0  m  2
 . Để hàm số đạt cực tiểu tại
x  0  g 0  0 2
m  4  0  2  m  2 .
Do m   nên m  1  ; 0  ;1 .
Vậy cả hai trường hợp ta được 4 giá trị nguyên của m thỏa ycbt.
Câu 57. (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y x  m   5 x   2 m   4 3
9 x 1 đạt cực tiểu tại x  0 ? A. 6 B. Vô số C. 4 D. 7 Lời giải Chọn A Ta có 8
y x  m   5 x   2 m   4 3 9 x 1 7
y  x  m   4 x   2 m   3 8 5 3 4 9 x . y  0 3  x  4
x  m   x   2 8 5 3 4 m  9  0 x  0   g   x 4
 8x  5m  3 x  4 2 m  9  0 
Xét hàm số g x 4
x  m   x   2 8 5 3
4 m  9 có g x 3
 32x  5m  3 .
Ta thấy g x  0 có một nghiệm nên g x  0 có tối đa hai nghiệm
+) TH1: Nếu g x  0 có nghiệm x  0  m  3 hoặc m  3 
Với m  3 thì x  0 là nghiệm bội 4 của g x . Khi đó x  0 là nghiệm bội 7 của y và y đổi
dấu từ âm sang dương khi đi qua điểm x  0 nên x  0 là điểm cực tiểu của hàm số. Vậy m  3 thỏa ycbt.  x  0 Với m  3
 thì g x 4 8x 30x 0      15 .  3 x   4 Bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào BBT x  0 không là điểm cực tiểu của hàm số. Vậy m  3  không thỏa ycbt. +) TH2:
g 0  0  m  3
 . Để hàm số đạt cực tiểu tại x  0  g 0  0 2
m  9  0  3  m  3 .
Do m   nên m  2  ; 1  ;0;1;  2 .
Vậy cả hai trường hợp ta được 6 giá trị nguyên của m thỏa ycbt.
Câu 58. (MĐ 103 BGD&ĐT NĂM 2017-2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y x  m   5 x   2 m   4 4
16 x  1 đạt cực tiểu tại x  0 . A. 8 B. Vô số C. 7 D. 9 Lời giải Chọn A Ta có 7
y x  m   4 x   2 m   3 ' 8 5 5 4 16 x 3 4
x x  m   x   2 8 5 4 4 m 16 3
x .g x  
Với g x 4
x  m   x   2 8 5 5 4 m 16 .
● Trường hợp 1: g 0  0  m  4  . Với 7
m  4  y '  8x . Suy ra x  0 là điểm cực tiểu của hàm số. Với 4
m    y x  3 4 ' 8
x  5 . Suy ra x  0 không là điểm cực trị của hàm số.
● Trường hợp 2 : g 0  0  m  4  .
Để hàm số đạt cực tiểu tại x  0 thì qua giá trị x  0 dấu của y ' phải chuyển từ âm sang dương do
đó g 0  0  4   m  4 .
Kết hợp hai trường hợp ta được 4   m  4 .
Do m    m  3  ; 2  ; 1  ;0;1; 2;3;  4 .
Vậy có 8 giá trị nguyên của tham số m thỏa mãn.
Câu 59. (KTNL GIA BÌNH NĂM 2018-2019) Có bao nhiêu giá trị nguyên của tham số m để hàm số 12 7 2 6
y x  (m  5)x  (m  25)x 1 đạt cực đại tại x  0 ? A. 8 B. 9 C. Vô số D. 10 Lời giải Chọn B Ta có 11 6 2 5
y '  12x  7(m  5)x  6(m  25)x TH1: 11
m  5  y '  12x . Khi đó y '  0  x  0 là nghiệm bội lẻ, đồng thời dấu của ’ y đổi từ
âm sang dương, nên x  0 là điểm cực tiểu của hàm số,do đó không thỏa mãn, m  5 loại.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 TH2: 6 5 m  5
  y '  x (12x  70)  0  x  0 là nghiệm bội chẵn, do đó ’
y không đổi dấu khi
đi qua x  0 , m  5  loại. TH3: 5 6 2 5
m  5  y '  x 1
 2x  7(m  5)x  6(m  25)  x .g(x)   Với 6 2
g(x)  12x  7(m  5)x  6(m  25) , ta thấy x  0 không là nghiệm của g x .
Để hàm số đạt cực đại tại x  0 thì y’ phải đổi dấu từ dương sang âm khi đi qua x  0 , xảy ra khi
 lim g (x)  0   và chỉ khi x0 2 
 6(m  25)  0  5  m  5 lim g (x)  0  x0
Vì m nguyên nên m   4  ; 3  ;...;3; 
4 , vậy có 9 giá trị của m thỏa mãn bài toán.
Câu 60. Tìm tất cả tham số thực m để hàm số y  m   4 x   2 m   2 1
2 x  2019 đạt cực tiểu tại x  1  A. m  0 . B. m  2  . C. m  1. D. m  2 . Lời giải
Tập xác định: D  . 
Ta có: y  m   3 x   2 4 1 2 m  2 x
* Điều kiện cần:
Điều kiện cần để hàm số đạt cực tiểu tại x  1  là f ' 
1  0   m     2 4 1 2 m  2  0 m  0 2
 2m  4m  0   . m  2 
* Điều kiện đủ:
Trường hợp 1: m  0 hàm số trở thành 4 2
y  x  2x  2019  x  1  Ta có: y '  0 3  4
x  4x  0  x  0   x  1  Bảng biến thiên:
Từ bảng biến thiên ta có hàm số đạt cực đại tại x  1
 nên loại m  0 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Trường hợp 2: m  2 hàm số trở thành 4 2
y x  2x  2019 .  x  1  Ta có: y '  0 3
 4x  4x  0  x  0   x  1  Bảng biến thiên:
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại x  1  . Chọn m  2 .
Vậy với m  2 thì hàm số y  m   4 x   2 m   2 1
2 x  2019 đạt cực tiểu tại x  1  .
Câu 61. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số y f x xác
định trên tập số thực  và có đạo hàm f x   x
x x m  x   m 3 2 ' sin 3 9 x    ( m là
tham số). Có bao nhiêu giá trị nguyên của m để hàm số y f x đạt cực tiểu tại x  0 ? A. 6 B. 7 C. 5 D. 4 Lời giải Điều kiện 2 9  m  0  3   m  3
TH 1: 0  m  3 ta có BTT
TH 2: 3  m  0 ta có BTT
TH 2: m  3 ta có BTT
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ đó suy ra 3  m  3  có 6 giá trị nguyên của m thỏa mãn.
Dạng 4. Tìm m để hàm số có n cực trị
Câu 62. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để hàm số
y  m   4
x  m   2 1 2
3 x 1 không có cực đại?
A. 1  m  3
B. m 1
C. m  1
D. 1  m  3 Lời giải Chọn D TH1: Nếu 2
m  1 y  4x 1. Suy ra hàm số không có cực đại.
TH2: Nếu m 1.
Để hàm số không có cực đại thì 2
 m  3  0  m  3. Suy ra 1  m  3.
Vậy 1  m  3 .
Câu 63. (MĐ 104 BGD&DT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 3 2 3
y x  3mx  4m có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với
O là gốc tọa độ. 1 1
A. m  0 B. m   ; m 4 2 4 2 C. m  1  ; m 1 D. m 1 Lời giải Chọn C 2
y  3x  6mx . 3
x  0  y  4m 2
y  0  3x  6mx  0   .
x  2m y  0 
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi m  0 .
Khi đó, hai điểm cực trị của đồ là A  3
0; 4m  và B 2 ;
m 0 , m  0 . 1 1 SO . A OB  4 3 4 
. 4m 2m  4  m  1  m  1  . OAB 2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 64. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tìm tất cả các giá trị của 3 x
tham số m để hàm số 2 y  
mx  2mx  1 có hai điểm cực trị. 3 m  2
A. 0  m  2. B. m  2 . C. m  0 . D.  . m  0  Lời giải Ta có: 2
y  x  2mx  2m 3 x Hàm số 2 y  
mx  2mx  1 có hai điểm cực trị  y  0 có hai nghiệm phân biệt 3 m  2 2
   m  2m  0   . m  0 
Câu 65. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  3x  2mx m có cực đại và cực tiểu? 3 3 3 3 A. m  . B. m   . C. m  . D. m  . 2 2 2 2 Lời giải + TXĐ: D   + 2
y  3x  6x  2m
+ Hàm số có cực đại và cực tiểu  y  0 có 2 nghiệm phân biệt. 3
   36  24m  0  m  . 2
Câu 66. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Tập hợp các giá trị của m để hàm 1 số 3 2 y
x mx  m  2 x 1 có hai cực trị là: 3 A.  ;    1  2;  B.  ;   
1  2;  C.  1  ; 2 D. 1; 2 Lời giải Chọn B Ta có 2
y  x  2mx m  2 . Để hàm số có hai cực trị thì y  0 có hai nghiệm phân biệt nên m  1 2
y  0    0  m m  2  0   m  2 
Câu 67. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hàm số 4 2
y mx x 1. Tập hợp
các số thực m để hàm số đã cho có đúng một điểm cực trị là A. 0;   . B. ;0 . C. 0;   . D. ;0 . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Tập xác định D   .
TH1: m  0 hàm số đã cho trở thành 2
y  x 1 là một hàm bậc hai nên luôn có một cực trị. TH2: m  0 , ta có 3
y  4mx  2x .  x  0 y  0 3
 4mx  2x  0  x  2 2 2mx   1  0   . 2
2mx 1  0  
Để hàm số có đúng một cực trị thì phương trình y  0 có đúng 1 nghiệm.
Ycbt  Phương trình  có một nghiệm x  0 hoặc vô nghiệm suy ra m  0 . Vậy m  0 .
Câu 68. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho hàm số 4 2
y mx  (2m 1)x 1.
Tìm tất cả các giá trị thực của tham số m để hàm số có đúng một điểm cực tiểu. 1 1
A. Không tồn tại m . B. m  0. C. m   . D.   m  0. 2 2 Lời giải Với m  0 , ta có 2
y x 1  y '  2x . Khi đó hàm số có 1 cực trị và cực trị đó là cực tiểu. Suy ra
m  0 thỏa mãn yêu cầu bài toán. (1) Với m  0 , ta có 3 2
y '  4mx  2(2m 1)x  2x(2mx  2m 1) m  0
Hàm số có một cực trị là cực tiểu   2
2mx  2m 1  0 vô nghiêm  m  0 m  0    1   2m 1   m   m  0 (2)  0   2   2m   m  0 
Từ (1) và (2) suy ra hàm số có một cực trị là cực tiểu khi m  0.
Câu 69. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số m để hàm số 4
y x   2
m m   2 2
6 x m 1 có ba điểm cực trị. A. 6 . B. 5 . C. 4 . D. 3 . Lời giải Ta có 3
y  x   2 m m    2 x x x    2 4 4 6 4
m m  6   . x  0  y  0   2 x    2
m m  6  0 (1) 
Hàm số có ba điểm cực trị  (1) có hai nghiệm phân biệt khác 0  2
m m  6  0  2  m  3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Ta có: m   , 2
  m  3  m   1;  0;1;  2 .
Vậy có 4 giá trị nguyên của tham số m để hàm số có ba điểm cực trị.
Câu 70. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số 4
y mx  m   2
1 x 1 2m có một điểm cực trị khi
A. 0  m  1.
B. m  0  m  1. C. m  0 .
D. m  0  m  1. Lời giải
Trường hợp 1: m  0 thì hàm số đã cho trở thành 2
y  x 1. Hàm số này có 1 cực trị là cực đại
m  0 thỏa mãn.
Trường hợp 2: m  0 thì hàm số đã cho trở thành 4
y mx  m   2 1 x 1 2m x  0 2x  0 Ta có 3
y  mx  m   x x  2 4 2 1 2
2mx m   1 ; y 0       1 m 2 2
2mx m 1  0 x     *  2m
YCBT  y đổi dấu một lần  Phương trình * vô nghiệm hoặc có nghiệm x  0 . 1 mm 1   0   2m m  0 
Kết hợp hai trường hợp ta được 0  m m  1. m 1
Giải nhanh: Với a khác 0 thì hàm số đã cho có 1 cực trị  ab  0  mm   1  0   . m  0 
Câu 71. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Có tất cả bao nhiêu giá
trị nguyên của m trên miền  1  0;10 để hàm số 4 y x   m   2 2 2
1 x  7 có ba điểm cực trị? A. 20 B. 10 C. Vô số D. 11 Lời giải Chọn D Ta có 2
y '  4x x  2m   1  x    . x  0 y  0   2
x  2m 1 * 
Hàm số đã cho có ba cực trị khi và chỉ khi y  0 có ba nghiệm phân biệt, hay (*) có hai nghiệm 1
phân biệt khác 0  2m 1  0  m   . 2 Do m  10 
;10 nên có 11 giá trị thỏa mãn.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 72. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số 4
y mx   2 m   2 6 x  4
. Có bao nhiêu số nguyên m để hàm số có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại ? A. 4 B. 3 C. 2 D. 5 Lời giải Chọn C
Tập xác định D   . Ta có 3
y  mx   2 4
2 m  6 x .
Hàm số đã cho có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại khi và 4m  0  chỉ khi   0  m  6 . m   2 m  6  0 
Do đó có hai giá trị nguyên của tham số m .
Câu 73. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Tìm tất cả các giá trị thực của
tham số m để hàm số 4
y mx  m   2
1 x 1 2m có một cực trị. A. m 1 B. m  0
C. 0  m  1
D. m  0  m  1 Lời giải Chọn D Ta có: 3
y  4mx  2m   1 x
 Trường hợp 1: Xét m  0  y  2x . Ta thấy phương trình y  0 đổi dấu một lần nên hàm số
có một điểm cực trị. Suy ra m  0 (thoả YCBT) (1)  Trường hợp 2: Xét 3
m  1  y  4x .Ta thấy phương trình y  0 đổi dấu một lần nên hàm số
có một điểm cực trị. Suy ra m 1 (thoả YCBT) (2) x  0
 Trường hợp 3: Xét m  0 , y 0     1 m 2 x   2m 1 mm  0
Để hàm số có một điểm cực trị thì  0   (3) 2m m  1  m  0
Từ (1), (2) và (3) suy ra  m  1 
Ghi chú: Dùng công thức tính nhanh
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 m  0
Hàm số có một điểm cực trị khi và chỉ khi m m   1  0  .  m  1 
Dạng 5. Đường thẳng đi qua 2 điểm cực trị
Câu 74. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị thực của tham số m để đường thẳng
d : y  2m  
1 x  3  m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 3 3 1 1 A. m B. m C. m   D. m  2 4 2 4 Lời giải Chọn B Ta có 2
y  3x  6x . Từ đó ta có tọa độ hai điểm cực trị A0;  1 , B 2; 3
  . Đường thẳng qua hai
điểm cực trị có phương trình y  2
x 1. Đường thẳng này vuông góc với đường thẳng 3
y  2m  
1 x  3  m khi và chỉ khi 2m  
1 2  1  m  . 4
Câu 75. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Đồ thị hàm số y  3 x  2
3x  9x  1 có hai cực trị A và B
. Điểm nào dưới đây thuộc đường thẳng AB ?
A. M 0; 1
B. N 1; 10
C. P 1; 0
D. Q 1;10 Lời giải Chọn B Ta có:  y  2
3x  6x  9 thực hiện phép chia y cho 
y ta được số dư là y  8x  2 .
Như thế điểm N 1; 10 thuộc đường thẳng AB .
Câu 76. (MĐ 105 BGD&ĐT NĂM 2017) Đồ thị của hàm số y   3 x  2
3x  5 có hai điểm cực trị A và
B . Tính diện tích S của tam giác OAB với O là gốc tọa độ. 10
A. S  5 B. S
C. S  10 D. S  9 3 Lời giải Chọn A Ta có y   2
3x  6x y  0  x  0  x  2
Dễ dàng xác định được tọa độ các điểm cực trị là A 0; 5; B2; 9
Vậy OA  5;OB  85; AB  2 5
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
AB OA OB Gọi p  2
Áp dụng công thức Heron tính diện tích tam giác OAB ta có S
p p OA p OB p AB  5 OAB    
Câu 77. Đồ thị của hàm số 3 2
y x  3x  9x 1 có hai điểm cực trị A và B . Điểm nào dưới đây thuộc đường thẳng AB .
A. P 1;0 .
B. M 0;   1 . C. N 1; 1  0 . D. Q  1  ;10 . Lời giải TXĐ: D   . 2
y '  3x  6x  9 .
x  1  y  6 2
y '  0  3x  6x  9  0  
x  3  y  26    Ta có A 1  ;6, B 3; 2
 6  AB  4; 32 nên ) Chọn n  8  ;1 . AB
Phương trình đường thẳng AB là: 8 x  
1 1 y  6  0  8x y  2  0 .
Thay tọa độ các điểm P, M , N , Q vào phương trình đường thẳng AB ta có điểm N 1; 1  0 thuộc đường thẳng.
Câu 78. (THPT Xuân Hòa-Vĩnh Phúc- Lần 1- 2018- BTN) Biết đồ thị hàm số 3
y x  3x 1 có hai điểm
cực trị A , B . Khi đó phương trình đường thẳng AB là
A. y  2x 1.
B. y  2x  1.
C. y  x  2.
D. y x  2 . Lời giải Chọn B  1 
Thực hiện phép chia y cho y ta được: y y .
x  2x     1 .  3 
Giả sử hai điểm cực trị của đồ thị hàm số lần lượt là: Ax ; y và B x ; y . 2 2  1 1    1 
y y x yx . x  2
x 1  2x 1  1  1   1   1   1  1   3  Ta có:  .  1 
y y x yx . x  2x 1  2  x 1 2  2   2   2   2  2    3 
Ta thấy, toạ độ hai điểm cực trị A và B thoả mãn phương trình y  2x  1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vậy phương trình đường thẳng qua hai điểm cực trị là: y  2x  1 .
Câu 79. (Lương Văn Chánh - Phú Yên – 2017 - 2018 - BTN) Tìm giá trị thực của tham số m để đường
thẳng d : y  3m  
1 x  3  m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 1 1 1 1 A. . B.  . C. m  . D.  . 3 6 6 3 Lời giải Chọn B Xét hàm số 3 2
y x  3x 1  1 1  Có : 2
y  3x  6x , y x y  2x 1   .  3 3 
Do đó, đường thẳng  qua hai điểm cực trị của đồ thị hàm số này có phương trình là y  2x 1 . 1
Để d vuông góc với  thì 3m   1 . 2    1   m   . 6 1
Vậy giá trị cần tìm của m là m   . 6
Câu 80. (THPT CHUYÊN VĨNH PHÚC - LẦN 1 - 2017 - 2018 - BTN) Tìm tất cả các giá trị của tham
số m để đồ thị hàm số 3 2
y x  2x  m  
3 x m có hai điểm cực trị và điểm M 9;  5 nằm trên
đường thẳng đi qua hai điểm cực trị của đồ thị. A. m  1  . B. m  5  .
C. m  3.
D. m  2. Lời giải Chọn C Ta có 2
y  3x  4x m  3 , để hàm số có hai điểm cực trị thì phương trình y  0 có hai nghiệm 13
phân biệt    0  m    * 3  1 2  2m 26 7m 2 Ta có y y .  x    x      
nên phương trình đường thẳng đi qua hai điểm  3 9  3 9  9 3  2m 26 7m 2 cực trị là y   x   .  
Theo giả thiết, đường thẳng này đi qua M 9;  5 nên m  3  3 9  9 3
(thỏa mãn điều kiện   * ).
Câu 81. (PTNK Cơ Sở 2 - TPHCM - 2017 - 2018 - BTN) Tìm giá trị thực của tham số m để đường thẳng
y  2m  
1 x m  3 song song với đường thẳng đi qua các điểm cực trị của đồ thị hàm số 3 2
y x  3x 1 3 1 3 1 A. m  . B. m  . C. m   . D. m   . 4 2 4 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn D x  0 Hàm số 3 2
y x  3x 1 có TXĐ: ; 2
y  3x  6x ; y '  0   x  2  
Suy ra đồ thị hàm số có hai điểm cực trị là A0; 
1 , B 2; 3  AB  2; 4 . x y 1
Đường thẳng d đi qua hai điểm A , B có phương trình: 
y  2x 1. 2 4 2m 1  2 1
Đường thẳng y  2m  
1 x m  3 song song với đường thẳng d    m   . m  3  1 2 
Câu 82. (TT Tân Hồng Phong - 2018 - BTN) Tìm tổng tất cả các giá trị thực của tham số m sao cho
đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y x  m   2 2 3
1 x  6m 1 2mx song
song đường thẳng y  4x . 1 2 2 A. m   . B. m  . C. m   .
D. m  1. 3 3 3 Lời giải Chọn A x m Ta có 2
y  6x  6m  
1 x  6m 1 2m , y  0   . x  1 2m  1
Để hàm số có hai cực trị thì m  1 2m m  . 3
Hai điểm cực trị của đồ thị hàm số là A 3 2
m ;  7m  3m  , B  3 2
1  2m ; 20m  24m  9m   1 . Do đó   2
AB    m m  3 1 3 ; 3
1  . Do đó AB có vectơ pháp tuyến là n  3m   1  ;1 .
Do đó AB m  2 3 2 : 3 1
x y  2m  3m m  0  y    m  2 3 2 3 1
x  2m  3m m .
Để đường thẳng AB song song với đường thẳng y  4x thì: m  1  1 m    3   3m  2 1  4  1 
 m  0  m   . 3 2
2m  3m m  0 3    1 m   2  m  1 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước
Câu 83. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Gọi S là tập hợp tất cả các giá trị thực của tham số 1
m để đồ thị của hàm số 3 2 y
x mx   2 m  
1 x có hai điểm cực trị A và B sao cho , A B nằm 3
khác phía và cách đều đường thẳng d : y  5x  9 . Tính tổng tất cả các phần tử của S . A. 3 B. 6 C. 6  D. 0 Lời giải Chọn D Cách 1: Ta có 2
y x mx   2 ' 2 m   1 3 x m 1 
m  3m  2  3 
m  3m  2   y '  0   A m 1;    và B m 1;   x m 1 3    3   m 2 m   1 2
Dễ thấy phương trình đường thẳng AB : y   x
nên AB không thể song song hoặc 3 3
trùng với d A, B cách đều đường thẳng d : y  5x  9 nếu trung điểm I của AB nằm trên d m  3 3 3  m  3m m  3m 3 I ; md
 5m  9  m 18m  27  0     3 3 3  3 5   m   2 Với m  3  ,
A B thỏa điều kiện nằm khác phía so với d . 3   3 5 Với m   ,
A B thỏa điều kiện nằm khác phía so với d . 2
Tổng các phần tử của S bằng 0.
Câu 84. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số 1 3 y
mx  m   2
1 x  3m  2 x  2018 với m là tham số. Tổng bình phương tất cả các giá trị 3
của m để hàm số có hai điểm cực trị x ; x thỏa mãn x  2x  1 bằng 1 2 1 2 40 22 25 8 A. B. C. D. 9 9 4 3 Lời giải Chọn A Ta có 2 y '  x m  2m  
1 x  3m  2
Để hàm số có hai điểm cực trị thì phương trình 2 x m  2m  
1 x  3m  2  0 phải có hai nghiệm phân biệt.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 m  0  m  0        m  2 1
 3m m  2 2  0
2m  4m  1  0    2 m   1 x .  x   1 2  m
Theo định lý Vi-ét ta có  3  m  2 x .x  1 2   m  3m  4  2m   1 x  1 x .   x   m 1 2  m
Theo bài ta có hệ phương trình  2 m   1 2   m x  2x  1 x  1   1 2 2   m m
m  2 t / m 3m  4 2  m 3m  2 .
32 mm 3m 42 m 0           2  m m m m  t / m  3 40 Vậy 2 2 m m  . 1 2 9
Câu 85. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm tất cả cả các giá trị của tham số m để 3 2
y  x  3x  mx 1 đạt cực trị tại x , x thỏa mãn 2 2
x x  6 1 2 1 2 A. m  3  B. m  3 C. m  1  D. m 1 Lời giải Chọn A 2
y '  3x  6x  m . Hàm số đạt cực trị tại x , x .Vậy x , x là nghiệm của phương trình y '  0 1 2 1 2 x x  2 1 2  Theo viet ta có  m x .x   1 2  3 2 2 2
x x  (x x )  2x x 1 2 1 2 1 2 2m 2m  4   4   6  m  3  3 3
Câu 86. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2
y x x   2 m   2 8
11 x  2m  2
có hai điểm cực trị nằm về hai phía của trục Ox . A. 4. B. 5. C. 6. D. 7. Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Yêu cầu bài toán  đồ thị hàm số cắt trục hoành tại ba điểm phân biệt 3 2
x x   2 m   2 8
11 x  2m  2  0 có ba nghiệm phân biệt 3 2
x x   2 m   2 8
11 x  2m  2  0   x   2 2 2
x  6x m   1  0 x  2   2 2
x  6x m 1  0(*) 
Suy ra phương trình (*) có hai nghiệm phân biệt khác 2 2 
 '  10  m  0  m  2  2     2 m  8  0   10  m  10 
Vậy có 7 giá trị nguyên của tham số thỏa mãn đề bài. Câu 87. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho hàm số 3
y x   m   2 2
1 x  m  
1 x m  1 . Có bao nhiêu giá trị của số tự nhiên m  20 để đồ thị hàm
số có hai điểm cực trị nằm về hai phía trục hoành? A. 18 . B. 19 . C. 21. D. 20 . Lời giải
+ Ta có: y   x    2
1 x  2mx  1  m .
+ Hàm số có hai điểm cực trị nằm về hai phía trục hoành khi và chỉ khi đồ thị y cắt trục hoành tại
ba điểm phân biệt.  y   x    2
1 x  2mx  1  m  0 có ba nghiệm phân biệt. 2
x  2mx  1  m  0 có hai nghiệm phân biệt khác 1.   1   5   m   2   2
m m  1  0  1   5     m  . 2 3m 0      2   2   m    3
+ Do m N , m  20 nên 1  m  20 . Vậy có 19 số tự nhiên thỏa mãn bài toán.
Câu 88. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số 3
y x  m   2 x   2 m   2 1
2 x m  3 có hai điểm cực trị và hai điểm cực trị đó
nằm về hai phía khác nhau đối với trục hoành? A. 2 . B. 1. C. 3 . D. 4 . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Ta có 2
y   x  m   2 0 3 2
1 x m  2  0 . 1 15 1 15
Để hàm số có hai điểm cực trị 2    0  2
m  2m  7  0   m  * . 2 2
Ta lần lượt thử bốn giá trị nguyên của m thỏa mãn   * là 1  ; 0;1; 2 . Ta được bốn hàm số 3 3 2 3 2 3 2
y x x  2; y x x  2x  3; y x  2x x  2; y x  3x x 1 .
Khi đó ta nhận thấy chỉ có m  1 thỏa mãn yêu cầu bài toán.
Câu 89. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hàm số 3
y x  m   2 2 3
1 x  6m  2x 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm
số có điểm cực đại và điểm cực tiểu nằm trong khoảng 2;  3 .
A. m  1; 
3 3; 4 . B. m  1;  3 .
C. m  3; 4 .
D. m  1; 4 . Lời giải Chọn A Ta có: 2
y '  6x  6m  
1 x  6m 2
Để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng 2; 
3  pt y'  0 có 2 nghiệm thuộc khoảng 2;  3 2
x m 
1 x m  2  0 có 2 nghiệm thuộc khoảng 2;  3  x  
1 x m  2  0
x 12;  3    x  2m  2  m  1  m  3   YCBT      2   2m  3  1   m  4  
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Tổng tất cả các giá trị
thực của tham số m để hàm số: 3
y x  m   2 3 2
1 x  3mx m  5 có hai điểm cực trị x ; x đồng 1 2
thời y x .y x  0 là: 1   2  A. 21 B. 3  9 C. 8  D. 3 11 13 Lời giải Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+) Để hàm số có hai cực trị thì phương trình y  0 phải có hai nghiệm phân biệt: 2
y  9x  4m  
1 x  3m có hai nghiệm phân biệt    m  2 4 1  27m  0
+) Xét y x .y x  0 nên ta có 3
y x  m   2 3 2
1 x  3mx m  5 phải tiếp xúc với trục hoành 1   2  3
x  m   2 3 2
1 x  3mx m  5  0 phải có nghiệm kép   x   2
1 3x  2m  5 x m  5  0  1   phải có nghiệm kép +) TH1: Phương trình 2
3x  2m  5 x m  5  0 có một nghiệm x  1  m  13 1 +) TH2: Phương trình 2
3x  2m  5 x m  5  0 có nghiệm kép khác 1
   2m  52 125  m 2
 0  4m  32m  35  0  m m  8 2 3
m m m  21 1 2 3
Câu 91. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Gọi S là tập các giá trị dương của
tham số m sao cho hàm số 3 2
y x  3mx  27x  3m  2 đạt cực trị tại x , x thỏa mãn x x  5 1 2 1 2 . Biết S   ;
a b . Tính T  2b a .
A. T  51  6
B. T  61  3
C. T  61  3
D. T  51  6 Lời giải Chọn C +) Ta có  2
y  3x  6mx  27 ,  2
y  0  x  2mx  9  0 (1)
+) Theo giả thiết hàm số đạt cực trị tại x , x  phương trình (1) có 2 nghiệm phân biệt 1 2 m  3     0 2
m  9  0   (*) m  3 
x x  2m
+) Với điều kiện (*) thì phương trình (1) có 2 nghiệm x , x , theo Vi-ét ta có: 1 2 1 2 x x  9  1 2 2 2
+) Ta lại có x x  5   x x
 25  x x  4x x  25  0 1 2   1 2  1 2 1 2 61 61 2
 4m  61  0    m  (**) 2 2 61
+) Kết hợp (*), (**) và điều kiện m dương ta được: 3  m  2 a  3   
T  2b a  61  3 61 . b    2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 92. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Gọi S là tập hợp các giá trị nguyên của 3 x
tham số m để hàm số 2 y
 2x mx  3 có hai điểm cực trị x , x  4 . Số phần tử của S bằng 3 1 2 A. 5 . B. 3 . C. 2 . D. 4 . Lời giải 3 x Ta có: 2 2 y
 2x mx  3  y '  x  4x m . 3
Hàm số có hai điểm cực trị x , x thì phương trình y '  0 có hai nghiệm phân biệt 1 2
  '  0  4  m  0  m  4 .
x  2  4  m
Khi đó giả sử x x , 1 y '  0   1 2
x  2  4  m  2
Yêu cầu bài toán trở thành x  4  2  4  m  4  0  m  4 . 2
Kết hợp với m  4 ta được 0  m  4 . Do m nguyên nên m 0;1; 2; 
3 . Vậy có 4 giá trị của m
thỏa mãn yêu cầu bài toán.
Câu 93. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Tìm giá trị thực của tham số m để hàm số 3
y x  m  2 4
2 x 7x 1 có hai điểm cực trị x ; x x x thỏa mãn x x  4  1 2  1 2 1 2 1 7
A. m  5 . B. m  .
C. m  3 . D. m  . 2 2 Lời giải Ta có 3
y x  m  2 4
2 x 7x 1 (1) 2
y '  3x 8m 
2 x 7 . Xét phương trình 2
3x 8m  2 x 7  0 (2)
   m  2 ' 4 2   21 0  
, với mọi m  hàm số (1) luôn có hai điểm cực trị x ; x với mọi m . 1 2
*Ta thấy ac  21 0  phương trình (2) có 2 nghiệm trái dấu
x  0; x  0  x  x ; x x 1 2 1 1 2 2 8m  2
*Ta có x x  4
  x x  4  x x  4    1 4  m  1 2  1 2 1 2 3 2
Câu 94. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Có bao nhiêu giá trị nguyên của tham số m để điểm 3
M (2m ; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số 3 2
y  2x  3(2m 1)x  6m(m 1)x 1 (C) một tam giác có diện tích nhỏ nhất? A. 0 B. 1 C. 2 D. không tồn tại Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn B Ta có 2
y '  6x  6(2m 1)x  6m(m 1) x m y '  0   m   R  , hàm số luôn có CĐ, CT x m 1 
Tọa độ các điểm CĐ, CT của đồ thị là 3 2 3 2 ( A ;
m 2m  3m 1), B(m 1; 2m  3m )
Suy ra AB  2 và phương trình đường thẳng 3 2
AB : x y  2m  3m m 1  0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất 2 3m 1 1
Ta có d (M , AB)  
, dấu "=" khi m  0 2 2
Câu 95. (HSG BẮC NINH NĂM 2018-2019) Tìm tất cả các giá trị thực của tham số thực m để đường
thẳng đi qua hai điểm cực đại, cực tiểu của đồ thị hàm số 3
y x  3mx  2 cắt đường tròn C  có tâm I 1 
;1 , bán kính bằng 1 tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. 2  3 2  3 1 3 2  5 A. m B. m C. m D. m  3 2 2 2 Lời giải Ta có: 2
y  3x  3m suy ra đồ thị hàm số có điểm cực đại và cực tiểu khi m  0 . Các điểm cực
đại, cực tiểu của đồ thị hàm số là C  m;2  2m m ; Dm;2  2m m .
Đường thẳng  đi qua các điểm CĐ, CT của đồ thị hàm số có phương trình là: y  2mx  2 . Do 2m 1
d I,  
R  1 (vì m > 0)   luôn cắt đường tròn tâm I 1; 
1 , bán kính R 1 tại 2 2 4m 1 1 điểm ,
A B phân biệt. Dễ thấy m  không thõa mãn do ,
A I , B thẳng hàng. 2 1 1 1 1 Với m
:  không đi qua I, ta có: 2 SI . A I . B sin AIB R  . 2 ABI 2 2 2 1 R 1 Do đó S lớn nhất bằng khi 
sin AIB  1 hay A
IB vuông cân tại I IH   IAB 2 2 2 2m 1 1 2  3    m
( H là trung điểm của AB ) 2 4m 1 2 2
Câu 96. (ĐỀ 04 VTED NĂM 2018-2019) Biết đồ thị hàm số 3 2
y x ax bx c có hai điểm cưc trị
M x ; y , N x ; y thỏa mãn x y y y x x . Giá trị nhỏ nhất của biểu thức 1  1 2  1  1 2  1 1   2 2 
P abc  2ab  3c bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 49 25 841 7 A. B. C. D.  4 4 36 6 Lời giải Chọn A Ta có 2
y  3x  2ax b 2  1 1   a 2b ab
Chia y cho y ta được y yx a    x c      .  3 9  9 3 9  
Do M x ; y , N x ; y là hai điểm cực trị nên y x  0, yx  0 1   2  1 1   2 2  2 2  a 2b aba 2b ab Do đó y    x c  ; y    x c  1   1 2   2 9 3 9 9 3 9    
Theo giả thiết x y yy x x
x y x y 1  1 2  1  1 2  1 2 2 1 2 2  a 2b ab   a 2b ab   x   x c   x   x c  1   2  2   1  9 3 9 9 3 9        ab   ab abx c   x c   c
 0(x x )  ab  9c 1   2   1 2  9   9  9 2  7  49 49 Ta có: 2
P abc  2ab  3c  9c  21c  3c        2  4 4 49
Vậy giá trị nhỏ nhất của biểu thức P abc  2ab  3c bằng  4
Dạng 7. Tam giác cực trị
Câu 97. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 4 2
y x  2mx 1 có ba điểm cực trị tạo thành một tam giác vuông cân 1 1 A. m  .
B. m  1. C. m   . D. m  1  . 3 9 3 9 Lời giải Chọn D Hàm số 4 2
y x  2mx 1 có tập xác định: D    x  0 Ta có: 3 3
y '  4x  4mx ; y '  0  4x  4mx  0  4x  2
x m  0   2
x  m  
Hàm số có 3 cực trị khi và chỉ khi phương trình  có 2 nghiệm phân biệt khác 0
 m  0  m  0 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vậy tọa độ 3 điểm lần lượt là: A  B 2  mm C  2 0;1 ; ;1 ; m;1 m    Ta có AB   2
 m m AC   2 ; ; m; m    Vì ABC vuông cân tại 2 2 2 4 4 A A .
B AC  0   m m .m  0   m m  0  m m  0  m  1  ( vì m  0 ) Vậy với m  1
 thì hàm số có 3 cực trị tạo thành một tam giác vuông cân.
Câu 98. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y  4 x  2
2mx có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1 .
A. 0  m  1
B. m  0 C. m  3 0 4
D. m  1 Lời giải Chọn A
Tập xác định D   ym m x O 2 m B H Ax  0 Ta có y  3
4x  4mx . y  0  3
4x  4mx  0   . 2 x   m
Hàm số có ba điểm cực trị khi và chỉ khi m  0 . Khi đó đồ thị hàm số có ba điểm cực trị là
O 0; 0 , Am  2
; m , B m  2 ; m . 1 1 Do đó SOH.AB  2 m .2 m  2 m
m  1  0  m  1. OAB 2 2
Câu 99. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị của tham
số m để đồ thị hàm số 4
y x  m   2 2 2
1 x m có ba điểm cực trị tạo thành ba đỉnh của một tam
giác vuông. Số phần tử của tập hợp S là A. 2 . B. 0 . C. 4 . D. 1 . Lời giải • 4
y x  m   2 2 3
x m y x  m   x x  2 2 1 ' 4 4 1 4 x m   1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
• Hàm số có 3 điểm cực trị  y '  0 có 3 nghiệm phân biệt. 2
x m 1  0 có 2 nghiệm phân biệt khác 0.  m 1  0 .  m  1  .
x   m 1 
Khi đó: y '  0  x  0  .  x m 1  • Giả sử ,
A B, C là ba điểm cực trị của đồ thị hàm số.
A m   m   B  2 1; 2 1 ,
0; m ,C m 1; 2m   1  
AB   m  m  2  CB   m  m  2 1; 1 , 1; 1    m   A
BC vuông tại B AB.CB  0   m    m  4 1 1 1  0   m  0  . m  0 
Câu 100. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho hàm số 4 2
y x  2mx 1   1 . Tổng
lập phương các giá trị của tham số m để đồ thị hàm số  
1 có ba điểm cực trị và đường tròn đi qua
3 điểm này có bán kính R  1 bằng 5  5 1 5 A. . B. . C. 2  5 . D. 1   5 . 2 2 Lời giải  TXĐ: D  .   3 2
y '  4x  4mx  4x(x m).
 Để đồ thị hs (1) có 3 điểm cực trị  m  0.  Gọi 2 2 (
A 0;1), B( m; m 1),C( m; m 1) là các điểm cực trị của đồ thị hs (1), 2
I (0; m 1) là trung điểm B . C 1 A . B AC.BC 2 AI Ta có 2 4
AI m , AB AC
m m . Suy ra AI.BC   R  2 4R A . B ACm  0 (l) m 1 (n)  2 2m  4 2 1   5 
 1  m  2m m  0  4 m  (l) m m 2   1   5 m  (n)  2
Câu 101. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2 2
y x  2m x m  4 có ba điểm cực trị tạo thành ba đỉnh của một tam giác đều?
A. m 0; 3;  3 B. m  6 6
0; 3;  3 C. m6 6 3;   3
D. m  3;  3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn C
Đồ thị hàm số có 3 điểm cực trị  m  0 .
Khi đó, 3 điểm cực trị của đồ thị hàm số là A0; m  4 , B  4
m ;  m m  4 , C  4
m ;  m m  4 .
Tam giác ABC có AB AC nên tam giác ABC cân tại A , suy ra tam giác ABC đều m  0  AB BC 2 8 8 2 2 
m m  2 m m m  4m   . 6 m   3 
Kết hợp điều kiện ta được m  6 6  3; 3.
Câu 102. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Tìm m để đồ thị hàm số 4 2 2
y x  2m x  1 có 3 điểm cực trị lập thành một tam giác vuông cân. A. m  1. B. m  1   ;1 . C. m  1  ;0  ;1 . D. m   . Lời giải 4 2 2
y x  2m x  1. + Cách 1: Hàm số có 3 cực trị 2
ab  0  2m  0  m  0 . 3 2
y  4x  4m x 3 2
y  0  4x  4m x  0  4x  2 2
x m   0 x  0  y  1 1 1   4
x m y  m  1 2   2 4 x  m   3 y  m  1  3 Giả sử A0;  1 , B  4
m ;  m   1 , C  4
m ;  m  
1 là 3 điểm cực trị của đồ thị hàm số.  AB   4 m ;  m  2 8  AB m m .  AC   4 m ;  m  2 8  AC m m . Yêu cầu bài toán  A
BC vuông cân tại A AB AC  m    2 6    
 m 1  m   0 2 8  A . B AC  0  m m  0 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 m  0 (l) 
m  1 (n) .  m  1  (n)  Vậy m  1   ;1 .
+ Cách 2: (Áp dụng công thức tính nhanh cực trị hàm trùng phương) 2  2  m  0   m  0 ab 0   m  0 
Yêu cầu bài toán    8 8a    
 m  1 (n) . 6  1  1 m  1  3     b  2  m 3 2 m  1  (n)   Vậy m  1   ;1 .
Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối
Câu 103. (ĐỀ THAM KHẢO BGD & ĐT 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 7 điểm cực trị? A. 5 B. 6 C. 4 D. 3 Lời giải. Chọn C
y f x 4 3 2
 3x  4x 12x m
Ta có: f  x 3 2
12x 12x  24x .; f  x  0  x  0 hoặc x  1 hoặc x  2 .
Do hàm số f x có ba điểm cực trị nên hàm số y f x có 7 điểm cực trị khi m  0 
 0  m  5 . Vậy có 4 giá trị nguyên thỏa đề bài là m  1; m  2; m  3; m  4 . m  5  0 
Câu 104. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Biết phương trình 3 2
ax bx cx d  0
a  0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số 3 2
y ax bx cx d có bao nhiêu điểm cực trị? A. 4 . B. 5 . C. 2 . D. 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Phương trình 3 2
ax bx cx d  0 , a  0 là sự tương giao của đồ thị hàm số 3 2
ax bx cx d  0 , a  0 và trục hoành. Do phương trình 3 2
ax bx cx d  0 , a  0 có đúng hai nghiệm thực nên phương trình 3 2
ax bx cx d  0 có thể viết dưới dạng a x x 2 x x  0 với x , x là hai nghiệm thực 1  2  1 2
của phương trình (giả sử x x ). Khi đó đồ thị hàm số 3 2
y ax bx cx d a  0 tiếp xúc 1 2
trục hoành tại điểm có hoành độ x và cắt trục hoành tại điểm có hoành độ x . 1 2 Đồ thị hàm số 3 2
y ax bx cx d a  0 ứng với từng trường hợp a  0 và a  0 : Đồ thị hàm số 3 2
y ax bx cx d a  0 tương ứng là Vậy đồ thị hàm số 3 2
y ax bx cx d a  0 có tất cả 3 điểm cực trị.
Câu 105. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Tìm số các giá trị nguyên của tham số
m để đồ thị hàm số 4 2 2
y x  2mx  2m m 12 có bảy điểm cực trị
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 1. B. 4 . C. 0 . D. 2 . Lời giải Đồ thị hàm số 4 2 2
y x  2mx  2m m 12 có bảy điểm cực trị khi và chỉ khi đồ thị hàm số 4 2 2
y x 2mx  2m m 1
 2 cắt trục hoành tại bốn điểm phân biệt  2 m     2
2m m 12 0  4 2 2
x  2mx  2m m 12  0 có bốn nghiệm phân biệt khi và chỉ khi 2  m  0   2 2
m m12  0 
4m3     1 97 m  0     m 3  4  1 97 1  97 m   m   4 4
Vậy không có giá trị nguyên của tham số m để đồ thị hàm số 4 2 2
y x  2mx  2m m 12 có
bảy điểm cực trị.
Câu 106. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số y   x   x  2 1 2 là A. 2 B. 2 C. 3 D. 4 Lời giải
Xét hàm số: y   x   x  2 3 2 1 2
x  5x  8x  4 .  x  2 2
y  3x 10x  8. Lúc đó: 2 y 0 3x 10x 8 0         4 .  x   3
Vẽ đồ thị hàm số y   x   x  2 1 2
bằng cách vẽ đồ thị 3 2
y x  5x  8x  4 , giữ nguyên phần
đồ thị nằm phía trên trục hoành, rồi lấy đối xứng qua trục hoành phần đồ thị ở dưới trục hoành,
sau đó xóa phần đồ thị nằm dưới trục hoành. 3 2.5 2 1.5 1 0.5 1 1 2 3 4 0.5 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào đồ thị hàm số y   x   x  2 1 2
ở trên, hàm số này có 3 điểm cực trị. Cách 2: Bảng biến thiên: 4 x  2  3 f '(x)  0  0  4  f (x)  27 0
Số điểm cực trị của hàm số y f x bằng tổng số điểm cực trị của hàm số y f x và số
nghiệm đơn, nghiệm bội lẻ của phương trình f x  0 . Hàm số 3 2
y x  5x  8x  4 có 2 điểm cực trị.
Phương trình y   x   x  2 1 2
có hai nghiệm nhưng chỉ có 1 nghiệm đơn x  1 .
Do đó số điểm cực trị của hàm số y   x   x  2 1 2 là 2 1  3.
Câu 107. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y f x có bảng biến thiên như sau
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 4 B. 2 C. 5 D. 3 Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ bảng biến thiên ta thấy đồ thị y f x có 2 điểm cực trị nằm phía trên trục Ox và cắt trục
Ox tại 1 điểm duy nhất. Suy ra đồ thị y f x sẽ có 3 điểm cực trị (tham khảo hình vẽ)
Câu 108. (KTNL GIA BÌNH NĂM 2018-2019) Cho hàm số y f (x) có bảng biến thiên như sau.
Hàm số y f x  3  có bao nhiêu điểm cực trị A. 5 B. 6 C. 3 D. 1 Lời giải Chọn C
y f x  3    1 ,Đặt t |
x  3 |, t  0 Thì (1) trở thành: y f (t)(t  0) x  3 Có 2 t
(x  3)  t '  2 (x  3) Có   
y t f (t) x xx  3  x  3  t  0  x   y  0  
t f (t)  0   t  2(
L)  x  7 x x   f (t) 0     t  4  x  1   
Lấy x=8 có t '(8) f '(5)  0 , đạo hàm đổi dấu qua các nghiệm đơn nên ta có bảng biến thiên:
Dựa vào BBT thì hàm số y f x  3  có 3 cực trị.
Câu 109. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y f (x) xác định, liên tục
trên  và có bảng biến thiên như sau:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5 Lời giải Chọn B
Từ bảng biến thiên ta thấy đồ thị y f x có 2 điểm cực trị nằm phía trên trục Ox và cắt trục Ox
tại 1 điểm duy nhất. Suy ra đồ thị y f x sẽ có 3 điểm cực trị (tham khảo hình vẽ)
Câu 110. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên như sau
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 5 B. 3 C. 4 D. 2 Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 73
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ bảng biến thiên ta thấy đồ thị y f x có 2 điểm cực trị nằm phía trên trục Ox và cắt trục Ox
tại 1 điểm duy nhất. Suy ra đồ thị y f x sẽ có 3 điểm cực trị (tham khảo hình vẽ) Câu 111. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số a   0,d  2019  f x 3 2
ax bx cx d (a, , b , c d  ) và 
. Số cực trị của hàm số a
 b c d 2019  0 
y g x ( với g x  f x 2019) bằng A. 2 . B. 5 . C. 3 . D. 1. Lời giải + Ta có
 lim gx x
g 0d20190     g x
0 có ba nghiệm phân biệt, mà g x là hàm số bậc g   
1  a b c d  2019  0
 lim gx x
ba. Suy ra, hàm số y g x có hai điểm cực trị.
+ Vậy đồ thị của hàm số y g x là đồ thị của hàm số bậc ba, có hai điểm cực trị và cắt trục Ox
tại ba điểm phân biệt. Do đó, số điểm cực trị của hàm số y g x bằng 5  số cực trị của hàm
số y g x bằng 2 hoặc bằng 3.
Câu 112. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Có bao nhiêu giá trị
nguyên của tham số m để hàm số 4 3 2 2
y  3x  4x 12x m có đúng 5 điểm cực trị? A. 5 . B. 7 . C. 6 . D. 4 . Lời giải Xét hàm số 4 3 2 2
f (x)  3x  4x 12x m ; 3 2 f (
x)  12x 12x  24x f (
x)  0  x  0; x  1
 ; x  2 . Suy ra, hàm số y f (x) có 3 điểm cực trị. 1 2 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 74
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  Hàm số 4 3 2 2
y  3x  4x 12x m có 5 điểm cực trị khi đồ thị hàm số y f (x) cắt trục hoành
tại 2 điểm phân biệt  4 3 2 2
3x  4x 12x m  0 có 2 nghiệm phân biệt. Phương trình 4 3 2 2 4 3 2 2
3x  4x 12x m  0  3
x  4x 12x m (1). Xét hàm số 4 3 2 g(x)  3
x  4x 12x ; 3 2 g (  x)  1
 2x 12x  24x . Bảng biến thiên: 2 m  0
Phương trình (1) cớ 2 nghiệm phân biệt    5  m  32 . 2 5  m  32  Vậy m 3; 4;5; 3  ; 4  ;   5 .
Câu 113. (HSG BẮC NINH NĂM 2018-2019) Số điểm cực trị của hàm số y   x   x  2 1 2 là A. 2 B. 2 C. 3 D. 4 Lời giải
Xét hàm số: y   x   x  2 3 2 1 2
x  5x  8x  4 .  x  2 2
y  3x 10x  8. Lúc đó: 2 y 0 3x 10x 8 0         4 .  x   3
Vẽ đồ thị hàm số y   x   x  2 1 2
bằng cách vẽ đồ thị 3 2
y x  5x  8x  4 , giữ nguyên phần
đồ thị nằm phía trên trục hoành, rồi lấy đối xứng qua trục hoành phần đồ thị ở dưới trục hoành,
sau đó xóa phần đồ thị nằm dưới trục hoành.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 75
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 2.5 2 1.5 1 0.5 1 1 2 3 4 0.5 1
Dựa vào đồ thị hàm số y   x   x  2 1 2
ở trên, hàm số này có 3 điểm cực trị. Cách 2: Bảng biến thiên: 4 x  2  3 f '(x)  0  0  4  f (x)  27 0
Số điểm cực trị của hàm số y f x bằng tổng số điểm cực trị của hàm số y f x và số
nghiệm đơn, nghiệm bội lẻ của phương trình f x  0 . Hàm số 3 2
y x  5x  8x  4 có 2 điểm cực trị.
Phương trình y   x   x  2 1 2
có hai nghiệm nhưng chỉ có 1 nghiệm đơn x  1 .
Do đó số điểm cực trị của hàm số y   x   x  2 1 2 là 2 1  3.
Câu 114. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Có bao nhiêu giá trị nguyên dương
của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 5 điểm cực trị. A. 16 B. 44 C. 26 D. 27 Lời giải Chọn C Đặt: 4 3 2
g(x)  3x  4x 12x m
x  2  y m  32  Ta có: 3 2
g '(x)  12x 12x  24x  0  x  1
  y m  5 
x  0  y m
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 76
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 m  0  m  0
Dựa vào bảng biến thiên, hàm số có y g(x) có 5 điểm cực trị khi m  5  0    .  5  m  32   m  32  0 
Vì m là số nguyên dương cho nên có 26 số m thỏa đề bài
Câu 115. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số 4 2
y x  2mx  2m 1 với m là tham số thực. Số giá trị nguyên trong khoảng  2
 ; 2 của m để
hàm số đã cho có 3 điểm cực trị là A. 2 B. 4 C. 3 D. 1 Lời giải Chọn B x  0
Đặt f x 4 2
x  2mx  2m 1, f  x 3
 4x  4mx , f  x  0   2 x m
+ Trường hợp 1: hàm số có một cực trị  m  2  ;0 .
Đồ thị hàm số y f x có một điểm cực trị là A0; 2m   1 . Do m  2
 ; 0  y  2m 1 0 nên đồ thị hàm số y f x cắt trục hoành tại 2 điểm phân biệt A
nên hàm số y f x có 3 cực trị  có 3 giá trị nguyên của m thỏa ycbt.
+ Trường hợp 2: hàm số có ba cực trị  m  0; 2 .
Khi đó đồ thị hàm số có 3 điểm cực trị là A0; 2m   1 , B  2
m; m  2m   1 , C  2
m; m  2m   1 .
Do a  1  0 nên hàm số y f x có 3 điểm cực trị khi hàm số y f x có y y  0 B C 2
 m  2m 1  0  m  1 .
Nếu y y  0 (trong bài toán này không xảy ra) thì hàm số có ít nhất 5 điểm cực trị. B C
Vậy có 4 giá trị của m thỏa ycbt.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 77
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 116. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số y f x có đồ
thị như hình vẽ bên dưới
Tìm tất cả các giá trị của tham số m để đồ thị hàm số h x 2
f x  2 f x  2m có đúng 3 điểm cực trị. A. m 1 B. m  1 C. m  2
D. m  2 Lời giải Chọn B
Số cực trị của hàm số h x 2
f x  2 f x  2m bằng số cực trị của hàm số y x 2
f x  2 f x  2m cộng với số giao điểm (khác điểm cực trị) của đồ thị hàm số y x 2
f x  2 f x  2m và y  0 .
Xét hàm số gx 2
f x  2 f x  2m
g x  2 f x.f  x  2 f  x  2 f  x  f x 1    
f  xx 1  0 
g x  0    x  3 
f  x  1 
x     0  BBT 1
Hàm số hx có 3 điểm cực trị  2m 0  m . Đáp án B là gần kết quả nhất 2
Câu 117. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Tập hợp các giá trị của m để hàm số 4 3 2
y  3x  4x 12x m 1 có 7 điểm cực trị là: A. (0; 6) B. (6;33) C. (1;33) D. (1; 6)
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 78
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn D Xét hàm số 4 3 2
f (x)  3x  4x 12x m 1 ,
Có lim f x   , lim f x   x x  3 2 f x x x x x  2 ( ) 12 12 24 12
x x  2  x  0 
f  (x)  0  x  1  .   x  2  Bảng biến thiên:
Từ bảng biến thiên, ta có hàm số y f (x) có 7 điểm cực trị  đồ thị hàm số y f (x) cắt Ox
tại 4 điểm phân biệt  m  6  0  m 1  1  m  6 .
------------- HẾT -------------
Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x)
Câu 118. (Mã đề 101 - BGD - 2019) Cho hàm số y f x , bảng biến thiên của hàm số f ' x như sau:
Số điểm cực trị của hàm số y f  2
x  2x là A. 9. B. 3. C. 7. D. 5. Lời giải Chọn C
Ta có y   x   f  2 2 1 . x  2x .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 79
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  1 x  1   2
x  2x a   ;    2 1
x  2x a  0, a   ;      1 (1) x  1   y  0   2
x  2x b   1  ; 0 2
x  2x b  0, b   1  ; 0 (2) . f      2
x  2x  0   2
x  2x c  0   2 ;1
x  2x c  0, c  0  ;1 (3)   2  x 2x d 1;  2      
x  2x d  0, d  1;   (4)  
Phương trình (1) vô nghiệm, các phương trình (2), (3), (4) đều có hai nghiệm phân biệt khác 1 và
do b, c, d đôi một khác nhau nên các nghiệm của phương trình (2), (3), (4) cũng đôi một khác
nhau. Do đó f  2
x  2x  0 có 6 nghiệm phân biệt.
Vậy y  0 có 7 nghiệm phân biệt, do đó số điểm cực trị của hàm số y f  2
x  2x là 7.
Câu 119. (Mã đề 104 - BGD - 2019) Cho hàm số f x , bảng biến thiên của hàm số f  x như sau:
Số điểm cực trị của hàm số y f  2
4x  4x là A. 5. B. 9. C. 7. D. 3. Lời giải Chọn C  1  x     Có  f  2
x x   x   f  2 4 4 8 4
4x  4x ,  f  2
4x  4x  0  2  .  f  2
4x  4x  0  2
4x  4x a  ;  1 1    2
4x  4x a  1; 0 2  
Từ bảng biến thiên trên ta có f  2
4x  4x  0   . (1) 2
4x  4x a  0;1  3    2
4x  4x a  1;  4   
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 80
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 Xét g x 2
 4x  4x , g x  8x  4 , g x  0  x   ta có bảng biến thiên 2
Kết hợp bảng biến thiên của g x và hệ (1) ta thấy: Phương trình 2
4x  4x a   ;  1  vô nghiệm. 1   1 Phương trình 2
4x  4x a  1
 ;0 tìm được hai nghiệm phân biệt khác  . 2   2 1 Phương trình 2
4x  4x a  0;1 tìm được thêm hai nghiệm mới phân biệt khác  . 2   2 1 Phương trình 2
4x  4x a  1;  tìm được thêm hai nghiệm phân biệt khác  . 2   2
Vậy hàm số y f  2
4x  4x có tất cả 7 điểm cực trị. f x f ' x
Câu 120. (Mã 102 - BGD - 2019) Cho hàm số
, bảng biến thiên của hàm số như sau x -∞ -1 0 1 +∞ +∞ 2 +∞ f'(x) -1 -3
Số điểm cực trị của hàm số y f  2
x  2x là A. 9. B. 5. C. 7 . D. 3. Lời giải Chọn C 2x  2  0  2
x  2x a, a  1   Ta có y '
2x 2 f ' 2 x 2x 2 0     
x  2x  , b 1   b  0  2
x  2x c, 0  c  1  2
x  2x d, d  1 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 81
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 8 6 4 2 d c b 15 10 5 5 10 15 a 2 4 6 8
Dựa vào đồ thị ta được y '  0 có 7 nghiệm đơn nên nó có 7 cực trị
Câu 121. (Mã 103 - BGD - 2019) Cho hàm số f x , bảng biến thiên của hàm số f  x như sau:
Số cực trị của hàm số y f  2
4x  4x là A. 3 . B. 9 . C. 5 . D. 7 . Lời giải Chọn D Từ bảng biến thiên
x a   ;    1
x b 1  ; 0
Ta thấy f x 0    
x c 0;  1 
x d  1;  
Với y f  2
4x  4x , ta có y   x   f  2 8 4 4x  4x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 82
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1 x   2  2
4x  4x a   ;     1   1  8x  4  0  2 y  0   
4x  4x b  1  ; 0 2 2     f  
4x  4x  0   2
 4x  4x c  0  ;1 3  2
4x  4x d  1;  4   1
Xét hàm số g x 2
 4x  4x , ta có g x  8x  4  0  x  2 Bảng biến thiên
Từ bảng biến thiên của g x ta có: a  ;    1   1 Vì nên vô nghiệm. Vì b  1
 ;0 nên 2 có 2 nghiệm phân biệt. Vì c  0 
;1 nên 3 có 2 nghiệm phân biệt.
Vì d 1;  nên 4 có 2 nghiệm phân biệt.
Vậy hàm số y f  2
4x  4x có 7 điểm cực trị Cách khác:
Ta có: y   x   f  2 8 4 . 4x  4x . 8x  4  0
y  0  8x  4. f  2
4x  4x  0   f    2
4x  4x  0  1
+ 8x  4  0  x  . 2 2
4x  4x a a    1   1  2
4x  4x b 1  b  0 2  + f  2
4x  4x  0  2
 4x  4x c0  c   1 3  2
 4x  4x d d   1 4  + Phương trình 2 2
4x  4x m  4x  4x m  0 có nghiệm khi   4  4m  0 hay m  1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 83
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ đó, ta có phương trình  
1 ; 2 ; 3 luôn có hai nghiệm phân biệt.
Phương trình 4 vô nghiệm.
Do đó, hàm số đã cho có 7 cực trị.
Câu 122. Cho hàm số y f x xác định trên  và có đồ thị hàm số y f  x là đường cong ở hình vẽ.
Hỏi hàm số y f x có bao nhiêu điểm cực trị? y a O c b x A. 2 . B. 3 . C. 4 . D. 1. Lời giải x a
Từ đồ thị hàm số y f  x ta có f  x  0  x b .  x c
Từ bảng biến thiên ta thấy hàm số đã cho có 1 điểm cực trị.
Câu 123. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số y f x có đồ thị
y f  x như hình vẽ sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 84
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đồ thị hàm số g x  f x 2 2
x có tối đa bao nhiêu điểm cực trị? A. 7 B. 5 C. 6 D. 3 Lời giải Chọn A
Xét hàm số h x  f x 2 2
x h ' x  2 f ' x  2x
Từ đồ thị ta thấy h ' x  0  f ' x  x x  2  x  2  x  4 2 4
 2 f 'x  2xdx  2x  2 f 'xdx  0 2 2
h x 2  h x 4  h 2  h 2   h 4  h 2  h 4  h 2 2 2 Bảng biến thiên
Vậy g x  f x 2 2
x có tối đa 7 cực trị
Câu 124. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hàm số f (x) xác định trên  và có
đồ thị f (x) như hình vẽ bên. Đặt g(x)  f (x)  x . Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 85
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3  1  A.  ;3    B.  2  ;  0 C. 0;  1 D.  ; 2 2  2  Lời giải x 1 
Ta có g x  f x1; g x  0  f x 1  x  1  x  2 
Bảng xét dấu của gx: x -∞ -1 1 2 +∞ g'(x) + 0 0 0 +
Từ bảng xét dấu nhận thấy g x đạt cực đại tại x  1   2  ;  0 .
Câu 125. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số y f (
x 1) có đồ thị như hình vẽ. Hàm số
2 f x 4x y   
đạt cực tiểu tại điểm nào? A. x  1 . B. x  0 . C. x  2 . D. x  1  . Lời giải: Ta có:     
2 f x  4 2  4 x y f x   ln    .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 86
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
y  0  2 f  x  4  0  f  x  2 .
Đồ thị hàm số y f  x nhận được từ việc tịnh tiến đồ thị hàm số y f  x   1 sang trái 1 đơn vị  x  2 
nên f  x  2  x  0 .   x  1  Do x  2
 và x  1 là nghiệm bội chẵn nên ta có bảng biến thiên sau: x  2 0 1  y  0  0  0    y
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại x  0 .
Câu 126. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số
y f x có đạo hàm trên  và có đồ thị là đường cong như hình vẽ. Đặt g x  3 f f x  4 .
Tìm số điểm cực trị của hàm số g x? y 3 1 1 2 3 4 O x A. 2 . B. 8 . C. 10 . D. 6 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 87
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải
g x  3 f  f x. f  x .
f x  0  
f  f x  0 f
  x  a
g x  0  3 f  f x. f  x  0   
, 2  a  3 .
f  x  0   x  0  x a
f x  0 có 3 nghiệm đơn phân biệt x , x , x khác 0 và a . 1 2 3
Vì 2  a  3 nên f x  a có 3 nghiệm đơn phân biệt x , x , x khác x , x , x , 0 , a. 4 5 6 1 2 3
Suy ra g x  0 có 8 nghiệm đơn phân biệt. Do đó hàm số g x  3 f f x  4 có 8 điểm cực trị.
Câu 127. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y f x xác
định và liên tục trên  , đồ thị của hàm số y f  x như hình vẽ. Điểm cực đại của hàm số
g x  f x  x là A. x  0 . B. x  1 . C. x  2 .
D. không có điểm cưc đại. Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 88
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta có: g x  f  x 1 x  0
g x  0  f  x 1  0  f  x 1   x  1 .  x  2  Bảng biến thiên:
Vậy hàm số g x đạt cực đại tại x 1.
Câu 128. Cho hàm số y f x có đạo hàm liên tục trên  và có đồ thị hàm số y f  x như hình vẽ. Đặt     3 g x f
x  . Tìm số điểm cực trị của hàm số y g x . y a b c O x A. 3 B. 5 C. 4 D. 2 Lời giải Chọn A Đặt     3 h x
f x       3 h x f x  . h x 2  x f  3 3 x
h x   x  3 3 3 0
0; a; b; c Bảng biến thiên:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 89
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vậy hàm số y g x có ba điểm cực trị.
Câu 129. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số y f x xác định trên 
và hàm số y f x có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số y f  2 x   3 . y 2 1 x -2 O A. 4 B. 2 C. 5 D. 3 Lời giải Chọn D
Quan sát đồ thị ta có y f  x  đổi dấu từ âm sang dương qua x  2 nên hàm số y f x  có
một điểm cực trị là x  2 . x  0 x  0     Ta có  y  f  2
x    x f  2 3 2 . x  2             3  0 x 3 2 x 1   .  2  x 3 1 x  2  
Mà x  2 là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số y f  2 x   3 có ba cực trị.
Câu 130. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo
hàm là f  x . Đồ thị của hàm số y f  x như hình vẽ bên. Tính số điểm cực trị của hàm số   2 y
f x  trên khoảng  5; 5 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 90
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 2 . B. 4 . C. 3 . D. 5 . Lời giải
Xét hàm số g x  f  2
x   g x  xf  2 2 x  . x  0 x  0  x  0
g x  0   2  x  0    . f    2 x   0  x   2 2  x  2  Ta có bảng xét dấu: Từ đó suy ra hàm số   2 y
f x  có 3 điểm cực trị.
Câu 131. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hàm số y  f  x có đạo hàm liên
tục trên và đồ thị hàm số y  f 'x như hình vẽ bên.
Số điểm cực trị của hàm số y  f x  2017  2018x  2019 là. A. 3 B. 4 C. 1 D. 2 Lời giải Chọn C
Ta có: f x  2017  2018x  2019 
  0  f x  2017  2018  0  f x  2017  2018  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 91
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 f x  2017  2018
Dựa vào đồ thị hàm số y  f 'x suy ra phương trình có 1 nghiệm đơn duy
nhất. Suy ra hàm số y  f x  2017  2018x  2019 có 1 điểm cực trị.
Câu 132. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số y f ( x) . Hàm số y f (
x) có đồ thị như hình vẽ dưới đây. y x 0 1 2 3
Tìm m để hàm số 2
y f (x m) có 3 điểm cực trị.
A. m  3; .
B. m 0;  3 .
C. m 0;3 .
D. m   ;  0 . Lời giải Chọn C Do hàm số 2
y f (x m) là hàm chẵn nên hàm số có 3 cực trị khi và chỉ khi hàm số này có
đúng 1 điểm cực trị dương. 2
y f x m y  xf  2 ( ) 2 x m  x  0  x  0  2  2 x  0 x m  0 x  m y 0         f    2 x m 2 2  0 x m  1  x  1 m    2 2 x m  3
x  3  m  
Đồ thị hàm số y f  x tiếp xúc trục hoành tại điểm có hoành độ là x 1 nên các nghiệm của pt 2
x  1  m (nếu có) không làm  2 f
x m  đổi dấu khi x đi qua, do đó các điểm cực trị của x  0  hàm số 2
y f (x m) là các điểm nghiệm của hệ 2 x  m  2 x  3  m  m  0
Hệ trên có duy nhất nghiệm dương khi và chỉ khi   0  m  3 . 3  m  0 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 92