Các dạng toán GTLN – GTNN của hàm số thường gặp trong kỳ thi THPTQG

Các dạng toán GTLN – GTNN của hàm số thường gặp trong kỳ thi THPTQG được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

66 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 3
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 1
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó ...................................... 1
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b] ..................................................... 7
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b) ................................................ 8
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế ............................................................................................... 9
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước ........................................................ 11
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm ................................................................................ 13
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số ............................................................................................... 18
PHẦN B. LỜI GIẢI THAM KHẢO ........................................................................................................................... 19
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó .................................... 19
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b] ................................................... 28
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b) .............................................. 32
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế ............................................................................................. 34
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước ........................................................ 41
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm ................................................................................ 51
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số ............................................................................................... 62
PHẦN A. CÂU HỎI
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó
Câu 1. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
( )
y f x
=
liên tục trên đoạn
1;3
-
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên
đoạn
1;3
-
. Giá trị của
M m-
bằng
A.
1
B.
4
C.
5
D.
0
Câu 2. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
=
liên tục trên đoạn
1;1
-
và có đồ thị như hình vẽ.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1-
. Giá trị của
M m-
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 3. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm
số
=
trên đoạn
2; 2
-
.
A.
5; 1m M= - = -
. B.
2; 2m M= - =
. C.
1; 0m M= - =
. D.
5; 0m M= - =
.
Câu 4. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số
( )
y f x
=
xác định, liên tục trên
và có bảng
biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
-1
.
C. Hàm số đạt cực đại tại
x = 0
và đạt cực tiểu tại
x = 1
.
D. Hàm số có đúng một cực trị.
Câu 5. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Cho hàm số
=
liên tục trên
3;2-
và có bảng biến thiên như sau. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
1;2-
. Tính
M m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 6. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét hàm số với có bảng biến
thiên như sau:
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn
B. Hàm số đã cho đạt GTNN tại và trên đoạn
C. Hàm số đã cho đạt GTNN tại và đạt GTLN tại trên đoạn
D. Hàm số đã cho đạt GTNN tại trên đoạn
Câu 7. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hàm số
=
liên tục trên
, có bảng biến thiên như hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3-
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng
( ) ( )
; 1 , 2;
- -
.
Câu 8. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
=
liên tục trên
và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
A. Phương trình
( )
0
f x
=
có
4
nghiệm phân biệt
B. Hàm số đồng biến trên khoảng
( )
0;

C. Giá trị nhỏ nhất của hàm số bằng
0
D. Hàm số có
3
điểm cực trị
Câu 9. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số
( )=y f x
liên tục và có bảng biến thiên trên đoạn
1;3
-
như hình vẽ bên. Khẳng định nào sau đây đúng?
( )y f x=
1;5
x -
1;5
-
1
x
= -
2
x
=
1;5
-
1
x
= -
5
x
=
1;5
-
0
x
=
1;5
-
x
– ∞
-2
0
2
+ ∞
y'
+
0
–
0
+
0
–
y
– ∞
4
0
4
– ∞
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
A.
1;3
max ( ) (0)f x f
-
=
. B.
( ) ( )
1;3
max 3
-
=f x f
. C.
( ) ( )
1;3
max 2
-
=f x f
. D.
( ) ( )
1;3
max 1
-
= -f x f
.
Câu 10. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số
( )
f x
liên tục trên
1;5-
và có
đồ thị trên đoạn
1;5-
như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
f x
trên
đoạn
1;5-
bằng
A.
1-
B.
4
C.
1
D.
2
Câu 11. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Cho hàm số
( )
f x
liên tục trên
và có đồ thị
như hình vẽ sau:
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
( )
f x
trên
3
1;
2
-
. Giá trị của
M m
bằng
A.
1
2
. B.
5
. C.
4
. D.
3
.
Câu 12. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
xác định, liên
tục trên
5
1,
2
-
và có đồ thị là đường cong như hình vẽ.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
( )
f x
trên
5
1,
2
-
là:
A.
4, 1
M m
= =
B.
= = -4, 1
M m
C.
7
, 1
2
M m
= = -
D.
7
, 1
2
M m
= =
Câu 13. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
( )
y f x
=
có đồ thị như
hình vẽ. Giá trị lớn nhất của hàm số
( )
f x
trên đoạn
0;2
là:
A.
( )
0;2
2
Max f x
=
. B.
( )
0;2
2
Max f x =
. C.
( )
0;2
4
Max f x
=
. D.
( )
0;2
0
Max f x
=
.
Câu 14. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
( )y f x=
liên tục trên đoạn
1;3
-
và có đồ thị như hình vẽ bên. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã
cho trên đoạn
1;3
-
. Giá trị của
M m
là
A.
2
B.
6-
C.
5-
D.
2-
Câu 15. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số
( )
y f x
=
có bảng biến thiên trên
)
5;7
-
như sau
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
Mệnh đề nào dưới đây đúng?
A.
)
( )
5;7
Min 6f x
-
=
. B.
)
( )
5;7
Min 2f x
-
=
. C.
)
( )
-5;7
Max 9f x =
. D.
)
( )
5;7
Max 6f x
-
=
.
Câu 16. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Cho ham sô
( )
f x
liên tuc trên
đoan
0;3
va co đô thi như hinh ve bên. Goi
M
va
m
lân lươt la gia tri lơn nhât va nho nhât cua ham sô đa
cho trên
0;3
. Gia tri cua
M m
băng?
A.
5
. B.
3
. C.
2
. D.
1
.
Câu 17. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số
( )
y f x=
liên tục
trên đoạn
2;6
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2;6
. Giá trị của
M m
bằng
A.
9
. B.
8-
. C.
9-
. D.
8
.
y = f(x)
y
x
-2
4
5
6
-1
-3
-4
-1
3
O
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 18. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Cho hàm số
=
liên tục và có đồ thị
trên đoạn
2;4
-
như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số
=
trên đoạn
2;4
-
bằng
A.
5
B.
3
C.
0
D.
2-
Câu 19. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
=
có bảng
xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng
A.
(
( ) ( )
1;1
max 0
f x f
-
=
B.
( )
( ) ( )
0;
max 1f x f

=
C.
( )
( ) ( )
; 1
min 1
f x f
- -
= -
D.
( )
( ) ( )
1;
min 0
f x f
- 
=
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b]
Câu 20. (Mã 102 - BGD - 2019) Giá trị nhỏ nhất của hàm số
( )
3
3 2
f x x x
= -
trên đoạn
3;3
-
bằng
A.
0
. B.
16-
. C.
20
. D.
4
.
Câu 21. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị lớn nhất
M
của hàm số
4 2
2 3
y x x
= -
trên đoạn
0; 3
.
A.
6
M
=
B.
1M =
C.
9
M
=
D.
M =
Câu 22. (Mã 103 - BGD - 2019) Giá trị lớn nhất của hàm số
( )
3
3f x x x= -
trên đoạn
[ 3;3]-
bằng
A.
2-
. B.
18
. C.
2
. D.
18-
.
Câu 23. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
=
-
x
y
x
trên đoạn
2;4
.
A.
2;4
min 3= -
y B.
2;4
19
min
3
=y
C.
2;4
y D.
2;4
min 2= -
y
Câu 24. (Mã đề 104 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số
4 2
13
y x x
= -
trên đoạn
[ 1;2]-
bằng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
A.
85
B.
51
4
C.
13
D.
25
Câu 25. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
=
trên đoạn
1
;2
2
.
A.
5
m
=
B.
3
m
=
C.
17
4
m
=
D.
10
m
=
Câu 26. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số
= - -
3 2
7 11 2
y x x x
trên đoạn
[0; 2]
.
A.
= 3m
B.
= 0m
C.
= -2m
D.
= 11m
Câu 27. (Mã đề 101 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số
4 2
4 9
y x x
= -
trên đoạn
2;3
-
bằng
A.
201
B.
2
C.
9
D.
54
Câu 28. (ĐỀ THAM KHẢO BGD & ĐT 2018) Giá trị lớn nhất của hàm số
( )
4 2
4 5
f x x x
= -
trêm đoạn
2;3
-
bằng
A.
122
B.
50
C.
5
D.
1
Câu 29. (MĐ 105 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số
= -
4 2
13
y x x
trên đoạn
-
2;3
.
A.
= 13m
B.
=
51
4
m
C.
=
51
2
m
D.
=
49
4
m
Câu 30. (Mã đề 104 - BGD - 2019) Giá trị nhỏ nhất của hàm số
( )
3
3= -f x x x
trên đoạn
3;3
-
bằng
A.
18.-
B.
2.-
C.
2.
D.
18.
Câu 31. (MĐ 103 BGD&ĐT NĂM 2017-2018) Giá trị nhỏ nhất của hàm số
3 2
3y x x
= trên đoạn
4; 1- -
bằng
A.
16-
B.
0
C.
4
D.
4-
Câu 32. (Mã đề 102 BGD&ĐT NĂM 2018) Giá trị nhỏ nhất của hàm số
3 2
2 7y x x x= -
trên đoạn
0;4
bằng
A.
259-
B.
68
C.
0
D.
4-
Câu 33. (Mã đề 101 - BGD - 2019) Giá trị lớn nhất của hàm số
( )
3
3 2
f x x x
= -
trên đoạn
3;3
-
là
A.
4
. B.
16-
. C.
20
. D.
0
.
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b)
Câu 34. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tính giá trị nhỏ nhất của hàm số
2
4
3y x
x
=
trên
khoảng
( )
0;

.
A.
( )
0;
33
min
5
y

=
B.
( )
3
0;
min 2 9
y

=
C.
( )
3
0;
min 3 9
y
=
D.
( )
0;
min 7
y

=
Câu 35. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Gọi
m
là giá trị nhở
nhất của hàm số
y x
trên khoảng
( )
0;

. Tìm
m
A.
4
m
=
. B.
2
m
=
. C.
1
m
=
. D.
3
m
=
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 36. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Gọi
a
là giá trị nhỏ nhất của hàm số
2
4
y x
x
=
trên khoảng
(0; )
. Tìm
a
.
A.
3
3 4
. B.
5
. C.
6
. D.
3
2 16
.
Câu 37. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Giá trị nhỏ nhất của hàm số
1
5y x
x
= -
trên khoảng
( )
0;

bằng bao nhiêu?
A.
0
B.
1-
C.
3-
D.
2-
Câu 38. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số
1
( )f x x
x
=
trên nửa khoảng
)
2;

là:
A.
2
B.
5
2
C.
0
D.
7
2
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế
Câu 39. (Mã đề 101 BGD&ĐT NĂM 2018) Ông
A
dự định dùng hết
2
6,5m
kính để làm một bể cá có dạng
hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung
tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 m
B.
3
1,61m
C.
3
1,33 m
D.
3
1,50 m
Câu 40. (MĐ 104 BGD&DT NĂM 2017) Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
= -
với
t
(giây) là
khoảng thời gian tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của
vật đạt được bằng bao nhiêu?
A.
243
(m/s) B.
27
(m/s) C.
144
(m/s) D.
36
(m/s)
Câu 41. (MĐ 103 BGD&ĐT NĂM 2017-2018) Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước
không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
B.
3
0,96 m
C.
3
1,33 m
D.
3
1,51 m
Câu 42. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người ta
cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập
tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn
nhất.
A.
3
x
=
B.
2
x
=
C.
4
x
=
D.
6
x
=
Câu 43. (KTNL GIA BÌNH NĂM 2018-2019) Một chất điểm chuyển động theo phương trình
3 2
3 2
S t t
= - -
, trong đó
t
tính bằng giây và
S
tính theo mét. Chuyển động có vận tốc lớn nhất là
A.
1
m/s. B.
4
m/s. C.
3
m/s. D.
2
m/s.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Câu 44. (THPT NĂM 2018-2019 LẦN 04) Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc
trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi
tiêm vào cơ thể trong
t
giờ được cho bởi công thức
( )
2
1
t
c t
t
=
( )
/mg L
. Sau khi tiêm thuốc bao lâu thì
nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Câu 45. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Đợt xuất khẩu gạo của tỉnh A thường
kéo dài trong
2
tháng (
60
ngày). Người ta nhận thấy số lượng xuất khẩu gạo tính theo ngày thứ
t
được xác
định bởi công thức
( )
3 2
2
63 3240 3100
5
= - -S t t t t
với
( )
1 60
t
. Hỏi trong
60
ngày đó thì ngày thứ mấy
có số lượng xuất khẩu gạo cao nhất.
A.
60
B.
45
C.
30
D.
25
Câu 46. (GKI NHÂN CHÍNH HÀ NỘI NĂM 2018-2019 LẦN 01) Một vật chuyển động theo quy luật
2 3
1
10
3
S t t
= -
, với
t
(giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và
( )
S m
là quãng đường
vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian
15
giây từ lúc vật bắt đầu chuyển động vận
tốc
( )
/v m s
của vật đạt giá trị lớn nhất tại thời điểm
( )
t s
bằng:
A.
( )
8 s
. B.
( )
20
s
C.
( )
10 s
. D.
( )
15 s
.
Câu 47. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Một sợi dây có chiều dài
28m
được cắt thành hai đoạn để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo đơn vị mét) của
đoạn dây làm thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất?
A.
56
4
. B.
112
4
. C.
84
4
. D.
92
4
.
Câu 48. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Một xưởng in có
15
máy in được cài đặt tự
động và giám sát bởi một kỹ sư, mỗi máy in có thể in được
30
ấn phẩm trong
1
giờ, chi phí cài đặt và bảo
dưỡng cho mỗi máy in cho
1
đợt hàng là
48.000
đồng, chi phí trả cho kỹ sư giám sát là
24.000
đồng/giờ.
Đợt hàng này xưởng in nhận
6000
ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là
A.
10
máy. B.
11
máy. C.
12
máy. D.
9
máy.
Câu 49. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật
( )
3 2
4 12
s t t t
= -
(m), trong đó
t
(s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất
điểm đó đạt giá trị bé nhất khi
t
bằng bao nhiêu?
A. 2 (s). B.
8
3
(s). C. 0 (s). D.
4
3
(s).
Câu 50. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho một tấm nhôm hình chữ nhật có chiều
dài bằng
10cm
và chiều rộng bằng
8cm
. Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng
nhau, mỗi hình vuông có cạnh bằng
( )
x cm
, rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp không
nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
A.
8 2 21
3
x
-
=
B.
10 2 7
3
x
-
=
C.
9 21
9
x
=
. D.
9 21
3
x
-
=
Câu 51. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Một đoàn cứu trợ lũ lụt đang ở vị trí
A
của
một tỉnh miền trung muốn đến xã
C
để tiếp tế lương thực và thuốc men. Để đi đến
C
, đoàn cứu trợ phải chèo
thuyền từ
A
đến vị trí
D
với vận tốc
( )
4 /km h
, rồi đi bộ đến vị trí
C
với vận tốc
. Biết
A
cách
B
một khoảng
5km
,
B
cách
C
một khoảng
7km
(hình vẽ). Hỏi vị trí điểm
D
cách
A
bao xa để đoàn cứu
trợ đi đến xã
C
nhanh nhất?
A.
5 3AD km=
. B.
2 5AD km=
. C.
5 2AD km=
. D.
3 5AD km=
.
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước
Câu 52. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số
=
- 1
x m
y
x
(
m
là tham số thực) thỏa mãn
=
[2;4]
min 3.y Mệnh đề nào dưới đây đúng?
A.
4m
B.
3 4m
C.
-1m
D.
1 3m
Câu 53. (ĐỀ THAM KHẢO BGD & ĐT 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao
cho giá trị lớn nhất của hàm số
3
3y x x m= -
trên đoạn
0;2
bằng 3. Số phần tử của S là
A. 0 B. 6 C. 1 D. 2
Câu 54. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số
1
x m
y
x
=
(
m
là tham số thực) thoả mãn
1;2
1;2
16
min max
3
y y =
. Mệnh đề nào dưới đây đúng?
A.
4m
B.
2 4m
C.
0m
D.
0 2m
Câu 55. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Có một giá trị
0
m
của tham số
m
để
hàm số
3 2
1 1y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là đúng?
A.
2
0 0
2018 0m m
. B.
0
2 1 0m
.
C.
2
0 0
6 0m m
. D.
0
2 1 0m
.
Câu 56. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
2y x x m= -
trên đoạn
1;2- bằng
5
.
A.
1-
. B.
2
. C.
2-
. D.
1
.
Câu 57. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số
2
1y x m x= -
có giá trị lớn nhất bằng
2 2
thì giá trị của
m
là
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
A.
2
2
. B.
2
-
. C.
2
. D.
2
2
-
.
Câu 58. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số
1
x m
y
x
(
m
là tham số
thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây đúng?
A.
1 3m
B.
6m
C.
1m
D.
3 6m
Câu 59. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên
1;2
bằng
8
(
m
là tham số thực). Khẳng định nào sau đây đúng?
A.
10
m
. B.
8 10
m
. C.
m
. D.
m
.
Câu 60. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
3 2
2 3
y x x m= - -
.
Trên
1;1
-
hàm số có giá trị nhỏ nhất là
1-
. Tính
m
?
A.
6
m
= -
. B.
3
m
= -
. C.
4
m
= -
. D.
5
m
= -
.
Câu 61. (THPT ĐÔNG SƠN THANH HÓA NĂM 2018-2019 LẦN 02) Tìm
m
để giá trị lớn nhất của hàm
số
3
3 2 1
y x x m
= - -
trên đoạn
0;2
là nhỏ nhất. Giá trị của
m
thuộc khoảng nào?
A.
3
; 1
2
- -
. B.
2
;2
3
. C.
1;0
-
. D.
( )
0;1
.
Câu 62. (HỌC MÃI NĂM 2018-2019-LẦN 02) Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá
trị nhỏ nhất của hàm số
4 2 3 2
2
y x m x x m= - - -
trên đoạn
0;1
bằng
16-
. Tính tích các phần tử của
S
.
A.
2
. B.
2-
. C.
15-
. D.
17-
.
Câu 63. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
,A B
lần lượt là giá trị nhỏ nhất, giá trị lớn
nhất của hàm số
2
1
x m m
y
x
=
-
trên đoạn
2;3
. Tìm tất cả các giá trị thực của tham số
m
để
13
2
A B
=
.
A.
1; 2
m m
= = -
. B.
2
m
= -
. C.
2
m
=
. D.
1; 2
m m
= - =
.
Câu 64. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1x mx
y
x m
=
liên tục và đạt giá trị nhỏ nhất trên đoạn
0;2
tại một điểm
( )
0
0;2
x
.
A.
0 1
m
B.
1
m
C.
2
m
D.
1 1
m
-
Câu 65. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Gọi
S
là tập hợp tất cả các giá trị thực
của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
y
x
=
trên
1;2
bằng
2
. Số phần tử của tập
S
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 66. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm
m
để giá trị nhỏ nhất của hàm số
2
( )
1
x m m
f x
x
-
=
trên đoạn (0;1) bằng –2
A.
1
2
m
m
=
=
.
B.
1
2
m
m
=
= -
.
C.
1
2
m
m
= -
=
. D.
1 21
2
m
=
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
Câu 67. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Cho hàm số
1 sin
cos 2
m x
y
x
-
=
. Có bao
nhiêu giá trị nguyên của tham số
m
thuộc đoạn
0;10
để giá trị nhỏ nhất của hàm số nhỏ hơn
2-
?
A.
1
. B.
9
. C.
3
. D.
6
.
Câu 68. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Xét hàm số
( )
2
f x x ax b=
, với
a
,
b
là tham số. Gọi
M
là giá trị lớn nhất của hàm số trên
1;3
-
. Khi
M
nhận giá trị nhỏ nhất có thể được,
tính
2a b
.
A.
2
. B.
4
. C.
4-
. D.
3
.
Câu 69. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Cho hàm số
3
, 0
y ax cx d a
=
có
( )
( ) ( )
;0
min 2
x
f x f
-
= -
. Giá trị lớn nhất của hàm số
( )
y f x
=
trên đoạn
1;3
bằng
A.
11d a-
. B.
16d a-
. C.
2d a
. D.
8d a
.
Câu 70. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x
-
=
-
trên đoạn
1;1
- bằng
3
. Tính tổng tất cả các phần tử của
S
.
A.
8
3
-
. B.
5
. C.
5
3
. D.
1-
.
Câu 71. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Tìm tất cả các giá trị của tham số m
để hàm số
2
1
x m
y
x x
=
có giá trị lớn nhất trên
nhỏ hơn hoặc bằng 1.
A.
1
m
. B.
1
m
. C.
1
m
-
. D.
1
m
-
.
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm
Câu 72. (Mã 102 - BGD - 2019) Cho hàm số
( )
f x
, hàm số
( )
y f x
¢
=
liên tục trên
và có đồ thị như hình
vẽ.
Bất phương trình
( )
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
x
khi và chỉ khi
A.
( )
0
m f
. B.
( )
0
m f
. C.
( )
2 2
m f
-
. D.
( )
2 2
m f
-
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Câu 73. (Mã 103 - BGD - 2019) Cho hàm số
( )
y f x=
, hàm số
( )
'y f x=
liên tục trên
và có đồ thị như
hình vẽ bên. Bất phương trình
( )
2
f x x m
(m là tham số thực) nghiệm đúng với mọi
( )
0;2
x
khi và chỉ
khi
A.
( )
0m f
. B.
( )
2 4m f -
. C.
( )
0m f
. D.
( )
2 4m f -
.
Câu 74. (Mã đề 101 - BGD - 2019) Cho hàm số
( )
y f x=
, hàm số
( )
'y f x=
liên tục trên
và co đồ thị
như hình vẽ bên dưới
Bất phương trình
( )
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
( )
0;2x
khi và chỉ khi
A.
( )
2 2.
m f
-
B.
( )
0 .
m f
C.
( )
2 2.
m f
-
D.
( )
0 .
m f
Câu 75. (Mã đề 104 - BGD - 2019) Cho hàm số
( )
f x
, hàm số
( )
f x
¢
liên tục trên
và có đồ thị như hình
vẽ.
Bất phương trình
( )
2f x x m
(
m
là tham số thực) nghiệm đúng với mọi
( )
0; 2x
khi và chỉ khi
A.
( )
2 4m f -
. B.
( )
2 4m f -
. C.
( )
0m f
. D.
( )
0m f
.
Câu 76. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
xác định
và liên tục trên
, đồ thị của hàm số
( )
y f x
¢
=
như hình vẽ.
x
y
2
2
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
Giá trị lớn nhất của hàm số
( )
y f x
=
trên đoạn
1;2
-
là
A.
( )
1f
. B.
( )
1
f
-
. C.
( )
2
f
. D.
( )
0
f
.
Câu 77. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
( )
f x
có đạo hàm
là
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình vẽ bên. Biết rằng
( ) ( ) ( ) ( ) ( )
0 1 2 3 5 4
f f f f f - = -
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
( )
f x
trên đoạn
0;5
.
A.
( ) ( )
5 , 3m f M f
= =
B.
( ) ( )
5 , 1m f M f
= =
C.
( ) ( )
0 , 3
m f M f= =
D.
( ) ( )
1 , 3
m f M f= =
Câu 78. (ĐÊ 04 VTED NĂM 2018-2019) Cho hàm số
( )
y f x
=
. Hàm số
/
( )y f x
= có bảng biến thiên như
sau:
Bất phương trình
( )
x x
f e e m
nghiệm đúng với mọi
( )
1;1
x -
khi và chỉ khi
A.
1 1
m f
e e
-
B.
( )
1
1m f
e
- -
C.
( )
1
1m f
e
- -
D.
1 1
m f
e e
-
Câu 79. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số
( )
y f x
=
có
bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
( )
( )
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
= - -
trên đoạn
1;3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
A. 15. B.
25
3
. C.
19
3
. D. 12.
Câu 80. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Cho hàm số
=
. Hàm số
( )
¢
=
y f x
có
bảng biến thiên như sau
Bất phương trình
( )
cos
2 3
x
f x m
đúng với mọi
0;
2
x
khi và chỉ khi
A.
( )
1
0 2
3
-
m f
. B.
( )
1
0 2
3
-
m f
. C.
1
1
3 2
-
m f
. D.
1
1
3 2
-
m f
.
Câu 81. (Đề minh họa 2019) Cho hàm số
( )
y f x
=
. Hàm số
/
( )y f x
= có bảng biến thiên như sau:
Bất phương trình
( )
x x
f e e m
nghiệm đúng với mọi
( )
1;1
x -
khi và chỉ khi
A.
1 1
m f
e e
-
B.
( )
1
1m f
e
- -
C.
( )
1
1m f
e
- -
D.
1 1
m f
e e
-
Câu 82. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
( )
f x
có bảng biến
thiên như sau:
Gọi
S
là tập hợp các số nguyên dương
m
để bất phương trình
( )
( )
3 2
3 5
f x m x x
-
có nghiệm thuộc đoạn
1;3
-
. Số phần tử của
S
là
A.
3
B. Vô số C.
2
D.
0
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
Câu 83. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
liên tục
trên
.
Đồ thị của hàm số
( )
y f x
¢
=
như hình bên. Đặt
( ) ( ) ( )
2
2 1 .g x f x x= -
Mệnh đề dưới đây đúng.
A.
( ) ( )
3;3
max 3 .g x g
-
=
B.
( ) ( )
3;3
min 1 .g x g
-
=
C.
( ) ( )
3;3
max 0 .g x g
-
=
D.
( ) ( )
3;3
max 1 .g x g
-
=
Câu 84. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho hàm số có đạo hàm cấp
hai trên . Biết , và bảng xét dấu của như sau:
Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A.
( )
; 2017- -
B.
( )
2017;
C.
( )
0;2
D.
( )
2017;0-
Câu 85. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số
( )
f x
liên tục trên
và có đồ
thị như hình vẽ bên. Bất phương trình
( )
3 2
2 2 3f x x m x
nghiệm đúng với mọi
( )
1;3
x -
khi và chỉ khi
A.
10.m -
B.
5.m -
C.
3.m -
D.
2.m -
Câu 86. (KTNL GV BẮC GIANG NĂM 2018-2019) Cho hàm số
( )
f x
có đạo hàm trên
và có đồ thị
của hàm
( )
y f x
¢
=
được cho như hình vẽ.
=
( )
0 3
f
¢
=
( )
2 2018
f
¢
= -
( )
f x
¢¢
( )
2017 2018y f x x
=
0
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Biết rằng
( ) ( ) ( ) ( )
3 0 4 1
f f f f
- = -
. Giá trị lớn nhất và giá trị nhỏ nhất của
( )
f x
trên đoạn
3;4
-
lần
lượt là:
A.
(4)f
và
( 3)
f
-
. B.
( 3)
f
-
và
(0)f
. C.
(4)f
và
(0)f
. D.
(2)f
và
( 3)
f
-
.
Câu 87. Cho hàm số
( )
f x
có đạo hàm là
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình vẽ dưới
đây:
Biết rằng
( ) ( ) ( ) ( )
1 0 1 2
f f f f-
. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
=
trên đoạn
1;2
-
lần lượt là:
A.
( )
1f
;
( )
2
f
. B.
( )
2
f
;
( )
0
f
. C.
( )
0
f
;
( )
2
f
. D.
( )
1f
;
( )
1
f
-
.
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số
Câu 88. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số
m
để
bất phương trình
( )( )
2
6 2 8 1
x x x x m
- -
nghiệm đúng với mọi
2;8 .
x -
A.
16
m
B.
15
m
C.
8
m
D.
2 16
m
-
Câu 89. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm
m
để bất phương trình
4
1
x m
x
-
có nghiệm trên khoảng
( )
;1-
.
A.
5
m
. B.
3
m
-
. C.
1
m
. D.
1
m
-
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Biết rằng tập nghiệm của
bất phương trình
2
6 4
2 4 2 2
5 1
x
x x
x
-
- -
là
;a b
. Khi đó giá trị của biểu thức
3 2P a b= -
bằng:
A.
2
B.
4
C.
2-
D.
1
Câu 91. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi
s
là tập hợp các giá trị
nguyên của tham số
0;2019
m
để bất phương trình
( )
3
2 2
1 0
x m x
- -
đúng với mọi
1;1
x -
. Số phần tử của tập
s
bằng
A.
1
. B.
2020
. C.
2019
. D.
2
.
Câu 92. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
M
là giá trị lớn nhất của hàm số
( )
2 2
4 4 6 4 1
f x x x x x
= - -
. Tính tích các nghiệm của phương trình
( )
f x M=
.
A.
2
. B.
4
. C.
2-
. D.
4-
.
Câu 93. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
2 2
2
x xy y
- =
. Giá trị nhỏ nhất
của
2 2
P x xy y=
bằng:
A.
2
3
B.
1
6
C.
1
2
D.
2
Câu 94. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
x
,
y
là các số thực thỏa mãn
1 2 2
x y x y
= -
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
( )( )
2 2
2 1 1 8 4
P x y x y x y= - -
. Tính giá trị
M m
A.
42
B.
41
C.
43
D.
44
Câu 95. (KTNL GIA BÌNH NĂM 2018-2019) Cho bất phương trình
( )
( )
2
2 2 1 2 0
m x x x x
- -
.
Hỏi có bao nhiêu số nguyên
m
không nhỏ hơn
2018-
để bất phương trình đã cho có nghiệm
0;1 3
x
?
A.
2018
B.
2019
C.
2017
D.
2020
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó
Câu 1. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
( )
y f x
=
liên tục trên đoạn
1;3
-
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm
số đã cho trên đoạn
1;3
-
. Giá trị của
M m-
bằng
A.
1
B.
4
C.
5
D.
0
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Lời giải
Chọn C
Dựa và đồ thị suy ra
( ) ( )
3 3; 2 2M f m f= = = = -
Vậy
5M m- =
Câu 2. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
( )
y f x=
liên tục trên đoạn
1;1-
và có đồ thị như hình vẽ.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1-
. Giá trị
của
M m-
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Từ đồ thị ta thấy
1, 0M m= =
nên
1M m- =
.
Câu 3. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
( )
y f x=
trên đoạn
2; 2-
.
A.
5; 1
m M
= - = -
. B.
2; 2m M= - =
. C.
1; 0m M= - =
. D.
5; 0m M= - =
.
Lời giải
Nhìn vào đồ thị ta thấy:
( )
2;2
max 1M f x
-
= = -
khi
1x = -
hoặc
2x =
.
( )
2;2
min 5m f x
-
= = -
khi
2x = -
hoặc
1x =
.
Câu 4. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số
( )
y f x=
xác định, liên tục trên
và có
bảng biến thiên:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
-1
.
C. Hàm số đạt cực đại tại
x
= 0
và đạt cực tiểu tại
x
= 1
.
D. Hàm số có đúng một cực trị.
Lơi giai
Chọn C
Đáp án A sai vì hàm số có
2
điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu
y
= -1
khi
x
= 0
.
Đáp án C sai vì hàm số không có GTLN và GTNN trên
.
Đáp án D đúng vì hàm số đạt cực đại tại
x
= 0
và đạt cực tiểu tại
x
= 1
.
Câu 5. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Cho hàm số
=
liên tục
trên
3;2
-
và có bảng biến thiên như sau. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số
=
trên đoạn
1;2
-
. Tính
M m
.
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Trên đoạn
1;2
-
ta có giá trị lớn nhất
3
M
=
khi
1
x
= -
và giá trị nhỏ nhất
0
m
=
khi
0
x
=
.
Khi đó
3 0 3
M m
= =
.
Câu 6. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét hàm số với có bảng biến
thiên như sau:
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn
B. Hàm số đã cho đạt GTNN tại và trên đoạn
C. Hàm số đã cho đạt GTNN tại và đạt GTLN tại trên đoạn
D. Hàm số đã cho đạt GTNN tại trên đoạn
Lời giải
( )y f x=
1;5
x -
1;5
-
1
x
= -
2
x
=
1;5
-
1
x
= -
5
x
=
1;5
-
0
x
=
1;5
-
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
A. Đúng. Vì
5
lim
x
y
-
= 
nên hàm số không có GTLN trên đoạn .
B. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn .
C. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn và .
D. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn .
Câu 7. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hàm số
=
liên tục trên
, có bảng biến thiên như hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3-
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng
( ) ( )
; 1 , 2;
- -
.
Lời giải
Dựa vào BBT ta thấy hàm số không có GTLN, GTNN.
Câu 8. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
=
liên tục trên
và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
A. Phương trình
( )
0
f x
=
có
4
nghiệm phân biệt
B. Hàm số đồng biến trên khoảng
( )
0;

C. Giá trị nhỏ nhất của hàm số bằng
0
D. Hàm số có
3
điểm cực trị
Lời giải
Chọn D
Dựa vào bảng biến thiên, hàm số có 3 điểm cực trị.
Câu 9. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số
( )=y f x
liên tục và có bảng biến thiên trên đoạn
1;3
-
như hình vẽ bên. Khẳng định nào sau đây
đúng?
1;5
-
2
x
=
1;5
-
2
x
=
1;5
-
5
lim
x
y
= 
2
x
=
1;5
-
x
– ∞
-2
0
2
+ ∞
y'
+
0
–
0
+
0
–
y
– ∞
4
0
4
– ∞
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
A.
1;3
max ( ) (0)f x f
-
=
. B.
( ) ( )
1;3
max 3
-
=f x f
.
C.
( ) ( )
1;3
max 2
-
=f x f
. D.
( ) ( )
1;3
max 1
-
= -f x f
.
Lời giải
Nhìn vào bảng biến thiên ta thấy
( ) ( )
1;3
max 0 .f x f
-
=
Câu 10. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số
( )
f x
liên tục trên
1;5-
và
có đồ thị trên đoạn
1;5-
như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm
số
( )
f x
trên đoạn
1;5
-
bằng
A.
1-
B.
4
C.
1
D.
2
Lời giải
Từ đồ thị ta thấy:
( )
( )
1;5
1;5
max 3
1.
min 2
M f x
M n
n f x
-
-
= =
=
= = -
Câu 11. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Cho hàm số
( )
f x
liên tục trên
và có đồ thị
như hình vẽ sau:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
( )
f x
trên
3
1;
2
-
. Giá trị của
M m
bằng
A.
1
2
. B.
5
. C.
4
. D.
3
.
Lời giải
Dựa vào đồ thị hàm số
( )
f x
ta có:
( )
3
1;
2
max 4
M f x
-
= =
;
( )
3
1;
2
min 1
m f x
-
= = -
.
Do đó
( )
4 1 3
M m
= - =
.
Câu 12. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Cho hàm số
=
xác định, liên
tục trên
5
1,
2
-
và có đồ thị là đường cong như hình vẽ.
Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
( )
f x
trên
5
1,
2
-
là:
A.
4, 1
M m
= =
B.
= = -4, 1
M m
C.
7
, 1
2
M m
= = -
D.
7
, 1
2
M m
= =
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Dựa vào đồ thị
= = -4, 1
M m
.
Câu 13. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
( )
y f x
=
có đồ thị
như hình vẽ. Giá trị lớn nhất của hàm số
( )
f x
trên đoạn
0;2
là:
A.
( )
0;2
2
Max f x
=
. B.
( )
0;2
2
Max f x =
.
C.
( )
0;2
4
Max f x
=
. D.
( )
0;2
0
Max f x
=
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy trên đoạn
0;2
hàm số
( )
f x
có giá trị lớn nhất bằng
4
khi
2
x =
Suy ra
( )
0;2
4
Max f x
=
Câu 14. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
( )y f x=
liên tục trên đoạn
1;3
-
và có đồ thị như hình vẽ bên. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số đã cho trên đoạn
1;3
-
. Giá trị của
M m
là
A.
2
B.
6-
C.
5-
D.
2-
Lời giải
Dựa vào đồ thị ta thấy GTLN của hàm số trên đoạn
1;3
-
là
2M =
đạt được tại
1
x
= -
và GTNN
của hàm số số trên đoạn
1;3
-
là
4
m
= -
đạt được tại
2
x
=
2 ( 4) 2
M m
= - = -
Câu 15. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số
( )
y f x
=
có bảng biến thiên trên
)
5;7
-
như sau
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
Mệnh đề nào dưới đây đúng?
A.
)
( )
5;7
Min 6f x
-
=
. B.
)
( )
5;7
Min 2f x
-
=
. C.
)
( )
-5;7
Max 9f x =
. D.
)
( )
5;7
Max 6f x
-
=
.
Lời giải
Dựa vào bảng biến thiên trên
)
5;7-
, ta có:
)
( ) ( )
5;7
Min 1 2f x f
-
= =
.
Câu 16. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Cho ham sô
( )
f x
liên tuc trên
đoan
0;3
va co đô thi như hinh ve bên. Goi
M
va
m
lân lươt la gia tri lơn nhât va nho nhât cua
ham sô đa cho trên
0;3
. Gia tri cua
M m
băng?
A.
5
. B.
3
. C.
2
. D.
1
.
Lời giải
Dưa vao hinh ve ta co:
3M =
,
2m = -
nên
1M m =
.
Câu 17. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số
( )
y f x=
liên
tục trên đoạn
2;6
và có đồ thị như hình vẽ bên dưới.
y = f(x)
y
x
-2
4
5
6
-1
-3
-4
-1
3
O
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2;6
. Giá trị
của
M m
bằng
A.
9
. B.
8-
. C.
9-
. D.
8
.
Lời giải
Từ đồ thị suy ra
( )
4 5
f x
-
2;6 ;
x -
( ) ( )
1 4; 4 5
f f
= - =
5
4
M
m
=
= -
9
M m
- =
.
Câu 18. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Cho hàm số
=
liên tục và có đồ thị
trên đoạn
2;4
-
như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số
=
trên
đoạn
2;4
-
bằng
A.
5
B.
3
C.
0
D.
2-
Lời giải
Chọn B
Dựa vào đồ thị hàm số ta có
( )
2;4
4
x
m Min f x
-
= = -
,
( )
2;4
7
x
M Max f x
-
= =
Khi đó
3
M m
=
Câu 19. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
=
có bảng
xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng
A.
(
( ) ( )
1;1
max 0
f x f
-
=
B.
( )
( ) ( )
0;
max 1f x f

=
C.
( )
( ) ( )
; 1
min 1
f x f
- -
= -
D.
( )
( ) ( )
1;
min 0
f x f
- 
=
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b]
Câu 20. (Mã 102 - BGD - 2019) Giá trị nhỏ nhất của hàm số
( )
3
3 2f x x x= -
trên đoạn
3;3-
bằng
A.
0
. B.
16-
. C.
20
. D.
4
.
Lời giải
Chọn B
Cách 1:Mode 7
( )
3
3 2f x x x= -
.
Start -3
end3step 1
Chọn B
Cách 2:
( )
2
3 3f x x
¢
= -
.
( )
0 1 3;3f x x
¢
= Û = -
.
( )
3 16f - = -
;
( )
1 4f - =
;
( )
1 0f =
;
( )
3 20f =
.
Giá trị nhỏ nhất là
16-
.
Câu 21. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị lớn nhất
M
của hàm số
4 2
2 3y x x= -
trên
đoạn
0; 3
.
A.
6M =
B.
1M =
C.
9M =
D.
8 3M =
Lời giải
Chọn A
Ta có:
( )
3 2
4 4 4 1y x x x x
¢
= - = -
0y
¢
=
Û
( )
2
4 1 0x x - =
0
1
1( )
x
x
x l
=
Û =
= -
Ta có :
( )
0 3y =
;
( )
1 2y =
;
( )
3 6y =
Vậy giá trị lớn nhất của hàm số
4 2
2 3y x x= -
trên đoạn
0; 3
là
( )
3 6M y= =
Câu 22. (Mã 103 - BGD - 2019) Giá trị lớn nhất của hàm số
( )
3
3f x x x= -
trên đoạn
[ 3;3]-
bằng
A.
2-
. B.
18
. C.
2
. D.
18-
.
Lời giải
Chọn B
Ta có
2
3 3 0 1y x x
¢
= - = Û =
( ) ( ) ( ) ( )
3 18; 1 2; 1 2; 3 18f f f f- = - - = = - =
.
Câu 23. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
=
-
x
y
x
trên đoạn
2;4
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
A.
2;4
min 3= -
y B.
2;4
19
min
3
=y
C.
2;4
y D.
2;4
min 2= -
y
Lời giải
Chọn C
Tập xác định:
\ 1
=
D
Hàm số
2
3
1
=
-
x
y
x
xác định và liên tục trên đoạn
2;4
Ta có
( )
2
2
2
2 3
; 0 2 3 0 3
1
- -
¢ ¢
= = Û - - = Û =
-
x x
y y x x x
x
hoặc
1= -
x
(loại)
Suy ra
( ) ( ) ( )
19
2 7; 3 6; 4
3
= = =y y y
. Vậy
2;4
min 6=y
tại
3=
x
.
Câu 24. (Mã đề 104 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số
4 2
13
y x x
= -
trên đoạn
[ 1;2]-
bằng
A.
85
B.
51
4
C.
13
D.
25
Lời giải
Chọn D
( )
4 2
13
y f x x x
= = -
3
' 4 2y x x= -
3
0 [ 1;2]
1
4 2 0 [ 1;2]
2
1
[ 1;2]
2
x
x x x
x
= -
- = Û = - -
= -
1 51 1 51
( 1) 13; (2) 25; (0) 13; ;
4 4
2 2
f f f f f
- = = = - = =
Giá trị lớn nhất của hàm số
4 2
13
y x x
= -
trên đoạn
[ 1;2]-
bằng
25.
Câu 25. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
=
trên đoạn
1
;2
2
.
A.
5
m
=
B.
3
m
=
C.
17
4
m
=
D.
10
m
=
Lời giải
Chọn B
Đặt
( )
2
2
y f x x
x
= =
.
Ta có
3
2 2
2 2 2
2
x
y x
x x
-
¢
= - =
,
1
0 1 ;2
2
y x
¢
= =
.
Khi đó
( ) ( )
1 17
1 3, , 2 5
2 4
f f f
= = =
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Vậy
( ) ( )
1
;2
2
min 1 3
m f x f
= = =
.
Câu 26. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số
= - -
3 2
7 11 2
y x x x
trên đoạn
[0; 2]
.
A.
= 3m
B.
= 0m
C.
= -2m
D.
= 11m
Lời giải
Chọn C
Xét hàm số trên đoạn
[0; 2]
. Ta có
¢
= -
2
3 14 11
y x x
suy ra
¢
= Û =0 1y x
Tính
( ) ( ) ( )
= - = =0 2; 1 3, 2 0
f f f
. Suy ra
( ) ( )
= = - =
0;2
min 0 2
f x f m
.
Câu 27. (Mã đề 101 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số
4 2
4 9
y x x
= -
trên đoạn
2;3
-
bằng
A.
201
B.
2
C.
9
D.
54
Lời giải
Chọn D
3
4 8
¢
= -y x x
;
0
0
2
=
¢
= Û
=
x
y
x
.
Ta có
( )
2 9
y
- =
;
( )
3 54
y
=
;
( )
0 9
y
=
;
( )
2 5
y
=
.
Vậy
2;3
max 54
y
-
=
.
Câu 28. (ĐỀ THAM KHẢO BGD & ĐT 2018) Giá trị lớn nhất của hàm số
( )
4 2
4 5
f x x x
= -
trêm đoạn
2;3
-
bằng
A.
122
B.
50
C.
5
D.
1
Lời giải
Chọn B
3
0
'( ) 4 8 0 2;3
2
=
= - = Û -
=
x
f x x x
x
;
( )
( )
( ) ( )
0 5; 2 1; 2 5; 3 50
f f f f
= = - = =
Vậy
2;3
50
Max y
-
=
Câu 29. (MĐ 105 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số
= -
4 2
13
y x x
trên đoạn
-
2;3
.
A.
= 13m
B.
=
51
4
m
C.
=
51
2
m
D.
=
49
4
m
Lời giải
Chọn B
¢
= -
3
4 2y x x
;
= -
¢
= Û
= -
0 2;3
0
1
2;3
2
x
y
x
;
Tính
( )
- =2 25
y
,
( )
=3 85
y
,
( )
=0 13
y
,
= =
1 51
12,75
4
2
y
;
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Kết luận: giá trị nhỏ nhất
m
của hàm số là
=
51
4
m
.
Câu 30. (Mã đề 104 - BGD - 2019) Giá trị nhỏ nhất của hàm số
( )
3
3= -f x x x
trên đoạn
3;3
-
bằng
A.
18.-
B.
2.-
C.
2.
D.
18.
Lời giải
Chọn A
Ta có
( )
2
1
3 3 0 .
1
=
¢
== - = Û
= -
x
f x x
x
Mà
( ) ( ) ( ) ( )
3 18; 1 2; 1 2; 3 18.
- = - - = = - =f f f f
Vậy giá trị nhỏ nhất của hàm số
( )
3
3= -f x x x
trên đoạn
3;3
-
bằng
18.-
Câu 31. (MĐ 103 BGD&ĐT NĂM 2017-2018) Giá trị nhỏ nhất của hàm số
3 2
3y x x
= trên đoạn
4; 1- -
bằng
A.
16-
B.
0
C.
4
D.
4-
Lời giải
Chọn A
Ta có
2
3 6y x x
¢
=
;
2
4; 1
0
0 3 6 0
4; 1
2
x
y x x
x
- -
=
¢
= = Û
- -
= -
.
Khi đó
( )
4 16
y
- = -
;
( )
2 4
y
- =
;
( )
1 2
y
- =
.
Nên
4; 1
min 16
y
- -
= -
.
Câu 32. (Mã đề 102 BGD&ĐT NĂM 2018) Giá trị nhỏ nhất của hàm số
3 2
2 7y x x x= -
trên đoạn
0;4
bằng
A.
259-
B.
68
C.
0
D.
4-
Lời giải
Chọn D
TXĐ
D .=
Hàm số liên tục trên đoạn
0;4
.
Ta có
2
3 4 7
y x x
¢
= -
0
y
¢
=
1 0 4
7
0 4
3
x ;
x ;
=
Û
= -
( ) ( ) ( )
0 0; 1 4; 4 68
y y y
= = - =
.
Vậy
0;4
min 4
y
= -
.
Câu 33. (Mã đề 101 - BGD - 2019) Giá trị lớn nhất của hàm số
( )
3
3 2
f x x x
= -
trên đoạn
3;3
-
là
A.
4
. B.
16-
. C.
20
. D.
0
.
Lời giải
Chọn C
( )
3
3 2
f x x x
= -
tập xác định
.
( )
2
' 0 3 3 0 1 3;3
f x x x= Û - = Û = -
.
( ) ( ) ( ) ( )
1 0; 1 4; 3 20; 3 16
f f f f
= - = = - = -
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
Từ đó suy ra
( )
3;3
max (3) 20
f x f
-
= =
.
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b)
Câu 34. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tính giá trị nhỏ nhất của hàm số
2
4
3y x
x
=
trên
khoảng
( )
0;

.
A.
( )
0;
33
min
5
y

=
B.
( )
3
0;
min 2 9
y

=
C.
( )
3
0;
min 3 9
y
=
D.
( )
0;
min 7
y

=
Lời giải
Chọn C
Cách 1:
3
3
2 2 2
4 3 3 4 3 3 4
3 3 . . 3 9
2 2 2 2
x x x x
y x
x x x
= = =
Dấu
" "=
xảy ra khi
3
2
3 4 8
2 3
x
x
x
= Û =
.
Vậy
( )
3
0;
min 3 9
y
=
Cách 2:
Xét hàm số
2
4
3y x
x
=
trên khoảng
( )
0;

Ta có
2 3
4 8
3 ' 3y x y
x x
= = -
Cho
3
3
3
8 8 8
' 0 3
3 3
y x x
x
= Û = Û = Û =
( )
3
3
0;
8
min 3 9
3
y y

= =
Câu 35. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Gọi
m
là giá trị nhở
nhất của hàm số
y x
trên khoảng
( )
0;

. Tìm
m
A.
4
m
=
. B.
2
m
=
. C.
1
m
=
. D.
3
m
=
.
Lời giải
( )
2
4
' 1
' 0 2; 2 0; .
y
x
y x x
= -
= Û = = 
Bảng biến thiên:
x
0

3
8
3
'y
y
3
3 9
0
-
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
Suy ra giá trị nhỏ nhất của hàm số bằng
2) 4(
4.
y m
= =
Câu 36. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Gọi
a
là giá trị nhỏ nhất của hàm số
2
4
y x
x
=
trên khoảng
(0; )
. Tìm
a
.
A.
3
3 4
. B.
5
. C.
6
. D.
3
2 16
.
Lời giải.
Ta có:
3
2
2 2
4 4 2 4
' 2
x
y x y x
x x x
-
= = - =
.
3
3
' 0 2 4 0 2
y x x= Û - = Û =
.
Bảng biến thiên
Nhìn vào BBT ta thấy giá trị nhỏ nhất của hàm số là
3
3 4
a =
.
Câu 37. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Giá trị nhỏ nhất của hàm số
1
5y x
x
= -
trên khoảng
( )
0;

bằng bao nhiêu?
A.
0
B.
1-
C.
3-
D.
2-
Lời giải
Chọn C
Áp dụng bất đẳng thức Cô – si ta có:
1 1
5 2 . 5 3
y x x
x x
= - - = -
Dấu bằng xảy ra khi
2
1
1 1x x x
x
= Û = Û =
(vì
0
x
).
Vậy
( )
0;
min 3
y

= -
.
Câu 38. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số
1
( )f x x
x
=
trên nửa khoảng
)
2;

là:
A.
2
B.
5
2
C.
0
D.
7
2
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
Áp dụng bất đẳng thức Cô-si, ta được:
1 3 1 3.2 1 5
( ) 2 .
4 4 4 4 2
x x x
f x x
x x x
= = =
.
Dấu bằng xảy ra khi
2
x
=
.
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế
Câu 39. (Mã đề 101 BGD&ĐT NĂM 2018) Ông
A
dự định dùng hết
2
6,5m
kính để làm một bể cá có
dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể).
Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 m
B.
3
1,61m
C.
3
1,33 m
D.
3
1,50 m
Lời giải
Chọn D
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá:
=V abc
Mặt khác theo giả thiết ta có:
2 2 6,5
2
=
=
ab bc ac
a b
2
2 6 6,5
2
=
Û
=
b bc
a b
2
6,5 2
6
2
-
=
Û
=
b
c
b
a b
Khi đó
2
2
6,5 2
2 .
6
-
=
b
V b
b
3
6,5 2
3
-
Û =
b b
V
.
Xét hàm số:
( )
3
6,5 2
3
-
=
b b
f b
. Có BBT
Vậy bể cá có dung tích lớn nhất là:
3
39
1,50
6
=
f m
.
Câu 40. (MĐ 104 BGD&DT NĂM 2017) Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
= -
với
t
(giây)
là khoảng thời gian tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển
được trong khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây kể từ khi bắt đầu chuyển động,
vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A.
243
(m/s) B.
27
(m/s) C.
144
(m/s) D.
36
(m/s)
Lời giải
c
b
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Chọn D
Ta có:
2
12v s t t
¢
= = -
;
2 12
v t
¢
= -
;
0 6v t
¢
= Û =
.
BBT
Nhìn bbt ta thấy vận tốc đạt giá trị lớn nhất khi
6t =
. Giá trị lớn nhất là
( )
6 36m/s
v =
.
Câu 41. (MĐ 103 BGD&ĐT NĂM 2017-2018) Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có
kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng
phần trăm)?
A.
3
1,01m
B.
3
0,96 m
C.
3
1,33 m
D.
3
1,51 m
Lời giải
Chọn A
Gọi
,x y
lần lượt là chiều rộng và chiều cao của bể cá (điều kiện
, 0
x y
).
Ta có thể tích bể cá
2
2
V x y
= .
Theo đề bài ta có:
2
2 2.2 2 5
xy xy x
=
2
6 2 5
xy x
Û =
2
5 2
6
x
y
x
-
Û =
(Điều kiện kiện
2
0 5 2 0
y x
Û -
5
0
2
x
)
2 3
2
5 2 5 2
2
6 3
x x x
V x
x
- -
= =
2
5 6
3
x
V
-
¢
=
2
0 5 6 0
V x
¢
= Û - =
5
6
xÛ =
3
max
5 30
1,01
27
V
m
=
.
Câu 42. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người ta
cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm),
rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để hộp nhận
được có thể tích lớn nhất.
y
x
2
x
C
D
A
D'
B
C'
B'
A'
t
v
¢
v
0
9
6
0
36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
A.
3
x
=
B.
2
x
=
C.
4
x
=
D.
6
x
=
Lơi giai
Chọn B
Ta có :
( )
h x cm
=
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
( )
12 2
x cm
-
Vậy diện tích đáy hình hộp
( )
( )
2
2
12 2
S x cm
= -
. Ta có:
( )
0 0
0;6
12 2 0 6
x x
x
x x
Û Û
-
Thể tích của hình hộp là:
( )
2
. 1.
2 2
V S xh
x
= -=
Xét hàm số:
( ) ( )
2
. 12 2 0;6
y x x x= -
Ta có :
( ) ( ) ( )( )
2
' 12 2 4 12 2 12 2 12 6y x x x x x
= - - - = - -
;
( ) ( )
' 0 12 2 . 12 6 0 2
y x x x
= Û - - = Û =
hoặc
6
x
=
(loại).
Suy ra với
2
x
=
thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là
( )
2 128
y =
.
Câu 43. (KTNL GIA BÌNH NĂM 2018-2019) Một chất điểm chuyển động theo phương trình
3 2
3 2
S t t
= - -
, trong đó
t
tính bằng giây và
S
tính theo mét. Chuyển động có vận tốc lớn nhất
là
A.
1
m/s. B.
4
m/s. C.
3
m/s. D.
2
m/s.
Lời giải
Chọn C.
( )
2
3 2 2
3 2 3 6 3 1 3 3
S t t v t t t
= - - = - = - -
.
Do đó
( )
max 3 /v m s
=
.
Câu 44. (THPT NĂM 2018-2019 LẦN 04) Một loại thuốc được dùng cho một bệnh nhân và nồng độ
thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của
bệnh nhân sau khi tiêm vào cơ thể trong
t
giờ được cho bởi công thức
( )
2
1
t
c t
t
=
( )
/mg L
. Sau
khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Lời giải
Xét hàm số
( )
2
1
t
c t
t
=
,
( 0)
t
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
( )
( )
2
2
2
1
1
t
c t
t
-
¢
=
.
( )
1
0
1
t
c t
t
=
¢
= Û
= -
.
Với
1t =
giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất.
Câu 45. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Đợt xuất khẩu gạo của tỉnh A thường
kéo dài trong
2
tháng (
60
ngày). Người ta nhận thấy số lượng xuất khẩu gạo tính theo ngày thứ
t
được xác định bởi công thức
( )
3 2
2
63 3240 3100
5
= - -S t t t t
với
( )
1 60 t
. Hỏi trong
60
ngày
đó thì ngày thứ mấy có số lượng xuất khẩu gạo cao nhất.
A.
60
B.
45
C.
30
D.
25
Lời giải
Chọn B
( ) ( )
3 2 2
2 6
63 3240 3100 126 3240
5 5
¢
= - - = - S t t t t S t t t
Ta có:
( )
45
0
60
=
¢
= Û
=
t
S t
t
Câu 46. (GKI NHÂN CHÍNH HÀ NỘI NĂM 2018-2019 LẦN 01) Một vật chuyển động theo quy luật
2 3
1
10
3
S t t= -
, với
t
(giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và
( )
S m
là
quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian
15
giây từ lúc vật
bắt đầu chuyển động vận tốc
( )
/v m s
của vật đạt giá trị lớn nhất tại thời điểm
( )
t s
bằng:
A.
( )
8 s
. B.
( )
20 s
C.
( )
10 s
. D.
( )
15 s
.
Lời giải
Chọn C.
Ta có:
2 3
1
10
3
S t t= -
( )
2
20v t S t t
¢
= = -
.
Xét hàm số
( )
; 0;15v t t
, ta có:
¢
v t
( )
= 20 - 2t = 0 Û t = 10
.
( ) ( ) ( )
0 0; 15 75; 10 100v v v= = =
. Do đó:
( )
0;15
max 100 10v t t= Û =
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
Câu 47. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Một sợi dây có chiều dài
28m
được cắt thành hai đoạn để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo
đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông
và hình tròn là nhỏ nhất?
A.
56
4
. B.
112
4
. C.
84
4
. D.
92
4
.
Lời giải
Gọi chiều dài của đoạn dây làm thành hình vuông là
x
(
m
) (
0 28
x
)
=> chiều dài của đoạn dây làm thành hình tròn là
28
x-
(
m
)
+) Diện tích hình vuông là:
2
2
4 16
x x
=
+) Bán kính hình tròn là: R =
28
2
x
-
=> Diện tích hình tròn:
2
2
2
28 784 56
.
2 4
x x x
R
- -
= =
+) Tổng diện tích hai hình:
2 2
2
784 56 4 14 196
16 4 16
x x x
x x
-
= -
Xét
2
4 14 196
( )
16
f x x x
= -
. Nhận thấy
( )f x
đạt giá trị nhỏ nhất tại
2
b
x
a
-
= =
( )
14 16 112
.
2 4 4
=
Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ
nhất là
112
4
m
Câu 48. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Một xưởng in có
15
máy in được cài đặt
tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in được
30
ấn phẩm trong
1
giờ, chi phí cài
đặt và bảo dưỡng cho mỗi máy in cho
1
đợt hàng là
48.000
đồng, chi phí trả cho kỹ sư giám sát là
24.000
đồng/giờ. Đợt hàng này xưởng in nhận
6000
ấn phẩm thì số máy in cần sử dụng để chi phí
in ít nhất là
A.
10
máy. B.
11
máy. C.
12
máy. D.
9
máy.
Lời giải
Chọn A
Gọi
x
( )
0 15
x
là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt và bảo dưỡng là
48000x
.
Số giờ in hết số ấn phẩm là
6000
30x
, chi phí giám sát là
6000 48000
.24000
30x x
.
Tổng chi phí in là
( )
4800000
48000P x x
x
=
.
( )
2
4800000
48000P x
x
¢
= -
;
( )
( )
2
10
0 100
10
x
P x x
x L
=
¢
= Û = Û
= -
.
Bảng biến thiên:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
Vậy chi phí in nhỏ nhất là
10
máy.
Câu 49. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật
( )
3 2
4 12
s t t t
= -
(m), trong đó
t
(s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc
của chất điểm đó đạt giá trị bé nhất khi
t
bằng bao nhiêu?
A. 2 (s). B.
8
3
(s). C. 0 (s). D.
4
3
(s).
Lời giải
( ) ( )
2
3 8v t s t t t
¢
= = -
.
( )
6 8v t t
¢
= -
. Có
( )
4
0
3
v t t
¢
= Û =
.
Dựa vào bảng biến thiên ta có
)
0;
4 16
min
3 3
v v
= = -
.
Vậy vận tốc của chất điểm đó đạt giá trị bé nhất khi
4
3
t
=
.
Câu 50. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho một tấm nhôm hình chữ nhật có
chiều dài bằng
10cm
và chiều rộng bằng
8cm
. Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
( )
x cm
, rồi gập tấm nhôm lại (như hình vẽ)
để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
8 2 21
3
x
-
=
B.
10 2 7
3
x
-
=
C.
9 21
9
x
=
. D.
9 21
3
x
-
=
Lơi giai
Chọn D
x
( )
P x
¢
( )
P x
0
15
10
0
-
( )
10
P
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
Ta có :
( )
h x cm=
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
( )
10 2x cm-
và
( )
8 2x cm-
Vậy diện tích đáy hình hộp
( )( )
( )
2
10 2 8 2S x x cm= - -
. Ta có:
( )
0
0
10 2 0 0;4
4
8 2 0
x
x
x x
x
x
- Û Û
-
Thể tích của hình hộp là:
( ) ( )
. 10 2 . 8 2.S xV x xh - -= =
Xét hàm số:
( ) ( ) ( )
. 10 2 . 8 2 0;4y x x x x= - -
Ta có :
2
' 12 72 80y x x= - ;
( )
( )
9 21
4
3
' 0
9 21
3
x l
y
x n
=
= Û
-
=
.
Suy ra với
9 21
3
x
-
=
thì thể tích hộp là lớn nhất và giá trị lớn nhất.
Câu 51. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Một đoàn cứu trợ lũ lụt đang ở vị trí
A
của
một tỉnh miền trung muốn đến xã
C
để tiếp tế lương thực và thuốc men. Để đi đến
C
, đoàn cứu
trợ phải chèo thuyền từ
A
đến vị trí
D
với vận tốc
( )
4 /km h
, rồi đi bộ đến vị trí
C
với vận tốc
( )
6 /km h
. Biết
A
cách
B
một khoảng
5km
,
B
cách
C
một khoảng
7km
(hình vẽ). Hỏi vị trí
điểm
D
cách
A
bao xa để đoàn cứu trợ đi đến xã
C
nhanh nhất?
A.
5 3AD km=
. B.
2 5AD km=
. C.
5 2AD km=
. D.
3 5AD km=
.
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
Đặt
( )
AD x km=
,
( )
0x
. Ta có
( )
2 2 2
25 5BD AD AB x x= - = -
2
7 25
CD BC BD x
= - = - -
Thời gian đi từ A đến C là:
( )
2
7 25
4 6 4 6
AD DC x x
T x
- -
= =
( )
2
2 2
1 2 3 25 2
4
12 25 12 25
x x x
T x
x x
- - -
¢
= =
- -
.
( )
2
0 3 25 2 3 5T x x x x
¢
= Û - = Û =
Bảng biến thiên
Do đó
)
( )
( )
5;
14 5 5
min 3 5
12
x
T x T

= =
Vậy
( )
3 5AD km=
.
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước
Câu 52. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số
=
- 1
x m
y
x
(
m
là tham số thực) thỏa mãn
=
[2;4]
min 3.y Mệnh đề nào dưới đây đúng?
A.
4m
B.
3 4m
C.
-1m
D.
1 3m
Lời giải
Chọn A
Ta có
( )
- -
=
-
2
1
'
1
m
y
x
* TH 1.
- - Û -1 0 1m m
suy ra
y
đồng biến trên
2; 4
suy ra
( ) ( )
= = = Û =
2;4
2
min 2 3 1
1
m
f x f m
(loại)
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
* TH 2.
- - Û -1 0 1m m
suy ra
y
nghịch biến trên
2; 4
suy ra
( ) ( )
= = = Û =
2;4
4
min 4 3 5
3
m
f x f m
suy ra
4m
.
Câu 53. (ĐỀ THAM KHẢO BGD & ĐT 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao
cho giá trị lớn nhất của hàm số
3
3
y x x m= -
trên đoạn
0;2
bằng 3. Số phần tử của S là
A. 0 B. 6 C. 1 D. 2
Lời giải
Chọn D
Xét hàm số
( )
3
3
f x x x m= -
, ta có
( )
2
3 3
f x x
¢
= -
. Ta có bảng biến thiên của
( )
f x
:
TH 1 :
2 0 2
m m
Û -
. Khi đó
( ) ( )
0;2
2 2
max f x m m=- - = -
2 3 1
m m
- = Û = -
(loại).
TH 2 :
2 0
2 0
0
m
m
m
Û -
. Khi đó :
2 2 2 2
m m m- = -
( ) ( )
0;2
2 2
max f x m m =- - = -
2 3 1
m m
- = Û = -
(thỏa mãn).
TH 3 :
0
0 2
2 0
m
m
m
Û
-
. Khi đó :
2 2 2 2
m m m- = -
( )
0;2
2
max f x m =
2 3 1
m m
= Û =
(thỏa mãn).
TH 4:
2 0 2
m m
- Û
. Khi đó
( )
0;2
2
max f x m=
2 3 1
m m
= Û =
(loại).
Câu 54. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số
1
x m
y
x
=
(
m
là tham số thực) thoả mãn
1;2
1;2
16
min max
3
y y
=
. Mệnh đề nào dưới đây đúng?
A.
4
m
B.
2 4
m
C.
0
m
D.
0 2
m
Lời giải
Chọn A
Ta có
( )
2
1
1
m
y
x
-
¢
=
.
Nếu
1 1, 1
m y x
= = -
. Không thỏa mãn yêu cầu đề bài.
Nếu
1
m
Hàm số đồng biến trên đoạn
1;2
.
Khi đó:
1;2
1;2
16
min max
3
y y
=
( ) ( )
16 1 2 16
1 2 5
3 2 3 3
m m
y y m
Û = Û = Û =
(loại).
Nếu
1
m
Hàm số nghịch biến trên đoạn
1;2
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
Khi đó:
( ) ( )
1;2
1;2
16 16 2 1 16
min max 2 1 5
3 3 3 2 3
m m
y y y y m
= Û = Û = Û =
( t/m)
Câu 55. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Có một giá trị
0
m
của tham số
m
để
hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau
đây là đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
.
C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.
Lời giải
+ Đặt
3 2
1 1
f x x m x m
.
+ Ta có:
2 2
3 1
y x m
. Dễ thấy rằng
0
y
với mọi
x
,
m
thuộc
nên hàm số đồng biến
trên
, suy ra hàm số đồng biến trên
0;1
. Vì thế
0;1
min y
0;1
min
f x
0f
1
m
.
+ Theo bài ra ta có:
m
, suy ra
4
m
.
+ Như vậy
0
4
m
và mệnh đề đúng là
2
0 0
2018 0
m m
.
Câu 56. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
2
y x x m= -
trên đoạn
1;2
- bằng
5
.
A.
1-
. B.
2
. C.
2-
. D.
1
.
Lời giải
Ta có
2
2 2
2
x
y
x x m
-
¢
=
-
,
0 1y x
¢
= =
.
Do đó yêu cầu bài toán tương đương
( ) ( ) ( )
max 1 , 2 , 1 5
y y y
- =
.
max 3 , , 1 5
m m m
Û - =
.
+ Trường hợp
1
m
-
, ta có
max 3 , , 1 5 3 5 2
m m m m m
- = Û = =
.
+ Trường hợp
1
m
-
ta có
max 3 , , 1 5 1 5 4
m m m m m
- = Û - = = -
.
Vậy tổng các giá trị
m
bằng
2-
.
Câu 57. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số
2
1
y x m x= -
có giá trị lớn nhất bằng
2 2
thì giá trị của
m
là
A.
2
2
. B.
2
-
. C.
2
. D.
2
2
-
.
Lời giải
Xét hàm số
2
1
y x m x= -
Tập xác định:
1;1
D = -
.
Ta có:
2
1
1
x
y
x
¢
= -
-
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
2
2
1
0
1 0
x x
y
x
- =
¢
= Û
-
2
1 0
1
x
x x
Û
- =
2
1 0
1
1 0
1
2
2 1
2
1
2
x
x
x
x
x
x
=
Û Û Û =
=
= -
.
Ta có:
( ) ( )
1
1 1 , 1 1 , 2
2
y m y m y m
- = - = =
.
Do hàm số
2
1
y x m x= -
liên tục trên
1;1
-
nên
1;1
Max 2
y m
-
=
.
Theo bài ra thì
1;1
Max 2 2
y
-
=
, suy ra
2 2 2 2
m m = Û =
.
Câu 58. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số
1
x m
y
x
(
m
là tham
số thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây đúng?
A.
1 3m
B.
6m
C.
1m
D.
3 6m
Lời giải
Chọn D
Tập xác định:
\ 1
D
.
Với
1m
1y
,
0;1
x
thì
0;1
min 3y
.
Suy ra
1m
. Khi đó
2
1
1
m
y
x
không đổi dấu trên từng khoảng xác định.
TH 1:
0 1y m
thì
0;1
min 0 3
y y m
(loại).
TH 2:
0 1y m
thì
0;1
min 1 5
y y m
( thỏa mãn).
Câu 59. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm
số
1
x m
y
x
trên
1;2
bằng
8
(
m
là tham số thực). Khẳng định nào sau đây đúng?
A.
10
m
. B.
8 10
m
. C.
m
. D.
m
.
Lời giải
Nếu
1
m
=
thì
1
y
(không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu
1
m
thì hàm số đã cho liên tục trên
1;2
và
2
1
'
1
m
y
x
.
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn
1;2
.
Do vậy
( ) ( )
1;2 1;2
1 2 41
1 2 8
2 3 5
x x
m m
Min y Max y y y m
= = = Û =
.
Câu 60. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
3 2
2 3
y x x m= - -
. Trên
1;1
-
hàm số có giá trị nhỏ nhất là
1-
. Tính
m
?
A.
6
m
= -
. B.
3
m
= -
. C.
4
m
= -
. D.
5
m
= -
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
Lời giải
Chọn C
Xét
1;1
-
có
2
6 6y x x
¢
= -
.
0
y
¢
=
2
6 6 0
x x
Û - =
0 1;1
1 1;1
x
x
= -
Û
= -
.
Khi đó
( )
1 5
y m- = - -
;
( )
0
y m= -
;
( )
1 1
y m= - -
Ta thấy
5 1
m m m- - - - -
nên
1;1
min 5
y m
-
= - -
.
Theo bài ra ta có
1;1
min 1
y
-
= -
nên
5 1
m
- - = -
4
m
Û = -
.
Câu 61. (THPT ĐÔNG SƠN THANH HÓA NĂM 2018-2019 LẦN 02) Tìm
m
để giá trị lớn nhất của
hàm số
3
3 2 1
y x x m
= - -
trên đoạn
0;2
là nhỏ nhất. Giá trị của
m
thuộc khoảng nào?
A.
3
; 1
2
- -
. B.
2
;2
3
. C.
1;0
-
. D.
( )
0;1
.
Lời giải
Xét hàm số
( )
3
3 2 1
y f x x x m
= = - -
trên đoạn
0;2
.
Ta có
( )
2
1 0;2
' 3 3 0
1
x
f x x
x
= -
= - = Û
=
.
Ta có
( )
0 2 1
f m
= -
,
( )
1 2 3
f m
= -
và
( )
2 2 1
f m
=
Suy ra
( )
0;2
2 1 ; 2 3 ; 2 1 2 3 ; 2 1
max f x max m m m max m m P= - - = - =
.
Trường hợp 1: Xét
( )
1
2 3 2 1 4 4 2 0
2
m m m m
- Û - - Û
.
Khi đó
2 3 2
P m
= -
,
1
2
m
. Suy ra
min
1
2
2
P m
= Û =
.
Trường hợp 2: Xét
( )
1
2 3 2 1 4 4 2 0
2
m m m m
- Û - - Û
.
Khi đó
2 1 2
P m
=
,
1
2
m
. Suy ra
min
P
không tồn tại.
Vậy
1
2
m
=
.
Câu 62. (HỌC MÃI NĂM 2018-2019-LẦN 02) Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá
trị nhỏ nhất của hàm số
4 2 3 2
2
y x m x x m= - - -
trên đoạn
0;1
bằng
16-
. Tính tích các phần tử
của
S
.
A.
2
. B.
2-
. C.
15-
. D.
17-
.
Lời giải
TXĐ:
D =
.
Ta có:
3 2 2
4 3 4y x m x x
¢
= - -
( )
3 2 2
2 2 2
0
0 4 3 4 0
4 3 4 0 9 64
x
y x m x x
x m x m
=
¢
= Û - - = Û
- - = =
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
2 4
2 4
0
3 9 64
1
8
3 9 64
0
8
x
m m
x
m m
x
=
Û =
-
=
Nên hàm số đơn điệu trên
( )
0;1
.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
0;1
bằng
16-
nên
( ) ( )
( )
2 2
0 1 16 1 16 2 15 0
y y m m m m m
= - Û - - - - = - Û - - =
.
Vậy
1 2
. 15
m m
= -
.
Câu 63. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
,A B
lần lượt là giá trị nhỏ nhất, giá trị
lớn nhất của hàm số
2
1
x m m
y
x
=
-
trên đoạn
2;3
. Tìm tất cả các giá trị thực của tham số
m
để
13
2
A B
=
.
A.
1; 2
m m
= = -
. B.
2
m
= -
. C.
2
m
=
. D.
1; 2
m m
= - =
.
Lời giải
Xét hàm số
2
1
x m m
y
x
=
-
trên đoạn
2;3
.
( )
( ) ( )
2 2 2
2
1 3 2
' 0 2;3 3 , 2
2 1
1
m m m m m m
y x A f B f
x
- - -
= = = = =
-
.
2 2
1
13 3 2 13
2
2 2 1 2
m
m m m m
A B
m
=
= Û = Û
= -
.
Câu 64. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1x mx
y
x m
=
liên tục và đạt giá trị nhỏ nhất trên đoạn
0;2
tại một điểm
( )
0
0;2
x
.
A.
0 1
m
B.
1
m
C.
2
m
D.
1 1
m
-
Lời giải
Chọn A
Tập xác định:
\
D m= -
. Hàm số liên tục trên
0;2
0 0
2 2
m m
m m
-
Û Û
- -
Ta có
( )
( )
( )
2
2 2
2 2
1
2 1
x m
x mx m
y
x m x m
-
-
¢
= =
. Cho
1
2
1
0
1
x m
y
x m
= - -
¢
= Û
= -
.
Ta có bảng biến thiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
Hàm số đạt giá trị nhỏ nhất tại
( )
0
0;2
x
nên
0 1 2 1 1m m - Û -
So với điều kiện hàm số liên tục trên đoạn
0;2
. Ta có
0 1m
.
CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định x m -
Hàm số liên tục trên đoạn
0;2
nên
( )
0 0
0;2 *
2 2
m m
m
m m
-
- Û
- -
( )
( )
( )
2
2 2
2 2
1
2 1
'
x m
x mx m
y
x m x m
-
-
= =
' 0y =
có hai nghiệm là
1
2
1
1
x m
x m
= -
= - -
,
1 2
2x x- =
nên chỉ có nhiều nhất một nghiệm thuộc
( )
0;2
Ta thấy
1 1,m m m- - -
và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên
0;2
tại một
điểm
( )
0
0;2x
thì
( )
0 1 2 1 1 **m m - Û -
Từ
( ) ( )
* , **
ta có
0 1m
Câu 65. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Gọi
S
là tập hợp tất cả các giá trị
thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
y
x
=
trên
1;2
bằng
2
. Số
phần tử của tập
S
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D
Xét
2
1
x mx m
y
x
=
. Ta có:
( )
( )
2
2
2
1
x x
f x
x
¢
=
,
( )
0 1;2
0
2 1;2
x
f x
x
=
¢
= Û
= -
.
Mà
( ) ( )
1;2
2 1 3 4 2 1 3 4
1 ,f 2 max ;
2 3 2 3
x
m m m m
f y
= = =
.
Trường hợp 1:
1;2
3
2 1
2
max 2
5
2
2
x
m
m
y
m
=
= =
= -
.
• Với
3 3 4 17
2
2 3 6
m
m
= =
(loại)
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
• Với
5 3 4 7
2
2 3 6
m
m
= - =
(thỏa mãn)
Trường hợp 2:
1;2
2
3 4 6
3 4
3
max 2
3 4 6 10
3
3
x
m
m
m
y
m
m
=
=
= = Û
= -
= -
.
• Với
2 2 1 7
2
3 2 6
m
m
= =
(thỏa mãn)
• Với
10 2 1 17
2
3 2 6
m
m
= - =
(loại)
Vậy có
2
giá trị của
m
thỏa mãn.
Câu 66. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm
m
để giá trị nhỏ nhất của hàm số
2
( )
1
x m m
f x
x
-
=
trên đoạn (0;1) bằng –2
A.
1
2
m
m
=
=
.
B.
1
2
m
m
=
= -
.
C.
1
2
m
m
= -
=
. D.
1 21
2
m
=
.
Lời giải
Chọn C
Ta có:
( )
2
2
1
' 0,
1
m m
y m
x
-
=
Hs luôn nghịc biến trên
0;1
( ) ( )
0;1
0
Max f x f =
2
2
2
1
m
m m
m
=
Û - = - Û
= -
Câu 67. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Cho hàm số
1 sin
cos 2
m x
y
x
-
=
. Có bao
nhiêu giá trị nguyên của tham số
m
thuộc đoạn
0;10
để giá trị nhỏ nhất của hàm số nhỏ hơn
2-
?
A.
1
. B.
9
. C.
3
. D.
6
.
Lời giải
Tập xác định:
D =
.
Ta có:
1 sin
cos 2
m x
y
x
-
=
cos sin 1 2y x m x yÛ = -
.
Phương trình có nghiệm khi và chỉ khi:
2 2 2
1 4 4y m y y
-
2 2
3 4 1 0
y y m
Û - -
2 2
2 1 3 2 1 3
3 3
m m
y
-
Û
.
Theo đề bài, ta có:
2
2 1 3
min 2
3
0;10
x
m
y
m
m
-
= -
2
1 3 8
0;10
m
m
m
Û
2
3 63
0;10
m
m
m
Û
2
21
0;10
m
m
m
Û
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
5,6,7,8,9,10
mÛ
.
Vậy có
6
giá trị nguyên của tham số
m
thỏa yêu cầu bài toán.
Câu 68. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Xét hàm số
( )
2
f x x ax b=
,
với
a
,
b
là tham số. Gọi
M
là giá trị lớn nhất của hàm số trên
1;3
-
. Khi
M
nhận giá trị nhỏ
nhất có thể được, tính
2a b
.
A.
2
. B.
4
. C.
4-
. D.
3
.
Lời giải
Xét hàm số
( )
2
f x x ax b=
. Theo đề bài,
M
là giá trị lớn nhất của hàm số trên
1;3
-
.
Suy ra
( )
( )
( )
1
3
1
M f
M f
M f
-
1
9 3
1
M a b
M a b
M a b
-
Û
4 1 9 3 2 1
M a b a b a b - - - -
1 9 3 2( 1 )a b a b a b - - - -
4 8
M
M
.
Nếu
2M =
thì điều kiện cần là
1 9 3 1 2
a b a b a b
- = = - - - =
và
1
a b-
,
9 3
,
1
a b- - -
cùng dấu
1 9 3 1 2
1 9 3 1 2
a b a b a b
a b a b a b
- = = - - - =
Û
- = = - - - = -
2
1
a
b
= -
Û
= -
.
Ngược lại, khi
2
1
a
b
= -
= -
ta có, hàm số
( )
2
2 1f x x x= - -
trên
1;3
-
.
Xét hàm số
( )
2
2 1g x x x= - -
xác định và liên tục trên
1;3
-
.
( )
2 2
g x x
¢
= -
;
( )
0 1 1;3
g x x
¢
= Û = -
M
là giá trị lớn nhất của hàm số
( )
f x
trên
1;3
-
( ) ( ) ( )
max 1 ; 3 ; 1
M g g g = -
=2
.
Vậy
2
1
a
b
= -
= -
. Ta có:
2 4
a b
= -
.
Câu 69. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Cho hàm số
3
, 0
y ax cx d a
=
có
( )
( ) ( )
;0
min 2
x
f x f
-
= -
. Giá trị lớn nhất của hàm số
( )
y f x
=
trên đoạn
1;3
bằng
A.
11d a-
. B.
16d a-
. C.
2d a
. D.
8d a
.
Lời giải
Vì
3
, 0
y ax cx d a
=
là hàm số bậc ba và có
( )
( ) ( )
;0
min 2
x
f x f
-
= -
nên
0
a
và
' 0
y
=
có hai
nghiệm phân biệt.
Ta có
2
' 3 0
y ax c
= =
có hai nghiệm phân biệt
0
ac
Û
.
Vậy với
0, 0
a c
thì
' 0
y
=
có hai nghiệm đối nhau
3
c
x
a
= -
Từ đó suy ra
( )
( )
;0
min
3
x
c
f x f
a
-
= - -
2 2 12
3 3
c c
c a
a a
Û - - = - Û - = Û = -
Ta có bảng biến thiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
Ta suy ra
( ) ( )
1;3
max 2 8 2 16
x
f x f a c d a d
= = = -
.
Câu 70. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x
-
=
-
trên đoạn
1;1
- bằng
3
. Tính tổng tất cả các
phần tử của
S
.
A.
8
3
-
. B.
5
. C.
5
3
. D.
1-
.
Lời giải
Xét hàm số
( )
2
2
2
x mx m
y f x
x
-
= =
-
trên
1;1
- có
( )
( )
2
4
1
2
f x
x
¢
= -
-
;
( )
0
0
4 1;1
x
f x
x
=
¢
= Û
= -
;
( ) ( ) ( )
3 1 1
1 ; 0 ; 1
3 1
m m
f f m f
- = = - =
- -
.
Bảng biến thiên
x
1 0 1-
( )
f x
¢
0
-
( )
f x
( )
0
f
( ) ( )
1 1f f
-
Trường hợp 1.
( )
0 0 0
f m
Û
. Khi đó
( ) ( ) ( )
1;1
3 max max 1 ; 1f x f f
-
= = - Û
3 1
3 max ; 1
3
m
m
=
1 3 2
m m
Û = Û =
.
Trường hợp 2.
( )
0 0 0
f m
Û
.
Khả năng 1.
( )
( )
1 0
1
1 0
f
m
f
-
Û -
. Khi đó
( ) ( )
1;1
3 max 0
f x f
-
= =
3
m
Û = -
.
Khả năng 2.
1
1
3
m
- -
. Khi đó
( )
( )
1 0
1 0
f
f
-
.
( ) ( ) ( )
1;1
3 max max 0 ; 1
f x f f
-
= =
3 max ; 1
m m
Û = -
: Trường hợp này vô nghiệm.
Khả năng 3.
1
0
3
m
-
. Khi đó
( ) ( ) ( ) ( )
1;1
3 max max 0 ; 1 ; 1
f x f f f
-
= = -
: Vô nghiệm.
Vậy có hai giá trị thỏa mãn là
1 2
3, 2
m m
= - =
. Do đó tổng tất cả các phần tử của
S
là
1-
.
Câu 71. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Tìm tất cả các giá trị của tham số
m để hàm số
2
1
x m
y
x x
=
có giá trị lớn nhất trên
nhỏ hơn hoặc bằng 1.
A.
1
m
. B.
1
m
. C.
1
m
-
. D.
1
m
-
.
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
Chọn A
+ TXĐ:
D =
.
+
lim 0
x
y

=
+
( )
2
2
2
2 1
1
x mx m
y
x x
- - -
¢
=
.
2
0 2 1 0 (*)
y x mx m
¢
= Û - - - =
2
(*)
1 0,m m m
¢
= -
nên (*) có 2 nghiệm phân biệt
1 2
,x x m
+ BBT:
Vậy hàm số đạt giá trị lón nhất là
( )
2
2
1
2 1
f x
x
=
với
2
2
1
x m m m
= - -
2
2
1
1 1 2 2 1 1
2 2 1 1
YCBT m m m
m m m
Û Û - -
- -
( vì
( )
2 2
0 2 1 0
f x x
)
2
2 2
0
0
1 1
1
m
m
m m m m
m m m
Û - Û Û
-
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm
Câu 72. (Mã 102 - BGD - 2019) Cho hàm số
( )
f x
, hàm số
( )
y f x
¢
=
liên tục trên
và có đồ thị như
hình vẽ.
Bất phương trình
( )
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
x
khi và chỉ khi
A.
( )
0
m f
. B.
( )
0
m f
. C.
( )
2 2
m f
-
. D.
( )
2 2
m f
-
.
Lời giải
Chọn C
Xét bất phương trình
( ) ( )
f x x m m f x x Û -
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
Xét hàm số
( ) ( )
g x f x x= -
với
x
. Ta có
( ) ( )
1
g x f x
¢ ¢
= -
.
( ) ( )
0 1
g x f x
¢ ¢
= Û =
. Từ đồ thị ta thấy đường thẳng
1y =
không cắt đồ thị
( )
y f x
¢
=
tại bất kỳ
điểm nào có hoành độ thuộc khoảng
( )
0;2
nên phương trình
( )
1
f x
¢
=
vô nghiệm với
( )
0;2
x
.
Ta có bảng biến thiên như sau:
(do
( )
1
f x
¢
với
x ).
Từ bảng biến thiên ta thấy để
( )
m g x
với
x
( ) ( )
2 2 2
m g m f
Û Û -
.
Câu 73. (Mã 103 - BGD - 2019) Cho hàm số
=
, hàm số
( )
'y f x
=
liên tục trên
và có đồ thị như
hình vẽ bên. Bất phương trình
( )
2
f x x m
(m là tham số thực) nghiệm đúng với mọi
( )
0;2
x
khi và chỉ khi
A.
( )
0
m f
. B.
( )
2 4
m f
-
. C.
( )
0
m f
. D.
( )
2 4
m f
-
.
Lời giải
Chọn A
( )
( )
( )
( )
0;2
2
2
max 2
f x x m
m f x x
m f x x
Û -
Û -
Ta tìm
( )
0;2
max 2f x x
-
Đặt
( ) ( )
2g x f x x= -
( ) ( )
( )
( ) ( ) ( )
0;2
' ' 2
0;2 , ' 2 0
max 0 0
g x f x
x f x
g x g f
= -
-
= =
Vậy
( )
0
m f
Câu 74. (Mã đề 101 - BGD - 2019) Cho hàm số
=
, hàm số
( )
'y f x
=
liên tục trên
và co đồ thị
như hình vẽ bên dưới
x
y
2
2
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
Bất phương trình
( )
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
( )
0;2x
khi và chỉ khi
A.
( )
2 2.m f -
B.
( )
0 .m f
C.
( )
2 2.m f -
D.
( )
0 .m f
Lời giải
Chọn D
( )
f x x m
( )
f x x mÛ -
.
Đặt
( )
( )
g x f x x= -
xét trên khoảng
( )
0;2
.
( )
( ) 1g x f x
¢ ¢
= -
.
Từ đồ thị ta thấy
( )
( ) 1 0g x f x
¢ ¢
= -
với mọi
( )
0;2x
. Suy ra hàm số
( )
( )g x f x x= -
luôn
nghịch biến trên khoảng
( )
0;2
.
Bất phương trình
( )
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
( )
0;2x
khi và chỉ
khi
( )
0
lim (0)
x
m g x f
=
.
Câu 75. (Mã đề 104 - BGD - 2019) Cho hàm số
( )
f x
, hàm số
( )
f x
¢
liên tục trên
và có đồ thị như
hình vẽ.
Bất phương trình
( )
2f x x m
(
m
là tham số thực) nghiệm đúng với mọi
( )
0; 2x
khi và chỉ
khi
A.
( )
2 4m f -
. B.
( )
2 4m f -
. C.
( )
0m f
. D.
( )
0m f
.
Lời giải
Chọn B
Hàm số
( ) ( )
2g x f x x= -
nghịch biến trên khoảng
( )
0; 2
vì
( ) ( ) ( )
2 0, 0;2g x f x x
¢ ¢
= -
(quan sát trên khoảng
( )
0; 2
, đồ thị hàm số
( )
f x
¢
nằm dưới đường thẳng
2y =
).
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
Suy ra
( ) ( ) ( ) ( )
2 0 , 0;2g g x g x
.
Bất phương trình đã cho nghiệm đúng với mọi
( )
0; 2x
khi và chỉ khi
( ) ( )
, 0; 2m g x x
( ) ( )
2 2 4
m g m f
Û Û -
.
Câu 76. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
xác
định và liên tục trên
, đồ thị của hàm số
( )
y f x
¢
=
như hình vẽ.
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;2-
là
A.
( )
1f
. B.
( )
1f -
. C.
( )
2f
. D.
( )
0f
.
Lời giải
( )
1
0 1
2
x
f x x
x
= -
¢
= Û =
=
.
Từ đồ thị hàm
y f x
ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên
1;2
là
1f
.
Câu 77. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
( )
f x
có đạo
hàm là
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình vẽ bên. Biết rằng
( ) ( ) ( ) ( ) ( )
0 1 2 3 5 4f f f f f - = -
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
( )
f x
trên
đoạn
0;5
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
A.
( ) ( )
5 , 3m f M f= =
B.
( ) ( )
5 , 1m f M f= =
C.
( ) ( )
0 , 3m f M f= =
D.
( ) ( )
1 , 3m f M f= =
Lời giải
Chọn A
Từ đồ thị ta có bảng biến thiên của
( )
f x
trên đoạn
0;5
( )
3M f =
và
( ) ( ) ( ) ( )
1 3 , 4 3f f f f
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
5 0 1 3 4 3 0 5 0 5f f f f f f f f m f- = - - =
.
Câu 78. (ĐÊ 04 VTED NĂM 2018-2019) Cho hàm số
( )
y f x=
. Hàm số
/
( )y f x= có bảng biến thiên như
sau:
Bất phương trình
( )
x x
f e e m
nghiệm đúng với mọi
( )
1;1x -
khi và chỉ khi
A.
1 1
m f
e e
-
B.
( )
1
1m f
e
- -
C.
( )
1
1m f
e
- -
D.
1 1
m f
e e
-
Lời giải
Chọn A
Ta có
( ) ( )
x x x x
f e e m f e e m Û -
,
( )
1;1x -
.
Đặt
( )
( )
x x
g x f e e= -
khi đó
( ) ( )
( )
1;1
1;1m g x x m Max g x
-
- Û
.
Xét
( )
( )
x x
g x f e e= -
trên
1;1-
.
Có
( )
( ) ( )
( )
1 0, 1;1
x x x x x
g x e f e e e f e x
¢ ¢ ¢
= - = - -
(Suy ra từ bảng biến thiên).
Do đó
( ) ( )
1;1
1 1
1Max g x
e
g f
e
-
= - =
-
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
Vậy
( ) ( )
1;1
1
1 1
fm Ma
e e
x g x g
-
-
= - =
là giá trị cần tìm.
Câu 79. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số
( )
y f x
=
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
( )
( )
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
= - -
trên đoạn
1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Lời giải
( ) ( )
( )
2 2
4 2 4 6 8g x x f x x x x
¢ ¢
= - - -
( )
( )
2
2 2 4 4
x f x x x
¢
= - - -
.
Với
1;3
x
thì
4 0
x
-
;
2
3 4 4
x x
-
nên
( )
2
4 0
f x x
¢
-
.
Suy ra
( )
2
2 4 4 0
f x x x
¢
- -
,
1;3
x
.
Bảng biến thiên
Suy ra
( ) ( )
1;3
max 2
g x g=
( )
4 7 12
f
= =
.
Câu 80. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Cho hàm số
=
. Hàm số
( )
¢
=
y f x
có
bảng biến thiên như sau
Bất phương trình
( )
cos
2 3
x
f x m
đúng với mọi
0;
2
x
khi và chỉ khi
A.
( )
1
0 2
3
-
m f
. B.
( )
1
0 2
3
-
m f
. C.
1
1
3 2
-
m f
. D.
1
1
3 2
-
m f
.
Lời giải
Ta có
( )
cos
2 3
x
f x m
0;
2
x
( )
cos
2 3
Û -
x
f x m
0;
2
x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
Xét hàm
( ) ( )
cos
2
= -
x
g x f x
trên
0;
2
.
Ta có
( ) ( )
cos
2 sin .ln 2
¢ ¢
=
x
g x f x x
Vì
¢
f x
0;
2
x
;
sin 0
x
0;
2
x
cos
2 sin .ln2 0
x
x
0;
2
x
nên ta suy ra
( ) ( )
cos
2 sin .ln 2 0
¢ ¢
=
x
g x f x x
0;
2
x
.
Vậy ta có bảng biến thiên
Từ bảng biến thiên ta có ycbt
( )
0 3
Û
g m
( )
3 0 2Û -
m f
( )
1
0 2
3
Û -
m f
.
Câu 81. (Đề minh họa 2019) Cho hàm số
( )
y f x
=
. Hàm số
/
( )y f x
= có bảng biến thiên như sau:
Bất phương trình
( )
x x
f e e m
nghiệm đúng với mọi
( )
1;1
x -
khi và chỉ khi
A.
1 1
m f
e e
-
B.
( )
1
1m f
e
- -
C.
( )
1
1m f
e
- -
D.
1 1
m f
e e
-
Lời giải
Chọn A
Ta có
( ) ( )
x x x x
f e e m f e e m Û -
,
( )
1;1
x -
.
Đặt
( )
( )
x x
g x f e e= -
khi đó
( ) ( )
( )
1;1
1;1
m g x x m Max g x
-
- Û
.
Xét
( )
( )
x x
g x f e e= -
trên
1;1
-
.
Có
( )
( ) ( )
( )
1 0, 1;1
x x x x x
g x e f e e e f e x
¢ ¢ ¢
= - = - -
(Suy ra từ bảng biến thiên).
Do đó
( ) ( )
1;1
1 1
1Max g x
e
g f
e
-
= - =
-
.
Vậy
( ) ( )
1;1
1
1 1
fm Ma
e e
x g x g
-
-
= - =
là giá trị cần tìm.
g(
π
2
)
g(0)
π
2
0
+
g(x)
g'(x)
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
Câu 82. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số
( )
f x
có bảng
biến thiên như sau:
Gọi
S
là tập hợp các số nguyên dương
m
để bất phương trình
( )
( )
3 2
3 5f x m x x -
có nghiệm
thuộc đoạn
1;3-
. Số phần tử của
S
là
A.
3
B. Vô số C.
2
D. 0
Lời giải
Chọn B
Gọi
( )
3 2
3 5g x x x= -
trên đoạn
1;3-
( )
2
0
' 0 3x 6x 0
2
x
g x
x
=
= Û - = Û
=
( ) ( ) ( ) ( )
1 1; 0 5; 2 1; 3 5g g g g- = = = =
( )
1 5, 1;3g x x -
( )
( )
( )
( )
( )
( )
3 2
1;3
3 5 , 1;3 , 1;3 min
f x f x
f x m x x x m x m
g x g x
-
- - Û - Û
Vì hàm số
( ) ( )
,f x g x
liên tục trên đoạn
1;3-
suy ra tồn tại giá trị nhỏ nhất của hàm số
( )
( )
f x
g x
trên đoạn
1;3
-
Suy ra
( )
( )
1;3
;min
f x
m
g x
-
-
Số phần tử của tập hợp
S
là vô số
Câu 83. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hàm số
( )
y f x=
liên
tục trên
.
Đồ thị của hàm số
( )
y f x
¢
=
như hình bên. Đặt
( ) ( ) ( )
2
2 1 .g x f x x= -
Mệnh đề
dưới đây đúng.
A.
( ) ( )
3;3
max 3 .g x g
-
=
B.
( ) ( )
3;3
min 1 .g x g
-
=
C.
( ) ( )
3;3
max 0 .g x g
-
=
D.
( ) ( )
3;3
max 1 .g x g
-
=
Lời giải
Chọn D
( ) ( ) ( ) ( ) ( ) ( )
2
2 1 2 2 1g x f x x g x f x x
¢ ¢
= - = -
Dựa vào đồ thị ta thấy
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
( ) ( )
3
0 1 1
3
x
g x f x x x
x
= -
¢ ¢
= Û = Û =
=
Và
với
( ) ( ) ( )
; 3 : 1 0
x f x x g x
¢ ¢
- -
với
( ) ( ) ( )
3;1 : 1 0
x f x x g x
¢ ¢
-
,
với
( ) ( ) ( )
1;3 : 1 0
x f x x g x
¢ ¢
với
( ) ( ) ( )
3; : 1 0
x f x x g x
¢ ¢
Bảng biến thiên
x
-
3-
1
3
( )
g x
¢
‒
0
+
0
‒
0
+
( )
g x
Dựa vào bảng biến thiên suy ra
( ) ( )
3;3
max 1 .
g x g
-
=
Câu 84. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho hàm số có đạo hàm
cấp hai trên . Biết , và bảng xét dấu của như sau:
Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A.
( )
; 2017
- -
B.
( )
2017;

C.
( )
0;2
D.
( )
2017;0
-
Lời giải
Dựa vào bảng xét dấu của
( )
f x
¢¢
ta có bảng biến thiên của hàm sồ
( )
f x
¢
Đặt
2017
t x
=
.
Ta có
( ) ( ) ( )
2017 2018 2018 2017.2018
y f x x f t t g t
= = - =
.
( ) ( )
2018
g t f t
¢ ¢
=
.
Dựa vào bảng biến thiên của hàm số
( )
f x
¢
suy ra phương trình
( )
g t
¢
có một nghiệm đơn
( )
;0
-
và một nghiệm kép
2
t
=
.
Ta có bảng biến thiên
( )
g t
Hàm số
( )
g t
đạt giá trị nhỏ nhất tại
( )
0
;0
t
= -
.
=
( )
0 3
f
¢
=
( )
2 2018
f
¢
= -
( )
f x
¢¢
( )
2017 2018y f x x
=
0
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
Suy ra hàm số đạt giá trị nhỏ nhất tại
0
x
mà
( ) ( )
0 0
2017 ;0 ; 2017
x x - Û - -
.
Câu 85. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số
( )
f x
liên tục trên
và có đồ
thị như hình vẽ bên. Bất phương trình
( )
3 2
2 2 3f x x m x
nghiệm đúng với mọi
( )
1;3
x -
khi
và chỉ khi
A.
10.
m
-
B.
5.
m
-
C.
3.
m
-
D.
2.
m
-
Hướng dẫn giải
Ta có
( ) ( )
3 2 3 2
2 2 3 2 3 2f x x m x f x x x m
Û -
Nhận xét
( )
( ) ( )
1;3
minf 2 3
x f
-
= = -
Đặt
( ) ( )
3 2
3 2m, 1;3
g x x x x= - -
( ) ( )
2
0
3 6 , 0
2
x
g x x x g x
x
=
¢ ¢
= - = Û
=
( ) ( ) ( )
0 2 ; 1 4 2 ; 3 2g m g m g m
= - = =
và
( )
2 4 2g m
=
( )
( ) ( )
1;3
max 2 4 2g x g m
-
= =
ycbt
( )
( )
( )
( )
1;3
1;3
2 min max 6 2 4 5
f x g x m m
-
-
Û Û - Û -
Câu 86. (KTNL GV BẮC GIANG NĂM 2018-2019) Cho hàm số
( )
f x
có đạo hàm trên
và có đồ thị
của hàm
( )
y f x
¢
=
được cho như hình vẽ.
Biết rằng
( ) ( ) ( ) ( )
3 0 4 1
f f f f
- = -
. Giá trị lớn nhất và giá trị nhỏ nhất của
( )
f x
trên đoạn
3;4
-
lần lượt là:
( )
2017 2018y f x x
=
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
A.
(4)f
và
( 3)
f
-
. B.
( 3)
f
-
và
(0)f
. C.
(4)f
và
(0)f
. D.
(2)f
và
( 3)
f
-
.
Lời giải
Chọn B.
Dựa vào đồ thị của hàm số
( )
y f x
¢
=
ta có bảng biến thiên của hàm số
=
:
x
-
-3
0
4

( )
f x
¢
-
-
0
0
-
( )
f x
( )
3
f
-
( )
0
f
( )
4
f
( ) ( )
0 4 0
f f
¢ ¢
= =
nên
0
x
=
và
4
x
=
là hai điểm cực trị của
=
.
Từ bảng biến thiên ta có
3;4
min ( ) (0)f x f
-
= , đồng thời
( ) ( )
1 0
f f-
. Do đó:
( ) ( ) ( ) ( )
3 0 4 1
f f f f
- = -
Û
( ) ( ) ( ) ( ) ( ) ( )
3 4 1 0 0 3 4
f f f f f f- - = - - -
.
3;4
max ( ) ( 3)
f x f
-
= -
. Chọn B
Câu 87. Cho hàm số
( )
f x
có đạo hàm là
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình vẽ
dưới đây:
Biết rằng
( ) ( ) ( ) ( )
1 0 1 2
f f f f-
. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
=
trên đoạn
1;2
-
lần lượt là:
A.
( )
1f
;
( )
2
f
. B.
( )
2
f
;
( )
0
f
. C.
( )
0
f
;
( )
2
f
. D.
( )
1f
;
( )
1
f
-
.
Lời giải
Từ đồ thị của hàm số
( )
y f x
¢
=
ta có bảng biến thiên của hàm số
=
trên đoạn
1;2
-
như sau
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
Nhận thấy
( ) ( )
1;2
min 1f x f
-
=
.
 Để tìm
( )
1;2
max
f x
-
ta so sánh
( )
1
f
-
và
( )
2
f
.
Theo giả thiết,
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
1 0 1 2 2 1 0 1f f f f f f f f
- Û - - -
.
Từ bảng biến thiên, ta có
( ) ( )
0 1 0
f f
-
. Do đó
( ) ( ) ( ) ( )
2 1 0 2 1
f f f f
- - Û -
.
Hay
( ) ( )
1;2
max 2
f x f
-
=
.
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số
Câu 88. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số
m
để
bất phương trình
( )( )
2
6 2 8 1
x x x x m
- -
nghiệm đúng với mọi
2;8 .
x -
A.
16
m
B.
15
m
C.
8
m
D.
2 16
m
-
Lời giải
Chọn B
Xét bất phương trình:
( )( ) ( )
2
6 2 8 1 1
x x x x m - -
, điều kiện
2;8 .
x -
Đặt
( )( )
2 8
t x x= -
,
2;8 .
x -
Ta có:
( )( )
3
'
2 8
x
t
x x
-
=
-
,
' 0 3
t x
= Û =
Bảng biến thiên
Suy ra
0; 5
t
. Khi đó
( )
1
trở thành:
( )
2
15 2
t t m -
.
Xét hàm số
( )
2
15
f t t t
= -
,
( )
' 2 1 0, 0; 5
f t t t=
Bất phương trình
( )
1
nghiệm đúng với mọi
2;8
x -
khi và chỉ khi
( )
2
nghiệm đúng với mọi
0;5
t
0;5
maxÛ
( )
15
f t m m
Û
.
Câu 89. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm
m
để bất phương trình
4
1
x m
x
-
có nghiệm trên khoảng
( )
;1-
.
A.
5
m
. B.
3
m
-
. C.
1
m
. D.
1
m
-
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
4
( )
1
f x x
x
=
-
( )
( )
( )
2
2 2
3( )
1 4
4
'( ) 1 0
1( )
1 1
x l
x
f x
x tm
x x
=
- -
= - = =
= -
- -
Bảng biến thiên
Vậy
3
m
-
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Biết rằng tập nghiệm
của bất phương trình
2
6 4
2 4 2 2
5 1
x
x x
x
-
- -
là
;a b
. Khi đó giá trị của biểu thức
3 2P a b= -
bằng:
A.
2
B.
4
C.
2-
D.
1
Lời giải
Chọn C
ĐK:
2 2
x
-
Ta có:
2 2
6 4 2 4 4(2 ) 6 4
2 4 2 2 0
2 4 2 2
5 1 5 1
x x x x
x x
x x
x x
- - - -
- - Û -
-
( )
( )
( )
( )
2
2
1 1
6 4 0
2 4 2 2
5 1
6 4 5 1 2 4 2 2 0 1
x
x x
x
x x x x
Û - -
-
Û - - -
Xét hàm số
( )
2 4 2 2
f x x x= -
với
2 2
x
-
Ta có
( )
1 1 2
0
3
2 4 2
f x x
x x
¢
= - = Û = -
-
. Do đó
( ) ( )
2
2 6; 2 4; 2 2 2
3
f f f
- = - = =
Suy ra
( )
2 2 2 6
f x
mà
2
5 1 5
x
nên
( )
2
5 1 2 4 2 2 0
x x x
- -
( )
2
1 6 4 0
3
x x
Û - Û
. Kết hợp với điều kiện ta có tập nghiệm là
2
;2
3
Vậy
3 2 2
P a b
= - = -
.
Câu 91. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi
s
là tập hợp các giá trị
nguyên của tham số
0;2019
m
để bất phương trình
( )
3
2 2
1 0
x m x
- -
đúng với mọi
1;1
x -
. Số phần tử của tập
s
bằng
A.
1
. B.
2020
. C.
2019
. D.
2
.
Lời giải
Đặt
2
1
t x= -
, với
1;1 0;1
x t -
. Bất phương trình
( )
( )
3
2 2
1 0 1
x m x- -
trở thành
( )
3 2 3 2
1 0 1 2
t t m m t t- - Û -
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
Bất phương trình
( )
1
đúng với mọi
1;1
x -
khi và chỉ khi bất phương trình
( )
2
nghiệm đúng
với mọi
0;1
t
. Hay
( )
3 2
0;1
ax 1 1
m m t t m
- Û
.
Mặt khác, m là số nguyên thuộc
0;2019
nên
1;2;3;...;2019
m
Vậy có 2019 giá trị của m thỏa mãn bài toán.
Câu 92. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
M
là giá trị lớn nhất của hàm số
( )
2 2
4 4 6 4 1
f x x x x x
= - -
. Tính tích các nghiệm của phương trình
( )
f x M=
.
A.
2
. B.
4
. C.
2-
. D.
4-
.
Lời giải
Đặt
( )
2
2
4 6 2 2 2
t x x x= - = -
.
Khi đó,
( )
)
( )
2;
max max
M f x g t

= =
, với
( )
2
4 7g t t t= -
trên
2;
.
Có
( ) ( )
2
2
4 7 11 2 11
g t t t t
= - = - -
, dấu đẳng thức xảy ra khi
2
2 4 6 2
t x x
= Û - =
2
4 2 0
x x
Û - =
2 2
2 2
x
x
=
Û
= -
.
Như vây,
( )
)
( )
2;
max max 11 2 2
M f x g t x

= = = Û =
, suy ra nghiệm của phương trình
( )
f x M=
là
2 2
x =
.
Vậy tích các nghiệm của phương trình
( )
f x M=
bằng
2
.
Câu 93. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
2 2
2
x xy y
- =
. Giá trị nhỏ
nhất của
2 2
P x xy y=
bằng:
A.
2
3
B.
1
6
C.
1
2
D.
2
Lời giải
Chọn A
Xét
2 2 2 2
2 2
2 2
P x xy y x xy y
x xy y
= =
-
+nếu
0
y
=
thì
2
2
x
=
. Do đó
2
2
P x
= =
suy ra
min 2P =
+nếu
0
y
ta chia tử mẫu cho
2
y
ta được
2
2 2
2
2 2
1
2
1
x x
y y
P x xy y
x xy y
x x
y y
= =
-
-
Đặt
x
t
y
=
, khi đó
2
2
1
2 1
P t t
t t
=
-
Xét
( ) ( )
( )
2 2
2
2
2
1 2 2
'
1
1
t t t
f t f t
t t
t t
-
= =
-
-
( )
1
' 0
1
t
f t
t
=
= Û
= -
Bảng biến thiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
Khi đó
1
min
2 3
P
=
do đó
2
min
3
P =
.
Câu 94. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
x
,
y
là các số thực thỏa mãn
1 2 2
x y x y
= -
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
( )( )
2 2
2 1 1 8 4P x y x y x y= - -
. Tính giá trị
M m
A.
42
B.
41
C.
43
D.
44
Lời giải
Chọn C
( )
( )
( )
2
2
1 2 1 3 0 3x y x y x y x y = - Û
( )( ) ( ) ( ) ( )
2
2 2
2 1 1 8 4 2 2 8 4
P x y x y x y x y x y x y= - - = -
Đặt
( )
4 , 1;2t x y t= -
.
Ta có:
( )
( ) ( )
2
2 2 4 2
4 2 4 2 8 10 8 26f t t t t t t t= - - = - .
( )
3
4 20 8f t t t
¢
= -
( )
2
2 1;2
2
0 1 2 1;2
2 1 0
1 2 1;2
t
t
f t t
t t
t
=
=
¢
= Û Û = -
- =
= - -
( ) ( )
1 25; 2 18
f f
= =
.
Suy ra
( ) ( )
( ) ( )
1;2
1;2
min 2 18; max 1 25m f t f M f t f= = = = = =
.
Vậy
43M m =
.
Câu 95. (KTNL GIA BÌNH NĂM 2018-2019) Cho bất phương trình
( )
( )
2
2 2 1 2 0m x x x x- -
.
Hỏi có bao nhiêu số nguyên
m
không nhỏ hơn
2018-
để bất phương trình đã cho có nghiệm
0;1 3x
?
A.
2018
B.
2019
C.
2017
D.
2020
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
Đặt
2
2 2t x x= -
, ta có
0;1 3 1;2x t
. Vì
( )
2 2 2
2 2 2 2t x x x x t= - Û - = -
.
Bất phương trình đã cho trở thành
( )
2
2
2
1 2
1
t
m t t m
t
-
- Û
( )
1
.
Xét hàm số
( )
2
2
1
t
f t
t
-
=
,
1;2t
. Ta có
( )
( )
( )
( )
2
2
2
2 2 1
1 0, 1;2
1
1
t t
f t t
t
t
¢
= =
.
Bất phương trình đã cho có nghiệm 0;1 3x
Û Bất phương trình
( )
1
có nghiệm
1;2t
2
3
mÛ
.
Theo giả thiết
2018m -
nên ta có
2
2018
3
m-
. Vậy có tất cả là
2019
số nguyên của
m
thỏa
yêu cầu bài toán.
| 1/66
| | Tải xuống

Có thể bạn quan tâm:

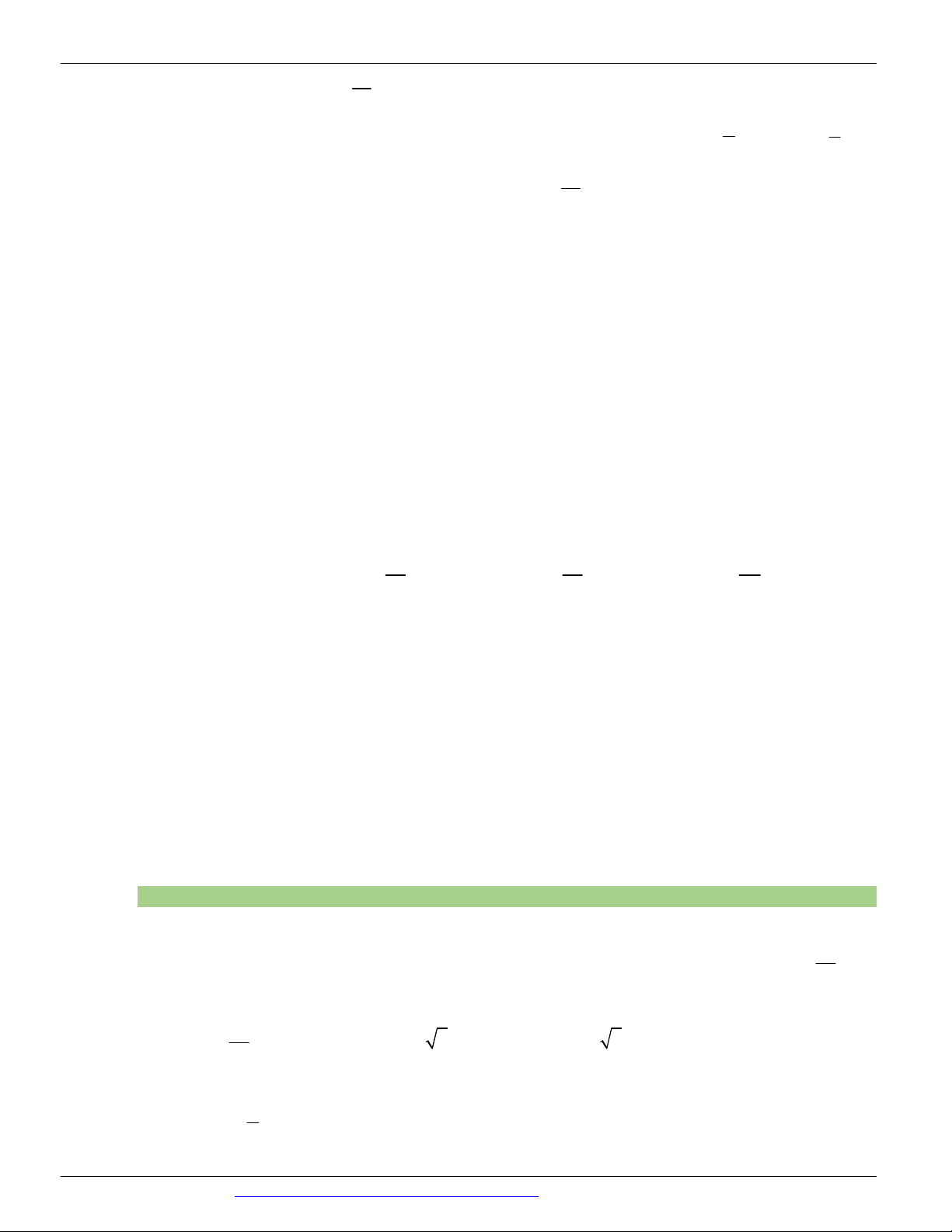
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ ĐỀ 3 MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 1
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó ...................................... 1
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b] ..................................................... 7
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b) ................................................ 8
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế ............................................................................................... 9
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước ........................................................ 11
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm ................................................................................ 13
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số ............................................................................................... 18
PHẦN B. LỜI GIẢI THAM KHẢO ........................................................................................................................... 19
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó .................................... 19
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b] ................................................... 28
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b) .............................................. 32
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế ............................................................................................. 34
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước ........................................................ 41
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm ................................................................................ 51
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số ............................................................................................... 62 PHẦN A. CÂU HỎI
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó
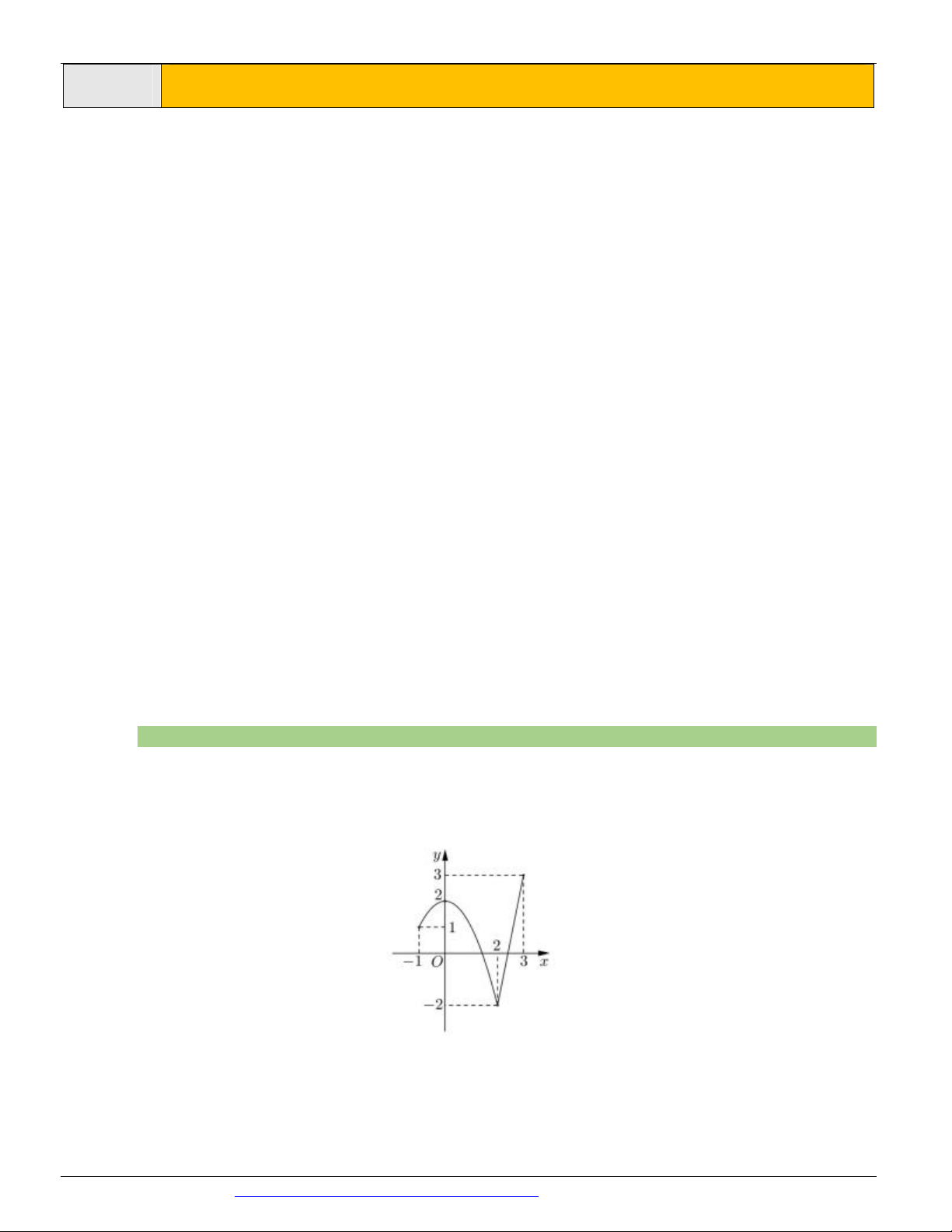
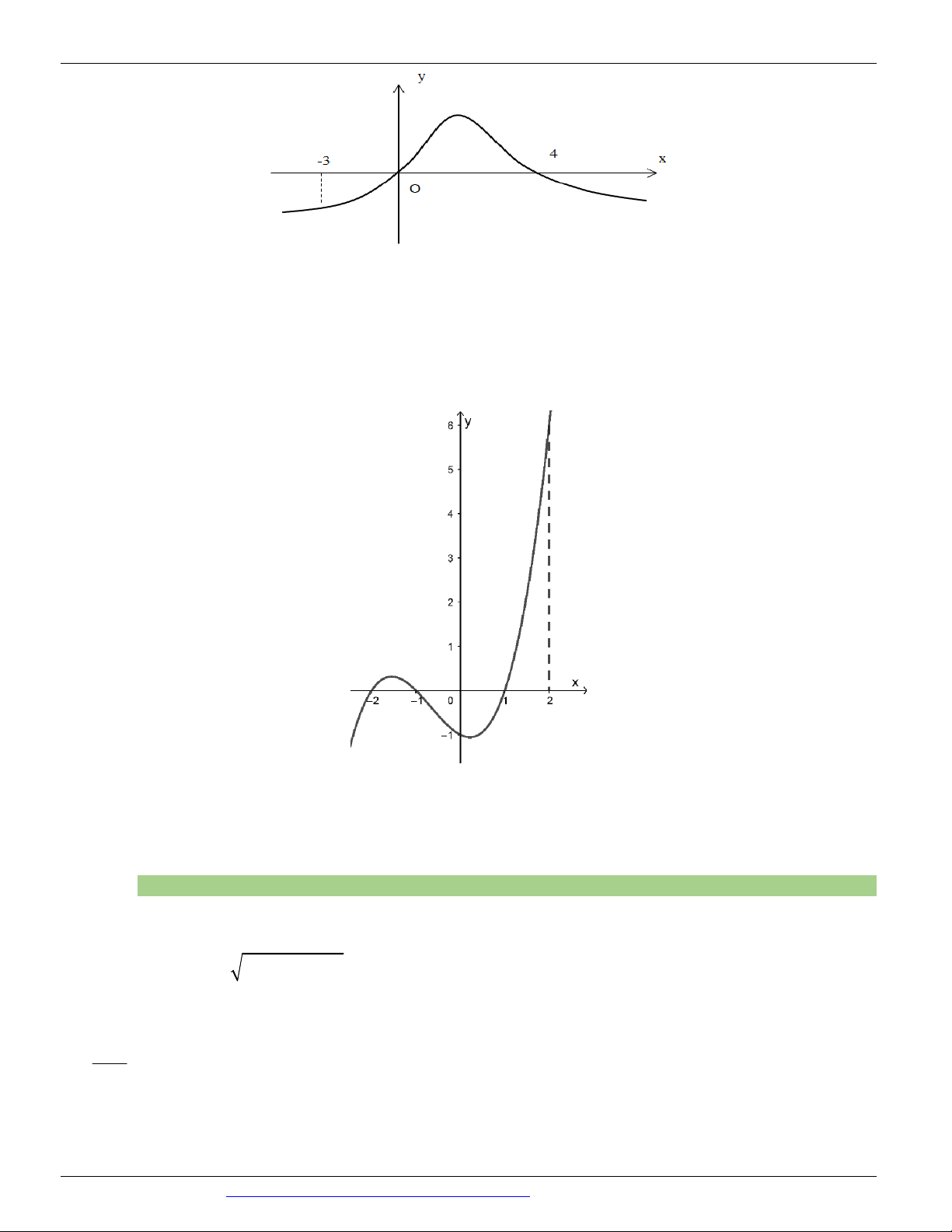
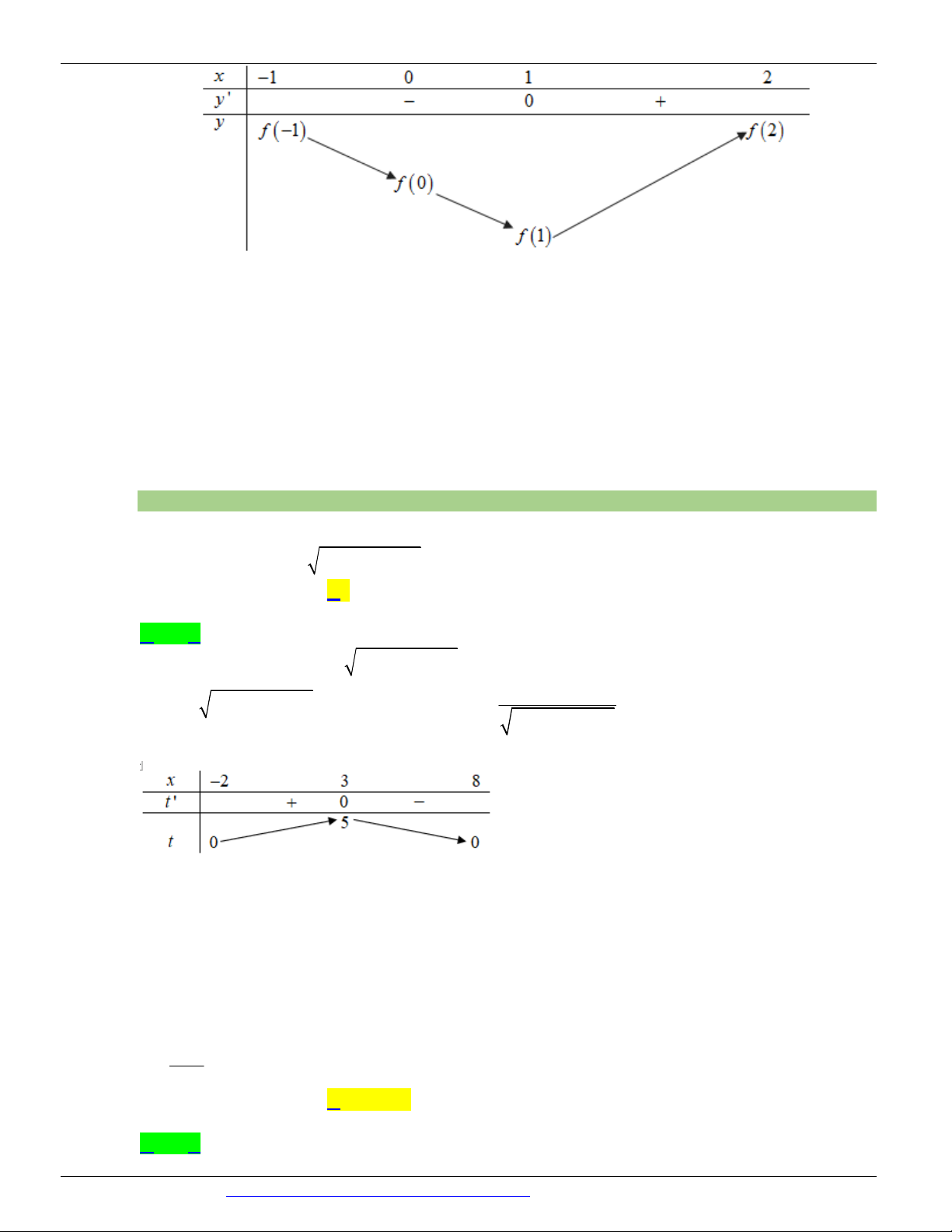
Câu 1. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y = f ( x) liên tục trên đoạn -1;3
và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên
đoạn -1;3 . Giá trị của M - m bằng A. 1 B. 4 C. 5 D. 0
Câu 2. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
y = f ( x) liên tục trên đoạn  1 - 
;1 và có đồ thị như hình vẽ.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 - 
;1 . Giá trị của M - m bằng A. 0 . B. 1. C. 2 . D. 3 .
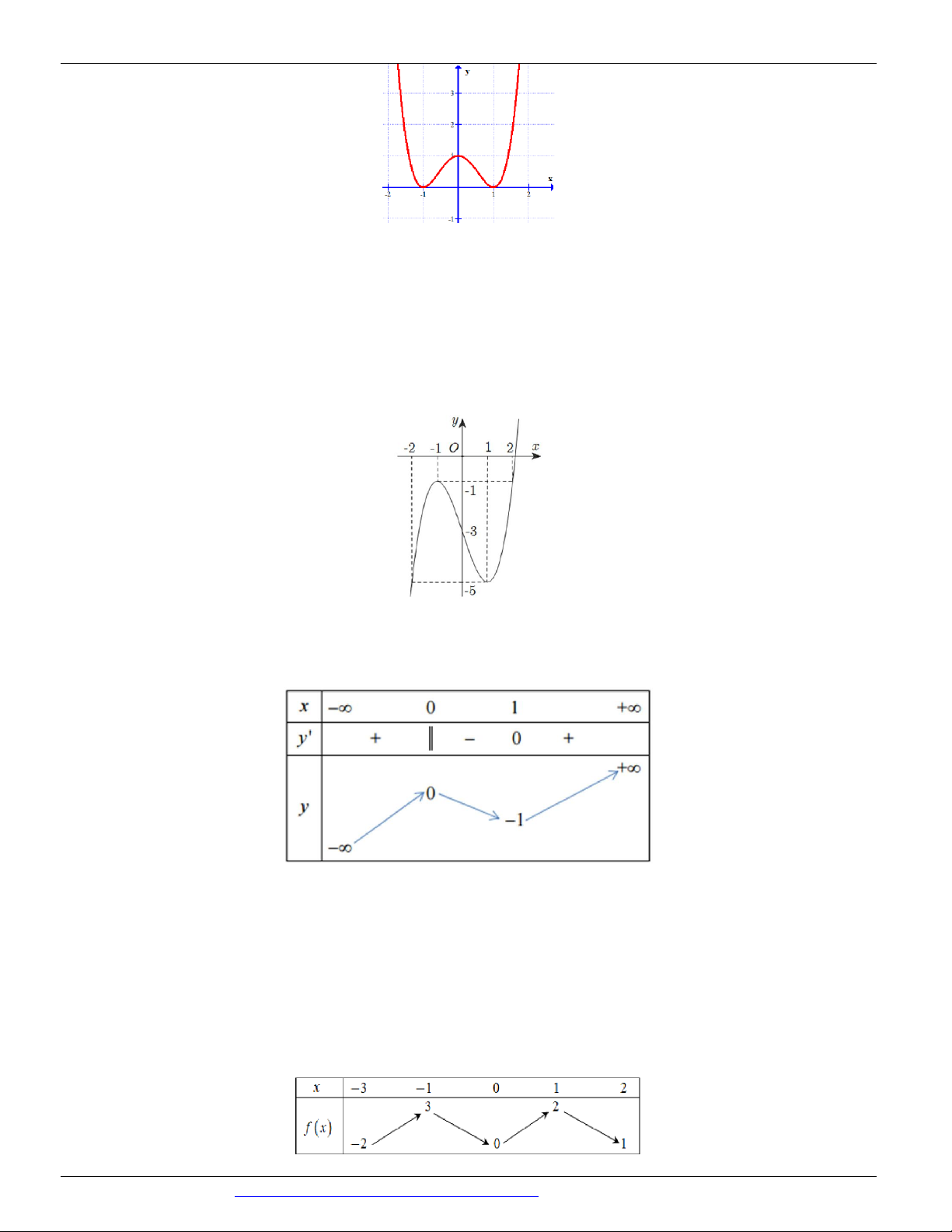
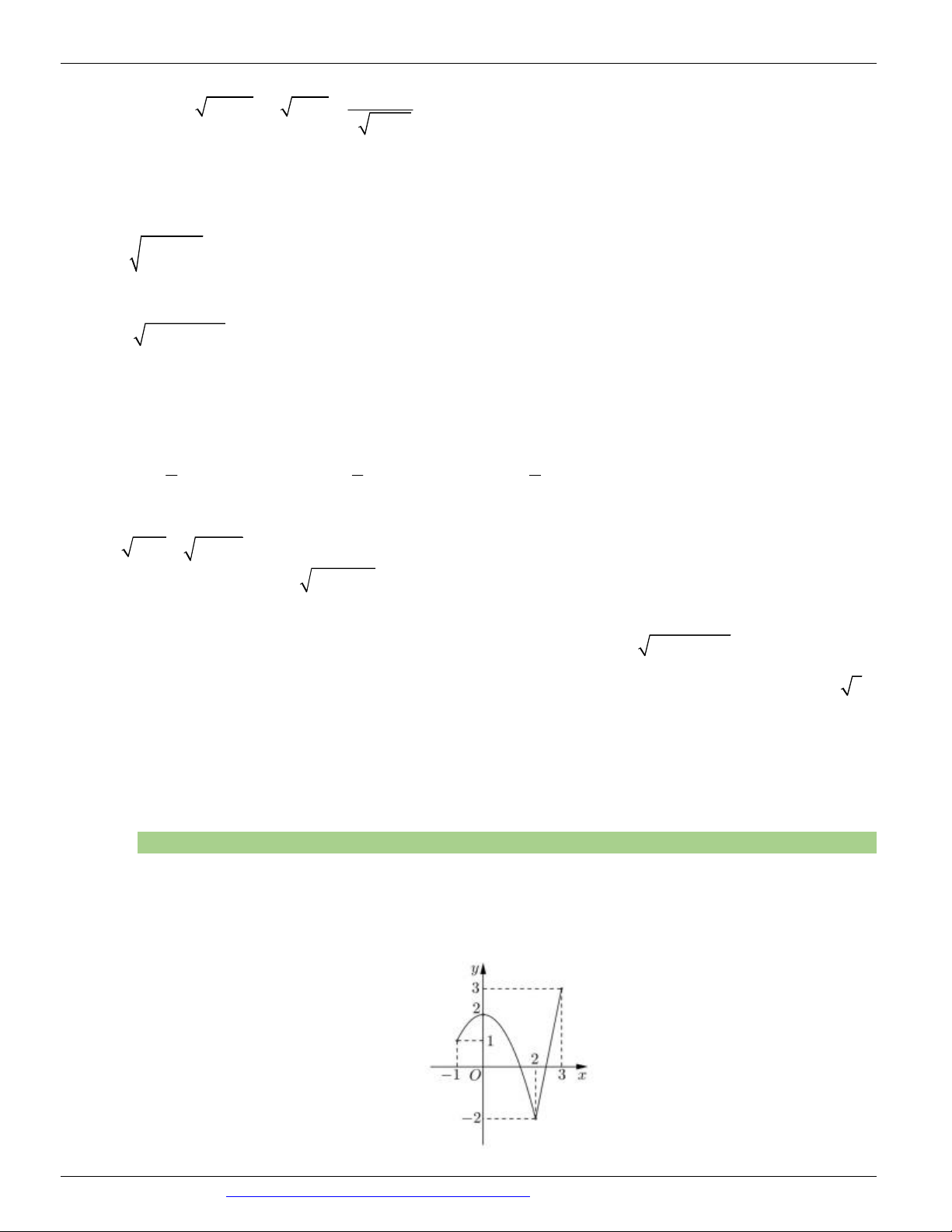
Câu 3. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x)
xác định và liên tục trên  có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm
số y = f ( x) trên đoạn -2; 2 . A. m = 5 - ; M = 1 - . B. m = 2 - ; M = 2 . C. m = 1 - ; M = 0 . D. m = 5 - ; M = 0 .
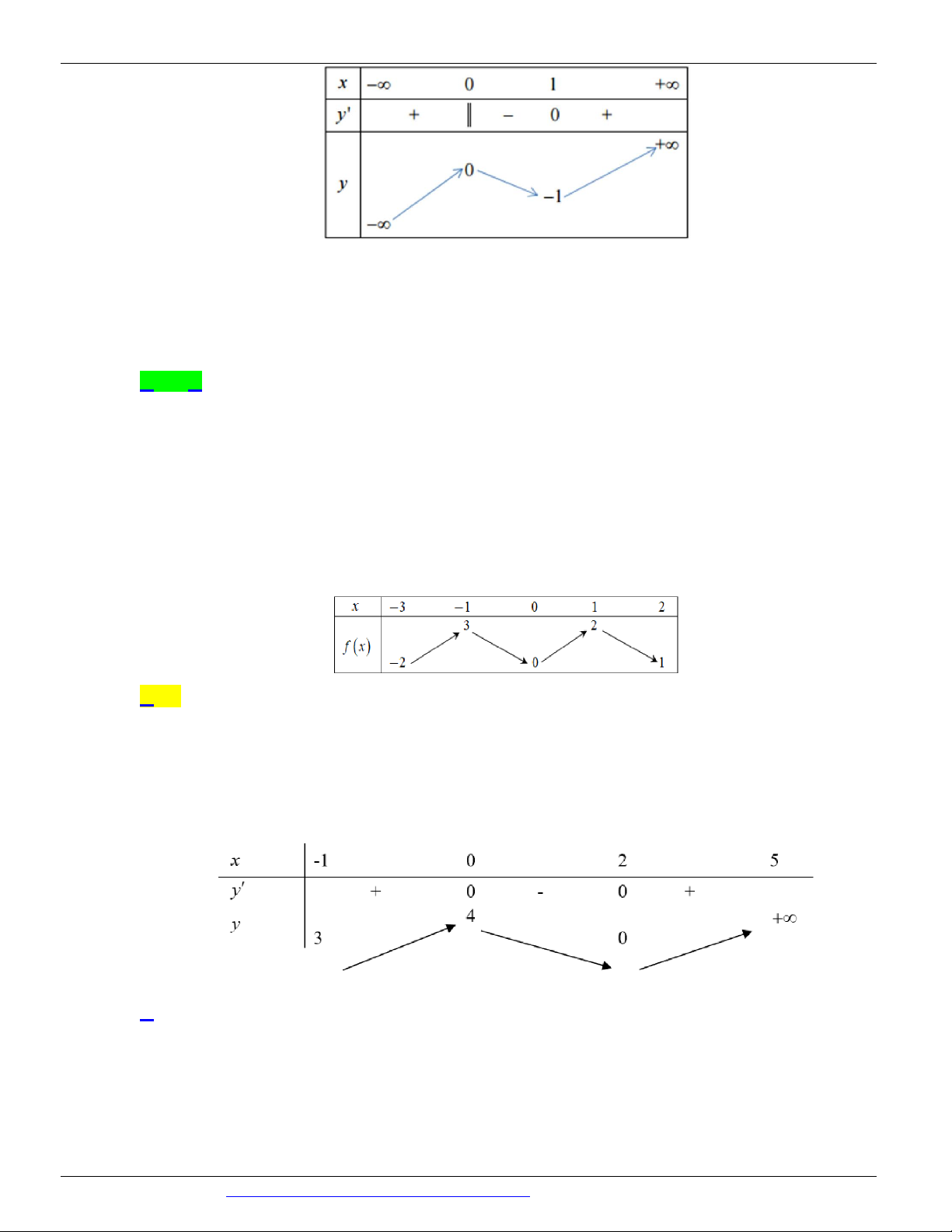
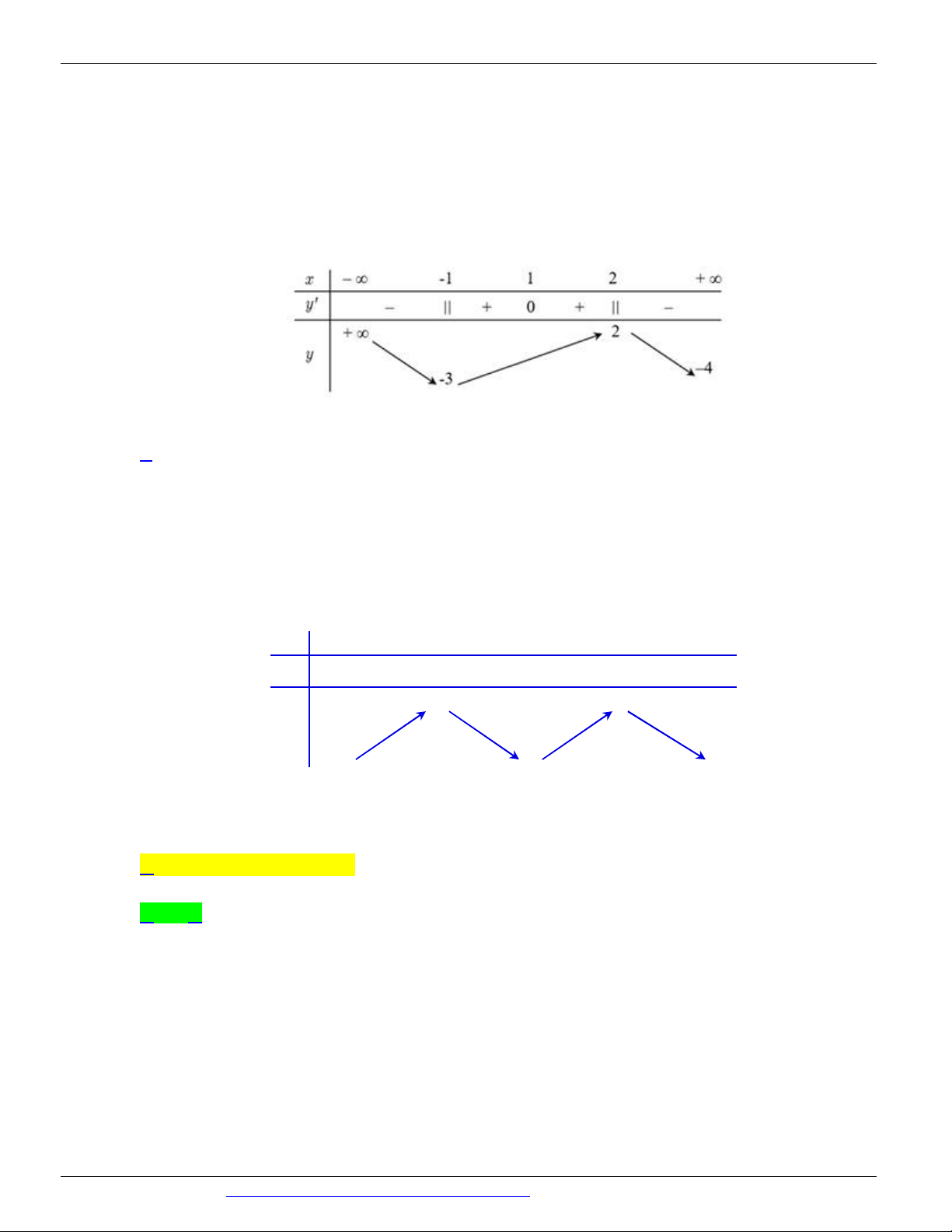
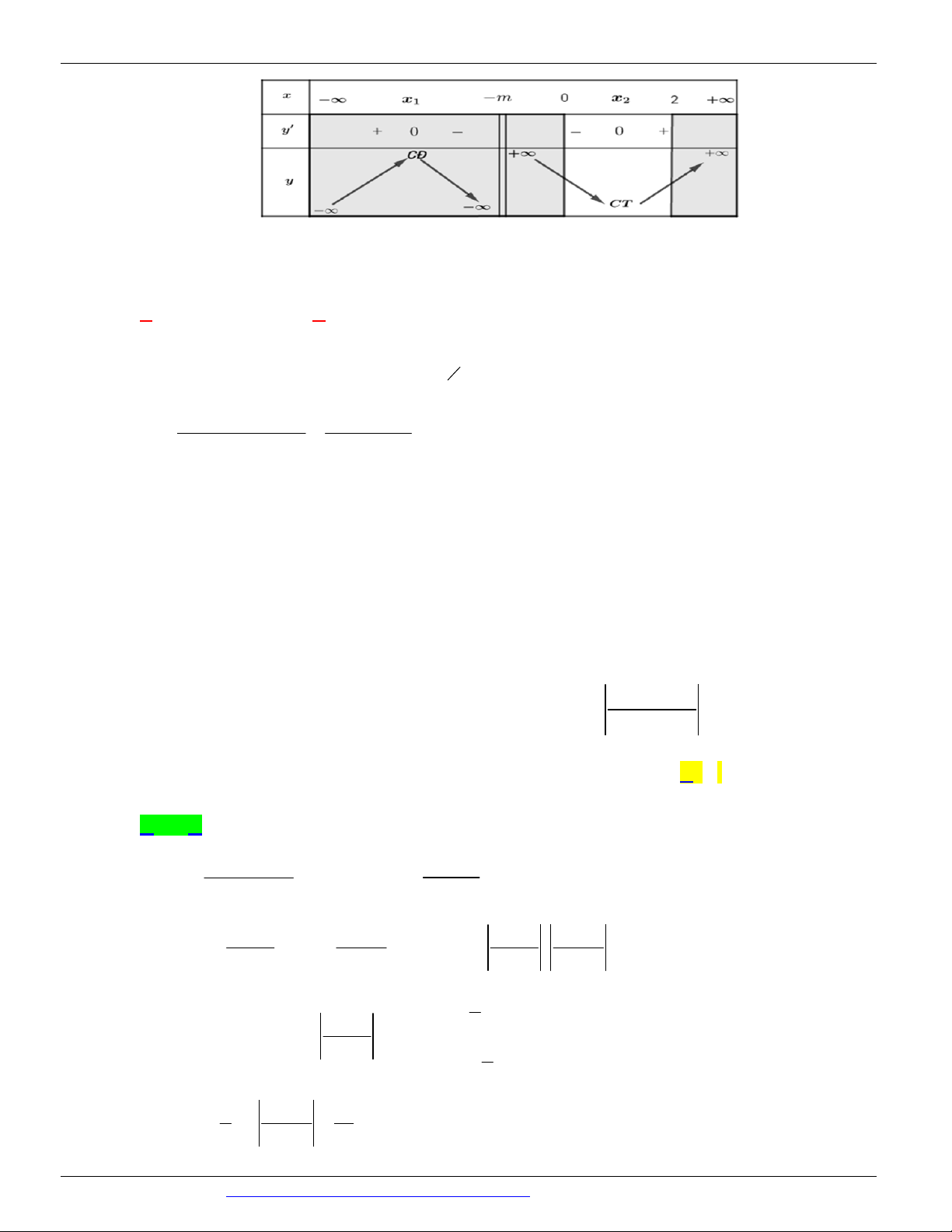
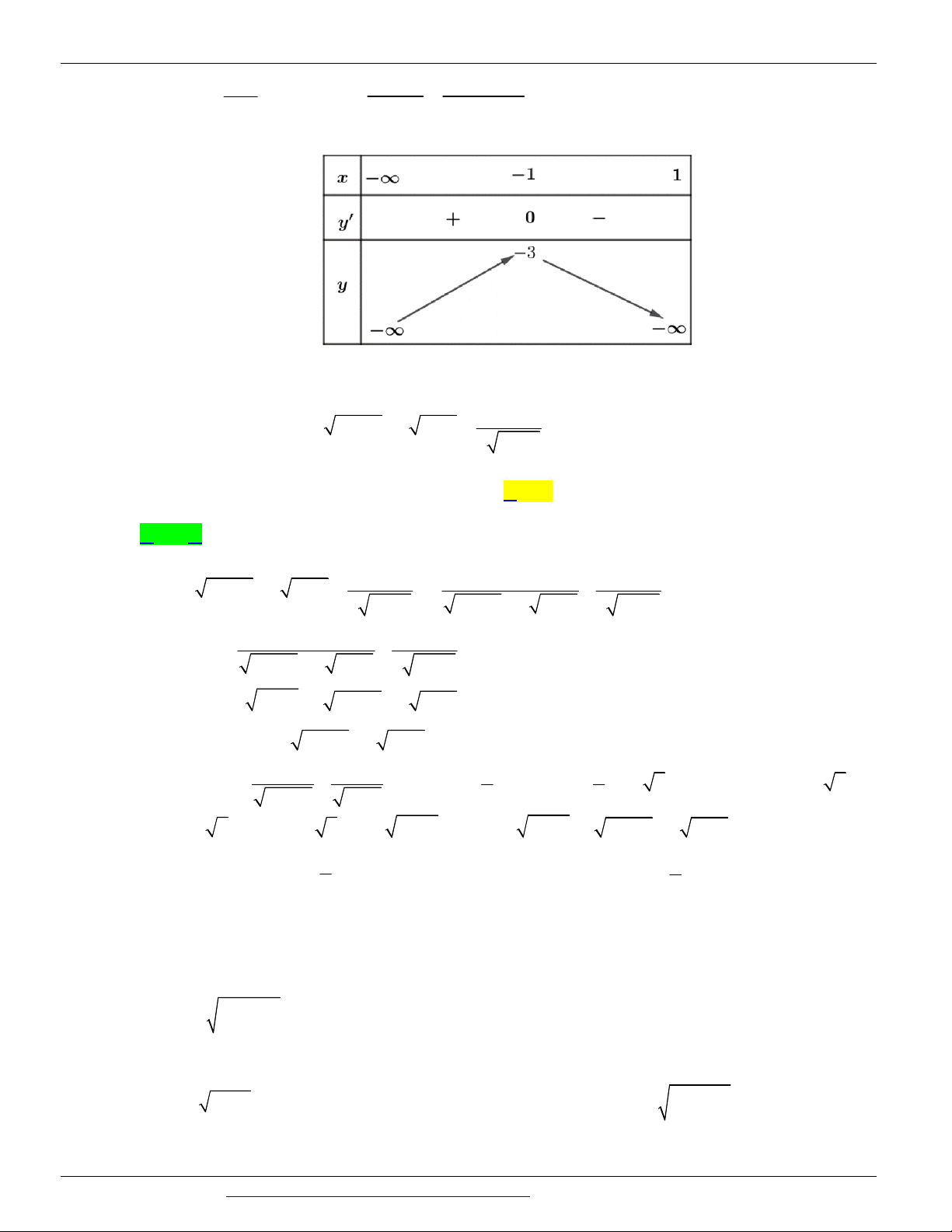
Câu 4. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số y = f ( x) xác định, liên tục trên  và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng 1 .
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1 .
C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 .
D. Hàm số có đúng một cực trị.
Câu 5. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Cho hàm số y = f ( x) liên tục trên  3
- ; 2 và có bảng biến thiên như sau. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = f ( x) trên đoạn  1
- ; 2. Tính M m .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 3 . B. 2 . C. 1. D. 4 .
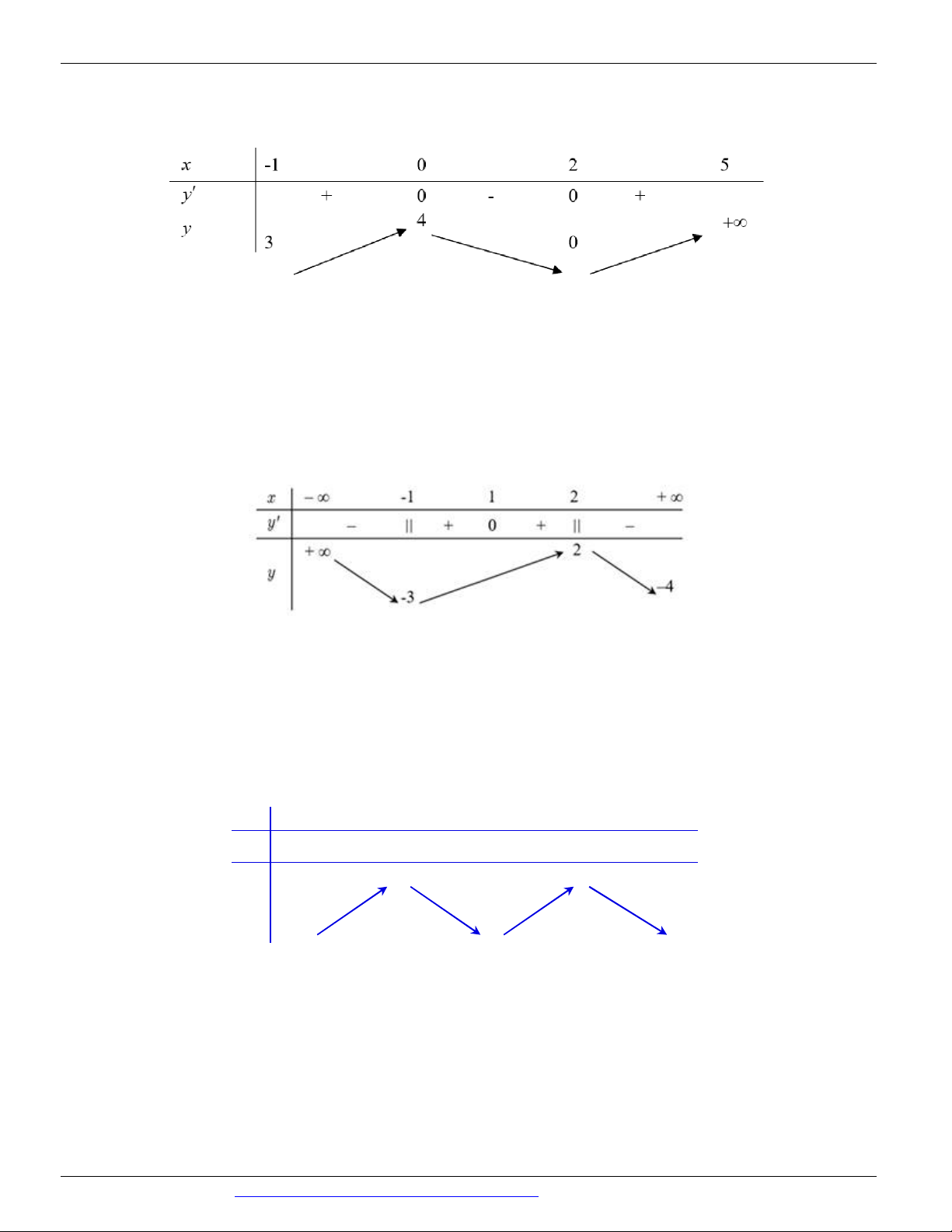
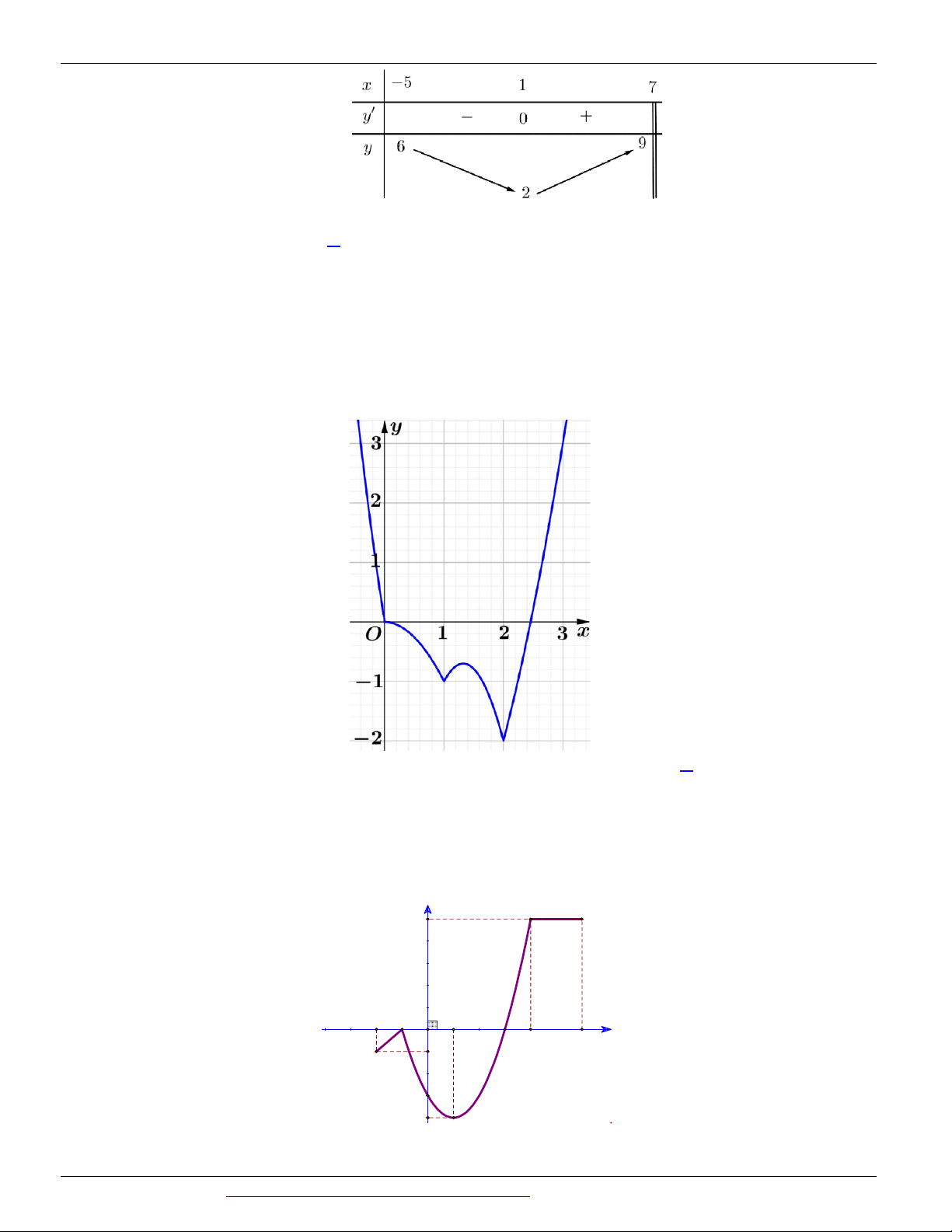
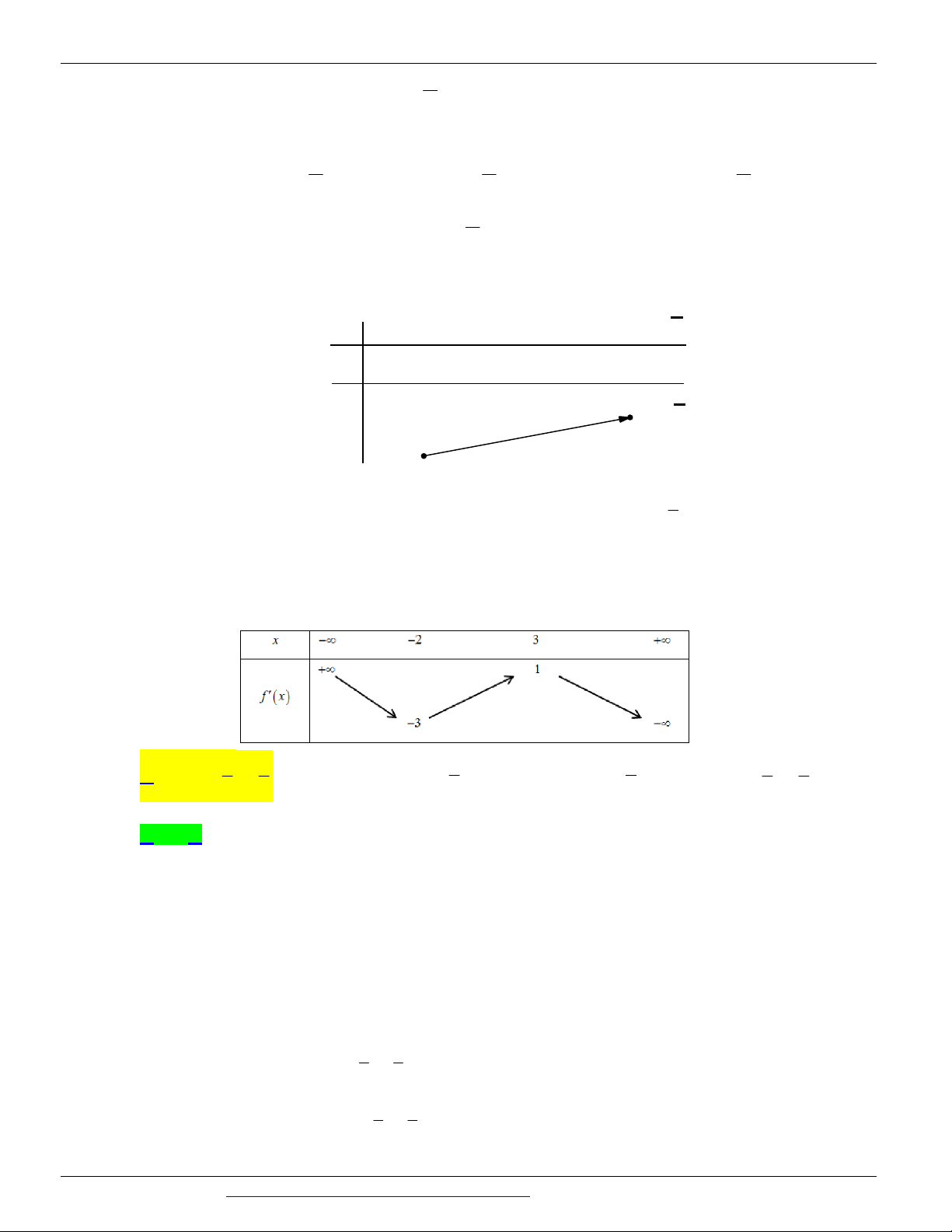
Câu 6. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét hàm số y = f (x) với x  1 - ;  5 có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn  1 - ;5
B. Hàm số đã cho đạt GTNN tại x = 1
- và x = 2 trên đoạn  1 - ;5
C. Hàm số đã cho đạt GTNN tại x = 1
- và đạt GTLN tại x = 5 trên đoạn  1 - ;5
D. Hàm số đã cho đạt GTNN tại x = 0 trên đoạn  1 - ;5
Câu 7. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) liên tục trên 
, có bảng biến thiên như hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3 .
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng (-; - ) 1 , (2;  ) .
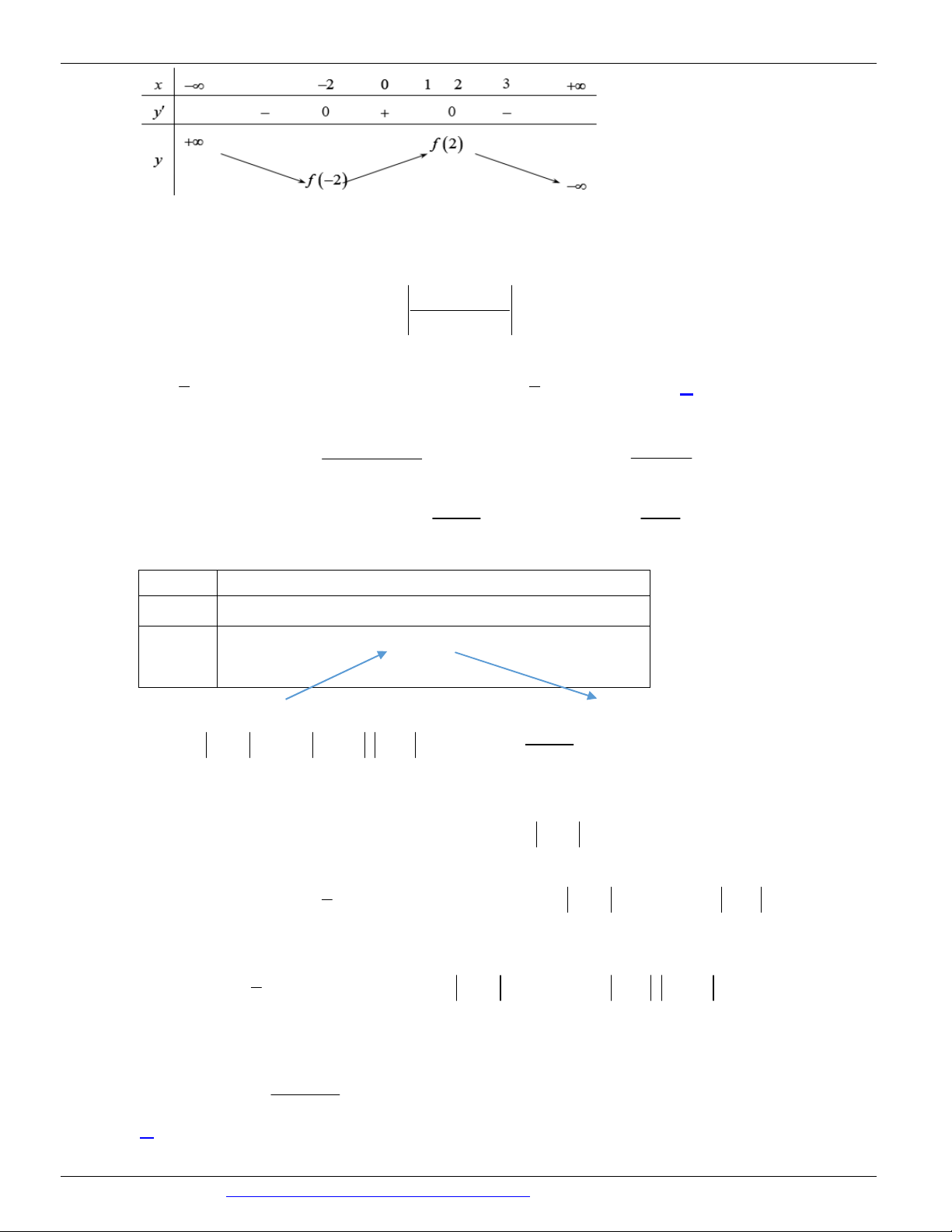
Câu 8. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x)
liên tục trên  và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng? x – ∞ -2 0 2 + ∞ y' + 0 – 0 + 0 – 4 4 y – ∞ 0 – ∞
A. Phương trình f ( x) = 0 có 4 nghiệm phân biệt
B. Hàm số đồng biến trên khoảng (0; )
C. Giá trị nhỏ nhất của hàm số bằng 0
D. Hàm số có 3 điểm cực trị
Câu 9. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số y = f (x)
liên tục và có bảng biến thiên trên đoạn -1;3 như hình vẽ bên. Khẳng định nào sau đây đúng?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. max f (x) = f (0) .
B. max f ( x) = f ( )
3 . C. max f ( x) = f (2) . D. max f ( x) = f (- ) 1 .  1 - ;  3  1 -  ;3  1 -  ;3  1 -  ;3
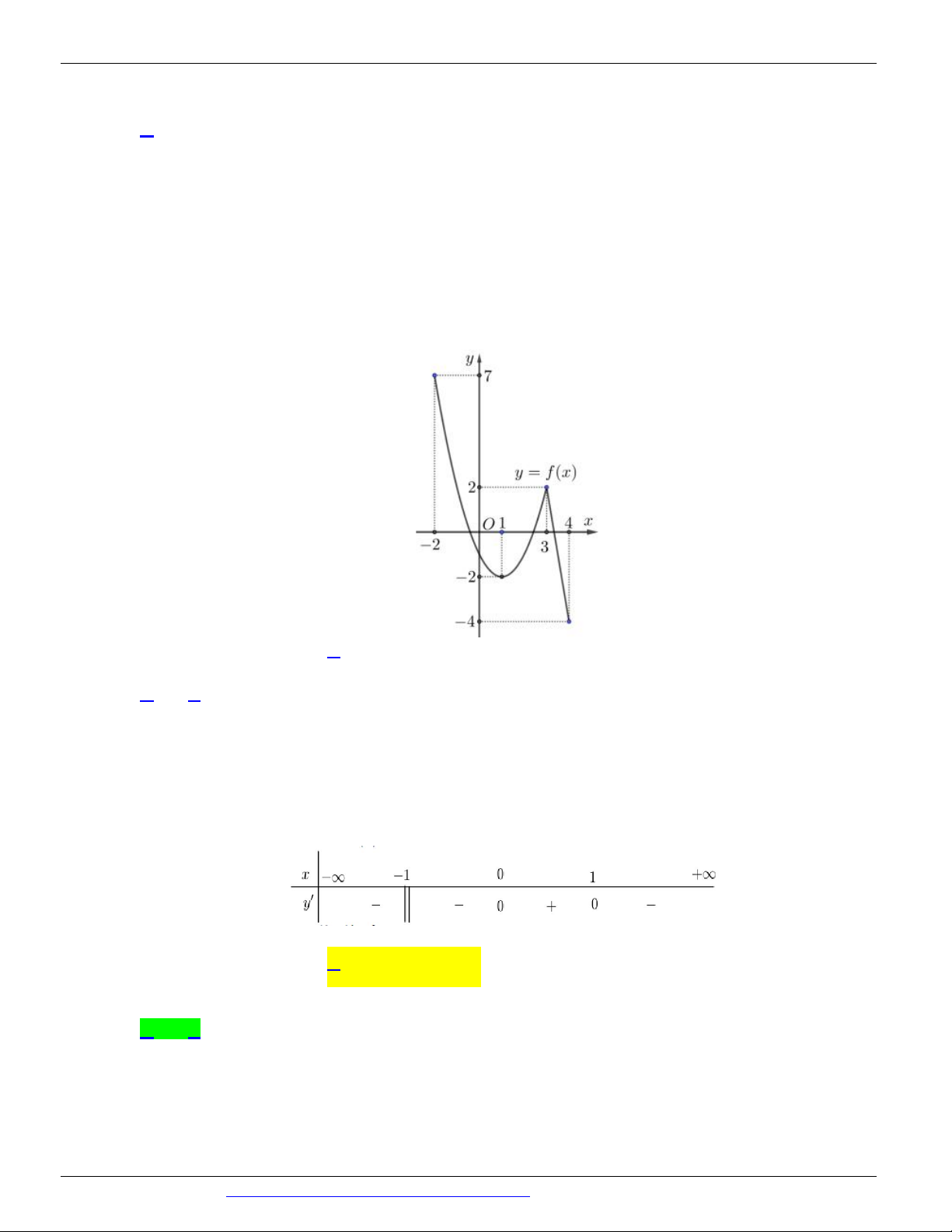
Câu 10. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số f ( x) liên tục trên  1 - ;5 và có
đồ thị trên đoạn  1
- ;5 như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x) trên đoạn  1 - ;5 bằng A. -1 B. 4 C. 1 D. 2
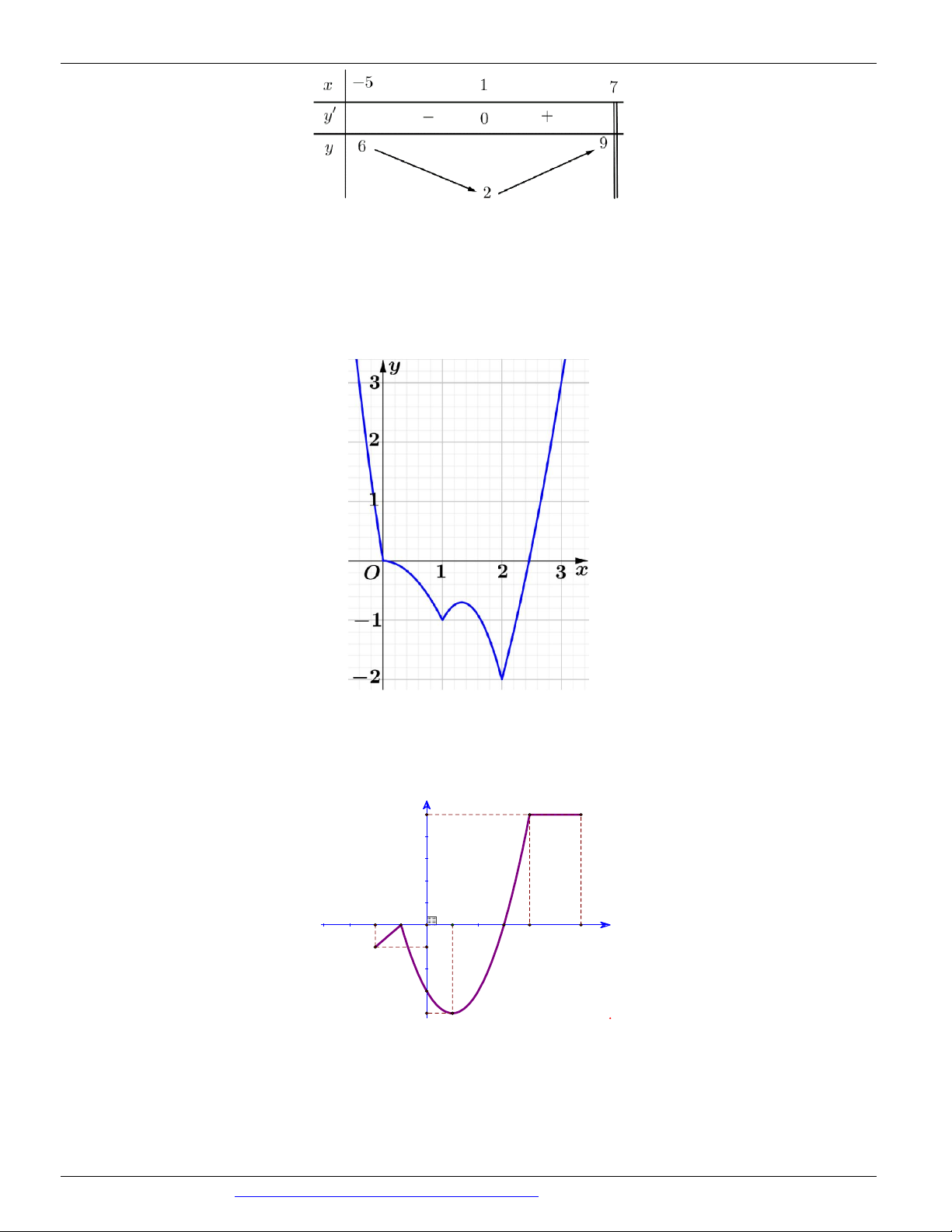
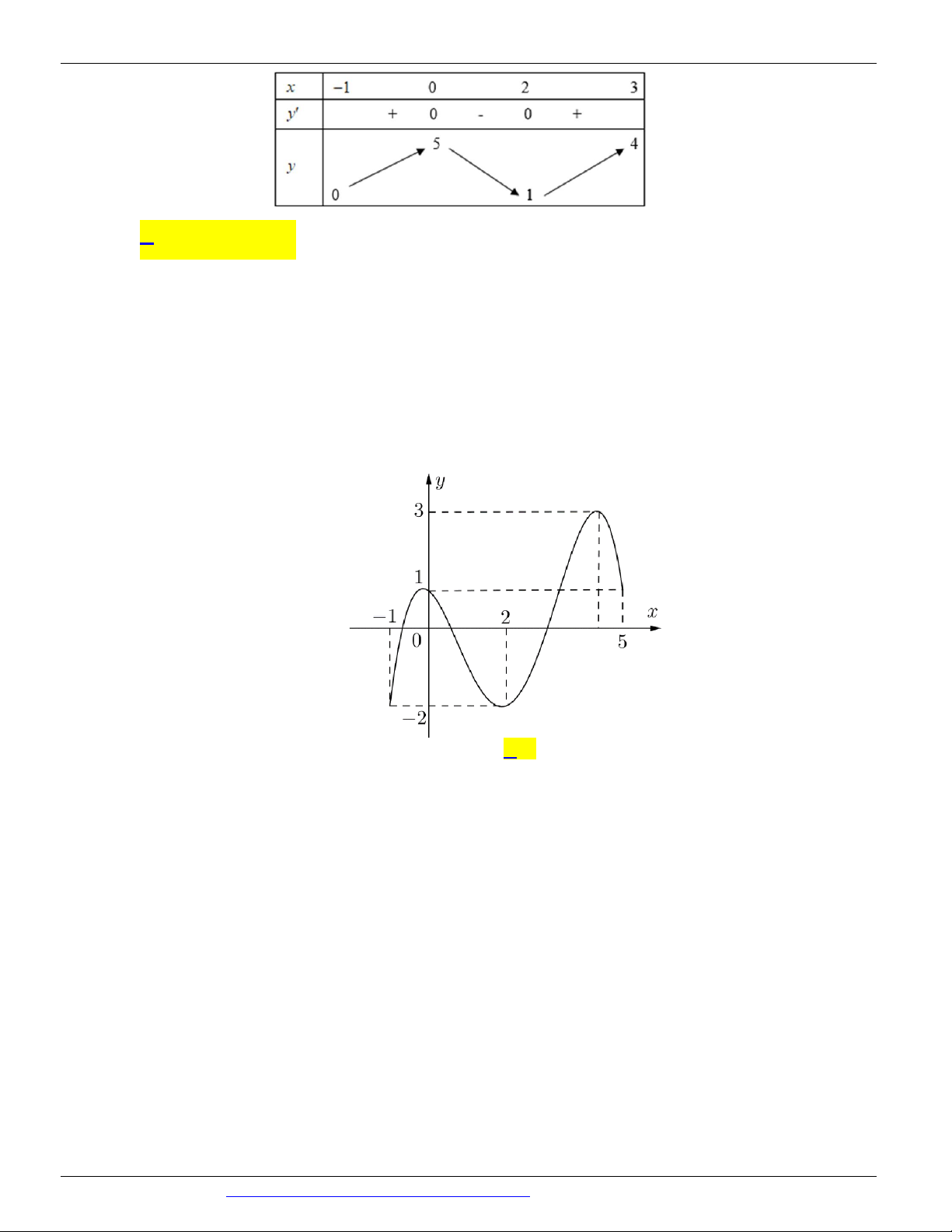
Câu 11. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Cho hàm số f ( x) liên tục trên  và có đồ thị như hình vẽ sau:  3 
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số f ( x) trên 1 - ;
. Giá trị của M m  2    bằng 1 A. . B. 5 . C. 4 . D. 3 . 2
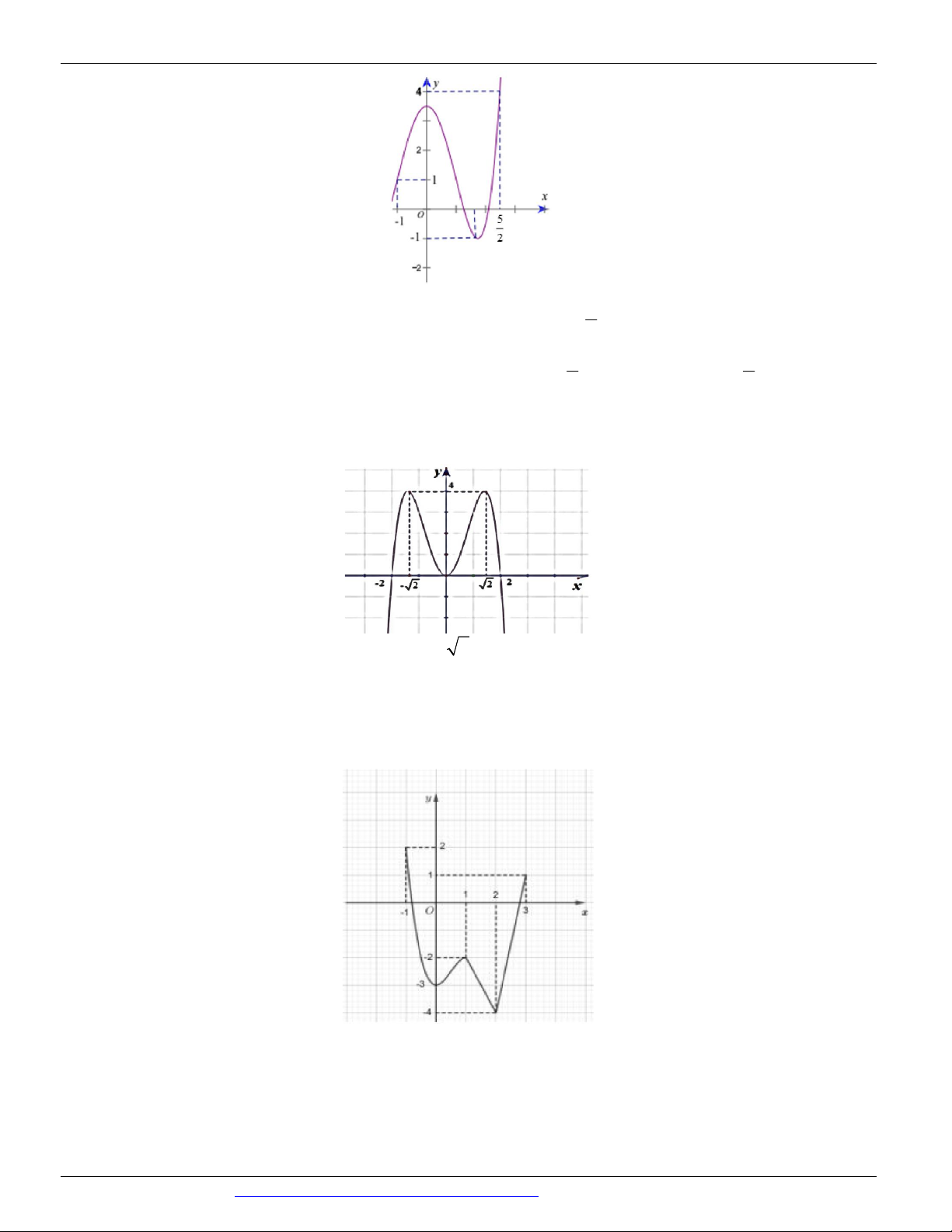
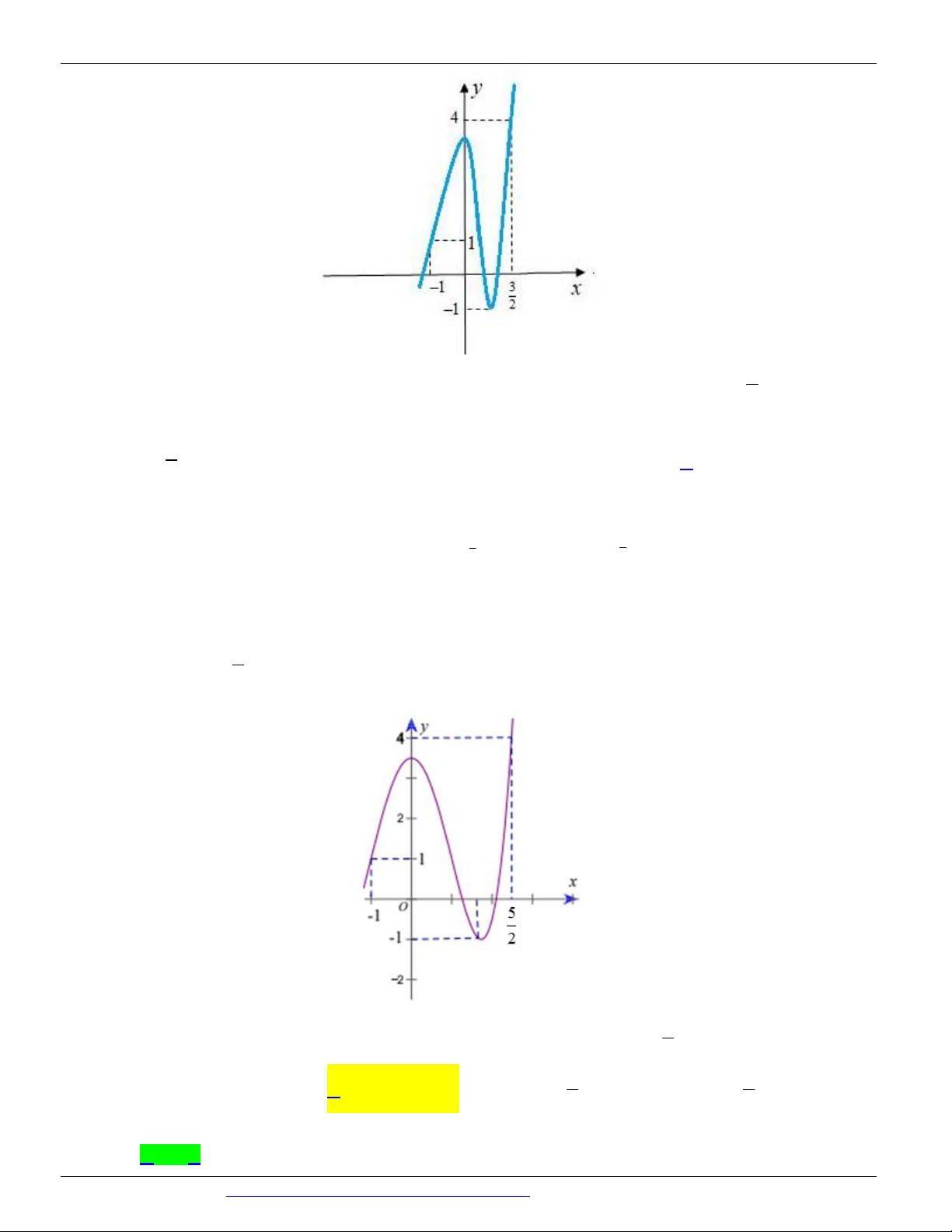
Câu 12. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) xác định, liên  5  tục trên 1 - , 
và có đồ thị là đường cong như hình vẽ. 2   
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  5 
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f ( x) trên -1,  là: 2    7 7
A. M = 4, m =1
B. M = 4,m = -1 C. M = , m = 1 - D. M = , m = 1 2 2
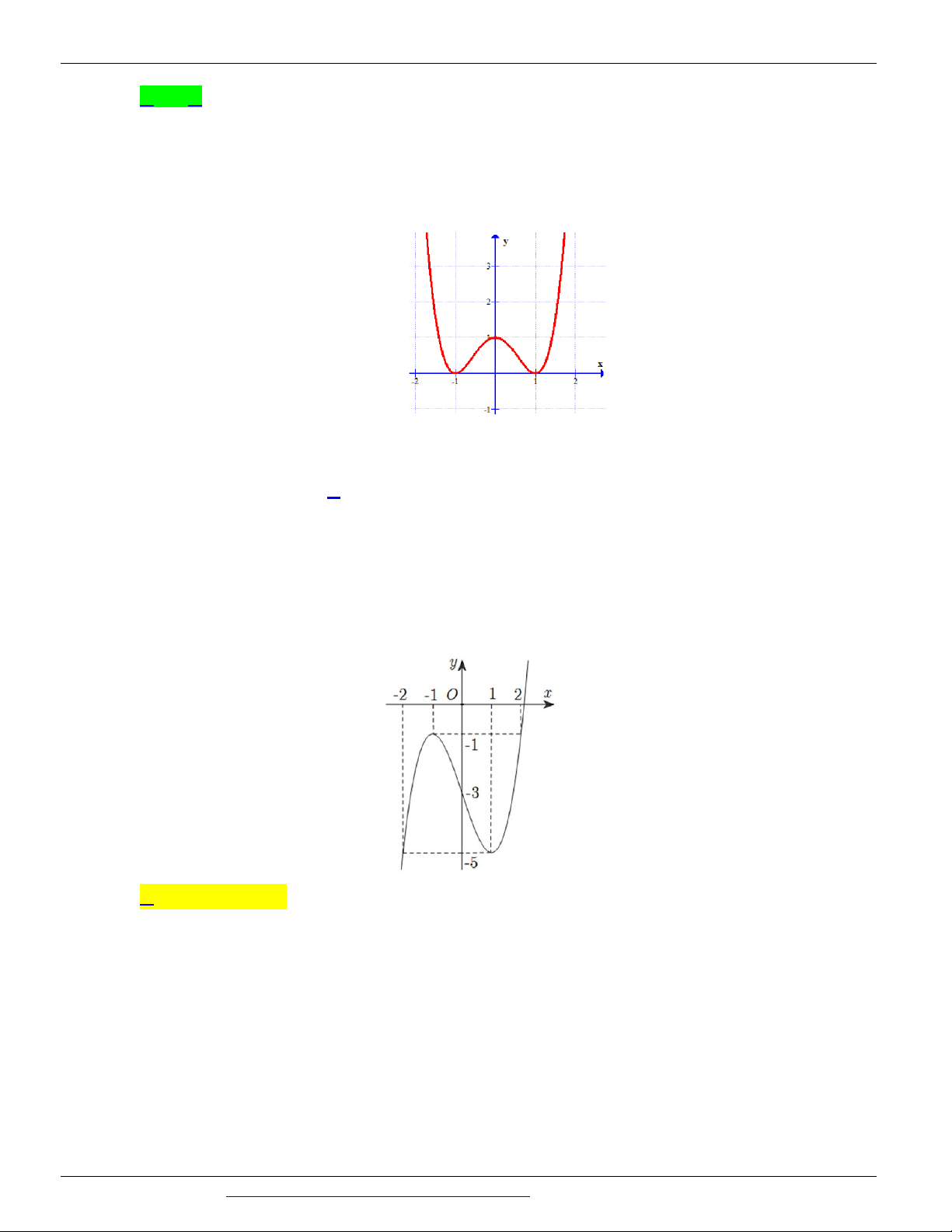
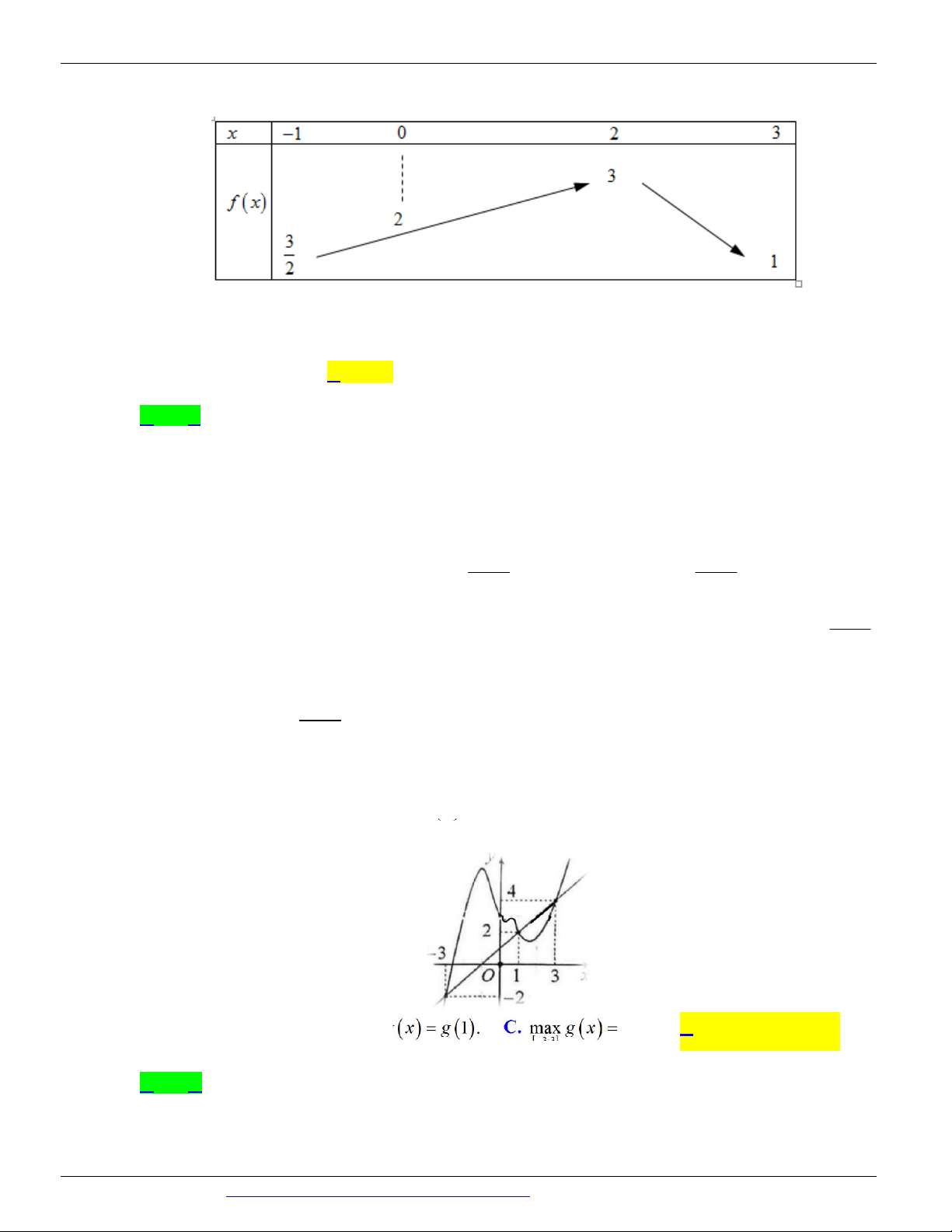
Câu 13. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số y = f ( x) có đồ thị như
hình vẽ. Giá trị lớn nhất của hàm số f ( x) trên đoạn 0; 2 là:
A. Max f ( x) = 2 .
B. Max f ( x) = 2 .
C. Max f ( x) = 4 .
D. Max f ( x) = 0 . 0;  2 0;2 0;  2 0;  2
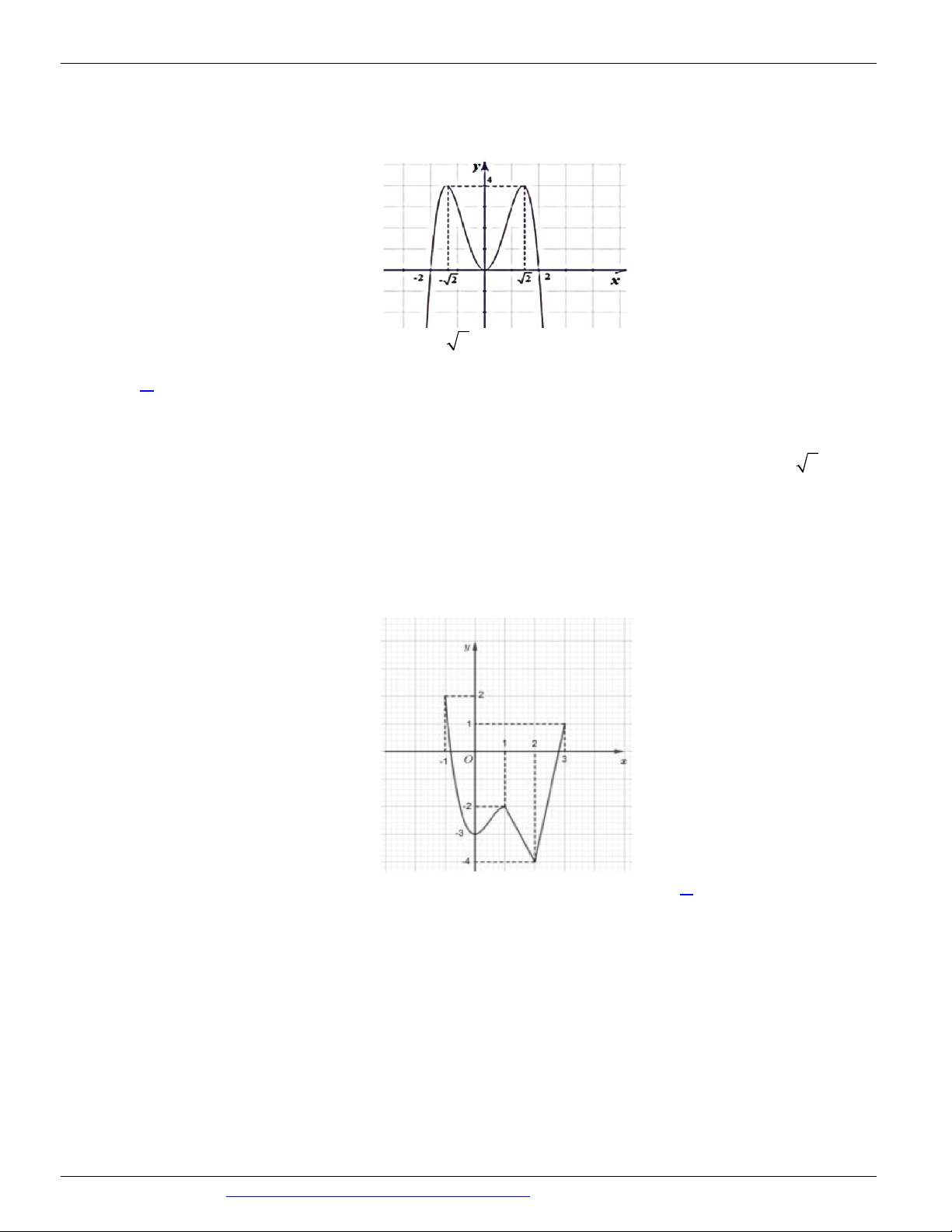
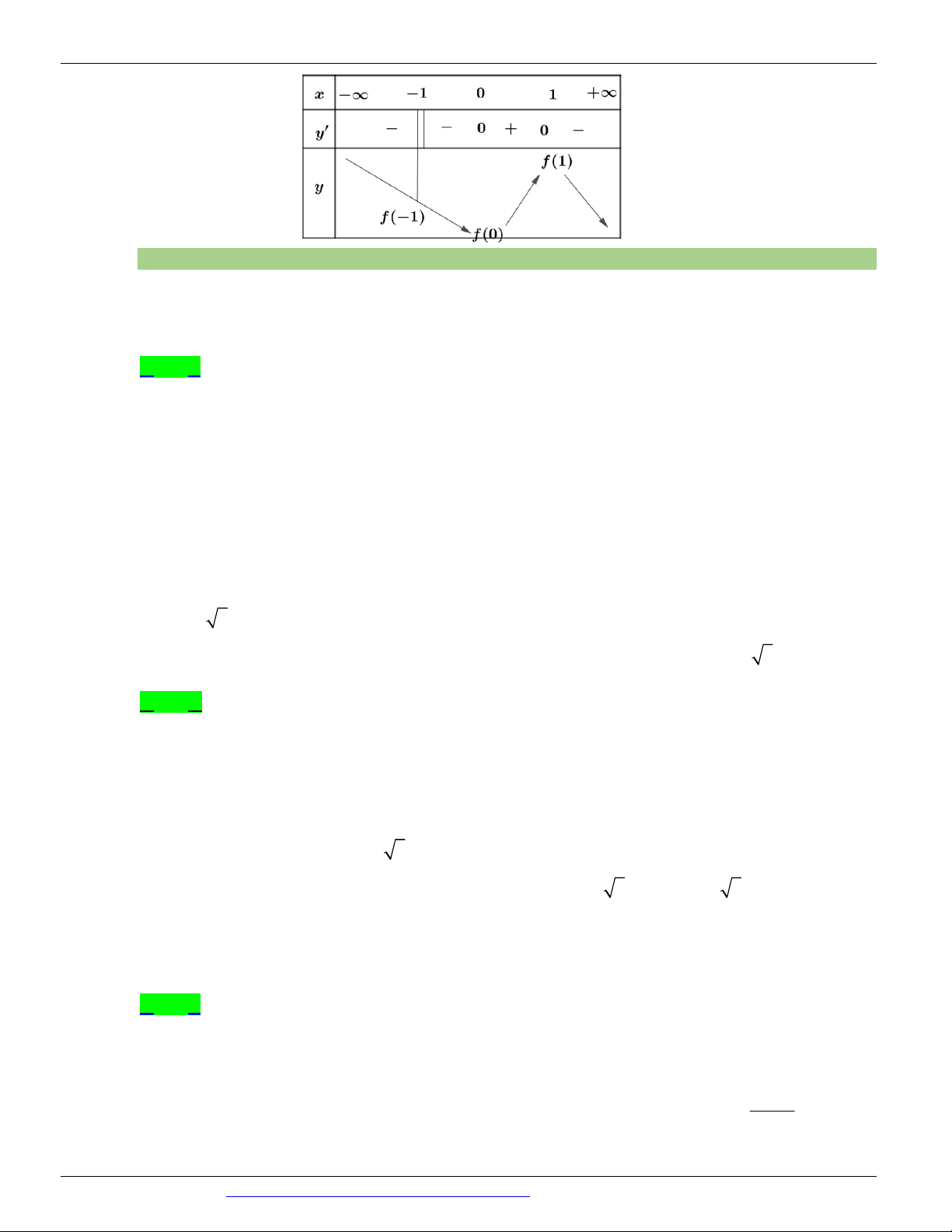
Câu 14. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số y = f (x) liên tục trên đoạn -1; 
3 và có đồ thị như hình vẽ bên. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn -1; 
3 . Giá trị của M m là A. 2 B. 6 - C. 5 - D. -2
Câu 15. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số y = f ( x) có bảng biến thiên trên -5;7) như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Mệnh đề nào dưới đây đúng?
A. Min f ( x) = 6 .
B. Min f ( x) = 2 .
C. Max f ( x) = 9 .
D. Max f ( x) = 6 .  5; - 7)  5; - 7) -5;7)  5 - ;7)
Câu 16. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hàm số f ( x ) liên tục trên
đoạn 0;3 và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã
cho trên 0;3 . Giá trị của M m bằng? A. 5 . B. 3 . C. 2 . D. 1.
Câu 17. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số y = f ( x) liên tục
trên đoạn 2 ; 6 và có đồ thị như hình vẽ bên dưới. y 5 -2 -1 O 1 3 4 6 x -1 y = f(x) -3 -4
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 2 ; 6. Giá trị của M m bằng A. 9 . B. 8 - . C. 9 - . D. 8 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
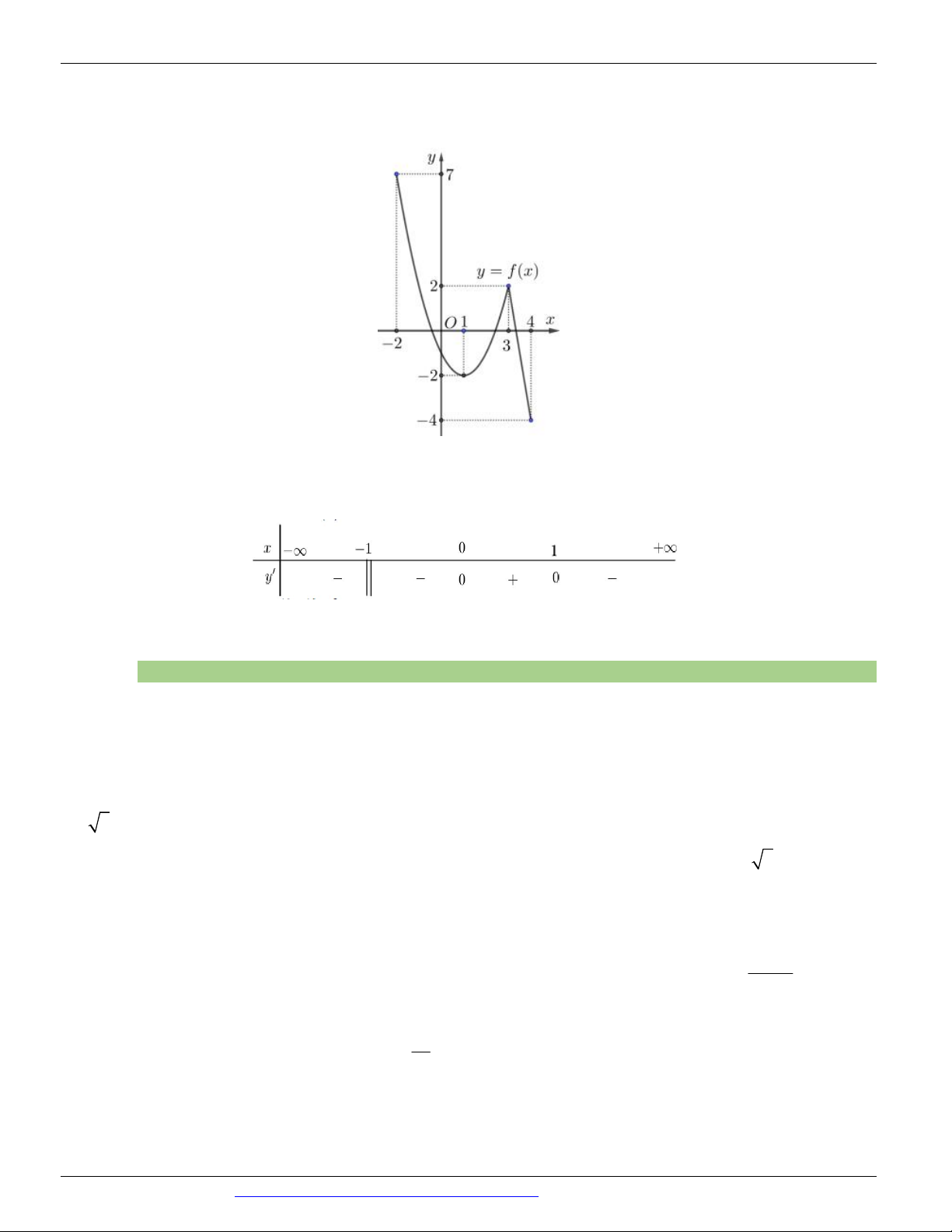
Câu 18. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Cho hàm số y = f ( x) liên tục và có đồ thị
trên đoạn -2; 4 như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f ( x) trên đoạn  2 - ; 4 bằng A. 5 B. 3 C. 0 D. -2
Câu 19. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) có bảng
xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng
A. max f ( x) = f (0)
B. max f ( x) = f ( ) 1
C. min f ( x) = f (- )
1 D. min f ( x) = f (0) ( 1 - ;  1 (0;) (- ;  - ) 1 ( 1 - ; )
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b]
Câu 20. (Mã 102 - BGD - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x - 3x  2 trên đoạn  3 - ;  3 bằng A. 0 . B. 16 - . C. 20 . D. 4 .
Câu 21. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị lớn nhất M của hàm số 4 2
y = x - 2x  3 trên đoạn 0; 3 .  
A. M = 6
B. M = 1
C. M = 9
D. M = 8 3
Câu 22. (Mã 103 - BGD - 2019) Giá trị lớn nhất của hàm số f ( x) 3
= x - 3x trên đoạn [ - 3;3] bằng A. -2 . B. 18 . C. 2 . D. -18 . 2 x  3
Câu 23. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số y = trên đoạn x -1 2; 4 . 19
A. min y = -3 B. min y =
C. min y = 6 D. min y= 2 - 2;4 2;4 3 2;4 2;4
Câu 24. (Mã đề 104 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số 4 2
y = x - x 13 trên đoạn [-1; 2] bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 51 A. 85 B. C. 13 D. 25 4 2  1 
Câu 25. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số 2 y = x  trên đoạn ; 2 . x  2    17
A. m = 5
B. m = 3 C. m = D. m =10 4
Câu 26. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số y = 3 x - 2 7x  11x - 2 trên đoạn [0 ; 2].
A. m = 3
B. m = 0
C. m = -2 D. m = 11
Câu 27. (Mã đề 101 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số 4 2
y = x - 4x  9 trên đoạn  2 - ;  3 bằng A. 201 B. 2 C. 9 D. 54
Câu 28. (ĐỀ THAM KHẢO BGD & ĐT 2018) Giá trị lớn nhất của hàm số f ( x) 4 2
= x - 4x  5 trêm đoạn  2 - ;  3 bằng A. 122 B. 50 C. 5 D. 1
Câu 29. (MĐ 105 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số y = 4 x - 2 x  13 trên đoạn -2;3   . 51 51 49
A. m = 13 B. m = C. m = D. m = 4 2 4
Câu 30. (Mã đề 104 - BGD - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x - 3x trên đoạn  3 - ;  3 bằng A. -18. B. 2 - . C. 2. D. 18.
Câu 31. (MĐ 103 BGD&ĐT NĂM 2017-2018) Giá trị nhỏ nhất của hàm số 3 2
y = x  3x trên đoạn -4; -  1 bằng A. -16 B. 0 C. 4 D. -4
Câu 32. (Mã đề 102 BGD&ĐT NĂM 2018) Giá trị nhỏ nhất của hàm số 3 2
y = x  2x - 7x trên đoạn 0; 4 bằng A. 259 - B. 68 C. 0 D. -4
Câu 33. (Mã đề 101 - BGD - 2019) Giá trị lớn nhất của hàm số f ( x) 3
= x - 3x  2 trên đoạn  3 - ;  3 là A. 4 . B. 16 - . C. 20 . D. 0 .
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b) 4
Câu 34. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tính giá trị nhỏ nhất của hàm số y = 3x  trên 2 x
khoảng (0;  ) . 33 A. min y = B. 3 min y = 2 9 C. 3 min y = 3 9
D. min y = 7 (0;) 5 (0;) (0;) (0;)
Câu 35. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Gọi m là giá trị nhở 4
nhất của hàm số y = x
trên khoảng (0; ) . Tìm m x A. m = 4 . B. m = 2 . C. m = 1. D. m = 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 36. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Gọi a là giá trị nhỏ nhất của hàm số 4 2 y = x  trên khoảng (0; )  . Tìm a . x A. 3 3 4 . B. 5. C. 6 . D. 3 2 16 . 1
Câu 37. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Giá trị nhỏ nhất của hàm số y = x - 5  x
trên khoảng (0; ) bằng bao nhiêu? A. 0 B. 1 - C. 3 - D. -2
Câu 38. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số 1
f (x) = x
trên nửa khoảng 2; ) là: x 5 7 A. 2 B. C. 0 D. 2 2
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế
Câu 39. (Mã đề 101 BGD&ĐT NĂM 2018) Ông A dự định dùng hết 2
6, 5m kính để làm một bể cá có dạng
hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung
tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 2, 26 m B. 3 1, 61 m C. 3 1,33 m D. 3 1,50 m 1
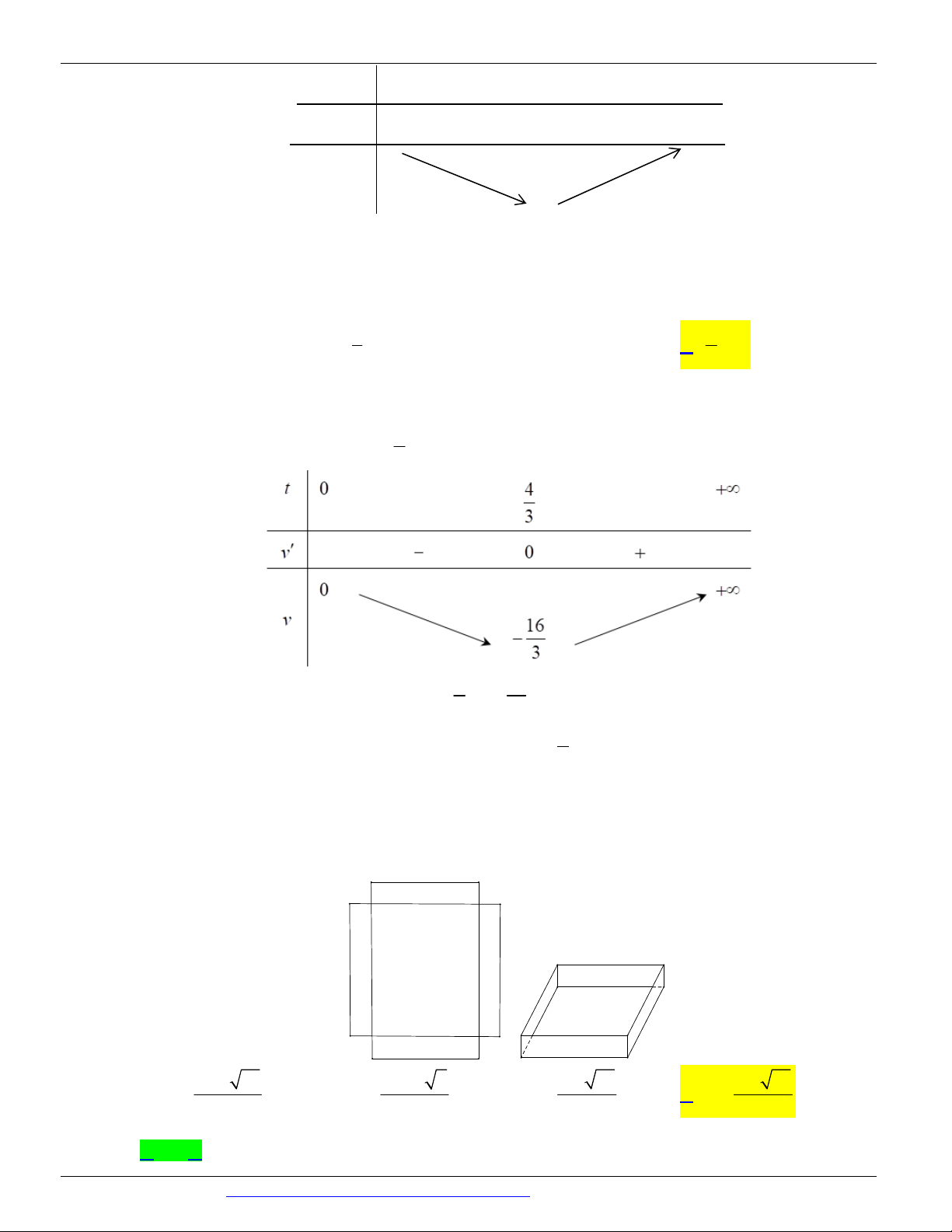
Câu 40. (MĐ 104 BGD&DT NĂM 2017) Một vật chuyển động theo quy luật 3 2
s = - t  6t với t (giây) là 3
khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của
vật đạt được bằng bao nhiêu? A. 243 (m/s) B. 27 (m/s) C. 144 (m/s) D. 36 (m/s)
Câu 41. (MĐ 103 BGD&ĐT NĂM 2017-2018) Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước
không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1, 01 m B. 3 0, 96 m C. 3 1,33 m D. 3 1,51 m
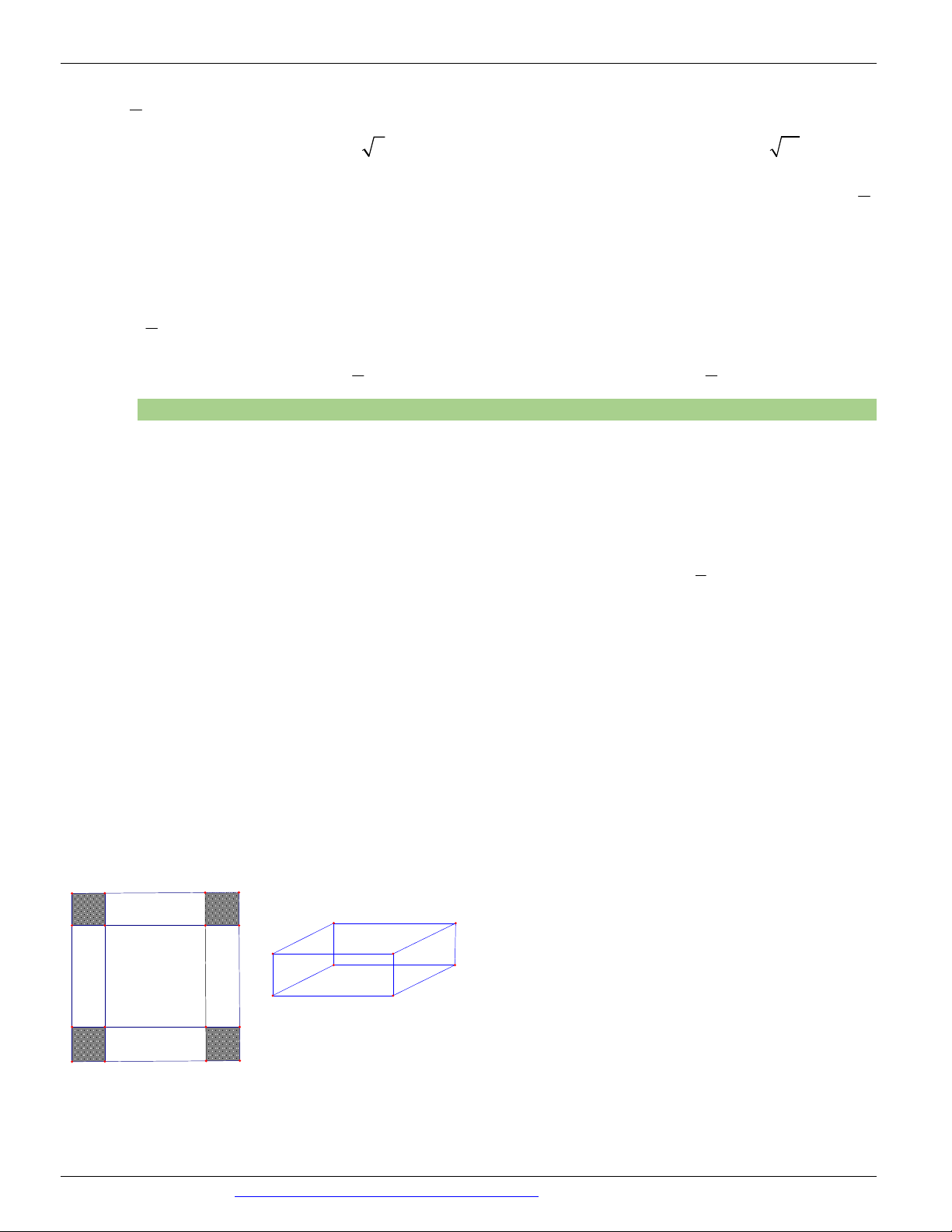
Câu 42. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta
cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập
tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. x = 3
B. x = 2
C. x = 4
D. x = 6
Câu 43. (KTNL GIA BÌNH NĂM 2018-2019) Một chất điểm chuyển động theo phương trình 3 2 S = t
-  3t - 2 , trong đó t tính bằng giây và S tính theo mét. Chuyển động có vận tốc lớn nhất là A. 1 m/s. B. 4 m/s. C. 3 m/s. D. 2 m/s.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 44. (THPT NĂM 2018-2019 LẦN 04) Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc
trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi t
tiêm vào cơ thể trong t giờ được cho bởi công thức c (t ) =
(mg / L) . Sau khi tiêm thuốc bao lâu thì 2 t 1
nồng độ thuốc trong máu của bệnh nhân cao nhất? A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Câu 45. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Đợt xuất khẩu gạo của tỉnh A thường
kéo dài trong 2 tháng ( 60 ngày). Người ta nhận thấy số lượng xuất khẩu gạo tính theo ngày thứ t được xác 2
định bởi công thức S (t ) 3 2 =
t - 63t  3240t - 3100 với (1  t  60) . Hỏi trong 60 ngày đó thì ngày thứ mấy 5
có số lượng xuất khẩu gạo cao nhất. A. 60 B. 45 C. 30 D. 25
Câu 46. (GKI NHÂN CHÍNH HÀ NỘI NĂM 2018-2019 LẦN 01) Một vật chuyển động theo quy luật 1 2 3
S = 10t - t , với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và S (m) là quãng đường 3
vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 15 giây từ lúc vật bắt đầu chuyển động vận
tốc v (m / s) của vật đạt giá trị lớn nhất tại thời điểm t (s) bằng: A. 8(s) . B. 20 (s) C. 10 (s) . D. 15(s) .
Câu 47. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Một sợi dây có chiều dài 28m
được cắt thành hai đoạn để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo đơn vị mét) của
đoạn dây làm thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất? 56 112 84 92 A. . B. . C. . D. . 4   4   4   4  
Câu 48. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Một xưởng in có 15 máy in được cài đặt tự
động và giám sát bởi một kỹ sư, mỗi máy in có thể in được 30 ấn phẩm trong 1 giờ, chi phí cài đặt và bảo
dưỡng cho mỗi máy in cho 1 đợt hàng là 48.000 đồng, chi phí trả cho kỹ sư giám sát là 24.000 đồng/giờ.
Đợt hàng này xưởng in nhận 6000 ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là A. 10 máy. B. 11 máy. C. 12 máy. D. 9 máy.
Câu 49. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s (t ) 3 2
= t - 4t 12 (m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất
điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu? 8 4 A. 2 (s). B. (s). C. 0 (s). D. (s). 3 3
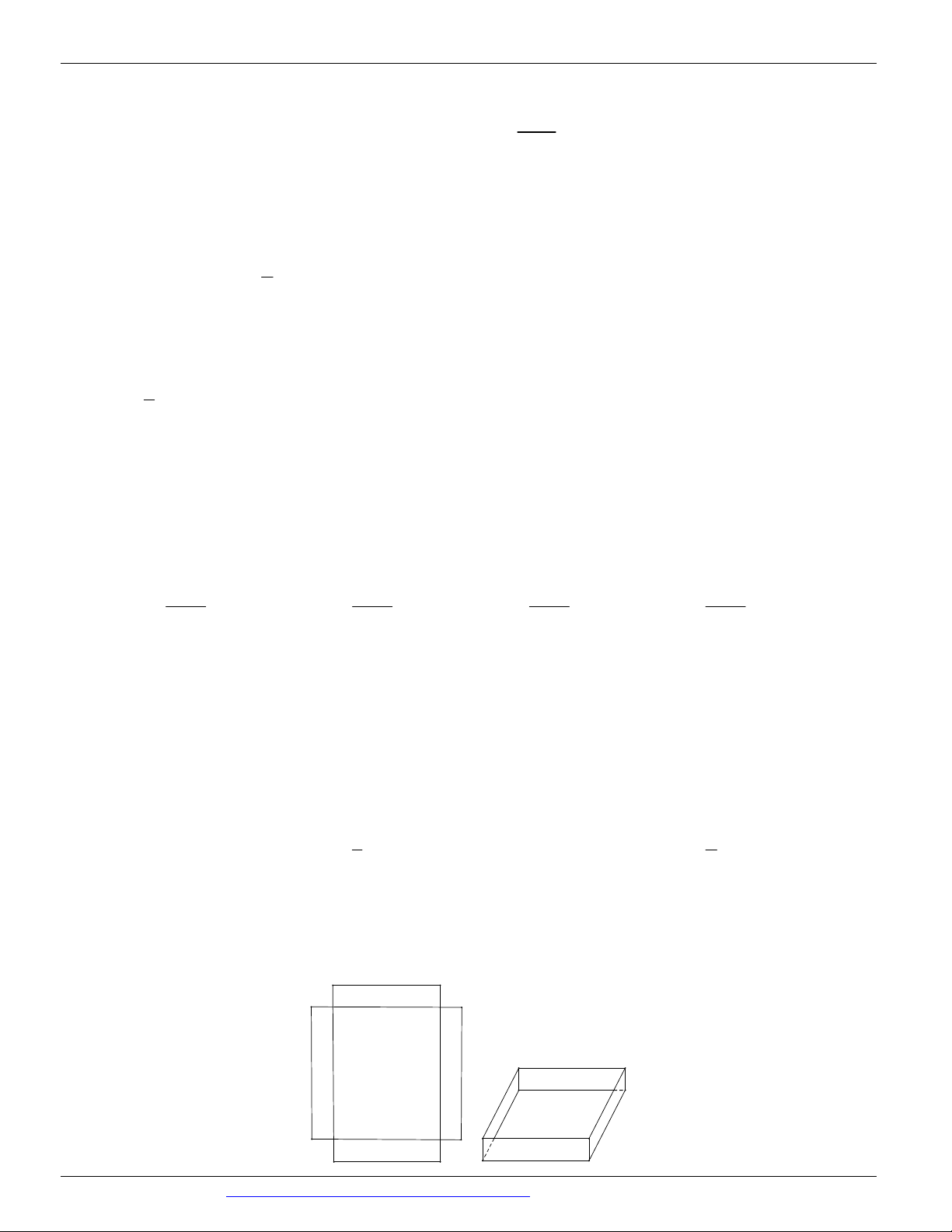
Câu 50. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho một tấm nhôm hình chữ nhật có chiều
dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng
nhau, mỗi hình vuông có cạnh bằng x (cm) , rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp không
nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
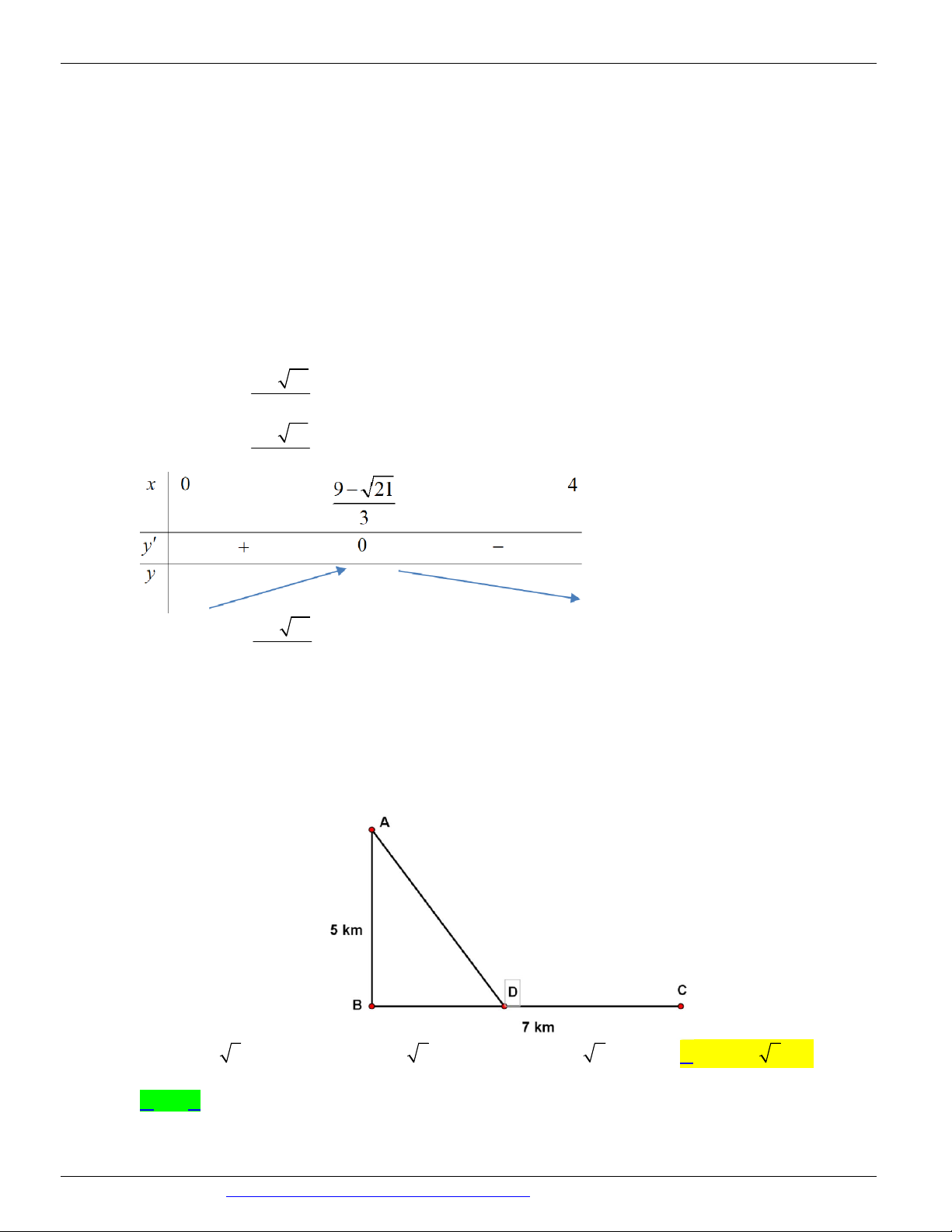
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 8 - 2 21 10 - 2 7 9  21 9 - 21 A. x = B. x = C. x = . D. x = 3 3 9 3
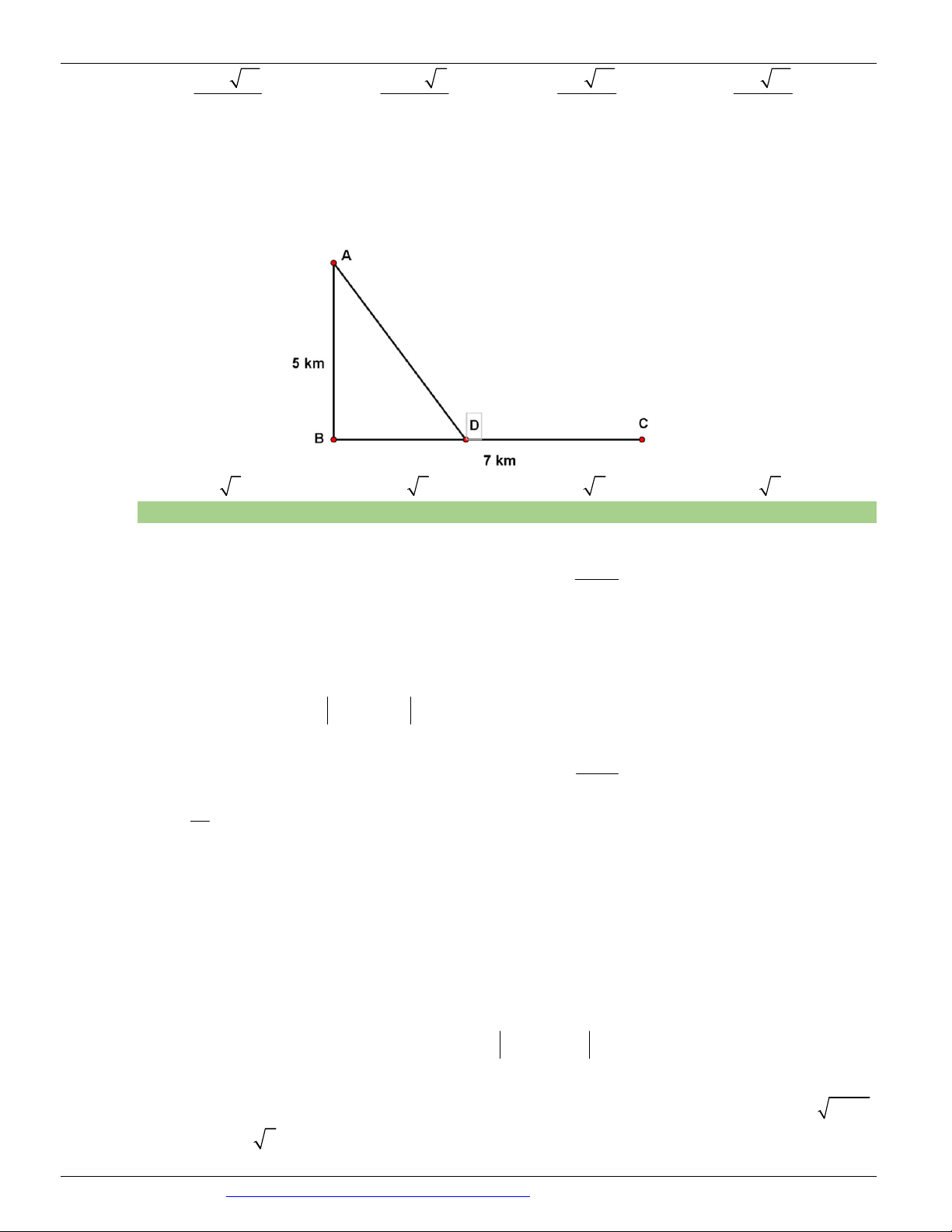
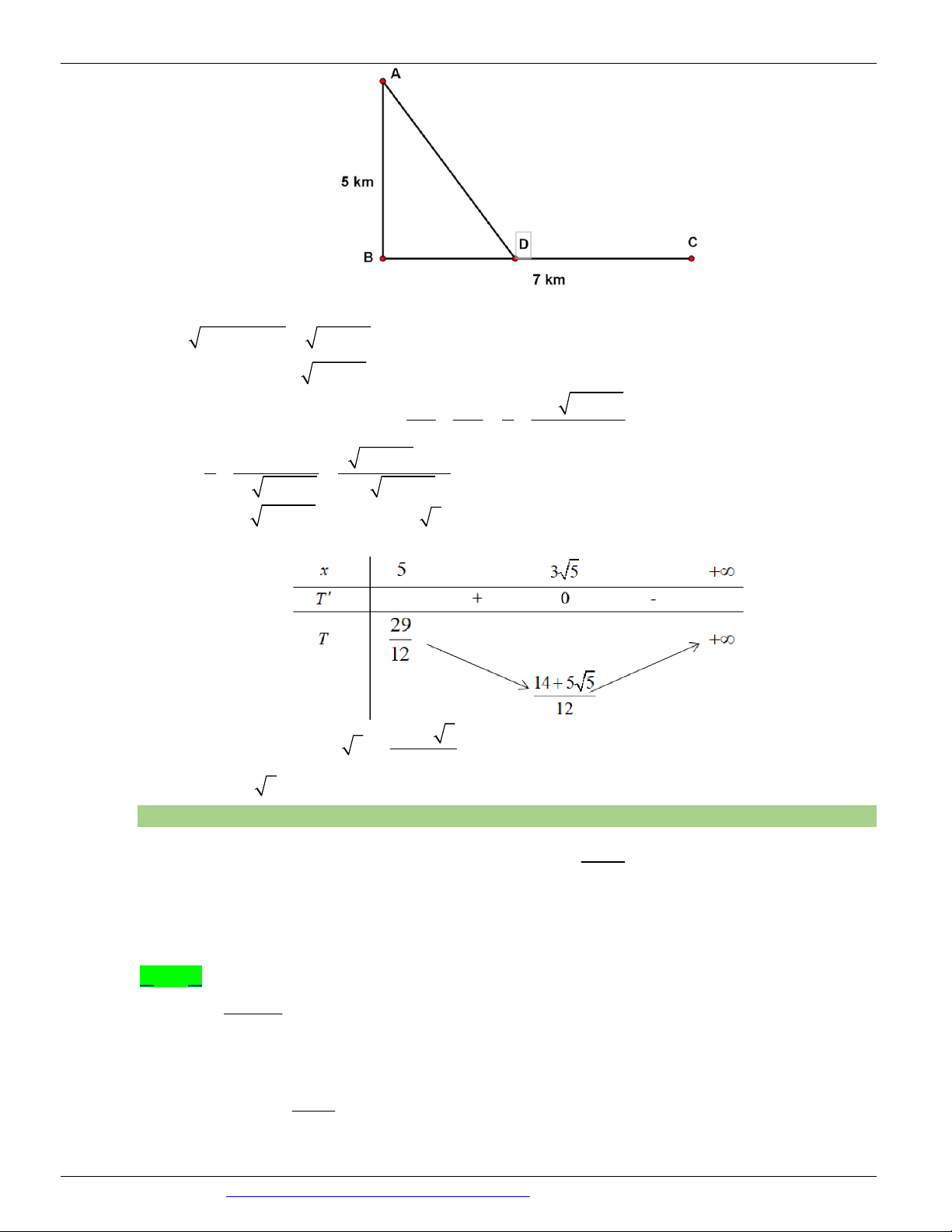
Câu 51. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Một đoàn cứu trợ lũ lụt đang ở vị trí A của
một tỉnh miền trung muốn đến xã C để tiếp tế lương thực và thuốc men. Để đi đến C , đoàn cứu trợ phải chèo
thuyền từ A đến vị trí D với vận tốc 4 (km / h) , rồi đi bộ đến vị trí C với vận tốc 6(km / h) . Biết A cách
B một khoảng 5km , B cách C một khoảng 7km (hình vẽ). Hỏi vị trí điểm D cách A bao xa để đoàn cứu
trợ đi đến xã C nhanh nhất?
A. AD = 5 3 km .
B. AD = 2 5 km .
C. AD = 5 2 km .
D. AD = 3 5 km .
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước x m
Câu 52. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y =
( m là tham số thực) thỏa mãn x - 1
min y = 3. Mệnh đề nào dưới đây đúng? [2;4]
A. m  4
B. 3  m  4
C. m  -1
D. 1  m  3
Câu 53. (ĐỀ THAM KHẢO BGD & ĐT 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao
cho giá trị lớn nhất của hàm số 3
y = x - 3x m trên đoạn 0; 
2 bằng 3. Số phần tử của S là A. 0 B. 6 C. 1 D. 2 x m
Câu 54. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y =
( m là tham số thực) thoả mãn x 1 16
min y  max y =
. Mệnh đề nào dưới đây đúng? 1;2 1;2 3
A. m  4
B. 2  m  4
C. m  0
D. 0  m  2
Câu 55. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Có một giá trị m của tham số m để 0 hàm số 3 y x  2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 5 trên đoạn 0; 
1 . Mệnh đề nào sau đây là đúng? A. 2
2018m m  0 . B. 2m 1   0 . 0 0 0 C. 2
6m m  0 .
D. 2m 1 0 . 0 0 0
Câu 56. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số m sao cho giá trị lớn nhất của hàm số 2
y = x - 2x m trên đoạn  1 - ; 2 bằng 5 . A. -1 . B. 2 . C. -2 . D. 1 .
Câu 57. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số 2
y = x m  1- x
có giá trị lớn nhất bằng 2 2 thì giá trị của m là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 A. . B. - 2 . C. 2 . D. - . 2 2 x m
Câu 58. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số y  ( m là tham số x  1
thực) thỏa mãn min y  3 . Mệnh đề nào dưới đây đúng? 0;1  
A. 1  m  3 B. m  6 C. m  1
D. 3  m  6
Câu 59. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số x m y
trên 1; 2 bằng 8 ( m là tham số thực). Khẳng định nào sau đây đúng? x 1 A. m  10 .
B. 8  m  10 .
C. 0  m  4 .
D. 4  m  8 .
Câu 60. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số 3 2
y = 2x - 3x - m . Trên  1 - 
;1 hàm số có giá trị nhỏ nhất là 1 - . Tính m ? A. m = 6 - . B. m = 3 - . C. m = 4 - . D. m = 5 - .
Câu 61. (THPT ĐÔNG SƠN THANH HÓA NĂM 2018-2019 LẦN 02) Tìm m để giá trị lớn nhất của hàm số 3
y = x - 3x  2m -1 trên đoạn 0; 2 là nhỏ nhất. Giá trị của m thuộc khoảng nào?  3   2  A. - ; -1   . B. ; 2   . C.  1 - ; 0 . D. (0 ) ;1 .  2   3 
Câu 62. (HỌC MÃI NĂM 2018-2019-LẦN 02) Biết S là tập giá trị của m để tổng giá trị lớn nhất và giá
trị nhỏ nhất của hàm số 4 2 3 2
y = x - m x - 2x - m trên đoạn 0; 
1 bằng -16 . Tính tích các phần tử của S . A. 2 . B. -2 . C. -15 . D. -17 .
Câu 63. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi ,
A B lần lượt là giá trị nhỏ nhất, giá trị lớn 2
x m m 13
nhất của hàm số y = trên đoạn 2; 
3 . Tìm tất cả các giá trị thực của tham số m để A B = . x -1 2
A. m = 1; m = -2 . B. m = -2 . C. m = 2 .
D. m = -1; m = 2 .
Câu 64. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số m 2 x mx 1 để hàm số y =
liên tục và đạt giá trị nhỏ nhất trên đoạn 0; 2 tại một điểm x  0; 2 . 0 ( ) x m
A. 0  m  1 B. m  1 C. m  2 D. 1 -  m  1
Câu 65. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị thực 2
x mx m
của tham số m sao cho giá trị lớn nhất của hàm số y =
trên 1;2 bằng 2 . Số phần tử của tập x 1 S A. 3 . B. 1. C. 4 . D. 2 .
Câu 66. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm m để giá trị nhỏ nhất của hàm số 2
x - m m f (x) =
trên đoạn (0;1) bằng –2 x 1 m = 1 m = 1 m = -1 1  21 A.B.C.  . D. m = . m = 2  m = -2 m = 2 2 .  . 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1- m sin x
Câu 67. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Cho hàm số y = . Có bao cos x  2
nhiêu giá trị nguyên của tham số m thuộc đoạn 0;10 để giá trị nhỏ nhất của hàm số nhỏ hơn -2 ? A. 1. B. 9 . C. 3 . D. 6 .
Câu 68. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Xét hàm số ( ) 2
f x = x ax b , với
a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên -1; 
3 . Khi M nhận giá trị nhỏ nhất có thể được,
tính a  2b . A. 2 . B. 4 . C. -4 . D. 3 .
Câu 69. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Cho hàm số 3
y = ax cx d, a  0
có min f ( x) = f (-2) . Giá trị lớn nhất của hàm số y = f ( x) trên đoạn 1;  3 bằng x (  -;0)
A. d -11a .
B. d -16a .
C. d  2a .
D. d  8a .
Câu 70. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi S là tập hợp các giá trị của tham số m 2
x - mx  2m
để giá trị lớn nhất của hàm số y = trên đoạn - 
1;1 bằng 3 . Tính tổng tất cả các phần tử của x - 2 S . 8 5 A. - . B. 5 . C. . D. 1 - . 3 3
Câu 71. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Tìm tất cả các giá trị của tham số m x m để hàm số y =
có giá trị lớn nhất trên  nhỏ hơn hoặc bằng 1. 2 x x 1 A. m  1. B. m  1. C. m  -1. D. m  1 - .
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm
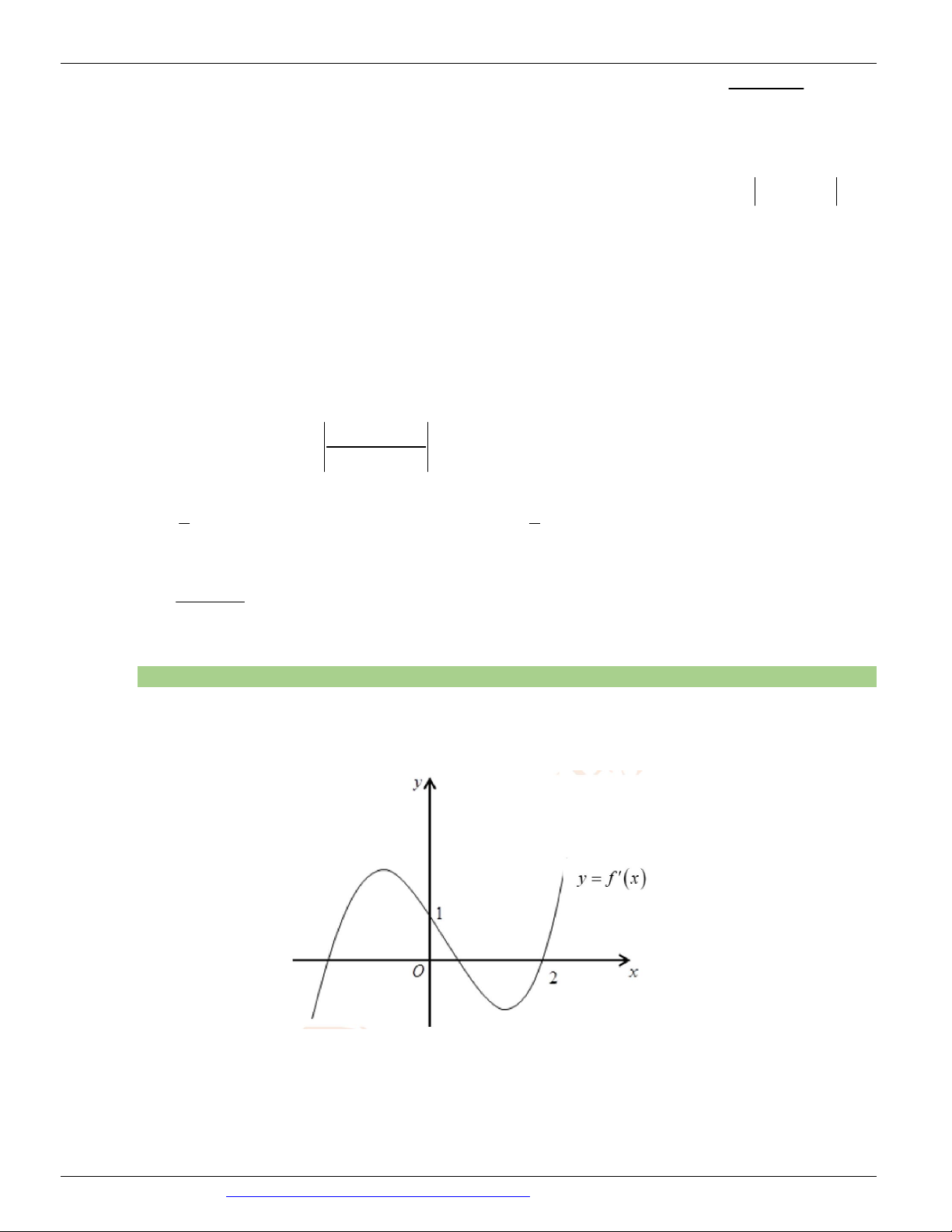
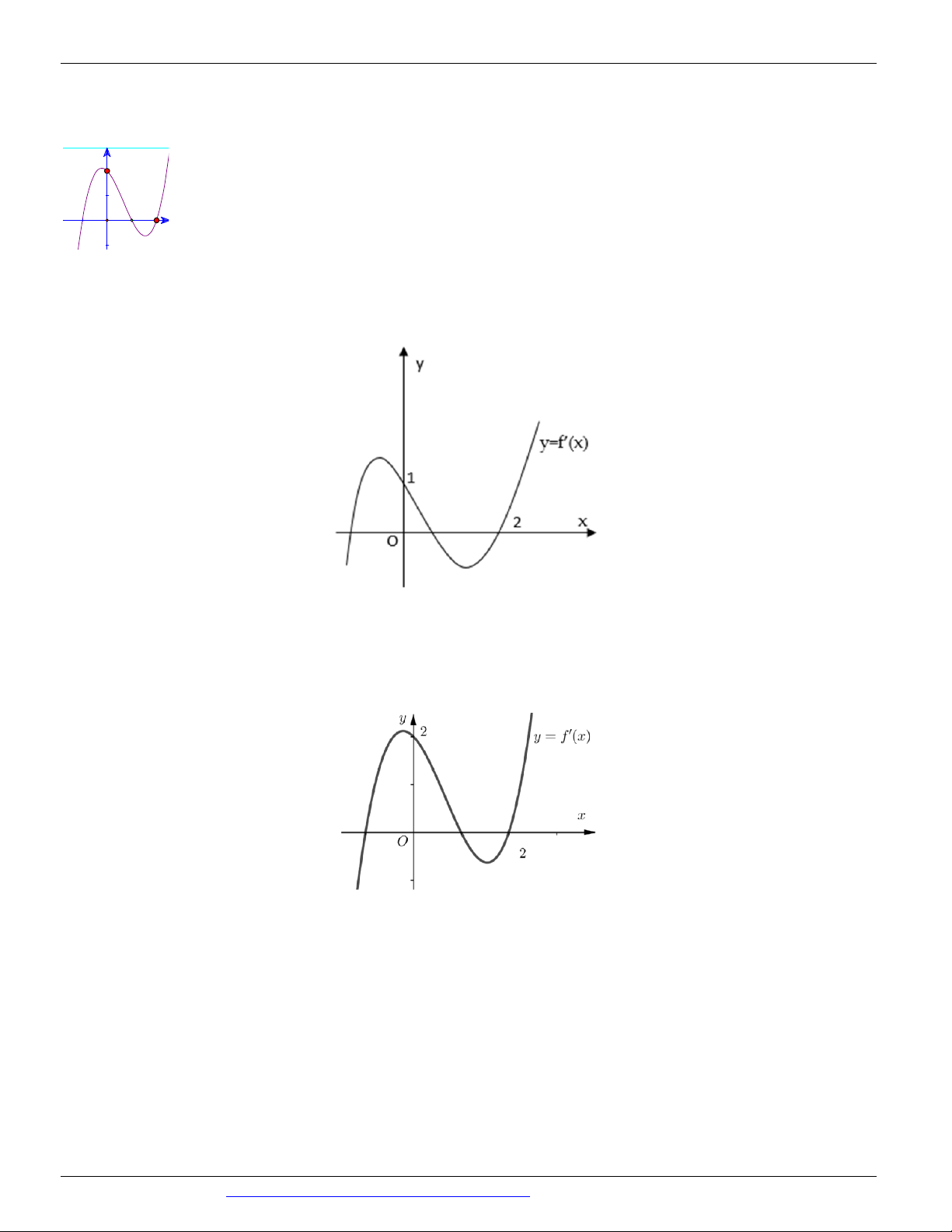
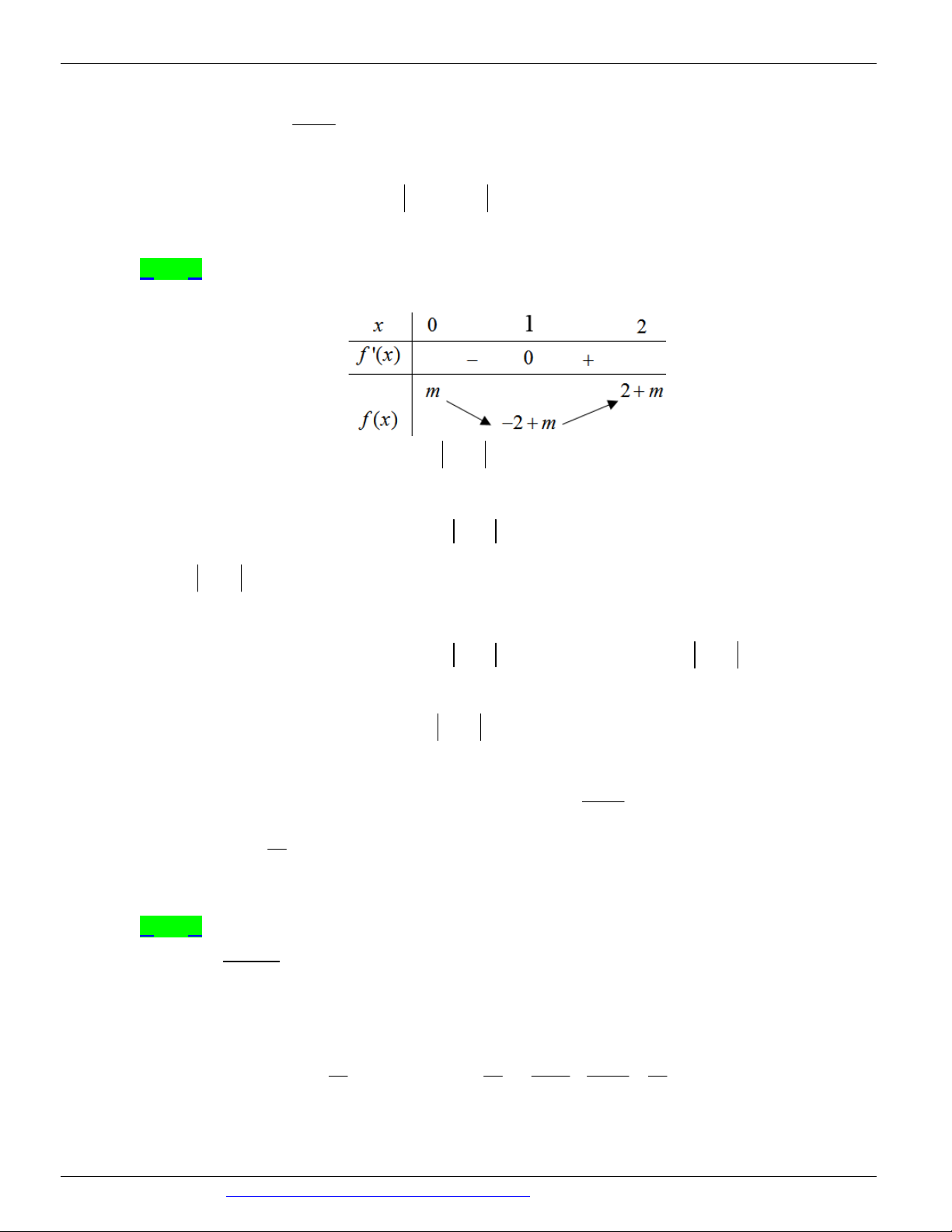
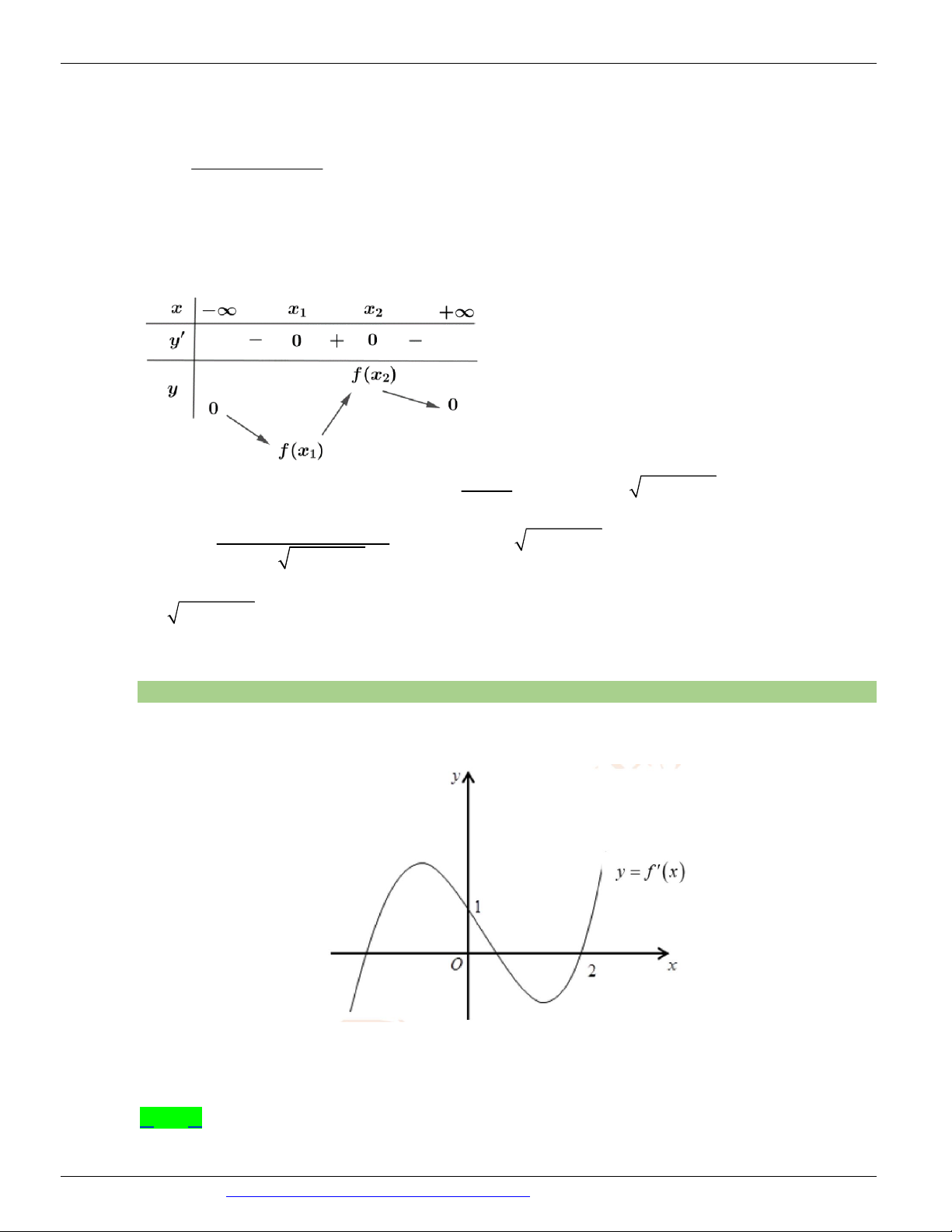
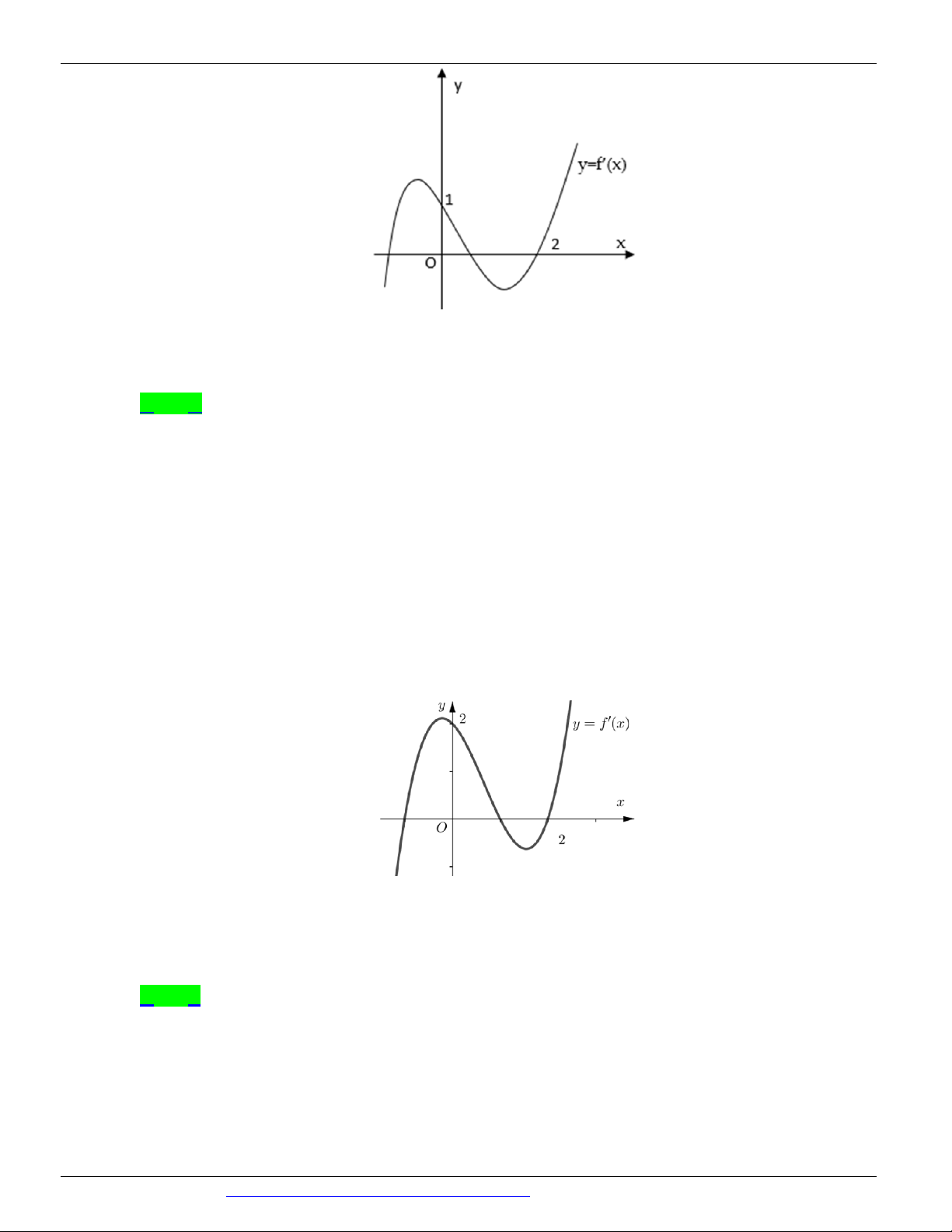
Câu 72. (Mã 102 - BGD - 2019) Cho hàm số f ( x) , hàm số y = f ¢( x) liên tục trên  và có đồ thị như hình vẽ.
Bất phương trình f ( x)  x m ( m là tham số thực) nghiệm đúng với mọi x (0; 2) khi và chỉ khi
A. m f (0) .
B. m f (0) .
C. m f (2) - 2 .
D. m f (2) - 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
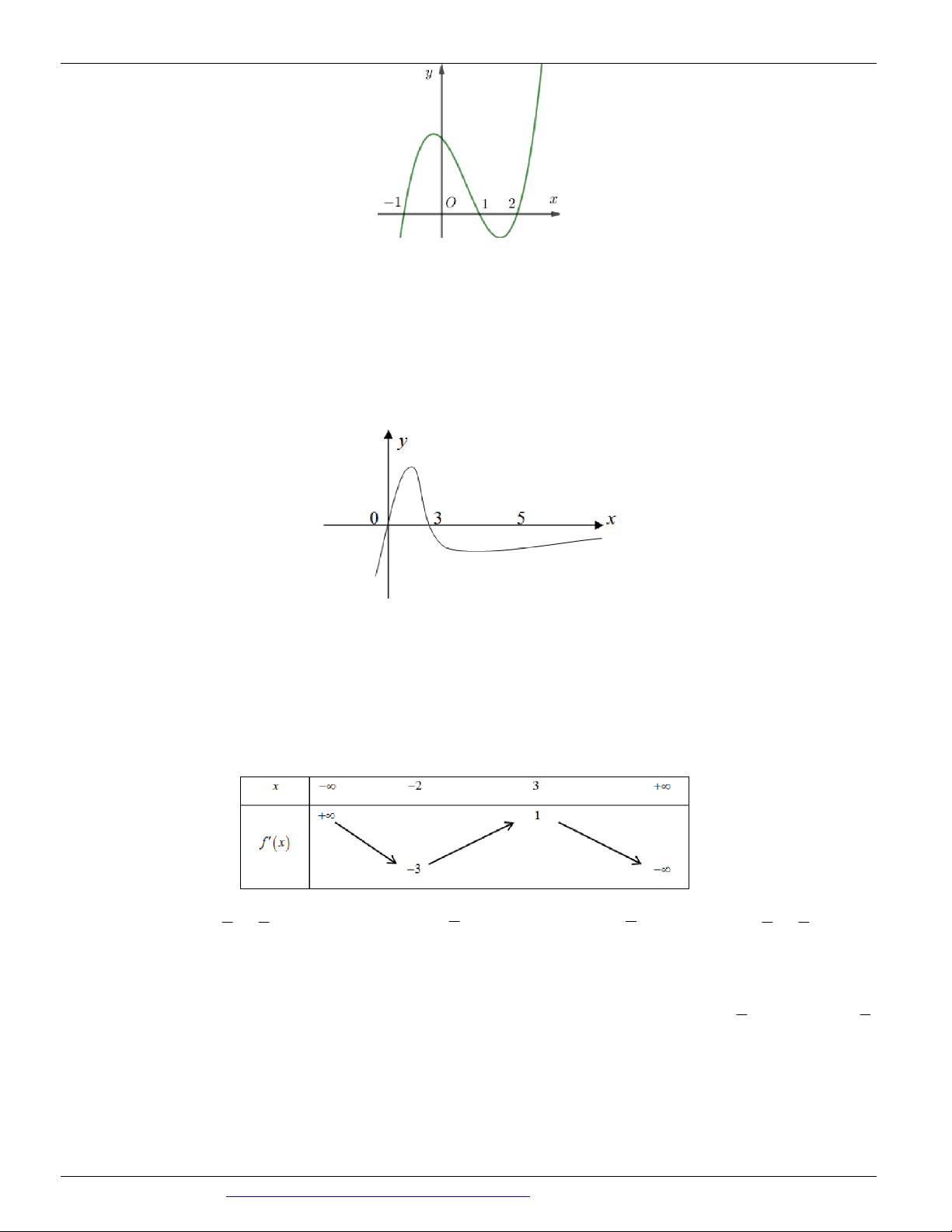
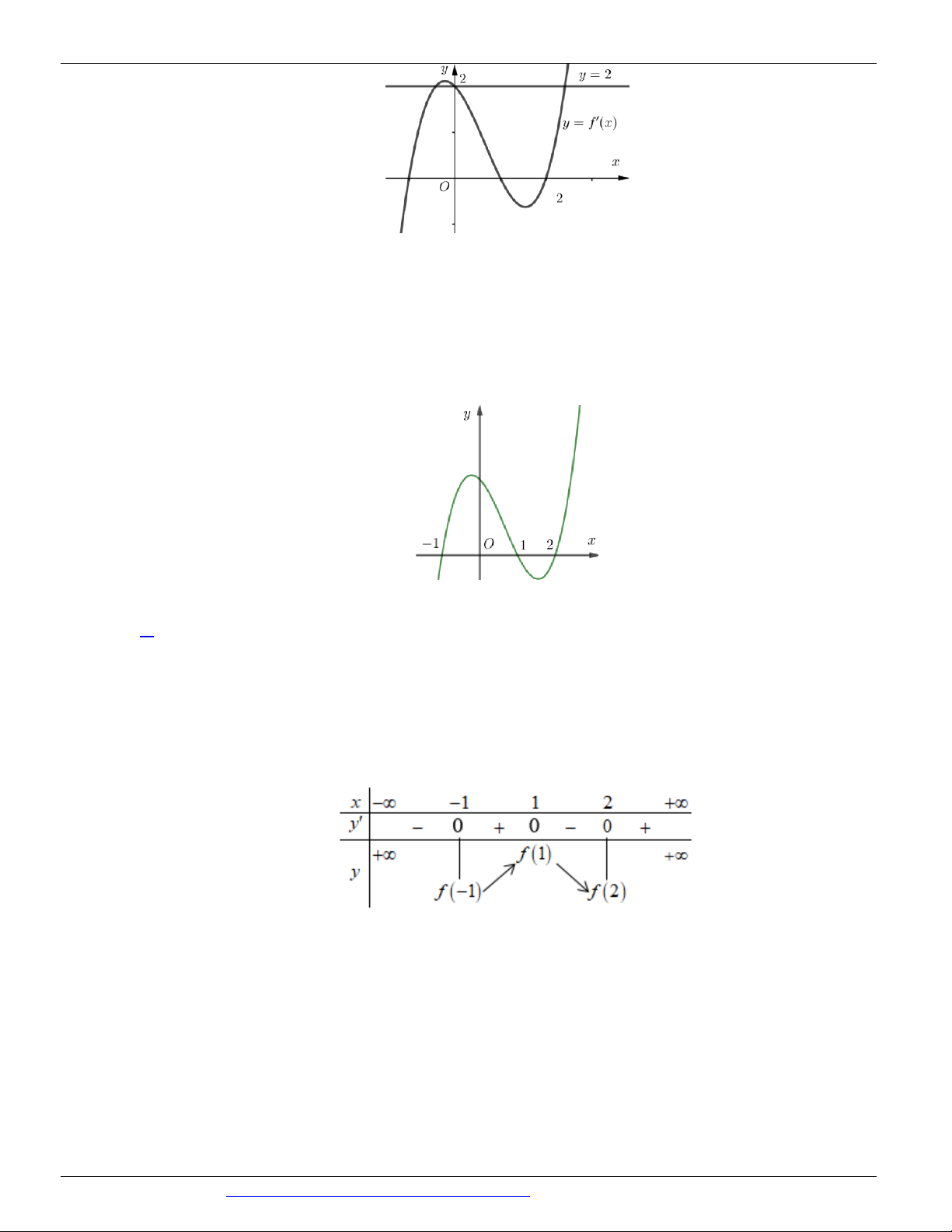
Câu 73. (Mã 103 - BGD - 2019) Cho hàm số y = f ( x) , hàm số y = f '( x) liên tục trên  và có đồ thị như
hình vẽ bên. Bất phương trình f ( x)  2x m (m là tham số thực) nghiệm đúng với mọi x  (0; 2) khi và chỉ khi y 2 2 1 x
A. m f (0) .
B. m f (2) - 4 .
C. m f (0) .
D. m f (2) - 4 .
Câu 74. (Mã đề 101 - BGD - 2019) Cho hàm số y = f ( x) , hàm số y = f '( x) liên tục trên  và có đồ thị như hình vẽ bên dưới
Bất phương trình f ( x)  x m ( m là tham số thực) nghiệm đúng với mọi x (0; 2) khi và chỉ khi
A. m f (2) - 2.
B. m f (0).
C. m f (2) - 2.
D. m f (0).
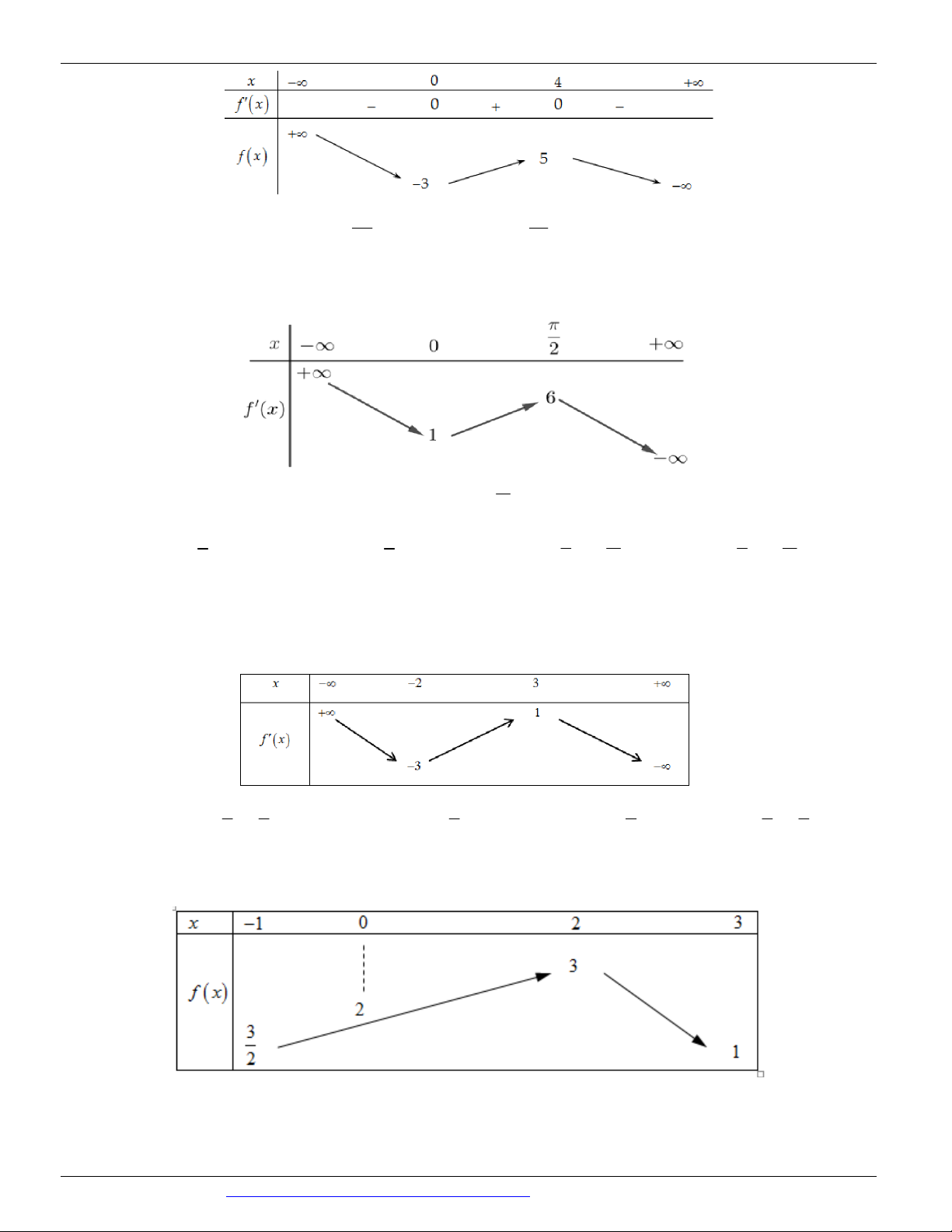
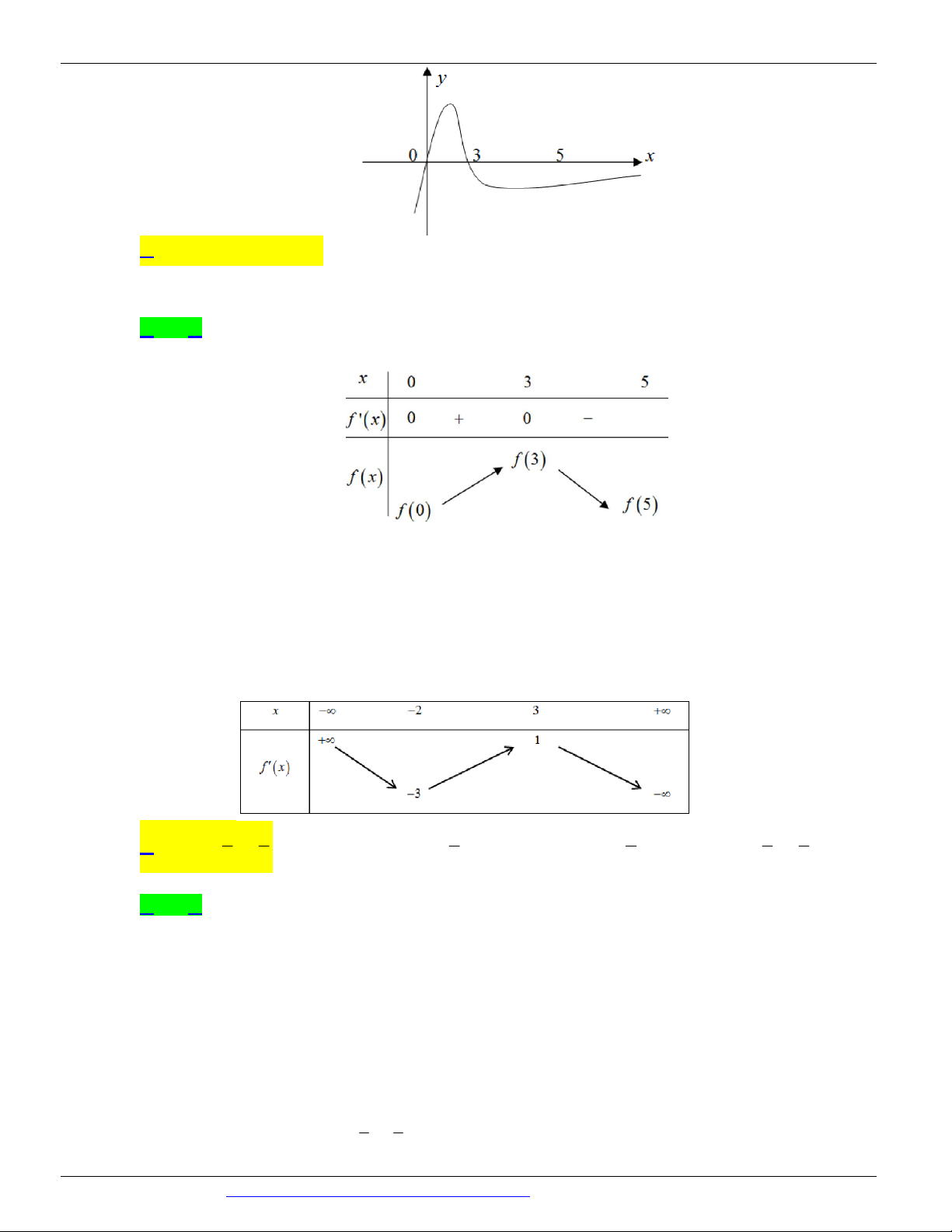
Câu 75. (Mã đề 104 - BGD - 2019) Cho hàm số f ( x) , hàm số f ¢( x) liên tục trên  và có đồ thị như hình vẽ.
Bất phương trình f ( x)  2x m ( m là tham số thực) nghiệm đúng với mọi x(0; 2) khi và chỉ khi
A. m f (2) - 4 .
B. m f (2) - 4 .
C. m f (0) .
D. m f (0) .
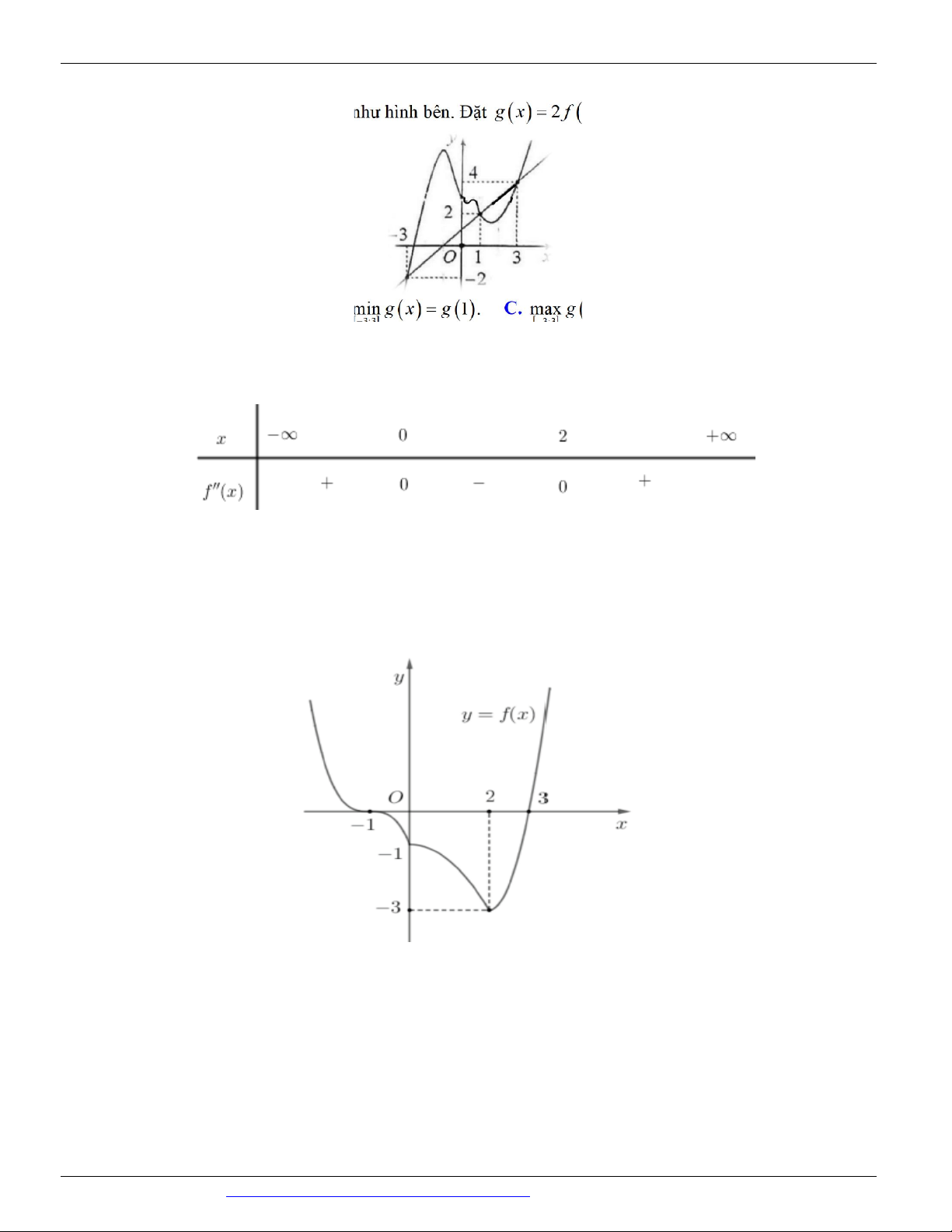
Câu 76. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) xác định
và liên tục trên  , đồ thị của hàm số y = f ¢( x) như hình vẽ.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Giá trị lớn nhất của hàm số y = f ( x) trên đoạn  1 - ; 2 là A. f ( ) 1 . B. f (- ) 1 . C. f (2) . D. f (0) .
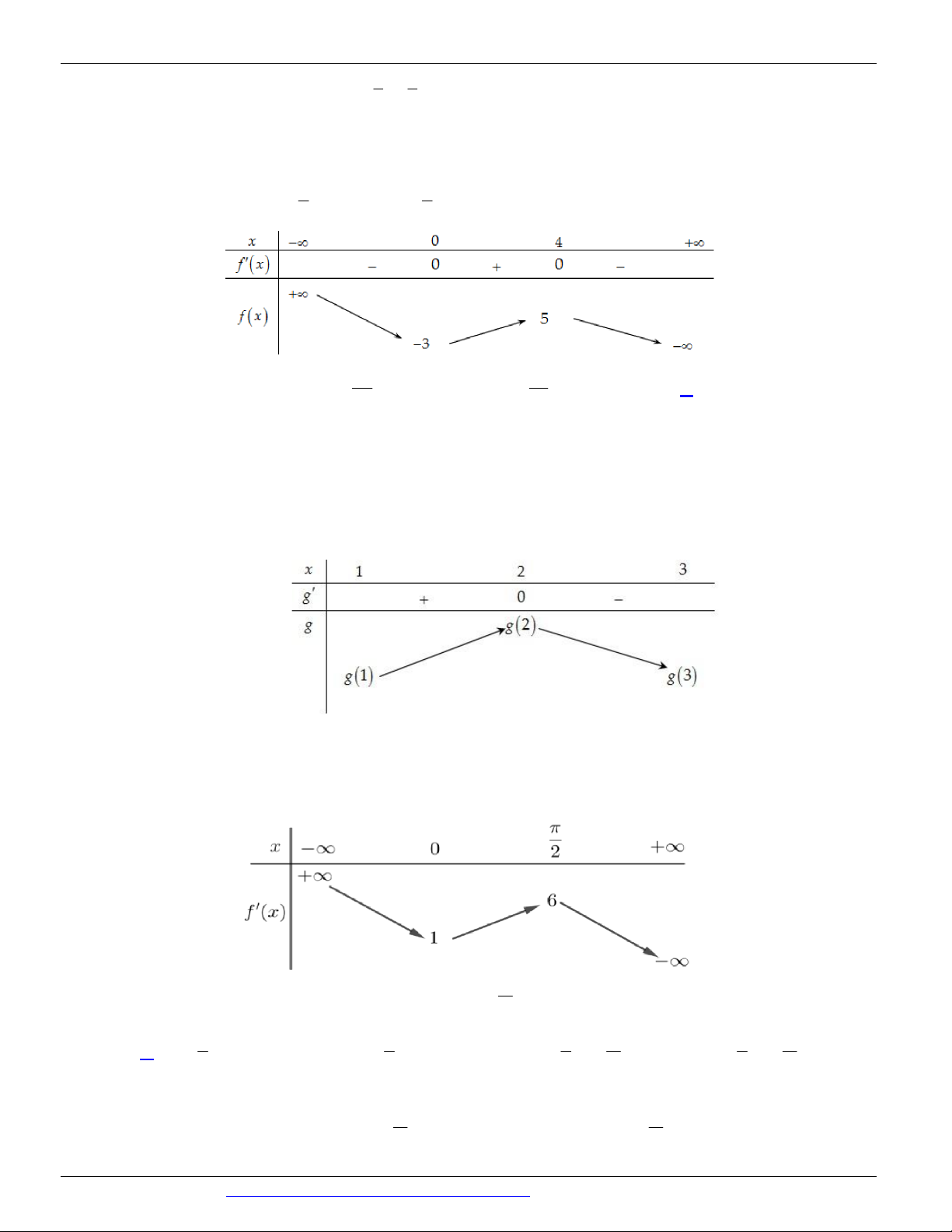
Câu 77. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số f ( x) có đạo hàm là
f ¢( x) . Đồ thị của hàm số
y = f ¢( x) được cho như hình vẽ bên. Biết rằng f (0)  f ( )
1 - 2 f (3) = f (5) - f (4) . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f ( x) trên đoạn 0;5 .
A. m = f (5), M = f (3) B. m = f (5), M = f ( ) 1
C. m = f (0), M = f (3) D. m = f ( ) 1 , M = f (3)
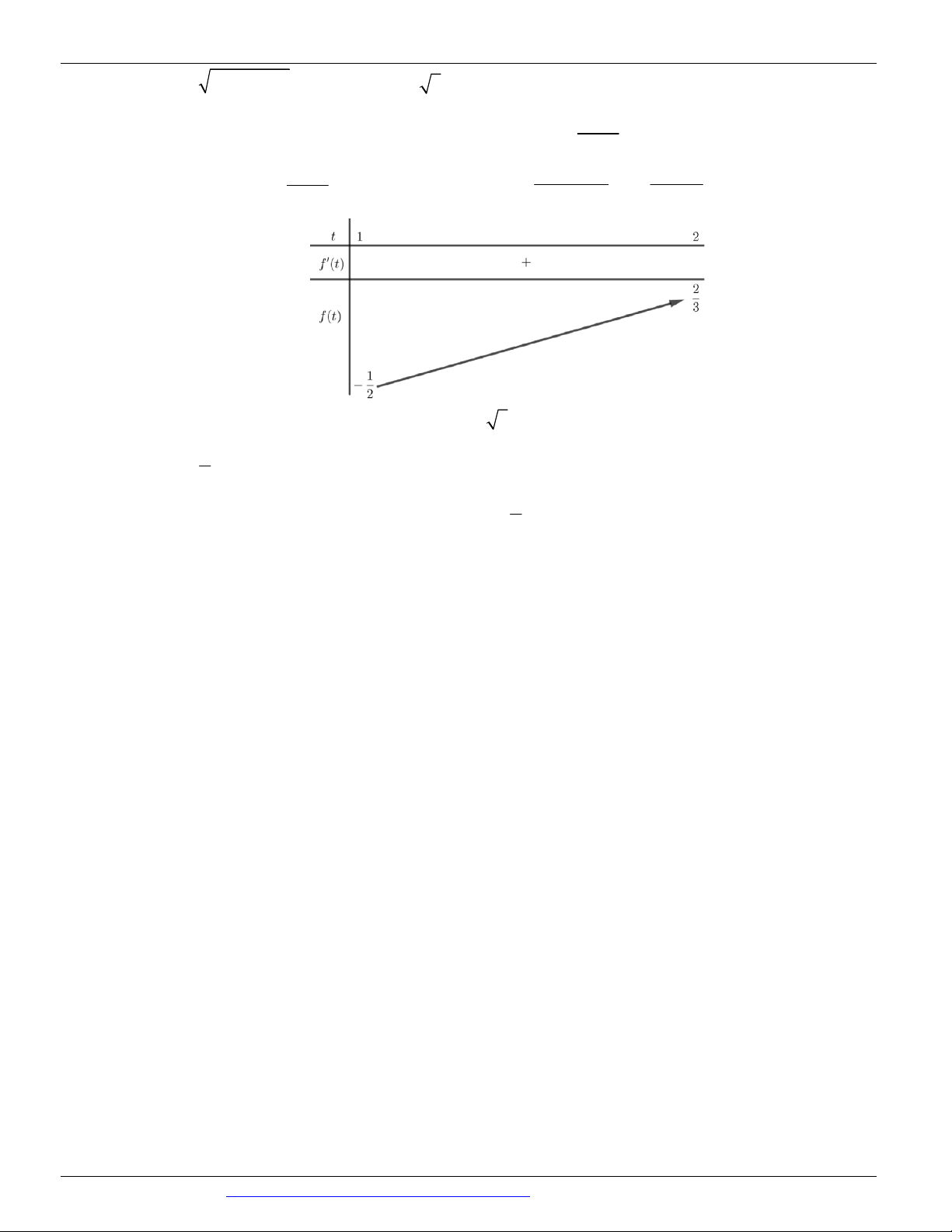
Câu 78. (ĐỀ 04 VTED NĂM 2018-2019) Cho hàm số y = f ( x) . Hàm số /
y = f (x) có bảng biến thiên như sau:
Bất phương trình ( x ) x f e
e m nghiệm đúng với mọi x ( 1 - ; ) 1 khi và chỉ khi  1  1 1 1  1  1
A. m f -  
B. m f (- ) 1 -
C. m f (- ) 1 -
D. m f -    e e e ee e
Câu 79. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số y = f ( x) có 1 1
bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số g ( x) = f ( 2 4x - x ) 3 2 
x - 3x  8x  3 3 trên đoạn 1;  3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 25 19 A. 15. B. . C. . D. 12. 3 3
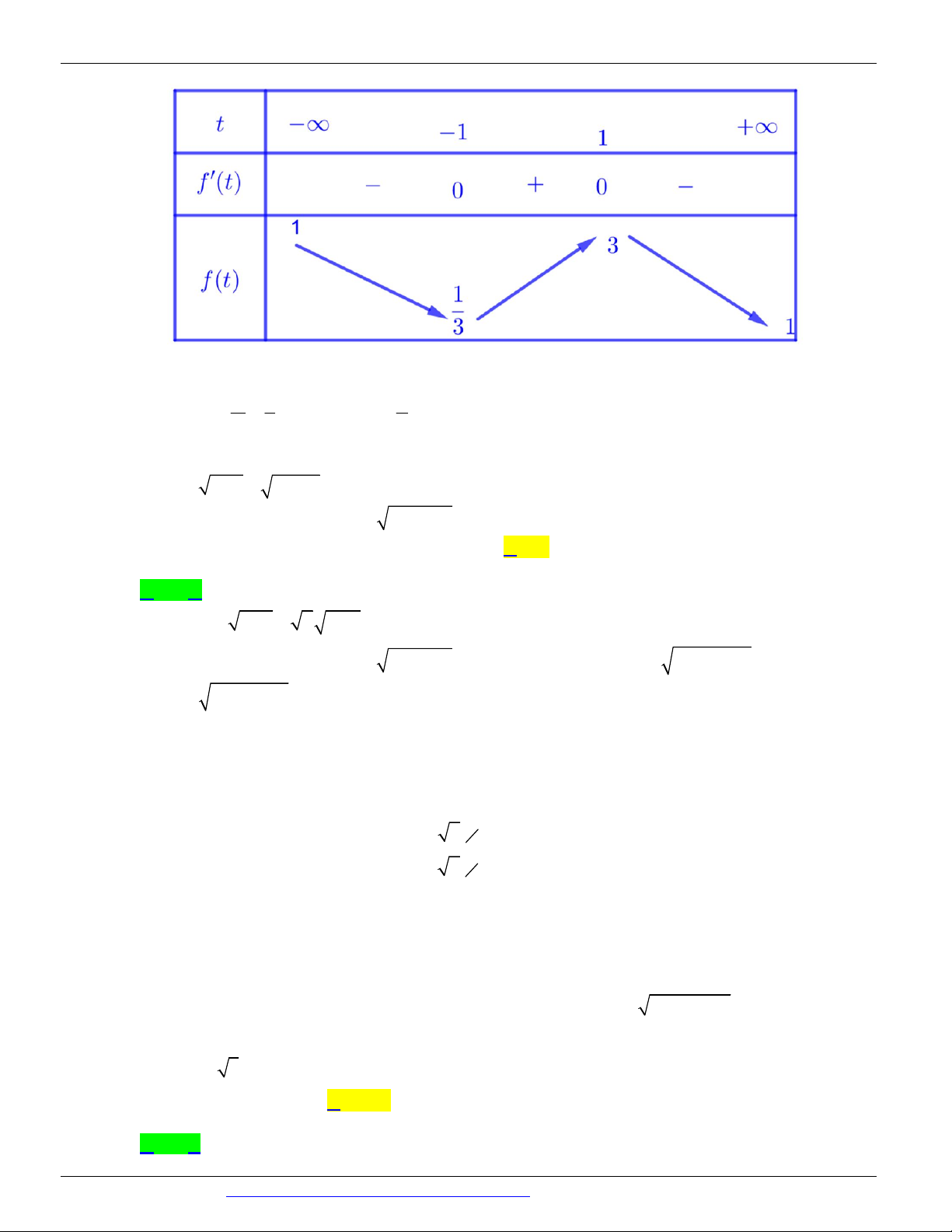
Câu 80. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Cho hàm số y = f ( x) . Hàm số y = f ¢( x) có bảng biến thiên như sau    Bất phương trình ( ) cos  2 x f x
 3m đúng với mọi x  0;   khi và chỉ khi  2  1 1 1      1      A. m   f (0) - 2 . B. m
f (0) - 2 . C. m f -1     . D. m f -1     . 3   3   3   2   3   2  
Câu 81. (Đề minh họa 2019) Cho hàm số y = f ( x) . Hàm số /
y = f (x) có bảng biến thiên như sau:
Bất phương trình ( x ) x f e
e m nghiệm đúng với mọi x ( 1 - ; ) 1 khi và chỉ khi  1  1 1 1  1  1
A. m f -  
B. m f (- ) 1 -
C. m f (- ) 1 -
D. m f -    e e e ee e
Câu 82. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số f ( x) có bảng biến thiên như sau:
Gọi S là tập hợp các số nguyên dương m để bất phương trình f ( x)  m( 3 2
x - 3x  5) có nghiệm thuộc đoạn -1; 
3 . Số phần tử của S là A. 3 B. Vô số C. 2 D. 0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 83. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) liên tục
trên . Đồ thị của hàm số y = f ¢ ( x) như hình bên. Đặt g ( x) = f ( x) - ( x  )2 2
1 . Mệnh đề dưới đây đúng.
A. max g ( x) = g (3).
B. min g ( x) = g ( )
1 . C. max g ( x) = g (0). D. max g ( x) = g ( ) 1 .  3; -  3  3; -  3 -3;  3  3; -  3
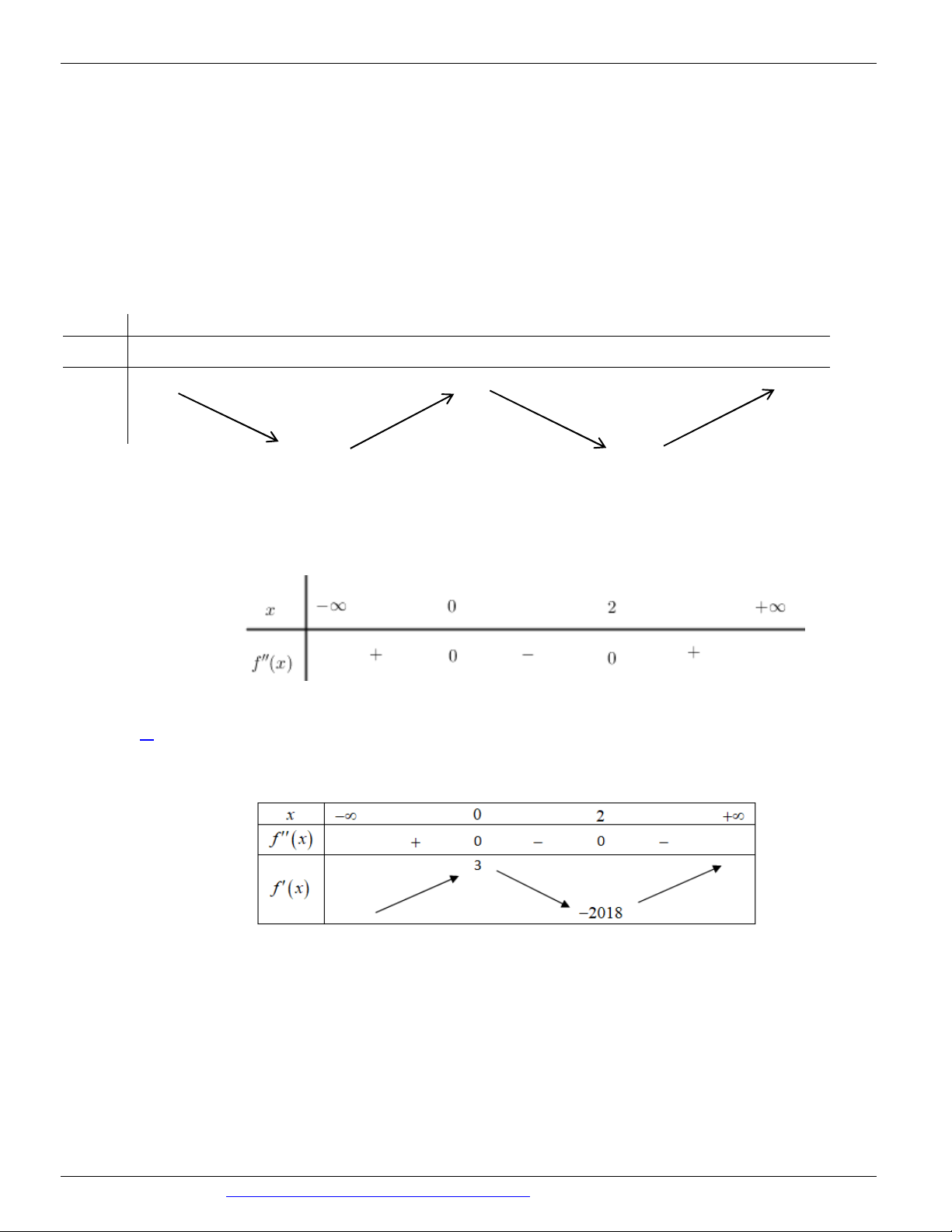
Câu 84. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho hàm số y = f ( x) có đạo hàm cấp
hai trên  . Biết f ¢(0) = 3 , f ¢(2) = 20 -
18 và bảng xét dấu của f ¢¢( x) như sau:
Hàm số y = f ( x  2017)  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A. ( ; - - 2017) B. (2017; ) C. (0; 2) D. ( 201 - 7;0)
Câu 85. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số f ( x) liên tục trên và có đồ
thị như hình vẽ bên. Bất phương trình f ( x) 3 2 2
x  2m  3x nghiệm đúng với mọi x  ( 1 - ;3) khi và chỉ khi A. m  10. - B. m  5. - C. m  3. - D. m  2. -
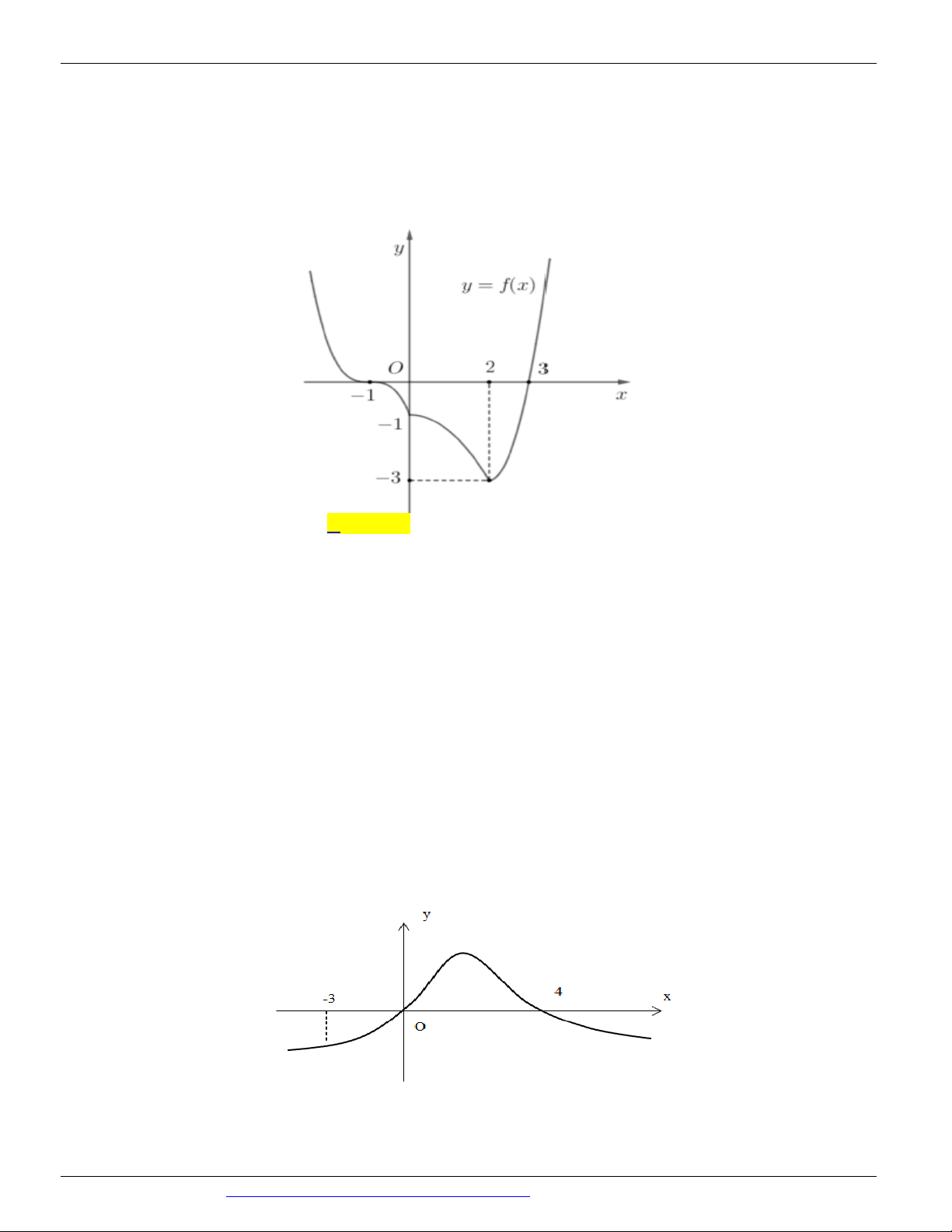
Câu 86. (KTNL GV BẮC GIANG NĂM 2018-2019) Cho hàm số f ( x) có đạo hàm trên  và có đồ thị
của hàm y = f ¢ ( x) được cho như hình vẽ.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Biết rằng f ( 3
- )  f (0) = f (4)  f (- )
1 . Giá trị lớn nhất và giá trị nhỏ nhất của f ( x) trên đoạn -3; 4 lần lượt là:
A. f (4) và f (-3) .
B. f (-3) và f (0) .
C. f (4) và f (0) .
D. f (2) và f (-3) .
Câu 87. Cho hàm số f ( x) có đạo hàm là f ¢( x) . Đồ thị của hàm số y = f ¢( x) được cho như hình vẽ dưới đây: Biết rằng f (- )
1  f (0)  f ( )
1  f (2) . Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f ( x) trên đoạn -1;2 lần lượt là: A. f ( ) 1 ; f (2) .
B. f (2) ; f (0) .
C. f (0) ; f (2) . D. f ( ) 1 ; f (- ) 1 .
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số
Câu 88. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số m để
bất phương trình x  (  x)( - x) 2 6 2 8
x m -1 nghiệm đúng với mọi x  2 - ;8.
A. m  16
B. m  15
C. m  8 D. 2 -  m  16
Câu 89. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm m để bất phương trình 4 x
m có nghiệm trên khoảng ( ; - ) 1 . x -1
A. m  5 . B. m  3 - .
C. m  1 . D. m  1 -
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Biết rằng tập nghiệm của 6x - 4
bất phương trình 2x  4 - 2 2 - x
là a;b . Khi đó giá trị của biểu thức P = 3a - 2b bằng: 2 5 x 1 A. 2 B. 4 C. -2 D. 1
Câu 91. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi s là tập hợp các giá trị
nguyên của tham số m 0; 2019 để bất phương trình
x - m  ( - x )3 2 2 1
 0 đúng với mọi x -1; 
1 . Số phần tử của tập s bằng A. 1. B. 2020 . C. 2019 . D. 2 .
Câu 92. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi M là giá trị lớn nhất của hàm số f ( x) 2 2
= 4 x - 4x  6  4x - x 1. Tính tích các nghiệm của phương trình f ( x) = M . A. 2 . B. 4 . C. -2 . D. -4 . 2 2
Câu 93. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho x - xy y = 2 . Giá trị nhỏ nhất 2 2
của P = x xy y bằng: 2 1 1 A. B. C. D. 2 3 6 2
Câu 94. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho x , y là các số thực thỏa mãn x y =
x -1  2 y  2 . Gọi M ,
m lần lượt là giá trị lớn nhất và nhỏ nhất của 2 2
P = x y  2( x  ) 1 ( y  )
1  8 4 - x - y . Tính giá trị M m A. 42 B. 41 C. 43 D. 44
Câu 95. (KTNL GIA BÌNH NĂM 2018-2019) Cho bất phương trình m ( 2
x - 2x  2  1)  x (2 - x)  0 .
Hỏi có bao nhiêu số nguyên m không nhỏ hơn 2018 -
để bất phương trình đã cho có nghiệm x  0;1 3   ? A. 2018 B. 2019 C. 2017 D. 2020
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị của nó Câu 1.
(ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y = f ( x) liên tục trên đoạn
-1;3 và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm
số đã cho trên đoạn -1;3 . Giá trị của M - m bằng A. 1 B. 4 C. 5 D. 0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn C
Dựa và đồ thị suy ra M = f (3) = 3; m = f (2) = -2
Vậy M - m = 5 Câu 2.
(ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số
y = f ( x) liên tục trên đoạn  1 - 
;1 và có đồ thị như hình vẽ.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 -  ;1 . Giá trị
của M - m bằng A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Từ đồ thị ta thấy M = 1, m = 0 nên M - m = 1 . Câu 3.
(CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x)
xác định và liên tục trên  có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất
M của hàm số y = f ( x) trên đoạn -2; 2 . A. m = 5 - ; M = 1 - . B. m = 2 - ; M = 2 . C. m = 1 - ; M = 0 . D. m = 5 - ; M = 0 . Lời giải
Nhìn vào đồ thị ta thấy:
M = max f ( x) = 1 - khi x = 1 - hoặc x = 2 .  2 - ;2
m = min f ( x) = 5 - khi x = 2
- hoặc x = 1 .  2 - ;2 Câu 4.
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số y = f ( x) xác định, liên tục trên  và có bảng biến thiên:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng 1 .
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1 .
C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 .
D. Hàm số có đúng một cực trị. Lời giải Chọn C
Đáp án A sai vì hàm số có 2 điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu y = -1 khi x = 0 .
Đáp án C sai vì hàm số không có GTLN và GTNN trên  .
Đáp án D đúng vì hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 . Câu 5.
(THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Cho hàm số y = f ( x) liên tục
trên -3; 2 và có bảng biến thiên như sau. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số y = f ( x) trên đoạn -1; 2. Tính M m . A. 3 . B. 2 . C. 1. D. 4 . Lời giải Trên đoạn  1
- ; 2 ta có giá trị lớn nhất M = 3 khi x = 1
- và giá trị nhỏ nhất m = 0 khi x = 0 .
Khi đó M m = 3  0 = 3. Câu 6.
(THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét hàm số y = f (x) với x  1 - ;  5 có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn  1 - ;5
B. Hàm số đã cho đạt GTNN tại x = 1
- và x = 2 trên đoạn  1 - ;5
C. Hàm số đã cho đạt GTNN tại x = 1
- và đạt GTLN tại x = 5 trên đoạn  1 - ;5
D. Hàm số đã cho đạt GTNN tại x = 0 trên đoạn  1 - ;5 Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. Đúng. Vì lim y =  nên hàm số không có GTLN trên đoạn  1 - ;5 . x 5- 
B. Sai. Hàm số đã cho chỉ đạt GTNN tại x = 2 trên đoạn  1 - ;5 .
C. Sai. Hàm số đã cho chỉ đạt GTNN tại x = 2 trên đoạn 1
- ;5 và lim y =  . x5
D. Sai. Hàm số đã cho chỉ đạt GTNN tại x = 2 trên đoạn 1 - ;5 . Câu 7.
(CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) liên tục trên
 , có bảng biến thiên như hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3 .
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng (-; - ) 1 , (2;  ) . Lời giải
Dựa vào BBT ta thấy hàm số không có GTLN, GTNN. Câu 8.
(THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x)
liên tục trên  và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng? x – ∞ -2 0 2 + ∞ y' + 0 – 0 + 0 – 4 4 y – ∞ 0 – ∞
A. Phương trình f ( x) = 0 có 4 nghiệm phân biệt
B. Hàm số đồng biến trên khoảng (0; )
C. Giá trị nhỏ nhất của hàm số bằng 0
D. Hàm số có 3 điểm cực trị Lời giải Chọn D
Dựa vào bảng biến thiên, hàm số có 3 điểm cực trị. Câu 9.
(CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số
y = f (x) liên tục và có bảng biến thiên trên đoạn -1;3 như hình vẽ bên. Khẳng định nào sau đây đúng?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. max f (x) = f (0) .
B. max f ( x) = f ( ) 3 .  1 - ;  3  1 -  ;3
C. max f ( x) = f (2) .
D. max f ( x) = f (- ) 1 .  1 -  ;3  1 -  ;3 Lời giải
Nhìn vào bảng biến thiên ta thấy max f ( x) = f (0).  1 -  ;3
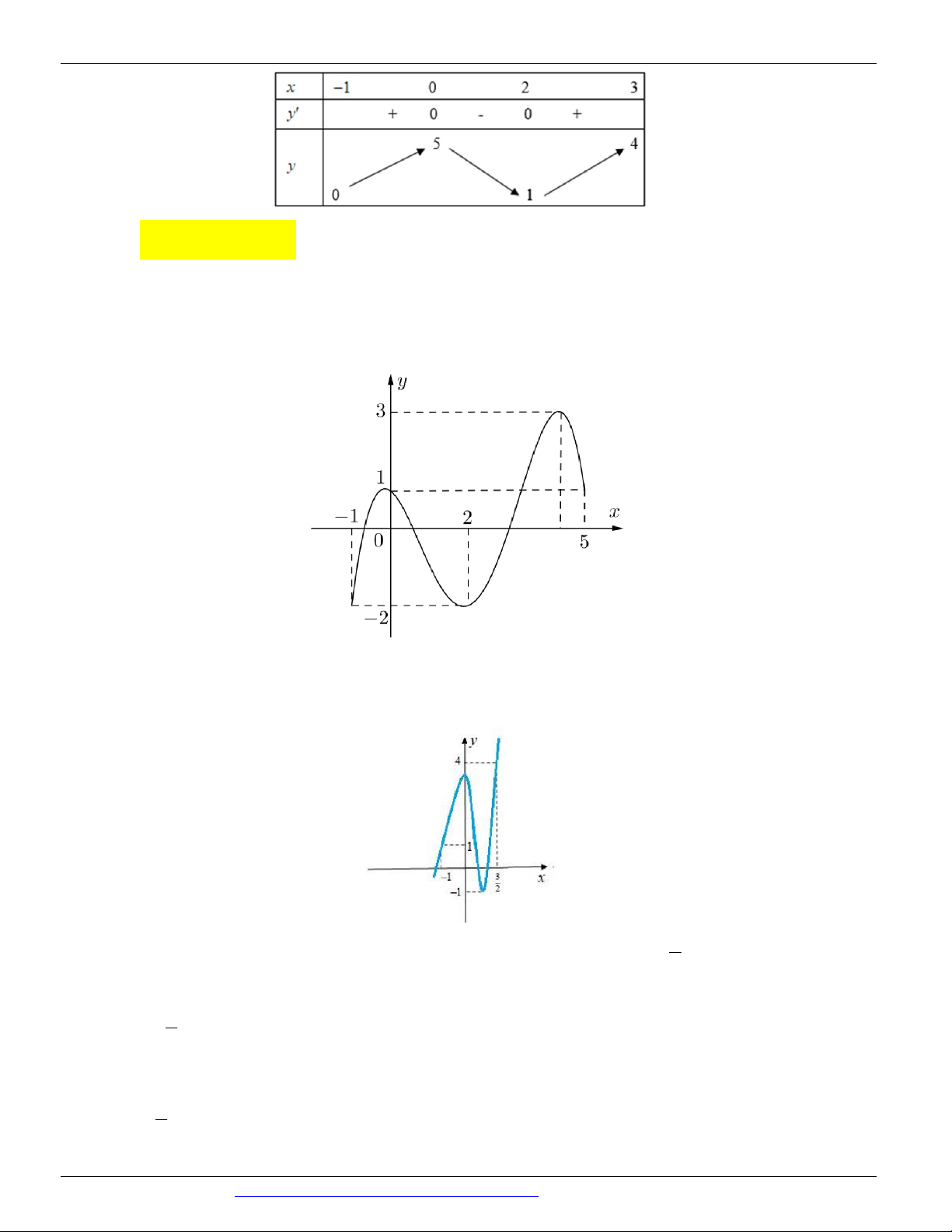
Câu 10. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số f ( x) liên tục trên  1 - ;5 và
có đồ thị trên đoạn  1
- ;5 như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm
số f ( x) trên đoạn  1 - ;5 bằng A. -1 B. 4 C. 1 D. 2 Lời giải
M = max f ( x) = 3   1 -  ;5
Từ đồ thị ta thấy: 
M n = 1. n = min f  ( x) = -2  1 - ;  5 
Câu 11. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Cho hàm số f ( x) liên tục trên  và có đồ thị như hình vẽ sau:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  3 
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số f ( x) trên 1 - ; . Giá trị của  2    M m bằng 1 A. . B. 5 . C. 4 . D. 3 . 2 Lời giải
Dựa vào đồ thị hàm số f ( x) ta có: M = max f ( x) = 4 ; m = min f ( x) = 1 - .  3   3  1 - ;  1 - ; 2       2 
Do đó M m = 4  (- ) 1 = 3 .
Câu 12. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) xác định, liên  5  tục trên -1, 
và có đồ thị là đường cong như hình vẽ. 2     5 
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f ( x) trên -1,  là: 2    7 7
A. M = 4, m =1
B. M = 4,m = -1 C. M = , m = 1 - D. M = , m = 1 2 2 Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào đồ thị M = 4, m = -1.
Câu 13. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số y = f ( x) có đồ thị
như hình vẽ. Giá trị lớn nhất của hàm số f ( x) trên đoạn 0; 2 là:
A. Max f ( x) = 2 .
B. Max f ( x) = 2 . 0;  2 0;2
C. Max f ( x) = 4 .
D. Max f ( x) = 0 . 0;  2 0;  2 Lời giải Chọn C
Dựa vào đồ thị ta thấy trên đoạn 0; 2 hàm số f ( x) có giá trị lớn nhất bằng 4 khi x = 2
Suy ra Max f ( x) = 4 0;  2
Câu 14. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số y = f (x) liên tục trên đoạn -1; 
3 và có đồ thị như hình vẽ bên. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số đã cho trên đoạn -1; 
3 . Giá trị của M m là A. 2 B. 6 - C. 5 - D. -2 Lời giải
Dựa vào đồ thị ta thấy GTLN của hàm số trên đoạn -1; 
3 là M = 2 đạt được tại x = 1 - và GTNN
của hàm số số trên đoạn -1;  3 là m = 4
- đạt được tại x = 2
M m = 2  (-4) = -2
Câu 15. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số y = f ( x) có bảng biến thiên trên -5;7) như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Mệnh đề nào dưới đây đúng?
A. Min f ( x) = 6 .
B. Min f ( x) = 2 .
C. Max f ( x) = 9 .
D. Max f ( x) = 6 .  5; - 7)  5; - 7) -5;7)  5 - ;7) Lời giải
Dựa vào bảng biến thiên trên -5;7) , ta có: Min f ( x) = f ( ) 1 = 2 .  5;7 - )
Câu 16. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hàm số f ( x ) liên tục trên
đoạn 0;3 và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của
hàm số đã cho trên 0;3 . Giá trị của M m bằng? A. 5 . B. 3 . C. 2 . D. 1. Lời giải
Dựa vào hình vẽ ta có: M = 3 , m = 2
- nên M m = 1.
Câu 17. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số y = f ( x) liên
tục trên đoạn 2 ; 6 và có đồ thị như hình vẽ bên dưới. y 5 -2 -1 O 1 3 4 6 x -1 y = f(x) -3 -4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 2 ; 6. Giá trị
của M m bằng A. 9 . B. 8 - . C. 9 - . D. 8 . Lời giải Từ đồ thị suy ra 4
-  f ( x)  5 x   2 - ;6; f ( ) 1 = 4 - ; f (4) = 5 M = 5  
M - m = 9 . m = -4 
Câu 18. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Cho hàm số y = f ( x) liên tục và có đồ thị
trên đoạn -2; 4 như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f ( x) trên đoạn  2 - ; 4 bằng A. 5 B. 3 C. 0 D. -2 Lời giải Chọn B
Dựa vào đồ thị hàm số ta có
m = Min f ( x) = -4 , M = Max f ( x) = 7 x   2 - ; 4 x   -2; 4
Khi đó M m = 3
Câu 19. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) có bảng
xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng
A. max f ( x) = f (0)
B. max f ( x) = f ( ) 1
C. min f ( x) = f (- )
1 D. min f ( x) = f (0) ( 1 - ;  1 (0;) (- ;  - ) 1 ( 1 - ; ) Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn [a;b]
Câu 20. (Mã 102 - BGD - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x - 3x  2 trên đoạn  3 - ;  3 bằng A. 0 . B. 16 - . C. 20 . D. 4 . Lời giải Chọn B
Cách 1:Mode 7 f ( x) 3
= x - 3x  2 . Start -3 end3step 1  Chọn B
Cách 2: f ¢( x) 2
= 3x - 3. f ¢( x) = 0 Û x = 1   3 - ;  3 . f (- ) 3 = 1 - 6 ; f (- ) 1 = 4 ; f ( ) 1 = 0 ; f (3) = 20 .
 Giá trị nhỏ nhất là 16 - .
Câu 21. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm giá trị lớn nhất M của hàm số 4 2
y = x - 2x  3 trên đoạn 0; 3 .  
A. M = 6
B. M = 1
C. M = 9
D. M = 8 3 Lời giải Chọn A Ta có: 3
y¢ = x - x = x ( 2 4 4 4 x - ) 1  x = 0  y¢ = 0 Û x ( 2 4 x - ) 1 = 0 Û x = 1  x = 1 - (l) 
Ta có : y (0) = 3 ; y ( ) 1 = 2 ; y ( 3) = 6
Vậy giá trị lớn nhất của hàm số 4 2
y = x - 2x  3 trên đoạn 0; 3 là M = y ( 3) = 6  
Câu 22. (Mã 103 - BGD - 2019) Giá trị lớn nhất của hàm số f ( x) 3
= x - 3x trên đoạn [ - 3;3] bằng A. -2 . B. 18 . C. 2 . D. -18 . Lời giải Chọn B Ta có 2
y¢ = 3x - 3 = 0 Û x = 1 
f (-3) = -18; f (- ) 1 = 2; f ( )
1 = -2; f (3) = 18 . 2 x  3
Câu 23. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số y = trên đoạn x -1 2; 4 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 19
A. min y = -3 B. min y =
C. min y = 6 D. min y= 2 - 2;4 2;4 3 2;4 2;4 Lời giải Chọn C
Tập xác định: D =  \   1 2 x  3 Hàm số y =
xác định và liên tục trên đoạn 2; 4 x -1 2 x - 2x - 3 Ta có 2 y¢ =
; y¢ = 0 Û x - 2x - 3 = 0 Û x = 3 hoặc x = 1 - (loại) ( x - )2 1 19
Suy ra y (2) = 7; y (3) = 6; y (4) =
. Vậy min y= 6 tại x = 3 . 3 2;4
Câu 24. (Mã đề 104 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số 4 2
y = x - x 13 trên đoạn [-1; 2] bằng 51 A. 85 B. C. 13 D. 25 4 Lời giải Chọn D
y = f ( x) 4 2
= x - x 13 3
y ' = 4x - 2x  x = 0[ -1;2]   1 3
4x - 2x = 0 Û x = - [ -1; 2]  2   1 x = [ -1; 2]   2  1  51  1  51
f (-1) = 13; f (2) = 25; f (0) = 13; f - = ; f =      2  4  2  4
Giá trị lớn nhất của hàm số 4 2
y = x - x 13 trên đoạn [-1; 2] bằng 25. 2  1 
Câu 25. (MĐ 104 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số 2 y = x  trên đoạn ; 2 x  2    . 17
A. m = 5
B. m = 3 C. m = D. m =10 4 Lời giải Chọn B 2
Đặt y = f ( x) 2 = x  . x 3 2 2x - 2  1 
Ta có y¢ = 2x - =
, y¢ = 0  x = 1 ;2 . 2 2 x x  2     1  17 Khi đó f ( ) 1 = 3, f = , f   (2) = 5 .  2  4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vậy m = min f ( x) = f ( ) 1 = 3.  1  ;2  2   
Câu 26. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số y = 3 x - 2 7x  11x - 2 trên đoạn [0 ; 2]. A. m = 3
B. m = 0
C. m = -2 D. m = 11 Lời giải Chọn C
Xét hàm số trên đoạn [0 ; 2]. Ta có y¢ = 2
3x - 14x  11suy ra y¢ = 0 Û x = 1
Tính f (0) = -2; f (1) = 3, f (2) = 0 . Suy ra min f (x) = f (0) = -2 = m. 0;2  
Câu 27. (Mã đề 101 BGD&ĐT NĂM 2018) Giá trị lớn nhất của hàm số 4 2
y = x - 4x  9 trên đoạn  2 - ;  3 bằng A. 201 B. 2 C. 9 D. 54 Lời giải Chọn D x = 0 3
y¢ = 4x - 8x ; y¢ = 0 Û  . x =  2  Ta có y ( 2
- ) = 9 ; y (3) = 54 ; y (0) = 9 ; y ( 2 ) = 5 .
Vậy max y = 54 . -2;3
Câu 28. (ĐỀ THAM KHẢO BGD & ĐT 2018) Giá trị lớn nhất của hàm số f ( x) 4 2
= x - 4x  5 trêm đoạn  2 - ;  3 bằng A. 122 B. 50 C. 5 D. 1 Lời giải Chọn B x = 0 3
f '(x) = 4x - 8x = 0 Û    2 - ;  3 ; x =  2 
f (0) = 5; f ( 2) =1; f ( 2
- ) = 5; f (3) = 50
Vậy Max y = 50  2 - ;  3
Câu 29. (MĐ 105 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số y = 4 x - 2 x  13 trên đoạn -2;3   . 51 51 49
A. m = 13 B. m = C. m = D. m = 4 2 4 Lời giải Chọn B x = 0  -2;3    y¢ = 3
4x - 2x ; y¢ = 0 Û  1 ; x =   -2;3     2  1  51
Tính y (-2) = 25 , y (3) = 85 , y (0) = 13 , y  = =   12,75 ;  2  4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 51
Kết luận: giá trị nhỏ nhất m của hàm số là m = . 4
Câu 30. (Mã đề 104 - BGD - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x - 3x trên đoạn  3 - ;  3 bằng A. -18. B. 2 - . C. 2. D. 18. Lời giải Chọn A x = 1 Ta có f ¢( x) 2 == 3x - 3 = 0 Û .  x = -1  Mà f (- ) 3 = 1 - 8; f (- ) 1 = 2; f ( ) 1 = 2 - ; f ( ) 3 =18.
Vậy giá trị nhỏ nhất của hàm số f ( x) 3
= x - 3x trên đoạn  3 - ;  3 bằng -18.
Câu 31. (MĐ 103 BGD&ĐT NĂM 2017-2018) Giá trị nhỏ nhất của hàm số 3 2
y = x  3x trên đoạn -4;-  1 bằng A. -16 B. 0 C. 4 D. -4 Lời giải Chọn A x = 0  4 - ; -1 2   Ta có 2
y¢ = 3x  6x ; y¢ = 0  3x  6x = 0 Û  . x = -2    4 - ; -  1 Khi đó y ( 4 - ) = 16 - ; y ( 2 - ) = 4 ; y (- ) 1 = 2 .
Nên min y = -16 . -4;-  1
Câu 32. (Mã đề 102 BGD&ĐT NĂM 2018) Giá trị nhỏ nhất của hàm số 3 2
y = x  2x - 7x trên đoạn 0; 4 bằng A. 259 - B. 68 C. 0 D. -4 Lời giải Chọn D TXĐ D = .
Hàm số liên tục trên đoạn 0; 4 . Ta có 2
y¢ = 3x  4x - 7
x = 10;4 y¢ = 0  Û 7
x = - 0;4  3 y (0) = 0; y( ) 1 = 4 - ; y(4) = 68 .
Vậy min y = -4 . 0;4
Câu 33. (Mã đề 101 - BGD - 2019) Giá trị lớn nhất của hàm số f ( x) 3
= x - 3x  2 trên đoạn -3;  3 là A. 4 . B. 16 - . C. 20 . D. 0 . Lời giải Chọn C f ( x) 3
= x - 3x  2 tập xác định  . f ( x) 2 '
= 0 Û 3x - 3 = 0 Û x = 1   3 - ;  3 . f ( ) 1 = 0; f (- )
1 = 4; f (3) = 20; f ( 3 - ) = -16 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ đó suy ra max f ( x) = f (3) = 20 .  3 - ;  3
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b) 4
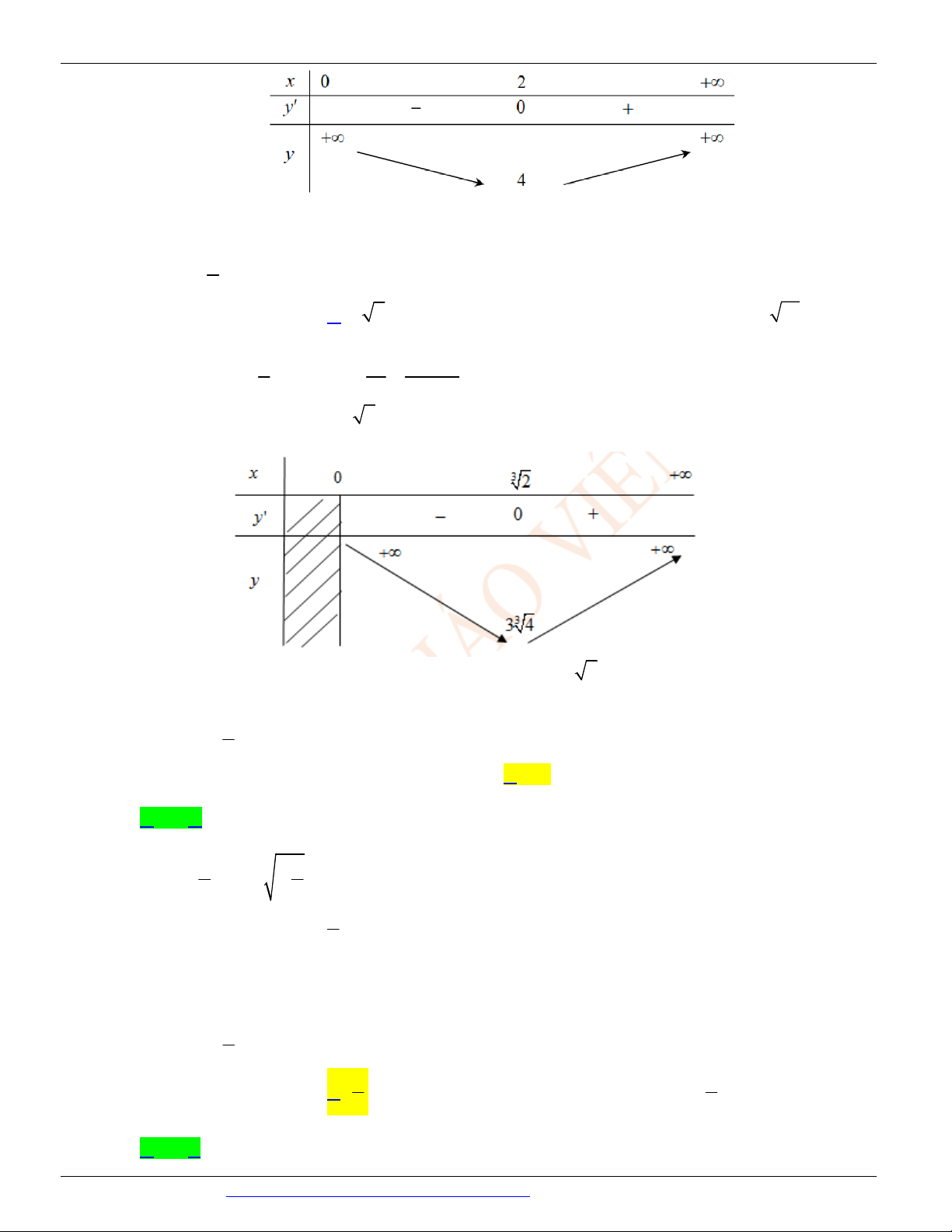
Câu 34. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tính giá trị nhỏ nhất của hàm số y = 3x  trên 2 x
khoảng (0;  ) . 33 A. min y = B. 3 min y = 2 9 C. 3 min y = 3 9
D. min y = 7 (0;) 5 (0;) (0;) (0;) Lời giải Chọn C Cách 1: 4 3x 3x 4 3x 3x 4 3 3 y = 3x  =    3 . . = 3 9 2 2 2 x 2 2 x 2 2 x 3x 4 8 Dấu " = " xảy ra khi 3 = Û x = . 2 2 x 3 Vậy 3 min y = 3 9 (0;) Cách 2: 4
Xét hàm số y = 3x  trên khoảng (0;  ) 2 x 4 8
Ta có y = 3x   y ' = 3 - 2 3 x x 8 8 8 Cho 3 3 y ' = 0 Û = 3 Û x = Û x = 3 x 3 3 8 x 0 3  3 y ' - 0  y 3 3 9  8  3 3
 min y = y   = 3 9 (0;)  3   
Câu 35. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Gọi m là giá trị nhở 4
nhất của hàm số y = x
trên khoảng (0; ) . Tìm m x A. m = 4 . B. m = 2 . C. m = 1. D. m = 3 . Lời giải 4 y ' = 1- 2 x y ' = 0 Û x = 2  ; x = 2  (0; ). Bảng biến thiên:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Suy ra giá trị nhỏ nhất của hàm số bằng y(2) = 4  m = 4.
Câu 36. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Gọi a là giá trị nhỏ nhất của hàm số 4 2 y = x  trên khoảng (0; )  . Tìm a . x A. 3 3 4 . B. 5. C. 6 . D. 3 2 16 . Lời giải. 3 4 4 2x - 4 Ta có: 2 y = x   y ' = 2x - = . 2 2 x x x 3 3
y ' = 0 Û 2x - 4 = 0 Û x = 2 . Bảng biến thiên
Nhìn vào BBT ta thấy giá trị nhỏ nhất của hàm số là 3 a = 3 4 .
Câu 37. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Giá trị nhỏ nhất của hàm số 1 y = x - 5 
trên khoảng (0; ) bằng bao nhiêu? x A. 0 B. 1 - C. 3 - D. -2 Lời giải Chọn C
Áp dụng bất đẳng thức Cô – si ta có: 1 1 y = x  - 5  2 . x - 5 = 3 - x x 1 Dấu bằng xảy ra khi 2 x =
Û x = 1 Û x = 1 (vì x  0 ). x Vậy min y = -3 . (0;)
Câu 38. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số 1
f (x) = x
trên nửa khoảng 2; ) là: x 5 7 A. 2 B. C. 0 D. 2 2 Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 3x x 1 3.2 x 1 5
Áp dụng bất đẳng thức Cô-si, ta được: f (x) = x  =     2 . = . x 4 4 x 4 4 x 2
Dấu bằng xảy ra khi x = 2 .
Dạng 4. Ứng dụng GTLN-GTNN vào bài toán thực tế
Câu 39. (Mã đề 101 BGD&ĐT NĂM 2018) Ông A dự định dùng hết 2
6, 5m kính để làm một bể cá có
dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể).
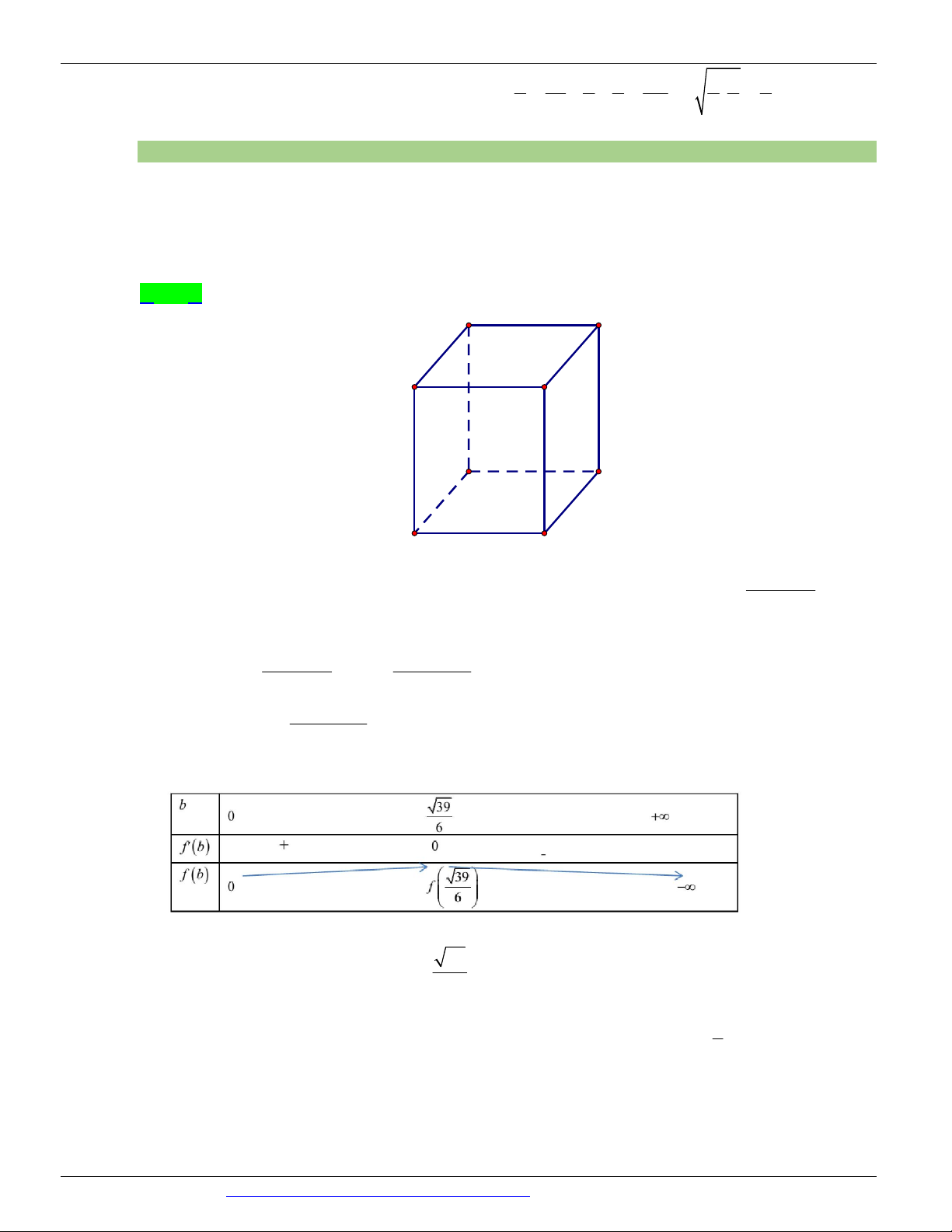
Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 2, 26 m B. 3 1, 61 m C. 3 1,33 m D. 3 1,50 m Lời giải Chọn D a c b
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá: V = abc 2  6,5 - 2b
ab  2bc  2ac = 6,5 2
2b  6bc = 6,5 c =
Mặt khác theo giả thiết ta có:  Û  Û  6b a = 2  b a = 2  ba = 2  b 2 6,5 - 2b 3 6,5b - 2b Khi đó 2 V = 2b . Û V = . 6b 3 3 6,5b - 2b
Xét hàm số: f (b) = . Có BBT 3  39 
Vậy bể cá có dung tích lớn nhất là: 3 f   = 1,50 m .  6    1
Câu 40. (MĐ 104 BGD&DT NĂM 2017) Một vật chuyển động theo quy luật 3 2
s = - t  6t với t (giây) 3
là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển
được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động,
vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. 243 (m/s) B. 27 (m/s) C. 144 (m/s) D. 36 (m/s) Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn D Ta có: 2
v = s¢ = -t 12t ; v¢ = 2
- t 12 ; v¢ = 0 Û t = 6. BBT t 0 6 9 v¢  0  36 v
Nhìn bbt ta thấy vận tốc đạt giá trị lớn nhất khi t = 6 . Giá trị lớn nhất là v (6) = 36m/s .
Câu 41. (MĐ 103 BGD&ĐT NĂM 2017-2018) Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có
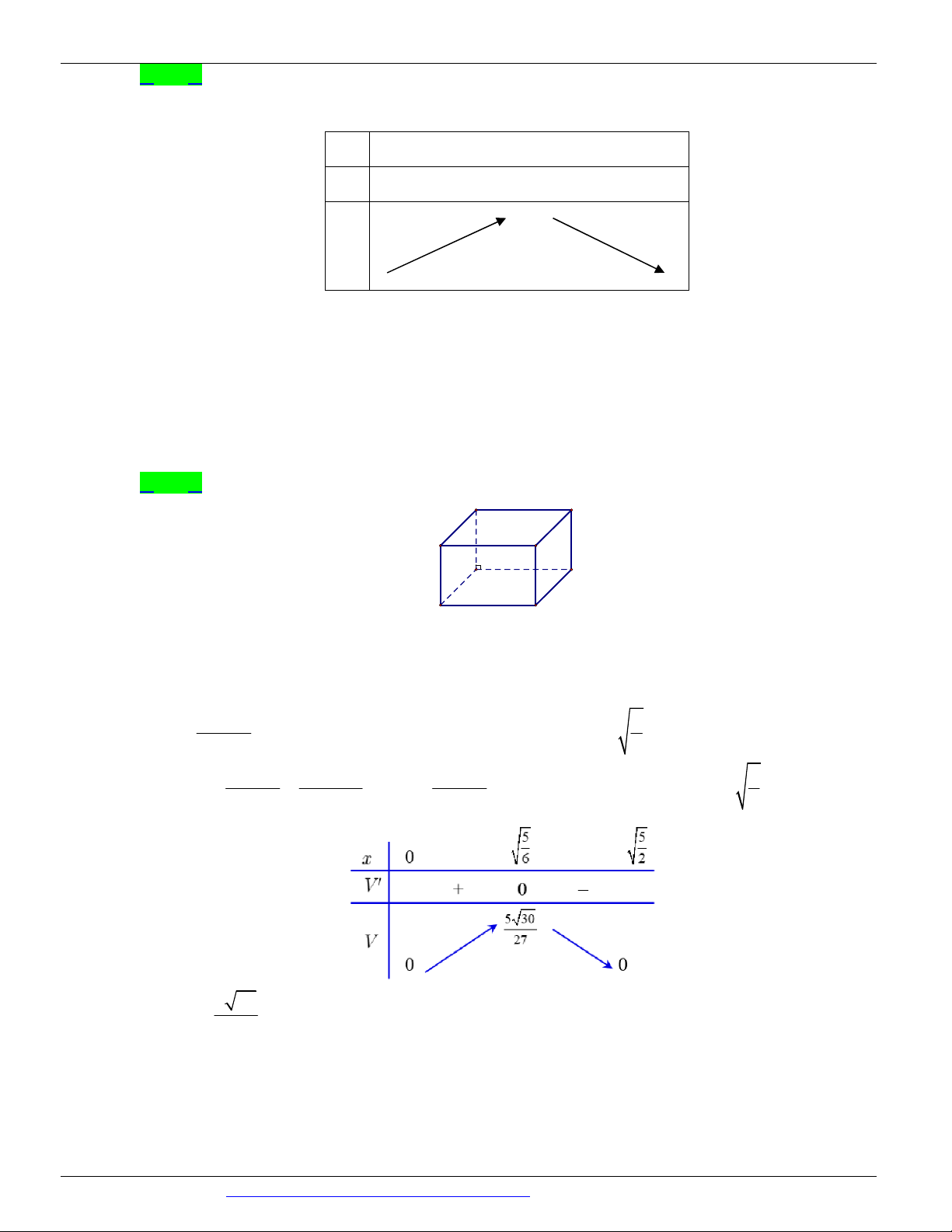
kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1, 01 m B. 3 0, 96 m C. 3 1,33 m D. 3 1,51 m Lời giải Chọn A A' D' B' C' y A 2 x D x B C
Gọi x, y lần lượt là chiều rộng và chiều cao của bể cá (điều kiện x, y  0 ). Ta có thể tích bể cá 2 V = 2x y . Theo đề bài ta có: 2
2xy  2.2xy  2x = 5 2
Û 6xy  2x = 5 2 5 - 2x 5 Û y = (Điều kiện kiện 2
y  0 Û 5 - 2x  0  0  x  ) 6x 2 2 3 5 - 2x 5x - 2x 2 5 - 6x 5 2  V = 2x =  V ¢ = 2
V ¢ = 0 Û 5 - 6x = 0 Û x = 6x 3 3 6 5 30 3  V =  1, 01 m . max 27
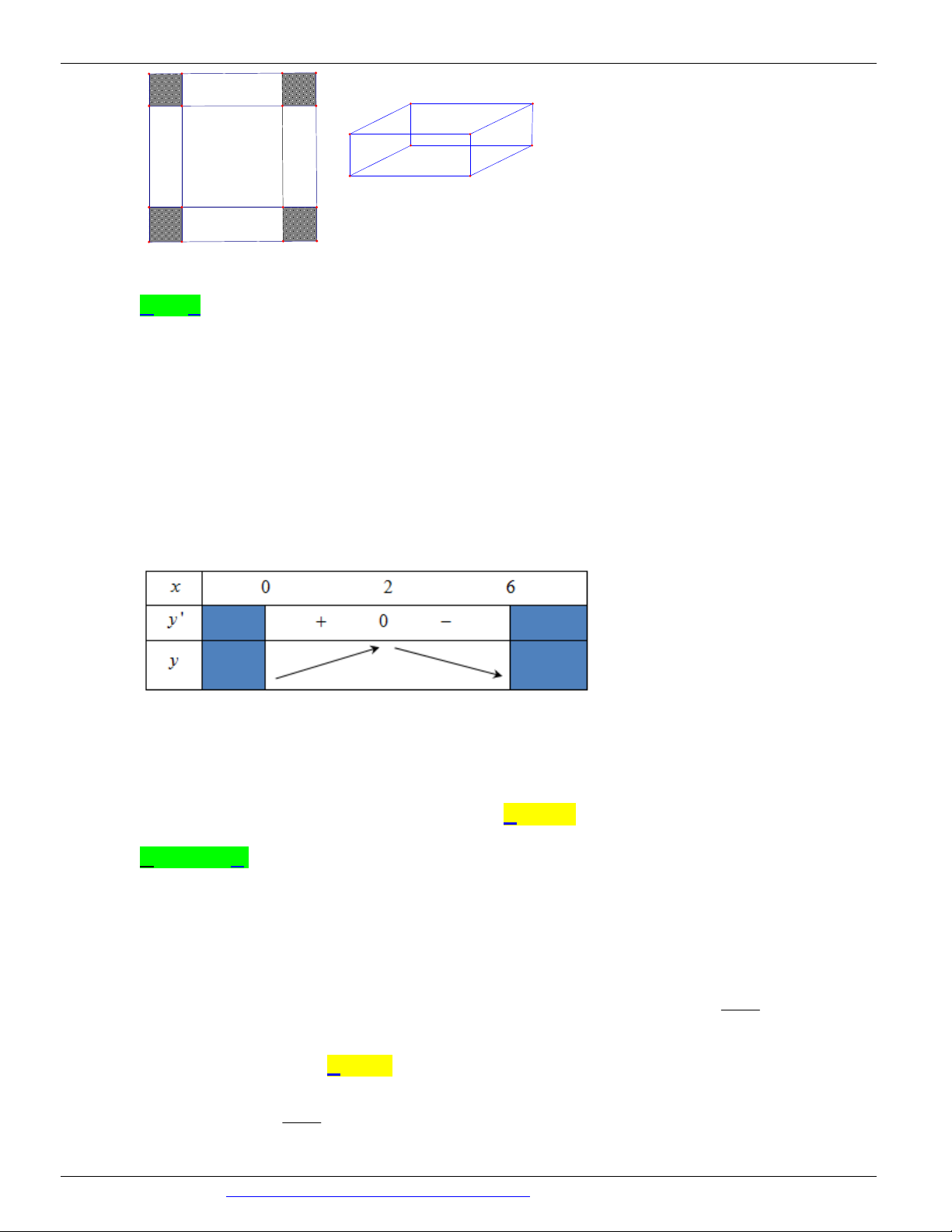
Câu 42. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta
cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm),
rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận
được có thể tích lớn nhất.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. x = 3
B. x = 2
C. x = 4
D. x = 6 Lời giải Chọn B
Ta có : h = x (cm) là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 12 - 2x (cm) 2 x  0 x  0
Vậy diện tích đáy hình hộp S = ( - x) ( 2 12 2 cm ) . Ta có:  Û  Û x  (0;6) 12 - 2x  0 x  6  
Thể tích của hình hộp là: V = S.h = x ( 2 - 2x)2 . 1 2 Xét hàm số: y = . x (12 - 2x) x   (0;6) 2
Ta có : y ' = (12 - 2x) - 4x (12 - 2x) = (12 - 2x)(12 - 6x) ;
y ' = 0 Û (12 - 2x).(12 - 6x) = 0 Û x = 2 hoặc x = 6 (loại).
Suy ra với x = 2 thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là y (2) = 128 .
Câu 43. (KTNL GIA BÌNH NĂM 2018-2019) Một chất điểm chuyển động theo phương trình 3 2 S = t
-  3t - 2 , trong đó t tính bằng giây và S tính theo mét. Chuyển động có vận tốc lớn nhất là A. 1 m/s. B. 4 m/s. C. 3 m/s. D. 2 m/s. Lời giải Chọn C.
S = -t t -  v = - t t = - (t - )2 3 2 2 3 2 3 6 3 1  3  3 .
Do đó max v = 3(m / s) .
Câu 44. (THPT NĂM 2018-2019 LẦN 04) Một loại thuốc được dùng cho một bệnh nhân và nồng độ
thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của t
bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức c (t ) = (mg / L) . Sau 2 t 1
khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất? A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ. Lời giải t
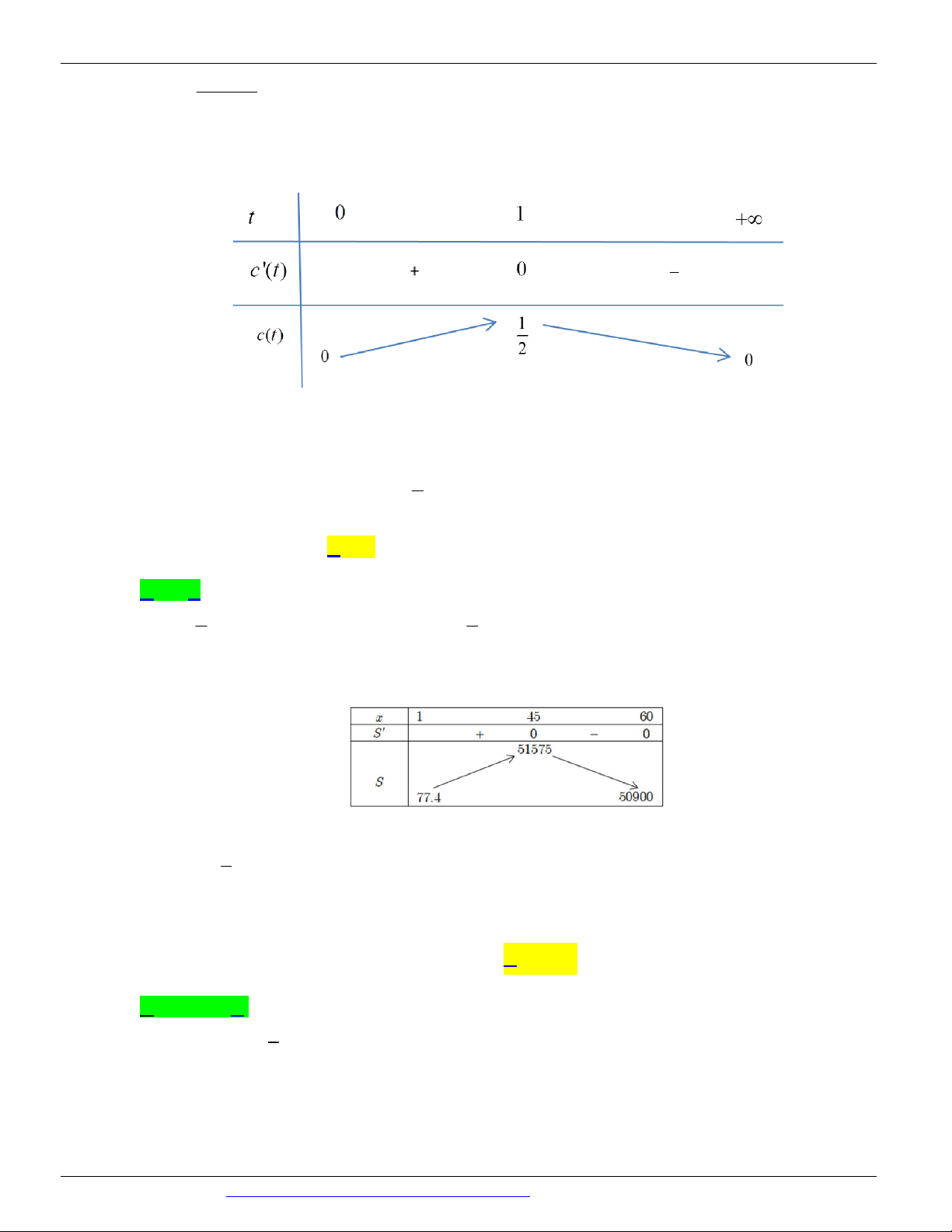
Xét hàm số c (t ) = , (t  0) . 2 t 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 1- t c¢(t ) = . (t  )2 2 1 t = 1
c¢(t ) = 0 Û  . t = 1 - 
Với t = 1 giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất.
Câu 45. (THPT YÊN MỸ HƯNG YÊN NĂM 2018-2019 LẦN 01) Đợt xuất khẩu gạo của tỉnh A thường
kéo dài trong 2 tháng ( 60 ngày). Người ta nhận thấy số lượng xuất khẩu gạo tính theo ngày thứ t 2
được xác định bởi công thức S (t ) 3 2 =
t - 63t  3240t - 3100 với (1  t  60) . Hỏi trong 60 ngày 5
đó thì ngày thứ mấy có số lượng xuất khẩu gạo cao nhất. A. 60 B. 45 C. 30 D. 25 Lời giải Chọn B 2 6 S (t ) 3 2 =
t - 63t  3240t - 3100  S¢(t ) 2 =
t -126t  3240 5 5 t = 45
Ta có: S¢(t ) = 0 Û  t = 60 
Câu 46. (GKI NHÂN CHÍNH HÀ NỘI NĂM 2018-2019 LẦN 01) Một vật chuyển động theo quy luật 1 2 3
S = 10t - t , với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và S (m) là 3
quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 15 giây từ lúc vật
bắt đầu chuyển động vận tốc v (m / s) của vật đạt giá trị lớn nhất tại thời điểm t (s) bằng: A. 8(s) . B. 20 (s) C. 10 (s) . D. 15(s) . Lời giải Chọn C. 1 Ta có: 2 3
S = 10t - t v (t ) 2
= S¢ = 20t - t . 3
Xét hàm số v (t );t 0 
;15 , ta có: v¢(t) = 20 - 2t = 0 Û t = 10.
v (0) = 0; v (15) = 75;v (10) = 100 . Do đó: max v (t ) = 100 Û t = 10 . 0;15
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 47. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Một sợi dây có chiều dài
28m được cắt thành hai đoạn để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo
đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông
và hình tròn là nhỏ nhất? 56 112 84 92 A. . B. . C. . D. . 4   4   4   4   Lời giải
Gọi chiều dài của đoạn dây làm thành hình vuông là x ( m ) ( 0  x  28 )
=> chiều dài của đoạn dây làm thành hình tròn là 28 - x ( m ) 2 2  x x
+) Diện tích hình vuông là: =    4  16 28 - x
+) Bán kính hình tròn là: R = 2 2 2  28 - x  784 - 56x x
=> Diện tích hình tròn: 2  R =  . =    2  4 2 2 x 784 - 56x x    4  14 196
+) Tổng diện tích hai hình: 2  = x - x    16 4  16       4  14 196 Xét 2 f (x) = x - x   
. Nhận thấy f (x) đạt giá trị nhỏ nhất tại  16    -b 14 16 112 x = = . = 2a  2(  4)   4
Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ 112 nhất là m 4  
Câu 48. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Một xưởng in có 15 máy in được cài đặt
tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in được 30 ấn phẩm trong 1 giờ, chi phí cài
đặt và bảo dưỡng cho mỗi máy in cho 1 đợt hàng là 48.000 đồng, chi phí trả cho kỹ sư giám sát là
24.000 đồng/giờ. Đợt hàng này xưởng in nhận 6000 ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là A. 10 máy. B. 11 máy. C. 12 máy. D. 9 máy. Lời giải Chọn A
Gọi x (0  x  15) là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt và bảo dưỡng là 48000x . 6000 6000 48000
Số giờ in hết số ấn phẩm là , chi phí giám sát là .24000  . 30x 30x x 4800000
Tổng chi phí in là P ( x) = 48000x  . x 4800000 x = 10
P¢( x) = 48000 - ; P¢( x) 2 = 0 Û x = 100 Û . 2  x x = -10 ( L)  Bảng biến thiên:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x 0 10 15 P¢ ( x) - 0  P ( x) P (10)
Vậy chi phí in nhỏ nhất là 10 máy.
Câu 49. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s (t ) 3 2
= t - 4t 12 (m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc
của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu? 8 4 A. 2 (s). B. (s). C. 0 (s). D. (s). 3 3 Lời giải
v (t ) = s¢(t ) 2 = 3t - 8t . 4
v¢(t ) = 6t - 8 . Có v¢(t ) = 0 Û t = . 3  4  16
Dựa vào bảng biến thiên ta có min v = v = -   . 0;)  3  3 4
Vậy vận tốc của chất điểm đó đạt giá trị bé nhất khi t = . 3
Câu 50. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho một tấm nhôm hình chữ nhật có
chiều dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm) , rồi gập tấm nhôm lại (như hình vẽ)
để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. 8 - 2 21 10 - 2 7 9  21 9 - 21 A. x = B. x = C. x = . D. x = 3 3 9 3 Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta có : h = x (cm) là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 10 - 2x (cm) và 8 - 2x (cm)
Vậy diện tích đáy hình hộp S = ( - x)( - x)( 2 10 2 8 2 cm ) . Ta có: x  0  x  0 1  0 - 2x  0 Û  Û x  (0; 4) x  4   8 - 2x  0 
Thể tích của hình hộp là: V = S.h = .
x (10 - 2x).(8 - 2x) Xét hàm số: y = .
x (10 - 2x).(8 - 2x)x  (0; 4) Ta có : 2
y ' = 12x - 72x  80 ;  9  21 x =  4  (l ) 3 y ' = 0 Û  .  9 - 21  x = (n)  3 9 - 21 Suy ra với x =
thì thể tích hộp là lớn nhất và giá trị lớn nhất. 3
Câu 51. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Một đoàn cứu trợ lũ lụt đang ở vị trí A của
một tỉnh miền trung muốn đến xã C để tiếp tế lương thực và thuốc men. Để đi đến C , đoàn cứu
trợ phải chèo thuyền từ A đến vị trí D với vận tốc 4 (km / h) , rồi đi bộ đến vị trí C với vận tốc
6(km / h) . Biết A cách B một khoảng 5km , B cách C một khoảng 7km (hình vẽ). Hỏi vị trí
điểm D cách A bao xa để đoàn cứu trợ đi đến xã C nhanh nhất?
A. AD = 5 3 km .
B. AD = 2 5 km .
C. AD = 5 2 km .
D. AD = 3 5 km . Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đặt AD = x (km) , ( x  0) . Ta có 2 2 2 BD = AD - AB =
x - 25 ( x  5) 2
CD = BC - BD = 7 - x - 25 2 AD DC x 7 - x - 25
Thời gian đi từ A đến C là: T ( x) =  =  4 6 4 6 2 1 -2x 3 x - 25 - 2 x T ¢ ( x) =  = . 2 2 4 12 x - 25 12 x - 25 T ¢( x) 2
= 0 Û 3 x - 25 = 2x Û x = 3 5 Bảng biến thiên 14  5 5
Do đó min T ( x) = T (3 5) = x   5;) 12
Vậy AD = 3 5 (km) .
Dạng 5. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước x m
Câu 52. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y =
( m là tham số thực) thỏa mãn x - 1
min y = 3. Mệnh đề nào dưới đây đúng? [2;4]
A. m  4
B. 3  m  4
C. m  -1
D. 1  m  3 Lời giải Chọn A -1 - m Ta có y ' = ( 2 x - ) 1
* TH 1. -1 - m  0 Û m  -1 suy ra y đồng biến trên 2; 4   suy ra m min f (x) f (2) 2  = = = 3 Û m = 1 (loại) 2;4   1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
* TH 2. -1 - m  0 Û m  -1 suy ra y nghịch biến trên 2; 4   suy ra m min f (x) f (4) 4  = =
= 3 Û m = 5 suy ra m  4 . 2;4   3
Câu 53. (ĐỀ THAM KHẢO BGD & ĐT 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao
cho giá trị lớn nhất của hàm số 3
y = x - 3x m trên đoạn 0; 
2 bằng 3. Số phần tử của S là A. 0 B. 6 C. 1 D. 2 Lời giải Chọn D
Xét hàm số f ( x) 3
= x -3x m , ta có f ¢( x) 2
=3x -3. Ta có bảng biến thiên của f ( x) :
TH 1 : 2  m  0 Û m  - 2 . Khi đó max f ( x) = -(- 2 m) = 2 - m 0;  2
2 - m = 3 Û m = -1 (loại). 2  m  0
TH 2 : 
Û - 2  m  0 . Khi đó : m- 2 = 2 - m 2  2  m m  0 
max f ( x) = -(- 2 m) = 2- m 0;  2
2 - m = 3 Û m = -1 (thỏa mãn). m  0
TH 3 : 
Û 0  m  2 . Khi đó : m- 2 = 2 - m 2 2 m max f ( x) = 2  m - 2  m  0  0;  2
2  m = 3 Û m =1 (thỏa mãn).
TH 4: - 2  m  0 Û m  2 . Khi đó max f ( x) = 2 m 0;  2
2  m = 3 Û m =1 (loại). x m
Câu 54. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y =
( m là tham số thực) thoả mãn x 1 16
min y  max y =
. Mệnh đề nào dưới đây đúng? 1;2 1;2 3
A. m  4
B. 2  m  4
C. m  0
D. 0  m  2 Lời giải Chọn A 1 - m Ta có y¢ = . ( x  )2 1
 Nếu m = 1  y = 1, x
  -1. Không thỏa mãn yêu cầu đề bài.
 Nếu m  1  Hàm số đồng biến trên đoạn 1;  2 . 16 16 m 1 m  2 16
Khi đó: min y  max y = Û y ( ) 1  y (2) = Û  = Û m = 5 (loại). 1;2 1;2 3 3 2 3 3
 Nếu m  1  Hàm số nghịch biến trên đoạn 1;  2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 16 16 2  m 1 m 16
Khi đó: min y  max y =
Û y (2)  y ( ) 1 = Û  = Û m = 5 ( t/m) 1;2 1;2 3 3 3 2 3
Câu 55. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Có một giá trị m của tham số m để 0 hàm số 3 y x  2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 5 trên đoạn 0;  1 . Mệnh đề nào sau đây là đúng? A. 2
2018m m  0 . B. 2m 1   0 . 0 0 0 C. 2
6m m  0 .
D. 2m 1 0 . 0 0 0 Lời giải
+ Đặt f x 3  x  2 m  
1 x m 1 . + Ta có: 2 2
y  3x m 1. Dễ thấy rằng y  0 với mọi x , m thuộc  nên hàm số đồng biến
trên  , suy ra hàm số đồng biến trên 0; 
1 . Vì thế min y  min f x  f 0  m 1. 0;  1 0;  1
+ Theo bài ra ta có: m 1  5 , suy ra m  4 .
+ Như vậy m  4 và mệnh đề đúng là 2
2018m m  0 . 0 0 0
Câu 56. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số m sao cho giá trị lớn nhất của hàm số 2
y = x - 2x m trên đoạn -1;2 bằng 5 . A. -1 . B. 2 . C. -2 . D. 1 . Lời giải 2x - 2 Ta có y¢ =
, y¢ = 0  x = 1. 2
x - 2x m
Do đó yêu cầu bài toán tương đương max y (- ) 1 , y (2), y ( ) 1  = 5 .
Û max3  m , m , m -1 = 5 .
+ Trường hợp m  1
- , ta có max3  m , m , m -1 = 5 Û 3  m = 5  m = 2 .
+ Trường hợp m  1
- ta có max3  m , m , m -1 = 5 Û m -1 = 5  m = -4 .
Vậy tổng các giá trị m bằng -2 .
Câu 57. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số 2
y = x m  1- x có giá trị lớn nhất bằng 2 2 thì giá trị của m là 2 2 A. . B. - 2 . C. 2 . D. - . 2 2 Lời giải Xét hàm số 2
y = x m  1- x
Tập xác định: D =  1 - ;  1 . x Ta có: y¢ = 1- 2 1- x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1   x  0  1 1   x  0   x = 1 2   1- x = x 1   x  0   Û  Û  2 Û x = y¢ = 0 Û  Û  2 2x = 1  2 . 2   1 2  - x  0   1- x = x   1  x = -    2  1  Ta có: y (- ) 1 = 1 -  , m y ( ) 1 = 1 , m y = 2  m   .  2  Do hàm số 2
y = x m  1- x liên tục trên  1 - ; 
1 nên Maxy = m  2 . -1;  1
Theo bài ra thì Maxy = 2 2 , suy ra m  2 = 2 2 Û m = 2 .  1 - ;  1 x m
Câu 58. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số y  (m là tham x  1
số thực) thỏa mãn min y  3 . Mệnh đề nào dưới đây đúng? 0;1  
A. 1  m  3 B. m  6 C. m  1
D. 3  m  6 Lời giải Chọn D
Tập xác định: D   \   1 .
Với m  1  y  1, x 0;1
    thì miny  3 . 0;1   1  m
Suy ra m  1. Khi đó y 
không đổi dấu trên từng khoảng xác định. x  2 1
TH 1: y  0  m  1 thì min y y  
0  m  3 (loại). 0;1  
TH 2: y  0  m  1 thì min y y  
1  m  5 ( thỏa mãn). 0;1  
Câu 59. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm x m số y
trên 1; 2 bằng 8 ( m là tham số thực). Khẳng định nào sau đây đúng? x 1 A. m  10 .
B. 8  m  10 .
C. 0  m  4 .
D. 4  m  8 . Lời giải
Nếu m = 1 thì y 1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8) 1 m
Nếu m  1 thì hàm số đã cho liên tục trên 1; 2 và y '  . x  2 1
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn 1; 2. m 1 m  2 41
Do vậy Min y Max y = y ( ) 1  y (2) =  = 8 Û m = . x   1;2 x   1;2 2 3 5
Câu 60. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số 3 2
y = 2x - 3x - m . Trên  1 - 
;1 hàm số có giá trị nhỏ nhất là 1 - . Tính m ? A. m = 6 - . B. m = 3 - . C. m = 4 - . D. m = 5 - .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn C Xét  1 -  ;1 có 2
y¢ = 6x - 6x . x = 0 -1  ;1 y¢ = 0 2
Û 6x - 6x = 0 Û  . x = 1-1  ;1  Khi đó y (- ) 1 = 5
- - m ; y (0) = -m ; y ( ) 1 = 1 - - m Ta thấy 5 - - m  1 - - m m
- nên min y = -5 - m .  1 - ;  1
Theo bài ra ta có min y = -1 nên 5 - - m = 1 - Û m = 4 - .  1 - ;  1
Câu 61. (THPT ĐÔNG SƠN THANH HÓA NĂM 2018-2019 LẦN 02) Tìm m để giá trị lớn nhất của hàm số 3
y = x - 3x  2m -1 trên đoạn 0; 2 là nhỏ nhất. Giá trị của m thuộc khoảng nào?  3   2  A. - ; -1   . B. ; 2   . C.  1 - ; 0 . D. (0 ) ;1 .  2   3  Lời giải
Xét hàm số y = f ( x) 3
= x - 3x  2m -1 trên đoạn 0; 2 . x = -1 0; 2 2  
Ta có f '( x) = 3x - 3 = 0 Û  . x = 1 
Ta có f (0) = 2m -1, f ( )
1 = 2m - 3 và f (2) = 2m 1
Suy ra max f ( x) = max 2m -1 ; 2m - 3 ; 2m 1 = max 2m - 3 ; 2m 1 = P . 0;2 1
Trường hợp 1: Xét 2m - 3  2m 1 Û 4
- (4m - 2)  0 Û m  . 2 1 1
Khi đó P = 2m - 3  2 , m   . Suy ra P = 2 Û m = . 2 min 2 1
Trường hợp 2: Xét 2m - 3  2m 1 Û 4
- (4m - 2)  0 Û m  . 2 1
Khi đó P = 2m 1  2 , m   . Suy ra P không tồn tại. 2 min 1 Vậy m = . 2
Câu 62. (HỌC MÃI NĂM 2018-2019-LẦN 02) Biết S là tập giá trị của m để tổng giá trị lớn nhất và giá
trị nhỏ nhất của hàm số 4 2 3 2
y = x - m x - 2x - m trên đoạn 0; 
1 bằng -16 . Tính tích các phần tử của S . A. 2 . B. -2 . C. -15 . D. -17 . Lời giải TXĐ: D =  . Ta có: 3 2 2
y¢ = 4x - 3m x - 4x x = 0 3 2 2
y¢ = 0 Û 4x - 3m x - 4x = 0 Û  2 2
4x - 3m x - 4 = 0  ( 2  = 9m  64) 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  x = 0  2 4  3m  9m  64 Û x =  1  8  2 4  3m - 9m  64 x =  0   8
Nên hàm số đơn điệu trên (0; ) 1 .
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0;  1 bằng -16 nên
y ( )  y ( ) = - Û -m  ( 2 -m - m - ) 2 0 1 16
1 = -16 Û -m - 2m 15 = 0 .
Vậy m .m = -15 . 1 2
Câu 63. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi ,
A B lần lượt là giá trị nhỏ nhất, giá trị 2
x m m
lớn nhất của hàm số y = trên đoạn 2; 
3 . Tìm tất cả các giá trị thực của tham số m để x -1 13 A B = . 2
A. m = 1; m = -2 . B. m = -2 . C. m = 2 .
D. m = -1; m = 2 . Lời giải 2
x m m Xét hàm số y = trên đoạn 2;  3 . x -1 2 2 2 -m - m -1 m m  3 m m  2 y ' =  0 x
  2;3  A = f 3 = , B = f 2 = . 2   ( ) ( ) ( x - ) 1 2 1 2 2 13 m m  3 m m  2 13 m = 1 A B = Û  = Û  . 2 2 1 2 m = -2 
Câu 64. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số 2 x mx 1
m để hàm số y =
liên tục và đạt giá trị nhỏ nhất trên đoạn 0; 2 tại một điểm x  0; 2 0 ( ) x m .
A. 0  m  1 B. m  1 C. m  2 D. 1 -  m  1 Lời giải Chọn A -m  0 m  0
Tập xác định: D =  \ - 
m . Hàm số liên tục trên 0; 2 Û Û   -m  2 m  -2  
x  2mx m -1 ( x m)2 2 2 -1  x = -m -1 Ta có y¢ = = . Cho 1 y¢ = 0 Û  . ( x m)2 ( x m)2 x = -m 1  2 Ta có bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Hàm số đạt giá trị nhỏ nhất tại x  0; 2 nên 0  -m 1  2 Û 1 -  m  1 0 ( )
So với điều kiện hàm số liên tục trên đoạn 0; 2. Ta có 0  m  1 . CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định x  -m -m  0 m  0
Hàm số liên tục trên đoạn 0; 2 nên -m  0; 2  Û   (*) -m  2 m  2 -  
x  2mx m -1 ( x m)2 2 2 -1 y ' = = ( x m)2 ( x m)2 x = -m 1
y ' = 0 có hai nghiệm là 1  , x = -m -1  2
x - x = 2 nên chỉ có nhiều nhất một nghiệm thuộc (0; 2) 1 2 Ta thấy m - 1  m - -1, m
 và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên 0;2 tại một
điểm x  0; 2 thì 0  -m 1  2 Û 1 -  m  1 (* ) * 0 ( ) Từ ( ) * ,(* ) * ta có 0  m  1
Câu 65. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị 2
x mx m
thực của tham số m sao cho giá trị lớn nhất của hàm số y =
trên 1;2 bằng 2 . Số x 1
phần tử của tập S A. 3 . B. 1. C. 4 . D. 2 . Lời giải Chọn D 2
x mx m 2 x  2xx = 0 1;2 Xét y =
. Ta có: f ¢( x) =
, f ¢( x) = 0 Û  . x 1 ( x  )2 1 x = 2 - 1;2  2m 1 3m  4
 2m 1 3m  4  Mà f ( ) 1 = ,f (2) =  max y =  ;  . x   1;2 2 3 2 3    3 m = 2m 1   2
Trường hợp 1: max y = = 2   . x   1;2 2 5 m = -  2 3 3m  4 17 • Với m =  =  2 (loại) 2 3 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 5 3m  4 7 • Với m = -  =  2 (thỏa mãn) 2 3 6  2 m = 3m  4 3m  4 = 6  3
Trường hợp 2: max y = = 2  Û   . x   1;2 3 3m  4 = -6 10  m = -  3 2 2m 1 7 • Với m =  =  2 (thỏa mãn) 3 2 6 10 2m 1 17 • Với m = -  =  2 (loại) 3 2 6
Vậy có 2 giá trị của m thỏa mãn.
Câu 66. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Tìm m để giá trị nhỏ nhất của hàm số 2
x - m m f (x) =
trên đoạn (0;1) bằng –2 x 1 m = 1 m = 1 m = -1 1  21 A. B. C.  . D. m = . m = 2  m = -2 m = 2 2 .  .  Lời giải Chọn C 2 -m m 1 Ta có: y ' =  0, m    ( x  )2 1
 Hs luôn nghịc biến trên 0;  1 m = 2
Max f ( x) = f (0) 2
Û -m m = -2 Û  0;  1 m = -1  1- m sin x
Câu 67. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Cho hàm số y = . Có bao cos x  2
nhiêu giá trị nguyên của tham số m thuộc đoạn 0;10 để giá trị nhỏ nhất của hàm số nhỏ hơn -2 ? A. 1. B. 9 . C. 3 . D. 6 . Lời giải
Tập xác định: D =  . 1- m sin x Ta có: y =
Û y cos x m sin x = 1- 2 y . cos x  2
Phương trình có nghiệm khi và chỉ khi: 2 2 2
y m  1- 4 y  4 y 2 2
Û 3y - 4 y 1- m  0 2 2 2 - 1 3m 2  1 3m Û  y  . 3 3 2  2 - 1 3m min y =  -2 2  2 2 x 3 1 3m  8 3  m  63 m  21      
Theo đề bài, ta có: m 0;10 Û m 0;10
Û m 0;10 Û m 0;10     m   m   m   m         
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Û m 5, 6, 7,8,9,1  0 .
Vậy có 6 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 68. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Xét hàm số ( ) 2
f x = x ax b ,
với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên -1; 
3 . Khi M nhận giá trị nhỏ
nhất có thể được, tính a  2b . A. 2 . B. 4 . C. -4 . D. 3 . Lời giải Xét hàm số ( ) 2
f x = x ax b . Theo đề bài, M là giá trị lớn nhất của hàm số trên -1;  3 . M f (- ) 1
M  1- a b  
Suy ra  M f (3) Û M  9  3a b  4M  1- a b  9  3a b  2 -1- a - b M f ( ) 1  
M  1 a b
 1 - a b  9  3a b  2 (-1 - a - b)  4M  8  M  2 .
Nếu M = 2 thì điều kiện cần là 1- a b = 9  3a b = 1
- - a - b = 2 và 1- a b , 9  3a b ,
 1- a b = 9  3a b = 1 - - a - b = 2 a = 2 - 1
- - a - b cùng dấu Û  Û  .
1- a b = 9  3a b = 1 - - a - b = 2 -  b = 1 -  a = 2 - Ngược lại, khi 
ta có, hàm số f ( x) 2
= x - 2x -1 trên -1;  3 . b = 1 - 
Xét hàm số g ( x) 2
= x - 2x -1 xác định và liên tục trên -1;  3 .
g¢ ( x) = 2x - 2 ; g¢( x ) = 0 Û x = 1-1;3
M là giá trị lớn nhất của hàm số f ( x) trên -1; 
3  M = max g (- )
1 ; g (3) ; g ( ) 1  =2 . a = 2 - Vậy 
. Ta có: a  2b = 4 - . b = 1 - 
Câu 69. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Cho hàm số 3
y = ax cx d, a  0
có min f ( x) = f (-2) . Giá trị lớn nhất của hàm số y = f ( x) trên đoạn 1;  3 bằng x (  -;0)
A. d -11a .
B. d -16a .
C. d  2a .
D. d  8a . Lời giải Vì 3
y = ax cx d, a  0 là hàm số bậc ba và có min f ( x) = f (-2) nên a  0 và y ' = 0 có hai x (  -;0) nghiệm phân biệt. Ta có 2
y ' = 3ax c = 0 có hai nghiệm phân biệt Û ac  0 . c
Vậy với a  0, c  0 thì y ' = 0 có hai nghiệm đối nhau x =  - 3ac c c
Từ đó suy ra min f ( x) = f  - -  Û - - = 2 - Û - = 2 Û c = 1 - 2a   x (  -;0) 3a   3a 3a Ta có bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta suy ra max f ( x) = f (2) = 8a  2c d = -16a d . x   1;  3
Câu 70. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi S là tập hợp các giá trị của tham số m 2
x - mx  2m
để giá trị lớn nhất của hàm số y = trên đoạn - 
1;1 bằng 3 . Tính tổng tất cả các x - 2 phần tử của S . 8 5 A. - . B. 5 . C. . D. 1 - . 3 3 Lời giải 2
x - mx  2m 4
Xét hàm số y = f ( x) = trên - 
1;1 có f ¢( x) = 1 - ; x - 2 ( x - 2)2  x = 0 3m  1 m  1
f ¢( x) = 0 Û  ; f (- ) 1 = ; f (0) = - ; m f ( ) 1 = . x = 4 -1;  1  3 - 1 - Bảng biến thiên x -1 0 1 f ¢( x)  0 - f ( x) f (0) f (- ) 1 f ( ) 1
Trường hợp 1. f (0)  0 Û m  0 . Khi đó 3m  1 
3 = max f ( x) = max f (- ) 1 ; f ( ) 1  Û 3 = max 
;m  1 Û m 1 = 3 Û m = 2 . -1;  1  3 
Trường hợp 2. f (0)  0 Û m  0 .  f  (- ) 1  0 Khả năng 1. 
Û m  -1. Khi đó 3 = max f ( x) = f (0) Û m = -3. f  ( ) 1  0  1 - ;  1  1  f  (- ) 1  0 Khả năng 2. 1
-  m  - . Khi đó 
. 3 = max f ( x) = max f (0); f ( ) 1  3 f  ( ) 1  0 -1;  1 
Û 3 = max -m; m  
1 : Trường hợp này vô nghiệm. 1 Khả năng 3. -
m  0 . Khi đó 3 = max f ( x) = max f (0); f ( ) 1 ; f (- ) 1 : Vô nghiệm. 3 -1;  1
Vậy có hai giá trị thỏa mãn là m = 3
- , m = 2 . Do đó tổng tất cả các phần tử của S là 1 - . 1 2
Câu 71. (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Tìm tất cả các giá trị của tham số x m
m để hàm số y =
có giá trị lớn nhất trên  nhỏ hơn hoặc bằng 1. 2 x x 1 A. m  1. B. m  1. C. m  -1. D. m  1 - . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn A + TXĐ: D =  . + lim y = 0 x 2
-x - 2mx 1- m + y¢ = . (x x  )2 2 1 2
y¢ = 0 Û -x - 2mx 1- m = 0 (*) 2
¢ = m - m 1  0, m
   nên (*) có 2 nghiệm phân biệt x x , m    (*) 1 2 + BBT: 1
Vậy hàm số đạt giá trị lón nhất là f ( x = với 2
x = -m m - m 1 2 ) 2x 1 2 2 1 2 YCBT Û
 1 Û 1- 2m  2 m - m 1  1 ( vì f ( x  0  2x 1  0 ) 2 ) 2 2 2
- m  2 m - m 1 1 m  0 2  Û
m - m 1  m Û m  0 Û m  1   2 2
m - m 1  m 
Dạng 6. Bài toán GTLN-GTNN liên quan đến đồ thị đạo hàm
Câu 72. (Mã 102 - BGD - 2019) Cho hàm số f ( x) , hàm số y = f ¢( x) liên tục trên  và có đồ thị như hình vẽ.
Bất phương trình f ( x)  x m ( m là tham số thực) nghiệm đúng với mọi x (0; 2) khi và chỉ khi
A. m f (0) .
B. m f (0) .
C. m f (2) - 2 .
D. m f (2) - 2 . Lời giải Chọn C
Xét bất phương trình f ( x)  x m Û m f ( x) - x .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Xét hàm số g ( x) = f ( x) - x với x (0; 2) . Ta có g¢( x) = f ¢( x) -1.
g¢( x) = 0 Û f ¢( x) = 1. Từ đồ thị ta thấy đường thẳng y =1 không cắt đồ thị y = f ¢( x) tại bất kỳ
điểm nào có hoành độ thuộc khoảng (0; 2) nên phương trình f ¢( x) = 1 vô nghiệm với x (0; 2) .
Ta có bảng biến thiên như sau:
(do f ¢( x)  1 với x (0; 2) ).
Từ bảng biến thiên ta thấy để m g ( x) với x (0; 2) Û m g (2) Û m f (2) - 2 .
Câu 73. (Mã 103 - BGD - 2019) Cho hàm số y = f ( x) , hàm số y = f '( x) liên tục trên  và có đồ thị như
hình vẽ bên. Bất phương trình f ( x)  2x m (m là tham số thực) nghiệm đúng với mọi x  (0; 2) khi và chỉ khi y 2 2 1 x
A. m f (0) .
B. m f (2) - 4 .
C. m f (0) .
D. m f (2) - 4 . Lời giải Chọn A
f ( x)  2x m
Û m f ( x) - 2x
Û m  max  f ( x) - 2x   (0;2)
Ta tìm max  f ( x) - 2x    0;2
Đặt g ( x) = f ( x) - 2x
g '( x) = f '( x) - 2 x
 0; 2, f '( x) - 2  0
 max g ( x) = g (0) = f (0) 0;2
Vậy m f (0)
Câu 74. (Mã đề 101 - BGD - 2019) Cho hàm số y = f ( x) , hàm số y = f '( x) liên tục trên  và có đồ thị như hình vẽ bên dưới
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Bất phương trình f ( x)  x m ( m là tham số thực) nghiệm đúng với mọi x (0; 2) khi và chỉ khi
A. m f (2) - 2.
B. m f (0).
C. m f (2) - 2.
D. m f (0). Lời giải Chọn D
f ( x)  x m Û f ( x) - x m .
Đặt g(x) = f ( x) - x xét trên khoảng (0; 2) . g (
¢ x) = f ¢( x) -1.
Từ đồ thị ta thấy g (
¢ x) = f ¢( x) -1  0 với mọi x (0;2) . Suy ra hàm số g(x) = f ( x) - x luôn
nghịch biến trên khoảng (0; 2) .
Bất phương trình f ( x)  x m ( m là tham số thực) nghiệm đúng với mọi x (0; 2) khi và chỉ
khi m  lim g ( x) = f (0) . x0
Câu 75. (Mã đề 104 - BGD - 2019) Cho hàm số f ( x) , hàm số f ¢( x) liên tục trên  và có đồ thị như hình vẽ.
Bất phương trình f ( x)  2x m ( m là tham số thực) nghiệm đúng với mọi x(0; 2) khi và chỉ khi
A. m f (2) - 4 .
B. m f (2) - 4 .
C. m f (0) .
D. m f (0) . Lời giải Chọn B
Hàm số g ( x) = f ( x) - 2x nghịch biến trên khoảng (0; 2) vì g¢( x) = f ¢( x) - 2  0, x  (0;2)
(quan sát trên khoảng (0; 2) , đồ thị hàm số f ¢( x) nằm dưới đường thẳng y = 2 ).
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Suy ra g (2)  g ( x)  g (0), x  (0;2) .
Bất phương trình đã cho nghiệm đúng với mọi x (0; 2) khi và chỉ khi m g ( x), x  (0; 2)
Û m g (2) Û m f (2) - 4 .
Câu 76. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) xác
định và liên tục trên  , đồ thị của hàm số y = f ¢( x) như hình vẽ.
Giá trị lớn nhất của hàm số y = f ( x) trên đoạn  1 - ; 2 là A. f ( ) 1 . B. f (- ) 1 . C. f (2) . D. f (0) . Lời giải x = 1 -  f ¢( x) = 0 Û x = 1 .   x = 2 
Từ đồ thị hàm y f x ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên  1  ;  2 là f   1 .
Câu 77. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số f ( x) có đạo
hàm là f ¢( x) . Đồ thị của hàm số y = f ¢( x) được cho như hình vẽ bên. Biết rằng f (0)  f ( )
1 - 2 f (3) = f (5) - f (4) . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f ( x) trên đoạn 0;5 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. m = f (5), M = f (3) B. m = f (5), M = f ( ) 1
C. m = f (0), M = f (3) D. m = f ( ) 1 , M = f (3) Lời giải Chọn A
Từ đồ thị ta có bảng biến thiên của f ( x) trên đoạn 0;5
M = f (3) và f ( )
1  f (3), f (4)  f (3)
f (5) - f (0) = f ( )
1 - f (3)  f (4) - f (3)  0  f (5)  f (0)  m = f (5) .
Câu 78. (ĐỀ 04 VTED NĂM 2018-2019) Cho hàm số y = f ( x) . Hàm số /
y = f (x) có bảng biến thiên như sau:
Bất phương trình ( x ) x f e
e m nghiệm đúng với mọi x ( 1 - ; ) 1 khi và chỉ khi  1  1 1 1  1  1
A. m f -  
B. m f (- ) 1 -
C. m f (- ) 1 -
D. m f -    e e e ee e Lời giải Chọn A Ta có ( x ) x   Û ( x ) x f e e m f e
- e m , x ( 1 - ; ) 1 . Đặt ( ) = ( x ) x g x f e
- e khi đó m g ( x) x   ( 1 - ; )
1 Û m Max g ( x) .  1 - ;  1 Xét ( ) = ( x ) x g x f e - e trên  1 - ;  1 . Có ¢( ) x = ¢( x ) x x - = ( ¢( x g x e f e e e f e ) - ) 1  0, x   1 - ; 
1 (Suy ra từ bảng biến thiên).  1  1
Do đó Max g ( x) = g (- ) 1 = f -   . -1;  1  e e
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1  1
Vậy m Max g ( x) = g (- ) 1 = f -   là giá trị cần tìm. -1;  1  e e
Câu 79. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số y = f ( x)
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số 1 1
g ( x) = f ( 2 4x - x ) 3 2 
x - 3x  8x  trên đoạn 1;  3 . 3 3 25 19 A. 15. B. . C. . D. 12. 3 3 Lời giải
g¢ ( x) = ( - x) f ¢( 2 x - x ) 2 4 2 4
x - 6x  8 = ( - x)  f ¢( 2 2 2
4x - x )  4 - x   . Với x 1;  3 thì 4 - x  0 ; 2
3  4x - x  4 nên f ¢( 2
4x - x )  0 . Suy ra f ¢( 2 2
4x - x )  4 - x  0 , x  1;  3 . Bảng biến thiên
Suy ra max g ( x) = g (2) = f (4)  7 =12 . 1;  3
Câu 80. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Cho hàm số y = f ( x) . Hàm số y = f ¢( x) có bảng biến thiên như sau    Bất phương trình ( ) cos  2 x f x
 3m đúng với mọi x  0;   khi và chỉ khi  2  1 1 1      1      A. m   f (0) - 2 . B. m
f (0) - 2 . C. m f -1     . D. m f -1     . 3   3   3   2   3   2   Lời giải       Ta có ( ) cos  2 x f x
 3m x  0; x   Û f ( x) cos - 2
 3m x  0;   .  2   2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489    Xét hàm ( ) = ( ) cos - 2 x g x f x trên 0;   .  2  Ta có ¢( ) = ¢( ) cos  2 x g x f x sin . x ln 2         
Vì f ¢( x)  1 x  0; cos x
 ; sin x  0 x  0;    2 sin .
x ln 2  0 x  0;   nên ta suy ra  2   2   2     ¢( ) = ¢( ) cos  2 x g x f x sin .
x ln 2  0 x  0;   .  2 
Vậy ta có bảng biến thiên π x 0 2 g'(x) + π g(x) g( ) 2 g(0) 1
Từ bảng biến thiên ta có ycbt Û g (0)  3m Û 3m f (0) - 2 Û m   f (0) - 2 . 3  
Câu 81. (Đề minh họa 2019) Cho hàm số y = f ( x) . Hàm số /
y = f (x) có bảng biến thiên như sau:
Bất phương trình ( x ) x f e
e m nghiệm đúng với mọi x ( 1 - ; ) 1 khi và chỉ khi  1  1 1 1  1  1
A. m f -  
B. m f (- ) 1 -
C. m f (- ) 1 -
D. m f -    e e e ee e Lời giải Chọn A Ta có ( x ) x   Û ( x ) x f e e m f e
- e m , x ( 1 - ; ) 1 . Đặt ( ) = ( x ) x g x f e
- e khi đó m g ( x) x  ( 1 - )
;1 Û m Max g ( x) . -1;  1 Xét ( ) = ( x ) x g x f e - e trên  1 - ;  1 . Có ¢( ) x = ¢( x ) x x - = ( ¢( x g x e f e e e f e ) - ) 1  0, x   1 - 
;1 (Suy ra từ bảng biến thiên).  1  1
Do đó Max g ( x) = g (- ) 1 = f -   . -1;  1  e e  1  1
Vậy m Max g ( x) = g (- ) 1 = f -   là giá trị cần tìm. -1;  1  e e
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 82. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hàm số f ( x) có bảng biến thiên như sau:
Gọi S là tập hợp các số nguyên dương m để bất phương trình f ( x)  m( 3 2
x - 3x  5) có nghiệm thuộc đoạn  1 - ; 
3 . Số phần tử của S là A. 3 B. Vô số C. 2 D. 0 Lời giải Chọn B Gọi g ( x) 3 2
= x - 3x  5 trên đoạn  1 - ;  3 x = 0 g '( x) 2 = 0 Û 3x - 6x = 0 Û  x = 2  g (- )
1 = 1; g (0) = 5; g (2) = 1; g (3) = 5  1  g ( x)  5, x   1 - ;  3 f x f x 3 2 ( ) ( )
f ( x)  m ( x - 3x  5), x   1 - ;  3 Û m  , x  -1;  3 Û m  min g ( x)  1 - ;3 g ( x) f ( x)
Vì hàm số f ( x), g ( x) liên tục trên đoạn  1 - ; 
3 suy ra tồn tại giá trị nhỏ nhất của hàm số g ( x) trên đoạn  1 - ;  3  f ( x)  Suy ra m   ; - min
  Số phần tử của tập hợp S là vô số  -1  ;3 g ( x)  
Câu 83. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hàm số y = f ( x) liên
tục trên . Đồ thị của hàm số y = f ¢ ( x) như hình bên. Đặt g ( x) = f ( x) - ( x  )2 2 1 . Mệnh đề dưới đây đúng.
A. max g ( x) = g (3).
B. min g ( x) = g ( )
1 . C. max g ( x) = g (0). D. max g ( x) = g ( ) 1 .  3; -  3  3; -  3 -3;  3  3; -  3 Lời giải Chọn D
g ( x) = f ( x) - ( x  )2 2 1
g¢( x) = 2 f ¢( x) - 2( x  ) 1
Dựa vào đồ thị ta thấy
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x = -3 
g¢( x) = 0 Û f ¢( x) = x 1 Û x = 1   x = 3  Và
với x  (-; -3) : f ¢( x)  x 1  g¢( x)  0 với x  (-3; )
1 : f ¢ ( x)  x 1  g¢( x)  0 ,
với x  (1;3) : f ¢( x)  x 1  g¢( x)  0
với x  (3; ) : f ¢( x)  x 1  g¢( x)  0 Bảng biến thiên x - -3 1 3  g¢( x) ‒ 0 + 0 ‒ 0 + g ( x)
Dựa vào bảng biến thiên suy ra max g ( x) = g ( ) 1 .  3 - ;  3
Câu 84. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho hàm số y = f ( x) có đạo hàm
cấp hai trên  . Biết f ¢(0) = 3 , f ¢(2) = 2
- 018 và bảng xét dấu của f ¢¢( x) như sau:
Hàm số y = f ( x  2017)  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A. ( ; - - 2017) B. (2017; ) C. (0; 2) D. ( 2017 - ; 0) Lời giải
Dựa vào bảng xét dấu của f ¢ ( x) ta có bảng biến thiên của hàm sồ f ¢( x)
Đặt t = x  2017 .
Ta có y = f ( x  2017)  2018x = f (t )  2018t - 2017.2018 = g (t ) .
g¢(t ) = f ¢(t )  2018 .
Dựa vào bảng biến thiên của hàm số f ¢( x) suy ra phương trình g¢(t ) có một nghiệm đơn
  (-;0) và một nghiệm kép t = 2 .
Ta có bảng biến thiên g (t )
Hàm số g (t ) đạt giá trị nhỏ nhất tại t =   -;0 . 0 ( )
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Suy ra hàm số y = f ( x  2017)  2018x đạt giá trị nhỏ nhất tại x mà 0
x  2017  -; 0 Û x  -; -2017 . 0 ( ) 0 ( )
Câu 85. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Cho hàm số f ( x) liên tục trên và có đồ
thị như hình vẽ bên. Bất phương trình f ( x) 3 2 2
x  2m  3x nghiệm đúng với mọi x  ( 1 - ;3) khi và chỉ khi A. m  10. - B. m  5. -
C. m  -3. D. m  2. - Hướng dẫn giải Ta có f ( x) 3 2
x m x Û f ( x) 3 2 2 2 3 2
 -x  3x  2m
Nhận xét minf ( x) = f (2) = -3 (-1;3) Đặt g ( x) 3 2
= -x  3x  2 m, x   (-1;3) x = 0 g¢( x) 2 = 3 - x  6 ,
x g¢( x) = 0 Û  x = 2  g (0) = 2 ; m g (- ) 1 = 4  2 ;
m g (3) = 2m và g (2) = 4  2m
 max g ( x) = g (2) = 4  2m (-1;3)
ycbt Û 2 min f ( x)  max g ( x) Û 6
-  2m  4 Û m  5 - (-1;3) ( 1 - ;3)
Câu 86. (KTNL GV BẮC GIANG NĂM 2018-2019) Cho hàm số f ( x) có đạo hàm trên  và có đồ thị
của hàm y = f ¢( x) được cho như hình vẽ. Biết rằng f ( 3
- )  f (0) = f (4)  f (- )
1 . Giá trị lớn nhất và giá trị nhỏ nhất của f ( x) trên đoạn  3 - ; 4 lần lượt là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. f (4) và f (-3) .
B. f (-3) và f (0) .
C. f (4) và f (0) .
D. f (2) và f (-3) . Lời giải Chọn B.
Dựa vào đồ thị của hàm số y = f ¢( x) ta có bảng biến thiên của hàm số y = f ( x) : x - -3 0 4  f ¢( x) - - 0  0 - f (4) f ( x) f ( 3 - ) f (0)
f ¢(0) = f ¢(4) = 0 nên x = 0 và x = 4 là hai điểm cực trị của y = f ( x) .
Từ bảng biến thiên ta có
min f (x) = f (0) , đồng thời f (- ) 1  f (0) . Do đó: -3;4 f ( 3
- )  f (0) = f (4)  f (- ) 1 Û f ( 3
- ) - f (4) = f (- )
1 - f (0)  0  f ( 3 - )  f (4) .
 max f (x) = f (-3) . Chọn B  3; - 4
Câu 87. Cho hàm số f ( x) có đạo hàm là f ¢( x) . Đồ thị của hàm số y = f ¢( x) được cho như hình vẽ dưới đây: Biết rằng f (- )
1  f (0)  f ( )
1  f (2) . Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f ( x) trên đoạn  1 - ; 2 lần lượt là: A. f ( ) 1 ; f (2) .
B. f (2) ; f (0) .
C. f (0) ; f (2) . D. f ( ) 1 ; f (- ) 1 . Lời giải
Từ đồ thị của hàm số y = f ¢( x) ta có bảng biến thiên của hàm số y = f ( x) trên đoạn  1 - ; 2 như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Nhận thấy
min f ( x) = f ( ) 1 -1;2 . f (- ) 1 f (2)
Để tìm max f ( x) ta so sánh và . -1;2
Theo giả thiết, f (- )
1  f (0)  f ( )
1  f (2) Û f (2) - f (- )
1  f (0) - f ( ) 1 .
Từ bảng biến thiên, ta có f (0) - f ( )
1  0 . Do đó f (2) - f (- )
1  0 Û f (2)  f (- ) 1 .
Hay max f ( x) = f (2) .  1; - 2
Dạng 7. Ứng dụng GTLN-GTNN vào bài toán đại số
Câu 88. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số m để
bất phương trình x  (  x)( - x) 2 6 2 8
x m -1 nghiệm đúng với mọi x -2;8.
A. m  16
B. m  15
C. m  8 D. 2 -  m  16 Lời giải Chọn B
Xét bất phương trình: x  (  x)( - x) 2 6 2 8
x m -1 ( )
1 , điều kiện x -2;8. 3 - x
Đặt t = (2  x)(8 - x) , x  2 - ;8. Ta có: t ' =
, t ' = 0 Û x = 3 (2  x)(8 - x) Bảng biến thiên
Suy ra t 0; 5 . Khi đó ( ) 1 trở thành: 2
t t -15  m (2) .
Xét hàm số f (t ) 2
= t t -15 , f '(t ) = 2t 1  0, t  0;  5 Bất phương trình ( )
1 nghiệm đúng với mọi x  2 - ; 
8 khi và chỉ khi (2) nghiệm đúng với mọi
t 0;5 Û max f (t )  m Û m  15 . 0;5
Câu 89. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm m để bất phương trình 4 x
m có nghiệm trên khoảng ( ; - ) 1 . x -1
A. m  5 . B. m  3 - .
C. m  1 . D. m  1 - Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 4 4 ( x - ) 1 - 4 x = 3(l)
f (x) = x   f '(x) = 1- = = 0   x -1 ( x - )2 1 ( x - )2 1 x = -1(tm)  Bảng biến thiên Vậy m  3 -
Câu 90. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Biết rằng tập nghiệm 6x - 4 của bất phương trình
2x  4 - 2 2 - x
là a;b . Khi đó giá trị của biểu thức 2 5 x 1
P = 3a - 2b bằng: A. 2 B. 4 C. -2 D. 1 Lời giải Chọn C
ĐK: -2  x  2 6x - 4
2x  4 - 4(2 - x) 6x - 4
Ta có: 2x  4 - 2 2 - x  Û -  0 2 2 5 x 1
2x  4  2 2 - x 5 x 1  1 1  Û (6x - 4) -   0 2
2x  4  2 2 - x  5 x 1  (6x 4) 2 5 x
1 ( 2x 4 2 2 x ) Û -  -   -  0( ) 1  
Xét hàm số f ( x) = 2x  4  2 2 - x với -2  x  2 1 1 2  2 
Ta có f ¢( x) = - = 0 Û x = - . Do đó f - = 2 6; f   (-2) = 4; f (2) = 2 2 2x  4 2 - x 3  3 
Suy ra 2 2  f ( x)  2 6 mà 2 5 x 1  5 nên 2
5 x 1 - ( 2x  4  2 2 - x )  0 2 ( )  2 
1 Û 6x - 4  0 Û x
. Kết hợp với điều kiện ta có tập nghiệm là ; 2 3  3   
Vậy P = 3a - 2b = 2 - .
Câu 91. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi s là tập hợp các giá trị
nguyên của tham số m 0; 2019 để bất phương trình
x - m  ( - x )3 2 2 1
 0 đúng với mọi x -1; 
1 . Số phần tử của tập s bằng A. 1. B. 2020 . C. 2019 . D. 2 . Lời giải 3 Đặt 2
t = 1- x , với x  -1;  1  t  0;  1 . Bất phương trình 2 x - m  ( 2 1- x )  0 ( ) 1 trở thành 3 2 3 2
t - t  1- m  0 Û m t - t  1 (2)
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Bất phương trình ( )
1 đúng với mọi x -1; 
1 khi và chỉ khi bất phương trình (2) nghiệm đúng
với mọi t 0; 
1 . Hay m max ( 3 2 t - t  ) 1 Û m  1. 0;  1
Mặt khác, m là số nguyên thuộc 0; 2019 nên m 1; 2;3;...; 201  9
Vậy có 2019 giá trị của m thỏa mãn bài toán.
Câu 92. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi M là giá trị lớn nhất của hàm số f ( x) 2 2
= 4 x - 4x  6  4x - x 1. Tính tích các nghiệm của phương trình f ( x) = M . A. 2 . B. 4 . C. -2 . D. -4 . Lời giải Đặt t = x - x  = ( x - )2 2 4 6 2  2  2 .
Khi đó, M = max f ( x) = max g (t ) , với g (t ) 2 = t -
 4t  7 trên  2;  .  )  2 ;  )
Có g (t ) = t -  t  = - (t - )2 2 4 7 11 2
 11, dấu đẳng thức xảy ra khi 2 t = 2 Û x - 4x  6 = 2  x = 2  2 2
Û x - 4x  2 = 0 Û  .  x = 2 - 2 
Như vây, M = max f ( x) = max g (t ) = 11 Û x = 2  2 , suy ra nghiệm của phương trình  2;  )
f ( x) = M là x = 2  2 .
Vậy tích các nghiệm của phương trình f ( x) = M bằng 2 . 2 2
Câu 93. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho x - xy y = 2 . Giá trị nhỏ 2 2
nhất của P = x xy y bằng: 2 1 1 A. B. C. D. 2 3 6 2 Lời giải Chọn A 2 2 2 2 P
x xy y
x xy y Xét = = 2 2 2 2
x - xy y +nếu y = 0 thì 2 x = 2 . Do đó 2
P = x = 2 suy ra min P = 2
+nếu y  0 ta chia tử mẫu cho 2 y ta được 2
x   x  1  2 2     P
x xy y y y     = = 2 2 2 2
x - xy y
x   x  1-      y y     x 2 P 1 t t Đặt t = , khi đó = y 2 2 1- t t 2 2 1 t t 2 - t  2 Xét f (t ) =  f ' t = 2 ( ) 1- t t ( 2 1- t t )2 t = 1
f '(t ) = 0 Û  t = 1 -  Bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 P 1 2 Khi đó min = do đó min P = . 2 3 3
Câu 94. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho x , y là các số thực thỏa mãn x y =
x -1  2 y  2 . Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của 2 2
P = x y  2( x  ) 1 ( y  )
1  8 4 - x - y . Tính giá trị M m A. 42 B. 41 C. 43 D. 44 Lời giải Chọn C 2
( x y)2 = ( x -1 2 y 1)  3(x y) Û 0  x y  3
P = x y  ( x  )( y  ) 
- x - y = ( x y)2 2 2 2 1 1 8 4
 2( x y)  2  8 4 - ( x y)
Đặt t = 4 - ( x y),t 1; 2. 2
Ta có: f (t ) = ( 2 - t )  ( 2 - t ) 4 2 4 2 4
 2  8t = t -10t  8t  26 . f ¢ (t ) 3
= 4t - 20t  8 t = 2 1; 2 t = 2  f ¢(t ) = 0 Û Û  t = 1 -  2  1; 2 2 t  2t -1 = 0   t = 1 - - 2  1; 2  f ( ) 1 = 25; f (2) = 18 .
Suy ra m = min f (t ) = f (2) = 18; M = max f (t ) = f ( ) 1 = 25 . 1;2 1;2
Vậy M m = 43 .
Câu 95. (KTNL GIA BÌNH NĂM 2018-2019) Cho bất phương trình m ( 2
x - 2 x  2  1)  x (2 - x)  0 .
Hỏi có bao nhiêu số nguyên m không nhỏ hơn 20 -
18 để bất phương trình đã cho có nghiệm x  0;1 3 ?   A. 2018 B. 2019 C. 2017 D. 2020 Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 2 Đặt 2
t = x - 2x  2 , ta có x  0;1 3  t 1; 2 . Vì t = x -2x  2 Û x( x -2) = t -2 .   2 t - 2
Bất phương trình đã cho trở thành m (t  ) 2
1  t - 2 Û m  ( ) 1 . t 1 2 t - 2 2 t  2t  2 1
Xét hàm số f (t ) = , t    1; 
2 . Ta có f ¢(t ) = = 1  0, t   1; 2 . 2 2 ( ) t 1 (t 1 ) (t  ) 1
Bất phương trình đã cho có nghiệm x  0;1 3 Û Bất phương trình ( ) 1 có nghiệm t   1;  2   2 Û m  . 3 2
Theo giả thiết m  20 -
18 nên ta có -2018  m
. Vậy có tất cả là 2019 số nguyên của m thỏa 3 yêu cầu bài toán.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66