Các dạng toán hệ thức lượng trong tam giác vuông Toán 9

PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Chương IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 11. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
A. KIẾN THỨC CẦN NHỚ
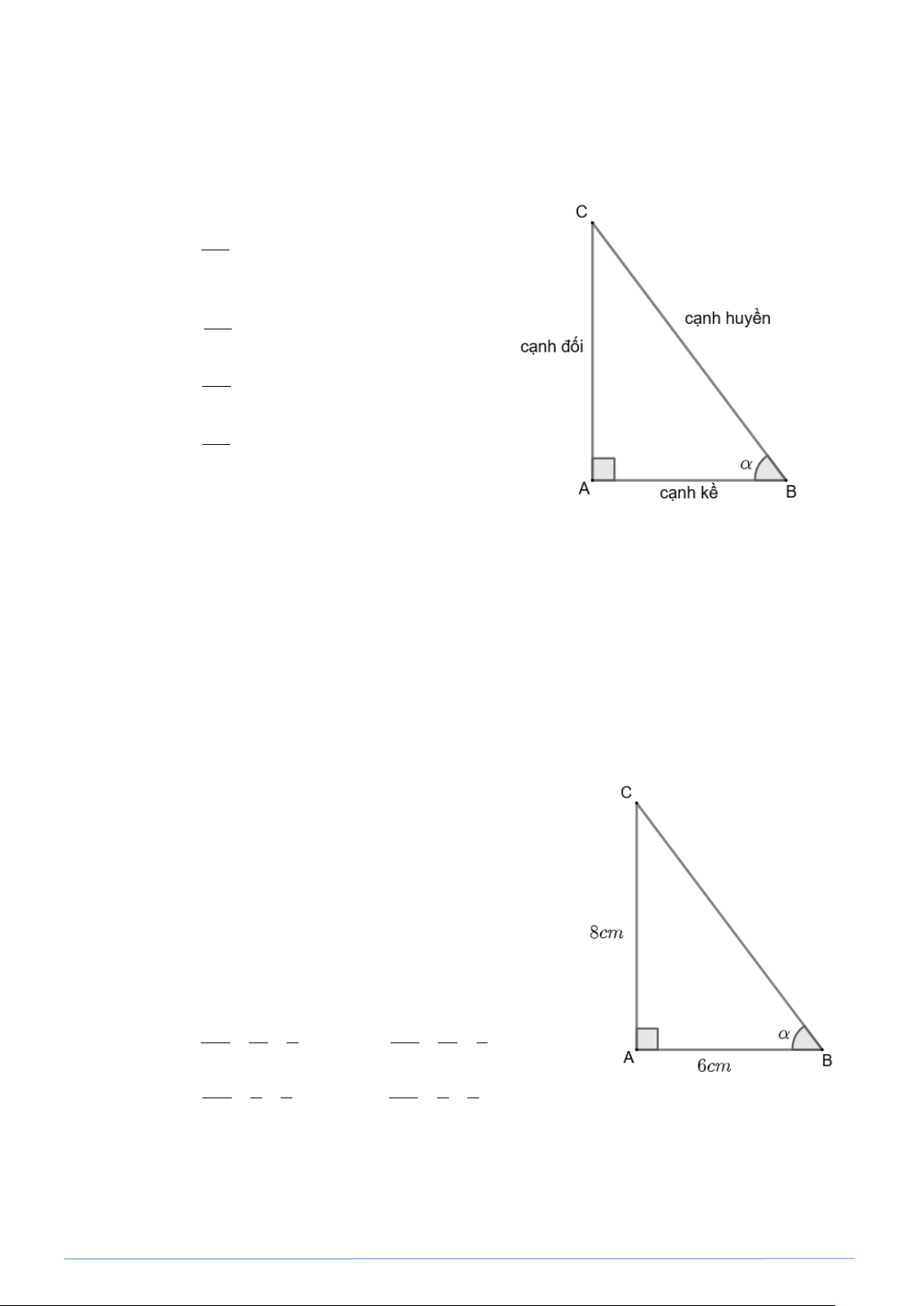
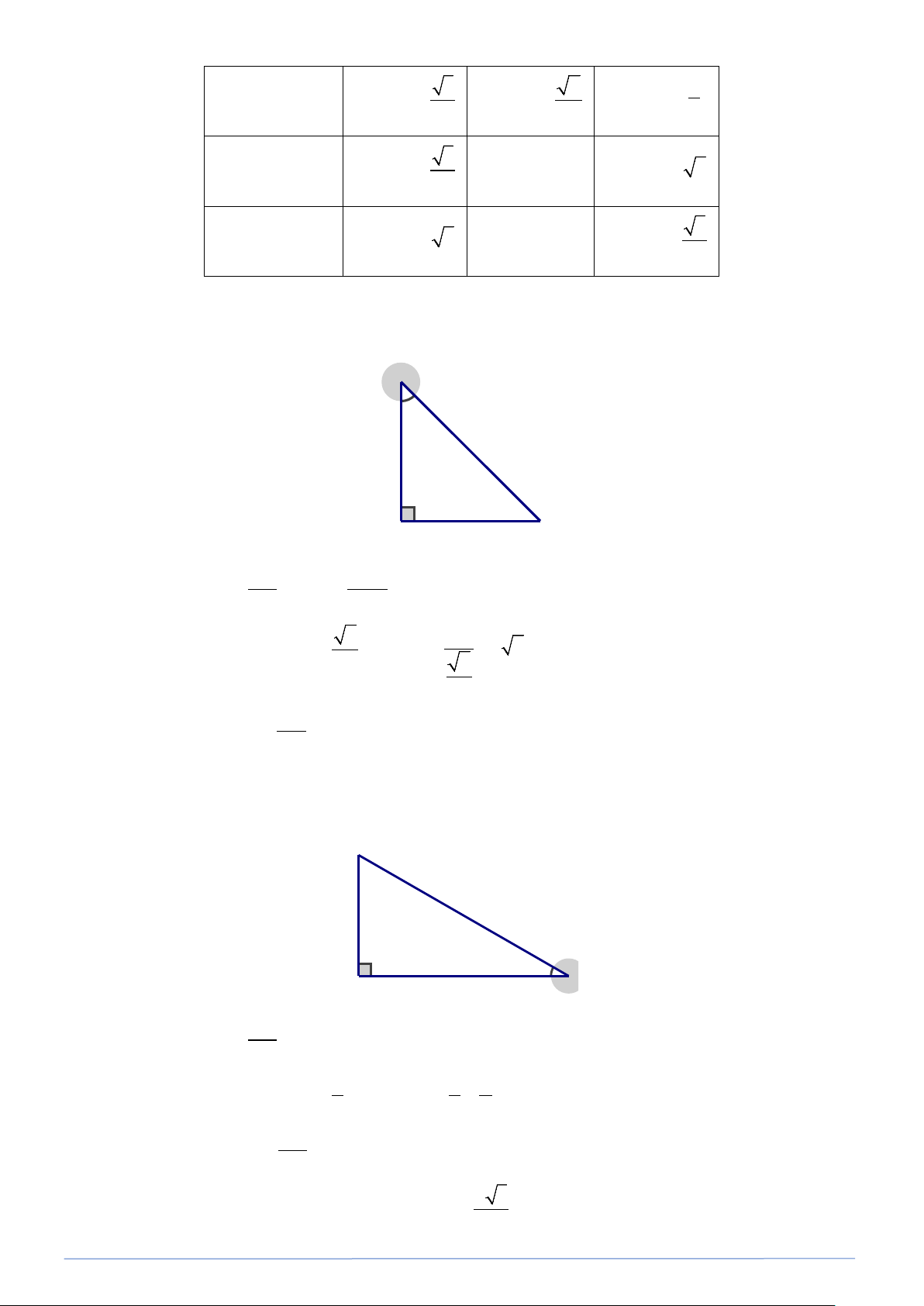
Cho góc nhọn α . Xét tam giác ABC vuông tại A , có góc nhọn bằng α (hình vẽ bên). Ta có: I. Định nghĩa AC sinα =
(tỉ số giữa cạnh đối và cạnh BC huyền) . AB cosα =
(tỉ số giữa cạnh kề và cạnh huyền) BC AC tanα =
(tỉ số giữa cạnh đối và cạnh kề) AB AB cotα =
(ti số giữa cạnh kề và cạnh đối) AC
Chú ý: 0 < sinα <1;0 < cosα <1.
II. Tỉ số lượng giác cưa hai góc phụ nhau sin (90° −α ) = cosα cos(90° −α ) = sinα tan (90° −α ) = cotα cot (90° −α ) = tanα
B. PHÂN LOẠI CÁC BÀI TẬP
I. Tính tỉ số lượng giác của một góc nhọn
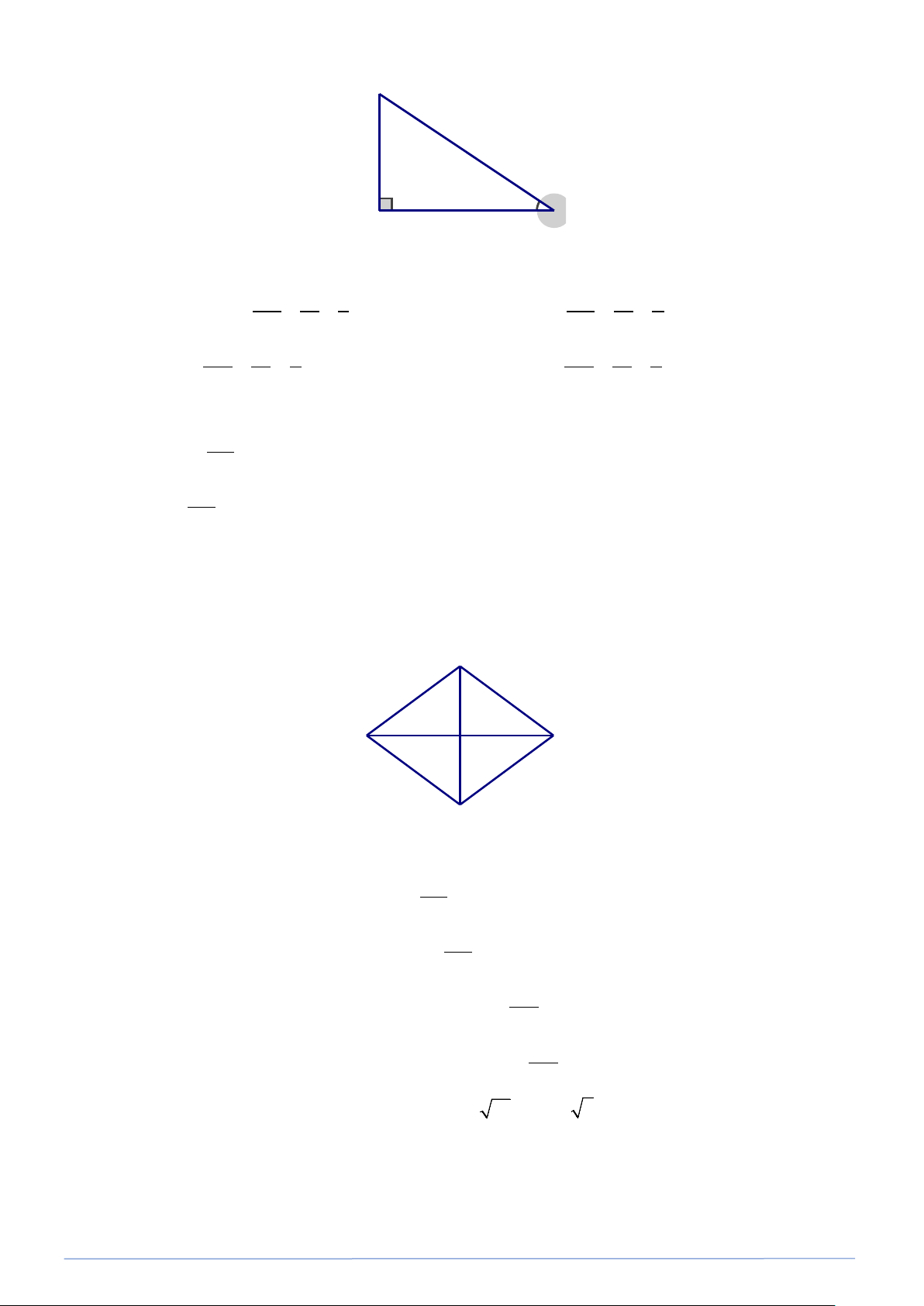
Bài toán 1. Cho tam giác ABC vuông tại A , có AB = 6 cm, AC = 8 cm . Hãy tính các tỉ số lượng giác
sinα,cosα, tanα,cotα với α = B . Lời giải Xét A
∆ BC vuông tại A co B = α(gt)
Theo định lí Pythagore, ta có: 2 2 2 2 2
BC = AB + AC = 6 + 8 =100 ⇒ BC =10( cm)
Theo định nghĩa của tỉ số lượng giác sin, cos, tan, cot, ta có: AC 8 4 sinα = = = ; AB 6 3 cosα = = = ; BC 10 5 BC 10 5 AC 8 4 tanα = = = ; AB 6 3 cotα = = = . AB 6 3 AC 8 4
Bài toán 2. Cho tam giác ABC vuông tại A , có AB =12, AC = 9, BC =15. Tính các tỉ số lượng giác
sinα, cosα, tanα, cotα với α = . B Lời giải
Trang: 1.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 C 15 9 α A 12 B Xét A
∆ BC vuông tại A có α = B (GT) Ta có: AC 9 3 sinα = = = ; AB 12 4 cosα = = = ; BC 15 5 BC 15 5 AC 9 3 tanα = = = ; AB 12 4 cotα = = = . AB 12 4 AC 9 3
Bài toán 3. Cho hình thoi ABCD có hai đường chéo cắt nhau tại điểm O (hình vẽ bên).
a) Tỉ số OB là sin của góc nhọn nào? AB
Tỉ số OB là cos của góc nhọn nào? BC
b) Viết tỉ số lượng giác của mỗi góc nhọn sau:  tan OCD,  cot OA . D Lời giải B O A C D
Ta có ABCD là hình thoi (GT) nên hai đường chéo AC và BD vuông góc với nhau tại O . a) Xét OA ∆
B vuông tại O nên tỉ số OB =  sin BA . O AB Tương tự OC ∆
B vuông tại O nên tỉ số OB =  cosCB . O BC b) Xét OC ∆
D vuông tại O nên tỉ số  tan OD OCD = . OC Tương tự OA ∆
D vuông tại O nên tỉ số  cot OA OAD = . OD
Bài toán 4. Cho tam giác ABC vuông tại B, có AB = 10, BC = 6 và góc nhọn A = β . Tính các tỉ số
lượng giác của góc nhọn β. Lời giải
Trang: 2.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 C 4 6 β B 10 A Xét A
∆ BC vuông tại B có α = B (GT).
Theo định lí Pythagore, ta có:
AC = BC + AB = ( )2 +( )2 2 2 2 6 10 =16 ⇒ AC = 4
Theo định lí của tỉ số lượng giác sin, cos, tan, cot. BC 6 AB 10 Ta có: sin β = = ; cos β = = ; AC 4 AC 4 BC 6 tan β = = ; AB 10 cot β = = . AB 10 BC 6
Bài toán 5. Cho tam giác ABC vuông cân tại ,
A có cạnh góc vuông bằng .
a Tính độ dài cạnh huyền
BC theo a rồi tính:
* Các tỉ số AB , AC . Từ đó suy ra sin 45 ,° os c 45 .° BC BC
* Các tỉ số AB , AC . Từ đó suy ra tan 45 ,° ot c 45 .° AC AB Lời giải B 45° a 45° A a C Xét A
∆ BC vuông cân tại A (GT)
Theo định lí Pythagore, ta có: 2 2 2 2 2 2
BC = AB + AC = a + a = 2a ⇒ BC = a 2. * Tỉ số AB a 1 2 = = = hay 2 sin C = . BC a 2 2 2 2
Tương tự tỉ số AC 2 = = cosC BC 2 Vậy 2 sin 45° = cos 45°= . 2
Trang: 3.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 * Tỉ số AB a = = 1 hay tan C =1. AC a
Tương tự tỉ số AC =1 hay cot C =1. AB Vậy tan 45° = cot 45°=1.
Bài toán 6. Cho tam giác đều ABC, có cạnh bằng 2a (xem hình vẽ).
a) Tính đường cao AH của tam giác ABC.
b) Tính sin 30 ,° cos30 ,° sin 60° và cos60 .°
c) Tính tan 30 ,° cot 30 ,° tan 60° và cot 60 .° Lời giải A 30° 2a 60° B H C a) A
∆ BC đều nên đường cao AH đồng thời cũng là đường phân giác của góc BAC .
Xét tam giác AHB vuông tại H có  BAH = 30° AB 2a BH = = = . a 2 2
Theo định lí Pythagore, ta có: 2 2 2
AB = AH + BH 2 2 2
⇒ AH = AB − BH = ( a)2 2 2 2 − a = 3a ⇒ AH = a 3. b) Ta có: BH a 1 sin 30° = sin BAH = = = . AB 2a 2 AH a 3 3 cos30° = cos BAH = = = . AB 2a 2 BH a 1 3 tan 30° = tan BAH = = = = . AH a 3 3 3 AH a 3 cot 30° = cot BAH = = = 3. BH a
Từ bài toán 5 và 6 ở trên, ta có bảng sau: α 30° 45° 60° sinα 1 2 3 2 2 2
Trang: 4.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 1 cosα 3 2 2 2 2 tanα 3 1 3 3 cotα 3 1 3 3
Bài toán 7. Cho tam giác ABC vuông tại A , có C = 45° và AB = c . Tính BC và AC theo .c Lời giải C 45° A c B Ta có sin AB AB C = ⇒ BC = BC sin C Theo bảng trên 2 c sin 45° = nên BC = = c 2 2 2 2 Tương tự cot AC C =
⇒ AC = AB ⋅cot C = c ⋅cot C = c ⋅1 = c AB
Bài toán 8. Cho tam giác ABC vuông tại A , có C = 30° và BC = .
a Tính các cạnh AB và AC theo . a Lời giải B a 30° A C Ta có sin AB C =
⇒ AB = BC ⋅sin C = a ⋅sin 30° BC Theo bảng trên 1 sin 30° = nên 1 a AB = a ⋅ = 2 2 2 Tương tự cos AC C = BC a 3
⇒ AC = BC ⋅cosC = a ⋅cosC = a ⋅cos30° = . 2
Trang: 5.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
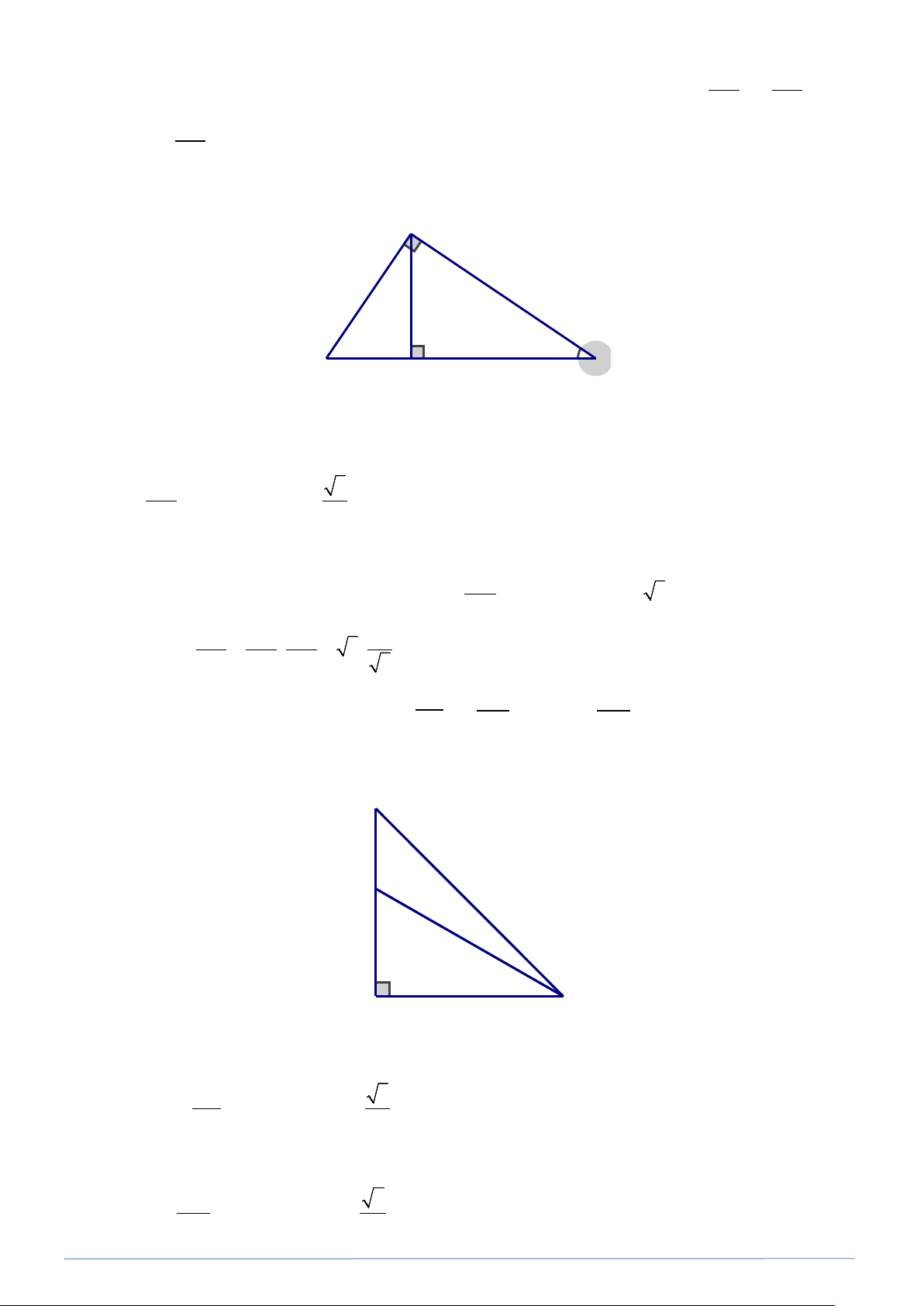
Bài toán 9. Cho tam giác ABC vuông tại A , có B = 30° , đường cao AH . Tính tỉ số AH và AH , từ đó BH CH tìm BH . CH Lời giải A a 30° C H B
Ta có AH ⊥ BC. Xét A
∆ HB vuông tại H, có B = 30° (GT) AH 3 = tan B = tan 30° = . BH 3 A
∆ BC vuông tại A có B = 30° (GT) ⇒ C = 90° − 30° = 60° Xét A
∆ HC vuông tại H, có C = 60° nên AH = tan C = tan 60° = 3. CH Do đó BH AH BH 3 = ⋅ = 3 ⋅ = 3. CH CH AH 3
Bài toán 10. Trong hình vẽ bên, hãy tính tỉ số PN và PN , từ đó tìm PQ . PQ PM PM Lời giải M 45° Q 60° N P Xét QN ∆
P vuông tại N, có Q = 60° (GT) Ta có NP 3 = sin Q = sin 60° = . PQ 2 Xét MN ∆
P vuông tại N, có  M = 45° PN 2 nên = sin M = sin 45° = . PM 2
Trang: 6.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Vậy PQ PQ PN 2 2 2 6 = ⋅ = ⋅ = = . PM PN PM 3 2 3 3
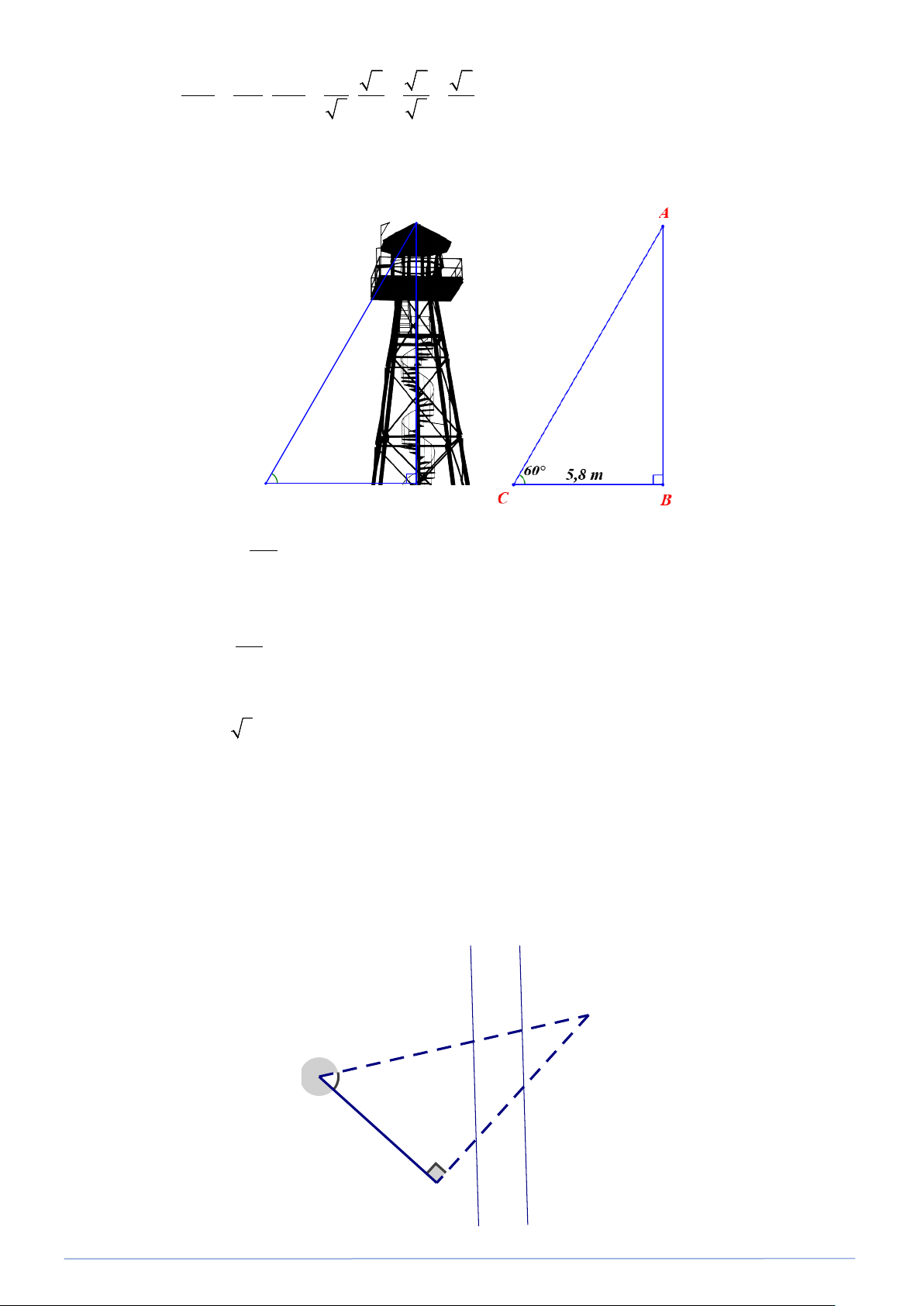
Bài toán 11. Tìm chiều cao của tháp canh trong hình vẽ bên (kết quả làm tròn đến hàng phần trăm). Lời giải A 60° 5,8 m C B Ta có tan AB C = BC
mà C = 60 ,° BC = 5,8 (GT) hay tan 60 AB ° = 5,8
⇒ AB = 5,8⋅ tan 60° AB = 5,8⋅ 3
⇒ AB ≈10,05(m)
Bài toán 12. Để tính khoảng cách giữa hai địa điểm ,
A B mà không đo trược tiếp được. Chẳng hạn A và
B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho A
∆ BC vuông tại B . Ở bên bờ sông chứa B người ta đo được 
ACB = 55° và BC = 70 m , với các
dữ liệu đó khoảng cách AB có tính được không và nếu được bạn hãy tính AB . Lời giải A C 70 B
Trang: 7.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Ta có A
∆ BC vuông tại B , có  ACB = 55°
và BC = 70 m (GT)
nên AB = tan C ⇒ AB = BC ⋅ tan C BC
= 70.tan 55° ≈ 99,97(m)
Trả lời: Khoảng cách AB tính được AB ≈ 99,97(m)
Bài toán 13. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45 .°
sin 65 ,° cos75 ,° tan85 ,° cot 71 .° Lời giải
Ta có: sin 65° = cos(90° − 65°) = cos 25 .°
cos75° = sin (90° − 75°) = sin15 .°
tan85° = cot (90° −85°) = cot 5 .°
cot 71° = tan (90° − 71°) = tan19 .°
Bài toán 14. Cho tam giác ABC vuông tại A , biết AB = 3c , m BC = 5c .
m Tính các tỉ số lượng giác của
hai góc B và C Lời giải A 4 3 B 5 C
Áp dụng định lý Pythagore ta có 2 2 2 2 2
AC = BC − AB = 5 − 3 =16 ⇒ AC = 4cm 4 4
sin B = ⇒ cosC = (Vì B và C là hai góc phụ nhau) 5 5 3 3
cos B = ⇒ sin C = 5 5 4 4
tan B = ⇒ cot C = 3 3 3 3
cot B = ⇒ tan C = . 4 4
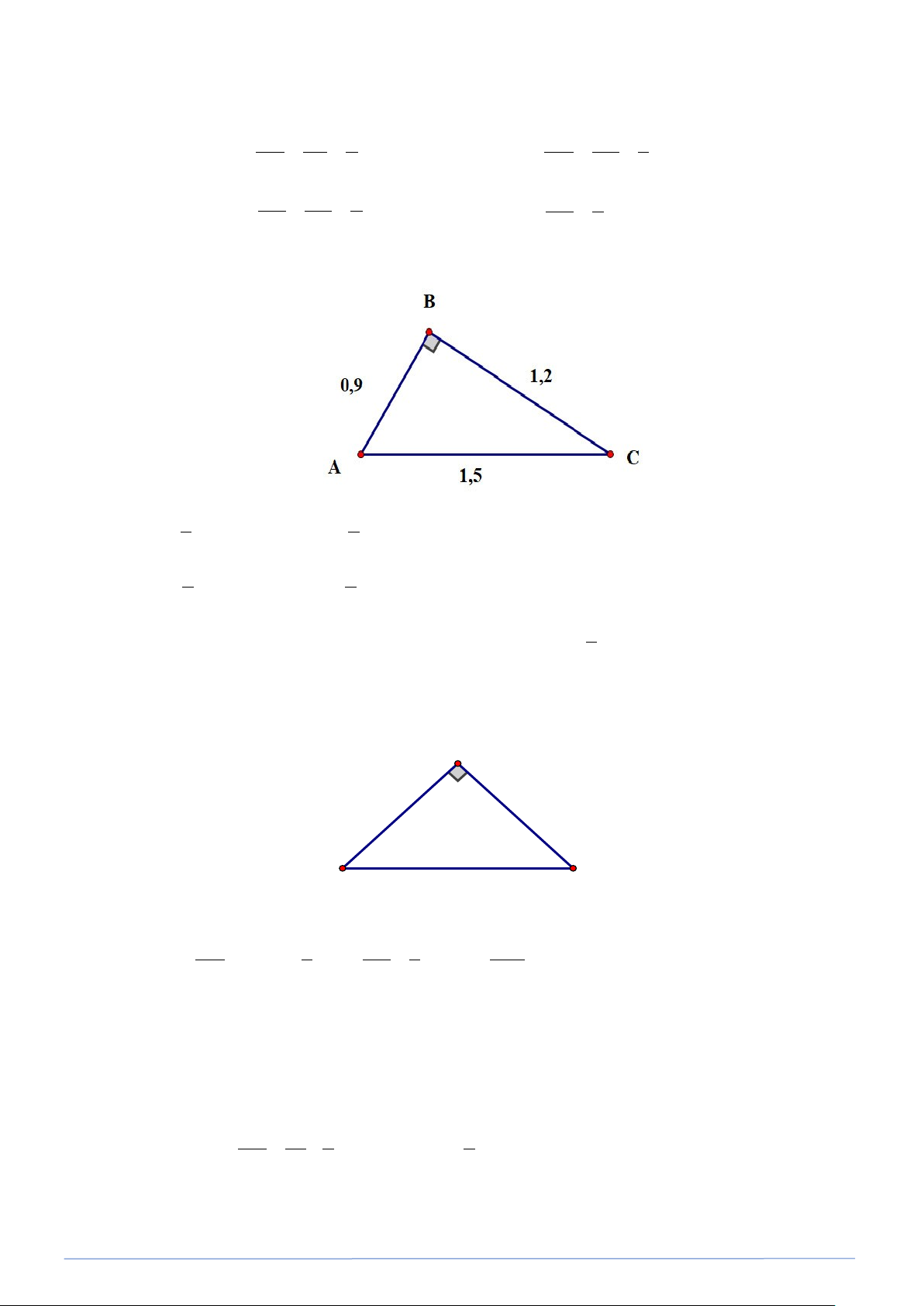
Bài toán 15. Cho tam giác ABC vuông tại B, trong đó AB = 0,9cm, BC =1,2c .
m Tính các tỉ số lượng
giác của góc A đó suy ra tỉ số lượng giác của góc C. Lời giải Ta có: 2 2 2
AC = AB + BC (định lý Pythagore)
Trang: 8.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 2 2 2 AC = 0,9 +1,2 = 2,25 ⇒ AC =1,5cm BC 1,2 4 sin A = = = ; AB 0,9 3 cos A = = = AC 1,5 5 AC 1,5 5 BC 1,2 4 tan A = = = AB 3 cot A = = AB 0,9 3 BC 4
Vì A và C là hai góc phụ nhau , ta có 3 sin C = 4 cosC = ; 5 5 3 tan C = 4 cot C = 4 3
Bài toán 16. Cho tam giác ABC vuông tại A có 3 AC =12c ,
m cosC = ..Tính tan B,cot . B 5 Lời giải A 21 C B Ta có AC 3 = cosC = hay 21 3 21.5 = ⇒ BC = = 35(cm) BC 5 BC 5 3
Áp dụng định lý Pythagore : 2 2 2
AB = BC − AC 2 2 = 35 − 21 = 784
⇒ AB = 28(cm) Vậy AC 21 3 tan B = = − và 4 ABC cot B = . AB 28 4 3
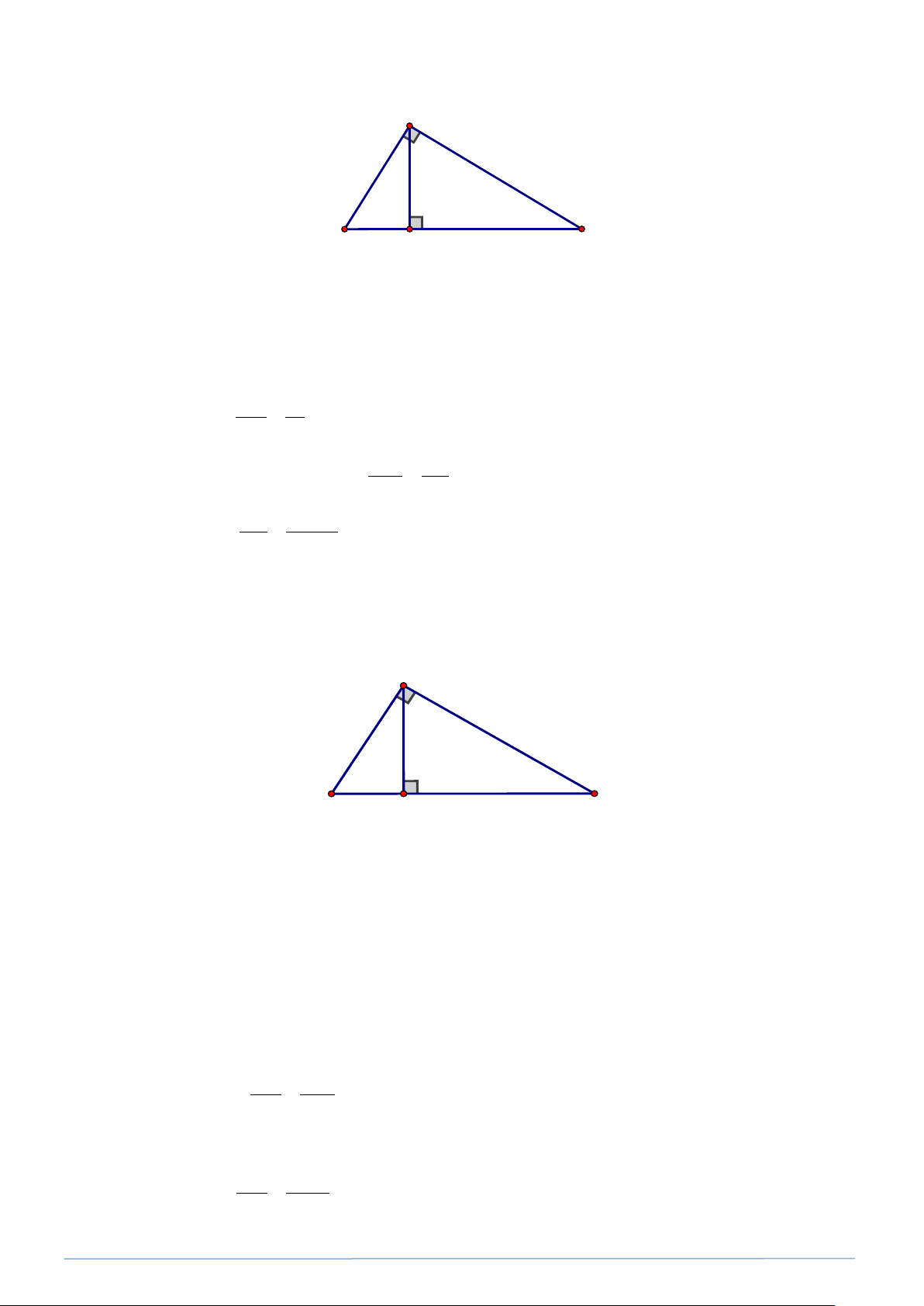
Bài toán 17. Cho tam giác ABC vuông tại A , đường cao AH . Biết AB =17, BH = 8. Tìm sin B,sinC.
(Kết quả làm tròn đến chữ số thập phân thứ hai).
Trang: 9.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Lời giải A 17 15 B H C
Xét tam giác AHB vuông tại H
Theo định lý Pythagore , tao có : 2 2 2 2 2
AH = AB − BH =17 −8 = 225 ⇒ AH =15 Vậy AH 15 sin B = = ≈ 0,88 AB 17 2 2 Ta có 2 AB 17
AB = BH.BC ⇒ BC = = = 36,125. BH 8 Vậy AB 17 Sin C = = ≈ 0,47. BC 36,125
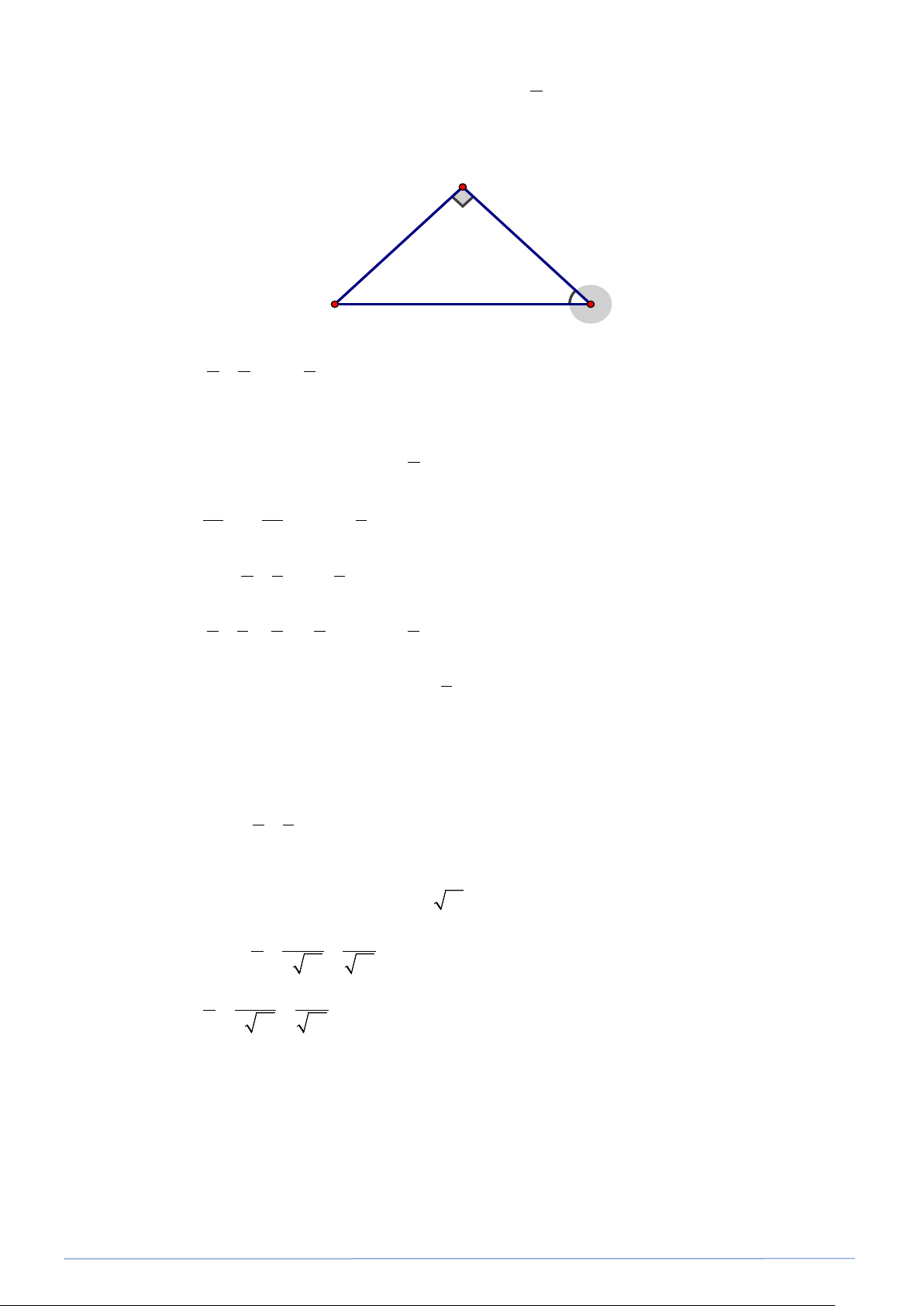
Bài toán 18. Cho tam giác ABC vuông tại A , đường cao AH . Biết HB = 4, HC = 9. Tính sin B,sinC.
(Kết quả làm tròn đến chữ số thập phân thứ hai). Lời giải A 6 B 4 H 9 C Ta có A
∆ BC vuông tại A có đường cao AH
Áp dụng hệ thức 2
h = b .′c′ , ta có : 2 AH = .
HB HC = 4.9 = 36 ⇒ AH = 6 Theo định lý Pythagore: 2 2 2
AB = AH + HB 2 2 = 6 + 4 = 52 ⇒ AB ≈ 7,21 AH 6 Do đó sin B = ≈
≈ 0,83. Lại có BC = BH + HC = 4 + 9 =13 AB 7,21 Ta có 2 2 2 2
AC = BC − AB =13 −52 −117 ⇒ AC ≈10,82 AH 6 Vậy sin C = ≈ ≈ 0,55. AC 10,82
Trang: 10.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Bài toán 19. Cho tam giác ABC vuông tại A ,  4
C = α,cosα = . Hãy tính sinα, tanα,cotα. 5 Lời giải A c b α B a C 4 b 4 cosα = = ⇒ b = . a 5 a 5
Theo định lý Pythagore, ta có: 2 2 2 2 2 2 2 2  4 a b c c a b a a = + ⇒ = − = −  5    2 16 2 9 2 3 = a − a = a ⇒ c = . a 25 25 5 Vậy c 3 3
sinα = = a : a = a 5 5 c 3 4 3 4
tanα = = a : a = ⇒ cotα = . b 5 5 4 3
Bài toán 20. Cho hình vẽ như bài 10, cho 1
tanα = . Tính sinα,cosα, (Kết quả làm tròn đến chữ số thập 3 phân thứ hai). Lời giải (Xem hình bài 19). Ta có c 1
tanα = = ⇒ b = 3c b 3
Theo định lý Pythagore, ta có:
a = b + c = ( c)2 2 2 2 2 2 3
+ c =10c ⇒ a = c 10 Do đó c c 1 sinα = = = ≈ 0.32 a c 10 10 b 3c 3 cosα = = = ≈ 0,95 a c 10 10
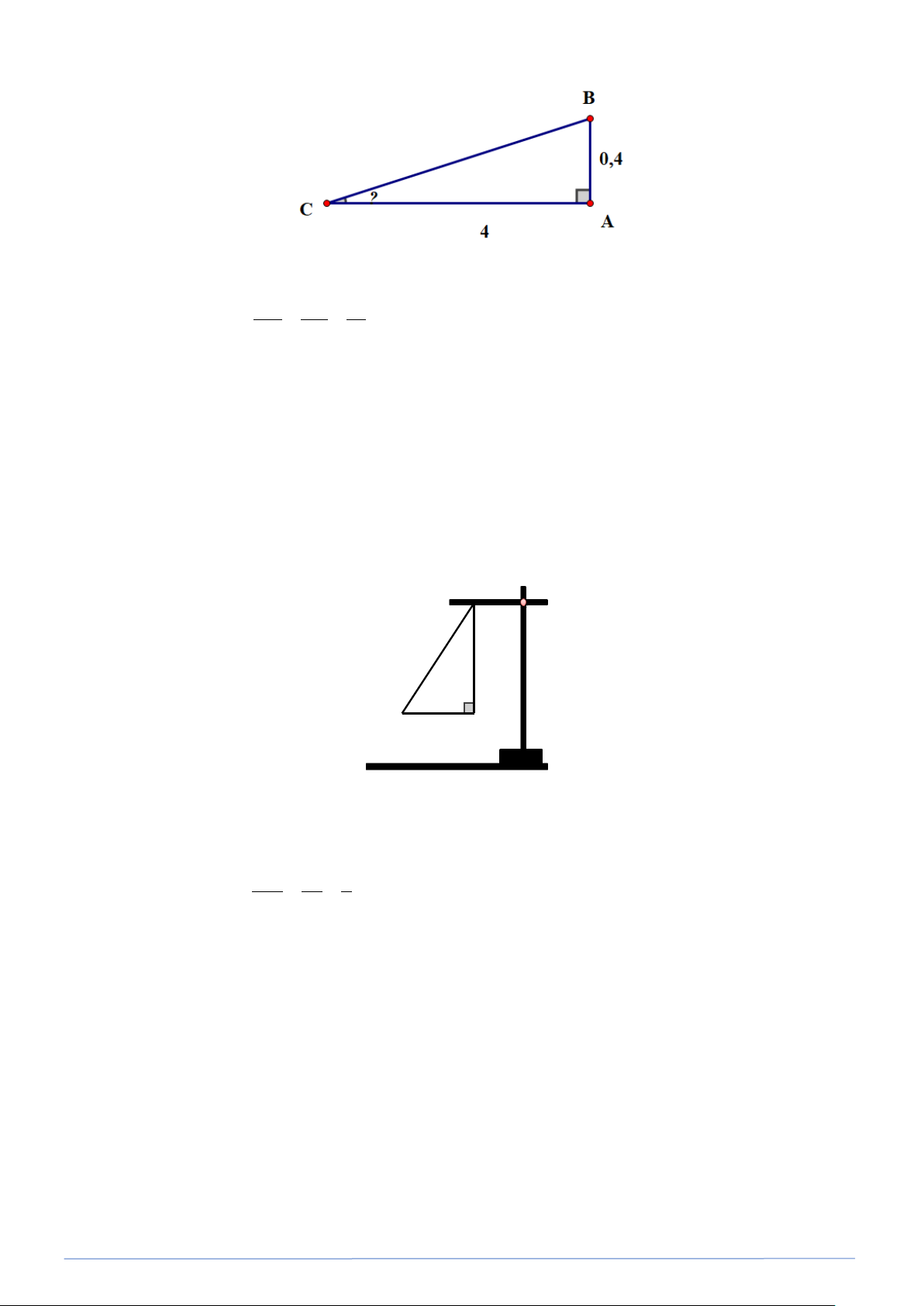
Bài toán 21. Trong các tòa nhà trung cư , người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc
dốc bé hơn 6°. Hãy tính góc dốc , biết rằng đoạn dốc vào sảnh nhà dài 4m , độ cao của đỉnh dốc bằng 0,4m Lời giải
Trang: 11.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 A
∆ BC vuông tại A có AC = 4 , m AB = 0,4m AB 0,4 1 Ta có tan C = = = AC 4 10 ⇒ C ≈ 5 42 ° ′.
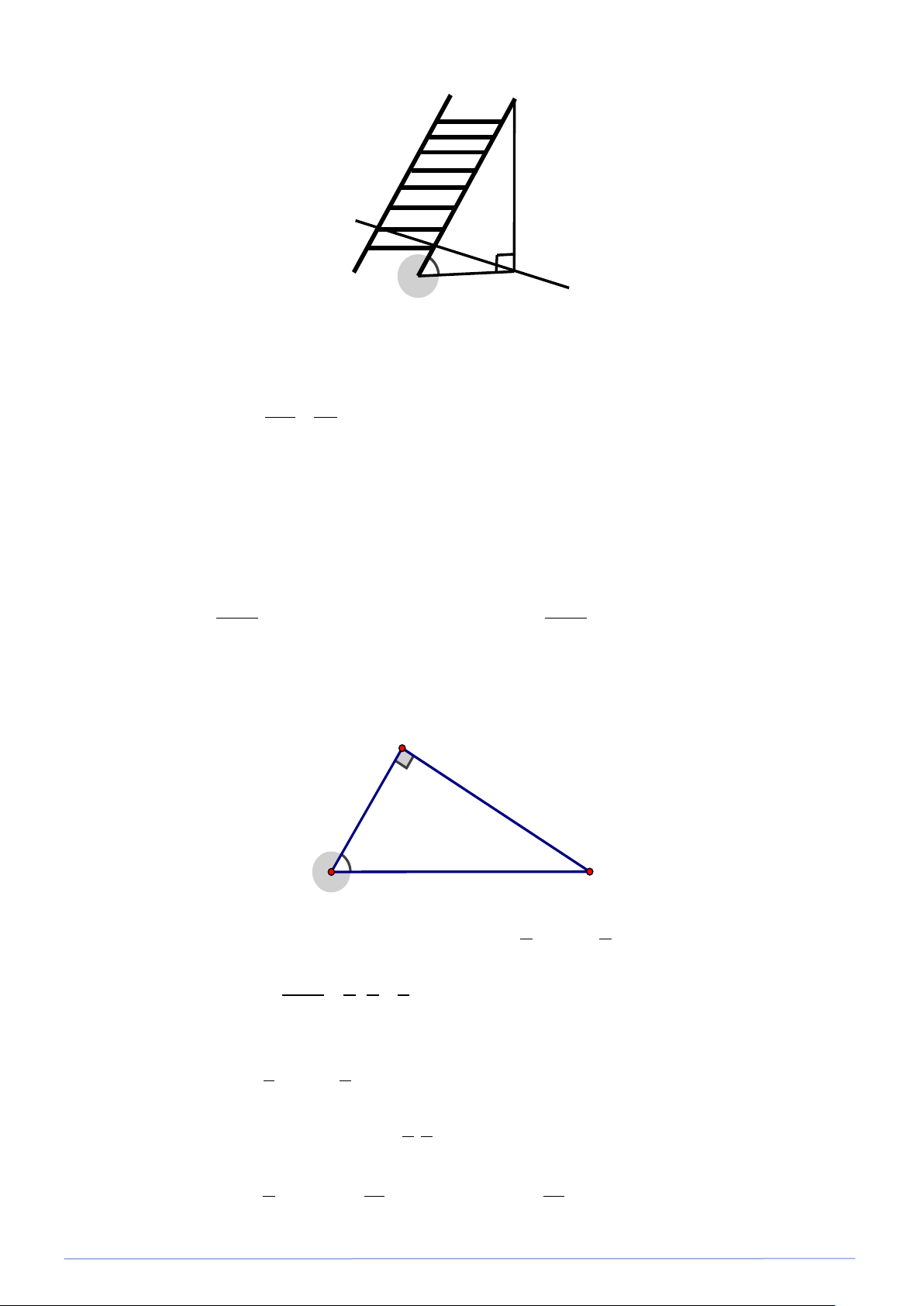
Bài toán 22. Treo quả cầu kim loại vào giá thí nghiệm bằng sợi dây mảnh nhẹ không dãn . Khi quả cầu
đứng yên tại vị trí cân bằng , dây treo có phương thẳng đứng . Kéo quả cầu khỏi vị trí cân bằng
một đoạn nhỏ rồi buông ra thì quả cầu sẽ chuyển động qua lại quanh vị trí cân bằng . Khi kéo quả
cầu khỏi vị trí cân bằng , giả sử tâm A của quả cầu cách B một khoảng AB = 60cm và cách vị trí
cân bằng một khoảng AH = 20cm ( hình vẽ ). Tính số đo góc α tạo bởi dây và vị trí cân bằng(
Làm tròn kết quả đến hàng đơn vị của độ ) . Lời giải B 60cm A 20cm H
Xét tam giác AHB vuông tại H có AH = 20c , m AB = 60cm.
Gọi α là góc tạo bởi dây AB và vị trí cân bằng ( Xem hình vẽ  ABH là α ) Ta có AH 20 1 sinα = = = ⇒ α ≈19° AB 60 3 Vâỵ α ≈19°.
Bài toán 23. Hình vẽ bên mô tả một chiếc thang có chiều dài AB = 4m được đặt dựa vào tường ,
khoảng cách từ chân thang đến chân tường là BH =1,5 .
m Tính góc tạo bởi cạnh AB và phương
nằm ngang trên mặt đất ( Làm tròn kết quả đến hàng đơn vị của độ ) . Lời giải
Trang: 12.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 A 4 α H B 1,5
Gọi α là góc tạo bởi cạnh AB và phương nằm ngang trên mặt đất ( góc  ABH ).
Xét tam giác AHB vuông tại H có BH =1,5 ,
m AB = 4m. Ta có : BH 1,5 cosα = = = 0,375 . AB 4 Do đó α ≈ 68°
Vậy góc tạo bởi cạnh AB và phương nằm ngang trên mặt đất khoảng 68°
II. Chứng minh các hệ thức lượng giác
Bài toán 24. Hãy sử dụng định nghĩa các tỷ số lượng giác của một góc nhọn để chứng minh : Với góc nhọn α tùy ý , ta có α α a) sin tanα = b) cos cotα = cosα sinα c) tanα.cotα =1 d) 2 2 sin α + cos α =1. Lời giải B b c α A a C
a) Theo định nghĩa tỷ số lượng giác ta có : sin b α = ;cos c α = a a α
Biến đổi vế phải : sin b = : c b = = tanα ( đpcm ) cosα a a c
b) Chứng minh tương tự câu a. c)Ta có tan b α = ;cot c α = c b
Khi đó ta có vế trái : tanα.cot b α = . c =1 ( đpcm ) c b 2 2 d)Ta có b 2 sinα = ⇒ sin b α = , tương tự 2 cos c α = 2 a a 2 a
Trang: 13.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 2 2 2 2 2 2 2 sin α cos b c b c a α + ⇒ + = + = = =1 ( đpcm ) 2 2 2 2 a a a a
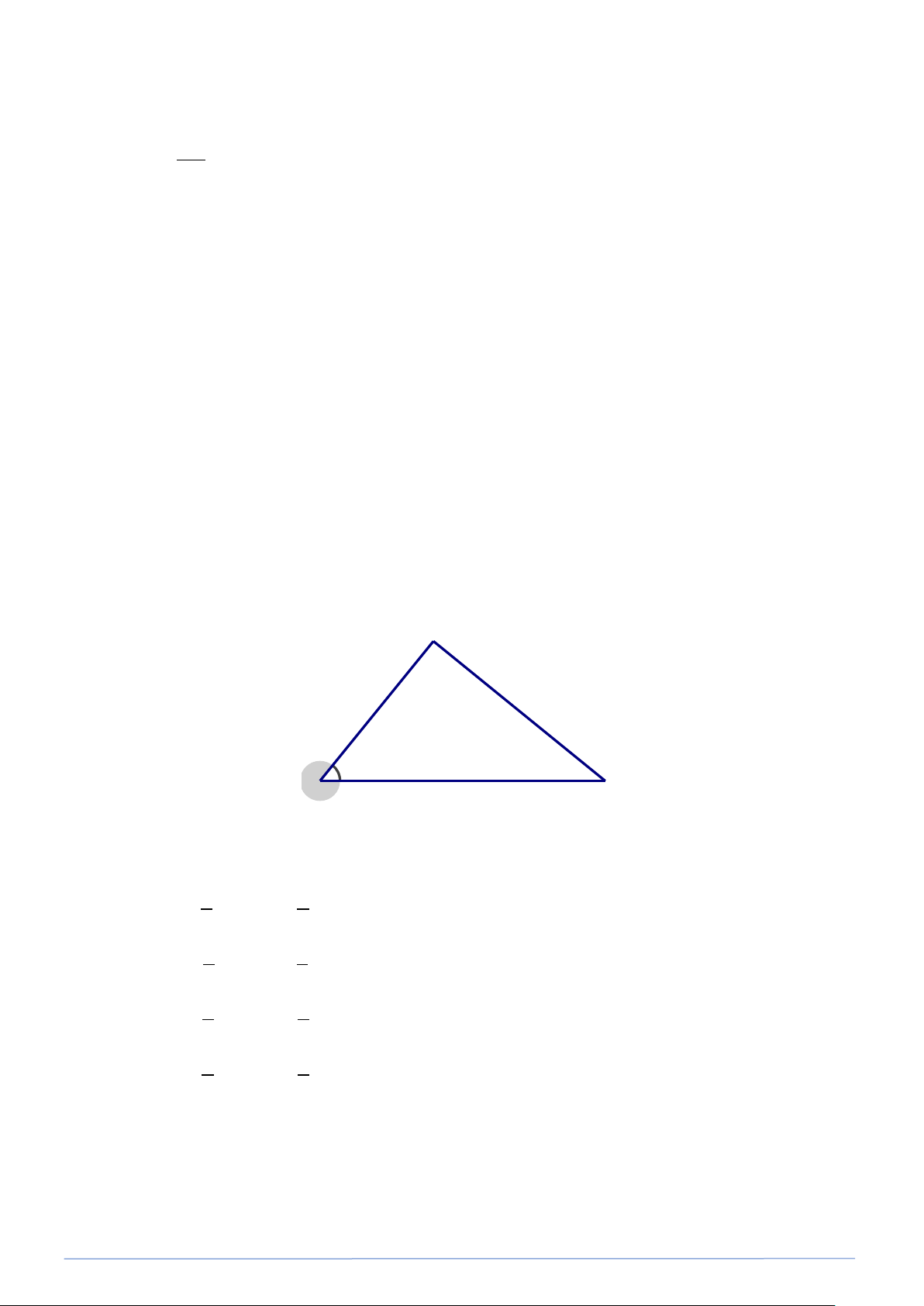
Bài toán 25. Cho tam giác ABC vuông tại A . Chứng minh rằng AC sin B = . AB sin C Lời giải A B C Ta có sin AC = ;sin AB B C = BC BC Vế phải : sin B AC = : AB AC = ( đpcm ) sin C BC BC AB
Bài toán 26. Cho tam giác ABC vuông tại A , và B = α . chứng minh rằng: a) 2 1 1+ tan α = b) 2 1 1+ cot α = 2 cos α 2 sin α Lời giải A α B C
a)Theo định nghĩa tỷ số lượng giác ta có 2 AC 2 tanα = ⇒ tan AC α = 2 AB AB 2 2 2 Vế trái 2 1+ tan α =1 AC AB + AC + = 2 2 AB AB 2 BC 1 1 = = ( đpcm ) 2 2 2 AB  AB  cos α  BC    2
b) Chứng minh tương tự , ta có AB 2 cotα = ⇒ cot AB α = 2 AC AC 2 Vế trái 2 1+ cot α =1 AB + 2 AC
Bài toán 27. Cho góc nhọnα . Hãy rút gọn các biểu thức sau:
Trang: 14.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 a) A = ( α + α )2 + ( 2 2 sin cos sin α − cos α )2 b) 6 6 2 2
B = sin α + cos α + 3sin α.cos α
Hướng dẫn: Sử dụng hằng đẳng thức ( ± )2
A B để khai triển rồi áp dụng hệ thức 2 2 sin α + cos α =1 ( Chứng minh ở bài 32) Lời giải a) A = ( α + α )2 + ( 2 2 sin cos sin α − cos α )2 = ( 2 2 α + α ) + α α + ( 2 2 sin cos 2sin cos
sin α + cos α ) − 2sinα cosα = 1+1 = 2 b) 6 6 2 2
B = sin α + cos α + 3sin α.cos α = ( α )3 +( α )3 2 2 2 2 + α α ( 2 2 sin cos 3sin cos sin α + cos α ) = ( α )3 +( α )3 2 2 4 2 2 4 sin cos
+ 3sin α cos α + 3sin α cos α = ( α + α )3 2 2 3 sin cos =1 =1.
Bài toán 28. Cho góc nhọnα . Chứng tỏ rằng giá trị của biểu thức sau không phụ thuộc vào góc nhọn α M = ( α + α )2 −( α − α )2 tan cot cot tan . Lời giải M = ( α + α )2 −( α − α )2 tan cot cot tan
= (tanα + cotα + cotα − tanα (tanα + cotα )−(cotα − tanα ))
= 2cotα [tanα + cotα − cotα + tanα]
= 2cotα.2 tanα = 4cotα.tanα = 4
Bài toán 29 . Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào góc α (0° < α < 90°) . ( α − α )2 −( α + α )2 cos sin cos sin cosα.sinα Lời giải ( α − α )2 −( α + α )2 cos sin cos sin Ta có cosα.sinα 2 2 α − sα α + α − ( 2 2 cos 2cos sin sin
cos α + 2sinα cosα + sin α ) = cosα.sinα − α α − − α α 1 2cos sin 1 2sin cos = cosα sinα − α 4cos sα sin = = 4 − cosα sinα
Chứng tỏ biểu thức không phụ thuộc vào góc α
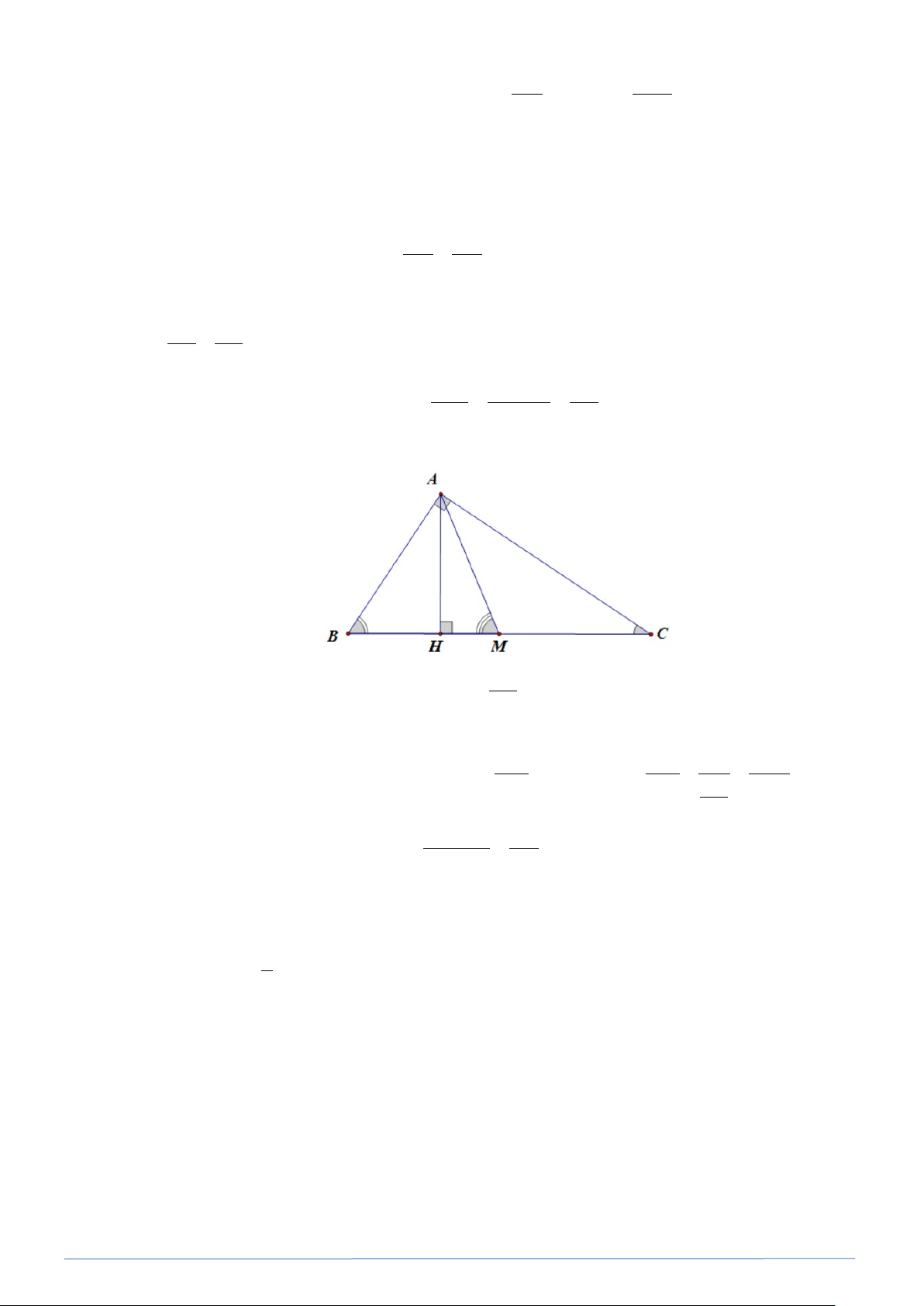
Bài toán 30. Cho tam giác nhọn ABC có BC = ; a CA = ;
b AB = c . Chứng minh rằng :
Trang: 15.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 a b c = =
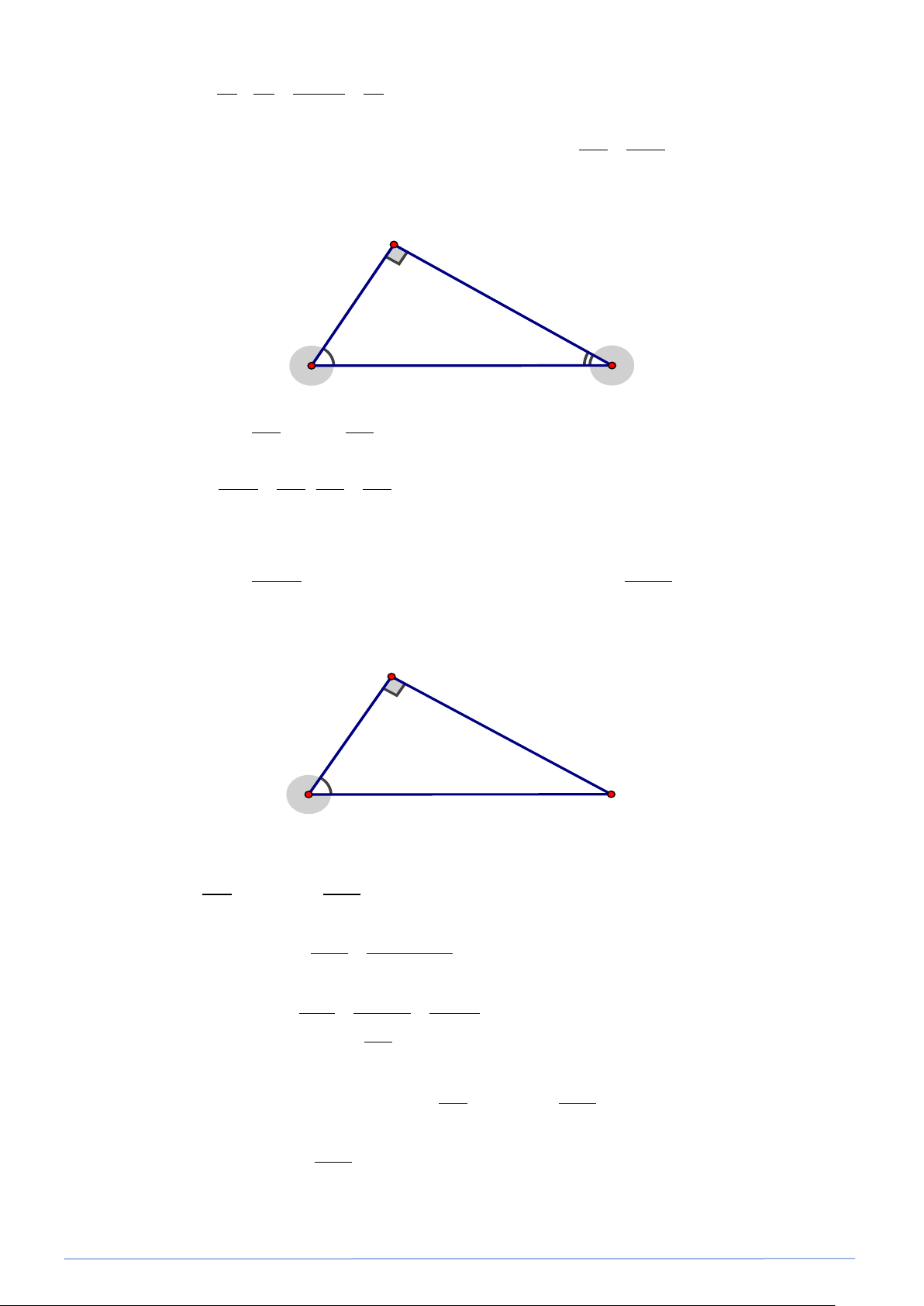
sin A sin B sin C Lời giải
Kẻ đường cao AH ta có : AH AH sin B = ;sin C = AB AC sin B AH ⇒ = : AH AC b = = sin C AB AC AB c b c ⇒ = . sin B sin C Tương tự : a b = sin A sin B Do đó : a b c = = ( đpcm ). sin A sin B sin C
Bài toán 31. Cho tam giác nhọn ABC . Chứng minh rằng : 1 S = AB ⋅ AC ⋅ A ABC sin 2 Lời giải Vẽ CH ⊥ AB (H ∈AB) Ta có : CH = AC⋅sin A Do đó : 1 S = AB ⋅ AC ⋅ A . ABC sin 2
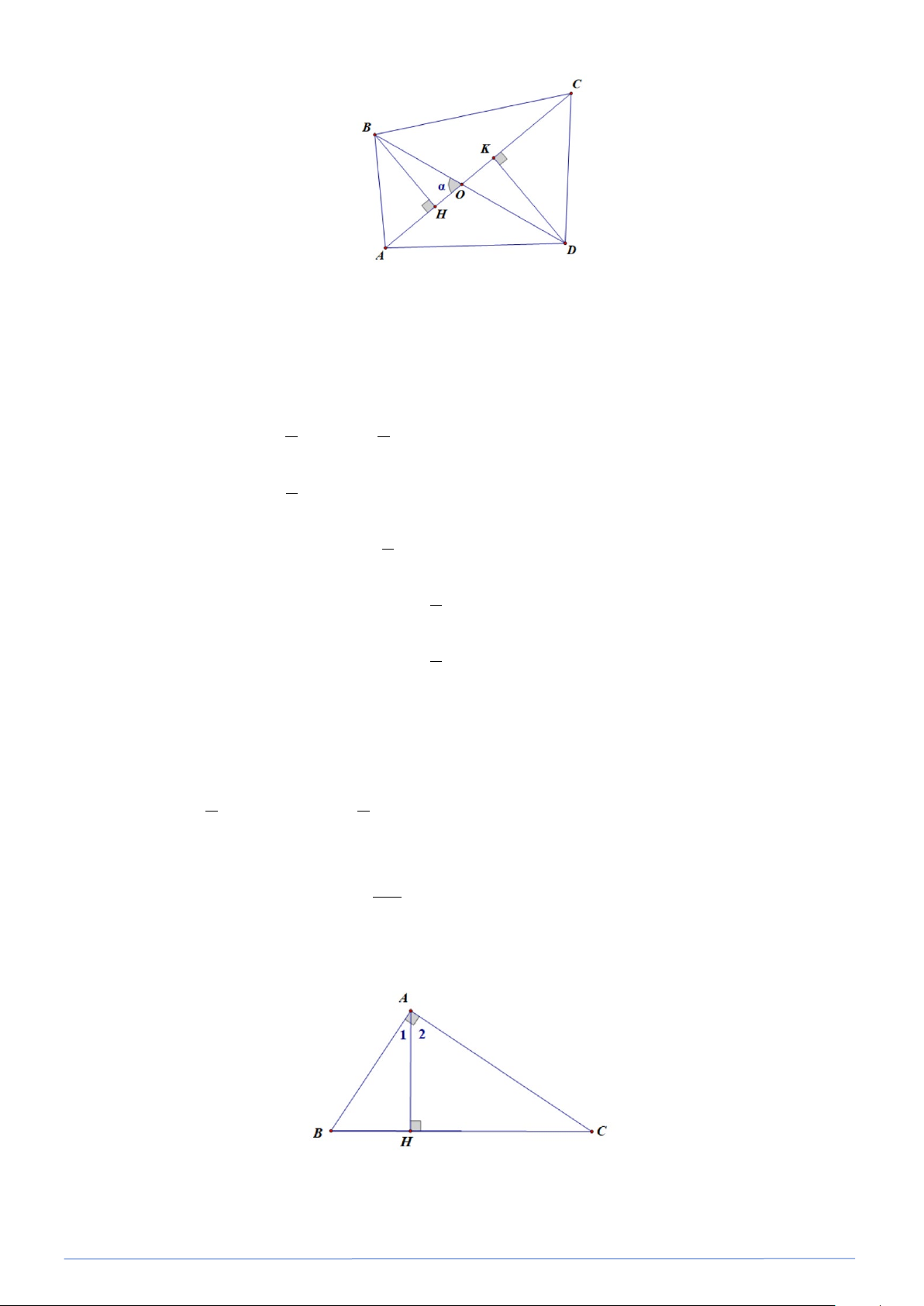
Bài toán 32. Cho α là góc nhọn tạo bởi hai đường chéo AC và BD của tứ giác ABCD . Chứng minh rằng : 1 S = AC⋅BDsinα . ABCD 2 Lời giải
Trang: 16.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9
Gọi O là giao điểm hai đường chéo AC và BD . Kẻ BH ⊥ AC,DK ⊥ AC.
Các tam giác vuông BHO và DKO có : BH = OB⋅sinα và DK = OD⋅sinα (1) Ta có : S = S + S ABCD ABC ADC 1 1 = AC⋅BH + AC⋅DK 2 2 1 = AC(BH + DK) (2) 2 Thay (1) và (2) , ta có : 1 S
= AC⋅(OB⋅sinα + OD⋅sinα) ABCD 2 1 = AC(OB + OD)sinα 2 1 = AC⋅BD⋅sinα 2
Áp dụng : Cho tứ giác ABCD , hai đường chéo AC và BD cắt nhau tại O , biết  AOB 60° =
; AC = 4,2 cm ;BD = 6,5 cm . Tính diện tích tứ giác ABCD .
Hướng dẫn : Sử dụng ngay kết quả của bài toán trên ta có : 1 ° 1 ° 2 S
= AC⋅BD⋅sin 60 = ⋅4,2⋅6,5⋅sin 60 ≈11,824 cm ABCD 2 2
Bài toán 33. Cho tam giác ABC vuông tại A . đường cao AH . a) Chứng minh rằng : 2 HC sin B = . BC
b) Chứng minh rằng : sin 2C = 2sin C ⋅cosC Lời giải
a) Xét tam giác vuông AHB
Trang: 17.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 2
Theo định nghĩa tỷ số lượng giác , ta có : AH 2 sin = ⇒ sin AH B B = (1) 2 AB AB Xét A ∆ HB và A
∆ HC vuông tại H Có :   1
A = C ( cùng phụ với B )
Tương tự có : A =  2
B ( cùng phụ với C ) Do đó : A ∆ HB∽ C
∆ HA(g − g) AH HB 2 ⇒ = ⇒ AH = HB⋅HC (*) HC AH
Chứng minh tương tự, ta có : A ∆ BC∽ H ∆ B ( A g ⋅ g) AB BC 2 ⇒ = ⇒ AB = HB⋅BC (**) HB AB 2
Thay (*) (**) vào (1) , ta có : 2 AH HB⋅HC HC sin B = = = . 2 AB HB⋅BC BC b)
Kẻ trung tuyến AM ta có: BC
MA = MC = MB = 2 hay A
∆ MC cân tại M ⇒  =  ⇒  =  MAC C
AMH 2.C ( góc ngoài của A ∆ MC )
Xét tam giác vuông AHM ta có :  sin AH AMH = hay AH AH 2 sin 2 AH C = = = (1) AM AM BC BC 2 Mà 2 AH ⋅CH AH
AC = BC⋅CH ⇒ sin C ⋅cosC = = (2) BC ⋅CH BC
Từ (1) và (2) có sin 2C = 2sin C ⋅cosC .
Bài toán 34. Cho tam giác ABC cân tại A có AB = AC =1cm và A 2α (0° α 45° = < < )các đường cao  1 AD và BE .  2 3 − x⋅ y ⋅   2x .  2 
a) Chứng minh rằng : A ∆ DC∽ B ∆ EC .
b) Chứng minh : sin A = 2sinα ⋅cosα
Hướng dẫn: Với câu b) để chứng minh đẳng thức , ta đưa hai biểu thức về cùng một biểu thức thứ ba . Dựa
vào các hệ thức lượng giác trong các tam giác vuông . Lời giải
Trang: 18.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 a) Dễ thấy : A ∆ DC∽ B ∆ EC (g.g) b) A
∆ BC cân tại A nên đường cao AD đồng thời là đường phân giác α  =  A 2 BAD CAD = = = α 2 2
Xét tam giác vuông ABD có : BD = ABsin BAD =1sinα A
∆ BC cân tại A nên đường cao AD đồng thời là đường trung tuyến nên BC = 2BD = 2sinα
Xét tam giác vuông CEB có :  = 
CBE CAD = α ( cùng phụ với C )
Ta có : BE = BC.cosCBE = BCcosα = 2sinαcosα (1)
Xét tam giác vuông AEB có : BE BE sin A = = = BE (2) AB 1
Từ (1) và (2) có : sin A = 2sinα ⋅cosα ( đpcm)
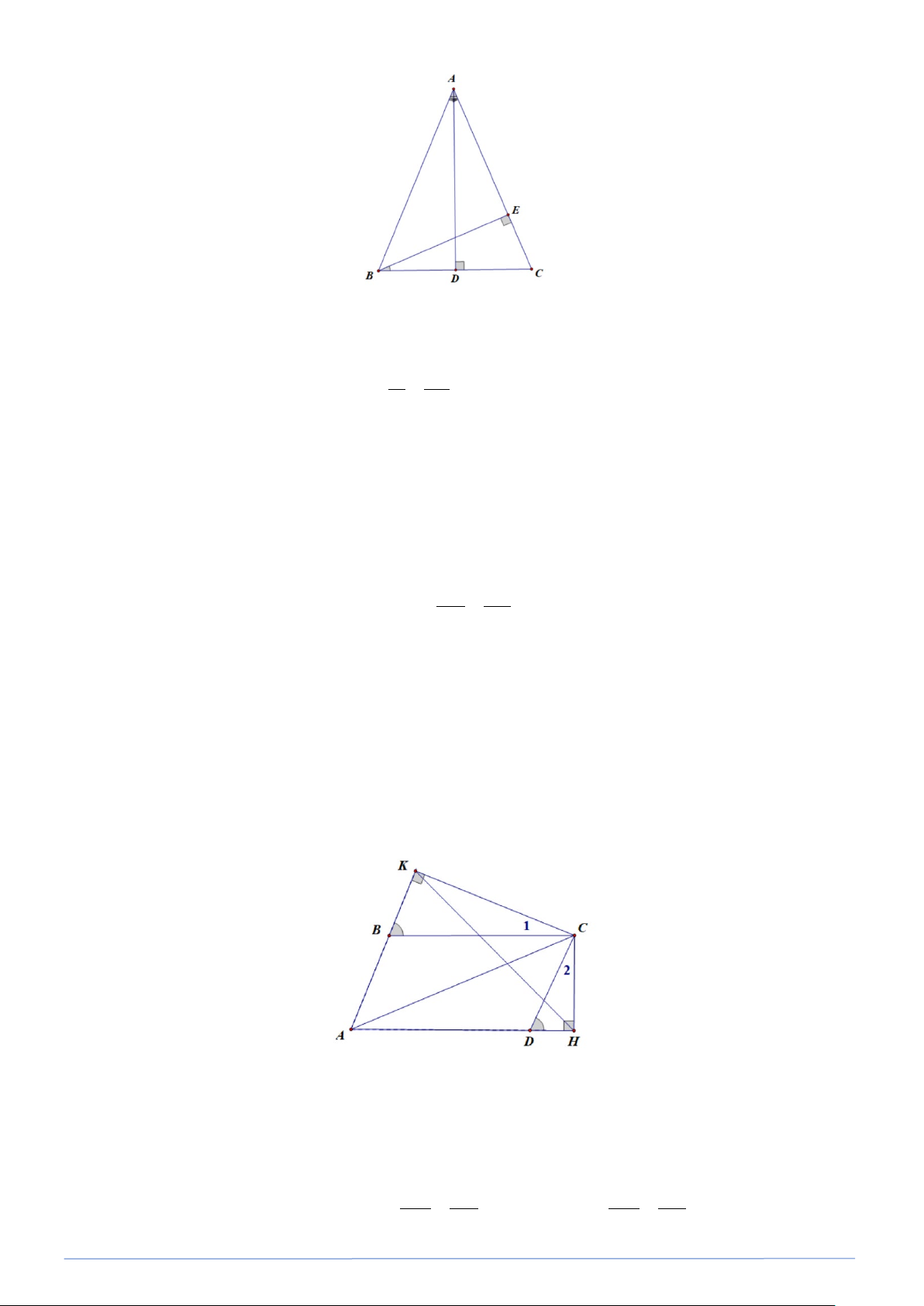
Bài toán 35. Cho hình bình hành ABCD có AC là đường chéo lớn . Kẻ CH vuông góc với AD(H ∈AD)
và CK vuông góc với AB(K∈AB) a) Chứng minh : C ∆ KH ∽ A ∆ BC . b) Chứng minh : =  HK ACsin BAD . Lời giải a) Ta có: ⇒  =  AB// CD(gt) BAD CDH ( đồng vị ) Tương tự : ⇒  =  AD // BC BAD KBC . Nên  =  KBC CDH Do đó : CK CB CK CB CKB ∆ ∽ CH ∆
D( g.g ) ⇒ = mà CD = AB ⇒ = (1) CH CD CH AB
Trang: 19.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG TOÁN 9 Lại có :   AB// CD mà AK CK CD CK hay KCD BKC 90° ⊥ ⇒ ⊥ = = Mặt khác 
ABC là góc ngoài của B ∆ KC nên    ° = + = +  ABC BKC 1 C 90 1 C Lại có :    ° = + = +  KCH KCD C2 90 C2 mà  =  1 C C2 (cmt) ⇒  =  ABC KCH (2)
Từ (1) và (2) có : CKH ∆ ∽ B
∆ CA( .cg.c) Ta có : CKH ∆ ∽ B ∆ CA (cmt) HK CK ⇒ = =  ⇒ = ⋅  sin KBC
HK CA sin KBC mà  =  BAD KBC (cmt) CA CB Do đó : =  HK ACsin BAD (đpcm)
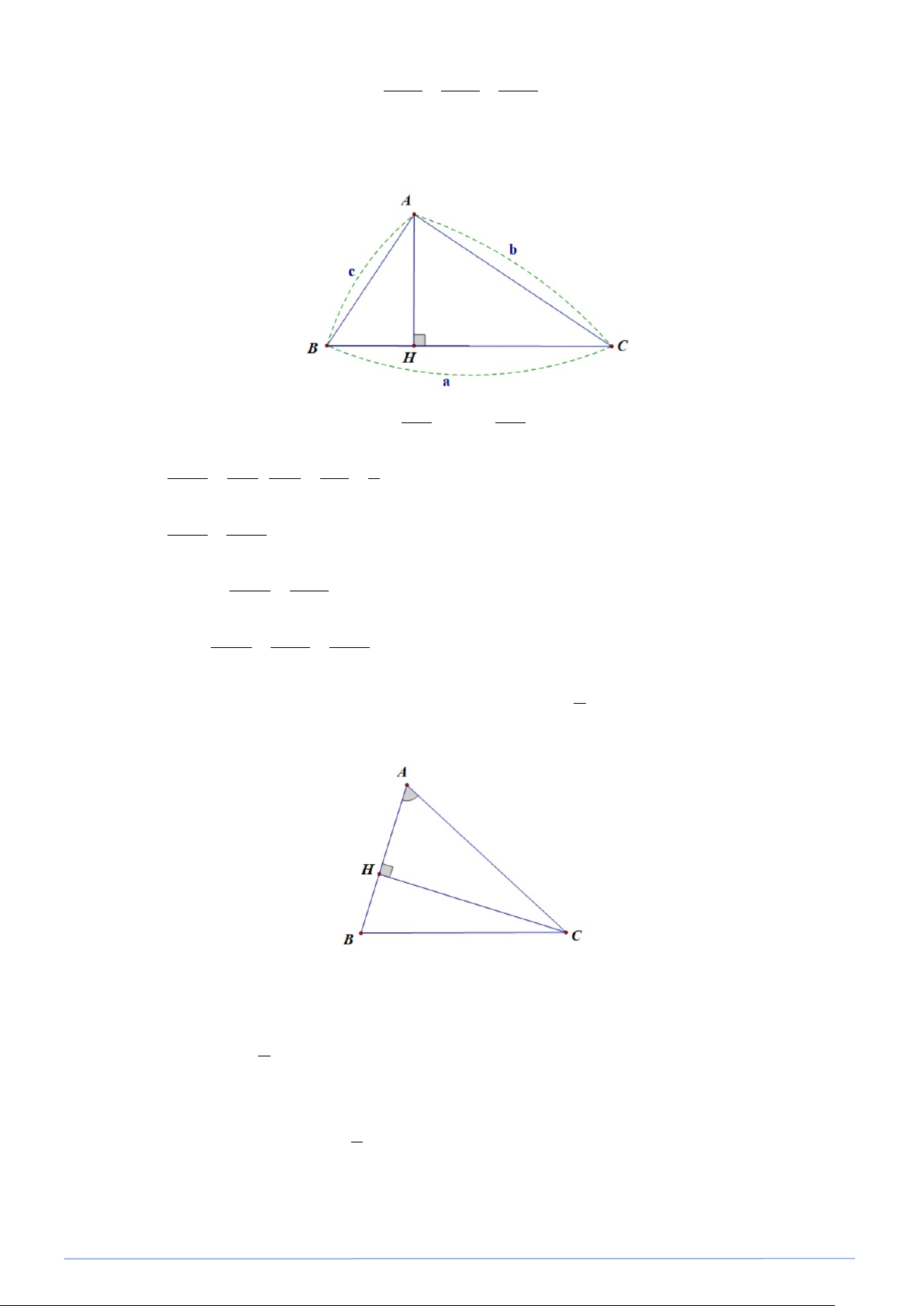
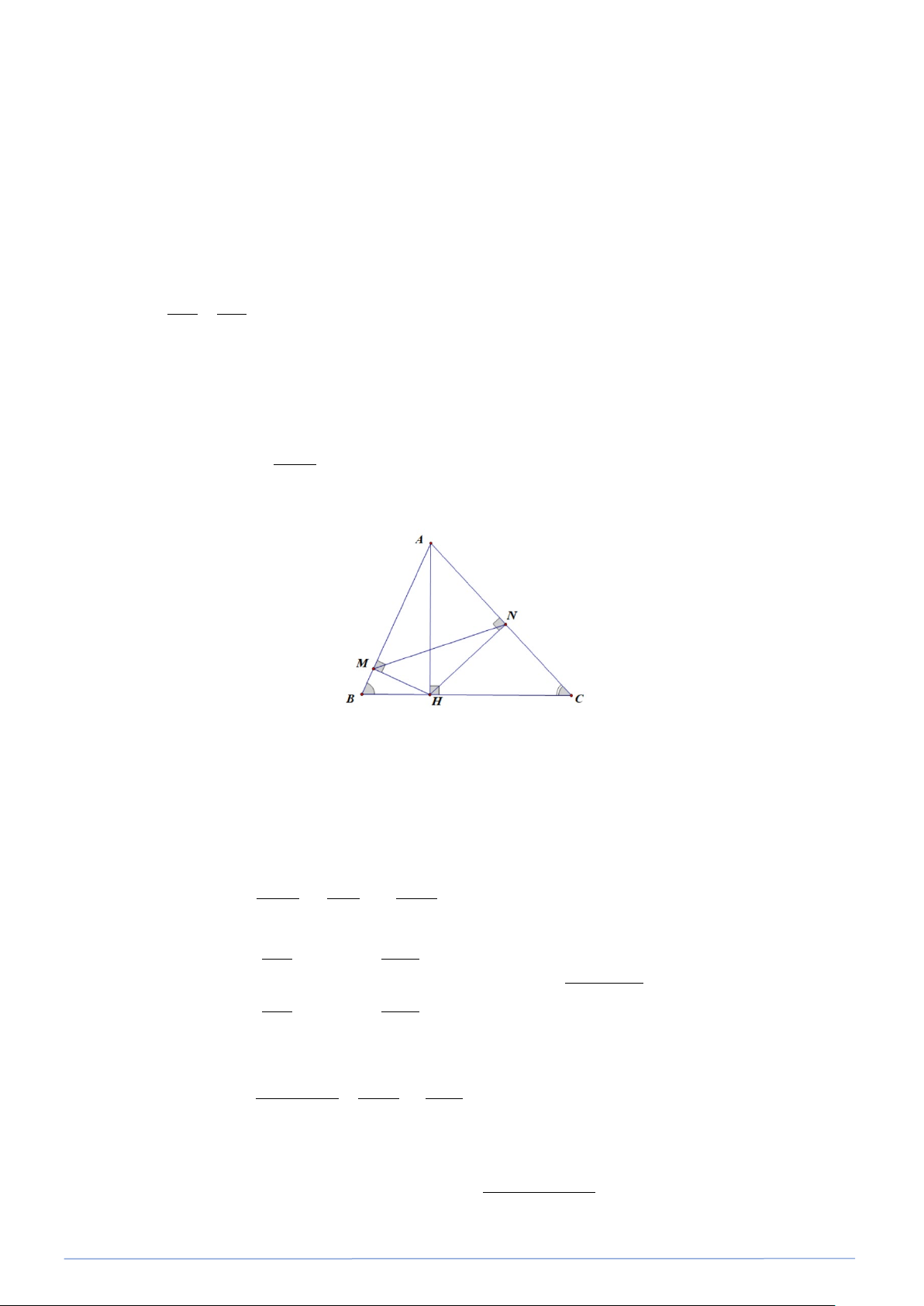
Bài toán 36. Cho A
∆ BC nhọn , đường cao AH . Gọi M , N lần lượt là hình chiếu của H trên AB và AC .
a) Chứng minh : AM.AB = AN.AC . b) Chứng minh : SAMN 2 2 = sin . B sin C . SABC Lời giải
a) Xét tam giác vuông AHB vuông tại H có đường cao HM (gt) Theo hệ thức 2 b a b′ = ⋅ , ta có : 2 AH = AM.AB (1)
Tương tự với AHC , ta có : 2 AH = AN.AC (2)
Từ (1) và (2) có : AM.AB = AN.AC . b) Dễ thấy : A ∆ MN ∽ A
∆ CB( .cg.c) 2 2 Nên : Vế trái : S  AM  AM AMM = =   2 S  AC  AC ACB 2 AH  2 AH sin B = ⇒ sin B = 2  4 Lại có : AB AB  2 2 AH  ⇒ sin Bsin C = (3) 2 2 2 AH AH AB ⋅AC 2 sin C sin C  = ⇒ = 2 AC AC  Thay 4 2 2 2
AH = (AB.AM) = AB .AM vào (3) , ta có : 2 2 2 2 2 AB ⋅AM AM SAMS 2 2 sin Bsin C = = ⇒ = sin Bsin C . 2 2 2 AC ⋅AB AC SABC
Bài toán 37. Cho A
∆ BC nhọn , đường cao AH . Chứng minh rằng :
a) sin A + cos A >1. b) BC AH = . cotg B + cotg C
Trang: 20.