Các dạng toán tiếp tuyến của đồ thị hàm số – Cao Văn Tuấn Toán 12

Các dạng toán tiếp tuyến của đồ thị hàm số – Cao Văn Tuấn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ

I. KIẾN THỨC CẦN NHỚ

Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số

 

y f x

tại điểm

là hệ số góc của tiếp

tuyến với đồ thị

 

của hàm số tại điểm

 

,.M x y

Khi đó, phương trình tiếp tuyến của

 

tại điểm

 

,M x y

là:

  

0 0 0

y y x x x y



  

Nguyên tắc chung để lập được phương trình tiếp tuyến là ta phải tìm được hoành độ tiếp điểm

II. MỘT SỐ DẠNG BÀI TẬP THƯỜNG GẶP

DẠNG 1:VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN KHI BIẾT TIẾP ĐIỂM

1. Phƣơng pháp

Bài toán: Viết phương trình tiếp tuyến của đồ thị

   

:C y f x

tại điểm

 

,.M x y

Phƣơng pháp giải:

 Bước 1: Tính đạo hàm

 

y f x





hệ số góc tiếp tuyến

 

.k y x





 Bước 2: Phương trình tiếp tuyến của đồ thị tại điểm

 

,M x y

có dạng:

  

0 0 0

y y x x x y



  

Chú ý:

 Nếu đề cho (hoành độ tiếp điểm)

thì tìm

bằng cách thế vào hàm số ban đầu,

tức là:

 

y f x

 Nếu đề cho (tung độ tiếp điểm)

thì tìm

bằng cách giải phương trình

 

.f x y

 Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị

   

:C y f x

và đường thẳng

:d y ax b

. Khi đó các hoành độ tiếp điểm là

nghiệm của phương trình hoành độ giao điểm giữa

và

 

Đặc biệt: Trục hoành

:0Ox y 

và trục tung

: 0.Oy x 

Sử dụng máy tính cầm tay:

Phương trình tiếp cần lập có dạng

:.d y kx m

 Đầu tiên tìm hệ số góc tiếp tuyến

 

.k y x





Bấm q y và nhập

 



, sau đó bấm = ta được k.

 Tiếp theo: Bấm phím ! để sửa lại thành

 

   

f X X f X





, sau đó

bấm phím r với

Xx

và bấm phím = ta được

Nhận xét: Sử dụng máy tính để lập phương trình tiếp tuyến tại điểm thực chất là rút gọn các

bước của cách 1. Sử dụng máy tính giúp ta nhanh chóng tìm ra kết quả và hạn chế được sai sót

trong tính toán. Nếu học sinh nào tính nhẩm tốt có thể bỏ qua cách này.

CHỦ ĐỀ

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

2. Ví dụ minh họa

Ví dụ 1: Phương trình tiếp tuyến của đồ thị

 

2 : C y x x

tại điểm

 

1; 3M

là

7 4.yx

7 4.yx

7 4.yx  

7 4.yx  

Lời giải:

Cách 1. Ta có:

 

3 4 1 7y x x k y



    

Phương trình tiếp tuyến tại

 

1; 3M

là:

   

0 0 0

: 7 1 3 7 4d y y x x y y x y x



          

Chọn đáp án B.

Cách 2 [Sử dụng máy tính cầm tay].

 Nhập

 





, sau đó bấm = ta được kết

quả là

 Bấm phím ! để sửa lại thành:

 

3 2 3 2

2 x 2

X X X X X



   

sau đó bấm phím r với

1X 

và bấm phím = ta

được kết quả

4.

Vậy phương trình tiếp tuyến của đồ thị

 

tại

là:

74yx  

Chọn đáp án B.

Ví dụ 2: Cho điểm

thuộc đồ thị

 







và có hoành độ bằng

1.

Phương trình tiếp

tuyến của đồ thị

 

tại điểm

là

yx

yx

yx  

yx  

Lời giải:

Cách 1. Ta có:

 

x y y     

và

 

y k y





    



Phương trình tiếp tuyến tại

là:

 

3 1 3 1

4 2 4 4

y x y        

Chọn đáp án D.

Cách 2 [Sử dụng máy tính cầm tay].

 Nhập

dx X



  







, sau đó bấm = ta được kết

quả là

0,75 .

  

 Bấm phím ! để sửa lại thành:

 

2 1 2 1

d X X

dx X X



   









sau đó bấm phím r với

1X 

và bấm phím =

ta được kết quả

0,25 .

  

Vậy phương trình tiếp tuyến tại

là:

y    

Chọn đáp án D.

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Ví dụ 3: Cho điểm

thuộc đồ thị

 

C y x x

có hoành độ

0x 

và

 

1yx





Phương trình tiếp tuyến của

 

tại điểm

là

yx  

yx

yx

yx  

Lời giải:

Ta có:

4y x x





34 .yx





Khi đó:

 

0 0 0 0

1 3 4 1 1 1 1

y x x x x x





         

Đến đây bạn đọc có thể giải tiếp bằng nhiều cách như hai ví dụ trình bày ở trên.

Cách 1.

Ta có:

 

1 1 .1 2.1

x y y      

và

 

1 1 4.1 3.ky



    

Phương trình tiếp tuyến tại

là:

 

3 1 3

y x y x        

Chọn đáp án A.

Cách 2 [Sử dụng máy tính cầm tay].

 Nhập











, sau đó bấm = ta được

kết quả là

3.

 Bấm phím ! để sửa lại thành:

 

4 2 4 2

2 x 2

X X X X X





   





sau đó bấm phím r với

1X 

và bấm phím = ta

được kết quả

Vậy phương trình tiếp tuyến tại

là:

yx   

Chọn đáp án A.

DẠNG 2: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN KHI BIẾT PHƢƠNG (Biết hệ số góc k)

1. Phƣơng pháp

Bài toán: Cho hàm số

 

y f x

có đồ thị

 

. Lập phương trình tiếp tuyến của đồ thị

 

với hệ số góc

cho trước.

Phƣơng pháp giải:

 Bước 1: Gọi

 

;M x y

là tiếp điểm và tính

 

.y f x





 Bước 2:

 Hệ số góc tiếp tuyến là

 

k f x





 Giải phương trình này tìm được

thay vào hàm số được

 Bước 3: Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng:

 

0 0 0

:d y y x x y



  

Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:

 Tiếp tuyến

// : .d y ax b k a    

Sau khi lập được phương trình tiếp tuyến thì nhớ kiểm tra lại xem tiếp tuyến có

bị trùng với đường thẳng



hay không? Nếu trùng thì phải loại đi kết quả đó.

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

 Tiếp tuyến

: . 1d y ax b k a k

          

 Tiếp tuyến tạo với trục hoành một góc



thì

tan .k





Tổng quát: Tiếp tuyến tạo với đường thẳng

: y ax b  

một góc



Khi đó:

tan .









Sử dụng máy tính cầm tay:

Phương trình tiếp cần lập có dạng

:.d y kx m

 Tìm hoành độ tiếp điểm

 Nhập

   

k X f X

(hoặc

 

f X kX

) sau đó bấm r với

Xx

rồi bấm = ta

được kết quả là

2. Ví dụ minh họa

Ví dụ 1: Phương trình tiếp tuyến của đồ thị

 

: 3 2C y x x  

có hệ số góc bằng 9 là

9 18; 9 22.y x y x   

9 14; 9 18.y x y x   

9 18; 9 22.y x y x   

9 14; 9 18.y x y x   

Lời giải:

Ta có:

33yx





. Gọi tiếp điểm của tiếp tuyến cầ tìm là

 

;.M x y



hệ số góc của tiếp tuyến là:

 

0 0 0 0

9 3 3 9 4 2.k y x x x x



         

Cách 1.

 Với

24xy  

ta có tiếp điểm

 

2; 4 .M

Phương trình tiếp tuyến tại

là:

 

: 9 2 4 : 9 14.d y x d y x     

 Với

20xy   

ta có tiếp điểm

 

2;0 .M 

Phương trình tiếp tuyến tại

là:

 

: 9 2 0 : 9 18.d y x d y x     

Vậy có hai tiếp tuyến cần tìm là

: 9 14; : 9 18d y x d y x    

Chọn đáp án B.

Cách 2 [Sử dụng máy tính cầm tay].

 Với

2x 

ta nhập

 

9 3 2X X X   

r với

2X 

rồi bấm = ta được kết quả là

14 .

: 9 14.d y x  

 Với

2x 

ta nhập

 

9 3 2X X X   

r với

2X 

rồi bấm = ta được kết quả là

18 .

: 9 18.d y x  



Chọn đáp án B.

Ví dụ 2: Tiếp tuyến của đồ thị

 







song song với đường thẳng

: 3 2 0xy   

có

phương trình là

3 4.yx

3 2.yx

3 14.yx

3 4.yx

Lời giải:

Ta có:

 







và

: 3 2 0 3 2.x y y x      

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Gọi tiếp điểm của tiếp tuyến cầ tìm là

 

;.M x y

Vì tiếp tuyến song song với đường thẳng



nên

 

2 1 1

3 2 1 .

2 1 3

     

      



    





Cách 1.

 Với

11xy    

ta có tiếp điểm

 

1; 1 .M 

Phương trình tiếp tuyến tại

là:

 

: 3 1 1 : 3 2.d y x d y x     

Lúc này:

d   

Loại.

 Với

35xy   

ta có tiếp điểm

 

3;5 .M 

Phương trình tiếp tuyến tại

là:

 

: 3 3 5 : 3 14.d y x d y x     

Vậy có một tiếp tuyến cần tìm là

: 3 14d y x

Chọn đáp án C.

Cách 2 [Sử dụng máy tính cầm tay].

 Với

1x 

ta nhập

 







r với

1X 

rồi bấm = ta được kết quả là

: 3 2d y x d      

Loại.

 Với

3x 

ta nhập

 







r với

3X 

rồi bấm = ta được kết quả là

14 .

: 3 14d y x  

Chọn đáp án C.

DẠNG 3: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN KHI BIẾT TIẾP TUYẾN ĐI QUA MỘT

ĐIỂM CHO TRƢỚC

1. Phƣơng pháp

Bài toán: Viết phương trình tiếp tuyến của đồ thị

 

, biết tiếp tuyến đi qua điểm

 

A x y

Phƣơng pháp giải:

Cách 1: Sử dụng điều kiện tiếp xức của hai đồ thị

 Bước 1: Phương trình tiếp tuyến đi qua

 

;

A x y

hệ số góc

có dạng:

   

d y k x x y  

 Bước 2: d là tiếp tuyến của

 

khi và chỉ khi hệ

   

 

f x k x x y

f x k



  













có nghiệm.

 Bước 3: Giải hệ trên tìm được

xk

và thế vào phương trình

 

, thu được

phương trình tiếp tuyến cần tìm.

Cách 2:

 Bước 1:

 Gọi

 

;M x f x

là tiếp điểm.

 Tính hệ số góc tiếp tuyến

 

k f x





theo

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

 Bước 2: Phương trình tiếp tuyến có dạng:

      

0 0 0

: * *d y f x x x f x



  

Vì điểm

 

;

A x y d

nên

    

0 0 0AA

y f x x x f x



  

. Giải phương trình này sẽ

tìm được

Bước 3: Thay

vừa tìm được vào

 

ta được phương trình tiếp tuyến cần tìm.

2. Ví dụ minh họa

Ví dụ 1: Tiếp tuyến của đồ thị

 

: 4 3 1C y x x   

đi qua điểm

 

1; 2A 

có phương trình là

9 7; 2.y x y x     

9 11; 2.y x y x     

9 11; 2.y x y   

9 7; 2.y x y   

Lời giải:

Ta có:

12 3.yx



  

Đường thẳng

đi qua

 

1; 2A 

với hệ số góc

có phương trình

 

: 1 2.d y k x  

Đường thẳng

là tiếp tuyến của

 

C 

hệ

   

 

4 3 1

1 2 1

12 3 2

x x k x



     





  





có nghiệm.

Thay k từ

 

vào

 

ta được:

 

4 3 1 12 3 1 2x x x x       

 

8 12 4 0 1 0

x x x x

  





        













 Với

19xk    

. Phương trình tiếp tuyến là:

9 7.yx  

 Với

xk  

. Phương trình tiếp tuyến là:

2.y 

Vậy có hai tiếp tuyến cần tìm là

9 7; 2y x y    

Chọn đáp án D.

Bình luận: Đối với dạng bài toán viết phương trình tiếp tuyến đi qua điểm việc tính toán tương đối mất

thời gian và dễ dẫn đến sai lầm đáng có. Do đó, ta có thể sử dụng máy tính bỏ túi để thử các đáp án như

 Cho

 

bằng kết quả các đáp án, từ đó ta thu được các phương trình.

 Sử dụng chức năng giải phương trình bậc ba của máy tính bỏ túi bằng cách bấm tổ hợp phím

w 5 4 và

nhập hệ số phương trình.

Thông thường máy tính cho số nghiệm thực nhỏ hơn số bậc của phương trình là 1 thì ta chọn đáp

án đó.

Cụ thể trong bài toán này:

 Đầu tiên thử với đáp án A, ta cho:

4 3 1 9 7 4 12 6 0.x x x x x          

Máy tính cho 3 nghiệm



Loại A.

 Thử với đáp án B, ta cho:

4 3 1 2 4 4 1 0.x x x x x          

Máy tính cho 3 nghiệm



Loại B.

 Thử với đáp án B, ta cho:

4 3 1 9 11 4 12 10 0.x x x x x          

Máy tính hiển thị 1 nghiệm thực và 2 nghiệm phức (phương trình có số nghiệm thực là một nhỏ

hơn bậc của phương trình là 2)



Loại C.



Chọn đáp án D.

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Đến đây ta có thể dừng được rồi, tuy nhiên có thể kiểm nghiệm thêm đáp án D, ta cho:



4 3 1 9 7 4 12 8 0x x x x x          

máy tính hiển thị 2 nghiệm

1;x 

2x 

(nhận).



4 3 1 2 4 3 1 0x x x x        

máy tính hiển thị 2 nghiệm

xx  

(nhận).

Ví dụ 2: Tiếp tuyến của đồ thị

 







đi qua điểm

 

1; 4A 

có phương trình là

1 13

yx

D. Không tồn tại tiếp tuyến.

Lời giải:

Điều kiện:

1.x 

Ta có:

 







Đường thẳng

đi qua

 

1; 4A 

với hệ số góc

có phương trình:

 

: 1 4.d y k x  

Đường thẳng

là tiếp tuyến của

 

C 

hệ

   

 

1 4 1



  

















có nghiệm.

Thay k từ

 

vào

 

ta được:

 

2 1 3

1 4.



  



10 8 0 4 .

x x x k

  



         







Phương trình tiếp tuyến là:

1 13

d y x  

Chọn đáp án A.

DẠNG 4: MỘT SỐ BÀI TOÁN CHỨA THAM SỐ

Ví dụ 1: Cho hàm số

3y x x

có đồ thị

 

. Gọi

là điểm thuộc đồ thị

 

có hoành độ

bằng 1. Với giá trị nào của tham số

thì tiếp tuyến của

 

tại

song song với đường thẳng

 

: 4 2 1?d y m x m   

1.m 

1.m 

2.m 

2.m 

Lời giải:

TXĐ:

.D 

Ta có:

3 6 .y x x





Phương trình tiếp tuyến của

tại

   

1; 2MC

là:

 

: 2 3.1 6.1 1 3 1.y x y x        

Khi đó:

// 1

2 1 1







  





      



















Chọn đáp án B.

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

Ví dụ 2: Cho hàm số

 

2 1 2y x m x m    

có đồ thị

 

. Gọi

là điểm thuộc đồ thị hàm

số có hoành độ bằng 1. Với giá trị nào của tham số

thì tiếp tuyến với đồ thị

 

tại

vuông

góc với đường thẳng

: 4 1 0?xy   

1.m 

1.m 

2.m 

2.m 

Lời giải:

TXĐ:

.D 

Ta có:

 

4 4 1 .y x m x



  

Gọi

là tiếp tuyến của

tại điểm

Khi đó

có hệ số góc:

   

1 4 4 1 4 .k y m m



    

: 4 1 0 .

x y y x      

Do đó:

4 4 4 1d k m m           

Chọn đáp án A.

Ví dụ 3: Cho hàm số

 

3 2 1 2 3y x x m x m      

có đồ thị

 

. Với giá trị nào của tham

số

thì tiếp tuyến có hệ số góc lớn nhất của đồ thị

 

vuông góc với đường thẳng

: 2 4 0?xy   

2.m 

1.m 

0.m 

4.m 

Lời giải:

TXĐ:

.D 

Ta có:

 

3 6 2 1 3 2 1 2 2 3 1 2 2 2 2, .y x x m x x m x m m x



                   

Do đó: GTLN của



là

22m 

, đạt tại

1.x 

Với

1 4 2.x y m   

Phương trình tiếp tuyến của

 

tại

 

1; 4 2Mm

là:

      

: 4 2 2 2 1 2 2 2 4.d y m m x y m x m         

Theo đề ra ta có:

: 2 4 0xy   

hay

yx

Khi đó:

2 2 2 2d m m         

Chọn đáp án A.

Ví dụ 4: Cho hàm số







có đồ thị

 

. Giả sử, đường thẳng

:d y kx m

là tiếp tuyến

của

 

, biết rằng

cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt

,AB

và tam giác

OAB

cân tại gốc tọa độ O. Tổng

km

có giá trị bằng

1.

3.

Lời giải:

TXĐ:









Ta có:

 









Tiếp tuyến

:d y kx m

cắt

,Ox Oy

lần lượt tại hai điểm

,AB

nên

0, 0.mk

A Ox

nên









B Oy

nên

 

0; .Bm

Do tam giác

OAB

cân tại gốc tọa độ O nên

1 0 .

OA OB m m

  



      











 







nên

1.k 

Suy ra:

 

1 2 3 1 .

    



     



   





https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

 Phương trình tiếp tuyến của

 

tại

 

1;1M 

là:

 

11y x y x      

(loại).

 Phương trình tiếp tuyến của

 

tại

 

2;0M 

là:

 

2 2.y x y x      

Khi đó:

1 2 3km      

Chọn đáp án D.

Ví dụ 5 [Sở GD & ĐT Vũng Tàu – 2017]: Tìm tập hợp tất cả các giá trị tham số thực

để đồ thị

 

của hàm số







cắt đường thẳng

2y x m

tại hai điểm phân biệt mà hai tiếp tuyến

của

 

tại hai điểm đó song song với nhau.

 

2; 2 .

 

1;1 .

 

2; 2 .

Lời giải:

Chọn đáp án D.

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

III. CÂU HỎI TRẮC NGHIỆM RÈN LUYỆN

Câu 1. Tiếp tuyến của đồ thị

 







tại điểm có hoành độ bằng

có phương trình là

yx

yx

yx  

yx  

Câu 2. Tiếp tuyến của

 

:2C y x x

tại điểm có hoành độ bằng

2

có phương trình là

24 40.yx  

24 40.yx  

24 40.yx

24 40.yx

Câu 3. Tiếp tuyến của

 

: 5 1

C y x

  



tại điểm

;







có phương trình là

yx

yx  

3 1.yx

3 1.yx

Câu 4. Tiếp tuyến của

 







tại điểm có tung độ bằng 3 có phương trình là

yx

yx

yx  

yx  

Câu 5. Tiếp tuyến của

 

: 2 3 1C y x x  

tại điểm có tung độ bằng 4 có phương trình là

12 8.yx  

12 8.yx  

12 8.yx

12 8.yx

Câu 6. Cho hàm số

2 3 2y x x   

có đồ thị

 

. Tiếp tuyến của

 

tại điểm có hoành độ là

nghiệm của phương trình





có phương trình là

yx

yx

yx  

yx  

Câu 7. Cho hàm số

31y x x x   

có đồ thị

 

. Tiếp tuyến của

 

tại điểm thuộc đồ thị

 

có hoành độ dương và là nghiệm của phương trình

. 11 0y x y

 

  

có phương trình là

3.yx  

4 2.yx  

2.yx  

4 3.yx  

Câu 8. Cho hàm số







có đồ thị

 

. Tiếp tuyến của

 

tại giao điểm của

 

với trục

tung có phương trình là

yx  

yx  

3 2.yx  

3 2.yx  

Câu 9. Cho hàm số







có đồ thị

 

. Phương trình tiếp tuyến của

 

tại các giao điểm

của

 

và đường

:3yx  

là

3 ; 1.y x x y x   

3; 1.y x y x     

3; 1.y x y x    

3; 1.y x y x    

Câu 10. Cho hàm số

32y x x   

có đồ thị

 

. Số phương trình tiếp tuyến của

 

tại giao

điểm

 

với đường thẳng

: 2 0xy   

là

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Câu 11. Cho hàm số







có đồ thị

 

. Biết điểm

 

MC

sao cho khoảng cách từ điểm

đến đường tiệm cận đứng của đồ thị

 

bằng 2. Phương trình tiếp tuyến của

 

tại

là

1 1 1 7

4 4 4 4

y x x y x   

1 1 1 5

4 4 4 4

y x y x   

1 1 1 5

4 4 4 4

y x y x     

1 1 1 5

4 4 4 4

y x x y x     

Câu 12. Cho hàm số







có đồ thị

 

. Tiếp tuyến của đồ thị

 

tại điểm

 

MC

có tọa

độ nguyên dương có phương trình là

1.y 

1.y 

1.yx  

5.yx  

Câu 13. Cho hàm số

y x x  

có đồ thị

 

. Biết điểm

 

MC

sao cho

x 

và

là

nghiệm của phương trình





. Viết phương trình tiếp tuyến của

 

tại điểm

có phương

trình là

24 16.yx

24 16.yx  

24 80.yx  

24 80.yx

Câu 14. Tiếp tuyến của đồ thị

 







có hệ số góc

1k 

có phương trình là

1; 5.y x y x   

1; 5.y x y x   

; 5.

y x y x   

1; .

y x y x   

Câu 15. Tiếp tuyến của đồ thị

 

: 3 3C y x x  

song song với đường thẳng

: 9 24xy  

có

phương trình là

9 24.yx

9 8.yx

9 10.yx

9 30.yx

Câu 16. Tiếp tuyến của đồ thị

 







song song với đường thẳng

: 5 13 0xy   

có

phương trình là

5 8; 5 2.y x y x     

5 2; 5 22.y x y x     

5 2; 5 22.y x y x     

5 2; 5 8.y x y x     

Câu 17. Phương trình tiếp tuyến của đồ thị

 







tại

có dạng

y kx m

. Biết tiếp

tuyến tại

song song với đường thẳng

: 3 2 19 0xy   

. Khi đó, tổng

km

có giá trị bằng

11.

8.

1.

Câu 18. Tiếp tuyến của đồ thị

 

: 3 5C y x x  

vuông góc với đường

: 9 0d x y

có phương

trình là

9 ; 9 32.y x y x  

9 22; 9 18.y x y x   

9 ; 9 32.y x y x  

9 22; 9 18.y x y x   

Câu 19. Tiếp tuyến của đồ thị

 

:6C y x x   

vuông góc với đường thẳng

yx  

có

phương trình là

6 2.yx  

6 2.yx  

6 10.yx  

6 10.yx  

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

Câu 20. Cho hàm số

2 3 5y x x  

có đồ thị

 

. Gọi

:d y kx m

là tiếp tuyến của

 

tại

điểm có hệ số góc tiếp tuyến nhỏ nhất. Tỉ số

2:T m k

có giá trị bằng

7.T 

5.T 

5.T 

7.T 

Câu 21. Cho hàm số

31y x x  

có đồ thị

 

. Hai điểm

, AB

thuộc

 

sao cho tiếp tuyến

của

 

tại A và B song song với nhau và độ dài đoạn

42AB 

là

   

2;1 ; 2; 3 .AB

   

3;1 ; 1; 3 .AB

   

0; 1 ; 4; 3 .AB

   

3;2 ; 1; 2 .AB

Câu 22. Tiếp tuyến của đồ thị

 







đi qua điểm

 

1; 3A 

có phương trình là

1 13

yx  

1 13

yx  

1 13

yx

1 13

yx

Câu 23. Cho hàm số







có đồ thị

 

. Giả sử đường thẳng

:d y kx m

là tiếp tuyến của

 

và tiếp tuyến này đi qua giao điểm của đường tiệm cận và trục hoành

. Tỉ số

:T k m

có giá trị bằng

2.

1.

Câu 24. Cho hàm số

69y x x x  

có đồ thị

 

. Tiếp tuyến của

 

tạo với đường thẳng

: 1 0xy   

một góc



sao cho

cos





và tiếp điểm có hoành độ nguyên có phương

trình là

9 ; 9 32.y x y x  

9 21; 9 7.y x y x   

9 ; 9 32.y x y x  

9 21; 9 7.y x y x   

Câu 25. Cho hàm số







có đồ thị

 

. Nếu điểm

thuộc

: 2 1 0d x y  

có hoành độ

âm và từ điểm M kẻ được duy nhất một tiếp tuyến tới

 

thì tọa độ điểm M là

 

1; 1 .M 

 

2; 3 .M 

 

3; 5 .M 

 

4; 7 .M 

Câu 26. Cho hàm số

32y x x  

có đồ thị

 

. Nếu điểm M thuộc

 

cùng với hai điểm

cực trị của đồ thị hàm số

 

tạo thành tam giác có diện tích bằng

thì phương trình tiếp

tuyến với đồ thị tại điểm M là

9 7; 9 25.y x y x     

9 25; 9 7.y x y x   

9 7; 9 25.y x y x     

9 25; 9 7.y x y x   

Câu 27. Có bao nhiêu tiếp tuyến của đồ thị

 







cách đều hai điểm

 

2; 4A 

và

 

4; 2B 

Câu 28. Cho hàm số







có đồ thị

 

. Gọi

là giao điểm hai đường tiệm cận của

 

Tiếp tuyến

của

 

tại điểm

thỏa mãn

IM d

có phương trình là

1; 5.y x y x     

1; 5.y x y x     

1; 5.y x y x     

1; 5.y x y x     

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Câu 29. [THPT Chuyên Thái Bình – Lần 4 – 2017] Đồ thị hàm số

21y x x  

có bao nhiêu

tiếp tuyến song song với trục hoành ?

Câu 30. [THPT Quốc Học Quy Nhơn – Bình Định – Lần 1 – 2017] Cho hàm số

 

y f x







có đồ thị

 

Viết phương trình tiếp tuyến của đồ thị

 

biết hoành độ tiếp điểm là nghiệm

của phương trình

   

7 11 . 10.x f x





2 1 5 1

; .

5 5 2 2

y x y x     

2 1 5 1

; .

5 5 2 2

y x y x    

2 9 5 9

; .

5 5 2 2

y x y x     

2 9 5 1

; .

5 5 2 2

y x y x     

Câu 31. [THPT Chuyên Lê Khiết – Quảng Ngãi – 2017] Cho hàm số

3 1yx x

có đồ thị là

 

Gọi



là tiếp tuyến của

 

tại điểm

 

1; 5A

và

là giao điểm thứ hai của



với

 

Tính diện tích

của tam giác

,OAB

với

là gốc tọa độ.

12.S 

6.S 

15.S 

24.S 

Câu 32. [THPT Chuyên Biên Hòa – Hà Nam – 2017] Cho hàm số

6 2.y x x  

Hỏi có bao

nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm

 

1; 3 ?A 

Câu 33. [THPT Chuyên Lê Quý Đôn – Đà Nẵng – Lần 2 – 2017] Cho hàm số







có hàm số

 

Biết

, ab

là các giá trị thực sao cho tiếp tuyến của

 

tại điểm

 

1; 2M 

song song với

đương thẳng

: 3 4 0.d x y

Tính

.ab

0.ab

1.ab  

2.ab

1.ab

Câu 34. [THPT Chuyên Sơn La – Lần 2 – 2017] Cho hàm số







có đồ thị

 

Gọi

là

khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của

 

Tìm

giá trị lớn nhất của

max

d  

max

5.d 

max

3.d 

max

6.d 

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

BẢNG ĐÁP ÁN

Câu

Đáp án

Câu

Đáp án

Câu

Đáp án

Câu

Đáp án

HƯỚNG DẪN GIẢI

Câu 1. TXĐ:

 

1\.D 

Ta có:

 







Với

 

,.x y y



   

Phương trình tiếp tuyến của

 

tại







là:

 

yx  

hay

.yx



Chọn đáp án B.

Câu 2. TXĐ:

D 

. Ta có:

44.y x x





Với

 

2 8 2 24,.x y y



      

Phương trình tiếp tuyến của

 

tại

 

28;M 

là:

 

24 2 8 24 40y x y x        

Chọn đáp án A.

Câu 3. TXĐ:

 

1\D 

. Ta có:

 

.yy





   







Phương trình tiếp tuyến của

 

tại điểm

;







là:

3 3 1

y x y x



      





Chọn đáp án D.

Câu 4. TXĐ:

 

2\D 

. Ta có:

 









Với

34yx  

. Khi đó:

 





Phương trình tiếp tuyến của

 

tại điểm

 

43;M

là:

 

4 3 5

y x y x        

Chọn đáp án C.

Câu 5. TXĐ:

D 

. Ta có:

66.y x x





Với

41yx  

. Khi đó:

 

1 12.y





Phương trình tiếp tuyến của

 

tại điểm

 

14;M

là:

 

12 1 4 12 8y x y x      

Chọn đáp án C.

Câu 6. TXĐ:

D 

. Ta có:

6 6 12 6;.y x x y x

 

     

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Khi đó:

 

0 0 0 0

0 12 6 0

y x x x y



        

và











Phương trình tiếp tuyến của

 

tại điểm







là:

3 1 5 3 7

2 2 2 2 4

y x y x



      





Chọn đáp án A.

Câu 7. TXĐ:

D 

. Ta có:

3 6 6 6;.y x x y x

 

   

Xét phương trình:

 

. 11 0 3 6 6 6 11 0 .

y x y x x x x





 

         









0x 

nên

2.x 

Với

25xy   

và

 

21.y





Phương trình tiếp tuyến của

 

tại điểm

 

25;M 

là:

 

2 5 3y x y x        

Chọn đáp án A.

Câu 8. TXĐ:

 

1\.D 

Ta có:

 







Giao điểm của

 

và trục tung là

 

02;M 

và

 

03.y





Phương trình tiếp tuyến của

 

tại điểm

 

02;M 

là:

32yx   

Chọn đáp án D.

Câu 9. TXĐ:

 

1\.D 

Ta có:

 







Phương trình hoành độ giao điểm của đồ thị

 

và đường thẳng



là:

 

3 2 0 .

x tm

x x x

x tm







     











 Với

03xy   

và

 

01.y





Phương trình tiếp tuyến của

 

tại điểm

 

03;M 

là:

3yx  

 Với

 

2 1 2 1,.x y y



     

Phương trình tiếp tuyến của

 

tại điểm

 

21;M 

là:

 

2 1 1.y x y x       



Chọn đáp án B.

Câu 10. TXĐ

.D 

Ta có:

33.yx



  

Phương trình hoành độ giao điểm của

 

và đường thẳng

2: yx   

là:

3 2 2 4 0 0 .

x x x x x x

  



           







Do có

tiếp điểm nên có

tiếp tuyến thỏa yêu cầu bài toán



Chọn đáp án C.

Câu 11. TXĐ:

 

\1D 

. Tiệm cận đứng là đường thẳng

: 1.x

Ta có:

 







Vì

 

MC

nên

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

Theo đề ra ta có:

 

1 , 1

; 2 1 2 .

3 , 3

x y y

d M x

x y y





     



     





    





 Phương trình tiếp tuyến tại

là:

hay

 Phương trình tiếp tuyến tại

là:

hay



Chọn đáp án A.

Câu 12. TXĐ:

 

\ 1 .D 

Ta có:

 









Lấy

 

;

M x C













Khi đó,

có tọa độ nguyên dương nên:

 

2 3, 2 1.

x y y







































       





  



  



  





  























Phương trình tiếp tuyến của

tại điểm

2; 3M

là:

 

2 3 5.y x y x       



Chọn đáp án D.

Câu 13.

4 2 3 2

8 4 16 ; 3 16.

y x x y x x y x

 

       

Gọi

     

; , 0

M M M

M x y C x

là tiếp điểm.

là nghiệm của phương trình





nên

3 16 4 .

  

   







x 

nên

2 32

xy    

và

 

2 24.y





Phương trình tiếp tuyến của đồ thị

 

tại

 

2; 32M 

là:

 

24 2 32 24 16y x y x      

Chọn đáp án A.

Câu 14. TXĐ:

 

\ 1 .D 

Ta có:

 







Gọi

;











là tiếp điểm của tiếp tuyến đồ thị

có hệ số góc

1k 

Khi đó:

 

1 1 1 1 1 1 .

k x x

    

         



  





 Phương trình tiếp tuyến tại

 

2; 3M 

là:

5.yx

 Phương trình tiếp tuyến tại

 

0;1M

là:

1.yx



Chọn đáp án A.

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Câu 15.

3 6 .y x x





Gọi

;M x y

là tiếp điểm của tiếp tuyến

song song với đường thẳng

: 9 24xy  

Vì

// d 

nên

có hệ số góc

9k 

. Khi đó:

3 6 9 .

     

  



  



 Phương trình tiếp tuyến tại

 

1; 1M 

là:

 

9 1 1 9 8.y x y x     

 Phương trình tiếp tuyến tại

 

3;3M

là:

 

9 3 3 9 24y x y x     

(loại).

Vậy phương trình tiếp tuyến

: 9 8d y x  

Chọn đáp án B.

Câu 16. TXĐ:

 

\ 2 .D

Ta có:

 









Gọi

;M x y

là tiếp điểm của tiếp tuyến

song song với đường thẳng

: 5 13xy  

Vì

// d 

nên

có hệ số góc

5k 

Khi đó:

 

5 2 1 .

    



     



  





 Phương trình tiếp tuyến tại

 

1; 5M 

là:

 

5 1 3 5 2.y x y x       

 Phương trình tiếp tuyến tại

 

3;7M

là:

 

5 3 7 5 22.y x y x       



Chọn đáp án C.

Câu 17. TXĐ:

 

\ 1 .D 

Ta có:

 







: 3 2 19 0xy   

hay

3 19

yx

Gọi

là tiếp tuyến của

song song với đường thẳng



và

;











là tiếp điểm.

// d 

nên

có hệ số góc là

k 

Khi đó:

 

3 3 6 3

2 2 2

k y x

    



     



   





 Phương trình tiếp tuyến tại điểm

 

1; 1M 

là:

 

3 3 5

1 1 .

2 2 2

y x y x     

 Phương trình tiếp tuyến tại điểm

 

3;5M 

là:

 

3 3 19

2 2 2

y x y x     

(loại).

Do đó

3 5 3 5

2 2 2 2

y kx m

d y x k m





         





Chọn đáp án D.

Câu 18. TXĐ:

.D 

Ta có:

3 6 .y x x





: 9 0d x y

hay

yx

Gọi



là tiếp tuyến của

vuông góc với

và có tiếp điểm làm

 

;.M x y





nên



có hệ số góc

9.k 

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

Khi đó:

 

0 0 0

9 9 3 6 9 .

k y x x x

   



      



   



 Phương trình tiếp tuyến tại điểm

 

1;9M

là:

 

9 1 9 9 .y x y x    

 Phương trình tiếp tuyến tại điểm

 

3;5M 

là:

 

9 3 5 9 32.y x y x     



Chọn đáp án A.

Câu 19. TXĐ:

.D 

Ta có:

4 2 .y x x



  

Gọi

là tiếp tuyến của

vuông góc với

yx  

và có tiếp điểm là

0 0 0

;M x y

d 

nên

có hệ số góc

6.k 

Khi đó:

 

0 0 0 0 0

6 6 4 2 6 1 4.k y x x x x y



             

Phương trình tiếp tuyến tại

 

1; 4M

là:

 

6 1 4 6 10y x y x        

Chọn đáp án C.

Câu 20.

TXĐ:

.D 

Ta có:

1 3 1 3 3

6 6 6 6 , .

4 2 2 2 2

y x x x x x x

   



            

   

   

Do đó: GTNN của



là



, đạt tại

x 

Với

xy  

Phương trình tiếp tuyến của

 

tại điểm

;







là:

3 1 9 3 21

2 2 2 2 4

y x y x



       





Do đó:

21 3

2 : 2. : 7

T m k



     





Chọn đáp án A.

Câu 21. Đối với bài toán này ta sử dụng phép thử:

Dễ thấy, điểm

ở đáp án A, B, D không thuộc

 

nên ta chọn đáp án B.



Chọn đáp án B.

Câu 22. Thế tọa độ điểm

 

1; 3A 

lần lượt vào các phương trình ở bốn đáp án, ta được đáp án C

có

 

1 13

   

Chọn đáp án C.

Câu 23. Đồ thị

 

có đường tiệm cận đứng là đường thẳng

x 

Giao điểm của tiệm cận đứng với trục hoành là

;0 .









Gọi



là đường thẳng đi qua









và có hệ số góc

Khi đó, phương trình của



là:

y k x











là tiếp tuyến của

 

khi hệ

 

2 1 2



   



























có nghiệm.

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Thay

 







cào phương trình

 

ta được:

 

1 3 1 3 1

. 1 .

2 1 2 2 1 2

x x x

       

      

   



   



 

2 4 0

x x x

x loai









       















Với

x 

thì

k 

Phương trình tiếp tuyến là

1 1 1 1

12 2 12 24

y x y x



      





d y kx m







   



    











Chọn đáp án A.

Câu 24. Đường thẳng

: 1 0xy   

có vectơ pháp tuyến là:

 

1;1 .n 

Goi

 

:d y kx m

là tiếp tuyến cần tìm

d

có vectơ pháp tuyến là:

 

; 1 .nk

Theo giả thiết, ta có:

 

4 4 4

cos ,

41 4



    

41 1 4 2. 1 9 82 9 0

k k k k





        









 Với

9k 

thì

: 9 .d y x m

tiếp xúc với

 

khi hệ

 

6 9 9 1

3 12 9 9 2

x x x x m



   





  





có nghiệm

Ta có:

 

0 0 9

2 3 12 0 .

4 32 9 32

x m y x

      

   



       



 Với

k 

thì

d y x m

tiếp xúc với

 

khi hệ

 

6 9 3

3 12 9 4

x x x x m



   







  





có nghiệm

Ta có:

 

18 2 21

4 27 108 80 0

x x x



       

loại.

Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán có phương trình là:

9;yx

9 32yx  

Chọn đáp án A.

Câu 25.

Vì

: 2 1 0M d x y   

nên

 

; 2 1 .M m m 

Tiếp tuyến của

 

qua

có phương trình dạng

 

2 1.y k x m m   

https://www.facebook.com/ThayCaoTuan

Cao Tuấn – 0975306275 Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN

Từ điểm M kẻ được duy nhất một tiếp tuyến tới

 



hệ

   

 

2 1 1

k x m m



   



















có nghiệm duy nhất.

Thay

 

vào

 

, ta được:

 

x m m



   



         

3 1 4 2 1 1 , 1x x x m m x x         

Lần lượt thử từng phương án:

Với

thì phương trình trên trở thành

2 4 2 0xx  

có nghiệm duy nhất là

1.x 

Vậy

 

1 1; 1mM     

Chọn đáp án A.

Câu 26.

 

có hai điểm cực trị là

 

0; 2A

và

 

2; 2 .B 

Gọi

 

; 3 2M m m m C  

Theo giả thiết, ta có:

 

6 ; . 6

MAB

S d M AB AB



  

 

2 3 2 2

. .2 5 6

2 3 6

3 2 6 3

3 2 6 4

m m m

   



   



   





    





Ta có:

 













Với

3m 

thì

 

3;2M

. Khi đó, tiếp tuyến tại

có phương trình

9 25.yx

Loại trừ các phương án, chỉ có B thỏa mãn



Chọn đáp án B.

Câu 27. Gọi

 

;

M x C













với

1.x 

Phương trình tiếp tuyến

 

của

 

tại

là:

 

     

0 0 0 0

: 1 2 2 1 0

y x x d x x y x x



         



 

cách đều hai điểm

 

2; 4A 

và

 

4; 2B 

   

 

   

 

0 0 0 0 0 0

0 0 0 0

2 1 4 2 2 1 4 1 2 2 2 1

1 1 1 1

6 12 0

2 6 1 4 6 1

2 2 0

d A d d B d

x x x x x x

x x x x

x loai



           



   











        





  













Vậy có 3 tiếp tuyến thỏa mãn yêu cầu bài toán



Chọn đáp án C.

https://www.facebook.com/ThayCaoTuan

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Câu 28. Giao điểm

của hai tiệm cận có tọa độ

 

2;1 .

Gọi

 

;

M x C













với

2.x 

Phương trình tiếp tuyến

 

của

 

tại

là:

 

     

0 0 0 0

: 2 2 2 0

y x x d x x y x x



         



Đường thẳng

có vectơ chỉ phương là

IM x



  







đường thẳng

có vectơ

pháp tuyến là

; 2 .













Khi đó:

  

. 0 2 2 0

IM d IM d

IM d n n n n x x



         



 

3 : 5

2 1 .

1 : 1

x d y x



    

  

    



  

    





Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là:

   

: 1, : 5.d y x d y x     



Chọn đáp án B.

Bấm Tải xuống để xem toàn bộ.

| 1/21

| | Tải xuống

Preview text:

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan 11 CHỦ ĐỀ
TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
I. KIẾN THỨC CẦN NHỚ
Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số y  f x tại điểm x là hệ số góc của tiếp 0
tuyến với đồ thị C của hàm số tại điểm M x , y . 0 0 
Khi đó, phương trình tiếp tuyến của C tại điểm M x , y là: y  yx
x  x  y 0   0  0 0  0
Nguyên tắc chung để lập được phương trình tiếp tuyến là ta phải tìm được hoành độ tiếp điểm x . 0
II. MỘT SỐ DẠNG BÀI TẬP THƯỜNG GẶP
DẠNG 1:VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN KHI BIẾT TIẾP ĐIỂM uan 1. Phƣơng pháp T
Bài toán: Viết phương trình tiếp tuyến của đồ thị C : y  f x tại điểm M x , y . 0 0  ayCao Phƣơng pháp giải:
 Bước 1: Tính đạo hàm y  f x  hệ số góc tiếp tuyến k  yx . 0  /Th
 Bước 2: Phương trình tiếp tuyến của đồ thị tại điểm Mx ,y có dạng: 0 0  com
y  yx
x  x  y 0   0  0 ook. Chú ý:
 Nếu đề cho (hoành độ tiếp điểm) x thì tìm y bằng cách thế vào hàm số ban đầu, 0 0 .faceb
tức là: y  f x 0  0 w
 Nếu đề cho (tung độ tiếp điểm) y thì tìm x bằng cách giải phương trình 0 0 //ww
f x  y . 0  0 tps:
 Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị ht
C: y  f x và đường thẳng d: y  axb. Khi đó các hoành độ tiếp điểm là
nghiệm của phương trình hoành độ giao điểm giữa d và C.
Đặc biệt: Trục hoành Ox : y  0 và trục tung Oy : x  0.
Sử dụng máy tính cầm tay:
Phương trình tiếp cần lập có dạng d : y  kx  . m
 Đầu tiên tìm hệ số góc tiếp tuyến k  yx . 0  d Bấm q y và nhập
 f X , sau đó bấm = ta được k. x dx  0 x  d
Tiếp theo: Bấm phím ! để sửa lại thành
 f X x X f X, sau đó x dx  0 x
bấm phím r với X  x và bấm phím = ta được . m 0
Nhận xét: Sử dụng máy tính để lập phương trình tiếp tuyến tại điểm thực chất là rút gọn các
bước của cách 1. Sử dụng máy tính giúp ta nhanh chóng tìm ra kết quả và hạn chế được sai sót
trong tính toán. Nếu học sinh nào tính nhẩm tốt có thể bỏ qua cách này. 1
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN 2. Ví dụ minh họa
Ví dụ 1: Phương trình tiếp tuyến của đồ thị C 3 2
: y  x  2x tại điểm M 1; 3 là
A. y  7x  4.
B. y  7x  4. C. y  7  x  4. D. y  7  x  4. Lời giải:
Cách 1. Ta có: 2
y  3x  4x  k  y  1  7 .
Phương trình tiếp tuyến tại M 1; 3 là:
d : y  y x  x  y  y  7 x  1  3  y  7x  4  Chọn đáp án B. 0  0  0  
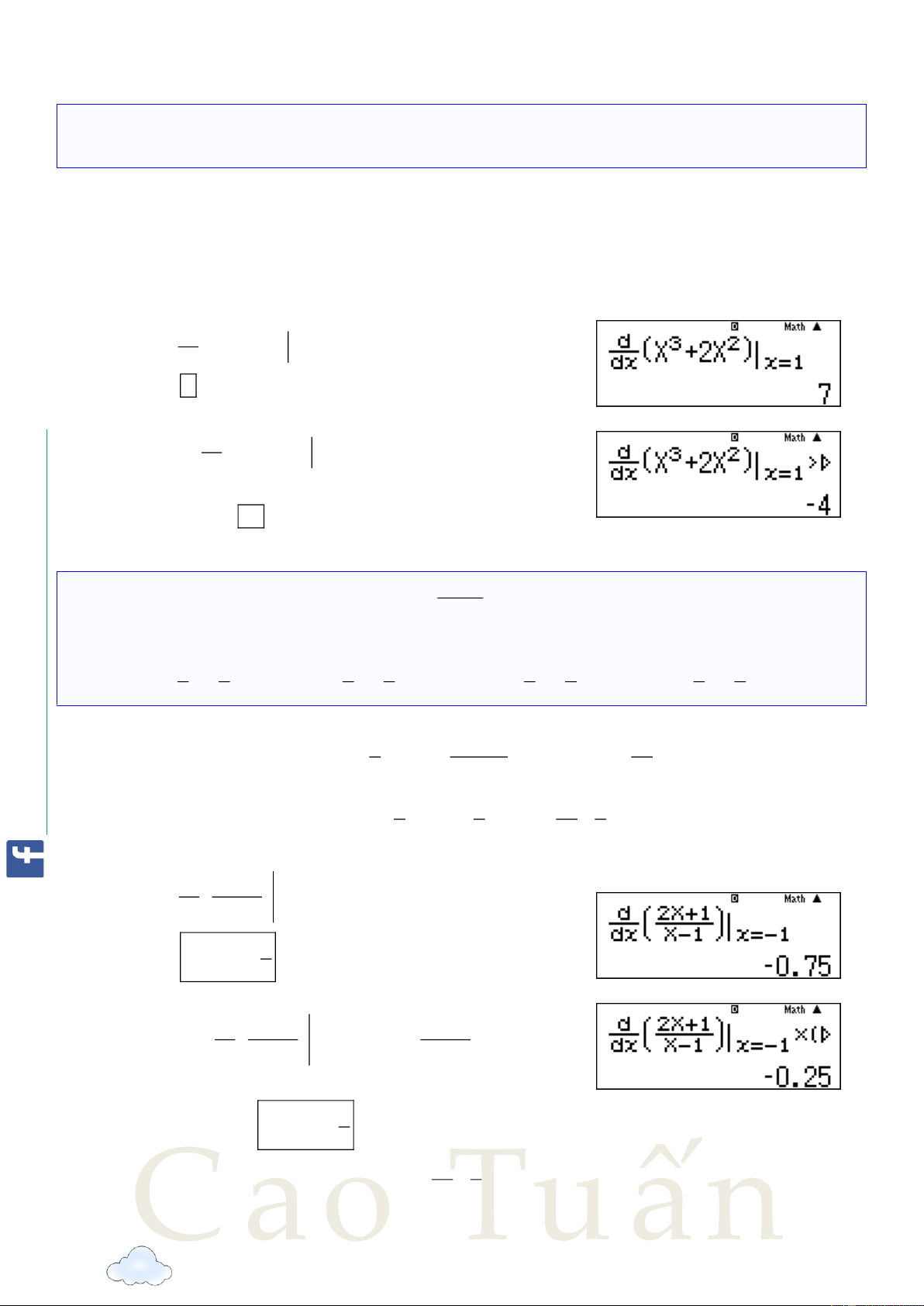
Cách 2 [Sử dụng máy tính cầm tay].  d Nhập  3 2 X  2X 
, sau đó bấm = ta được kết x 1 dx  quả là 7 .
 Bấm phím ! để sửa lại thành: d  3 2 X  2X  x X 3 2 uan  X  2X T x 1 dx 
sau đó bấm phím r với X  1 và bấm phím = ta được kết quả 4  . ayCao
Vậy phương trình tiếp tuyến của đồ thị C tại M là: y  7x  4  Chọn đáp án B. /Th x  1 
com Ví dụ 2: Cho điểm M thuộc đồ thị C 2 : y
và có hoành độ bằng 1.  Phương trình tiếp x  1
tuyến của đồ thị C tại điểm M là ook. 3 1 3 1 3 1 3 1 A. y  x  . B. y  x  .
C. y   x  .
D. y   x  . .faceb 4 4 4 4 4 4 4 4 w Lời giải: 1 3  3 
Cách 1. Ta có: x  1
  y  y 1   và y   k  y 1   . 2   0 0   //ww 2 x  4 1 tps: 3 1 3x 1
Phương trình tiếp tuyến tại M là: y   x   1   y  
  Chọn đáp án D. ht 4 2 4 4
Cách 2 [Sử dụng máy tính cầm tay].     d 2X 1 Nhập  
, sau đó bấm = ta được kết
dx  X  1  x 1  3 quả là 0  ,75   . 4
 Bấm phím ! để sửa lại thành:
d  2X  1    X 2X 1 x   
dx  X 1  X  1 x 1 
sau đó bấm phím r với X  1  và bấm phím = 1 ta được kết quả 0  ,25   . 4 3x 1
Vậy phương trình tiếp tuyến tại M là: y  
  Chọn đáp án D. 4 4 2
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan 1
Ví dụ 3: Cho điểm M thuộc đồ thị C 4 2 : y 
x  2x có hoành độ x  0 và y x  1  . 0  4 0
Phương trình tiếp tuyến của C tại điểm M là 5 5 19 19 A. y  3  x  .
B. y  3x  .
C. y  3x  . D. y  3  x  . 4 4 4 4 Lời giải: Ta có: 3
y  x  4x , 2
y  3x  4. x  0
Khi đó: y x  2 2 0  1   3x  4  1   x  1 x  1    x  1 o 0 0 0 0
Đến đây bạn đọc có thể giải tiếp bằng nhiều cách như hai ví dụ trình bày ở trên. Cách 1. 1 7
Ta có: x  1  y  y   4 2
1  .1  2.1   và k  y  3 1  1  4.1  3  . 0 0 4 4
Phương trình tiếp tuyến tại M là: y   x   7 5 3 1   y  3
 x   Chọn đáp án A. 4 4 uan
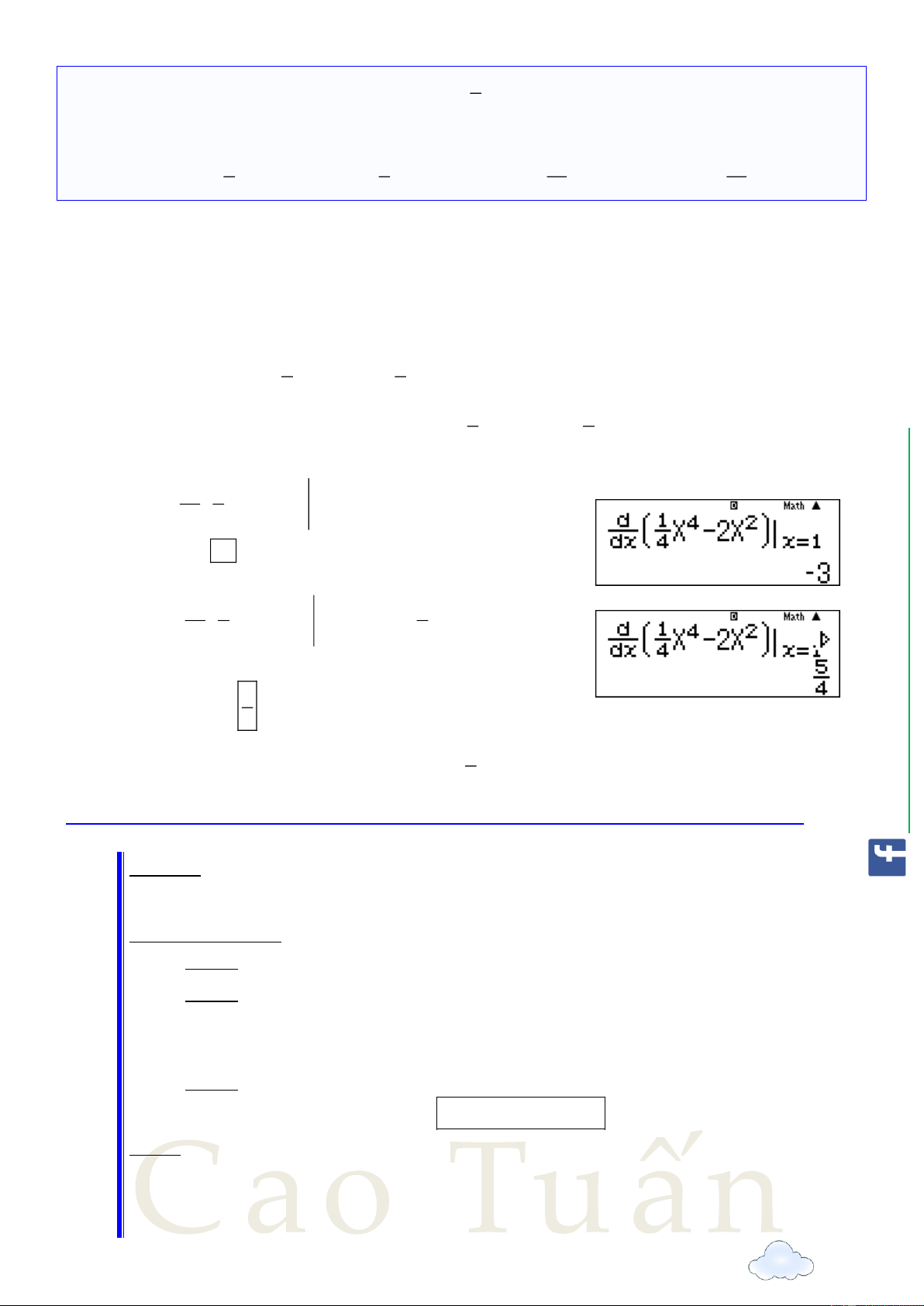
Cách 2 [Sử dụng máy tính cầm tay]. T    d 1 Nhập 4 2 X   2X 
, sau đó bấm = ta được dx  4  x 1  ayCao kết quả là 3  . /Th
 Bấm phím ! để sửa lại thành: d  1  4 2 1 4 2 com X  2X
x X  X    2X dx  4  4 x 1  ook.
sau đó bấm phím r với X  1 và bấm phím = ta 5 được kết quả . .faceb 4 w 5
Vậy phương trình tiếp tuyến tại M là: y  3
 x   Chọn đáp án A. //ww 4 tps:
DẠNG 2: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN KHI BIẾT PHƢƠNG (Biết hệ số góc k) ht 1. Phƣơng pháp
Bài toán: Cho hàm số y  f x có đồ thị C . Lập phương trình tiếp tuyến của đồ thị
C với hệ số góc k cho trước. Phƣơng pháp giải:
 Bước 1: Gọi Mx ; y là tiếp điểm và tính y  f x. 0 0   Bước 2:
 Hệ số góc tiếp tuyến là k  f x . 0 
 Giải phương trình này tìm được x , thay vào hàm số được y . 0 0
 Bước 3: Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng:
d : y  y x  x  y 0  0  0
Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:
 Tiếp tuyến d //  : y  ax  b  k  . a
Sau khi lập được phương trình tiếp tuyến thì nhớ kiểm tra lại xem tiếp tuyến có
bị trùng với đường thẳng  hay không? Nếu trùng thì phải loại đi kết quả đó. 3
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN  1
Tiếp tuyến d   : y  ax  b  k.a  1   k    a
 Tiếp tuyến tạo với trục hoành một góc  thì k  tan.
Tổng quát: Tiếp tuyến tạo với đường thẳng  : y  ax  b một góc  . k  a Khi đó:  tan. 1  ka
Sử dụng máy tính cầm tay:
Phương trình tiếp cần lập có dạng d : y  kx  . m
 Tìm hoành độ tiếp điểm x . 0
 Nhập kX  f X (hoặc f X  kX ) sau đó bấm r với X  x rồi bấm = ta 0 được kết quả là . m 2. Ví dụ minh họa
Ví dụ 1: Phương trình tiếp tuyến của đồ thị C 3
: y  x  3x  2 có hệ số góc bằng 9 là uan T
A. y  9x 18; y  9x  22.
B. y  9x 14; y  9x  18.
C. y  9x  18; y  9x  22.
D. y  9x 14; y  9x 18. ayCao Lời giải: Ta có: 2
y  3x  3 . Gọi tiếp điểm của tiếp tuyến cầ tìm là M x ; y . 0 0  /Th
 hệ số góc của tiếp tuyến là: k  yx  2 2
 9  3x  3  9  x  4  x  2  . 0 0 0 0 com Cách 1.
 Với x  2  y  4 ta có tiếp điểm M 2; 4 . 1   ook. 0 0
Phương trình tiếp tuyến tại M là: d : y  9 x  2  4  d : y  9x 14. 1   1 1 .faceb       w Với x 2 y
0 ta có tiếp điểm M 2; 0 . 2   0 0
Phương trình tiếp tuyến tại M là: d : y  9 x  2  0  d : y  9x  18. 2   2 2 //ww
Vậy có hai tiếp tuyến cần tìm là d : y  9x 14; d : y  9x  18  Chọn đáp án B. 1 2 tps:
Cách 2 [Sử dụng máy tính cầm tay]. ht
 Với x  2 ta nhập X 3 9
 X  3X  2 r với X  2 0
rồi bấm = ta được kết quả là 1  4 .
 d : y  9x 14. 1  Với x  2
 ta nhập X 3 9
 X  3X  2 r với 0 X  2
 rồi bấm = ta được kết quả là 18 .
 d : y  9x 18. 2
 Chọn đáp án B. x 
Ví dụ 2: Tiếp tuyến của đồ thị C 2 1 : y 
song song với đường thẳng  : 3x  y  2  0 có x  2 phương trình là
A. y  3x  4.
B. y  3x  2.
C. y  3x  14.
D. y  3x  4. Lời giải: 3 Ta có: y          và : 3x y 2 0 y 3x 2. x  22 4
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan
Gọi tiếp điểm của tiếp tuyến cầ tìm là M x ; y . 0 0 
Vì tiếp tuyến song song với đường thẳng  nên 3 x  2  1 x  1  k 
 3  x  2  1     . 2  0 2 0 0 x  x  2  1  x  3 2    0  0 0 Cách 1.  Với x  1   y  1
 ta có tiếp điểm M 1  ; 1  . 1   0 0
Phương trình tiếp tuyến tại M là: d : y  3 x  1 1  d : y  3x  2. 1   1 1
Lúc này: d    Loại. 1  Với x  3
  y  5 ta có tiếp điểm M 3  ; 5 . 2   0 0
Phương trình tiếp tuyến tại M là: d : y  3 x  3  5  d : y  3x  14. 2   2 2
Vậy có một tiếp tuyến cần tìm là d : y  3x  14 Chọn đáp án C. 2
Cách 2 [Sử dụng máy tính cầm tay].   X Với x  1
 ta nhập X 2 1 3  r với X  1  uan 0 X  2 T
rồi bấm = ta được kết quả là 2 .
 d : y  3x  2  d    Loại. 1 1 ayCao X  /Th  Với x  3
 ta nhập X 2 1 3  r với X  3  0 X  2 com
rồi bấm = ta được kết quả là 14 .
d : y  3x  14  Chọn đáp án C. 2 ook.
DẠNG 3: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN KHI BIẾT TIẾP TUYẾN ĐI QUA MỘT .faceb w ĐIỂM CHO TRƢỚC 1. Phƣơng pháp //ww
Bài toán: Viết phương trình tiếp tuyến của đồ thị C , biết tiếp tuyến đi qua điểm tps:
Ax ; y . A A ht Phƣơng pháp giải:
Cách 1: Sử dụng điều kiện tiếp xức của hai đồ thị
 Bước 1: Phương trình tiếp tuyến đi qua Ax ; y hệ số góc k có dạng: A A 
d : y  k x  x   y * A A 
 f x  kx  x   y A 
 Bước 2: d là tiếp tuyến của C khi và chỉ khi hệ A  có nghiệm. f   x   k
 Bước 3: Giải hệ trên tìm được x  k và thế vào phương trình * , thu được
phương trình tiếp tuyến cần tìm. Cách 2:  Bước 1:
 Gọi Mx ; f x là tiếp điểm. 0  0
 Tính hệ số góc tiếp tuyến k  f x theo x . 0  0 5
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN
 Bước 2: Phương trình tiếp tuyến có dạng: d : y  f x x  x  f x * * 0   0   0  
Vì điểm Ax ; y d nên y  f  x
x  x  f x . Giải phương trình này sẽ A
 0 A 0  0 A A  tìm được x . 0
Bước 3: Thay x vừa tìm được vào * * ta được phương trình tiếp tuyến cần tìm. 0 2. Ví dụ minh họa
Ví dụ 1: Tiếp tuyến của đồ thị C 3 : y  4
 x  3x 1 đi qua điểm A 1
 ; 2 có phương trình là A. y  9
 x 7; y  x  2. B. y  9
 x 11; y  x  2. C. y  9
 x 11; y  2. D. y  9
 x 7; y  2. Lời giải: Ta có: 2 y  1  2x  3.    
Đường thẳng d đi qua A 1; 2 với hệ số góc k có phương trình d : y k x 1 2. 3  4
 x  3x  1  k x   1   2   uan 1 T
Đường thẳng d là tiếp tuyến của C  hệ  có nghiệm. 2 k  1  2x   3   2
Thay k từ 2 vào 1 ta được: ayCao 3
 x  x    2 4 3 1 1
 2x  3x  1  2 /Th x  1    com 1 8x 12x 4 0 x x 12 3 2 0             1  2   x   2 ook.  Với x  1   k  9
 . Phương trình tiếp tuyến là: y  9  x  7. .faceb  1 Với x 
 k  0 . Phương trình tiếp tuyến là: y  2. w 2
Vậy có hai tiếp tuyến cần tìm là y  9
 x 7; y  2  Chọn đáp án D. //ww
Bình luận: Đối với dạng bài toán viết phương trình tiếp tuyến đi qua điểm việc tính toán tương đối mất tps:
thời gian và dễ dẫn đến sai lầm đáng có. Do đó, ta có thể sử dụng máy tính bỏ túi để thử các đáp án như ht sau:
 Cho f x bằng kết quả các đáp án, từ đó ta thu được các phương trình.
 Sử dụng chức năng giải phương trình bậc ba của máy tính bỏ túi bằng cách bấm tổ hợp phím
w 5 4 và nhập hệ số phương trình.
Thông thường máy tính cho số nghiệm thực nhỏ hơn số bậc của phương trình là 1 thì ta chọn đáp án đó.
Cụ thể trong bài toán này:
 Đầu tiên thử với đáp án A, ta cho: 3 3 4
 x  3x 1  9  x 7  4
 x 12x 6  0.
Máy tính cho 3 nghiệm  Loại A.
 Thử với đáp án B, ta cho: 3 3 4
 x  3x 1  x  2  4
 x  4x 1  0.
Máy tính cho 3 nghiệm  Loại B.
 Thử với đáp án B, ta cho: 3 3 4
 x  3x 1  9  x 11  4
 x 12x 10  0.
Máy tính hiển thị 1 nghiệm thực và 2 nghiệm phức (phương trình có số nghiệm thực là một nhỏ
hơn bậc của phương trình là 2)  Loại C.
 Chọn đáp án D. 6
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan
Đến đây ta có thể dừng được rồi, tuy nhiên có thể kiểm nghiệm thêm đáp án D, ta cho:  3 3 4
 x  3x 1  9  x 7  4
 x 12x  8  0
máy tính hiển thị 2 nghiệm x  1;
 x  2 (nhận).  3 3 4
 x  3x 1  2  4
 x  3x 1  0 1
máy tính hiển thị 2 nghiệm x  1;
 x  (nhận). 2 x 
Ví dụ 2: Tiếp tuyến của đồ thị C 2 1 : y  đi qua điểm A 1
 ; 4 có phương trình là x  1 1 13 1 1 1
A. y  x  .
B. y  x  .
C. y  x  4. 3 3 3 3 3
D. Không tồn tại tiếp tuyến. Lời giải: 3
Điều kiện: x  1.
 Ta có: y   x  1 . 2
Đường thẳng d đi qua A 1
 ; 4 với hệ số góc k có phương trình: d : y  kx   1  4. uan T 2x 1  k 
x1 4  1  x  1
Đường thẳng d là tiếp tuyến của C  hệ  3 có nghiệm. ayCao k  2 2    x 1 /Th 2x  1 3
Thay k từ 2 vào 1 ta được:  x  1  4. 2   com x  1 x 1 ook. x  1    2 x 1 1
 x 10x  8  0    x  4   k  . x  4   3 .faceb 1 13    w
Phương trình tiếp tuyến là: d : y x
Chọn đáp án A. 3 3 //ww
DẠNG 4: MỘT SỐ BÀI TOÁN CHỨA THAM SỐ tps: ht
Ví dụ 1: Cho hàm số 3 2
y  x  3x có đồ thị C . Gọi M là điểm thuộc đồ thị C có hoành độ
bằng 1. Với giá trị nào của tham số m thì tiếp tuyến của C tại M song song với đường thẳng d y   2 :
m  4 x  2m 1?
A. m  1. B. m  1. 
C. m  2. D. m  2.  Lời giải: TXĐ: D  . Ta có: 2
y  3x  6 . x
Phương trình tiếp tuyến của C tại M 1; 2  C là:  y    2 : 2 3.1  6.  1 x   1  y  3  x 1. m  1 2  3   m  4 
Khi đó:  // d    m  1   m  1
  Chọn đáp án B. 2m 1  1 m   1 7
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN
Ví dụ 2: Cho hàm số 4
y  x  m   2 2
1 x  m  2 có đồ thị C . Gọi A là điểm thuộc đồ thị hàm
số có hoành độ bằng 1. Với giá trị nào của tham số m thì tiếp tuyến với đồ thị C tại A vuông
góc với đường thẳng  : x  4y  1  0?
A. m  1. B. m  1. 
C. m  2. D. m  2.  Lời giải: TXĐ: D  . Ta có: 3
y  4x  4m   1 . x
Gọi d là tiếp tuyến của C tại điểm A .
Khi đó d có hệ số góc: k  y 
1  4  4m   1  4 . m 1 1
 : x  4y 1  0  y  x  . 4 4
Do đó: d    k  4   4  m  4
  m  1 Chọn đáp án A.
Ví dụ 3: Cho hàm số 3 2
y  x  3x  2m  
1 x  2m  3 có đồ thị C . Với giá trị nào của tham m 
số m thì tiếp tuyến có hệ số góc lớn nhất của đồ thị C vuông góc với đường thẳng m  uan T
 : x  2y  4  0? A. m  2.  B. m  1. 
C. m  0.
D. m  4. ayCao Lời giải: TXĐ: D  . /Th
Ta có: y   x  x  m    x  x    m    x  2 2 2 3 6 2 1 3 2 1 2 2 3
1  2m  2  2m  2, x   . com
Do đó: GTLN của y là 2m  2 , đạt tại x  1. Với x  1  y  4m  2. 0 0 0
Phương trình tiếp tuyến của C
tại M 1; 4m  2 là: m  ook.
d : y  4m  2  2m  2x  
1  y  2m  2 x  2m  4. .faceb 1 w
Theo đề ra ta có:  : x  2y  4  0 hay y  x  2 . 2
Khi đó: d    2m  2  2   m  2
  Chọn đáp án A. //ww x  2   
tps: Ví dụ 4: Cho hàm số y
C . Giả sử, đường thẳng d : y
kx m là tiếp tuyến
2x  có đồ thị   3
ht của C , biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A,B và tam giác O
 AB cân tại gốc tọa độ O. Tổng k  m có giá trị bằng A. 1. B. 3. C. 1.  D. 3.  Lời giải:  3 1  TXĐ: D 
\ . Ta có: y  .  2 2x32
Tiếp tuyến d : y  kx  m cắt Ox,Oy lần lượt tại hai điểm A, B nên m  0, k  0.  m 
Do AOx nên A  
; 0  , BOy nên B0; m.  k  Do tam giác O
 AB cân tại gốc tọa độ O nên m  1  k  1   2 1 OA  OB   m  m   1   0   . Do k   0 nên k  1.  2 k  k  k  1 2x 32 0 1  x  1   y  1 Suy ra:  1
  2x  3  1   . 2  0 2 0 0  x  x  2   y   0 2 3  0 0 0 8
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan
 Phương trình tiếp tuyến của C tại M 1
 ;1 là: y  x  
1  1  y  x (loại). 1  
 Phương trình tiếp tuyến của C tại M 2;
 0 là: y  x  2  y  x  2. 2  
Khi đó: k  m  1   2  3
  Chọn đáp án D.
Ví dụ 5 [Sở GD & ĐT Vũng Tàu – 2017]: Tìm tập hợp tất cả các giá trị tham số thực m để đồ thị  2x  3
C  của hàm số y  cắt đường thẳng 2
y  2x  m tại hai điểm phân biệt mà hai tiếp tuyến x  1
của C tại hai điểm đó song song với nhau. A.   2 .
B.  2; 2. C.  1  ;  1 . D.  2  ;  2 . Lời giải:
Chọn đáp án D. uan T ayCao /Th com ook. .faceb w //ww tps: ht 9
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN
III. CÂU HỎI TRẮC NGHIỆM RÈN LUYỆN x 
Câu 1. Tiếp tuyến của đồ thị C 2 1 : y   x 
tại điểm có hoành độ bằng 1 có phương trình là 1 3 1 3 1 3 1 3 1 A. y  x  . B. y  x  .
C. y   x  .
D. y   x  . 4 4 4 4 4 4 4 4
Câu 2. Tiếp tuyến của C 4 2
: y  x  2x tại điểm có hoành độ bằng 2
 có phương trình là A. y  2  4x  40. B. y  2
 4x  40. C. y  24x  40.
D. y  24x  40. 1  1 5 
Câu 3. Tiếp tuyến của C : y  5x  1
tại điểm A  ;  có phương trình là 2x   1  2 2  3 3
A. y  2x  . B. y  2  x  .
C. y  3x 1.
D. y  3x  1. 2 2 x 
Câu 4. Tiếp tuyến của C 2 2 : y   x 
tại điểm có tung độ bằng 3 có phương trình là 2 1   1   1    1    uan A. y x 5. B. y x 5. C. y x 5. D. y x 5. T 2 2 2 2
Câu 5. Tiếp tuyến của C 3 2
: y  2x  3x  1 tại điểm có tung độ bằng 4 có phương trình là A. y  1  2x  8. B. y  1  2x  8.
C. y  12x  8.
D. y  12x  8. ayCao Câu 6. Cho hàm số 3 2 y  2
 x  3x  2 có đồ thị C . Tiếp tuyến của C tại điểm có hoành độ là /Th
nghiệm của phương trình y  0 có phương trình là com 3 7 3 7 9 3 9 3 A. y  x  . B. y  x  .
C. y   x  .
D. y   x  . 2 4 2 4 2 4 2 4 ook. Câu 7. Cho hàm số 3 2
y  x  3x  x  1 có đồ thị C . Tiếp tuyến của C tại điểm thuộc đồ thị .faceb
C có hoành độ dương và là nghiệm của phương trình y .xy 11 0 có phương trình là w
A. y  x  3. B. y  4  x  2.
C. y  x  2. D. y  4  x  3.  //ww x 2
Câu 8. Cho hàm số y 
C . Tiếp tuyến của C tại giao điểm của C với trục
x  có đồ thị   1 tps: tung có phương trình là ht 1 2 1 2
A. y   x  .
B. y   x  . C. y  3  x  2. D. y  3  x  2. 3 3 3 3 2  x  3
Câu 9. Cho hàm số y 
C . Phương trình tiếp tuyến của C tại các giao điểm x  có đồ thị   1
của C và đường  : y  x  3 là
A. y  x  3 ;
x y  x  1.
B. y  x  3; y  x  1.
C. y  x  3; y  x  1.
D. y  x  3; y  x  1. Câu 10. Cho hàm số 3
y  x  3x  2 có đồ thị C . Số phương trình tiếp tuyến của C tại giao
điểm C với đường thẳng  : x  y  2  0 là A. 1. B. 2. C. 3. D. 4. 10
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan x  2
Câu 11. Cho hàm số y 
C . Biết điểm M C sao cho khoảng cách từ điểm M
x  có đồ thị   1
đến đường tiệm cận đứng của đồ thị C bằng 2. Phương trình tiếp tuyến của C tại M là 1 1 1 7 1 1 1 5 A. y 
x  x; y  x  . B. y  x  ; y  x  . 4 4 4 4 4 4 4 4 1 1 1 5 1 1 1 5
C. y   x  ; y   x  .
D. y   x  x; y   x  . 4 4 4 4 4 4 4 4 2x  1
Câu 12. Cho hàm số y 
C . Tiếp tuyến của đồ thị C tại điểm M C có tọa
x  có đồ thị   1
độ nguyên dương có phương trình là
A. y  1. B. y  1. 
C. y  x 1.
D. y  x  5. 1 Câu 13. Cho hàm số 4 2 y 
x  8x  4 có đồ thị C . Biết điểm M C sao cho x  0 và x là 4 M M
nghiệm của phương trình y  4
 . Viết phương trình tiếp tuyến của C tại điểm M có phương trình là uan           T
A. y 24x 16. B. y 24x 16. C. y 24x 80.
D. y 24x 80. x 
Câu 14. Tiếp tuyến của đồ thị C 2 1 : y 
k  có phương trình là x  có hệ số góc 1 1 ayCao
A. y  x  1; y  x  5.
B. y  x 1; y  x  5. /Th 1 5
C. y  x  ; y  x  5.
D. y  x  1; y  x  . 2 4 com
Câu 15. Tiếp tuyến của đồ thị C 3 2
: y  x  3x  3 song song với đường thẳng  : 9x  y  24 có ook. phương trình là
A. y  9x  24.
B. y  9x  8.
C. y  9x 10.
D. y  9x  30. .faceb x  w
Câu 16. Tiếp tuyến của đồ thị C 2 1 : y   x  y   có x 
song song với đường thẳng : 5 13 0 2 phương trình là //ww A. y  5
 x 8; y  5  x  2. B. y  5
 x  2; y  5  x  22. tps: C. y  5
 x  2; y  5  x  22. D. y  5
 x  2; y  5  x 8. ht x 
Câu 17. Phương trình tiếp tuyến của đồ thị C 2 4 : y    . Biết tiếp x 
tại M có dạng y kx m 1
tuyến tại M song song với đường thẳng  : 3x  2y  19  0 . Khi đó, tổng k  m có giá trị bằng A. 11. B. 4. C. 8.  D. 1. 
Câu 18. Tiếp tuyến của đồ thị C 3 2
: y  x  3x  5 vuông góc với đường d : x  9y  0 có phương trình là A. y  9 ;
x y  9x  32.
B. y  9x  22; y  9x  18. C. y  9 ;
x y  9x  32.
D. y  9x  22; y  9x 18. 1
Câu 19. Tiếp tuyến của đồ thị C 4 2
: y  x  x  6 vuông góc với đường thẳng  : y  x  1 có 6 phương trình là A. y  6  x  2. B. y  6  x  2. C. y  6  x 10. D. y  6  x 10. 11
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN Câu 20. Cho hàm số 3 2
y  2x  3x  5 có đồ thị C . Gọi d : y  kx  m là tiếp tuyến của C tại
điểm có hệ số góc tiếp tuyến nhỏ nhất. Tỉ số T  2m : k có giá trị bằng A. T  7.  B. T  5. 
C. T  5.
D. T  7. Câu 21. Cho hàm số 3 2
y  x  3x  1 có đồ thị C . Hai điểm A, B thuộc C sao cho tiếp tuyến
của C tại A và B song song với nhau và độ dài đoạn AB  4 2 là A. A 2;  1; B2; 3  . B. A3;  1 ; B 1  ; 3  .
C. A0;  
1 ; B4; 3. D. A 3  ; 2; B1; 2  . x 
Câu 22. Tiếp tuyến của đồ thị C 2 1 : y  A 1
 ; 3 có phương trình là x  đi qua điểm   1 1 13 1 13 1 13 1 13
A. y   x  .
B. y   x  . C. y  x  . D. y  x  . 4 4 4 4 4 4 4 4 x  1   
Câu 23. Cho hàm số y
C . Giả sử đường thẳng d : y
kx m là tiếp tuyến của
2x  có đồ thị   1 uan
C và tiếp tuyến này đi qua giao điểm của đường tiệm cận và trục hoành Ox . Tỉ số T  k :m T có giá trị bằng A. 2. B. 2.  C. 1. D. 1.  ayCao Câu 24. Cho hàm số 3 2
y  x  6x  9x có đồ thị C . Tiếp tuyến của C tạo với đường thẳng /Th  4
: x  y 1  0 một góc  sao cho cos 
và tiếp điểm có hoành độ nguyên có phương com 41 trình là        ook. A. y 9 ;
x y 9x 32.
B. y 9x 21; y 9x 7. C. y  9 ;
x y  9x  32.
D. y  9x  21; y  9x  7. .faceb x  3 w
Câu 25. Cho hàm số y 
C . Nếu điểm M thuộc d : 2x  y  1  0 có hoành độ
x  có đồ thị   1
âm và từ điểm M kẻ được duy nhất một tiếp tuyến tới C thì tọa độ điểm M là //ww A. M  1  ;   1 . B. M  2;  3  . C. M  3  ; 5  . D. M  4;  7  . tps: ht Câu 26. Cho hàm số 3 2
y  x  3x  2 có đồ thị C . Nếu điểm M thuộc C cùng với hai điểm
cực trị của đồ thị hàm số C tạo thành tam giác có diện tích bằng 6 thì phương trình tiếp
tuyến với đồ thị tại điểm M là A. y  9
 x 7; y  9  x  25.
B. y  9x  25; y  9x  7. C. y  9
 x 7; y  9  x  25.
D. y  9x  25; y  9x  7. x 
Câu 27. Có bao nhiêu tiếp tuyến của đồ thị C 2 1 : y  A 2;  4 và x  cách đều hai điểm   1 B4; 2   ? A. 1. B. 2. C. 3. D. 4. x  1
Câu 28. Cho hàm số y 
C . Gọi I là giao điểm hai đường tiệm cận của C .
x  có đồ thị   2
Tiếp tuyến d của C tại điểm M thỏa mãn IM  d có phương trình là
A. y  x  1; y  x  5.
B. y  x  1; y  x  5.
C. y  x 1; y  x  5.
D. y  x 1; y  x  5. 12
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan
Câu 29. [THPT Chuyên Thái Bình – Lần 4 – 2017] Đồ thị hàm số 4 2
y  x  2x  1 có bao nhiêu
tiếp tuyến song song với trục hoành ? A. 0. B. 1. C. 2. D. 3. x 
Câu 30. [THPT Quốc Học Quy Nhơn – Bình Định – Lần 1 – 2017] Cho hàm số y  f x 3 1  x  3
có đồ thị C. Viết phương trình tiếp tuyến của đồ thị C , biết hoành độ tiếp điểm là nghiệm
của phương trình 7x 1 
1 . f x  10. 2 1 5 1 2 1 5 1
A. y   x  ; y   x  .
B. y   x  ; y  x  . 5 5 2 2 5 5 2 2 2 9 5 9 2 9 5 1
C. y   x  ; y   x  .
D. y   x  ; y   x  . 5 5 2 2 5 5 2 2
Câu 31. [THPT Chuyên Lê Khiết – Quảng Ngãi – 2017] Cho hàm số 3 2
y  x  3x  1 có đồ thị là
C. Gọi  là tiếp tuyến của C tại điểm A1;5 và B là giao điểm thứ hai của  với C.
Tính diện tích S của tam giác OAB, với O là gốc tọa độ. uan
A. S  12.
B. S  6.
C. S  15.
D. S  24. T
Câu 32. [THPT Chuyên Biên Hòa – Hà Nam – 2017] Cho hàm số 3
y  x  6x  2. Hỏi có bao
nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm A1; 3  ? ayCao A. 3. B. 2. C. 0. D. 1. /Th x  b
Câu 33. [THPT Chuyên Lê Quý Đôn – Đà Nẵng – Lần 2 – 2017] Cho hàm số y  có hàm số ax  2 com
C. Biết a, b là các giá trị thực sao cho tiếp tuyến của C tại điểm M1; 2   song song với ook.
đương thẳng d : 3x  y  4  0. Tính a  . b
A. a  b  0.
B. a  b  1. 
C. a  b  2.
D. a  b  1. .faceb x  1 w
Câu 34. [THPT Chuyên Sơn La – Lần 2 – 2017] Cho hàm số y 
có đồ thị C. Gọi d là x  2
khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của C. Tìm //ww
giá trị lớn nhất của . d tps: 2 ht A. d   B. d  5. C. d  3. D. d  6. max 2 max max max 13
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án B A D C C A A D B C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án A D A A B C D A C A Câu 21 22 23 24 25 26 27 28 29 30 Đáp án B C A A A B C B B A Câu 31 32 33 34 Đáp án A B C D HƯỚNG DẪN GIẢI 3
Câu 1. TXĐ: D   \  
1 . Ta có: y   x   . 2 1 1 3
Với x  1 y  , y 1  . 0 0   uan 2 4 T  1  3 1 3 1
Phương trình tiếp tuyến của C tại M 1
 ;  là: y  x   1  hay y  x  .  2  4 2 4 4 ayCao
 Chọn đáp án B. /Th
Câu 2. TXĐ: D  . Ta có: 3
y  4x  4 . x        com Với x 2 y 8, y 2 24. 0 0  
Phương trình tiếp tuyến của C tại M  2  ;8 là: ook. y  2
 4x  28  y  2
 4x  40  Chọn đáp án A. .faceb 1  1 
Câu 3. TXĐ: D   \ 
1 . Ta có: y  5   y  3   . w x 2  2 2 1   1 5  //ww
Phương trình tiếp tuyến của C tại điểm A ;  là:  2 2  tps:  1  5 ht y  3 x 
  y  3x 1  
Chọn đáp án D.  2  2 2 
Câu 4. TXĐ: D   \ 
2 . Ta có: y   . x  22
Với y  3  x  4 . Khi đó: y  1 4   . 0 0 2
Phương trình tiếp tuyến của C tại điểm M 4;3 là: 1
y   x   1
4  3  y   x  5  Chọn đáp án C. 2 2
Câu 5. TXĐ: D  . Ta có: 2
y  6x  6 . x
Với y  4  x  1. Khi đó: y  1  12. 0 0
Phương trình tiếp tuyến của C tại điểm M 1; 4 là:
y 12x  
1  4  y  12x  8  Chọn đáp án C.
Câu 6. TXĐ: D  . Ta có: 2 y  6  x  6 ; x y  1  2x  6. 14
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan 1 5  1  3
Khi đó: y x  0  1
 2x  6  0  x   y  và y    . 0  0 0 0 2 2  2  2  1 5 
Phương trình tiếp tuyến của C tại điểm M  ;  là:  2 2  3  1  5 3 7 y  x 
  y  x    
Chọn đáp án A. 2  2  2 2 4
Câu 7. TXĐ: D  . Ta có: 2
y  3x  6 ;
x y  6x  6. x  2 
Xét phương trình: y  .
x y  11  0   2
3x  6x  x6x  6 11  0  . 2  x    3
Do x  0 nên x  2.
Với x  2  y  5
 và y2  1  . 0 0
Phương trình tiếp tuyến của C tại điểm M 2; 5   là:
y  x  2  5  y  x  3  Chọn đáp án A. uan T 3
Câu 8. TXĐ: D   \ 
1 . Ta có: y    x   . 2 1 ayCao
Giao điểm của C và trục tung là M 0; 2
  và y0  3  . /Th
Phương trình tiếp tuyến của C tại điểm M 0; 2   là: y  3
 x  2  Chọn đáp án D. com 1
Câu 9. TXĐ: D   \ 
1 . Ta có: y    x   . 2 1 ook.
Phương trình hoành độ giao điểm của đồ thị C và đường thẳng  là: .faceb    x  0 2 3 tm x  2 w
 x  3  x  2x  0   x  x   tm. 1 2 //ww
 Với x  0  y  3
 và y0  1  . 0 0 tps:
Phương trình tiếp tuyến của C tại điểm M 0; 3
  là: y  x 3 ht
 Với x  2  y  1  , y 2  1  . 0 0  
Phương trình tiếp tuyến của C tại điểm M 2;   1 là:
y  x  2 1  y  x  1.
 Chọn đáp án B.
Câu 10. TXĐ D  . Ta có: 2 y  3  x  3.
Phương trình hoành độ giao điểm của C và đường thẳng  : y  x  2 là: x  2   3 3
x  3x  2  x  2  x  4x  0  x  0 .  x  2 
Do có 3 tiếp điểm nên có 3 tiếp tuyến thỏa yêu cầu bài toán  Chọn đáp án C.
Câu 11. TXĐ: D   \ 
1 . Tiệm cận đứng là đường thẳng  : x  1. 1 x 2 Ta có: y   
Vì M C nên 0 M x ; . 0 x   . 2 1 x 1 0 15
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN  3 1 x  1
  y  , y 1    0 0  
Theo đề ra ta có: d M  2 4 ;
 2  x 1  2   . 0  1 1
x   3  y  , y 3  0 0    2 4  3 3 1 1 7
Phương trình tiếp tuyến tại M 1; là: y x 1 hay y x . 1 2 2 4 4 4  1 1 1 1 1
Phương trình tiếp tuyến tại M 3; là: y x 3 hay y x . 2 2 2 4 4 4
 Chọn đáp án A. 1   2x  1 
Câu 12. TXĐ: D   \ 
1 . Ta có: y  0    Lấy M x ; C . 0 0   x   . 2 1 x  1  0 
Khi đó, M có tọa độ nguyên dương nên: x  0 x  0 0 0 x  0   0   1  1 uan   2x  1 x  x     T 0 0 0  0  2  2  x 1     0   x  1   x  1         0 0 x 2 y 3, y 2 1. 0 0   x   0     ayCao x x0 0  1   2    1 x  0 /Th 0  x  1     0 x  1 x   2 0  0 com
Phương trình tiếp tuyến của C tại điểm M 2; 3 là: y  x  2  3  y  x  5. 0  ook.
Chọn đáp án D. 1 Câu 13. 4 2 3 2 y 
x  8x  4  y  x  16x; y  3x  16. .faceb 4 w
Gọi M x ; y C , x  0 là tiếp điểm. M M M  x  2  //ww
Do x là nghiệm của phương trình y  4  3x  16  4 M    . M nên 2 M x  2  M tps: Do x  0
x    y  
và y2  24. ht M nên 2 32 M M
Phương trình tiếp tuyến của đồ thị C tại M 2; 3  2 là:
y  24x  2  32  y  24x  16  Chọn đáp án A. 1
Câu 14. TXĐ: D   \  
1 . Ta có: y   x  1 . 2  2x  1  Gọi 0 M  x ;
 là tiếp điểm của tiếp tuyến đồ thị C có hệ số góc k  1 . 0 x  1  0  1 x  2   y  3 Khi đó: k  1 
 1  x  1  1  x  1  1   . 2  0 2 0 0 x  0
x  0  y   1 1  0 0 0
 Phương trình tiếp tuyến tại M 2;
 3 là: y  x  5. 1  
 Phương trình tiếp tuyến tại M 0;1 là: y  x 1. 2  
 Chọn đáp án A. 16
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan Câu 15. 2
y  3x  6 . x
Gọi M x ; y là tiếp điểm của tiếp tuyến d song song với đường thẳng  : 9x  y  24 . 0 0 x  1   y  1 
Vì d //  nên d có hệ số góc k  9 . Khi đó: 2 0 0
3x  6x  9   . 0 0
x  3  y  3  0 0
 Phương trình tiếp tuyến tại M 1  ; 1
 là: y  9x  
1  1  y  9x  8. 1  
 Phương trình tiếp tuyến tại M 3; 3 là: y  9x  3 3  y  9x  24 (loại). 2  
Vậy phương trình tiếp tuyến d : y  9x  8  Chọn đáp án B. 5 
Câu 16. TXĐ: D   \ 
2 . Ta có: y   x  2 . 2
Gọi M x ; y là tiếp điểm của tiếp tuyến d song song với đường thẳng  : 5x  y 13 . 0 0
Vì d //  nên d có hệ số góc k  5  . 5 
x  1 y  5  Khi đó: 0 0  5
  x  2  1   . 2 0
x  3  y   7  uan x 2 0 0 0 T
 Phương trình tiếp tuyến tại M 1; 5  là: y  5  x   1  3  y  5  x  2. 1  
 Phương trình tiếp tuyến tại M 3;7 là: y  5
 x  37  y  5  x  22. 2   ayCao
 Chọn đáp án C. /Th
Câu 17. TXĐ: D   \   1 . com 6 Ta có: y  . ook. x12  3 19
: 3x  2y  19  0 hay y  x  .faceb 2 2 w  2x  4 
Gọi d là tiếp tuyến của C song song với đường thẳng  và 0 M  x ;  là tiếp điểm. 0 x  1  0  //ww 3
Do d //  nên d có hệ số góc là k  . tps: 2 ht 3 3 6 3
x  1  y  1  Khi đó: k   yx  0 0      . 0 2 2 x 2 2 x  3   y   5 1  0 0 0  3 3 5
Phương trình tiếp tuyến tại điểm M 1; 1
 là: y  x   1  1  y  x  . 1   2 2 2  3 3 19
Phương trình tiếp tuyến tại điểm M 3
 ; 5 là: y  x  3  5  y  x  (loại). 2   2 2 2 3 5
y  kx  m 3  5 
Do đó d : y 
x  
k  m     1    
Chọn đáp án D. 2 2 2  2 
Câu 18. TXĐ: D  . 1 Ta có: 2
y  3x  6 .
x d : x  9y  0 y   . x hay 9
Gọi d là tiếp tuyến của C vuông góc với d và có tiếp điểm làm M x ; y . 0 0 
Do d  d nên d có hệ số góc k  9. 17
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN
x  1 y  9
Khi đó: k  9  yx  2 0 0
 9  3x  6x  9   . 0 0 0 x  3   y  5  0 0
 Phương trình tiếp tuyến tại điểm M 1;9 là: y  9x   1  9  y  9 . x 1  
 Phương trình tiếp tuyến tại điểm M 3
 ; 5 là: y  9x  3  5  y  9x  32. 2  
 Chọn đáp án A.
Câu 19. TXĐ: D  . Ta có: 3 y  4  x  2 . x 1
Gọi d là tiếp tuyến của C vuông góc với  : y  x  1 và có tiếp điểm là M x ; y . 6 0 0 0
Do d   nên d có hệ số góc k  6.  Khi đó: k  6
  yx  3  6   4
 x  2x  6
  x  1 y  4. 0 0 0 0 0
Phương trình tiếp tuyến tại M 1; 4 là: y  6
 x        1 4 y 6x 10
Chọn đáp án C. Câu 20. uan T 2     TXĐ: D  . Ta có: 2 2 1 3 1 3 3
y  6x  6x  6 x  x    6 x     , x       .  4  2  2  2 2 ayCao 3 1 1 9
Do đó: GTNN của y là  , đạt tại x  . Với x   y  . 2 0 2 0 0 2 2 /Th  1 9 
Phương trình tiếp tuyến của C tại điểm M  ;  là: com  2 2  3  1  9 3 21         ook. y  x  y x . 2  2  2 2 4 21  3  .faceb
Do đó: T  2m : k  2. :   7    
Chọn đáp án A. w 4  2 
Câu 21. Đối với bài toán này ta sử dụng phép thử: //ww
Dễ thấy, điểm A ở đáp án A, B, D không thuộc C nên ta chọn đáp án B. tps:
 Chọn đáp án B. ht
Câu 22. Thế tọa độ điểm A 1
 ; 3 lần lượt vào các phương trình ở bốn đáp án, ta được đáp án C 1 13 có 3    1 
 Chọn đáp án C. 4 4 1
Câu 23. Đồ thị C có đường tiệm cận đứng là đường thẳng x   . 2  1 
Giao điểm của tiệm cận đứng với trục hoành là A   ; 0 .  2   1 
Gọi  là đường thẳng đi qua A  
; 0  và có hệ số góc k .  2   1 
Khi đó, phương trình của  là: y  k x   .  2  x 1  1   k x     1  2x  1  2 
 là tiếp tuyến của C khi hệ  có nghiệm. 3    k 2 2   2x1 18
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan 3  Thay  
k cào phương trình 1 ta được: 2x  12 x 1 3   1  3   1   x   x   x      2x  1  x  . 1 . 2  2  2x  1  2 2 1   5 x  5 1    2 2  2
 x  4x   0 x      2  2   1 x   loai  2 5 1 Với x  thì k   . 2 12 1  1  1 1
Phương trình tiếp tuyến là y   x   y   x    . 12  2  12 24  1   k d : y kx m       12 k   T 
 2  Chọn đáp án A. uan 1 m    T m  24
Câu 24. Đường thẳng  : x  y 1  0 có vectơ pháp tuyến là: n  1;1 . 1   ayCao
Goi d : y  kx  m là tiếp tuyến cần tìm  d có vectơ pháp tuyến là: n  k; 1  . 1   /Th 4 4 n .n 4
Theo giả thiết, ta có: c s o  
 cosn ,n  1 2    1 2 com 41 41 n . n 1 2 41 k  9 ook. 2 2 41 k 1 4 2. k 1 9k 82k 9 0           1  k   9 .faceb
 Với k  9 thì d : y  9x  . m w 3 2
x  6x  9x  9x   m 1
d tiếp xúc với C khi hệ  có nghiệm //ww 2
3x  12x  9   9  2 tps:
x  0  m  0  y  9x Ta có: 2 2
 3x 12x  0   . ht
x  4   m  3
 2  y  9x   32  1 1 Với k  thì d : y  x  . m 9 9  3 2 1
x  6x  9x  x  m  3 
d tiếp xúc với C khi hệ 9  có nghiệm  2 1
3x  12x  9  4  9   Ta có:   2 18 2 21
4  27x  108x  80  0  x    loại. 9
Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán có phương trình là: y  9 ;
x y  9x  32  Chọn đáp án A. Câu 25.
Vì M d : 2x  y  1  0 nên M  ; m 2m   1 .
Tiếp tuyến của C qua M có phương trình dạng y  k x  m  2m  1. 19
Cao Tuấn – 0975306275
Số 135A/ Ngõ 189/ Hoàng Hoa Thám, BĐ, HN
Từ điểm M kẻ được duy nhất một tiếp tuyến tới C x  3  k 
xm 2m1  1  x 1  hệ  4  có nghiệm duy nhất.   k 2 2   x1 x  3 4 
Thay 2 vào 1 , ta được: 
x  m  2m  1 2   x  1 x 1 2
 x  3x   1  4
 x  m2m  1 x   1 , x   1
Lần lượt thử từng phương án: Với m
1 thì phương trình trên trở thành 2
2x  4x  2  0 có nghiệm duy nhất là x  1.  Vậy m  1   M 1  ;  
1  Chọn đáp án A. 3 2
Câu 26. C có hai điểm cực trị là A0; 2 và B2; 2  . Gọi M ;
m m  3m  2C . uan 1    T
Theo giả thiết, ta có: S 6 d M AB AB M  AB  ; . 6 2 3 2
2m  m  3m  2  2 1  . .2 5  6 ayCao 2 5 /Th 3 2
 2m  m  3m  6 3 2
m  3m  2m  6 3 com   3 2
m  3m  2m  6   4 ook. m  Ta có:   3 3   . .faceb m   2 w
Với m  3 thì M 3; 2 . Khi đó, tiếp tuyến tại M có phương trình y  9x  25. //ww
Loại trừ các phương án, chỉ có B thỏa mãn  Chọn đáp án B.  2x  1  tps: Câu 27. Gọi 0 M  x ;
 C với x  1. 0   x  1   0 ht 0
Phương trình tiếp tuyến d của C tại M là: 1  2x  1 y  x  x 
 d : x  x 1 y  2x  2x 1  0 2   0 0    0 2 2 x  0 0 x   1 1 0 0
d cách đều hai điểm A 2;  4 và B4; 2  
 dA,d  d ; B d 2
  x 12 4  2x  2x 1 4  x  12 2  2   2
 2x  2x 1 0 0 0 0 0 0   1  x  14 1  x  14 2 2 0 0 x  0 0  2
6x 12x  0 x  2 2 2 0 0  0
 2x  6x  1  4
 x  6x  1    0 0 0 0 2  2  x  2  0 x  1   0 0  x  1 loai  0  
Vậy có 3 tiếp tuyến thỏa mãn yêu cầu bài toán  Chọn đáp án C. 20
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan
Câu 28. Giao điểm I của hai tiệm cận có tọa độ 2;  1 .  x  1  Gọi 0 M  x ;
 C với x  2. 0   x  2  0 0 
Phương trình tiếp tuyến d của C tại M là: 1  x  1 y  x  x 
 d : x  x  2 y  x  2x  2  0 2   0 0    0 2 2 x  0 0 x   2 2 0 0  1 
Đường thẳng IM có vectơ chỉ phương là IM   x  2;
  đường thẳng IM có vectơ 0 x  2  0   1   pháp tuyến là n   ; x  2 . IM 0 x  2  0  1 
Khi đó: IM  d  n
 n  n .n  0   x  x   IM d IM d  2 22 0 0 0 x  2 0          4 x 2 1 x 3 d : y x 5 0 0 uan
 x  2  1     . 0    T x  2  1 
x  1  d : y  x  1 0  0  
Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là: d : y  x 1, d : y  x  5. 1   2 ayCao
 Chọn đáp án B. /Th com ook. .faceb w //ww tps: ht 21

Các dạng toán tiếp tuyến của đồ thị hàm số – Cao Văn Tuấn Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số