Các dạng toán tính đơn điệu của hàm số thường gặp trong kỳ thi THPTQG

Các dạng toán tính đơn điệu của hàm số thường gặp trong kỳ thi THPTQG được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

80 40 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

59 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 1
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
MỤC LỤC
PHẦN A. CÂU HỎI ........................................................................................................................................ 1
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị .......................................... 1
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước .................................................................................. 3
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó ....................................................... 4
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước ....................................................... 5
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước .............................................................. 6
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước ............................................................... 7
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x) .............................................. 9
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x) 12
PHẦN B. LỜI GIẢI THAM KHẢO ............................................................................................................ 14
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị ........................................ 14
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước ................................................................................ 18
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó ..................................................... 21
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước ..................................................... 26
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước ............................................................ 28
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước ............................................................. 35
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x) ............................................ 42
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x) 52
PHẦN A. CÂU HỎI
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị
Câu 1: (Mã 103 - BGD - 2019) Chohàmsố
f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàosauđây?
A.
; 1 .
B.
0;1 .
C.
1;0 .
D.
1; . 
Câu 2: (MĐ 104 BGD&DT NĂM 2017) Chohàmsố
y f x
cóbảngxétdấuđạohàmnhưsau
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 2
Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
; 2
B. Hàmsốđồngbiếntrênkhoảng
2;0
C. Hàmsốđồngbiếntrênkhoảng
;0
D. Hàmsốnghịchbiếntrênkhoảng
0;2
Câu 3: (Mãđề101BGD&ĐTNĂM2018)Chohàmsố
y f x
cóbảngbiếnthiênnhưsau
Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?
A.
1;0
B.
;0
C.
1;
D.
0;1
Câu 4: (Mã 102 - BGD - 2019) Chohàmsố
f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây
A.
0;
. B.
0;2
. C.
2;0
. D.
; 2
.
Câu 5: (MĐ 103 BGD&ĐT NĂM 2017-2018) Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
0;1
B.
1;
C.
;1
D.
1;0
Câu 6: (Mã đề 101 - BGD - 2019) Chohàmsốcóbảngbiếnthiênnhưsau
Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?
A.
0;2 .
B.
0; .
C.
2;0 .
D.
2; .
Câu 7: (Mã đề 102 BGD&ĐT NĂM 2018) Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 3
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
1;

. B.
1;

. C.
1;1
. D.
;1
.
Câu 8: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Chohàmsố
y f x
cóđồthịnhưhìnhvẽ
bên.Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
B.
1;1
C.
1;0
D.
0;1
Câu 9: (Mã đề 104 BGD&ĐT NĂM 2018) Chohàmsố
y f x
cóbảngbiếnthiênnhưsau
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
2;3
B.
3;
C.
; 2
D.
2;
Câu 10: (ĐỀTHAMKHẢOBGD&ĐT2018)Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Hàmsố
y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
0;
B.
; 2
C.
0;2
D.
2;0
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước
Câu 11: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Hàmsốnàodướiđâyđồngbiếntrênkhoảng
;
?
A.
1
2
x
y
x
B.
3
y x x
C.
3
3y x x
D.
1
3
x
y
x
Câu 12: (ĐỀTHAMKHẢOBGD&ĐTNĂM2017)Chohàmsố
2
1
x
y
x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
;
 
B. Hàmsốnghịchbiếntrênkhoảng
1;

C. Hàmsốnghịchbiếntrênkhoảng
; 1
D. Hàmsốđồngbiếntrênkhoảng
; 1
Câu 13: (ĐỀTHAMKHẢOBGD&ĐTNĂM2017)Hàmsốnàodướiđâyđồngbiếntrênkhoảng
;
 
?
A.
4 2
3y x x
. B.
2
1
x
y
x
. C.
3
3 3 2
y x x
. D.
3
2 5 1y x x
.
x
y
-2
-1
O
1-1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 4
Câu 14: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Chohàmsố
3 2
3y x x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốđồngbiếntrênkhoảng
0;2
B. Hàmsốnghịchbiếntrênkhoảng
0;2
C. Hàmsốnghịchbiếntrênkhoảng
;0
D. Hàmsốnghịchbiếntrênkhoảng
2;
Câu 15: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Hỏihàmsố
4
2 1
y x
đồngbiếntrênkhoảngnào?
A.
;0 .

B.
1
;
2

. C.
0;

. D.
1
;
2

.
Câu 16: (MĐ 105 BGD&ĐT NĂM 2017) Chohàmsố
y f x
cóđạohàm
2
1
f x x
,
x
.Mệnh
đềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng

1;
B. Hàmsốnghịchbiếntrênkhoảng
1;1
C. Hàmsốđồngbiếntrênkhoảng

;
D. Hàmsốnghịchbiếntrênkhoảng

; 0
Câu 17: Chohàmsố
3 2
2 1 y x x x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
1;

B. Hàmsốnghịchbiếntrênkhoảng
1
;1
3
C. Hàmsốnghịchbiếntrênkhoảng
1
;
3

D. Hàmsốđồngbiếntrênkhoảng
1
;1
3
Câu 18: (MĐ 105 BGD&ĐT NĂM 2017) Chohàmsố
4 2
2y x x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
 ; 2
B. Hàmsốđồngbiếntrênkhoảng
1;1
C. Hàmsốnghịchbiếntrênkhoảng
1;1
D. Hàmsốđồngbiếntrênkhoảng
 ; 2
Câu 19: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Hàmsố
2
2
1
y
x
nghịchbiếntrênkhoảngnàodướiđây?
A.
 ( ; )
B.
(0; )
C.
( ; 0)
D.
( 1; 1)
Câu 20: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Chohàmsố
3
3 2
y x x
.Mệnhđềnàodướiđâylàđúng?
A. Hàmsốnghịchbiếntrênkhoảng

; 0
vàđồngbiếntrênkhoảng

0;
B. Hàmsốđồngbiếntrênkhoảng

; 0
vàđồngbiếntrênkhoảng

0;
C. Hàmsốđồngbiếntrênkhoảng

;
D. Hàmsốnghịchbiếntrênkhoảng

;
Câu 21: (MĐ 104 BGD&DT NĂM 2017) Chohàmsố
2
2 1
y x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốđồngbiếntrênkhoảng
0;
B. Hàmsốđồngbiếntrênkhoảng
;0
C. Hàmsốnghịchbiếntrênkhoảng
0;
D. Hàmsốnghịchbiếntrênkhoảng
1;1
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Câu 22: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịchbiếntrênkhoảng
;
 
.
A.
0
B.
3
C.
2
D.
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 5
Câu 23: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Chohàmsố
3 2
4 9 5
y x mx m x
,vớimlàtham
số.Hỏicóbaonhiêugiátrịnguyêncủamđểhàmsốnghịchbiếntrênkhoảng

;
A.
5
B.
4
C.
6
D.
7
Câu 24: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số hàm số
2 3 2
1
2 3 2
3
y m m x mx x
đồngbiếntrênkhoảng
;

?
A.
4
. B.
5
. C.
3
. D.
0
.
Câu 25: Tìmtấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1 2
y mx mx m m x
đồngbiếntrên
.
A.
4
3
m
và
0
m
. B.
0
m
hoặc
4
3
m
. C.
4
3
m
. D.
4
3
m
.
Câu 26: Chohàmsố
3 2
1
3 2 1
3
y x mx m x
.Tìmtấtcảgiátrịcủa
m
đểhàmsốnghịchbiếntrên
.
A.
1
2
m
m
. B.
2 1
m
. C.
2 1
m
. D.
1
2
m
m
.
Câu 27: Tìm
m
đểhàmsố
3 2
3 3 2 1 1
y x mx m
đồngbiếntrên
.
A. Khôngcógiátrị
m
thỏamãn. B.
1
m
.
C.
1
m
. D. Luônthỏamãnvớimọi
m
.
Câu 28: Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
3 2
2 3 5
3
m
y x mx m x
đồngbiến
trên
.
A.
4
. B.
2
. C.
5
. D.
6
.
Câu 29: Tìmtậphợptấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1
4
3
y x mx x m
đồngbiếntrên
khoảng
;
 
.
A.
2;2
. B.
;2

. C.
; 2
. D.
2;

.
Câu 30: Chohàmsố
3 2
1
2 2 1 3 2
3
y x x a x a
(
a
làthamsố).Vớigiátrịnàocủa
a
thìhàm
sốnghịchbiếntrên
?
A.
1a
. B.
5
2
a
. C.
5
2
a
. D.
1a
.
Câu 31: Tìmtấtcảcácgiátrịcủa
m
đểhàmsố
3 2
1 3 1 3 2
y m x m x x
đồngbiếnbiếntrên
?
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
Câu 32: Giátrịcủa
m
đểhàmsố
3 2
1
– 2 3 – 5
3
y x mx m x m
đồngbiếntrên
là.
A.
3
1
4
m
. B.
3
4
m
. C.
3
1
4
m
. D.
1
m
.
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
Câu 33: (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 6
2
3
x
y
x m
đồngbiếntrênkhoảng
; 6
.
A.
2
B.
6
C. Vôsố D.
1
Câu 34: (MĐ 103 BGD&ĐT NĂM 2017-2018) Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
1
3
x
y
x m
nghịchbiếntrênkhoảng
6;

?
A.
0
B.
6
C.
3
D. Vôsố
Câu 35: (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
5
x
y
x m
đồngbiếntrênkhoảng
; 10

?
A.
2
B. Vôsố C.
1
D.
3
Câu 36: (MĐ 104 BGD&DT NĂM 2017) Chohamsô
4mx m
y
x m
vơi
m
lathamsô.Goi
S
latâphơptât
cacacgiatringuyêncua
m
đêhamsônghichbiêntrêncackhoangxacđinh.Timsôphântưcua
S
.
A.
4
B. Vôsô C.
3
D.
5
Câu 37: (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
x m
nghịchbiếntrênkhoảng
10;
?
A. Vôsố B.
4
C.
5
D.
3
Câu 38: (MĐ 105 BGD&ĐT NĂM 2017) Chohàmsố
2 3mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợp
tấtcảcácgiátrịnguyêncủa
m
đểhàmsốđồngbiếntrêncáckhoảngxácđịnh.Tìmsốphầntửcủa
S
.
A. Vôsố B.
3
C.
5
D.
4
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Câu 39: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Tậphợptấtcảcácgiátrịthựccủathamsố
m
để
hàmsố
3 2
6 4 9 4
y x x m x
nghịchbiếntrênkhoảng
; 1
là
A.
3
;
4

B.
0;

C.
;0

D.
3
;
4

Câu 40: Chohàmsố
3 2
3 4y x x mx
.Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsốđồngbiếntrên
khoảng
;0

là
A.
1;5
. B.
; 3
. C.
; 4
. D.
1;
.
Câu 41: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3
2
( ) 7 14 2
3
mx
y f x mx x m
giảm
trênnửakhoảng
[1; )
?
A.
14
;
15

. B.
14
2;
15
. C.
14
;
15

. D.
14
;
15

.
Câu 42: Xácđịnhcácgiátrịcủathamsốmđểhàmsố
3 2
3
y x mx m
nghịchbiếntrênkhoảng
0;1 ?
A.
0m
. B.
1
2
m
. C.
0m
. D.
1
2
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 7
Câu 43: Tìmtấtcảcácgiátrịcủathamsố
m
đểhàmsố
3 2
3 1y x x mx
đồngbiếntrênkhoảng
;0

.
A.
0
m
. B.
2
m
. C.
3
m
. D.
1
m
.
Câu 44: Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
3 2 2
3 9
y x mx m x
nghịchbiếntrênkhoảng
0;1
.
A.
1
1
3
m
. B.
1
3
m
. C.
1
m
. D.
1
3
m
hoặc
1
m
.
Câu 45: Tìmcácgiátrịcủathamsố
m
đểhàmsố
3 2
1
2 1 2
3
y x mx m x m
nghịchbiếntrênkhoảng
2;0 .
.
A.
0
m
. B.
1
m
. C.
1
2
m
. D.
1
2
m
.
Câu 46: Tìmtấtcảcácgiátrị
m
đểhàmsố
3 2
3 2y x x mx
tăngtrênkhoảng
1;
.
A.
3
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Câu 47: Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsố
3 2
6 1y x mx m x
đồngbiếntrênkhoảng
0;4
là:
A.
;3

. B.
;3

. C.
3;6
. D.
;6

.
Câu 48: Tìmtấtcảcácgiáthựccủathamsố
m
saochohàmsố
3 2
2 3 6
y x x mx m
nghịchbiếntrên
khoảng
1;1
.
A.
1
4
m
. B.
1
4
m
. C.
2
m
. D.
0
m
.
Câu 49: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3 2
6 1y x x mx
đồngbiếntrênkhoảng
0;

?
A.
12
m
. B.
12
m
. C.
0
m
. D.
0
m
.
Câu 50: Tậphợpcácgiátrị
m
đểhàmsố
3 2
3 2
y mx x x m
đồngbiếntrên
3;0
là
A.
1
;0
3
. B.
1
;
3

. C.
1
;
3

. D.
1
;
3

.
Câu 51: Tìm
m
đểhàmsố
3 2
3 3 1
y x x mx m
nghịchbiếntrên
0;

.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
Câu 52: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàm
số
tan 2
tan
x
y
x m
đồngbiếntrênkhoảng
0; .
4
A.
0
m
hoặc
1 2
m
B.
0
m
C.
1 2
m
D.
2
m
Câu 53: (ĐỀTHAMKHẢOBGD&ĐT2018)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
đểhàmsố
3
5
1
5
y x mx
x
đồngbiếntrênkhoảng
0;
A.
0
B.
4
C.
5
D.
3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 8
Câu 54: (THPTBẠCHĐẰNGQUẢNGNINHNĂM2018-2019)Gọi
S
làtậphợptấtcảcácgiátrịcủa
thamsố
m
đểhàmsố
2 5 3 2 2
1 1
10 20
5 3
f x m x mx x m m x
đồngbiếntrên
.Tổnggiátrịcủatất
cảcácphầntửthuộc
S
bằng
A.
5
2
. B.
2
. C.
1
2
. D.
3
2
.
Câu 55: (THPTLÊQUÝĐÔNĐÀNẴNGNĂM2018-2019)Tậphợpcácgiátrịthựccủathamsốmđể
hàmsố
1
2
m
y x
x
đồngbiếntrênmỗikhoảngxácđịnhcủanólà
A.
0;1
. B.
;0

. C.
0; \ 1
. D.
;0

.
Câu 56: (THPTMINHKHAIHÀTĨNHNĂM2018-2019)Tìmtấtcảcácgiátrịthựccủathamsốđểhàm
số
cos 3
cos
x
y
x m
nghịchbiếntrênkhoảng
;
2
A.
0 3
1
m
m
. B.
0 3
1
m
m
. C.
3
m
. D.
3
m
.
Câu 57: (TTHOÀNGHOATHÁM-2018-2019)Chohàmsố
(4 ) 6 3
6
m x
y
x m
.Cóbaonhiêugiátrị
nguyêncủamtrongkhoảng
10;10
saochohàmsốđồngbiếntrên
8;5
?
A.
14
. B.
13
. C.
12
. D.
15
.
Câu 58: (THPTLƯƠNGTHẾVINHHÀNỘINĂM2018-2019LẦN1)Cóbaonhiêugiátrịnguyênâm
củathamsố
m
đểhàmsố
4
1 3
4 2
y x mx
x
đồngbiếntrênkhoảng
0;
.
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 59: (THPTCHUYÊNBẮCGIANGNAM2018-2019LẦN01)Chohàmsố
ln 4
ln 2
x
y
x m
với
m
là
thamsố.Gọi
S
làtậphợpcácgiátrịnguyêndươngcủa
m
đểhàmsốđồngbiếntrênkhoảng
1;e
.Tìmsố
phầntửcủa
S
.
A.
3
B.
2
C.
1
D.
4
Câu 60: (THPTCHUYÊNVĨNHPHÚCNĂM2018-2019LẦN01)Tìm
m
đểhàmsố
cos 2
cos
x
y
x m
đồng
biếntrênkhoảng
0;
2
A.
2
2
m
m
B.
2
m
C.
0
1 2
m
m
D.
1 1
m
Câu 61: (CHUYÊNLƯƠNGTHẾVINHĐỒNGNAINĂM2018-2019LẦN01)Cóbaonhiêugiátrị
nguyênâmcủathamsố
m
đểhàmsố
4 2
3 9
2 15 3 1
4 2
y x x m x m
đồngbiếntrênkhoảng
0;
?
A.
2.
B.
3.
C.
5.
D.
4.
Câu 62: Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
3
3
1
m m
y x
x
đồngbiếntrêntừng
khoảngxácđịnhcủanó?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 9
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 63: Tìmmđểhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
A.
2m
. B.
0
1 2
m
m
. C.
2m
. D.
2m
.
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x)
Câu 64: (ĐỀTHAMKHẢOBGD&ĐT2018)Chohàmsố
( )y f x
.Hàmsố
'( )y f x
cóđồthịnhưhình
bên.Hàmsố
(2 ) y f x
đồngbiếntrênkhoảng
A.
2;
B.
2;1
C.
; 2
D.
1;3
Câu 65:
(Mã đề 104 - BGD - 2019) Chohàmsố
f x
,bảngxétdấucủa
f x
nhưsau:
Hàmsố
5 2
y f x
đồngbiếntrênkhoảngnàodướiđây?
A.
3;4
.
B.
1;3
.
C.
; 3
.
D.
4;5
.
Câu 66: (Mã 103 - BGD - 2019) Chohàmsố
( )f x
,bảngxétdấucủa
( )f x
nhưsau:
Hàmsố
3 2y f x
đồngbiếntrênkhoảngnàodướiđây?
A.
0;2
. B.
2;3
. C.
; 3
. D.
3;4
.
Câu 67: (Mã 102 - BGD - 2019) Chohàmsố
( )f x
cóbảngdấu
( )f x
nhưsau:
Hàmsố
(5 2 )y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
3;5
. B.
5;
. C.
2;3
. D.
0;2
.
Câu 68: (Mã đề 101 - BGD - 2019) Chohamsô
f x
,bảngxétdấucủa
'f x
nhưsau:
Hamsô
3 2y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
2;1 .
B.
2;4 .
C.
1;2 .
D.
4; .
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 10
Câu 69: (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Chohàmsố
( )f x
cóbảngxétdấu
nhưsau:
Hàmsố
2
2y f x x
nghịchbiếntrênkhoảngnàodướiđây?
A.
2;1
. B.
4; 3
. C.
0;1
. D.
2; 1
.
Câu 70: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Chohàmsố
y f x
cóđạo
hàm
'f x
trên
.Hìnhvẽbênlàđồthịcủahàmsố
'y f x
.Hàmsố
2
g x f x x
nghịchbiến
trênkhoảngnàotrongcáckhoảngdướiđây?
A.
3
;
2

. B.
3
;
2

. C.
1
;
2

. D.
1
;
2

.
Câu 71: (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Chohàmsố
'y f x
cóđồthịnhưhìnhvẽ
Hàmsố
2
2y f x
đồngbiếntrênkhoảngnàodướiđây
A.
;0
. B.
0;1
. C.
1;2
. D.
0;
.
Câu 72: (THPTGIALỘCHẢIDƯƠNGNĂM2018-2019LẦN01)Chohàmsố
( )f x
,đồthịhàmsố
( )y f x
nhưhìnhvẽdướiđây.
Hàmsố
3y f x
đồngbiếntrênkhoảngnàodướiđây?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 11
A.
4;6
. B.
1;2
. C.
; 1 .
D.
2;3
.
Câu 73: (THPTMINHCHÂUHƯNGYÊNNĂM2018–2019)Chohàmsố
y f x
.Hàmsố
'y f x
cóđồthịnhưhìnhvẽ.Hàmsố
2
( ) ( 2).
g x f x
Mệnhvđềnàosai?
A. Hàmsố
g x
nghịchbiếntrên
; 2
B. Hàmsố
g x
đồngbiếntrên
2;

C. Hàmsố
g x
nghịchbiếntrên
1;0
D. Hàmsố
g x
nghịchbiếntrên
0;2
Câu 74: (GKITHPTVIỆTĐỨCHÀNỘINĂM2018-2019)Chohàmsố
y f x
cóđạohàmliêntục
trên
vàđồthịhàmsố
'y f x
nhưhìnhbên.
Hỏihàmsố
3 2g x f x
nghịchbiếntrênkhoảngnàotrongcáckhoảngsau?
A.
1;

B.
; 1
C.
1;3
D.
0;2
Câu 75: (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Chohàmsố
y f x
cóđạohàm
trên
vàcóđồthị
y f x
nhưhìnhvẽ.
Xéthàmsố
2
2
xfxg .
Mệnhđềnàosauđâysai?
A.Hàmsố
g x
nghịchbiếntrên
0;2
B.Hàmsố
g x
đồngbiếntrên
2;

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 12
C.Hàmsố
g x
nghịchbiếntrên
; 2
D.Hàmsố
g x
nghịchbiếntrên
1;0
Câu 76: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Chohàmsố
y f x
cóbảng
xétdấuđạohàmnhưsau:
Hàmsố
2
2y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
2; 1
. B.
2;
. C.
0;2
. D.
1;0
.
Câu 77: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Chohàmsố
y f x
cóđạohàmliêntụctrên
.Biếthàmsố
y f x
cóđồthịnhưhìnhvẽ.Gọi
S
làtậphợpcácgiátrịnguyên
5;5m
đểhàmsố
g x f x m
nghịchbiếntrênkhoảng
1;2
.Hỏi
S
cóbaonhiêuphầntử?
A.
4
. B.
3
. C.
6
. D.
5
.
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x)
Câu 78: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Chohàmsố
f x
cóbảngxétdấucủađạohàm
nhưsau

1 2 3 4
0
0
0
0
Hàmsố
3
3 2 3y f x x x
đồngbiếntrênkhoảngnàodướiđây?
A.
; 1 .
B.
1;0 .
C.
0;2 .
D.
1; .
Câu 79: (CHUYÊNLÊQUÝĐÔNĐIỆNBIÊNNĂM2018-2019LẦN02)Chohàmsố
f x
cóbảng
xétdấucủađạohàmnhưsau
Hàmsố
3
1 12 2019y f x x x
nghịchbiếntrênkhoảngnàodướiđây?
A.
1;
. B.
1;2
. C.
;1
. D.
3;4
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 13
Câu 80: (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Chohàmsố
f x
cóbảng
xétdấuđạohàmnhưsau:
Hàmsố
2
2 1 1
y f x x x
nghịchbiếntrênnhữngkhoảngnàodướiđây
A.
; 2
. B.
;1

. C.
2;0
. D.
3; 2
.
Câu 81: (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Chohàmsố
f x
cóbảngxétdấucủađạohàm
nhưsau:
x

1 2 3 4
'f x
0
0 + 0
0 +
Hàmsố
2
2 1 1
y f x x x
nghịchbiếntrênkhoảngnàodướiđây?
A.
;1
. B.
; 2
. C.
2;0
. D.
3; 2
.
Câu 82: (SỞGIÁODỤCĐÀOTẠOVĨNHPHÚCNĂM2018 -2019LẦN01)Chohàmsốbậcbốn
( )y f x
cóđồthịcủahàmsố
( )y f x
nhưhìnhvẽbên.
Hàmsố
3 2
3 ( ) 6 9y f x x x x
đồngbiếntrênkhoảngnàotrongcáckhoảngsauđây?
A.
0;2
. B.
1;1
. C.
1;

. D.
2;0
.
Câu 83: (HỌCMÃINĂM2018-2019-LẦN02)Chohàmsố
y f x
cóđạohàmtrên
.Đồthịhàmsố
y f x
nhưhìnhbên.Hỏiđồthịhàmsố
2y f x x
cóbaonhiêuđiểmcựctrị?
A.
4
. B.
3
. C.
2
. D.
1
.
x
y
O
-4
-2 2-3
-3
1
-1
-2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 14
Câu 84: (TRƯƠNGTHPTHOANGHOATHAMHƯNGYÊNNĂM2018-2019)Chohàmsố
y f x
liêntụctrên
.Hàmsố
y f x
cóđồthịnhưhìnhvẽ.Hàmsố
2019 2018
1
2018
x
g x f x
đồngbiến
trênkhoảngnàodướiđây?
A.
2;3
. B.
0;1
. C.
-1;0
. D.
1;2
.
Câu 85: (SỞGD&ĐTNINHBÌNHLẦN01NĂM2018-2019)Chohàmsố
y f x
cóbảngxétdấucủa
đạohàmnhưsau
Hàmsố
2 2019
y f x
nghịchbiếntrênkhoảngnàotrongcáckhoảngdướiđây?
A.
4;2
. B.
1;2
. C.
2; 1
. D.
2;4
.
Câu 86: (GKITHPTLƯƠNGTHẾVINHHÀNỘINĂM2018-2019)Chohàmsố
y f x
.Biếtđồthị
hàmsố
y f x
cóđồthịnhưhìnhvẽbên.Hàmsố
2
3 2018
y f x
đồngbiếntrênkhoảngnàodưới
đây?
A.
1; 0
B.
2; 3
C.
2; 1
D.
0; 1
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị
Câu 1: (Mã 103 - BGD - 2019) Chohàmsố
f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàosauđây?
O
x
y
1
1
1
2
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 15
A.
; 1 .
B.
0;1 .
C.
1;0 .
D.
1; . 
Lời giải
Chọn C
Hàmsốđãchođồngbiếntrênkhoảng
1;0 .
Câu 2: (MĐ 104 BGD&DT NĂM 2017) Chohàmsố
y f x
cóbảngxétdấuđạohàmnhưsau
Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
; 2
B. Hàmsốđồngbiếntrênkhoảng
2;0
C. Hàmsốđồngbiếntrênkhoảng
;0

D. Hàmsốnghịchbiếntrênkhoảng
0;2
Lờigiải
Chọn D
Theobảngxétdấuthì
' 0
y
khi
(0;2)
x
nênhàmsốnghịchbiếntrênkhoảng
(0;2)
.
Câu 3: (Mãđề101BGD&ĐTNĂM2018)Chohàmsố
y f x
cóbảngbiếnthiênnhưsau
Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?
A.
1;0
B.
;0

C.
1;

D.
0;1
Lờigiải
Chọn D
Dựavàobảngbiếnthiêntacóhàmsốđãchonghịchbiếntrêncáckhoảng
0;1
và
; 1
.
Câu 4: (Mã 102 - BGD - 2019) Chohàmsố
f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây
A.
0;

. B.
0;2
. C.
2;0
. D.
; 2
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 16
Lời giải
Chọn C
Từbảngbiếnthiên,suyratrênkhoảng
2;0
hàmsốđồngbiến.
Câu 5: (MĐ 103 BGD&ĐT NĂM 2017-2018) Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
0;1
B.
1;
C.
;1
D.
1;0
Lời giải
Chọn A
Câu 6: (Mã đề 101 - BGD - 2019) Chohàmsốcóbảngbiếnthiênnhưsau
Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?
A.
0;2 .
B.
0; .
C.
2;0 .
D.
2; .
Lời giải
Chọn A
Dựavàobảngbiếnthiêntathấytrênkhoảng
0;2
thì
' 0f x
.
Vậyhàmsốnghịchbiếntrênkhoảng
0;2
.
Câu 7: (Mã đề 102 BGD&ĐT NĂM 2018) Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
1; 
. B.
1;
. C.
1;1
. D.
;1
.
Lời giải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 17
Chọn B
Câu 8: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Chohàmsố
y f x
cóđồthịnhưhìnhvẽ
bên.Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
B.
1;1
C.
1;0
D.
0;1
Lời giải
Chọn C
Từđồthị,tathấyhàmsốđồngbiếntrêncáckhoảng
1;0
và
1;

.Chọn
Câu 9: (Mã đề 104 BGD&ĐT NĂM 2018) Chohàmsố
y f x
cóbảngbiếnthiênnhưsau
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
2;3
B.
3;
C.
; 2
D.
2;
Lời giải
Chọn A
Câu 10: (ĐỀTHAMKHẢOBGD&ĐT2018)Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Hàmsố
y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
0;
B.
; 2
C.
0;2
D.
2;0
Lờigiải
Chọn D
x
y
-2
-1
O
1-1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 18
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước
Câu 11: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Hàmsốnàodướiđâyđồngbiếntrênkhoảng
;
?
A.
1
2
x
y
x
B.
3
y x x
C.
3
3y x x
D.
1
3
x
y
x
Lời giải
Chọn B
Vì
3
y x x
2
3 1 0,y x x
.
Câu 12: (ĐỀTHAMKHẢOBGD&ĐTNĂM2017)Chohàmsố
2
1
x
y
x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
;
 
B. Hàmsốnghịchbiếntrênkhoảng
1;

C. Hàmsốnghịchbiếntrênkhoảng
; 1
D. Hàmsốđồngbiếntrênkhoảng
; 1
Lờigiải
Chọn D
Tậpxácđịnh:
1
\
.
Tacó
2
3
' 0
1
y
x
,
1
\x
.
Câu 13: (ĐỀTHAMKHẢOBGD&ĐTNĂM2017)Hàmsốnàodướiđâyđồngbiếntrênkhoảng
;
 
?
A.
4 2
3y x x
. B.
2
1
x
y
x
. C.
3
3 3 2
y x x
. D.
3
2 5 1y x x
.
Lờigiải
Chọn C
Hàmsố
3
3 3 2
y x x
cóTXĐ:
D
.
2
9 3 0,y x x
,suyrahàmsốđồngbiếntrênkhoảng
;
 
.
Câu 14: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Chohàmsố
3 2
3y x x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốđồngbiếntrênkhoảng
0;2
B. Hàmsốnghịchbiếntrênkhoảng
0;2
C. Hàmsốnghịchbiếntrênkhoảng
;0
D. Hàmsốnghịchbiếntrênkhoảng
2;
Lời giải
Chọn B
Tacó
2
3 6y x x
;
0
0
2
x
y
x
.
Lậpbảngbiếnthiênrồisuyrahàmsốnghịchbiếntrênkhoảng
0;2
Câu 15: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Hỏihàmsố
4
2 1
y x
đồngbiếntrênkhoảngnào?
A.
;0 .

B.
1
;
2

. C.
0;

. D.
1
;
2

.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 19
Lời giải
Chọn C
4
2 1
y x
.Tậpxácđịnh:
D
Tacó:
3
8y x
;
3
0 8 0 0
y x x
suyra
y
Giớihạn:
lim
x
y


;
lim
x
y


Bảngbiếnthiên:
Vậyhàmsốđồngbiếntrênkhoảng
0;

.
Câu 16: (MĐ 105 BGD&ĐT NĂM 2017) Chohàmsố
y f x
cóđạohàm
2
1
f x x
,
x
.Mệnh
đềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng

1;
B. Hàmsốnghịchbiếntrênkhoảng
1;1
C. Hàmsốđồngbiếntrênkhoảng

;
D. Hàmsốnghịchbiếntrênkhoảng

; 0
Lời giải
Chọn C
Dohàmsố
y f x
cóđạohàm
2
1 0
f x x
x
nênhàmsốđồngbiếntrênkhoảng

;
.
Câu 17: Chohàmsố
3 2
2 1 y x x x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
1;

B. Hàmsốnghịchbiếntrênkhoảng
1
;1
3
C. Hàmsốnghịchbiếntrênkhoảng
1
;
3

D. Hàmsốđồngbiếntrênkhoảng
1
;1
3
Lời giải
Chọn B
Tacó
2
1
3 4 1 0
1
3
x
y x x y
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 20
Bảngbiếnthiên:
Vậyhàmsốnghịchbiếntrênkhoảng
1
;1
3
.
Câu 18: (MĐ 105 BGD&ĐT NĂM 2017) Chohàmsố
4 2
2y x x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng
 ; 2
B. Hàmsốđồngbiếntrênkhoảng
1;1
C. Hàmsốnghịchbiếntrênkhoảng
1;1
D. Hàmsốđồngbiếntrênkhoảng
 ; 2
Lời giải
Chọn A
TXĐ:
.D
3 3
0
4 4 ; 0 4 4 0 1
1
x
y x x y x x x
x
Suyrahàmsốđồngbiếntrêncáckhoảng
1; 0
,
1;
;hàmsốnghịchbiếntrêncáckhoảng
 ; 1
,
0;1
.Vậyhàmsốnghịchbiếntrênkhoảng
 ; 2
.
Cách2:Dùngchứcnăngmode7trênmáytínhkiểmtratừngđápán.
Câu 19: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Hàmsố
2
2
1
y
x
nghịchbiếntrênkhoảngnàodướiđây?
A.
 ( ; )
B.
(0; )
C.
( ; 0)
D.
( 1; 1)
Lờigiải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 21
Chọn B
Tacó
2
2
4
0 0
1
x
y x
x
Câu 20: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Chohàmsố
3
3 2
y x x
.Mệnhđềnàodướiđâylàđúng?
A. Hàmsốnghịchbiếntrênkhoảng

; 0
vàđồngbiếntrênkhoảng

0;
B. Hàmsốđồngbiếntrênkhoảng

; 0
vàđồngbiếntrênkhoảng

0;
C. Hàmsốđồngbiếntrênkhoảng

;
D. Hàmsốnghịchbiếntrênkhoảng

;
Lờigiải
Chọn C
Tacó:
+)TXĐ:
D
.
+)
2
' 3 3 0,y x x
,dođóhàmsốđồngbiếntrên
.
Câu 21: (MĐ 104 BGD&DT NĂM 2017) Chohàmsố
2
2 1
y x
.Mệnhđềnàodướiđâyđúng?
A. Hàmsốđồngbiếntrênkhoảng
0;
B. Hàmsốđồngbiếntrênkhoảng
;0
C. Hàmsốnghịchbiếntrênkhoảng
0;
D. Hàmsốnghịchbiếntrênkhoảng
1;1
Lờigiải
Chọn A
Tacó
D
,
2
2
2 1
x
y
x
;
0 0
y x
.
Vậyhàmsốnghịchbiếntrênkhoảng
;0
vàđồngbiếntrênkhoảng
0;
.
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Câu 22: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịchbiếntrênkhoảng
;
 
.
A.
0
B.
3
C.
2
D.
1
Lờigiải
Chọn C
TH1:
1
m
.Tacó:
4y x
làphươngtrìnhcủamộtđườngthẳngcóhệsốgócâmnênhàmsốluôn
nghịchbiếntrên
.Dođónhận
1
m
.
TH2:
1
m
.Tacó:
2
2 4
y x x
làphươngtrìnhcủamộtđườngParabolnênhàmsốkhôngthểnghịch
biếntrên
.Dođóloại
1
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 22
TH3:
1
m
.Khiđóhàmsốnghịchbiếntrênkhoảng
;
 
0y x
,dấu“=”chỉxảyraở
hữuhạnđiểmtrên
.
2 2
3 1 2 1 1 0
m x m x
,
x
2
2
2
2
1 1
1 0
1 0
0
1
1
1
0
2
1
1 4 2 0
1 3 1 0
2
m
m
m
a
m
m
m m
m m
.Vì
m
nên
0
m
.
Vậycó
2
giátrị
m
nguyêncầntìmlà
0
m
hoặc
1
m
.
Câu 23: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Chohàmsố
3 2
4 9 5
y x mx m x
,vớimlàtham
số.Hỏicóbaonhiêugiátrịnguyêncủamđểhàmsốnghịchbiếntrênkhoảng

;
A.
5
B.
4
C.
6
D.
7
Lờigiải
Chọn D
Tacó:
+)TXĐ:
D
+)
2
' 3 2 4 9
y x mx m
.
Hàmsốnghịchbiếntrên

;
khi
 
' 0, ;y x
2
3 0
' 3 4 9 0
a
m m
9; 3
m
có7giátrịnguyêncủamthỏamãn.
Câu 24: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số hàm số
2 3 2
1
2 3 2
3
y m m x mx x
đồngbiếntrênkhoảng
;

?
A.
4
. B.
5
. C.
3
. D.
0
.
Lời giải
Chọn A
2 2
4 3y m m x mx
Hàmsốđãchođồngbiếntrênkhoảng
;

0
y
với
x
.
+Với
0
m
tacó
3 0
y
với
x
Hàmsốđồngbiếntrênkhoảng
;

.
+Với
1
m
tacó
3
4 3 0
4
y x x
1
m
khôngthảomãn.
+Với
1
0
m
m
tacó
0
y
với
x
2
2
0
3 0
m m
m m
1
0
3 0
m
m
m
3 0
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 23
Tổnghợpcáctrườnghợptađược
3 0
m
.
3; 2; 1;0
m m
.
Vậycó
4
giátrịnguyêncủa
m
thỏamãnbàira.
Câu 25: Tìmtấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1 2
y mx mx m m x
đồngbiếntrên
.
A.
4
3
m
và
0
m
. B.
0
m
hoặc
4
3
m
.
C.
4
3
m
. D.
4
3
m
.
Lời giải
Chọn C
TH1:
0 2
m y
làhàmhằngnênloại
0
m
.
TH2:
0
m
.Tacó:
2
3 2 1
y mx mx m m
.
Hàmsốđồngbiếntrên
'( ) 0f x x
2 2
3 1 0
3 0
m m m
m
2
4 3 0
0
m m
m
4
4
3
3
0
m
m
m
Câu 26: Chohàmsố
3 2
1
3 2 1
3
y x mx m x
.Tìmtấtcảgiátrịcủa
m
đểhàmsốnghịchbiếntrên
.
A.
1
2
m
m
. B.
2 1
m
. C.
2 1
m
. D.
1
2
m
m
.
Lời giải
Chọn B
TXĐ:
D
,
2
2 3 2
y x mx m .
Hàmsốnghịchbiếntrên
khivàchỉkhi
0
y
,
x
2
1 0
3 2 0
a
m m
2 1
m
.
Câu 27: Tìm
m
đểhàmsố
3 2
3 3 2 1 1
y x mx m
đồngbiếntrên
.
A. Khôngcógiátrị
m
thỏamãn. B.
1
m
.
C.
1
m
. D. Luônthỏamãnvớimọi
m
.
Lờigiải
Chọn C
2
3 6 3 2 1
y x mx m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 24
Tacó:
2
3 3.3. 2 1
m m
.Đểhàmsốluônđồngbiếntrên
thì
0
2
2 2
9 18 9 0 9 2 1 0 9 1 0
m m m m m
1
m
.
Câu 28: Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
3 2
2 3 5
3
m
y x mx m x
đồngbiến
trên
.
A.
4
. B.
2
. C.
5
. D.
6
.
Lời giải
Chọn D
Tacó
2
4 3 5
y mx mx m
.
Với
0 0
a m
5 0
y
.Vậyhàmsốđồngbiếntrên
.
Với
0 0
a m
.Hàmsốđãchođồngbiếntrên
khivàchỉkhi
0
0,
0
a
y x
2
0
2 3 5 0
m
m m m
2
0
0
0 5
0 5
5 0
m
m
m
m
m m
.
Vì
0;1;2;3;4;5
m m
.
Câu 29: Tìmtậphợptấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1
4
3
y x mx x m
đồngbiếntrên
khoảng
;
 
.
A.
2;2
. B.
;2

. C.
; 2
. D.
2;

.
Lời giải
Chọn A
Tacó:
2
2 4y x mx
.
Hàmsốđồngbiếntrênkhoảng
;
 
khivàchỉkhi
0, ;y x
 
.
2
4 0 2 2
m m
.
Câu 30: Chohàmsố
3 2
1
2 2 1 3 2
3
y x x a x a
(
a
làthamsố).Vớigiátrịnàocủa
a
thìhàm
sốnghịchbiếntrên
?
A.
1a
. B.
5
2
a
. C.
5
2
a
. D.
1a
.
Lời giải
Chọn C
Tìmđiềukiệncủathamsốthực
m
đểhàmsố
3 2
3 3 1 2
y x x m x
đồngbiếntrên
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 25
A.
2
m
. B.
2
m
. C.
0
m
. D.
0
m
.
Lời giải
Chọn D
Tậpxácđịnh:
D
.
Tacó:
2
3 6 3 1
y x x m
0, 9 0 0
YCBT y x m m
.
Câu 31: Tìmtấtcảcácgiátrịcủa
m
đểhàmsố
3 2
1 3 1 3 2
y m x m x x
đồngbiếnbiếntrên
?
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
Lời giải
Chọn C
Tacó
2
3 1 6 1 3y m x m x
.
Hàmsốđãchođồngbiếntrên
khivàchỉkhi
0,y x
1 0
1 0
0
m
m
2
1
1
9 1 9 1 0
m
m
m m
1
1
1 2
m
m
m
1 2
m
.
Câu 32: Giátrịcủa
m
đểhàmsố
3 2
1
– 2 3 – 5
3
y x mx m x m
đồngbiếntrên
là.
A.
3
1
4
m
. B.
3
4
m
. C.
3
1
4
m
. D.
1
m
.
Lơi giải
Chọn A
Tacótậpxácđịnh
D
.
2
– 4 3
y x mx m
.
2
0 – 4 3 0
y x mx m
.
Hàmsốđãchođồngbiếntrên
khivàchỉkhi
0,y x
,đẳngthứcchỉxảyratạihữuhạnđiểm
2
2
3
0 2 1. 3 0 4 3 0 1
4
m m m m m
.
Vậy
3
1
4
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 26
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
Câu 33: (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
3
x
y
x m
đồngbiếntrênkhoảng
; 6
.
A.
2
B.
6
C. Vôsố D.
1
Lời giải
Chọn A
Tậpxácđịnh:
; 3 3 ;D m m
 
.
Tacó
2
3 2
3
m
y
x m
Hàmsốđổngbiếntrênkhoảng
; 6
2
3 2 0
3
6 3
2
m
m
m
m
2
2
3
m
.
Mà
m
nguyênnên
1;2
m
.
Câu 34: (MĐ 103 BGD&ĐT NĂM 2017-2018) Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
1
3
x
y
x m
nghịchbiếntrênkhoảng
6;

?
A.
0
B.
6
C.
3
D. Vôsố
Lời giải
Chọn C
Tậpxácđịnh
\
3D m
;
2
3 1
3
m
y
x m
.
Hàmsố
1
3
x
y
x m
nghịchbiếntrênkhoảng
6;

khivàchỉkhi:
0
6;
y
D
3 1 0
3 6
m
m
1
3
2
m
m
1
2
3
m
.
Vì
m
2; 1;0
m
.
Câu 35: (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
5
x
y
x m
đồngbiếntrênkhoảng
; 10

?
A.
2
B. Vôsố C.
1
D.
3
Lờigiải
Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 27
TXĐ:
\ 5D m
.
2
5 2
'
5
m
y
x m
.
Hàmsốđồngbiếntrênkhoảng
; 10

khivàchỉkhi
5 2 0
5 10;
m
m

2
5
5 10
m
m
2
2
5
m
.
Vì
m
nguyênnên
1;2
m
.Vậycó
2
giátrịcủathamsố
m
.
Câu 36: (MĐ 104 BGD&DT NĂM 2017) Chohamsô
4mx m
y
x m
vơi
m
lathamsô.Goi
S
latâphơptât
cacacgiatringuyêncua
m
đêhamsônghichbiêntrêncackhoangxacđinh.Timsôphântưcua
S
.
A.
4
B. Vôsô C.
3
D.
5
Lờigiải
ChonD
\
D m
;
2
2
4m m
y
x m
.
Hamsônghichbiêntrêncackhoangxacđinhkhi
0,
y x D
2
4 0
m m
0 4
m
.
Ma
m
nênco
3
giatrithoamãn.
Câu 37: (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
x m
nghịchbiếntrênkhoảng
10;
?
A. Vôsố B.
4
C.
5
D.
3
Lời giải
Chọn B
Tậpxácđịnh
\ 5D m

.
2
5 6
5
m
y
x m
Hàmsốnghịchbiếntrên
10;
khivàchỉkhi
0,
5 10;
y x D
m

5 6 0
5 10
m
m
6
5
2
m
m
.
Mà
m
nên
2; 1;0;1
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 28
Câu 38: (MĐ 105 BGD&ĐT NĂM 2017) Chohàmsố
2 3mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợp
tấtcảcácgiátrịnguyêncủa
m
đểhàmsốđồngbiếntrêncáckhoảngxácđịnh.Tìmsốphầntửcủa
S
.
A. Vôsố B.
3
C.
5
D.
4
Lời giải
Chọn B
2
2
2 3
'
m m
y
x m
hàmsốđồngbiếntrênkhoảngxácđịnhkhi
1 3m
nêncó3giátrịcủamnguyên
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Câu 39: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Tậphợptấtcảcácgiátrịthựccủathamsố
m
để
hàmsố
3 2
6 4 9 4
y x x m x
nghịchbiếntrênkhoảng
; 1
là
A.
3
;
4

B.
0;

C.
;0

D.
3
;
4

Lời giải
Chọn A
Tacó
2
3 12 4 9
y x x m
Đểhàmsố nghịchbiếntrênkhoảng
; 1
thì
2
3 6 4 9 0 ; 1
y x x m x

2
4 3 12 9 ; 1
m x x x

; 1
4 min ,m f x

2
3 12 9
f x x x
Tacó
' 6 12;
f x x
' 0 2
f x x
.
Khiđó,tacóbảngbiếnthiên
Suyra
;0
3
min 3 4 3
4
f x m m

.
Câu 40: Chohàmsố
3 2
3 4y x x mx
.Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsốđồngbiếntrên
khoảng
;0

là
A.
1;5
. B.
; 3
. C.
; 4
. D.
1;
.
Lời giải
Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 29
Tacó
2
3 6
y x x m
.
Đểhàmsốđồngbiếntrênkhoảng
;0

thì
0, ;0
y x

2
3 6 0, ;0
x x m x 
2
3 6 , ;0
m x x x 
.
Đặt
2
3 6g x x x
,hàmsố
g x
cóbảngbiếnthiên
Dựavàobảngbiếnthiêntacó
2
3 6 , ;0
m x x x 
3
m
.
Câu 41: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3
2
( ) 7 14 2
3
mx
y f x mx x m
giảm
trênnửakhoảng
[1; )
?
A.
14
;
15

. B.
14
2;
15
. C.
14
;
15

. D.
14
;
15

.
Lời giải
Chọn A
Tậpxácđịnh
D
,yêucầucủabàitoánđưađếngiảibấtphươngtrình
2
14 14 0, 1mx mx x
,tươngđươngvới
2
14
( )
14
g x m
x x
(1)
Dễdàngcóđược
( )g x
làhàmtăng
1;x
,suyra
1
14
min ( ) (1)
15
x
g x g
Kếtluận:(1)
1
14
min ( )
15
x
g x m m
Câu 42: Xácđịnhcácgiátrịcủathamsốmđểhàmsố
3 2
3
y x mx m
nghịchbiếntrênkhoảng
0;1 ?
A.
0m
. B.
1
2
m
. C.
0m
. D.
1
2
m
.
Lời giải
Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 30
2
2
' 3 6 0
0
x m
y x mx
x
Hàmsố
3 2
3
y x mx m
nghịchbiếntrênkhoảng
1
0;1 2 1
2
m m
Câu 43: Tìmtấtcảcácgiátrịcủathamsố
m
đểhàmsố
3 2
3 1y x x mx
đồngbiếntrênkhoảng
;0

.
A.
0
m
. B.
2
m
. C.
3
m
. D.
1
m
.
Lờigiải
Chọn C
Tậpxácđịnh:
D
.
Đạohàm:
2
3 6
y x x m
.
Hàmsốđồngbiếntrênkhoảng
;0

khivàchỉkhi
0
y
,
0
x
2
3 6 0
x x m
,
0
x
.
Cách1:
2
3 6 0
x x m
,
0
x
2
3 6
x x m
,
0
x
.
Xéthàmsố
2
3 6f x x x
trênkhoảng
;0

,tacó:
6 6f x x
.Xét
0
f x
6 6 0
x
1
x
.Tacó
1 3
f
.
Bảngbiếnthiên:
Dựavàobảngbiếnthiên,tacó:
3
m
.
Cách2:
Tacó
9 3m
.
Nếu
0 3
m
thì
0
y
x
0
y
0
x
.
Nếu
0
thì
y
cóhainghiệmphânbiệt
1 2
,x x
.Khiđóđể
0
y
0
x
thìtaphảicó
1 2
0
x x
.Điềunàykhôngthểxảyravì
1 2
2 0
S x x
.
Vậy
3
m
.
Cách3:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 31
PhươngánB:Với
3
m
tacó
3
3 2
3 3 1 1
y x x x x
.Khiđó
2
3 1 0
y x
x
.
Suyrahàmsốđồngbiếntrênkhoảng
;0

.VậyBlàđápánđúng.
Câu 44: Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
3 2 2
3 9
y x mx m x
nghịchbiếntrênkhoảng
0;1
.
A.
1
1
3
m
. B.
1
3
m
.
C.
1
m
. D.
1
3
m
hoặc
1
m
.
Lời giải
Chọn D
Tậpxácđịnh
D
.
2 2
3 6 9
y x mx m
;
2 2 2 2
0 3 6 9 0 2 3 0
3
x m
y x mx m x mx m
x m
.
Nếu
3 0
m m m
thì
0;
y x
nênhàmsốkhôngcókhoảngnghịchbiến.
Nếu
3 0
m m m
thìhàmsốnghịchbiếntrênkhoảng
;3
m m
.
Dođóhàmsốnghịchbiếntrênkhoảng
0;1
0
1
3 1
3
m
m
m
.
Kếthợpvớiđiềukiệntađược
1
3
m
.
Nếu
3 0
m m m
thìhàmsốnghịchbiếntrênkhoảng
3 ;
m m
.
Dođóhàmsốnghịchbiếntrênkhoảng
0;1
3 0
1
1
m
m
m
.
Kếthợpvớiđiềukiệntađược
1
m
.
Vậyhàmsốnghịchbiếntrênkhoảng
0;1
khi
1
m
hoặc
1
3
m
.
Câu 45: Tìmcácgiátrịcủathamsố
m
đểhàmsố
3 2
1
2 1 2
3
y x mx m x m
nghịchbiếntrênkhoảng
2;0 .
.
A.
0
m
. B.
1
m
. C.
1
2
m
. D.
1
2
m
.
Lơi giải
Chọn C
Tacó:
2
2 2 1.
y x mx m
Cho
2
1
0 2 2 1 0 .
2 1
x
y x mx m
x m
.
Nếu
1 2 1
m
thìtacóbiếnđổi
0 1 2 1
y x m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 32
(trườnghợpnàyhàmsốkhôngthểnghịchbiếntrênkhoảng
2;0
).
Xét
2 1 1
m
tacóbiếnđổi
0 2 1;1
y x m
.
.
Vậy,hàmsốnghịchbiếntrênkhoảng
2;0
thì
2;0 2 1;1
m
.
1
2 1 2 .
2
m m
.
Câu 46: Tìmtấtcảcácgiátrị
m
đểhàmsố
3 2
3 2y x x mx
tăngtrênkhoảng
1;
.
A.
3
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Lờigiải
Chọn B
Đạohàm:
2
3 6
y x x m
YCBT
0, 1;y x
.
2 2
3 6 0, 1; 3 6 , 1;x x m x m x x x
Xéthàmsố:
2
3 6 , 1; 6 6 0 1f x x x x f x x f x x
.
lim
x
f x


,
1 3
f
.Dođó:
, 1; 3
m f x x m
.
Câu 47: Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsố
3 2
6 1y x mx m x
đồngbiếntrênkhoảng
0;4
là:
A.
;3

. B.
;3

. C.
3;6
. D.
;6

.
Lời giải
Chọn B
2
3 2 6
y x mx m
.Đểhàmsốđồngbiếntrênkhoảng
0;4
thì:
0
y
,
0;4
x
.
tứclà
2
3 2 6 0 0;4
x mx m x
2
3 6
0;4
2 1
x
m x
x
Xéthàmsố
2
3 6
2 1
x
g x
x
trên
0;4
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 33
2
2
6 6 12
2 1
x x
g x
x
,
1 0;4
0
2 0;4
x
g x
x
Tacóbảngbiếnthiên:
Vậyđể
2
3 6
0;4
2 1
x
g x m x
x
thì
3m
.
Câu 48: Tìmtấtcảcácgiáthựccủathamsố
m
saochohàmsố
3 2
2 3 6y x x mx m nghịchbiếntrên
khoảng
1;1
.
A.
1
4
m
. B.
1
4
m
. C.
2m
. D.
0m
.
Lời giải
Chọn C
Tacó
2
6 6 6y x x m
.
Hàmsốnghịchbiếntrênkhoảng
1;1
khivàchỉkhi
0y
với
1;1x
hay
2
m x x
với
1;1x
.
Xét
2
f x x x
trênkhoảng
1;1
tacó
2 1f x x
;
1
0
2
f x x
.
Bảngbiếnthiên
Dựavàobảngbiếnthiêntacó
m f x
với
1;1x
2m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 34
*Cóthểsửdụng
0y
với
1;1x
1 0
1 0
y
y
6 0
12 6 0
m
m
0
2
m
m
2m
.
Câu 49: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3 2
6 1y x x mx đồngbiếntrênkhoảng
0;
?
A.
12m
. B.
12m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
Cách 1:Tậpxácđịnh:
D
.Tacó
2
3 12y x x m
Trườnghợp1:
Hàmsốđồngbiếntrên
0,y x
3 0 ( )
12
36 3 0
hn
m
m
Trườnghợp2:Hàmsốđồngbiếntrên
0;
0y
cóhainghiệm
1 2
,x x thỏa
1 2
0x x (*)
Trườnghợp2.1:
0y
cónghiệm
0x
suyra
0m
.Nghiệmcònlạicủa
0y
là
4x
(khôngthỏa
(*))
Trườnghợp2.2:
0y
cóhainghiệm
1 2
,x x thỏa
1 2
0
0 0
0
x x S
P
36 3 0
4 0( )
0
3
m
vl
m
khôngcó
m
.Vậy
12m
Cách 2:Hàmsốđồngbiếntrên
0;
2
12 3 ( ), (0; )m x x g x x  .
Lậpbảngbiếnthiêncủa
( )g x
trên
0;
.
Câu 50: Tậphợpcácgiátrị
m
đểhàmsố
3 2
3 2y mx x x m đồngbiếntrên
3;0
là
A.
1
;0
3
. B.
1
;
3

. C.
1
;
3

. D.
1
;
3

.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 35
Lời giải
Chọn D
TXĐ:
D
Tacó
2
3 2 3y' mx x
.Hàmsốđồngbiếntrênkhoảng
3;0
khivàchỉkhi:
0y'
,
3;0
x
(Dấu
'' ''
xảyratạihữuhạnđiểmtrên
3;0
)
2
3 2 3 0
mx x
,
3;0
x
2
2 3
3
x
m g x
x
3;0
x
Tacó:
3
2 6
; 0 3
3
x
g x g x x
x
BBT
Vậy
3;0
1
max
3
m g x
.
Câu 51: Tìm
m
đểhàmsố
3 2
3 3 1
y x x mx m
nghịchbiếntrên
0;

.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Lơi giải
Chọn A
Tacó
2 2
3 6 3 3 2
y x x m x x m
.
Vìhàmsốliêntụctrênnửakhoảng
0;

nênhàmsốnghịchbiếntrên
0;

cũngtươngđươnghàm
sốnghịchtrên
0;

khichỉkhi
0, 0,y x
.
2 2
0;
2 0 0; 2 0;
min 1 1
x x m x m x x f x x
m f x f

 
.
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
Câu 52: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàm
số
tan 2
tan
x
y
x m
đồngbiếntrênkhoảng
0; .
4
A.
0
m
hoặc
1 2
m
B.
0
m
C.
1 2
m
D.
2
m
Lời giải
Chọn A
x
3
0
1
3

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 36
Đặt
,vì
0; 0;1
4
x t
Xéthàmsố
2
0;1
t
f t t
t m
.Tậpxácđịnh:
\
D m
Tacó
2
2
m
f t
t m
.
Tathấyhàmsố
tan
t x x
đồngbiếntrênkhoảng
0;
4
.Nênđểhàmsố
tan 2
tan
x
y
x m
đồngbiếntrên
khoảng
0;
4
khivàchỉkhi:
0 0;1
f t t
2
2
2 0
2
0 0;1 ;0 1;2
0
0;1
1
m
m
m
t m
m
m
t m
m

CASIO: Đạohàmcủahàmsốtađược
2 2
2
1 1
tan tan 2
cos cos
tan
x m x
x x
y
x m
Tanhậpvàomáytínhthằng
y
\CALC\Calc
8
x
(Chọngiátrịnàythuộc
0;
4
)
\=\
?
m
1giátrịbấtkỳtrong4đápán.
ĐápánD
2
m
.Tachọn
3
m
.Khiđó
0,17 0
y
(Loại)
ĐápánC
1 2
m
Tachọn
1,5
m
.Khiđó
0,49 0
y
(nhận)
ĐápánB
0
m
Tachọn
0
m
.Khiđó
13,6 0
y
(nhận)
VậyđápánBvàCđềuđúngnênchọnđápán A.
Câu 53: (ĐỀTHAMKHẢOBGD&ĐT2018)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
đểhàmsố
3
5
1
5
y x mx
x
đồngbiếntrênkhoảng
0;
A.
0
B.
4
C.
5
D.
3
Lờigiải
Chọn B
2
6
1
3y x m
x
Hàmsốđồngbiếntrên
0;
khivàchỉkhi
2
6
1
3 0, 0;y x m x
x
2
6
1
3 , 0;x m x
x
.Xéthàmsố
2
6
1
( ) 3
g x x m
x
,
0;x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 37
8
7 7
6( 1)
( ) 6
6
x
g x x
x x
,
1
( ) 0
1(loai)
x
g x
x
Bảngbiếnthiên:
DựavàoBBTtacó
4
m
,suyracácgiátrịnguyênâmcủathamsố
m
là
4; 3; 2; 1
Câu 54: (THPTBẠCHĐẰNGQUẢNGNINHNĂM2018-2019)Gọi
S
làtậphợptấtcảcácgiátrịcủa
thamsố
m
đểhàmsố
2 5 3 2 2
1 1
10 20
5 3
f x m x mx x m m x
đồngbiếntrên
.Tổnggiátrịcủatất
cảcácphầntửthuộc
S
bằng
A.
5
2
. B.
2
. C.
1
2
. D.
3
2
.
Lờigiải
Tacó
2 4 2 2 2 4 2
20 20 1 1 20 1
f x m x mx x m m m x m x x
2 2
1 1 1 1 1 20 1
m x x x m x x x
2 2
1 1 1 1 20
x m x x m x
2 2
1
0
1 1 1 20 0 *
x
f x
m x x m x
Tacó
0
f x
cómộtnghiệmđơnlà
1
x
,dođónếu
*
khôngnhận
1
x
lànghiệmthì
f x
đổidấuqua
1
x
.Dođóđể
f x
đồngbiếntrên
thì
0,f x x
hay
*
nhận
1
x
làm
nghiệm(bậclẻ).
Suyra
2 2
1 1 1 1 1 1 20 0 4 2 20 0
m m m m
.
Tổngcácgiátrịcủa
m
là
1
2
.
Câu 55: (THPTLÊQUÝĐÔNĐÀNẴNGNĂM2018-2019)Tậphợpcácgiátrịthựccủathamsốmđể
hàmsố
1
2
m
y x
x
đồngbiếntrênmỗikhoảngxácđịnhcủanólà
A.
0;1
. B.
;0

. C.
0; \ 1
. D.
;0

.
Lờigiải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 38
•Tậpxácđịnh:
\ 2
D
.
Hàmsốđãchođồngbiếntrênmỗikhoảngxácđịnhcủanókhivàchỉkhi:
' 0,
y x D
2
1 0,
2
m
x D
x
2
2 ,
m x x D
Xéthàmsố
2
2
f x x
tacó:
' 2 4 ' 0 2
f x x f x x
Bảngbiếnthiên:
Vậy,đểhàmsốđãchođồngbiếntrênmỗikhoảngxácđịnhcủanóthì
0
m
.
Câu 56: (THPTMINHKHAIHÀTĨNHNĂM2018-2019)Tìmtấtcảcácgiátrịthựccủathamsốđểhàm
số
cos 3
cos
x
y
x m
nghịchbiếntrênkhoảng
;
2
A.
0 3
1
m
m
. B.
0 3
1
m
m
. C.
3
m
. D.
3
m
.
Lờigiải
Điềukiện:
cosx m
.Tacó:
2 2
( 3) ( 3)
.( s in ) .sin
cos cos
m m
y x x
x m x m
Vì
; sin 0
2
x x
,
2
cos 0, ; : cos
2
x m x x m
.
Đểhàmsốnghịchbiếntrênkhoảng
;
2
0 ;
2
y x
3
3 0
3 0
0 3
1
cos ; 1;0
1
0
2
m
m
m
m
m
x m x m
m
m
.
Chúý:Tậpgiátrịcủahàmsố
cos , ;
2
y x x
là
1;0
.
Câu 57: (TTHOÀNGHOATHÁM-2018-2019)Chohàmsố
(4 ) 6 3
6
m x
y
x m
.Cóbaonhiêugiátrị
nguyêncủamtrongkhoảng
10;10
saochohàmsốđồngbiếntrên
8;5
?
A.
14
. B.
13
. C.
12
. D.
15
.
Lờigiải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 39
Đặt 6
t x
vì
8;5
x
14; 1
t và 6
t x
đồngbiếntrên
8;5
.
Hàmsốtrởthành
(4 ) 3m t
y
t m
tậpxácđịnh
\
D m
2
2
4 3
'
( )
m m
y
t m
.
Đểhàmsốđồngbiếntrênkhoảng
14; 1
2
4 3 0
14
1
m m
m
m
14
1 1
3
m
m
m
.
9, 8, 7, 6, 5, 4, 1,0,4,5,6,7,8,9
m
có14giátrị.
Câu 58: (THPTLƯƠNGTHẾVINHHÀNỘINĂM2018-2019LẦN1)Cóbaonhiêugiátrịnguyênâm
củathamsố
m
đểhàmsố
4
1 3
4 2
y x mx
x
đồngbiếntrênkhoảng
0;
.
A.
2
. B.
1
. C.
3
. D.
0
.
Lờigiải
Tậpxácđịnh:
.
D
3
2
3
2
y x m
x
.
Tacó:hàmsốđãchođồngbiếntrênkhoảng
0;
khivàchỉkhi
0
y
với
0;x
3
2
3
0, 0;
2
x m x
x
3
2
3
, 0;
2
x m x
x
0;
Min
m f x
,với
3
2
3
1
2
f x x
x
.
Cách1:
TheobấtđẳngthứcCauchytacó
3 3
3
5
2 2 2 2 5
3 1 1 1 1 5
5
2 2 2 2 2 2 2 2
x x
f x x
x x x x
.
Dấubằngxảyrakhivàchỉkhi
1x
.Dođó
0;
5
Min 2
2
f x
.
Từ
1
và
2
tacó
5 5
2 2
m m
.Do
m
nguyênâmnên
1
m
hoặc
2
m
.
Vậycóhaigiátrịnguyênâmcủathamsố
m
thỏamãnđiềukiệnbàira.
Cách2:
Xéthàmsố
3
2
3
, 0;
2
f x x x
x
.
Tacó
2
3
3
3 , 0 1f x x f x x
x
.
Bảngbiếnthiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 40
Từbảngbiếnthiêntacó
5 5
2 2
m m
.Do
m
nguyênâmnên
1
m
hoặc
2
m
.
Vậycóhaigiátrịnguyênâmcủathamsố
m
thỏamãnđiềukiệnbàira.
Câu 59: (THPTCHUYÊNBẮCGIANGNAM2018-2019LẦN01)Chohàmsố
ln 4
ln 2
x
y
x m
với
m
là
thamsố.Gọi
S
làtậphợpcácgiátrịnguyêndươngcủa
m
đểhàmsốđồngbiếntrênkhoảng
1;e
.Tìmsố
phầntửcủa
S
.
A.
3
B.
2
C.
1
D.
4
Lờigiải
ChọnC
ln 4
ln 2
x
y f x
x m
Đặt
lnt x
,điềukiện
0;1
t
4
2
t
g t
t m
;
2
2 4
2
m
g t
t m
Đểhàmsố
f x
đồngbiếntrên
1;e
thìhàmsố
g t
đồngbiếntrên
0;1
0, t 0;1
g t
2
2 4
0, 0;1
2
m
t
t m
1
2 4 0
2
2
2 0;1
0
m
m
m
m
S
làtậphợpcácgiátrịnguyêndương
1
S
.
Vậysốphầntửcủatập
S
là
1
.
Câu 60: (THPTCHUYÊNVĨNHPHÚCNĂM2018-2019LẦN01)Tìm
m
đểhàmsố
cos 2
cos
x
y
x m
đồng
biếntrênkhoảng
0;
2
A.
2
2
m
m
B.
2
m
C.
0
1 2
m
m
D.
1 1
m
–
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 41
Lờigiải
ChọnC
Tacó
2
2
' . sin ,sin 0 0;
2
cos
m
y x x x
x m
.
Dođó:Hàmsốnghịchbiếntrênkhoảng
0;
2
khivàchỉkhi
2 0
2
cos 0 0; 0;1
2
m
m
x m x m
0
1 2
m
m
.
Câu 61: (CHUYÊNLƯƠNGTHẾVINHĐỒNGNAINĂM2018-2019LẦN01)Cóbaonhiêugiátrị
nguyênâmcủathamsố
m
đểhàmsố
4 2
3 9
2 15 3 1
4 2
y x x m x m
đồngbiếntrênkhoảng
0;
?
A.
2.
B.
3.
C.
5.
D.
4.
Lờigiải
Yêucầubàitoán
3
3 9 2 15 0 0;y x x m x

vàdấubằngxảyratạihữuhạnđiểmthuộc
0;

3
3 9 15 2 0;x x m x

.
Xéthàmsố:
3
( ) 3 9 15
g x x x
trên
0;
.
Tacó:
2
( ) 9 9
g x x
0
g x
1
1 ( )
x
x l
.
Bảngbiếnthiên:
TừBBTtacó:
9
2 9
2
m m
Vậy
{ 4; 3; 2; 1}
m
.
Câu 62: Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
3
3
1
m m
y x
x
đồngbiếntrêntừng
khoảngxácđịnhcủanó?
A.
4
. B.
2
. C.
1
. D.
3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 42
Lờigiải
Tậpxácđịnh
\ 1
D
.
2
3
3
1
m m
y x
x
2
2
2
3 1 3
1
x m m
y
x
.
Hàmsốđồngbiếntrêntừngkhoảngxácđịnhkhi
0
y
,
1
x
2
3 0
m m
3 0
m
.
Do
m
3; 2; 1;0
m
.
Vậycó
4
giátrịnguyêncủa
m
thỏayêucầubàitoán.
Câu 63: Tìmmđểhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
A.
2m
. B.
0
1 2
m
m
. C.
2m
. D.
2m
.
Lờigiải
Đặt
.
Tacó:
sin 0, 0;
2
t x x
.
hàmsố
nghịchbiếntrênkhoảng
0;
2
.
Dođóhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
hàmsố
2
t
y
t m
đồngbiếntrên
khoảng
0;1
.
Tậpxácđịnh
\
D m
.
Hàmsố
2
t
y
t m
đồngbiếntrênkhoảng
0;1
2
2
0, 0;1
m
y t
t m
.
2 0 2
1 2
1 1
0
0 0
m m
m
m m
m
m m
.
Vậyvới
0
1 2
m
m
thìhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
.
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x)
Câu 64: (ĐỀTHAMKHẢOBGD&ĐT2018)Chohàmsố
( )y f x
.Hàmsố
'( )y f x
cóđồthịnhưhình
bên.Hàmsố
(2 ) y f x
đồngbiếntrênkhoảng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 43
A.
2;
B.
2;1
C.
; 2
D.
1;3
Lờigiải
Chọn B
Cách1:
Tathấy
'( ) 0
f x
với
(1;4)
1
x
x
nên
( )f x
nghịchbiếntrên
1;4
và
; 1
suyra
( ) ( )g x f x
đồngbiếntrên
( 4; 1)
và
1;

.Khiđó
(2 )f x
đồngbiếnbiếntrênkhoảng
( 2;1)
và
3;

Cách2:
Dựavàođồthịcủahàmsố
y f x
tacó
1
0
1 4
x
f x
x
.
Tacó
2 2 . 2 2
f x x f x f x
.
Đểhàmsố
2
y f x
đồngbiếnthì
2 0 2 0
f x f x
2 1 3
1 2 4 2 1
x x
x x
.
Câu 65:
(Mã đề 104 - BGD - 2019) Chohàmsố
f x
,bảngxétdấucủa
f x
nhưsau:
Hàmsố
5 2
y f x
đồngbiếntrênkhoảngnàodướiđây?
A.
3;4
.
B.
1;3
.
C.
; 3
.
D.
4;5
.
Lời giải
Chọn D
Tacó
5 2
y f x
2 5 2
f x
.
0
y
2 5 2 0
f x
5 2 3
5 2 1
5 2 1
x
x
x
4
3
2
x
x
x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 44
5 2 0
f x
5 2 3
1 5 2 1
x
x
4
2 3
x
x
;
5 2 0
f x
5 2 1
3 5 2 1
x
x
2
3 4
x
x
.
Bảngbiếnthiên
Dựavàobảngbiếnthiênhàmsố
5 2
y f x
đồngbiếntrênkhoảng
4;5
.
Câu 66: (Mã 103 - BGD - 2019) Chohàmsố
( )f x
,bảngxétdấucủa
( )f x
nhưsau:
Hàmsố
3 2y f x
đồngbiếntrênkhoảngnàodướiđây?
A.
0;2
. B.
2;3
. C.
; 3
. D.
3;4
.
Lời giải
Chọn D
Tacó
2. 3 2 0 3 2 0
y f x f x
3 2 3 3
1 3 2 1 1 2.
x x
x x
Vậychọn A.
Câu 67: (Mã 102 - BGD - 2019) Chohàmsố
( )f x
cóbảngdấu
( )f x
nhưsau:
Hàmsố
(5 2 )y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
3;5
. B.
5;
. C.
2;3
. D.
0;2
.
Lời giải
Chọn D
Hàmsố
( )y f x
cótậpxácđịnhlà
suyrahàmsố
(5 2 )y f x
cótậpxácđịnhlà
.
Hàmsố
(5 2 )y f x
có
y 2. (5 2 ), xf x
.
3 5 2 1 3 4
y 0 (5 2 ) 0
5 2 1 2
x x
f x
x x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 45
Vậyhàmsốnghịchbiếntrêncáckhoảng
;2

;
3;4
.DođóBphươngánchọn.
Câu 68: (Mã đề 101 - BGD - 2019) Chohamsô
f x
,bảngxétdấucủa
'f x
nhưsau:
Hamsô
3 2y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
2;1 .
B.
2;4 .
C.
1;2 .
D.
4; .
Lời giải
Chọn A
2. 3 2y f x
.
Hàmsốnghịchbiếnkhi
0 2. 3 2 0 3 2 0
y f x f x
3 3 2x 1
3 2x 1
2 3
1
x
x
.
Vậychọnđápán
B.
Câu 69: (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Chohàmsố
( )f x
cóbảngxétdấu
nhưsau:
Hàmsố
2
2y f x x
nghịchbiếntrênkhoảngnàodướiđây?
A.
2;1
. B.
4; 3
. C.
0;1
. D.
2; 1
.
Lời giải
Tacó:Đặt:
2
( ) 2y g x f x x
;
2 2
( ) ( 2 ) 2 2 . ( 2 )g x f x x x f x x
2
( ) 0 2 2 . ( 2 ) 0
g x x f x x
2
2 2
2
1
1
1 2
2 2 0 2 2( )
1 2
( 2 ) 0 2 1
1
2 3
3
x
x
x
x x x VN
x
f x x x x
x
x x
x
(Trongđó:
1 2 ; 1 2
x x
làcácnghiệmbộichẵncủaPT:
2
2 1
x x
)
+Tacóbảngbiếnthiên
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 46
Dựavàobảngbiếnthiên,suyrahàmsố
2
2y f x x
nghịchbiếntrênkhoảng
2; 1
.
Chú ý: Cáchxétdấu
( )g x
:
Chọngiátrị
2
0 1; 1 2 2 0 (0) (0) 0
x x x g f
(dựatheobảngxétdấucủahàm
( )f x
).Suyra
( ) 0 1; 1 2
g x x
,sửdụngquytắcxétdấuđathức“lẻđổi,chẵnkhông”suyra
dấucủa
( )g x
trêncáckhoảngcònlại
Câu 70: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Chohàmsố
y f x
cóđạo
hàm
'f x
trên
.Hìnhvẽbênlàđồthịcủahàmsố
'y f x
.Hàmsố
2
g x f x x
nghịchbiến
trênkhoảngnàotrongcáckhoảngdướiđây?
A.
3
;
2

. B.

. C.
1
;
2

. D.

.
Lời giải
Phương pháp
Hàmsố
y g x
nghịchbiếntrên
; ' 0 ;
a b g x x a b
vàbằng0tạihữuhạnđiểm.
Cách giải
Tacó:
2
' 1 2 '
g x x f x x
.
Hàmsố
y g x
nghịchbiếntrên
; ' 0 ;
a b g x x a b
vàbằng0tạihữuhạnđiểm.
Tacó
' 1 3 ' 2 0
g f
LoạiđápánA,BvàD
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 47
Câu 71: (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Chohàmsố
'y f x
cóđồthịnhưhìnhvẽ
Hàmsố
2
2y f x
đồngbiếntrênkhoảngnàodướiđây
A.
;0
. B.
0;1
. C.
1;2
. D.
0;
.
Lời giải
Chọn B
Hàmsố
2
2y f x
có
2
' 2 . ' 2y x f x
2
2
2
2
0
0
1 2 2
1 1
0 1
0
' 2 . ' 2 0
0
1
1
2 1
1
2 2
x
x
x
x
x
x
y x f x
x
x
x
x
x
x
Dođóhàmsốđồngbiếntrên
0;1
.
Câu 72: (THPTGIALỘCHẢIDƯƠNGNĂM2018-2019LẦN01)Chohàmsố
( )f x
,đồthịhàmsố
( )y f x
nhưhìnhvẽdướiđây.
Hàmsố
3y f x
đồngbiếntrênkhoảngnàodướiđây?
A.
4;6
. B.
1;2
. C.
; 1 .
D.
2;3
.
Lờigiải
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 48
Tacó:
3
3 3 3 ( 3)
3
3 0
3
3 0 3 0
3
3 0
x
y f x f x f x x
x
f x
x
f x f x
x
x
3 1
1
3 1
7
2
3 4
4
3
x L
x
x N
x
x
x N
x
x L
Tacóbảngxétdấucủa
3 :f x
Từbảngxétdấutathâyhàmsố
3
y f x
đồngbiếntrênkhoảng
1;2 .
Câu 73: (THPTMINHCHÂUHƯNGYÊNNĂM2018–2019)Chohàmsố
y f x
.Hàmsố
'y f x
cóđồthịnhưhìnhvẽ.Hàmsố
2
( ) ( 2).
g x f x
Mệnhvđềnàosai?
A. Hàmsố
g x
nghịchbiếntrên
; 2
B. Hàmsố
g x
đồngbiếntrên
2;

C. Hàmsố
g x
nghịchbiếntrên
1;0
D. Hàmsố
g x
nghịchbiếntrên
0;2
Lờigiải
ChọnA
Tacó
2 2
2
2
0
0
0
'( ) 2 . '( 2) 0 2 1 1
( 2) 0
2
2 2
x
x
x
g x x f x x x
f x
x
x
Từđồthị
'( )f x
tacó
2 2
2
'( 2) 0 2 0
2
x
f x x
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 49
BBT
TừBBTtathấyđápánCsai
Câu 74: (GKITHPTVIỆTĐỨCHÀNỘINĂM2018-2019)Chohàmsố
y f x
cóđạohàmliêntục
trên
vàđồthịhàmsố
'y f x
nhưhìnhbên.
Hỏihàmsố
3 2g x f x
nghịchbiếntrênkhoảngnàotrongcáckhoảngsau?
A.
1;

B.
; 1
C.
1;3
D.
0;2
Lờigiải
ChọnB
Tacó
2
' 0 2
5
x
f x x
x
Khiđó
' 2 ' 3 2g x f x
Với
5
2
3 2 2
1
' 0 ' 3 2 0 3 2 2
2
3 2 5
1
x
x
g x f x x x
x
x
Bảngbiếnthiên:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 50
Câu 75: (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hàm số
y f x
có đạo hàm
trên
và có đồ thị
y f x
như hình vẽ.
Xét hàm số
2
2
xfxg .
Mệnh đề nào sau đây sai?
A. Hàm số
g x
nghịch biến trên
0;2
B. Hàm số
g x
đồng biến trên
2;

C. Hàm số
g x
nghịch biến trên
; 2
D. Hàm số
g x
nghịch biến trên
1;0
Lờigiải
ChọnD
Ta có
2
2
xfxg
xxfxg 2.2''
2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 51
2
2
1
1
0
22
12
0
02'
0
0'
2
2
2
x
x
x
x
x
x
x
x
xf
x
xg
Ta có
3 6. 7 0
g f
,
g x
đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các
nghiệm bội chẵn nên ta có bảng xét dấu
g x
:
x
2
1
0
1
2
g x
0
0
0
0
0
Suy ra đáp án là D.
Câu 76: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Chohàmsố
y f x
cóbảng
xétdấuđạohàmnhưsau:
Hàmsố
2
2y f x
nghịchbiếntrênkhoảngnàodướiđây?
A.
2; 1
. B.
2;
. C.
0;2
. D.
1;0
.
Lời giải
Xéthàmsố
2
2g x f x
.Tacó:
2
' 2 . ' 2g x x f x
.
2
0
' 0
' 2 0
x
g x
f x
2 2
2 2
0
0 0
1
2 1 1 1
2
2 2 4
2
x
x x
x
x x x
x
x x
x
.
Tacóbảngxétdấu
'g x
:
Dựavàobảngxétdấu
'g x
tathấyhàmsố
2
2y f x
nghịchbiếntrêncáckhoảng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 52
Câu 77: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Chohàmsố
y f x
cóđạohàmliêntụctrên
.Biếthàmsố
y f x
cóđồthịnhưhìnhvẽ.Gọi
S
làtậphợpcácgiátrịnguyên
5;5
m
đểhàmsố
g x f x m
nghịchbiếntrênkhoảng
1;2
.Hỏi
S
cóbaonhiêuphầntử?
A.
4
. B.
3
. C.
6
. D.
5
.
Lời giải
Tacó
g x f x m
.Vì
y f x
liêntụctrên
nên
g x f x m
cũngliêntụctrên
.
Căncứvàođồthịhàmsố
y f x
tathấy
0 0
g x f x m
1 1
1 3 1 3
x m x m
x m m x m
.
Hàmsố
g x f x m
nghịchbiếntrênkhoảng
1;2
2 1
3 2
1 1
m
m
m
3
0 1
m
m
.
Mà
m
làsốnguyênthuộcđoạn
5;5
nêntacó
5; 4; 3;0;1
S
.
Vậy
S
có5phầntử.
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x)
Câu 78: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Chohàmsố
f x
cóbảngxétdấucủađạohàm
nhưsau
x

1 2 3 4
f x
0
0
0
0
Hàmsố
3
3 2 3y f x x x
đồngbiếntrênkhoảngnàodướiđây?
A.
; 1 .
B.
1;0 .
C.
0;2 .
D.
1; .
Lời giải
Chọn B
Tacó:
2
3 2 3
y f x x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 53
Với
1;0 2 1;2 2 0x x f x
,lạicó
2
3 0 0; 1;0x y x
Vậyhàmsố
3
3 2 3y f x x x
đồngbiếntrênkhoảng
1;0 .
Chúý:
+)Taxét
2
1;2 1; 2 3;4 2 0; 3 0x x f x x

Suyrahàmsốnghịchbiếntrênkhoảng
1;2
nênloạihaiphươngán
A,D.
+)Tươngtựtaxét
2
; 2 2 ;0 2 0; 3 0 0; ; 2x x f x x y x
  
Suyrahàmsốnghịchbiếntrênkhoảng
; 2
nênloạihaiphươngán
B.
Câu 79: (CHUYÊNLÊQUÝĐÔNĐIỆNBIÊNNĂM2018-2019LẦN02)Chohàmsố
f x
cóbảng
xétdấucủađạohàmnhưsau
Hàmsố
3
1 12 2019y f x x x
nghịchbiếntrênkhoảngnàodướiđây?
A.
1;
. B.
1;2
. C.
;1
. D.
3;4
.
Lờigiải
Tacó
2 2 2
1 3 12 3 6 9 3 6 9y f x x f t t t f t t t
,với
1t x
Nghiệmcủaphươngtrình
0y
làhoànhđộgiaođiểmcủacácđồthịhàmsố
2
; 3 6 9y f t y t t
.
Vẽđồthịcủacáchàmsố
2
; 3 6 9y f t y t t
trêncùngmộthệtrụctọađộnhưhìnhvẽsau:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 54
Dựavàođồthịtrên,tacóBXDcủahàmsố
2
3 6 9y f t t t
nhưsau:
0
1t
Vậyhàmsốnghịchbiếntrênkhoảng
0
;1t t
.Dođóhàmsốnghịchbiếntrênkhoảng
0
1;2 1;1x t
.
Câu 80: (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Chohàmsố
f x
cóbảng
xétdấuđạohàmnhưsau:
Hàmsố
2
2 1 1y f x x x
nghịchbiếntrênnhữngkhoảngnàodướiđây
A.
; 2
. B.
;1
. C.
2;0
. D.
3; 2
.
Lời giải.
2
2 1 1
1
x
y f x
x
.
Có
2
1 0
1
x
x
,
2;0x
.
Bảngxétdấu:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 55
2 1 0, 2;0
f x x
2
2 1 1 0, 2;0
1
x
f x x
x
.
Câu 81: (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Chohàmsố
f x
cóbảngxétdấucủađạohàm
nhưsau:
x

1 2 3 4
'f x
0
0 + 0
0 +
Hàmsố
2
2 1 1
y f x x x
nghịchbiếntrênkhoảngnàodướiđây?
A.
;1
. B.
; 2
. C.
2;0
. D.
3; 2
.
Lời giải
Tacó:
2
2 2
1
' 2 ' 1 1 2 ' 1
1 1
x x x
y f x f x
x x
Chúý:
2
2
1
0, .
1
x x
x R
x
+)Với
;1 1 0;x x
 
(loạivìkhôngthểkếtluậnđược)
+)Với
; 2 1 3;x x
 
(loạivìkhôngthểkếtluậnđược)
+)Với
3; 2 1 3;4
x x
(loạivìkhôngthểkếtluậnđược)
+)Với
2;0 1 1;3 ' 1 0 ' 0
x x f x y
(thỏamãn).
Câu 82: (SỞGIÁODỤCĐÀOTẠOVĨNHPHÚCNĂM2018 -2019LẦN01)Chohàmsốbậcbốn
( )y f x
cóđồthịcủahàmsố
( )y f x
nhưhìnhvẽbên.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 56
Hàmsố
3 2
3 ( ) 6 9y f x x x x
đồngbiếntrênkhoảngnàotrongcáckhoảngsauđây?
A.
0;2
. B.
1;1
. C.
1;

. D.
2;0
.
Lờigiải
Hàmsố
4 3 2
( ) ,( 0)
f x ax bx cx dx e a
;
3 2
( ) 4 3 2
f x ax bx cx d
.
Đồthịhàmsố
( )y f x
điquacácđiểm
( 4;0),( 2;0),(0; 3),(2;1)
nêntacó:
5
96
256 48 8 0
7
32 12 4 0
24
3
7
32 12 4 1
24
3
a
a b c d
a b c d
b
d
c
a b c d
d
Dođóhàmsố
3 2 2 3 2
5 15 55
3 ( ) 6 9 ; 3 ( ) 4 3 3
24 8 12
y f x x x x y f x x x x x x
11
0 0
2
x
y x
x
.Hàmsốđồngbiếntrêncáckhoảng
( 11;0)
và
2;

.
Câu 83: (HỌCMÃINĂM2018-2019-LẦN02)Chohàmsố
y f x
cóđạohàmtrên
.Đồthịhàmsố
y f x
nhưhìnhbên.Hỏiđồthịhàmsố
2y f x x
cóbaonhiêuđiểmcựctrị?
x
y
O
-4
-2 2-3
-3
1
-1
-2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 57
A.
4
. B.
3
. C.
2
. D.
1
.
Lờigiai
ChonB
Đặt
2g x f x x
.
2
g x f x
.
Vẽđườngthẳng
2
y
.
phươngtrình
0
g x
có3nghiệmbộilẻ.
đồthịhàmsố
2y f x x
có3điểmcựctrị.
Câu 84: (TRƯƠNGTHPTHOANGHOATHAMHƯNGYÊNNĂM2018-2019)Chohàmsố
y f x
liêntụctrên
.Hàmsố
y f x
cóđồthịnhưhìnhvẽ.Hàmsố
2019 2018
1
2018
x
g x f x
đồngbiến
trênkhoảngnàodướiđây?
A.
2;3
. B.
0;1
. C.
-1;0
. D.
1;2
.
Lờigiải
Tacó
1 1
g x f x
.
0 1 1 0 1 1
g x f x f x
1 1 0
.
1 2 3
x x
x x
Từđósuyrahàmsố
2019 2018
1
2018
x
g x f x
đồngbiếntrênkhoảng
-1;0
.
Câu 85: (SỞGD&ĐTNINHBÌNHLẦN01NĂM2018-2019)Chohàmsố
y f x
cóbảngxétdấucủa
đạohàmnhưsau
O
x
y
1
1
1
2
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 58
Hàmsố
2 2019
y f x
nghịchbiếntrênkhoảngnàotrongcáckhoảngdướiđây?
A.
4;2
. B.
1;2
. C.
2; 1
. D.
2;4
.
Lờigiải
Xét
2 2019
y g x f x
.
Tacó
2 2019 2
g x f x f x
,
2
1
0
2
4
x
x
g x
x
x
.
Dựavàobảngxétdấucủa
f x
,tacóbảngxétdấucủa
g x
:
Dựavàobảngxétdấu,tathấyhàmsố
y g x
nghịchbiếntrênkhoảng
1;2
.
Câu 86: (GKITHPTLƯƠNGTHẾVINHHÀNỘINĂM2018-2019)Chohàmsố
y f x
.Biếtđồthị
hàmsố
y f x
cóđồthịnhưhìnhvẽbên.Hàmsố
2
3 2018
y f x
đồngbiếntrênkhoảngnàodưới
đây?
A.
1; 0
B.
2; 3
C.
2; 1
D.
0; 1
Lờigiải
ChọnA
Tacó
2 2
3 2018 2 . 3
f x x f x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 59
2
2
2
2
0
0
3 6
3
2 . 3 0
2
3 1
1
3 2
x
x
x
x
x f x
x
x
x
x
.
Bảngxétdấucủađạohàmhàmsốđãcho
Từbảngxétdấusuyrahàmsốđồngbiếntrên
1; 0
.
x
3
2
1
0
1
2
3

2
3
f x
0
0
0
0
0
0
0
2
2 3
xf x
0
0
0
0
0
0
0
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

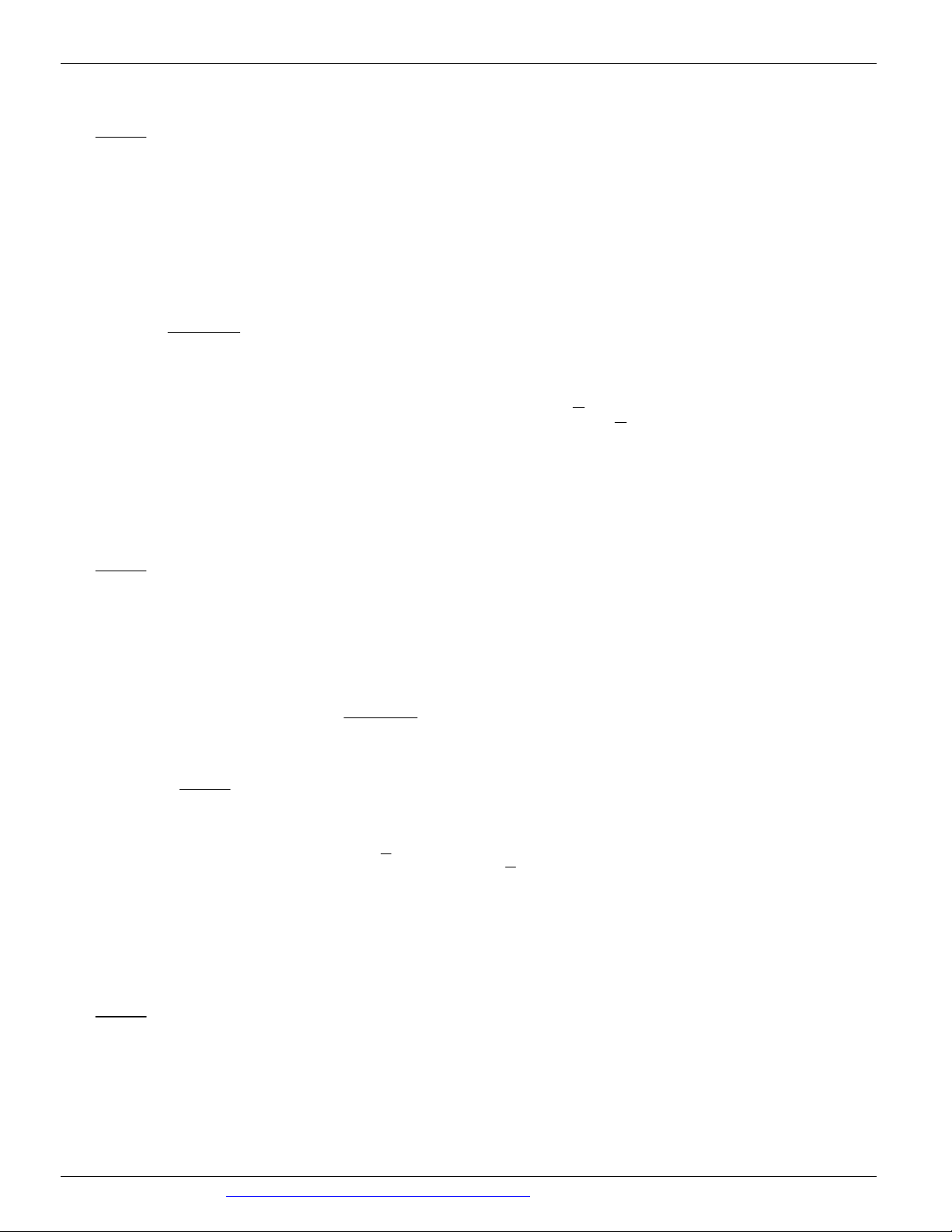
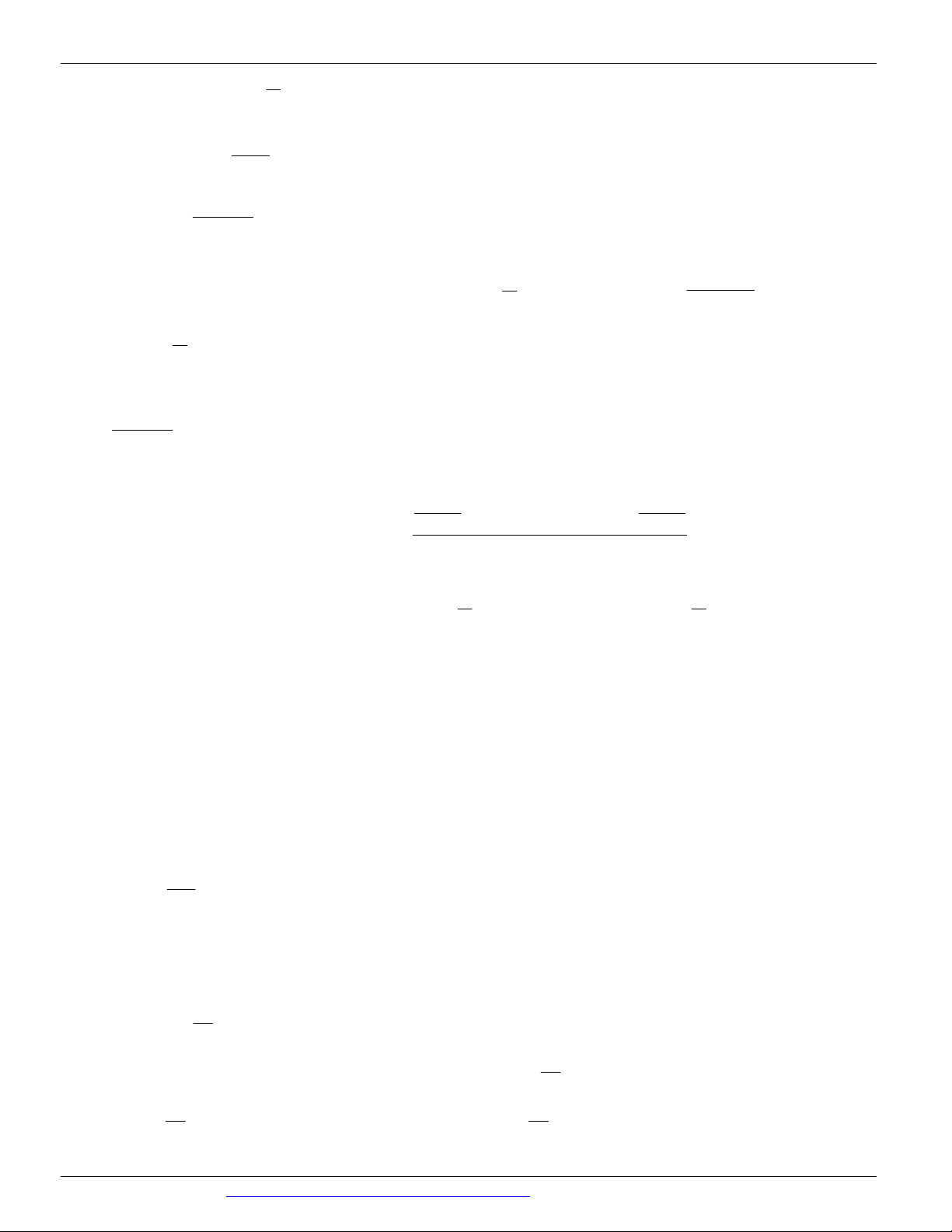
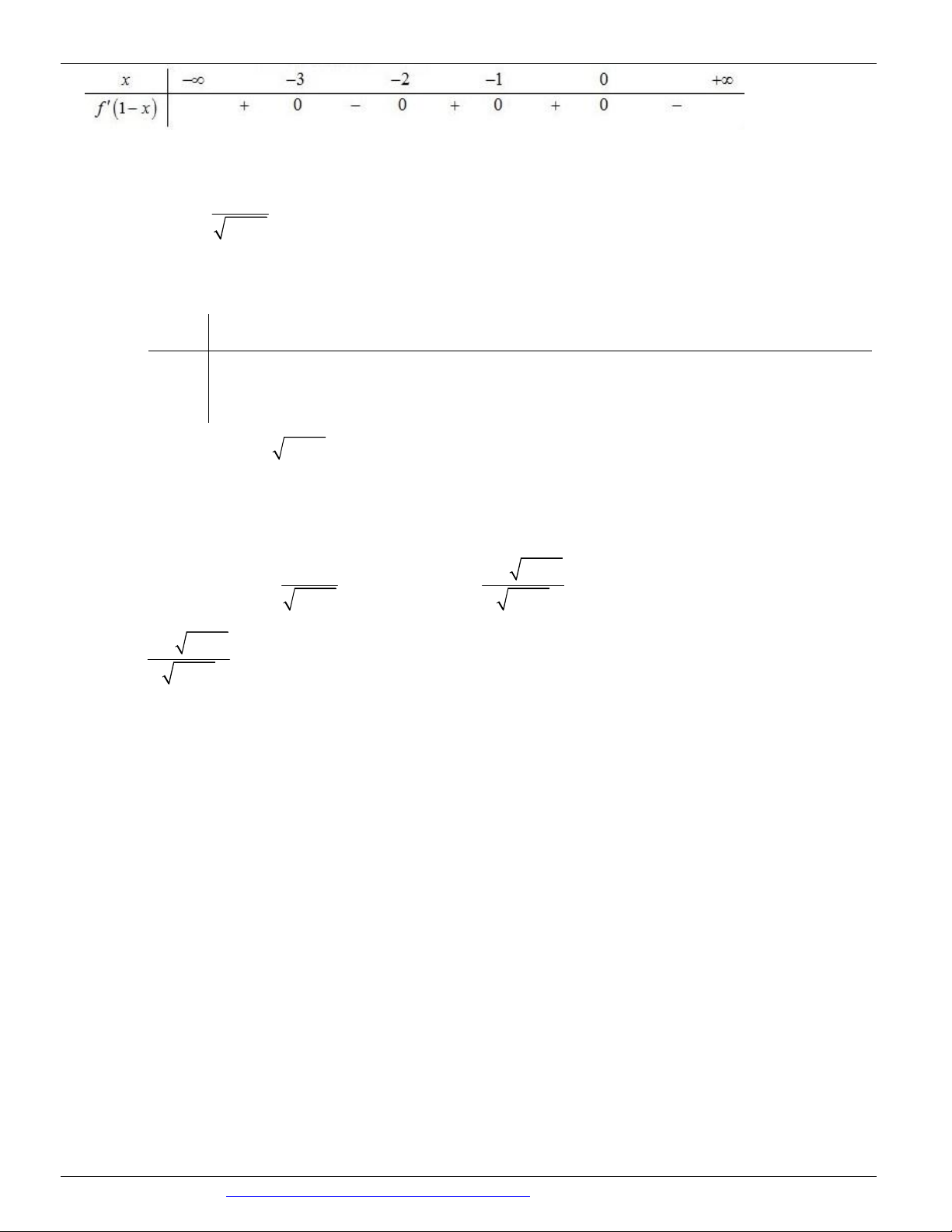
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ĐỀ 1 MỤC LỤC
PHẦN A. CÂU HỎI ........................................................................................................................................ 1
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị .......................................... 1
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước .................................................................................. 3
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó ....................................................... 4
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước ....................................................... 5
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước .............................................................. 6
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước ............................................................... 7
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x) .............................................. 9
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x) 12
PHẦN B. LỜI GIẢI THAM KHẢO ............................................................................................................ 14
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị ........................................ 14
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước ................................................................................ 18
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó ..................................................... 21
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước ..................................................... 26
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước ............................................................ 28
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước ............................................................. 35
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x) ............................................ 42
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x) 52 PHẦN A. CÂU HỎI
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị
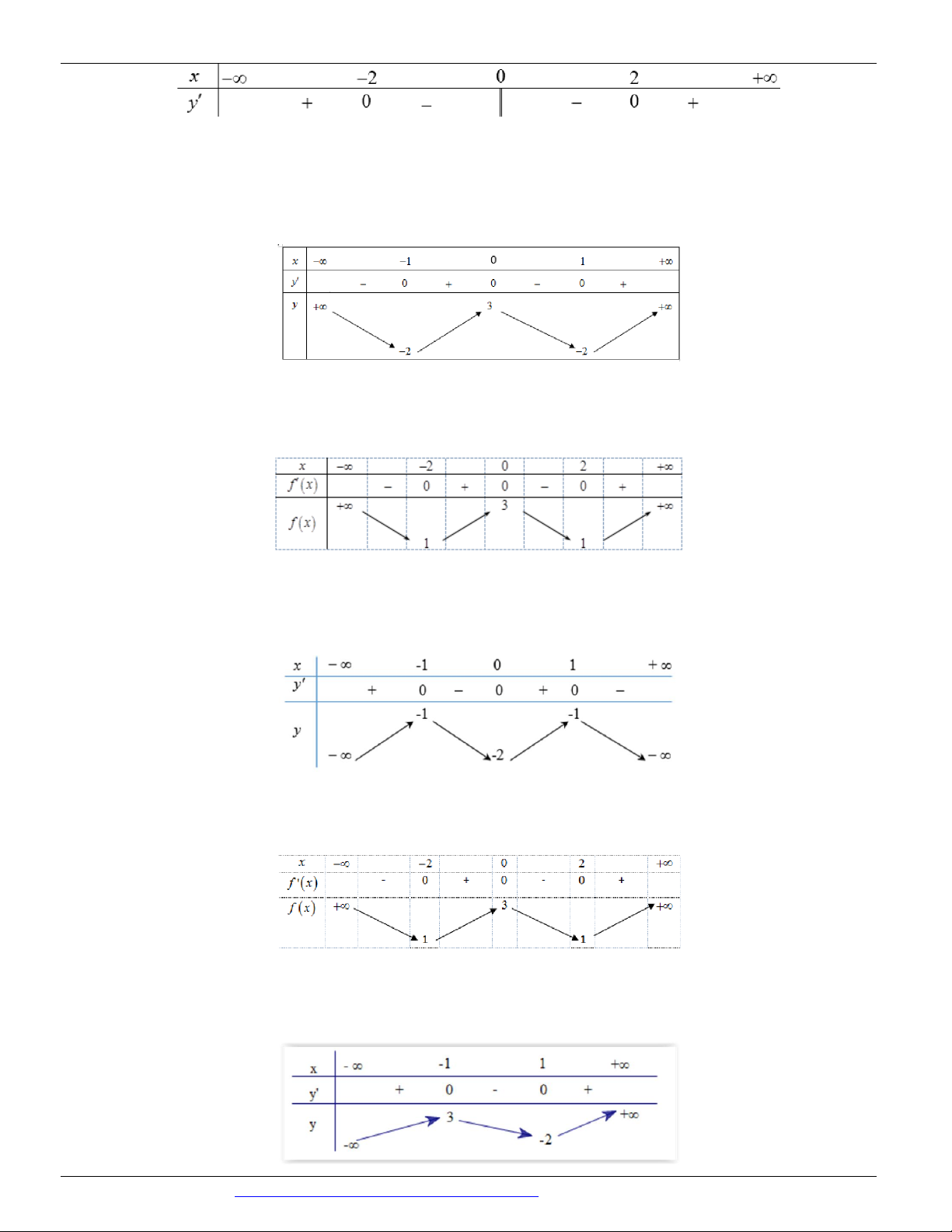
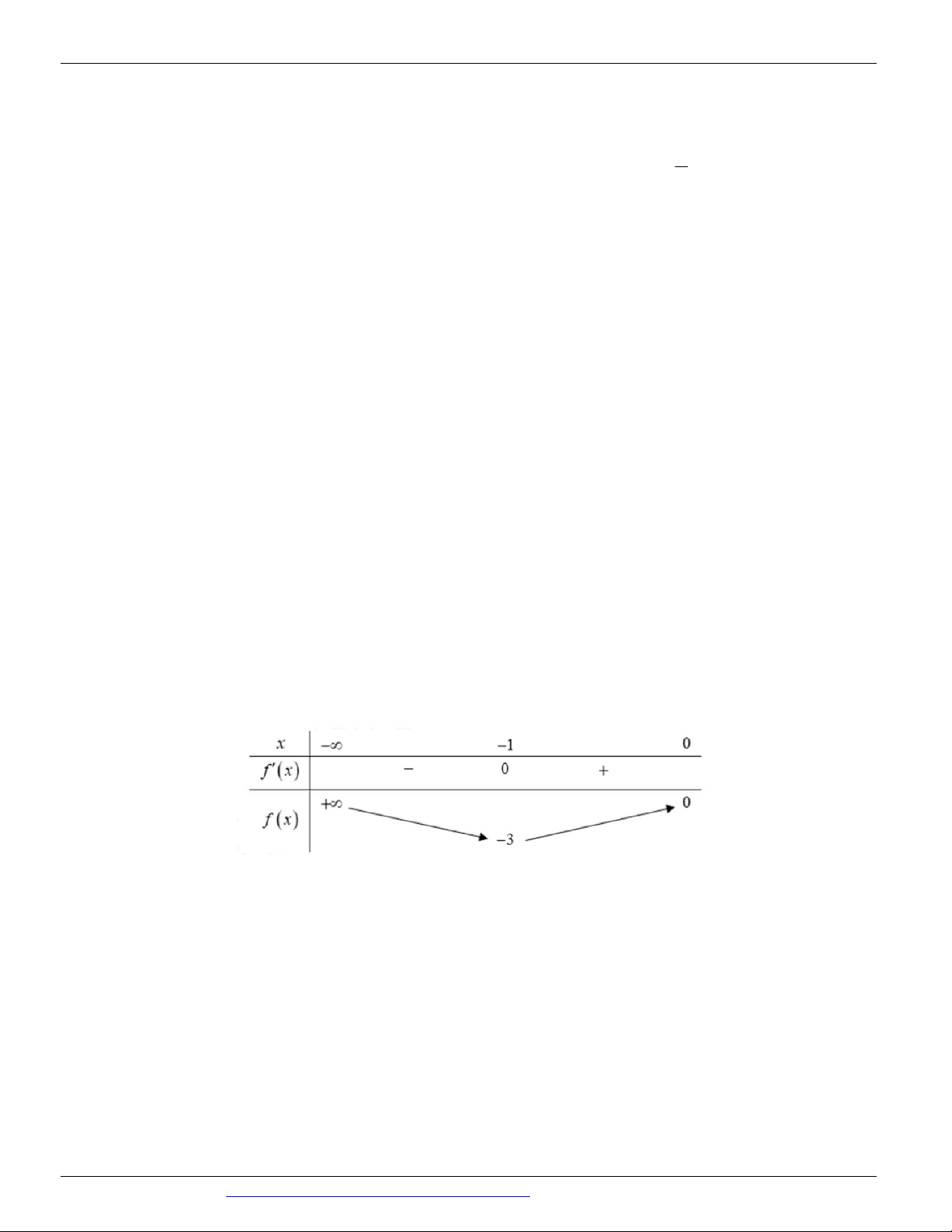
Câu 1: (Mã 103 - BGD - 2019) Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào sau đây? A.  ;    1 . B. 0  ;1 . C.  1  ;0. D.  1  ; .
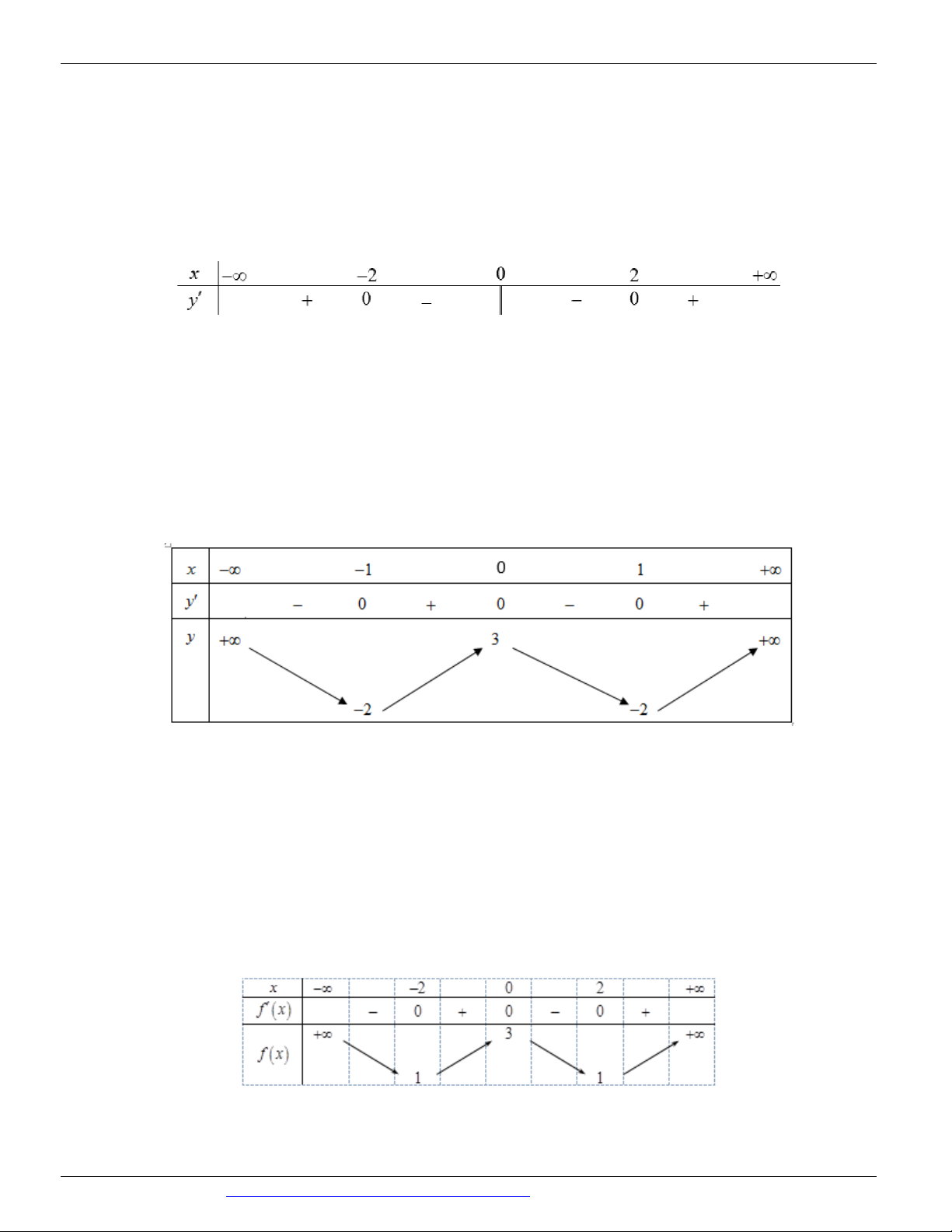
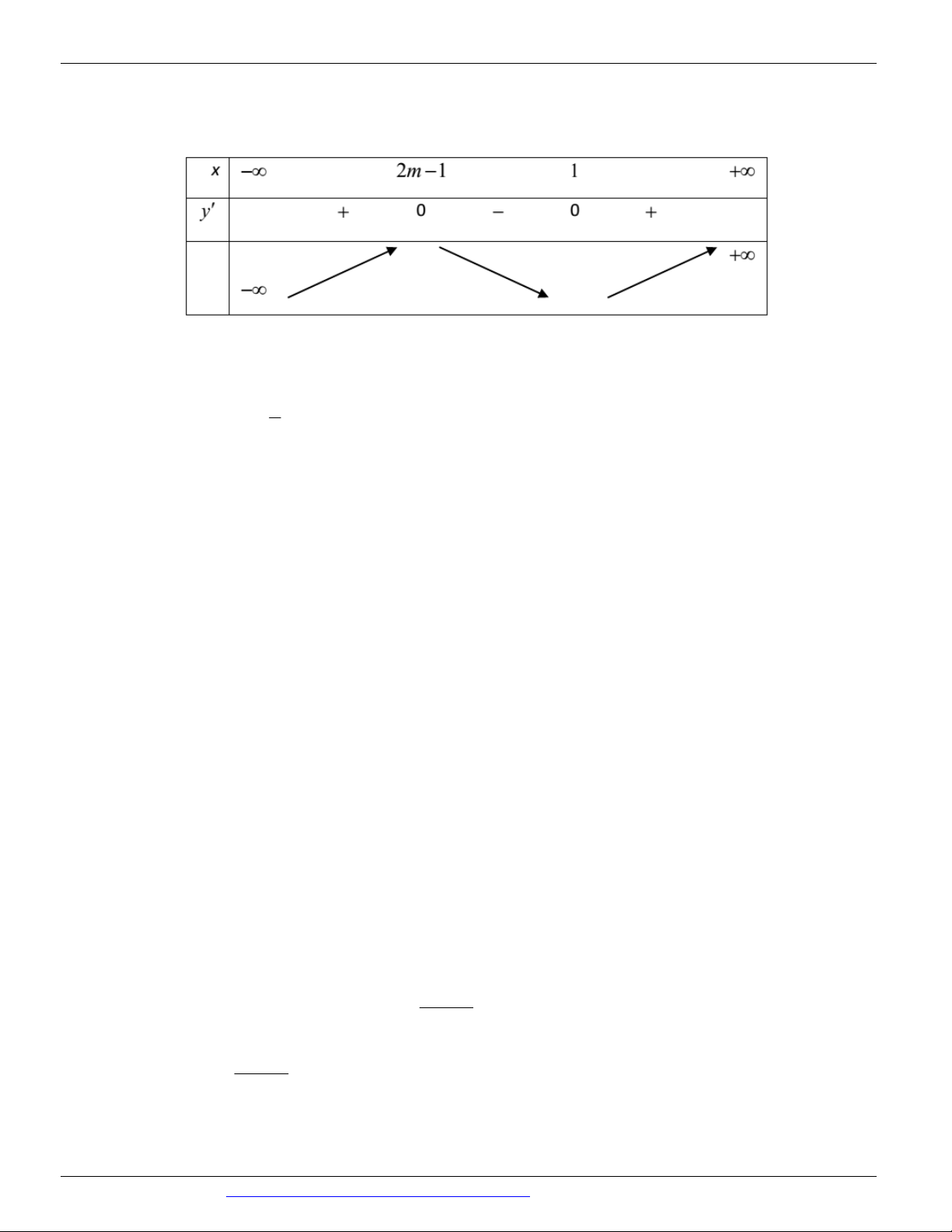
Câu 2: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số y f x có bảng xét dấu đạo hàm như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng  ;
 2 B. Hàm số đồng biến trên khoảng 2; 0
C. Hàm số đồng biến trên khoảng  ;
 0 D. Hàm số nghịch biến trên khoảng 0; 2
Câu 3: (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số y f x có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. 1;0 B.  ;  0
C. 1;  D. 0  ;1
Câu 4: (Mã 102 - BGD - 2019) Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A. 0;  . B. 0; 2 .
C. 2;0 . D.  ;  2   .
Câu 5: (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số y f x có bảng biến thiên như sau :
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 0  ;1
B. 1;  C.  ;   1 D. 1;0
Câu 6: (Mã đề 101 - BGD - 2019) Cho hàm số có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; 2.
B. 0; . C.  2  ; 0. D. 2; .
Câu 7: (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số y f x có bảng biến thiên như sau:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  1  ;  .
B. 1;  . C.  1  ;  1 . D.  ;   1 .
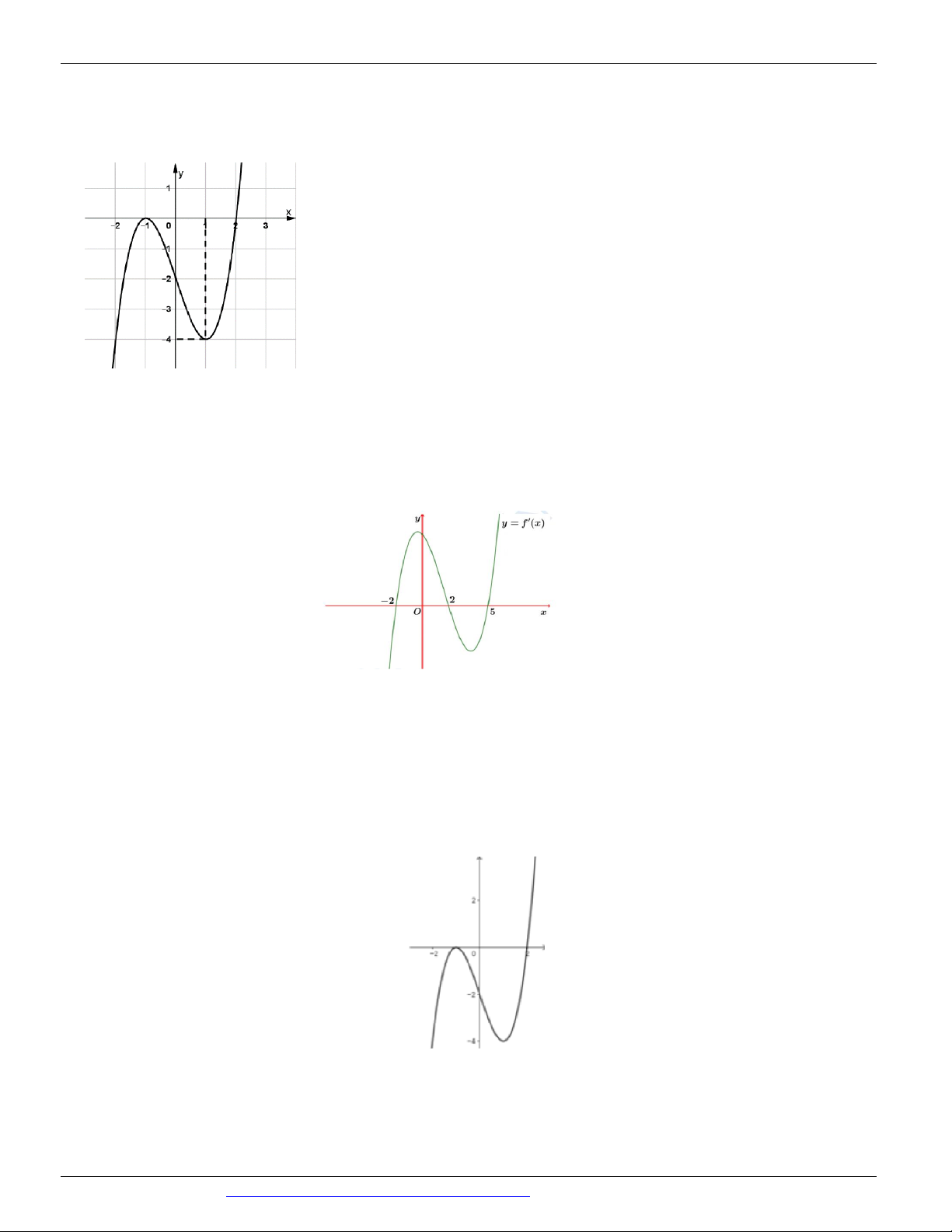
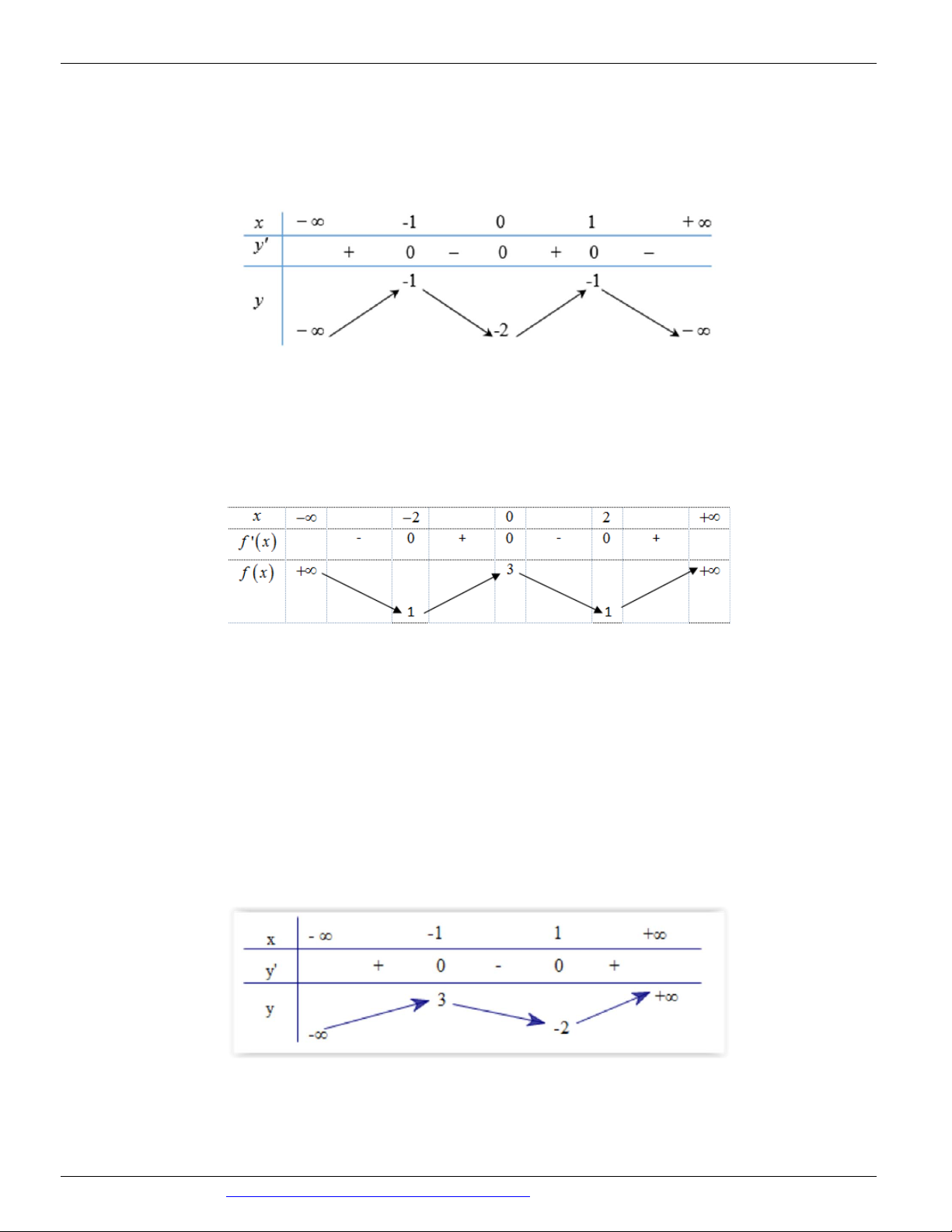
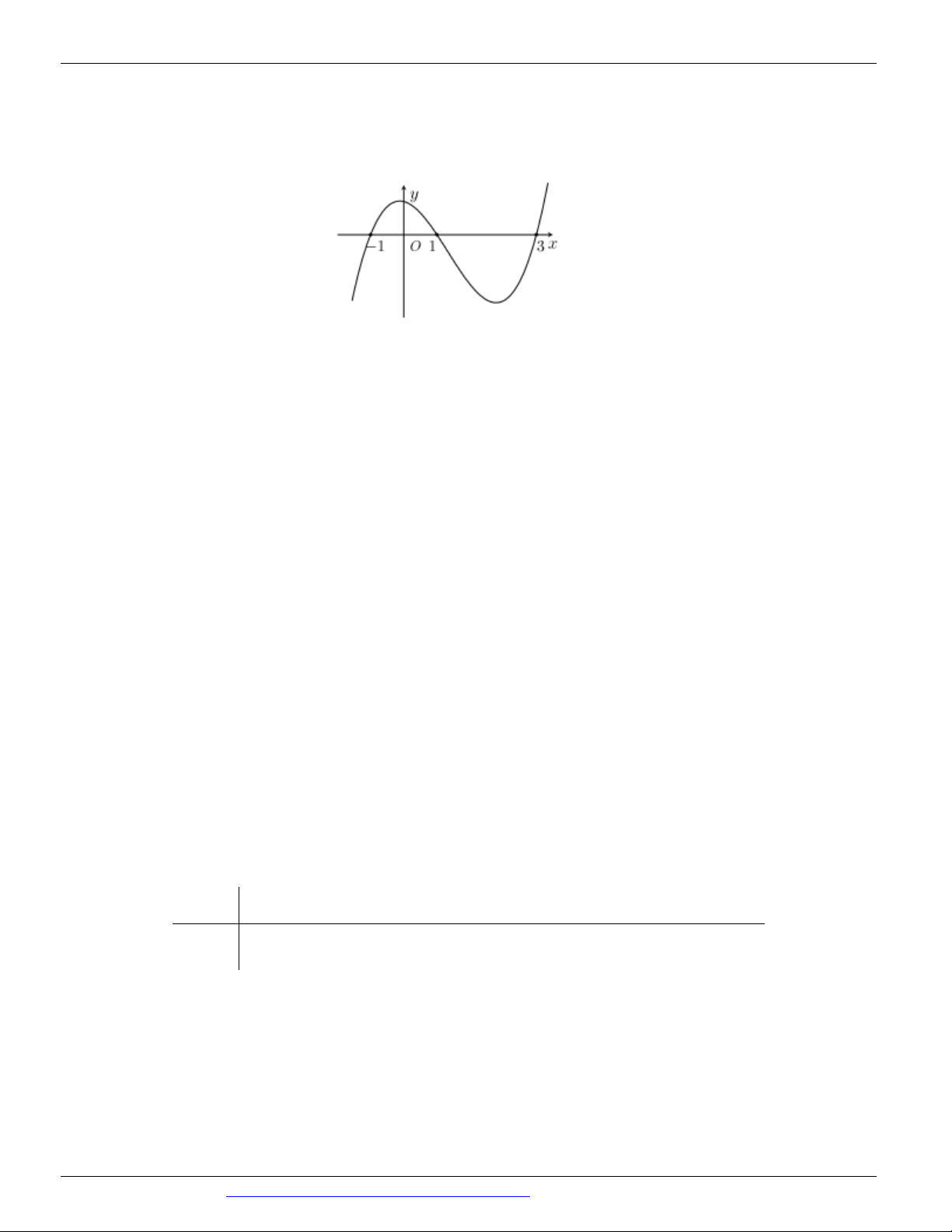
Câu 8: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y f x có đồ thị như hình vẽ
bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? y -1 1 O x -1 -2 A.    1 B.  1  ;  1
C. 1;0 D. 0;  1
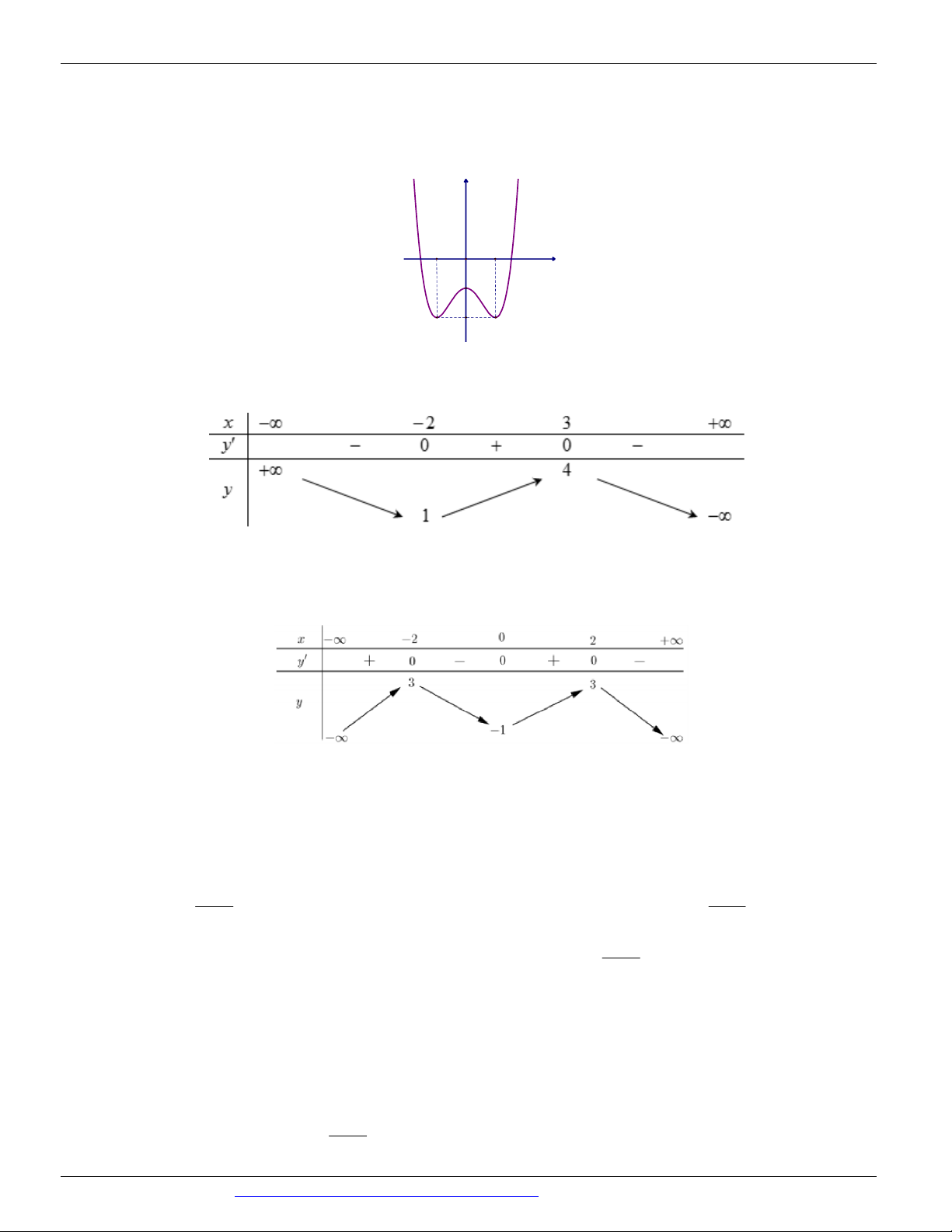
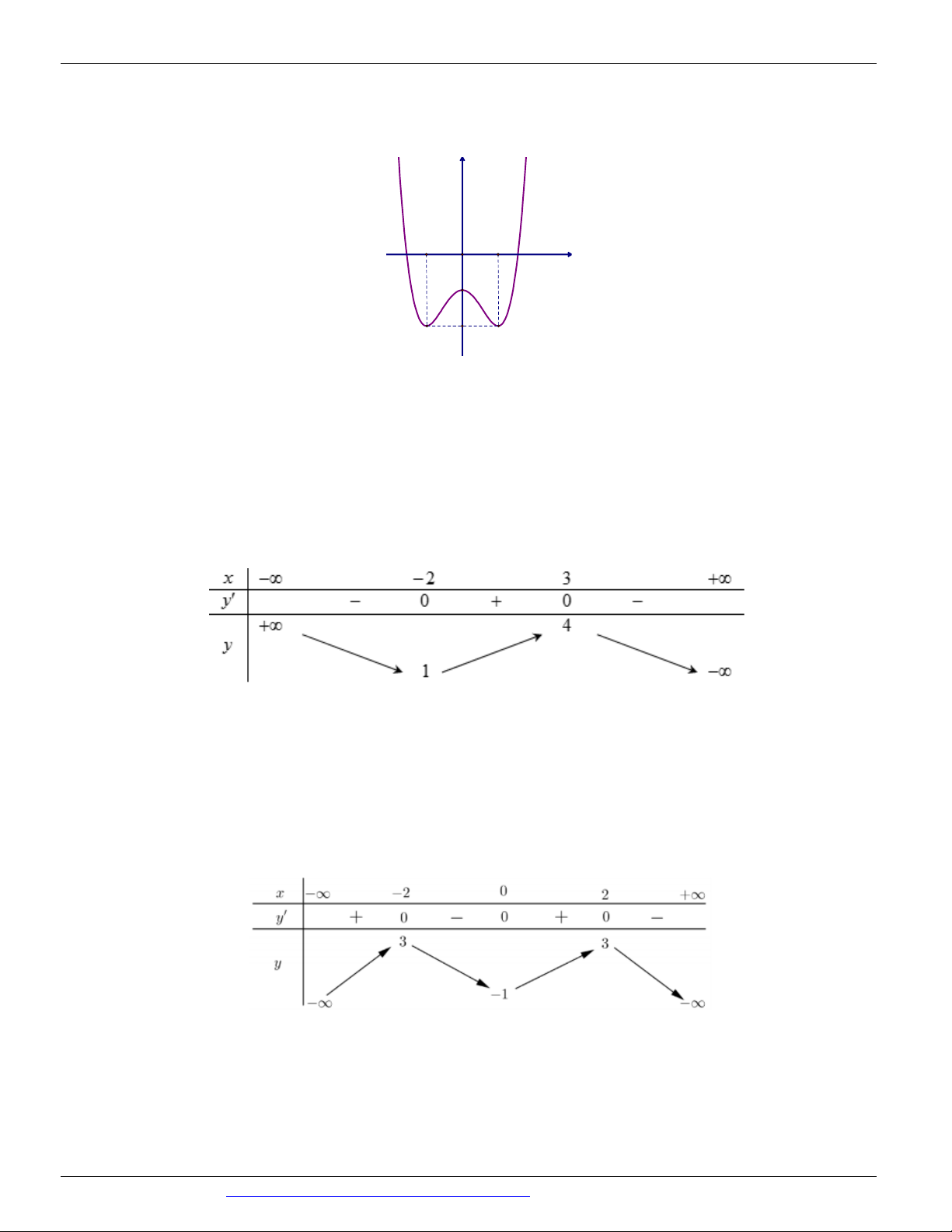
Câu 9: (Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số y f x có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 2;3
B. 3;   C.  ;   2 D.  2  ;  
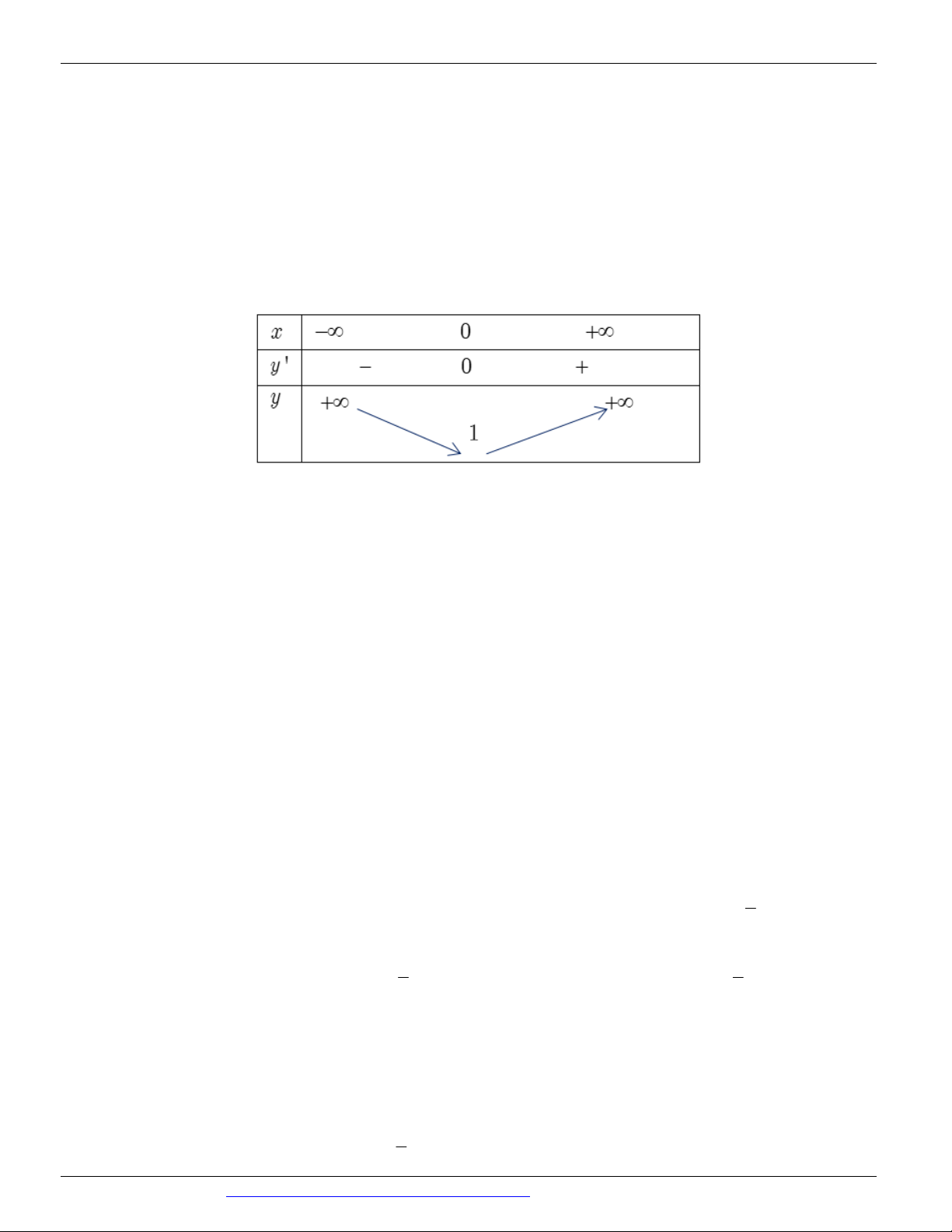
Câu 10: (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y f x có bảng biến thiên như sau:
Hàm số y f x nghịch biến trên khoảng nào dưới đây?
A. 0; B.  ;  2   C. 0;2 D.  2  ;0
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước
Câu 11: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x 1 x  1 A. y B. 3
y x x C. 3
y  x  3x D. y x  2 x  3 x  2
Câu 12: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số y
. Mệnh đề nào dưới đây đúng? x 1
A. Hàm số nghịch biến trên khoảng  ;
  B. Hàm số nghịch biến trên khoảng  1  ; 
C. Hàm số nghịch biến trên khoảng  ;    1
D. Hàm số đồng biến trên khoảng  ;    1
Câu 13: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x  2 A. 4 2
y x  3x . B. y  . C. 3
y  3x  3x  2 . D. 3
y  2x  5x 1. x 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 14: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số 3 2
y x  3x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0; 2 B. Hàm số nghịch biến trên khoảng 0; 2
C. Hàm số nghịch biến trên khoảng  ;  0
D. Hàm số nghịch biến trên khoảng 2;
Câu 15: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Hỏi hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1   1  A.  ;  0. B. ;    .
C. 0;  . D.  ;    .  2   2 
Câu 16: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y f x có đạo hàm f x  2
x  1 , x   . Mệnh
đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 1; 
B. Hàm số nghịch biến trên khoảng 1;1
C. Hàm số đồng biến trên khoảng ; 
D. Hàm số nghịch biến trên khoảng ; 0 Câu 17: Cho hàm số 3 2
y x  2x x 1 . Mệnh đề nào dưới đây đúng?  1 
A. Hàm số nghịch biến trên khoảng 1; 
B. Hàm số nghịch biến trên khoảng ;1    3   1   1 
C. Hàm số nghịch biến trên khoảng ;   
D. Hàm số đồng biến trên khoảng ;1    3   3 
Câu 18: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y  4 x  2
2x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ;  2 B. Hàm số đồng biến trên khoảng 1;1
C. Hàm số nghịch biến trên khoảng 1;1 D. Hàm số đồng biến trên khoảng ;  2 2
Câu 19: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Hàm số y
nghịch biến trên khoảng nào dưới đây? 2 x  1
A. (; ) B. (0; ) C. (; 0) D. (1; 1)
Câu 20: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y  3
x  3x  2 . Mệnh đề nào dưới đây là đúng?
A. Hàm số nghịch biến trên khoảng ; 0 và đồng biến trên khoảng 0; 
B. Hàm số đồng biến trên khoảng ; 0 và đồng biến trên khoảng 0; 
C. Hàm số đồng biến trên khoảng ; 
D. Hàm số nghịch biến trên khoảng ; 
Câu 21: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số 2 y
2x  1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0;    B. Hàm số đồng biến trên khoảng ; 0
C. Hàm số nghịch biến trên khoảng 0;   
D. Hàm số nghịch biến trên khoảng 1;1
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Câu 22: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hỏi có bao nhiêu số nguyên m để hàm số y   2 m   3
x  m   2 1
1 x x  4 nghịch biến trên khoảng  ;   . A. 0
B. 3 C. 2 D. 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 23: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y   3 x  2
mx  4m  9 x  5 , với m là tham
số. Hỏi có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng ;  A. 5 B. 4 C. 6 D. 7
Câu 24: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số hàm số 1 y   2 m m 3 2
x  2mx  3x  2 đồng biến trên khoảng  ;    ? 3 A. 4 .
B. 5 . C. 3 . D. 0 .
Câu 25: Tìm tất cả các giá trị của tham số thực m để hàm số 3 2
y mx mx m m  
1 x  2 đồng biến trên  . 4 4 4 4 A. m m  .
B. m  0 hoặc m  . C. m  . D. m  . 3 và 0 3 3 3 1 Câu 26: Cho hàm số 3 2 y  
x mx  3m  2 x 1. Tìm tất cả giá trị của m để hàm số nghịch biến trên  3 . m  1  m  1  A.  . B. 2   m  1  . C. 2   m  1  . D.  . m  2   m  2  
Câu 27: Tìm m để hàm số 3 2
y x  3mx  32m  
1 1 đồng biến trên  .
A. Không có giá trị m thỏa mãn.
B. m  1.
C. m  1.
D. Luôn thỏa mãn với mọi m . m
Câu 28: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y
x  2mx  3m  5 x đồng biến 3 trên  . A. 4 .
B. 2 . C. 5 . D. 6 . 1
Câu 29: Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số 3 2 y
x mx  4x m đồng biến trên 3 khoảng  ;   . A.  2  ; 2. B.  ;  2 . C.  ;  2  .
D. 2;  . 1 Câu 30: Cho hàm số 3 2
y   x  2x  2a  
1 x  3a  2 (a là tham số). Với giá trị nào của a thì hàm 3
số nghịch biến trên  ? 5 5
A. a  1 . B. a   . C. a   .
D. a  1 . 2 2
Câu 31: Tìm tất cả các giá trị của m để hàm số y  m   3
x  m   2 1 3
1 x  3x  2 đồng biến biến trên  ?
A. 1  m  2 .
B. 1  m  2 .
C. 1  m  2 .
D. 1  m  2 1
Câu 32: Giá trị của m 3 2 để hàm số y
x – 2mx  m  3 x – 5  m đồng biến trên  là. 3 3 3 3 A.
m  1. B. m   . C.   m  1.
D. m  1. 4 4 4
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
Câu 33: (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  2 y
đồng biến trên khoảng  ;  6 . x  3m A. 2 B. 6 C. Vô số D. 1
Câu 34: (MĐ 103 BGD&ĐT NĂM 2017-2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x 1 y
nghịch biến trên khoảng 6;  ? x  3m A. 0 B. 6 C. 3 D. Vô số
Câu 35: (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x  2 y
đồng biến trên khoảng  ;  1  0 ? x  5m A. 2 B. Vô số C. 1 D. 3 mx  4m
Câu 36: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số y
với m là tham số. Gọi S là tập hợp tất x m
cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S . A. 4 B. Vô số C. 3 D. 5
Câu 37: (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x  6 y
nghịch biến trên khoảng 10; ? x  5m A. Vô số B. 4 C. 5 D. 3 mx  2m  3
Câu 38: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y
với m là tham số. Gọi S là tập hợp x m
tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S . A. Vô số B. 3 C. 5 D. 4
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Câu 39: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2
y  x  6x  4m  9 x  4 nghịch biến trên khoảng  ;    1 là  3   3  A. ;  
B. 0;  C.  ;  0 D.  ;    4     4  Câu 40: Cho hàm số 3 2
y x  3x mx  4 . Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng  ;  0 là A.  1  ;5 . B.  ;    3 . C.  ;   4. D.  1  ;   . 3 mx
Câu 41: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 2
y f (x) 
 7mx 14x m  2 giảm 3 trên nửa khoảng [1;  )  ?  14   14   14   14  A.  ;    . B. 2;  . C.  ;    . D.  ;     . 15       15   15   15 
Câu 42: Xác định các giá trị của tham số m để hàm số 3 2
y x  3mx m nghịch biến trên khoảng 0;  1 ? 1 1
A. m  0 . B. m  .
C. m  0 . D. m  . 2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 43: Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  3x mx 1 đồng biến trên khoảng ;0 .
A. m  0 . B. m  2  . C. m  3  . D. m  1  .
Câu 44: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2 2
y x  3mx  9m x nghịch biến trên khoảng 0  ;1 . 1 1 1
A. 1  m  . B. m  . C. m  1  . D. m  hoặc m  1  . 3 3 3 1
Câu 45: Tìm các giá trị của tham số m 3 2 để hàm số y
x mx  2m  
1 x m  2 nghịch biến trên khoảng 3  2  ; 0. . 1 1
A. m  0 .
B. m  1. C. m   . D. m   . 2 2
Câu 46: Tìm tất cả các giá trị m để hàm số 3 2
y x  3x mx  2 tăng trên khoảng 1;   .
A. m  3 .
B. m  3 .
C. m  3 .
D. m  3 .
Câu 47: Tập hợp tất cả các giá trị của tham số m để hàm số 3 2
y x mx  m  6 x 1 đồng biến trên khoảng 0;4 là: A.  ;  3 . B.  ;   3 . C. 3;6 . D.  ;  6 .
Câu 48: Tìm tất cả các giá thực của tham số m sao cho hàm số 3 2
y  2x  3x  6mx m nghịch biến trên khoảng  1   ;1 . 1 1 A. m   . B. m  .
C. m  2 .
D. m  0 . 4 4
Câu 49: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y x  6x mx 1 đồng biến trên khoảng 0; ?
A. m  12 .
B. m  12 .
C. m  0 .
D. m  0 .
Câu 50: Tập hợp các giá trị m để hàm số 3 2
y mx x  3x m  2 đồng biến trên 3;0 là  1   1   1    1   A. ;0   . B. ;    . C. ;   . D. ;    .  3   3   3   3 
Câu 51: Tìm m để hàm số 3 2
y  x  3x  3mx m 1 nghịch biến trên 0;  .
A. m  1 .
B. m  1 .
C. m  1. D. m  1.
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
Câu 52: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m sao cho hàm tan x  2    số y
đồng biến trên khoảng 0; .   tan x m  4 
A. m  0 hoặc1  m  2 B. m  0
C. 1  m  2
D. m  2
Câu 53: (ĐỀ THAM KHẢO BGD & ĐT 2018) Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 1 3
y x mx
đồng biến trên khoảng 0; 5 5x A. 0 B. 4 C. 5 D. 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 54: (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị của 1 1
tham số m để hàm số f x 2 5 3 2 
m x mx  10x   2
m m  20 x đồng biến trên  . Tổng giá trị của tất 5 3
cả các phần tử thuộc S bằng 5 1 3 A. . B. 2  . C. . D. . 2 2 2
Câu 55: (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Tập hợp các giá trị thực của tham số m để m
hàm số y x 1 
đồng biến trên mỗi khoảng xác định của nó là x  2 A. 0;  1 . B.  ;  0 .
C. 0;   \   1 . D.  ;  0 .
Câu 56: (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Tìm tất cả các giá trị thực của tham số để hàm cos x  3    số y
nghịch biến trên khoảng ;   cos x m  2  0  m  3 0  m  3 A.  . B.  . C. m  3 . D. m  3 . m  1  m  1  (4  ) m 6  x  3
Câu 57: (TT HOÀNG HOA THÁM - 2018-2019) Cho hàm số y  . Có bao nhiêu giá trị 6  x m
nguyên của m trong khoảng 10;10 sao cho hàm số đồng biến trên 8;5 ? A. 14 . B. 13 . C. 12. D. 15 .
Câu 58: (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Có bao nhiêu giá trị nguyên âm 1 3
của tham số m để hàm số 4 y x mx
đồng biến trên khoảng 0;   . 4 2x A. 2 . B. 1. C. 3 . D. 0 . ln x  4
Câu 59: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hàm số y  với m là ln x  2m
tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng 1; e . Tìm số phần tử của S . A. 3 B. 2 C. 1 D. 4 cos x  2
Câu 60: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Tìm m để hàm số y  đồng cos x m    biến trên khoảng 0;    2  m  2 m  0 A. B. m  2 C.
D. 1  m  1 m  2  1  m  2 
Câu 61: (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị
nguyên âm của tham số m để hàm số 3 9 4 2 y x
x  2m 15 x  3m 1 đồng biến trên khoảng 0;   ? 4 2 A. 2.
B. 3. C. 5. D. 4. 2 m  3m
Câu 62: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y  3x  đồng biến trên từng x 1
khoảng xác định của nó?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 4 .
B. 2 . C. 1. D. 3 . cosx  2   
Câu 63: Tìm m để hàm số y
nghịch biến trên khoảng 0;   cosx m  2  m  0 A. m  2 . B. . C. m  2 . D. m  2 . 1   m 2 
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x)
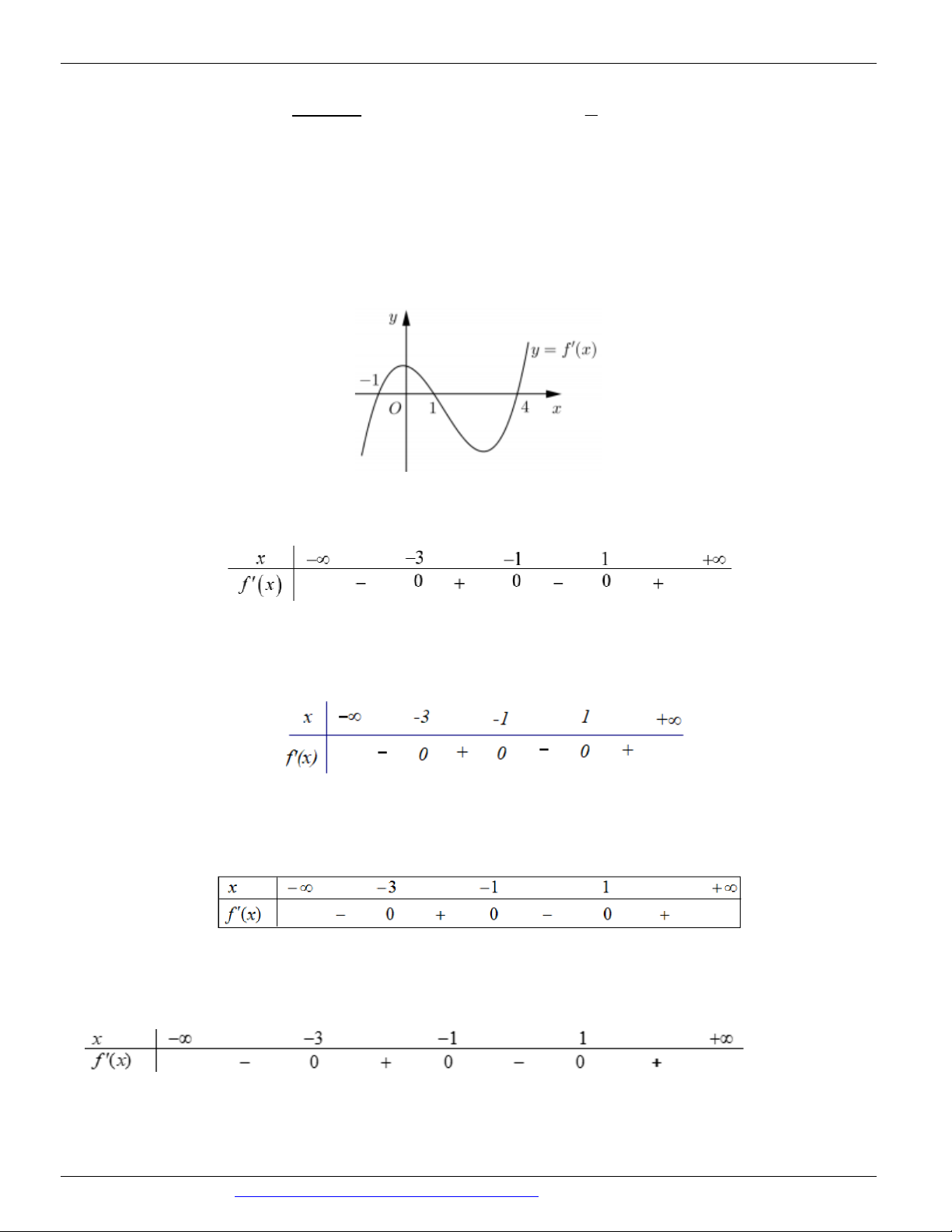
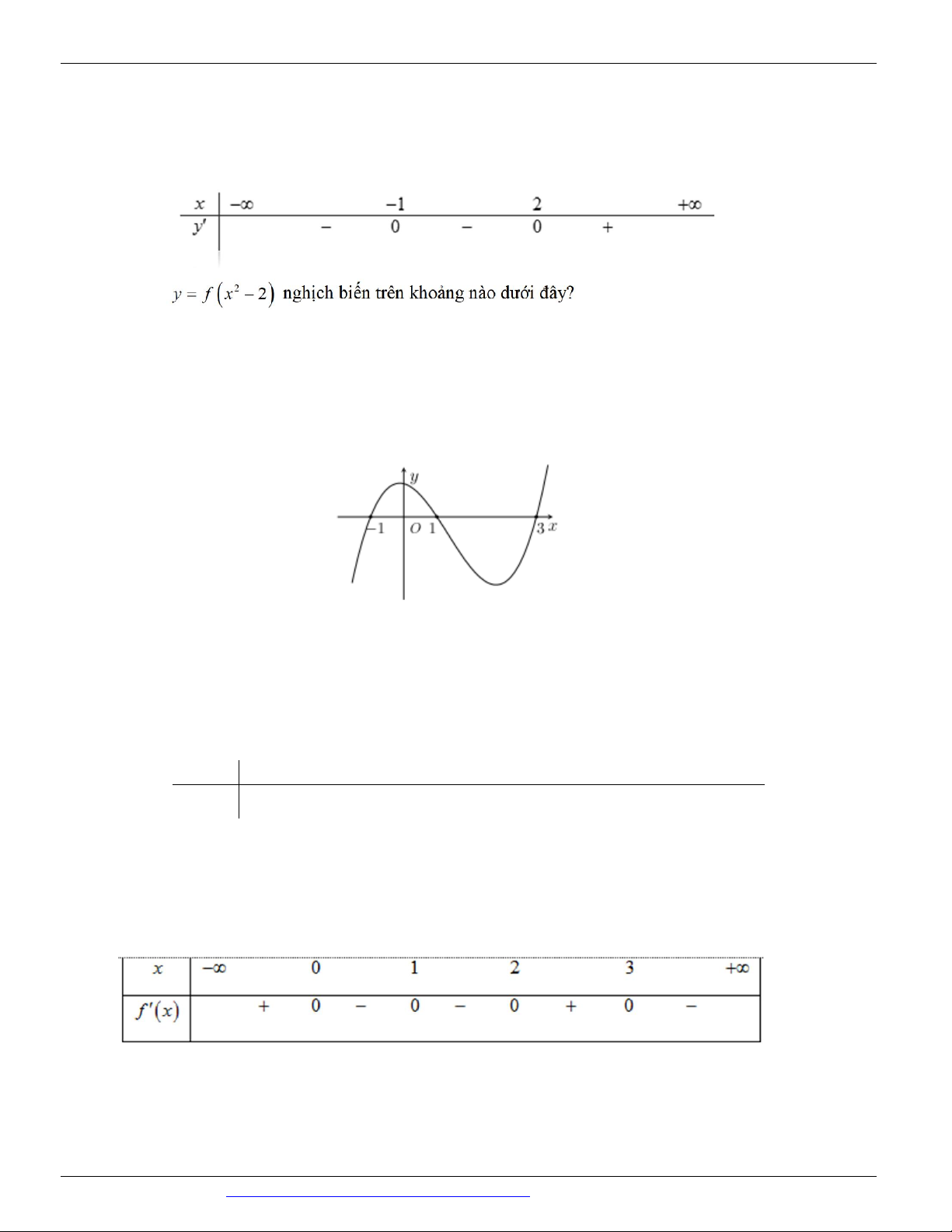
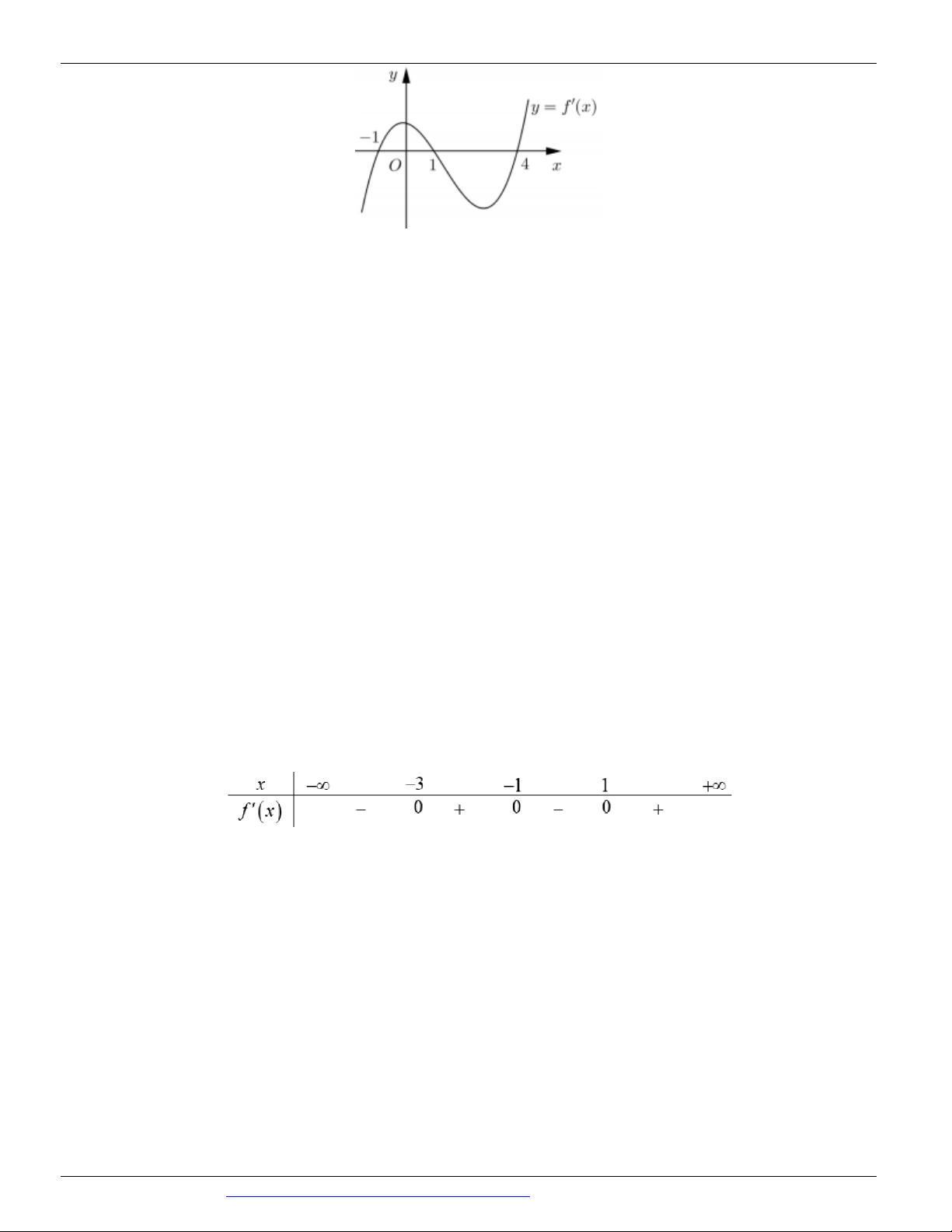
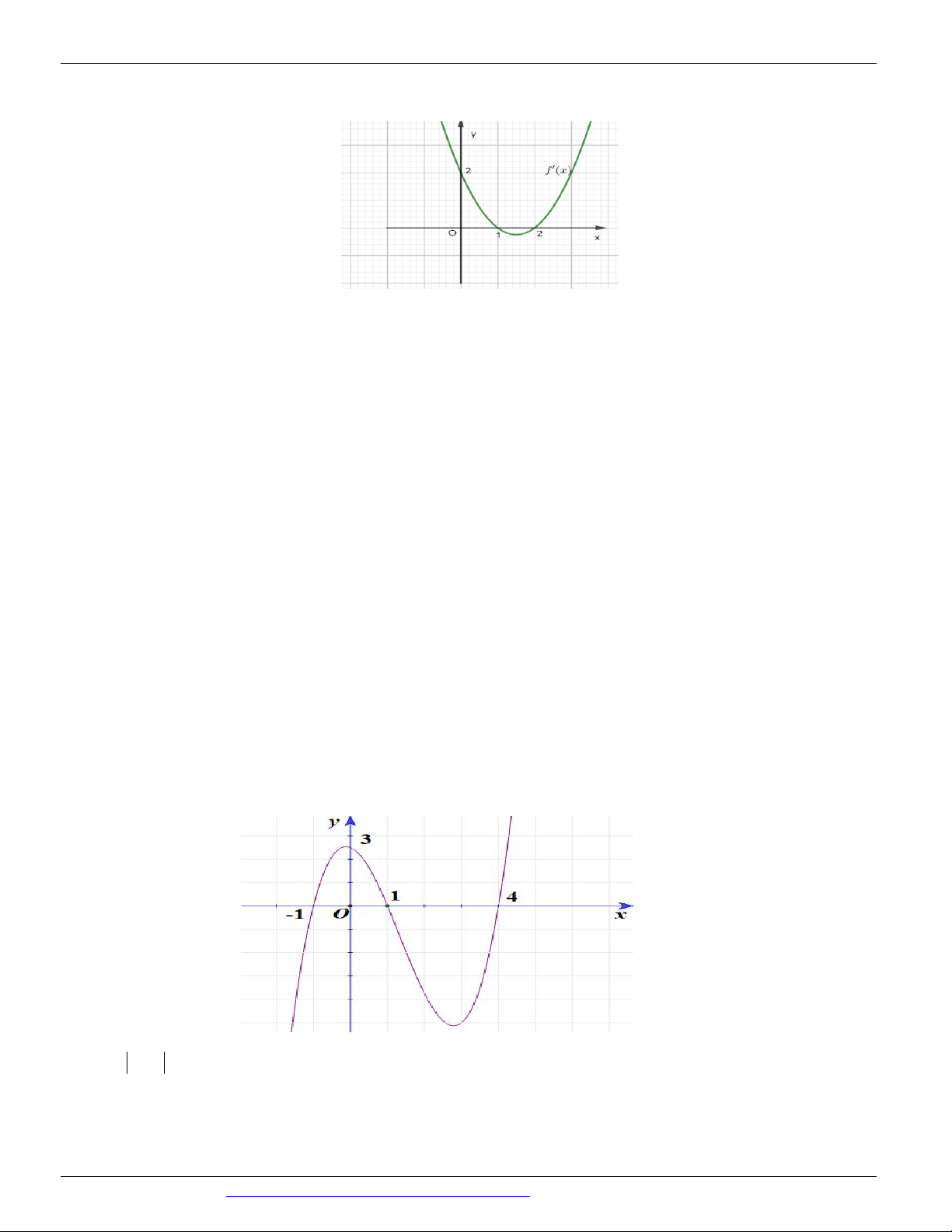
Câu 64: (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y f (x) . Hàm số y f '(x) có đồ thị như hình
bên. Hàm số y f (2  x) đồng biến trên khoảng
A. 2; B.  2  ;  1 C.  ;  2   D. 1;  3
Câu 65: (Mã đề 104 - BGD - 2019) Cho hàm số f x , bảng xét dấu của f  x như sau:
Hàm số y f 5  2x đồng biến trên khoảng nào dưới đây? A. 3;4 . B. 1;  3 . C. ;  3 . D. 4;5 .
Câu 66: (Mã 103 - BGD - 2019) Cho hàm số f (x) , bảng xét dấu của f (  x) như sau:
Hàm số y f 3  2x đồng biến trên khoảng nào dưới đây? A. 0;2 . B. 2;  3 . C. ;  3 . D. 3;4 .
Câu 67: (Mã 102 - BGD - 2019) Cho hàm số f (x) có bảng dấu f (  x) như sau:
Hàm số y f (5  2x) nghịch biến trên khoảng nào dưới đây? A. 3;5 .
B. 5;  . C. 2;3 . D. 0; 2 .
Câu 68: (Mã đề 101 - BGD - 2019) Cho hàm số f x , bảng xét dấu của f ' x như sau:
Hàm số y f 3  2x nghịch biến trên khoảng nào dưới đây? A.  2  ;  1 . B. 2; 4. C. 1;2. D. 4; .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 69: (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Cho hàm số f (
x) có bảng xét dấu như sau:
Hàm số y f  2
x  2x nghịch biến trên khoảng nào dưới đây? A.  2   ;1 . B.  4  ; 3   . C. 0  ;1 . D.  2  ;   1 .
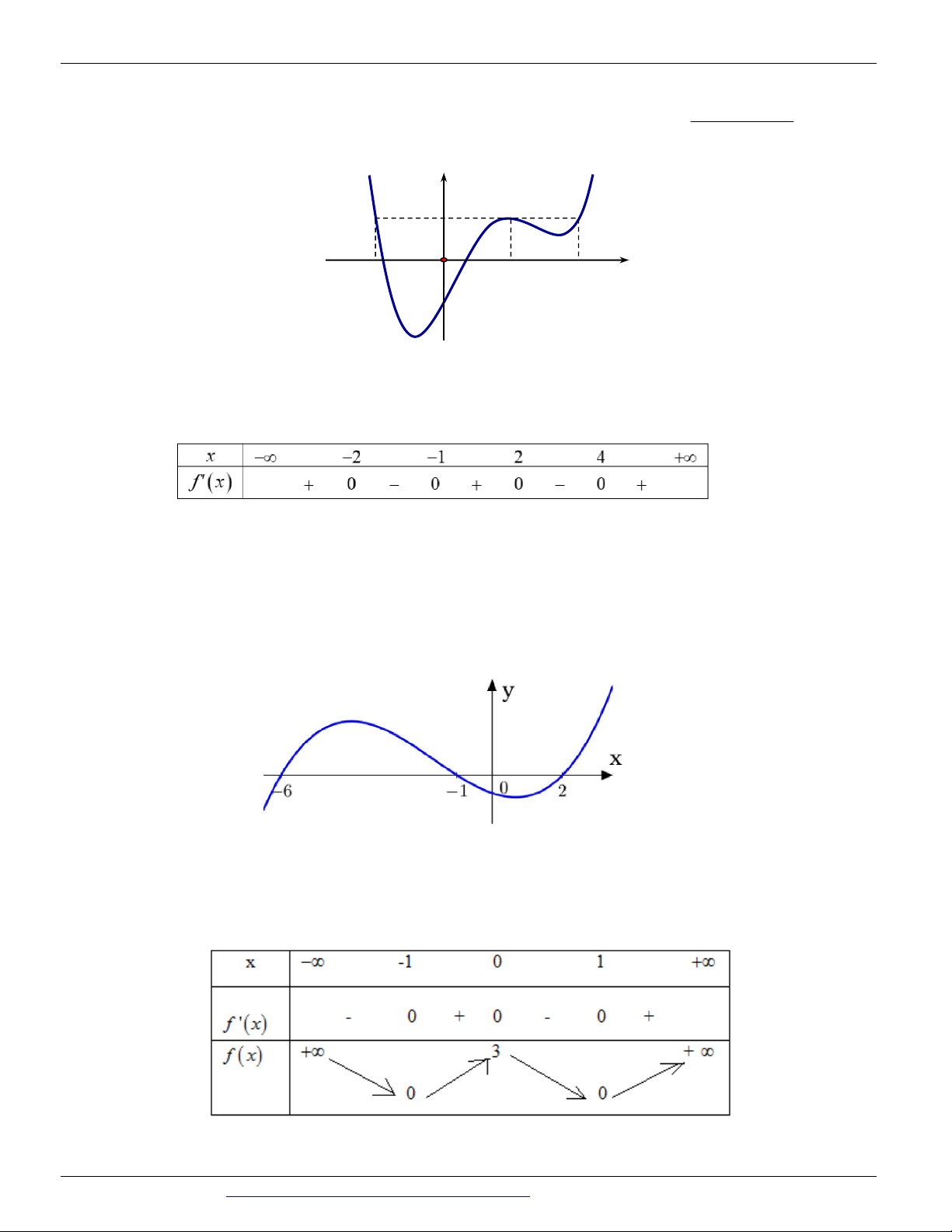
Câu 70: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Cho hàm số y f x có đạo
hàm f ' x trên  . Hình vẽ bên là đồ thị của hàm số y f ' x . Hàm số     2 g x
f x x  nghịch biến
trên khoảng nào trong các khoảng dưới đây?  3   3   1   1  A.  ;    . B.  ;    . C. ;    . D.  ;    .  2   2   2   2 
Câu 71: (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Cho hàm số
y f ' x có đồ thị như hình vẽ
Hàm số y f  2
2  x  đồng biến trên khoảng nào dưới đây A.  ;  0 . B. 0  ;1 . C. 1; 2 . D. 0;  .
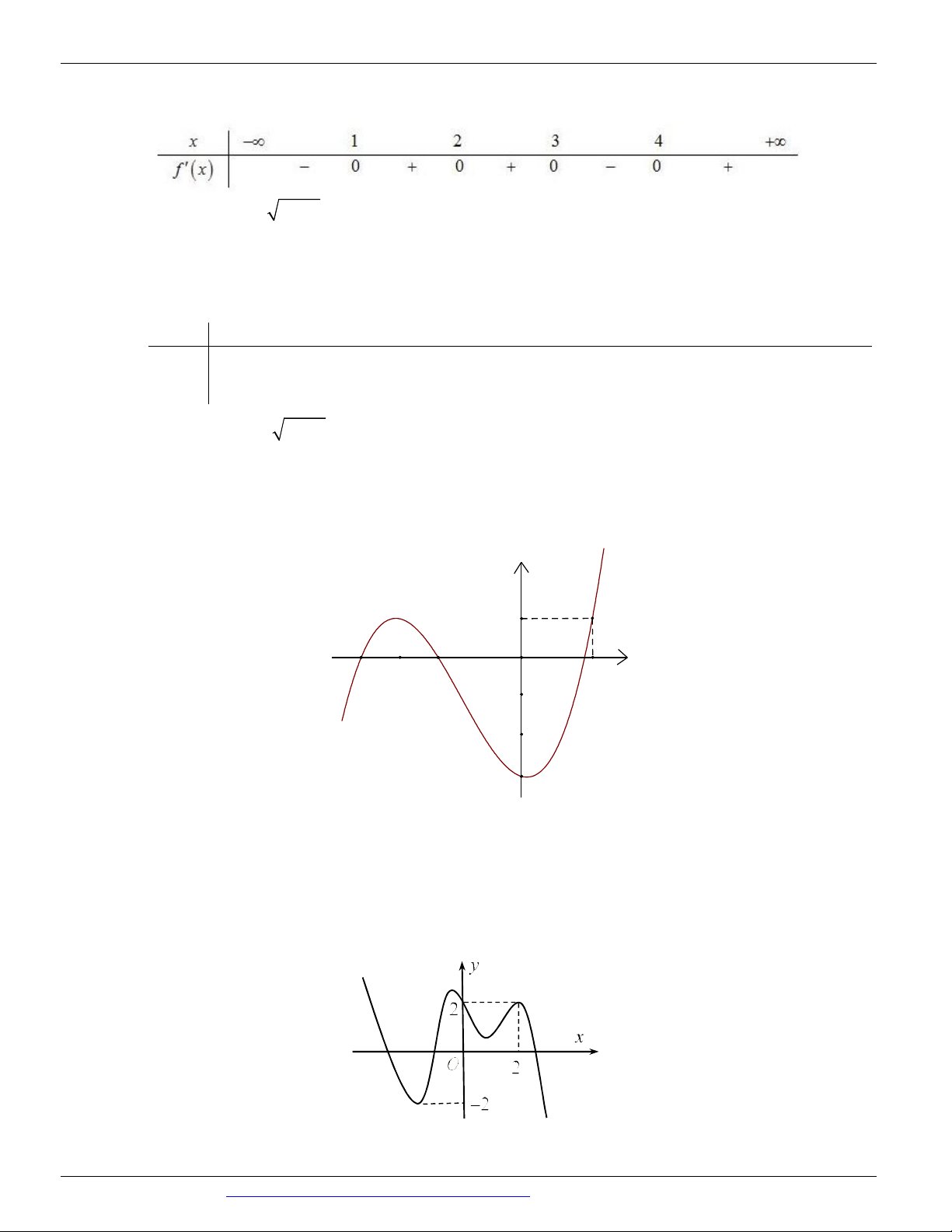
Câu 72: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số f (x) , đồ thị hàm số y f (
x) như hình vẽ dưới đây.
Hàm số y f  3  x  đồng biến trên khoảng nào dưới đây?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 4;6 . B.  1  ;2 . C. ;  1 . D. 2;  3 .
Câu 73: (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hàm số y f x . Hàm số y f ' x
có đồ thị như hình vẽ. Hàm số 2
g(x)  f (x  2). Mệnhvđề nào sai?
A. Hàm số g x nghịch biến trên  ;  2  
B. Hàm số g x đồng biến trên 2; 
C. Hàm số g x nghịch biến trên  1
 ; 0 D. Hàm số g x nghịch biến trên 0; 2
Câu 74: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có đạo hàm liên tục
trên  và đồ thị hàm số y f ' x như hình bên.
Hỏi hàm số g x  f 3  2x nghịch biến trên khoảng nào trong các khoảng sau? A.  1  ;  B.  ;    1 C. 1;  3 D. 0;2
Câu 75: (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hàm số y f x có đạo hàm
trên  và có đồ thị y f  x như hình vẽ.
Xét hàm số gx  f  2 x  2.
Mệnh đề nào sau đây sai?
A. Hàm số g x nghịch biến trên 0; 2 g xB. Hàm số
đồng biến trên 2; 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
C. Hàm số g x nghịch biến trên  ;  2  
D. Hàm số g x nghịch biến trên  1  ;0
Câu 76: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số y f x có bảng
xét dấu đạo hàm như sau:
Hàm số y f  2
x  2 nghịch biến trên khoảng nào dưới đây? A. 2;   1 . B. 2;  . C. 0;2 . D.  1  ;0 .
Câu 77: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số y f x
có đạo hàm liên tục trên . Biết hàm số y f  x có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên m  5  ; 
5 để hàm số g x  f x m nghịch biến trên khoảng 1;2 . Hỏi S có bao nhiêu phần tử? A. 4 . B. 3 . C. 6 . D. 5 .
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x)
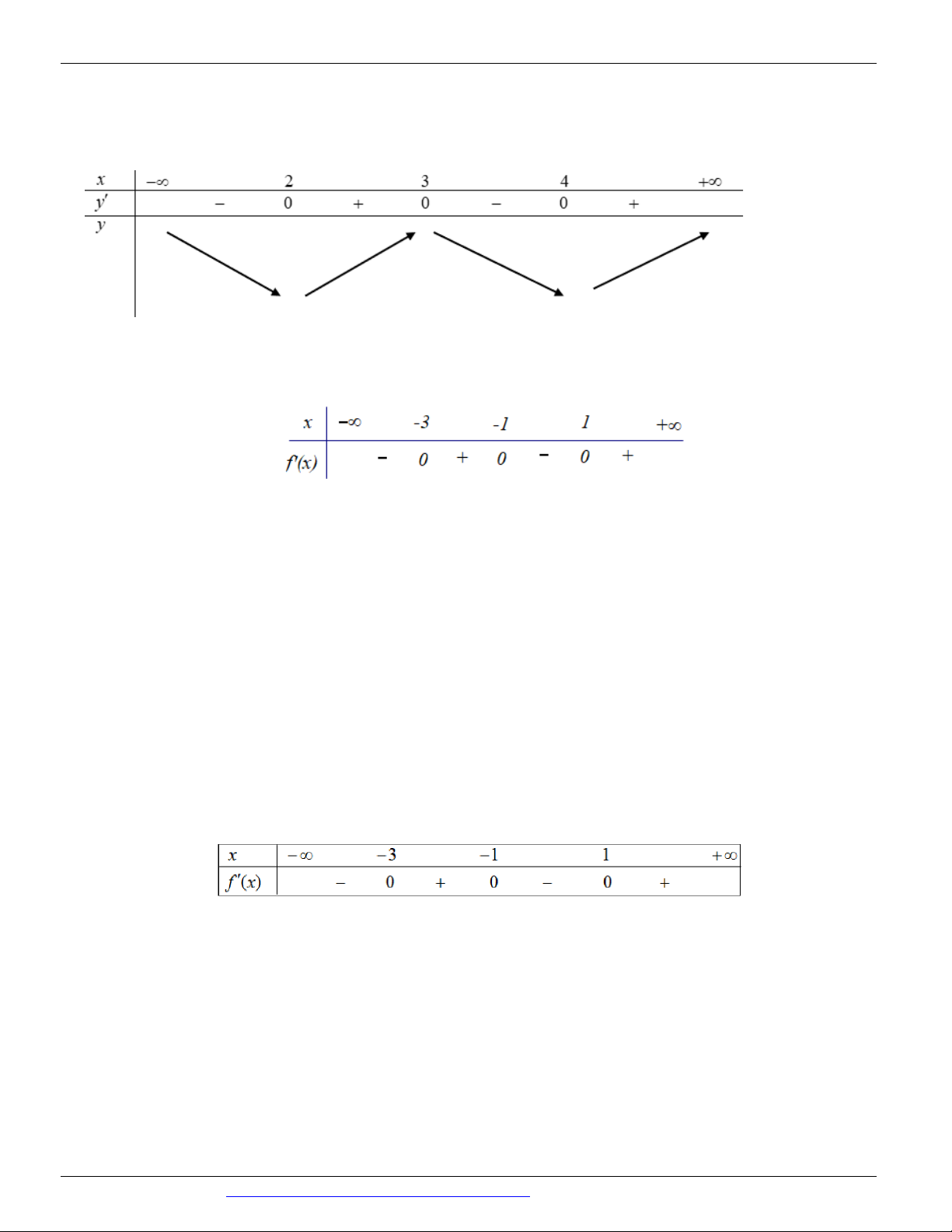
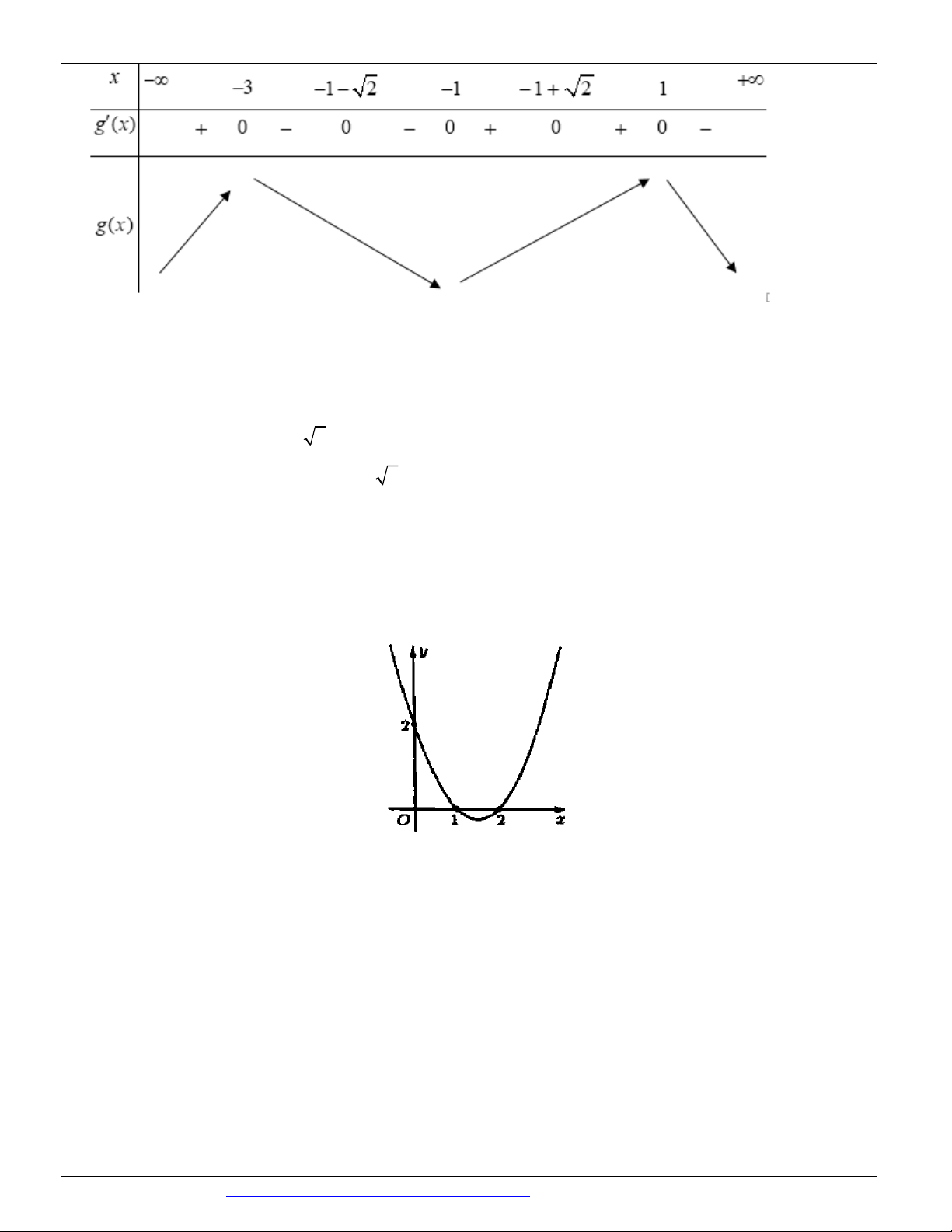
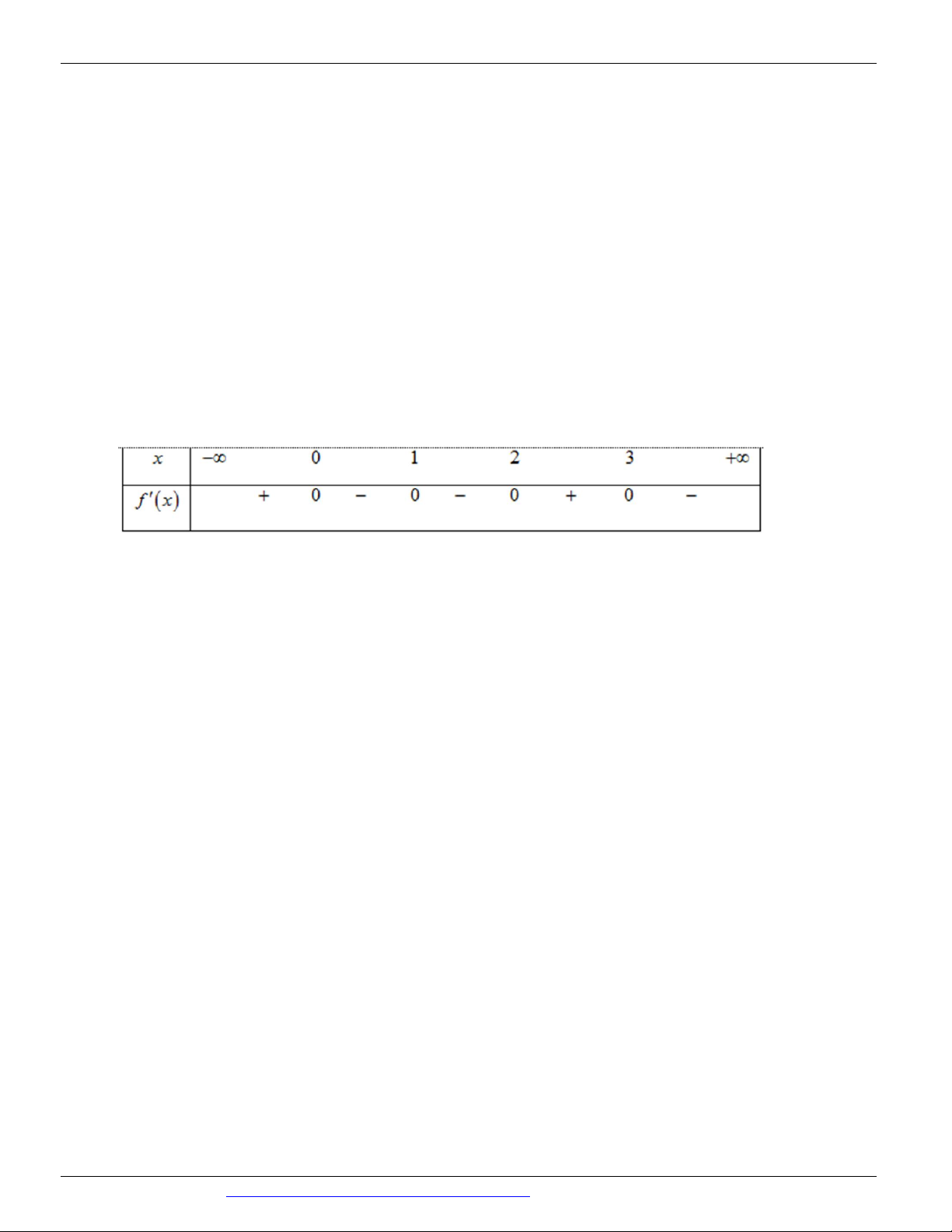
Câu 78: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số f x có bảng xét dấu của đạo hàm như sau x  1 2 3 4  f  x  0  0  0  0 
Hàm số y f x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A.  ;    1 . B.  1  ;0. C. 0;2. D. 1; .
Câu 79: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Cho hàm số f x có bảng
xét dấu của đạo hàm như sau
Hàm số y f x   3
1  x 12x  2019 nghịch biến trên khoảng nào dưới đây? A. 1;   . B. 1; 2 . C.   ;1 . D. 3; 4 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 80: (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Cho hàm số f x có bảng
xét dấu đạo hàm như sau: Hàm số y f   x 2 2 1 
x 1  x nghịch biến trên những khoảng nào dưới đây
A. ;  2 . B.   ;1 . C. 2;0 . D. 3;  2 .
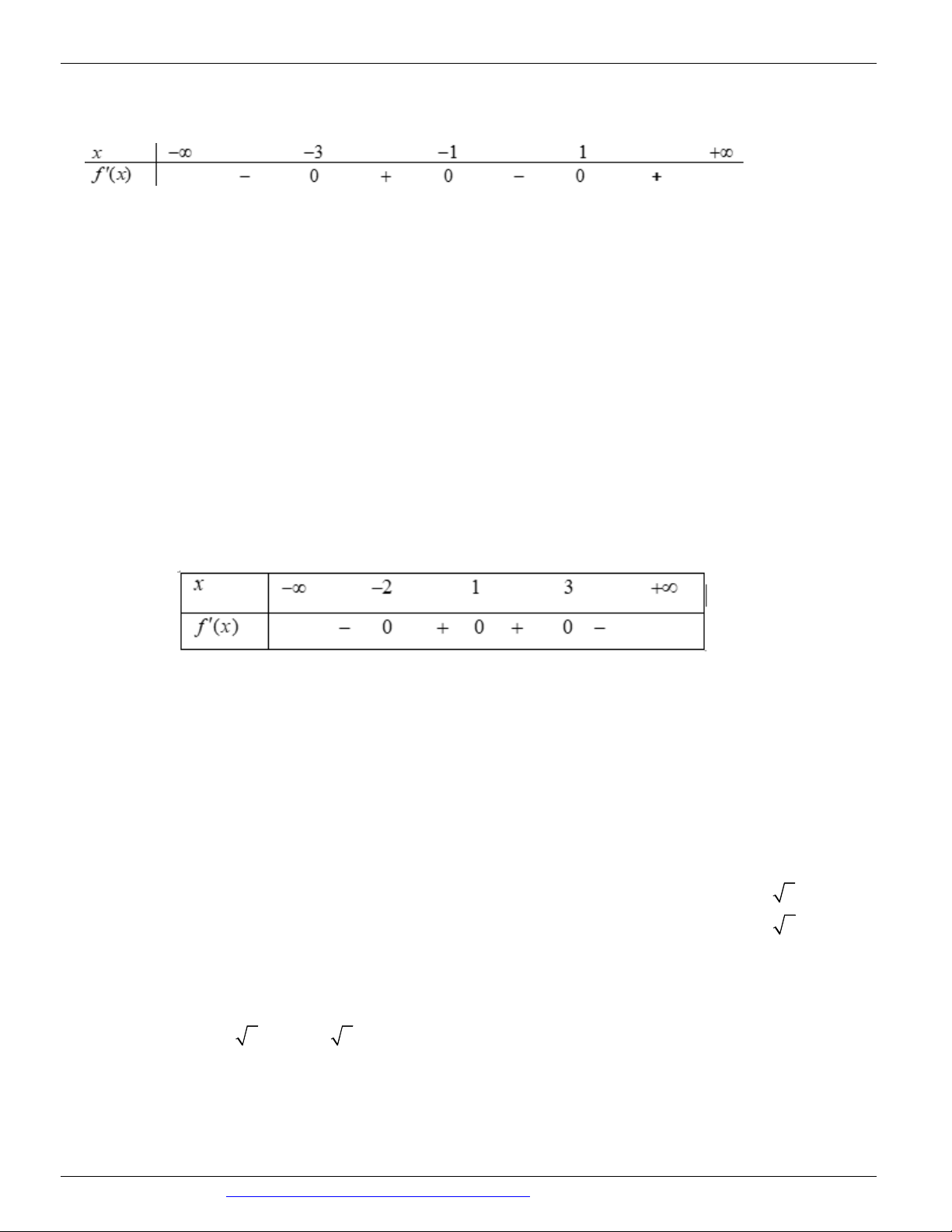
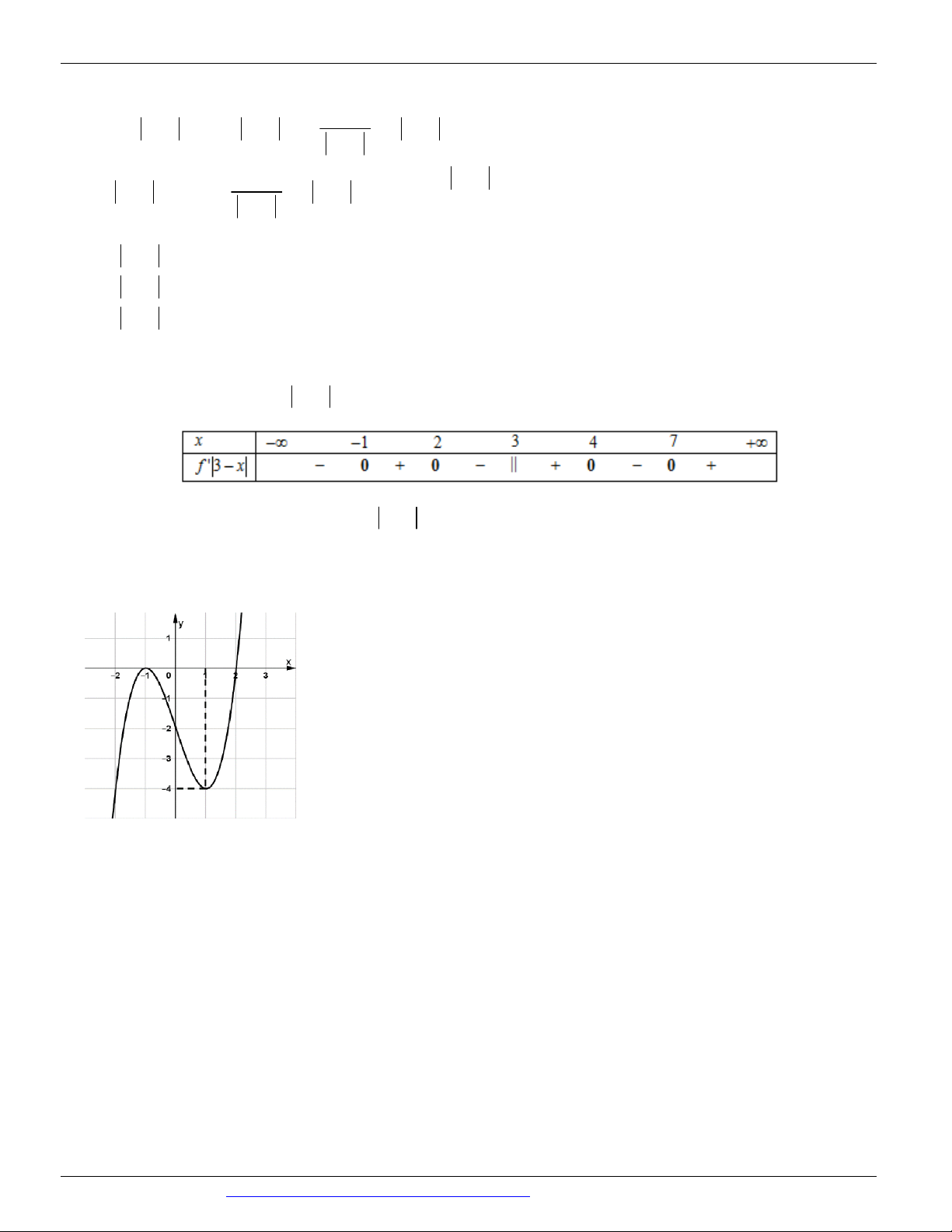
Câu 81: (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Cho hàm số f x có bảng xét dấu của đạo hàm như sau : x  1 2 3 4  f ' x  0  0 + 0  0 + Hàm số y f   x 2 2 1
x 1  x nghịch biến trên khoảng nào dưới đây ? A.  ;   1 . B.  ;  2   . C.  2  ;0 . D.  3  ; 2   .
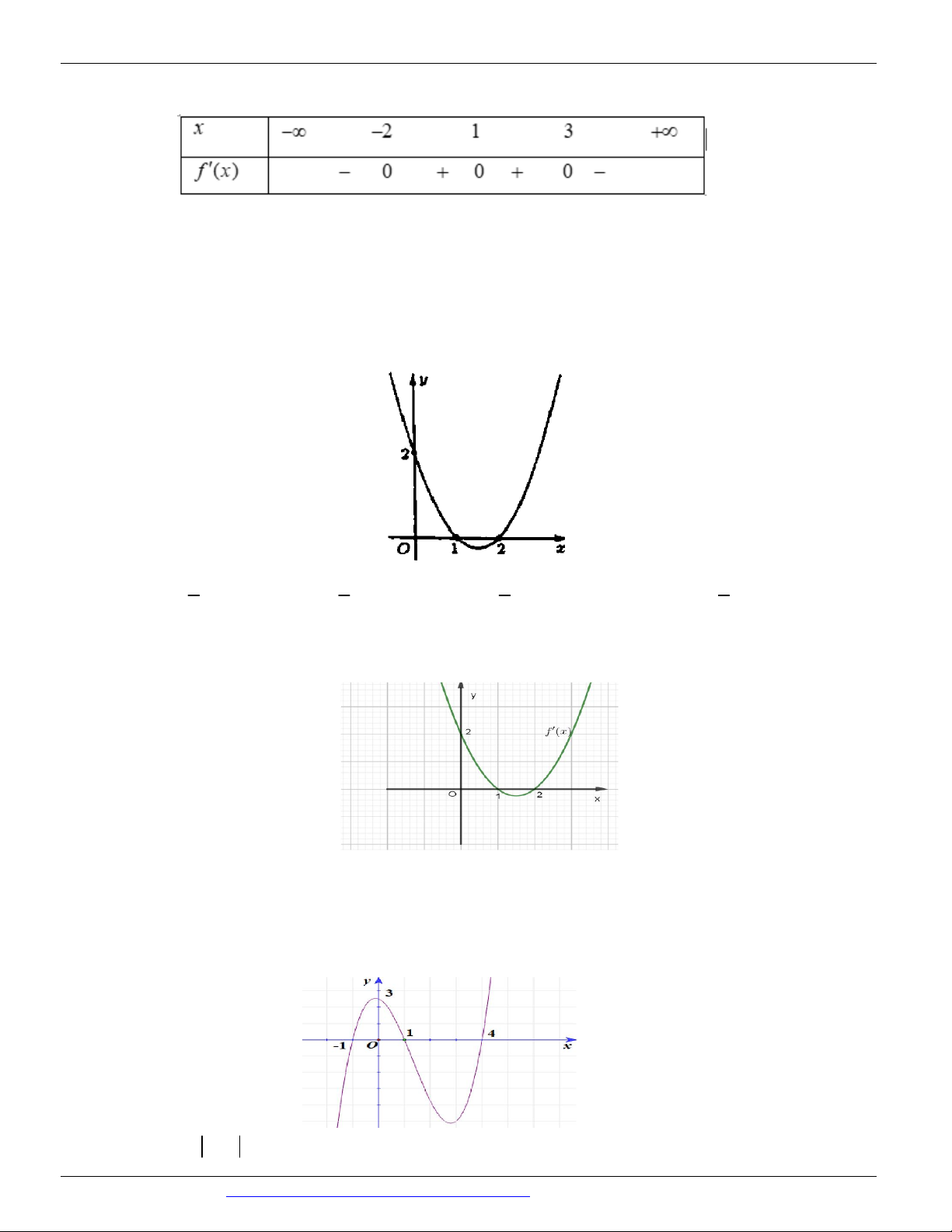
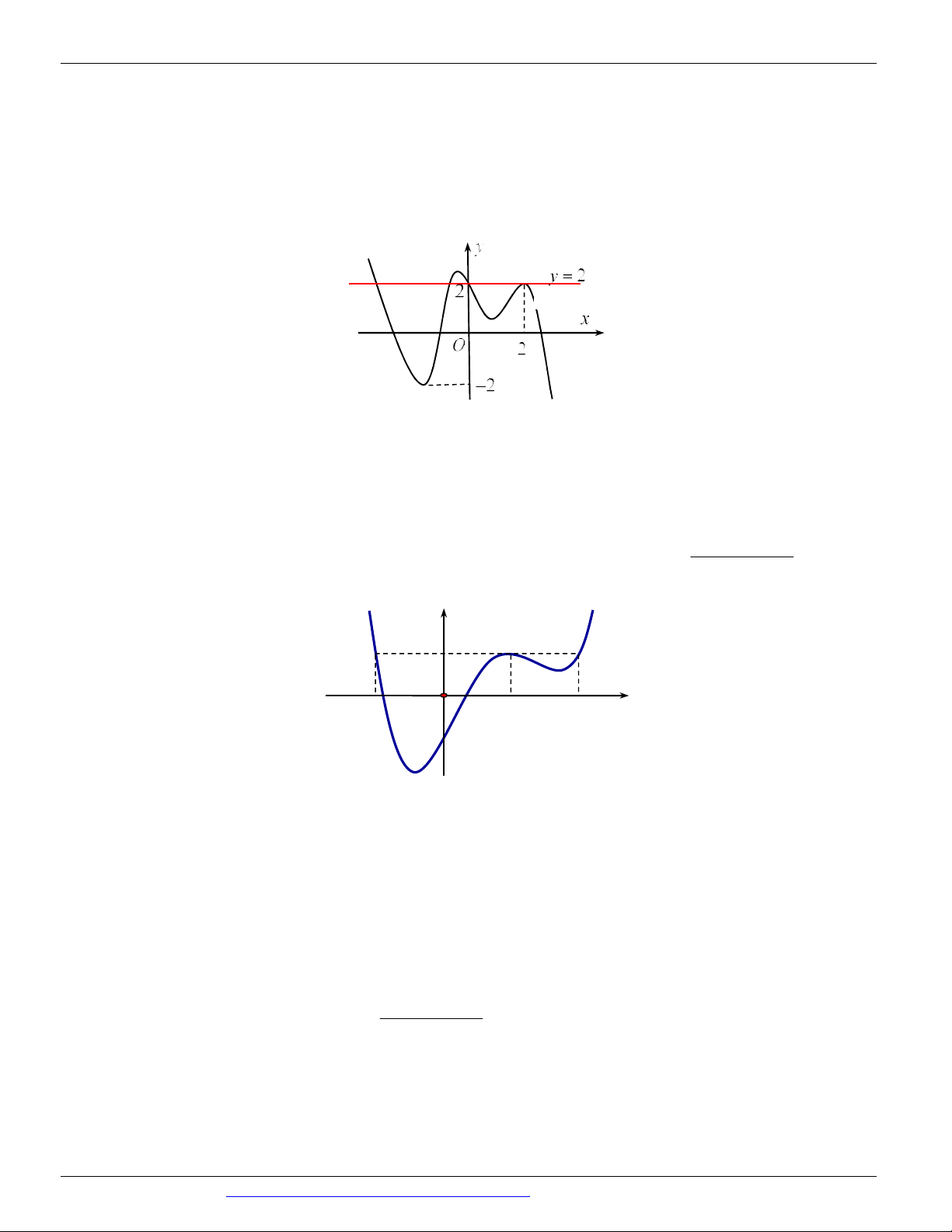
Câu 82: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hàm số bậc bốn
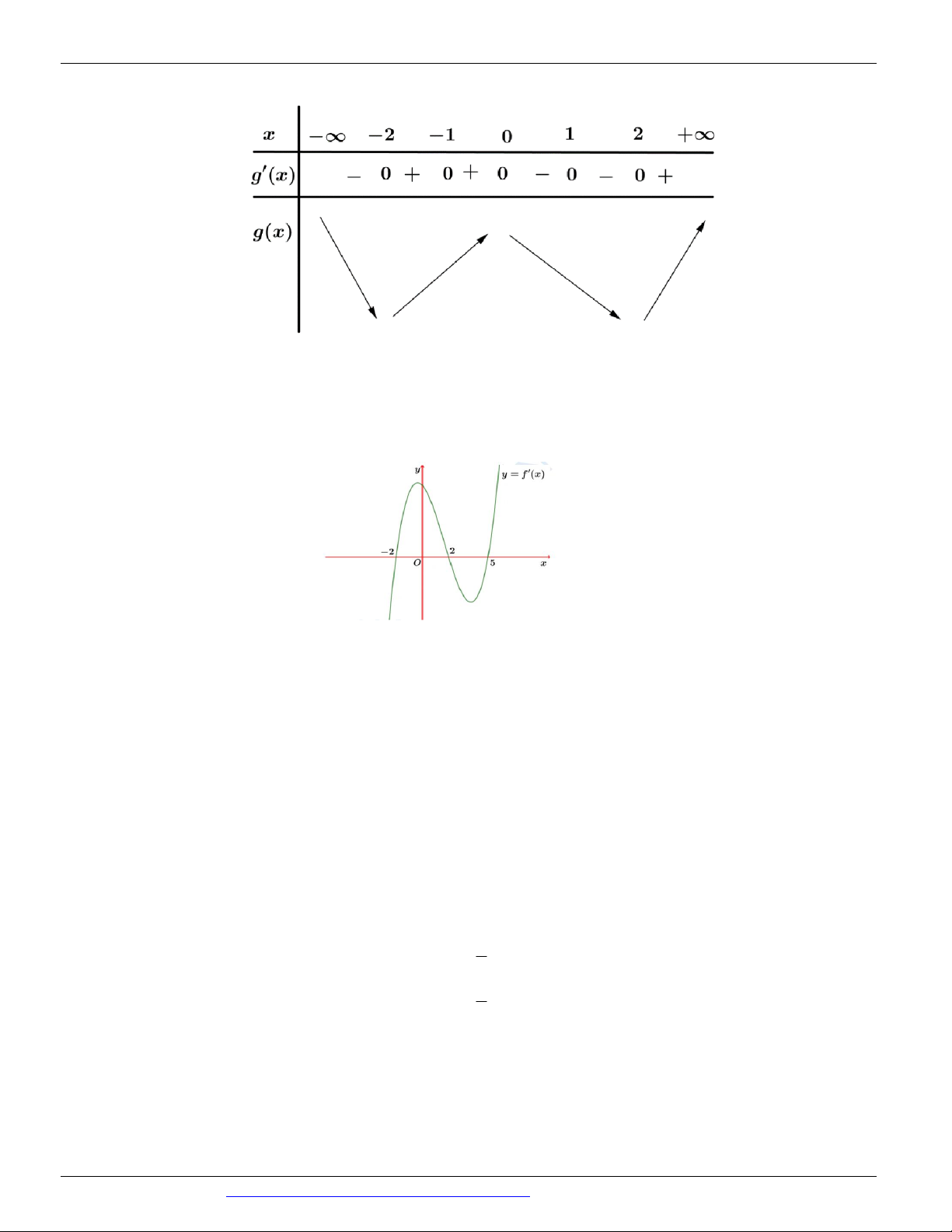
y f (x) có đồ thị của hàm số y f (
x) như hình vẽ bên. y 1 O -4 -3 -2 2 x -1 -2 -3 Hàm số 3 2
y  3 f (x)  x  6x  9x đồng biến trên khoảng nào trong các khoảng sau đây? A. 0; 2 . B. 1;  1 . C. 1;  . D. 2; 0 .
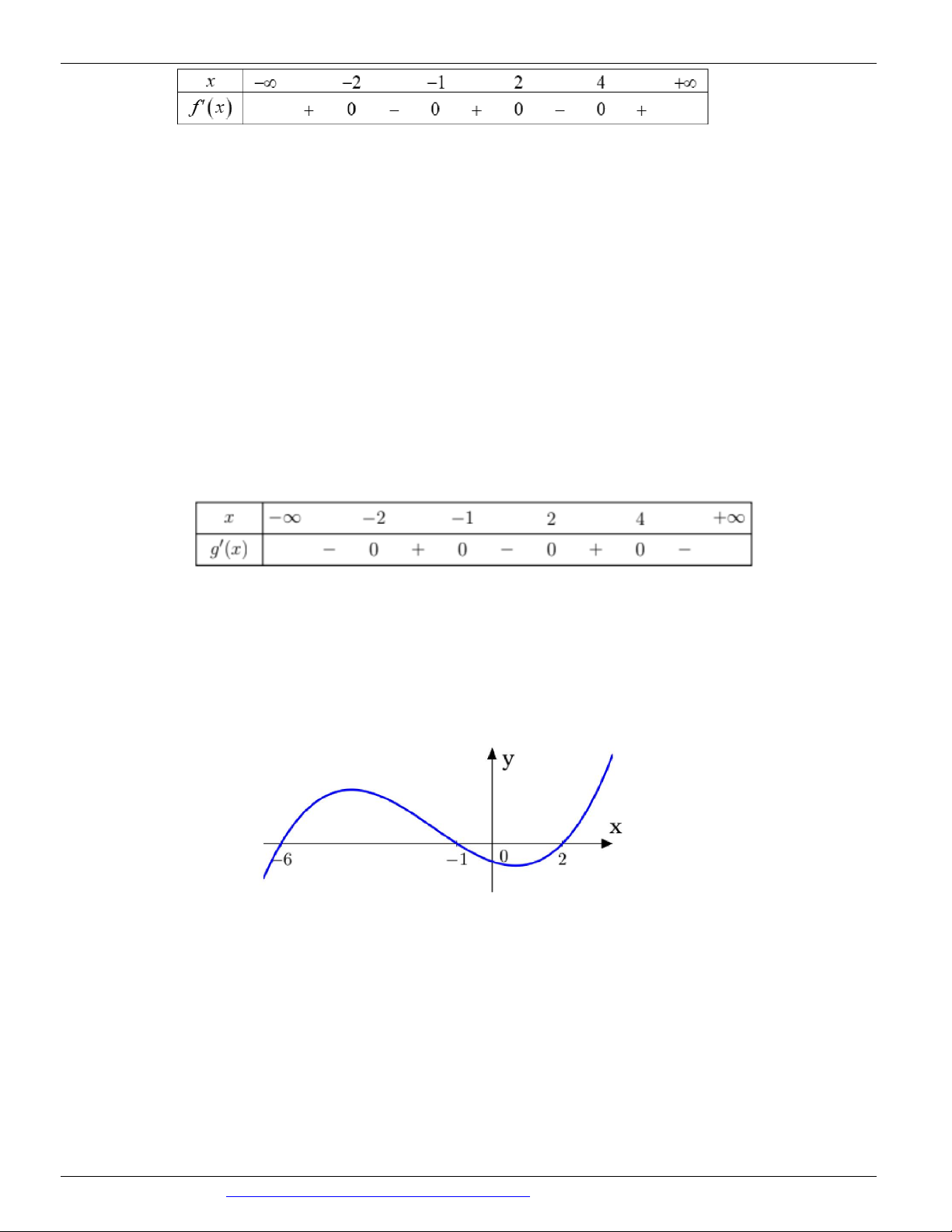
Câu 83: (HỌC MÃI NĂM 2018-2019-LẦN 02) Cho hàm số y f x có đạo hàm trên  . Đồ thị hàm số
y f  x như hình bên. Hỏi đồ thị hàm số y f x  2x có bao nhiêu điểm cực trị? A. 4 . B. 3 . C. 2 . D. 1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 84: (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số y f x 2019  2018x
liên tục trên  . Hàm số y f  x có đồ thị như hình vẽ. Hàm số g x  f x   1  đồng biến 2018
trên khoảng nào dưới đây? y 1  1 O 1 2 x  1 A. 2 ; 3 . B. 0 ;  1 . C. -1 ; 0 . D. 1 ; 2 .
Câu 85: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hàm số y f x có bảng xét dấu của đạo hàm như sau Hàm số y  2
f x  2019 nghịch biến trên khoảng nào trong các khoảng dưới đây? A.  4  ; 2 . B.  1  ; 2 . C.  2  ;   1 . D. 2; 4 .
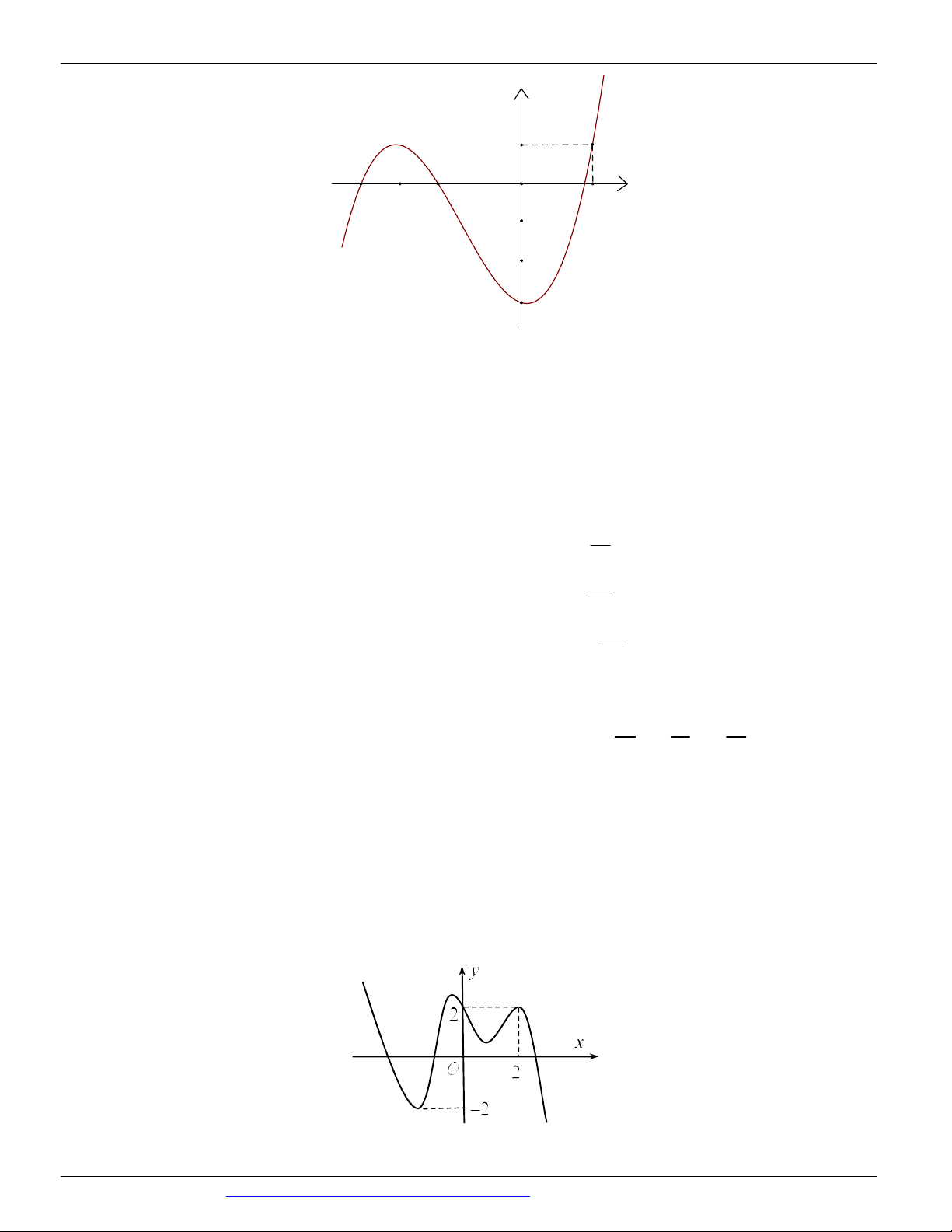
Câu 86: (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số y f x . Biết đồ thị
hàm số y f x có đồ thị như hình vẽ bên. Hàm số y f  2
3 x  2018 đồng biến trên khoảng nào dưới đây? A.  1  ;  0 B. 2;  3 C.  2  ;   1 D. 0;  1
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị
Câu 1: (Mã 103 - BGD - 2019) Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào sau đây?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A.  ;    1 . B. 0  ;1 . C.  1  ;0. D.  1  ; . Lời giải Chọn C
Hàm số đã cho đồng biến trên khoảng  1  ;0.
Câu 2: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số y f x có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng  ;  2
B. Hàm số đồng biến trên khoảng 2; 0
C. Hàm số đồng biến trên khoảng  ;  0
D. Hàm số nghịch biến trên khoảng 0; 2 Lời giải Chọn D
Theo bảng xét dấu thì y '  0 khi x (0;2) nên hàm số nghịch biến trên khoảng (0; 2) .
Câu 3: (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số y f x có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. 1;0 B.  ;  0
C. 1;  D. 0  ;1 Lời giải Chọn D
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng 0  ;1 và  ;    1 .
Câu 4: (Mã 102 - BGD - 2019) Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A. 0;  . B. 0; 2 .
C. 2;0 . D. ; 2   .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn C
Từ bảng biến thiên, suy ra trên khoảng 2;0 hàm số đồng biến.
Câu 5: (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số y f x có bảng biến thiên như sau :
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 0  ;1
B. 1;  C.  ;   1 D. 1;0 Lời giải Chọn A
Câu 6: (Mã đề 101 - BGD - 2019) Cho hàm số có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; 2.
B. 0; . C.  2  ; 0. D. 2; . Lời giải Chọn A
Dựa vào bảng biến thiên ta thấy trên khoảng 0; 2 thì f ' x  0 .
Vậy hàm số nghịch biến trên khoảng 0; 2 .
Câu 7: (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  1  ;  .
B. 1;  . C.  1  ;  1 . D.  ;   1 . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn B
Câu 8: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y f x có đồ thị như hình vẽ
bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? y -1 1 O x -1 -2 A.    1 B.  1  ;  1
C. 1;0 D. 0;  1 Lời giải Chọn C
Từ đồ thị, ta thấy hàm số đồng biến trên các khoảng 1;0 và 1;  . Chọn
Câu 9: (Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số y f x có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 2;3
B. 3;   C.  ;   2 D.  2  ;   Lời giải Chọn A
Câu 10: (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y f x có bảng biến thiên như sau:
Hàm số y f x nghịch biến trên khoảng nào dưới đây?
A. 0; B.  ;  2   C. 0;2 D.  2  ;0 Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước
Câu 11: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x 1 x  1 A. y B. 3
y x x C. 3
y  x  3x D. y x  2 x  3 Lời giải Chọn B Vì 3
y x x 2
y  3x 1  0, x    . x  2
Câu 12: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số y
. Mệnh đề nào dưới đây đúng? x 1
A. Hàm số nghịch biến trên khoảng  ;  
B. Hàm số nghịch biến trên khoảng  1  ; 
C. Hàm số nghịch biến trên khoảng  ;    1
D. Hàm số đồng biến trên khoảng  ;    1 Lời giải Chọn D
Tập xác định: \  1 . 3 Ta có y '   0 , x   \  1 .  x  2 1
Câu 13: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x  2 A. 4 2
y x  3x . B. y  . C. 3
y  3x  3x  2 . D. 3
y  2x  5x 1. x 1 Lời giải Chọn C Hàm số 3
y  3x  3x  2 có TXĐ: D   . 2
y  9x  3  0, x
   , suy ra hàm số đồng biến trên khoảng  ;   .
Câu 14: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số 3 2
y x  3x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0; 2
B. Hàm số nghịch biến trên khoảng 0; 2
C. Hàm số nghịch biến trên khoảng  ;  0
D. Hàm số nghịch biến trên khoảng 2; Lời giải Chọn B x  0 Ta có 2
y  3x  6x ; y  0   . x  2 
Lập bảng biến thiên rồi suy ra hàm số nghịch biến trên khoảng 0; 2
Câu 15: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Hỏi hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1   1  A.  ;  0. B. ;    .
C. 0;  . D.  ;    .  2   2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn C 4
y  2x 1 . Tập xác định: D   Ta có: 3 y  8x ; 3
y  0  8x  0  x  0 suy ra y 0  1
Giới hạn: lim y   ; lim y   x x Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng 0;  .
Câu 16: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y f x có đạo hàm f x  2
x  1 , x   . Mệnh
đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 1; 
B. Hàm số nghịch biến trên khoảng 1;1
C. Hàm số đồng biến trên khoảng ; 
D. Hàm số nghịch biến trên khoảng ; 0 Lời giải Chọn C
Do hàm số y f x có đạo hàm f x  2
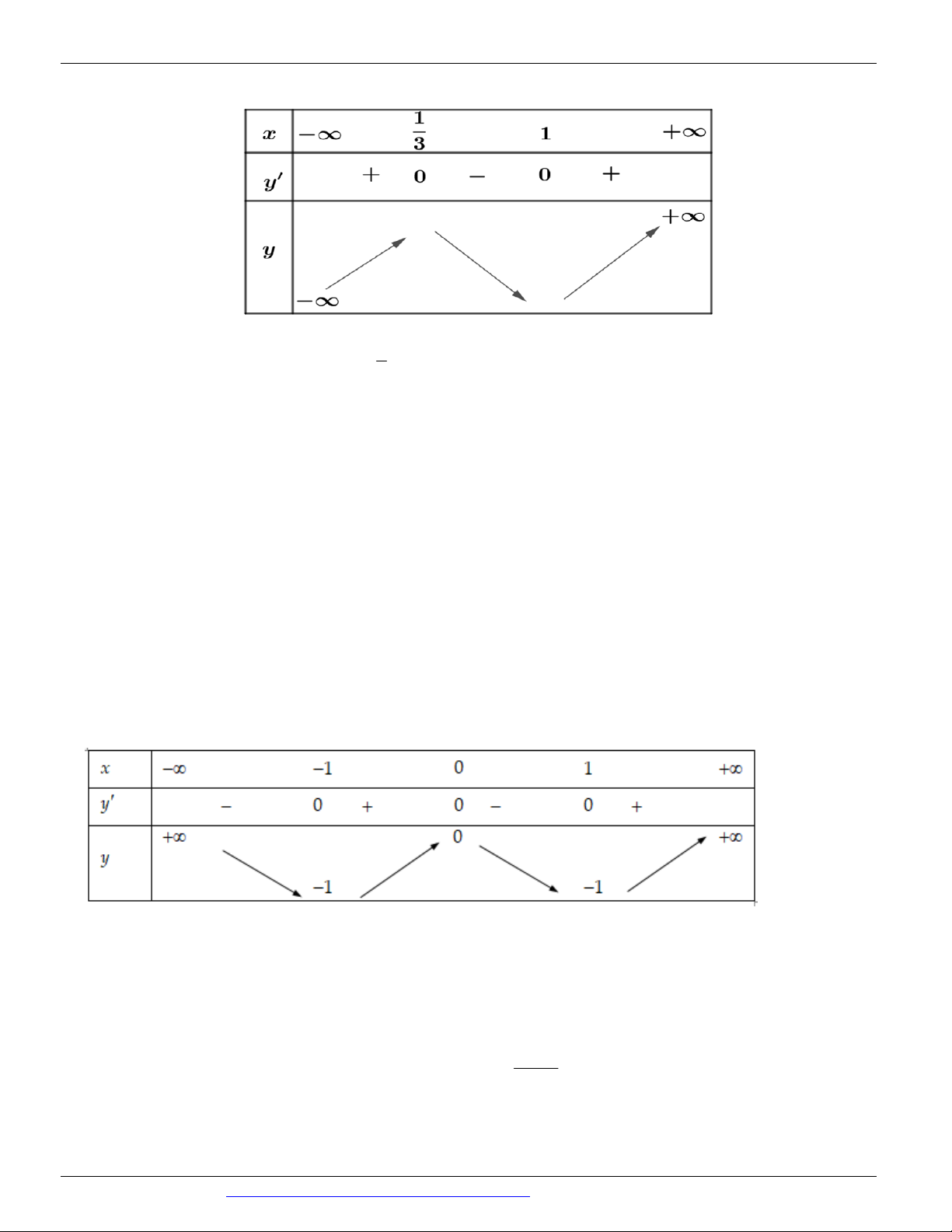
x  1  0 x   nên hàm số đồng biến trên khoảng ; . Câu 17: Cho hàm số 3 2
y x  2x x 1 . Mệnh đề nào dưới đây đúng?  1 
A. Hàm số nghịch biến trên khoảng 1; 
B. Hàm số nghịch biến trên khoảng ;1    3   1   1 
C. Hàm số nghịch biến trên khoảng ;   
D. Hàm số đồng biến trên khoảng ;1    3   3  Lời giải Chọn B x  1 Ta có 2
y  3x  4x  1  y  0     1 x   3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Bảng biến thiên:  1 
Vậy hàm số nghịch biến trên khoảng ;1   .  3 
Câu 18: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y  4 x  2
2x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ;  2
B. Hàm số đồng biến trên khoảng 1;1
C. Hàm số nghịch biến trên khoảng 1;1
D. Hàm số đồng biến trên khoảng ;  2 Lời giải Chọn A TXĐ: D  . x  0 3 3 
y  4x  4x; y  0  4x  4x  0  x   1 x    1
Suy ra hàm số đồng biến trên các khoảng 1; 0 , 1;   ; hàm số nghịch biến trên các khoảng ;  1
, 0;1 . Vậy hàm số nghịch biến trên khoảng ;  2 .
Cách 2: Dùng chức năng mode 7 trên máy tính kiểm tra từng đáp án. 2
Câu 19: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Hàm số y
nghịch biến trên khoảng nào dưới đây? 2 x  1
A. (; ) B. (0; ) C. (; 0) D. (1; 1) Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn B 4x Ta có y 
 0  x  0  2 2 x   1
Câu 20: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y  3
x  3x  2 . Mệnh đề nào dưới đây là đúng?
A. Hàm số nghịch biến trên khoảng ; 0 và đồng biến trên khoảng 0; 
B. Hàm số đồng biến trên khoảng ; 0 và đồng biến trên khoảng 0; 
C. Hàm số đồng biến trên khoảng ; 
D. Hàm số nghịch biến trên khoảng ;  Lời giải Chọn C Ta có: +) TXĐ: D   . +) y  2
' 3x  3  0,x   , do đó hàm số đồng biến trên  .
Câu 21: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số 2 y
2x  1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0;   
B. Hàm số đồng biến trên khoảng ; 0
C. Hàm số nghịch biến trên khoảng 0;   
D. Hàm số nghịch biến trên khoảng 1;1 Lời giải Chọn A 2x
Ta có D   , y 
; y  0  x  0 . 2 2x 1
Vậy hàm số nghịch biến trên khoảng ; 0 và đồng biến trên khoảng 0;    .
Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Câu 22: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hỏi có bao nhiêu số nguyên m để hàm số y   2 m   3
x  m   2 1
1 x x  4 nghịch biến trên khoảng  ;   .
A. 0 B. 3 C. 2 D. 1 Lời giải Chọn C
TH1: m  1. Ta có: y  x  4 là phương trình của một đường thẳng có hệ số góc âm nên hàm số luôn
nghịch biến trên  . Do đó nhận m  1. TH2: m  1  . Ta có: 2 y  2
x x  4 là phương trình của một đường Parabol nên hàm số không thể nghịch
biến trên  . Do đó loại m  1  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 TH3: m  1
 . Khi đó hàm số nghịch biến trên khoảng  ;
   y  0 x   , dấu “=” chỉ xảy ra ở
hữu hạn điểm trên  .   2 m   2 3
1 x  2 m  
1 x 1  0 , x    2 2  1   m  1 m 1  0 a  0   m 1  0  1         1  
m  1 . Vì m     0  m   2 1  3 2 m   1  0 m    1 4m  2  0   m  1 2     2 nên m  0 .
Vậy có 2 giá trị m nguyên cần tìm là m  0 hoặc m 1.
Câu 23: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y   3 x  2
mx  4m  9 x  5 , với m là tham
số. Hỏi có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng ;  A. 5 B. 4 C. 6 D. 7 Lời giải Chọn D Ta có: +) TXĐ: D   +) y   2 '
3x  2mx  4m  9 . a  3   0
Hàm số nghịch biến trên ;  khi y '  0,x ;     '  2
m  34m  9    0
m  9; 3 
  có 7 giá trị nguyên của m thỏa mãn.
Câu 24: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số hàm số 1 y   2 m m 3 2
x  2mx  3x  2 đồng biến trên khoảng  ;    ? 3 A. 4 . B. 5 . C. 3 . D. 0 . Lời giải Chọn A y   2 m m 2
x  4mx  3
Hàm số đã cho đồng biến trên khoảng  ;
    y  0 với x    .
+ Với m  0 ta có y  3  0 với x
    Hàm số đồng biến trên khoảng  ;    . 3
+ Với m  1 ta có y  4x  3  0  x  
m  1 không thảo mãn. 4 m  1 m  1 2  m m  0  + Với 
ta có y  0 với x        m  0   3   m  0 . m  0  2
  m  3m  0  3  m  0 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Tổng hợp các trường hợp ta được 3   m  0 .
m    m  3  ;  2; 1;  0 .
Vậy có 4 giá trị nguyên của m thỏa mãn bài ra.
Câu 25: Tìm tất cả các giá trị của tham số thực m để hàm số 3 2
y mx mx m m  
1 x  2 đồng biến trên  . 4 4 A. m m  .
B. m  0 hoặc m  . 3 và 0 3 4 4 C. m  . D. m  . 3 3 Lời giải Chọn C
TH1: m  0  y  2 là hàm hằng nên loại m  0 .
TH2: m  0 . Ta có: 2
y  3mx  2mx m m   1 .
Hàm số đồng biến trên   f '(x)  0 x     4 2 2  2
  m  3m m   1  0 
m 4  3m  0 m  4      3  m 3m  0  m  0  3  m  0  1 Câu 26: Cho hàm số 3 2 y  
x mx  3m  2 x 1. Tìm tất cả giá trị của m để hàm số nghịch biến trên  3 . m  1  m  1  A.  . B. 2   m  1  . C. 2   m  1  . D.  . m  2   m  2   Lời giải Chọn B TXĐ: D   , 2
y  x  2mx  3m  2 .
Hàm số nghịch biến trên  khi và chỉ khi y  0 , x    a  1   0    2   m  1  . 2 
  m  3m  2  0 
Câu 27: Tìm m để hàm số 3 2
y x  3mx  32m  
1 1 đồng biến trên  .
A. Không có giá trị m thỏa mãn.
B. m  1.
C. m  1.
D. Luôn thỏa mãn với mọi m . Lời giải Chọn C 2
y  3x  6mx  32m   1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2
Ta có:   3m  3.3.2m  
1 . Để hàm số luôn đồng biến trên  thì   0  m
m    m m     m  2 2 2 9 18 9 0 9 2 1 0 9
1  0  m  1 . m
Câu 28: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y
x  2mx  3m  5 x đồng biến 3 trên  . A. 4 . B. 2 . C. 5 . D. 6 . Lời giải Chọn D Ta có 2
y  mx  4mx  3m  5 .
Với a  0  m  0  y  5  0 . Vậy hàm số đồng biến trên  .
Với a  0  m  0 . Hàm số đã cho đồng biến trên  khi và chỉ khi a  0 m  0  y  0, x          0 2  2m
  m3m  5  0  m  0 m  0      0  m  5 . 2 m  5m  0 0  m  5  
Vì m    m 0;1; 2;3; 4;  5 . 1
Câu 29: Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số 3 2 y
x mx  4x m đồng biến trên 3 khoảng  ;   . A.  2  ; 2. B.  ;  2 . C.  ;  2  .
D. 2;  . Lời giải Chọn A Ta có: 2
y  x  2mx  4 .
Hàm số đồng biến trên khoảng  ;
  khi và chỉ khi y  0, x   ;   . 2
   m  4  0  2  m  2 . 1 Câu 30: Cho hàm số 3 2
y   x  2x  2a  
1 x  3a  2 (a là tham số). Với giá trị nào của a thì hàm 3
số nghịch biến trên  ? 5 5
A. a  1 . B. a   . C. a   .
D. a  1 . 2 2 Lời giải Chọn C
Tìm điều kiện của tham số thực m để hàm số 3 2
y x  3x  3m  
1 x  2 đồng biến trên  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. m  2 .
B. m  2 .
C. m  0 .
D. m  0 . Lời giải Chọn D
Tập xác định: D   . Ta có: 2
y  3x  6x  3m   1
YCBT y  0, x       9
m  0  m  0 .
Câu 31: Tìm tất cả các giá trị của m để hàm số y  m   3
x  m   2 1 3
1 x  3x  2 đồng biến biến trên  ?
A. 1  m  2 .
B. 1  m  2 .
C. 1  m  2 .
D. 1  m  2 Lời giải Chọn C
Ta có y  m   2 3
1 x  6 m   1 x  3 . m 1  0 
Hàm số đã cho đồng biến trên  khi và chỉ khi y  0, x    m 1  0      0  m  1 m  1    m  1   m  1 
 1  m  2 .    9   m  2 1  9 m   1  0  1  m  2   1
Câu 32: Giá trị của m 3 2 để hàm số y
x – 2mx  m  3 x – 5  m đồng biến trên  là. 3 3 3 3 A.   m  1. B. m   . C.   m  1.
D. m  1. 4 4 4 Lời giải Chọn A
Ta có tập xác định D   . 2
y  x – 4mx  m  3 . 2
y  0  x – 4mx  m  3  0 .
Hàm số đã cho đồng biến trên  khi và chỉ khi y  0, x
   , đẳng thức chỉ xảy ra tại hữu hạn điểm 3    0   2
m2 1.m  3 2
 0  4m m  3  0    m  1. 4 3 Vậy   m  1. 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
Câu 33: (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x  2 y
đồng biến trên khoảng  ;  6 . x  3m
A. 2 B. 6 C. Vô số D. 1 Lời giải Chọn A
Tập xác định: D   ;  3  m   3  ; m  . 3m  2 Ta có y   x  3m2  2 3  m  2  0 m  2
Hàm số đổng biến trên khoảng  ;  6     3   m  2 . 6   3  m   3 m  2 
Mà m nguyên nên m  1;  2 .
Câu 34: (MĐ 103 BGD&ĐT NĂM 2017-2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x 1 y
nghịch biến trên khoảng 6;  ? x  3m
A. 0 B. 6 C. 3 D. Vô số Lời giải Chọn C 3m 1
Tập xác định D  \ 3   m ; y  .  x  3m2 x 1 Hàm số y
nghịch biến trên khoảng 6;  khi và chỉ khi: x  3m  1  y  0  3  m 1  0 m  1    3  2  m  .    6;     D  3m  6   3 m  2 
Vì m    m  2  ; 1  ;  0 .
Câu 35: (Mã đề 101 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x  2 y
đồng biến trên khoảng  ;  1  0 ? x  5m
A. 2 B. Vô số C. 1 D. 3 Lời giải Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 TXĐ: D   \  5   m . 5m  2 y '  .  x  5m2 5  m  2  0 
Hàm số đồng biến trên khoảng  ;  1  0 khi và chỉ khi  5
m 10;      2 m  2   5   m  2 .  5 5m  10 
Vì m nguyên nên m 1; 
2 . Vậy có 2 giá trị của tham số m . mx  4m
Câu 36: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số y
với m là tham số. Gọi S là tập hợp tất x m
cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S .
A. 4 B. Vô số C. 3 D. 5 Lời giải Chọn D 2 m  4m D   \   m ; y  .  x m2
Hàm số nghịch biến trên các khoảng xác định khi y  0, x   D 2
m  4m  0  0  m  4 .
Mà m nên có 3 giá trị thỏa mãn.
Câu 37: (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số x  6 y
nghịch biến trên khoảng 10; ? x  5m A. Vô số B. 4 C. 5 D. 3 Lời giải Chọn B
Tập xác định D \ 5   m . 5m  6 y   x  5m2  6
y  0, x   D  5  m  6  0 m
Hàm số nghịch biến trên 10; khi và chỉ khi      5 . 5m  10;     5m  10  m  2 
Mà m   nên m  2  ; 1  ; 0  ;1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 mx  2m  3
Câu 38: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y
với m là tham số. Gọi S là tập hợp x m
tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S . A. Vô số B. 3 C. 5 D. 4 Lời giải Chọn B  2 m  2m  3 y ' 
hàm số đồng biến trên khoảng xác định khi 1  m  3 nên có 3 giá trị của m nguyên  2 x m
Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Câu 39: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2
y  x  6x  4m  9 x  4 nghịch biến trên khoảng  ;    1 là  3   3  A. ;  
B. 0;  C.  ;  0 D.  ;    4     4  Lời giải Chọn A Ta có 2
y  3x 12x  4m  9
Để hàm số nghịch biến trên khoảng  ;    1 thì 2
y  3x  6x  4m  9  0 x    ;    1 2
 4m  3x 12x  9 x    ;   
1 4m  min f x, f x 2
 3x  12x  9 ;  1
Ta có f ' x  6x 12; f ' x  0  x  2  .
Khi đó, ta có bảng biến thiên 3 
Suy ra min f x  3   4m  3   m  . ;0 4 Câu 40: Cho hàm số 3 2
y x  3x mx  4 . Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng  ;  0 là A.  1  ;5 . B.  ;    3 . C.  ;   4. D.  1  ;   . Lời giải Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Ta có 2
y  3x  6x m .
Để hàm số đồng biến trên khoảng  ;
 0 thì y  0, x    ;  0 2
 3x  6x m  0, x   ;  0 2
m  3x  6x, x   ;  0 .
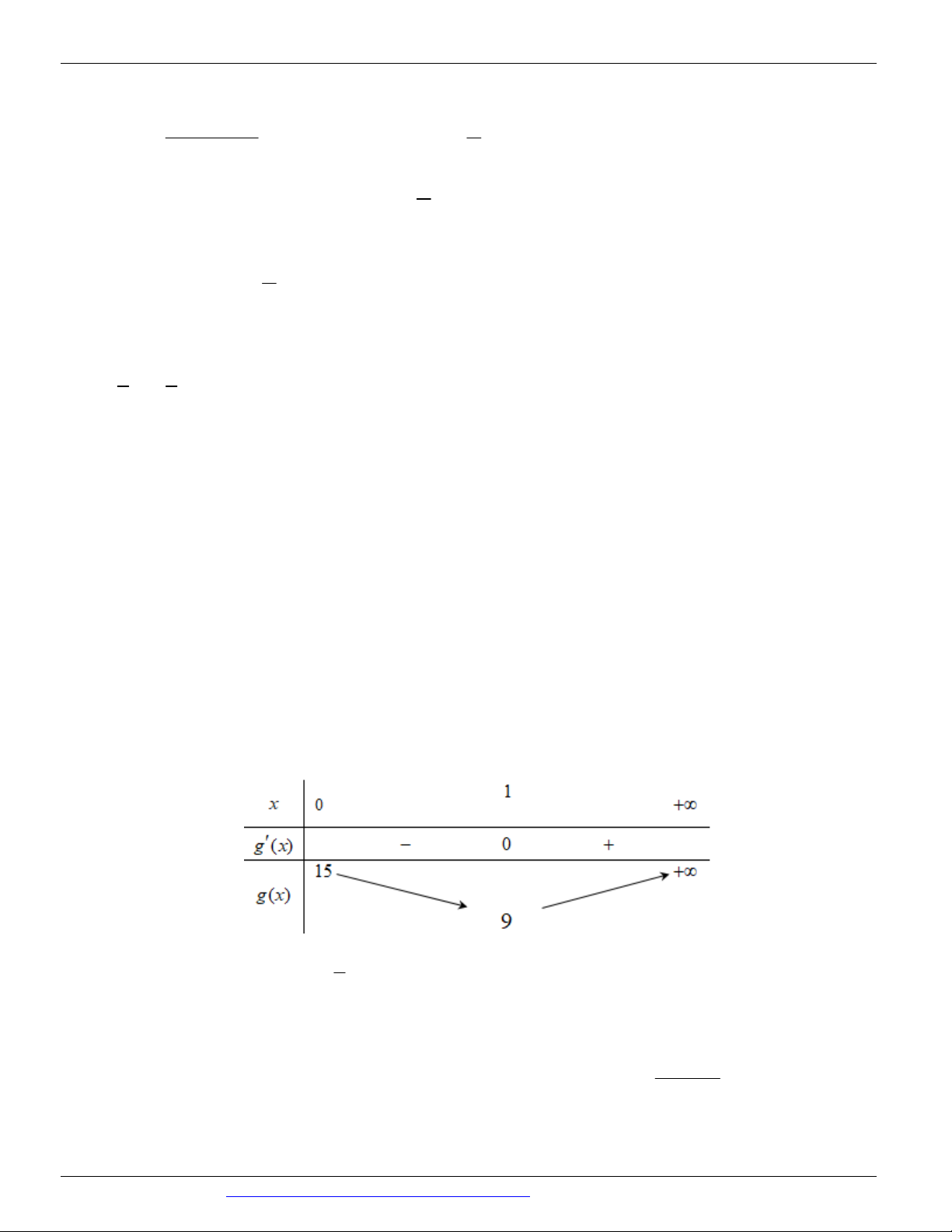
Đặt g x 2
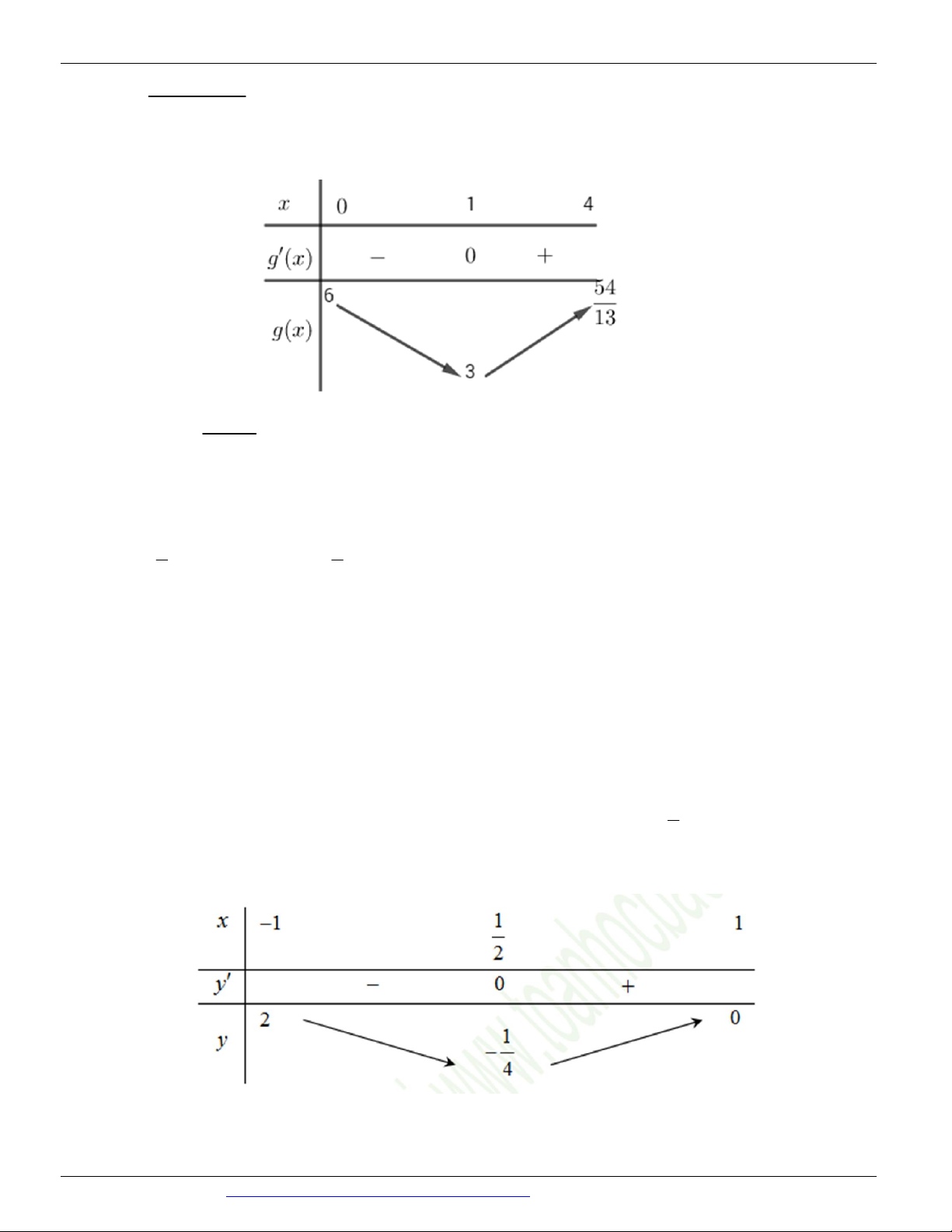
 3x  6x , hàm số g x có bảng biến thiên
Dựa vào bảng biến thiên ta có 2
m  3x  6x, x    ;  0  m  3  . 3 mx
Câu 41: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 2
y f (x) 
 7mx 14x m  2 giảm 3 trên nửa khoảng [1;  )  ?  14   14   14   14  A.  ;    . B. 2;  . C.  ;    . D.  ;     . 15       15   15   15  Lời giải Chọn A
Tập xác định D , yêu cầu của bài toán đưa đến giải bất phương trình 1  4 2
mx 14mx 14  0, x
  1, tương đương với g(x)   m (1) 2 x 14x 14
Dễ dàng có được g( )
x là hàm tăng x 1;  , suy ra min g(x)  g(1)   x 1  15 14
Kết luận: (1)  min g(x)  m    m x 1  15
Câu 42: Xác định các giá trị của tham số m để hàm số 3 2
y x  3mx m nghịch biến trên khoảng 0;  1 ? 1 1
A. m  0 . B. m  .
C. m  0 . D. m  . 2 2 Lời giải Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  2m 2
y '  3x  6mx  0  x  0  1 Hàm số 3 2
y x  3mx m nghịch biến trên khoảng 0 
;1  2m  1  m 2
Câu 43: Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  3x mx 1 đồng biến trên khoảng ;0 .
A. m  0 . B. m  2  . C. m  3  . D. m  1  . Lời giải Chọn C
Tập xác định: D   . Đạo hàm: 2
y  3x  6x m .
Hàm số đồng biến trên khoảng ;0 khi và chỉ khi y  0 , x   0 2
 3x  6x m  0 , x   0 . Cách 1: 2
3x  6x m  0 , x   0 2
 3x  6x m , x   0 .
Xét hàm số f x 2
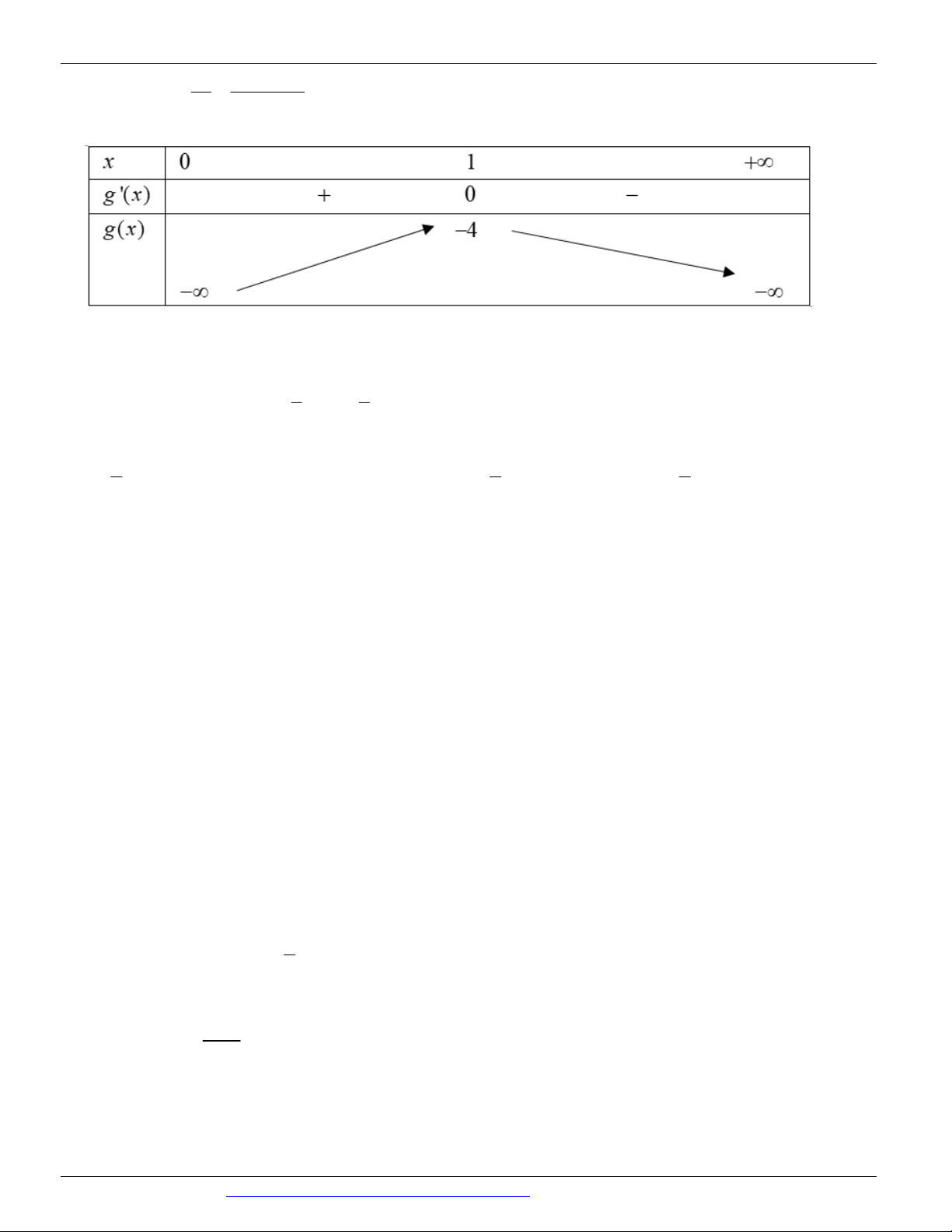
 3x  6x trên khoảng ;0 , ta có:
f  x  6x  6 . Xét f  x  0  6x  6  0  x  1
 . Ta có f   1  3  . Bảng biến thiên:
Dựa vào bảng biến thiên, ta có: m  3  . Cách 2:
Ta có   9  3m .
Nếu   0  m  3  thì y  0 x
    y  0 x   0 .
Nếu   0 thì y có hai nghiệm phân biệt x , x . Khi đó để y  0 x   0 thì ta phải có 1 2
0  x x . Điều này không thể xảy ra vì S x x  2  0 . 1 2 1 2 Vậy m  3  . Cách 3:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Phương án B: Với m  3
 ta có y x x x    x  3 3 2 3 3 1
1 . Khi đó y   x  2 3 1  0 x  .
Suy ra hàm số đồng biến trên khoảng ;0 . Vậy B là đáp án đúng.
Câu 44: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2 2
y x  3mx  9m x nghịch biến trên khoảng 0  ;1 . 1 1 A. 1   m  . B. m  . 3 3 1 C. m  1  . D. m  hoặc m  1  . 3 Lời giải Chọn D
Tập xác định D   . x  m 2 2
y  3x  6mx  9m ; 2 2 2 2
y  0  3x  6mx  9m  0  x  2mx  3m  0   . x  3  m
Nếu m  3m m  0 thì y  0;x   nên hàm số không có khoảng nghịch biến.
Nếu m  3m m  0 thì hàm số nghịch biến trên khoảng  ; m 3m . m  0 1
Do đó hàm số nghịch biến trên khoảng 0  ;1    m  . 3m  1 3  1
Kết hợp với điều kiện ta được m  . 3
Nếu m  3m m  0 thì hàm số nghịch biến trên khoảng 3 ; m m . 3  m  0
Do đó hàm số nghịch biến trên khoảng 0  ;1    m  1. m  1 
Kết hợp với điều kiện ta được m  1  . 1
Vậy hàm số nghịch biến trên khoảng 0  ;1 khi m  1
 hoặc m  . 3 1
Câu 45: Tìm các giá trị của tham số m 3 2 để hàm số y
x mx  2m  
1 x m  2 nghịch biến trên khoảng 3  2  ; 0. . 1 1
A. m  0 .
B. m  1. C. m   . D. m   . 2 2 Lời giải Chọn C x  1 Ta có: 2
y  x  2mx  2m 1.  Cho 2
y  0  x  2mx  2m 1  0  . x  2m 1  .
Nếu 1  2m 1 thì ta có biến đổi y  0  1  x  2m 1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
(trường hợp này hàm số không thể nghịch biến trên khoảng  2  ;0 ).
Xét 2m 1  1 ta có biến đổi y  0  x 2m 1  ;1 . .
Vậy, hàm số nghịch biến trên khoảng  2  ;0 thì  2
 ;0  2m 1  ;1 . 1  2m 1  2
  m   .. 2
Câu 46: Tìm tất cả các giá trị m để hàm số 3 2
y x  3x mx  2 tăng trên khoảng 1;   .
A. m  3 .
B. m  3 .
C. m  3 .
D. m  3 . Lời giải Chọn B Đạo hàm : 2
y  3x  6x m
YCBT  y  0, x   1;   . 2
x x m x     2 3 6 0, 1;  m  3
x  6x, x  1;  
Xét hàm số: f x 2  3
x  6x, x
 1;    f  x  6
x  6  f  x  0  x  1.
lim f x   , f  
1  3 . Do đó : m f x, x 1;    m  3. x
Câu 47: Tập hợp tất cả các giá trị của tham số m để hàm số 3 2
y x mx  m  6 x 1 đồng biến trên khoảng 0;4 là: A.  ;  3 . B.  ;   3 . C. 3;6 . D.  ;  6 . Lời giải Chọn B 2
y  3x  2mx  m  6 . Để hàm số đồng biến trên khoảng 0; 4 thì: y  0 , x  0; 4 . 2 3x  6 tức là 2
3x  2mx  m  6  0 x  0; 4   m x   0; 4 2x 1 2 3x  6
Xét hàm số g x  trên 0; 4 . 2x 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 6x  6x 12
x  1 0; 4 g x 
, g x  0   2x  2 1  x  2   0; 4  Ta có bảng biến thiên: 2 3x  6
Vậy để g x   m x
 0; 4 thì m  3 . 2x 1
Câu 48: Tìm tất cả các giá thực của tham số m sao cho hàm số 3 2
y  2x  3x  6mx m nghịch biến trên khoảng  1   ;1 . 1 1 A. m   . B. m  .
C. m  2 .
D. m  0 . 4 4 Lời giải Chọn C Ta có 2
y  6x  6x  6m .
Hàm số nghịch biến trên khoảng  1  
;1 khi và chỉ khi y  0 với x   1   ;1 hay 2
m x x với x   1   ;1 . 1 Xét   2
f x x x trên khoảng  1  
;1 ta có f  x  2x 1; f  x  0  x  . 2 Bảng biến thiên
Dựa vào bảng biến thiên ta có m f x với x   1   ;1  m  2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 y    1  0  6  m  0 m  0
* Có thể sử dụng y  0 với x   1   ;1        m  2 . y    1  0  12  6m  0  m  2 
Câu 49: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y x  6x mx 1 đồng biến trên khoảng 0; ?
A. m  12 .
B. m  12 .
C. m  0 .
D. m  0 . Lời giải Chọn A
Cách 1:Tập xác định: D   . Ta có 2
y  3x 12x m Trường hợp 1: 3   0 (hn)
Hàm số đồng biến trên   y  0, x      m  12 36  3m  0 
Trường hợp 2: Hàm số đồng biến trên 0;   y  0 có hai nghiệm x , x thỏa x x  0 (*) 1 2 1 2
Trường hợp 2.1: y  0 có nghiệm x  0 suy ra m  0 . Nghiệm còn lại của y  0 là x  4 (không thỏa (*))
Trường hợp 2.2: y  0 có hai nghiệm x , x thỏa 1 2    0 3  6  3m  0  
x x  0  S  0  4  0(vl)
 không có m .Vậy m  12 1 2 P  0   m   0  3
Cách 2:Hàm số đồng biến trên 0;  2
m  12x  3x g(x), x
  (0; ) .
Lập bảng biến thiên của g( )
x trên 0;  .
Câu 50: Tập hợp các giá trị m để hàm số 3 2
y mx x  3x m  2 đồng biến trên 3;0 là  1   1   1   1   A. ;0   . B. ;    . C. ;   . D. ;    .  3   3   3   3 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn D TXĐ: D   Ta có 2
y'  3mx  2x  3 . Hàm số đồng biến trên khoảng  3  ;0 khi và chỉ khi: y'  0 , x   3
 ; 0 (Dấu '  ' xảy ra tại hữu hạn điểm trên 3;0 ) 2
 3mx  2x  3  0 , x   3  ; 0 2x  3  m
g x x   3  ;0 2   3x 2x  6
Ta có: g x 
; gx  0  x  3 3   3x x 0 BBT 3  1 Vậy 1
m  max g x   .   3;0 3 3
Câu 51: Tìm m để hàm số 3 2
y  x  3x  3mx m 1 nghịch biến trên 0;  .
A. m  1 .
B. m  1 .
C. m  1.
D. m  1. Lời giải Chọn A Ta có 2
y   x x m   2 3 6 3
3 x  2x m .
Vì hàm số liên tục trên nửa khoảng 0;  nên hàm số nghịch biến trên 0;  cũng tương đương hàm
số nghịch trên 0;  khi chỉ khi y  0, x  0,  . 2
 x  2x m  0 x  0;  2
m x  2x f xx  0;  .
m  min f x  f   1  1  0;
Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
Câu 52: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m sao cho hàm tan x  2    số y
đồng biến trên khoảng 0; .   tan x m  4 
A. m  0 hoặc1  m  2 B. m  0
C. 1  m  2
D. m  2 Lời giải Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   
Đặt t  tan x , vì x  0;  t    0  ;1  4  t  2
Xét hàm số f t   t   0; 
1 . Tập xác định: D   \   m t m 2  m
Ta có f t   . t m2    tan x  2
Ta thấy hàm số t x  tan x đồng biến trên khoảng 0; 
 . Nên để hàm số y  đồng biến trên  4  tan x m    khoảng 0; 
 khi và chỉ khi: f t   0 t  0  ;1  4  m  2  2  m  0 2 m     0 t   0;1  
 m  0  m  ;  0  1; 2 2       t mm   0  ;1  m 1  1 1
tan x m  tan x  2 2     2
CASIO: Đạo hàm của hàm số ta được cos x cos x y 
tan x m2    
Ta nhập vào máy tính thằng y \ CALC\Calc x
( Chọn giá trị này thuộc 0;   ) 8  4 
\= \ m  ? 1 giá trị bất kỳ trong 4 đáp án.
Đáp án D m  2 . Ta chọn m  3 . Khi đó y  0,17  0 ( Loại)
Đáp án C 1  m  2 Ta chọn m  1, 5 . Khi đó y  0, 49  0 (nhận)
Đáp án B m  0 Ta chọn m  0 . Khi đó y  13, 6  0 (nhận)
Vậy đáp án B và C đều đúng nên chọn đáp án A.
Câu 53: (ĐỀ THAM KHẢO BGD & ĐT 2018) Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 1 3
y x mx
đồng biến trên khoảng 0; 5 5x
A. 0 B. 4 C. 5 D. 3 Lời giải Chọn B 1 2
y  3x m 6 x 1
Hàm số đồng biến trên 0; khi và chỉ khi 2
y  3x m
 0, x  0;   6 x 1 1 2  3x
m, x  0;  . Xét hàm số 2
g(x)  3x
m , x 0; 6 x 6 x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 8 6 6(  x 1)  x  1 g (  x)  6  x   , g (  x)  0  7 7  x x x  1(loai) 
Bảng biến thiên:
Dựa vào BBT ta có m  4 , suy ra các giá trị nguyên âm của tham số m là 4; 3  ; 2; 1
Câu 54: (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị của 1 1
tham số m để hàm số f x 2 5 3 2 
m x mx  10x   2
m m  20 x đồng biến trên  . Tổng giá trị của tất 5 3
cả các phần tử thuộc S bằng 5 1 3 A. . B. 2  . C. . D. . 2 2 2 Lời giải
Ta có f  x 2 4 2
m x mx x   2 m m   2  m  4
x    m  2 20 20 1 x   1  20  x   1 2
m x    x    2 1 1 x  
1  m x   1  x   1  20  x   1   x   2
m x   2 1 1 x  
1  m x   1  20    x  1
f  x  0   2 m   x   1  2 x  
1  m x   1  20  0   * 
Ta có f  x  0 có một nghiệm đơn là x  1  , do đó nếu   * không nhận x  1
 là nghiệm thì f  x
đổi dấu qua x  1
 . Do đó để f x đồng biến trên  thì f  x  0,x   hay   * nhận x  1  làm nghiệm (bậc lẻ). Suy ra 2
m        m    2 1 1 1 1 1 1  20  0  4
m  2m  20  0 . 1
Tổng các giá trị của m là . 2
Câu 55: (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Tập hợp các giá trị thực của tham số m để m
hàm số y x 1 
đồng biến trên mỗi khoảng xác định của nó là x  2 A. 0;  1 . B.  ;  0 .
C. 0;   \   1 . D.  ;  0 . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
• Tập xác định: D   \   2 .
Hàm số đã cho đồng biến trên mỗi khoảng xác định của nó khi và chỉ khi: m y '  0, x   D  1  0, x   D x  22
m   x  2 2 , x   D
Xét hàm số f x   x  2 2 ta có:
f ' x  2x  4  f ' x  0  x  2 Bảng biến thiên:
Vậy, để hàm số đã cho đồng biến trên mỗi khoảng xác định của nó thì m  0 .
Câu 56: (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Tìm tất cả các giá trị thực của tham số để hàm cos x  3    số y
nghịch biến trên khoảng ;   cos x m  2  0  m  3 0  m  3 A.  . B.  . C. m  3 . D. m  3 . m  1  m  1  Lời giải (m  3) (m  3)
Điều kiện: cos x m . Ta có: y  .( s in x)  .sin x
cos x m2
cos x m2       Vì x  ;  s in x  0   ,  x m2 cos  0, x
; : cos x m   .  2   2       
Để hàm số nghịch biến trên khoảng ;    y  0 x   ;    2   2  m  3  0 m  3  m  3  0   0  m  3         m  1   . cos x m x ; m      1;0       m  1       2  m  0    
Chú ý : Tập giá trị của hàm số y  cos x, x  ;   là  1; 0 .  2  (4  ) m 6  x  3
Câu 57: (TT HOÀNG HOA THÁM - 2018-2019) Cho hàm số y  . Có bao nhiêu giá trị 6  x m
nguyên của m trong khoảng 10;10 sao cho hàm số đồng biến trên 8;5 ? A. 14 . B. 13 . C. 12. D. 15 . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đặt t   6  x vì x  8
 ;5  t   14; 
1 và t   6  x đồng biến trên  8  ;5 .
(4  m)t  3 2 m  4m  3
Hàm số trở thành y
tập xác định D   \   m y '  . t   m 2 ( t   m) 2
m  4m  3  0 m   14  
Để hàm số đồng biến trên khoảng  14; 
1  m   14  1  m  1  .   m  1 m  3    m   9  , 8  , 7,  6  , 5  , 4  , 1  , 0, 4,5, 6, 7,8,  9 có 14 giá trị.
Câu 58: (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Có bao nhiêu giá trị nguyên âm 1 3
của tham số m để hàm số 4 y x mx
đồng biến trên khoảng 0;   . 4 2x A. 2 . B. 1. C. 3 . D. 0 . Lời giải 3
Tập xác định : D  .  3
y  x m  . 2 2x
Ta có: hàm số đã cho đồng biến trên khoảng 0;   khi và chỉ khi y  0 với x  0;   3 3 3  x m   0, x   0;   3  x    , m x   0;   2   2   2x 2x 3
 m  Min f x ,với f x 3  x  1 . 2   0; 2x Cách 1: 3 3 3 x x 1 1 1 1 5
Theo bất đẳng thức Cauchy ta có f x 3 5  x        5  . 2 2 2 2 5 2x 2 2 2x 2x 2x 2 2 5
Dấu bằng xảy ra khi và chỉ khi x  1 . Do đó Min f x  2 . 0; 2 5 5 Từ  
1 và 2 ta có m   m   . Do m nguyên âm nên m  1  hoặc m  2  . 2 2
Vậy có hai giá trị nguyên âm của tham số m thỏa mãn điều kiện bài ra. Cách 2: 3
Xét hàm số f x 3  x
, x  0;   . 2   2x 3
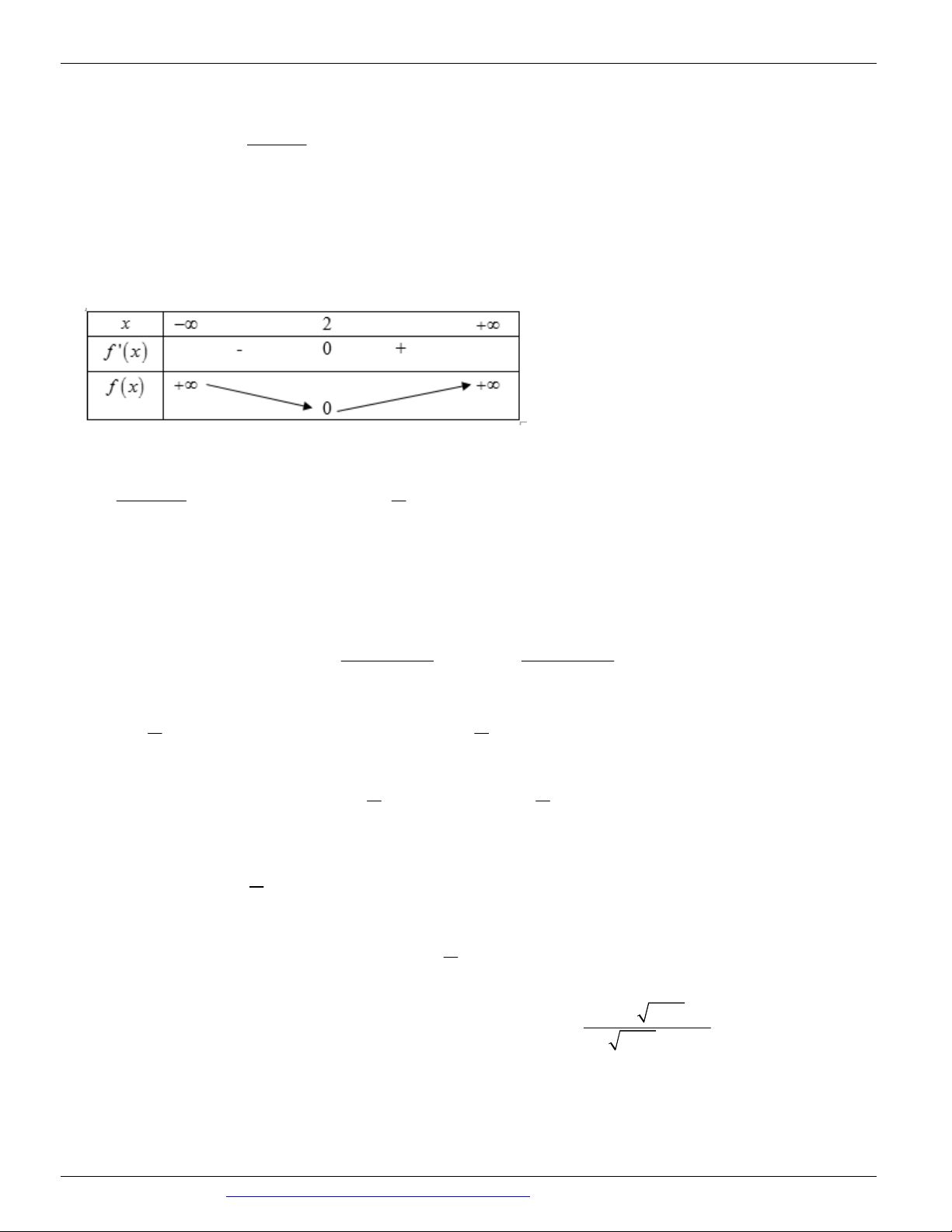
Ta có f  x 2  3x
, f x  0  x  1. 3   x Bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 – 5 5
Từ bảng biến thiên ta có m   m  
. Do m nguyên âm nên m  1  hoặc m  2  . 2 2
Vậy có hai giá trị nguyên âm của tham số m thỏa mãn điều kiện bài ra. ln x  4
Câu 59: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hàm số y  với m là ln x  2m
tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng 1; e . Tìm số phần tử của S . A. 3 B. 2 C. 1 D. 4 Lời giải Chọn C ln x  4
y f x  ln x  2m
Đặt t  ln x , điều kiện t  0  ;1 t  4 2m  4 g t  
; gt   t  2mt  2m2
Để hàm số f x đồng biến trên 1; e thì hàm số g t  đồng biến trên 0 
;1  gt   0, t 0  ;1 2m  4   0, t  0;1 2   t  2m  1  2  m  4  0   m  2     2 2m   0  ;1   m  0 
S là tập hợp các giá trị nguyên dương  S    1 .
Vậy số phần tử của tập S là 1. cos x  2
Câu 60: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Tìm m để hàm số y  đồng cos x m    biến trên khoảng 0;    2  m  2 m  0 A. B. m  2 C.
D. 1  m  1 m  2  1  m  2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải Chọn C 2  m    Ta có y ' 
. sin x,sin x  0x  0;   .
cos x m2  2    
Do đó: Hàm số nghịch biến trên khoảng 0;   khi và chỉ khi  2  2  m  0  m  2  m  0        .
cos x m  0x  0; m       0  ;1 1  m  2    2  
Câu 61: (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị
nguyên âm của tham số m để hàm số 3 9 4 2 y x
x  2m 15 x  3m 1 đồng biến trên khoảng 0;   ? 4 2
A. 2. B. 3. C. 5. D. 4. Lời giải Yêu cầu bài toán 3
y  3x  9x  2m 15  0 x
  0;  và dấu bằng xảy ra tại hữu hạn điểm thuộc 0; 3
 3x  9x 15  2  m x   0;  . Xét hàm số: 3
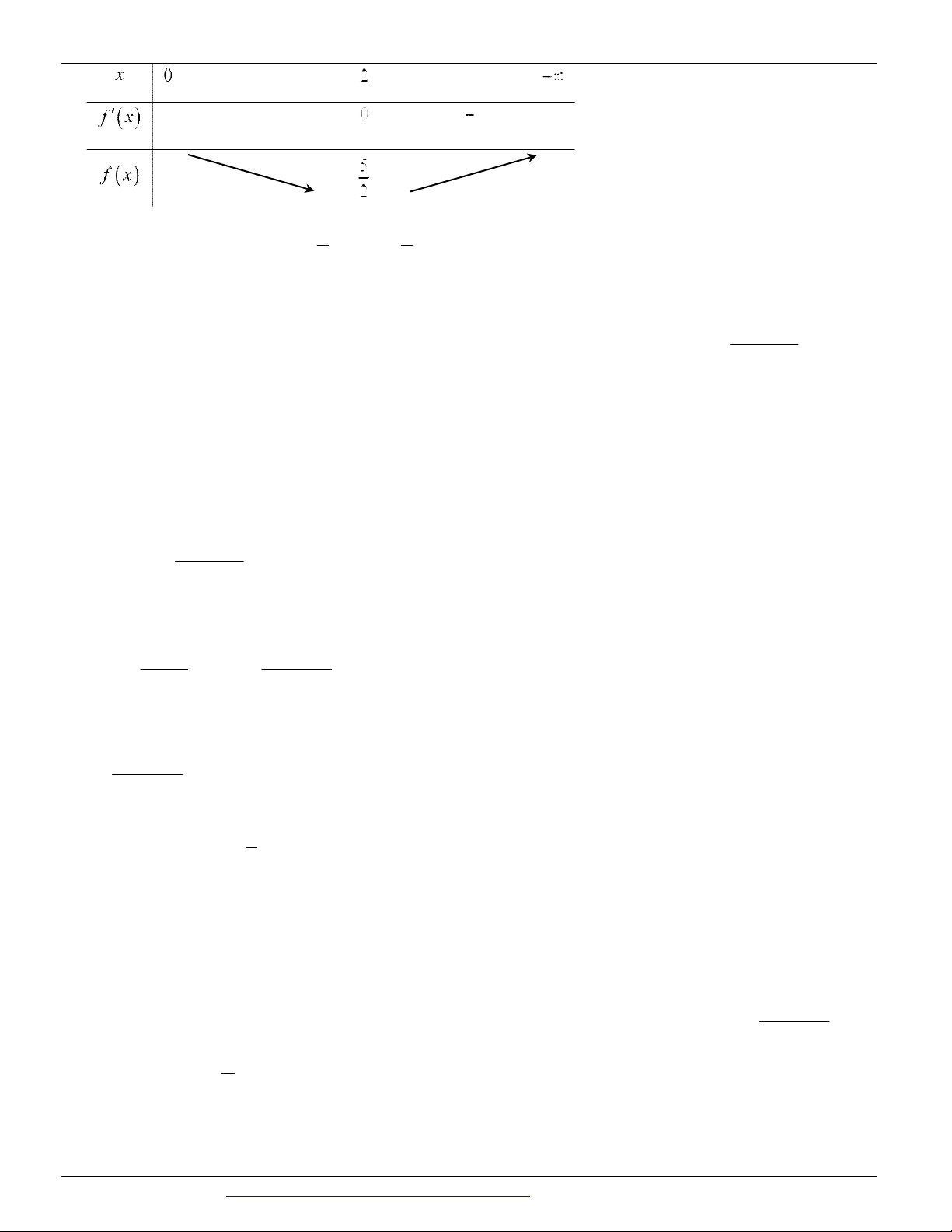
g(x)  3x  9x 15 trên 0;  . Ta có: 2 g (
x)  9x  9  x  1
g x  0   . x  1 (l)  Bảng biến thiên: 9 Từ BBT ta có: 2
m  9  m   2
Vậy m {  4;  3;  2; 1} . 2 m  3m
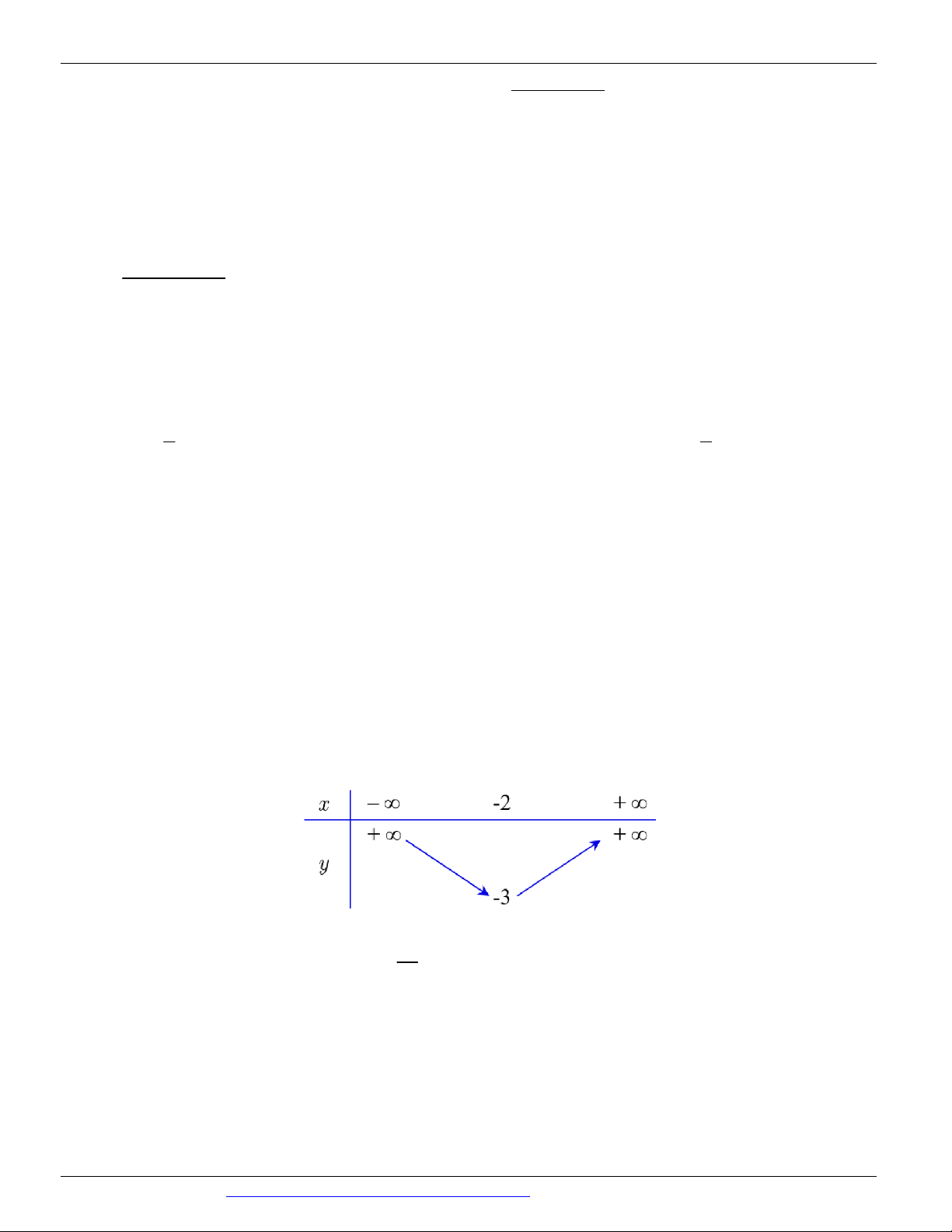
Câu 62: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y  3x  đồng biến trên từng x 1
khoảng xác định của nó? A. 4 . B. 2 . C. 1. D. 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Lời giải
Tập xác định D   \   1 . 2 2 2 m  3m 3x  
1 m 3my  3x   y  . x 1 x  2 1
Hàm số đồng biến trên từng khoảng xác định khi y  0 , x   1   2
m  3m  0  3
  m  0 .
Do m    m   3  ; 2  ; 1  ;  0 .
Vậy có 4 giá trị nguyên của m thỏa yêu cầu bài toán. cosx  2   
Câu 63: Tìm m để hàm số y
nghịch biến trên khoảng 0;   cosx m  2  m  0 A. m  2 . B. . C. m  2 . D. m  2 . 1   m 2  Lời giải
Đặt t  cos x .   
Ta có: t   sin x  0 ,x  0;   .  2    
 hàm số t  cos x nghịch biến trên khoảng 0;   .  2  cosx  2    t  2 Do đó hàm số y
nghịch biến trên khoảng 0;    hàm số y  đồng biến trên cosx m  2  t m khoảng 0  ;1 .
Tập xác định D   \   m . t  2 2  m Hàm số y
đồng biến trên khoảng 0  ;1  y 
 0 , t  0;1 . 2   t mt m 2  m  0 m  2   1   m  2   1   m   1   m   . m  0    m  0 m  0   m  0 cosx  2    Vậy với thì hàm số y
nghịch biến trên khoảng 0;   . 1   m 2  cosx m  2 
Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x)
Câu 64: (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y f (x) . Hàm số y f '(x) có đồ thị như hình
bên. Hàm số y f (2  x) đồng biến trên khoảng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. 2; B.  2  ;  1 C.  ;  2   D. 1;  3 Lời giải Chọn B Cách 1: x  (1; 4)
Ta thấy f '(x)  0 với 
nên f (x) nghịch biến trên 1; 4 và  ;   
1 suy ra g(x)  f (x) x  1 
đồng biến trên (4; 1) và 1;  . Khi đó f (2  x) đồng biến biến trên khoảng (2;1) và 3;  Cách 2: x  1 
Dựa vào đồ thị của hàm số y f  x ta có f  x  0   . 1  x  4  
Ta có  f 2  x  2  x . f 2  x   f 2  x . 
Để hàm số y f 2 x đồng biến thì  f 2  x  0  f 2  x  0 2  x  1   x  3     . 1  2  x  4 2  x  1  
Câu 65: (Mã đề 104 - BGD - 2019) Cho hàm số f x , bảng xét dấu của f  x như sau:
Hàm số y f 5  2x đồng biến trên khoảng nào dưới đây? A. 3;4 . B. 1;  3 . C. ;  3 . D. 4;5 . Lời giải Chọn D Ta có 
y f 5 2x  2
f 5 2x . 5  2x  3 x  4 y  0  2
f 5 2x  0  
 5  2x  1  x  3 .   5  2x  1  x  2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 5  2x  3  x  4 5  2x  1  x  2
f 5 2x  0    
; f 5  2x  0     . 1  5  2x  1  2  x  3 
3  5  2x  1  3  x  4  Bảng biến thiên
Dựa vào bảng biến thiên hàm số y f 5  2x đồng biến trên khoảng 4;5 .
Câu 66: (Mã 103 - BGD - 2019) Cho hàm số f (x) , bảng xét dấu của f (  x) như sau:
Hàm số y f 3  2x đồng biến trên khoảng nào dưới đây? A. 0;2 . B. 2;  3 . C. ;  3 . D. 3;4 . Lời giải Chọn D Ta có y  2.
f 3  2x  0  f 3  2x  0 3  2x  3   x  3     1   3  2x  1 1  x  2.   Vậy chọn A.
Câu 67: (Mã 102 - BGD - 2019) Cho hàm số f (x) có bảng dấu f (  x) như sau:
Hàm số y f (5  2x) nghịch biến trên khoảng nào dưới đây? A. 3;5 .
B. 5;  . C. 2;3 . D. 0; 2 . Lời giải Chọn D
Hàm số y f (x) có tập xác định là  suy ra hàm số y f (5  2x) có tập xác định là  .
Hàm số y f (5  2x) có y  2  . f (
 5  2x), x   .  3   5  2x  1  3  x  4 y  0  f (  5  2x)  0     . 5  2x  1 x  2  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vậy hàm số nghịch biến trên các khoảng ; 2 ; 3; 4 . Do đó B phương án chọn.
Câu 68: (Mã đề 101 - BGD - 2019) Cho hàm số f x , bảng xét dấu của f ' x như sau:
Hàm số y f 3  2x nghịch biến trên khoảng nào dưới đây? A.  2  ;  1 . B. 2; 4. C. 1;2. D. 4; . Lời giải Chọn A y  2.
f 3  2x . 3  3  2x  1 2  x  3
Hàm số nghịch biến khi y  0  2.
f 3  2x  0  f 3  2x  0     . 3  2x  1  x  1  Vậy chọn đáp án B.
Câu 69: (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Cho hàm số f (
x) có bảng xét dấu như sau:
Hàm số y f  2
x  2x nghịch biến trên khoảng nào dưới đây? A.  2   ;1 . B.  4  ; 3   . C. 0  ;1 . D.  2  ;   1 . Lời giải
Ta có: Đặt: y g x f  2 ( ) x  2x ; 2
gx   f x x    x   2 ( ) ( 2 ) 2 2 . f (  x  2x)   x  1  x  1 x  1 2   2 2x  2  0
x  2x  2(VN )   gx    x   2 ( ) 0 2 2 . f (
x  2x)  0    x  1 2  2 2 f (x 2x) 0     x  2x  1    x  1 2
x  2x  3   x  3  (Trong đó: x  1   2 ; x  1
  2 là các nghiệm bội chẵn của PT: 2
x  2x  1 ) + Ta có bảng biến thiên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào bảng biến thiên, suy ra hàm số y f  2
x  2x nghịch biến trên khoảng  2  ;   1 .
Chú ý: Cách xét dấu g (  x) :
Chọn giá trị x       2 0 1; 1
2  x  2x  0  g (  0)  f (
 0)  0 ( dựa theo bảng xét dấu của hàm f (
x) ). Suy ra g (  x)  0 x
  1;1 2  , sử dụng quy tắc xét dấu đa thức “ lẻ đổi, chẵn không” suy ra dấu của g (
x) trên các khoảng còn lại
Câu 70: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Cho hàm số y f x có đạo
hàm f ' x trên  . Hình vẽ bên là đồ thị của hàm số y f ' x . Hàm số     2 g x
f x x  nghịch biến
trên khoảng nào trong các khoảng dưới đây?  3   3   1   1  A.  ;    . B.  ;    . C. ;    . D.  ;    .  2   2   2   2  Lời giải Phương pháp
Hàm số y g x nghịch biến trên a;b  g ' x  0 x
  a;b và bằng 0 tại hữu hạn điểm. Cách giải
Ta có: g x    xf  2 ' 1 2 ' x x  .
Hàm số y g x nghịch biến trên a;b  g ' x  0 x
  a;b và bằng 0 tại hữu hạn điểm. Ta có g '  1  3 f ' 2
   0  Loại đáp án A, B và D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 71: (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Cho hàm số
y f ' x có đồ thị như hình vẽ
Hàm số y f  2
2  x  đồng biến trên khoảng nào dưới đây A.  ;  0 . B. 0  ;1 . C. 1; 2 . D. 0;  . Lời giải Chọn B
Hàm số y f  2
2  x  có y   x f  2 ' 2 . ' 2  x  x  0 x  0  2  1  2  x  2  1   x  1   0  x  1 y '  2  . x f ' 2 2  x   0   x 0    x  0     x  1     2    2  x  1 x  1      2 x  1  2  x  2  
Do đó hàm số đồng biến trên 0  ;1 .
Câu 72: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số f (x) , đồ thị hàm số y f (
x) như hình vẽ dưới đây.
Hàm số y f  3  x  đồng biến trên khoảng nào dưới đây? A. 4;6 . B.  1  ;2 . C. ;  1 . D. 2;  3 . Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Ta có: 3  x
y f  3  x   f  3  x   
f  3  x (x  3) 3  x 3  x
f  3  x   0
f  3  x   0  
f  3  x   0   3  x 3  x  0 
 3  x  1 L  x  1  3 x 1   N     x  7   
 3 x  4N   x  2 
x  Lx  4 3  
Ta có bảng xét dấu của f  3  x  :
Từ bảng xét dấu ta thây hàm số y f  3  x  đồng biến trên khoảng  1  ;2.
Câu 73: (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hàm số y f x . Hàm số y f ' x
có đồ thị như hình vẽ. Hàm số 2
g(x)  f (x  2). Mệnhvđề nào sai?
A. Hàm số g x nghịch biến trên  ;  2  
B. Hàm số g x đồng biến trên 2; 
C. Hàm số g x nghịch biến trên  1  ; 0
D. Hàm số g x nghịch biến trên 0; 2 Lờigiải ChọnA x  0 x  0 x  0  Ta có 2 2  g '(x)  2 .
x f '(x  2)  0   x  2  1   x  1   2  f (x 2) 0     2 x  2  2 x  2    x  2
Từ đồ thị f '(x) ta có 2 2
f '(x  2)  0  x  2  0   x  2  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 BBT
Từ BBT ta thấy đáp án C sai
Câu 74: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có đạo hàm liên tục
trên  và đồ thị hàm số y f ' x như hình bên.
Hỏi hàm số g x  f 3  2x nghịch biến trên khoảng nào trong các khoảng sau? A.  1  ;  B.  ;    1 C. 1;  3 D. 0;2 Lời giải Chọn B x  2  Ta có 
f ' x  0  x  2   x  5 
Khi đó g ' x  2
f '3  2x  5 x   2 3  2x  2   1
Với g ' x 0 f '3 2x 0 3 2x 2          x    2 3  2x  5   x  1   Bảng biến thiên:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 75: (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hàm số y f x có đạo hàm
trên và có đồ thị y f  x như hình vẽ.
Xét hàm số gx  f  2 x  2.
Mệnh đề nào sau đây sai?
A. Hàm số g x nghịch biến trên 0; 2 g xB. Hàm số
đồng biến trên 2; 
C. Hàm số g x nghịch biến trên  ;  2  
D. Hàm số g x nghịch biến trên  1  ;0 Lời giải Chọn D
Ta có gx  f  2 x  2
g'x  f 'x2  22 . x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  0  x  0 x  1  x  0 g'x   0   2
x  2  1    x 1 2
f 'x  2     0   2 x 2  2 x  2 x  2
Ta có g3  6. f 7  0 , g x đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các
nghiệm bội chẵn nên ta có bảng xét dấu g x: x   2
1 0 1 2  
g x 0 0 0 0 0
Suy ra đáp án là D.
Câu 76: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số y f x có bảng
xét dấu đạo hàm như sau:
Hàm số y f  2
x  2 nghịch biến trên khoảng nào dưới đây? A. 2;   1 . B. 2;  . C. 0;2 . D.  1  ;0 . Lời giải
Xét hàm số g x  f  2
x  2 . Ta có: g x  x f  2 ' 2 . ' x  2 .  x  0 x 0 x 0    x  1  x  0   
g ' x  0   2 2
x  2  1  x  1   x  1  . f '     2 x  2  0   2 2 x  2  2 x  4 x  2     x  2  
Ta có bảng xét dấu g '  x :
Dựa vào bảng xét dấu g '  x ta thấy hàm số y f  2
x  2 nghịch biến trên các khoảng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 77: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số y f x
có đạo hàm liên tục trên . Biết hàm số y f  x có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên m  5  ; 
5 để hàm số g x  f x m nghịch biến trên khoảng 1;2 . Hỏi S có bao nhiêu phần tử? A. 4 . B. 3 . C. 6 . D. 5 . Lời giải
Ta có g x  f  x m . Vì y f  x liên tục trên nên g x  f  x m cũng liên tục trên .
Căn cứ vào đồ thị hàm số y f  x ta thấy x m  1  x  1   m
g x  0  f  x m  0     .
1  x m  3
1 m x  3  m  
Hàm số g x  f x m nghịch biến trên khoảng 1;2 2  1   m  m  3   3   m  2    .  0  m  1   1 m  1 
Mà m là số nguyên thuộc đoạn  5  ; 
5 nên ta có S   5  ; 4  ; 3  ;0;  1 .
Vậy S có 5 phần tử.
Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x)
Câu 78: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số f x có bảng xét dấu của đạo hàm như sau x  1 2 3 4  f  x  0  0  0  0 
Hàm số y f x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A.  ;    1 . B.  1  ;0. C. 0;2. D. 1; . Lời giải Chọn B
Ta có: y   f  x     2 3 2 x  3  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Với x  1
 ;0  x  21; 2  f  x  2  0 , lại có 2
x  3  0  y  0; x    1  ;0
Vậy hàm số y f x   3 3
2  x  3x đồng biến trên khoảng  1  ;0. Chú ý: +) Ta xét x 
     x  
  f  x   2 1; 2 1; 2 3; 4 2  0; x  3  0
Suy ra hàm số nghịch biến trên khoảng 1;2 nên loại hai phương án A, D.
+) Tương tự ta xét x     x     f  x   2 ; 2 2 ;0
2  0; x  3  0  y  0; x    ;  2  
Suy ra hàm số nghịch biến trên khoảng  ;  2
  nên loại hai phương án B.
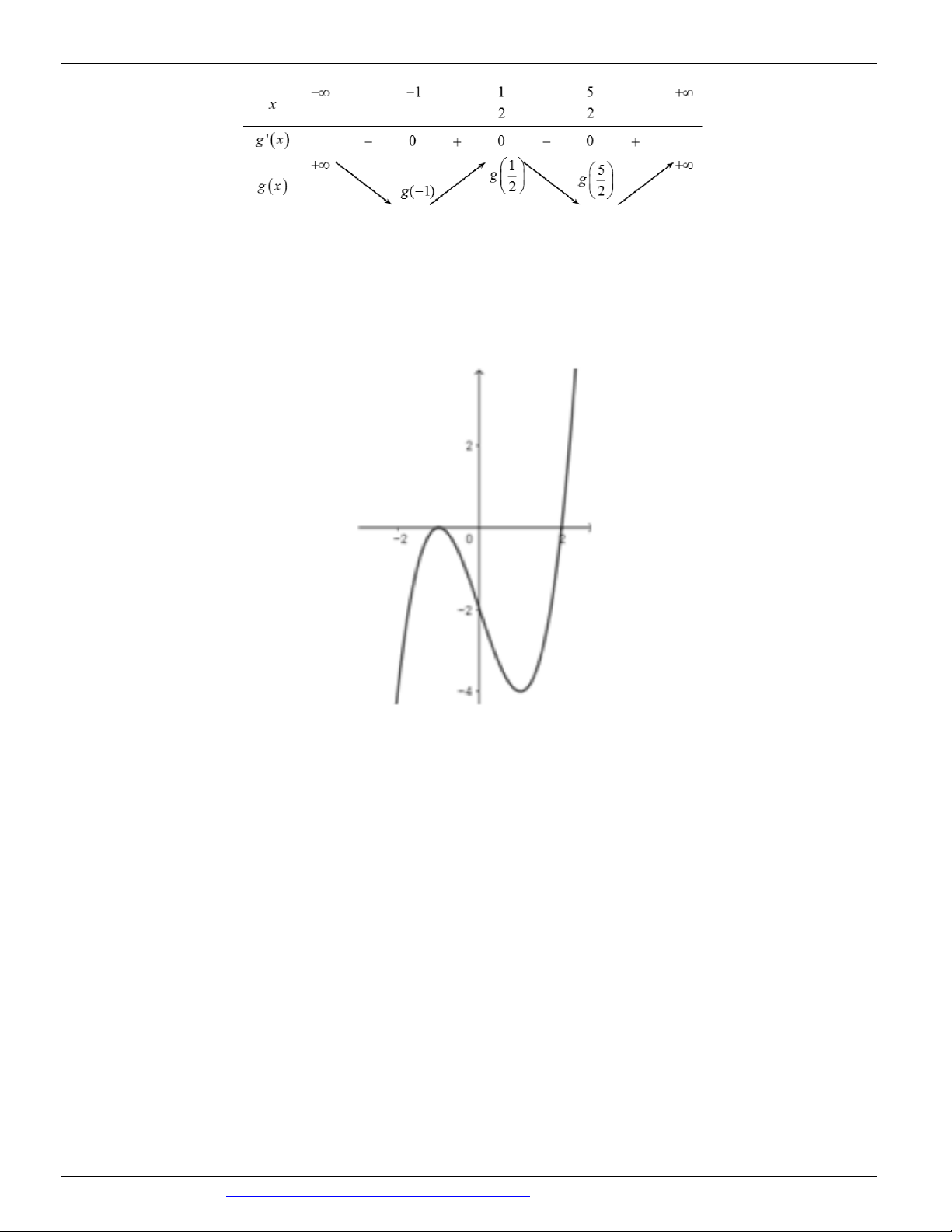
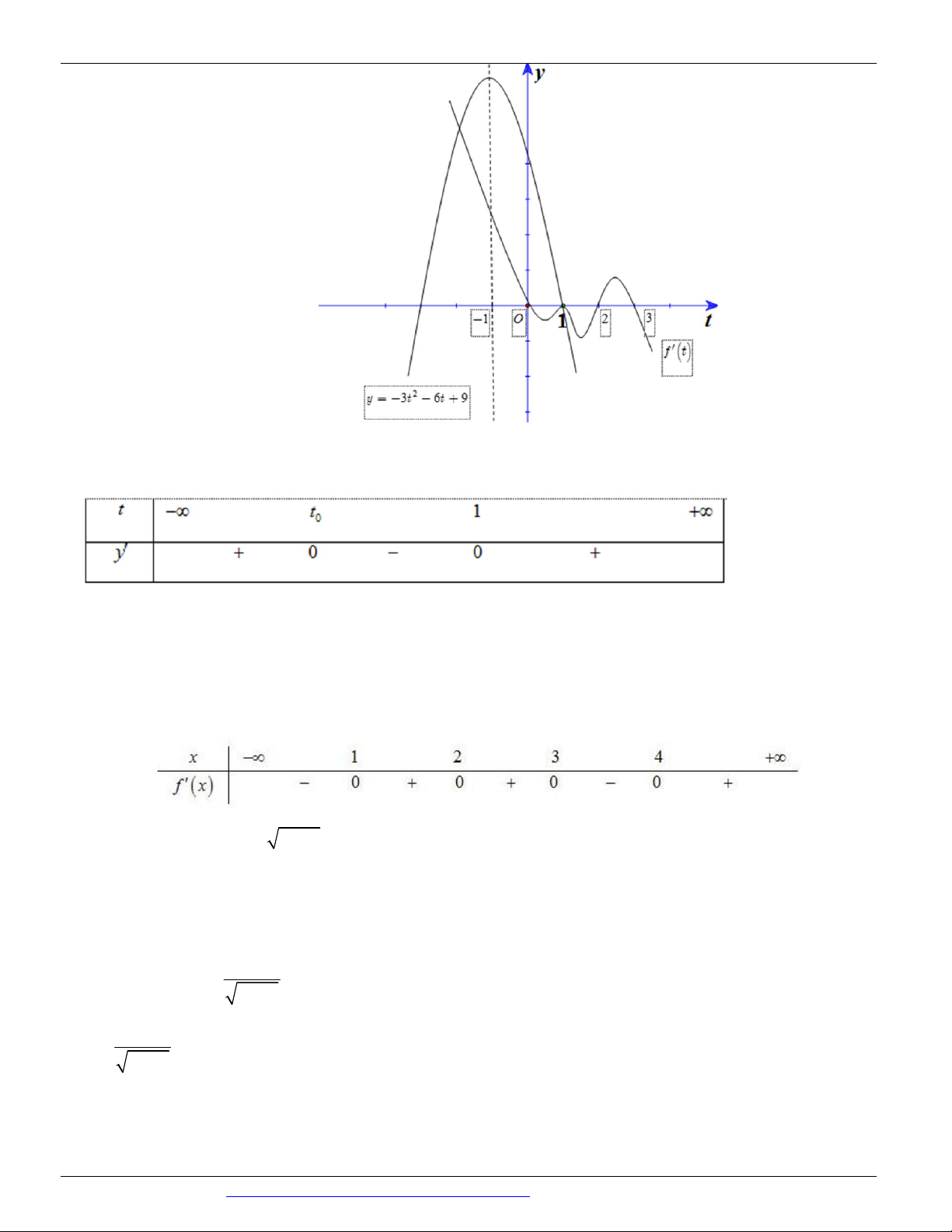
Câu 79: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Cho hàm số f x có bảng
xét dấu của đạo hàm như sau
Hàm số y f x   3
1  x 12x  2019 nghịch biến trên khoảng nào dưới đây? A. 1;   . B. 1; 2 . C.   ;1 . D. 3; 4 . Lời giải
Ta có y  f  x   2  x
f t  2
t t   f t    2 1 3 12 3 6 9 3
t  6t  9 , với t x 1
Nghiệm của phương trình y  0 là hoành độ giao điểm của các đồ thị hàm số
y f t  2 ; y  3
t  6t  9 .
Vẽ đồ thị của các hàm số y f t  2 ; y  3
t  6t  9 trên cùng một hệ trục tọa độ như hình vẽ sau:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dựa vào đồ thị trên, ta có BXD của hàm số y  f t    2
3t  6t  9 như sau: t  1  0 
Vậy hàm số nghịch biến trên khoảng t t ;1 . Do đó hàm số nghịch biến trên khoảng 0 
x  1; 2  t 1;1 . 0 
Câu 80: (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Cho hàm số f x có bảng
xét dấu đạo hàm như sau: Hàm số y f   x 2 2 1 
x 1  x nghịch biến trên những khoảng nào dưới đây
A. ;  2 . B.   ;1 . C.  2  ; 0 . D. 3;  2 . Lời giải. x y  2
f 1 x  1. 2 x 1 x Có 1  0 , x   2;0 . 2 x 1 Bảng xét dấu:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
 2 f 1 x  0, x   2;0 x  2
f 1 x  1  0, x   2  ; 0 . 2 x 1
Câu 81: (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Cho hàm số f x có bảng xét dấu của đạo hàm như sau : x  1 2 3 4  f ' x  0  0 + 0  0 + Hàm số y f   x 2 2 1
x 1  x nghịch biến trên khoảng nào dưới đây ? A.  ;   1 . B.  ;  2   . C.  2  ;0 . D.  3  ; 2   . Lời giải 2 x x x 1 Ta có : y '  2
f '1 x  1  2
f '1 x  2 2 x 1 x 1 2 x x 1 Chú ý :  0, x   . R 2 x 1
+) Với x   
;1  1 x  0;  (loại vì không thể kết luận được) +) Với x   ;  2
   1 x 3;  (loại vì không thể kết luận được) +) Với x   3  ; 2
  1 x 3; 4 (loại vì không thể kết luận được) +) Với x   2
 ;0  1 x 1;3  f '1 x  0  y '  0 (thỏa mãn).
Câu 82: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hàm số bậc bốn
y f (x) có đồ thị của hàm số y f (
x) như hình vẽ bên.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 y 1 O -4 -3 -2 2 x -1 -2 -3 Hàm số 3 2
y  3 f (x)  x  6x  9x đồng biến trên khoảng nào trong các khoảng sau đây? A. 0; 2 . B. 1;  1 . C. 1;  . D. 2; 0 . Lời giải Hàm số 4 3 2
f (x)  ax bx cx dx  , e (a  0) ; 3 2 f (
x)  4ax  3bx  2cx d .
Đồ thị hàm số y f (
x) đi qua các điểm ( 4  ; 0), ( 2  ; 0), (0; 3  ), (2;1) nên ta có:  5 a   96
256a  48b  8c d  0   7
 32a 12b 4c d 0       b     24 d  3   7 32  12  4   1 c a b c d    24  d  3   5 15 55  Do đó hàm số 3 2
y  3 f (x)  x  6x  9 ; x y  3 2 f (
x)  x  4x  3 3 2  3 x x x    24 8 12  x  1  1 
y  0  x  0
. Hàm số đồng biến trên các khoảng ( 1  1;0) và 2; .  x  2 
Câu 83: (HỌC MÃI NĂM 2018-2019-LẦN 02) Cho hàm số y f x có đạo hàm trên  . Đồ thị hàm số
y f  x như hình bên. Hỏi đồ thị hàm số y f x  2x có bao nhiêu điểm cực trị?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn B
Đặt g x  f x  2x .
g x  f  x  2 .
Vẽ đường thẳng y  2 .
 phương trình g x  0 có 3 nghiệm bội lẻ.
 đồ thị hàm số y f x  2x có 3 điểm cực trị.
Câu 84: (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số y f x 2019  2018x
liên tục trên  . Hàm số y f  x có đồ thị như hình vẽ. Hàm số g x  f x   1  đồng biến 2018
trên khoảng nào dưới đây? y 1  1 O 1 2 x  1 A. 2 ; 3 . B. 0 ;  1 . C. -1 ; 0 . D. 1 ; 2 . Lời giải
Ta có g x  f  x   1 1. x 1  1 x  0
g x  0  f  x  
1 1  0  f  x   1  1   .   x 1  2 x  3   2019  2018x
Từ đó suy ra hàm số g x  f x   1 
đồng biến trên khoảng -1 ; 0 . 2018
Câu 85: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hàm số y f x có bảng xét dấu của đạo hàm như sau
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Hàm số y  2
f x  2019 nghịch biến trên khoảng nào trong các khoảng dưới đây? A.  4  ; 2 . B.  1  ; 2 . C.  2  ;   1 . D. 2; 4 . Lời giải
Xét y g x  2
f x  2019 . x  2    x  1 
Ta có g x   2
f x  2019  2
f  x , g x  0   . x  2 x  4 
Dựa vào bảng xét dấu của f  x , ta có bảng xét dấu của g x :
Dựa vào bảng xét dấu, ta thấy hàm số y g x nghịch biến trên khoảng  1  ; 2 .
Câu 86: (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số y f x . Biết đồ thị
hàm số y f x có đồ thị như hình vẽ bên. Hàm số y f  2
3 x  2018 đồng biến trên khoảng nào dưới đây? A.  1  ;  0 B. 2;  3 C.  2  ;   1 D. 0;  1 Lời giải Chọn A  Ta có  f   2  x      x f     2 3 2018 2 . 3 x   .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  0 x  0    2  x   x    2 . x f  3 6 3 2 3 x   0     . 2  3 x  1 x  2    2 3 x  2 x  1  
Bảng xét dấu của đạo hàm hàm số đã cho
Từ bảng xét dấu suy ra hàm số đồng biến trên  1  ;  0 . 3 x  3 2 1  0 1 2  f  2 3 x   0  0  0  0  0  0  0   xf  2 2 3 x   0  0  0  0  0  0  0 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59