Các dạng toán về căn bậc hai và căn bậc ba

Tài liệu gồm 44 trang, phân loại và hướng dẫn giải các dạng toán về căn bậc hai và căn bậc ba, giúp học sinh lớp 9 tham khảo khi học chương trình Toán 9 (tập 1) phần Đại số chương 1. Mời bạn đọc đón xem.

54 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

44 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
MỤC LỤC
VẤN ĐỀ 1. CĂN BẬC HAI .............................................................................................................................. 3
A. TÓM TẮT LÝ THUYẾT .......................................................................................................................... 3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................................... 3
Dạng 1. Tìm căn bậc hai và căn bậc hai số học của một số ................................................................ 3
Dạng 2. So sánh các căn bậc hai số học................................................................................................. 4
C. BÀI TẬP VỀ NHÀ ................................................................................................................................... 5
VẤN ĐỀ 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
=
2
AA
............................................... 7
A. TÓM TẮT LÝ THUYẾT .................................................................................................................... 7
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................... 7
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai ........................................................................... 7
Dạng 2. Rút gọn biểu thức chứa căn bậc hai ....................................................................................... 8
C. BÀI TẬP VỀ NHÀ ................................................................................................................................... 8
VẤN ĐỀ 3. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
=
2
AA
............................................. 10
A. TÓM TẮT LÝ THUYẾT .................................................................................................................. 10
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 10
Dạng 3: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa ...................................................... 10
Dạng 4. Giải phương trình chứa căn bậc hai. .................................................................................... 10
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 11
VẤN ĐỀ 4. LIÊN HỆ PHÉP NHÂN, PHÉP CHIA VỚI PHÉP KHAI PHƯƠNG (PHẦN 1) ............... 12
A.Tóm tắt lý thuyết .................................................................................................................................... 12
B. Bài tập và các dạng toán. ....................................................................................................................... 12
Dạng 1. Thực hiện phép tính. .............................................................................................................. 12
Dạng 2. Rút gọn biểu thức. ................................................................................................................... 13
C.BÀI TẬP VỀ NHÀ .................................................................................................................................. 14
VẤN ĐỀ 5. LIÊN HỆ PHÉP NHÂN, PHẾP CHIAVỚI PHÉP KHAI PHƯƠNG (PHẦN II) ................ 15
A. TÓM TẮT LÝ THUYẾT ........................................................................................................................ 15
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................................... 15
Dạng 4. Rút gọn biểu thức .................................................................................................................... 15
Dạng 5. Giải phương trình ................................................................................................................... 16
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 16
VẤN ĐỀ 6. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI. ............................................. 18
A. TÓM TẮT LÍ THUYẾT .................................................................................................................... 18
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 18
Dạng
1. Dưa thừa số ra ngoài dấu căn hoặc vào trong dấu căn ..................................................... 18
Dạng 2. So sánh các căn bậc hai ........................................................................................................... 19
Dạng 3. Rút gọn biểu thức chứa căn bậc hai ..................................................................................... 19
Dạng 4. Trục căn thức ở mẫu ............................................................................................................... 20
1
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 21
VẤN ĐỀ 7: RÚT GỌN BIỂU THỨC CHỨA CĂN VÀ CÁC BÀI TOÁN LIÊN QUAN ........................ 23
A. TÓM TẮT LÝ THUYẾT .................................................................................................................. 23
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 23
Dạng 1.Rút gọn biểu thức chứa căn bậc hai ...................................................................................... 23
Dạng 2: Chứng minh đẳng thức chứa căn thức bậc hai ................................................................... 24
Dạng 3. Rút gọn biểu thức và các bài toán liên quan ....................................................................... 24
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 25
VẤN ĐỀ 8. CĂN BẬC BA .............................................................................................................................. 27
A. TÓM TẮT LÝ THUYẾT ................................................................................................................. 27
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 27
Dạng 1. Thực hiện phép tính có chứa căn bậc ba .............................................................................. 27
Dạng 2. So sánh các căn bậc ba ............................................................................................................ 28
Dạng 3. Giải phương trình chứa căn bậc ba ...................................................................................... 28
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 29
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I) ....................................................................................................................... 30
A. TÓM TẮT LÝ THUYẾT ............................................................................................................................. 30
1. Căn bậc hai số học ............................................................................................................................. 30
2. Căn thức bậc hai ................................................................................................................................ 30
3. Liên hệ giữa phép nhân, phép chia với phép khai phương ........................................................ 30
4. Biến đổi đơn giản
biểu thức chứa căn bậc hai ............................................................................... 30
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................................... 30
Dạng 1. Tìm điều kiện cho các biểu thức có nghĩa ........................................................................... 30
Dạng 2: Tính và rút gọn biểu thức ...................................................................................................... 31
Dạng 3. Giải phương trình và bất phương trình ............................................................................... 32
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II) ..................................................................................................................... 34
A. TÓM TẮT LÍ THUYẾT ......................................................................................................................... 34
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................................... 34
Dạng 4. Tìm các giá trị nguyên của biến để các biểu thức cho trước có giá trị nguyên .............. 34
Dạng 5. Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của biểu thức ................................................... 34
Dạng 6. Rút gọn biểu thức và các bài toán liên quan ....................................................................... 34
Một số bài tập nâng cao ........................................................................................................................ 36
HƯỚNG DẪN – ĐÁP SỐ ............................................................................................................................... 37
VẤN ĐỀ 1. ................................................................................................................................................... 37
VẤN ĐỀ 2. ................................................................................................................................................... 38
VẤN ĐỀ 3 .................................................................................................................................................... 39
VẤN ĐỀ 4 .................................................................................................................................................... 39
VẤN ĐỀ 5 .................................................................................................................................................... 40
VẤN ĐỀ 6 .................................................................................................................................................... 41
VẤN ĐỀ 7.
................................................................................................................................................... 42
VẤN ĐỀ 8 .................................................................................................................................................... 42
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I) ................................................................................................................ 43
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II) .............................................................................................................. 43
2
Chủ đề 1. CĂN BẬC HAI. CĂN BẬC BA
VẤN ĐỀ 1. CĂN BẬC HAI
A. TÓM TẮT LÝ THUYẾT
• Căn bậc hai của số thực
a
không âm là số thực
x
sao cho
=
2
xa
.
* Chú ý:
+) Số dương
a
có đúng hai căn bậc hai, là hai số đối nhau:
- Số dương kí hiệu là
a
- Số âm kí hiệu là
− a
.
+) Căn bậc hai của số 0 là 0.
+) Số âm không có căn bậc hai.
• Với số
a
không âm, số
a
được gọi là căn bậc hai số học của
a
.
• Ta có
≥
= ⇔
=
2
0x
ax
xa
• So sánh hai căn bậc hai số học:
.
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tìm căn bậc hai và căn bậc hai số học của một số
Phương pháp giải: Ta sử dụng kiến thức sau:
1. Nếu
a
là số thực dương, các căn bậc hai của
a
là
a
và
− a
; căn bậc hai số học của
a
là
a
.
2. Nếu
a
là số 0 thì căn bậc hai của
a
và căn bậc hai số học của
a
cũng bằng 0.
3. Nếu
a
là số thực âm thì
a
không có căn bậc hai và do đó không có căn bậc hai số học.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tìm các căn bậc hai và căn bậc hai số học của các số sau:
a) 0; b) 64;
c)
9
16
;
d) 0,04.
Bài 2. Mỗi số sau đây là căn bậc hai số học của số nào?
a) 12;
b)
−0,36
;
c)
2
2
7
;
d)
0,2
3
.
Bài 3. Tính:
a)
9
;
b)
4
25
;
c)
−
2
3
;
d)
( )
−−
2
6
;
e)

−



2
3
4
;
f)
( )
−
2
7
.
Bài 4. Tính giá trị của các biểu thức sau:
a)
−
21
81 16
32
;
b)
+0,5 0,04 5 0,36
;
3
c)
−
2 25 1 4
5 16 2 9
; d)
−−
− +−
−
25 9
45
16 25
.
Bài 5. Tìm giá trị
x
, biết:
a)
−=
2
16 0x
;
b)
=
2
13x
;
c)
+=
2
90x
;
d)
= 5x
; e)
− +=20
3
x
;
f)
− +=
2
2 14xx
.
* Học sinh tự luyện các bài tập sau tại lớp
Bài 6. Tìm các căn bậc hai và căn bậc hai số học của các số sau:
a) 81; b) 0, 25; c) 1, 44;
d)
40
1
81
.
Bài 7. Mỗi số sau đây là căn bậc hai số học của số nào?
a) 13;
b)
−
3
4
;
c)
12
25
;
d)
0,12
0,3
.
Bài 8. Tính
a)
121
;
b)
16
25
;
c)
( )
−−
2
8
;
d)
( )
−
2
2
;
e)

−



2
1
4
;
f)



2
3
5
.
Bài 9. Tính giá trị của các biểu thức sau:
a)
−
21
25 4
52
;
b)
+0,5 0,09 5 0,81
;
c)
−
2 25 5 4
5 36 2 25
; d)
−−
− +−
−
36 81
25
16 25
.
Bài 10. Tìm giá trị của
x
biết:
a)
=
2
1
3
x
;
b)
+=
2
36 0x
;
c)
−=
1
5
3
x
;
d)
− −=8 11x
; e)
−−=113x
;
f)
− + −=
2
4 413xx
.
Dạng 2. So sánh các căn bậc hai số học
Phương pháp giải: Ta có
< ⇔≤<0a b ab
.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 11. So sánh
a)
−2
và
3
;
b) 3 và
22
;
c) 11 và
99
;
d) 5 và
+17 1
;
e) 3 và
−15 1
;
f)
−13
và
0,2
.
Bài 12. Tìm giá trị của
x
biết:
a)
≥ 6x
;
b)
< 1x
;
c)
−+ ≥16x
;
d)
+≤2 12x
.
Bài 13. Tìm giá trị của
x
biết:
a)
≥2xx
; b) *
≤
2
2xx
.
* Học sinh tự luyện các bài sau tại lớp:
Bài 14. So sánh
a) 2 và
+12
; b)
3 11
và 12;
c) 1 và
−31
;
d)
3
và
−25
;
e)
−10
và
−2 23
;
f)
−3 29
và
−15
.
4
Bài 15. Tìm các giá trị của
x
biết:
a)
+≥15x
; b)
+<12x
; c)
− +>2 28x
; d)
+≤2 13x
.
C. BÀI TẬP VỀ NHÀ
Bài 16. Tìm các căn bậc hai và căn bậc hai số học của các số sau:
a) 225;
b) 324;
c)
169
100
;
d)
49
289
;
e) 2, 25;
f) 0, 16.
Bài 17. Mỗi số sau đây là căn bậc hai số học của số nào?
a) 7;
b)

−−


3
4
;
c)
32
23
;
d)
0,25
0,5
;
Bài 18. Tính
a)
225
9
; b)
49
25
;
c)
( )
−−
2
111
;
d)
2
13
;
e)
( )
−
2
7
;
f)

−



2
1
400
.
Bài 19.Tính giá trị của các biểu thức sau:
a)
−+
2 9 16
25 144
5 2 81
; b)
−+
1
0,5 0,09 2 0,25
4
;
c)
−
9 3 64
1
16 2 9
; d)
−−
− +−
−
289 0,09
10
16 9
.
Bài 20. Tìm giá trị của
x
biết:
a)
−=
2
196 0x
;
b)
=
2
1
15
x
;
c)
−+ =
2
324 0x
;
d)
+=
2
100 0x
;
e)
= 7x
;
f)
−=
1
3
3
x
.
Bài 21. Tìm giá trị của
x
biết:
a)
−−=3 1 4 13x
;
b)
− +=
2
9 6 1 18xx
;
c)
+=
1
2
2
x
;
d)
− +=2 30x
;
e)
+
=
24
3
2
x
;
f)
=
−
2
4
3x
.
Bài 22. Tìm giá trị của
x
biết:
a)
+≤9 31x
; b)
−>2 16x
;
c)
+≥35x
; d)
−+<2 152x
.
Bài 23. So sánh các số sau:
a) 4 và
+17
;
b)
25
và 8;
c)
−6
và
−27
;
d) 4 và
−23 1
;
e)
0,5
và
−32
;
f)
+2015 2018
và
+2016 2017
.
Bài 24*. Chứng minh
3
và
7
là các số vô tỉ.
Bài 25*. Cho biểu thức
=−+22Ax x
.
5
a) Đặt
= + 2yx
. Hãy biểu thị
A
theo
y
;
b) Tìm giá trị nhỏ nhất của
A
.
Bài 26*. So sánh
a)
+++ +
111 1
.............
1 2 3 100
và 10; b)
+++ +4 4 4 ......... 4
và 3.
Bài 26*. So sánh:
a)
+ + ++
111 1
...
1 2 3 100
và
10;
b)
++++4 4 4 ... 4
và
3;
6
VẤN ĐỀ 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
=
2
AA
(PHẦN I)
A. TÓM TẮT LÝ THUYẾT
Hằng đẳng thức
≥
= =
−<
2
khi 0
khi 0
AA
AA
AA
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai
Phương pháp giải:
Sử dụng hằng đẳng thức
≥
= =
−<
2
khi 0
khi 0
AA
AA
AA
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tính:
a)
( )
−−
2
4
0,4 ;
3
b)
( ) ( )
−+ −
64
4 3 5 2;
c)
49
144. . 0,01;
64
d)
+− −
22 22
72 : 3 4 3 5 3 .
Bài 2. Rút gọn biểu thức:
a)
( )
+−
2
5 55;
b)
( )
( )
− +−
22
4 11 1 3 ;
c)
( )
−+
2
22 7 22;
d)
( )
( )
− +−
22
2 3 1 3.
Bài 3. Chứng minh:
a)
( )
+=+
2
11 6 2 3 2 ;
b)
( )
−=−
2
8 27 7 1 ;
c)
+ +− =11 6 2 11 6 2 6;
d)
− −+ =−8 27 8 27 2.
Bài 4.Thực hiện các phép tính sau:
a)
+ −−5 26 5 26;
b)
− −+41 12 5 41 12 5 ;
c)
− ++49 12 5 49 12 5 ;
d)
+ +−29 12 5 29 12 5.
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 5. Tính:
a)

−


2
1
5;
5
b)
( )
( )
− −−
22
3 1,5 4 0,5 ;
c)
( )
−+0,25 225 2,25 : 169;
d)
( )
+−0,04 121 1,44 81.
Bài 6. Rút gọn biểu thức:
a)
( )
−+
2
3 5 5;
b)
( )
−+
2
7 5 7;
c)
( ) ( )
−+ +
22
11 4 11 4 ;
d)
( ) ( )
− +−
22
2 33 8 33 .
7
Bài 7. Chứng minh:
a)
( )
−=−
2
28 10 3 3 5 ;
b)
( )
−=−
2
193 132 2 11 6 2 ;
c)
− ++ =28 10 3 28 10 3 10;
d)
− ++ =193 132 2 193 132 2 22.
Bài 8. Thực hiện các phép tính sau:
a)
+ −−10 4 6 10 4 6 ;
b)
− ++39 12 3 39 12 3 ;
c)
− −+31 12 3 31 12 3 ;
d)
+ +−21 12 3 21 12 3 .
Dạng 2. Rút gọn biểu thức chứa căn bậc hai
Phương pháp giải:Sử dụng hằng đẳng thức
≥
= =
−<
2
khi 0
khi 0
AA
AA
AA
Bài 9. Rút gọn các biểu thức sau:
a)
−
2
5 25 25aa
với
≤ 0;a
b)
+
2
49 3aa
với
≥ 0;a
c)
+
42
16 6 ;aa
d)
−
63
39 6aa
với
≤ 0.a
Bài 10. Rút gọn các biểu thức sau:
a)
− −+
2
4 44xx x
với
≥ 2;x
b)
+++
2
3 96x xx
với
≤−3;x
c)
( )( )
++ −
− −+
−
2
69 3
4 44
9
xx x
x xx
x
với
≤≠0 9;x
d)
++
+
2
44
2
xx
x
với
≠−2.x
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 11. Rút gọn các biểu thức sau:
a)
−
2
4 16 16aa
với
≤ 0;a
b)
+
2
64 3aa
với
≥ 0;a
c)
+
42
25 6 ;aa
d)
−
63
3 81 6aa
với
≤ 0.a
Bài 12. Rút gọn các biểu thức sau:
a)
− −+
2
4 21xx x
với
≥ 1;x
b)
+ −+
2
3 96x xx
với
≥ 3;x
c)
( )( )
++ −
−
−
10 25 5
5
25
xx x
x
x
với
≤≠0 25;x
d)
−+
−
2
44
2
xx
x
với
≠ 2.x
C. BÀI TẬP VỀ NHÀ
Bài 13. Tính:
a)
( )
−−
2
7
. 0.81 ;
9
b)

−


2
61
;
5 36
c)
+49. 144 256 : 64;
d)
−
22
72 : 2 .3 .36 225.
Bài 14. Rút gọn biểu thức:
a)
( )
( )
− ++
22
11 6 2 11 6 2 ;
b)
( ) ( )
− −+
22
10 4 6 10 4 6 ;
8
c)
( )
( )
− +−
22
4 5 1 5;
d)
( ) ( )
+ −−
22
7 2 1 2.
Bài 15. Chứng minh:
a)
( )
+=+
2
7 43 2 3 ;
b)
( )
−=−
2
6 25 5 1 ;
c)
( )
−=−
2
5 2 27 10 2;
d)
+ −− =9 45 9 45 4.
Bài 16.Thực hiện các phép tính sau:
a)
+ +−6 25 6 25;
b)
− −+8 27 8 27;
c)
+ −−11 6 2 11 6 2 ;
d)
+ +−17 12 2 17 12 2.
Bài 17. Rút gọn các biểu thức sau:
a)
+
2
64 2 ;aa
b)
−
63
39 6 .aa
Bài 18. Rút gọn các biểu thức sau:
a)
+ ++ − +
22
69 69aa aa
với
−≤ ≤3 3;a
b)
+ −+ − −21 21aa aa
với
≤≤1 2.a
Bài 19. Rút gọn các biểu thức sau:
a)
−+ −
−
82 4
;
4
aa a a
a
b)
+ −−
12 6
.
7 26 7 26
9
VẤN ĐỀ 3. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
=
2
AA
(PHẦN II)
A. TÓM TẮT LÝ THUYẾT
Hằng đẳng thức
≥
= =
−<
2
khi 0
khi 0
AA
AA
AA
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 3: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Phương pháp giải:Chú ý rằng biểu thức
A
có nghĩa khi và chỉ khi
≥ 0.A
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Với giá trị nào của x thì các căn thức sau có nghĩa:
a)
−
2 4;x
b)
−
7 6;x
c)
−
−
2
;
31x
d)
−
−+
2
32
.
24
x
xx
* Chú ý rằng với a là số dương ta luôn có:
≥
≥⇔
≤−
22
xa
xa
xa
≤ ⇔− ≤ ≤
22
.x a axa
Bài 2.Với giá trị nào của x thì các căn thức sau có nghĩa:
a)
( )( )
−−3 5 6;xx
b)
−
−
24
;
5
x
x
c)
−−
2
8 9;xx
d)
−
2
16 .
x
*Học sinh luyện bài tập sau đây tại lớp
Bài 3.Với giá trị nào sau đây của
x
thì căn thức có nghĩa:
a)
−23x
; b)
−7x
; c)
14x−
; d)
2
3 1x +
.
Bài 4. Với giá trị nào sau đây của
x
thì căn thức có nghĩa:
a)
2
1x −
; b)
7
3
x−−
; c)
3
4
x
x
−
−
; d)
+
−
+
2
4
3
2
2
x x
x
.
Bài 5. Với giá trị nào sau đây của
x
thì căn thức có nghĩa:
a)
( )( )
26xx−−
; b)
2
4 5x x− −
; c)
2
9x −
; d)
2
1 x−
.
Dạng 4. Giải phương trình chứa căn bậc hai.
Phương pháp giải: Ta chú ý một số phép biến đổi tương đương liên quan đến căn thức
bậc hai sau đây:
2
0B
AB
AB
≥
= ⇔
=
;
2
A B AB=⇔=
( )
00AB
AB
AB
≥ ∨≥
= ⇔
=
;
22
A B AB A B= ⇔ = ⇔=±
10
Giáo viên hướng dẫn HS giải bài tập sau:
Bài 6. Giải các phương trình:
a)
6 13x −=
; b)
2
412 xxx +=−−
;
c)
2
168 91xxx +=−−
; d)
2
4 1xxx−−= −
;
e)
22
441 942xxxx−−+= +
; f)
2 12xx+ −=
.
Học sinh tự luyện bài tập sau tại lớp:
Bài 7. Giải các phương trình:
a)
93x +=
; b)
= −+
2
2x 3 12 x
;
c)
+=− −
2
112 19x x x
; d)
2
6 3xxx−−= −
;
e)
22
41 34261xxxx++= ++
; f)
4 42xx+ −=
.
C. BÀI TẬP VỀ NHÀ
Bài 8. Với giá trị nào sau đây của
x
thì căn thức có nghĩa:
a)
5 10x−−
; b)
2
2 1x x− +
; c)
2
2 4 5x x+ +
; d)
2
44xx− + −
.
Bài 9.Với giá trị nào sau đây của
x
thì căn thức có nghĩa:
a)
5
7x
−
−−
; b)
2
3 2x x− +
; c)
3
5
x
x
+
−
; d)
2
1
5 6x x− +
.
Bài 10. Giải các phương trình:
a)
93x +=
; b)
2
412 xxx +=−−
;
c)
2
946 xxx +=−−
; d)
22
32 441xxxx+ −+ +=−
.
Bài 11. Giải các phương trình:
a)
2
4 2xx+ = −
; b)
2
2510 3 19xxx +=−−
;
c)
22
9690xxx−−+ +=
; d)
22223 2138235x xx x−+ − + + + − =
.
Bài 12. a) Chứng minh rằng nếu
22
1x y+=
thì
22xy− ≤+≤
.
b) Cho
, ,zxy
là số thực dương. Chứng minh:
111 1 1 1
xyz
yz zx xy
++≥ + +
.
Bài 13*. Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
22
4 14 1 942xxxx−−++ +
; b)
22
22 2249x 9 49 9xxx++ + +−
.
11
Bài 14 .*Tìm các số
, ,zxy
thỏa mãn đẳng thức:
8214263xyz x y z+++= −+ −+ −
.
VẤN ĐỀ 4. LIÊN HỆ PHÉP NHÂN, PHÉP CHIA VỚI PHÉP KHAI PHƯƠNG (PHẦN 1)
A.Tóm tắt lý thuyết
*Khai phương một tích:
Với
0, 0,AB≥≥
ta có
..AB A B=
.
*Khai phương một thương:
Với
0, 0,AB≥>
ta có
AA
B
B
=
.
B. Bài tập và các dạng toán.
Dạng 1. Thực hiện phép tính.
Phương pháp giải:Áp dụng công thức khai phương một tích và khai phương một
thương ở trên.
*Giáo viên hướng dẫn học sinh làm các bài tập sau:
Bài 1. Tính:
a)
45.80
; b)
2,5.14,4
; c)
10. 40
; d)
52. 13
.
Bài 2. Tính:
a)
9
169
; b)
9
1
16
; c)
2300
23
; d)
12,5
0.5
.
Bài 3. Thực hiện phép tính:
a)
91
.2
22

−



; b)
( )
12 27 3 . 3+−
;
c)
8 50
24 . 6
33

−+



; d)
1
26 43 52 8.36
4

−+−


.
Bài 4. Thực hiện phép tính:
a)
( )
45 20 5 : 5−+
; b)
1 16
7:7
77

−+



;
c)
( )
325 117 2 208 : 13−+
; d)
1123 21 21
:
323276 78

−+



;
*Học sinh tự luyện các bài sau tại lớp:
Bài 5. Tính:
12
a)
32.200
; b)
9 25
:
16 36
; c)
11. 1100
; d)
13. 52
.
Bài 6. Tính:
a)
25
64
; b)
9
1
16
; c)
999
111
−
; d)
643. 34,3
567
.
Bài 7. Thực hiện phép tính:
a)
16 1
.3
33

−



; b)
( )
20 45 5 . 5+−
;
c)
8 50
66
23

−+



; d)
( )( )
62 3 2+−
.
Bài 8. Thực hiện phép tính:
a)
1 16
11 : 11
11 11

−+



; b)
( )
20 300 15 675 5 75 : 15−+
;
c)
14
3:3
33

−+



; d)
3 5: 2−
.
Dạng 2. Rút gọn biểu thức.
Phương pháp giải: Áp dụng công thức khai phương của một phương hoặc khai
phương của một tích.
*Giáo viên hướng dẫn học sinh làm bài tập sau:
Bài 9. Rút gọn:
a)
10 15
8 12
−
−
; b)
15 5 5 2 5
3 1 25 4
−−
−
−−
;
c)
2 8 12 5 27
18 48 30 162
−+
−
−+
; d)
( )
3 23 2 2
23
3 21
++
+ −+
+
.
Bài 10. Rút gọn:
a)
1
aa
a
−
−
; b)
x xy
xy
−
−
với
0, 0,xyxy≥≥≠
.
c)
2
xy yx
x xy y
+
++
d)
3 21
44 1
aa
aa
−−
−+
* Học sinh tự luyện các bài tập sau tại lớp.
Bài 11. Tính:
13
a)
15 6
35 14
−
−
; b)
55
10 2
+
+
:
c)
5 25 5 35
( 2).( 2);
25 35
−+
−−
−+
d)
41 1
(323).(1,224)
33 5
++ +−
.
Bài 12. Rút gọn biểu thức sau:
a)
x xy
xy
+
−
với
0, 0, ;xyxy≥≥≠
b)
;
1
aa
a
+
+
c)
4 44
;
22
aa a
aa
++ −
+
+−
d)
xy yx
x xy y
−
−+
.
C.BÀI TẬP VỀ NHÀ
Bài 13. Tính :
a)
2. 18;
b)
5. 125;
c)
9
196
; d)
7
2
81
.
Bài 14. Tính :
a)
16. 25 196 : 49;+
b)
( 28 63 7) : 7;−+
c)
2,5. 30. 48;
d)
1 14 34
3 .2 .2 .
16 25 81
Bài 15. Thực hiện phép tính:
a)
3
( 12 2 27) 150;
2
+−
b)
( 28 12 7). 7 2 21;−− +
c)
(1 2 3)(1 2 3);+− ++
d)
2
3(2 3) (3 2).− −−
Bài 16. Rút gon biểu thức sau:
a)
2
3
;
3
x
x
−
+
b)
2
;
4
x
x
−
−
c)
2
2
2 22
;
2
xx
x
−+
−
d)
2
5
.
2 55
x
xx
+
++
14
VẤN ĐỀ 5. LIÊN HỆ PHÉP NHÂN, PHẾP CHIAVỚI PHÉP KHAI PHƯƠNG (PHẦN II)
A. TÓM TẮT LÝ THUYẾT
Nhác lại các công thức khai phương ở vấn đề 4:
Khai phương một tích:
Với
0,B 0A ≥≥
ta có
. ..AB A B=
Khai phương một thương:
Với
0,B 0A ≥>
ta có
.
AA
B
B
=
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tính:
a)
15 5
62
−
−
; b)
3 5.(3 5)
;
10 2
−+
+
c)
2 10 30 2 2 6
;
2 10 2 2
+−−
−
d)
2
(1 2006) . 2017 2 2016.−+
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 2. Tính:
a)
12,1.360;
b)
0,4. 6,4
; c) -0,4
2
( 0,4)−
; d)
42
2 .( 7) .−
Bài 3. Tính:
a)
2
( 15 2 3) 12 5;++
b)
2
2 5(2 3 5) (1 2 5) 6 5;− +− +
Dạng 4. Rút gọn biểu thức
Phương pháp giải: Sử dụng hằng đẳng thức
2
,0
,0
AA
AA
AA
≥
= =
−<
Và phép khai phương của một tích hoặc một thương.
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
a)
2
27.48(1 )a−
với a<1. b)
42
1
()aab
ab
−
−
với a<b.
c)
23
.
38
aa
với
0a ≥
c)
5 . 45 3a aa−
với
0a ≥
.
Bài 5. Rút gọn các biểu thức sau:
a)
33
ab a b
ab
ab
−+
−
−
−
với
0, 0, ;a b ab≥≥≠
b)
23
25 3
a ab b
a ab b
+−
−+
với
0, 0,4 9 .a b ab≥≥ ≠
* Học sinh tự luyện các bài tập sau tại lớp.
Bài 6. Rút gọn các biểu thức sau:
15
a)
24
(3 ) 0,2. 180 ;aa−−
b)
2
27( 3)
48
a −
với a<3;
c)
3
63
7
y
y
với y>0 ; d)
46
62
16
128
ab
ab
với
0, 0.ab<≠
Bài 7. Rút gọn biểu thức sau :
a)
2
;
21
aa
a
−
−
b)
2
2
;
2
x
x
−
−
c)
3
9
x
x
−
−
; d)
x xy
xy
+
−
.
Dạng 5. Giải phương trình
Phương pháp giải : chú ý rằng:
*
2
0
.
B
AB
AB
≥
= ⇔
=
*
0( 0)
.
B hayA
AB
AB
≥ ≥
= ⇔
=
* Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 8. Giải các phương trình sau:
a)
23
2;
1
x
x
−
=
−
b)
2
4 9 2 2 3;xx−= +
c)
2
2 40xx−− −=
d)
1
4 20 5 9 45 4.
3
xx x− + −− − =
Bài 9. Giải các phương trình sau:
a)
2
8 16 5xx−+=
; b)
97
75
75
x
x
x
−
= +
+
;
c)
2
3 2 9 0;xx−− −=
d)
11
2 9 27 25 75 49 147 20.
57
xxx−− −− − =
Bài 10. Giải các phương trình sau:
a)
3
2;
21
x
x
−
=
+
b)
10 7
3 5;
35
x
x
x
−
= +
+
c)
2
2 2 4 0;xx−− −=
d)
1
2 4 8 9 18 2.
2
xx x−− −− − =
C. BÀI TẬP VỀ NHÀ
Bài 11.tính:
a)
2.80
; b)
25
144
; c)
5. 45;
d)
14
2.
25
Bài 12. Thưc hiện phép tính:
a)
5 55 5
;
5 55 5
+−
+
−+
b)
2 8 12 5 27
;
18 48 30 162
−+
−
−+
c)
(2 5 3)(2 5 3);++ +−
d)
23 23
.
23 23
−+
+
+−
Bài 13. Rút gọn các biểu thức sau :
16
a)
−+
++
21
21
xx
xx
với
≥ 0;x
b)
++
−
22
22
363
2
4
x xy y
xy
với
+>0;xy
c)
+
++
2
7
;
2 77
x
xx
d)
+
++
.
2
xy yx
x xy y
Bài 14. Giải các phương trình sau :
a)
− +=
2
10 25 7;xx
b)
−
=
+
3
2;
21
x
x
c)
−= −
2
25 9 2 5 3;xx
d)
−+ − − − =
1
5 4 20 9 45 3.
5
xx x
Bài 15. Giải các phương trình sau :
a)
−
=
−
23
2;
1
x
x
b)
−
=
+
3
2;
21
x
x
c)
−
= +
+
10 3
2 1;
21
x
x
x
d)
−= −
2
4 9 2 2 3.xx
Bài 16. Cho
x
là số thực bất kì. Chứng minh ta luôn có :
+
>
+
4
4
5
2.
4
x
x
17
VẤN ĐỀ 6. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI.
A. TÓM TẮT LÍ THUYẾT
• Đưa thừa số
2
A
ra ngoài dấu căn :
=
2
AB A B
với
≥ 0.B
• Đưa thừa số vào trong dấu căn :
≥
=
−<
2
2
0
.
0
A B khi A
AB
A B khi A
• Khử mẫu của biểu thức dưới dấu căn bậc hai :
= =
2
.1
.
A AB
AB
B
B
B
với
≠≥0, . 0.B AB
• Trục căn thức ở mẫu :
( )
( )
=
−
=
−
+
+
=
−
−
;
;
.
A AB
B
B
mA B
m
AB
AB
mA B
m
AB
AB
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Dưa thừa số ra ngoài dấu căn hoặc vào trong dấu căn
Phương pháp giải :
1. Cách đưa thừa số
2
A
ra ngoài dấu căn :
=
2
AB A B
với
≥ 0.B
2. Cách đưa thừa số vào trong dấu căn :
≥
=
−<
2
2
0
.
0
A B khi A
AB
A B khi A
• Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 1. Đưa thừa số ra ngoài dấu căn :
a)
2
7x
với
≥ 0;x
b)
2
7y
với
≤ 0;y
c)
2
25x
với
≥ 0;x
d)
4
48 .y
Bài 2.Đưa thừa số vào trong dấu căn :
a)
13x
với
≥ 0;x
b)
2x
với
≤ 0;x
c)
15
x
x
với
≥ 0;x
d)
−15
x
x
với
< 0.x
• Học sinh tự luyện các bài tập sau tại lớp :
Bài 3. Đưa thừa số ra ngoài dấu căn
a)
2
13x
với
≥ 0;x
b)
2
12y
với
≤ 0;y
c)
3
81x
với
≥ 0;x
d)
8
48 .y
18
Bài 4. Đưa các thừa số vào trong dấu căn
a)
13x
với
≥ 0;x
b)
3x
với
≤ 0;x
c)
7
2y
y
với
> 0;y
d)
−7
2y
y
với
< 0.y
Dạng 2. So sánh các căn bậc hai
Phương pháp giải : Đưa thừa số ra ngoài hoặc vào trong đấu căn rồi so sánh.
• Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 5. So sánh các số
a)
52
và
4 3;
b)
51
26
và
1
6;
37
c)
2 29
và
3 13;
d)
5
2
4
và
33
.
22
Bài 6. Sắp xếp theo thứ tự tăng dần
a)
3 5;2 6; 29;4 2;
b)
6 2; 38; 3 7;2 14.
• Học sinh tự luyện các bài tập sau tại lớp :
Bài 7. So sánh các số :
a)
35
và
2 7;
b)
31
23
và
1
6;
14
c)
3 21
và
2 47;
d)
5
3
9
và
2
14.
7
Bài 8. Sắp xếp theo thứ tự giảm dần :
a)
7 2;2 8; 28;5 2;
b)
2 5;2 40;3 8;5 30.
Dạng 3. Rút gọn biểu thức chứa căn bậc hai
Phương pháp giải : Đưa các thừa số ra ngoài hoặc vào trong dấu căn rồi rút gọn.
• Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 9. Rút gọn các biểu thức sau :
a)
−−+5 48 4 27 2 57 108;
b)
−− +5 16 4 25 2 100 169aa aa
với
≥ 0.a
Bài 10. Rút gọn biểu thức sau :
a)
−
2
35aa
với
≤ 0;a
b)
−
63
34 5aa
với
≤ 0;a
c)
+ +−4 23 4 23;
d)
−− − +
2
2 44x xx
với
≥ 2.x
19
• Học sinh tự luyện các bài sau tại lớp :
Bài 11. Rút gọc các biểu thức sau :
a)
− +−2 24 2 54 3 6 150;
b)
−−
2
5 4 4 100aa a
với
> 0.a
Bài 12. Rút gọn biểu thức sau :
a)
+
2
45aa
với
≥ 0;a
b)
+
2
25 3xx
với
≤ 0;x
c)
−− − +
2
2 44x xx
với
≤ 2;x
d)
−+ + +
2
3 99x xx
với
≤−3.x
Dạng 4. Trục căn thức ở mẫu
Phương pháp giải :
1. Cách khử mẫu của biểu thức dưới dấu căn bậc hai :
= =
2
.1
.
A AB
AB
B
B
B
với
≠≥0, . 0.B AB
2. Cách trục căn thức ở mẫu :
( )
( )
=
−
=
−
+
+
=
−
−
;
;
.
A AB
B
B
mA B
m
AB
AB
mA B
m
AB
AB
• Giáo viên hướng dẫn học sinh làm các bài tập sau :
Bài 13. Khử mẫu của mỗi biểu thức lấy căn và rút gọn ( nếu được) :
a)
2
;
3
b)
2
5
x
với
≥ 0;x
c)
3
5
49
a
b
với
≥>0, 0;ab
d)
−
3
7xy
xy
với
<>0, 0.xy
Bài 14. Trục căn thức ở mẫu và rút gọn:
a)
+
+
10 2 10
;
52
b)
−
−
2 8 12
;
18 48
c)
−
2
;
53
d)
−
+
23
.
23
Bài 15. Trục căn thức và thực hiện phép tính:
a)
( )

+− +

+ −−

15 4 12
6 11 ;
61 623 6
b)
−
−−
11
;
3 5 51
c)
+−−
+ −−
111
5;
51 523 5
d)
+
+−
11
.
5 32 5 32
20
*Học sinh tự luyện tập các bài tập sau tại lớp:
Bài 16. Khử mẫu của mỗi biểu thức lấy căn và rút gọn (nếu được):
a)
2
;
7
b)
2
31
x
với
≥ 0;x
c)
3
5
49
b
a
với
>≥0, 0;ab
d)
−
16
7xy
xy
với
<<0, 0.xy
Bài 17. Trục căn thức ở mẫu và rút gọn:
a)
+
+
5 25
;
52
b)
−
−
2 6 10
;
43 25
c)
−
1
;
22 33
d)
−
+
35
.
35
Bài 18. Trục căn thức và thực hiện phép tính:
a)
( )
++
+ −+
+
3 23 2 2
2 3;
3 21
b)

+−
−−


+−

5555
1.1;
15 15
c)

−+
−−


−+

5 25 5 35
2 2;
25 35
d)
−+
−− +
321
.
5 22 2 3 2
C. BÀI TẬP VỀ NHÀ
Bài 19. Rút gọn các biểu thức sau:
a)
−−+125 2 20 3 80 4 45;
b)
−− −
3
10 28 2 75 3 343 396;
2
c)
+
+−
11
;
7 43 7 43
d)
−
1
.
211 37
Bài 20. Rút gọn các biểu thức sau:
a)
+
42
9 2;aa
b)
−
2
92xx
với
≥ 0;x
c)
−−4 23 3
d)
−+ + +
2
3 69xx x
với
>−3.x
Bài 21. Tính:
a)
( )
+−2 45 80 125 . 5;
b)
−−
16 1 4
236;
5 45 20
c)
+− −3 7 2 6 3 6;
d)
−+
+− −
3 41
.
5 2 3 5 21
Bài 22. Tính:
21
b)
−++3 5 3 5;
b)
−−
16 1 4
2 3 6;
3 27 75
c)
−
+−
+−
1 62 4
175 ;
87 32
d)
−−+10 84 34 2 189.
Bài 23. Tính:
a)

++

− −− +

2 3 15 1
.;
31 32 3 3 35
b)
−
+− ++
33
;
311 311
c)
+−
31 1
2;
20 60 15
d)

−−
+


−− −

14 7 15 5 1
:.
12 13 7 5
Bài 24. Giải phương trình:
a)
−+ − =5 2 25 125 22;xx
b)
+− ++ +=
1
18 9 8 4 2 1 4;
3
xx x
c)
−−
=
−−
24
;
56
xx
xx
d)
−− −+ − =
1
4 8 2 9 18 9.
2
x xx
Bài 25. Giải phương trình:
a)
−= +
2
4 9 2 2 3;xx
b)
−
−+ − −=
51
4 20 3 9 45 4
;
93
x
xx
c)
−
−− − + =
21 1
9 9 16 16 27 4;
3 4 81
x
xx
d)
−− −
− − −+ =
2
2
9 27 4 12 9 81
5 7 7 9 18 0.
25 9 81
xx x
x
Bài 26. Tìm
,,xyz
biết rằng:
a)
+ ++ = +2 1 4 4;xy yy
b)
( )
++ −+ −= ++
1
131 .
2
x y z xyz
Bài 27. Rút gọn:
=++++
+ + + −+
111 1
... .
12 23 34 1
A
nn
Bài 28. Tìm giá trị nhỏ nhất của biểu thức:
22
= − −+ + −21 21.Ax x x x
Bài 29. Chứng minh với mọi số tự nhiên
n
khác
0
, ta luôn có:
( )
+ + + + > +−
11 1
1 ... 2 1 1 .
23
n
n
Bài 30. Chứng minh:
+ >+
2002 2003
2002 2003.
2003 2002
VẤN ĐỀ 7: RÚT GỌN BIỂU THỨC CHỨA CĂN VÀ CÁC BÀI TOÁN LIÊN QUAN
A. TÓM TẮT LÝ THUYẾT
Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần biết vận dụng linh hoạt thích hợp
các phép biến đổi đơn giản như: Đưa thừa số ra ngoài dấu căn, đưa thừa số vào trong
dấu căn, khử căn ở mẫu và trục căn thức ở mẫu để làm xuất hiện các căn thức bậc hai có
cùng một biểu thức dưới dấu căn …
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1.Rút gọn biểu thức chứa căn bậc hai
Phương pháp giải:
Bước 1. Vận dụng thích hợp các phép tính và các phép biến đổi đã biết làm xuất hiện căn
thức cùng loại.
Bước 2. Cộng, trừ các căn thức bậc hai cùng loại.
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Rút gọn các biểu thức sau:
a)
+−+32 50 2 8 18;
b)
++
1
4,5 12,5;
2
c)
( )
− −−
2
123 4 23;
d)
− + −−
+
23
96 6 10 4 6.
3
36
Bài 2. Rút gọn các biểu thức sau:
a)
+−+
4
56 5
4
a
aa
a
với
> 0;a
b)
−+ −
32
5 4 25 5 16 9a b a a ab a
với
≥≥0, 0.ab
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 3. Rút gọn các biểu thức sau:
a)
−−
27 48 2 75
2;
4 9 5 16
b)
( )
−− +99 18 11 11 3 22;
c)
( )
+−5 3 8 2 15 ;
d)
( )
−+ −48 23 25 5 245: 3.
Bài 4. Rút gọn các biểu thức sau:
23
a)
( )

−+

−+

+
2
11 1
1. ;
52 52
21
b)
−+ +
32 5
2
42
2 9 25a aa a
a
a
với
> 0.a
Dạng 2: Chứng minh đẳng thức chứa căn thức bậc hai
Phương pháp giải: Thực hiện các phép biến đổi căn thức và các hằng đẳng thức đáng nhớ
để thực hiện phép chứng minh.
*Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 5. Chứng minh các đẳng thức sau:
a)

−−
+=


−
−

2
11
1
1
1
aa a
a
a
a
với
≥≠0, 1.aa
b)
+
=
++
24
22 2
2
a b ab
a
b a ab b
với
+>0ab
và
≠ 0.b
*Học sinh tự luyện tập bài tập sau tại lớp:
Bài 6. Chứng minh các đẳng thức sau:
a)

−−
−=


−

2 3 6 216 1 3
.;
32
82 6
b)
+−
− −=
−
−+ −
22
22 22
ab ab b b
ba
a b a b ab
với
≠ab
và
≥≥0, 0.ab
Dạng 3. Rút gọn biểu thức và các bài toán liên quan
*Phương pháp giải:
1. Để rút gọn biểu thức, ta thực hiện các phép biến đổi căn thức và các hằng đẳng thức
đáng nhớ.
2. Các bài toán liên quan thường gặp là:
- Tính giá trị của biểu thức với giá trị của biến cho trước.
- Giải phương trình hoặc bất phương trình chứa căn bậc hai.
- Tìm giá trị nguyên của biểu thức.
- So sánh biểu thức với một số.
- Tìm giá trị lớn nhất, nhỏ nhất của biểu thức.
* Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 7. Cho biểu thức
− ++
= −−
−+ − −
2 9 32 1
.
5 6 23
x xx
M
xx x x
a) Rút gọn
;M
b) Tính giá trị của
M
khi
= −11 6 2;x
c) Tìm các giá trị thực của x để
= 2;M
d) Tìm các giá trị thực của
x
để
< 1;M
e) Tìm các giá trị nguyên để
M
nguyên.
* Học sinh tự luyện các bài tập sau tại lớp:
24
Bài 8. Với
> 0x
, cho các biểu thức
= −
+
1
1
x
A
xx
và
=
+
.
x
B
xx
a) Tính giá trị của
A
khi
= 4.x
b) Tìm các giá trị thực của
x
để
=
1
;
3
B
c) So sánh
B
với
1;
d) Đặt
= :.P AB
Tìm
x
thỏa mãn
( )
+ − = − −+2 5 1 3 2 4 3.Px x x x
Bài 9. Cho biểu thức

+
=−+


+
− −+− +++

12 1
:
1
11 1
x xx
P
x
x xx x x xx x x
với
≥≠0, 1;xx
a) Rút gọn
;P
b) Tìm
x
để
<
1
;
2
P
c) Tìm giá trị của
x
để
=
1
;
3
P
d) Tìm
x
nguyên để
P
nguyên;
e) Tìm giá trị nhỏ nhất cuả
.P
C. BÀI TẬP VỀ NHÀ
Bài 10. Rút gọn các biểu thức sau:
a)
+−−5 27 3 48 2 12 6 3;
b)

−+
++


−

3 3 21 7
3 2;
13 7
c)
− + −−
+
23
96 6 10
4 6
;
3
36
d)
−− −
5 11
6 2 6.
22
Bài 11. Rút gọn các biểu thức sau
a)
−−
471
10 6 ;
7 25 28
b)
( )
+−10 2 3 5 ;
c)
+ −−
+
6 11 7 33
;
62
d)
−+
+−
−+ +
53 35 2 55 33
.
5 3 4 15 5 3
Bài 12. Cho biểu thức
+− + −
= −+
+− + −
39312
.
2 21
xx x x
Q
xx x x
a) Rút gọn
;Q
b) Tính giá trị của
Q
khi
= +4 2 3;x
c) Tìm các giá trị của
x
để
= 3;Q
d) Tìm các giá trị của
x
để
>
1
;
2
Q
e) Tìm
∈x
để
∈.Q
Bài 13. Cho biểu thức


−−
=−+



+


1 11
:.
xx
Px
x x xx
a) Rút gọn
;P
b) Tính giá trị của
P
biết
=
+
2
;
23
x
25
c) Tìm
x
thỏa mãn
= −− −6 3 4.Px x x
Bài 14. Cho biểu thức


+−
=−−



−
++


24
:.
1
11
x xx
Px
x
xx
a) Rút gọn
;P
b) Tính giá trị của
x
thỏa mãn
< 0;P
c) Tìm giá trị nhỏ nhất của
.P
Bài 15. Cho biểu thức
( )
−
−+
= −+
++ −
2
21
2
.
11
x
x x xx
P
xx x x
a) Rút gọn
;P
b) Tìm giá trị nhỏ nhất của
;P
c) Tìm
x
để biểu thức
=
2 x
Q
P
nhận giá trị là số nguyên.
Bài 16 . Cho các biểu thức
++
=−=
−−
−
29 5
;
9 25
3
xxx xx
AB
xx
x
, với
≥≠0, 9xx
và
≠ 25.x
a) Rút gọn các biểu thức
A
và
;P
b) Đặt
= :.P AB
So sánh
P
với
1;
c) Tìm giá trị nhỏ nhất của
.P
26
VẤN ĐỀ 8. CĂN BẬC BA
A. TÓM TẮT LÝ THUYẾT
• Căn bậc ba của một số thực
a
là số thực
x
sao cho:
=
3
,xa
kí hiệu là
3
.a
• Mọi số thực
a
đều có duy nhất một căn bậc ba. Căn bậc ba của số dương là số dương;
của một số âm là số âm; của 0 là 0.
• Các công thức liên quan đến căn bậc ba:
<⇔ <
= ⇔=
=
33
33
33
3
.
.
. ..
AB A B
A B AB
AB A B
=
3
3
3
AA
B
B
với
≠ 0.B
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Thực hiện phép tính có chứa căn bậc ba
Phương pháp giải: Áp dụng công thức:
( )
= =
3
3
3
3
a aa
và các hằng đẳng thức:
( )
( )
3
3 2 23
3
3 2 23
33
33
a b a a b ab b
a b a a b ab b
+=+ + +
−=− + −
( )
( )
( )
( )
33 2 2
33 2 2
a b a b a ab b
a b a b a ab b
+=+ −+
−=− ++
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tính:
a)
3
27;
b)
3
1
;
125
c)
3
3
64 ;a
d)
−
3
36
8;ab
Bài 2. Thực hiện các phép tính sau:
a)
−+
3
33
2 24 81 4 192;
b)
−−
−
3
33
3
2
4 2.
21
Bài 3. Thực hiện các phép tính sau
a)
=+ +−
33
2 5 2 5;A
b)
= +− −
33
17 5 38 17 5 38.B
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 4. Tính
a)
3
729;
b)
3
1
;
216
c)
3
3
343 ;a
d)
3
36
512 .ab−
Bài 5. Thực hiện các phép tính sau
a)
3
33
2 27 3 8 4 125;−+
b)
3
3
3
27 1
64 1000;
512 3
−
+−
27
c)
3
33
3
3
9 3;
31
−−
−
d)
3
32
125 75 15 1.xxx+ ++
Bài 6. Thực hiện các phép tính sau:
a)
( )( )
3
5 1 6 2 5;++
b)
( )
( )
3
4 2 3 3 1;++
c)
3
33
27 64 216;−− +
d)
( ) ( )
33
33
91 91.+− −
Bài 7. Thực hiện các phép tính sau:
a)
33
7 52 7 52;A =+ +−
b)
33
9 45 9 45;B =+ +−
c)
36 3
2 5. 9 4 5 2 5 ;C

=− + ++


d)
33
11
2 10 2 10 .
27 27
D =+ +−
Dạng 2. So sánh các căn bậc ba
Phương pháp giải: Ta có
33
.A B AB< ⇔<
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 8. So sánh:
a)
3
23A =
và
3
23;B =
b)
33A =
và
3
3 133B =
.
Bài 9. So sánh:
33
20 40 2 20 14 2A =+ +−
và
2 5.B =
Bài 10. Tìm
x
biết:
a)
3
2 1 5;x + >−
b)
3
32
3 6 4 1. xxx x+ + +>+
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 11. So sánh:
a)
3
32A =
và
3
42;B =
b)
22A =
và
3
3 122;B =
c)
3
26A =
và
3
54;B =
d)
3
56A =
và
3
6 5.B =
Bài 12. So sánh:
33
7 52 7 52A =+ +−
và
2.B =
Bài 13. Tìm
x
biết:
a)
3
32 4x−>
; b)
3
32
3 6 3 1.xxx x− − + − >− −
Dạng 3. Giải phương trình chứa căn bậc ba
Phương pháp giải: Áp dụng
3
3
AB AB=⇔=
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 14. Giải các phương trình sau:
a)
3
2 1 3;x +=
b)
3
2 3 2.x−=−
Bài 15. Giải các phương trình sau:
a)
33
2 1 3;xx−+ +=
b)
33
13 22 5.xx−+ +=
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 16. Giải các phương trình sau:
28
a)
3
11 ;xx−+=
b)
3
5 5.xx+−=
Bài 17. Giải các phương trình sau:
a)
3
2 1 2 2 3;xx−+ + =
b)
33
12 2 23 2 5.xx−+ +=
C. BÀI TẬP VỀ NHÀ
Bài 18. Tính:
a)
3
512;
b)
3
1
;
125
−
c)
36
3
343
;
216
ab
−
d)
3
66
64 .ab−
Bài 19. Tính:
a)
3
33
1
27 8 125;
5
−−− −
b)
3
3
125 1
125 27;
512 3
+−
c)
3
32
3 3 1;xxx+ ++
d)
32
3
(8 12 6 1.x xx+ ++
Bài 20. Thực hiện các phép tính sau:
a)
3
3
3
3
135
54. 4;
5
−
b)
( )( )
33
33 3
25 10 4 5 2 ;−+ +
c)
3 33
64 125 216;−− +
d)
( )
( )
33
33
41 41.+− −
Bài 21. Thực hiện các phép tính sau:
a)
33
6 3 10 6 3 10;A = +− −
b)
33
7 52 7 52;B =+ +−
c)
3
3 3 10 6 3 ;C =++ +
d)
33 3
2 5. 9 4 5 2 5 .D

=− + ++


Bài 22. Thực hiện các phép tính sau:
a)
( )( )
3
2 1 3 2 2;++
b)
( )( )
3
4 2 3 3 1;−−
c)
( )
( )
33
33 3
96432−+ +
d)
33
5 31 5 31
4. 4. .
33 33
+ +−
Bài 23. Giải các phương trình sau:
a)
3
2 1 1;x +=
b)
3
2 3 3.x−=−
Bài 24. Giải các phương trình sau:
a)
3
22 ;xx−+=
b)
3
32
2 2.x xx+=+
Bài 25. Giải các phương trình sau:
a)
33
2 8 2;xx−+ +=
b)
33
1 7 2.xx++ − =
29
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I)
A. TÓM TẮT LÝ THUYẾT
1. Căn bậc hai số học
• Căn bậc hai của một số không âm là số
x
sao cho
2
.xa=
• Số dương
a
có đúng hai căn bậc hai là
a
(và gọi là căn bậc hai số học của
a
) và
.a−
• Số
0
có đúng một căn bậc hai là chính số
0
và nó cũng là căn bậc hai số học của
0.
• Với hai số không âm
,,ab
ta có
.ab a b<⇔ <
2. Căn thức bậc hai
• Với
A
là một biểu thức đại số, ta gọi
A
là căn thức bậc hai của
A
.
•
A
xác định (hay có nghĩa) khi
A
lấy giá trị không âm.
•
2
khi 0
.
khi 0
AA
AA
AA
≥
= =
−<
3. Liên hệ giữa phép nhân, phép chia với phép khai phương
• Khai phương một tích:
. . ( 0, 0)AB A B A B= ≥≥
• Nhân các căn bậc hai:
. . ( 0, 0)A B AB A B= ≥≥
• Khai phương một thương:
( 0, 0)
AA
AB
B
B
= ≥>
• Chia căn bậc hai:
( )
0, 0
AA
AB
B
B
= ≥>
4. Biến đổi đơn giản biểu thức chứa căn bậc hai
• Với
0A ≥
và
0B ≥
thì
2
AB A B=
• Với
0A <
và
0B ≥
thì
2
AB A B= −
• Với
0A ≥
và
0B ≥
thì
2
A B AB=
• Với
0A <
và
0B ≥
thì
2
A B AB= −
• Với
.0AB≥
và
0B ≠
thì
A AB
B
B
=
• Với
0B >
thì
A AB
B
B
=
• Với
0A >
và
2
AB≠
thì
2
()C CAB
AB
AB
=
−
±
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tìm điều kiện cho các biểu thức có nghĩa
Bài 1. Với giá trị nào của
x
thì các biểu thức sau có nghĩa:
30
a)
32x−+
b)
2
9 61xx−+
c)
2
23xx++
d)
2
1xx−+
e)
4
23x +
g)
5
.
11x−−
Bài 2. Với giá trị nào của
x
thì các biểu thức sau có nghĩa:
a)
21
2
x
x
−
−
b)
3
5
x
x
−
−
c)
2
4x −
d)
1
1
x
x
−
+
e)
2
3
1
x
x
−
−
g)
2
.
2x −
Dạng 2: Tính và rút gọn biểu thức
Bài 3. Thực hiện phép tính
a)
12 27 108 ;−+
b)
3 2 4 18 32 50− +−
;
c)
27 2 3 2 48 3 75−+ −
d)
3
10 28 2 275 3 343 396
2
−−−
.
Bài 4. Thực hiện phép tính
a)
1
8 18 6 200 ;
2
+− −
b)
3 23
62 4
2 32
+−
;
c)
8 32 18
6 5 14
9 25 49
−+
d)
16 1 4
236
3 27 75
−−
.
Bài 5. Thực hiện phép tính
a)
16 1 4
2 3 6 . 3 ;
3 27 75

−−



b)
8 32 18 1
6 5 14 .
9 25 49 2

−+



;
c)
( )
( )
5 22. 5 22+−
; d)
( )( )
2 32 3+−
.
Bài 6. Thực hiện phép tính
a)
( )
20 12 15 27 : 5 3 ;−
b)
( )
75 243 48 : 3+−
;
c)
( ) ( )
22
21 21++ −
;
d)
( )
28 2 3 7 7 84−+ +
.
Bài 7. Trục căn thức ở mẫu
a)
3
;
5
b)
23
;
2
c)
23
;
23
+
−
d)
1
;
32+
e)
21
;
21
+
−
g)
32
.
31+
Bài 8. Rút gọn biểu thức
a)
10 2 10 8
+ ;
5 21 5
+
+−
b)
2 8 12 5 27
18 48 30 162
−+
−
−+
;
31
c)
16 1 4
2. 3. 6 ;
3 27 75
−−
d)
23 23
23 23
−+
+
+−
;
Bài 9. Rút gọn biểu thức:
a)
( )
3 5. 3 5
;
10 2
−+
+
b)
416
31 32 33
++
+−−
;
c)
4 9 4 2 ;−+
d)
11
223 223
+
++ −−
;
Bài 10. Rút gọn biểu thức:
a)
3 5 3 5 ;−++
b)
;
c)
5 55 5
11
1515

+−
−−


+−

d)
4 10 2 5 4 10 2 5+ + +− +
.
Dạng 3. Giải phương trình và bất phương trình
Bài 11. Giải phương trình
a)
1 4 4 25 25 2 0 ;xx x−+ −− − +=
b)
16 16 9 9 4 4 1 16 ;x x xx+ − ++ ++ +=
c)
1
4 20 5 9 45 4 ;
3
xx x+ + +− + =
d)
1
2 8 18 10 2 ;
3
xx x− + −=
Bài 12. Giải các phương trình
a)
2
6 9 3 ;xx− +=
b)
2
8 16 2 ;xx x−+=+
c)
2
6 9 3 6 ;xx x− += −
d)
2
44250 ;xx x−+−+=
.
Bài 13. Giải các phương trình
a)
53 ;xx−=−
b)
45 25 ;xx−=−
c)
6 3 4 ;xx−= −
d)
5 9 2 ;xx−=−
.
Bài 14. Giải các phương trình
a)
5 3 ;xx−= −
b)
45 25 ;xx−=−
;
c)
22
21 4 41 ;xx xx−+= −+
d)
22
10 25 6 9 ;x x xx− += −+
.
Bài 15. Giải các phương trình
a)
1
3.
2
x
x
−
=
−
b)
11
.
2
1
x
x
+
=
−
c)
10
2.
2
x
x
+
= −
−
d)
35
.
31
x
x
x
+
=
+
Bài 16. Giải các phương trình
a)
2
45223.xx x+ += +
b)
2
9 20 2 3 10.xx x++= +
c)
2
7 14 2 4xx x++= +
d)
2
4 1 5 14x xx+= − +
Bài 17. Giải các phương trình
32
a)
55 1xx−+ −=
b)
2 3 32 0xx−+ − =
c)
( )
1
323
2
x y z xyz++ −+ −= ++
d)
42 4 1xy x y++= + −
Bài 18. Giải các phương trình
a)
2
4 3 3 4 3 22 1x x xx x+ += ++ −
b)
43 1 7x xx+− −=+
c)
2
4 6 10 27x xx x−+ −= − +
d)
2
2 6 48x xx x++ −= − +
Bài 19. Giải các bất phương trình
a)
1
1
2
x
x
−
<
−
b)
11
2
1
x
x
+
>
−
c)
10
2
2
x
x
−
≥−
+
d)
31
1
x
x
x
−+
>−
+
33
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II)
A. TÓM TẮT LÍ THUYẾT
Xem lại Tóm tắt lí thuyết trong ôn tập chủ đề 1, Phần I
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 4. Tìm các giá trị nguyên của biến để các biểu thức cho trước có giá trị nguyên
Bài 1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên
a)
1
3
x
x
−
−
b)
3
3
x
x −
Bài 2. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên
a)
61
x
x +
b)
2
3
x
x
−
−
Dạng 5. Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của biểu thức
Bài 3. Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
42Ax= −−
b)
4 10Bx x=−+
c)
Cx x= −
d)
2
2 41Dx x= − ++
Bài 4. Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
1
3
x
P
x
−
=
+
b)
3
1
x
Q
x
+
=
+
Bài 5. Tìm giá trị lớn nhất của các biểu thức sau:
a)
31Mx=−−
b)
61N xx= −−
c)
1
1
P
xx
=
−+
d)
5
3
x
Q
x
+
=
+
Dạng 6. Rút gọn biểu thức và các bài toán liên quan
Bài 6. Cho các biểu thức
2 1 3 11
9
33
xx x
A
x
xx
+−
=++
−
+−
và
3
1
x
B
x
−
=
+
với
09x≤≠
a) Tính giá trị của B khi
36;x =
b) Rút gọn biểu thức A;
c) Tìm số nguyên x để P = A.B là một số nguyên.
Bài 7. Cho biểu thức
364
1
11
xx
P
x
xx
−
=+−
−
−+
với
0; 1xx≥≠
.
a) Rút gọn P; b) Tìm giá trị của x để P = -1;
c) Tìm
x ∈
để
P ∈
; d) So sánh P với 1;
e) Tìm giá trị nhỏ nhất của P.
Bài 8. Cho biểu thức
11 2
:
21 1
xx x x
E
x x x xx x

++ −
= −+


−+ − −

với
0x ≥
và
1x ≠
a) Rút gọn E; b) Tìm giá trị của x để E > 1;
c) Tìm giá trị nhỏ nhất của E với
1x >
; d) Tìm
x ∈
để
E∈
;
34
e) Tìm x để
9
2
E =
.
Bài 9. Cho biểu thức
( )
2
1
22
.
12
21
x
xx
P
x
xx

−
−+
= −


−
++

với
0x ≥
và
1x ≠
a) Rút gọn P;
b) Tính giá trị của P khi
7 43x = −
;
c) Tìm giá trị của x để biểu thức P có giá trị lớn nhất.
Bài 10. Cho biểu thức
12 2
:2
1
11
xx
B
x
x xx x x


−
=−−



+
+ ++ +


với
0x ≥
a) Rút gọn B;
b) Tính giá trị của B khi
6 25x = +
;
c) Tìm giá trị nguyên của x để B có giá trị nguyên.
Bài 11. Cho biểu thức
26 19 2 3
23 1 3
xx x x x
P
xx x x
+− −
= −+
+− − +
với
0x ≥
và
1x ≠
a) Rút gọn P; b) Tính giá trị của x khi
4P =
;
c) Tìm giá trị nhỏ nhất của P; d) Tính P khi
3 22x = −
.
Bài 12. Cho biểu thức
( )
( )
25 3
:1
12
12
x
P
x xx
xx

−


=−+


− +−
−+


a) Rút gọn biểu thức
P
;
b) Tính
P
khi
6 25x = −
;
c) Tìm giá trị của
x
để
1
P
x
=
;
d) Tìm
x ∈
để
P ∈
;
e) Tìm
x
để
1Px<−
;
f) Tìm giá trị nhỏ nhất của
P
.
Bài 13. Cho biểu thức
1
:
1
xx
P
x x xx

= +

++

với
0x >
.
a) Rút gọn
P
;
b) Tìm
x
để
1P = −
;
c) Tính
P
tại
88
51 51
x = −
−+
;
d) Tìm
x
để
2Px>+
;
e) So sánh
P
với
1
;
f) Tìm giá trị nhỏ nhất của
P
.
Bài 14. Cho các biểu thức
13
11
xx
A
x xx
−+
= −
−−
và
2
1
x
B
xx
+
=
++
.
a) Tính giá trị
B
tại
36x =
;
b) Rút gọn
A
;
c) Cho biết
( )
:1PA B= −
. Tìm
x
để
1P ≤
.
35
Bài 15. Cho biểu thức
1 11
:
xx
Px
x x xx

−−

=−+


+


.
a) Rút gọn
P
;
b) Tính giá trị của
P
biết
2
23
x =
+
;
c) Tìm
x
thỏa mãn :
63 4Px x x= −− −
.
Bài 16. Cho biểu thức
11
1:1
11 1 1
xy x xy x
xx
P
xy xy xy xy

++
++
= + +− −


+− − +

.
a) Rút gọn
P
;
b) Cho
11
6
xy
+=
. Tìm giá trị lớn nhất của
P
.
Một số bài tập nâng cao
Bài 17. Giải phương trình:
a)
( )
1
2 2009 2010
2
x y z xyz−+ + + − = ++
.
b)
( )
2
3 3 1 3 2 1 11x x x x xx− − = + −− ++
.
Bài 18. Cho
22
, 0; 16ab a b> +≤
. Tìm giá trị lớn nhất của biểu thức:
( ) ( )
98 98M a ba b b ab a= ++ +
.
Bài 19. Cho
25
,,
4
abc>
. Tìm giá trị nhỏ nhất của biểu thức:
2 52 5
25
abc
P
ca
b
=++
−−
−
.
Bài 20. Cho
,, 0abc>
và
1ab bc ca++=
. Chứng minh:
( )
222
1 1 12a b c abc++ ++ +≤ ++
.
Bài 21. Cho hai số thực
,ab
thay đổi, thỏa mãn điều kiện
1ab+≥
và
0a >
. Tìm giá trị nhỏ
nhất của
2
2
8
4
ab
Ab
a
+
= +
.
Bài 22. Cho
,xy
thỏa mãn điều kiện
22
22xyyx+− = +−
. Tìm giá trị nhỏ nhất của
22
2 2 2 10A x xy y y=+ − ++
.
Bài 23. Với mọi
1a >
, chứng minh :
1
3
3
a
a
+≥
−
.
36
HƯỚNG DẪN – ĐÁP SỐ
CHỦ ĐỀ 1. CĂN BẬC HAI. CĂN BẬC BA
VẤN ĐỀ 1.
Bài 1. Căn bậc hai của các số đã cho lần
lượt là:
±± ±
3
0; 8; ; 0,2
4
;
Căn bậc hai số học của các số đã cho lần
lượt là:
3
0;8; ;0,2.
4
Bài 2. a)
144;
b) Không tồn tại;
c)
8
;
7
d)
1
.
75
Bài 3. a)
3;
b)
2
;
5
c)
3;−
d)
6;−
e)
3
;
4
−
g)
7.
Bài 4. a)
4;
b)
3,1;
c)
1
;
6
d)
2.−
Bài 5. a)
4;x = ±
b)
13;x = ±
c) Không có giá trị nào của
;x
d)
25;x =
e)
36;x =
g)
3x = −
hoặc
5.x =
Bài 6. Căn bậc hai của các số đã cho lần
lượt là:
11
9; 0,5; 1,2; ;
9
±± ± ±
Căn bậc hai số học của các số đã cho lần
lượt là:
11
9;0;5;1,2; .
9
Bài 7. a)
169;
b) Không tồn tại;
c)
1
;
10
d)
6
.
125
Bài 8. a)
11;
b)
4
;
5
c)
8;−
d)
2;
e)
1
;
4
−
g)
3
.
5
Bài 9. a)
1;
b)
4,65;
c)
2
;
3
−
d)
6.
Bài 10. a)
1
;
3
x = ±
b)
;x ∈∅
c)
256
;
9
x =
d) Không có giá trị nào của
x
e)
17;x =
g)
6x =
hoặc
2.x = −
Bài 11. a)
2 3;−<
b)
3 2 2;>
c)
11 99;>
d)
25 18 2 17;<+
e)
3 15 1;>−
g)
1 3 0,2.−<
Bài 12. a)
36;x ≥
b)
0 1;x≤<
c)
35;x ≤−
d)
13
.
22
x
−
≤≤
Bài 13. a)
2 0 0;xx x⇔ ≥≥⇔≥
b)
2
02 0xx x⇔≤ ≤ ⇔=
hoặc
2.x ≥
Bài 14. a)
2 1 2;<+
b)
3 11 12;<
c)
1 3 1;>−
d)
3 2 5;>−
e)
10 2 23;
− <−
g)
3 29 15.
− <−
Bài 15. a)
24;x ≥
b)
1 3;x−≤ <
c)
31;x <−
d)
13
.
22
x
−
≤≤
Bài 16. Căn bậc hai của các số đã cho lần
lượt là:
±±± ± ± ±
13 7
15; 18; ; ; 1,5; 0,4;
10 17
Căn bậc hai số học của các số đã cho lần
lượt là:
13 7
15;18; ; ;1,5;0,4.
10 17
Bài 17. a)
49;
b)
9
;
16
c)
3
;
2
d)
1
.
8
Bài 18. a)
5;
b)
7
;
5
c)
−111;
d)
13;
e)
7;
g)
−
1
.
400
Bài 19. a)
12;
b)
−
7
;
20
c)
−
11
;
4
d)
−
13
.
4
Bài 20. a)
= ±14;x
b)
= ±
1
;
15
x
c)
= ±18;x
d) Không có giá trị nào của
;x
e)
= 7;x
g)
=
100
.
9
x
37
Bài 21. a)
=
290
;
3
x
b)
=
19
3
x
hoặc
= −
17
;
3
x
c) Không có giá trị nào của
;x
d)
=
9
;
4
x
e)
= 16;x
g)
=
13
.
4
x
Bài 22. a)
≤≤0 484;x
b)
>
37
;
2
x
c)
≥ 22;x
d) Không có giá trị nào của
.x
Bài 23. a)
>+4 1 7;
b)
<2 5 8;
c)
− <−6 2 7;
d)
>−4 23 1;
e)
>−0,5 3 2;
g) So sánh:
( )
+
2
2005 2008
và
( )
+
2
2016 2017
.
Từ đó quy về so sánh:
( )
2015.2018 2016 1 2018
2016.2018 2018
= −
= −
và
( )
= −2016.2017 2016 2018 1
= −2016.2018 2016
⇒+<+2015 2018 2016 2017.
Bài 24. * Giả sử
( )
∃∈ =, :, 1mn mn
và
=⇒=
22
33
m
mn
n
⇒ ⇒ ⇒∃ ∈ =
2
3 3 : 3.m m k mk
⇒ = ⇒= ⇒
2 22 22
93 3 3k nnkn
( )
⇒⇒ ≠3 ,1n mn
. Vô lý!
* Chứng minh tương tự ta được
7
là số
vô tỷ.
Bài 25. a) Đặt
= + 2yx
⇒ =+⇒= −
22
22y x xy
⇒= − −
2
2 2;Ay y
b) Ta có:
( )
= − − ≥−
2
133Ay
Từ đó tìm được:
= −
min
3A
tại
= 1y
hay
= −1.x
Bài 26. a) Ta có:
>>
11 1
1 ; ;...;
100 2 100
>⇒
11
99 100
đpcm
b) Ta có:
<43
⇒+ <+<
⇒++ <+<
⇒++++
< +<
4 4 43 3
444 433
4 4 4 ... 4
4 3 3.
VẤN ĐỀ 2.
Bài 1. a)
−8
;
15
b)
128;
c)
21
;
20
d)
12
.
5
Bài 2. a)
5;
b)
4;
c)
7;
d)
1.
Bài 3. a) Ta có:
( )
+=+ +
= +
2
11 6 2 9 2.3. 2 2
3 2;
b) Ta có:
( )
−=− +
= −
2
8 2 7 7 2. 7.1 1
71
c) Áp dụng kết quả câu a);
d) Áp dụng kết quả câu b).
Bài 4. a)
2 2;
b)
−2 5;
c)
6 5;
d)
4 5.
Bài 5. a)
1;
b)
2,5;
c)
−1;
d)
90.
Bài 6. a)
3;
b)
5;
c)
8;
d)
6.
Bài 7. Tương tự Bài 3.
Bài 8. a)
4;
b)
12;
c)
−4;
d)
4 3.
Bài 9. a)
−50 ;a
b)
10 ;a
c)
2
10 ;a
d)
−
3
15 .a
Bài 10. a)
+3 2;x
b)
+4 3;x
c)
−3 3;x
d)
>
−<
1 khi 2
.
1 khi 2
x
x
Bài 11. a)
−32 ;a
b)
11 ;a
c)
2
11 ;a
d)
−
3
33 .a
Bài 12. a)
+3 1;x
b)
−4 3;x
c)
−4 5;x
d)
>−
− <−
1 khi 2
.
1 khi 2
x
x
Bài 13. a)
−0,63;
b)
1
;
30
c)
86;
d)
−13.
Bài 14. a)
22;
b)
−8 6;
c)
3;
d)
8.
Bài 15. Tương tự Bài 3.
38
Bài 16. a)
2 5;
b)
−2;
c)
2 2;
d)
6.
Bài 17. a)
≥
−<
10 khi 0
;
6 khi 0
aa
aa
b)
≥
−<
3
3
3 khi 0
.
12 khi 0
aa
aa
Bài 18. a)
6;
b)
2.
Bài 19. a)
+ 2;a
b)
6 6.
VẤN ĐỀ 3
Bài 1. a)
≥ 2;x
b)
≤
7
;
6
x
c)
<
1
;
3
x
d)
≥
2
.
3
x
Bài 2. a)
≤≤
3
6;
5
x
b)
≤<2 5;x
c)
≥ 9;x
≤−1;x
d)
−≤ ≤4 4.x
Bài 3. a)
≥
3
;
2
x
b)
≤ 0;x
c)
≤
1
;
4
x
d)
∈.x
Bài 4. a)
> 1;x
b)
≤−7;x
c)
≤<3 4;x
d)
>
2
.
3
x
Bài 5. a)
2x ≤
hoặc
6x ≥
b)
1x ≤−
hoặc
5x ≥
c)
3x ≤−
hoặc
3x ≥
d)
11x−≤ ≤
Bài 6 . a)
175x =
;b)
x ∈∅
; c)
1
2
x =
;
d)
3x =
; e)
1x =
hoặc
5
3
x =
g)
2x =
.
Bài 7. a)
0x =
; b)
1x =
;c)
1
10
x =
;
d)
3x =
; e)
5x =
hoặc
7
3
x = −
g)
4x =
.
Bài 8. a)
2x ≤−
b)
x ∈
; c)
x ∈
d)
2x =
.
Bài 9.a)
7x >−
; b)
1x ≤
hoặc
2x ≥
;
c)
35x−≤ ≤
; d)
2; 3xx<>
.
Bài 10. a)
0x =
; b)
x ∈∅
; c)
7
2
x =
;
d)
0x =
hoặc
3x =
.
Bài 11. a)
x ∈∅
;b)
1
9
x
−
=
; c)
3x = −
;
d)
3
2
x =
.
Bài 12.Cách 1. Ta có :
( )
2
22
12 1 2x y xy x y+ =+ ≤+ + =
⇒
đpcm.
Cách 2. Sử dụng BĐT Cauchy –
Schwartz :
( )
( )( )
2
2222
.ab cd a c b d+ ≤+ +
b) Cách 1 . Theo BĐT AM-CM, ta có :
111111 111
22
11 1 1 1 1
2
xyz xy yz
zx
xy yz xz

++= + + +



+ +≥ + +


Cách 2. Xét hiệu :
2
2
2
11 1
2
11 1 11 1
0.
22
VT VP
xy
yz zx


−= −





+ −+ −≥




Bài 13. a)
2 1 3 2 2;Ax x≥−+−=
min
2A =
khi
12
23
x≤≤
.
b) Áp dụng
22 22
ab cd++ +
( ) ( )
22
ac bd≥ + ++
, ta có :
2
11 320
7
7 49
Bx

= −+


+
2
11 320
7 6.
7 49
x

+ +≥


Từ đó
min
6B =
tại
0.x =
Bài 14.Ta có :
( ) ( )
22
11 22xy−− + −−
( )
2
33 0z+ −− =
2, 6, 12xyz⇔= = =
.
VẤN ĐỀ 4
Bài 1. a)
60
; b)
6
; c)
20
; d)
26
.
39
Bài 2 .a)
3
13
; b)
5
4
c)
10
; d)
5
.
Bài 3. a)
2;
b)
12
; c)
2
;
d)
36 36 2 27 3.−+
Bài 4. a)
30
3
; b)
4
7
; c)
10
; d)
7 12 3
3
−
.
Bài 5.a)
80
;
9
10
; c)
110
; d)
26
.
Bài 6. a)
5
8
; b)
5
3
; c)
3
; d)
56
9
.
Bài 7. a)
3
; b)
20
; c)
4 26+
; d)
2
.
Bài 8 . a)
8
11
; b)
0
; c)
2
3
; d)
51
2
−
.
Bài 9.a)
5
2
; b)
5
2
; c)
6
2
−
d)
22−
.
Bài 10. a)
a−
; b)
x
xy+
;
c)
xy
xy+
; d)
1
21
a
a
−
−
.
Bài 11.a)
21
7
;b)
10
2
; c)
1−
; d)
4
.
Bài 12. a)
x
xy−
; b)
a
; c)
0
;
d)
xy
xy−
.
Bài 13. a)
6
; b)
25
; c)
3
14
; d)
13
9
.
Bài 14. a)
22
; b)
0
; c)
60
; d)
196
45
.
Bài 15. a)
12 5 6−
; b)
7
; c)
22
;
d)
43 72−
.
Bài 16. a)
3x −
; b)
1
2x +
;
c)
2
2
x
x
−
+
; d)
1
5x +
.
VẤN ĐỀ 5
Bài 1. a)
10
2
; b)
1
; c)
23
2
+
;
d)
2015
.
Bài 2. a)
66
; b)
1,6
; c)
0,16−
; d)
28
.
Bài 3. a)
27 24 5+
; b)
65 9−
.
Bài 4. a)
( )
36 1 a−
; b)
2
a−
; c)
2
a
; d)
12 .a
Bài 5. a)
2ab b
ab
−
−
; b)
23
23
ab
ab
+
−
.
Bài 6. a)
2
96 5aa−−
; b)
( )
3
3
4
a−
;
c)
3y
; d)
2
22
b
a
−
.
Bài 7. a)
a−
; b)
2x +
; c)
1
3x +
;
d)
x
xy−
.
Bài 8. a)
1
2
x =
; b)
3
2
x
−
=
,
7
2
x =
;
c)
2x =
hoặc
3x = −
; d)
9x =
.
Bài 9. a)
1x = −
hoặc
9x =
; b)
6x =
;
c)
3x =
; d)
28x =
.
Bài 10. a)
1x = −
; b)
12
7
x =
; c)
2x =
;
d)
34
9
x =
.
Bài 11. a)
4 10
; b)
5
12
; c)
15
; d)
8
5
.
Bài 12. a)
3
; b)
6
2
−
; c)
6 45+
; d)
4.
Bài 13. a)
1
1
x
x
−
+
; b)
3
xy−
;
c)
1
7x +
; d)
xy
xy+
.
Bài 14. a)
2, 12xx=−=
; b)
1x = −
;
c)
3
5
x =
; d)
105
16
x =
.
Baì 15. a) Vô nghiệm; b)
1x = −
;
c)
1
2
x =
; d)
3
2
x =
.
40
Bài 16: Ta có:
( )
44 4
5 4 12 4xx x+= + +≥ +
4
4
5
2
4
x
x
+
⇒≥
+
. Dấu “ = “ không
xảy ra nên ta có đpcm.
VẤN ĐỀ 6
Bài 1. a)
7x
; b)
22y−
; c)
5xx
;
d)
2
43y
.
Bài 2. a)
2
13x
; b)
2
2x−
; c)
15x
;
d)
15x−−
.
Bài 3. a)
13x
; b)
23y−
; c)
9xx
;
d)
4
43y
.
Bài 4. a)
2
13x
; b)
2
3x−
; c)
27y
;
d)
27y−−
.
Bài 5. a)
52 43>
; b)
51 1
6
2 6 37
>
.
c)
2 29 3 13<
; d)
5 33
2
4 22
>
.
Bài 6. a)
2 6; 29;4 2;3 5
;
b)
38;2 14;3 7;6 2
.
Bài 7. a)
35 27>
; b)
31 1
6
2 3 14
<
;
c)
3 21 2 47>
;d)
52
3 14
97
<
.
Bài 8. a)
7 2;5 2;2 8; 28
;
b)
5 30;2 40;3 8;2 5
.
Bài 9. a)
43
; b)
7 a−
.
Bài 10. a)
8a−
; b)
3
9a−
; c)
23
;d)
0
.
Bài 11. a)
46−
; b)
4a−
.
Bài 12. a)
7a
; b)
2x−
; c)
2x
; d) -
2x
.
Bài 13. a)
6
3
; b)
5
5
x
; c)
5
7
a ab
b
;
d)
73xy−
.
Bài 14. a)
25
; b)
6
3
−
; c)
10 6
2
+
;
d)
23−
.
Bài 15. a)
115−
; b)
1
2
; c)
1
; d)
10
7
.
Bài 16. a)
14
7
;b)
31
31
x
; c)
5
7
bb
a
;
d)
7 13xy−
Bài 17. a)
5
; b)
2
2
; c)
33 22
19
−+
;
d)
35
2
−
.
Bài 18.
) 2 ; )4; ) 1;a bc
)5 3 22d 
Bài 19.
) 5 ; ) 19 11 7;ab
211 37
) 14; )
19
cd

Bài 20.
2
) 5 ; ) ; ) 1; )6.aa b x c d
Bài 21.
5
) 25; ) ; )2 2 6; ) 2.
5
a bc d
Bài 22.
23 3
) 10 ; ) ; )4 7; ) 8.
15
a b cd
Bài 23.
1
) ; )2; )0; )2.
2
a bcd
Bài 24.
) 9; ) 4;a x bx
) 64; ) 6.cx dx
Bài 25
37
) ; ) 9;
22
a x x bx
) 2; ) 3.cx dx
Bài 26.
) 0; ) 0; 4; 2a x y bx y z
Bài 27.
1n
.
Bài 28.
1 1 11 2A xx  
Dấu “=” xảy ra khi
12x
.
Bài 29.
Chú ý:
12
2( 1 )
1
kk
k kk


41
Bài
30.
2002 2003
( 2003) ( 2002)
2003 2002

11
0
2002 2003

.
VẤN ĐỀ 7.
Bài 1.
92
) 8 2 ; ) ; ) 3; )5.
2
a b cd
Bài 2.
) 6 5 ; )2a a ba
.
Bài 3.
73
) ; )22; )2; )10.
6
a b cd
Bài 4.
1
) ; )12 .
3
a b a aa
Bài 5. a) Học sinh tự làm.
2
2
).
ab
ab
b VT a VP
a
b
b

.
Bài 6.
6( 2 1) 6 6 1
) ( ).
3
2( 2 1) 6
6 13
( 2 6)
22
6
44
)
2( )( )
2
()
a VT a
VP
V
P
ab b
b VT
a ba b
b
VP
ab




Bài 7.
1
) ) 1 2
2 ) 49
3
)0 9; 4 ) 1;16;25;49
x
aM bM cx
x
d x x ex


Bài 8.
7
) )4)1)5
6
aA bx cB dx 
.
Bài 9.
1
) )0 9;
1
1
x
aP b x x
x

max
) 4 ) 0 ) 1; 0cx dx cP x 
.
Bài 10.
) 17 3 ; )6; ) 5; ) 6 3a bc d
Bài 11.
15 7 1
) ; ) 4; ) ; )0.
72
a bc d
Bài 12.
1 3 23
) ;) ;
3
1
x
aQ b
x

) 4; ) 1 ) 0;4;9cx dx e
Bài 13.
2
( 1) 3( 3 1)
) );
2
x
aP b
x

) 4.cx
Bài 14.
1
) ; )0
1;
2
x
aP b
x
x

min
1
) ; 0.
2
cP x
Bài
15.
) 1;aP x x
min
3 7 35
) ; 0) .
42
bP x c x

Bài 16.
) ;) ;
35
xx
a A bB
xx


) 64; ) 6.cx dx
VẤN ĐỀ 8
Bài 1.
2
1
) 3 ) ; )4 ) 2
5
a b c a d ab
Bài 2.
3
) 11 3; )2ab
.
Bài 3.
) 1; ) 4aA bB
.
Bài 4.
2
1
)9; ) ; )7 ; ) 8 .
6
a b c a d ab
Bài 5.
33
7 393
)20; ) ; )
24 2
ab c

)5 1.cx
Bài
6.
) 5 1; ) 3 1; ) 1; )18 3 2.a b cd 
Bài 7.
) 2 2 ; )3; ) 2; )2a bc d
.
Bài 8.
) ;) .aAB bAB
Bài 9.
AB
.
Bài 10.
) 63; ) 1ax bx 
.
Bài 11.
) )) )aABbABcABdAB 
Bài 12.
AB
.
Bài 13.
61 2
))
29
ax bx
.
42
Bài 14.
10
) 13 )
3
ax bx
.
Bài 15.
) 3 ) 14; 5ax bx x 
.
Bài 16.
) 0;1;2 ) 6; 5; 4ab
.
Bài 17.
15
) 1) ; 2
2
ax bx x 
.
Bài 18.
2 22
17
)8 ) ) ) 4
56
a b c ab d a b
.
Bài 19.
45
)6 ) 3 ) 1 )2 1
8
a b cx d x
.
Bài 20.
3
)18 )7 ) 3 )6 16 2a bc d
.
Bài 21.
)2 )2 2 ) 3 1 ) 2ab c d
.
Bài 22.
)2 1 )3 1)5 )1a b cd
.
Bài 23.
29
) 0)
3
ax bx
.
Bài 24.
) 3; 1; 2 ) 2; 1ab
.
Bài 25.
) 1 ) 1; 7ax bx x 
.
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I)
Bài 1.
2
) ; ) ;) ;
3
a x bx c x
3
) ; ) )1 2.
2
dx ex g x 
Bài 2.
1
) 2; )3 5;
2
a x bx 
) 2; 2 ) 0;
) 0; 1 ) 0; 4
cx x dx
exx gxx

 
Bài 3.
) 5 3 ; ) 10 2;ab
) 6 3 ) 19 11 7cd 
.
Bài 4.
6 23 3
) 82 ) ;)62 )
6 15
a bcd
.
Bài 5.
23
) ; )6; ) 3; )21.
5
a bc d
Bài 6.
) 1; )10; )6; )21.a b cd
Bài 7.
35
) ; ) 6; )7 4 3;
5
a bc
36 32
) 3 2; )3 2 2 ) .
2
d dg

Bài 8.
6 23 3
) 2 ) ; ) )4
2 15
ab c d
.
Bài 9.
) 1; ) 7; ) 2 1; ) 2.ab c d
Bài 10.
) 10; )14; )4; )1 5 .a b cd
Bài 11.
) 2; ) 15;ax bx
81
) 1; ) .
2
cx dx
Bài
12.
9
) 0; 6 ; ) 1; ) ) 3.
2
axx bxcxdx
Bài 13.a) Vô nghiệm.
19
) 0; ) 2; ) .
4
bx cx dx 
Bài 14. b) Vô nghiệm. c) Vô nghiệm.
2
) 0; ; ) 4.
3
cx x dx
Bài 15.
25
);
4
ax
b) Vô nghiệm.
c) Vô nghiệm.;
25
).
9
dx
Bài 16.
) 1; ) 3;ax bx 
) 3; ) 3.cx dx
Bài 17. a) Vô nghiệm.
3
)
2
bx
) 2, 3, 4 ; ) 1 ; 5.cx y z dx y
Bài 18.
) 1; ) 1; ) 5; ) 2.axbxcx dx
.
Bài 19.
)0 4 ) 1;a x bx
) 4; ) 0; 1.cx dx x 
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II)
Bài 1
) 1; 4;16;25 ;ax
) 0;4;16;36;144 .bx
Bài 2.
) 0 ) 4;16;100 .ax bx
Bài 3.
min
) 2; 4;aA x
min
) 6; 4.bB x
c)
min
1
4
C = −
khi
1
;
4
x =
d)
min
31D = +
khi
1.x =
Bài 4. a)
min
1
3
E = −
khi
0;x =
b)
min
22 2F = −
khi
1.x =
43
Bài 5. a)
max
3M =
khi
1;x =
b)
max
8N =
khi
9;x =
c)
max
4
3
P =
khi
1
;
4
x =
d)
max
5
3
Q =
khi
0;x =
Bài 6. a)
3
;
7
B =
b)
3
;
3
x
A
x
=
−
c)
0x =
hoặc
4.x =
Bài 7. a)
1
;
1
x
P
x
−
=
+
b)
x 0;=
c)
0;x =
d)
1;P <
e)
max
1P = −
khi
0.x =
Bài 8. a)
( )
1
;
1
xx
E
x
+
=
−
b)
x 1;>
c)
min
9E =
khi
4;x =
d)
{ }
4;0;9 ;x ∈
e) Vô nghiệm.
Bài 9. a)
( )
1;P xx=−−
b)
3 3 5;P = −
c)
max
1
4
P =
khi
1
.
4
x =
Bài 10. a)
( )
1
;
21
x
B
x
−
=
+
b)
5 25
;
2
B
−
=
c)
1.x =
Bài 11. a)
16
;
3
x
P
x
+
=
+
b)
4;x =
c)
min
4P =
khi
4;x =
d)
42 23 2
.
2
−
Bài 12. a)
21
;
1
x
P
x
−
=
+
b)
10 5 3
;
5
−
c)
23
;
2
x
+
=
d)
0, 4;xx= =
e)
0 3 1;x≤≤ −
g)
min
1P =
khi
0.x =
Bài 13. a)
21
;
x
P
x
+
=
b) Vô nghiệm; c)
5
;
2
P =
d)
0 1;x<<
e)
1;P >
f) Không có GTNN.
Bài 14. a)
38
;
43
B =
b)
2
;
1
A
xx
=
++
c)
01x≤<
hoặc
9.x ≥
Bài 15. a)
( )
2
1
;
x
P
x
+
=
b)
3 33
;
2
+
c)
4.x =
Bài 16. a)
1
;P
xy
=
b)
max
9P =
khi
1
.
9
xy= =
Bài 17. a)
3; y 2008;z 2011.x ==−=
b)
( )( )
31 31 10x xx x−− −− + =
1x⇔=
hoặc
35
.
2
x
±
=
Bài 18. Ta có
max
20736M =
khi
2 2.ab= =
Bài 19.
Đặt
2 5 ,2 5 ,2 5 .a xb yc z−= −= −=
Biến đổi
P
theo
,,,xyz
ta được:
min
33
4
P =
khi
25.abc= = =
Bài 20. Ta có
( )( )
22
1
2
.
2
a ab bc ca a
abc
abac
+ = +++
++
= + +≤
Áp dụng tương tự với
2
1 b+
và
2
1.c+
Bài 21.
min
3
2
A =
khi
1
.
2
ab= =
Bài 22
min
9A =
khi
1.xy= = −
Bài 23. Ta có
( )
1
1 1.
1
VT a
a
=−+ +
−
44
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

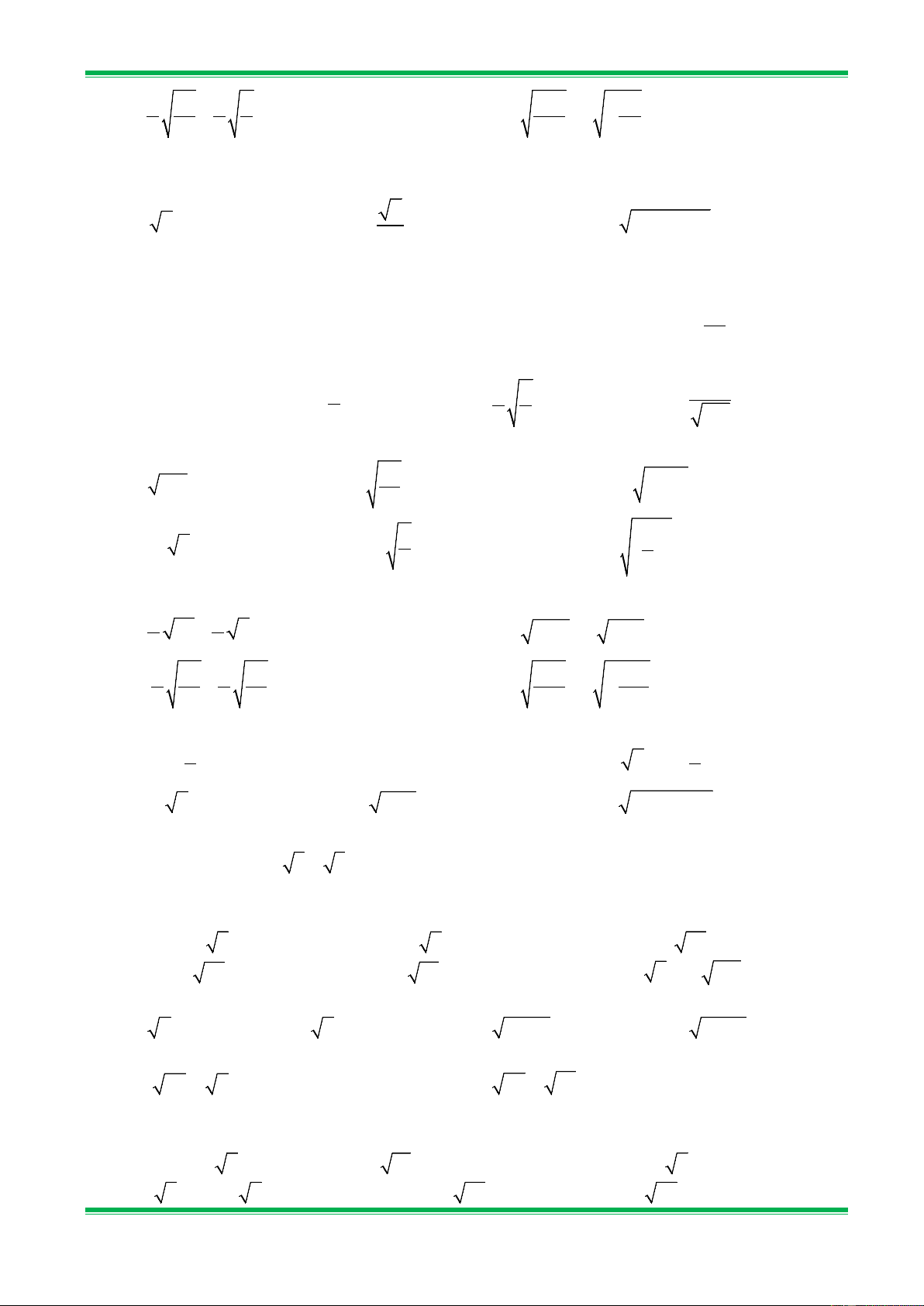
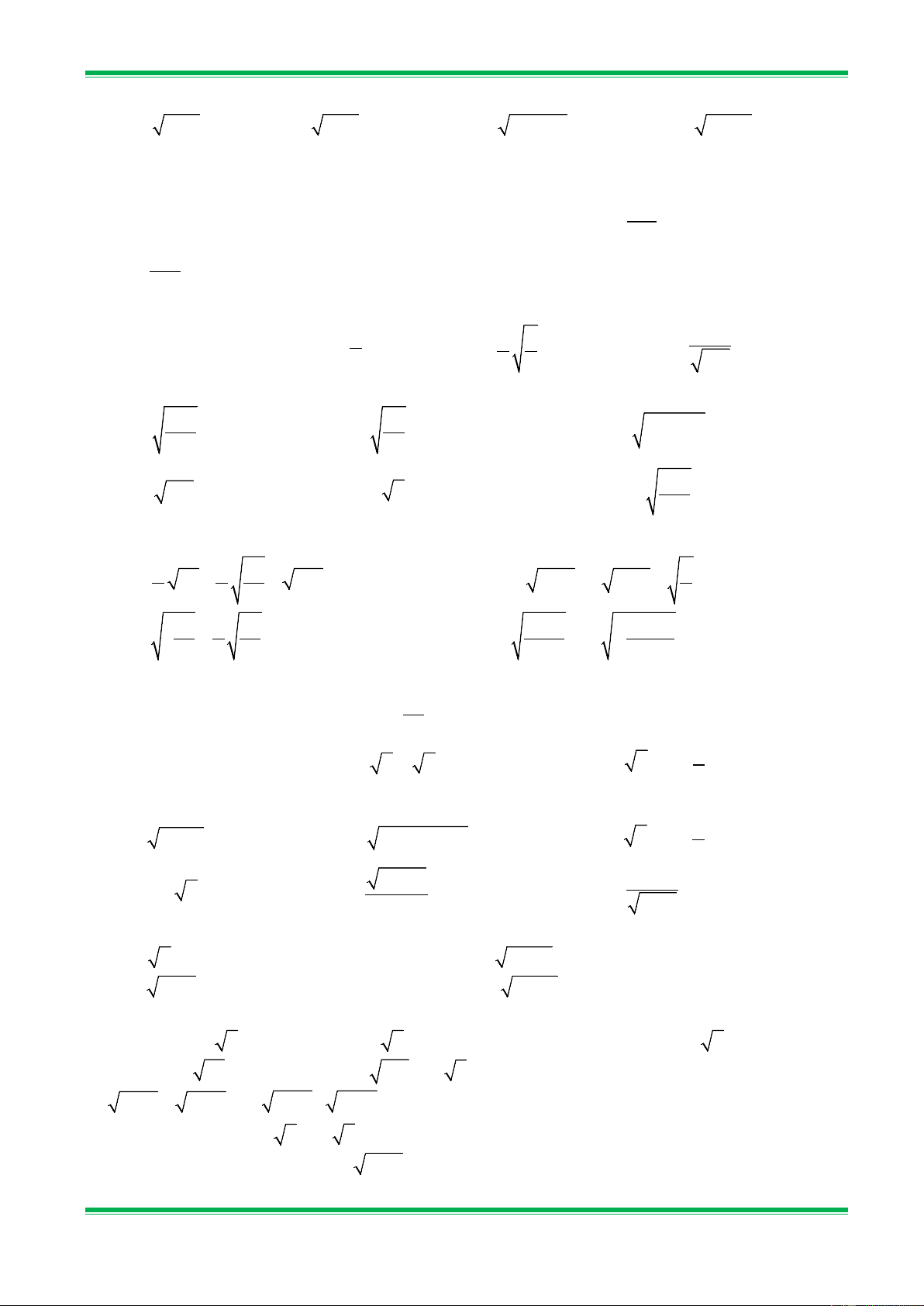
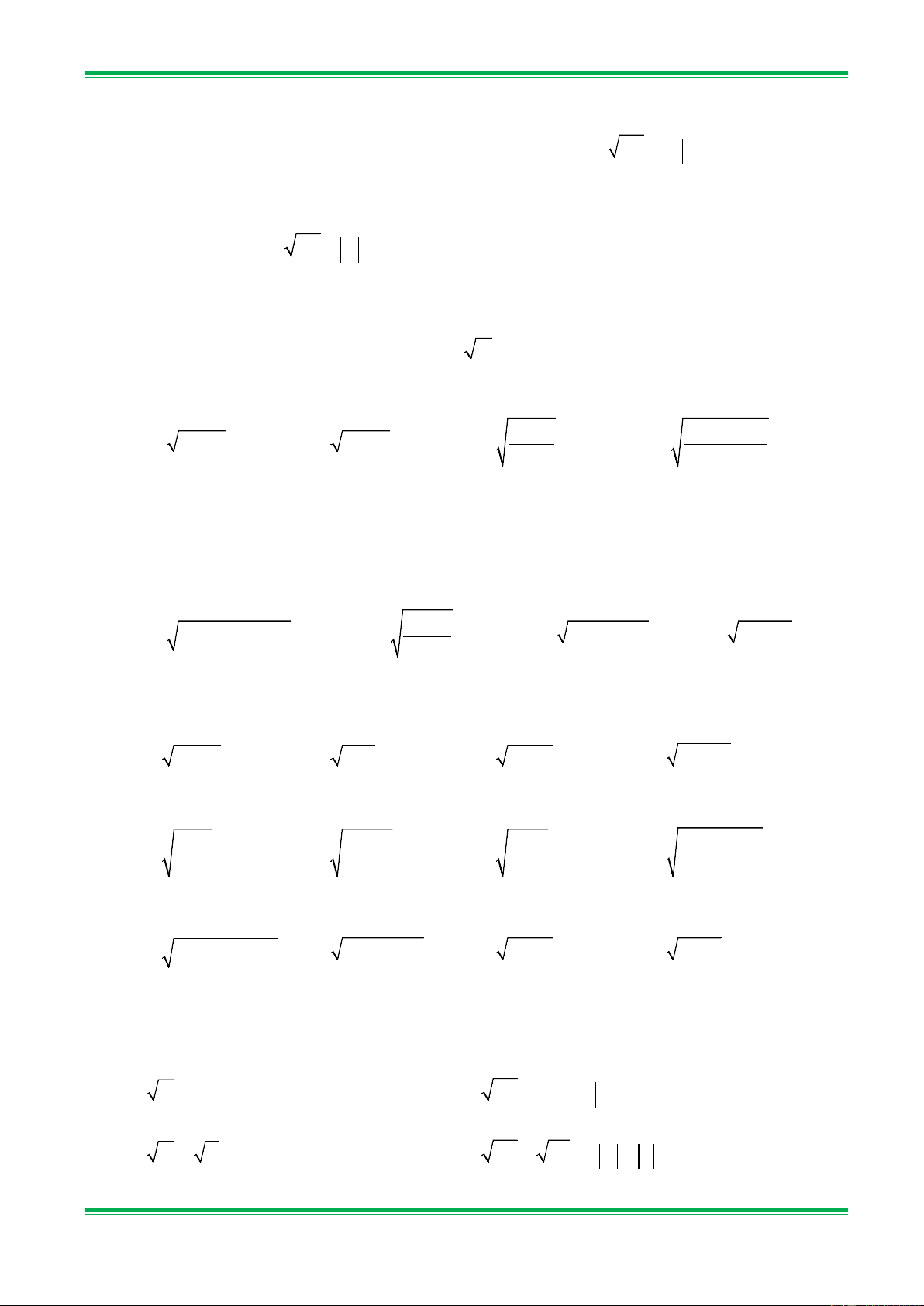
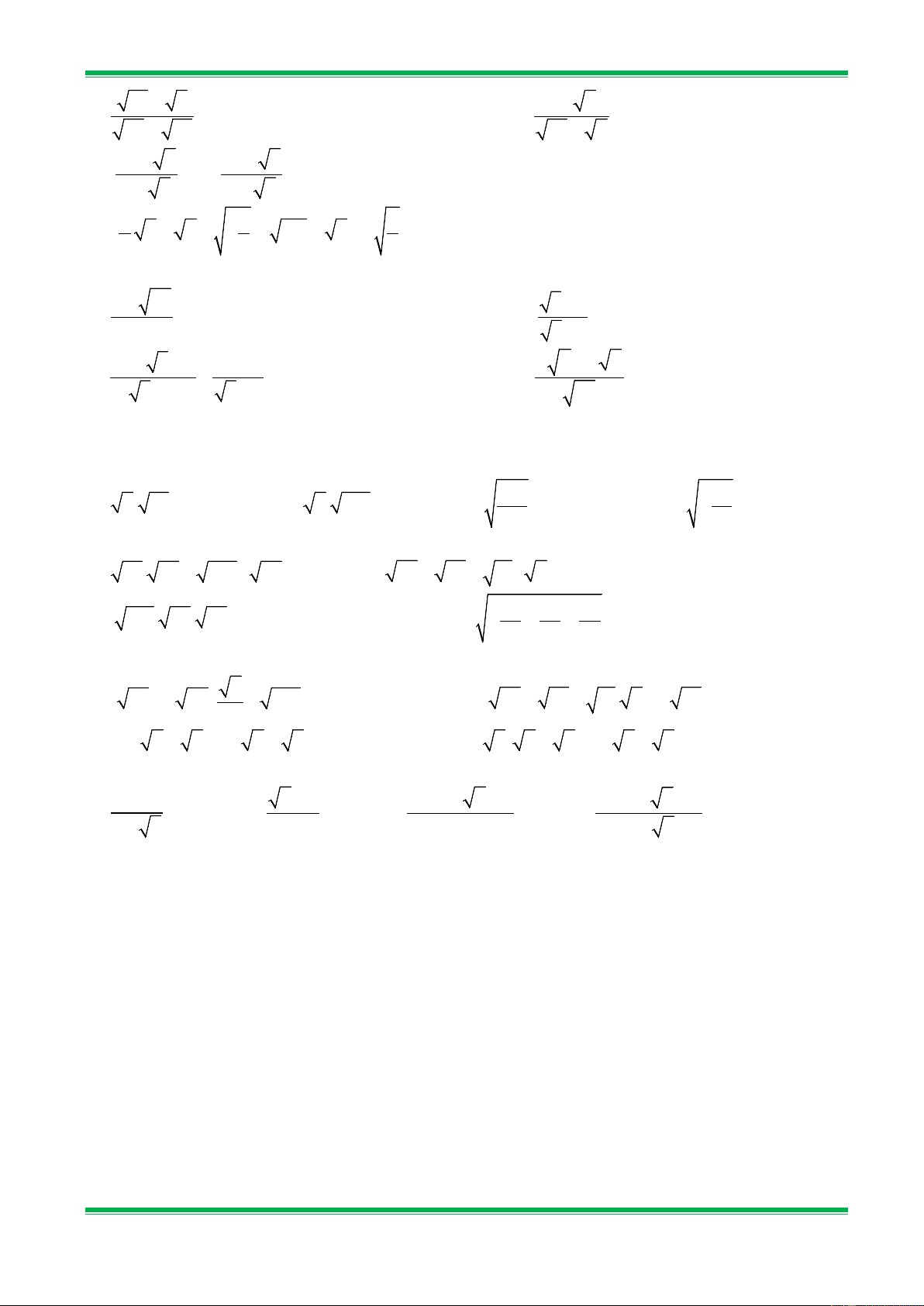
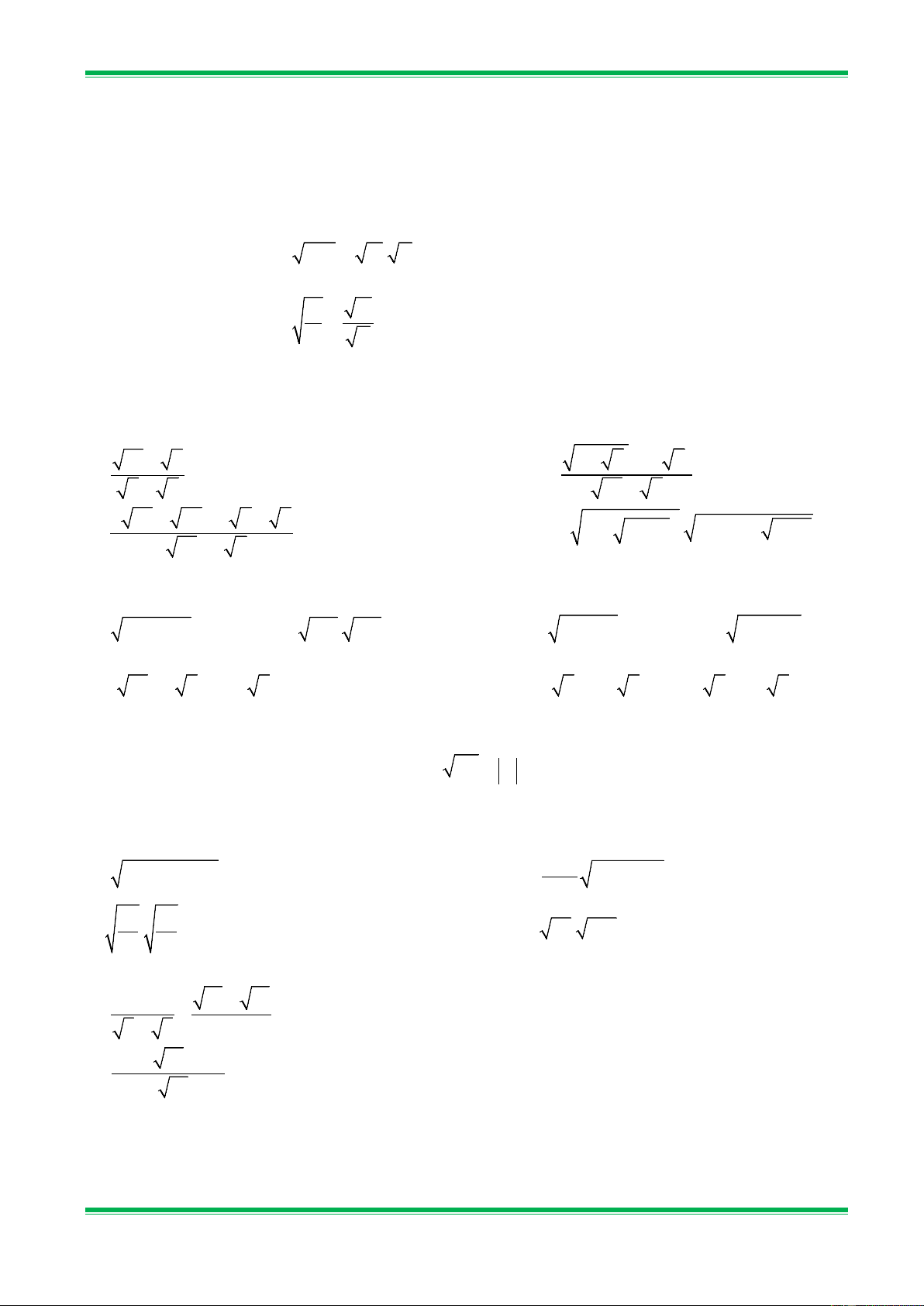
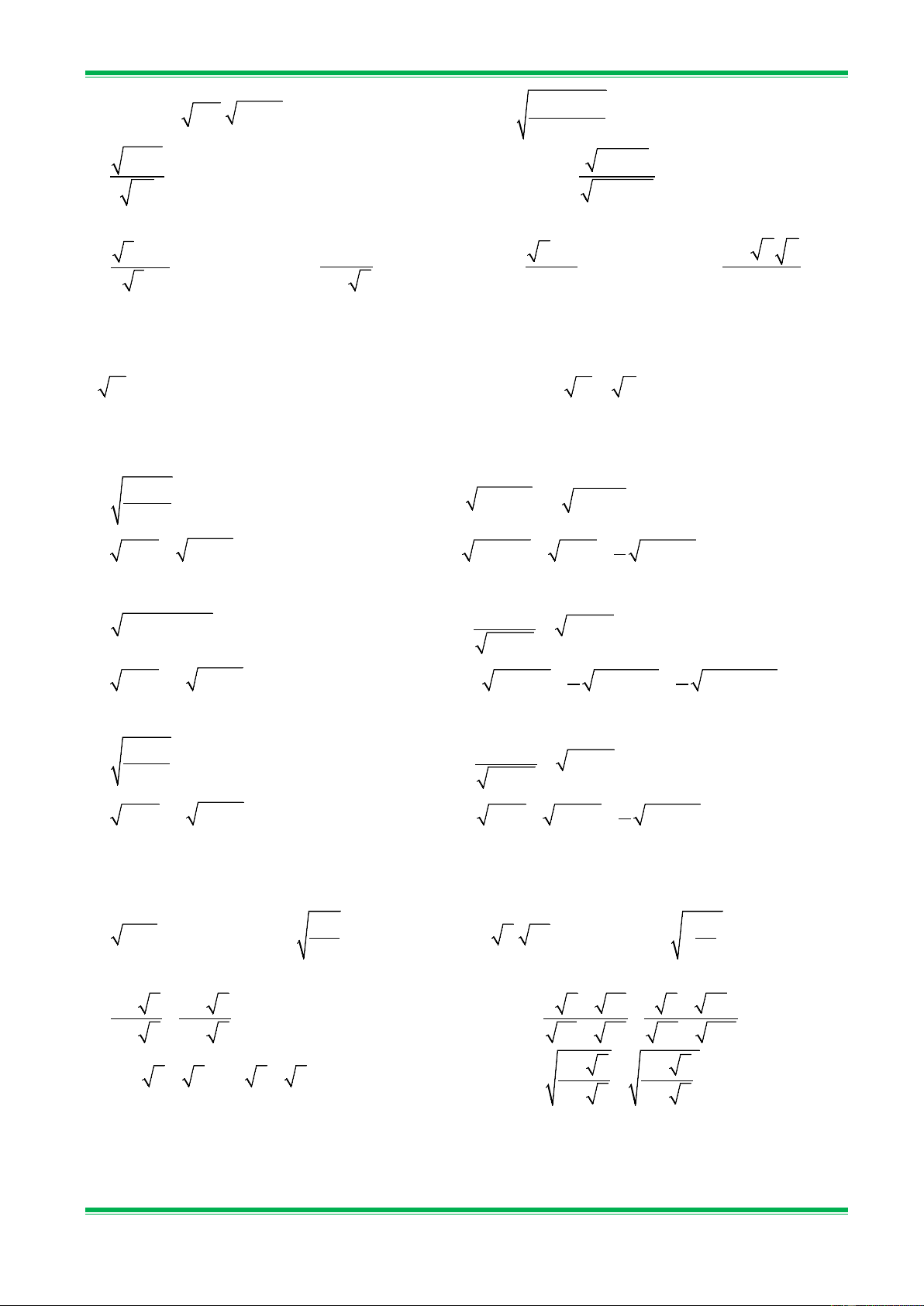
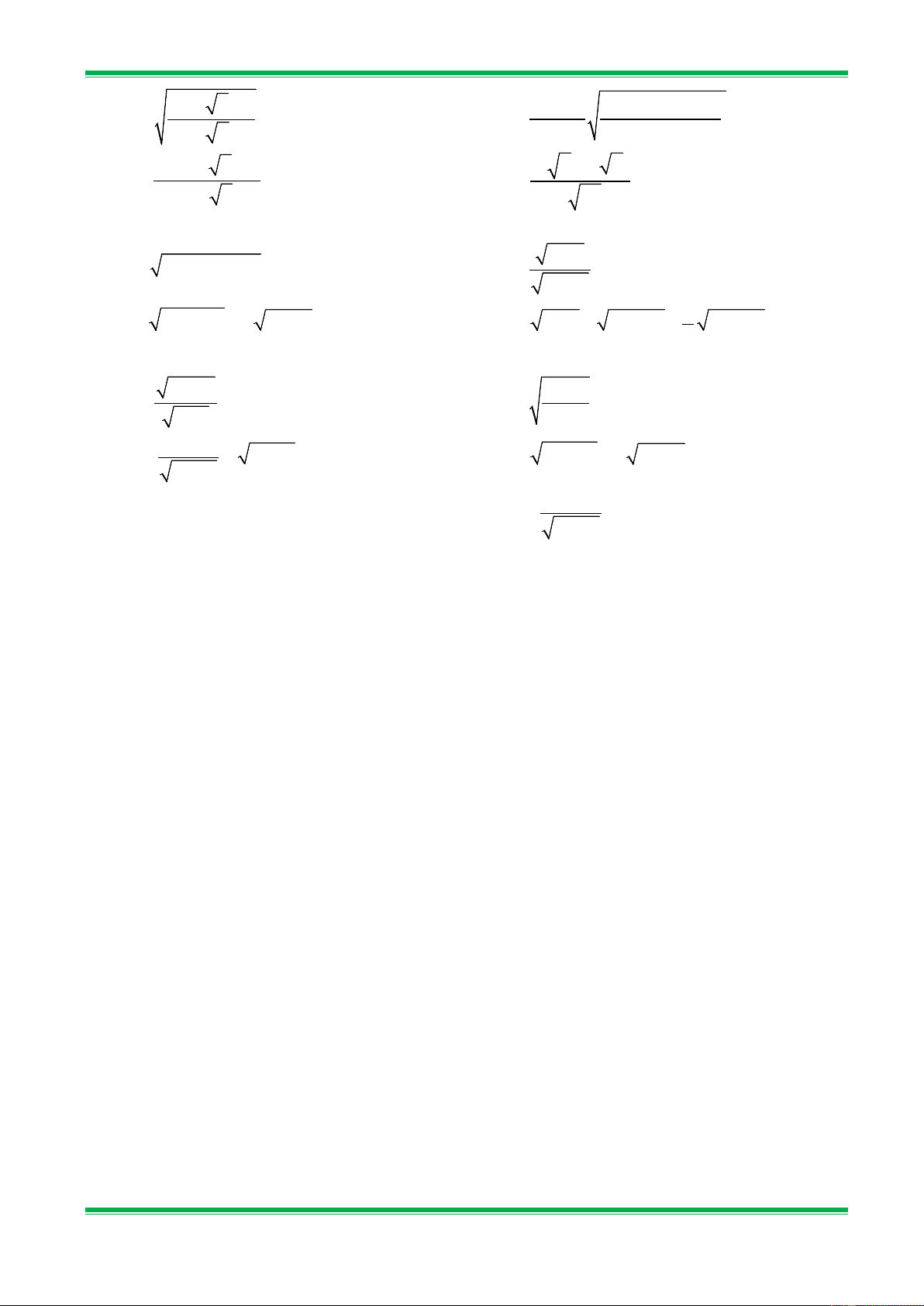
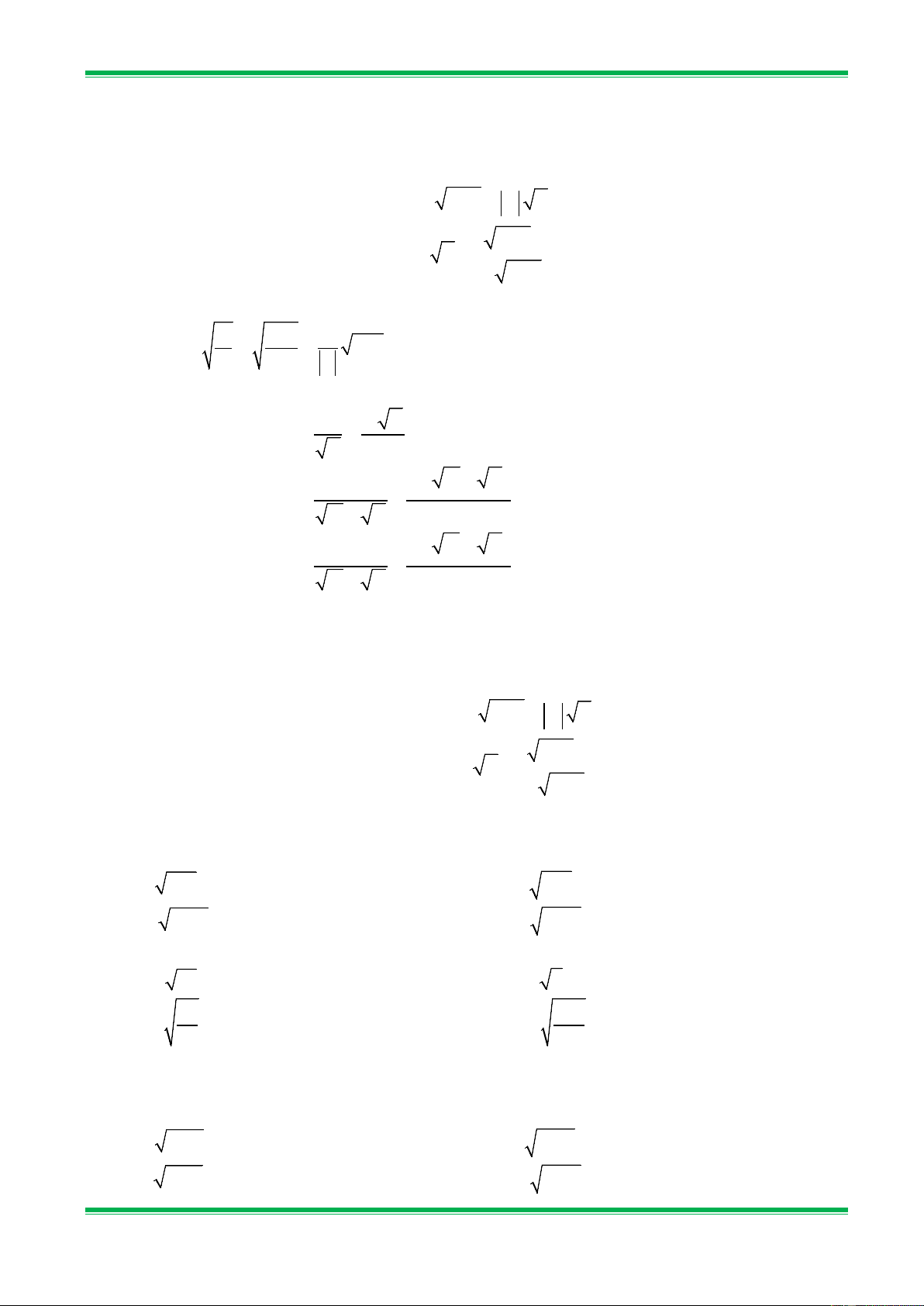
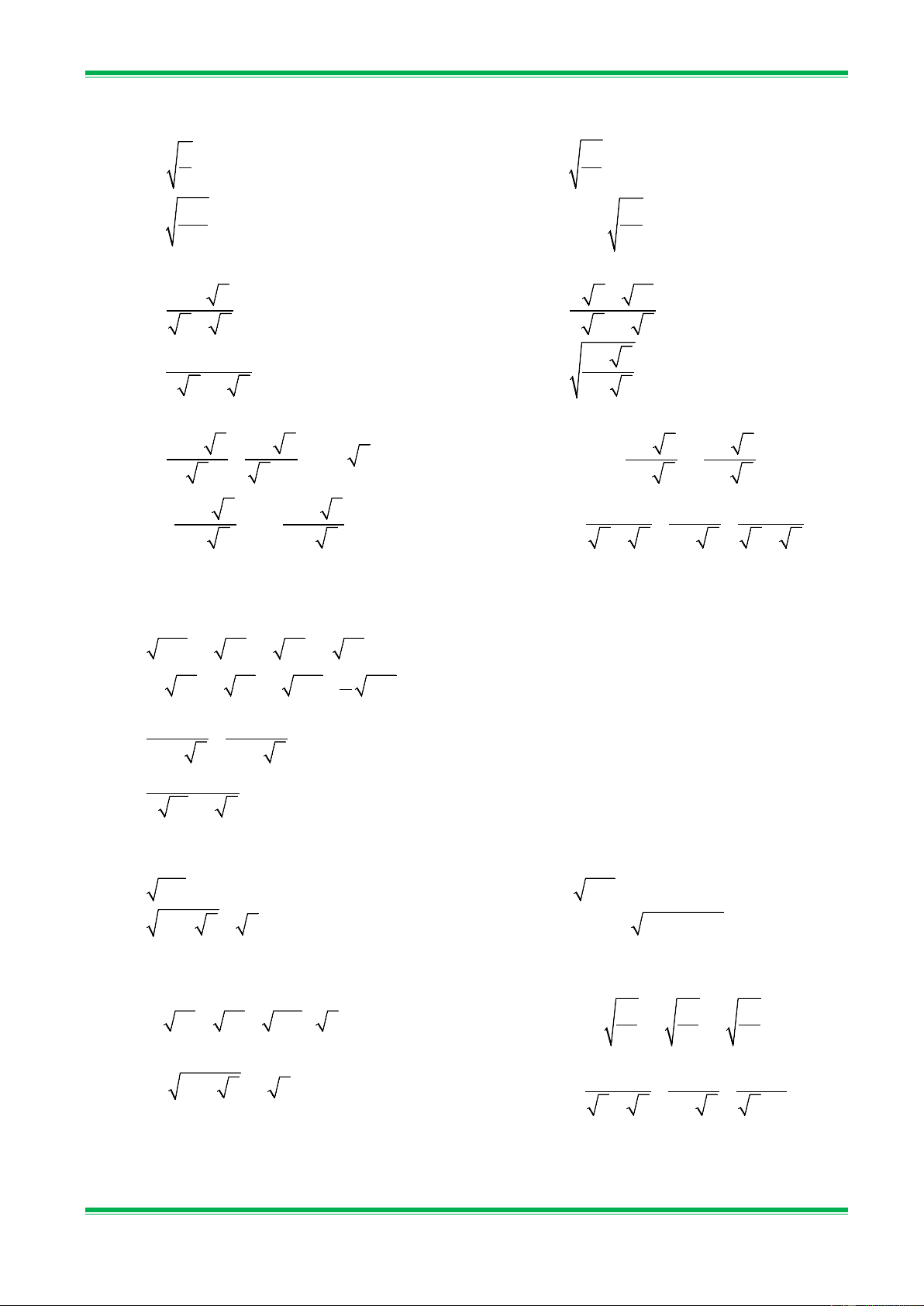
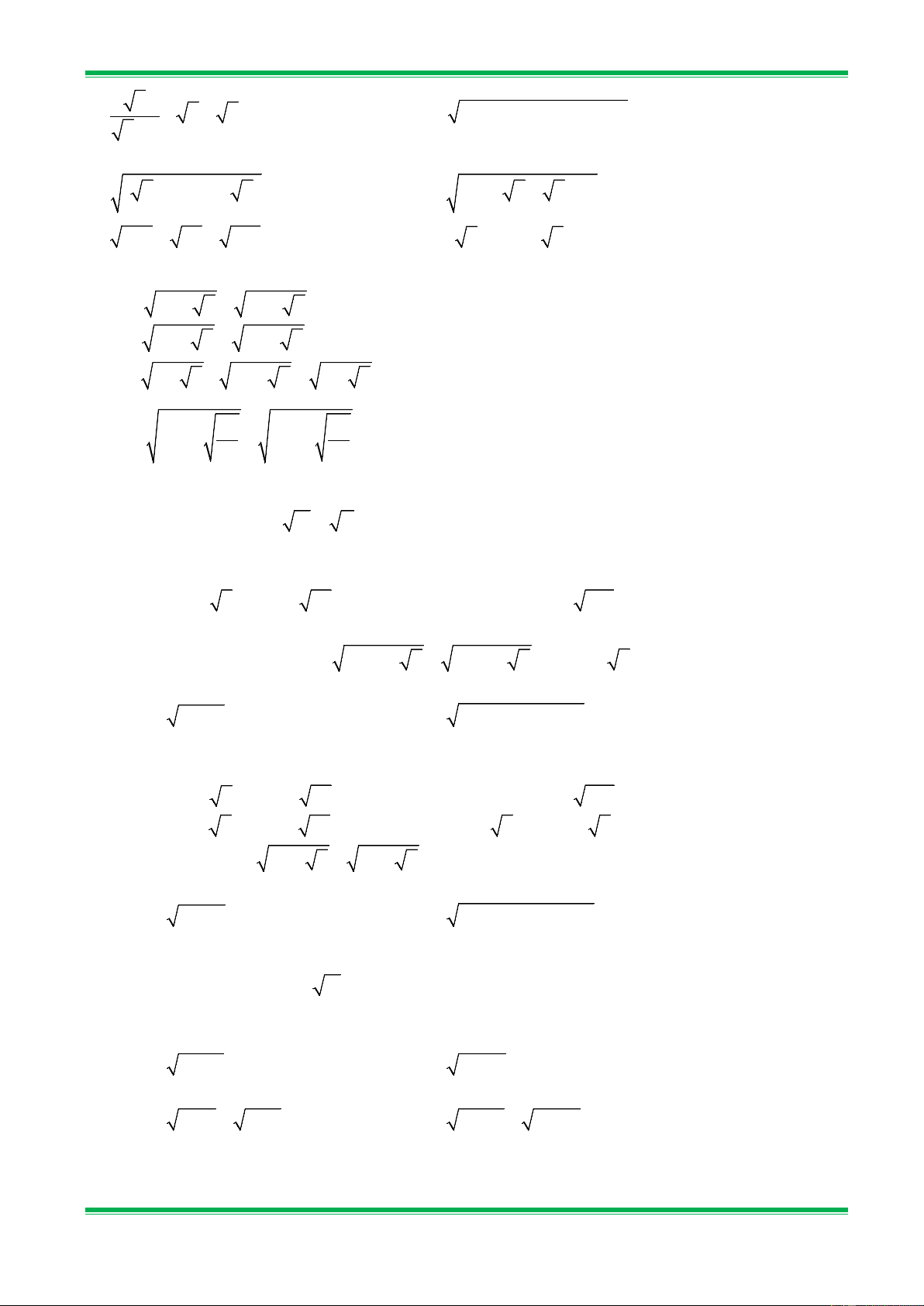
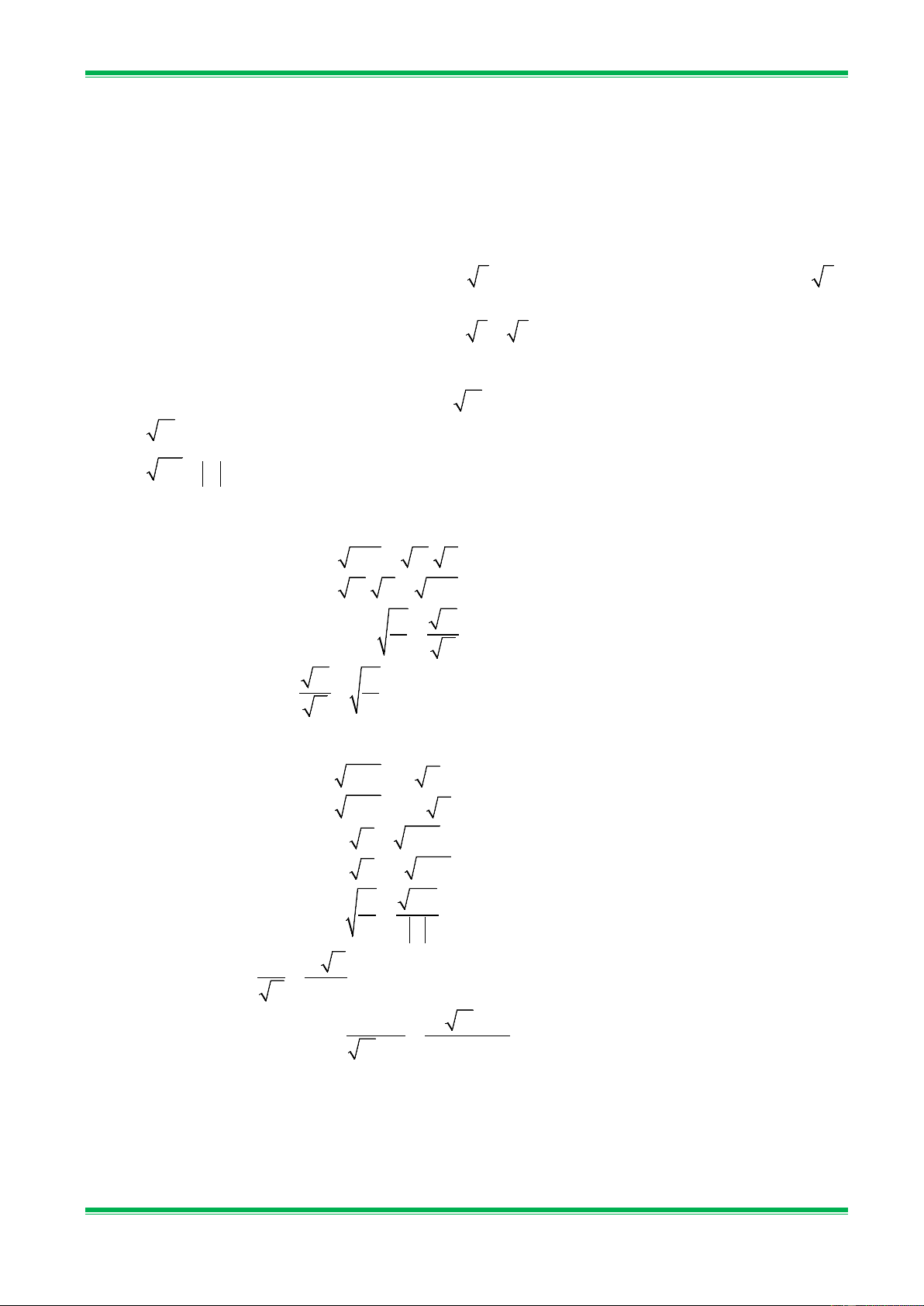
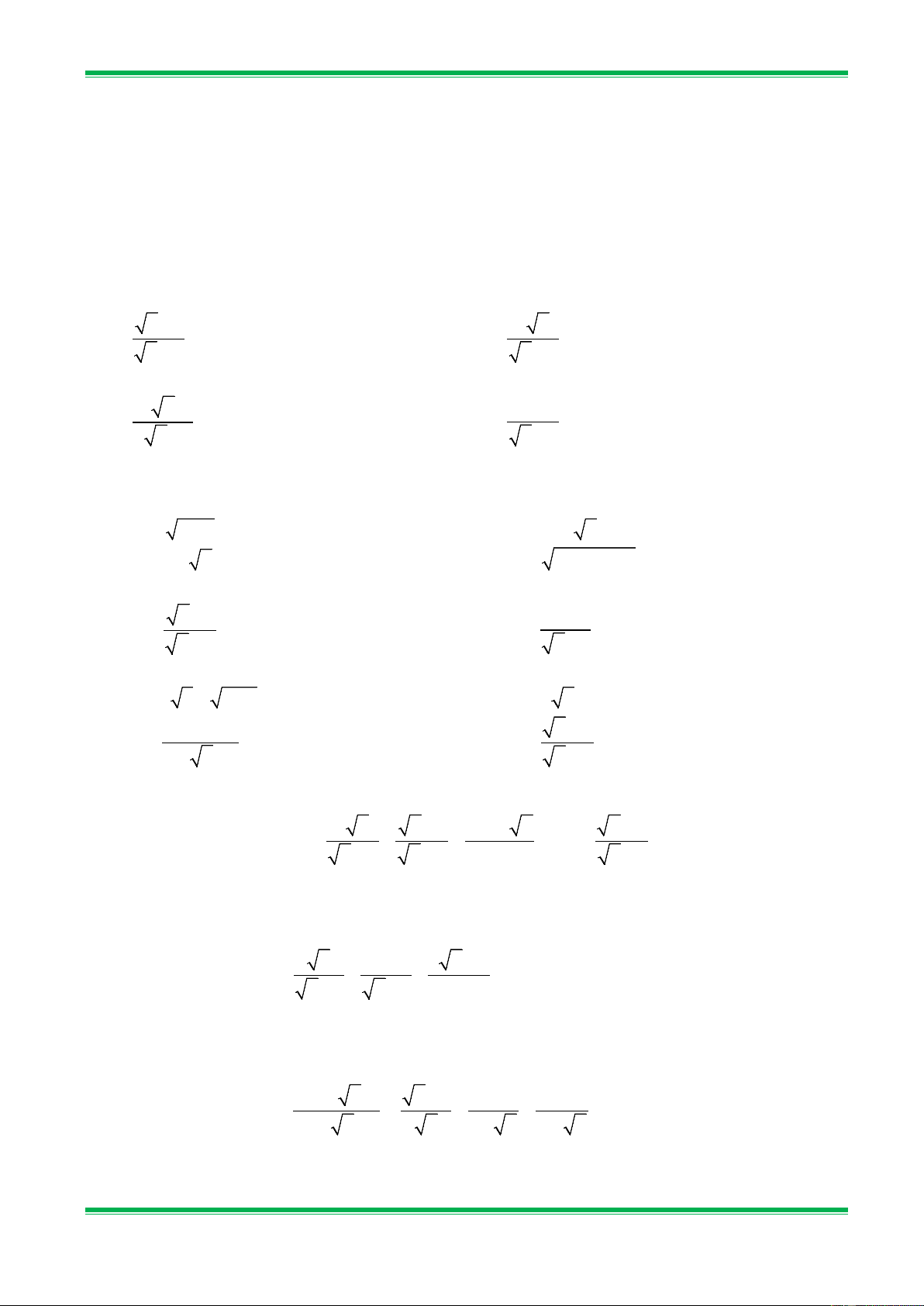
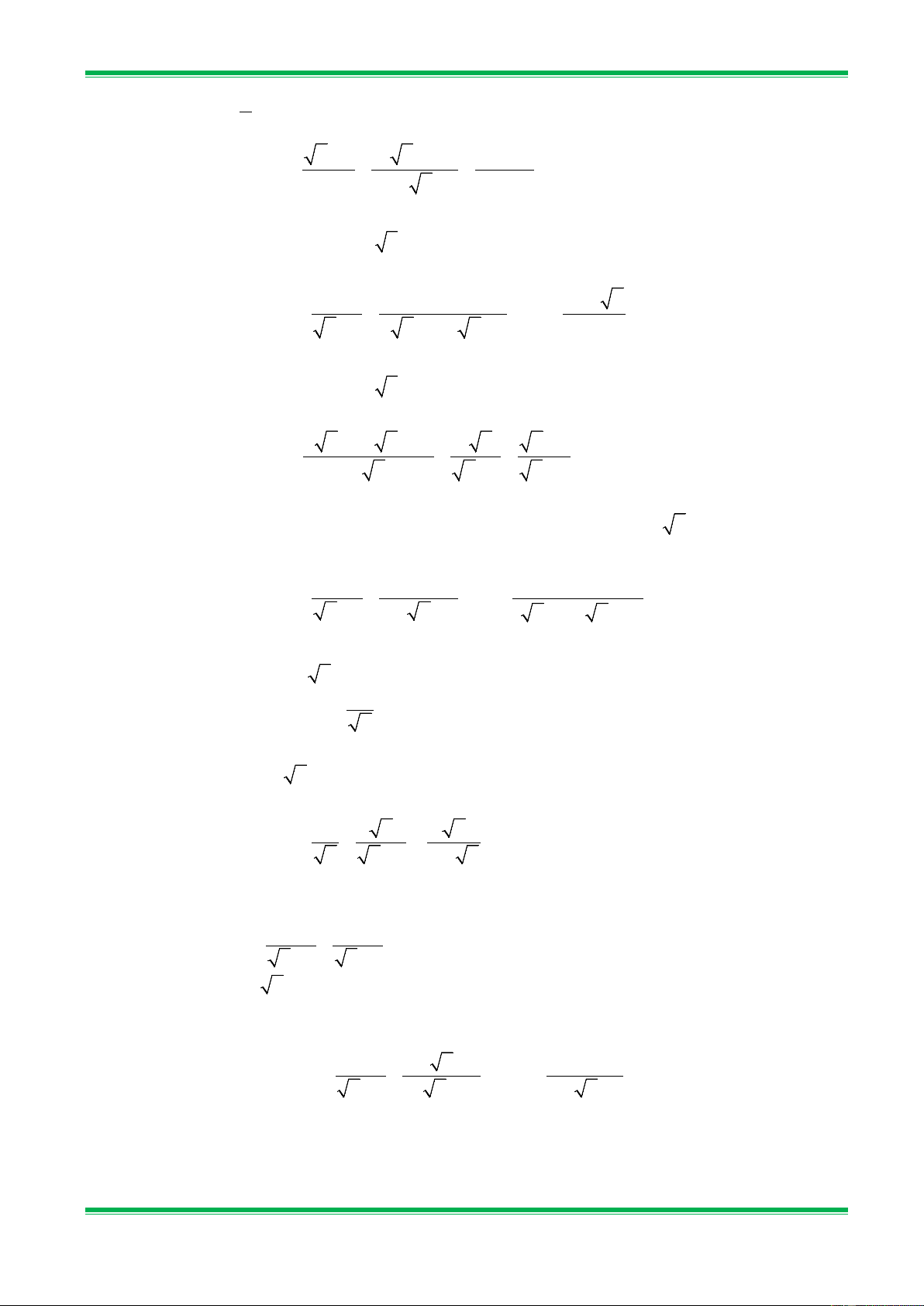
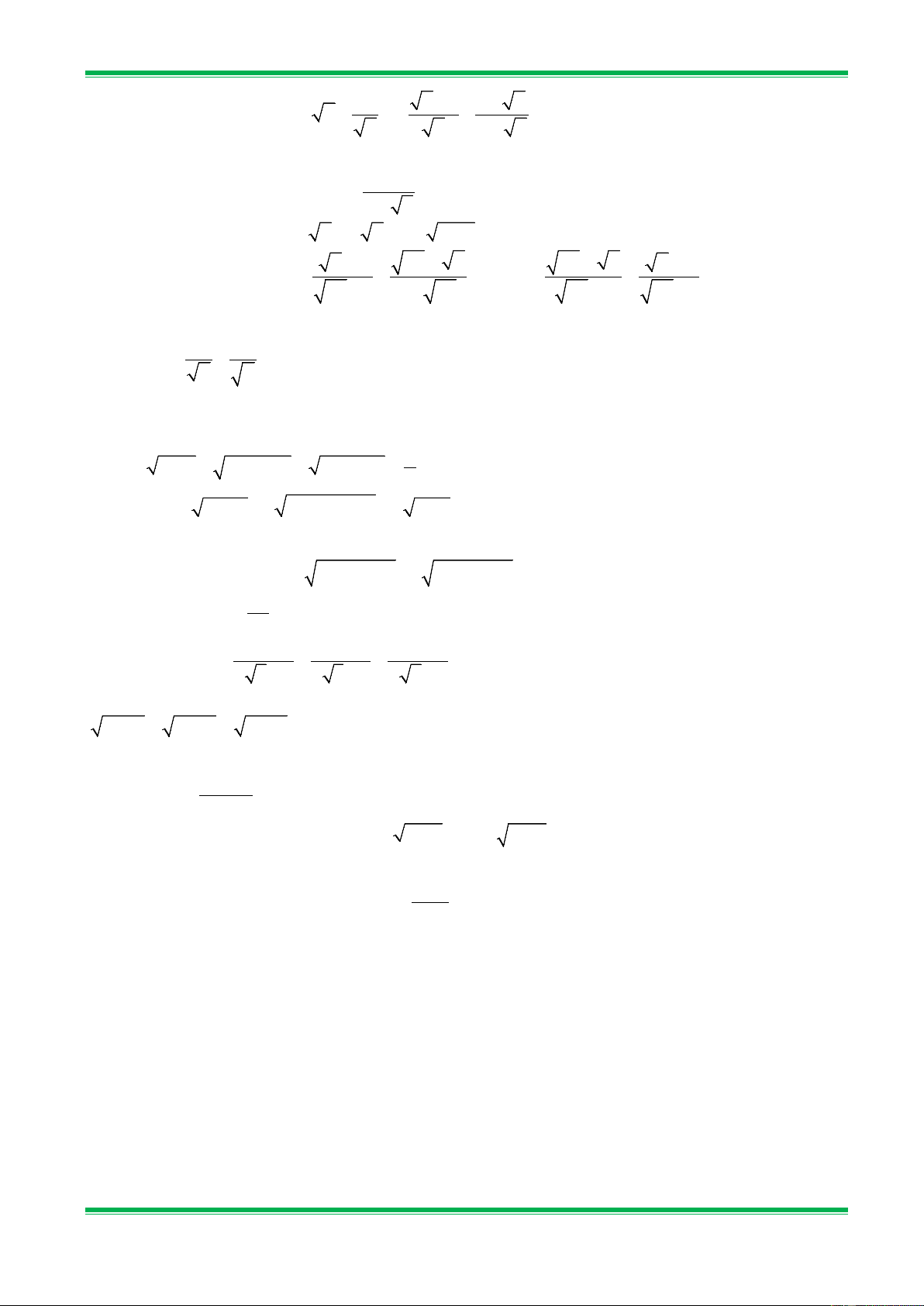
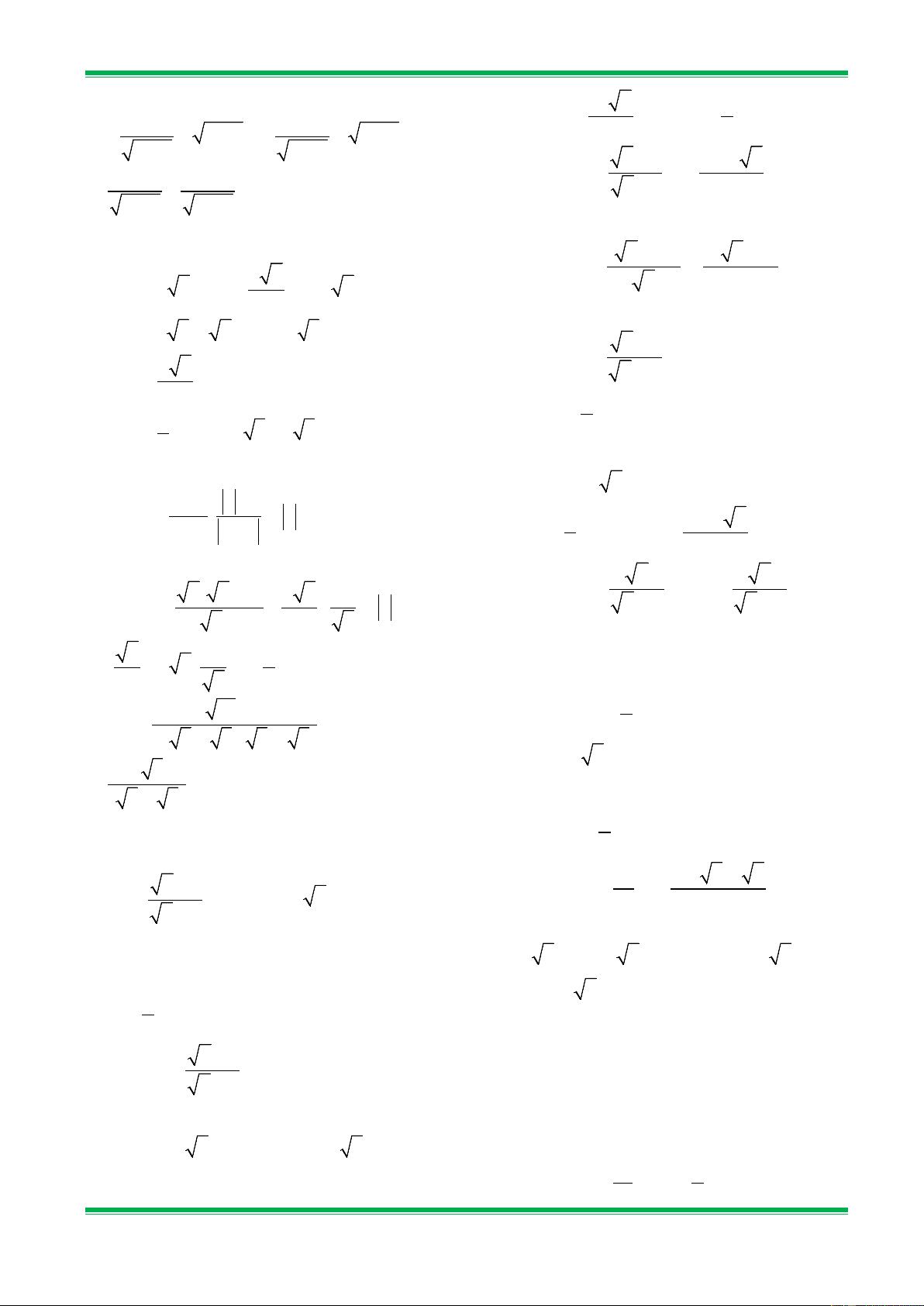
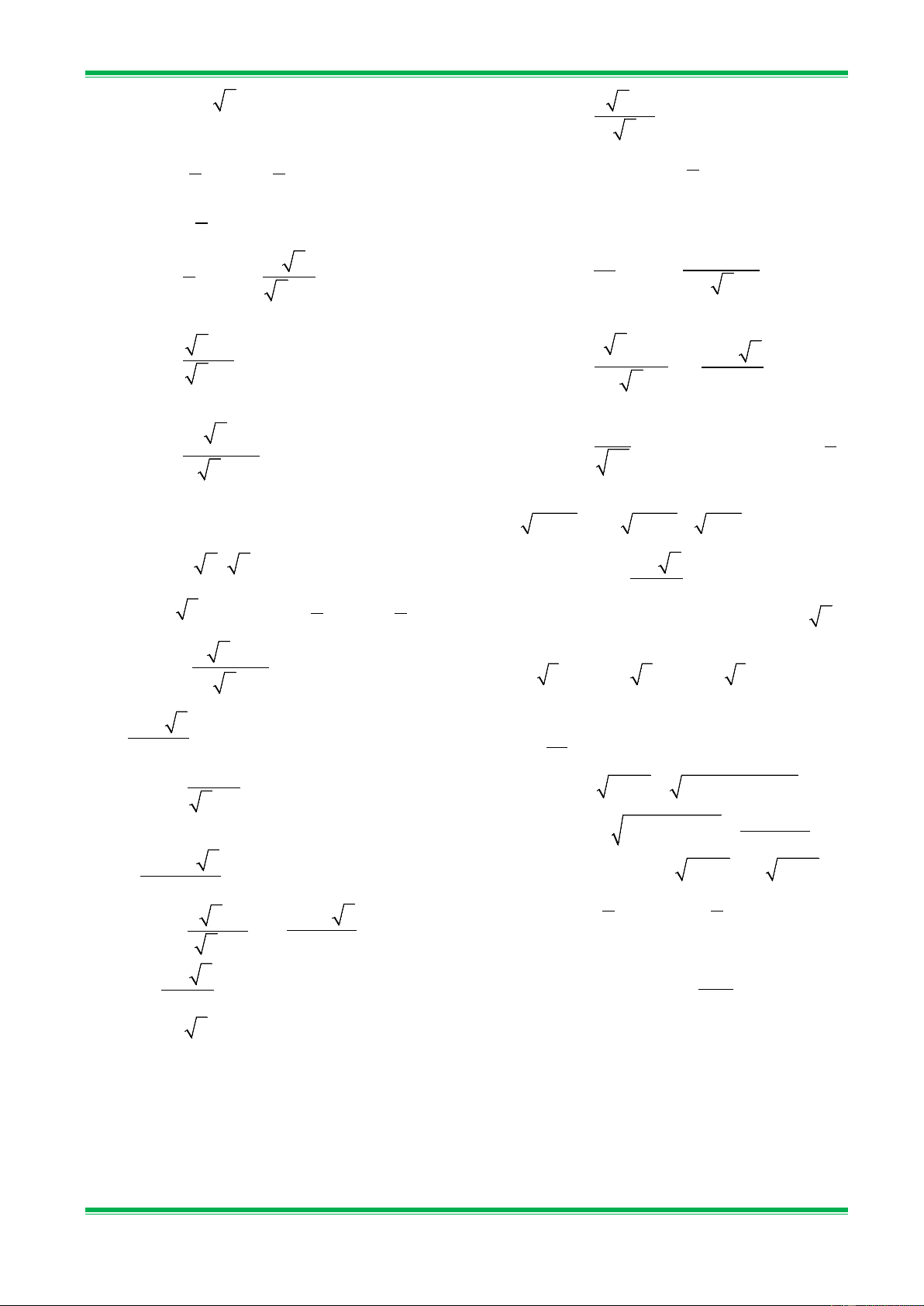
Preview text:

MỤC LỤC
VẤN ĐỀ 1. CĂN BẬC HAI .............................................................................................................................. 3
A. TÓM TẮT LÝ THUYẾT .......................................................................................................................... 3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................................... 3
Dạng 1. Tìm căn bậc hai và căn bậc hai số học của một số ................................................................ 3
Dạng 2. So sánh các căn bậc hai số học................................................................................................. 4
C. BÀI TẬP VỀ NHÀ ................................................................................................................................... 5
VẤN ĐỀ 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2
A = A ............................................... 7 A.
TÓM TẮT LÝ THUYẾT .................................................................................................................... 7 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................... 7
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai ........................................................................... 7
Dạng 2. Rút gọn biểu thức chứa căn bậc hai ....................................................................................... 8
C. BÀI TẬP VỀ NHÀ ................................................................................................................................... 8
VẤN ĐỀ 3. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2
A = A ............................................. 10 A.
TÓM TẮT LÝ THUYẾT .................................................................................................................. 10 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 10
Dạng 3: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa ...................................................... 10
Dạng 4. Giải phương trình chứa căn bậc hai. .................................................................................... 10
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 11
VẤN ĐỀ 4. LIÊN HỆ PHÉP NHÂN, PHÉP CHIA VỚI PHÉP KHAI PHƯƠNG (PHẦN 1) ............... 12
A.Tóm tắt lý thuyết .................................................................................................................................... 12
B. Bài tập và các dạng toán. ....................................................................................................................... 12
Dạng 1. Thực hiện phép tính. .............................................................................................................. 12
Dạng 2. Rút gọn biểu thức. ................................................................................................................... 13
C.BÀI TẬP VỀ NHÀ .................................................................................................................................. 14
VẤN ĐỀ 5. LIÊN HỆ PHÉP NHÂN, PHẾP CHIAVỚI PHÉP KHAI PHƯƠNG (PHẦN II) ................ 15
A. TÓM TẮT LÝ THUYẾT ........................................................................................................................ 15
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................................... 15
Dạng 4. Rút gọn biểu thức .................................................................................................................... 15
Dạng 5. Giải phương trình ................................................................................................................... 16
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 16
VẤN ĐỀ 6. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI. ............................................. 18 A.
TÓM TẮT LÍ THUYẾT .................................................................................................................... 18 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 18
Dạng 1. Dưa thừa số ra ngoài dấu căn hoặc vào trong dấu căn ..................................................... 18
Dạng 2. So sánh các căn bậc hai ........................................................................................................... 19
Dạng 3. Rút gọn biểu thức chứa căn bậc hai ..................................................................................... 19
Dạng 4. Trục căn thức ở mẫu ............................................................................................................... 20 1
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 21
VẤN ĐỀ 7: RÚT GỌN BIỂU THỨC CHỨA CĂN VÀ CÁC BÀI TOÁN LIÊN QUAN ........................ 23 A.
TÓM TẮT LÝ THUYẾT .................................................................................................................. 23 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 23
Dạng 1.Rút gọn biểu thức chứa căn bậc hai ...................................................................................... 23
Dạng 2: Chứng minh đẳng thức chứa căn thức bậc hai ................................................................... 24
Dạng 3. Rút gọn biểu thức và các bài toán liên quan ....................................................................... 24
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 25
VẤN ĐỀ 8. CĂN BẬC BA .............................................................................................................................. 27 A.
TÓM TẮT LÝ THUYẾT ................................................................................................................. 27 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN ................................................................................................. 27
Dạng 1. Thực hiện phép tính có chứa căn bậc ba .............................................................................. 27
Dạng 2. So sánh các căn bậc ba ............................................................................................................ 28
Dạng 3. Giải phương trình chứa căn bậc ba ...................................................................................... 28
C. BÀI TẬP VỀ NHÀ ................................................................................................................................. 29
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I) ....................................................................................................................... 30
A. TÓM TẮT LÝ THUYẾT ............................................................................................................................. 30
1. Căn bậc hai số học ............................................................................................................................. 30
2. Căn thức bậc hai ................................................................................................................................ 30
3. Liên hệ giữa phép nhân, phép chia với phép khai phương ........................................................ 30
4. Biến đổi đơn giản biểu thức chứa căn bậc hai ............................................................................... 30
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................................... 30
Dạng 1. Tìm điều kiện cho các biểu thức có nghĩa ........................................................................... 30
Dạng 2: Tính và rút gọn biểu thức ...................................................................................................... 31
Dạng 3. Giải phương trình và bất phương trình ............................................................................... 32
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II) ..................................................................................................................... 34
A. TÓM TẮT LÍ THUYẾT ......................................................................................................................... 34
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................................... 34
Dạng 4. Tìm các giá trị nguyên của biến để các biểu thức cho trước có giá trị nguyên .............. 34
Dạng 5. Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của biểu thức ................................................... 34
Dạng 6. Rút gọn biểu thức và các bài toán liên quan ....................................................................... 34
Một số bài tập nâng cao ........................................................................................................................ 36
HƯỚNG DẪN – ĐÁP SỐ ............................................................................................................................... 37
VẤN ĐỀ 1. ................................................................................................................................................... 37
VẤN ĐỀ 2. ................................................................................................................................................... 38
VẤN ĐỀ 3 .................................................................................................................................................... 39
VẤN ĐỀ 4 .................................................................................................................................................... 39
VẤN ĐỀ 5 .................................................................................................................................................... 40
VẤN ĐỀ 6 .................................................................................................................................................... 41
VẤN ĐỀ 7. ................................................................................................................................................... 42
VẤN ĐỀ 8 .................................................................................................................................................... 42
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I) ................................................................................................................ 43
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II) .............................................................................................................. 43 2
Chủ đề 1. CĂN BẬC HAI. CĂN BẬC BA
VẤN ĐỀ 1. CĂN BẬC HAI A. TÓM TẮT LÝ THUYẾT
• Căn bậc hai của số thực a không âm là số thực x sao cho 2 x = a . * Chú ý:
+) Số dương a có đúng hai căn bậc hai, là hai số đối nhau:
- Số dương kí hiệu là a
- Số âm kí hiệu là − a .
+) Căn bậc hai của số 0 là 0.
+) Số âm không có căn bậc hai.
• Với số a không âm, số a được gọi là căn bậc hai số học của a . x ≥ 0
• Ta có a = x ⇔ x =  2 a
• So sánh hai căn bậc hai số học: a < b ⇔ 0 ≤ a < b .
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tìm căn bậc hai và căn bậc hai số học của một số
Phương pháp giải: Ta sử dụng kiến thức sau:
1. Nếu a là số thực dương, các căn bậc hai của a là a và − a ; căn bậc hai số học của a là a .
2. Nếu a là số 0 thì căn bậc hai của a và căn bậc hai số học của a cũng bằng 0.
3. Nếu a là số thực âm thì a không có căn bậc hai và do đó không có căn bậc hai số học.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tìm các căn bậc hai và căn bậc hai số học của các số sau: a) 0; b) 64; c) 9 ; d) 0,04. 16
Bài 2. Mỗi số sau đây là căn bậc hai số học của số nào? a) 12; b) −0,36 ; c) 2 2 ; d) 0,2 . 7 3 Bài 3. Tính: a) 9 ; b) 4 ; c) − 2 3 ; 25  2 3 2 d) − (− )2 6 ; e) −    ; f) (− 7 ) .  4 
Bài 4. Tính giá trị của các biểu thức sau: a) 2 1 81 − 16 ; b) 0,5 0,04 + 5 0,36 ; 3 2 3 c) 2 25 1 4 25 9 − ; d) − − −4 + 5 − . 5 16 2 9 −16 25
Bài 5. Tìm giá trị x , biết: a) 2 x −16 = 0; b) 2 x = 13 ; c) 2 x + 9 = 0 ; d) x x = 5 ; e) − + 2 = 0 ; f) 2
x − 2x + 1 = 4 . 3
* Học sinh tự luyện các bài tập sau tại lớp
Bài 6. Tìm các căn bậc hai và căn bậc hai số học của các số sau: a) 81; b) 0, 25; c) 1, 44; d) 40 1 . 81
Bài 7. Mỗi số sau đây là căn bậc hai số học của số nào? a) 13; b) 3 − ; c) 1 2 ; d) 0,12 . 4 2 5 0,3 Bài 8. Tính a) 121 ; b) 16 ; c) − (− )2 8 ; 25 2 2   2 d)(− 2) ; e) 1 −  3   ; f)     .  4   5 
Bài 9. Tính giá trị của các biểu thức sau: a) 2 1 25 − 4 ; b) 0,5 0,09 + 5 0,81 ; 5 2 c) 2 25 5 4 36 81 − ; d) − − −2 + 5 − . 5 36 2 25 −16 25
Bài 10. Tìm giá trị của x biết: a) 2 1 x 1 = ; 2 x 36 0 x 5 ; 3 b) + = ; c) − = 3 d) − x − 8 = 11; e) x −1 −1 = 3 ; f) 2
x − 4x + 4 −1 = 3 .
Dạng 2. So sánh các căn bậc hai số học
Phương pháp giải: Ta có a < b ⇔ 0 ≤ a < b .
* Giáo viên hướng dẫn học sinh giải các bài tập sau: Bài 11. So sánh a) −2 và 3 ; b) 3 và 2 2 ; c) 11 và 99 ; d) 5 và 17 + 1; e) 3 và 15 −1 ; f)1− 3 và 0,2 .
Bài 12. Tìm giá trị của x biết: a) x ≥ 6 ; b) x < 1; c) −x + 1 ≥ 6; d) 2x + 1 ≤ 2 .
Bài 13. Tìm giá trị của x biết: a) 2x ≥ x ; b) * ≤ 2 2x x .
* Học sinh tự luyện các bài sau tại lớp: Bài 14. So sánh a) 2 và 1+ 2 ; b) 3 11 và 12; c) 1 và 3 −1; d) 3 và 2 − 5 ; e) −10 và −2 23 ; f) −3 29 và −15. 4
Bài 15. Tìm các giá trị của x biết: a) x + 1 ≥ 5 ; b) x + 1 < 2 ; c) −2x + 2 > 8 ; d) 2x + 1 ≤ 3 . C. BÀI TẬP VỀ NHÀ
Bài 16. Tìm các căn bậc hai và căn bậc hai số học của các số sau: a) 225; b) 324; c) 169 ; 100 d) 49 ; e) 2, 25; f) 0, 16. 289
Bài 17. Mỗi số sau đây là căn bậc hai số học của số nào? 3 a) 7; b)   − −   ; c) 3 2 ; d) 0,25 ;  4  2 3 0,5 Bài 18. Tính a) 225 ; b) 49 ; c) − (− )2 111 ; 9 25 2 2   1 d) 2 13 ; e)(− 7 ) ; f) −    .  400 
Bài 19.Tính giá trị của các biểu thức sau: a) 2 9 16 25 1 − + 144 ; b) 0,5 0,09 − 2 0,25 + ; 5 2 81 4 c) 9 3 64 1 289 0,09 − ; d) − − − + 10 − . 16 2 9 −16 9
Bài 20. Tìm giá trị của x biết: a) 2 x −196 = 0; b) 2 1 x = ; 2 15 c) −x + 324 = 0 ; 1 d) 2 x + 100 = 0 ; e) x = 7 ; f) x − 3 = . 3
Bài 21. Tìm giá trị của x biết: 1
a) 3x −1 − 4 = 13 ; b) 2
9x − 6x + 1 = 18 ; c) x + 2 = ; 2 2 d) 2x 4 −2 x + 3 = 0 ; e) + = 3; f) = 4 . 2 x − 3
Bài 22. Tìm giá trị của x biết: a) x + 9 ≤ 31; b) 2x −1 > 6 ; c) x + 3 ≥ 5 ;
d) 2x −1 + 5 < 2 .
Bài 23. So sánh các số sau: a) 4 và 1+ 7 ; b) 2 5 và 8; c) −6 và −2 7 ; d) 4 và 23 −1; e) 0,5 và 3 − 2;
f) 2015 + 2018 và 2016 + 2017 .
Bài 24*. Chứng minh 3 và 7 là các số vô tỉ.
Bài 25*. Cho biểu thức A = x − 2 x + 2 . 5
a) Đặt y = x + 2 . Hãy biểu thị A theo y ;
b) Tìm giá trị nhỏ nhất của A . Bài 26*. So sánh a) 1 1 1 1 + + + .............+ và 10;
b) 4 + 4 + 4 + .........+ 4 và 3. 1 2 3 100 Bài 26*. So sánh: a) 1 1 1 1 + + + ...+ và 10; b) 4 + 4 + 4 + ...+ 4 và 3; 1 2 3 100 6
VẤN ĐỀ 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2 A = A (PHẦN I)
A. TÓM TẮT LÝ THUYẾT
A khi A ≥ 0 Hằng đẳng thức 2
A = A = −A khi A <  0 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai Phương pháp giải:
A khi A ≥ 0
Sử dụng hằng đẳng thức 2
A = A = −A khi A <  0
*Giáo viên hướng dẫn học sinh giải các bài tập sau: Bài 1. Tính: a) 4 − (−0,4)2 ; b) (− )6 + (− )4 4 3 5 2 ; 3 c) 49 144. . 0,01; d) 2 + 2 − 2 − 2 72 : 3 4 3 5 3 . 64
Bài 2. Rút gọn biểu thức: 2 2 2 a) 5 + ( 5 −5) ; b) (4 − 11) + (1− 3) ; 2 2 2 c) (2 2 −7) + 2 2; d) (2 − 3) + (1− 3) . Bài 3. Chứng minh: 2 2 a)11+ 6 2 = (3+ 2) ; b) 8 − 2 7 = ( 7 −1) ; c) 11+ 6 2 + 11− 6 2 = 6;
d) 8 − 2 7 − 8 + 2 7 = −2.
Bài 4.Thực hiện các phép tính sau: a) 5 + 2 6 − 5 − 2 6 ; b) 41−12 5 − 41+ 12 5 ; c) 49 −12 5 + 49 + 12 5 ; d) 29 + 12 5 + 29 −12 5 .
*Học sinh tự luyện các bài tập sau tại lớp: Bài 5. Tính: 2 a)  −1  5 2 2   ; b) 3 (−1,5) − 4 (−0,5) ;  5 
c) ( 0,25 − 225 + 2,25): 169; d) ( 0,04 + 121 − 1,44) 81.
Bài 6. Rút gọn biểu thức: 2 2 a) (3− 5) + 5; b) ( 7 −5) + 7; 2 2 2 2 c) ( 11 −4) + ( 11 + 4) ; d) (2 −3 3) + (8−3 3) . 7 Bài 7. Chứng minh: 2 2 a) 28 −10 3 = ( 3 −5) ; b) 193 −132 2 = (11−6 2) ;
c) 28 −10 3 + 28 + 10 3 = 10;
d) 193 −132 2 + 193 + 132 2 = 22.
Bài 8. Thực hiện các phép tính sau: a) 10 + 4 6 − 10 − 4 6 ; b) 39 −12 3 + 39 + 12 3 ; c) 31−12 3 − 31+ 12 3 ; d) 21+ 12 3 + 21−12 3.
Dạng 2. Rút gọn biểu thức chứa căn bậc hai
A khi A ≥ 0
Phương pháp giải:Sử dụng hằng đẳng thức 2
A = A = −A khi A <  0
Bài 9. Rút gọn các biểu thức sau: a) 2
5 25a − 25a với a ≤ 0; b) 2
49a + 3a với a ≥ 0; c) 4 a + 2 16 6a ; d) 6 a − 3 3 9
6a với a ≤ 0.
Bài 10. Rút gọn các biểu thức sau: a) x − 2 4
x − 4x + 4 với x ≥ 2; b) x + + x + 2 3 9 6
x với x ≤ −3;
(x+6 x +9)( x −3) c) 4 x − 2
x − 4x + 4 với 0 ≤ x ≠ 9; x − 9 2
d) x + 4x + 4 với x ≠ −2. x + 2
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 11. Rút gọn các biểu thức sau: a) 2
4 16a −16a với a ≤ 0; b) 2
64a + 3a với a ≥ 0; c) 4 a + 2 25 6a ; d) 6 a − 3 3 81
6a với a ≤ 0.
Bài 12. Rút gọn các biểu thức sau: a) x − 2 4
x − 2x + 1 với x ≥ 1; b) x + − x + 2 3 9 6
x với x ≥ 3;
(x+10 x +25)( x −5) c) 5 x − với 0 ≤ x ≠ 25; x − 25 2
d) x − 4x + 4 với x ≠ 2. x − 2 C. BÀI TẬP VỀ NHÀ Bài 13. Tính: 2 a) 7 6 −1 − . (−0.81)2 ; b)   ; 9   5  36  c) 49. 144 + 256 : 64; d) 2 2 72 : 2 .3 .36 − 225.
Bài 14. Rút gọn biểu thức: 2 2 2 2 a) (11−6 2) + (11+6 2) ; b) (10−4 6) − (10+ 4 6) ; 8 2 2 2 2 c) (4− 5) + (1− 5) ; d) (7 + 2) − (1− 2) . Bài 15. Chứng minh: 2 2 a)7 + 4 3 = (2 + 3) ; b) 6 − 2 5 = ( 5 −1) ; 2 c)(5− 2) = 27 −10 2; d) 9 + 4 5 − 9 − 4 5 = 4.
Bài 16.Thực hiện các phép tính sau: a) 6 + 2 5 + 6 − 2 5 ; b) 8 − 2 7 − 8 + 2 7 ; c) 11+ 6 2 − 11− 6 2 ; d) 17 + 12 2 + 17 −12 2 .
Bài 17. Rút gọn các biểu thức sau: a) 2 64a + 2a; b) 6 a − 3 3 9 6a .
Bài 18. Rút gọn các biểu thức sau: a) 2 a + a + + 2 6 9
a − 6a + 9 với −3 ≤ a ≤ 3;
b) a + 2 a −1 + a − 2 a −1 với 1 ≤ a ≤ 2.
Bài 19. Rút gọn các biểu thức sau:
a) a a − 8 + 2a − 4 a ; b) 12 6 . a − 4 7 + 2 6 − 7 − 2 6 9
VẤN ĐỀ 3. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2 A = A (PHẦN II)
A. TÓM TẮT LÝ THUYẾT
A khi A ≥ 0 Hằng đẳng thức 2
A = A = −A khi A <  0
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 3: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Phương pháp giải:Chú ý rằng biểu thức A có nghĩa khi và chỉ khi A ≥ 0.
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Với giá trị nào của x thì các căn thức sau có nghĩa: a) x 2x 2 3 2 − 4; b) 7 − 6x; c) − ; d) − . 3x −1 2 x − 2x + 4
* Chú ý rằng với a là số dương ta luôn có: x ≥ a 2 x ≥ 2
a ⇔ x ≤ −  a 2 x ≤ 2
a ⇔ −a ≤ x ≤ .a
Bài 2.Với giá trị nào của x thì các căn thức sau có nghĩa: a) ( 2x 4
3 − 5x)(x − 6); b) − ; c) 2 x − 8x − 9; d) − 2 16 x . 5 − x
*Học sinh luyện bài tập sau đây tại lớp
Bài 3.Với giá trị nào sau đây của x thì căn thức có nghĩa: a) 2x − 3 ; b) −7x ; c) 1− 4x ; d) 2 3x + 1 .
Bài 4. Với giá trị nào sau đây của x thì căn thức có nghĩa: 2 a) 2 ; b) 7 − − x ; c) x − 3 ; d) x + 2x + 4 . x −1 3 4 − x 2x − 3
Bài 5. Với giá trị nào sau đây của x thì căn thức có nghĩa:
a) (x − 2)(x − 6) ; b) 2
x − 4x − 5 ; c) 2 x − 9 ; d) 2 1− x .
Dạng 4. Giải phương trình chứa căn bậc hai.
Phương pháp giải: Ta chú ý một số phép biến đổi tương đương liên quan đến căn thức bậc hai sau đây: B ≥ 0 A = B ⇔  ; 2
A = B ⇔ A = B 2 A = B
A ≥ 0(∨B ≥ 0) A = B ⇔  ; 2 2
A = B ⇔ A = B ⇔ A = ±B A = B 10
Giáo viên hướng dẫn HS giải bài tập sau:
Bài 6. Giải các phương trình: a) x − 6 = 13 ; b) 2
x − 2x + 4 = x −1 ; c) 2
x − 8x + 16 = 9x −1 ; d) 2
x − x − 4 = x −1 ; e) 2 2
x − 4x + 4 = 4x −12x + 9 ;
f) x + 2 x −1 = 2 .
Học sinh tự luyện bài tập sau tại lớp:
Bài 7. Giải các phương trình: a) x + 9 = 3 ; b) 2 2x + 2 = 3x −1 ; c) 2
x − 2x + 1 = 19x −1; d) 2
x − x − 6 = x − 3 ; e) 2 2
4x + 4x + 1 = x + 2 1 x + 36 ;
f) x + 4 x − 4 = 2 . C. BÀI TẬP VỀ NHÀ
Bài 8. Với giá trị nào sau đây của x thì căn thức có nghĩa: a) 5 − x −10 ; b) 2 x − 2x + 1 ; c) 2 2x + 4x + 5 ; d) 2
−x + 4x − 4 .
Bài 9.Với giá trị nào sau đây của x thì căn thức có nghĩa: − + a) 5 ; b) x 1 2 x − 3x + 2 ; c) 3 ; d) . −x − 7 5 − x 2 x − 5x + 6
Bài 10. Giải các phương trình: a) x + 9 = 3 ; b) 2
x − 2x + 4 = x −1; c) 2
x − 6x + 9 = 4 − x ; d) 2 2
x − 2x + 1 + x − 4x + 4 = 3 .
Bài 11. Giải các phương trình: a) 2
x + 4 = x − 2 ; b) 2
x −10x + 25 = 3 −19x ; c) 2 2
x − 9 + x − 6x + 9 = 0 ;
d) 2x − 2 + 2 2x − 3 + 2x + 13 + 8 2x − 3 = 5.
Bài 12. a) Chứng minh rằng nếu 2 2
x + y = 1 thì − 2 ≤ x + y ≤ 2 .
b) Cho x, y,z là số thực dương. Chứng minh: 1 1 1 1 1 1 + + ≥ + + . x y z yz zx xy
Bài 13*. Tìm giá trị nhỏ nhất của các biểu thức sau: a) 2 2
4x − 4x + 1 + 4x −12x + 9 ; b) 2 2
49x − 22x + 9 + 49x + 22x + 9 . 11
Bài 14 .*Tìm các số x, y,z thỏa mãn đẳng thức:
x + y + z + 8 = 2 x −1 + 4 y − 2 + 6 z − 3 .
VẤN ĐỀ 4. LIÊN HỆ PHÉP NHÂN, PHÉP CHIA VỚI PHÉP KHAI PHƯƠNG (PHẦN 1)
A.Tóm tắt lý thuyết
*Khai phương một tích:
Với A ≥ 0,B ≥ 0, ta có .
A B = A. B . *Khai phương một thương:
Với A ≥ 0,B > 0, ta có A A = . B B
B. Bài tập và các dạng toán.
Dạng 1. Thực hiện phép tính.
Phương pháp giải:Áp dụng công thức khai phương một tích và khai phương một thương ở trên.
*Giáo viên hướng dẫn học sinh làm các bài tập sau: Bài 1. Tính: a) 45.80 ; b) 2,5.14,4 ; c) 10. 40 ; d) 52. 13 . Bài 2. Tính: a) 9 ; b) 9 1 ; c) 2300 ; d) 12,5 . 169 16 23 0.5
Bài 3. Thực hiện phép tính:   a) 9 1  − . 2  ; b)( 12 + 27 − 3). 3 ; 2 2      c) 8 50    − 24 + . 6  ; d) 1 2 6 − 4 3 + 5 2 −  8 .3 6 . 3 3     4 
Bài 4. Thực hiện phép tính:   a)( 45 − 20 + 5) : 5 ; b) 1 16  − + 7  : 7  ; 7 7       
c)( 325 − 117 + 2 208) : 13 ; d) 1 1 2 3 2 1 2 1  − +  :    ; 3 2 3 2 7 6   7 8     
*Học sinh tự luyện các bài sau tại lớp: Bài 5. Tính: 12 a) 32.200 ; b) 9 25 : ; c) 11. 1100 ; d) 13. 52 . 16 36 Bài 6. Tính: a) 25 ; b) 9 1 ; c) 999 − ; d) 643. 34,3 . 64 16 111 567
Bài 7. Thực hiện phép tính:   a) 16 1  − . 3  ; b)( 20 + 45 − 5). 5 ; 3 3      c) 8 50  − 6 +  6  ; d)( 6 + 2)( 3 − 2). 2 3   
Bài 8. Thực hiện phép tính:   a) 1 16  − + 11  : 11  ;
b)(20 300 −15 675 + 5 75) : 15 ; 11 11      c) 1 4  − + 3  : 3  ; d) 3 − 5 : 2 . 3 3   
Dạng 2. Rút gọn biểu thức.
Phương pháp giải: Áp dụng công thức khai phương của một phương hoặc khai phương của một tích.
*Giáo viên hướng dẫn học sinh làm bài tập sau: Bài 9. Rút gọn: a) 10 − 15 ; b) 15 − 5 5 − 2 5 − ; 8 − 12 3 −1 2 5 − 4 c) 2 8 − 12 5 + 27 3 + 2 3 2 + 2 − ; d) + − (2 + 3). 18 − 48 30 + 162 3 2 + 1 Bài 10. Rút gọn: x − xy a) a − a ; b)
với x ≥ 0, y ≥ 0,x ≠ y . a −1 x − y x y + y x c)
d) 3 a − 2a −1
x + 2 xy + y 4a − 4 a + 1
* Học sinh tự luyện các bài tập sau tại lớp. Bài 11. Tính: 13 a) 15 − 6 ; b) 5 + 5 : 35 − 14 10 + 2 c) 5 − 2 5 5 + 3 5 ( − 2).( − 2); 2 − 5 3 + 5 d) 4 1 1 ( 3 + 2 + 3 ).( 1,2 + 2 − 4 ). 3 3 5
Bài 12. Rút gọn biểu thức sau: x + xy a)
với x ≥ 0, y ≥ 0,x ≠ y; b) a + a ; x − y a + 1 x y − y x c) a + 4 a + 4 4 − a + ; d) . a + 2 a − 2
x − xy + y C.BÀI TẬP VỀ NHÀ Bài 13. Tính : a) 2. 18; b) 5. 125; c) 9 ; d) 7 2 . 196 81 Bài 14. Tính : a) 16. 25 + 196 : 49; b) ( 28 − 63 + 7) : 7; c) 2,5. 30. 48; d) 1 14 34 3 .2 .2 . 16 25 81
Bài 15. Thực hiện phép tính: a) 3 ( 12 + 2 27) − 150;
b) ( 28 − 12 − 7). 7 + 2 21; 2 c) (1+ 2 − 3)(1+ 2 + 3); d) 2 3( 2 − 3) −( 3 − 2).
Bài 16. Rút gon biểu thức sau: 2 2 a) x − 3 ; b) x − 2 ;
c) x − 2x 2 + 2 ; d) x + 5 . x + 3 x − 4 2 x − 2 2 x + 2x 5 + 5 14
VẤN ĐỀ 5. LIÊN HỆ PHÉP NHÂN, PHẾP CHIAVỚI PHÉP KHAI PHƯƠNG (PHẦN II) A. TÓM TẮT LÝ THUYẾT
Nhác lại các công thức khai phương ở vấn đề 4: Khai phương một tích:
Với A ≥ 0,B ≥ 0 ta có .
A B = A. B. Khai phương một thương:
Với A ≥ 0,B > 0 ta có A A = . B B
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
* Giáo viên hướng dẫn học sinh giải các bài tập sau: Bài 1. Tính: a) 15 − 5 ; b) 3 − 5.(3 + 5) ; 6 − 2 10 + 2 2 c) 2 10 + 30 − 2 2 − 6 ;
d) (1− 2006) . 2017 + 2 2016 . 2 10 − 2 2
* Học sinh tự luyện các bài tập sau tại lớp: Bài 2. Tính: a) 12,1.360; b) 0,4. 6,4 ; c) -0,4 2 ( 0 − ,4) ; d) 4 2 2 .( 7 − ) . Bài 3. Tính: a) 2 ( 15 + 2 3) + 12 5; b) 2
2 5(2 − 3 5) + (1− 2 5) + 6 5;
Dạng 4. Rút gọn biểu thức A, A ≥ 0
Phương pháp giải: Sử dụng hằng đẳng thức 2
A = A = −A,A <  0
Và phép khai phương của một tích hoặc một thương.
*Giáo viên hướng dẫn học sinh giải các bài tập sau: a) 2
27.48(1− a) với a<1. b) 1 4 2
a (a − b) với aa − b c) 2a 3
. a với a ≥ 0
c) 5a. 45a − 3a với a ≥ 0 . 3 8
Bài 5. Rút gọn các biểu thức sau: 3 3 a) a − b a + b −
với a ≥ 0,b ≥ 0,a ≠ b; a − b a − b
b) 2a + ab − 3b với a ≥ 0,b ≥ 0,4a ≠ 9 . b
2a − 5 ab + 3b
* Học sinh tự luyện các bài tập sau tại lớp.
Bài 6. Rút gọn các biểu thức sau: 15 2 a) 2 4
(3 − a) − 0,2. 180a ;
b) 27(a − 3) với a<3; 48 3 63y 4 6 c) với y>0 ;
d) 16a b với a < 0,b ≠ 0. 7y 6 2 128a b
Bài 7. Rút gọn biểu thức sau : 2 x + x y a) a − 2a x − 2 ; b) ; c) x − 3 ; d) . 2 a −1 x − 2 x − 9 x − y
Dạng 5. Giải phương trình
Phương pháp giải : chú ý rằng: B ≥ 0
B ≥ 0(hayA ≥ 0) * A = B ⇔  . * A = B ⇔  . 2 A = B A =  B
* Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 8. Giải các phương trình sau: a) 2x − 3 = 2; b) 2
4x − 9 = 2 2x + 3; x −1 c) 2
2 − x − x − 4 = 0 d) 1
4x − 20 + x − 5 − 9x − 45 = 4. 3
Bài 9. Giải các phương trình sau: a) 2 x x − − 8x + 16 = 5 ; b) 9 7 = 7x+5 ; 7x + 5 c) 2
x − 3 − 2 x − 9 = 0; d) 1 1 2 9x − 27 − 25x − 75 − 49x −147 = 20. 5 7
Bài 10. Giải các phương trình sau: a) x − 3 = 2;
b) 10x − 7 = 3x + 5; 2x + 1 3x + 5 c) 2
x − 2 − 2 x − 4 = 0; d) 1
x − 2 − 4x − 8 − 9x −18 = 2. 2 C. BÀI TẬP VỀ NHÀ Bài 11.tính: a) 2.80 ; b) 25 ; c) 5. 45; d) 14 2 . 144 25
Bài 12. Thưc hiện phép tính: a) 5 + 5 5 − 5 − + + ; b) 2 8 12 5 27 − ; 5 − 5 5 + 5 18 − 48 30 + 162 c) (2 + 5 + 3)(2 + 5 − 3); d) 2 − 3 2 + 3 + . 2 + 3 2 − 3
Bài 13. Rút gọn các biểu thức sau : 16 2 2
a) x − 2 x + 1 với 2 3x 6xy 3y x ≥ 0; b) + +
với x + y > 0; x + 2 x + 1 2 x − 2 y 4 x y + y x c) x + 7 ; d) . 2 x + 2x 7 + 7
x + 2 xy + y
Bài 14. Giải các phương trình sau : a) 2 x x 3 − 10x + 25 = 7; b) − = 2; 2x + 1 c) 2 25x 1 − 9 = 2 5x − 3;
d) x − 5 + 4x − 20 − 9x − 45 = 3. 5
Bài 15. Giải các phương trình sau : a) 2x − 3 = 2; b) x − 3 = 2; x −1 2x + 1
c) 10x − 3 = 2x + 1; d) 2
4x − 9 = 2 2x − 3. 2x + 1 4
Bài 16. Cho x là số thực bất kì. Chứng minh ta luôn có : x + 5 > 2. 4 x + 4 17
VẤN ĐỀ 6. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI. A. TÓM TẮT LÍ THUYẾT • Đưa thừa số 2
A ra ngoài dấu căn : 2
A B = A B với B ≥ 0.  2 A B khi A ≥ 0
• Đưa thừa số vào trong dấu căn : A B =  . − 2 A B khi A <  0
• Khử mẫu của biểu thức dưới dấu căn bậc hai : A . A B 1 = = .
A B với B ≠ 0, . A B ≥ 0. 2 B B B
• Trục căn thức ở mẫu : A A B = ; B B
m( A − B m ) = ; A + B A − B m( A + B m ) = . A − B A − B
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Dưa thừa số ra ngoài dấu căn hoặc vào trong dấu căn
Phương pháp giải : 1. Cách đưa thừa số 2
A ra ngoài dấu căn : 2
A B = A B với B ≥ 0.  2 A B khi A ≥ 0
2. Cách đưa thừa số vào trong dấu căn : A B =  . − 2 A B khi A <  0
• Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 1. Đưa thừa số ra ngoài dấu căn : a) 2
7x với x ≥ 0; b) 2
7y với y ≤ 0; c) 2
25x với x ≥ 0; d) 4 48y .
Bài 2.Đưa thừa số vào trong dấu căn :
a) x 13 với x ≥ 0;
b) x 2 với x ≤ 0; c) 15 x với x ≥ 0; d) −15 x với x < 0. x x
• Học sinh tự luyện các bài tập sau tại lớp :
Bài 3. Đưa thừa số ra ngoài dấu căn a) 2
13x với x ≥ 0; b) 2
12y với y ≤ 0; c) 3
81x với x ≥ 0; d) 8 48y . 18
Bài 4. Đưa các thừa số vào trong dấu căn
a) x 13 với x ≥ 0;
b) x 3 với x ≤ 0; c) 7 2y với y > 0; d) −7 2y với y < 0. y y
Dạng 2. So sánh các căn bậc hai
Phương pháp giải : Đưa thừa số ra ngoài hoặc vào trong đấu căn rồi so sánh.
• Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 5. So sánh các số a) 5 2 và 4 3; b) 5 1 và 1 6 ; 2 6 37 c) 2 29 và 3 13; d) 5 2 và 3 3. 4 2 2
Bài 6. Sắp xếp theo thứ tự tăng dần a) 3 5; 2 6; 29; 4 2; b) 6 2; 38; 3 7; 2 14.
• Học sinh tự luyện các bài tập sau tại lớp :
Bài 7. So sánh các số : a) 3 5 và 2 7; b) 3 1 và 1 6 ; 2 3 14 c) 3 21 và 2 47; d) 5 3 và 2 14. 9 7
Bài 8. Sắp xếp theo thứ tự giảm dần : a) 7 2; 2 8; 28; 5 2; b) 2 5; 2 40; 3 8; 5 30.
Dạng 3. Rút gọn biểu thức chứa căn bậc hai
Phương pháp giải : Đưa các thừa số ra ngoài hoặc vào trong dấu căn rồi rút gọn.
• Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 9. Rút gọn các biểu thức sau :
a) 5 48 − 4 27 − 2 57 + 108; b)
5 16a − 4 25a − 2 100a + 169a với a ≥ 0.
Bài 10. Rút gọn biểu thức sau : a) 2
3 a − 5a với a ≤ 0; b) 6 a − 3 3 4
5a với a ≤ 0; c) 4 + 2 3 + 4 − 2 3 ; d) x − − − x + 2 2 4 4
x với x ≥ 2. 19
• Học sinh tự luyện các bài sau tại lớp :
Bài 11. Rút gọc các biểu thức sau :
a) 2 24 − 2 54 + 3 6 − 150; b) a − 2 5 4
4 a − 100a với a > 0.
Bài 12. Rút gọn biểu thức sau : a) 2
4a + 5a với a ≥ 0; b) 2
25x + 3x với x ≤ 0; c) x − − − x + 2 2 4 4
x với x ≤ 2; d) − x + + x + 2 3 9 9
x với x ≤ −3.
Dạng 4. Trục căn thức ở mẫu
Phương pháp giải :
1. Cách khử mẫu của biểu thức dưới dấu căn bậc hai : A . A B 1 = = .
A B với B ≠ 0, . A B ≥ 0. 2 B B B
2. Cách trục căn thức ở mẫu : A A B = ; B B
m( A − B m ) = ; A + B A − B m( A + B m ) = . A − B A − B
• Giáo viên hướng dẫn học sinh làm các bài tập sau :
Bài 13. Khử mẫu của mỗi biểu thức lấy căn và rút gọn ( nếu được) : 2 a) 2 x ; b) với x ≥ 0; 3 5 3 c) 5a với a 3 ≥ 0,b > 0; d) −7xy
với x < 0, y > 0. 49b xy
Bài 14. Trục căn thức ở mẫu và rút gọn: a) 10 + 2 10 ;b) 2 8 − 12 ; 5 + 2 18 − 48 c) 2 ; d) 2 − 3 . 5 − 3 2 + 3
Bài 15. Trục căn thức và thực hiện phép tính:  15 4 12  a) 1 1  + − ( 6 +11); b) − ;  6 + 1 6 − 2 3 − 6  3 − 5 5 −1 c) 1 1 1 1 1 + − − 5; d) + . 5 + 1 5 − 2 3 − 5 5 + 3 2 5 − 3 2 20
*Học sinh tự luyện tập các bài tập sau tại lớp:
Bài 16. Khử mẫu của mỗi biểu thức lấy căn và rút gọn (nếu được): 2
a) 2 ; b) x với x ≥ 0; 7 31 3 c) 5b với a 16 > 0,b ≥ 0; d) −7xy
với x < 0, y < 0. 49a xy
Bài 17. Trục căn thức ở mẫu và rút gọn: a) 5 + 2 5 ; b) 2 6 − 10 ; 5 + 2 4 3 − 2 5 c) 1 ; d) 3 − 5 . 2 2 − 3 3 3 + 5
Bài 18. Trục căn thức và thực hiện phép tính:  5 +   5 5 −  a) 3 + 2 3 2 + 2 + − (2 + 3); b) 5 1− . − 1; 3 2 + 1     1+ 5 1−    5   5 −  2 5 5 +  c) 3 5 3 2 1  − 2 − 2   ; d) − + . 2 − 5 3 +   5  5 − 2 2 − 2 3 + 2 C. BÀI TẬP VỀ NHÀ
Bài 19. Rút gọn các biểu thức sau:
a) 125 − 2 20 − 3 80 + 4 45; b) 3 10 28 − 2 75 − 3 343 − 396; 2 c) 1 1 + ; 7 + 4 3 7 − 4 3 d) 1 . 2 11 − 3 7
Bài 20. Rút gọn các biểu thức sau: a) 4 a + 2 9 2a ; b) 2
9x − 2x với x ≥ 0; c) 4 − 2 3 − 3 d) − x + 2 3
x + 6x + 9 với x > −3. Bài 21. Tính: a) (2 45 16 1 4 + 80 − 125 ). 5; b) 2 − 3 − 6 ; 5 45 20 c) 3 3 4 1 + 7 − 2 6 − 3 6; d) − + . 5 + 2 3 − 5 2 −1 Bài 22. Tính: 21 b) 16 1 4 3 − 5 + 3 + 5 ; b) 2 − 3 − 6 ; 3 27 75 c) 1 6 2 − 4 + 175 − ; d) 10 − 84 − 34 + 2 189 . 8 + 7 3 − 2 Bài 23. Tính:  2 3 15  a) 1  + + . ;  3 − 1 3 − 2 3 − 3  3 + 5 b) 3 3 − ; 3 + 1 −1 3 + 1 + 1 c) 3 1 1 + − 2 ; 20 60 15  14 − 7 15 −  d) 5 1  +    : . 1− 2 1− 3 7 −   5
Bài 24. Giải phương trình: a) 1
x − 5 + 2 25x −125 = 22; b) 18x + 9 − 8x + 4 + 2x + 1 = 4; 3 c) x − 2 x − 4 1 = ; d) 4x − 8 −
x − 2 + 9x −18 = 9. x − 5 x − 6 2
Bài 25. Giải phương trình: a) 2
4x − 9 = 2 2x + 3; b) x − 5 1 4x − 20 + 3 − 9x − 45 = 4; 9 3 2 1 x −1 c) 9x − 9 − 16x −16 + 27 = 4; 3 4 81 2 d) 9x − 27 4x −12 2 9x − 81 5 − 7 − 7 x − 9 + 18 = 0. 25 9 81
Bài 26. Tìm x, y,z biết rằng:
a) x + 2 y + 1 + y = 4y + 4; b) 1
x + 1 + y − 3 + z −1 = (x + y + z). 2 Bài 27. Rút gọn: 1 1 1 1 A = + + + ...+ . 1 + 2 2 + 3 3 + 4 n −1 + n
Bài 28. Tìm giá trị nhỏ nhất của biểu thức: 22
A = x − 2 x −1 + x + 2 x −1.
Bài 29. Chứng minh với mọi số tự nhiên n khác 0 , ta luôn có: 1 1 1 1+ + + ...+ > 2( n+1 −1). 2 3 n Bài 30. Chứng minh: 2002 2003 + > 2002 + 2003. 2003 2002
VẤN ĐỀ 7: RÚT GỌN BIỂU THỨC CHỨA CĂN VÀ CÁC BÀI TOÁN LIÊN QUAN A. TÓM TẮT LÝ THUYẾT
Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần biết vận dụng linh hoạt thích hợp
các phép biến đổi đơn giản như: Đưa thừa số ra ngoài dấu căn, đưa thừa số vào trong
dấu căn, khử căn ở mẫu và trục căn thức ở mẫu để làm xuất hiện các căn thức bậc hai có
cùng một biểu thức dưới dấu căn …
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1.Rút gọn biểu thức chứa căn bậc hai Phương pháp giải:
Bước 1. Vận dụng thích hợp các phép tính và các phép biến đổi đã biết làm xuất hiện căn thức cùng loại.
Bước 2. Cộng, trừ các căn thức bậc hai cùng loại.
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Rút gọn các biểu thức sau: a) 1 32 + 50 − 2 8 + 18; b) + 4,5 + 12,5; 2 2 c) 2 3 (1−2 3) − 4−2 3; d) 96 − 6 + − 10 − 4 6 . 3 3 + 6
Bài 2. Rút gọn các biểu thức sau: a) a 4 5 a + 6 − a + 5 với a > 0; 4 a b) a − 3 b a + 2 5 4 25
5a 16ab − 9a với a ≥ 0,b ≥ 0.
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 3. Rút gọn các biểu thức sau: a) 27 48 2 75 2 − − ;
b) ( 99 − 18 − 11) 11 + 3 22; 4 9 5 16 c) ( 5 + 3) 8 − 2 15;
d) ( 48 −2 3 + 2 5) 5 −2 45 : 3.
Bài 4. Rút gọn các biểu thức sau: 23  1 1  a) 1  − + 1. ;  5 − 2 5 + 2  ( 2 2 + 1) b) 4 2 2 a − 3 9a + 2 a + 5
25a với a > 0. 2 a a
Dạng 2: Chứng minh đẳng thức chứa căn thức bậc hai
Phương pháp giải: Thực hiện các phép biến đổi căn thức và các hằng đẳng thức đáng nhớ
để thực hiện phép chứng minh.
*Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 5. Chứng minh các đẳng thức sau:  2 1−  a a 1−  a) a  + a   =  
1 với a ≥ 0,a ≠ 1. 1− a 1−    a a + 2 4 b) b a b
= a với a + b > 0 và b ≠ 0. 2 2 b a + ab + 2 2 b
*Học sinh tự luyện tập bài tập sau tại lớp:
Bài 6. Chứng minh các đẳng thức sau:  2 3 −  a) 6 216 1 −3  − . =   ; 8 −  2 3  6 2 b) a + b a − b 2b 2 b − − =
với a ≠ b và a ≥ 0,b ≥ 0.
2 a − 2 b 2 a + 2 b b − a a − b
Dạng 3. Rút gọn biểu thức và các bài toán liên quan *Phương pháp giải:
1. Để rút gọn biểu thức, ta thực hiện các phép biến đổi căn thức và các hằng đẳng thức đáng nhớ.
2. Các bài toán liên quan thường gặp là:
- Tính giá trị của biểu thức với giá trị của biến cho trước.
- Giải phương trình hoặc bất phương trình chứa căn bậc hai.
- Tìm giá trị nguyên của biểu thức.
- So sánh biểu thức với một số.
- Tìm giá trị lớn nhất, nhỏ nhất của biểu thức.
* Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 7. Cho biểu thức 2 x − 9 x + 3 2 x + 1 M = − − . x − 5 x + 6 x − 2 3 − x a) Rút gọn M;
b) Tính giá trị của M khi x = 11 − 6 2;
c) Tìm các giá trị thực của x để M = 2;
d) Tìm các giá trị thực của x để M < 1;
e) Tìm các giá trị nguyên để M nguyên.
* Học sinh tự luyện các bài tập sau tại lớp: 24
Bài 8. Với x > 0 , cho các biểu thức 1 x A x = − và B = . x x + 1 x + x
a) Tính giá trị của A khi x = 4.
b) Tìm các giá trị thực của x để 1 B = ; 3 c) So sánh B với 1;
d) Đặt P = A : .
B Tìm x thỏa mãn P x + (2 5 −1) x = 3x −2 x −4 + 3.    1 2 x x + 
Bài 9. Cho biểu thức x 1 P =  −  :  +     với
x −1 x x − x + x −1
x x + x + x + 1 x +     1
x ≥ 0,x ≠ 1; a) Rút gọn P; b) Tìm x để 1 P < ; 2
c) Tìm giá trị của x để 1 P = ;
d) Tìm x nguyên để P nguyên; 3
e) Tìm giá trị nhỏ nhất cuả . P C. BÀI TẬP VỀ NHÀ
Bài 10. Rút gọn các biểu thức sau:  3 −  3 21 +  7
a) 5 27 + 3 48 − 2 12 − 6 3; b)  3 +  + 2   ; 1−  3  7  c) 2 3 96 − 6 + − 10 − 4 6 ; d) 5 11 − 6 − − 2 6 . 3 3 + 6 2 2
Bài 11. Rút gọn các biểu thức sau a) 4 7 1 − 10 − 6 ; b) ( 10 + 2) 3− 5; 7 25 28 c) 6 + 11 − 7 − 33 ; d) 5 3 − 3 5 2 5 5 + 3 3 + − . 6 + 2 5 − 3 4 + 15 5 + 3
Bài 12. Cho biểu thức 3x + 9x − 3 x + 1 x − 2 Q = − + . x + x − 2 x + 2 1− x a) Rút gọn Q;
b) Tính giá trị của Q khi x = 4 + 2 3;
c) Tìm các giá trị của x để Q = 3;
d) Tìm các giá trị của x để 1 Q > ; 2
e) Tìm x∈ để Q∈.  1   x −1 1− 
Bài 13. Cho biểu thức x P =  x −  :  +   .  x x x +  x  a) Rút gọn P;
b) Tính giá trị của P biết 2 x = ; 2 + 3 25
c) Tìm x thỏa mãn P x = 6 x − 3 − x − 4.  x + 2   x x − 
Bài 14. Cho biểu thức 4 P =  x −  :  −   .  x + 1 x + 1 1−   x  a) Rút gọn P;
b) Tính giá trị của x thỏa mãn P < 0;
c) Tìm giá trị nhỏ nhất của . P 2 x − x
2x + x 2(x −1)
Bài 15. Cho biểu thức P = − + . x + x + 1 x x −1 a) Rút gọn P;
b) Tìm giá trị nhỏ nhất của P;
c) Tìm x để biểu thức 2 x
Q = P nhận giá trị là số nguyên.
Bài 16 . Cho các biểu thức 2 x x + 9 x x + 5 x A = − ; B =
, với x ≥ 0,x ≠ 9 và x ≠ 25. x − 3 x − 9 x − 25
a) Rút gọn các biểu thức A và P;
b) Đặt P = A : .
B So sánh P với 1;
c) Tìm giá trị nhỏ nhất của . P 26
VẤN ĐỀ 8. CĂN BẬC BA
A. TÓM TẮT LÝ THUYẾT
• Căn bậc ba của một số thực a là số thực x sao cho: 3
x = a, kí hiệu là 3 a.
• Mọi số thực a đều có duy nhất một căn bậc ba. Căn bậc ba của số dương là số dương;
của một số âm là số âm; của 0 là 0.
• Các công thức liên quan đến căn bậc ba:
A < B ⇔ 3 A < 3 B.
3 A = 3 B ⇔ A = . B 3 . A B = 3 3 A. B. 3 A A 3 = với B ≠ 0. 3 B B
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Thực hiện phép tính có chứa căn bậc ba
Phương pháp giải: Áp dụng công thức: 3 3 3 = (3 a a ) = a
và các hằng đẳng thức: (a+b)3 3 2 2 3
= a + 3a b + 3ab + b (a−b)3 3 2 2 3
= a − 3a b + 3ab − b 3 3
a + b = (a + b)( 2 2
a − ab + b ) 3 3
a − b = (a − b)( 2 2
a + ab + b )
* Giáo viên hướng dẫn học sinh giải các bài tập sau: Bài 1. Tính: a) 3 27; b) 1 3 ; c) 3 3 64a ; d) 3 − 3 6 8a b ; 125
Bài 2. Thực hiện các phép tính sau: 3 a) 3 − 3 + 3 2 24 81 4 192; b) 2 − 3 4 − 3 2. 3 2 −1
Bài 3. Thực hiện các phép tính sau a) A = 3 + + 3 2 5 2 − 5 ; b) B = 3 + − 3 17 5 38 17 5 − 38.
* Học sinh tự luyện các bài tập sau tại lớp: Bài 4. Tính a) 3 729; b) 1 3 ; c) 3 3 343a ; d) 3 3 6 512 − a b . 216
Bài 5. Thực hiện các phép tính sau a) 3 3 3 2 27 − 3 8 + 4 125; b) 27 − 3 1 3 3 + 64 − 1000; 512 3 27 3 c) 3 3 3 − 9 − 3; d) 3 3 2
125x + 75x + 15x + 1. 3 3 −1
Bài 6. Thực hiện các phép tính sau: a) 3 ( 5 +1)(6 + 2 5); b) 3 (4 + 2 3)( 3 +1); 3 3 c) 3 3 3 27 − − 64 + 216; d) (3 + ) −(3 9 1 9 −1) .
Bài 7. Thực hiện các phép tính sau: a) 3 3
A = 7 + 5 2 + 7 − 5 2 ; b) 3 3
B = 9 + 4 5 + 9 − 4 5 ; c) 3  6 3 C 2 5. 9 4 5 2 5  = − + + + ;   d) 1 1 3 3 D = 2 + 10 + 2 −10 . 27 27
Dạng 2. So sánh các căn bậc ba
Phương pháp giải: Ta có 3 3
A < B ⇔ A < . B
* Giáo viên hướng dẫn học sinh giải các bài tập sau: Bài 8. So sánh: a) 3 A = 2 3 và 3 B = 23; b) A = 33 và 3 B = 3 133 . Bài 9. So sánh: 3 3
A = 20 + 40 2 + 20 −14 2 và B = 2 5.
Bài 10. Tìm x biết: a) 3 2x + 1 > 5; − b) 3 3 2
x + 3x + 6x + 4 > x + 1.
* Học sinh tự luyện các bài tập sau tại lớp: Bài 11. So sánh: a) 3 A = 3 2 và 3 B = 42; b) A = 22 và 3 B = 3 122; c) 3 A = 2 6 và 3 B = 54; d) 3 A = 5 6 và 3 B = 6 5. Bài 12. So sánh: 3 3
A = 7 + 5 2 + 7 − 5 2 và B = 2.
Bài 13. Tìm x biết: a) 3 3 − 2x > 4 ; b) 3 3 2
−x − 3x + 6x − 3 > −x −1.
Dạng 3. Giải phương trình chứa căn bậc ba
Phương pháp giải: Áp dụng 3 3
A = B ⇔ A = B
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 14. Giải các phương trình sau: a) 3 2x + 1 = 3; b) 3 2 − 3x = 2. −
Bài 15. Giải các phương trình sau: a) 3 3
x − 2 + x + 1 = 3; b) 3 3
13 − x + 22 + x = 5.
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 16. Giải các phương trình sau: 28
a) 3 x −1 + 1 = x;
b) 3 5 + x − x = 5.
Bài 17. Giải các phương trình sau:
a) 3 2x −1 + 2x + 2 = 3; b) 3 3
12 − 2x + 23 + 2x = 5. C. BÀI TẬP VỀ NHÀ Bài 18. Tính: 3 6 a) 3 512; b) 1 343a b 3 − ; c) 3 ; d) 3 6 6 64 − a b . 125 216 − Bài 19. Tính: a) 3 3 1 3 27 − 8 − − 125 − ; b) 125 3 1 3 + 125 − 27; 5 512 3 c) 3 3 2
x + 3x + 3x + 1; d) 3 3 2
(8x + 12x + 6x + 1.
Bài 20. Thực hiện các phép tính sau: 3 a) 135 3 3 − 54. 4; b) (3 3 3 25 − 10 + 4 )(3 3 5 + 2 ); 3 5 3 3 c) 3 3 3 64 − − 125 + 216; d) (3 + ) −(3 4 1 4 −1) .
Bài 21. Thực hiện các phép tính sau: a) 3 3
A = 6 3 + 10 − 6 3 −10; b) 3 3
B = 7 + 5 2 + 7 − 5 2 ; c) 3 C = 3 + 3 + 10 + 6 3 ; d) 3  3 3 D 2 5. 9 4 5 2 5  = − + + + .  
Bài 22. Thực hiện các phép tính sau: a) 3 ( 2 +1)(3+ 2 2); b) 3 (4 −2 3)( 3 −1); c) (3 3 3 9 5 31 5 31 − 6 + 4 )( 3 3 3 + 2 ) d) 3 3 4 + . + 4 − . . 3 3 3 3
Bài 23. Giải các phương trình sau: a) 3 2x + 1 = 1; b) 3 2 − 3x = 3. −
Bài 24. Giải các phương trình sau:
a) 3 x − 2 + 2 = x; b) 3 3 2
x + 2x = x + 2.
Bài 25. Giải các phương trình sau: a) 3 3
x − 2 + x + 8 = 2; b) 3 3
x + 1 + 7 − x = 2. 29
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I) A. TÓM TẮT LÝ THUYẾT
1. Căn bậc hai số học
• Căn bậc hai của một số không âm là số x sao cho 2 x = .a
• Số dương a có đúng hai căn bậc hai là a (và gọi là căn bậc hai số học của a ) và − a.
• Số 0 có đúng một căn bậc hai là chính số 0 và nó cũng là căn bậc hai số học của 0.
• Với hai số không âm a,b, ta có a < b ⇔ a < b.
2. Căn thức bậc hai
• Với A là một biểu thức đại số, ta gọi A là căn thức bậc hai của A . •
A xác định (hay có nghĩa) khi A lấy giá trị không âm. A khi 0 A ≥ • 2 A = A =  . −A khi 0 A < 
3. Liên hệ giữa phép nhân, phép chia với phép khai phương • Khai phương một tích: .
A B = A. B (A ≥ 0,B ≥ 0) • Nhân các căn bậc hai: A. B = .
A B (A ≥ 0,B ≥ 0)
• Khai phương một thương: A A =
(A ≥ 0,B > 0) B B
• Chia căn bậc hai: A A =
(A ≥ 0,B > 0) B B
4. Biến đổi đơn giản biểu thức chứa căn bậc hai
• Với A ≥ 0 và B ≥ 0 thì 2 A B = A B
• Với A < 0 và B ≥ 0 thì 2 A B = −A B
• Với A ≥ 0 và B ≥ 0 thì 2 A B = A B
• Với A < 0 và B ≥ 0 thì 2 A B = − A B • Với .
A B ≥ 0 và B ≠ 0 thì A AB = B B
• Với B > 0 thì A A B = B B • Với A C C( A  ) B > 0 và 2 A ≠ B thì = 2 A ± B A − B
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tìm điều kiện cho các biểu thức có nghĩa
Bài 1. Với giá trị nào của x thì các biểu thức sau có nghĩa: 30 a) 3 − x + 2 b) 2 9x − 6x + 1 c) 2 x + 2x + 3 d) 2 x − x + 1 e) 4 g) 5 . 2x + 3 1− x −1
Bài 2. Với giá trị nào của x thì các biểu thức sau có nghĩa: a) 2x −1 b) x − 3 c) 2 x − 4 2 − x 5 − x d) x −1 e) 3 − x g) 2 . x + 1 2 x −1 x − 2
Dạng 2: Tính và rút gọn biểu thức
Bài 3. Thực hiện phép tính a) 12 − 27 + 108 ; b) 3 2 − 4 18 + 32 − 50 ; c) 27 − 2 3 + 2 48 − 3 75 d) 3 10 28 − 2 275 − 3 343 − 396 . 2
Bài 4. Thực hiện phép tính a) 1 8 + 18 − 6 − 200 ; b) 3 2 3 6 + 2 − 4 ; 2 2 3 2 c) 8 32 18 6 − 5 + 14 d) 16 1 4 2 − 3 − 6 . 9 25 49 3 27 75
Bài 5. Thực hiện phép tính     a) 16 1 4  2 − 3 − 6 . 3 ;  b) 8 32 18 1 6 − 5 + 14 . ; 3 27 75      9 25 49 2   c) ( 5 + 2 2).( 5 −2 2) ; d) (2 + 3)(2 − 3) .
Bài 6. Thực hiện phép tính a) (20 12 −15 27 ) : 5 3 ; b) ( 75 + 243 − 48): 3 ; 2 2 c) ( 2 +1) +( 2 −1) ; d) ( 28 −2 3 + 7 ) 7 + 84 .
Bài 7. Trục căn thức ở mẫu a) 3 ; b) 2 3 ; c) 2 + 3 ; 5 2 2 − 3 d) 1 ; e) 2 + 1 ; g) 3 2 . 3 + 2 2 −1 3 + 1
Bài 8. Rút gọn biểu thức a) 10 + 2 10 8 + ; b) 2 8 − 12 5 + 27 − ; 5 + 2 1− 5 18 − 48 30 + 162 31 c) 16 1 4 2. − 3. − 6 ; − + 3 27 75 d) 2 3 2 3 + ; 2 + 3 2 − 3
Bài 9. Rút gọn biểu thức: 3 − 5.(3+ 5) b) 4 1 6 + + ; a) ; 3 + 1 3 − 2 3 − 3 10 + 2 c) 4 − 9 + 4 2 ; d) 1 1 + ; 2 + 2 + 3 2 − 2 − 3
Bài 10. Rút gọn biểu thức: a) 3 3 3 − 5 + 3 + 5 ; b) ( 2 +1) −( 2 −1) ;  +  −  c) 5 5 5 5 1−  − 1
d) 4 + 10 + 2 5 + 4 − 10 + 2 5 .  1 5  1 5  + −   
Dạng 3. Giải phương trình và bất phương trình
Bài 11. Giải phương trình
a) x −1 + 4x − 4 − 25x − 25 + 2 = 0 ;
b) 16x + 16 − 9x + 9 + 4x + 4 + x + 1 = 16 ; c) 1
4x + 20 + x + 5 − 9x + 45 = 4 ; 3
d) 1 2x − 8x + 18x −10 = 2 ; 3
Bài 12. Giải các phương trình a) 2
x − 6x + 9 = 3 ; b) 2
x − 8x + 16 = x + 2 ; c) 2
x − 6x + 9 = 3x − 6 ; d) 2
x − 4x + 4 − 2x + 5 = 0 ; .
Bài 13. Giải các phương trình
a) x − 5 = 3 − x ;
b) 4 − 5x = 2 − 5x ;
c) 6 − x = 3x − 4 ;
d) 5 − x = 9 − 2x ;.
Bài 14. Giải các phương trình
a) x − 5 = 3 − x ;
b) 4 − 5x = 2 − 5x ; ; c) 2 2
x − 2x + 1 = 4x − 4x + 1 ; d) 2 2
x −10x + 25 = x − 6x + 9 ; .
Bài 15. Giải các phương trình a) x −1 x + = 3. b) 1 1 = . x − 2 x −1 2 c) x + 10 x + = 2. − d) 3 5 = x. x − 2 3 x + 1
Bài 16. Giải các phương trình a) 2
x + 4x + 5 = 2 2x + 3. b) 2
x + 9x + 20 = 2 3x + 10. c) 2
x + 7x + 14 = 2 x + 4 d) 2
4 x + 1 = x − 5x + 14
Bài 17. Giải các phương trình 32
a) x − 5 + 5 − x = 1
b) 2x − 3 + 3 − 2x = 0 c) 1
x + 3 + y − 2 + z − 3 = (x + y + z)
d) x + y + 4 = 2 x + 4 y −1 2
Bài 18. Giải các phương trình a) 2
4x + 3x + 3 = 4x x + 3 + 2 2x −1
b) 4 x + 3 − x −1 = x + 7 c) 2
x − 4 + 6 − x = x −10x + 27 d) 2
x + 2 + 6 − x = x − 4x + 8
Bài 19. Giải các bất phương trình a) x −1 x + < 1 b) 1 1 > x − 2 x −1 2 c) x −10 − x + ≥ 2 − d) 3 1 > − x x + 2 x + 1 33
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II) A. TÓM TẮT LÍ THUYẾT
Xem lại Tóm tắt lí thuyết trong ôn tập chủ đề 1, Phần I
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 4. Tìm các giá trị nguyên của biến để các biểu thức cho trước có giá trị nguyên
Bài 1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên a) x −1 b) 3 x x − 3 x − 3
Bài 2. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên a) x b) x − 2 6 x + 1 x − 3
Dạng 5. Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của biểu thức
Bài 3. Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = x − 4 − 2
b) B = x − 4 x + 10
c) C = x − x d) 2
D = x − 2x + 4 + 1
Bài 4. Tìm giá trị nhỏ nhất của các biểu thức sau: a) x −1 + P x = b) 3 Q = x + 3 x + 1
Bài 5. Tìm giá trị lớn nhất của các biểu thức sau:
a) M = 3 − x −1
b) N = 6 x − x −1 c) 1 P = d) x + 5 Q = x − x + 1 x + 3
Dạng 6. Rút gọn biểu thức và các bài toán liên quan
Bài 6. Cho các biểu thức 2 x x + 1 3 −11 x A x − = + + và 3 B = với 0 ≤ x ≠ 9 x + 3 x − 3 9 − x x + 1
a) Tính giá trị của B khi x = 36;
b) Rút gọn biểu thức A;
c) Tìm số nguyên x để P = A.B là một số nguyên.
Bài 7. Cho biểu thức x 3 6 x − 4 P = + −
với x ≥ 0; x ≠ 1. x −1 x + 1 x −1 a) Rút gọn P;
b) Tìm giá trị của x để P = -1;
c) Tìm x∈ để P∈ ;
d) So sánh P với 1;
e) Tìm giá trị nhỏ nhất của P. +  + − 
Bài 8. Cho biểu thức x x x 1 1 2 = : x E  − +
 với x ≥ 0 và x ≠ 1 x 2 x 1  x 1 x x x  − + − −   a) Rút gọn E;
b) Tìm giá trị của x để E > 1;
c) Tìm giá trị nhỏ nhất của E với x > 1;
d) Tìm x∈ để E∈ ; 34 e) Tìm x để 9 E = . 2  x − 2
x + 2  ( − x)2 1
Bài 9. Cho biểu thức P =  − . 
với x ≥ 0 và x ≠ 1 x −1 x + 2 x +  1 2  a) Rút gọn P;
b) Tính giá trị của P khi x = 7 − 4 3 ;
c) Tìm giá trị của x để biểu thức P có giá trị lớn nhất.    − 
Bài 10. Cho biểu thức 1 2 2 =  −  :  2 x x B −  với x ≥ 0
x + 1 x x + x + x + 1   x + 1    a) Rút gọn B;
b) Tính giá trị của B khi x = 6 + 2 5 ;
c) Tìm giá trị nguyên của x để B có giá trị nguyên.
Bài 11. Cho biểu thức x x + 26 x −19 2 x x − 3 P = − +
với x ≥ 0 và x ≠ 1 x + 2 x − 3 x −1 x + 3 a) Rút gọn P;
b) Tính giá trị của x khi P = 4 ;
c) Tìm giá trị nhỏ nhất của P;
d) Tính P khi x = 3 − 2 2 .  
Bài 12. Cho biểu thức  2 5  3 = −   : 1 − x P + 
x − 1 x + x − 2   ( x −1)( x + 2) 
a) Rút gọn biểu thức P ;
b) Tính P khi x = 6 − 2 5 ;
c) Tìm giá trị của x để 1 P = ; x
d) Tìm x∈ để P∈ ;
e) Tìm x để P < 1− x ;
f) Tìm giá trị nhỏ nhất của P .  
Bài 13. Cho biểu thức 1 x =  +  : x P với x > 0 . x x + 1 x +   x a) Rút gọn P ;
b) Tìm x để P = 1 − ; c) Tính P tại 8 8 x = − ; 5 −1 5 + 1
d) Tìm x để P > x + 2 ; e) So sánh P với 1;
f) Tìm giá trị nhỏ nhất của P .
Bài 14. Cho các biểu thức 1 x − x + 3 A x + = − và 2 B = . x −1 x x −1 x + x + 1
a) Tính giá trị B tại x = 36 ; b) Rút gọn A ;
c) Cho biết P = A : (1− B). Tìm x để P ≤ 1. 35    − − 
Bài 15. Cho biểu thức 1 1 1 = −   : x x P x  + .  x   x x + x  a) Rút gọn P ;
b) Tính giá trị của P biết 2 x = ; 2 + 3
c) Tìm x thỏa mãn : P x = 6 x − 3 − x − 4 .  x + xy + x   xy + x + 
Bài 16. Cho biểu thức 1 x 1 P =  + + 1 : 1− −   . xy 1 1 xy   xy 1 xy 1 + − − +     a) Rút gọn P ; b) Cho 1 1 +
= 6 . Tìm giá trị lớn nhất của P . x y
Một số bài tập nâng cao
Bài 17. Giải phương trình: a) 1
x − 2 + y + 2009 + z − 2010 = (x + y + z) . 2
b) x( − x − ) 2 3 3
1 = 3x + 2x −1 − x x + 1 + 1. Bài 18. Cho 2 2
a,b > 0; a + b ≤ 16. Tìm giá trị lớn nhất của biểu thức:
M = a 9b(a + 8b) + b 9a(b + 8a) . Bài 19. Cho 25
a,b,c >
. Tìm giá trị nhỏ nhất của biểu thức: 4a b c P = + + .
2 b − 5 2 c − 5 2 a − 5
Bài 20. Cho a,b,c > 0 và ab + bc + ca = 1 . Chứng minh: 2 2 2
a + 1 + b + 1 + c + 1 ≤ 2(a + b + c) .
Bài 21. Cho hai số thực a,b thay đổi, thỏa mãn điều kiện a + b ≥ 1 và a > 0 . Tìm giá trị nhỏ 2 nhất của 8a + b 2 A = + b . 4a
Bài 22. Cho x, y thỏa mãn điều kiện 2 2
x + 2 − y = y + 2 − x . Tìm giá trị nhỏ nhất của 2 2
A = x + 2xy − 2y + 2y + 10 .
Bài 23. Với mọi a > 1, chứng minh : 1 a + ≥ 3 . a − 3 36
HƯỚNG DẪN – ĐÁP SỐ
CHỦ ĐỀ 1. CĂN BẬC HAI. CĂN BẬC BA VẤN ĐỀ 1.
d) Không có giá trị nào của x e) x = 17;
g) x = 6 hoặc x = 2. −
Bài 1. Căn bậc hai của các số đã cho lần Bài 11. a) 2 − < 3; b) 3 > 2 2; lượt là: 3 0; ±8; ± ; ±0,2 ; c) 11 > 99; d) 25 < 18 + 2 17; 4 e) 3 > 15 −1; g) 1− 3 < 0,2.
Căn bậc hai số học của các số đã cho lần
Bài 12. a) x ≥ 36; b) 0 ≤ x < 1; lượt là: 3 0;8; ;0,2. − 4 c) x ≤ 35; − d) 1 3 ≤ x ≤ . Bài 2. a) 144; b) Không tồn tại; 2 2
Bài 13. a) ⇔ 2x ≥ x ≥ 0 ⇔ x ≥ 0; c) 8 ; d) 1 . b) 2
⇔ 0 ≤ 2x ≤ x ⇔ x = 0 hoặc x ≥ 2. 7 75
Bài 14. a) 2 < 1+ 2; b) 3 11 < 12;
Bài 3. a) 3; b) 2 ; c) 3; − 5 c) 1 > 3 −1; d) 3 > 2 − 5; d) 6; − e) 3 − ; g) 7. e) 10 − < 2 − 23; g) 3 − 29 < 15. − 4
Bài 15. a) x ≥ 24; b) 1 − ≤ x < 3;
Bài 4. a) 4; b) 3,1; c) 1 ; d) 2. − − 6 c) x < 3 − 1; d) 1 3 ≤ x ≤ . 2 2
Bài 5. a) x = 4; ± b) x = ± 13;
Bài 16. Căn bậc hai của các số đã cho lần
c) Không có giá trị nào của x; lượt là: 13 7 ±15; ±18; ± ; ± ; ±1,5; ±0,4; d) x = 25; e) x = 36; 10 17 g) x = 3 − hoặc x = 5.
Căn bậc hai số học của các số đã cho lần
Bài 6. Căn bậc hai của các số đã cho lần lượt là: 13 7 15;18; ; ;1,5;0,4. 10 17 lượt là: 11 9; ± 0 ± ,5; 1 ± ,2; ± ; 9
Bài 17. a) 49; b) 9 ; c) 3 ; d) 1 .
Căn bậc hai số học của các số đã cho lần 16 2 8 lượt là: 11 9;0; 5;1,2; .
Bài 18. a) 5; b) 7 ; c) −111; d) 13; 9 5 Bài 7. a) 169; b) Không tồn tại; e) 7; g) 1 − . 400 c) 1 ; d) 6 . 10 125 Bài 19. a) 12; b) 7 11 13 − ; c) − ; d) − . 20 4 4
Bài 8. a) 11; b) 4 ; c) 8; − d) 2; 5
Bài 20. a) x = ±14; b) 1 x = ± ; e) 1 − ; g) 3 . 15 4 5
c) x = ±18; d) Không có giá trị nào của x; e)
Bài 9. a) 1; b) 4,65; c) 2 − ; d) 6. x = 7; g) 100 x = . 3 9 Bài 10. a) 1 x = ± ; b) x∈∅; 3 c) 256 x = ; 9 37 Bài 21. a) 290 x 19 1 1 = ; b) x = hoặc > ⇒ đpcm 3 3 99 100 17 x = −
; c) Không có giá trị nào của x; d) 3 b) Ta có: 4 < 3 9 x 13
= ; e) x = 16; g) x = . 4 4 ⇒ 4 + 4 < 4 + 3 < 3
Bài 22. a) 0 ≤ x ≤ 484; b) 37 x > ;
⇒ 4 + 4 + 4 < 4 + 3 < 3 2
c) x ≥ 22; d) Không có giá trị nào của . x ⇒ 4 + 4 + 4 + ...+ 4
Bài 23. a) 4 > 1+ 7; b) 2 5 < 8; < 4 + 3 < 3. c) −6 < −2 7; d) 4 > 23 −1; VẤN ĐỀ 2. e) 0,5 > 3 − 2; 2
Bài 1. a) −8 ; b) 128; c) 21 ; d) 12 .
g) So sánh: ( 2005 + 2008) và 15 20 5 ( 2
Bài 2. a) 5; b) 4; c) 7; d) 1. 2016 + 2017 ) . Bài 3. a) Ta có: Từ đó quy về so sánh: 11+ 6 2 = 9 + 2.3. 2 + 2 2015.2018 = (2016 −1)2018 2 = (3+ 2) ; = 2016.2018 − 2018 b) Ta có: và 8 − 2 7 = 7 − 2. 7.1+ 1 2016.2017 = 2016(2018 −1) 2 = ( 7 −1) = 2016.2018 − 2016
⇒ 2015 + 2018 < 2016 + 2017.
c) Áp dụng kết quả câu a);
d) Áp dụng kết quả câu b).
Bài 24. * Giả sử ∃m,n∈ : (m,n) = 1
Bài 4. a) 2 2; b) −2 5; c) 6 5; d) và m = ⇒ 2 m = 2 3 3n 4 5. n
Bài 5. a) 1; b) 2,5; c) −1; d) 90. ⇒ 2
m 3 ⇒ m3 ⇒ ∃k ∈ : m = 3k.
Bài 6. a) 3; b) 5; c) 8; d) 6. ⇒ 2 k = 2 n ⇒ 2 n = 2 k ⇒ 2 9 3 3 n 3
Bài 7. Tương tự Bài 3.
⇒ n3 ⇒ (m,n) ≠ 1. Vô lý!
Bài 8. a) 4; b) 12; c) −4; d) 4 3.
* Chứng minh tương tự ta được 7 là số
Bài 9. a) −50a; b) 10a; c) 2 10a ; d) − 3 15a . vô tỷ.
Bài 10. a) 3x + 2; b) 4x + 3;
Bài 25. a) Đặt y = x + 2 1 khi x > 2 c) 3 x − 3; d)  . ⇒ 2
y = x + ⇒ x = 2 2 y − 2 −1 khi x <  2 ⇒ A = 2 y − 2y − 2;
Bài 11. a) −32a; b) 11a; c) 2 11a ; d) − 3 33a .
b) Ta có: A = (y − )2 1 − 3 ≥ −3
Bài 12. a) 3x + 1; b) 4x − 3; 1 khi x > − Từ đó tìm được: 2 A = −3 tại y = 1 hay c) 4 x − 5; d) . min −1 khi x < −2 x = −1.  Bài 26. a) Ta có: 1 1 1 1 > ; > ;...;
Bài 13. a) −0,63; b) 1 ; c) 86; d) −13. 100 2 100 30
Bài 14. a) 22; b) −8 6; c) 3; d) 8.
Bài 15. Tương tự Bài 3. 38
Bài 16. a) 2 5; b) −2; c) 2 2; d) 6.
Bài 11. a) x∈∅ ;b) 1 x − = ; c) x = 3 − ;
10a khi a ≥ 0 9 Bài 17. a)  ; −6a khi a <  0 d) 3 x = . 2  3 3a khi a ≥ 0 b)  .
Bài 12.Cách 1. Ta có : − 3 12a khi a <  0 (x+ y)2 2 2
= 1+ 2xy ≤ 1+ x + y = 2 Bài 18. a) 6; b) 2. ⇒ đpcm.
Bài 19. a) a + 2; b) 6 6.
Cách 2. Sử dụng BĐT Cauchy – VẤN ĐỀ 3 Schwartz :
(ab+cd)2 ≤ ( 2 2 a + c )( 2 2 b + d ).
Bài 1. a) x ≥ 2; b) 7 x 1 ≤ ; c) x < ; 6 3
b) Cách 1 . Theo BĐT AM-CM, ta có : d) 2 x ≥ .
1 1 1 1  1 1  1  1 1  3 + + =  +  +  + x y z 2 x y 2 y z     
Bài 2. a) 3 ≤ x ≤ 6; b) 2 ≤ x < 5; 5 1  1 1  1 1 1 + + ≥ + +  
c) x ≥ 9; x ≤ −1; d) −4 ≤ x ≤ 4. 2  z x xy yz xz Bài 3. a) 3
x ≥ ; b) x ≤ 0; Cách 2. Xét hiệu : 2 2 1  1 1  c) 1 x − =  −  ≤ ; d) x∈ VT VP .   4 2 x y  
Bài 4. a) x > 1; b) x ≤ −7; 2 2 1  1 1  1  1 1  +  −  +  −  ≥ 0. c) 3 ≤ x < 4; d) 2 x > . 2  y z  2 3  z x   
Bài 5. a) x ≤ 2 hoặc x ≥ 6
Bài 13. a) A ≥ 2x −1+ 3 − 2x = 2; b) x ≤ 1 − hoặc x ≥ 5 c) x ≤ 3 − hoặc x ≥ 3 A = 2 khi 1 2 ≤ x ≤ . min 2 3 d) 1 − ≤ x ≤ 1 b) Áp dụng 2 2 2 2
a + b + c + d
Bài 6 . a) x = 175 ;b) x∈∅ ; c) 1 x = ; 2 2 2
≥ (a + c) + (b + d) , ta có :
d) x = 3 ; e) x = 1 hoặc 5 x = 2 3  11  320 B = − 7x +   g) x = 2 .  7  49 2
Bài 7. a) x = 0 ; b) x = 1 ;c) 1 x = ;  11  320 10 + + 7x + ≥   6.  7  49
d) x = 3 ; e) x = 5 hoặc 7 x = − 3
Từ đó B = 6 tại x = 0. min g) x = 4 . 2 2
Bài 14.Ta có : ( x −1 −1) +( y −2 −2)
Bài 8. a) x ≤ 2
− b) x∈  ; c) x∈ d) x = 2 . + ( z − − )2 3 3 = 0
Bài 9.a) x > 7
− ; b) x ≤ 1 hoặc x ≥ 2 ;
⇔ x = 2, y = 6,z = 12 . c) 3
− ≤ x ≤ 5 ; d) x < 2; x > 3 . Bài 10. a) x VẤN ĐỀ 4 = 0 ; b) x∈∅ ; c) 7 x = ; 2
Bài 1. a) 60 ; b) 6 ; c) 20 ; d) 26 .
d) x = 0 hoặc x = 3 . 39
Bài 2 .a) 3 ; b) 5 c) 10 ; d) 5 . VẤN ĐỀ 5 13 4 + Bài 3. a) 2; b)12 ; c) 2 ; Bài 1. a) 10 ; b) 1 ; c) 2 3 ; 2 2 d) 36 − 36 2 + 27 3. d) 2015 . Bài 2. a) 66 ; b)1,6 ; c) 0 − ,16 ; d) 28 . Bài 4. a) 30 ; b) 4 ; c) − 10 ; d) 7 12 3 . 3 7 3
Bài 3. a) 27 + 24 5 ; b) 6 5 − 9.
Bài 5.a) 80 ; 9 ; c)110 ; d) 26 . a 10
Bài 4. a) 36(1− a); b) 2 −a ; c) ; d) 12 . a 2
Bài 6. a) 5 ; b) 5 ; c) 3 ; d) 56 . ab − b a + b 8 3 9 Bài 5. a) 2 ; b) 2 3 . a − b 2 a − 3 b
Bài 7. a) 3 ; b) 20 ; c) 4 + 2 6 ; d) 2 . Bài 6. a) 2
9 − 6a − 5a ; b) 3 (3 − a); Bài 8 . a) 8 ; b) − 0 ; c) 2 ; d) 5 1 . 4 11 3 2 2
c) 3y ; d) −b . Bài 9.a) 5 ; b) 5 ; c) 6 − 2 2a 2 2 2
Bài 7. a) − a ; b) x + 2 ; c) 1 ; d) 2 − 2 . x + 3 Bài 10. a) − a ; b) x ; d) x . x + y x − y xy c) ; d) 1− a . Bài 8. a) 1 x = ; b) 3 x − = , 7 x = ; x + y 2 a −1 2 2 2
c) x = 2 hoặc x = 3 − ; d) x = 9 . Bài 11.a) 21 ;b) 10 ; c) 1 − ; d) 4 . Bài 9. a) x = 1
− hoặc x = 9 ; b) x = 6 ; 7 2
c) x = 3 ; d) x = 28 . Bài 12. a) x ; b) a ; c) 0 ; Bài 10. a) x = 1 − ; b) 12 x = ; c) x = 2 ; x − y 7 xy d) . d) 34 x = . 9 x − y
Bài 11. a) 4 10 ; b) 5 ; c) 15 ; d) 8 .
Bài 13. a) 6 ; b) 25 ; c) 3 ; d) 13 . 12 5 14 9 Bài 12. a) − 3 ; b) 6 ; c) 6+4 5 ; d) 4.
Bài 14. a) 22 ; b) 0 ; c) 60 ; d) 196 . 2 45 x −1
Bài 15. a) 12 − 5 6 ; b) 7 ; c) 2 2 ; Bài 13. a) ; b) 3 ; d) 4 3 − 7 2 . x + 1 x − y xy
Bài 16. a) x − 3 ; b) 1 ; c) 1 ; d) . x + 2 x + 7 x + y Bài 14. a) x = 2
− ,x = 12 ; b) x = 1 − ; c) x − 2 ; d) 1 . x + 2 x + 5 c) 3 x = ; d) 105 x = . 5 16
Baì 15. a) Vô nghiệm; b) x = 1 − ; c) 1 x = ; d) 3 x = . 2 2 40 Bài 16: Ta có: Bài 15. a) 115 − ; b) 1 ; c) 1 ; d) 10 . 4 x + = ( 4 x + ) 4 5 4 + 1 ≥ 2 x + 4 2 7 4 x + 5 x b b ⇒
≥ 2 . Dấu “ = “ không Bài 16. a) 14 ;b) 31 ; c) 5 ; 7 31 7a 4 x + 4 d) 7 − 13xy xảy ra nên ta có đpcm. Bài 17. a) 5 ; b) 2 ; c) 3 − 3 + 2 2 ; 2 19 VẤN ĐỀ 6 − Bài 1. a) x 7 ; b) 2
− y 2 ; c) 5x x ; d) 3 5 . 2 d) 2 4y 3 . Bài 18. a) 2 ; b)4; c) 1; Bài 2. a) 2 13x ; b) 2
− 2x ; c) 15x ; d) 5  3  2 2 d) − 15 − x . Bài 19. a) 5 ; b)19 11 7; Bài 3. a) 13x ; b) 2
− y 3 ; c) 9x x ; 2 11  3 7 d) 4 4y 3 . c) 14; d) 19 Bài 4. a) 2 13x ; b) 2
− 3x ; c) 2 7y ; Bài 20. 2 a) 5a ;
b)x; c)1; d)6. d) 2 − 7 − y . Bài 21. 5 a) 25; b)
; c)22 6; d)2. 5
Bài 5. a) 5 2 > 4 3 ; b) 5 1 1 > 6 . 2 6 37 Bài 22. c) 2 29 23 3 < 3 13 ; d) 5 3 3 2 > . a) 10 ; b) ; c)4 7; d) 8. 4 2 2 15
Bài 6. a) 2 6; 29; 4 2; 3 5 ; Bài 23. 1 a) ;
b)2; c)0; d)2. b) 38; 2 14; 3 7;6 2 . 2
Bài 24. a) x  9; b)x  4;
Bài 7. a) 3 5 > 2 7 ; b) 3 1 1 < 6 ; 2 3 14 c)x  64; d)x  6. c) 3 21 > 2 47 ;d) 5 2 3 < 14 . Bài 25 3 7
a) x   ; x b)x  9; 9 7 2 2 Bài 8. a)7 2; 5 2; 2 8; 28 ; c)x  2; d)x  3. b) 5 30; 2 40; 3 8; 2 5 . Bài 26. Bài 9. a) 4 3 ; b) 7 − a .
a) x y  0; b)x  0; y  4; z  2 Bài 10. a) 8 − a ; b) 3 9 − a ; c) 2 3 ;d) 0 .
Bài 27. n 1. Bài 11. a) 4 − 6 ; b) 4 − a .
Bài 28. A  1 x1  x1 1  2 Bài 12. a)7a ; b) 2
− x ; c) 2x ; d) - 2x .
Dấu “=” xảy ra khi 1 x  2 .
Bài 13. a) 6 ; b) x 5 ; c) a 5ab ; Bài 29. 3 5 7b d) 7 3 − xy . Chú ý: 1 2 
 2( k 1  k) k k k 1
Bài 14. a) 2 5 ; b) − 6 ; c) 10 + 6 ; 3 2 d) 2 − 3 . 41 Bài Bài 11. 15 7 1 a) 
; b) 4; c) ; d)0. 30. 2002 2003 (  2003)(  2002) 7 2 2003 2002 x   1 1 Bài 12. 1 3 2 3 a) Q  ; b) ;    0 . x 1 3 2002 2003
c)x  4; d)x  1 e)0;4;  9 VẤN ĐỀ 7. 2 Bài 13. ( x 1) 3( 3 1) a) P b) ; Bài 1. 9 2 a) 8 2 ; b) ; c) 3; d)5. x 2 2 c)x  4.
Bài 2. a) 6 a  5 ; b)2 a . Bài 14. x 1 a) P
; b)0  x 1; Bài 3. 7 3 a) ;
b)22; c)2; d)10. x  2 6 1
c) P   ; x  0. Bài 4. 1 a) ; b)12 a min a a. 2 3 Bài
Bài 5. a) Học sinh tự làm.
15. a) P xx 1; 2 a b a b b)VT  .  a VP . 2 b a b 3 7 3 5 b)P
; x 0 c) x     . min 4 2 Bài 6. x x 6( 2 1) 6 6 1
Bài 16. a) A  ; b)B  ; a)VT  (  ).  a VP x  3 x 5 2( 2 1) 3 6 c)x  64; d)x  6. 6 1 3  ( 2 6)    VP 2 6 2 VẤN ĐỀ 8 4 ab  4 1 ) b b VT Bài 1. 2 a) 3
b) ; c)4a d)2ab 5
2( a b)( a b) Bài 2. 3
a) 11 3; b)2 . 2 b   VP a A b B . ( a Bài 3. ) 1; )  4  b) Bài 4. 1 2
a)9; b) ; c)7a; d)8ab . Bài 7. 6 3 3 x 7 3 9  3 1 a) M
Bài 5. a)20; b) ; c) c)5x 1. 
b)M  12 2 c)x  49 24 2 x 3 Bài
d)0  x  9; x  4 e)x 1;16;25;  49
6. a) 5 1; b) 3 1; c)1; d)18 3  2. Bài 8. 7 Bài 7. a) 2 2 ;
b)3; c)2; d)2 . a)A
b)x  4 c)B 1 d) x  5 . 6
Bài 8. a) A B; b)A  . B
Bài 9. A B . Bài 9. x 1 a)P
b)0  x  9; x  1 x 1
Bài 10. a) x 63; b)x 1.
c)x  4 d)x  0 c)P  1; x  0 .
Bài 11. a)A B b)A B c) A B d)A B max
Bài 10. a) 17 3 ; b)6; c) 5; d) 6 3
Bài 12. A B. Bài 13. 61 2 a)x  b)x  . 2 9 42 Bài 14. 10
a)x  13 b)x  .
Bài 9. a) 1; b)7; c) 2 1; d) 2. 3
Bài 15. a)x
Bài 10. a) 10; b)14; c)4; d)1 5 .
 3 b)x  14; x  5 .
Bài 11. a)x  2; b)x  15;
Bài 16. a)0;1; 
2 b)6;5;  4 . 81 c)x  1; d)x  . Bài 17. 15
a)x  1 b)x   ; x  2 . 2 2 Bài Bài 18. 1 7 2 2 2 a)8 b)
c) ab d)4a b . 12. 5 6 9
a) x  0; x  6; b)x  1; c) x d)x  3. Bài 19. 45 a)6 b)
 3 c)x 1 d)2x 1 . 2 8
Bài 13.a) Vô nghiệm. Bài 20. 3
a)18 b)7 c)3 d)6 16  2 . 19
b)x  0 ; c)x  2 ; d)x  .
Bài 21. a)2 b)2 2 c) 3 1 d)2 . 4
Bài 22. a) 2 1 b) 3 1 c)5 d)1.
Bài 14. b) Vô nghiệm. c) Vô nghiệm. 2
c)x  0; x  ; d)x  4. Bài 23. 29
a)x  0 b)x  . 3 3
Bài 24. a)3;1;  2 b)2;  1 . Bài 15. 25 a)x  ; b) Vô nghiệm. 4
Bài 25. a)x  1 b)x  1; x  7 . c) Vô nghiệm.; 25 d)x  .
ÔN TẬP CHỦ ĐỀ 1 (PHẦN I) 9
Bài 16. a) x  1; b)x  3; Bài 1. 2
a) x  ; b)x  ; c) x  ; 3 c)x  3; d)x  3. 3
d)x  ; e)x  g)1 x  2.
Bài 17. a) Vô nghiệm. 3 b)x  2 2
c)x  2, y  3,z  4 ; d)x  1 ; y  5. Bài 2. 1
a)  x  2; b)3  x  5; 2
Bài 18. a)x  1; b)x  1; c)x  5; d)x  2..
c)x 2; x  2 d)x  0;
Bài 19. a)0  x  4 b)x  1;
e)x  0; x  1 g)x  0; x  4
c)x  4; d)x  0; x  1.
Bài 3. a) 5 3 ; b)10 2;
ÔN TẬP CHỦ ĐỀ 1 (PHẦN II)
c)6 3 d)19 11 7 .
Bài 1 a)x 1;4;16;  25 ; Bài 4. 6 23 3 a) 8 2 b) ; c)6 2 d) .
b)x 0;4;16;36;  144 . 6 15
Bài 2. a)x  0 b)x 4;16;  100 . Bài 5. 23 a)
; b)6; c)3; d)21. 5
Bài 3. a)A  2; x  4; min
Bài 6. a)1; b)10; c)6; d)21.
b)B  6; x  4. min 1 Bài 7. 3 5 a)
; b) 6; c)7  4 3; c) C = − khi 1 x = ; min 5 4 4 3 6 3 2 d) D = 3 + 1 khi x = 1. min
d) 3  2; d)3 2 2 g) . 2 Bài 4. a) 1 E = − khi x = 0; min 3 Bài 8. 6 23 3 a) 2 b) ; c) d)4 . 2 15
b) F = 2 2 − 2 khi x = 1. min 43 Bài 5. a) M = 3 khi x = 1; x + max Bài 13. a) 2 1 P = ; b) N = 8 khi x = 9; x max c) 4 P = khi 1 x = ; b) Vô nghiệm; c) 5 P = ; max 3 4 2
d) 0 < x < 1; e) P > 1; d) 5 Q = khi x = 0; max 3 f) Không có GTNN. Bài 6. a) 3 B x = ; b) 3 A = ; Bài 14. a) 38 B = ; b) 2 A = ; 7 x − 3 43 x + x + 1
c) x = 0 hoặc x = 4.
c) 0 ≤ x < 1 hoặc x ≥ 9. ( x +1)2 Bài 7. a) x −1 P = ; b) x = 0; + x + 1 Bài 15. a) P = ; b) 3 3 3 ; x 2
c) x = 0; d) P < 1;e) P = 1 − khi x = 0. max c) x = 4. x( x +1) Bài 8. a) E = ; b) x > 1; Bài 16. a) 1 P = ; b) P = 9 khi 1 x = y = . max 9 x −1 xy
c) E = 9 khi x = 4;
Bài 17. a) x = 3; y = 2008 − ; z = 2011. min d) x∈{4;0; } 9 ; e) Vô nghiệm.
b)( 3x −1 − x)( 3x −1 − x +1) = 0
Bài 9. a) P = − x ( x −1); ⇔ x = 1 hoặc 3 5 x ± = . 2 b) P = 3 3 − 5; c) 1 P = khi 1 x = . max 4 4
Bài 18. Ta có M
= 20736 khi a = b = 2 2. max − Bài 19. Bài 10. a) x 1 B = ( x+ ); 2 1
Đặt 2 a − 5 = x,2 b − 5 = y,2 c − 5 = . z
Biến đổi P theo x, y,z,ta được: b) 5 2 5 B − = ; c) x = 1. 33 2 P =
khi a = b = c = 25. min 4 Bài 11. a) x + 16 P = ; b) x = 4; 2 2
1+ a = ab + bc + ca + a x + 3 Bài 20. Ta có c) P
2a + b + c = 4 khi x = 4;
= (a + b)(a + c) ≤ . min 2 d) 42 − 23 2 . Áp dụng tương tự với 2 1+ b và 2 1+ c . 2 Bài 21. 3 A = khi 1 a = b = . Bài 12. a) 2 x −1 − P = ; b) 10 5 3 ; min 2 2 x + 1 5 Bài 22 A
= 9 khi x = y = 1. − min c) 2 3 x + =
; d) x = 0,x = 4;
Bài 23. Ta có VT = (a − ) 1 1 + + 1. 2 a −1
e) 0 ≤ x ≤ 3 −1; g) P = 1 khi x = 0. min 44
Document Outline

  • VẤN ĐỀ 1. CĂN BẬC HAI
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1. Tìm căn bậc hai và căn bậc hai số học của một số
      • Dạng 2. So sánh các căn bậc hai số học
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai
      • Dạng 2. Rút gọn biểu thức chứa căn bậc hai
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 3. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 3: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
      • Dạng 4. Giải phương trình chứa căn bậc hai.
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 4. LIÊN HỆ PHÉP NHÂN, PHÉP CHIA VỚI PHÉP KHAI PHƯƠNG (PHẦN 1)
    • A.Tóm tắt lý thuyết
    • B. Bài tập và các dạng toán.
      • Dạng 1. Thực hiện phép tính.
      • Dạng 2. Rút gọn biểu thức.
    • C.BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 5. LIÊN HỆ PHÉP NHÂN, PHẾP CHIAVỚI PHÉP KHAI PHƯƠNG (PHẦN II)
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 4. Rút gọn biểu thức
      • Dạng 5. Giải phương trình
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 6. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI.
    • A. TÓM TẮT LÍ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1. Dưa thừa số ra ngoài dấu căn hoặc vào trong dấu căn
      • Dạng 2. So sánh các căn bậc hai
      • Dạng 3. Rút gọn biểu thức chứa căn bậc hai
      • Dạng 4. Trục căn thức ở mẫu
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 7: RÚT GỌN BIỂU THỨC CHỨA CĂN VÀ CÁC BÀI TOÁN LIÊN QUAN
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1.Rút gọn biểu thức chứa căn bậc hai
      • Dạng 2: Chứng minh đẳng thức chứa căn thức bậc hai
      • Dạng 3. Rút gọn biểu thức và các bài toán liên quan
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 8. CĂN BẬC BA
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1. Thực hiện phép tính có chứa căn bậc ba
      • Dạng 2. So sánh các căn bậc ba
      • Dạng 3. Giải phương trình chứa căn bậc ba
    • C. BÀI TẬP VỀ NHÀ
  • ÔN TẬP CHỦ ĐỀ 1 (PHẦN I)
  • A. TÓM TẮT LÝ THUYẾT
    • 1. Căn bậc hai số học
    • 2. Căn thức bậc hai
    • 3. Liên hệ giữa phép nhân, phép chia với phép khai phương
    • 4. Biến đổi đơn giản biểu thức chứa căn bậc hai
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1. Tìm điều kiện cho các biểu thức có nghĩa
      • Dạng 2: Tính và rút gọn biểu thức
      • Dạng 3. Giải phương trình và bất phương trình
  • ÔN TẬP CHỦ ĐỀ 1 (PHẦN II)
    • A. TÓM TẮT LÍ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 4. Tìm các giá trị nguyên của biến để các biểu thức cho trước có giá trị nguyên
      • Dạng 5. Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của biểu thức
      • Dạng 6. Rút gọn biểu thức và các bài toán liên quan
      • Một số bài tập nâng cao
  • HƯỚNG DẪN – ĐÁP SỐ
    • VẤN ĐỀ 1.
    • VẤN ĐỀ 2.
    • VẤN ĐỀ 3
    • VẤN ĐỀ 4
    • VẤN ĐỀ 5
    • VẤN ĐỀ 6
    • VẤN ĐỀ 7.
    • VẤN ĐỀ 8
    • ÔN TẬP CHỦ ĐỀ 1 (PHẦN I)
    • ÔN TẬP CHỦ ĐỀ 1 (PHẦN II)