Cách xét tính đơn điệu của hàm số

Cách xét tính đơn điệu của hàm số
1. Tính đơn điệu của hàm số
Tính đơn điệu của hàm số là một thuộc tính quan trọng để nghiên cứu sự
biến đổi của hàm số trên một khoảng cụ thể. Một hàm số được coi là đơn
điệu trên một khoảng nào đó nếu giá trị của hàm này luôn thay đổi theo cùng
một hướng khi biến đổi độc lập của biến đầu vào trên khoảng đó.
Có hai loại tính đơn điệu quan trọng chính:
Tính đơn điệu tăng (increasing monotonicity): Một hàm số f(x) được gọi là
đơn điệu tăng trên một khoảng [a, b] nếu với mọi x1 và x2 thuộc khoảng [a, b]
với x1 < x2, ta có f(x1) ≤ f(x2). Nghĩa là, khi biến đổi x từ x1 đến x2, giá trị của
hàm số luôn tăng hoặc không giảm.
Tính đơn điệu giảm (decreasing monotonicity): Một hàm số f(x) được gọi là
đơn điệu giảm trên một khoảng [a, b] nếu với mọi x1 và x2 thuộc khoảng [a, b]
với x1 < x2, ta có f(x1) ≥ f(x2). Nghĩa là, khi biến đổi x từ x1 đến x2, giá trị của
hàm số luôn giảm hoặc không tăng.
Tính đơn điệu có thể được xác định bằng cách sử dụng đạo hàm của hàm số.
Nếu đạo hàm của hàm số luôn dương (hoặc không âm) trên khoảng cần xem
xét, thì hàm số là đơn điệu tăng. Nếu đạo hàm luôn âm (hoặc không dương)
trên khoảng đó, thì hàm số là đơn điệu giảm.
Tính đơn điệu của hàm số là một khái niệm quan trọng trong toán học và có
nhiều ứng dụng trong tối ưu hóa, thống kê, và các lĩnh vực khác.
Cho hàm số y = f(x) xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn.
Hàm số y = f(x) đồng biến (tăng) trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).
2. Cách xét tính đơn điệu của hàm số
Để xét tính đơn điệu của một hàm số, bạn có thể sử dụng đạo hàm của hàm
số và áp dụng một số quy tắc cơ bản. Dưới đây là các bước cơ bản để xét
tính đơn điệu của hàm số:
Tìm khoảng cần xét tính đơn điệu: Xác định khoảng trên đó bạn muốn kiểm
tra tính đơn điệu của hàm số. Điều này thường đòi hỏi bạn phải biết rõ miền xác định của hàm số.
Tính đạo hàm của hàm số: Tính đạo hàm của hàm số ban đầu. Điều này có
thể được thực hiện bằng cách sử dụng quy tắc đạo hàm của các hàm cơ bản
và luật chuỗi nếu cần.
+ Đạo hàm của hàm số mũ: Nếu bạn có hàm số dạng f(x) = a^x, với a là hằng
số dương, thì đạo hàm của nó là f'(x) = a^x * ln(a).
+ Đạo hàm của hàm số lũy thừa: Nếu bạn có hàm số dạng f(x) = x^n, với n là
một số thực, thì đạo hàm của nó là f'(x) = n * x^(n-1).
+ Đạo hàm của tổng và hiệu của các hàm số: Nếu bạn có hàm số f(x) = g(x) +
h(x) hoặc f(x) = g(x) - h(x), thì đạo hàm của nó là f'(x) = g'(x) + h'(x) hoặc f'(x) = g'(x) - h'(x) tương ứng.
Kiểm tra dấu của đạo hàm: Xem xét dấu của đạo hàm trên khoảng cần xét.
Điều này sẽ giúp bạn xác định tính đơn điệu của hàm số. Cụ thể: Nếu đạo
hàm luôn dương (hoặc không âm) trên khoảng đó, thì hàm số là đơn điệu
tăng trên khoảng đó. Nếu đạo hàm luôn âm (hoặc không dương) trên khoảng
đó, thì hàm số là đơn điệu giảm trên khoảng đó. Nếu đạo hàm không thay đổi
dấu trên khoảng đó (không dương cũng không âm), thì hàm số không đơn điệu trên khoảng đó.
Kết luận tính đơn điệu: Dựa trên kết quả kiểm tra dấu của đạo hàm, bạn có
thể kết luận về tính đơn điệu của hàm số trên khoảng đó. Lưu ý rằng tính đơn
điệu của hàm số có thể khác nhau trên các khoảng khác nhau. Điều này đòi
hỏi bạn phải xét tính đơn điệu cho từng khoảng cụ thể trên miền xác định của hàm số.
Dưới đây là một ví dụ cụ thể:
Ví dụ: Xét hàm số f(x) = x^2 trên khoảng [-2, 2].
Khoảng cần xét: Khoảng [-2, 2].
Đạo hàm của hàm số: f'(x) = 2x.
Kiểm tra dấu của đạo hàm:
- Khi x < 0, f'(x) < 0, nên hàm số là đơn điệu giảm trên khoảng này.
- Khi x > 0, f'(x) > 0, nên hàm số là đơn điệu tăng trên khoảng này. - Khi x = 0, f'(x) = 0.
Kết luận tính đơn điệu: Hàm số f(x) = x^2 là đơn điệu giảm trên khoảng [-2, 0]
và đơn điệu tăng trên khoảng [0, 2].
3. Điều kiện để làm số đơn điệu
Điều kiện cần để hàm số đơn điệu:
Nếu hàm số đồng biến trên khoảng K, thì f'(x) ≥ 0 cho mọi x ∈ K và f'(x) = 0
tại một số điểm hữu hạn trên khoảng K.
Nếu hàm số nghịch biến trên khoảng K, thì f'(x) ≤ 0 cho mọi x ∈ K và f'(x) = 0
tại một số điểm hữu hạn trên khoảng K.
Điều kiện đủ để hàm số đơn điệu:
Nếu f'(x) > 0 cho mọi x ∈ K, thì hàm số đồng biến trên khoảng K.
Nếu f'(x) < 0 cho mọi x ∈ K, thì hàm số nghịch biến trên khoảng K. Nếu f'(x) =
0 cho mọi x ∈ K, thì hàm số không đổi trên khoảng K.
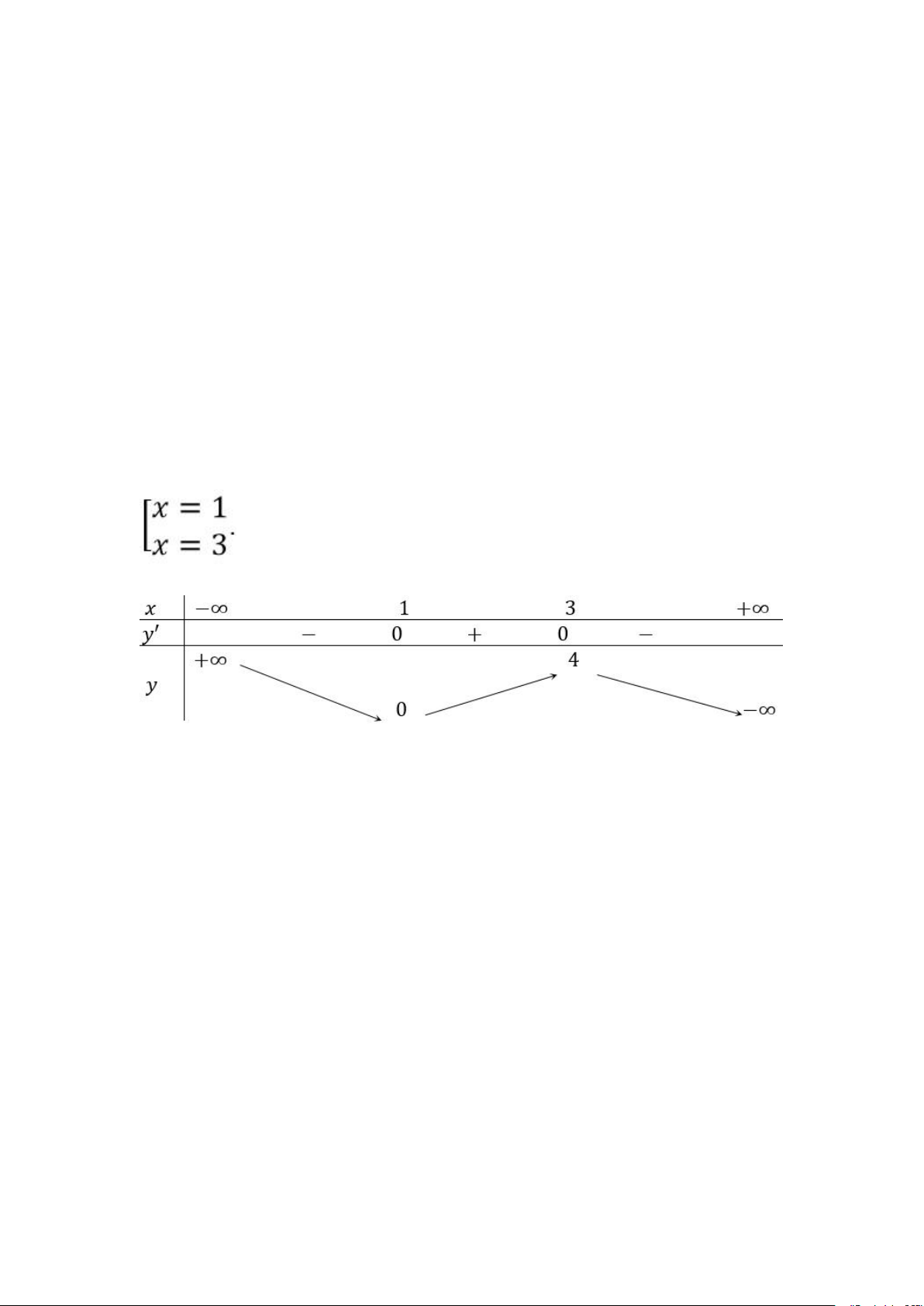
Ví dụ: Xét tính đồng biến và nghịch biến của hàm số sau: y= -x3+ 6x2 -9x + 4 giải
Hàm số đã cho xác định trên D= R Tính y' = -3x2 + 12x -9 cho y' = 0 <=> -3x2 + 12x - 9= 0 Bảng biến thiên
Dựa vào bảng biến thiên, hàm số đồng biến trên (1;3)
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
Các điều kiện này cho phép bạn xác định tính đơn điệu của hàm số dựa trên
thông tin về đạo hàm của nó. Tính đơn điệu quan trọng trong việc hiểu cách
hàm số biến đổi trên các khoảng cụ thể và có nhiều ứng dụng trong toán học và khoa học tự nhiên.
4. Một số bài tập về đồng biến, nghịch biến
Dưới đây là thêm một số bài tập về tính đồng biến và tính nghịch biến của hàm số:
Bài tập 1: Xét tính đồng biến hoặc nghịch biến của hàm số y = 2x^3 - 3x^2 - 12x trên khoảng [-2, 3].
Bài tập 2: Xác định tất cả các khoảng con trên đó hàm số y = x^4 - 4x^3 +
6x^2 - 2x + 1 là đồng biến và nghịch biến.
Bài tập 3: Xét tính đồng biến hoặc nghịch biến của hàm số y = e^x + 2x trên khoảng (-∞, 0).
Bài tập 4: Xét tính đồng biến hoặc nghịch biến của hàm số y = ln(x^2) trên khoảng (1, ∞).
Bài tập 5: Xét tính đồng biến hoặc nghịch biến của hàm số y = 1/(x^3) trên khoảng (-∞, -1).
Bài tập 6: Xét tính đồng biến hoặc nghịch biến của hàm số y = sin(x) - cos(x) trên khoảng [0, π/2].
Bài tập 7: Xét tính đồng biến hoặc nghịch biến của hàm số y = x^2 - 4x + 4 trên khoảng [0, 3].
Bài tập 8: Xét tính đồng biến hoặc nghịch biến của hàm số y = 1/(x^4) trên khoảng (0, ∞).
Bài tập 9: Xét tính đồng biến hoặc nghịch biến của hàm số y = tan(2x) trên khoảng (-π/4, π/4).
Bài tập 10: Xác định khoảng trên đó hàm số y = 3x^3 - 9x^2 + 6x - 2 là đồng biến và nghịch biến.
Bài tập 11: Xét tính đồng biến và nghịch biến của hàm số sau y = (3 - 2x)/(x + 7)
Bài tập 12: Xét tính đồng biến và nghịch biến của hàm số sau y = x4 + 4x + 6
Bài tập 13: Xét tính đồng biến và nghịc biến của hàm số sau y= |x2 - 2x - 3|
Bài tập 14: Xét tính đồng biến và nghịch biến của hàm số sau y = 2sinx + cos2x,x ∈ [0; π]
Hãy sử dụng đạo hàm và kiểm tra dấu của đạo hàm để xác định tính đồng
biến hoặc tính nghịch biến của hàm số trên các khoảng xác định. Nếu có bất
kỳ câu hỏi hoặc khúc mắc nào, xin vui lòng hỏi thêm.
Mong rằng thông qua những nội dung và thông tin mà chúng tôi cung cấp ở
phía trên để giúp cho các bạn có thêm thông tin hữu ích về tính đơn điệu của
hàm số và làm được các bài tập có liên quan đến hàm số nghịch biến và
đồng biến một cách dễ dàng và nhanh chóng hơn bao giờ hết.
Document Outline

• Cách xét tính đơn điệu của hàm số
  • 1. Tính đơn điệu của hàm số
  • 2. Cách xét tính đơn điệu của hàm số
  • 3. Điều kiện để làm số đơn điệu
  • 4. Một số bài tập về đồng biến, nghịch biến