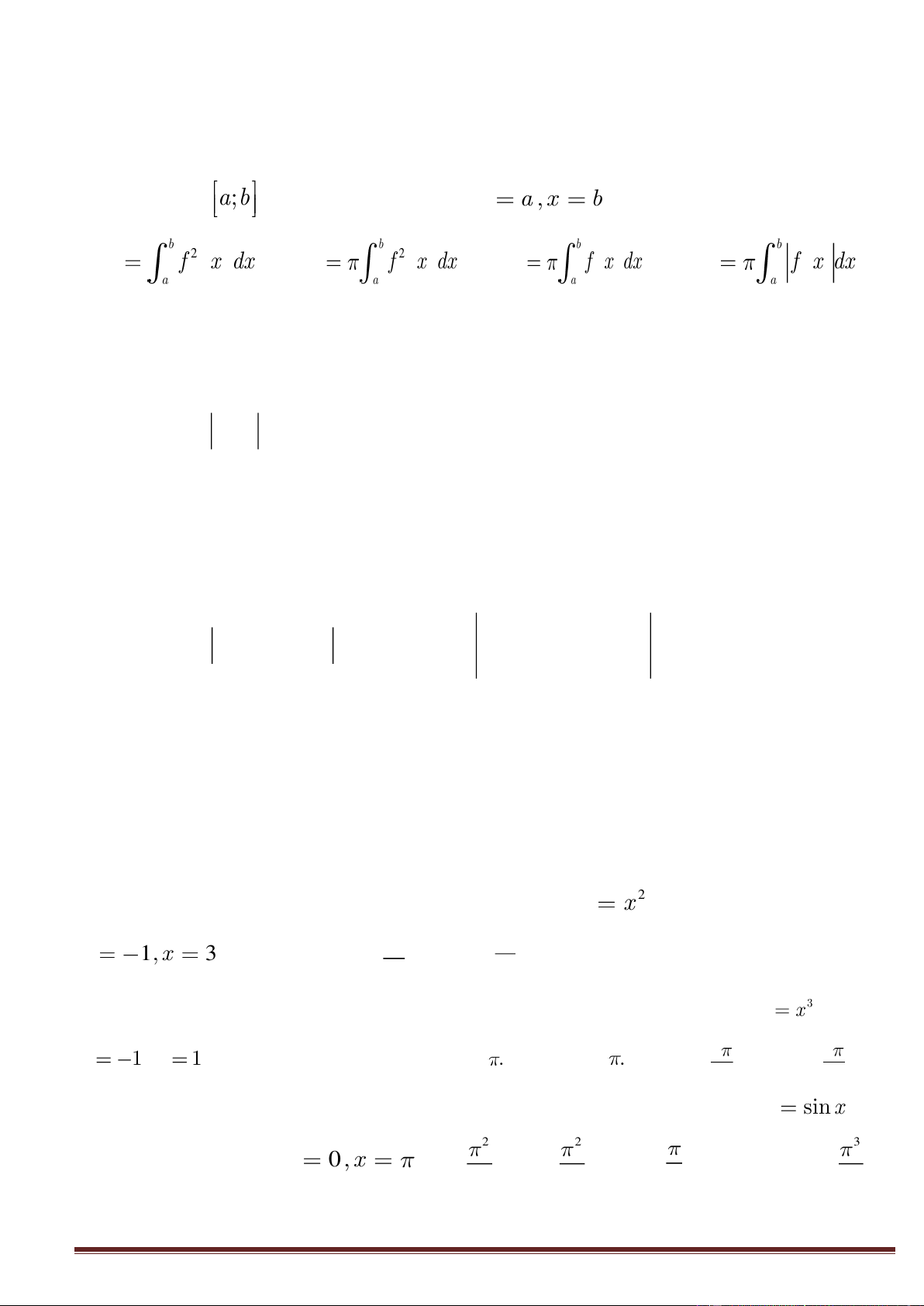








Preview text:
BÀI TẬP TRẮC NGHIỆM ỨNG DỤNG CỦA TÍCH PHÂN Mức độ nhận biết.
Câu 1. Thể tích của khối tròn xoay khi quay quanh trục Ox hình phẳng được giới hạn bởi đồ thị hàm số f(x)
liên tục trên đoạn a;b , trục Ox và hai đường thẳngx a , x
b có công thức tính là: b b b b 2 2 A. V f x dx . B.V f x dx . C. V f x dx . D.V f x dx . a a a a
Câu 2. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f (x ) liên tục trên a;b , trục hoành
và hai đường thẳng x = a ,x = b được tính theo công thức: b b
A. S = f (x ) dx.
B. S = f (x )dx. a a 0 b 0 b C. S =
f (x )dx +
f (x)dx. D. S = f (x)dx −
f (x)dx. a 0 a 0
Câu 3. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f
x ,y = f x liên tục trên a;b 1 ( ) 2 ( )
và hai đường thẳng x = a ,x = b được tính theo công thức: b b A. S = f B. S = (f 1 (x ) −
f2 (x ) dx . 1 (x ) −
f2 (x ) dx. a a b b b C. S = f D. S = f 1 (x )dx −
f2 (x)dx. 1 (x ) −
f2 (x )dx. a a a
Câu 4. Thể tích khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng (H) được giới hạn bởi các
đường sau:y = f (x ) , trục Ox và hai đường thẳng x = a ,x = b (a b) là: b b b b 2 2 2
A. V = f (x )dx.
B. V = f (x )dx. C. V = f (x )dx. D. V =
2 f (x )dx. a a a a 2
Câu 5. Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y
x , trục hoành và hai đường thẳng x 26 1, x 3 28 là: A.8. B. . C. . D. 28 . 3 3 3
Câu 6. Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường y x , trục Ox, x 1 6 2 , x
1 một vòng quanh trục Ox là: A. . B. 2 . C. . D. . 7 7
Câu 7. Thể tích của khối tròn xoay khi quay quanh trục Ox hình phẳng được giới hạn bởi: y sin x , trục 2 2 3
hoành và hai đường thẳng x 0, x là:A. . B. . C. . D. . 4 2 2 3 Trang 1
Câu 8. Diện tích hình phẳng được giới hạn bởi các đường y
ln x , trục hoành và hai đường thẳng 1 1 2 1 2 x ,x e là:A. e . B. . C. e . D. 2 . e e e e e 3
Câu 9. Diện tích hình phẳng được giới hạn bởi các đường y x 3x ,y
x và đường thẳng x 2 5 99 1 là: A. . B. 12. C. . D. . 99 5 12
Câu 10. Diện tích hình phẳng giới hạn bởi 3
y = x , y = 0, x = 1 − , x = 2 là: 17 15 14 A. . B. 4. C. . D. . 4 4 4
Câu 11. Diện tích hình phẳng giới hạn bởi 2
y = −x + 5 x+ 6, y = 0, x = 0, x = 2 là: 58 56 55 52 A. . B. . C. . D. . 3 3 3 3 2
Câu 12. Cho hình phẳng (H) được giới hạn bởi parabol (P) : y x
2x , trục Ox và các đường thẳng 2 4 8 x 1, x
3 . Diện tích của hình phẳng (H) là : A. . B. . C.2. D. . 3 3 3
Câu 22. Diện tích của hình phẳng giới hạn bởi (C ) 3
: y = x ; y = 0; x = −1; x = 2 là: 1 17 15 19 A. . B. . C. . D. . 4 4 4 4
Câu 13. Diện tích của hình phẳng giới hạn bởi (C ) 4 2
: y = 3x − 4x + 5;Ox ; x = 1; x = 2 là: 212 213 214 43 A. . B. . C. . D. . 15 15 15 3
Câu 14. Cho hai hàm số f ( x) và g ( x) liên tục trên a;b và thỏa mãn: 0 g ( x) f ( x), x ; a b .
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng ( H ) giới hạn bởi các đường:
y = f ( x), y = g ( x) , x = a; x = b . Khi đó V được tính bởi công thức nào sau đây? b b 2 A. V = f (x)−g(x) dx. B. 2 V = f (x) 2 − g (x)dx. a a 2 b b C. V = f (x)−g(x)dx . D. V = f (x)−g(x) dx. a a
Câu 15. Diện tích của hình phẳng giới hạn bởi (C ) 2
: y = −x + 6x − 5; y = 0 ; x = 0; x = 1 là: 5 7 7 5 A. . B. . C. − . D. − . 2 3 3 2
Câu 16. Diện tích của hình phẳng giới hạn bởi (C ) : y = sin ;
x Ox ; x = 0; x = là: A. 1. B. 2. C. 3. D. 4.
Câu 17. Gọi ( H ) là hình phẳng giới hạn bởi các đường: y = sin x;Ox; x = 0; x = . Quay ( H ) xung quanh 2
trục Ox ta được khối tròn xoay có thể tích là:A. . B. . C. 2. D. 2 . 2 2
Câu 18. Diện tích hình phẳng giới hạn bởi các đường 3
y = x − 4x ; Ox ; x = 3 − x = 4 bằng ? Trang 2 119 201 A. . B. 44. C. 36. D. . 4 4
Câu 19. Diện tích hình phẳng giới hạn bởi các đường y = cos ; x O ; x O ; y x = bằng ? A. 1. B. 2. C. 3. D. 4.
Câu 20. Gọi ( H ) là hình phẳng giới hạn bởi các đường y = tan ; x O ; x x = 0; x =
. Quay ( H ) xung quanh 4
trục Ox ta được khối tròn xoay có thể tích bằng ? 2 2 A. 1− . B. 2 . C. − . D. −. 4 4 4 2
Câu 21. Diện tích hình phẳng được giới hạn bởi đường cong (C ) : y
sin x , trục Ox và các đường thẳng x 0,x bằng: A. . B. . C. . D. . 2 3 4
Câu 22. Diện tích hình phẳng giới hạn bởi y = x + sin ;
x y = x; x = 0; x = là: A. 1. B. 2. C. 3. D. 4.
Câu 23. Diện tích hình phẳng giới hạn bởi 2
y = sin x+ sinx+1; y = 0; x = 0; x = / 2 là: 3 3 3 3 A. . B. +1. C. −1. D. . 4 4 4 4 Mức độ thông hiểu.
Câu 1. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 y = 5
− x + 5 và trục hoành là: A. 4. B. 8. C. 3108. D. 6216.
Câu 2. Thể tích của khối tròn xoay được giới hạn bởi các đường 2 y x. o c s x sin x , y 0, x 0, y là: 2 3 4 5 4 3 4 3 4 A. . B. . C. . D. . 4 4 4 5
Câu 3. Diện tích hình phẳng được giới hạn bởi các đường y sin 2x,y o
c sx và hai đường thẳng x 1 1 3 1 0, x là :A. . B. . C. . D. . 2 4 6 2 2
Câu 4. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi y = ln ,
x y = 0, x = e là: A. . e B. (e − ) 1 . C. (e − 2). D. (e + ) 1 .
Câu 5. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi y = ln ,
x y = 0, x =1, x = 2 là: A. ( − )2 2 ln 2 1 . B. ( + )2 2 ln 2 1 . C. ( + )2 2 ln 2 1 . D. ( − )2 2 ln 2 1 .
Câu 6. Diện tích hình phẳng được giới hạn bởi các đường 2 y x 2x và y x là : 9 7 9 A. . B. . C. . D. 0. 2 2 2 3 3
Câu 7. Cho hình phẳng (H) được giới hạn bởi đường cong (C ) : y
x , trục Ox và đường thẳng x . 2 65 81 81
Diện tích của hình phẳng (H) là : A. . B. . C. . D.4. 64 64 4 Trang 3 2
Câu 8. Diện tích hình phẳng được giới hạn bởi các đường 3 y x x và y x x là : 37 27 8 5 A. . B. . C. . D. . 12 4 3 12
Câu 9. Cho hình phẳng (H) được giới hạn bởi đường cong ( ) : x C y
e , trục Ox, trục Oy và đường thẳng 2 e x 2 2 2
. Diện tích của hình phẳng (H) là : A.e 4. B.e e 2. C. 3. D.e 1. 2 2x 1
Câu 10. Cho hình phẳng (H) được giới hạn bởi đường cong (C ) : y
, trục Ox và trục Oy. Thể tích x 1
của khối tròn xoay khi cho hình (H) quay quanh trục Ox là : A. 3 . B. 4 ln 2. C.(3 4 ln 2) . D.(4 3 ln 2) .
Câu 11. Cho hình phẳng (H) được giới hạn bởi đường cong (C) : y
ln x , trục Ox và đường thẳng x e . 1
Diện tích của hình phẳng (H) là : A.1. B. 1. C. . e D.2. e 3 2
Câu 12. Cho hình phẳng (H) được giới hạn đường cong (C ) : y x
2x và trục Ox. Diện tích của hình 4 5 11 68 phẳng (H) là: A. . B. . C. . D. . 3 3 12 3
Câu 13. Diện tích hình phẳng được giới hạn bởi các đường 2 y x x 1 và 4 y x x 1 là: 8 7 7 4 A. . B. . C. . D. . 15 15 15 15
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y = x − 3x và trục hoành là: 27 3 27 A. − . B. . C. . D. 4. 4 4 4
Câu 15. Diện tích hình phẳng giới hạn bởi y = sin ; x y = cos ; x x = 0; x = là: A. 2. B. 3. C. 3 2. D. 2 2.
Câu 16. Diện tích hình phẳng được giới hạn bởi đường 2 y x x
3 và đường thẳng y 2x 1 là: 1 1 A. 7 . B. . C. . D. 5. 6 6 6
Câu 17. Diện tích hình phẳng giới hạn bởi 2
y = x + 3, y = x − 4x + 3 có kết quả là : 2 5 3 5 4 5 3 5 −1 A. . B. . C. . D. . 6 6 6 6 3 x
Câu 18. Diện tích hình phẳng giới hạn bởi y = ; y = x 2 1− là: x A. 1. B. 1 – ln2. C. 1 + ln2. D. 2 – ln2.
Câu 19. Diện tích của hình phẳng giới hạn bởi (C ) 2
: y = 4x − x ;Ox là: Trang 4 31 31 32 33 A. . B. − . C. . D. . 3 3 3 3 2
Câu 20. Gọi ( H ) là hình phẳng giới hạn bởi các đường: y = 3x − x ;Ox . Quay ( H ) xung quanh trục 81 83 83 81
Ox ta được khối tròn xoay có thể tích là: A. . B. . C. . D. . 11 11 10 10
Câu 21. Diện tích của hình phẳng giới hạn bởi (C ) 2
: y = x + 2x ; y = x + 2 là: 5 7 9 11 A. . B. . C. . D. . 2 2 2 2
Câu 22. Diện tích của hình phẳng giới hạn bởi (C ) 1 : y = và d : y = 2 − x + 3là: x 3 1 3 1 A. − ln 2. B. . C. ln 2 − . D. . 4 25 4 24
Câu 23. Diện tích của hình phẳng giới hạn bởi (C ) 2
: y = x và (d ) : x + y = 2 là: 7 9 11 13 A. . B. . C. . D. . 2 2 2 2
Câu 24. Diện tích của hình phẳng giới hạn bởi (C ) 2
: y = x và (d ) : y = x là: 2 4 5 1 A. . B. . C. . D. . 3 3 3 3
Câu 25. Gọi ( H ) là hình phẳng giới hạn bởi các đường: y =
x −1;Ox; x = 4 . Quay ( H ) xung quanh
trục Ox ta được khối tròn xoay có thể tích là: 7 5 7 5 A. . B. . C. 2 . D. 2 . 6 6 6 6
Câu 26. Diện tích hình phẳng giới hạn bởi các đường 2 y = 3
− x + 3 với x 0 ;Ox ;Oy là: A. 4. − B. 2. C. 4. D. 44.
Câu 27. Cho hình (H) giới hạn bởi các đường y =
x ; x = 4 ; trục hoành. Quay hình (H) quanh trục Ox ta đượ 15 14 16
c khối tròn xoay có thể tích là:A. . B. . C. 8. D. . 2 3 3 6
Câu 28. Diện tích hình phẳng giới hạn bởi các đường y = 2x −1; y = ; x = 3 là: x 2 443 25 A. 4 − 6ln 6. B. 4 + 6 ln . C. . D. . 3 24 6
Câu 29. Diện tích hình phẳng giới hạn bởi hai đường 3
y = x +11x − 6 và 2 y = 6x là: 1 1 A. 52. B. 14. C. . D. . 4 2
Câu 30. Diện tích hình phẳng giới hạn bởi hai đường 3
y = x và y = 4x là: 2048 A. 4. B. 8. C. 40. D. . 105 2
Câu 31. Cho hình phẳng (H) được giới hạn bởi đường cong y x x
3 và đường thẳng y 2x 1. 23 5 1
Diện tích của hình (H) là: A. . B.4. C. . D. . 6 6 6
Câu 32. Gọi ( H ) là hình phẳng giới hạn bởi các đường 2
y = 1− x ; Ox . Quay ( H ) xung quanh trục Ox ta đượ 16 16 4 4
c khối tròn xoay có thể tích bằng ?A. . B. . C. . D. . 15 15 3 3 Trang 5
Câu 33. Diện tích hình phẳng giới hạn bởi các đường x
y = e ; y = 1 và x = 1 là: A. e − 2. B. . e C. e +1. D. 1− . e
Câu 34. Diện tích hình phẳng giới hạn bởi các đường y = 3 x ; x = 4 ; Ox là: 16 A. . B. 24. C. 72. D. 16. 3
Câu 35. Diện tích hình phẳng giới hạn bởi các đường 3 y = x − ; x Ox bằng ? 1 1 1 − A. . B. . C. 2. D. . 2 4 4 2
Câu 36. Diện tích hình phẳng được giới hạn bởi các đường y 2x
x và đường thẳng x y 2 1 5 6 1 là: A. . B. . C. . D. . 6 2 5 2
Câu 37. Diện tích hình phẳng giới hạn bởi các đường 2
y = x ; y = x + 2 bằng ? 15 9 − 9 15 − A. . B. . C. . D. . 2 2 2 2
Câu 38. Diện tích hình phẳng giới hạn bởi các đường 4 2
y = x − 4x ; Ox bằng ? 1792 128 128 A. 128. B. . C. . D. − . 15 15 15
Câu 39. Diện tích hình phẳng giới hạn bởi các đường 3 y = x + 4 ; x O ; x x = 1 − bằng ? 9 9 A. 24. B. . C. 1. D. − . 4 4
Câu 40. Diện tích hình phẳng giới hạn bởi các đường 2
y = x − 4 ; Ox bằng ? 32 16 32 − A. . B. . C. 12. D. . 3 3 3
Câu 41. Cho hình (H) giới hạn bởi các đường 2
y = x ; x = 1; trục hoành. Quay hình (H) quanh trục Ox ta đượ 2 2
c khối tròn xoay có thể tích là:A. . B. . C. . D. . 5 3 3 5
Câu 42. Diện tích hình phẳng giới hạn bởi 4 2 y = 1
− , y = x − 2x −1 có kết quả là 6 2 28 16 2 27 A. . B. . C. . D. . 5 3 15 4
Câu 43. Diện tích hình phẳng giới hạn bởi 2 y = − ,
x y = 2x − x là 9 7 A. 4. B. . C.5. D. . 2 2
Câu 44: Cho đồ thị hàm số y=f(x) . diện tích hình phẳng (phần tô đậm trong hình)là: 4 0 0
A. f (x)dx. B. f (x)dx + f (x)dx . −3 −3 4 1 4 −3 4
C. f (x)dx + f (x)dx . D. f (x)dx + f (x)dx . −3 1 0 0
Câu 46: Diện tích hình phẳng (phần bôi đen) trong hình sau được tích theo công thức: Trang 6 c b c b c c A. S = f
(x)dx + f
(x)dx B.S = f
(x)dx − f (x)dx C. f (x)dx D. S = f (x)dx a b b a a a Mức độ vận dụng. 2 2 x y
Câu 1. Thể tích khối tròn xoay khi cho Elip + =1 quay quanh trục Ox : 2 2 a b 4 4 2 2 A. 2 a . b B. 2 ab . C. 2 a . b D. 2 − ab . 3 3 3 3 1 1 5 3 2
Câu 2. Cho (C) :y x mx 2x 2m . Giá trị m 0; sao cho hình phẳng giới 3 3 6
hạn bởi đồ thị (C) , y 0, x 0, x
2 có diện tích bằng 4 là: 3 1 2 5 A. m . B. m . C. m . D. m . 4 2 3 7
Câu 3. Cho (H) là hình phẳng giới hạn bởi đường cong (L): 3
y = x ln(1+ x ) , trục Ox và đường thẳng x =1.
Thể tích của vật thể tròn xoay tạo ra khi cho (H) quay quanh trục Ox là. A.V = (ln 4 −1). B. V = (ln 4 + 2). C. V = (ln 3 + 2). D. V = ln 3. 3 3 3 3
Câu 4. Diện tích hình phẳng giới hạn bởi các đường y = mx cos x ; Ox ; x = 0; x = bằng 3 . Khi đó giá trị của m là: A. m = 3. − B. m = 3. C. m = 4. − D. m = 3. 8
Câu 5. Diện tích hình phẳng giới hạn bởi các đường y = 2x ; y = ; x = 3 là: x 2 14 A. 5 −8ln 6. B. 5 + 8ln . C. 26. D. . 3 3
Câu 6. Diện tích hình phẳng được giới hạn bởi các đường y e 1 x , 1 x y e x là: e e e e A. 2. B. 1. C. 1. D. 1. 2 2 3 2
Câu 7. Diện tích của hình phẳng giới hạn bởi: ( ) : x C
y = e ;d : y = −x + 1; x = 1 là: 1 3 A. . e B. e + . C. e +1. D. e − . 2 2
Câu 8. Diện tích hình phẳng giới hạn bởi x −x
y = e − e ;O ; x x = 1 là: 1 1 1 A. 1. B. e + −1. C. e + . D. e + − 2. e e e Trang 7
Câu 9. Để tìm diện tích của hình phẳng giới hạn bởi (C ) 3
: y = x ; y = 0; x = -1; x = 2 một học sinh thực hiện theo các bước như sau: 2 2 4 x 1 15 Bước I. 3 S = x dx Bước II. S = Bước III. S = 4 − = 4 4 4 1 − 1 −
Cách làm trên đúng hay sai từ bước nào? A. Bước I. B. Bước II. C. Bước III.
D. Không có bước nào sai.
Câu 10. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y = 1 − x , y = 0 quanh trục a Ox có kết quả dạng
. Khi đó a+b có kết quả là: b A. 11. B. 17. C. 31. D. 25.
Câu 11. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x +11x − 6 , 2
y = 6x , x = 0, x = 2 có kết quả a dạng
khi đó a − b bằng b
A.2. B. -3. C. 3. D. 59.
Câu 12. Thể tích vật thể khi quay quanh trục Ox hình phẳng giới hạn bởi 3
y = x , y = 8, x = 3 là: A. ( 7 5 3 − 9.2 ). B. ( 7 6 3 − 9.2 ). C. ( 7 7 3 − 9.2 ). D. ( 7 8 3 − 9.2 ). 7 7 7 7
Mức độ vận dụng cao.
Câu 1. Cho đường cong (C ) : y = 2 − ln x . Gọi d là tiếp tuyến của (C ) tại điểm M (1; 2) . Khi đó diện tích
của hình phẳng giới hạn bởi : (C ); d;Ox là: 2 2 A. e − 3. B. 2 e −1. C. 2 e . D. e − 5.
Câu 2. Diện tích hình phẳng giới hạn bởi các đồ thị 2
y = x − 4x + 3 và y = x + 3 là: 55 205 109 126 A. . B. . C. . D. . 6 6 6 5
Câu 3. Diện tích hình phẳng giới hạn bởi y |
= ln x |; y =1 là: 3 1 A. 2 e − 2e + 2. B. e − + 2. C. 2
e + 2e −1. D. e + − 2 . e e 2 x 2 x
Câu 4. Diện tích hình phẳng được giới hạn bởi các đường: y 4 ; y là: 4 4 2 4 2 4 4 4 A. 2 . B. . C. . D. 2 . 3 3 3 3
Câu 5. Diện tích của hình phẳng giới hạn bởi: (C ) : y = x;(d ) : y = x − 2;Ox là: 10 16 122 128 A. . B. . C. . D. . 3 3 3 3
Câu 6. Diện tích của hình phẳng giới hạn bởi: (C ) : y = ln ; x d : y = 1; ; Ox Oy là: A. e − 2. B. e + 2. C. e −1. D. . e
Câu 7. Diện tích của hình phẳng giới hạn bởi: (C ) : y = ln ;
x d : y = 1; d : y = −x +1 là: 1 2 Trang 8 1 3 1 3 A. e − . B. e − . C. e + . D. e + . 2 2 2 2
Câu 8. Diện tích của hình phẳng giới hạn bởi: ( ) : x C
y = e ;d : y = ;
e d : y = 1 − e x + 1 là: 1 2 ( ) e −1 e + 1 e + 3 e A. . B. . C. . D. . 2 2 2 2
Câu 9. Cho đường cong (C ) : y = x . Gọi d là tiếp tuyến của (C ) tại điểm M (4, 2) . Khi đó diện tích của
hình phẳng giới hạn bởi: (C ); d;Ox là: 8 2 16 22 A. . B. . C. . D. . 3 3 3 3
Câu 10. Tính diện tích hình phẳng tạo bởi Parabol(P): 2
y = x − 4x + 5và hai tiếp tuyến tại các điểm
A (1; 2), B(4;5) nằm trên (P): 7 11 9 13 A. S = . B. S = . C. S = . D. S = . 2 6 4 8
Câu 11. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường
y = xln x, y = ,
0 x = e có giá trị bằng ( 3
b.e − 2) trong đó a, b là hai số thực nào dưới đây? a
A. a = 27, b = 5. B. a = 24, b = 6. C. a = 27, b = 6. D. a = 24, b = 5. Trang 9




