46 trang 31 lượt tải

Chủ đề tiệm cận của đồ thị hàm số ôn thi tốt nghiệp THPT môn Toán

61

Tài liệu gồm 46 trang, được biên soạn bởi thầy giáo Phan Nhật Linh, tổng hợp lý thuyết trọng tâm, ví dụ minh họa và các dạng bài tập chủ đề tiệm cận của đồ thị hàm số ôn thi tốt nghiệp THPT môn Toán, có đáp án và lời giải chi tiết.

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/46
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
LÝ THUYẾT
CHỦ ĐỀ 04: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
❖ Đường tiệm cận ngang
▪ Cho hàm số
= ()y f x
xác định trên một khoảng vô hạn (là khoảng dạng
( ) ( )
+ −; , ;ab
hoặc
( )
− +;
). Đường thẳng
=
0
yy
là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị
hàm số
= ()y f x
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
→+ →−
==
00
lim ( ) , lim ( )
xx
f x y f x y
.
❖ Đường tiệm cận đứng
▪ Đường thẳng
được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
= ()y f x
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
+−
→→
= + = −
00
lim ( ) , lim ( ) ,
x x x x
f x f x
+−
→→
= − = +
00
lim ( ) , lim ( )
x x x x
f x f x
Lưu ý:
▪ Với đồ thị hàm phân thức dạng
( )
+
= −
+
0; 0
ax b
y c ad bc
cx d
luôn có tiệm cận ngang là
=
a
y
c
và tiệm cận đứng
=− .
d
x
c
❖ Dấu hiệu nhận biết các đường tiệm cận của đồ thị hàm số
▪ Hàm phân thức mà nghiệm của mẫu không là nghiệm của tử có tiệm cận đứng.
▪ Hàm phân thức mà bậc của tử
bậc của mẫu có TCN.
▪ Hàm căn thức dạng:
( ) ( ) ( ) ( ) ( ) ( )
= − = − = −,,y f x g x y f x g x y g x f x
có tiệm cận
ngang. (dùng liên hợp)
▪ Hàm
( )
= , 0 1
x
y a a
có tiệm cận ngang
= 0y
.
▪ Hàm số
( )
= log , 0 1
a
y x a
có tiệm cận đứng
= 0x
.
❖ Cách tìm các đường tiệm cận của đồ thị hàm số
▪ Tiệm cận đứng: ta đi tìm nghiệm của mẫu không là nghiệm của tử.
▪ Tiệm cận ngang: tính 2 giới hạn:
hoặc
❖ Một số chú ý trong quá trình tìm tiệm cận.
▪ Nếu
→ + = =
2
0x x x x x
.
▪ Nếu
→ − = = −
2
0x x x x x
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
VÍ DỤ MINH HỌA
Lời giải
Chọn B
Vì
( )
+
→
= +
1
lim
x
fx
nên đồ thi hàm số có tiệm cận đứng
= 1x
.
Lời giải
Chọn C
Xét phương trình
=−
+ + =
=−
2
1
5 4 0
4
x
xx
x
, hai nghiệm này đều không là nghiệm của tử số nên
đây là hai đường tiệm cận đứng của đồ thị hàm số.
Mặt khác:
→
−
=
++
2
2
2
lim 2
54
x
xx
xx
, nên đường
= 2y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có ba đường tiệm cận.
Lời giải
Chọn D
Ta có:
( )( )
( )
( )
( )
+ − −
= =
−+
− − + + − + +
2
3 2 1 1
,1
32
1 2 3 2 2 3 2
xx
x
xx
x x x x x
.
Khi đó ta thấy
= 2x
là đường tiệm cận đứng của đồ thị hàm số.
Mặt khác:
( )
( )
→+
=
− + +
1
lim 0
2 3 2
x
xx
, nên đồ thị hàm số nhận
= 0y
làm tiệm cận ngang.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Lời giải
Chọn B
VÍ DỤ 2. Cho hàm số
−
=
++
2
2
2
54
xx
y
xx
. Số đường tiệm cận của đồ thị hàm số là:
A.
2
B.
1
C.
3
D.
4
VÍ DỤ 3. Cho hàm số
+−
=
−+
2
32
32
x
y
xx
. Đồ thị hàm số có bao nhiêu đường tiệm cận.
A.
3
B.
1
C.
4
D.
2
VÍ DỤ 4. Đường tiệm cận ngang của đồ thị hàm số
=
− − −
22
1
()
2 5 2 3
fx
x x x x
A.
= = −2; 2yy
. B.
= = −2; 2yy
. C.
= 2y
. D.
= 2y
.
VÍ DỤ 1. Cho hàm số
( )
=y f x
có
( )
+
→
= +
1
lim
x
fx
và
( )
−
→
=
1
lim 2
x
fx
. Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số không có tiệm cận. B. Đồ thị hàm số có tiệm cận đứng
= 1x
.
C. Đồ thị hàm số có hai tiệm cận. D. Đồ thị hàm số có tiệm cận ngang
= 2y
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
Tập xác định
( )

= − +


5
;0 ;
2
D
. Ta có
→+ →+
− + −
= = −
−
22
2 5 2 3
lim ( ) lim 2
2
xx
x x x x
fx
x
Và
→− →−
− + −
==
−
22
2 5 2 3
lim ( ) lim 2
2
xx
x x x x
fx
x
.
Vậy đồ thị hàm số có hai tiệm cận ngang là đường thẳng
= 2y
Lời giải
Chọn A
Điều kiện xác định:
( ) 0fx
.
Từ đồ thị ta thấy
=( ) 0fx
khi
=−4x
,
=−1x
và
= 2x
.
Khi đó
= + + −( ) ( 4)( 1)( 2)f x a x x x
có 3 nghiệm.
Do đó đồ thị hàm số
( )
=y g x
có 3 đường tiệm cận đứng.
Lời giải
Chọn A
Đồ thị hàm số
( )
− + +
=
−
2
35
2
x ax b
y
x
không có tiệm cận đứng
( )
= − + + =3 5 0f x x ax b
có nghiệm kép
= 2x
.
( )
( )
+ + =
=
=−
+=
=

=
−
1 2 0
3
20
3
2
0
20
2
2 2.3 5
ab
f
a
a
f
b
.
Vậy

− = − − = −


3
4 4. 2 8
2
ab
.
VÍ DỤ 5. Cho hàm số
= = + + +
32
()y f x ax bx cx d
có đồ thị như hình bên dưới.
Hỏi đồ thị hàm số
( )
( )
==
2x
y g x
fx
có bao nhiêu đường tiệm cận đứng?
A.
3
B.
1
C.
4
D.
2
VÍ DỤ 6. Biết đồ thị hàm số
( )
− + +
=
−
2
35
2
x ax b
y
x
không có tiệm cận đứng. Khi đó
bằng:
A.
−8
. B.
10
. C.
−4
. D.
8
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
Lời giải
Chọn A
Ta có
( )
( )
− + +
2
1 3 3 0 1x x x x
Trường hợp 1:
Nếu
= 0m
thì đồ thị hàm số không có tiệm cận ngang. Do đó đồ thị hàm số không thể có ba
đường tiệm cận.
Trường hợp 2:
Nếu
0m
thì đồ thị hàm số có một đường tiệm cận ngang
= 0.y
Do đó đồ thị hàm số có đúng ba đường tiệm cận
+ − =
2
2 3 0mx x
có hai nghiệm phân biệt
12
,xx
thuộc nửa khoảng
)
+
1;
( )( )
( ) ( )

− −
− + −
12
12
'0
1 1 0
1 1 0
xx
xx
+
−
−
−


−
+

1
1 3 0
3
11
0 0 0
3
1
1
0
m
m
mm
m
m
m
m
. Vậy

−


1
;0
3
m
Lời giải
Chọn C
Ta có
( )
=
+
2
3
2
y
x
.
Với
=−2xm
= −
3
1y
m
:
( )

− −


3
2;1 0A m m
m
.
Phương trình tiếp tuyến
d
của
( )
C
:
( )
= − + + −
2
33
21y x m
m
m
.
Đồ thị
( )
C
có tiệm cận ngang
= 1y
và tiệm cận đứng
=−2x
.
VÍ DỤ 7. Tìm tập hợp các giá trị của tham số
m
để đồ thị hàm số
( )
( )
− + +
=
+−
2
2
1 3 3
23
x x x
y
mx x
có đúng 3
đường tiệm cận.
A.

−


1
;0
3
m
. B.

− +


1
;
3
m
C.

−

1
;0
3
m
. D.

−

1
;0
3
m
.
VÍ DỤ 8. Cho hàm số
−
=
+
1
2
x
y
x
có đồ thị
( )
C
, gọi
d
là tiếp tuyến với
( )
C
tại điểm có hoành độ bằng
− 2m
. Biết đường thẳng
d
cắt tiệm cận đứng của
( )
C
tại điểm
( )
11
; A x y
và cắt tiệm cận ngang của
( )
C
tại điểm
( )
22
; B x y
. Gọi
S
là tập hợp các số
m
sao cho
+ = −
21
5xy
. Tính tổng bình phương các
phần tử của
S
.
A.
0
. B.
4
. C.
10
. D.
9
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
Tọa độ điểm
A
là nghiệm của hệ:
( )
= − + + −
=−
2
33
21
2
y x m
m
m
x
=−
=−
6
1
2
y
m
x
nên
=−
1
6
1y
m
.
Tọa độ điểm
B
là nghiệm của hệ:
( )
= − + + −
=
2
33
21
1
y x m
m
m
y
=
=−
1
22
y
xm
nên
=−
2
22xm
.
Suy ra
+=
21
xy
− − = −
6
2 1 5m
m
+ − =
2
2 4 6 0mm
=
=−
1
3
m
m
.
Vậy tổng bình phương các phần tử của
S
là
( )
+ − =
2
2
1 3 10
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
Câu 1: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 4 1
1
xx
y
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 2: Tìm số tiệm cận của đồ thị hàm số
2
2
54
1
xx
y
x
−+
=
−
.
A.
2
B.
3
C.
0
D.
1
Câu 3: Đồ thị hàm số
2
2
4
x
y
x
−
=
−
có mấy tiệm cận.
A.
3
B.
1
C.
2
D.
0
Câu 4: Số tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là
A.
1
B.
2
C.
0
D.
3
Câu 5: Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
2 1 3
56
− − + +
=
−+
x x x
y
xx
.
A.
3=x
và
2=x
. B.
3=x
. C.
3=−x
và
2=−x
. D.
3=−x
.
Câu 6: Số tiệm cận đứng của đồ thị hàm số
2
16 4x
y
xx
+−
=
+
là
A.
3
B.
2
C.
1
D.
0
Câu 7: Số tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
+−
=
+
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 8: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
4 6 2
2
xx
y
x
+−
=
+
là?
A.
1
B.
3
C.
2
D.
4
Câu 9: Cho hàm số
2
42
23
32
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 10: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
21
32
−+
=
−+
x
y
xx
là
A.
4
B.
1
C.
3
D.
2
Câu 11: Đồ thị hàm số
2
2
31
x x x
y
x
+−
=
+
có tất cả bao nhiêu đường tiệm cận?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 12: Đồ thị hàm số
2
5 1 1
2
xx
y
xx
+ − +
=
−
có tất cả bao nhiêu đường tiệm cận?
Cơ bản về tiệm cận của đồ thị hàm số
DẠNG 1
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 13: Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
xx
−
=
+ − −
.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 14: Cho hàm số
2
42
23
32
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 15: Đồ thị hàm số
2
4 2 1
1
x x x
y
x
+ − +
=
+
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 16: Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
2
2
62
+
=
−+
x
y
x x m
có hai đường tiệm
cận đứng. Số phần tử của
S
là
A. vô số. B.
12
. C.
14
. D.
13
.
Câu 17: Có bao nhiêu giá trị nguyên dương của tham số
m
để đồ thị hàm số
2
1
8
x
y
x x m
−
=
−+
có 3 đường
tiệm cận?
A.
14
. B.
8
. C.
15
. D.
16
.
Câu 18: Cho hàm số
( )
3 2 2
3
3 2 1
x
y
x mx m x m
−
=
− + + −
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc
đoạn
2020;2020−
để đồ thị hàm số có 4 đường tiệm cận?
A. 4039. B. 4040. C. 4038. D. 4037.
Câu 19: Có bao nhiêu số nguyên của
m
thuộc đoạn
100;100−
để đồ thị hàm số
( )
2
1
2
y
x m x x
=
−−
có đúng hai đường tiệm cân?
A.
200.
B.
2.
C.
199.
D.
0.
Câu 20: Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
32
xm
y
xx
+
=
−+
có đúng hai đường
tiệm cận.
A.
1m =−
B.
{1;4}m
C.
4m =
D.
{ 1; 4}m − −
Câu 21: Cho hàm số
( )
2
1
24
x
x
yf
m
x
x
+
=
−+
=
. Tìm tất cả các giá trị của tham số
m
để đồ thị có ba đường
tiệm cận
A.
2m
B.
2
5
2
m
m
−
−
C.
2
2
5
2
m
m
m
−
−
D.
2
2
m
m
−
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
Câu 22: Biết rằng đồ thị của hàm số
( )
3 2017
3
n x n
y
xm
− + −
=
++
(
,mn
là các số thực) nhận trục hoành làm
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng
mn+
.
A.
0
B.
3−
C.
3
D.
6
Câu 23: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
82
−
=
−+
x
y
mx x
có đúng bốn
đường tiệm cận?
A.
8
B.
6
C.
7
D. Vô số
Câu 24: Với giá trị nào của hàm số
m
để đồ thị hàm số
2
37= − − +y x mx x
có tiệm cạn ngang.
A.
1=m
B.
1=−m
C.
1=m
D. Không có
m
Câu 25: Cho hàm số
1
.
2
+
=
−
ax
y
bx
Tìm
,ab
để đồ thị hàm số có
1=x
là tiệm cận đứng và
1
2
=y
là tiệm
cận ngang.
A.
1; 2= − =ab
. B.
4; 4==ab
. C.
1; 2==ab
. D.
1; 2= − = −ab
.
Câu 26: Có bao nhiêu giá trị nguyên
10;10m−
sao cho đồ thị hàm số
2
1
2 6 3
x
y
x x m
−
=
+ − −
có hai
đường tiệm cận đứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Câu 27: Có bao nhiêu giá trị nguyên của
m
để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm
số
2
34
2
mx mx
y
x
++
=
+
bằng 3?
A.
4
. B.
2
. C. Vô số. D.
3
.
Câu 28: Tổng các giá trị của tham số
m
để đồ thị của hàm số
( )
22
1
2 1 2
x
y
x m x m
−
=
+ − + −
có đúng một
tiệm cận đứng.
A.
1
2
−
. B.
2
. C.
3−
. D.
3
2
.
Câu 29: Cho hàm số
3 2 2
3
3 2 1
x
y
x mx m x m
. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
Câu 30: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
2
23++
=
−
x x m
y
xm
không có tiệm
cận đứng.
A.
1=m
. B.
1m
. C.
1=m
và
0=m
. D.
0m
.
Câu 31: Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để đồ thị hàm số
2
2
4
x
y
x x m
có hai tiệm cận đứng.
A.
2019
. B.
2021
. C.
2018
. D.
2020
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
Câu 32: Cho hàm số
()y f x
thỏa mãn
lim ( ) 2019
x
f x m
,
4
lim ( ) 2020
x
f x m
. Hỏi có tất cả bao
nhiêu giá trị của
m
để đồ thị của hàm số
()y f x
có duy nhất một tiệm cận ngang?
A. 4. B. 2. C. 3. D. 1.
Câu 33: Cho hàm số
( )
2
1
2 1 2
y
x m x m x m
=

− + + −

. Tìm tất cả các giá trị thực của tham số
m
để đồ
thị hàm số có 4 đường tiệm cận.
A.
01
1
2
m
m

. B.
1
1
2
m
m
. C.
1m
. D.
01
1
2
m
m

.
Câu 34: Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
( )( )
22
63
6 3 9 6 1
x
y
mx x x mx
−
=
− + + +
có đúng
1 đường tiệm cận?
A.
0.
B. 2. C.
1.
D. Vô số.
Câu 35: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số:
2
1y x mx
có tiệm cận ngang.
A.
0 1.m
B.
1.m
C.
1.m
D.
1.m
Câu 36: Cho hàm số
2
2
24
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị của tham số
m
để đồ thị hàm số có
đúng hai đường tiệm cận?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 37: Gọi S là tập các giá trị nguyên của
m
sao cho đồ thị hàm số
2
2019
17 1
x
y
x m x
=
−−
có bốn đường
tiệm cận. Tính số phần tử của tập S.
A. Vô số B. 3 C. 5 D. 4
Câu 38: Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 4 2
()
11
x
fx
x mx x x m x
=
+ + − + + +
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
1
3
. D.
1
3
−
.
Câu 39: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( ) 1
2
x x m
y
x
có
đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Câu 40: Cho hàm số
32
1
31
y
x x m
=
− + −
với
m
là tham số. Tìm tất cả các giá trị của
m
để đồ thị hàm
số đã cho có
4
đường thẳng tiệm cận.
A.
15m
. B.
12m−
. C.
1m
hoặc
5m
. D.
2m
hoặc
1m −
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
Câu 41: Hàm số
( )
2
31
1
x ax b
y
x
+ + +
=
−
không có tiệm cận đứng. Khi đó hiệu
ab−
bằng:
A.
1
2
.
B.
3
4
−
. C.
5
4
−
.
D.
1
2
−
.
Câu 42: Có bao nhiêu giá trị nguyên của tham để
m
đồ thị hàm số
2
2016 2017 24 7xx
y
xm
− + + −
=
−
có
tiệm cận đứng?
A. vô số.
B.
2
. C.
2017
D.
2019
.
Câu 43: Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 4 2
()
11
x
fx
x mx x x m x
=
+ + − + + +
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
1
3
. D.
1
3
−
.
Câu 44: Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( ) 1
2
x x m
y
x
có
đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Câu 45: Tìm tất cả các giá trị thực của
m
sao cho đồ thị hàm số
1
1
2
+
+
=
x
mx
y
có đúng một đường tiệm
cận.
A.
01 − m
. B.
01 − m
. C.
1−m
. D.
0m
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
BẢNG ĐÁP ÁN
1.C
2.A
3.C
4.A
5. B
6.C
7.C
8.C
9.A
10.D
11.A
12.C
13.A
14.B
15.C
16.B
17.A
18.D
19.A
20.D
21.C
22.A
23.B
24.A
25.C
26.C
27.B
28.A
29.B
30.C
31.D
32.B
33.A
34.C
35.B
36.D
37.C
38.B
39.A
40.A
41.C
42.C
43.B
44.A
45.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn C
Tiệm cận ngang:
Ta có:
2
2
2
2
2
2
2
2
41
41
5
5
5 4 1
lim lim lim lim 5
1
1
1
1
1
x x x x
x
xx
x
x
x
x
y
x
x
x
x
→+ →+ →+ →+

−−
−−

−−

= = = =

−
−
−


nên đồ thị hàm
số có một tiệm cận ngang
5y =
.
Tiệm cận đứng:
Cho
2
1
1
1
x
x
x
=
=
=−
Ta có:
( )( )
( )( )
2
2
1 1 1 1
5 1 1
5 4 1 5 1 6
lim lim lim lim 3
1 1 1 2
1
x x x x
xx
x x x
y
x x x
x
→ → → →
+−
− − +
= = = = =
+ − +
−
nên
1x =
không là tiệm
cận đứng.
( ) ( ) ( )
( )( )
( )
2 2 2
2
1 1 1 1
5 4 1 5 4 1 1 5 4 1
lim lim lim lim .
1 1 1 1
1
x x x x
x x x x x x
y
x x x x
x
+ + + +
→ − → − → − → −

− − − − − −
= = = = −


+ − + −
−

vì
( )
( )
1
2
1
1
lim
1
5 4 1
lim 4 0
1
x
x
x
xx
x
+
+
→−
→−
= +
+
−−
= −
−
.
Khi đó, đồ thị hàm số có một tiệm cận đứng
1x =−
.
Tổng cộng đồ thị hàm số có 2 tiệm cận.
Câu 2: Chọn A
Tập xác định:
\1D =
Ta có:
2
2
2
2
54
1
54
lim lim lim 1
1
1
1
x x x
xx
xx
y
x
x
→ → →
−+
−+
= = =
−
−
1y=
là đường tiệm cận ngang.
Mặc khác:
( )( )
( )( )
( )
( )
2
2
11
11
1 4 4
5 4 3
lim lim lim lim
1 1 1 1 2
xx
xx
x x x
xx
y
x x x x
→→
→→
− − −
−+
= = = = −
− − + +
1x=
không là đường tiệm cận đứng.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
( ) ( )
( )( )
( )( )
( )
( )
( )
2
2
1
1 1 1
1 4 4
54
lim lim lim lim
1 1 1 1
x
x x x
x x x
xx
y
x x x x
+ + + +
→
→ − → − → −
− − −
−+
= = = = −
− − + +
( ) ( ) ( )
( )( )
( )( )
( )
( )
( )
2
2
1 1 1 1
1 4 4
54
lim lim lim lim
1 1 1 1
x x x x
x x x
xx
y
x x x x
− − − −
→ − → − → − → −
− − −
−+
= = = = +
− − + +
1x = −
là đường tiệm cận đứng.
Vậy đồ thị hàm số có 2 đường tiệm cận
Câu 3: Chọn C
Ta có
2
4 0 2xx− = =
2
2
21
lim
44
x
x
x
→
−

=

−

nên đường thẳng
2x =
không phải là tiệm cân đứng của đồ thị hàm số.
2
22
21
lim lim ,
42
xx
x
xx
++
→− →−
−

= = +

−+

( ) ( )
2
22
21
lim lim ,
42
xx
x
xx
−−
→ − → −
−

= = −

−+

nên đường thẳng
2x =−
là tiệm cân đứng của đồ thị hàm số.
2
2
lim 0
4
x
x
x
→
−

=

−

nên đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số.
Vậy có đồ thị có hai đường tiệm cận.
Câu 4: Chọn A
Tập xác định của hàm số:
)
9; \ 0; 1D = − + −
Ta có:
( )
1
lim
x
y
+
→−
=
( )
2
1
93
lim
x
x
xx
+
→−
+−
+
= +
và
( )
1
lim
x
y
−
→−
( )
2
1
93
lim
x
x
xx
−
→−
+−
=
+
= −
.
TCĐ:
1x =−
.
0
lim
x
y
+
→
=
2
0
93
lim
x
x
xx
+
→
+−
+
( )
( )
2
0
lim
93
x
x
x x x
+
→
=
+ + +
( )
( )
0
1
lim
1 9 3
x
xx
+
→
=
+ + +
1
6
=
.
0
lim
x
y
−
→
=
2
0
93
lim
x
x
xx
−
→
+−
+
( )
( )
2
0
lim
93
x
x
x x x
−
→
=
+ + +
( )
( )
0
1
lim
1 9 3
x
xx
−
→
=
+ + +
1
6
=
.
0=x
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
1
tiệm cận đứng.
Câu 5: Chọn B
Tập xác định
2;3\=D
( )
( )
( )
(
)
( )
( )
( )
(
)
2
2
2
2
22
22
2
2
22
2
2 1 3
2 1 3
lim lim
56
5 6 2 1 3
2 1 3
lim
5 6 2 1 3
xx
x
x x x
x x x
xx
x x x x x
x x x
x x x x x
++
+
→→
→
− − + +
− − + +
=
−+
− + − + + +
− − + +
=
− + − + + +
( )
(
)
2
2
(3 1) 7
lim
6
3 2 1 3
+
→
+
= = −
− − + + +
x
x
x x x x
Tương tự
2
2
2
2 1 3 7
lim
5 6 6
−
→
− − + +
=−
−+
x
x x x
xx
. Suy ra đường thẳng
2=x
không là tiệm cận đứng của
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
đồ thị hàm số đã cho.
22
22
33
2 1 3 2 1 3
lim ; lim
5 6 5 6
+−
→→
− − + + − − + +
= + = −
− + − +
xx
x x x x x x
x x x x
. Suy ra đường thẳng
3=x
là tiệm
cận đứng của đồ thị hàm số đã cho.
Câu 6: Chọn C
Tập xác định hàm số
)
16; \ 1;0D = − + −
.
Ta có
( )
( )
( )
( )
( )
0 0 0 0
16 4 1 1
lim lim lim lim
18
1 16 4 1 16 4
x x x x
xx
y
xx
x x x x x
→ → → →
+−
= = = =
+
+ + + + + +
.
( ) ( )
( )
( )
( )
( )
1 1 1
16 4 1
lim lim lim
1
1 16 4
x x x
x
y
xx
xx
+ + +
→ − → − → −
+−
= = = +
+
+ + +
.
vì
( )
( )
1
lim 16 4 15 4 0
x
x
+
→−
+ + = +
,
( )
( )
1
lim 1 0
x
x
+
→−
+=
và
( )
1x
+
→−
thì
1 1 0xx − +
.
Tương tự
( ) ( )
( )
( )
11
1
lim lim
1 16 4
xx
y
xx
−−
→ − → −
= = −
+ + +
.
Vậy đồ thị hàm số đã cho có tiệm cận đứng là
1x =−
.
Câu 7: TXĐ:
)
4; \ 1;0D = − + −
.
Ta có:
( ) ( )
2
11
42
lim lim
xx
x
y
xx
++
→ − → −
+−
= = −
+
Nên đường thẳng
1x =−
là một đường tiệm cận đứng của đồ thị hàm số đã cho.
( )( )
( )
( )
( )
( )
2
0 0 0 0
4 2 4 2
4 2 1 1
lim lim lim lim
4
1 4 2 1 4 2
x x x x
xx
x
y
xx
x x x x x
→ → → →
+ − + +
+−
= = = =
+
+ + + + + +
Nên đường thẳng
0x =
không là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có một tiệm cận đứng
1x =−
.
Câu 8: Chọn C
( )
62
4
4 6 2
lim lim 2
2
2
1
xx
xx
xx
x
x
→+ →+
+−
+−
==
+
+
( )
62
4
4 6 2
lim lim 2
2
2
1
xx
xx
xx
x
x
→− →−
− + −
+−
= = −
+
+
( )
( )( )
( ) ( )
( )
( )
2 2 2
4 6 2
2 4 2
4 2 5
lim lim lim
22
4 6 2
2 4 6 2
x x x
xx
xx
x
x
xx
x x x
→− →− →−
+−
+−
−−
= = =
+
++
+ + +
Vậy hàm số có hai tiệm cận ngang
2y =
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
Câu 9: Điều kiện:
( )
( )
( )
; 2 1;1 2;x − − − +
.
Do
lim lim
xx
yy
→+ →−
=
2
42
23
lim
32
x
xx
xx
→
++
=
−+
2
24
23
1
lim 1
32
1
x
xx
xx
→
++
==
−+
1y=
là đường tiệm cận
ngang của đồ thị hàm số.
Có
1
lim
x
y
−
→
= +
nên đường thẳng
1x =
là đường tiệm cận đứng.
Có
( ) ( )
( )( )
( )
( )
( )
( )
( )
( ) ( )
( )
( )
( )
1 1 1
12
12
lim lim lim 0
1 2 1 2 2 1 2
x x x
xx
xx
y
x x x x x x x
+ + +
→ − → − → −
++
++
= = =
+ + − − + − −
nên
đường thẳng
1x =−
không là đường tiệm cận đứng.
Có
( )
2
lim
x
y
+
→
= +
nên đường thẳng
2x =
là đường tiệm cận đứng.
Có
( )
2
lim
x
y
−
→−
= +
nên đường thẳng
2x =−
là đường tiệm cận đứng.
Vậy đồ thị hàm số có
4
đường tiệm cận (
1
tiệm cận ngang,
3
tiệm cận đứng).
Câu 10: Chọn D
Đkxđ:
2
20
2
2
2, 1
3 2 0
−


− +
x
x
x
xx
xx
Ta có:
2
2
21
lim
32
+
→

−+
= +


−+

x
x
xx
nên đường thẳng
2=x
là tiệm cận đứng của đồ thị hàm số.
2
21
lim 0
32
→+

−+
=


−+

x
x
xx
nên đường thẳng
0=y
là tiệm cận ngang của đồ thị hàm số.
Câu 11: Chọn A
Xét hàm số
2
2
31
x x x
y
x
+−
=
+
có tập xác định
(
)
1
;0 1; \
3
D

= − + −


.
Ta có
2
1
3
2
lim
31
x
x x x
x
→−
+−
+
( )
(
)
2
1
2
3
3
lim
3 1 2
x
xx
x x x x
→−
+
=
+ − −
1
2
3
lim
2
x
x
x x x
→−
=
−−
1
4
=
;
2
0
2
lim 0
31
x
x x x
x
−
→
+−
=
+
và
2
1
21
lim
3 1 2
x
x x x
x
+
→
+−
=
+
nên đồ thị không có tiệm cận đứng.
2
11
33
11
2 1 2 1
21
lim lim lim
1
3 1 3 1 3
3
x
xx
xx
x x x
xx
xx
x
→−
→− →−
− − − −
+−
= = =
++
+
,
và
2
11
33
11
2 1 2 1
2
lim lim lim 1
1
3 1 3 1
3
x
xx
xx
x x x
xx
xx
x
→+
→− →−
+ − + −
+−
= = =
++
+
nên đồ thị có hai tiệm cận ngang
là
1
3
y =
và
1y =
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
Vậy đồ thị hàm số có tất cả hai đường tiệm cận.
Câu 12: Chọn C
Tập xác định của hàm số là
) ( )
1;0 2;D = − +
. Ta có
( )
( )
( )
( )
2
2
0 0 0
25 9 25 9 9
lim lim lim
4
2 5 1 1 2 5 1 1
x x x
x x x
y
x x x x x x x
→ − → − → −
++
= = = −
− + + + − + + +
.
2
lim
x
y
→+
= +
.
2 3 4
5 1 1 1
lim lim 0
2
1
xx
x x x x
y
x
→+ →+
+ − +
==
−
.
Vậy đồ thị của hàm số có hai đường tiệm cận có phương trình
2x =
và
0y =
.
Câu 13: Chọn A
Tập xác định:
1
; \ 1
3
D

= − +

+ Ta có:
( )
( )
( )
( )
2
1 1 1
1 4 3 1 3 5
1 4 3 1 3 5
lim lim lim
91
4 3 1 3 5
91
x x x
x x x
x x x
x
xx
x
+ + +
→ → →
− + + +
− + + +
= = = −
−−
+ − −
−−
do đó đường thẳng
1x =
là đường tiệm cận đứng của đồ thị hàm số.
+
2
1
1
11
lim lim
3
4 3 1 3 5 3 1 5
43
xx
x
x
xx
x x x
→+ →+
−
−
= = −
+ − −
+ − −
do đó đường thẳng
1
3
y =−
là đường
tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 14: Chọn B
Tập xác định
( )
( )
( )
; 2 1;1 2;D = − − − +
.
( ) ( )
( ) ( )
11
22
lim lim lim lim
xx
xx
y y y y
− + + −
→ − →
→ − →
= = = = +
.
Các đường tiệm cận đứng của đồ thị là
2x =
,
1x =
.
lim lim 1
xx
yy
→− →+
==
đồ thị có một tiệm cận ngang
1y =
.
Câu 15: Chọn C
Hàm số
2
4 2 1
1
x x x
y
x
+ − +
=
+
xác định
2
15
4
4 2 1 0
15
10
4
1
x
xx
x
x
x
−−
+ −


−+
+
−
.
Tập xác định của hàm số đã cho là
( )
1 5 1 5
; 1 1; ;
44
D
− − − +
= − − − +



.
2
2
21
4
4 2 1
lim lim lim
11
x x x
xx
x x x
xx
y
xx
→− →− →−
+ − +
+ − +
==
++
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
11 | Facebook tác giả: Phan Nhật Linh
22
2 1 2 1
4 4 1
lim lim 1
1
1
1
xx
xx
x x x x
x
x
→− →−
− + − + − + − +
= = = −
+
+
.
1y = −
là đường tiệm cận ngang của đồ thị hàm số khi
x → −
.
2
2
21
4
4 2 1
lim lim lim
11
x x x
xx
x x x
xx
y
xx
→+ →+ →+
+ − +
+ − +
==
++
22
2 1 2 1
4 4 1
lim lim 3
1
1
1
xx
xx
x x x x
x
x
→+ →−
+ − + + − +
= = =
+
+
.
3y=
là đường tiệm cận ngang của đồ thị hàm số khi
x → +
.
( )
(
)
( )( )
( )
(
)
2 2 2
1 1 1 1
22
1 3 1
4 2 1 4 2 1
lim lim lim lim 2.
1
1 4 2 1 1 4 2 1
x x x x
xx
x x x x x x
y
x
x x x x x x x x
→− →− →− →−
+−
+ − + + − −
= = = = −
+
+ + − − + + − −
Vậy đồ thị hàm số
2
4 2 1
1
x x x
y
x
+ − +
=
+
có
2
đường tiệm cận.
Câu 16: Chọn B
Điều kiện xác định
2
20
6 2 0
+
− +
x
x x m
.
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình
2
6 2 0− + =x x m
có hai nghiệm
phân biệt
12
,xx
lớn hơn
2−
( ) ( )
12
2
9
9 2 0
9
2
2 3 2
2
8
4 12 2 0
2 6 2 2 0
= −

+ − −
−
+ +
− − − +
m
m
m
xx
m
m
m
.
Do đó tập
7; 6; 5;...;4= − − −S
có
12
giá trị.
Câu 17: Chọn A
Ta có
22
11
lim lim 0
88
xx
xx
x x m x x m
→− →+
−−
==
− + − +
nên hàm số có một tiện cận ngang
0y =
.
Hàm số có 3 đường tiệm cận khi và chỉ khi hàm số có hai đường tiệm cận đứng
phương trình
2
80x x m− + =
có hai nghiệm phân biệt khác
1
Δ 16 0 16
7 0 7
mm
mm
= −



−

.
Kết hợp với điều kiện
m
nguyên dương ta có
1;2;3;...;6;8;...;15m
. Vậy có
14
giá trị của
m
thỏa mãn đề bài.
Câu 18: Chọn D
Ta có
lim 0, lim 0
xx
yy
→+ →−
==
đồ thị hàm số đã cho có 1 tiệm cận ngang.
Do đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi nó có 3 tiệm cận đứng
( )
*
.
Có
( )
( )
( )
3 2 2 2
3 2 1 2 1x mx m x m x m x mx− + + − = − − +
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12
( )
( )
3 2 2
2
3 2 1 0
2 1 0 2
xm
x mx m x m
x mx
=
− + + − =
− + =
( )
*
( )
3 2 2
3 2 1 0x mx m x m− + + − =
có 3 nghiệm phân biệt khác
3
.
3m
và
( )
2
có 2 nghiệm phân biệt khác
m
và khác 3.
2
2
2
2
3
5
3,
2 . 1 0
3
1
3 2 .3 1 0
1
10
m
mm
m m m
m
m
m
m

− +



− +


−
= −
Do đó tập tất cả giá trị nguyên của
m
thỏa ycbt là
2020; 2019;...; 2;2;4;5;...;2020− − −
.
Vậy có 4037 giá trị
m
thỏa ycbt.
Câu 19: Chọn A
Ta có điều kiện xác định là
( )
0;2
xm
x
, khi đó đồ thị hàm số sẽ không có tiệm cận ngang.
Ta có
02
lim , lim
xx
yy
+−
→→
= =
Suy ra
0, 2xx==
là hai đường tiệm cận đứng
Vậy để đồ thị hàm số có đúng hai đường tiệm cận thì
0
2
m
m
, theo bài
m
thuộc đoạn
100;100−
. Vậy có 200 số nguyên của
m
thỏa mãn đầu bài.
Câu 20:
( )( )
22
2
3 2 1 2
x m x m
y
x x x x
++
==
− + − −
.
lim 1
x
y
→
=
1y =
là đường tiệm cận ngang.
Đồ thị hàm số
2
2
32
xm
y
xx
+
=
−+
có đúng hai đường tiệm cận
đồ thị hàm số có đúng một tiệm
cận đứng
pt
2
0xm+=
nhận nghiệm
1x =
hoặc
2x =
.
Khi đó:
1
4
m
m
=−
=−
.
Với
1m =−
có một tiệm cận đứng
2x =
.
Với
4m =−
có một tiệm cận đứng
1x =
.
Vậy
{ 1; 4}m − −
.
Câu 21: Chọn C
Để đồ thị có ba đường tiệm cận thì
2
2 4 0x mx− + =
có hai nghiệm phân biệt
1−
( ) ( )
2
2
0
2
1 2 1 4 0
5
2
m
m
m
m



−


− − − +
−
Câu 22: Chọn A
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
13 | Facebook tác giả: Phan Nhật Linh
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số
ax b
y
cx d
=
+
+
ta có
Đồ thị hàm số nhận
30
d
xm
c
= − = − − =
làm TCĐ
3m = −
Đồ thị hàm số nhận
30
a
yn
c
= = − =
làm TCN
3n=
.
Vậy
0mn+=
.
Câu 23: Trường hợp 1:
0m
suy ra tập xác định của hàm số là
( )
12
;=D x x
, (
12
;xx
là nghiệm của
phương trình
2
8 2 0− + =mx x
). Do đó
0m
không thỏa yêu cầu của bài toán.
Trường hợp 2:
1
0
82
−
= = =
−+
x
my
x
suy ra tập xác định của hàm số là
( )
;4= −D
.
4
lim ; lim
−
→−
→
= − = −
x
x
yy
. Khi đó ta có
4=−x
là đường tiệm cận đứng của đồ thị hàm số.
Do đó
0=m
không thỏa yêu cầu của bài toán
Trường hợp 3:
0m
suy ra tập xác định của hàm số là
( ) ( )
12
;;= − +D x x
(
12
;xx
là
nghiệm của phương trình
2
8 2 0− + =mx x
). Do đó đồ thị hàm số có bốn đường tiệm cận khi
phương trình
2
8 2 0− + =mx x
có hai nghiệm phân biệt khác
16 2 0 8
1 0; 0; 1;2;3;4;5;7
8 2 0 6
−


=

− +

mm
m m m m m
mm
. Suy ra có tất cả
6
giá trị nguyên của
tham số
m
thỏa mãn yêu cầu của bài toán.
Câu 24: Chọn A
Đồ thị hàm số có tiệm cận ngang
Hàm số xác định trên một trong các miền
( ) (
( )
; , ; , ,− − +a a a
hoặc
)
;+a
0m
Trường hợp 1:
0 3 7, lim
→
= = − − + = 
x
m y x x y
đồ thị không có tiệm cận ngang
Trường hợp 2:
2
0, 3 7 = − − +m y x mx x
Khi
2
3 7 3
lim lim
2
→+
→+

= − − + =



x
x
y x x m
xx
đồ thị hàm số có tiệm cận ngang khi và chỉ khi
1=m
.
Vậy
1=m
Cách trắc nghiệm:
Thay
1=m
(
)
22
3
3 7 lim 3 7
2
→+
= − − + − − + =
x
y x x x x x x
đồ thị hàm số có tiệm cận ngang
(
)
2
lim 3 7
→−
− − + = −
x
x x x
không có tiệm cận ngang.
Thay
1=−m
(
)
22
3 7 lim 3 7
→+
= − − − + − − − +
x
y x x x x x x
không xác định.
(
)
2
lim 3 7
→−
− − − +
x
x x x
không xác định. Vậy
1=m
Câu 25: Chọn C
+
0=b
đồ thị hàm số
1
2
+
=
−
ax
y
không có tiệm cận.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14
+
0b
, tập xác định của hàm số
1
2
+
=
−
ax
y
bx
là
2
\

=


DR
b
.
1
1
lim lim lim
2
2
→ → →
+
+
= = =
−
−
x x x
a
ax a
x
y
bx b
b
x
.
đồ thị hàm số
1
2
+
=
−
ax
y
bx
có tiệm cận ngang là đường thẳng
1
2
2
= = =
aa
y b a
bb
.
22
1
lim lim
2
++
→→
+
+
==
−
−
xx
bb
ax
y
bx
.
đồ thị hàm số
1
2
+
=
−
ax
y
bx
có tiệm cận đứng là đường thẳng
22
1 2 1= = = =x b a
bb
.
Vậy
1; 2==ab
.
Câu 26: Chọn C
Ta có đồ thị hàm số
2
1
2 6 3
x
y
x x m
−
=
+ − −
có hai đường tiệm cận đứng khi phương trình
2
2 6 3 0x x m+ − − =
có hai nghiệm phân biệt khác
1
( )
2
2
3 2 3 0
2.1 6.1 3 0
m
m
− − −
+ − −
15
2
5
m
m
−
Từ đó ta suy ra tập các giá trị nguyên của
m
thỏa mãn là
7, 6, 5, 4, 3, 2, 1,0,1,2,3,4,6,7,8,9,10− − − − − − −
. Vậy có
17
giá trị nguyên của
m
thỏa mãn.
Câu 27: Chọn B
Đồ thị hàm số
2
34
2
mx mx
y
x
++
=
+
có nhiều nhất một tiệm cận đứng và hai tiệm cận ngang.
Điều kiện để đồ thị hàm số
2
34
2
mx mx
y
x
++
=
+
có 3 tiệm cận là nó có đúng 1 tiệm cận đứng và
2 tiệm cận ngang.
Xét điều kiện tồn tại
lim
x
y
→+
và
lim
x
y
→−
Trường hợp 1:
( )
2
3 4 0g x mx mx= + +
với
x
2
0
16
0
0
9
9 16 0
m
m
m
mm
=
= −
Trường hợp 2:
( )
2
3 4 0g x mx mx= + +
với
( ) ( )
12
;;x x x − +
với
1
x
;
2
x
là nghiệm
của
( )
gx
2
0
16
9
9 16 0
m
m
mm
= −
Vậy
0m
thì tồn tại
lim
x
y
→+
và
lim
x
y
→−
Khi đó:
2
2
34
34
lim lim lim
2
2
1
x x x
m
m
mx mx
xx
ym
x
x
→+ →+ →+
++
++
= = =
+
+
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
15 | Facebook tác giả: Phan Nhật Linh
2
2
34
34
lim lim lim
2
2
1
x x x
m
m
mx mx
xx
ym
x
x
→− →− →−
− + +
++
= = = −
+
+
Vậy điều kiện để đồ thị hàm số có hai đường tiệm cận ngang là
0m
Xét trường hợp
2x =−
là nghiệm của tử số
2x = −
là nghiệm của
( )
2
34g x mx mx= + +
( )
2 0 2gm− = =
Khi đó
2
2 6 4
2
xx
y
x
++
=
+
( )( )
( )
22
2 1 2
21
lim lim
22
xx
xx
x
y
xx
−−
→− →−

++
+
= = − = −

++


Đồ thị hàm số có một tiệm cận đứng
2x =−
2m =
thỏa mãn
Xét trường hợp
2x =−
không là nghiệm của tử số, để
2x =−
là tiệm cận đứng của đồ thị hàm
số thì
( )
( )
( )
20
2 0 4 2 0 2
20
g
g m m
g
−
− −
−
đồ thị hàm số có một đường tiệm cận đứng
2x =−
với
(
0;2m
Vậy điều kiện để đồ thị hàm số
2
34
2
mx mx
y
x
++
=
+
có 3 tiệm cận là
(
0;2m
Vậy có hai giá trị nguyên của
m
thỏa mãn đề bài là
1m =
;
2m =
.
Câu 28: Chọn A
Đặt
( ) ( )
22
2 1 2x m mfx x+ − + −=
Đồ thị hàm số có đúng một tiệm cận đứng khi và chỉ khi
( )
0fx=
có 2 nghiệm phân biệt trong
đó có 1 nghiệm
1x =
hoặc
( )
0fx=
có nghiệm kép
( )
( )
( )
( )
2
2
2
3
1 2 0
0
1
2
1 2 1 2 0
1 0 3
1; 3
3
3
3
0
2
2
2
mm
m
m
mm
fm
mm
m
m
m
− − −


=

+ − + − =

= = −
= = −
=
=
=
=
.
Vậy tổng các giá trị
m
thỏa mãn là:
1
2
−
.
Câu 29: Chọn B
lim lim 0
xx
yy
nên đồ thị hàm số có tiệm cận ngang là đường thẳng
0y
.
Do đó, đồ thị hàm số có bốn đường tiệm cận khi phương trình
3 2 2
3 2 1 0x mx m x m
có 3 nghiệm phân biệt
3x
.
Xét phương trình
3 2 2
3 2 1 0x mx m x m
ta có
3 2 2
3 2 1 0x mx m x m
2
2 1 0x m x mx
2
2 1 0
xm
x mx
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16
Phương trình có ba nghiệm phân biệt
3x
khi và chỉ khi
3m
và phương trình
2
2 1 0x mx
có hai nghiệm phân biệt
3x
2
2
3
3
1
10
1
3 2.3. 1 0
5
3
m
m
m
m
m
m
m
.
Do
m
nguyên và
6;6m
nên
6; 5; 4; 3; 2;2;4;5;6m
.
Vậy có
9
giá trị nguyên của
m
thỏa mãn đề bài.
Câu 30: Chọn C
Tập xác định:
\ m
.
Có
22
2 3 2 2
lim lim 2 2 3
→→

− + −
= + − +

−−

x m x m
x x m m m
xm
x m x m
.
Để đồ thị hàm số không có tiệm cận đứng thì phải tồn tại
2
23
lim
→
−+
−
xm
x x m
xm
,
2
0
2 2 0
1
=
− =
=
m
mm
m
Câu 31: Chọn D
Để đồ thị hàm số
2
2
4
x
y
x x m
có hai tiệm cận đứng thì phương trình
2
40x x m
có
hai nghiệm phân biệt khác
2
2017 4
40
12 2017; 2016;..;3 \ 12
12 0
m
m
mm
m
m
.
Do đó số giá trị nguyên của tham số
m
thỏa đề bài là:
3 ( 2017) 1 1 2020
giá trị.
Câu 32: Chọn B
Đồ thị hàm số
( )
y f x=
có duy nhất một tiệm cận ngang
4
3
0
2019 2020
2019
2020
m
mm
m
=
=
=
.
Vậy có 2 giá trị của
m
thỏa bài toán
Câu 33: Chọn A
Điều kiện
.xm
Ta có
lim 0 0
x
yy
→+
= =
là tiệm cận ngang của đồ thị hàm số.
Xét phương trình
( )
( )
2
2
2 1 2 0
2 1 2 0(*)
xm
x m x m x m
x m x m
=

− + + − =

− + + =
Để hàm số có 4 đường tiệm cận thì phương trình
(*)
có 2 nghiệm phân biệt
12
m x x
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
17 | Facebook tác giả: Phan Nhật Linh
( )
( )( ) ( )
2
22
1 2 1 2 1 2
12
11
2 1 0
22
1
0 0 0
2
01
10
2 2 1 2
mm
m
m
x m x m x x m x x m m m
m
x x m m m



−

− − − + − −

+ +



.
Câu 34: Chọn C
Đặt
( )
2
63f x mx x= − +
và
( )
2
9 6 1g x x mx= + +
. Ta xét các trường hợp:
Trường hợp 1:
0m =
khi đó ta có
( )
( )
2
63
6 3 9 1
x
y
xx
−
=
− + +
đồ thị hàm số có 1 đường tiệm cận
ngang là đường thẳng
0y =
do đó
0m =
thỏa mãn yêu cầu bài toán.
Trường hợp 2:
0m
và cả hai tam thức
( )
fx
và
( )
gx
đều vô nghiệm
2
'0
9 3 0
3
' 0 1 1
9 9 0
f
g
m
m
m
m
m

−

−
−
.
Trường hợp 3: Tam thức
( )
gx
nhận
1
2
x =
làm nghiệm
1 13
0
2 12
gm

= = −


khi đó
( )
fx
luôn có 2 nghiệm phân biệt nên đồ thị hàm số đã cho có nhiều hơn 1 đường tiệm cận.
Vậy có 1 giá trị nguyên của
m
để đồ thị hàm số
( )( )
22
63
6 3 9 6 1
x
y
mx x x mx
−
=
− + + +
có đúng 1
đường tiệm cận
Câu 35: Chọn B
Điều kiện cần và đủ để đồ thị hàm số:
2
1y x mx
có tiệm cận ngang là tồn tại số thực k
sao cho:
2
2
lim ( 1) k
lim ( 1) k
x
x
x
x mx
x mx
Hiển nhiên nếu
0m
thì giới
2
lim ( 1)
x
x mx
không hữu hạn
Nếu
0m
ta có
2
lim ( 1) .
x
x mx
2
2
2
2
1
x(1 )
(1 ) 1
lim y lim ( 1) lim lim
1
1
1
x x x x
m
xm
x
x mx
x mx
m
x
Để giới hạn trên hữu hạn khi và chỉ khi m=1.
Câu 36: Chọn D
Với
0m =
; ta có hàm số
2
2
24
x
y
x
−
= = −
−+
Không thỏa mãn yêu cầu bài toán.
Với
0m
, ta có:
2
2
lim 0
24
x
x
mx x
→
−
=
−+
0y =
là tiệm cận ngang của đồ thị hàm số.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18
Đồ thị hàm số có đúng hai đường tiệm cận
đồ thị hàm số có đúng 1 tiệm cận đứng
2
2 4 0mx x− + =
có nghiệm duy nhất hoặc
2
2 4 0mx x− + =
có hai nghiệm phân biệt trong đó có
một nghiệm
2x =
.
2
2 4 0mx x− + =
có nghiệm duy nhất
1
0 1 4 0
4
mm
= − = =
.
2
2 4 0mx x− + =
có hai nghiệm phân biệt trong đó có một nghiệm
2x =
.
1
0
4
40
0
m
m
m



=
=
0m =
không thỏa mãn điều kiện.
Vậy chỉ có một giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 37: Chọn C
2019 2019
lim , lim
17 17
xx
yy
mm
→− →+
==
−−
.
Với
17m
thì đồ thị hàm số có hai đường tiệm cận ngang là
2019 2019
,
17 17
yy
mm
==
−−
.
Khi đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi phương trình
( )
2
17 1 0 1x m x− − =
có hai nghiệm phân biệt khác 0.
Ta có:
( )
( )
( )
2
22
2 2 2
0
0
1 17 1
17 1 2
17 1
m
m
x m x
mx
x m x
− =

−=
−=
Phương trình có 2 nghiệm phân biệt khác 0 khi và chỉ khi phương trình có hai nghiệm phân biệt
khác 0
2
0
0 17
17 0
m
m
m
−
.
Suy ra
0,1,2,3,4S =
.
Câu 38: Chọn B
Ta có:
3
3 4 2
00
1
lim ( ) lim
11
xx
fx
x mx x x m x
x
→→
=
+ + − + + +
.
Mà
3
3 4 2
0
11
lim
x
x mx x x m x
x
→
+ + − + + +
3
3 4 2
0
34
2
3
3 4 2 4
0
3
1 1 1 1
lim
lim .
( 1 1) ( ( 1) 1 1)
x
x
x mx x x m x
x x x
x mx x x
m
x x mx x x x x x
→
→

+ + − + + −
= − +




++
= − +

+ + + + + + + + +

Đồ thị hàm số
()fx
nhận trục tung làm tiệm cận đứng
23
22
3
3 4 2 4
0
3
( ) ( 1) 1
lim( ) 0 0
23
( 1 1) ( 1) 1 1
x
x m x m
mm
x mx x x x x
→
++
− + = − + =
+ + + + + + + + +
.
2
6 3 2 0mm + − =
Vậy
12
1
.
2
mm+ = −
Câu 39: Chọn A
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
19 | Facebook tác giả: Phan Nhật Linh
Xét
1g x x x m
.
Ta có
( ) 1
lim 1
2
x
x x m
x
và
( ) 1
lim 1
2
x
x x m
x
. Nên đồ thị hàm số luôn có hai
đường tiệm cận ngang
1y
và
1y
.
Trường hợp 1:
0m
khi đó hàm số là
1
2
x
y
x
. Đồ thị hàm số có tiệm cận đứng là
2x
.
Vậy
0m
thỏa mãn yêu cầu đề bài.
Trường hợp 2:
0m
. Hàm số
gx
có tập xác định là
;0 ;Dm
.
2xD
.
( 2) 2 2 1 0gm
nên
2x
là tiệm cận đứng của đồ thị hàm số
Vậy
1m
,
2m
,.
9m
thỏa mãn. Nên có
9
giá trị
m
.
Trường hợp 3:
0m
. Hàm số
gx
có tập xác định là
; 0;Dm
.
Để
2x
là tiệm cận đứng của đồ thị hàm số thì trước hết
2xD
hay
2m
. Nên chỉ
có
2m
,
1m
thỏa mãn
Với
1m
ta có
( ) 1 1g x x x
,
( 2) 2 1 0g
nên
2x
là tiệm cận đứng của
đồ thị hàm số.
Với
2m
ta có
( ) 2 1g x x x
,
( 2) 2 1 1 0g x x
nên
2x
là
tiệm cận đứng của đồ thị hàm số.
Vậy
12
giá trị
m
nguyên thỏa mãn yêu cầu.
Câu 40: Ta có
32
1
lim lim 0
31
xx
y
x x m
→+ →+
==
− + −
,
32
1
lim lim
31
xx
y
x x m
→− →−
=
− + −
không tồn tại. Suy ra
0y =
là đường tiệm cận ngang của đồ thị hàm số.
Do đó, để đồ thị hàm số đã cho có
4
đường thẳng tiệm cận thì phương trình
32
3 1 0x x m− + − =
có
3
nghiệm phân biệt.
Xét hàm số
( )
32
31g x x x m= − + −
. Tập xác định
D =
.
( )
2
36g x x x
=−
;
( )
0
0
2
x
gx
x
=
=
=
.
Bảng biến thiên:
Từ bảng biến thiên, ta thấy phương trình
32
3 1 0x x m− + − =
có
3
nghiệm phân biệt khi và chỉ
khi
5 0 1 1 5m m m− −
.
Câu 41: Chọn A
Do hàm số không có tiệm cận đứng nên
( ) ( ) ( )
2
3 1 1f x x ax b x g x= + + + = −
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20
Suy ra
( )
( )
3
20
10
1
4
3
5
2
0
' 1 0
4
4
ab
a
f
ab
a
f
b
+ + =
=−
=
− =
+=
=

=−
→
đáp án A.
Chú ý: Với
( ) ( ) ( )
0
n
f x x x g x=−
thì ta luôn có
( ) ( ) ( )
( )
( )
1
0 0 0 0
' '' ... 0
n
f x f x f x f x
−
= = = = =
.
Câu 42: Chọn C
Biểu thức:
2
2016 2017xx− + +
có nghĩa khi
2
2016 2017 0 1 2017x x x− + + −
.
Đặt
( )
2
2016 2017f x x x= − + +
.
Xét
0x m x m− = =
. Vậy đồ thị nếu có tiệm cận đứng chỉ có thể là
xm=
, khi đó điều kiện
là:
( )
( )
( )
2
1;2017 1
1 2017
0
2016 2017
24 7 *
m
x
fm
mm
−
−


− + +
Ta có
( ) ( )
2
1
* 2016 2015 0 2
2015
m
mm
m
− +
Từ
( ) ( )
1 , 2 1;2017 \ 1;2015
m
m
− ⎯⎯⎯→
có
2019 2 2017−=
số nguyên
m
thỏa mãn bài
toán
→
đáp án C.
Câu 43: Chọn B
Ta có:
3
3 4 2
00
1
lim ( ) lim
11
xx
fx
x mx x x m x
x
→→
=
+ + − + + +
.
Mà
3
3 4 2
0
11
lim
x
x mx x x m x
x
→
+ + − + + +
3
3 4 2
0
34
2
3
3 4 2 4
0
3
1 1 1 1
lim
lim .
( 1 1) ( ( 1) 1 1)
x
x
x mx x x m x
x x x
x mx x x
m
x x mx x x x x x
→
→

+ + − + + −
= − +




++
= − +

+ + + + + + + + +

Đồ thị hàm số
()fx
nhận trục tung làm tiệm cận đứng
23
22
3
3 4 2 4
0
3
( ) ( 1) 1
lim( ) 0 0
23
( 1 1) ( 1) 1 1
x
x m x m
mm
x mx x x x x
→
++
− + = − + =
+ + + + + + + + +
.
2
6 3 2 0mm + − =
Vậy
12
1
.
2
mm+ = −
Câu 44: Chọn A
Xét
1g x x x m
.
Ta có
( ) 1
lim 1
2
x
x x m
x
và
( ) 1
lim 1
2
x
x x m
x
. Nên đồ thị hàm số luôn có hai
đường tiệm cận ngang
1y
và
1y
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
21 | Facebook tác giả: Phan Nhật Linh
Trường hợp 1:
0m
khi đó hàm số là
1
2
x
y
x
. Đồ thị hàm số có tiệm cận đứng là
2x
.
Vậy
0m
thỏa mãn yêu cầu đề bài.
Trường hợp 2:
0m
. Hàm số
gx
có tập xác định là
;0 ;Dm
.
2xD
.
( 2) 2 2 1 0gm
nên
2x
là tiệm cận đứng của đồ thị hàm số
Vậy
1m
,
2m
,.
9m
thỏa mãn. Nên có
9
giá trị
m
.
Trường hợp 3:
0m
. Hàm số
gx
có tập xác định là
; 0;Dm
.
Để
2x
là tiệm cận đứng của đồ thị hàm số thì trước hết
2xD
hay
2m
. Nên chỉ
có
2m
,
1m
thỏa mãn
Với
1m
ta có
( ) 1 1g x x x
,
( 2) 2 1 0g
nên
2x
là tiệm cận đứng của
đồ thị hàm số.
Với
2m
ta có
( ) 2 1g x x x
,
( 2) 2 1 1 0g x x
nên
2x
là
tiệm cận đứng của đồ thị hàm số.
Vậy
12
giá trị
m
nguyên thỏa mãn yêu cầu.
Câu 45: Chọn A
Nếu
0m =
thì
1
1
y
x
=
+
. Hàm số này có tập xác định
\1D =−
.
Ta có
1
lim 0
1
x
x
→+
=
+
nên đồ thị hàm số có tiệm cận ngang là
0y =
.
( )
1
1
lim
1
x
x
+
→−
= +
+
nên đồ thị hàm số có tiệm cận đứng
1x =−
.
Vậy với
0m =
thì đồ thị hàm số có hai đường tiệm cận.
Nếu
0m
thì
2
10mx +
với mọi
x
và tập xác định của hàm số là
\1D =−
.
2
1
lim
1
x
mx
x
→+
+
+
2
1
lim
1
1
x
m
x
m
x
→+
+
==
+
,
2
1
lim
1
x
mx
x
→−
+
+
2
1
lim
1
1
x
m
x
m
x
→+
−+
= = −
+
. Suy ra đồ thị
hàm số có hai tiệm cận ngang là
ym=
và
ym=−
.
( )
2
1
1
lim
1
x
mx
x
+
→−
+
= +
+
nên
1x =−
là đường tiệm cận đứng của đồ thị hàm số.
Vậy
0m
không thỏa mãn.
Nếu
0m
thì tập xác định của hàm số là
11
; \ 1D
mm

= − − − −


.
Trường hợp này đồ thị hàm số không có tiệm cận ngang. Để đồ thị hàm số có đúng một đường
tiệm cận thì đồ thị hàm số phải có một tiệm cận đứng. Điều này xảy ra khi
1
1
m
− − −
1
1
m
−
1
1
m
−
1m −
.
Vậy với
10m−
thì đồ thị hàm số có đúng một đường tiệm cận.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
Câu 1: Cho hàm số . Có bao nhiêu giá trị nguyên thuộc đoạn
của tham số để đồ thị hàm số có 4 đường tiệm cận?
A. . B. . C. . D. .
Câu 2: Cho hàm số . Tìm tất cả các giá trị của sao cho đồ thị hàm số có đúng hai
đường tiệm cận đứng
A. . B. . C. . D. .
Câu 3: Cho hàm số bậc bốn có đồ thị như hình vẽ.
Số đường tiệm cận của đồ thị hàm số là
A. . B. . C. . D. .
Câu 4: Cho đồ thị hàm số như hình vẽ dưới đây:
Đồ thị của hàm số có bao nhiêu đường tiện cận đứng
A. . B. . C. . D. .
3 2 2
3
3 (2 1)x m
−
=
− + + −
x
y
x mx m
2020;2020−
m
4039
4040
4038
4037
2
2
20 6
82
xx
y
x x m
+−
=
−+
m
)
6;8m
( )
6;8m
)
12;16m
( )
0;16m
( )
y f x=
( )
( )
( )
( )
( )
4
23
4 3 1
1
x x x
y
f f x
− − +
=
−
6
5
3
4
32
y ax bx cx d= + + +
( )
( ) ( )
2
2
32
36
xx
gx
f x f x
−−
=
−
5
4
3
2
Bài tập tiệm cận của đồ thị hàm số nâng cao
DẠNG
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
Câu 5: Cho hàm số bậc ba có bảng biến thiên như hình bên dưới.
Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận
ngang
A. . B. . C. . D. .
Câu 6: Cho hàm số bậc ba có đồ thị như hình vẽ. Hỏi đồ thị hàm số
có bao nhiêu đường tiệm cận?
A. . B. . C. . D. .
Câu 7: Cho hàm trùng phương có đồ thị như hình vẽ. Hỏi đồ thị hàm số
có tổng cộng bao nhiêu tiệm cận đứng?
A. . B. . C. . D. .
Câu 8: Biết đồ thị hàm số
( )
+ + +
=
−
2
31
5
x ax b
y
x
không có tiệm cận đứng. Tính
+
23
ab
A.
−4841
152
. B.
−4814
152
. C.
4841
152
. D.
4814
152
.
( )
y f x=
( )
( )
2 7 3 4 5
1
xx
gx
fx
+ − +
=
−
4
3
2
5
( )
32
f x ax bx cx d= + + +
( )
( ) ( )
2
2
3 2 1x x x
gx
x f x f x
− + −
=

−

3
5
6
4
42
y ax bx c= + +
( )( )
( ) ( )
22
2
42
23
x x x
y
f x f x
−+
=
+−


5
2
3
4
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
Câu 9: Biết rằng tích phân
−
−

= + + = −


2
2
3
2
1
3
41
1 . d 3.
3
ac
x
x b d
I x e x e e
x
, trong đó các phân số
;
ac
bd
tối giản.
Hãy xác định phương trình đường tiệm cận ngang của đồ thị hàm số
+
=
+
ax b
y
cx d
.
A.
=
25
3
y
. B.
=
25
53
y
. C.
=
25
9
y
. D.
= 3y
.
Câu 10: Cho hàm số bậc ba
( )
=y f x
có đồ thị như hình vẽ.
Tổng các giá trị nguyên của tham số
m
để đồ thị hàm số
( )
( )
( )
=
+−
2020
1
gx
f f x m
có
4
đường
tiệm cận bằng
A.
15
. B.
1
. C.
13
. D.
11
.
Câu 11: Có bao nhiêu giá trị thực của tham số
m
để đồ thị hàm số
− + − −
==
− + −
32
6 3 2 3
()
3 14 20 8
x mx m
y f x
x x x
có
đúng hai đường tiệm cận?
A.
1
. B.
2
. C.
3
. D. Vô số.
Câu 12: Số đường tiệm cận của đồ thị hàm số:
( )
(
)
( )
− − +
=
−
3
2
3
9 2 ln 1xx
fx
xx
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 13: Cho hàm số bậc ba
( )
=y f x
có đồ thị như sau
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
Gọi
,Mm
lần lượt là số tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
( )
( )
( )
− − − − +
=
−−
2 2 4 2
2
2 3 . . 17 16
2 . 2 3
x x x x x x
y
f x x x
. Khi đó mệnh đề nào đúng?
A.
=23Mm
. B.
= 3Mm
. C.
= 2Mm
. D.
=Mm
.
Câu 14: Đồ thị hàm số
( )
( )
(
)
− + −
=
+ − + + +
2
2
2 3 2 8
2 1 . 4 4 2
x x x
y
x x x x
có tổng số đường tiệm cận đứng, tiệm cận
ngang là
A.
2
. B.
3
. C.
4
. D.
6
.
Câu 15: Đồ thị hàm số
( )
( )
−+
==
−
+ + +
2
2
2
22
2
2
4 1 2 2
xx
khi x
y f x
xx
x x x khi x
có tất cả bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 16: Cho hàm số
( )
( )
( )
− + + −
==
+ + − + +
32
22
4 20 24 2
20 14 9 14 11 2 1
x x m x m
y f x
x x x x
có đồ thị là
( )
C
. Gọi
S
là tập hợp
các giá trị của
m
để
( )
C
có đúng một tiệm cận đứng. Tổng các giá trị trong
S
là
A.
−1
. B.
−3
. C.
−5
. D.
−7
.
Câu 17: Cho đồ thị hàm số
( )
=y f x
liên tục trên và có đúng hai đường tiệm cận ngang
= − =5, 1 yy
. Tìm giá trị của tham số
m
sao cho đồ thị hàm số
( )
=+y f x m
có đúng một đường tiệm cận
ngang.
A.
= 1m
. B.
=−2m
. C.
= 2m
. D.
= 3m
.
Câu 18: Cho hàm số
( )
(
)
= + − − − +
3
3 2 2
. 1 2 1f x x ax bx x x
. Biết rằng đồ thị hàm số có một đường tiệm
cận ngang bằng
=
5
4
y
. Giá trị
+ab
thuộc khoảng nào trong các khoảng sau?
.
A.
( )
−−5; 3
. B.
( )
−3;0
. C.
( )
0; 3
. D.
( )
3;5
.
Câu 19: Cho hàm số bậc ba
( )
32
f x ax bx cx d= + + +
( )
, , ,a b c d
có đồ thị như hình vẽ sau đây:
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
Đồ thị hàm số
( )
( ) ( )
2
( 2)
2
xx
gx
f x f x
−
=
−
có bao nhiêu đường tiệm cận đứng?
A. 2 B. 4. C. 3. D. 1.
Câu 20: Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
2
1
24
x
y
x mx
−
=
−+
có 3 đường
tiệm cận.
A.
2m
. B.
22m−
. C.
2
2
5
2
m
m
m

−
. D.
2
2
m
m
−
.
Câu 21: Gọi
S
là tập các giá trị của
m
sao cho đồ thị hàm số
22
1
2 2 6
x
y
x mx m m
−
=
− + − −
có đúng hai
đường tiệm cận. Số phần tử của
S
là:
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 22: Cho hàm số
( )
32
= = + + +y f x ax bx cx d
( )
0a
có đồ thị như hình dưới đây.
Gọi
S
là tập các giá trị nguyên của
m
thuộc khoảng
( )
2019;2020−
để đồ thị hàm số
( )
( ) ( )
( )
( )
( )
2
1
2 2 2
x f x
gx
f x x mx m
+
=
− − + +
có 5 đường tiệm cận (tiệm cận đứng hoặc tiệm cận ngang).
Số phần tử của tập
S
là
A.
2016.
B.
4034.
C.
4036.
D.
2017.
Câu 23: Cho hàm số bậc ba
( )
32
f x ax bx cx d= + + +
có đồ thị như hình vẽ. Hỏi đồ thị hàm số
( )
( )
( ) ( ) ( )
2
2
21
33
x x x
gx
x f x f x
−−
=

−+

có bao nhiêu đường tiệm cận đứng?
A.
4
. B.
3
. C.
5
. D.
6
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
BẢNG ĐÁP ÁN
1.B
2.B
3.A
4.C
5.B
6.C
7.D
8.A
9.B
10.D
11.B
12.C
13.C
14.A
15.C
16.C
17.C
18.D
19.
20.
21.
22.
23.
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn B
Ta có suy ra là tiệm cận ngang của đồ thị hàm số.
Để đồ thị hàm số có đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng đường tiệm cận
đứng, hay khi có nghiệm phân biệt khác
Ta có
Để phương trình có nghiệm phân biệt khác khi phương trình có nghiệm phân
biệt khác và khi
Vì là số nguyên thuộc đoạn nên có giá trị của tham số .
Câu 2: Chọn B
Ta có tập xác định của hàm số phải thỏa mãn .
Điều kiện để đồ thị hàm số có 2 tiệm cận đứng là phương trình có 2 nghiệm
phân biệt thỏa mãn .
Ta có: . Đặt .
Ta có bảng biến thiên của hàm trên đoạn .
Yêu cầu bài toán .
Câu 3: Chọn A
Hàm số bậc bốn có dạng . Ta có: .
lim lim 0,
xx
yy
→+ →−
==
0y =
4
3
( )
3 2 2
3 (2 1)x m 0 1x mx m− + + − =
3
3.
( )
( )
3 2 2 2
3 (2 1)x m 0 2 1 0x mx m x m x mx− + + − = − − + =
( ) ( )
2
2 1 0 2
xm
f x x mx
=
= − + =
( )
1
3
3
( )
2
2
3
m
( )
( )
2
2
22
1
1
10
0
1
5
3 0 3 6 1 0 .
1
3
2 1 0
0
1
m
m
m
m
f m m
m
mm
fm
m

−
−

−
− +
− +

m
2020;2020−
4038
m
2
6 0 0 6x x x−
2
8 2 0x x m− + =
12
,xx
12
06xx
2
82x x m− = −
( )
2
8f x x x=−
( )
fx
0;6
16 2 12 6 8mm − − −
( )
4 3 2
0y ax bx cx dx e a= + + + +
32
4 3 2y ax bx cx d
= + + +
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
Từ đồ thị trong hình vẽ đã cho ta thấy: Đồ thị hàm số có ba điểm cực trị
với . Ngoài ra đồ thị hàm số đi qua các điểm .
Từ đó ta có: .
Suy ra bậc bốn .
Ta có: .
Từ đó ta có hàm số
.
Xét .
Ta có: ; ; ; ; ;
; .
Suy ra đồ thị hàm số có tiệm cận đứng và tiệm cận ngang.
Câu 4: Chọn C
( ) ( ) ( )
00
1;0 , ; , 2;0xy−
00
0 1; 0xy
( ) ( )
2;3 , 3;3−
( )
( )
( )
( )
( )
( )
10
4 3 2 0
1
20
32 12 4 0
2
10
0
3
16 8 4 2 0
20
4
16 8 4 2 3
23
4
81 27 9 3 3
33
y
a b c d
a
y
a b c d
b
y
a b c d e
c
a b c d e
y
d
a b c d e
y
e
a b c d e
y
−=
− + − + =
=
=
+ + + =
=−
−=
− + − + =

= −
+ + + + =
=
=
− + − + =
−=
=
+ + + + =
=
( )
4 3 2
2 3 4 4y f x x x x x= = − − + +
( ) ( ) ( )
22
4 3 2
2 3 4 4 1 2f x x x x x x x= − − + + = + −
( )
( )
( )
( )
( )
4
23
4 3 1
1
x x x
y
f f x
− − +
=
−
( )
( )
( )
( ) ( )
( )
4
23
22
4 3 1
1 2 1
x x x
y
f x x
− − +
=
+ − −
( ) ( ) ( )( )
( )
( ) ( )
( )
( ) ( )
( )
44
2
22
2 2 2 2
2 2 3 1 1
1 2 1 2 3
x x x x x x
y
x x x x
− + − + − +
=
+ − + − −
( ) ( ) ( )( )
( )
( ) ( ) ( ) ( )
( )
44
2
2
4 4 2 2
2 2 3 1 1
1 2 1 2 3
x x x x x x
y
x x x x
− + − + − +
=
+ − + − −
( )
( ) ( ) ( )( )
( )
( ) ( )
( ) ( )
44
2
22
44
22
2 2 3 1 1
1 2 2 3 2 3
x x x x x x
y g x
x x x x x x
− + − + − +
= =
+ − − − − − − +
( ) ( )
( ) ( )
22
44
22
1 2 2 3 2 3 0x x x x x x+ − − − − − − + =
1
2
3
4
1
2
1 9 4 3
2
1 9 4 3
2
1 9 4 3
2
1 9 4 3
2
x
x
xx
xx
xx
xx
=−
=
++
==
−+
==
+−
==
−−
==
( )
1
lim
x
gx
→−
= −
( )
2
256
lim
81
x
gx
→
−
=
( )
1
lim
xx
gx
→
= −
( )
2
lim
xx
gx
→
= +
( )
3
lim
xx
gx
→
= −
( )
4
lim
xx
gx
→
= −
( )
lim 0
x
gx
→
=
5
1
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
Xét phương trình .
Dựa vào đồ thị ta suy ra:
Phương trình , với là nghiệm đơn và là nghiệm kép.
Suy ra: .
Phương trình , các nghiệm đều là nghiệm đơn.
Suy ra .
Khi đó:
Vậy đồ thị hàm số có đường tiệm cận đứng
Cách 2: Chọn hàm số . Ta có
Đồ thị hàm số qua 4 điểm .
suy ra hay
Khi đó:
Vậy đồ thị hàm số có đường tiệm cận đứng
Câu 5: Chọn B
Hàm số xác định khi
Ta có là hàm bậc ba và dựa vảo bảng biến thiên ta có
.
( ) ( )
( )
( )
2
0
3 6 0
2
fx
f x f x
fx
=
− =
=
( )
2
0
1
x
fx
x
=−
=
=
2x =−
1x =
( ) ( )( ) ( )
2
2 1 , 0f x a x x a= + −
( ) ( )
( )
0
2 2 1
1
x
f x x m m
x n n
=
= = − −
=
( ) ( )( ) ( )
2 , 0f x ax x m x n a− = − −
( )
( )( )
( ) ( )
( )( )
( )( ) ( )( )
2
2
1 3 2 1 3 2
32
3 2 1
x x x x
gx
f x f x
a x x x x m x n
− + − +
==
−

+ − − −

( )
( )( )( )( )
( )
2
32
,0
3 2 1
x
a
a x x x x m x n
+
=
+ − − −
( )
gx
5
( )
fx
( )
32
f x ax bx cx d= + + +
( ) ( ) ( ) ( )
2;0 , 1;4 , 0;2 , 1;0A B C D−−
1
0
3
2
a
b
c
d
=
=
=−
=
( )
3
32f x x x= − +
( )
( ) ( )
( ) ( )
( )
( )( )
( )( )
( )( )
( )
2 2 2
2
33
2
2
3 2 3 2 3 2
36
32
3 3 2 3
1 3 2
3 2 1 3
x x x x x x
gx
f x f x
f x f x
x x x x
xx
x x x x
− − − − − −
= = =
−
−
− + −
−+
=
+ − −
( )
gx
5
( )
gx
( )
5
4
1
x
fx
−

( )
y f x=
( )
2
1y a x
=−
3
3
a
y x ax b = − +
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
là tiệm cận ngang của đồ thị hàm số.
(vì
là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tiện cận ngang là và tiệm cận đứng là
Câu 6: Chọn C
Điều kiện xác định của hàm số
( )
gx
là .
( )
( )
3
3
13
3
3
31
11
1
1
3
a
ab
y
a
y x x
y
ab
ab
− + + =
−=
=

= − +
=−
=
− + = −
( )
2 3 5 6
3
2 3 3
2 7 4 5
3
2 7 3 4 5
lim lim lim 0
3 1 1
3 1 1
1
x x x
xx
x x x x
gx
xx
x x x
→+ →+ →+
+ − +
+ − +
= = =
− + −
− + −
0y=
( )
( )
( )
( )
( )
( )
( )
( )
2
2
4 8 4 1
2 7 3 4 5
1
1 2 7 3 4 5
x x f x
xx
gx
fx
f x x x
− + +
+ − +
==
−
− + + +
( ) ( )
( )
( )
( )
( )
( )
( )
2
4 1 1
1 1 2 7 3 4 5
x f x
f x f x x x
−+
=
− + + + +
( ) ( )
( )
( )( )
( )( )
( )
2
2
4 1 1
3 3 2 1 2 7 3 4 5
x f x
x x x x x x x
−+
=
+ − + − + + +
( )
( )
( )( )
( )
( )
41
3 3 2 2 7 3 4 5
fx
x x x x x x
+
=
+ − + + + +
( )( )
( )
( )
0
3 3 2 2 7 3 4 5
3
x
x x x x x x
x
=
+ − + + + +
=
5
4
x −
( )
( )
0
0
lim
0
lim
x
x
gx
x
gx
+
−
→
→
= −
=
= +
( )
( )
3
3
lim
3
lim
x
x
gx
x
gx
+
−
→
→
= +
=
= −
0y =
3y =
1x
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
Xét phương trình
( ) ( )

−=

2
0x f x f x
.
Xét phương trình
( )
= 0fx
có nghiệm kép và nghiệm đơn .
Xét phương trình
( )
= 1fx
có ba nghiệm đơn . Ta thấy
( )
( )
→+
→−
= +
= −
lim
lim
x
x
fx
fx
Nên không mất tính tổng quát, ta có
+
+
Do đó:
Khi đó
+ không tồn tại giới hạn không là tiệm cận đứng của đồ thị hàm số
+ .
là tiệm cận đứng của đồ thị hàm số .
+
là tiệm cận đứng của đồ thị hàm số .
+
là tiệm cận đứng của đồ thị hàm số .
+
là tiệm cận đứng của đồ thị hàm số .
( ) ( )
. . 1 0x f x f x −=


( )
( )
0
0
1
x
fx
fx
=
=
=
2x =
1x =
, 1 2
, 1 2,
,2
x a a
x b b b a
x c c
=
=
=
( )
0fx=
( )( )
2
1 2 0xx− − =
( )
1fx=
( )( )( )
0x a x b x c− − − =
( )
( ) ( )
( )( ) ( )( )( )
22
2
2
3 2 1 3 2 1
12
x x x x x x
gx
x f x f x
x x x x a x b x c
− + − − + −
==

−
− − − − −

( )
( )
0
0
lim
lim
x
x
gx
gx
+
−
→
→
0x =
( )
gx
( )
( )( ) ( )( )( )
2
2
11
3 2 1
lim lim
12
xx
x x x
gx
x x x x a x b x c
++
→→
− + −
= = +
− − − − −
1x =
( )
gx
( )
( )( ) ( )( )( )
( )
( )( ) ( )( )( )
2
2
22
2
2
22
3 2 1
lim lim
12
3 2 1
lim lim
12
xx
xx
x x x
gx
x x x x a x b x c
x x x
gx
x x x x a x b x c
++
−−
→→
→→
− + −
= = −
− − − − −
− + −
= = +
− − − − −
2x =
( )
gx
( )
( )( ) ( )( )( )
( )
( )( ) ( )( )( )
2
2
2
2
3 2 1
lim lim
12
3 2 1
lim lim
12
x a x a
x a x a
x x x
gx
x x x x a x b x c
x x x
gx
x x x x a x b x c
++
−−
→→
→→
− + −
= = −
− − − − −
− + −
= = +
− − − − −
xa=
( )
gx
( )
( )( ) ( )( )( )
( )
( )( ) ( )( )( )
2
2
2
2
3 2 1
lim lim
12
3 2 1
lim lim
12
x b x b
x b x b
x x x
gx
x x x x a x b x c
x x x
gx
x x x x a x b x c
++
−−
→→
→→
− + −
= = +
− − − − −
− + −
= = −
− − − − −
xb=
( )
gx
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
11 | Facebook tác giả: Phan Nhật Linh
+
là tiệm cận đứng của đồ thị hàm số .
+ .
là tiệm cận ngang của đồ thị hàm số .
Vậy đồ thị hàm số có 6 đường tiệm cận.
Câu 7: Chọn D
Ta có: .
Xét .
Dựa vào đồ thị ta thấy các nghiệm là các nghiệm kép (nghiệm bội 2).
Do đó đa thức có bậc là 8.
Suy ra .
Vậy đồ thị hàm số có 4 đường tiệm cận đứng là .
Câu 8: Chọn A
Xét hàm số
( )
= + + +31f x x ax b
có
( )
=+
+
3
2 3 1
f x a
x
Để hàm số không có tiệm cận đứng:
( ) ( ) ( )
=−
2
5.f x x g x
( )
( )
+ + + =
=



+=
=
+
3.5 1 .5 0
50
3
0
50
2 3.5 1
ab
f
a
f
−
+ = −
=



−
−
=

=
17
54
8
3
3
8
8
ab
b
a
a
Nên
− − −
+ = + =
23
23
1 3 4814
2 2 152
ab
Câu 9: Chọn B
Ta có
−−

= + +



22
22
33
2
11
33
4
e d . d
xx
xx
I x x e x
x
=+
12
II
, với
−
=
2
2
3
1
1
3
ed
x
x
Ix
;
−

=+


2
2
3
2
2
1
3
4
.d
x
x
I x e x
x
.
( )
( )( ) ( )( )( )
( )
( )( ) ( )( )( )
2
2
2
2
3 2 1
lim lim
12
3 2 1
lim lim
12
x c x c
x c x c
x x x
gx
x x x x a x b x c
x x x
gx
x x x x a x b x c
++
−−
→→
→→
− + −
= = +
− − − − −
− + −
= = −
− − − − −
xc=
( )
gx
( )
( )( ) ( )( )( )
2
2
3 2 1
lim lim 0
12
xx
x x x
gx
x x x x a x b x c
→ →
− + −
==
− − − − −
0y =
( )
gx
( )
gx
( )( )
( ) ( )
22
2
42
23
x x x
y
f x f x
−+
=

+−

( )( ) ( )
( ) ( )
( )( )
( ) ( )
2
22
2 2 2 2 2
2 3 2 3
x x x x x x x
f x f x f x f x
− + + − +
==
+ − + −
( ) ( )
2
2 3 0f x f x

+ − =

( )
( )
1
3
fx
fx
=
=−
,2
0
,2
2
2
x m m
x
x n n
x
x
= −
=
=
=
=−
0; 2xx= =
( ) ( )
2
23f x f x+−


( )( )
( ) ( ) ( )( )
2
22
22
22
22
x x x
y
a x x x x m x n
−+
=
+ − − −
( )( )( )
2
1
2a x x x m x n
=
− − −
0, 2, ,x x x m x n= = = =
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12
Tính
−
=
2
2
3
1
1
3
ed
x
x
Ix
. Đặt
−
−

=+

=



=
=
2
2
2
2
3
4
d 1 d
dd
x
x
x
x
u e x
ue
x
vx
vx
.
Ta có
−−

= − +


22
3
22
3
1
2
1
1
3
3
4
. . d
xx
xx
I x e x e x
x
−
= − −
25 53
93
2
1
3
3
e e I
.
Do vậy
−
= + = −
25 53
93
12
1
3
3
I I I e e
.
Ta có
= = = =25; 9; 53; 3.a b c d
Suy ra hàm số
+
=
+
25 9
53 3
x
y
x
.
Khi đó đồ thị hàm số
+
=
+
25 9
53 3
x
y
x
có phương trình đường tiệm cận ngang
=
25
53
y
.
Câu 10: Chọn D
Ta thấy đồ thị hàm số
( )
gx
có
1
đường tiệm cận ngang là
= 0y
.
Để đồ thị hàm số
( )
gx
có
4
đường tiệm cận thì phương trình
( )
( )
+ − =10f f x m
có
3
nghiệm
phân biệt.
Đặt
( ) ( )
( )
=+1h x f f x
. Khi đó,
( ) ( ) ( )
( )
=+.1h x f x f f x
.
( )
= 0hx
( )
( )
( )
=
+=
0
10
fx
f f x
( )
( )
( )
=
+=
+=
0
11
12
fx
fx
fx
( )
( )
( )
=
=
=
0
0
1
fx
fx
fx
1 2 3
4 5 6
1,2
;;
;;
x
x x x x
x x x x
.
( )
1 4 5 2 3 6
12x x x x x x
Ta có
( ) ( ) ( ) ( )
( )
= = = + =
1 2 3 1
12h x h x h x f f x
;
( ) ( ) ( ) ( )
( )
= = = + = −
4 5 6 4
11h x h x h x f f x
;
( ) ( )
( )
= + =1 1 1 14h f f
;
( ) ( )
( )
= + = −2 2 1 13h f f
Bảng biến thiên:
Căn cứ vào bảng biến thiên để phương trình
( )
( )
+ − =10f f x m
có ba nghiệm phân biệt thì:

− −
2 14
13 1
m
m
.
Câu 11: Chọn B
Điều kiện xác định:
1
2
2
2
3
x
x
x
. Ta có
→+
− + − −
=
− + −
32
6 3 2 3
lim 0
3 14 20 8
x
x mx m
x x x
với mọi
m
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
13 | Facebook tác giả: Phan Nhật Linh
Suy ra đồ thị hàm số có một đường tiệm cận ngang
= 0y
.
Ta có
( ) ( )
− + − −
==
−−
2
6 3 2 3
()
2 3 2
x mx m
y f x
xx
.
Yêu cầu bài toán trở thành, tìm
m
để đồ thị hàm số có đúng một đường tiệm cận đứng
= 2x
hoặc
=
2
3
x
.
Nếu
− + − −6 3 2 3x mx m
nhận
=
2
3
x
là nghiệm thì
=−
3
2
m
. Khi đó
( ) ( )
( )
→→
−−
−
==

−−
− − +


2
22
33
3
63
39
2
lim lim
32
3
2 3 2
4 2 6 3
2
xx
xx
xx
x x x
( ) ( )
( )
++
→→
−−
−
= = −

−−
− − +


2
22
3
63
3
2
lim lim
3
2 3 2
4 2 6 3
2
xx
xx
xx
x x x
.
Suy ra
= 2x
là đường tiệm cận đứng duy nhất của đồ thị hàm số.
Nếu
( )

− + − − = − +

−+

6
6 3 2 3 2
6 3 3
x mx m x m
x
nhận
= 2x
là nghiệm kép thì
=−1m
.
Khi đó
( ) ( )
( )
( )
++
→→
− − − −
= = −
− − + +
−−
2
22
33
6 3 1 1
lim lim
3 2 6 3 1
2 3 2
xx
xx
x x x
xx
( ) ( )
( )
( )
→→
− − − −
= = −
− − + +
−−
2
22
6 3 1 1 1
lim lim
24
3 2 6 3 1
2 3 2
xx
xx
x x x
xx
Suy ra
=
2
3
x
là đường tiệm cận đứng duy nhất của đồ thị hàm số.
Vậy có hai giá trị của

− −


3
1;
2
m
thỏa mãn bài toán.
Câu 12: Chọn C
Tập xác định:
( )
= − +1; \ 0;1D
.
Ta có :
( )



− − +
=
→+
−
3
2
9 2 ln 1
0
lim
3
xx
x
xx
.
( )
( )
− − + − −
+
= = −
++
−−
→→
33
22
9 2 ln 1 9 2
ln 1
3
. 2 9
lim lim
32
1
00
x x x
x
x
x x x
xx
.
( )
( )
− − + − −
+
= = −
−−
−−
→→
33
22
9 2 ln 1 9 2
ln 1
3
. 2 9
lim lim
32
1
00
x x x
x
x
x x x
xx
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14
( )
(
)
( )
(
)
(
)







− − +
−+
=
++
−
→ − → −
− − + − +
3
2
2
9 2 ln 1
1 ln 1
lim lim
3
2
3
2 2 2
3
11
1 9 2 9 4
xx
xx
xx
xx
x x x x
( )
(
)







−+
= = −
+
→−
− + − +
ln 1
.
lim
2
3
22
3
1
9 2 9 4
x
x
x x x
( )
(
)
( )
(
)
(
)







− − +
−+
=
++
−
→→
− − + − +
3
2
2
9 2 ln 1
1 ln 1
lim lim
3
2
11
3
2 2 2
3
1 9 2 9 4
xx
xx
xx
xx
x x x x
( )
(
)




−+
==
+
→
− + − +
ln 1
1
ln2.
lim
12
2
1
3
22
3
9 2 9 4
x
x
x x x
Tương tự
( )



− − +
=
−
−
→
3
2
9 2 ln 1
1
ln 2
lim
3
12
1
xx
xx
x
.
Vậy đồ thị hàm số đã cho có 2 tiệm cận
= 0y
và
=−1x
.
Câu 13: ChọnC
Từ giả thiết, ta có
( )
= − +
32
34f x x x
.
Gọi
( )
C
là đồ thị hàm số
( )
( )
( )
− − − − +
==
− + −
2 2 4 2
3 2 2
2 3 . . 17 16
3 2 . 2 3
x x x x x x
y g x
x x x x
.
Điều kiện xác định:
( )
−
− +
− + −
2
42
3 2 2
0
17 16 0
3 2 . 2 3 0
xx
xx
x x x x
−
− −
4
1 1 3 0
4
x
x
x
.
Ta có:
( )
( )
→+ →+
→− →−

− − − − +


==
− + −


− − − − − +





==
− − + −
2 2 4
3
2 2 4
3
2 3 1 17 16
1 . 1 . 1
1
lim lim
2
3 2 3
1 . 2
2 3 1 17 16
1 . 1 . 1
1
lim lim
2
3 2 3
1 . 2
xx
xx
xx
x x x
gx
xx
x
xx
x x x
gx
xx
x
đường thẳng
=
1
2
y
là tiệm cận ngang của
( )
C
.
( )
( )
( )
( )
( )
−−
→→
− − − − +
= = −
− + − −
2 4 2
32
00
2 3 . 1 . 17 16
lim lim
3 2 . . 2 3
xx
x x x x x
gx
x x x x
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
15 | Facebook tác giả: Phan Nhật Linh
đường thẳng
= 0x
là tiệm cận đứng của
( )
C
.
( )
( )
( )
( )
( )
−−
→ − → −
− − − − +
= = −
− + −
2 2 4 2
3 2 2
1 3 1 3
2 3 . . 17 16
lim lim
3 2 . 2 3
xx
x x x x x x
gx
x x x x
đường thẳng
=−13x
là tiệm cận đứng của
( )
C
. Vậy
==2; 1Mm
nên
= 2Mm
.
Câu 14: Chọn A
Gọi
( )
C
là đồ thị hàm số
( )
( )
( )
(
)
− + −
==
+ − + + +
2
2
2 3 2 8
2 1 . 4 4 2
x x x
y f x
x x x x
.
Ta có
( )
(
)
+ − + + + =
2
2 1 . 4 4 2 0x x x x
+=
+ + = −
2
21
4 4 2
x
x x x
+ =
+=
21
0
40
x
x
x
= −
= −
=−
1
3
4
x
x
x
.
Suy ra tập xác định của hàm số
( )
=y f x
là:
( ) )
= − − +
; 4 2;D
.
+)
( ) ( )
( )
( )
(
)
−−
→ − → −
− + −
=
+ − + + +
2
2
44
2 3 2 8
lim lim
2 1 . 4 4 2
xx
x x x
y
x x x x
( )
( ) ( )( )
(
)
( ) ( )
−
→−
− − + − − + + −
=
− − +
2
4
2 3 2 4 4 4 2
lim
3 . 4
x
x x x x x x
xx
( )
( )
(
)
( )
−
→−
− − + + + −
= = +
+ − −
2
4
2 3 2 4 4 2
lim
3 . 4
x
x x x x x
xx
Suy ra đường thẳng
=−4x
là tiệm cận đứng của
( )
C
.
+)
( )
( )
(
)
→+ →+
− + −
=
+ + + +
2
2
2 3 2 8
lim lim
1 . 4 4 2
xx
x x x
y
x x x x
→+

− + −


==


+ + + +





2
2
3 2 8
21
1
lim
2
1 1 4
1 . 4 2
x
xx
x
xx
x
.
+)
( )
( )
(
)
→− →−
− + −
=
− − + + +
2
2
2 3 2 8
lim lim
3 . 4 4 2
xx
x x x
y
x x x x
( )
(
)
( )( )
→−
− + − + + −
=
− − +
22
2 3 2 8 4 4 2
lim
34
x
x x x x x x
xx
( )
→−

− + − − + + −


= − = +


− − +


22
2 8 1 4
1 4 2
lim 2 3 .
34
11
x
xx
xx
x
xx
.
Suy ra đường thẳng
=
1
2
y
là tiệm cận ngang của
( )
C
.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Câu 15: Chọn C
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16
Gọi
( )
C
là đồ thị hàm số
( )
=y f x
;
( )
→+ →+ →+
−+
−+
= = =
−

−


2
56
22
1 1 2
2
22
lim lim lim 0
2
2
1
x x x
xx
x
xx
y
xx
x
.
Suy ra
( )
C
nhận đường thẳng
= 0y
là đường tiệm cận ngang.
(
)
→− →− →− →−
+
+
= + + + = = = −
+ + −
− + + −
2
2
2
1
1
11
lim lim 4 1 2 lim lim
4
11
4 1 2
42
x x x x
x
x
y x x x
x x x
x
x
.
Suy ra
( )
C
nhận đường thẳng
=−
1
4
y
là tiệm cận ngang.
( )
( )
( )
( )
( )
( )
+ + + +
→ → → →
−+
− + + + +
= = = = +
− + +
− − + +
4
2 3 2
22
2
2
2 2 2 2
42
2 2 2 4 4
lim lim lim lim
2 2 2
2 2 2 2
x x x x
xx
x x x x x
y
x x x x
x x x x x x
.
Suy ra
( )
C
nhận đường thẳng
= 2x
là tiệm cận đứng.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Câu 16: Chọn C
Ta có
( ) ( )
+ + + + + =
22
20 14 9 14 11 2 1 0 1x x x x
( )
+ + + + + =
22
315 35
350 245 14 11 2 1 0
22
x x x x
( )
+ + + + + + + + + + =
2
2 2 2 2
35 35 35 1225 7 315 35
14 2 14 . 2 1 2 1 2 1 0
4 4 4 16 8 8 8
x x x x x x
( )

+ + + + + + + =


2
2 2 2
35 35 7 315 35
14 2 1 2 1 0 2
4 4 8 8 8
x x x x
.
Nhận thấy phương trình (2) vô nghiệm nên phương trình (1) vô nghiệm.
Do đó
( )
+ + − + +
22
20 14 9 14 11 2 1x x x x
( )
( )
( )
( )
+ + − + +
=
+ + + + +
2
2
22
22
20 14 9 14 11 2 1
20 14 9 14 11 2 1
x x x x
x x x x
( )
− + − −
=
+ + + + +
4 3 2
22
8 56 118 5 40
20 14 9 14 11 2 1
x x x x
x x x x
( )
( )
( )
− − −
=
+ + + + +
2
2
22
2 2 4 12 5
20 14 9 14 11 2 1
x x x
x x x x
.
Khi đó hàm số
( )
( )
( )
( )
( )
( )
− − +

= = + + + + +


− − −
2
22
2
2
2 4 12
. 20 14 9 14 11 2 1
2 2 4 12 5
x x x m
y f x x x x x
x x x
( )
( )
( )
−+

= + + + + +


− − −
2
22
2
4 12
. 20 14 9 14 11 2 1
2 2 4 12 5
x x m
y x x x x
x x x
.
Hàm số
( )
=y f x
có TXĐ là


=


3 14
\ 2;
2
D
.
Dễ thấy để đồ thị
( )
C
của hàm số
( )
=y f x
có đúng 1 tiệm cận đứng thì phương trình
( )
− + =
2
4 12 0 1x x m
phải có đúng hai trong ba nghiệm
3 14
2;
2
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
17 | Facebook tác giả: Phan Nhật Linh
Nếu
( )
1
có hai nghiệm phân biệt
12
,xx
thì
+ =
12
3xx
. Do đó,
( )
1
phải có hai nghiệm là
3 14
2
, suy ra
=−5m
. Do đó
=−5S
.
Vậy tổng các giá trị trong
S
là
−5
.
Câu 17: Chọn C
Đồ thị hàm số
( )
=y f x
có hai đường tiệm cận ngang
= − =5, 1 yy
.
Đồ thị hàm số
( )
=+y f x m
có hai đường tiệm cận ngang
= − + = +5 , 1y m y m
Do đó đồ thị hàm số
( )
=+y f x m
có đúng một đường tiệm cận ngang khi và chỉ khi hai đường
thẳng
= − + = +5 , 1y m y m
đối xứng qua trục
Ox
− + + + =5 1 0mm
=2m
.
Câu 18: Chọn D
Trường hợp 1:
( )
(
)
→+ →+

= + − − − + =


3
3 2 2
55
lim lim . 1 2 1
44
xx
f x x ax bx x x
→+

+ − − − + =



2
3
2
1 1 5
lim . 1 2 1
4
x
b
xa
xx
x
Suy ra
− = =
3
2 0 8aa
. Thay lại ta được
(
)
( ) ( )
(
)
( )
(
)
( ) ( )
( )
→+
→+
→+

+ − − − + =



+ − − − + − − − + =




+−
−
+ =

− + − +

+ − + − + − + −


3
3 2 2
3
3 2 2
32
2
2
2
33
3 2 3 2
5
lim . 8 1 2 1
4
5
lim . 8 1 2 1 2 1 4 4 4
4
12 6
35
lim
4
2 1 4 4 4
8 1 2 1 8 1 2 1
x
x
x
x x bx x x
x x bx x x x x
b x x
x
x x x
x bx x x bx x
Do
( )
→+

−−

=

− + − +

2
33
lim
4
2 1 4 4 4
x
x
x x x
và
( )
→+
=
5
lim
4
x
fx
nên
( )
(
)
( ) ( )
→+


+−


+ − + − + − + −


32
2
2
33
3 2 3 2
12 6
lim
8 1 2 1 8 1 2 1
x
b x x
x bx x x bx x
phải hữu han.
Do đó
( )
+ = = −12 0 12bb
thay lại ta được
(
)
( ) ( )
→+


−−
=


− − + − − − + −


2
2
2
33
3 2 3 2
61
lim
2
8 12 1 2 1 8 12 1 2 1
x
x
x x x x x x
Thay lai được
( )
→+
=−
5
lim
4
x
fx
không thỏa mãn
Trường hợp 2: Xét
( )
(
)
→− →−

= + − − − + =


3
3 2 2
55
lim lim . 1 2 1
44
xx
f x x ax bx x x
→−

+ − + − + =



2
3
2
1 1 5
lim . 1 2 1
4
x
b
xa
xx
x
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18
Suy ra
+ = = −
3
2 0 8aa
.
Thay lại ta được
(
)
→−

− + − − − + =


3
3 2 2
5
lim . 8 1 2 1
4
x
x x bx x x
( ) ( )
(
)
→−

− + − + − − − − − + =


3
3 2 2
5
lim . 8 1 2 1 2 1 4 4 4
4
x
x x bx x x x x
( )
(
)
( ) ( )
( )
→−


−+
−
− =

− − − +

− + − − − − + − + −


32
2
2
2
33
3 2 3 2
12 6
35
lim
4
2 1 4 4 4
8 1 2 1 8 1 2 1
x
b x x
x
x x x
x bx x x bx x
Do
( )
→−

−

=−

− − − +

2
33
lim
4
2 1 4 4 4
x
x
x x x
và
( )
→−
=
5
lim
4
x
fx
nên
( )
(
)
( ) ( )
→−


−+


− + − + − − + − + −


32
2
2
33
3 2 3 2
12 6
lim
8 1 2 1 8 1 2 1
x
b x x
x bx x x bx x
hữu han.
Do đó
( )
− = =12 0 12bb
thay lại ta được
(
)
( ) ( )
→−


=


− + − + − − + − + −


2
2
2
33
3 2 3 2
61
lim
2
8 12 1 2 1 8 12 1 2 1
x
x
x x x x x x
Từ đó suy ra
( )
→−
=
5
lim
4
x
fx
thỏa mãn. Vậy ta được
( )
+=4 3; 5ab
.
Câu 19: Chọn C
Điều kiện:
( ) ( )
2
0
20
x
f x f x
−
. Xét phương trình:
( ) ( )
( )
( )
2
0
20
2
fx
f x f x
fx
=
− =
=
Từ đồ thị
phương trình
( )
1
0
2
x
fx
x
=−
=
=
1x =−
không là tiệm cận đứng do đk
0x
.
2x =
là nghiệm kép và tử số có một nghiệm
22xx= =
là một đường tiệm cận đứng.
Từ đồ thị
phương trình
( )
0
21
( 2)
xa
f x x
x b b
=
= =
=
xa=
không là tiệm cận đứng (vì
0x
)
1,x x b==
là hai đường tiệm cận đứng.
Vậy tổng số đường tiệm cận đứng của đồ thị hàm số
( )
gx
là 3.
Câu 20: Chọn C
lim 0, lim 0
xx
yy
→− →+
==
nên đồ thị hàm số có đường tiệm cận ngang
0,ym=
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
19 | Facebook tác giả: Phan Nhật Linh
Do đó đồ thị hàm số đã cho có 3 đường tiệm cận
phương trình
2
2 x 4 0xm− + =
có hai nghiệm phân biệt khác
1
2
0
40
5
5
2
2
m
m
m

−



5
2
2
2
m
m
m
−
.
Câu 21: Chọn B
Ta có
2
2
2
11
lim lim 0
2 2 6
1
xx
x
x
y
m m m
x
x
→ →
−
==
−−
−+
.
Nên đồ thị hàm số luôn có một đường tiệm cận ngang là
0y =
.
Do đó để đồ thị hàm số có đúng hai đường tiệm cận thì phương trình:
22
2 2 6 0x mx m m− + − − =
có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có 1 nghiệm
bằng 1.
Khi đó
2
2 6 0
2 6 0
4 5 0
+=
+
− − =
m
m
mm
3
3
1
5
=−
−
=−
=
m
m
m
m
3
1
5
m
m
m
=−
= −
=
.
Vậy
3; 1;5S = − −
. Nên tập
S
có
3
phần tử.
Câu 22: Chọn A
Điều kiện.
( )
( )
2
0
2
2 2 0
fx
fx
x mx m
− + +
Nếu
( )
0fx
2x −
Nếu
( )
2fx=
2
1
x
x
=
=−
(
1x =
là nghiệm kép).
Nếu
( )
0fx=
2
1
x
x
=−
=
(
1x =
là nghiệm kép).
Khi đó.
( )
( ) ( )( )
( )( )
( )
2
2
2
1 2 1
2 1 2 2
+ + −
=
− + − + +
x a x x
gx
a x x x mx m
( )
( )( )
( )
( )
2
12
0
2 1 2 2
−+
=
− + − + +
x a x
a
a x x x mx m
.
Ta có
( )
lim 0
x
gx
→+
=
, nên hàm số có 1 tiện cận ngang
0y =
( )
2
lim
x
gx
→
=
, nên hàm số có tiện cận đứng
2x =
( )
1
lim
x
gx
→−
=
, nên hàm số có tiện cận đứng
1x =−
Để hàm số
( )
gx
có 5 đường tiệm cận (tiệm cận đứng hoặc tiệm cận ngang). Thì phương trình
( )
2
2 2 0h x x mx m= − + + =
có 2 nghiệm phân biệt lớn hơn
2−
và
1;1;2x −
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20
( )
( )
( )
( )
( )
'0
. 2 0
2
2
10
10
20
hx
ah
S
h
h
h

−
−
−
2
20
5 6 0
2
3 3 0
30
6 3 0
mm
m
m
m
m
m
− −
+
−
+
−
−
1
2
6
5
2
1
3
2
m
m
m
m
m
m
m
−
−
−
−
6
1
5
2
3
− −
m
m
m
.
Do
m
có giá trị là nguyên và
m
thuộc khoảng
( )
2019;2020−
Vậy có 2016 giá trị nguyên của
m
thuộc khoảng
( )
2019;2020−
là
4;5;6.....;2019
Câu 23:
Điều kiện:
( ) ( )
( ) ( )
2
2
1
1
30
30
30
x
x
x
f x f x
f x f x
−

+
+
.
Ta có
( ) ( ) ( )
( )
( )
( )
2
3 L
3 3 0 0
3
x
x f x f x f x
fx
=

− + = =

=−
. Dựa vào đồ thị ta có
( )
( )
( )
1
2
3
1;0
( ) 0 0;1
2;
xx
f x x x
xx
= −
= =
= +
(loại
3
2x
), do đó có 2 tiệm cân đứng
1
xx=
,
2
xx=
.
44
, 0
( ) 3
2 (L)
x x x
fx
x
=
= −
=
, do đó có 1 tiệm cận đứng
4
xx=
.
Vậy đồ thị hàm số
( )
gx
có 3 đường tiệm cận đứng.

Tài liệu khác của Toán 12

Preview text:

Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
CHỦ ĐỀ 04: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ LÝ THUYẾT
❖ Đường tiệm cận ngang
▪ Cho hàm số y = f (x) xác định trên một khoảng vô hạn (là khoảng dạng (a;+),(−;b) hoặc
(−;+)). Đường thẳng y = y là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị 0
hàm số y = f (x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f (x) = y , lim f (x) = y . x→+ 0 x→− 0
❖ Đường tiệm cận đứng
▪ Đường thẳng x = x được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số 0
y = f (x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f (x) = +, lim f (x) = −, lim f (x) = −, lim f (x) = + + − + − x→x x→x x→x x→x 0 0 0 0 Lưu ý: ax + ▪ b
Với đồ thị hàm phân thức dạng y =
(c  0; ad − bc  0) luôn có tiệm cận ngang là = a y cx + d c
và tiệm cận đứng = − d x . c
❖ Dấu hiệu nhận biết các đường tiệm cận của đồ thị hàm số
▪ Hàm phân thức mà nghiệm của mẫu không là nghiệm của tử có tiệm cận đứng.
▪ Hàm phân thức mà bậc của tử  bậc của mẫu có TCN.
▪ Hàm căn thức dạng: y = f (x) − g(x),y = f (x) − g(x),y = g(x) − f (x) có tiệm cận ngang. (dùng liên hợp) ▪ Hàm = x y
a ,(0  a  )
1 có tiệm cận ngang y = 0 .
▪ Hàm số y = log x,(0  a  1 có tiệm cận đứng x = 0 . a )
❖ Cách tìm các đường tiệm cận của đồ thị hàm số
▪ Tiệm cận đứng: ta đi tìm nghiệm của mẫu không là nghiệm của tử.
▪ Tiệm cận ngang: tính 2 giới hạn: lim y hoặc lim y x→+ x→−
❖ Một số chú ý trong quá trình tìm tiệm cận.
▪ Nếu x → +  x   2 0
x = x = x .
▪ Nếu x → −  x   2 0
x = x = −x . 1 |
Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số VÍ DỤ MINH HỌA
VÍ DỤ 1. Cho hàm số y = f (x) có lim f x = + và lim f x = 2 . Mệnh đề nào sau đây đúng? − ( ) + ( ) x→1 x→1
A. Đồ thị hàm số không có tiệm cận.
B. Đồ thị hàm số có tiệm cận đứng x = 1.
C. Đồ thị hàm số có hai tiệm cận.
D. Đồ thị hàm số có tiệm cận ngang y = 2 . Lời giải Chọn B
Vì lim f x = + nên đồ thi hàm số có tiệm cận đứng x . + ( ) = 1 x→1 2 2x − x
VÍ DỤ 2. Cho hàm số y =
. Số đường tiệm cận của đồ thị hàm số là: 2 x + 5x + 4 A. 2 B. 1 C. 3 D. 4 Lời giải Chọn Cx = −1 Xét phương trình 2
x + 5x + 4 = 0  
, hai nghiệm này đều không là nghiệm của tử số nên x = −  4
đây là hai đường tiệm cận đứng của đồ thị hàm số. 2 2x − Mặt khác: x lim
= 2 , nên đường y = 2 là tiệm cận ngang của đồ thị hàm số. x→ 2 x + 5x + 4
Vậy đồ thị hàm số có ba đường tiệm cận. x + 3 − 2
VÍ DỤ 3. Cho hàm số y =
. Đồ thị hàm số có bao nhiêu đường tiệm cận. 2 x − 3x + 2 A. 3 B. 1 C. 4 D. 2 Lời giải Chọn D x + 3 − 2 x − 1 1 Ta có: = = , x  1 . 2 x − 3x + 2
(x −1)(x − 2)( x+3 +2) (x−2)( x+3 +2)
Khi đó ta thấy x = 2 là đường tiệm cận đứng của đồ thị hàm số. Mặt khác: 1 lim
= 0 , nên đồ thị hàm số nhận y = 0 làm tiệm cận ngang.
x→+ (x − 2)( x + 3 + 2)
Vậy đồ thị hàm số có 2 đường tiệm cận. 1
VÍ DỤ 4. Đường tiệm cận ngang của đồ thị hàm số f (x) = 2 2x − 5x − 2 2x − 3x
A. y = 2; y = −2 .
B. y = 2; y = − 2 . C. y = 2 . D. y = 2 . Lời giải Chọn B
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 2 x − x + 2 2 5 2x − Tập xác định 3x D ( ;0)  5  = −  ; + 
. Ta có lim f (x) = lim = − 2  2  x→+ x→+ −2x 2 x − x + 2 2 5 2x − 3x
Và lim f (x) = lim = 2 . x→− x→− −2x
Vậy đồ thị hàm số có hai tiệm cận ngang là đường thẳng y =  2
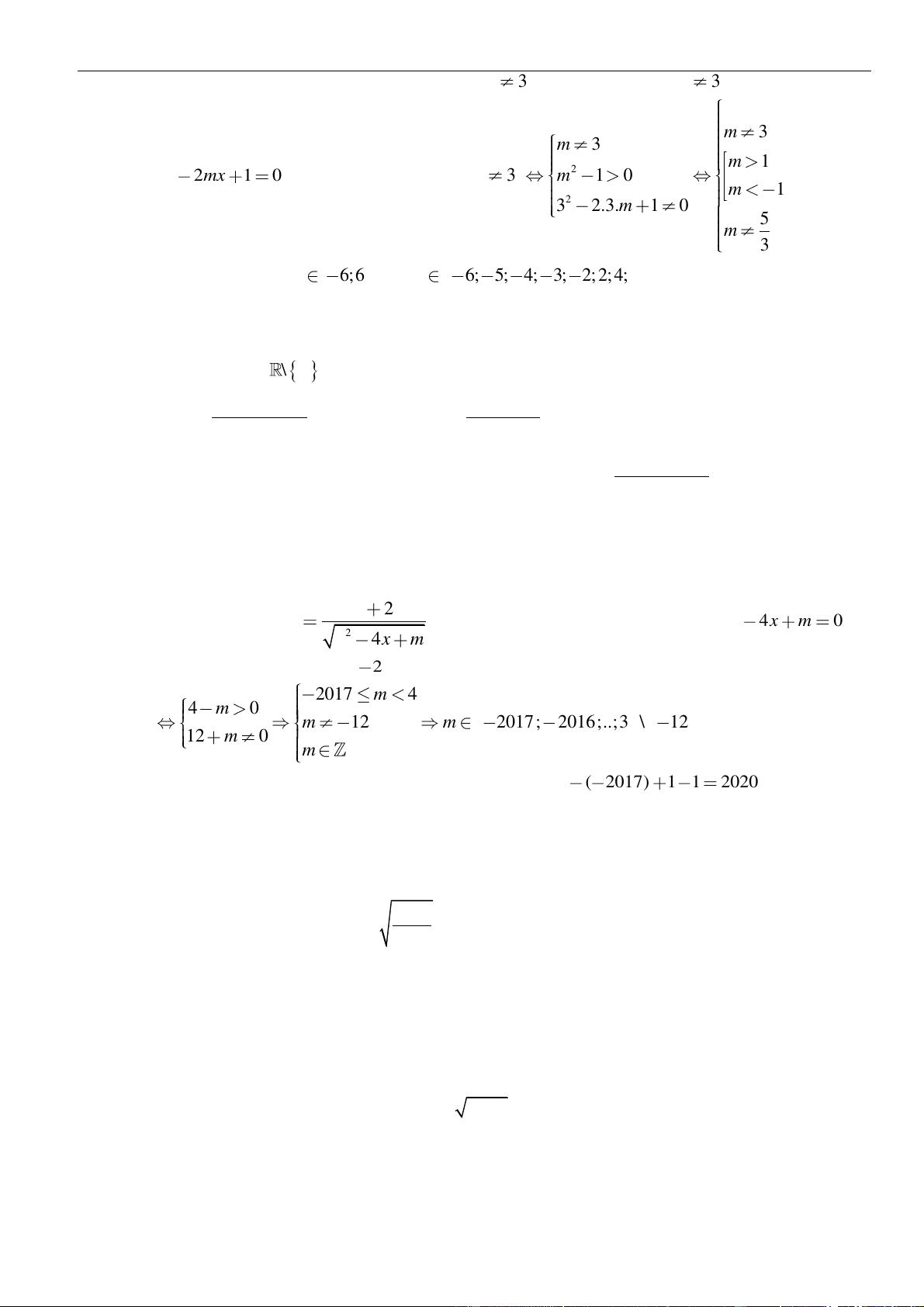
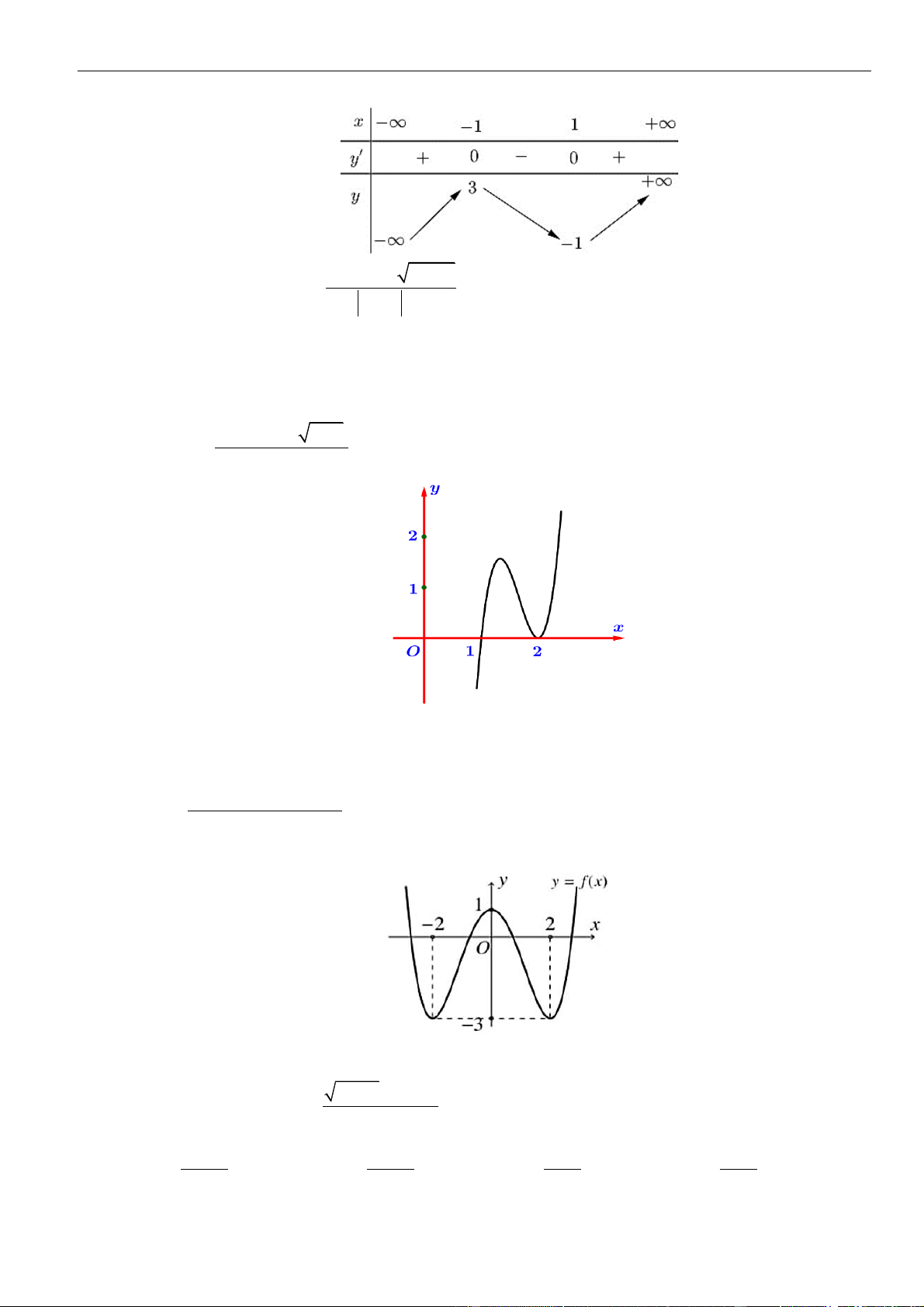
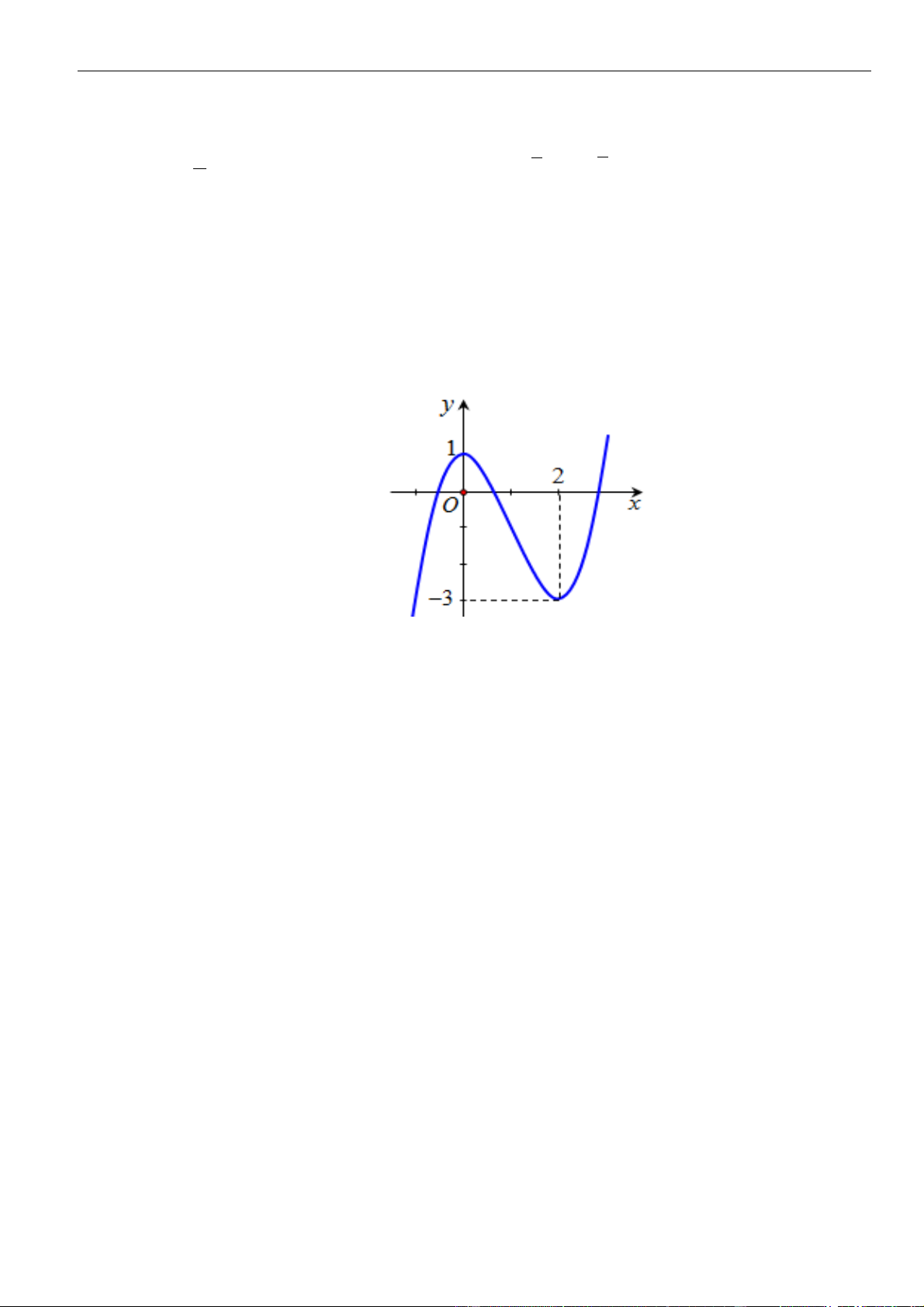
VÍ DỤ 5. Cho hàm số y = f x = 3 ax + 2 ( )
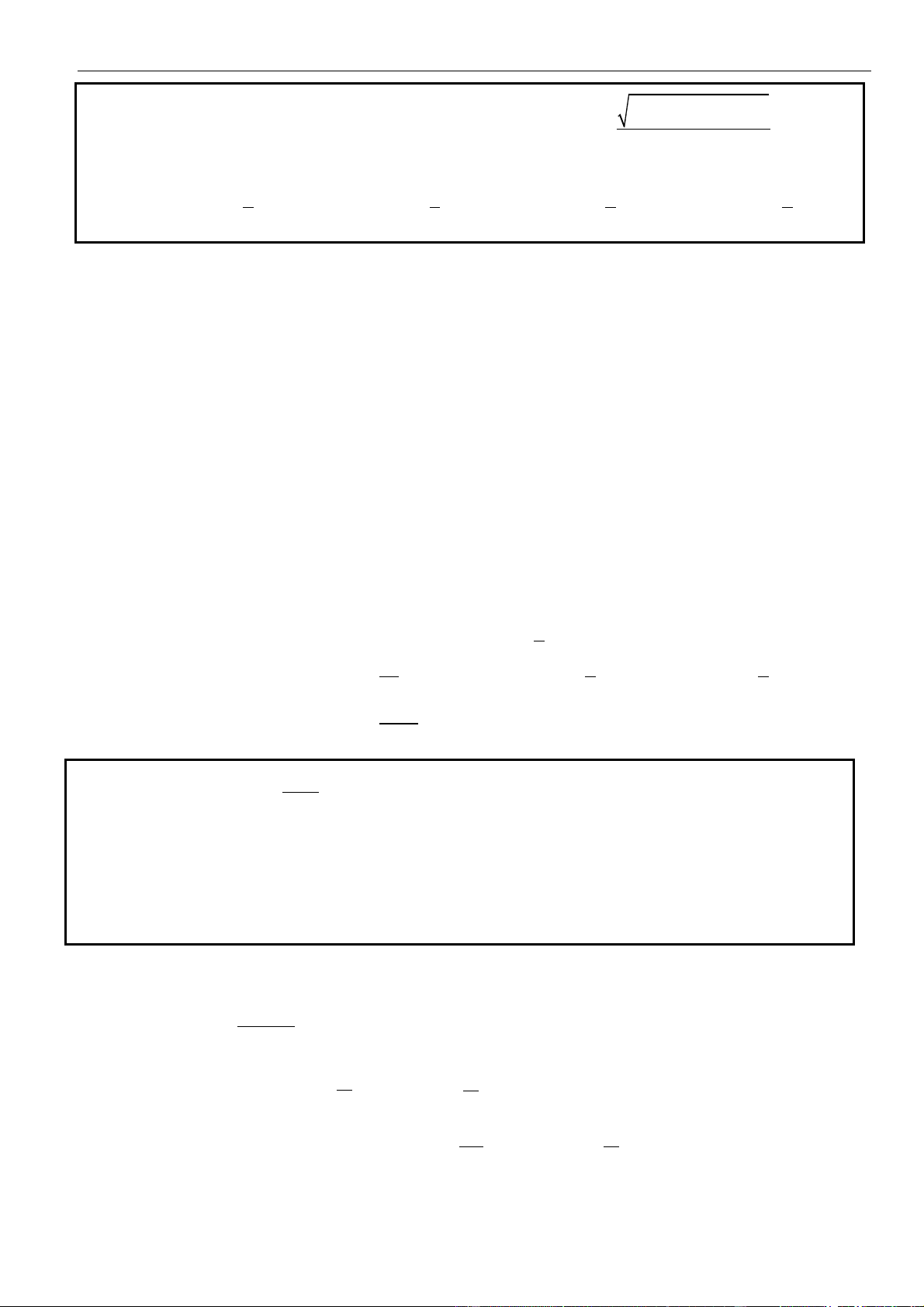
bx + cx + d có đồ thị như hình bên dưới.
Hỏi đồ thị hàm số = ( ) = 2x y g x
có bao nhiêu đường tiệm cận đứng? f (x) A. 3 B. 1 C. 4 D. 2 Lời giải Chọn A
Điều kiện xác định: f (x)  0 .
Từ đồ thị ta thấy f (x) = 0 khi x = −4 , x = −1 và x = 2 .
Khi đó f (x) = (
a x + 4)(x + 1)(x − 2) có 3 nghiệm. Do đó đồ thị hàm số
y = g (x) có 3 đường tiệm cận đứng.
3x − 5 + ax + b
VÍ DỤ 6. Biết đồ thị hàm số y = (
không có tiệm cận đứng. Khi đó 4a − b bằng: x − 2)2 A. −8 . B. 10 . C. −4 . D. 8 . Lời giải Chọn A 3x − 5 + ax + Đồ thị hàm số = b y (
không có tiệm cận đứng x − 2)2
f (x) = 3x − 5 + ax + b = 0 có nghiệm kép x = 2 . 1 2a b 0  f ( )  + + =   =  a = − 3 2 0   . f  3 2  (2)     = 0 + a =  0 b =  −  2 2 2.3 5  3 
Vậy 4a − b = 4. − − 2 = −   8 .  2 
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
(x− )1( 2x +3x+3)
VÍ DỤ 7. Tìm tập hợp các giá trị của tham số m để đồ thị hàm số y = có đúng 3 2 mx + 2x − 3 đường tiệm cận.  1   1   1   1  A. m  −  ;0  .
B. m  − ; +   C. m  −  ;0  . D. m  −  ;0 .  3   3   3   3  Lời giải Chọn A Ta có (x − )( 2
1 x + 3x + 3)  0  x  1 Trường hợp 1:
Nếu m = 0 thì đồ thị hàm số không có tiệm cận ngang. Do đó đồ thị hàm số không thể có ba đường tiệm cận. Trường hợp 2:
Nếu m  0 thì đồ thị hàm số có một đường tiệm cận ngang y = 0.
Do đó đồ thị hàm số có đúng ba đường tiệm cận  2
mx + 2x − 3 = 0 có hai nghiệm phân biệt
x , x thuộc nửa khoảng  + 1; ) 1 2   1  1+ 3m  0 m  − '  0   3 ( −1   1  1   x − 1 x 1 0    0
 m  0  −  m  0 . Vậy m − ;0 1 )( − 2 )    (  m  3  3  x − 1 x 1 0 m  −1 1 )+( − 2 )   1+ m    0   m x − 1
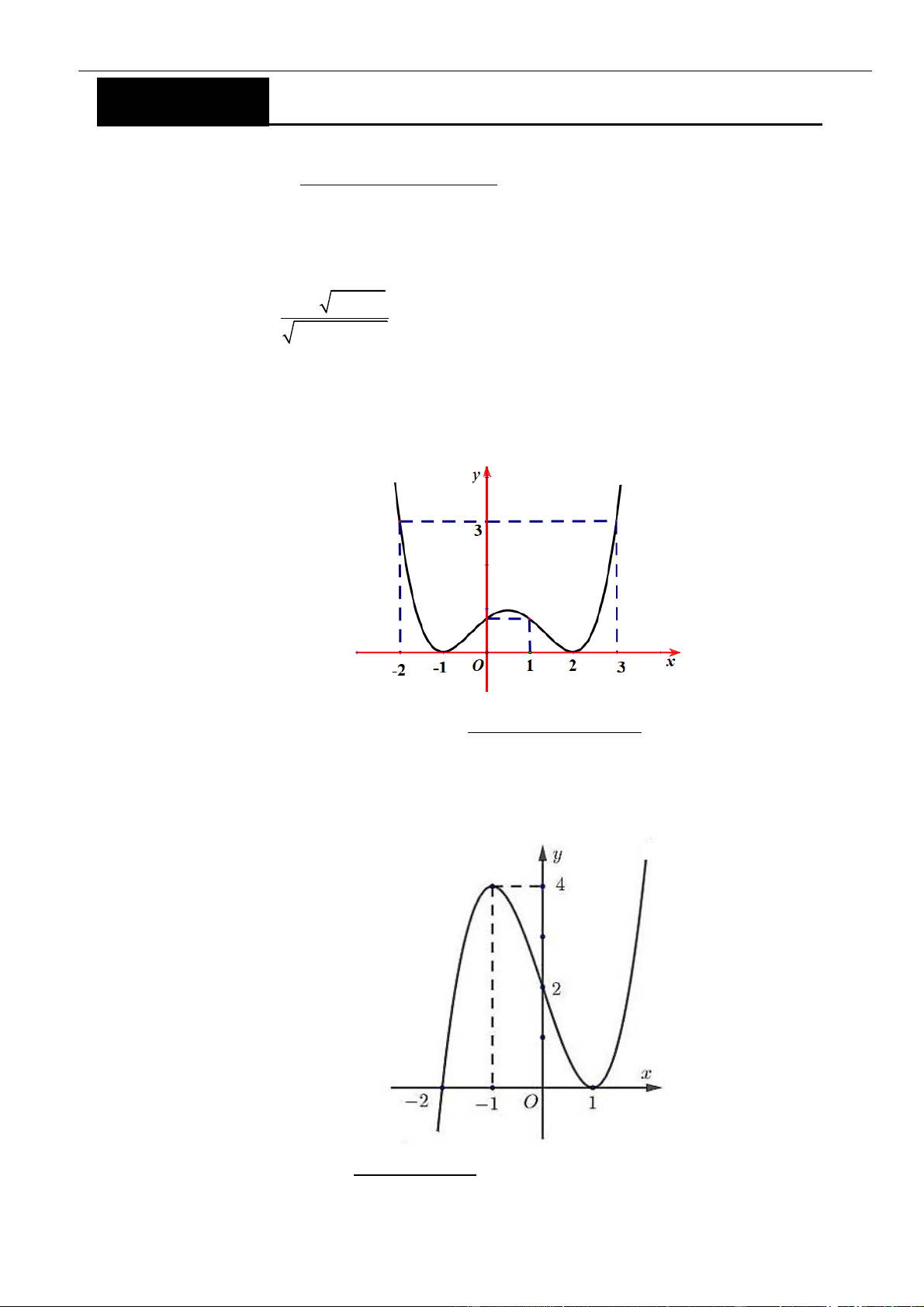
VÍ DỤ 8. Cho hàm số y =
có đồ thị (C) , gọi d là tiếp tuyến với (C) tại điểm có hoành độ bằng x + 2
m − 2 . Biết đường thẳng d cắt tiệm cận đứng của (C) tại điểm A(x ; y và cắt tiệm cận ngang của 1 1 )
(C) tại điểm B(x ; y . Gọi S là tập hợp các số m sao cho x + y = −5. Tính tổng bình phương các 2 2 ) 2 1 phần tử của S . A. 0 . B. 4 . C. 10 . D. 9 . Lời giải Chọn C 3 Ta có y = ( . x + 2)2  3 
Với x = m − 2  y = − 3 1 : A m − 2;1 − (m    0) . mm
Phương trình tiếp tuyến 3 3
d của (C) : y =
(x−m+ 2)+1− . 2 m m
Đồ thị (C) có tiệm cận ngang y = 1 và tiệm cận đứng x = −2 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023    6 y = 3 3 x m 2 1 y = 1 − 6 2 ( − + ) + −
Tọa độ điểm A là nghiệm của hệ:  m m  
m nên y = 1 − .  1 m x = −  2 x = −  2  y = 3 3 x m 2 1 y = 1 2 ( − + ) + −
Tọa độ điểm B là nghiệm của hệ:  m m  
nên x = 2m − 2 .  x = 2m − 2 2 y =  1  6 m = 1
Suy ra x + y = 2m − −1 = −5  2
2m + 4m − 6 = 0   . 2 1 m m = −  3
Vậy tổng bình phương các phần tử của 2 S là 2 1 + (−3) = 10 .
5 | Facebook tác giả: Phan Nhật Linh Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 DẠNG 1
Cơ bản về tiệm cận của đồ thị hàm số 2 5x 4x 1
Câu 1: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y là 2 x 1 A. 0. B. 1. C. 2. D. 3. 2 x − 5x + 4 Câu 2:
Tìm số tiệm cận của đồ thị hàm số y = . 2 x −1 A. 2 B. 3 C. 0 D. 1 x − 2 Câu 3:
Đồ thị hàm số y = 2
x − có mấy tiệm cận. 4 A. 3 B. 1 C. 2 D. 0 x + 9 − 3 Câu 4:
Số tiệm cận đứng của đồ thị hàm số y = là 2 x + x A. 1 B. 2 C. 0 D. 3 2
2x −1− x + x + 3 Câu 5:
Tìm tất cả các tiệm cận đứng của đồ thị hàm số y = . 2 x − 5x + 6
A. x = 3 và x = 2 .
B. x = 3 .
C. x = −3 và x = −2 . D. x = −3 . x +16 − 4 Câu 6:
Số tiệm cận đứng của đồ thị hàm số y = 2 x + là x A. 3 B. 2 C. 1 D. 0 x + 4 − 2 Câu 7:
Số tiệm cận đứng của đồ thị hàm số y = là 2 x + x A. 3 . B. 0 . C. 1. D. 2 . x (4x + 6) − 2 Câu 8:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là? x + 2 A. 1 B. 3 C. 2 D. 4 2 x + 2x + 3 Câu 9: Cho hàm số y =
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x − 3x + 2 A. 4 . B. 5 . C. 3 . D. 6 . x − 2 +1
Câu 10: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là 2 x − 3x + 2 A. 4 B. 1 C. 3 D. 2 2
2x + x − x
Câu 11: Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận? 3x +1 A. 2 . B. 3 . C. 0 . D. 1. 5x +1− x +1
Câu 12: Đồ thị hàm số y = 2 x −
có tất cả bao nhiêu đường tiệm cận? 2x
1 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số A. 0 . B. 1 . C. 2 . D. 3 . x −
Câu 13: Tìm số đường tiệm cận của đồ thị hàm số 1 y = .
4 3x +1 − 3x − 5 A. 2 . B. 3 . C. 1. D. 0 . 2 x + 2x + 3
Câu 14: Cho hàm số y =
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x − 3x + 2 A. 4 . B. 5 . C. 3 . D. 6 . 2
4x + 2x −1 + x
Câu 15: Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? x +1 A. 1. B. 0 . C. 2 . D. 3 . x + 2
Câu 16: Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = có hai đường tiệm 2
x − 6x + 2m
cận đứng. Số phần tử của S là A. vô số. B. 12 . C. 14 . D. 13 . x −1
Câu 17: Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số y = có 3 đường 2
x − 8x + m tiệm cận? A. 14 . B. 8 . C. 15 . D. 16 . x − 3
Câu 18: Cho hàm số y =
. Có bao nhiêu giá trị nguyên của tham số m thuộc 3 2 x − 3mx + ( 2 2m + ) 1 x − m đoạn  2020 −
; 2020 để đồ thị hàm số có 4 đường tiệm cận? A. 4039. B. 4040. C. 4038. D. 4037. 1
Câu 19: Có bao nhiêu số nguyên của m thuộc đoạn  10
− 0;100để đồ thị hàm số y = (x−m) 2 2x − x
có đúng hai đường tiệm cân? A. 200. B. 2. C. 199. D. 0. 2 x + m
Câu 20: Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = có đúng hai đường 2 x − 3x + 2 tiệm cận. A. m = −1 B. m {1; 4} C. m = 4
D. m { −1; 4 − } x +1
Câu 21: Cho hàm số y = f ( x) =
. Tìm tất cả các giá trị của tham số m để đồ thị có ba đường 2 x − 2mx + 4 tiệm cận  m  2  m  −2   m  2 − m  2 − A. m  2 B.  5 C. D. m  −   m  2   5 2 m  −  2
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
(n −3) x + n −2017
Câu 22: Biết rằng đồ thị của hàm số y =
( m, n là các số thực) nhận trục hoành làm x + m + 3
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n. A. 0 B. 3 − C. 3 D. 6 x −1
Câu 23: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = có đúng bốn 2 mx − 8x + 2
đường tiệm cận? A. 8 B. 6 C. 7 D. Vô số
Câu 24: Với giá trị nào của hàm số m để đồ thị hàm số 2
y = x − mx − 3x + 7 có tiệm cạn ngang. A. m = 1 B. m = −1 C. m = 1
D. Không có m ax +1 1
Câu 25: Cho hàm số y =
. Tìm a, b để đồ thị hàm số có x = 1 là tiệm cận đứng và y = là tiệm bx − 2 2 cận ngang.
A. a = −1;b = 2 .
B. a = 4;b = 4 .
C. a = 1;b = 2 .
D. a = −1;b = −2 . x −1
Câu 26: Có bao nhiêu giá trị nguyên m  10
− ;10 sao cho đồ thị hàm số y = có hai 2
2x + 6x − m − 3
đường tiệm cận đứng? A. 19 . B. 15 . C. 17 . D. 18 .
Câu 27: Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm 2 + + số mx 3mx 4 y = bằng 3? x + 2 A. 4 . B. 2 . C. Vô số. D. 3 . x −1
Câu 28: Tổng các giá trị của tham số m để đồ thị của hàm số y = 2 x + 2(m − ) 2
1 x + m − có đúng một 2 tiệm cận đứng. 1 3 A. − . B. 2 . C. 3 − . D. . 2 2 x 3
Câu 29: Cho hàm số y
. Có bao nhiêu giá trị nguyên thuộc đoạn 6;6 3 2 2 x 3mx 2m 1 x m
của tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12 . B. 9 . C. 8 . D. 11. 2
2x + 3x + m
Câu 30: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = không có tiệm x − m cận đứng. A. m = 1. B. m  1.
C. m = 1và m = 0 . D. m  0 .
Câu 31: Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn
2017 ; 2017 để đồ thị hàm số x 2 y
có hai tiệm cận đứng. 2 x 4x m A. 2019 . B. 2021 . C. 2018 . D. 2020 .
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
Câu 32: Cho hàm số y
f (x) thỏa mãn lim f (x) 2019m , 4 lim f (x)
2020m . Hỏi có tất cả bao x x
nhiêu giá trị của m để đồ thị của hàm số y
f (x) có duy nhất một tiệm cận ngang? A. 4. B. 2. C. 3. D. 1. 1
Câu 33: Cho hàm số y =
. Tìm tất cả các giá trị thực của tham số m để đồ 2 x − (2m + )
1 x + 2mx − m  
thị hàm số có 4 đường tiệm cận. 0  m 1       m 1  0 m 1  A.  1 . B.  1 . C. m  1. D.  1 . m   m m     2  2  2 6x − 3
Câu 34: Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y = ( có đúng 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 1 đường tiệm cận? A. 0. B. 2. C. 1. D. Vô số.
Câu 35: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số: 2 y x mx 1 có tiệm cận ngang. A. 0 m 1. B. m 1. C. m 1. D. m 1. x − 2
Câu 36: Cho hàm số y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có 2 mx − 2x + 4
đúng hai đường tiệm cận? A. 0 . B. 2 . C. 3 . D. 1. 2019x
Câu 37: Gọi S là tập các giá trị nguyên của m sao cho đồ thị hàm số y = có bốn đường 2 17x −1 − m x
tiệm cận. Tính số phần tử của tập S. A. Vô số B. 3 C. 5 D. 4
Câu 38: Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số x f (x) =
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần 3 3 4 2
x + mx +1 − x + x +1 + m x
tử của S bằng 1 1 1 1 A. . B. − . C. . D. − . 2 2 3 3 x(x m) 1
Câu 39: Có bao nhiêu giá trị m nguyên thuộc khoảng
10;10 để đồ thị hàm số y có x 2
đúng ba đường tiệm cận? A. 12 . B. 11. C. 0 . D. 10 . 1
Câu 40: Cho hàm số y =
với m là tham số. Tìm tất cả các giá trị của m để đồ thị hàm 3 2
x − 3x + m −1
số đã cho có 4 đường thẳng tiệm cận.
A. 1  m  5 .
B. −1  m  2 .
C. m  1 hoặc m  5 . D. m  2 hoặc m  −1 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
3x +1 + ax + b
Câu 41: Hàm số y = − (
không có tiệm cận đứng. Khi đó hiệu a b bằng: x − )2 1 1 3 5 1 A. . B. − . C. − . D. − . 2 4 4 2 2
−x + 2016x + 2017 − 24 7
Câu 42: Có bao nhiêu giá trị nguyên của tham để m đồ thị hàm số y = có x − m tiệm cận đứng? A. vô số. B. 2 . C. 2017 D. 2019 .
Câu 43: Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số x f (x) =
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần 3 3 4 2
x + mx +1 − x + x +1 + m x
tử của S bằng 1 1 1 1 A. . B. − . C. . D. − . 2 2 3 3 x(x m) 1
Câu 44: Có bao nhiêu giá trị m nguyên thuộc khoảng
10;10 để đồ thị hàm số y có x 2
đúng ba đường tiệm cận? A. 12 . B. 11. C. 0 . D. 10 . 2 mx + 1
Câu 45: Tìm tất cả các giá trị thực của m sao cho đồ thị hàm số y =
có đúng một đường tiệm x + 1 cận.
A. −1  m  0 .
B. −1  m  0 . C. m  −1 . D. m  0 .
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số BẢNG ĐÁP ÁN 1.C 2.A 3.C 4.A 5. B 6.C 7.C 8.C 9.A 10.D 11.A 12.C 13.A 14.B 15.C 16.B 17.A 18.D 19.A 20.D 21.C 22.A 23.B 24.A 25.C 26.C 27.B 28.A 29.B 30.C 31.D 32.B 33.A 34.C 35.B 36.D 37.C 38.B 39.A 40.A 41.C 42.C 43.B 44.A 45.A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn C Tiệm cận ngang: 2  4 1  4 1 − −   − − 2 x 5 5 2 2 − − Ta có: 5x 4x 1  x x x lim = lim = lim = lim x y = 5 nên đồ thị hàm 2 x→+ x→+ x −1 x→+ 2  1  x→+ 1 x 1− 1−   2 2  x x
số có một tiệm cận ngang y = 5 . Tiệm cận đứng:  = Cho 2 x 1 x = 1   x = 1 − 2 5x − 4x −1 (5x + ) 1 ( x − ) 1 5x +1 6 Ta có: lim y = lim = lim = lim
= = 3 nên x = 1không là tiệm 2 x 1 → x 1 → − x 1 x 1 → ( x + ) 1 ( x − ) 1 x 1 → x +1 2 cận đứng. 2 2 2 5x − 4x −1 5x − 4x −1
 1 5x − 4x −1 lim y = lim = lim = lim  .  = − + + + +   x ( → − ) x ( → − ) 2 1 1 x −1 x ( → − ) 1
(x + )1(x − )1 x ( → − ) 1 x +1 x −1    1 lim = +  + x ( → − ) 1 x +1 vì  . 2 5x − 4x −1  lim = −4  0 + x  ( → − ) 1 x −1
Khi đó, đồ thị hàm số có một tiệm cận đứng x = −1 .
Tổng cộng đồ thị hàm số có 2 tiệm cận. Câu 2: Chọn A Tập xác định: D = \   1 5 4 − + 2 1 2 x − 5x + 4 Ta có: lim = lim = lim x x y
=1  y = 1 là đường tiệm cận ngang. 2 x→ x→ x −1 x→ 1 1− 2 x Mặc khác: 2 x − 5x + 4 (x − ) 1 ( x − 4) (x − 4) 3 lim y = lim = lim = lim = − 2 x 1 → x 1 → x 1 x −1 → ( x − ) 1 ( x + ) x 1 1 → ( x + ) 1 2
x = 1 không là đường tiệm cận đứng.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 2 x − 5x + 4 (x − ) 1 ( x − 4) (x − 4) lim y = lim = lim = lim = − + + + + x ( → − ) 1 x ( → − ) 2 1 − x 1 x 1 → (x − ) 1 ( x + ) 1 x→(− ) 1 (x + ) 1 2 x − 5x + 4 (x − ) 1 ( x − 4) (x − 4) lim y = lim = lim = lim = + − − − − x ( → − ) x ( → − ) 2 1 1 x −1 x ( → − ) 1 (x − ) 1 ( x + ) 1 x ( → − ) 1 (x + ) 1  x = 1
− là đường tiệm cận đứng.
Vậy đồ thị hàm số có 2 đường tiệm cận Câu 3: Chọn C Ta có 2
x − 4 = 0  x = 2  x − 2  1 lim =  
nên đường thẳng x = 2 không phải là tiệm cân đứng của đồ thị hàm số. 2
x→2  x − 4  4  x − 2  1  x − 2  1 lim = lim = +,   lim = lim = −,  
nên đường thẳng x = −2 + 2 + − 2 − x 2 →− x 2  x − 4 →−  x + 2 x ( → 2 − )  x − 4 x  ( → 2 − ) x + 2
là tiệm cân đứng của đồ thị hàm số.  x − 2  lim = 0  
nên đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. 2
x→  x − 4 
Vậy có đồ thị có hai đường tiệm cận. Câu 4: Chọn A
Tập xác định của hàm số: D =  9 − ;+) \0;−  1 x + 9 − 3 x + 9 − 3 Ta có: lim y = lim = + và lim y = lim = −. + + − − x ( → − ) 1 x ( → − ) 2 1 x + x x→(− ) 1 x ( → − ) 2 1 x + x  TCĐ: x = −1. x + 9 − 3 x 1 1 lim y = lim = lim = lim = . + + 2 x→0 + + x→0 x + x x→ ( 2 0
x + x)( x + 9 + 3) x→0 ( x + ) 1 ( x + 9 + 3) 6 x + 9 − 3 x 1 1 lim y = lim = lim = lim = . − x→0 − 2 − − x→0 x + x x→ ( 2 0
x + x)( x + 9 + 3) x→0 ( x + ) 1 ( x + 9 + 3) 6
x = 0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng. Câu 5: Chọn B Tập xác định D = \2;  3 x − − x + x + (2x − )2 1 − ( 2 2 x + x + 3 2 1 3 ) lim = lim + 2 + x→2 − + x→2 x 5x 6 ( 2x −5x+6)( 2 2x −1+ x + x + 3 ) (2x − )2 1 − ( 2 x + x + 3) = lim+ x→2 ( 2 x − 5x + 6)( 2 2x −1+ x + x + 3 ) (3x + 1) 7 = lim = − + x→2 (x − )( 2 x − + x + x + ) 6 3 2 1 3 2
x − − x + x + Tương tự 2 1 3 7 lim
= − . Suy ra đường thẳng x = 2 không là tiệm cận đứng của − 2 x→2 x − 5x + 6 6
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
đồ thị hàm số đã cho. 2 2
2x −1− x + x + 3
2x −1− x + x + 3 lim = + ;  lim
= − . Suy ra đường thẳng x = 3 là tiệm + 2 − 2 x 3 → x − x + x 3 5 6 → x − 5x + 6
cận đứng của đồ thị hàm số đã cho. Câu 6: Chọn C
Tập xác định hàm số D =  16 − ;+) \−1;  0 . Ta có x +16 − 4 x 1 1 lim y = lim = lim = lim = . x→0 x→0 (x + ) x→0 1 x x ( x + )
1 ( x +16 + 4) x→0 ( x + ) 1 ( x +16 + 4) 8 x +16 − 4 1 lim y = lim = lim = + . + + + x→(− ) 1 x→(− ) 1 (x + )1 x x→(− ) 1
(x + )1( x+16 + 4) + vì lim + + = +  , lim ( x + ) 1 = 0 và x → (− )
1 thì x  −1  x +1  0 . + ( x 16 4) 15 4 0 + x ( → − ) 1 x→(− ) 1 1
Tương tự lim y = lim = − . − − x ( → − ) 1 x ( → − ) 1
(x + )1( x+16 +4)
Vậy đồ thị hàm số đã cho có tiệm cận đứng là x = −1 . Câu 7: TXĐ: D =  4 − ;+) \ 1 − ;  0 . x + 4 − 2 Ta có: lim y = lim = − + + x ( → − ) x→(− ) 2 1 1 x + x
Nên đường thẳng x = −1 là một đường tiệm cận đứng của đồ thị hàm số đã cho. + − + + x + − ( x 4 2)( x 4 2 4 2 ) 1 1 lim y = lim = lim = lim = 2 x→0 x→0 x→0 x + x x ( x + ) 1 ( x + 4 + 2) x→0 ( x + ) 1 ( x + 4 + 2) 4
Nên đường thẳng x = 0 không là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có một tiệm cận đứng x = −1 . Câu 8: Chọn C 6 2 + − x ( x + ) 4 4 6 − 2 x x lim = lim = 2 x→+ x + 2 x→+ 2 1+ x 6 2 − + − x ( x + ) 4 4 6 − 2 x x lim = lim = 2 − x→− x + 2 x→− 2 1+ x x (4x + 6) − 2
(x + 2)(4x − 2) 4x − 2 5 − lim = lim = lim =    x→ 2 − + x→ 2 x 2 −
(x + 2)( x(4x+6) +2) x→ 2− x(4x+6) +2 2
Vậy hàm số có hai tiệm cận ngang y = 2 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Câu 9:
Điều kiện: x (− ;  − 2 )( 1 − ) ;1  ( 2;+). 2 3 + + 2 1 x + 2x + 3 2
Do lim y = lim y = lim = lim x x
=1  y = 1 là đường tiệm cận x→+ x→− x→ 4 2 x − 3x + 2 x→ 3 2 1− + 2 4 x x
ngang của đồ thị hàm số.
Có lim y = + nên đường thẳng x = 1 là đường tiệm cận đứng. − x 1 → (x + ) 1 ( x + 2) (x + ) 1 ( x + 2) Có lim y = lim = lim = 0 nên + + + x→(− ) 1 x→(− ) 1 ( → − x + )
1 ( x + 2 )( x − )
1 ( x − 2 ) x ( )1 (x + 2 )( x − ) 1 (x − 2 )
đường thẳng x = −1 không là đường tiệm cận đứng.
Có lim y = + nên đường thẳng x = 2 là đường tiệm cận đứng. + x→( 2) Có lim
y = + nên đường thẳng x = − 2 là đường tiệm cận đứng. − x→(− 2)
Vậy đồ thị hàm số có 4 đường tiệm cận (1 tiệm cận ngang, 3 tiệm cận đứng). Câu 10: Chọn D x − 2  0 x  2 Đkxđ:     x  2 2
x − 3x + 2  0
x  2, x  1  x − 2 +1  Ta có: lim 
 = + nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số. + 2 x→   2 x − 3x + 2    x − 2 +1  lim 
 = 0 nên đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. 2 x→+   x − 3x + 2   Câu 11: Chọn A 2 + −   Xét hàm số 2x x x y =
có tập xác định D = (−   +) 1 ;0 1; \ −  . 3x +1  3 Ta có 2 2x + x − x 2 3x + x x 1 lim = lim = lim = ; 1 + 1 2 1 2 x→− 3x 1 x→−
3x +1 2x − x − x x→− 2x − x − x 4 3 ( )( ) 3 3 2
2x + x − x 2
2x + x − x 1 lim = 0 và lim
= nên đồ thị không có tiệm cận đứng. − + x→0 3x +1 x 1 → 3x +1 2 1 1 − − − − 2 2x x 1 2 1
2x + x − x x x 1 lim = lim = lim = , x→− 1 1 3x +1 + x→− 3x 1 →− 1 x 3 + 3 3 3 x 1 1 + − + − 2 2x x 1 2 1 2x + x − x và x x lim = lim = lim
=1 nên đồ thị có hai tiệm cận ngang x→+ 1 1 3x +1 + x→− 3x 1 →− 1 x + 3 3 3 x 1 là y = và y = 1. 3
9 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
Vậy đồ thị hàm số có tất cả hai đường tiệm cận. Câu 12: Chọn C
Tập xác định của hàm số là D =  1 − ;0) (2;+). Ta có 2 25x + 9x 25x + 9 9 lim y = lim = lim = − . x→0− x→0− ( 2
x − 2x)(5x +1+ x +1) x→0− ( x − 2)(5x +1+ x +1) 4 lim y = + . x→2+ 5 1 1 1 + − + 2 3 4 x x x x lim y = lim = 0. x→+ x→+ 2 1− x
Vậy đồ thị của hàm số có hai đường tiệm cận có phương trình x = 2 và y = 0 . Câu 13: Chọn A   Tập xác định: 1 D = − ; + \     1  3  − + + + x − (x ) 1 (4 3x 1 3x 5 1 ) 4 3x +1 + 3x + 5 + Ta có: lim = lim = = − + + + x→
4 3x +1 − 3x − 5 x→ 9 − (x − ) lim 2 1 1 x 1 1 → 9 − (x − ) 1
do đó đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số. 1 1− x −1 1 1 + lim = lim x
= − do đó đường thẳng y = − là đường
x→+ 4 3x +1 − 3x − 5 x→+ 3 1 5 3 3 4 + − 3− 2 x x x
tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận. Câu 14: Chọn B
Tập xác định D = (− ;  − 2 )( 1 − ) ;1  ( 2;+) . lim
y = lim y = lim y = lim y = + . ( → − )− ( → )+ + − x ( → − ) 1 x x x ( → ) 1 2 2
Các đường tiệm cận đứng của đồ thị là x =  2 , x = 1.
lim y = lim y = 1 đồ thị có một tiệm cận ngang y = 1. x→− x→+ Câu 15: Chọn C  1 − − 5 x  4 2 + − + 2 
4x + 2x −1 0   Hàm số 4x 2x 1 x y = xác định     1 − + 5 . x +1 x +1  0 x   4  x  1 −  − −  − + 
Tập xác định của hàm số đã cho là D = (− − ) 1 5 1 5 ; 1   1 − ;    ; +    . 4 4     2 1 + − + 2 x 4 x 2
4x + 2x −1 + x x x lim y = lim = lim x→− x→− x +1 x→− x + 1
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 2 1 2 1 −x 4 + − + x − 4 + − +1 2 2 x x x x = lim = lim = 1 − . x→− x +1 x→− 1 1+ xy = 1
− là đường tiệm cận ngang của đồ thị hàm số khi x → −. 2 1 + − + 2 x 4 x 2
4x + 2x −1 + x x x lim y = lim = lim x→+ x→+ x +1 x→+ x + 1 2 1 2 1 x 4 + − + x 4 + − +1 2 2 x x x x = lim = lim = 3 . x→+ x +1 x→− 1 1+ x
y = 3 là đường tiệm cận ngang của đồ thị hàm số khi x → +. 2 2 2
4x + 2x −1 + x
4x + 2x −1− x
(x + )1(3x − )1 lim y = lim = lim = lim = −2. x→ 1 − x→−1 x→−1 x +1 ( →− x + ) 1 ( 2
4x + 2x −1 − x) x 1 (x + ) 1 ( 2
4x + 2x −1 − x) 2 + − + Vậy đồ thị hàm số 4x 2x 1 x y = có 2 đường tiệm cận. x +1 Câu 16: Chọn B x + 2  0
Điều kiện xác định  . 2
x − 6x + 2m  0
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình 2
x − 6x + 2m = 0 có hai nghiệm  9 m
 = 9 − 2m  0  2  9   m
phân biệt x , x lớn hơn −2  x + x  −2  3   −2   2 . 1 2 1 2 (    + + m   − −  − + m  m  − 2  )2 6 ( 2) 4 12 2 0 8 2 0   Do đó tập S =  7 − ; 6 − ; 5 − ;...;  4 có 12 giá trị. Câu 17: Chọn A x −1 x −1 Ta có lim = lim
= 0 nên hàm số có một tiện cận ngang y = 0 . 2 2
x→− x − 8 x x + m
→+ x − 8x + m
Hàm số có 3 đường tiệm cận khi và chỉ khi hàm số có hai đường tiệm cận đứng  phương trình
Δ =16 − m  0 m 16 2
x − 8x + m = 0 có hai nghiệm phân biệt khác 1     . m − 7  0 m  7
Kết hợp với điều kiện m nguyên dương ta có m 1;2;3;...;6;8;...;1 
5 . Vậy có 14 giá trị của
m thỏa mãn đề bài. Câu 18: Chọn D
Ta có lim y = 0, lim y = 0  đồ thị hàm số đã cho có 1 tiệm cận ngang. x→+ x→−
Do đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi nó có 3 tiệm cận đứng (*) . Có 3 2 x − mx + ( 2
m + ) x − m = ( x − m)( 2 3 2 1 x − 2mx + ) 1
11 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số x = m 3 2 x − 3mx + ( 2 2m + )
1 x − m = 0   2 x − 2mx +1 = 0  (2) (*)  3 2 x − mx + ( 2 3 2m + )
1 x − m = 0 có 3 nghiệm phân biệt khác 3 .
m  3 và (2) có 2 nghiệm phân biệt khác m và khác 3. m  3  5  m  3, m  2  m − 2 . m m +1  0  3     2 − +  m  1 3 2 .3 m 1 0    2   = −  m  1 − m 1 0  2
Do đó tập tất cả giá trị nguyên của m thỏa ycbt là  2 − 020; 2 − 019;...; 2 − ;2;4;5;...;202  0 .
Vậy có 4037 giá trị m thỏa ycbt. Câu 19: Chọn A x m
Ta có điều kiện xác định là 
, khi đó đồ thị hàm số sẽ không có tiệm cận ngang. x   (0;2) Ta có lim y = ,  lim y =  + − x 0 → x→2
Suy ra x = 0, x = 2 là hai đường tiệm cận đứng m  0
Vậy để đồ thị hàm số có đúng hai đường tiệm cận thì 
, theo bài m thuộc đoạn  10 − 0;100 m  2
. Vậy có 200 số nguyên của m thỏa mãn đầu bài. 2 2 x + m x + m Câu 20: y = = . 2 x − 3x + 2 (x − ) 1 ( x − 2)
lim y = 1  y = 1 là đường tiệm cận ngang. x→ 2 + Đồ thị hàm số x m y =
có đúng hai đường tiệm cận  đồ thị hàm số có đúng một tiệm 2 x − 3x + 2 cận đứng  pt 2
x + m = 0 nhận nghiệm x = 1 hoặc x = 2 . m = 1 − Khi đó:  . m = 4 −
Với m = −1 có một tiệm cận đứng x = 2 .
Với m = −4 có một tiệm cận đứng x = 1 . Vậy m { −1; 4 − } . Câu 21: Chọn C
Để đồ thị có ba đường tiệm cận thì 2
x − 2mx + 4 = 0 có hai nghiệm phân biệt  −1   m  2    0     m  2 −    (  −  )  2 1 − 2m (− ) 1 + 4  0  5 m  −   2 Câu 22: Chọn A
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 +
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số ax b y = ta có cx + d Đồ thị hàm số nhận d x = −
= −m − 3 = 0 làm TCĐ m = 3 − c Đồ thị hàm số nhận a y =
= n − 3 = 0 làm TCN  n = 3. c
Vậy m + n = 0 .
Câu 23: Trường hợp 1: m  0 suy ra tập xác định của hàm số là D = ( x ; x , ( x ; x là nghiệm của 1 2 ) 1 2 phương trình 2
mx − 8x + 2 = 0 ). Do đó m  0 không thỏa yêu cầu của bài toán. x −1
Trường hợp 2: m = 0 = y =
suy ra tập xác định của hàm số là D = (− ;  4) . 8 − x + 2 lim y = − ;
 lim y = − . Khi đó ta có x = −4 là đường tiệm cận đứng của đồ thị hàm số. − x→− x→4
Do đó m = 0 không thỏa yêu cầu của bài toán
Trường hợp 3: m  0 suy ra tập xác định của hàm số là D = (− ;
x x ;+ ( x ; x là 1 ) ( 2 ) 1 2
nghiệm của phương trình 2
mx − 8x + 2 = 0 ). Do đó đồ thị hàm số có bốn đường tiệm cận khi phương trình 2
mx − 8x + 2 = 0 có hai nghiệm phân biệt khác 1  6 − 2m  0 m  8  
1  m  0; m   m  0; m   m = 1; 2;3; 4;5; 
7 . Suy ra có tất cả 6 giá trị nguyên của   m − 8 + 2  0 m  6  
tham số m thỏa mãn yêu cầu của bài toán.
Câu 24: Chọn A
Đồ thị hàm số có tiệm cận ngang
Hàm số xác định trên một trong các miền (− ;  a),(− ;
a,(a,+) hoặc a;+) m  0
Trường hợp 1: m = 0  y = x − 3
− x + 7, lim y =  đồ thị không có tiệm cận ngang x→ Trường hợp 2: 2
m  0, y = x − mx − 3x + 7  3 7  3
Khi lim y = lim  x − x m − +
 = đồ thị hàm số có tiệm cận ngang khi và chỉ khi m = 1. 2 x→+   x→+ x x 2   Vậy m = 1
Cách trắc nghiệm: 3 Thay m = 1 2
y = x − x − 3x + 7  lim x − x − x +
= đồ thị hàm số có tiệm cận ngang x→+ ( 2 3 7 ) 2  ( 2 lim x −
x − 3x + 7 = − không có tiệm cận ngang. x→− ) Thay m = −1 2
y = x − −x − x +  x x x không xác định. x ( 2 3 7 lim − − − 3 + 7 →+ ) x x x
không xác định. Vậy m = 1 x ( 2 lim − − − 3 + 7 →− ) Câu 25: Chọn C ax +1
+ b = 0  đồ thị hàm số y = không có tiệm cận. 2 −
13 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số ax +1 2
+ b  0 , tập xác định của hàm số y =
là D = R \   . bx − 2 b  1 a + ax +1 a lim = lim = lim x y = . x→
x→ bx − 2 x→ 2 − b b x ax +  1 a a 1
đồ thị hàm số y =
có tiệm cận ngang là đường thẳng y =
 =  b = 2a . bx − 2 b b 2 ax +1 + lim y = lim =  . + + 2 2 bx − 2 x x − → → b b ax +  1 2 2
đồ thị hàm số y =
có tiệm cận đứng là đường thẳng x =
 =1  b = 2  a =1. bx − 2 b b
Vậy a = 1;b = 2 . Câu 26: Chọn C − Ta có đồ thị hàm số x 1 y =
có hai đường tiệm cận đứng khi phương trình 2
2x + 6x − m − 3  2 15 3
 − 2(−m −3)  0 m  − 2
2x + 6x − m − 3 = 0 có hai nghiệm phân biệt khác 1     2 2
2.1 + 6.1− m − 3  0 m  5 Từ đó ta suy ra tập các giá trị nguyên của m thỏa mãn là  7, − 6 − , 5 − , 4 − , 3 − , 2 − , 1 − ,0,1,2,3,4,6,7,8,9, 
10 . Vậy có 17 giá trị nguyên của m thỏa mãn. Câu 27: Chọn B 2 mx + 3mx + 4
Đồ thị hàm số y =
có nhiều nhất một tiệm cận đứng và hai tiệm cận ngang. x + 2 2 mx + 3mx + 4
Điều kiện để đồ thị hàm số y = x +
có 3 tiệm cận là nó có đúng 1 tiệm cận đứng và 2 2 tiệm cận ngang.
Xét điều kiện tồn tại lim y và lim y x→+ x→− m = 0  16
Trường hợp 1: g ( x) 2
= mx + 3mx + 4  0 với x   m  0  0  m    9 2
 = 9m −16m  0
Trường hợp 2: g ( x) 2
= mx + 3mx + 4  0 với x  (− ;
x x ;+ với x ; x là nghiệm 1 ) ( 2 ) 1 2 m  0 của 16 g ( x)    m  2
 = 9m −16m  0 9
Vậy m  0 thì tồn tại lim y và lim y x→+ x→− 3m 4 + + 2 m 2 mx + 3mx + 4 Khi đó: x x lim y = lim = lim = m x→+ x→+ x + 2 x→+ 2 1+ x
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 3m 4 − + + 2 m 2 mx + 3mx + 4 x x lim y = lim = lim = − m x→− x→− x + 2 x→− 2 1+ x
Vậy điều kiện để đồ thị hàm số có hai đường tiệm cận ngang là m  0
Xét trường hợp x = −2 là nghiệm của tử số  x = −2 là nghiệm của g ( x) 2 = + + mx 3mx 4  g ( 2 − ) = 0  m = 2 2 + + 2 ( x + ) 1 ( x + 2)  2 ( x + )  Khi đó 2x 6x 4 1 y =  lim y = = lim −  = − x + 2 − − x→ 2 − + x→−2 x 2  x + 2   
 Đồ thị hàm số có một tiệm cận đứng x = −2  m = 2 thỏa mãn
Xét trường hợp x = −2 không là nghiệm của tử số, để x = −2 là tiệm cận đứng của đồ thị hàm g  (−2)  0 số thì 
g (−2)   −    g  (− ) 0 4 2m 0 m 2 2  0
 đồ thị hàm số có một đường tiệm cận đứng x = −2 với m  (0;2 2 mx + 3mx + 4
Vậy điều kiện để đồ thị hàm số y = m   0;2 x + có 3 tiệm cận là (  2
Vậy có hai giá trị nguyên của m thỏa mãn đề bài là m = 1; m = 2 . Câu 28: Chọn A Đặt f ( x) 2 = x + (m − ) 2 2 1 x + m − 2
Đồ thị hàm số có đúng một tiệm cận đứng khi và chỉ khi f ( x) = 0 có 2 nghiệm phân biệt trong
đó có 1 nghiệm x = 1 hoặc f ( x) = 0 có nghiệm kép  (     m −  )2 −( 2 m − ) 3 1 2  0       0 mm =1   2       =   + − + − = f  ( ) 1 2  (m ) 2 1 m 2 0 1 0    m =1;m = 3 −  m = 3 −  .   3    = 0 3 3 m =  m = m =  2  2  2
Vậy tổng các giá trị m thỏa mãn là: 1 − . 2 Câu 29: Chọn B lim y lim y
0 nên đồ thị hàm số có tiệm cận ngang là đường thẳng y 0 . x x
Do đó, đồ thị hàm số có bốn đường tiệm cận khi phương trình 3 2 2 x 3mx 2m 1 x m 0
có 3 nghiệm phân biệt x 3 . Xét phương trình 3 2 2 x 3mx 2m 1 x m 0 ta có x m 3 2 2 x 3mx 2m 1 x m 0 2 x m x 2mx 1 0 . 2 x 2mx 1 0
15 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
Phương trình có ba nghiệm phân biệt x 3 khi và chỉ khi m 3 và phương trình m 3 m 3 m 1 2 x 2mx 1
0 có hai nghiệm phân biệt x 3 2 m 1 0 . m 1 2 3 2.3.m 1 0 5 m 3
Do m nguyên và m 6; 6 nên m 6; 5; 4; 3; 2; 2; 4;5; 6 .
Vậy có 9 giá trị nguyên của m thỏa mãn đề bài. Câu 30: Chọn C Tập xác định: \   m . 2 2
2x − 3x + m  2m − 2m  Có lim
= lim 2x + 2m −3+  . x→m x→ x − m mx − m  2 x − x +
Để đồ thị hàm số không có tiệm cận đứng thì phải tồn tại 2 3 m lim , x→m x − mm = 0 2
 2m − 2m = 0   m =1 Câu 31: Chọn D Để đồ thị hàm số x 2 y
có hai tiệm cận đứng thì phương trình 2 x 4x m 0 có 2 x 4x m
hai nghiệm phân biệt khác 2 2017 m 4 4 m 0 m 12 m 2017; 2016;..;3 \ 12 . 12 m 0 m
Do đó số giá trị nguyên của tham số m thỏa đề bài là: 3 ( 2017) 1 1 2020 giá trị. Câu 32: Chọn B
Đồ thị hàm số y = f ( x) có duy nhất một tiệm cận ngang m = 0 4 
 2019m = 2020m  2019  . 3 m =  2020
Vậy có 2 giá trị của m thỏa bài toán Câu 33: Chọn A Điều kiện x  . m
Ta có lim y = 0  y = 0 là tiệm cận ngang của đồ thị hàm số. x→+ x = m Xét phương trình 2 x −(2m + )
1 x + 2mx − m = 0     2 x − 
(2m+ )1 x + 2m= 0(*)
Để hàm số có 4 đường tiệm cận thì phương trình (*) có 2 nghiệm phân biệt m x x . 1 2
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023  1  1 ( m m   2m − )2 1  0   2 2  1   (   − )( − )   m x m x
m  0  x x − m ( x + x ) 2 2
− m  0  m − m  0   2 . 1 2 1 2 1 2    
x + x  2m 2m +1  2m 1  0 0  m 1 1 2      Câu 34: Chọn C Đặt f ( x) 2
= mx − 6x + 3 và g (x) 2
= 9x + 6mx +1. Ta xét các trường hợp: 6x − 3
Trường hợp 1: m = 0 khi đó ta có y = (
đồ thị hàm số có 1 đường tiệm cận 6 − x + 3)( 2 9x + ) 1
ngang là đường thẳng y = 0 do đó m = 0 thỏa mãn yêu cầu bài toán.
Trường hợp 2: m  0 và cả hai tam thức f ( x) và g ( x) đều vô nghiệm  '  0   −     f 9 3m 0 m 3        m . 2  '  0   m −  −  m g 9 9 0 1 1 1  
Trường hợp 3: Tam thức g ( x) nhận x = làm nghiệm 1 13 g = 0  m = −  
khi đó f ( x) 2  2  12
luôn có 2 nghiệm phân biệt nên đồ thị hàm số đã cho có nhiều hơn 1 đường tiệm cận. −
Vậy có 1 giá trị nguyên của 6x 3
m để đồ thị hàm số y = ( có đúng 1 2
mx − 6x + 3)( 2 9x + 6mx + ) 1 đường tiệm cận Câu 35: Chọn B
Điều kiện cần và đủ để đồ thị hàm số: 2 y x mx
1 có tiệm cận ngang là tồn tại số thực k 2 lim (x mx 1) k x sao cho: 2 lim (x mx 1) k x x Hiển nhiên nếu m 0 thì giới 2 lim (x mx 1) không hữu hạn x Nếu m 0 ta có 2 lim (x mx 1) . x 1 2 x(1 m) x (1 m) 1 2 lim y lim ( 1) lim lim x x mx x x x 2 x mx 1 x 1 1 m 2 x
Để giới hạn trên hữu hạn khi và chỉ khi m=1. Câu 36: Chọn D − Với x
m = 0 ; ta có hàm số 2 y = = 2
−  Không thỏa mãn yêu cầu bài toán. 2 − x + 4 − Với x 2 m  0 , ta có: lim
= 0  y = 0 là tiệm cận ngang của đồ thị hàm số. 2
x→ mx − 2x + 4
17 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
Đồ thị hàm số có đúng hai đường tiệm cận  đồ thị hàm số có đúng 1 tiệm cận đứng  2
mx − 2x + 4 = 0 có nghiệm duy nhất hoặc 2
mx − 2x + 4 = 0 có hai nghiệm phân biệt trong đó có một nghiệm x = 2 . 2
mx − 2x + 4 = 0 có nghiệm duy nhất 1
  = 0  1− 4m = 0  m = . 4  1    0 m  2
mx − 2x + 4 = 0 có hai nghiệm phân biệt trong đó có một nghiệm x = 2 .     4 4m = 0 m = 0
m = 0 không thỏa mãn điều kiện.
Vậy chỉ có một giá trị của m thỏa mãn yêu cầu bài toán. Câu 37: Chọn C 2019 2019 lim y = , lim y = . x→− m − 17 x→+ 17 − m 2019 2019
Với m  17 thì đồ thị hàm số có hai đường tiệm cận ngang là y = , y = . m − 17 17 − m
Khi đó đồ thị hàm số đã cho có 4 đường tiệm cận khi và chỉ khi phương trình 2
17x −1 − m x = 0 ( )
1 có hai nghiệm phân biệt khác 0. m  0 m  0  Ta có: ( ) 2
1  17x −1 = m x     2 2 2 1
 7x −1 = m x ( 2 17 − m  ) 2x =1 (2)
Phương trình có 2 nghiệm phân biệt khác 0 khi và chỉ khi phương trình có hai nghiệm phân biệt m  0 khác 0    0  m  17 . 2 1  7 − m  0
Suy ra S = 0,1, 2,3,  4 . Câu 38: Chọn B 1
Ta có: lim f (x) = lim . x→0 x→0 3 3 4 2
x + mx +1 − x + x +1 + m x x 3 3 4 2
x + mx +1 − x + x +1 + m x Mà lim x→0 x 3 3 4 2  x mx 1 1 x x 1 1 m x  + + − + + − = lim  − +  x→0  x x x    3 4  x + mx x + x 2 = lim  − + m . x→0 3 4 2 3 4 3
x( x + mx +1 +1) x( (x + x +1) + x + x +1 +1)   
Đồ thị hàm số f (x) nhận trục tung làm tiệm cận đứng 2 3 (x + ) m (x +1) m 1 2 2  lim( − + m ) = 0  − + m = 0 . x→0 3 4 2 3 4 3 + + + + + + + + + 2 3 ( x mx 1 1) (x x 1) x x 1 1 1 2
 6m + 3m − 2 = 0 Vậy m + m = − . 1 2 2 Câu 39: Chọn A
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Xét g x x x m 1. x(x ) m 1 x(x m) 1 Ta có lim 1 và lim
1 . Nên đồ thị hàm số luôn có hai x x 2 x x 2
đường tiệm cận ngang y 1 và y 1. x 1
Trường hợp 1: m
0 khi đó hàm số là y
. Đồ thị hàm số có tiệm cận đứng là x 2 x 2 . Vậy m
0 thỏa mãn yêu cầu đề bài.
Trường hợp 2: m
0 . Hàm số g x có tập xác định là D ; 0 m; . x 2 D . g( 2) 2 m 2 1 0 nên x
2 là tiệm cận đứng của đồ thị hàm số Vậy m 1, m 2 ,. m
9 thỏa mãn. Nên có 9 giá trị m .
Trường hợp 3: m
0 . Hàm số g x có tập xác định là D ; m 0; . Để x
2 là tiệm cận đứng của đồ thị hàm số thì trước hết x 2 D hay m 2 . Nên chỉ có m 2 , m 1 thỏa mãn Với m 1 ta có g(x) x x 1 1 , g( 2) 2 1 0 nên x
2 là tiệm cận đứng của đồ thị hàm số. Với m 2 ta có g(x) x x 2 1 , g( 2) x x 2 1 1 0 nên x 2 là
tiệm cận đứng của đồ thị hàm số.
Vậy 12 giá trị m nguyên thỏa mãn yêu cầu. 1 1
Câu 40: Ta có lim y = lim = 0, lim y = lim không tồn tại. Suy ra x→+ x→+ 3 2
x − 3x + m −1 x→− x→− 3 2
x − 3x + m −1
y = 0 là đường tiệm cận ngang của đồ thị hàm số.
Do đó, để đồ thị hàm số đã cho có 4 đường thẳng tiệm cận thì phương trình 3 2
x − 3x + m −1 = 0 có 3 nghiệm phân biệt.
Xét hàm số g ( x) 3 2
= x − 3x + m −1. Tập xác định D = . x = g( x) 2
= 3x − 6x ; g(x) 0 = 0   . x = 2 Bảng biến thiên:
Từ bảng biến thiên, ta thấy phương trình 3 2
x − 3x + m −1 = 0 có 3 nghiệm phân biệt khi và chỉ
khi m − 5  0  m −1  1  m  5 . Câu 41: Chọn A
Do hàm số không có tiệm cận đứng nên f ( x) =
x + + ax + b = ( x − )2 3 1 1 g ( x) .
19 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số  3  ( ) a + b + 2 = 0 = − 1 = 0 a f    4 1 Suy ra     
a − b = → đáp án A. f '  ( ) 3 1 = 0 a + = 0 5 2    4 b = −  4 n −
Chú ý: Với f ( x) = ( x − x
g x thì ta luôn có f ( x ) = f '( x ) = f ' ( x ) (n )1 = ... = f x = 0 . 0 0 0 ( 0 ) 0 ) ( ) Câu 42: Chọn C Biểu thức: 2
−x + 2016x + 2017 có nghĩa khi 2
−x + 2016x + 2017  0  −1  x  2017 . Đặt f ( x) 2
= −x + 2016x + 2017 .
Xét x − m = 0  x = m . Vậy đồ thị nếu có tiệm cận đứng chỉ có thể là x = m , khi đó điều kiện  1 −  x  2017 m    1 − ;2017 ( ) 1 là:     f  (m) 2  0
 −m + 2016m + 2017  24 7  (*) m  1 Ta có ( ) 2
*  m − 2016m + 2015  0   (2) m  2015 Từ ( ) 1 ,(2)  1;2017\1;201  5 m m    − ⎯⎯⎯
→ có 2019 − 2 = 2017 số nguyên m thỏa mãn bài toán → đáp án C. Câu 43: Chọn B 1
Ta có: lim f (x) = lim . x→0 x→0 3 3 4 2
x + mx +1 − x + x +1 + m x x 3 3 4 2
x + mx +1 − x + x +1 + m x Mà lim x→0 x 3 3 4 2  x mx 1 1 x x 1 1 m x  + + − + + − = lim  − +  x→0  x x x    3 4  x + mx x + x 2 = lim  − + m . x→0 3 4 2 3 4 3
x( x + mx +1 +1) x( (x + x +1) + x + x +1 +1)   
Đồ thị hàm số f (x) nhận trục tung làm tiệm cận đứng 2 3 (x + ) m (x +1) m 1 2 2  lim( − + m ) = 0  − + m = 0 . x→0 3 4 2 3 4 3 + + + + + + + + + 2 3 ( x mx 1 1) (x x 1) x x 1 1 1 2
 6m + 3m − 2 = 0 Vậy m + m = − . 1 2 2 Câu 44: Chọn A Xét g x x x m 1. x(x ) m 1 x(x m) 1 Ta có lim 1 và lim
1 . Nên đồ thị hàm số luôn có hai x x 2 x x 2
đường tiệm cận ngang y 1 và y 1.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 x 1
Trường hợp 1: m
0 khi đó hàm số là y
. Đồ thị hàm số có tiệm cận đứng là x 2 x 2 . Vậy m
0 thỏa mãn yêu cầu đề bài.
Trường hợp 2: m
0 . Hàm số g x có tập xác định là D ; 0 m; . x 2 D . g( 2) 2 m 2 1 0 nên x
2 là tiệm cận đứng của đồ thị hàm số Vậy m 1, m 2 ,. m
9 thỏa mãn. Nên có 9 giá trị m .
Trường hợp 3: m
0 . Hàm số g x có tập xác định là D ; m 0; . Để x
2 là tiệm cận đứng của đồ thị hàm số thì trước hết x 2 D hay m 2 . Nên chỉ có m 2 , m 1 thỏa mãn Với m 1 ta có g(x) x x 1 1 , g( 2) 2 1 0 nên x
2 là tiệm cận đứng của đồ thị hàm số. Với m 2 ta có g(x) x x 2 1 , g( 2) x x 2 1 1 0 nên x 2 là
tiệm cận đứng của đồ thị hàm số.
Vậy 12 giá trị m nguyên thỏa mãn yêu cầu. Câu 45: Chọn A Nếu 1 m = 0 thì y =
. Hàm số này có tập xác định D = \ −  1 . x +1 1 Ta có lim
= 0 nên đồ thị hàm số có tiệm cận ngang là y = 0 . x→+ x +1 1 lim
= + nên đồ thị hàm số có tiệm cận đứng x = −1 . + x ( → − ) 1 x +1
Vậy với m = 0 thì đồ thị hàm số có hai đường tiệm cận. Nếu m  0 thì 2
mx +1  0 với mọi x và tập xác định của hàm số là D = \ −  1 . 1 + 1 − + 2 m m mx +1 2 2 mx +1 2 lim x = x lim = m , lim = lim
= − m . Suy ra đồ thị x→+ x +1 x→+ 1 x→− x +1 x→+ 1 1+ 1+ x x
hàm số có hai tiệm cận ngang là y = m và y = − m . 2 mx +1 lim
= + nên x = −1 là đường tiệm cận đứng của đồ thị hàm số. + x ( → − ) 1 x +1
Vậy m  0 không thỏa mãn.  1 1 
Nếu m  0 thì tập xác định của hàm số là D = − − ; −  \−  1 . m m  
Trường hợp này đồ thị hàm số không có tiệm cận ngang. Để đồ thị hàm số có đúng một đường
tiệm cận thì đồ thị hàm số phải có một tiệm cận đứng. Điều này xảy ra khi 1 − −  1 1 −  −  1 1  − 1  m  −1 . m m m
Vậy với −1  m  0 thì đồ thị hàm số có đúng một đường tiệm cận.
21 | Facebook tác giả: Phan Nhật Linh Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 DẠNG
Bài tập tiệm cận của đồ thị hàm số nâng cao x − 3 Câu 1: Cho hàm số y =
. Có bao nhiêu giá trị nguyên thuộc đoạn 3 2 2
x − 3mx + (2m +1) x− m  2020 −
; 2020 của tham số m để đồ thị hàm số có 4 đường tiệm cận? A. 4039 . B. 4040 . C. 4038 . D. 4037 . 2 20 + 6x − x Câu 2: Cho hàm số y =
. Tìm tất cả các giá trị của m sao cho đồ thị hàm số có đúng hai 2
x − 8x + 2m
đường tiệm cận đứng
A. m 6;8) .
B. m  (6;8) .
C. m 12;16) .
D. m  (0;16) . Câu 3:
Cho hàm số bậc bốn y = f ( x) có đồ thị như hình vẽ. (x − )4 2 (x − )( 3 4 3 x + ) 1
Số đường tiệm cận của đồ thị hàm số y = là
f ( f ( x) − ) 1 A. 6 . B. 5 . C. 3 . D. 4 . Câu 4: Cho đồ thị hàm số 3 2
y = ax + bx + cx + d như hình vẽ dưới đây: 2 − − Đồ 3x x 2
thị của hàm số g ( x) =
có bao nhiêu đường tiện cận đứng 2
3 f ( x) − 6 f ( x) A. 5 . B. 4 . C. 3 . D. 2 .
1 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số Câu 5:
Cho hàm số bậc ba y = f ( x) có bảng biến thiên như hình bên dưới.
2x + 7 − 3 4x + 5
Đồ thị hàm số g ( x) =
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận f ( x) −1 ngang A. 4 . B. 3 . C. 2 . D. 5 . Câu 6: Cho hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ. Hỏi đồ thị hàm số − + − g ( x) 2 x 3x 2 x 1 =
có bao nhiêu đường tiệm cận? 2
x f ( x) − f ( x)   A. 3 . B. 5 . C. 6 . D. 4 . Câu 7: Cho hàm trùng phương 4 2
y = ax + bx + c có đồ thị như hình vẽ. Hỏi đồ thị hàm số
( 2x −4)( 2x +2x) y =
có tổng cộng bao nhiêu tiệm cận đứng?  f  ( x) 2  + 2 f  (x)−3 A. 5 . B. 2 . C. 3 . D. 4 .
3x + 1 + ax + b Câu 8:
Biết đồ thị hàm số y =
không có tiệm cận đứng. Tính 2 a + 3 ( b x − 5)2 −4841 −4814 4841 4814 A. . B. . C. . D. . 152 152 152 152
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 3 2 a − −  4  1 c x a c Câu 9: Biết rằng tích phân = 1 + + 2 . x d = 3. b −  d I x e x e
e , trong đó các phân số ; tối giản. 2  x 3 b d 1   3 ax +
Hãy xác định phương trình đường tiệm cận ngang của đồ thị hàm số = b y . cx + d A. y = 25 . B. y = 25 . C. y = 25 . D. y = 3 . 3 53 9
Câu 10: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ.
Tổng các giá trị nguyên của tham số 2020
m để đồ thị hàm số g(x) = có 4 đường
f ( f (x) + ) 1 − m tiệm cận bằng A. 15 . B. 1 . C. 13 . D. 11 .
6x − 3 + mx − 2m − 3
Câu 11: Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số y = f (x) = có 3 3x − 2 14x + 20x − 8
đúng hai đường tiệm cận? A. 1 . B. 2 . C. 3 . D. Vô số.
(3 9− 2x −2)ln(x+1)
Câu 12: Số đường tiệm cận của đồ thị hàm số: f (x) = là: 3 x − x A. 0 . B. 1 . C. 2 . D. 3 .
Câu 13: Cho hàm số bậc ba y = f (x) có đồ thị như sau
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
Gọi M,m lần lượt là số tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
( 2x −2x−3) 2 . x − 4 x. x − 2 17x + 16 y =
. Khi đó mệnh đề nào đúng? f (x) − 2 .( 2 2x − 3x)
A. 2M = 3m .
B. M = 3m .
C. M = 2m .
D. M = m .
(2x −3) 2x + 2x −8
Câu 14: Đồ thị hàm số y = (
có tổng số đường tiệm cận đứng, tiệm cận x + 2 − 1).( 2
4x + x + 4 + 2x) ngang là A. 2 . B. 3 . C. 4 . D. 6 .  2 x − 2 x +  2 khi x   2 2
Câu 15: Đồ thị hàm số y = f (x) =  x(x − 2)
có tất cả bao nhiêu đường tiệm cận?   2
4x + x + 1 + 2x khi x   2 A. 1 . B. 2 . C. 3 . D. 4 . 3 4x − 2
20x + m + 24 x − 2m
Câu 16: Cho hàm số y = f (x) ( ) =
có đồ thị là (C) . Gọi S là tập hợp 2
20x + 14x + 9 − (14x + 11) 2 2x + 1
các giá trị của m để (C) có đúng một tiệm cận đứng. Tổng các giá trị trong S là A. −1. B. −3 . C. −5 . D. −7 .
Câu 17: Cho đồ thị hàm số y = f (x) liên tục trên và có đúng hai đường tiệm cận ngang y = −5, y = 1
. Tìm giá trị của tham số m sao cho đồ thị hàm số y = f (x) + m có đúng một đường tiệm cận ngang. A. m = 1 . B. m = −2 . C. m = 2 . D. m = 3 .
Câu 18: Cho hàm số f (x) = x ( 3 3 ax + 2 bx − − 2 .
1 2 x − x + 1) . Biết rằng đồ thị hàm số có một đường tiệm
cận ngang bằng y = 5 . Giá trị a + b thuộc khoảng nào trong các khoảng sau? 4 . A. (−5; −3) . B. (−3;0) . C. (0; 3) . D. (3; 5) .
Câu 19: Cho hàm số bậc ba ( ) 3 2
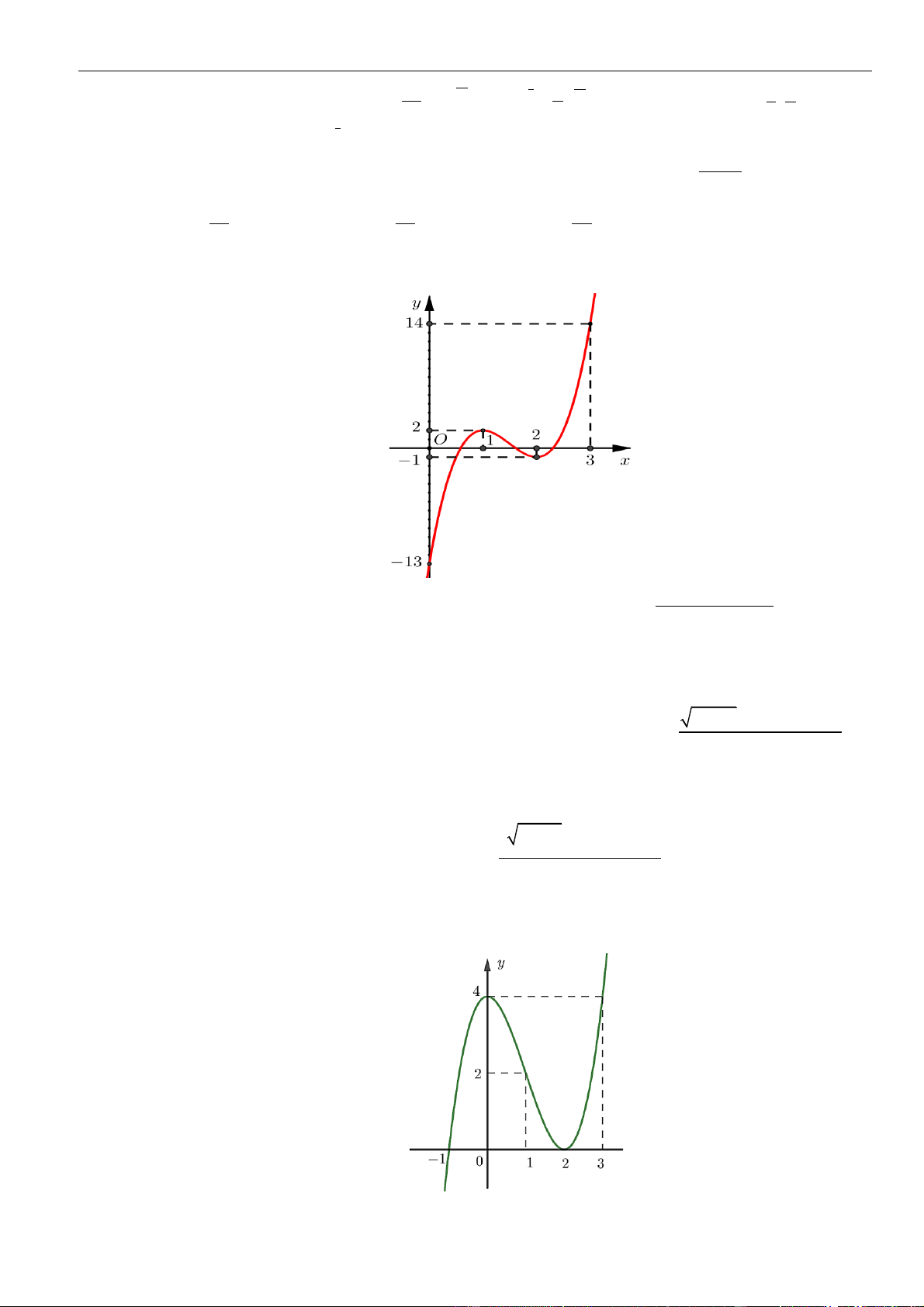
f x = ax + bx + cx + d (a ,b , c , d  ) có đồ thị như hình vẽ sau đây:
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 x (x − 2)
Đồ thị hàm số g ( x) =
có bao nhiêu đường tiệm cận đứng? 2
f ( x) − 2 f ( x) A. 2 B. 4. C. 3. D. 1. x −1
Câu 20: Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = có 3 đường 2 x − 2mx + 4 tiệm cận. m  2  m  2 − m  2
A. m  2 . B. 2
−  m  2 . C.  . D.  .  5 m  2 − m   2 x −1
Câu 21: Gọi S là tập các giá trị của m sao cho đồ thị hàm số y = có đúng hai 2 2
x − 2mx + m − 2m − 6
đường tiệm cận. Số phần tử của S là: A. 2 . B. 3 . C. 0 . D. 1.
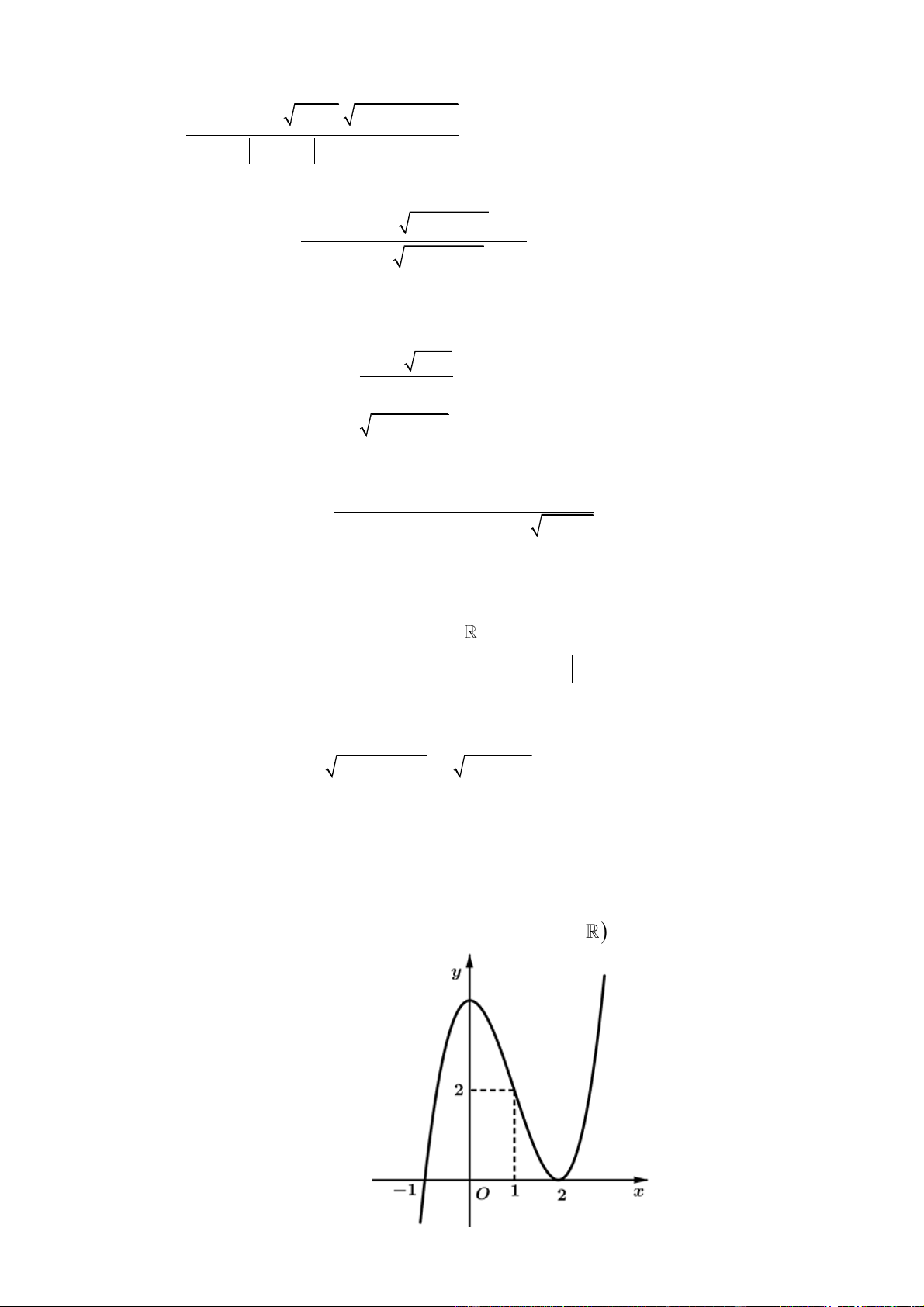
Câu 22: Cho hàm số y f ( x) 3 2 =
= ax + bx + cx + d (a  0) có đồ thị như hình dưới đây.
Gọi S là tập các giá trị nguyên của m thuộc khoảng ( 2019 −
; 2020) để đồ thị hàm số
(x + )1 f (x) g ( x) = (
có 5 đường tiệm cận (tiệm cận đứng hoặc tiệm cận ngang). f ( x) − 2)( 2
x − 2mx + m + 2)
Số phần tử của tập S là A. 2016. B. 4034. C. 4036. D. 2017.
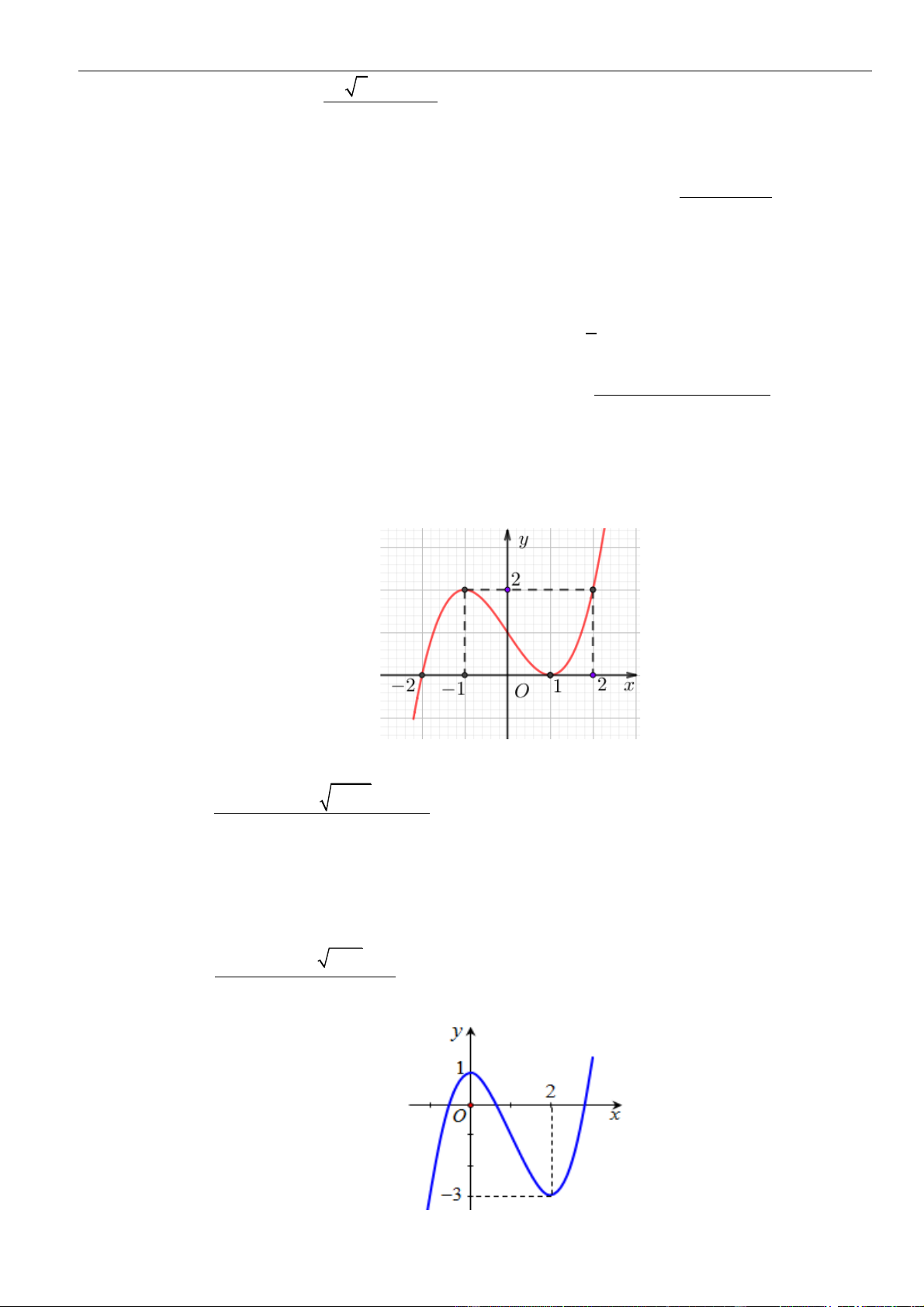
Câu 23: Cho hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ. Hỏi đồ thị hàm số ( 2x −2x) ( ) 1− x g x = (
có bao nhiêu đường tiệm cận đứng? x − 3) 2
f (x) + 3 f (x)   A. 4 . B. 3 . C. 5 . D. 6 .
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số BẢNG ĐÁP ÁN 1.B 2.B 3.A 4.C 5.B 6.C 7.D 8.A 9.B 10.D 11.B 12.C 13.C 14.A 15.C 16.C 17.C 18.D 19. 20. 21. 22. 23.
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn B
Ta có lim y = lim y = 0, suy ra y = 0 là tiệm cận ngang của đồ thị hàm số. x→+ x→−
Để đồ thị hàm số có 4 đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng 3 đường tiệm cận đứng, hay khi 3 2 2
x − 3mx + (2m +1) x− m = 0 ( )
1 có 3 nghiệm phân biệt khác 3. Ta có 3 2 2 x − mx + m +
− =  (x − m)( 2 3 (2 1) x m 0 x − 2mx + ) 1 = 0 x = m   f  ( x) 2
= x − 2mx +1 = 0(2) Để phương trình ( )
1 có 3 nghiệm phân biệt khác 3 khi phương trình (2) có 2 nghiệm phân m 1     −    − 2 m 1 0 m 1 0    5 m  1 −
biệt khác 3 và m khi  f (3) 2  0  3
 − 6m +1  0  m   .       f  (m) 3 m 1 2 2  0
m − 2m +1  0  m  1   
Vì m là số nguyên thuộc đoạn  2020 −
; 2020 nên có 4038 giá trị của tham số m . Câu 2: Chọn B
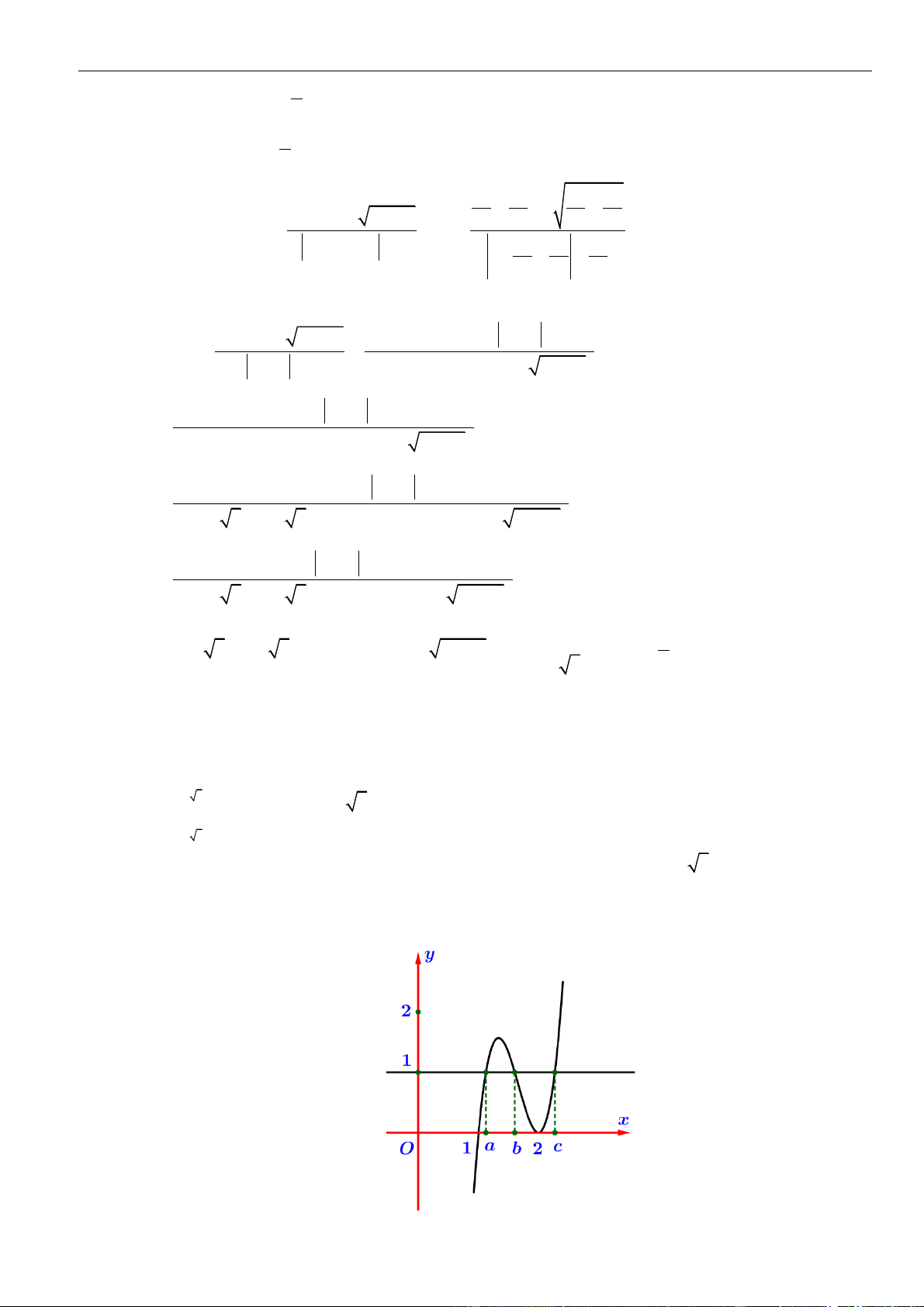
Ta có tập xác định của hàm số phải thỏa mãn 2
6x − x  0  0  x  6 .
Điều kiện để đồ thị hàm số có 2 tiệm cận đứng là phương trình 2
x − 8x + 2m = 0 có 2 nghiệm
phân biệt x , x thỏa mãn 0  x x  6 . 1 2 1 2 Ta có: 2
x − 8x = −2m . Đặt f ( x) 2 = x − 8x .
Ta có bảng biến thiên của hàm f ( x) trên đoạn 0;6.
Yêu cầu bài toán  −16  −2m  −12  6  m  8 . Câu 3: Chọn A
Hàm số bậc bốn có dạng 4 3 2
y = ax + bx + cx + dx + e (a  0) . Ta có: 3 2
y = 4ax + 3bx + 2cx + d .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Từ đồ thị trong hình vẽ đã cho ta thấy: Đồ thị hàm số có ba điểm cực trị ( 1
− ;0),(x ; y , 2;0 0 0 ) ( )
với 0  x  1; y  0 . Ngoài ra đồ thị hàm số đi qua các điểm ( 2 − ;3),(3;3) . 0 0 y(− ) 1 = 0  4
− a + 3b − 2c + d = 0    =   = y ( ) a 1 2 0
32a +12b + 4c + d = 0    = − y  (− ) b 2 1 = 0
a − b + c − d + e = 0  Từ đó ta có:     c = 3 − . y  (2) = 0
16a + 8b + 4c + 2d + e = 0  d = 4   − + − + =  y (− ) 16a 8b 4c 2d e 3 2 = 3   e = 4   =  + + + + = y  ( ) 81a 27b 9c 3d e 3 3 3
Suy ra bậc bốn y = f ( x) 4 3 2
= x − 2x − 3x + 4x + 4 . 2 2 Ta có: f ( x) 4 3 2
= x − 2x − 3x + 4x + 4 = (x + ) 1 ( x − 2) . ( 4 x − )4 2 (x − )( 3 4 3 x + ) 1
( 2x −4) (x−3)( 3x + )1 Từ đó ta có hàm số y =  y =
f ( f ( x) − ) 1 f (( x + )2 1 ( x − 2)2 − ) 1
(x − 2)4 (x + 2)4 (x −3)(x + ) 1 ( 2 x − x + ) 1
y = ( x+ )1 (x−2) )2( x+ )1 (x−2) −3)2 2 2 2 2
(x − 2)4 (x + 2)4 (x −3)(x + ) 1 ( 2 x − x + ) 1  y = (x + )
1 ( x − 2) ( x + ) 1 ( x − 2) − 3)2 4 4 2 2
(x − 2)4 (x + 2)4 (x −3)(x + ) 1 ( 2 x − x + )
y = g (x) 1 = . (x + )
1 ( x − 2) ( x − x − 2 − 3)2 ( x − x − 2 + 3)2 4 4 2 2 x = 1 − x = 2   1+ 9 + 4 3 x = = x1  2  2 2 4 4   − +
Xét ( x + ) ( x − ) ( 2 x − x − − ) ( 2 1 2 2 3
x − x − 2 + 3 ) = 0 1 9 4 3 = = . x x2  2   1+ 9 − 4 3 x = = x  3 2   1− 9 − 4 3 x = = x4  2 256 −
Ta có: lim g ( x) = − ; lim g ( x) =
; lim g ( x) = − ; lim g ( x) = + ; lim g ( x) = − ; x 1 →− x→2 81 x→ → → 1 x x 2 x x 3 x
lim g ( x) = − ; lim g ( x) = 0 . x→ x→ 4 x
Suy ra đồ thị hàm số có 5 tiệm cận đứng và 1 tiệm cận ngang.
Câu 4: Chọn C
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số  f (x) = 0 Xét phương trình 2
3 f ( x) − 6 f ( x) = 0   .  f  ( x) = 2
Dựa vào đồ thị ta suy ra: x = −
Phương trình f ( x) 2 = 0 
, với x = −2 là nghiệm đơn và x = 1 là nghiệm kép.  x =1 2
Suy ra: f ( x) = a ( x + 2)( x − ) 1 , (a  0) . x = 0 
Phương trình f ( x) = 2  x = m( 2 −  m  − )
1 , các nghiệm đều là nghiệm đơn.
x = n(n   ) 1
Suy ra f ( x) − 2 = ax ( x − m)( x − n),(a  0) . x −1 3x + 2 (x − ) 1 (3x + 2) Khi đó: g ( x) ( )( ) = =
3 f ( x)  f
 ( x) − 2 3a ( x + 2)( x − )2 2
1 x ( x − m)( x − n) (3x + 2) = , a  0 2
3a x ( x + 2)( x − )
1 ( x − m)( x − n) ( )
Vậy đồ thị hàm số g ( x) có 5 đường tiệm cận đứng
Cách 2: Chọn hàm số f ( x) . Ta có ( ) 3 2
f x = ax + bx + cx + d
Đồ thị hàm số qua 4 điểm A( 2 − ;0), B( 1
− ;4),C (0;2), D(1;0) . a = 1  b = 0 suy ra  hay f ( x) 3 = x − 3x + 2 c = −3  d = 2  Khi đó: − − − − − − g ( x) 2 2 2 3x x 2 3x x 2 3x x 2 = = = 2
3 f ( x) − 6 f ( x)
3 f ( x)( f ( x) − 2) 3( 3 x − 3x + 2)( 3 x − 3x) (x − ) 1 (3x + 2) =
3( x + 2)( x − )2 1 x ( 2 x − 3)
Vậy đồ thị hàm số g ( x) có 5 đường tiệm cận đứng Câu 5: Chọn B  5 x  −
Hàm số g ( x) xác định khi  4  f (x)  1  
Ta có y = f ( x) là hàm bậc ba và dựa vảo bảng biến thiên ta có y = a ( 2 x − ) 1 a 3
y = x − ax + b . 3
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023  a − + + = y(− ) a b 3 1 = 3  a = 3 3 3     
y = x − 3x +1  y  ( ) 1 = 1 − a  b =1 − a + b = 1 −  3 2 7 4 5 + − 3 +
2x + 7 − 3 4x + 5 x x x x
lim g ( x) 2 3 5 6 = lim = lim = 0 3 x→+ x→+ x − 3x +1 −1 x→+ 3 1 1 1− + − 2 3 3 x x x
y = 0 là tiệm cận ngang của đồ thị hàm số. ( 2
4x − 8x + 4)( f ( x x x ) + + − + ) g ( x) 1 2 7 3 4 5 = = f ( x) −1
( 2f (x)− )1(2x+7+3 4x+5) (x − )2 4 1 ( f ( x) + ) 1 =
( f (x)− )1( f (x)+ )1(2x+7+3 4x+5) 4 ( x − )2 1 ( f ( x) + ) 1 =
x ( x + 3)( x − 3)( x + 2)( x − )2
1 (2x + 7 + 3 4x + 5 ) 4 ( f ( x) + ) 1 =
x ( x + 3)( x − 3)( x + 2)(2x + 7 + 3 4x + 5 )  = 5 x (x +
)(x− )(x+ )( x+ + x+ ) x 0 3 3 2 2 7 3 4 5   (vì x  − x = 3 4
 lim g (x) = − +  → x 0 
x = 0 là tiệm cận đứng của đồ thị hàm số.
lim g ( x) = +  − x→0
 lim g (x) = + + x→ 3
x = 3 là tiệm cận đứng của đồ thị hàm số.
lim g ( x) = −  − x→ 3
Vậy đồ thị hàm số có tiện cận ngang là y = 0 và tiệm cận đứng là y = 3 Câu 6: Chọn C
Điều kiện xác định của hàm số g(x) là x  1.
9 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số x = 0 
Xét phương trình x  2
f (x) − f (x) =   0  .
x f ( x). f  ( x) −1 = 0  f x = 0 .   ( )  f  ( x) =1
Xét phương trình f (x) = 0 có nghiệm kép x = 2 và nghiệm đơn x = 1 .
x = a, 1  a  2
lim f (x) = +  
Xét phương trình f (x) = 1 có ba nghiệm đơn x = b, 1 b  2, b a . Ta thấy x→+  
lim f (x) = − 
x = c, c  2 x→− 
Nên không mất tính tổng quát, ta có
+ f ( x) = 0  ( x − )( x − )2 1 2 = 0
+ f ( x) = 1  ( x − a)( x − b)( x − c) = 0 Do đó: − + − − + − g ( x) 2 2 x 3x 2 x 1 x 3x 2 x 1 = = 2
x f ( x) − f ( x) x   (x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c) Khi đó lim g (x) +  → + x 0 
không tồn tại giới hạn  x = 0 không là tiệm cận đứng của đồ thị hàm số g ( x) lim g  (x) − x→0 2
x − 3x + 2 x −1
+ lim g ( x) = lim = + . + + x→ x→ x ( x − ) 1 ( x − 2)2 1 1
(x −a)(x −b)(x −c)
x = 1 là tiệm cận đứng của đồ thị hàm số g ( x) .  − + −  g ( x) 2 x 3x 2 x 1 lim = lim = − + + x→ x→  x ( x − ) 1 ( x − 2)2 2 2
(x − a)(x −b)(x −c) +   − + − g ( x) 2 x 3x 2 x 1 lim = lim = +  − − x→ x→ x  (x − ) 1 ( x − 2)2 2 2
(x − a)(x −b)(x −c)
x = 2 là tiệm cận đứng của đồ thị hàm số g ( x) .  − + −  g ( x) 2 x 3x 2 x 1 lim = lim = − + + x→a x→ax ( x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c) +   − + − g ( x) 2 x 3x 2 x 1 lim = lim = +  − − x→a x→a x  (x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c)
x = a là tiệm cận đứng của đồ thị hàm số g ( x) .  − + −  g ( x) 2 x 3x 2 x 1 lim = lim = + + + x→b x→bx ( x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c) +   − + − g ( x) 2 x 3x 2 x 1 lim = lim = −  − − x→b x→b x  (x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c)
x = b là tiệm cận đứng của đồ thị hàm số g ( x) .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023  − + −  g ( x) 2 x 3x 2 x 1 lim = lim = + + + x→c x→cx ( x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c) +   − + − g ( x) 2 x 3x 2 x 1 lim = lim = −  − − x→c x→c x  (x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c)
x = c là tiệm cận đứng của đồ thị hàm số g ( x) . 2
x − 3x + 2 x −1
+ lim g ( x) = lim = 0 . x→
x→ x ( x − )
1 ( x − 2)2 ( x − a)( x − b)( x − c)
y = 0 là tiệm cận ngang của đồ thị hàm số g ( x) .
Vậy đồ thị hàm số g ( x) có 6 đường tiệm cận. Câu 7: Chọn D
( 2x −4)( 2x +2x) (x−2)(x+2)x(x+2)
(x − 2)(x + 2)2 x Ta có: y = = = .  2 2 f  ( x) 2  + 2 f  (x)−3  f
 ( x) + 2 f  (x)−3  f
 ( x) + 2 f  (x)−3 x = , m m  2 −  x = 0  2  f (x) =1 Xét  f  (x) + 2 f  (x)−3 = 0  
  x = n, n  2 . f ( x) = 3 −   x = 2   x = 2 −
Dựa vào đồ thị ta thấy các nghiệm x = 0; x = 2 là các nghiệm kép (nghiệm bội 2). 2
Do đó đa thức  f
 ( x) + 2 f
(x)−3 có bậc là 8.
(x − 2)(x + 2)2 x 1 Suy ra y = = . 2
a x ( x + 2)2 ( x − 2)2 2 2
(x − m)(x − n) a x(x − 2)(x −m)(x −n)
Vậy đồ thị hàm số có 4 đường tiệm cận đứng là x = 0, x = 2, x = , m x = n . Câu 8: Chọn A Xét hàm số 3
f (x) = 3x + 1 + ax + b có f (x) = + a 2 3x + 1
Để hàm số không có tiệm cận đứng: f (x) = (x − )2 5 .g (x)  − 5a + b = −4 b = 17 f ( )  3.5 +1 + .5 a + b =  =   0 5 0      8 3   −  3   f (5)    = 0 + a =  0 a = −   3   a = 2 3.5 + 1 8  8
 −12  −3 3 −4814 Nên 2 a + 3 b = + =      2   2  152 Câu 9: Chọn B 3 3 2 3 2 x− 2 3 x− 2 x− x−  4  2  4  Ta có = e x d + +   . x I x x e
dx = I + I , với = e x I dx ; = + . x I x e dx . 2  2 1  2  2  2  2 x 1 2 x 1   1 1   1 3 3 3 3
11 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số  x−  x  4  2 2 3 − 2 x− 2  2 d = 1+ =  x x u e dx u e 3  Tính = e x I dx . Đặt    . 1  2  x  1 dv = dx   v = x 3  3 25 − x− 2 3 x− 2 53 2  4  1 Ta có = . x − + . x I x e x e dx = 9 3e − 3 e − I . 1  2  2 2 1 x 3 1   3 3 25 −53
Do vậy I = I + I = 1 9 3e − 3 e . 1 2 3 25x + 9
Ta có a = 25; b = 9 ; c = 53;d = 3. Suy ra hàm số y = . 53x + 3 25x +
Khi đó đồ thị hàm số y =
9 có phương trình đường tiệm cận ngang y = 25 . 53x + 3 53 Câu 10: Chọn D
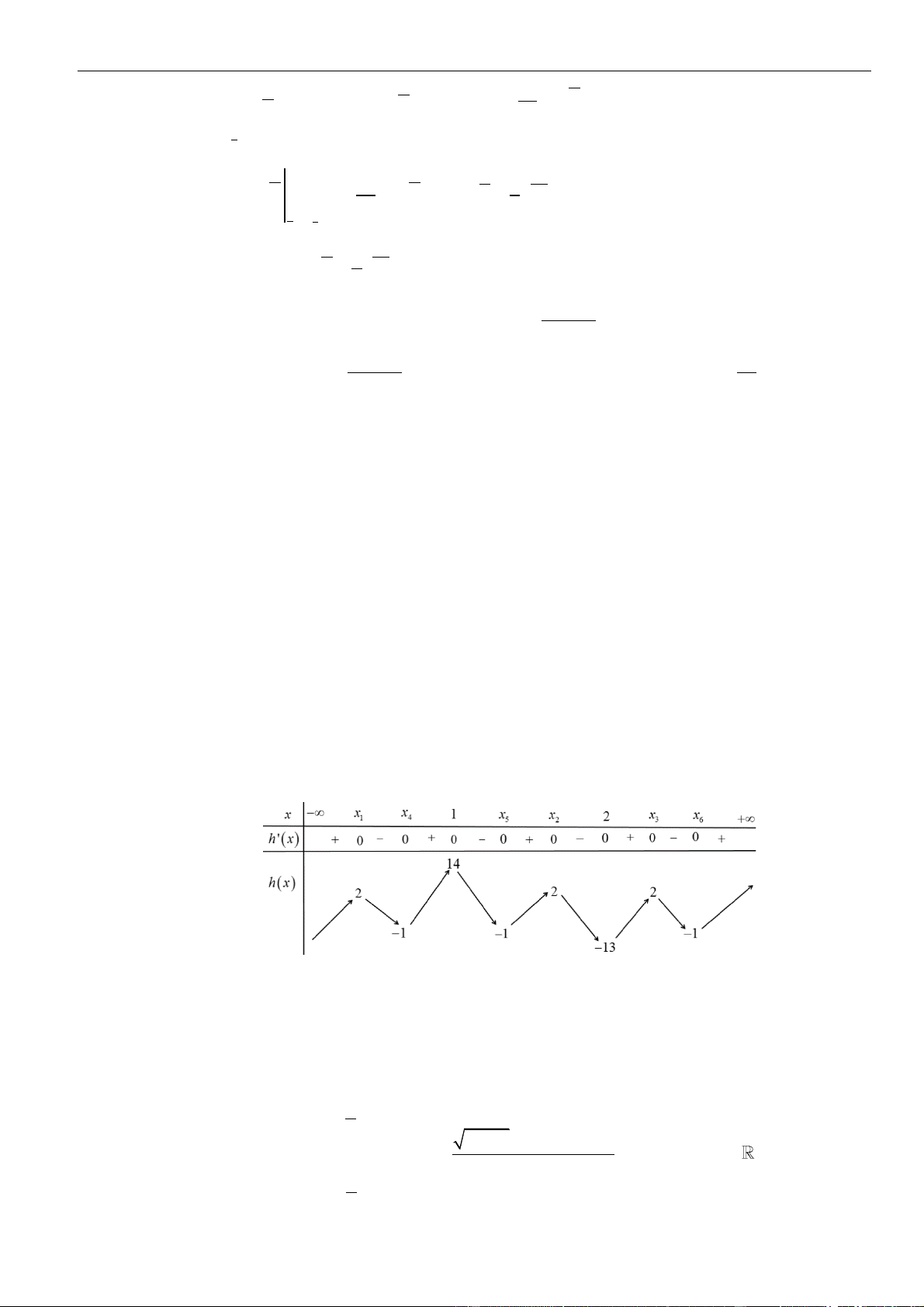
Ta thấy đồ thị hàm số g(x) có 1đường tiệm cận ngang là y = 0 .
Để đồ thị hàm số g(x) có 4 đường tiệm cận thì phương trình f ( f (x) +1) − m = 0 có 3 nghiệm phân biệt.
Đặt h(x) = f ( f (x) + ) 1 . Khi đó, 
h (x) = f (x). f ( f (x) + ) 1 .  f (x) =  f (x) = x 1,   0 0 2 f (x) = 0   
h(x) = 0  
  f (x) + 1 = 1   f (x) = 0  xx ;x ;x . 1 2 3   f
 ( f (x) + 1) = 0    f (x) + 1 =  2 f (x) =  1 x  
x ;x ;x 4 5 6 
(x x  1 x x  2  x x 1 4 5 2 3 6 )
Ta có h(x ) = h(x ) = h(x ) = f ( f (x ) + ) 1 = 2 ; 1 2 3 1
h(x ) = h(x ) = h(x ) = f ( f (x ) + ) 1 = −1; h( ) 1 = f ( f ( )
1 + 1) = 14 ; h(2) = f ( f (2) + ) 1 = −13 4 5 6 4 Bảng biến thiên:
Căn cứ vào bảng biến thiên để phương trình f ( f (x) +1) − m = 0 có ba nghiệm phân biệt thì: 2  m  14  . −13  m  −  1 Câu 11: Chọn B x  1   2
6x − 3 + mx − 2m − 3
Điều kiện xác định: x  2 lim = 0 với mọi m  .  . Ta có x→+ 3 3x − 2 14x + 20x − 8 x  2  3
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Suy ra đồ thị hàm số có một đường tiệm cận ngang y = 0 .
6x − 3 + mx − 2m − 3
Ta có y = f (x) = ( .
x − 2)2 (3x − 2)
Yêu cầu bài toán trở thành, tìm m để đồ thị hàm số có đúng một đường tiệm cận đứng x = 2 hoặc x = 2 . 3
Nếu 6x − 3 + mx − 2m − 3 nhận x = 2 là nghiệm thì m = − 3 . Khi đó 3 2 x − − 3 6 3 x − = 3 = 9 2 lim lim 2
x→ 2 (x − 2) (3x − 2) x→ 2 3 32 3 3 4 ( x − 2)  6x − 3 +  x   2  x − − 3 6 3 x − = 3 2 lim lim = − + . x (x−2)2 2 (3x −2) + →
x→2 4(x − 2) 3  6x − 3 +  x   2 
Suy ra x = 2 là đường tiệm cận đứng duy nhất của đồ thị hàm số.
Nếu 6x 3 mx 2m 3 (x 2) 6  − + − − = − 
+ m nhận x = 2 là nghiệm kép thì m = −1.  6x − 3 + 3 
6x − 3 − x − 1 − Khi đó = 1 lim lim = − + x x − 2 2 2 3x − 2 2 x 3x − 2 6x − 3 + x +   ( ) ( ) +     → →  ( ) 1 3 3 ( )    
6x − 3 − x − 1 − = 1 = − 1 lim lim x→ (x − 2)2 2
(3x − 2) x→2 ( x − )( x− + x+ ) 24 3 2 6 3 1
Suy ra x = 2 là đường tiệm cận đứng duy nhất của đồ thị hàm số. 3  3 
Vậy có hai giá trị của m −1;−  thỏa mãn bài toán.  2  Câu 12: Chọn C
Tập xác định: D = (−1;+)  \ 0;  1 . Ta có :  3 2 
 9 − x − 2ln(x + 1)   = 0 . →+ lim 3 x x − x  3 2 
9 − x − 2 ln(x + 1)  3 2     9 − x − 2     ln(x + ) = 1 = −3 . 2 9 li . + m lim → 3 − + x 0 → 2 − x 0 1 x x x x  3 2 
9 − x − 2 ln(x + )  3 2    1  9 − x − 2     ln(x + ) = 1 = −3 . 2 9 li − →m x 0 − li − →m 3 2 x 0 − 1 x x x x
13 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số  3 2  
− x −  (x + ) − 2 9 2 ln 1 1 x ln x +   ( ) ( 1) = lim + x − lim 3 x +  2      x 1 x 1 2 3 2 3  → −   → −  x −  1 x 9 − x + 2 9 − 2 x +      ( ) 4  ( )    −ln(x + ) = 1 = −. lim +  2    x 1 3 2 3  → −   x 9 − x + 2 9 − 2 x +    4  ( )     3 2  
− x −  (x + ) − 2 9 2 ln 1 1 x ln x +   ( ) ( 1) = li + m lim → 3 x x − x + → x ( 2 1 1 2 x − ) 3 1 x (9− 2x)   + 3 2 9 − 2 x +  4     −ln(x + ) = 1 = 1 ln2. + lim  → x 1 3 x ( 2 12 9 − 2 x )   + 3 2 9 − 2 x +  4      3 2 
 9 − x − 2ln(x + 1)   1 Tương tự = ln 2 . − → lim 3 x x − 12 1 x
Vậy đồ thị hàm số đã cho có 2 tiệm cận y = 0 và x = −1. Câu 13: ChọnC
Từ giả thiết, ta có f (x) = 3 x − 2 3x + 4 .
( 2x −2x−3) 2 . x − 4 x. x − 2 17x + 16
Gọi (C) là đồ thị hàm số y = g(x) = . 3 x − 2 3x + 2 .( 2 2x − 3x)  2 x − x  x  −4  0  
Điều kiện xác định:  4 x − 2 17x + 16  0
 −1  x  1− 3  0 .   3 x − 2 3x + 2 .( 2 2x − 3x)   x   0  4   2 3   1 − − . 1 − 1 . 1 − 17 + 16  2   x x x x x lim g(x)   2 4 = lim = 1 x→+ x→+  3 2   3  2  1 − + . 2 −  3      x x   x  Ta có:    2 3    1 − − 1 17 16  . 1 . 1 2   − −  − +    2 4 ( )  x x   x   x x g x = = 1 lim lim x→− x→−   3 2   3  − 1− + . 2 − 2   3      x x   x
 đường thẳng y = 1 là tiệm cận ngang của (C) . 2
( 2x −2x−3). 1− 4 x. x − 2 17x + 16 lim g x = lim = − − ( ) − x→0 x→0 ( 3x − 2
3x + 2).(− x ).(2x − 3)
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
 đường thẳng x = 0 là tiệm cận đứng của (C) .
( 2x −2x−3) 2 . x − 4 x. x − 2 17x + 16 lim g x = lim = − − ( ) x (1 3) x (1 3)− 3 2 2 → − → −
x − 3x + 2 .(2x − 3x)
 đường thẳng x = 1− 3 là tiệm cận đứng của (C) . Vậy M = 2;m = 1 nên M = 2m. Câu 14: Chọn A 2x − 2 3 x + 2x − 8
Gọi (C) là đồ thị hàm số y = f (x) ( ) = ( . x + 2 − 1).( 2
4x + x + 4 + 2x)  x + 2 = 1 x = −1 x + 2 = 1   Ta có ( x + − ) ( 2 2 1 .
4x + x + 4 + 2x) = 0    x  0  x = −3 .    4x + x + 4 = −  2 2x   x + 4 =  0 x = −  4
Suy ra tập xác định của hàm số y = f (x) là: D = (−;−4)  2;+  ) .
(2x −3) 2x + 2x −8 +) lim y = lim x ( )− x ( )− → − → − ( x+2 −1).( 2 4 4
4x + x + 4 + 2x)
(2x −3) (−x + 2)(−x −4)( 2
4x + x + 4 − 2x) = lim x ( 4)− → −
(−x − 3).(x + 4)
(2x −3) −x + 2( 2
4x + x + 4 − 2x) = lim = + x ( 4)− → −
(x + 3). −x − 4
Suy ra đường thẳng x = −4 là tiệm cận đứng của (C) .  3  2 8 ( 2 − 1 + − 2x − 3) 2 x + 2x − 8    x  2 x x 1 +) lim y = lim = lim = . x→+ x→+ ( x→+ x + 1).( 2
4x + x + 4 + 2x)  1    2 1 + 1 4  . 4 + + + 2  2   x   x x  (
( x − ) 2x + x − ( 2 2 3 2 8
4x + x + 4 − 2x) 2x − 3) 2 x + 2x − 8 +) lim y = lim = lim x→− x→− (− x→−
(−x − 3)(x+ 4) x − 3).( 2
4x + x + 4 + 2x)        − + 2 − 8  − + 1 + 4 1 4 − 2  2  2   x x x x = lim (2x − 3)     . = +   . x→−  3  4   −1− 1 +       x  x    
Suy ra đường thẳng y = 1 là tiệm cận ngang của (C) . 2
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận. Câu 15: Chọn C
15 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số 1 − 1 2 + 2 2 x − 2 x + 5 6 Gọi ( 2 C) x
là đồ thị hàm số y = f (x) ; lim = lim = lim x x y = 0 . x→+ x→+ x(x − 2)2 x→+  2 2 1 −    x
Suy ra (C) nhận đường thẳng y = 0 là đường tiệm cận ngang. 1 + 1 x + = 2 + + + = 1 = x y x x x = − 1 lim lim 4 1 2 lim lim . x→− x→− ( ) x→− 2 x→−
4x + x + 1 − 2x − 4 + 1 + 1 − 4 2 2 x x
Suy ra (C) nhận đường thẳng y = − 1 là tiệm cận ngang. 4 x − 2 x + 4 2 x − 2 4(x + 2) 3 x + 2 2x + 4x + y = = = 4 lim lim lim lim = + . + + x 2 x 2 x(x − 2)2 + x
2 x(x − 2)2 ( 2 x + 2 x + 2 ) + → → →
x→2 x(x − 2)( 2 x + 2 x + 2 )
Suy ra (C) nhận đường thẳng x = 2 là tiệm cận đứng.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận. Câu 16: Chọn C Ta có 2 x + x + + ( x + ) 2 20 14 9 14 11 2x + 1 = 0 (1)  2 x + x + 315 + 35 350 245 (14x+1 ) 2 1 2x + 1 = 0 2 2  35 2  35   x + + x + 35 2 x + + 1225 ( 2 x + ) + 7 2 x + 315 2 x + + 35 14 2 14 . 2 1 2 1 2 1 =     0  4   4  4 16 8 8 8  35 35 2  x + + 2 x + + 7 2 x + 315 2 x + + 35 14 2 1 2 1 =   0 (2) .  4 4  8 8 8
Nhận thấy phương trình (2) vô nghiệm nên phương trình (1) vô nghiệm.
(20x +14x+9)2 −(14x+11)2 2 ( 2 2x + 1) Do đó 2 x + x + − ( x + ) 2 20 14 9 14 11 2x + 1 = 2
20x + 14x + 9 + (14x + 11) 2 2x + 1 2 4 2(x − 2) ( 2
4x − 12x − 5) 8x − 3 56x + 2 118x − 5x − = 40 = . 2
20x + 14x + 9 + (14x + 1 ) 2 1 2x + 1 2
20x + 14x + 9 + (14x + 11) 2 2x + 1 x − 2
2 4x − 12x + m Khi đó hàm số y f (x) ( )( )  2 2  = =
. 20x + 14x + 9 + 14x + 11 2x + 2(x 2) 1 2 ( 2 4x 12x 5) ( )   − − − 2
4x − 12x + m  2 2   y = x x x x . 2(x 2)( . 20 14 9 14 11 2 1 2 4x 12x 5) + + + ( + ) +   − − −  3   14 
Hàm số y = f (x) có TXĐ là D = \2;  .  2 
Dễ thấy để đồ thị (C) của hàm số y = f (x) có đúng 1 tiệm cận đứng thì phương trình 3  2 14
4x − 12x + m = 0 (1) phải có đúng hai trong ba nghiệm 2; . 2
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Nếu ( )
1 có hai nghiệm phân biệt x , x thì x + x = 3  . Do đó, ( ) 1 phải có hai nghiệm là 1 2 1 2
3  14 , suy ra m = −5 . Do đóS = −  5 . 2
Vậy tổng các giá trị trong S là −5 .
Câu 17: Chọn C
Đồ thị hàm số y = f (x) có hai đường tiệm cận ngang y = −5,y = 1 .
 Đồ thị hàm số y = f (x) + m có hai đường tiệm cận ngang y = −5 + m, y = 1 + m
Do đó đồ thị hàm số y = f (x) + m có đúng một đường tiệm cận ngang khi và chỉ khi hai đường
thẳng y = −5 + m,y = 1 + m đối xứng qua trục Ox
 −5 + m + 1 + m = 0  m = 2 .
Câu 18: Chọn D Trường hợp 1: 5  3 3 2 2  5
lim f (x) =  lim . x
ax + bx − 1 − 2 x − x + 1 = x→+ x→+  4  ( ) 4    2 b lim x . 1 1 5 3 a + −1 − 2 1− +  = x→+  2   x x x  4
Suy ra 3 a − 2 = 0  a = 8 . Thay lại ta được  3 3 2 2  x x + bx − − x − x + = 5 lim . 8 1 2 1 x→+   ( ) 4  3 3 2 2   x x + bx − − x − + x − − x − x + = 5 lim . 8 1 2 1 2 1 4 4 4 x→+   ( ( ) ( ) ) 4  (b+12)   3 x − 2 6x −    + 3x  = 5 lim x→+  2  ( 3 2 8x bx 1) (2x 1) 3 2 8x bx 1 (2x 1)2 3 3 ( x− )+ 2 x − x +  + − + − + − + −  4 2 1 4 4 4     −3x −3 Do   lim = và f (x) = 5 lim nên x→+  ( x ) 2  − + x − x + x→+   4 2 1 4 4 4 4  (b+12)   3 x − 2 6x  lim   phải hữu han. x→+  2  ( 3 2 8x bx 1) (2x ) 3 2 1 8x bx 1 (2x 1)2 3 3  + − + − + − + −   
Do đó (b + 12) = 0  b = −12 thay lại ta được    − 2  6x −   = 1 lim x→+  2  ( 3 2 8x 12x 1) (2x 1) 3 2 8x 12x 1 (2x 1)2 3 3  − − + − − − + −  2   Thay lai được f (x) = − 5 lim không thỏa mãn x→+ 4 Trường hợp 2: 5  3 3 2 2  5
Xét lim f (x) =  lim . x
ax + bx − 1 − 2 x − x + 1 = x→− x→−  4  ( ) 4    2 b lim x . 1 1 5 3 a + −1 + 2 1− +  = x→−  2   x x x  4
17 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số
Suy ra 3 a + 2 = 0  a = −8 . Thay lại ta được  3 3 2 2  x
− x + bx − − x − x + = 5 lim . 8 1 2 1 x→−   ( ) 4  3 3 2 2   x
− x + bx − + x − − x − − x − x + = 5 lim . 8 1 2 1 2 1 4 4 4 x→− ( ( ) ( ) ) 4  (b−12)   3 x + 2 6x −    − 3x  = 5 lim x→−  2  ( 3 2 8x bx 1) (2x ) 3 2 1 8x bx 1 (2x 1)2 3 3 ( x− )− 2 x − x +  − + − − − − + − + −  4 2 1 4 4 4     −3x 3 Do   lim = − và f (x) = 5 lim
x→−  ( x ) 2  − − x − x + x→−   4 2 1 4 4 4 4  (b−12)   3 x + 2 6x  nên lim   hữu han. x→−  2  ( 3 2 8x bx 1) (2x ) 3 2 1 8x bx 1 (2x 1)2 3 3  − + − + − − + − + −   
Do đó (b −12) = 0  b = 12 thay lại ta được    2   6x  = 1 lim x→−  2  ( 3 2 8x 12x 1) (2x 1) 3 2 8x 12x 1 (2x 1)2 3 3  − + − + − − + − + −  2   Từ đó suy ra f (x) = 5 lim
thỏa mãn. Vậy ta được a + b = 4  (3;5) . x→− 4 Câu 19: Chọn C x  0   f ( x) = 0 Điều kiện:  . Xét phương trình: 2
f ( x) − 2 f ( x) = 0   2  f
 ( x) − 2 f (x)  0  f  ( x) = 2 x = −
Từ đồ thị  phương trình f ( x) 1 = 0   x = 2
x = −1 không là tiệm cận đứng do đk x  0 .
x = 2 là nghiệm kép và tử số có một nghiệm x = 2  x = 2 là một đường tiệm cận đứng. x = a  0 
Từ đồ thị  phương trình f ( x) = 2  x = 1 
x = b (b  2) 
x = a không là tiệm cận đứng (vì x  0 )
x = 1, x = b là hai đường tiệm cận đứng.
Vậy tổng số đường tiệm cận đứng của đồ thị hàm số g ( x) là 3. Câu 20: Chọn C
lim y = 0, lim y = 0 nên đồ thị hàm số có đường tiệm cận ngang y = 0 , m  . x→− x→+
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Do đó đồ thị hàm số đã cho có 3 đường tiệm cận  phương trình 2 x − 2 x
m + 4 = 0 có hai nghiệm phân biệt khác 1  5 2   0   m − 4  0 m      2  5   5   m    m    m 2   2  2  m  −2 . Câu 21: Chọn B 1 1 − 2 Ta có lim = lim x x y = 0 . 2 x→ x→ 2m m − 2m − 6 1 − + 2 x x
Nên đồ thị hàm số luôn có một đường tiệm cận ngang là y = 0 .
Do đó để đồ thị hàm số có đúng hai đường tiệm cận thì phương trình: 2 2
x − 2mx + m − 2m − 6 = 0 có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có 1 nghiệm bằng 1. m = −3 2m + 6 = 0  m = 3 −  m  −3 Khi đó    2m + 6  0     m = 1 − .  m = −1  2
m −4m−5 = 0  m = 5  m = 5
Vậy S = −3; −1; 
5 . Nên tập S có 3 phần tử. Câu 22: Chọn A f (x)  0 
Điều kiện.  f ( x)  2  2
x − 2mx + m + 2  0 
Nếu f ( x)  0  x  −2 x =
Nếu f ( x) = 2  2 
( x = 1 là nghiệm kép). x = 1 − x = −
Nếu f ( x) = 0  2 
( x = 1 là nghiệm kép). x =1
(x + )1 a(x + 2)(x − )2 1
x −1 a ( x + 2)
Khi đó. g ( x) = = a  0 .
a ( x − 2)( x + )2 1 ( 2
x − 2mx + m + 2)
a ( x − 2)( x + )
1 ( x − 2mx + m + 2) ( ) 2
Ta có lim g ( x) = 0 , nên hàm số có 1 tiện cận ngang y = 0 x→+
lim g ( x) =  , nên hàm số có tiện cận đứng x = 2 x→2
lim g ( x) =  , nên hàm số có tiện cận đứng x = −1 x 1 →−
Để hàm số g ( x) có 5 đường tiệm cận (tiệm cận đứng hoặc tiệm cận ngang). Thì phương trình h ( x) 2
= x − 2mx + m + 2 = 0 có 2 nghiệm phân biệt lớn hơn −2 và x   1 − ;1;  2 .
19 | Facebook tác giả: Phan Nhật Linh
Chủ đề 04: Tiệm cận của đồ thị hàm số   '  0 m  1 −   2  − −    a .h −  m m 2 0  m 2 h x ( 2) ( ) 0   5m + 6  0   6  6 S  m  − −  m  −1   2 −   −    m 2 5  5 2        3m + 3  0 m  2 − m  2 . h (− ) 1  0      −  m  1 − m  3  3 m 0 h ( ) 1  0    6 − 3m  0 m  3  h  (2)  0 m  2
Do m có giá trị là nguyên và m thuộc khoảng ( 2019 − ; 2020)
Vậy có 2016 giá trị nguyên của m thuộc khoảng ( 2019 −
; 2020) là 4;5;6.....; 201  9 Câu 23: x 1  x 1 
Điều kiện: x − 3  0   . 2   f
(x)+3 f (x)  0 2 f
(x)+3 f (x)  0 x = 3 (L)  Ta có ( x − 3) 2
f (x) + 3 f (x) = 0     f ( x) = 0
. Dựa vào đồ thị ta có  f (x) = 3 −  x = x  1 − ;0 1 ( ) 
f (x) = 0  x = x  0;1 (loại x  2 ), do đó có 2 tiệm cân đứng x = x , x = x . 2 ( ) 3 1 2
x = x  2;+  3 ( )
x = x , x  0 4 4 f (x) = 3 −  
, do đó có 1 tiệm cận đứng x = x . x = 2 (L) 4
Vậy đồ thị hàm số g ( x) có 3 đường tiệm cận đứng.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20
Document Outline

  • [04.D0] Lý thuyết và ví dụ minh họa tiệm cận
  • [04.D1] Bài tập cơ bản về tiệm cận của đồ thị hàm số
  • [04.D2] Bài tập về tiệm cận của đồ thị hàm số nâng cao

Tài liệu liên quan: