Chương 05 : Các định luật về chuyển động | Tài liệu môn Vật lý 1 trường đại học sư phạm kĩ thuật TP. Hồ Chí Minh

5.1 Các khái niệm về lực; Có thể phân các loại lực thành hai nhóm: (1) Lực do có tiếp xúc (lực đàn hồi của lò xo, lực căng dây, lực đàn hồi ở các điểm tiếp xúc giữa các vật…) (2) Lực của một trường lực (lực hấp dẫn, lực tĩnh điện, lực từ ); Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

4 2 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: vật lý 1, 2

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

26 trang 2 tuần trước

Tác giả:

Profile Lê Kim Dung
1
Chương 5: Các định luật v chuyề ển động
Khái ni l c ệm về ự
Có th phân các lo i l c thành hai nhóm: (1) L c do có ti p xúc (l i c a lò xo, ể ạ ự ự ế ực đàn hồ ủ
lực căng dây, lực đàn hồ các điểi ở m tiếp xúc gi a các v c c a m ng lữ ật…) (2) Lự ủ ột trườ ực
(lự ự ừc hấp dẫn, l n, lực tĩnh điệ c t )
Hình 5.1: a, b, c l c do có ti p xúc; d, e, f l c c a m ng ự ế ự ủ ột trườ
Bản chất vectơ củ ực là đại lượng vectơ nên khi tìm lự ần chú ý đến điểm đặa lực: L c c t,
phương, chiều và độ lớn của lực. Khi tổng hợp các l c, c n chú ý qui t c cự ầ ắ ộng vectơ.
Hình 5.2 minh h a 2 l c tác d ng vào móc c a l c k theo 2 cách khác nhau: 2 l c cùng ọ ự ụ ủ ự ế ự
phương và 2 lực vuông góc v i nhau. Khi tác d ng d c theo tr c lò xo, l c F và F lớ ụ ọ ụ ự
1 2
ần lượt
làm lò xo giãn ra 1cm và 2cm (hình 5.2 a,b). Nhưng hai lực này tác d ng vuông góc v i nhau ụ ớ
thì lò xo giãn ra 2,24cm (hình 5.2d).
Hình 5.2: Các l c tác d ng lên l c k : a. l c F ; b. l c F ; c. 2 l c F và Fự ụ ự ế ự
1
ự
2
ự
1 2
cùng phương
chiều; d. 2 l c F và F vuông góc v nhau. ự
1 2
ới
2
Định lu t Newton th t và các h qui chi u quán tính ậ ứ nhấ ệ ế
5.2.1 Định luật Newton thứ nhất:
Nếu m t v i các v t khác thì ta có th nh m t h qui chi u ộ ật không tương tác vớ ậ ể xác đị ộ ệ ế
trong đó vật có gia tốc bằng 0.
Hình 5.3: Mi ng nh m khí. ế ựa đặt trên đệ
5.2.2 Hệ qui chi u quán tính ế
Một h qui chi nh lu t Newton th nhệ ếu mà đị ậ ứ ất được thỏa mãn gọi là hệ qui chi u quán ế
tính.
Một d ng phát bi u khác c nh lu t Newton th nh ạ ể ủa đị ậ ứ ất:
Khi không có ngo i l c tác dạ ự ụng và được quan sát từ m t h qui chi u quán tính, mộ ệ ế ột vật
đứng yên s vẽ ẫn đứng yên và m t v t chuy ng s p t c chuyộ ậ ển độ ẽ tiế ụ ển động với v n t c không ậ ố
đổ ứi (t c là chuy ng vển độ ới t i theo m ng thốc độ không đổ ột đườ ẳng).
Ví dụ như khi xét một miếng nhựa tròn đặt trên bàn đệm khí, và bàn này đặ ặt đất trên m t
thì mi ng nh a i v c c a nó ế ự này không tương tác vớ ật nào khác theo phương ngang nên gia tố ủ
theo phương ngang bằng không. Nếu bàn đệm khí này được đặt trên một con tàu chuy ng ển độ
thẳng đều thì ta cũng quan sát đượ ện tượng tương tự ển độc hi . Tuy nhiên, nếu tàu chuy ng có
gia t c thì h qui chi u g n vố ệ ế ắ ới tàu không còn là h qui chi u quán tính n a. Mệ ế ữ ột người đứng
trên tàu s ẽ thấy mi ng nh a chuy ng có gia t c. H qui chi u g n vế ự ển độ ố ệ ế ắ ới tàu là hệ qui chiếu
phi quán tính. M c d u v y, mặ ầ ậ ột người quan sát đứng yên trên m t v n y mi ng nhặt đấ ẫ thấ ế ựa
chuyển độ ẳng đềng th u.
Một h qui chi u chuy ng v i v n tệ ế ển độ ớ ậ ốc không đổi đối với các ngôi sao ở rất xa là một
xấp x tỉ ốt nh t cho mấ ột hệ qui chi u quán tính. Trong nhi ng hế ều trườ ợp, Trái Đất cũng có thể
xem là m t h qui chi u quán tính. ộ ệ ế
Khoảng trước năm 1600 thì người ta cho rằng trạng thái tự nhiên của vật chất là trạng
thái ngh ng yên). Galileo ỉ (đứ là người đầu tiên đưa ra cách nhìn nhận mới về ng và chuyển độ
trạng thái t nhiên c a v t chự ủ ậ ất. Theo ông thì “Vận tốc mà ta truy n cho m t v t chuy ng ề ộ ậ ển độ
sẽ được b o toàn n u các nguyên nhân bên ngoài làm ch m chuy ng bả ế ậ ển độ ị loại bỏ”. Lúc đó
vật không tìm về “trạ ỉng thái ngh bản ch a. ất” nữ
Câu h i 5.1:ỏ Hãy ch n phát biọ ểu đúng trong các phát biểu sau:a) M t v t có th ộ ậ ể chuyển động
khi không có l c tác d ng lên vự ụ ật đó. b) Một vật có thể không chuy ng khi có l c tác ển độ ự
dụng lên vật đó. c) Cả (a) và (b) đề đúng. d) Cả (a) và (b) đều u sai.
3
5.2.3 Cách phát bi u khác c a t Newton th t ể ủ định luậ ứ nhấ
Nếu không có ngo i l c tác d c quan sát t m t h qui chi u quán tính thì mạ ự ụng và đượ ừ ộ ệ ế ột
vật đứng yên s ng yên và mẽ đứ ột vật chuy ng s p t c chuy ng vển độ ẽ tiế ụ ển độ ới vận tốc không
đổ ứi (t c là chuy ng th u). ển độ ẳng đề
Nói cách khác, n u không có l c tác d ng lên v t thì gia t c c a v t b ng không. B t k ế ự ụ ậ ố ủ ậ ằ ấ ỳ
vật cô l ng yên ho c chuy ng th ng ch ng l i s thay ập nào cũng đứ ặ ển độ ẳng đều. Khuynh hướ ố ạ ự
đổ ố ọi vận t c của một v c gật đượ i là quán tính.
5.2.4 Đị nghĩanh lực
Lực là nguyên nhân làm thay đổ ển đội chuy ng của một vật
Khối lượng
5.3.1 Định nghĩa khối lượng
Khối lượng là m t thu c tính c a v nh m ng l i s i v n t c cộ ộ ủ ật xác đị ức độ chố ạ ự thay đổ ậ ố ủa
nó. Đơn vị c a kh ng trong h ng qu c t là kilôgram (kg). Các thí nghiủ ối lượ ệ đo lườ ố ế ệm đã cho
thấy, dướ ực cho trướ ối lượ thu đượi tác dụng của một l c thì vật có kh ng càng lớn sẽ c gia tốc
càng nh u cho cùng m t l c tác d ng lên hai v t có kh ng l t là m và m . ỏ. Nế ộ ự ụ ậ ối lượ ần lượ
1 2
Các kh ng có th a t c t o ra b i m t l c tác d ng lên ối lượ ể định nghĩa theo gi ố ạ ở ộ ực cho trướ ụ
chúng:
Độ ủ lớn c a gia tốc tác dụng lên một vật t lỉ ệ ngh ch vị ới kh ng cối lượ ủa vật.
Khối lượng là thuộc tính cố hữu của một vật, không ph ng xung ụ thuộc vào môi trườ
quanh v ng nó. Khật và phương pháp được dùng để đo lườ ối lượng là đại lượng vô hướng.
Khối lượ ọc thông thường tuân theo các phép tính số h ng.
Khối lượ ọng lượng và tr ng:
Khối l ng và trượ ọng lượng (weight) là hai đại lượ ọng lượng là động khác nhau. Tr lớn
của l c hự ấp dẫn tác d ng lên v t. Tr ng có th i tùy theo v trí c a v t. ụ ậ ọng lượ ể thay đổ ị ủ ậ
Ví d ụ:
w
earth
= 180 lb; w ~ 30 lb
moon
m
earth
= 2 kg; m = 2 kg
moon
Định lu t Newton th hai ậ ứ
Khi xem xét t m t h quy chi u quán tính, gia t c c a m t v t t l n tr c ti p vừ ộ ệ ế ố ủ ộ ậ ỉ ệ thuậ ự ế ới
lực t ng h p tác d ng lên v t và tổ ợ ụ ậ ỉ l nghệ ịch v i kh ng c a nó. ớ ối lượ ủ
Lực là nguyên nhân c trong chuy gia t ủa các thay đổi ển động, được đo thông qua ốc.
1 2
2 1
m a
m a
(5.1)
4
Cần lưu ý là một vật có th chuyể ển động mà không c n có l c tác dầ ự ụng. Không được diễn
giải r ng l c là nguyên nhân c a chuy ng. ằ ự ủ ển độ
Về m i sặt đạ ố thì:
ở đây, hệ số t lỉ ệ c ch n b ng 1 và các tđượ ọ ằ ốc độ ển độ chuy ng c a các v t ph i nh ủ ậ ả ỏ hơn nhiều
so v i tớ ốc độ ánh sáng. Trong đó,
F
là l c t ng h p, là tự ổ ợ ổng vectơ của tất cả các lực tác
dụng lên v t (còn gậ ọi là l c toàn ph n). ự ầ
Đị ứ đượnh luật Newton th 2 cũng có thể c biểu diễn theo các thành phần:
F
x
= ma
x
F
y
= ma
y
F
z
= ma
z
Lưu ý:
am
không ph i là m t l c. ả ộ ự
Tổng t t c các l c b ng tích c a kh ng c a v t v i gia t c c a nó. ấ ả ự ằ ủ ối lượ ủ ậ ớ ố ủ
Đơn vị của lực: Trong SI, đơn vị của lực là newton (N)
1 N = 1 kg·m / s
2
Theo h c a M c a l c là ệ đơn vị ủ ỹ thì đơn vị ủ ự pound (lb).
1 lb = 1 slug·ft / s
2
Quy đổi đơn vị: 1 N ~ ¼ lb
Câu h i 5.2:ỏ M t v t chuy ng không gia t c. Hãy ch n phát bi u trong các ộ ậ ển độ ố ọ ể không đúng
phát bi u sau:a) Ch có m t l c tác d ng lên vể ỉ ộ ự ụ ật đó. b) Không có lực nào tác dụng lên vật. c)
Các l c tác d ng lên vự ụ ật, nhưng không gây ra tác dụng.
Câu h i 5.3:ỏ Khi đẩy một vật từ trạng thái ngh t qua m t m t sàn không ma sát v i lỉ trượ ộ ặ ớ ực
không đổi trong kho ng thả ời gian Δt, kết quả vật thu được tốc độ v. Sau đó, lặ p lại thí nghiệm
trên với l y lực đẩ ớn hơn 2 lầ ỏi đển. H c v n t c cuđạt đượ ậ ố ối cùng như thí nghiệm trên thì thời
gian đẩ ật là?a) 4Δt; b) 2 Δt; c) Δt; d) Δt. y v
Bài t p m u 5.1: ng có gia t c c a qu bóng khúc côn c u. ậ ẫ Chuyển độ ố ủ ả ầ
M t qu bóng Khúc côn c u có kh t không ma sát trên mộ ả ầ ối lượng 0,3kg trượ ặt băng
phẳng. Hai cây g y Khúc côn c bóng cùng mậ ầu đánh vào quả ột lúc như hình 5.4. Lực
F
1
lcó độ ớn 5N và theo phương nghiêng mộ 0 đột góc 2 ở dưới trục Ox. Còn lực F
2
có
a F a
m
m
(5.2)
5
độ lớn 8N có phương nghiêng một góc 60 độ ục Ox. Hãy xác định độ phía trên tr lớn
và phương củ ển độa gia tốc chuy ng của quả bóng.
Giải.
Khái ni m hóa:ệ T hình 5.4: s d ng ki n thừ ử ụ ế ức
cộng vectơ ở chương 3, có thể tính được tổng hợp
lực tác d ng lên qu Khúc côn c u. Tụ ả ầ ừ đó, suy ra
gia t c chuy ng c a qu Khúc côn c u s cùng ố ển độ ủ ả ầ ẽ
phương chiều với tổng h p lợ ực đó.
Phân loại: Bởi vì bài toán có thể tính ra t ng h p ổ ợ
lực, và m c tiêu là tìm gia tụ ốc. Do đó, mô hình được
sử d ng là mô hình ch i tác dụ ất điểm dướ ụng của
tổng h p lợ ực.
Phân tích:
Tìm l c t ng h p lên v ự ổ ợ ật theo phương Ox:
cos cos
1 2 1 2x x x
F F F F F
Tổng h p l ợ ực theo phương Oy:
Áp d nh lu t Newton 2 theo t ụng đị ậ ừng phương:
2
cos cos cos cos
m/s
1 2
5 ( 20) 8 60
29
0,3
x
x
F
F F
a
m m
2
sin sin sin sin
m/s
1 2
5 ( 20) 8 60
17
0,3
y
y
F
F F
a
m m
Gia t c c a v t là: ố ủ ậ
2
m/s
2 2
29 17 34a
Phương củ ốc đốa gia t i với trục Ox:
01 1
17
tan tan 31
29
y
x
a
a
Hoàn t t: ấ Sử ứ dụng phương pháp cộng vectơ trên hình 5.4, có thể kiểm ch ng lại kết
quả thu được.
Lực h p d n và i ấ ẫ khố lượng
Lực h p d n ấ ẫ
F
g
là l t tác d ng lên m t v t. L ng v tâm c a Trái ực mà Trái đấ ụ ộ ậ ực này hướ ề ủ
đấ độ ủt, và lớn c c gủa nó đượ ọi là trọng lượng c a vật.
Theo định luật Newton thứ 2 thì:
Hình 5.4: Qu Khúc côn cả ầu
chuyển động trên bề mặt không
ma sát dưới tác dụng của 2 lực.
6
Do đó, trọng lượng của vật:
Nói thêm v ề trọng lượng:
Do tr ng ph c vào gia t c tr ng (g) nên nó s i theo v ọng lượ ụ thuộ ố ọng trườ ẽ thay đổ ị trí.
Càng lên cao thì g và tr ng càng gi ọng lượ ảm.
Điều này cũng áp dụng được cho các hành tinh khác, nhưng g thay đổi theo hành tinh
nên tr i t hành tinh này sang hành tinh khác. ọng lượng cũng thay đổ ừ
Trọng lượng không ph i là thu c tính c h u c a v t. Tr ng l ng là thu c tính cả ộ ố ữ ủ ậ ọ ượ ộ ủa một
hệ các v t: v t. Vậ ật và Trái đấ ề đơn vị thì kg không ph c a tr ng. Công thải là đơn vị ủ ọng lượ ức
1kg=2,2lb là công thức tương đương và chỉ đúng trên mặt đấ t.
Khối lượ ối lượng hấp dẫn và kh ng quán tính:
Trong các định luật của Newton, kh ng là kh ng ối lượ ối lượ quán tính và đo bằng s cự ản
trở i vđố ới s i chuy ng c a v t. Còn trong công th c (5.6) kh ng ự thay đổ ển độ ủ ậ ứ ối lượ m cho biết
lực h p d n gi a vấ ẫ ữ ật và Trái Đất. Các thí nghi m cho th y khệ ấ ối lượng quán tính và kh ng ối lượ
hấp d n có cùng giá tr . ẫ ị
Câu h i 5.4:ỏ Giả s r ng b i m t cu n tho i liên hành tinh v i b n c a b ử ằ ạn đang gọ ộ ộc điệ ạ ớ ạ ủ ạn ở
trên M i bặt Trăng. Ngườ ạn đó kể rằng anh ta m i thớ ắng được 1 Newton vàng trong m t cuộ ộc
thi. Anh ta khuyên b n nên tham dạ ự cuộc thi đó phiên bản Trái Đấ ắng cũng t và nếu chiến th
được 1 Newton vàng. H i nỏ ếu điều đó xảy ra, ai s ẽ giàu hơn?, a) Bạn sẽ giàu hơn; b) Bạn của
bạn giàu hơn; c) Cả 2 giàu bằng nhau.
Định lu t Newton th 3 ậ ứ
Nếu hai vật tương tác, lực
12
F
do v t 1 tác d ng lên v t 2 b ng v lậ ụ ậ ằ ề độ ớn nhưng ngược
chiều v i lớ ực
21
F
do v t 2 tác d ng lên v t 1. ậ ụ ậ
Lưu ý về ký hiệu:
AB
F
là l c do A tác d ng lên B. ự ụ
Một cách phát bi u khác c nh luể ủa đị ật:
F g
g
m
(5.5)
g
F = mg
(5.6)
12 21
F F
(5.7)
7
Lực tác d ng và l c ph n tác d ng (ph n l c) b ng ụ ự ả ụ ả ự ằ
nhau v l c chi u. ề độ ớn nhưng ngượ ề
Một trong hai lực là lực tác d ng, lụ ực kia là ph n ả
lực.
Lực và ph n l c ph i tác d ng lên hai v t khác nhau ả ự ả ụ ậ
và cùng lo i nhau. ại vớ
Ví d 1 vụ ề ả l phực – n l hình 5.5, hai v t tác d ng ực: Ở ậ ụ
vào nhau b i các l l n bở ực có độ ớ ằng nhau nhưng ngược
chiều nhau.
Ví d 2 v l ph n l Trong hình 5.6a trên, l c pháp tuy (normal force) do m
ụ ề ực – ả ực: ở ự ến
1
ặt
bàn tác d ng lên màn hình (ụ
tm
n = F
) là ph n l c c a l c tác d ng c a màn hình lên m t bàn (ả ự ủ ự ụ ủ ặ
mt
F
).
a
b
c
Hình 5.6: Các l c tác d ng lên m t n m yên trên m t mự ụ ột màn hình máy tính được đặ ằ ộ ặt
bàn
Lực tác d ng c t lên màn hình (ụ ủa Trái đấ
g Em
F F
) có độ lớn bằng với l c mà màn hình ự
tác d t (ụng lên Trái đấ
mE
F
) nhưng ngược chiều.
Khi gi i toán b ng cách v n dả ằ ậ ụng các định luật c a Newton, ta có th v các l c tác d ng ủ ể ẽ ự ụ
lên v l c). M t cách khác là ta có th v l c trong ật như trong hình b (còn gọi là sơ đồ ự ộ ể ẽ sơ đồ ự
đó sử ất điể ật, ta đượ ột sơ đồ như trong hình c (gọ dụng mô hình ch m cho v c m i là free-body
diagram).
Khi v , c v nh ng l c tác d ng lên v c các lẽ các sơ đồ ần lưu ý là chỉ ẽ ữ ự ụ ật đang xét (kể ả ực
do tr ng l c gây ra). Các l c tác d ng lên v ng lên ch m thay th ườ ự ự ụ ật xem như là tác dụ ất điể ế
1
Còn g i là ph n l c, lọ ả ự ực đàn hồi vuông góc
Hình 5.5: Định luật 3 Newton
8
cho v này giúp ta tách các l c tác d ng lên v qua các l c khác khi ật. Sơ đồ ự ụ ật đang xét mà bỏ ự
phân tích.
Câu h i 5.5:ỏ i) N u m t con ru i va ch m vào kính ch n gió c a m t ế ộ ồ ạ ắ ủ ộ chiếc xe buýt đang chạy
rất nhanh, thì l a con ru i tác d ng vào xe, b)c a xe buýt tác ực nào sau đây lớn hơn? a) củ ồ ụ ủ
dụng vào ruồi, c)2 v t tác dậ ụng các l c b ng nhau. ự ằ
ii) V t nào có gia t c l i, b) Xe buýt, c) 2 v t có gia t c b ng nhau. ậ ố ớn hơn? a) Con ruồ ậ ố ằ
Các mô hình phân tích s d nh lu t 2 Newton ử ụng đị ậ
Trong ph n này, ta th o lu n vầ ả ậ ề hai mô hình phân tích để ải toán trong đó vậ gi t cân b ng ằ
hoặc chịu tác d ng c a các lụ ủ ực không đổi. Để ải các bài toán ta đơn giả gi n hóa mô hình bằng
các gi nh sau: ả đị
Các v t có th c mô hình hóa thành các ch m (particle). ậ ể đượ ất điể
Chỉ quan tâm đến các ngo i l c tác d ng lên v t (có th b qua ph n lạ ự ụ ậ ể ỏ ả ực – vì ph n lả ực
tác d ng lên v t khác). ụ ậ
Tạm th i b qua ma sát các b mờ ỏ ở ề ặt.
Khối lượ ợi dây là không đáng kể ật hướng của các s : Lực của dây tác dụng lên v ng ra
xa v t và song song v c bu c vào vậ ới dây. Khi dây đượ ộ ật và kéo v lật đi thì độ ớn của
lực này là l ực căng dây
Mô hình phân tích: H ng thái cân b ạt ở trạ ằng
Nếu gia t c c a m t v t (xem là m t ch m) b ng không, vố ủ ộ ậ ộ ất điể ằ ật
được gọi là ở trạng thái cân bằng. Mô hình này gọi là mô hình chất
điể ựm ở trạng thái cân bằng. Về mặt toán học, l c tổng h p tác d ng ợ ụ
lên v t b ng không: ậ ằ
hay
0
x
F
và
0
y
F
Ví d v cân b ng: m c treo b ng m t dây xích nh ụ ề ằ ột cái đèn đượ ằ ộ ẹ
(hình 5.7). Các l c tác d ự ụng lên đèn gồm:
Lực h p d ng xu i ấ ẫn hướ ống dướ
Lực căng của dây xích hướng lên trên.
Áp d u ki n cân b c ụng điề ệ ằng, ta đượ
0 0
y g g
F T F T F
Mô hình phân tích: H i tác d ng c a m t l c t ng h p ạt dướ ụ ủ ộ ự ổ ợ
Nếu một vật được mô hình hóa như mộ ất điểt ch m ch u m t gia t c, ph i có l c t ng hị ộ ố ả ự ổ ợp
khác không tác d ng lên nó. Mô hình dùng trong ụ trường h p này là mô hình chợ ất điểm dưới
tác d ng c a m t l c t ng h p. Ta gi c sau: ụ ủ ộ ự ổ ợ ải bài toán theo các bướ
0
F
Hình 5.7: Một chiếc đèn
được treo trên trần nhà
nhờ s i xích. ợ
9
Vẽ sơ đồ lực.
Viết định luật 2 Newton:
.F m a
Xét theo các phương x, y.
Một ngườ ột cái thùng như hình 5.8 a. Các lựi kéo m c tác d ng lên thùng: lụ ực căng dây
T
, trọng lực
F
g
, và ph n l c pháp tuy n ả ự ế
n
tác d ng b i sàn nhà. ụ ở
Áp d nh lu : ụng đị ật 2 Newton theo các phương x, y
x x
F T ma
0
y g g
F n F n F
Giải h n. ệ phương trình theo các ẩ
Nếu l i thì gia t là h ng s , ta có ực căng dây là không đổ ốc a ằ ố
thể áp dụng các phương trình độ ọc để đầy đủ hơn vềng h mô tả
chuyển động của thùng.
Lưu ý về phản lực pháp tuyến
n
:
Lực pháp tuy n không ph i là luôn b ng tr ng l c tác d ng lên ế ả ằ ọ ự ụ
vật. Ví d nh thì ụ như trong hình bên cạ
0
y g
F n F F
nên:
n mg F
Nó cũng có thể hơn trọ nhỏ ng lực.
Gợi ý để ụng các đị giải toán: Áp d nh luật Newton
Khái ni m hóa: ệ
Vẽ một sơ đồ
Chọn h t thích h p cho m i vệ ọa độ ợ ỗ ật
Phân lo i: ạ
Mô hình ch m cân b ng: ất điể ằ
0
F
Mô hình ch m ch u tác d ng c a l c t ng h p: ất điể ị ụ ủ ự ổ ợ
m
F a=
Phân tích:
Vẽ sơ đồ lực cho mỗi vật
Chỉ ự vẽ các l c tác dụng lên vật
Tìm các thành ph n theo các tr c t ầ ụ ọa độ
Bảo đả ằng các đơn vịm r là nhất quán
Áp d i d ng thành ph n ụng các phương trình thích hợp dướ ạ ầ
Giải phương trình để tìm các ẩn số
Hoàn thành bài gi i ả
Hình 5.8: M t cái hộ ộp
được kéo trên mặt sàn
không ma sát.
10
Kiểm tra các k t qu xem có phù h p v l c không ế ả ợ ới sơ đồ ự
Kiểm tra các giá tr c bi t ị đặ ệ
Bài t p m u 5.2 ậ ẫ : đèn giao thông
Một hộp đèn giao thông có trọng lượng 122 N được treo trên m t s i dây bu c vào hai ộ ợ ộ
sợi dây khác như hình 5.10a. Các sợi dây phía trên không ch c b ng dây th ng ắ ằ ẳng đứ
nên s b d t n u l N. H i hẽ ị ứ ế ực căng lớn hơn 100 ỏ ộp đèn có đứng yên được không hay
là m t trong các s i dây s bộ ợ ẽ ị đứt.
Hình 5.10: Đèn giao thông được treo nhờ các sợi dây cáp
Giải
Khái ni m hóa.ệ H p ộ đèn giao thông
Giả thiết là các s i dây không b t ợ ị đứ
Không có cái gì chuy ển động
Phân loại. Bài toán t bài toán v cân b ng như là mộ ề ằ
Không có chuy ng, v y gia t c b ng không ển độ ậ ố ằ
Mô hình ch m cân b ng ất điể ằ
Phân tích.
Vẽ sơ đồ ộp đèn các lực tác dụng lên h
Vẽ sơ đồ l c tác d ng lên nút bu v trí các dây n i v i nhau: Nút buự ụ ộc ở ị ố ớ ộc là điểm phù
hợp để chọn vì mọi l c ta quan tâm tác d ng d ng dây s n nút ự ụ ọc theo các đườ ẽ đi đế
buộc.
Áp d ng cho nút bu c ụng các phương trình cân bằ ộ
11
Với h ộp đèn, ta có:
3
0 0
y g
F T F
hay
3
g
T F
Với nút bu ộc:
1 1 2 2
cos cos 0
x
F T T
1 1 2 2
sin sin 0
y g
F T T F
Giải các phương trình, ta được:
1
122N
73,4N
sin37,0 cos37,0 tan53,0
T
2
cos37,0
(73,4N) 97,4N
cos53,0
T
Bài t p m u 5.3: M t ph ng nghiêng ậ ẫ ặ ẳ
Một chi c xe kh trên m ng dế ối lượng m đỗ ột đườ ốc nghiêng có đóng băng như trong
hình 5.11a.
(A) Tìm gia t c c a xe, gi t mố ủ ả thiế ặt
đường không có ma sát
Giải:
Khái ni m hóa:ệ dùng hình 5.11a để
khái ni m hóa tình hu ng c a bài ệ ố ủ
toán. T kinh nghi m h ng ngày, ta ừ ệ ằ
biết r ng m t chi c xe trên dằ ộ ế ốc
nghiêng s ng nhanh dẽ chuyển độ ần
xuống dưới.
Phân loại: đây là chất điểm dưới tác
dụng của l c tự ổng h p do xe chuy n ợ ể
độ ống có gia t c.
Phân tích: Các l c tác d ng vào v t: ự ụ ậ
Phản l c vuông góc v i mự ớ ặt
nghiêng.
Trọng l ng th ng xu i. ực hướ ẳng đứ ống dướ
Chọn h c t v i x d c theo m t nghiêng và y vuông góc v i m t nghiêng. ệ trụ ọa độ ớ ọ ặ ớ ặ
Thay tr ng l c b i các thành ph n c a nó (theo x và y). ọ ự ở ầ ủ
Hình 5.11: M t chi c t ph ng ộ ế xe hơi trên mặ ẳ
nghiêng không ma sát
12
Áp d ng mô hình ch m chuyụ ất điể ển động dưới tác dụng c a l c t ng hủ ự ổ ợp theo phương
x và ch m cân b . ất điể ằng theo phương y
sin
x x
F mg ma
cos 0
y
F n mg
Giải phương trình thứ ất, ta đượ nh c
sin
x
a g
(B) Gi s c th t ng thái ngh t nh d c và kho ng cách t c c cả ử xe đượ ả ừ trạ ỉ ừ đỉ ố ả ừ ản trướ ủa
xe đế ất bao lâu để ản trướn chân dốc là . Xe phd ải m c c của nó chạm chân dốc và tốc
độ c n chân dủa xe lúc đế ốc.
Giải:
Đây là nội dung liên quan đế ần độ ốc tìm đượ câu a đển ph ng học. Dùng gia t c ở thay
vào các phương trình độ đó tìm đượng học. Từ c:
2
sin
d
t
g
và
2 sin
xf
v gd
Trường hợp có nhi u v ề ật:
Khi có hai hay nhi u v t k t n i v i nhau ho c ti p xúc nhau, có th áp d nh ề ậ ế ố ớ ặ ế ể ụng các đị
lu thật Newton cho h t v t t ng ệ như mộ ậ ổ ể hay t ng v t riêng r . Ta có th n m ừ ậ ẽ ể chọ ột cách để
gi kiải bài toán và dùng cách khác để ểm tra l i k t qu . ạ ế ả
Bài t p m u 5.4 ậ ẫ : Động cơ Atwood
Khi hai v t có khậ ối lượng khác nhau được
treo th ng trên m t ròng r c nh và ẳng đứ ộ ọ ẹ
không có ma sát ở trục như hình 5.12a thì hệ
vật được gọi là động cơ Atwood. Thiết bị này
thường được dùng trong phòng thí nghiệm để
tìm giá tr c . Hãy tìm gia t c c a các vị ủa g ố ủ ật
và l a s dây nh . ực căng củ ợ ẹ
Giải
Khái ni m hóa:ệ Hãy tưởng tượng tình hu ng ố
trong hình 5.12a: khi m t v t chuy ng ộ ậ ển độ
xuống dưới thì vật kia chuy ng lên trên. ển độ
Vì chúng được nối với nhau bằng một sợ dây
không giãn nên gia t c c l n ố ủa chúng có độ ớ
bằng nhau
Hình 5.12: Động cơ Atwood
13
Phân loại: Các v t trong máy Atwood ch u tác d ng c a tr ng l c cậ ị ụ ủ ọ ực cũng như lự ủa
các dây bu c vào chúng nên ta có th phân loộ ể ại bài toán này như là bài toán có hai chất
điểm dưới tác dụng của lực tổng hợp.
Phân tích: Các l c tác d ng lên các v t: ự ụ ậ
Lực căng dây như nhau ở ( hai vật và n dây) ở các đoạ
Trọng l c ự
Các v t có gia t c n i v i nhau. ậ ốc như nhau do chúng đượ ố ớ
Vẽ sơ đồ lực
Áp d nh lu : ụng các đị ật Newton
Cho v t th nh ậ ứ ất
1 1
y y
F T m g m a
Cho v t th 2: ậ ứ
2 2
y y
F m g T m a
Giải để tìm các ẩn
2 1
1 2
y
m m
a g
m m
và
1 2
1 2
2
m m
T g
m m
Hoàn tất: Giá tr ị tìm được của gia t c có th ố ể diễn giải như là tỉ ữa độ số gi chênh lệch
về lực c a h và t ng kh ng c a h nh lu t 2 Newton. ủ ệ ổ ối lượ ủ ệ, như dự đoán của đị ậ
Bài t p m u 5.5 Hai v ng có gia ậ ẫ : ật chuyển độ
tốc n i nhau b ng m t s i dây. ố ằ ộ ợ
Một qu c u khả ầ ối lượng m
1
và m t kh i h p khộ ố ộ ối
lượng c n i v i nhau b i mm
2
đượ ố ớ ở ột dây nhẹ vắt
qua m ròng r c nh quaột ọ ẹ y không ma sát như
hình 5.15a. i h p n m trên m t m t nghiêng Khố ộ ằ ộ ặ
không có ma sát v i góc nghiêng ớ
. Tìm độ lớn
của gia t c c a hai vố ủ ật và s ức căng dây.
Giải:
Khái ni m hóa: ệ Hãy hình dung các v t trong ậ
hình 5.13 đang chuyển độ đi xuống. Nếu m
2
ng
thì m
1
s c n i v i nhau ẽ đi lên. Do các vật đượ ố ớ
bằng s i dây nên gia tợ ốc của chúng có cùng độ
lớn. Sử d ng h t ng cho qu cụ ệ ọa độ bình thườ ả ầu
và h t i h p. ệ ọa độ “nghiêng” cho khố ộ
Phân loại: Theo các phương y và x’ thì đây là
bài toán thì là bài toán v t cân vật ch u tác d ng c a l c t ng hị ụ ủ ự ổ ợp. Theo phương y’ ậ
bằng.
Hình 5.13: Hai v c n i vật đượ ố ới
nhau b ng s i dây nhé v t qua ằ ợ ắ
một ròng r c không có ma sát. ọ
14
Phân tích: Xét các sơ đồ ực như trong hình 5.13b và 5.13c thì có thể ụng đị l áp d nh
luật 2 Newton cho các v ật như sau:
Với qu c u: ả ầ
1 1 1
y y
F T m g m a m a
Với kh i h p: ố ộ
' 2 2 ' 2
sin
x x
F m g T m a m a
' 2
cos 0
y
F n m g
Giải các phương trình trên, ta được:
2 1
1 2
sin
m m
a g
m m
và
1 2
1 2
sin 1
m m
T g
m m
Hoàn tất: Khối h p chuy ng có gia t c xu i n u ộ ển độ ố ống dướ ế m
2
sin
> c l i, m
1
. Ngượ ạ
gia t c c a kh i h ng lên trên và gia t c c a qu c ng xu i. T kố ủ ố ộp hướ ố ủ ả ầu hướ ống dướ ừ ết
quả gia t c, có th y r ng gia t c là tố ể thấ ằ ố ỉ số giữa độ lớn của ngoại lực tác dụng lên hệ
với tổng kh ng c a các v t trong h . ối lượ ủ ậ ệ
Các l c ma sát ự
Khi m t v t chuy ng trên b mộ ậ ển độ ề ặt hoặc
xuyên qua m ng nh t thì s xu t hi n sột môi trườ ớ ẽ ấ ệ ức
cản chuyển động. Đó là do các tương tác giữa vật và
môi trườ ản này đượng quanh nó. Sức c c gọi là lực
ma sát.
5.8.1 Lực ma sát nghỉ (tĩnh)
Lực ma sát ngh cho v t không chuy n ỉ giữ ậ ể
độ ừng. Ch ng nào v ng thì lật chưa chuyển độ ực ma
sát ngh ng l ng t bên ngoài = F ỉ đúng bằ ực tác độ ừ ƒ
s
Nếu F tăng thì f
s
tăng và ngược lại.
Gọi µ
s
là h s ma sát ngh ệ ố ỉ thì ƒ
s
µ
s
n
Lưu ý: dấ ắt đầu bằng xảy ra khi các mặt b u
trượt lên nhau.
5.8.2 Lực ma sát trượt (động)
Lực ma sát trượt tác dụng khi vật chuy ng. ển độ
Hệ s ố ma sát trượt µ
k
có th ể thay đổi theo tốc độ
của v t, tuy nhiên, ta b qua s i này. ậ ỏ ự thay đổ
ƒ
k
= µ
k
n
Khảo sát lực ma sát: Để ảo sát, ta tăng dần độ kh lớn c a ngo i l F và ghi l i giá tr củ ạ ực ạ ị ủa
lực ma sát. Chú ý th m v t bời điể ậ ắt đầu trượt. Đồ thị bi u di n quan h a l c ma sát và ể ễ ệ giữ ự
ngoại lực cho trên hình 5.16c.
Hình 5.14: Kéo m t v t b u ộ ậ ắt đầ
chuyển độ ắng đượng khi th c lực ma
sát ngh . ỉ
15
Lưu ý:
Các phương trình này chỉ quan tâm đến độ lớn của các l c, chúng không ph i là ự ả
phương trình vec-tơ.
Với ma sát ngh ( u b ng chỉ f
s
), dấ ằ ỉ đúng khi vậ ển độ ắp trượt sắp chuy ng, các bề mặt s t
lên nhau. N u các b m t lên nhau thì dùng d u nh ế ề ặt chưa trượ ấ ỏ hơn
Hệ s ma sát ph c vào các m t ti p xúc. ố ụ thuộ ặ ế
Lực ma sát ngh ng l ng). ỉ (tĩnh) thườ ớn hơn lực ma sát trượt (độ
Hướng c a l c v ng c a chuy ng và song song v i các mủ ực ma sát ngượ ới hướ ủ ển độ ớ ặt
tiếp xúc.
Hệ s ma sát h c vào di n tích m t ti p xúc. ố ầu như không phụ thuộ ệ ặ ế
5.8.3 Ma sát trong các bài toán dùng nh lu t Newton các đị ậ
Ma sát là m t l c n thêm nó vào tron nh lu t Newton. ộ ực, do đó chỉ ầ g các đị ậ
Các qui t c vắ ề ma sát cho phép ta xác định hướng và
độ ự lớn của l c ma sát.
Bài t p m u 5.6: thí nghiậ ẫ ệm xác định
s
và
k
Một kh i hố ộp đang nằm trên m t mộ ặt nghiêng như
hình 5.15. Nâng d n khi h p ần góc nghiêng cho đế ộ
bắt đầu trượt. Ch ng t r ng có thứ ỏ ằ ể tìm được hệ s ố
ma sát ngh ỉ
s
theo góc t i h n ớ ạ
.
Giải:
Khái ni m hóa:ệ Tưởng tượng r ng kh i h p có xu ằ ố ộ
hướng trược xuống dưới do tác d ng c a tr ng l c. ụ ủ ọ ự
Hộp trượt xuống nên ma sát sẽ hướng lên phía
trên.
Phân loại: Khối h p ch u tác d ng c a nhi u lộ ị ụ ủ ề ực
khác nhau, tuy nhiên, nó chưa trượt xu ng d c nên ố ố
đây là bài toán chất điểm cân bằng.
Phân tích: Sơ đồ lực trên hình 5.15 cho th y các l c tác d ng vào h p g m: tr ng lấ ự ụ ộ ồ ọ ực
g
m
, ph n lả ực
n
và l c ma sát ngh ự ỉ
f
s
. Ch n tr d c theo m t nghiêng và vuông ọ ục x ọ ặ y
góc v i m t nghiêng. ớ ặ
sin 0
x s
F mg f
cos 0
y
F n mg
Giải hệ phương trình ta có
sin tan
s
f mg n
Với góc nghiêng t i h n ớ ạ
c
thì l c ma sát ngh b ng ự ỉ ằ
s s
f n
nên
tan
s c
.
Hình 5.15: M t kh i hộ ố ộp trượt
trên m t m t ph ng nghiêng có ộ ặ ẳ
ma sát
16
Hoàn tất: Khi h p b t thì ộ ắt đầu trượ

≥
c
. Hộp trượ ống dướt có gia tốc xu i thì lực ma
sát trượt
k k
f n
. Tuy nhiên, n u gi m góc q thì v t xu ng, n u vế ả ật cũng có thể trượ ố ế ật
trượt th u thì ẳng đề
tan
k c
với
c c
Lưu ý: V i b trí thí nghiớ ố ệm như trên thì ta có thể xác đị nh hệ số ma sát b ng thằ ực
nghiệm: = tan µ
Với µ
s
, sử d ng góc nghiêng khi kh i h p b t. ụ ố ộ ắt đầu trượ
Với µ
k
, sử d ng góc nghiêng khi mà kh i h t xu ng v i t i. ụ ố ộp trượ ố ớ ốc độ không đổ
Bài t p m u 5.7: M t qu bóng khúc côn c t ậ ẫ ộ ả ầu đang trượ
Một qu bóng khúc côn c t trên mả ầu trượ ặt băng vớ ốc độ ban đầi t u là 20,0 m/s. Quả
bóng trượt đượ m trướ ại. Hãy xác đị ma sát trược 115 c khi dừng l nh hệ số t giữa qu ả
bóng và băng.
Giải:
Khái ni m hóa: ệ Giả sử qu bóng chuyả ển
động sang ph c ma sát ải như hình 5.16. Lự
trượt tác dụng về ả ả bên ph i và làm qu bóng
chuyển động ch m lậ ại cho đến khi d ng h n. ừ ẳ
Phân loại: Các l c tác d ng lên qu bóng ự ụ ả
như trong hình 5.16, nhưng bài toán lại cho
các bi n s v ng h phân ế ố ề độ ọc. Do đó, có thể
loại bài toán b ng nhi u cách khác nhau. ằ ề
Theo phương thẳng đứng, đây là bài toán
chất điểm cân b ng (t ng l c tác d ng lên vằ ổ ự ụ ật
bằng 0). Theo phương ngang, là bài toán chất
điểm có gia tốc không đổi.
Phân tích: Vẽ sơ đồ ật, lưu ý đế ực ma sát (ngượ lực tác dụng lên v n l c chiều chuyển
động, song song với mặt tiếp xúc).
Áp d ng mô hình ch m ch u tác d ng c a l c t ng h : ụ ất điể ị ụ ủ ự ổ ợp theo phương x
x k x
F f ma
Áp d ng mô hình ch m cân b : ụ ất điể ằng theo phương y
0
y
F n mg
Giải h ệ phương trình, với định nghĩa lực ma sát trượt, ta được:
x k
a g
Sau khi tìm đượ ụng mô hình độ ọc, ta tìm được gia tốc, áp d ng h c
Hình 5.16: qu khúc con c t có ả ầu trượ
ma sát trên m ặt băng
17
2
2
xi
k
f
v
gx
thay số:
0,117
k
Hoàn tất: Lưu ý rằng
k
không có th nguyên và có giá tr i v i m t vứ ị bé, không đổ ớ ộ ật
trượt trên m ặt băng.
Bài t p m u 5.8: Gia t c cậ ẫ ố ủa hai v i v i nhau khi có ma sát ật nố ớ
Một kh i h p có kh ng n m trên mố ộ ối lượ m
2
ằ ột m c nặt ngang, nhám đượ ối v i mớ ột qu ả
cầu kh ng bối lượ m
1
ằng m t s i dây nh v t qua m t ròng r c nhộ ợ ẹ ắ ộ ọ ẹ, không ma sát như
trong hình 5.20a. Tác d ng vào kh i h p m t l l n h p vụ ố ộ ộ ực có độ ớ F ợ ới phương ngang
một góc
và kh i h p chuy ng sang ph i. H số ộ ển độ ả ệ ố ma sát trượt giữa kh i h p và ố ộ
mặt ngang là
k
Tìm độ lớn của gia tốc của hai vật.
Hình 5.17: h 2 v t n i nhau khi có ma sát. ệ ậ ố
Giải:
Khái ni m hóa: ệ Hình dung xem chuy n gì x y ra khi tác d ng lệ ả ụ ực
F
vào kh i h p. ố ộ
Giả s l l c ma sát nghử ực đủ ớn hơn lự ỉ nhưng không đủ ớn để l nhất hộp lên, h p s ộ ẽ
trượt sang phải và quả c c kéo lên. ầu đượ
Phân loại: Bài toán này là bài toán hai . Vì chất điểm dưới tác dụng của lực tổng hợp
khối h p không b nh c lên nên the ng, kh i h c xem là ộ ị ấ o phương thẳng đứ ố ộp đượ chất
điểm cân bằng.
Phân tích: Vẽ sơ đồ lực cho từng v t (hình 5.17b và 5.17c). ậ
Áp d ng mô hình ch m ch u tác d ng c a l c t ng h p cho kh i hụ ất điể ị ụ ủ ự ổ ợ ố ộp theo phương
ngang:
2 2
cos
x k x
F F f T m a m a
(1)
Áp d ng mô hình ch m cân b ng cho kh i hụ ất điể ằ ố ộp theo phương thẳng đứng
2
sin 0
y
F n F m g
(2)
Áp d ng mô hình ch m ch u tác d ng c a l c t ng h p cho qu cụ ất điể ị ụ ủ ự ổ ợ ả ầu theo phương
thẳng đứng:
18
1 1 1
y y
F T m g m a m a
(3)
Giải h ệ phương trình, ta tìm được:
1 2
1 2
cos sin
k k
F m m g
a
m m
(4)
Hoàn tất: Gia t c c a kh i h p có th ng sang ph i ho c trái tùy theo d u c a t ố ủ ố ộ ể hướ ả ặ ấ ủ ử
số trong phương trình (4). Nế ộp hướ ải đổu vận tốc của khối h ng sang trái thì ph i dấu
của f
k
trong (1). Trong trườ ợp đó, chỉ ần đổng h c i hai dấu cộng (+) trong tử số của (4)
thành d u tr ( ấ ừ –).
Câu h i lý thuyỏ ết chương 5:
1. Trong bức tranh It Happened One Night (Columbia Pictures, 1934), Clark Gable đang
đứng trên xe bus, đằng sau là Claudette Colbert đang ngồi. Xe bus độ ột đi vềt ng phía
trước và Clark ngã vào long Claudette. T y ra? ại sao điều đó xả
2. Một ngườ trái banh trên tay. (a) Xác địi giữ nh t t c các ngo i l c tác d ng lên trái banh ấ ả ạ ự ụ
và xác định ph n lả ực theo định lu t 3 Newton c a m i lậ ủ ỗ ực đó. (b) Nếu trái banh rơi xuống,
lực gì tác dụng vào nó khi nó đang rơi? Xác định ph n l c c a nó. (B qua l c c n không ả ự ủ ỏ ự ả
khí).
3. S ợi dây B m nh, nhả ẹ, không co giãn nối
vật 1 và v t 2, bi t v t 2 nậ ế ậ ặng hơn vật 1
(hình). Dây A tác d ng l c lên vụ ự ật 1 làm
nó chuy ng có gia t c v c. ển độ ố ề phía trướ
(a) So sánh độ lớn l c dây A tác d ng lên ự ụ
vật 1 với l c do dây B tác d ng lên v t 2? ự ụ ậ
(b) So sánh gia t c c a v t 1 và v t 2. (c) ố ủ ậ ậ
Xác định lực do dây B tác dụng lên vật 1
và so sánh l c do dây B tác d ng lên hai v ự ụ ật.
Bài tập chương 5:
1. qu Một động cơ tên lửa đồ chơi đượ c gắn vào một ả bóng l n, chúng có th t không ớ ể trượ
ma sát trên m ng n m ngang. Qu bóng n ng 4 kg có v n t c 3.00ặt phẳ ằ ả ặ ậ ố i m/s tại 1 thời
điểm, và 8s sau vận tốc nó là (8.00i+ 10.00j) m/s. Gi s ng l c không ả ử động cơ đã tác dụ ự
đổi theo phương ngang lên quả ần và (b) độ bóng, tìm (a) các thành ph lớn của lực trên.
ĐS: 1
,53m; 5,29
o
2.
Một electron n ng 9,1.10 kg có vặ
-31
ận t u 3.10 c 5cm thì t ốc đầ
5
m/s. Nó đi thẳng đượ ốc độ
c
ủa nó tăng lên 7.10
5
m/s. Gi s gia t c c a nó là h ng s . (a) X l n c a lả ử ố ủ ằ ố ác định độ ớ ủ ực
tác d ng vào electron và (b) so sánh l c này v i tr ng c a electron. ụ ự ớ ọng lượ ủ
ĐS: 3
,64.10
-18
N; 4,08.10 l
11
ần
19
3. Một xe hơi nặng 1000kg đang kéo một toa moóc 300kg. C 2 cùng ti n vả ế ề c vphía trướ ới
gia t c 2.15m/s qua l c c nh:
ố
2
. Bỏ ự ản không khí và ma sát. Xác đị
(a) Tổng l c tác d ự ụng lên xe hơi.
(b) Tổng l c tác d ng lên toa moóc. ự ụ
(c) Lực do toa moóc tác d . ụng lên xe hơi
(d) Lực do xe hơi tác dụng lên đường.
ĐS: 2
,15.10
3
N; 645N; 645N; 1,02.10 N
4
4. Một s i dây dài 35, u trên c i treo m t bulong s t nợ 7cm đầ ố định, đầu dướ ộ ắ ặng 65g. Đặt
một nam châm l i g n bên ph i bulong s m), bulong s t b hút v phía ạ ầ ả ắt đó (không chạ ắ ị ề
nam châm theo phương ngang, nó đi được 28m r i d ng l t tr ng thái cân b ng). ồ ừ ại (đạ ạ ằ
(a) Vẽ sơ đồ lực tác dụng lên bulong.
(b) Tính l ực căng trên dây.
(c) Tính l d ng lên bulong. ực từ tác ụ
ĐS: 1,03N; 0,805N
5. Hình bên bi u di n các lể ễ ực theo phương ngang tác dụng
vào con thuy ng b c v i vền đang di chuyển theo hướ ắ ớ ận
tốc không đổ ốc đội khi nhìn từ trên cao. Lúc t con thuyền
đạ ị ựt giá tr xác định, nước tác dụng l c 220N lên thân tàu,
góc θ = 40
o
. Hãy viết 2 phương trình thành phần biểu di n ễ
định lu nh ật 2 Newton, sau đó giải phương trình để xác đị
P – l c gió tác d ng lên thuy n và l c n lự ụ ề ự – ực nước tác
dụng lên đáy thuyền trong 2 trường hợp sau:
(a) Chọn chi u trề ục x theo hướng đông, trục y theo hướng
bắc;
(b) Chọn trục x theo hướng đông bắc, phương tạo góc θ = 40o so với phương đông; trục
y theo hướ ắc, phương tạo góc θ = 40o so với phương bắng tây b c.
(c) So sánh 2 k t qu câu (a) và (b): chúng có bế ả ằng nhau không? Phương pháp nào dễ
làm hơn?
ĐS: 262N; 262N; 342N
6. Bốn cơ hệ như trên hình bên đều đang ở trạng
thái cân b ng. Lằ ực k c ch nh theo ế lò xo đượ ỉ
đơn vị đọc đượ Newton. Hỏi giá trị c từ các lực
kế trên. Gi sả ử bỏ qua kh ng ròng r c và ối lượ ọ
ma sát gi a dây v i ròng rữ ớ ọc cũng như ma sát
giữa v t v i m t ph ng nghiêng. ậ ớ ặ ẳ
ĐS: 49N-49N-98N-24.5N
20
7. Một cơ hệ cho như hình vẽ bên. Các
vật trượt không ma sát trên mặt
ngang và l c tác d ng vào kh i 3kg ự ụ ố
là 42N. Xác định (a) gia t c c a hố ủ ệ,
(b) lực căng dây giữa khối 3kg và
1kg và (c) l c tác d ng c a kh i 1kg ự ụ ủ ố
lên kh i 2kg. ố
ĐS: 7
m/s
2
; 21N; 14N
8. Khoảng cách giữa hai c n tho i 50m. Chú chim n u chính giột điệ ạ ặng 1kg đậ ở ữa m t dây ộ
điện thoai n i hai c n tho i trên làm dây b chùng xu ng m t ố ột điệ ạ ị ố ộ đoạn 0.2m, b qua khỏ ối
lượng dây.
(a) Vẽ sơ đồ lực các lực tác dụng lên chú chim.
(b) Tính l do chú chim tác d ng lên dây. ực căng ụ
ĐS: 613N
9. Một vật đang chuyển động trên m t mộ ặt phẳng, với t x và cho bọa độ ởi phương trình x =
5t
2
– 1 (m), y = 3t l n t ng l
3
+ 2 (m). Tính độ ớ ổ ực tác d ng lên ụ
vật t i th m t = 2s. ạ ời điể
ĐS: 112N
10. Một bao xi măng có trọng lượng 325N treo cân b ng nh 3 sằ ờ ợi
dây như hình bên. Cho θ , θ ực căng
1
= 60
o
2
= 40 . Tính các l
o
dây T , T khi h ng thái cân b ng.
1
, T
2 3
ệ ở trạ ằ
ĐS: 253N, 165N, 325N
11. Hai ngườ ợi dây theo phương i kéo một con thuyền bằng 2 s
ngang. N u h kéo cùng chi u thì con thuy n chuy ng vế ọ ề ề ển độ ới
gia t c 1,52 m/s v
ố
2
ề ả phía ph i. Còn nếu họ kéo ngược chiều
nhau thì con thuy n chuy ng v i gia t c 0,518 m/s v
ề ển độ ớ ố
2
ề
phía trái. Xác định độ lớn lực do mỗi người tác dụng lên thuyền. Giả sử không quan tâm
đến các l c tác dực theo phương ngang khá ụng lên thuyền.
ĐS: 100N; 204N
12. Các qu nả ặng được treo trên các dây nối
với tr n c a thang máy, bi t thang máy ầ ủ ế
đang di chuyển với vận tốc không đổi.
Tính giá tr các l T Tị ực căng dây T
1 2 3
ở
2 ng h p trên.trườ ợ
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chương 5: Các định luật về chuyển động
Khái niệm về lực
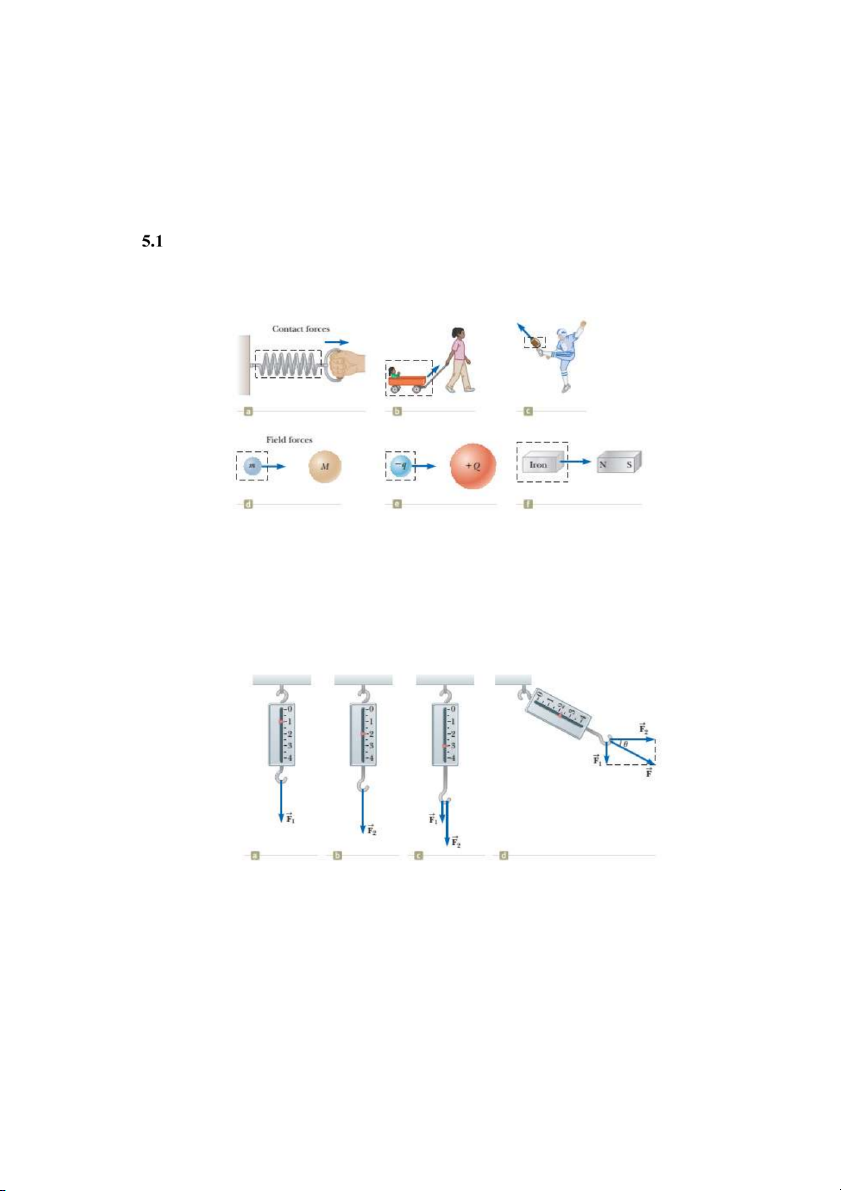
Có thể phân các loại lực thành hai nhóm: (1) Lực do có tiếp xúc (lực đàn hồi của lò xo,
lực căng dây, lực đàn hồi ở các điểm tiếp xúc giữa các vật…) (2) Lực của một trường lực
(lực hấp dẫn, lực tĩnh điện, lực từ)
Hình 5.1: a, b, c lực do có tiếp xúc; d, e, f lực của một trường
Bản chất vectơ của lực: Lực là đại lượng vectơ nên khi tìm lực cần chú ý đến điểm đặt,
phương, chiều và độ lớn của lực. Khi tổng hợp các lực, cần chú ý qui tắc cộng vectơ.
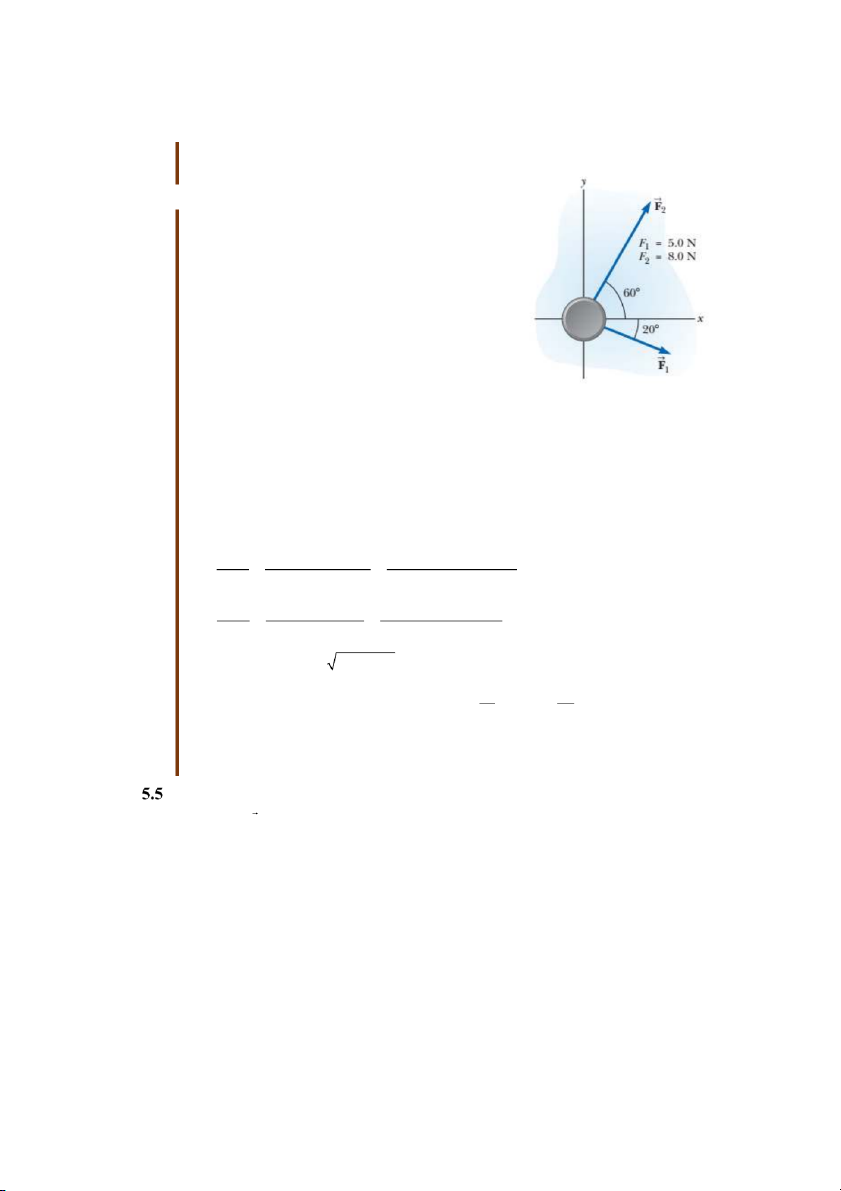
Hình 5.2 minh họa 2 lực tác dụng vào móc của lực kế theo 2 cách khác nhau: 2 lực cùng
phương và 2 lực vuông góc với nhau. Khi tác dụng dọc theo trục lò xo, lực F1 và F2 lần lượt
làm lò xo giãn ra 1cm và 2cm (hình 5.2 a,b). Nhưng hai lực này tác dụng vuông góc với nhau
thì lò xo giãn ra 2,24cm (hình 5.2d).
Hình 5.2: Các lực tác dụng lên lực kế: a. lực F1; b. lực F2; c. 2 lực F1 và F2 cùng phương
chiều; d. 2 lực F1 và F2 vuông góc với nhau. 1
Định luật Newton thứ nhất và các hệ qui chiếu quán tính
5.2.1 Định luật Newton thứ nhất:
Nếu một vật không tương tác với các vật khác thì ta có thể xác định một hệ qui chiếu
trong đó vật có gia tốc bằng 0.
Hình 5.3: Miếng nhựa đặt trên đệm khí.
5.2.2 Hệ qui chiếu quán tính
Một hệ qui chiếu mà định luật Newton thứ nhất được thỏa mãn gọi là hệ qui chiếu quán tính.
Một dạng phát biểu khác của định luật Newton thứ nhất:
Khi không có ngoại lực tác dụng và được quan sát từ một hệ qui chiếu quán tính, một vật
đứng yên sẽ vẫn đứng yên và một vật chuyển động sẽ tiếp tục chuyển động với vận tốc không
đổi (tức là chuyển động với tốc độ không đổi theo một đường thẳng).
Ví dụ như khi xét một miếng nhựa tròn đặt trên bàn đệm khí, và bàn này đặt trên mặt đất
thì miếng nhựa này không tương tác với vật nào khác theo phương ngang nên gia tốc của nó
theo phương ngang bằng không. Nếu bàn đệm khí này được đặt trên một con tàu chuyển động
thẳng đều thì ta cũng quan sát được hiện tượng tương tự. Tuy nhiên, nếu tàu chuyển động có
gia tốc thì hệ qui chiếu gắn với tàu không còn là hệ qui chiếu quán tính nữa. Một người đứng
trên tàu sẽ thấy miếng nhựa chuyển động có gia tốc. Hệ qui chiếu gắn với tàu là hệ qui chiếu
phi quán tính. Mặc dầu vậy, một người quan sát đứng yên trên mặt đất vẫn thấy miếng nhựa
chuyển động thẳng đều.
Một hệ qui chiếu chuyển động với vận tốc không đổi đối với các ngôi sao ở rất xa là một
xấp xỉ tốt nhất cho một hệ qui chiếu quán tính. Trong nhiều trường hợp, Trái Đất cũng có thể
xem là một hệ qui chiếu quán tính.
Khoảng trước năm 1600 thì người ta cho rằng trạng thái tự nhiên của vật chất là trạng
thái nghỉ (đứng yên). Galileo là người đầu tiên đưa ra cách nhìn nhận mới về chuyển động và
trạng thái tự nhiên của vật chất. Theo ông thì “Vận tốc mà ta truyền cho một vật chuyển động
sẽ được bảo toàn nếu các nguyên nhân bên ngoài làm chậm chuyển động bị loại bỏ”. Lúc đó
vật không tìm về “trạng thái nghỉ bản chất” nữa.
Câu hỏi 5.1: Hãy chọn phát biểu đúng trong các phát biểu sau:a) Một vật có thể chuyển động
khi không có lực tác dụng lên vật đó. b) Một vật có thể không chuyển động khi có lực tác
dụng lên vật đó. c) Cả (a) và (b) đều đúng. d) Cả (a) và (b) đều sai. 2
5.2.3 Cách phát biểu khác của định luật Newton thứ nhất
Nếu không có ngoại lực tác dụng và được quan sát từ một hệ qui chiếu quán tính thì một
vật đứng yên sẽ đứng yên và một vật chuyển động sẽ tiếp tục chuyển động với vận tốc không
đổi (tức là chuyển động thẳng đều).
Nói cách khác, nếu không có lực tác dụng lên vật thì gia tốc của vật bằng không. Bất kỳ
vật cô lập nào cũng đứng yên hoặc chuyển động thẳng đều. Khuynh hướng chống lại sự thay
đổi vận tốc của một vật được gọi là quán tính.
5.2.4 Định nghĩa lực
Lực là nguyên nhân làm thay đổi chuyển động của một vật
Khối lượng
5.3.1 Định nghĩa khối lượng
Khối lượng là một thuộc tính của vật xác định mức độ chống lại sự thay đổi vận tốc của
nó. Đơn vị của khối lượng trong hệ đo lường quốc tế là kilôgram (kg). Các thí nghiệm đã cho
thấy, dưới tác dụng của một lực cho trước thì vật có khối lượng càng lớn sẽ thu được gia tốc
càng nhỏ. Nếu cho cùng một lực tác dụng lên hai vật có khối lượng lần lượt là m1 và m2.
Các khối lượng có thể định nghĩa theo gia tốc tạo ra bởi một lực cho trước tác dụng lên chúng: m a 1 2  (5.1) m a 2 1
Độ lớn của gia tốc tác dụng lên một vật tỉ lệ nghịch với khối lượng của vật.
Khối lượng là thuộc tính cố hữu của một vật, không phụ thuộc vào môi trường xung
quanh vật và phương pháp được dùng để đo lường nó. Khối lượng là đại lượng vô hướng.
Khối lượng tuân theo các phép tính số học thông thường.
Khối lượng và trọng lượng:
Khối lượng và trọng lượng (weight) là hai đại lượng khác nhau. Trọng lượng là độ lớn
của lực hấp dẫn tác dụng lên vật. Trọng lượng có thể thay đổi tùy theo vị trí của vật. Ví dụ:
 wearth = 180 lb; wmoon ~ 30 lb
 mearth = 2 kg; mmoon = 2 kg
Định luật Newton thứ hai
Khi xem xét từ một hệ quy chiếu quán tính, gia tốc của một vật tỉ lệ thuận trực tiếp với
lực tổng hợp tác dụng lên vật và tỉ lệ nghịch với khối lượng của nó.
Lực là nguyên nhân của các thay đổi trong chuyển động, được đo thông qua gia tốc. 3
Cần lưu ý là một vật có thể chuyển động mà không cần có lực tác dụng. Không được diễn
giải rằng lực là nguyên nhân của chuyển động. Về mặt đại số thì:  a   F a m (5.2) m
ở đây, hệ số tỉ lệ được chọn bằng 1 và các tốc độ chuyển động của các vật phải nhỏ hơn nhiều
so với tốc độ ánh sáng. Trong đó, F là lực tổng hợp, là tổng vectơ của tất cả các lực tác
dụng lên vật (còn gọi là lực toàn phần).
Định luật Newton thứ 2 cũng có thể được biểu diễn theo các thành phần: Fx = maxFy = mayFz = maz
Lưu ý: ma không phải là một lực.
Tổng tất cả các lực bằng tích của khối lượng của vật với gia tốc của nó.
Đơn vị của lực: Trong SI, đơn vị của lực là newton (N)  1 N = 1 kg·m / s2
Theo hệ đơn vị của Mỹ thì đơn vị của lực là pound (lb).  1 lb = 1 slug·ft / s2
Quy đổi đơn vị: 1 N ~ ¼ lb
Câu hỏi 5.2: Một vật chuyển động không gia tốc. Hãy chọn phát biểu không đúng trong các
phát biểu sau:a) Chỉ có một lực tác dụng lên vật đó. b) Không có lực nào tác dụng lên vật. c)
Các lực tác dụng lên vật, nhưng không gây ra tác dụng.
Câu hỏi 5.3: Khi đẩy một vật từ trạng thái nghỉ trượt qua một mặt sàn không ma sát với lực
không đổi trong khoảng thời gian Δt, kết quả vật thu được tốc độ v. Sau đó, lặp lại thí nghiệm
trên với lực đẩy lớn hơn 2 lần. Hỏi để đạt được vận tốc cuối cùng như thí nghiệm trên thì thời
gian đẩy vật là?a) 4Δt; b) 2 Δt; c) Δt; d) Δt.
Bài tập mẫu 5.1: Chuyển động có gia tốc của quả bóng khúc côn cầu.
Một quả bóng Khúc côn cầu có khối lượng 0,3kg trượt không ma sát trên mặt băng
phẳng. Hai cây gậy Khúc côn cầu đánh vào quả bóng cùng một lúc như hình 5.4. Lực
F1 có độ lớn 5N và theo phương nghiêng một góc 20 độ ở dưới trục Ox. Còn lực F2 có 4
độ lớn 8N có phương nghiêng một góc 60 độ phía trên trục Ox. Hãy xác định độ lớn
và phương của gia tốc chuyển động của quả bóng. Giải.
Khái niệm hóa: Từ hình 5.4: sử dụng kiến thức
cộng vectơ ở chương 3, có thể tính được tổng hợp
lực tác dụng lên quả Khúc côn cầu. Từ đó, suy ra
gia tốc chuyển động của quả Khúc côn cầu sẽ cùng
phương chiều với tổng hợp lực đó.
Phân loại: Bởi vì bài toán có thể tính ra tổng hợp
lực, và mục tiêu là tìm gia tốc. Do đó, mô hình được
sử dụng là mô hình chất điểm dưới tác dụng của tổng hợp lực. Phân tích:
Tìm lực tổng hợp lên vật theo phương Ox:
Hình 5.4: Quả Khúc côn cầu
F F F F   F   cos cos
chuyển động trên bề mặt không x 1x 2x 1 2
ma sát dưới tác dụng của 2 lực.
Tổng hợp lực theo phương Oy:
F F F F    sin F si n y 1y 2y 1 2
Áp dụng định luật Newton 2 theo từng phương: F F F x co 5 ( 20) 8 60 1  s co 2  s cos   a    cos2 29m/s x m m 0,3 F F F y sin  sin 5sin(20)  a   8 60 1 2  sin2 1 m 7 /s y m m 0,3
Gia tốc của vật là: a  2  2 29 17  2 3 m 4 /s a y 17 1 1  
Phương của gia tốc đối với trục Ox:     tan    tan    0 31  ax   29 
Hoàn tất: Sử dụng phương pháp cộng vectơ trên hình 5.4, có thể kiểm chứng lại kết quả thu được.
Lực hấp dẫn và khối lượng
Lực hấp dẫn F là lực mà Trái đất tác dụng lên một vật. Lực này hướng về tâm của Trái g
đất, và độ lớn của nó được gọi là trọng lượng của vật.
Theo định luật Newton thứ 2 thì: 5 F g m (5.5) g
Do đó, trọng lượng của vật: F = mg (5.6) g
Nói thêm về trọng lượng :
Do trọng lượng phụ thuộc vào gia tốc trọng trường (g) nên nó sẽ thay đổi theo vị trí .
 Càng lên cao thì g và trọng lượng càng giảm.
 Điều này cũng áp dụng được cho các hành tinh khác, nhưng g thay đổi theo hành tinh
nên trọng lượng cũng thay đổi từ hành tinh này sang hành tinh khác.
Trọng lượng không phải là thuộc tính cố hữu của vật. Trọng lượng là thuộc tính của một
hệ các vật: vật và Trái đất. Về đơn vị thì kg không phải là đơn vị của trọng lượng. Công thức
1kg=2,2lb là công thức tương đương và chỉ đúng trên mặt đất.
Khối lượng hấp dẫn và khối lượng quán tính:
Trong các định luật của Newton, khối lượng là khối lượng quán tính và đo bằng sự cản
trở đối với sự thay đổi chuyển động của vật. Còn trong công thức (5.6) khối lượng m cho biết
lực hấp dẫn giữa vật và Trái Đất. Các thí nghiệm cho thấy khối lượng quán tính và khối lượng
hấp dẫn có cùng giá trị.
Câu hỏi 5.4: Giả sử rằng bạn đang gọi một cuộc điện thoại liên hành tinh với bạn của bạn ở
trên Mặt Trăng. Người bạn đó kể rằng anh ta mới thắng được 1 Newton vàng trong một cuộc
thi. Anh ta khuyên bạn nên tham dự cuộc thi đó phiên bản Trái Đất và nếu chiến thắng cũng
được 1 Newton vàng. Hỏi nếu điều đó xảy ra, ai sẽ giàu hơn?, a) Bạn sẽ giàu hơn; b) Bạn của
bạn giàu hơn; c) Cả 2 giàu bằng nhau.
Định luật Newton thứ 3
Nếu hai vật tương tác, lực F do vật 1 tác dụng lên vật 2 bằng về độ lớn nhưng ngược 12
chiều với lực F do vật 2 tác dụng lên vật 1. 21
F  F (5.7) 12 21
Lưu ý về ký hiệu: F là lực do A tác dụng lên B. AB
Một cách phát biểu khác của định luật: 6
Lực tác dụng và lực phản tác dụng (phản lực) bằng
nhau về độ lớn nhưng ngược chiều.
 Một trong hai lực là lực tác dụng, lực kia là phản lực.
 Lực và phản lực phải tác dụng lên hai vật khác nhau và cùng loại với nhau.
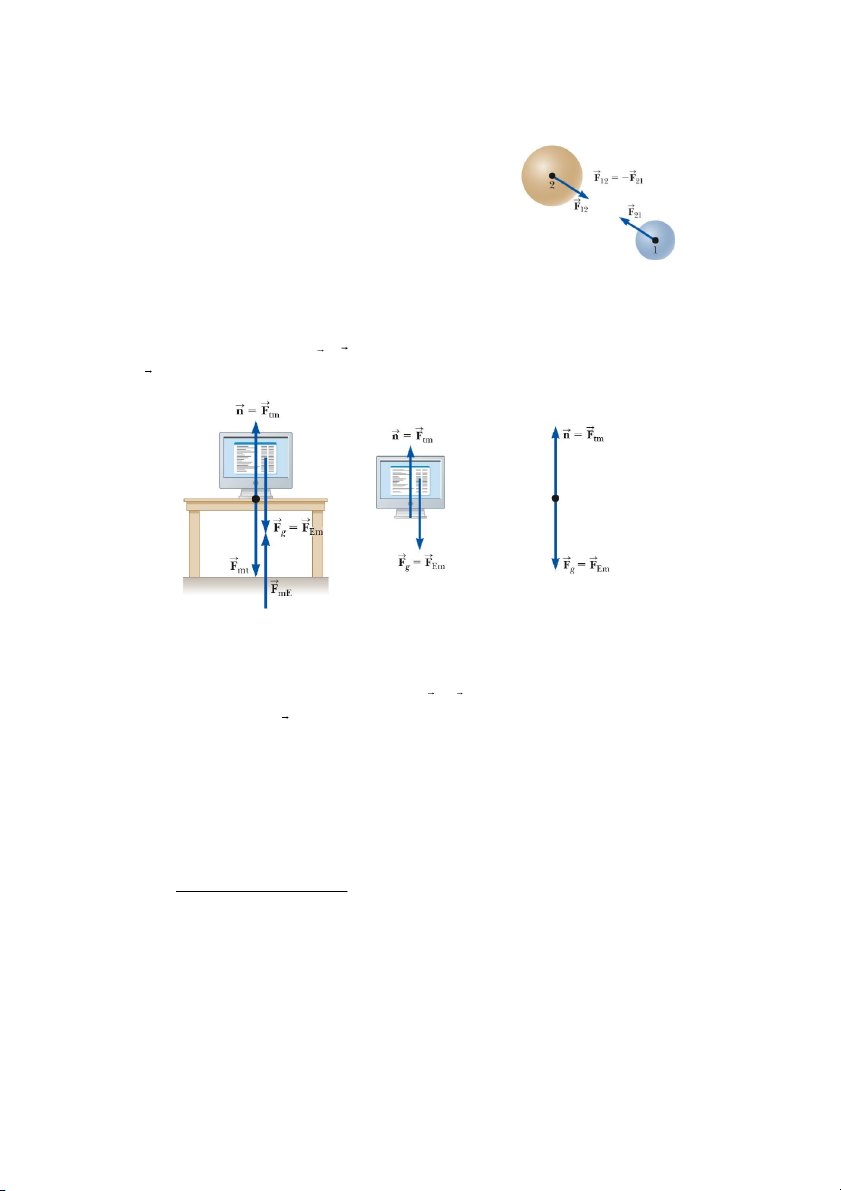
Ví dụ 1 về lực – phản lực: Ở hình 5.5, hai vật tác dụng
vào nhau bởi các lực có độ lớn bằng nhau nhưng ngược Hình 5.5: Định luật 3 Newton chiều nhau.
Ví dụ 2 về lực – phản lực: Trong hình 5.6a ở trên, lực pháp tuyến1 (normal force) do mặt
bàn tác dụng lên màn hình ( n = F ) là phản lực của lực tác dụng của màn hình lên mặt bàn ( tm F ). mt b c a
Hình 5.6: Các lực tác dụng lên một màn hình máy tính được đặt nằm yên trên một mặt bàn
Lực tác dụng của Trái đất lên màn hình (F F ) có độ lớn bằng với lực mà màn hình g Em
tác dụng lên Trái đất ( F ) nhưng ngược chiều. mE
Khi giải toán bằng cách vận dụng các định luật của Newton, ta có thể vẽ các lực tác dụng
lên vật như trong hình b (còn gọi là sơ đồ lực). Một cách khác là ta có thể vẽ sơ đồ lực trong
đó sử dụng mô hình chất điểm cho vật, ta được một sơ đồ như trong hình c (gọi là free-body diagram).
Khi vẽ các sơ đồ, cần lưu ý là chỉ vẽ những lực tác dụng lên vật đang xét (kể cả các lực
do trường lực gây ra). Các lực tác dụng lên vật xem như là tác dụng lên chất điểm thay thế
1 Còn gọi là phản lực, lực đàn hồi vuông góc 7
cho vật. Sơ đồ này giúp ta tách các lực tác dụng lên vật đang xét mà bỏ qua các lực khác khi phân tích.
Câu hỏi 5.5: i) Nếu một con ruồi va chạm vào kính chắn gió của một chiếc xe buýt đang chạy
rất nhanh, thì lực nào sau đây lớn hơn? a) của con ruồi tác dụng vào xe, b)của xe buýt tác
dụng vào ruồi, c)2 vật tác dụng các lực bằng nhau.
ii) Vật nào có gia tốc lớn hơn? a) Con ruồi, b) Xe buýt, c) 2 vật có gia tốc bằng nhau.
Các mô hình phân tích sử dụng định luật 2 Newton
Trong phần này, ta thảo luận về hai mô hình phân tích để giải toán trong đó vật cân bằng
hoặc chịu tác dụng của các lực không đổi. Để g ả
i i các bài toán ta đơn giản hóa mô hình bằng các giả định sau:
 Các vật có thể được mô hình hóa thành các chất điểm (particle).
 Chỉ quan tâm đến các ngoại lực tác dụng lên vật (có thể bỏ qua phản lực – vì phản lực
tác dụng lên vật khác).
 Tạm thời bỏ qua ma sát ở các bề mặt.
 Khối lượng của các sợi dây là không đáng kể: Lực của dây tác dụng lên vật hướng ra
xa vật và song song với dây. Khi dây được buộc vào vật và kéo vật đi thì độ lớn của
lực này là lực căng dây
Mô hình phân tích: Hạt ở trạng thái cân bằng
Nếu gia tốc của một vật (xem là một chất điểm) bằng không, vật
được gọi là ở trạng thái cân bằng. Mô hình này gọi là mô hình chất
điểm ở trạng thái cân bằng. Về mặt toán học, lực tổng hợp tác dụng lên vật bằng không:  0 F hay F  0  và F  0  x y
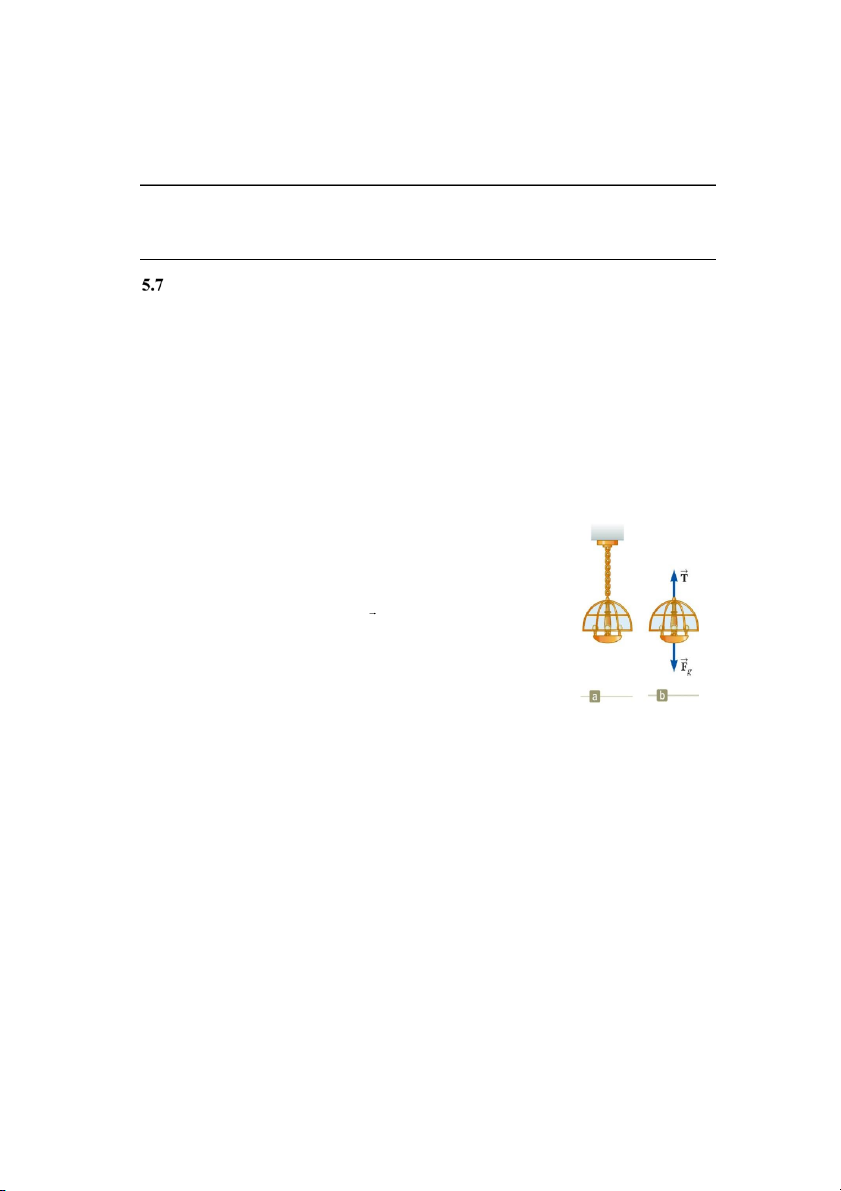
Ví dụ về cân bằng: một cái đèn được treo bằng một dây xích nhẹ
(hình 5.7). Các lực tác dụng lên đèn gồm: 
Lực hấp dẫn hướng xuống dưới
 Lực căng của dây xích hướng lên trên.
Hình 5.7: Một chiếc đèn
Áp dụng điều kiện cân bằng, ta được
được treo trên trần nhà
nhờ sợi xích.
F  0 T F  0 T   F y g g
Mô hình phân tích: Hạt dưới tác dụng của một lực tổng hợp
Nếu một vật được mô hình hóa như một chất điểm chịu một gia tốc, phải có lực tổng hợp
khác không tác dụng lên nó. Mô hình dùng trong trường hợp này là mô hình chất điểm dưới
tác dụng của một lực tổng hợp. Ta giải bài toán theo các bước sau: 8  Vẽ sơ đồ lực.
 Viết định luật 2 Newton: F  . m a
 Xét theo các phương x, y.
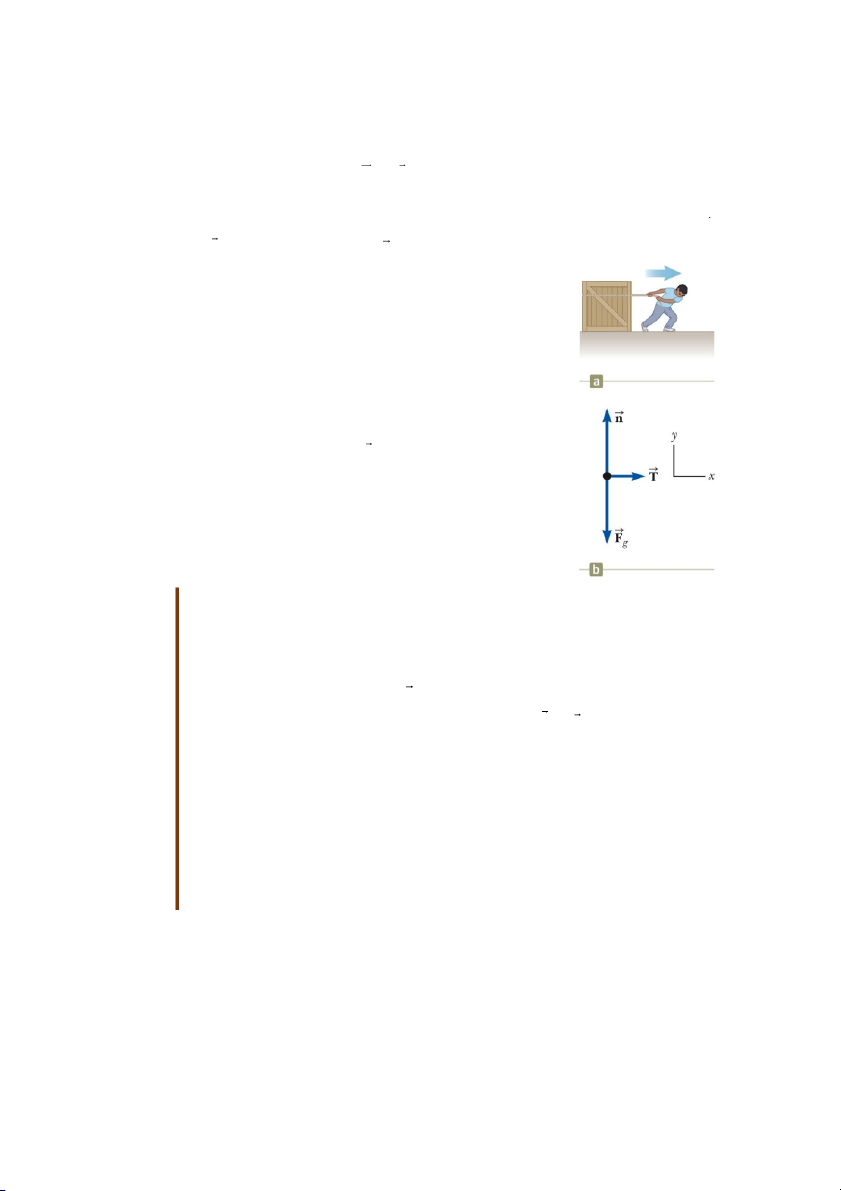
Một người kéo một cái thùng như hình 5.8 a. Các lực tác dụng lên thùng: lực căng dây T
, trọng lực F , và phản lực pháp tuyến n tác dụng bởi sàn nhà. g
Áp dụng định luật 2 Newton theo các phương x, y: F T   ma x x
F n F  0  n   F y g g
Giải hệ phương trình theo các ẩn.
Nếu lực căng dây là không đổi thì gia tốc a là hằng số, ta có
thể áp dụng các phương trình động học để mô tả đầy đủ hơn về
chuyển động của thùng.
Lưu ý về phản lực pháp tuyến n:
Lực pháp tuyến không phải là luôn bằng trọng lực tác dụng lên
vật. Ví dụ như trong hình bên cạnh thì
F n F F  0 
nên: n mg F y g
Nó cũng có thể nhỏ hơn trọng lực.
Gợi ý để giải toán: Áp dụng các định luật Newton
Khái niệm hóa:
Hình 5.8: Một cái hộp
 Vẽ một sơ đồ
được kéo trên mặt sàn
 Chọn hệ tọa độ thích hợp cho mỗi vật không ma sát. Phân loại:
 Mô hình chất điểm cân bằng: F  0
 Mô hình chất điểm chịu tác dụng của lực tổng hợp: = mF a Phân tích:
 Vẽ sơ đồ lực cho mỗi vật
 Chỉ vẽ các lực tác dụng lên vật
 Tìm các thành phần theo các trục tọa độ
 Bảo đảm rằng các đơn vị là nhất quán
 Áp dụng các phương trình thích hợp dưới dạng thành phần
 Giải phương trình để tìm các ẩn số
Hoàn thành bài giải 9
 Kiểm tra các kết quả xem có phù hợp với sơ đồ lực không
 Kiểm tra các giá trị đặc biệt
Bài tập mẫu 5.2: đèn giao thông
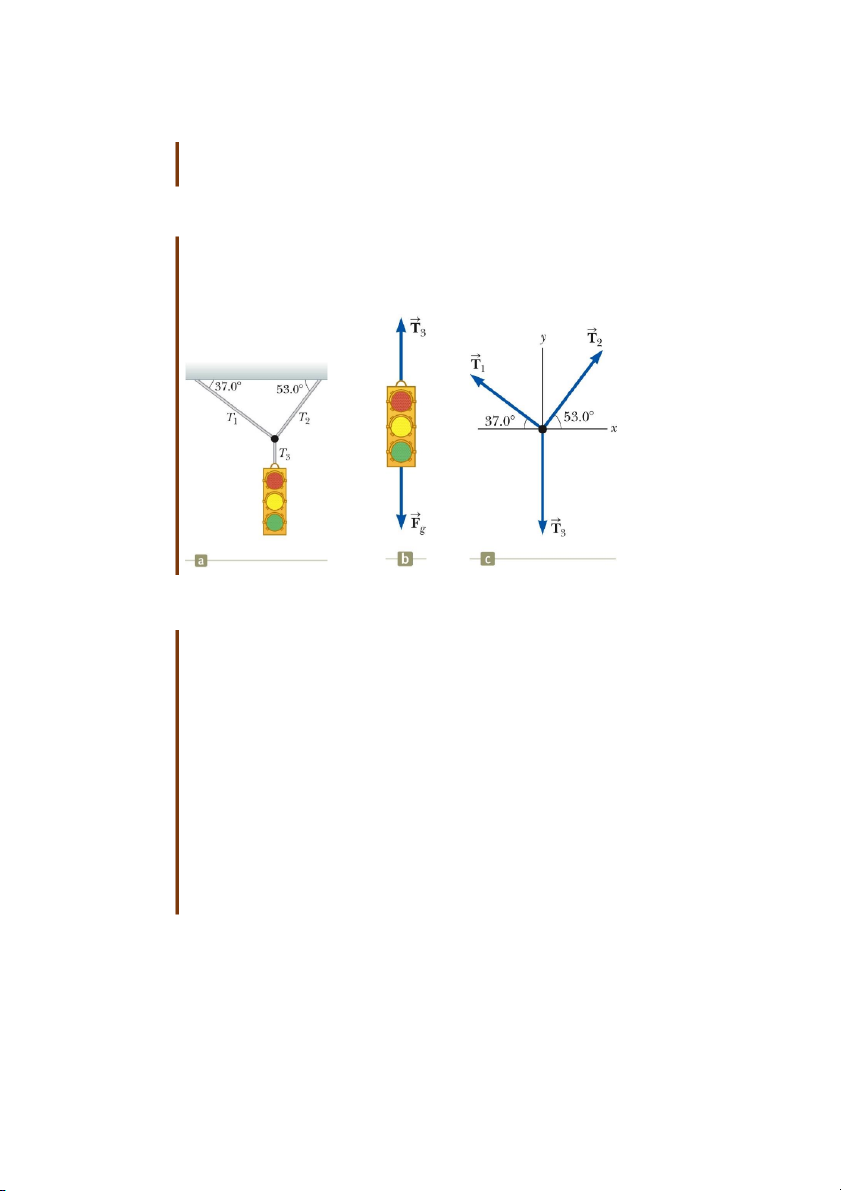
Một hộp đèn giao thông có trọng lượng 122 N được treo trên một sợi dây buộc vào hai
sợi dây khác như hình 5.10a. Các sợi dây phía trên không chắc bằng dây thẳng đứng
nên sẽ bị dứt nếu lực căng lớn hơn 100 N. Hỏi hộp đèn có đứng yên được không hay
là một trong các sợi dây sẽ bị đứt.
Hình 5.10: Đèn giao thông được treo nhờ các sợi dây cáp Giải
Khái niệm hóa. Hộp đèn giao thông
Giả thiết là các sợi dây không bị đứt
Không có cái gì chuyển động
Phân loại. Bài toán như là một bài toán về cân bằng
Không có chuyển động, vậy gia tốc bằng không
Mô hình chất điểm cân bằng Phân tích.
Vẽ sơ đồ các lực tác dụng lên hộp đèn
Vẽ sơ đồ lực tác dụng lên nút buộc ở vị trí các dây nối với nhau: Nút buộc là điểm phù
hợp để chọn vì mọi lực ta quan tâm tác dụng dọc theo các đường dây sẽ đi đến nút buộc.
Áp dụng các phương trình cân bằng cho nút buộc 10 Với hộp đèn, ta có:
F  0  T F  0  hay T F y 3 g 3 g Với nút buộc:
F  T cos T cos   0 x 1 1 2 2
F T sin T sin  F   0 y 1 1 2 2 g
Giải các phương trình, ta được: 122N T   73,4N 1
sin37,0  cos37,0 tan53,0  cos37,0  T  (73,4N)  97,4N 2    cos53,0 
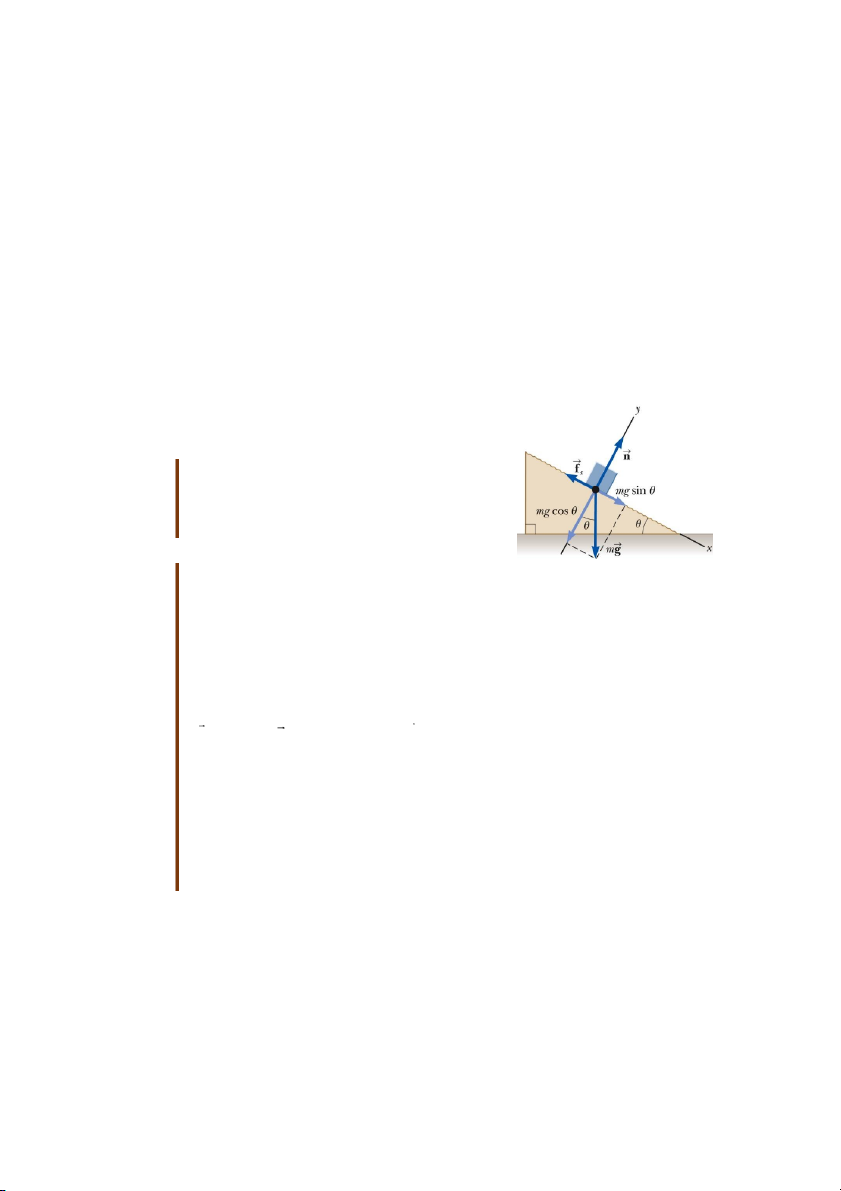
Bài tập mẫu 5.3: Mặt phẳng nghiêng
Một chiếc xe khối lượng m đỗ trên một đường dốc nghiêng có đóng băng như trong hình 5.11a.
(A) Tìm gia tốc của xe, giả thiết mặt đường không có ma sát Giải:
Khái niệm hóa: dùng hình 5.11a để
khái niệm hóa tình huống của bài
toán. Từ kinh nghiệm hằng ngày, ta
biết rằng một chiếc xe trên dốc
nghiêng sẽ chuyển động nhanh dần xuống dưới.
Phân loại: đây là chất điểm dưới tác
dụng của lực tổng hợp do xe chuyển động có gia tốc.
Hình 5.11: Một chiếc xe hơi trên mặt phẳng
Phân tích: Các lực tác dụng vào vật:
nghiêng không ma sát
Phản lực vuông góc với mặt nghiêng.
Trọng lực hướng thẳng đứng xuống dưới.
Chọn hệ trục tọa độ với x dọc theo mặt nghiêng và y vuông góc với mặt nghiêng.
Thay trọng lực bởi các thành phần của nó (theo x và y). 11
Áp dụng mô hình chất điểm chuyển động dưới tác dụng của lực tổng hợp theo phương
x và chất điểm cân bằng theo phương y.
F mg sin  ma x x
F n mgcos   0 y
Giải phương trình thứ nhất, ta được a g sin x
(B) Giả sử xe được thả từ trạng thái nghỉ từ đỉnh dốc và khoảng cách từ cản trước của
xe đến chân dốc là d. Xe phải mất bao lâu để cản trước của nó chạm chân dốc và tốc
độ của xe lúc đến chân dốc. Giải:
Đây là nội dung liên quan đến phần động học. Dùng gia tốc tìm được ở câu a để thay
vào các phương trình động học. Từ đó tìm được: 2  d t
và v  2gdsin gsin xf
Trường hợp có nhiều vật:
Khi có hai hay nhiều vật kết nối với nhau hoặc tiếp xúc nhau, có thể áp dụng các định
luật Newton cho hệ như một vật tổng thể hay từng vật riêng rẽ. Ta có thể chọn một cách để
giải bài toán và dùng cách khác để kiểm tra lại kết quả.
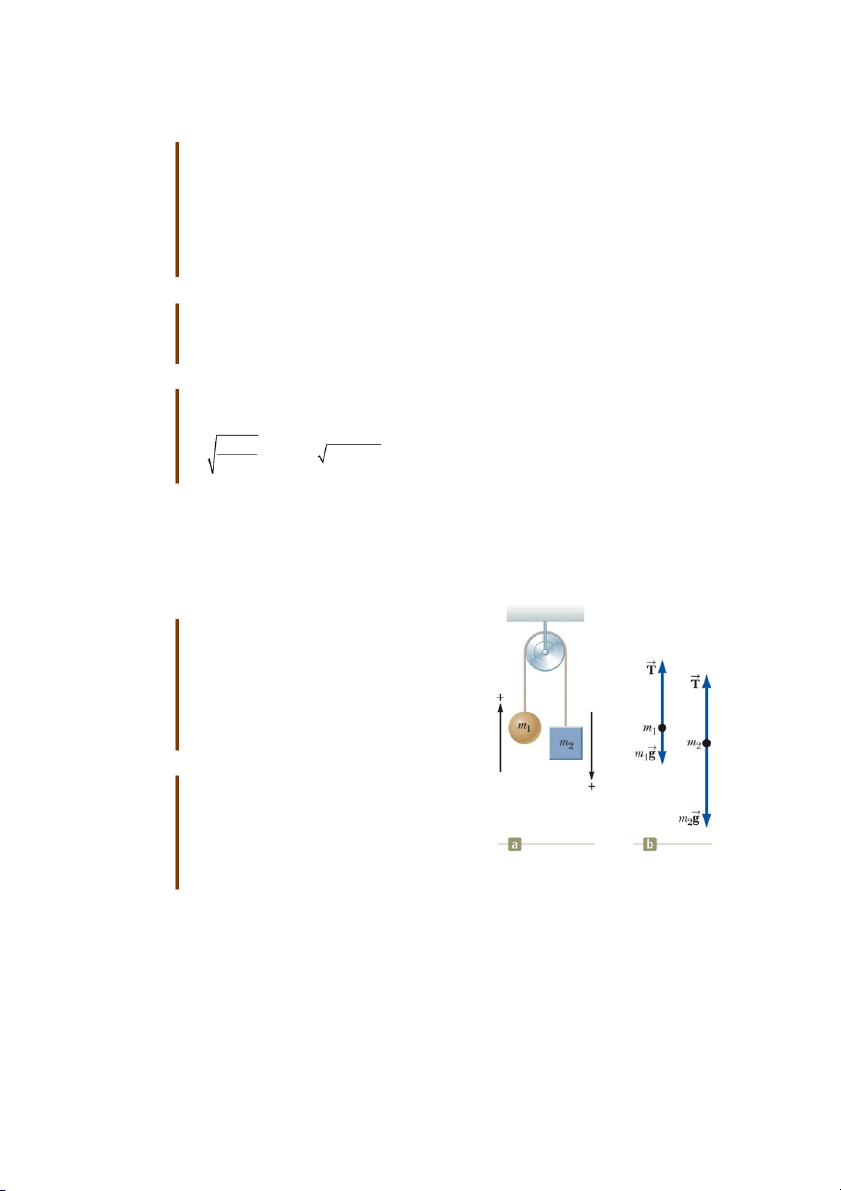
Bài tập mẫu 5.4: Động cơ Atwood
Khi hai vật có khối lượng khác nhau được
treo thẳng đứng trên một ròng rọc nhẹ và
không có ma sát ở trục như hình 5.12a thì hệ
vật được gọi là động cơ Atwood. Thiết bị này
thường được dùng trong phòng thí nghiệm để
tìm giá trị của g. Hãy tìm gia tốc của các vật
và lực căng của sợ dây nhẹ. Giải
Khái niệm hóa: Hãy tưởng tượng tình huống
trong hình 5.12a: khi một vật chuyển động
xuống dưới thì vật kia chuyển động lên trên.
Vì chúng được nối với nhau bằng một sợ dây
không giãn nên gia tốc của chúng có độ lớn bằng nhau
Hình 5.12: Động cơ Atwood 12
Phân loại: Các vật trong máy Atwood chịu tác dụng của trọng lực cũng như lực của
các dây buộc vào chúng nên ta có thể phân loại bài toán này như là bài toán có hai chất
điểm dưới tác dụng của lực tổng hợp.
Phân tích: Các lực tác dụng lên các vật:
 Lực căng dây (như nhau ở hai vật và ở các đoạn dây)  Trọng lực
Các vật có gia tốc như nhau do chúng được nối với nhau. Vẽ sơ đồ lực
Áp dụng các định luật Newton:
Cho vật thứ nhất F T m g   m a y 1 1 y
Cho vật thứ 2: F m g T m a y 2 2 y Giải để tìm các ẩn  m m   2m m  2 1 a g và 1 2 T g y     m   m m m 1 2   1 2 
Hoàn tất: Giá trị tìm được của gia tốc có thể diễn giải như là tỉ số g ữ i a độ chênh lệch
về lực của hệ và tổng khối lượng của hệ, như dự đoán của định luật 2 Newton.
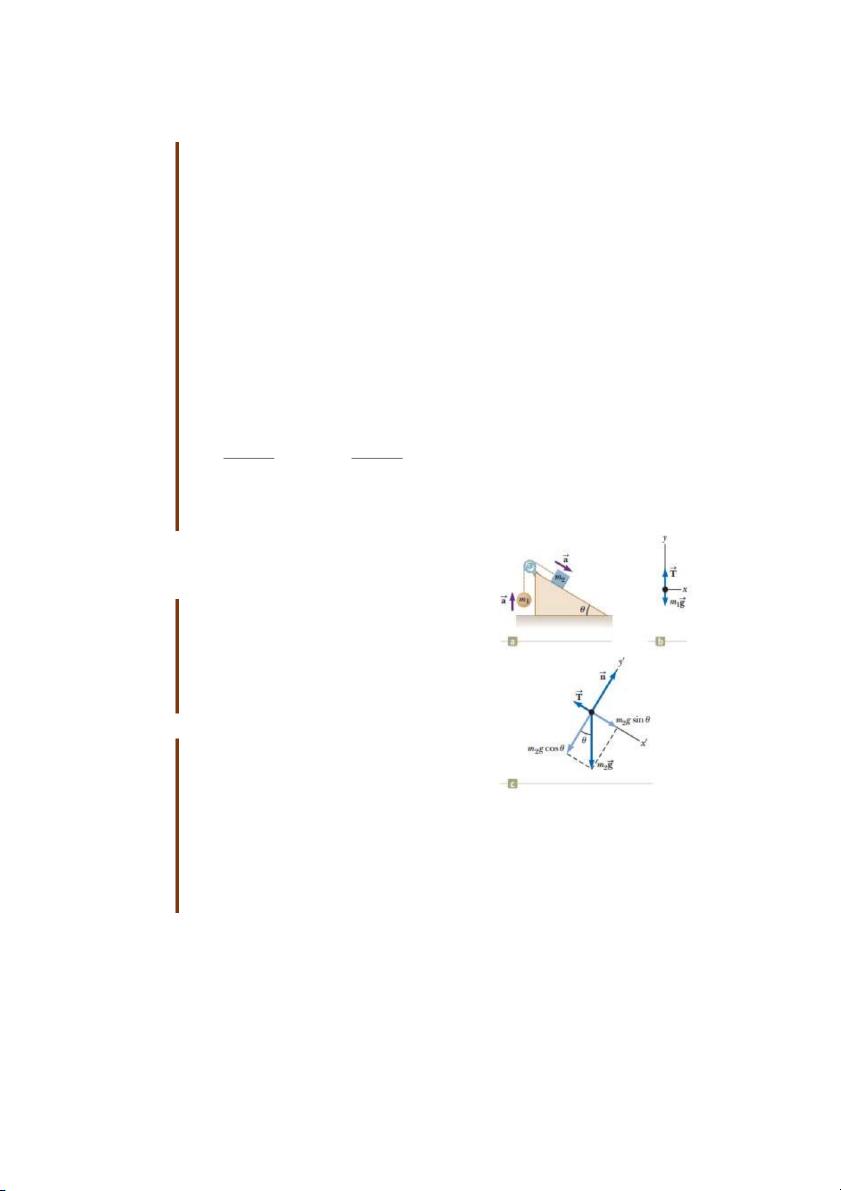
Bài tập mẫu 5.5: Hai vật chuyển động có gia
tốc nối nhau bằng một sợi dây.
Một quả cầu khối lượng m1 và một khối hộp khối
lượng m2 được nối với nhau bởi một dây nhẹ vắt
qua một ròng rọc nhẹ quay không ma sát như
hình 5.15a. Khối hộp nằm trên một mặt nghiêng
không có ma sát với góc nghiêng . Tìm độ lớn
của gia tốc của hai vật và sức căng dây. Giải:
Khái niệm hóa: Hãy hình dung các vật trong
hình 5.13 đang chuyển động. Nếu m2 đi xuống
thì m1 sẽ đi lên. Do các vật được nối với nhau
bằng sợi dây nên gia tốc của chúng có cùng độ ật đượ ố ớ
lớn. Sử dụng hệ tọa độ bình thường cho quả cầu Hình 5.13: Hai v c n i v i
và hệ tọa độ “nghiêng” cho khối hộp.
nhau bằng sợi dây nhé vắt qua
một ròng rọc không có ma sát.
Phân loại: Theo các phương y và x’ thì đây là
bài toán vật chịu tác dụng của lực tổng hợp. Theo phương y’ thì là bài toán vật cân bằng. 13
Phân tích: Xét các sơ đồ lực như trong hình 5.13b và 5.13c thì có thể áp dụng định
luật 2 Newton cho các vật như sau:
Với quả cầu: F T m g m a m a y 1 1 y 1 Với khối hộp:
F m g sin T m a   m a x' 2 2 x' 2
F n m g cos   0 y' 2 m m sin  1 1 2  
Giải các phương trình trên, ta được: m sin  m 2 1 a g và T g m m m m 1 2 1 2
Hoàn tất: Khối hộp chuyển động có gia tốc xuống dưới nếu m2 sin > m1. Ngược lại,
gia tốc của khối hộp hướng lên trên và gia tốc của quả cầu hướng xuống dưới. Từ kết
quả gia tốc, có thể thấy rằng gia tốc là tỉ số giữa độ lớn của ngoại lực tác dụng lên hệ
với tổng khối lượng của các vật trong hệ.
Các lực ma sát
Khi một vật chuyển động trên bề mặt hoặc
xuyên qua một môi trường nhớt thì sẽ xuất hiện sức
cản chuyển động. Đó là do các tương tác giữa vật và
môi trường quanh nó. Sức cản này được gọi là lực ma sát.
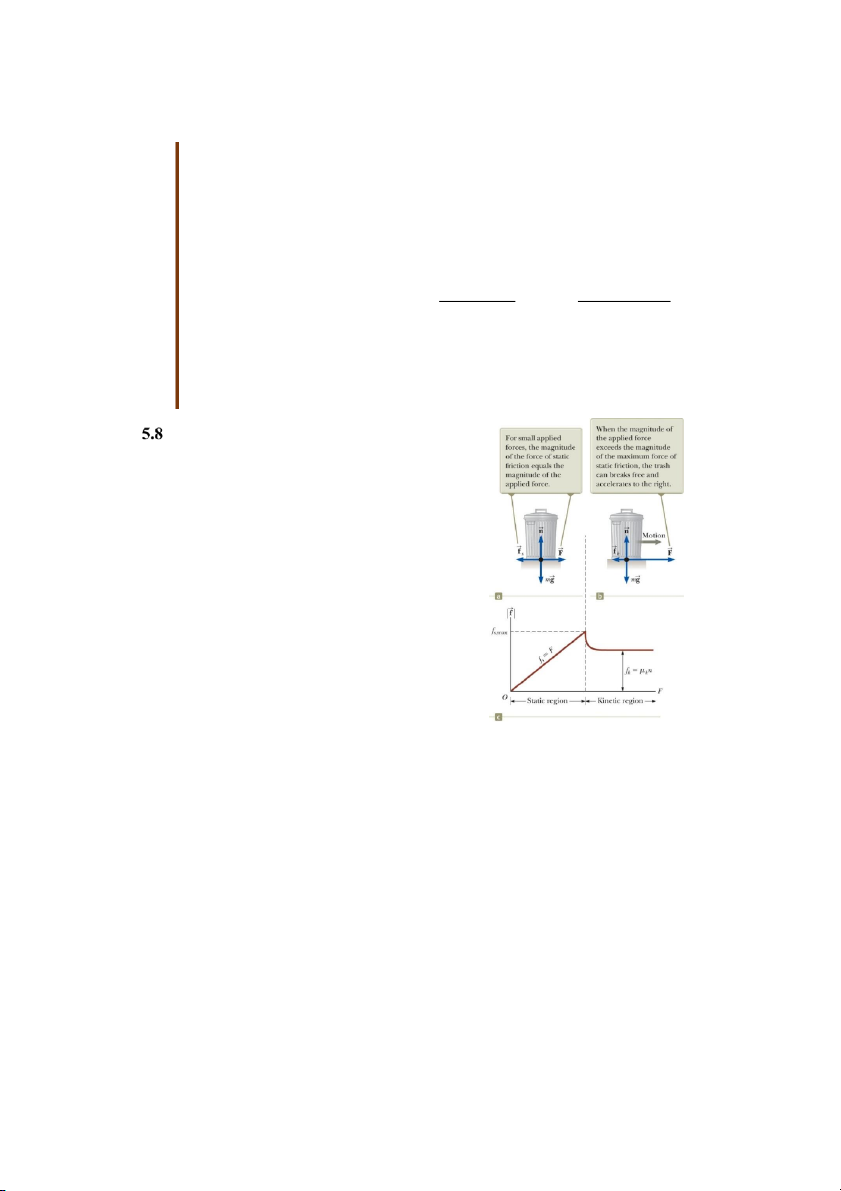
5.8.1 Lực ma sát nghỉ (tĩnh)
Lực ma sát nghỉ giữ cho vật không chuyển
động. Chừng nào vật chưa chuyển động thì lực ma
sát nghỉ đúng bằng lực tác động từ bên ngoài ƒs = F
Nếu F tăng thì fs tăng và ngược lại.
Gọi µs là hệ số ma sát nghỉ thì ƒsµs n
 Lưu ý: dấu bằng xảy ra khi các mặt bắt đầu trượt lên nhau.
5.8.2 Lực ma sát trượt (động)
Lực ma sát trượt tác dụng khi vật chuyển động.
Hình 5.14: Kéo một vật bắt đầu
Hệ số ma sát trượt µk có thể thay đổi theo tốc độ chuyển động khi thắng được lực ma
của vật, tuy nhiên, ta bỏ qua sự thay đổi này. sát nghỉ. ƒk = µk n
Khảo sát lực ma sát: Để khảo sát, ta tăng dần độ lớn của ngoại lực F và ghi lại giá trị của
lực ma sát. Chú ý thời điểm vật bắt đầu trượt. Đồ thị biểu diễn quan hệ giữa lực ma sát và
ngoại lực cho trên hình 5.16c. 14 Lưu ý:
 Các phương trình này chỉ quan tâm đến độ lớn của các lực, chúng không phải là phương trình vec-tơ.
 Với ma sát nghỉ (fs), dấu bằng chỉ đúng khi vật sắp chuyển động, các bề mặt sắp trượt
lên nhau. Nếu các bề mặt chưa trượt lên nhau thì dùng dấu nhỏ hơn
 Hệ số ma sát phụ thuộc vào các mặt tiếp xúc.
 Lực ma sát nghỉ (tĩnh) thường lớn hơn lực ma sát trượt (động).
 Hướng của lực ma sát ngược với hướng của chuyển động và song song với các mặt tiếp xúc.
 Hệ số ma sát hầu như không phụ thuộc vào diện tích mặt tiếp xúc.
5.8.3 Ma sát trong các bài toán dùng các định luật Newton
Ma sát là một lực, do đó chỉ cần thêm nó vào trong các định luật Newton.
Các qui tắc về ma sát cho phép ta xác định hướng và
độ lớn của lực ma sát.
Bài tập mẫu 5.6: thí nghiệm xác định s và k
Một khối hộp đang nằm trên một mặt nghiêng như
hình 5.15. Nâng dần góc nghiêng cho đến khi hộp
bắt đầu trượt. Chứng tỏ rằng có thể tìm được hệ số
ma sát nghỉ s theo góc tới hạn . Giải:
Khái niệm hóa: Tưởng tượng rằng khối hộp có xu
hướng trược xuống dưới do tác dụng của trọng lực.
Hộp trượt xuống nên ma sát sẽ hướng lên phía trên.
Hình 5.15: Một khối hộp trượt Phân lo ộ ặ ẳ
ại: Khối hộp chịu tác dụng của nhiều lực trên m t m t ph ng nghiêng có ma sát
khác nhau, tuy nhiên, nó chưa trượt xuống dốc nên
đây là bài toán chất điểm cân bằng.
Phân tích: Sơ đồ lực trên hình 5.15 cho thấy các lực tác dụng vào hộp gồm: trọng lực g
m , phản lực nvà lực ma sát nghỉ f . Chọn trục x dọc theo mặt nghiêng và y vuông s góc với mặt nghiêng.
F mg sin  f   0 x s
F n mg cos   0 y
Giải hệ phương trình ta có f mgsin   ntan s
Với góc nghiêng tới hạn c thì lực ma sát nghỉ bằng f   n nên   tan . s s s c 15
Hoàn tất: Khi hộp bắt đầu trượt thì ≥c. Hộp trượt có gia tốc xuống dưới thì lực ma
sát trượt f   n . Tuy nhiên, nếu giảm góc q thì vật cũng có thể trượt xuống, nếu vật k k
trượt thẳng đều thì   tan  với     k c c c
Lưu ý: Với bố trí thí nghiệm như trên thì ta có thể xác định hệ số ma sát bằng thực nghiệm: µ = tan 
 Với µs, sử dụng góc nghiêng khi khối hộp bắt đầu trượt.
 Với µk, sử dụng góc nghiêng khi mà khối hộp trượt xuống với tốc độ không đổi.
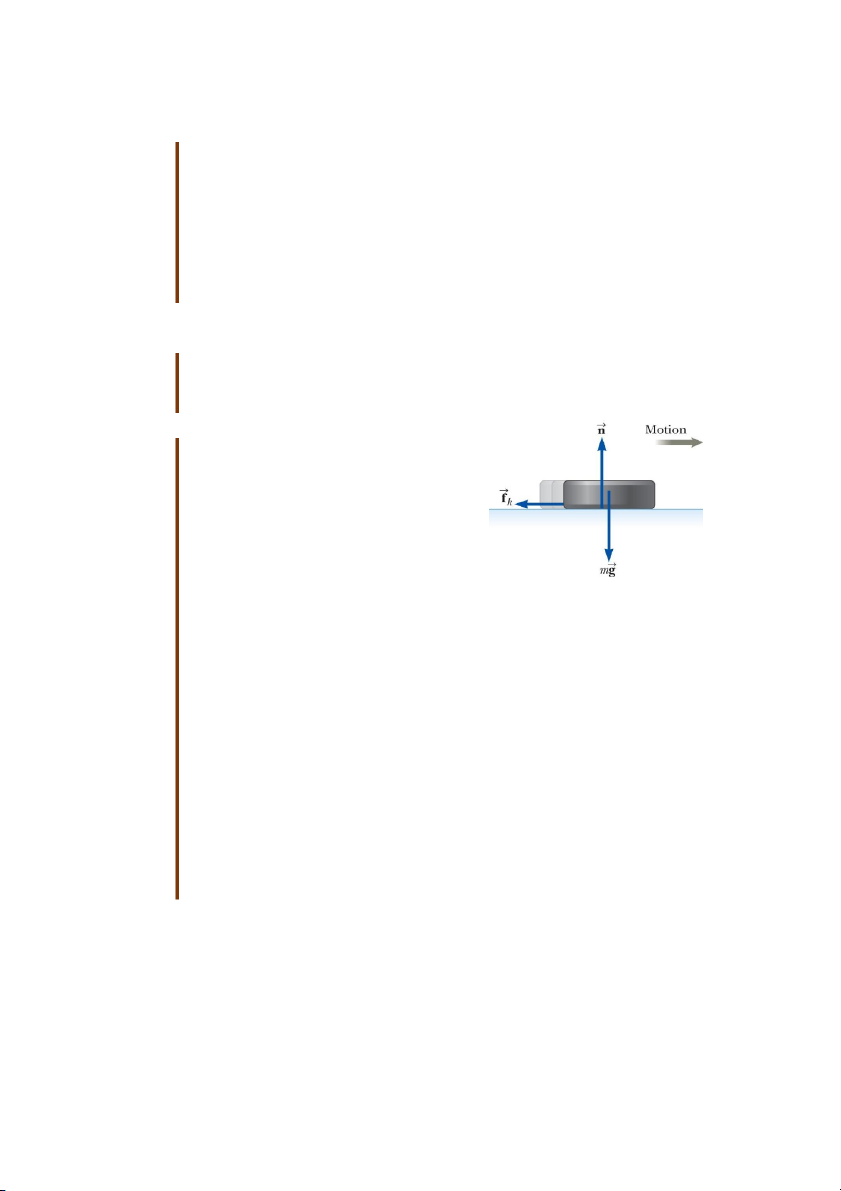
Bài tập mẫu 5.7: Một quả bóng khúc côn cầu đang trượt
Một quả bóng khúc côn cầu trượt trên mặt băng với tốc độ ban đầu là 20,0 m/s. Quả
bóng trượt được 115 m trước khi dừng lại. Hãy xác định hệ số ma sát trượt giữa quả bóng và băng. Giải:
Khái niệm hóa: Giả sử quả bóng chuyển
động sang phải như hình 5.16. Lực ma sát
trượt tác dụng về bên phải và làm quả bóng
chuyển động chậm lại cho đến khi dừng hẳn.
Phân loại: Các lực tác dụng lên quả bóng
như trong hình 5.16, nhưng bài toán lại cho
các biến số về động học. Do đó, có thể phân
loại bài toán bằng nhiều cách khác nhau.
Theo phương thẳng đứng, đây là bài toán
chất điểm cân bằng (tổng lực tác dụng lên vật
Hình 5.16: quả khúc con cầu trượt có
bằng 0). Theo phương ngang, là bài toán chất
ma sát trên mặt băng
điểm có gia tốc không đổi.
Phân tích: Vẽ sơ đồ lực tác dụng lên vật, lưu ý đến lực ma sát (ngược chiều chuyển
động, song song với mặt tiếp xúc).
Áp dụng mô hình chất điểm chịu tác dụng của lực tổng hợp theo phương x: F  f   ma x k x
Áp dụng mô hình chất điểm cân bằng theo phương y:
F n mg  0  y
Giải hệ phương trình, với định nghĩa lực ma sát trượt, ta được: a   g x k
Sau khi tìm được gia tốc, áp dụng mô hình động học, ta tìm được 16 2
  vxi thay số:   0,117 k 2gx k f
Hoàn tất: Lưu ý rằng k không có thứ nguyên và có giá trị bé, không đổi với một vật trượt trên mặt băng.
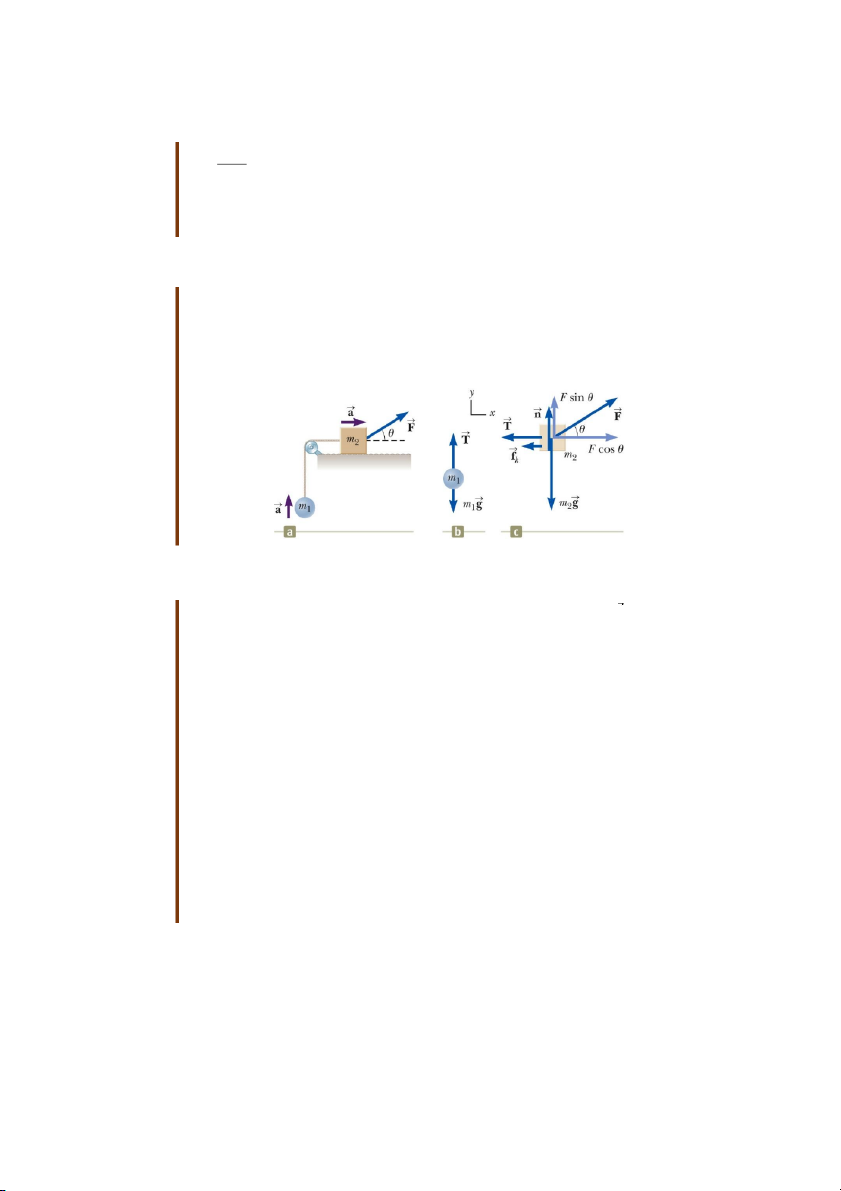
Bài tập mẫu 5.8: Gia tốc của hai vật nối với nhau khi có ma sát
Một khối hộp có khối lượng m2 nằm trên một mặt ngang, nhám được nối với một quả
cầu khối lượng m1 bằng một sợi dây nhẹ vắt qua một ròng rọc nhẹ, không ma sát như
trong hình 5.20a. Tác dụng vào khối hộp một lực có độ lớn F hợp với phương ngang
một góc  và khối hộp chuyển động sang phải. Hệ số ma sát trượt giữa khối hộp và
mặt ngang là k Tìm độ lớn của gia tốc của hai vật.
Hình 5.17: hệ 2 vật nối nhau khi có ma sát. Giải:
Khái niệm hóa: Hình dung xem chuyện gì xảy ra khi tác dụng lực F vào khối hộp.
Giả sử lực đủ lớn hơn lực ma sát nghỉ nhưng không đủ lớn để nhất hộp lên, hộp sẽ
trượt sang phải và quả cầu được kéo lên.
Phân loại: Bài toán này là bài toán hai chất điểm dưới tác dụng của lực tổng hợp. Vì
khối hộp không bị nhấc lên nên theo phương thẳng đứng, khối hộp được xem là chất
điểm cân bằng.
Phân tích: Vẽ sơ đồ lực cho từng vật (hình 5.17b và 5.17c).
Áp dụng mô hình chất điểm chịu tác dụng của lực tổng hợp cho khối hộp theo phương ngang:
F F cos f T m a m a (1) x k 2 x 2
Áp dụng mô hình chất điểm cân bằng cho khối hộp theo phương thẳng đứng
F n F sin  m g   0 (2) y 2
Áp dụng mô hình chất điểm chịu tác dụng của lực tổng hợp cho quả cầu theo phương thẳng đứng: 17
F T mg ma ma(3) y 1 1 y 1
Giải hệ phương trình, ta tìm được:
F cos   sin m m g k      1 k 2  a  (4) m m 1 2
Hoàn tất: Gia tốc của khối hộp có thể hướng sang phải hoặc trái tùy theo dấu của tử
số trong phương trình (4). Nếu vận tốc của khối hộp hướng sang trái thì phải đổi dấu
của fk trong (1). Trong trường hợp đó, chỉ cần đổi hai dấu cộng (+) trong tử số của (4) thành dấu trừ (–).
Câu hỏi lý thuyết chương 5:
1. Trong bức tranh It Happened One Night (Columbia Pictures, 1934), Clark Gable đang
đứng trên xe bus, đằng sau là Claudette Colbert đang ngồi. Xe bus đột ngột đi về phía
trước và Clark ngã vào long Claudette. Tại sao điều đó xảy ra?
2. Một người giữ trái banh trên tay. (a) Xác định tất cả các ngoại lực tác dụng lên trái banh
và xác định phản lực theo định luật 3 Newton của mỗi lực đó. (b) Nếu trái banh rơi xuống,
lực gì tác dụng vào nó khi nó đang rơi? Xác định phản lực của nó. (Bỏ qua lực cản không khí).
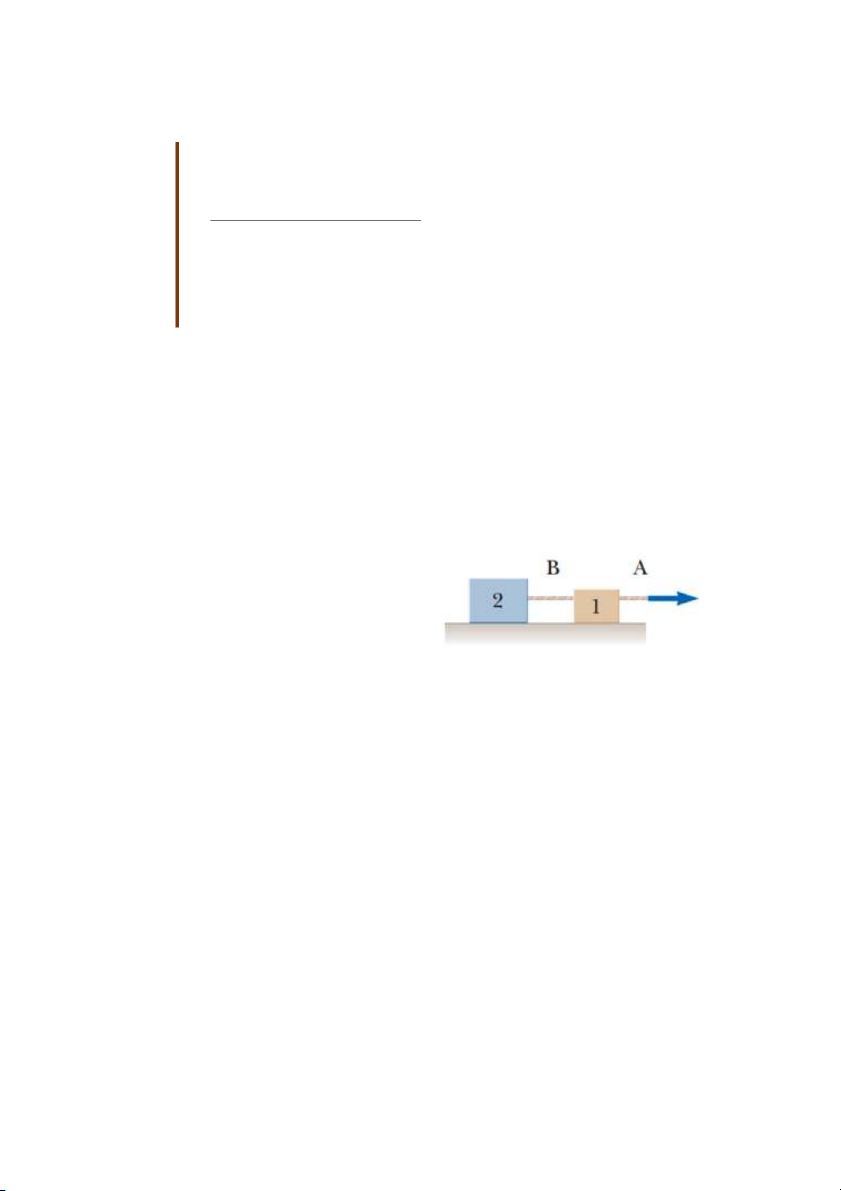
3. Sợi dây B mảnh, nhẹ, không co giãn nối
vật 1 và vật 2, biết vật 2 nặng hơn vật 1
(hình). Dây A tác dụng lực lên vật 1 làm
nó chuyển động có gia tốc về phía trước.
(a) So sánh độ lớn lực dây A tác dụng lên
vật 1 với lực do dây B tác dụng lên vật 2?
(b) So sánh gia tốc của vật 1 và vật 2. (c)
Xác định lực do dây B tác dụng lên vật 1
và so sánh lực do dây B tác dụng lên hai vật .
Bài tập chương 5:
1. Một động cơ tên lửa đồ chơi được gắn vào một quả bóng lớn, chúng có thể trượt không
ma sát trên mặt phẳng nằm ngang. Quả bóng nặng 4 kg có vận tốc 3.00i m/s tại 1 thời
điểm, và 8s sau vận tốc nó là (8.00i+ 10.00j) m/s. Giả sử động cơ đã tác dụng lực không
đổi theo phương ngang lên quả bóng, tìm (a) các thành phần và (b) độ lớn của lực trên. ĐS: 1,53m; 5,29o
2. Một electron nặng 9,1.10-31kg có vận tốc đầu 3.105m/s. Nó đi thẳng được 5cm thì tốc độ
của nó tăng lên 7.105m/s. Giả sử gia tốc của nó là hằng số. (a) Xác định độ lớn của lực
tác dụng vào electron và (b) so sánh lực này với trọng lượng của electron.
ĐS: 3,64.10-18N; 4,08.1011 lần 18
3. Một xe hơi nặng 1000kg đang kéo một toa moóc 300kg. Cả 2 cùng tiến về phía trước với
gia tốc 2.15m/s2. Bỏ qua lực cản không khí và ma sát. Xác định:
(a) Tổng lực tác dụng lên xe hơi.
(b) Tổng lực tác dụng lên toa moóc.
(c) Lực do toa moóc tác dụng lên xe hơi.
(d) Lực do xe hơi tác dụng lên đường.
ĐS: 2,15.103N; 645N; 645N; 1,02.104N
4. Một sợi dây dài 35,7cm đầu trên cố định, đầu dưới treo một bulong sắt nặng 65g. Đặt
một nam châm lại gần bên phải bulong sắt đó (không chạm), bulong sắt bị hút về phía
nam châm theo phương ngang, nó đi được 28m rồi dừng lại (đạt trạng thái cân bằng).
(a) Vẽ sơ đồ lực tác dụng lên bulong.
(b) Tính lực căng trên dây. (c) Tính lực từ tá c dụng lên bulong. ĐS: 1,03N; 0,805N
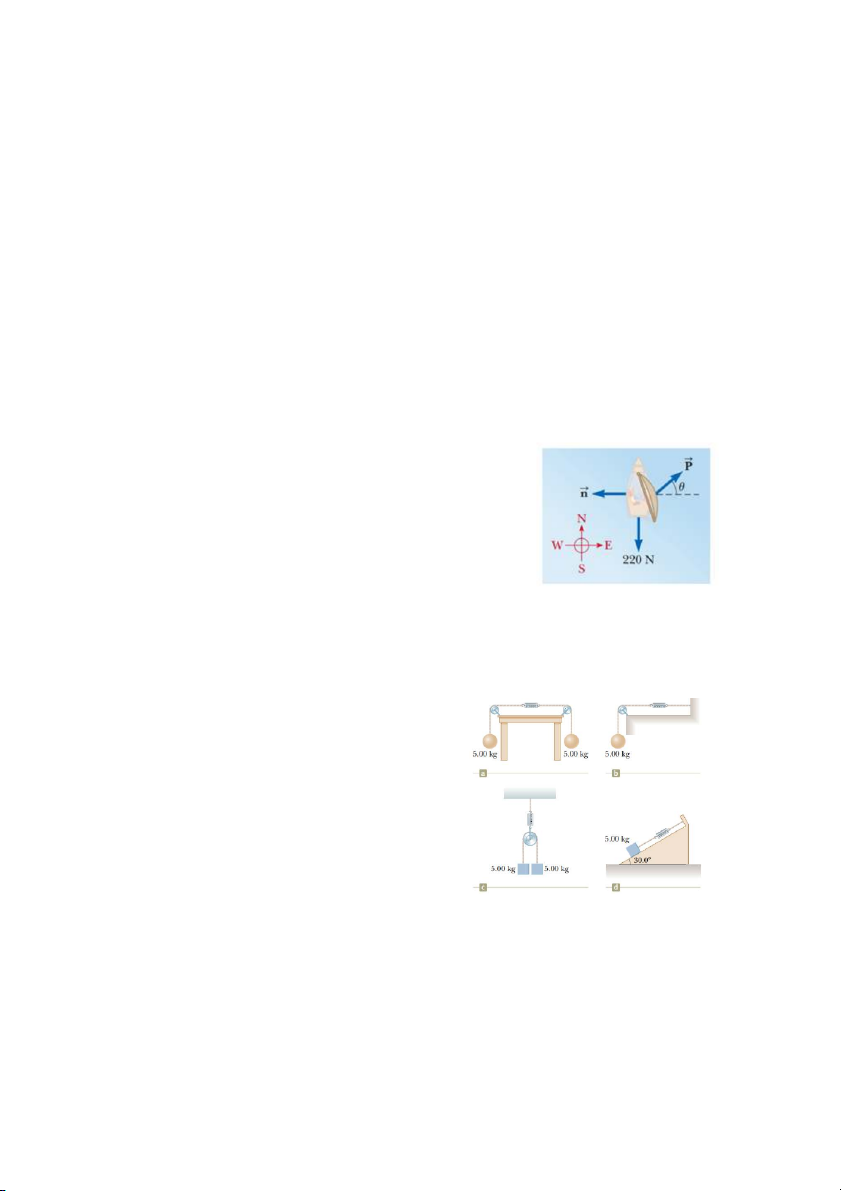
5. Hình bên biểu diễn các lực theo phương ngang tác dụng
vào con thuyền đang di chuyển theo hướng bắc với vận
tốc không đổi khi nhìn từ trên cao. Lúc tốc độ con thuyền
đạt giá trị xác định, nước tác dụng lực 220N lên thân tàu,
góc θ = 40o. Hãy viết 2 phương trình thành phần biểu diễn
định luật 2 Newton, sau đó giải phương trình để xác định
P – lực gió tác dụng lên thuyền và lực n – lực nước tác
dụng lên đáy thuyền trong 2 trường hợp sau:
(a) Chọn chiều trục x theo hướng đông, trục y theo hướng bắc;
(b) Chọn trục x theo hướng đông bắc, phương tạo góc θ = 40o so với phương đông; trục
y theo hướng tây bắc, phương tạo góc θ = 40o so với phương bắc.
(c) So sánh 2 kết quả câu (a) và (b): chúng có bằng nhau không? Phương pháp nào dễ làm hơn? ĐS: 262N; 262N; 342N
6. Bốn cơ hệ như trên hình bên đều đang ở trạng
thái cân bằng. Lực kế lò xo được chỉnh theo
đơn vị Newton. Hỏi giá trị đọc được từ các lực
kế trên. Giả sử bỏ qua khối lượng ròng rọc và
ma sát giữa dây với ròng rọc cũng như ma sát
giữa vật với mặt phẳng nghiêng. ĐS: 49N-49N-98N-24.5N 19
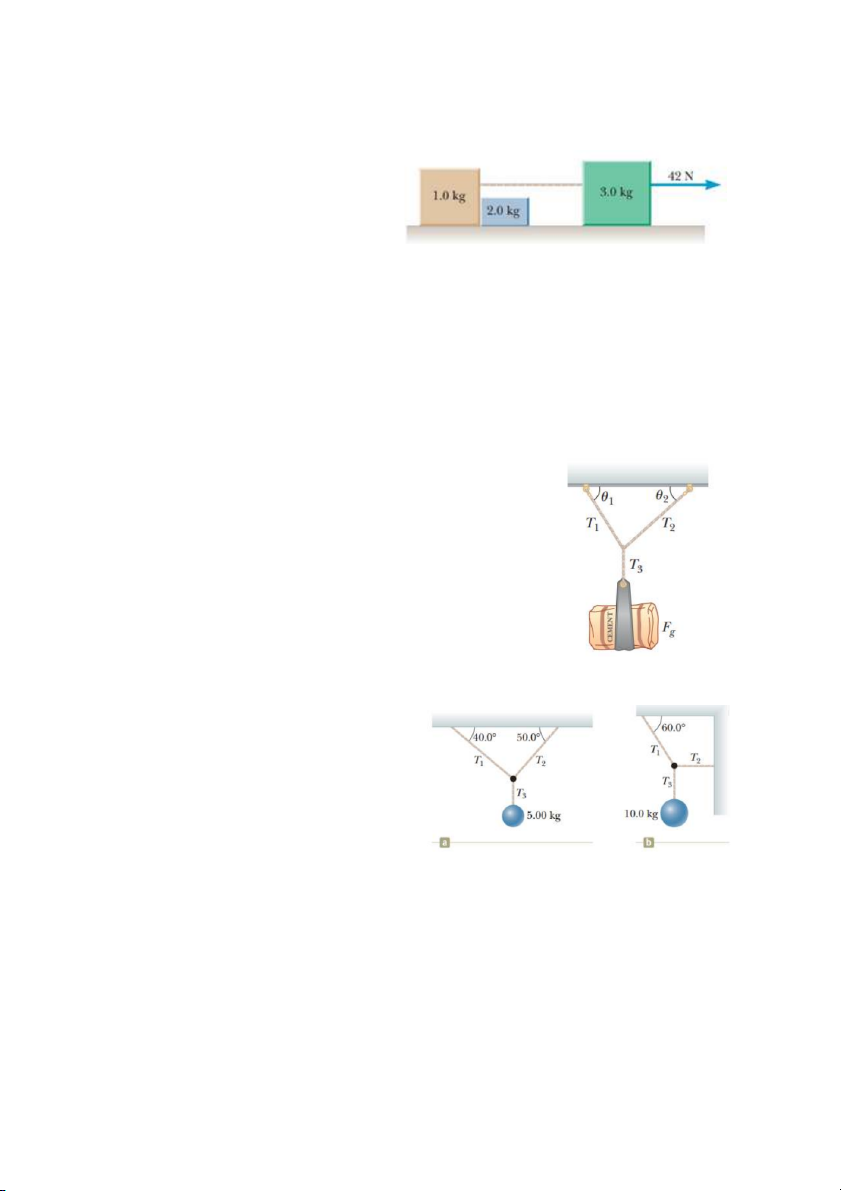
7. Một cơ hệ cho như hình vẽ bên. Các
vật trượt không ma sát trên mặt
ngang và lực tác dụng vào khối 3kg
là 42N. Xác định (a) gia tốc của hệ,
(b) lực căng dây giữa khối 3kg và
1kg và (c) lực tác dụng của khối 1kg lên khối 2kg. ĐS: 7m/s2; 21N; 14N
8. Khoảng cách giữa hai cột điện thoại 50m. Chú chim nặng 1kg đậu ở chính giữa một dây
điện thoai nối hai cột điện thoại trên làm dây bị chùng xuống một đoạn 0.2m, bỏ qua khối lượng dây.
(a) Vẽ sơ đồ lực các lực tác dụng lên chú chim.
(b) Tính lực căng do chú chim tác dụng lên dây. ĐS: 613N
9. Một vật đang chuyển động trên một mặt phẳng, với tọa độ x và cho bởi phương trình x =
5t2 – 1 (m), y = 3t3 + 2 (m). Tính độ lớn tổng lực tác dụng lên
vật tại thời điểm t = 2s. ĐS: 112N
10. Một bao xi măng có trọng lượng 325N treo cân bằng nhờ 3 sợi dây như hình bên. Cho θ o
1 = 60o, θ2 = 40 . Tính các lực căng
dây T1, T2, T3 khi hệ ở trạng thái cân bằng. ĐS: 253N, 165N, 325N
11. Hai người kéo một con thuyền bằng 2 sợi dây theo phương
ngang. Nếu họ kéo cùng chiều thì con thuyền chuyển động với
gia tốc 1,52 m/s2 về phía phải. Còn nếu họ kéo ngược chiều
nhau thì con thuyền chuyển động với gia tốc 0,518 m/s2 về
phía trái. Xác định độ lớn lực do mỗi người tác dụng lên thuyền. Giả sử không quan tâm
đến các lực theo phương ngang khác tác dụng lên thuyền. ĐS: 100N; 204N
12. Các quả nặng được treo trên các dây nối
với trần của thang máy, biết thang máy
đang di chuyển với vận tốc không đổi.
Tính giá trị các lực căng dây T1 T2 T3 ở 2 trường hợp trên. 20