







Preview text:
Mục Lục Chương 7
7.1. GIỚI THIỆU: ..................................................................................................... 1
7.2. MÔ HÌNH CỦA BJT .......................................................................................... 1
7.2.1. Mạng 2 cửa: ................................................................................................... 1
7.2.2. Mô hình tương đương của transistor: ............................................................. 2
7.2.3. Cấu hình mạch CE: ........................................................................................ 3
7.2.4. Cấu hình mạch CB ......................................................................................... 4
7.2.5. Cấu hình mạch CC ......................................................................................... 4
7.2.6. Xác định các giá trị thông số của BJT bằng đồ thị .......................................... 5
7.3. CÁC CHỈ TIÊU CỦA BỘ KHUẾCH ĐẠI: ....................................................... 8
7.4. PHÂN TÍCH MẠCH KHUẾCH ĐẠI TÍN HIỆU NHỎ .................................... 9
7.4.1. Cấu hình mạch khuếch đại CE, phân cực cố định: .......................................... 9
7.4.2. Cấu hình mạch khuếch đại CE, phân cực kiểu định dòng điện có điện trở RE13
7.4.3. Cấu hình mạch khuếch đại CE, phân cực kiểu cầu phân áp: ......................... 20
7.4.4. Cấu hình mạch khuếch đại CE, phân cực hồi tiếp từ cực C. .......................... 23
7.4.5. Cấu hình mạch khuếch đại CC ..................................................................... 29
7.4.6. Cấu hình mạch khuếch đại CB ..................................................................... 33
7.5. MÔ HÌNH CỦA FET........................................................................................ 35
7.5.1. JFET: ........................................................................................................... 35
7.5.2. MOSFET ..................................................................................................... 36
7.5.3. Các chỉ tiêu của bộ khuếch đại dùng FET: ................................................... 37
7.5.4. Cấu hình mạch khuếch đại CS: .................................................................... 38
7.5.5. Cấu hình mạch khuếch đại CD ..................................................................... 40
7.5.6. Cấu hình mạch CG ...................................................................................... 42
7.6. ĐÁP ỨNG TẦN SỐ CỦA MẠCH KHUẾCH ĐẠI .......................................... 46
7.6.1. Phân tích giản đồ bode của mạch lọc thông thấp và thông cao: ..................... 47
7.6.2. Phân tích mạch khuếch đại tại vùng tần số trung bình: ................................. 50
7.6.3. Phân tích mạch khuếch đại ở tần số thấp: ..................................................... 50
7.6.4. Phân tích mạch khuếch đại tại vùng tần số cao ............................................. 57
7.7. ĐÁP ỨNG TẦN SỐ CỦA MẠCH KHUẾCH ĐẠI ĐA TẦNG: ...................... 63
7.8. BÀI TẬP ............................................................................................................ 65
TÀI LIỆU THAM KHẢO ........................................................................................... 86 CHƯƠNG 7
MẠCH KHUẾCH ĐẠI TÍN HIỆU NHỎ. 7.1. GIỚI THIỆU:
Cấu trúc cơ bản, kí hiệu và các đặc tính của transistor BJT và FET đã được giới
thiệu ở chương 3 và 5. Phân cực cho transistor đã trình bày chi tiết ở chương 4 và 6.
Trong chương 7 chúng ta sẽ khảo sát đáp ứng tín hiệu ac của mạch khuếch đại transistor
đối với tín hiệu nhỏ.
Một trong những vấn đề quan tâm trong quá trình phân tích các mạch transistor là
biên độ của tín hiệu ngõ vào và ngõ ra. Trước tiên cần phải xác định biên độ tín hiệu vào
lớn hay nhỏ để kỹ thuật nào được áp dụng. Không có một ranh giới nào để phân biệt
nhưng trong các ứng dụng biên độ có thể thay đổi liên quan đến các đặc tính của linh
kiện. Trong chương này sẽ trình bày phần phân tích biên độ tín hiệu vào nhỏ.
Một mô hình thường được sử dụng trong phân tích ac tín hiệu nhỏ của mạch
transistor là: mô hình thông số lai -h (hybrid). 7.2. MÔ HÌNH CỦA BJT
Chìa khóa để phân tích tín hiệu nhỏ là dùng mạch tương đương – còn gọi là mô hình.
Một mô hình là một tổ hợp của các phần tử được lựa chọn một cách hợp lí mà nó
gần chính xác với linh kiện bán dẫn thật trong một số điều kiện đặc biệt. 7.2.1. Mạng 2 cửa:
Một mạng 2 cửa tuyến tính có thể đưa về mô hình tương đương là mô hình , T
hay mô hình h theo các tham số vi phân y, z hay h. Ở đây ta chỉ khảo sát mô hình h theo tham số h.
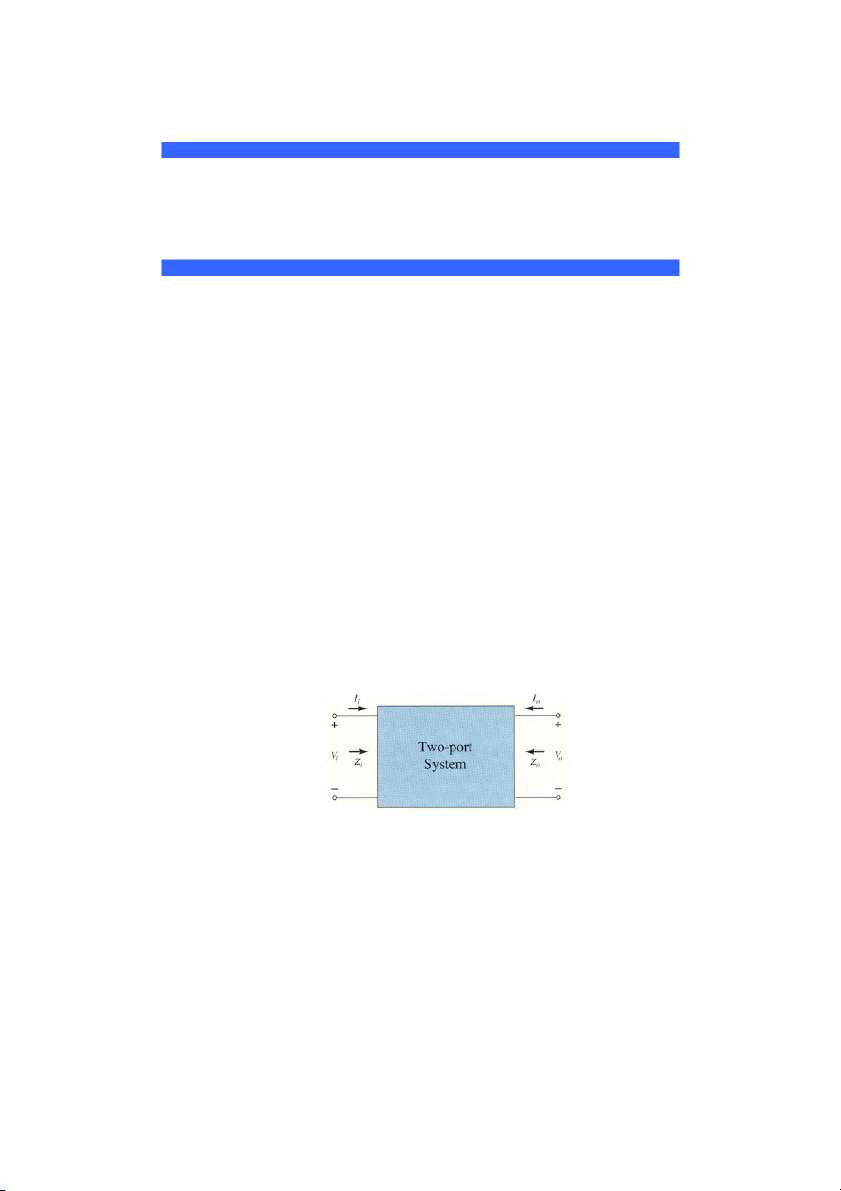
Xét mô hình mạng hai cửa tuyến tính như hình 7.1. Hình 7.1. Mạng hai cửa. Trong đó
i , v : là dòng điện và điện áp ngõ vào của mạng hai cửa. i i
i , v : là dòng điện và điện áp ngõ ra của mạng hai cửa. o o 1
Ta có phương trình theo tham số vi phân h của mạng hai cửa tuyến tính là: v h i h v (7.1) i 11 i 12 o i h i h v (7.2) o 21 i 22 o
Từ phương trình (7.1) và (7.2) , ta có: vi h
h là điện trở ngõ vào khi ngõ ra bị ngắn mạch (7.3) 11 i i v 0 i o vi h
là hệ số truyền ngược điện áp khi ngõ vào hở mạch (7.4) 12 hr v i 0 o i io h
là hệ số truyền thuận dòng điện khi ngõ ra ngắn mạch (7.5) 21 hf i v 0 i o i o h
h là điện dẫn ngõ ra khi ngõ vào hở mạch (7.6) 22 O v i 0 o i
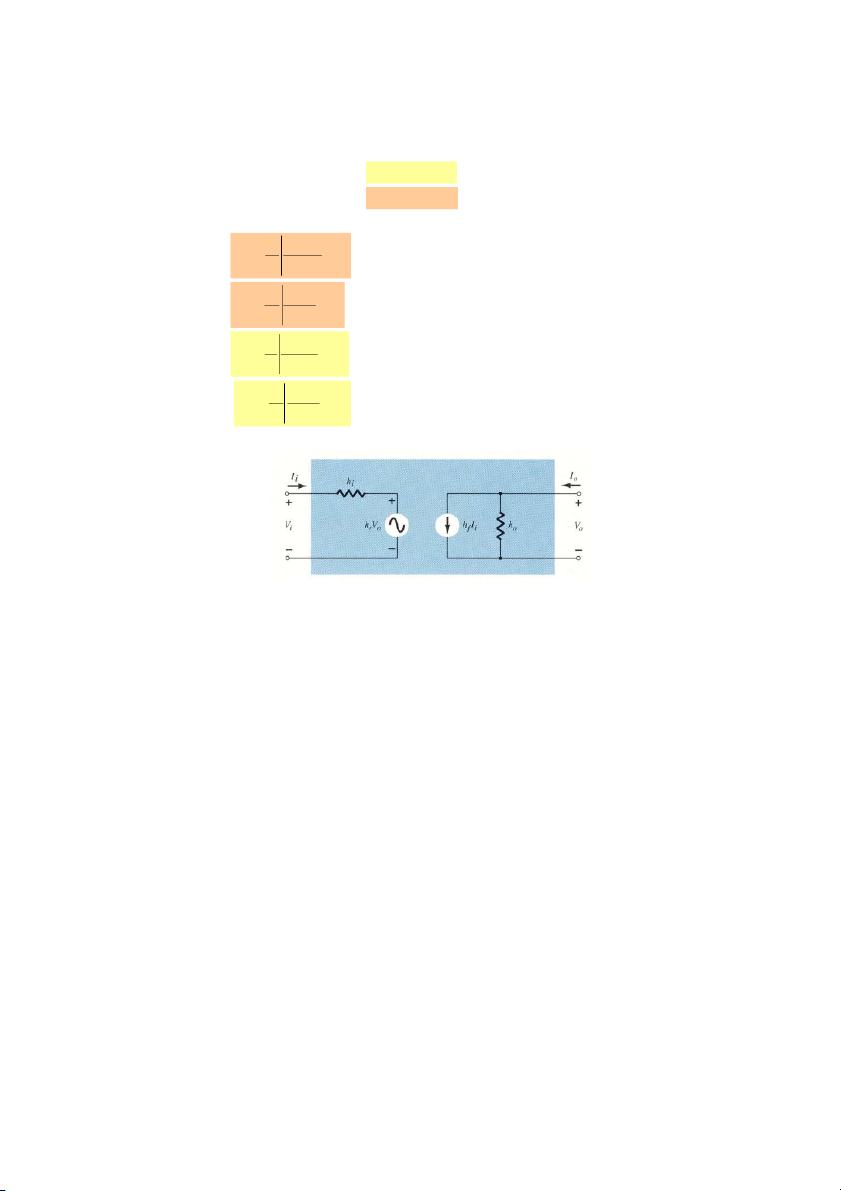
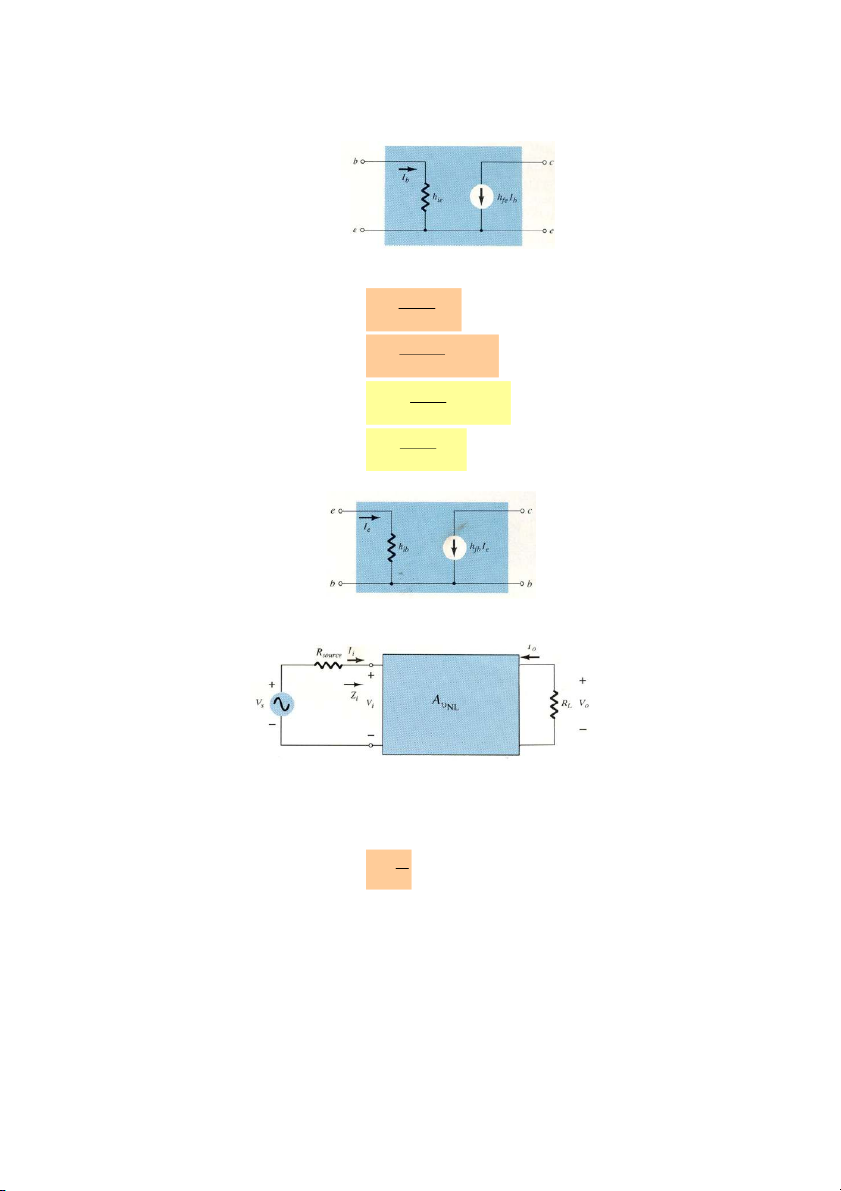
Từ phương trình (7.1) và (7.2), ta vẽ được mô hình h theo tham số h như hình 7.2.
Hình 7.2. Mô hình theo thông số h của mạng hai cửa tuyến tính. 7.2.2.
Mô hình tương đương của transistor:
Khi BJT làm việc với tín hiệu nhỏ, có nghĩa là trên cơ sở điện áp một chiều phân
cực cho hai chuyển tiếp JE và JC (xác định điểm làm việc tĩnh Q) khi có thêm tín hiệu
xoay chiều ở ngõ vào có biên độ nhỏ thì BJT khuếch đại để đưa tín hiệu xoay chiều này
đến ở ngõ ra nhưng có biên độ lớn hơn. Ở trạng thái đó (trạng thái động tín hiệu nhỏ),
một cách gần đúng có thể coi BJT như một phần tử tuyến tính. Điều này hoàn toàn cho
phép, vì ta đã thấy trên các đường đặc tuyến vôn-ampe của BJT ở chương 3 có thể xem là
một đường thẳng tuyến tính trong những vùng lân cận của điểm làm việc của BJT nằm trong vùng khuếch đại.
Mặc dù BJT có nhiều cách mắc khác nhau (CE, CB, CC) nhưng tất cả có thể xem là
một mạng hai cửa, vậy có thể thay BJT ở trạng thái động tín hiệu nhỏ bằng một mạng hai
cửa tuyến tính. Khi đó có thể dùng mô hình tương đương của mạng hai cửa cho mô hình
tương đương của BJT với các tham số vi phân được thể hiện bằng sự biến thiên nhỏ của
dòng hay áp khi BJT hoạt động được gọi là tham số vi phân của BJT. Tuỳ theo yêu cầu
kỹ thuật mà chọn đại lượng phụ thuộc và không phụ thuộc thông qua các tham số để biễu
diễn khả năng hoạt động của BJT. 2
Lưu ý: các tham số vi phân h chính là các tham số xoay chiều chúng biểu thị cho độ
dốc (hoặc nghịch đảo độ dốc) của các đặc tuyến tĩnh tương ứng, vì vậy chúng thay đổi
theo điểm làm việc tương ứng.
Mạch điện hình 7.2 có thể áp dụng đối với bất kỳ linh kiện điện tử 3 cực tuyến tính
hoặc các hệ thống không có nguồn độc lập bên trong. Do đó đối với transistor có 3 cấu
hình cơ bản thì mạch điện tương cũng có dạng như hình 7.3.
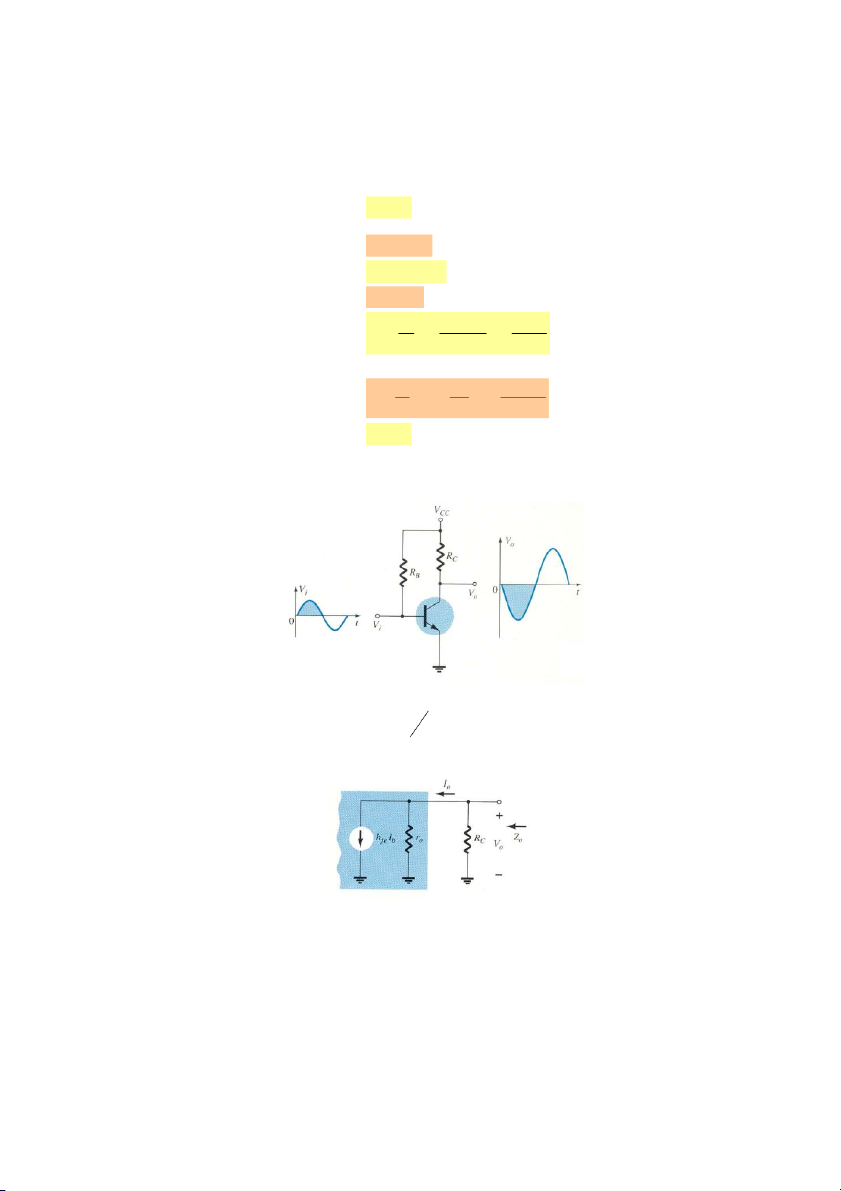
Hình 7.3. Cấu hình mạch tương đương của transistor. 7.2.3. Cấu hình mạch CE:
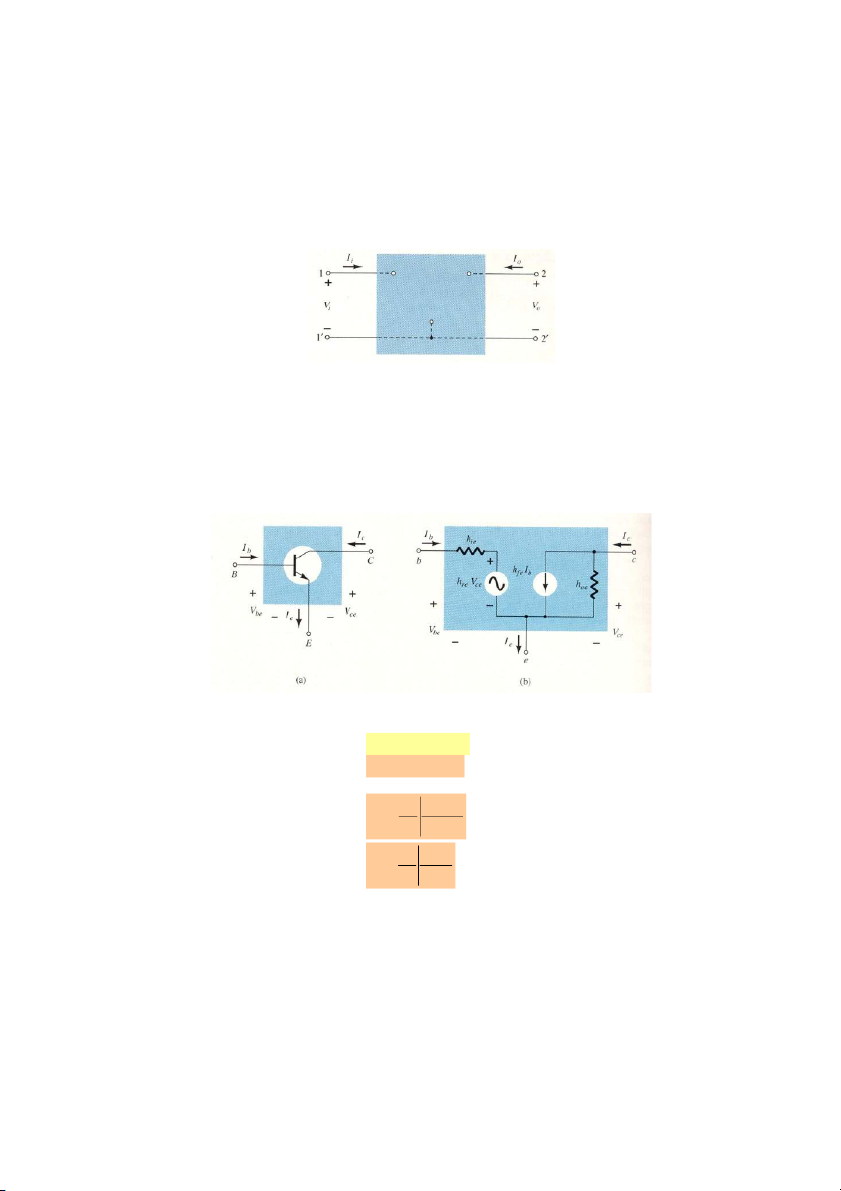
Cấu hình mạch tương đương của transistor cực E chung như hình 7.4, trong đó các
thông số được thêm vào chữ e để phân biệt đây là cấu hình mạch tương đương cực E
chung. Chú ý dòng vào i i và dòng ra i i . Dòng i i i , điện áp vào là v và i b o c e b c be điện áp ra là v . ce
Mạch CE trong hình 7.4a và mô hình tương đương của BJT mắc CE như hình 7.4b.
Hình 7.4. a. Mạch CE; b. mô hình tương đương của mạch CE
Phương trình của mạch CE: v h i h v (7.7) be ie b re ce i h i h v (7.8) c fe b oe ce
Trong đó các tham số vi phân của CE v h be ie i v 0 b ce v h be re v i 0 ce b 3 i h c fe i v b ce 0 i h c oe v i 0 ce b 7.2.4. Cấu hình mạch CB
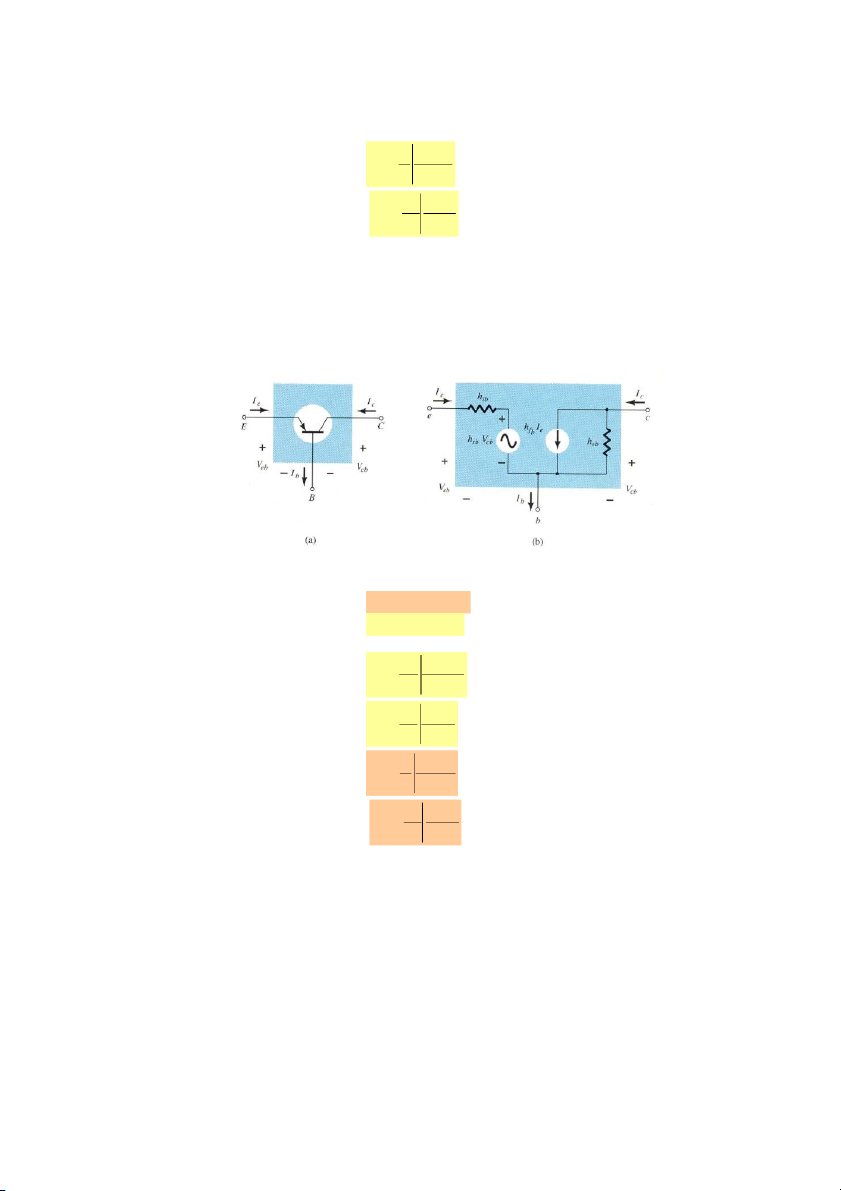
Cấu hình mạch tương đương của transistor cực B chung như hình 7.6, trong đó các
thông số được thêm vào chữ b để phân biệt đây là cấu hình mạch tương đương cực B
chung. Chú ý dòng vào i i và dòng ra i i . Điện áp vào là v v và điện áp ra là i e o c i be v v . o cb
Mạch CB trong hình 7.5a và mô hình tương đương của BJT mắc CE như hình 7.5b.
Hình 7.5. a. Mạch CB; b. Mô hình tương đương của mạch CB.
Phương trình của mạch CE: v h i h v (7.9) eb ib e rb cb i h i h v (7.10) c fb e ob cb
Trong đó các tham số vi phân của CB v h eb ib i v 0 e cb v h eb rb v i 0 cb e i h c fb i v 0 e cb i h c ob v i 0 cb e 7.2.5. Cấu hình mạch CC
Mô hình mạch CC của BJT ít được sử dụng, nên ở đây không xây dựng mô hình cho mạch CC của BJT. 4
Phương trình của mạch CC: v h i h v (7.11) bc ic b rc ec i h i h v (7.12) e fc b oc ec
Trong đó các tham số vi phân của CC v h bc ic i v 0 b ec v h bc rc v i 0 ec b i h c fc i v 0 b ec i h c oc v i ec b 0 7.2.6.
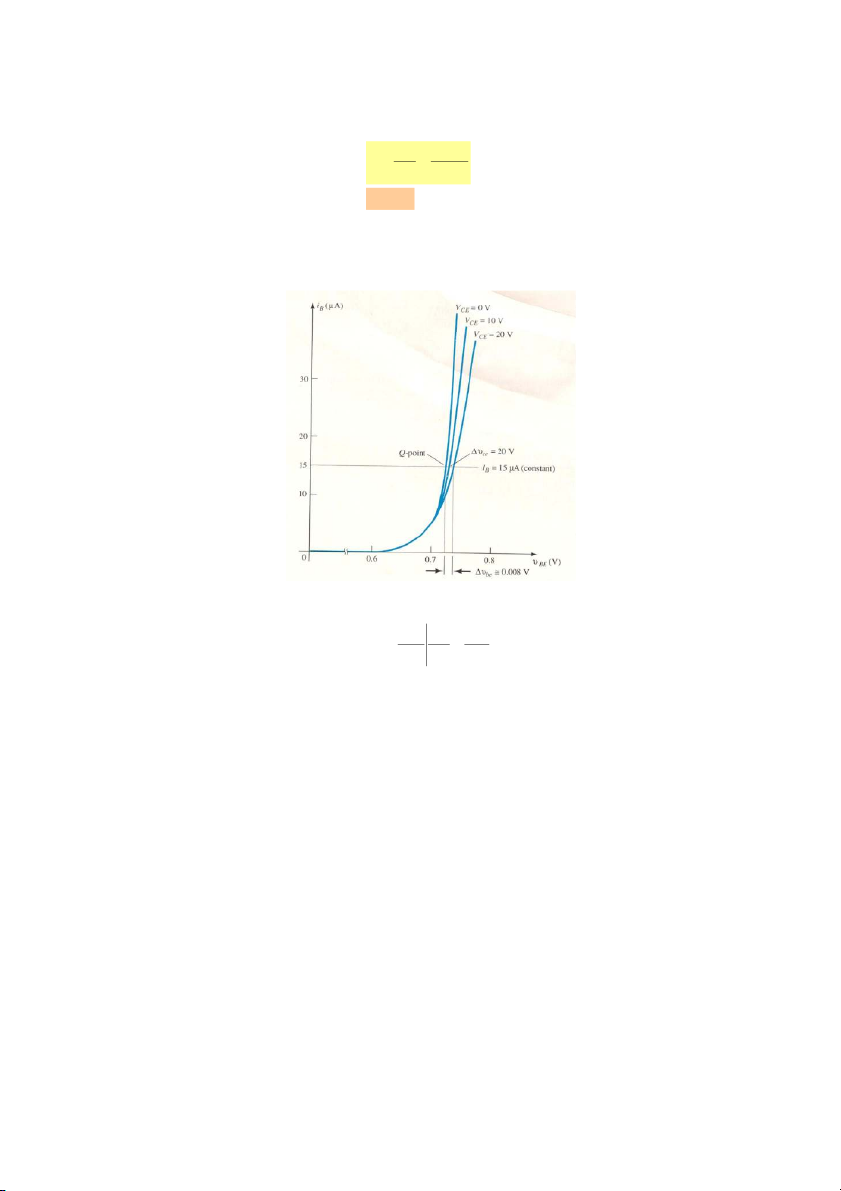
Xác định các giá trị thông số của BJT bằng đồ thị a. hie
Xét đường đặc tuyến ngõ vào khi cố định V V như hình 7.6 CE CEQ
Hình 7.6. Đặc tuyến ngõ vào. v v V Từ hình 7.6 ta có: be be T h (7.13) ie i V 0 i I b CEQ b EQ 26mV
tại nhiệt độ phòng t = 25oC h (7.14a) ie IEQ 5 V mV 26 Đặt T r e I I EQ EQ Vậy h r (7.14b) ie e
Chú ý chữ e trong điện trở r được chọn để nhấn mạnh rằng dòng điện dc tại cực E e
xác định giá trị điện trở của mối nối JE. b. hre
Xét đường đặc tuyến ngõ vào khi cố định I I như hình 7.7 B BQ
Hình 7.7. Đặc tuyến ngõ vào. Từ hình 7.7 ta có: v v be h (5.15) re be 0 v I v ce BQ ce c. hfe
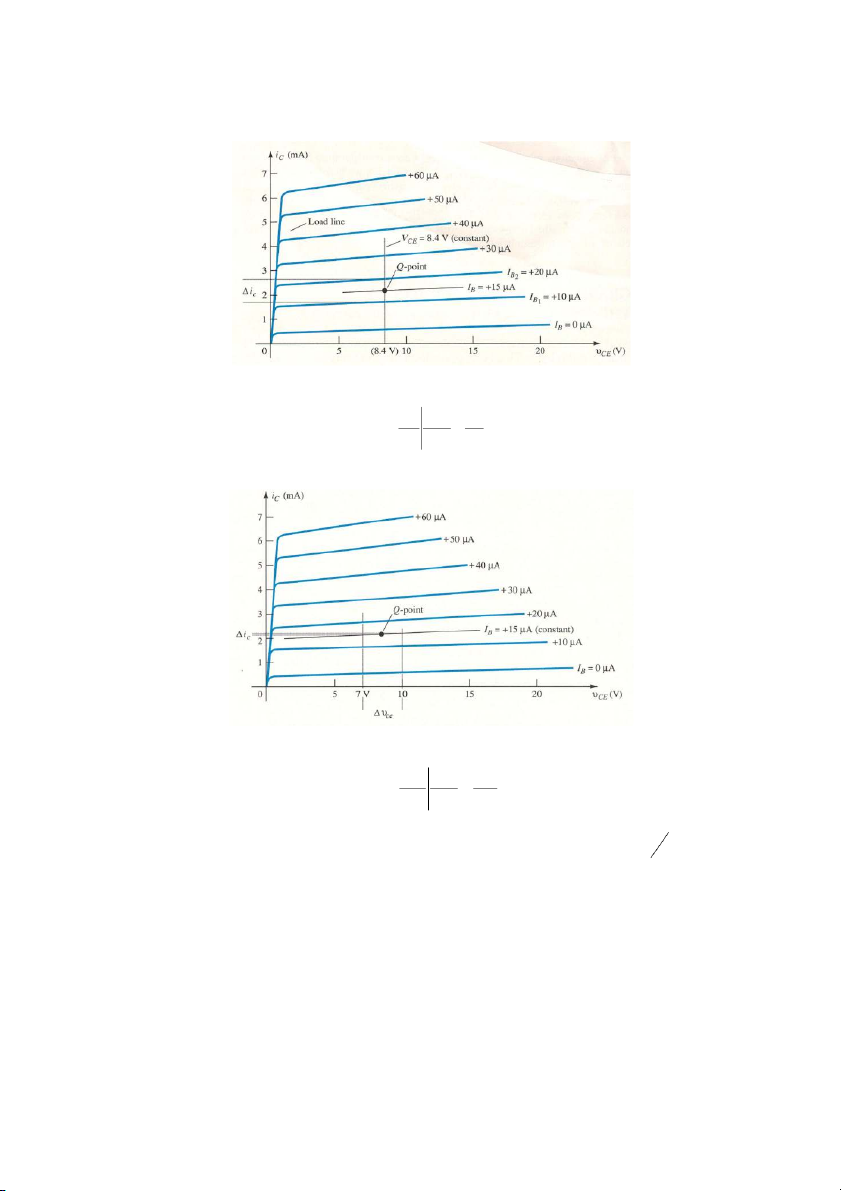
Xét đường đặc tuyến ngõ ra, khi cố định V V như hình 7.8 CE CEQ 6
Hình 7.8. Đặc tuyến ngõ ra. Từ hình 7.8 ta có: i i c h (7.16) fe c i V i b CEQ b d. hoe
Xét đường đặc tuyến ngõ ra, khi cố định I I như hình 7.9 B BQ
Hình 7.9. Đặc tuyến ngõ ra. Từ hình 7.9 ta có: i i c h c 0 (7.17) oe v V v ce CEQ ce
Đối với cấu hình cực E chung thì giá trị của thông số hr là một đại lượng tương đối
nhỏ có thể xem h 0 nên h v 0 , kết quả là ngắn mạch phần tử này. Đại lượng 1 r r o h o
thường có giá trị rất lớn nên có thể bỏ qua nếu so sánh với 1 điện trở tải, kết quả mô hình
tương đương gần đúng của transistor cấu hình cực E chung như hình 7.11 7
Hình 7.10. Mô hình tương đương gần đúng của BJT.
Bảng chuyển đổi thông số giữa các dạng mạch CE và CB cùng BJT: h ie h (7.18) ib re 1 hfe h h ie h h (7.19) rb oe re 0 1 h fe h h fe 1 (7.20) fb 1 h fe h h oe 0 (7.21) ob 1 hfe
Sơ đồ tương đương gần đúng của BJT mắc CB trong hình 7.12
Hình 7.11. Mạch tương đương.
7.3. CÁC CHỈ TIÊU CỦA BỘ KHUẾCH ĐẠI:
Hình 7.12. Sơ đồ khối của mạch khuếch đại.
Từ sơ đồ khối của bộ khuếch đại, ta có: Tổng trở vào Zi:
Tổng trở vào Z i được xác định bởi định luật Ohm có phương trình: V i Z (7.22) i Ii Tổng trở ra Zo: 8
Tổng trở ra thường được xác định tại các đầu ngõ ra nhưng hoàn toàn khác với tổng
trở ngõ vào: tổng trở ra được xác định tại các đầu ngõ ra nhìn vào hệ thống khi không có tín hiệu ở ngõ vào.
Tổng trở ra xác định theo phương trình: V O Z (7.23) O IO Độ lợi điện áp:
Một trong những đặc tính quan trọng nhất của mạch khuếch đại là độ lợi điện áp,
chính là tỷ số điện áp ngõ ra và ngõ vào: V O A (7.24) V VI
Đối với hệ thống hình 7.13, độ lợi áp toàn mạch là: V Z o i A A (7.25) Vs V V Z R s i s Độ lợi dòng điện:
Độ lợi dòng điện được xác định bởi phương trình: I O A (7.26) i I I
Đối với hệ thống như hình 7.13 dòng điện ngõ vào và dòng điện ngõ ra được xác định: V V i I và O I i Z O R i L
Khi đó độ lợi dòng điện: Vo I R V Z Z o L o i i A A (7.27) i V I Vi V R R i i L L Z i Độ lợi công suất: P V I O o O A A A (7.28) P v i P V I I i i Mối quan hệ về pha:
Mối quan hệ và pha của tín hiệu vào và tín hiệu ra dạng sin rất quan trọng. Đối với
các mạch khuếch đại transistor ở dãi tần trung bình cho phép bỏ qua ảnh hưởng của các
phần tử dung kháng, tín hiệu vào và tín hiệu ra có thể cùng pha hoặc ngược pha nhau
180 tùy theo đặc tính của mạch.
7.4. PHÂN TÍCH MẠCH KHUẾCH ĐẠI TÍN HIỆU NHỎ
Các mô hình đã giới thiệu bây giờ được sử dụng để thực hiện việc phân tích ac của
một số cấu hình mạch chuẩn dùng transistor. 7.4.1.
Cấu hình mạch khuếch đại CE, phân cực cố định:
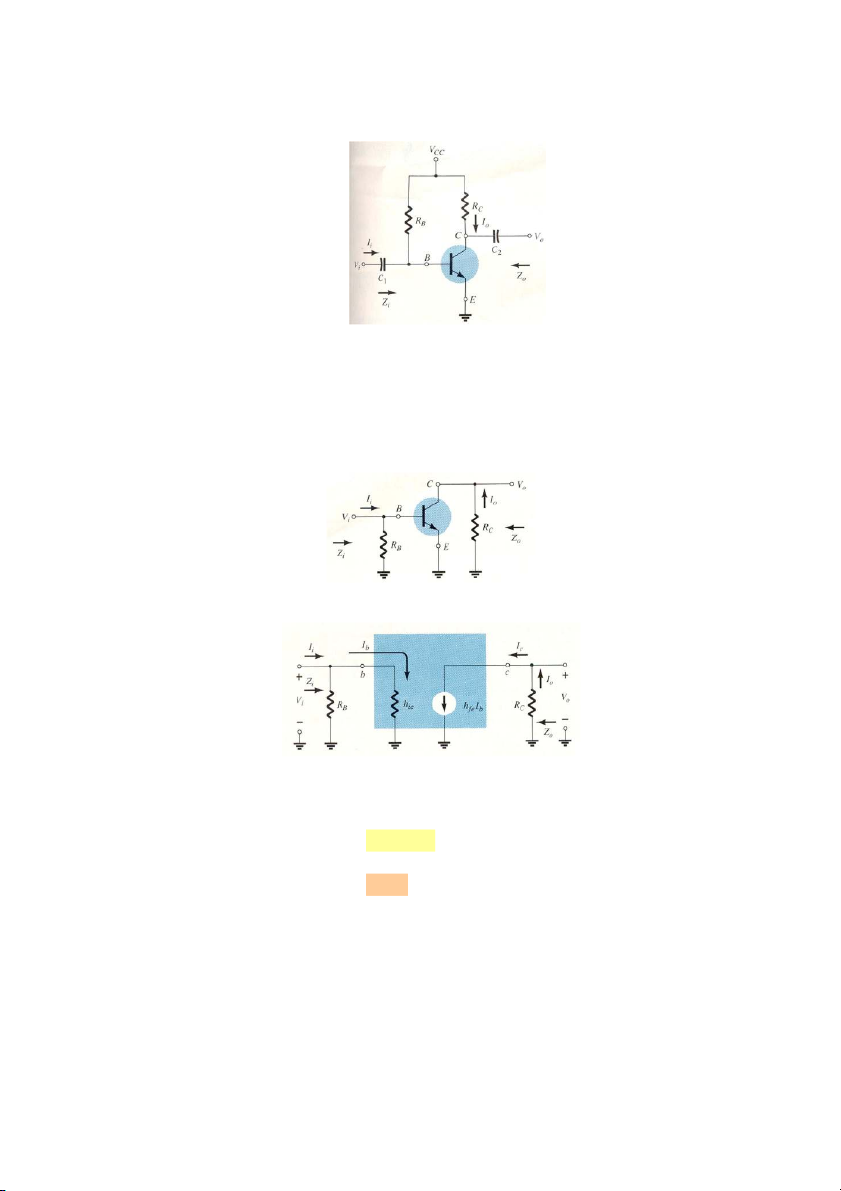
Ví dụ xét mạch điện như hình 7.13: 9
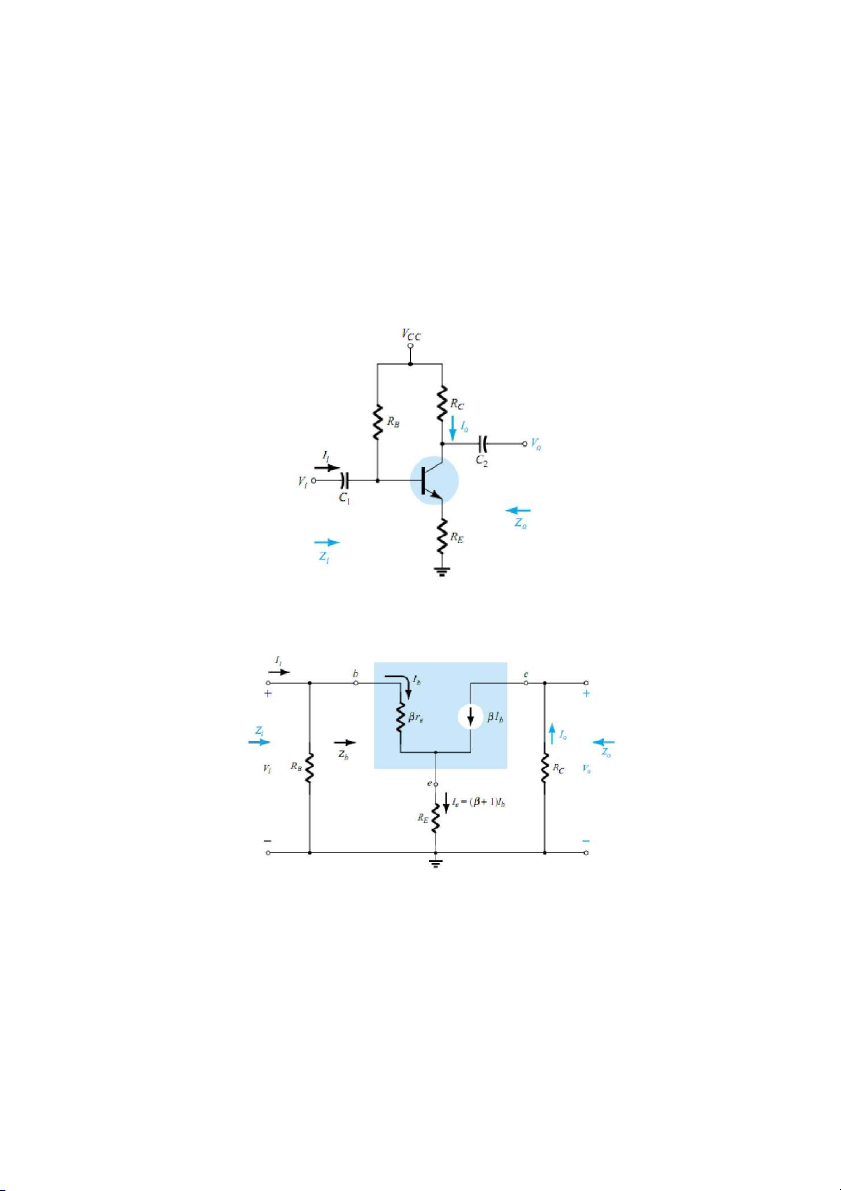
Hình 7.13. Mạch khuếch đại E chung.
Mạch điện tương đương được phân tích như sau: giả sử tín hiệu vào là ac đã được
xác định. Do chỉ xét đến tín hiệu ac nên tất cả các nguồn dc có thể xem như ngắn mạch
do chúng chỉ xác định điện áp dc ở ngõ ra mà không xác định biên độ dao động ngõ ra.
Mạch điện tương đương như hình 7.14. Các tụ liên lạc ac xem như nối tắt C1 và C2
và tụ bypass C3 được chọn sao cho có tổng trở rất nhỏ tại tần số của tín hiệu và nối tắt điện trở RE.
Sơ đồ mạch hình 7.14 được vẽ lại như hình 7.15.
Hình 7.14. Mạch điện khi chỉ xét tín hiệu xoay chiều.
Sơ đồ tương đương tín hiệu nhỏ của mạch hình 7.15 như hình 7.16.
Hình 7.15. Mạch tương đương tín hiệu nhỏ.
Xác định các thông số: tổng trở vào, tổng trở ra, hệ số khuếch đại điện áp, hệ số
khuếch đại dòng điện: Tổng trở vào: Z R | h (7.29) i B ie
Nếu điện trở R lớn hơn h gấp 10 lần thì có thể xem: B ie Z h (7.30) i ie 10 Tổng trở ra:
Được xác định khi tín hiệu vào v 0 , suy ra i i 0 nên có thể xem là hở mạch i i b
nguồn dòng và kết quả là tổng trở ra: Z R (7.31) o C
Hệ số khuếch đại điện áp: Điện áp ra: V I R o o C Suy ra điện áp ra Vo: V h I R (7.32) o fe b C Điện áp vào: V I h i b ie V h I R h R
Hệ số khuếch đại điện áp: o fe b C fe C A (7.33) v i V Ib ie h ie h
Hệ số khuếch đại dòng: dòng điện ngõ ra được xác định: I Z R o i B A A h (7.34) i V fe I R R h i C B ie Nếu h R thì: A h ie B i fe (7.35)
Mối liên hệ về pha: dấu trừ <-= trong hệ số khuếch đại áp chứng tỏ tín hiệu ra đảo
pha 180 so với tín hiệu vào như hình 7.17:
Hình 7.16. Minh họa tín vào và ra đảo pha.
Ảnh hưởng của điện trở r ( hay 1
): nếu xét thêm điện trở r ( trường hợp o h o oe
nếu điện trở r không lớn hơn điện trở R hơn 10 lần) thì trong mạch điện hình 7.13 o C
mạch điện phần ngõ ra có dạng như hình 7.17. 11
Hình 7.17. Xét ảnh hưởng của r . o
Khi đó tổng trở ra Zo được xác định: Z r // R (7.36) O O C
Khi đó hệ số khuếch đại điện áp: R // r C o A h (7.37) v fe hie
Hệ số khuếch đại dòng điện: Dòng điện ngõ ra: ro I h I o fe b r R o C I r R
Suy ra hệ số khuếch đại: O o B A h (7.38) i fe I r R R h i o C B ie
Vậy mạch khuếch đại CE có độ lợi áp và độ lợi dòng lớn nên thường được sử dụng
để khuếch đại tín hiệu, độ lệch pha giữa tín hiệu vào và ra là 1800.
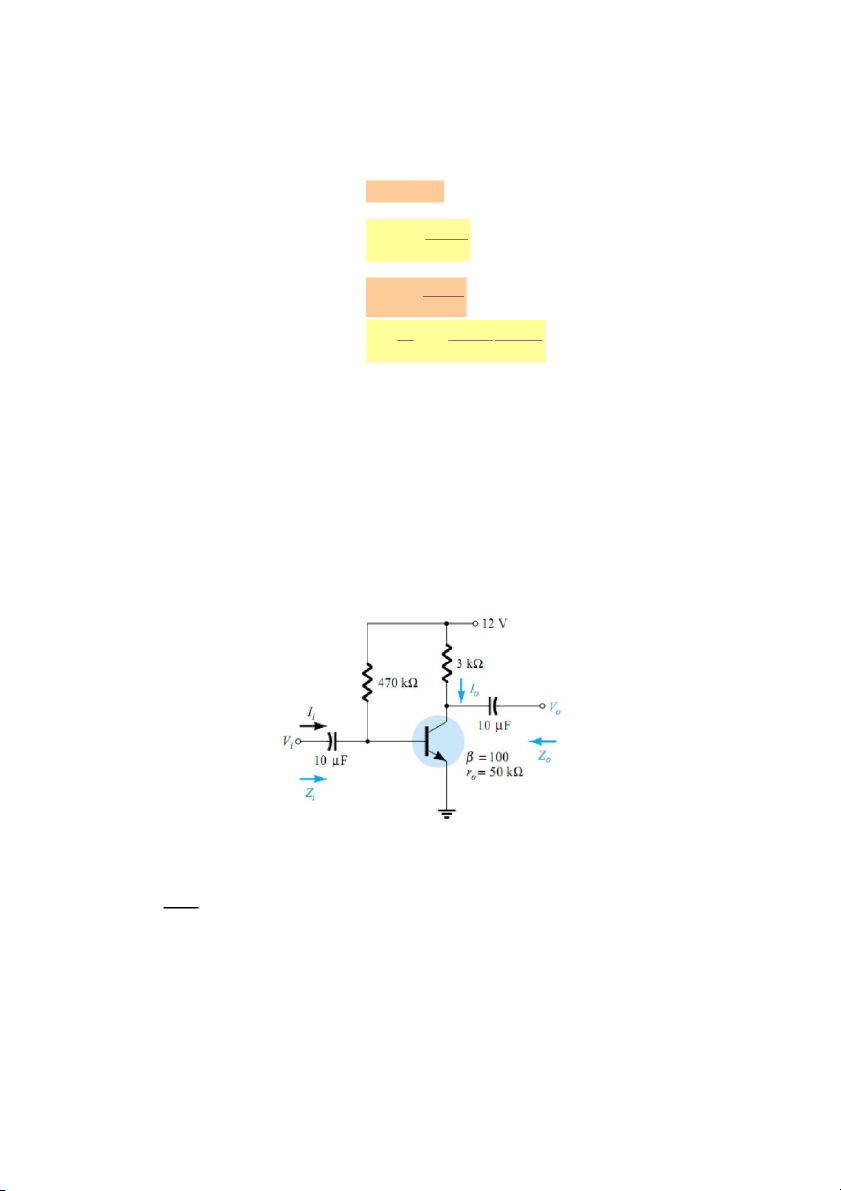
Ví dụ 7.1 Cấu hình mạch khuếch đại CE, phân cực cố định Cho mạch như hình 7.18. a) Xác định re,
b) Xác định tổng trở ngõ vào Zi
c) Tính tổng trở ngõ ra Z0 d) Xác định AV, AI
e) Khi r0 = 50 kΩ, tính lại các giá trị Z0, AV, AI.
Hình 7.18. Mạch khuếch đại CE, phân cực cố định cho ví dụ 7.1 Giải: 12 a) Phân tích DC ta có: V V 12V 0,7V CC BE I 24,04 A B R 470k B Do đó 26mV 26mV r 10, 71 e I 2, 428mA E Với I ø ù 1 I ø 10 ù 1 ø 24,04 ù A 2, 428mA E B
hie r ø100ùø10, 71 ù 1,071k e b) Tổng trở ngõ vào Zi Z = R Phie = 47OkW 1 P , 071kW= 1,069kW i B c) Tổng trở ngõ ra Zo Z R 3k 0 C
d) Độ lợi điện áp, độ lợi dòng điện Độ lợi áp AV R 3k C A V 280,11 r 10,71k e
Do R ? 10b r (470kW> 10,71kW B e ) Độ lợi dòng AI A I 100
b) Khi xét đến ảnh hưởng của ro Z = r PR = 50kWP 3kW= 2,83kW 0 0 C r R P 2,83kW 0 C A = - = - = - 264, 24 V r 10,71kW e R r 100 470k 50k B 0 ø ù ø ùø ù A I ø 94,13 r R R r
50k 3k 470k 1,071k 0 C ù ø B e ù ø ùø ù 7.4.2.
Cấu hình mạch khuếch đại CE, phân cực kiểu định dòng điện có điện trở RE 13
Trong cấu hình mạch này, điện trở RE có thể có hoặc không bị bypass trong miền
ac. Đầu tiên ta xem xét RE không bị bypass bởi tụ CE, sau đó ta mở rộng kết quả
cho trường hợp RE bị bypass.
Trường hợp không có tụ bypass CE
Cho mạch điện như hình 7.19, mạch tương đương như hình 7.20, ta giả sử rằng bỏ
qua ảnh hưởng của điện trở ngõ ra r0 của transistor. Tuy nhiên ở phần sau, ta sẽ
xem xét đến ảnh hưởng của r0.
Hình 7.19. Mạch khuếch đại CE không có tụ CE, mạch phân cực cố định có điện trở RE
Hình 7.20. Mạch tương đương tín hiệu nhỏ 14
Áp dụng định luật Kirchoff cho hình 7.20, ta có: v I r I R i b e e E v I r I R i b ø ù 1 b E
Trở kháng ngõ vào bên phải của RB là: vi Z r R (7.39) b e ø ù1 E Ib
Do β thông thường lớn hơn 1 rất nhiều nên: Z r R b e E Z r R (7.40) b ø e E ù
Do RE thường lớn hơn re nhiều nên (8.21) có thể viết Z R (7.41) b E Tổng trở Zi: Từ mạch 7.20 ta có: Z = R PZ (7.42) i B b Tổng trở Z0:
Đặt Vi = 0, Ib = 0 và βIb = 0 bằng cách ngắn mạch ngõ vào, ta có: Z0 = RC (7.43) A V v: i I (7.44) b Zb Với Z r R b ø e E ù Độ lợi AV: V R 0 C A (7.45) V V Z i B Nếu Z R thì: b E RC A (7.46) V RE Độ lợi AI:
Áp dụng luật phân dòng cho ngõ vào của mạch ta có: 15 R I B i I b R Z B b Suy ra: I R b B I R Z i B b Ta có: I0 = βIb Nên I 0 I b Do đó: I I I R 0 0 A . b . B i I I I R Z i b i B b RB A (7.47) i R Z B b Z Hoặc: A A . i (7.48) i V RC
Mối quan hệ về pha: biểu thức (5.46) cho thấy tín hiệu vào ra lệch pha nhau 180o Xét ảnh hưởng của r0:
Các công thức dưới đây cho thấy điện trở r0 của transitor ảnh hưởng trong mạch: ø ù 1 R / r Z C 0 i: Z r R (7.49) b e 1 øR r ù/ E r C e 0
Do tỷ số RC/r0 luôn nhỏ hơn (β+1) rất nhiều, nên: ø 1ù RE Z r b e 1ø R r r C e ù / 0 Nếu r0 ≥ 10(RC + RE) Z r ø ù 1 R b e E Dob + 1 ; b Nên Z r R (7.50) b ø e E ù é ù ê ú ê b (r + r ú 0 e ) Z0: Z = R P r ê + ú (7.51) 0 C 0 ê b r ú ê 1 e + ú ê RE ú ë û 16 Tuy nhiên r ? r , nên: 0 e é ù ê ú ê b ú Z @ R P r ê + ú 0 C 0 ê b r ê 1 e ú + ú ê R ë E ú û é ù ê ú ê 1 ú Z @ R P r ê + ú 0 C 0 ê 1 re ú ê + ú ê b RE ú ë û 1
Thông thường và re nhỏ hơn 1 rất nhiều nên tổng của chúng cũng nhỏ hơn 1. RE
Giả sử với β = 100, re = 10 Ω, RE = 1 kΩ 1 1 50 1 10 0,02 100 1k Z = R P 51r 0 C 0 Do đó để đơn giản: Z0 = RC (7.52) R r R C 1 e C V Z r r A 0 b v: 0 0 A (7.53) V V R i 1 C r0 Tỷ số: re = 1 r0 R R C C V Z r 0 b 0 A V V R i 1 C r0 Nếu r 10R 0 C V R 0 C A V V Z i b 17 A Z i: A A . i i v RC
Trường hợp có tụ bypass CE: Nếu điện trở RE trong mạch hình 7.19 được bypass
bởi tụ CE thì mạch tương đương trở thành mạch tương đương như hình 7.13. Các
công thức từ 5.29 đến 5.35 đều dùng được.
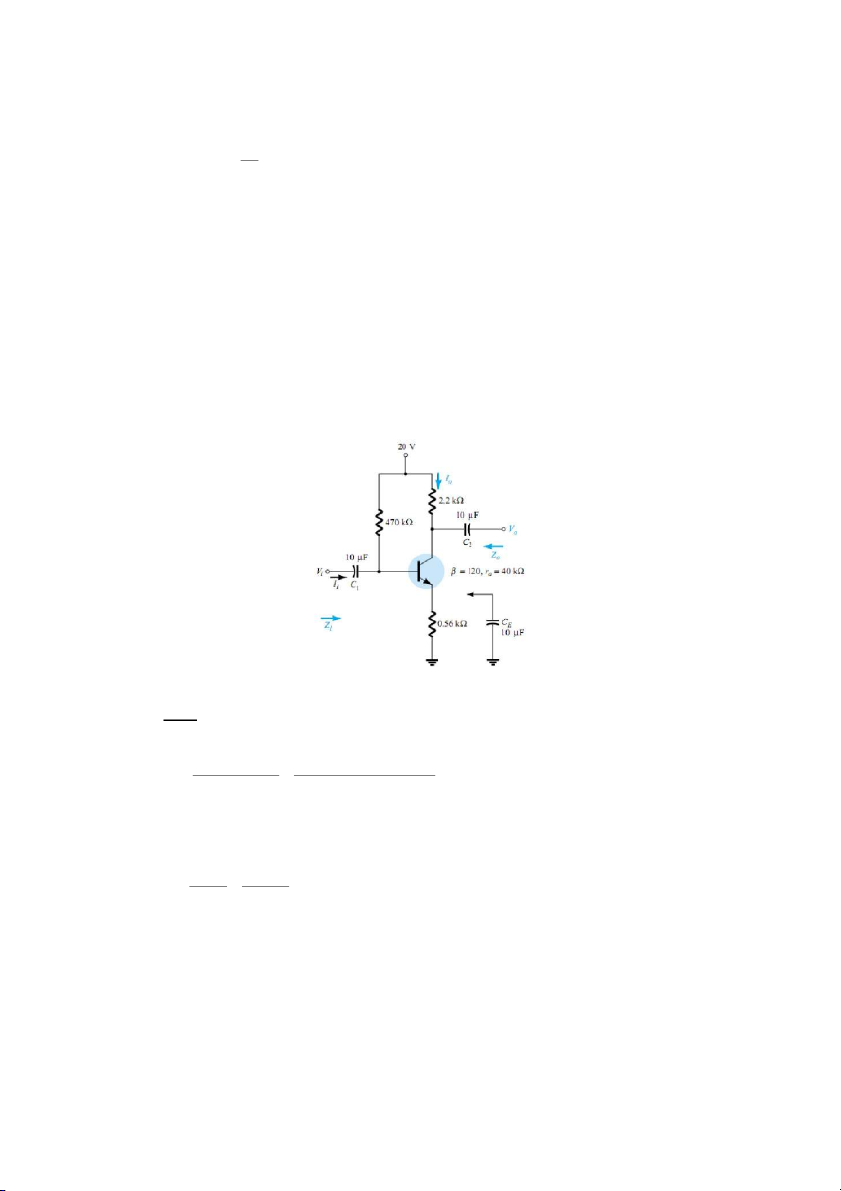
Ví dụ 7.2: Cho mạch điện như hình 7.21, không có tụ CE, xác định: a) re b) Zi c) Z0 d) Av e) Ai
Hình 7.21. Mạch khuếch đại CE, cho ví dụ 7.2 Giải: a) Phân tích DC, ta có: V V V CC BE 20 0,7 I A B R R k k B ø ù E ø ùø ù 35,89 1 470 121 0,56 Do đó I ø ù 1 I ø 12 ù 1 ø35,89Aù 4,34mA E B 26mV 26mV r 5, 99 e I 4,34mA E 18
b) Kiểm tra điều kiện: r 10 R R 0 ø C E ù 40k 1 ø 0 2, 2k 0,56k ù
40k 27,6k (thỏa mãn)
Do đó: Z ø r R ù 12 ø
0 5,99 560 ù 67,92k b e E
Z = R PZ = 470kWP67,92kW= 59,34kW i B i c) Zb = RC = 2,2 kΩ
d) r0 ≥ 10RC thỏa mãn, do đó: V R 120 2,2k 0 ø ùø ù C A 3,89 V V Z 67,92 k i b So sánh với A R
V=-3,93 khi sử dụng công thức (5.46) C A V RE Z 59,34k e) A A . i i v ø 3,89ù ø ù . 104,92 R 2,2k C R
So sánh với AI=104,92 khi sử dụng công thức (7.47) B A i R Z B b
Ví dụ 7.3. Cho mạch điện như hình 7.21 với tụ bypass CE, tính lại các giá trị như ví dụ 7.2. Giải: a) Phân tích DC ta có re = 5,99 Ω
b) RE bị ngắn mạch bởi CE, do đó: Z = R PZ = R Pbr = 470kW ( P 120)(5,99 ) W = 717,70W i B b B e c) Z R 2, 2k 0 C d) R k C 2, 2 A
367, 28 (tăng đáng kể khi có tụ CE) V r 5,99k e R ø120ùø470k ù e) B A 119,82 i R Z 470k 718,8k B b 19




