Đề thi học kỳ I năm học 2023-2024 Môn: Vật lý 1 | Khoa khoa học ứng dụng Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI HỌC KỲ I NĂM HỌC 2023-2024 THÀNH PHỐ HỒ CHÍ MINH Môn: Vật lý 1
KHOA KHOA HỌC ỨNG DỤNG Mã môn học: PHYS130902
Đề số:01. Đề thi có 02 trang.
-------------------------
Ngày thi: 25/12/2023. Thời gian: 90 phút.
Được phép sử dụng một tờ giấy A4 chép tay.
Câu 1:(1,0 điểm)
Hai ly uống nước có cùng diện tích đáy nhưng hình dạng khác nhau được đổ đầy với
cùng một mực nước. Hãy so sánh áp suất ở đáy hai ly và lực tác dụng vào đáy hai ly. Giải thích.
Câu 2: (1,0 điểm)
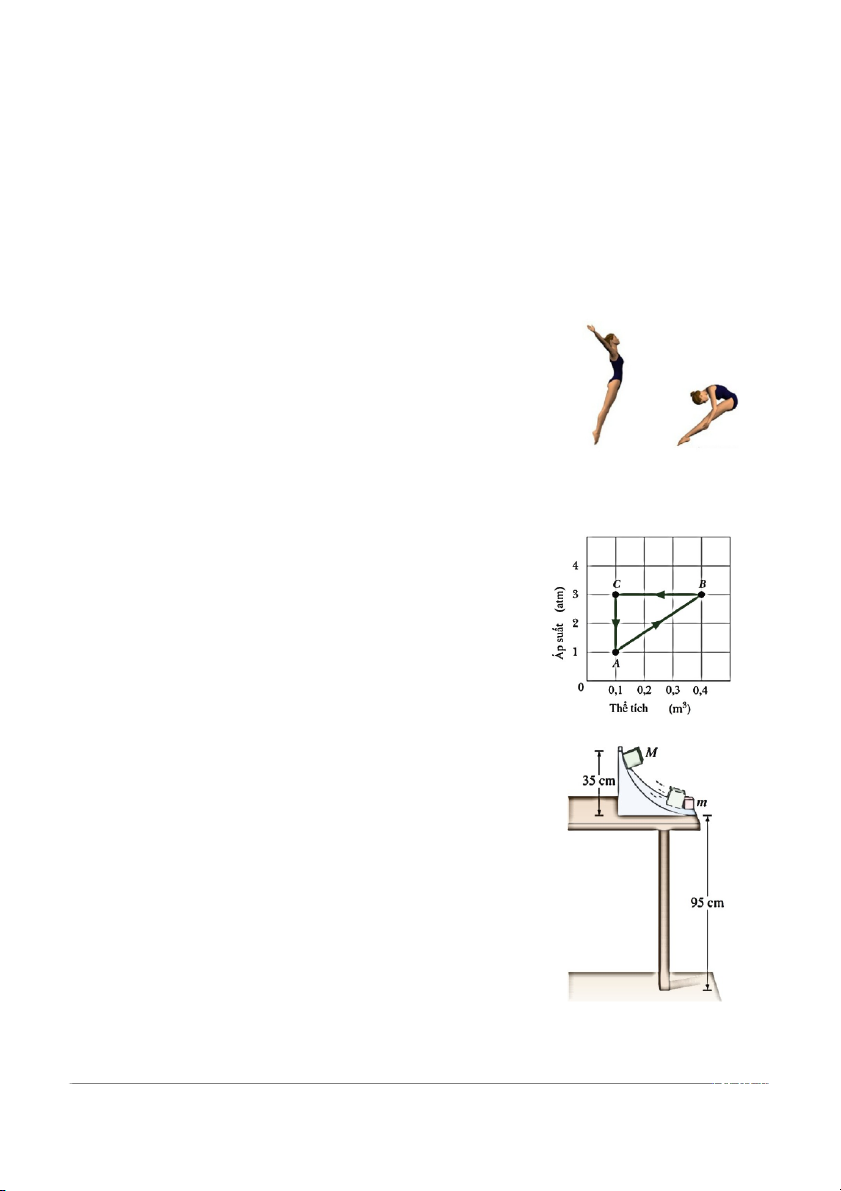
Một nữ vận động viên nhảy cầu trong tư thế duỗi thẳng
người và quay chậm quanh trục quay nằm ngang (vuông góc
với mặt phẳng hình vẽ) đi qua khối tâm (hình A). Nếu vận
động viên gập người lại như hình B thì tốc độ quay của cô sẽ
tăng hay giảm so với tư thế ban đầu? Giải thích. (A) (B)
Câu 3: (1,0 điểm)
Một bi sắt là khối cầu đặc khối lượng M bắt đầu lăn không trượt trên một dốc nghiêng
có độ cao h. Xác định động năng tịnh tiến của bi sắt khi nó đến chân dốc.
Câu 4: (1,0 điểm)
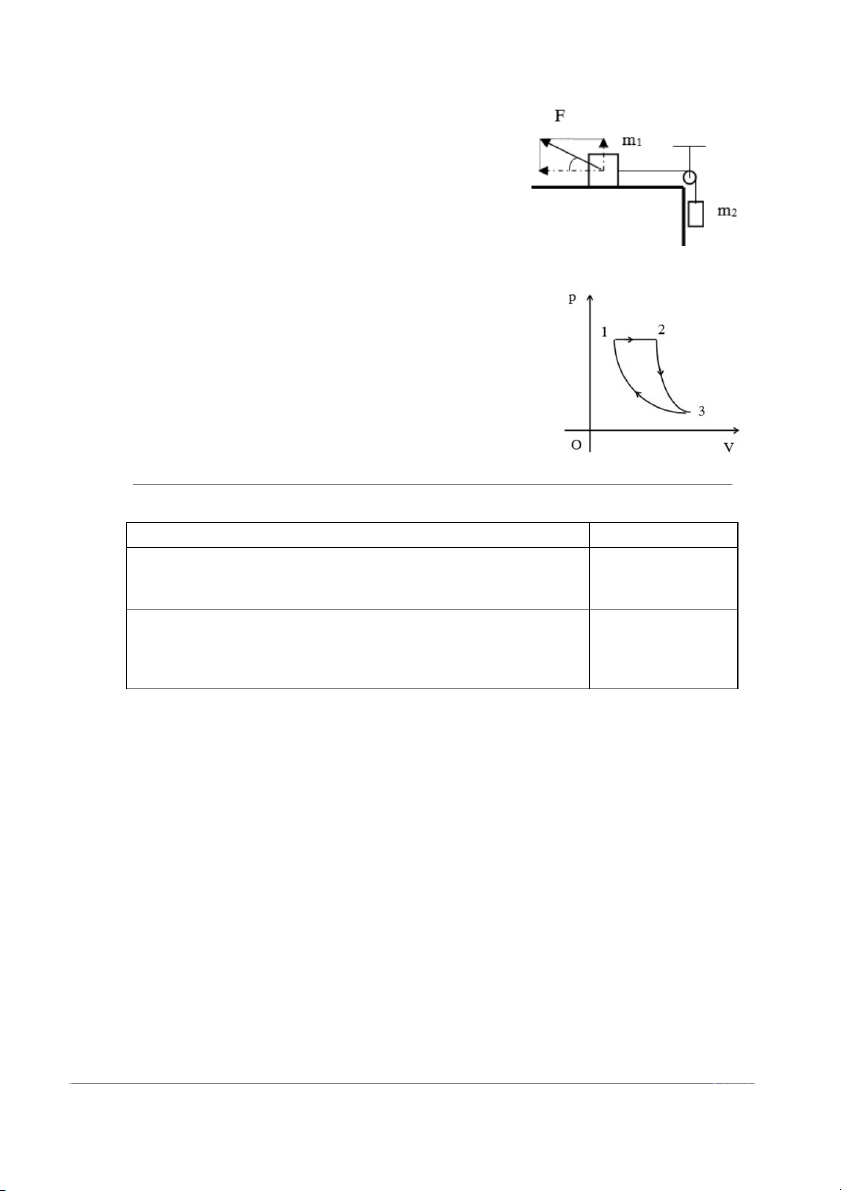
Một khối khí lý tưởng hoạt động theo chu trình ABCA
như hình vẽ bên. Hãy tính công và nhiệt lượng trao đổi sau chu
trình này và cho biết sau một chu trình hệ sinh công hay nhận
công, tỏa nhiệt hay nhận nhiệt?
Câu 5: (2,0 điểm)
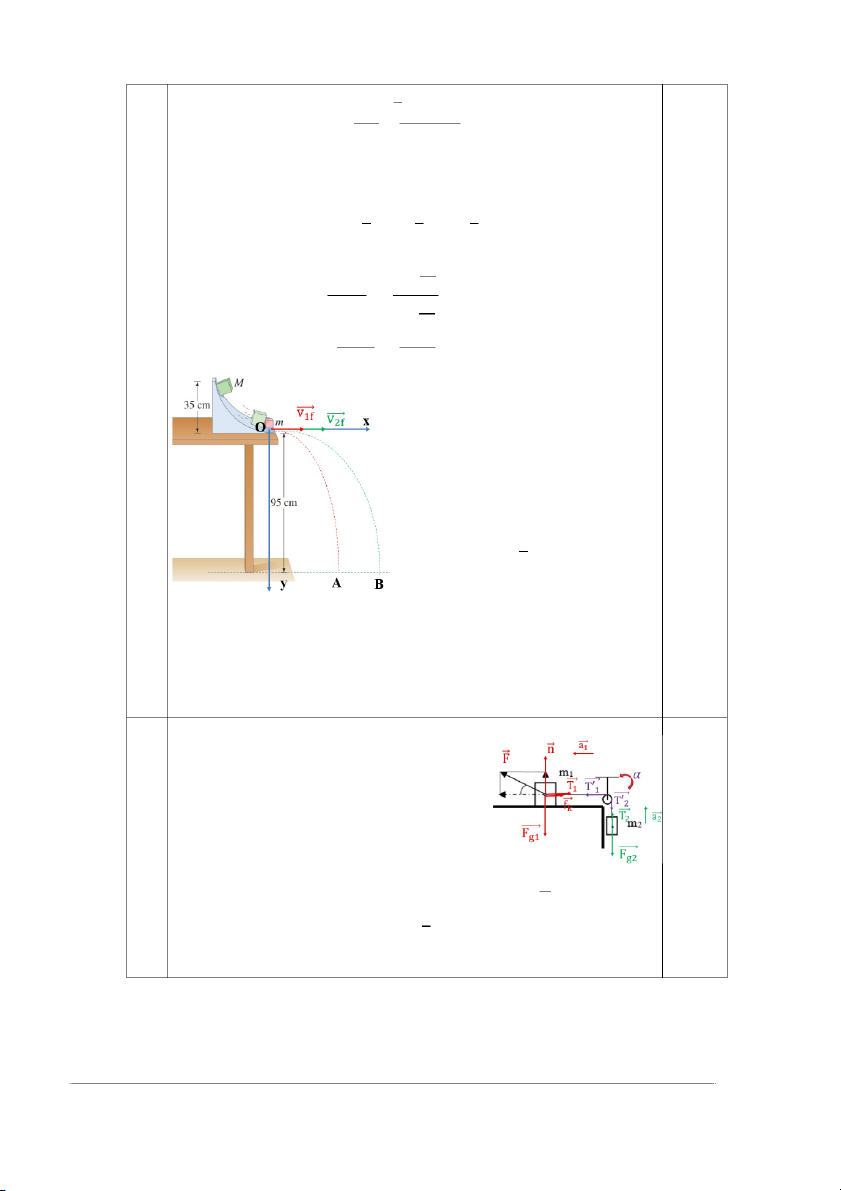
Trong một phòng thí nghiệm vật lý, một khối hộp bắt đầu
trượt từ trạng thái nghỉ trên một rãnh không ma sát, khi đến điểm
cuối rãnh thì va chạm đàn hồi với khối hộp khác chỉ nặng bằng
một nửa nó đang đứng yên ở đó. Biết độ cao của rãnh là 35 cm và
độ cao của bàn so với sàn là 95 cm. Cả hai vật rời khỏi rãnh trên
bàn theo phương ngang. Hãy xác định:
a. Tốc độ sau va chạm của mỗi khối hộp.
b. Mỗi khối hộp sẽ chạm đất ở đâu? Lấy g = 9,8 m/s2 Trang 1
Câu 6: (2,0 điểm)
Cho hệ như hình: vật m 1 và m2 đều có khối lượng
3kg, ròng rọc là một trụ đặc đồng chất khối lượng M = 1 kg.
Biết dây không co giãn, có khối lượng không đáng kể và
không trượt trên mặt ròng rọc. Hệ số ma sát trượt giữa vật
m1 và mặt phẳng ngang là 0,15. Phải kéo vật m 1một lực F
bằng bao nhiêu để vật m 2
2 đi lên với gia tốc a = 2 m/s . Biết góc hợp bởi lực 
F và phương ngang là α = 30o. Lấy g = 9,8 m/s2
Câu 7: (2,0 điểm)
Một động cơ nhiệt có tác nhân là khí lý tưởng lưỡng
nguyên tử thực hiện một chu trình gồm ba quá trình: quá trình12
là quá trình đẳng áp, 23 - quá trình đoạn nhiệt và 31 - quá trình
nén đẳng nhiệt. Biết nhiệt độ ở trạng thái 1 là t o 1 = 27 C và V 3 = 5V1. Hãy tính:
a. Nhiệt độ cao nhất và thấp nhất của chu trình.
b. Hiệu suất của động cơ nhiệt hoạt động theo chu trình này.
Cho hằng số khí lý tưởng R = 8,31 J/mol.K; 1 atm = 1,013.10 N/m 5 .2
Ghi chú:Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 1.1] Hiểu rõ các khái niệm, định lý, định luật liên quan đến cơ học Câu 1, 2, 3, 5, 6
chất điểm, hệ chất điểm, cơ học vật rắn và cơ học chất lỏng.
[CĐR 2.1] Vận dụng kiến thức về cơ học để giải bài tập có liên quan.
[CĐR 1.3] Hiểu rõ các khái niệm, các quá trình biến đổi và các nguyên lý Câu 4,7
nhiệt động học của chất khí.
[CĐR 2.3] Vận dụng kiến thức về nhiệt học để giải thích các hiện tượng liên
quan đến nhiệtđộ và giải bài tập về nhiệt học Thông qua Bộ môn Trang 2
Đáp án và thang điểm Vật lý 1 Thi ngày 25-12-2022 Người soạn: Câu Lời giải Điểm 1
Áp suất ở đáy hai ly bằng nhau và lực tác dụng vào đáy hai ly cũng bằng 0,5 nhau. Giải thích:
Áp suất ở bề mặt cả hai ly đều bằng nhau, là áp suất Po. Ta có áp suất ở đáy
ly tuân theo quy luật: P=P + ρghvới ρlà mật độ khối lượng của nước, h là 0,5 o
độ cao của mực nước trong ly. Vì cả hai ly đổ cùng mực nước nên áp suất tại đáy là bằng nhau.
Mặc khác ta có P= F suy ra lực tác dụng vào đáy ly: F=P . A . Vì hai ly có A
cùng diện tích đáy A và có cùng áp suất ở đáy, nên lực tác dụng vào đáy ly là như nhau. 2
Khi vận động viên gập người lại, tốc độ quay của cô sẽ tăng. 0,25 Giải thích:
Vận động viên đang quay chậm thì gập người lại, tổng momen ngoai lực 0,5
tác dụng vào cô ấy lúc này bằng 0 nên momen động lượng bảo toàn:
∑ →τ=0⇒L=I ω=const
Mặc khác momen quán tính I tỉ lệ với ∑ mr2. Khi cô ấy gập người lại thì r 0,25
giảm nên I giảm, suy ra ω tăng hay tốc độ quay tăng. 3
Xét hệ bi sắt – Trái đất, áp dụng bảo toàn cơ năng từ vị trí đầu đến chân 0,5
mặt nghiêng (có độ cao h), chọn gốc thế năng tại chân mặt nghiêng.
∆ K + ∆ U =0 ↔[(1 M v2+1 I ω2)−0]+(0−Mgh)=0 g 2 2 1 ↔
M v2+ 1(2 M R2)( v )2=Mgh 0,5 2 2 5 R 1
↔ (M+2 M)v2=Mg h 2 5 1 7 ↔ . M v2=Mg h 2 5 1 ↔ . M v2= 5 Mg h 2 7
Vậy động năng tịnh tiến của bi sắt tại chân mặt nghiêng là
K = 1 M v2= 5 Mg h 2 7 4
Chu trình ABCA là chu trình ngược, sau một chu trình ngược hệ nhận 0,5 công.
Công hệ nhận được sau một chu trình bằng diện tích của chu trình. W = A
= 1 .(2.1,013 . 105) .(0,3 )=30390 J ABCA ABC 2
Sau một chu trình: ∆ E∫¿= 0,5 0 ↔ W +Q =0 ¿ ABCA ABCA
Suy ra nhiệt lượng hệ trao đổi sau một chu trình ABCA là: Q =−W =−30390 J <0 ABCA ABCA
Vậy hệ tỏa nhiệt. 5
a. Xét giai đoạn vật M trượt xuống không vận tốc đầu trên rãnh (ở độ cao 0,5
h = 35 cm) cho đến trước khi va chạm vật m vật đạt tốc độ vi, do M trượt
không ma sát nên cơ năng bảo toàn. Chọn gốc thế năng ở cuối rãnh. Trang 3
∆ K + ∆ U =0 →(1 M v2−0)+(0−Mgh)=0 g 2 i
→ v =√2 gh=√ 2.9,8.0,35=2,62 m/s i
- Tại vị trí va chạm: do vật m = M/2 va chạm đàn hồi với M nên động
lượng và cơ năng của hệ hai vật bảo toàn. Ta có: 0,5 → → → → →
P =P ⇔ M v =M v + m v (1) i f i 1 f 2 f 1 K =K ⇔
M v 2= 1 M v2 + 1 m v2 ( 2) i f 2 i 2 1 f 2 2 f
Từ (1) và (2) ta tính được vận tốc của M và m sau va chạm lần lượt là: M − M 2
v = M −m v = .2,62=0,87 m/ s 1 f M +m i M + M 2
v = 2 M v = 2 M .2,62=3,5 m/s 2 f M + m i 1,5 M
Ta thấy v >0 và v >0 chứng tỏ cả hai 1 f 2 f
vật cùng bay ra khỏi rãnh về phía phải
theo phương ngang, tương đương chuyển động ném ngang.
b. Xét M trong chuyển động ném 0,5
ngang khi rời khỏi rãnh. Chọn gốc tọa
độ Oxy như hình vẽ. Phương trình chuyển động của M: {x=v t(3) f 1 f 1 y = g t 2(4 ) f 2
Khi M chạm sàn tại A, ta có yA =
0,95m, thế vào (4) ta tính được thời
gian M đi từ O đến A là tA = 0,45s. Thế vào (3) ta tính được xA = 0,87.0,45 0,5 = 0,39 m.
Tương tự khi xét đối với vật m bay ra khỏi rãnh và chạm sàn tại B có xB = 3,5.0,45 =1,58 m.
Kết luận: vật M và m chạm sàn lần lượt tại hai điểm A (39 cm, 95 cm)
và B (158 cm, 95cm) so với điểm cuối của rãnh. 6
Phân tích lực tác dụng vào các vật như hình vẽ. Hình
Chọn chiều dương là chiều chuyển động. (0,5)
PTĐLH của các vật như sau:
=Fcosα−f −T = a (1) PTĐLH k 1 m
Vật m : {∑ F1x 1 1 1 ∑ (0,5)
F =n+ Fsinα −F =0 1 y g 1
Ròng rọc: ∑ τ=I α →R .T ' −R .T ' =I . α(2) 1 2 Biến Vật mo: ∑ đổi ra  F =m 
a → ∑ F =T −F =m a (3) 2 2 2 2 x 2 g 2 2 2 biểu
Do dây không giãn, ta có: T =T' ;a =a =a=a =Rα → α= a thức a 1 1 1 2 RR R (0,5)
Theo bài ra, ròng rọc là trụ đặc nên có I = 1 M R2 2
Thế vào các phương trình (1), (2), (3), và cộng vế theo vế chúng ta được biểu Tính F
thức tính gia tốc của m và m (0,5) 1 2: Trang 4
Fcos α−f −F
Fcos α−μ ( F −Fsinα )−F g 1 g 2 a= k g 2 = k m +m + M m + m + M 1 2 2 1 2 2
Như vậy, độ lớn lực F kéo m để m 2 1
đi lên với gia tốc a = 1 m/s 2 là:
(m +m +M)a+F +μ F 1 2 2 g 2 k g 1 (3+3+0,5).2+3.9,8+0,15.3.9,8 F= = =50 N
cos α + μ . sinα
cos 30o+0,15. sin 30o k 7
a. Theo bài ra, nhiệt độ ở trạng thái 1 là T o
1 = 27 C + 273 = 300K. Khí lý 0,5
tưởng lưỡng nguyên tử nên i = 5, suy ra hệ số nhiệt dung phân tử γ=1,4
Quá trình 3 1 là đẳng nhiệt nên T  3 = T = 300 K 1
Xét quá trình đẳng nhiệt 3 1 có:  V p p V = p V → 3 = 1=5 (1) 3 3 1 1 V p 1 3
Xét quá trình đoạn nhiệt: 2 3 có:  p V
p V γ= p V γ ↔ p V γ= p Vγ →(V2)1,4= 3= −51→ 2=0,32(2) 2 2 3 3 1 2 3 3 V p V 3 1 3 Từ (1) và (2) ta suy ra: V 0,5 2=1,6 V 1
Xét quá trình đẳng áp 12: V V V
2= 1 → T = 2 . T =480 K T T 2 V 1 2 1 1
Vậy nhiệt độ thấp nhất của chu trình là 300K và cao nhất của chu trình là 480K.
b. Nhiệt lượng trao đổi trong từng quá trình: 0,5
Q =n C (T −T ) >0 12 p 2 1 Q =0 23 V Q =nR T ln 1 <0 31 3 V 3
Nhiệt lượng hệ nhận vào là: Q =Q h 12
Nhiệt lượng hệ tỏa ra là: Q =Q c 31
Hiệu suất của động cơ nhiệt: V V 3 3 | nR T ln T ln 0,5 Q | |Q | 3 3 c 31 V V e=1− =1− =1− 1 =1− 1 Q Q i+ 2 i+ 2 h 12 n
R(T −T ) (T −T ) 2 2 1 2 2 1
→ e=1− 300. ln5 =23,4 % 3,5.180 Trang 5