Chương 1: Giải phóng phương trình | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

Chương 1: Giải phóng phương trình. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính và matlab CTTT

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

20 trang 1 tháng trước

Tác giả:

Profile Lê Na
C
C
h
h
ö
ö
ô
ô
n
n
g
g
I
I
:
G
G
i
i
a
a
û
û
i
i
p
p
h
h
ö
ö
ô
ô
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
f
f
(
(
x
x
)
=
=
0
0
1
1
1
)
)
)
Ñ
Ñ
Ñ
ò
ò
ò
n
n
n
h
h
h
n
n
n
g
g
g
h
h
h
ó
ó
ó
a
a
a
:
:
:
Khoaûng
]
,
[
b
a
goïi laø moät
k
k
h
h
o
o
a
a
û
û
n
n
g
g
c
c
a
a
ù
ù
c
c
h
h
l
l
y
y
n
n
g
g
h
h
i
i
e
e
ä
ä
m
m
neáu trong khoaûng ñoù
phöông trình
0
)
(
=
x
f
chæ coù duy nhaát moät
nghie
äm .
nghie
äm .
Ñ
Ñ
Ñ
ò
ò
ò
n
n
n
h
h
h
l
l
l
y
y
y
ù
ù
ù
:
:
:
N
N
N
e
e
e
á
á
á
u
u
u
)
(
x
f
khaû vi lieân tuïc treân
]
,
b
a
1)
)
(
'
x
f
giöõ daáu treân
]
,
b
a
2)
0
)
(
)
(
<
b
f
a
f
t
t
t
h
h
h
ì
ì
ì
]
,
b
a
laø khoaûng caùch ly nghieäm .
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
:
:
:
Phöông trình
014
4
=−− xx
0
94
.
1
5
.
1
<
−
=
f
0
7
2
>
=
f
.
Haøm ñôn ñieäu trong
2
,
5
.
1
[
0
)
(
'
>
x
f
khoaûng caùch ly nghieäm :
]
2
,
5
.
1
[
khoaûng caùch ly nghieäm thứ 2 :
]
0
,
1
[
−
(BTập)
2
2
)
)
C
C
o
o
â
â
n
n
g
g
t
t
h
h
ö
ö
ù
ù
c
c
s
s
a
a
i
i
s
s
o
o
á
á
t
t
o
o
å
å
n
n
g
g
q
q
u
u
a
a
ù
ù
t
t
:
:
d
x
: nghieäm ñuùng cuûa
0
)
(
=
x
f
gd
x
: nghieäm gaàn ñuùng.
Coâng thöùc sai soá :
(1)
( )
gd
gd d
f x
x x
m
− ≤
m
Kyù hieäu :
)('
)
1
(
xfMinm =
,
∈
∀
x
]
,
[
b
a
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
:
:
:
Phöông trình
014
4
=−− xx
xeùt trong
khoaûng caùch ly nghieäm :
]
2
,
5
.
1
[
giaû söû
663
.
1
=
gd
x
. Ñaùnh giaù sai soá tuyeät ñoái
(1.663) 0.003629
f
=
=
)
1
(
m
9.5
=
)
1
(
m
9.5
sai soá :
0.0004
0.003629
1.663 *
9.5
x− ≤ ≈
3
3
3
)
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
c
c
c
h
h
h
i
i
i
a
a
a
ñ
ñ
ñ
o
o
o
â
â
â
i
i
i
:
a
a
a
)
)
)
N
N
N
o
o
o
ä
ä
ä
i
i
i
d
d
d
u
u
u
n
n
n
g
g
g
:
:
:
Neáu
]
,
[
b
a
laø khoaûng caùch ly nghieäm thì
]
2
,
[
b
a
a
+
hoaëc
],
2
[
b
b
a
+
seõ laø khoaûng caùch
ly nghieäm môùi .
ly nghieäm môùi .
Laëp laïi quaù trình phaân chia naøy nhieàu laàn .
b
b
b
)
)
)
Ñ
Ñ
Ñ
a
a
a
ù
ù
ù
n
n
n
h
h
h
g
g
g
i
i
i
a
a
a
ù
ù
ù
s
s
s
a
a
a
i
i
i
s
s
s
o
o
o
á
á
á
:
:
:
1
( )
2
n d
n
b a
x x
+
−
− ≤
c
c
c
)
)
)
N
N
N
h
h
h
a
a
a
ä
ä
ä
n
n
n
x
x
x
e
e
e
ù
ù
ù
t
t
t
:
:
:
Luoân cho nghieäm gaàn ñuùng.
Luoân cho nghieäm gaàn ñuùng.
Giaûi thuaät ñôn giaûn.
Toác ñoä hoäi tuï khaù chaäm .
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
1
1
1
:
:
:
Phöông trình
0
cos
=
−
x
x
vôùi
khoaûng caùch ly nghieäm
]
1
,
0
[
, chia ñoâi tôùi
4
x
Keát quaû cho theo baûng sau
Sai soá
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
c
c
c
h
h
h
i
i
i
a
a
a
đ
đ
đ
ô
ô
ô
i
i
i
laø
5
1
0.3125
32
2
b a
−
= =
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
2
2
2
:
:
:
Giaûi phöông trình
0
=
−
−
x
e
x
vôùi
khoaûng caùch ly nghieäm
]
1
,
0
[
ñeán
3
x
0.5
0.75
0.625
0.5625
0.5625
2
2
2
)
)
)
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
l
l
l
a
a
a
ë
ë
ë
p
p
p
ñ
ñ
ñ
ô
ô
ô
n
n
n
(
(
(
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
ñ
ñ
ñ
i
i
i
e
e
e
å
å
å
m
m
m
b
b
b
a
a
a
á
á
á
t
t
t
ñ
ñ
ñ
o
o
o
ä
ä
ä
n
n
n
g
g
g
,
,
,
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
a
a
a
ù
ù
ù
n
n
n
h
h
h
x
x
x
a
a
a
ï
ï
ï
c
c
c
o
o
o
)
)
)
a
a
a
)
)
)
N
N
N
o
o
o
ä
ä
ä
i
i
i
d
d
d
u
u
u
n
n
n
g
g
g
:
:
:
*) Ñöa phöông trình
0
)
(
=
x
f
veà daïng
töông ñöông
)
(
x
x
ϕ
=
*)
Kieåm tra
ñ
ñ
ñ
i
i
i
e
e
e
à
à
à
u
u
u
k
k
k
i
i
i
e
e
e
ä
ä
ä
n
n
n
ñoái vôùi haøm
)
(
x
ϕ
:
*)
Kieåm tra
ñ
ñ
ñ
i
i
i
e
e
e
à
à
à
u
u
u
k
k
k
i
i
i
e
e
e
ä
ä
ä
n
n
n
ñoái vôùi haøm
)
(
x
ϕ
:
'( ) 1 [ , ]
Max x q x a b
ϕ
= < ∀ ∈
*) Laáy
0
x
laø moät giaù trò ban ñaàu
t
t
t
u
u
u
ø
ø
ø
y
y
y
y
y
y
ù
ù
ù
∈
[ a,
b ]
Xaây döïng daõy laëp :
)
(
0
1
x
x
ϕ
=
)
(
1
2
x
x
ϕ
=
)
(
2
3
x
x
ϕ
=
Laáy
n
n
n
h
h
h
ö
ö
ö
õ
õ
õ
u
u
u
h
h
h
a
a
a
ï
ï
ï
n
n
n
gdn
x
x
=
b
b
b
)
)
)
Ñ
Ñ
Ñ
a
a
a
ù
ù
ù
n
n
n
h
h
h
g
g
g
i
i
i
a
a
a
ù
ù
ù
s
s
s
a
a
a
i
i
i
s
s
s
o
o
o
á
á
á
:
:
:
1)
q
xxq
xx
n
n
−
−
≤−
1
*
01
(
ñaùnh giaù
t
t
t
i
i
i
e
e
e
â
â
â
n
n
n
n
n
n
g
g
g
h
h
h
i
i
i
e
e
e
ä
ä
ä
m
m
m
)
(
ñaùnh giaù
t
t
t
i
i
i
e
e
e
â
â
â
n
n
n
n
n
n
g
g
g
h
h
h
i
i
i
e
e
e
ä
ä
ä
m
m
m
)
2)
q
x
x
q
xx
nn
n
−
−
≤−
−
1
*
1
( ñaùnh giaù
h
h
h
a
a
a
ä
ä
ä
u
u
u
n
n
n
g
g
g
h
h
h
i
i
i
e
e
e
ä
ä
ä
m
m
m
)
c
c
c
)
)
)
N
N
N
h
h
h
a
a
a
ä
ä
ä
n
n
n
x
x
x
e
e
e
ù
ù
ù
t
t
t
:
:
:
Coù
v
v
v
o
o
o
â
â
â
s
s
s
o
o
o
á
á
á
caùch choïn haøm
)
(
x
ϕ
Haøm
)
(
x
ϕ
coù tính chaát
1
<
q
goïi laø
h
h
h
a
a
a
ø
ø
ø
m
m
m
c
c
c
o
o
o
q
laø
h
h
h
e
e
e
ä
ä
ä
s
s
s
o
o
o
á
á
á
c
c
c
o
o
o
q
caøng nhoû thì toác ñoä hoäi tuï caøng cao
1
q
≥
Khoâng söû duïng ñöôïc
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
1
1
1
:
:
:
Xeùt phöông trình
01000
3
=−+ xx
trong khoaûng caùch ly nghieäm
]
10
,
9
[
a
a
a
)
)
)
01000
3
=−+ xx
3
1000 xx −=
3
1000
)
(
x
x
−
=
ϕ
1000
)
(
x
x
−
=
ϕ
2
3)(' xx −=ϕ
2
3)(' xx =ϕ
300)('
=
ϕ
=
xMaxq
>
>
>
1
1
1
Khoâng söû duïng ñöôïc
b
b
b
)
)
)
01000
3
=−+ xx
xx −=1000
3
3
1000 xx −=
3
1000)( xx −=ϕ
1
)
(
'
x
−
=
ϕ
3
2
)1000(3
)
(
'
x
x
−
=
ϕ
3
2
)1000(3
1
)('
x
x
−
=ϕ
3
2
)1000(3
1
x
Maxq
−
=
0.003355742403
=
9.966554934
9.966667166
9.966666789
9.966666791
x
0
=10.0
9.966666791
12
6.74 10
−
×
Sai số hậu nghiệm x
4
c
c
c
)
)
)
01000
3
=−+ xx
xx −=1000
3
x
x
x
−
=
1000
2
x
x
x
−
=
1000
x
x
x
x
−
=ϕ
1000
)(
Vôùi
10
0
=
x
ta coù
966666791
,
9
=
gd
x
vôùi soá
böôùc laëp
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
N
N
N
e
e
e
w
w
w
t
t
t
o
o
o
n
n
n
(
(
(
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
T
T
T
i
i
i
e
e
e
á
á
á
p
p
p
t
t
t
u
u
u
y
y
y
e
e
e
á
á
á
n
n
n
)
)
)
a
a
a
)
)
)
N
N
N
o
o
o
ä
ä
ä
i
i
i
d
d
d
u
u
u
n
n
n
g
g
g
:
:
:
Ñöa
0
)
(
=
x
f
veà daïng laëp
)(
)('
)
(
x
xf
x
f
xx ϕ=−=
.
Choïn
0
x
Choïn
0
x
)('
)
(
0
0
01
xf
x
f
xx −=
)('
)
(
1
1
12
xf
x
f
xx −=
b
b
b
)
)
)
Ñ
Ñ
Ñ
a
a
a
ù
ù
ù
n
n
n
h
h
h
g
g
g
i
i
i
a
a
a
ù
ù
ù
s
s
s
a
a
a
i
i
i
s
s
s
o
o
o
á
á
á
:
:
:
Sai soá theo coâng thöùc sai soá toång quaùt
)1(
)(
*
m
xf
xx
gd
gd
≤−
c
c
c
)
)
)
N
N
N
h
h
h
a
a
a
ä
ä
ä
n
n
n
x
x
x
e
e
e
ù
ù
ù
t
t
t
:
:
:
Phöông phaùp s
ử dụ
ng đ
ượ
c
neáu
)
(
'
x
f
vaø
)
(
'
'
x
f
Phöông phaùp s
ử dụ
ng đ
ượ
c
neáu
)
(
'
x
f
vaø
)
(
'
'
x
f
khoâng ñoåi daáu treân khoaûng caùch ly nghieäm .
Ñieåm
0
x
laø ñieåm Fourier neáu
)
(
0
x
f
cuøng daáu
vôùi
0
''( )
f x
Choïn
0
,
x a x b
= =
neáu a , b laø
ñ
ñ
ñ
i
i
i
e
e
e
å
å
å
m
m
m
F
F
F
o
o
o
u
u
u
r
r
r
i
i
i
e
e
e
r
r
r
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
:
:
:
Phöông trình
01000
3
=−+xx
vôùi khoaûng
caùch ly nghieäm
]
10
,
9
[
Ñieåm naøo laø ñieåm Fourier trong hai ñieåm 9 , 10
Vôùi
0
x
tìm ñöôïc , tính
2
x
.
Ñaùnh giaù sai soá cuûa
2
x
0.3
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

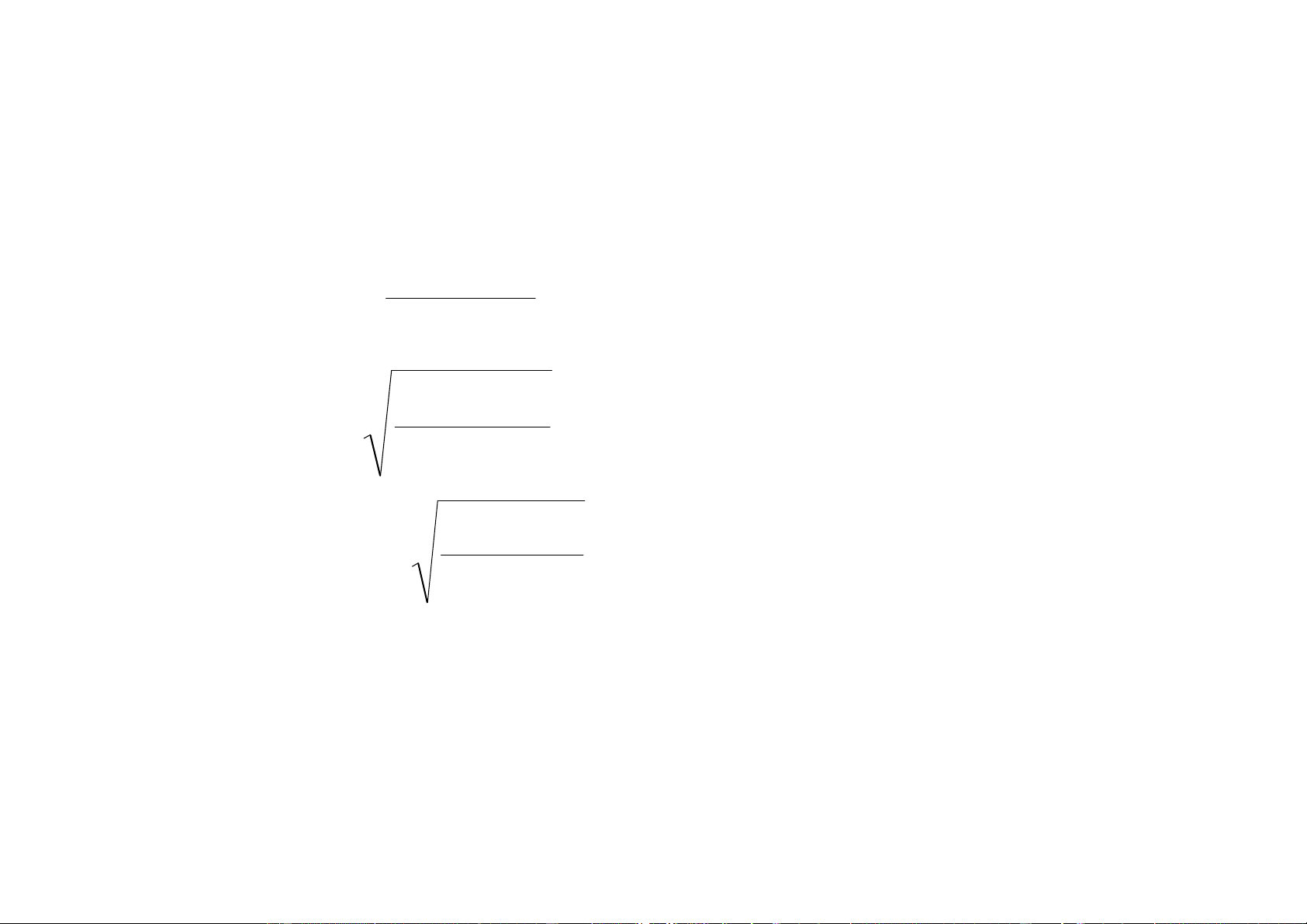
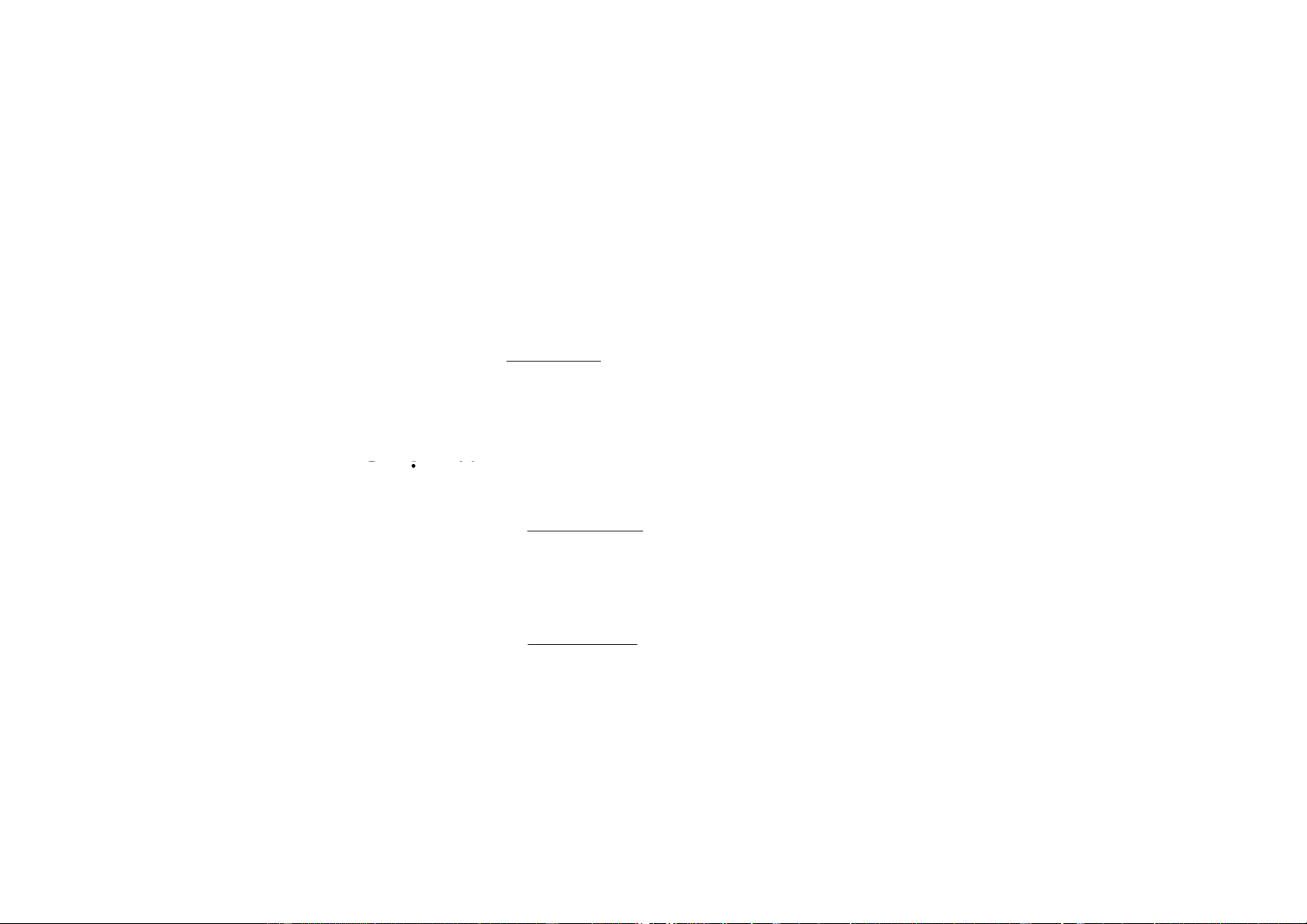
Preview text:

Chöông I : Giaûi phöông trình f(x)=0
1)Ñònh nghóa: Khoaûng [ a , b ] goïi laø moät
khoaûng caùch ly nghieäm neáu trong khoaûng ñoù
phöông trình f (x) =0 chæ coù duy nhaát moät ng n h g i h e i äem m . Ñònh lyù:
Neáu f (x) khaû vi lieân tuïc treân [ a ,b ]
1) f '(x) giöõ daáu treân [a,b]
2) f (a) f (b) < 0
thì [ a,b] laø khoaûng caùch ly nghieäm .
Ví duï : Phöông trình 4
x − 4x −1= 0 f ) 5 . 1 ( =− 9 . 1 4< 0 f (2) = 7 > 0 . Haøm ñôn ñieäu trong 1 [ 5 . , 2] f '(x) > 0
khoaûng caùch ly nghieäm : [ . 1 5 , 2 ]
khoaûng caùch ly nghieäm thứ 2 : [ 1 − , 0] (BTập)
2)Coâng thöùc sai soá toång quaùt : d
x : nghieäm ñuùng cuûa f (x) = 0
xgd : nghieäm gaàn ñuùng. f (x ) Coâng thöùc sai soá : gd x − ≤ gd d x (1) m Kyù hieäu : ) 1 ( m = Min f '( )
x , ∀ x∈[ a ,b ]
Ví duï : Phöông trình 4
x − 4x −1= 0 xeùt trong
khoaûng caùch ly nghieäm : [ . 1 5, 2 ] giaû söû x
. Ñaùnh giaù sai soá tuyeät ñoái gd = 6 . 1 63 f (1.663) = 0.003629 ) 1 ( m =9. 9 5 . sai soá : 0.003629 1.663 − x * ≤ ≈ 0.0004 9.5
3)Phöông phaùp chia ñoâi : a)Noäi dung :
Neáu [ a,b ] laø khoaûng caùch ly nghieäm thì a + b a + b [ a , ] hoaëc [
, b ] seõ laø khoaûng caùch 2 2 ly l y ng n h g i h e i äem m mô m ùôi i. .
Laëp laïi quaù trình phaân chia naøy nhieàu laàn .
b) Ñaùnh giaù sai soá : (b − a) − ≤ n x d x n 1 + 2 c)Nhaän xeùt :
Luoân cho nghieäm gaàn ñuùng. Giaûi thuaät ñôn giaûn.
Toác ñoä hoäi tuï khaù chaäm .
Ví duï 1: Phöông trình x − cos x = 0 vôùi
khoaûng caùch ly nghieäm [0, 1] , chia ñoâi tôùi 4 x
Keát quaû cho theo baûng sau
Sai soá phöông phaùp chia đôi laø b − a 1 = = 0.3125 5 32 2
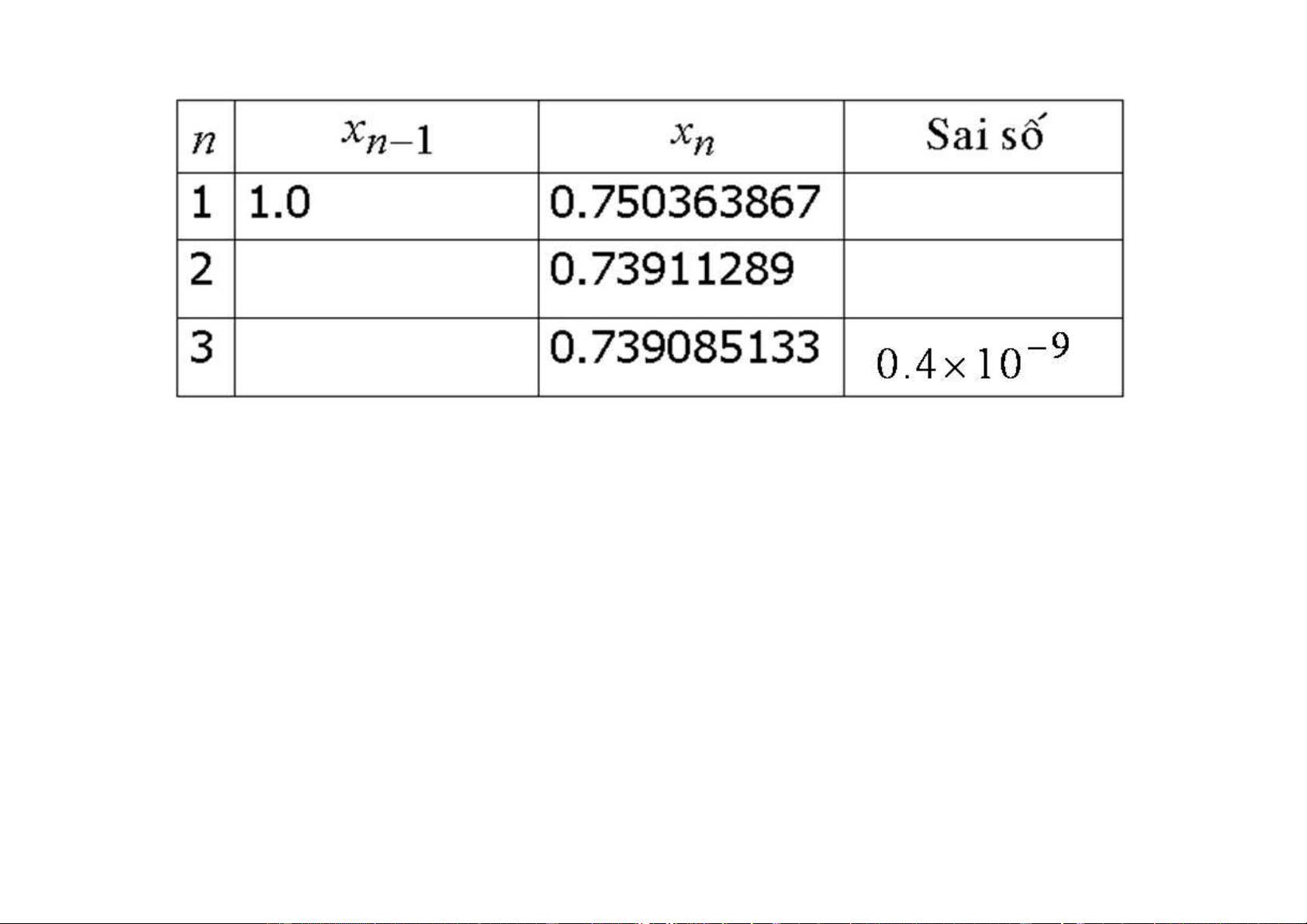
Ví duï 2 : Giaûi phöông trình x − −x e = 0 vôùi
khoaûng caùch ly nghieäm [0,1] ñeán 3 x 0.5 0.75 0.625 0.5 . 625
2) Phöông phaùp laëp ñôn
(phöông phaùp ñieåm baát ñoäng, phöông phaùp aùnh xaï co ) a) Noäi dung :
*) Ñöa phöông trình f (x) = 0 veà daïng töông ñöông x = ( ϕ x) *) * Kie i åem trta ñie i àeu kieäen ñ o ñ áoi ivô v ùôi iha h øm ( ϕ x) : :
Max ϕ '(x) = q < 1 x ∀ [ ∈ a,b] *) Laáy ø ù 0
x laø moät giaù trò ban ñaàu tuøy y ∈[ a, b ]
Xaây döïng daõy laëp : x = ( ϕ x ) 1 0 x = ( ϕ x ) 2 1 x = ( ϕ x ) 3 2
Laáy n höõu haïn n x = xgd
b) Ñaùnh giaù sai soá : n 1− 1) q x x x − x 0 n * ≤ 1 − q ( (ñaùnh gia i ù ti t eâen n gh g ieäem m ) ) − 2) q x x x − − x n n 1 n * ≤ 1 − q
( ñaùnh giaù haäu nghieäm ) c) Nhaän xeùt :
Coù voâ soá caùch choïn haøm ( ϕ x) Haøm (
ϕ x) coù tính chaát q < 1 goïi laø haøm co
q laø heä soá co
q caøng nhoû thì toác ñoä hoäi tuï caøng cao
q ≥ 1 Khoâng söû duïng ñöôïc
Ví duï1 : Xeùt phöông trình 3
x + x −1000 = 0
trong khoaûng caùch ly nghieäm 9 [ , 10 ] a) 3
x + x − 1000 = 0 3 x = 1000 − x 3 (
ϕ x) =1000− x 2 ϕ'(x) =−3x 2 ϕ'(x) = 3x q = Max '
ϕ (x) = 300 > 1
Khoâng söû duïng ñöôïc b) 3
x + x −1000 = 0 x3 = 1000 − x 3 x = 1000 − x 3 (
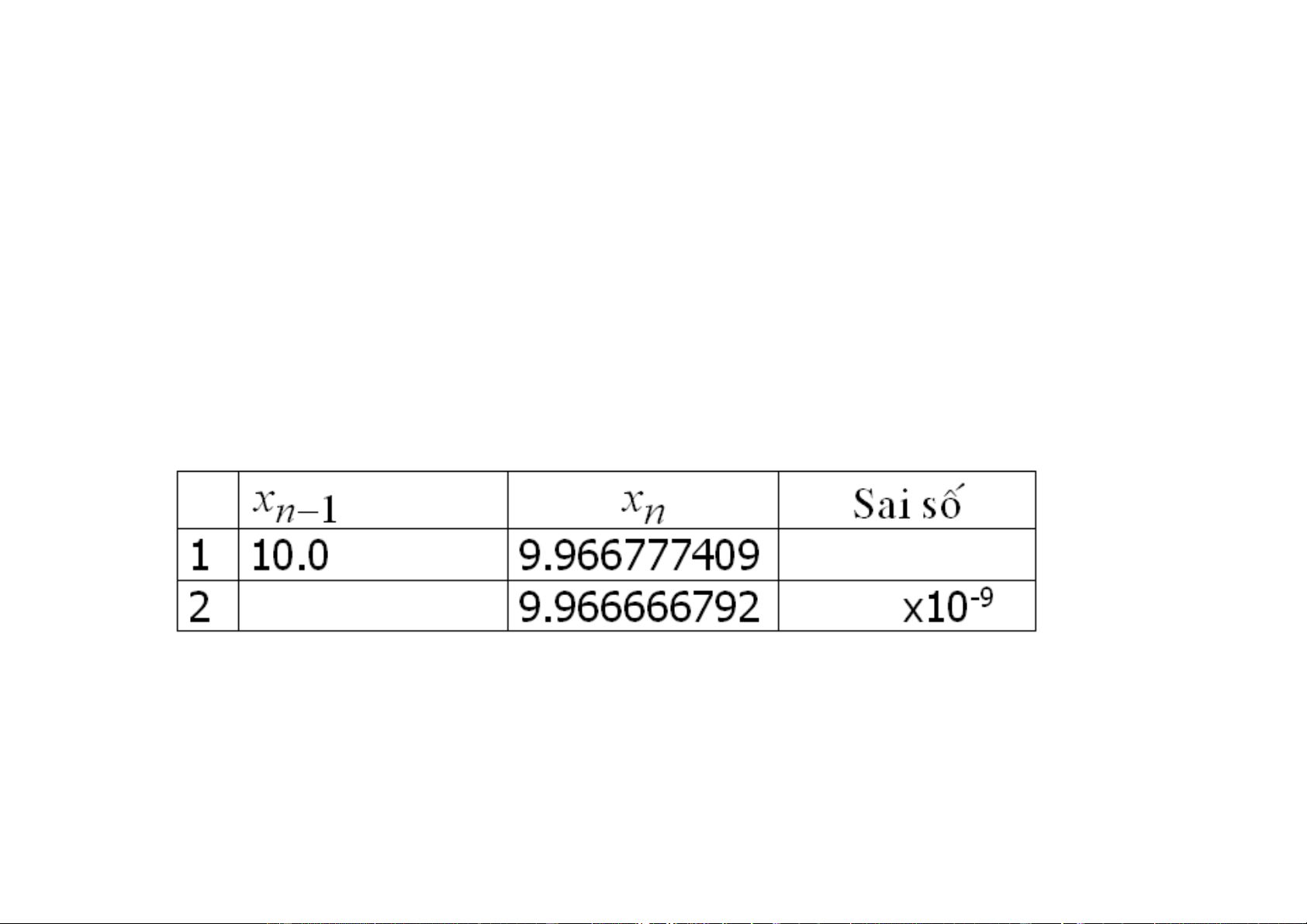
ϕ x)= 1000− x −1 ' ϕ (x)= 3 2 3 1 ( 000 − x) 1 ' ϕ (x) = 3 2 3 1 ( 000 − x) 1 q = Max = 0.003355742403 3 2 3 1 ( 000 − x) x =10.0 0 9.966554934 9.966667166 9.966666789 9. 9 96 9 6 6 6 6 6 6 6 6 7 6 9 7 1 9 −12 Sai số hậu nghiệm x 6.74 4 ×10 c) 3
x + x −1000 = 0 x3 = 1000 − x 2 − x x = 1000 x − x x = 1000 x − x ϕ 1000 (x) = x Vôùi x 10 ta coù xgd = vôùi soá 0 = 9 , 9 66666791 böôùc laëp Phöông phaùp Newton
( Phöông phaùp Tieáp tuyeán )
a) Noäi dung : Ñöa f (x) = 0 veà daïng laëp f ( ) x x = x − = ( ϕ ) x . f '( ) x Ch C oïn 0 x 0 x f (x ) 0 1 x = 0
x − f '(x ) 0 f (x ) 1 2 x = 1 x − f '(x ) 1
b) Ñaùnh giaù sai soá :
Sai soá theo coâng thöùc sai soá toång quaùt f (x ) gd x − x * gd ≤ ) 1 ( m c)Nhaän xeùt : Phö h ô ö ng n g ph p a h ùp p sử s ử dụng đượ ư c c ne n áu
u f '(x) vaøa f ''(x)
khoâng ñoåi daáu treân khoaûng caùch ly nghieäm . Ñieåm cuøng daáu 0
x laø ñieåm Fourier neáu f ( ) 0 x vôùi f ' ( 0 x ) Choïn x = a, = å 0 x
b neáu a , b laø ñiem Fourier
Víduï: Phöông trình 3
x + x −1000=0 vôùi khoaûng caùch ly nghieäm 9 [ , 1 ] 0
Ñieåm naøo laø ñieåm Fourier trong hai ñieåm 9 , 10 Vôùi 0
x tìm ñöôïc , tính 2 x . Ñaùnh giaù sai soá cuûa 2 x 0.3