





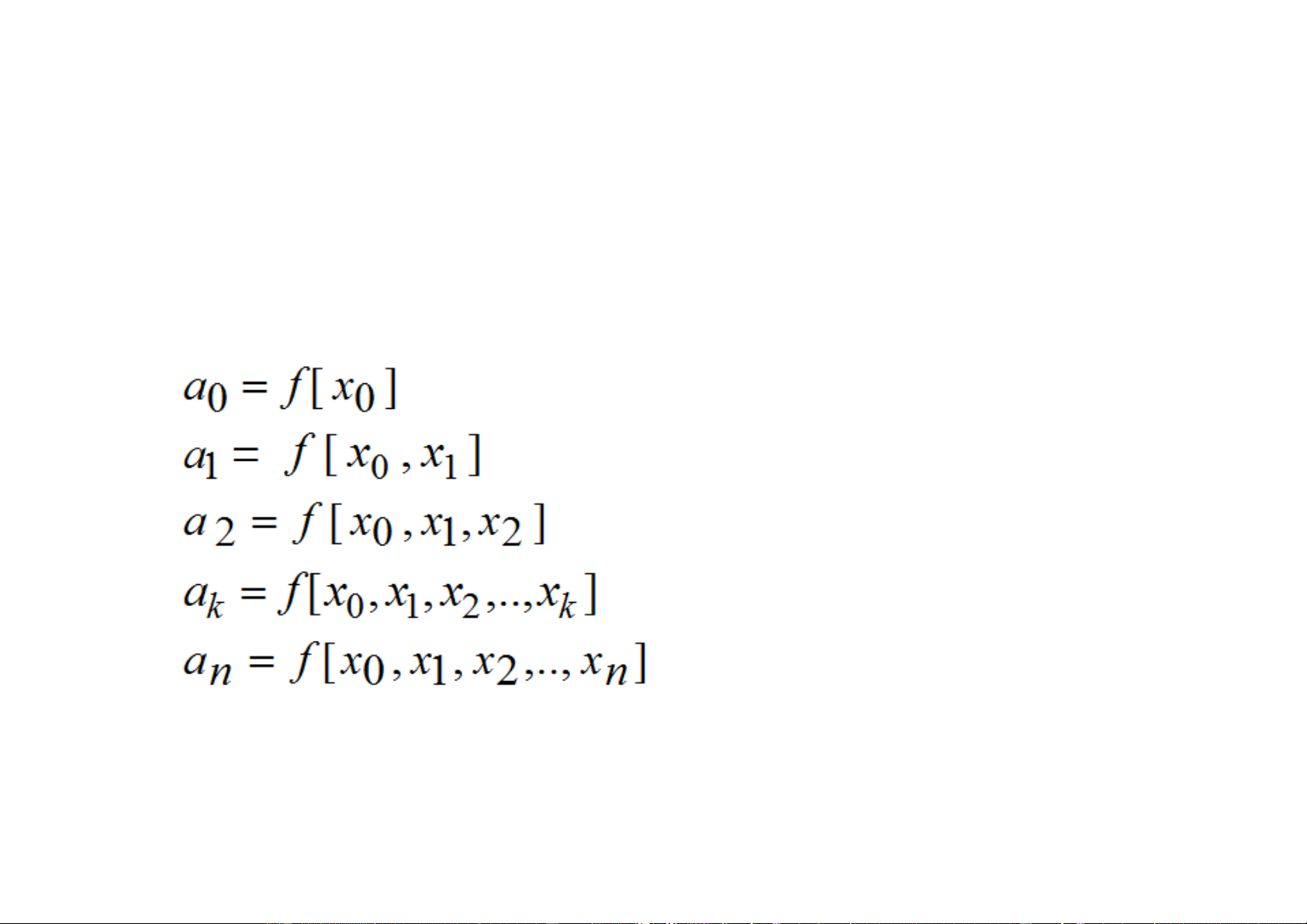






Preview text:
Chương III : NOÄI SUY
1) Noäi suy ña thöùc
2) Noäi suy Spline baäc 3
3) Phöông phaùp bình phöông toái thieåu
Ngô Thu Lương – Phương Pháp Tính 1
1.1) Noäi suy ña thöùc theo Lagrange
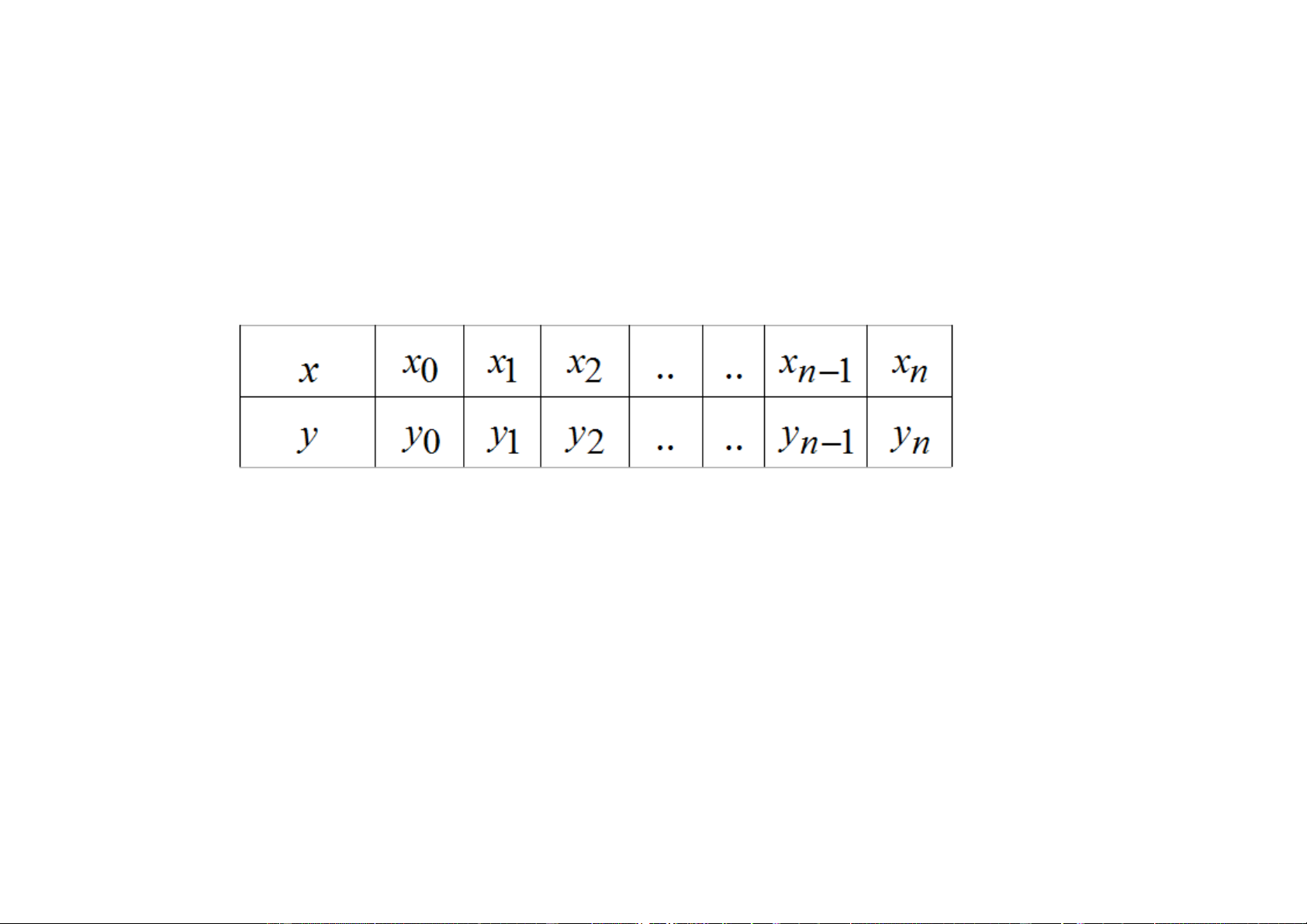
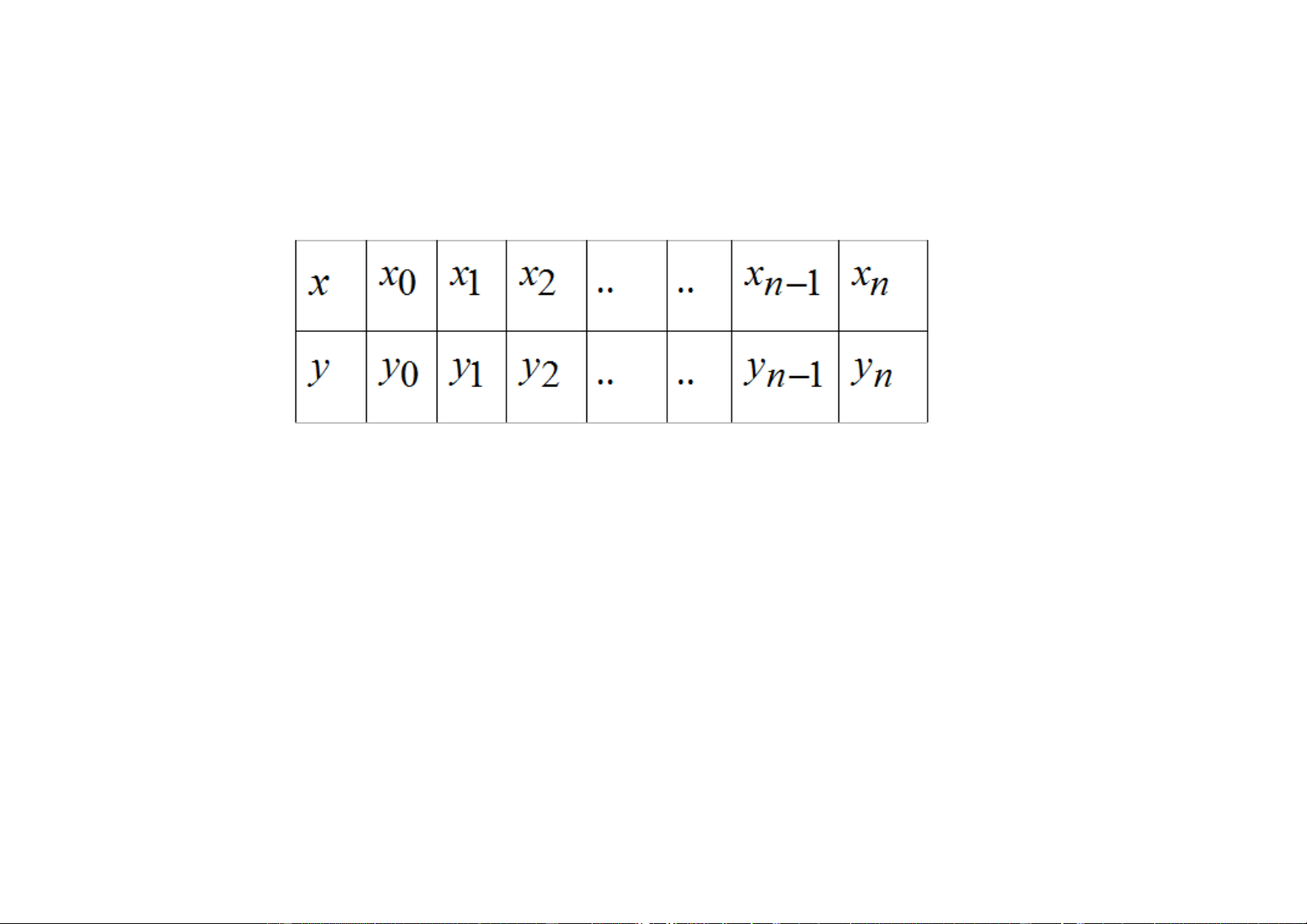
a) Noäi dung : Bieát caùc giaù trò y = f (x ) cuûa haøm i i y = f ( )
x taïi caùc ñieåm x i theo baûng
Tìm haøm laïi haøm f (x)
Lôøi giaûi : Voâ soá haøm
Tìm f (x) = P(x) chæ laø ña thöùc baäc n
thoûa P( ix) = iy
Lôøi giaûi laø duy nhaát
Ngô Thu Lương – Phương Pháp Tính 2
Caùc böôùc tìm ña thöùc P(x)
Böôùc 1 : Thieát laäp ña thöùc cô sôû Lagrange n ( x − ) L ( x ) = ∏ xk i ( x 0, i − k = k ≠ i xk )
Ví duï : L ( ) 0 x = (x − x ). ) . . . . ( . x ( − − − − 1 x − x )( ) x i−1 − x ).)..(.x ( i x ) n =
(x − x )...(x − x )(x −
− x )..(x − x ) 0 1 0 i 1 0 i 0 n
Ngô Thu Lương – Phương Pháp Tính 3
Böôùc 2 : Coâng thöùc tính P(x) n
P( x) = ∑ yiL i (x) = i =0
y L ( x) + y L ( x) + ... + y L ( x) 0 0 1 1 n n b) Sai soá :
f ( x) − P ( x) ≤ (n + ) 1 M ≤
( x − x )( x − x )....( x − x ) 0 1 n (n + ) 1 !
Ngô Thu Lương – Phương Pháp Tính 4 c) Nhaän xeùt :
*) Soá moác noäi suy caøng lôùn thì sai soá caøng nhoû , tuy
nhieân baäc cuûa ña thöùc seõ lôùn, tính toaùn seõ daøi .
*)Sai soá phuï thuoäc vaøo (n+ ) 1 M , thöïc teá khoâng bieát
vì haøm f (x) chöa bieát
*)Ña thöùc noäi suy P(x) laø duy nhaát
Ngô Thu Lương – Phương Pháp Tính 5 Ví duï :
Tìm ña thöùc noäi suy P(x) töø baûng soá lieäu
x = −1 , x = 0 , x = 1 0 1 2 1 y = , y = 1 , y = 3 0 1 2 3
Tính gaàn ñuùng giaù trò cuûa bảng taïi x = 0.7
Ngô Thu Lương – Phương Pháp Tính 6
Giaûi : Ta tìm caùc ña thöùc Lagrange 2 − − − (x ) 0 (x ) 1 x x L (x) 0 = = ( 1 − − ) 0 ( 1 − − ) 1 2 2 x − − x − x − [ ( ) 1 ]( ) 1 1 L (x) 1 = = 0 [ − (− ) 1 ] 0 ( − ) 1 −1 2 [x − (− ) 1 ](x − ) 0 x + [x ( ) 1 ](x ) 0 x x L (x) 2 = = 1 [ − (− ) 1 ] 1 ( − ) 0 2 1 2 2 x + 4 + 3 ( P ) x = x L ( ) x +1L ( ) x + 3L ( ) x = 0 1 2 3 3 2.(0.7)2 + 4.(0.7) + 3 P(0.7) = = 2.26 3
Ngô Thu Lương – Phương Pháp Tính 7 d) Tyû sai phaân
Tyû sai phaân baäc 0 cuûa f taïi 0 x :
f [x ] = f (x ) 0 0
Tyû sai phaân baäc 1 cuûa f taïi x , : 0 1 x
f [x ] − f [x ] 1 0 f [ 0 x , x1] = x1 − 0 x
Tyû sai phaân baäc 2 cuûa f taïi x , x , 0 1 x 2
f [x1, x 2] − f [ 0 x , x1] f [ 0
x , x1, x2] = x 2 − 0 x
Töông töï cho tyû sai phaân baäc cao hôn
Ngô Thu Lương – Phương Pháp Tính 8
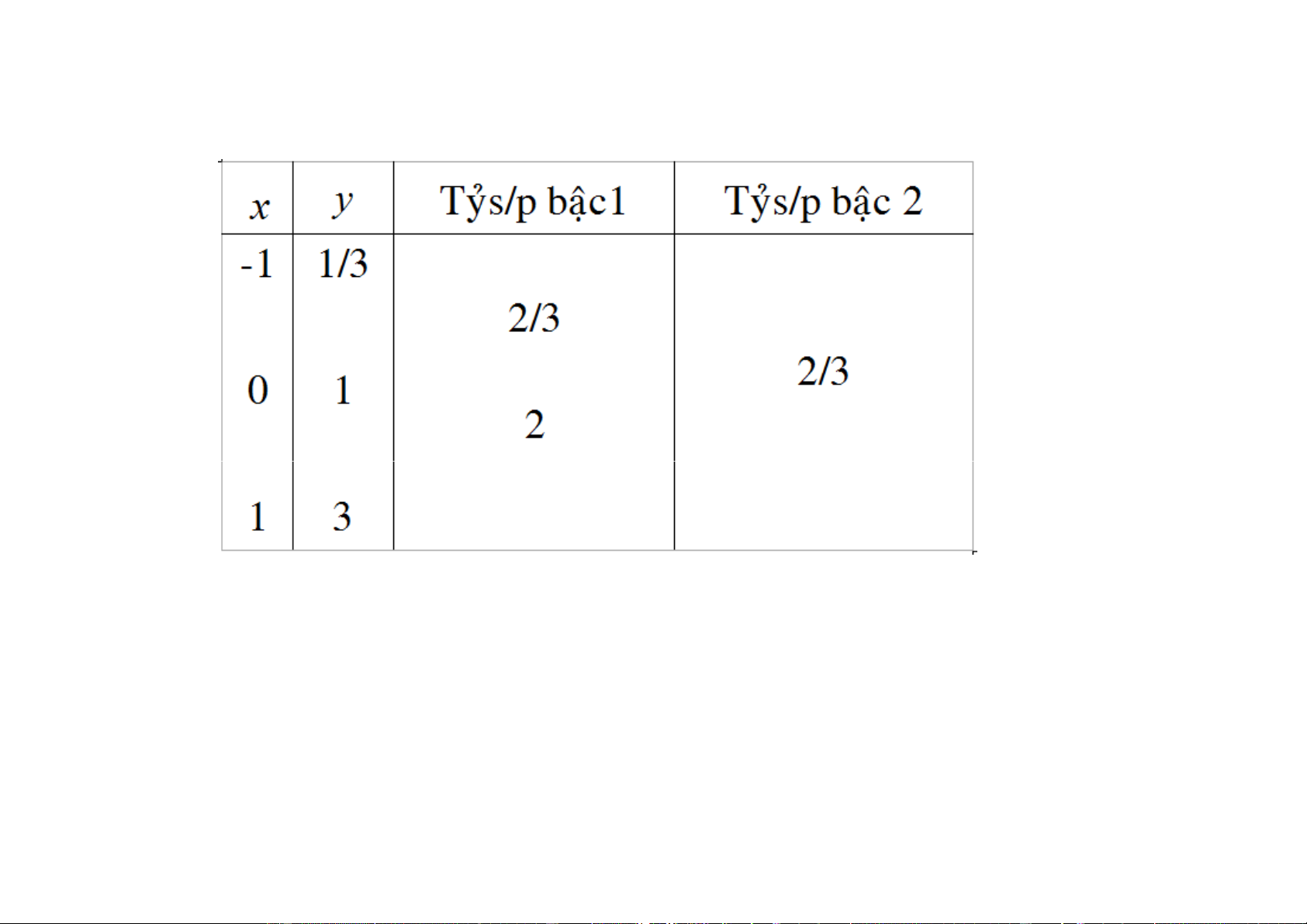
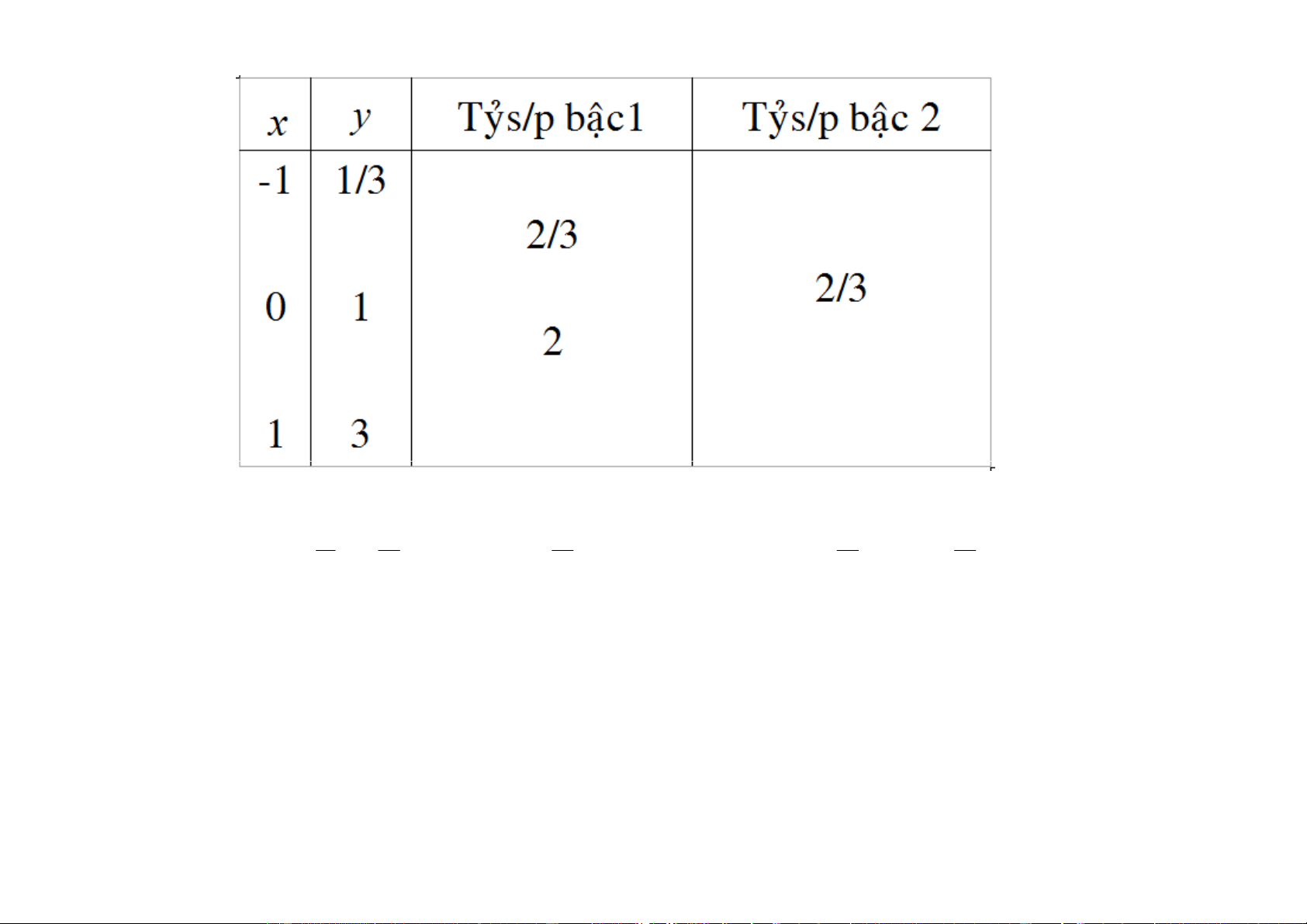
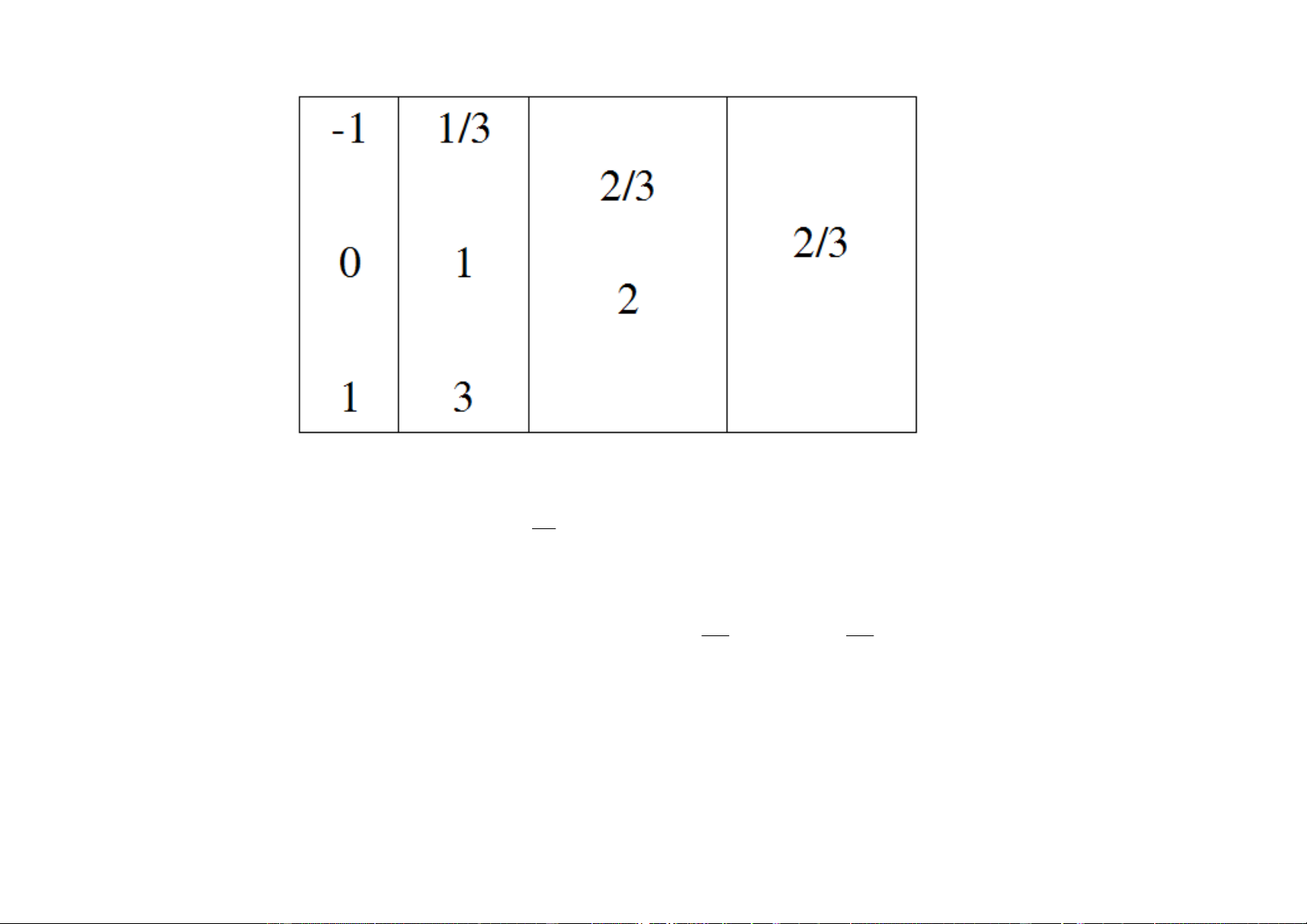
e) Baûng tyû sai phaân
Ngô Thu Lương – Phương Pháp Tính 9
f) Noäi suy Newton tieán theo baûng tyû sai phaân
Ña thöùc P(x) coù theå tìm döôùi daïng
P(x) = a + a (x − x ) + a (x − x )(x − x ) + .. 0 1 0 2 0 1 .. + a (
n x − x )(x − x )..(x − x ) 0 1 n 1 −
Ngô Thu Lương – Phương Pháp Tính 10 1 2 2 2 2 4 ( P ) x = + (x + ) 1 + (x + ) 1 (x − ) 0 = x + x +1 3 3 3 3 3
Ngô Thu Lương – Phương Pháp Tính 11
g) Noäi suy Newton luøi ( P )
x = a + a (x − x )
n + a (x − x )( n x − x ) − n +.. 0 1 2 1
... + a (x − x )(x − x )..( x − − x ) n n n 1 1
a0 = f [ x ] 0 n . 1
a = f [x , x ] n n 1 − a
= f [ x , x , x ] 2 n n 1 − n−2
a = f [x , x x , x ] k n n− , 1 ... n−k 1 + n−k
a = f [ x , x
1 , ..x3 , x2 , 1 x , x − 0 ] n n n
Ngô Thu Lương – Phương Pháp Tính 12 2
P( x) = 3 + 2( x − ) 1 + ( x − ) 1 ( x − 0) 3 2 2 4 = x + x + 1 3 3
Ngô Thu Lương – Phương Pháp Tính 13
2) Noäi suy Spline baäc 3
a) Noäi dung : Cho baûng soá lieäu Tì T m ì moäot t h a
h øam S(x) th t oûoa ca c ùc c ñie i àeu kie i äen : :
S(x) : Đi qua các điểm đã cho trong bảng
S(x) laø ña thöùc baäc 3 treân moãi ñoaïn nhoû [ x , ] j x j +1
( caùc ña thöùc naøy coù caùc heä soá khaùc nhau)
Ngô Thu Lương – Phương Pháp Tính 14 Goïi S ( )
j x laø ña thöùc treân moãi ñoaïn nhoû [ x , x 1] j j + S ( )
j x thoûa caùc ñieàu kieän :
a) S j (x j ) = y j S ( j x j+1) = y j 1 + b) / S (x ) / j j+1 = S (x ) +1 + j j+ j j +1 1 c) // S (x ) // j j = S (x ) +1 + j j +1 1 d) // / / S = 0 ( 0 x ) S 1(x ) n− n
ñieàu kieän bieân töï nhieân
Ngô Thu Lương – Phương Pháp Tính 15 h = +1 − j x j x j a j = y j (c j c 1 − j ) d j = + h 3 j
(a + − a ) h (c + + 2c ) j 1 j j j 1 j b = − j h 3 j
Ngô Thu Lương – Phương Pháp Tính 16
Ñeå tìm c ta giaûi töø heä j Ax = b 1 0 0 0 0 0 h 2( 0 0 h + h ) h . . 0 1 1 0 h 2( 1 h1 + h ) h . 0 A = 2 2 0 0 . . . 0 0 0 . n h − 2( 2 n h −2 + n h − ) 1 n h − 1 0 0 0 0 0 1 c 0 0 c 3 3 1 ( a − a ) − ( a − a ) 2 1 1 0 h h 1 0 x = . . B = . cn −1 3 3 ( a − a ) − ( a − a ) n n −1 n −1 n − 2 c h h n n −1 n − 2 0
Ngô Thu Lương – Phương Pháp Tính 17
Ví duï : Noäi suy Spline baäc 3 cuûa baûng x = 0 x = 1 x = 2 x = 3 0 1 2 3 y = 0 y = 1 y = 4 y = 0 0 1 2 3 a = y = 0 a = y = 1 0 0 1 1 a = y = 4 2 2 a = y = 0 3 3
Caùc heä soá ic tính theo heä phöông trình 1 0 0 0 c 0 0 c c 0 0 0 c 1 4 1 0 1 c 6 = 1 c 3 = 0 1 4 1 c c 2 − 6 2 − 2 1 0 0 0 1 3 c 0 3 c 0 = = = 0 b 0 1 b 3 2 b 0 d = 1 d = −3 d = 2 0 1 2
Ngô Thu Lương – Phương Pháp Tính 18
Ta coù haøm : S (x) = ( 1 x − ) 0 3 0≤ x ≤1 1+ ( 3 x − ) 1 + ( 3 x − ) 1 2 − ( 3 x − ) 1 3 1≤ x ≤ 2 4 − ( 6 x − ) 2 2 + ( 2 x − ) 2 3 2≤ x ≤ 3
Ngô Thu Lương – Phương Pháp Tính 19
Spline với ñieàu kieän bieân raøng buoäc / / d ) S = = 0 ( 0 x ) f '( 0
x ) , S 1(x ) f '( x ) n− n n
trong ñoù f '(x ), f '( ) laø caùc ñaïi löôïng cho tröôùc 0 n x 2 0 h 0 h 0 0 0 0 + 0 h 2( 0 h h1) 1 h . . 0 0 + 1 h 2( 1 h 2 h ) 2 h . 0 A = 0 0 . . . 0 0 0 . + n h 2 2( − n h 2 − n h 1) − n h 1 − 0 0 0 0 n h 1 2 − n h 1 −
Ngô Thu Lương – Phương Pháp Tính 20



