Chương 5: Giải gần đúng phương trình vi phân | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

Chương 5: Giải gần đúng phương trình vi phân. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính và matlab CTTT

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

9 trang 1 tháng trước

Tác giả:

Profile Lê Na
C
C
C
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
5
5
5
G
G
G
i
i
i
a
a
a
û
û
û
i
i
i
g
g
g
a
a
a
à
à
à
n
n
n
ñ
ñ
ñ
u
u
u
ù
ù
ù
n
n
n
g
g
g
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
t
t
t
r
r
r
ì
ì
ì
n
n
n
h
h
h
v
v
v
i
i
i
p
p
p
h
h
h
a
a
a
â
â
â
n
n
n
Cho phöông trình vi phaân caáp1
))
(
,
(
)
(
'
x
y
x
f
x
y
=
vôùi ñieàu kieän ban ñaàu
0
0
)
(
y
x
y
=
.
Tính gaàn ñuùng giaù trò
)
(
b
y
vôùi
b
baát kyø cho tröôùc
1
1
1
)
)
)
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
E
E
E
u
u
u
l
l
l
e
e
e
r
r
r
:
:
:
Ngô Thu Lương – Phương Pháp Tính
1
a
a
a
)
)
)
N
N
N
o
o
o
ä
ä
ä
i
i
i
d
d
d
u
u
u
n
n
n
g
g
g
: Chia ñoaïn
]
,
[
b
a
thaønh
n
phaàn ñeàu
nhau , bôûi caùc ñieåm chia
<
+
=
<
+
=
<
=
h
x
x
h
x
x
a
x
2
0
2
0
1
0
nh
a
b
x
n
+
=
=
<
<
...
=
+
1
i
y
k
y
i
+
)
,
(
i
i
y
x
f
h
k
=
b
b
b
)
)
)
S
S
S
a
a
a
i
i
i
s
s
s
o
o
o
á
á
á
:
:
:
)
(2)
(
( ) ( ) [ 1]
2
gd d
L b a
hM
y b y b e
L
−
− ≤ −
( , )
f
L Max x y
y
∂
=
∂
Ngô Thu Lương – Phương Pháp Tính
2
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
: Phöông trình
2
)(1)(' yxxy −+=
vôùi ñieàu kieän ban ñaàu
1
)
2
(
=
y
.
Tính gaàn ñuùng nghieäm
)
6
.
2
(
y
vôùi böôùc
2
.
0
=
h
2
2
2
)
)
)
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
E
E
E
u
u
u
l
l
l
e
e
e
r
r
r
c
c
c
a
a
a
û
û
û
i
i
i
t
t
t
i
i
i
e
e
e
á
á
á
n
n
n
Ngô Thu Lương – Phương Pháp Tính
3
2
2
2
)
)
)
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
E
E
E
u
u
u
l
l
l
e
e
e
r
r
r
c
c
c
a
a
a
û
û
û
i
i
i
t
t
t
i
i
i
e
e
e
á
á
á
n
n
n
a
a
a
)
)
)
N
N
N
o
o
o
ä
ä
ä
i
i
i
d
d
d
u
u
u
n
n
n
g
g
g
:
2
21
1
k
k
yy
ii
+
+=
+
)
,
(
1
i
i
y
x
hf
k
=
)
,
(
1
1
2
k
y
x
hf
k
i
i
+
=
+
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
: Giaûi phöông trình
2
)(1)(' yxxy −+=
vôùi
ñieàu kieän ban ñaàu
1
)
2
(
=
y
trong ví duï tröôùc theo
phöông phaùp Euler caûi tieán , keát quaû nhö sau :
Ngô Thu Lương – Phương Pháp Tính
4
3
3
3
)
)
)
C
C
C
o
o
o
â
â
â
n
n
n
g
g
g
t
t
t
h
h
h
ö
ö
ö
ù
ù
ù
c
c
c
R
R
R
u
u
u
n
n
n
g
g
g
e
e
e
–
–
–
K
K
K
u
u
u
t
t
t
t
t
t
a
a
a
b
b
b
a
a
a
ä
ä
ä
c
c
c
4
4
4
:
:
:
a
a
a
)
)
)
C
C
C
o
o
o
â
â
â
n
n
n
g
g
g
t
t
t
h
h
h
ö
ö
ö
ù
ù
ù
c
c
c
(
)
43211
22
6
1
)()( kkkkxyxy
ii
++++=
+
)
,
(
1
i
i
y
x
hf
k
=
)
,
(
1
k
y
h
x
hf
k
+
+
=
Ngô Thu Lương – Phương Pháp Tính
5
)
2
,
2
(
1
2
k
y
h
x
hf
k
ii
+
+
=
)
2
,
2
(
2
3
k
y
h
xhfk
ii
++=
)
,
(
3
1
4
k
y
x
f
h
k
i
i
+
=
+
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
: Giaûi phöông trình
2
)(1)(' yxxy −+=
vôùi
ñieàu kieän ban ñaàu
1
)
2
(
=
y
trong ví duï tröôùc theo
phöông phaùp Runge-Kutta , keát quaû nhö sau :
Ngô Thu Lương – Phương Pháp Tính
6
4
4
4
)
)
)
G
G
G
i
i
i
a
a
a
û
û
û
i
i
i
h
h
h
e
e
e
ä
ä
ä
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
t
t
t
r
r
r
ì
ì
ì
n
n
n
h
h
h
v
v
v
i
i
i
p
p
p
h
h
h
a
a
a
â
â
â
n
n
n
c
c
c
a
a
a
á
á
á
p
p
p
1
1
1
:
:
:
Giaû söû ta caàn giaûi heä :
=
=
),,('
)
,
,
(
'
zyxGz
z
y
x
F
y
trong ñoù
)
(
x
y
y
=
,
)
(
x
z
z
=
laø nhöõng haøm phaûi tìm vaø thoûa
ñieàu kieän ban ñaàu
0
0
)
(
y
x
y
=
,
0
0
)
(
z
x
z
=
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
E
E
E
u
u
u
l
l
l
e
e
e
r
r
r
Ngô Thu Lương – Phương Pháp Tính
7
P
P
P
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
p
p
p
h
h
h
a
a
a
ù
ù
ù
p
p
p
E
E
E
u
u
u
l
l
l
e
e
e
r
r
r
)
,
,
(
1
z
y
x
F
h
y
y
+
=
+
)
,
,
(
1
z
y
x
G
h
z
z
+
=
+
V
V
V
í
í
í
d
d
d
u
u
u
ï
ï
ï
:
:
:
Cho heä
+−=
=
xxyxzxz
x
z
x
y
)()(2)('
)
(
)
(
'
vôùi ñieàu kieän
1
)
0
(
=
y
,
0
)
0
(
=
z
.
Tìm
)
1
(
y
vaø
)
1
(
z
neáu soá böôùc chia laø
4
=
n
Ngô Thu Lương – Phương Pháp Tính
8
5
5
5
)
)
)
G
G
G
i
i
i
a
a
a
û
û
û
i
i
i
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
t
t
t
r
r
r
ì
ì
ì
n
n
n
h
h
h
v
v
v
i
i
i
p
p
p
h
h
h
a
a
a
â
â
â
n
n
n
c
c
c
a
a
a
á
á
á
p
p
p
c
c
c
a
a
a
o
o
o
:
:
:
Giaûi phöông trình vi phaân caáp 2
)
(
)
(
)
(
)
(
'
)
(
)
(
'
'
x
f
x
y
x
q
x
y
x
p
x
y
=
+
+
vôùi ñ
ñ
ñ
i
i
i
e
e
e
à
à
à
u
u
u
k
k
k
i
i
i
e
e
e
ä
ä
ä
n
n
n
ñ
ñ
ñ
a
a
a
à
à
à
u
u
u
0
0
)
(
y
x
y
=
,
/
0
0
)(' yxy =
Ñ
Ñ
Ñ
ö
ö
ö
a
a
a
v
v
v
e
e
e
à
à
à
h
h
h
e
e
e
ä
ä
ä
p
p
p
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
t
t
t
r
r
r
ì
ì
ì
n
n
n
h
h
h
v
v
v
i
i
i
p
p
p
h
h
h
a
a
a
â
â
â
n
n
n
c
c
c
a
a
a
á
á
á
p
p
p
1
1
1
baèng pheùp
ñoåi bieán
,
Ngô Thu Lương – Phương Pháp Tính
9
ñoåi bieán
)
(
)
(
'
x
z
x
y
=
,
)
(
'
)
(
'
'
x
z
x
y
=
Heä
+−−=
=
)()()('
'
xfyxqzxpz
z
y
vôùi ñieàu kieän
ban ñaàu
0
0
)
(
y
x
y
=
vaø
0
/
0
0
)( zyxz ==
.
Heä naøy ñaõ bieát caùch giaûi
| 1/9
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chöông 5 :Giaûi gaàn ñuùng phöông trình vi phaân
Cho phöông trình vi phaân caáp1
y '(x) = f (x, y(x))
vôùi ñieàu kieän ban ñaàu y(x = . 0 ) y0
Tính gaàn ñuùng giaù trò y(b) vôùi b baát kyø cho tröôùc
1) Phöông phaùp Euler :
a)Noäi dung : Chia ñoaïn [ a ,b] thaønh n phaàn ñeàu
nhau , bôûi caùc ñieåm chia
x0 = a < x1 = x0 + h < x2 = x0 + 2h <
< ... < x = b = a nh n +
Ngô Thu Lương – Phương Pháp Tính 1 i y +1 = y k i +
k = h f (x , y ) i i (2) b) Sai soá : h M L(b−a) y
(b) − y (b) ≤ [ e −1] gd d 2 L f ∂ L = Max (x, y) y ∂
Ví duï : Phöông trình 2
y '(x) = 1+ (x − y)
vôùi ñieàu kieän ban ñaàu y(2) = 1 .
Tính gaàn ñuùng nghieäm y( ) 6 . 2 vôùi böôùc h = 2 . 0
Ngô Thu Lương – Phương Pháp Tính 2 2) 2 ) P h P ö h ô ö n ô g n g p h p a h ùap p E u E l u e l r e r c a c ûai it i t e i áen n a) Noäi dung : 1 k + k2 y i 1 + = yi + 2
k = hf ( x , ) 1 i yi
k = hf ( x , y + + k ) 2 i 1 i 1
Ngô Thu Lương – Phương Pháp Tính 3
Ví duï : Giaûi phöông trình 2
y '(x) = 1+ (x − y) vôùi
ñieàu kieän ban ñaàu y( )
2 = 1 trong ví duï tröôùc theo
phöông phaùp Euler caûi tieán , keát quaû nhö sau :
Ngô Thu Lương – Phương Pháp Tính 4
3) Coâng thöùc Runge – Kutta baäc 4 : a) Coâng thöùc 1 y(x i 1) + = y(x ) i + ( 1k + 2k2 + 2 3 k + k4 ) 6
k = hf (x , y ) 1 i i h k
k2 = hf (xi + , 1 k , yi + ) 2 2 k k = hf ( h x + , 2 y + ) 3 i i 2 2
k = h f (x , y + + k ) 4 i 1 i 3
Ngô Thu Lương – Phương Pháp Tính 5
Ví duï : Giaûi phöông trình 2
y '(x) = 1+ (x − y) vôùi
ñieàu kieän ban ñaàu y( )
2 = 1 trong ví duï tröôùc theo
phöông phaùp Runge-Kutta , keát quaû nhö sau :
Ngô Thu Lương – Phương Pháp Tính 6
4) Giaûi heä phöông trình vi phaân caáp 1 : y ' =
Giaû söû ta caàn giaûi heä : 
F (x, y, z)  trong ñoù
z ' = G(x, y, z)
y = y(x), z = z(x) laø nhöõng haøm phaûi tìm vaø thoûa ñieàu kieän ban ñaàu ( y 0 x ) = , 0 y z( 0 x ) = z0 Ph P ö h ô ö n ô g n g p h p a h ùap p E u E l u e l r e r
y + = y + h F(x , y , z ) i 1 i i i i
z + = z + hG(x , y ,z ) i 1 i i i i
Ngô Thu Lương – Phương Pháp Tính 7
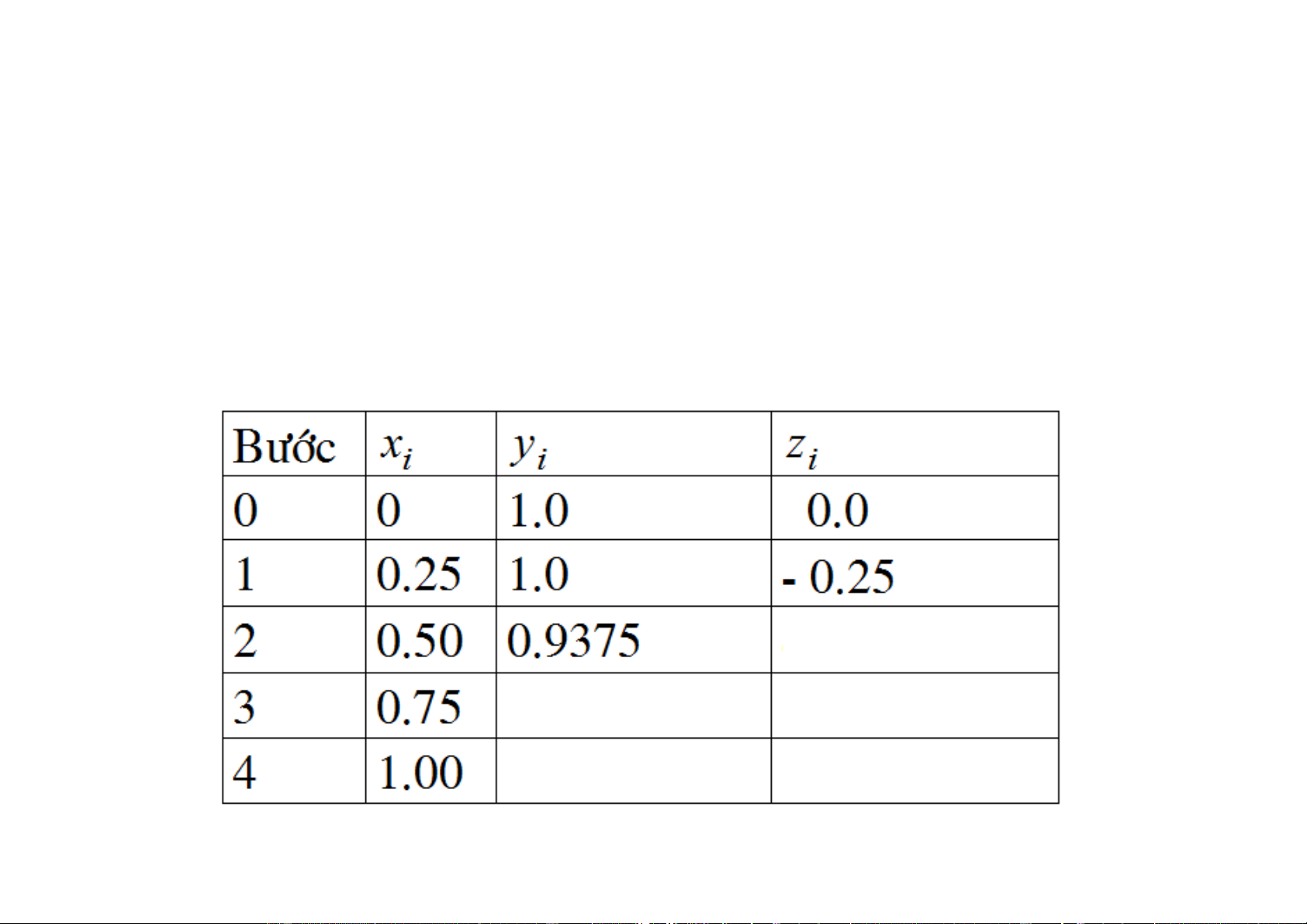
y '(x) = z(x) Ví duï : Cho heä 
z '(x) = 2z(x) − y(x) + x
vôùi ñieàu kieän y(0) = 1 , z(0) = 0 . Tìm y ) 1 ( vaø z ) 1
( neáu soá böôùc chia laø n = 4
Ngô Thu Lương – Phương Pháp Tính 8
5) Giaûi phöông trình vi phaân caáp cao :
Giaûi phöông trình vi phaân caáp 2
y ' '(x) + p(x) y '(x) + q(x) y(x) = f (x)
vôùi ñieàu kieän ñaàu y( 0 x ) = , / 0 y y '( 0 x ) = y0
Ñöa veà heä phöông trình vi phaân caáp 1 baèng pheùp ño ñ åoi ibi b e i án e
n y '(x) = z(x) , y ''(x) = z '(x) y '= z Heä  vôùi ñieàu kieän
z ' = − p(x) z − q(x) y + f (x) ban ñaàu y( / . 0 x ) = vaø 0 y z( 0
x ) = y = z0 0
Heä naøy ñaõ bieát caùch giaûi
Ngô Thu Lương – Phương Pháp Tính 9