Chương 4: Tính gần đúng tích phân xác định và đạo hàm | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

Chương 4: Tính gần đúng tích phân xác định và đạo hàm. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

37 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính và matlab CTTT

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

12 trang 1 tháng trước

Tác giả:

Profile Lê Na
C
C
C
h
h
h
ö
ö
ö
ô
ô
ô
n
n
n
g
g
g
V
V
V
:
:
:
T
T
T
í
í
í
n
n
n
h
h
h
g
g
g
a
a
a
à
à
à
n
n
n
ñ
ñ
ñ
u
u
u
ù
ù
ù
n
n
n
g
g
g
t
t
t
í
í
í
c
c
c
h
h
h
p
p
p
h
h
h
a
a
a
â
â
â
n
n
n
x
x
x
a
a
a
ù
ù
ù
c
c
c
ñ
ñ
ñ
ò
ò
ò
n
n
n
h
h
h
v
v
v
a
a
a
ø
ø
ø
ñ
ñ
ñ
a
a
a
ï
ï
ï
o
o
o
h
h
h
a
a
a
ø
ø
ø
m
m
m
1
1
1
)
)
)
T
T
T
í
í
í
n
n
n
h
h
h
g
g
g
a
a
a
à
à
à
n
n
n
ñ
ñ
ñ
u
u
u
ù
ù
ù
n
n
n
g
g
g
t
t
t
í
í
í
c
c
c
h
h
h
p
p
p
h
h
h
a
a
a
â
â
â
n
n
n
x
x
x
a
a
a
ù
ù
ù
c
c
c
ñ
ñ
ñ
ò
ò
ò
n
n
n
h
h
h
1
1
1
.
.
.
1
1
1
)
)
)
C
C
C
o
o
o
â
â
â
n
n
n
g
g
g
t
t
t
h
h
h
ö
ö
ö
ù
ù
ù
c
c
c
h
h
h
ì
ì
ì
n
n
n
h
h
h
t
t
t
h
h
h
a
a
a
n
n
n
g
g
g
:
:
:
a
a
a
)
)
)
N
N
N
o
o
o
ä
ä
ä
i
i
i
d
d
d
u
u
u
n
n
n
g
g
g
:
Chia ñoaïn
]
,
[
b
a
thaønh
n
phaàn baèng nhau bôûi caùc
Ngô Thu Lương
1
Chia ñoaïn
]
,
[
b
a
thaønh
phaàn baèng nhau bôûi caùc
ñieåm :
n
x
x
x
x
,
...
,
,
210
vôùi böôùc chia ñeàu
n
ab
h
−
=
<
=
+
<
=
+
<
=
2
0
1
0
0
2
x
h
x
x
h
x
a
x
b
x
nh
x
n
=
=
+
<
0
Xaáp xæ haøm
)
(
x
f
treân ñoaïn
]
,
[
1
0
x
x
bôûi
ña thöùc noäi
suy
b
b
b
a
a
a
ä
ä
ä
c
c
c
n
n
n
h
h
h
a
a
a
á
á
á
t
t
t
P(x) treân
h
h
h
a
a
a
i
i
i
m
m
m
o
o
o
á
á
á
c
c
c
noäi suy
]
,
[
1
0
x
x
≈
∫
1
0
)(
x
x
dxxf
dxxP
x
x
)(
1
0
∫
0 1
[ ]
2
h
y y
= +
C
C
C
o
o
o
â
â
â
n
n
n
g
g
g
t
t
t
h
h
h
ö
ö
ö
ù
ù
ù
c
c
c
h
h
h
ì
ì
ì
n
n
n
h
h
h
t
t
t
h
h
h
a
a
a
n
n
n
g
g
g
:
:
:
Ngô Thu Lương
2
C
C
C
o
o
o
â
â
â
n
n
n
g
g
g
t
t
t
h
h
h
ö
ö
ö
ù
ù
ù
c
c
c
h
h
h
ì
ì
ì
n
n
n
h
h
h
t
t
t
h
h
h
a
a
a
n
n
n
g
g
g
:
:
:
( )
nn
b
a
yyyyy
h
dxxf +++++≈
−
∫
1210
2...22
2
)(
b
b
)
)
S
S
a
a
i
i
s
s
o
o
á
á
:
:
(2) 2
( )
12
M h
b a
−
Ngô Thu Lương
3
1
1
X
+
CALC
? 0
X
=
CALC
4
5
0 6
1
2
2
i
i
h
I y y y
=
= + +
∑
? 0.1
X
=
0.470510739
=
CALC
Sai sSai số ố ::
(2) 2
( )
12
M h b a
−
0.6
b a
− =
0.1
h
=
0.001
=
0
>
1
( )
1
f x
x
=
+
2
1
'( )
(1 )
f x
x
−
=
+
3
2
''( )
(1 )
f x
x
=
+
5
0.1
h
=
(2)
''( )
M Max f x
=
3
2
(1 )
Max
x
=
+
3
2
(1 )
Max
x
=
+
2
=
[0, 0.6]
x
∈
0
>
1.
2)
C
C
o
o
â
â
n
n
g
g
t
t
h
h
ö
ö
ù
ù
c
c
S
S
i
i
m
m
p
p
s
s
o
o
n
n
:
:
a
a
)
)
N
N
o
o
ä
ä
i
i
d
d
u
u
n
n
g
g
:Chia ñoaïn
]
,
[
b
a
thaønh
n
phaàn ñeàu
nhau ( n chaün :
n
m
2
=
). Xaáp xæ haøm
)
(
x
f
treân
ñoaïn
]
,
[
2
0
x
x
bôûi ña thöùc noäi suy baäc hai treân
caùc moác noäi suy
2
1
0
,
,
x
x
x
[
]
2
2
h
x
x
Ngô Thu Lương
6
[
]
2102
4
3
)()(
2
0
2
0
yyy
h
dxxPdxxf
x
x
x
x
++=≈
∫∫
C
C
o
o
â
â
n
n
g
g
t
t
h
h
ö
ö
ù
ù
c
c :
( )
b
a
f x dx
≈
∫
1
0 2 2 1 2
1 1
4 2
3
m m
m k k
k k
h
y y y y
−
−
= =
+ + +
∑ ∑
b
b
)
)
S
S
a
a
i
i
s
s
o
o
á
á
:
180
)(
4
)
4
(
abhM −
(4)
max ''''( )
a x b
M f x
≤ ≤
=
Ngô Thu Lương
7
VVíí dụ dụ : : tính gần đúng
theo công thức SimpsonSimpson với số khoảng chia n=6
0.6
0
1
1
dx
x
+
∫
8
44
0 6 1 3 5 2 4
[ 4( ) 2( )]
3
h
I y y y y y y y
= + + + + + + =
0.47000638
=
11
9
44
44
44
22
22
11
Sai số :Sai số :
(4) 4
( )
180
M h b a
−
0.6
b a
− =
0.1
h
=
0.000008
=
10
0.1
h
=
(4)
''''( )
M Max f x
=
5
24
(1 )
Max
x
=
+
5
24
(1 )
Max
x
=
+
24
=
[0, 0.6]
x
∈
2
2
2
)
)
)
T
T
í
í
n
n
h
h
g
g
a
a
à
à
n
n
ñ
ñ
u
u
ù
ù
n
n
g
g
ñ
ñ
a
a
ï
ï
o
o
h
h
a
a
ø
ø
m
m
:
:
a
)
)
)
T
T
í
í
n
n
h
h
g
g
a
a
à
à
n
n
ñ
ñ
u
u
ù
ù
n
n
g
g
ñ
ñ
a
a
ï
ï
o
o
h
h
a
a
ø
ø
m
m
c
c
a
a
á
á
p
p
1
1
:
:
Cho baûng soá lieäu vôùi moác caùch ñeàu ( h ) :
Tính gaàn ñuùng giaù trò
)
(
'
x
y
,
)
(
'
'
x
y
Ngô Thu Lương
11
Tính gaàn ñuùng giaù trò
)
(
'
i
x
y
,
)
(
'
'
i
x
y
Coâng thöùc
t
t
r
r
u
u
n
n
g
g
t
t
a
a
â
â
m
m
tính gaàn ñuùng ñaïo haøm caáp 1:
1 1
' '( )
2
i i
i i
y y
y y x
h
+ −
−
= ≈
b
b
)
)
C
C
o
o
â
â
n
n
g
g
t
t
h
h
ö
ö
ù
ù
c
c
t
t
í
í
n
n
h
h
g
g
a
a
à
à
n
n
ñ
ñ
u
u
ù
ù
n
n
g
g
ñ
ñ
a
a
ï
ï
o
o
h
h
a
a
ø
ø
m
m
c
c
a
a
á
á
p
p
2
2
2
11
2
'')(''
h
y
y
y
yxy
iii
ii
+−
+
−
≈=
Tính gaàn ñuùng giaù trò
)
1
(
'
'
,
)
1
(
'
y
y
neáu haøm
)(cos)(
3
4
xxy =
, vôùi
1
.
0
=
h
Ngô Thu Lương
12
3573462
.
0
)
1
(
'
'
=
y
'(1) 0.17824017
y
=−
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chöông IV : Tính gaàn ñuùng tích phaân xaùc ñònh vaø ñaïo haøm
1) Tính gaàn ñuùng tích phaân xaùc ñònh
1.1) Coâng thöùc hình thang : a) Noäi dung : Chia i ñoa o ïan [ a [ ,b] ] t h t aøanh h n ph p aàan ba b èang nha h u u bô b ûi icaùac b−a
ñieåm : x , x , x ..., x = 0 1 2
n vôùi böôùc chia ñeàu h n 0 x = a < 0 x + h = 1 x < 0
x + 2h = x2 <
< x0 + nh = x = b n Ngô Thu Lương 1
Xaáp xæ haøm f (x) treân ñoaïn [ x , x ] 0 1 bôûi ña thöùc noäi
suy baäc nhaát P(x) treân hai moác noäi suy [x , x ] 0 1 x 1 x 1 h
∫ f (x) dx ≈ ∫ P( x) dx = [ + 0 y 1 y ] 2 0 x x0 Coâong n thö h ùöc c hì h n ì h h th t a h ng : : b h
∫ f (x)dx ≈
(y0 +2y1+2y2 +... +2 n y −1 + n y ) 2 a (2) 2 b) Sai soá : M h (b − a) 12 Ngô Thu Lương 2 Ngô Thu Lương 3 1 1+ X CALC X = ? 0 CAL A C X = ? 0.1  5 hI =  + + ∑ 0 y 6 y 2 i y  = 0.470510739 2  i 1 =  4 Sai s ai ố ố :: 1
f ( x) = 1+ x (2) 2 M
h (b − a) 1 − = 0.001 f '( x) = 2 12 (1 + x) 2 f ' ( x) = b − a = 0.6 3 (1 + x) h = 0. 0 1 > 0 (2) 2 M
= Max f '(x) = Max x ∈ [0, 0.6] 3 (1+ x) 2 = Max = 2 3 (1+ x) 5
1.2)Coâng thöùc Simpson :
a) Noäi dung :Chia ñoaïn [a,b ] thaønh n phaàn ñeàu
nhau ( n chaün : n= 2m ). Xaáp xæ haøm f (x) treân
ñoaïn [x , x ] bôûi ña thöùc noäi suy baäc hai treân 0 2 caùc moác noäi suy 0 x , 1 x , x2 x2 x 2 2 h
∫ f (x) dx ≈ ∫ 2
P ( x) dx = [y0 + 4 1 y + y2 ] 3 x0 x0 Coâng thöùc : b m m  −1  ∫ h
f ( x)dx ≈ y  + + ∑ + ∑ 0 y2 4 m y2k −1 2 y2  3 k ak =1 k =1  Ngô Thu Lương 6 (4) 4 M
h (b − a) b) Sai soá : 180 (4) M = max f ' '(x)
a≤ x≤b Ngô Thu Lương 7 0.6 1 Ví d
dụ : tính gần đúng ∫ dx 1+ x 0 theo công thức Si S m i p m s
p on với số khoảng chia n=6 8 h I = [ + + + + + + = 0 y 6 y 4( 1 y 3 y 5 y ) 2( y2 y4)] 3 = 0.47000638 1 4 2 4 2 4 1 9 Sai ai s ố : ố (4) 4 M
h (b − a) = 0.000008 180 b − a = 0.6 h = 0. 0 1 (4) 24 M
= Max f ''(x) = Max x ∈ [0, 0.6] 5 (1+ x) 24 = Max = 24 5 (1+ x) 10
2) Tính gaàn ñuùng ñaïo haøm :
a) Tính gaàn ñuùng ñaïo haøm caáp 1 :
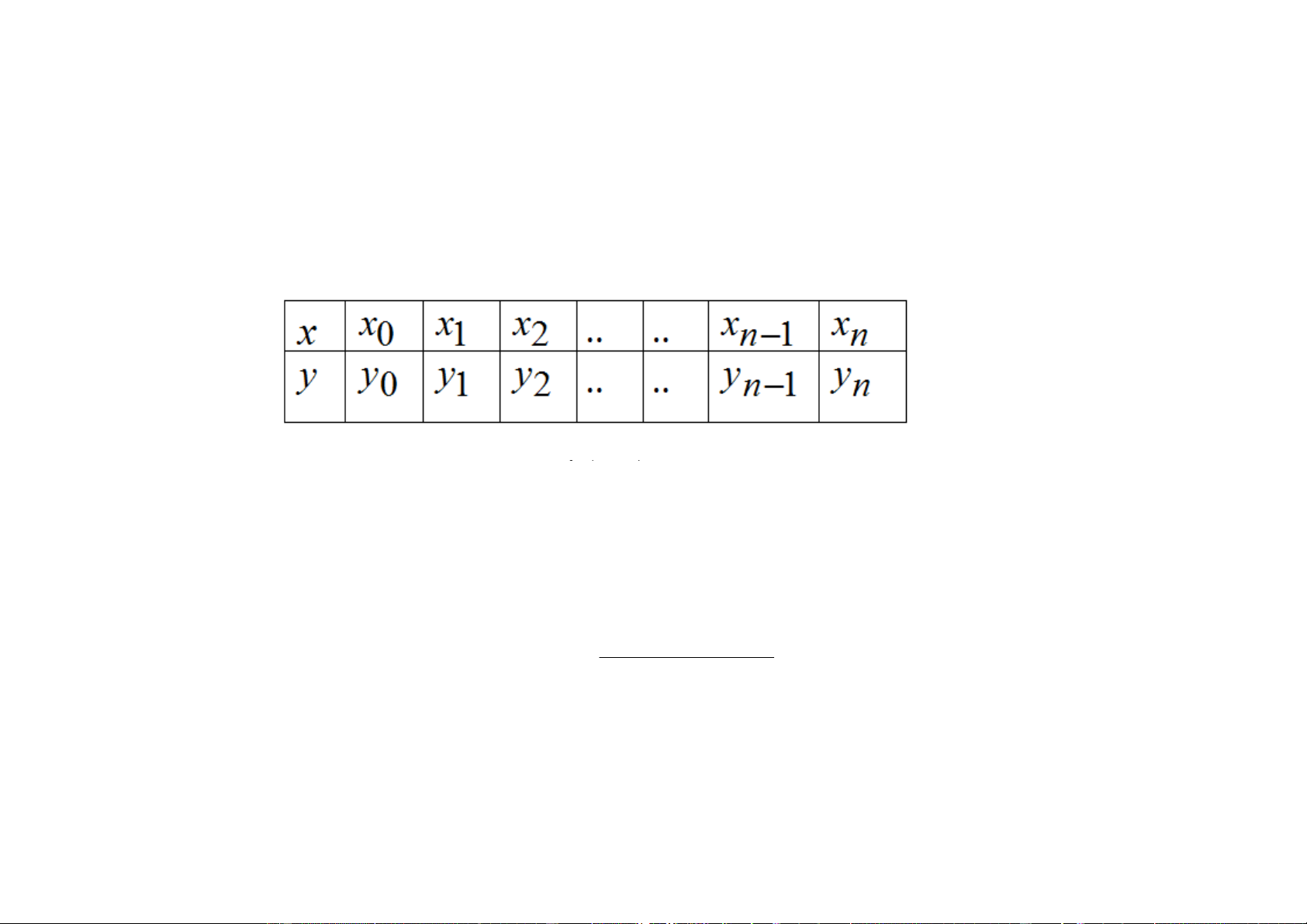
Cho baûng soá lieäu vôùi moác caùch ñeàu ( h ) :
Tính gaàan ñuùung giaùa trò ò y '(x ) , , y ''(x ) i x i x
Coâng thöùc trung taâm tính gaàn ñuùng ñaïo haøm caáp 1: − i y 1 + i y 1
y ' = y '(x ) − ≈ i i 2h Ngô Thu Lương 11
b) Coâng thöùc tính gaàn ñuùng ñaïo haøm caáp 2
yi−1 − 2 y + y i i +1
y ' ' ( x ) = y ' ' i i ≈ 2 h
Tính gaàn ñuùng giaù trò y' ) 1 ( , y'' ) 1 ( neáu haøm
y(x) = cos4 (3 x ) , vôùi h = 0.1 y '(1) = − 0.17824017 y'' ) 1 ( = 3 . 0 573462 Ngô Thu Lương 12