lOMoAR cPSD| 49519085 12/2/2021 1/12/2021 1 Định thức
của A, bỏ đi dòng 𝑖 và cột 𝑗 của ma trận A thì ta 1 lOMoAR cPSD| 49519085 12/2/2021
được ma trận vuông cấp 𝑛 − 1, Ký hiệu 𝑀 được
gọi là ma trận con tương ứng với phần tử 𝑎 2 Cho ma trận . Tìm các ma trận 3 2 lOMoAR cPSD| 49519085 12/2/2021 4
• Định nghĩa của định thức:
• Cho ma trận vuông cấp 𝑛 : 𝐴 = 𝑎 lOMoAR cPSD| 49519085 12/2/2021 × • 4 lOMoAR cPSD| 49519085 12/2/2021
Định thức của ma trận A được ký hiệu là
𝐷𝑒𝑡(𝐴) hoặc 𝐴 được định nghĩa như sau:
• Định thức cấp 1: 𝐴 = [𝑎 ] thì det 𝐴 = 𝑎 𝑎 𝑎
• Định thức cấp 2: 𝐴 = 𝑎 𝑎 thì 𝑎 𝑎 • det 𝐴 = 𝑎 𝑎 = 𝑎 𝑎 − 𝑎 𝑎 5
Định nghĩa của định thức • Quy tắc Sarius lOMoAR cPSD| 49519085 12/2/2021 6 7 Ví dụ: 6 lOMoAR cPSD| 49519085 12/2/2021
Hãy tìm các định thức của các ma trận sau: 0 2 0 8 9 lOMoAR cPSD| 49519085 12/2/2021 𝒂𝟏𝟏 ⋯ 𝒂𝟏𝒏 • Nếu 𝑨 = ⋮ ⋱ ⋮ , với 𝑛 ≥ 3 𝒂𝒏𝟏 ⋯ 𝒂𝒏𝒏 8 lOMoAR cPSD| 49519085 12/2/2021
• Khai triển công thức khai triển theo hàng lOMoAR cPSD| 49519085 12/2/2021 thứ i • 𝐴 = ∑ −1 𝑎 𝑀
• Khai triển công thức khai triển theo cột thứ j • 𝐴 = ∑ −1 𝑎 𝑀 • Với 𝑀
là ma trận con cấp (n -1) được tao
ra từ ma trận A bằng cách bỏ đi hàng thứ I và cột j 10
• Ví dụ: Compute the determinant of matrix 11 10 lOMoAR cPSD| 49519085 12/2/2021 12
Tính chất của định thức
• Định lý 1: Với A là 1 ma trận vuông cấp n
• a. Nếu cộng 1 dòng của ma trận A và 1 dòng
khác thì định thức của ma trận mới sinh ra không đổi
• b. Nếu đổi chỗ 2 dòng của ma trận A thì định
thức ma trận mới đổi dấu lOMoAR cPSD| 49519085 12/2/2021
• c. Nếu nhân 1 dòng của ma trận A với 1 số 𝑘
thì định thức ma trận mới tăng k lần ( với 𝑘 ≠ 0 ) 13
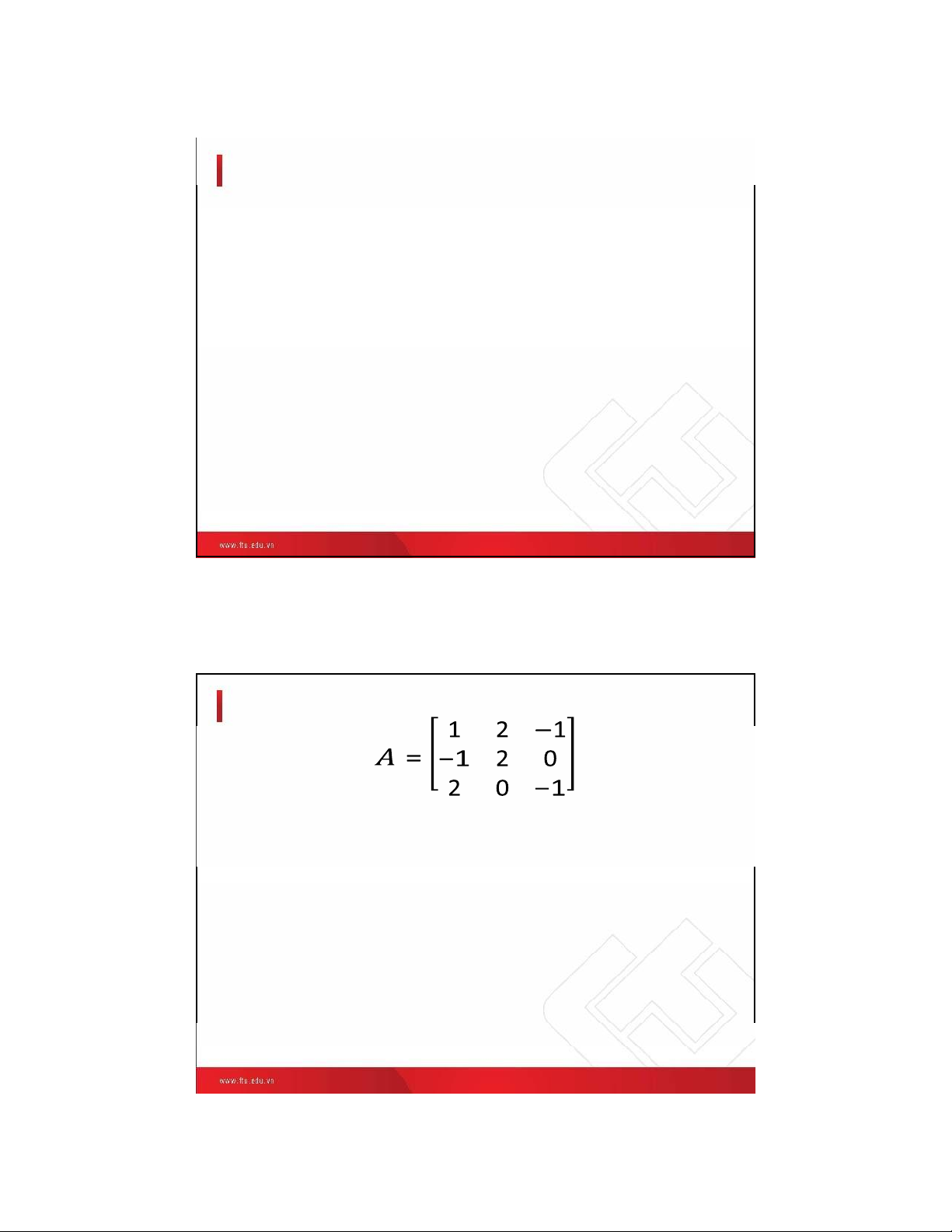
• Ví dụ: Tính định thức ma trận 𝐴 với 𝐴 = 14 12 lOMoAR cPSD| 49519085 12/2/2021 15 Bài tập lOMoAR cPSD| 49519085 12/2/2021 16
• 2. Chứng minh rằng định thức của ma trận
tam giác chính là tích các phần tử nằm trên đường chéo chính. 17 14 lOMoAR cPSD| 49519085 12/2/2021
Phương pháp tìm định thức
• Sử dụng phép biến đổi sơ cấp để biến đổi ma
trận A về dạng ma trận tam giác.
• Áp dụng: Định thức của ma trận tam giác
chính là tích của các phần tử nằm trên đường chéo chính 18