Biên dịch: Huỳnh Tấn Liêm Chương 1 PHƯƠNG PHÁP TOÁN HỌC 1.1. Các định nghĩa
Trong kinh tế học, người ta thường cố gắng đưa ra những suy nghĩ chính xác và
một trong những cách chúng ta thực hiện điều này đó là sử dụng toán học. Bắt đầu cho
việc này là phải làm rõ được những gì chúng ta đang nói và với mục đích này chúng ta
cần đến các định nghĩa.
Chúng ta bắt đầu với lý thuyết số sơ cấp để minh hoạ các phương pháp toán học
mà sau này chúng ta sẽ áp dụng vào các mô hình kinh tế. Giả sử chúng ta quan tâm đến
các tính chất về số chẵn và số lẻ. Một cách trực giác, ta biết 4 là số chẵn và 5 là số lẻ. Tuy
nhiên, nếu chúng ta muốn chứng minh các vấn đề về số chẵn và số lẻ, ta phải định nghĩa
những gì chúng ta hiểu về các số chẵn và các số lẻ.
Ta xét bài toán: Chứng minh rằng tích của một số lẻ và một số chẵn luôn là một số
chẵn. Ta không thể liệt kê hết danh sách như sau: 4 5  20 2 3  6 12 37  444 etc.
và chú ý rằng 20, 6 và 444 là các số chẵn. Đây không phải là một phép chứng minh ngay
cả khi danh sách trên có dài thêm bao nhiêu đi nữa bởi vì có vô hạn các tổ hợp giữa số chẵn và số lẻ.
Nếu không có các định nghĩa, ta sẽ không thể bắt đầu. Bây giờ một định nghĩa về
các số chẵn và số lẻ sẽ là: Định nghĩa 1.1.
Số nguyên m là một số chẵn nếu và chỉ nếu tồn tại một số nguyên n sao cho m  2 n Định nghĩa 1.2.
Số nguyên m là một số lẻ nếu và chỉ nếu tồn tại một số nguyên n sao cho m  2  n 1
Biên dịch: Huỳnh Tấn Liêm
Ví dụ 1.1. Theo định nghĩa 16 là số chẵn, vì ta có thể viết 16  2  n , trong đó n  8 và 7
là số lẻ, vì ta có thể viết 7  2 n 1 , trong đó n  3.
Với các định nghĩa trên, bây giờ ta có thể chứng minh định lý sau: Định lý 1.3.
Tích của một số lẻ và một số chẵn là một số chẵn. Chứng minh.
Nếu a là số chẵn và b là số lẻ thì a  2m và b  2n 1 và a b  2m (2n  1)  2 (m  (2n 1))  2 r
trong đó r  (m(2n 1) là một số nguyên. Do đó, a b  là một số chẵn.
Chú thích: Hãy chú ý đến sức mạnh của loại lý luận này. Trong vài dòng ngắn chúng ta
có thể chứng minh một kết quả mà áp dụng cho vô hạn con số. Tính vô hạn này là một
danh sách các con số sẽ đi qua mặt trăng hay ngay cả đi qua vì sao xa nhất và chúng ta
chưa thể nói điều gì đó rõ ràng để định nghĩa điều đó. Đây là phép kỳ diệu của toán học.
1.2. Sự khác nhau giữa ' = ' và ' ≡ '
Đôi khi các sự việc là bằng nhau một cách đơn giản theo định nghĩa. Chẳng hạn nếu
A  ”số các cử nhân ở Montreal”
B  ”số các đàn ông độc thân ở Montreal”
thì A và B là bằng nhau theo định nghĩa. Không có gì để chứng minh ở đây và điều đó
không nói gì cả về thế giới hay Montreal.
Để nhấn mạnh bản chất của loại đẳng thức này, chúng ta sử dụng một loại dấu
bằng đặc biệt: ' ≡ ' sao cho với các cử nhân và các đàn ông độc thân ở Montreal ta viết A  B
Khi đó, điều này nói rằng A và B là bằng nhau theo định nghĩa hay đây là sự đồng nhất kế toán.
Khi bạn thấy dấu đẳng thức này, bạn có thể bớt căng thẳng. Không có gì để chứng
minh. Các điều này đơn thuần là các ký hiệu khác nhau để chỉ cùng sự vật. 2
Biên dịch: Huỳnh Tấn Liêm
Trong Kinh tế học, một ví dụ tốt của sự đồng nhất kế toán là đẳng thức GNP mà
bạn biết trong môn Kinh tế học vĩ mô:
Y  C  I  G  X  M
trong đó Y là GNP ,C là lượng tiêu thụ, I là sự đầu tư, G là sự tiêu xài của chính phủ,
X là số xuất khẩu và M là số nhập khẩu.
Mặt khác, đôi khi các sự vật là bằng nhau theo một cách quan trọng hơn. Ví dụ 2
E  mc biểu thị một sự kiện quan trọng trong vật lý, trong khi 2 f (x)  x hay f '( ) x  2 x
cho ta thông tin thật về hàm số f . Trong các trường hợp này, ta sử dụng dấu "  " như là
một cách để nhấn mạnh thông tin thật đang được cung cấp. 1.3. Phép kéo theo
Trong toán kinh tế, chúng ta bắt đầu với các điều giả sử và từ đó cố gắng để suy
luận các phép kéo theo đúng của các giả sử này. Cơ bản đối với loại lý luận này là ý
tưởng của phép kéo theo logic :
Nếu A là đúng thì điều đó kéo theo B cũng phải đúng. Ta viết điều này một cách
hình thức như sau: A  B ; đọc là A kéo theo B. Ví dụ 1.2: Nếu
A  ”Ông Nam sống ở Nha Trang”
B  ”Ông Nam sống ở Việt Nam”
thì A  B vì Nha Trang là một thành phố của Việt Nam.
Ta thường cố gắng để xây dựng các phép chứng minh của các mệnh đề theo kiểu: A  B .
Mối liên hệ giữa A và B thường không rõ ràng và ta cần tìm một chuỗi các phép
kéo theo trung gian sao cho một phép chứng minh thường có dạng:
A  S  S  ... S  B 1 2 n
Từ đó ta kết luận: A  B . Do đó, chiến lược chung trong việc chứng minh A  B
là bắt đầu với A và sử dụng một chuỗi các phép kéo theo đúng để cuối cùng thu được mệnh đề B. Ta có định lý sau: 3
Biên dịch: Huỳnh Tấn Liêm Định lý 1.4.
Tổng của hai số lẻ là một số chẵn. Chứng minh. Đặt
A  " a là số lẻ và b là số lẻ "
B  " a  b là số chẵn "
Từ giả sử A , ta có a  2r1 và b  2s1 , với r và s là các số nguyên. Do đó
A  a  2r 1,b  2s 1
 a b  (2r 1)  (2s 1)
 a b  2(r  s 1)
 a b  2t,t  r  s 1  'a b là số chẵn’ B
Chú thích: Chú ý rằng ta chỉ có một chiều đối với mũi tên: . Điều này nghĩa là chân lý
của mệnh đề A được truyền đến chân lý của mệnh đề B nhưng không cần thiết là chân lý
của B kéo theo chân lý của A . Do đó không đúng để kết luận từ A  B thì B  A.
Ví dụ 1.3. Nếu B = “ a  b là một số chẵn ”, ta không thể suy ra A = “ a và b đều là các
số lẻ”. Chẳng hạn nếu a  4 và b  6 thì B là đúng vì 4 6 10 nhưng A không đúng vì
cả hai a và b đều không là số lẻ. Do đó, A B là đúng trong khi B  A là sai. 1.4. Phép phủ định
Ký hiệu  A là phép phủ định của mệnh đề A, nghĩa là “không” A hay A là không đúng hay A là sai.
Ví dụ 1.4. Nếu A là mệnh đề: “Ông Nam sống ở Nha Trang” thì  A là mệnh đề: “Ông
Nam không sống ở Nha Trang”.
Dấu phủ định tác dụng như dấu âm trong số học vì:  ( A )  A
Như đã biết nếu A  B là đúng thì ta chưa thể kết luận B  A cũng đúng. Tuy nhiên,
ta có thể kết luận một cách chính xác rằng nếu A  B là đúng thì  B  A là đúng hay nói một cách khác A  B thì  B  A Ví dụ 1.5. 4
Biên dịch: Huỳnh Tấn Liêm
A  ”Ông Nam sống ở Nha Trang”
B  ”Ông Nam sống ở Việt Nam”
Ở đây ta thấy A  B là đúng nên  B  A cũng đúng; nghĩa là nếu ông Nam
không sống ở Việt Nam thì chắc chắn ông ta không thể sống ở Nha Trang được. Ví dụ 1.6.
A  " a là số lẻ và b là số lẻ "
B  " a  b là số chẵn "
Trong số học, ta có thể kết luận một cách chính xác nếu  B , nghĩa là “ a b
không phải là một số chẵn” thì  A , nghĩa là “không phải cả hai a và b đều lẻ”.
1.5. Phép chứng minh phản chứng
Chứng minh bằng phản chứng hay 'Reductio ad absurdum' là chứng minh một
mệnh đề A bằng cách giả sử mệnh đề phủ định  A là đúng và suy ra một điều mâu thuẫn. Do đó, nếu
 A  B và  A  B
thì  A phải sai và như vậy A phải đúng. Định lý 1.5.
2 là số vô tỉ, nghĩa là không tồn tại các số nguyên a và b sao cho a 2  b Chứng minh
Giả sử 2 không phải số vô tỷ (tức là số hữu tỷ), nghĩa là tồn tại 2 số nguyên a, b sao cho a 2  b
Không mất tính tổng quát, giả sử a và b không đồng thời là số chẵn vì nếu a và b đều chẵn thì a 2 r r 2    b 2s s Ta có 5
Biên dịch: Huỳnh Tấn Liêm a 2 2 2   a  2b b 2  a là số chẵn  a là số chẵn
Do đó ta có thể viết a  2 n , với n là số nguyên. Ta lại có 2 2 2 2b  a 4n 2 2  b  2n  b là số chẵn
Ở đây ta suy ra cả a và b đều chẵn, mâu thuẫn với giả thiết ban đầu. Do đó giả sử 2
không phải số vô tỷ là sai. Vậy 2 là số vô tỷ là đúng.
Ví dụ 1.7. Chứng minh hàm số f ( )
x  x không bị chặn với mọi x. Chứng minh
Giả sử hàm f (x)  x bị chặn, nghĩa là tồn tại hằng số c   sao cho x  c, x 
Nếu ta chọn x  c  2 1 thì ta có x  c  2 1  c 1
  c 1  0 (vô lý)
Vậy điều giả sử ban đầu là sai. Do đó hàm số f (x)  x không bị chặn với mọi x.
1.6. Điều kiện cần và điều kiện đủ
Trong toán học, bạn thường nghe về “các điều kiện cần” và “các điều kiện đủ”. Ví
dụ, điều kiện cần để ông Nam sống tại Nha Trang là ông ta phải sống tại Việt Nam, trong
khi điều kiện đủ để ông Nam sống tại Việt Nam là ông ta sống tại Nha Trang. Tuy nhiên,
sống tại Nha Trang không phải là điều kiện cần để sống tại Việt Nam và sống tại Việt
Nam không phải là điều kiện đủ để sống tại Nha Trang. Ta có các định nghĩa sau:
Định nghĩa 1.6. (Điều kiện cần)
Nếu  B  A hay tương đương A  B , thì B là điều kiện cần đối với A .
Định nghĩa 1.7. (Điều kiện đủ) 6
Biên dịch: Huỳnh Tấn Liêm
Nếu A  B hay tương đương  B  A , thì A là điều kiện đủ đối với B Chú thích:
 Nếu ta chứng minh một mệnh đề có dạng A  B thì A là điều kiện đủ đối với B và
B là điều kiện cần đối với A
 Nếu A là điều kiện đủ của B thì không có nghĩa A là điều kiện cần của B và tương
tự nếu B là điều kiện cần của A thì cũng không có nghĩa B sẽ là điều kiện đủ của A.
Ví dụ 1.8. Ta chứng minh mệnh đề
"a là số lẻ và b là số lẻ"  " a  b là số chẵn "
Điều kiện đủ để tổng a b là một số chẵn là cả hai a và b đều là số lẻ, trong khi
điều kiện cần để cả hai a và b đều là số lẻ là a  b là số chẵn.
Tuy nhiên, a b là một số chẵn không phải là điều kiện đủ để cả hai a và b là số
lẻ vì chẳng hạn nếu a  2 và b  4 thì a  b  6 .
1.7. Điều kiện cần và đủ
Đôi khi ta có thể chứng minh cả hai mệnh đề A  B và B  A . Trong trường
hợp này, A à điều kiện cần và đủ đối với B và B là điều kiện cần và đủ đối với A, vì khi
đó ta có các mệnh đề đúng A  B và  A  B B  A và  B  A
Do đó, ta có định nghĩa sau: Định nghĩa 1.8.
Nếu A  B và B  A thì A là điều kiện cần và đủ đối với B và ta viết A  B Chú thích:
 Với A  B thì mũi tên chỉ theo hai chiều. Điều này chỉ ra rằng chân trị của A
truyền sang B cũng như chân trị của B được truyền sang A
 Nếu bạn có thể chứng minh được A B thì bạn có một mệnh đề mạnh mẽ hơn
một trong hai mệnh đề A  B hay B  A . Định lý 1.9. 7
Biên dịch: Huỳnh Tấn Liêm
Ta có a và b là các số lẻ khi và chỉ khi tích a × b là một số lẻ. Chứng minh
Đặt A  ”Các số nguyên a và b là các số lẻ”
B  “Tích của các số nguyên a b là một số lẻ”.
Trước tiên ta sẽ chứng minh A  B
Vì a, b là các số lẻ nên ta có a  2n 1; b  2m 1  a b  2n  1  2m  1  2 2mn m  n 1 là số lẻ Vậy A B (1)
Sau đó ta tiếp tục chứng minh chiều ngược lại B  A
Từ giả thiết B ta có a b 2s 1, bằng phương pháp phản chứng ta giả sử A sai, nghĩa là
một trong 2 số a, b phải là số chẵn. Không mất tính tổng quát, giả sử a chẵn, tức là
a  2n a b  2n b  2s 1 1
 n b  s  2 (vô lý)
Vậy A đúng, nghĩa là B  A (2)
Từ (1) và (2) ta kết luận A  B 1.8. 'Or' và 'And'
Trong đời sống và trong toán học ta thường nối các mệnh đề khác nhau bằng cách sử
dụng từ “hoặc” được ký hiệu:  . Ví dụ 1.9.
Nếu A là mệnh đề “ n là số lẻ” và B là mệnh đề “ n 10 ” thì A B nghĩa là n là
số lẻ hoặc n lớn hơn 10 .
Nếu n  13 thì A  B là mệnh đề đúng vì n thoả cả hai A và B.
Nếu n  7 thì A B cũng là mệnh đề đúng vì n thoả A và ta không cần thỏa B.
Tương tự, nếu n  22 thì A B là mệnh đề đúng vì n thoả B và lúc đó ta không cần thỏa A
Mệnh đề A B chỉ sai nếu cả hai A và B là sai. Vì thế nếu n  8 thì A  B là sai. 8
Biên dịch: Huỳnh Tấn Liêm
Định lý 1.10. (The Law of the Excluded Middle)
Với bất kỳ mệnh đề A, mệnh đề A  A là đúng. Định lý 1.11.
Với bất kỳ mệnh đề A và B , ta có ( A  B )  ( A B  )
Một từ nối quan trọng khác giữa các mệnh đề là từ “và” được ký hiệu:  . Do đó,
trong ví dụ trên A B nghĩa là n là số lẻ và n lớn hơn 10 . Nếu mệnh đề A B đúng thì cả hai A và B là đúng.
Việc phủ định các mệnh đề chứa  thì tương đương với việc phủ định mỗi mệnh
đề thành phần và đổi  thành  . Tương tự, việc phủ định các mệnh đề chứa  thì tương
đương với việc phủ định mỗi mệnh đề thành phần và đổi  thành  . Định lý 1.12.
Với bất kỳ mệnh đề A và B , ta có
 ( A B )  A   B
 ( A  B )  A  B 1.9. Lượng từ ∃ ∃ và ∀ ∀
Đôi khi trong toán học ta sử dụng lượng từ  để nói rằng một điều nào đó tồn tại.
Ví dụ để biểu thị ý tưởng số nguyên a là số lẻ, ta có thể viết n | (a  2n 1)
Điều này nói rằng tồn tại một số nguyên n sao cho a  2 n1. Chúng ta muốn tạo
ra một mệnh đề tổng quát trong đó tất cả các phần tử thuộc một lớp nào đó cùng thỏa một
tính chất bằng cách sử dụng lượng từ  . Ví dụ ta có thể viết: n(n  n  1)
Điều này nói rằng tất cả các số nguyên n đều lớn hơn n 1 .
Trong toán học và kinh tế học trung cấp, các ký hiệu  và  đôi khi được sử dụng
như một cách viết tắt tiện lợi nhưng không quan trọng. Chúng được sử dụng nhiều trong
toán học và kinh tế học cao cấp.
1.10. Chứng minh bằng phản ví dụ 9
Biên dịch: Huỳnh Tấn Liêm
Trong toán học ta thường bị dẫn dắt bởi trực giác để tin mà không có một phép
chứng minh là một điều gì đó luôn đúng. Do đó, ta thường tạo ra một gợi ý hay một
phỏng đoán là mệnh đề này là luôn đúng.
Ví dụ 1.10. Vào thế kỷ 17, nhà toán học người Pháp Fermat đã phỏng đoán rằng nếu n là
một số nguyên thì tất cả các số có dạng 2
2 n 1 là các số nguyên tố.
Vì thế với n  0,1,2,3,4, ta có 2
2 n  1 =3, 2 2 1 +1=5, 2 2 2 +1=17, 2 2 3 +1=257, 2 2 4 +1=65537
và 3,5,17,257 và 65537 đều là các số ngyên tố (số nguyên n là số nguyên tố nếu các ước
của nó chỉ là 1 và n ).
Vì ta không biết khi nào một phỏng đoán là đúng hay sai, do đó có hai chiến lược
đối với một phỏng đoán:
1. Chứng minh điều phỏng đoán là đúng.
2. Dùng phép chứng minh bằng phản ví dụ để tìm một trường hợp trong đó điều phỏng đoán là sai.
Một cách tổng quát, chiến lược đầu tiên là chiến lược khó nhất vì ta phải chứng
minh một điều gì đó là đúng với vô hạn các trường hợp.
Đối với phỏng đoán của Fermat, đó là một chứng minh rất khó khăn và sâu xa mà
sẽ chứng tỏ rằng tất cả các số có dạng 2
2 n 1 đều là nguyên tố. Dĩ nhiên, nếu điều phỏng
đoán thật sự là đúng, đây là chiến lược duy nhất dẫn đến thành công.
Tuy nhiên, bạn thường sẽ thấy là dù bạn cố gắng thế nào đi nữa bạn không thể
chứng minh được điều phỏng đoán. Trong trường hợp này, bạn có thể thử chiến lược thứ
hai và tìm một phản ví dụ. Nếu bạn may mắn điều này có thể dễ dàng hơn nhiều vì không
giống như chiến lược đầu tiên, bạn chỉ cần một phản ví dụ để chứng minh điều phỏng đoán là sai.
Fermat đã chết mà không thể chứng minh điều phỏng đoán của ông ta. Sau này
Euler đã có thể chứng tỏ rằng điều phỏng đoán của Fermat thật ra là sai vì với n  5: 5 2
2  1 4294967297  641  6700417 và do đó 52
2 không là số nguyên tố. 10
Biên dịch: Huỳnh Tấn Liêm
1.11. Chứng minh bằng qui nạp
Các sinh viên thường cố gắng chứng minh các kết quả một cách đơn giản bằng
cách liệt kê vài trường hợp đầu tiên rồi kiểm tra rằng mệnh đề là đúng và khi đó bằng
cách đặt dấu ' … ' hay 'etc.'. Giả sử bạn muốn chứng minh phỏng đoán sau đây: Phỏng đoán:
Tổng của n số nguyên đầu tiên là n (n 1) 1 2  3  ...  n  2 Do đó, ta có thể viết: 1 11  1  =1 2 2(2 1  ) 1 2   3 2 3 3 1   1  2 3   6 2 etc.
và kết luận mệnh đề là đúng.
Việc kết luận này không đúng vì nó không loại trừ khả năng điều phỏng đoán có
thể sai với n  4 hay tại một con số lớn nào đó chẳng hạn như 10 10 n 1  0 .
Một phương pháp chính xác đối với phép chứng minh loại các phỏng đoán này là
phép chứng minh bằng qui nạp. Phép chứng minh bằng qui nạp tiến hành như sau:
Cho trước một dãy các mệnh đề , S ,S ... và ta muốn chứng minh rằng mỗi S là 1 2 i
đúng. Ví dụ ta muốn chứng minh rằng S là đúng, trong đó S là mệnh đề: n n n(n 1)
S ="1  2 3  ...  n  " n 2
Chứng minh bằng qui nạp được tiến hành theo hai bước:
1. Chứng minh rằng S là đúng. Điều này thường là hiển nhiên qua một phép tính 1 toán. 2. Giả sử S ,S ,...,S 1 2
n1 là đúng (đây được gọi là giả thiết qui nạp) và ta sử dụng
điều này để chứng minh rằng S là đúng. n
Ví dụ 1.11. Chứng minh rằng 11
Biên dịch: Huỳnh Tấn Liêm n(n  1) 1 2 3 ... n  2 Chứng minh.
Bước đầu tiên là kiểm tra mệnh đề đúng với n  1. Điều này dễ dàng vì 1 11  1  2
Bây giờ giả sử giả thiết qui nạp là đúng, nghĩa là mệnh đề đúng đến n 1, nghĩa là
 n1   n1  1  nn1 
1 2 3 ... n  1 = 2 2
Ta cần chứng minh mệnh đề đúng đến n. Ta có n n1  1 +2+3+... n 1 n=  n  2  n n 1   2  (n 1)  = n +1    2   (n 1)  2   n   2  n(n 1)  2
Ví dụ 1.12. Sử dụng quy nạp toán học chứng minh rằng 3 2 2 2 2 2 n n n
S =1  2  3  ... n    n 3 2 6 Chứng minh. 3 2 Dễ dàng ta có 2 1 1 1 S 1    1 3 2 6
Với giả thiết qui nạp là đúng, nghĩa là 3 2 (n1) (n1) (n1) 2 2 2 2
S =1  2  3  ... (n1)    n 1  3 2 6 Ta có 12
Biên dịch: Huỳnh Tấn Liêm 2 2 2 2 2 S
1  2  3 ...  (    n 1) n n 1 3 2 (n1) (n1) (n 1) 2 =    n 3 2 6 3 2 2
n  3n  3n  1 n  2n  1 n  1 2 =    n 3 2 6 3 2 n n n =   dfcm 3 2 6 1.12. Hàm số
Đối tượng cơ bản trong toán học mà ta sẽ làm việc là hàm số được định nghĩa như sau:
Định nghĩa 1.13. (Hàm số)
Một hàm số y  f (x) là một qui tắc gán duy nhất một số y với mỗi giá trị của x. Ví dụ 1.13. Hàm số 2
y  f (x)  x gán giá trị x  2 một giá trị duy nhất 2 y  2  4 . Ví dụ 1.14.
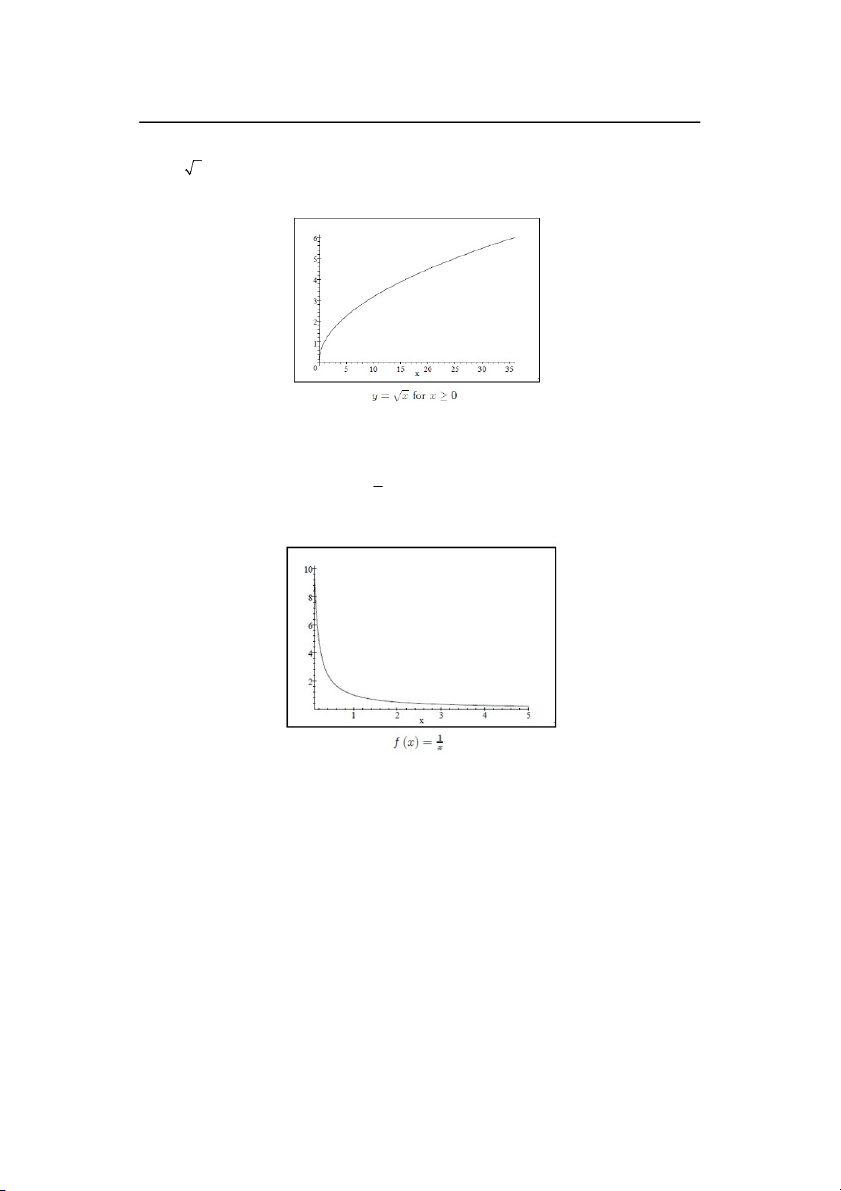
y  f (x)  x không phải là một hàm số vì với x  4 nó gán hai giá trị y  2 và y  2
 , trong khi với x  4 nó không gán giá trị nào cả vì 4 không xác định. Định nghĩa 1.14.
Miền xác định (domain) của hàm số y  f (x ) là tập hợp tất cả các giá trị của x
sao cho f (x) được xác định. Định nghĩa 1.15.
Miền giá trị (range) của hàm số y  f (x) là tập hợp các giá trị y trên miền xác định của hàm số.
Chú thích: Thông thường ta có thể bảo đảm rằng f là một hàm số bằng cách hạn chế
miền xác định và miền giá trị của nó. Ví dụ 1.15. Hàm số f ( )
x  x có thể được xác định bằng cách:
1) hạn chế miền xác định là x  0 13
Biên dịch: Huỳnh Tấn Liêm
2) hạn chế miền giá trị là y  0 hay nói cách khác giải thích như căn bậc hai dương
(ví dụ 4  2 và không là -2 ).
Với những hạn chế này, ta có một hàm số tốt như được thấy bởi đồ thị sau:
Thật ra, đây là một ví dụ của hàm sản xuất Cobb-Douglas, là một trong những
kiến thức cơ bản của lý thuyết kinh tế.
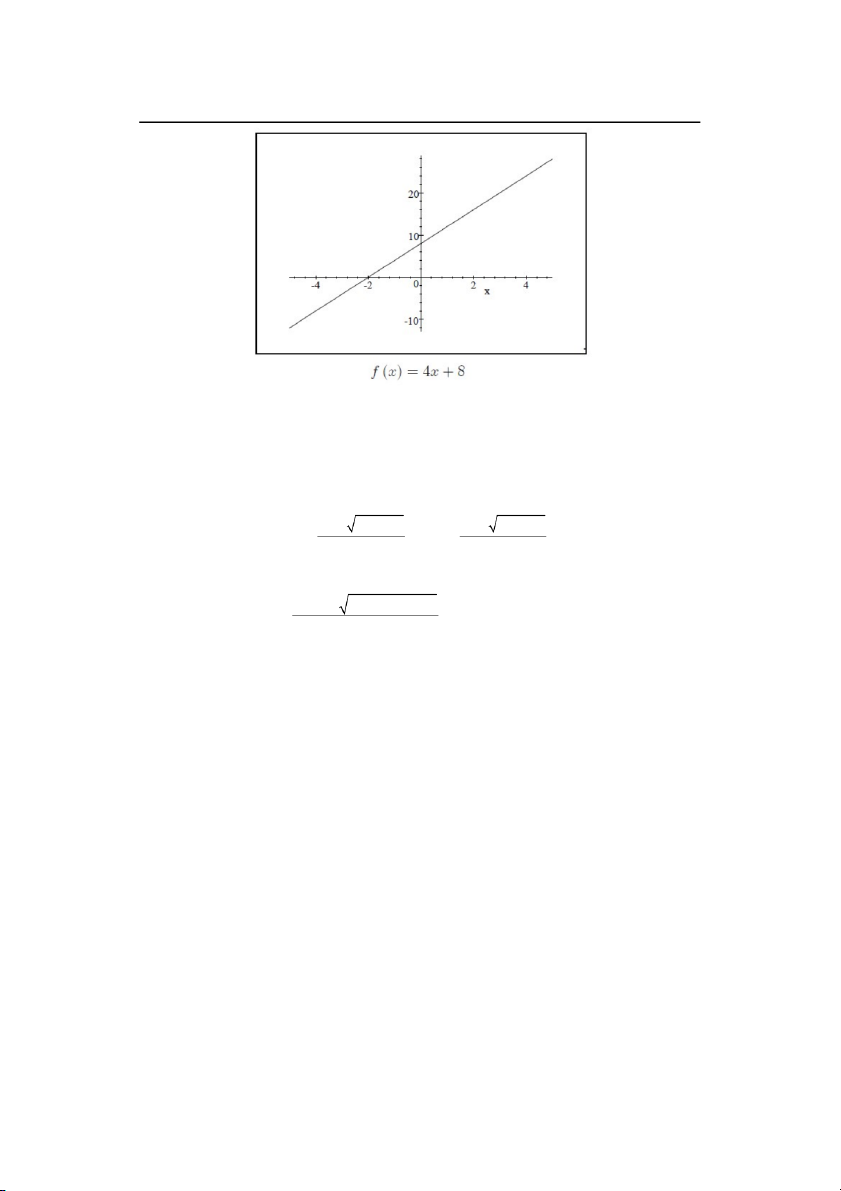
Tương tự, bài toán với 1
f (x)  có thể được xác định bằng cách hạn chế miền xác x
định là x  0 và ta có đồ thị:
Chú thích: Ta thường xác định miền giá trị và miền xác định sao cho bảo đảm rằng hàm
số có ý nghĩa kinh tế. Ví dụ nếu Q  f (P) 14
Biên dịch: Huỳnh Tấn Liêm
là một hàm cầu với P là giá và Q là lượng cầu thì miền xác định của f (P) sẽ là P  0 và
miền giá trị là Q  0 vì giá và lượng cầu không thể âm.
1.12.1 Hàm luỹ thừa với số mũ nguyên
Một lớp hàm quan trọng có dạng: ( ) n f x  x
trong đó n là một số nguyên. Ý nghĩa của n
x với n  0 là x được nhân n lần. Ví dụ 1.16. 3 x  x x x .
Trong trường hợp này, miền xác định của f là mọi x , nghĩa là   x  
Ta cũng có thể cho phép các số mũ nguyên âm (nghĩa là 1,2,3,... ) . Khi đó, n x  nghĩa là 1 . Chẳng hạn n x  1 1 1 1 3 x     3 x x x x
Chú ý đối với các số mũ nguyên âm, ta cần loại trừ x  0 ra khỏi miền xác định
của hàm số, vì 1   không xác định. Các số mũ nguyên tuân theo các qui tắc sau: 0 Định lý 1.16.
Nếu m vàn là các số nguyên âm hay dương thì 1. m n m n x x x   2. ( m )n mn x  x 3. 0 x  1 4. n 1 x  n x 5. ( )n n n xy  x y
Chú thích: Chú ý rằng (  ) n n n x y  x  y
Ví dụ với n  2 , ta có 2 2 2 2 2
(x  y)  x  2xy  y  x  y 1.12.2. Hàm đa thức 15
Biên dịch: Huỳnh Tấn Liêm Định nghĩa 1.17.
Một đa thức bậc n là một hàm số có dạng n n1 f ( )
x  a x  a x  ... a x a n n 1  1 0 trong đó a  0 . n
Một tính chất quan trọng của đa thức là các nghiệm của nó: Định nghĩa 1.18.
Nghiệm của hàm số f (x) là các giá trị r thỏa mãn f (r) 0 .
Đối với một đa thức có nghiệm r thì nó phải thỏa n n 1
f (r )  a r  a r   ... a r  a  0 n n1 1 0
Một trong những kết quả quan trọng trong toán học là: Một đa thức bậc n có n
nghiệm (có thể là nghiệm phức). Kết quả này đủ quan trọng và được gọi là Định Lý Cơ
Bản của Đại Số. Gauss là người đầu tiên chứng minh định lý này.
Định lý 1.19. (Định Lý Cơ Bản của Đại Số):
Đa thức bậc n có n nghiệm: r ,r ,...,r ; nghĩa là n nghiệm (có thể phức) 1 2 n đối với phương trình n n 1
f (r )  a r  a r   ... a r  a  0 n n1 1 0
Hai trường hợp đặc biệt quan trọng là: Định nghĩa 1.20.
Hàm tuyến tính là một đa thức bậc 1: y  f (x)  ax  b Định nghĩa 1.21.
Hàm bậc hai là một đa thức bậc 2: 2
y  f (x )  ax  bx  c
Ví dụ 1.17. Đa thức bậc một: f (x)  ax  b có một nghiệm là b r   như là nghiệm đối a
với f (r)  ar  b  0 .
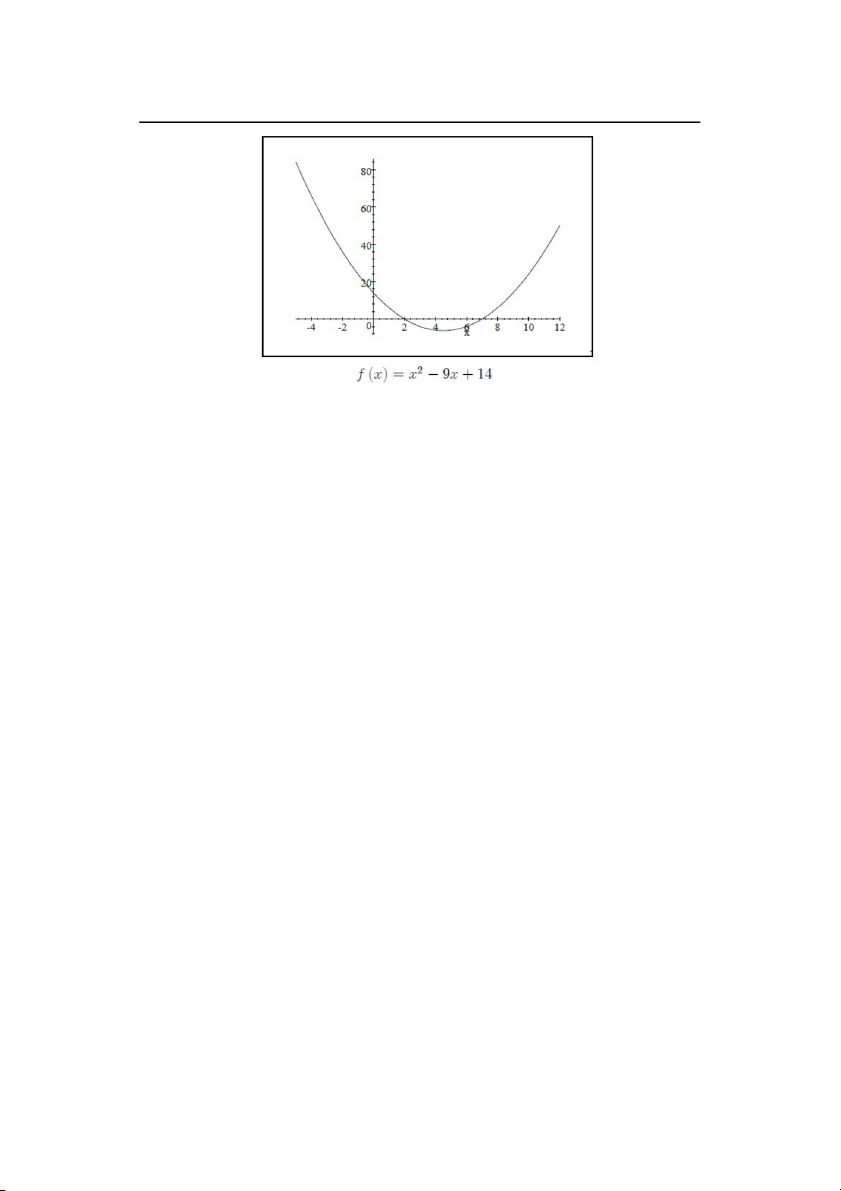
Do đó f ( x)  4 x 8 có nghiệm duy nhất là r  2 và được minh họa dưới đây: 16
Biên dịch: Huỳnh Tấn Liêm Định lý 1.22. Phương trình bậc hai 2 f ( ) x  ax  bx  c
có hai nghiệm r và r được cho bởi 1 2 2 b   b 4ac 2  b b  4ac r  và r  1 2a 2 2a
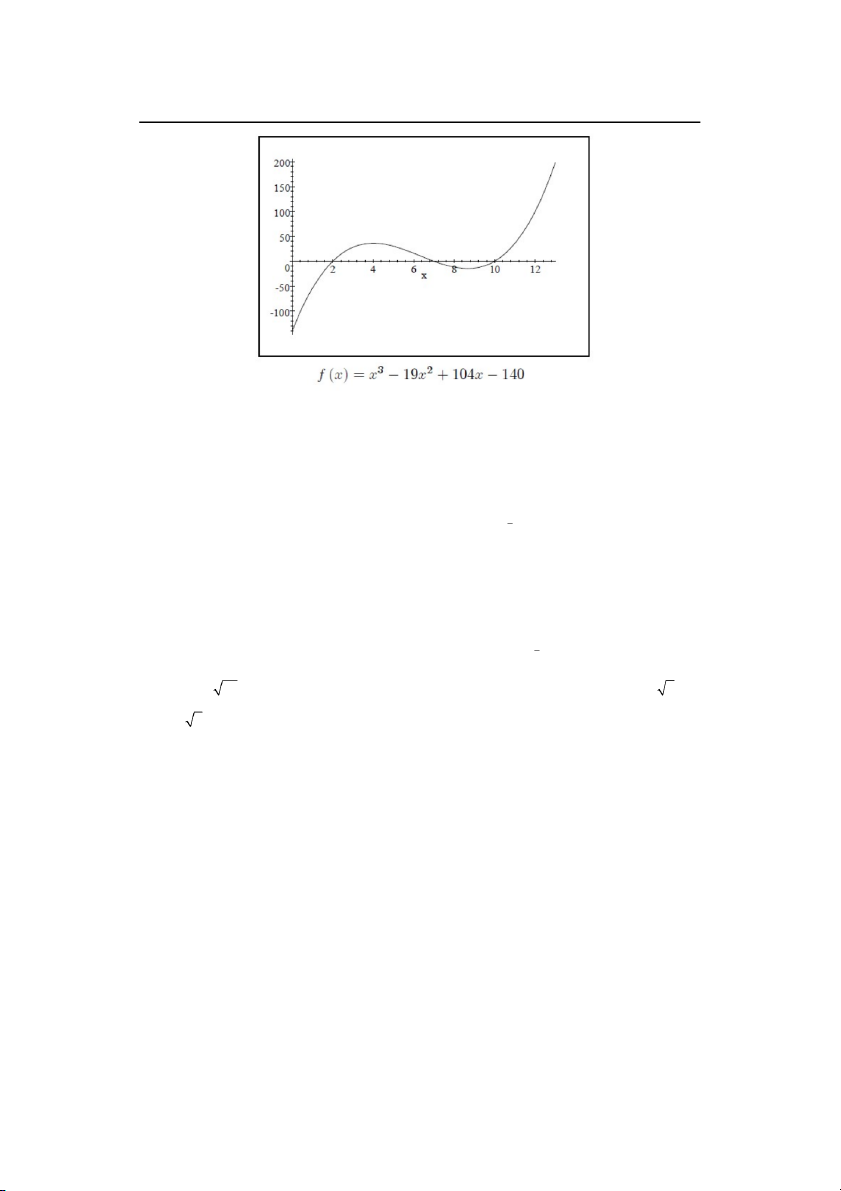
Ví dụ 1.18. Phương trình bậc hai 2
x  9 x  14 có hai nghiệm là 2
(9) (9)  4(1)(14) r  hay r  2 và r  7 2 1 2
và có thể được nhìn thấy bởi đồ thị dưới đây, trong đó f (x) cắt trục Ox. 17
Biên dịch: Huỳnh Tấn Liêm
Một hệ quả của Định Lý Cơ Bản của Đại Số là: Một đa thức luôn có thể được
phân tích thành các thừa số như sau: Định lý 1.23.
Cho r ,r ,...,r là n nghiệm của đa thức 1 2 n n n1 f ( )
x  a x  a x  ... a x a n n 1  1 0 Khi đó, f ( )
x có thể được phân tích thành các thừa số như sau:
f  x  a x  r  x  r ... x  r n 1   2   n 
Ví dụ 1.19. Phương trình bậc hai 2
3x  27 x  60 có hai nghiệm r  5 và r  4 1 2
Do đó ta có thể phân tích f ( ) x  3( x  5)( x  4)
Ví dụ 1.20. Phương trình bậc ba 3 2
x 19x 104x  140 có các nghiệm r  2,r  7 và 1 2
r  10 và có thể được nhìn thấy bởi đồ thị bên dưới. 3 Vì vậy 3 2
x -19x 104x 140   x  2 x  7 x 10 18
Biên dịch: Huỳnh Tấn Liêm
1.12.3. Hàm luỹ thừa với số mũ không nguyên
Trong kinh tế, ta thường muốn xét các hàm lũy thừa với số mũ không nguyên: ( ) a
f x  x , trong đó a không phải là số nguyên.
Ví dụ 1.21. Hai hàm số với số mũ không nguyên là 1 0,3143 f (x)  x và 2 Q  f (L)  L
trong đó với trường hợp thứ nhất a  0,3143 và với trường hợp thứ hai a  0,5 . Trường
hợp sau là một ví dụ của hàm sản xuất Cobb-Douglas.
Đối với hàm số với số mũ không nguyên a
y  x , ta rơi vào vấn đề toán học sâu xa 1
và khó khăn nếu ta cho phép x hay y là âm. Ví dụ với 2 f ( )
x  x , nếu ta cho phép x  1
thì f (1)  1 không xác định, trong khi nếu x  4 và ta cho phép y  0 thì y  4  2 và y  4  2  .
Vì lý do này, bất kỳ khi nào ta làm việc với a
y x với số mũ a không nguyên, ta
luôn giả sử x  0 và y  0 .
Với hạn chế này các hàm số với số mũ không nguyên tuân theo cùng các qui luật
như các hàm số với số mũ nguyên. Do đó: Định lý 1.24. 19
Biên dịch: Huỳnh Tấn Liêm
Nếu x  0 và a là số thực bất kỳ (nguyên hay không nguyên, âm hay dương) thì a x được xác định và 1. a x  0 2. a b a b x x x   3. ( a )b ab x  x 4. ( )a a a xy  x y 5. 0 x  1 6. a 1 x  . a x
Thường ta sẽ cần tìm nghiệm dương duy nhất của hàm số ( ) b f x  Ax  c
với x  0 và b không phải là số nguyên. Ta có: Định lý 1.25.
Nghiệm dương duy nhất của ( ) b
f r  Ar  c 0 cho bởi 1 b c r    A    Ví dụ 1.22. Cho 7,3 f (x)  10x  23
trong đó A  10,b  7,3 và c  23 . 1 7,3  23 Ta thấy  r   1,120 
hấylà nghiệm dương duy nhất của f(x). Điều này có thể thấy 10   
trong đồ thị dưới đây 20