Chương 1: Phương pháp toán học | Tài liệu học tập Môn Toán kinh tế 1 Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh
Trong kinh tế học, ngưßi ta thưßng cố gắng đưa ra những suy nghĩ chính xác và một trong những cách chúng ta thực hiện điều này đó là sử dụng toán học. Bắt đầu cho việc này là phải làm rõ được những gì chúng ta đang nói và với mục đích này chúng ta cần đến các định nghĩa. Chúng ta bắt đầu với lý thuyết số sơ cấp để minh hoạ các phương pháp toán học mà sau này chúng ta sẽ áp dụng vào các mô hình kinh tế. Giả sử chúng ta quan tâm đến các tính chất về số chẵn và số lẻ. Một cách trực giác, ta biết 4 là số chẵn và 5 là số lẻ. Tuy nhiên, nếu chúng ta muốn chứng minh các vấn đề về số chẵn và số lẻ, ta phải định nghĩa những gì chúng ta hiểu về các số chẵn và các số lẻ. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Toán kinh tế 1,2
Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
TÀI LIỆU HỌC TẬP
TOÁN KINH TẾ 1 Tháng 02/2021 MĀC LĀC
Ch°¢ng 1: Ph°¢ng pháp toán hác ...........................................................2
1.1. Các định nghĩa ....................................................................................2
1.2. Sự khác nhau giữa < = = và < ≡ < ........................................................3
1.3. Phép kéo theo ......................................................................................4
1.4. Phép phủ định .....................................................................................5
1.5. Chứng minh bằng phản chứng ............................................................6
1.6. Điều kiện cần và điều kiện đủ .............................................................7
1.7. Điều kiện cần và đủ.............................................................................8
1.8. 1.9. Lượng từ Ǝ và Ɐ ...............................................................................10
1.10. Chứng minh ằng phản ví dụ b
............................................................10
1.11. Chứng minh quy nạp .........................................................................12
1.12. Hàm số ..............................................................................................14
1.12.1. Hàm lũy thừa với số mũ nguyên ........................................16
1.12.2. Hàm đa thức .......................................................................16
1.12.3. Hàm lũy thừa với số mũ không nguyên .............................19
1.12.4. Cấp số nhân ........................................................................21
Bài tập chương 1 .......................................................................................23 Ch°¢ng 1
PH¯¡NG PHÁP TOÁN HàC
Chương 1 s cung c Āp ki Ān thư뀁c cơ bn nh Āt v ccc phương phcp toc 漃 n h
⌀c như ph攃Āp ph đ椃⌀nh, 攃 ph
Āp k攃Āo theo, ph攃Āp ph n chư뀁ng, 攃 ph
Āp quy n愃⌀p,… vc m t s Ā hcm sơ c Āp cơ bn
như뀃ng tknh ch Āt vc ư뀁ng d甃⌀ng ca ch ng t w rong kinh t Ā.
Sau khi h漃⌀c xong chương ncy, ngươ i
ꄀ h漃⌀c c漃Ā kh năng
• Sư뀉 d甃⌀ng ccc phương phcp tocn h漃⌀c cơ bn đ chư뀁ng minh m t s Ā bci tocn nh.
• 䄃Āp d甃⌀ng đươꄣc tknh ch Āt ca ccc d愃⌀ng c
h m ly thư뀀a vc ư뀁ng d甃⌀ng ch ng t w rong kinh t Ā s Ā nhân).
1.1. Các đßnh nghĩa
Trong kinh tế học, ngưßi ta ng thưß
cố gắng đưa ra những suy nghĩ chính xác và m t ộ
trong những cách chúng ta thực hiện điều này đó là sử d ng ụ toán h c
ọ . Bắt đầu cho việc này là
phải làm rõ được ững nh
gì chúng ta đang nói và với mục đích này chúng ta cần đến các định nghĩa.
Chúng ta bắt đầu với lý thuyết số sơ cấp để minh hoạ các phương pháp toán c họ mà sau này chúng ta sẽ áp d ng ụ
vào các mô hình kinh tế. Giả sử chúng ta quan tâm đến các tính chất về số chẵn và số lẻ. M t ộ cách tr c ự giác, ta biết 4 là s ố chẵn và 5 là s
ố lẻ. Tuy nhiên, nếu chúng ta
muốn chứng minh các vấn đề về số chẵn và số lẻ, ta phải định nghĩa ng nhữ gì chúng ta hiểu về các s c ố hẵn và các s l ố ẻ. Ta xét bài toán: ch ng ứ minh rằng tích c a ủ m t ộ số lẻ và m t ộ s ố chẵn luôn là m t ộ s ố chẵn.
Ta không thể liệt kê hết danh sách như sau: 4ô 5 = 20 2ô 3 = 6 12ô37 = 444 ...
và chú ý rằng 20, 6 và 444 là các s
ố chẵn. Đây không phải là m t ộ phép ch ng ứ minh ngay cả khi
danh sách trên có dài thêm bao nhiêu đi nữa bái vì có vô hạn các t h ổ ợp gi a
ữ số chẵn và số lẻ.
Nếu không có các định nghĩa, ta sẽ không thể bắt đầu. Bây giß một định nghĩa về các số
chẵn và số lẻ sẽ là:
Đßnh nghĩa 1.1. S Ā nguyên m là m t s Ā ch n n ẵ
Āu và chỉ n Āu t n t
ồ 愃⌀i m t s Ā nguyên n sao cho m = 2ô n 2
Đßnh nghĩa 1.2. S Ā nguyên m là m t s Ā lẻ n Āu và chỉ n Āu t n t
ồ 愃⌀i m t s Ā nguyên n sao cho m = 2ô n +1
Ví dā 1.1. Theo định nghĩa 16 là số chẵn, vì ta có thể viết 16 = 2ôn , trong đó n = 8 và 7 là số
lẻ, vì ta có thể viết 7 = 2ô n +1 , trong đó n = 3 .
Với các định nghĩa trên, bây giß ta có thể chứng minh định lý sau:
Đßnh lý 1.3. Tích ca m t s Ā lẻ và m t s Ā chẵn là m t s Ā chẵn. Chứng minh. Nếu a là s c
ố hẵn và b là s l
ố ẻ thì a = 2m và b = 2n +1 và
aô b = 2mô (2n +1)
= 2ô (mô (2n +1)) = 2ô r
trong đó r = (mô(2n +1) là m t ộ s nguyên ố
. Do đó, a ôb là m t ộ s c ố hẵn.
Chú thích: Hãy chú ý đến sức mạnh của loại lý luận này. Trong vài dòng ngắn chúng ta có thể
chứng minh một kết quả mà áp dụng cho vô hạn con số. Tính vô hạn này là một danh sách các con s
ố sẽ đi qua mặt trăng hay ngay cả đi qua vì sao xa nhất và chúng ta chưa thể nói điều gì đó
rõ ràng để định nghĩa điều đó. Đây là phép kỳ diệu của toán học.
1.2. Sự khác nhau giữa ' = ' và ' ≡ '
Đôi khi các sự việc là bằng nhau một cách đơn giản theo định nghĩa. Chẳng hạn nếu A = =s c ố nhân ử á Montreal= B = =s
ố đàn ông độc thân á Montreal=
thì A và B là bằng nhau theo định nghĩa. Không có gì để chứng minh á đây và điều đó không
nói lên điều gì cả về thế giới hay Montreal. Để ấ nh n mạnh bản chất c a ủ loại đẳng th c ứ này, chúng ta sử d ng ụ m t
ộ loại dấu bằng đặc
biệt: ' ≡ ' sao cho với các cử nhân và các đàn ông độ c thân á Montreal ta viết A ú B
Khi đó, điều này nghĩa là A và B là bằng nhau theo định nghĩa hay đây là sự <đồng
nhất kế toán”.
Khi bạn thấy dấu đẳng thức này, bạn có thể bớt căng thẳng. Không có gì để ch ng ứ minh.
Các điều này đơn thuần là các ký hiệu khác nhau để chỉ cùng sự vật. 3 Trong Kinh tế h c ọ , m t ộ ví d t ụ t ố c a ủ sự ng nh đồ
ất kế toán là đẳng thức GNP mà bạn biết trong môn Kinh tế h ọc vĩ mô:
Y ú C + I + G + X − M
trong đó Y là GNP, C là lượng tiêu dwng, I là lượng đầu tư, G là lượng chi tiêu của chính phủ, X ng xu là lượ ất khẩu và M ng nh là lượ ập khẩu.
Mặt khác, đôi khi các sự vật là bằng nhau theo một cách quan trọng hơn. Ví dụ 2 E = mc
biểu thị một tính chất quan trọng trong vật lý, trong khi 2 f ( )
x = x hay f '(x) = 2x cho ta thông tin thật về hàm s
ố f . Trong các trưßng hợp này, ta sử dụng dấu " = " như là một cách để nhấn mạnh thông tin th c
ật đang đượ cung cấp. 1.3. Phép kéo theo
Trong toán kinh tế, chúng ta bắt đầu với các điều giả sử và từ đó cố gắng để suy luận các
phép kéo theo đúng của các giả sử này. Cơ bản i
đố với loại lý luận này là ý ng tưá c a ủ phép kéo theo logic :
Nếu A là đúng thì điều đó kéo theo B cũng phải đúng. Ta viết điều này một cách hình
thức như sau: A B ; đọc là A kéo theo B.
Ví dā 1.2: Nếu A = ng =Ông Nam số á Nha Trang= B = ng =Ông Nam số á Vi ệt Nam=
thì A B vì Nha Trang là m t ộ thành phố c a ủ Việt Nam. Ta thưßng cố ắng g để xây d ng ự các phép chứng minh c a
ủ các mệnh đề theo kiểu: A B . Mối liên hệ gi a ữ A và B ng thưß
không rõ ràng và ta cần tìm m t ộ chu i ỗ các phép kéo theo
trung gian sao cho một phép chứng minh thưßng có dạng:
A S S .. 1 2 S B n
Từ đó ta kết luận: A B . Do đó, chiến lược chung trong việc chứng minh A B là
bắt đầu với A và sử dụng một chuỗi các phép kéo theo đúng để cu c
ối cwng thu đượ mệnh đề B. Ta có định lý sau:
Đßnh lý 1.4. Tổng ca hai s Ā lẻ là m t s Ā chẵn. Chứng minh. 4 Đặt A = " a là s l ố ẻ và b là s l ố ẻ "
B = " a + b là s c ố hẵn "
Từ giả sử A , ta có a = 2r +1 và b = 2s +1 , với r và s là các số nguyên. Do đó
A a = 2r +1, b = 2s + 1
a+ b= (2r+ 1)+ (2s+ 1)
a+ b = 2(r + s+ 1)
a + b = 2t, t = r + s +1 'a + b là s c ố hẵn9 = B
Chú thích: Chú ý rằng ta chỉ có m t ộ chiều i
đố với mũi tên: . Điều này nghĩa là chân lý của
mệnh đề A được truyền đến chân lý c a
ủ mệnh đề B nhưng không cần thiết là chân lý của B kéo theo chân lý c a
ủ A . Do đó không đúng để kết luận từ A B thì B A .
Ví dā 1.3. Nếu B = <a + b là m t
ộ số chẵn =, ta không thể suy ra A = < a và b đều là các s l ố ẻ=.
Chẳng hạn nếu a = 4 và b = 6 thì B là đúng vì 4 + 6 =10 nhưng A không đúng vì cả hai a và
b đều không là s l
ố ẻ. Do đó, A B là đúng trong khi B A là sai.
1.4. Phép phủ đßnh Ký hiệu là phép phủ định c a
ủ mệnh đề A, nghĩa là A hay A là không đúng hay A là sai.
Ví dā 1.4. Nếu A là mệnh đề: <Ông Nam sống á Nha Trang= thì
là mệnh đề: <Ông Nam không s ng ố á Nha Trang=.
Dấu phủ định tác dụng như dấu âm trong số học vì:
Như đã biết nếu A B là đúng thì ta chưa thể kết luận B A cũng đúng. Tuy nhiên, ta có
thể kết luận một cách chính xác rằng nếu A B là đúng thì là đúng hay nói một cách khác A B thì Ví dā 1.5. A = ng =Ông Nam số á Nha Trang= B = ng =Ông Nam số á Vi ệt Nam=
à đây ta thấy A B là đúng nên
cũng đúng; nghĩa là nếu ông Nam không
sống á Việt Nam thì chắc chắn ông ta không thể sống á Nha Trang được. 5 Ví dā 1.6. A = " a là s l ố ẻ và b là s l ố ẻ "
B = " a + b là s c ố hẵn " Trong s ố h c
ọ , ta có thể kết luận m t ộ cách chính xác nếu
, nghĩa là < a + b không phải là một số ch t ẵn= hì
, nghĩa là a và b đều lẻ= .
1.5. Phép chứng minh phản chứng
Chứng minh bằng phản chứng hay 'Reductio ad absurdum' là chứng minh một mệnh đề
A bằng cách giả sử mệnh đề ph ủ định
là đúng và suy ra một điều mâu thuẫn. Do đó, nếu và thì
phải sai và như vậy A phải đúng.
Đßnh lý 1.5. 2 là s Ā vô t n t
ỉ, nghĩa lc không tồ 愃⌀i các s Ā nguyên a và b sao cho 2 a = b Chứng minh
Giả sử 2 không phải s vô t ố ( ỷ tức là s h
ố ữu tỷ), nghĩa là tồn tại 2 s nguyên a, b sa ố o cho 2 a = b
Không mất tính t ng quát, gi ổ ả s
ử a và b không đồng thßi là s c ố hẵn vì n u c ếu a và b đề hẵn thì a 2r r 2 = = = b 2s s Ta có a 2 2 2 = a = 2b b 2 a là s c ố hẵn a là s c ố hẵn
Do đó ta có thể viết a = 2n, với n là s nguyên. ố Ta lại có 2 2 2
2 b = a = 4 n 2 2 b = 2n b là s c ố hẵn 6
à đây ta suy ra cả a và b đều chẵn, mâu thuẫn với giả thiết ban đầu. Do đó giả sử 2 không phải số vô t l
ỷ à sai. Vậy 2 là s vô t ố ỷ là đúng.
Ví dā 1.7. Chứng minh hàm số f (x) = x không bị chặn với m i ọ x. Chứng minh
Giả sử hàm f (x) = x bị chặn, nghĩa là tồn tại hằng s ố c ü sao cho x c, x
Nếu ta chọn x =( c + )2 1 thì ta có x = (c + )2
1 = c +1 c 1 0 (vô lý)
Vậy điều giả sử ban đầu là sai. Do đó hàm số
f (x) = x không bị chặn với mọi x.
1.6. Điều kiện cần và điều kiện đủ Trong toán h c ọ , bạn ng thưß nghe về dụ
điều kiện cần để ông Nam sống tại Nha Trang là ông ta phải sống tại Việt Nam, trong khi điều
kiện đủ để ông Nam sống tại Việt Nam là ông ta sống tại Nha Trang. Tuy nhiên, sống tại Nha
Trang không phải là điều kiện cần để s ng t ố ại Việt Nam và s ng ố
tại Việt Nam không phải là điều
kiện đủ để sống tại Nha Trang. Ta có các định nghĩa sau:
Đßnh nghĩa 1.6. (Điều kiện cần) . N Ā u
hay tương đương A B , thì B lc điu kiện
cần đ Āi vơꄁi A .
Đßnh nghĩa 1.7. (Điều kiện đủ). N Āu A B hay tương đương
, thì A lc điu kiện
đ đ Āi vơꄁ Bi Chú thích:
✓ Nếu ta chứng minh một mệnh đề có dạng A B thì A là điều kiện đủ đối với B và B là
điều kiện cần đối với A
✓ Nếu A là điều kiện đ
ủ của B thì không có nghĩa A là điều kiện cần của B và tương tự nếu B u ki là điề ện cần của A B
thì cũng không có nghĩa sẽ u ki là điề ện đủ của A.
Ví dā 1.8. Ta chứng minh mệnh đề " a là s l ố ẻ và b là s l
ố ẻ" "a + b là số chẵn " 7
Điều kiện đủ để tổng a + b là m t ộ s
ố chẵn là cả hai a và b đều là số lẻ, trong khi điều kiện c c
ần để ả hai a và b đều là số lẻ là a + b là s c ố hẵn.
Tuy nhiên, a + b là một s
ố chẵn không phải là điều kiện đủ để cả hai a và b là s ố lẻ vì
chẳng hạn nếu a = 2 và b = 4 thì a + b = 6 .
1.7. Điều kiện cần và đủ
Đôi khi ta có thể chứng minh cả hai mệnh đề A B và B A . Trong trưßng hợp này,
A à điều kiện cần và đủ đối với B
và B là điều kiện cần và
đủ đối với A, vì khi đó ta có các mệnh đề đúng A B và B A và Do đó, ta có đị nghĩa sau: nh
Đßnh nghĩa 1.8. N Āu A B và B A thì A lc điu kiện cần vc đ đ Āi vơꄁi B và ta vi Āt A û B Chú thích:
✓ Với A û B thì mũi tên chỉ theo hai chiều. Điều này chỉ ra rằng chân trị của A truyền
sang B cũng như chân trị c a
ủ B được truyền sang A
✓ Nếu bạn có thể chứng minh được A û B thì bạn có m t
ộ mệnh đề mạnh mẽ hơn một trong hai m
ệnh đề A B hay B A .
Đßnh lý 1.9. Ta có a và b là các s Ā lẻ khi và chỉ khi tích a × b là m t s Ā lẻ. Chứng minh Đặt A = nguyên =Các số
a và b là các số l ẻ=
B = a ô b là m t ộ số lẻ= .
Trước tiên ta sẽ chứng minh A B
Vì a, b là các số lẻ nên ta có
a = 2n +1; b = 2m +1
aôb = (2n + ) 1 ô(2m+ )
1 = 2(2mn + m + n) +1 là s l ố ẻ Vậy A B (1)
Sau đó ta tiếp tục chứng minh chiều ngược lại B A
Từ giả thiết B ta có aôb = 2s +1, b n c ằng phương pháp phả hứng ta giả sử A t sai, nghĩa là mộ trong 2 s a ố , b phải là s c
ố hẵn. Không mất tính t ng quát, gi ổ ả s a ử chẵn, t c ứ là 8
a = 2n a ô b = 2nôb = 2s +1 1
nôb = s + 2 (vô lý)
Vậy A đúng, nghĩa là B A (2)
Từ (1) và (2) ta kết luận A û B 1.8. 'Or' và 'And'
Trong đßi sống và trong toán ọc ta h
thưßng nối các mệnh đề khác nhau bằng cách sử dụng từ Ví dā 1.9.
Nếu A là mệnh đề < n là s
ố lẻ= và B là mệnh đề < n þ10 = thì A ú B nghĩa là n là số
lẻ hoặc n lớn hơn 10 .
Nếu n =13 thì A ú B là mệnh đề đúng vì n thoả cả hai A và B.
Nếu n = 7 thì A ú B cũng là mệnh đề đúng vì n thoả A và ta không cần th a ỏ B.
Tương tự, nếu n = 22 thì A ú B là mệnh đề đúng vì n thoả B và lúc đó ta không n cầ thỏa A
Mệnh đề A ú B chỉ sai nếu cả hai A và B là sai. Vì thế nếu n = 8 thì A ú B là sai.
Đßnh lý 1.10. (The Law of the Excluded Middle) . Vơꄁi b Āt kỳ mệnh đ A, mệnh đ A ú là đwng.
Đßnh lý 1.11. Vơꄁi b Āt kỳ m A
ệnh đ và B , ta có
( A B ) û ( A ú B ) Một t ừ n i ố quan tr ng ọ khác gi a
ữ các mệnh đề là từ Do đó, trong ví d t
ụ rên A ù B nghĩa là n là s l
ố ẻ và n lớn hơn 10. Nếu m
ệnh đề A ù B ha đúng thì cả i A và B là đúng.
Việc phủ định các mệnh đề chứa ú thì tương đương với việc phủ định m i ỗ mệnh đề thành phần và i
đổ ú thành ù . Tương tự, việc phủ định các mệnh đề chứa ù thì tương đương
với việc phủ định mỗi m t
ệnh đề hành phần và đổi ú thành ù .
Đßnh lý 1.12. Vơꄁi b Āt kỳ m A
ệnh đ và B , ta có
( Aú B ) û A ù B
( A ù B ) û Aú B
1.9. L°ÿng từ ∃ và ∃ ∀ ∀ 9
Đôi khi trong toán học ta sử ụng d
lượng từ để nói rằng một điều nào đó tồn tại. Ví d ụ để biểu thị ng s ý tưá ố nguyên a là s l ố ẻ, ta có thể viết n
| (a = 2n +1)
Điều này nói rằng tồn tại một số nguyên n sao cho a = 2n +1. Chúng ta mu n t ố ạo ra m t ộ
mệnh đề tổng quát trong đó tất cả các phần tử thuộc một lớp nào đó cwng thỏa một tính chất bằng cách s d
ử ụng lượng từ . Ví d t ụ a có thể viết: n
(n þ n −1)
Điều này nói rằng tất cả các s
ố nguyên n đều lớn hơn n −1 . Trong toán h c ọ và kinh tế
học, các ký hiệu và đôi khi được sử ụng d
như một cách viết tắt tiện lợi nhưng không quan
trọng. Chúng được sử dụng nhiều trong toán học và kinh tế học cao cấp.
1.10. Chứng minh bằng phản ví dā
Trong toán học ta thưßng bị dẫn dắt bái trực giác để tin mà không có m t ộ phép ch ng ứ
minh một điều gì đó luôn đúng. Do đó, ta thưßng tạo ra m t ộ gợi ý hay m t ộ phỏng đoán là nh mệ đề này là luôn đúng.
Ví dā 1.10. Vào thế kỷ 17, nhà toán học ngưßi Pháp Fermat đã phỏng ng đoán rằ nếu n là m t ộ số
nguyên thì tất cả các s c ố ó dạng 2 2 n 1 + là các số nguyên t . ố
Vì thế với n = 0,1, 2,3, 4 , ta có 0 2 2 +1 = 2 +1 = 3 1 2 2 2 + 1= 2 + 1= 5 2 2 4 2 +1 = 2 +1 =17 3 2 8 2 +1 = 2 +1 = 257 4 2 16 2 +1 = 2 +1 = 65537
và 3, 5, 17, 257 và 65537 đều là các số ngyên t
ố (số nguyên n là số nguyên tố nếu các ước của
nó chỉ là 1 và n).
Vì ta không biết khi nào m t
ộ phỏng đoán là đúng hay sai, do đó có hai cách i đố với m t ộ phỏng đoán: 1. Chứng minh điề ỏng đoán là đúng u ph .
2. Dùng phép chứng minh bằng phản ví dụ để tìm một trưßng hợp trong đó điều ph ng ỏ đoán là sai. 10 Một cách t ng ổ
quát, cách đầu tiên là cách khó nhất vì ta phải ch ng ứ minh một điều gì đó
là đúng với vô hạn các trưßng hợp.
Đối với phỏng đoán của Fermat, đó
là một chứng minh rất khó khăn và sâu xa mà sẽ
chứng tỏ rằng tất cả các s c ố ó dạng 2 2 n 1
+ đều là nguyên tố. Dĩ nhiên, nếu u điề phỏng đoán thật
sự là đúng, đây là cách duy nhất dẫn đến thành công.
Tuy nhiên, bạn thưßng sẽ thấy là dù bạn cố gắng thế nào đi nữa bạn không thể chứng
minh được điều phỏng đoán. Trong trưßng hợp này, bạn có thể thử cách thứ hai là tìm một phản ví d . ụ Nếu bạn may mắn u
điề này có thể dễ dàng hơn u
nhiề vì không giống như cách đầu tiên,
bạn chỉ cần một phản ví dụ để ch u ph ứng minh điề ỏng đoán là sai.
Fermat đã chết mà không thể chứng minh điều ỏng ph
đoán của ông ta. Sau này Euler đã có thể chứng t r
ỏ ằng điều phỏng đoán của Fermat thật ra là sai vì với n = 5 : 5 2
2 +1= 4294967297 = 641 ô 6700417 và do đó 52 2 không là s nguyên t ố . ố
1.11. Chứng minh bằng qui nạp Các sinh viên ng thưß c
ố gắng chứng minh các kết quả một cách đơn giản bằng cách liệt kê vài trưßng ợp h
đầu tiên rồi kiểm tra rằng mệnh đề là đúng và khi đó bằng cách đặt dấu . 8…9
Giả sử bạn muốn chứng minh phỏng đoán sau đây:
Phỏng đoán: n(n +1)
Tổng của n số nguyên đầu tiên là 1 +2 +3 +... +n = 2 Ta có thể liệt kê ( 1 1+1 ) 1 = =1 2 2(2+ 1) 1 + 2 = = 3 2 3 ( 3 +1 ) 1 + 2 +3 = = 6 2 ..... và kết luận mệnh đề là đúng.
Tuy nhiên, việc kết luận này không đúng vì nó không loại trừ khả năng điều ỏng ph đoán
có thể sai với n = 4 hay tại m t ộ con s l ố ng h ớn nào đó chẳ ạn như 10 10 n = 10 . 11
Một phương pháp chính xác đối với phép chứng minh loại các ỏng ph đoán này là phép
chứng minh bằng qui nạp. Phép chứng minh bằng qui nạp tiến hành như sau:
Cho trước một dãy các mệnh đề , S , S ... và ta mu n c ố h ng m ứ inh rằng m i ỗ S là đúng. Ví 1 2 i
dụ ta muốn chứng minh rằng S là đúng, trong đó S là mệnh đề: n n ( n n +1) S ="1+ 2 + 3+...+ n = " n 2 Chứng minh bằng qui n c
ạp đượ tiến hành theo hai bước: 1. Chứng minh rằng
là đúng. Điều này thưß ể ộ 1 S
ng là hi n nhiên qua m t phép tính toán.
2. Giả sử S ,S ,. .,
là đúng (đây được gọi là giả thiết qui nạp) và ta sử dụng u điề này 1 2 Sn−1
để chứng minh rằng S là đúng. n
Ví dā 1.11. Chứng minh rằng ( n n +1) 1 +2 +3 +... +n = 2 Chứng minh.
Bước đầu tiên là kiểm tra mệnh đề đúng vớ
i n = 1. Điều này dễ dàng vì 1( 1+1 ) 1 = 2 Bây giß giả s gi ử ả thiết qui n
ạp là đúng, nghĩa là mệnh đề đúng đến n −1 , nghĩa là
(n− 1 )( (n− 1 )+ 1 ) n (n− 1 ) 1 +2 +3 +... +n 1 − = = 2 2 Ta cần ch ng m ứ inh m ệnh đề đúng đến . T n a có ( n n− 1 ) 1 + − + + n n( 2 n −1 ) 2 ö (n −1) ö = n÷ +1 ÷ ø 2 ø ö (n −1) + 2 ö = n÷ ÷ ø 2 ø ( n n+ 1) = 2
Ví dā 1.12. Sử d ng quy n ụ ạp toán h c ọ ch ng m ứ inh rằng 12 3 2 2 2 2 2 n n n S + + + + n = + + n =1 2 3 ... 3 2 6 Chứng minh. 3 2 1 1 1 Dễ dàng ta có 2 S = 1 = + + 1 3 2 6
Với giả thiết qui nạp là đúng, nghĩa là 3 2 2 2 2 2 (n −1) (n −1) (n −1) S =1 + 2 + 3 + ...+ ( − = + + − n 1) n 1 3 2 6 Ta có 2 2 2 2 2 S
= 1 + 2 + 3 + ...+ (n −1) + n n 1 − 3 2 (n −1) (n −1) (n −1) 2 = + + + n 3 2 6 3 2 2
n − 3n + 3n −1
n − 2n +1 n −1 2 = + + + n 3 2 6 3 2 = n n n + + (dfcm) 3 2 6 1.12. . Hàm số
Đối tượng cơ bản trong toán học mà ta sẽ làm việc là hàm số được định nghĩa như sau:
Đßnh nghĩa 1.13. (Hàm số) . M t hàm s Ā y = f (x) là m t qui t c
ắ gán duy nh Āt m t s Ā y vơꄁi
mỗi giá tr椃⌀ ca x. Ví dā 1.13. 2
y = f (x) = x là m t ộ hàm s v ố ì n ó gán m i
ỗ giá trị x là m t
ộ giá trị y duy nhất. Ví dụ giá trị x = 2 m t ộ giá trị duy nhất 2 y = 2 = 4.
Ví dā 1.14. y = f (x) = x không phải là m tộ hàm s ốvì với x = 4 nó gán hai giá trị y = 2 và y = 2
− , trong khi với x = 4
− nó không gán giá trị nào cả vì 4 − không xác định.
Ví dā 1.15. Dân số thế giới P phụ thuộc vào thßi gian t như sau Năm Dân s ( ố tri i ệu ngưß ) 1900 1650 1910 1750 1920 1860 13 1930 2070 1940 2300 1950 2560 1960 3040 1970 3710 1980 4450 1990 5280 2000 6080 Bảng s
ố liệu cho thấy với m i
ỗ giá trị t sẽ được gán duy nhất m t
ộ giá trị P, do đó P(t) là một hàm s . ố
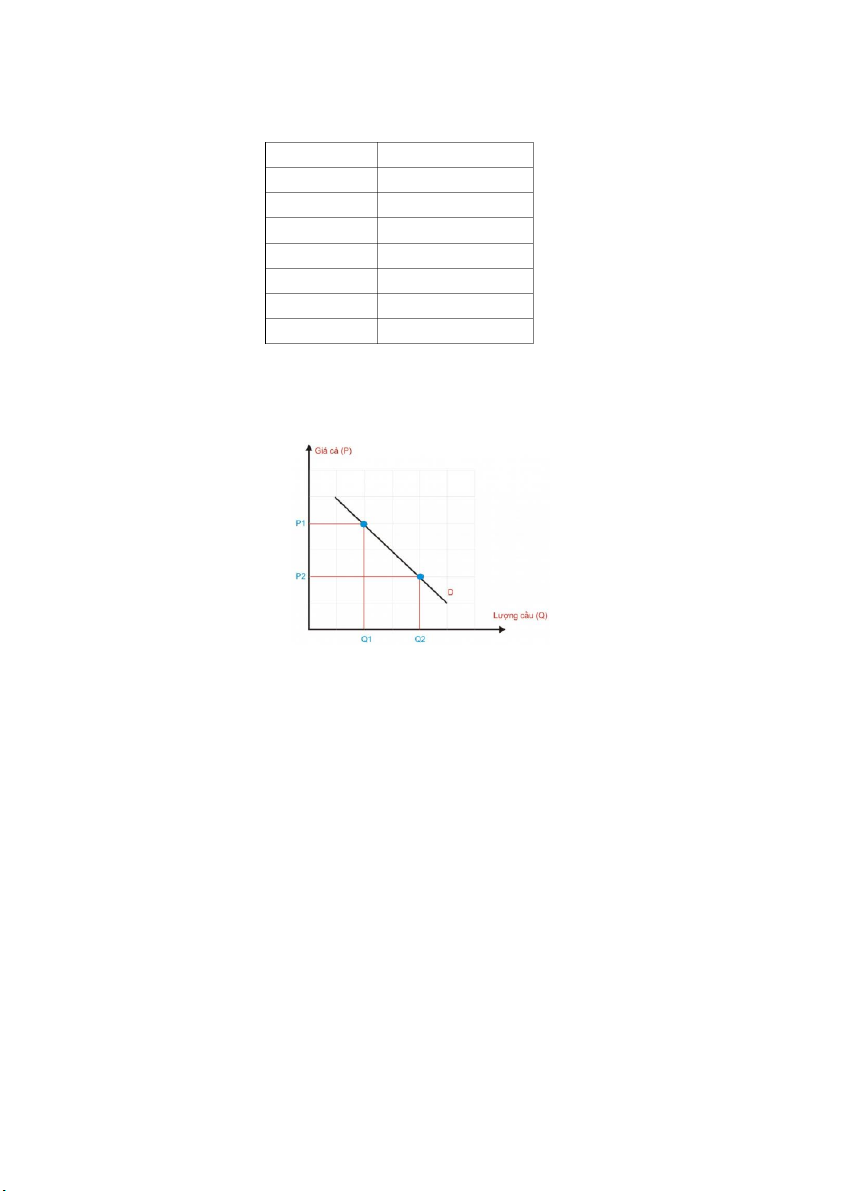
V1 dā 1.16. Cho hàm cầu c a ủ m t
ộ loại hàng hóa như sau
Ta thấy á mỗi mức giá P đều xác định duy nhất một lượng hàng h a ó Q h , do đó àm cầu là
Q = f (P) và cụ thể hơn sẽ c d
ó ạng Q(P) = a − bP
Đßnh nghĩa 1.14. Min xcc đ椃⌀nh (domain) ca hàm sy Ā
= f (x) là t p
ậ hơꄣp t Āt c
các giá tr椃⌀
ca x sao cho f (x) đươꄣc xcc đ椃⌀nh.
Đßnh nghĩa 1.15. Min giá tr椃⌀ (range) ca hàm sy Ā
= f (x) là tập hơꄣp các giá tr椃 y ⌀ t rên min
xcc đ椃⌀nh ca hàm s Ā.
Chú thích: Thông thưßng ta có thể bảo đảm rằng f là m t ộ hàm s
ố bằng cách hạn chế miền xác
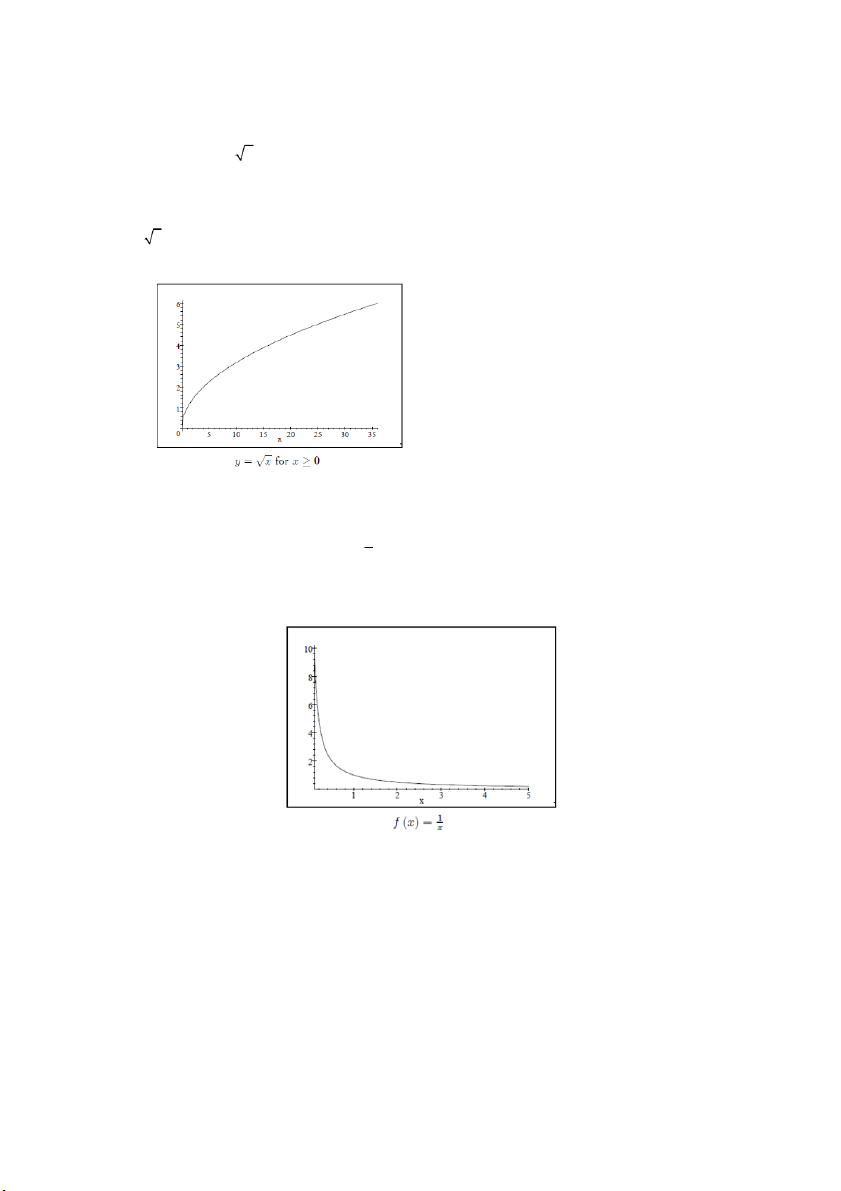
định và miền giá trị của nó. Ví dā 1.17. 14 Hàm s
ố f (x) = x có thể được xác định bằng cách: 1) hạn chế mi nh l ền xác đị à x ó 0
2) hạn chế miền giá trị là y ó 0 hay nói cách khác giải thích như căn bậc hai dương (ví dụ 4 = 2 và không là -2 ).
Với những hạn chế này, ta có một hàm số t c ốt như đượ thấy b t ái đồ hị sau:
Thật ra, đây là một ví dụ của hàm sản xuất Cobb-Douglas, là m t ộ trong những kiến th c ứ
cơ bản của lý thuyết kinh tế. 1
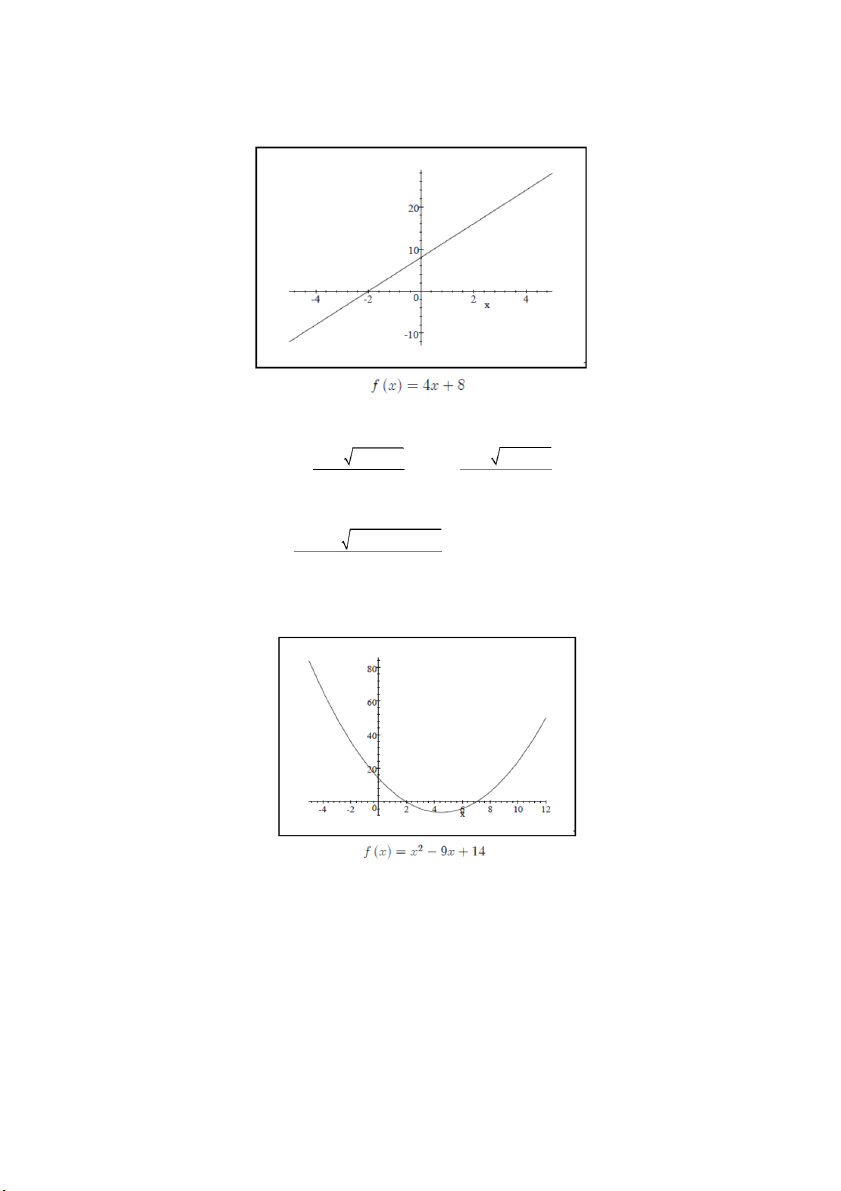
Tương tự, bài toán với f (x) = có thể được xác định bằng cách hạn chế miền xác định x
là x þ 0 và ta có đồ thị: Chú thích: Ta thưßng xác định miền giá trị và mi nh sao cho b ền xác đị m
ảo đả rằng hàm số có ý nghĩa kinh tế. Ví dụ nếu 15
Q = f (P) là m t
ộ hàm cầu với P là giá và Q là lượng cầu thì miền xác định của f ( )
P sẽ là P ó 0 và miền
giá trị là Q ó 0 vì giá và lượng cầu không thể âm.
1.12.1 Hàm luỹ thừa với số mũ nguyên
Một lớp hàm quan tr ng có d ọ ạng: ( ) n f x = x
trong đó n là một s nguyên. ố Ý nghĩa của n
x với n þ 0 là x được nhân n lần. Ví dā 1.18. 3
x = x ô x ô x .
Trong trưßng hợp này, miề ác đị n x nh của f là m i ọ x , nghĩa là − x
Ta cũng có thể cho phép các số mũ nguyên âm (nghĩa là 1 − , 2 − , 3
− ,... ) . Khi đó, n x− 1 nghĩa là . Chẳng hạn n x − 3 1 1 1 1 x = = ô ô 3 x x x x
Chú ý đối với các số mũ nguyên âm, ta cần loại trừ x = 0 ra kh i ỏ miền xác định c a ủ hàm 1
số, vì = không xác định. Các s ố c
mũ nguyên tuân theo các qui tắ sau: 0
Đßnh lý 1.16. N Āu m và n là các s Ā nguyên âm hay dương thì 1. m n m n x x x + = 2. ( m )n mn x = x 3. 0 x = 1 n − 1 4. x = n x 5. ( )n n n xy = x y
Chú thích: Chú ý rằng ( + )n n n x y
ù x + y . Ví d v
ụ ới n = 2 , ta có 2 2 2 2 2
(x + y) = x + 2xy + y ù x + y 16
1.12.2. Hàm đa thức
Đßnh nghĩa 1.17. M t đa thư뀁c bậc
n là m t hàm s Ā có d愃⌀ng n n 1 f ( )
x = a x + a x − + + + − ... a x a n n 1 1 0 trong đ漃Ā a ù 0 . n
Một tính chất quan trọng của đa thức là các nghiệm c a ủ nó:
Đßnh nghĩa 1.18. Nghiệm ca hàm s f (x) là các giá tr椃⌀ r th a m ãn f (r) = 0 .
Đối với một đa thức có nghiệm r thì nó phải thỏa n n 1
f (r) = a r + a r − + + a r + a = n n −1 ... 1 0 0
Một trong những kết quả quan tr ng ọ trong toán h c
ọ là: M t đa thư뀁c bậc
n có n nghiệm
(có th là nghiệm phư뀁c). Kết quả này
đủ quan trọng và được gọi là Định Lý Cơ Bản của i Đạ Số.
Gauss là ngưßi đầu tiên chứng minh định lý này.
Đßnh lý 1.19. (Đßnh Lý C¢ Bản của Đại Số): Đa thư뀁c bậc
n có n nghiệm: r, r ,..., 1 2 r ; nghĩa lc n
n nghiệm (có th phư뀁c) đ Āi vơꄁ i phương trình n n 1 −
f (r) = a r + a r
+ ...+ a r + a = 0 n n −1 1 0 Hai trưß ợp đặ ng h
c biệt quan trọng là:
Đßnh nghĩa 1.20. Hàm tuy Ān tính là m t đa thư c 뀁 bậc 1:
y = f (x) = ax + b
Đßnh nghĩa 1.21. Hàm b c
ậ hai là m t đa thư c 뀁 b c ậ 2: 2
y = f (x) = ax + bx + c
Ví dā 1.19. Đa thức bậc nhất b
f (x) = ax + b có một nghiệm là r = −
như là nghiệm đối với a
f (r) = ar + b = 0 .
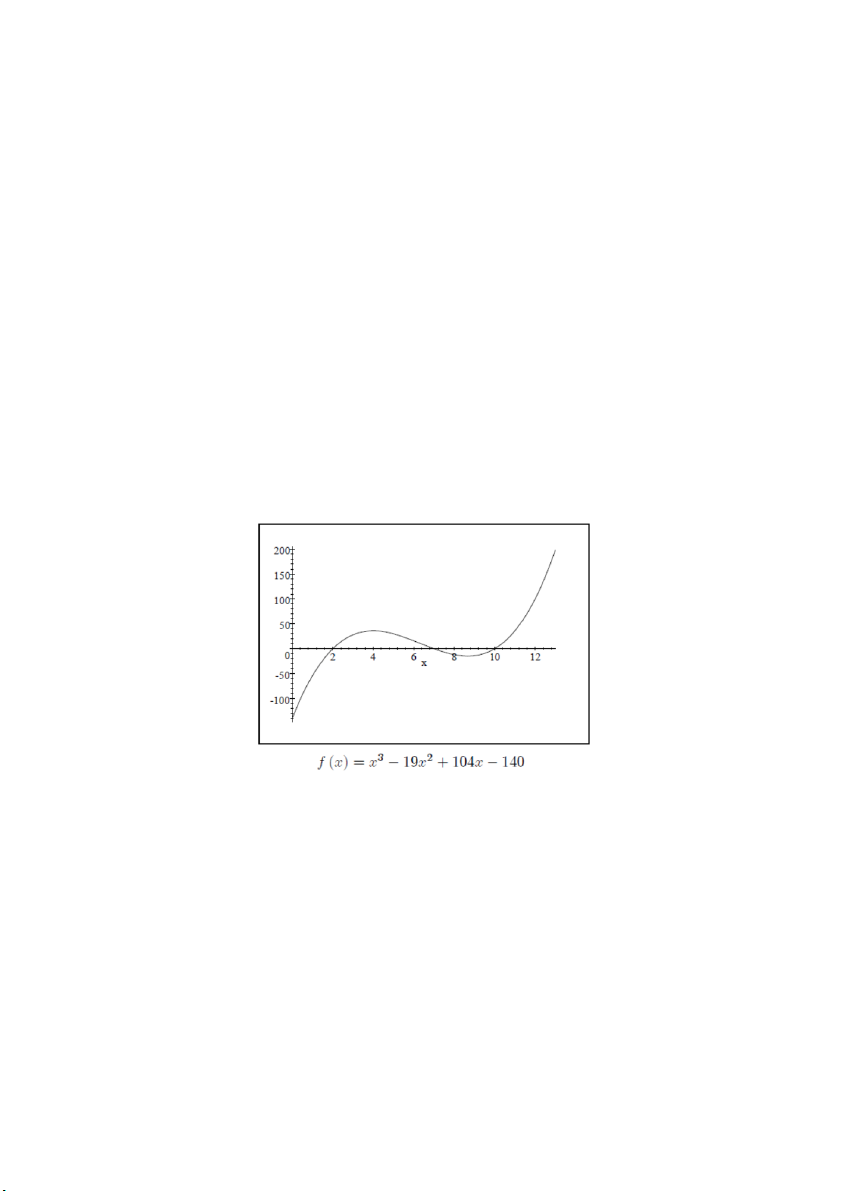
Do đó f (x) = 4x + 8 có nghiệm duy nhất là r = −2 và được minh họa dưới đây chính là
giao điểm giữa đồ thị hàm f(x) với trục Ox. 17
Đßnh lý 1.22. Đa thư c 뀁 bậ 2 c hai
f (x) = ax + bx + c có hai nghiệm đươꄣ ở 1 r và r c cho b i 2 2
−b+ b − 4ac 2 b
− − b − 4ac r = = 1 và r 2a 2 2a
Ví dā 1.20. Đa thức bậc hai 2
x − 9x +14 có hai nghiệm là 2
−(−9) (−9) − 4(1)(14) r =
hay r = 2 và r = 7 2 1 2
và có thể được nhìn thấy bái đồ thị dưới đây, trong đó f (x) cắt tr c ụ Ox t m ại hai điể c ó hoành độ lần lượt là 2 và 7. 18
Một hệ quả của Định Lý Cơ Bản c a
ủ Đại Số là: M t đa thư뀁c luôn có th đươꄣc phân tích
thành các thư뀀a s Ā như sau:
Đßnh lý 1.23. Cho r, r ,..., r ệ a đa thư뀁 1 2 là n nghi m c c n n n− 1 f ( )
x = a x + a x + ...+ a x+ a n n 1 − 1 0 Khi đ漃Ā
f ,(x) có th đươꄣc phân tích thành các thư뀀a s Ā như sau:
f ( x) = a ( x − r ô x − r ô...ô x − r n 1 ) ( 2 ) ( n )
Ví dā 1.21. Phương trình bậc hai 2
3x − 27x + 60 = 0 có hai nghiệm r = 5 và r = 4 1 2 phân tích Do đó ta có thể
f (x) = 3(x − 5)(x − 4)
Ví dā 1.22. Phương trình bậc ba 3 2
x −19x +104x −140 = 0 có các nghiệm r = 2, r = 7 và 1 2
r = 10 và có thể được nhìn thấy bái đồ thị bên dưới. 3 Vì vậy 3 2
x -19x +104x −140 = ( x − )
2 ( x −7)( x −1 ) 0
1.12.3. Hàm luỹ thừa với số mũ không nguyên
Trong kinh tế, ta thưßng mu n
ố xét các hàm lũy thừa với số mũ không nguyên: ( ) a
f x = x , trong đó a không phải là s nguyên. ố
Ví dā 1.23. Hai hàm s v ố ới s ố mũ không nguyên là 19