Chương 2 Phép tính vi phân hàm một biến | Tài liệu môn Kinh tế học Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

Chương 2
PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN
Chương 2 sẽ cung cấp các kiến thức cơ bản về phép tính vi phân hàm một biến: đạo hàm,
độ co giãn, biên tế, tính đơn điệu và tính lồi lõm của hàm số, cực trị, chuỗi Taylor và các
ứng dụng của chúng trong các bài toán kinh tế.
Sau khi học xong chương này, người học có khả năng
 Áp dụng đạo hàm, biên tế, độ co giãn của hàm số để đánh giá sự thay đổi của các đại lượng kinh tế.
 Áp dụng cực trị để giải quyết các vấn đề tối ưu trong các mô hình kinh tế: mô hình
sản xuất, mô hình chi phí, mô hình lợi nhuận…. 2.1. Đạo hàm 2.1.1. Độ dốc
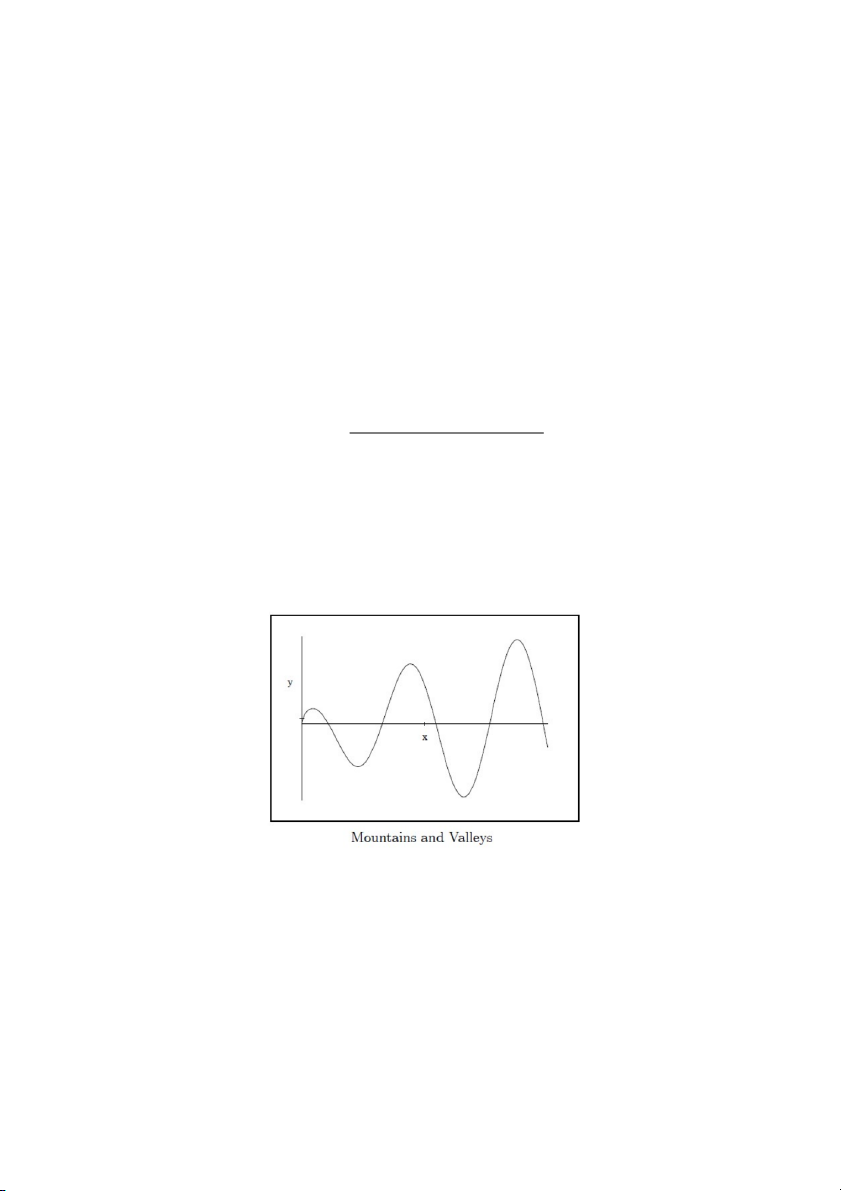
Bạn có thể nghĩ hàm số f(x) như một hệ thống các ngọn núi và thung lũng với x chỉ
vị trí của bạn dọc theo trục – x (để nói về khoảng cách đối với hướng đông hay tây từ một
điểm nào đó) và y chỉ độ cao của bạn ở trên trục - y (hay để nói về độ cao của bạn ở trên
mực nước biển). Điều này được minh họa bởi đồ thị dưới đây:
Khi đó, một xem xét quan trọng cho cả người đi bộ và nhà kinh tế chính là độ dốc.
Những người đi bộ rõ ràng lo lắng khi họ đang leo lên núi hay đang leo xuống núi, và các
nhà kinh tế lo lắng khi một hàm số có độ dốc hướng lên (như một đường cong cung) hay
có độ dốc hướng xuống (như một đường cong cầu).
Độ dốc tại điểm x bất kỳ có thể được đo bằng khoảng dịch chuyển x  (chẳng hạn x
  5 hay dịch chuyển 5 đơn vị về bên phải), đo sự thay đổi về độ cao bằng y  (chẳng y  hạn y
  20 hay dịch xuống 20 feet dưới mực nước biển) và lấy tỉ số như độ dốc (ở x  y đây  20   4
 , do đó với mỗi foot tiến về phía trước bạn rơi 4 feet với số âm chỉ độ x  5
dốc hướng xuống). Điều này dẫn đến định nghĩa sau:
Định nghĩa 2.1. Độ dốc của f (x) tại x đối với sự thay đổi đã cho theo x là x  được định nghĩa bởi y  và bằng x  y f ( x  ) x  f ( ) x  x  x   y  Nếu
 0 thì hàm số có độ dốc hướng lên sao cho việc tăng (giảm) của x dẫn x 
đến việc tăng (giảm) của y .   y Nếu
 0 thì hàm số có độ dốc hướng xuống sao cho việc tăng (giảm) của x dẫn x 
đến việc giảm (tăng) của y . Ví dụ 2.1. Nếu 2
f (x )  x và ta muốn đo độ dốc tại x 1 với x
  2 thì khi đó ta được: 2 2  y ( x  ) x  x  x x 2 2 (1  2) 1   4 2
Mặt khác, nếu ta sử dụng x  0, 25 ta được: 2 2 2 y (x  x)  x  x x 2 2 (1 0, 25) 1    2,25 0, 25
Trong khi nếu ta sử dụng x   0, 001 ta được: 2 2 y (1 0,001)  1  x 0,001  2,001 Chú ý khi ta làm x
 nhỏ hơn thì độ dốc xuất hiện sẽ tiến đến 2. Tổng quát, ta có định lý sau: Định lý 2.2. Với 2 f (x)  x , độ dốc là y  2x x x 2.1.2 Đạo hàm
Bài toán với các độ dốc là bài toán mà ta có thể nhận được các độ dốc khác nhau phụ thuộc vào x
 mà ta chọn. Ví dụ với 2
x tại x = 1 thì độ dốc là 2 x  và vì thế ta
nhận các độ dốc 2,25 và 2,001 đối với x
  0, 25 và  x  0, 001 .
Vì vậy, ta nhận các độ dốc khác nhau đối với các x khác nhau. Vậy thì sự chọn
lựa tốt nhất đối với x là bao nhiêu? Câu hỏi này có câu trả lời khá bất ngờ. Đó là sự
chọn lựa tốt nhất là làm cho x
 bằng không, cụ thể: x  0
Chú thích: Theo các ý kiến trước đây về phép toán vi tích phân thì: x   dx
trong đó dx ( , delta, là mẫu tự Hy Lạp đối với d ), được biết như là đại lượng vi phân,
là đại lượng gần với zero mà không thật sự là 0 .
Khi chúng ta làm cho các bước dịch chuyển x
 vô cùng bé, lượng thay đổi mà
chúng ta nhận được cũng vô cùng bé sao cho:  y  dy 3
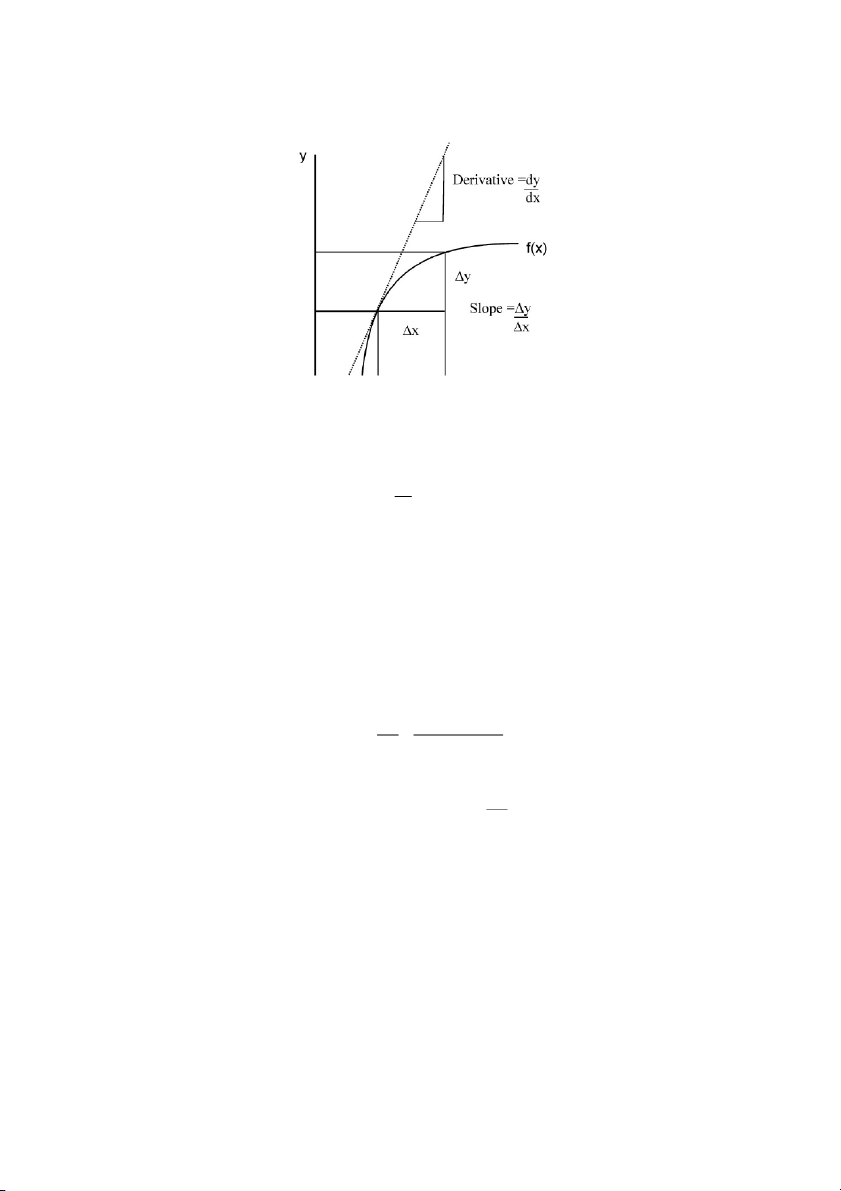
Tuy nhiên, tỉ số của hai đại lượng trên hay độ dốc sẽ tiến tới một đại lượng có ý
nghĩa, đó chính là đạo hàm của hàm số: dy  f '(x) dx
Việc sử dụng các đại lượng vô cùng bé không được tán thành bởi nhiều người,
chẳng hạn nhà triết học người Anh Berkeley. Tuy vậy, không có gì thay đổi cho đến hơn
100 năm sau khi mà Cauchy có thể đưa ra các cơ sở đối với phép toán vi tích phân mà
không cần sử dụng các đại lượng vô cùng bé. Tuy nhiên, các đại lượng vô cùng bé là sự
trợ giúp thực sự cho trực giác và đặc biệt trong công trình ứng dụng mà họ sử dụng. Ví dụ 2.2. Nếu 2
y  x , từ định lý 2.2, ta có khi x  0 : y  2x  x   2x dx  2x x
trong đó ta không quan tâm đến dx vì nó khá bé. Điều này đưa đến một kết quả nổi tiếng: dy d 2  ( x )  2 x dx dx
Do đó, tại x  1 ta thu được độ dốc dy  f '(1)  2 dx
Tổng quát, đạo hàm được định nghĩa như sau: dy
Định nghĩa 2.3. Đạo hàm của hàm số y  f (x ) , được ký hiệu bởi f '( ) x hay , là giới dx hạn của độ dốc khi x   0 hay: y f ( x  ) x  f ( ) x lim  lim x0 x0 x  x 
Một mô tả sự khác nhau giữa độ dốc và đạo hàm được cho bởi đồ thị dưới đây: 4 Định lý 2.4. Cho ( ) n f x  x , khi đó: 1 '( ) n f x nx   Ví dụ 2.3. Cho hàm số 7 f ( ) x  x . Khi đó ta có df ' 7 1  6 f (x)   7x  7x dx
2.1.3. Việc sử dụng từ 'Biên tế' trong kinh tế học
Trong kinh tế học ta thường sử dụng từ biên tế: ví dụ sản lượng biên tế của lao
động, tiện ích biên tế của quả táo, khuynh hướng biên tế của tiêu thụ,...
Ý nghĩa nguồn gốc của từ “biên tế”, chẳng hạn sản lượng biên tế của lao động là
ảnh hưởng của việc thêm một đơn vị vào lượng lao động L đối với sản lượng đầu ra Q .
Giải thích điều này trong toán học như sau: nếu ta viết hàm sản xuất là Q  f ( ) L thì sản
lượng biên tế của lao động là Q f ( L 1)  f ( ) L MP   L L  1 trong đó L  1 và Q
  f (L 1)  f (L) . Q
Do đó, sản lượng biên tế của lao động chính là độ dốc: khi L  1 . L
Trong kinh tế học cao cấp, người ta muốn có các công cụ của phép toán vi tích
phân để tùy ý sử dụng. Với lý do này, sử dụng đạo hàm sẽ tiện lợi hơn nhiều so với độ 5 Q 
dốc để đo sản lượng biên tế của lao động. Bởi thế thay vì đặt L   1 và sử dụng , ta L  dQ cho L
  0 và sử dụng đạo hàm  f '(L) . dL
Khi đó, việc tinh lọc khái niệm biên tế này được mở rộng cho tất cả các khái niệm biên tế ngày nay.
Định nghĩa 2.5. Trong kinh tế học khi ta nói đến các khái niệm biên tế, ta hiểu là đạo hàm.
Ví dụ 2.4. Cho hàm sản xuất Cobb-Douglas: 1 2 Q  f ( ) L  L
Sản lượng biên tế của lao động là đạo hàm của f(L) hay 1 1 2 MP (L)  f '(L)  L L 2
Ví dụ 2.5. Cho hàm tiện ích của các quả táo: 2 3 U( ) Q  Q
Tiện ích biên tế của các quả táo là 1 2 3 MU (Q) U '(Q)  Q 3
Ví dụ 2.6. Sản lượng hàng ngày của một nhà máy là 1 3
Q(L)  60000L (đơn vị sản phẩm)
trong đó L là số giờ lao động. Hiện tại nhà máy có 1000 giờ lao động mỗi ngày. Sử dụng
đạo hàm ước tính số sản phẩm giảm xuống nếu nhà máy giảm số giờ lao động xuống còn 940 giờ mỗi ngày. Giải 2  Ta có ' ' 3
Q (L)  20000L  Q (1000)  200
Khi số giờ lao động giảm từ 1000 giờ xuống 940 giờ, nghĩa là L   6  0 6 Suy ra ' Q  Q ( ) L .L  200*( 6  0)  1
 2000 hay nhà máy sẽ giảm 12000 đơn vị sản phẩm. 2.1.4. Độ co dãn
Thường thì các nhà kinh tế làm việc với độ co dãn nhiều hơn là với đạo hàm. Bài
toán với các đạo hàm là bài toán mà chúng phụ thuộc vào các đơn vị mà x và y đo được.
Ví dụ giả sử ta có đường cong cầu $ Q  100 3P dQ trong đó giá $
P được tính bằng dollars và đạo hàm là  3. dL
Nếu ta quyết định tính giá bằng cents, ta có $ P = c P /100 và 3  100 c Q  P 100 dQ 3 Khi đó   . dP 100 dQ 3
Vậy sự thay đổi về đơn vị làm cho đạo hàm
thay đổi từ 3 đến  . dL 100
Độ co dãn sẽ tránh được vấn đề này bằng cách làm việc với sự thay đổi về tỷ lệ y 
phần trăm. Trong khi độ dốc là sự thay đổi của y chia cho sự thay đổi của x hay , độ x  y
co dãn  là sự thay đổi về phần trăm của y : 1
 00% chia cho sự thay đổi về phần y x trăm của x: 100% hay x y 100% y y  x     x 100% x y x Chú ý rằng độ co dãn 
 bằng độ dốc y nhân với x . Đây được gọi là “độ co x  y
dãn cung” và được sử dụng trong kinh tế học sơ cấp. 7 dy
Trong kinh tế học cao cấp, ta cho x
  0 và sử dụng đạo hàm trong độ co dãn: dx y
thay vì độ dốc:  . Điều này dẫn đến khái niệm độ co dãn điểm hay đơn giản là độ co x  dãn. Định nghĩa 2.6.
Độ co dãn của hàm số y  f( )
x tại x , được ký hiệu bởi ( ) x , là dy x x (x)   f '(x) dx y f (x ) Chú thích:
 Trong kinh tế học thường x  0 và y  0 . Điều này có nghĩa là đạo hàm f '(x ) và độ co dãn ( )
x luôn có cùng dấu. Do đó, nếu độ co dãn của cầu là âm, điều này
tương đương với cách nói rằng đường cong cầu có độ nghiêng xuống.  Nếu (  ) x  2
 thì khi x tăng 1% dẫn đến y giảm 2% . Nếu (  x)  3 thì khi x tăng 1% dẫn đến y tăng 3%.
 Độ co dãn có thể được tính đối với bất kỳ hàm số y  f( ) x nào chứ không chỉ
riêng đối với các đường cong cầu.  Nếu (  ) x 1
 thì ta nói hàm f co giãn không đáng kể tại x (hàm số có phản ứng
chậm với sự thay đổi của biến số).
 Nếu  (x )  1 thì ta nói hàm f co giãn đáng kể tại x (hàm số có phản ứng nhanh với
sự thay đổi của biến số).
 Nếu  (x )  1 thì ta nói hàm f đẳng co tại x.
Ví dụ 2.7. Xét hàm y  4  2 x Ta có độ co giãn là dy x x   .  2  . dx y y
Để thu được độ co dãn như một hàm số của x, ta thay y bằng 4 2 x như sau: 8 x x (x)  2   2  y 4 2x 1 Do đó, tại x  , ta có 2  1   2x  1         1
 2   4  2x | x 3 2 1 1
Ý nghĩa: Tại mức x   y  4 2*  3 , nếu tăng x thêm 1% (nghĩa là 2 2 1 1 x   0,01*  0,505) thì dẫn đến y sẽ giảm 0.33% (nghĩa là 2 2
y  3  0,0033*3  2,9901 ).
Chú ý rằng trong khi đạo hàm bằng -2 với mọi x, độ co dãn giảm khi x tăng như
được chỉ ra bằng đồ thị dưới đây: Ví dụ 2.8. Xét hàm 2 y  x  5 Ta có độ co giãn là 2 dy x x 2 x   .  2 . x  dx y y y
Để thu được độ co dãn như một hàm số của x , ta thay y bằng 2 x  5 : 9 2 x 2 x ( ) x 2 x  2 2 x  5 x  5
Ví dụ 2.9. Giả sử hàm cầu của một loại hàng hóa được cho như sau Q  600  3P d
Tính hệ số co giãn của cầu theo giá tại các mức giá P = 50, P = 100 và P= 150 và phát
biểu ý nghĩa của kết quả thu được.
Ta có hệ số co giãn của cầu theo giá là dQ P P 3P   .  3  .   dP Q Q 600  3P 1
+ Tại P = 50:    , điều này có nghĩa là nếu giá tăng 1% thì lượng cầu sẽ giảm 0,33% 3 1
Vì   1 nên lượng cầu co giãn không đáng kể và như thế thì việc tăng giá ở thời 3
điểm này có lợi cho doanh nghiệp. + Tại P = 100:   1
 , điều này có nghĩa là nếu giá tăng 1% thì lượng cầu cũng giảm 1%.
Như vậy ở mức giá này thì lượng cầu đẳng co.
+ Tại P = 150:   3 , điều này có nghĩa là nếu giá tăng 1% thì lượng cầu sẽ giảm 3%.
Vì   3 1 nên lượng cầu co giãn đáng kể và việc tăng giá có ảnh hưởng lớn đến doanh
nghiệp. Do đó ở thời điểm này doanh nghiệp nên cân nhắc cẩn thận về việc tăng giá hay không.
2.1.5. Hàm có độ co dãn là hằng số.
Một cách tổng quát độ co dãn (x) thay đổi theo x . Ta biết rằng tồn tại một hàm số dạng f ( ) x  ax b trong đó đạo hàm f '( )
x  a không thay đổi theo x mặc dù độ co dãn: x ax (x)  f '( ) x  y ax  b thay đổi theo x . 10
Với sự quan trọng của các độ co dãn trong kinh tế học, một câu hỏi tự nhiên đặt ra
là liệu có thể tồn tại một dạng hàm mà độ co dãn  ( )
x không thay đổi theo x hay không?
Điều này rất hữu ích vì điều đó có nghĩa là đường cong cầu Q P  sẽ có cùng độ co dãn ở bất kỳ mức giá nào.
Hàm số có tính chất này có dạng ( ) b f x  Ax
Thật ra, ta có một kết quả mạnh hơn:
Định lý 2.7. Hàm số f (x) có cùng độ co dãn với mọi x nếu và chỉ nếu nó có thể được viết dưới dạng: ( ) b f x  Ax Chứng minh: Từ b ' b 1 f (x) Ax f (x) Abx    
Suy ra độ co giãn của f(x) bằng b x  x Abx ' b 1
 (x)  f (x).  Abx .   b  hằng số. b y y Ax
Chứng minh chiều ngược lại đòi hỏi phải sử dụng đến kiến thức về giải phương trình vi
phân nên chúng ta sẽ không đề cập ở đây. Ví dụ 2.10. Đường cong cầu 3 Q 1000P   có dạng hàm b
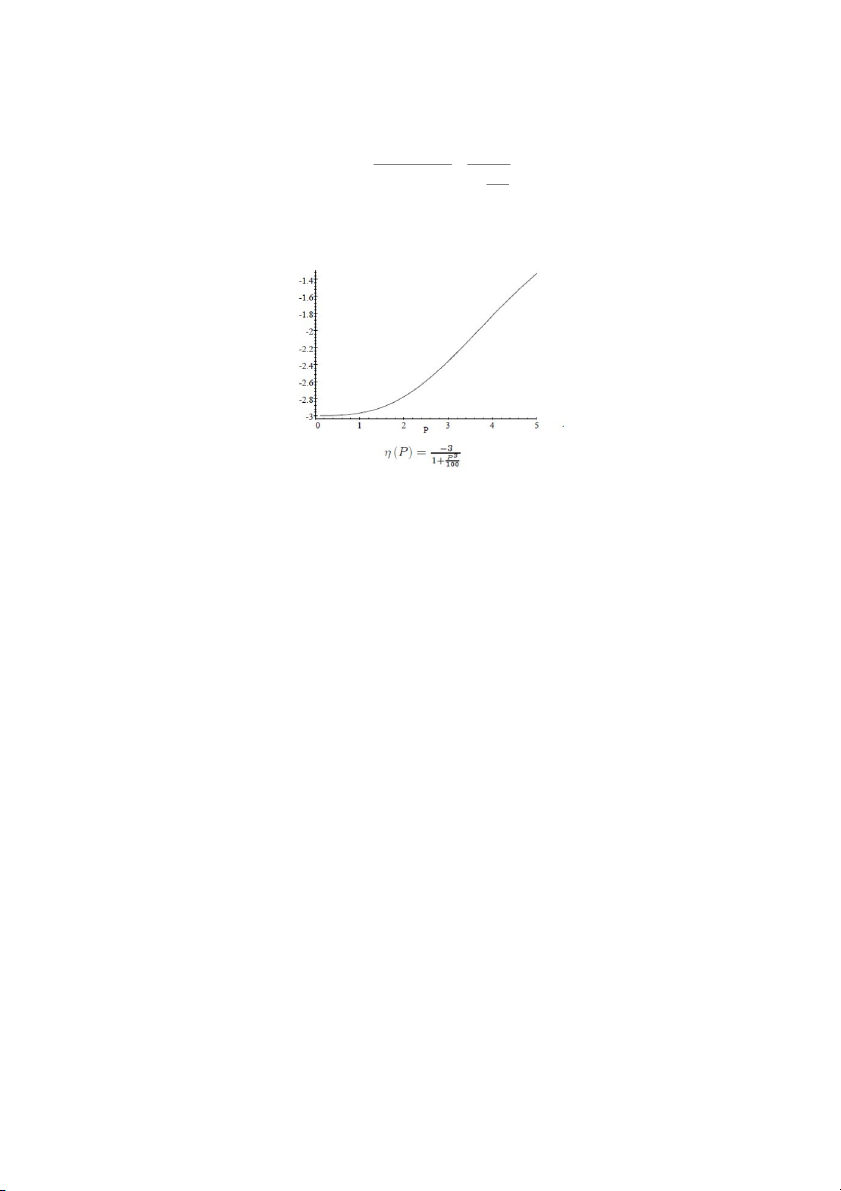
Ax và do đó độ co dãn của cầu là  (P)  3  , là số mũ của P . Ví dụ 2.11.
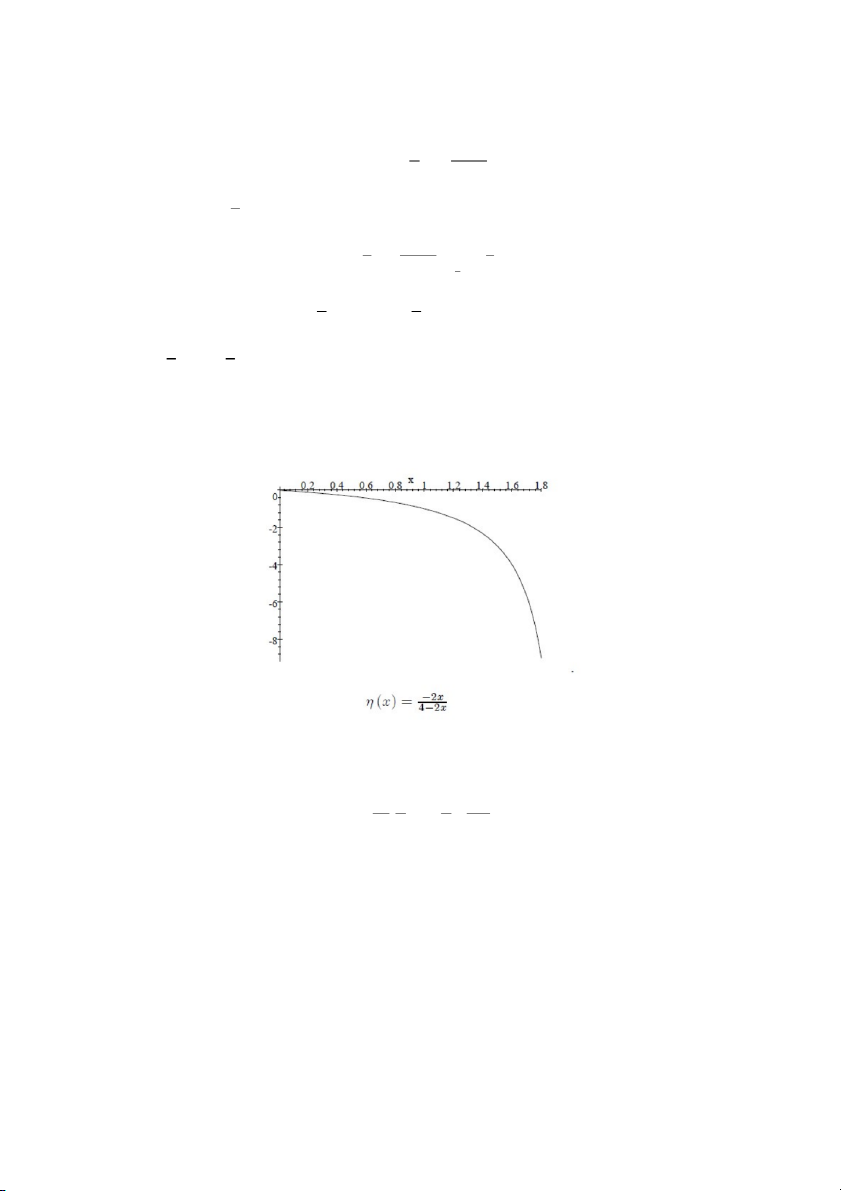
Nếu ta thêm vào hằng số 10 vào đường cong cầu trong ví dụ trên như sau: 3 Q 1000P  10
thì đường cong cầu không có dạng hàm b
Ax và vì thế không có cùng độ co dãn với mọi P . Thật vậy 11 3 3000P 3 ( ) P    3 3 1000P 10 P 1 100
và do đó sự thay đổi của P làm thay đổi độ co dãn và được minh họa bởi đồ thị dưới dây:
2.1.6. Tính chất địa phương và tính chất toàn cục
Khi người đi bộ nói rằng: “sau dòng suối là một đường mòn lên dốc”, nghĩa là anh
ta đang nói về một tính chất địa phương của đường mòn, vì phía sau nữa của đường mòn
có thể là xuống dốc. Mặt khác, nếu anh ta nói: 'Hôm nay trời mưa và cả đường mòn đầy
bùn”, nghĩa là anh ta đang thực hiện một phát biểu toàn cục, một phát biểu áp dụng cho
cả đường mòn. Ta có định nghĩa sau:
Định nghĩa 2.8. (Tính chất địa phương) Ta nói f ( )
x có tính chất địa phương tại x nếu tồn tại một lân cận xung quanh x 0 0
(có lẽ là rất nhỏ) mà trong đó f (x) có tính chất đó.
Định nghĩa 2.9. (Tính chất toàn cục)
Ta nói f (x) có tính chất toàn cục nếu hàm số có tính chất đó với mọi x trong
miền xác định của f ( ) x .
Thực hiện một phát biểu toàn cục thì luôn mạnh hơn thực hiện một phát biểu địa phương. 12
Nếu đường mòn một cách toàn cục đầy bùn thì một cách địa phương nó đầy bùn
sau dòng suối. Tuy nhiên, nếu một cách địa phương nó đầy bùn sau dòng suối thì không
suy ra rằng nó đầy bùn về mặt toàn cục (đầy bùn trên toàn đường mòn). Định lý 2.10.
Nếu A là phát biểu “ f (x) có tính chất P một cách toàn cục” và B là phát biểu
“ f (x) có tính chất P một cách địa phương” thì A  B
nhưng B  A là không đúng.
Một hàm số có thể tăng, giảm một cách địa phương hay toàn cục theo các định nghĩa sau:
Định nghĩa 2.11. (Tăng địa phương)
Nếu f '(x )  0 thì hàm số tăng địa phương (có độ dốc hướng lên) tại x  x . 0 0
Định nghĩa 2.12. (Tăng toàn cục) Nếu f '( )
x  0 với mọi x trong miền xác định của f (x) thì hàm số tăng toàn cục
hay còn gọi là hàm số đơn điệu.
Định nghĩa 2.13. (Giảm địa phương)
Nếu f '(x )  0 thì hàm số giảm địa phương (có độ dốc hướng xuống) tại x  x . 0 0
Định nghĩa 2.14. (Giảm toàn cục) Nếu f '( )
x  0 vơi mọi x trong miền xác định của f (x) thì hàm số giảm toàn cục. Ví dụ 2.12.
Các đường cong cầu có độ dốc hướng xuống toàn cục, trong khi các đường cong
cung có độ dốc hướng lên toàn cục hay nói một cách khác thì đường cong cầu và đường
cong cung là các hàm đơn điệu.
Ví dụ 2.13. Xét hàm số có đồ thị dưới đây: 13
Ta thấy hàm số này tăng địa phương chẳng hạn tại x  4 và tổng quát với bất kỳ 0
x  6 . Nó giảm địa phương tại x  8 và tổng quát với bất kỳ x  6 . 0
Vì nó tăng với một số giá trị x và giảm với những giá trị x khác nên nó không tăng
toàn cục hay giảm toàn cục.
Ví dụ 2.14. Xét hàm số có đồ thị dưới đây:
Bạn có thể kiểm tra từ đồ thị là hàm số này tăng địa phương tại x 1 và tại x 3 . 0 0
Thật ra, nó tăng với mọi x và do đó hàm số này tăng toàn cục hay đơn điệu tăng.
2.1.7. Các công thức tổng, tích và thương của đạo hàm
Có một số công thức để nhớ khi tính các đạo hàm. Ba trong số những công thức
quan trọng hơn là các công thức tổng, tích và thương được đưa ra dưới đây:
Định lý 2.15. (Luật tổng) 14
Nếu h x   af x  bg  x , trong đó a vàb là các hằng số thì ' h  
x  af ' x bg'  x
Định lý 2.16. (Luật tích) Nếu h 
x  f  xg  x  thì
h ' x  f 'x g(x)  f (x)g ' x
Định lý 2.17. (Luật thương) Nếu h x f (x)  thì g (x )   x g( ) x f '( ) x f (x)g '( ) x h '  2 g(x) Ví dụ 2.15. Cho f x  5 3  3x  4x
Áp dụng luật tổng ta có d d f ' x  5 3  3 (x )  4 (x ) dx dx 4 2 15x 12x Ví dụ 2.16. Cho 2 h(x)  x f (x)
Áp dụng luật tích ta có: 2 h'(x)  2xf ( ) x  x f '(x) Ví dụ 2.17. Giả sử ( P )
Q là đường cầu ngược mà một nhà độc quyền đối mặt với P'( )
Q  0 nghĩa là đường cầu ngược có độ dốc hướng xuống.
Tổng doanh thu như một hàm số theo Q lúc đó bằng R(Q)  P(Q) Q
Doanh thu biên (tế) lúc đó được xác định bởi: M ( R ) Q  ' R ( ) Q
Áp dụng luật tích, ta thu được:     MR(Q)  P'(Q)Q  ( P Q) 15
Vì P '(Q)  0 và Q  0 nên suy ra: MR(Q) P(Q)
nghĩa là đường cong doanh thu biên tế luôn nhỏ hơn giá.
Sự chênh lệch giữa giá và doanh thu biên tế này là lý do tại sao một nhà độc quyền
sản xuất hàng hóa ở mức độ thấp hơn thì về mặt xã hội là tối ưu (một cách chính xác hơn là tối ưu Pareto).
Tuy nhiên, với một công ty có sức cạnh tranh tốt thì P sẽ không phụ thuộc vào Q (P là một hằng số).
Vì đạo hàm của hằng số là 0 nên suy ra P '(Q)  0 và như vậy MR(Q)  P
Ví dụ 2.18. Tính đạo hàm của f ( ) x ( h ) x  2 x
Áp dụng luật thương ta có: 2 x f '(x)  2xf (x) h '(x)  2 2 (x ) Ví dụ 2.19.
Nếu C(Q) là hàm chi phí của công ty thì chi phí biên tế được cho bởi: MC (Q)  C '(Q)
trong khi chi phí trung bình là C( ) Q AC (Q)  Q Lấy đạo hàm AC( )
Q và áp dụng luật thương, ta thấy QC '(Q ) C (Q ) AC '( ) Q  2 Q 1  C( ) Q   C '(Q)  Q  Q    MC (Q ) AC (Q )  Q 16
Từ điều này ta nhận thấy
AC '(Q)  0  MC (Q)  AC (Q)
AC '(Q)  0  MC (Q)  AC (Q )
nghĩa là AC '(Q)  0 khi chi phí biên tế vượt quá chi phí trung bình và đường cong chi phí
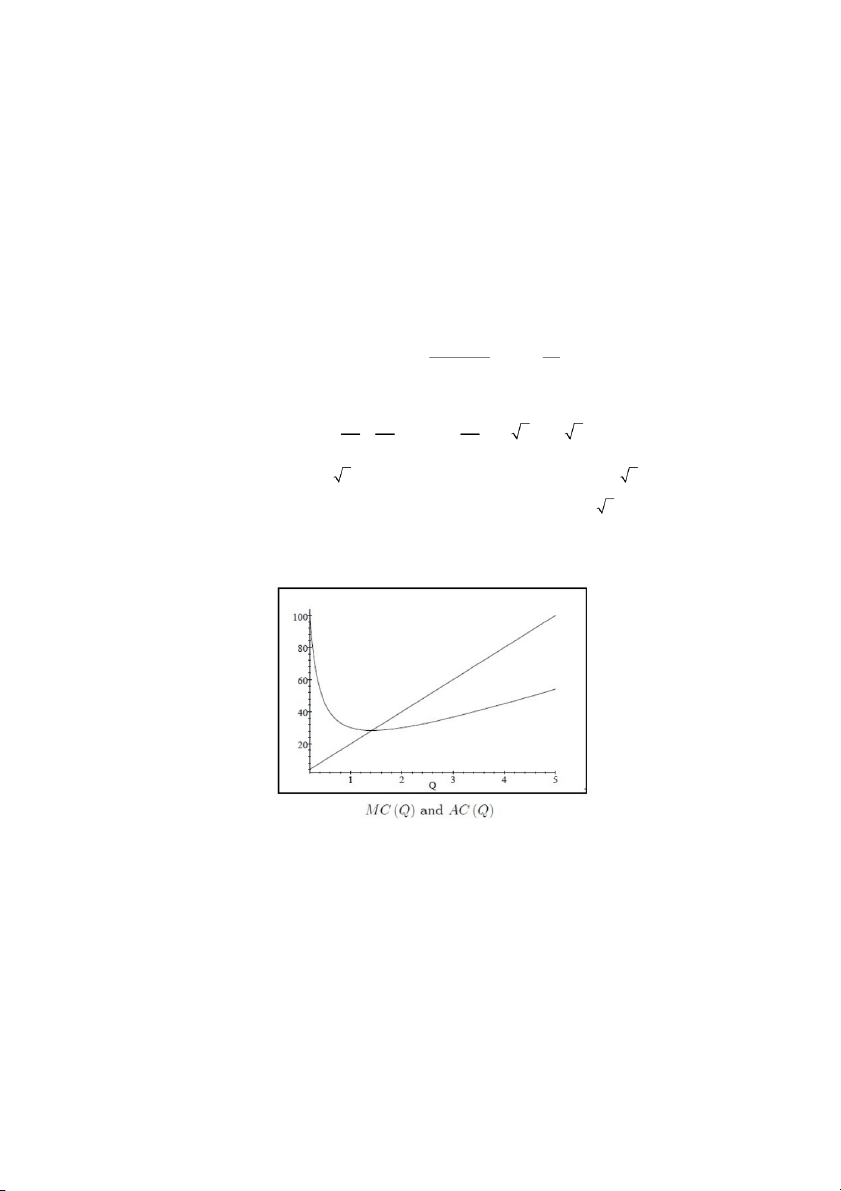
trung bình giảm và AC '(Q)  0 khi chi phí biên tế nhỏ hơn chi phí trung bình. Ví dụ 2.20. Nếu 2 C( ) Q  10Q  20 thì 2 10Q  20 20 MC( ) Q  20 , Q A ( C ) Q  10Q  Q Q Ta có 20 10 2 10 AC'( ) Q 1  0   ( Q 2)  (Q  2)(Q  2) 2 2 2 Q Q Q
nghĩa là AC (Q) giảm với Q  2 và do đó AC  MC , AC (Q ) tăng với Q  2 và do đó
AC  MC . Hơn nữa chi phí biên tế bằng với chi phí trung bình khi Q  2 , đây là điểm
cực tiểu của đường cong chi phí trung bình.
Bạn có thể thấy các mối quan hệ này dưới đây trong đó đường thẳng là MC(Q) :
2.1.8. Đạo hàm hàm hợp (Luật móc xích)
Chúng ta thường sẽ làm việc với hàm số của một hàm số. Ví dụ xét hàm số: 17 1 ( h ) x  2 1 x 1
Ta có thể nghĩ h(x) gồm hai hàm số: hàm số bên ngoài f (x)  và hàm số bên x trong 2 ( g ) x 1  x , nghĩa là 1 1 ( h ) x  f ( g( ) x )   2 g( ) x 1 x
Tổng quát, ta có định nghĩa: Định nghĩa 2.18. Cho ( h ) x  f (g( ) x )
Ta gọi f (x) là hàm số bên ngoài và ( g ) x là hàm số bên trong.
Vào lúc này ta không có công thức để tìm h'( )
x . Tuy nhiên, giả sử rằng ta biết
cách để tính đạo hàm của hàm số bên ngoài f ( )
x và hàm số bên trong g (x) . Khi đó,
công thức đạo hàm hàm hợp cho phép ta tính đạo hàm của ( h ) x  f (g( ) x ) như sau:
Định lý 2.19. Nếu h(x)  f (g(x)) thì h '(x)  f '(g (x))g '(x)
Lúc đầu sinh viên thường gặp khó khăn đối với công thức đạo hàm của hàm hợp.
Dần dần điều này trở nên dễ dàng hơn. Công thức đạo hàm của hàm hợp có thể được hiểu như thuật toán sau đây:
1. Nhận ra hàm bên ngoài f (x) và hàm bên trong g(x) . (Nếu bạn không chắc
chắn, hãy kiểm tra bằng cách đặt hàm g (x) vào bên trong f (x) như f (g (x )) và chắc
chắn bạn nhận được h(x) ).
2. Lấy đạo hàm của hàm bên ngoài: f '(x) .
3. Thay x trong f '(x) ở bước 2 bằng hàm bên trong g(x) để thu được f '(g (x)) .
4. Lấy đạo hàm của hàm bên trong: g '( ) x
5. Nhân kết quả ở bước 3 với kết quả ở bước 4 để nhận được: h '(x)  f '(g(x))g '(x) 18 Chú thích:
Nhận ra một cách chính xác các hàm bên ngoài và hàm bên trong là vô cùng quan trọng. Ví dụ, với 1 2 f ( ) x  ; g( ) x 1 x x
Nếu thay vì f(g(x)) ta lại tính 2 g( f (x)) 1  f (x) 2  1 1     x    1  1 2 x 1
không giống như f (g(x))  . 2 1 x 1 Ví dụ 2.21. Với h(x) 
2 và theo công thức, ta có: 1  x 1
1. Hàm bên ngoài là f (x)  và hàm bên trong là 2 g( ) x  1 x x 1
2. Lấy đạo hàm của hàm bên ngoài, ta được: f '(x)  2 x
3. Đặt hàm bên trong vào trong kết quả ở bước 2, ta được: 1 1 f '(g (x ))     2 2 2 g (x) (1 x )
4. Lấy đạo hàm của hàm bên trong, ta được: g '(x)  2x .
5. Nhân 3. và 4., ta được:  1  2x h '(x )     2x    2 2  2 2  (1 x )  tu buoc 4 (1 x )    tu buoc 3 Ví dụ 2.22. Với 4 h(x)  1 x ta có 19 1 1. Hàm bên ngoài là 2
f (x)  x  x và hàm bên trong là 4 g(x)  1 x . Ta kiểm tra điều này như sau: 4 f ( g( ) x )  g(x)  1 x . 1 
2. Lấy đạo hàm của hàm bên ngoài, ta được: 1 1 2 f '(x)  x  . 2 2 x
3. Đặt hàm bên trong vào trong kết quả ở bước 2, ta được: 1 f '(g (x))  2 g(x)
4. Lấy đạo hàm của hàm bên trong, ta được: 3 g '(x)  4x .
5. Nhân 3. và 4., ta được: 3 3  1  4x 2x 3 h'( ) x    4 x     4 4 4
 2 1 x  tu buoc 4 2 1 x 1 x  tu buoc 3 Ví dụ 2.23. Hàm cầu   8000 D p 
(đơn vị sản phẩm) cho biết nhu cầu tiêu thụ hằng p
tháng của một loại sản phẩm khi giá của sản phẩm là p (đơn vị tiền tệ). Sau t tháng tính từ
bây giờ, giá của sản phẩm là p t  3/2
 0,04t  15. Nhu cầu tiêu thụ của sản phẩm thay đổi
như thế nào sau 25 tháng? Giải
Để trả lời câu hỏi của bài toán chúng ta cần tính ' D t  Ta có
D t   D  p(t)  D '(t)  D ' p(t).p '(t) 12 1 8000 3 480t 2   . t   2 p 50  32 0,04t 1  52 Khi t = 25: D'(25)  6
 , nghĩa là sau 25 tháng thì nhu cầu tiêu thụ sẽ giảm 6 (đơn vị sản phẩm) 20