Chuyên đề căn bậc ba

Tài liệu gồm 19 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề căn bậc ba. Mời bạn đọc đón xem.

65 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ CĂN BẬC BA
A.KIẾN THỨC TRỌNG TÂM
a) Định nghĩa: Căn bậc ba của một số a, kí hiệu
3
,a
là số x sao cho
3
xa
Cho

3
3
33
,aaxxaa
Mỗi số thực a đều có duy nhất một căn bậc ba.
Nếu
0a
thì
3
0a
Nếu
0a
thì
3
0a
Nếu
0a
thì
3
0a
b) Tính chất
33
0 aab
333
.ab a b

3
3
3
0
aa
b
bb

c) Các phép biến đổi căn bậc ba
3
3
3
AB AB
3
3
3
AB A B

3
2
3
1
0
A
AB B
BB


33
22
3
33
1 AABB
AB
AB
AB
Mở rộng: Căn bậc n
a) Định nghĩa: Cho
a
và
;2.nn
Căn bậc n của a là một số mà lũy thừa bậc n của nó bằng a.
Trường hợp n lẻ

21; nk k
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Mỗi số thực a đều có một căn bậc lẻ duy nhất:
21
21
k
k
ax x a

Nếu
0a
thì
21
0
k
a
Nếu
0a
thì
21
0
k
a
Nếu
0a
thì
21
0
k
a
Trường hợp 11 chẵn

2; nkk
Mỗi số thực
0a
đều có hai căn bậc chẵn đối nhau. Căn bậc chẵn dương kí hiệu là
2k
a
(gọi là căn bậc
2k số học của a), căn bậc chẵn âm kí hiệu là
2k
a
2
0
k
ax x
và
2k
xa
2
0
k
ax x và
2k
xa
Mọi số
0a
đều không có căn bậc chẵn.
b) Tính chất của căn bậc n

;2.nn


*
1 0, ,
nnk
mmk
AA Akm

2 0, , 2
m
nmn
AA Amm

. 3 0, 0
nnn
AB A B A B

4 0, 0
n
n
n
AA
AB
B
B




*
5 0,
m
n
m
n
AA Am
Ứng dụng:
- Công thức (1 ) dùng để hạ bậc một căn thức hoặc quy đồng chỉ số các căn thức.
- Công thức (2) dùng để khai căn một căn thức.
- Công thức (3) dùng để khai căn một tích, nhân các căn thức cùng chỉ số, để đưa một thừa số ra ngoài
hoặc vào trong dấu căn.
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
- Công thức (4) dùng để khai căn một thương và chia các căn thức cùng chỉ số, để khử mẫu của biểu thức
lấy căn.
- Công thức (5) dùng để nâng một căn thức lên một lũy thừa.
B.CÁC DẠNG BÀI MINH HỌA
I.Dạng toán cơ bản
Ví dụ 1: Thực hiện phép tính:
a)
3
3
54 : 2 b)
33
837.837
Lời giải
a)
3
333
54 : 2 54 : 2 27 3
b)

33
3
837.837 837837
33
64 37 27 3
Ví dụ 2: Rút gọn biểu thức:
a) b)
Lời giải
a)
b)
Ví dụ 3: Rút gọn
33 3
1
8 2 27 125
5

33
33
125 64 5aaa
33 3
1
8 2 27 125
5


3
3
3
33
3
1
22 3 5
5


1
22.3 .5
5

2617
33
33
125 64 5aaa
 
33
33
545aaa
545aaa
4a
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a)
33
26 15 3 26 15 3A 
b)
33
84 84
11
99
B 
Lời giải
a) Ta có:
33
8 12 3 18 3 3 8 12 3 18 3 3A  

33
33
23 23 23234A 
b)
33
84 84
11
99
B 
Áp dụng hằng đẳng thức
 
3
33
3ab a b abab
ta có:
3
3
3
3
84 84 84 84
113.1 1.
33 9 9
84
23.1 2
81
BB
BB B





 


32
20 1 2 0BB B BB 
mà
2
20BB
Suy ra
1.B
II.Dạng bài nâng cao phát triển tư duy
Ví dụ 1: Hãy tính giá trị biểu thức:

2020
32
31 ,Qxx biết:

3
33
26 15 3. 2 3
980 980
x


Lời giải
Xét
33
980 980a 



3
3
3
3
33
32
9 80 9 80 3. 9 80 9 80 .
18 3. 81 80.
18 3 3 18 0
27 3 9 0 3 3 6 0
aa
aa
aaaa
aa aaa



 
Ta có
2
2
315
36 0
24
aa a




nên
30 3aa
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Do đó


3
3
3
32 2 3
33 18 123 8.2 3
33
x




322 3
43 1
333
x


Vậy

2020
2020
11
3. 1 1 1
27 9
Q




Ví dụ 2: Rút gọn biểu thức:

5
10
1
19 610.32 25
2
Q 
Lời giải
Ta có

5
10
1
38 12 10 . 3 2 2 5
4
Q 

 

2
5
10
5
55
5
5
1
32 25 .32 25
4
11
3225.3225 32253225
22
1
18 20 1 1
2
Q
Q
Q

 

Ví dụ 3: Tính giá trị biếu thức:
2
44
44
21
1
4212
2
2
12 2 12
T








Lời giải
Đặt
4
2 a
thì
42
4
2; 4 2.aa
Khi đó
2
22
24
2
21
1
1
11
aa a
aa
T
aa a








2
22
22
22
1111
0
1
aa
Ta
aaa
aa





Vậy
0T
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
BÀI TẬP TỰ LUYỆN
Cơ bản
Bài 1. Rút gọn biểu thức:
a) b)
c)
Bài 2. Tính:
a) b)
c) d)
Bài 3. Rút gọn:
a) b)
c)
Bài 4. So sánh:
a) b)
Bài 5. Giải phương trình:
a) b)
c)
Nâng cao và phát triển tư duy
Bài 1. Cho biểu thức
183111
:
10
31 3111
xx x
P
x
xxxx







a) Rút gọn biếu thức P.
b) Tính giá trị của P khi
44
322 322
322 322
x



Bài 2. Tính giá trị của biểu thức
a)

2020
3
12 9 ,Bx x
biết

33
451 451x 
333
27 8 125
333
1000 27 729 
33 3 3
48 135 384 40
3
3
39
.
416
3
3
54 : 2
33
837.837
33
3
16
0,5. 1, 25.
10

33
33
11aa
32
3
1
1
a
aa


3
3
3
3
13 1 1xxx x
3
3
32 32 và
33
78 87 và
3
312x 
3
3210x
3
42 53x
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b)
3
,Cx axb biết
23 23
3
2 4 27 2 4 27
bba bba
x 
Bài 3. Hãy tính giá trị của biểu thức:
3
32Px x
với
3
3
1
21
21
x 
Bài 4. Hãy tính giá trị của biểu thức:

2020
3
382,Txx biết

3
17 5 38
.52
51465
x


Bài 5. Cho x, y thỏa mãn
22
33
11.xyy yy
Tính giá trị của biểu thức:
43 2 2
321Ax xy x xy y 
Bài 6. Tính giá tri biểu thức

2013
2
42 ,Px x
với

3
31 1063
21 4 5 3
x


Bài 7. Cho
0; 1.aa
Rút gọn biểu thức:

3
3
1
6 4 2. 20 14 2 3 3 1 : 1
22
a
Saaa
a




Bài 8. Tính giá trị biểu thức:
3
32
32
452
aa
P
aaa


biết:
33
55 3024 55 3024.a 
HƯỚNG DẪN GIẢI
Cơ bản
Bài 1. Rút gọn biểu thức:
a) Biểu thức
b) Biểu thức
333
27 8 125
 
33
3
3
33
32 5

32 5
6
333
1000 27 729 
 
33
33
33
10 3 9

10 3 9 22
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
c) Biểu thức
Bài 2. Tính:
a) Biểu thức
b) Biểu thức
c) Biểu thức
d) Biểu thức
Bài 3. Rút gọn:
a) Biểu thức
b) Biểu thức
c) Biểu thức
Bài 4. So sánh:
a) Ta có: . Nên
b) Ta có: và mà . Nên
Bài 5. Giải phương trình:
Chú ý: Khi giải phương trình, căn thức bậc ba không cần điều kiện của biểu thức trong căn, chỉ cần chú
ý đến các điề
u kiện của mẫu, hoặc căn bậc chẵn nếu có.
33 3 3
48 135 384 40
33333333
2.6 3.5 4.6 2.5
3333
26 35 46 25
33
526
333
3
3
33
3
3
3
39 39 3 3 3
..
416 416 4 4
4


3
3
33
3
3
54
54 : 2 27 3 3
2


3
2
33
3
3
8 37. 8 37 8 37 8 37 8 37 27 3
3
33
33
16 16
0,5. 1, 25. 0,5.1, 25. 1 1
10 10


33
33
11112aaaaa
3
2
33
33 3
3
33 3
22 2
33 3
11
11
1
11 1
aaa
aa
a
aa aa aa



  

3
3
3
3
13 1 1xxx x

3
3
32
3
331 1xxx x

33
33
11xx
112xx
3
3
3
33
32 3.2 54 32
3
3
32 32
33
33
7 8 7 .8 2744
33
33
8 7 8 .7 3584
33
2744 3584
33
78 87
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a)
Vậy nghiệm của phương trình là .
b)
Vậy nghiệm của phương trình là .
c)
Vậy nghiệm của phương trình là .
Nâng cao phát triển tư duy
Bài 1.
Đặt
1xa
biểu thức P có dạng:



 


2
22
2
22
9311
:
39 3
39
31( 3)
:
33 3
39313
:
33 3
39 24
.
33 (3)
3( 3) ( 3)
.
(3 )(3 ) 2( 2)
3
22
aa a
P
aaaaa
aaa
aa
P
aa aa
aa a a a
P
aaaa
aa
P
aaaa
aaa
P
aaa
a
P
a


















Vậy

31
212
x
P
x


b) Ta có:




22
44
22
21 21
21 21
21 21
21 21
x







22
21 21
21 21 2
21 21
x



Vậy

321 3 1
2.3 2
2212
P



3
312 318 3xxx
3x
33
32103212721 13xxxx
13x
33
42 53 42 2 42 8 2 12 6xxxxx
6x
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 2.
a) Xét
 
3
3
4514513.451.451.xx
33
812 12 9 1xxxx
Vậy
2020
11B 
b) Xét
23 23 23 23
3
3
3. .
2 4 27 2 4 27 2 4 27 2 4 27
bbbbbb bba bba
xx





2
3
33
23
3.
44
0
27
xb x
xbaxxaxb
bba


Vậy
0C
Bài 3.
Ta có
333
3
1
21 21 21
21
x  
Xét

3
3
21 21 3. 21 21.xx
33
23 3 20xxxx
Vậy
0P
Bài 4.
Ta có

3
5 5 30 12 5 8
.52
59655
x





 
3
3
2
52
52
.52 .52
53 5
535
54 1
33
x
x




Suy ra

2020
2020
11
3. 8. 2 1 1
27 9
T



11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 5.
Xét
32 2 2 2
3
113.11.xy y y y y y y y x

3
3
22
3
3
23. 1.
32320*
yy x
xx xy
xy
xy


Ta có

432
33
2
3321
32 32
2
1
Ax x xy xyxy y
Axx x y yx x y


Kết hợp với (*) suy ra
1A
Bài 6.
Ta có




3
3
3
2
22
31. 31
31 339331
20 4 5 1 3
25 1 3
31. 31
31 1 5 2
1
25 13 25 4 5 2
25 445 41
x
x
xxxxx









 
Vậy

2013
12 1P 
Bài 7
Ta có


3
3
23 3
33
1
4422.81221222 3 3 1: 1
2
12
22.22 1:
2
2
22.22 1.
1
422 4
a
Saaaa
a
Sa
Sa
a
S








Bài 8.
Xét

3
3
55 3024 55 3024 3 55 3024 55 3024 .aa 
33
3
110 3. 3025 3024. 3 110 0aaaa 
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com





3
2
2
125 3 15 0
5525350
55220
aa
aaa a
aaa
 
 
 
Nhận xét:
2
2
563
522 0
24
aa a




nên
50 5aa
Từ đó suy ra
3
32
53.52 1127
54.55.52483
P



C.TRẮC NGHIỆM RÈN PHẢN XẠ
Câu 1. Khẳng định nào sau đây đúng?
A.
3
3
ax a x= =
. B.
3
3
axa x=- =-
.
C.
3
3
ax ax==
. D.
3
3
axax=- =
.
Câu 2. Khẳng định nào sau đây là đúng?
A.
3
3
22
axa x==
. B.
3
3
22
ax ax==
.
C.
3
3
22axax==
. D.
3
3
28axax==
.
Câu 3. Khẳng định nào sau đây là đúng?
A.
33
abab>>
. B.
33
abab><
. C.
33
abab³=
. D.
33
abab<>
.
Câu 4. Khẳng định nào sau đây là sai?
A.
33 3
.ab ab=
. B.
3
3
3
aa
b
b
=
. C.
()
3
3
aa=
. D.
3
3
aa=
.
Câu 5. Khẳng định nào sau đây là đúng?
A.
3
.ab a b=
. B.
3
3
aa
b
b
=
với
0b ¹
. C.
()
3
3
0aakhia=- <
. D.
3
3
3
aa
b
b
=
với
0b ¹
.
Câu 6. Chọn khẳng định đúng.
A.
3
27 9=
. B.
3
27 3=
. C.
3
27 3=-
. D.
3
27 9=-
.
Câu 6. Đáp án B.
Ta có
3
3
3
27 3 3==.
Câu 7. Chọn khẳng định đúng, với
0a ¹
ta có:
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
3
3
11
2
8
a
a
-=-
. B.
3
3
11
2
8
a
a
-=
. C.
3
3
11
4
8
a
a
-=
. D.
3
32
11
82aa
-=-
.
Câu 8. Thu gọn
3
3
1
27a
-
với 0a ¹ ta được
A.
1
3a
. B.
1
4a
. C.
1
3a
- . D.
1
8a
- .
Câu 9. Rút gọn biểu thức
33
33 3
3
27 1
64 1000
512 3
aa a
-
+-
ta được
A.
7
24
a
. B.
5
24
a
. C.
7
8
a
. D.
5
8
a
.
Câu 10. Rút gọn biểu thức
33
3
33 3
2 27 3 8 4 125aa a-+ ta được
A.
14a
. B.
20a
. C.
9a
. D.
8a-
.
Câu 11. Rút gọn biểu thức
33
17 5 38 17 5 38B =+--
ta được
A.
4
. B.
5
. C.
25
. D.
2
.
Câu 12. Rút gọn biểu thức
33
945 945A =+ +-
ta được:
A.
3A =
. B.
3A =
. C.
6A =
. D.
27A =
.
Câu 13. Cho
3
23A =
và
3
25B =
. Chọn khẳng định đúng
A.
AB<
. B.
AB>
. C. AB³ . D.
0AB+=
.
Câu 14. Cho
3
32A =
và
3
42B =
. Chọn khẳng định đúng.
A.
AB<
. B.
AB>
. C. AB³ . D.
0AB+=
.
Câu 15. Tìm
x
biết
3
21 3x +>-
A.
14x =-
. B.
14x <-
. C.
14x >-
. D.
12x >-
.
Câu 16. Tìm
x
biết
3
42 4x->
.
A.
30x <
. B.
30x >-
. C.
30x <-
. D.
30x >
.
Câu 17. Tìm số nguyên nhỏ nhất thỏa mãn bất phương trình
3
3
32 4x-£
.
A.
31x =-
. B.
30x =-
. C.
32x =-
. D.
29x =-
.
Câu 18. Thu gọn biểu thức
36
3
343
125
ab
-
ta được:
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
2
7
5
ab-
. B.
2
7
5
ab
. C.
2
5
ab
-
. D.
2
5
ab
.
Câu 19. Rút gọn biểu thức
3
55
3
22
64ab
ab
-
ta được:
A.
4ab
. B.
8ab-
. C.
16ab
. D.
4ab-
.
Câu 20. Số nghiệm của phương trình
3
213x +=
là
A.
2
. B. 0 . C.
1
. D.
3
.
Câu21. Kết luận nào đúng khi nói về nghiệm của phương trình
3
32 2x -=-
.
A. Là số nguyên âm. B. Là phân số. C. Là số vô tỉ. D. Là số nguyên.
Câu 22. . Kết luận nào đúng khi nói về nghiệm của phương trình
32
3
62xxx+=+.
A. Là số nguyên âm. B. Là phân số. C. Là số vô tỉ. D. Là số nguyên.
Câu 23. Số nghiệm của phương trình
3
55xx+-=
là:
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 24. Tổng các nghiệm của phương trình
3
22xx-+=
là
A.
6
. B. 5. C.
2
. D.
3
.
Câu 25. Tổng các nghiệm của phương trình
3
3
12 2 23 2 5xx-+ +=
là
A.
2
. B.
1
2
. C.
11
2
- . D.
19
2
.
Câu 26. Tập nghiệm của phương trình
3
3
17 2xx++ - =
là
A.
{}
1; 7S =-
. B.
{}
1; 7S =-
. C.
{}
7S =
. D.
{}
1S =-
.
Câu 27. Thu gọn biểu thức
32 3 2
33
33181261xxx x xx+++- + ++
ta được:
A.
x
. B.
x
-
. C.
2x
. D.
2x-
.
Câu 28. Thu gọn biểu thức
32 3 2
33
3 3 1 125 75 15 1xxx x x x-+-- + ++ ta được
A.
4x-
. B.
6x-
. C.
4x
. D.
6x
.
HƯỚNG DẪN
Câu 1. Đáp án C.
Với
a
ta có
3
3
ax ax==
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Và
3
33
()axa x ax=- = - =-
Câu 2. Đáp án D.
Với
a
ta có
3
33
2(2)8axa x ax== =
Câu 3. Đáp án A.
Với mọi
,ab
ta có
33
abab>>
.
Câu 4. Đáp án D.
333
.ab a b=
Với
0b
¹
, ta có
3
3
3
aa
b
b
=
()
3
3
3
3
aaa==
.
Câu 5. Đáp án D.
33
ab a b< <
333
.ab a b=
Với
0b
¹
, ta có
3
3
3
aa
b
b
=
()
3
3
3
3
aaa==
.
Câu 7. Đáp án A.
Ta có
3
3
3
3
111
22
8
aa
a
æö
÷
ç
÷
-=- =-
ç
÷
ç
÷
ç
èø
Câu 8. Đáp án C.
3
3
3
3
111
33
27
aa
a
æö
÷
ç
÷
-=-=-
ç
÷
ç
÷
ç
èø
Câu 9. Đáp án A.
Ta có
33
33 3
3
27 1
64 1000
512 3
aa a
-
+-
() ()
3
33
33
3
31
410
83
aa a
æö
÷
ç
÷
=- + -
ç
÷
ç
÷
ç
èø
3107
4
8324
a
aa a
-
=+-=.
Câu 10. Đáp án B.
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
33
3
33 3
2 27 3 8 4 125aa a-+
33 3
333
2 (3) 3 (2) 4 (5)aaa=-+
2.3 3.2 4.5 20aaaa=-+=
Câu 11. Đáp án A.
Ta có
33
17 5 38 17 5 38B =+--
() () () ()
23 3 2
32 23
33
2 3.2 . 5 3.2. 5 5 5 3. 5 .2 3. 5.2 2=+ + + - - + -
()()
33
33
2 5 52 52 524=+ - -=+-+=
Câu 12. Đáp án A.
Ta có
33
945 945A =+ +-
Suy ra:
3
33
3
945 945A
æö
÷
ç
=+ +-
÷
ç
÷
ç
èø
33
33 3
33 3
945 945 3945
.9 45 9 45 9 45
æöæö
÷÷
çç
=+ +- ++
÷÷
çç
÷÷
çç
èøèø
æö
÷
ç
-++-
÷
ç
÷
ç
èø
()()
3
9459453.945945.A=+ +- + + -
(vì
33
945 945A =+ +-
)
()
2
2
3
18 3 9 4 5 .A=+ -
18 3A=+
hay
33
318 3180AA AA=+--=
3
27 3 9 0AA--+=
2
(3)( 39)3(3)0AAA A- + +- -=
2
(3)( 36)0AAA- + +=
2
2
3
30
315
360
0
2
)
4
(
A
A
AA
AVN
é
=
ê
é
-=
ê
ê

æö
ê
ê
÷
ç
++=
÷
++=
ç
ê
ê
÷
ë
ç
÷
ç
ê
èø
ë
Vậy
3A
=
.
Câu 13. Đáp án A.
3333
23 8.3 24A == =
Vì
33 33
24 25 24 25 2 3 25< < <
hay
AB<
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 14. Đáp án B.
Ta có:
333
3
3 2 27. 2 54A == =
Vì
33 33
54 42 54 42 3 2 42> > >
hay
AB>
Câu 15. Đáp án C.
Ta có
3
21 3x +>-
3
21(3)x+>-
21 27x+>-
228x>-
14x>-
Câu 16. Đáp án C.
Ta có
3
3
42 4 42 4 42 64 2 60 30xx xxx->->-><-<-
Câu 17. Đáp án B.
Ta có
3
3
32 4 32 4xx-£-£
32 64x- £ 261x³-
61
2
x³-
Nên số nguyên nhỏ nhất thỏa mãn bất phương trình trên là
30
-
Câu 18. Đáp án A.
Ta có:
36
3
343
125
ab
-
3
22
3
77
55
ab ab
æö
÷
ç
÷
==-
ç
÷
ç
÷
÷
ç
-
èø
Câu 19. Đáp án D.
Ta có
3
55
3
22
64ab
ab
-
55
3
33 3
3
3
22
64
64 ( 4 ) 4
ab
ab ab ab
ab
-
==-=-=-
Câu 20. Đáp án C.
Ta có
3
3
213213xx+= +=
21272 26xx+==
13x=
Vậy phương trình đã cho có 1 nghiệm là
13.x
=
Câu 21. Đáp án A.
Ta có
3
32 2x -=-
3
32(2) 32 83 6 2xxxx-=--=-=-=-
Vậy nghiệm của phương trình là số nguyên âm.
Câu 22. Đáp án B.
Ta có
32
3
62xxx+=+
32 3
6(2)xxx+ =+
3232
66128xxxx x+ =+ + +
2
12 8 0
3
xx+==-
Vậy nghiệm của phương trình là phân số.
Câu 23. Đáp án D.
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
33
5555xx x x+-= +=+
33
5 ( 5) ( 5) ( 5) 0xx x x+= + + - + =
2
(5)(5)10(5)(51)(51)0xx xx x
éù
+ + -=+ +- ++=
êú
ëû
5
(5 4 60 4
6
)( )( )
x
xxx x
x
é
=-
ê
ê
+++==-
ê
ê
=-
ê
ë
Vậy phương trình có ba nghiệm phân biệt.
Câu 24. Đáp án A.
Ta có
33
22 2 2xxxx-+= -=-
33
2( 2) ( 2) ( 2)0xx x x-= - - - - =
2
( 2) ( 2) 1 0 ( 2)( 2 1)( 2 1) 0xx xx x
éù
- - -= - -- -+=
êú
ëû
2
2310()() 3
1
()
x
xxx x
x
é
=
ê
ê
- - -==
ê
ê
=
ê
ë
Vậy tổng các nghiệm của phương trình là
2316.++=
Câu 12. Đáp án C.
Ta có
3
3
12 2 23 2 5xx-+ +=
()
3
3
3
3
12 2 23 2 5xx-++=
()
3
3
3
12 2 3 (12 2 )(23 2 ) 12 2 23 2 23 2 125xxxxxx-+ - + -+ + ++=
Mà
3
3
12 2 23 2 5xx-+ +=
Nên ta có phương trình
3
3. (12 2 )(23 2 ).5 35 125xx-++=
3
(12 2 )(23 2 ) 6xx- +=
(12 2 )(23 2 ) 216xx- +=
2
422600xx- - + =
2
211300xx+-=
2
2 4 15 30 0xxx-+-=
2( 2) 15( 2) 0xx x-+-=
(2 15)( 2) 0xx+ -=
152
2
x
x
é
=-
ê
ê
=
ê
ë
Nên tổng các nghiệm của phương trình là
15 11
2
22
æö
-
÷
ç
÷
+- =
ç
÷
ç
÷
ç
èø
Câu 26. Đáp án B.
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có:
3
3
17 2xx++ - =
()
3
33
3
17 2xx++-=
()
3
3
3
17 3( 1)(7 ) 1 7 8xxxxx x++-+ + - ++ - =
Mà
3
3
17 2xx++ - =
nên ta có phương trình
33
3( 1)(7 ).2 8 8 6( 1)(7 ) 0xx xx+-+= +-=
3
10 1
(1)(7)0 17 0(
70 7
)( )
xx
xx xx
xx
éé
+= =-
êê
+ - = + - =
êê
-= =
êê
ëë
Tập nghiệm của phương trình là
{}
1; 7S =-
.
Câu 27. Đáp án B.
Ta có
32 3 2
33
33181261xxx x xx+++- + ++
33
33
(1) (21)xx=+- +
12 1xx x=+- -=-
.
Câu 28. Đáp án A.
32 3 2
33
3 3 1 125 75 15 1xxx x x x-+-- + ++
33
33
(1) (51)xx=-- +
15 1 4.xx x=+- -=-
------------------------- Toán Học Sơ Đồ -------------------------
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

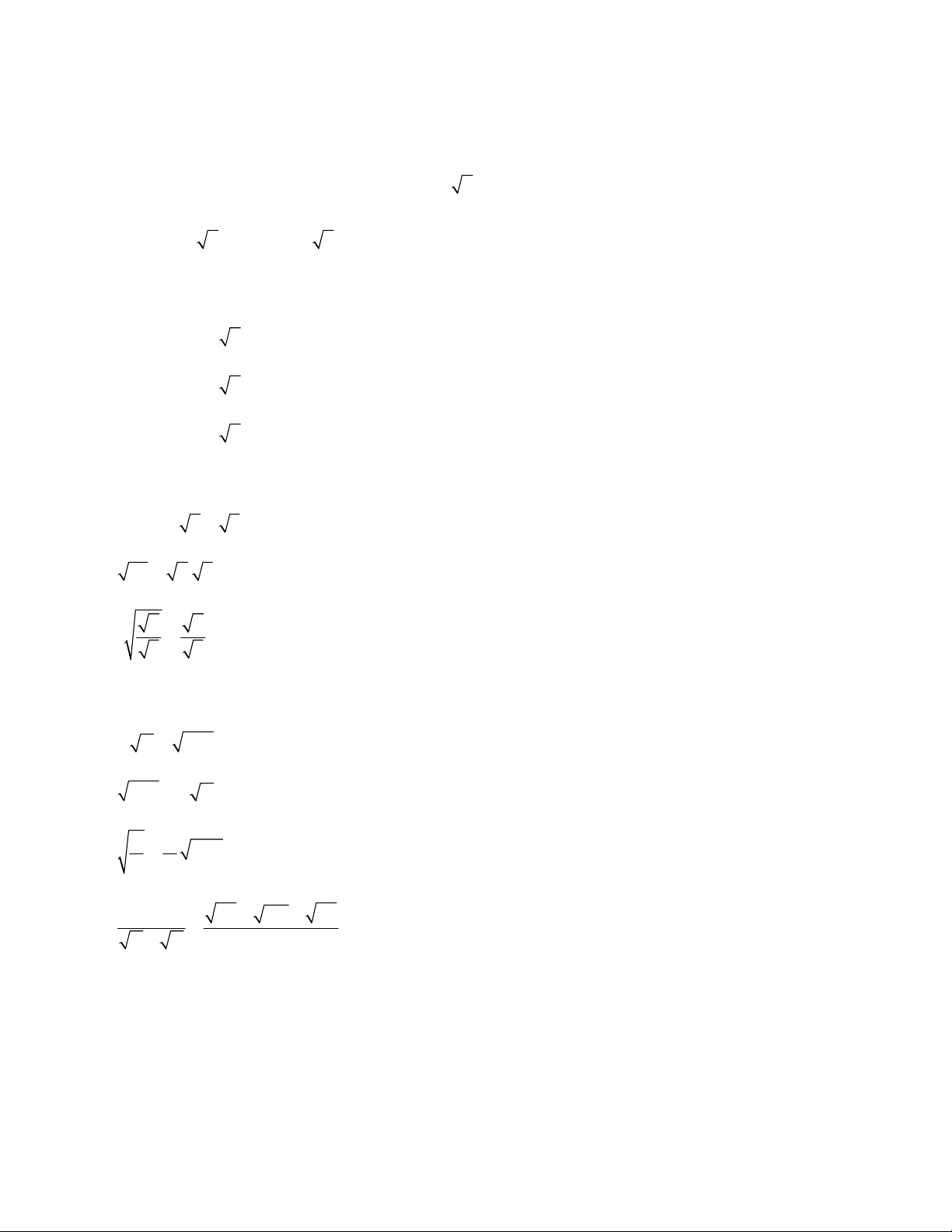
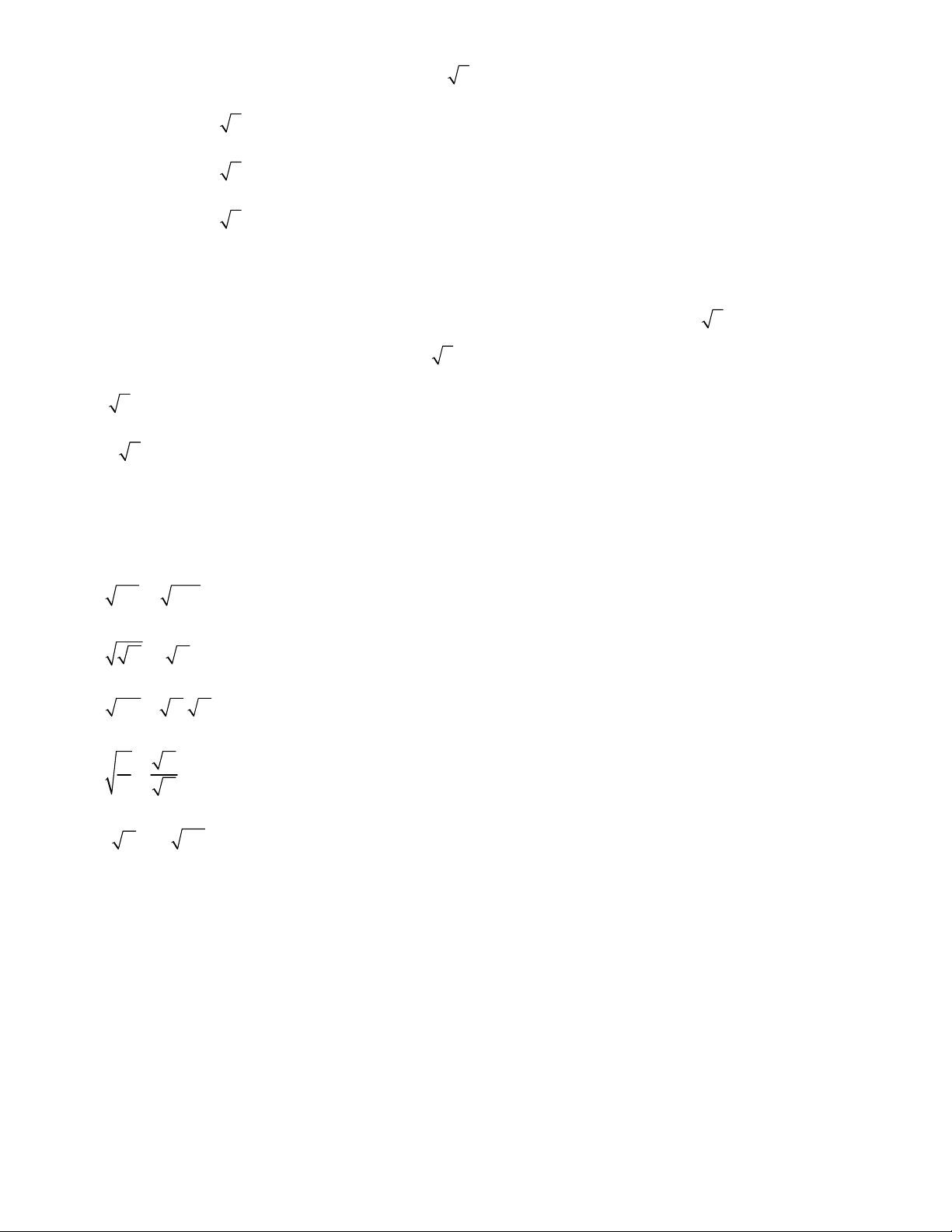
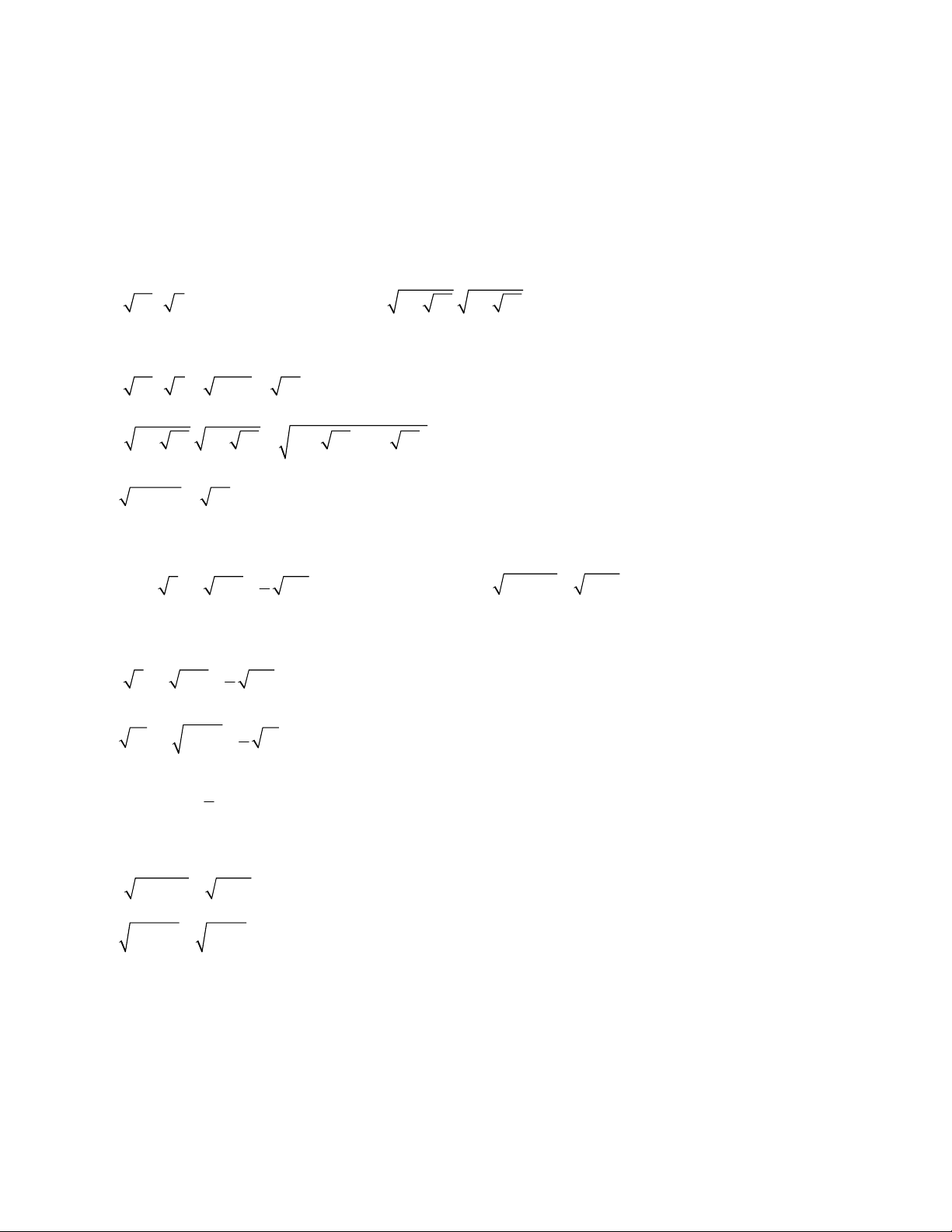
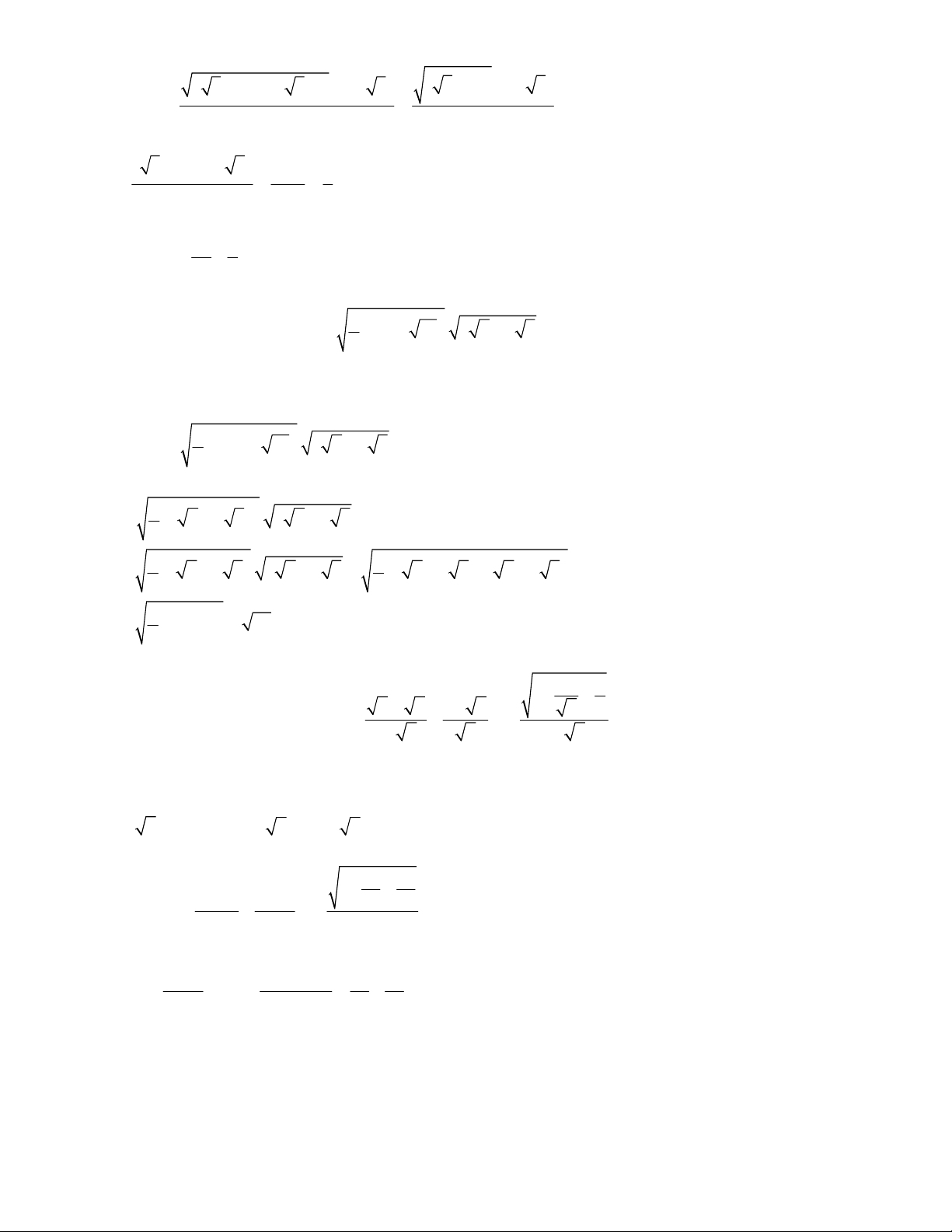
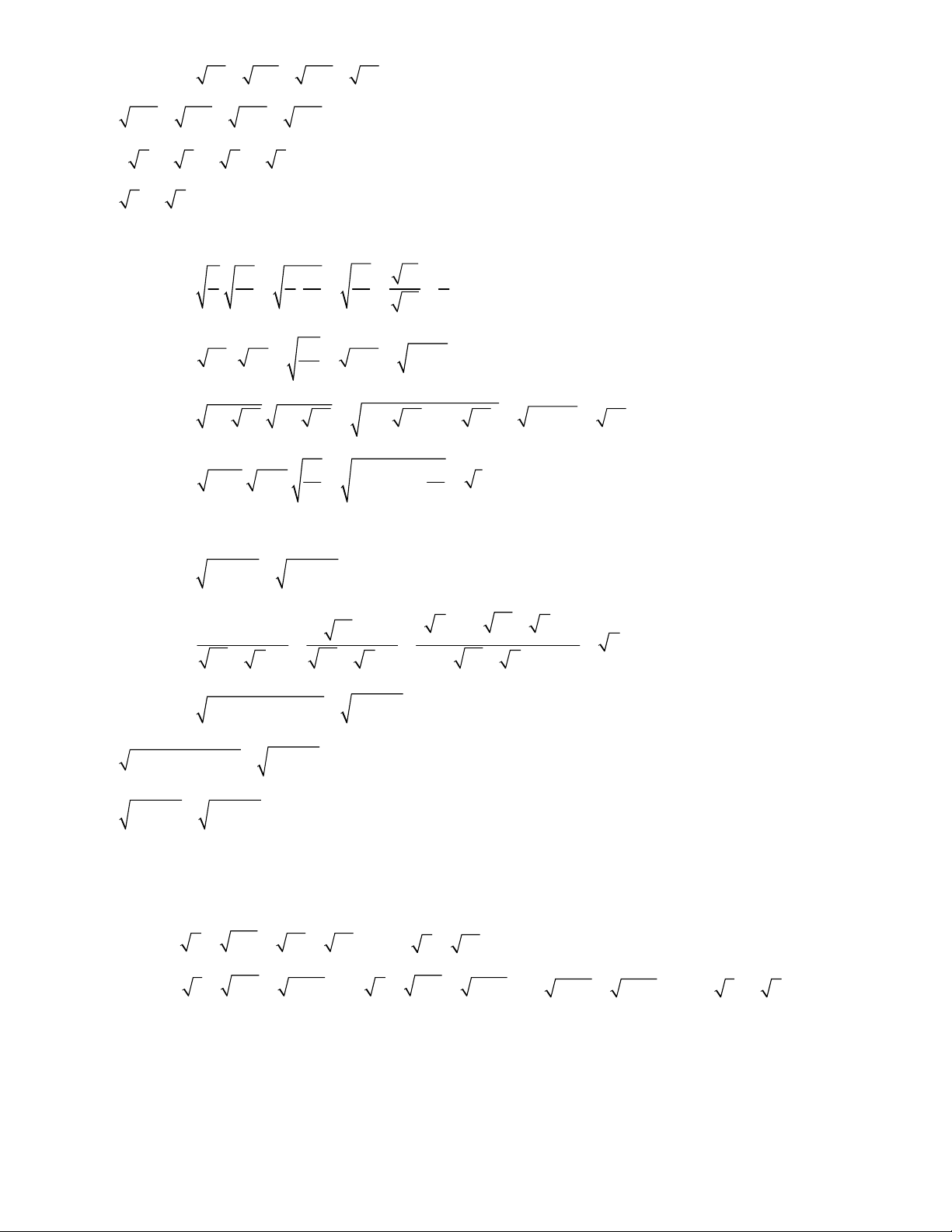
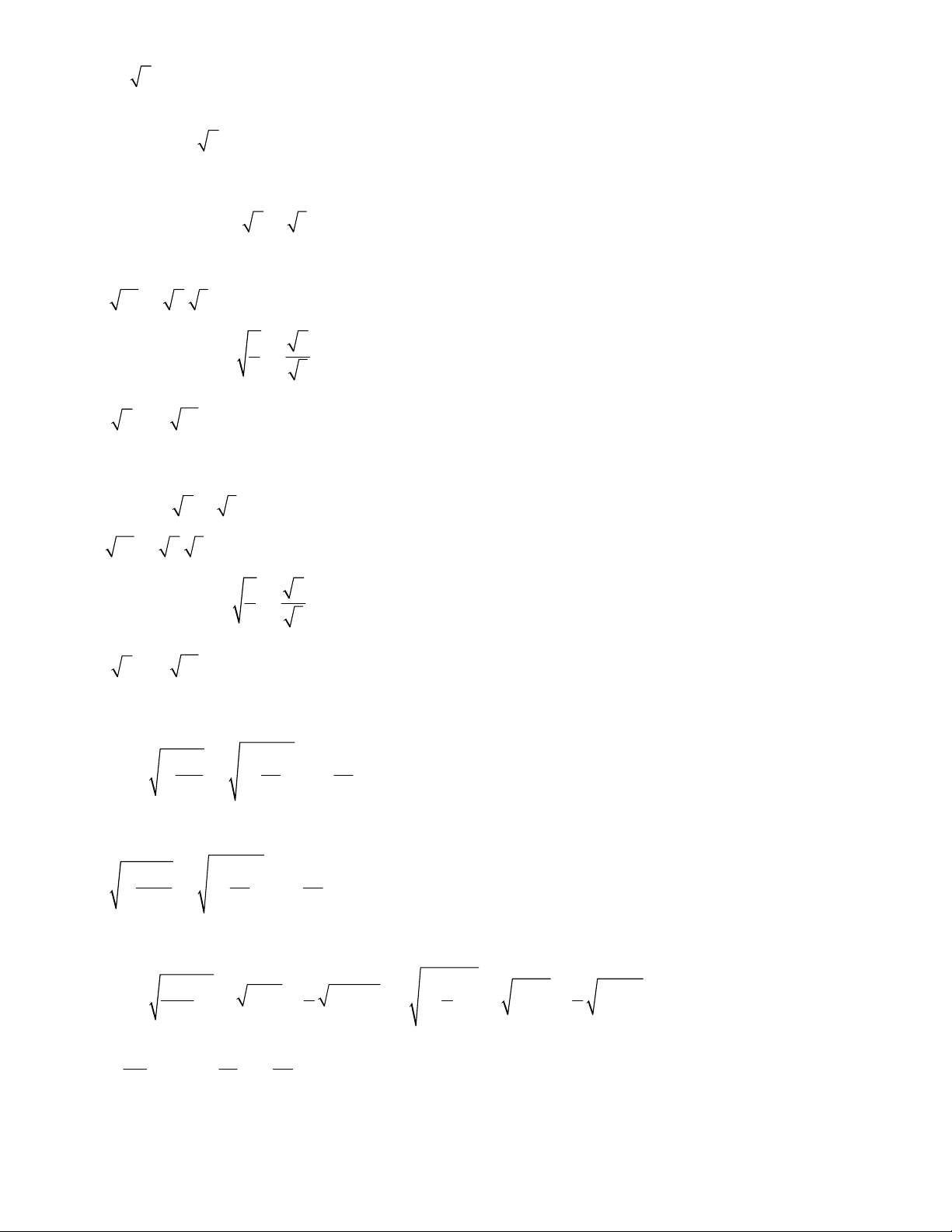
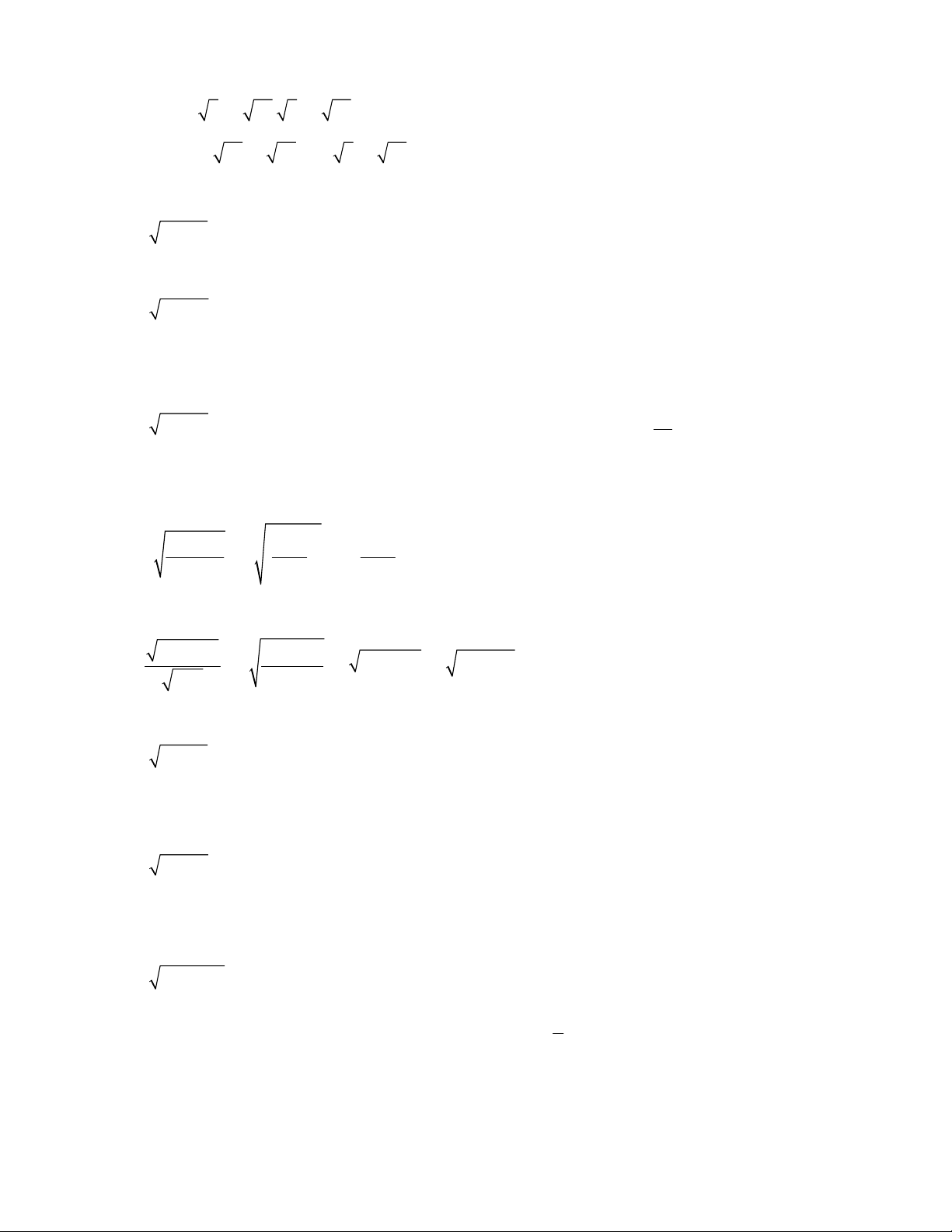
Preview text:


CHUYÊN ĐỀ CĂN BẬC BA
A.KIẾN THỨC TRỌNG TÂM
a) Định nghĩa: Căn bậc ba của một số a, kí hiệu 3 a, là số x sao cho 3 x a  Cho 3
a   a x x   3 , a 3 3  a
 Mỗi số thực a đều có duy nhất một căn bậc ba.
 Nếu a  0 thì 3 a  0
 Nếu a  0 thì 3 a  0
 Nếu a  0 thì 3 a  0 b) Tính chất  3 3
a  0  a b  3 3 3
ab a. b 3 a a  3  b  0 3 b b
c) Các phép biến đổi căn bậc ba  3 3 3 A B A B  3 3 3 A B A B A 1  3 2 3 
AB B  0 B B 3 2 3 3 2 1
A AB B    AB 3 3 A B A B
Mở rộng: Căn bậc n
a) Định nghĩa: Cho a  và n  ; n  2. Căn bậc n của a là một số mà lũy thừa bậc n của nó bằng a.
Trường hợp n lẻn  2k 1; k  
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Mỗi số thực a đều có một căn bậc lẻ duy nhất: 2k 1  2k 1
a x x   a
Nếu a  0 thì 2k 1  a  0
Nếu a  0 thì 2k 1  a  0
Nếu a  0 thì 2k 1  a  0
Trường hợp 11 chẵnn  2k; k 
Mỗi số thực a  0 đều có hai căn bậc chẵn đối nhau. Căn bậc chẵn dương kí hiệu là 2k a (gọi là căn bậc
2k số học của a), căn bậc chẵn âm kí hiệu là 2ka
2k a x x  0 và 2k x a 2k
a x x  0 và 2k x a
Mọi số a  0 đều không có căn bậc chẵn.
b) Tính chất của căn bậc nn ;  n  2. n m nk mk A A   *
1 A  0, k, m    m n mn A
A 2 A  0, m ,m  2 n n  .n AB
A B 3 A  0, B  0 n A A n
4 A  0, B  0 n B Bn Am n mA   *
5 A  0, m    Ứng dụng:
- Công thức (1 ) dùng để hạ bậc một căn thức hoặc quy đồng chỉ số các căn thức.
- Công thức (2) dùng để khai căn một căn thức.
- Công thức (3) dùng để khai căn một tích, nhân các căn thức cùng chỉ số, để đưa một thừa số ra ngoài
hoặc vào trong dấu căn.
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
- Công thức (4) dùng để khai căn một thương và chia các căn thức cùng chỉ số, để khử mẫu của biểu thức lấy căn.
- Công thức (5) dùng để nâng một căn thức lên một lũy thừa.
B.CÁC DẠNG BÀI MINH HỌA
I.Dạng toán cơ bản
Ví dụ 1: Thực hiện phép tính: a) 3 3 54 : 2 b) 3 3 8  37 . 8  37 Lời giải a) 3 3 3 3
54 : 2  54 : 2  27  3 b) 3 3 3
8  37 . 8  37  8  37 8  37  3 3  64  37  27  3
Ví dụ 2: Rút gọn biểu thức: 1 a) 3 3 3 8  2 27  125 b) 3 3 3 3 125 
a  64a  5a 5 Lời giải 1 a) 3 3 3 8  2 27  125 5 1 3  2  2 33 3 3 3 3  5 5     1 2 2. 3  .5 5  2  6 1  7 b) 3 3 3 3 125 
a  64a  5a
  a3   a3 3 3 5 4  5a  5
a  4a  5a  4a Ví dụ 3: Rút gọn
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 84 84 a) 3 3
A  26 15 3  26 15 3 b) 3 3 B  1  1 9 9 Lời giải a) Ta có: 3 3
A  8 12 3 18  3 3  8 12 3 18  3 3
A    3    3 3 3 2 3 2 3  2  3  2  3  4 84 84 b) 3 3 B  1  1 9 9
Áp dụng hằng đẳng thức a b3 3 3
a b  3aba b ta có: 84 84  84  84  3 B  1 1  3.3 1 1 .B 3 3  9  9     84 3 3 B  2  3 . B 1  2  B 81 3
B B    B   2 2 0
1 B B  2  0 mà 2
B B  2  0 Suy ra B 1.
II.Dạng bài nâng cao phát triển tư duy 3 26 15 3.2  3
Ví dụ 1: Hãy tính giá trị biểu thức: Q   x x  2020 3 2 3 1 , biết: x  3 3 9  80  9  80
Lời giải Xét 3 3
a  9  80  9  80 3 3
a  9  80  9  80  3. 9 809 80.a 3 3
a 18  3. 8180.a 3 3
a 18  3a a  3a 18  0 3
a  27  3a  9  0  a 3 2
a  3a  6  0 2  3  15 Ta có 2
a  3a  6  a    0  
nên a  3  0  a  3  2  4
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
3 3 18 12 3  8.2  3   3 3 3 3 2 2  3 Do đó x   3 3
 322 3 43 1 x    3 3 3 2020  1 1  Vậy Q  3.  1     2020 1  1  27 9  1
Ví dụ 2: Rút gọn biểu thức: Q  196 10 5 10 . 3 2  2 5 2
Lời giải 1 Ta có Q  3812 10 5 10 . 3 2  2 5 4 1 Q  3 2 2 52 5 10 . 3 2  2 5 4 1 Q  3 2 2 5 1 5 5 5 . 3 2  2 5 
3 2 2 53 2 2 5 2 2 1 Q  18 20 5 5  1  1  2 2 1 2 1  4 4  4  2 1 2  2 2
Ví dụ 3: Tính giá trị biếu thức: T       4 4 1 2 2   1 2  
Lời giải
Đặt 4 2  a thì 4 4 2
a  2; 4  a  2. 2 1 2   2 2 1 2 4
a a 1 a  Khi đó a a T      2  1 a a  1 a 2 2 2 1 aa 1 1 1  T    a      0 2  aa  2 1 a  2 2 a a Vậy T  0
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
BÀI TẬP TỰ LUYỆN Cơ bản
Bài 1. Rút gọn biểu thức: a) 3 3 3 27  8  125  b) 3 3 3 1000  27   729  c) 3 3 3 3 48  135  384  40 Bài 2. Tính: 3 9 a) 3 3 . b) 3 3 54 : 2  4 16 16 c) 3 3 8  37 . 8  37 d) 3 3 3 0,  5. 1,25. 10 Bài 3. Rút gọn: a 1 a)
a  3  a  3 3 3 1 1 b) 3 2 3 a a 1 c)
3 x 1 3x x   1   x  3 3 3 1 Bài 4. So sánh: a) 3 3 3 2 và 32 b) 3 3 7 8 và 8 7
Bài 5. Giải phương trình: a) 3 3x 1  2 b) 3 3  2x 1  0 c) 3 4  2x  5  3
Nâng cao và phát triển tư duy x 1
x  8   3 x 1 1 1 
Bài 1. Cho biểu thức P     :    
3  x 1 10 x   x  3 x 1 1 x 1      
a) Rút gọn biếu thức P. 3  2 2 3  2 2
b) Tính giá trị của P khi 4 4 x   3  2 2 3  2 2
Bài 2. Tính giá trị của biểu thức
a) B  x x  2020 3 12 9 , biết 3 x     3 4 5 1  4 5   1
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 3 2 3 b b a b b a b) 3
C x ax b, biết 3 x         2 4 27 2 4 27 1
Bài 3. Hãy tính giá trị của biểu thức: 3
P x  3x  2 với 3 x  2 1  3 2 1 3 17 5  38
Bài 4. Hãy tính giá trị của biểu thức: T   x x  2020 3 3 8 2 , biết x  . 5  2 5  14  6 5
Bài 5. Cho x, y thỏa mãn 3 2 3 2
x y y 1  y y 1. Tính giá trị của biểu thức: 4 3 2 2
A x x y  3x xy  2y 1   3 3 1 10  6 3
Bài 6. Tính giá tri biểu thức P  x x  2013 2 4 2 , với x  21 4 5  3
Bài 7. Cho a  0; a  1. Rút gọn biểu thức:  a 1  3 3
S  6  4 2. 20 14 2  a  3 a  3a 1 : 1   2 a  2  3 a  3a  2
Bài 8. Tính giá trị biểu thức: P  biết: 3 3
a  55  3024  55  3024 . 3 2
a  4a  5a  2 HƯỚNG DẪN GIẢI Cơ bản
Bài 1. Rút gọn biểu thức: a) Biểu thức 3 3 3 27  8  125  
  3   3 3 3 3 3 3 2 5  3 2   5    6 b) Biểu thức 3 3 3 1000  27   729  
  3   3 3 3 3 3 10 3 9 10   3    9    22
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com c) Biểu thức 3 3 3 3 48  135  384  40 3 3 3 3 3 3 3 3
 2 .6  3 .5  4 .6  2 .5 3 3 3 3
 2 6  3 5  4 6  2 5 3 3  5  2 6 Bài 2. Tính: 3 3 3 3 9 3 9 3 3 3 a) Biểu thức 3 3 3 3 .  .    3 3 3 4 16 4 16 4 4 4 54 b) Biểu thức 3 3 3 3 54 : 2    27    3  3 3  3  2  c) Biểu thức 3 3         3 2 3 3 8 37 . 8 37 8 37 8 37  8  37  27  3 16 16 d) Biểu thức 3 3 3 3 3 0  ,5. 1,25.  0  ,5.1, 25.  1 1 10 10 Bài 3. Rút gọn: a) Biểu thức
a  3  a  3 3 3 1
1  a 1 a 1  2a 3 a  13 2 3 3 3 3 a a a a    1 1 1 b) Biểu thức 3    a 1 3 2 3 3 2 3 3 2 3 a a 1 a a 1 a a 1 c) Biểu thức
3 x 1 3x x   1   x  3 3 3 1
x x x   x  3 3 3 2 3 3 3 1 1
 x  3  x  3 3 3 1 1
x 1 x   1  2 Bài 4. So sánh: a) Ta có: 3 3 3 3 3
3 2  3 .2  54  32 . Nên 3 3 3 2  32 b) Ta có: 3 3 3 3 7 8  7 .8  2744 và 3 3 3 3 8 7  8 .7  3584 mà 3 3 2744  3584 . Nên 3 3 7 8  8 7
Bài 5. Giải phương trình:
Chú ý: Khi giải phương trình, căn thức bậc ba không cần điều kiện của biểu thức trong căn, chỉ cần chú
ý đến các điều kiện của mẫu, hoặc căn bậc chẵn nếu có.
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com a)
3 3x 1  2  3x 1  8  x  3
Vậy nghiệm của phương trình là x  3. b) 3 3
3  2x 1  0  3  2x 1  27  2x 1  x  13
Vậy nghiệm của phương trình là x  13 . c) 3 3
4  2x  5  3  4  2x  2   4  2x  8   2  x  1  2  x  6
Vậy nghiệm của phương trình là x  6 .
Nâng cao phát triển tư duy Bài 1.
Đặt x 1  a biểu thức P có dạng: 2  a
a  9   3a 1 1  P     :  2  2 
 3  a 9  a   a  3a a a 3 a 2
a  9 3a 1 (a  3)
P   a a : 3 3 a a  3 2 2
3a a a  9 3a 1 a  3
P   a a : 3 3 a a  3 3a  9 2a  4
P   a a. 3 3 a(a  3) 3(a  3) a(a  3) P  .
(3  a)(3  a) 2(a  2) 3  a
P  2a2 3 x 1 Vậy P  2 x 1  2  2  2 1  2  2 1 2 1 2 1 b) Ta có: x  4     4   2   2 2 1 2 1 2 1 2 1   2   2 2 1 2 1 x     2   1   2   1  2 2 1 2 1 3 2 1 3 1 Vậy P    2 2 1  2 2.3 2
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Bài 2. a) Xét 3
x         3 4 5 1 4 5 1  3. 4 5   1 .4 5   1 .x 3 3
x  8 12x x 12x  9  1 Vậy 2020 B  1  1 2 3 2 3 2 3 2 3 b b b b b bb b a  b b a  b) Xét 3 x         3.3         .x 2 4 27 2 4 27  2 4 27  2 4 27     2 2 3 b b a 3 x b   3   .x 4 4 27 3 3 x b
  ax x ax b  0 Vậy C  0 Bài 3. 1 Ta có 3 3 3 x  2 1   2 1  2 1 3 2 1 Xét 3 x       3 2 1 2 1  3.  2   1  2   1 .x 3 3
x  2  3x x  3x  2  0 Vậy P  0 Bài 4. 3 5 5  30 12 5  8 Ta có x  . 5  2 5  9  6 5  5  523 3 5  2 x  . 5  2  . 5  2 2         5  3  5 5 3 5 5  4 1 x   3 3 2020  1 1  Suy ra T  3.  8.  2     2020 1  1  27 9 
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Bài 5. Xét 3 2 2
x y y   y y    2
y y   2 3 1 1 3.
1 y y 1.x 3 3 2 2
x  2y  3. y y 1.x 3 3
x  2y  3x x  3x  2y  0* 4 2 3 2
A x  3x  2xy x y  3xy  2 y 1 Ta có A x  3
x  3x  2 y  y 3
x  3x  2 y 1
Kết hợp với (*) suy ra A  1 Bài 6.
 3 1 3 393 31  3 1.  3 3 3 3 1 x   20  4 5 1  3 2 5 2 1  3
 3 1. 3 1 31 1 5  2 Ta có x     2 5 1 3 2 5  4 5  2 1 2 2
x  2  5  x  4x  4  5  x  4x 1
Vậy P    2013 1 2  1 Bài 7 Ta có  a 1  3 3
S  4  4 2  2. 8 12 2 12  2 2  a a  3a  3 a 1 :  1 2   2 3 3 a 1 2
S  2  2  3. 2  2  3   a   1 : 2 S   
    a   2 2 2 . 2 2 1 . a 1
S  4  2  2  4 Bài 8. Xét 3 3
a  55  3024  55  3024  3 55  302455  3024.a 3 3 3
a  110  3. 3025  3024.a a  3a 110  0
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3
a 125  3a 15  0  a 5 2
a  5a  25  3a 5  0  a 5 2
a  5a  22  0 2  5  63 Nhận xét: 2
a  5a  22  a    0  
nên a  5  0  a  5  2  4 3 5  3.5  2 112 7 Từ đó suy ra P    3 2 5  4.5  5.5  2 48 3
C.TRẮC NGHIỆM RÈN PHẢN XẠ
Câu 1. Khẳng định nào sau đây đúng? A. 3 3
a = x a = x . B. 3 3 a = x -  a = x - . C. 3 3
a = x a = x . D. 3 3 a = x -  a = x .
Câu 2. Khẳng định nào sau đây là đúng? A. 3 3
a = 2x a = 2x . B. 3 3
a = 2x  2a = x . C. 3 3
a = 2x a = 2x . D. 3 3
a = 2x a = 8x .
Câu 3. Khẳng định nào sau đây là đúng? A. 3 3
a > b a > b . B. 3 3
a > b a < b . C. 3 3
a ³ b a = b . D. 3 3
a < b a > b .
Câu 4. Khẳng định nào sau đây là sai? 3 a a A. 3 3 3
a . b = ab . B. 3 = . C. ( )3 3 a = a . D. 3 3 a = a . 3 b b
Câu 5. Khẳng định nào sau đây là đúng? 3 a a 3 a a
A. 3 ab = a. b . B.
= với b ¹ 0 . C. ( a)3 3 = a
- khi a < 0 . D. 3 = với b ¹ 0 . 3 b b 3 b b
Câu 6. Chọn khẳng định đúng. A. 3 27 = 9 . B. 3 27 = 3 . C. 3 27 = 3 - . D. 3 27 = 9 - . Câu 6. Đáp án B. Ta có 3 3 3 27 = 3 = 3 .
Câu 7. Chọn khẳng định đúng, với a ¹ 0 ta có:
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 1 1 1 1 1 1 1 A. 3 - = - . B. 3 - = . C. 3 - = . D. 3 - = - . 3 8a 2a 3 8a 2a 3 8a 4a 3 2 8a 2a 1 Câu 8. Thu gọn 3 -
với a ¹ 0 ta được 3 27a 1 1 1 1 A. . B. . C. - . D. - . 3a 4a 3a 8a -27 1
Câu 9. Rút gọn biểu thức 3 3 3 3 3 3 a + 64a - 1000a ta được 512 3 7a 5a 7a 5a A. . B. . C. . D. . 24 24 8 8
Câu 10. Rút gọn biểu thức 3 3 3 3 3 3
2 27a - 3 8a + 4 125a ta được
A. 14a . B. 20a . C. 9a . D. -8a .
Câu 11. Rút gọn biểu thức 3 3
B = 17 5 + 38 - 17 5 - 38 ta được A. 4 . B. 5 . C. 2 5 . D. 2 .
Câu 12. Rút gọn biểu thức 3 3
A = 9 + 4 5 + 9 - 4 5 ta được: A. A = 3 . B. A = 3 . C. A = 6 . D. A = 27 . Câu 13. Cho 3 A = 2 3 và 3
B = 25 . Chọn khẳng định đúng
A. A < B .
B. A > B .
C. A ³ B .
D. A + B = 0 . Câu 14. Cho 3 A = 3 2 và 3
B = 42 . Chọn khẳng định đúng.
A. A < B .
B. A > B .
C. A ³ B .
D. A + B = 0 .
Câu 15. Tìm x biết 3 2x + 1 > -3 A. x = -14 . B. x < 14 - . C. x > 14 - . D. x > 12 - .
Câu 16. Tìm x biết 3 4 - 2x > 4 . A. x < 30. B. x > 30 - . C. x < 30 - . D. x > 30.
Câu 17. Tìm số nguyên nhỏ nhất thỏa mãn bất phương trình 3 3 3 - 2x £ 4 . A. x = -31. B. x = -30 . C. x = -32 . D. x = -29 . 3 6 343a b
Câu 18. Thu gọn biểu thức 3 ta được: -125
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 -7ab 2 7ab 2 ab 2 ab A. . B. . C. - . D. . 5 5 5 5 3 5 5 -64a b
Câu 19. Rút gọn biểu thức ta được: 3 2 2 a b
A. 4ab . B. -8ab . C. 16ab . D. -4ab .
Câu 20. Số nghiệm của phương trình 3 2x + 1 = 3 là A. 2 . B. 0 . C. 1 . D. 3 .
Câu21. Kết luận nào đúng khi nói về nghiệm của phương trình 3 3x - 2 = -2 .
A. Là số nguyên âm. B. Là phân số. C. Là số vô tỉ. D. Là số nguyên.
Câu 22. . Kết luận nào đúng khi nói về nghiệm của phương trình 3 3 2
x + 6x = x + 2 .
A. Là số nguyên âm. B. Là phân số. C. Là số vô tỉ. D. Là số nguyên.
Câu 23. Số nghiệm của phương trình 3 5 + x - x = 5 là: A. 2 . B. 0 . C. 1 . D. 3 .
Câu 24. Tổng các nghiệm của phương trình 3 x - 2 + 2 = x là A. 6 . B. 5 . C. 2 . D. 3 .
Câu 25. Tổng các nghiệm của phương trình 3 3
12 - 2x + 23 + 2x = 5 là 1 11 19 A. 2 . B. . C. - . D. . 2 2 2
Câu 26. Tập nghiệm của phương trình 3 3
x + 1 + 7 - x = 2 là A. S = {1;-7} . B. S = {-1;7}. C. S = {7}. D. S = {- } 1 .
Câu 27. Thu gọn biểu thức 3 3 2 3 3 2
x + 3x + 3x + 1 - 8x + 12x + 6x + 1 ta được: A. x . B. x - . C. 2x . D. -2x .
Câu 28. Thu gọn biểu thức 3 3 2 3 3 2
x - 3x + 3x - 1 - 125x + 75x + 15x + 1 ta được
A. -4x . B. -6x . C. 4x . D. 6x . HƯỚNG DẪN Câu 1. Đáp án C. 3 Với a ta có 3
a = x a = x
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Và 3 3 3 a = x -  a = ( x - )  a = x - Câu 2. Đáp án D. 3 3 3
Với a ta có a = 2x a = (2x)  a = 8x Câu 3. Đáp án A. 3 3
Với mọi a,b ta có a > b a > b . Câu 4. Đáp án D. 3 3 3
ab = a . b 3 a a
Với b ¹ 0 , ta có 3 = 3 b b (3 )3 3 3 a = a = a . Câu 5. Đáp án D. 3 3
a < b a < b 3 3 3
ab = a . b 3 a a Với b ¹ 0 , ta có 3 = 3 b b (3 )3 3 3 a = a = a . Câu 7. Đáp án A. 3 1 æ 1 ö ç ÷ 1 Ta có 3 3 - = - ç ÷ = - 3 ç ÷ 8a çè 2a ÷ø 2a Câu 8. Đáp án C. 3 1 æ 1 ö ç ÷ 1 3 3 - = - ç ÷ = - 3 ç ÷ 27a çè 3a ÷ø 3a Câu 9. Đáp án A. 3 -27 1 æ 3 ö 3 ç ÷ 1 3 Ta có 3 3 3 3 3 3 a + 64a - 1000a 3 = - ç a÷ + ç ÷ (4a) 3 3 - (10a) 512 3 çè 8 ÷ø 3 3 - 10 7a = a + 4a - a = . 8 3 24 Câu 10. Đáp án B.
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3 3 3 3 3 3
2 27a - 3 8a + 4 125a 3 3 3 3 3 3
= 2 (3a) - 3 (2a) + 4 (5a) = 2.3a - 3.2a + 4.5a = 20a Câu 11. Đáp án A. Ta có 3 3
B = 17 5 + 38 - 17 5 - 38 = + + ( )2 +( )3 - ( )3 - ( )2 3 2 2 3 3 3 2 3.2 . 5 3.2. 5 5 5 3. 5 .2 + 3. 5.2 - 2 = ( + )3 - ( - )3 3 3 2 5 5 2 = 5 + 2 - 5 + 2 = 4 Câu 12. Đáp án A. Ta có 3 3 A = 9 + 4 5 + 9 - 4 5 3 æ ö Suy ra: 3 3 3
A = ç 9 + 4 5 + 9 - 4 5 ÷ ç ÷ ç ÷ è ø 3 3 æ ö æ ö 3 3 3 = ç 9 + 4 5 ÷ ç ÷ + ç 9 - 4 5 ÷ ç ÷ ç ÷ + 3 9 + 4 5 è ø ç ÷ è ø æ ö 3 3 3
. 9 - 4 5 ç 9 + 4 5 + 9 - 4 5 ÷ ç ÷ ç ÷ è ø = + + - + 3 9 4 5 9 4 5
3. (9 + 4 5)(9 - 4 5).A (vì 3 3
A = 9 + 4 5 + 9 - 4 5 ) = + - ( )2 2 3 18 3 9
4 5 .A = 18 + 3A hay 3 3
A = 3A + 18  A - 3A - 18 = 0 3
A - 27 - 3A + 9 = 0 2
 (A - 3)(A + 3A + 9) - 3(A - 3) = 0 2
 (A - 3)(A + 3A + 6) = 0 A é = 3 A é - 3 = 0 ê ê ê 2   æ ö ê 2 ê 3 + + = ç ÷ 15 A 3A 6 0 ê A çê + ÷ + = 0(VN ) ë çêè 2÷÷ø 4 ë Vậy A = 3 . Câu 13. Đáp án A. 3 3 3 3
A = 2 3 = 8. 3 = 24 3 3 3 3
Vì 24 < 25  24 < 25  2 3 < 25 hay A < B
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 14. Đáp án B. Ta có: 3 3 3 3
A = 3 2 = 27. 2 = 54 3 3 3 3
Vì 54 > 42  54 > 42  3 2 > 42 hay A > B Câu 15. Đáp án C.
Ta có 3 2x + 1 > 3 - 3
 2x + 1 > (-3)  2x + 1 > 2
- 7  2x > 2
- 8 x > 14 - Câu 16. Đáp án C. Ta có 3 3
4 - 2x > 4  4 - 2x > 4  4 - 2x > 64  2x < -60  x < -30 Câu 17. Đáp án B. 61 Ta có 3 3
3 - 2x £ 4  3 - 2x £ 4  3 - 2x £ 64  2x ³ 6 - 1 x ³ - 2
Nên số nguyên nhỏ nhất thỏa mãn bất phương trình trên là -30 Câu 18. Đáp án A. 3 3 6 343a b æ 2 ö 2 7ab ç ÷ 7ab Ta có: 3 3 = ç ÷ = - - ç ÷ 125 çè -5 ÷ø 5 Câu 19. Đáp án D. 3 5 5 -64a b 5 5 64 - a b Ta có 3 3 3 3 3 3 = = 64 - a b = ( 4 - ab) = 4 - ab 3 2 2 a b 2 2 a b Câu 20. Đáp án C. Ta có 3 3
2x + 1 = 3  2x + 1 = 3  2x + 1 = 27  2x = 26  x = 13
Vậy phương trình đã cho có 1 nghiệm là x = 13. Câu 21. Đáp án A.
Ta có 3 3x - 2 = -2 3
 3x - 2 = (-2)  3x - 2 = -8  3x = -6  x = -2
Vậy nghiệm của phương trình là số nguyên âm. Câu 22. Đáp án B. Ta có 3 3 2
x + 6x = x + 2 3 2 3
x + 6x = (x + 2) 3 2 3 2 2
x + 6x = x + 6x + 12x + 8  12x + 8 = 0  x = - 3
Vậy nghiệm của phương trình là phân số. Câu 23. Đáp án D.
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3 3
5 + x - x = 5  x + 5 = x + 5 3 3
x + 5 = (x + 5)  (x + 5) - (x + 5) = 0 é 2 (x 5) (x 5) 1ù  + +
- = 0  (x + 5)(x + 5 - 1)(x + 5 + 1) = 0 êë úû x é = -5 ê (x 5)(x 4)(x 6) 0 x ê + + + =  = -4 ê x ê ê = -6 ë
Vậy phương trình có ba nghiệm phân biệt. Câu 24. Đáp án A. Ta có 3 3
x - 2 + 2 = x x - 2 = x - 2 3 3
x - 2 = (x - 2)  (x - 2) - (x - 2) = 0 é 2 (x 2) (x 2) 1ù  - -
- = 0  (x - 2)(x - 2 - 1)(x - 2 + 1) = 0 êë úû x é = 2 ê (x 2)(x 3)(x 1) 0 x ê  - - - =  = 3 ê x ê ê = 1 ë
Vậy tổng các nghiệm của phương trình là 2 + 3 + 1 = 6. Câu 12. Đáp án C. Ta có 3 3
12 - 2x + 23 + 2x = 5  ( 3
12 - 2x + 23 + 2x )3 3 3 = 5 3
 12 - 2x + 3 (12 - 2x)(23 + 2x) (3 3
12 - 2x + 23 + 2x ) + 23 + 2x = 125 Mà 3 3
12 - 2x + 23 + 2x = 5 Nên ta có phương trình 3
 3. (12 - 2x)(23 + 2x).5 + 35 = 125 3
 (12 - 2x)(23 + 2x) = 6  (12 - 2x)(23 + 2x) = 216 2  4
- x - 22x + 60 = 0 2
 2x + 11x - 30 = 0 2
 2x - 4x + 15x - 30 = 0  2x(x - 2) + 15(x - 2) = 0 x é = -152
 (2x + 15)(x - 2) = 0 ê  x ê = 2 êë æ 15ö ç ÷ 11 -
Nên tổng các nghiệm của phương trình là 2 + - ç ÷ = ç çè 2 ÷÷ø 2 Câu 26. Đáp án B.
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
 (3 x +1 + 7 -x )3 3 3 = 3 3 2
Ta có: x + 1 + 7 - x = 2 3
x + 1 + 7 - x + 3 (x + 1)(7 - x) (3 3
x + 1 + 7 - x ) = 8 3 3
Mà x + 1 + 7 - x = 2 nên ta có phương trình 3 3
3 (x + 1)(7 - x).2 + 8 = 8  6 (x + 1)(7 - x) = 0 x é 1 0 é + = x = -1 3 (x 1)(7 x) 0 (x 1 7 )( x) 0 ê ê + - =  + - =   ê7 x 0 ê - = x = 7 êë êë
Tập nghiệm của phương trình là S = {-1;7}. Câu 27. Đáp án B. Ta có 3 3 2 3 3 2
x + 3x + 3x + 1 - 8x + 12x + 6x + 1 3 3 3 3
= (x + 1) - (2x + 1)
= x + 1 - 2x -1 = x - . Câu 28. Đáp án A. 3 3 2 3 3 2
x - 3x + 3x - 1 - 125x + 75x + 15x + 1 3 3 3 3
= (x - 1) - (5x + 1) = x + 1 - 5x -1 = 4 - x.
------------------------- Toán Học Sơ Đồ -------------------------
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com