Chuyên đề căn bậc hai, căn thức bậc hai và hằng đẳng thức

Tài liệu gồm 46 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề căn bậc hai, căn thức bậc hai và hằng đẳng thức . Mời bạn đọc đón xem.

125 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

46 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
CĂN BẬC HAI - CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
2
AA=
A. KIẾN THỨC TRỌNG TÂM
I. Căn bậc hai số học
• Căn bậc hai của một số không âm a là số x sao cho
2
xa=
• Số dương a có đúng hai căn bậc hai là hai số đối nhau:
Số dương kí hiệu là
a
, số âm kí hiệu là
a−
• Số 0 có đúng một căn bậc hai là chính số 0, ta viết
00=
• Với số dương a, số
a
được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học
của 0.
• Với hai số không âm a, b, ta có
ab a b
<⇔ <
II. Căn thức bậc hai
• Với A là một biểu thức đại số, ta gọi
A
là căn thức bậc hai của A.
•
A
xác định (hay có nghĩa) khi A
≥
0.
B. BÀI MINH HỌA
I. BÀI TẬP VÀ CÁC DẠNG BÀI TỰ LUẬN
Dạng 1. Tìm điều kiện để biểu thức chứa căn có nghĩa
Bài 1. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa:
Bài 2. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa:
2
xxx
a) x2 b) x2 c) x2
x2 x2 x 4
142
d)e)f)
3 2x 2x 3 x 1
+− +− +−
−+ −
−
− ++
Bài 3. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa:
22 2
22
a) x 1 b) 4x 3 c) 9x 6x 1
d) x 2x 1 e) x 5 f ) 2x 1
+ + −+
− + − −+ − −
Bài 4. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa:
( )
22 2
22
a)4 x b)x 16 c)x 3
d)x 2x 3 e)xx 2 f)x 5x 6
− −−
−− + −+
Lời giải
Bài 1:
2
a)x 0 b)x 2 c)x
3
12 1
d)x e)x f )x
39 6
≤ ≤≤
−
≥≥≥
Bài 2:
a) 3x b) 4 2x c) 3x 2
d) 3x 1 e) 9x 2 f ) 6x 1
− − −+
+−−
2. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
x
a) x 2
x2
+−
−
Điều kiện của biểu thức là
x20 x 2
x2
x20 x 2
−≥ ≥

⇔ ⇔>

−≠ ≠

Vậy điều kiện của biểu thức là
x2>
x
b) x 2
x2
+−
+
Điều kiện của biểu thức là
x20 x2
x2
x20 x 2
−≥ ≥

⇔ ⇔≥

+ ≠ ≠−

Vậy điều kiện của biểu thức là
x2≥
c)
2
x
x2
x4
+−
−
Điều kiện
2
x20
x2
x2
x2
x 40
−≥
≥
⇔ ⇔>

≠±
−≠
Vậy điều kiện của biểu thức là
x2
>
1
d)
3 2x−
dạng
A
B
với
A0>
⇒ Điều kiện
13
0 3 2x 0 x
3 2x 2
≥⇔− >⇔<
−
Vậy điều kiện của biểu thức là
3
x
2
<
e)
4
2x 3+
. Dạng
A
B
với
A0>
⇒ Điều kiện
43
0 2x 3 0 x
2x 3 2
≥⇔ +>⇔>−
+
Vậy điều kiện của biểu thức là
3
x
2
>−
f)
2
x1
−
+
dạng
A
B
với
A0<
⇒ Điều kiện
2
0x10x1
x1
−
≥⇔+<⇔<−
+
Vậy điều kiện của biểu thức là
x1<−
Bài 3.
a) Vì
2
x 1 0x+>∀
. Vậy hàm số luôn xác định
x∀∈
b) Vì
2
4x 3 0 x+>∀
. Vậy hàm số luôn xác định
x∀∈
c)
( )
2
2
9x 6x 1 3x 1− += −
. Vì
(
)
2
3x 1 0 x− ≥∀∈
Vậy hàm số xác định với mọi x
d)
( )
( )
2
22
x 2x 1 x 2x 1 x 1− + −=− − + =− −
Hàm số xác định
( )
2
x1 0 x10 x 1⇔− − ≥ ⇔ − = ⇔ =
Vậy hàm số xác định khi
x1=
3. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
e)
x5−+
Điều kiện
x5 0 x50 x 5− + ≥⇔+=⇔ =−
f)
2
2x 1−−
Điều kiện
( )
22
2x 1 2x 1 0 x− −=− + <∀
Vậy không tồn tại giá trị x để hàm số có nghĩa
Bài 4. Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
a) Điều kiện của biểu thức là
22
4x 0 x 4 2x 2− ≥ ⇔ ≤ ⇔− ≤ ≤
Vậy điều kiện của biểu thức là
2x2
−≤ ≤
b) Điều kiện của biểu thức là
22
x 16 0 x 16 x 4− ≥⇔ ≥ ⇔≥
hoặc
x4≤−
Vậy điều kiện của biểu thức là
x4≥
hoặc
x4≤−
c) Điều kiện của biểu thức là
22
x 30 x 3 x 3
−≥⇔ ≥⇔ ≥
hoặc
x3≤−
Vậy điều kiện của biểu thức là
x3≥
hoặc
x3≤−
d)
( )(
)
2
x10 x 1
x3
x30 x3
x 2x3 0 x1x3 0
x10 x 1
x1
x30 x3
+ ≥ ≥−

⇔ ⇔≥

−≥ ≥

− −≥⇔ + − ≥⇔
+ ≤ ≤−

⇔ ⇔ ≤−

−≤ ≤

Vậy biểu thức xác định khi
x3≥
hoặc
x1≤−
e) Điều kiện của biểu thức là
(
)
xx 2 0 x 2+ ≥ ⇔ ≤−
hoặc
x0
≥
Vậy điều kiện của biểu thức là
x2≤−
hoặc
x0
≥
f) Điều kiện của biểu thức là
( )( )
2
x 5x60 x2x3 0 x2
− +≥⇔ − − ≥⇔≤
hoặc
x3≥
Vậy điều kiện của biểu thức là
x2≤
hoặc
x3≥
Dạng 2. Tính giá trị biểu thức
Trong các bài toán tính giá trị biểu thức và bài toán rút gọn thường xuất hiện các dạng biểu thức “ẩn” của
các hằng đẳng thức. Để tính toán và giải quyết nhanh bài toán, các em cần biến đổi, và sử dụng thành thạo
các dạng của các hằng đẳng thức đáng nhớ.
Để đơn giản hoá việc nhận dạng và xử lý bài toán, các em có thể tham khảo sơ đồ bên dưới.
Sử dụng hằng đẳng thức trong bài toán chứa căn
Chú ý:
( ) (
)
23
x x x 0; x x x= ≥=
Các hằng đẳng thức đáng
nhớ
Ví dụ minh họa
(
)
2
22
a b a 2ab b
+=++
( )
( )
( )
( )
( )
( )
22
22
22
1.6 25 5 25 1 5 25 1 5 1
2.423 3231 3 231 31 31
3.x2x1 x 2x1 x1
+ = + += + += +
+ = + += + += + = +
+ += + += +
4. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
( )
2
22
a b a 2ab b−=−+
(
)
(
)
( )
(
)
(
)
(
)
(
)
22
2 22
2222
22
22 2
1.6 25 5 25 1 5 25 1 5 1
2. 7 2 10 5 2 5. 2 2 5 2 5. 2 2 5 2
3.x34x5 x54x544
x5 4x544 x52 42
− =− += − += −
−=−+=−+=−
+− − = −− −++
= − − −++= −− +≥
( )( )
22
a b abab−=− +
( ) ( )( )
( ) ( )( )
2
2
2
x 1 x1 x1
x1
1. x 1
x1 x1 x1
2 a 2 a2 a
4a
2. 2 a
2a 2a 2a
− −+
−
= = = −
++ +
− −+
−
= = = +
−− −
( )
( )
33 2 2
a b a b a ab b−=− ++
( )
( )
( ) ( )( )
( )
32
3
2
1.x 27 x 3 x 3x 9
1 a 1 a1 aa
1aa
2. a a a
1a 1a 1a
1aa a1a
−=− ++
− − ++
−
+= += +
−− −
=+ ++ = +
( )
( )
33 2 2
a b a b a ab b+=+ −+
( )
( )
32
1.x 27 x 3 x 3x 9
−=− ++
( )
( )
( )( )
(
)
3
2
xx1
xxx1 x x1x x1
xx
2.
x x1 x x1 x x1 x x1
x x1

+
+ + −+

+

= = =
−+ −+ −+ −+
= +
( )
3
3 2 23
a b a 3a b 3ab b
+=+++
( )
(
)
3
33
3
3
1063 339331 31 31
x1 xx3x3x1
+ = ++ += + = +
+= ++ +
(
)
3
3 2 23
a b a 3a b 3ab b−=− + −
(
)
(
)
3
33
3
3
6310 339331 31 31
x1 xx3x3x1
− = −+ −= − = −
−= −+ −
Bài 1. Thực hiện các phép tính sau:
( ) ( )
( ) ( )
22
26
a) 0,8 0,125 b) 2 c) 3 2 d) 2 2 3−− − − −
Bài 2. Thực hiện các phép tính sau:
( ) ( ) (
) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
22 22
22 22
2 2 22
a) 3 22 3 22 b) 5 26 5 26
c) 2 3 1 3 d) 3 2 1 2
e) 5 2 5 2 f ) 2 1 2 5
− ++ − −+
− +− + −−
− + + +− −
Bài 3. Thực hiện các phép tính sau:
5. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
a) 5 2 6 5 2 6 b) 7 2 10 7 2 10 c) 4 2 3 4 2 3
d) 24 8 5 9 4 5 e) 17 12 2 9 4 2 f ) 6 4 2 22 12 2
+ −− − −+ − ++
+ +− − ++ − + −
Bài 4. Thực hiện các phép tính sau:
( )
22
8 43 4 23
a) 3 2 5 2 6 b)
6 2 13
c) 5 9 29 12 5 d) 13 30 2 9 4 2

−+
−+ −


−+

−− − + ++
Lời giải
Bài 1:
a) Biến đổi biểu thức
(
)
2
0,8 0,125 0,8 0,125 0,8.0,125 0,1− − =−− =− =−
Vậy biểu thức có giá trị là: -0,1
b) Biến đổi biểu thức
(
)
( )
63
2 2 88− =− =−=
Vậy biểu thức có giá trị là: 8
c) Biến đổi biểu thức:
( )
2
32 32 2 3
− = −=−
vì
320
−<
Vậy biểu thức có giá trị là
23
−
d) Biến đổi biểu thức
( )
2
22 3 22 3 3 22− = −=−
vì
3223 8 9 80− =−=−>
Vậy biểu thức có giá trị là
3 22−
Bài 2:
a) Biến đổi biểu thức:
( )
( )
22
3 22 3 22 3 22 3 22 3 22 3 22 6− + + = − + + =− ++ =
(vì
3 2 2 0)−>
Vậy biểu thức có giá trị là: 6
b) Biến đổi biểu thức
( )
( )
( )
( )
22
5 26 5 26 5 26 5 26 5 26 5 26 46− − + =− −+ = − − + =−
(vì
5 2 6 0)−>
Vậy biểu thức có giá trị là:
46
−
c) Biến đổi biểu thức
( )
( )
22
23 13 231323311− + − = − +− = − + −=
(Vì
2 3 0;1 3 0)−>−<
Vậy biểu thức có giá trị là: 1
d) Biến đổi biểu thức
( )
( )
(
)
22
32 12 321232 214+ − − = + −− =+ − − =
(vì
3 2 0;1 2 0)+>−<
Vậy biểu thức có giá trị là: 4
e) Biến đổi biểu thức
( )
( )
22
52 52 52 52 525225− + + = − + + =−++=
vì
5 20;5 20−> +>
6. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy biểu thức có giá trị là:
25
f) Biến đổi biểu thức
(
)
(
)
(
)
22
21 25 21 25 21 5 2 224
+ − − = + − − = +− − = −
(Vì
2 1 0; 2 5 0+> −<
)
Vậy biểu thức có giá trị là
22 4−
Bài 3:
a) 5 26 5 26
+ −−
Ta có:
( )
( )
22
5 26 3 232 2 3 2 ;5 26 3 23.2 2 3 2+ =+ += + − =− += −
Nên
( ) ( ) (
)
( )
22
526526 32 32 32 32 32 32+ −− = + − − = + − − = + − −
22=
vì
3 20;3 20+> −>
Vậy biểu thức có giá trị là
22
b)
7 2 10 7 2 10− −+
Ta có:
( ) ( )
22
7 2 10 5 2 5. 2 2 5 2 ; 7 2 10 5 2 5. 2 2 5 2− =− += − + =+ += +
Nên
( )
( )
( )
( )
22
72107210 52 52 52 52 52 52 22
− −+ = − − + = − − + = − − + =−
vì
5 20;5 20−> +>
Vậy biểu thức có giá trị là
22−
c) Biến đổi biểu thức
( )
(
)
2
3. 3 1
33
423 31 31 31 31 31 23
33
+
+
− + = − + = −+ += −+ +=
Vậy biểu thức có giá trị
23
d) Biến đổi biểu thức
( )
( )
(
)
( )
( )
22
2
22
24 85 9 45 46 25 9 45 45 25 1 5 45 4
4 5 25 1 5 25.2 2
4 51 52
251 52
25 2 5 2 35
+ +− = + +− = + ++− +
= + ++ − +
= ++ −
= ++ −
= ++ −=
Vậy biểu thức có giá trị
35
e) Biến đổi biểu thức
7. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
(
) ( )
( ) ( )
22
22
22
17 12 2 9 4 2
9122 8 8 42 1
3 2.3.2 2 2 2 2 2 2.2 2 1
3 22 22 1
3 22 22 1
3 22 22 1 4
− ++
= − ++ + +
=− + + ++
=−+ +
=−++
=− + +=
Vậy biểu thức có giá trị là 4
f) Biến đổi biểu thức
(
)
(
) ( )
2
2
22
22
6 4 2 22 12 2
4 4 2 2 18 12 2 4
2 2.2 2 2 3 2 2.3. 2.2 2
2 2 32 2
2 2 32 2
2 2 32 2 22
− +−
= − ++ − +
=− ++ − +
=−+ −
=−+ −
=− + −=
Vậy biểu thức có giá trị
22
Bài 4.
a) Biến đổi biểu thức
( )
( ) ( )
( )
( )
( )
( ) ( )
2
22
3 2 5 26
32 32
3 23 2
3232
3 2 321
−+
=−+
=−+
=−+
= − =−=
b) Ta có:
( )
(
)
2
31
4 23
31
31 31
−
−
= = −
−−
và
( )
( )
2
31
4 23
31
13 13
+
+
= = +
++
Suy ra
( ) ( ) ( ) ( )
22
22
4 23 4 23
3 1 3 1 4 23 4 23 43
31 1 3

−+
− = − − + =− −+ =−


−+

Vậy biểu thức có giá trị
43−
c) Biến đổi biểu thức
8. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
( )
( )
( ) (
)
2
2
5 9 29 12 5
5 9 20 12 5 9 5 9 2 5 3
5 9 25 3 5 6 25
5 51 5 51 11
−− −
= −− − += −− +
= −− += −−
= − − = − −= =
Vậy biểu thức có giá trị 1
d) Biến đổi biểu thức
( ) ( )
( )
( )
( )
2
2
2
13 30 2 9 4 2
13 30 2 2 2 1 13 30 2 2 2 1
13 30 3 2 2 13 30 2 1
13 30 2 1 43 30 2
25 2.5.3 2 18 5 3 2 5 3 2
+ ++
=++ +=+++
=++=+ +
= + += +
= + += + =+
Vậy biểu thức có giá trị
5 32+
Dạng 3. Rút gọn biểu thức
Bài 1. Rút gọn các biểu thức sau:
(
)
( )
( )
( )
2 22
22
a)x 3 x 6x 9 x 3 b) x 4x 4 x 2 x 0
x 2x 1 x 4x 4
c) x 1 d) x 2 x 2
x1 x2
++−+≤ ++− −≤≤
−+ −+
> −+ <
−−
Bài 2. Rút gọn các biểu thức sau:
( )
2 22
2
2 42
42
2
2
2
a) 1 4a 4a 2a b)x 2y x 4xy 4y
x 10x 25
c)x x 8x 16 d)2x 1
x5
x 4x 4 x 4
e) f ) x 4
x2
x 8x 16
−+ − −− − +
−+
+ − + −−
−
−+ −
−+
−
−+
Bài 3. Cho biểu thức
22 22
A x 2x 1 x 2x 1= + −− − −
a) Với giá trị nào của x thì A có nghĩa?
b) Tính A nếu
x2
≥
Bài 4. Cho 3 số dương x,y,z thỏa điều kiện
xy yz xz 1++=
Tính
( )( ) ( )( ) ( )( )
22 2 2 2 2
222
1y 1z 1z 1x 1x 1y
Ax y z
1x 1y 1z
++ ++ ++
=++
+++
Lời giải
Bài 1.
9. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
( )
( )
2
2
a)x3 x 6x9x3
x3 x3 x3 x3
++−+≤
= ++ − = ++ −
(vì
x3≤
nên
(
)
x3 x3
−=− −
)
( )
x3 x3 6= +− − =
( )
( )
22
2
2
b) x 4x 4 x 2 x 0
x2 x x2 x
+ + − −≤ ≤
= + + =++
vì
x2≥−
nên
x2 x2
+=+
và
x0≤
nên
xx= −
x2x 2
=+−=
( )
( )
2
2
x 2x 1
c) x 1
x1
x1
x1
x1
1
x1 x1 x1
−+
>
−
−
−
−
= = = =
− −−
Vì
x1>
nên
x1 x1−=−
d)
( )
2
2
x2
x 4x 4
x2 x2
x2 x2
−
−+
−+ =−+
−−
vì x < 2 nên
( )
x2 x2
−=− −
Biểu thức
(
)
( )
x2
x2
x2 x2 x21 x1
x2 x2
−
−−
= − + =− − + =−+−=−+
−−
Bài 2.
a) Biến đổi biểu thức
( )
2
2
1 4a 4a 2a 1 2a 2a 1 2a 2a−+ −= − −=−−
Với
1
a
2
≤
thì
1 2a 0−≥
nên
1 2a 1 2a−=−
ta có:
2
1 4a 4a 2a 1 2a 2a 1 2a 2a 1 4a−+ −=−−=−−=−
Với
1
a
2
≥
thì
1 2a 0
−≤
nên
1 2a 2a 1−=−
ta có:
2
1 4a 4a 2a 1 2a 2a 2a 1 2a 1−+ −=−−=−−=−
b) Biến đổi biểu thức
( )
2
22
x 2y x 4xy 4y x 2y x 2y x 2y x 2y−− − + =−− − =−−−
Với
x 2y 0−≤
thì
( )
x 2y x 2y− =−−
ta có
( )
22
x 2y x 4xy 4y x 2y x 2y x 2y x 2y 2x 4y−− − + =−−− =−+− =−
Với
x 2y 0−≥
thì
x 2y x 2y−=−
ta có
( )
22
x 2y x 4xy 4y x 2y x 2y x 2y x 2y 0−− − + =−−− =−−− =
c)
( )
2
2 4 2 2 2 22
x x8x16x x4 x x4+ − +=+ − =+−
với
22
x 40 x 4 2x2− ≤ ⇔ ≤ ⇔− ≤ ≤
thì
( )
22
x4 x4−=− −
ta có:
( )
2 4 2 22 2 2
x x8x16x x4x x44+ − + = + −= − − =
10. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Với
22
x40x4x2− ≥ ⇔ ≥ ⇔ ≤−
hoặc
x2≥
thì
22
x4x4−= −
ta có:
( )
2 4 2 22 2 2 2
x x8x16x x4x x42x4+ − + = + −= + − = −
d)
( )
2
2
x5
x5
x 10x 25
2x 1 2x 1 2x 1
x5 x5 x5
−
−
−+
−− = −− = −−
− −−
Với
x50 x 5−≤⇔ ≤
thì
( )
x5 x5−=− −
ta có:
2
x5
x 10x 25 x 5
2x 1 2x 1 2x 1 2x
x5 x5 x5
−
−+ −
−− = −− = −+ =
− −−
Với
x50 x 5−≥⇔ ≥
thì
( )
x5 x5−= −
ta có:
2
x5
x 10x 25 x 5
2x 1 2x 1 2x 1 2x 2
x5 x5 x5
−
−+ −
−− = −− = −− = −
− −−
Bài 3. Biểu thức
22 22
A x 2x 1 x 2x 1
= + −− − −
a) Biểu thức xác định khi
22
x 10 x 1 x 1− ≥ ⇔ ≥ ⇔ ≤−
hoặc
x1≥
b) Tính A với
x2≥
( ) ( )
(
)
(
)
22 22
22 22
22
22
22
A x 2x 1 x 2x 1
x12x11 x12x11
x11 x11
x11 x11
= + −− − −
= − + −+− − − −+
= −+ − −−
= −++ −−
Với
x2≥
thì
22 2 2
x 2 x11 x11 x110≥ ⇔ −≥⇒ −≥⇔ −−≥
Vậy
2 2 22 2
A x11 x11 x11 x112x1= −++ −− = −++ −−= −
Bài 4. Cho 3 số dương x,y,z thỏa điều kiện: xy + yz + zx = 1.
Tính
( )( )
( )
( )
( )( )
22 2 2 2 2
222
1y 1z 1z 1x 1x 1y
Ax y z
1x 1y 1z
++ ++ ++
=++
+++
Ta có:
( ) ( ) ( ) ( )( )
2 22
1 y xy yz xz y xy y yz zx y x y z y x x y y z+= ++ +=+++= ++ +=+ +
Tương tự
( )( )
2
1z yzzx+=+ +
( )( )
2
1x zx xy+=+ +
Suy ra
( )( )
( )( )( )( )
( )( )
( ) ( )
22
2
2
1y 1z
xyyzxzyz
*x x x yz xyz
1x x yxz
++
++++
= = += +
+ ++
( )(
)
( )( )
( )( )
( )( )
( ) (
)
22
2
2
1z 1x
zxyzxzxy
*y y y xz yxz
1y xyyz
++
++++
= = += +
+ ++
( )( )
( )
( )( )( )
( )( )
( )
( )
22
2
2
1x 1y
xyxzxyyz
*z z zxy zxy
1z xz yz
++
++++
= = +=+
+ ++
11. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy
( ) ( ) ( ) ( )
A x y z y x z z x y 2 xy yz xz 2= ++ ++ + = ++ =
Dạng 4. Giải phương trình
Để đơn giản hoá việc nhận dạng và xử lý bài toán, các em có thể tham khảo sơ đồ bên dưới.
Một số dạng phương trình cơ bản
Dạng toán
Ví dụ minh họa
22
AB A B= ⇔=±
2 22
1.x4x2 x2=⇔ = ⇔=
hoặc
x2= −
( )
( )
2
2
x1x 0x1PTVN
2. x 1 x
1
x 1 x 2x 1 x
2
−= ⇔ =
−=⇔
−=−⇔ =⇔ =
Vậy phương trình có nghiệm là
1
x
2
=
( )
A 0 hay B 0
AB
AB
≥≥
= ⇔
=
x3
3x 0
2x 5 3 x
2
2x 5 3 x
x
3
≤
−≥
+= −⇔ ⇔
−

+=−
=
(thỏa)
2
B0
AB
AB
≥
= ⇔
=
Nếu B < 0 thì phương trình vô nghiệm
( )
2
2
22
2
x10
x1
1x x1
1 x x 2x 1
1x x1
−≥
≥
− = −⇔ ⇔

−=−+
−=−
( )
( )
( )
2
x1
x1
x1
x 0 loai
2x x 1 0
2x 2x 0
x 1 TM
≥
≥
≥
=
⇔⇔ ⇔

−=
−=
=
Vậy nghiệm của phương trình là
x1=
B0
AB
AB
AB
≥
= ⇔
=
= −
x1
2 3x 5
2 3x 5
7
2 3x 5
x
3
= −
−=
−=⇔ ⇔
−=−
=
Vậy tập nghiệm của phương trình là
7
S 1;
3

= −


2
11
x x 2x x 2x
42
++ = ⇔ + =
( )
( )
x0
2x 0
1
1
x TM
x 2x
2
2
1
1
x loai
x 2x
6
2
≥
≥
=
+=
⇔⇔



= −
+=−
Vậy tập nghiệm của phương trình
1
x
2
=
A B A B hay A B= ⇔= =−
3x 1 x 3
3x 1 x 3
3x 1 x 3
+= +
+= +⇔
+=−−
2x 2 x 1
4x4 x1
= =

⇔⇔

=−=−

Vậy tập nghiệm của phương trình
{ }
S 1; 1= −
12. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
A0
AB0
B0
=
+=⇔
=
2
2
x5
x50
x 5 x 25 0 x 5
x5
x 25 0
x5
= −
+=
++ − =⇔ ⇔ ⇔=−
=

−=
= −
Vậy nghiệm của phương trình:
x5= −
A0
A B0
B0
=
+=⇔
=
2
1x x1 0− + +=
22
x1
1x 0 x 1
x1
x1
x10 x 1
= ±

−= =
⇔ ⇔⇔⇔=−

= −
+= =−

Vậy nghiệm của phương trình: x = -1
Bài 1. Giải các phương trình sau:
( )
2
2
2
a) x 3 3 x b) 4x 20x 25 2x 5
c) 1 12x 36x 5 d) x 2 x 1 2
− =− − ++=
− + = + −=
Bài 2. Giải các phương trình sau:
2
2
a) 2x 5 1 x b) x x 3 x
c) 2x 3 4x 3 d) 2x 1 x 1
+= − −= −
−= − −= −
Bài 3. Giải các phương trình sau:
22
2 22
a)x x x b)1x x1
c) x 4x 3 x 2 d) x 1 x 1 0
+= − =−
− + = − −− +=
Bài 4. Giải các phương trình sau:
22 2
42 2
a) x 2x 1 x 1 b) 4x 4x 1 x 1
1
c) x 2x 1 x 1 d) x x x
4
− += − − += −
− += − ++ =
Bài 5. Giải các phương trình sau:
2
2 2 22
a)3x1 x1 b)x 3 x 3
c) 9x 12x 4 x d) x 4 x 4x 4 0
+= + −= −
− += −+ + +=
Lời giải
Bài 1. Giải các phương trình sau:
( )
2
a) x3 3x x3 3x
3x0 x3 x3
x3
x 3 3 x 2x 6 x 3
x 3 x 3 0x 0 0x 0
− =−⇔ −=−
−≥ ≤ ≤


⇔ ⇔ ⇔ ⇔≤
−=− = =




−=− = =


Vậy tập nghiệm của PT là
x3≤
( )
2
2
b) 4x 20x 25 2x 5 2x 5 5 2x
− ++=⇔ − =−
13. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
( )
5
x
2
5 2x 0
5
5
x TM
2x 5 5 2x x
2x 5 5 2x
2
2
2x 5 2x 5
5
0x 0 dung x
2
≤
−≥

=
⇔ −=− ⇔ ⇔ ⇔≤
−=−


−= −

= ∀≤


Vậy tập nghiệm của PT là
5
x
2
≤
c) Biến đổi biểu thức
2
1 12x 36x 5−+ =
( )
2
1 6x 5 1 6x 5
2
1 6x 5
x
3
1 6x 5
x1
⇔ − =⇔− =
−=
= −
⇔⇔
−=−
=
Vậy tập nghiệm của phương trình là
2
S ;1
3

= −


d)
x 2x1 2+ −=
ĐK:
x1≥
Biến đổi biểu thức
x 2x1 2 x12x11 2+−=⇔−+−+=
( )
( )
( )
2
x11 2 x11 2
x1 3
x11 2
x 1 1 PTVN
x11 2
x 1 9 x 10 TM
⇔ −− = ⇔ −− =
−=
−−=
⇔⇔
−=−
−−=−
⇔ −= ⇔ =
Vậy nghiệm của phương trình là x = 10
Bài 2.
a) Biến đổi biểu thức
x1
1x 0 x 1
4
2x 5 1 x x
4
2x 5 1 x 3x 4
3
x
3
≤
−≥ ≤

+= −⇔ ⇔ ⇔ ⇔=−

+=− =−
= −

Vậy nghiệm của PT là
4
x
3
= −
b) Biến đổi biểu thức
(
)
(
)
2
22
x3
3x 0 x 3
x 3 TM
x x 3x
x x 3x x 3
x 3 TM
≤
−≥ ≤

=
−= −⇔ ⇔ ⇔

−=− =

= −
Vậy tập nghiệm của phương trình là
{ }
S 3; 3= −
c) Biến đổi biểu thức
( )
( )
2
2
2
3
x
3
4
4x 3 0
x
2x 3 4x 3
4
x 0 k TM
2x 3 4x 3
2x 4x 0
x 2 TM
≥
−≥
≥

−= −⇔ ⇔ ⇔

=
−= −

−=
=
Vậy nghiệm của phương trình là x = 2
14. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
d)
( )
x1
x10
2x1 x1
x 0 kTM
2x1 x1
≥
−≥
−= −⇔ ⇔

=
−= −
Vậy phương trình vô nghiệm
Bài 3.
a) Biến đổi biểu thức
2
22
x0
x0
x xx x0
x0
x xx
≥
≥
+=⇔ ⇔ ⇔=

=
+=
Vậy nghiệm của phương trình là x = 0
b) Biến đổi biểu thức
( ) ( )
2
22
22
x10 x1
1x x1
1x x1 x1 x 10
−≥ ≥


− = −⇔ ⇔

− = − − + −=


( ) ( )( )
( ) ( ) ( )
( )
( )
( )
2
x1
x1
x1 x1 x1 0
x1 x1x1 0
x1
x1
x 0 kTM
x1
x 1 2x 0
x 1 TM
≥
≥

⇔⇔

− −+ + =

− + − +=

≥
≥
=
⇔ ⇔ ⇔=

−=
=
Vậy nghiệm của phương trình là x = 1
c) Biến đổi biểu thức
( )
(
)
2
2
22
2
x20
x2
x2
x 4x 3 x 2 PTVN
0x 1
x 4x 3 x 4x 4
x 4x 3 x 2
−≥
≥
≥
− +=−⇔ ⇔ ⇔

=
−+=−+
− += −
Vậy phương trình vô nghiệm
d) Biến đổi biểu thức
( )
2
22 2 2
2
22
x 10
x1x10 x1x1
x1x1
−≥
−− += ⇔ −= −⇔
−= −
( )
( )
( )
( )
2
22
22
x1
x1
x1
x11x1 0
x 12x 0
≥
≥
≤−
⇔⇔


− − −=


− −=
( )
22
22
x1 x1
x1
x1 x1
x1
x1
x 10 x 1
TM
x2
2x 0 x 2
≥ ≥
≥



≤− ≤−
≤−


⇔ ⇔⇔

= ±

−= =



= ±
−= =


{ }
x 2 ; 1; 1; 2⇔=− −
Vậy tập nghiệm của phương trình là
{ }
x 2 ; 1; 1; 2=−−
Bài 4. Giải các phương trình sau:
a) Biến đổi biểu thức
22
x 2x 1 x 1− += −
( )
2
22
x1 x 1 x1 x 1⇔ − = −⇔ − = −
15. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
(
)
( )( )
( )
( )( )
( )
( )
( )
( )
2
2
2
2
2
x1
x1
x1
x 10
x1
x1
x 0 KTM
x1 x 1
x x0
x x 1 0 x 1 TM
x1 x 1 x1 x1x1 0
x1x2 0 x1TM
x 2 TM
≥
≤−
≥
−≥
≥
≤−
=

−= −
⇔⇔ ⇔ ⇔
−=

−= =

−=− − −+ − + =

− += =
= −
Vậy tập nghiệm của phương trình là
{ }
S 2;1= −
b, Biến đổi biểu thức
2
4x 4x 1 x 1− += −
( )
(
)
( )
( )
2
2x1 x1 2x1 x1
x1
x10
x1
x 0 KTM
2x1 x1
x0
2
2x1 x1
3x 2 0
x KTM
3
⇔ − = −⇔ − = −
≥
−≥
≥
=

−= −
⇔ ⇔⇔
=


−=− −
−=
=
Vậy phương trình vô nghiệm
c) Biến đổi biểu thức
42
x 2x 1 x 1− += −
(
)
( )
( )
( )
( )
( )
( )
( )
(
)
( )(
)
(
)
( )
2
22
2
2
2
2
x 1 x1 x 1 x1
x1
x10
x x0
x 1 x1
x 1 x1 0
x 1 x1
x1 x1
xx 1 0 xx 1 0
x1x1 x1 0 x1x 2 0
x1
x 0 KTM
x1
x1
x1
x 2 KTM
⇔ − = −⇔ − = −
≥
−≥
−=
−= −
⇔⇔


−+ −=
−=− −
≥≥


−= −=

⇔⇔



− ++−= − +=



≥
=
⇔
=
⇔=
=
= −
Vậy tập nghiệm của phương trình là x = 1
d) Biến đổi biểu thức
2
1
xx x
4
++ =
16. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
( )
(
)
2
11
x xx x
22
x0 x0 x0
1 11
x x 0x 0x PTVN
2 22
1 11
x x 2x x KTM
2 24

⇔ + =⇔+=


≥ ≥≥




+= =− =−

⇔ ⇔⇔





+=− =− =−



Vậy phương trình vô nghiệm
Bài 5. Giải các phương trình sau:
a) Biến đổi biểu thức
3x1 x1+= +
( )
x0
3x1x1
2x 0
1
3x1 x1
4x 2
x
2
=
+= +
=
⇔ ⇔⇔
+=− +
= −
= −
Vậy tập nghiệm của phương trình là
1
S ;0
2

= −


b) Biến đổi biểu thức
( )
2
2
2
x 3x 3
x3x 3
x3 x 3
−=−
−=− ⇔
−=− −
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
x3x3 x30
x3x3 x30
x 3 x 31 0
x 3 x 31 0
x 30
x 310
x 30
x 310
x3
x1 3
x3
x 13
− + −− =
⇔
− + +− =
− + −=
⇔
− + +=
−=
+ −=
⇔
−=
+ +=
=
= −
⇔
=
=−−
Vậy tập nghiệm của phương trình là
{ }
S 1 3;1 3; 3=−− −
c) Biến đổi biểu thức
22
9x 12x 4 x− +=
( )
2
2
3x 2 x 3x 2 x
x1
3x 2 x 2x 2
1
3x 2 x 4x 2
x
2
⇔ − = ⇔ −=
=
−= =

⇔ ⇔⇔

−=− =
=

17. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy tập nghiệm của phương trình là
1
S ;1
2

=


d) Biến đổi biểu thức
22
x 4 x 4x 4 0−+ + +=
( )( )
( )
2
2
2
x20 x 2
x2x2 0
x 40
x2
x20 x 2
x 4x 4 0
x2 0
x20 x 2
−= =

− +=
−=


⇔ ⇔ ⇔ ⇔ ⇔=−
+= =−


+ +=
+=

+= =−

Vậy nghiệm của phương trình là x = -2
Bài 5. Giải các phương trình sau
a)
22 2
6 9 70xx x− ++ −=
;
b)
2 4 62 5 2 4 22 5 4x xx x
+− −+ −+ − =
.
Lời giải
a)
( )
2
22 2
6 9 70 3 70xx x x x− ++ −=⇔ − + −=
3 70xx⇔ −+ −=
Trường hợp 1: Xét
3x ≥
phương trình có dạng:
3 70 5 5xx x x
−+ − = ⇔ =⇔ =±
.
Trường hợp 2: Xét
03x≤<
phương trình có nghiệm:
3 70xx− + −=
vô nghiệm.
Vậy tập nghiệm của phương trình là
{ }
5; 5
S = −
.
b)
2 4 62 5 2 4 22 5 4
x xx x
+− −+ −+ − =
256259 2522514xx xx
⇔ −− −++ −+ −+=
( ) ( )
22
253 251 4xx⇔ −− + −+ =
253 2514xx⇔ −−+ −+=
Ta có:
2533 253 25x xx−−=−−≥−−
Vậy vế trái
3 2 5 2 514
xx
≥− − + + +=
.
Do vậy vế trái bằng vế phải khi:
5
2530259 7
2
x xx−≤⇔≤ −≤⇔ ≤≤
.
Vậy tập nghiệm của phương trình là:
5
/7
2
Sx x

= ≤≤


.
Dạng 6.Nâng cao
Bài 1: Rút gọn biểu thức sau:
a)
6 25 6 25A =+ −−
; b)
2
1 21Ba a a= +− − +
với
1a <
Bài 2: Tìm giá trị nhỏ nhất của biểu thức sau:
a)
2
3 2 8 33A xx=+ −+
; b)
2
8 18 1Bxx= −+−
;
c)
22 2
2 2 2 10 2 8 2020C x y xy x y y y= +− +−++ −+
.
Bài 3: Tìm giá trị nhỏ nhất của biểu thức:
18. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
a)
22
12 36 16 64Axx xx= −++ −+
b)
( ) ( ) ( )
22 2
2 9 1945Bx x x=−+−+−
.
Bài 4. Cho
,,abc
là các số hữu tỉ thỏa mãn
2020ab bc ca++=
. Chứng minh rằng biểu thức
( )( )
22
2
2020 2020
2020
ab
A
c
++
=
+
là một số hữu tỉ.
Bài 5. Cho
,,abc
là các số thực thỏa mãn
22
2ab
+=
.Chứng minh rằng:
( )
42 4 2
8 8 61ab ba++ +=
Bài 6. Tìm giá trị nhỏ nhất của biểu thức:
a)
( ) ( )
22
2019 2020Ax x=− +−
;
b)
( ) ( )
(
)
222
2018 2019 2020Bx y x=− +− +−
;
c)
(
)
(
)
( )
( )
2222
2017 2018 2019 2020Cx x x x
=− +− +− +−
.
Bài 7. Tìm giá trị nhỏ nhất của:
3 4 1 15 8 1Aa a a a= +− −+ + − −
.
Bài 8. Cho
,
xy
thỏa mãn
0 1, 0 1xy<< <<
và
1
11
xy
xy
+=
−−
.Tính giá trị của biểu thức
22
P x y x xy y
=++ − +
.
Bài 9. Tính
x
y
biết
1; 0
xy><
và
( )
(
)
( )
( )
( )
2
33
22 3 4
1 41
6
1 41
xyx y x
x x y xy y
+ − −−
= −
− − ++
Lời giải
Bài 1: Rút gọn biểu thức sau:
a)
6 25 6 25A =+ −−
; b)
2
1 21Ba a a= +− − +
với
1a <
Lời giải
a) Ta có
6 25 6 25A =+ −−
5 25 1 5 25 1
A = + +− − +
( ) ( )
22
51 51A = +− −
( )
( )
51 51 2A = +− −=
.
b)
2
1 21Ba a a= +− − +
với
1a
<
( )
2
11Ba a= +− −
( )
1 1 11 2Ba a a a a= +− − = +− − =
.
Bài 2: Tìm giá trị nhỏ nhất của biểu thức sau:
a)
2
3 2 8 33A xx=+ −+
; b)
2
8 18 1Bxx
= −+−
;
c)
22 2
2 2 2 10 2 8 2020C x y xy x y y y= +− +−++ −+
.
Lời giải
a) Ta có:
( )
2
2
3 2 8 33 3 2 2 25 3 25 8A xx x=+ − + =+ − + ≥+ =
.
Vậy giá trị nhỏ nhất của biểu thức A là 8 khi
2x =
.
19. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
b) Ta có:
( )
2
2
8 181 4 21 21Bxx x= −+−= − +−≥ −
Vậy giá trị nhỏ nhất của biểu thức B là
21−
khi
4x =
.
c) Ta có:
22 2
2 2 2 10 2 8 2020C x y xy x y y y= +− +−++ −+
( ) ( )
22
1 9 2 2 2012C xy y⇒ = −+ ++ − +
9 2012 2015C⇒≥ + =
.
Vậy giá trị nhỏ nhất của C là 2015.
Khi
10 1
20 2
xy x
yy
− += =

⇔

−= =

.
Bài 3: Tìm giá trị nhỏ nhất của biểu thức:
a)
22
12 36 16 64Axx xx= −++ −+
b)
( ) ( ) ( )
22 2
2 9 1945Bx x x=−+−+−
.
Lời giải
a) Ta có:
( ) ( )
22
22
12 36 16 64 6 8Axx xx x x= −++ −+= −+ −
6 8 6 8 68 2
Ax x x x x x
=−+−=−+−≥−+−=
Vậy giá trị nhỏ nhất của A là 2 khi
( )( )
68 0xx− −≥
hay
68x≤≤
.
b) Ta có:
( ) ( ) ( )
22 2
2 9 1945Bx x x=−+−+−
2 9 1945Bx x x=−+−+−
2 1945 9 2 1945 0 1943Bx xx x x=−+ −+−≥−+ −+=
.
Vậy giá trị nhỏ nhất của B là 1943 khi
( )(
)
2 1945 0xx− −≥
và
90x −=
tức là
9
x =
.
Bài 4. Cho
,,
abc
là các số hữu tỉ thỏa mãn
2020ab bc ca++=
. Chứng minh rằng biểu thức
( )( )
22
2
2020 2020
2020
ab
A
c
++
=
+
là một số hữu tỉ.
Lời giải
• Ta có:
22
2020
a a ab bc ca+ =+++
( )
( ) ( )
2
2020 1a abac⇒+ =+ +
• Tương tự, ta có:
( )
( )
( )
2
2020 2
b babc+ =++
( )( ) ( )
2
2020 3c cacb+ =++
Từ (1) ,(2), (3) suy ra
( )( )( )( )
( )( )
( )
2
abacbcba
A ab ab
cacb
++++
= = +=+
++
A ab⇒=+
.
Vì a, b là các số hữu tỉ nên
ab+
cũng là số hữu tỉ. Vậy A là một số hữu tỉ.
Lưu ý: Các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa của các số hữu tỉ có kết quả cũng là một số
hữu tỉ.
Bài 5. Cho
,,abc
là các số thực thỏa mãn
22
2ab+=
20. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Chứng minh rằng:
( )
42 4 2
8 8 61
ab ba++ +=
Lời giải
Cách 1. Thay
22
2ab+=
vào (1) ta có:
Vế trái:
(
)
( )
4 22 2 4 22 2
44a bab b aab+ ++ + +
4222 4224
44 44
a ab b b ab a=+++++
( ) ( )
22
22 22 2222
2 2 22ab ba abba= + + + =+ ++
( )
22
3 3.2 6ab= +==
.
Vế trái bằng vế phải. Suy ra điều phải chứng minh.
Cách 2. Từ giả thiết suy ra:
2 22 2
2; 2
b aa b
=−=−
thay vào (1) ta được:
(
)
(
)
( )
( )
22
4 24 2 2 2
82 82 4 4
a ab b a b+−+ +−= −+ −
22
44ab= −+ −
(do
22
4; 4ab<<
)
22
446
ab=− +− =
. Vế trái bằng vế phải. Suy ra điều phải chứng minh.
Bài 6. Tìm giá trị nhỏ nhất của biểu thức:
a)
( )
( )
22
2019 2020
Ax x=− +−
;
b)
(
)
(
)
( )
222
2018 2019 2020Bx y x=− +− +−
;
c)
( ) ( ) ( ) ( )
2222
2017 2018 2019 2020Cx x x x=− +− +− +−
.
Lời giải
a)
2019 2020Ax x=− +−
2019 2020 2019 2020 1x xx x= − + −≥− + −=
Vậy giá trị nhỏ nhất của A là 1 khi
2019 0x −≥
và
2020 0x−≥
hay
2019 2020x≤≤
.
b) Giá trị nhỏ nhất của B là 2 khi
2018 2020
x≤≤
và
2019y =
.
c) Giá trị nhỏ nhất của C là 4 khi
2018 2019x≤≤
.
Bài 7. Tìm giá trị nhỏ nhất của:
3 4 1 15 8 1
Aa a a a= +− −+ + − −
.
Lời giải
Ta có:
1 4 1 4 1 8 1 16Aa a a a= −− −+ + −− −+
( ) ( )
22
12 14Aa a⇔ = −− + −−
12 4 1 124 1Aa a a a
⇒ = −− + − − ≥ −−+− −
2A⇒≥
.
Đẳng thức xảy ra khi
2 1 4 4 1 16aa≤ −≤ ⇔ ≤ −≤
.
Vậy giá trị nhỏ nhất của A là 2 khi
5 17a≤≤
.
Bài 8. Cho
,xy
thỏa mãn
0 1, 0 1xy<< <<
và
1
11
xy
xy
+=
−−
.
21. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Tính giá trị của biểu thức
22
P x y x xy y=++ − +
.
Lời giải
Từ giả thiết, suy ra:
(
) ( ) ( )( )
1 1 11x yy x x y
−+ −=− −
(
) ( ) ( )
22
22
2 2 13 2 1 1x y xy x xyy xy xy xy
⇔ + −= ⇔ − + = + − + += + −
Vậy
22
1Pxy x xyy xyxy=++ − + =+++−
Từ giả thiết, ta lại có:
1
1
12
x
x
x
<⇒ <
−
Tương tự ta có:
1
2
y <
. Suy ra
01xy
<+<
, ta có
11
Pxy xy
= + +− − =
.
Bài 9. Tính
x
y
biết
1; 0xy><
và
( )
( )
( )
( )
( )
2
33
22 3 4
1 41
6
1 41
xyx y x
x x y xy y
+ − −−
= −
− − ++
Lời giải
Ta có: Với
14 4413 410 3xx x x>⇒ > ⇒ −> ⇒ − >
Do đó
( )
2
1 41 411xx− − = −−
Từ đó
(
)
(
)
(
)
( )
( )
33
22 3 4
4 11
6
1 41
xyx y x
x x y xy y
+ − −−
= −
− − ++
(
)
(
)
( )(
)
(
)
( )
33 2 2
22 3 4
22 2
66
xyx y xyxyx xyy
x y xy y
y x xy y
+ − + − ++
⇔=⇔ =
++
++
22 2 2 2
67 7
x
xyyxy
y
⇔−= ⇔= ⇔ =
Mà
1; 0xy><
nên
7
x
y
= −
.
22. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
II. TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Cho số thực
0a
. Số nào sau đây là căn bậc hai số học của
a
?
A.
a
. B.
a
. C.
2
a
. D.
2 a
.
Câu 2. Số nào sau đây là căn bậc hai số học của số
0.36a
?
A.
0, 6
. B.
0, 6
. C.
0, 9
. D.
0, 18
.
Câu 3. Khẳng định nào sau đây sai?
A.
2
0A A khi A
. B.
2
0A A khi A

.
C.
0A B AB 
. D.
0AB A B 
.
Câu 3. Biểu thức
10 100x
có nghĩa khi
A.
10x
. B.
1
10
x 
. C.
1
10
x
. D.
10
x
.
Câu 4. So sánh hai số
5
và
50 2
A.
5 50 2
. B.
5 50 2

. C.
5 50 2
. D. Chưa đủ điều kiện so sánh.
Câu 5. Tìm các số
x
không âm thỏa mãn
5 10x
A.
0 20x
. B.
20x
. C.
0
x
. D.
2x
.
Câu 6. Tìm giá trị biểu thức
22
23 13 
.
A.
3
. B.
1
. C.
23
. D.
2
.
Câu 8. Tính giá trị biểu thức
2
2
8
9 ( 0, 8)
3



.
A.
24,64
. B.
32
. C.
24, 8
. D.
24, 8
.
Câu 9. Tính giá trị biểu thức
22
6 ( 2, 5) 8 ( 0, 5) 
.
A.
15
. B.
11
. C.
11
. D.
13
.
Câu 10. Tìm điều kiện xác định của
125 5x
A.
15x
. B.
25x
. C.
25x
. D.
0x
.
Câu 11. Tìm điều kiện xác định của
53x
A.
5
3
x
. B.
5
3
x
. C.
3
5
x
. D.
3
5
x
.
Câu 12. Rút gọn biểu thức
2
144 9A aa

với
0
a
.
A.
9a
. B.
3a
. C.
3a
. D.
9a
.
Câu 13. Tìm
x
để
2
( 5)
63x
có nghĩa
A.
2x
. B.
2x
. C.
2x
. D.
2x
.
Câu 14. Tìm
x
để
2
31
x
có nghĩa
A.
1
3
x
. B.
1
3
x
. C.
1
3
x
. D.
1
3
x
.
23. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Câu 15. Giá trị của biểu thức
2 9 16
25 169
5 2 81

là:
A.
12
. B.
13
. C.
14
. D.
15
.
Câu 16. Tìm giá trị của
x
không âm biết
2 30 0x 
.
A.
15x 
. B.
225x
. C.
25
x
. D.
15
x
.
Câu 17. Tìm giá trị của
x
không âm biết
5 2 125 0
x

A.
25
2
x
. B.
125x
. C.
25
x
. D.
625
2
x
.
Câu 18. Tính giá trị biểu thức
19 8 3 19 8 3 
.
A.
23
. B.
8 23
. C.
6
. D.
8
.
Câu 19. Tính giá trị biểu thức
15 6 6 15 6 6

A.
26
. B.
6
. C.
6
. D.
12
.
Câu 20. Rút gọn biểu thức
22
8 16 8 16
aa aa 
với
44a
ta được:
A.
2
a
. B.
8
. C.
8
. D.
a
.
Câu 21. Rút gọn biểu thức
22
4 12 9 4 12 9aa aa 
với
33
22
a
ta được:
A.
4
a
. B.
4
a
. C.
6
. D.
6
.
Câu 22. Tìm
x
thỏa mãn phương trình
2
63
xx x
.
A.
2x
. B.
4x
. C.
1x
. D.
3x
.
Câu 24. Tìm
x
thỏa mãn phương trình
2
2 3 34xx x
.
A.
2x
. B.
4x
. C.
1x
. D.
1; 2xx
.
Câu 24. Nghiệm của phương trình
2
2x 2 3 1x
là:
A.
2x
. B.
5x
. C.
1
x
. D.
3x
.
Câu 24. Số nghiệm của phương trình
2
4 4 1 34xx x 
là:
A.
0
. B.
4
. C.
1
. D.
2
.
Câu 26. Nghiệm của phương trình
2
6 94xx x 
là:
A.
2
x
. B.
1
4
x
. C.
1
2
x
. D.
3x
.
Câu 27. Rút gọn biểu thức
2
10 25
5
xx
x


với
5x 
ta được:
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 28.Trong các khẳng định sau, khẳng định nào sai?
A.
( )
( )
3
4 43xy xy
xy
−=−
−
với mọi
0xy>>
.
B.
2
11 1a
aa a
+
+=
với mọi
0a >
.
24. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
C.
( ) ( )
2
1 3 23 3
12 3
−−
=
.
D.
15
500 50
=
.
Câu 29. Tìm giá trị nhỏ nhất của biểu thức:
22
4 4 1 4 12 9B aa a a 
A.
2
. B.
1
. C.
4
. D.
10
.
Câu 30. Tìm giá trị nhỏ nhất của biểu thức:
22
2 1 8 16
Am m m m

A.
2
. B.
9
. C.
5
. D.
10
.
25. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
HƯỚNG DẪN
Câu 1. Đáp án A.
Với số dương
a
, số
a
được gọi là căn bậc hai số học của
a
.
Câu 2. Đáp án B.
Căn bậc hai số học của
0, 36
a
là
0, 36 0, 6
.
Câu 3. Đáp án D.
- Với hai số
,ab
không âm ta
ab a b
nên C đúng.
- Với hai số
,ab
không âm ta có
0ab a b
nên D sai.
- Sử dụng hằng đẳng thức
2
|
0
|
0
A khi A
AA
A khi A


nên A, B đúng.
Câu 3. Đáp án B.
Ta có:
10 100
x
có nghĩa khi
10 100 0 100 10 110x xx  
.
Câu 4. Đáp án C.
Tách
5 7 2 49 2
Vì
49 50 49 50

7 50 7 2 50 2 
5 50 2
. Câu 5. Đáp án A.
Điều kiện:
50 0
xx

Vì
10 100
nên
5 10x
5 100
x

5 100 20xx 
Kết hợp điều kiện
0
x
ta có
0 20x
Vậy
0 20x

.
Câu 6. Đáp án B.
2
23 23 
mà
243
(vì
43
) nên
2 30
.
Từ đó
2
23 2323 
.
Ta có
2
13 13 
mà
113
(vì
13
) nên
1 30
. Từ đó
2
13 13 31

.
Nên
22
23 13 23 311 
.
Câu 8. Đáp án D.
Ta có:
2
8 88
3 33



và
2
( 0, 8) 0, 8 0, 8 
Nên
2
2
88
9 ( 0,8) 9. 0,8 24 0,8 24,8
33

 

.
Câu 9. Đáp án C.
26. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Ta có
2
( 2, 5) 2, 5 2, 5 
và
2
( 0, 5) 0, 5 0, 5 
Nên
22
6 ( 2, 5) 8 ( 0, 5) 6.2, 5 8.0, 5 15 4 11
.
Câu 10. Đáp án C.
Ta có:
125 5x
có nghĩa khi
125 5 0 5 125 25xx x 
.
Câu 11. Đáp án A.
Ta có
53x
có nghĩa khi
5
53 0 3 5
3
x xx  
.
Câu 12. Đáp án C.
Ta có:
22
144 (12 ) 12a aa
mà
0 12 0
aa

nên
12 12aa
hay
2
144 12aa
Từ đó:
2
144 9 12 9 3 .A a a aa a
 
.
Câu 13. Đáp án A.
Ta có:
2
( 5)
63x
có nghĩa khi
2
( 5) 25
00
63 63
xx


mà
25 0
63 0 63 2x xx
.
Câu 14. Đáp án A.
Ta có
2
31x
có nghĩa khi
2
0
31x
mà
20

3 10x

1
3
x
.
Câu 15. Đáp án B.
Ta có:
2
2
16 4 4 4
25 5 5 5;
81 9 9 9



2
169 13 13 13 
Nên
2 9 16
25 169
5 2 81

2 94
.5 . 13 2 2 13 13
5 29

.
Câu 16. Đáp án B.
Với
x
không âm ta có
2 30 0 2 30xx 
15x
mà
15 0
nên
15x
2
15 225xx 
(thỏa mãn).
Vậy
225x
.
Câu 17. Đáp án D.
Điều kiện:
20 0xx

Ta có:
5 2 125 0 5 2 125 2 25x xx 
mà
25 0
nên
2
625
2 25 2 25 2 625
2
xx xx 
(thỏa mãn).
Vậy
625
2
x
.
Câu 18. Đáp án D.
27. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Ta có:
2
2
19 8 3 4 2.4. 3 3 4 3 4 3 4 3 
Và
2
2
19 8 3 4 2.4. 3 3 4 3 4 3 4 3 
(vì
4 16 3 4 3 0

)
Nên
19 8 3 19 8 3 4 3 4 3 8 
.
Câu 19. Đáp án A.
Ta có
2
2
15 6 6 3 2.3. 6 6 3 6 
3636 
Và
2
2
15 6 6 3 2.3. 6 6 3 6 
3636 
(vì
3 9 6 3 60 
)
Nên
15 6 6 15 6 6 
3636363626
 
.
Câu 20. Đáp án B.
Ta có
22
8 16 ( 4) 4aa a a

Mà
4 4 40aa

44aa 
Hay
2
8 16 4aa a 
với
44a
Ta có
22
8 16 ( 4)
aa a
Mà
4 4 40aa

44aa

Hay
2
8 16 4aa a 
với
44a
Khi đó
22
8 16 8 16 4 4 8aa aa a a 
.
Câu 21. Đáp án D.
Ta có:
2 2 22
4 12 9 (2 ) 2.3.2 3 (2 3) 2 3aa a a a a 
Mà
2302323
33
32 3
||
2 30 3 3| 2
22
| 2
a aa
aa
a aa

 

Hay:
2
4 12 9 2 3aa a 
và
2
4 12 9 3 2aa a 
với
33
22
a

Khi
đó:
22
4 12 9 4 12 9 2 3 3 2 6aa aa a a 
.
Câu 22. Đáp án D.
ĐK:
30 3xx
Với điều kiện trên, ta có
2
63xx x
2 22
6 3 2 30 3 30
(3)(3)0(3)(1)0
x x x x x x xx
xx x x x
  

28. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
30 3
10 1
()
()
x xN
x xL








Vậy phương trình có nghiệm
3x
.
Câu 24. Đáp án A.
ĐK:
4
3 40 3 4
3
x xx

Với điều kiện trên, ta có:

2
2 3 34xx x
  
22 2
2 3 3 4 2 3 3 40 2 6 40xxx xxx xx
22
()() ()
3 20 2
(
20
12 1 )0 1 20
x x xxx
xx x x x
  
 
10 1
20 2
()
()
x xL
x xN








Vậy phương trình có nghiệm
2x
.
Câu 24. Đáp án C.
ĐK:
1
3 10
3
xx
Với điều kiện trên ta có:
2 2 22 2
22
2x2312 2(31) 2 29 61
7 6 1 0 7 7 1 0 7 ( 1) ( 1) 0
1
7 10
7
()
()
10
1
x x x x xx
xxxxxxxx
x
xL
x
xN
 
 




Câu 25. Đáp án D.
22
4 4 1 34 (2 1) 34xx x x x  
2 1 34 6 2
2 1 34
21
|
3
|
4 24
x xx
xx
xx x








1
3
2
x
x
Vậy phương trình có hai nghiệm
1
;2
3
xx

.
Câu 26. Đáp án C.
22
6 9 4 ( 3) 4
34 : 4
1
34
21
2
34
3
||
()4
()
xx x x x
x x ÐK x
xx
x x TM
xx
L
 






Vậy phương trình có nghiệm
1
2
x
.
Câu 27. Đáp án B.
Ta có:
22
10 25 ( 5) 5 ( 5)xx x x x 
(vì
5x 
).
29. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Nên
2
10 25 ( 5)
1
5 ( 5)
xx x
xx



.
Câu 28.Trong các khẳng định sau, khẳng định nào sai?
A.
(
) (
)
3
4 43xy xy
xy
−=−
−
với mọi
0xy>>
.
B.
2
11 1a
aa a
+
+=
với mọi
0a >
.
C.
( ) ( )
2
1 3 23 3
12 3
−−
=
.
D.
15
500 50
=
.
Chọn C
Ta có
( )
( )
2
1 3 23 3
13
31 3 3
12 6 3
23 23
−−
−
−−
= = = ≠
.
Câu 29. Đáp án A.
Ta có
22
4-4 1 4-12 9B aa a a 
22
(2 1) (2 3) 2 1 2 3a a aa 
Ta có
21232132 2132 2
a a a aa a 
Dấu “=” xảy ra khi
2 1 32 4 4 1a aa a
Suy ra GTNN của
B
là
21
a
.
Câu 30. Đáp án C.
Ta có

22
2 1 8 16Am m m m

22
(1) (4) 1 4m m mm
.
Ta có
1 4 1 4 14 5m m m mm m 
Dấu “=” xảy ra khi
3
14 2 3
2
m mm m

Suy ra GTNN của
B
là
3
5
2
m
.
30. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
III.TỰ LUYỆN
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai
Bài 1: Tính
a.
64
25
b.
( )
2
2,5
c.
( )
2
2−
d.
36
169
−

−


Bài 2: Tính
a.
196. 25 5 81−
b.
( )
2
10 3 10−−
c.
(
)
2
5 7 8 27
+ −−
d.
(
)
81: 9 169 . 225+
Bài 3. Thực hiện các phép tính sau:
a.
5 26 5 26.+ −−
b.
49 12 5 49 12 5.
− ++
c.
31 12 3 31 12 3.− −+
d.
21 12 3 21 12 3.+ +−
Bài 4:Tính
1)
3 2 4 18 2 32 50−+−
2)
2 24 2 54 3 6 150
− +−
3)
2 28 2 63 3 175 112+− +
4)
3
10 28 2 175 3 343 448
2
+−−
5)
13 4 3
−
6)
7 43 2−−
7)
15 6 6 33 12 6
− +−
Bài 5:Tính:
1)
(
)
(
)
25 7 25 7
−+
2)
16 1 4
236
3 27 75
−−
3)
10 15
8 12
−
−
4)
15 5 5 2 6
3 1 25 4
−−
−
−−
5)
2 8 12 5 27
18 48 30 162
−+
−
−+
Bài 6:Tính:
1)
( )
3 4 19 8 3+−
2)
17 3 32 17 3 32− ++
3)
(
)
(
)
(
)
5 42 3 21 2 3 21 2+ ++ −+
4)
(
)
5 26 2 3−+
5)
2 17 49 45+−+
6)
2 2 3 18 8 2+ +−
7)
4 5 3 5 48 10 7 4 3+ +−+
Bài 7:Tính:
1)
3 22 3 22
17 12 2 17 12 2
−+
−
−+
2)
1 62 4
175
87 32
−
+−
+−
3)
1
7 48
2
+−
4)
22
22 3 5 22 3 5
+
++ −−
5)
( )( )
5 26 49 206 5 26
9 3 11 2
+− −
−
31. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
6)
33
11
22
33
11 11
22
+−
+
++ −−
7)
11 1
...
1 2 2 3 24 25
+ ++
++ +
Dạng 2: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 1: Với giá trị nào của
x
thì mỗi căn thức sau có nghĩa:
a.
15
2x −
b.
17
12 x
−
−
c.
72x
d.
24 10x+
e.
13
3x
−
f.
27 6x−
Bài 2: Với giá trị nào của
x
thì mỗi căn thức sau có nghĩa:
a.
2
11x +
b.
2
56xx++
c.
2
10 3
31
x
x
−
+
d.
2
42
45
x
xx
+
++
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Rút gọn các biểu thức sau:
a.
( )
2
32
−
b.
( )
2
11 3
+
c.
4 23−
d.
7 43+
Bài 2: Rút gọn các biểu thức sau:
a.
2
2 a−
với
0a ≥
b.
2
16 4aa
+
với
0a <
c.
(
)
2
1
a −
với
1a ≥
d.
2
9 6 13aa a
− ++
với
1
3
a <
e.
2
69
aa++
với
3a ≥−
f.
42
25 3aa−
Dạng 4: So sánh
Bài 1. So sánh
a. 5 và
17 1.+
b. 3 và
15 1.
−
Bài 2. Tìm giá trị của
x
biết
a.
1 6.x−+≥
b.
2
2.xx≤
Bài 3:So sánh
A
và
B
:
a)
2013 2015A = +
;
2 2014B =
.
b)
12 12 12 6 6 6 6A = + + ++++
;
12 11B
= +
.
c)
11 1
...
1.2014 2.2013 2014.1
A = + ++
;
4028
2015
B =
.
Dạng 4: Phân tích đa thức thành nhân tử
Bài 1: Phân tích đa thức thành nhân tử
a.
2
7x −
b.
2
43x −
c.
2
27 7xx++
d.
2
9 62 2xx++
Bài 2: Phân tích đa thức thành nhân tử
a.
2
3x −
b.
2
95x −
c.
2
22 2xx++
d.
2
4 43 3xx++
32. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Dạng 5: Giải phương trình
Bài 1: Giải phương trình
a.
2
3x =
b.
2
9 10x =
c.
2
4 19 0x
−=
d.
2
49 14x = −
Bài 2: Giải phương trình
a.
( )
2
22x +=
b.
2
44 3xx−+=
c.
2
4 43xx x− +=+
d.
2
9 61 1xx x+ +=−
e.
2
23 3 0xx+ +=
f.
4 40xx− +=
Bài 3: Giải phương trình:
1)
2
95x +=
2)
2
4 20 25 1xx− +=
3)
12 2 2
xx
−+ − =
4)
2
22xx x−−= −
5)
2
93
xx
−= −
6)
11xx−+=
7)
2
25 30 9 7xx x− +=+
8)
32 5xx++ −=
9)
22
20xx xx−+ +−=
10)
( )
2
2
1 44
x xx− + ++
11)
2 1 9 18
25 50 8
2 16
xx
x
−+ −
−− =
12)
1227 622x x xx−+ − + + + − =
33. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
HƯỚNG DẪN
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai
Bài 1: Tính
a.
64
25
b.
( )
2
2,5
c.
( )
2
2−
d.
36
169
−

−


Lời giải
a.
64 8
25 5
=
b.
( )
2
2,5 2,5=
c.
( )
2
22−=
d.
36 6
169 13
−

−=


Bài 2: Tính
a.
196. 25 5 81−
b.
( )
2
10 3 10−−
c.
( )
2
5 7 8 27+ −−
d.
( )
81: 9 169 . 225+
Lời giải
a.
196. 25 5 81−
13.5 5.9
65 45
20
= −
= −
=
b.
( )
2
10 3 10−−
10 3 10
10 3 10
3
= −−
= −−
= −
c.
( )
2
5 7 8 27
+ −−
( )
2
57 17
5 71 7
5 71 7
6
=+−−
=+ −−
= + +−
=
d.
( )
81: 9 169 . 225+
( )
81: 3 13 .15
30.15
450
= +
=
=
Bài 3. Thực hiện các phép tính sau:
a.
5 26 5 26.+ −−
b.
49 12 5 49 12 5.− ++
c.
31 12 3 31 12 3.− −+
d.
21 12 3 21 12 3.+ +−
Lời giải
34. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
a.
5 26 5 26+ −−
( )
( )
22
32 32
32 32
= +−−
=+−−
323222=+−+ =
.
b.
49 12 5 49 12 5− ++
( ) ( )
22
35 2 35 2
35 2 35 2
6 5.
= −+ +
= −+ +
=
c.
31 12 3 31 12 3− −+
( ) ( )
22
33 2 33 2
4.
= −− +
= −
d.
21 12 3 21 12 3
+ +−
( )
( )
22
23 3 23 3
4 3.
= ++ −
=
Bài 4:Tính
1)
3 2 4 18 2 32 50−+−
2)
2 24 2 54 3 6 150
− +−
3)
2 28 2 63 3 175 112+− +
4)
3
10 28 2 175 3 343 448
2
+−−
5)
13 4 3−
6)
7 43 2−−
7)
15 6 6 33 12 6
− +−
Lời giải
1)
3 2 4 18 2 32 50 3 2 12 2 8 2 5 2 6 2− + −=− +−=−
.
2)
2 24 2 54 3 6 150 4 6 6 6 3 6 5 6 4 6− +− =−+−=−
.
3)
2 28 2 63 3 175 112 4 7 6 7 15 7 4 7 7+ − + =+− +=−
4)
3
10 28 2 175 3 343 448 20 7 10 7 21 7 12 7 3 7
2
+ − − = +−−=−
.
5)
( )
2
743 42.233 23 2323− = − += − =− =−
.
6)
( )
2
7432 32 2 32 22 32 3− −= − −= −−=− −=−
.
7)
15 6 6 33 12 6 9 2.3. 6 6 9 2.3.2 6 24− + − = − ++ − +
(
) ( )
22
3 6 3 26=− +−
3 6 26 3 6=− + −=
Bài 5:Tính:
1)
(
)( )
25 7 25 7
−+
2)
16 1 4
236
3 27 75
−−
3)
10 15
8 12
−
−
4)
15 5 5 2 6
3 1 25 4
−−
−
−−
5)
2 8 12 5 27
18 48 30 162
−+
−
−+
Lời giải
1)
( )( )
25 7 25 7−+
=
( )
( )
22
25 7−
=
20 7 13−=
35. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
2)
16 1 4
236
3 27 75
−−
=
22
22
412
23 6
3 3 .3 5 .3
−−
=
1 31 21
2.4 6.
3 3 .3 5 3
−−
=
3 12 1
8
35 3

−−


=
23 3
15
.
3)
10 15
8 12
−
−
=
(
)
( )
2 35
5.2 5.3
4.2 4.3
2 34
−
−
=
−
−
=
5
4
=
5
2
4)
15 5 5 2 6
3 1 25 4
−−
−
−−
=
5.3 5 5 2 6
3 1 25 4
−−
−
−−
=
(
)
5 31
5 26
3 1 25 4
−
−
−
−−
=
5 26
5
25 4
−
−
−
=
( )
525 4
5 26
25 4 25 4
−
−
−
−−
=
10 4 5 5 2 6
25 4 25 4
−−
−
−−
=
10 4 5 5 2 6
25 4
− −+
−
=
5 45 26
25 4
−+
−
5)
2 8 12 5 27
18 48 30 162
−+
−
−+
=
=
(
) ( )
42 23 5 33
6322 6533
−+
−
−+
( )
( )
2 3 22
13 6
2
66
6 3 22
−−
−
= −==−
−
Bài 6:Tính:
1)
( )
3 4 19 8 3+−
2)
17 3 32 17 3 32− ++
3)
( )
(
)
(
)
5 42 3 21 2 3 21 2
+ ++ −+
4)
(
)
5 26 2 3−+
5)
2 17 49 45
+−+
6)
2 2 3 18 8 2+ +−
7)
4 5 3 5 48 10 7 4 3+ +−+
Lời giải
1)
( )
3 4 19 8 3+−
=
( )
3 4 16 2.4 3 3+−+
=
( ) ( )
2
2
3 4 4 2.4 3 3+−+
=
( ) ( )
2
34 4 3+−
=
( )
( )
344 3+−
=
16 3 13
−=
.
2)
17 3 32 17 3 32− ++
=
17 3.4 2 17 3.4 2− ++
=
17 2.6 2 17 2.6 2− ++
=
( )
(
)
22
9 2.3.2 2 2 2 9 2.3.2 2 2 2− + ++ +
=
( ) ( )
22
3 22 3 22− ++
=
3 22 3 22− ++
=
6
.
3)
( )
(
)
(
)
5 42 3 21 2 3 21 2+ ++ −+
=
( ) ( )
( )
2
5 4 2 3 41 2+ −+
=
( )
5 42+
( )
5 42−
=
25 16.2−
=
7
−
36. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
4)
(
)
5 26 2 3
−+
=
15 2.3 6 6
−+
=
9 2.3 6 6 6− ++
=
( )
2
36 6
−+
=
3 6 63−+=
.
5)
2 17 49 45+−+
=
2 17 45 45 4+−+ +
=
(
)
2
2 17 4 5 2+− +
=
( )
2 17 4 5 2+− +
=
2 9 45+−
=
2 5 45 4+− +
=
( )
2
2 52+−
=
2 52 5+ −=
6)
2 2 3 18 8 2+ +−
=
2 2 3 16 2.4 2 2++− +
=
(
)
2
2 23 4 2+ +−
=
2 23 4 2+ +−
=
23 4+
=
3 23 1++
=
( )
2
31+
=
31+
7)
4 5 3 5 48 10 7 4 3+ +−+
=
4 5 3 5 48 10 4 4 3 3+ + − ++
=
( )
2
4 5 3 5 48 10 2 3+ +− +
=
( )
4 5 3 5 48 10 2 3+ + −+
=
4 5 3 5 28 10 3+ +−
=
4 5 3 5 25 10 3 3
+ +−+
=
( )
4 5 3 55 3
+ +−
=
4 53 25 53+ +−
=
45
+
=
3
Bài 7:Tính:
1)
3 22 3 22
17 12 2 17 12 2
−+
−
−+
2)
1 62 4
175
87 32
−
+−
+−
3)
1
7 48
2
+−
4)
22
22 3 5 22 3 5
+
++ −−
5)
( )
( )
5 26 49 206 5 26
9 3 11 2
+− −
−
6)
33
11
22
33
11 11
22
+−
+
++ −−
7)
11 1
...
1 2 2 3 24 25
+ ++
++ +
Lời giải
1)
3 22 3 22
17 12 2 17 12 2
−+
−
−+
( )
( )
( )
( )
22
22
21 21
3 22 3 22
−+
= −
−+
21 21
3 22 3 22
−+
= −
−+
( )( ) ( )( )
( )( )
2 13 22 2 13 22
3 22 3 22
−+ −+−
=
−+
37. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
32 432232 4322
1
+−− − +−+
=
2=
2)
1 62 4
175
87 32
−
+−
+−
(
)
( )
8 7 2 2.3 2 2. 2
57
32
8787
−−
= +−
−
−+
( )
2 23 2
87
57
87
32
−
−
= +−
−
−
8 7 57 22=−+ −
22 47 22
=+−
47=
3)
1
7 48
2
+−
3
7 43
2
=+−
( )
2
2
23
2
=+−
2
23
2
=+−
22 3 2
2
+−
=
2. 4 2 3 2
2
+−
=
( )
2
2. 3 1 2
2
+−
=
(
)
2. 3 1 2
622 6
2 22
+−
+−
= = =
4)
23684
234
++++
++
( )
( )
2 32 6 82
234
+++ ++
=
++
( )
( )
2 32 2. 2 32
12
234
+++ ++
= = +
++
5)
23
2
2 32 23
2
6 23
+
++
−+
( )
4 23
2 2. 2 3
2 2.2 2 2. 2 3
2
6 23
+
=
+
+
−+
31
43 4 23
26
3
3
+
=
+
+− +
31
43 3 1
26
3
3
+
=
+
+− +
( ) ( )
31
3 3. 2 6 4.3 3 3 1
23
+
=
+ −+ +
38. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
31 31
33 32 3 3 6 3
3
++
= =
+ − +−
6)
(
)
(
)
33
11
4 23 4 23
22
33
22 4 2 3 22 4 2 3
11 11
22
+−
+−
+= +
++ −−
++ −−
( )
( )
(
)
( )
( ) ( )
2 2 22
31 31 31 31
6 23 6 23
4231 4231
+ − +−
=+=+
+−
++−−
( )
( )
( )
( )
22
31 31
31 31
1
23 23
23 3 1 23 3 1
+−
+−
= + =+=
+−
7)
11 1
...
1 2 2 3 24 25
+ ++
++ +
( ) ( ) ( ) ( ) ( ) ( )
1 2 2 3 24 25
...
1 2 . 1 2 2 3 . 2 3 24 25 . 24 25
−− −
= + ++
+− +− + −
1 2 2 3 24 25
...
11 1
−− −
= + ++
−− −
(
)
1 2 2 3 ... 24 25=− − + − ++ −
(
)
1 25 4
=−− =
Dạng 2: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 1: Với giá trị nào của
x
thì mỗi căn thức sau có nghĩa:
a.
15
2x −
b.
17
12 x
−
−
c.
72x
d.
24 10x+
e.
13
3x
−
f.
27 6x−
Lời giải
a.
15
2x −
có nghĩa
20x⇔−≥
2x⇔≥
b.
17
12 x
−
−
có nghĩa
12 0x⇔ −≤
12x⇔≥
c.
72x
có nghĩa
72 0x⇔≥
0x⇔≥
d.
24 10x+
có nghĩa
24 10 0x
⇔+ ≥
12
5
x
−
⇔≥
39. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
e.
13
3
x
−
có nghĩa
13
0
3x
−
⇔≥
0x⇔<
f.
27 6x−
có nghĩa
27 6 0x⇔−≥
27
6
x
⇔≤
Bài 2: Với giá trị nào của
x
thì mỗi căn thức sau có nghĩa:
a.
2
11x +
b.
2
56xx++
c.
2
10 3
31
x
x
−
+
d.
2
42
45
x
xx
+
++
Lời giải
a.
2
11x +
có nghĩa
2
11 0x⇔ +≥
x
⇔∈
b.
2
56xx++
có nghĩa
2
5 60xx
⇔ + +≥
( )( )
2 30xx⇔+ +≥
3
2
x
x
≤−
⇔
≥−
c.
2
10 3
31
x
x
−
+
có nghĩa
2
10 3
0
31
x
x
−
≥
+
vì
2
3 11x
+≥
nên
10 3 0x−≥
10 3x⇔≥
10
3
x⇔≤
d.
2
42
45
x
xx
+
++
có nghĩa
2
42
0
45
x
xx
+
≥
++
vì
( )
2
2
4 5 2 11xx x
+ + = + +≥
nên
4 20x +≥
42x⇔ ≥−
1
2
x
−
⇔≥
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Rút gọn các biểu thức sau:
a.
( )
2
32
−
b.
( )
2
11 3+
c.
4 23−
d.
7 43+
Lời giải
a.
(
)
2
32 3232− =−=−
b.
( )
2
11 3 11 3 11 3+ = += +
c.
( )
2
423 13 13 31− =− =−=−
d.
( )
2
743 23 2323
+ = + =+=+
Bài 2: Rút gọn các biểu thức sau:
a.
2
2 a−
với
0a ≥
b.
2
16 4aa
+
với
0a <
c.
( )
2
1a −
với
1a ≥
d.
2
9 6 13aa a− ++
với
1
3
a <
e.
2
69aa++
với
3a ≥−
f.
42
25 3aa−
Lời giải
40. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
a.
2
2 a
−
với
0a
≥
=
22aa−=−
b.
2
16 4aa+
với
0a <
=
4 4 44
aa
+=− +
c.
( )
2
1a −
với
1a ≥
( )
1 11a aa= −=− ≥
d.
2
9 6 13aa a− ++
với
1
3
a <
=
( )
2
1
31 3113
3
a a aa

− = −=− <


e.
2
69aa++
với
3
a
≥−
( )
2
3 33a aa= + =+=+
f.
42
25 3aa−
22 2
53 2aa a=−=
Dạng 4: So sánh
Bài 1. So sánh
a. 5 và
17 1.+
b. 3 và
15 1.−
Lời giải
a. Ta có
16 1 17 1
+< +
5 17 1.⇔< +
b. Ta có
16 1 15 1−> −
3 15 1.⇔> −
Bài 2. Tìm giá trị của
x
biết
a.
1 6.x−+≥
Lời giải
a. Điều kiện
10 1xx−+≥ ⇔ ≤
. Ta có
1 36 35xx−+≥ ⇔ ≤−
(thỏa mãn điều kiện).
b.
2
2.xx≤
Lời giải
b. Điều kiện
0
x ≥
. Ta có
(
)
2
2
2 20
0
x
x x xx
x
≥
≤ ⇔ − ≥⇔
≤
Kết hợp điều kiện ta có
0x =
hoặc
2x ≥
.
Bài 3:So sánh
A
và
B
:
a)
2013 2015A
= +
;
2 2014B =
.
b)
12 12 12 6 6 6 6A = + + ++++
;
12 11B = +
.
c)
11 1
...
1.2014 2.2013 2014.1
A = + ++
;
4028
2015
B =
.
Lời giải
a)
2013 2015
A = +
;
2 2014B =
.
Ta có:
2013 2015<
⇒
0 2013 2014 2015 2014<+<+
⇒
11
2013 2014 2015 2014
>
++
⇒
( )
( )
( )( )
2014 2013 2015 2014
2014 2013 2014 2013 2015 2014 2015 2014
−−
>
+− +−
41. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
⇒
2014 2013 2015 2014−>−
⇒
2 2014 2015 2013>+
⇒
BA
>
.
Cách khác :
Ta có
22
2013 2015 0 4028 2 2013.2015 2.2014 2 2014 1AA= + >⇔ = + = + −
2
2.2014 2.2014 4.2014A <+=
2
2 2014 0 4.2014BB= >⇔ =
Suy ra
22
A B AB< ⇔<
(do
,0
AB>
)
b) So sánh
12 12 12 6 6 6 6A = + + ++++
;
12 11B = +
.
Ta có:
2
2
12 12 12 6 6 6 6A

= + + ++++



2
12 12 12 6 6 6 6 2. 12 12 12 . 6 6 6 6A =+ + ++++ + + + +++
2
18 12 12 6 6 6 2. 12 12 12 . 6 6 6 6A =+ + +++ + + + +++
( )
2
2
12 11 23 2. 132B
=+=+
Dễ thấy
12 12 9
+>
và
666 4
++ >
⇒
18 12 12 6 6 6 23+ + +++ >
.
⇒ Để so sánh
2
A
và
2
B
ta chỉ cần so sánh
12 12 12 . 6 6 6 6+ + +++
và
132
.
Ta có:
(
)
12 12 12 . 6 6 6 6

+ + +++


72 12 6 6 6 6 12 12 12 12 . 6 6 6=+ ++ + + + + ++
Mà
666 93++ > =
và
12 12 9 3+ >=
nên
6 12 12 6.3 18+ >=
12 12 . 6 6 6 3.3 9+ ++ > =
⇒
72 12 6 6 6 6 12 12 12 12 . 6 6 6 72 36 18 9+ ++ + + + + ++ >+++
.
⇒
72 12 6 6 6 6 12 12 12 12 . 6 6 6 135+ ++ + + + + ++ >
.
⇒
72 12 6 6 6 6 12 12 12 12 . 6 6 6 132+ ++ + + + + ++ >
.
⇒
12 12 12 . 6 6 6 6 132+ + +++ >
.
⇒
2
A
>
2
B
.
⇒
AB>
(Do
0A >
và
0B >
).
Dạng 4: Phân tích đa thức thành nhân tử
42. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Bài 1: Phân tích đa thức thành nhân tử
a.
2
7x −
b.
2
43x −
c.
2
27 7xx
++
d.
2
9 62 2xx++
Lời giải
a.
(
)
(
)
2
7 77
x xx−= + −
b.
(
)
( )
2
4 3 2 32 3x xx−= + −
c.
( )
2
2
27 7 7
x xx+ += +
d.
( )
2
2
9 62 2 3 2xx x+ += +
Bài 2: Phân tích đa thức thành nhân tử
a.
2
3
x −
b.
2
95
x −
c.
2
22 2xx++
d.
2
4 43 3
xx++
Lời giải
a.
(
)(
)
2
3 33x xx−= + −
b.
(
)
(
)
2
9 5 3 53 5
x xx−= + −
c.
(
)
2
2
22 2 2x xx+ += +
d.
( )
2
2
4 43 3 2 3
xx x
+ += +
Dạng 5: Giải phương trinh
Bài 1: Giải phương trình
a.
2
3
x
=
b.
2
9 10x =
c.
2
4 19 0x −=
d.
2
49 14
x
= −
Lời giải
a.
2
3x =
3x⇔=
3
3
x
x
=
⇔
= −
Vậy
{ }
3; 3S = −
b.
2
9 10x =
( )
2
3 10x⇔=
3 10x⇔=
3 10
3 10
x
x
=
⇔
= −
10
3
10
3
x
x
=
⇔
−
=
Vậy
10 10
;
33
S
−

=


c.
2
4 19 0x −=
2 19x⇔=
2 19
2 19
x
x
=
⇔
= −
d.
2
49 14x = −
7 14x⇔=
7 14
7 14
x
x
=
⇔
= −
2
2
x
x
=
⇔
= −
43. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
19
2
19
2
x
x
=
⇔
−
=
Vậy
19 19
;
22
S
−

=


Vậy
{
}
2; 2
S
= −
Bài 2: Giải phương trình
a.
( )
2
22x +=
b.
2
44 3xx−+=
c.
2
4 43xx x− +=+
d.
2
9 61 1xx x+ +=−
e.
2
23 3 0xx
+ +=
f.
4 40
xx− +=
Lời giải
a.
( )
2
22x +=
22
22
x
x
+=
⇔
+=−
0
4
x
x
=
⇔
= −
Vậy
{ }
0; 4
S = −
b.
2
44 3xx
−+=
(
)
2
23
x⇔ −=
23x⇔−=
23
23
x
x
−=
⇔
−=−
1
5
x
x
= −
⇔
=
Vậy
{
}
5; 1S = −
c.
2
4 43xx x
− +=+
30
23
x
xx
+≥
⇔
−=+
( )
3
23
23
x
xx
xx
≥−
−=+
⇔
−=− +
05
21
x
x
=
⇔
= −
1
2
x
−
⇔=
(nhận)
Vậy
1
2
S
−

=


d.
2
9 61 1xx x+ +=−
10
31 1
x
xx
−≥
⇔
+=−
( )
1
31 1
31 1
x
xx
xx
≥
+= −
⇔
+=− −
22
40
x
x
= −
⇔
=
1
2
x
−
⇔=
Vậy
1
2
S
−

=


e.
2
23 3 0xx+ +=
(
)
2
30x⇔+ =
3x
⇔=−
f.
4 40xx− +=
( )
2
20x⇔+ =
2x⇔=−
Vậy
{ }
2S = −
44. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy
{ }
3
S
= −
Bài 4: Giải phương trình:
1)
2
95x +=
2)
2
4 20 25 1xx− +=
3)
12 2 2
xx−+ − =
4)
2
22xx x−−= −
5)
2
93xx−= −
6)
11
xx
−+=
7)
2
25 30 9 7
xx x
− +=+
8)
32 5xx++ −=
9)
22
20xx xx−+ +−=
10)
( )
2
2
1 44
x xx
− + ++
11)
2 1 9 18
25 50 8
2 16
xx
x
−+ −
−− =
12)
1227 622x x xx−+ − + + + − =
Lời giải
1)
2
95x +=
( ĐK :
2
90x +≥
với mọi
x
)
2
9 25x
⇔ +=
2
16 0x⇔−=
( ) ( )
4. 4 0xx⇔− +=
40
40
x
x
+=
⇔
−=
4
4
x
x
= −
⇔
=
Vậy nghiệm của phương trình là
4, 4xx
= = −
2)
2
4 20 25 1xx− +=
( )
2
25 1
x⇔ −=
2 51x
⇔ −=
3
x⇔=
Vậy nghiệm của phương trình là
3
x =
3)
12 2 2xx−+ − =
Đk:
2
x
≥
12 2 2
xx−+ − =
22 21 2xx⇔ −+ −+=
( )
2
21 2x⇔ −+ =
21 2x
⇔ −+=
212x⇔ − +=
(vì với
2x ≥
thì
20x −≥
nên
2110x − +≥>
)
21x⇔ −=
21x⇔−=
3x⇔=
(thoả mãn điều kiện)
4)
2
22xx x−−= −
ĐK:
2x ≥
2
22xx x⇔ −−=−
2
220x xx⇔ −−−+=
2
20xx⇔−=
( )
20xx
⇔ −=
0
20
x
x
=
⇔
−=
0(KTM)
2 (TM)
x
x
=
⇔
=
{
}
2S =
45. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
5)
2
93xx−= −
Đk :
2
3
3
90
3
3
30
3
x
x
x
x
x
x
x
≤−
≤−
−≥
⇔⇔
≥

=
−≥
≤
2
93
xx
⇔ −=−
2
12 0xx
⇔ +− =
2
4 3 12 0
x xx⇔+−−=
( )
( )
43 4 0
xx x⇔ +− +=
( )( )
4 30xx⇔+ −=
40
30
x
x
+=
⇔
−=
( )
( )
4
3
x TM
x TM
= −
⇔
=
{ }
4;3S
= −
6)
11
xx−+=
11xx⇔ −= −
1
x ≥
2
1 21
x xx⇔ −= − +
2
3 20xx⇔ − +=
2
2 20xx x⇔ −− +=
( )
( )
1 20
xx⇔− −=
10
20
x
x
−=
⇔
−=
1
(TM)
2
x
x
=
⇔
=
{ }
S 1; 2=
7)
2
25 30 9 7xx x− +=+
ĐK:
7x ≥−
22
25 30 9 14 49xx xx⇔ − += + +
2
24 44 40 0xx
⇔ − −=
2
6 11 10 0
xx⇔ − −=
2
6 4 15 10 0xxx
⇔ −+ −=
( )( )
2 53 2 0xx⇔ + −=
2 50
3 20
x
x
+=
⇔
−=
25
32
x
x
= −
⇔
=
5
2
(TM)
2
3
x
x
−
=
⇔
=
25
S;
32
−

=


8)
3 2 5(*)xx
++ −=
ĐK:
32x−≤ ≤
Đặt
3
2
xu
xv
+=
−=
( )
,0uv≥
( )
2
22 2
2
5
5 5 (1)
(*)
5 5 10 0 (2)
55
vu
uv v u
uv u u
uu
= −
+= =−

⇔⇔ ⇔

+= −+=
+− =

Xét (2)
2
5 10 0
uu−+=
có
15 0∆=− <
nên phương trình (2) vô nghiệm
Suy ra hệ phương trình trên vô nghiệm
Vậy phương trình (*) vô nghiệm
9)
22
20xx xx−+ +−=
ĐK:
1x ≥
( )( )
1 1 20xx x x⇔ −+ − + =
( )
1 20x xx⇔ − + +=
46. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
10
20
x
xx
−=
⇔
+ +=
1
2 0,
x
xx x
=
⇔
+ +>∀
1(TM)x⇔=
{ }
S1=
10)
( )
2
2
1 4 40x xx− + + +=
(
)
(
)
22
1 20
xx
⇔ −+ + =
(*)
Ta có :
( )
2
1 0,xx− ≥∀
( )
2
2 0,
xx+ ≥∀
(*)
10
20
x
x
−=
⇔
+=
1
()
2
x
L
x
=
⇔
= −
Vậy phương trình vô nghiệm
11)
2 1 9 18
25 50 8
2 16
xx
x
−+ −
−− =
21
5. 2 6 2
2
x
xx
−+
⇒ −− = −
21
5. 2 6 2
2
12 2 2 10 2 1
22
x
xx
xx x
−+
⇔ −− = −
−+ −− −
⇔=−
3 21x⇔ −=−
(vô lý)
Vậy phương trình vô nghiệm
12)
1227 622x x xx−+ − + + + − =
(
)
(
)
22
2221 26292xx xx
⇔ − + −++ − + −+=
( ) ( )
22
21 23 2xx⇔ −+ + −+ =
21 232xx⇔ −++ −+=
2 22x
⇔ −=−
21x⇔ −=−
( vô lý)
Vậy phương trình vô nghiệm
------------------------- TOÁN HỌC SƠ ĐỒ -------------------------
| 1/46
| | Tải xuống

Có thể bạn quan tâm:

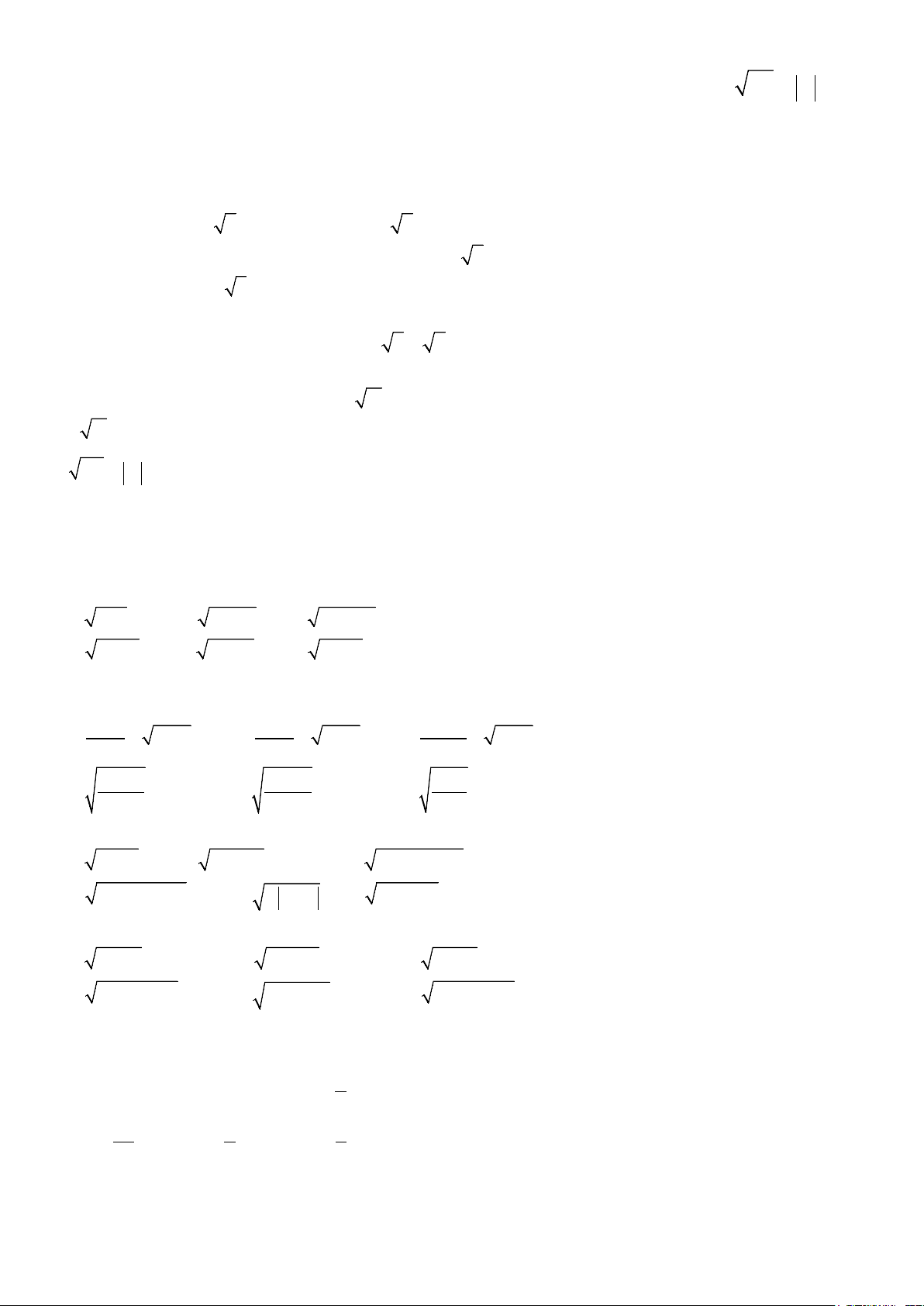
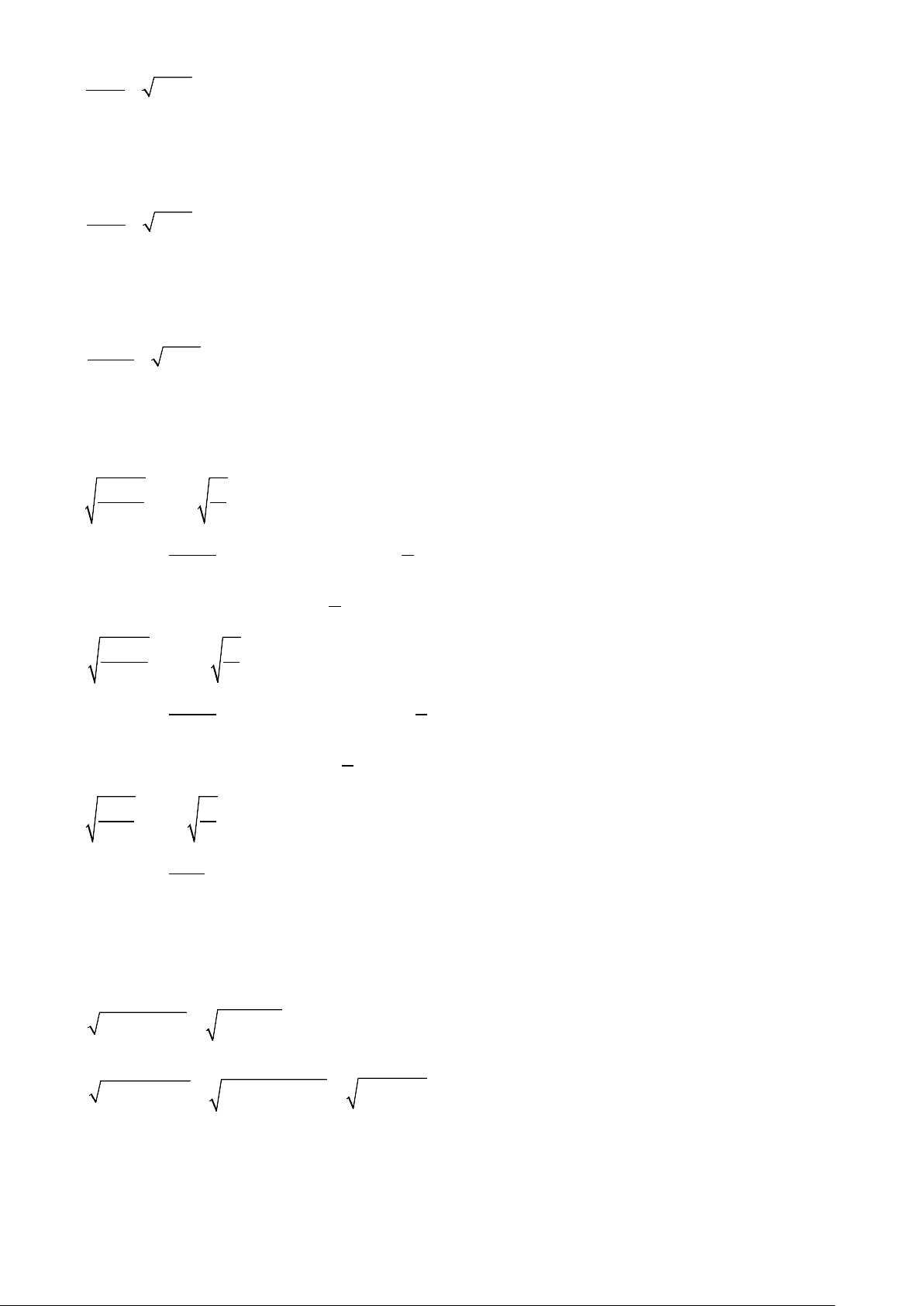
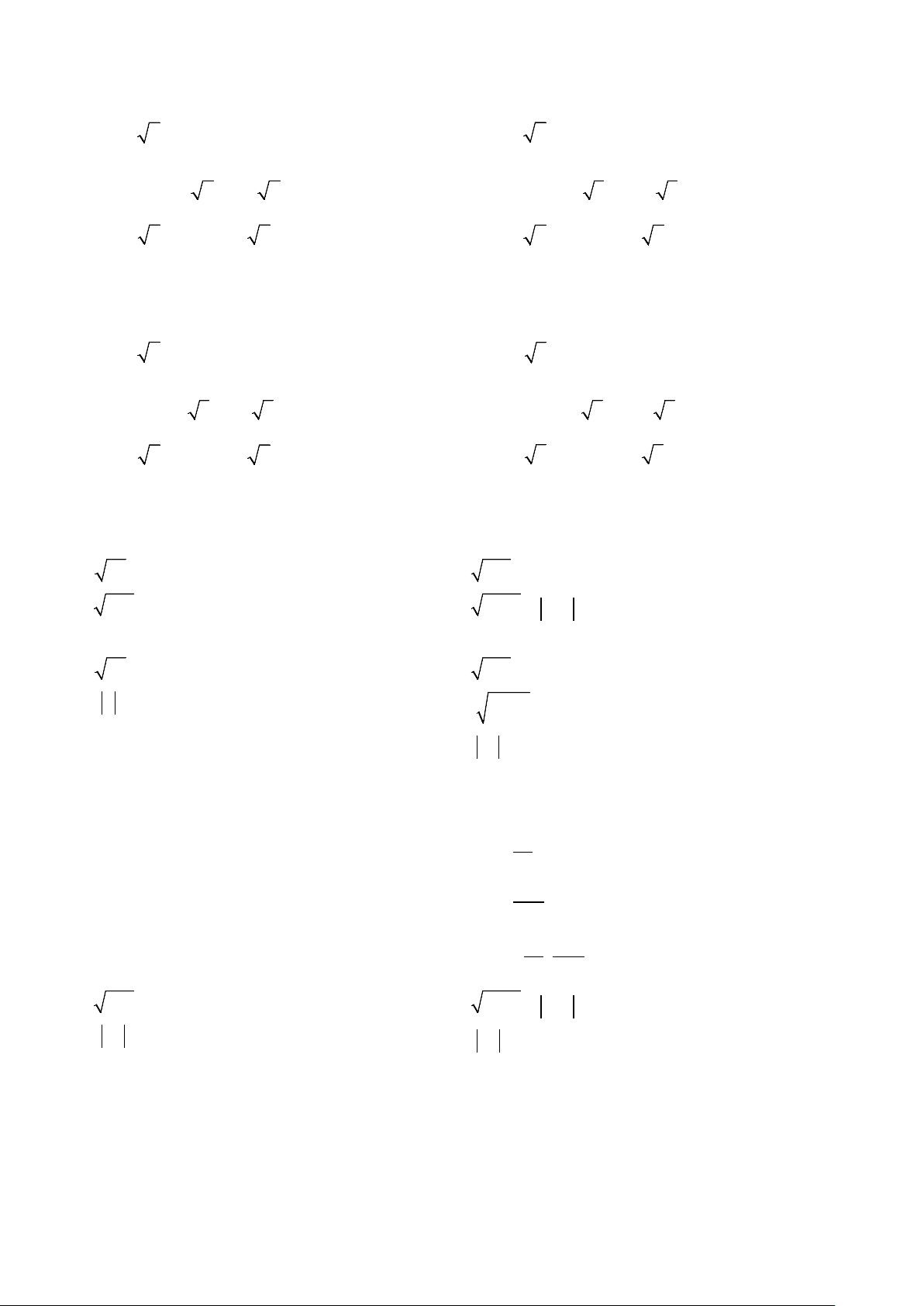
Preview text:

CĂN BẬC HAI - CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2 A = A
A. KIẾN THỨC TRỌNG TÂM
I. Căn bậc hai số học
• Căn bậc hai của một số không âm a là số x sao cho 2 x = a
• Số dương a có đúng hai căn bậc hai là hai số đối nhau:
Số dương kí hiệu là a , số âm kí hiệu là − a
• Số 0 có đúng một căn bậc hai là chính số 0, ta viết 0 = 0
• Với số dương a, số a được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.
• Với hai số không âm a, b, ta có a < b ⇔ a < b II. Căn thức bậc hai
• Với A là một biểu thức đại số, ta gọi A là căn thức bậc hai của A.
• A xác định (hay có nghĩa) khi A ≥ 0. A .A ≥ 0 2 A = A =  −A .A < 0 B. BÀI MINH HỌA
I. BÀI TẬP VÀ CÁC DẠNG BÀI TỰ LUẬN
Dạng 1. Tìm điều kiện để biểu thức chứa căn có nghĩa
Bài 1. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa: a) 3x − b) 4 − 2x c) 3x − + 2 d) 3x +1 e) 9x − 2 f ) 6x −1
Bài 2. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa: x x x a) + x − 2 b) + x − 2 c) + x − 2 2 x − 2 x + 2 x − 4 1 4 2 d) e) f ) − 3− 2x 2x + 3 x +1
Bài 3. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa: 2 2 2 a) x +1 b) 4x + 3 c) 9x − 6x +1 2 2 d) −x + 2x −1 e) − x + 5 f ) 2x − −1
Bài 4. Với giá trị nào của x thì mỗi biểu thức sau có nghĩa: 2 2 2 a) 4 − x b) x −16 c) x − 3 2 d) x − 2x − 3 e) x (x + 2) 2 f ) x − 5x + 6 Lời giải Bài 1: 2 a)x ≤ 0 b)x ≤ 2 c)x ≤ 3 1 − 2 1 d)x ≥ e)x ≥ f )x ≥ 3 9 6 Bài 2:
1. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com x a) + x − 2 x − 2 x − 2 ≥ 0 x ≥ 2
Điều kiện của biểu thức là  ⇔  ⇔ x > 2 x − 2 ≠ 0 x ≠ 2
Vậy điều kiện của biểu thức là x > 2 x b) + x − 2 x + 2 x − 2 ≥ 0 x ≥ 2
Điều kiện của biểu thức là  ⇔  ⇔ x ≥ 2 x + 2 ≠ 0 x ≠ 2 −
Vậy điều kiện của biểu thức là x ≥ 2 c) x + x − 2 2 x − 4 x − 2 ≥ 0 x ≥ 2 Điều kiện  ⇔  ⇔ x > 2 2 x − 4 ≠ 0 x ≠ 2 ±
Vậy điều kiện của biểu thức là x > 2 1 d) dạng A với A > 0 3− 2x B ⇒ Điều kiện 1 3
≥ 0 ⇔ 3− 2x > 0 ⇔ x < 3− 2x 2
Vậy điều kiện của biểu thức là 3 x < 2 e) 4 . Dạng A với A > 0 2x + 3 B ⇒ Điều kiện 4 3
≥ 0 ⇔ 2x + 3 > 0 ⇔ x > − 2x + 3 2
Vậy điều kiện của biểu thức là 3 x > − 2 f) 2 − dạng A với A < 0 x +1 B ⇒ Điều kiện 2
− ≥ 0 ⇔ x +1< 0 ⇔ x < 1 − x +1
Vậy điều kiện của biểu thức là x < 1 − Bài 3. a) Vì 2 x +1 > 0 x
∀ . Vậy hàm số luôn xác định x ∀ ∈  b) Vì 2 4x + 3 > 0 x
∀ . Vậy hàm số luôn xác định x ∀ ∈  c) 2 9x − 6x +1 = (3x − )2 1 . Vì ( − )2 3x 1 ≥ 0 x ∀ ∈ 
Vậy hàm số xác định với mọi x d) 2 − + − = −( 2 x 2x 1 x − 2x + ) 1 = −(x − )2 1
Hàm số xác định ⇔ −( − )2
x 1 ≥ 0 ⇔ x −1 = 0 ⇔ x =1
Vậy hàm số xác định khi x =1
2. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com e) − x + 5
Điều kiện − x + 5 ≥ 0 ⇔ x + 5 = 0 ⇔ x = 5 − f) 2 2x − −1 Điều kiện 2 − − = −( 2 2x 1 2x + ) 1 < 0 x ∀
Vậy không tồn tại giá trị x để hàm số có nghĩa
Bài 4. Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
a) Điều kiện của biểu thức là 2 2
4 − x ≥ 0 ⇔ x ≤ 4 ⇔ 2 − ≤ x ≤ 2
Vậy điều kiện của biểu thức là 2 − ≤ x ≤ 2
b) Điều kiện của biểu thức là 2 2
x −16 ≥ 0 ⇔ x ≥16 ⇔ x ≥ 4 hoặc x ≤ 4 −
Vậy điều kiện của biểu thức là x ≥ 4 hoặc x ≤ 4 −
c) Điều kiện của biểu thức là 2 2
x − 3 ≥ 0 ⇔ x ≥ 3 ⇔ x ≥ 3 hoặc x ≤ − 3
Vậy điều kiện của biểu thức là x ≥ 3 hoặc x ≤ − 3 x +1≥ 0 x ≥ 1 −  ⇔  ⇔ x ≥ 3 x − 3 ≥ 0 x ≥ 3 d) 2
x − 2x − 3 ≥ 0 ⇔ (x + ) 1 (x −3) ≥ 0 ⇔  x +1 ≤ 0 x ≤ 1 −  ⇔  ⇔ x ≤ 1 − x −3 ≤ 0 x ≤ 3
Vậy biểu thức xác định khi x ≥ 3 hoặc x ≤ 1 −
e) Điều kiện của biểu thức là x (x + 2) ≥ 0 ⇔ x ≤ 2 − hoặc x ≥ 0
Vậy điều kiện của biểu thức là x ≤ 2 − hoặc x ≥ 0
f) Điều kiện của biểu thức là 2
x − 5x + 6 ≥ 0 ⇔ (x − 2)(x −3) ≥ 0 ⇔ x ≤ 2 hoặc x ≥ 3
Vậy điều kiện của biểu thức là x ≤ 2 hoặc x ≥ 3
Dạng 2. Tính giá trị biểu thức
Trong các bài toán tính giá trị biểu thức và bài toán rút gọn thường xuất hiện các dạng biểu thức “ẩn” của
các hằng đẳng thức. Để tính toán và giải quyết nhanh bài toán, các em cần biến đổi, và sử dụng thành thạo
các dạng của các hằng đẳng thức đáng nhớ.
Để đơn giản hoá việc nhận dạng và xử lý bài toán, các em có thể tham khảo sơ đồ bên dưới.
Sử dụng hằng đẳng thức trong bài toán chứa căn 2 3
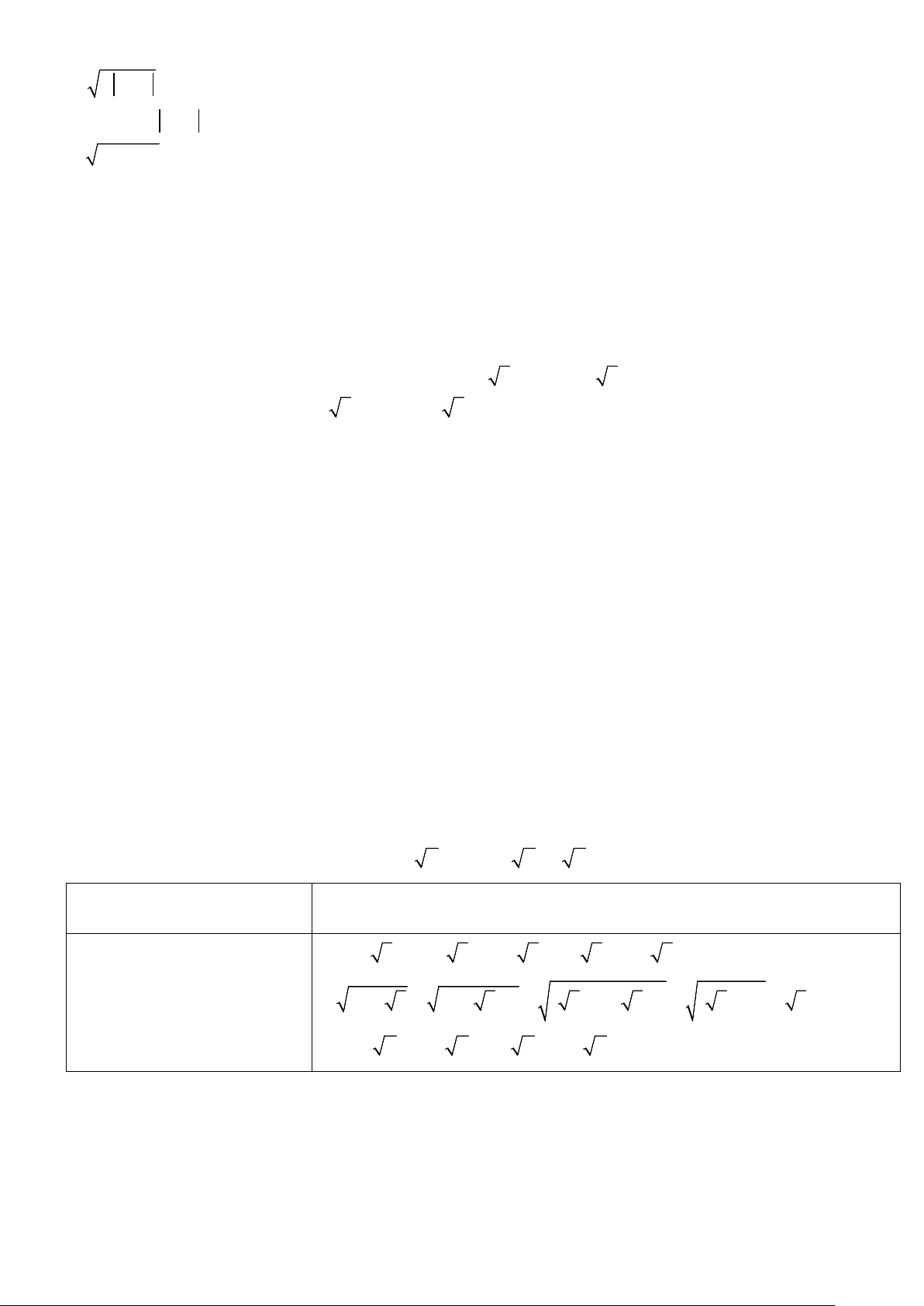
Chú ý: x = ( x ) x ≥ 0;x x = ( x )
Các hằng đẳng thức đáng Ví dụ minh họa nhớ ( + )2 2 2 a b = a + 2ab + b
1.6 + 2 5 = 5 + 2 5 +1 = ( 5)2 + 2 5 +1= ( 5 + )2 1
2. 4 + 2 3 = 3+ 2 3 +1 = ( 3)2 + 2 3 +1 = ( 3 + )2 1 = 3 +1
3.x + 2 x +1 = ( x )2 + 2 x +1= ( x + )2 1
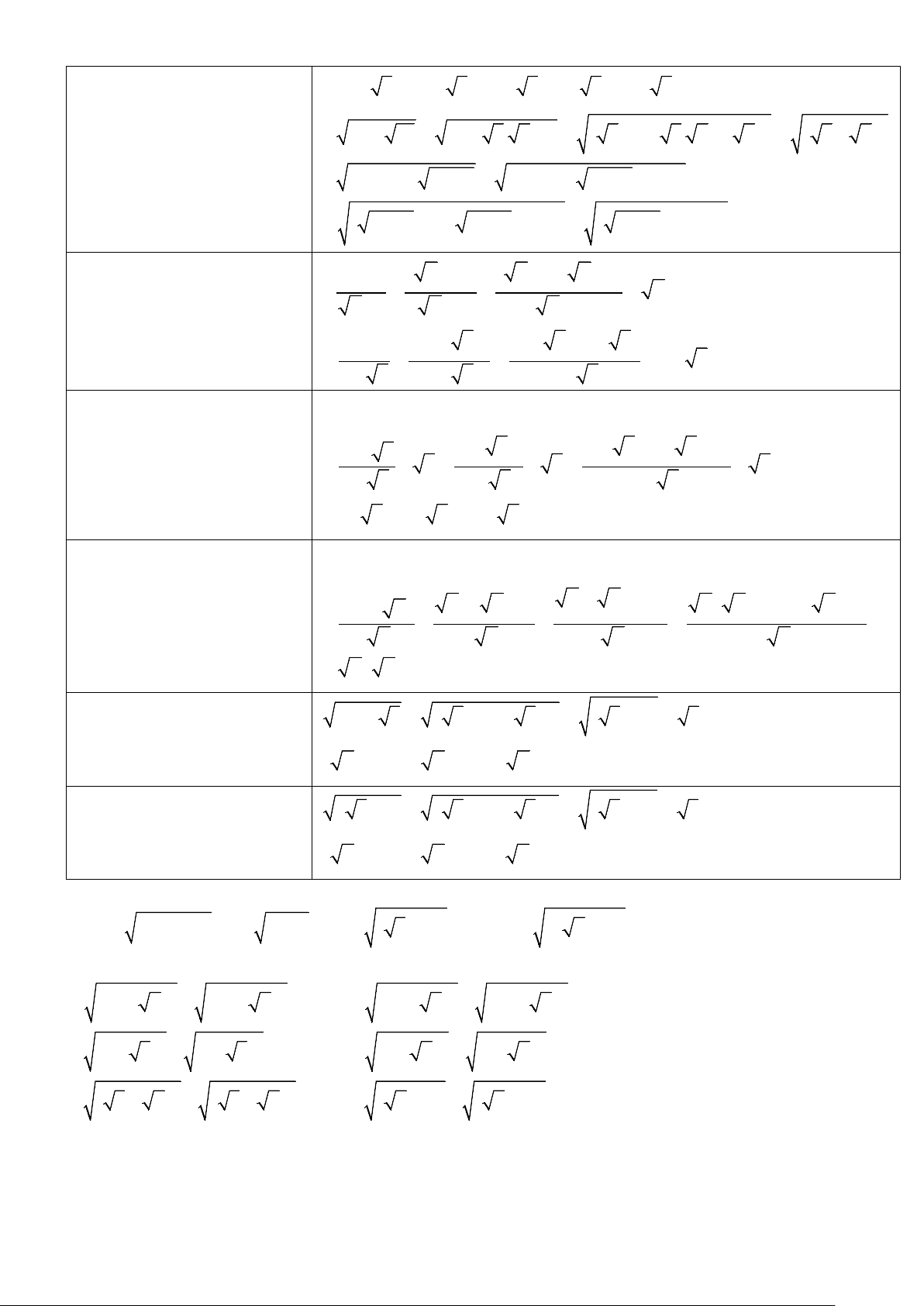
3. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com ( − )2 2 2 a b = a − 2ab + b
1.6 − 2 5 = 5 − 2 5 +1 = ( 5)2 − 2 5 +1= ( 5 − )2 1
2. 7 − 2 10 = 5 − 2 5. 2 + 2 = ( 5)2 − 2 5. 2 +( 2)2 = ( 5 − 2)2 2 2 2 2
3. x + 3− 4 x − 5 = x − 5 − 4 x − 5 + 4 + 4
= ( x −5)2 −4 x −5 + 4+ 4 = ( x −5 −2)2 2 2 2 + 4 ≥ 2 2 2 a − b = (a − b)(a + b) ( x)2 −1 ( x − )1( x + − )1 x 1 1. = = = x −1 x +1 x +1 x +1 2 − ( a )2 2 (2− a)(2+ − a 4 a ) 2. = = = 2 + a 2 − a 2 − a 2 − a 3 3 − = ( − )( 2 2 a b a b a + ab + b ) 3 1.x − 27 = (x −3)( 2 x + 3x + 9) 1− ( a )3 (1− a)(1+ a + − a 1 a a ) 2. + a = + a = + a 1− a 1− a 1− a = 1+ a + a + a = (1+ a )2 3 3 + = ( + )( 2 2 a b a b a − ab + b ) 3 − = ( − )( 2 1.x 27 x 3 x + 3x + 9) + ( ) ( )3  2 x x + + 1 x x x 1 x   ( x + )1(x− x +   )1 x x 2. = = = x − x +1 x − x +1 x − x +1 x − x +1 = x ( x + ) 1 ( + )3 3 2 2 3 a b = a + 3a b + 3ab + b
10 + 6 3 = 3 3 + 9 + 3 3 +1 = ( 3 + )3 3 3 3 1 = 3 +1 ( x + )3 1 = x x + 3x + 3 x +1 ( − )3 3 2 2 3 a b = a − 3a b + 3ab − b
6 3 −10 = 3 3 − 9 + 3 3 −1 = ( 3 − )3 3 3 3 1 = 3 −1 ( x − )3 1 = x x − 3x + 3 x −1
Bài 1. Thực hiện các phép tính sau: − (− ) (− ) ( − )2 ( − )2 2 6 a) 0,8 0,125 b) 2 c) 3 2 d) 2 2 3
Bài 2. Thực hiện các phép tính sau: a) (3− 2 2)2 + (3+ 2 2)2 b) (5− 2 6)2 − (5+ 2 6)2 c) (2− 3)2 + (1− 3)2 d) (3+ 2)2 − (1− 2)2 e) ( 5 − 2)2 + ( 5 + 2)2 f ) ( 2 + )2 1 − ( 2 −5)2
Bài 3. Thực hiện các phép tính sau:
4. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com a) 5 + 2 6 − 5 − 2 6 b) 7 − 2 10 − 7 + 2 10 c) 4 − 2 3 + 4 + 2 3 d) 24 + 8 5 + 9 − 4 5 e) 17 −12 2 + 9 + 4 2 f ) 6 − 4 2 + 22 −12 2
Bài 4. Thực hiện các phép tính sau: 2 2 ( − )
 8− 4 3   4 + 2 3  a) 3 2 5 + 2 6 b)  −    6 2   1 3  − +     c) 5 − 9 − 29 −12 5 d) 13+ 30 2 + 9 + 4 2 Lời giải Bài 1:
a) Biến đổi biểu thức − (− )2 0,8 0,125 = 0 − ,8 0 − ,125 = 0 − ,8.0,125 = 0 − ,1
Vậy biểu thức có giá trị là: -0,1
b) Biến đổi biểu thức (− )6 = (− )3 2 2 = 8 − = 8
Vậy biểu thức có giá trị là: 8
c) Biến đổi biểu thức: ( − )2
3 2 = 3 − 2 = 2 − 3 vì 3 − 2 < 0
Vậy biểu thức có giá trị là 2 − 3
d) Biến đổi biểu thức ( − )2
2 2 3 = 2 2 − 3 = 3− 2 2 vì 3− 2 2 = 3− 8 = 9 − 8 > 0
Vậy biểu thức có giá trị là3− 2 2 Bài 2: 2 2
a) Biến đổi biểu thức: (3− 2 2) + (3+ 2 2) = 3− 2 2 + 3+ 2 2 = 3− 2 2 +3+ 2 2 = 6 (vì 3− 2 2 > 0)
Vậy biểu thức có giá trị là: 6 2 2
b) Biến đổi biểu thức (5− 2 6) − (5+ 2 6) = 5− 2 6 − 5+ 2 6 = (5− 2 6)−(5+ 2 6) = 4 − 6 (vì 5 − 2 6 > 0)
Vậy biểu thức có giá trị là: 4 − 6 2 2
c) Biến đổi biểu thức (2− 3) + (1− 3) = 2− 3 + 1− 3 = 2− 3 + 3 −1=1
(Vì 2 − 3 > 0;1− 3 < 0)
Vậy biểu thức có giá trị là: 1 2 2
d) Biến đổi biểu thức (3+ 2) − (1− 2) = 3+ 2 − 1− 2 = 3+ 2 −( 2 − )1 = 4
(vì 3+ 2 > 0;1− 2 < 0)
Vậy biểu thức có giá trị là: 4 2 2
e) Biến đổi biểu thức ( 5 − 2) + ( 5 + 2) = 5 − 2 + 5 + 2 = 5 − 2 + 5 + 2 = 2 5
vì 5 − 2 > 0; 5 + 2 > 0
5. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy biểu thức có giá trị là: 2 5 2 2
f) Biến đổi biểu thức ( 2 + )1 − ( 2 −5) = 2 +1 − 2 −5 = 2 +1−(5− 2) = 2 2 − 4
(Vì 2 +1 > 0; 2 − 5 < 0 )
Vậy biểu thức có giá trị là 2 2 − 4 Bài 3: a) 5 + 2 6 − 5 − 2 6 Ta có: + = + + = ( + )2 − = − + = ( − )2 5 2 6 3 2 3 2 2 3 2 ; 5 2 6 3 2 3. 2 2 3 2 2 2
Nên 5 + 2 6 − 5 − 2 6 = ( 3 + 2) − ( 3 − 2) = 3 + 2 − 3 − 2 = ( 3 + 2)−( 3 − 2)
= 2 2 vì 3 + 2 > 0; 3 − 2 > 0
Vậy biểu thức có giá trị là 2 2 b) 7 − 2 10 − 7 + 2 10 Ta có: − = − + = ( − )2 + = + + = ( + )2 7 2 10 5 2 5. 2 2 5 2 ;7 2 10 5 2 5. 2 2 5 2 Nên − − + = ( − )2 − ( + )2 7 2 10 7 2 10 5 2 5
2 = 5 − 2 − 5 + 2 = ( 5 − 2)−( 5 + 2) = 2 − 2
vì 5 − 2 > 0; 5 + 2 > 0
Vậy biểu thức có giá trị là 2 − 2
c) Biến đổi biểu thức − + = ( − )2 3.( 3 + + )1 3 3 4 2 3 3 1 +
= 3 −1 + 3 +1 = 3 −1+ 3 +1 = 2 3 3 3
Vậy biểu thức có giá trị 2 3
d) Biến đổi biểu thức
24 + 8 5 + 9 − 4 5 = 4(6+ 2 5) + 9− 4 5 = 4(5+ 2 5 + )1 + 5− 4 5 + 4 = 4( 25 + 2 5 + ) 2 2 1 + 5 − 2 5.2 + 2 = 4( 5 + )2 1 + ( 5 − 2)2 = 2 5 +1 + 5 − 2 = 2 5 + 2 + 5 − 2 = 3 5
Vậy biểu thức có giá trị 3 5
e) Biến đổi biểu thức
6. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 17 −12 2 + 9 + 4 2 = 9 −12 2 + 8 + 8 + 4 2 +1
= 3 − 2.3.2 2 + (2 2)2 + (2 2)2 2 2 + 2.2 2 +1 = (3− 2 2)2 + (2 2 + )2 1 = 3− 2 2 + 2 2 +1 = 3− 2 2 + 2 2 +1 = 4
Vậy biểu thức có giá trị là 4
f) Biến đổi biểu thức 6 − 4 2 + 22 −12 2
= 4 − 4 2 + 2 + 18 −12 2 + 4 2 2 = 2 − 2.2 2 + 2 + (3 2)2 2 − 2.3. 2.2 + 2 = (2− 2)2 + (3 2 − 2)2 = 2 − 2 + 3 2 − 2 = 2 − 2 + 3 2 − 2 = 2 2
Vậy biểu thức có giá trị 2 2 Bài 4.
a) Biến đổi biểu thức ( 3− 2) 5+2 6 = ( 3 − 2) ( 3 + 2)2 = ( 3 − 2) 3 + 2 = ( 3 − 2)( 3 + 2) = ( 3)2 −( 2)2 = 3− 2 =1 4 2 3 ( − − )2 3 1 b) Ta có: = = ( 3 − ) 1 3 −1 3 −1 4 2 3 ( + + )2 3 1 và = = ( 3 + ) 1 1+ 3 1+ 3 2 2  −   +  Suy ra   −   =     ( − )2 −( + )2 4 2 3 4 2 3 3 1
3 1 = (4− 2 3)−(4+ 2 3) = 4 − 3 3 −1 1+    3 
Vậy biểu thức có giá trị 4 − 3
c) Biến đổi biểu thức
7. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 5 − 9 − 29 −12 5 = 5 − 9 − 20 −12 5 + 9 = 5 − 9 − (2 5 +3)2 =
5 − 9 − (2 5 +3) = 5 − 6− 2 5 = 5 − ( 5 − )2 1 = 5 − ( 5 − )1 = 1 =1
Vậy biểu thức có giá trị 1
d) Biến đổi biểu thức 13+ 30 2 + 9 + 4 2 = 13+ 30 2 + (2 2 + )2 1 = 13+ 30 2 + (2 2 + )1
= 13+ 30 3+ 2 2 = 13+ 30 ( 2 + )2 1 = 13+ 30( 2 + ) 1 = 43+ 30 2
= 25 + 2.5.3 2 +18 = (5+3 2)2 = 5+3 2
Vậy biểu thức có giá trị 5 + 3 2
Dạng 3. Rút gọn biểu thức
Bài 1. Rút gọn các biểu thức sau: 2
a)x + 3+ x − 6x + 9 (x ≤ 3) 2 2 b) x + 4x + 4 − x ( 2 − ≤ x ≤ 0) 2 2 x − 2x +1 ( > ) x − 4x + 4 c) x 1 d) x − 2 + (x < 2) x −1 x − 2
Bài 2. Rút gọn các biểu thức sau: 2 2 2 a) 1− 4a + 4a − 2a b)x − 2y − x − 4xy + 4y 2 2 4 2 x −10x + 25 c)x + x −8x +16 d)2x −1− x − 5 4 2 x − 4x + 4 ( − )2 x − 4 e) f ) x 4 + 2 2 x − 2 x −8x +16
Bài 3. Cho biểu thức 2 2 2 2
A = x + 2 x −1 − x − 2 x −1
a) Với giá trị nào của x thì A có nghĩa? b) Tính A nếu x ≥ 2
Bài 4. Cho 3 số dương x,y,z thỏa điều kiện xy + yz + xz =1 ( 2 1+ y )( 2 1+ z ) ( 2 1+ z )( 2 1+ x ) ( 2 1+ x )( 2 1+ y ) Tính A = x + y + z 2 2 2 1+ x 1+ y 1+ z Lời giải Bài 1.
8. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 2
a)x + 3+ x − 6x + 9 (x ≤ 3)
= x + 3+ (x − 3)2 = x + 3+ x − 3
(vì x ≤ 3 nên x − 3 = −(x −3) ) = x + 3− (x − 3) = 6 2 2 b) x + 4x + 4 − x ( 2 − ≤ x ≤ 0) = (x + 2)2 2 + x = x + 2 + x vì x ≥ 2
− nên x + 2 = x + 2 và x ≤ 0 nên x = −x = x + 2 − x = 2 2 x − 2x +1 c) (x > ) 1 x −1 (x − )2 1 x −1 x −1 = = = = 1 x −1 x −1 x −1
Vì x >1 nên x −1 = x −1 x − 4x + 4 ( − )2 2 x 2 d) x − 2 + = x − 2 + x − 2 x − 2
vì x < 2 nên x − 2 = −(x − 2) x − 2 − x − 2 Biểu thức = x − 2 + = −(x − 2) ( ) + = −x + 2 −1 = −x +1 x − 2 x − 2 Bài 2.
a) Biến đổi biểu thức 2
1− 4a + 4a − 2a = (1− 2a)2 − 2a = 1− 2a − 2a Với 1
a ≤ thì 1− 2a ≥ 0 nên 1− 2a =1− 2a ta có: 2 2
1− 4a + 4a − 2a = 1− 2a − 2a =1− 2a − 2a =1− 4a Với 1
a ≥ thì 1− 2a ≤ 0 nên 1− 2a = 2a −1 ta có: 2
1− 4a + 4a − 2a = 1− 2a − 2a = 2a −1− 2a = 1 − 2
b) Biến đổi biểu thức 2 2
x − 2y − x − 4xy + 4y = x − 2y − (x − 2y)2 = x − 2y − x − 2y
Với x − 2y ≤ 0 thì x − 2y = −(x − 2y) ta có 2 2
x − 2y − x − 4xy + 4y = x − 2y − x − 2y = x − 2y + (x − 2y) = 2x − 4y
Với x − 2y ≥ 0 thì x − 2y = x − 2y ta có 2 2
x − 2y − x − 4xy + 4y = x − 2y − x − 2y = x − 2y − (x − 2y) = 0 c) + − + = + ( − )2 2 4 2 2 2 2 2 x x 8x 16 x x 4 = x + x − 4 với 2 2
x − 4 ≤ 0 ⇔ x ≤ 4 ⇔ 2
− ≤ x ≤ 2 thì 2 − = −( 2 x 4 x − 4) ta có: 2 4 2 2 2 2 + − + = + − = − ( 2 x x 8x 16 x x 4 x x − 4) = 4
9. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Với 2 2
x − 4 ≥ 0 ⇔ x ≥ 4 ⇔ x ≤ 2 − hoặc x ≥ 2 thì 2 2 x − 4 = x − 4 ta có: 2 4 2 2 2 2 + − + = + − = + ( 2 − ) 2 x x 8x 16 x x 4 x x 4 = 2x − 4 x −10x + 25 ( − )2 2 x 5 x − 5 d) 2x −1− = 2x −1− = 2x −1− x − 5 x − 5 x − 5
Với x − 5 ≤ 0 ⇔ x ≤ 5 thì x − 5 = −(x −5) ta có: 2 x −10x + 25 x − 5 x − 5 2x −1− = 2x −1− = 2x −1+ = 2x x − 5 x − 5 x − 5
Với x − 5 ≥ 0 ⇔ x ≥ 5 thì x − 5 = (x − 5) ta có: 2 x −10x + 25 x − 5 x − 5 2x −1− = 2x −1− = 2x −1− = 2x − 2 x − 5 x − 5 x − 5 Bài 3. Biểu thức 2 2 2 2
A = x + 2 x −1 − x − 2 x −1
a) Biểu thức xác định khi 2 2
x −1≥ 0 ⇔ x ≥1 ⇔ x ≤ 1 − hoặc x ≥1 b) Tính A với x ≥ 2 2 2 2 2
A = x + 2 x −1 − x − 2 x −1 = ( 2 x − ) 2 1 + 2 x −1 +1 − ( 2 x − ) 2 1 − 2 x −1 +1 = ( x −1+ )2 1 − ( x −1− )2 2 2 1 2 2 = x −1 +1 + x −1 −1 Với x ≥ 2 thì 2 2 2 2
x ≥ 2 ⇔ x −1≥1⇒ x −1 ≥1 ⇔ x −1 −1≥ 0 Vậy 2 2 2 2 2
A = x −1 +1 + x −1 −1 = x −1 +1+ x −1 −1 = 2 x −1
Bài 4. Cho 3 số dương x,y,z thỏa điều kiện: xy + yz + zx = 1. ( 2 1+ y )( 2 1+ z ) ( 2 1+ z )( 2 1+ x ) ( 2 1+ x )( 2 1+ y ) Tính A = x + y + z 2 2 2 1+ x 1+ y 1+ z Ta có: 2 + = ( + + ) 2 2 1 y
xy yz xz + y = xy + y + yz + zx = y(x + y) + z(y + x) = (x + y)(y + z) Tương tự 2 1+ z = (y + z)(z + x) 2 1+ x = (z + x)(x + y) Suy ra ( 2 1+ y )( 2 1+ z ) (x + y)(y + z)(x + z)(y + z) 2 *x = x = x y + z = x y + z 2 1+ x (x + y)(x + z) ( ) ( ) ( 2 1+ z )( 2 1+ x ) (z + x)(y + z)(x + z)(x + y) 2 *y = y = y x + z = y x + z 2 1+ y (x + y)(y + z) ( ) ( ) ( 2 1+ x )( 2 1+ y ) (x + y)(x + z)(x + y)(y + z) 2 *z = z = z x + y = z x + y 2 1+ z (x + z)(y + z) ( ) ( )
10. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy A = x (y + z) + y(x + z) + z(x + y) = 2(xy + yz + xz) = 2
Dạng 4. Giải phương trình
Để đơn giản hoá việc nhận dạng và xử lý bài toán, các em có thể tham khảo sơ đồ bên dưới.
Một số dạng phương trình cơ bản Dạng toán Ví dụ minh họa 2 2 A = B ⇔ A = ±B 2 2 2
1.x = 4 ⇔ x = 2 ⇔ x = 2 hoặc x = 2 − x −1 = x ⇔ 0x =1(PTVN) 2.(x )2 2 1 x  − = ⇔  1
x −1 = −x ⇔ 2x =1 ⇔ x =  2
Vậy phương trình có nghiệm là 1 x = 2 A ≥ 0(hay B ≥ 0) x ≤ 3 A = B ⇔  3  − x ≥ 0  A = B 2x + 5 = 3− x ⇔  ⇔  2 (thỏa) 2x + 5 = 3 − x x − =  3 B ≥ 0 x −1 ≥ 0 A   ≥ = B ⇔ x 1  2 − = − ⇔  ⇔ 2 1 x x 1  A = B 2 1  − x =  (x − )2 2 2 1 1  − x = x − 2x +1
Nếu B < 0 thì phương trình vô nghiệm x ≥ 1 x ≥ 1 x ≥1  ⇔  ⇔  ⇔   x = 0(loai) 2 2x − 2x = 0 2x  (x − ) 1 = 0  x =1  (TM)
Vậy nghiệm của phương trình là x =1 B ≥ 0 x = 1 2 − 3x = 5 − A B  = ⇔  A = B 2 − 3x = 5 ⇔ ⇔  7  − = −   2 3x 5 x = A = −B  3
Vậy tập nghiệm của phương trình là  7 S  1;  = − 3   2 1 1 x + x + = 2x ⇔ x + = 2x 4 2 2x ≥ 0 x ≥ 0  1  1  x + = 2x  x = (TM) ⇔   2 ⇔   2    1  1  x + = 2x −  x = − (loai)   2   6
Vậy tập nghiệm của phương trình 1 x = 2 A = B ⇔ A = Bhay A = −B 3x +1 = x + 3 3x +1 = x + 3 ⇔  3x +1 = −x − 3 2x = 2 x =1 ⇔ ⇔  4x 4  = − x = 1 −
Vậy tập nghiệm của phương trình S = { 1; − } 1
11. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com A = 0 x = 5 − A + B = 0 ⇔  x + 5 = 0  B = 0 2 x + 5 + x − 25 = 0 ⇔  ⇔ x = 5 ⇔ x = 5 − 2 x − 25 = 0  x = 5 −
Vậy nghiệm của phương trình: x = 5 − A = 0 2 A + B = 0 ⇔  1− x + x +1 = 0 B = 0 2 2 1  − x = 0 x =1 x = 1 ± ⇔  ⇔  ⇔  ⇔ x = 1 − x +1 = 0 x = 1 − x = 1 −
Vậy nghiệm của phương trình: x = -1
Bài 1. Giải các phương trình sau: a) (x −3)2 2 = 3− x b) 4x − 20x + 25 + 2x = 5 2 c) 1−12x + 36x = 5 d) x + 2 x −1 = 2
Bài 2. Giải các phương trình sau: 2 a) 2x + 5 = 1− x b) x − x = 3− x 2
c) 2x − 3 = 4x − 3 d) 2x −1 = x −1
Bài 3. Giải các phương trình sau: 2 2 a) x + x = x b) 1− x = x −1 2 2 2 c) x − 4x + 3 = x − 2 d) x −1 − x +1 = 0
Bài 4. Giải các phương trình sau: 2 2 2 a) x − 2x +1 = x −1 b) 4x − 4x +1 = x −1 4 2 2 1 c) x − 2x +1 = x −1 d) x + x + = x 4
Bài 5. Giải các phương trình sau: 2 a) 3x +1 = x +1 b) x − 3 = x − 3 2 2 2 2 c) 9x −12x + 4 = x d) x − 4 + x + 4x + 4 = 0 Lời giải
Bài 1. Giải các phương trình sau: ( − )2
a) x 3 = 3− x ⇔ x − 3 = 3− x 3  − x ≥ 0 x ≤ 3 x ≤ 3  x − 3 = 3 − x  2x = 6  ⇔ ⇔ ⇔ x = 3 ⇔ x ≤ 3  x − 3 = x − 3  0x = 0  0x = 0
Vậy tập nghiệm của PT là x ≤ 3 2
b) 4x − 20x + 25 + 2x = 5 ⇔ (2x −5)2 = 5− 2x
12. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com  5 x ≤  2 5  − 2x ≥ 0    5
⇔ 2x − 5 = 5 − 2x ⇔ 2x −5 = 5 − 2x ⇔ =  ( ) 5 x TM ⇔  x ≤ 2  2 2x − 5 = 2x − 5    5 0x = 0 dung x  ∀ ≤      2 
Vậy tập nghiệm của PT là 5 x ≤ 2
c) Biến đổi biểu thức 2 1−12x + 36x = 5 ⇔ ( − )2 1 6x = 5 ⇔ 1− 6x = 5  2 1  − 6x = 5 x = −  ⇔ ⇔  3 1  − 6x = 5 −  x =1
Vậy tập nghiệm của phương trình là  2 S  ;1 = − 3   
d) x + 2 x −1 = 2 ĐK: x ≥1
Biến đổi biểu thức x + 2 x −1 = 2 ⇔ x −1+ 2 x −1 +1 = 2 ⇔ ( − − )2 x 1 1 = 2 ⇔ x −1 −1 = 2  x −1 −1= 2  x −1 = 3 ⇔  ⇔   x −1 −1= 2 −  x −1 = 1 −  (PTVN) ⇔ x −1 = 9 ⇔ x =10(TM)
Vậy nghiệm của phương trình là x = 10 Bài 2. x ≤1 1  − x ≥ 0 x ≤1
a) Biến đổi biểu thức  4 2x + 5 = 1− x ⇔  ⇔  ⇔  4 ⇔ x = − 2x + 5 = 1− x 3x  = 4 − x = − 3  3 Vậy nghiệm của PT là 4 x = − 3 x ≤ 3 3  − x ≥ 0 x ≤ 3 
b) Biến đổi biểu thức 2 x − x = 3− x  ⇔  ⇔  ⇔   x = 3 (TM) 2 2 x − x = 3 − x x = 3  x = −  3  (TM)
Vậy tập nghiệm của phương trình là S = {− 3; 3}  3 x  3 ≥ 4x 3 0 x  − ≥ ≥ 4
c) Biến đổi biểu thức 2 2x 3 4x 3   4  − = − ⇔ ⇔ ⇔ 2   − = − x = 0(k TM) 2x 3 4x 3  2 2x 4x 0  − =  x = 2  (TM)
Vậy nghiệm của phương trình là x = 2
13. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com x −1 ≥ 0 x ≥1 d) 2x −1 = x −1 ⇔  ⇔ 2x −1 = x −1  x = 0  (kTM)
Vậy phương trình vô nghiệm Bài 3. x ≥ 0 x ≥ 0
a) Biến đổi biểu thức 2 x + x = x ⇔  ⇔  ⇔ x = 0 2 2 x + x = x x = 0
Vậy nghiệm của phương trình là x = 0 x −1 ≥ 0 x ≥1
b) Biến đổi biểu thức 2 1 x x 1   − = − ⇔  ⇔  2 1  − x =  (x − )2 1 (  x −  )2 2 1 + x −1 = 0 x ≥1   x ≥1 ⇔ ( ⇔   x −  )2 1 + (x − ) 1 (x + ) 1 = 0 (  x − ) 1   (x − ) 1 + (x + ) 1  = 0  x ≥1 x ≥1  ⇔  ⇔   x = 0(kTM) (  −  ) ⇔ x =1 x 1 2x = 0  x =1  (TM)
Vậy nghiệm của phương trình là x = 1
c) Biến đổi biểu thức x − 2 ≥ 0  x ≥ 2 x ≥ 2 2 x − 4x + 3 = x − 2 ⇔  ⇔  ⇔  PTVN 2 2 ( ) x − 4x + 3 =  (x − 2) 2 2 x − 4x + 3 = x − 4x + 4 0x = 1
Vậy phương trình vô nghiệm 2 x −1≥ 0
d) Biến đổi biểu thức 2 2 2 2 x 1 x 1 0 x 1 x 1  − − + = ⇔ − = − ⇔  x −1 =  (x − )2 2 2 1 x ≥1 2 x ≥1   ⇔ ( ⇔ x ≤ 1 − 2 x − ) 1 1  −   ( 2 x − ) 1  =  0  ( 2x −  )1( 2 2 − x ) = 0 x ≥1 x ≥1 x ≥1  x 1  x 1  ≤ − ≤ − x ≤ −1 ⇔  ⇔  ⇔  2 2 x −1= 0 x =   1 x = ±1     (TM)  2  2 2 − x = 0 x = 2  x = ± 2 ⇔ x = {− 2; 1; − 1; 2}
Vậy tập nghiệm của phương trình là x = {− 2; 1; − 1; 2}
Bài 4. Giải các phương trình sau:
a) Biến đổi biểu thức 2 2 x − 2x +1 = x −1 ⇔ ( − )2 2 2
x 1 = x −1 ⇔ x −1 = x −1
14. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com x ≥1  x ≥1  x ≤ 1 − 2 2 x −1≥ 0 x ≥1    x 1  ≤ − x = 0  (KTM) 2 2 ⇔   x −1 = x −1 ⇔ x − x = 0 ⇔  ⇔      − =   = x −1 = −  ( x x 1 0 x 1 TM 2 x − ) ( ) ( ) 1 x −1+  (x − ) 1 (x + ) 1 = 0   (x − ) 1 (x + 2) = 0 x =1(TM)  x = 2 −  (TM)
Vậy tập nghiệm của phương trình là S = { 2; − } 1
b, Biến đổi biểu thức 2 4x − 4x +1 = x −1 ⇔ ( − )2
2x 1 = x −1 ⇔ 2x −1 = x −1 x ≥ 1 x −1 ≥ 0 x ≥ 1    x = 0(KTM) ⇔ 2x −1 = x −1 ⇔ x = 0 ⇔   − = −  ( − )    − =  2 2x 1 x 1 3x 2 0 x = (KTM)   3
Vậy phương trình vô nghiệm
c) Biến đổi biểu thức 4 2 x − 2x +1 = x −1 ⇔ (x − )2 2 2 1 = x −1 ⇔ x −1 = x −1 x −1 ≥ 0 x ≥1   2 2 ⇔   x −1 = x −1 ⇔   x − x = 0    2 x −1 = −  (x − )1  ( 2 x − ) 1 + (x − ) 1 = 0 x ≥1 x ≥1  ⇔   x (x )1 0  − = ⇔   x (x − ) 1 = 0   (   x )1(x )1 (x )1 0  − + + − =  (x − ) 1 (x + 2) = 0 x ≥1 x = 0  (KTM)  ⇔ x =1 ⇔ x =1 x =1  x = 2 −  (KTM)
Vậy tập nghiệm của phương trình là x = 1
d) Biến đổi biểu thức 2 1 x + x + = x 4
15. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 2  1  1 ⇔ x + = x ⇔ x + =   x  2  2 x ≥ 0 x ≥ 0 x ≥ 0  1  1     1  x + = x  0x = −  0x = − (PTVN) ⇔   2 ⇔   2 ⇔   2     1  1     1  x + = −x  2x = −  x = − (KTM)   2   2   4
Vậy phương trình vô nghiệm
Bài 5. Giải các phương trình sau:
a) Biến đổi biểu thức 3x +1 = x +1 x = 0 3x +1 = x +1 2x = 0  ⇔  + = −  ( + ) ⇔ ⇔  1 3x 1 x 1 4x = 2 − x = −  2
Vậy tập nghiệm của phương trình là  1 S  ;0 = − 2    2 x −3 = x − 3
b) Biến đổi biểu thức 2 x − 3 = x − 3 ⇔  2 x − 3 = −  (x− 3)
(x − 3)(x + 3)−(x − 3) = 0 
⇔ (x− 3)(x+ 3)+(x− 3)=0 (x − 3)(x + 3 − )1 = 0 
⇔ (x− 3)(x+ 3+ )1=0 x − 3 = 0  x + 3 −1 = 0 ⇔ x− 3 =  0  x + 3 +1 = 0  x = 3   x =1− 3 ⇔  x =  3  x = 1 − − 3
Vậy tập nghiệm của phương trình là S = { 1 − − 3;1− 3; 3}
c) Biến đổi biểu thức 2 2 9x −12x + 4 = x ⇔ ( − )2 2 3x 2 = x ⇔ 3x − 2 = x x =1 3x − 2 = x 2x = 2  ⇔ ⇔ ⇔   1 3x − 2 = −x 4x = 2 x =  2
16. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Vậy tập nghiệm của phương trình là 1 S ;1 =  2   
d) Biến đổi biểu thức 2 2 x − 4 + x + 4x + 4 = 0 x − 2 = 0 x = 2 2 x − 4 = 0 (  x − 2  )(x + 2) = 0    x + 2 = 0  ⇔ ⇔ ⇔ ⇔ x = 2 − ⇔ x = 2 − 2 x + 4x + 4 = 0 (  x + 2  )2 = 0  x + 2 = 0  x = 2 −
Vậy nghiệm của phương trình là x = -2
Bài 5. Giải các phương trình sau a) 2 2 2
x − 6 x + 9 + x − 7 = 0 ;
b) 2x + 4 − 6 2x − 5 + 2x − 4 + 2 2x − 5 = 4 . Lời giải a) x −
x + + x − = ⇔ ( x − )2 2 2 2 6 9 7 0 3 + x − 7 = 0
⇔ x − 3 + x − 7 = 0
Trường hợp 1: Xét x ≥ 3 phương trình có dạng:
x − 3+ x − 7 = 0 ⇔ x = 5 ⇔ x = 5 ± .
Trường hợp 2: Xét 0 ≤ x < 3 phương trình có nghiệm: 3− x + x − 7 = 0 vô nghiệm.
Vậy tập nghiệm của phương trình là S = { 5; − } 5 .
b) 2x + 4 − 6 2x − 5 + 2x − 4 + 2 2x − 5 = 4
⇔ 2x − 5 − 6 2x − 5 + 9 + 2x − 5 + 2 2x − 5 +1 = 4
⇔ ( x − − )2 + ( x − + )2 2 5 3 2 5 1 = 4
⇔ 2x − 5 − 3 + 2x − 5 +1 = 4
Ta có: 2x − 5 − 3 = 3− 2x − 5 ≥ 3− 2x − 5
Vậy vế trái ≥ 3− 2x − 5 + 2x + 5 +1 = 4 .
Do vậy vế trái bằng vế phải khi: 5
2x − 5 ≤ 3 ⇔ 0 ≤ 2x − 5 ≤ 9 ⇔ ≤ x ≤ 7 . 2
Vậy tập nghiệm của phương trình là:  5 S x / x 7 = ≤ ≤ . 2    Dạng 6.Nâng cao
Bài 1: Rút gọn biểu thức sau:
a) A = 6 + 2 5 − 6 − 2 5 ; b) 2
B = a +1− a − 2a +1 với a <1
Bài 2: Tìm giá trị nhỏ nhất của biểu thức sau: a) 2
A = 3+ 2x −8x + 33 ; b) 2
B = x −8x +18 −1; c) 2 2 2
C = x + y − 2xy + 2x − 2y +10 + 2y −8y + 2020 .
Bài 3: Tìm giá trị nhỏ nhất của biểu thức:
17. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com a) 2 2
A = x −12x + 36 + x −16x + 64 b) B = (x − )2 + (x − )2 + (x − )2 2 9 1945 .
Bài 4. Cho a, b, c
là các số hữu tỉ thỏa mãn ab + bc + ca = 2020 . Chứng minh rằng biểu thức
( 2a +2020)( 2b +2020) A = là một số hữu tỉ. 2 c + 2020
Bài 5. Cho a, b, c
là các số thực thỏa mãn 2 2
a + b = 2 .Chứng minh rằng: 4 2 4 2
a + 8b + b + 8a = 6 ( ) 1
Bài 6. Tìm giá trị nhỏ nhất của biểu thức: a) A = (x − )2 + (x − )2 2019 2020 ; b) B = (x − )2 + ( y − )2 + (x − )2 2018 2019 2020 ; c) C = (x − )2 + (x − )2 + (x − )2 + (x − )2 2017 2018 2019 2020 .
Bài 7. Tìm giá trị nhỏ nhất của: A = a + 3− 4 a −1 + a +15 −8 a −1 . Bài 8. Cho x y
x, y thỏa mãn 0 < x <1, 0 < y <1 và +
=1.Tính giá trị của biểu thức 1− x 1− y 2 2
P = x + y + x − xy + y .
(x + y)(x − y ) (1− 4x−1)2 3 3
Bài 9. Tính x biết x >1; y < 0 và = 6 − y (1− 4x−1)( 2 2 3 4
x y + xy + y ) Lời giải
Bài 1: Rút gọn biểu thức sau:
a) A = 6 + 2 5 − 6 − 2 5 ; b) 2
B = a +1− a − 2a +1 với a <1 Lời giải
a) Ta có A = 6 + 2 5 − 6 − 2 5 b) 2
B = a +1− a − 2a +1 với a <1
A = 5 + 2 5 +1 − 5 − 2 5 +1
B = a + − (a − )2 1 1 A = ( + )2 − ( − )2 5 1 5 1
B = a +1− a −1 = a +1− (1− a) = 2a . A = ( 5 + ) 1 − ( 5 − ) 1 = 2 .
Bài 2: Tìm giá trị nhỏ nhất của biểu thức sau: a) 2
A = 3+ 2x −8x + 33 ; b) 2
B = x −8x +18 −1; c) 2 2 2
C = x + y − 2xy + 2x − 2y +10 + 2y −8y + 2020 . Lời giải a) Ta có: 2
A = 3+ 2x −8x + 33 = 3+ 2(x − 2)2 + 25 ≥ 3+ 25 = 8.
Vậy giá trị nhỏ nhất của biểu thức A là 8 khi x = 2 .
18. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com b) Ta có: 2
B = x −8x +18 −1 = (x − 4)2 + 2 −1≥ 2 −1
Vậy giá trị nhỏ nhất của biểu thức B là 2 −1 khi x = 4 . c) Ta có: 2 2 2
C = x + y − 2xy + 2x − 2y +10 + 2y −8y + 2020
⇒ C = (x − y + )2 + + ( y − )2 1 9 2 2 + 2012
⇒ C ≥ 9 + 2012 = 2015.
Vậy giá trị nhỏ nhất của C là 2015.
x − y +1 = 0 x =1 Khi  ⇔ . y 2 0  − = y = 2
Bài 3: Tìm giá trị nhỏ nhất của biểu thức: a) 2 2
A = x −12x + 36 + x −16x + 64 b) B = (x − )2 + (x − )2 + (x − )2 2 9 1945 . Lời giải a) Ta có: 2 2
A = x −12x + 36 + x −16x + 64 = (x − 6)2 + (x −8)2
A = x − 6 + x −8 = x − 6 + 8 − x ≥ x − 6 + 8 − x = 2
Vậy giá trị nhỏ nhất của A là 2 khi (x − 6)(8 − x) ≥ 0 hay 6 ≤ x ≤ 8 . b) Ta có:
B = (x − )2 + (x − )2 + (x − )2 2 9 1945
B = x − 2 + x − 9 + x −1945
B = x − 2 + 1945 − x + x − 9 ≥ x − 2 +1945 − x + 0 =1943.
Vậy giá trị nhỏ nhất của B là 1943 khi (x − 2)(1945− x) ≥ 0 và x −9 = 0 tức là x = 9 .
Bài 4. Cho a, b, c
là các số hữu tỉ thỏa mãn ab + bc + ca = 2020 . Chứng minh rằng biểu thức
( 2a +2020)( 2b +2020) A = là một số hữu tỉ. 2 c + 2020 Lời giải • Ta có: 2 2
a + 2020 = a + ab + bc + ca 2
⇒ a + 2020 = (a + b)(a + c) ( ) 1 • Tương tự, ta có: 2
b + 2020 = (b + a)(b + c) (2) 2
c + 2020 = (c + a)(c + b) (3)
(a +b)(a + c)(b + c)(b + a)
Từ (1) ,(2), (3) suy ra A = ( + )( + )
= (a + b)2 = a + b c a c b
⇒ A = a + b .
Vì a, b là các số hữu tỉ nên a + b cũng là số hữu tỉ. Vậy A là một số hữu tỉ.
Lưu ý: Các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa của các số hữu tỉ có kết quả cũng là một số hữu tỉ.
Bài 5. Cho a, b, c
là các số thực thỏa mãn 2 2 a + b = 2
19. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Chứng minh rằng: 4 2 4 2
a + 8b + b + 8a = 6 ( ) 1 Lời giải Cách 1. Thay 2 2
a + b = 2 vào (1) ta có: Vế trái: 4 2 a + b ( 2 2 a + b ) 4 2 + b + a ( 2 2 4 4 a + b ) 4 2 2 2 4 2 2 4
= a + 4a b + 4b + b + 4a b + 4a
= (a + b )2 + (b + a )2 2 2 2 2 2 2 2 2 2 2
= a + 2b + b + 2a = ( 2 2
3 a + b ) = 3.2 = 6.
Vế trái bằng vế phải. Suy ra điều phải chứng minh.
Cách 2. Từ giả thiết suy ra: 2 2 2 2
b = 2 − a ;a = 2 − b thay vào (1) ta được:
a + ( − a ) + b + ( −b ) = (a − )2 + (b − )2 4 2 4 2 2 2 8 2 8 2 4 4 2 2
= a − 4 + b − 4 (do 2 2
a < 4;b < 4 ) 2 2
= 4 − a + 4 − b = 6 . Vế trái bằng vế phải. Suy ra điều phải chứng minh.
Bài 6. Tìm giá trị nhỏ nhất của biểu thức: a) A = (x − )2 + (x − )2 2019 2020 ; b) B = (x − )2 + ( y − )2 + (x − )2 2018 2019 2020 ; c) C = (x − )2 + (x − )2 + (x − )2 + (x − )2 2017 2018 2019 2020 . Lời giải
a) A = x − 2019 + x − 2020
= x − 2019 + 2020 − x ≥ x − 2019 + 2020 − x =1
Vậy giá trị nhỏ nhất của A là 1 khi x − 2019 ≥ 0 và 2020 − x ≥ 0 hay 2019 ≤ x ≤ 2020 .
b) Giá trị nhỏ nhất của B là 2 khi 2018 ≤ x ≤ 2020 và y = 2019 .
c) Giá trị nhỏ nhất của C là 4 khi 2018 ≤ x ≤ 2019.
Bài 7. Tìm giá trị nhỏ nhất của: A = a + 3− 4 a −1 + a +15 −8 a −1 . Lời giải Ta có:
A = a −1− 4 a −1 + 4 + a −1−8 a −1 +16
⇔ A = ( a − − )2 + ( a − − )2 1 2 1 4
⇒ A = a −1 − 2 + 4 − a −1 ≥ a −1 − 2 + 4 − a −1 ⇒ A ≥ 2 .
Đẳng thức xảy ra khi 2 ≤ a −1 ≤ 4 ⇔ 4 ≤ a −1≤16 .
Vậy giá trị nhỏ nhất của A là 2 khi 5 ≤ a ≤17 . Bài 8. Cho x y
x, y thỏa mãn 0 < x <1, 0 < y <1 và + =1. 1− x 1− y
20. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Tính giá trị của biểu thức 2 2
P = x + y + x − xy + y . Lời giải
Từ giả thiết, suy ra: x(1− y) + y(1− x) = (1− x)(1− y) 2 2
⇔ 2x + 2y −1 = 3xy ⇔ x − xy + y = (x + y)2 − 2(x + y) +1 = (x + y − )2 1 Vậy 2 2
P = x + y + x − xy + y = x + y + x + y −1
Từ giả thiết, ta lại có: x 1 < 1⇒ x < 1− x 2 Tương tự ta có: 1
y < . Suy ra 0 < x + y <1, ta có P = x + y +1− x − y =1. 2
(x + y)(x − y ) (1− 4x−1)2 3 3
Bài 9. Tính x biết x >1; y < 0 và = 6 − y (1− 4x−1)( 2 2 3 4
x y + xy + y ) Lời giải
Ta có: Với x >1⇒ 4x > 4 ⇒ 4x −1 > 3 ⇒ 4x −10 > 3 Do đó ( − x − )2 1 4 1 = 4x −1 −1 (x + y)( 3 3
x − y )( 4x −1− )1 Từ đó ( = − 1− 4x −1)( 6 2 2 3 4
x y + xy + y ) (x + y)( 3 3 x − y )
(x + y)(x − y)( 2 2
x + xy + y ) ⇔ = 6 ⇔ = 6 2 2 3 4 2
x y + xy + y y ( 2 2
x + xy + y ) 2 2 2 2 2 ⇔ − = 6 ⇔ = 7 x x y y x y ⇔ = 7 y Mà x
x >1; y < 0 nên = − 7 . y
21. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
II. TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Cho số thực a  0 . Số nào sau đây là căn bậc hai số học của a ? A. a . B.a . C. 2a . D. 2 a .
Câu 2. Số nào sau đây là căn bậc hai số học của số a  0.36 ? A.0,6 . B. 0,6. C. 0,9. D. 0,18 .
Câu 3. Khẳng định nào sau đây sai? A. 2
A A khi A  0 . B. 2 A Akhi A  0 .
C. A B  0  A B .
D. A B  0  A B .
Câu 3. Biểu thức 10  100x có nghĩa khi A. x  10 . B. 1 x   . C. 1 x  . D. x  10 . 10 10
Câu 4. So sánh hai số 5 và 50  2 A. 5  50  2 . B. 5  50  2 . C. 5  50  2 .
D. Chưa đủ điều kiện so sánh.
Câu 5. Tìm các số x không âm thỏa mãn 5x  10
A. 0  x  20. B. x  20 . C. x  0. D. x  2 . 2 2
Câu 6. Tìm giá trị biểu thức 2  3  1 3 . A. 3 . B. 1. C. 2 3 . D. 2 . 2  
Câu 8. Tính giá trị biểu thức 8   2 9     (0, 8)  .  3 A. 24,64 . B. 32 . C. 24,8 . D. 24,8.
Câu 9. Tính giá trị biểu thức 2 2 6 (2,5)  8 (0,5) . A. 15 . B. 11. C. 11. D. 13.
Câu 10. Tìm điều kiện xác định của 125  5x A. x  15 . B. x  25 . C. x  25 . D. x  0.
Câu 11. Tìm điều kiện xác định của 5  3x A. 5 x  . B. 5 x  . C. 3 x  . D. 3 x  . 3 3 5 5
Câu 12. Rút gọn biểu thức 2
A  144a  9a với a  0 . A. 9a . B. 3a . C. 3a . D. 9a . 2 Câu 13. Tìm (5) x để có nghĩa 6  3x A. x  2 . B. x  2 . C. x  2 . D. x  2 . Câu 14. Tìm  x để 2 có nghĩa 3x  1 A. 1 x  . B. 1 x  . C. 1 x  . D. 1 x  . 3 3 3 3
22. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Câu 15. Giá trị của biểu thức 2 9 16 25   169 là: 5 2 81 A. 12 . B. 13 . C. 14 . D. 15 .
Câu 16. Tìm giá trị của x không âm biết 2 x  30  0 .
A. x  15 . B. x  225 . C. x  25 . D. x  15 .
Câu 17. Tìm giá trị của x không âm biết 5 2x 125  0 A. 25 x  . B. x  125. C. x  25 . D. 625 x  . 2 2
Câu 18. Tính giá trị biểu thức 19  8 3  19  8 3 . A. 2 3 . B. 8  2 3 . C. 6. D. 8 .
Câu 19. Tính giá trị biểu thức 15  6 6  15  6 6 A. 2 6 . B. 6 . C. 6. D. 12 .
Câu 20. Rút gọn biểu thức 2 2
a  8a  16  a  8a  16 với 4  a  4 ta được: A. 2a . B. 8 . C. 8 . D. a .
Câu 21. Rút gọn biểu thức 2 2
4a  12a  9  4a  12a  9 với 3 3
  a  ta được: 2 2 A. 4a . B. 4a . C. 6 . D. 6.
Câu 22. Tìm x thỏa mãn phương trình 2
x x  6  x  3 . A. x  2 . B. x  4 . C. x  1. D. x  3 .
Câu 24. Tìm x thỏa mãn phương trình 2
2x  3x  3x  4 . A. x  2 . B. x  4 . C. x  1.
D. x  1;x  2 .
Câu 24. Nghiệm của phương trình 2
2x  2  3x  1 là: A. x  2 . B. x  5 . C. x  1. D. x  3 .
Câu 24. Số nghiệm của phương trình 2
4x  4x  1  3  4x là: A. 0 . B. 4 . C. 1. D. 2 .
Câu 26. Nghiệm của phương trình 2
x  6x  9  4  x là: A. x  2 . B. 1 x  . C. 1 x  . D. x  3 . 4 2 2
Câu 27. Rút gọn biểu thức x  10x  25 với x  5 ta được: 5  x A. 1. B. 1. C. 2 . D. 2.
Câu 28.Trong các khẳng định sau, khẳng định nào sai?
A. (x − y) 3 4
= 4 3(x − y) với mọi x > y > 0 . x − y B. 1 1 1+ a + =
với mọi a > 0 . 2 a a a
23. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com ( − )2 1 3 2(3− 3) C. = . 12 3 D. 1 5 = . 500 50
Câu 29. Tìm giá trị nhỏ nhất của biểu thức: 2 2
B  4a  4a  1  4a  12a  9 A. 2 . B. 1. C. 4 . D. 10 .
Câu 30. Tìm giá trị nhỏ nhất của biểu thức: 2 2
A m  2m  1  m  8m  16 A. 2 . B.9. C. 5. D. 10 .
24. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com HƯỚNG DẪN Câu 1. Đáp án A.
Với số dương a , số a được gọi là căn bậc hai số học của a . Câu 2. Đáp án B.
Căn bậc hai số học của a  0,36 là 0,36  0,6. Câu 3. Đáp án D.
- Với hai số a,b không âm ta a b a b nên C đúng.
- Với hai số a,b không âm ta có a b  0  a b nên D sai. A  khi A  0
- Sử dụng hằng đẳng thức 2 A | A |     nên A, B đúng.  Akhi A  0  Câu 3. Đáp án B.
Ta có: 10  100x có nghĩa khi 10  100x  0  100x  10  x  110 . Câu 4. Đáp án C.
Tách 5  7  2  49  2
Vì 49  50  49  50  7  50  7  2  50  2  5  50  2 . Câu 5. Đáp án A.
Điều kiện: 5x  0  x  0
Vì 10  100 nên 5x  10  5x  100  5x  100  x  20
Kết hợp điều kiện x  0 ta có 0  x  20 Vậy 0  x  20. Câu 6. Đáp án B.   2 2 3
 2  3 mà 2  4  3 (vì 4  3 ) nên 2  3  0 . Từ đó   2 2 3  2  3  2  3 . Ta có   2 1 3
 1  3 mà 1  1  3 (vì 1  3 ) nên 1  3  0 . Từ đó   2 1 3  1  3  3  1. 2 2
Nên 2  3  1 3  2  3  3 1  1. Câu 8. Đáp án D. 2   Ta có: 8   8 8        và 2
(0, 8)  0, 8  0, 8  3 3 3 2   Nên 8   2 8 9  
  (0, 8)  9.  0, 8  24  0, 8  24, 8  .  3 3 Câu 9. Đáp án C.
25. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Ta có 2
(2,5)  2,5  2,5 và 2 (0,5)  0,5  0,5 Nên 2 2
6 (2,5)  8 (0,5)  6.2,5  8.0,5  15  4  11. Câu 10. Đáp án C.
Ta có: 125  5x có nghĩa khi 125  5x  0  5x  125  x  25 . Câu 11. Đáp án A.
Ta có 5  3x có nghĩa khi 5
5  3x  0  3x  5  x  . 3 Câu 12. Đáp án C. Ta có: 2 2
144a  (12a)  12a mà a  0  12a  0 nên 12a  12a hay 2 144a  12a Từ đó: 2
A  144a  9a  12a  9a  3a. . Câu 13. Đáp án A. 2 2
Ta có: (5) có nghĩa khi (5) 25  0   0 mà 25  0 6  3x 6  3x 6  3x
 6  3x  0  6  3x x  2 . Câu 14. Đáp án A. Ta có
2 có nghĩa khi 2  0 mà 2  0  3x 1  0 1  x  . 3x  1 3x  1 3 Câu 15. Đáp án B. 2   Ta có: 2 16 4   4 4 25  5  5  5;      81 9 9 9 2 169  13  13  13 Nên 2 9 16 25   169 2 9 4
 .5  .  13  2  2  13  13 . 5 2 81 5 2 9 Câu 16. Đáp án B.
Với x không âm ta có 2 x  30  0  2 x  30
x  15 mà 15  0 nên x  15 2
x  15  x  225 (thỏa mãn). Vậy x  225 . Câu 17. Đáp án D.
Điều kiện: 2x  0  x  0
Ta có: 5 2x 125  0  5 2x  125  2x  25 mà 25  0 nên 2 625
2x  25  2x  25  2x  625  x  (thỏa mãn). 2 Vậy 625 x  . 2 Câu 18. Đáp án D.
26. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Ta có:        2 2 19 8 3 4 2.4. 3 3 4 3  4  3  4  3 Và        2 2 19 8 3 4 2.4. 3 3 4 3  4  3  4  3
(vì 4  16  3  4  3  0 )
Nên 19  8 3  19  8 3  4  3  4  3  8 . Câu 19. Đáp án A. Ta có        2 2 15 6 6 3 2.3. 6 6 3 6  3  6  3  6 Và        2 2 15 6 6 3 2.3. 6 6 3 6  3  6  3  6
(vì 3  9  6  3  6  0 )
Nên 15  6 6  15  6 6  3  6 3  6  3  6  3  6  2 6 . Câu 20. Đáp án B. Ta có 2 2
a  8a  16  (a  4)  a  4
Mà 4  a  4  a  4  0  a  4  a  4 Hay 2
a  8a  16  a  4 với 4  a  4 Ta có 2 2
a  8a  16  (a  4)
Mà 4  a  4  a  4  0  a  4  4 a Hay 2
a  8a  16  4 a với 4  a  4 Khi đó 2 2
a  8a  16  a  8a  16  a  4  4 a  8 . Câu 21. Đáp án D. Ta có: 2 2 2 2
4a  12a  9  (2a)  2.3.2a  3  (2a  3)  2a  3 3 3 2  a  3  0 |
 2a  3 | 2a  3 Mà a 3 2a 3           2 2 2  a  3  0 |
 2a  3 | 3  2a  Hay: 2
4a  12a  9  2a  3 và 2
4a  12a  9  3  2a với 3 3   a  Khi 2 2 đó: 2 2
4a  12a  9  4a  12a  9  2a  3  3  2a  6 . Câu 22. Đáp án D.
ĐK: x  3  0  x  3
Với điều kiện trên, ta có 2
x x  6  x  3 2 2 2
x x  6  x  3  x  2x  3  0  x  3x x  3  0
x(x  3)  (x  3)  0  (x  3)(x  1)  0
27. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com x  3 0 x     3(N )     x  1 0 x     1(L)  
Vậy phương trình có nghiệm x  3 . Câu 24. Đáp án A. ĐK: 4
3x  4  0  3x  4  x  Với điều kiện trên, ta có: 2
2x  3x  3x  4 3  2
x x x   2
x x x    2 2 3 3 4 2 3 3 4 0
2x  6x  4  0 2 2
x  3x  2  0  x x  2x  2  0  x(x  ) 1  ( 2 x  ) 1  0  (x  ) 1 (x  ) 2  0 x  1 0 x     1(L)     x  2 0 x     2(N )  
Vậy phương trình có nghiệm x  2 . Câu 24. Đáp án C. ĐK: 1
3x  1  0  x  3
Với điều kiện trên ta có: 2 2 2 2 2
2x  2  3x  1  2x  2  (3x  1)  2x  2  9x  6x  1 2 2
 7x  6x  1  0  7x  7x x  1  0  7x(x  1)  (x  1)  0   1 7x  1  0 x    (L)      7 x  1  0  x    ( 1 N )  Câu 25. Đáp án D. 2 2
4x  4x  1  3  4x  (2x  1)  3  4x  2  x 1 3 4x     6x  2 1 x   | 2x 1 | 3 4x           2  x 1 4x 3 2     x  4 3     x   2 
Vậy phương trình có hai nghiệm 1
x  ;x  2 . 3 Câu 26. Đáp án C. 2 2
x  6x  9  4  x  (x  3)  4  x |
x  3 | 4  x ÐK : x  4   1
x  3  4  x 2
x  1  x  (TM)      2
x  3  x  4   3   ( 4 L) 
Vậy phương trình có nghiệm 1 x  . 2 Câu 27. Đáp án B. Ta có: 2 2
x  10x  25  (x  5)  x  5  (
x  5) (vì x  5 ).
28. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 2
Nên x  10x  25 (  x  5)   1. 5  x (  x  5)
Câu 28.Trong các khẳng định sau, khẳng định nào sai?
A. (x − y) 3 4
= 4 3(x − y) với mọi x > y > 0 . x − y B. 1 1 1+ a + =
với mọi a > 0 . 2 a a a ( − )2 1 3 2(3− 3) C. = . 12 3 D. 1 5 = . 500 50 Chọn C ( − )2 1 3 1− 3 − − 2 3 1 3 3 (3− 3) Ta có = = = ≠ . 12 2 3 2 3 6 3 Câu 29. Đáp án A. Ta có 2 2
B  4a - 4a  1  4a - 12a  9 2 2
 (2a  1)  (2a  3)  2a  1  2a  3
Ta có 2a 1  2a  3  2a 1  3  2a  2a 1  3  2a  2
Dấu “=” xảy ra khi2a 1  3  2a  4a  4  a  1
Suy ra GTNN của B là 2  a  1. Câu 30. Đáp án C. Ta có A  2 m m   2 2 1 m  8m  16  m  2  m  2 ( 1) (
4)  m  1  m  4 .
Ta có m  1  m  4  m  1  4  m m  1  4  m  5 Dấu “=” xảy ra khi 3
m  1  4  m  2m  3  m  2
Suy ra GTNN của B là 3 5  m  . 2
29. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com III.TỰ LUYỆN
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai Bài 1: Tính a. 64 b. ( )2 2,5 25 c. ( )2 2 −  − d. 36  − 169    Bài 2: Tính a. 196. 25 − 5 81 b. ( − )2 10 3 − 10 c. ( + )2 5 7 − 8 − 2 7 d.(81: 9 + 169). 225
Bài 3. Thực hiện các phép tính sau: a. 5 + 2 6 − 5 − 2 6. b. 49 −12 5 + 49 +12 5. c. 31−12 3 − 31+12 3. d. 21+12 3 + 21−12 3. Bài 4:Tính 1) 3 2 − 4 18 + 2 32 − 50
2) 2 24 − 2 54 + 3 6 − 150
3) 2 28 + 2 63 − 3 175 + 112 4) 3 10 28 + 2 175 − 3 343 − 448 2
5) 13− 4 3 6) 7 − 4 3 − 2 7) 15 − 6 6 + 33−12 6 Bài 5:Tính: 16 1 4 10 − 15 1) (2 5 − 7)(2 5 + 7) 2) 2 − 3 − 6 3) 4) 3 27 75 8 − 12 15 − 5 5 − 2 6 − + − 2 8 12 5 27 5) − 3 −1 2 5 − 4 18 − 48 30 + 162 Bài 6:Tính: 1) ( 3 + 4) 19 −8 3 2) 17 − 3 32 + 17 + 3 32
3) (5 + 4 2)(3+ 2 1+ 2 )(3− 2 1+ 2 ) 4) ( 5− 2 6 + 2) 3 5) 2 + 17 − 4 9 + 4 5 6)
2 + 2 3 + 18 −8 2 7) 4 + 5 3 + 5 48 −10 7 + 4 3 Bài 7:Tính: − 1) 3− 2 2 3+ 2 2 − 2) 1 6 2 4 + 175 − 3) 1 7 + 48 − 17 −12 2 17 +12 2 8 + 7 3− 2 2 (5+2 6)(49−20 6) 5−2 6 4) 2 2 + 5) 2 2 + 3+ 5 2 2 − 3− 5 9 3 −11 2
30. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 3 3 1+ 1− 6) 2 2 + 3 3 1+ 1+ 1− 1− 2 2 7) 1 1 1 + +...+ 1 + 2 2 + 3 24 + 25
Dạng 2: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 1: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: a. 15 b. 17 − c. 72x d. 24 +10x e. 13 − f. 27 − 6x x − 2 12 − x 3x
Bài 2: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: a. 2 x +11 b. 2 x + 5x + 6 c. 10 − 3x d. 4x + 2 2 3x +1 2 x + 4x + 5
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Rút gọn các biểu thức sau: a. ( − )2 3 2 b. ( + )2 11 3 c. 4 − 2 3 d. 7 + 4 3
Bài 2: Rút gọn các biểu thức sau: a. 2 2
− a với a ≥ 0 b. 2
16a + 4a với a < 0 c. (a − )2 1 với a ≥1 d. 2
9a − 6a +1 + 3a với 1 a < 3 e. 2
a + 6a + 9 với a ≥ 3 − f. 4 2 25a − 3a Dạng 4: So sánh Bài 1. So sánh a. 5 và 17 +1. b. 3 và 15 −1.
Bài 2. Tìm giá trị của x biết a. −x +1 ≥ 6. b. 2 2x ≤ x .
Bài 3:So sánh A và B :
a) A = 2013 + 2015 ; B = 2 2014 .
b) A = 12 + 12 + 12 + 6 + 6 + 6 + 6 ; B = 12 + 11 . c) 1 1 1 A = + +...+ ; 4028 B = . 1.2014 2.2013 2014.1 2015
Dạng 4: Phân tích đa thức thành nhân tử
Bài 1: Phân tích đa thức thành nhân tử a. 2 x − 7 b. 2 4x − 3 c. 2 x + 2 7x + 7 d. 2 9x + 6 2x + 2
Bài 2: Phân tích đa thức thành nhân tử a. 2 x − 3 b. 2 9x − 5 c. 2 x + 2 2x + 2 d. 2 4x + 4 3x + 3
31. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Dạng 5: Giải phương trình
Bài 1: Giải phương trình a. 2 x = 3 b. 2 9x =10 c. 2 4x −19 = 0 d. 2 49x = 14 −
Bài 2: Giải phương trình a. (x + )2 2 = 2 b. 2
4 − 4x + x = 3 c. 2
x − 4x + 4 = 3+ x d. 2
9x + 6x +1 = x −1 e. 2
x + 2 3x + 3 = 0
f. x − 4 x + 4 = 0 Bài 3: Giải phương trình: 1) 2 x + 9 = 5 2) 2
4x − 20x + 25 =1
3) x −1+ 2 x − 2 = 2 4) 2
x − x − 2 = x − 2 5) 2
x − 9 = 3 − x
6) x −1 +1 = x 7) 2
25x − 30x + 9 = x + 7 8) x + 3 + 2 − x = 5 9) 2 2
x − x + x + x − 2 = 0 10) (x − )2 2 1 + x + 4x + 4 11) x − 2 +1 9x −18 25x − 50 − = 8 2 16
12) x −1+ 2 x − 2 + 7 + x + 6 x − 2 = 2
32. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com HƯỚNG DẪN
Dạng 1: Tính giá trị của biểu thức chứa căn bậc hai Bài 1: Tính a. 64 b. ( )2 2,5 25 c. ( )2 2 −  − d. 36  − 169    Lời giải a. 64 8 = b. ( )2 2,5 = 2,5 25 5 c. (− )2 2 = 2  − d. 36  6 − =  169    13 Bài 2: Tính a. 196. 25 − 5 81 b. ( − )2 10 3 − 10 c. ( + )2 5 7 − 8 − 2 7 d.(81: 9 + 169). 225 Lời giải a. 196. 25 − 5 81 b. ( − )2 10 3 − 10 =13.5 − 5.9 = 65 − 45 = 10 − 3 − 10 = 20 = 10 − 3− 10 = 3 − d. (81: 9 + 169). 225 c. ( + )2 5 7 − 8 − 2 7 = (81:3+13).15 = 30.15 = + − ( − )2 5 7 1 7 = 450 = 5 + 7 − 1− 7 = 5 + 7 +1− 7 = 6
Bài 3. Thực hiện các phép tính sau: a. 5 + 2 6 − 5 − 2 6. b. 49 −12 5 + 49 +12 5. c. 31−12 3 − 31+12 3. d. 21+12 3 + 21−12 3. Lời giải
33. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com a. 5 + 2 6 − 5 − 2 6 b. 49 −12 5 + 49 +12 5 2 2 = ( + )2 − ( − )2 3 2 3 2 = (3 5 − 2) + (3 5 + 2) = 3 + 2 − 3 − 2 = 3 5 − 2 + 3 5 + 2 = 3 + 2 − 3 + 2 = 2 2 . = 6 5. c. 31−12 3 − 31+12 3 d. 21+12 3 + 21−12 3 2 2 = ( − )2 − ( + )2 3 3 2 3 3 2 = (2 3 +3) + (2 3 −3) = 4. − = 4 3. Bài 4:Tính 1) 3 2 − 4 18 + 2 32 − 50
2) 2 24 − 2 54 + 3 6 − 150
3) 2 28 + 2 63 − 3 175 + 112 4) 3 10 28 + 2 175 − 3 343 − 448 2 5) 13− 4 3
6) 7 − 4 3 − 2 7) 15 − 6 6 + 33−12 6 Lời giải
1) 3 2 − 4 18 + 2 32 − 50 = 3 2 −12 2 + 8 2 − 5 2 = 6 − 2 .
2) 2 24 − 2 54 + 3 6 − 150 = 4 6 − 6 6 + 3 6 − 5 6 = 4 − 6 .
3) 2 28 + 2 63 − 3 175 + 112 = 4 7 + 6 7 −15 7 + 4 7 = − 7 4) 3 10 28 + 2 175 − 3 343 −
448 = 20 7 +10 7 − 21 7 −12 7 = 3 − 7 . 2 5) − = − + = ( − )2 7 4 3 4 2.2 3 3 2 3 = 2 − 3 = 2 − 3 . 6) − − = ( − )2 7 4 3 2
3 2 − 2 = 3 − 2 − 2 = 2 − 3 − 2 = − 3 .
7) 15 − 6 6 + 33−12 6 = 9 − 2.3. 6 + 6 + 9 − 2.3.2 6 + 24 = ( − )2 + ( − )2 3 6
3 2 6 = 3− 6 + 2 6 − 3 = 6 Bài 5:Tính: 16 1 4 1) (2 5 − 7)(2 5 + 7) 2) 2 − 3 − 6 3 27 75 10 − 15 15 − 5 5 − 2 6 3) 4) − 8 − 12 3 −1 2 5 − 4 2 8 − 12 5 + 27 5) − 18 − 48 30 + 162 Lời giải 2 2
1) (2 5 − 7)(2 5 + 7) = (2 5) −( 7) = 20 − 7 =13
34. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 16 1 4 2 2 4 1 2 2) 2 − 3 − 6 = 2 − 3 − 6 3 27 75 2 2 3 3 .3 5 .3 1 3 1 2 1  3 12  1 23 3 = 2.4 − − 6. = 8 − − = . 3 3 .3 5 3 3 5    3 15 10 − 15 ( 2 − − 3) 5 5.2 5.3 5 5 3) = = = = 8 − 12 4.2 − 4.3 ( 2 − 3) 4 4 2 15 − 5 5 − 2 6 5.3 − 5 5 − 2 6 5 ( 3 − )1 5− 2 6 5 − 2 6 4) − = − = − = 5 − 3 −1 2 5 − 4 3 −1 2 5 − 4 3 −1 2 5 − 4 2 5 − 4
5 (2 5 − 4) 5− 2 6 10 − 4 5 5− 2 6 10 − 4 5 −5+ 2 6 5− 4 5 + 2 6 = − = − = = 2 5 − 4 2 5 − 4 2 5 − 4 2 5 − 4 2 5 − 4 2 5 − 4 2 8 − 12 5 + 27 5) − = 18 − 48 30 + 162 4 2 − 2 3 5 + 3 3 2 − ( 3 − 2 2) 1 3 − 6 = − = − = = − 6 ( 3 − 2 2) 6 ( 5 + 3 3) 6 ( 3 − 2 2) 6 6 2 Bài 6:Tính: 1) ( 3 + 4) 19 −8 3 2) 17 − 3 32 + 17 + 3 32
3) (5 + 4 2)(3+ 2 1+ 2 )(3− 2 1+ 2 ) 4) ( 5− 2 6 + 2) 3 5) 2 + 17 − 4 9 + 4 5 6) 2 + 2 3 + 18 −8 2
7) 4 + 5 3 + 5 48 −10 7 + 4 3 Lời giải
1) ( 3 + 4) 19 −8 3 = ( 3 + 4) 16 − 2.4 3 + 3 = ( + ) − + ( )2 2 3 4 4 2.4 3 3 = ( + ) ( − )2 3 4 4
3 = ( 3 + 4)(4 − 3) = 16 −3 =13.
2) 17 − 3 32 + 17 + 3 32 = 17 − 3.4 2 + 17 + 3.4 2 2 2
= 17 − 2.6 2 + 17 + 2.6 2 = 9 − 2.3.2 2 + (2 2) + 9 + 2.3.2 2 + (2 2) 2 2
= (3− 2 2) + (3+ 2 2) = 3− 2 2 + 3+ 2 2 = 6.
3) (5 + 4 2)(3+ 2 1+ 2 )(3− 2 1+ 2 ) = ( + )( 2 5 4 2 3 − 4(1+ 2)
= (5+ 4 2) (5− 4 2) = 25−16.2 = 7 −
35. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
4) ( 5− 2 6 + 2) 3 = 15− 2.3 6 + 6 = 9− 2.3 6 + 6 + 6 = ( − )2 3 6 + 6 = 3 − 6 + 6 = 3.
5) 2 + 17 − 4 9 + 4 5 = 2 + 17 − 4 5 + 4 5 + 4 = + − ( + )2 2 17 4 5 2
= 2 + 17 − 4( 5 + 2) = 2 + 9 − 4 5 = 2 + 5 − 4 5 + 4 = + ( − )2 2 5 2 = 2 + 5 − 2 = 5 6) 2 + 2 3 + 18 −8 2 = 2 + 2 3 + 16 − 2.4 2 + 2 = + + ( − )2 2 2 3 4 2 =
2 + 2 3 + 4 − 2 = 2 3 + 4 = 3 + 2 3 +1= ( + )2 3 1 = 3 +1
7) 4 + 5 3 + 5 48 −10 7 + 4 3 = 4 + 5 3 + 5 48 −10 4 + 4 3 + 3 = + + − ( + )2 4 5 3 5 48 10 2
3 = 4 + 5 3 + 5 48 −10(2 + 3)
= 4 + 5 3 + 5 28 −10 3 = 4 + 5 3 + 5 25 −10 3 + 3
= 4 + 5 3 + 5(5− 3) = 4 + 5 3 + 25−5 3 = 4 + 5 = 3 Bài 7:Tính: 1) 3− 2 2 3+ 2 2 − − 2) 1 6 2 4 + 175 − 17 −12 2 17 +12 2 8 + 7 3− 2 3) 1 7 + 48 − 4) 2 2 + 2 2 2 + 3+ 5 2 2 − 3− 5 ( 3 3 5 + 2 6)(49− 20 6) 5− 2 6 1+ 1− 5) 6) 2 2 + 9 3 −11 2 3 3 1+ 1+ 1− 1− 2 2 7) 1 1 1 + +...+ 1 + 2 2 + 3 24 + 25 Lời giải ( 2 − )2 1 ( 2 + )2 1 1) 3− 2 2 3+ 2 2 − = − 17 −12 2 17 +12 2 (3−2 2)2 (3+2 2)2 2 −1 2 +1
( 2 − )1(3+2 2)−( 2 + )1(3−2 2) = − = 3− 2 2 3+ 2 2 (3−2 2)(3+2 2)
36. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
3 2 + 4 − 3− 2 2 − 3 2 + 4 − 3+ 2 2 = = 2 1 − 2) 1 6 2 4 + 175 − 8 + 7 3− 2 8 − 7 2 2.3− 2 2. 2 = ( + − 8 − 7 )( 8 + 7) 5 7 3− 2 2 2 (3− − 2 8 7 ) = + 5 7 − = 8 − 7 + 5 7 − 2 2 8 − 7 3− 2 = 2 2 + 4 7 − 2 2 = 4 7 3) 1 7 + 48 − 3 = 7 + 4 3 − = ( + )2 2 2 3 − 2 2 2 2 = 2 + 3 − 2 2 2 + 3 − 2 + − ( + )2 2. 3 1 − 2 = 2. 4 2 3 2 = = 2 2 2 2.( 3 + )1− 2 6 + 2 − 2 6 = = = 2 2 2 + + + + 4) 2 3 6 8 4 2 + 3 + 4
( 2 + 3+2)+( 6 + 8+2) ( 2 + 3+2)+ 2.( 2 + 3+2) = = =1+ 2 2 + 3 + 4 2 + 3 + 4 2 + 3 5) 2 2 + 3 2 2 + 3 − + 2 6 2 3 4 + 2 3 3 +1 = = 2 2.( 2 + 3) 2 2.2 2 2. 2+ 3 4 3 4 + 2 3 − + 2 + 6 − + 2 6 2 3 3 3 3 +1 = 3 +1 = 4 3 3 +1 2 3 3.(2+ 6)− 4.3+3( 3 + ) + 6 − + 1 3 3 2 3
37. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com 3 +1 3 +1 = = 3 3 + 3 2 − 3 3+ 6 − 3 3 3 3 1+ 1− 6) 2 2 4 + 2 3 4 − 2 3 + = + 3 3 2 + + − − (2+ 4+2 3) 2(2− 4−2 3 1 1 1 1 ) 2 2 ( + )2 ( − )2 ( + )2 ( − )2 3 1 3 1 3 1 3 1 = + = +
4 + 2( 3 + )1 4− 2( 3 − )1 6+ 2 3 6− 2 3 ( + )2 ( − )2 3 1 3 1 3 +1 3 −1 = + = + = 2 3 ( 3 + )1 2 3( 3 − ) 1 1 2 3 2 3 7) 1 1 1 + +...+ 1 + 2 2 + 3 24 + 25 1 − 2 2 − 3 24 − 25 = ( +
) ( − ) + ( + ) ( − ) +...+ 1 2 . 1 2 2 3 . 2 3 ( 24 + 25).( 24 − 25) 1 − 2 2 − 3 24 − 25 = + + ...+ 1 − 1 − 1 −
= −( 1− 2 + 2 − 3 +...+ 24 − 25) = −(1− 25) = 4
Dạng 2: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 1: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: a. 15 b. 17 − x − 2 12 − x c. 72x d. 24 +10x e. 13 − f. 27 − 6x 3x Lời giải
a. 15 có nghĩa ⇔ x − 2 ≥ 0 b. 17 −
có nghĩa ⇔ 12 − x ≤ 0 x − 2 12 − x ⇔ x ≥ 2 ⇔ x ≥12
c. 72x có nghĩa ⇔ 72x ≥ 0
d. 24 +10x có nghĩa ⇔ 24 +10x ≥ 0 ⇔ x ≥ 0 12 x − ⇔ ≥ 5
38. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com e. 13 − có nghĩa 13 − − ⇔ − ≥ ⇔ ≥ 0 f. 27 6x có nghĩa 27 6x 0 3x 3x 27 ⇔ x ≤ ⇔ x < 0 6
Bài 2: Với giá trị nào của x thì mỗi căn thức sau có nghĩa: a. 2 x +11 b. 2 x + 5x + 6 c. 10 − 3x d. 4x + 2 2 3x +1 2 x + 4x + 5 Lời giải a. 2 x +11 có nghĩa 2 ⇔ x +11≥ 0 b. 2
x + 5x + 6 có nghĩa 2
⇔ x + 5x + 6 ≥ 0 ⇔ x∈
⇔ (x + 2)(x + 3) ≥ 0 x ≤ 3 − ⇔  x ≥ 2 −
c. 10 − 3x có nghĩa 10 − 3x 4x + 2 + ≥ 0 d. có nghĩa 4x 2 ≥ 0 2 3x +1 2 3x +1 2 x + 4x + 5 2 x + 4x + 5 vì 2
3x +1≥1 nên 10 − 3x ≥ 0 vì 2
x + 4x + 5 = (x + 2)2 +1≥1 ⇔ 10 ≥ 3x nên 4x + 2 ≥ 0 10 ⇔ x ≤ ⇔ 4x ≥ 2 − 3 1 x − ⇔ ≥ 2
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Rút gọn các biểu thức sau: a. ( − )2 3 2 b. ( + )2 11 3 c. 4 − 2 3 d. 7 + 4 3 Lời giải a. ( − )2 3 2 = 3− 2 = 3− 2 b. ( + )2 11 3 = 11 + 3 = 11 + 3 c. − = ( − )2 4 2 3 1 3 = 1− 3 = 3 −1 d. + = ( + )2 7 4 3 2 3 = 2 + 3 = 2 + 3
Bài 2: Rút gọn các biểu thức sau: a. 2 2
− a với a ≥ 0 b. 2
16a + 4a với a < 0 c. (a − )2 1 với a ≥1 d. 2
9a − 6a +1 + 3a với 1 a < 3 e. 2
a + 6a + 9 với a ≥ 3 − f. 4 2 25a − 3a Lời giải
39. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com a. 2 2
− a với a ≥ 0 b. 2
16a + 4a với a < 0 = 2 − a = 2 − a = 4 a + 4 = 4 − a + 4 c. (a − )2 1 với a ≥1 d. 2
9a − 6a +1 + 3a với 1 a < 3
= a −1 = a −1(a ≥ ) 1 = ( a )2  1 3 1 3a 1 1 3a a  − = − = − <  3    e. 2
a + 6a + 9 với a ≥ 3 − f. 4 2 25a − 3a 2 2 2 = (a + )2
3 = a + 3 = a + 3
= 5a − 3a = 2a Dạng 4: So sánh Bài 1. So sánh a. 5 và 17 +1. b. 3 và 15 −1. Lời giải
a. Ta có 16 +1< 17 +1
b. Ta có 16 −1 > 15 −1 ⇔ 5 < 17 +1. ⇔ 3 > 15 −1.
Bài 2. Tìm giá trị của x biết a. −x +1 ≥ 6. b. 2 2x ≤ x . Lời giải Lời giải
a. Điều kiện −x +1≥ 0 ⇔ x ≤1. Ta có
b. Điều kiện x ≥ 0 . Ta có
−x +1≥ 36 ⇔ x ≤ 35
− (thỏa mãn điều kiện). x ≥ 2 2
2x ≤ x ⇔ x(x − 2) ≥ 0 ⇔  x ≤ 0
Kết hợp điều kiện ta có x = 0 hoặc x ≥ 2 .
Bài 3:So sánh A và B :
a) A = 2013 + 2015 ; B = 2 2014 .
b) A = 12 + 12 + 12 + 6 + 6 + 6 + 6 ; B = 12 + 11 . c) 1 1 1 A = + +...+ ; 4028 B = . 1.2014 2.2013 2014.1 2015 Lời giải
a) A = 2013 + 2015 ; B = 2 2014 . Ta có: 2013 < 2015
⇒ 0 < 2013 + 2014 < 2015 + 2014 ⇒ 1 1 > 2013 + 2014 2015 + 2014 2014 − 2013 2015 − 2014 ⇒ ( >
2014 + 2013)( 2014 − 2013) ( 2015 + 2014)( 2015 − 2014)
40. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
⇒ 2014 − 2013 > 2015 − 2014 ⇒ 2 2014 > 2015 + 2013 ⇒ B > A . Cách khác : Ta có 2 2
A = 2013 + 2015 > 0 ⇔ A = 4028 + 2 2013.2015 = 2.2014 + 2 2014 −1 2
A < 2.2014 + 2.2014 = 4.2014 2
B = 2 2014 > 0 ⇔ B = 4.2014 Suy ra 2 2
A < B ⇔ A < B (do , A B > 0 )
b) So sánh A = 12 + 12 + 12 + 6 + 6 + 6 + 6 ; B = 12 + 11 . 2   Ta có: 2
A =  12 + 12 + 12 + 6 + 6 + 6 + 6      2
A =12 + 12 + 12 + 6 + 6 + 6 + 6 + 2. 12 + 12 + 12 . 6 + 6 + 6 + 6 2
A =18 + 12 + 12 + 6 + 6 + 6 + 2. 12 + 12 + 12 . 6 + 6 + 6 + 6 B = ( + )2 2 12 11 = 23+ 2. 132
Dễ thấy 12 + 12 > 9 và 6+ 6+ 6 > 4 ⇒ 18+ 12+ 12 + 6+ 6+ 6 > 23. ⇒ Để so sánh 2 A và 2
B ta chỉ cần so sánh 12 + 12 + 12 . 6 + 6 + 6 + 6 và 132 .
Ta có: (12 12 12 ).6 6 6 6  + + + + +    
= 72 +12 6 + 6 + 6 + 6 12 + 12 + 12 + 12. 6 + 6 + 6
Mà 6 + 6 + 6 > 9 = 3 và 12 + 12 > 9 = 3 nên 12 6 + 6 + 6 >12.3 = 36 6 12 + 12 > 6.3 =18
12 + 12. 6 + 6 + 6 > 3.3 = 9
⇒ 72 +12 6 + 6 + 6 + 6 12 + 12 + 12 + 12. 6 + 6 + 6 > 72 + 36 +18 + 9 .
⇒ 72 +12 6 + 6 + 6 + 6 12 + 12 + 12 + 12. 6 + 6 + 6 >135 .
⇒ 72 +12 6 + 6 + 6 + 6 12 + 12 + 12 + 12. 6 + 6 + 6 >132 .
⇒ 12 + 12 + 12 . 6 + 6 + 6 + 6 > 132 . ⇒ 2 A > 2 B .
⇒ A > B (Do A > 0 và B > 0 ).
Dạng 4: Phân tích đa thức thành nhân tử
41. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Bài 1: Phân tích đa thức thành nhân tử a. 2 x − 7 b. 2 4x − 3 c. 2 x + 2 7x + 7 d. 2 9x + 6 2x + 2 Lời giải a. 2
x − 7 = (x + 7)(x − 7) b. 2
4x − 3 = (2x + 3)(2x − 3) c. x + x + = (x + )2 2 2 7 7 7 d. x + x + = ( x + )2 2 9 6 2 2 3 2
Bài 2: Phân tích đa thức thành nhân tử a. 2 x − 3 b. 2 9x − 5 c. 2 x + 2 2x + 2 d. 2 4x + 4 3x + 3 Lời giải a. 2
x − 3 = (x + 3)(x − 3) b. 2
9x − 5 = (3x + 5)(3x − 5) c. x + x + = (x + )2 2 2 2 2 2 d. x + x + = ( x + )2 2 4 4 3 3 2 3
Dạng 5: Giải phương trinh
Bài 1: Giải phương trình a. 2 x = 3 b. 2 9x =10 c. 2 4x −19 = 0 d. 2 49x = 14 − Lời giải a. 2 x = 3 b. 2 9x =10 ⇔ x = 3 ⇔ ( x)2 3 =10 x = 3 ⇔  ⇔ 3x =10 x = 3 − 3x =10 Vậy S = { 3 − ; } 3 ⇔  3x = 10 −  10 x =  3 ⇔  10 x −  =  3 Vậy 10  10 S ; −  =  3 3    c. 2 4x −19 = 0 d. 2 49x = 14 − ⇔ 2x =19 ⇔ 7x =14 2x =19 ⇔ 7x =14  ⇔ 2x = 19 −  7x = 14 − x = 2 ⇔  x = 2 −
42. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com  19 x − = Vậy S = {2; } 2  2 ⇔  19 x −  =  2 Vậy 19  19 S ; −  =  2 2   
Bài 2: Giải phương trình a. (x + )2 2 = 2 b. 2
4 − 4x + x = 3 c. 2
x − 4x + 4 = 3+ x d. 2
9x + 6x +1 = x −1 e. 2
x + 2 3x + 3 = 0
f. x − 4 x + 4 = 0 Lời giải a. (x + )2 2 = 2 b. 2
4 − 4x + x = 3 x + 2 = 2 ⇔ ( − x)2 2 = 3 ⇔  x + 2 = 2 − ⇔ 2 − x = 3 x = 0 ⇔  2 − x = 3 x = 4 − ⇔  2 − x = 3 − Vậy S = {0;− } 4 x = 1 − ⇔  x = 5 Vậy S = {5;− } 1 c. 2
x − 4x + 4 = 3+ x d. 2
9x + 6x +1 = x −1 3  +  x ≥ 0 x −1≥ 0 ⇔  ⇔ 
x − 2 = 3 + x
 3x +1 = x −1  x ≥ 3 − x ≥ 1  
⇔ x − 2 = 3+ x
⇔ 3x +1 = x −1 x − 2 = −   (3+ x)
3x +1 = −(x −  ) 1 0x = 5 2x = 2 − ⇔  ⇔  2x = 1 − 4x = 0 1 x − ⇔ = (nhận) 1 x − ⇔ = 2 2 Vậy  1 S −  =    Vậy 1 S − = 2       2  e. 2
x + 2 3x + 3 = 0
f. x − 4 x + 4 = 0 ⇔ (x + )2 3 = 0 ⇔ (x + )2 2 = 0 ⇔ x = 2 − ⇔ x = − 3 Vậy S = {− } 2
43. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Vậy S = {− 3}
Bài 4: Giải phương trình: 1) 2 x + 9 = 5 2) 2
4x − 20x + 25 =1
3) x −1+ 2 x − 2 = 2 4) 2
x − x − 2 = x − 2 5) 2
x − 9 = 3 − x
6) x −1 +1 = x 7) 2
25x − 30x + 9 = x + 7 8) x + 3 + 2 − x = 5 9) 2 2
x − x + x + x − 2 = 0 10) (x − )2 2 1 + x + 4x + 4 11) x − 2 +1 9x −18 25x − 50 − = 8
12) x −1+ 2 x − 2 + 7 + x + 6 x − 2 = 2 2 16 Lời giải 1) 2 x + 9 = 5 ( ĐK : 2
x + 9 ≥ 0 với mọi x ) 2 ⇔ x + 9 = 25 x + 4 = 0 x = 4 − 2
⇔ x −16 = 0 ⇔ (x − 4).(x + 4) = 0 ⇔  ⇔  x − 4 = 0 x = 4
Vậy nghiệm của phương trình là x = 4, x = 4 − 2) 2
4x − 20x + 25 =1 ⇔ ( x − )2 2 5 =1
⇔ 2x − 5 =1 ⇔ x = 3
Vậy nghiệm của phương trình là x = 3
3) x −1+ 2 x − 2 = 2 Đk: x ≥ 2
x −1+ 2 x − 2 = 2
⇔ x − 2 + 2 x − 2 +1 = 2 ⇔ ( x − + )2 2 1 = 2 ⇔ x − 2 +1 = 2
⇔ x − 2 +1 = 2 (vì với x ≥ 2 thì x − 2 ≥ 0 nên x − 2 +1≥1 > 0) ⇔ x − 2 =1 ⇔ x − 2 =1
⇔ x = 3 (thoả mãn điều kiện) 4) 2
x − x − 2 = x − 2 ĐK: x ≥ 2 2
⇔ x − x − 2 = x − 2 2
⇔ x − x − x − 2 + 2 = 0 2
⇔ x − 2x = 0 ⇔ x(x − 2) = 0 x = 0 x = 0(KTM) ⇔  ⇔  x − 2 = 0 x = 2(TM) S = { } 2
44. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com x ≤ 3 − 2 x −9 ≥ 0  x ≤ 3 − 5) 2
x − 9 = 3 − x Đk :  ⇔ x ≥ 3 ⇔ 3  − x ≥ 0   x = 3 x ≤ 3 2
⇔ x − 9 = 3− x 2
⇔ x + x −12 = 0 2
⇔ x + 4x − 3x −12 = 0 ⇔ x(x + 4) − 3(x + 4) = 0 ⇔ (x + 4)(x − 3) = 0 x + 4 = 0 x = 4 − (TM ) ⇔  ⇔  x − 3 = 0 x = 3  (TM ) S = { 4; − } 3
6) x −1 +1 = x
⇔ x −1 = x −1 x ≥1 2
⇔ x −1 = x − 2x +1 2
⇔ x − 3x + 2 = 0 2
⇔ x − x − 2x + 2 = 0 x −1 = 0 x = 1 ⇔ (x − ) 1 (x − 2) = 0 ⇔  ⇔  (TM) x − 2 = 0 x = 2 S = {1; } 2 7) 2
25x − 30x + 9 = x + 7 ĐK: x ≥ 7 − 2 2
⇔ 25x − 30x + 9 = x +14x + 49 2
⇔ 24x − 44x − 40 = 0 2
⇔ 6x −11x −10 = 0 2
⇔ 6x − 4x +15x −10 = 0 ⇔ (2x + 5)(3x − 2) = 0  5 − 2x + 5 = 0 2x = 5 − x =  ⇔ 2  ⇔  ⇔  (TM) 3x − 2 = 0 3x = 2  2 x =  3 2 5 S ; −  =  3 2   
8) x + 3 + 2 − x = 5(*) ĐK: 3 − ≤ x ≤ 2  x + 3 = u Đặt  (u,v ≥ 0)
 2 − x = v u  + v = 5 v = 5 − u  v = 5 − u (1) (*) ⇔  ⇔  ⇔ 2 2  2 u  + v = 5 u  +  (5−u)2 2 = 5 u  − 5u +10 = 0 (2) Xét (2) 2
u − 5u +10 = 0 có ∆ = 15
− < 0 nên phương trình (2) vô nghiệm
Suy ra hệ phương trình trên vô nghiệm
Vậy phương trình (*) vô nghiệm 9) 2 2
x − x + x + x − 2 = 0 ĐK: x ≥1
⇔ x x −1 + (x − ) 1 (x + 2) = 0
⇔ x −1( x + x + 2) = 0
45. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com x −1 = 0 x = 1 ⇔  ⇔  ⇔ x = 1(TM)
 x + x + 2 = 0
x + x + 2 > 0, x ∀ S = { } 1 10) (x − )2 2
1 + x + 4x + 4 = 0
⇔ (x − )2 + (x + )2 1 2 = 0 (*) Ta có : (x − )2 1 ≥ 0, x ∀ (x + )2 2 ≥ 0, x ∀ x −1 = 0 x =1 (*) ⇔  ⇔  (L) x + 2 = 0 x = 2 −
Vậy phương trình vô nghiệm 11) x − 2 +1 9x −18 25x − 50 − = 8 2 16 x − 2 +1 ⇒ 5. x − 2 − = 6 x − 2 2 x − 2 +1 ⇔ 5. x − 2 − = 6 x − 2 2
12 x − 2 + x − 2 −10 x − 2 1 ⇔ = − 2 2 ⇔ 3 x − 2 = 1 − (vô lý)
Vậy phương trình vô nghiệm
12) x −1+ 2 x − 2 + 7 + x + 6 x − 2 = 2
⇔ ( x − )2 + x − + + ( x − )2 2 2 2 1 2 + 6 x − 2 + 9 = 2
⇔ ( x − + )2 + ( x − + )2 2 1 2 3 = 2
⇔ x − 2 +1+ x − 2 + 3 = 2 ⇔ 2 x − 2 = 2 − ⇔ x − 2 = 1 − ( vô lý)
Vậy phương trình vô nghiệm
------------------------- TOÁN HỌC SƠ ĐỒ -------------------------
46. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Document Outline

  • ĐS9-C1-CD1. CĂN BẬC HAI – CĂN THỨC BẬC HAI
    • Câu 28.Trong các khẳng định sau, khẳng định nào sai?
    • Câu 28.Trong các khẳng định sau, khẳng định nào sai?