Chuyên đề căn bậc hai và căn bậc ba – Diệp Tuân

Tài liệu gồm 127 trang, được biên soạn bởi thầy giáo Diệp Tuân, trình bày tóm tắt lý thuyết, phân dạng và bài tập minh họa chuyên đề căn bậc hai và căn bậc ba, giúp học sinh lớp 9 tham khảo khi học chương trình Toán 9 tập 1 phần Đại số chương 1.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

127 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
1
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
1
CĂN BẬC HAI – CĂN BẬC BA
A. TÓM TẮT LÝ THUYẾT
I. Căn bậc hai số học.
1. Định nghĩa: Với số dương
a
, số
a
được gọi là
căn bậc hai số học
của
a
.
2. Tính chất:
Tính chất 1. Số
0
cũng được gọi là căn bậc hai số học của
.
Tính chất 2. Với
a0
, ta có:
2
0
x
ax
xa

Nhận xét. Đây gọi là phương pháp bình phương hai vế.
Ví dụ 1. Giải phương trình:
2 3 12.x
Lời giải
ĐKXĐ:
0.x
Ta có :
2 3 12 3 6 3 36 12x x x x
( thỏa mãn điều kiện).
Ví dụ 2. Tính tổng các giá trị của
x
thỏa mãn đẳng thức
2
25 13.x 
Lời giải
Ta có :
2
25 13x 
2
25 169x
2
169 25x
2
144x
12.x
Vậy tổng các giá trị của
x
thỏa mãn đẳng thức đã cho là
12 12 0
.
Tính chất 3. Với
0a
:
2
x a x a
.
Ví dụ 3. Giải các phương trình sau:
a).
2
5 80x
b).
2
3 0,75.x
Lời giải
a).
2
5 80x
Ta có
22
5 80 16.xx
Do đó
16 4.x
b).
2
3 0,75.x
Ta có
22
3 0,75 0,25.xx
Do đó
0,25 0,5.x
Tính chất 4. Với
2
0 x a khi x a
.
Ví dụ 4. Tìm số
x
không âm, biết
a).
1
5 10.
2
x
b).
36x
Lời giải
§BI 1. CĂN BẬC HAI
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
2
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a).
1
5 10.
2
x
Với
0x
ta có :
1
5 10 5 20
2
xx
5 400 80.xx
Vậy
0 80.x
b).
36x
Với
0x
ta có :
3 6 3 36xx
12.x
Vậy
0 12.x
II. Căn bậc hai.
1. Định nghĩa: Căn bậc hai của số không âm
a
là số
sao cho
2
.xa
2. Tính chất:
Số dương
a
có đúng hai căn bậc hai là hai số đối nhau là số dương kí hiệu là
a
và số âm kí
hiệu là
.a
Ví dụ 5. Tìm căn bậc hai số học rồi tìm căn bậc hai của:
a).
121
. b).
2
2
5



Lời giải
a) Ta có
121 11
vì
11 0
và
2
11 121.
Do đó số
121
có hai căn bậc hai là
11
và
11
.
b) Ta có
2
22
55




vì
2
0
5
và
22
22
.
55

Do đó số
2
2
5



có hai căn bậc hai là
2
5
và
2
5
.
III. So sánh các căn bậc hai số học
Với
0; 0ab
. Ta có
a b a b
.
Ví dụ 6. Không dung máy tính hoặc bảng số , hãy so sánh
8
và
65.
Lời giải
Cách 1:
Ta có
8 64
.
Vì
64 65
nên
8 65
.
Cách 2:
Vì
2
2
8 64; 65 65
Nên
2
2
8 65
, suy ra
8 65.
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
3
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Cách giải này dựa vào tính chất: Nếu
0, 0ab
và
22
ab
thì
ab
.
Như vậy, để so sánh hai số dương ta có thể so sánh các bình phương của chúng.
Ví dụ 7. Không dung máy tính hoặc bảng số , hãy so sánh
15 1
và
10.
Lời giải
Ta có
15 16 15 16
15 1 16 1 4 1 3
.
10 9 3
Vậy
15 1 10.
Ví dụ 8. Với
0a
thì số nào lớn hơn trong hai số
a
và
2a
?
Lời giải
Ta có
12
nên
2aa
(vì
0a
).
Do đó
2aa
.
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
DẠNG 1. TÌM CĂN BẬC HAI SỐ HỌC CỦA MỘT SỐ
1. Phương pháp.
Căn bậc hai số học của số dương
a
là
a
( giá trị dương của căn bậc hai).
Với
0a
, ta có:
Nếu
xa
thì
0x
và
2
.xa
Nếu
0x
và
2
xa
thì
xa
.
⋆⋆Nhận xét.
Nếu
0a
thì các căn bậc hai của
a
là
a
; căn bậc hai số học của
a
là
a
.
Nếu
0a
thì căn bậc hai của
a
và căn bậc hai số học của
a
cùng bằng 0.
Nếu
0a
thì
không có căn bậc hai và do đó không có căn bậc hai hai số học.
2. Bài tập minh họa.
Bài tập 1. Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng:
64;81;100;196.
Lời giải
Ta có:
2
8 64
nên
8
là căn bậc hai số học của
64
.
Từ đó suy ra căn bậc hai của
64
là
8
và
8
.
Tương tự căn bậc hai của
64;81;100;196
lần lượt là :
8;9;10;14
Bài tập 2. Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm
tròn đến chữ số thập phân thứ ba):
a)
2
4,5x
. b)
2
5x
. c)
2
7,5x
. d)
2
9,12x
.
Lời giải
a) Nghiệm của phương trình
2
xa
( với
0a
) là các căn bậc hai của
.
Phương trình
2
4,5x
có hai nghiệm là
1
4,5x
và
2
4,5x 
.
Dùng máy tính ta tìm được
1
2,121x
và
2
2,121x 
.
b)
2
5x
có hai nghiệm
5 2,236x
.
c)
2
7,5x
có hai nghiệm
7,5 2,739x
.
d)
2
9,12x
có hai nghiệm
9,12 3,020x
.
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
4
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
3. Bài tập rèn luyện.
Bài 1. Tìm căn bậc hai số học của các số sau
a).
12
; b).
121
; c).
4
9
; d).
0,09.
e).
40
1
81
f).
; g).
64
; h).
81
; n).
9
16
; m).
0,04.
Lời giải
a)
12
có căn bậc hai số học là:
12
b).
121
có căn bậc hai số học là:
121
c).
4
9
có căn bậc hai số học là:
4
9
d).
0,09
có căn bậc hai số học là:
0,3.
e).
40
1
81
có căn bậc hai số học là:
11
9
f). 0 có căn bậc hai số học là 0
g).
64
có căn bậc hai số học là:
8.
h).
81
không có căn bậc hai số học.
k).
9
16
có căn bậc hai số học là:
3
4
m).
0,04
có căn bậc hai số học là:
0,02
.
DẠNG 2. TÌM SỐ CÓ CĂN BẬC HAI SỐ HỌC LÀ MỘT SỐ CHO TRƯỚC
1. Phương pháp.
Với số thực
0a
cho trước ta có
2
a
chính là số có căn bậc hai số học bằng
.a
2. Bài tập minh họa.
Bài tập 3. Mỗi số sau đây là căn bậc hai số học của số nào?
a).
12;
b).
0,36;
c).
2
2;
7
d).
0,2
;
3
e).
13;
f).
3
;
4
g).
12
;
25
h).
0,12
;
0,3
n).
0,49;
m).
1
;
7
l).
12
;
27
r).
0,12
.
0,7
Lời giải
a). Số có căn bậc hai số học bằng
12
là
144.
b). Vì
0,36 0
nên không tồn tại số nào có căn bậc hai số học bằng
0,36;
c). Tương tự, số có căn bậc hai số học bằng
2
2
7
là
8
7
.
d). Số có căn bậc hai số học bằng
0,2
3
và
0,04
3
.
e). Số có căn bậc hai số học bằng
13
là
169.
f). Vì
3
0
4

nên không tồn tại
g). Số có căn bậc hai số học bằng
12
25
là
1
10
.
h). Số có căn bậc hai số học bằng
0,12
0,3
là
0,144
3
n). Vì
0,49 0
nên không tồn tại số nào có căn bậc hai số học là
0,49
.
m). Không tồn tại số nào có căn bậc hai số học bằng
1
7
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
5
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
l). Số có căn bậc hai số học bằng
12
27
là
1
10
r). Số có căn bậc hai số học bằng
0,12
0,7
là
0,12
7
DẠNG 3. SO SÁNH HAI SỐ
1. Phương pháp.
Áp dụng: Với
0, 0ab
ta có:
a b a b
.
2. Bài tập minh họa.
Bài tập 4. So sánh:
a). 3 và
5
b).
8
và
63
c).
9
và
79
Lời giải
a) Ta có
39
và
9 5 9 5
. Vậy
35
.
b) Ta có
8 64
và
64 63 64 63
. Vậy
8 63
.
c) Ta có
9 81
và
81 79 81 79
. Vậy
9 79
.
Bài tập 5. Không dùng máy tính hoặc bảng số, hãy so sánh:
a).
26 3
và
63
; b).
1
2
và
31
2
.
Lời giải
a).
26 3 63
b).
3 1 1
22
.
Bài tập 6. So sánh các số sau
a).
5
và
17 1
. b).
3
và
15 1
c ).
13
và
0,2
Lời giải
a).
5
và
17 1
.
Ta có
5 4 1 16 1.
Mà
16 17
(Do16 17) nª n 5 17 1
b). Tương tự câu b,
3 4 1 16 1.
Vì
16 15 (v× 16 15) nªn 3 > 15 1
c). Ta có
1 3 1 - 3 0
mµ 0 0,2 nªn 1- 3 0,2
Bài tập 7. So sánh các số sau
a).
7 15
và 7 b).
3 26
và 15 c).
2 11
và
35
d).
30
và
5 35
e).
30 2 45
4
và
17
f).
15 24
và
101 1
g).
17 2 15
6
và
2
Lời giải
a). Ta có:
7 9 9; 15 16 4 7 15 3 4 7
b). Ta có:
26 25 5 3. 26 3.5 3. 26 15
c). Ta có :
2 3; 11 25 2 11 3 5
d). Ta có :
35 36 6 5. 35 5. 36 30 5 35 30
e). Ta có :
30 2 45 30 2 49 30 2.7
4 16 17
4 4 4
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
6
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
f). Ta có
15 24 16 25 4 5 9; 101 1 100 1 10 1 9 101 1 15 24
Vậy
101 1 15 24
g). Ta có
2
2
17 2 15 17 2 16 3 17 2 15 17 2 15
2,25 2 2
6 6 2 6 6




Vậy
17 2 15
2
6
.
Bài tập 8. So sánh các số sau
a).
23
và
10
b).
52
và
26
c).
32
và
26
d).
8
và
15 7
e).
3 2 2
và
2
f).
71
3 12
và
7
43
Lời giải
Đưa về so sánh
2
A
và
2
B
a). Xét
22
2 3 5 2 6 5 24; 10 10 5 25
Vì
22
24 25 2 3 10 2 3 10
b). Xét
22
5 2 9 4 5 9 80; 2 6 8 2 12 8 48
Vì
22
9 80 8 48 5 2 2 6 5 2 2 6
c). Xét
2 2 2 2
3 2 7 4 3 7 48; 2 6 8 2 12 8 48 3 2 2 6
3 2 2 6 3 2 2 6
d). Xét
2
2
15 7 22 2 105;8 22 2 441
2
2
15 7 8
15 7 8 15 7 8
e). Xét
2
3 2 2 17 12 2 17 288
và
2
2 17 169
Vì
2
2
17 288 17 169 3 2 2 2 3 2 2 2
f). Ta có
2
2
7 1 49 7 49
.;
3 12 108 48
43








Vì
2
2
49 49 7 7 1 7 7 1
..
48 108 3 12 3 12
4 3 4 3







Bài tập 9. So sánh các số sau
a).
30 29
và
29 28
b).
27 6 1
và
48
c).
21 2
và
14 3
d).
17 6
và
21 2
Lời giải
a). Ta có
30 29 30 29 1; 29 28 29 28 1
11
30 29 29 28 30 29 29 28
30 29 29 28

b).
27 6 1 3 3 6 1
và
48 4 3 3 3 3
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
7
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Mà
6 1 3 1 3 27 6 1 48.
c). Ta có
2 2 2
21 2 21 2. 21. 2 2 23 2 42
2 2 2
14 3 14 2. 14. 3 3 14 2 42 3 17 2 42
Vì
22
23 17 23 2 42 17 2 42 21 2 14 3
21 2 14 3
Vậy
21 2 14 3
.
d). Ta có
22
17 6 23 2 102; 21 2 23 2 42
Vì
22
23 2 102 23 2 42 17 6 21 2 17 6 21 2
Vậy
17 6 21 2
.
Nhận xét: Khi so sánh
ab
và
cd
mà
2 2 2 2
a b c d
thì ta sẽ đi so
sánh bình phương của hai số, rồi từ đó suy ra kết quả.
Bài tập 10. Sắp xếp theo thứ tự tăng dần
23;2 7;5 6; 8 2; 127
Lời giải
Ta có
2
8 2 8 .2 128 127 0
Ta so sánh các số dương
23;2 7;5 6
như sau:
2 2 2
23 23 529;2 7 2 .7 28;5 6 5 .6 150
Do
28 150 529 28 15 529 2 7 5 6 23
Vậy
128 127 2 7 5 6 23.
Bài tập 11. So sánh hai số sau
29 28
và
28 27
Lời giải
Xét
1
29 28 29 28 29 28 1 29 28
29 28
1
28 27 28 27 28 27 1 28 27
28 27
Vì
11
27 29 28 27 29 28
28 27 29 28

28 27 29 28
Vậy
28 27 29 28
Nhận xét: Để so sánh hai số dạng
ab
và
bd
(
, , ,a b c d
là các số dương) mà
a b b d
ta làm như sau:
;a b a b a b
b d b d b d
Sau đó từ việc so sánh hai số
ab
và
bd
ta sẽ só sánh được hai số
ab
và
bd
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
8
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 12. So sánh
a).
2 2 2 2 2
và
2
b).
13 15; 11 17xy
c).
23 21; 19 17xy
d).
12 5; 20 3xy
Lời giải
a).
2 2 2 2 2 2 2 2 2 4 2
b). Ta có:
(13 15 11 17); , 0xy
Khi đó
2
2
28 2 13.15;
28 2 11.17
x
y


22
x y x y
c). Ta có:
(23 21 19 17);
23 21 2 2
;
23 21 23 21 19 17
xy
Vì
23 21 19 17 xy
Chú ý:
,0
ab
a b a b a b a b a b
ab
d). Ta có
12.5 20.3;
2
2
17 2 60
;
23 2 60
x
y


22
,0x y x y x y
Bài tập 13. So sánh:
a).
1 1 1 1
...
1 2 3 100
và
10.
b).
4 4 4 ..... 4
và
3.
Lời giải
a).
1 1 1 1
...
1 2 3 100
và
10.
Đặt
1 1 1 1
...
1 2 3 100
a
Ta có
1 1 1 1 1
.... 100. 10
1 2 3 100 100
a
b).
4 4 4 ..... 4
và
3.
Ta có
4 3 4 4 4 3 3
4 4 4 4 3 3
4 4 4 .... 4 4 3 3
DẠNG 3. TÌM
THỎA ĐIỀU KIỆN CHO TRƯỚC
1. Phương pháp.
Áp dụng:
2
0x a a x a
Với
., 0:a b a b a b
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
9
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2. Bài tập minh họa.
Bài tập 14. Tìm số
x
không âm, biết:
a)
15;x
b)
2 14;x
c)
2;x
d)
2 4.x
Lời giải
a) Ta có
2
15 15 225.x x x
Vậy
225x
.
b) Ta có
2 14 7 49 49.x x x x
Vậy
49.x
c) Ta có
2 2.xx
Kết hợp điều kiện
0 2.x
d) Ta có
2 4 2 16 0 2 16 0 8.x x x x
Vậy
0 8.x
Bài tập 15. Tìm
x
không âm biết :
a).
5x
b).
2x
c).
2x 
d).
1
23
3
x 
e).
2 1 3 0x
f).
2
4 13 3xx
.
Lời giải
a) Ta có
2
5 5 25xx
b) Ta có
2
2 ( 2) 2xx
c) Ta có
2 ông xx kh
d) Ta có
1 13
23
33
xx
e) Ta có
2 1 3 0xx
f) Ta có
2
4 13 3 2.x x x
Bài tập 16. Tìm giá trị của
x
biết :
a).
2
9 16 0x 
. b).
2
4 13.x
c).
2
2 9 0.x 
d).
21
20
3
x
e).
1 3( 0)xx
f).
2
12x 
g).
2
5 20 4xx
n).
1
23
3
x 
m).
2 1 3 0x
l).
2
4 13 3.xx
Lời giải
a) Ta có
2
22
44
9 16 0
33
x x x x



b) Ta có
2
22
13 13
4 13
22
x x x




c) Vì
22
0 2 9 0x x x
d) Ta có
2
35
2 1 6 2 1 6
2
x x x
e) Ta có
1 3( 0) 4 16x x x x
f) Ta có
2 2 2
1 2 1 2 1 1x x x x
g) Ta có
2 2 2
1
5 20 4 5 20 16 5 4 0
4
x
x x x x x x
x


h)
13
3
x
m).
x
l).
2.x
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
10
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 17. Tìm giá trị của
x
, biết:
a).
1
2
3
x
b).
1
35
2
x
c).
2 1 7x
d).
3
21
2
x 
e).
3x
f).
39x
Lời giải
a) Ta có
1 1 1 1
2 2 0 2 0
3 9 9 18
x x x x
b) Điều kiện:
11
30
26
xx
Ta có
1 1 49
3 5 3 25
2 2 6
x x x
(TMĐK)
c) Điều kiện:
1
.
2
x
Ta có
3
21
2
x
2 1 49 24xx
(TMĐK)
d) Điều kiện:
1
.
2
x
Ta có
3
21
2
x
9 13
21
48
xx
Kết hợp điều kiện ta được
1 13
28
x
e). Ta có
3 9 0 9x x x
.
f). Ta có
3 9 3 81 3 81 27x x x x
Bài tập 18.
Đố.
Tính cạnh của một hình vuông, biết diện tích của nó bằng diện tích của hình chữ
nhật có chiều rộng
3,5
m và chiều dài
14
m.
Lời giải
Diện tích hình chữ nhật là
2
3,5.14 49(m ).
Gọi cạnh của hình vuông là
0.xx
Ta có:
2
49 7.xx
Vậy cạnh của hình vuông là
7m.
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
11
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT LÝ THUYẾT
1. Căn thức bậc hai:
Nếu
A
là một biểu thức đại số thì
A
gọi là căn thức bậc hai của
.A
A
xác định (hay có nghĩa) khi
0.A
Ví dụ 1. Tìm
x
để căn thức
52x
có nghĩa.
Lời giải
Ta có
52x
có nghĩa khi
5
5 2 0 2 5 .
2
x x x
Ví dụ 2. Có bao nhiêu giá trị nguyên của
x
để biểu thức
42M x x
có nghĩa?
Lời giải
Ta có
M
có nghĩa khi
4 0 4
2 0 2
xx
xx



Vì
xZ
nên
4; 3; 2; 1;0;1;2x
Vậy có 7 giá trị nguyên của
x
để biểu thức
M
có nghĩa
2. Hằng đẳng thức
2
.AA
Với mọi số
,a
ta có
2
| |.aa
Khi đó
2
0
0
A khi A
A
A khi A

Ví dụ 3. Tính giá trị của biểu thức:
0,09 7. 0,36 3 2,25.
Lời giải
Ta có
0,09 7. 0,36 3 2,25
2 2 2
0,3 7. 0,6 3 1,5
0,3 7.0,6 3.1,5 0,3 4,2 4,5 0
.
Ví dụ 4. Giá trị của biểu thức sau là số vô tỉ hay hữu tỉ:
99
1 - .18?
16 16




Lời giải
Ta có
9 9 25 9 5 3
1 - .18 - .18 .18 9 3.
16 16 16 16 4 4



Vậy giá trị của biểu thức đã cho là một số hữu tỉ, hơn nữa còn là một số tự nhiên.
Ví dụ 5. Tính giá trị của biểu thức
3 2 2 6 4 2C
.
Lời giải
Ta có
22
3 2 2 6 4 2 2 1 2 2C
2 1 2 2
2 1 (2 2) 2 2 3.
Ví dụ 6. Rút gọn biểu thức
2
1
.
4
A x x
Lời giải
§BI 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
12
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
2
2
1 1 1
4 2 2
A x x x x



Nếu
1
2
x
thì
1
2
Ax
Nếu
1
2
x
thì
1
2
Ax
Ví dụ 7. Rút gọn biểu thức
46
.B x x
Lời giải
Ta có
22
4 6 2 3
B x x x x
2 3 2 3
.x x x x
Nếu
0x
thì
23
;B x x
Nếu
0x
thì
23
.B x x
Ví dụ 8. Cho biểu thức:
2
3 10 25.P x x x
a). Rút gọn biểu thức
P
;
b). Tính giá trị của
P
khi
2x
.
Lời giải
a). Rút gọn biểu thức
P
;
Ta có
2
3 10 25P x x x
2
35xx
3 5 .xx
Nếu
5x
thì
3 ( 5) 2 5P x x x
.
Nếu
5x
thì
3 ( 5) 4 5P x x x
.
b). Khi
25x 
thì giá trị của biểu thức là :
4.2 5 3.P
Ví dụ 9. Cho biểu thức:
2
2 2 1.Q x x x
a). Rút gọn biểu thức
Q
;
b). Tính các giá trị của
x
để
7Q
.
Lời giải
a). Rút gọn biểu thức
Q
;
Ta có
22
2 2 1 2 ( 1) 2 1Q x x x x x x x
Nếu
1x 
thì
2 ( 1) 1Q x x x
Nếu
1x 
thì
2 ( 1) 3 1Q x x x
b). Tính các giá trị của
để
7Q
.
Ta phải xét hai trường hợp:
7 1 7 8Q x x
( Không thỏa mãn
1x
)
7 3 1 7 2Q x x
( Không thỏa mãn
1x
).
Vậy
7Q
khi
8x
Ví dụ 10. Tìm giá trị nhỏ nhất của biểu thức
2
4 4 1 3.D x x
Lời giải
Ta có
2
4 4 1 3D x x
=
2
2 1 3 2 1 3 3xx
với mọi
x
.
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
13
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Vậy minD = 3 khi
1
2
x
.
Ví dụ 11. Tìm
x
, biết
2
6 9 7 13.x x x
Lời giải
Ta có
2
6 9 7 13x x x
2
3 7 13xx
3 7 13 (1)xx
Nếu
3x
thì
3 3.xx
Khi đó (1) trở thành
3 7 13 8 16 2x x x x
(không thuộc khoảng đang xét )
Nếu
3x
thì
3 3 .xx
Khi đó (1) trở thành
5
3 7 13 6 10
3
x x x x
( thuộc khoảng đang xét )
Vậy giá trị của
x
thỏa mãn đẳng thức đã cho là
5
3
x
.
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
Dạng 1. TÌM ĐIỀU KIỆN ĐỂ
A
CÓ NGHĨA
1. Phương pháp.
①
A
có nghĩa
0.A
②
1
A
có nghĩa
0.A
2. Bài tập minh họa.
Bài tập 1. (Bài 6, tr. 10 SGK). Với giá trị nào của
a
thì mỗi căn thức sau có nghĩa:
a).
;
3
a
b).
4;a
c).
5;a
d).
3 7.a
Lời giải
a)
3
a
có nghĩa
0 0.
3
a
a
b)
5a
có nghĩa
5 0 0.aa
c)
4 a
có nghĩa
4 0 4.aa
d)
37a
có nghĩa
7
3 7 0 .
3
aa
Bài tập 2. (Bài 12, tr. 11 SGK) Tìm
,x
để mỗi căn thức sau có nghĩa:
a).
2 7;x
b).
3 4;x
c).
1
;
1 x
d).
2
1.x
Lời giải
a)
27x
có nghĩa
7
2 7 0 .
2
xx
b)
34x
có nghĩa
4
3 4 0 3 4 .
3
x x x
c)
1
1 x
có nghĩa
1 0 1.xx
d) Vì
2
10x
với mọi
x
nên
2
1 x
có nghĩa với mọi
x
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
14
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 3. (Bài 37, tr. 20 SGK) Với giá trị nào của
a
thì mỗi căn thức sau có nghĩa:
a).
2
1
;
a
b).
2
1
;
12
a
a
c).
2
1;a
d).
2
4.a
Lời giải
a)
2
1
a
có nghĩa
2
1
0 0.a
a
b)
2
1
12
a
a
có nghĩa
1 2 0a
(vì
2
1 0,aa
)
1
.
2
a
c)
2
1a
có nghĩa
22
1 0 1aa
| | 1 1aa
hoặc
1.a
d)
2
4 a
có nghĩa
22
4 0 4aa
| | 2 2 2.aa
3. Bài tập rèn luyện.
Bài 1. Tìm
x
để căn thức
2
1
44xx
có nghĩa.
Lời giải
Ta có
2
1
44xx
có nghĩa khi
2
1
( 2)x
có nghĩa.
Điều đó xảy ra khi
2
( 2) 0 2.xx
Bài 2. Với giá trị nào của
x
thì biểu thức
2
25 x
có nghĩa?
Lời giải
Ta có
2
25 x
có nghĩa khi
2
25 0x
2
25x
2
25x
5x
5 5.x
Bài 3. Tìm các giá trị của x để biểu thức
2
1
100x
có nghĩa
Lời giải
Ta có
2
1
100x
có nghĩa khi
2
100 0x 
2
100x
10x
10
10
x
x

Bài 4. Biểu thức sau xác định với giá trị nào của
x
?
a).
32x
; b).
4
23x
; c).
2
2
x
; d).
2xx
;
e).
2
9 6 1xx
f).
21
2
x
x
g).
2
5 3 8xx
h).
2
5 4 7xx
.
Lời giải
a) Đk:
2
3 2 0 3 2 .
3
x x x
b) Đk:
4
0
3
2 3 0 2 3 .
23
2
2 3 0
x x x
x
x

c) Đk:
2
2
2
2
0
0 0.
0
xx
x
x
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
15
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
d) Đk:
00
2 0 2
0
2 0 .
2
00
2 0 2
xx
xx
x
xx
x
xx
xx














e) Đk:
2
2
9 6 1 0 3 1 0, .x x x x
f) Đk:
1
2 1 0
2
1
2 0 2
2
2 1 1
02
2
22
2 1 0 1
2
20
2
x
x
xx
x
x
x
x
x
x
x
x
x







.
g) Đk:
22
5 3 8 0 5 8 5 8 0x x x x
2
5 8 5 8 0 5 8 1 0x x x x x
5 8 0
10
5 8 0
10
x
x
x
x



8
.
5
1
x
x

h) Đk:
22
5 4 7 0 25 20 35 0x x x x
2
2
25 2.5 .2 4 31 0 5 2 31 0, .x x x x
Bài 5. Tìm
x
để biểu thức sau có nghĩa:
a).
2
39xx
b).
1
2
5
x
x

c).
2
2
52
9
x
x

d).
2 4 8xx
e).
2
4
9
1
x
x
x

f).
2
4 2 2xx
g).
2
2
x
x
x

h).
2
2
x
x
x

i).
2
2
4
x
x
x

j).
3
3xx
x
k).
1
2
2
x
x
x

l).
21
2
2
x
x
x

m).
2
2
2
2
4
x
xx
x

Lời giải
a) Biểu thức đã cho có nghĩa khi
2
3 0 3 0
30
3
3
3 3 0 3 0
3
90
xx
x
x
x
x x x
x
x







b) Biểu thức đã cho có nghĩa khi
2 0 2
5 0 5
xx
xx



c) Biểu thức đã cho có nghĩa khi
2
33
90
55
5 2x 0
22
xx
x
xx








d)
2
2
x
x
x

có nghĩa
2 0 2
2
2 0 2
xx
x
xx



e)
2
2
x
x
x

có nghĩa
2 0 2
2
2 0 2
xx
x
xx



Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
16
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
f)
2
2
4
x
x
x

có nghĩa
2
2
2
x
x
x

g).
3
3xx
x
có nghĩa
2
3
3
0
0
30
0
x
x
x
x
x
x
x





h)
1
2
2
x
x
x

có nghĩa khi
2 0 2
2
2 0 2
xx
x
xx

i)
21
2
2
x
x
x

có nghĩa khi
2 0 2
2
2 0 2
xx
x
xx

j)
2
2
2
2
4
x
xx
x

có nghĩa khi
2
2 0 2
2
4 0 2
xx
x
xx

Bài 6. Chứng minh rằng các biểu thức sau luôn có nghĩa với mọi
x
a).
2
2
2
1.
2
A x x
x
b).
2
2
21
22
1
x
B x x
xx

Lời giải
a). Ta có
2
20x 
với mọi
x
và
2
2
13
10
24
x x x



với mọi
.x
Do đó biểu thức đa cho luôn có nghĩa với mọi
.x
b). Ta có
2
2
1 15
2 2 2 0
48
x x x



với mọi
.x
Lại có
2 2 2
1 0 1 | | 0x x x x x x x
với mọi
x
Vậy biểu thức đã cho luôn xác định với mọi
x
.
Bài 7. Chứng minh rằng các biểu thức sau luôn có nghĩa với mọi x
a).
2
2
2
1
1
A x x
x
b).
2
2
35
1
23
x
B x x
xx

Lời giải
a). Ta có
2
1 0,xx
và
2
2
13
1 0,
24
x x x x



Do đó biểu thức luôn có nghĩa với mọi
x
.
b). Ta có
22
2 3 ( 1) 2 0,x x x x
Và
2
2
13
1 0,
24
x x x x



Do đó biểu thức đã cho luôn có nghĩa với mọi
x
.
Dạng 2. TÍNH GIÁ TRỊ BIỂU THỨC
1. Phương pháp.
Áp dụng:
2
0
0
A khi A
A
A khi A

2. Bài tập minh họa.
Bài tập 4. Tính
a).
2
0,1 ;
b).
2
0,3 ;
c).
2
1,3 ;
d).
2
0,4 0,4 .
Lời giải
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
17
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a)
2
0,1 | 0,1| 0,1.
b)
2
0,3 | 0,3| 0,3.
c)
2
1,3 | 1,3| 1,3.
d)
2
0,4 0,4 0,4.| 0,4| 0,16.
Bài tập 5.(Bài 11, tr. 11 SGK) Tính:
a).
16. 25 196 : 49;
b).
2
36: 2.3 .18 169;
c).
81;
d).
22
3 4 .
Lời giải
a) Ta có
16. 25 196 : 49 4.5 14:7 20 2 22.
b)
22
36: 2.3 .18 169 36: 18 13 36:18 13 2 13 11.
c)
81 9 3.
d)
22
3 4 25 5.
Bài tập 6. Thực hiện phép tính
a).
2
(2 2 3)A 
b).
2
(0,1 0,1)B 
c).
22
(2 2 3) (2 2 3)C
d).
22
(2 6 5) (2 6 5)D
Lời giải
a). Ta có
2
(2 2 3) | 2 2 3| 3 2 2A
b). Ta có
2
(0,1 0,1) |0,1 0,1| 0,1 0,1B
c). Ta có
22
(2 2 3) (2 2 3) | 2 2 3| | 2 2 3| 6C
d). Ta có
22
(2 6 5) (2 6 5) | 2 6 5| | 2 6 5| 4 6D
Bài tập 7. Rút gọn biểu thức:
a).
2
(4 3 2)
b).
2
(2 5)
c).
2
(4 2)
d).
2
2 3 (2 3)
e).
2
(2 3)
f).
2
(2 5)
g)
22
( 3 1) ( 3 2)
h).
22
(2 5) ( 5 1)
Lời giải
a). Ta có:
2
(4 3 2) 4 3 2 3 2 4
b). Ta có:
2
(2 5) 2 5 2 5
c). Ta có:
2
(4 2) 4 2
d). Ta có:
2
2 3 (2 3) 2 3 2 3 2 3
e). Ta có:
2
(2 3) 2 3
f). Ta có:
2
(2 5) 5 2
g). Ta có:
22
( 3 1) ( 3 2) 3 1 2 3 1
h). Ta có:
22
(2 5) ( 5 1) 5 2 5 1 1
Bài tập 8. Thực hiện phép tính
a).
2(5 16 4 25) 64A
b).
2015 36 25A
Lời giải
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
18
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a).
2 2 2
2(5 4 4 5 ) 8 2(5.4 4.5) 8 2(20 20) 8 8A
b).
22
2015 6 5 2015 6 5 2016.A
Loại
2.mn
1. Phương pháp
① Cách 1.
Nhẩm hai số
và
b
sao cho
.a b n
và
a b m
Sử dụng các hằng đẳng thức:
2 2 2
2 ( )a ab b a b
hoặc
2 2 2
2 ( )a ab b a b
② Cách 2: Dùng máy tính:
Nhấn Mode
53
Nhập
1; ;a b m c n
sẽ cho được hai số
a
và
b
cần tìm.
Sử dụng các hằng đẳng thức như cách 1.
③ Chú ý: Sử dụng công thức:
..a b a b
với
,0ab
.
2. Bài tập minh họa
Bài tập 9. Rút gọn
a).
3 2 2
b).
8 2 15
c).
23 2 120
Lời giải
a).
3 2 2
Bấm máy Mode/5/3: nhập
1; 3; 2a b c
ta được
2; 1ab
Khi đó
22
2
3 2 2 3 2 2.1 3 2 2 1 2 2 2. 1 1 ( 2 1)
2 1 2 1
b).
8 2 15
Bấm máy Mode/5/3 nhập
1; 8; 15a b c
ta được
5; 3ab
Khi đó
22
2
8 2 15 8 2 5.3 8 2 5 3 5 2 5. 3 3 ( 5 3)
5 3 5 3
c).
23 2 120
Bấm máy Mode/5/3 nhập
1; 23; 120a b c
ta được
15; 8.ab
Khi đó
22
23 2 120 23 2 15.8 23 2 15. 8 15 2 15. 8 8
2
( 15 8)
15 8 15 8 15 2 2
Loại
m k n
1. Phương pháp
① Trường hợp 1: Nếu
k
là số chẵn thì tách sao cho
2kk
Đưa
k
vào căn bậc hai bằng công thức:
2
kk

Bài toán về dạng 2.
Chú ý: Sử dụng công thức đưa vào căn bậc hai:
2
aa
với
a
là một số không âm.
2. Bài tập minh họa
Bài tập 10. Rút gọn
a).
27 10 2
b).
36 12 5
c).
49 12 5 49 12 5
Lời giải
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
19
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a).
27 10 2
Ta tách số
10 2.5
và đưa số
2
5 5 25
Khi đó
22
2
27 10 2 27 2.5. 2 27 2. 25 2 25 2 25 2 2 ( 25 2)
25 2 25 2 5 2
Nhận xét: Ta thấy
25 2 27
. Vậy
25a
và
2b
.
b).
36 12 5
Ta tách số
12 2.6
và đưa số
2
6 6 36
Khi đó
36 12 5 36 2.6. 5 36 2. 36. 5 36 2 180 36 2 30. 6
2
36 2 30. 6 30 2 30. 6 6 ( 30 6) 30 6) 30 6
Nhận xét: Ta thấy
36 5 36
nên ta phải nhân
36.5 180
để đưa bài toán về dạng
2.mn
c).
22
49 12 5 49 12 5 2 3 5 2 3 5 4.
② Trường hơp 2:
Nếu
là số lẻ thì nhân cả tử và mẫu của
m k n
cho
2.
Sử dụng công thức:
aa
b
b
Với
a
là một số không âm,
b
là một số dương.
Bài toán về dạng 2.
3. Bài tập minh họa
Bài tập 11. Rút gọn
a).
5 21
b).
47
8 2 7.
2
Lời giải
a).
5 21
Ta nhân vào trong căn thức cả tử và mẫu cho
2
Khi đó
2(5 21) 10 2 21 10 2 21
5 21
22
2
22
10 2 7. 3 7 2 7. 3 3
22

2
73
( 7 3)
73
2 2 2
b).
47
8 2 7.
2
Ta có
2
4 7 8 2 7
8 2 7 1 7
24

2
71
1 7 7 1
6
1 7 . 3
2 2 2

Bài tập 12. Rút gọn các biểu thức sau
a).
2
4 15 15A
b).
22
2 3 1 3B
c).
49 12 5 49 12 5C
d).
29 12 5 29 12 5D
Lời giải
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
20
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a).
2
4 15 15 4 15 15 4 4 15A
b).
22
2 3 1 3 2 3 1 3 1B
c).
22
49 12 5 49 12 5 2 3 5 2 3 5 4CC
d).
22
29 12 5 29 12 5 3 2 5 3 2 5 6DD
Bài tập 13. Rút gọn các biểu thức sau
a).
8 2 15 6 2 5
b).
17 2 72 19 2 18
c).
12 2 32 9 4 2
d).
29 2 180 9 4 5
e).
4 7 4 7 2
f).
6 11 6 11 3 2
g).
8 2 15 7 2 10
h).
10 2 21 9 2 14
i).
8 3 7 4 7
j).
5 21 5 21
k).
9 3 5 9 3 5
l) .
( 10 2) 4 6 2 5
Lời giải
a).
8 2 15 6 2 5 3 2 3. 5 5 5 2 5.1 1
.
22
3 5 5 1 3 5 5 1 3 1
.
b).
17 2 72 19 2 18 9 2. 9. 8 8 18 2 18.1 1
.
22
3 2 2 18 1 3 2 2 18 1 4 2 2 18
.
c).
12 2 32 9 4 2 8 2 8. 4 4 8 2.2. 2.1 1
.
22
2 2 2 2 2 1 2 2 2 2 2 1 4 2 1
.
d).
29 2 180 9 4 5 20 2. 20. 9 9 5 4 5 4
.
22
20 3 5 2 20 3 5 2 5 1 5
.
e).
4 7 4 7 2
.
Ta có:
2
4 7 4 7 4 7 4 7 2 4 7 4 7 8 2 16 7
8 2 9 8 6 2
Do đó
4 7 4 7 2
Vì
4 7 4 7
.
Suy ra
4 7 4 7 2 2 2 0
.
f).
6 11 6 11 3 2
.
Ta có:
2
6 11 6 11 6 11 6 11 2 6 7 6 11
.
12 2 36 11 12 2 25 12 10 2
.
Do đó
6 11 6 11 2
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
21
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Vì
6 11 6 11
.
Suy ra
6 11 6 11 3 2 2 3 2 4 2
.
g).
8 2 15 7 2 10 5 2 5. 3 3 5 2 5. 2 2
22
5 3 5 2 5 3 5 2 2 3
.
h).
10 2 21 9 2 14 7 2 7. 3 3 7 2 7. 2 2
.
22
7 3 7 2 7 3 7 2 2 3
.
i).
8 3 7 4 7
.
Ta có:
2
8 3 7 4 7 12 4 7 2 8 3 7. 4 7
12 4 7 2 53 20 7
2
12 4 7 2 2 7 5 12 4 7 2 2 7 5 12 10 2
.
Do đó
8 3 7 4 7 2
(vì
8 3 7 4 7 0
).
j).
5 21 5 21
.
Ta có:
2
5 21 5 21 5 21 5 21 2 5 21. 5 21
10 2 25 21 10 4 6
Suy ra
5 21 5 21 6
Vì
5 21 5 21
.
k).
9 3 5 9 3 5
.
Ta có:
2
9 3 5 9 3 5 9 3 5 9 3 5 2 9 3 5. 9 3 5
18 2 81 45 18 12 6
Suy ra
9 3 5 9 3 5 6
Vì
9 3 5 9 3 5
.
l).
2
10 2 4 6 2 5 10 2 4 5 2 5.1 1 10 2 4 5 1
.
10 2 4 5 1 2 5 1 3 5
.
Bài tập 14. Tính giá trị của các biểu thức sau
a).
6 4 2 22 12 2
b).
2
( 3 2) 2
c).
2
3 5 (1 5)
d).
17 12 2 9 4 2
e).
6 2 5 6 2 5
f).
3 2 2 6 4 2
g).
24 8 5 9 4 5
h).
41 12 5 41 12 5
Lời giải
a).
22
6 4 2 22 12 2 (2 2) (3 2 2) 2 2
b).
2
( 3 2) 2 3 2 2 3
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
22
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c).
2
3 5 (1 5) 3 5 1 5 3 5 1 5 3 5 ( 5 1) 2 5 1
d).
22
17 12 2 9 4 2 (3 2 2) (2 2 1) 4
e).
22
6 2 5 6 2 5 ( 5 1) ( 5 1) 2 5
f).
22
3 2 2 6 4 2 ( 2 1) (2 2) 3
g).
2
24 8 5 9 4 5 4(6 2 5) ( 5 2) 2 5 1 5 2 3 5
h).
22
41 12 5 41 12 5 6 5 6 5 2 5
4. Bài tập rèn luyện.
Bài 8. Tính:
a).
2
0,8 0,125
; b).
6
2
; c).
2
32
; d).
2
2 2 3
;
e).
2
11
23



; f).
2
0,1 0,1
; g).
4 2 3
; h).
3 2 2
;
i).
9 4 5
; j).
16 6 7
.
Lời giải
a)
2
0,8 0,125 0,8 0,125 0,8.0,125 0,1.
b)
2
6 3.2 3 3
3
2 2 2 2 2 8.


c)
2
3 2 3 2 2 3.
d)
2
2 2 3 2 2 3 3 2 2.
e)
2
1 1 1 1 1 1
.
2 3 2 3 2 3



f)
2
0,1 0,1 0,1 0,1 0,1 0,1 1 0,1 1 0,1 0,1 1.
g)
2
4 2 3 3 2 3.1 1 3 1 3 1 3 1.
h)
2
3 2 2 2 2. 2.1 1 2 1 2 1 2 1.
i)
2
9 4 5 5 2. 5.2 4 5 2 5 2 5 2.
j)
2
16 6 7 7 2. 7.3 9 7 3 7 3 3 7.
Dạng 3. RÚT GỌN BIỂU THỨC
1. Phương pháp.
① Áp dụng
2
0
0
A khi A
AA
A khi A


Xét các trường hợp
0A
,
0A
để bỏ dấu giá trị tuyệt đối.
②
A
xác định ( có nghĩa)
0A
.
③ Áp dụng hằng đẳng thức đáng nhớ
2
22
2a b a ab b
hoặc
2
22
2a b a ab b
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
23
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2. Bài tập minh họa.
Bài tập 15. Rút gọn các biểu thức sau:
a).
2
4 15 15
; b).
22
2 3 1 3
;
c).
7 4 3 7 4 3
; d).
2
49a
, với
0a
.
Lời giải
a) Ta có
2
4 15 15
4 15 15
4 15 15
4
.
( Vì
4 15 0
nên
4 15 4 15
)
b) Ta có
22
2 3 1 3
2 3 1 3
2 3 1 3


2 3 3 1
1
( Vì
2 3 0
nên
2 3 2 3
và
1 3 0
nên
1 3 3 1
)
c) Ta có
7 4 3 7 4 3
22
22
3 2. 3.2 2 3 2. 3.2 2
22
3 2 3 2
3 2 3 2
3 2 2 3
3 2 2 3 4
.
d) Ta có
2
49a
2
7a
7a
7a
. ( Vì
0a
nên
70a
, suy ra
77aa
)
Bài tập 16. Rút gọn các biểu thức sau:
a).
2
25 3aa
, với
0a
; b).
42
16 6aa
;
c).
63
3 9 6aa
, với
0a
; d).
22
6 9 6 9a a a a
, với
33a
.
Lời giải
a). Ta có
2
25 3aa
2
53aa
53aa
5 3 2a a a
.
(Vì
0a
nên
50a
, suy ra
55aa
)
b). Ta có
42
16 6aa
2
22
46aa
22
46aa
2 2 2
4 6 10a a a
.
(Vì
2
0a
, với mọi
a
nên
2
40a
, với mọi
a
, suy ra
22
44aa
)
c). Ta có
63
3 9 6aa
2
33
3 3 6aa
33
3 3 6aa
3 3 3
3. 3 6 15a a a
.
(Vì
0a
nên
3
30a
, suy ra
33
33aa
)
d). Ta có
22
6 9 6 9a a a a
22
33aa
33aa
33aa
3 3 6aa
.
(Vì
33a
nên
30a
và
30a 
, do đó
33aa
và
33aa
)
Bài tập 17. Rút gọn các biểu thức sau:
a).
2
4
a
a
, với
0, 4aa
; b).
21
1
aa
a

, với
0, 1aa
;
Lời giải
a). Với
0, 4aa
ta có
2
2
42aa
22aa
nên:
2
4
a
a
2
22
a
aa

1
2a
.
b). Với
0, 1aa
ta có
21
1
aa
a

2
2
21
1
aa
a

2
1
11
a
aa

1
1
a
a
.
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
24
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 18. Rút gọn biểu thức sau
a).
2
92xx
với
0x
. b).
2
2 x
với
0.x
c).
2
3 ( 2)x
với
2.x
d).
2
2 x
5x với
0x
e).
2
25 3xx
với
0.x
f).
42
93xx
với
x
bất kỳ
g).
2
4 16 8x x x
với
4.x
Lời giải
a) Ta có:
2
9 2 3 2 3 2 5x x x x x x x
b) Ta có:
2
2 2 2x x x
c) Ta có:
2
3 ( 2) 3. 2 3. 2 6 2x x x x
d) Ta có:
2
2 5 2 5 2 5 7x x x x x x x
e) Ta có:
2
25 3 5 3 5 3 8x x x x x x x
f) Ta có:
4 2 2 2 2
9 3 3 3 6x x x x x
g) Ta có:
2
2
4 16 8 4 4 4 4 4 4 2 8x x x x x x x x x x
Bài tập 19. Rút gọn biểu thức sau
a).
2
4 12 9 2 1A x x x
b).
2
5
10 25
x
B
xx

c).
2
2
1
( 1)
21
x
Cx
xx

d).
2
69
3
xx
D
x

e).
2 4 2
8 16E x x x
f).
2
1 4 4 2F a a a
Lời giải
a) Ta có:
2
4 12 9 2 1 2 3 2 1A x x x x x
3
2 3 2 1 4 4
2
3
2 3 2 1 2
2
x A x x x
x A x x
b) Điều kiện xác định
5x
Khi đó
2
55
5
10 25
xx
B
x
xx



5
51
5
5
51
5
x
xC
x
x
xC
x
c) Điều kiện xác định
1x
2
2
11
( 1) 1
1
21
1
1 1 1 1
1
1
1 1 1 1
1
xx
C x x
x
xx
x
x D x x x
x
x
x D x x x
x



d) Điều kiện xác định
3x
2
3
69
33
3
31
3
3
31
3
x
xx
D
xx
x
xE
x
x
xE
x




e) Ta có:
2 4 2 2 2
8 16 4F x x x x x
22
44xx
f)
2
2
1 4 4 2 2 1 2F a a a a a
1
2 1 2
2
2 1 2
1
2 1 2
2
a a khi a
aa
a a khi a
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
25
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 20. Chứng tỏ:
2
2 2 4 ( 2 2)x x x
với
2x
.
Áp dụng rút gọn biểu thức sau:
2 2 4 2 2 4x x x x
với
2x
.
Lời giải
Thật vậy
2
2
( 2 2) 2 2. 2. 2 2 2 2 4VP x x x x x VT
Ta có:
2 2 4 2 2 4 2 2 2 2 2 2 2x x x x x x x
Bài tập 21. Rút gọn biểu thức sau
(loại bỏ dấu căn và dấu trị tuyệt đối)
:
a).
44xx
với
4.x
b).
2 2 3xx
với
3.x
c).
2 1 2 1x x x x
với
1.x
d).
2 1 2 1x x x x
với
0.x
Lời giải
a) Ta có
2
4 4 4 4 4 4 4 2 4 2x x x x x x
b) Ta có
2
2 2 3 3 1 3 1 3 1x x x x x
c) Ta có
22
2 1 2 1 1 1 1 1 1 1 1 1C x x x x x x x x
2 1 1 1 1 2. 1
1 2 1 1 1 1 2
x C x x x
x C x x
d) Ta có
22
2 1 2 1 1 1 1 1D x x x x x x x x
1 1 1 2
0 1 1 1 2
x D x x x
x D x x

Bài tập 22. Rút gọn các biểu thức sau
a).
6 9 3
4 0 ; 9
9
x x x
A x x x
x
b).
2
9 12 4 2
3 2 3
xx
Bx
x




Lời giải
a). Ta có:
2
33
4 3 1 0 9
33
xx
A x A x x
xx


b). Ta có:
2
2
1
32
9 12 4
3
2
3 2 3 2
1
3
khi x
x
xx
B
xx
khi x



Bài tập 23. Rút gọn các biểu thức sau
a).
2 1 2 1(1 2)A a a a a a
b).
2
4 4 4 ( 2)B x x x x
c).
2
44
( 2)
2
xx
Cx
x


d).
2
10 25
21
5
xx
Dx
x

e).
( 6 9)( 3)
4 (0 9)
9
x x x
E x x
x
Lời giải
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
26
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a).
2 1 2 1(1 2) 1 1 1 1A a a a a a a a
Với
1 2 1 1 0; 1 1 0a a a
Ta được:
1 1 1 1 1 1 1 1 2A a a a a
b).
2
4 4 4( 2) 4 2 4 ( 2) 3 2B x x x x x x x x x
c).
2
2
44
( 2)
22
x
xx
Cx
xx


Nếu
2x 
thì
1A 
Nếu
2x 
thì
1A
d).
2
5
10 25
2 1 2 1
55
x
xx
D x x
xx


Nếu
5 0 5 2 1 1 2x x A x x
Nếu
5 2 2x A x
e).
( 6 9)( 3)
4 (0 9)
9
x x x
E x x
x
Ta có
2
( 6 9)( 3) ( 3) ( 3)
4 4 3( 1) (0 9)
9
( 3)( 3)
x x x x x
E x x x x
x
xx

Bài tập 24. Cho biểu thức
2 2 2 2
2 1 2 1A x x x x
a). Với giá trị nào của
x
thì
A
có nghĩa.
b). Tính
A
nếu
2x
.
Lời giải
a).
2 2 2 2 2 2 2 2
2 1 2 1 ( 1 1) ( 1 1)A x x x x x x
22
1 1 1 1xx
A
có nghĩa
22
1
1 0 1
1
x
xx
x

b).
2 2 2 2
2 2 1 1 1 1 1 1 0x x x x x
2 2 2
1 1 1 1 2 1A x x x
Bài tập 25. Với giá trị nào của
a
và
b
thì:
a).
22
11
2
ba
a ab b

. b).
22
( 2 1) (1 )a b b a b
.
Lời giải
a). Điều kiện
ab
Ta có
2 2 2
1 1 1 1
2 ( )
b a b a
a ab b a b

Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
27
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
0a b b a a b a b
b).
22
0
1
( 2 1) (1 ) | ( 1) | (1 ) ( 1) 0
0
1
a
b
a b b a b a b a b a b
a
b

Bài tập 26. Rút gọn rồi tính giá trị của biểu thức:
a).
2
9 12 4 1 3A x x x
tại
1
3
x
.
b).
2
2 6 2 9B x x
tại
32x
Lời giải
a).
2
9 12 4 1 3A x x x
Ta có
22
9 12 4 1 3 (3 2) 1 3 |3 2| 1 3A x x x x x x x
Thay
1
3
x
vào biểu thức A ta được:
11
|3. 2| 1 3. 1 1 1 1
33
A
Vậy
1A
tại
1
3
x
b).
22
2 6 2 9 ( 2 3) | 2 3|B x x x x
Thay
32x
vào biểu thức
B
ta được
|3 2. 2 3| 3B
Vậy
3B
tại
32x
3. Bài tập rèn luyện.
Bài 9. Rút gọn biểu thức:
a).
2
2 x
, với
0x
; b).
10
1
2
x
, với
0x
;
c).
2
5a
, với
5a
; d).
10
10x
, với
10x
;
e).
2
4 8 16x x x
, với
4x
; f).
22
x y x y
, với
0 xy
.
Lời giải
a)
2
2 2 2 .x x x
b)
2
10 5.2 5 5 5
1 1 1 1 1
.
2 2 2 2 2
x x x x x
c) Ta có:
5 5 0aa
2
5 5 5a a a
d) Ta có:
55
10 10 0 10 0 10 0.x x x x
2
10 5 5 5 5
10 10 10 10 10 .x x x x x


e) Ta có:
4 4 0xx
2
2
4 8 16 4 4 4 4 4 4 0x x x x x x x x x
f) Ta có:
0 0 0x y x y y x
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
28
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2
2
22
22
x y x y x y x y x y




2
.x y x y x y y x
Bài 10. Rút gọn biểu thức:
a).
3
, 0, 9
9
x
xx
x

b).
56
, 0, 9
3
xx
xx
x


; c).
2
6 2 9 6 , 3x x x x
.
Lời giải
a).
3 3 1
.
9
3
33
xx
x
x
xx


b).
32
56
2.
33
xx
xx
x
xx



c).
2
2
6 2 9 6 6 2 3 6 2 3 6 2 3 3 .x x x x x x x x x x
DẠNG 4. GIẢI PHƯƠNG TRÌNH
1. Phương pháp.
Áp dụng
2
AA
.
22
A B A B
.
2. Bài tập minh họa.
Bài tập 27. Tìm
x
, biết:
a)
2
7.x
b)
2
8.x 
c)
2
4 6.x
d)
2
9 12 .x 
Lời giải
a) Ta có
2
7 7 7x x x
. Vậy
7x 
.
b) Ta có
2
8 8 8x x x
. Vậy
8x 
.
c) Ta có
2
4 6 2 6 3 3x x x x
.Vậy
3x 
.
d) Ta có
2
9 12 3 12 4 4x x x x
. Vậy
4x 
.
Bài tập 28. Giải các phương trình sau:
a).
2
5 0.x 
b).
2
2 11 11 0.xx
Lời giải
a) Ta có
2
22
5 0 5 5 5x x x x
. Vậy
5x 
.
b) Ta có
22
22
2 11 11 0 2. 11. 11 0 11 0x x x x x
11x
.
Vậy
11x
.
Bài tập 29. Giải các phương trình sau:
a).
2 5 3xx
b).
2
11xx
c).
2
1
2
4
x x x
d).
3 1 3xx
e).
2
5 25 0xx
f).
22
( 1)xx
.
Lời giải
a).
3
30
2 5 3 ( / )
2
2 5 3
3
x
x
x x t m
xx
x


Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
29
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b).
2
2 2 2 2
1
1 0 1
11
0 ( )
1 ( 1) 1 2 1
1 ( / )
x
xx
xx
x Ktm
x x x x x
x t m


c).
2
0
20
1
1
11
( / )
2
22
2
2
42
1
1
()
2
6
2
x
x
x t m
xx
x x x x x
x loai
xx




d).
3 1 3 1
3 1 3
3 1 3 1
x x x
xx
x x x



e).
2
5
5 25 0 5
5
5
x
x x x
x
x

f).
22
0 1( )
1
( 1)
1
1
2
vn
xx
xx
xx
x

Bài tập 30. Giải phương trình:
a).
2
9 2 1xx
b).
4
7x
c).
2
6 9 3 1x x x
d).
2
7x
e).
2
8x 
f).
2
1 4 4 5xx
g).
4
9x
h).
2
( 2) 2 1xx
i).
2
6 9 5xx
j).
2
4 12 9 3x x x
k).
22
4 4 1 2 1x x x x
l).
22
4 12 9 9 24 16x x x x
Lời giải
a).
2
9 2 1 3| | 2 1x x x x
Trường hợp 1:
0x
, phương trình trở thành:
3 2 1 1x x x
(TM
0x
)
Trường hợp 2:
0x
, phương trình trở thành:
1
3 2 1
5
x x x
(TM
0x
)
Vậy
1
{ ;1}
5
S 
b).
42
7 7 7x x x
.
Vậy tập nghiệm của phương trình
{ 7; 7}S 
c).
22
6 9 3 1 ( 3) 3 1x x x x x
| 3| 3 1 1xx
Cách 1:
3 3 1xx
Trường hợp 1: Nếu
3x 
Khi đó
1
trở thành
3 3 1xx
3 1 3
2 4 2( )
xx
x x TM
Trường hợp 1: Nếu
3x 
Khi đó
1
trở thành
3 3 1xx
3 1 3 4 2x x x
1
2
x
( Loại vì không TMĐK)
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
30
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Vậy phương trình đã cho có một nghiệm
{2}S
Cách 2: ĐK :
1
3
x
. Bình phương hai vế ta có:
22
( 3) (3 1)xx
22
( 3) (3 1) 0
( 3 3 1).( 3 3 1) 0
4 2 0 2( )
(4 2 ).(4 2) 0
1
4 2 0 ( )
2
xx
x x x x
x x TM
xx
x x khôngTM
Vậy phương trình đã cho có một nghiệm
{2}S
d).
2
7x
77xx
Vậy pt có hai nghiệm x =
7
e).
2
8x 
88xx
Vậy phương trình có tập nghiệm là
{-8;8}S
.
f).
2
1 4 4 5xx
2
(1 2 ) 5 1 2 5xx
1 2 5 2
1 2 5 3
xx
xx
Vậy phương trình có tập nghiệm là
{-3;2}S
.
g).
4
9x
2
93xx
Vậy phương trình có tập nghiệm là
{ 3;3}S 
.
h).
2
( 2) 2 1xx
( ĐK:
1
2
x
)
22
( 2) (2 1) 0 ( 2 2 1).( 2 2 1) 0
(1 ).(3 3) 0
1 0 1 ( )
3 3 0 1 ( )
x x x x x x
xx
x x TMĐK
x x khôngTM




Vậy phương trình có tập nghiệm là
{1}S
.
i).
2
6 9 5xx
2
( 3) 5 3 5xx
3 5 8
3 5 2
xx
xx
Vậy phương trình có tập nghiệm là
{ 2;8 }S 
.
j).
2
4 12 9 3x x x
(ĐK:
3)x
2 2 2
(2 3) 3 (2 3) ( 3) 0
(2 3 3).(2 3 3) 0
0 0 ( )
.(3 6) 0
3 6 0 2 ( )
x x x x
x x x x
x x KhôngTM
xx
x x khôngTM




Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
31
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Vậy phương trình có tập nghiệm là
S 
.
k).
22
4 4 1 2 1x x x x
2 2 2 2
(2 1) ( 1) (2 1) ( 1) 0
(2 1 1).(2 1 1) 0
0
0
.(3 2) 0
2
3 2 0
3
x x x x
x x x x
x
x
xx
x
x

Vậy phương trình có tập nghiệm là
2
{0; }
3
S
.
l).
22
4 12 9 9 24 16x x x x
2 2 2 2
(2 3) (3 4) (2 3) (3 4) 0x x x x
(2 3 3 4).(2 3 3 4) 0
1
10
(1 ).(5 7) 0
7
5 7 0
5
x x x x
x
x
xx
x
x


Vậy phương trình có tập nghiệm là
7
{1; }
5
S
.
Bài tập 31. Giải các phương trình sau
a).
2
2 4 2 2x x x
b).
2 1 2xx
c).
2
2 2 1 2 1x x x
d).
4 4 2xx
Lời giải
a).
2
2
2
2 2 0
2 4 2 2 2
2 4 2 2
x
x x x x
x x x

Vậy phương trình có tập nghiệm là
{2}S
.
b).
2 1 2xx
Cách 1: Ta có
2
2 1 2 2 1 2x x x x
2
40
2 1 4 2
4 1 4
x
xx
xx

Vậy phương trình có tập nghiệm là
{2}S
.
Cách 2: Ta có
2 1 2 1 1 2 2x x x x
c)
2
2
2
2 1 0
2 2 1 2 1 1
2 2 1 2 1
x
x x x x
x x x

(thỏa mãn)
d)
2
2
4 4 2 4 2.2 4 2 2x x x x
2
4 2 2 4 2 2 4 2 2x x x
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
32
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
4 0 4 0 4x x x
Vậy phương trình có tập nghiệm là
{4}S
.
Bài tập 32. Giải các phương trình sau
a).
2
3 2 1x x x
b).
22
4 4 4 12 9x x x x
Lời giải
a). Ta có
2
2
1
10
3 2 1
3 2 1
3
x tm
x
x x x
x x x
x tm

Vậy phương trình có tập nghiệm là
{1;3}S
.
b).
22
1
4 4 4 12 9 2 2 3
5
3
x tm
x x x x x x
x t m
Vậy phương trình có tập nghiệm là
5
{1; }
3
S
Bài tập 33. Giải các phương trình sau
a).
2
( 3) 3xx
b).
2
4 20 25 2 5x x x
c).
2
(3 2 ) 4x
d).
2 1 2 ( 1)x x x
Lời giải
a).
2
( 3) 3 3 3 3 0 3x x x x x x
b).
22
4 20 25 2 5 (5 2 ) 5 2x x x x x
5
5 2 5 2 5 2 0
2
x x x x
c).
2
3 2 4 1,5
(3 2 ) 4 3 2 4
3 2 4 3,5
xx
xx
xx



Vậy phương trình có tập nghiệm là
{ 1,5; 3,5}S
.
d).
2 1 2( 1) 1 2 1 1 2x x x x x
2
( 1 1) 2x
13
1 1 2 1 9 10
1 1( )
x
x x x
x loai

Vậy phương trình có tập nghiệm là
{10}S
.
Bài tập 34. Giải các phương trình sau
a).
22
2 1 6 9 1x x x x
b).
2
2 3 4 3xx
c).
2
11xx
Lời giải
a).
22
2 1 6 9 1x x x x
22
( 1) ( 3) 1 1 3 1 (1)x x x x
Với
1x
10
3
(1) 1 3 1 ( )
30
2
x
x x x loai
x


Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
33
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
10
1 3 (1) 1 3 1 0 1 ( )
30
x
x x x x loai
x


Với
3x
10
5
(1) 1 3 1 ( )
30
2
x
x x x loai
x


Vậy phương trình vô nghiệm.
b).
2
2
3
4 3 0
4
2 3 4 3
0( )
2 3 4 3
2( / )
x
x
xx
x loai
xx
x t m


c).
2
2 2 2
1
1
10
1 1 1; 2
1
1 ( 1)
( / )
2
x
x
x
x x x
x
xx
tm
x






Bài tập 35. Giải các phương trình sau
a).
22
2 1 1x x x
b).
2
33xx
c).
22
4 4 4 0x x x
d).
2 2 2
3 18 28 4 24 45 5 6x x x x x x
Lời giải
a).
22
2 1 1x x x
2 2 2
2
2
2
2
2
( 1) 1 1 1
10
1
11
0
( 1)( 2) 0
1 ( 1)
1
1
1; 2
0( )
1( / )
2( / )
x x x x
x
x
xx
xx
xx
xx
x
x
x
x loai
x t m
x t m








Vậy phương trình có tập nghiệm là
{ 2;1}S 
.
b).
2
33xx
2
2
33
3 ( 3)
( 3)( 3) ( 3) 0
( 3)( 3) ( 3) 0
3 0 3
3 1 0 1 3
3 0 3
3 1 0 1 3
xx
xx
x x x
x x x
xx
xx
xx
xx








Vậy phương trình có nghiệm
{ 2;1}S 
.
c).
2
22
2
2
40
4 4 4 0
22
4 4 0
2
x
x
x x x
xx
xx
x





d).
2 2 2
3 18 28 4 24 45 5 6x x x x x x
2 2 2
3( 3) 1 4( 3) 9 4 ( 3) (1)x x x
Ta có:
14
14
VT
VT
phương trình có nghiệm khi hai vế đều bằng 4
2
( 3) 0 3xx
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
34
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 36.
Đố
: Hãy tìm chỗ sai trong phép chứng minh “con muỗi nặng bằng con voi”dưới đây.
Gỉa sử con muỗi nặng
m
(gam), còn con voi nặng
V
(gam).Ta có :
2 2 2 2
m V V m
Cộng cả hai vế với
2mV
, ta có:
2 2 2 2
22m mV V V mV m
hay
22
m V V m
Lấy căn bậc hai mỗi vế của đẳng thức trên, ta được:
m V V m
Từ đó ta có
22mV
, Suy ra
Vm
. Vậy con muỗi nặng bằng con voi (!).
Lời giải
Sai lầm ở chỗ: Sau khi lấy căn bậc hai mỗi vế của đẳng thức
22
m V V m
phải được kết
quả
m V V m
chứ không thể có
m V V m
( chú ý rằng
2
AA
).
3. Bài tập rèn luyện.
Bài 11. Tìm
x
biết
a).
2
33xx
; b).
2
25 20 4 2 5x x x
;
c).
2
1 1 1
2 16 4
x x x
; d).
2 1 1 1x x x
;
e).
2
1 12 36 5xx
; g).
2 1 2xx
.
Lời giải
a).
2
33xx
Ta có biến đổi:
33xx
Ta có hai trường hợp:
TH 1: Nếu
3x
thì
3 3 3x x x TM
TH 2: Nếu
3x
thì
3 3 0 0x x TM
Vậy tất cả
3x
đều thỏa mãn.
b).
2
25 20 4 2 5x x x
Ta có biến đổi:
2
5 2 5 2xx
5 2 5 2xx
Ta có hai trường hợp:
TH 1: Nếu
5
2
x
thì
5 2 5 2 0 0x x TM
TH 2: Nếu
5
2
x
thì
5
2 5 5 2
2
x x x
(L)
Vậy tất cả
5
2
x
đều thỏa mãn.
c).
2
1 1 1
2 16 4
x x x
Ta có biến đổi:
2
1 1 1 1
4 4 4 4
x x x x



Tương tự ta có: tất cả
1
4
x
đều thỏa mãn.
d).
2 1 1 1x x x
.
Điều kiện:
1x
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
35
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có biến đổi:
2
1 1 1 1 1 1 1 1x x x x
Ta có hai trường hợp:
Nếu:
1 1 2xx
:
1 1 1 1xx
(TM)
Nếu:
1 1 2xx
:
1 1 1 1 2x x x l
(TM)
Vậy:
2x
đều thỏa mãn.
e).
2
1 12 36 5xx
.
Ta có biến đổi:
2
1 6 5 1 6 5xx
Ta có hai trường hợp:
Nếu:
1
6
x
thì
2
1 6 5
3
xx
(TM)
Nếu:
1
6
x
thì
6 1 5 1xx
(TM)
Vậy:
2
3
x 
và
1x
là giá trị cần tìm.
g).
2 1 2xx
.
Điều kiện:
1x
Ta có biến đổi:
2
1 1 2 1 1 2xx
Ta có hai trường hợp:
TH1:
1 1 2 1 1 1 1 2x x x x
TH2:
1 1 2 1 3x x VL
.
Vậy
2x
là giá trị cần tìm.
Dạng 5: PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
1. Phương pháp.
Áp dụng các hằng đẳng thức đáng nhớ:
2
AA
(với
0A
) .
22
A B A B A B
.
2
22
2A B A AB B
2. Bài tập minh họa.
Bài tập 37. Phân tích thành nhân tử:
a).
2
2x
. b).
2
7x
.
c).
2
2 15 15xx
. d).
2
4 4 3 3xx
.
Lời giải
a). Ta có
2
22
2 2 2 2x x x x
.
b). Ta có
2
22
7 7 7 7x x x x
.
c). Ta có
22
22
2 15 15 2. . 15 15 15x x x x x
.
d). Ta có
22
2
2
4 4 3 3 2 2.2 . 3 3 2 3x x x x x
.
3. Bài tập rèn luyện.
Bài 9. Phân tích đa thức thành nhân tử.
a).
2
11x
; b).
2
2 2 2xx
;
c).
5x
(với
0x
) ; d).
2
57x
(với
0x
) .
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
36
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
e).
34x
(với
0x
) ;
Lời giải
a).
2
11 11 11x x x
.
b).
2
2
2 2 2 2x x x
.
c).
5 5 5x x x
(với
0x
)
d).
2
5 7 5 7 5 7x x x
(với
0x
)
e).
22
3 4 3 4 3 4 3 4x x x x
(với
0x
)
Dạng 6. CHỨNG MINH BẤT ĐẲNG THỨC
1. Phương pháp.
Áp dụng
Các hằng đẳng thức đáng nhớ.
và
2
AA
để biến đổi vế trái thành vế phải hoặc ngược lại.
2. Bài tập minh họa.
Bài tập 38. Chứng minh:
a).
2
5 1 6 2 5
. b).
6 2 5 5 1
.
Lời giải
a). Ta có
22
2
5 1 5 2. 5.1 1 5 2 5 1 6 2 5
.
b). Áp dụng câu a, ta có:
2
6 2 5 5 5 1 5 5 1 5 5 1 5 1
.
3. Bài tập rèn luyện.
Bài 12. Chứng minh đẳng thức:
a).
2
9 4 5 5 2
; b).
9 4 5 5 2
;
c).
23 8 7 7 4
; d).
4 2 2 4 2 2 4a a a a
(với
26a
).
Lời giải
a).
2
9 4 5 5 2
2
2
2
5 2. 5.2 4 5 2. 5.2 2 5 2VT VT
b). Ta có biến đổi:
2
2
2
5 2. 5.2 4 5 5 2. 5.2 2 5
5 2 5 5 2 5 5 2 5 2
VT
VP
c).
2
2
16 2.4. 7 7 7 4 2.4. 7 7 7VT
2
4 7 7 4 7 7 4 7 7 4 VP
d).
2 2. 22 4 2 2. 2.2 4VT a a a a
2 2 2 2 2 2 2 2 4a a a a VP
(Vì
26a
)
Dạng 7. TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC
1. Phương pháp.
Áp dụng bất đẳng thức:
A B A B
, dấu “=”
.0AB
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
37
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2. Bài tập minh họa.
Bài tập 39. Tìm GTNN của các biểu thức sau
a).
22
2 1 2 1A x x x x
b).
2 1 3 2B x x
c).
22
4 4 1 4 12 9C x x x x
d).
22
49 42 9 49 42 9D x x x x
Lời giải
a).
22
2 1 2 1 1 1A x x x x A x x
Cách 1:
Nếu
1 1 1 2 2(1)x A x x x
Nếu
1 1 1 1 2(2)x A x x
Nếu
1 1 1 2 2(3)x A x x x
Từ (1)(2)(3)
2 1 1MinA x
Cách 2: Áp dụng bất đẳng thức
A B A B
1 1 1 1 1 1 2A x x x x x x
Vậy
2 ( 1)(1 ) 0 1 1MinA x x x
b).
13
2 1 3 2 2
22
B x x MinB x
c).
22
4 4 1 4 12 9 2 1 3 2 (2 1) (3 2 ) 2C x x x x x x x x
13
(2 1)(3 2 ) 0
22
x x x
d).
33
6
77
min
Dx
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
38
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT LÍ THUYẾT
1. Quy tắc khai phương một tích
Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số rồi nhân
các kết quả với nhau.
Nếu
0, 0AB
thì
.AB A B
.
Ví dụ 1. Tính:
a).
12,1.160
b).
2500.4,9.0,9
.
Lời giải
a).
12,1.160 121. 16 11.4 44
b).
2500.4,9.0,9 25.49.9 25. 49. 9 5.7.3 105
Ví dụ 2. Tính:
a).
22
41 40
b).
81.6,25 2,25.81
Lời giải
a).
22
41 40 (41 40)(41 40) 1.81 1.9 9
b).
81.6,25 2,25.81 81.(6,25 2,25) 81. 4 9.2 18
Ví dụ 3. Rút gọn các biểu thức sau:
a).
3
60
15x .
x
b).
2
16( 6x 9)x 
.
Lời giải
a).
3
60
15 .x
x
ĐK:
0x
.
Ta có
32
30 0
60
15 . 900 30 .
30 0
x khi x
x x x
x khi x
x

b).
22
4( 3) 3
16( 6x 9) 16( 3) 4 3 .
4( 3) 3
x khi x
x x x
x khi x

Ví dụ 4. Rút gọn biểu thức
2
25 2 1M x x x
với
01x
.
Lời giải
Ta có
2
2
25 2 1 25 1 5 1M x x x x x
.
Vì
0x
nên
xx
.
Vì
01x
nên
1x
. Do đó
11xx
Vậy
51M x x
Ví dụ 5. Đẳng thức
(1 ) . 1x y x y
đúng với những giá trị nào của x và y.
Lời giải
Theo địnhlí khai phương một tích thì
(1 ) . 1x y x y
khi
0 à 1- 0 hay 0 và 1x v y x y
.
Ví dụ 6. Cho cac biểu thức
( 1)( 3) à 1. 3M x x v N x x
a). Tìm các giá trị của
x
để
M
có nghĩa;
N
có nghĩa.
b). Với giá trị nào của
x
thì
MN
?
§BI 3. LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
39
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Lời giải
a). Tìm các giá trị của
x
để
M
có nghĩa;
N
có nghĩa.
M
có nghĩa khi
( 1)( 3) 0.xx
Trường hợp 1:
1 0 1
1
3 0 3
xx
x
xx



Trường hợp 2:
1 0 1
3
3 0 3
xx
x
xx



Vậy
M
có nghĩa khi
1x
hoặc
3x 
.
N
có nghĩa khi
1 0 1
1
3 0 3
xx
x
xx



b). Để
M
và
N
đồng thời có nghĩa thì
1x
Khi đó ta có
MN
theo định lí khai phương một tích.
2. Quy tắc nhân các căn bậc hai
Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới dấu căn với nhau
rồi khai phương kết quả đó.
Nếu
0, 0AB
thì
.A B AB
Ví dụ 7. Tính:
a).
72. 50
b).
12,8. 0,2
Lời giải
a).
72. 50
72.50 36.100 6.10 60
b).
12,8. 0,2
12,8.0,2 128.0,02 64.0,04 8 .0,2 1,6
Ví dụ 8. Tính:
a).
40. 20. 4,5
. b).
2 12 1
..
3 25 2
.
Lời giải
a).
40. 20. 4,5
40.20.0,5 400.9 20.3 60
b).
2 12 1
..
3 25 2
2 12 1 4 2
..
3 25 2 25 5
Ví dụ 9. Thực hiện các phép tính:
a).
20 45 5 . 5
b).
12 3 27 3
c).
5 3 1 5 1
Lời giải
a).
20 45 5 . 5
100 225 25 10 15 5 20
b).
12 3 27 3
324 36 81 9 18 6 9 3 18
c).
5 3 1 5 1
5 5 15 3 5 1 4 15 3
.
Ví dụ 10. Tính:
a).
2
73
b).
2
82
c).
3 5 2 7 3 5 2 7
Lời giải
a).
2
73
22
7 2 7. 3 3 7 2 21 3 10 2 21
b).
2
82
22
8 2 8. 2 2 8 2 16 2 2
c).
3 5 2 7 3 5 2 7
22
5 3 2 7 25.3 4.7 47
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
40
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ví dụ 11. Rút gọn các biểu thức sau:
a).
35
.
5 27
xx
với
0.x
b).
62
.( 2)xx
với
2x
.
Lời giải
a).
2
3 5 3 5
..
5 27 5 27 9 3 3
x
x x x x x x
(Vì
0.x
)
b).
62
.( 2)xx
6 2 3 3
. ( 2) . 2 ( 2)x x x x x x
(vì
2x
).
Ví dụ 12. Rút gọn các biểu thức sau:
a).
21xx
b).
2 2 1xx
Lời giải
a).
2
2 1 1 2 1 1 1 1 1 1x x x x x x
( ĐK:
1x
)
b).
2
2 2 1 1 2 1 1 1 1 1 1x x x x x x
( ĐK
1x 
)
Nếu
0x
thì
1 1 1 1xx
Nếu
0x
thì
1 1 1 1xx
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA.
Dạng 1. THỰC HIỆN PHÉP TÍNH
1. Phương pháp.
Sử dụng các quy tắc khai phương một tích và quy tắc nhân các căn bậc hai
Nếu
0, 0AB
thì
.AB A B
2. Bài tập minh họa.
Bài tập 1. Áp dụng quy tắc khai phương một tích, hãy tính:
a).
0,16.81
; b).
2
4
3 . 5
; c).
16,9.250
; d).
24
5 .4
.
Lời giải
a) Ta có:
0,16.81 0,16. 81 0,4.9 3,6
.
b) Ta có:
22
4 4 2
3 . 5 3 . 5 3 . 5 9.5 45
.
c) Ta có:
16,9.250 169.25 169. 25 13.5 65
.
d) Ta có:
2 4 2 4 2
5 .4 5 . 4 5.4 80
.
Bài tập 2. Áp dụng quy tắc nhân các căn bậc hai, hãy tính:
a).
5. 80
; b).
2,45. 40. 50
; c).
0,6. 5,4
; d).
8,1. 5. 4,5
.
Lời giải
a) Ta có:
5. 80 5.80 400 20
.
b) Ta có:
2,45. 40. 50 2,45.40.50 4900 70
.
c) Ta có:
0,6. 5,4 0,6.5,4 3,24 1,8
.
d) Ta có:
8,1. 5. 4,5 8,1.5.4,5 182,25 13,5
.
Bài tập 3. Khai phương tích
13.25.52
được:
a). 2600. b).130. c). 13. d). 260.
Hãy chọn kết quả đúng.
Lời giải
Ta có:
13.25.52 16900 130
(chọn B).
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
41
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 4. Biến đổi các biểu thức dưới dấu căn thành dạng tích rồi tính
a).
22
25 24
; b).
22
26 10
; c).
22
137 88
; d).
22
481 480
.
Lời giải
a) Ta có:
22
25 24 25 24 25 24 49 7
.
b) Ta có:
22
26 10 26 10 26 10 16.36 4.6 24
.
c) Ta có:
22
137 88 137 88 137 88 49.225 7.15 105
.
d) Ta có:
22
481 480 481 480 481 480 961 31
.
Bài tập 5. Tính giá trị của các biểu thức sau:
a).
4 2 3
b).
8 2 15
c).
9 4 5
Lời giải
a)
2
4 2 3 3 2. 3.1 1 3 1 3 1
b)
2
8 2 15 5 2 5. 3 3 5 3 5 3
c)
2
9 4 5 5 2.2. 5 4 5 2 5 2
Nhận xét: Phương pháp giải trong ví dụ này là biến đổi biểu thức lấy căn thành bình phương của
tổng hay hiệu hai số rồi áp dụng hằng đẳng thức
2
AA
3. Bài tập rèn luyện.
Bài 1. Tính
a).
2 50
24 . 6
33





b).
3 5. 2
c).
34
3 5 . 12
43





d).
3 5. 8
Lời giải
a).
2 50 2 50
24 . 6 .6 .6 24.6 0
3 3 3 3




b).
2
3 5. 2 3.2 2 5 5 1 5 1
c).
34
3 5 . 12 7
43




d).
3 5. 8 2 5 1
Bài 2. Tính
a).
55.77.35
b).
11
. 2. 125.
85
c).
2 1. 2 1
d).
2
2 2.( 3 2) (1 2 2) 2 6
Lời giải
a).
55.77.35 5.11.7.11.5.7 5.7.11 385
b).
1 1 1 1 2.125 25 5
. 2. 125. .2.125.
8 5 8 5 8.5 4 2
c).
2 1. 2 1 ( 2 1).( 2 1) 2 1 1
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
42
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
d).
2
2 2.( 3 2) (1 2 2) 2 6 2 6 4 2 1 4 2 8 2 6 9
Bài 3. Tính
a).
2 3. 2 3
b).
3 2 2 3. 3 2 2 3
c).
2
( 3 2 3 2)
d).
(1 2 3).(1 2 3)
Lời giải
a).
2 3. 2 3 2 3 2 3 4 3 1 1
.
b).
22
3 2 2 3. 3 2 2 3 3 2 2 3 18 12 6
.
c).
2 2 2
3 2 3 2 3 2 2 3 2. 3 2 3 2
3 2 2 3 2 3 2 3 2 2 3 2 3 2 2 3 2 2 3 1
.
d).
2
2
1 2 3 . 1 2 3 1 2 3 1 2 3 2 2.3 4 2 6
.
Bài 4. Tính
a).
(4 15)( 10 6) 4 15A
b).
(3 5) 3 5 (3 5) 3 5B
c).
2 3. 2 2 3. 2 2 2 3 . 2 2 2 3C
Lời giải
a).
(4 15)( 10 6) 4 15 ( 10 6) 4 15. 4 15. 4 15A
( 10 6) 4 15. (4 15)(4 15) 10 6. ( 10 6)(4 15)
10 6. 4 10 150 4 6 90 10 6. 10 6 ( 10 6)( 10 6)
42

b).
(3 5) 3 5 (3 5) 3 5 3 5. 3 5. 3 5 (3 5) 3 5B
3 5. 3 5 3 5 3 5 2( 3 5 3 5)
2( 3 5. 2 3 5. 2)
22
2( 6 2 5 6 2 5) 2( ( 5 1) ( 5 1)
2( 5 1 5 1) 2 10
c.
2 3. 2 2 3. 2 2 2 3 . 2 2 2 3C
2 3. 2 2 3. 2 2 3C
22
2 3.( 2 ( 2 3) ) 2 3. 2 3 1C
Bài 5. Tính
a).
3 5 2 3. 3 5 2 3A
b).
4 8. 2 2 2 . 2 2 2
c).
( 12 3 15 4 135) 3
d).
2 40 12 2 75 3 5 48
Lời giải
a).
22
3 5 2 3. 3 5 2 3 3 ( 5 2 3) 9 (5 2 3)A
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
43
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2
9 5 2 3 4 2 3 ( 3 1) 3 1
b).
22
4 8. 2 2 2 . 2 2 2 4 4. 2. 2 ( 2 2)
4 2 2. 2 2 2.(2 2)(2 2) 2.2 2
c).
2
( 12 3 15 4 135) 3 36 3 9.5 4 9 .5
6 9 5 36 5 6 27 5
d).
2 40 12 2 75 3 5 48 2 40 12 2 5 3 3 20 3
2 80 3 2 5 3 6 5 3
8 5 3 2 5 3 6 5 3 5 3(8 2 6) 0
Bài 6. Thực hiện phép tính
a).
(4 2 3)(13 4 3)
b).
( 3 2)( 6 2) 3 2
c).
(3 5)( 10 2) 3 5
d).
(4 15)( 10 6) 4 15
e).
4 15 4 15 2 3 5
f).
4 8. 2 2 2 . 2 2 2
g).
(5 4 2).(3 2 1 2).(3 2 1 2)
h).
2 3. 2 2 3 . 2 2 2 3 . 2 2 2 3
Lời giải
a).
22
4 2 3 13 4 3 3 1 . 2 3 1 3 1 . 2 3 1
.
b).
3 2 6 2 3 2 3 2 6 2 6 2 2 3 2 2 6 3 2
.
2 1 3 3 2 2 4 2 3 3 2 2 2 2
.
c).
3 5 10 2 3 5 2 5 1 3 5 3 5 2. 2 2 5 . 3 5
.
2
2 2 1 5 . 3 5
2 2 6 2 5 3 5 2 2. 8 8
d).
4 15 10 6 4 15 2. 4 15 5 3 4 15
.
2
2 5 3 4 15
2 5 3 4 15 2. 2 2
.
e).
8 2 15 8 2 15 2 6 2 5
4 15 4 15 2 3 5
2
.
5 3 5 3 2 5 1
2
2
22
f).
4 8. 2 2 2 . 2 2 2 2. 2 2. 4 2 2
.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
44
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2. 2 2. 2 2 2. 4 2 2
.
g).
5 4 2 . 3 2 1 2 . 3 2 1 2 5 4 2 . 9 4 1 2


.
2
5 4 2 . 5 4 2 5 4 2
.
h).
2 3. 2 2 3 . 2 2 2 3 . 2 2 2 3
.
2 3. 2 2 3. 4 2 2 3 2 3. 2 2 3. 2 2 3 2 3. 4 2 3
.
2 3. 2 3 4 3 1
.
DẠNG 2. RÚT GỌN BIỂU THỨC VÀ TÍNH GIÁ TRỊ BIỂU THỨC
1. Phương pháp.
Trước hết tìm điều kiện của biến để biểu thức có nghĩa (nếu cần).
Áp dụng các quy tắc
① Khai phương một tích
.AB A B
(
0, 0AB
) và
2
AA
,
② Quy tắc nhân các căn bậc hai
.A B AB
.
③ Các hằng đẳng thức để rút gọn.
Thay giá trị của biến vào biểu thức đã rút gọn rồi tính.
2. Bài tập minh họa.
Bài tập 6. Rút gọn biểu thức sau:
a).
2
0,49a
với
0a
; b).
4
2
62
2
a
a



với
3a
;
c).
2
19.76 2 a
với
2a
; d).
2
2 2 2
1
. a a b
ab
với
0ab
.
Lời giải
a) Ta có:
2
0,49 0,7 0,7a a a
(do
0a
).
b) Ta có:
42
2
2
2
.2 3
3
6 2 6 2
2 2 4 2
aa
aa
aa
aa
(do
3a
).
c) Ta có:
22
19.76 2 1444 2 38 2 38 2a a a a
(do
2a
).
d) Ta có:
2
2 2 2 2 2
1 1 1
. . . . .a a b a a b a a b a b a a b
a b a b a b
(do
0ab
).
Bài tập 7. Rút gọn các biểu thức sau:
a).
25
.
5 18
aa
với
0a
; b).
99
11 .a
a
với
0a
;
c).
21 11 . 44a a a
với
0a
; d).
2
2
4 0,4. 160aa
Lời giải
a) Ta có:
22
2 5 10
.
5 18 90 9 3
a a a a a
(do
0a
).
b) Ta có:
99 99
11 . 11 . 1089 33aa
aa
.
c) Ta có:
2
21 11 . 44 21 484 21 22a a a a a a a a
(do
0a
)
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
45
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
d) Ta có:
2 2 2
2 2 2
4 0,4. 160 4 64 4 8 16 8 8a a a a a a a a a
Nếu
0a
thì
2
22
4 0,4. 160 16a a a
.
Nếu
0a
thì
2
22
4 0,4. 160 16 16a a a a
.
Bài tập 8. Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
a).
2
2
9 4 20 25xx
tại
5x 
; b).
22
2 2 12 18a b b
tại
3, 3ab
.
Lời giải
a) Ta có:
2
42
2
9 4 20 25 9. 2 5 3 2 5x x x x
.
Thay
5x 
vào biểu thức đã rút gọn, ta được:
2
2
3 2 5 3 2 5 5 3 129 20 5 252,836x
.
b) Ta có:
2
2 2 2 2 2
2 2 12 18 4 6 9 4 . 3 2 . 3a b b a b b a b a b
Thay
3, 3ab
vào biểu thức đã rút gọn, ta được:
2 . 3 2 3. 3 3 6 3 3 7,608ab
.
3. Bài tập rèn luyện.
Bài 7. Rút gọn các biểu thức sau:
a).
75 48 300
b).
98 72 0,5 8
c).
9 16 49a a a
0a
d).
160 2 40 3 90b b b
0b
Lời giải
a).
75 48 300 5 3 4 3 10 3 3
b).
98 72 0,5 8 7 2 6 2 2 2 2
c).
9 16 49 3 4 7 6a a a a a a a
d).
160 2 40 3 90 4 10 4 10 9 10 10b b b b b b b
Bài 8. Rút gọn các biểu thức sau:
a).
3 2 4 18 2 32 50
b).
5 48 4 27 2 75 108
c).
125 2 20 3 80 4 45
d).
2 28 2 63 3 175 112
Lời giải
a).
3 2 4 18 2 32 50 3 2 12 2 8 2 5 2 7 2
b).
5 48 4 27 2 75 108 20 3 12 3 10 3 6 3 4 3
c).
125 2 20 3 80 4 45 5 5 4 5 12 5 12 5 5
d).
2 28 2 63 3 175 112 4 7 6 7 15 7 4 7 7
Bài 9. Rút gọn các biểu thức sau:
a).
(2 3 5) 3 60
b).
(5 2 2 5) 5 250
c).
( 28 12 7) 7 2 21
d).
( 99 18 11) 11 3 22
Lời giải
a).
2 3 5 . 3 60 6 2 15 2 15 6
b).
5 2 2 5 . 5 250 5 10 10 5 10 10
c).
28 12 7 . 7 2 21 14 2 21 7 2 21 7
d).
99 18 11 . 11 3 22 33 3 22 11 3 22 22
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
46
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài 10. Rút gọn các biểu thức sau:
a).
2 40 12 2 75 3 5 48
b).
2 80 3 2 5 3 3 20 3
Lời giải
a).
2 40 12 2 75 3 5 48 8 5 3 2 5 3 6 5 3 0
b).
2 80 3 2 5 3 3 20 3 8 5 3 2 5 3 6 5 3 0
Bài 11. Rút gọn
a).
10 15
8 12
A
b).
6 15
35 14
B
c).
55
10 2
C
d).
15 5 5 2 5
3 1 2 5 4
D



e).
33
3 1 .
23
E

f).
3 18 2 8
50
F
g).
6 14
2 3 28
G
h).
2 3 6 8 4
234
H

i).
3 8 2 12 20
3 18 2 27 45
K


Lời giải
a).
10 15 5. 2 5. 3 5
2
8 12 4. 2 4. 3
AA


b).
6 15 3 21
7
35 14 7
B
c).
5 5 5 10
2
10 2 2
C
d).
15 5 5 2 5 5( 3 1) 5( 5 2) 5 3 5
5
22
3 1 2 5 4 3 1 2( 5 2)
D
e).
33
3 1 .
23
E

3(1 3)
3 1 .
23

3 1 . 3 1
2


31
1
2
f).
3 18 2 8 3.3 2 2.2 2 9 2 4 2 5 2
1
50 5 2 5 2 5 2
F
g).
6 14 2. 3 2. 7 2 1
2
2 3 28 2 3 4. 7 2
G


h).
2 3 6 8 4 2 3 4 4 6 8
21
2 3 4 2 3 4
H
i).
3 8 2 12 20 3.2 2 2.2 3 2 5 2(3 2 2 3 5) 2
3
3 18 2 27 45 3.3 2 2.3 3 3 5 3(3 2 2 3 5)
K
Bài 12. Rút gọn biểu thức sau
(loại bỏ dấu căn và dấu trị tuyệt đối)
:
a).
2
0,36x
với
0x
b).
5x
với
3x
c).
2
27.48(1 )x
với
1x
d).
42
1
. ( )x x y
xy
e).
2
4.( 3)x
với
3x
f).
2
9.( 2)x
với
2x
g).
14 7 15 5 1
:2
1 2 1 3 7 5





với
0x
h).
22
( 1)xx
với
0x
i).
23
.
38
xx
với
0x
j).
52
13x
x
với
0x
k).
1
6
2
với
x
bất kỳ. l).
22
(3 ) 0,2. 180 ,x x x
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
47
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Lời giải
a).
2
0,36x
với
0x
.
Ta có:
2
2
0,36 0,36 0,36 0,36x x x x
(vì
0x
).
b)
2
4
3xx
với
3x
.
Ta có:
2
2
4 2 2 2
3 3 3 3x x x x x x x x


(vì
3x
).
c).
2
27.48(1 )x
với
1x
.
Ta có:
2
2
2 3 4 2 2 2 2
27.48(1 ) 3 .2 .3. 1 3 .2 . 1 3 .2 . 1 36. 1x x x x x


(vì
1x
).
d).
42
1
. ( )x x y
xy
0xy
.
Ta có:
2
2
4 2 2 2
1 1 1
. x x y x x y x x y x
x y x y x y


(vì
0xy
).
e).
2
4.( 3)x
với
3x
.
Ta có:
2
2
4.( 3) 2 3 2 3 2 3x x x x


(vì
3x
).
f).
2
9.( 2)x
với
2x
.
Ta có:
2
2
9.( 2) 3 2 3 2 3 2x x x x


(vì
2x
).
g).
2
2
1xx
với
0x
.
Ta có:
2
2
2
1 1 1 1x x x x x x x x


(vì
0x
).
h)
22
( 1)xx
với
0x
.
Ta có:
2
22
( 1) 1 1 1x x x x x x x x


(vì
0x
).
i).
23
.
38
xx
với
0x
.
Ta có:
2
2 3 2 .3
.
3 8 3.8 4 2
x x x x x x
(vì
0x
).
j).
52
13x
x
với
0x
.
Ta có:
52 13 .52
13 13.13.4 13.2 26
x
x
xx
.
k).
5 . 45 3x x x
với
bất kỳ.
Ta có:
2
5 . 45 3 5.5.9 3 5.3 3x x x x x x x
.
Khi đó
5 . 45 3 12x x x x
nếu
0x
.
Hoặc
5 . 45 3 18x x x x
nếu
0x
.
l).
22
(3 ) 0,2. 180xx
,
x
.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
48
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có:
22
2 2 2 2
(3 ) 0,2. 180 3 0,2.180. 3 2.2.9x x x x x x
.
2
36xx
.
Khi đó
2
2 2 2
(3 ) 0,2. 180 3 6 12 9x x x x x x
nếu
0x
.
Hoặc
2
2 2 2
(3 ) 0,2. 180 3 6 9x x x x x
nếu
0x
.
Bài 13. Rút gọn các biểu thức sau
a).
23
.0
38
tt
At

b).
6
4
28
0
7
y
By
y

c).
22
1. 1 1C x x x x x
d).
4 2 4 2
4 . 4D x x x x
Lời giải
a).
2
2 3 2 3
. . 0
3 8 3 8 4 2
t t t t t t
At



b).
6
4
28
02
7
y
B y B y
y
c).
2
2 2 2 2
1. 1 1 1C x x x x x x
d).
4 2 4 2 4 2 4 2
4 . 4 ( 4 )( 4 )x x x x x x x x
4 2 2
( 4) ( ) 4 2xx
Bài 14. Rút gọn các biểu thức
a).
0; 0; 0
2
x y y x
A x y xy
x xy y

b).
( 0; 0; )
2
x y y x
B x y x y
x xy y

c).
3 2 1 1
( 0; )
4
4 4 1
aa
aa
aa



d).
4 4 4
( 0; 4)
22
a a a
D a a
aa

Lời giải
a).
2
2
x y x y
x y y x xy
AA
x xy y x y
xy
b).
2
x y y x xy
B
x xy y x y

c).
2
3 2 1 (2 1)(1 ) 1
4 4 1 (2 1) 2 1
a a a a a
a a a a

d).
4 4 4
0
22
a a a
D
aa

Bài 15. Rút gọn các biểu thức sau:
a).
21
21
xx
xx


với x 0 b).
2
4
( 2 1)
1
1, 1, 0
( 1)
1
yy
x
x y y
x
y

Lời giải
a)
21
21
xx
xx


với
1x
.
Ta có :
2
2
2
1
2 1 1 1
2 1 1 1
1
x
x x x x
x x x x
x




.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
49
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b)
2
4
( 2 1)
1
( 1)
1
yy
x
x
y

,
1; 1; 0x y y
.
Ta có :
2
2
4 2 2
21
2 1 2 1 1
1 1 1
.
( 1) ( 1) ( 1) 1
1 1 1
yy
y y y y y
x x x
x x x x
y y y





.
Bài 16. Rút gọn rồi tính giá trị của các biểu thức sau:
a).
22
4(1 6 9 )xx
tại
2x 
b).
22
9 ( 4 4 )a b b
tại
2; 3ab
c).
32
2
48
2
xx
x
x

tại
2x 
d).
42
2
( 2) 1
(3 ) 3
xx
xx


(với
3x
) tại
0,5x
Lời giải
a).
22
4(1 6 9 )xx
tại
2x 
.
Ta có:
4
2
22
2
4 1 6 9 2 1 3 2 1 3x x x x


.
Thay
2x 
, ta được:
2
2 1 3. 2 2 1 6 2 18 2 19 6 2
.
b).
22
9 ( 4 4 )a b b
tại
2; 3ab
.
Ta có:
2
22
9 ( 4 4 ) 3 2 3 2a b b a b a b
.
Thay
2; 3ab
, ta được:
3 2 3 2 6 3 2
.
c).
32
2
48
2
xx
x
x

tại
2x 
.
Ta có:
32
2
2
4 8 4 8 4 8
22
xx
xx
x x x x
xx

.
Thay
2x 
, ta được:
4 2 8 2 3 2 8
.
d).
42
2
( 2) 1
(3 ) 3
xx
xx


(với
3x
) tại
0,5x
.
Ta có:
2
22
4 2 2 2
2
22
( 2) 1 1 1
(3 ) 3 3 3 3 3
xx
x x x x
x x x x x x





.
Thay
0,5x
, ta được:
2
2
0,5 2
0,5 1 6
3 0,5 0,5 3 5


.
Dạng 3. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
1. Phương pháp.
Áp dụng một số cách sau
① Phương pháp thừa số chung với
⋆
0x
thì
.x x x
⋆
0x
thì
3
x x x
⋆
0, 0xa
thì
22
x a x a x a x a
② Phương pháp hằng đẳng thức đáng nhớ.
③ Phương pháp nhóm hạng tử.
④ Phương pháp thêm, bớt và tách hạng tử.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
50
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
2. Bài tập minh họa.
Bài tập 9. Phân tích thành nhân tử:
a).
33
b).
3x xy
c).
x y y x
d).
x x xy y
Lời giải
a).
3 3 3 3 1
b).
33x xy x x y
( Điều kiện
0; 0xy
)
c).
x y y x xy x y
( Điều kiện
0; 0xy
)
d).
11x x xy y x x y y
1x x y
( Điều kiện
0; 0xy
)
Bài tập 10. Phân tích thành nhân tử:
a).
3
25xx
b).
96x xy y
c).
33
xy
d).
2
9 2 3xx
Lời giải
a).
32
25 25 5 5x x x x x x x
(Điều kiện:
0x
)
b).
2
9 6 3x xy y x y
(Điều kiện:
,0xy
).
c).
33
x y x y x xy y
(Điều kiện:
,0xy
).
d).
2
9 2 3 3 3 2x x x x
(Điều kiện:
3x
).
Bài tập 11. Phân tích thành nhân tử
a).
5aa
; b).
7a
với
0a
;
c).
44aa
; d).
4 3 12xy x y
.
Lời giải
a).
5aa
; b).
77aa
; c).
2
2a
; d).
34xy
.
Bài tập 12. Rút gọn biểu thức:
14 6 5 21
.
Lời giải
Ta có
14 6 5 21 2 7 3 5 21
2
7 3 10 2 7.3 7 3 7 3
7 3 7 3 4
.
Bài tập 13. Tìm
x
và
y
, biết
13 2 2 3x y x y
.
Lời giải
Ta có
13 4 6x y x y
(ĐK:
,0xy
)
22
2
4 4 6 9 0 2 3 0x x y y x y
2
20x
và
2
30y 
4x
và
9y
.
Bài tập 14. Tính giá trị của biểu thức
7 13 7 13A
.
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
51
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
2
2
7 13 7 13 7 13 2 7 13 7 13 7 13A
14 2 49 13 14 2 36 14 12 2
Khi đó
2
2 2.AA
Dạng 4. GIẢI PHƯƠNG TRÌNH
1. Phương pháp.
Để giải một phương trình chứa căn, ta tiến hành các bước sau:
Bước 1. Trước tiên tìm điều kiện để căn thức có nghĩa.
Bước 2. Áp dụng một số cách sau
① Sử dụng hằng đẳng thức
2
22
2a b a ab b
hoặc
2
22
2a b a ab b
để đưa
phương trình chứa căn thức về phương trình chứa dấu giá trị tuyệt đối với
2
AA
;
② Áp dụng
22
AB
AB
AB


.
③ Đặt thừa số chung để đưa về phương trình tích:
.
0
.0
0
A
AB
B

④ Bình phương hai vế
2
0B
AB
AB

2. Bài tập minh họa.
Bài tập 15. Tìm
x
biết:
a).
2
5x
; b).
2
25 10x
;
b).
2
4 28 49 7xx
; c).
10 25 3xx
.
Lời giải
a). Ta có
2
5x
5x
5
5
x
x

. Vậy
5;5x
.
b). Ta có
2
25 10x
2
5 10x
5 10x
5 10
5 10
x
x

2
2
x
x

. Vậy
2;2x
.
c). Ta có
2
4 28 49 7xx
2
2 7 7x
2 7 7x
2 7 7
2 7 7
x
x

2 14
20
x
x
7
0
x
x
.
Vậy
0;7x
.
d). Ta có
10 25 3xx
2
53x
53x
53
53
x
x

8
2
x
x
64
4
x
x
.
Vậy
4;64x
.
Bài tập 16. Giải các phương trình sau:
a).
2
4 64 0x 
; b).
4
70x 
;
c).
2
9 2 1xx
; d).
22
4 4 4 4 0x x x x
.
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
52
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a). Ta có
2
4 64 0x 
2
4 64x
2
16x
4
4
x
x

.
Vậy
4;4S 
.
b). Ta có
4
70x 
2
2
7x
2
7x
2
7x
7
7
x
x

. Vậy
7; 7S 
.
c). Ta có
2
9 2 1xx
2
3 2 1xx
3 2 1xx
30
3 2 1
30
3 2 1
x
xx
x
xx


0
1
0
1
5
x
x
x
x


1
1
5
x
x

. Vậy
1
;1
5
S




.
d). Ta có
22
4 4 4 4 0x x x x
22
4 4 4 4x x x x
22
22xx
22xx
22
22
xx
xx
04
20
x
x

0
0
x
x
x

. Vậy
0S
.
Bài tập 17. Giải các phương trình:
a).
23
2
1
x
x
b).
23
2
1
x
x
c).
43
3
1
x
x
d).
43
3
1
x
x
Lời giải
a).
23
2
1
x
x
Điều kiện xác định:
2 3 0
23
0
10
1
x
x
x
x



hoặc
2 3 0
10
x
x


3
2
1
x
x
hoặc
3
2
1
x
x
3
2
x
hoặc
1x
Khi đó
2 3 2 3 1
2 4 2 3 4 1
1 1 2
xx
x x x
xx


(Thỏa mãn điều kiện)
b).
23
2
1
x
x
.
Điều kiện xác định:
3
2 3 0
3
.
2
10
2
1
x
x
x
x
x



Khi đó
1
2 3 4 1
2
23
2 2 3 2 1 1 0 1
1
2 3 0 3
2
x
xx
x
x x x x x
x
x
x



.
c).
43
3
1
x
x
.
Điều kiện xác định:
4 3 0
43
0
10
1
x
x
x
x



hoặc
4 3 0
10
x
x


Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
53
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
3
4
1
x
x


hoặc
3
4
1
x
x


3
4
x
hoặc
1x 
Khi đó
4 3 4 3 6
3 9 4 3 9 9
1 1 5
xx
x x x
xx


(thỏa mãn điều kiện).
d).
43
3
1
x
x
Điều kiện xác định:
3
4 3 0
3
.
4
10
4
1
x
x
x
x
x





Khi đó
6
5
4 3 9 1
4 3 3
3 4 3 3 1 4 3 0
4
1
10
1
x
xx
x
x x x x x
x
x
x





.
Bài tập 18. Giải phương trình ẩn
y
a).
1
4 20 5 9 45 4
3
y y y
b).
11
2 9 27 25 75 49 147 20
57
y y y
Lời giải
a).
1
4 20 5 9 45 4
3
y y y
1
4 20 5 9 45 4
3
y y y
1
4 5 5 9 5 4
3
1
2 5 5 .3 5 4
3
2 5 4
50
5 2 9
54
y y y
y y y
y
y
yy
y


b).
11
2 9 27 25 75 49 147 20
57
y y y
11
2 9 3 25 3 49 3 20
57
y y y
6 3 3 3 20yyy
4 3 20
3 0 3
3 5 28
3 25 28
y
yy
yy
yy



Bài tập 19. Giải phương trình:
2
25. 5 15.x 
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
54
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
2
25. 5 15x 
5 3 2
5 5 15 5 3
5 3 8.
xx
xx
xx



Bài tập 20. Giải phương trình:
2
9 90 225 6.xx
Lời giải
Ta có:
2
9 90 225 6xx
2
2
9 10 25 6 9 5 6 3 5 6x x x x
5 2 7
52
5 2 3.
xx
x
xx



Bài tập 21. Giải phương trình:
2
25 2 5.xx
Lời giải
Điều kiện:
22
25 0 25
5.
5 0 5
xx
x
xx



Khi đó
2
25 2 5xx
5 5 2 5 0x x x
5 5 2 0xx
5
5 0 5 0 5 0
54
1.
5 2 0 5 2
x TM
x x x
x
x
xx
L






Bài tập 22. Giải phương trình:
11
5 9 45 25 125 6.
35
x x x
Lời giải
Điều kiện:
5.x
Ta có
11
5 9 45 25 125 6
35
x x x
11
5 9. 5 25 5 6
35
x x x
5 5 5 6x x x
56x
5 36x
41x
(thỏa mãn điều kiện).
Bài tập 23. Giải phương trình:
1
2.x
x

Lời giải
Điều kiện:
0.x
Ta có:
1
2x
x

2
1 1 2
2 0 0 1 0
xx
xx
xx

1 0 1xx
(thỏa mãn điều kiện)
Bài tập 24. Tính cạnh của hình vuông, biết diện tích hình vuông đó bằng diện tích tam giác vuông
có hai cạnh góc vuông là
12,8 m
và
40 m
.
Lời giải
Gọi
0, mxx
là cạnh hình vuông, khi đó diện tích hình vuông bằng:
22
m
hv
Sx
.
Diện tích tam giác vuông là:
2
1
12,8.40 256 m
2
tgv
S
.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
55
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Theo giả thiết ta có:
hv tgv
SS
2
256x
256 16 mx
.
Vậy cạnh của hình vuông là
16 m
.
3. Bài tập rèn luyện.
Bài 17. Giải các phương trình
a).
2
2 4 2 2x x x
b).
2
2 2 3x x x
c).
2
43x x x
d).
2
3 2 9 0xx
Lời giải
a).
2
2
2
2 2 0
2 2 0
2 4 2 2 2
2
2 4 2 2
x
x
x x x x
x
x x x



b).
2
2
2
2
2 3 0
2 2 3 2
3
2 2 3
20
x
x
x x x x
x x x
xx


c).
2
2
2
30
30
1
43
43
5
2
x
x
x
x x x x
x x x
x




d). Cách 1:
2
2
3
30
3 2 9 0 3
11
3 4 9
4
x tm
x
x x x
xx
x loai

Cách 2: Với
2
3 9 3. 3 3 1 2 3 0 3x x x x x x x tm
Bài 18. Giải các phương trình sau
a).
2
9.(2 3 ) 6x
b).
2
4 9 2 2 3xx
c).
10( 3) 20x 
d).
2
6 9 3 6x x x
Lời giải
a).
2
4
9.(2 3 ) 6 3 2 3 6 2 3 2
3
0
x
x x x
x
b).
2
4 9 2 2 3 (2 3)(2 3) 2 2 3x x x x x
2 3. 2 3 2 2 3x x x
3
2 3 0
2
2 3.( 2 3 2) 0
7
2 3 0
2
x
x
xx
x
x





c).
10( 3) 20x 
Điều kiện
3.x
Ta có
10( 3) 20x 
10( 3) 20 5xx
(thỏa mãn điều kiện)
d).
2
6 9 3 6x x x
2
2
3 6 0
9
( / )
( 3) 3 6 3 3 6
3 3 6
2
3 3 6 3
()
4
x
x
x t m
x x x x
xx
xx
x loai



Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
56
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Dạng 5. CHỨNG MINH BẤT ĐẲNG THỨC
1. Phương pháp.
Để chứng minh một bất đẳng thức, ta có thể dùng các phương pháp sau:
① Với
0a
;
0b
thì
22
a b a b
;
② Biến đổi tương đương.
2. Bài tập minh họa.
Bài tập 25. Chứng minh:
a).
(2 3)(2 3) 1
b).
9 17. 9 17 8
c).
( 2014 2013)
.
( 2014 2013)
=1 d).
2
2 2( 3 2) (1 2 2) 2 6 9
Lời giải
a).
2 3 2 3 1
.
Ta có
2 3 2 3 4 3 1
.
b).
9 17. 9 17 8
.
Ta có
9 17. 9 17 81 17 64 8
.
c).
2014 2013
.
2014 2013 1
Ta có
2014 2013
.
2014 2013
2014 2013 1
.
d).
2
2 2 3 2 1 2 2 2 6 9
.
Ta có
2
2 2 3 2 1 2 2 2 6 2 6 4 2 1 8 4 2 2 6 9
.
Bài tập 26. Không dùng máy tính hoặc bảng số, chứng minh rằng:
5 8 6 7.
Lời giải
Ta có
5 8 6 7
22
5 8 6 7
(vì hai vế đều dương)
5 2 40 8 6 2 42 7 13 2 40 13 2 42
40 42 40 42.
Bất đẳng thức cuối cùng hiển nhiên đúng nên bất đẳng thức đã cho là đúng.
Bài tập 27. Không dùng máy tính hoặc bảng số, chứng minh rằng:
3 2 2 3 1 .
Lời giải
Ta có
2
3 2 3 4 3 4 7 4 3
;
2
2
2 3 1 2 3 1 2 3 2 3 1 8 4 3.


Vì
7 4 3 8 4 3
nên
2
2
3 2 2 3 1


.
Do đó
3 2 2 3 1
.
Bài tập 28. Chứng minh rằng:
7 3 6 2
.
Lời giải
Ta có
7 3 6 2
22
7 2 6 3 7 2 6 3
9 2 14 9 2 18 2 14 2 18
.
Bất đẳng thức cuối cùng đúng nên bất đẳng thức đã cho là đúng.
Bài tập 29. Cho
0a
, chứng minh rằng:
93aa
.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
57
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Lời giải
Ta có
2
99aa
;
2
3 6 9.a a a
Do
0a
nên
9 9 6a a a
, do đó
22
9 3 .aa
Vậy
9 3.aa
Bài tập 30. Cho
, , 0abc
. Chứng minh rằng:
a).
2a b ab
; b).
.a b c ab bc ca
Lời giải
a).
2a b ab
Ta có
2a b ab
20a b ab
2
0ab
(dấu
""
xảy ra khi và chỉ khi
ab
).
Bất đẳng thức cuối này đúng nên bất đẳng thức đã cho là đúng.
NHẬN XÉT:
Bất đẳng thức
2a b ab
với
,0ab
gọi là bất đẳng thức Cô – si.
b).
.a b c ab bc ca
Ta có
, , 0abc
. Áp dụng bất đẳng thức Cô – si đối với hai số ta được:
2a b ab
2b c bc
2c a ca
.
Công từng vế ba bất đẳng thức trên ta được
22a b c ab bc ca
.
Suy ra
a b c ab bc ca
(dấu
""
xảy ra khi và chỉ khi
abc
).
Bài tập 31. Chứng minh bất đẳng thức:
22
a b a b
với
,0ab
.
Lời giải
Với
,0ab
ta có
22
2 2 2 2
a b a b a b a b
2.
2 2 .
24
a b a a b b
a b a a b b
22
2 . 0 2 . 0a a b b a a b b
2
0,ab
luôn đúng với
,0ab
. Vậy
22
a b a b
.
Bài tập 32. Cho
1
2
a
, chứng minh rằng:
21aa
.
Lời giải
Từ bất đẳng thức Cô – si
2a b ab
suy ra
2
ab
ab
.
Áp dụng bất đẳng thức này cho các số không âm
21a
và 1 ta được:
2 1 1
2 1 2 1 .1
2
a
a a a

.
Vậy
21aa
(dấu
""
xảy ra khi và chỉ khi
1a
).
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
58
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT KIẾN THỨC
1. Quy tắc phép khai phương của một phương
Muốn khai phương một thương
A
B
, trong đó số
A
không âm và số
B
dương, ta có thể khai
phương lần lượt số
A
và số
B
, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai
AA
B
B
(với
0, 0AB
)
Ví dụ 1. Tính
a).
4 49
:
25 121
; b).
36
49
a
với
0a
.
Lời giải
a).
4 49 4 49 2 7 22
. : :
25 121 25 121 5 11 35
.
b).
36 36 36. 6
49 7
49 49
a a a a
.
Nhận xét: Vì
0a
nên
a
có nghĩa.
Ví dụ 2. Tính
a).
22
65 52
225
; b).
11 7
:1,44 :1,44
99
.
Lời giải
a).
22
2
65 52 65 52
65 52 13.117 13.13.9 13.3 39
225 225 225 15 15 15

.
b).
11 7 11 7 144
:1,44 :1,44 :
9 9 9 9 100



4 144 4 144 2 12 5
: : :
9 100 9 100 3 10 9
.
Ví dụ 3. Đẳng thức
55
2
2
xx
y
y

đúng với những giá trị nào của
x
và
y
?
Lời giải
Theo định lí khai phương một thương thì
55
2
2
xx
y
y

Khi
50x 
và
20y 
hay
5x
và
2y 
.
2. Quy tắc phép chia căn bậc hai
Muốn chia căn bậc hai của số
A
không âm cho căn bậc hai của số
B
dương, ta có thể chia số
A
cho số
B
rồi khai phương kết quả đó
AA
B
B
( với
0, 0AB
)
§BI 4. LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
59
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ví dụ 4. Tính
a).
45 : 80
; b).
5
35
2.3 : 2 .3
.
Lời giải
a).
45 9 3
45 : 80
80 16 4
. b).
55
5
3 5 2
35
2 .3
2.3 : 2 .3 2 2
2 .3
.
Ví dụ 5. Tính
a).
54 : 2 : 3
; b).
3 52
:
75 117
.
Lời giải
a).
54 : 2 : 3 54:2 : 3 27:3 9 3
.
b).
3 52 3 52 1 4 1 2 3
: : : :
75 117 25 9 5 3 10
75 117
.
Ví dụ 6. Thực hiện các phép tính
a).
45 125 20 : 5
; b).
2 18 3 8 6 2 : 2
.
Lời giải
a).
45 125 20 : 5 9 25 4 3 5 2 0
.
b).
2 18 3 8 6 2 : 2 2 9 3 4 6 2.3 3.2 6 6
.
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA.
Dạng 1. THỰC HIỆN PHÉP TÍNH
1. Phương pháp.
Sử dụng các quy tắc khai phương một thương và quy tắc chia hai căn bậc hai để tính
Với
0, 0AB
thì
AA
B
B
2. Bài tập minh họa.
Bài tập 1.( Bài 28, tr. 18 SGK) Tính :
a).
289
225
. b).
14
2
25
. c).
0,25
9
. d)
8,1
1,6
.
Lời giải
a) Ta có:
289 289 17
225 15
225

.
b) Ta có
14 64 64 8
2
25 25 5
25

.
c) Ta có:
0,25 0,25 0,5
99
9

.
d)
8,1 81 81 9
1,6 16 4
16

.
Bài tập 2. ( Bài 29, tr. 19 SGK) Tính :
a).
2
18
b).
15
735
. c).
12500
500
. d).
5
35
6
2 .3
.
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
60
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a) Ta có:
2 2 1 1
18 9 3
18
.
b) Ta có
15 15 1 1
735 49 7
735
.
c) Ta có:
12500 12500
25 5
500
500
.
d)
5 5 5
3 5 3 5
6 2 .3
42
2 .3 2 .3
.
Bài tập 3.(Bài 32, tr. 19 SGK) Tính :
a).
94
1 .5 .0,01
16 5
. b)
1,44.1,21 1,44.0,4
. c).
22
165 124
164
. d)
22
22
149 76
457 384
.
Lời giải
a) Ta có:
9 4 25 49 5 7 7
1 .5 .0,01 . . 0,01 . .0,1
16 5 16 9 4 3 24
.
b) Ta có
1,44.1,21 1,44.0,4 1,44. 1,21 0,4 1,44.0,81 1,44. 0,81 1,2.0,9 1,08
.
c) Ta có:
22
165 124 165 124
165 124 41.289 289 17
164 164 164 4 2

.
d)
22
22
149 76 73.225 225 15
457 384 73.841 29
841
.
3. Bài tập rèn luyện.
Bài 1. Tính
a).
7
2;
81
và
6
;
150
b).
5 7 7 5 : 35;
c).
2 8 3 3 1 : 6.
Lời giải
a) Ta có
7 169 169 13
2.
81 81 9
81
và
6 6 1 1
.
150 25 5
150
b) Ta có
5 7 7 5 5 7
5 7 7 5 : 35 5 7.
35 35 5 7
c) Ta có
2 8 3 3 1 4 3 3 2 6
2 8 3 3 1 : 6 .
3 2 6
6 6 6
Bài 2. Tính
1 1 3 2 4 1
4,5 50 :
2 2 2 5 15 8
Lời giải
Tính
1 1 3 2
4,5 50
2 2 2 5
2
1 9 2 2
1 1 3 9 2 1 9
25.2 2 2 0
2 2 2 2 5
2 2 2 2 2 2
Vậy
1 1 3 2 4 1
4,5 50 : 0
2 2 2 5 15 8
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
61
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài 3. Tính
a).
1 16
7 : 7
77





b).
36 12 5 : 6
c).
14
3 : 3
33





d).
3 5 : 2
e).
2 12 3 27 5 3
3

f).
32 50 8
2

g).
( 12 75 27): 15
h).
(12 50 8 200 7 450): 10
i).
22
32 6. 3
11

Lời giải
a).
1 16 1 16 1 4
7 : 7 7 .
7 7 7
7 7 7
b).
36 12 5 : 6 6 2 5 5 1
c).
1 4 2
3 : 3
3 3 3




d).
6 2 5 5 1
3 5 : 2 2. 3 5 :2
22

e).
22
3 2.2 3.3 4
2 12 3 27 5 3 2 2 .3 3. 3 .3 5 3
2.2 3.3 4 1
3 3 3

f).
52
2 4 5 2
32 50 8 2 2.5 2 2
1
2 2 2

.
g).
12 75 27 4 9
( 12 75 27): 15 5
15 15 15 5 5
2 3 5
5 5 2 5
5 5 5
h).
(12 50 8 200 7 450): 10 12 5 8 20 7 45
12 5 16 5 21 5 17 5
i).
22
32 6. 3
11

22
16.2 18 4 2 3 2 2 2 2
11
Bài 4. Thực hiện phép tính
a).
7 5 2 7 4 1A
b).
5
4 3 6 3 15 3
2
B
c).
1 2 5 5 11 5 2C
d).
1 2 27 2 38 5 3 2
3 2 4
D
e).
5 2 2 2 2 2 1 2 1E



f).
2 3 2 3
g).
3 5 3 5 2
h).
6,5 12 6,5 12 2 6
Lời giải
a).
7 5 2 7 4 1 7 4 2 7 4.1 1 1A
2
7 4 1 1
2
71
2 7 8
7 4 1 1 7 4
22
2 7 1
71
2
2

.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
62
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b).
5 8 2 3 2 6 3 15 2 3 5
4 3 6 3 15 3
2
2
B
.
2
2 3 5 3 2 3 5
5 2 3 2 3 2 3 5 3 2 3 5
22

.
2 3 5 3 2 3 5 6
2
2

.
c).
2
1 2 5 5 11 5 2 5 2 3 5 5 2C
5 2 3 5 5 2
2
11
3 5 6 2 5 5 1
22
.
2 5 1
1
51
2
2
d).
1 2 27 2 38 5 3 2
3 2 4
D
2
5 3 2 3 2 4 5 3 2
3 2 4
5 3 2 3 2 4 5 3 2 3 2 4
1
3 2 4 3 2 4

.
e).
5 2 2 2 2 2 1 2 1E



.
Ta có
2 1 2 1. 2 1 2 1 2 1 2 1
.
Khi đó
5 2 2 2 2 5 2 2. 2 1 2 2 2 3 2 2 2 2. 2 1
.
2
2 2 1 2 1 2 2. 2 1 2 1
2
2 2 2 2 1
5 2 2 2 2 2 2 2 2 1
.
Do đó
5 2 2 2 2 2 1 2 1 2 2 2. 2 1 2E



.
f).
22
3 1 3 1
( 3 1) ( 3 1)
4 2 3 4 2 3 2
2
22
2 2 2 2 2



g).
22
( 5 1) ( 5 1) 5 1 5 1
3 5 3 5 2 2 0
22
2
h).
6,5 12 6,5 12 2 6 4 6
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
63
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Dạng 2. RÚT GỌN BIỂU THỨC
1. Phương pháp.
Tìm điều kiện của biến để căn thức có nghĩa.
Áp dụng phép khai phương một thương:
AA
B
B
(
0, 0AB
)
Quy tắc phép chia các căn bậc hai
AA
B
B
(
0, 0AB
)
Áp dụng
2
,0
,0
A khi A
AA
A khi A


.
Xét các trường hợp
0, 0AA
để bỏ dấu giá trị tuyệt đối.
Thay giá trị của biến vào biểu thức đã rút gọn rồi thực hiện các phép tính.
2. Bài tập minh họa.
Bài tập 4. Rút gọn biểu thức
16 12
12 8
33
33
.
Lời giải
Ta có
12 4
16 12
4
84
12 8
3 3 1
33
39
3 3 1
33
.
Bài tập 5. Rút gọn
22
165 124
.
369
Ax
rồi tính giá trị của biểu thức sau với
6x
.
Lời giải
Ta có
22
165 124
165 124 165 124
..
369 369
A x x


289.41 289 17
. . .
369 9 3
x x x
.
Với
6x
thì
17
.6 34
3
A 
.
Bài tập 6. (Bài 30, tr. 19 SGK) Rút gọn các biểu thức sau:
a).
2
4
yx
xy
với
0, 0xy
. b).
4
2
2
2
4
x
y
y
với
0y
.
c).
2
6
25
5
x
xy
y
với
0, 0xy
. d)
33
48
16
0,2xy
xy
với
0, 0xy
.
Lời giải
a) Ta có:
2
4 2 2
1
..
x
y x y y x
x y x y x y y

( do
0, 0xy
).
b) Ta có
4 4 2 2
2 2 2 2 2
22
2 2 2 2 .
4 4 2 2
x x x x
y y y y x y
y y y y
.
c) Ta có:.
2 2 2
6 3 2
3
6
5
25 25 5 25
5 5 . 5 . 5 .
x
x x x x
xy xy xy xy
y y y
y
y
(do
0, 0xy
).
d)
3 3 3 3
4 8 2 4
16 4 0,8
0,2 0,2 . .
x
x y x y
x y x y y

Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
64
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 7. ( Bài 34, tr. 19 SGK) Rút gọn các biểu thức sau:
a).
2
24
3
ab
ab
với
0,b 0a 
. b).
2
27 3
48
a
với
3a
.
c).
2
2
9 12 4aa
b

với
0, 1,5ba
. d).
2
ab
ab
ab
với
0ab
.
Lời giải
a) Ta có:
2 2 2
2 4 2
2
3 3 3
. . 3ab ab ab
a b ab
ab
( do
0,b 0a 
).
b) Ta có
22
33
27 3 9 3 3 3
48 16 4 4
a
a a a
(do
3a
).
c) Ta có:
2
2
22
32
32
9 12 4 3 2
a
a
a a a
b b b b
. (do
0, 1,5ba
).
d)
2
2
ab ab ab ab
a b a b a b a b ab
a b b a
ab
ab

(do
0)ab
Bài tập 8. Cho biểu thức
1
1
:
11
y
x
B
yx

. Rút gọn rồi tính giá trị của
B
với
5x
;
10y
.
Lời giải
Ta có
1
1
:
11
y
x
B
yx

. Điều kiện:
1x
;
1y
.
Khi đó
11
1
11
:
1
11
11
xx
y
xx
B
y
yx
yy




.
Với
5x
;
10y
thì
5 1 4 2
10 1 9 3
B
.
Bài tập 9. Rút gọn biểu thức rồi tính
a).
11
:
11
ab
A
ba


tại
7,25 ; 3,25ab
b).
2
15 8 15 16B a a
tại
3 5 8
53
15
a
c).
32
5
5 125 ( 0)
5
xx
C x x
x
tại
5x
d).
2 2 2 2
2 1 2 1E a a a a
với
5a
Lời giải
a).
( 1)( 1) 1 5
7,25, 3,25
13
( 1)( 1)
a a a
A a b
b
bb

b).
22
88
15 8 15 16 15.( ) 8. . 15 16
15 15
B a a
22
8 8 16 16 4
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
65
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c).
32
5
5 125 ( 0)
5
xx
C x x
x
Do
2 2 2
( 6) ( 36) 2 12
5 5 0 5 5 16
55
x x x x
x x x x C
xx

d).
2 2 2 2
2 1 2 1D a a a a
Ta có :
32
05x x x
và
5x
luôn có nghĩa.
Vậy
D
luôn xác định.
Với
3 2 2
5 . 5
5 125 5 125
55
x x x x
D x x
xx


5 125 6 5 5( 0) 5x x x x D
e).
2 2 2 2
2 1 2 1E a a a a
2 2 2 2
( 1) 2 1 1 ( 1) 2 1 1a a a a
2 2 2 2 2 2
22
( 1 1) ( 1 1) 1 1 1 1
( 5) 1 1 ( 5) 1 1
a a a a
Bài tập 10. Cho biểu thức
2
69
x xy y
C
x xy y


với
0x
,
0y
.
Rút gọn rồi tính giá trị của
C
với
25x
;
81y
.
Lời giải
Ta có
2
2
2
6 9 3
3
xy
xy
x xy y
C
x xy y x y
xy

.
Với
25x
;
81y
thì
25 81
59
41
5 3.9 32 8
25 3 81
C
. Vậy
1
.
8
C
3. Bài tập rèn luyện.
Bài 5. Rút gọn biểu thức
a).
2
;
x x y y
xy
xy
b).
21
,0
21
xx
x
xx
c).
2
4
21
1
. , 1, 1, 0
1
1
yy
x
x y y
y
x
.
Lời giải
a).
2
;
x x y y
xy
xy
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
66
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
2
2x xy y x y
x x y y x x y y
xy
x y x y x y
22
22
22
.
x x y y x x x y x y xy y x y y
xy
xy x y
x y x y y x y x x y y x
xy
x y x y x y
b).
2
2
1
1
21
.
2 1 1
1
x
x
xx
x x x
x
c).
2 4 2
4 4 2
2 1 1 1
1
1 1 1
. . . .
1
1 1 1
1 1 1
y y y y
y
x x x
x
y y y
x x x
Bài 6. Rút gọn và tính:
a).
2a ab b
A
ab

(với
0ab
) tại
36; 25.ab
b).
33
:
3
xx
B
x
x

(với
3x
) tại
81.x
c).
4
2
2
5
25
( 4)
4
4
x
x
Cx
x
x
, tại
3.x
d).
32
3
3 27 ( 0)
3
xx
M x x
x
, tại
3.x
Lời giải
a).
2a ab b
A
ab

Với
0ab
ta có
2
22
(1)
ab
a ab b a ab b
A a b
a b a b
ab

Ta thấy
36; 25ab
thỏa mãn điều kiện.
Thay
36; 25ab
vào (1) ta có
36 25 1 1A
.
b) Với
3x
ta có;
3 3 3 3 ( 3)( 3)
: : . (1)
3 3 3
3
x x x x x x x
Bx
x x x x x
x
Ta thấy
81x
thỏa mãn điều kiện.
Thay
81x
vào
1
ta có
81 9B 
.
c) Với
4x
ta có
2
4
4
2 2 2
2
2
22
2
22
5
5
5
25 25 25
4 4 4 4
4
4
5 5 25
25 2 10
(1)
4 4 4 4
x
x
x
x x x
C
x x x x
x
x
x x x
x x x
x x x x

Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
67
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta thấy
3x
thỏa mãn điều kiện.
Thay
3x
vào (1) ta có
2
2.3 10.3
12
43
C
.
d) Với
0x
ta có
2
32
2
3
3
3 27 3 27 3 27
3
3
3 27 3 27 4 27 (1)
xx
xx
M x x x x
x
x
x x x x x
Ta thấy
3x
thỏa mãn điều kiện.
Thay
3x
vào (1) ta có
4 3 27 4 3 3 3 3M
.
Dạng 3. GIẢI PHƯƠNG TRÌNH
1. Phương pháp.
Tìm điều kiện để căn thức có nghĩa.
Áp dụng:
.0, 0
AA
AB
B
B
2
;AA
và
AB
AB
AB


(với
0B
).
Đặt biệt. Nếu hai
vế không âm
thì có thể bình phương hai vế để khử dấu căn.
2. Bài tập minh họa.
Bài tập 11. (Bài 33, tr. 19 SGK) Giải phương trình:
a).
2. 50 0;x 
c).
2
3. 12 0;x 
b).
2. 8 0;x 
d).
2
20 0.
5
x

Lời giải
a) Ta có
2. 50 0 2. 5 2 5.x x x
Vậy
5.x
b)
8
2. 8 0 4 2.
2
xx
Vậy
2.x
c)
2 2 2
12
3. 12 0 3 12 4 2.
3
x x x
2.x
Vậy
12
2, 2.xx
d)
22
2
20 0 20 5. 20 10
55
xx
x
.
10.x
Vậy
12
10, 10.xx
Bài tập 12. Tìm
x
biết:
a).
2
3 9;x 
b).
2
4 4 1 6.xx
Lời giải
a) Ta có
2
3 9 12
3 9 3 9 .
3 9 6
xx
xx
xx



Vậy
12
12, 6.xx
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
68
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b)
2
2
4 4 1 6 2 1 6 2 1 6x x x x
5
2 1 6
2
.
2 1 6 7
2
x
x
x
x



Vậy
12
57
,.
22
xx
Bài tập 13. Giải các phương trình sau
a).
4
4 20 3 5 9 45 6
3
x x x
b).
15 1
25 25 6 1
29
x
xx
c).
1
4 20 9 45 5 4
3
x x x
d).
1
4 20 9 45 5 4
3
x x x
.
Lời giải
a).
4
4 20 3 5 9 45 6
3
x x x
Điều kiện xác định:
5x 
2 5 3 5 4 5 6x x x
3 5 6x
52x
54x
1x
(thỏa mãn)
Vậy phương trình có nghiệm là:
1x 
b).
15 1
25 25 6 1
29
x
xx
Điều kiện xác định:
1x
Ta có
15 1
25 25 6 1
29
x
xx
15
5 1 1 6 1
2.3
x x x
10 1 5 1 12 2 1
3 1 12 1 4
1 16
17( )
x x x
xx
x
x TM

Vậy phương trình có nghiệm là:
17x
c).
1
4 20 9 45 5 4
3
x x x
Điều kiện xác định:
5x
2 5 5 5 4
2 5 4 5 2
5 4 9( )
x x x
xx
x x TM
Vậy phương trình có nghiệm là:
9x
d)
16 16 9 9 4 4 16 1 x x x x
Điều kiện xác định:
1x 
4 1 3 1 2 1 16 1
4 1 16
1 4 1 16 15( )
x x x x
x
x x x TM
Vậy phương trình có nghiệm là:
15x
Bài tập 14. Giải các phương trình
a).
31
2
2
x
x
. b).
57
1
21
x
x
.
Lời giải
a).
31
2
2
x
x
.
ĐKXĐ:
31x
và
2x
cùng dấu hoặc
1
3
x
.
Trường hợp 1:
1
3 1 0
1
3
20
3
2
x
x
x
x
x




.
Trường hợp 2:
1
3 1 0
2
3
20
2
x
x
x
x
x




.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
69
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Vậy ĐKXĐ là
1
3
x
hoặc
2x 
.
Bình phương hai vế của phương trình ta được:
31
4
2
x
x
3 1 4 2xx
3 1 4 8xx
9x
(thỏa mãn điều kiện).
b).
57
1
21
x
x
.
ĐKXĐ:
7
5 7 0
7
5
2 1 0
1
5
2
x
x
x
x
x



.
Bình phương hai vế ta được:
57
1
21
x
x
5 7 2 1xx
36x
2x
(thỏa mãn điều kiện).
Bài tập 15.(Bài 37, tr. 20 SGK)
Đố.
Trên lưới ô vuông, mỗi ô vuông cạnh
1,cm
cho 4 điểm
, , ,M N P Q
(H.3).
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác
.MNPQ
Lời giải
Tứ giác
MNPQ
có:
Các cạnh bằng nhau và cùng bằng đường chéo hình chữ nhật có chiều dài
2,cm
chiều rộng
1.cm
Do đó độ dài cạnh của tứ giác
MNPQ
là:
22
1 2 5 .cm
Các đường chéo bằng nhau và cùng bằng đường chéo hình chữ nhật có chiều dài
3,cm
chiều rộng
1.cm
Do đó độ dài đường chéo là:
22
1 3 10 .cm
Vậy tứ giác
MNPQ
là hình vuông cạnh
5 cm
nên có diện tích là
2
2
5 5 .cm
4. Bài tập rèn luyện.
Bài 7. Giải phương trình
a).
41
3
1
x
x
; b).
41
3
1
x
x
;
c).
2
49 98 14 3 2 8
49
x
xx
; d).
15 1
25 25 6 1
29
x
xx
.
Lời giải
a) ĐKXĐ:
1x 
hoặc
1
4
x
.
Ta có
4 1 4 1
3 9 4 1 9 9 2
11
xx
x x x
xx


(thỏa mãn ĐKXĐ).
Vậy phương trình có nghiệm là
2x 
.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
70
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b) ĐKXĐ:
1
4
x
.
Ta có
4 1 4 1 4 1
3 3 9 2
11
1
x x x
x
xx
x

(không thỏa mãn ĐKXĐ).
Vậy phương trình vô nghiệm.
c) ĐKXĐ:
2x
.
Ta có
2
49 98 14 3 2 8
49
x
xx
14 2
49( 2) 3 2 8
49
7 2 2 2 3 2 8
2 2 8 2 4 2 16 18
x
xx
x x x
x x x x
Ta thấy
18x
(thỏa mãn ĐKX Đ). Vậy phương trình có nghiệm
18.x
d) ĐKXĐ:
1x
.
Ta có
15 1
25 25 6 1
29
x
xx
15 1
25 1 . 6 1
2
9
51
5 1 6 1
2
5 1 12 2 1
3 1 12 1 4 1 16 17.
x
xx
x
xx
xx
x x x x
Ta thấy
17x
thỏa mãn ĐKXĐ.
Vậy phương trình có nghiệm là
17.x
Bài 8. Giải phương trình
a).
3 6.x
b).
23
2.
1
x
x
c).
23
2.
1
x
x
d).
2
9 6 1 5.xx
e).
64 64 25 25 4 4 20.x x x
f).
2
2 25 10 12.x x x
Lời giải
a)
3 6.x
Điều kiện
0.x
Ta có
6
3 6 3. 6 2 2 .
3
x x x x x tm
Vậy
2.x
b)
23
2.
1
x
x
Điều kiên
3
2 3 0
3
.
2
10
2
1
x
x
x
x
x



Ta có
22
23
2 2 3 2 1 2 3 2 1
1
x
x x x x
x
1
2 3 4 1 2 1 .
2
x x x x ktm
Vậy phương trình vô nghiệm.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
71
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c)
23
2.
1
x
x
Điều kiên
1
23
1
0
3
1
3
.
2
11
2
1
x
x
x
x
x
x
x
x





Ta có
2
2 3 2 3 2 3
2 4 4
1 1 1
x x x
x x x




1
2 3 4 1 2 1 .
2
x x x x tm
Vậy
1
.
2
x
d)
2
2
2
3 1 5
9 6 1 5 3 1 5 3 1 5 .
4
3 1 5
3
x
x
x x x x
x
x


Vậy
12
4
2, .
3
xx
e)
64 64 25 25 4 4 20.x x x
Điều kiện
1.x 
Ta có
64 64 25 25 4 4 20x x x
64 1 25 1 4 1 20x x x
8 1 5 1 2 1 20 5 1 20x x x x
2
1 4 1 4 17x x x tm
Vậy
17.x
f)
2
2 25 10 12.x x x
Ta có
22
2
2 12 0
2 25 10 12 25 10 2 12
5 2 12
x
x x x x x x
xx

6
5 2 12
x
xx
6
6
17
5 2 12
3
5 12 2
7
x
x
x ktm
xx
xx
x tm




. Vậy
7.x
Bài 9. Giải các phương trình sau
a).
2
11xx
b).
2
4 4 2x x x
c).
2
2 7 2xx
d).
2
4 3 2x x x
e).
2
4 2 0xx
f).
2
4 4 2 1x x x
g).
(2 4)( 1) 1x x x
h).
2
2 4 1 2x x x
.
Lời giải
a).
2
11xx
Điều kiện
1x
2 2 2
2
1 1 1 2 1
0( )
2 2 0 2 ( 1) 0
1( )
x x x x x
x KTM
x x x x
x TM
Vậy nghiệm của phương trình là:
1.x
b).
2
4 4 2x x x
Điều kiện
2x
2
22
4 4 2
4 4 4 4
4 4 0 0( )
x x x
x x x x
x x x KTM
Vậy phương trình trên vô nghiệm.
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
72
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c).
2
2 7 2xx
Điều kiện
2x
Ta có
2 2 2
2 7 2 2 7 4 4x x x x x
2
1( )
4 3 0
3( )
x TM
xx
x TM


Vậy nghiệm của phương trình là:
1, 3.xx
d).
2
4 3 2x x x
Điều kiện
2x
2
22
4 3 2
4 3 4 4
1
8 1 ( )
0
x x x
x x x x
x x KTM
Vậy phương trình trên vô nghiệm.
e).
2
4 2 0xx
Điều kiện
2x
2
22
42
4 4 4
4 8 2( )
xx
x x x
x x TM
Vậy nghiệm của phương trình là:
2.x
f).
2
4 4 2 1x x x
Điều kiện
1
2
x
Ta có
2
4 4 2 1x x x
2
2 2 1xx
| 2| 2 1xx
2 2 1 1( )
2 1 2 1( )
x x x KTM
x x x TM




Vậy nghiệm của phương trình là:
1x
g).
(2 4)( 1) 1x x x
Điều kiện
1x 
22
2
2 2 4 2 1
5( )
50
5( )
x x x x
x KTM
x
x TM

Vậy nghiệm của phương trình là:
5x
h).
2
2 4 1 2x x x
.
Điều kiện
2x
22
2
22
2 4 1 4 4
8 5 0
8 16 21 0 ( 4) 21 0
4 21 4 21( )
4 21 4 21( )
x x x x
xx
x x x
x x KTM
x x KTM

Vậy phương trình đã cho vô nghiệm.
Bài 10. Giải các phương trình sau
a).
4 4 5xx
b).
2 1 2 1 2x x x x
c).
2 4 2 7 6 2 1x x x x
d).
2 3 2 5 2 3 2 5 2 2x x x x
.
Lời giải
a).
4 4 5xx
Điều kiện
4x
2
4 4 4 4 5 ( 4 2) 5
4 2 5 4 3 4 9 13( )
x x x
x x x x TM
Vậy nghiệm của phương trình là:
13x
b).
2 1 2 1 2x x x x
Điều kiện
1x
22
2 1 2 1 2
1 2 1 1 1 2 1 1 2
( 1 1) ( 1 1) 2
1 1 | 1 1| 2
x x x x
x x x x
xx
xx
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
73
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Nếu
1 1 0 2xx
thì
1 1 1 1 2 2 2xx
Vậy phương trình có nghiệm đúng với mọi
12x
Nếu
1 1 0 2xx
thì
1 1 1 1 2xx
2 1 2 1 1 1 1 2( )x x x x TM
Vậy phương trình có nghiệm đúng với mọi
2x
c).
2 4 2 7 6 2 1x x x x
Điều kiện
2x
22
2 4 2 4 2 6 2 9 1
( 2 2) ( 2 3) 1
| 2 2| | 2 3| 1
x x x x
xx
xx
Nếu
26x
thì
2 2 2 3 1xx
2 2 4 2 2 2 4 6( )x x x x TM
Vậy phương trình có nghiệm
6x
Nếu
6 11x
thì
2 2 2 3 1xx
0 2 0x
Vậy phương trình có nghiệm đúng với mọi
6 11x
Nếu
11x
ta có:
2 2 2 3 1xx
3 2 6 2 2 6(KTM)x x x
Vậy không có giá trị nào của
x
.
d).
2 3 2 5 2 3 2 5 2 2x x x x
Điều kiện
5
2
x
22
2 5 6 2 5 9 2 5 6 2 5 9 4
( 2 5 3) ( 2 5 3) 4
| 2 5 3| 2 5 3 4
x x x x
xx
xx
Nếu
5
7
2
x
Ta có:
3 2 5 2 5 3 4 6 4( )x x VL
Vậy không có giá trị nào của
.x
Nếu
7x
thì
2 5 3 2 5 3 4xx
2 2 5 4 2 5 2
9
2 5 4 ( )
2
xx
x x KTM
Vậy không có giá trị nào của
.x
.
Bài 11. Giải các phương trình sau
a).
22
3 5 3 7x x x x
b).
22
5 5 28 5 4x x x x
c).
22
2 2 3 5 2 3 6x x x x
d).
22
2 3 9 2 3 33x x x x
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
74
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Lời giải
a).
22
3 5 3 7x x x x
22
3 5 3 5 12x x x x
Đặt
2
3 5 ( 0)x x t t
Ta có:
22
4 ( )
12 12 0
3 ( )
t KTM
t t t t
t TM

Khi
3t
ta có:
2
3 5 3xx
22
1
3 5 9 0 3 4 0
4
x
x x x x
x

Vậy phương trình có nghiệm là:
1; 4.xx
b).
22
5 5 28 5 4x x x x
22
5 5 28 5 28 24x x x x
Đặt
2
5 28 ( 0)x x t t
Ta có:
22
8 ( )
5 24 5 24 0
3 ( )
t TM
t t t t
t KTM

Khi
8t
ta có:
2
5 28 8xx
22
4
5 28 64 0 5 36 0
9
x
x x x x
x

Vậy phương trình có nghiệm là:
9; 4.xx
c).
22
2 2 3 5 2 3 6x x x x
22
2 2 3 5 2 3 5 11x x x x
Đặt
2
2 3 5 ( 0)x x t t
Ta có:
22
10 1 ( )
2 11 2 11 0
1 10 ( )
t TM
t t t t
t KTM


Khi
1 10t 
ta có:
2
2 3 5 1 10xx
2
2
2 3 5 11 2 10 0
3 57 16 10
4
2 3 6 2 10 0
3 57 16 10
4
xx
x
xx
x


Vậy phương trình có nghiệm là
3 57 16 10 3 57 16 10
;
44
xx

d).
22
2 3 9 2 3 33x x x x
22
2 3 9 2 3 9 42x x x x
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
75
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Đặt
2
2 3 9 ( 0)x x t t
Ta có:
22
6 ( )
42 42 0
7 ( )
t TM
t t t t
t KTM

Khi
6t
ta có:
2
2 3 9 6xx
22
3
2 3 9 36 0 2 3 27 0
9
2
x
x x x x
x
Vậy phương trình có nghiệm là
9
3;
2
xx

Bài 12. Giải các phương trình sau
a).
1 3 1 3xx
b).
2
6 9 3 6x x x
c).
2 3 5 1xx
d).
57
4
3
x
x
Lời giải
a).
1 3 1 3xx
Điều kiện:
1
3
x
2
0( )
(1) 3 1 3 1 (3 1) 3 1 9 ( 1) 0
1( )
x loai
x x x x x x
x tm
b).
22
6 9 3 6 ( 3) 3 6 3 3 6x x x x x x x
2
3 6 0
9
()
3 3 6
2
3 3 6 3
()
4
x
x
x tm
xx
xx
x loai




c).
2 3 5 1xx
Điều kiện:
3 5 0
5
10
3
x
x
x



2
2 3 5 1 2 3 5 1
2( )
3 5 1 3 5 2 1 ( 3)( 2) 0
3( )
x x x x
x tm
x x x x x x x
x tm
d).
57
4
3
x
x
Điều kiện:
7
5 7 0
5
3 0 3
5 7 7
03
35
5 7 0 7
5
30
3
x
x
xx
x
x
x
x
x
x
x





Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
76
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
5 7 5 7 41
4 16 ( )
3 3 11
xx
x tm
xx

Dạng 4. CHỨNG MINH BẤT ĐẲNG THỨC
1. Phương pháp.
Sử dụng phương pháp biến đổi tương đương.
Ta biến đổi bất đẳng thức cần chứng minh tương đương với bất đẳng thức đúng.
Bất đẳng thức đúng thường có dạng
2
0.A
2. Bài tập minh họa.
Bài tập 16. (Bài 31, tr. 19 SGK)
a). So sánh
25 16
và
25 16;
b). Chứng minh rằng, với
0ab
thì
.a b a b
Lời giải
a) Ta có
25 16 9 3; 25 16 5 4 1
Mà
13
do đó
25 16 25 16.
b) Với
0ab
thì
0.ab
Ta có:
22
a b a b a a b b a a b b
2 0 2a a b b a b b b a b
(luôn đúng).
Vậy
.a b a b
Bài tập 17. (Bài 36, tr. 20 SGK) Mỗi khẳng định sau đúng hay sai? Vì sao?
a).
0,01 0,0001;
b).
0,5 0,25;
c).
39 7
và
39 6;
d).
4 13 .2 3. 4 13 2 3.xx
Lời giải
a) Đúng, vì
2
0,01 0,0001.
b)
Sai, vì
0,25
không có nghĩa.
c) Đúng, vì
2
2
39 7
và
2
2
39 6 .
d) Đúng, vì nhân hai vế của bất phương trình với cùng một số dương
1
4 13
thì không đổi chiều
bất đẳng thức.
Bài tập 18.
a). Cho
0.a
Chứng minh
1
2;a
a

b). Cho
0, 0.ab
Chứng minh
;
22
a b a b
c). Cho
, 0.ab
Chứng minh
;
ab
ab
ba
d). Chứng minh
2
2
2
2
1
x
x
với mọi
.x
Lời giải
a). Cho
0.a
Chứng minh
1
2;a
a

Ta có
2
2
1
1 1 2
2 0 0
a
aa
a
a a a

(đúng với mọi
0a
).
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
77
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b). Cho
0, 0.ab
Chứng minh
;
22
a b a b
Với
0 , 0ab
ta có
22
2
2 2 2 2 2 4
a b a b a b a b a b a b ab
2
2 2 2 0 0a b a b ab a b ab a b
(đúng).
c). Cho
, 0.ab
Chứng minh
;
ab
ab
ba
Với
0, 0ab
ta có
0
ab
a b a b b a a a b b a b a b b a
ba
00b a a b b a a b a b
2
0b a a b
(đúng).
d). Chứng minh
2
2
2
2
1
x
x
với mọi
.x
Ta có
2
2
2 2 2 2 2
2
2
2 2 2 1 1 2 1 1 0 1 1 0
1
x
x x x x x
x
.
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
39
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT KIẾN THỨC
1. Đưa thừa số ra ngoài dấu căn
Với
0B
ta có
2
neáu A 0
neáu 0.
AB
A B A B
A B A
Ví dụ 1. Đưa thừa số ra ngoài dấu căn
a).
45
; b).
2400
; c).
147
; d).
1,25
.
Lời giải
a).
45 9.5 3 5
; b).
2400 400.6 20 6
;
c).
147 49.3 7 3
; d).
1,25 0,25.5 0,5 5
.
Ví dụ 2. Đưa thừa số ra ngoài dấu căn
a).
50.6
; b).
14.21
; c).
32.45
; d).
125.27
.
Lời giải
a).
50.6 100.3 10 3
;
b).
14.21 7.7.2.3 7 6
;
c).
32.45 16.2.9.5 16.9.10 4.3. 10 12 10
;
d).
125.27 25.5.9.3 25.9.15 5.3 15 15 15
.
Ví dụ 3. Đưa thừa số ra ngoài dấu căn
a).
18x
; b).
2
75xy
; c).
32
605xy
.
Lời giải
a).
18 9.2 3 2x x x
(với
0x
).
b).
22
75 25 .3 5 3x y x y x y
0y
5 3 0
5 3 0.
x y khi x
x y khi x

c).
3 2 2 2
605 121 . .5 11 5x y x y x x y x
0x
11 5 0
11 5 0.
xy x khi y
xy x khi y

Ví dụ 4. Đưa thừa số ra ngoài dấu căn
a).
2
128 xy
; b).
2
150 4 4 1xx
; c).
32
6 12 8x x x
.
Lời giải
a).
22
128 64 .2 8 2x y x y x y
82
8 2 .
x y khi x y
y x khi x y


§BI 6 BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
40
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b).
2
2
150 4 4 1 25.6 2 1x x x
1
5 2 1 6
2
5 2 1 6
1
5 1 2 6 .
2
x khi x
x
x khi x


c).
32
32
6 12 8 2 2 . 2x x x x x x
22xx
(với
2x
).
2. Đưa thừa số vào trong dấu căn
Với
0, 0AB
thì
2
.A B A B
Với
0, 0AB
thì
2
.A B A B
Ví dụ 5. Đưa thừa số vào trong dấu căn
a).
35
; b).
56
; c).
2
35
7
.
Lời giải
a).
2
3 5 3 .5 45
;
b).
2
5 6 5 .6 150
;
c).
2
2 2 20
35 .35
7 7 7




.
Ví dụ 6. Đưa thừa số vào trong dấu căn:
a).
1
4
8
; b).
0,06 250
.
Lời giải
a).
2
11
4 4 2
88
b).
2
0,06 250 0,06 .250 0,9
Ví dụ 7. Đưa thừa số vào trong dấu căn
a).
xx
b).
x
y
y
c).
xy
yx
.
Lời giải
a).
23
.0x x x x x x
b).
x
y
y
ĐK:
. 0; 0x y y
Xét trường hợp
0x
,
0y
, ta có
2
xx
y y xy
yy

Xét trường hợp
0; 0xy
,ta có
2
xx
y y xy
yy
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
41
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c).
xy
yx
ĐK: xy > 0, ta có
2
2
x y x y x
y x y x y

Ví dụ 8. Đưa thừa số vào trong dấu căn:
a).
3
x
x
với
0.x
b).
1
x
x
với
0.x
Lời giải
a) Ta có
2
33
3x x x
xx
với
0.x
b) Ta có
2
11
()x x x
xx




với
0.x
Ví dụ 9. Chỉ ra chỗ sai trong các biến đổi sau:
a).
2
33
77
x
x
b).
2
.
yy
xy y x y xy
xx

Lời giải
a). Biến đổi
2
33
77
x
x
chỉ đúng khi
0x
Nếu
0x
thì
2
33
77
x
x 
b). Biến đổi
2
.
yy
xy y x y xy
xx

chỉ đúng khi
0x
Nếu
0x
x < 0 thì
2
.
yy
xy y x y xy
xx
B. CÁC DẠNG TOÁN:
Dạng 1: ĐƯA THỪA SỐ RA NGOÀI DẤU CĂN VÀ ĐƯA THỪA SỐ VÀO TRONG DẤU CĂN
1. Phương pháp giải
① Đưa thừa số ra ngoài dấu căn:
Biến đổi biểu thức lấy căn thành
dạng tích
2
AB
trong đó có thừa số là bình phương của một
số hoặc một biểu thức.
Thực hiện việc đưa thừa số ra ngoài dấu căn bằng cách áp dụng
2
A B A B
(với
0B
).
② Đưa thừa số vào trong dấu căn:
Chú ý đến dấu của thừa số trước dấu căn.
Nếu
0A
thì ta nâng
A
lên lũy thừa bậc hai rồi viết kết quả vào trong dấu căn:
2
A B A B
(với
0A
;
0B
).
Nếu
0A
thì ta coi
A
như là
A
. Ta nâng
A
lên lũy thừa bậc hai rồi viết kết quả
vào trong dấu căn. Còn dấu
""
vẫn để đằng trước dấu căn:
2
A B A B
(với
0A
;
0B
).
2. Bài tập minh họa.
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
42
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 1.(Bài 43, tr. 27 SGK) Viết các số hoặc biểu thức dưới dấu căn thành dạng tích một cách
thích hợp rồi đưa thừa số ra ngoài dấu căn :
a).
54
. b).
108
. c).
0,1 2000
. d)
0,05 28800
. e).
2
7.63.a
Lời giải
a) Ta có
54 9.6 3 6.
b) Ta có
108 36.3 6 3
.
c) Ta có
0,1 20000 0,1 10000.2 0,1.100 2 10 2
.
d) Ta có
2
0,05 28800 0,05 10 . 144. 2 0,05.10.12 2 6 2.
e) Ta có
2 2 2
7.63. 7 9. 7.3 21 .a a a a
Bài tập 2. ( Bài 44, tr. 27 SGK) Đưa thừa số vào trong dấu căn (với
x0
và
0y
):
a).
35
. b).
52
. c).
2
3
xy
. d).
2
x
x
.
Lời giải
a) Ta có
2
3 5 3 5 45.
b) Ta có
2
5 2 5 .2 50.
c) Ta có: Với
0x
và
0y
:
24
39
xy
xy
d) Ta có: Với :
0x
và
2
22
2.
x
xx
xx
3. Bài tập rèn luyện.
Bài 1. Đưa thừa số ra ngoài dấu căn:
a).
96.125
. b).
45
ab
.
c).
6 11
ab
. d).
4
3
11a a a
.
e).
3
75a
; f).
52
98a ( 6 9).bb
Lời giải
a)
5 3 4 2
96.125 2 .3.5 2 .5 .30 20 30
.
b)
4 5 2 2
a b a b b
.
c)
6 11 3 5
.a b a b b
.
d) Với
1:a
2
4 2 2
32
1 . . 1 1a a a a a a a a


.
e)
3 2 2
5 3 0
75 5 .3. . 5 3 .
5 3 0
a a khi a
a a a a a
a a khi a

f)
2
22
5 2 2 4 2 2
98 ( 6 9) 7 .2. . . 3 7 .2. . . 3a b b a a b a a b
2
2
2
7 ( 3) 2 3
7 3 2 .
7 (3 ) 2 3
a b a khi b
a b a
a b a khi b


Bài 2. Đưa thừa số vào trong dấu căn:
a).
13x
với
0x
. b).
2x
với
0x
. c).
11
x
x
với
0x
.
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
43
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a) Với
0x
:
2
13 13xx
.
b) Với
0x
:
2
22xx
.
c) Với
0x
:
2
11 11
11x x x
xx
.
Dạng 2: SO SÁNH PHÂN SỐ
1. Phương pháp.
① Sử dụng đưa thừa số vào trong dấu căn hoặc ra ngoài dấu căn và chú ý rằng:
Nếu
0 AB
thì
A C B C
(với
0C
).
② Sử dụng đưa thừa số vào trong dấu căn rồi so sánh các số trong dấu căn.
Nếu
0 AB
thì
.AB
2. Bài tập minh họa.
Bài tập 3. ( Bài 45, tr. 27 SGK) So sánh :
a)
33
và
12
. b)
7
và
35
.
c)
1
51
3
và
1
150
5
. d)
1
6
2
và
1
6
2
.
Lời giải
a) Ta có
12 4.3 2 3
.
Vì
23
và
30
nên
2 3 3 3
. Vậy
12 33
.
b) Ta có
7 49,3 5 45.
Vì
49 45 7 3 5.
Vậy
7 3 5.
c) Ta có
1 51 17 1 150
51 ; 150 6
3 9 3 5 25
.
Vì
17 1 1
6 51 150
3 3 5
. Vậy
11
51 150
35
d) Ta có
1 6 3 1 36
6 ; 6 18
2 4 2 2 2
.
Vì
3 1 1
18 6 6
2 2 2
. Vậy
11
66
22
.
Bài tập 4. Không dùng máy tính hoặc bảng số , hãy so sánh :
a).
56
và
73
. b).
2
32
3
và
1
51
5
.
Lời giải
a)
56
và
73
.
Ta có
5 6 25.6 150
;
7 3 49.3 147
Vì
150 147
nên
5 6 7 3
.
b)
2
32
3
và
1
51
5
.
Ta có
28
3 2 9. 24
33

16
5 1 25. 30
55

Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
44
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Vì
24 30
nên
21
3 2 5 1
35
Bài tập 5. Không dùng máy tính hoặc bảng số , hãy so sánh :
a).
5
2
4
và
2
7
3
. b).
3 11
và
2 23
.
Lời giải
a) Ta có
5 25 25 1
2 .2 3
4 16 8 8
2 4 28 1
7 .7 3
3 9 9 9
Vì
11
33
89
nên
52
27
43
b) Ta có
3 11 9.11 99
2 23 4.23 92
Vì
99 92
nên
3 11 2 23
Bài tập 6. Sắp xếp theo thứ tự tăng dần
a).
22
6 3,7 2,15 ,9 1
59
b).
21
71, 12, 21, 5 3
32

Lời giải
a) Ta có
6 3 36.3 108;7 2 49.2 98;
2 2 2 11
15 225. 90;9 1 81. 99
5 5 9 9
Vì
90 98 99 108
nên
22
15 7 2 9 1 6 3
59
b) Ta có
2 4 16 1
12 .12 5 ;
3 9 3 3
1 1 21 1
21 .21 5 ;
2 4 4 4
5 3 25.3 75.
Vì
11
75 71 5 5
43
nên
12
5 3 71 21 12.
23
3. Bài tập rèn luyện.
Bài 3. So sánh các cặp số:
a).
47
và
3 13
. b).
1
82
4
và
1
6
7
.
Lời giải
a) Ta có:
2
4 7 4 .7 112
,
2
3 13 13.3 117
Vì
112 117
nên
112 117
. Vậy
4 7 3 13
.
b) Ta có:
2
1 82 41
82
4 4 8

,
2
1 6 36
6
7 7 7

.
Vì
41 36
87
nên
41 36
87
. Vậy
11
82 6
47
.
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
45
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
DẠNG 3. RÚT GỌN BIỂU THỨC
1. Phương pháp.
Đưa thừa số ra ngoài dấu căn rồi rút gọn các căn thức đồng dạng
0A
()p A q A r A p q r A
.
2. Bài tập minh họa.
Bài tập 7. Rút gọn các biểu thức sau:
a).
20 80 45;
b).
18 50 98
.
Giải
a) Ta có
5 20 80 45 2 5 4 5 3 5
b) Ta có
18 50 98 3 2 5 2 7 2 5 2
Bài tập 8. Rút gọn các biểu thức sau :
a).
2 125 5 45 6 20;
b).
3 72 4,5 12,5
. c).
2 75 4 27 12.
Lời giải
a)
2 2 2
2 125 5 45 6 20 2 5 .5 5 3 .5 6 2 .5 10 5 15 5 12 5
10 5 15 5 12 5 10 15 12 5 7 5.
b)
3 72 4,5 12,5 216 13,5 37,5
27 75 3 5
6 6 6 6 6 6 5 6
2 2 2 2
.
c)
2 2 2
2 75 4 27 12 2 5 .5 4 3.3 2 .2
10 5 12 3 2 2 10 12 2 2 0.
Bài tập 9. Rút gọn các biểu thức sau với
0x
:
a).
2 3 4 3 27 3 3x x x
b).
3 2 5 8 7 18 28x x x
.
Lời giải
a) Ta có
2 3 4 3 27 3 3 (2 4 3) 3 27 5 3 27x x x x x
.
b) Ta có
3 2 5 8 7 18 28 3 2 10 2 21 2 28x x x x x x
(3 10 21) 2 28 14 2 28xx
.
Bài tập 10. Rút gọn biểu thức
3 3 3 3
2 16 7 25 3 36M x xy x y y x y
với
0; 0xy
Lời giải
Ta có
3 3 3 3
2 16 7 25 3 36M x xy x y y x y
8 35 18 25xy xy xy xy xy xy xy xy
Bài tập 11. Rút gọn
a).
2
22
2 3( )
2
xy
xy
với
0, 0 và x y x y
.
b).
22
2
5 1 4 4
21
a a a
a

với
a > 0,5.
Lời giải
a) Ta có
2
2 2 2 2
2 3( ) | | 4.3 6
.6
2 2 ( )( )
x y x y x y
x y x y x y x y x y
(vì
0xy
) .
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
46
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b)
2 2 2 2
22
5 1 4 4 5 (1 2 )
2 1 2 1
a a a a a
aa

2 2 5 1
| |.|1 2 | 5 . .(2 1) do 2 5a.
2 1 2 1 2
a a a a a
aa




3. Bài tập rèn luyện.
Bài 4. Rút gọn các biểu thức
a).
50 32 3 8
; b).
25 2 160 3 10a a a
với
0a
.
c).
2 7 3 7 84
. d).
63 8 7 7 2 14
.
Lời giải
a) Ta có
50 32 3 8 25.2 16.2 3 4.2 5 2 4 2 3.2. 2 7 2
.
b)
25 2 160 3 10 25.10 2. 16.10 3 10a a a a a a
5 10 2.4. 10 3 10 10 10a a a a
.
c)
2 7 3 7 84 2 7. 7 3. 7 4.21 2.7 21 2 21 14 21
.
d)
63 8 7 7 2 14 63. 7 8. 7 7. 7 2 14
9.7.7 2 2. 7 7 2 14 3.7 2 14 7 2 14 14
.
Bài 5. Khai triển và rút gọn biểu thức (với
0; 0xy
)
a).
2 1 2 2 1x x x
. b).
2 2 4x y x xy y
. c).
2x y x y
Lời giải
a)
23
2
2 1 2 2 1 2 1 2 2 .1 1 2 1 2 2 1x x x x x x x x x
.
b)
22
2 2 4 2 .2 2x y x xy y x y x x y y



33
28x y x x y y
.
c)
2 .2 . .2 .x y x y x x x y y x y y
2 2 2x xy xy y x xy y
.
Bài 6. Chứng minh rằng:
a).
22
2
x y y x y x
xy
xy


với
0, 0xy
.
b).
2
2 5 25 5 5x x x
với
5x
.
Lời giải
a) Với
0, 0xy
:
2 2 2.
22
x y y x y x xy x y x y
xy xy
.x y x y x y
Vậy
22
2
x y y x y x
xy
xy


với
0, 0xy
.
b) Với
5x
:
2 2 2
5 5 5 2. 5. 5 5x x x
5 2 5 25 5 2 5 25x x x x
.
Vậy
2
2 5 25 5 5x x x
với
5x
.
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
47
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT KIẾN THỨC
1. Khử mẫu của biểu thức lấy căn:
Với
,AB
mà
0AB
và
0,B
ta có:
2
.
A AB AB
B B B

Ví dụ 1. Khử mẫu của các biểu thức lấy căn sau a).
5
72
; b).
3
80
c).
2
75
Lời giải
a). Ta có
5 5.2 10 1
. 10
72 72.2 144 12
Nhận xét :
Nếu bạn nhân cả tử và mẫu của phân số
5
72
với
72
thì vẫn ra kết quả nhưng biến đổi phức
tạp hơn :
2
5 5.72 360 6 1
. 10 . 10
72 72.72 72 72 12
Vậy tìm thừa số phụ như nào cho hợp lý ?
Trước hết bạn phân tích mẫu số ra thừa số nguyên tố:
22
72 2 .3
.
Bạn thấy ngay thừa số phụ là
2,
lúc đó số mũ của các thừa số nguyên tố đều chẵn.
b). Ta có
2 2 2
3 3 3.5 15 1
15.
80 16.5 4 .5 20 20
c). Ta có
2 2 2
2 2 2.3 6 1
6.
75 25.3 5 .3 15 15
Ví dụ 2. Khử mẫu của biểu thức lấy căn
a).
11
27x
b).
3
3
5
x
y
Lời giải
a).
2
11 11.3 33 1
33
27 27 .3x 81 9
xx
x
x x x x
(ĐK:
0x
)
b).
3 3 4 2
3 3 .5 15 1
15
5 5 .5 25 5
x x y xy
xy
y y y y y
( ĐK:
0; 0xy y
)
Ví dụ 3. Khử mẫu của biểu thức lấy căn
b).
32
1
3 3 1x x x
b).
23
11
xx
Lời giải
a).
3 4 2
32
1 1 1 1
1
3 3 1
1 1 1
x
x
x x x
x x x
(ĐK:
1x 
)
b).
2 3 3 4 2
1 1 1 .( 1) 1
.1
x x x
xx
x x x x x

( ĐK:
1x
hoặc
0x
)
Ví dụ 4. Rút gọn các biểu thức sau :
a).
1
200 50 4
8

b).
3 72 4,5 12,5
.
Lời giải
§BI 7. TRỤC CĂN THỨC Ở MẪU
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
48
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a)
11
200 50 4 10 2 5 2 4. . 2 6 2.
84
b)
3 72 4,5 12,5 216 13,5 37,5
27 75 3 5
6 6 6 6 6 6 5 6
2 2 2 2
.
Ví dụ 5. Rút gọn các biểu thức sau :
a).
23
12
32




; b).
2 1 1
42
9 2 18

Lời giải
a)
2 3 1 1
12 12 6 6 4 6 6 6 2 6
3 2 3 2







.
b)
2 1 1 4 1 1
4 2 2 2 2 2 2
9 2 18 3 2 6
.
Ví dụ 6. Rút gọn các biểu thức sau :
1
9 7 5 3
ab
P ab ab
b a ab
với
,0ab
.
Lời giải
Ta có
1
9 7 5 3
ab
P ab ab
b a ab
7 5 1 7 5
3 3 .P ab ab ab ab ab ab
b a ab b a



2. Trục căn thức ở mẫu:
Với
0B
, ta có
;
A A B
B
B
Với
0A
và
2
,AB
ta có:
2
;
C A B
C
AB
AB
Với
0; 0AB
và
,AB
ta có:
.
C A B
C
AB
AB
Ví dụ 7. Trục căn thức ở mẫu
a).
33
53
b).
22
21
Lời giải
a) Ta có
3 3 3.( 3 1) ( 3 1)
5
5 3 5 3

b) Ta có
2 2 2.( 2 1)
2
2 1 2 1



Ví dụ 8. Trục căn thức ở mẫu
a).
3
7
; b)
2
31
; c)
3
15 4
;
Lời giải
a)
3 3. 7 3. 7
7
7 7. 7

Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
49
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b)
2 2.( 3 1) 2.( 3 1)
31
31
3 1 ( 3 1).( 3 1)

c)
3 3.( 15 4) 3.( 15 4)
3.(4 15)
15 16
15 4 ( 15 4).( 15 4)

Ví dụ 9. Trục căn thức ở mẫu
a).
5 3 3 5
5 3 3 5
b).
2
1 2 3
Lời giải
a) Ta có
2
5 3 3 5 (5 3 3 5) 75 45 30 15
75 45
5 3 3 5 (5 3 3 5).(5 3 3 5)

30.(4 15)
4 15
30
b)
2
2 2(1 2 3) 2(1 2 3) 2(1 2 3)
1 2 3 (1 2 3)(1 2 3) (1 2) 3 (1 2 2 2 3
2(1 2 3) 3 2 1
2
22

Ví dụ 10. Rút gọn các biểu thức
3 4 1
5 2 6 2 6 5
B 
Lời giải
Ta có
3 4 1 3( 5 2) 4( 6 2) ( 6 5)
5 2 6 2 6 5
5 2 6 2 6 5
B
( 5 2) ( 6 2) 6 5 2 6B
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
Dạng 1. KHỬ MẪU CỦA BIỂU THỨC LẤY CĂN
1. Phương pháp.
① Bằng cách nhân tử và mẫu của biểu thức trong căn cho mẫu số rồi rút mẫu ra ngoài căn bằng
công thức:
2
A AB AB
B B B

( Với
,AB
mà
0AB
và
0).B
② Trong thực hành, cụ thể gồm các bước sau :
Biến đổi mẫu thành bình phương của một số hoặc một biểu thức (nếu cần );
Khai phương mẫu và đưa ra ngoài dấu căn.
2. Bài tập minh họa.
Bài tập 1. (Bài
48, 49
tr.
19
SGK). Khử mẫu của biểu thức lấy căn
a).
2
13
1 11 3 5
; ; ; ; .
600 540 50 98 27
b).
;
a
ab
b
;
ab
ba
2
11
;
bb
3
9
;
36
a
b
2
3.xy
xy
(Giả thiết các biểu thức có nghĩa).
Lời giải
a).
2
1 600 6.100 10 6 6
;
600 600 600 600 60
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
50
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
11 11 11 11. 15 165
;
540 6.15 90
9.4.15 6 15
2
3 3.50 6.25 5 6 6
;
50 50 50 50 10
5 5 5 10
;
98 14
49.2 7 2
b).
2
0
;
0
a ab khi b
a ab ab
ab ab ab
b b b
a ab khi b

2
0
0
ab
khi a
a b a ab a
b
ab
b a b a b a
ab
khi a
b


22
1 1 1 1
;
bb
b b b b

33
9
36 2 2 2
a ab
a a b a ab
b b b b
(
0; 0).ab b
2
2
3 3 . 3 2
xy
xy xy xy
xy xy

(vì
0).xy
3. Bài tập rèn luyện.
Bài 1. Khử mẫu các biểu thức dưới dấu căn rồi thực hiện phép tính:
3 1 1
2
20 60 15

.
Lời giải
Ta có:
3 60 2 15 15
2 2 2.
20 20 20 5
1 60 2 15 15
60 60 60 30
1 15
15 15
Vậy
3 1 1 15 15 15 1 1 1 15
2 15
20 60 15 5 30 15 5 30 15 6



.
Dạng 2. TRỤC CĂN Ở MẪU
1. Phương pháp
Nhân cả tử và mẫu với biểu thức liên hợp của mẫu để làm mất dấu căn ở mẫu.
Cụ thể áp dụng các công thức sau:
①.
;
A A B
B
B
②.
2
;
A B C
A
BC
BC
③.
.
A B C
A
BC
BC
Nhận xét. Ta gọi
BC
và
BC
là hai biểu thức liên hợp.
2. Bài tập minh họa.
Bài tập 2. (Bài
50, 51, 52
tr.30 SGK). Trục căn ở mẫu với giả thiết các biểu thức chữ đều có nghĩa.
a).
5
;
10
5
;
25
1
;
3 20
2 2 2
;
52
y b y
by
với
0; 0.by
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
51
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b).
3
;
31
2
;
31
23
;
23
3
b
b
với
0;b
21
p
p
với
1
0, .
4
pp
c).
2
;
65
3
;
10 7
1
xy
với
0, 0, ;x y x y
2ab
ab
với
0, 0, .a b a b
Lời giải
a).
5 5 10 10
;
10 2
10

2
5
55
;
2
2 5 2 5

1 1 1 5
;
30
3 20 3 4.5 6 5
2 2 2
2 2 2 2 2
;
5
5 2 5 2


.
y y b
y b y y b
b
b y b y


b).
3 3 1 3 3 1
3
;
3 1 2
31


2 3 1
2
3 1;
31
3 1 3 1

2
23
2 3 7 4 3
7 4 3;
43
23
2 3 2 3


3
;
9
3
bb
b
b
b
21
2
;
4 1 4 1
21
pp
p p p
p
pp
p


c).
2
2 6 5 ;
65

3 10 7
3
10 7;
10 7
10 7
1
;
xy
xy
xy
2
2
.
ab a b
ab
ab
ab
Bài tập 3. Trục căn thức ở mẫu.
a).
1
1
a
a
với
0; 1aa
b).
1
1ab
với
0, 0ab
và
1
4
ab
Lời giải
a)
2
1 (1 ) 1 2
1
1 (1 )(1 )
a a a a
a
a a a

b)
1 1.( 1) ( 1)
1 ( 1)( 1) 2 1
a b a b
a b a b a b a b ab

Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
52
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
11
1
21
4
a b a b
ab
ab

3. Bài tập rèn luyện.
Bài 2. Trục căn ở mẫu:
a).
9
3
b).
3
52
; c).
21
21
;
d).
53
53
e).
1
1
aa
a
; f).
1
18 8 2 2
.
g).
2
;
1 2 3
h).
1
3 2 5
Lời giải
a). Ta có
9 9 3
33
3
3

b).
3 5 2
3
52
52
52
c).
2
21
21
3 2 2
21
21
d).
2
53
5 3 8 2 15
4 15
5 3 2
53

e).
11
1
1
11
a a a
aa
aa
aa

f).
1 1 1 2
6
18 8 2 2 3 2 2 2 2 2 3 2
g).
2 1 2 3
2 1 2 3
2
1 2 3 3 2 2 3



h).
1 3 2 5 3 2 5 3 2 2 3 30
12
3 2 5 5 2 6 5 2 6

.
Bài 3. Rút gọn biểu thức:
a).
11
7 4 3 7 4 3
A 

; b).
15 4 12
6
6 1 6 2 3 6
B
.
Lời giải
a).
1 1 7 4 3 7 4 3
14
49 48
7 4 3 7 4 3
A

b).
15 6 1 4 6 2 12 3 6
15 4 12
66
6 1 6 4 9 6
6 1 6 2 3 6
B
.
3 6 1 2 6 2 4 3 6 6 11
Bài 4. Cho
75 12
147 48
x
. Chứng minh rằng
3x
là một số nguyên.
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
53
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
22
22
5 3 2 3 7 3 4 3
75 12 5 .3 2 .3 5 3 2 3
147 48 7 3 4 3
7 3 2 3 7 3 4 3
3.7 4 .3
x



22
5 3 2 3 7 3 4 3
105 60 42 24 231 7
.
147 48 99 3
7 3 4 3

Tính
x
được
7
3
x
, do đó
37xZ
Bài 5. Biến đổi
26
10 4 3
về dạng
3ab
. tính tích
.ab
Lời giải
Ta có
2
13 5 2 3
26 13 65 26 3 65 26 3
5 2 3
13
10 4 3 5 2 3
5 2 3 5 2 3
25 2 3



Vậy
5; 2.ab
do đó
. 5.( 2) 10ab
Bài 6. Tính
1 1 1 1
...
1 2 2 3 3 4 99 100
Lời giải
Ta có
1 1 1 1
...
1 2 2 3 3 4 99 100
1 2 2 3 3 4 99 100
...
1 2 1 2 2 3 2 3 3 4 3 4 99 100 99 100
1 2 2 3 3 4 99 100
...
1 2 2 3 3 4 99 100
1 2 2 3 3 4 99 100
...
1 1 1 1
2 1 3 2 4 3 ... 100 99 100 1 10 1 9.
Dạng 3. RÚT GỌN BIỂU THỨC
1. Phương pháp.
Thực hiện các phép biến đổi căn thức:
①.
2
.AA
②.
A AB
BB
(với
0, 0AB
).
③.
2
A B A B
(với
0B
).
. ④
A B C
A
BC
BC
(
0, 0,B C B C
).
.
2. Bài tập minh họa.
Bài tập 4. Rút gọn các biểu thức sau (giả sử các biểu thức chữ đều có nghĩa):
a).
2
18 2 3 ;
c)
34
;
aa
bb
b).
22
1
1;ab
ab
d)
.
a ab
ab
Lời giải
a).
22
18 2 3 2.9 2 3 3 2 3 2 3 3 2 2 3 6 6.
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
54
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b).
22
22
2 2 2 2
11
11
a b ab
ab ab a b
ab
a b a b
22
22
10
1 0.
a b neu ab
a b neu ab

c).
3 4 4 2
.
a a ab a ab a
b b b b

d).
.
a a b
a ab
a
a b a b


Cách khác:
.
a ab a b a a b a b
a a b
a ab
a
a b a b a b
ab
Bài tập 5. Rút gọn các biểu thức sau (giả sử các biểu thức chữ đều có nghĩa):
2
2 2 15 5 2 3 6
; ; ; ; .
1 2 1 3 8 2 1 2
pp
aa
ap
Lời giải
Ta có:
2 1 2
22
2;
1 2 1 2


5 3 1
15 5
5;
1 3 1 3

6 2 1
2 3 6 6
;
2
82
2 2 1

1
;
1
1
aa
aa
a
ra
a
2
2
.
22
pp
pp
p
pp


Bài tập 6. Xét biểu thức:
2
2
1
1
a a a a
A
a a a


a). Rút gọn
A
;
b). Biết
a 1
, hãy so sánh
A
và
A
;
c). Tìm
a
để
2A
;
d). Tìm giá trị nhỏ nhất của
A
.
Lời giải
a). (ĐK
a 0
)
2
3
2
1
1
1
11
(2 1)
1 (2 1) 1
11
2 1 1
a a a a
A
a a a
aa
a a a a
aa
a
a a a a a
a a a a a


Với
a 1 1 1 0.aa
và
10aa
Suy ra
10A a a a a
Khi đó
0A A A
. Vậy
AA
.
c). Tìm
a
để
2A
2 2 0 2 2 0
1 2 1 0 1 2 0
a a a a a a a
a a a a a
1 0 1( )
4
2 0 2
a a VN
a
aa




Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
55
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Đối chiếu điều kiện ta được
4a
thì
A=2
.
d).
2
1 1 1 1 1
2
2 4 4 2 4
A a a a a a



Vì
2
1
0
2
a




với mọi a.
Nên
2
1 1 1
2 4 4
a



với mọi a.
Vậy giá trị nhỏ nhất của A bằng
1
4
khi và chỉ khi
11
0
24
aa
Bài tập 7. Xét biểu thức:
2
33
1 : 1
1
1
Ba
a
a






a). Rút gọn
B
;
b). Tìm giá trị của
B
nếu
3
;
23
a
c). Với giá trị nào của a thì
BB
.
Lời giải
a). Điều kiện
11a
2
22
22
33
1 : 1
1
1
3 1 . 1 3 1 3 1 1. 1
: . 1
11
1 3 1
Ba
a
a
a a a a a a
a
aa
aa















b). Với
3
;
23
a
Khi đó:
2
2. 2 3 3 1
3 2 3 3
1 1 3 1
43
2 3 2 3
2 3 2 3
Ba




c). Với
11a
, ta có:
(1 ) 0B B B B
0
0
1 0
01
1
0
()
1 0
B
B
B
B
B
B
VN
B



Khi đó
0 1 1 0 1 1 0 1.a a a
Kết hớp với điều kiện
11a
ta được
01a
Vậy
01a
thì
BB
.
Bài tập 8. Cho a > b > 0, chứng minh rằng
22
2
4
82
2
6
75 15
a ab b
ab
b
a b a b

Lời giải
Ta có
2 2 2 2 2
44
8( 2 ) 8( ) .
75 75 .
a b a ab b a b a b b
a b a b a b a bb

2
2
2( ) 2 2 2 .3 2
. . . 6 .
5 3 5 9 15
a b a b b b
b
a b a b
Ta thấy vế trái đúng bằng vế phải.
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
56
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
3. Bài tập rèn luyện.
Bài 7. Rút gọn các biểu thức sau (giả sử các biểu thức chữ đều có nghĩa):
a).
11 6 2;
e).
21
21
xx
xx


(với
0x
).
.
b).
52
;
3 5 3 2
c).
13 2 4 6
;
24 4 3
d).
6 14
;
2 3 28
g).
23
;
2
f).
2 3 6 8 16
;
234

h).
8 15
.
30 2
Lời giải
a)
2
11 6 2 9 2.3 2 2 3 2 3 2.
b)
22
2
2
5 2 5 2
5 2 5 2 5 2 5 2
.
33
3
3 5 2 3 5 2 5 2
3 5 3 2




c)
2
2 13 4 3 2 12 2.2 3.1 1 2 2 3 1
13 2 4 6 2 3 1
.
24 4 3 2 6
4 3 2 3 1 4 3 2 3 1 4 3 2 3 1

d)
2 3 7 2 3 7
6 14 2
.
2
2 3 28 2 3 2 7
2 3 7



e)
2
2
2
2
1
1
1
21
2 1 1
1
1
x
x
x
xx
x x x
x
x


Với
01x
thì
1
1
.
11
x
x
xx

Với
1x
thì
1
0
0.
11
x
xx


Với
1x
thì
1
1
.
11
x
x
xx

f)
2 3 2 2 2 6 2
2 3 6 8 16 2 3 6 2 2 4
2 3 4 2 3 2 2 3 2

2 3 2 2 2 3 2 2 3 2 1 2
1 2.
2 3 2 2 3 2
g)
2
31
2 3 2. 2 3 4 2 3 3 2. 3 1 3 1
.
2 2 2 2
2 2. 2
h)
211
16 2 15 15 2. 15.1 1
15 1
8 15 15 1 1
22
.
2
30 2
2 15 1 2 15 1 2 15 1 2 15 1

Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
57
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài 8. Chứng minh đẳng thức:
a).
2
1 (a 0,b 0,a 0);
a b b
ab
a b a b

b).
22
2
0
2
a b b ab b ab
a b b a b
ab
a a b b

Lời giải
a). Ta có
2
(a 0,b 0,a 0);
a b b
ab
a b a b

2
=
.
2
1
a a b b a b
b
ab
a b a b
a ab ab b b
a b a b
ab
ab




b). Ta có
23
2
0
2
a b b ab b ab
a b a b
ab
a a b b

2
2
2
2
2
.
..
b a b b a b ab
ab
a a b b
a b a b
b a b b a b b a b b a b
b
a b a b a b
ab



Dạng 4. PHÂN TÍCH THÀNH NHÂN TỬ
1. Phương pháp.
Áp dụng:
①
2
AA
(với
0A
).
②
2
A B A B
(với
0B
).
2. Bài tập minh họa.
Bài tập 9. Phân tích thành nhân tử (với
, , ,a b x y
là các số không âm).
a).
1;ab b a a
b).
3 3 2 2
.x y x y xy
Lời giải
a)
2
11ab b a a b a b a a
1 1 1 1 .b a a a a b a
b)
3 3 2 2
x y x y xy x x y y x y y x x x x y y y y x
.x x y y x y x y x y
Bài tập 10. Tính
a).
1 2 3 6;
b).
6 55 10 33.
Lời giải
a)
1 2 3 6 1 2 3 1 2 1 2 1 3 .
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
58
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b)
6 55 10 33 6 10 33 55 2 3 5 11 3 5
3 5 2 11
Dạng 5. SO SÁNH CÁC SỐ
1. Phương pháp.
Đưa thừa số vào trong căn rồi so sánh các số trong căn.
0.A B A B
2. Bài tập minh họa.
Bài tập 11. Sắp xếp theo thứ tự tăng dần
a).
3 5, 2 6, 29, 4 2;
b).
6 2, 38, 3 7, 2 14.
Lời giải
Đưa các thừa số vào trong dấu căn rồi so sánh các số trong căn.
a)
3 5 9.5 45; 2 6 4.6 24; 4 2 16.2 32.
Vì
24 29 32 45
nên
2 6 29 4 2 3 5.
b)
6 2 36.2 72; 3 7 9.7 63; 2 14 4.14 56.
Vì
38 56 63 72
nên
38 2 14 3 7 6 2.
Bài tập 12. So sánh
a).
33
và
12;
b).
20
và
3 5;
c).
1
54
3
và
1
150;
5
d).
30 29
và
29 28;
Lời giải
a)
33
và
12;
Ta có
3 3 9.3 27
và
12
Vì
27 12
nên
3 3 12.
b)
20
và
3 5;
Ta có
2
20 20 400
và
3 5 9.5 45
Vì
400 45
nên
20 3 5.
c)
1
54
3
và
1
150;
5
Ta có
1 1 1
54 9.6 .3 6 6
3 3 3
và
1 1 1
150 25.6 .5 6 6.
5 5 5
Vì
66
nên
11
54 150.
35
d)
30 29
và
29 28;
Ta có
30 29 30 29
1
30 29
30 29
30 29

và
29 28 29 28
1
29 28
29 28
29 28

Vì
30 29 29 28
nên
11
30 29 29 28

Vậy
30 29 29 28.
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
59
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Dạng 6. GIẢI PHƯƠNG TRÌNH
1. Phương pháp giải
① Đặt điều kiện để phương trình có nghĩa:
A
có nghĩa
0A
.
② Đưa thừa số ra ngoài dấu căn:
2
A B A B
.
③ Rút gọn các căn thức đồng dạng.
④ Biến đổi phương trình về dạng:
2
A B A B
(với
0A
).
2. Bài tập minh họa.
Bài tập 13. Giải phương trình:
a).
1
18 9 3 4 12 9
2
x x x
;
b).
25 50 16 32 9 18 12 4 2x x x x
.
Lời giải
a). Điều kiện:
1
2
x 
1
18 9 3 4 12 9
2
x x x
3 2 1 3 3 9x x x
2 1 3 2 1 9 4x x x
(nhận)
Vậy phương trình có nghiệm
4x
b). Điều kiện:
2x
25 50 16 32 9 18 12 4 2x x x x
5 2 4 2 3 2 12 4 2x x x x
2 6 2 36 38x x x
(nhận)
Vậy phương trình có nghiệm
38x
Bài tập 14. Giải phương trình:
a).
1 3 1
1 9 9 24 17;
2 2 64
x
xx
b).
3 7 4 0;xx
c).
5 7 12 0;xx
Lời giải
a). Điều kiện:
1x
2
1 3 1
1 9 9 24 17 290.
2 2 64
1 3 1
1 9( 1) 24 17
2 2 8
1 9 24
1 1 1 17 1 17 1 17
2 2 8
1 289 290.
x
x x x
x
xx
x x x x x
xx
Đối chiếu với điều kiện ta được:
290.x
b). (Điều kiện
0x
Ta có
3 7 4 0 3 3 4 4 0x x x x x
3 1 4 1 0x x x
4
16
3 4 0
3
1 3 4 0
9
10
1
1
x
x
x
xx
x
x
x


Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
60
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Đối chiếu với điều kiện ta được:
16
;1
9
xx
.
c). Điều kiện
0x
5 7 12 0
5 5 12 12 0
5 . 1 12 1 0 1 5 12 0
1 (vn)
10
144
.
12
25
5 12 0
5
xx
x x x
x x x x x
x
x
x
x
x


Đối chiếu điều kiện ta được:
144
.
25
x
Bài tập 15. Tìm
x
, biết:
a).
11
2 9 27 25 75 49 147 20;
57
x x x
b).
3 5 2 7
1;
23
xx
x

c).
22
22
1 5 1 25 125
9 45 16 80 3 9;
12 16 4 9
xx
xx

d).
4,5 50 32 72 5 12 0.
2
x
x x x x
Lời giải
a).
11
2 9 27 25 75 49 147 20
57
x x x
ĐKXĐ:
3x
11
2 9 27 25 75 49 147 20
57
11
2 9 3 25 3 49 3 20
57
6 3 3 3 20 4 3 20
3 5 3 25
x x x
x x x
x x x x
xx
28x
( Thỏa ĐK)
Vậy
28.x
b).
3 5 2 7
1
23
xx
x

ĐKXĐ:
0x
3 5 2 7
1
23
3 5 .3 2 7 .2
66
6 6 6 6
9 15 4 14 6 6 9 4 6 15 14 6
55
xx
x
xx
x
x x x x x x
xx


25x
( Thỏa ĐK). Vậy
25.x
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
61
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c).
22
22
1 5 1 25 125
9 45 16 80 3 9;
12 16 4 9
xx
xx

22
22
2
2
22
2 2 2 2 2
2 2 2
1 5 1 25 125
9 45 16 80 3 9
12 16 4 9
25 5
1 5 1
9 5 16 5 3 9
12 4
16 9
1 3 5
3 5 5 5 5 9 3 5 9
3 4 12
5 3 5 9 4
xx
xx
x
x
xx
x x x x x
x x x

2x
hoặc
2.x
Vậy
2x 
hoặc
2.x
d).
4,5 50 32 72 5 12 0.
2
x
x x x x
ĐKXĐ:
0x
222
4,5 50 32 72 5 12 0
2
9
5 .2 4 .2 6 .2 5 12 0
22
35
2 5 2 4 2 6 2 2 12 6 2 12
22
2 2 2 4
x
x x x x
xx
xxx
x x x x x x
xx
2x
( Thỏa ĐK). Vậy
2.x
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
62
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT LÝ THUYẾT
Rút gọn biểu thức:
Để thực hiện phép tính, rút gọn biểu thức ta sử dụng các phép biến đổi đơn giản như:
Đưa thừa số ra ngoài dấu căn,.
Đưa thừa số vào trong dấu căn.
Khử căn ở mẫu và trục căn thức ở mẫu để làm xuất hiện các căn thức bậc hai có cùng một
biểu thức dưới dấu căn (căn đồng dạng).
Cộng trừ các căn thức đồng dạng:
p A q A r A m p q r A m
Ví dụ 1. Rút gọn các biểu thức sau:
a).
11
4,5 72 5
22

b).
25 3 98
42 10 12
6 2 3

Lời giải
a) Ta có
1 1 9.2 1 5
4,5 72 5 .6 2 2
2 2 2.2 2 2
35
2 3 2 2 2
22
b) Ta có
25 3 98 5 1 7
42 10 12 42. 6 10. 6 12. 6
6 2 3 6 2 3
35 6 5 6 28 6 2 6.
Ví dụ 2. Rút gọn biểu thức
33
11
22
N
Lời giải
Ta có:
33
11
22
N
=
2 3 2 3 4 2 3 4 2 3
2 2 4 4
22
11
( 3 1) ( 3 1)
22
1
3 1) ( 3 1) 1
2


Ví dụ 3. Biến đổi biểu thức
1
54
aa
b b ab

về dạng
x y z
ab
a b c




, với
, 0; , ,a b x y z Z
Tính tổng
x y z
Lời giải
Ta có
1 5 4 1 5 4 1
54
aa
ab ab ab ab
b b ab a b ab a b ab



Vậy
5; 4; 1.x y z
do đó
0x y z
Ví dụ 4. Rút gọn biểu thức
y
x
P
xy x y xy


Lời giải
Điều kiện:
0; 0; .x y x y
khi đó ta có:
( ) ( ) ( )
y
x y x
P
x y x y y x xy y x
§BI 8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
63
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
=
()
y x y x
yx
xy y x xy

Ví dụ 6. Rút gọn biểu thức
3:
3
xy
x
P
y x xy





Lời giải
Điều kiện:
0; 0.xy
khi đó ta có:
3 ( 3 )
9
3 : . .
3
xy x y x x y
x x y
P
y
y x xy y xy





Ví dụ 7. Rút gọn biểu thức
:( )
x x y y
P xy x y
xy




Lời giải
Ta có
( )( )
:( )
x y x xy y
P xy x y
xy




2
1
2 . .
xy
xy
x xy y
xy
xy
x y x y

Ví dụ 8. rút gọn biểu thức
1
1:
11
xx
P
x x x x





Lời giải
Điều kiện:
0; 1xx
. Khi đó ta có:
11
.
11
x x x x x
P
x x x




2
2 1 1
.
11
( 1) ( 1).( 1)
.1
11
x x x x
x x x
x x x x
x
x x x
Ví dụ 9. Rút gọn biểu thức
1 2 3 1 2 2
.
1
11
x x x
P
xx
x x x









Lời giải
Điều kiện
0; 1xx
. Khi đó ta có
2
( 1) 2 ( 1) 3 1 2 2
.
( 1)( 1)
x x x x x
P
x
xx

2 1 2 2 3 1 2( 1)
.
( 1)( 1)
3 ( 1) 2( 1) 6
.
( 1)( 1)
x x x x x x
x
xx
x x x
x
x x x




B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
DẠNG 1. RÚT GỌN CÁC BIỂU THỨC
1. Phương pháp.
Thực hiện các phép biến đổi đơn giản của căn thức bậc hai để làm xuất hiện căn thức đồng
dạng.
Cộng, trừ các căn thức đồng dạng.
2. Bài tập minh họa.
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
64
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 1. (Bài 58, tr. 32 SGK) Rút gọn các biểu thức sau:
a).
11
5 20 5
52

; b).
1
4,5 12,5
2

;
c).
20 45 3 18 72
; d).
0,1 200 2 0,08 0,4 50
.
Lời giải
a)
1 1 25 20
5 20 5 5 3 5;
5 2 5 4
b)
1 2 9 25 2 3 2 5 2 9 2
4,5 12,5 .
2 4 2 2 2 2 2 2
c)
20 45 3 18 72 4.5 9.5 3 9.2 36.2
2 5 3 5 9 2 6 2 15 2 5.
d)
0,1 200 2 0,08 0,4 50 0,1 100.2 2 0,04.2 0,4 25.2
2 0,4 2 2 2 3,4 2.
Bài tập 2. Rút gọn biểu thức sau:
a).
1 33 1
48 2 75 5 1 ;
23
11
b).
2
150 1,6 60 4,5 2 6
3
;
c).
28 2 3 7 7 84
; d).
2
6 5 120
Lời giải
a)
1 33 1 1 11 3 4
48 2 75 5 1 16.3 2 25.3 5
2 3 2 3
11 11
3 17
2 3 10 3 3 10 3.
33
b)
28
150 1,6 60 4,5 2 6 25.6 16.6 4,5 6
33
24
5 6 4 6 4,5 6 8 6 1,5.2 6
9
8 6 3 6 11 6.
c)
28 2 3 7 7 84 4.7 7 2 21 7 4.21
14 2 21 7 2 21 21.
2
6 5 120 6 2 30 5 4.30 6 2 30 5 2 30 11.
Bài tập 3. Rút gọn biểu thức sau (với
0, 0ab
);
a).
32
5 4 25 5 16 2 9a b a ab a
b).
3 3 3 3
5 64 3 12 2 9 5 81 .a ab a b ab ab b a b
Lời giải
a)
32
5 4 25 5 16 2 9 5 20 20 6 .a b a ab a a ab a ab a a a
b)
3 3 3 3
5 64 3 12 2 9 5 81a ab a b ab ab b a b
40 6 6 45 5 .ab ab ab ab ab ab ab ab ab ab
Bài tập 4. Cho biểu thức:
16 16 9 9 4 4 1B x x x x
với
1.x 
a). Rút gọn biểu thức
B
;
b). Tìm
x
sao cho
B
có giá trị bằng
16
.
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
65
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Lời giải
a)
4 1 3 1 2 1 1 4 1.B x x x x x
b)
16 4 1 16 1 4 1 16 15.B x x x x
Bài tập 5.
a).
a a b
ab
b b a

với
0a
và
0b
;
b).
2
2
4 8 4
.
1 2 81
m m mx mx
xx


với
0m
và
1x
.
Lời giải
a)
22
1 1 2
1
a a b ab a ab
ab ab ab ab ab ab
b b a b b a b b b



.
b)
2
2 2 2
2
2
41
4 8 4 4 4 2
. . .
1 2 81 81 81 9
81
1
mx
m m mx mx m m m m
xx
x


( với
0m
và
1x
)
Bài tập 6. Rút gọn rồi so sánh giá trị của
M
với
1
, biết:
1 1 1
:
1 2 1
a
M
a a a a a




với
0a
và
1a
.
Lời giải
Ta có:
1 1 1 1
1
1 1 1
aa
a a a
a a a a a a

Do đó:
2
1
1 1 1 1 1
: . 1 .
2 1 1
11
a
a a a a
M
a a a a a
a a a a

Vì
0a
nên
1
11
a

suy ra
1.M
Bài tập 7. Giá trị của biểu thức
11
2 3 2 3

bằng:
A).
1
2
; B).
1
; C).
4
; D).
4
.
Chọn câu trả lời đúng.
Lời giải
Ta có:
1 1 2 3 2 3 4
4
1
2 3 2 3
2 3 2 3


Chọn D).
Bài tập 8. Cho
2 9 3 2 1
5 6 2 3
x x x
B
x x x x
a). Xác định
x
để cho
B
có nghĩa;
b). Rút gọn
B
;
c). Tìm
x
để
1B
;
d). Tìm
x
x
nguyên để
B
là số nguyên.
Lời giải
a) Ta có
5 6 3 2x x x x
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
66
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Điều kiện
0
0
39
4
2
x
x
xx
x
x


b)
2 9 3 2 1
23
32
x x x
B
xx
xx


2 9 3 3 2 1 2
32
x x x x x
xx

2 9 9 2 4 2 2
3 2 3 2
x x x x x x x
x x x x

21
1
.
3
23
xx
x
x
xx



c) Ta có
3 4 4
1
33
x
B
xx


4
1 0 3 9
3
B x x
x
Vậy với
9x
thì
1.B
d) Vì
4
1
3
B
x

nên
3B Z x
là ước của 4. Do đó
3x
nhận các giá trị
1, 2, 4
Suy các giá trị thích hợp của
x
là
1, 4, 16, 25, 49
.
3. Bài tập rèn luyện
Bài 1. Rút gọn biểu thức:
a).
3
1
3 2 18 4 128
24
a
a a a
(với
0a
)
b).
32
1
2
a
y x y x x x x y
x y ax ay

( với
0xy
)
c).
a b a b
a b a b


(với
0, 0,a b a b
)
Lời giải
a). Với
0a
, ta có:
3
1
3 2 18 4 128
24
a
a a a
3 2 3 2 2 2 2 2a a a a a
3 2 3 2 3 1 2 .a a a a a
b). Với
0xy
, ta có:
32
1
2
a
y x y x x x x y
x y ax ay

2
1
2
a
y x y x x x x y
x y a x y

11
2y x y x x y x x
xy xy
2x y y x 
(do
0x
).
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
67
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
c). Với
0, 0,a b a b
, ta có:
22
a b a b
a b a b
a b a b
a b a b




2 2 2 2a ab b a ab b a b
ab
a b a b

.
Bài 2 (Dạng 1). Rút gọn biểu thức:
a).
2 1 2 2 1
2 2 2 2 2



b).
2 5 2 5
2 3 5 2 3 5

Lời giải
a). Ta có:
2
21
2 1 2 2 1 2 1 2
2 2 2 2 2 2(1 2) 2( 2 1) 2( 2 1)
3 2 1
2 1 2 2 2 2 1 3 2 3
3 2 1
21
2( 2 1) 2( 2 1) 2 1
b). Ta có:
2 5 2 5 2 2 10 2 2 10
2 3 5 2 3 5 2 6 2 5 2 6 2 5
22
2 2 10 2 2 10
2 5 1 2 5 1


2 2 10 2 2 10 2 2 10 2 2 10
2 5 1 2 5 1 3 5 3 5

2 2 10 3 5 2 2 10 3 5
3 5 3 5

6 2 2 10 3 10 50 6 2 2 10 3 10 50
95
12 2 2 50 12 2 10 2 2 2 2
.
4 4 4 2

DẠNG 2. CHỨNG MINH ĐẲNG THỨC
1. Phương pháp.
Thực hiện các phép biến đổi căn thức và các hằng đẳng thức đáng nhớ để biến đổi vế trái
bằng vế phải hoặc vế phải bằng vế trái của đẳng thức.
2. Bài tập minh họa.
Bài tập 9. Chứng minh các đẳng thức sau:
a).
3 2 3 6
6 2 4
2 3 2 6
. b).
6 2 1
6 : 6 2
33
x
x x x
x




với
0x
.
Lời giải
a) Ta có:
3 2 3 3 6 6
VT 6 2 4 6 2 4
2 3 2 2 9 4
3 2 3 2 6
6 6 2 6 2 6 VP
2 3 2 3 6



(đpcm).
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
68
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b) b) Ta có
6 2 6
VT 6 : 6 6 6 : 6
33
xx
x x x x x x
x
7 7 1
6 : 6 2 VP
3 3 3
xx
(đpcm).
Bài tập 10. Chứng minh các đẳng thức sau:
a).
2
11
1
1
1
a a a
a
a
a


với a
0
và
1a
.
b).
24
2 2 2
2
a b a b
a
b a ab b

với
0ab
và
0b
.
Lời giải
a) Ta có:
3
1
1
1
11
a
aa
a a a a a
aa

2
1 2 1a a a
và
1 1 1
1
1
11
aa
a
a
aa



Do đó:
2
2
2
1 1 1
VT 1 1 VP
1
1
1
a a a
aa
a
a
a

(đpcm).
b) Ta có:
2
2 4 2 4
2
2 2 2 2 2
.
VT . VP
2
ab
a b a b a b a b a b
a
b a ab b b b a b
ab
(đpcm).
(do
0ab
và
0b
).
3. Bài tập rèn luyện.
Bài 3. Chứng minh đẳng thức sau với
0; 0;x y x y
:
1
4
:
x y x y y
x
xy
x y x y y y





Lời giải
Rút gọn vế trái được
4
14
.
xy
x
x y x y
y

.
Bài 4. Chứng minh đẳng thức sau với
0 ; 0 x y và x y
:
4
:
x y xy x y
x
xy
x y x x y







Lời giải
Xét vế trái
4
:
x y xy x y
xy
x y x






2
( ) 4
.
( )( )
x y xy
x
x y x y x y





24
.
( )( )
x xy y xy
x
x y x y x y




2
()
.
( )( )
xy
x
x y x y x y





x
xy
Ta thấy vế trái đúng bằng vế phải nên đẳng thức đã cho là đúng.
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
69
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài 5. Chứng minh đẳng thức sau với
0 ; 0 x y và x y
:
2
:( ) 1
x x y y y
xy x y
x y x y





Lời giải
Xét vế trái
:( )
x x y y
T xy x y
xy




( )( )
1
.
x y x xy y
xy
xy
xy




2
()
( )( )
xy
x y x y

xy
xy
Xét vế phải
2x y y x y
P
x y x y


Rõ ràng
TP
, suy ra điều phải chứng minh.
Bài 6. Chứng minh rằng giá trị của biểu thức
2
2
.
()
x y x y y x
x
A
xy y xy x x y






là hằng số
với mọi giá trị thích hợp của
x
và
y
:
Lời giải
Điều kiện:
0 ; 0 ; x y x y
.
Khi đó ta có
2
2 ( )
.
( ) ( ) ( )
x y xy x y
x
A
y x y x y x x y






2
2 ( )
.
( ) ( )
x xy y xy x y
xy x y x y

2
2
( ) ( )
.1
( ) ( )
x y xy x y
xy x y x y



Vậy giá trị của biểu thức A luôn là hằng số với mọi giá trị thích hợp
x
và
y
.
DẠNG 3. CHỨNG MINH BIỂU THỨC KHÔNG PHỤ THUỘC VÀO BIẾN.
1. Phương pháp.
Thực hiện các phép biến đổi căn để biến đổi biểu thức không còn chứa biến.
2. Bài tập minh họa.
Bài tập 11. Chứng minh biểu thức sau không phụ thuộc vào biến
a
:
2
2
1 1 1 1
.1
1
2 2 2 2
a
aa
aa







với
0, 1aa
.
Lời giải
Ta có:
1 1 1 1
2 2 2 2 2(1 ) 2(1 )a a a a
1 1 2 1
2(1 ) 1
2(1 )(1 )
aa
aa
aa


Do đó biểu thức đã cho bằng:
2
1 1 1
1 1 1
aa
a a a a





2
2
1 1 1
1
a a a
aa
2
1
1
1
1
aa
a
aa
.
Vậy biểu thức đã cho không phụ thuộc vào biến
a
.
Bài tập 12. ( Dạng 3). Chứng minh biểu thức sau không phụ thuộc vào biến:
2
2
.
2
xy x y y
x
xy
x y y x
xy






với
0, 0, .x y x y
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
70
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có:
2
2
.
2
xy x y y
x
xy
x y y x
xy






2
2
4
2
.
2
2
.
2
xy x y
y
x
x y y x
x y x y
xy
y
x
x y y x
x y x y







yy
xx
x y y x x y x y
1
xy
xy

(đpcm).
Vậy biểu thức đã cho không phụ thuộc vào biến.
DẠNG 4. RÚT GỌN RỒI TÍNH GIÁ TRỊ CỦA BIỂU THỨC TẠI
.xa
1. Phương pháp.
Bước 1. tìm điều kiện để biểu thức có nghĩa
Bước 2. rút gọn biểu thức.
Bước 3. thay giá trị của biến
.xa
vào biểu thức đã được rút gọn rồi thực hiện các phép tính.
Nhận xét:
Nhiều lúc có thể phải sử dụng kết quả rút gọn, lập phương trình hoặc bất phương trình rồi
giải ra để tìm giá trị của biến.
2. Bài tập minh họa.
Bài tập 13. Cho biểu thức
1 2 2 5
4
22
x x x
P
x
xx


a). Rút gọn
.P
b). Tính giá trị của
P
với
2
23
x
.
Lời giải
a) Điều kiện:
0; 4xx
.
Khi đó ta có:
( 1)( 2) 2 ( 2) (2 5 )
( 2)( 2)
x x x x x
P
xx

3 2 2 4 2 5
( 2)( 2)
2 ( 2)
( 2)( 2) ( 2)( 2) 2
x x x x x
xx
x x x x x
x x x x x


b) Ta có
2
2
2(2 3) ( 3 1) 3 1
23
xx
Do đó
2
3 1 3 1 ( 3 1) 4 2 3
(2 3)
22
2 ( 3 1) 1 3
P

Bài tập 14. Cho biểu thức
2
2 2 4
:
1 ( 1)
21
x x x
P
xx
xx








a). Rút gọn
.P
b). Tính giá trị của
P
biết
54x 
.
Lời giải
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
71
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
a) Điều kiện:
0; 1.xx
Khi đó ta có
2
2
2 2
1 1
1
1
.
4
x
P
x
xx
x
x
x




2
2
2 1 2 1
( 1)
.
4
11
x x x x
x
x
xx

2
2
2 2
( 1)
.
4
11
x x x x
x
x
xx

2
2
2
( 1) 1
2
.
4
11
xx
x
x
xx


1
2
x
x
b) Ta có
5 4 9
| 5| 4
5 4 1
xx
x
xx



Với
9x
, ta có
9 1 4 2
63
29
P
Với
1x
, không thỏa mãn điều kiện đã nêu nên biểu thức
P
không có giá trị.
Bài tập 15. Cho biểu thức
2
2
.
22
xy x y
x
P
xy
x y x y






a). Rút gọn
.P
b). Tính giá trị của
P
biết
4
9
x
y
.
Lời giải
a) Điều kiện:
0 ; 0 ; x y x y
.
Khi đó ta có
2
2
.
2( )
xy x y
x
P
xy
x y x y






2
4 ( )
2
.
2( )( )
xy x y
x
x y x y x y

42
2
.
2( )( )
xy x xy y
x
x y x y x y
( 2 )
2
.
2( )( )
x xy y
x
x y x y x y
2
()
2
.
2( )( )
xy
x
x y x y x y


x
xy
b) Ta có
4
9
x
y
9
4
x
y
Do đó
2
35
5
9
22
4
x x x
P
x x x
xx
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
72
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 16. Cho
1 2 2 1
:
4
2 4 4 2
P
x
x x x x


a). Rút gọn
.P
b). Tìm
x
để
1
2
P 
.
Lời giải
a) Điều kiện:
0 ; 4xx
.
Khi đó ta có:
2
1 2 2 1
:
4
2 ( 2) 2
P
x
x x x






2
2 2 2 ( 2)
:
4
( 2)
xx
x
x
2
( 2)( 2) 2
.
( 2) 2
x x x x
x x x

b) Ta có
1
2
P 
21
2
2
x
x
2 4 2xx
6x
36x
(thỏa mãn điều kiện).
Bài Tập 17. Cho biểu thức
1 1 3 3
:
3 9 3 3
xx
P
x x x x x x x







a). Rút gọn
.P
b). Tìm
x
để
1.P
Lời giải
a) Điều kiện:
0 ; 9xx
.
Khi đó ta có:
( 3) 3 3 3
:
( 3)( 3) ( 3)
x x x x
P
x x x x x
3 3 ( 3)
.
( 3)( 3) 3 3
x x x x
x x x x x
1
3x
b) Để
1P
11
1 1 0
33xx

13
0
3
x
x


4
0
3
x
x

40
30
x
x


hoặc
40
30
x
x


9 < < 16 x
(thỏa mãn điều kiện)
Bài tập 18. Cho biểu thức
1 6 1
2:
2 3 (2 3)( 1) 1
x x x
D
x x x x




.
a). Rút gọn
.D
. b). Chứng minh rằng
3
2
D
Lời giải
a) Điều kiện:
9
0 ; .
4
xx
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
73
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Khi đó ta có:
2(2 3) ( 1) 6 1 (2 3)
:
2 3 (2 3)( 1)
x x x x x
D
x x x
4 6 1 6 1 2 3
:
2 3 (2 3)( 1)
x x x x x
x x x
3 5 (2 3)( 1)
.
2 3 2 3 1
x x x
x x x
3 5 (2 3)( 1)
.
2 3 (2 1)( 1)
x x x
x x x
35
21
x
x
b) Xét hiệu
3 5 6 10 6 3 13
0
2 1 2(2 1) 2
2
(2 1
3
2
)
3
D
x x x
x x x


. Vậy
3
2
D
Nhận xét:
Về mặt phương pháp, muốn chứng minh
3
2
D
ta chứng minh
3
0
2
D 
Bài tập 19. Cho biểu thức
2 1 1
1 1 1
xx
B
x x x x x

a). Rút gọn
B
.
b). Chứng minh rằng
B
luôn luôn có giá trị không âm với mọi giá trị thích hợp của
.
Lời giải
a) Điều kiện
0 x
.
Khi đó ta có:
2 ( 1)( 1) ( 1)
( 1)( 1)
x x x x x
B
x x x
2 1 1
( 1)( 1)
x x x x
x x x
( 1)( 1)
xx
x x x
( 1)
( 1)( 1)
xx
x x x
1
x
xx

b) Ta cos
0 x
nên
0x
Khi đó
2
1 3 3
1 ( ) 0
2 4 4
x x x
với mọi
x
.
Do đó
0
1
x
B
xx


với mọi
0x
.
Bài tập 20. Cho biểu thức C =
12
:1
1
11
x
x
x x x x x








a). Rút gọn
C
.
b). Chứng minh rằng
C
luôn luôn có giá trị âm với mọi giá trị thích hợp của
x
.
Lời giải
a) Điều kiện
0 ; 1xx
.
Khi đó ta có:
1 2 1
:
1
1 ( 1)( 1)
xx
C
x
x x x





1 2 ( 1)
.
( 1)(x 1) 1
xx
x x x
( 1)( 1) ( 1)
.
( 1)(x 1) 1
x x x
x x x
( 1)
1
x
xx


b) Ta có
0 ; 1xx
nên
( 1) 0.x
Khi đó
2
13
1 0.
24
x x x



Do đó
( 1)
0
1
x
C
xx



với mọi giá trị thích hợp của
x
.
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
74
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 21. (Dạng 1). Cho biểu thức:
1 2 2 5
4
22
x x x
A
x
xx



a). Rút gọn
A
nếu
0x
và
4x
;
b). Tìm
x
để
2A
.
Lời giải
a). Với
0x
và
4x
,
ta có:
1 2 2 5
4
22
x x x
A
x
xx



1 2 2 2
25
2 2 2 2 2 2
x x x x
x
x x x x x x
3 2 2 4 2 5
22
x x x x x
xx

32
3 6 3
2
2 2 2 2
xx
x x x
x
x x x x

b). Khi
2A
ta được
3
2 3 2 2 4 16 (tm 0, 4)
2
x
x x x x x x
x
Vậy
16x
.
Bài tập 22. (Dạng 1). Cho biểu thức:
2 2 2 2 2 2
1:
a a b
B
a b a b a a b



với
0.ab
a). Rút gọn
B
;
b). Tính
B
nếu
3
2
a
b
;
c). Tìm điều kiện của
,ab
để
1B
Lời giải
a) Với điều kiện:
0ab
, ta có:
2 2 2 2 2 2
1:
a a b
B
a b a b a a b



2 2 2 2
2 2 2 2
2 2 2 2
.
a b a a a b
a
b
a b a b
a b a b a b
ab
ab
a b a b




b) Ta có:
3
2
a
b
3
2
ab
thay vào ta được
31
15
22
.
35
55
22
b b b
B
b b b
c) Khi
1B
ta có:
1
ab
ab

1
ab
a b a b
ab
2 0 0.a b a b b b b b
Vậy với
0ab
thì
1.B
Bài tập 23. Rút gọn
36
.
9
33
xx
P
x
xx

rồi tính giá trị của biểu thức
P
với
0,36x
.
Lời giải
Rút gọn ta được
3
3
x
P
x
với điều kiện
0 ; 9.xx
Khi đó
0,36x
ta có
2
.
3
P 
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
75
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
DẠNG 5. RÚT GỌN RỒI TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC
1. Phương pháp.
Bước 1. tìm điều kiện để biểu thức có nghĩa
Bước 2. rút gọn biểu thức ta được biểu thức
Q
.
① Nếu
Q
là một biểu thức có dạng bậc hai, tức là
2
,0Q ax bx c a
thì ta đưa về dạng
bình phương thiếu:
22
2 2 2
22
2. .
2 4 4
b c b b b c
Q ax bx c a x x a x x
a a a a a a






22
22
2
44
2 4 2 4
b b ac b b ac
a x a x
a a a a





2
24
b
ax
aa
khi đó:
⋆ Nếu
0a
thì
2
4
ax bx c
a

dấu bằng xảy ra khi
.
2
b
x
a

Suy ra GTNN là
4a

.
⋆ Nếu
0a
thì
2
4
ax bx c
a

dấu bằng xảy ra khi
.
2
b
x
a

Suy ra GTLN là
4a

.
② Nếu
Q
là một biểu thức có dạng phân thức
2
0
fx
k
hoặc
2
0
fx
k
2. Bài tập minh họa.
Bài tập 24. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
2
21
2
m
A
m
.
Lời giải
Xét
22
2
2 2 1
2
km m k
Ak
m

.
Khi đó để biểu thức đạt giá trị lớn nhất, nhỏ nhất thì tử số là biếu thức
22
2 2 1f m km m k
phải biểu diễn được dưới dạng bình phương
hay
2
1
0 1 1 2 0 2 1 0
1
2
m
k
k k k k
k

.
Khi đó
2
2
2 2 2
1
2 1 2 1 2
1 1 0, 1,
2 2 2
m
m m m
A m A m
m m m
Dấu bằng xảy ra khi và chỉ khi
1m
Và
2
2
2
22
2 2 1 2 2
1 2 1 1 1
0, ,
2 2 2 2
2 2 2 2
m m m
m
A m A m
m
mm

Dấu bằng xảy ra khi và chỉ khi
2m 
Vậy
max 1A
khi và chỉ khi
1m
,
1
min
2
A 
khi và chỉ khi
2m 
Bài tập 25. Tìm giá trị lớn nhất của biểu thức
1
1
A
xx

Lời giải
Điều kiện xác định
0x
Để
A
đạt giá trị lớn nhất thì
1xx
đạt giá trị nhỏ nhất
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
76
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Có
2
1 1 1 1 3
1 2 1
2 4 4 2 4
x x x x x



Lại có
22
1 1 3 3
0, 0 , 0
2 2 4 4
x x x x
Dấu "="xảy
11
24
ra x x
Khi đó
31
Min 1
44
x x x
Vậy
41
Max
34
Ax
Bài tập 26. Cho biểu thức
2
1 1 1
:
1 ( 1)
x
A
x x x x




a). Rút gọn
.A
b). Tìm giá trị lớn nhất của biểu thức
9P A x
Lời giải
a).
2
1 1 1
:
1 ( 1)
x
A
x x x x




với
0, 1xx
2
1 1 1
:
( 1) 1 ( 1)
x
x x x x




22
1 ( 1) ( 1) 1
( 1) 1 ( 1)
x x x x
x x x x x x
b).
11
9 9 1 9
x
P A x x x
xx



với
0, 1xx
Với
0, 1xx
, áp dụng bất đẳng thức Cauchy có:
11
9 2 9 6xx
xx
11
9 6 1 9 1 6 5 5x x P
xx
Dấu "="xảy ra
11
9
9
xx
x
(thỏa mãn). Vậy max
1
5
9
Px
Bài tập 27. Cho biểu thức
6
4
22
x x x
A
x
xx





với
0; 4xx
a). Rút gọn
.A
b).Tìm giá trị nhỏ nhất của
A
.
Lời giải
a).
6
4
22
x x x
A
x
xx





với
0; 4xx
(2 ) (2 ) 6
(2 )(2 ) (2 )(2 )
x x x x x
x x x x

2 2 6
(2 )(2 ) (2 )(2 )
x x x x x
x x x x

4 6 3 6
(2 )(2 ) (2 )(2 )
x x x
x x x x

3 ( 2) 3
(2 )(2 ) 2
x
x x x

b). Có
3 3 3 3
0 0 2 2
22
22
x x x
xx


Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
77
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Dấu "=" xảy ra
0x
Vậy
3
min 0
2
Ax
Bài tập 28. Cho biểu thức:
2
1
22
.
12
21
x
xx
C
x
xx







a). Rút gọn
C
nếu
0, 1;xx
b). Tìm
x
để
C
dương;
c). Tìm giá trị lớn nhất của
C
.
Lời giải
a) ĐK:
0, 1xx
, ta có:
22
2
2 1 2 1
11
22
..
1 2 2
21
11
x x x x
xx
xx
C
x
xx
xx













22
22
11
2 2 2
..
22
1 1 1 1
xx
x x x x x
x x x x


2
11
1
1 1 1
x x x x
xx
x x x
b) Ta có:
0 1 0 1 0 1 0 1.C x x x x x
c) Với
0, 1xx
, ta có
1C x x x x x x
2
1 1 1 1 1
2.
2 4 4 2 4
x x x
Vì
2
1
0
2
x



với mọi
0x
nên
2
1 1 1
2 4 4
x



với mọi
0x
.
Do đó:
1
4
C
với mọi
0x
GTLN của
1
4
C
khi
1 1 1
0.
2 2 4
x x x
Vậy GTLN của
1
4
C
khi
1
4
x
.
Bài tập 29. Cho biểu thức P =
1 1 4
: 2 .
1
11
x
x
xx









a). Rút gọn
.P
b). Tìm giá trị lớn nhất của
.P
Lời giải
a) Điều kiện:
0 ; 1xx
.
Khi đó ta có
( 1) 1 2.( 1) ( 4)
:
( 1)( 1) 1
x x x
P
x x x
21
.
( 1)( 1) 2
xx
x x x


1
1x
.
b) Ta có
11
1
1
1
P
x
vì
0x
Do đó
max 1P
đạt được khi
00xx
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
78
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 30. Cho biểu thức Q =
3 3 14 3
.
92
33
x x x
x
xx






a). Rút gọn
.Q
.
b). Tìm giá trị nhỏ nhất của
.Q
Lời giải
a) Điều kiện:
0 ; 9xx
.
Khi đó ta có:
22
( 3) 3) 14 3
.
2
( 3)( 3)
x x x
Q
xx

6 9 6 9 14 3
.
2
( 3)( 3)
x x x x x
xx

2 32 3
.
2
( 3)( 3)
xx
xx



16
3
x
x
b) Ta có
16
3
x
Q
x
=
9 25 25
3
33
x
x
xx


25
36
3
x
x
25
2 ( 3). 6
3
x
x
(bất đẳng thức cô si)
10 6 4.
Dấu “ = “ xảy ra khi và chỉ khi
25
3
3
x
x

2
( 3) 25 3 5xx
2
( 3) 25 3 5xx
4x
(thỏa mãn điều kiện)
Vậy minQ = 4 khi
4.x
3. Bài tập rèn luyện.
Bài 7. Cho biểu thức P =
6 36
:
36
6 2( 3)( 2 3)
x x x x x
P
x
x x x x x






.
a). Rút gọn
P
.
b). Với giá trị nào của
x
thì
P
có giá trị lớn nhất ? Giá trị lớn nhất đó là bao nhiêu?
Lời giải
a) Rút gọn ta được
6
23xx
với điều kiện
0; 9; 36xxx
.
b)
2
66
3
2
( 1) 2
P
x

( vì
2
( 1) 0x 
).
Suy ra max
P
= 3 đạt được khi
1x
.
Bài 8. Cho biểu thức P =
2 3 3 2 15 11
3 1 2 3)
x x x
x x x x

a). Rút gọn
P
.
b). Tìm giá trị nhỏ nhất của
P
.
Lời giải
a)
52
( 0; 1)
3
x
P x x
x
.
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
79
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
b)
5 15 17 17 17
55
3
33
x
P
xx


17
5
3
P
( vì
√
𝑥 ≥ 0 ).
2
3
P 
( dấu bằng xảy ra khi
0.x
). Vậy min =
2
3
, đạt được khi
0.x
DẠNG 6. RÚT GỌN RỒI TÌM GIÁ TRỊ CỦA
x
NGUYÊN ĐỂ BIỂU THỨC NHẬN GIÁ TRỊ NGUYÊN
1. Phương pháp.
Bước 1. tìm điều kiện để biểu thức có nghĩa
Bước 2. Ta xét hai trường hợp sau:
① Loại 1. Biểu thức
Q
sẽ có dạng
()
()
fx
gx
trong đó
()fx
và
()gx
là các đa thức và
( ) 0gx
Khi đó:
⋆ Bước 1: Tách về dạng
()
()
k
Q m x
gx

trong đó
mx
là một biểu thức nguyên khi
x
nguyên và
có giá trị là số nguyên.
⋆ Bước 2: Để
Q
nhận giá trị nguyên thì
()
k
gx
nguyên hay
: ( )k g x
nghĩa là
()gx
thuộc tập
ước của
.k
⋆ Bước 3: Lập bảng để tính các giá trị của
.x
⋆ Bước 4: Kết hợp với điều kiện đề bài, loại bỏ những giá trị không phù hợp, sau đó kết
luận bài toán.
2. Bài tập minh họa.
Bài tập 31. Tìm các giá trị nguyên của biến số
để biểu thức đã cho cũng có giá trị nguyên
a).
2
.
1x
b).
2
.
1
x
x
c).
3
.
1
x
x
Lời giải
a).
2
1x
có điều kiện
1x
Để
2
1x
nhận giá trị nguyên thì
2:( 1) 1 (2) { 1; 2}x x U
Ta có bảng:
1x
2
1
1
2
x
1
(thỏa mãn)
0
(thỏa mãn)
2
(thỏa mãn)
3
(thỏa mãn)
Vậy với
{ 1;0;2;3}x
thì biểu thức
2
1x
nhận giá trị nguyên.
b).
2
1
x
x
có điều kiện
1x
Ta có:
2 1 1 1 1 1
1
1 1 1 1 1
x x x
x x x x x
Để
2
1
x
x
nhận giá trị nguyên thì
1:( 1) 1 (1) { 1}x x U
Ta có bảng:
1x
1
1
0
(thỏa mãn)
2
(thỏa mãn)
Vậy với
{0;2}x
thì biểu thức
2
1
x
x
nhận giá trị nguyên
c).
3
1
x
x
có điều kiện là
0x
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
80
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
3 3( 1) 3 3( 1) 3 3
3
1 1 1 1 1
x x x
x x x x x
Để
3
1
x
x
nhận giá trị nguyên thì
3:( 1) 1 (3) { 1; 3}x x U
Ta có bảng:
1x
3
1
1
3
x
4
(loại)
2
(loại)
0
(thỏa mãn)
2
0
(thỏa mãn)
(thỏa mãn)
Vậy với
{0;4}x
thì biểu thức
3
1
x
x
nhận giá trị nguyên
② Loại 2. Đây là một dạng nâng cao hơn của dạng bài tập tìm gá trị nguyên của
x
để biểu thức
Q
nhận giá trị nguyên bởi ta chưa xác định giá trị của biến
x
có nguyên hay không để biến
đổi biểu thức A về dạng
()
()
k
A m x
gx

.
Bởi vậy, để làm được dạng bài tập này, chúng ta sẽ thực hiện các bước sau:
⋆ Bước 1: Áp dụng điều kiện cùng với các bất đẳng thức đã được, chứng minh
m A M
trong đó
m,M
là các số nguyên.
⋆ Bước 2: Trong khoảng từ
m
đến
M
, tìm các giá trị nguyên.
⋆ Bước 3: Với mỗi giá trị nguyên ấy, tìm giá trị của biến
.
⋆ Bước 4: Kết hợp với điều kiện đề bài, loại bỏ những giá trị không phù hợp rồi kết luận.
Nhận xét: Trong dạng này ta hay sử dụng bất đẳng thức Cô-Si: cho
0, 0ab
2a b ab
Dấu
'' ''
xảy khi khi
.ab
3. Bài tập minh họa.
Bài tập 32. Tìm giá trị của
x
để các biểu thức dưới đây nhận giá trị nguyên.
a).
2
3
x
x
b).
2
1
x
xx
Lời giải
a).
2
3
x
x
có điều kiện là
0x
Có
20
0
3 3 0
x
x
x

. Suy ra ta có
2
00
3
x
x
x
(1)
Lại có
22
3
3
x
x
x
x
Áp dụng bất đẳng thức Cauchy cho
0x
có
33
2 2 3xx
xx
2 2 3
(2)
3
3
23
x
x
Từ (1) và (2) ta có:
23
0
33
x
x

mà biểu thức nhận giá trị nguyên nên
2
0
3
x
x
Giải phương trình tính được
0x
Vậy với
0x
thì biểu thức nhận giá trị nguyên
b).
2
1
x
xx
có điều kiện là
0x
.
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
81
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Có
20
0 0 (1)
10
x
xx
xx
Lại có
22
1
1
1
x
xx
x
x


Áp dụng bất đẳng thức Cauchy cho
0x
có
1 1 2 2
2 1 3
1
3
1
xx
xx
x
x

(2)
Từ (1) va (2) ta có
22
0
3
1
x
xx


mà biểu thức nhận giá trị nguyên nên
2
0
3
x
x
.
Giải phương trình được
0x
Vậy với
0x
thì biểu thức nhận giá trị nguyên.
Bài tập 33. Cho biểu thức P =
1 1 1
.
11
x
x
x x x x








a). Rút gọn
.P
b). Tìm các giá trị nguyên của
x
để
P
có giá trị nguyên.
Lời giải
a).
2
( 0);
x
Px
x

b).
1;4x
.
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
82
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
A. TÓM TẮT LÝ THUYẾT
1. Định nghĩa.
Căn bậc ba của một số
là số
x
sao cho
3
.xa
Mỗi số
a
đều có duy nhất một căn bậc ba.
⋆ Nhận xét :
Căn bậc ba của một số dương là số dương ;
Căn bậc ba của một số âm là một số âm ;
Căn bậc ba của số 0 là số 0 ;
Ví dụ 1. Hãy tìm :
a).
3
216
b).
3
729
c).
3
331
.
Lời giải
a)
3
3
3
216 6 6
b).
3
3
3
729 9 9
c).
3
3
3
331 11 11
Ví dụ 2. Hãy tìm :
a).
3
343
b).
3
1000
c).
3
1728
.
Lời giải
a)
3
3
3
343 7 7
b)
3
3
3
1000 10 10
c)
3
3
3
1728 12 12
Ví dụ 3. Hãy tìm :
a).
3
8
27
b).
3
125
512
c).
3
0,064
Lời giải
a).
3
8
27
3
3
22
33



b).
3
125
512

3 3 3
3 27.12 1 324 1 343 1 7 1 6
c).
3
0,064
3
3
0,4 0,4
.
2. Tính chất
3
3
;aa
3
3
.aa
So sánh:
33
.a b a b
Phép khai phương
3 3 3
;ab a b
Phép khai phương
3
3
3
. ( 0)
aa
b
b
b

Ví dụ 4. So sánh
a). 7 và
3
345
b).
3
2 6
và
3
32
.
Lời giải
a). 7 và
3
345
Ta có
33
7 343 345
;
b).
3
2 6
và
3
32
.
§BI 9. CĂN BẬC ba
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
83
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Ta có
3
3
3
3
22 86 .6 4
3
3
3
3
33 42 .2 5
48 54
nên
3
3
3
23 4625
Ví dụ 5. So sánh
a).
3
2
18
3
và
3
3
12
4
b).
3
130 1
và
3
3 12 1
.
Lời giải
a) . Ta có
3
2
18
3
=
3
3
33
2 16 1
.18 5
3 3 3




3
3
12
4
=
3
3
33
3 81 1
.12 5
4 16 16




Vì
11
55
3 16
nên
3
2
18
3
>
3
3
12
4
b) Ta có
3
130 1
>
3
125 1 5 1 6
;
3
3 12 1
=
3 3 3
3 27.12 1 324 1 343 1 7 1 6
;
Vậy
3
130 1
>
3
3 12 1
.
Ví dụ 6. Cho
0a
, hỏi số nào lớn hơn trong hai số
3
2a
và
3
3a
Lời giải
Ta có
23
nên
23aa
( vì
0a
).
Do đó
3
2a
>
3
3a
.
Ví dụ 7. Rút gọn các biểu thức
a).
3 3 3
8 27 64
; b).
3 3 3
54 16 128
.
Lời giải
a) Ta có
3 3 3
8 27 64
2 3 4 5
b) Ta có
3 3 3
54 16 128
=
33
3 3 3
3 3 3 3
3
3 .2 ( 2) .2 4 .2 3 2 2 2 4 2 9 2.
Ví dụ 8. Tính
a).
3 3 3 3
16. 13.5 120 : 15
; b).
3 3 3
( 2 1)( 4 2 1).
Lời giải
a)
3 3 3 3
16. 13.5 120 : 15
=
33
16.13.5 120:15
=
33
216 8
6 – 2 4
6 – 2 4
b)
3 3 3
( 2 1)( 4 2 1)
=
3 3 3 3
3
8 4 2 4 2 1
2 1 3
Nhận xét:
Để tính tích trên có thể sử dụng hằng đẳng thức :
2 2 3 3
()a b a ab b a b
Ta có
33
3 3 3 3
( 2 1)( 4 2 1) ( 2) 1 2 1 3.
Ví dụ 9. Tính
a).
3
3 3 3
( 5 1) 3 5( 5 1)
; b).
3
3 3 3
3
( 4 3) 6 2( 2 1)
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
84
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Lời giải
a) Ta có
3
3 3 3
( 5 1) 3 5( 5 1)
=
3 3 3 3
5 3 25 3 5 1 3 25 3 5 6.
b) Ta có
3
3 3 3 3 3
3 3 3
( 4 3) 6 2( 2 1) 4 3 32 3 16 2 6 4 6 2
=
3 3 3 3
6 6 4 6 2 2 6 4 6 2 2
.
Ví dụ 10. Tính
33
5 2 5 2A
.
Lời giải
Ta có
3
A
(
33
5 2 5 2
)
3
3
A
3 3 3
5 2 5 2 3 5 2 5 2 5 2 5 2



3
43AA
3
3 – 4 0AA
2
( 1)( 4) 0A A A
10A
( vì
2
40AA
)
Vậy
1A
Ví dụ 11. Rút gọn biểu thức.
a).
3
3
1 3 ( 1)x x x
; b).
2
3
3
1
1
x
xx

.
Lời giải
a) Ta có
3
3
1 3 ( 1)x x x
=
3
3
( 1) 1xx
.
b)
2
3
3
1
1
x
xx

=
3
2
33
3
3
2
3
( 1)( 1)
1.
1
x x x
x
xx


B. PHÂN DẠNG VÀ VI DỤ MINH HỌA.
DẠNG 1. THỰC HIỆN PHÉP TÍNH
1. Phương pháp.
Áp dụng
3
3
3
3
;.a a a a
2. Bài tập minh họa.
Bài tập 1. (Bài 67, tr 36 SGK) Hãy tìm
33
3 3 3
512; 729; 0,064; 0,216; 0,008.
Lời giải
Ta có:
3
3
3
512 8 8.
3
3
3
729 9 9.
3
3
3
0,064 (0,4) 0,4.
3
3
3
0,216 ( 0,6) 0,6.
3
3
3
0,008 ( 0,2) 0,2.
Bài tập 2. (Bài 68, tr. 36 SGK) Tính:
a).
3 3 3
27 8 125;
b).
3
3
3
3
135
54. 4.
5
Lời giải
a).
3
33
3 3 3
3 3 3
27 8 125 3 2 5 3 2 5 0
b).
3
3
3 3 3 3
3
3
135 135
54. 4. 54.4. 27 216 3 6 3
5
5
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
85
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 3. Thực hiện phép tính
a).
33
3 3 3
9 6 4 3 2A
b).
33
2 5 2 5.B
Lời giải
a). Ta có:
22
3 3 3 3 3
3 3 3 3 3 3
9 6 4 3 2 3 3 2 2 3 2A
33
3
3
3 2 3 2 1
b). Áp dụng hằng đẳng thức
3
33
3 ( )a b a b ab a b
Ta có:
3
3
3 3 3 3 3 3
2 5 2 5 2 5 2 5 3 2 5 2 5 2 5 2 5B
3
3
4 3 2 5 2 5 4 3 4 5 4 3B B B
3 3 2
3 4 0 1 3 3 0 ( 1)( 4) 0B B B B B B B
2
22
1 1 15 1 15
1 4 2 0
2 4 4 2 4
B B B B B B







Vậy
33
2 5 2 5 1.B
3. Bài tập rèn luyện.
Bài 1. Thực hiện phép tính
a).
33
3
1
18 3
2
. b).
33
2 1 3 2 2 ; 4 2 3 3 1
.
c).
33
3
11
2 16 4
24




. d).
33
33
1 1 1
9 2 3 3 :2
2 3 3





.
e).
33
3 3 3
9 6 4 3 2
.
Lời giải
a).
3 3 3
33
11
18 3 ( 18) 3 27 3
22
.
b).
23
33
3
2 1 3 2 2 2 1 2 1 2 1 2 1
.
23
33
3
4 2 3 3 1 3 1 3 1 3 1 3 1
.
c).
3 3 3 3 3
3
1 1 1 1
2 16 4 2 2 4 0
22 4 2
.
d).
3 3 3 3 3 3 3 3 3 3
33
1 1 1 1 2 2 9
9 2 3 3 :2 9 2 3 9 :
3
3
9 9 2 3 : 9 9
2 3 2 3 2 3 4




.
e).
33
3
3
2
3 3 3 3
3 3 3 3 3 3
2
9 6 4 3 2 2 3 2 3 2 3 2 53 3 2
.
Bài 2. Thực hiện phép tính
3 3 3
64 125 216
a).
33
33
4 1 4 1
b).
3 3 3
3
3
1
12 2 16 2 2 5 4 3
2




.
Lời giải
a)
3 3 3
64 125 216 4 5 6 3
b) Ta có
33
33
4 1 4 1
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
86
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
22
3 3 3 3 3 3
4 1 4 1 4 1 4 1 4 1 4 1



3 3 3
3 3 3 3
2. 16 2 4 1 16 1 16 2 4 1 2 3 16 1 2 6 2 1
c) Ta có
3 3 3
3
3
1
12 2 16 2 2 5 4 3
2




3 3 3 3 3 3
33
11
12 2 2 2 2 2 5 4 3 12 2 5 4 3 120 36 84
22
Bài 3. Cho
33
2
2 2 2 4
x
và
33
6
2 2 2 4
y
. Tính
33
xy x y
.
Lời giải
Ta có
22
3 3 3
3
3 3 3 3
2 2 2
2 2 2 4 16 2 4
4 2. 4 2
x
33
33
2 4 2
42
42
Tương tự
33
33
6
42
2 2 2 4
y
Do đó:
33
3 3 2 2
8 2 2 4xy x y xy y x xy y x y x
Bài 4. Trục căn ở mẫu số biểu diễn
3
33
1
16 12 9
Lời giải
Ta có:
3
3
3
3
22
3
33
3
33
1 1 4 3
4 3.
43
16 12 9
4 3. 4 3
DẠNG 2. CHỨNG MINH ĐẲNG THỨC
1. Phương pháp.
biến đổi hai vế của đẳng thức cùng bằng một biểu thức.
2. Bài tập minh họa.
Bài tập 4. Chứng minh rằng nếu:
3 3 3
ax by cz
và
1 1 1
1
x y z
thì
2 2 2
3 3 3
3
.ax by cz a b c
Lời giải
Ta đặt
3 3 3
ax by cz t
suy ra
3 3 3
,,
t t t
a b c
x y z
Ta có:
2 2 2 2 2 2
3
3
3
33
3 3 3
1 1 1
(1)
t t t t t t
ax by cz x y z t t
x y z x y z x y z



Ta lại có:
333
3 3 3 3 3
3
3
3
3 3 3
1 1 1
(2)
t t t t t t
a b c t t
x y z x y z x y z



Từ (1) và (2) ta có:
2 2 2
3 3 3
3
.ax by cz a b c
(ĐPCM)
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
87
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Bài tập 5. Chứng minh đẳng thức:
2 2 2
3 3 3
3 3 3
3 3 3 3
1
3.
2
x y z xyz x y z x y y z z x



Từ đó suy ra bất đẳng thức Cô-si cho
3
số không âm
, , :x y z
3
.
3
x y z
xyz

Lời giải
3
33
3 3 3 3 3
3
3 3 3 3
3 3 3 3
3 3 3 3 3
3 3 3
33
VT x y z xyz x y xy x y z xyz
x y z x y z x y z xy x y z
2
33
3 3 3
3 3 3 3
3
3
2 2 2
3
33
3
3 3 3
3x y z x y z xy yz zx
x y z x y z xy yz zx



3
3
2 2 2
3
33
3
3 3 3
2 2 2
3 3 3
3 3 3
3 3 3
1
2 2 2 2 2 2
2
1
2
.
x y z x y z xy yz zx
x y z x y y z z x
VP



Vậy ta có đẳng thức
2 2 2
3 3 3
3 3 3
3 3 3 3
1
3.
2
x y z xyz x y z x y y z z x



Suy ra với 3 số không âm
, , :x y z
2 2 2
3 3 3
3 3 3
3 3 3 3
1
30
2
x y z xyz x y z x y y z z x



Do đó
33
3.
3
x y z
x y z xyz xyz

Dấu “
” xảy ra khi
.x y z
DẠNG 3. SO SÁNH HAI SỐ
1. Phương pháp.
Đưa thừa số vào căn bậc ba rồi so sánh hai số trong căn:
3
3
3
A B A B
.
33
A B A B
.
2. Bài tập minh họa.
Bài tập 6. So sánh
a).
6
và
3
215
. b).
3
45
và
3
54
.
Lời giải
a). Ta có
33
6 216 215
. Vậy
3
6 215
.
b).
3
3
33
4 5 4 5 320
;
3
3
3
3
5 4 5 4 500
.
Vì
320 500
nên
3
3
4 5 5 4
.
Bài tập 7. So Sánh:
a).
3
23
và
3
23
; b).
33
và
3
3 133
.
Lời giải
a) Ta có:
3
3 3 3 3
2 3 8. 3 24 23
. Do đó
33
2 3 23.
b) Ta có:
33
33 3 11 3 1331 3 133.
Do đó
3
33 3 133.
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
88
Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
DẠNG 4. GIẢI PHƯƠNG TRÌNH
1. Phương pháp.
Áp dụng:
3
3
A B A B
.
2. Bài tập minh họa.
Bài tập 8. Giải các phương trình
a).
3
2 1 2x 
. b).
3
1 2 2x
. c).
3
22xx
.
Lời giải
a).
3
7
2 1 2 2 1 8
2
x x x
.
Vậy phương trình có nghiệm
7
2
x
.
b).
3
9
1 2 2 1 2 8
2
x x x
.
Vậy phương trình có nghiệm
9
2
x
.
c).
3
33
2 2 2 2 2 ( 2)x x x x x x
2
2
20
3
( 2) 1
1
x
x
x
x
x


.
Vậy phương trình có 3 nghiệm
1; 2; 3x x x
.
Bài tập 9. Giải phương trình:
a).
3
32
93x x x
; b).
3
5 5.xx
Lời giải
a)
3
32
93x x x
3
3
32
3
3
3 2 3 2
93
9 3 9 27 27
27 27 0 1.
x x x
x x x x x x
xx
b)
3
55xx
3
3
2
2
5 5 5 5
5 0 5
50
5 5 1 0 5 1 4.
51
5 1 6
x x x x
xx
x
x x x x
x
xx









| 1/127
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học 1
CĂN BẬC HAI – CĂN BẬC BA §BÀI 1. CĂN BẬC HAI A. TÓM TẮT LÝ THUYẾT I. Căn bậc hai số học.
1. Định nghĩa: Với số dương a , số a được gọi là căn bậc hai số học của a . 2. Tính chất:
Tính chất 1. Số 0 cũng được gọi là căn bậc hai số học của 0 .
Tính chất 2. Với a  0 , ta có: x  0 a x   2 x a
Nhận xét. Đây gọi là phương pháp bình phương hai vế.
Ví dụ 1. Giải phương trình: 2 3x  12. Lời giải ĐKXĐ: x  0.
Ta có : 2 3x  12  3x  6  3x  36  x  12 ( thỏa mãn điều kiện).
Ví dụ 2. Tính tổng các giá trị của x thỏa mãn đẳng thức 2 x  25  13. Lời giải Ta có : 2 x  25  13 2  x  25 169 2  x 169  25 2
x 144  x  12. 
Vậy tổng các giá trị của x thỏa mãn đẳng thức đã cho là  1  2 12  0 .
Tính chất 3. Với a  0 : 2
x a x   a .
Ví dụ 3. Giải các phương trình sau: a). 2 5x  80 b). 2 3x  0, 75. Lời giải a). 2 5x  80 b). 2 3x  0, 75. Ta có 2 2
5x  80  x  16. Ta có 2 2
3x  0, 75  x  0, 25.
Do đó x   16  4.
Do đó x   0, 25  0  ,5. Tính chất 4. Với 2
x a khi 0  xa .
Ví dụ 4. Tìm số x không âm, biết 1 a). 5x  10. b). 3x  6 2 Lời giải
1 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học 1 a). 5x  10. 2 1 Với x  0 ta có :
5x  10  5x  20 2
 5x  400  x  80. Vậy 0  x  80. b). 3x  6
Với x  0 ta có : 3x  6  3x  36  x 12. Vậy 0  x 12. II. Căn bậc hai.
1. Định nghĩa: Căn bậc hai của số không âm a là số x sao cho 2 x  . a 2. Tính chất:
Số dương a có đúng hai căn bậc hai là hai số đối nhau là số dương kí hiệu là a và số âm kí hiệu là  a.
Ví dụ 5. Tìm căn bậc hai số học rồi tìm căn bậc hai của: 2  2  a). 121. b).     5  Lời giải
a) Ta có 121  11 vì 11  0 và 2 11  121.
Do đó số 121 có hai căn bậc hai là 11 và 11. 2  2  2 2 2 2  2   2  b) Ta có     vì  0 và   .      5  5 5  5   5  2  2  2 2 Do đó số  
 có hai căn bậc hai là và  .  5  5 5
III. So sánh các căn bậc hai số học
Với a  0;b  0 . Ta có a b a b .
Ví dụ 6. Không dung máy tính hoặc bảng số , hãy so sánh 8 và 65. Lời giải Cách 1: Ta có 8  64 . Vì 64  65 nên 8  65 . Cách 2: Vì   2 2 8 64; 65  65 Nên   2 2 8 65 , suy ra 8  65.
2 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
Cách giải này dựa vào tính chất: Nếu a  0,b  0 và 2 2
a b thì a b .
Như vậy, để so sánh hai số dương ta có thể so sánh các bình phương của chúng.
Ví dụ 7. Không dung máy tính hoặc bảng số , hãy so sánh 15 1 và 10. Lời giải
Ta có 15  16  15  16  15 1  16 1  4 1  3 . 10  9  3 Vậy 15 1  10.
Ví dụ 8. Với a  0 thì số nào lớn hơn trong hai số a và 2a ? Lời giải
Ta có 1  2 nên a  2
a (vì a  0 ).
Do đó a  2a .
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
DẠNG 1. TÌM CĂN BẬC HAI SỐ HỌC CỦA MỘT SỐ 1. Phương pháp.
Căn bậc hai số học của số dương a là a ( giá trị dương của căn bậc hai).
Với a  0 , ta có:
 Nếu x a thì x  0 và 2 x  . a  Nếu x  0 và 2
x a thì x a . ⋆⋆Nhận xét.
Nếu a  0 thì các căn bậc hai của a là  a ; căn bậc hai số học của a là a .
Nếu a  0 thì căn bậc hai của a và căn bậc hai số học của a cùng bằng 0.
Nếu a  0 thì a không có căn bậc hai và do đó không có căn bậc hai hai số học.
2. Bài tập minh họa.
Bài tập 1. Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng: 64;81;100;196. Lời giải Ta có: 2
8  64 nên 8 là căn bậc hai số học của 64 .
Từ đó suy ra căn bậc hai của 64 là 8 và 8  .
Tương tự căn bậc hai của 64;81;100;196 lần lượt là : 8;9;10;14
Bài tập 2. Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm
tròn đến chữ số thập phân thứ ba): a) 2 x  4, 5 . b) 2 x  5 . c) 2 x  7, 5 . d) 2 x  9,12 . Lời giải
a) Nghiệm của phương trình 2
x a ( với a  0 ) là các căn bậc hai của a . Phương trình 2
x  4, 5 có hai nghiệm là x  4,5 và x   4,5 . 1 2
Dùng máy tính ta tìm được x  2,121 và x  2  ,121. 1 2 b) 2
x  5 có hai nghiệm x   5  2  ,236. c) 2
x  7, 5 có hai nghiệm x   7,5  2  ,739 . d) 2
x  9,12 có hai nghiệm x   9,12  3  ,020 .
3 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
3. Bài tập rèn luyện.
Bài 1. Tìm căn bậc hai số học của các số sau 4 40 a).12 ; b). 121; c). ; d). 0, 09. e).1 9 81 9 f). 0 ; g). 64 ; h). 81  ; n). ; m). 0, 04. 16 Lời giải
a) 12 có căn bậc hai số học là: 12
b). 121 có căn bậc hai số học là: 121 4 4
c). có căn bậc hai số học là:
d). 0, 09 có căn bậc hai số học là: 0,3. 9 9 40 11 e). 1
có căn bậc hai số học là:
f). 0 có căn bậc hai số học là 0 81 9
g). 64 có căn bậc hai số học là: 8. h). 81
 không có căn bậc hai số học. 9 3 k).
có căn bậc hai số học là:
m). 0, 04 có căn bậc hai số học là: 0, 02 . 16 4
DẠNG 2. TÌM SỐ CÓ CĂN BẬC HAI SỐ HỌC LÀ MỘT SỐ CHO TRƯỚC 1. Phương pháp.
Với số thực a  0 cho trước ta có 2
a chính là số có căn bậc hai số học bằng . a
2. Bài tập minh họa.
Bài tập 3. Mỗi số sau đây là căn bậc hai số học của số nào? 2 0, 2 a). 12; b). 0  ,36; c). 2 ; d). ; e).13; 7 3 3 1 2 0,12 1  f).  ; g). ; h). ; n). 0  ,49; m). ; 4 2 5 0,3 7 1 2 0,12 l). ; r). . 2 7 0, 7 Lời giải
a). Số có căn bậc hai số học bằng 12 là 144. b). Vì 0
 ,36 0 nên không tồn tại số nào có căn bậc hai số học bằng 0  ,36; 2 8
c). Tương tự, số có căn bậc hai số học bằng 2 là . 7 7 0, 2 0, 04
d). Số có căn bậc hai số học bằng và . 3 3
e). Số có căn bậc hai số học bằng 13 là 169. 3
f). Vì   0 nên không tồn tại 4 1 2 1
g). Số có căn bậc hai số học bằng là . 2 5 10 0,12 0,144
h). Số có căn bậc hai số học bằng là 0, 3 3 n). Vì 0
 , 49  0 nên không tồn tại số nào có căn bậc hai số học là 0  ,49 . 1 
m). Không tồn tại số nào có căn bậc hai số học bằng 7
4 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học 1 2 1
l). Số có căn bậc hai số học bằng là 2 7 10 0,12 0,12
r). Số có căn bậc hai số học bằng là 0, 7 7 DẠNG 3. SO SÁNH HAI SỐ 1. Phương pháp.
Áp dụng: Với a  0,b  0 ta có: a b a b .
2. Bài tập minh họa. Bài tập 4. So sánh: a). 3 và 5 b). 8 và 63 c). 9 và 79 Lời giải
a) Ta có 3  9 và 9  5  9  5 . Vậy 3  5 .
b) Ta có 8  64 và 64  63  64  63 . Vậy 8  63 .
c) Ta có 9  81 và 81  79  81  79 . Vậy 9  79 .
Bài tập 5. Không dùng máy tính hoặc bảng số, hãy so sánh: 1 3 1 a). 26  3 và 63 ; b). và . 2 2 Lời giải 3 1 1 a). 26  3  63 b).  . 2 2
Bài tập 6. So sánh các số sau a). 5 và 17 1. b). 3 và 15 1 c ). 1 3 và 0,2 Lời giải a). 5 và 17 1.
Ta có 5  4 1  16 1.
Mà 16  17 (Do16  17) nª n 5  17 1
b). Tương tự câu b, 3  4 1  16 1.
Vì 16  15 (v× 16  15) nªn 3 > 15 1
c). Ta có 1 3  1 - 3  0 mµ 0  0,2 nªn 1- 3  0,2
Bài tập 7. So sánh các số sau a). 7  15 và 7 b). 3 26 và 15 c). 2  11 và 3  5 30  2 45 d). 30  và 5 35 e). và 17 f). 15  24 và 101 1 4 17  2 15 g). và 2 6 Lời giải
a). Ta có: 7  9  9; 15  16  4  7  15  3  4  7
b). Ta có: 26  25  5  3. 26  3.5  3. 26  15
c). Ta có : 2  3; 11  25  2  11  3  5
d). Ta có : 35  36  6  5. 35  5. 36  30  5  35  30  30  2 45 30  2 49 30  2.7 e). Ta có :    4  16  17 4 4 4
5 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
f). Ta có 15  24  16  25  4  5  9; 101 1  100 1 10 1  9  101 1  15  24 Vậy 101 1  15  24 2      2 17 2 15 17 2 16 3 17 2 15 17  2 15 g). Ta có       2, 25     2   2 6 6 2 6 6   17  2 15 Vậy  2 . 6
Bài tập 8. So sánh các số sau a). 2  3 và 10 b). 5  2 và 2  6
c).  3  2 và  2  6 7 1 7 d). 8  và  15  7 e). 3  2 2 và 2 f). và 3 12 4 3 Lời giải Đưa về so sánh 2 A và 2 B 2 2
a). Xét  2  3  5  2 6  5  24; 10  10  5  25 2 2
Vì 24  25   2  3   10  2  3  10 2 2
b). Xét  5  2  9  4 5  9  80; 2  6   8 2 12  8  48 2 2
Vì 9  80  8  48   5  2   2  6   5  2  2  6 2 2 2 2
c). Xét  3  2  7  4 3  7  48; 2  6   8  2 12  8  48   3  2   2  6   3  2  2  6  3   2   2  6 d). Xét   2 2 15 7
 22  2 105;8  22  2 441    2 2 15 7  8
 15  7  8   15  7  8  e). Xét   2 3 2 2
17 12 2 17  288 và 2 2  17  169 Vì       2 2 17 288 17 169 3 2 2  2  3 2 2  2 2 2  7 1  49  7  49 f). Ta có  .   ;      3 12 108    4 3  48 2 2 49 49  7   7 1  7 7 1 Vì       .    .   48 108  4 3  3 12 4 3 3 12  
Bài tập 9. So sánh các số sau a). 30  29 và 29  28 b). 27  6 1 và 48 c). 21  2 và 14  3 d). 17  6 và 21  2 Lời giải
a). Ta có  30  29 30  29 1; 29  28 29  28 1 1 1 30  29  29  28    30  29  29  28 30  29 29  28
b). 27  6 1  3 3  6 1 và 48  4 3  3 3  3
6 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
Mà 6 1  3 1  3  27  6 1  48. 2 2 2
c). Ta có  21  2   21  2. 21. 2   2   23 2 42   2  2    2 14 3 14 2. 14. 3 3
14  2 42  3 17  2 42 2 2
Vì 23  17  23  2 42  17  2 42   21  2    14  3  21  2  14  3 Vậy 21  2  14  3 . 2 2
d). Ta có  17  6  23 2 102; 21  2   23 2 42 2 2
Vì 23  2 102  23  2 42   17  6    21  2   17  6  21  2 Vậy 17  6  21  2 . 2 2 2 2
Nhận xét: Khi so sánh a b và c d mà  a    b    c    d  thì ta sẽ đi so
sánh bình phương của hai số, rồi từ đó suy ra kết quả.
Bài tập 10. Sắp xếp theo thứ tự tăng dần 23;2 7;5 6; 8  2; 127 Lời giải Ta có 2 8
 2   8 .2   128   127  0
Ta so sánh các số dương 23; 2 7;5 6 như sau: 2 2 2
23  23  529; 2 7  2 .7  28;5 6  5 .6  150
Do 28  150  529  28  15  529  2 7  5 6  23
Vậy  128   127  2 7  5 6  23.
Bài tập 11. So sánh hai số sau 29  28 và 28  27 Lời giải Xét      1 29 28 29 28  29  28  1  29  28  29  28      1 28 27 28 27  28  27  1  28  27  28  27 1 1
Vì 27  29  28  27  29  28   28  27 29  28  28  27  29  28 Vậy 28  27  29  28
Nhận xét: Để so sánh hai số dạng a b và
b d ( a, , b ,
c d là các số dương) mà
a b b d ta làm như sau:  a b  a b   a  ; b
b d  b d   b d
Sau đó từ việc so sánh hai số a b và b d ta sẽ só sánh được hai số a b và b d
7 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học Bài tập 12. So sánh
a). 2  2  2  2 2 và 2
b). x  13  15; y  11  17
c). x  23  21; y  19  17
d). x  12  5; y  20  3 Lời giải
a). 2  2  2  2 2  2  2  2  2 4    2
b). Ta có: (13 15  1117); , x y  0 2
x  28 2 13.15; Khi đó   2 2
x y x y 2
y  28 2 11.17
c). Ta có: (23  21  19 17); 23  21 2 2 x   ; y  23  21 23  21 19  17
Vì 23  21  19  17  x y a b
Chú ý: a,b  0  a b   a b  a b   a b a b d). Ta có12.5  20.3; 2 x 17  2 60  ; 2 2
x y  ,
x y  0  x y 2 y  23 2 60 Bài tập 13. So sánh: 1 1 1 1 a).    ... và 10.
b). 4  4  4  .....  4 và 3. 1 2 3 100 Lời giải 1 1 1 1 a).    ... và 10. 1 2 3 100 1 1 1 1 Đặt a    ... 1 2 3 100 1 1 1 1 1 Ta có    ....   a  100.  10 1 2 3 100 100
b). 4  4  4  .....  4 và 3.
Ta có 4  3  4  4  4  3  3
 4  4  4   4  3  3
 4  4  4  .... 4  4  3  3
DẠNG 3. TÌM x THỎA ĐIỀU KIỆN CHO TRƯỚC 1. Phương pháp. Áp dụng:
x a a   2 0  x a
Với a,b  0 : a b a  . b
8 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
2. Bài tập minh họa.
Bài tập 14. Tìm số x không âm, biết: a) x 15; b) 2 x  14; c) x  2; d) 2x  4. Lời giải a) Ta có 2 x  15 
x  15  x  225. Vậy x  225 .
b) Ta có 2 x  14  x  7  x  49  x  49. Vậy x  49.
c) Ta có x  2  x  2. Kết hợp điều kiện 0  x  2.
d) Ta có 2x  4  2x  16  0  2x  16  0  x  8. Vậy 0  x  8.
Bài tập 15. Tìm x không âm biết : a). x  5 b). x  2 c). x  2  1 d). 2x   3
e). 2x 1  3  0 f). 2
x  4x 13  3 . 3 Lời giải a) Ta có 2
x  5  x  5  25 b) Ta có 2
x  2  x  ( 2)  2
c) Ta có x  2   k ô h ng x  1 13 d) Ta có 2x   3  x  3 3
e) Ta có 2x 1  3  0  x  f) Ta có 2
x  4x 13  3  x  2.
Bài tập 16. Tìm giá trị của x biết : a). 2 9x 16  0 . b). 2 4x  13. c). 2 2x  9  0. 2x 1 d).   2  0
e). x 1  3(x  0) f). 2 x 1  2 3 1 g). 2
x  5x  20  4 n). 2x   3
m). 2x 1  3  0 3 l). 2
x  4x 13  3. Lời giải 2  4  4 a) Ta có 2 2
9x 16x  0  x   x      3  3 2  13  13 b) Ta có 2 2
4x  13  x     x     2 2   c) Vì 2 2
x  0  2x  9  0  x  35 d) Ta có 2
2x 1  6  2x 1  6  x  2
e) Ta có x 1  3(x  0)  x  4  x  16 f) Ta có 2 2 2
x 1  2  x 1  2  x  1  x  1  x  1  g) Ta có 2 2 2
x  5x  20  4  x  5x  20  16  x  5x  4  0   x  4  13 h) x  m). x  l). x  2. 3
9 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Bậc Hai Số Học
Bài tập 17. Tìm giá trị của x , biết: 1 1 a). 2x  b). 3  x   5 c). 2  x 1  7 3 2 3 d). 2x 1  e). x  3 f). 3x  9 2 Lời giải 1 1 1 1 a) Ta có 2x
 2x   0  2x   0  x  3 9 9 18 1 1 b) Điều kiện: 3
x   0  x  2 6 1 1 49 Ta có 3  x   5  3
x   25  x   (TMĐK) 2 2 6 1
c) Điều kiện: x  . 2 3 Ta có 2x 1   2
x  1 49  x  2  4 (TMĐK) 2 1
d) Điều kiện: x  . 2 3 Ta có 2x 1   9 13 2x 1   x  2 4 8 1 13
Kết hợp điều kiện ta được  x  2 8
e). Ta có x  3  x  9  0  x  9 .
f). Ta có 3x  9  3x  81  3x  81  x  27
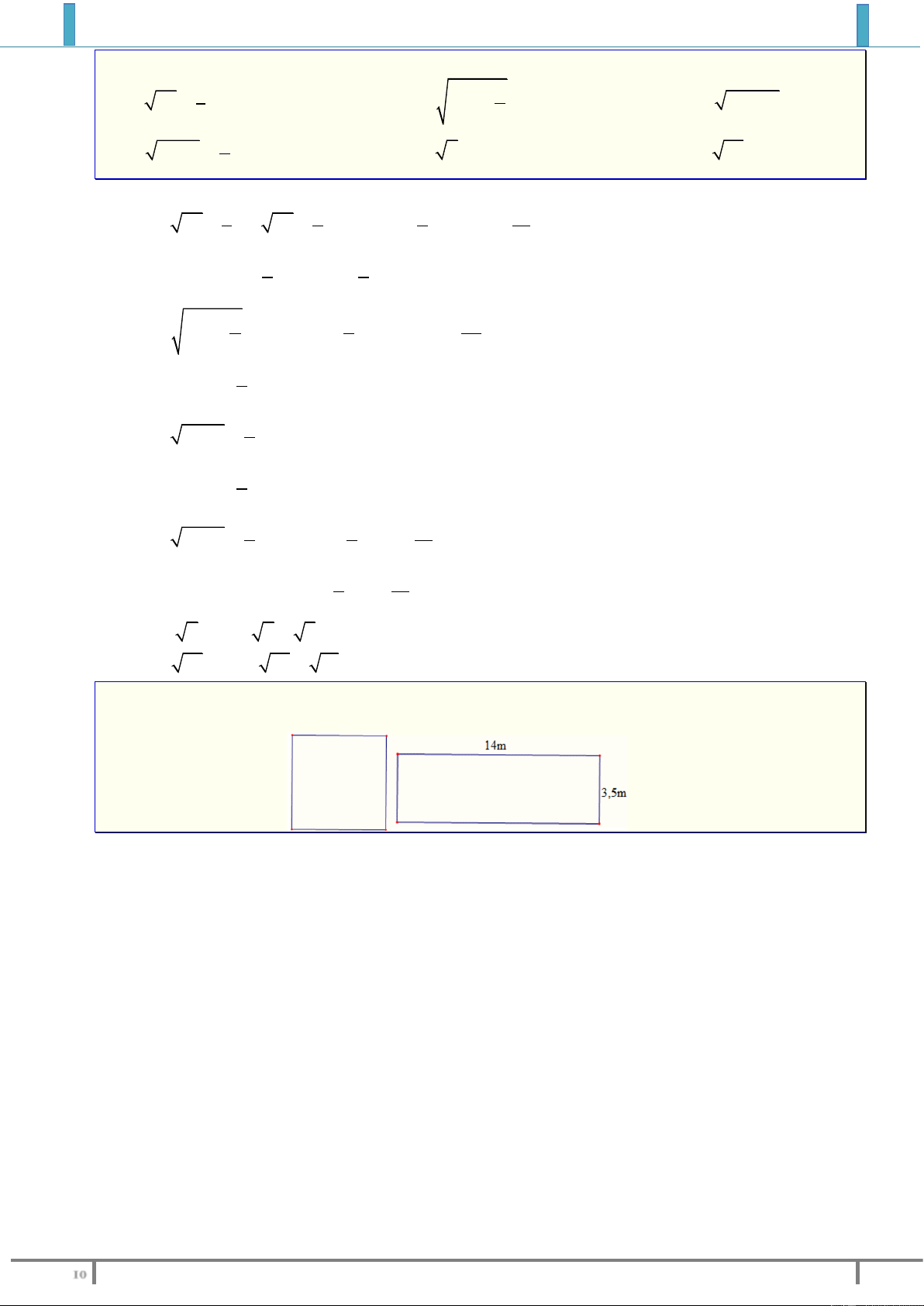
Bài tập 18. Đố. Tính cạnh của một hình vuông, biết diện tích của nó bằng diện tích của hình chữ
nhật có chiều rộng 3,5 m và chiều dài 14 m. Lời giải
Diện tích hình chữ nhật là 2 3, 5.14  49(m ).
Gọi cạnh của hình vuông là x x  0. Ta có: 2
x  49  x  7.
Vậy cạnh của hình vuông là 7m.
10 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
§BÀI 2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC A. TÓM TẮT LÝ THUYẾT 1. Căn thức bậc hai:
Nếu A là một biểu thức đại số thì A gọi là căn thức bậc hai của . A A x
ác định (hay có nghĩa) khi A  0.
Ví dụ 1. Tìm x để căn thức 5  2x có nghĩa. Lời giải 5
Ta có 5  2x có nghĩa khi 5  2x  0  2  x  5   x  . 2
Ví dụ 2. Có bao nhiêu giá trị nguyên của x để biểu thức M x  4  2  x có nghĩa? Lời giải x  4  0 x  4 
Ta có M có nghĩa khi    2  x  0 x  2
Vì x Z nên x  4  ; 3  ; 2  ; 1  ;0;1;  2
Vậy có 7 giá trị nguyên của x để biểu thức M có nghĩa 2. Hằng đẳng thức 2 A A .
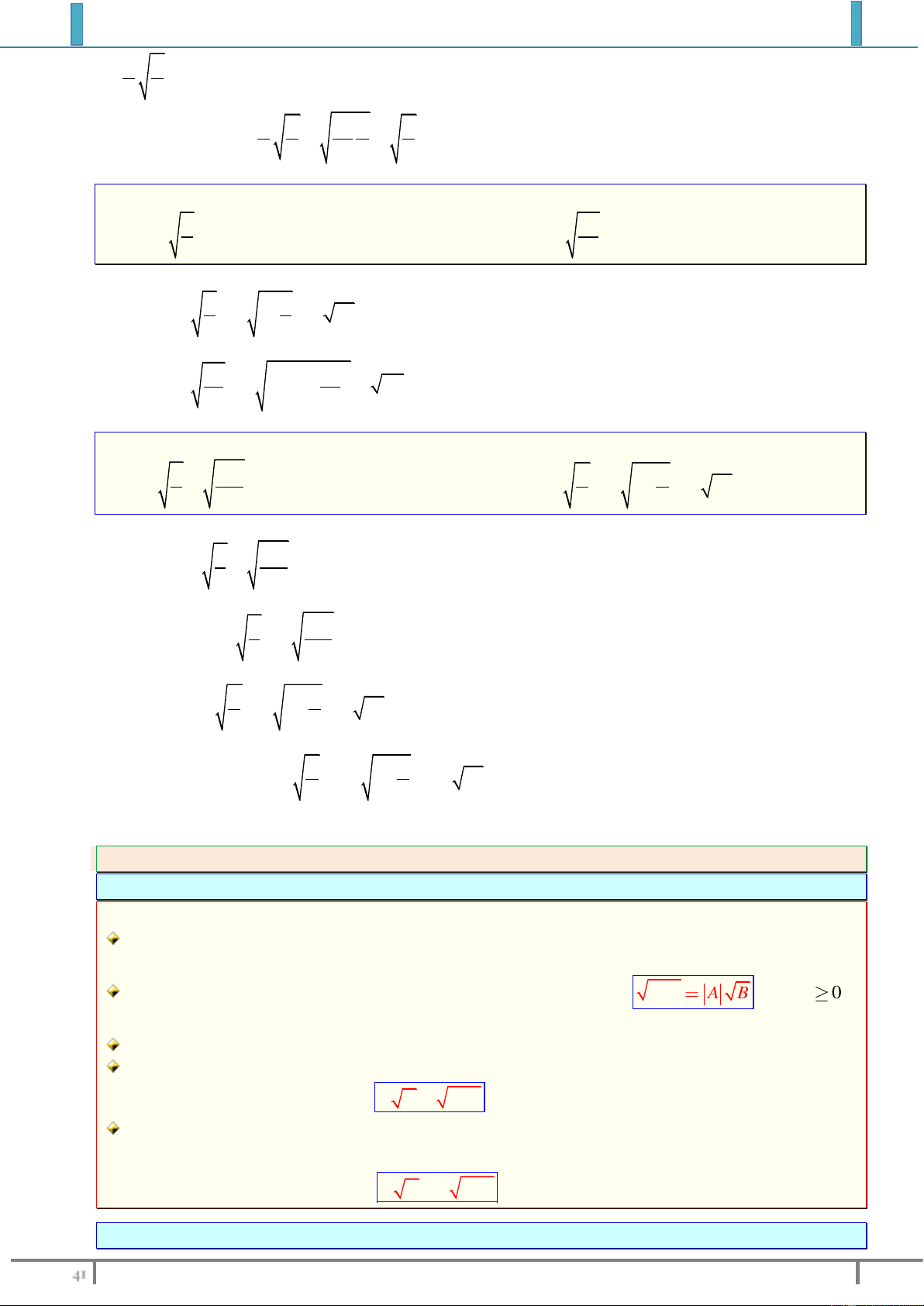
Với mọi số a, ta có 2 a |  a | . A khi A  0 Khi đó 2 A   A khi A  0
Ví dụ 3. Tính giá trị của biểu thức: 0,09  7. 0,36  3 2, 25. Lời giải
Ta có 0,09  7. 0,36  3 2, 25   2   2   2 0,3 7. 0, 6 3 1,5
 0,3  7.0, 6  3.1,5  0,3  4, 2  4,5  0 .  9 9 
Ví dụ 4. Giá trị của biểu thức sau là số vô tỉ hay hữu tỉ:  1 - .18 ?   16 16   Lời giải  9 9   25 9   5 3  Ta có  1 - .18   - .18   .18  9  3.       16 16 16 16      4 4 
Vậy giá trị của biểu thức đã cho là một số hữu tỉ, hơn nữa còn là một số tự nhiên.
Ví dụ 5. Tính giá trị của biểu thức C  3  2 2  6  4 2 . Lời giải 2 2
Ta có C  3  2 2  6  4 2   2   1  2 2 
2 1  2  2  2 1 (2  2)  2 2  3. 1
Ví dụ 6. Rút gọn biểu thức 2 A x x  . 4 Lời giải
11 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai 2 1  1  1 Ta có 2 A x x   x   x    4  2  2  1 1 Nếu x
thì A x  2 2  1 1 Nếu x  thì A   x 2 2
Ví dụ 7. Rút gọn biểu thức 4 6 B x x . Lời giải 2 2 Ta có 4 6     2    3 B x x x x  2 3 2 3
x x x x .  Nếu x  0 thì 2 3
B x x ;  Nếu x  0 thì 2 3
B x x .
Ví dụ 8. Cho biểu thức: 2
P  3x x 10x  25.
a). Rút gọn biểu thức P ;
b). Tính giá trị của P khi x  2 . Lời giải
a). Rút gọn biểu thức P ; Ta có 2
P  3x x 10x  25  x   x  2 3 5
 3x x  5 .
 Nếu x  5 thì P  3x  (x 5)  2x  5 .
 Nếu x  5 thì P  3x  (x 5)  4x 5 .
b). Khi x  2  5 thì giá trị của biểu thức là : P  4.2  5  3.
Ví dụ 9. Cho biểu thức: 2
Q  2x x  2x 1.
a). Rút gọn biểu thức Q ;
b). Tính các giá trị của x để Q  7 . Lời giải
a). Rút gọn biểu thức Q ; Ta có 2 2
Q  2x x  2x 1  2x  (x 1)  2x x 1  Nếu x  1
 thì Q  2x  (x 1)  x 1  Nếu x  1
 thì Q  2x  (x 1)  3x 1
b). Tính các giá trị của x để Q  7 .
Ta phải xét hai trường hợp:
Q  7  x 1  7  x  8 ( Không thỏa mãn x  1)
Q  7  3x 1  7  x  2 ( Không thỏa mãn x 1).
Vậy Q  7 khi x  8
Ví dụ 10. Tìm giá trị nhỏ nhất của biểu thức 2
D  4x  4x 1  3. Lời giải Ta có 2
D  4x  4x 1  3 =  x  2 2 1
 3  2x 1  3  3 với mọi x .
12 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai 1
Vậy minD = 3 khi x  . 2
Ví dụ 11. Tìm x , biết 2
x  6x  9  7x  13. Lời giải Ta có 2
x  6x  9  7x  13   x  2 3  7x 13
x  3  7x 13 (1)
 Nếu x  3 thì x  3  x  3.
Khi đó (1) trở thành x  3 7x 13  8x 16  x  2 (không thuộc khoảng đang xét )
 Nếu x  3 thì x 3  3 . x 5
Khi đó (1) trở thành 3  x  7x  13  6x  10  x
( thuộc khoảng đang xét ) 3 5
Vậy giá trị của x thỏa mãn đẳng thức đã cho là x  . 3
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
Dạng 1. TÌM ĐIỀU KIỆN ĐỂ A CÓ NGHĨA 1. Phương pháp. 1 ①
A có nghĩa  A  0. ② có nghĩa  A  0. A
2. Bài tập minh họa.
Bài tập 1. (Bài 6, tr. 10 SGK). Với giá trị nào của a thì mỗi căn thức sau có nghĩa: a a). ; b). 4  a; c). 5  a; d). 3a  7. 3 Lời giải a a a)    a  3 có nghĩa 0 0. 3 b) 5a      có nghĩa 5a 0 a 0. c) 4  a      có nghĩa 4 a 0 a 4. 7 d) 3a  7       có nghĩa 3a 7 0 a . 3
Bài tập 2. (Bài 12, tr. 11 SGK) Tìm x, để mỗi căn thức sau có nghĩa: 1 a). 2x  7; b). 3  x  4; c). ; d). 2 1 x . 1   x Lời giải 7 a) 2x  7       có nghĩa 2x 7 0 x . 2 4 b) 3  x  4         có nghĩa 3x 4 0 3x 4 x . 3 1 c)
   x   x  1   x có nghĩa 1 0 1. d) Vì 2 1 x  0  với mọi x nên 2
1 x có nghĩa với mọi x
13 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
Bài tập 3. (Bài 37, tr. 20 SGK) Với giá trị nào của a thì mỗi căn thức sau có nghĩa: 1 2 a 1 a). ; b). ; c). 2 a 1; d). 2 4  a . 2 a 1 2a Lời giải 1 1 a)   0  a  0. 2 có nghĩa a 2 a 2 a 1 1 b)   a  (vì 2 a 1  0, a   )  a  . 1 2a có nghĩa 1 2 0 2 c) 2 a 1      có nghĩa 2 2 a 1 0 a 1 |
a |1  a  1  hoặc a 1. d) 2 4  a      có nghĩa 2 2 4 a 0 a 4 |  a | 2  2   a  2.
3. Bài tập rèn luyện. 1
Bài 1. Tìm x để căn thức có nghĩa. 2 x  4x  4 Lời giải 1 1 Ta có có nghĩa khi có nghĩa. 2 x  4x  4 2 (x  2) Điều đó xảy ra khi 2
(x  2)  0  x  2.
Bài 2. Với giá trị nào của x thì biểu thức 2 25  x có nghĩa? Lời giải Ta có 2
25  x có nghĩa khi 2 25  x  0 2  x  25  2
x  25  x  5  5   x  5. 1
Bài 3. Tìm các giá trị của x để biểu thức có nghĩa 2 x 100 Lời giải 1 x 10 Ta có có nghĩa khi 2 x 100  0 2
x 100  x 10   2 x 100 x  10 
Bài 4. Biểu thức sau xác định với giá trị nào của x ? 4 2 a). 3  x  2 ; b). ; c). ;
d). x x  2 ; 2x  3 2 x 2x 1 e). 2 9x  6x 1 f). g). 2 5x  3x  8 h). 2
5x  4x  7 . 2  x Lời giải 2 a) Đk: 3  x  2  0  3  x  2   x  . 3  4   0 3 
b) Đk: 2x  3
 2x  3  0  2x  3   x  . 2 2x 3  0  2   0 c) Đk: 2 2  x
x  0  x  0. 2 x  0
14 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai x  0 x  0   x  2  0 x  2 x  0
d) Đk: x x  2  0    .   x  0 x  0 x  2   x  2  0 x  2
e) Đk: x x     x  2 2 9 6 1 0 3 1  0, . x  1    x  2x 1 0  2        1 2 x 0 x  2 2x 1  x  2 1 f) Đk: 0      2   x  2 .    2 x 2x 1  0  1  2    x  x  2  x  0  2  x  2 g) Đk: 2 2
5x  3x  8  0  5x  8  5 x  8  0   2
5x  8x  5x 8  0  5x 8 x   1  0 5x  8  0   8 x 1  0   x    5 . 5x  8  0   x  1  x 1 0 h) Đk: 2 2
5x  4x  7  0  25x  20x  35  0   x x       x  2 2 25 2.5 .2 4 31 0 5 2  31  0, . x
Bài 5. Tìm x để biểu thức sau có nghĩa: 1 2 a). 2
x  3  x  9 b). x  2  c).  5  2x x  5 2 x  9 4  x
d). 2x  4  8  x e). 2  9  x f). 2
x  4  2 x  2 x 1 x x x g).  x  2 h).  x  2 i).  x  2 x  2 x  2 2 x  4 3 x 1 2x 1 j). x   3  x k).  x  2 l).  x  2 x x  2 x  2 2x m). 2  x x  2 2 x  4 Lời giải
a) Biểu thức đã cho có nghĩa khi x  3  0 x  3  0  x  3  0  x  3          x  3 2 x  9  0   x  3  x 3  0   x  3    0 x  3 x  2  0 x  2
b) Biểu thức đã cho có nghĩa khi    x  5  0 x  5 x  3  x  3 2 x  9  0  
c) Biểu thức đã cho có nghĩa khi    5   5 5   2x  0 x x     2  2 xx  2  0 x  2 d)
x  2 có nghĩa      x  2 x  2 x  2  0 x  2 xx  2  0 x  2 e)
x  2 có nghĩa      x  2 x  2 x  2  0 x  2 
15 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai xx  2 f)
x  2 có nghĩa    x  2 2 x  4 x  2  2  3  x  3 3 x   0   0 g). x   3
x có nghĩa   x   xx  x  3  x  0 x  0 x 1 x  2  0 x  2 h)
x  2 có nghĩa khi     x  2 x  2 x  2  0  x  2  2x 1 x  2  0 x  2 i)
x  2 có nghĩa khi     x  2 x  2 x  2  0  x  2 2xx  2  0 x  2 j) 2
x x  2 có nghĩa khi     x  2 2 x  4 2 x  4  0  x  2 
Bài 6. Chứng minh rằng các biểu thức sau luôn có nghĩa với mọi x 2 2x 1 a). 2 A x x 1  . b). 2 B
 2x x  2 2 x  2 2 x 1  x Lời giải 2  1  3 a). Ta có 2
x  2  0 với mọi x và 2
x x 1  x    0   với mọi . x  2  4
Do đó biểu thức đa cho luôn có nghĩa với mọi . x 2  1  15 b). Ta có 2
2x x  2  2 x    0   với mọi . x  4  8 Lại có 2 2 2 x 1  0  x 1  x x x |
x | x  0 với mọi x
Vậy biểu thức đã cho luôn xác định với mọi x .
Bài 7. Chứng minh rằng các biểu thức sau luôn có nghĩa với mọi x 2 3x  5 a). 2 A x x 1  b). 2 B
x x 1 2 x 1 2 x  2x  3 Lời giải 2  1  3 a). Ta có 2 x 1  0, x  và 2
x x 1  x    0, x     2  4
Do đó biểu thức luôn có nghĩa với mọi x . b). Ta có 2 2
x  2x  3  (x 1)  2  0, x  2  1  3 Và 2
x x 1  x    0, x     2  4
Do đó biểu thức đã cho luôn có nghĩa với mọi x .
Dạng 2. TÍNH GIÁ TRỊ BIỂU THỨC 1. Phương pháp. A khi A  0 Áp dụng: 2 A   A khi A  0
2. Bài tập minh họa. Bài tập 4. Tính a).  2 0,1 ; b).  2 0,3 ; c).   2 1,3 ; d).   2 0, 4 0, 4 . Lời giải
16 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai a)  2 0,1 |  0,1| 0,1. b)  2 0,3 |  0  ,3| 0,3. c)   2 1,3   | 1  ,3| 1  ,3. d)   2 0, 4 0, 4  0  ,4.| 0  ,4 | 0  ,16.
Bài tập 5.(Bài 11, tr. 11 SGK) Tính: a). 16. 25  196 : 49; b). 2 36 : 2.3 .18  169; c). 81; d). 2 2 3  4 . Lời giải
a) Ta có 16. 25  196 : 49  4.5 14 : 7  20  2  22. b) 2 2
36 : 2.3 .18  169  36 : 18 13  36 :18 13  2 13  1  1. c) 81  9  3. d) 2 2 3  4  25  5.
Bài tập 6. Thực hiện phép tính a). 2 A  (2 2  3) b). 2 B  (0,1 0,1) c). 2 2 C  (2 2  3)  (2 2  3) d). 2 2 D  (2 6  5)  (2 6  5) Lời giải a). Ta có 2 A  (2 2  3) |  2 2  3 | 3  2 2 b). Ta có 2 B  (0,1 0,1) |
 0,1 0,1 | 0,1  0,1 c). Ta có 2 2
C  (2 2  3)  (2 2  3) |
 2 2  3 |  | 2 2  3 | 6 d). Ta có 2 2
D  (2 6  5)  (2 6  5) |
 2 6  5 |  | 2 6  5 | 4  6
Bài tập 7. Rút gọn biểu thức: a). 2 (4  3 2) b). 2 (2  5) c). 2 (4  2) d). 2 2 3  (2  3) e). 2 (2  3) f). 2 (2  5) g) 2 2 ( 3 1)  ( 3  2) h). 2 2 (2  5)  ( 5 1) Lời giải a). Ta có: 2
(4  3 2)  4  3 2  3 2  4 b). Ta có: 2
(2  5)  2  5  2  5 c). Ta có: 2 (4  2)  4  2 d). Ta có: 2
2 3  (2  3)  2 3  2  3  2  3 e). Ta có: 2 (2  3)  2  3 f). Ta có: 2 (2  5)  5  2 g). Ta có: 2 2
( 3 1)  ( 3  2)  3 1 2  3  1 h). Ta có: 2 2
(2  5)  ( 5 1)  5  2   5   1  1 
Bài tập 8. Thực hiện phép tính
a). A  2(5 16  4 25)  64
b). A  2015  36  25 Lời giải
17 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai a). 2 2 2
A  2(5 4  4 5 )  8  2(5.4  4.5)  8  2(20  20)  8  8 b). 2 2
A  2015  6  5  2015  6  5  2016.
Loại m  2. n 1. Phương pháp ① Cách 1.
Nhẩm hai số a và b sao cho .
a b n và a b m
Sử dụng các hằng đẳng thức: 2 2 2
a  2ab b  (a b) hoặc 2 2 2
a  2ab b  (a  ) b
② Cách 2: Dùng máy tính:
Nhấn Mode 5 3 Nhập a  1; b  m; c n sẽ cho được hai số a và b cần tìm.
Sử dụng các hằng đẳng thức như cách 1.
③ Chú ý: Sử dụng công thức: . a b
a. b với a,b  0 .
2. Bài tập minh họa Bài tập 9. Rút gọn a). 3  2 2 b). 8  2 15 c). 23  2 120 Lời giải a). 3  2 2
Bấm máy Mode/5/3: nhập a  1;b  3
 ;c  2 ta được a  2;b 1 2 2 Khi đó 2
3  2 2  3  2 2.1  3  2 2 1 
2  2 2. 1  1  ( 2  1)  2  1  2 1 b). 8  2 15
Bấm máy Mode/5/3 nhập a  1;b  8
 ;c 15 ta được a  5;b  3 2 2 Khi đó 2
8  2 15  8  2 5.3  8  2 5 3 
5  2 5. 3  3  ( 5  3)  5  3  5  3 c). 23  2 120
Bấm máy Mode/5/3 nhập a  1;b  2
 3;c 120 ta được a 15;b  8. 2 2
Khi đó 23  2 120  23  2 15.8  23  2 15. 8  15  2 15. 8  8 2
 ( 15  8)  15  8  15  8  15  2 2
Loại m k n 1. Phương pháp
① Trường hợp 1: Nếu k là số chẵn thì tách sao cho k  2k
Đưa k vào căn bậc hai bằng công thức:    2 k k Bài toán về dạng 2.
Chú ý: Sử dụng công thức đưa vào căn bậc hai: 2 a a
với a là một số không âm.
2. Bài tập minh họa Bài tập 10. Rút gọn a). 27 10 2 b). 36 12 5 c). 49 12 5  49 12 5 Lời giải
18 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai a). 27 10 2
Ta tách số 10  2.5 và đưa số 2 5  5  25 2 2 Khi đó 2
27 10 2  27  2.5. 2  27  2. 25 2 
25  2 25 2  2  ( 25  2) 
25  2  25  2  5  2
Nhận xét: Ta thấy 25  2  27 . Vậy a  25 và b  2 . b). 36 12 5
Ta tách số 12  2.6 và đưa số 2 6  6  36
Khi đó 36 12 5  36  2.6. 5  36  2. 36. 5  36  2 180  36  2 30. 6 2  36  2 30. 6 
30  2 30. 6  6  ( 30  6)  30  6)  30  6
Nhận xét: Ta thấy 36  5  36 nên ta phải nhân 36.5 180 để đưa bài toán về dạng m  2. n 2 2
c). 49 12 5  49 12 5  2 3 5  2  3 5  4. ② Trường hơp 2:
Nếu k là số lẻ thì nhân cả tử và mẫu của m k n cho 2. a a Sử dụng công thức: 
Với a là một số không âm, b là một số dương. b b Bài toán về dạng 2.
3. Bài tập minh họa Bài tập 11. Rút gọn 4  7 a). 5  21 b). 8  2 7 . 2 Lời giải a). 5  21
Ta nhân vào trong căn thức cả tử và mẫu cho 2 2(5  21) 10  2 21 10  2 21 Khi đó 5  21    2 2 2 2 2  10  2 7. 3 7  2 7. 3  3 2 7 3 ( 7  3) 7  3      2 2 2 2 2 4  7 b). 8  2 7 . 2   Ta có     2 4 7 8 2 7 8 2 7 1 7 2 4 2 7 1 1 7 7 1 6  1 7       .    3 2 2 2
Bài tập 12. Rút gọn các biểu thức sau 2 2 a). A    2 4 15  15
b). B  2  3  1 3
c). C  49 12 5  49 12 5
d). D  29 12 5  29 12 5 Lời giải
19 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai 2
a). A  4  15  15  4  15  15  44  15 2 2
b). B  2  3  1 3  2  3  1 3 1 2 2
c). C  49 12 5  49 12 5  2 3 5  2 3 5  C  4 2 2
d). D  29 12 5  29 12 5  3 2 5  3 2 5  D  6
Bài tập 13. Rút gọn các biểu thức sau a). 8  2 15  6  2 5
b). 17  2 72  19  2 18
c). 12  2 32  9  4 2
d). 29  2 180  9  4 5
e). 4  7  4  7  2
f). 6  11  6  11  3 2
g). 8  2 15  7  2 10
h). 10  2 21  9  2 14 i). 8  3 7  4  7 j). 5  21  5  21 k). 9  3 5  9  3 5
l) . ( 10  2) 4  6  2 5 Lời giải
a). 8  2 15  6  2 5  3  2 3. 5  5  5  2 5.11 .
   2    2 3 5 5 1
 3  5  5 1  3 1.
b). 17  2 72  19  2 18  9  2. 9. 8  8  18  2 18.11 . 2 2
 3 2 2   18   1
 3 2 2  18 1  4  2 2  18 .
c). 12  2 32  9  4 2  8  2 8. 4  4  8  2.2. 2.11 .    2    2 2 2 2 2 2 1
 2 2  2  2 2 1  4 2 1.
d). 29  2 180  9  4 5  20  2. 20. 9  9  5  4 5  4 .    2    2 20 3 5 2
 20  3 5  2  5 1 5.
e). 4  7  4  7  2 . 2
Ta có:  4 7  4 7   4 7  4 7  2 4 74 7  8 2 167
 8  2 9  8  6  2
Do đó 4  7  4  7   2 Vì 4  7  4  7 .
Suy ra 4  7  4  7  2   2  2  0 .
f). 6  11  6  11  3 2 . 2
Ta có:  6 11  6 11  6 11 6 11 2 6 76 11 .
 12  2 36 11  12  2 25  12 10  2 .
Do đó 6  11  6  11  2
20 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai Vì 6  11  6  11 .
Suy ra 6  11  6  11  3 2  2  3 2  4 2 .
g). 8  2 15  7  2 10  5  2 5. 3  3  5  2 5. 2  2 2 2
  5  3   5  2  5  3  5  2  2  3 .
h). 10  2 21  9  2 14  7  2 7. 3  3  7  2 7. 2  2 .
   2    2 7 3 7 2
 7  3  7  2  2  3 . i). 8  3 7  4  7 . Ta có:     2 8 3 7 4 7
12  4 7  2 8  3 7. 4  7
 12  4 7  2 53  20 7 2
 12  4 7  2 2 7 5 12  4 7  22 7 5 12 10  2 .
Do đó 8  3 7  4  7  2 (vì 8  3 7  4  7  0 ). j). 5  21  5  21 . Ta có:     2 5 21 5 21
 5  21  5  21  2 5  21. 5  21
 10  2 25  21  10  4  6
Suy ra 5  21  5  21  6 Vì 5  21  5  21 . k). 9  3 5  9  3 5 . Ta có:     2 9 3 5 9 3 5
 9  3 5  9  3 5  2 9  3 5. 9  3 5
 18  2 81 45  18 12  6
Suy ra 9  3 5  9  3 5   6 Vì 9  3 5  9  3 5 . l).                    2 10 2 4 6 2 5 10 2 4 5 2 5.1 1 10 2 4 5 1 .
  10  2 4  5 1  2  5   1 3  5 .
Bài tập 14. Tính giá trị của các biểu thức sau a). 6  4 2  22 12 2 b). 2 ( 3  2)  2 c). 2 3 5  (1 5) d). 17 12 2  9  4 2 e). 6  2 5  6  2 5 f). 3  2 2  6  4 2 g). 24  8 5  9  4 5    h). 41 12 5 41 12 5 Lời giải a). 2 2
6  4 2  22 12 2  (2  2)  (3 2  2)  2 2 b). 2 ( 3  2)  2  3  2  2  3
21 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai c). 2
3 5  (1 5)  3 5  1 5  3 5  1 5  3 5  ( 5 1)  2 5 1 d). 2 2
17 12 2  9  4 2  (3  2 2)  (2 2 1)  4 e). 2 2
6  2 5  6  2 5  ( 5 1)  ( 5 1)  2 5 f). 2 2
3  2 2  6  4 2  ( 2 1)  (2  2)  3 g). 2
24  8 5  9  4 5  4(6  2 5)  ( 5  2)  2 5 1  5  2  3 5 2 2
h). 4112 5  4112 5  6  5  6  5  2  5
4. Bài tập rèn luyện. Bài 8. Tính: a).   2 0,8 0,125 ; b).  6 2  ; c).   2 3 2 ; d).   2 2 2 3 ; 2  1 1  e).    ; f).   2 0,1 0,1 ; g). 4  2 3 ; h). 3  2 2 ;  2 3  i). 9  4 5 ; j). 16  6 7 . Lời giải a)   2 0,8 0,125  0  ,8 0  ,125  0  ,8.0,125  0  ,1. 2 b) 6 3.2 3 3
    
       3 2 2 2 2  2  8.   c)   2 3 2  3  2  2  3. d)   2 2 2 3  2 2  3  3 2 2. 2  1 1  1 1 1 1 e)      .    2 3  2 3 2 3 2
f) 0,1 0,1  0,1 0,1  0,1 0,1  
1  0,1 1 0,1  0,1 1. g)        2 4 2 3 3 2 3.1 1 3 1  3 1  3 1. h)        2 3 2 2 2 2. 2.1 1 2 1  2 1  2 1. i)        2 9 4 5 5 2. 5.2 4 5 2  5  2  5  2. j)          2 16 6 7 7 2. 7.3 9 7 3  7 3  3 7.
Dạng 3. RÚT GỌN BIỂU THỨC 1. Phương pháp.
A khi A  0 ① Áp dụng 2 A A  
A khi A  0
Xét các trường hợp A  0, A  0 để bỏ dấu giá trị tuyệt đối. ②
A xác định ( có nghĩa)  A  0 .
③ Áp dụng hằng đẳng thức đáng nhớ a b2 2 2
a  2ab b hoặc a b2 2 2
a  2ab b
22 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
2. Bài tập minh họa.
Bài tập 15. Rút gọn các biểu thức sau: 2 2 a).   2 4 15  15 ;
b). 2  3  1 3 ;
c). 7  4 3  7  4 3 ; d). 2
49a , với a  0 . Lời giải a) Ta có   2 4 15
 15  4  15  15  4  15  15  4 .
( Vì 4  15  0 nên 4  15  4  15 ) 2 2
b) Ta có 2  3  1 3  2  3  1 3  2  3  
 1 3  2  3  3 1  1
( Vì 2  3  0 nên 2  3  2  3 và 1 3  0 nên 1 3  3 1) 2 2
c) Ta có 7  4 3  7  4 3    2      2 3 2. 3.2 2 3  2. 3.2  2 2 2
  3  2   3  2  3  2  3  2   3  2  2  3  3  2  2  3  4 . d) Ta có 2 49a   2 7a  7a  7
a . ( Vì a  0 nên 7a  0 , suy ra 7a  7  a )
Bài tập 16. Rút gọn các biểu thức sau: a). 2
25a  3a , với a  0 ; b). 4 2 16a  6a ; c). 6 3
3 9a  6a , với a  0 ; d). 2 2
a  6a  9  a  6a  9 , với 3   a  3. Lời giải a). Ta có 2
25a  3a   a2 5
 3a  5a  3a  5
a 3a  2  a .
(Vì a  0 nên 5a  0 , suy ra 5a  5  a ) b). Ta có 4 2
16a  6a   a 2 2 2 4  6a 2 2  4a  6a 2 2 2
 4a  6a 10a . (Vì 2
a  0 , với mọi a nên 2
4a  0 , với mọi a , suy ra 2 2 4a  4a ) c). Ta có 6 3 3 9a  6a   a 2 3 3 3 3  6a 3 3
 3 3a  6a   3  a  3 3 3. 3  6a  15  a . (Vì a  0 nên 3 3a  0 , suy ra 3 3 3a  3  a ) d). Ta có 2 2 2 2
a  6a  9  a  6a  9  a  3  a  3  a  3  a  3  a  3  3  a
a  3 3 a  6 . (Vì 3
  a  3 nên a 3  0 và a 3  0, do đó a  3  a  3 và a 3  3 a )
Bài tập 17. Rút gọn các biểu thức sau: a  2 a  2 a 1 a).
, với a  0, a  4 ; b).
, với a  0, a  1 ; a  4 a 1 Lời giải
a). Với a  0, a  4 ta có a    a 2 2 4
 2   a  2 a 2 nên: a  2 a  2  1  . a  4
a 2 a 2 a 2  2 a 2  a   a  2 a 1  2 a 1 1 a 1
b). Với a  0, a  1 ta có    . a 1 
a  1 a    a 2 1 1 a 1
23 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
Bài tập 18. Rút gọn biểu thức sau a). 2
9x  2x với x  0 . b). 2
2 x với x  0. c). 2
3 (x  2) với x  2. d). 2
2 x  5x với x  0 e). 2
25x  3x với x  0. f). 4 2
9x  3x với x bất kỳ g). 2
x  4  16  8x x với x  4. Lời giải a) Ta có: 2
9x  2x  3 x  2x  3
x  2x  5  x b) Ta có: 2
2 x  2 x  2x c) Ta có: 2
3 (x  2)  3. x  2  3.2  x  6  2x d) Ta có: 2
2 x  5x  2 x  5x  2
x  5x  7  x e) Ta có: 2
25x  3x  5 x  3x  5x  3x  8x f) Ta có: 4 2 2 2 2
9x  3x  3x  3x  6x
g) Ta có: x  
x x x   x  2 2 4 16 8 4 4
x  4  x  4  x  4  x  4  2x  8
Bài tập 19. Rút gọn biểu thức sau 5  x x 1 a). 2
A  4x 12x  9  2x 1 b). B  c). 2 C  (x 1)  2 x 10x  25 2 x  2x 1 2 x  6x  9 d). D  e). 2 4 2
E x x  8x 16 f). 2
F  1 4a  4a  2a x  3 Lời giải a) Ta
có: b) Điều kiện xác định x  5 2   A
4x 12x  9  2x 1  2x  3  2x 1 5 x 5 x Khi đó B   2   5 10 25  x x x 3
x   A  2x  3 2x 1  4x  4 2 5  x       3 x 5 C 1
x   A  2
x  3 2x 1  2 x  5 2 5  x
x  5  C   1 5  x
c) Điều kiện xác định x  1
d) Điều kiện xác định x  3 x 1 x 1 2 2   
C  (x 1)   x 1  x 6x 9 x 3   2   x 1 D x 2x 1 x  3 x  3 x 1  x  3
x  1  D x 1
x 11  x
x  3  E   1 x 1 x  3 x 1  x  3
x  1  D  x 1
 x 11  x        x 3 E 1 x 1 x  3 e) Ta có: 2 4 2 2 2
F x x  8x 16  x x  4 f) F
a a a   a  2 2 1 4 4 2 2 1  2a 2  x   2 x  4  4  1 2a 1 2a khi a   2
 2a 1  2a   1
2a 1 2a khi a   2
24 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai Bài tập 20. Chứng tỏ: 2
x  2 2x  4  ( 2  x  2) với x  2 .
Áp dụng rút gọn biểu thức sau: x  2 2x  4  x  2 2x  4 với x  2 . Lời giải Thật vậyVP   x   
x    x  2 2 ( 2 2) 2 2. 2. 2 2
x  2 2x  4  VT
Ta có: x  2 2x  4  x  2 2x  4  2  x  2  2 
x  2  2  2  x  2 
Bài tập 21. Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
a). x  4 x  4 với x  4.
b). x  2  2 x  3 với x  3.
c). x  2 x 1  x  2 x 1 với x  1.
d). x  2 x 1  x  2 x 1 với x  0. Lời giải a) Ta có x x   x   x     x   2 4 4 4 4 4 4 4 2  x  4  2
b) Ta có x   x    x   2 2 2 3 3 1
x  3 1  x  3 1 2 2
c) Ta có C x  2 x 1  x  2 x 1   x 1   1   x 1  1
x 1 1  x 1 1
x  2  C x 1 1 x 1 1  2. x 1 1
  x  2  C x 1 1 x 1 1  2 2 2
d) Ta có D x  2 x 1  x  2 x 1   x   1   x   1
x 1  x 1
x 1 D x 1 x 1  2 x
0  x 1 D   x 1 x 1  2
Bài tập 22. Rút gọn các biểu thức sau
x6 x 9 x 3 2
9x 12x  4  2  
a). A  4 x  0  ;x x  9 b). B x    x  9 3x  2  3  Lời giải  x  2 3  x  3
a). Ta có: A  4 x    A x   x
x  3 x  3 3 1 0 9  2 1 khi x  2 9x 12x  4 3x  2  b). Ta có: 3 B     3x  2 3x  2 2  1  khi x   3
Bài tập 23. Rút gọn các biểu thức sau
a). A a  2 a 1  a  2 a 1(1  a  2) b). 2
B  4x x  4x  4 (x  2) 2 x  4x  4 2 x 10x  25 c). C  (x  2) D  2x 1 x  2 d). x  5
(x  6 x  9)( x  3)
e). E  4 x  (0  x  9) x  9 Lời giải
25 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
a). A a  2 a 1  a  2 a 1(1  a  2)  a 1 1  a 1 1
 Với 1 a  2  a 1 1 0; a 1 1 0
 Ta được: A a 1 1  a 1 1  a 1 1 a 1 1 2 b). 2
B  4x x  4x  4(x  2)  4x x  2  4x  (x  2)  3x  2 2 x  4x  4 x  2 c). C  (x  2)  x  2 x  2  Nếu x  2  thì A  1  Nếu x  2  thì A  1 2 x 10x  25 x  5
d). D  2x 1  2x 1 x  5 x  5
 Nếu x 5  0  x  5  A  2x 11 2x
 Nếu x  5  A  2x  2
(x  6 x  9)( x  3)
e). E  4 x  (0  x  9) x  9 2
(x  6 x  9)( x  3)
( x  3) ( x  3)
Ta có E  4 x   4 x
 3( x 1) (0  x  9) x  9
( x  3)( x  3)
Bài tập 24. Cho biểu thức 2 2 2 2 A
x  2 x 1  x  2 x 1
a). Với giá trị nào của x thì A có nghĩa.
b). Tính A nếu x  2 . Lời giải a). 2 2 2 2 2 2 2 2 A
x  2 x 1  x  2 x 1  ( x 1 1)  ( x 1 1) 2 2
x 1 1  x 1 1 x  1  A có nghĩa 2 2
x 1 0  x 1   x 1 b). 2 2 2 2
x  2  x  2  x 1  1  x 1  1 
x 1 1  0 2 2 2
A x 1 1 x 1 1  2 x 1
Bài tập 25. Với giá trị nào của a và b thì: 1 1 a).  . b). 2 2
a (b  2b 1)  a(1 b) . 2 2  2  b a a ab b Lời giải
a). Điều kiện a b 1 1 1 1 Ta có    2 2 2  2  b a (  ) b a a ab b a b
26 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
a b b a a b  0  a b a  0 b   1 b). 2 2
a (b  2b 1)  a(1 b) |
a(b 1) | a(1 b)  a(b 1)  0  a  0   b   1
Bài tập 26. Rút gọn rồi tính giá trị của biểu thức: 1 a). 2
A  9x 12x  4 1 3x tại x  . 3 b). 2
B  2x  6x 2  9 tại x  3 2 Lời giải a). 2
A  9x 12x  4 1 3x Ta có 2 2
A  9x 12x  4 1 3x  (3x  2) 1 3x |  3x  2 | 1   3x 1 1 1
Thay x  vào biểu thức A ta được: A |  3.  2 | 1   3. 111 1 3 3 3 1
Vậy A  1 tại x  3 b). 2 2 B
2x  6x 2  9  (x 2  3) |  x 2  3 |
Thay x  3 2 vào biểu thức B ta được B |  3 2. 2 3| 3
Vậy B  3 tại x  3 2
3. Bài tập rèn luyện.
Bài 9. Rút gọn biểu thức: 1 a). 2
2 x , với x  0 ; b). 10
x , với x  0 ; 2 c). a  2 5 , với a  5; d).  x  10 10 , với x 10 ; 2 2 e). 2
x  4  x  8x 16 , với x  4 ;
f).  x y   x y  , với 0  x y . Lời giải a) 2
2 x  2 x  2  . x 1 1 1 1 1 b) xx  x 2 10 5.2 5 5 5
x   x . 2 2 2 2 2 c) Ta có:
a  5  a 5  0  a  2 5
a  5  5  a d) Ta có:  5 5
x  10  x 10  0   x 10  0  10  x  0. 2  10 5 5 5 5
x 10   x 10    x 10  10  x  10  x .   e) Ta có:
x  4  x  4  0  2 2
x  4  x  8x 16  x  4   x  4  x  4  x  4  x  4   x  4  0 f) Ta có:
 0  x y x y  0  y x  0
27 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai 2 2 2
             2 2 2 x y x y x y x y    x y    
  x y2  x y   x y  y  . x
Bài 10. Rút gọn biểu thức: 3  x x  5 x  6 a).
,  x  0, x  9 b).
,  x  0, x  9 ; c). 2
6  2x  9  6x x ,  x  3 . x  9 x  3 Lời giải 3  x 3  x 1 a).    x
x 3 x 3 . 9 x  3   x x
x 3 x 2 5 6  b).   x  2. x  3 x  3 c).  x
x x   x    x2 2 6 2 9 6 6 2 3
 6  2x  3 x  6  2x  3 x  3 . x
DẠNG 4. GIẢI PHƯƠNG TRÌNH 1. Phương pháp. Áp dụng 2 A A . 2 2
A B A  B .
2. Bài tập minh họa.
Bài tập 27. Tìm x , biết: a) 2 x  7. b) 2 x  8 . c) 2 4x  6. d) 2 9x  12  . Lời giải a) Ta có 2
x  7  x  7  x  7 . Vậy x  7  . b) Ta có 2 x  8
  x  8  x  8  . Vậy x  8  . c) Ta có 2
4x  6  2x  6  x  3  x  3  .Vậy x  3  . d) Ta có 2 9x  12 
 3x  12  x  4  x  4 . Vậy x  4  .
Bài tập 28. Giải các phương trình sau: a). 2 x  5  0. b). 2
x  2 11x 11  0. Lời giải
a) Ta có x    x   x   2 2 2 5 0 5 5
x   5 . Vậy x   5 . 2 2 b) Ta có 2 2
x  2 11x 11  0  x  2. 11.x   11  0  x  11  0  x  11 . Vậy x  11 .
Bài tập 29. Giải các phương trình sau: 1
a). 2x  5  3  x b). 2
1 x x 1 c). 2 x x   2x 4
d). 3x 1  x  3 e). 2
x  5  x  25  0 f). 2 2
(x 1)  x . Lời giải x  3 3   x  0 
a). 2x  5  3  x     2  (t / m)
2x  5  3 x x   3
28 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai x 1 x 1 0 x 1  b). 2
1 x x 1    
 x  0 (Ktm) 2 2 2 2 1
  x  (x 1) 1
  x x  2x 1 
x 1 (t / m) 2x  0 x  0    1  1 1 1      c). 2 x 2x x (t / m) x x   2x x   2x      2  2 4 2     1 1     x   2  xx  (loai)   2   6
3x 1  x  3 x 1
d). 3x 1  x  3    
3x 1  x  3 x  1  x  5   e). 2
x  5  x  25  0  x  5  x  5   x  5  0  1(vn) x 1  x f). 2 2 (x 1) x       1
x 1  xx   2
Bài tập 30. Giải phương trình: a). 2 9x  2x 1 b). 4 x  7 c). 2
x  6x  9  3x 1 d). 2 x  7 e). 2 x  8    f). 2 1 4x 4x 5 g). 4 x  9 h). 2
(x  2)  2x 1 i). 2
x  6x  9  5 j). 2
4x 12x  9  x  3 k). 2 2
4x  4x 1 
x  2x 1 l). 2 2
4x 12x  9  9x  24x 16 Lời giải a). 2
9x  2x 1  3 | x | 2x 1
Trường hợp 1: x  0 , phương trình trở thành: 3x  2x 1  x 1 (TM x  0 ) 1
Trường hợp 2: x  0 , phương trình trở thành: 3
x  2x 1  x   (TM x  0 ) 5 1 Vậy S  {  ;1} 5 b). 4 2
x  7  x  7  x   7 .
Vậy tập nghiệm của phương trình S  { 7; 7} c). 2 2
x  6x  9  3x 1 
(x  3)  3x 1 |
x  3| 3x 1   1
Cách 1: x  3  3x 1
Trường hợp 1: Nếu x  3 
Trường hợp 1: Nếu x  3  Khi đó  
1 trở thành  x  3  3x 1 Khi đó  
1 trở thành x  3  3x 1
x  3x  1   3
 x 3x  1   3  4  x  2  2  x  4
  x  2(TM )   1 x  ( Loại vì không TMĐK) 2
29 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
Vậy phương trình đã cho có một nghiệm S  {2} 1
Cách 2: ĐK : x  . Bình phương hai vế ta có: 2 2
(x  3)  (3x 1) 3 2 2
 (x  3)  (3x 1)  0
 (x  3  3x 1).(x  3  3x 1)  0
4  2x  0  x  2(TM ) (4 2x).(4x 2) 0       1 
4x  2  0  x  (khôngTM )  2
Vậy phương trình đã cho có một nghiệm S  {2} d). 2
x  7  x  7  x  7 
Vậy pt có hai nghiệm x = 7  e). 2
x  8  x  8  x  8 
Vậy phương trình có tập nghiệm là S  {-8;8}. f). 2
1 4x  4x  5 2
 (1 2x)  5  1 2x  5 1
  2x  5  x  2    1   2x  5   x  3
Vậy phương trình có tập nghiệm là S  {-3; 2}. g). 4 x  9 2
x  9  x  3 
Vậy phương trình có tập nghiệm là S  { 3  ;3}. 1  h). 2
(x  2)  2x 1 ( ĐK: x  ) 2 2 2
 (x  2)  (2x 1)  0  (x  2  2x 1).(x  2  2x 1)  0
 (1 x).(3x  3)  0 1   x  0 x  1 (TMĐK )     3x  3  0 x  1  (khôngTM )
Vậy phương trình có tập nghiệm là S  {1 } . i). 2
x  6x  9  5 2
 (x  3)  5  x  3  5
x  3  5  x  8   x  3  5   x  2 
Vậy phương trình có tập nghiệm là S  { 2  ;8 }. j). 2
4x 12x  9  x  3 (ĐK: x  3) 2 2 2
 (2x  3)  x  3  (2x  3)  (x  3)  0
 (2x  3  x  3).(2x  3  x  3)  0 x  0 x  0 (KhôngTM )  .(
x 3x  6)  0     3x  6  0 x  2 (khôngTM )
30 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
Vậy phương trình có tập nghiệm là S   . k). 2 2
4x  4x 1  x  2x 1 2 2 2 2
 (2x 1)  (x 1)  (2x 1)  (x 1)  0
 (2x 1 x 1).(2x 1 x 1)  0 x  0 x  0   .(3 x x  2)  0    2 3x  2  0 x   3 2
Vậy phương trình có tập nghiệm là S  {0; }. 3 l). 2 2
4x 12x  9  9x  24x 16 2 2 2 2
 (2x  3)  (3x  4)  (2x  3)  (3x  4)  0
 (2x  3  3x  4).(2x  3  3x  4)  0 x 1 1   x  0  
(1 x).(5x  7)  0    7 5x  7  0 x   5 7
Vậy phương trình có tập nghiệm là S  {1; } . 5
Bài tập 31. Giải các phương trình sau a). 2
x  2x  4  2x  2
b). x  2 x 1  2 c). 2
2x  2x 1  2x 1
d). x  4 x  4  2 Lời giải 2x  2  0  a). 2
x  2x  4  2x  2    x
x  2x  4   2x  2 2 2 2
Vậy phương trình có tập nghiệm là S  {2}.
b). x  2 x 1  2 Cách 1: Ta có 2
x  2 x 1  2  x  2 x 1  2 4  x  0 
 2 x 1  4    x  4   x   1  4  x 2 2
Vậy phương trình có tập nghiệm là S  {2}.
Cách 2: Ta có x  2 x 1  2 
x 1 1  2  x  2 2x 1  0  c) 2
2x  2x 1  2x 1  
x  (thỏa mãn)
2x  2x 1   2x   1 2 2 1 d) x x     x  2 2 4 4 2 4
 2.2 x  4  2  2   x   2 4 2
 2  x  4  2  2  x  4  2  2
31 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
x  4  0  x  4  0  x  4
Vậy phương trình có tập nghiệm là S  {4}.
Bài tập 32. Giải các phương trình sau a). 2
x  3x  2  x 1 b). 2 2
x  4x  4  4x 12x  9 Lời giải x 1 0
x 1tm a). Ta có 2
x  3x  2  x 1     2
x  3x  2  x 1 x  3  tm
Vậy phương trình có tập nghiệm là S  {1;3} .
x  1 tm b). 2 2 
x  4x  4 
4x 12x  9  x  2  2x  3  5  x  tm  3 5
Vậy phương trình có tập nghiệm là S  {1; } 3
Bài tập 33. Giải các phương trình sau a). 2
(x  3)  3  x b). 2
4x  20x  25  2x  5 c). 2 (3  2x)  4
d). x  2 x 1  2 (x  1) Lời giải a). 2
(x  3)  3  x x  3  3  x x  3  0  x  3 b). 2 2
4x  20x  25  2x  5 
(5  2x)  5  2x 5
 5  2x  5  2x  5  2x  0  x  2 3 2x  4 x  1  ,5 c). 2
(3  2x)  4  3  2x  4     3 2x  4  x  3  ,5
Vậy phương trình có tập nghiệm là S  {1,5;  3,5} .
d). x  2 x 1  2(x  1)  x 1 2 x 1 1  2 x   2  ( x 1 1)  1 3 2 
x 1 1  2  
x 1  9  x  10  x 1  1  (loai)
Vậy phương trình có tập nghiệm là S  {10}.
Bài tập 34. Giải các phương trình sau a). 2 2
x  2x 1  x  6x  9  1 b). 2
2x  3  4x  3 c). 2
1 x x 1 Lời giải a). 2 2
x  2x 1  x  6x  9  1 2 2
 (x 1)  (x  3)  1  x 1  x  3  1 (1)     x 1 0 3 Với x  1  
 (1)  1 x  3 x 1  x  (loai) x  3  0 2
32 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai     x 1 0 1  x  3  
 (1)  x 1 3 x 1  0x  1  (loai) x  3  0     x Với x  1 0 5 3  
 (1)  x 1 x  3  1 x  (loai) x  3  0 2
Vậy phương trình vô nghiệm.  3 x   4x  3  0  4 b). 2 2x  3  4x  3     2    
x  0(loai) 2x 3 4x 3 
x  2(t / m) x 1  x 1  0 x  1  c). 2
1 x x 1      x  1; 2 2 2 2  
x 1  (x 1) x  1   (t / m)  x   2
Bài tập 35. Giải các phương trình sau a). 2 2
x  2x 1  x 1 b). 2
x  3  x  3 c). 2 2
x  4  x  4x  4  0 d). 2 2 2
3x 18x  28  4x  24x  45  5   x  6x Lời giải a). 2 2
x  2x 1  x 1 b). 2
x  3  x  3 2  2 2 2    
(x 1)  x 1  x 1  x 1 x 3 x 3   2 2      2 x 1 0  x 3 (x 3) x  1   2 2   
x 1  x 1
 x x  0
(x  3)(x  3)  (x  3)  0     2
x 1  (x 1)
(x 1)(x  2)  0
(x  3)(x  3)  (x  3)  0 x 1 x  3  0 x  3    x  1  x  3 1  0 x  1 3       
x  0(loai)  x 1;   2 x  3  0 x  3   
x  1(t / m)    x  3 1  0 x  1 3 x  2(  t / m) 
Vậy phương trình có nghiệm S  { 2;1}.
Vậy phương trình có tập nghiệm là S  { 2;1}. x  2 2 x  4  0  c). 2 2 x  4 
x  4x  4  0    x  2   x  2  2
x  4x  4  0  x  2  d). 2 2 2
3x 18x  28  4x  24x  45  5
  x  6x 2 2 2
 3(x  3) 1  4(x  3)  9  4  (x  3) (1) VT    1  4 Ta có: 
 phương trình có nghiệm khi hai vế đều bằng 4 2
 (x  3)  0  x  3 VT    1  4
33 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
Bài tập 36. Đố: Hãy tìm chỗ sai trong phép chứng minh “con muỗi nặng bằng con voi”dưới đây.
Gỉa sử con muỗi nặng m (gam), còn con voi nặng V (gam).Ta có : 2 2 2 2
m V V m Cộng cả hai vế với 2 2 2  mV , ta có: 2 2 2 2
m  2mV V V  2mV m hay m V   V m
Lấy căn bậc hai mỗi vế của đẳng thức trên, ta được: m V V m
Từ đó ta có 2m  2V , Suy ra V m . Vậy con muỗi nặng bằng con voi (!). Lời giải
Sai lầm ở chỗ: Sau khi lấy căn bậc hai mỗi vế của đẳng thức   2    2 m V V
m phải được kết
quả m V V m chứ không thể có m V V m ( chú ý rằng 2 A A ).
3. Bài tập rèn luyện.
Bài 11. Tìm x biết a).  x  2 3  3 x ; b). 2
25  20x  4x  2x  5 ; 1 1 1 c). 2 x x    x ;
d). x  2 x 1  x 1 1; 2 16 4 e). 2
112x  36x  5 ;
g). x  2 x 1  2 . Lời giải a).  x  2 3  3 x
Ta có biến đổi: x  3  3  x Ta có hai trường hợp:
TH 1: Nếu x  3 thì x  3  3  x x  3TM
TH 2: Nếu x  3 thì 3  x  3  x  0  0TM
Vậy tất cả x  3 đều thỏa mãn. b). 2
25  20x  4x  2x  5
Ta có biến đổi:   x2 5 2  5  2x
 5  2x  5  2x Ta có hai trường hợp: 5 TH 1: Nếu x
thì 5  2x  5  2x  0  0TM  2 5 5 TH 2: Nếu x
thì 2x  5  5  2x x  (L) 2 2 5 Vậy tất cả x  đều thỏa mãn. 2 1 1 1 c). 2 x x    x 2 16 4 2  1  1 1 1 Ta có biến đổi: x
  x x    x    4  4 4 4 1
Tương tự ta có: tất cả x  đều thỏa mãn. 4
d). x  2 x 1  x 1 1.
Điều kiện: x  1
34 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
Ta có biến đổi:  x   2 1 1
x 1 1  x 1 1  x 1 1 Ta có hai trường hợp:
Nếu: x 1  1  x  2 : x 1 1  x 1 1(TM)
Nếu: x 1  1  x  2 : 1 x 1  x 1 1  x  2l  (TM)
Vậy: x  2 đều thỏa mãn. e). 2
112x  36x  5 .
Ta có biến đổi:   x2 1 6
 5  1 6x  5 Ta có hai trường hợp: 1 2
Nếu: x  thì 1 6x  5  x   (TM) 6 3 1 Nếu: x
thì 6x 1  5  x 1 (TM) 6 2
Vậy: x   và x  1 là giá trị cần tìm. 3
g). x  2 x 1  2 .
Điều kiện: x  1
Ta có biến đổi:  x   2 1 1
 2  x 1 1  2 Ta có hai trường hợp:
TH1: x 1 1  2  x 1  1  x 1  1  x  2 TH2: x 1 1  2   x 1  3  VL .
Vậy x  2 là giá trị cần tìm.
Dạng 5: PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ 1. Phương pháp.
Áp dụng các hằng đẳng thức đáng nhớ:   2 A A (với A  0) . 2 2
A B   A B A B .  A B2 2 2
A  2AB B
2. Bài tập minh họa.
Bài tập 37. Phân tích thành nhân tử: a). 2 x  2 . b). 2 x  7 . c). 2
x  2 15x 15 . d). 2
4x  4 3x  3 . Lời giải 2 a). Ta có 2 2
x  2  x   2   x  2x  2  . 2 b). Ta có 2 2
x  7  x   7   x  7 x  7  . 2 2 c). Ta có 2 2
x  2 15x 15  x  2. .
x 15   15  x  15 . 2 2 d). Ta có x
x    x2 2 4 4 3 3 2  2.2 .
x 3   3  2x  3 .
3. Bài tập rèn luyện.
Bài 9. Phân tích đa thức thành nhân tử. a). 2 x 11 ; b). 2
x  2 2x  2 ;
c). x  5 (với x  0 ) ; d). 2
5  7x (với x  0 ) .
35 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 1. Căn Thức Bậc Hai
e). 3  4x (với x  0 ) ; Lời giải a). 2
x 11  x  11x  11 . b). x
x   x  2 2 2 2 2 2 .
c). x  5   x  5 x  5 (với x  0 ) d). 2
5  7x   5  7x  5  7x  (với x  0 ) 2 2
e). 3  4x  3  4x   3  4x  3  4x  (với x  0 )
Dạng 6. CHỨNG MINH BẤT ĐẲNG THỨC 1. Phương pháp. Áp dụng
Các hằng đẳng thức đáng nhớ. và   2 A A
để biến đổi vế trái thành vế phải hoặc ngược lại.
2. Bài tập minh họa. Bài tập 38. Chứng minh: a).   2 5 1  6  2 5 . b). 6  2 5  5  1  . Lời giải 2 2 a). Ta có       2 5 1 5
 2. 5.11  5  2 5 1  6  2 5 .
b). Áp dụng câu a, ta có:      2 6 2 5 5 5 1
 5  5 1  5  5 1 5  1  .
3. Bài tập rèn luyện.
Bài 12. Chứng minh đẳng thức: a).     2 9 4 5 5 2 ; b). 9  4 5  5  2 ; c). 23  8 7  7  4 ;
d). a  4 a  2  2  a  4 a  2  2  4 (với 2  a  6 ). Lời giải a).     2 9 4 5 5 2 2 2
VT  5  2. 5.2  4  5  2. 5.2  2   5  22  VT b). Ta có biến đổi: 2 2
VT  5  2. 5.2  4  5  5  2. 5.2  2  5
  5  22  5  5  2  5  5  2 5  2 VP 2 c). 2
VT  16  2.4. 7  7  7  4  2.4. 7  7  7    2 4 7
 7  4  7  7  4  7  7  4  VP
d). VT a  2  2. a  22  4  a  2  2. a  2.2  4  a  2  2 
a  2  2  a  2  2  2  a  2  4  VP (Vì 2  a  6 )
Dạng 7. TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC 1. Phương pháp.
Áp dụng bất đẳng thức: A B A B , dấu “=”  . A B  0
36 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học AMSTERDAM Chương I-Bài 2. Căn Thức Bậc Hai
2. Bài tập minh họa.
Bài tập 39. Tìm GTNN của các biểu thức sau a). 2 2 A
x  2x 1  x  2x 1
b). B  2x 1  3  2x c). 2 2
C  4x  4x 1  4x 12x  9 d). 2 2
D  49x  42x  9  49x  42x  9 Lời giải a). 2 2 A
x  2x 1 
x  2x 1  A x 1  x 1 Cách 1:  Nếu x  1
  A  x 1 x 1 2  x  2(1)  Nếu 1
  x 1 A x 1 x 1 2(2)
 Nếu x 1 A x 1 x 1  2x  2(3)
 Từ (1)(2)(3)  MinA  2  1   x 1
Cách 2: Áp dụng bất đẳng thức A B A B
A x 1  x 1  x 1  1 x x 11 x  2
Vậy MinA  2  (x 1)(1 x)  0  1   x 1 1 3
b). B  2x 1  3  2x MinB  2   x  2 2 c). 2 2 C
4x  4x 1  4x 12x  9  2x 1  3  2x  (2x 1)  (3  2x)  2 1 3
 (2x 1)(3 2x)  0   x  2 2 3  3 d). D  6   x min 7 7
37 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
§BÀI 3. LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG A. TÓM TẮT LÍ THUYẾT
1. Quy tắc khai phương một tích
Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả với nhau.
Nếu A  0, B  0 thì AB A. B . Ví dụ 1. Tính: a). 12,1.160 b). 2500.4,9.0,9 . Lời giải
a). 12,1.160  121. 16 11.4  44
b). 2500.4,9.0,9  25.49.9  25. 49. 9  5.7.3 105 Ví dụ 2. Tính: a). 2 2 41  40 b). 81.6, 25  2, 25.81 Lời giải a). 2 2
41  40  (41 40)(41 40)  1.81  1.9  9
b). 81.6, 25  2, 25.81  81.(6, 25  2, 25)  81. 4  9.2 18
Ví dụ 3. Rút gọn các biểu thức sau: 60 a). 3 15x . b). 2 16(x  6x  9) . x Lời giải 60 a). 3 15x . x ĐK: x  0 . 60  30x khi x 0 Ta có 3 2 15x .
 900x  30 x   . x  30  x khi x  0
 4(x  3) khi x  3 b). 2 2
16(x  6x  9)  16(x  3)  4 x  3   .  4
 (x  3) khi x  3
Ví dụ 4. Rút gọn biểu thức 2
M  25x x  2 x   1 với 0  x 1. Lời giải Ta có M x x x     x  2 2 25 2 1 25 1  5 x 1 .
Vì x  0 nên x x .
Vì 0  x 1 nên x  1 . Do đó
x 1  1 x
Vậy M  5x 1 x
Ví dụ 5. Đẳng thức x(1 y)  x. 1 y đúng với những giá trị nào của x và y. Lời giải
Theo địnhlí khai phương một tích thì x(1 y) 
x. 1 y khi x  0 à
v 1- y  0 hay x  0 và y 1.
Ví dụ 6. Cho cac biểu thức M  (x 1)(x  3) à v N x 1. x  3
a). Tìm các giá trị của x để M có nghĩa; N có nghĩa.
b). Với giá trị nào của x thì M N ?
38 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương Lời giải
a). Tìm các giá trị của x để M có nghĩa; N có nghĩa.
M có nghĩa khi (x 1)(x  3)  0. x 1  0 x 1 Trường hợp 1:     x 1 x  3 0 x   3 x 1  0 x 1 Trường hợp 2:     x   3 x  3 0 x   3
Vậy M có nghĩa khi x  1 hoặc x  3  .       x 1 0 x 1 N có nghĩa khi     x 1 x  3 0 x   3
b). Để M và N đồng thời có nghĩa thì x  1
Khi đó ta có M N theo định lí khai phương một tích.
2. Quy tắc nhân các căn bậc hai
Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới dấu căn với nhau
rồi khai phương kết quả đó.
Nếu A  0, B  0 thì A. B AB Ví dụ 7. Tính: a). 72. 50 b). 12,8. 0, 2 Lời giải
a). 72. 50  72.50  36.100  6.10  60
b). 12,8. 0, 2  12,8.0, 2  128.0,02  64.0,04  8 .0, 2 1,6 Ví dụ 8. Tính: 2 12 1 a). 40. 20. 4,5 . b). . . . 3 25 2 Lời giải
a). 40. 20. 4,5  40.20.0,5  400.9  20.3  60 2 12 1 2 12 1 4 2 b). . .  . .   3 25 2 3 25 2 25 5
Ví dụ 9. Thực hiện các phép tính:
a).  20  45  5. 5 b).  12  3 27  3 c).  5  3   1  5   1 Lời giải
a).  20  45  5. 5  100  225  25 10 155  20
b).  12  3 27  3  324  36  81  9 18  6  9 3 18 c).  5  3   1  5  
1  5  5  15  3  5 1  4  15  3 . Ví dụ 10. Tính: a).   2 7 3 b).   2 8 2
c). 3 5  2 73 5  2 7  Lời giải 2 2 a).   2 7 3
  7  2 7. 3  3  7  2 213 10 2 21 2 2 b).   2 8 2
  8  2 8. 2  2  8 2 16  2  2 2 2
c). 3 5  2 73 5  2 7   5 3 2 7   25.3 4.7  47
39 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
Ví dụ 11. Rút gọn các biểu thức sau: 3x 5x a). . với x  0. b). 6 2
x .(x  2) với x  2 . 5 27 Lời giải 2 3x 5x 3x 5x x x x a). .  .    (Vì x  0.) 5 27 5 27 9 3 3 b). 6 2 x .(x  2) 6 2 3 3
x . (x  2)  x . x  2  x (x  2) (vì x  2 ).
Ví dụ 12. Rút gọn các biểu thức sau:
a). x  2 x 1
b). x  2  2 x 1 Lời giải a). x x   x  
x     x   2 2 1 1 2 1 1 1 1
x 1 1 ( ĐK: x 1) b). x   x   x  
x     x   2 2 2 1 1 2 1 1 1 1
x 1 1 ( ĐK x  1  ) Nếu x  0 thì x 1 1  x 1 1 Nếu x  0 thì
x 1 1  1 x 1
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA.
Dạng 1. THỰC HIỆN PHÉP TÍNH 1. Phương pháp.
Sử dụng các quy tắc khai phương một tích và quy tắc nhân các căn bậc hai
Nếu A  0, B  0 thì AB A. B
2. Bài tập minh họa.
Bài tập 1. Áp dụng quy tắc khai phương một tích, hãy tính: a). 0,16.81 ; b).  2 4 3 . 5  ; c). 16,9.250 ; d). 2 4 5 .4 . Lời giải
a) Ta có: 0,16.81  0,16. 81  0, 4.9  3,6 . b) 2 2 Ta có: 4   4    2 3 . 5 3 . 5  3 . 5   9.5  45 .
c) Ta có: 16,9.250  169.25  169. 25  13.5  65 . d) Ta có: 2 4 2 4 2
5 .4  5 . 4  5.4  80 .
Bài tập 2. Áp dụng quy tắc nhân các căn bậc hai, hãy tính: a). 5. 80 ; b). 2, 45. 40. 50 ; c). 0,6. 5, 4 ; d). 8,1. 5. 4,5 . Lời giải
a) Ta có: 5. 80  5.80  400  20 .
b) Ta có: 2, 45. 40. 50  2, 45.40.50  4900  70 .
c) Ta có: 0,6. 5, 4  0,6.5, 4  3, 24 1,8 .
d) Ta có: 8,1. 5. 4,5  8,1.5.4,5  182, 25 13,5 .
Bài tập 3. Khai phương tích 13.25.52 được: a). 2600. b).130. c). 13. d). 260.
Hãy chọn kết quả đúng. Lời giải
Ta có: 13.25.52  16900  130 (chọn B).
40 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
Bài tập 4. Biến đổi các biểu thức dưới dấu căn thành dạng tích rồi tính a). 2 2 25  24 ; b). 2 2 26 10 ; c). 2 2 137  88 ; d). 2 2 481  480 . Lời giải a) Ta có: 2 2
25  24  25  2425  24  49  7 . b) Ta có: 2 2
26 10  26 1026 10  16.36  4.6  24 . c) Ta có: 2 2
137  88  137  88137  88  49.225  7.15  105 . d) Ta có: 2 2
481  480  481 480481 480  961  31.
Bài tập 5. Tính giá trị của các biểu thức sau: a). 4  2 3 b). 8  2 15 c). 9  4 5 Lời giải a)        2 4 2 3 3 2. 3.1 1 3 1  3 1 b)        2 8 2 15 5 2 5. 3 3 5 3  5  3 c)        2 9 4 5 5 2.2. 5 4 5 2  5  2
Nhận xét: Phương pháp giải trong ví dụ này là biến đổi biểu thức lấy căn thành bình phương của
tổng hay hiệu hai số rồi áp dụng hằng đẳng thức 2 A A
3. Bài tập rèn luyện. Bài 1. Tính  2 50  a).    24 . 6   b). 3  5. 2 3 3    3 4  c).   3  5 . 12   d). 3  5. 8 4 3   Lời giải  2 50  2 50 a).    24 . 6  .6  .6  24.6  0   3 3 3 3   b).       2 3 5. 2 3.2 2 5 5 1  5 1  3 4  c).   3  5 . 12  7   4 3  
d). 3  5. 8  2 5   1 Bài 2. Tính 1 1 a). 55.77.35 b). . 2. 125. 8 5 c). 2 1. 2 1 d). 2
2 2.( 3  2)  (1 2 2)  2 6 Lời giải
a). 55.77.35  5.11.7.11.5.7  5.7.11  385 1 1 1 1 2.125 25 5 b). . 2. 125.  .2.125.    8 5 8 5 8.5 4 2 c). 2 1.
2 1  ( 2 1).( 2 1)  2 1  1
41 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương d). 2
2 2.( 3  2)  (1 2 2)  2 6  2 6  4 2 1 4 2  8  2 6  9 Bài 3. Tính a). 2  3. 2  3 b). 3 2  2 3. 3 2  2 3 c). 2 ( 3  2  3  2 )
d). (1 2  3).(1 2  3) Lời giải
a). 2  3. 2  3  2  32  3  4 3  1 1. 2 2
b). 3 2  2 3. 3 2  2 3  3 2 2 3  18 12  6 . 2 2 2
c).  3  2  3  2    3  2   2 3  2. 3  2  3  2 
 3  2  2  3  2 3  2  3  2  2 3  2 32  2 3  2  2 3   1 . d).   
       2 2 1 2 3 . 1 2 3 1 2 3 1 2  3 2 2.3  4   2 6 . Bài 4. Tính
a). A  (4  15)( 10  6) 4  15
b). B  (3  5) 3  5  (3  5) 3  5
c). C  2  3. 2  2  3 . 2  2  2  3 . 2  2  2  3 Lời giải
a). A  (4  15)( 10  6) 4  15  ( 10  6) 4  15. 4  15. 4  15
 ( 10  6) 4  15. (4  15)(4  15) 
10  6 . ( 10  6)(4  15) 
10  6 . 4 10  150  4 6  90  10  6 .
10  6  ( 10  6)( 10  6)  4  2
b). B  (3  5) 3  5  (3  5) 3  5  3  5. 3  5. 3  5  (3  5) 3  5
 3 5. 3  5  3 5  3 5   2( 3 5  3 5)
 2( 3  5. 2  3  5. 2) 2 2
 2( 6  2 5  6  2 5 )  2( ( 5 1)  ( 5 1)
 2( 5 1 5 1)  2 10
c. C  2  3. 2  2  3 . 2  2  2  3 . 2  2  2  3
C  2  3. 2  2  3 . 2  2  3 2 2
C  2  3.( 2  ( 2  3) )  2  3. 2  3 1 Bài 5. Tính
a). A  3  5  2 3 . 3  5  2 3
b). 4  8. 2  2  2 . 2  2  2
c). ( 12  3 15  4 135) 3 d). 2 40 12  2 75  3 5 48 Lời giải a). 2 2
A  3  5  2 3 . 3  5  2 3  3  ( 5  2 3 )  9  (5  2 3)
42 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương 2
 9  5  2 3  4  2 3  ( 3 1)  3 1 b). 2 2
4  8. 2  2  2 . 2  2  2  4  4. 2 . 2  ( 2  2 )  4  2 2 . 2  2  2.(2  2)(2  2)  2.2  2 c). 2
( 12  3 15  4 135) 3  36  3 9.5  4 9 .5
 6  9 5  36 5  6  27 5 d). 2 40 12  2
75  3 5 48  2 40 12  2 5 3  3 20 3  2 80 3  2 5 3  6 5 3
 8 5 3  2 5 3  6 5 3  5 3(8  2  6)  0
Bài 6. Thực hiện phép tính a). (4  2 3)(13  4 3) b). ( 3  2)( 6  2) 3  2
c). (3  5)( 10  2) 3  5
d). (4  15)( 10  6) 4  15
e). 4  15  4  15  2 3  5
f). 4  8. 2  2  2 . 2  2  2
g). (5  4 2).(3  2 1 2 ).(3  2 1 2 )
h). 2  3. 2  2  3 . 2  2  2  3 . 2  2  2  3 Lời giải 2 2
a). 4  2 313 4 3   3   1 .2 3   1   3   1 .2 3   1 .
b).  3  2 6  2
3  2  3 2  6  2 6  2 2  3  2   2  6  3  2 .
 2 1 3 3  2  2 4 2 3 3  2  2 2  2 .
c). 3 5 10  2 3 5  2  5  
1 3 5 3 5  2.2  2 5. 3 5 .    2 2 2 1 5 . 3  5
 2 2 6  2 53  5  2 2. 8  8
d). 4  15 10  6 4  15  2.4  15 5  3 4  15 .  2  5  3 4 15 .
 2  5  32 4 15  2. 2  2
8  2 15  8  2 15  2 6  2 5
e). 4  15  4  15  2 3  5  . 2
5  3  5  3  2  5   1 2    2 2 2
f). 4  8. 2  2  2 . 2  2  2  2. 2  2. 4  2  2  .
43 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
 2. 2  2. 2  2  2. 4  2  2.
g). 5 4 2.3 2 1 2 .32 1 2   5 4 2. 9   4  1 2.         2 5 4 2 . 5 4 2 5 4 2 .
h). 2  3. 2  2  3 . 2  2  2  3 . 2  2  2  3 .
 2  3. 2  2  3 . 4  2 2 3   2 3. 2 2 3. 2 2 3  2 3. 42 3
.  2  3. 2  3  4  3  1.
DẠNG 2. RÚT GỌN BIỂU THỨC VÀ TÍNH GIÁ TRỊ BIỂU THỨC 1. Phương pháp.
Trước hết tìm điều kiện của biến để biểu thức có nghĩa (nếu cần). Áp dụng các quy tắc ① Khai phương một tích AB
A. B ( A  0, B  0 ) và 2 A A ,
② Quy tắc nhân các căn bậc hai A. B AB .
③ Các hằng đẳng thức để rút gọn.
Thay giá trị của biến vào biểu thức đã rút gọn rồi tính.
2. Bài tập minh họa.
Bài tập 6. Rút gọn biểu thức sau: 4  a  a). 2 2
0, 49a với a  0 ;
b).   6  2a với a  3;  2  1 c).   2 19.76 2 a với a  2 ; d).
. a a b 2 2 2 2
với a b  0 . a b Lời giải a) Ta có: 2
0, 49a  0, 7 a  0
 ,7a (do a  0 ). 4 2 2 2  a   a aa a a  b) 2 .2 3 3 Ta có: 62a    6  2a       (do a  3).  2   2  4 2 c) 2 2
Ta có: 19.762  a  14442  a  38 2  a  38a  2 (do a  2 ). 2 1 1 1 d) Ta có: 2 . a  2 2 a b  2 2 
. a . a b  . .
a a ba b  a a b (do a b  0 ). a b a b a b
Bài tập 7. Rút gọn các biểu thức sau: 2a 5a 99 a). . với a  0 ; b). 11a. với a  0 ; 5 18 a
c). 21a  11a. 44a với a  0 ; d).   a2 2 4  0,4. 160a Lời giải 2 2 2a 5a 10a a a a) Ta có: .    (do a  0 ). 5 18 90 9 3 99 99 b) Ta có: 11a.  11 . a  1089  33. a a c) Ta có: 2
21a  11a. 44a  21a  484a  21a  22a  a (do a  0 )
44 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương 2 2 2
d) Ta có:   a 2 
a    a 2 
a    a 2 4 0, 4. 160 4 64 4
8 a 16  a  8a 8 a
Nếu a  0 thì   a2 2 2 4
 0,4. 160a 16  a .
Nếu a  0 thì   a2 2 2 4
 0,4. 160a 16  a 16a .
Bài tập 8. Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau: a).
  xx 2 2 9 4 20 25 tại x   5 ; b). 2 a  2 2
2b 12b 18 tại a  3  ,b  3 . Lời giải 2 4 2 a) Ta có:  2
9 4  20x  25x   9. 2  5x  32  5x .
Thay x   5 vào biểu thức đã rút gọn, ta được: 2   x2 3 2 5
 325 5  3129 20 5  252,836. b) Ta có:
a b b   
a b b    ab  2 2 2 2 2 2 2 2 12 18 4 6 9 4 . 3
 2 a . b  3 Thay a  3
 ,b  3 vào biểu thức đã rút gọn, ta được:
2 a . b  3  2 3
 . 3 3  63 3  7,608.
3. Bài tập rèn luyện.
Bài 7. Rút gọn các biểu thức sau: a). 75  48  300 b). 98  72  0,5 8
c). 9a  16a  49a a  0
d). 160b  2 40b  3 90b b  0 Lời giải
a). 75  48  300  5 3  4 3 10 3   3
b). 98  72  0,5 8  7 2  6 2  2  2 2
c). 9a  16a  49a  3 a  4 a  7 a  6 a
d). 160b  2 40b  3 90b  4 10b  4 10b  9 10b   10b
Bài 8. Rút gọn các biểu thức sau:
a). 3 2  4 18  2 32  50
b). 5 48  4 27  2 75  108
c). 125  2 20  3 80  4 45
d). 2 28  2 63  3 175  112 Lời giải
a). 3 2  4 18  2 32  50  3 2 12 2  8 2  5 2  7 2
b). 5 48  4 27  2 75  108  20 3 12 3 10 3  6 3  4 3
c). 125  2 20  3 80  4 45  5 5  4 5 12 5 12 5  5
d). 2 28  2 63  3 175  112  4 7  6 7 15 7  4 7   7
Bài 9. Rút gọn các biểu thức sau: a). (2 3  5) 3  60 b). (5 2  2 5) 5  250
c). ( 28  12  7) 7  2 21
d). ( 99  18  11) 11  3 22 Lời giải
a). 2 3  5. 3  60  6  2 15  2 15  6
b). 5 2  2 5. 5  250  5 10 10 5 10 10
c).  28  12  7. 7  2 21 14  2 21 7  2 21  7
d).  99  18  11. 11 3 22  333 22 113 22  22
45 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
Bài 10. Rút gọn các biểu thức sau: a). 2 40 12  2 75  3 5 48
b). 2 80 3  2 5 3  3 20 3 Lời giải a). 2 40 12  2
75  3 5 48  8 5 3  2 5 3  6 5 3  0
b). 2 80 3  2 5 3  3 20 3  8 5 3  2 5 3  6 5 3  0 Bài 11. Rút gọn 10  15 6  15 5  5 a). A  b). B  c).C  8  12 35  14 10  2 15  5 5  2 5  3 18  2 8 d). D   e). E     3 3 3 1 . f). F  3 1 2 5  4 2 3 50 6  14 2  3  6  8  4 3 8  2 12  20 g). G  h). H  i). K  2 3  28 2  3  4 3 18  2 27  45 Lời giải 10  15 5. 2  5. 3 5 a). A    A  8  12 4. 2  4. 3 2 6  15  3  21 b). B    35  14 7 7 5  5 5 10 c). C    10  2 2 2 15  5 5  2 5 5( 3 1) 5( 5  2) 5 3 5 d). D      5   3 1 2 5  4 3 1 2( 5  2) 2 2    3 1. 3 1  e). E     3 3 3 1 .     3(1 3) 3 1 .   3 1    1 2 3 2 3 2 2 3 18  2 8 3.3 2  2.2 2 9 2  4 2 5 2 f). F     1 50 5 2 5 2 5 2 6  14 2. 3  2. 7 2 1 g). G     2 3  28 2 3  4. 7 2 2 2  3  6  8  4
2  3  4  4  6  8 h). H    2 1 2  3  4 2  3  4 3 8  2 12  20 3.2 2  2.2 3  2 5 2(3 2  2 3  5) 2 i). K     3 18  2 27  45 3.3 2  2.3 3  3 5 3(3 2  2 3  5) 3
Bài 12. Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối): a). 2
0,36x với x  0
b). x 5 với x  3 1 c). 2
27.48(1 x) với x  1 d). 4 2
. x (x y) x y e). 2
4.(x  3) với x  3 f). 2
9.(x  2) với x  2  14  7 15  5  1 g).    :  2    với x  0 h). 2 2
x (x 1) với x  0 1 2 1 3 7  5   2x 3x 52 i). . với x  0 j). 13x với x  0 3 8 x 1 k). 6 với x bất kỳ. l). 2 2
(3  x)  0, 2. 180x , x  2
46 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương Lời giải a). 2
0,36x với x  0 . Ta có: x   x2 2 0,36 0,36  0,36x  0
 ,36x (vì x  0 ).
b) x   x2 4 3 với x  3 . 2
Ta có: x   x2 4 2
 x   x 2
  x   x 2 3 3 3
x x  3   (vì x  3 ). c). 2
27.48(1 x) với x  1. 2 Ta có:  x    x2 2 3 4 2 2     x 2 2 27.48(1 ) 3 .2 .3. 1 3 .2 . 1
  3 .2 .1 x  36.x   1   (vì x  1). 1 d). 4 2
. x (x y) x y  0 . x y 2 1 1 1 Ta có:
. x x y2 4 2 
x x y 2  
x x y 2  x   x y x y x y
(vì x y  0 ). e). 2
4.(x  3) với x  3 . 2 Ta có: 2 4.(x  3)  2
  x  3  2 
x 3  2x 3 (vì x  3). f). 2
9.(x  2) với x  2 . 2 Ta có: 2 9.(x  2)  3
  x  2  3 
x  2  32 x (vì x  2 ).
g). x x  2 2 1 với x  0 . 2 2 Ta có: 2 x x   1  x   x   1   x  x  
1  x x   1 (vì x  0 ). h) 2 2
x (x 1) với x  0 . 2 Ta có: 2 2 x (x 1)  x   x   1   x  x  
1  x x   1 (vì x  0 ). 2x 3x i). . với x  0 . 3 8 2 2x 3x 2 . x 3x x x Ta có: .    (vì x  0 ). 3 8 3.8 4 2 52 j). 13x với x  0 . x 52 13 . x 52 Ta có: 13x   13.13.4 13.2  26 . x x
k). 5x. 45x  3x với x bất kỳ. Ta có: 2
5x. 45x  3x  5.5.9x  3x  5.3x  3x .
Khi đó 5x. 45x  3x  12x nếu x  0 .
Hoặc 5x. 45x  3x  18x nếu x  0 . l). 2 2
(3  x)  0, 2. 180x , x  .
47 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương Ta có:  x
x    x2 
x    x2 2 2 2 2 (3 ) 0, 2. 180 3 0, 2.180. 3  2.2.9x .    x2 3  6 x . Khi đó  x
x    x2 2 2 2 (3 ) 0, 2. 180 3
 6x x 12x  9 nếu x  0 . Hoặc  x
x    x2 2 2 2 (3 ) 0, 2. 180 3
 6x x  9 nếu x  0 .
Bài 13. Rút gọn các biểu thức sau 2  t 3t 6 28 y a). A  . t  0 b). B   y  0 3 8 4 7 y c). 2 2 C
x x 1. x x 1  x   1 d). 4 2 4 2 D x  4  x . x  4  x Lời giải 2 2  t 3t 2  t  3  t t t  a). A  .  .     t  0 3 8 3  8  4 2 6 28 y b). B
y  0  B  2  y 4 7 y
c). C x x
x x   x   x  2 2 2 2 2 1. 1 1 1 d). 4 2 4 2 4 2 4 2 x  4  x .
x  4  x  ( x  4  x )( x  4  x ) 4 2 2
 (x  4)  (x )  4  2
Bài 14. Rút gọn các biểu thức x y y x x y y x a). A
x  0; y  0;xy  0 b). B
(x  0; y  0; x y)
x  2 xy y
x  2 xy y 3 a  2a 1 1 a  4 a  4 4  a c).
(a  0; a  ) d). D  
(a  0; a  4) 4a  4 a 1 4 a  2 a  2 Lời giải x y   x y x y y xxy a). A     x xy y    A 2 2 x y x y x y y x xy b). B  
x  2 xy y x y 3 a  2a 1
(2 a 1)(1 a ) 1 a c).   2 4a  4 a 1 (2 a 1) 2 a 1 a  4 a  4 4  a d). D    0 a  2 a  2
Bài 15. Rút gọn các biểu thức sau: x  2 x 1 2 x 1
( y  2 y 1) a). với x  0 b).
x  1, y  1, y  0 4   x  2 x 1 y 1 (x 1) Lời giải x  2 x 1 a) với x  1. x  2 x 1    x x x 2 2 1 2 1  x 1 x 1 Ta có :        . x  2 x 1  x  2 x 1 x 1 1  
48 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương 2 x 1
( y  2 y 1) b)
, x  1; y  1; y  0 . 4 y 1 (x 1)   x 1 y 2 y 2 2 1 x 1
y  2 y 1 x 1 y  2 y 1 y 1 Ta có :     .  . 4 2 2   y 1 (x 1) y 1 (x 1) y 1 (x 1) x 1  
Bài 16. Rút gọn rồi tính giá trị của các biểu thức sau: a). 2 2
4(1 6x  9x ) tại x   2 b). 2 2
9a (b  4  4b) tại a  2;b   3 3 2 x  2x 4 2 (x  2) x 1 c). 4x  8  tại x   2 d). 
(với x  3 ) tại x  0,5 x  2 2 (3  x) x  3 Lời giải a). 2 2
4(1 6x  9x ) tại x   2 . 4 2 Ta có:
  xx      x2    x2 2 4 1 6 9 2 1 3 2 1 3   . 2
Thay x   2 , ta được: 213. 2  21 6 2 18  219  6 2 . b). 2 2
9a (b  4  4b) tại a  2;b   3 . Ta có:
a b   b ab 2 2 2 9 ( 4 4 ) 3 2  3 a b  2 .
Thay a  2;b   3 , ta được: 3 2  3  2  6 3  2 . 3 2 x  2x c). 4x  8  tại x   2 . x  2 3 2 x  2x x x  2 Ta có: 4x  8   4x 8 
 4x 8  x . x  2 x  2
Thay x   2 , ta được: 4  2 8   2  3  2 8. 4 2 (x  2) x 1 d). 
(với x  3 ) tại x  0,5. 2 (3  x) x  3 (x  2) x 1 x  2 2 2  x 1 x  22 4 2 2 2 x 1 Ta có:        . 2 (3  x) x  3  3  x x  3 3  x x  3     2 2 0, 5 2 0, 5 1 6
Thay x  0,5, ta được:   . 3  0, 5 0, 5  3 5
Dạng 3. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ 1. Phương pháp.
Áp dụng một số cách sau
① Phương pháp thừa số chung với
⋆ x  0 thì x
x. x ⋆ x  0 thì   3 x x x 2 2
⋆ x  0, a  0 thì x a   x    a    x a  x a
② Phương pháp hằng đẳng thức đáng nhớ.
③ Phương pháp nhóm hạng tử.
④ Phương pháp thêm, bớt và tách hạng tử.
49 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
2. Bài tập minh họa.
Bài tập 9. Phân tích thành nhân tử: a). 3  3 b). x  3 xy
c). x y y x
d). x x xy y Lời giải
a). 3  3  3  3   1
b). x  3 xy
x x  3 y  ( Điều kiện x  0; y  0 )
c). x y y x
xy x y  ( Điều kiện x  0; y  0 )
d). x x xy y x x   1  y y   1   x  
1  x y  ( Điều kiện x  0; y  0 )
Bài tập 10. Phân tích thành nhân tử: a). 3 x  25 x
b). 9x  6 xy y c). 3 3 x y d). 2
x  9  2 x  3 Lời giải a). 3 x x x  2 25
x  25   x x  5 x  5 (Điều kiện: x  0 ) b). x xy y   x y 2 9 6 3
(Điều kiện: x, y  0 ). c). 3 3 x
y   x y x xy y (Điều kiện: x, y  0 ). d). 2
x  9  2 x  3 
x  3  x  3  2 (Điều kiện: x  3).
Bài tập 11. Phân tích thành nhân tử
a). a  5 a ;
b). a  7 với a  0 ;
c). a  4 a  4 ;
d). xy  4 x  3 y 12 . Lời giải
a). a a 5 ; b).  a  7 a  7 ; c).  a  2 2 ;
d).  x 3 y  4.
Bài tập 12. Rút gọn biểu thức:  14  6  5  21 . Lời giải
Ta có  14  6  5  21  2  7  3 5  21            2 7 3 10 2 7.3 7 3 7 3
  7  3 7  3  4 .
Bài tập 13. Tìm x và y , biết x y 13  22 x  3 y  . Lời giải
Ta có x y 13  4 x  6 y (ĐK: , x y  0 ) 2 2  x x     2 4 4
y  6 y  9  0   x  2   y  3  0   x  2 2
 0 và  y  2 3
 0  x  4 và y  9 .
Bài tập 14. Tính giá trị của biểu thức A  7  13  7  13 . Lời giải
50 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương 2 Ta có 2
A   7  13  7  13   7  13  2 7  137  13  7  13
 14  2 49 13  14  2 36  14 12  2 Khi đó 2
A  2  A  2.
Dạng 4. GIẢI PHƯƠNG TRÌNH 1. Phương pháp.
Để giải một phương trình chứa căn, ta tiến hành các bước sau:
Bước 1. Trước tiên tìm điều kiện để căn thức có nghĩa.
Bước 2. Áp dụng một số cách sau
① Sử dụng hằng đẳng thức a b2 2 2
a  2ab b hoặc a b2 2 2
a  2ab b để đưa
phương trình chứa căn thức về phương trình chứa dấu giá trị tuyệt đối với 2 A A ;  A B ② Áp dụng 2 2 A B   . A  BA  0
③ Đặt thừa số chung để đưa về phương trình tích: . A B  0  .  B  0  B  0 ④ Bình phương hai vế A B   2 A B
2. Bài tập minh họa.
Bài tập 15. Tìm x biết: a). 2 x  5 ; b). 2 25x  10 ; b). 2
4x  28x  49  7 ;
c). x 10 x  25  3 . Lời giải  x  a). Ta có 2
x  5  x  5 5   . Vậy x  5  ;  5 . x  5   x   x  2 b). Ta có 2
25x  10   x2 5 10  5x  5 10 10     . Vậy x  2  ;  2 . 5x  1  0 x  2   x   c). Ta có 2
4x  28x  49  7   x  2 2 7  7  2x  7  2 7 7 7   2x  7  7  2x 14 x  7     .  2x  0 x  0 Vậy x 0;  7 .  x  
d). Ta có x 10 x  25  3   x  2 5  3  x  5  5 3 3    x 5  3   x  8    x 64    .  x  2  x  4 Vậy x 4;6  4 .
Bài tập 16. Giải các phương trình sau: a). 2 4x  64  0 ; b). 4 x  7  0 ; c). 2
9x  2x 1 ; d). 2 2
x  4x  4  x  4x  4  0 . Lời giải
51 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương  x  4 a). Ta có 2 4x  64  0 2  4x  64 2  x 16   . x  4  Vậy S   4  ;  4 .  x  7 b). Ta có 4
x  7  0   x 2 2  7 2  x  7 2  x  7  
. Vậy S   7; 7. x   7 c). Ta có 2
9x  2x 1   x2 3
 2x 1  3x  2x 1      x 0 3x  0       x  1   3 x 1
  x  2x 1      1     
. Vậy S   ;1 .  x 0 1 3x  0        x 5    5  1
3x  2x 1 x     5 d). Ta có 2 2 2 2
x  4x  4  x  4x  4  0 2 2
x  4x  4  x  4x  4  x  2  x  2           x 2 x 2 0x 4 x
x  2  x  2       x  0  . Vậy S    0 . x  2    x  2  2x  0  x  0
Bài tập 17. Giải các phương trình: 2x  3 2x  3 4x  3 4x  3 a).  2 b).  2 c).  3 d).  3 x 1 x 1 x 1 x 1 Lời giải 2x  3 a).  2 x 1 2x  3 2x  3  0 2x  3  0 Điều kiện xác định:  0   hoặc  x 1 x 1  0 x 1 0  3   3 x     x 3  2 hoặc  2  x  hoặc x  1  2 x  1 x 1 2x  3 2x  3 1 Khi đó  2 
 4  2x  3  4x   1  x  (Thỏa mãn điều kiện) x 1 x 1 2 2x  3 b).  2 . x 1  3 2x  3  0 x  3
Điều kiện xác định:    2  x  . x 1  0 2 x 1  1  2  3  4   1 x x x  2 2x  3   Khi đó
 2  2x  3  2 x 1  x 1 0
 x 1  x . x 1   2x  3  0 3  x   2 4x  3 c).  3 . x 1 4x  3 4x  3  0 4x  3  0 Điều kiện xác định:  0   hoặc  x 1 x 1  0 x 1 0
52 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương  3   3 x       x 3  4 hoặc  4  x   hoặc x  1   4 x  1  x  1  4x  3 4x  3 6 Khi đó  3 
 9  4x  3  9x  9  x   (thỏa mãn điều kiện). x 1 x 1 5 4x  3 d).  3 x 1  3 4x  3  0 x   3
Điều kiện xác định:    4  x   . x 1  0 4 x  1  6 x   
x   x   5 4 3 9 1  4x  3   3 Khi đó
 3  4x  3  3 x 1  4x  3  0
 x    x . x 1 4   x 1  0  x  1  
Bài tập 18. Giải phương trình ẩn y 1
a). 4 y  20  y  5  9 y  45  4 3 1 1 b). 2 9 y  27  25y  75  49 y 147  20 5 7 Lời giải 1
a). 4 y  20  y  5  9 y  45  4 3 1
 4y  20  y  5  9 y  45  4 3   y   1 4 5  y  5  9  y  5  4 3   y   1 2 5 
y  5  .3 y  5  4 3  2 y  5  4 y  5  0
y  5  2    y  9 y  5  4 1 1 b). 2 9 y  27  25y  75  49 y 147  20 5 7   y   1   y   1 2 9 3 25 3 
49  y  3  20 5 7
 6  y 3   y  3   y  3  20
 4  y  3  20 y  3  0 y  3
y  3  5      y  28 y  3  25 y  28
Bài tập 19. Giải phương trình: x  2 25. 5 15. Lời giải
53 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương Ta có x  2 25. 5 15 x  5  3 x  2 
 5 x  5 15  x  5  3     x  5  3  x  8  .
Bài tập 20. Giải phương trình: 2
9x  90x  225  6. Lời giải Ta có: 2
9x  90x  225  6 
x x    x 2 2 9 10 25 6 9 5
 6  3 x  5  6 x  5  2 x  7  x  5  2     x  5  2  x  3.
Bài tập 21. Giải phương trình: 2
x  25  2 x  5. Lời giải 2 2 x  25  0 x  25 Điều kiện:     x  5. x  5  0 x  5 Khi đó 2
x  25  2 x  5
  x  5 x  5  2 x  5  0
x  5  x  5  2  0  x 5  0  x 5  0
x  5  0 x  5TM                x  5  4 x 5 2 0 x 5 2 x  1   L. 1 1
Bài tập 22. Giải phương trình: x  5  9x  45  25x 125  6. 3 5 Lời giải
Điều kiện: x  5. 1 1 Ta có x  5  9x  45  25x 125  6 3 5 1 1  x  5  9. x  5  25 x  5  6 3 5
x  5  x  5  x  5  6  x  5  6
x  5  36  x  41 (thỏa mãn điều kiện). 1
Bài tập 23. Giải phương trình: x   2. x Lời giải
Điều kiện: x  0. 1 x   x Ta có: x   2  x        x  2 1 1 2 2 0 0 1  0 x x x
x 1  0  x  1 (thỏa mãn điều kiện)
Bài tập 24. Tính cạnh của hình vuông, biết diện tích hình vuông đó bằng diện tích tam giác vuông
có hai cạnh góc vuông là 12,8 m và 40 m . Lời giải
Gọi xx  0, m là cạnh hình vuông, khi đó diện tích hình vuông bằng: 2 Sx  2 m . hv  1
Diện tích tam giác vuông là: S  12,8.40  256 . tgv  2 m  2
54 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
Theo giả thiết ta có: S S 2
x  256  x  256 16 m. hv tgv
Vậy cạnh của hình vuông là 16 m .
3. Bài tập rèn luyện.
Bài 17. Giải các phương trình a). 2
x  2x  4  2x  2 b). 2
x  2x  2  3x c). 2
x x  4  x  3 d). 2
x  3  2 x  9  0 Lời giải 2x  2  0  2x  2  0 a). 2
x  2x  4  2x  2      x
x  2x  4   2x  2 2 2 2 x  2  2 2  3x  0 x  b). 2
x  2x  2  3x     3  x  2  2
x  2x  2  3x 2
x x2  0 x  3  0 x  3  0   x 1 c). 2
x x  4  x  3      x  
x x  4   x 32 2  5 x   2
x  3tm x  3  0  d). Cách 1: 2 
x  3  2 x  9  0       x     x 3 2 x   11 3 4 9 x  loai  4 Cách 2: Với 2 x  3  x  9 
x  3. x  3 
x  3 1 2 x  3  0  x  3tm
Bài 18. Giải các phương trình sau a). 2 9.(2  3x)  6 b). 2
4x  9  2 2x  3
c). 10(x  3)  20 d). 2
x  6x  9  3x  6 Lời giải  4 x  a). 2 
9.(2  3x)  6  3 2  3x  6  2  3x  2  3  x  0 b). 2
4x  9  2 2x  3 
(2x  3)(2x  3)  2 2x  3
2x  3. 2x  3  2 2x  3  3 x   2x  3  0  2 
2x  3.( 2x  3  2)  0        7 2x 3 0 x   2 c). 10(x  3)  20
Điều kiện x  3.
Ta có 10(x  3)  20  10(x  3)  20  x  5 (thỏa mãn điều kiện) d). 2
x  6x  9  3x  6 x  2 3  x  6  0  9    2 x (t / m)
 (x  3)  3x  6  x  3  3x  6  x  3  3x  6    2    x  3  3  x  6 3   x  (loai)   4
55 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương
Dạng 5. CHỨNG MINH BẤT ĐẲNG THỨC 1. Phương pháp.
Để chứng minh một bất đẳng thức, ta có thể dùng các phương pháp sau:
① Với a  0 ; b  0 thì 2 2
a b a b ;
② Biến đổi tương đương.
2. Bài tập minh họa. Bài tập 25. Chứng minh: a). (2  3)(2  3)  1 b). 9  17 . 9  17  8
c). ( 2014  2013) . ( 2014  2013) =1 d). 2
2 2( 3  2)  (1 2 2)  2 6  9 Lời giải
a). 2  32  3 1.
Ta có 2  32  3  4 3 1.
b). 9  17 . 9  17  8.
Ta có 9  17 . 9  17  8117  64  8 .
c).  2014  2013 . 2014  2013 1
Ta có  2014  2013 . 2014  2013  2014 2013 1. d).     2 2 2 3 2 1 2 2  2 6  9 . Ta có     2 2 2 3 2 1 2 2
 2 6  2 6  4 2 1 8  4 2  2 6  9 .
Bài tập 26. Không dùng máy tính hoặc bảng số, chứng minh rằng: 5  8  6  7. Lời giải Ta có 5  8  6  7 2 2
  5  8   6  7 (vì hai vế đều dương)
 5  2 40  8  6  2 42  7  13 2 40 13 2 42  40  42  40  42.
Bất đẳng thức cuối cùng hiển nhiên đúng nên bất đẳng thức đã cho là đúng.
Bài tập 27. Không dùng máy tính hoặc bảng số, chứng minh rằng: 3  2  2  3   1 . Lời giải Ta có   2 3 2
 3 4 3  4  7  4 3 ; 2 2  2   3 1  2 
 3 1  232 3 184 3. 2
Vì 7  4 3  8  4 3 nên  3  2   2  3    2 1  .
Do đó 3  2  2  3   1 .
Bài tập 28. Chứng minh rằng: 7  3  6  2 . Lời giải 2 2
Ta có 7  3  6  2  7  2  6  3   7  2   6  3
 9  2 14  9  2 18  2 14  2 18 .
Bất đẳng thức cuối cùng đúng nên bất đẳng thức đã cho là đúng.
Bài tập 29. Cho a  0 , chứng minh rằng: a  9  a  3 .
56 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 3. Liên Hệ Giữa Phép Nhân Và Khai Phương Lời giải Ta có  a  2 9  a  9 ;  a  2 3
a  6 a  9. 2 2
Do a  0 nên a  9  a  9  6 a , do đó  a  9   a  3 . Vậy a  9  a  3. Bài tập 30. Cho a, ,
b c  0 . Chứng minh rằng:
a). a b  2 ab ;
b). a b c ab bc ca. Lời giải
a). a b  2 ab
Ta có a b  2 ab
a b  2 ab  0
  a b2  0 (dấu "  " xảy ra khi và chỉ khi a b ).
Bất đẳng thức cuối này đúng nên bất đẳng thức đã cho là đúng.
NHẬN XÉT: Bất đẳng thức a b  2 ab với a,b  0 gọi là bất đẳng thức Cô – si.
b). a b c ab bc ca. Ta có a, ,
b c  0 . Áp dụng bất đẳng thức Cô – si đối với hai số ta được: a b  2 ab
b c  2 bc
c a  2 ca .
Công từng vế ba bất đẳng thức trên ta được 2a b c  2 ab bc ca .
Suy ra a b c ab bc ca (dấu "  " xảy ra khi và chỉ khi a b c ). a b a b
Bài tập 31. Chứng minh bất đẳng thức: 
với a,b  0 . 2 2 Lời giải 2 2 a b a ba b   a b
Với a,b  0 ta có            2 2 2 2     a b a  2 . a b b  
 2a b  a  2 . a b b 2 4 2 2  a  2 .
a b b  0   a   2 .
a b   b   0 a b a b
  a b2  0, luôn đúng với a,b  0 . Vậy  . 2 2 1
Bài tập 32. Cho a
, chứng minh rằng: 2a 1  a . 2 Lời giải a b
Từ bất đẳng thức Cô – si a b  2 ab suy ra ab  . 2
Áp dụng bất đẳng thức này cho các số không âm 2a 1 và 1 ta được: 2a 1 1
2a 1  2a     1 .1   a . 2
Vậy 2a 1  a (dấu "  " xảy ra khi và chỉ khi a  1).
57 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
§BÀI 4. LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG A. TÓM TẮT KIẾN THỨC
1. Quy tắc phép khai phương của một phương A
Muốn khai phương một thương
, trong đó số A không âm và số B dương, ta có thể khai B
phương lần lượt số A và số B , rồi lấy kết quả thứ nhất chia cho kết quả thứ hai A A
(với A  0, B  0 ) B B Ví dụ 1. Tính 4 49 36  a a). : ; b). với a  0 . 25 121 49 Lời giải 4 49 4 49 2 7 22 a). .  :  :  . 25 121 25 121 5 11 35 3  6a 3  6a 36. a 6 a b).    . 49 49 49 7
Nhận xét: Vì a  0 nên a có nghĩa. Ví dụ 2. Tính 2 2 65  52 11 7 a). ; b). :1, 44  :1, 44 . 225 9 9 Lời giải 2 2 65  52 655265 52 13.117 13.13.9 13.3 39 a).      . 2 225 225 225 15 15 15 11 7 11 7  144 4 144 4 144 2 12 5 b). :1, 44  :1, 44   :    :  :  :  . 9 9  9 9  100 9 100 9 100 3 10 9 x  5 x  5 Ví dụ 3. Đẳng thức 
đúng với những giá trị nào của x và y ? y  2 y  2 Lời giải x  5 x  5
Theo định lí khai phương một thương thì  y  2 y  2
Khi x  5  0 và y  2  0 hay x  5 và y  2  .
2. Quy tắc phép chia căn bậc hai
Muốn chia căn bậc hai của số A không âm cho căn bậc hai của số B dương, ta có thể chia số A A A
cho số B rồi khai phương kết quả đó 
( với A  0, B  0 ) B B
58 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương Ví dụ 4. Tính a). 45 : 80 ; b).  5 3 5 2.3 : 2 .3 . Lời giải 45 9 3 2 .3 a). 45 : 80    . b). 2.3 5 5 5 3 5 2 : 2 .3   2  2 . 80 16 4 3 5 2 .3 Ví dụ 5. Tính 3 52 a). 54 : 2 : 3 ; b). : . 75 117 Lời giải
a). 54 : 2 : 3  54 : 2 : 3  27 : 3  9  3 . 3 52 3 52 1 4 1 2 3 b). :  :  :  :  . 75 117 75 117 25 9 5 3 10
Ví dụ 6. Thực hiện các phép tính
a).  45  125  20: 5 ;
b). 2 18 3 8 6 2: 2 . Lời giải
a).  45  125  20: 5  9  25  4  35 2  0.
b). 2 18 3 8 6 2: 2  2 9 3 4 6  2.33.2 6  6 .
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA.
Dạng 1. THỰC HIỆN PHÉP TÍNH 1. Phương pháp.
Sử dụng các quy tắc khai phương một thương và quy tắc chia hai căn bậc hai để tính A A
Với A  0, B  0 thì  B B
2. Bài tập minh họa.
Bài tập 1.( Bài 28, tr. 18 SGK) Tính : 289 14 0, 25 8,1 a). . b). 2 . c). . d) . 225 25 9 1, 6 Lời giải 289 289 17 a) Ta có:   . 225 225 15 14 64 64 8 b) Ta có 2    . 25 25 25 5 0, 25 0, 25 0,5 c) Ta có:   . 9 9 9 8,1 81 81 9 d)    . 1, 6 16 16 4
Bài tập 2. ( Bài 29, tr. 19 SGK) Tính : 2 15 12500 5 6 a). b). . c). . d). . 18 735 500 3 5 2 .3 Lời giải
59 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 2 2 1 1 a) Ta có:    . 18 18 9 3 15 15 1 1 b) Ta có    . 735 735 49 7 12500 12500 c) Ta có:   25  5. 500 500 5 5 5 6 2 .3 d)   4  2 . 3 5 3 5 2 .3 2 .3
Bài tập 3.(Bài 32, tr. 19 SGK) Tính : 9 4 2 2 165 124 2 2 149  76 a). 1 .5 .0, 01 . b) 1, 44.1, 211, 44.0, 4 . c). . d) . 16 5 164 2 2 457  384 Lời giải 9 4 25 49 5 7 7 a) Ta có: 1 .5 .0, 01  . . 0, 01  . .0,1  . 16 5 16 9 4 3 24
b) Ta có 1, 44.1, 211, 44.0, 4  1, 44.1, 21 0, 4  1, 44.0,81  1, 44. 0,81  1, 2.0,9  1,08 . 2 2 165 124 165124165124 41.289 289 17 c) Ta có:     . 164 164 164 4 2 2 2 149  76 73.225 225 15 d)    . 2 2 457  384 73.841 841 29
3. Bài tập rèn luyện. Bài 1. Tính 7 6 a). 2 ; và ; b). 5 7 7 5 : 35; c). 2 8 3 3 1 : 6. 81 150 Lời giải 7 169 169 13 6 6 1 1 a) Ta có 2 . và . 81 81 81 9 150 150 25 5 5 7 7 5 5 7 b) Ta có 5 7 7 5 : 35 5 7. 35 35 5 7 2 8 3 3 1 4 3 3 2 6 c) Ta có 2 8 3 3 1 : 6 . 6 6 6 3 2 6 1 1 3 2 4 1 Bài 2. Tính 4,5 50 : 2 2 2 5 15 8 Lời giải 1 1 3 2 Tính 4,5 50 2 2 2 5 2 1 9 2 2 1 1 3 9 2 1 9 25.2 2 2 0 2 2 2 2 5 2 2 2 2 2 2 1 1 3 2 4 1 Vậy 4,5 50 : 0 2 2 2 5 15 8
60 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương Bài 3. Tính  1 16   1 4  a).    7  : 7   b). 36 12 5 : 6 c).    3  : 3   7 7   3 3   2 12  3 27  5 3 32  50  8 d). 3  5 : 2 e). f). 3 2 22 g). ( 12  75  27) : 15
h). (12 50 8 200  7 450) : 10 i). 32  6. 3  11 Lời giải  1 16   1 16  1 4 a).    7  : 7     7 .      7 7 7 7 7 7    
b). 36 12 5 : 6  6  2 5  5 1  1 4  2 c).    3  : 3    3 3 3   6  2 5 5 1
d). 3  5 : 2  2. 3  5 : 2   2 2 2 2 2 12  3 27  5 3 2 2 .3  3. 3 .3  5 3 3 2.2  3.3  4 e).    2.2  3.3 4  1  3 3 3 5 2 32  50  8 2  2.5  2 2 2 4  5  2 f).   1. 2 2 2 12 75 27 4 9
g). ( 12  75  27) : 15      5  15 15 15 5 5 2 3 5   5    5  2 5 5 5 5
h). (12 50 8 200  7 450) : 10 12 5 8 20  7 45
 12 5 16 5  21 5  17 5 22 i). 32  6. 3  22  16.2  18   4 2 3 2  2  2 2 11 11
Bài 4. Thực hiện phép tính 5 a). A  7  5  2 7  4 1
b). B  4  3  6 3 15  3  2
1 2 27 2  38  5  3 2
c). C  1 2 5 5 11  5  2 d). D  3 2  4   e). E  5  2 2 2  2  2 1 2 1   f). 2  3  2  3  
g). 3  5  3  5  2
h). 6,5  12  6,5  12  2 6 Lời giải a). A  7  5  2
7  4 1   7  4  2 7  4.11 1     2 7 4 1 1    2 7 1 2  7    2 7 8 1 7 1  7  4 11  7  4     . 2 2 2 2
61 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 5
8  2 3  2 6 3 15  2 3  5
b). B  4  3  6 3 15  3   . 2 2
5  2 3  2 32 3  5  3  2 3  5    2 2 3 5 3  2 3  5   . 2 2 2 3  5  3  2 3  5 6   . 2 2 c). C           2 1 2 5 5 11 5 2 5 2 3 5  5  2  5  2  3  5  5  2        2 1 1 3 5 6 2 5 5 1 . 2 2 2 5 1 1   5    1  2 2
1 2 27 2  38  5  3 2 d). D  3 2  4     2 5 3 2 3 2 4  5  3 2  3 2  4
5  3 2  3 2  4  5  3 2 3 2  4   1. 3 2  4 3 2  4   e). E  5  2 2 2  2  2 1 2 1   .   Ta có 2 1  2 1.  2   1  2   1   2   1 2 1 .
Khi đó 5  2 2 2  2  5  2 2.
2 1  2  2 2  3  2 2  2 2. 2 1 . 2  2 2   1   2   1  2 2. 2 1  2   1      2 2 2 2
2 1  5  2 2 2  2  2  2 2  2 1 .   Do đó E  5  2 2 2  2  2 1 2 1  2  2 2 . 2 1  2   .   2 2 3 1 3 1 4  2 3 4  2 3 ( 3 1) ( 3 1) 2 f).        2 2 2 2 2 2 2 2 2 2 ( 5 1) ( 5 1) 5 1 5 1
g). 3  5  3  5  2    2   0 2 2 2
h). 6,5  12  6,5  12  2 6  4 6
62 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
Dạng 2. RÚT GỌN BIỂU THỨC 1. Phương pháp.
Tìm điều kiện của biến để căn thức có nghĩa. A A
Áp dụng phép khai phương một thương: 
( A  0, B  0 ) B B A A
Quy tắc phép chia các căn bậc hai 
( A  0, B  0 ) B B  , A khi A  0 Áp dụng 2 A A   .   , A khi A  0
Xét các trường hợp A  0, A  0 để bỏ dấu giá trị tuyệt đối.
Thay giá trị của biến vào biểu thức đã rút gọn rồi thực hiện các phép tính.
2. Bài tập minh họa. 16 12 3  3
Bài tập 4. Rút gọn biểu thức . 12 8 3  3 Lời giải 12  3  4 16 12 3   1 3 3 Ta có    . 3  3 3 3   4 3 9 8 4 12 8 1  2 2 165 124 
Bài tập 5. Rút gọn A
.x rồi tính giá trị của biểu thức sau với x  6 . 369 Lời giải  2 2 165 124  165124165124 Ta có A  .x  289.41 289 17 .x  .x  .x  .x . 369 369 369 9 3 17
Với x  6 thì A  .6  34 . 3
Bài tập 6. (Bài 30, tr. 19 SGK) Rút gọn các biểu thức sau: 2 y x 4 x a).
với x  0, y  0 . b). 2 2 y với y  0 . 4 x y 2 4 y 2 25x 16 c). 5xy
với x  0, y  0 . d) 3 3 0, 2x y
với x  0, y  0 . 6 y 4 8 x y Lời giải 2 y x y x y x 1 a) Ta có:  .  .
 ( do x  0, y  0 ). 4 2 2 x y x y x y y 4 4 2 2 x x x x b) Ta có 2 2 2 2 2 2 y  2y  2y  2y .  x y . 2 2 4 y 4 y 2 y 2  y 2 2 2 25x 25x 5 x 5  x 25x c) Ta có:. 5xy  5x . y  5x . y  5x . y  
(do x  0, y  0 ). 6 3 3 2 6 y y y y y 16 4 0,8x d) 3 3 3 3 0, 2x y  0, 2x y .  . 4 8 2 4 x y x y y
63 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
Bài tập 7. ( Bài 34, tr. 19 SGK) Rút gọn các biểu thức sau: 3 a  2 27 3 a). 2 ab
với a  0, b  0 . b). với a  3. 2 4 a b 48 2 9 12a  4a ab c).
với b  0, a  1  ,5.
d). a b
với a b  0. 2 ba b2 Lời giải 3 3 3 a) Ta có: 2 2 2 abab .  ab .
  3 ( do a  0,b  0 ). 2 4 2 2 a b abab 27 a  32 9 a  32 3 a  3 3a  3 b) Ta có    (do a  3). 48 16 4 4 9 12a  4a 3 2a2 2 3  2a 3  2a c) Ta có:   
. (do b  0, a  1  ,5). 2 2 b b b bab ab ab ab
d) a b  a ba ba b
  ab (do a b  0) 2       a b    a b2 a b b a x 1 y 1
Bài tập 8. Cho biểu thức B  :
. Rút gọn rồi tính giá trị của B với x  5; y  10 . y 1 x 1 Lời giải x 1 y 1 Ta có B  :
. Điều kiện: x  1; y  1. y 1 x 1   x 1   x 1 x y 1 1 x 1 Khi đó B  :   . y 1 x 1
y  1 y  1 y1 5 1 4 2
Với x  5; y  10 thì B    . 10 1 9 3
Bài tập 9. Rút gọn biểu thức rồi tính a 1 b 1 a). A  :
tại a  7, 25 ; b  3, 25 b 1 a 1 3 5 8 b). 2
B  15a  8a 15 16 tại a    5 3 15 3 2 x  5x
c). C  5x  125 
(x  0) tại x  5 x  5 d). 2 2 2 2 E
a  2 a 1  a  2 a 1 với a  5 Lời giải
( a 1)( a 1) a 1 5 a). A  
 a  7,25,b  3,25 ( b 1)( b  1) b 1 3 8 8 b). 2 2
B  15a  8a 15 16  15.( )  8. . 15 16 15 15 2 2  8 8 16  16  4
64 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 3 2 x  5x
c). C  5x  125  (x  0) x  5 2 2 2
(x  6)  (x  36) 2x 12x
Do x  5  5  x  0  5  x  5  x C    16  5  x 5  x d). 2 2 2 2 D
a  2 a 1  a  2 a 1 Ta có : 3 2 x  0 
x  5x và x  5 luôn có nghĩa.
Vậy D luôn xác định. 3 2 2 x  5x x . x  5
Với D  5x  125   5x  125  x  5 x  5
 5x  125  x  6x  5 5(x  0)  D  5 e). 2 2 2 2 E
a  2 a 1  a  2 a 1 2 2 2 2
 (a 1)  2 a 1 1  (a 1)  2 a 1 1 2 2 2 2 2 2
 ( a 1 1)  ( a 1 1)  a 1 1  a 1 1 2 2
 ( 5) 1 1  ( 5) 1 1
x  2 xy y
Bài tập 10. Cho biểu thức C
với x  0 , y  0 .
x  6 xy  9 y
Rút gọn rồi tính giá trị của C với x  25 ; y  81. Lời giải  2   x y2 x y x xy y Ta có C    .
x  6 xy  9 y   2 x 3 3 y x y 25  81 5  9 4 1 1
Với x  25 ; y  81 thì C     . Vậy C  . 25  3 81 5  3.9 32 8 8
3. Bài tập rèn luyện.
Bài 5. Rút gọn biểu thức 2 x x y y a). x y ; x y x 2 x 1 b). , x 0 x 2 x 1 2 y 2 y 1 x 1 c). .
, x 1,y 1,y 0 . 4 y 1 x 1 Lời giải 2 x x y y a). x y ; x y
65 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 2 x 2 xy y x y x x y y x x y y Ta có x y x y x y x y 2 2
x x y y x x x y 2 x y 2 xy y x y y x y 2 2 xy x y x y x y y x y x x y y x . xy x y x y x y 2 x 1 x 1 x 2 x 1 b). . 2 x 2 x 1 x 1 x 1 2 4 2 y 2 y 1 y 1 y 1 x 1 x 1 x 1 y 1 c). . . . . 4 4 2 y 1 x 1 y 1 x 1 y 1 x 1 x 1 Bài 6. Rút gọn và tính:
a  2 ab b a). A
(với a b  0 ) tại a  36;b  25. a b x  3 x  3 b). B  :
(với x  3) tại x  81.  3 x xx 54 2 x  25 c). C     x , tại x  3. 4  x ( 4) 2 x  4 3 2 x  3x
d). M  3x  27 
(x  0) , tại x  3. x  3 Lời giải
a  2 ab b a). A a b      a b a ab b a ab b 2 2 2
Với a b  0 ta có A     a b (1)  a b a b a b
Ta thấy a  36;b  25 thỏa mãn điều kiện.
Thay a  36;b  25 vào (1) ta có A  36  25  1  1.
b) Với x  3 ta có; x  3 x  3 x  3 x  3
( x  3)( x  3) x B  :  :  .  x (1)  x x  3 x x  3 x  3 x 3
Ta thấy x  81thỏa mãn điều kiện.
Thay x  81vào  
1 ta có B  81  9 .
c) Với x  4 ta có x 54 2    x 25 x  2  x 5 5 2 4 2 x 25 x  25 C       4 x2 x  4     4  x2 x 4 4 x x 4 x 52 2 x  25 x 52 2 2
x  25 2x 10x     (1) 4  x 4  x 4  x 4  x
66 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
Ta thấy x  3 thỏa mãn điều kiện. 2 2.3 10.3
Thay x  3 vào (1) ta có C   12  . 4  3
d) Với x  0 ta có 3 2 2 x  3x x x  3 2
M  3x  27   3x  27 
 3x  27  x x  3 x  3
 3x  27  x  3x  27  x  4x  27 (1)
Ta thấy x  3 thỏa mãn điều kiện.
Thay x  3 vào (1) ta có M  4 3  27  4 3  3 3  3 .
Dạng 3. GIẢI PHƯƠNG TRÌNH 1. Phương pháp.
Tìm điều kiện để căn thức có nghĩa. A A Áp dụng: 
A  0, B  0. B BA B 2
A A ; và A B   (với B  0). A  B
Đặt biệt. Nếu hai vế không âm thì có thể bình phương hai vế để khử dấu căn.
2. Bài tập minh họa.
Bài tập 11. (Bài 33, tr. 19 SGK) Giải phương trình: a). 2.x  50  0; c). 2 3.x  12  0; 2 x b). 2.x  8  0; d).  20  0. 5 Lời giải
a) Ta có 2.x  50  0  2.x  5 2  x  5. Vậy x  5. 8
b) 2.x  8  0  x
 4  2. Vậy x  2. 2 c) 2 2 2 12
3.x  12  0  3x  12  x   4  2. 3
x   2. Vậy x   2, x  2. 1 2 2 2 x x d) 2  20  0 
 20  x  5. 20 10 . 5 5  x   10.
Vậy x   10, x  10. 1 2
Bài tập 12. Tìm x biết: a).  x  2 3  9; b). 2
4x  4x 1  6. Lời giải x   x
a) Ta có  x  2 3 9 12 3
 9  x  3  9   .   x  3  9  x  6 
Vậy x  12, x  6.  1 2
67 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương b) 2
4x  4x 1  6  2x  2 1
 6  2x 1  6  5 x  2x 1  6  2   5 7  
. Vậy x  , x   . 2x 1  6  7  1 2 2 2 x    2
Bài tập 13. Giải các phương trình sau 4 15 x 1
a). 4x  20  3 5  x  9x  45  6 b). 25x  25   6  x 1 3 2 9 1 1 c). 4x  20  9x  45  x  5  4 d). 4x  20  9x  45  x  5  4 . 3 3 Lời giải 4 a). 
4x  20  3 5  x  9x  45  6 15 x 1 b). 25x  25   6  x 1 3 2 9
Điều kiện xác định: x  5 
Điều kiện xác định: x  1
 2 x  5  3 x  5  4 x  5  6 15 x 1 Ta có 25x  25   6  x 1  3 x  5  6 2 9  x  5  2 15  5 x 1  x 1  6  x 1  x 5  4 2.3  x  1  (thỏa mãn)
 10 x 1  5 x 1 12  2 x 1
Vậy phương trình có nghiệm là: x  1 
 3 x 1  12  x 1  4  x 1  16
x  17(TM )
Vậy phương trình có nghiệm là: x 17 1         c). d) 4x  20  9x  45  x  5  4 16x 16 9x 9 4x 4 16 x 1 3
Điều kiện xác định: x  1 
Điều kiện xác định: x  5
 4 x 1  3 x 1  2 x 1 16  x 1
 2 x  5  x  5  x  5  4  4 x 1 16
 2 x  5  4  x  5  2
x 1  4  x 1 16  x 15(TM )
x  5  4  x  9(TM )
Vậy phương trình có nghiệm là: x 15
Vậy phương trình có nghiệm là: x  9
Bài tập 14. Giải các phương trình 3x 1 5x  7 a).  2 . b). 1. x  2 2x 1 Lời giải 3x 1 a).  2 . x  2 1
ĐKXĐ: 3x 1 và x  2 cùng dấu hoặc x  . 3  1 3  x 1  0 x  1 Trường hợp 1:    3  x  . x  2  0 3 x  2   1 3  x 1  0 x  Trường hợp 2:    3  x  2  . x  2  0 x  2 
68 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 1
Vậy ĐKXĐ là x  hoặc x  2  . 3 3x 1
Bình phương hai vế của phương trình ta được:  4 x  2
 3x 1  4x  2  3x 1 4x 8  x  9
 (thỏa mãn điều kiện). 5x  7 b). 1. 2x 1  7 x  5  x  7  0  5 7 ĐKXĐ:     x  . 2x 1  0 1 5 x   2 5x  7
Bình phương hai vế ta được:
1  5x 7  2x 1  3x  6 2x 1
x  2 (thỏa mãn điều kiện).
Bài tập 15.(Bài 37, tr. 20 SGK)
Đố. Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho 4 điểm M , N, P, Q (H.3).
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNP . Q Lời giải Tứ giác MNPQ có:
Các cạnh bằng nhau và cùng bằng đường chéo hình chữ nhật có chiều dài 2 , cm chiều rộng 1 .
cm Do đó độ dài cạnh của tứ giác MNPQ là: 2 2
1  2  5 cm.
Các đường chéo bằng nhau và cùng bằng đường chéo hình chữ nhật có chiều dài 3 , cm chiều rộng 1 .
cm Do đó độ dài đường chéo là: 2 2
1  3  10 cm. 2
Vậy tứ giác MNPQ là hình vuông cạnh 5 cm nên có diện tích là     2 5 5 cm .
4. Bài tập rèn luyện.
Bài 7. Giải phương trình 4x 1 4x 1 a).  3 ; b).  3 ; x 1 x 1 x  2 15 x 1 c). 49x  98 14  3 x  2 8 ; d). 25x  25   6  x 1 . 49 2 9 Lời giải 1 a) ĐKXĐ: x  1  hoặc x  . 4 4x 1 4x 1 Ta có  3 
 9  4x 1  9x  9  x  2  (thỏa mãn ĐKXĐ). x 1 x 1
Vậy phương trình có nghiệm là x  2  .
69 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 1 b) ĐKXĐ: x  . 4 4x 1 4x 1 4x 1 Ta có  3   3   9  x  2
 (không thỏa mãn ĐKXĐ). x 1 x 1 x 1
Vậy phương trình vô nghiệm. c) ĐKXĐ: x  2 . x  2 Ta có 49x  98 14  3 x  2 8 49 14 x  2  49(x  2)   3 x  2  8 49
 7 x  2  2 x  2  3 x  2  8
 2 x  2  8  x  2  4  x  2  16  x  18
Ta thấy x 18 (thỏa mãn ĐKX Đ). Vậy phương trình có nghiệm x  18. d) ĐKXĐ: x  1. 15 x 1 Ta có 25x  25   6  x 1 2 9    x   15 x 1 25 1  .  6  x 1 2 9 5 x 1  5 x 1   6  x 1 2
 5 x 1 12  2 x 1
 3 x 1 12  x 1  4  x 1 16  x  17.
Ta thấy x 17 thỏa mãn ĐKXĐ.
Vậy phương trình có nghiệm là x  17.
Bài 8. Giải phương trình 2x  3 2x  3 a). 3x  6. b).  2. c).  2. d). 2
9x  6x 1  5. x 1 x 1
e). 64x  64  25x  25  4x  4  20. f). 2
2x  25 10x x  12. Lời giải a) 3x  6.
Điều kiện x  0. 6
Ta có 3x  6  3. x  6  x
x  2  x  2 tm. 3 Vậy x  2. 2x  3 b)  2. x 1  3 2x  3  0 x  3 Điều kiên    2  x  . x 1  0 2 x 1  2 2 2x 3 Ta có
 2  2x  3  2 x 1   2x 3  2 x 1 x 1
x   x   1 2 3 4
1  2x  1  x  ktm. 2
Vậy phương trình vô nghiệm.
70 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 2x  3 c)  2. x 1 x 1 2x  3  x 1   0  3 Điều kiên      x 1  x   3  2 x  .  x 1  1   2 x 1 2 2x  3  2x 3  2x  3 Ta có  2     4   4   x 1 x 1 x 1   1
 2x  3  4 x  
1  2x  1  x  tm. 2 1 Vậy x  . 2 x  2 3x 1  5 4 d) 2 
9x  6x 1  5  3x  2 1
 5  3x 1  5   
4 . Vậy x  2, x   .  1 2 3x 1  5  x   3  3
e) 64x  64  25x  25  4x  4  20. Điều kiện x  1. 
Ta có 64x  64  25x  25  4x  4  20  64x   1  25 x   1  4  x   1  20
 8 x 1  5 x 1  2 x 1  20  5 x 1  20 2
x 1  4  x 1  4  x 17tm Vậy x 17. f) 2
2x  25 10x x  12.  2x 12  0  Ta có 2 2
2x  25 10x x  12 
25 10x x  2x 12  
 5  x2  2x 12  x  6 x  6   x  6    17  
 5  x  2x 12   x
ktm. Vậy x  7.  
5  x  2x 12  3  
5  x 12  2x  x  7  tm
Bài 9. Giải các phương trình sau a). 2
1 x x 1 b). 2
x  4x  4  x  2 c). 2
2x  7  2  x d). 2
x  4x  3  x  2 e). 2
x  4  2  x  0 f). 2
x  4x  4  2x 1
g). (2x  4)(x 1)  x 1 h). 2
2x  4x 1  x  2 . Lời giải a). 2
1 x x 1 b). 2
x  4x  4  x  2 Điều kiện x  1 Điều kiện x  2 2 2 2
1 x x 1  1 x x  2x 1 2
x  4x  4  x  2
x  0(KTM ) 2 2
x  4x  4  x  4x  4 2 
2x  2x  0  2x(x 1)  0  x 1(TM)
 4x  4x  0  x  0(KTM )
Vậy nghiệm của phương trình là: x  1.
Vậy phương trình trên vô nghiệm.
71 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương c). 2
2x  7  2  x d). 2
x  4x  3  x  2
Điều kiện x  2 Điều kiện x  2 Ta có 2 2 2
2x  7  2  x  2x  7  4  4x x 2
x  4x  3  x  2 x  1  (TM ) 2 2       2  x 4x 3 x 4x 4
x  4x  3  0   x  3  (TM ) 1
 8x 1  x  (KTM )
Vậy nghiệm của phương trình là: 0 x  1  , x  3  .
Vậy phương trình trên vô nghiệm. e). 2
x  4  2  x  0 f). 2
x  4x  4  2x 1 Điều kiện x  2 1 Điều kiện x  2
x  4  x  2 2 2 2
x  4  x  4x  4 Ta có 2     x 4x 4 2x 1
 4x  8  x  2(TM )  x  2 2  2x 1 |
x  2 | 2x 1
Vậy nghiệm của phương trình là: x  2.
x  2  2x 1 x  1  (KTM )    
x  2 1 2xx 1(TM )
Vậy nghiệm của phương trình là: x  1
g). (2x  4)(x 1)  x 1 h). 2
2x  4x 1  x  2 . Điều kiện x  1  Điều kiện x  2 2 2
 2x  2x  4  x  2x 1 2 2
 2x  4x 1  x  4x  4  2
x   5(KTM )
x  8x  5  0 2
x  5  0   2 2 
 x 8x 16 x  5(TM )
 21  0  (x  4)  21  0
Vậy nghiệm của phương trình là: x  5 x  4  21
x  4  21(KTM )     x  4   21  
x  4  21(KTM )
Vậy phương trình đã cho vô nghiệm.
Bài 10. Giải các phương trình sau
a). x  4 x  4  5
b). x  2 x 1  x  2 x 1  2
c). x  2  4 x  2  x  7  6 x  2  1
d). x  2  3 2x  5  x  2  3 2x  5  2 2 . Lời giải
a). x  4 x  4  5 Điều kiện x  4 2
x  4  4 x  4  4  5  ( x  4  2)  5
x  4  2  5  x  4  3  x  4  9  x  13(TM )
Vậy nghiệm của phương trình là: x 13
b). x  2 x 1  x  2 x 1  2 Điều kiện x  1
x  2 x 1 
x  2 x 1  2
x 1 2 x 1 1  x 1 2 x 1 1  2 2 2
 ( x 1 1)  ( x 1 1)  2
x 1 1 | x 1 1| 2
72 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương
Nếu x 1 1  0  x  2 thì x 1 11 x 1  2  2  2
Vậy phương trình có nghiệm đúng với mọi 1 x  2
Nếu x 1 1  0  x  2 thì x 1 11 x 1  2  2 x 1  2 
x 1  1  x 1  1  x  2(TM )
Vậy phương trình có nghiệm đúng với mọi x  2
c). x  2  4 x  2  x  7  6 x  2  1 Điều kiện x  2
x  2  4 x  2  4  x  2  6 x  2  9  1 2 2
 ( x  2  2)  ( x  2  3)  1 |
x  2  2 |  | x  2  3 | 1
Nếu 2  x  6 thì  x  2  2  x  2  3  1  2  x  2  4
  x  2  2  x  2  4  x  6(TM )
Vậy phương trình có nghiệm x  6
Nếu 6  x 11 thì x  2  2  x  2  3 1  0 x  2  0
Vậy phương trình có nghiệm đúng với mọi 6  x 11
Nếu x  11 ta có: x  2  2  x  2  3  1  3 x  2  6  x  2  2  x  6(KTM)
Vậy không có giá trị nào của x .
d). x  2  3 2x  5  x  2  3 2x  5  2 2 5 Điều kiện x  2
 2x  5  6 2x  5  9  2x  5  6 2x  5   9  4 2 2
 ( 2x  5  3)  ( 2x  5  3)  4 |
 2x  5  3 |  2x  5  3  4 5 Nếu  x  7 2
Ta có: 3  2x  5  2x  5  3  4  6  4(V ) L
Vậy không có giá trị nào của . x
Nếu x  7 thì 2x  5  3  2x  5  3  4
 2 2x  5  4  2x  5  2 9
 2x  5  4  x  (KTM ) 2
Vậy không có giá trị nào của . x .
Bài 11. Giải các phương trình sau a). 2 2
x  3x  5  x  3x  7 b). 2 2
5 x  5x  28  x  5x  4 c). 2 2
2 2x  3x  5  2x  3x  6 d). 2 2
2x  3x  9  2x  3x  33
73 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương Lời giải a). 2 2
x  3x  5  x  3x  7 2 2
x 3x  5  x 3x  5 12 Đặt 2
x  3x  5  t (t  0) t  4  (KTM ) Ta có: 2 2
t t  12  t t 12  0   t  3 (TM ) Khi t  3 ta có: 2
x  3x  5  3 x  1  2 2
x  3x  5  9  0  x  3x  4  0   x  4
Vậy phương trình có nghiệm là: x  1  ; x  4. b). 2 2
5 x  5x  28  x  5x  4 2 2
 5 x  5x  28  x  5x  28  24 Đặt 2
x  5x  28  t (t  0) t  8 (TM ) Ta có: 2 2
5t t  24  t  5t  24  0   t  3  (KTM ) x  4 Khi t  8 ta có: 2
x  5x  28  8 2 2
x  5x  28  64  0  x  5x  36  0   x  9 
Vậy phương trình có nghiệm là: x  9  ; x  4. c). 2 2
2 2x  3x  5  2x  3x  6 2 2
 2 2x 3x  5  2x 3x  5 11 Đặt 2
2x  3x  5  t (t  0)
t  10 1 (TM ) Ta có: 2 2
2t t 11  t  2t 11  0  
t 1 10 (KTM )
Khi t  1 10 ta có: 2
2x  3x  5  1 10 2
 2x  3x  5 11 2 10  0  3  57 16 10   x 2  4 
2x  3x  6  2 10  0   3  57 16 10 x   4 3  57 16 10 3  57 16 10
Vậy phương trình có nghiệm là x  ; x  4 4 d). 2 2
2x  3x  9  2x  3x  33 2 2
 2x  3x  9  2x  3x  9  42
74 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương Đặt 2
2x  3x  9  t (t  0) t  6 (TM ) Ta có: 2 2
t t  42  t t  42  0   t  7  (KTM ) Khi t  6 ta có: 2
2x  3x  9  6 x  3  2 2
 2x  3x  9  36  0  2x  3x  27  0  9   x   2 9 
Vậy phương trình có nghiệm là x  3; x  2
Bài 12. Giải các phương trình sau
a). 1 3x 1  3x b). 2
x  6x  9  3x  6      5x 7  c). 2 3x 5 x 1 d). 4 x  3 Lời giải
a). 1 3x 1  3x 1 Điều kiện: x  3 x  0(loai) 2
(1)  3x 1  3x 1  (3x 1)  3x 1  9x(x 1)  0   x 1(tm) b). 2 2
x  6x  9  3x  6 
(x  3)  3x  6  x  3  3x  6 x  2 3  x  6  0  9   x  (tm)
 x  3  3x  6    2    x  3  3  x  6 3   x  (loai)   4
c). 2  3x  5  x 1 3  x  5  0 5 Điều kiện:   x  x 1 0 3 2  3x  5 
x 1  2  3x  5  x 1 x  2(tm) 2
 3x  5  x 1  3x  5  x  2x 1  (x  3)(x  2)  0  x 3(tm) 5x  7 d).  4 x  3  7     x  5x 7 0  5    x  3  0  x  3 5x 7  7  Điều kiện:  0     x  3    x 3 5  x  7  0  7  5    x  x  3  0  5  x  3 
75 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương 5x  7 5x  7 4  1 Ta có  4  16  x  ( ) tm x  3 x  3 11
Dạng 4. CHỨNG MINH BẤT ĐẲNG THỨC 1. Phương pháp.
Sử dụng phương pháp biến đổi tương đương.
 Ta biến đổi bất đẳng thức cần chứng minh tương đương với bất đẳng thức đúng.
 Bất đẳng thức đúng thường có dạng 2 A  0.
2. Bài tập minh họa.
Bài tập 16. (Bài 31, tr. 19 SGK)
a). So sánh 25 16 và 25  16;
b). Chứng minh rằng, với a b  0 thì a b a b. Lời giải
a) Ta có 25 16  9  3; 25  16  5  4 1
Mà 1  3 do đó 25  16  25 16.
b) Với a b  0 thì a b  0. 2 2
Ta có: a b a b a a b b   a    a b b
a a b  2 ba b  b  0  2 ba b (luôn đúng).
Vậy a b a b.
Bài tập 17. (Bài 36, tr. 20 SGK) Mỗi khẳng định sau đúng hay sai? Vì sao? a). 0,01  0,0001; b). 0  ,5  0  ,25; c). 39  7 và 39  6;
d). 4  13.2x  3.4  13  2x  3. Lời giải a) Đúng, vì 2 0,01  0,0001. b) Sai, vì 0  ,25 không có nghĩa. c) Đúng, vì  2 2 39  7 và  2 2 39  6 . 1
d) Đúng, vì nhân hai vế của bất phương trình với cùng một số dương thì không đổi chiều 4  13 bất đẳng thức. Bài tập 18. 1
a). Cho a  0. Chứng minh a   2; a a b a b
b). Cho a  0, b  0. Chứng minh  ; 2 2 a b
c). Cho a,b  0. Chứng minh a b   ; b a 2 x  2 d). Chứng minh  2 với mọi . x 2 x 1 Lời giải 1
a). Cho a  0. Chứng minh a   2; a 1 a 1 2aa  2 2 1 Ta có a   2   0 
 0 (đúng với mọi a  0 ). a a a
76 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Chương I-Bài 4. Liên Hệ Giữa Phép Chia Và Khai Phương a b a b
b). Cho a  0, b  0. Chứng minh  ; 2 2 2 2 a b a ba b   a b a b
a b  2 ab
Với a  0 ,b  0 ta có              2 2 2 2 2 4    
 a b  a b
ab a b ab
  a b2 2 2 2 0  0 (đúng). a b
c). Cho a,b  0. Chứng minh a b   ; b a
Với a  0,b  0 ta có a b a b  
a b b a a a b b a b a   bb a   0 b a
  b aa b  0   b a a b a b  0
  b a 2  a b  0 (đúng). 2 x  2 d). Chứng minh  2 với mọi . x 2 x 1 2 2 x  2 Ta có 2 2
 2  x  2  2 x 1   2 x   2
1  2 x 1 1  0   2 x 1 1  0 . 2  x 1
77 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
§BÀI 6 BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI A. TÓM TẮT KIẾN THỨC
1. Đưa thừa số ra ngoài dấu căn A B neáu A 0 Với B  0 ta có 2 A B A B A B neáu A 0.
Ví dụ 1. Đưa thừa số ra ngoài dấu căn a). 45 ; b). 2400 ; c). 147 ; d). 1, 25 . Lời giải a). 45  9.5  3 5 ; b). 2400  400.6  20 6 ; c). 147  49.3  7 3 ;
d). 1, 25  0, 25.5  0,5 5 .
Ví dụ 2. Đưa thừa số ra ngoài dấu căn a). 50.6 ; b). 14.21 ; c). 32.45 ; d). 125.27 . Lời giải a). 50.6  100.3  10 3 ;
b). 14.21  7.7.2.3  7 6 ;
c). 32.45  16.2.9.5  16.9.10  4.3. 10  12 10 ;
d). 125.27  25.5.9.3  25.9.15  5.3 15  15 15 .
Ví dụ 3. Đưa thừa số ra ngoài dấu căn a). 18x ; b). 2 75x y ; c). 3 2 605x y . Lời giải
a). 18x  9.2x  3 2x (với x  0 ). b). 2 2 75x y
25x .3y  5 x
3y y  0 5
x 3y khi x  0   
5x 3y khi x  0.  c). 3 2 2 2
605x y  121x .y .5x  11x y
5x x  0 11
xy 5x khi y  0     11
xy 5x khi y  0. 
Ví dụ 4. Đưa thừa số ra ngoài dấu căn a).   2 128 x y ; b).  2
150 4x  4x   1 ; c). 3 2
x  6x 12x  8 . Lời giải 8
 x y 2 khi x y a).
x y2  x y2 128 64 .2  8 x y 2   8
  y x 2 khi x  .y
39 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức b).
x x    x  2 2 150 4 4 1 25.6 2 1   x  1 5 2 1 6 khi x   2  5 2x 1 6      x 1 5 1 2 6 khi x  .  2 c). x x
x    x  3   x  2 3 2 6 12 8 2
2 . x  2   x  2 x  2 (với x  2 ).
2. Đưa thừa số vào trong dấu căn Với A 0, B 0 thì 2 A B A B. Với A 0, B 0 thì 2 A B A B.
Ví dụ 5. Đưa thừa số vào trong dấu căn 2 a). 3 5 ; b). 5 6 ; c). 35 . 7 Lời giải a). 2 3 5  3 .5  45 ; b). 2 5 6  5 .6  150 ; 2 2  2  20 c). 35  .35    . 7  7  7
Ví dụ 6. Đưa thừa số vào trong dấu căn: 1 a). 4  ; b). 0  ,06 250 . 8 Lời giải 1 1 a). 2 4    4   2 8 8 b).     2 0, 06 250 0, 06 .250   0,9
Ví dụ 7. Đưa thừa số vào trong dấu căn x x y a). x x b). y c). . y y x Lời giải a). 2 3 x x x .x
x x  0 x b). y y ĐK: .
x y  0; y  0 x x
Xét trường hợp x  0 , y  0 , ta có 2 yyxy y y x x
Xét trường hợp x  0; y  0 ,ta có 2 y   y   xy y y
40 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức x y c). y x 2 x y x y x ĐK: xy > 0, ta có   2 y x y x y
Ví dụ 8. Đưa thừa số vào trong dấu căn: 3 1  a). x với x  0. b). x với x  0. x x Lời giải 3 3 a) Ta có 2 x   x
  3x với x  0. x x 1   1   b) Ta có 2 x   (x)  x   với x  0. xx
Ví dụ 9. Chỉ ra chỗ sai trong các biến đổi sau: 2 3 3x y y a). x  b). 2 xy
y x .  y xy 7 7 x x Lời giải 2 3 3x a). Biến đổi x
chỉ đúng khi x  0 7 7 2 3 3x
Nếu x  0 thì x   7 7 y y b). Biến đổi 2 xy
y x .  y xy chỉ đúng khi x  0 x x y y
Nếu x  0 x < 0 thì 2 xy
 y x .  y xy x x B. CÁC DẠNG TOÁN:
Dạng 1: ĐƯA THỪA SỐ RA NGOÀI DẤU CĂN VÀ ĐƯA THỪA SỐ VÀO TRONG DẤU CĂN
1. Phương pháp giải
① Đưa thừa số ra ngoài dấu căn:
Biến đổi biểu thức lấy căn thành dạng tích 2
A B trong đó có thừa số là bình phương của một
số hoặc một biểu thức.
Thực hiện việc đưa thừa số ra ngoài dấu căn bằng cách áp dụng 2 A B A B (với B 0 ).
② Đưa thừa số vào trong dấu căn:
Chú ý đến dấu của thừa số trước dấu căn.
Nếu A  0 thì ta nâng A lên lũy thừa bậc hai rồi viết kết quả vào trong dấu căn: 2 A B
A B (với A  0 ; B  0 ).
Nếu A  0 thì ta coi A như là  A . Ta nâng A lên lũy thừa bậc hai rồi viết kết quả
vào trong dấu căn. Còn dấu " " vẫn để đằng trước dấu căn: 2
A B   A B (với A  0 ; B  0 ).
2. Bài tập minh họa.
41 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
Bài tập 1.(Bài 43, tr. 27 SGK) Viết các số hoặc biểu thức dưới dấu căn thành dạng tích một cách
thích hợp rồi đưa thừa số ra ngoài dấu căn : a). 54 . b). 108 . c). 0,1 2000 . d) 0  ,05 28800 . e). 2 7.63.a Lời giải
a) Ta có 54  9.6  3 6. b) Ta có 108 36.3 6 3 . c) Ta có 0,1 20000 0,1 10000.2 0,1.100 2 10 2 . d) Ta có 2 0, 05 28800 0, 05 10 . 144. 2 0, 05.10.12 2 6 2. e) Ta có 2 2 2 7.63.a 7 9.a 7.3 a 21 a .
Bài tập 2. ( Bài 44, tr. 27 SGK) Đưa thừa số vào trong dấu căn (với x 0 và y 0 ): 2 2 a). 3 5 . b). 5  2 . c).  xy . d). x . 3 x Lời giải a) Ta có 2 3 5 3 5 45. b) Ta có 2 5 2 5 .2 50. 2 4xy
c) Ta có: Với x 0 và y 0 : xy 3 9 2 2 2x
d) Ta có: Với : x 0 và x 2x. x x
3. Bài tập rèn luyện.
Bài 1. Đưa thừa số ra ngoài dấu căn: a). 96.125 . b). 4 5 a b . c). 6 11 4 a b . d). 3
a 1 a a   1 . e). 3 75a ; f). 5 2
98a (b  6b  9). Lời giải a) 5 3 4 2
96.125  2 .3.5  2 .5 .30  20 30 . b) 4 5 2 2 a b a b b . c) 6 11 3 5 a ba .b b . 2 d) 4 2 2 Với a  1: 3 a   a 2 1  a . .
a 1 a   a 1 aa   . 5  a 3a khi a  0 e) 3 2 2
75a  5 .3.a .a  5 3 a a   .  5
a 3a khi a  0 2 f) 2 2 5 2 2 4 a b b   a a b   2   2 98 ( 6 9) 7 .2. . . 3 7 .2. a  . . a b  3 2
7a (b 3) 2a khi b  3 2
 7a b  3 2a   . 2
7a (3b) 2a khi b  3
Bài 2. Đưa thừa số vào trong dấu căn: 11
a). x 13 với x  0 .
b). x 2 với x  0 . c). x  với x  0 . x Lời giải
42 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
a) Với x  0 : 2 x 13  13x .
b) Với x  0 : 2
x 2   2x . 11 11
c) Với x  0 : 2 x     x   11  x . x x Dạng 2: SO SÁNH PHÂN SỐ 1. Phương pháp.
① Sử dụng đưa thừa số vào trong dấu căn hoặc ra ngoài dấu căn và chú ý rằng: Nếu 0 A B thì A C B C (với C 0 ).
② Sử dụng đưa thừa số vào trong dấu căn rồi so sánh các số trong dấu căn. Nếu 0 A B thì A B.
2. Bài tập minh họa.
Bài tập 3. ( Bài 45, tr. 27 SGK) So sánh : a) 3 3 và 12 . b) 7 và 3 5 . 1 1 1 1 c) 51 và 150 . d) 6 và 6 . 3 5 2 2 Lời giải a) Ta có 12 4.3 2 3 .
Vì 2  3 và 3  0 nên 2 3 3 3 . Vậy 12 3 3 . b) Ta có 7 49,3 5 45. Vì 49 45 7 3 5. Vậy 7 3 5. 1 51 17 1 150 c) Ta có 51 ; 150 6 . 3 9 3 5 25 17 1 1 1 1 Vì 6 51 150 . Vậy 51 150 3 3 5 3 5 1 6 3 1 36 d) Ta có 6 ; 6 18 . 2 4 2 2 2 3 1 1 1 1 Vì 18 6 6 . Vậy 6 6 . 2 2 2 2 2
Bài tập 4. Không dùng máy tính hoặc bảng số , hãy so sánh : 2 1 a). 5 6 và 7 3 . b). 3 2 và 5 1 . 3 5 Lời giải a) 5 6 và 7 3 . Ta có 5 6  25.6  150 ; 7 3  49.3  147
Vì 150  147 nên 5 6  7 3 . 2 1 b) 3 2 và 5 1 . 3 5 2 8 Ta có 3 2  9.  24 3 3 1 6 5 1  25.  30 5 5
43 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức 2 1 Vì 24  30 nên 3 2  5 1 3 5
Bài tập 5. Không dùng máy tính hoặc bảng số , hãy so sánh : 5 2 a). 2 và 7 . b). 3 11 và 2 23 . 4 3 Lời giải 5 25 25 1 a) Ta có 2  .2   3 4 16 8 8 2 4 28 1 7  .7   3 3 9 9 9 1 1 5 2 Vì 3  3 nên 2  7 8 9 4 3 b) Ta có 3
 11   9.11   99 2
 23   4.23   92 Vì  99   92 nên 3  11  2  23
Bài tập 6. Sắp xếp theo thứ tự tăng dần 2 2 2 1 a). 6 3, 7 2,15 ,9 1 b).  71, 12, 21, 5  3 5 9 3 2 Lời giải
a) Ta có 6 3  36.3  108;7 2  49.2  98; 2 2 2 11 15  225.  90;9 1  81.  99 5 5 9 9 2 2
Vì 90  98  99  108 nên 15  7 2  9 1  6 3 5 9 2 4 16 1 b) Ta có 12  .12   5 ; 3 9 3 3 1 1 21 1 21  .21   5 ; 2 4 4 4 5
 3   25.3   75. 1 1 1 2 Vì  75   71  5  5 nên 5  3  71  21  12. 4 3 2 3
3. Bài tập rèn luyện.
Bài 3. So sánh các cặp số: 1 1 a). 4 7 và 3 13 . b). 82 và 6 . 4 7 Lời giải a) Ta có: 2 4 7  4 .7  112 , 2 3 13  13.3  117
Vì 112 117 nên 112  117 . Vậy 4 7  3 13 . 1 82 41 2 1 6 36 b) Ta có: 82   , 6   . 2 4 4 8 7 7 7 41 36 41 36 1 1 Vì  nên  . Vậy 82  6 . 8 7 8 7 4 7
44 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức
DẠNG 3. RÚT GỌN BIỂU THỨC 1. Phương pháp.
Đưa thừa số ra ngoài dấu căn rồi rút gọn các căn thức đồng dạng A  0
p A q A r A  ( p q r) A .
2. Bài tập minh họa.
Bài tập 7. Rút gọn các biểu thức sau: a). 20  80  45; b). 18  50  98 . Giải
a) Ta có 20  80  45  2 5  4 5  3 5  5
b) Ta có 18  50  98  3 2  5 2  7 2  5 2
Bài tập 8. Rút gọn các biểu thức sau :
a). 2 125  5 45  6 20; b). 3  72  4,5  12,5. c). 2 75  4 27  12. Lời giải a) 2 2 2
2 125  5 45  6 20  2 5 .5  5 3 .5  6 2 .5  10 5 15 5 12 5
 10 5 15 5 12 5  10 15 12 5  7 5.
b) 3  72  4,5  12,5  216  13,5  37,5 27 75 3 5  6 6    6 6  6  6  5 6 . 2 2 2 2 c) 2 2 2
2 75  4 27  12  2 5 .5  4 3.3  2 .2
 10 5 12 3  2 2  10 12  2 2  0.
Bài tập 9. Rút gọn các biểu thức sau với x  0 :
a). 2 3x  4 3x  27  3 3x
b). 3 2x  5 8x  7 18x  28 . Lời giải
a) Ta có 2 3x  4 3x  27  3 3x  (2  4  3) 3x  27  5  3x  27 .
b) Ta có 3 2x  5 8x  7 18x  28  3 2x 10 2x  21 2x  28
 (3 10  21) 2x  28 14 2x  28.
Bài tập 10. Rút gọn biểu thức 3 3 3 3
M  2x 16xy  7 25x y  3y 36x y với x  0; y  0 Lời giải Ta có 3 3 3 3
M  2x 16xy  7 25x y  3y 36x y
 8xy xy  35xy xy 18xy xy  25xy xy Bài tập 11. Rút gọn 2 2 3(x y) a).
với x  0, y  0 và x y . 2 2 x y 2 2 b). 2 5a  2
1 4a  4a  với a > 0,5. 2a 1 Lời giải 2 2 3(x y) | x y | 4.3 x y 6 a) Ta có   . 6 
(vì x y  0 ) . 2 2 2 2 x y 2 x y 2
(x y)(x y) x y
45 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 6. Biến Đổi Đơn Giản Biểu Thức Chứa Căn Thức 2 2 b) 2 5a  2
1 4a  4a  2 2  5a (1 2a) 2a 1 2a 1 2 2 5  1  
| a | . |1 2a | 5  . . a (2a 1) do a   2 5a.   2a 1 2a 1  2 
3. Bài tập rèn luyện.
Bài 4. Rút gọn các biểu thức a). 50  32  3 8 ;
b). 25a  2 160a  3 10a với a  0 .
c). 2 7  3 7  84 .
d).  63  8  7 7  2 14 . Lời giải
a) Ta có 50  32  3 8  25.2  16.2  3 4.2  5 2  4 2  3.2. 2  7 2 .
b) 25a  2 160a  3 10a  25.10a  2. 16.10a  3 10a  5 10a  2.4. 10a  3 10a  10 10a .
c) 2 7  3 7  84  2 7. 7  3. 7  4.21  2.7  21  2 21 14  21 .
d)  63  8  7 7  2 14  63. 7  8. 7  7. 7  2 14
 9.7.7  2 2. 7  7  2 14  3.7  2 14  7  2 14  14 .
Bài 5. Khai triển và rút gọn biểu thức (với x  0; y  0 ) a).  2x  
1 2x  2x  
1 . b).  x  2 y x  2 xy  4y .
c).  x y 2 x y  Lời giải 2 3
a) x   x x     x   x  2 2 1 2 2 1 2 1 2
 2x.11    2x 1 2x 2x1. 2 2  
b) x  2 y x  2 xy  4y   x  2 y   x   x.2 y   2 y   3 3
  x   2 y   x x  8y y .
c) x y 2 x y   x.2 x x. y y.2 x y. y
 2x xy  2 xy y  2x xy y . Bài 6. Chứng minh rằng:
x y y x2 y 2 x a).
x y với x  0, y  0 . 2 xy b). x x     x  2 2 5 25 5 5 với x  5 . Lời giải
a) Với x  0, y  0 :
x y y x2 y 2 xxyx y2. x y 
  x y x y  x  .y 2 xy 2 xy
x y y x2 y 2 x Vậy
x y với x  0, y  0 . 2 xy
b) Với x  5 :
  x 2  2 
x    x  2 5 5 5 2. 5. 5 5
 5  2 5x  25  x  5  x  2 5x  25 . Vậy x x     x  2 2 5 25 5 5 với x  5 .
46 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu §BÀI 7.
TRỤC CĂN THỨC Ở MẪU A. TÓM TẮT KIẾN THỨC
1. Khử mẫu của biểu thức lấy căn: A AB AB Với ,
A B mà AB  0 và B  0, ta có:   . 2 B B B 5 3 2
Ví dụ 1. Khử mẫu của các biểu thức lấy căn sau a). ; b). c). 72 80 75 Lời giải 5 5.2 10 1 a). Ta có    . 10 72 72.2 144 12 Nhận xét : 5
Nếu bạn nhân cả tử và mẫu của phân số
với 72 thì vẫn ra kết quả nhưng biến đổi phức 72 5 5.72 360 6 1 tạp hơn :    . 10  . 10 2 72 72.72 72 72 12
Vậy tìm thừa số phụ như nào cho hợp lý ?
Trước hết bạn phân tích mẫu số ra thừa số nguyên tố: 2 2 72  2 .3 .
Bạn thấy ngay thừa số phụ là 2, lúc đó số mũ của các thừa số nguyên tố đều chẵn. 3 3 3.5 15 1 b). Ta có     15. 2 2 2 80 16.5 4 .5 20 20 2 2 2.3 6 1 c). Ta có     6. 2 2 2 75 25.3 5 .3 15 15
Ví dụ 2. Khử mẫu của biểu thức lấy căn 11 3x a). b). 27x 3 5 y Lời giải 11 11.3x 33x 1 a).   
33x (ĐK: x  0 ) 2 27x 27 . x 3 x 81x 9x 3x 3 .5 x y 15xy 1 b).   
15xy ( ĐK: xy  0; y  0 ) 3 3 4 2 5y 5y .5y 25y 5y
Ví dụ 3. Khử mẫu của biểu thức lấy căn 1 1 1 b). b).  3 2
x  3x  3x 1 2 3 x x Lời giải 1 1 x 1 1 a).   
x 1 (ĐK: x  1  ) 3 2
x  3x  3x 1 x  3 1 x  4 1 x  2 1 1 1 x 1 . x (x 1) 1 b).     .
x x 1 ( ĐK: x  1 hoặc x  0 ) 2 3 3 4 2   x x x x x
Ví dụ 4. Rút gọn các biểu thức sau : 1 a). 200  50  4
b). 3  72  4,5  12,5. 8 Lời giải
47 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 1 1 a) 200  50  4
10 2 5 2  4. . 2  6 2. 8 4
b) 3  72  4,5  12,5  216  13,5  37,5 27 75 3 5  6 6    6 6  6  6  5 6 . 2 2 2 2
Ví dụ 5. Rút gọn các biểu thức sau :  2 3  2 1 1 a). 12     ; b). 4  2  3 2   9 2 18 Lời giải  2 3   1 1  a) 12   12 6  6  4 6  6 6  2  6     . 3 2    3 2  2 1 1 4 1 1 b) 4  2   2  2  2  2 2 . 9 2 18 3 2 6 a b 1
Ví dụ 6. Rút gọn các biểu thức sau : P  9ab  7  5  3ab
với a,b  0 . b a ab Lời giải a b 1
Ta có P  9ab  7  5  3ab b a ab 7 5 1  7 5  P  3 ab ab ab  3 . ab ab   ab   b a abb a
2. Trục căn thức ở mẫu: A A B
Với B  0 , ta có  ; B B C A B C  Với A  0 và 2
A B , ta có:  ; 2 A B A B C A B C
Với A  0; B  0 và A B, ta có:  . A B A B
Ví dụ 7. Trục căn thức ở mẫu 3  3 2  2 a). b). 5 3 2 1 Lời giải 3  3 3.( 3 1) ( 3 1) a) Ta có   5 3 5 3 5 2  2 2.( 2 1) b) Ta có   2 2 1 2 1
Ví dụ 8. Trục căn thức ở mẫu 3 2 3 a). ; b) ; c) ; 7 3 1 15  4 Lời giải 3 3. 7 3. 7 a)   7 7. 7 7
48 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 2 2.( 3 1) 2.( 3 1) b)    3 1 3 1 ( 3 1).( 3 1) 3 1 3 3.( 15  4) 3.( 15  4) c)    3.(4  15) 15  4 ( 15  4).( 15  4) 15 16
Ví dụ 9. Trục căn thức ở mẫu 5 3  3 5 2 a). b). 5 3  3 5 1 2  3 Lời giải 2 5 3  3 5 (5 3  3 5) 75  45  30 15 a) Ta có   5 3  3 5 (5 3  3 5).(5 3  3 5) 75  45 30.(4  15)   4  15 30 2 2(1 2  3) 2(1 2  3) 2(1 2  3) b)    2 1 2  3 (1 2  3)(1 2  3) (1 2)  3 (1 2 2  2  3 2(1 2  3) 3  2 1   2  2 2 3 4 1
Ví dụ 10. Rút gọn các biểu thức B    5  2 6  2 6  5 Lời giải 3 4 1 3( 5  2) 4( 6  2) ( 6  5) Ta có B       5  2 6  2 6  5 5  2 6  2 6  5
B  ( 5  2)  ( 6  2)  6  5  2 6
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
Dạng 1. KHỬ MẪU CỦA BIỂU THỨC LẤY CĂN 1. Phương pháp.
① Bằng cách nhân tử và mẫu của biểu thức trong căn cho mẫu số rồi rút mẫu ra ngoài căn bằng A AB AB công thức:   ( Với ,
A B mà AB  0 và B  0). 2 B B B
② Trong thực hành, cụ thể gồm các bước sau :
Biến đổi mẫu thành bình phương của một số hoặc một biểu thức (nếu cần );
Khai phương mẫu và đưa ra ngoài dấu căn.
2. Bài tập minh họa.
Bài tập 1. (Bài 48, 49 tr.19 SGK). Khử mẫu của biểu thức lấy căn   2 1 3 1 11 3 5 a). ; ; ; ; . 600 540 50 98 27 a a b 1 1 3 9a 2 b). ab ; ;  ; ; 3xy . b b a 2 b b 36b xy
(Giả thiết các biểu thức có nghĩa). Lời giải 1 600 6.100 10 6 6 a).     ; 2 600 600 600 600 60
49 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 11 11 11 11. 15 165     ; 540 9.4.15 6 15 6.15 90 3 3.50 6.25 5 6 6     ; 2 50 50 50 50 10 5 5 5 10    ; 98 49.2 7 2 14 a ab ab a ab khi b  0 b). ababab   ; 2 b b b
a ab khi b  0  abkhi a  0 a b a ab ab   ab   2 b a b a b aabkhi a  0  b 1 1 1 b 1 b    ; 2 2 b b b b 3 3 9a a b a ab a ab   
( ab  0;b  0). 36b 2 b 2 b 2b 2 2xy 3xy  3x . y
 3 2xy (vì xy  0). xy xy
3. Bài tập rèn luyện. 3 1 1
Bài 1. Khử mẫu các biểu thức dưới dấu căn rồi thực hiện phép tính: 2   . 20 60 15 Lời giải 3 60 2 15 15 Ta có: 2  2  2.  20 20 20 5 1 60 2 15 15    60 60 60 30 1 15  15 15 3 1 1 15 15 15  1 1 1  15 Vậy 2       15      . 20 60 15 5 30 15  5 30 15  6
Dạng 2. TRỤC CĂN Ở MẪU 1. Phương pháp
Nhân cả tử và mẫu với biểu thức liên hợp của mẫu để làm mất dấu căn ở mẫu.
Cụ thể áp dụng các công thức sau: AB C AB C AAA A B ①.  ; ②.  ; ③.  . B B 2 B C B C B C B C
Nhận xét. Ta gọi B C và B C là hai biểu thức liên hợp.
2. Bài tập minh họa.
Bài tập 2. (Bài 50, 51, 52 tr.30 SGK). Trục căn ở mẫu với giả thiết các biểu thức chữ đều có nghĩa. 5 5 1 2 2  2 y b y a). ; ; ; ;
với b  0; y  0. 10 2 5 3 20 5 2 b y
50 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 3 2 2  3 b p 1 b). ; ; ; với b  0;
với p  0, p  . 3 1 3 1 2  3 3  b 2 p 1 4 2 3 1 2ab c). ; ;
với x  0, y  0, x y;
với a  0,b  0, a  . b 6  5 10  7 x y a b Lời giải  5 5 2 5 5 10 10 5 a).   ;   ; 10 10 2 2 5 2 5 2 1 1 1 5    ; 3 20 3 4.5 6 5 30 2  2 2 2 2 2  2 2   ; 5 2 5 2 5 y   y b y b yy b   . b y b y b 3 3   1 3 3   1 3 b).   ; 3 1 3 1 2 2  3   1 2  
      31; 3 1 3 1 3 1    2 2 3 2 3 7  4 3     2  3 2 32 3 7 4 3; 4  3 b 3 b pp 2 p b  1   2 p p p ;   ; 3  b 9  b 2 p 1 4 p 1 4 p 1 2 c).  2 6  5; 6  5 3 10  7 3    10  7; 10  7 10  7 1 x y  ; x y x y 2  2 ab a b ab   . a b a b
Bài tập 3. Trục căn thức ở mẫu. 1 a 1 1 a).
với a  0; a  1 b).
với a  0,b  0 và ab  1 a a b 1 4 Lời giải 2 1 a (1 a ) 1 2 a a a)   1 a
(1 a )(1 a ) 1 a 1
1.( a b 1) ( a b 1) b)   a b 1
( a b 1)( a b 1)
a b  2 ab 1
51 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu a b 1 a b 1   1 a b a b  2 1 4
3. Bài tập rèn luyện.
Bài 2. Trục căn ở mẫu: 9 3 2 1 a). b). ; c). ; 3 5  2 2 1 5  3 1 a a 1 d). e). ; f). . 5  3 1 a 18  8  2 2 2 1 g). ; h). 1 2  3 3  2  5 Lời giải 9 9 3 a). Ta có   3 3 3 3 3 5  2 3  b).   5  2 5  2 5  2    2 2 1 2 1 c).   3 2 2 2 1 2 1    2 5 3 5 3 8  2 15 d).    4  15 5  3 5  3 2  1 a1  1 a a a a  e). 
1 a a 1 a 1 a 1 1 1 2 f).    18  8  2 2 3 2  2 2  2 2 3 2 6 2 1 2  3 2  1 2  3 g).   1 2  3 3  2 2  3 2 1 3  2  5 3  2  5 3 2  2 3  30 h).    . 3  2  5 5  2 6  5 2 6 12
Bài 3. Rút gọn biểu thức: 1 1 15 4 12 a). A   ; b). B     6 . 7  4 3 7  4 3 6 1 6  2 3  6 Lời giải 1 1 7  4 3  7  4 3 a). A    14 7  4 3 7  4 3 49  48 15 6   1 4  6  2 123  6 15 4 12  b). B     6     6 . 6 1 6  2 3  6 6 1 6  4 9  6  3 6  
1  2 6  2  43 6  6  1  1 75  12 Bài 4. Cho x
. Chứng minh rằng 3x là một số nguyên. 147  48 Lời giải
52 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 2 2    5 32 37 34 3 75 12 5 .3 2 .3 5 3 2 3  Ta có x     2 2 147  48 3.7  4 .3 7 3  4 3 7 32 37 34 3
5 32 37 34 3 105604224 231 7       . 2  2 147  48 99 3 7 3 4 3 7
Tính x được x
, do đó 3x  7  Z 3 26 Bài 5. Biến đổi
về dạng a b 3 . tính tích . a b 10  4 3 Lời giải 135  2 3 26 13  65  26 3 65  26 3 Ta có       10  4 3 5  2 3
52 352 3 252 3 5 2 3 2 13
Vậy a  5;b  2  . do đó . a b  5.( 2  )  1  0 1 1 1 1 Bài 6. Tính   ... 1  2 2  3 3  4 99  100 Lời giải 1 1 1 1 Ta có   ... 1  2 2  3 3  4 99  100 1  2 2  3 3  4 99  100
             ... 1 2 1 2 2 3 2 3 3 4 3 4
 99  100 99  100 1  2 2  3 3  4 99  100     ... 1 2 2  3 3  4 99 100 1  2 2  3 3  4 99  100     ... 1  1  1  1 
 2  1  3  2  4  3  ... 100  99  100  1  10 1  9.
Dạng 3. RÚT GỌN BIỂU THỨC 1. Phương pháp.
Thực hiện các phép biến đổi căn thức: A AB ①. 2 A A . ②. 
(với A  0, B  0 ). B B AB C A  ③. 2 A B A
B (với B  0 ).. ④  B C B C ).. B  ( 0, 0, C B C
2. Bài tập minh họa.
Bài tập 4. Rút gọn các biểu thức sau (giả sử các biểu thức chữ đều có nghĩa): a a a).   2 18 2 3 ; c)  ; 3 4 b b 1 a ab b). ab 1 ; d) . 2 2 a b a b Lời giải 2 2
a). 18 2  3  2.9 2  3  3 2  3 2  3 3  2  2  3 6 6.
53 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 2 2  1 a b 1 ab 2 2
a b 1 neu ab  0 b). 2 2 ab 1  aba b 1   2 2 2 2 a b a b ab 2 2
 a b 1 neu ab  0. a a ab a ab a c).    . 3 4 4 2 b b b b a   a b a ab  d).   a. a b a b     a ab
a ab a baa b a baab Cách khác:     a. a b a b a b a b
Bài tập 5. Rút gọn các biểu thức sau (giả sử các biểu thức chữ đều có nghĩa): 2  2
15  5 2 3  6 a a p  2 p ; ; ; ; . 1 2 1 3 8  2 1 a p  2 Lời giải 2  1 2 5  3    2 2  1 15 5 Ta có:   2;    5; 1 2 1 2 1 3 1 3 6  2   1 a   a a a  2 3 6 6 1      a; 8  2 2 2   ; 1 2 1 a 1 ra p p pp 2 2    p. p  2 p  2 2 a a 2a a
Bài tập 6. Xét biểu thức: A   1 a a 1 a a). Rút gọn A ;
b). Biết a 1, hãy so sánh A và A ;
c). Tìm a để A  2 ;
d). Tìm giá trị nhỏ nhất của A . Lời giải a). (ĐK a  0 ) 2 a a 2a a A   1 a a 1 a a  3 a   1 a
a  1aa a a 1 (2 1)   1   (2 a 1) 1 a a 1 a a a 1
a a  2 a 11  a a
Với a  1  a  1  a 1  0. và a 1 a  0
Suy ra A a a a a   1  0
Khi đó A  0  A A . Vậy A A .
c). Tìm a để A  2
a a  2  a a  2  0  a a  2 a  2  0
a a   1  2 a  
1  0   a   1  a  2  0  a 1 0  a  1  (VN)      a  4  a  2  0  a  2
54 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
Đối chiếu điều kiện ta được a  4 thì A=2 . 2 1 1 1  1  1
d). A a a a  2 a    a     2 4 4  2  4 2  1  Vì a   0   với mọi a.  2  2  1  1 1 Nên a       với mọi a.  2  4 4 1 1 1
Vậy giá trị nhỏ nhất của A bằng  khi và chỉ khi a   0  a  4 2 4  3   3 
Bài tập 7. Xét biểu thức: B   1 a :    1 2  a 1   1 a  a). Rút gọn B ; 3
b). Tìm giá trị của B nếu a  ; 2  3
c). Với giá trị nào của a thì B B . Lời giải a). Điều kiện 1   a 1  3   3  B   1 a :    1 2  a 1   1 a  2 2
 3 1 a. a 1   3 1 a  3 1 a a 1. 1 a    :    .  1 a    2  2 a 1   1 a a 1 3  1 a   3 b). Với a  ; Khi đó: 2  3        2 2. 2 3 3 1 3 2 3 3
B  1 a  1      2  3 2  3 2 32 3 3 1 4  3 c). Với 1
  a 1, ta có: B B B(1 B)  0  B  0   1   B  0 B  0       0  B 1    B 1 B 0  (VN )  1   B  0
Khi đó 0  1 a  1  0  1 a  1  0  a  1.
Kết hớp với điều kiện 1
  a 1 ta được 0  a 1
Vậy 0  a 1thì B B . 8 2 2 2
a  2ab b a b  2
Bài tập 8. Cho a > b > 0, chứng minh rằng  6b 4 a b 75a b 15 Lời giải 2 2 2 2 2 a b
8(a  2ab b ) a b
8(a b) .b Ta có  4 4 a b 75a b a b 75a . b b 2
a b 2(a b) 2b 2 2 . b 3 2  . .  .  6b. 2 a b 5a b 3 5 9 15
Ta thấy vế trái đúng bằng vế phải.
55 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
3. Bài tập rèn luyện.
Bài 7. Rút gọn các biểu thức sau (giả sử các biểu thức chữ đều có nghĩa): x  2 x 1 5  2 a). 11 6 2 ; e). x  ).. b). ;
x  2 x  (với 0 1 3 5  3 2 13 2  4 6 6  14 2  3 c). ; ; ; 24  d). 4 3 2 3  g). 28 2 2  3  6  8  16 8  15 f). ; h). . 2  3  4 30  2 Lời giải a)        2 11 6 2 9 2.3 2 2 3 2  3 2.    5 22  5 2 5 2 5 2 2 2  5  2  5  2 b)        3 5  3 2 3 5  2 
3 5  2  5  2  . 2 3 3 3             2 2 13 4 3 2 12 2.2 3.1 1 2 2 3 1 13 2 4 6 2 3 1 c)      4 3 2 3   1 4 3 2 3   1 4 3 2 3   . 24 4 3 1 2 6 2   3 7 2 3 7 6 14  2 d)    2 3  28 2 3  2 7 2 3  7  . 2    x x   x 2 1  x 2 1 x 1 2 1 e)    x  2 x 1   x  2  x  2 x 1 1 1 x 1 1 x
Với 0  x 1 thì  . x 1 x  1 x 1 0 Với x 1 thì   0. x 1 x  1 x 1 x 1 Với x 1 thì  . x 1 x  1        
 2  322 2 62 2 3 6 8 16 2 3 6 2 2 4  f)   2  3  4 2  3  2 2  3  2
 2  32 22 3 2  2  321 2   1 2. 2  3  2 2  3  2        2 3 1 2 3 2. 2 3 4 2 3 3 2. 3 1 3 1 g)      . 2 2. 2 2 2 2 2 1    1 16 2 15
152. 15.1 1  15  2 1 8 15 15 1 1 h) 2      30  2 2  15   2 1 2  15   1 2 15   1 2 15   . 1 2
56 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
Bài 8. Chứng minh đẳng thức: a b 2b a).  
1 (a  0,b  0,a  0); a b a b a b 2 2 a b b
ab b  2 ab b).  
a b b a b a b a a  2 b     0  b Lời giải a b 2b a). Ta có   (a  0,b  0,a  0); a b a b a b
a a b   b a b  2b =  
a b . a b a b
a ab ab b 2b   a b a b a b  1 a b 2 3 a b b
ab b  2 ab b). Ta có   a b a b a b a a  2 b     0  b
b a b
b a b  2 ab     a b a b . a b  2  
a  2a b b
b a b ba b 2
b a b b a b      a b  .    . b 2
a b  a b a b
Dạng 4. PHÂN TÍCH THÀNH NHÂN TỬ 1. Phương pháp. Áp dụng: ①   2 A A 2 (với A  0 ). ② A B A
B (với B  0 ).
2. Bài tập minh họa.
Bài tập 9. Phân tích thành nhân tử (với a, , b ,
x y là các số không âm).
a). ab b a a 1; b). 3 3 2 2 x y x y xy . Lời giải
a) ab b a a   ba 2 1
b a a 1  b a a   1   a   1   a   1 b a   1 . b) 3 3 2 2 x
y x y xy x x y y x y y x  x x x y    y y y x
xx y yx y   x y x y. Bài tập 10. Tính a). 1 2  3  6; b). 6  55  10  33. Lời giải
a) 1 2  3  6 1 2  3 1 2  1 21 3.
57 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
b) 6  55  10  33   6  10 33  55  2 3  5 11 3  5
  3  5 2  11 Dạng 5. SO SÁNH CÁC SỐ 1. Phương pháp.
Đưa thừa số vào trong căn rồi so sánh các số trong căn. 0  A B A B.
2. Bài tập minh họa.
Bài tập 11. Sắp xếp theo thứ tự tăng dần a). 3 5, 2 6, 29, 4 2; b). 6 2, 38, 3 7, 2 14. Lời giải
Đưa các thừa số vào trong dấu căn rồi so sánh các số trong căn.
a) 3 5  9.5  45; 2 6  4.6  24; 4 2  16.2  32.
Vì 24  29  32  45 nên 2 6  29  4 2  3 5.
b) 6 2  36.2  72; 3 7  9.7  63; 2 14  4.14  56.
Vì 38  56  63  72 nên 38  2 14  3 7  6 2. Bài tập 12. So sánh a). 3 3 và 12; b). 20 và 3 5; 1 1 c). 54 và 150; d). 30  29 và 29  28; 3 5 Lời giải a) 3 3 và 12;
Ta có 3 3  9.3  27 và 12 Vì 27 12 nên 3 3  12. b) 20 và 3 5; Ta có 2 20  20  400 và 3 5  9.5  45
Vì 400  45 nên 20  3 5. 1 1 c) 54 và 150; 3 5 1 1 1 1 1 1 Ta có 54  9.6  .3 6  6 và 150  25.6  .5 6  6. 3 3 3 5 5 5 1 1 Vì 6  6 nên 54  150. 3 5
d) 30  29 và 29  28;
 30  29 30  29 Ta có 1 30  29    và 30  29  30  29
 29  28 29  28 1 29  28    29  28  29  28 1 1
Vì 30  29  29  28 nên  30  29 29  28
Vậy 30  29  29  28.
58 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu
Dạng 6. GIẢI PHƯƠNG TRÌNH
1. Phương pháp giải
① Đặt điều kiện để phương trình có nghĩa:
A có nghĩa  A  0 .
② Đưa thừa số ra ngoài dấu căn: 2 A B A B .
③ Rút gọn các căn thức đồng dạng.
④ Biến đổi phương trình về dạng: 2
A B A B (với A  0 ).
2. Bài tập minh họa.
Bài tập 13. Giải phương trình: 1
a). 18x  9  x  3  4x 12  9 ; 2
b). 25x  50  16x  32  9x 18  12  4 x  2 . Lời giải 1
a). Điều kiện: x   2 1
18x  9  x  3  4x 12  9 2
 3 2x 1  x  3  x  3  9
 2x 1  3  2x 1  9  x  4 (nhận)
Vậy phương trình có nghiệm x  4
b). Điều kiện: x  2
25x  50  16x  32  9x 18  12  4 x  2
 5 x  2  4 x  2  3 x  2  12  4 x  2
x  2  6  x  2  36  x  38 (nhận)
Vậy phương trình có nghiệm x  38
Bài tập 14. Giải phương trình: 1 3 x 1 a). x 1  9x  9  24  1  7; 2 2 64
b). 3x  7 x  4  0; c). 5
x  7 x 12  0; Lời giải
a). Điều kiện: x  1 1 3 x 1 x 1  9x  9  24
 17  x  290. 2 2 64 1 3 x 1  x 1  9(x 1)  24  17  2 2 2 8 1 9 24  x 1  x 1 
x 1  17   x 1  17  x 1  17 2 2 8
x 1  289  x  290.
Đối chiếu với điều kiện ta được: x  290.
b). (Điều kiện x  0
Ta có 3x  7 x  4  0  3x  3 x  4 x  4  0
 3 x x   1  4 x   1  0  4      x   x x    
x 1 3 x  4 16 3 4 0  0    3  9    x 1 0  x 1 x  1
59 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 16
Đối chiếu với điều kiện ta được: x  ; x  1. 9
c). Điều kiện x  0 5
x  7 x 12  0  5
x  5 x 12 x 12  0  5  x. x   1 12  x  
1  0   x   1  5  x 12  0  x  1  (vn)  x 1  0  144     x  . 12   x   x  25 5 12 0  5 144
Đối chiếu điều kiện ta được: x  . 25
Bài tập 15. Tìm x , biết: 1 1 a). 2 9x  27  25x  75  49x 147  20; 5 7 3 x  5 2 x  7 b).  1  x; 2 3 2 2 1 x  5 1 25x 125 c). 2 2 9x  45  16x  80  3   9; 12 16 4 9 x
d). 4,5x  50x  32x  72x  5 12  0. 2 Lời giải 1 1 a). 2 9x  27  25x  75  49x 147  20 5 7 ĐKXĐ: x  3 1 1 2 9x  27  25x  75  49x 147  20 5 7  x   1  x   1 2 9 3 25 3 
49  x  3  20 5 7
 6 x  3  x  3  x  3  20  4 x  3  20
x  3  5  x  3  25
x  28 ( Thỏa ĐK) Vậy x  28. 3 x  5 2 x  7 b).  1  x 2 3 ĐKXĐ: x  0 3 x  5 2 x  7  1  x 2 3
3 x 5.3 2 x 7.2 6 6     x 6 6 6 6
 9 x 15  4 x 14  6  6 x  9 x  4 x  6 x 15 14  6   x  5   x  5
x  25 ( Thỏa ĐK). Vậy x  25.
60 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 7. Trục Căn Thức Ở Mẫu 2 2 1 x  5 1 25x 125 c). 2 2 9x  45  16x  80  3   9; 12 16 4 9 2 2 1 x  5 1 25x 125 2 2 9x  45  16x  80  3   9 12 16 4 9 2 x x   9 25 5 1 5 1 2 x  5  16  2 x  5 2    3   9 12 16 4 9 1 3 5 2 2 2 2 2  3 x  5  x  5  x  5 
x  5  9  3 x  5  9 3 4 12 2 2 2
x  5  3  x  5  9  x  4  x  2
 hoặc x  2. Vậy x  2  hoặc x  2. x
d). 4,5x  50x  32x  72x  5 12  0. 2 ĐKXĐ: x  0 x
4, 5x  50x  32x  72x  5 12  0 2 9x x 2 2 2 
 5 .2x  4 .2x  6 .2x  5 12  0 2 2 3 5 
2x  5 2x  4 2x  6 2x
2x  12  6 2x  12 2 2
 2x  2  2x  4
x  2 ( Thỏa ĐK). Vậy x  2.
61 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
§BÀI 8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI A. TÓM TẮT LÝ THUYẾT Rút gọn biểu thức:
Để thực hiện phép tính, rút gọn biểu thức ta sử dụng các phép biến đổi đơn giản như:
Đưa thừa số ra ngoài dấu căn,.
Đưa thừa số vào trong dấu căn.
Khử căn ở mẫu và trục căn thức ở mẫu để làm xuất hiện các căn thức bậc hai có cùng một
biểu thức dưới dấu căn (căn đồng dạng).
Cộng trừ các căn thức đồng dạng: p A q A r A m   p q r A m
Ví dụ 1. Rút gọn các biểu thức sau: 1 1 25 3 98 a). 4,5  72  5 b). 42 10 12 2 2 6 2 3 Lời giải 1 1 9.2 1 5 a) Ta có 4,5  72  5   .6 2  2 2 2 2.2 2 2 3 5  2  3 2  2  2 2 2 25 3 98 5 1 7 b) Ta có 42 10 12  42. 6 10. 6 12. 6 6 2 3 6 2 3
 35 6  5 6  28 6  2 6. 3 3
Ví dụ 2. Rút gọn biểu thức N  1  1 2 2 Lời giải 3 3 2  3 2  3 4  2 3 4  2 3 Ta có: N  1  1 =    2 2 2 2 4 4 1 1 2 2  ( 3 1)  ( 3 1) 2 2 1
  3 1)( 3 1) 1 2  a a 1  x y z
Ví dụ 3. Biến đổi biểu thức 5  4  về dạng   ab  
, với a,b  0; ,
x y, z Z b b aba b c
Tính tổng x y z Lời giải a a 1 5 4 1  5 4 1  Ta có 5  4   ab ab ab    ab   b b ab a b aba b ab
Vậy x  5; y  4  ; z  1
 . do đó x y z  0 y x
Ví dụ 4. Rút gọn biểu thức P   xy x y xy Lời giải y x y x
Điều kiện: x  0; y  0; x  .
y khi đó ta có: P   
x ( y x )
y ( y x )
xy ( y x )
62 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
y x y xy x = 
xy ( y x ) xyxxy
Ví dụ 6. Rút gọn biểu thức P    3 :   y x  3 xy   Lời giải
Điều kiện: x  0; y  0. khi đó ta có:  xxy x  3 y
x ( x  3 y ) x  9 y P    3 :  .  .   y x  3 xy y xy y    x x y y
Ví dụ 7. Rút gọn biểu thức P  
xy  : (x y)   x y   Lời giải
 ( x y)(x xy y)  Ta có P  
xy  : (x y)   x y   2  1 x y x y
 x  2 xy y   .   x y
x y x y . x yxx 1
Ví dụ 8. rút gọn biểu thức P  1  :   x x 1 x x 1   Lời giải
x x 1 x x x 1
Điều kiện: x  0; x  1. Khi đó ta có: P   .   x x 1 x 1  
x  2 x 1 x x 1  . x x 1 x 1 2 ( x 1) ( x 1).(x x 1)  .  x 1 x x 1 x 1  x 1 2 x 3 x 1   2 2 
Ví dụ 9. Rút gọn biểu thức P     .      x 1 x 1 1 x    x x  Lời giải 2
( x 1)  2 x ( x 1)  3 x 1 2 x  2
Điều kiện x  0; x  1. Khi đó ta có P  .
( x 1)( x 1) x
x  2 x 1 2x  2 x  3 x 1 2( x 1)  .
( x 1)( x 1) x 3 x ( x 1) 2( x 1) 6  . 
( x 1)( x 1) x x
B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA
DẠNG 1. RÚT GỌN CÁC BIỂU THỨC 1. Phương pháp.
Thực hiện các phép biến đổi đơn giản của căn thức bậc hai để làm xuất hiện căn thức đồng dạng.
Cộng, trừ các căn thức đồng dạng.
2. Bài tập minh họa.
63 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
Bài tập 1. (Bài 58, tr. 32 SGK) Rút gọn các biểu thức sau: 1 1 1 a). 5  20  5 ; b).  4,5  12,5 ; 5 2 2
c). 20  45  3 18  72 ;
d). 0,1 200  2 0,08  0, 4 50 . Lời giải 1 1 25 20 a) 5  20  5    5  3 5; 5 2 5 4 1 2 9 25 2 3 2 5 2 9 2 b)  4,5  12,5        . 2 4 2 2 2 2 2 2
c) 20  45  3 18  72  4.5  9.5  3 9.2  36.2
 2 5  3 5  9 2  6 2  15 2  5.
d) 0,1 200  2 0, 08  0, 4 50  0,1 100.2  2 0, 04.2  0, 4 25.2
 2  0, 4 2  2 2  3, 4 2.
Bài tập 2. Rút gọn biểu thức sau: 1 33 1 2 a). 48  2 75   5 1 ; b). 150  1, 6 60  4,5 2  6 ; 2 11 3 3
c).  28  2 3  7  7  84 ; d).   2 6 5  120 Lời giải 1 33 1 1 11 3 4 a) 48  2 75   5 1  16.3  2 25.3   5 2 11 3 2 11 3 3 17  2 3 10 3  3 10   3. 3 3 2 8
b) 150  1, 6 60  4,5 2
 6  25.6  16.6  4,5  6 3 3 24  5 6  4 6  4,5
 6  8 6 1,5.2 6  8 6  3 6 11 6. 9
c)  28  2 3  7 7  84  4.7 7  2 21  7  4.21 14  2 21  7  2 21  21.   2 6 5
 120  6  2 30  5  4.30  6  2 30  5  2 30 11.
Bài tập 3. Rút gọn biểu thức sau (với a  0, b  0 ); a). 3 2
5 a  4b 25a  5 16ab  2 9a b). 3 3 3 3
5a 64ab  3 12a b  2ab 9ab  5b 81a b. Lời giải a) 3 2
5 a  4b 25a  5 16ab  2 9a  5 a  20ab a  20ab a  6 a   a. b) 3 3 3 3
5a 64ab  3 12a b  2ab 9ab  5b 81a b
 40ab ab  6ab ab  6ab ab  45ab ab  5  ab ab.
Bài tập 4. Cho biểu thức: B  16x 16  9x  9  4x  4  x 1 với x  1. 
a). Rút gọn biểu thức B ;
b). Tìm x sao cho B có giá trị bằng 16 .
64 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai Lời giải
a) B  4 x 1  3 x 1  2 x 1  x 1  4 x 1.
b) B  16  4 x 1  16  x 1  4  x 1  16  x  15. Bài tập 5. a a b a).  ab
với a  0 và b  0 ; b b a 2 m
4m  8mx  4mx b). .
với m  0 và x  1. 2 1 2x x 81 Lời giải a a b ab a ab 1 1  2  a) ab    ab   ab ab ab  1 ab   . 2 2 b b a b b a b bbm
4m  8mx  4mx m 4m 1 x2 2 2 2 4m 4m 2m b) .  .    . ( với m  0 và 2 1 2x x 81 1 x2 81 81 81 9 x  1)
Bài tập 6. Rút gọn rồi so sánh giá trị của M với 1, biết:  1 1  a 1 M   :  
với a  0 và a  1.  a a
a 1  a  2 a 1 Lời giải 1 1 1 a 1 a Ta có:     a a a 1 a a   1 a a   1 a a   1    a   a a a 2 1 1 1 1 a 1 1 Do đó: M     
a a   : 1 a a
a a   . 1 . 2 1 1 a 1 a a 1 Vì a  0 nên 1  1 suy ra M 1. a 1 1
Bài tập 7. Giá trị của biểu thức  bằng: 2  3 2  3 1 A). ; B). 1 ; C). 4 ; D). 4 . 2
Chọn câu trả lời đúng. Lời giải 1 1 2  3  2  3 4 Ta có:     2  3 2  3 2 32 3 4 1 Chọn D). 2 x  9 x  3 2 x 1 Bài tập 8. Cho B    x  5 x  6 x  2 3  x
a). Xác định x để cho B có nghĩa; b). Rút gọn B ;
c). Tìm x để B  1 ;
d). Tìm x x nguyên để B là số nguyên. Lời giải
a) Ta có x  5 x  6   x 3 x  2
65 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai x  0 x  0  
Điều kiện  x  3  x  9    x  4 x 2   2 x  9 x  3 2 x 1 b) B    
x  3 x  2 x  2 x  3
2 x  9   x  3 x  3  2 x   1  x  2  
x  3 x  2
2 x  9  x  9  2x  4 x x  2 x x  2   
x  3 x  2
x 3 x 2
x 2 x  1 x 1   
x  2 x  3 . x  3 x  3  4 4 c) Ta có B  1 x  3 x  3 4 B  1 
 0  x  3  x  9 x  3
Vậy với x  9 thì B 1. 4
d) Vì B  1
nên B Z x  3 là ước của 4. Do đó x  3 nhận các giá trị 1  ,  2,  4 x  3
Suy các giá trị thích hợp của x là 1, 4, 16, 25, 49 .
3. Bài tập rèn luyện
Bài 1. Rút gọn biểu thức: a 1 a). 3
3 2a  18a  4 
128a (với a  0 ) 2 4 1 a b). 3 2
2 y x y xx
x x y ( với x y  0 ) x y ax ay a b a b c). 
(với a  0,b  0, a b ) a b a b Lời giải a 1
a). Với a  0 , ta có: 3
3 2a  18a  4 
128a  3 2a  3a 2a  2 2a  2 2a 2 4
 3 2a  3a 2a  31 a 2a. 1 a
b). Với x y  0 , ta có: 3 2
2 y x y xxx x y x y ax ay 1 a 2
 2y x y xx   x y
a x yx x y 1 1
 2y x y x x y xx x y x y
x y 2y x (do x  0 ).
66 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai   2     2 a b a b a b a b
c). Với a  0,b  0, a b , ta có:   a b a b
a b a b
a  2 ab b a  2 ab b 2a  2b    .
a b  a b a b
Bài 2 (Dạng 1). Rút gọn biểu thức: 2 1 2 2 1 2  5 2  5 a).   b).  2  2 2  2 2 2  3  5 2  3  5 Lời giải      2 2 1 2 1 2 2 1 2 1 2 a). Ta có:      2  2 2  2 2 2(1 2) 2( 2 1) 2( 2 1) 3 2       1 2 1 2 2 2 2 1 3 2 3      3 2   1 2( 2 1) 2( 2 1) 2 1 2 1 2  5 2  5 2 2  10 2 2  10 b). Ta có:    2  3  5 2  3  5 2  6  2 5 2  6  2 5 2 2  10 2 2  10       2 2 10 2 2 10 2 2 10 2 2 10     2  5 1 2  5 1 3  5 3  5 2   5  2 1 2   5  2 1
2 2  103 52 2  103 5   3  5 3 5
6 2  2 10  3 10  50  6 2  2 10  3 10  50  9  5 12 2  2 50 12 2 10 2 2 2 2     . 4 4 4 2
DẠNG 2. CHỨNG MINH ĐẲNG THỨC 1. Phương pháp.
Thực hiện các phép biến đổi căn thức và các hằng đẳng thức đáng nhớ để biến đổi vế trái
bằng vế phải hoặc vế phải bằng vế trái của đẳng thức.
2. Bài tập minh họa.
Bài tập 9. Chứng minh các đẳng thức sau: 3 2 3 6  6 2x  1 a). 6  2  4  . b).  x
 6x  : 6x  2 với x  0 . 2 3 2 6   x 3 3   Lời giải 3 2 3 3 6 6 a) Ta có: VT  6  2  4  6  2  4 2 3 2 2 9 4 3 2  3 2  6  6  6  2 6    2 6   VP   (đpcm). 2 3  2 3  6
67 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai  6 2x   6x
b) b) Ta có VT   x
 6x  : 6x   6x
 6x  : 6x     x 3 3     7 7 1  6x : 6x   2  VP (đpcm). 3 3 3
Bài tập 10. Chứng minh các đẳng thức sau: 2 1 a a 1 a  a).   a   1   
với a  0 và a  1. 1 a 1 a    2 4 a b a b b).
a với a b  0 và b  0 . 2 2 2 b
a  2ab b Lời giải    a a a 3 1 1 a) Ta có:  a
a  1 a a a  
a a    a 2 1 2 1 1 a 1 a 1 a 1 a 1 và   1 a
1 a1 a 1 a 2      2 1 a a 1 a 1 Do đó: VT    a       1 a    (đpcm). 1 a 1 a    1 a 1 VP 2 2 4 2 4 2 a b a b a b a b
a b a .b b) Ta có: VT    .  a  VP (đpcm). 2 2 2 2 b
a  2ab b ba b2 2 b a b
(do a b  0 và b  0 ).
3. Bài tập rèn luyện.
Bài 3. Chứng minh đẳng thức sau với x  0; y  0; x y :  x y x y y 1 4 x    :    x y x y y y x y   Lời giải 4 xy 1 4 x
Rút gọn vế trái được .  . x y y x y
Bài 4. Chứng minh đẳng thức sau với x  0 ; y  0 và x y :
x y 4 xy x y x    :    x y x y x x y   Lời giải
x y 4 xy x y 2
 ( x y)  4 xy x Xét vế trái    :     .   x y x y x   ( x y )( x y ) x y  
x  2 xy y  4 xy x   .   ( x y )( x y ) x y   2  ( x y )  x x   .    ( x y )( x y ) x y   x y
Ta thấy vế trái đúng bằng vế phải nên đẳng thức đã cho là đúng.
68 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
Bài 5. Chứng minh đẳng thức sau với x  0 ; y  0 và x y :  x x y y  2 y
xy  : (x y) 1   x y x y   Lời giải  x x y y
 ( x y)(x xy y)  1
Xét vế trái T  
xy  : (x y)      xy .   x y   x y x y   2 ( x y ) x y   ( x y )( x y ) x y x y  2 y x y Xét vế phải P   x y x y
Rõ ràng T P , suy ra điều phải chứng minh.  x 2 x
y x y y x
Bài 6. Chứng minh rằng giá trị của biểu thức A    .   là hằng số 2 xy y xy x ( x y )  
với mọi giá trị thích hợp của x và y : Lời giải
Điều kiện: x  0 ; y  0 ; xy .  x 2 x y
xy( x y)
Khi đó ta có A    .   2 y ( x y )
x ( y x ) ( x y )  
x  2 xy y xy ( x y ) 2 ( x y ) xy ( x y )  .  . 1 2 xy ( x y ) ( x y ) 2 xy ( x y ) ( x y )
Vậy giá trị của biểu thức A luôn là hằng số với mọi giá trị thích hợp x và y .
DẠNG 3. CHỨNG MINH BIỂU THỨC KHÔNG PHỤ THUỘC VÀO BIẾN. 1. Phương pháp.
Thực hiện các phép biến đổi căn để biến đổi biểu thức không còn chứa biến.
2. Bài tập minh họa.
Bài tập 11. Chứng minh biểu thức sau không phụ thuộc vào biến a : 2  1 1 a 1   1     . 1 
 với a  0,a 1 . 2
 2  2 a 2  2 a 1 a   a  Lời giải 1 1 1 1 Ta có:    2  2 a 2  2 a 2(1 a ) 2(1 a ) 1 a 1 a 2 1   
2(1 a )(1 a ) 2(1 a) 1 a 2  1 a 1  a 1 2
1 a a 1 a 1
Do đó biểu thức đã cho bằng:       1 a
1 a1 a     a  2 1 a a
a 1 aa 1    1. 2 1 a a
Vậy biểu thức đã cho không phụ thuộc vào biến a .
Bài tập 12. ( Dạng 3). Chứng minh biểu thức sau không phụ thuộc vào biến:   2 xy x y x y 2     với     x 0, y 0, x . y x y   x y . 2  x y y x  Lời giải
69 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai   2 xy x y 2 x y Ta có:      x y   x y . 2  x y y x
4 xy   x y 2 2 x y    x
y  x y . 2 x y y xx y 2 2 x y    x
y  x y . 2 x y y x x y x y x y       1 (đpcm). x y y x x y x y x y
Vậy biểu thức đã cho không phụ thuộc vào biến.
DẠNG 4. RÚT GỌN RỒI TÍNH GIÁ TRỊ CỦA BIỂU THỨC TẠI x  . a 1. Phương pháp.
Bước 1. tìm điều kiện để biểu thức có nghĩa
Bước 2. rút gọn biểu thức.
Bước 3. thay giá trị của biến x  .
a vào biểu thức đã được rút gọn rồi thực hiện các phép tính. Nhận xét:
Nhiều lúc có thể phải sử dụng kết quả rút gọn, lập phương trình hoặc bất phương trình rồi
giải ra để tìm giá trị của biến.
2. Bài tập minh họa. x 1 2 x 2  5 x
Bài tập 13. Cho biểu thức P    x  2 x  2 4  x a). Rút gọn . P 2
b). Tính giá trị của P với x  . 2  3 Lời giải
a) Điều kiện: x  0; x  4 .
( x 1)( x  2)  2 x ( x  2)  (2  5 x ) Khi đó ta có: P
( x  2)( x  2)
x  3 x  2  2x  4 x  2  5 x
( x  2)( x  2) x  2 xx( x  2) x   
( x  2)( x  2)
( x  2)( x  2) 2  x 2 b) Ta có 2 x
 2(2  3)  ( 3 1)  x  3 1 2  3 2 3 1 3 1 ( 3 1) 4  2 3 Do đó P      (2  3) 2  ( 3 1) 1 3 2  2   x  2 x  2  4x
Bài tập 14. Cho biểu thức P     :   2 x 1 x  2 x 1 (x 1)   a). Rút gọn . P
b). Tính giá trị của P biết x  5  4 . Lời giải
70 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
a) Điều kiện: x  0; x  1.   x  2
x  2   x   2 1
Khi đó ta có P      x   . 1  x   1   x  2 1 4x 
x 2 x  1 x 2 x   2 1 (x 1)     . 2    4 1 1 x x x
xx 2xx 2 2 (x 1)     . 2    4 1 1 x x x
( x 1)  x x 2 2 1 2   x 1     . 2    4 1 1 x x x 2 xx  5  4 x  9
b) Ta có | x  5 | 4     x  5  4  x 1 9 1 4 2
Với x  9 , ta có P    2 9 6 3
Với x  1, không thỏa mãn điều kiện đã nêu nên biểu thức P không có giá trị.  2 xy x y  2 x
Bài tập 15. Cho biểu thức P    .  x y   2 x  2 y x y   a). Rút gọn . P x 4
b). Tính giá trị của P biết  . y 9 Lời giải
a) Điều kiện: x  0 ; y  0 ; x y . 2 xy x y  2 x
Khi đó ta có P    .
x y 2( x y)   x y  2 4 xy  ( x y ) 2 x  . 2( x y )( x y ) x y
4 xy x  2 xy y 2 x     (x 2 xy y) 2 x .  . 2( x y )( x y ) x y 2( x y )( x y ) x y 2 ( x y) 2 xx  .  2( x y )( x y ) x y x y x 4 9x b) Ta có   y y 9 4  xxx 2  Do đó P     3 5 9 5  x x x x x 2 2 4
71 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai  1 2   2 1 
Bài tập 16. Cho P   :     
x  2 x  4 x  4  x  4 x  2  a). Rút gọn . P 1
b). Tìm x để P   . 2 Lời giải
a) Điều kiện: x  0 ; x  4 .  1 2   2 1 
Khi đó ta có: P     :    2
x  2 ( x  2)   x  4 x  2 
x  2  2 2  ( x  2)  : 2 ( x  2) x  4 x
( x  2)( x  2) 2  x  .  2 ( x  2)  x 2  x 1  x
b) Ta có P   2 1    2 2  x 2
 2 x  4  x  2  x  6  x  36 (thỏa mãn điều kiện).  1 1   x 3 x  3 
Bài Tập 17. Cho biểu thức P   :       
x  3 x x  9 x x  3 x  3 x   a). Rút gọn . P
b). Tìm x để P 1. Lời giải
a) Điều kiện: x  0 ; x  9 .
x ( x  3)  3 x  3 x  3 Khi đó ta có: P  :
x ( x  3)( x  3) x ( x  3) x  3 x  3 x ( x  3) 1  . 
x ( x  3)( x  3) x  3 x  3 x  3 1 1
b) Để P  1  1  1  0 x  3 x  3 1 x  3 x  4   0   0 x  3 x  3  x  4  0  x  4  0   hoặc 
 9 < x < 16 (thỏa mãn điều kiện)  x 3  0  x 3  0  x 1   6 x 1 x
Bài tập 18. Cho biểu thức D   2   :      . 2 x  3
(2 x  3)( x 1) x 1     3 a). Rút gọn . D .
b). Chứng minh rằng D  2 Lời giải 9
a) Điều kiện: x  0 ; x  . 4
72 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
2(2 x  3)  ( x 1) 6 x 1 x (2 x  3) Khi đó ta có: D  : 2 x  3
(2 x  3)( x 1)
4 x  6  x 1 6 x 1 2x  3 x  : 2 x  3
(2 x  3)( x 1)
3 x  5 (2 x  3)( x 1)
3 x  5 (2 x  3)( x 1) 3 x  5  .  .  2 x  3 2x  3 x 1
2 x  3 (2 x 1)( x 1) 2 x 1 3 3 x  5 3
6 x 10  6 x  3 13  3
b) Xét hiệu D       0 . Vậy D  2 2 x 1 2 2(2 x 1) 2(2 x 1) 2 3 3
Nhận xét: Về mặt phương pháp, muốn chứng minh D
ta chứng minh D   0 2 2 x  2 x 1 1
Bài tập 19. Cho biểu thức B    x x 1 x x 1 x 1 a). Rút gọn B .
b). Chứng minh rằng B luôn luôn có giá trị không âm với mọi giá trị thích hợp của x . Lời giải
a) Điều kiện x  0 .
x  2  ( x 1)( x 1)  (x x 1)
x  2  x 1 x x 1 Khi đó ta có: B  
( x 1)(x x 1)
( x 1)(x x 1) x x x ( x 1) x   
( x 1)(x x 1)
( x 1)(x x 1) x x 1
b) Ta cos x  0 nên x  0 1 3 3 Khi đó 2
x x 1  ( x  ) 
  0 với mọi x . 2 4 4 x Do đó B
 0 với mọi x  0 . x x 1  1 2   x
Bài tập 20. Cho biểu thức C =  :    1  
x 1 x x x x 1 x 1   a). Rút gọn C .
b). Chứng minh rằng C luôn luôn có giá trị âm với mọi giá trị thích hợp của x . Lời giải
a) Điều kiện x  0 ; x  1 .  1 2  x x 1 x 1 2 (x 1)
Khi đó ta có: C     :  .
x 1 ( x 1)( x 1) x 1 
( x 1)(x1) x x 1
( x 1)( x 1) (x 1) ( x 1)  .  ( x 1)(x1) x x 1 x x 1 2  1  3
b) Ta có x  0 ; x  1 nên (
x 1)  0. Khi đó x x 1  x    0.    2  4 ( x 1) Do đó C
 0 với mọi giá trị thích hợp của x . x x 1
73 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai x  1 2 x 2  5 x
Bài tập 21. (Dạng 1). Cho biểu thức: A    x  2 x  2 4  x
a). Rút gọn A nếu x  0 và x  4 ;
b). Tìm x để A  2 . Lời giải x  1 2 x 2  5 x
a). Với x  0 và x  4 , ta có: A    x  2 x  2 4  x
x  1 x 2 2 xx 2 2  5 x    
x  2 x  2  x  2 x  2  x  2 x  2 3 xx xx 2 3 6 
x  3 x  2  2x  4 x  2  5 x  3 x    
x  2 x  2
x 2 x 2  x 2 x 2 x 2 3 x
b). Khi A  2 ta được
 2  3 x  2 x  2  x  4  x 16 (tm x  0,x  4) x  2 Vậy x  16 . aab
Bài tập 22. (Dạng 1). Cho biểu thức: B   1  :
với a b  0. 2 2 2 2 2 2 a b
a b a a b a). Rút gọn B ; a 3 b). Tính B nếu  ; b 2
c). Tìm điều kiện của a,b để B  1 Lời giải aab
a) Với điều kiện: a b  0 , ta có: B   1  : 2 2 2 2 2 2 a b
a b a a b  2 2
a b a  2 2
a a b a    . 2 2 2 2   b a b a b a b a b a b     2 2 2 2 a b a b a b a b 3 1 b b b a 3 1 5 b) Ta có:  3
a b thay vào ta được 2 2 B     . b 2 2 3 5 5 5 b b b 2 2 a b a b
c) Khi B  1 ta có: 1 
1  a b a b a b a b
a b a b b
  b  2b  0  b  0.
Vậy với a b  0 thì B 1. x 3 6 x
Bài tập 23. Rút gọn P   
. rồi tính giá trị của biểu thức P với x  0,36 . x  3 3  x x  9 Lời giải x  3
Rút gọn ta được P
với điều kiện x  0 ; x  9. x  3 2
Khi đó x  0,36 ta có P   . 3
74 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
DẠNG 5. RÚT GỌN RỒI TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC 1. Phương pháp.
Bước 1. tìm điều kiện để biểu thức có nghĩa
Bước 2. rút gọn biểu thức ta được biểu thức Q .
① Nếu Q là một biểu thức có dạng bậc hai, tức là 2
Q ax bx  ,
c a  0 thì ta đưa về dạng 2 2  b c   b b b c  bình phương thiếu: 2 2 2
Q ax bx c a x x   a    x  2. . x     2 2  a a   2a 4a 4a a  2 2 2 2  b
b  4ac   b
b  4ac   a x        a x       2  2a    4a   2a    4a  2  b      a x       khi đó:  2a   4a   b 
⋆ Nếu a  0 thì 2
ax bx c
dấu bằng xảy ra khi x   . Suy ra GTNN là . 4a 2a 4a  b 
⋆ Nếu a  0 thì 2
ax bx c
dấu bằng xảy ra khi x   . Suy ra GTLN là . 4a 2a 4a f xf x
② Nếu Q là một biểu thức có dạng phân thức  0 hoặc  0 2 k 2 k
2. Bài tập minh họa. 2m 1
Bài tập 24. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức A  . 2 m  2 Lời giải 2 2
km  2m  2k 1 Xét A k  . 2 m  2
Khi đó để biểu thức đạt giá trị lớn nhất, nhỏ nhất thì tử số là biếu thức f m 2 2
 km  2m  2k 1 phải biểu diễn được dưới dạng bình phương  k  1 hay 0 1 k k k k              . m 1 2  2 0 2 1 0 1 k    2 2m 1
2m 1 m  2 m 2 2 1 Khi đó A 1  1     0, m
  A 1, m  2 2 2 m  2 m  2 m  2
Dấu bằng xảy ra khi và chỉ khi m 1 1 2m 1 1 22m   1  m  2 m  22 2 1 Và A       0, m
  A   , m  2 2 m  2 2 2  2 m  2 2  2 m  2 2
Dấu bằng xảy ra khi và chỉ khi m  2  1
Vậy max A 1 khi và chỉ khi m 1, min A   khi và chỉ khi m  2  2 1
Bài tập 25. Tìm giá trị lớn nhất của biểu thức A x x 1 Lời giải
Điều kiện xác định x  0
Để A đạt giá trị lớn nhất thì x x 1 đạt giá trị nhỏ nhất
75 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai 2 1 1 1  1  3
Có x x 1  x  2   x   1  x     2 4 4  2  4 2 2  1   1  3 3 Lại có x   0, x   0  x    , x   0      2   2  4 4 1 1
Dấu "="xảy ra x   x  Khi đó
xx   3 1 Min 1   x  2 4 4 4 4 1 Vậy Max A   x  3 4  1 1  x 1
Bài tập 26. Cho biểu thức A   :   2  x x
x 1  ( x 1) a). Rút gọn . A
b). Tìm giá trị lớn nhất của biểu thức P A  9 x Lời giải  1 1  x 1 a). A   :  
với x  0, x  1 2  x x
x 1  ( x 1)  1 1  x 1 2 2 1 x ( x 1) ( x 1) x 1     :     2  x( x 1)
x 1  ( x 1) x ( x 1) x 1 x ( x 1) x x 1  1 
b). P A  9 x   9 x 1  9 x
 với x  0, x  1 xx  1 1
Với x  0, x  1, áp dụng bất đẳng thức Cauchy có:  9 x  2 9 x  6 x x  1   1     9 x  6  1  9 x 1 6  5   P  5       x   x  1 1 1 Dấu "="xảy ra 
 9 x x  (thỏa mãn). Vậy max P  5   x x 9 9  x x  6  x
Bài tập 27. Cho biểu thức A       
với x  0; x  4 2  x 2  x 4  x   a). Rút gọn . A
b).Tìm giá trị nhỏ nhất của A . Lời giải  x x  6  x a). A       
với x  0; x  4 2  x 2  x 4  x   x (2  x )  x (2  x ) 6  x   (2  x )(2  x ) (2  x )(2  x )
2 x x  2 x x 6  x 4 x  6  x 3 x  6     (2  x )(2  x ) (2  x )(2  x ) (2  x )(2  x ) (2  x )(2  x ) 3 ( x  2) 3    (2  x )(2  x ) 2  x 3 3 3  3 
b). Có x  0  x  0  x  2  2     x  2 2 x  2 2
76 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai
Dấu "=" xảy ra  x  0 3  Vậy min A   x  0 2  x  2 x  2    x2 1
Bài tập 28. Cho biểu thức: C    .   x 1 x  2 x  1 2  
a). Rút gọn C nếu x  0, x 1;
b). Tìm x để C dương;
c). Tìm giá trị lớn nhất của C . Lời giải
a) ĐK: x  0, x 1, ta có:             x 2 x 2 
2   x 2 x 1  x 2 x x 1 1  1 x2 C    .      x 1 x  2 x  1 2   
x  1 x    . 2 2 1   x
x  2  x
x  2 1  x2 2  x 1 x2   
x   x   . . 2 2
x   x  2 2 1 1 1 1
x   x2 1 x 1 x        x x
x 1  x   1  x   1  1
b) Ta có: C  0  x 1 x   0 1 x  0 1 x  0  x 1.
c) Với x  0, x 1, ta có C x 1 x   x x  x x  2  1 1 1   1  1
  x  2 x.     x        2 4 4   2  4 2  2 1   1  1 1 Vì  x   0  
với mọi x  0 nên  x      với mọi x  0 .  2   2  4 4 1 Do đó: C  với mọi x  0 4 1 1 1 1 GTLN của C  khi x
 0  x   x  . 4 2 2 4 1 1 Vậy GTLN của C  khi x  . 4 4  1 1   x  4 
Bài tập 29. Cho biểu thức P =  :    2  .  
x 1 x 1 x 1   a). Rút gọn . P
b). Tìm giá trị lớn nhất của . P Lời giải
a) Điều kiện: x  0 ; x  1 . ( x 1) 1
2.( x 1)  ( x  4) Khi đó ta có P  :
( x 1)( x 1) x 1 x  2 x 1 1  .  .
( x 1)( x 1) x  2 x 1 1 1 b) Ta có P    1 vì x  0 x 1 1
Do đó max P 1đạt được khi x  0  x  0
77 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai  x 3 x  3 14  x  3
Bài tập 30. Cho biểu thức Q =    .   x  3 x  3 x  9 2   a). Rút gọn . Q .
b). Tìm giá trị nhỏ nhất của . Q Lời giải
a) Điều kiện: x  0 ; x  9 . 2 2 ( x  3)  x  3) 14 x  3 Khi đó ta có: Q  .
( x  3)( x  3) 2
x  6 x  9  x  6 x  9 14 x  3  .
( x  3)( x  3) 2 2x  32 x  3 x 16  . 
( x  3)( x  3) 2 x  3 x 16 x  9  25 25 b) Ta có Q  =  x  3 x  3 x  3 x  3 25 25  x  3   6  2 ( x  3).
 6 (bất đẳng thức cô si) x  3 x  3 10  6  4. 25
Dấu “ = “ xảy ra khi và chỉ khi x  3  x  3 2
 ( x  3)  25  x  3  5 2
 ( x  3)  25  x  3  5
x  4(thỏa mãn điều kiện)
Vậy minQ = 4 khi x  4.
3. Bài tập rèn luyện.  x x  6  x x  36 x
Bài 7. Cho biểu thức P = P     :   . x  36 x  6 x
2( x  3)(x  2 x  3)   a). Rút gọn P .
b). Với giá trị nào của x thì P có giá trị lớn nhất ? Giá trị lớn nhất đó là bao nhiêu? Lời giải 6
a) Rút gọn ta được
với điều kiện x  0; x  9; x  36 . x  2 x  3 6 6 b) P    3 ( vì 2 ( x 1)  0 ). 2 ( x 1)  2 2
Suy ra max P = 3 đạt được khi x  1. 2 x  3 3 x  2 15 x 11 Bài 8. Cho biểu thức P =   x  3 x 1 x  2 x  3) a). Rút gọn P .
b). Tìm giá trị nhỏ nhất của P . Lời giải 5 x  2 a) P
(x  0; x  1) . x  3
78 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai 5 x 15 17 17 17 17 b) P   5   5   P  5  ( vì √𝑥 ≥ 0 ). x  3 x  3 3 3 2 2 P  
( dấu bằng xảy ra khi x  0.). Vậy min = 
, đạt được khi x  0. 3 3
DẠNG 6. RÚT GỌN RỒI TÌM GIÁ TRỊ CỦA x NGUYÊN ĐỂ BIỂU THỨC NHẬN GIÁ TRỊ NGUYÊN 1. Phương pháp.
Bước 1. tìm điều kiện để biểu thức có nghĩa
Bước 2. Ta xét hai trường hợp sau: f (x)
① Loại 1. Biểu thức Q sẽ có dạng
trong đó f (x) và g(x) là các đa thức và g(x)  0 g(x) Khi đó: k
⋆ Bước 1: Tách về dạng Q m(x) 
trong đó m x là một biểu thức nguyên khi x g(x)
nguyên và k có giá trị là số nguyên. k
⋆ Bước 2: Để Q nhận giá trị nguyên thì
nguyên hay k : g(x) nghĩa là g(x) thuộc tập g(x) ước của k.
⋆ Bước 3: Lập bảng để tính các giá trị của . x
⋆ Bước 4: Kết hợp với điều kiện đề bài, loại bỏ những giá trị không phù hợp, sau đó kết luận bài toán.
2. Bài tập minh họa.
Bài tập 31. Tìm các giá trị nguyên của biến số x để biểu thức đã cho cũng có giá trị nguyên 2 x  2 3 x a). . b). . c). . x 1 x 1 x 1 Lời giải 2 a).
có điều kiện x  1 x 1 2 Để
nhận giá trị nguyên thì 2 : (x 1)  x 1U (2)  { 1  ; 2  } x 1 Ta có bảng: x 1 2 1 1 2 x 1(thỏa mãn) 0 (thỏa mãn) 2 (thỏa mãn) 3 (thỏa mãn) 2 Vậy với x { 1
 ;0;2;3} thì biểu thức nhận giá trị nguyên. x 1 x  2 b).
có điều kiện x  1 x 1 x  2 x 11 x 1 1 1 Ta có:    1 x 1 x 1 x 1 x 1 x 1 x  2 Để
nhận giá trị nguyên thì 1: (x 1)  x 1U (1)  { 1  } x 1 Ta có bảng: x 1 1 1 x 0 (thỏa mãn) 2 (thỏa mãn) x  2
Vậy với x {0; 2} thì biểu thức nhận giá trị nguyên x 1 3 x c).
có điều kiện là x  0 x 1
79 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai 3 x 3( x 1)  3 3( x 1) 3 3 Ta có     3 x 1 x 1 x 1 x 1 x 1 3 x Để
nhận giá trị nguyên thì 3: ( x 1)  x 1U (3)  { 1  ; 3  } x 1 Ta có bảng: x 1 3  1 1 3 x 4 (loại) 2 (loại) 0 (thỏa mãn) 2 x 0 (thỏa mãn) 4 (thỏa mãn) 3 x
Vậy với x {0; 4} thì biểu thức nhận giá trị nguyên x 1
② Loại 2. Đây là một dạng nâng cao hơn của dạng bài tập tìm gá trị nguyên của x để biểu thức
Q nhận giá trị nguyên bởi ta chưa xác định giá trị của biến x có nguyên hay không để biến k
đổi biểu thức A về dạng A m(x)  . g(x)
Bởi vậy, để làm được dạng bài tập này, chúng ta sẽ thực hiện các bước sau:
⋆ Bước 1: Áp dụng điều kiện cùng với các bất đẳng thức đã được, chứng minh m A M
trong đó m, M là các số nguyên.
⋆ Bước 2: Trong khoảng từ m đến M , tìm các giá trị nguyên.
⋆ Bước 3: Với mỗi giá trị nguyên ấy, tìm giá trị của biến x .
⋆ Bước 4: Kết hợp với điều kiện đề bài, loại bỏ những giá trị không phù hợp rồi kết luận.
Nhận xét: Trong dạng này ta hay sử dụng bất đẳng thức Cô-Si: cho a  0,b  0
a b  2 ab Dấu '  ' xảy khi khi a  . b
3. Bài tập minh họa.
Bài tập 32. Tìm giá trị của x để các biểu thức dưới đây nhận giá trị nguyên. 2 x 2 x a). b). x  3 x x 1 Lời giải 2 x a).
có điều kiện là x  0 x  3 2 x  0 2 x Có x  0   . Suy ra ta có  0 x   0 (1)
x  3  3  0 x  3 2 x 2 Lại có  x  3 3 x x 3 3
Áp dụng bất đẳng thức Cauchy cho x  0 có x   2 x   2 3 x x 2 2 3    (2) 3 2 3 3 x x 2 x 3 2 x Từ (1) và (2) ta có: 0  
mà biểu thức nhận giá trị nguyên nên  0 x  3 3 x  3
Giải phương trình tính được x  0
Vậy với x  0 thì biểu thức nhận giá trị nguyên 2 x b).
có điều kiện là x  0 . x x 1
80 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 8. Rút Gọn Biểu Thức Chứa Căn Bậc Hai 2 x  0 Có x  0   x   0 (1)
x x 1 0 2 x 2 Lại có    1 x x 1 x 1 x
Áp dụng bất đẳng thức Cauchy cho x  0 có 1 1 2 2 x   2  x  1 3   (2) 1 x x 3 x 1 x 2 x 2 2 x Từ (1) va (2) ta có 0 
 mà biểu thức nhận giá trị nguyên nên  0 . x x 1 3 x  3
Giải phương trình được x  0
Vậy với x  0 thì biểu thức nhận giá trị nguyên.  1   x 1 1 
Bài tập 33. Cho biểu thức P = x     .   
x x x 1 x 1   a). Rút gọn . P
b). Tìm các giá trị nguyên của x để P có giá trị nguyên. Lời giải x  2 a). P  (x  0); b). x 1;4. x
81 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba §BÀI 9. CĂN BẬC ba A. TÓM TẮT LÝ THUYẾT 1. Định nghĩa.
Căn bậc ba của một số a là số x sao cho 3 x  . a
Mỗi số a đều có duy nhất một căn bậc ba. ⋆ Nhận xét :
Căn bậc ba của một số dương là số dương ;
Căn bậc ba của một số âm là một số âm ;
Căn bậc ba của số 0 là số 0 ; Ví dụ 1. Hãy tìm : a). 3 216 b). 3 729 c). 3 331 . Lời giải a) 3 3 3 216  6  6 b). 3 3 3 729  9  9 c). 3 3 3 331  11  11 Ví dụ 2. Hãy tìm : a). 3 343 b). 3 1000  c). 3 1728  . Lời giải a) 3 3 3 3  43  7   7  b) 3 3 3 1  000  1  0  1  0 c) 3 3 3 1  728  1  2  1  2 Ví dụ 3. Hãy tìm : 8 125 a). 3 b). 3  c). 3 0  ,064 27 512 Lời giải 3 8  2  2 a). 3  3    27  3  3 125 b). 3   3 3 3
3 27.12 1  324 1  343 1  7 1  6 512 c). 3 0  ,064   3 3 0, 4  0  ,4 . 2. Tính chất  a 3 3  a; 3 3 a  . a So sánh: 3 3 a b a b. Phép khai phương 3 3 3 ab a b; 3 a a Phép khai phương 3  . (b  0) 3 b b Ví dụ 4. So sánh a). 7 và 3 345 b). 3 2 6 và 3 3 2 . Lời giải a). 7 và 3 345 Ta có 3 3 7  343  345 ; b). 3 2 6 và 3 3 2 .
82 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba Ta có 3 3 3 3 2 6  2 .6  8 4 3 3 3 3 3 2  3 .2  4 5 48  54 nên 3 3 3 2 6  3 2  4 5 Ví dụ 5. So sánh 2 3 a). 3 18 và 3 12 b). 3 130 1 và 3 3 12 1. 3 4 Lời giải 3 2  2  16 1 a) . Ta có 3 18 = 3 3 3 .18   5   3  3  3 3 3 3  3  81 1 3 12 = 3 3 3 .12   5   4  4  16 16 1 1 2 3 Vì 5  5 nên 3 18 > 3 12 3 16 3 4
b) Ta có 3 130 1 > 3 125 1  5 1  6 ; 3 3 12 1= 3 3 3
3 27.12 1  324 1  343 1  7 1  6 ; Vậy 3 130 1 > 3 3 12 1.
Ví dụ 6. Cho a  0 , hỏi số nào lớn hơn trong hai số 3 2a và 3 3a Lời giải
Ta có 2  3 nên 2a  3a ( vì a  0 ).
Do đó 3 2a > 3 3a .
Ví dụ 7. Rút gọn các biểu thức a). 3 3 3 8  27   64 ; b). 3 3 3 54  16   128 . Lời giải a) Ta có 3 3 3 8  27   64  2   3     4    5  b) Ta có 3 3 3 54  16   128 = 3 3 3 3 3 3 3 3 3 3 3 .2  ( 2
 ) .2  4 .2  3 2  2 2  4 2  9 2. Ví dụ 8. Tính a). 3 3 3 3 16. 13.5  120 : 15 ; b). 3 3 3 ( 2 1)( 4  2 1). Lời giải a) 3 3 3 3 16. 13.5  120 : 15 = 3 3 16.13.5  120 :15 = 3 3 216  8
 6 – 2  4  6 – 2  4 b) 3 3 3 ( 2 1)( 4  2 1) = 3 3 3 3 3
8  4  2  4  2 1  2  1  3
Nhận xét: Để tính tích trên có thể sử dụng hằng đẳng thức : a b  2 2
a ab b  3 3 ( )  a b Ta có 3 3 3 3 3 3
( 2 1)( 4  2 1)  ( 2) 1  2 1  3. Ví dụ 9. Tính a). 3 3 3 3 ( 5 1)  3 5( 5 1) ; b). 3 3 3 3 3 ( 4  3)  6 2( 2 1)
83 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba Lời giải a) Ta có 3 3 3 3 ( 5 1)  3 5( 5 1) = 3 3 3 3
5  3 25  3 5 1 3 25  3 5  6. b) Ta có 3 3 3 3 3 3 3 3 3
( 4  3)  6 2( 2 1)  4  3 32  3 16  2  6 4  6 2 = 3 3 3 3
6  6 4  6 2  2  6 4  6 2  2 . Ví dụ 10. Tính 3 3 A  5  2  5  2 . Lời giải Ta có 3 A  ( 3 3 5  2  5  2 )3   3 A       3 
     3    3 5 2 5 2 3 5 2 5 2 5 2   5  2    3
A  4  3A 3  A  3 A – 4  0 2
 (A 1)(A A  4)  0  A1 0 ( vì 2
A A  4  0 ) Vậy A  1
Ví dụ 11. Rút gọn biểu thức. x 1 a). 3
3 x 1 3x(x 1) ; b). . 3 2 3 x x 1 Lời giải a) Ta có 3
3 x 1 3x(x 1) = 3
3 (x 1)  x 1. x 1 3 3 2 3
( x 1)( x x 1) b) = 3  x 1. 3 2 3 3 2 x x 1 3 x x 1
B. PHÂN DẠNG VÀ VI DỤ MINH HỌA.
DẠNG 1. THỰC HIỆN PHÉP TÍNH 1. Phương pháp.
Áp dụng  3 a 3 3 3  ; a a  . a
2. Bài tập minh họa.
Bài tập 1. (Bài 67, tr 36 SGK) Hãy tìm 3 3 3 3 3 512; 7  29; 0,064; 0  ,216; 0  ,008. Lời giải Ta có: 3 3 3 512  8  8. 3 3 3 7  29  9   9  . 3 3 3 0, 064  (0, 4)  0, 4. 3 3 3 0  , 216  ( 0  ,6)  0  ,6. 3 3 3 0  ,008  ( 0  , 2)  0  , 2.
Bài tập 2. (Bài 68, tr. 36 SGK) Tính: 3 135 a). 3 3 3 27  8   125; b). 3 3  54. 4. 3 5 Lời giải a). 3 3 3 3 3 3 3 3 3 27  8
  125  3  2  5  3 2 5  0 3 135 135 b). 3 3 3 3 3 3  54. 4. 
 54.4.  27  216  3  6  3  3 5 5
84 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
Bài tập 3. Thực hiện phép tính a). A   3 3 3 9  6  4  3 3 3  2  b). 3 3 B  2  5  2  5. Lời giải 2 2 a). Ta có: A   3 3 3 9  6  4  3 3 3  2    3 3 3 3
 3 2   3 2 3 3 3  2    3 33  23 3  3  2 1
b). Áp dụng hằng đẳng thức a b3 3 3
a b  3ab(a b) 3 Ta có: 3 B   3 3     3 3        3 3 2 5 2 5 2 5 2 5 3 2 5 2 5 2  5  2  5         3 3 4 3 2 5 2
5 B  4  3 4  5B  4  3B 3 3 2
B  3B  4  0  B 1 3B  3  0  (B 1)(B B  4)  0 2  1 1 15 1 15    2 2
B 1  B B  4  B  2 B    B    0     2 4 4 2 4      Vậy 3 3 B  2  5  2  5  1.
3. Bài tập rèn luyện.
Bài 1. Thực hiện phép tính 1 a). 3 3 3  1  8  3 . b). 3      3 2 1 3 2 2 ; 42 3 3  1. 2  1 1   1 1  1 c). 3 3 3 2  16  4   . d). 3 3 3 3  9  2 3  3  : 2 .  2 4    2 3 3   e).  3 3 3 9  6  4  3 3 3  2 . Lời giải 1 1 a). 3 3 3 3 3  1  8  3  ( 1  8)3  2  7  3  . 2 2 2 3 b). 3  2   1 3 2 2 3   2   1  2   3 1   2   1  2 1. 3 4  2 3 3   1   3  2 1  3   1   3  3 3 3 1  3 1.  1 1   1 1  c). 3 3 3 3 3 3 2  16  4  2  2  4  0     .  2 4   2 2   1 1  1  1  2  3  2 9 d). 3 3 3 3 3 3 3 3 3 3 3 3  9  2 3  3  : 2  9  2 3  9 : 9  9  2 3 : 9   9       . 2 3 3    2  3  2  3 4 3 3 e).  3 3 3 9  6  4  3 3 3  2    3 2 3 3 2 3  3 2  2  3 3
3  2    3 3   3 2   3  2  5 .
Bài 2. Thực hiện phép tính 3 3 3 64   125  216 3 3  1  a).  3    3 4 1 4   1 b).  3 3 3 12 2  16  2 2  3 3 5 4  3    . 2   Lời giải a) 3 3 3 64 
 125  216  4  5  6  3 3 3
b) Ta có  3    3 4 1 4   1
85 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba    
   2        2 3 3 3 3 3 3 4 1 4 1 4 1 4 1 4 1 4 1     3 3 3 3 3           3 2. 16 2 4 1 16 1 16 2 4 1 2 3 16   1  2  3 6 2   1  1  c) Ta có  3 3 3 12 2  16  2 2  3 3 5 4  3    2      1   1  3 3 3 12 2  2 2  2 2  3 3 3 3 3 5 4 3  12 2 5 4 3  120 36  84     2 2     2 6 Bài 3. Cho x và y . Tính 3 3 xy x y . 3 3 2 2 2 4 3 3 2 2 2 4 Lời giải 2 2 2 Ta có x 3 3 3 3 2 2 2 2 2 4 16 2 4 3 3 3 3 4 2. 4 2 3 3 2 4 2 3 3 4 2 4 2 6 Tương tự 3 3 y 4 2 3 3 2 2 2 4 Do đó: 3 3 2 2 3 3 xy x y xy y x xy y x y x 8 2 2 4 1
Bài 4. Trục căn ở mẫu số biểu diễn 3 3 3 16 12 9 Lời giải 3 3 1 1 4 3 Ta có: 3 3 4 3. 3 3 3 2 2 16 12 9 3 3 3 4 3 4 3. 4 3
DẠNG 2. CHỨNG MINH ĐẲNG THỨC 1. Phương pháp.
biến đổi hai vế của đẳng thức cùng bằng một biểu thức.
2. Bài tập minh họa.
Bài tập 4. Chứng minh rằng nếu: 1 1 1 3 3 3
ax by cz và   1 thì 2 2 2 3 3 3 3
ax by cz
a b c. x y z Lời giải t t t Ta đặt 3 3 3
ax by cz t suy ra a  , b  , c  3 3 3 x y z t t t t t t  1 1 1  Ta có: 2 2 2 2 2 2 3 3
ax by cz  3 x y z  3    3 t    t (1)   3 3 3 x y z x y zx y z  3 3 3 t t t t t t  1 1 1  Ta lại có: 3 3 3 3 3 3 3
a b c   3      t    t (2)   3 3 3 x y z x y zx y z  Từ (1) và (2) ta có: 2 2 2 3 3 3 3
ax by cz
a b c. (ĐPCM)
86 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
Bài tập 5. Chứng minh đẳng thức: 2 2 2 1  
x y z  3 xyz  3 3 x y
z   3 x y    3 y z    3 3 3 3 3 3 z x  . 2  
x y z
Từ đó suy ra bất đẳng thức Cô-si cho 3 số không âm x, y, z : 3  xyz. 3 Lời giải
VT   x y  z  3 xyz   x y 3 3  3 xy  3 3 3 3 3 x y  3  z  3 xyz   3 3 x y z 3 3  3 3 3 x y  3 z  3 3 3 x y z  3  3 xy  3 3 3 x y z     
3 x y z   3 x y z 2 3 3  3 3 3 3 3 3 xy yz zx      3 3 3 x y z  3 2 2 3 2 3 3 3 3 x y z xy yz zx    1 3 3 3 x y z   3 2 2 3 2 3 3 3 3
2 x  2 y  2 z  2 xy  2 yz  2 zx  2 1    
3 x y z   3 x y 2   y z 2   3 3 3 3 z x 2 3 3 3 2    . VP Vậy ta có đẳng thức 1  
x y z  3 xyz
3 x y z3 x y2  y z2  3 3 3 3 3 z x 2 3 3 3 . 2  
Suy ra với 3 số không âm x, y, z : 1  
x y z  3 xyz
3 x y z3 x y2  y z2  3 3 3 3 3 z x 2 3 3 3  0 2  
x y z Do đó 3 3
x y z  3 xyz
xyz. Dấu “ ” xảy ra khi x y  . z 3 DẠNG 3. SO SÁNH HAI SỐ 1. Phương pháp.
Đưa thừa số vào căn bậc ba rồi so sánh hai số trong căn: 3 3 3 A B A B . 3 3 A B A B .
2. Bài tập minh họa. Bài tập 6. So sánh a). 6 và 3 215 . b). 3 4 5 và 3 5 4 . Lời giải a). Ta có 3 3 6  216  215 . Vậy 3 6  215 . b). 3 3 3 3 4 5  4 5  320 ; 3 3 3 3 5 4  5  4  500 . Vì 320  500 nên 3 3 4 5  5 4 . Bài tập 7. So Sánh: a). 3 2 3 và 3 23 ; b). 33 và 3 3 133 . Lời giải a) Ta có: 3 3 3 3 3 2 3 8. 3 24 23 . Do đó 3 3 2 3 23. b) Ta có: 3 3
33  3 11  3 1331  3 133. Do đó 3 33  3 133.
87 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi AMSTERDAM Bài 9. Căn Bậc Ba
DẠNG 4. GIẢI PHƯƠNG TRÌNH 1. Phương pháp. Áp dụng: 3 3
A B A B .
2. Bài tập minh họa.
Bài tập 8. Giải các phương trình a). 3 2x 1  2 . b). 3 1 2x  2  .
c). 3 x  2  2  x . Lời giải 7
a). 3 2x 1  2  2x 1  8  x  . 2 7
Vậy phương trình có nghiệm x  . 2 9 b). 3 1 2x  2   1 2x  8   x  . 2 9
Vậy phương trình có nghiệm x  . 2 x  2 x  2  0  c). 3 3 3
x  2  2  x
x  2  x  2  x  2  (x  2)    x  3 . 2  (x  2) 1 x 1 
Vậy phương trình có 3 nghiệm x  1; x  2; x  3 .
Bài tập 9. Giải phương trình: a). 3 3 2
x  9x x  3 ;
b). 3 5  x x  5. Lời giải a) 3 3 2
x  9x x  3
x  9x  x  33 3 3 2 3
x  9x  x  33 3 2 3 2
x  9x  27x  27
 27x  27  0  x  1. 
b) 3 5  x x  5
 5  x x  5  x  5  x  53 3 x  5  0 x  5       x  
x  5  x  5 5 0 2 1  0            x x   x  5 5 1 4. 2 1 x  5  1  x  6   
88 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880