































































Preview text:
Trường THPT Tạ Quang Bửu 0976071956 MATH.ND ? Lớp TOÁN THẦY DŨNG ? NGUYỄN NGỌC DŨNG CHUYÊN ĐỀ 12 CHỌN LỌC TOÁN
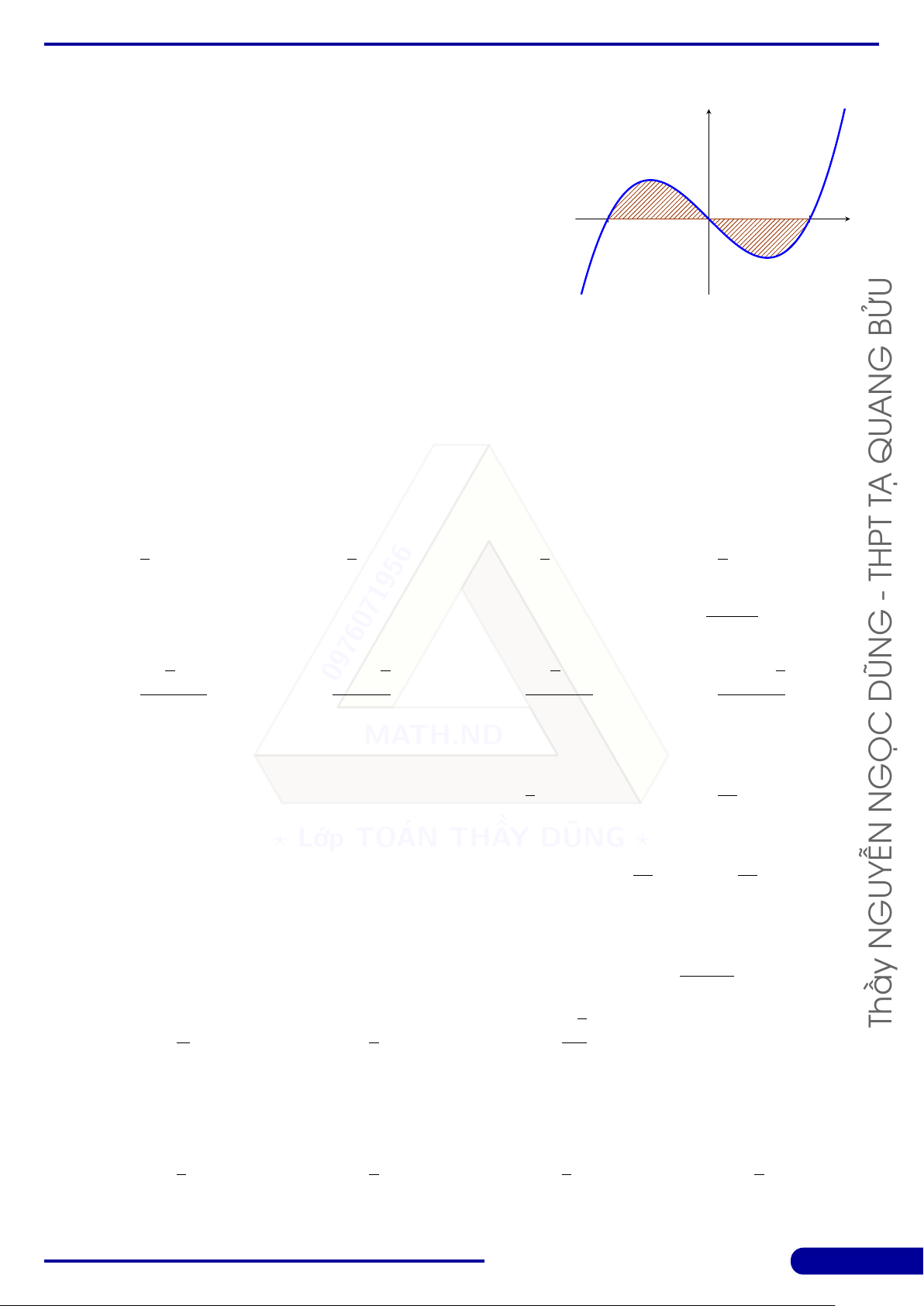
NGUYÊN HÀM - TÍCH PHÂN y f (x) 2 4 Z Z g(x) S = (f (x) − g(x)) dx + (h(x) − g(x)) dx 4 0 2 2 h(x) x O 2 4 MATHEMATICS
Sài Gòn 2023 - Lớp toán thầy Dũng - Tài liệu lưu hành nội bộ
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ MỤC LỤC Chương 3
Nguyễn hàm, tích phân và ứng dụng Trang 3 Bài 1
Nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 A
Các khái niệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 BỬU B
Tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 G C
Các dạng bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Dạng 1. Sử dụng bảng nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 AN
Dạng 2. Nguyên hàm hàm phân thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 QU Bài 2
Tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 TẠ A
Các khái niệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 B
Tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 C
Các dạng bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 THPT -
Dạng 1. Biến đổi và sử dụng bảng nguyên hàm. . . . . . . . . . . . . . . . . . . . . . . 11 G Bài 3
Phương pháp đổi biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Dạng 1. N 0976071956
guyên hàm đổi biến loại 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 DŨN
Dạng 2. Nguyên hàm đổi biến loại 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 Dạng 3. Tích MA phân TH.ND
đổi biến. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 Bài 4
Nguyên hàm, tích phân bằng phương pháp từng phân . . . . . . . . . . . . . . . 33 GỌC N
Dạng 1. Nguyên hàm từng phần . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 ? Lớp TOÁN THẦY DŨNG ?
Dạng 2. Tích phân từng phần . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 Bài 5
Ứng dụng của tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 GUYỄN
Dạng 1. Tính diện tích hình phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 N
Dạng 2. Tính thể tích vật thể . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 Bài 6
Các dạng toán nâng cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 Thầy
Dạng 1. Các bài toán lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Dạng 2. Tích phân hàm ẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
Dạng 3. Tích phân hàm số cho bởi nhiều biểu thức. . . . . . . . . . . . . . . . . . . 71
Dạng 4. Ứng dụng tích phân giải các bài toán khảo sát hàm số . . . . . . . 77
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 1 Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 3
Nguyễn hàm, tích phân và ứng dụng Chương
| Chủ đề 1. Nguyên hàm A CÁC KHÁI NIỆM
Cho hàm số f(x) xác định trên K. BỬU G
• F(x) được gọi là nguyên hàm của f(x) trên K nếu F0(x) = f(x), ∀x ∈ K. Z AN • Kí hiệu:
f (x) dx = F(x) + C, C là hằng số. QU Z • Như vậy
f (x) dx = F(x) + C ⇔ F0(x) = f(x), ∀x ∈ K TẠ B TÍNH CHẤT THPT - Z 1.
f 0(x) dx = f(x) + C; G Z Z 0976071956 2.
kf (x) dx = k
f (x) dx, k = const;
(kéo hằng số ra ngoài) DŨN Z Z MATH.ND Z 3.
[f(x) ± g(x)] dx =
f (x) dx ±
g (x) dx. (nguyên hàm của tổng bằng tổng các nguyên hàm) GỌC N ? Lớp TOÁN THẦY DŨNG ? C CÁC DẠNG BÀI TẬP
{ DẠNG 1. Sử dụng bảng nguyên hàm GUYỄN N
cccVÍ DỤ MINH HỌAccc
VÍ DỤ 1. Tính các nguyên hàm sau: Thầy Z Z 1 Z √ a x2017dx b dx c xdx x2 Z 1 Z 4x Z 3x d √ dx e dx. f dx 5 x3 2x 2x
VÍ DỤ 2. Tính các nguyên hàm sau: 3
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Z Å 2 1 ã Z a I = − x5 − + 2 dx b J =
(x − 2) x2 + x + 1 dx x3 3x Z
x3 + x2 − 1 Z c K = dx d I =
ex (e−x + 1) dx. x5
VÍ DỤ 3. Tính các nguyên hàm sau: Thầy Z Z a I =
(sin x + cos x) dx b I = cos 3x dx Z Z dx c I =
sin (3x − 1) dx d I = . N sin2 x. cos2 x GUYỄN
VÍ DỤ 4. Tính các nguyên hàm sau: Z Z 1 a x8dx b dx x5 N Z √ Z Å √ ã GỌC 3 1 2 3 c xdx d I = − x − + dx x x2 5 Å e−x ã DŨN
VÍ DỤ 5. Tìm nguyên hàm của hàm số f (x) = ex. 2 + cos2 x √ √ x + 3 x + 1
VÍ DỤ 6. Tìm nguyên hàm của hàm số f (x) = x G x2 Z 0976071956 cos3 x -
VÍ DỤ 7. Tìm nguyên hàm I = dx. THPT 1 − sin x
(CÁC VÍ DỤMATH.ND
TRẮC NGHIỆM ĐIỂN HÌNH) Z TẠ VÍ DỤ 8. Cho
f (x) dx = 3x2 + 2x − 3 + C. Hỏi f(x) là hàm số nào sau đây? QU
A. f(x) = 6x + 2 + C.
B. f(x) = x3 + x2 − 3x + C. ? Lớp TOÁN THẦY DŨNG ?
C. f(x) = 6x + 2.
D. f(x) = x3 + x2 − 3x. AN
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G VÍ DỤ 9. Cho F (x) là một nguyên hàm của hàm số f (x). Tìm Z BỬU I =
[4x + 1 − f(x)] dx.
A. I = 4x + 1 − F(x) + C.
B. I = 2x2 + x − F(x).
C. I = 2x2 + x − F(x) + C.
D. I = (2x2 + x) · F(x) + C.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . π
VÍ DỤ 10. Cho hàm số f (x) thỏa mãn f 0(x) = 2 + cos 2x và f = 2 2
π. Mệnh đề nào sau đây sai? sin 2x
A. f(0) = π.
B. f(x) = 2x + + 2 π. sin 2x π
C. f(x) = 2x − + = 0. 2 π. D. f − 2
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
VÍ DỤ 11. Họ nguyên hàm của hàm số f (x) = x3 + 3x2 là
A. x4 + x3 + C.
B. x4 + x3 + + 4 3 C. C. x4 4 x3 + C.
D. 3x2 + 6x + C.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
VÍ DỤ 12. Cho hàm số f (x) =
. Trong các khẳng định sau, khẳng định nào đúng? 3x + 1 Z 1 Z 1 A.
f (x) dx = ln ln 2
|3x + 1| + C. B.
f (x) dx = 3 |3x + 1| + C. Z 1 Z C.
f (x) dx = ln(3 3 x + 1) + C. D.
f (x) dx = ln |3x + 1| + C.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BỬU
VÍ DỤ 13. Họ nguyên hàm của hàm số f (x) = sin 2x − cos 3x là G 1 1 1 1 A. − cos 2 sin 3 cos 2 sin 3 2 x − 3 x + C. B. 2 x − 3 x + C.
C. cos 2x + sin 3x + C.
D. − cos 2x − sin 3x + C. AN
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . QU
VÍ DỤ 14. Họ nguyên hàm của hàm số f (x) = sin 5x sin 2x là TẠ cos 3x cos 7x sin 3x sin 7x A. + + 6 − 14 C. B. 6 − 14 C. cos 3x cos 7x sin 3x cos 7x C. + + + 6 14 C. D. 6 − 14 C. THPT
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -
VÍ DỤ 15. Họ các nguyên hàm của hàm số f (x) = e3x + 1 là G 1 1
A. 3e3x + x + C. B. 0976071956 3e3x + C. C. e3x + e3x + 3 C. D. 3 x + C.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . DŨN
VÍ DỤ 16. Họ nguyên hàm của MA hàm TH.ND
số y = 32x · 7x là21x 63x
A. 63x · ln 63 + C.
B. 63x + C. C. + + ln 21 C. D. ln63 C. GỌC
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N 9
VÍ DỤ 17. Họ tất cả ? các Lớp nguyênTOÁN hàm của THẦ hàm số Y f (x DŨNG ) = (2x + 5) ?là 1 1 A. (2 (2
10 x + 5)10 + C. B. 18(2x + 5)8 + C.
C. 9(2x + 5)8 + C.
D. 20 x + 5)10 + C.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GUYỄN
VÍ DỤ 18. Cho hàm số y = f (x) có đạo hàm trên (0; +∞). Biết x2 là một nguyên hàm của N
x2f 0(x) trên (0; +∞) và f(1) = 1. Tính f(e). A. 2e + 1. B. 3. C. 2. D. e. Thầy
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc
CÂU 1. Cho f (x), g (x) là các hàm số xác định và liên tục trên R. Trong các công thức sau, công thức nào sai? Z Z Z A.
f (x) · g(x) dx =
f (x) dx · g (x) dx. Z Z B.
2f(x) dx = 2 f (x) dx.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 5
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Z Z Z C.
[f(x) − g(x)] dx =
f (x) dx − g (x) dx. Z Z Z D.
[f(x) + g(x)] dx =
f (x) dx + g (x) dx. π
CÂU 2. Một nguyên hàm F (x) của hàm số f (x) = cos 2x thỏa mãn F = 2 2 π là 1 3π A. sin 2 . 2 x + 2π.
B. x + sin 2x + 2
C. sin x + 2π.
D. 2x + 2π. Thầy
CÂU 3. Cho hàm số f (x) = 2x3 + 3. Trong các khẳng định sau, khẳng định nào đúng? Z 1 Z A.
f (x) dx = 2x4 + 3x + C. B.
f (x) dx = 2x4 + 3x + C. Z 1 Z 1 N C.
f (x) dx = 2x4 + C. D.
f (x) dx = 4x4 + 3x + C. GUYỄN Z 1 CÂU 4. d 2 x bằng x − 1 1
A. ln |2x − 1| + C. B. ln 2
|2x − 1| + C. N
C. 2 ln |2x − 1| + C.
D. −2 ln |2x − 1| + C. GỌC 2
CÂU 5. Họ nguyên hàm của hàm số f (x) = là 7x − 5 2
A. 2 ln |7x − 5| + C. B. ln 7
|7x − 5| + C. 1 2 1 DŨN C. ln + 7
|7x − 5| + C.
D. −7 · (7 C. x − 5)2
CÂU 6. Cho hàm số f (x) = 2x + 4x3. Tìm khẳng định đúng trong các khẳng định sau. G Z Z A.
f (x) dx = 3x4 + x2 + C. 0976071956 B.
f (x) dx = x4 + x2 + C. - Z Z THPT C.
f (x) dx = 3x4 + 2x2 + C. D.
f (x) dx = x4 + 2x2 + C. MATH.ND 1 1
CÂU 7. Họ nguyên hàm của hàm số f (x) = − x2 − là T x2 3 Ạ x3 1 x
A. −x4 + x2 + 3 + C. B. − − + C. QU 3x 3 − x 3 x3 1 x ? Lớp TOÁN THẦY 2 DŨNG ? C. − + + 3 − C. D. −
− 2x + C. x 3 x2 AN
CÂU 8. Họ nguyên hàm của hàm số f (x) = cos(2x + 3) là 1 G A. − sin(2 2 x + 3) + C.
B. sin(2x + 3) + C. BỬU 1 C. sin(2 2 x + 3) + C.
D. − sin(2x + 3) + C. 2
CÂU 9. Họ tất cả các nguyên hàm của hàm số f (x) = sin x + là x 2 A. cos x − + C.
B. − cos x + 2 ln |x| + C. x2
C. − cos x − 2 ln |x| + C.
D. cos x + 2 ln |x| + C.
CÂU 10. Họ nguyên hàm của hàm số f (x) = tan2 x là
A. tan x + C.
B. tan x − x + C.
C. x − tan x + C.
D. tan x + x + C.
CÂU 11. Họ nguyên hàm của hàm số f (x) = 3x2 − sin x là
A. 3x3 − cos x + C.
B. x3 + cos x + C.
C. 3x3 + cos x + C.
D. x3 − cos x + C. 6
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 12. Nguyên hàm của hàm số f (x) = sin 3x là cos 3x cos 3x sin 3x A. − + + + 3 C. B. 3 C. C. − 3 C.
D. − cos 3x + C.
CÂU 13. Họ nguyên hàm của hàm số f (x) = 3x2 + 8 sin x là
A. x3 − 8 cos x + C.
B. 6x − 8 cos x + C.
C. 6x + 8 cos x + C.
D. x3 + 8 cos x + C.
CÂU 14. Cho hàm số f (x) = sin(3x + 1). Khẳng định nào sau đây đúng? Z 1 Z A.
f (x) dx = − cos(3 3 x + 1) + C. B.
f (x) dx = −3 cos(3x + 1) + C. Z 1 Z C.
f (x) dx = cos(3 3 x + 1) + C. D.
f (x) dx = 3 cos(3x + 1) + C. BỬU
CÂU 15. Họ nguyên hàm của hàm số f (x) = sin x cos x là G 1 1 A. cos 2 cos 2 4 x + C. B. −4 x + C.
C. sin 2x + C.
D. − sin x cos x + C. AN 1
CÂU 16. Biết F (x) là một nguyên hàm của hàm f (x) =
và đồ thị hàm số y = F(x) đi sin2 x π π QU qua điểm M ; 0. Tính . 6 F 3 √ √ π 2 π π 2 3 π 3 − 1 TẠ A. F = . = 0. = . = √ . 3 3 B. F 3 C. F 3 3 D. F 3 3
CÂU 17. Nguyên hàm của hàm số y = e−2x+1 là THPT 1 1
A. 2e−2x+1 + C.
B. −2e−2x+1 + C. C.
e−2x+1 + C.
D. − e−2x+1 + C. - 2 2 Z G CÂU 18. Biết
f (x) dx = ex + sin x + C. Mệnh đề nào sau đây đúng?
A. f(x) = ex − sin x. B. 0976071956
f (x) = ex − cos x. C. f(x) = ex + cos x. D. f(x) = ex + sin x. DŨN
CÂU 19. Họ nguyên hàm của hàm số y = 2x − 3 là 2x MA 3 TH.ND 2x A. + 3 + ln 2 x + C. B. 2x − C.
C. 2x − 3x + C. D. x
ln 2 − 3x + C. GỌC
CÂU 20. Họ nguyên hàm của hàm số y = 32x · 7x là21x 63x N
A. 63x · ln 63 + C.
B. 63x + C. C. + C. D. + C. ? Lớp TOÁN THẦY DŨNG ln 21 ? ln 63
CÂU 21. Họ tất cả các nguyên hàm của hàm số f (x) = (2x − 1)8 là (2x − 1)9 (1 − 2x)9 (2x − 1)9 (1 − 2x)9 A. + + + + 9 C. B. 18 C. C. 18 C. D. 9 C. GUYỄN
CÂU 22. Họ tất cả các nguyên hàm của hàm số f (x) = 22x · 3x · 7x là N 84x
22x · 3x · 7x A. + + ln 84 C. B. ln4 C. · ln 3 · ln 7
C. 84x + C.
D. 84x · ln 84 + C. Thầy 1
CÂU 23. Cho hàm số f (x) = 2e2x−1+ . Trong các khẳng định sau, khẳng định nào đúng? x Z 1 Z 1 A.
f (x) dx = e2x−1 − + C. B.
f (x) dx = 4e2x−1 − + C. x2 x2 Z Z C.
f (x) dx = 2e2x−1 + ln |x| + C. D.
f (x) dx = e2x−1 + ln |x| + C. 1
CÂU 24. Cho hàm số f (x) =
. Mệnh đề nào sau đây đúng? (3x − 2)3
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 7
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Z 1 Z 1 A.
f (x) dx = + + 6(3 C. B.
f (x) dx = − C. x − 2)2 6(3x − 2)2 Z 1 Z 1 C.
f (x) dx = − + + 3(3 C. D.
f (x) dx = C. x − 2)2 3(3x − 2)2 Z CÂU 25. Cho
f (x) dx = x3 + 13 + C
A. f(x) = 3 x3 + 12.
B. f(x) = 3x2 x3 + 12. Thầy
C. f(x) = 9x2 x3 + 12.
D. f(x) = 18x2 x3 + 12.
CÂU 26. Cho hàm sồ f (x) thỏa mãn f 0(x) = x + sin x và f (0) = 1. Khi đó hàm số f (x) là 1 N A. x2 + cos . + cos 2 − cos x + 2. B. x2
2 − cos x − 2. C. x2 2 x + 2 D. x2 2 x. GUYỄN
CÂU 27. Cho hàm số f (x) thỏa mãn 2xf (x) + x2f 0(x) = 1, ∀x ∈ R \ {0} và f (1) = 0. Giá trị của Å 1ã f bằng 2 A. −2. B. 1. C. 6. D. −1. N
ccc BẢNG ĐÁP ÁN ccc GỌC 1. A 2. A 3. A 4. B 5. B 6. B 7. B 8. C 9. B 10. B 11. B 12. A 13. A 14. A 15. B 16. C 17. D 18. C 19. D 20. D DŨN 21. C 22. A 23. D 24. B 25. C 26. A 27. A G
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc 0976071956 -
Câu 27. Ta có 2xf(x) + x2f(x) = 1 ⇔ x2f(x)0 = 1 ⇔ x2f(x) = x + C (C là hằng số). THPT
Với x = 1 Ñ 12 · f(1) = 1 + C ⇔ C = MA f (1) TH.ND
− 1 = 0 − 1 = −1. 1 Å 1ã 2 − 1 T
Suy ra x2f(x) = x − 1 Ñ f(x) = x − 1 Ñ f = = −2. Ạ x2 2 Å 1ã2 QU 2 ? Lớp TOÁN THẦY DŨNG ?
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AN G
{ DẠNG 2. Nguyên hàm hàm phân thức BỬU
cccVÍ DỤ MINH HỌAccc Z x + 1 VÍ DỤ 1. Biết
dx = a ln |x − 1| + b ln |x − 2| + C với a, b nguyên. Tính giá trị
x2 − 3x + 2
T = a + b. A. T = 1. B. T = 0. C. T = 6. D. T = 5.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
VÍ DỤ 2. Cho một nguyên hàm của hàm số f (x) = x + 1 là F (x) và F (0) = 3. Khi đó F (x) x − 1 bằng 2 A. x + + 3. (
B. x − 2 ln |x − 1| + 3. x − 1)2 8
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
C. x + 2 ln(x − 1) + 3.
D. x + 2 ln |x − 1| + 3.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2x + 1
VÍ DỤ 3. Họ tất cả các nguyên hàm của hàm số f (x) = trên khoảng ( ( −1; +∞) là x + 1)2 1 2 A. 2 ln(x + 1) + + C.
B. ln(x + 1) − . x + 1 x + 1 2 1 C. 2 ln(x + 1) + + C.
D. 2 ln(x + 1) − . x + 1 x + 1
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc BỬU
CÂU 1. Tìm họ tất cả các nguyên hàm của hàm số y = x . x + 1 G
A. x − ln(x + 1) + C.
B. x + ln |x + 1| + C.
C. x + ln(x + 1) + C.
D. x − ln |x + 1| + C. AN
CÂU 2. Tìm họ nguyên hàm của hàm số f (x) = x2 − 2x + 1 . QU x − 2 1 A. x + + C.
B. x2 + ln |x − 2| + C. TẠ x − 2 2 1
C. x2 + ln |x − 2| + C. D. 1 + + ( C. x − 2)2 THPT
CÂU 3. Tìm họ tất cả các nguyên hàm của hàm số y = (x + 1)2 . - x2 1 1 A G
. x + 2 ln |x| + + C.
B. x − 2 ln |x| − + C. x x 1 1
C. x − 2 ln |x| + + C. 0976071956
D. x + 2 ln |x| − + C. x x DŨN 1
CÂU 4. Tìm họ tất cả các MA nguyên TH.ND
hàm của hàm số f(x) = . 2x2 + 3x + 1 2x + 1 x + 1 2x − 1 1 2x + 1 A. ln + + + ln + C. B. ln C. C. ln C. D. C. x + 1 2x + 1 x − 1 2 x + 1 GỌC N
CÂU 5. Tìm họ tất cả các nguyên hàm của hàm số y = x2 + 2x + 3 ? ? Lớp TOÁN THẦY DŨNG x + ? 1 A. x2 + + 2
x + 2 ln |x − 1| + C. B. x2 2
x + ln |x + 1| + C.
C. (x + 1)2 + 2 ln 2
|x + 1| + C. D. x2
2 − x + 2 ln |x + 1| + C. GUYỄN 1 N
CÂU 6. Tìm họ tất cả các nguyên hàm của hàm số y = .
x2 − 3x + 2 x − 2 x − 1 A. ln + C. B. ln + C. x − 1 x − 2 1 1 Thầy
C. ln x − 2 x − 1 + C. D. ln + C.
x − 2 − ln x − 1
CÂU 7. Tìm nguyên hàm của hàm số f (x) = x . x2 − 16 Z x2 + 16 Z 1 A.
f (x)dx = − + ln + ( C. B. f (x)dx = x2 − 16 C. x2 − 16)2 2 Z 1 x − 4 Z C. f (x)dx = ln + + 8 C. D.
f (x)dx = ln x2 − 16 C. x + 4
CÂU 8. Họ nguyên hàm của hàm số f (x) = x + 3 là x2 + 3x + 2
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 9
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
A. F(x) = 2 ln |x + 2| − ln |x + 1| + C.
B. F(x) = 2 ln |x + 1| + ln |x + 2| + C.
C. F(x) = 2 ln |x + 2| + ln |x + 1| + C.
D. F(x) = 2 ln |x + 1| − ln |x + 2| + C. 1
CÂU 9. Cho hàm số f (x) =
. Mệnh đề nào sau đây đúng? x(x + 2) Z x Z 1 x A.
f (x) dx = ln + C. B.
f (x) dx = ln + C. x + 2 2 x + 2 Z x + 2 Z 1 x + 2 C.
f (x) dx = ln + ln + C. D.
f (x) dx = C. Thầy x 2 x
CÂU 10. Tìm nguyên hàm của hàm số f (x) = x + 1 . x − 1 Z Z N A.
f (x) dx = −x + 2 ln |x − 1| + C. B.
f (x) dx = −x − 2 ln |x − 1| + C . GUYỄN Z Z C.
f (x) dx = x + 2 ln |x − 1| + C. D.
f (x) dx = x − 2 ln |x − 1| + C .
CÂU 11. Tìm nguyên hàm của hàm số f (x) = x2 + x + 4 . x + 3 Z Z N A.
f (x) dx = x2 − 2x 2
− 10 ln |x + 3| + C. B.
f (x) dx = x2 + 4x 2
− 10 ln |x + 3| + C . GỌC Z Z C.
f (x) dx = x2 + 2x + 10 ln + 10 ln 2
|x + 3| + C. D.
f (x) dx = x2 − 4x 2
|x + 3| + C . 5 − x
CÂU 12. Tìm một nguyên hàm của hàm số f (x) = . 3 DŨN − 2x − x2 Z (x + 3)2 Z (x + 3)2 A.
f (x) dx = ln . B.
f (x) dx = − ln + C . |x − 1| |x − 1| Z Z G (x + 3)2 (x − 3)2 C.
f (x) dx = ln + C. D.
f (x) dx = − ln + C. |x − 1| 0976071956 |x + 1| - 2 THPT x
CÂU 13. Họ nguyên hàm của hàm số f (x) = là MATH.ND (1 − x)3 2 1 2 1 A. F(x) = + + C. B. F(x) = + C . x − 1 x − 1 − T (x − 1)2 (x − 1)2 Ạ 1 1 1 1 C. F(x) = + + C. D. F(x) = − + C . QU 1 − x 4(1 − x)4 1 − x 4(1 − x)4 ? Lớp TOÁN THẦY DŨNG ? là AN
CÂU 14. Họ nguyên hàm của hàm số f (x) = x2 − x (x + 1)2 3 2 2 + + G
A. F(x) = x + 1 − C.
B. F(x) = x + 1 − 3 ln |x + 1| − C .
(x + 1)2 − x + 1 x + 1 3 2 2 BỬU
C. F(x) = x + 1 − + + C.
D. F(x) = x + 1 − 3 ln |x + 1| + + C. (x + 1)2 x + 1 x + 1 4x − 3
CÂU 15. Họ nguyên hàm của hàm số f (x) = là
x2 − 3x + 2 x − 1 x − 1
A. F(x) = 4 ln |x − 2| + ln + + C.
B. F(x) = 4 ln |x − 2| − ln C . x − 2 x − 2 x − 2 x − 2
C. F(x) = −4 ln |x − 2| − ln + + C.
D. F(x) = 4 ln |x − 2| − ln C . x − 1 x − 1
ccc BẢNG ĐÁP ÁN ccc 1. A 2. B 3. D 4. A 5. C 6. A 7. B 8. D 9. B 10. C 11. D 12. A 13. A 14. B 15. D 10
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc
| Chủ đề 2. Tích phân A CÁC KHÁI NIỆM
Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].
Hiệu số F(a) − F(b) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là BỬU G b Z b
f (x) dx = F(x) =
F (b) − F(a) AN a a QU b 4 Z Ta gọi
là dấu tích phân, a là cận dưới, b là cận trên, f(x) dx là biểu thức dưới dấu TẠ a
tích phân và f(x) là hàm số dưới dấu tích phân. THPT - B TÍNH CHẤT G b a Z Z a
f 0(x) dx = f(b) − f(a). 0976071956 b
f (x) dx = 0. DŨN a a b a MATH.ND b b Z Z Z Z c
f (x) dx = − f (x) dx d
f (x) dx = f (t) dt GỌC a b a a N b b b Z ? Z Lớp TOÁN THẦYZ DŨNG ? e
kf (x) dx = k f (x) dx f
k dx = k(b − a), k = const. a a a b b b b c b GUYỄN Z Z Z Z Z Z N g
[f(x) ± g(x)] dx =
f (x) dx±
g (x) dx h
f (x) dx =
f (x) dx + f (x) dx a a a a a c Thầy C CÁC DẠNG BÀI TẬP
{ DẠNG 1. Biến đổi và sử dụng bảng nguyên hàm
B1. Biến đổi để đưa f(x) về các hàm đơn giản (có thể tìm nguyên hàm được nhờ bảng nguyên hàm).
B2. Tìm một nguyên hàm của các hàm đơn giản đó.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 11
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 b Z
B3. Áp dụng công thức
f (x) dx = F(b) − F(a), với F(x) là một nguyên hàm của f(x). a
cccBÀI TẬP TỰ LUẬNccc
BÀI 1. Tính các tích phân sau: Thầy 2 3 4 Z Z Å 1 1ã Z Å 1 ã2 a I =
(3x2 − 4x + 3) dx b J = − x2 + dx c K = x + dx x2 2 x 1 2 2 N GUYỄN
BÀI 2. Tính các tích phân sau: 2 −1 Z
6x3 − 2x + 3 Z (x − 1)2 a I = dx b J = dx x2 x4 1 −2 N GỌC
BÀI 3. Tính các tích phân sau: 1 2 5 Z Z √ Z 1 a I =
(x + ex) dx b J =
4x3 + x dx c K = √ dx x − 1 DŨN 0 1 1
BÀI 4. Tính các tích phân sau: G 3 4 √ √ Z √ √ 0976071956 Z x x + 3 x - a I =
x − 2 5 x dx b J = dx THPT x2 1 1 MATH.ND
BÀI 5. Tính các tích phân sau: TẠ 1 4 2 Z Å 3 ã Z √ Z Å√ 1 ã2 3 QU a I = e2x + dx b J = x − 12 dx c K = x + √ dx
x + 1 ? Lớp TOÁN THẦY DŨNG ? x 0 1 1 AN
BÀI 6. Tính giá trị của hằng số a để có đẳng thức G 2 Z BỬU
a2 + (4 − 4a)x + 4x3 dx = 12. 1
cccVÍ DỤ MINH HỌAccc 1 Z Å 1 1 ã
VÍ DỤ 1 (THPTQG 2017). Cho
dx = a ln 2 + b ln 3 với a, b là các số nguyên. x + 1 − x + 2 0
Mệnh đề nào dưới đây đúng?
A. a + b = 2.
B. a − 2b = 0.
C. a + b = −2.
D. a + 2b = 0.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ π π 2 2 Z Z
VÍ DỤ 2 (THPTQG 2017). Cho
f (x) dx = 5. Tính I =
[f(x) + 2 sin x] dx. 0 0 A. 7. B. 5 + π . 2 C. 3. D. 5 + π.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
VÍ DỤ 3 (THPT Chuyên Lê Khiết - Quảng Ngãi - 2017). π 4 Z 1 √ √ Tính tích phân
− sin3 x dx, ta được kết quả là a 3 + b 2 + c, với a,b,c ∈ sin2 Q. Khi đó, x π 6 BỬU
tổng a + b + c bằng A. 1. B. −1. C. 2. D. 0. G
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AN
VÍ DỤ 4 (THPT Chuyên ĐH Sư Phạm Hà Nội - lần 4 - 2017). 0 QU Z Tìm α < 0 để
(3−2x − 2.3−x)dx ≥ 0. TẠ α
A. −1 ≤ α < 0. B. α ≤ −1. C. α ≤ −3.
D. α = −3.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . THPT -
cccBÀI TẬP TRẮC NGHIỆMccc a Z G
CÂU 1. Tìm a ∈ R để
(a − 4x)dx ≥ 6 − 5a. 1 0976071956 A. a ∈ ∅. B. a = 2. C. a > 0. D. a 6= 2. DŨN 2 Z MATH.ND
CÂU 2. Tính I = min 1; x2 dx. 0 GỌC 8 4 A. 2. B. . C. 0. D. . N 3 3 ? Lớp e Z TOÁN THẦY DŨNG ? dx
CÂU 3. Tích phân I = bằng x − 3 1 3 − e 3 − e 3 + e e − 3 A. ln . B. ln . C. ln . D. ln . GUYỄN 2 4 4 2 N a Z 29
CÂU 4. Cho a ∈ 0; π . Tính d 2 J = cos x theo a. 2 x 0 Thầy 1 A. J = tan 29 a.
B. J = −29 tan a.
C. J = 29 tan a.
D. J = 29 cot a. m Z Å 1 ã
CÂU 5. Cho số thực m > 1. Tính K = + 2 dx theo m. x3 1 4m3 − 1 3 3 A. K = + . . 2
B. K = 3 − .m2 2 m4 2 4m3 − 1 3
C. K = 2m − . D. K = − . m2 2.m2 2
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 13
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 1 Z dx CÂU 6. Cho = ln 2
c. Giá trị của c là x + 1 0 √ A. 9. B. 3. C. 3. D. 1. 0 Z
CÂU 7. Tìm số b âm để tích phân
(x2 + x)dx có giá trị nhỏ nhất. b Thầy A. −3. B. −1. C. 0. D. −2. 3 Z
CÂU 8. Cho tích phân I =
(x2 + x + 1)dx. Ta có N 2 3 3 GUYỄN
A. I = x2 + x + 1 . .
B. I = 3x3 + 2x2 + x 2 2 Å x3 ã 3 3 C. I = + x2 + . . 3 2 x
D. I = (2x + 1) 2 2 2017π N Z sin 2xdx. GỌC
CÂU 9. Tính giá trị của tích phân 0 1 1 A. 1. B. − . . 2 C. 2 D. 0. DŨN b Z
CÂU 10. Giá trị nào của b để
(2x − 6) dx = 0? 1 G
A. b = 0 hoặc b = 3.
B. b = 0 hoặc b = 1. 0976071956 -
C. b = 5 hoặc b = 0.
D. b = 1 hoặc b = 5. THPT a Z CÂU 11. Biết
(2x − 4) dx = −4, MA hãy tìmTH.ND a. 0 TẠ
A. a = −4. B. a = 4.
C. a = −2. D. a = 2. 1 QU Z Å 3 ã e2 CÂU 12. Biết e2x + ? Lớp dx TO = ÁN + a lnTHẦ 2 + b, Y DŨNG trong đó a, b ?
là các số hữu tỉ, tính giá x + 1 2 AN 0
trị của a + b. 3 5 9 7 G A. . . . . 2 B. 2 C. 2 D. 2 BỬU 2017π 2 Z
CÂU 13. Tính tích phân I = cos xdx. 0 1 A. I = . 2
B. I = −1. C. I = 0. D. I = 1. a Z 875
CÂU 14. Tìm số thực a < 0 thỏa mãn
x3 − 6x dx = . 4 1
A. a = −4.
B. a = −5.
C. a = −6.
D. a = −3. Z 2 CÂU 15. Tính
(2ax + b)dx. 1 A. a + b.
B. 3a + 2b.
C. a + 2b.
D. 3a + b. 14
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 3 Z 1 CÂU 16. Biết d 2
x = m ln 5 + n ln 3, (m, n ∈ R). Tính P = m − n. x + 3 1 3 3 A. P = 0.
B. P = −1. C. P = . . 2
D. P = −2 1 2 5 Z 1 Z dx CÂU 17. Cho xn dx = và = ln 64 2
m, với m, n là các số nguyên dương. Khẳng x − 1 0 1
định nào sau đây luôn đúng?
A. 1 < n + m < 5. B. n = m. C. n > m. D. n < m. m BỬU Z 32
CÂU 18. Tìm số thực m sao cho
x2 − 2x + 5 dx = . G 3 1 A. m = 4. B. m = 5. C. m = 3. D. m = 2. AN a Z
CÂU 19. Có bao nhiêu số thực a ∈ (0; 2017) sao cho I = cos x dx = 0? QU 0 A. 642. B. 321. C. 643. D. 322. TẠ
CÂU 20. Tìm tham số thực m > 1 thỏa mãn m Z THPT
(2x − 3) dx = 2. - 1 17 G A. m = 3. B. m = 4. C. m = 2. D. m = . 9 2 0976071956 Z x − 1 DŨN CÂU 21. Biết rằng
dx = a − ln b, với a, b ∈ Z. Tính tích P = a.b. x 1 MATH.ND
A. P = −4. B. P = 4.
C. P = −2. D. P = 2. 3 Å 1ã GỌC
CÂU 22. Biết F (x) là một nguyên hàm của hàm số f (x) = e2x và F (0) = 2. Tính F 2 . N Å 1ã 1 1 Å 1ã 1 Å 1ã Å 1ã 1 A. F = e + ?. Lớp B. F TOÁN = e THẦ + 2. Y C. F DŨNG = 2e ? + 1. = e + 1. 2 2 2 2 2 2 D. F 2 2 a Z
CÂU 23. Có bao nhiêu số thực a thuộc khoảng (0; 2017) sao cho sin x dx = 0? GUYỄN 0 A. 1008. B. 320. C. 322. D. 321. N 2017π Z
CÂU 24. Tính tích phân
(sin x + cos x) dx. 0 Thầy A. I = 3. B. I = 1. C. I = 0. D. I = 2. 1 Z
CÂU 25. Tính I =
x 1 + x2 dx. 0 5 3 3 5 A. I = . . . . 2 B. I = 4 C. I = 2 D. I = 4
CÂU 26. Biết F (x) là một nguyên hàm của hàm số f (x) = 2x + 1 và F (1) = 3. Tính F (0). A. F(0) = 1. B. F(0) = 0. C. F(0) = 5. D. F(0) = 3.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 15
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 2 Z 1
CÂU 27. Xét I =
dx. Khẳng định nào sau đây là đúng? x2 1 1 2 1 1 2 1 1
A. I = − = = = 1 = . − −1. B. I = − x 1 2 − 1 x 1 2 2 1 2 Å 1 ã 1 2
C. I = − = = . = ln 4. −
D. I = ln |x|2 x 1 2 − 1 2 1 Thầy π 4 √ Z 2
CÂU 28. Giả sử I =
sin 3xdx = a + b · , với 2
a, b ∈ Q. Khi đó giá trị a − b là 0 N 3 1 1 A. − . B. − . C. 0. D. . GUYỄN 10 6 5 1 Z 1
CÂU 29. Tính tích phân I = e2017xdx. 0 1 A. I = e−2017 − 1.
B. I = 2017 e−2017 − 1. N 2017 Å 1 ã GỌC 1 C. I = e2017 e2017 . 2017 − 1. D. I = 2017 − 1 Z a
CÂU 30. Có bao nhiêu giá trị của a thỏa
(2x + 5) dx = a − 4? 0 DŨN A. 0. B. 1. C. −2. D. vô số. Z b √ 2 CÂU 31. Nếu x dx = (
3 a ≥ 0, b ≥ 0) thì G a √ √ √ √
A. b2 − a2 = 1. B. b 0976071956 b − a a = 1. C. b − a = 1.
D. b + a = 1. - THPT
CÂU 32. Cho hàm số f (x) = ax2 + bx, trong đó a, b là các hằng số, biết f 0(1) = 3 và 1 Z MATH.ND
f (x) dx = 1. Tính giá trị của b. T 0 Ạ 3 3
A. b = −1. B. b = 2. C. b = . D. b = . QU 2 4 ?4 Lớp TOÁN THẦY DŨNG ? Z dx 1 AN
CÂU 33. Biết tích phân = ln b với 3
a, b, c là các số nguyên dương nhỏ hơn 10. − 2x a c 2 G
Tính a + b − c. BỬU A. −2. B. 2. C. 0. D. 4. √ √
CÂU 34. Cho a, b là các số thực dương thỏa mãn a −
b + 1 = 0. Tính tích phân I = b Z dx √ . x a 1
A. I = −2. B. I = 1. C. I = . 2 D. I = 2. 1
CÂU 35. Cho F (x) là một nguyên hàm của hàm số f (x) = √
và F(3) = 3. Tính F(8). x + 1 A. F(8) = 5. B. F(8) = 3. C. F(8) = 7. D. F(8) = 2.
ccc BẢNG ĐÁP ÁN ccc 16
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 1. B 2. D 3. A 4. C 5. D 6. B 7. B 8. C 9. D 10. D 11. D 12. B 13. D 14. C 15. D 16. D 17. B 18. C 19. A 20. A 21. D 22. D 23. D 24. C 25. B 26. A 27. C 28. C 29. D 30. B 31. B 32. C 33. A 34. A 35. A
| Chủ đề 3. Phương pháp đổi biến
{ DẠNG 1. Nguyên hàm đổi biến loại 1 BỬU Z Z G Công thức:
f u(x)u0(x) dx =
f (t) dt với t = u(x)) AN
B1: Đặt t = u(x). QU
B2: Tính vi phân dt = u0(x) dx. Z Z TẠ
B3: Viết lại nguyên hàm ban đầu theo biến t:
f (x) dx = g (t) dt.
B4: Tính nguyên hàm theo biến t rồi chuyển lại biến x. THPT - 4
• Nguyên tắc: đặt t bằng cái gì thì dt phải là phần còn lại, do đó cần nhẩm G
trước xem đặt vậy có phù hợp hay không. 0976071956
• Trong một số trường hợp, ta không dễ dàng nhìn ra cách đặt ẩn ngay mà phải DŨN qua một số phép biến MA đổi TH.ND trung gian. DẤU HIỆU CHUNG: GỌC N
? Nếu có căn thì đặt t = căn.
? Nếu có mẫu thì đặt t = mẫu. ? Lớp TOÁN THẦY DŨNG ?
? Nếu có lũy thừa bậc cao thì đặt t = lũy thừa bậc cao.
DẤU HIỆU CỤ THỂ: GUYỄN N DẤU HIỆU CÓ THỂ ĐẶT VÍ DỤ CÁCH ĐẶT Z √ Có x2 pf(x)
Đặt t = pf(x) √ dx
Đặt t = x + 1 x + 1 Thầy Z
Có (ax + b)α
Đặt t = ax + b
x(2x − 1)9 dx
Đặt t = 2x − 1 Z etanx+1 Có af(x)
Đặt t = f(x) d cos x
Đặt t = tan x+1 2 x √ d Z 2 + ln √ Có ln x x x và
Đặt t = ln x hoặc t =
dx t = 2 + ln x x x
biểu thức chứa ln x
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 17
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Z √ √ Có ex dx
Đặt t = ex hoặc biểu
e2x 2ex − 1 dx t = 2ex − 1 thức chứa ex Z Có sin x dx Đặt t = cos x
cos4 x sin x dx Đặt t = cos x Z √ Có cos 3 x dx Đặt t = sin x
cos x sin x dx Đặt t = sin x Thầy d Z 1 + tan2 Có x Đặt x d cos t = tan x x
Đặt t = tan x 2 x cos2 x d Z ecotx N Có x Đặt t = cot x dx
Đặt t = cot x GUYỄN sin2 x 2 sin2 x
cccVÍ DỤ MINH HỌAccc
VÍ DỤ 1 (Hàm căn thức và lũy thừa bậc cao). N Tính các nguyên hàm sau: GỌC Z x2 Z √ 3 a √ dx b x x + 1 dx x + 1 DŨN Z Z c
x(2x − 1)20 dx d
x 2 − 3x28 dx G Z x Z 1 e √ dx f √ dx 1 + 2x + 1 0976071956 1 + 3 x + 1 - THPT Z Z 3 » (x − 1)20 g x5 ·
(1 − 2x2)2 dx MATH.ND h d ( x x + 2)22 TẠ QU
VÍ DỤ 2 (Hàm loga và mũ). Tính các nguyên hàm sau: ? Lớp TOÁN THẦY √ DŨNG ? Z 1 + ln2 x Z 2 + ln x ln x AN a dx b dx x x G Z x ln(x2 + 1) Z 1 c dx d √ dx BỬU x2 + 1 2x 2 + ln x Z 2ex Z √ e d f e2x 2ex e x − 1 dx x + 1 Z 1 Z ecotx g d h d 2e x x −x − 1 1 − cos 2x Z
VÍ DỤ 3 (Hàm lượng giác dạng
cosn x · sinm x dx).
Ghi nhớ: Nếu sin mũ lẻ thì đặt t bằng cos, nếu cos mũ lẻ thì đặt t bằng sin, còn nếu cả
hai đều mũ chẵn thì hạ bậc. 18
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ Z Z a
cos4 x · sin x dx b
cos3 x · sin2 x dx Z Z √ 3 c
cos2 x · sin2 x dx d
cos x · sin x dx Z √ Z sin5 x e
sin3 x · cos x dx f d cos x 3 x
VÍ DỤ 4 (Hàm lượng giác tổng hợp). Z sin3 x Z 1 + tan x a x b x BỬU d d 1 + 2 cos x cos2 x G Z tan x Z sin 2x + cos x c d d √ d cos x x 3 x 3 sin x + 1 AN QU
VÍ DỤ 5 (Đổi biến theo tan của góc chia đôi).
Tính các nguyên hàm sau: TẠ Z 1 Z 1 a d b d sin x x x cos x THPT Z 1 Z tan4 x - c d d d cos x x x − sin x + 1 cos 2x G 0976071956
cccBÀI TẬP TỰ LUẬNccc DŨN
CÂU 1. Tính các nguyên hàm MA sau: TH.ND Z √ Z √ Z √ a x x + 1 dx b
x 1 − x2 dx c
(x + 2) 3 1 − x dx GỌC Z Z Z N x x2 (x + 1)8 d √ dx e dx f dx 3 2x + 2 ? Lớp TOÁN (x THẦ − 3)21 Y DŨNG ? (2x − 1)10 Z x g √ √ dx 3x + 2 + x + 2 GUYỄN
CÂU 2. Tính các nguyên hàm sau: N Z Z sin3 x Z a
sin x cos3 x dx b d cos x c
e2 cos x sin x dx 5 x Thầy Z etanx+1 d d cos x 2 x
CÂU 3. Tính các nguyên hàm sau: Z 1 Z 2 − ln3 x Z ln2 x dx a dx b dx c √ x ln x x ln x Ä x 1 + ln x + 1ä Z ex dx d √ 1 + ex + 2
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 19
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
cccBÀI TẬP TRẮC NGHIỆMccc Z 1 + ln x CÂU 1. Nguyên hàm
dx (x > 0) bằng x
A. x + ln2 x + C.
B. ln2 x + ln x + C. 1 1 C. ln2 ln2 2
x + ln x + C.
D. x + 2 x + C.
CÂU 2. Tìm hàm số F (x) là một nguyên hàm của hàm số f (x) = − sin x(4 cos x + 1) thỏa π Thầy mãn F = 2 −1.
A. F(x) = cos 2x + cos x − 1.
B. F(x) = −2 cos 2x + cos x − 3.
C. F(x) = cos 2x + cos x.
D. F(x) = − cos 2x − cos x − 2. N GUYỄN
CÂU 3. Tìm nguyên hàm của hàm số f (x) = x(x + 1)20. Z A.
f (x) dx = 22(x + 1)22 − 22(x + 1)22 + C. Z (x + 1)22 (x + 1)22 B.
f (x) dx = + 22 − 22 C. Z N C.
f (x) dx = 22(x + 1)22 + 22(x + 1)22 + C. GỌC Z (x + 1)22 (x + 1)22 D.
f (x) dx = + + 22 22 C. √
CÂU 4. Họ nguyên hàm của hàm số f (x) = x2 4 + x3 là DŨN √ 2» » 1»
A. 2 x3 + 4 + C. B. (4 + (4 + (4 + 9 x3)3 + C. C. 2 x3)3 + C. D. 9 x3)3 + C. G π
CÂU 5. Cho F (x) là một 0976071956
nguyên hàm của hàm số f(x) = tan x trên khoảng − ; π và 2 2 - π
F (0) = 1. Giá trị F bằng THPT 3 A. 2 − ln 2. B. −1 + lnMA 2. TH.ND C. 1 + ln 2. D. 1 − ln 2. √ T sin x + 1. Ạ
CÂU 6. Tìm nguyên hàm F (x) của hàm số f (x) = cos x 1 √
1 − 2 sin x − 3 sin2 x QU
A. F(x) = (sin sin √ . 3 x + 1) x + 1 + C. B. F(x) = ? √ Lớp TOÁN THẦY DŨNG 2 √ ? sin x + 1 2 1
C. F(x) = (sin x + 1) sin x + 1 + C. D. F(x) =
sin x sin x + 1 + C. AN 3 3 π
CÂU 7. Nguyên hàm F (x) của hàm số f (x) = sin2 2x · cos3 2x thỏa F = 0 là G 4 BỬU 1 1 1 1 1 1 A. F(x) = sin3 2 sin5 2 . sin3 2 sin5 2 . 6 x − 10 x + 15
B. F(x) = 6 x + 10 x − 15 1 1 1 1 1 4 C. F(x) = sin3 2 sin5 2 . sin3 2 sin5 2 . 6 x − 10 x − 15
D. F(x) = 6 x + 10 x − 15 Z CÂU 8. Cho
2x (3x − 2)6 dx = A (3x − 2)8 + B (3x − 2)7 + C với A, B ∈ Q và C ∈ R. Giá trị
của biểu thức 12A + 7B bằng 23 241 52 7 A. . . . . 252 B. 252 C. 9 D. 9 Z CÂU 9. Xét I =
x3 4x4 − 35 dx. Bằng cách đặt u = 4x4 − 3, khẳng định nào dưới đây đúng? 20
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 1 Z 1 Z 1 Z Z
A. I = 4 u5 du.
B. I = 12 u5 du.
C. I = 16 u5 du. D. I = u5 du. Z (x − 2)10 CÂU 10. Nguyên hàm dx bằng (x + 1)12 1 Åx − 2ã11 1Åx − 2ã11 A. − + + 11 C. B. C. x + 1 3 x + 1 1 Åx − 2ã11 1 Åx − 2ã11 C. + + 11 C. D. C. x + 1 33 x + 1
ccc BẢNG ĐÁP ÁN ccc BỬU G 1. C 2. C 3. B 4. B 5. C 6. C 7. C 8. D 9. C 10. D AN
{ DẠNG 2. Nguyên hàm đổi biến loại 2 QU • Có π
a2 + x2 thì đặt x = |a| tan t với t ∈ − ; π hoặc 2 2
x = |a| cot t với t ∈ (0; π). Z TẠ 1 Ví dụ: d 1 +
x ta đặt x = tan t hoặc x = cot t. x2 √ • Có π
a2 + x2 thì đặt x = |a| tan t với t ∈ − ; π
hoặc x = |a| cot t với t ∈ (0; π). THPT 2 2 Z √ - Ví dụ:
4 + x2 dx ta đặt x = 2 tan t hoặc x = 2 cot t. G √ • Có h π i
a2 − x2 thì đặt 0976071956
x = |a| sin t với t ∈ − ; π hoặc 2 2
x = |a| cot t với t ∈ [0; π]. Z √ DŨN Ví dụ:
4 − x2 dx ta đặt x = 2 sin t hoặc x = 2 cos t. MATH.ND √ • Có h π i
x2 − a2 thì đặt x = |a| với ; π với sin t ∈ −
\ {0} hoặc x = |a| t ∈ t 2 2 cos t n o GỌC [0; π π] \ . N 2 Z √ 3 3 Ví dụ: x2? − Lớp 9 dx taTO đặt ÁN x = THẦY hoặc x DŨNG = . ? sin t cos t
cccVÍ DỤ MINH HỌAccc GUYỄN
VÍ DỤ 1. Tính các nguyên hàm sau: N Z 1 Z √ a d b 4 + 1 + x x2 dx x2 Thầy Z √ Z √ c 4 − x2 dx d
x2 − 9 dx Z √ Z 1 e 1 + x2 dx f √ dx 1 − x2 Z … 2 + x Z » g d h ( 2 x
x − 1)(2 − x) dx − x
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 21
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
cccBÀI TẬP TRẮC NGHIỆMccc Z 1
CÂU 1. Tìm nguyên hàm dx. x2 + 3 √ √ 3x 1 3x A. arctan + arctan + √ 3 C. B. √ 3 3 C. √ 3 3x √ 3x C. arctan + 3 arctan + 3 3 C. D. 3 C. Z 1 Thầy
CÂU 2. Tìm nguyên hàm dx. x2 + 2x + 4 1 + x √ A. √ + C .
B. arctan(1 + x) 3 + C . N 3 GUYỄN √3 1 + x 1 − x C. arctan √ + √ + 3 C. D. arctan C. 3 3 Z x3
CÂU 3. Tìm nguyên hàm d 1 + x. x8 N 1 1 1 GỌC A. arctan arctan arctan 4 x4 + C.
B. arctan x4 + C. C. 8 x4+C. D. 2 x4 + C. Z cos x
CÂU 4. Tìm nguyên hàm dx. 1 + sin2 x
A. arctan(sin x) + C.
B. arcsin(sin x) + C. DŨN
C. 2 arctan(sin x) + C.
D. arctan(sin x ) + 2 C. √ Z x2 G
CÂU 5. Nếu đặt x =
3 sin t thì nguyên hàm √ dx trở thành Z Z 0976071956 3 − x2 - Z Z A. sin2 t dt. B. cos2 dt. C. 3 sin2 t dt. D. 3 sin2 t dx. THPT MATH.ND Z »
CÂU 6. Nếu đặt x = 2 sin t thì nguyên hàm
(4 − x2)3 dx trở thành T Z Z Ạ A.
4(1 + cos 2t)2 dt. B.
4(1 − cos 2t)2 dt. QU Z Z C.
4(cos 2t − 1)2 dt. ? Lớp TOÁN THẦ D. Y 4(1DŨNG + cos 2t) dt?. AN Z dx
CÂU 7. Tìm nguyên hàm .
x2 − 2x + 10 G
A. arctan x − 1 + C.
B. 3 arctan x − 1 + C. BỬU 3 3 1 1
C. √ arctan x − 1 + C. D.
arctan x − 1 + C. 3 3 3 3 Z … 5 + x
CÂU 8. Tính nguyên hàm d 5 x. − x Å 1√ ã Å 1√ ã A. 5 arccos x + 4 + arccos 4 + 5 2 − x2 C . B. 10 x + 2 − x2 C . √ Å ã 1√ C. 5 arccos x + 4 + arccos x 4 + 5 − x2 C. D. 5 5 − 2 − x2 C.
ccc BẢNG ĐÁP ÁN ccc 22
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 1. C 2. C 3. A 4. A 5. C 6. A 7. D 8. A
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc Z 1 Z 1 Câu 2. Ta có dx = √ dx. x2 + 2x + 4 (x + 1)2 + ( 3)2 √ √ Đặt π x + 1 =
3 tan t, t ∈ − ; π , suy ra d 3(1 + tan2 2 2 x =
t) dt. Khi đó, ta có √ √ Z 1 3 Z 3 1 + d x x = dt = √ + C. x2 + 2x + 4 3 3 t + C = arctan 3 BỬU
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G AN Z x3 Z x3 Câu 3. Ta có d d 1 + x = x. x8 1 + (x4)2 QU 1 Đặt π
x4 = tan t, t ∈ − ; π , suy ra (1 + tan2 2 2 x3 dx = 4 t) dt. Khi đó TẠ Z x3 Z 1 Z 1 + tan2 1 Z 1 1 d x3 d t d d arctan 1 + x = x = t = t = x4 + C. x8 1 + (x4)2 4 1 + tan2 t 4 4t + C = 4 THPT -
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G 0976071956 π
Câu 4. Đặt sin x = tan t, t ∈ − ; π , suy ra cos x dx = (1 + tan2 t) dt. Khi đó DŨN 2 2 Z cos x Z MA 1 + TH.ND tan2 Z d t x = dt =
dt = t + C = arctan(sin x) + C. 1 + sin2 x 1 + tan2 x GỌC N
¤ Chọn đáp án A . .?.. Lớp . . . . . . . TO . . . . . .ÁN . . . . . . THẦ . . . . . . . Y . . . . DŨNG
. . . . . . . . . . . . ?... . . . . . . . . . . . . . . . . . . . . . . . . . √ √ Câu 5. x =
3 sin t, suy ra dx = 3 cos t dt. Khi đó √ GUYỄN Z x2 Z
3 sin2 t · 3 cos t Z N √ dx = √ dt = 3 sin2 t dt. 3 − x2 3 cos t Thầy
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6. Đặt x = 2 sin t, suy ra dx = 2 cos t dt. Khi đó Z Z Z Z
»(4 − x2)3 dx = 16 cos4 t dt = 16(cos2 t)2 dt = 4(1 + cos 2t)2 dt.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 23
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Z dx Z dx Câu 7. Ta có = .
x2 − 2x + 10 (x − 1)2 + 9
Đặt x − 1 = 3 tan t, ta có Z dx Z 1 3 1 1 = d arctan x − 1 + ( · t = C. x − 1)2 + 9 9 cos2 t 3t + C = 3 3 cos2 t Thầy
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i
Câu 8. Đặt x = 5 cos 2t, t ∈ 0; π , suy ra dx = −10 sin 2t dt. Khi đó N 2 GUYỄN Z … 5 + x Z 5(1 + cos 2 Z d t) sin2 cos2 5 x = −10 t dt = 20 t dt − x 5(1 − cos 2t) Z Å 1 1√ ã
= 10 (1 + cos 2t) dt = 10 arccos x + 4 + 2 5 4 − x2 C N GỌC
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
{ DẠNG 3. Tích phân đổi biến DŨN
cccVÍ DỤ MINH HỌAccc G 7 Z x dx VÍ DỤ 1. Tích phân 0976071956
bằng a ln 2 − b ln 5 với a, b ∈ -
Q. Giá trị của 2a + b bằng x2 + 1 THPT 2 3 1 A. . B. . MATH.ND 2 2 C. 1. D. 2.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ 1 Z √ 1 √ Ä ä QU VÍ DỤ 2. Biết x x2 + 4 dx =
b3 − c (với a, b, c ∈ ? Lớp
N). Tính Q = abc. a TOÁN THẦY DŨNG ? 0 AN A. Q = 120. B. Q = 15.
C. Q = −120. D. Q = 40.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G ln 6 Z dx BỬU
VÍ DỤ 3. Biết I =
= 3 ln a − ln b, với a, b là các số nguyên dương. Tính
ex + 2e−x − 3 ln 3 P = ab. A. P = 15. B. P = 10. C. P = 20.
D. P = −10.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . e √ √ Z 3 + ln x c VÍ DỤ 4. Biết dx = a − b
, trong đó a, b, c là các số nguyên dương và c < 4. x 3 1
Tính giá trị S = a + b + c. A. S = 13. B. S = 28. C. S = 25. D. S = 16.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ π 4 Z 5 sin x + cos x
VÍ DỤ 5. Biết tích phân d sin
x = aπ + ln b với a, b là các số hữu tỉ. Tính x + cos x 0
S = a + b. 5 11 3 A. S = . . . 4 B. S = 4 C. S = 4 D. S = 2.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc 4 √ Z 2x + 1 CÂU 1. Cho biết √
dx = a + b ln 2, (a, b ∈ 1 + 2
Q). Khi đó, đẳng thức nào sau đây x + 1 BỬU 0 đúng? G A. a − b = 0.
B. a2 − 4b − 1 = 0.
C. a2 − 4b + 1 = 0.
D. a2 − 4b = 0. 2 Z AN x3 dx √ √ CÂU 2. Biết √
= a 5 + b 2 + c với a, b, c là các số hữu tỷ. Giá trị của P = x2 + 1 − 1 QU 1
a + b + c là 5 7 5 TẠ A. − . . . 2 B. 2 C. 2 D. 2. 1 Z √ √ CÂU 3. Cho I =
x3 3 1 − x4 dx. Đặt t = 3 1 − x4 thì I bằng THPT - 0 1 1 1 1 Z Z Z Z G 3 3 A. − t3 dt. B. d 4t3 dt. C. t3 dt. D. − 4 t. 0 0976071956 0 0 0 4 √ √ DŨN Z 25 Ç å − x2 √ 5 6 + 12 CÂU 4. Cho
dx = a + b · 6 + c · ln √
+ d · ln 2 với a, b, c, d là các số x MATH.ND 5 6 − 12 1
hữu tỉ. Tính tổng a + b + c + d. GỌC 3 3 3 3 A. − . B. − . C. − . D. − . N 20 2 24 25 3 ? Lớp TOÁN THẦY DŨNG ? Z (x + 6)2017 CÂU 5. Cho
dx = a2018 − 32018 . Tính a. x2019 6 · 2018 1 A. 7. B. 9. C. 6. D. 8. GUYỄN √ 2 2 N Z x
CÂU 6. Biết I = √
dx = a ln 5 + b ln 2, với a, b là các số hữu tỉ. Tính tổng x2 − 1 + x2 + 1 √3
S = 3a + 2b. Thầy 2 1 5 A. . . . 3 B. 0. C. −3 D. −3 e Z 3 ln x + 1
CÂU 7. Cho tích phân I =
dx. Nếu đặt t = ln x thì x 1 e 1 1 1 Z Z Z 3t + 1 Z 3t + 1 A. I = (3t + 1) dt. B. I = (3t + 1) dt. C. I = dt. D. I = dt. t et 1 0 0 0
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 25
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 3 √ √ Z 1 + Ç å x2 1 √ c 10 CÂU 8. Giả sử dx = b 2 −
(với a, b, c ∈ N và b là phân số tối giản). x4 a a3 a 1
Khi đó giá trị a + bc bằng A. 43. B. 23. C. y = 33. D. 13. π 2 Z CÂU 9. Tích phân
sin2 x · cos x dx bằng Thầy 0 1 1 1 1 A. . . . . 4 B. 3 C. 2 D. 5 N π 2 GUYỄN Z √
CÂU 10. Cho tích phân I =
2 + cos x · sin x dx. Nếu đặt t = 2 + cos x thì kết quả nào sau 0 đây đúng? π 3 3 2 2 Z √ Z √ Z √ Z √ N A. I = t dt. B. I = 2 t dt. C. I = t dt. D. I = t dt. GỌC 2 2 0 3 a Z i sin x
CÂU 11. Có bao nhiêu giá trị của a trong đoạn h π ; 2 thỏa mãn √ d 4 π x = 1 + 3 cos x DŨN 0 2? 3 A. 4. B. 1. C. 2. D. 3. G π 4 √ Z 0976071956 - 2 + 3 tan x √ √
dx = a 5 + b 2, (a, b ∈ THPT CÂU 12. Cho 1 + cos 2
Q). Tính giá trị của biểu thức A = x 0 a + b. MATH.ND 1 7 2 4 A. . B. . C. . D. . T 3 12 3 3 Ạ π 2 QU Z
−4 sin x + 7 cos x
CÂU 13. Biết rằng I = ? Lớp TOÁNd THẦ x = a Y + 2 DŨNG ln b, với a ?
∗; b tối giản. 2 sin
> 0; b, c ∈ N x + 3 cos x c c AN 0
Hãy tính giá trị biểu thức P = a − b + c. G A. π − 1. B. π + 1. 2 C. π 2 − 1. D. 1. BỬU √3 Z dx √ √ 1 √ CÂU 14. Biết √
= a 3 + b 2 + c + ln(3 2 − 3) với a, b, c là các số hữu 1 + x + 1 + x2 2 1
tỉ. Tính P = a + b + c. 1 1 5 A. P = . . . 2
B. P = −1.
C. P = − 2 D. P = 2 2 Z … 1 1 √ √
CÂU 15. Cho tích phân +
dx = a 2 − b 5 với a, b là các số hữu tỷ. Giá trị của x8 x6 1
biểu thức a + b bằng 7 11 7 11 A. . . . . 8 B. 24 C. 5 D. 5 26
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 2 Z dx √ √ √ ä CÂU 16. Biết √ √
= ln Äa 6 + b 3 + c 2 + d với a, b, c, d là các số nguyên. x + 1 x + 2 1
Tính P = a + b + c + d. A. P = 45. B. P = 65. C. P = 93. D. P = 17. 1 √ Z dx Å 2 + a ã CÂU 17. Biết rằng √ = 2 ln √
với a, b là các số nguyên dương. Giá x2 + 4x + 3 1 + b 0
trị của a + b bằng A. 3. B. 5. C. 9. D. 7. 12 BỬU Z Å 1 ã c
CÂU 18. Cho tích phân I = 1 + x −
ex+ 1x dx = a · ed trong đó a, b, c, d là các số G x b 1 12 c AN nguyên dương và a,
là các phân số tối giản. Tính bc − ad. b d 1 QU A. 24. B. . 6 C. 12. D. 1. 2 TẠ Z
x(1 + ex) + ln x + 1 2
CÂU 19. Biết I = dx = a +
với a, b, c là các số nguyên.
(x ln x + ex)2 b ln 2 + ec e 1
Tính P = a + b + c. THPT - A. P = 3. B. P = 6. C. P = 1. D. P = 7. π 2 G Z
x sin x + cos x + 2x CÂU 20. Biết d + ln b với sin x = π2
a, b, c là các số nguyên dương và b x + 0976071956 2 a c c 0 DŨN
là phân số tối giản. Tính P = a · b · c. A. P = 24. B. P MA
= 13. TH.NDC. P = 48. D. P = 96. π 2 Z
x2 + (2x + cos x) cos x + 1 − sin x dx = aπ2 + b − ln c với a,b,c GỌC
CÂU 21. Cho tích phân x + cos x π N 0
là các số hữu tỷ. Tính? Lớp giá trị TO của ÁN biểu THẦ thức P = a Y c3 DŨNG + b. ? 5 3 A. P = . . 4 B. P = 2. C. P = 3. D. P = 4 π 2 Z x2 GUYỄN
+ sin2 x − sin x CÂU 22. Biết
dx = aπ2 + b ln π + c với a, b, c là các số hữu tỷ. Tính N x + cos x 2 0
giá trị của biểu thức T = 8a + b + c. A. 8. B. 3. C. 0. D. 1. Thầy
ccc BẢNG ĐÁP ÁN ccc 1. A 2. C 3. B 4. B 5. A 6. B 7. B 8. B 9. B 10. A 11. C 12. A 13. B 14. C 15. A 16. D 17. B 18. A 19. C 20. C 21. B 22. D
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 27
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 4 √ 4 √ Z 25 − x2 Z x 25 − x2 √
− t dt = xdx Câu 4. Ta có dx =
dx = I. Đặt t = 25 − x2 Ñ . x x2
x2 = 25 − t2 1 1 √
Đổi cận x = 1 Ñ t = 2 6, x = 4 Ñ t = 3. Khi đó, 3 Z −t2 dt I = Thầy 25 − t2 √ 2 6 3 Z ï 25 ò = 1 − dt N 25 − t2 √ GUYỄN 2 6 3 Z ï 5 Å 1 1 ãò = 1 − + d 2 5 t − t 5 + t √ 2 6 3 N 5 5 = − t t + ln GỌC 2 5 + t √ 2 6 √ 5 1 √ 5 5 6 = 3 + ln 6 ln − 2√ 2 4 − 2 − 2 5 + 2 6 √ DŨN √ 5 5 6 + 12
= 3 − 5 ln 2 − 2 6 + ln √ 2 . 5 6 − 12 G 5 0976071956 3 -
Vậy a = 3, b = −2, c = , d = −5 suy ra a + b + c + d = − . THPT 2 2 MATH.ND
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G 3 3 3 BỬU Z (x + 6)2017 Z (x + 6)2017 1 Z Å 6 ã2017 1
Câu 5. Ta có I = dx = · dx = 1 + · dx. x2019 x2017 x2 x x2 1 1 1 6 1 Đặt t = 1 +
Ñ nếu x = 1 thì t = 7; nếu x = 3 thì t = 3; dt = − dx. x 6x2 7 1 Z 72018 Khi đó − 32018
I = 6 t2017 dt = 6 · 2018 Ñ a = 7. 3
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ Câu 13. Ta có π π 2 2 Z
4 cos x − 6 sin x Z I = d 1 d 2 sin x + x x + 3 cos x 0 0 π 2 Z 2 = d(2 sin 2 sin
x + 3 cos x) + π x + 3 cos x 2 0 π
= 2 ln |2 sin x + 3 cos x| 2 0 + π 2
= 2 ln 2 − 2 ln 3 + π BỬU 2 2 G = 2 ln + π 3 2 . AN Vậy P = π + 1.
2 − 2 + 3 = π2 QU
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ √ √ √ 3 3 √ √ 3 √ Z dx Z
(1 + x − 1 + x2) dx Å 1
1 ã 3 Z x 1 + x2 Câu 14. √ − THPT Ta có = = ln x + dx. 1 + x + 1 + x2 2x 2 2x 1 2x2 - 1 1 1 √ 1 √ 3 − 1 G = ln 3 + 2 √ 2 − I. 3 √ Z 0976071956 1 + Xét x x2 I = dx. DŨN 2x2 1√ MATH.ND
Đặt t = 1 + x2, khi đó t dt = x dx. Ta có GỌC 2 Z t2 N I = d 2( t t2 − 1) √ ? Lớp TOÁN THẦY DŨNG ? 2 2 1 2 1 Z Å 1 1 ã = + d 2 t t √ 2 2
t − 1 − t + 1 √ GUYỄN 2 N 1 ï 1 ò 2 = ln t − 1 2 t + 2 t + 1 √ 2 √ 1 ñ √ 1 1 1 2 ô − 1 Thầy = 2 2 + ln ln √ 2 − 2 3 − 2 2 + 1 1 √ √ √ = î2 2 ln 3 2 2 − − ln( − 1)ó . 1√ 1√ 3 1 √ Vậy I = 3 + 2 + ln(3 2 2 2 − 2 2 − 3). 1
Do đó P = a + b + c = − . 2
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 29
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 2 2 2 Z … 1 1 Z 1 Å 1 ã Z 1 … 1
Câu 15. Ta có I = + dx = 1 + = 1 + dx. x8 x6 x6 x2 x3 x2 1 1 1 1 Đặt t = . Khi đó x 1
+) với x = 1 Ñ t = 1, với x = 2 Ñ t = . 2 d +) d x t = − . Thầy x2 12 1 Z √ Z √ Do đó I = − t · 1 + t2dt = t t2 + 1dt. N 1 1 2 GUYỄN
Đặt u = t2 + 1. Khi đó 1 5 +) với t = , với 3 Ñ u = 4 t = 1 Ñ u = 2.
+) du = 2tdt. 2 1 Z √ 1 Ç√ … 5 å 2√ 5 √ Do đó I = udu = 23 − ( )3 = 2 − 5. N 2 3 4 3 24 GỌC 5 4 2 5 7 Suy ra a = , .
3 b = 24 Ñ a + b = 8 DŨN
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G Câu 16. 0976071956 - 1 x + 1 = THPT … 1 • Đặt x + 2 u2 − 1 u =
ta có u2 = x + 2 = 1 + nên x + 1 x MA + 1 TH.ND x + 1 2u d d x = − u. (u2 − 1)2 … … T 3 4 Ạ
Đổi cận x = 1 thì u = , . 2 x = 2 thì u = 3 QU • Ta có ? Lớp TOÁN THẦY DŨNG ? √ √ AN 2u 2 2 4 4 3 − du 3 Z dx Z dx Z (u2 − 1)2 Z −2du √ √ = = = G x + 1 x + 2 … x + 2 1 u2 − 1 1 1 (x + 1) √ √ 3 3 x + 1 2
u2 − 1 · u 2 BỬU √ 43 Z Å 1 1 ã = du √
u + 1 − u − 1 3 2 √ 4 = (ln( 3
u + 1) − ln(u − 1)) √ 3 2 √ √ √ (2 + 3)( 3 2) √ √ √ = ln − √ √ √ = ln(2 + 3)2( 3 − 2)2 (2 − 3)( 3 + 2) √ √ √
= ln(−14 6 + 20 3 − 24 2 + 35).
• Vậy a + b + c + d = 17. 30
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 Z dx Z dx Câu 17. Ta có √ = . p x2 + 4x + 3 (x + 1)(x + 3) 0 0 √ √ 1 Å 1 1 ã
Đặt t = x + 3 + x + 1 Ñ dt = √ + √ d 2 x x √ √ + 3 x + 1 1 Ç å x + 1 + x + 3 1 t 2 dt dx ⇔ dt = d = . 2 ⇔ dt = x ⇔ p( p p x + 1)(x + 3) 2 · (x + 1)(x + 3) t (x + 1)(x + 3) √ √ BỬU
Khi x = 0 thì t = 1 + 3; khi x = 1 thì t = 2 + 2. √ 1 2+ 2 √ Z Z √ a G dx dt 2+ 2 2 + 2 = 2 √ = 2
= 2 ln |t| √ = 2 ln √ Ñ Ñ a + b = 5. x2 + 4x + 3 t 1+ 3 1 + 3 b = 3 0 √ AN 1+ 3
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . QU 12 12 12 TẠ Z Å 1 ã Z Z Å 1 ã
Câu 18. Ta có I = 1 + x −
ex+ 1x dx =
ex+ 1x dx + x −
ex+ 1x dx. x x 1 1 1 12 12 12 THPT 12 Z - Xét I1 =
ex+ 1x dx. G 1 12 Å ã 0976071956 1 du = 1 − ex+ 1x dx u = ex+ 1 x x2 DŨN Đặt Ñ dv = dx v = x. MATH.ND Do đó 12 Z Å ã 12 1 GỌC
I1 = xex+ 1x − x −
ex+ 1x dx. 1 x N 12 ? Lớp TOÁN THẦ 1 12 Y DŨNG ? Suy ra 12 143 145
I = xex+ 1x = e 12 . 1 12 12 GUYỄN
Vậy a = 143, b = 12 , c = 145, d = 12 và bc − ad = 24. N
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Thầy Câu 19. Ta có 2 2 Z
x(1 + ex) + ln x + 1 Z Å x + 1 ã x + 1 2 2 I = dx = − d = − = −3 +
(x ln x + ex)2
x ln x + ex
x ln x + ex 1 2 ln 2 + e2 e. 1 1
Suy ra a = −3, b = c = 2. Vậy
P = a + b + c = −3 + 2 + 2 = 1.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 31
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 20. π π 2 2 Z
x sin x + cos x + 2x Z d
x(sin x + 2) + cos x x = dx Thầy sin x + 2 sin x + 2 0 0 π 2 Z cos = x x + dx N sin x + 2 0 GUYỄN π ï ò 2 = x2 + ln 2
| sin x + 2| 0 3 = π2 + ln 8 2. N
P = a · b · c = 48. GỌC
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . DŨN Câu 21. Ta có π G 2 Z
x2 + (2x + cos x) cos x + 1 − sin x I = 0976071956 dx - x + cos x THPT 0 π 2 Z (x + MA cos x TH.ND )2 + 1 =
− sin x dx x + cos x T 0 Ạ π 2 Z Å ã QU 1 − sin x ?= Lớp x TO + cos ÁN x + dx x THẦ + cos Y x DŨNG ? 0 AN π π 2 2 Z Z d (x + cos x) G =
(x + cos x) dx + x + cos x 0 0 BỬU π Å ã 2 = x2 + sin 2
x + ln |x + cos x| 0
= π2 + 1 + ln π 8 2 1 2
= 8 · π2 + 1 − ln . π 1
Suy ra a = 8,b = 1,c = 2.
Vậy P = ac3 + b = 2.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ Câu 22. Ta có π π 2 2 Z
x2 + sin2 x − sin x Z
x2 − cos2 x + 1 − sin x I = dx = dx x + cos x x + cos x 0 0 π π 2 2 Z Z 1 = − sin x
(x − cos x) dx + dx. x + cos x 0 0 π 2 π Z Å ã 2 Xét x2 A =
(x − cos x) dx = = π2 BỬU 2 − sin x 0 8 − 1. 0π G 2 Z 1 Xét − sin x B = dx. AN x + cos x 0
Đặt x + cos x = t Ñ (1 − sin x) dx = dt. QU π 2 π Z 1 2 TẠ Suy ra B = dt = ln |t| = ln π . t 1 2 1 1 a = 8 THPT 1
Vậy I = A + B = Ñ T = 1. -
8π2 + ln π2 − 1 và do đó b = 1 G c = −1
¤ Chọn đáp án D . . . . . . . . . 0976071956
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . DŨN MATH.ND
| Chủ đề 4. Nguyên hàm, tích phân bằng phương pháp GỌC từng phân N ? Lớp TOÁN THẦY DŨNG ?
{ DẠNG 1. Nguyên hàm từng phần Z Z
1. Công thức nguyên hàm từng phần
u dv = uv − v du . GUYỄN N Z
2. Để tính nguyên hàm
f (x)dx bằng từng phần ta làm như sau:
• Bước 1. Chọn u, v sao cho f Thầy
(x) dx = udv (chú ý dv = v0 (x) dx). Sau đó tính Z v =
dv và du = u0.dx. Z
• Bước 2. Thay vào công thức (∗) và tính vdu.
4 Việc lựa chọn u nên theo thứ tự sau: Lô - Đa - Lượng - Mũ.
cccVÍ DỤ MINH HỌAccc
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 33
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 VÍ DỤ 1. Hãy tính Z Z Z a
(1 − 2x) ex dx b xe−x dx c
x sin2 x dx
VÍ DỤ 2. Tìm nguyên hàm các hàm số sau Z Z Z a ln c ex Thầy I = x dx. b I =
x ln x2 + 1 dx. I =
. sin x dx. N
Sơ đồ đường chéo GUYỄN
Để đơn giản trong quá trình tính toán, ta có thể sử dụng sơ đồ đường chéo như sau: a Chia thành 3 cột:
• Cột 1 (cột trái: cột u) luôn lấy đạo hàm tới 0. N GỌC
• Cột 2 (cột giữa: cột dấu): Bắt đầu từ dấu +, sau đó đan dấu +, −, + . . .
• Cột 3 (cột phải: cột dv), luôn lấy nguyên hàm cho tới khi tương ứng với cột 1. DŨN
b Nhân chéo kết quả cột 1 và 3 với nhau với dấu là dấu của cột 2. G
c Cộng các kết quả vừa 0976071956 nhân lại. - THPT (đạo hàm) dấu (nguyên hàm) u MATH.ND dv u0 + v TẠ − Z QU
u00? Lớp TOÁN THẦY DŨNG ? v ... ... ... AN G 0 BỬU
L Nếu biểu thức cùng 1 dòng có thể rút gọn được thì ta phải rút gọn trước rồi mới làm tiếp.
L Chú ý bước chọn v, ta chọn +C linh hoạt sao cho rút gọn được u0.
L Sơ đồ đường chéo dừng lại khi hai cột nhân nhau ta tính nguyên hàm được.
L Trong trường hợp nguyên hàm xoay vòng, ta dừng lại khi cột 1 và cột 3 trở lại như
dòng đầu tiên. Khi đó, ta nối 2 phần tử ở dòng dừng lại, thêm dấu nguyên hàm ở 34
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
trước kết quả và coi gạch nối là 1 đường chéo, sử dụng quy tắc đan dấu.
cccVÍ DỤ MINH HỌAccc Z
VÍ DỤ 1. Tính nguyên hàm I =
2x3 − 3x ex dx. Lời giải. (đạo hàm) dấu (nguyên hàm)
u = 2x3 − 3x
dv = ex dx 6x2 − 3 + ex BỬU 12x − ex G 12 + ex AN − QU 0 ex TẠ
Vậy I = (2x3 − 3x)ex − (6x2 + 3)ex + 12x(ex) − 12ex + C. Z THPT
VÍ DỤ 2. Tính nguyên hàm I =
3x3 − 2x2 sin x dx. - Lời giải. G (đạo hàm) dấu (nguyên hàm)
u = 3x3 − 0976071956 2x2
dv = sin x dx DŨN
9x2 − 4x + − cos x MATH.ND 18x − 4 − − sin x GỌC + cos x N 18 ? Lớp TOÁN THẦY DŨNG ? 0 − sin x GUYỄN
Vậy I = (3x3 − 2x2)(− cos x) − (9x2 − 4x)(− sin x) + (18x − 4) cos x − 18 sin x + C. N Z
VÍ DỤ 3. Tính nguyên hàm I =
x ln x dx. Lời giải. Thầy (đạo hàm) dấu (nguyên hàm) u = ln x dv = x dx 1 + x2 1 Ở đây, ta thấy và x2 có thể x 2 x 2 1
rút gọn được với nhau nên ta rút x 2
gọn sẽ được 1 và x . 2 0 − x2 4
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 35
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Vậy x2 I = x2 ln + 2 x − 4 C. Z
VÍ DỤ 4. Tính nguyên hàm I =
(2x + 1) ln3 x dx. Lời giải. (đạo hàm) dấu (nguyên hàm) u = ln3 x
dv = (2x + 1) dx Thầy 3 ln2 + x x2 + x x 3 ln2 x x + 1 N GUYỄN 6 ln x − x2 + x x 2 6 ln x x + 1 2 N 6 + x2 + x GỌC x 4 6 x + 1 4 − DŨN 0 x2 + 8 x Å x2 ã Å x2 ã Å x2 ã G
Vậy I = (x2 + x) ln3 x − + (3 ln2 + (6 ln + + 2 x x) + x x) − 6 x C. 0976071956 4 8 - Z THPT
VÍ DỤ 5. Tính nguyên hàm I = sin xex dx. Lời giải. MATH.ND T (đạo hàm) dấu (nguyên hàm) Ạ u = ex
dv = sin x dx QU ex + ? Lớp TOÁN THẦY DŨNG − cos?x AN ex −
− sin x (dừng lại) G + BỬU Z
Vậy I = ex(− cos x) − ex(− sin x) +
ex(− sin x) + C = ex(− cos x) − ex(− sin x) − I + C. sin Suy ra 2 xex − cos xex
I = sin xex − cos xex + C Ñ I = + 2 C.
Làm các ví dụ trắc nghiệm sau bằng sơ đồ đường chéo
VÍ DỤ 6. Tìm nguyên hàm của hàm số f (x) = xex. Z Z A.
f (x) dx = (x + 1)ex + C. B.
f (x) dx = (x − 1)ex + C. Z Z C.
f (x) dx = xex + C. D.
f (x) dx = −xex + C.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
VÍ DỤ 7. Tìm họ nguyên hàm của hàm số y = x sin x.
A. −x cos x + sin x + C.
B. x cos x + sin x + C.
C. x cos x − sin x + C.
D. x sin x + cos x + C.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
VÍ DỤ 8. Tìm họ nguyên hàm của hàm số f (x) = x ln(x + 2). Z x2 + 4x A.
f (x) dx = x2 ln( + 2 x + 2) − 4 C. Z x2 − 4x B.
f (x) dx = x2 − 4 ln( + 2 x + 2) − 4 C. Z x2 + 4x BỬU C.
f (x) dx = x2 − 4 ln( + 2 x + 2) − 4 C. G Z D.
f (x) dx = x2 ln( + 2
x + 2) + x2 + 4x 4 C. AN
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z ln (1 + x) QU
VÍ DỤ 9. Nguyên hàm I = dx có kết quả là x2 TẠ
A. x ln |x| − (x + 1) ln (x + 1) + C.
B. x ln x − (x + 1) ln (x + 1) + C. x x
ln |x| + (x + 1) ln (x + 1)
ln x + (x + 1) ln (x + 1) C. + C. D. + C. x x THPT
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . - Z
VÍ DỤ 10. Tính F (x) =
x2 cos x dx. Chọn kết quả đúng? G
A. F(x) = (x2 − 2) sin x + 2x cos x + C.
B. F(x) = 2x2 sin x − x cos x + sin x + C. 0976071956
C. F(x) = x2 sin x − 2x cos x + 2 sin x + C.
D. F(x) = (2x + x2) cos x − x sin x + C. DŨN
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . MA Z TH.ND
VÍ DỤ 11. Tính nguyên hàm I =
2x3 − 3x ex dx. GỌC
A. I = (2x3 − 3x)ex − (6x2 + 3)ex + 12x(ex) − 12ex + C. N
B. I = (3x − 2x3)ex?+ Lớp (6x2 + TO 3)ex ÁN − 12x(THẦ ex) + Y 12ex DŨNG + C. ?
C. I = (2x3 − 3x)ex + (6x2 + 3)ex + 12x(ex) − 12ex + C.
D. I = (3x − 2x3)ex − (6x2 + 3)ex + 12x(ex) − 12ex + C. GUYỄN
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z N
VÍ DỤ 12. Tính nguyên hàm I =
3x3 − 2x2 sin x dx.
A. I = −(3x3 − 2x2) cos x − (9x2 − 4x) sin x + (18x − 4) cos x − 18 sin x + C. Thầy
B. I = −(3x3 − 2x2) cos x + (9x2 − 4x) sin x + (18x − 4) cos x − 18 sin x + C.
C. I = (3x3 − 2x2) cos x − (9x2 − 4x) sin x + (18x − 4) cos x − 18 sin x + C.
D. I = (3x3 − 2x2) cos x + (9x2 − 4x) sin x + (18x − 4) cos x − 18 sin x + C.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z
VÍ DỤ 13. Tính nguyên hàm I =
x ln x dx. x2
A. I = x2 ln + ln + 2 x + x2 4 C. B. I = x2 4 x − 2 C.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 37
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 x2
C. I = x2 ln + ln + 2 x − 4 C. D. I = x2 4 x + x2 2 C.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z
VÍ DỤ 14. Tính nguyên hàm I = sin x · ex dx.
cos xex − sin xex
sin xex + cos xex A. I = + + 2 C. B. I = 2 C. sin +
xex − cos xex + Thầy
C. I = − sin xex − cos xex 2 C. D. I = 2 C.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc N Z GUYỄN CÂU 1. Biết
x sin 3x dx = ax cos 3x − b sin 3x + C, với a, b ∈ Q. Khi đó giá trị của a + 6b là A. −21. B. −7. C. −5. D. −1. Z CÂU 2. Cho I =
(x − 1) sin 2x dx. Chọn khẳng định đúng trong các khẳng định sau. N Z Z GỌC
A. I = − (x − 1) cos 2x + cos 2x dx.
B. I = − (x − 1) cos 2x cos 2x dx. 1 1 Z 1 1 Z
C. I = − ( cos 2 ( cos 2
2 x − 1) cos 2x + 2 x dx.
D. I = −2 x − 1)cos 2x − 2 x dx. DŨN Z
CÂU 3. Tính F (x) =
x sin x cos x dx. Chọn kết quả đúng? 1 x 1 x A. F(x) =
sin 2x − cos 2x + C. B. F(x) =
cos 2x − sin 2x + C. G 8 4 4 2 1 x C x x 0976071956 -
. F(x) = sin 2 + x cos 2 + sin 2 cos 2 4 8 C.
D. F(x) = −1 4 x − 8 x + C. THPT
CÂU 4. Tìm nguyên hàm của hàm Z 1 MA số f( 8 TH.ND
x) = (8x − 9) · 7x. A.
f (x) dx = (8
ln 7 x − 9).7x − ln 7.7x + C. T Z 1 8 Ạ B.
f (x) dx = (8
ln 7 x − 9).7x + ln 7.7x. QU Z C.
f (x) dx = 7x. ln 7. ? (8xLớp − 9 − TO 8 ln ÁN 7) + C. THẦY DŨNG ? AN Z 1 Å 8 ã D.
f (x) dx = 8 + ln 7.7x. x − 9 − ln7 C. G Z
CÂU 5. F (x) =
x · ex3 dx. Chọn kết quả đúng? BỬU
A. F(x) = 3(x − 3)ex3 + C.
B. F(x) = (x + 3)ex3 + C.
C. F(x) = x − 3ex3 + ex3 + 3 C.
D. F(x) = x + 3 3 C.
CÂU 6. Tìm nguyên hàm của hàm số f (x) = (2x − 1)e3x. Z 1 Z
(2x − 1)e3x 2e3x A.
f (x)dx = ( +
3 x2 − x)e3x + C. B. f (x)dx = 3 − 9 C. Z Z
(2x − 1)e3x 2e3x C.
f (x)dx = (x2 − x)e3x + c. D. f (x)dx = + 3 − 3 C. Z
CÂU 7. Kết quả của
x · 2x dx bằng 2x 2x (x − 1) A. x.2x + + ln 2 − C. B. C.
C. 2x(x + 1) + C.
D. 2x(x − 1) + C. ln2 2 ln 2 38
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 8. Tìm nguyên hàm của hàm số y = x3 ln x 1 1 1 1
A. F (x) = 4x4.lnx + 16x4 + C.
B. F (x) = 4x4.lnx − 16x4 + C. 1 1 1 1
C. F (x) = 4x4.ln2x − 16x4 + C.
D. F (x) = 4x4.lnx − 16x3 + C. Z CÂU 9. Biết
x ln(x + 1) dx = ax2 + bx + c ln (x + 1) + mx2 + nx + p với ,a, b, c, m, n, p ∈
R. Tính S = a2 + b2 + c2. 1 1 A. S = 1. B. S = . . 4 C. S = 2 D. S = 2. Z
CÂU 10. Nguyên hàm I =
2x ln (1 + x) dx có kết quả là BỬU 1 1
A. x2 − 1 ln (x + 1) − G
2 x2 − 2x + C.
B. x2 + 1 ln (x + 1) − 2 x2 − 2x + C.
C. x2 − 1 ln (x + 1) − x2 − x + C.
D. x2 − 1 ln (x + 1) − 2 x2 − 2x + C. AN
CÂU 11. Cho F (x) = x2 là một nguyên hàm của hàm số f (x)e2x. Tìm nguyên hàm của hàm QU
số f0(x)e2x. Z Z A.
f 0(x)e2x dx = −x2 + 2x + C. B.
f 0(x)e2x dx = −x2 + x + C. TẠ Z Z C.
f 0(x)e2x dx = x2 − 2x + C. D.
f 0(x)e2x dx = −2x2 + 2x + C. Z 2x THPT CÂU 12. Cho I =
dx = ax cot x + b ln |sin x| + C. Giá trị của biểu thức T = a + b - sin2 x bằng bao nhiêu? G A. T = 0. B. T = 1. C. T = 2. D. T = 3. Z 0976071956
CÂU 13. Nguyên hàm I =
x log x dx có kết quả là DŨN
A. x2 (2 ln x + 1) + C. MATH.ND + 4 ln 10
B. x (2 ln x − 1) 4 ln 10 C.
C. x2 (2 ln x − 1) + C.
D. x (2 ln x + 1) + C. GỌC 4 ln 10 4 ln 10 √ N Z x ln Äx + x2 + 1ä CÂU 14. Nguyên ? hàm I Lớp = TOÁN √ THẦY dx DŨNG có kết quả ? là x2 √ + 1 √
A. I = 2x ln Äx +
x2 + 1ä − x + C.
B. I = x ln Äx +
x2 + 1ä − x + C. √ √ √ √ C. I = x2 + 1 ln Äx +
x2 + 1ä − x + C. D. I = x2 + 1 ln Äx +
x2 + 1ä + x + C. GUYỄN 1 1 N
CÂU 15. Nguyên hàm của hàm số y = có kết quả là ln − x ln2x 1 x A. I = + C.
B. I = x2 + C.
C. I = − + C.
D. I = x + C. x ln x ln x ln x ln x Thầy
CÂU 16. Tìm họ nguyên hàm của hàm số f (x) = ecos x sin 2x. Z Z A.
f (x) dx = −2ecos x cos x + 2ecos x + C. B.
f (x) dx = 2ecos x cos x − 2ecos x + C. Z Z 1 C.
f (x) dx = −2ecos x + C. D.
f (x) dx = − esin x cos 2 2 x + C. Z
CÂU 17. Tìm họ nguyên hàm F (x) =
ex ln(ex + 1) dx.
A. F(x) = ex ln(ex + 1) + ex + C.
B. F(x) = ex ln(ex + 1) − ex + C.
C. F(x) = (ex + 1) ln(ex + 1) + ex + C.
D. F(x) = (ex + 1) ln(ex + 1) − ex + C.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 39
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
CÂU 18. Một nguyên hàm của hàm số f (x) = x2 + 2xex là A. x2ex.
B. x2 − 2xex.
C. 2x + 2ex.
D. x2 + xex. Z
CÂU 19. Tính I =
x3 · sin x dx.
A. I = x3 cos x − 3x2 sin x − 6x cos x + 6 sin x + C.
B. I = −x3 cos x − 3x2 sin x + 6x cos x − 6 sin x + C. Thầy
C. I = −x3 cos x + 3x2 sin x + 6x cos x − 6 sin x + C.
D. I = −x3 cos x + 3x2 sin x − 6x cos x + 6 sin x + C. N
ccc BẢNG ĐÁP ÁN ccc GUYỄN 1. D 2. C 3. A 4. D 5. A 6. B 7. A 8. B 9. C 10. A 11. D 12. A 13. C 14. C 15. D 16. A 17. D 18. A 19. C ccc N
HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc GỌC Z
Câu 11. Vì F(x) = x2 là một nguyên hàm của hàm số f(x)e2x nên
f (x)e2x dx = x2 + C1
và f(x)e2x = 2x. d u = e2x
u = 2e2xdx DŨN Đặt , ta có . Do đó
dv = f 0(x)dx
v = f (x) Z Z
f 0(x)e2x dx = f(x)e2x − 2
f (x)e2x dx = 2x − 2x2 + C. G 0976071956 - THPT
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . MATH.ND u = 2x d u = 2 dx T Câu 12. Đặt , ta có . Do đó Ạ 1 dv = dx
v = − cot x sin2 QU x Z
I = −2x cot x + 2 cot x ? dx Lớp = −2xTO cot xÁN + 2 lnTHẦ |sin x| Y + CDŨNG . ? AN
Vậy T = a + b = 0. G
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BỬU 1 du = dx u = log x x ln 10 Câu 13. Đặt , ta có . Do đó
dv = x dx v = x2 2 1 Z x2 I =x2 log log + 2
x − 2ln10 x dx = x22 x − 4ln10 C =x2 ln x x2 + + 2 ln 10 − 4 ln 10
C = x2 (2 ln x − 1) 4 ln 10 C.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ √ 1 u = ln Äx + x2 + 1ä du = √ dx Câu 14. Đặt , ta có x2 + 1 . Do đó d d √ v = x √ x x2 + 1 v = x2 + 1 √ √ Z √ √ I = x2 + 1 ln Äx + x2 + 1ä −
dx = x2 + 1 ln Äx + x2 + 1ä − x + C.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z Å 1 1 ã Z 1 Z 1 Câu 15. I = d d d ln − x = x − x. x ln2 x ln x ln2 x BỬU 1 1 Z 1 du = − dx u = G Xét A = d ln x , ta có x ln2 x ln x. Đặt . x dv = dx v = x Z AN 1 Do đó A = x + d ln x. x ln2x Z Z QU 1 1 Vậy I = x + d d + ln x − x = x C. x ln2x ln2x ln x TẠ
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . THPT Z Z - Câu 16.
ecosx sin 2x dx =
ecosx · 2 sin x cos x dx. G
Đặt t = cos x, ta có dt = − sin x dx. Do đó Z Z
ecosx sin 2x dx =
(−2t)et 0976071956 dt. DŨN d
u = −2t
u = −2 dt Đặt , ta có MATH.ND . Do đó
dv = et dt v = et GỌC Z Z N
ecosx sin 2x dx = −2tet +
2et dt = −2tet + 2et + C ? Lớp TOÁN THẦY DŨNG ?
= −2ecosx cos x + 2ecosx + C. GUYỄN
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N Z Z
Câu 17. Đặt t = ex + 1, ta có dt = ex dx. Do đó
ex ln(ex + 1) dx = ln t dt. Thầy 1 d d u = ln t u = t Đặt , ta có t . Do đó dv = dt v = t Z Z
ln t dt = t ln t −
dt = t ln t − t + C = (ex + 1) ln(ex + 1) − ex + C.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 41
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
{ DẠNG 2. Tích phân từng phần
cccVÍ DỤ MINH HỌAccc π 2 Z
VÍ DỤ 1. Tính tích phân I =
x cos x dx 0 Thầy 1
A. I = π . . . 2 B. I = π 2 − 1. C. I = π 3 − 2 D. I = π 3
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N 1 Z GUYỄN
VÍ DỤ 2. Cho I =
xe2x dx = ae2 + b (a, b là các số hữu tỷ). Khi đó tổng a + b bằng 0 1 1 A. 0. B. . . 4 C. 1. D. 2
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N b Z GỌC
VÍ DỤ 3. Cho b > a > −1. Tích phân I =
ln(x + 1) dx bằng biểu thức nào sau đây? a b b
A. I = (x + 1) ln(x + 1) − a + b.
B. I = (x + 1) ln(x + 1) − b + a. a a DŨN b 1 Z b b x C. I = .
D. I = x ln(x + 1) + dx. x + 1a a x + 1 a G
¤ Chọn đáp án B . . . . . . . . . . . . . 0976071956
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . - 1 THPT Z
VÍ DỤ 4. Cho hàm số f (x) có đạo hàm liên tục trên [0; 1] và thỏa mãn
x (f0(x) − 2) dx = f(1). MATH.ND 0 1 Z TẠ Giá trị của I =
f (x) dx bằng QU 0 A. 1. ? B. Lớp 2. TOÁN THẦ C. −Y
1. DŨNG ? D. −2. AN
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc G 1 Z BỬU CÂU 1. Cho biết
xe−x dx = a + b với e
a, b ∈ Z. Giá trị của a2 + b2 bằng 0 A. 7. B. 5. C. 3. D. 4. π 2 Z ea + 1
CÂU 2. Biết I =
ex sin x dx =
với a ∈ R, b ∈ N. Khi đó sin a + cos 2a + b bằng b 0 A. 2. B. 4. C. 1. D. 0. 2 2 Z Z
CÂU 3. Cho hàm số y = f (x) liên tục trên đoạn [1; 2] và
(x − 1)f0(x) dx = a. Tính f (x) dx 1 1
theo a và b = f(2). A. a − b. B. a + b. C. b − a. D. −b − a. 42
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 3 Z CÂU 4. Biết
x ln(x2 + 16) dx = a ln 5 + b ln 2 + c trong đó 2
a, b, c là các số nguyên. Tính 0
giá trị của biểu thức T = a + b + c. A. T = 2.
B. T = −16.
C. T = −2. D. T = 16. 2 Z
CÂU 5. Biết I =
(3x2 + ln x) dx = a + b ln 2 với a, b là các số nguyên. Tính S = a + b. 1 A. S = 4. B. S = 6. C. S = 2. D. S = 8. 1 Z x b a, b, c BỬU
CÂU 6. Biết I =
ln(2 + x2) dx = a ln 3 + ln 2 + c với
là các số nguyên. Tính tổng 2 2 0 G
a + b + c. A. 3. B. 0. C. 1. D. 2. AN
CÂU 7. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0; 2] và thỏa mãn f (2) = 16, QU 2 2 Z Z
f (x) dx = 4. Tính tích phân I =
x · f 0 (2x) dx. TẠ 0 0 A. I = 12. B. I = 7. C. I = 13. D. I = 20. 2 Z THPT
CÂU 8. Cho hàm số f (x) có đạo hàm liên tục trên [0; 2] và thỏa mãn
x(f0(x)−1) dx = 2f(2). - 0 G 2 Z
Tính giá trị của I =
f (x) d 0976071956 x. 0 DŨN A. 1. B. 2. C. −1. D. −2. MATH.ND
CÂU 9. Cho hàm số y = f (x) có đạo hàm cấp hai f 00(x) liên tục trên đoạn [0; 1] đồng thời
thỏa mãn điều kiện f(0) = f(1) = 1; f0(0) = 2021. Mệnh đề nào sau đây là đúng? GỌC 1 1 Z Z N A.
f 00(x)(1 − x) d ? x Lớp = − TO 2021. ÁN THẦ BY . DŨNG
f 00(x)(1 − x ? ) dx = 2021. 0 0 1 1 Z Z C.
f 00(x)(1 − x) dx = 1. D.
f 00(x)(1 − x) dx = −1. GUYỄN 0 0 N
CÂU 10. Cho f (x) và g (x) là hai hàm số có đạo hàm liên tục trên R và thỏa mãn f (0) = 1, 1 1 Z Z
f (1) = 2, g(0) = −2, g(1) = 4 và
f 0(x)g(x) dx = 7. Tính
f (x)g0(x) dx. Thầy 0 0
A. I = −3. B. I = 17. C. I = 3.
D. I = −17. 1
CÂU 11. Cho hàm số f (x) liên tục trên (0; +∞). Biết
là một nguyên hàm của hàm số x2 2 1 Z f (x)
y = f0(x) ln x và f(2) = . Khi đó d ln 2 x bằng x 1 7 1 1 7 A. − . . . . 4 B. 2 C. −2 D. 4
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 43
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 2 Z ln x CÂU 12. Biết
dx = b + a ln 2 (với a là số thực, b; c là số nguyên dương và b là phân x2 c c 1
số tối giản). Tính giá trị T = 2a + 3b + c.
A. T = −6. B. T = 6. C. T = 4. D. T = 5. 2 Z x + ln x 1 CÂU 13. Cho I = d ln 2 với là ( x = a −
a, b, c là các số nguyên dương và a x + 1)2 b c b Thầy 1
phân số tối giản. Tính giá trị của biểu thức S = a + b. c 2 1 1 5 A. . B. . C. . D. . N S = 3 S = 2 S = 3 S = 6 GUYỄN e Z ln x 2 CÂU 14. Biết d + + (1 + x = a b ln
c, với a, b, c ∈ Z. Tính a + b + c. x)2 e + 1 e + 1 1 A. 1. B. −1. C. 3. D. 2. N
CÂU 15. Cho hàm số y = f (x) có đạo hàm f 0(x) liên tục trên [0; 1] thỏa mãn f (1) = 1 và 1 1 GỌC Z Z √
f (x) dx = 2. Tích phân I = f 0 x dx bằng 0 0 A. I = 2.
B. I = −2.
C. I = −1. D. I = 1. DŨN 1 Z 1
CÂU 16. Cho hàm số y = f (x) liên tục trên R đồng thời thỏa mãn f (1) = 1 và
f (x) dx = . 3 0 G π 2 Z 0976071956 - Tính tích phân I =
sin 2x · f0(sin x) dx. THPT 0 2 4 4 2 A. I = .
B. I = − MA . TH.ND . . 3 3 C. I = 3
D. I = −3 TẠ
ccc BẢNG ĐÁP ÁN ccc QU 1. B 2. A 3. ? C Lớp 4. B TO 5. ÁN D THẦ 6. C Y DŨNG 7. B 8. ?D 9. A 10. C AN 11. D 12. C 13. D 14. A 15. B 16. C G
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc BỬU 1 Z
Câu 1. Xét tích phân I =
xe−x dx. 0 d u = x u = dx Đặt , ta có . Do đó
dv = e−x dx
v = −e−x 1 Z 1 1 1 2
I = −xe−x +
e−x dx = −e−1 − e−x = − . 0 0
e − e−1 − 1 = 1 − e 0
Suy ra a = 1, b = −2. Vậy a2 + b2 = 5.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Câu 2. Ta dùng sơ đồ đường chéo để giải tích phân này như sau (đạo hàm) dấu (nguyên hàm) u = ex
dv = sin x dx ex + − cos x ex −
− sin x (dừng lại) + BỬU Do đó G π Z 2
I = (−ex cos x + ex sin x) − ex sin x 0 AN π 2
⇔ 2I = (−ex cos x + ex sin x) 0 QU eπ2 + 1 ⇔ I = TẠ 2 .
Suy ra a = π và 2 b = 2. THPT
Vậy sin a + cos 2a + b = 2. - G
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0976071956 DŨN 2 x du = dx
u = ln(x2 + 16) MATH.ND Câu 4. Đặt , ta có x2 + 16 1 . Do đó
dv = x dx v = (x2 + 16) GỌC 2 N 3 3 Z ? Lớpï TO 1 ÁN THẦY DŨNG ò 3 Z 2x 1 ?
x ln(x2 + 16) dx = ( (
2 x2 + 16) · ln(x2 + 16) − x2 + 16) dx 0 x2 + 16 · 2 0 0 3 1 1 Z GUYỄN
= 2 · 25 · ln25 − 2 · 16 · ln16 − x dx N 0 3 = 25 ln 5 x2 − 16 ln 4 − 2 0 Thầy 9
= 25 ln 5 − 32 ln 2 − 2.
Suy ra a = 25, b = −32, c = −9.
Vậy T = a + b + c = 25 − 32 − 9 = −16.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 45
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 d u = 1 − x
u = − dx Câu 9. Đặt , ta có . Do đó
dv = f 00(x) dx
v = f 0(x) 1 1 Z 1 Z
f 00(x)(1 − x) dx = (1 − x)f0(x) + f 0(x) dx 0 0 0 1 Thầy
= 0 − f0(0) + f(x) =
−f 0(0) + f(1) − f(0) 0
= −2021 + 1 − 1 = −2021. N GUYỄN
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d
u = f (x)
u = f0(x) dx N Câu 10. Đặt , ta có . Do đó
dv = g 0(x) dx
v = g (x) GỌC 1 1 Z 1 Z
f (x)g0(x) dx = f(x)g(x) −
f 0(x)g(x) dx 0 DŨN 0 0
= f(1)g(1) − f(0)g(0) − 7 = 2 · 4 − 1 · (−2) − 7 = 3. G 0976071956 -
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . THPT MATH.ND
u = f (x) d
u = f0(x) dx T Câu 11. Đặt dx , ta có . Do đó Ạ dv = v = ln x x QU 2 2 Z f (x) Z 2 1 2 7 ? Lớp TOÁN THẦ Y DŨNG ?
dx = f(x) · ln x −
f 0(x) ln x dx = 1 − = . 4 AN x 1 x2 1 1 1 G
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BỬU 1 u = ln x du = dx Câu 12. Đặt x 1 , ta có 1 . Do đó dv = dx v = − x2 x 2 2 Z ln x ln 2 Z 1 ln 2 1 2 1 ln 2 d x x = − + d = . x = − x2 x 1 x2 2 − x 1 2 − 2 1 1 1 Suy ra a = − ,
2 b = 1, c = 2. Vậy T = 4.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
u = x + ln x
du = x + 1 dx Câu 13. Đặt x 1 , ta có 1 . Do đó dv = dx (x + 1)2 v = − x + 1 2 2 2 ( x + ln x) Z 1 2 + ln 2 1 2 1 I = − + dx = −
+ + ln x = ln 2 − x + 1 x 3 2 3 6. 1 1 1
Suy ra a = 2, b = 3, c = 6. 5
Vậy S = a + b = . c 6 BỬU
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G 1 u = ln x du = dx AN Câu 14. Đặt x 1 , ta có 1 . Do đó dv = (1 + + 1 = x x)2 v = − QU 1 + x 1 + x e e Z e Z TẠ ln x 1 d d (1 +
x = x ln x − x x)2 1 + x 1 1 + x 1 1 e e THPT
= 1 + e − ln|1 + x| - 1 Å 1 ã − G = ln (1 + e) + ln 2 1 + e − 1 0976071956 1 2 = + ln 1 + e 1 + e − 1. DŨN
Suy ra a = 1, b = 1, c = −1. VậyMA a + TH.ND b + c = 1. GỌC
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N ? Lớp TOÁN THẦY DŨNG 1 ? √ Z
Câu 15. Đặt t =
x, ta có t2 = x và 2tdt = dx. Do đó I = 2
tf 0(t) dt. 0 1 Z GUYỄN d u = t u = dt 1 Đặt , ta có
. Do đó I = tf(t) −
f (t) dt = −1. N 2 0
dv = f 0(t)dt
v = f (t) 0
Vậy I = −2. Thầy
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . π 2 Z
Câu 16. Ta có I =
2 sin x cos x · f0(sin x) dx. 0 d u = 2 sin x
u = 2 cos x dx Đặt , ta có . Do đó
du = cos x · f 0(sin x) dx
v = f (sin x)
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 47
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 π π π 2 2 2 Z Z
I = (2 sin x · f(sin x)) 2 cos cos −
x · f (sin x) dx = 2 − 2
x · f (sin x) dx. 0 0 0 π Thầy 2 Z Tính I1 =
cos x · f(sin x) dx. Đặt t = sin x, ta có dt = cos x dx. Do đó 0 N GUYỄN 1 1 Z Z 1 I1 =
f (t) dt =
f (x) dx = 3. 0 0 N GỌC 1 4
Vậy I = 2 − 2 · = . 3 3
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . DŨN G 0976071956 - THPT MATH.ND T | Ạ
Chủ đề 5. Ứng dụng của tích phân QU ? Lớp TOÁN THẦY DŨNG ? { AN
DẠNG 1. Tính diện tích hình phẳng G BỬU
cccBÀI TẬP TRẮC NGHIỆMccc
CÂU 1. Tìm diện tích S của miền phẳng gạch chéo trong hình y bên. f (x) b b Z Z
A. S = − f (x) dx. B. S = f (x) dx. a a a b Z Z x
C. S = − f (x) dx. D. S =
−f (x) dx. 0 a b b a 48
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 2. Cho đồ thị hàm số y = h(x). Diện tích hình y
phẳng gạch chéo trong hình vẽ bên bằng y = h(x) 0 1 Z Z A. h(x) dx + h(x) dx. −1 0 x 1 −1 0 1 Z B. h(x) dx. −10 0 Z Z BỬU C. h(x) dx + h(x) dx. −1 1 G 0 1 Z Z D. − h(x) dx + h(x) dx. AN −1 0 QU
CÂU 3. Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = 2x − x2 và trục TẠ hoành.4 4 4 4 A. . . 3
B. −3π. C. −3 D. 3π. THPT - √
CÂU 4. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x
x2 + 1, trục Ox và G
đường thẳng x = 1. √ √ √ √ 2 2 − 1 0976071956 3 − 2 3 2 − 1 3 − 2 2 A. . B. . C. . D. . DŨN 3 3 3 3 MATH.ND
CÂU 5. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 − x2 và y = x. 9 11 GỌC A. 5. B. 7. C. . . 2 D. 2 N ? Lớp TOÁN THẦY DŨNG ? x2
CÂU 6. Tính diện tích hình phẳng giới hạn bởi hai parabol y = x2 và + 3 4 y = − 2 x. A. 12. B. 8. C. 4. D. 16. GUYỄN N 1
CÂU 7. Tính diện tích S của hình phẳng giới hạn bởi các đường y = , trục hoành và 2x + 3
hai đường thẳng x = −1, x = 2. √ Thầy 1 2
A. S = π ln 7. ln 7. ln 7. 6 B. S = 2 C. S = 3 D. S = 2 ln 7.
CÂU 8. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = −x3 + 3x2 − 2, hai trục
tọa độ và đường thẳng x = 2 là 5 3 7 9 A. S = . . . . 2 B. S = 2 C. S = 2 D. S = 2
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 49
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
CÂU 9. Người ta cần sơn trang trí một bề mặt của một cổng chào y 9
có hình dạng như hình vẽ sau đây. Các biên của hình tương ứng
là các parabol có phương trình y = −x2 +6x, y = −2x2 + 12x − 10
(đơn vị đo độ dài bằng mét). Hỏi cần ít nhất bao nhiêu lít sơn? Biết
tỉ lệ phủ của sơn là 10 m2/lít. Thầy A. 3.6 lít. B. 2.2 lít. C. 1.5 lít. D. 2.4 lít. N x O 1 5 6 GUYỄN
CÂU 10. Cho hình thang cong (H) giới hạn bởi các đường y = 2x, y 16
y = 0, x = 0, x = 4. Đường thẳng x = a (0 < a < 4) chia (H) N GỌC
thành hai phần có diện tích là S1 và S2 như hình vẽ bên. Tìm a x = a để S2 = 4S1. x = 4 A. a = 3. B. a = log2 13. DŨN 16 C. a = 2. D. a = log2 . 5 S2 G S1 0976071956 a x O 4 - THPT MATH.ND y T
CÂU 11. Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô 2 Ạ
đậm như hình bên được giới hạn bởi một đồ thị hàm số đa thức bậc QU
ba và một đường thẳng. ? Lớp Diện tíchTO S ÁN của THẦ phần tô Y đậm DŨNG đó bằng ? bao −2 O 1 x −1 2 AN nhiêu?
A. S = 8 (đvdt). B. S = 6 (đvdt). C. S = 2 (đvdt). D. S = 4 (đvdt). −2 G BỬU
CÂU 12. Cho hàm số f (x) liên tục trên R. Đồ thị của hàm số y y = f0(x)
y = f0(x) được cho như hình vẽ bên. Diện tích các hình phẳng 5 8 19
(K), (H) lần lượt là và 12
3. Biết f(−1) = 12, tính f(2). −1 (K) O 1 2 11 2 x A. f(2) = . . 6
B. f(2) = −3 (H) C. f(2) = 3. D. f(2) = 0. 50
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 13. Tính diện tích hình phẳng giới hạn bởi các đường (P) : y
y = x2 − 1, trục tung và tiếp tuyến của (P) tại điểm M(−1; 0). 1 2 4 5 A. . . . 3 B. 3 C. 3
D. −3π . −1 1 x O −2 BỬU G
CÂU 14. Cho hình phẳng giới hạn bởi các đường (C) : y = x2, trục hoành và tiếp tuyến của
(C) tại điểm x0 = 1. Tính diện tích S của hình phẳng đó. AN 1 1 1
A. S = 3 (đvtt). B. S = (đvtt). (đvtt). (đvtt). 3 C. S = 4 D. S = 12 QU TẠ
CÂU 15. Tính diện tích S của phần hình phẳng giới hạn bởi đường y A B THPT
parabol y = x2 và hai đoạn thẳng AC và BC như hình vẽ bên. 4 - 25 20 10 A. S = . B. S = . C. S = . D. S = 9. 3 C G 6 3 3 2 0976071956 1 D E x DŨN −2 −1 0 1 2 MATH.ND GỌC
CÂU 16. Parabol y = x2 chia hình tròn có tâm tại gốc tọa độ, y N √ 2 bán kính bằng 2 2 3 ? Lớp thành hai TO phần ÁN có THẦ diện tích Y S1, SDŨNG 2 như hình ? vẽ bên. Tính S2 . S1 S1 9π − 1 9π − 2 23 9π − 2 A. . . . . x 2 3 3 B. C. D. π + 2 3π − 2 10 3π + 2 S2 GUYỄN N Thầy y
CÂU 17. Tính diện tích hình phẳng được tô đậm ở hình bên. √ 2 28 3
A. S = 2 3 − . . y = x2 3 B. S = 3 26 √ 1 C. S = . 2 . 3 D. S = 3 − 3 1 −1 O x
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 51
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
CÂU 18. Ông Bình có một mảnh vườn hình chữ nhật 2π m A B
ABCD có AB = 2π m, AD = 4 m và dự định trồng hoa
trên giải đất giới hạn bởi đường trung bình MN và một
đường hình sin như hình vẽ trên. Kinh phí trồng hoa M N π
là 100 000 đồng/1 m2. Hỏi ông Bình cần bao nhiêu tiền m 4 Thầy
để trồng hoa trên mảnh đất đó? (Số tiền được làm tròn D C đến hàng nghìn) N A. 1 600 000 đồng. B. 800 000 đồng. GUYỄN C. 900 000 đồng. D. 400 000 đồng.
CÂU 19. Một cái cổng hình parabol như hình vẽ. Chiều cao G
GH = 4 m, chiều rộng AB = 4 m, AC = BD = 0,9 m. Chủ nhà N
làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm E F GỌC
giá là 1200000 đồng/m2, còn các phần để trắng làm xiên hoa có
giá là 900000 đồng/m2. Hỏi tổng chi phí để là hai phần nói trên
gần nhất với số tiền nào dưới đây? DŨN A. 11445000 (đồng). B. 7368000 (đồng). C. 4077000 (đồng). D. 11370000 (đồng). A C H D B G
CÂU 20. Ông An muốn làm 0976071956 cửa rào sắt có hình - THPT
dạng và kích thước như hình vẽ bên, biết đường 1,5 m 2 m
cong phía trên là một Parabol. GiáMA 1m2 TH.ND của rào
sắt là 700.000 đồng. Hỏi ông An phải trả bao nhiêu T 5 m Ạ
tiền để làm cái cửa sắt như vậy (làm tròn đến hàng QU phần nghìn). ? Lớp TOÁN THẦY DŨNG ? A. 6 520 000 đồng. B. 6 320 000 đồng. C. 6 417 000 đồng. D. 6 620 000 đồng. AN G
CÂU 21. Một mảnh vườn hoa dạng hình tròn có BỬU
bán kính bằng 5 m. Phần đất trồng hoa là phần A B
tô trong hình vẽ bên. Kinh phí trồng hoa là 50.000
đồng/ m2. Hỏi số tiền cần để trồng hoa trên diện M N
tích phần đất đó là bao nhiêu, biết hai hình chữ
nhật ABCD và MNPQ có AB = MQ = 5 m?
A. 3.641.528 đồng.
B. 3.533.057 đồng.
C. 3.641.529 đồng.
D. 3.533.058 đồng. Q P D C 52
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 22. Cho hàm số y = x4 − 3x2 + m, có đồ thị (Cm), với y
m là tham số thực. Giả sử (Cm) cắt trục Ox như hình vẽ bên. (Cm)
Gọi S1, S2, S3 là diện tích các miền gạch chéo được cho trên
hình vẽ. Tìm m để S1 + S2 = S3. S3 5 5 5 5
A. m = − . . . . 2
B. m = −4 C. m = 2 D. m = 4 x S1 S2 BỬU G
ccc BẢNG ĐÁP ÁN ccc AN QU 1. C 2. C 3. B 4. B 5. C 6. C 7. C 8. D 9. C 10. D TẠ
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc THPT
Câu 13. Phương trình tiếp tuyến của (P) tại M(−1; 0) là y = −2x − 2. -
Gọi (H1) là hình phẳng giới hạn bởi (P) và trục tung. Thể tích V1 của khối tròn xoay thu được G
khi quay hình (H1) quanh trục Ox là: 0976071956 0 DŨN Z MA V1 = TH.ND π
(x2 − 1)2dx (đvtt) −1 GỌC
Gọi (H2) là hình phẳng giới hạn bởi y = −2x − 2 trục hoành và trục tung. Thể tích V2 của N khối tròn xoay thu ? được Lớp khi TO quay ÁN hình (HTHẦ 2) Y quanh DŨNG trục Ox là: ? 0 Z V1 = π
(−2x − 2)2dx (đvtt) GUYỄN −1 N
Thể tích V của khối tròn xoay thu được khi quay hình (H) quanh trục Ox là: 0 Z Thầy 4
V = V1 − V2 = π
(x2 − 1)2 − (−2x − 2)2 dx = 5π (đvtt) −1
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 19.
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 53
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox, A trùng O y
khi đó parabol có đỉnh G (2; 4) và đi qua gốc tọa độ. G 4
Gọi phương trình của parabol là y = ax2 + bx + c. c = 0 a = −1 E F Do đó ta có −b = 2 ⇔ . 2a b = 4 Thầy c = 0
22a + 2b + c = 4
Nên phương trình parabol là y = f(x) = −x2 + 4x. 0,9 2 3,1 A B
Diện tích của cả cổng là x O C H D N 4 GUYỄN Z Å x3 ã 4 32 S =
(−x2 + 4) dx = − + 2 = 3 x2 0
3 ≈ 10,67(m2) 0
Do vậy chiều cao CF = DE = f(0,9) = 2,79 (m), CD = 4 − 2 · 0,9 = 2,2 (m).
Diện tích hai cánh cổng là SCDEF = CD · CF = 6,138 ≈ 6,14 (m2). N
Diện tích phần xiên hoa là S GỌC
xh = S − SCDEF = 10,67 − 6,14 = 4,53 (m2).
Nên tiền là hai cánh cổng là 6,14 · 1200000 = 7368000 (đồng) và tiền làm phần xiên hoa
là 4,53 · 900000 = 4077000 (đồng). DŨN
Vậy tổng chi phí là 11445000 đồng.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G 0976071956 - THPT Câu 20. MATH.ND y 2 C TẠ A B QU ? Lớp TOÁN THẦY DŨNG ?
−3 −2 −1 O 1 2 3 x AN G
Chọn hệ trục tọa độ như hình vẽ. Trong đó A(−2,5; 1,5), B(2,5; 1, 5), C(0; 2). BỬU
Giả sử đường cong trên là một Parabol có dạng y = ax2 + bx + c, với a, b, c ∈ R.
Do Parabol đi qua các điểm A(−2,5; 1,5), B(2,5; 1, 5), C(0; 2) nên ta có hệ phương trình 2
a(−2,5)2 + b(−2,5) + c = 1, 5 a = − 25
a(2,5)2 + b(2,5) + c = 1, 5 ⇔ b = 0 c = 2 c = 2. 2
Khi đó phương trình Parabol là y = −25x2 + 2. 2
Diện tích S của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số y = −25x2+2,
trục hoành và hai đường thẳng x = −2,5, x = 2,5. 54
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 2,5 Z Å 2 ã 55 Ta có S = − d . 25x2 + 2 x = 6 −2,5 55
Vậy ông An phải trả số tiền để làm cái cửa sắt là S ·700.000 = 6 ·700.000 ≈ 6.417.000 (đồng).
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 21. y BỬU 5 A B G 4 AN 3 M E N 2 QU 1 TẠ x
−5 −4 −3 −2 −1 1 2 3 4 5 −1 THPT −2 - Q P −3 G 0976071956 −4 D C DŨN −5 MATH.ND
Đặt hệ trục Oxy như hình vẽ. √ GỌC
Phương trình đường tròn x2 + y2 = 25 ⇔ y = ± 25 − x2. √ N Ç 5 3 5å 5 Tìm được tọa độ ? điểm NLớp TO ; ÁN (một THẦ giao Y điểm DŨNG của đường ? tròn và đường thẳng ). 2 2 y = 2 √ 5 3 2 Z Å√ 5ã
Diện tích 4 phần trắng (không trồng cây) là: S1 = 4 25 − x2 − d 2 x. GUYỄN 5 2 N
Diện tích phần trồng rau bằng diện tích hình tròn trừ cho S1, tức là √ 5 3 2 Z Å√ 5ã S x Thầy
= πr2 − S1 = π.52 − 4 25 − x2 − d 2 5 2 √ Ç 25 5 Ç5 3 5åå 50 √ = 25 π π π − 4 = + 25 3 12 − 2. 2 − 2 3 − 25.
Số tiền cần để trồng hoa là 50000 · S ≈ 3533057 đồng.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 55
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
{ DẠNG 2. Tính thể tích vật thể
cccBÀI TẬP TRẮC NGHIỆMccc
CÂU 1. Cho hai hàm số y = f1(x) và y = f2(x) liên y Thầy
tục trên đoạn [a; b] và có đồ thị như hình bên. Gọi y = f1(x)
S là hình phẳng giới hạn bởi hai đồ thị hàm số trên
và các đường thẳng x = a, x = b. Thể tích V của N S GUYỄN
vật thể tròn xoay tạo thành khi quay S xung quanh
trục Ox được tính bởi công thức nào sau đây? y = f2(x) b Z A. V = π f 2 1 (x) − f 2 2 (x)dx. 0 a a b x N b Z GỌC B. V = π
f1(x) − f2(x)dx. a b Z C. V = f 2 DŨN 1 (x) − f 2 2 (x)dx. a b Z G D. V = π
f1(x) − f2(x)2dx. a 0976071956 - THPT
CÂU 2. Thể tích của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi y = ln x, y =
0, x = e quanh trục Ox được tính MA theo TH.ND công thức nào sau đây? e 1 e e Z Z Z Z T A. π ln xdx. B. π (ln x)2dx. C. π (ln x)2dx. D. (ln x)2dx. Ạ 1 e 1 1 QU
CÂU 3. Gọi (H) là hình ? Lớp phẳng giớiTO hạn ÁN bởi y THẦ = ex, y Y = DŨNG 0, x = 0 và ?
x = 1. Tính thể tích của AN
khối tròn xoay sinh ra bởi (H) khi quay quanh trục Ox.
A. π (e − 1).
B. π(e − 1).
C. π(e2 − 1).
D. π (e2 − 1). G 2 2 BỬU
CÂU 4. Tính thể tích vật thể tròn xoay khi quay hình (H) quanh trục Ox với (H) được giới √
hạn bởi đồ thị hàm số y = 4x − x2 và trục hoành là 34π 35π 31π 32π A. . . . . 3 B. 3 C. 3 D. 3
CÂU 5. Gọi (H) là hình phẳng giới hạn bởi các đường y = x2, y = 1. Tính thể tích khối tròn
xoay thu được khi quay (H) quanh trục Ox. 8π 6π 2π A. . . . . 5 B. 5 C. 5 D. π 5
CÂU 6. Thể tích khối tròn xoay được tạo nên khi quay miền D quanh trục Ox, biết miền D
được giới hạn bởi các đường y = 4 − x2 và y = x2 + 2, là A. 16π. B. 12π. C. 14π. D. 10π. 56
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 7. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi elip có
phương trình x2 + y2 = 1 và trục hoành quay xung quanh trục 3 Ox. b2 √ √ √ 2 3 4 3 5 3 A. 4πb. B. 3 πb2. C. 3 πb2. D. 3 πb2.
CÂU 8. Thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi ba đường √ y =
x, y = 2 − x và y = 0 quay quanh trục Ox bằng 3π 5π 2π A. . . . 2 B. 6 C. π. D. 3
CÂU 9. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng BỬU
khi cắt vật thể bởi mặt phẳng tuỳ ý vuông góc với trục Ox tại điểm có hoành độ x (1 ≤ x ≤ 3) √ G
thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3x2 − 2. √ 124π
A. V = 32 + 2 15. B. V = . AN 3 124 √ C. V = . 15) 3 D. V = (32 + 2 π. QU
CÂU 10. Thể tích vật thể giới hạn giữa hai mặt phẳng x = 0, x = 2 và có mặt cắt là hình √ TẠ
vuông cạnh bằng x x2 + 1 là 8 136 64 A. . . . 15 B. 15 C. 2. D. 15 THPT -
ccc BẢNG ĐÁP ÁN ccc G 1. A 2. C 3. D 0976071956 4. D 5. A 6. A 7. C 8. B 9. C 10. B DŨN ccc MA HƯỚNGTH.ND
DẪN GIẢI MỘT SỐ CÂU ccc GỌC | N
Chủ đề 6. Các dạng toán nâng cao ? Lớp TOÁN THẦY DŨNG ?
{ DẠNG 1. Các bài toán lý thuyết GUYỄN N
cccVÍ DỤ MINH HỌAccc 1 1 1 Z Z Z VÍ DỤ 1. Nếu
f (x) dx = −2,
g (x) dx = 1 thì
[2020f(x) + 2021g(x)] dx bằng 0 0 0 Thầy A. −2019. B. −2020. C. −2018. D. −1.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 Z Z VÍ DỤ 2. Biết
f (x) dx = 2. Giá trị của
[3 + 2f(x)] dx bằng 1 1 A. 5. B. 7. C. 10. D. 6.
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 57
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 2 2 2 Z Z Z VÍ DỤ 3. Nếu
[f(x) + 3g(x)] dx = 5 và
[−f(x) + g(x)] dx = −1 thì
[2f(x) + 3g(x) − 1] dx −1 −1 −1 bằng A. 7. B. 6. C. 4. D. 5.
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 4 4 Thầy Z Z Z VÍ DỤ 4. Nếu
f (x) dx = 1 và
f (y) dy = 5 thì
f (z) dz bằng 0 0 2 A. −4. B. 6. C. −6. D. 4. N
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GUYỄN
VÍ DỤ 5. Cho đồ thị hàm số y = f (x) trên đoạn [−2; 2] như y 22 76
hình vẽ ở bên và có diện tích S1 = S2 = . Tính f (x) N 15, S3 = 15 2 GỌC Z tích phân I = f (x) dx. −2 S3 x 18 32 98 −2 2 A. I = . B. I = . C. I = . D. I = 8. S1 S2 DŨN 5 15 15
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G
VÍ DỤ 6. Cho hàm số f (x) có 0976071956
đạo hàm liên tục trên [2; 3], f(2) = −1, f(3) = −2. Tính tích - 3 THPT Z phân I = f 0(x)dx. MATH.ND 2
A. I = −1.
B. I = −3. C. I = 1. D. I = 2. TẠ
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . QU ? Lớp TOÁN THẦY DŨNG ? 1 Z
VÍ DỤ 7. Cho hàm số f (x) thỏa mãn f (0) = 4 và f 0(x) = ex + x, ∀x ∈ R. Khi đó f (x) dx AN 0 bằng G 6e + 13 6e + 25 6e + 25 6e + 19 A. . . . . 6 B. 6 C. 3 D. 6 BỬU
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc 3 Z
CÂU 1. Biết F (x) = x3 là một nguyên hàm của hàm số f (x) trên R. Tính I =
[2 − f(x)] dx. 1 A. I = 20.
B. I = −26.
C. I = −22. D. I = 28.
CÂU 2. Cho F (x) là nguyên hàm của hàm số f (x) trên [a; b]. Phát biểu nào sau đây sai? b b b Z Z Z A.
f (x)dx = F(b) − F(a). B.
f (x)dx 6= f (t)dt. a a a 58
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ b b a Z Z Z C.
f (x)dx = 0. D.
f (x)dx = − f (x)dx. a a b b b c Z Z Z
CÂU 3. Cho a < b < c,
f (x) dx = 5,
f (x) dx = 2. Tính tích phân f (x) dx. a c a c c c c Z Z Z Z A.
f (x) dx = 7. B.
f (x) dx = 3. C.
f (x) dx = −3. D.
f (x) dx = 10. a a a a 2 2 2 Z Z Z f g BỬU CÂU 4. Cho (x) dx = 2 và
(x) dx = 3. Tích phân
[2f(x) − g(x)] dx bằng 0 0 0 G A. 5. B. 7. C. −1. D. 1. 1 3 3 Z Z Z AN CÂU 5. Nếu
f (x)dx = 3 và
f (x)dx = 7 thì
f (x)dx bằng 0 0 1 QU A. 10. B. 4. C. −4. D. 21. 10 6 Z Z TẠ
CÂU 6. Cho hàm số f (x) liên tục trên đoạn [0; 10] thoả mãn
f (x)dx = 7,
f (x)dx = 3. 0 2 2 10 Z Z THPT
Tính giá trị của biểu thức P = f (x)dx + f (x)dx. - 0 6 G A. 10. B. 4. C. 3. D. −4. 1 5 5 Z 0976071956 Z Z CÂU 7. Cho
f (x) dx = −2 và
2f(x) dx = 6, khi đó
f (x) dx bằng DŨN 0 1 0 A. 1.
B. 4. MATH.NDC. 3. D. 2. 3 5 5 5 Z Z Z Z h CÂU 8. Biết
f (x)dx = 2,
f (x)dx = 4,
g (x)dx = 8. Tính I =
3f(x) − g(x)idx. GỌC N 1 3 1 1 A. 4. ? Lớp B. 2. TOÁN THẦY C. DŨNG 26. ? D. 10.
CÂU 9. Cho các hằng số a, b, k (k 6= 0) và hàm số f (x) liên tục trên [a; b]. Mệnh đề nào dưới đây sai? b b b c b GUYỄN Z Z Z Z Z A.
k.f (x) dx = k f (x) dx. B.
f (x) dx =
f (x) dx + f (x) dx. N a a a a c b a b b Z Z Z Z C.
f (x) dx = − f (x) dx. D.
f (x) dx 6= f (t) dt. Thầy a b a a 1 1 Z Z CÂU 10. Cho
5f(x) + x2021 + x dx = 20. Tính f (x)dx. −1 −1 A. 5. B. 4. C. 1. D. 0. 1 2 2 2 Z Z Z Z CÂU 11. Biết
f (x)dx = 3,
[f(x) − g(x)] dx = 3,
[f(x) + g(x)] dx = 7. Tính I = f (x)dx. 0 0 0 1
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 59
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 A. I = 0.
B. I = −2. C. I = 3. D. I = 2.
CÂU 12. Cho hàm số F (x) có đạo hàm cấp 2 trên đoạn 2; 4. Biết f 0(2) = 1, f 0(4) = 5. Giá trị 4 Z của I =
f ”(x)dx là Thầy 2 A. I = 4. B. I = 3. C. I = 2. D. I = 1. N GUYỄN 4 0 4 Z Z Z CÂU 13. Nếu
f (x) dx = 3,
f (x) dx = 2 thì
4e2x + 3f(x) dx bằng −1 −1 0 A. 4e8 − 1. B. 2e8. C. 2e8 + 2. D. 2e8 + 1. N GỌC
CÂU 14. Cho hàm số y = f (x) có f 0(x − 1) = 3x2 + 2x + 2. Biết f (1) = 5, giá trị của f (5) bằng DŨN A. 161. B. 149. C. 253. D. 265. G 0976071956 - THPT
CÂU 15. Gọi S là diện tích hình MA phẳng TH.ND
(H) giới hạn bởi các y
đường y = f(x), trục hoành và 2 đường thẳng x = −1, x = 2 2 Z 0 Z 2 TẠ
(như hình vẽ bên). Đặt a =
f (x)dx, b =
f (x)dx. Mệnh 1 −1 0 QU
đề nào sau đây là đúng? ? Lớp TOÁN THẦY DŨNG ?−1
A. S = b − a.
B. S = b + a. x 0 1 2 AN
C. S = −b + a.
D. S = −b − a. G BỬU f CÂU 16.
Cho hàm số f(x) có đồ thị như hình vẽ. Biết y 3 Z
f (x) dx = 2,3 và F0(x) = f(x) với mọi x ∈ [0; 4]. Tính hiệu 3 1 2 F (3) − F(0)? 1 A. 0,3. B. 1,3. C. 3,3. D. 4,3. x O 1 2 3 4 60
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ y = f(x)
CÂU 17. Cho hàm số y = f (x) có đồ thị như hình vẽ x
dưới đây. Diện tích hình phẳng S (phần tô màu trong
hình vẽ) được tính bởi công thức nào? 0 b Z Z a b y A. S = f (x)dx + f (x)dx. O a 0 b Z B. S = 2 f (x)dx. 0 BỬU 0 b Z Z C. S =
f (x)dx − f (x)dx. G a 0 b AN Z D. S = f (x)dx. QU a TẠ THPT
CÂU 18. Cho hàm số y = f (x) và phần hình phẳng (H) được y -
gạch chéo như hình vẽ bên. Diện tích hình phẳng (H) là G 2 0 0 2 Z Z Z Z A.
f (x) dx −
f (x) dx. 0976071956 B.
f (x) dx − f (x) dx. − − DŨN 0 1 1 0 2 2 −1 2 x O Z Z C f MA D TH.ND . . . (x) dx f (x) dx. −1 −1 GỌC N ? Lớp TOÁN THẦY DŨNG ? y
CÂU 19. Cho đồ thị hàm số y = f (x) như hình vẽ. Diện GUYỄN N
tích S của hình phẳng (phần tô màu) được xác định bởi −2 O 1 2 công thức x 2 1 2 Z Z Z A f f f Thầy . (x) dx. B. (x) dx + (x) dx. −2 −2 1 −2 2 1 2 Z Z Z Z C.
f (x) dx + f (x) dx. D.
f (x) dx − f (x) dx. 1 1 −2 1
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 61
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
CÂU 20. Cho hàm số y = f (x) có đồ thị như hình vẽ. y
Diện tích hình phẳng phần tô đậm trong hình vẽ là 0 2 Z Z A. S =
f (x) dx + f (x) dx. −2 0 −2 1 Z Z Thầy B. S =
f (x) dx + f (x) dx. −2 1 x O 0 0 0 1 Z Z N C. S =
f (x) dx − f (x) dx. GUYỄN −2 0 1 Z D. S = f (x) dx. −2 N
ccc BẢNG ĐÁP ÁN ccc GỌC 1. C 2. B 3. B 4. D 5. B 6. B 7. A 8. D 9. D 10. B 11. D 12. A 13. C 14. C 15. A 16. D 17. C 18. A 19. C 20. C DŨN
{ DẠNG 2. Tích phân hàm ẩn G
Tích phân của hàm số chẵn, hàm số lẻ: 0976071956 - a Z THPT
• Nếu hàm số f(x) liên tục và là hàm số lẻ trên [−a; a] thì
f (x) dx = 0. MATH.ND −a a a T Z Z Ạ
• Nếu hàm số f(x) liên tục và là hàm số chẵn trên [−a; a] thì
f (x) dx = 2 f (x) dx. QU −a 0 ? Lớp TOÁN THẦY DŨNG ?
• Nếu f(x) liên tục và là hàm chẵn trên R thì AN α α Z f (x) Z G dx = f (x) dx (với α ∈ + R và a > 0) ax + 1 BỬU −α 0 π π 2 2 Z Z • Nếu i
f (x) liên tục trên h0; π thì 2
f (sin x) dx =
f (cos x) dx. 0 0
• Nếu f(x) liên tục và f(a+b−x) = f(x) hoặc f(a+b−x) = −f(x) thì đặt t = a+b−x.
cccVÍ DỤ MINH HỌAccc1 1 3 2 Z Z
VÍ DỤ 1. Cho hàm số f (x) liên tục trên đoạn [0; 1] và thỏa mãn
f (x) dx = 1,
f (2x) dx = 13. 0 1 6 62
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 1 Z Tính tích phân I =
x2f x3 dx. 0 A. I = 6. B. I = 8. C. I = 7. D. I = 9. Lời giải.
Gọi F(X) là một nguyên hàm của f(x). 1 3 Z
f (x) dx = 1 Å ã 1 F − F (0) = 1 1 3 1 ⇔
Ñ F (1) − F(0) = 27. Å ã 2 1 Z F (1) − F = 26 BỬU 3
f (2x) dx = 13 G 1 6 1 1 Z 1 Z 1 AN Vậy I =
x2f x3 dx = [ 3
f x3 d x3 = 3 F(1) − F(0)] = 9. 0 0 QU
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ 1 Z
VÍ DỤ 2. Cho hàm số f (x) có đạo hàm liên tục trên [0; 1] và thỏa mãn
x (f0(x) − 2) dx = f(1). THPT 0 1 - Z Giá trị của I =
f (x) dx bằng G 0 A. 1. B. 0976071956 2. C. −1. D. −2. Lời giải. DŨN d u = x u = dx Ñ MATH.ND Đặt . Ta có
dv = (f 0(x) − 2) dx
v = f (x) − 2x GỌC 1 Z 1 N ? Lớpf TO (1) = ÁN
x (f(x) THẦ
− 2x) −
(f(x) − 2x) dx 0 Y DŨNG ? 0 1 Z
⇔ f (1) = f(1) − 2 − f (x) dx GUYỄN 0 N 1 Z ⇔
f (x) dx = −2. 0 Thầy
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Z
VÍ DỤ 3. Cho y = f (x) là hàm số chẵn, có đạo hàm trên đoạn [−6; 6]. Biết rằng
f (−x) dx = −1 3 6 Z Z 6,
f (2x) dx = 5. Tính I = f (x) dx. 1 −1
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 63
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 A. I = 11. B. I = 17. C. I = 8. D. I = 16. Lời giải. 2 2 Z Z - Ta có
f (−x) dx =
f (x) dx = 6, vì f(x) là hàm chẵn. −1 −1 3 3 6 6 Z 1 Z 1 Z Z - Ta có
f (2x) dx = 2 f(2x)d(2x) = 2 f(u)d(u) = 5. Từ đó suy ra f(x)d(x) = 10. Thầy 1 1 2 2 - Vậy I = 16.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N GUYỄN ï 1 ò Å 1 ã
VÍ DỤ 4. Cho hàm số y = f (x) liên tục trên đoạn ; 2 và thỏa mãn = 3 2
f (x) + 2f x, x 2 Z f (x) ∀x ∈ ∗
R . Tính tích phân I = dx. x N 1 GỌC 2 3 5 15 15 A. I = . . . . 2 B. I = 2
C. I = 4 ln 2 − 8
D. I = 4 ln 2 + 8 Lời giải.1 1 DŨN
Đặt x = Ñ dx = − dt. t t2 1 1 Đổi cận: x = .
2 Ñ t = 2, x = 2 Ñ t = 2 G 1 Å 1ã Å 1 ã 2 2 2 f 2 f Z f (x) Z Å 1ã 0976071956 Å 1 ã Z Z - Khi đó t x I = dx = f · t · − dt = dt = dx. THPT x t t2 t x 1 2 1 1 2 MA Å TH.ND 2 2 1 ã
f (x) + 2f Å 1 ã T x Ạ
Ta có f(x) + 2f = 3x ⇔ = 3 x x Å ã Å ã Å ã QU 1 1 1
2 f(x) + 2f 2 2 3f 2 f Z x ?Z Lớp TO Z ÁN x THẦ9Y DŨNG Z x ? 3 Ñ dx = 3 dx Ñ dx = dx = . AN x x 2 Ñ x 2 1 1 1 1 2 2 2 2 G
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BỬU 1 1 Z Z
f (|x|) dx VÍ DỤ 5. Cho biết
f (x) dx = 2018. Tính tích phân I = . 1 + 2018x 0 −1 A. I = e2018. B. I = 2018. C. I = 1009. D. I = 2019. Lời giải.
Đặt x = −t Ñ dx = −dt. Đổi cận x = 1 Ñ t = −1; x = −1 Ñ t = 1. Ta có 1 −1 1 1 Z
f (|x|) dx Z
f (| − t|) dt Z
2018t · f(|t|) dt Z
2018x · f(|x|) dx I = = = = 1 + 2018 − . x 1 + 2018−t 1 + 2018t 1 + 2018x −1 1 −1 −1 64
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 1 1 1 Z Z Z Khi đó 2I =
f (|x|) dx = 2
f (|x|) dx Ñ I =
f (|x|) dx. −1 0 0 1 1 Z Z
Vì hàm y = f(|x|) là hàm số chẵn trên [−1; 1], nên I =
f (|x|) dx =
f (x) dx = 2018. 0 0
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
VÍ DỤ 6. Cho hàm số f (x) xác định, liên tục và có đạo hàm trên R thỏa mãn f (x) 6= 0 với BỬU
mọi x ∈ R và 3f0(x) + 2f2(x) = 0. Tính f(1) biết rằng f(0) = 1. 1 4 3 2 A. . B. . C. . D. . G 5 5 5 5 Lời giải. AN 2 Ta có 3 f 0(x)
f 0(x) + 2f2(x) = 0 ⇔
= − . Lấy tích phân hai vế ta được f 2(x) 3 QU 1 1 Z f 0(x) Z 2 1 1 2 1 1 2 1 5 3 TẠ dx = − dx ⇔ − = − ⇔ = f 2(x) 3 f (x)0 3x0
f (1) − 1 = 3 ⇔ f(1) 3 ⇔ f(1) = 5. 0 0 THPT -
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G
VÍ DỤ 7. Cho hàm số f (x) 0976071956
thỏa mãn f(x) + x · f0(x) = 3x2 + 2x, ∀x ∈ R. Tính f(1). DŨN A. 2. B. 3. C. 4. D. 5. Lời giải. MATH.ND
Theo giả thiết f(x) + x · f0(x) = 3x2 + 2x, ∀x ∈ R. GỌC 1 1 Z Z 1 N
Ta có (xf(x))0 = 3x2 + 2x Ñ
(xf(x))0 dx = (3x2 + 2x) dx = 2 Ñ (xf(x)) = 2 Ñ f (1) = 2. ? Lớp TOÁN THẦY DŨNG ? 0 0 0
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GUYỄN 9
VÍ DỤ 8. Cho hàm số f (x) có đạo hàm liên tục đến cấp 2 trên R và f (0) = 0, f 0(1) = , N 2 1 1 2 Z 39 Z 5 Z
[f0(x)]2 dx = , ( . Tính tích phân 4
x2 + x)f00(x) dx = 2 I = f (x) dx. Thầy 0 0 0 14 7 A. I = . . 3 B. I = 14. C. I = 3 D. I = 7. Lời giải. 1 1 1 5 Z Z Z Ta có = ( ( (2 2
x2 + x)f00(x) dx =
x2 + x) df0(x) = (x2 + x)f0(x)|10 −
x + 1)f0(x) dx 0 0 0 1 Z 13 Ñ
(2x + 1)f0(x) dx = (1) 2 . 0
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 65
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 1 Z Ñ
4[f0(x)]2 − 12(2x + 1)f0(x) + 9(2x + 1)2 dx = 0 0 1 Z Ñ
2f0(x) − 3(2x + 1)2 dx = 0 0 3(x2 + x)
Ñ 2f0(x) − 3(2x + 1) = 0 Ñ f(x) = + 2 C Thầy 2 3( Z 3( Từ x2 + x) x2 + x)
f (0) = 0 Ñ f(x) = . Vậy d 2 I = 2 x = 7. 0 N
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GUYỄN
VÍ DỤ 9. Cho hàm số f (x) = x3 + ax2 + bx + c với a, b, c là các số thực. Biết hàm số
g (x) = f(x) + f0(x) + f00(x) có hai giá trị cực trị là −3 và 6. Diện tích hình phẳng giới hạn bởi N các đường y = f (x) và y = 1 bằng GỌC g (x) + 6 A. 2 ln 3. B. ln 3. C. ln 18. D. 2 ln 2. Lời giải. Ta có DŨN
• f0(x) = 3x2 + 2ax + b. G
• f00(x) = 6x + 2a. 0976071956 - THPT • f000(x) = 6. MATH.ND T
Xét hàm số g(x) = f(x) + f0(x) + f00(x), ta có g0(x) = f0(x) + f00(x) + f000(x) = f0(x) + f00(x) + 6. Ạ
g (m) = −3 QU Theo giả thiết ta có ? phương Lớp trình TO g 0(x) ÁN = 0 cóTHẦ hai Y DŨNG
nghiệm m, n và ?
g (n) = 6. AN x = m Xét phương trình f (x)
= 1 ⇔ g(x) + 6 − f(x) = 0 ⇔ f0(x) + f00(x) + 6 = 0 ⇔ G g (x) + 6 x = n.
Diện tích hình phẳng cần tính là BỬU n n n Z Å f (x) ã Z
g (x) + 6 − f(x) Z
f 0(x) + f00(x) + 6 S = 1 d = d = d − x x x g (x) + 6 g (x) + 6 g (x) + 6 m m m n =
ln |g(x) + 6| = |ln |g(n) + 6| − ln |g(m) + 6|| = |ln 12 − ln 3| = ln 4 = 2 ln 2. m
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cccBÀI TẬP TRẮC NGHIỆMccc 66
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 3 1 Z Z CÂU 1. Cho
f (x) dx = 9. Tính I =
f (3x) dx. 0 0 9 A. I = . 2 B. I = 9. C. I = 27. D. I = 3. √2 3 16 √ Ä ä 4 Z Z Z f t Z CÂU 2. Cho biết
xf (x2) dx = 4,
f (z) dz = 2, √ dt = 2. Tính f (x) dx. t 0 2 9 0 A. 10. B. 11. C. 9. D. 1. 1 π 2 Z Z BỬU CÂU 3. Biết
xf (x) dx = 2, tính
sin 2x · f(cos x) dx. 0 0 G A. 6. B. 3. C. 8. D. 4. 2 4 AN Z Z
CÂU 4. Cho hàm số y = f (x) liên tục trên [0; 4] và
f (x) dx = 1,
f (x) dx = 3. Tính QU 0 0 1 Z TẠ I =
f (|3x − 1|) dx. −1 4 A. I = 4. B. I = 2. C. I = . D. I = 1. THPT 3 -
CÂU 5. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn f (0) = 6, 1 1 G Z Z
(2x − 2)f0(x) dx = 6. Tích phân 0976071956
f (x) dx có giá trị bằng 0 0 DŨN A. −3. B. −9. C. 3. D. 6. MATH.ND 2 2 Z Z
CÂU 6. Cho hàm số y = f (x) liên tục trên đoạn [1; 2] và
(x − 1)f0(x) dx = a. Tính f (x) dx GỌC 1 1
theo a và b = f(2). N A. a − b. ? Lớp B. a TO + b. ÁN THẦY C. b DŨNG − a. ? D. −b − a.
CÂU 7. Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [0; 1] thỏa mãn f (1) = 1 và 1 1 Z Z √ GUYỄN
f (x) dx = 2. Tích phân f 0 x dx bằng N 0 0 A. 3. B. −2. C. 1. D. 4. 0 2 Z Z Thầy
CÂU 8. Cho f (x) là một hàm số chẵn liên tục trên R và
f (x) dx = 2018,
f (x) dx = 2017. −2 −1 0 Z Giá trị của I =
f (x) dx bằng −1 A. I = 2. B. I = 1. C. I = 0.
D. I = −1. 2 Z
CÂU 9. Cho y = f (x) là hàm số chẵn, có đạo hàm trên đoạn [−6; 6]. Biết rằng
f (x) dx = 8 −1
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 67
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 3 6 Z Z và
f (−2x) dx = 3. Tính f (x) dx. 1 −1 A. I = 11. B. I = 5. C. I = 2. D. I = 14. 0 Z
CÂU 10. Cho hàm số y = f (x) là hàm lẻ, liên tục trên [−4; 4]. Biết
f (−x) dx = 2 và −2 2 4 Thầy Z Z
f (−2x) dx = 4. Tính I = f (x) dx. 1 0
A. I = −10.
B. I = −6. C. I = 6. D. I = 10. N GUYỄN
CÂU 11. Cho hàm số f (x) liên tục trên đoạn [0; 1] thỏa mãn điều kiện f (x) + 2f (1 − x) = 1 Z
3x2 − 6x, ∀x ∈ [0; 1]. Tính tích phân I =
f 1 − x2 dx. 0 4 2 2
A. I = − . B. I = 1.
C. I = − . D. I = . N 15 15 15 GỌC Å 2 ã 15x
CÂU 12. Cho hàm số y = f (x) liên tục trên R \ {0} và thỏa mãn 2 · f (3x) + 3 · f = − , x 2 3 9 2 Z Z Å 1 ã DŨN
f (x) dx = k. Tính I = f dx. x 3 1 2 45 + 45 45 + 45 G k − k k − 2k
A. I = − . . . . 9 B. I = C. I = D. I = 0976071956 9 9 9 - THPT
CÂU 13. Xét hàm số f (x) liên tục trên đoạn [0; 1] và thỏa mãn điều kiện 2f (x) + 3f (1 − x) = 1 √ Z x f MATH.ND
1 − x. Tính tích phân I = (x) dx. T 0 Ạ 4 1 4 1
A. I = − . . . . 15 B. I = 15 C. I = 75 D. I = 25 QU
CÂU 14. Cho hàm số f ( ? x) Lớp liên tụcTO trênÁN THẦY DŨNG ?
R thỏa mãn f (x) + f (2018 − x) = 2 với mọi x ∈ R. 2018 AN Z
Tính giá trị của tích phân f (x)dx. G 0 A. 1009. B. 4036. C. 2018. D. 10092. BỬU
CÂU 15. Cho hàm số f (x) nhận giá trị dương, có đạo hàm liên tục trên [0; 2]. Biết f (0) = 1 2 Z ( và
x3 − 3x2)f0(x)
f (x) · f(2 − x) = e2x2−4x, với mọi x ∈ [0; 2]. Tính tích phân dx. f (x) 0 16 16 14 32
A. I = − . . . . 3
B. I = − 5
C. I = − 3
D. I = − 5
CÂU 16. Cho hàm số y = f (x) liên tục trên đoạn [1; 3] thỏa f (4 − x) = f (x) ∀x ∈ [1; 3] và 3 3 Z Z
x.f (x) dx = −2. Giá trị
f (x) dx bằng 1 1 A. 2. B. −1. C. −2. D. 1. 68
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 17. Cho hàm số y = f (x) thỏa mãn y0 = x2y và f (−1) = 1. Tính f (2). A. e + 1. B. e3. C. 2e. D. e2.
CÂU 18. Cho hàm số f (x) liên tục trên R và f (x) 6= 0 với mọi x ∈ R thỏa mãn f 0(x) = 2017 (2 X
x + 1)f2(x) và f(1) = −0,5. Biết rằng tổng
f (i) = a , a ∈ Z, b ∈ N và a là phân số tối b b i=1
giản. Mệnh đề nào dưới đây đúng?
A. a + b = −1.
B. a ∈ (−2017; 2017). C. a < −1.
D. b − a = 4035. b BỬU
CÂU 19. Cho hàm số f (x) có đạo hàm liên tục trên (0; +∞), biết f 0(x) + (2x + 4)f 2(x) = 0, 1 G
f (x) > 0 ∀x > 0 và f(2) = . Tính 15
S = f(1) + f(2) + f(3). 7 11 11 7 A. S = . B. S = . C. S = . D. S = . AN 15 15 30 30 1 2 , f0(1) = và QU
CÂU 20. Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [1; 4], f (1) = 3 5 4 √ Z TẠ
thỏa mãn 2f0(x) + xf00(x) = x, ∀x ∈ [1; 4]. Tính I = f (x) dx. 1 139 213 263 119 A. I = . B. I = . C. I = . D. I = . THPT 75 25 75 25 -
CÂU 21. Cho hàm số y = f (x) có đạo hàm liên tục trên [1; 4] và thỏa mãn 2xf 0(x) − f (x) = 4 G √ Z 2 f (x)
x x, ∀x ∈ [1; 4]. Biết rằng f(1) = 0, tính I = dx. 0976071956 x 1 DŨN 22 20 8 14 A. I = . . . . 3 B. I = C. I = D. I = MA 3 TH.ND 3 3
ccc BẢNG ĐÁP ÁN ccc GỌC N 1. D 2. B ? 3. Lớp D 4. TO C ÁN 5. THẦ C 6. YC DŨNG 7. B ? 8. D 9. D 10. C 11. C 12. A 13. C 14. C 15. B 16. B 17. B 18. D 19. D 20. C 21. C GUYỄN ccc N
HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc Å 2 ã 15x
Câu 12. Từ giả thiết 2 · f(3x) + 3 · f = − , suy ra x 2 Thầy 3 3 3 Z Z Å 2 ã Z Å 15 ã 2 x
f (3x) dx + 3 f dx = −
dx = −30. x 2 1 1 1 3 Z Xét tích phân K =
f (3x) dx. 1 1
Đặt t = 3x Ñ dx = d
3 t. Với x = 1 Ñ t = 3; x = 3 Ñ t = 9. Suy ra
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 69
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 9 Z 1 K = f (t) d 3 t = k3. 3 3 Z Å 2 ã Xét tích phân L = f dx. x 1 Thầy 1 2 1 3 Đặt =
⇔ x = 2t Ñ dx = 2 dt. Với x = 1 Ñ t = ; x = 3 Ñ t = . Suy ra t x 2 2 3 N 2 Z Å 1ã GUYỄN L = f 2 dt = 2I. t 1 2 Vậy ta có k 45 + k N 2 · + 3 3
· 2I = −30 ⇔ I = − 9 . GỌC
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . DŨN 1
Câu 15. Có f(x) · f(2 − x) = e2x2−4x, thay x = 0 ta được f(0) · f(2) = 1 Ñ f(2) = = 1. G f (0) 0976071956 - 2 2 THPT Z
(x3 − 3x2)f0(x) 2 Z I =
dx = (x3 − 3x2) ln f(x) ln
f (x) d(x3 − 3x2) f (x) MATH.ND 0 − 0 0 2 2 T Z Z Ạ
= −4 ln f(2) − (3x2 − 6x) ln f(x) dx = − (3x2 − 6x) ln f(x) dx. QU ? Lớp 0 TOÁN THẦY0 DŨNG ? 2 AN Z
Xét A = (3x2 − 6x) ln f(x) dx. G 0
Đặt x = 2 − t, suy ra BỬU
• dx = −dt
• 3x2 − 6x = 3(2 − t)2 − 6(2 − t) = 12 − 12t + 3t2 − 12 + 6t = 3t2 − 6t. 2 0 Z Z A =
(3x2 − 6x) ln f(x) dx = − (3t2 − 6t) ln f(2 − t) dt 0 2 2 2 Z Z =
(3t2 − 6t) ln f(2 − t) dt = (3x2 − 6x) ln f(2 − x) dx. 0 0 70
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Lại có f(x) · f(2 − x) = e2x2−4x Ñ f(2 − x) = e2x2−4x
f (x) Ñ ln f(2 − x) = 2x2 − 4x − ln f(x). 2 Z
Nên A = (3x2 − 6x)(2x2 − 4x − ln f(x)) dx. 0 Suy ra 2 2 Z Z 2A =
(3x2 − 6x)(2x2 − 4x) dx = (6x4 − 12x3 − 12x3 + 24x2) dx 0 0 2 Z 32 BỬU =
(6x4 − 24x3 + 24x2) dx = 5 0 G 16 Ñ A = AN 5 . 16 QU Vậy I = − . 5 TẠ
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . THPT
{ DẠNG 3. Tích phân hàm số cho bởi nhiều biểu thức - G 0976071956
cccVÍ DỤ MINH HỌAccc 3 Z x nếu x ≥ 1 DŨN
VÍ DỤ 1. Cho hàm số f (x) = . Tính tích phân f (x) dx. 1 MATH.ND nếu x < 1 0 3 3 3 3 Z Z Z 9 Z 5 A.
f (x) dx = 3. B.
f (x) dx = 5. C.
f (x) dx = . D.
f (x) dx = . GỌC 2 2 N 0 0 0 0 Lời giải. 3 1 ? Lớp 3 TOÁN 1 THẦ 3 Y DŨNG ? Z Z Z Z Z 3 1
f (x) dx =
f (x) dx +
f (x) dx = 1 dx +
x dx = x + x2 = 5 0 2 . 1 0 0 1 0 1
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GUYỄN N 3 Z
VÍ DỤ 2. Tính tích phân I = 4 d
x2 − 4 x. Thầy −3 180 168 172 176 A. . . . . 3 B. 3 C. 3 D. 3 Lời giải.
4x2 − 4 = 0 ⇔ x = ±1. Bảng xét dấu của 4x2 − 4 trên [−3; 3] là: x −3 −1 1 3 4x2 − 4 + 0 − 0 +
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 71
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 −1 1 3 Z Z Z 176 Do đó: I =
4x2 − 4 dx −
4x2 − 4 dx +
4x2 − 4 dx = . 3 −3 −1 1
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1 Z Z Thầy
VÍ DỤ 3. Cho hàm số f (x) liên tục trên R và có
f (x)dx = 3. Tính
f (|2x|)dx. 0 −1 3 A. 3. B. 6. C. . 2 D. 0. N Lời giải. GUYỄN 1
Đặt t = 2x Ñ dt = 2dx Ñ dx = d 2 t.
Do x ∈ [−1; 1] nên t ∈ [−2; 2]. 1 2 2 2 Z 1 Z 1 Z Z I =
f (|2x|)dx = 2 f(|t|)dt = 22 f(|t|)dx = f(t)dx = 3 N −1 −2 0 0 GỌC
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . e4 Ä ä DŨN
x2 − 3x khi x < 8 Z ln2 f x
VÍ DỤ 4. Cho hàm số f (x) = 40 . Tích phân I = dx bằng x ln x khi x ≥ 8 x − 7 e2 G 40 15 40 20 A. −36 + ln 2 ln 3. ln 2 + ln 3. 7 − 7 0976071956 B. 36 + 7 7 - 40 15 20 40 THPT C. 36 − ln 2 + ln 3. ln 2 + ln 3. 7 7 D. 6 − 7 7 Lời giải. MATH.ND e4 Ä ä e4 Ä ä Z f ln2 x Z
f ln2 x · ln x T Ta có dx = dx. Ạ x ln x x ln2 x e2 e2 QU 2 ln Đặt x dx
t = ln2 x Ñ dt = ? Lớp . TOÁN THẦY DŨNG ? x AN
Đổi cận x = e2 Ñ t = 4, x = e4 Ñ t = 16. 16 16 8 16 Z f (t) dt Z f (x) dx Z f (x) dx Z f (x) dx G Vậy I = d d d d 2 t = x = x + x. t 2x 2x 2x 4 4 4 8 BỬU 8 8 Z f (x) dx Z 1 Å ã 8 d
x2 − 3x d x2 = 6. 2 x = x = x 2x 2 2 − 3x 4 4 4 16 16 16 Z f (x) dx Z 20 Z 20 Å 1 1 ã d d d 2 x = x = x x x(x − 7) 7 x − 7 − x 8 8 8 20 16 20 9 40 20 = ln x − 7 = ln = ln 3 ln 2 7 − . x 8 7 2 7 7 20 40 Vậy I = 6 − ln 2 + ln 3. 7 7
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
cccBÀI TẬP TRẮC NGHIỆMccc 1 Z x CÂU 1. Tích phân dx bằng
x2 − 5|x| + 6 −1 A. 2. B. 1. C. 0. D. −1. 1 Z
CÂU 2. Tính tích phân I =
(|3x − 1| − 2|x|) dx. 0 1 11 7
A. I = − . . . 6
B. I = − 6
C. I = −6 D. I = 0. 1 Z BỬU 2 x + 1 khi x > 3
CÂU 3. Cho hàm số f (x) =
với a là tham số thực. Nếu f (ex + G ax − 3a + 7 khi x ≤ 3 0
1)ex dx = e2 thì a bằng AN 3e2 + 4e − 6 A. . e B. 6e − 6. C. 6e + 6. D. −6e + 6. − 1 QU 2 1 Z x + 1 khi x > 3
CÂU 4. Cho hàm số f (x) =
với a là tham số thực. Nếu f (ex + TẠ ax − 3a + 7 khi x ≤ 3 0
1)ex dx = e2 thì a bằng 3e2 + 4e − 6 A B − C D − THPT . . . 6e 6. . 6e + 6. . 6e + 6. e − 1 - π 2 Z G x2 − 1 khi x ≥ 2
CÂU 5. Cho hàm số f (x) = . Tích phân
f (2 sin x + 1) cos x dx 0976071956
x2 − 2x + 3 khi x < 2 0 bằng DŨN 23 23 17 17 A. . B. . MATH.ND . . 3 6 C. 6 D. 3 e e x + 2 Z x + 1 khi x < 0 1 GỌC
CÂU 6. Cho hàm số f (x) = . Tích phân I =
f (2 ln x − 1) dx x N
− 3x2 + 2x + 2 khi x ≥ 0 1 bằng ? Lớp TOÁN THẦY DŨNG ? 1 3 1 3 1 5 1 3 A. + . . . + . 2e 2 B. 2e − 2
C. −2e − 2 D. −2e 2 π 2 Z GUYỄN 2 x2 + x − 1 khi x ≥ 1
CÂU 7. Cho hàm số f (x) = . Tích phân I =
f (3 cos x − 1) sin x dx N − x2 + 3x khi x < 1 0 bằng 3 3 31 2 A. − . B. . C. . D. − . Thầy 2 2 18 9 2x + 5 2 ln 2 khi Z x > 2
CÂU 8. Cho hàm số f (x) = x + 1 . Tích phân I =
f (ex − 1) ex dx bằng 6x2 − 21 khi x ≤ 2 0 4 4 3 3
A. −24 + 3 ln . . . . 3
B. −26 + 3 ln 3
C. −24 + 3 ln 4
D. −26 + 3 ln 4
ccc BẢNG ĐÁP ÁN ccc
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 73
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 1. C 2. A 3. B 4. B 5. B 6. D 7. B 8. A
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc
Câu 3. Ta có f(3) = lim f(x) = 7 và lim f(x) = lim (2x + 1) = 7. x→3− x→3+ x→3+
Nhận xét lim f(x) = lim f(x) = f(3) = 7 nên hàm số f(x) liên tục tại x = 3. x→3− x→3+
Đặt t = ex + 1 Ñ dt = ex dx. Thầy
Đổi cận x = 0 Ñ t = 2; x = 1 Ñ t = e + 1. Khi đó N 1 e+1 e+1 3 e+1 GUYỄN Z Z Z Z Z
f (ex + 1)ex dx =
f (t) dt =
f (x) dx =
f (x) dx + f (x) dx 0 2 2 2 3 3 e+1 Z Z =
(ax − 3a + 7) dx + (2x + 1) dx N 2 3 GỌC 3 Å ã e+1 = ax2 + (
2 − 3ax + 7x x2 + x) 3 2 Å 9 ã =
− (2a − 6a + 14) + (e + 1)2 + (e + 1) − (32 + 3) DŨN 2a − 9a + 21 1
= −2a + e2 + 3e − 3 G 1 Z 0976071956 - 1 Theo giả thiết
f (ex + 1)ex dx = e2 nên − THPT
2a + e2 + 3e − 3 = e2 ⇔ a = 6e − 6. 0 MATH.ND
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ QU
Câu 4. Ta có f(3) = lim f(x) = 7 và lim f(x) = lim (2x + 1) = 7.
x→3− ? Lớp TO x→ ÁN 3+ THẦ x→3+ Y DŨNG ?
Nhận xét lim f(x) = lim f(x) = f(3) = 7 nên hàm số f(x) liên tục tại x = 3. AN x→3− x→3+
Đặt t = ex + 1 Ñ dt = ex dx. G
Đổi cận x = 0 Ñ t = 2; x = 1 Ñ t = e + 1. BỬU Khi đó 1 e+1 e+1 3 e+1 Z Z Z Z Z
f (ex + 1)ex dx =
f (t) dt =
f (x) dx =
f (x) dx + f (x) dx 0 2 2 2 3 3 e+1 Z Z =
(ax − 3a + 7) dx + (2x + 1) dx 2 3 3 Å ã e+1 = ax2 + (
2 − 3ax + 7x x2 + x) 3 2 Å 9 ã =
2a − 9a + 21 − (2a − 6a + 14) + (e + 1)2 + (e + 1) − (32 + 3) 74
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½ 1
= −2a + e2 + 3e − 3 1 Z 1 Theo giả thiết
f (ex + 1)ex dx = e2 nên −2a + e2 + 3e − 3 = e2 ⇔ a = 6e − 6. 0
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Câu 5. Đặt 2 sin x + 1 = t Ñ cos x dx = d 2 t. π 2 3 3 2 3 BỬU Z 1 Z 1 Z 1 Z 1 Z Suy ra I =
f (2 sin x + 1) cos x dx = 2 f(t)dt = 2 f(x)dx = 2 f(x)dx + 2 f(x)dx. G 0 1 1 1 2 2 3 1 Z 1 Z 23 AN Vậy I = . 2
x2 − 2x + 3 dx + 2
x2 − 1 dx = 6 1 2 QU
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ Câu 6. THPT 2 -
• Đặt t = 2 ln x − 1 Ñ dt = dx. x G
• Đổi cận x = 1 Ñ t = −1 và x = e Ñ t = 1. Ta có 0976071956 DŨN 1 1 Z I = MA f (t) d TH.ND 2 t −1 1 GỌC 1 Z N = f (x) dx ? Lớp 2 − TO 1 ÁN THẦY DŨNG ? 0 1 1 Z 1 Z
= 2 f(x)dx + 2 f(x)dx −1 0 GUYỄN 0 1 Z Z N 1 1 = (ex + 2 2 x + 1) dx + 2
−3x2 + 2x + 2 dx −1 0 0 1 1 1 Thầy = ex + + 2 x2 + x
2 −x3 + x2 + 2x −1 0 1 = 1 2 − e−1 + 1 1 3 = − + 2e 2.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 75
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 Câu 7.
• Đặt t = 3 cos x − 1 Ñ dt = −3 sin x dx.
• Đổi cận x = 0 Ñ t = 2 và x = π2 Ñ t = −1. Ta có −1 2 1 Z 1 Z Thầy I
= −3 f(t)dt = 3 f(x)dx 2 −1 1 2 1 Z 1 Z =
f (x) dx + f (x) dx N 3 3 GUYỄN −1 1 1 2 1 Z 1 Z = 2 3
−x2 + 3x dx + 3
x2 + x − 1 dx −1 1 1 2 1 Å x3 3x2 ã Å ã 1 2x3 N = + + + x2 3 − 3 2 3 3 2 − x GỌC −1 1 2 31 3 = − + = 9 18 2. DŨN
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G Câu 8. 0976071956 - THPT
• Đặt t = ex − 1 Ñ dt = ex dx. MATH.ND
• Đổi cận x = 0 Ñ t = 0 và x = 2 ln 2 Ñ t = 3. T Ta có Ạ 3 3 Z Z QU ? Lớp I = TO f (t)ÁN dt = THẦ f (x) Y dx DŨNG ? 0 0 AN 2 3 Z Z =
f (x) dx + f (x) dx G 0 2 BỬU 2 3 Z Z 2 = 6 x + 5
x2 − 21 dx + dx x + 1 0 2 2 3 = 2
x3 − 21x + (2x + 3 ln |x + 1|) 0 2
= −26 + (6 + 3 ln 4 − 4 − 3 ln 3) 4
= −24 + 3 ln 3.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
{ DẠNG 4. Ứng dụng tích phân giải các bài toán khảo sát hàm số
cccVÍ DỤ MINH HỌAccc
VÍ DỤ 1. Cho hàm số y = f (x) có đạo hàm và liên tục trên y 3
R và đồ thị của hàm số y = f 0(x) trên đoạn [−2; 6] như hình 2
vẽ. Tìm mệnh đề đúng trong các mệnh đề sau. O BỬU x −2 −1 2 6 −1 G
A. max f(x) = f(−2).
B. max f(x) = f(2). x∈[−2;6] x∈[−2;6] C f f AN
. max (x) = f(6).
D. max (x) = f(−1). x∈[−2;6] x∈[−2;6] Lời giải. QU
Từ đồ thị của hàm số f0(x) ta có bảng biến thiên hàm số y = f(x) trên [−2; 6]. TẠ x −2 −1 2 6 THPT - y0 + 0 − 0 + G f (− ( 1) f (6) y 0976071956 DŨN f (− ( 2) f (2) MATH.ND GỌC N
Do đó hàm số y = f(x) đạt giá trị lớn nhất chỉ có thể tại x = −1 hoặc x = 6. Gọi S ? Lớp TOÁN THẦY DŨNG ?
1, S2 là diện tích hình phẳng giới hạn được tô như hình y vẽ. Ta có 3 2 6 S2 Z O GUYỄN
f (6) − f(−1) = f 0(x) dx S x −2 −1 1 2 6 N −1 −1 2 6 Z Z =
f 0(x) dx + f 0(x) dx Thầy −1 2
= −S1 + S2 > 0
Suy ra f(6) > f(−1). Vậy max f(x) = f(6). x∈[−2;6]
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 77
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
VÍ DỤ 2. Cho hàm số y = f (x) có đạo hàm và liên tục trên R. y
Biết rằng đồ thị hàm số y = f0(x) như dưới đây. Xét hàm số 5
g (x) = f(x) − x2 − x. Mệnh đề nào sau đây đúng?
A. g(−1) > g(1) > g(2).
B. g(−1) > g(2) > g(1). 3
C. g(2) > g(1) > g(−1).
D. g(1) > g(2) > g(−1). Thầy −1 x O 1 2 N −1 GUYỄN Lời giải.
Ta có g0(x) = f0(x) − 2x − 1 ⇔ f0(x) = 2x + 1 (∗). y
Dựa vào đồ thị hàm số y = f0(x), ta thấy đường thẳng y = 2x + 1 5
cắt đồ thị hàm số y = f0(x) tại ba điểm lần lượt có hoành độ là N GỌC x = −1 3 S2 S1
−1, 1, 2. Do đó (∗) ⇔ x = 1 x = 2. DŨN −1 x O 1 2 −1 G
Bảng biến thiên của hàm số g(x 0976071956 ) - THPT x −1 1 2 MATH.ND g 0(x) 0 + 0 − 0 TẠ g (1) QU g (x)
? Lớpg TOÁN THẦY DŨNG g ? (− ( 1) (2) AN
Từ bảng biến thiên suy ra max g(x) = g(1). G [−1;2]
Gọi S1 là diện tích hình phẳng giới hạn bởi 2 đồ thị y = f0(x), y = 2x + 1, x = −1 và x = 1. BỬU
Gọi S2 là diện tích hình phẳng giới hạn bởi 2 đồ thị y = f0(x), y = 2x+1, x = 1 và x = 2. Khi đó 2 2 Z Z
g (2) − g(−1) =
g 0(x) dx =
f0(x) − (2x + 1) dx −1 −1 1 2 Z Z =
f0(x) − (2x + 1) dx +
f0(x) − (2x + 1) dx −1 1
= S1 − S2 > 0
Ñ g (2) > g(−1). 78
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
VÍ DỤ 3. Cho hàm số y = f (x) có đạo hàm f 0(x) xác định y và liên tục trên 3 y = f0(x)
R. Hàm số y = f 0(x) có đồ thị như hình
bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ BỬU
nhất của hàm số y = f (|x|) trên đoạn [−4; 3]. Tính giá trị G của M − m. 1
A. f(3) − f(2).
B. f(3) − f(0). −1 O 2 x 3 AN
C. f(4) − f(0).
D. f(4) − f(2). Lời giải. QU
Ta có f0(x) = 0 ⇔ x ∈ {−1; 0; 1; 2}. TẠ
Mặt khác hàm số y = f (|x|) là hàm số chẵn.
Ta có bảng biến thiên của hàm số f(x) và f(|x|). THPT - G x −∞ −1 0 1 2 +∞ 0976071956 DŨN f 0(x) − 0 + 0 − 0 − 0 + +∞ MATH.ND f (0) +∞ f (x) GỌC N f (− ( 1) f (2) ? Lớp TOÁN THẦY DŨNG ? GUYỄN N x −4 −2 0 2 3 f (4) f (0) f (3) Thầy f (|x|) f (2) f (2)
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 79
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
Gọi S1, S2, S3 là diện tích hình phẳng giới hạn được tô như y hình vẽ. Ta có 3 y = f0(x) 3 S3 Z f (3) − f(0) = f 0(x) dx 0 2 3 1 Z Z −1 O S 2 x Thầy =
f 0(x) dx + f 0(x) dx 1 3 S2 0 2
= −(S1 + S2) + S3 > 0 N GUYỄN
Suy ra f(3) > f(0). Vì hàm số f(x) đồng biến trên khoảng (2; +∞) nên f(3) < f(4).
Vậy f(0) < f(3) < f(4).
Từ đó ta có min f (|x|) = f(2) = m và max f (|x|) = f(4) = M. Vậy M − m = f(4) − f(2). [−4;3] [−4;3]
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N GỌC
VÍ DỤ 4. Cho hàm số y = f (x). Đồ thị y = f 0(x) y DŨN trên [ 3
−2; 4] được hợp bởi một parabol và một
đoạn thẳng như hình vẽ. Biết f(2) = 7. Tìm giá 2 G
trị lớn nhất của hàm số f(x) trên0976071956 [−2; 4]. 1 - 9 A. 9. B. . C. 3. D. 7. THPT 2 −2 −1 MATH.ND x O 1 2 3 4 −1 T Lời giải. Ạ Từ giả thiết ta có QU ? Lớp TO+ 2 khi x2 ÁN x THẦY − 2 DŨNG ≤ x ≤ 1 ? f 0(x) = AN −x + 4
khi 1 ≤ x ≤ 4. Suy ra G 1
3x3 + x2 + C1 khi −2 ≤ x ≤ 1 BỬU f (x) = x2 + 4 − 2 x + C2 khi 1 < x ≤ 4.
Từ đồ thị của y = f0(x), suy ra bảng biến thiên của y = f(x) như sau x −2 0 4 y0 − 0 + f (−2) f (4) y f (0)
Từ đó ta được max f(x) = max{f(−2); f(4)}. [−3;2] 80
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Do hàm số f(x) có đạo hàm tại mọi điểm thuộc [−2; 4] nên f(x) liên tục trên [−2; 4].
Hàm số f(x) liên tục tại x = 1 nên lim f(x) = lim f(x) x→1− x→1+ 4 7 13 ⇔ + + (1). 3
C1 = 2 C2 ⇔ C1 − C2 = 6
Mà f(2) = 7 ⇔ 6 + C2 = 7 ⇔ C2 = 1 (2). 19
Từ (1), (2) suy ra C1 = . 6 1 19
khi −2 ≤ x ≤ 1 Ñ f (x) = 3x3 + x2 + 6 x2 + 4 − 2 x + 1 khi 1 < x ≤ 4. BỬU 9 Ta có f(−2) =
và f(4) = 9. Suy ra f(−2) < f(4). Vậy max f(x) = 9. G 2 [−3;2]
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AN QU y TẠ
VÍ DỤ 5. Cho hàm số y = f (x) xác định, liên tục trên R và f (2) < 0.
Hàm số y = f0(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của hàm số g(x) = |f(x)| trên THPT −1 2 3 -
[−1; 3]. Khi đó M, m lần lượt là x O
A. f(−1), f(3).
B. |f(3)|, |f(−1)|. G
C. |f(−1)|, |f(2)|. Lời giải. 0976071956
D. |f(−1)|, |f(3)|. DŨN
Từ đồ thị ta có bảng biến thiên của hàm số f(x) x −1 2 3 MATH.ND
trên đoạn [−1; 3] như hình bên. f 0(x) + 0 −
Mà f(2) < 0 nên ta có bảng biến thiên của hàm f (2) GỌC
số |f(x)| [−1; 3] như hình bên dưới. f (x) N ( (3) ? Lớp TOÁN THẦY DŨNG f (−1) − ? f
Từ đó suy ra M = max |f(x)| = |f(2)|. [−1;3]
Để xác định m = min |f(x)|, ta cần so sánh x −1 2 3 [−1;3] |f | (−1) − | |f | (3)| GUYỄN
|f (−1)| và |f(3)|. |f (x)| N |f | (2)|
hay −f(−1) và −f(3).
Từ đồ thị trên đề bài ta có Thầy 2 3 Z Z
f 0(x) dx >
−f 0(x) dx ⇔ f(2) − f(−1) > −f(3) + f(2) −1 2
Từ đó suy ra −f(−1) > −f(3) Ñ |f(−1)| > |f(3)|.
Vậy m = max |f(x)| = |f(−1)| và M = max |f(x)| = |f(2)|. [−1;3] [−1;3]
¤ Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 81
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
cccBÀI TẬP TRẮC NGHIỆMccc
CÂU 1. Cho hàm số y = f (x) có đạo hàm f 0(x) liên tục trên y 3
R và đồ thị của hàm số f 0(x) trên đoạn [−2; 6] như hình vẽ 2
bên. Tìm khẳng định đúng trong các khẳng định sau 1 Thầy x −2 − O 1 2 4 6 −1
A. min f(x) = f(−2).
B. min f(x) = f(2).
C. min f(x) = f(6).
D. min f(x) = f(−1). N [−2;6] [−2;6] [−2;6] [−2;6] GUYỄN
CÂU 2. Cho hàm số f (x) có đạo hàm f 0(x). Đồ thị hàm số y = f 0(x) y
được cho như hình vẽ bên. Giá trị nhỏ nhất, giá trị lớn nhất của 2 f (x) 1
trên đoạn [0; 3] lần lượt là N x O −1 2 3 GỌC
A. f(0), f(3).
B. f(2), f(0).
C. f(1), f(3).
D. f(2), f(3).
CÂU 3. Cho hàm số y = f (x) xác định và liên tục trên y DŨN
đoạn [−1; 2], có đồ thị hàm số y = f0(x) như hình vẽ bên.
Mệnh đề nào sau đây là đúng? G
A. max f(x) = f(−1).
B. max f(x) = f(2). −1 [−1;2] 0976071956 - [−1;2] Å 3ã x O 1 3 2 THPT
C. max f(x) = f(1).
D. max f(x) = f . 2 [−1;2] [− MA 1;2] TH.ND 2 −1 TẠ
CÂU 4. Cho hàm số y = f (x). Đồ thị y = f 0(x) trên [−3; 2] như hình vẽ (phần cong của đồ QU
thị là một phần của para ? bol Lớp y = a TO x2 + ÁN bx + c THẦ ). Y DŨNG ? AN y G 2 BỬU 1 x −3 −2 −1 O 2
Biết f(1) = 0. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x)
trên [−3; 2]. Tính m + M. 10 10 5 5 A. . . . . 3 B. − 3 C. −3 D. 3 82
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
CÂU 5. Cho hàm số f (x). Biết hàm số y = f 0(x) có đồ thị như y
hình vẽ bên. Hỏi giá trị nhỏ nhất của hàm số f(x) trên đoạn 1 [−1; 3] là
A. f(−1). B. f(3). C. f(0). D. f(2). x −1 O 1 3 BỬU
CÂU 6. Cho hàm số y = f (x) có đạo hàm liên tục trên R và có y G
đồ thị f0(x) như hình vẽ sau Gọi M và m là giá trị lớn nhất và 4 AN
giá trị nhỏ nhất của hàm số y = f(|x|) trên đoạn [−2; 1]. Tính M + m. QU
A. f(1) + f(0).
B. f(1) + f(2). x
−2 −1 O 1 2 TẠ
C. f(−2) + f(−1).
D. f(−1) + f(0).
CÂU 7. Cho hàm số f (x) có đạo hàm f 0(x). Hàm số f 0(x) liên tục trên R và có đồ thị như THPT - hình vẽ. G y 0976071956 DŨN MATH.ND GỌC x −1 O 1 2 4 N ? Lớp TOÁN THẦY DŨNG ?
Tìm giá trị lớn nhất và nhỏ nhất của hàm số f(|x|) trên đoạn [−1; 4].
A. max f(|x|) = f(1); min f(|x|) = f(0).
B. max f(|x|) = f(4); min f(|x|) = f(0). GUYỄN [−1;4] [−1;4] [−1;4] [−1;4] N
C. max f(|x|) = f(4); min f(|x|) = f(2).
D. max f(|x|) = f(1); min f(|x|) = f(0). [−1;4] [−1;4] [−1;4] [−1;4] Thầy
CÂU 8. Cho hàm số f (x) có đồ thị hàm số f 0(x) như hình vẽ sau y
Tìm giá trị nhỏ nhất của hàm số f(|x|) trên đoạn [−1; 4].
A. f(−1). B. f(1). C. f(0). D. f(4). x −1O 1 4
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 83
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
CÂU 9. Cho hàm số y = f (x) liên tục trên R có đồ thị y f 0(x)
y = f0(x) như hình vẽ dưới đây và f(1) < 0. Khi đó giá trị
lớn nhất của hàm số y = |f(x)| trên đoạn [−1; 4] bằng
A. |f(0)|.
B. |f(1)|.
C. |f(−1)|.
D. |f(4)|. −1 1 4 x O Thầy N
CÂU 10. Cho hàm số y = f (x) có đạo hàm f 0(x) trên R. Đồ thị y GUYỄN
f 0(x) như hình vẽ sau và f(−1) < −2. Khi đó gọi giá trị lớn nhất và
nhỏ nhất của hàm số g(x) = |f(x) + 2| trên đoạn [−2; 1] lần lượt
là M, m. Tổng M + m bằng
A. g(−2) + g(1).
B. g(−2) + g(−1). x O −2 −1 1 N GỌC
C. |f(−1) + 2| + |f(1) + 2|.
D. |f(−1) + f(1) + 4|. −2 DŨN
CÂU 11. Cho hàm số y = f (x) liên tục trên R có đồ thị của y hàm số y = f0(x)
y = f0(x) như hình bên. Tìm giá trị nhỏ nhất của 4 G
hàm số g(x) = 2f(x) − (x + 1)2. 0976071956 3 -
A. g(−3). B. g(3). C. g(1).
D. g(−1). THPT 2 MATH.ND 1
−3 −2 −1 T x O 1 2 3 Ạ −1 QU ? Lớp TOÁN THẦY DŨNG ? −2 AN
CÂU 12. Cho hàm số y = f (x). Đồ thị y = f 0 (x) trên [−3; 0] y 2
như hình vẽ (phần cong của đồ thị là một phần của parabol y = G 1 Z f (ln x) 2 1 BỬU
ax2 + bx + c). Biết
dx = . Tính giá trị f (0). x 3 e−3 14 7 x −3 −2 −1 O A. 1. B. 2. C. . . 9 D. −9
ccc BẢNG ĐÁP ÁN ccc 1. C 2. A 3. B 4. B 5. B 6. D 7. B 8. A
ccc HƯỚNG DẪN GIẢI MỘT SỐ CÂU ccc
Câu 3. Ta có f(3) = lim f(x) = 7 và lim f(x) = lim (2x + 1) = 7. x→3− x→3+ x→3+
Nhận xét lim f(x) = lim f(x) = f(3) = 7 nên hàm số f(x) liên tục tại x = 3. x→3− x→3+ 84
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Đặt t = ex + 1 Ñ dt = ex dx.
Đổi cận x = 0 Ñ t = 2; x = 1 Ñ t = e + 1. Khi đó 1 e+1 e+1 3 e+1 Z Z Z Z Z
f (ex + 1)ex dx =
f (t) dt =
f (x) dx =
f (x) dx + f (x) dx 0 2 2 2 3 3 e+1 Z Z =
(ax − 3a + 7) dx + (2x + 1) dx 2 3 3 Å ã BỬU e+1 = ax2 + (
2 − 3ax + 7x x2 + x) 3 G 2 Å 9 ã =
− (2a − 6a + 14) + (e + 1)2 + (e + 1) − (32 + 3) AN 2a − 9a + 21 1 = − QU
2a + e2 + 3e − 3 1 TẠ Z 1 Theo giả thiết
f (ex + 1)ex dx = e2 nên −2a + e2 + 3e − 3 = e2 ⇔ a = 6e − 6. 0 THPT
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . - G
Câu 4. Ta có f(3) = lim f(x) = 7 và lim f(x) = lim (2x + 1) = 7. x→3− 0976071956x→3+ x→3+
Nhận xét lim f(x) = lim f(x) = f(3) = 7 nên hàm số f(x) liên tục tại x = 3. x→3− x→3+ DŨN
Đặt t = ex + 1 Ñ dt = ex dx. MATH.ND
Đổi cận x = 0 Ñ t = 2; x = 1 Ñ t = e + 1. Khi đó GỌC 1 e+1 e+1 3 e+1 N Z Z Z Z Z
f (ex + 1)ex dx ? = Lớp f (t)TO dt =ÁN f ( THẦ
x) dx = Yf DŨNG (x) dx + ? f (x) dx 0 2 2 2 3 3 e+1 Z Z =
(ax − 3a + 7) dx + (2x + 1) dx GUYỄN 2 3 N 3 Å ã e+1 = ax2 + (
2 − 3ax + 7x x2 + x) 3 2 Å ã Thầy 9 =
2a − 9a + 21 − (2a − 6a + 14) + (e + 1)2 + (e + 1) − (32 + 3) 1
= −2a + e2 + 3e − 3 1 Z 1 Theo giả thiết
f (ex + 1)ex dx = e2 nên −2a + e2 + 3e − 3 = e2 ⇔ a = 6e − 6. 0
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 85
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956 1
Câu 5. Đặt 2 sin x + 1 = t Ñ cos x dx = d 2 t. π 2 3 3 2 3 Z 1 Z 1 Z 1 Z 1 Z Suy ra I =
f (2 sin x + 1) cos x dx = 2 f(t)dt = 2 f(x)dx = 2 f(x)dx + 2 f(x)dx. 0 1 1 1 2 2 3 1 Z 1 Z 23 Vậy I = . 2
x2 − 2x + 3 dx + 2
x2 − 1 dx = 6 Thầy 1 2
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N GUYỄN Câu 6. 2
• Đặt t = 2 ln x − 1 Ñ dt = dx. x N
• Đổi cận x = 1 Ñ t = −1 và x = e Ñ t = 1. GỌC Ta có 1 1 Z DŨN I
= 2 f(t)dt −1 1 Z G 1 = 2 0976071956 f (x) dx - −1 THPT 0 1 1 Z 1 Z = f (x MA ) dx TH.ND + 2 2 f (x) dx −1 0 T 0 1 Ạ 1 Z 1 Z =
(ex + 2x + 1) dx +
−3x2 + 2x + 2 dx QU 2 2 ? Lớp −1 TOÁN THẦY 0 DŨNG ? 0 1 AN 1 1 = e x + + 2 x2 + x
2 −x3 + x2 + 2x 0 G −1 1 = 1 − e−1 + 1 BỬU 2 1 3 = − + 2e 2.
¤ Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 7.
• Đặt t = 3 cos x − 1 Ñ dt = −3 sin x dx. 86
Lớp Toán Thầy Dũng — ĐT: 0976.071.956
Thầy NGUYỄN NGỌC DŨNG — 0976.071.956
½ Địa chỉ: Tạ Quang Bửu, P4, Q8, HCM ½
• Đổi cận x = 0 Ñ t = 2 và x = π2 Ñ t = −1. Ta có −1 2 1 Z 1 Z I
= −3 f(t)dt = 3 f(x)dx 2 −1 1 2 1 Z 1 Z
= 3 f(x)dx + 3 f(x)dx −1 1 1 2 1 Z 1 Z =
−x2 + 3x dx +
2x2 + x − 1 dx BỬU 3 3 −1 1 G 1 2 1 Å 3 ã 1 Å2 ã = x3 x2 x3 − + + + x2 AN 3 3 2 3 3 2 − x −1 1 2 31 3 = − + = QU 9 18 2. TẠ
¤ Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . THPT - Câu 8. G
• Đặt t = ex − 1 Ñ dt = e0976071956 x dx. DŨN
• Đổi cận x = 0 Ñ t = 0 và x = 2 ln 2 Ñ t = 3. MATH.ND Ta có 3 3 Z Z GỌC I =
f (t) dt = f (x) dx N ? Lớp TO 0 ÁN THẦ 0 Y DŨNG ? 2 3 Z Z =
f (x) dx + f (x) dx 0 2 GUYỄN 2 3 Z Z 2x + 5 N =
6x2 − 21 dx + dx x + 1 0 2 2 3 Thầy
= 2x3 − 21x + (2x + 3 ln |x + 1|) 0 2
= −26 + (6 + 3 ln 4 − 4 − 3 ln 3) 4
= −24 + 3 ln 3.
¤ Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp Toán Thầy Dũng — ĐT: 0976.071.956 87




