ĐỊNH LÍ TA-LÉT TRONG TAM GIÁC I. KIẾN THỨC CẦN NHỚ 1.
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng đơn vị đo (tỉ số này
không phụ thuộc vào cách chọn đơn vị đo). 2. Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng AB và C D
  nếu có tỉ lệ thức AB AB  hay AB CD .        A CD C D A B C D 3.
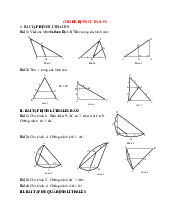
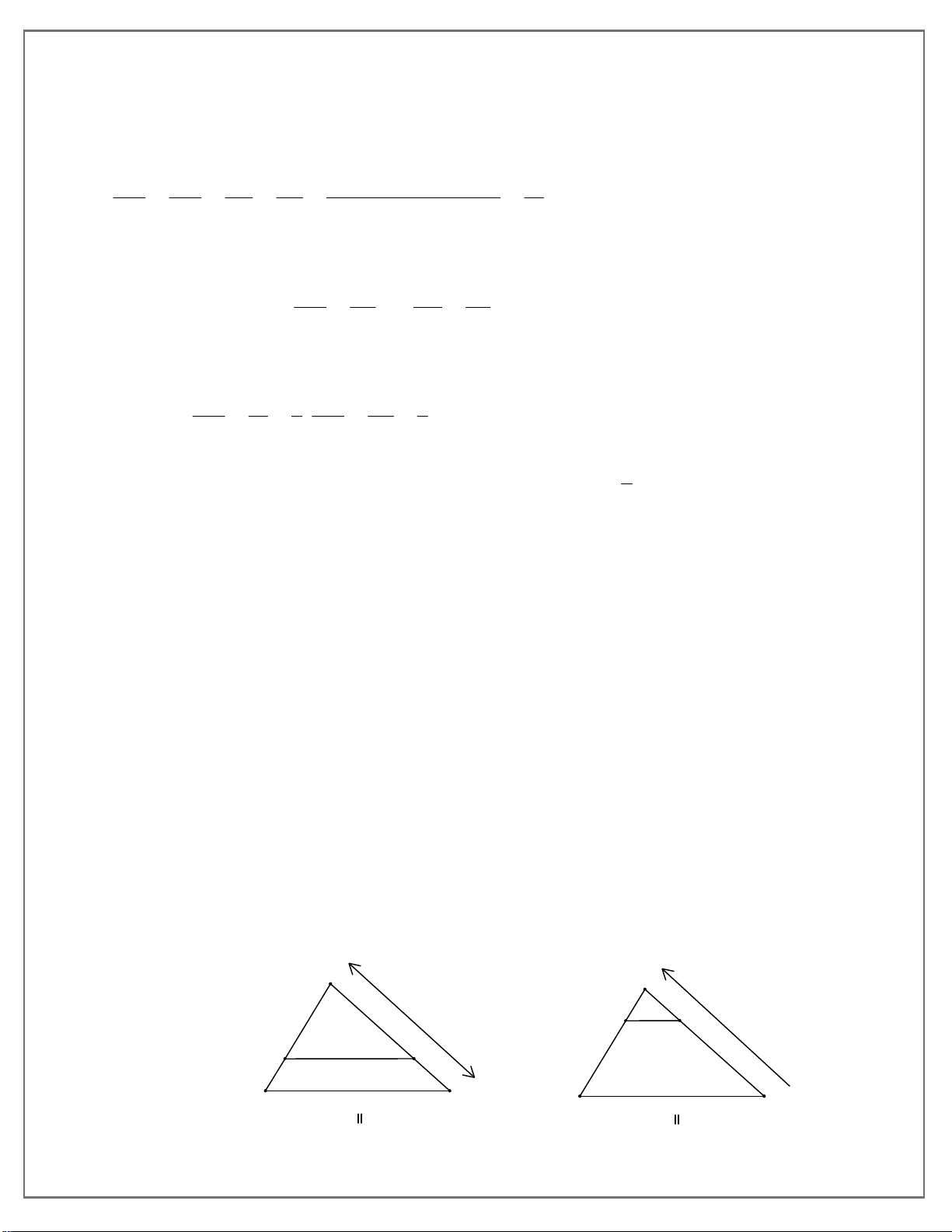
Định lí Ta-lét trong tam giác D E
Nếu một đường thẳng song song với một cạnh của tam giác và
cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn B C
thẳng tương tứng tỉ lệ. Hình 259  A  BC  AD AE    , DB EC  , AD AE . D  E BC   AB AC BA CA DB EC   4.
Nhớ lại tỉ lệ thức và tính chất của dãy tỉ số bằng nhau a)
Tỉ lệ thức là đẳng thức của hai tỉ số a c  . b d b) Tính chất
Tính chất 1 (Tính chất cơ bản của tỉ lệ thức): Nếu a c  thì ad  bc . b d
Tính chất 2: Nếu ad  bc và abcd  0 thì ta có bốn tỉ lệ thức sau: a c  ; a b  ;d c  ; d b  . b d c d b a c a c)
Tính chất của dãy tỉ số bằng nhau
Từ dãy tỉ số bằng nhau a c e   , suy ra a c e a c e a c e     . b d f b d f b d  f b d  f 5.
Từ định lí Ta-lét ta thu được kinh nghiệm thứ năm
1. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Cứ nói đến tỉ số của hai đoạn thẳng phải nghĩ đến định lí Ta-lét, ta cứ nói đến định lí Ta-lét phải
nghĩ đến đường thẳng song song.
Ý nghĩa của kinh nghiệm này là: Với các bài toán đề cập đến tỉ số của hai đoạn thẳng mà
phải vẽ thêm đường phụ, ta vẽ thêm đường thẳng song song để sử dụng định lí Ta-lét. II.BÀI TẬP MINH HỌA
A. CÁC DẠNG TOÁN CƠ BẢN
DẠNG 1. Tính tỉ số hai đoạn thẳng. Chia đoạn thẳng theo tỉ số cho trước I. PHƯƠNG PHÁP GIẢI 1.
Sử dụng định nghĩa tỉ số của hai đoạn thẳng. 2.
Một điểm C thuộc đoạn thẳng AB (hoặc đường thẳng AB ), được gọi là chia đoạn
thẳng AB theo tỉ số m  1 (m,n là các số dương), nếu ta có: CA m  . n CB n 3.
Sử dụng kĩ thuật đại số hóa hình học:  Nếu ta có: CA m   thì CA mt  (với t  0 ) CB n C  B  nt  4.
Lập tỉ lệ thức giữa các đoạn thẳng tỉ lệ rồi áp dụng tính chất của dãy tỉ số bằng nhau. II. VÍ DỤ
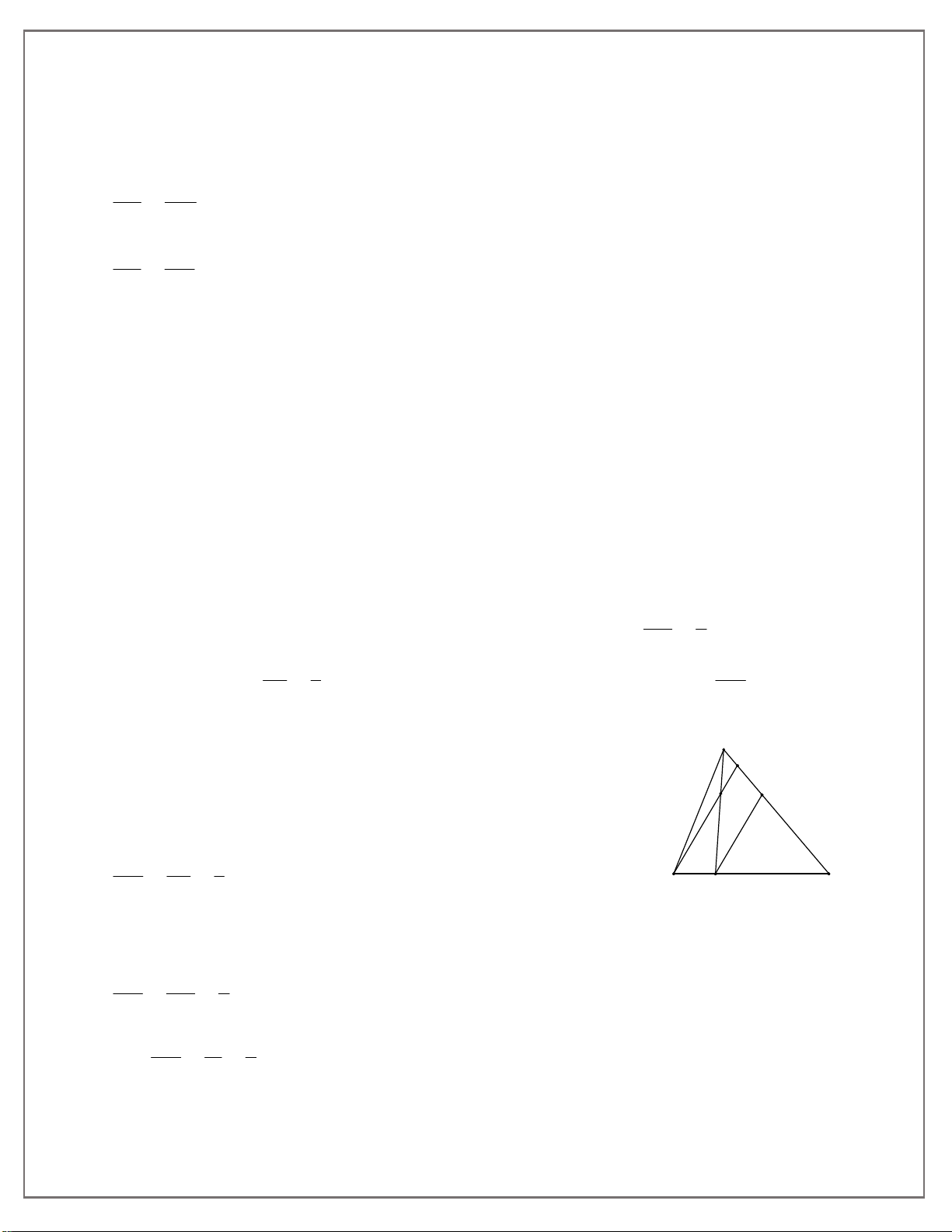
Ví dụ 1. Điểm C thuộc đoạn thẳng AB và chia AB theo tỉ số 3 . Hãy tính các tỉ số: 5 AB ;AB . AC CB Lời giải (hình 260)
Vì C chia đoạn AB theo tỉ số 3 nên: 5 8 CA 3 C  A  3t     với .  t  0 A CB 5 CB  5t C B  3 5  Hình 260
Do đó AB  AC CB  8t . Vậy AB 8t 8 AB 8t 8   ,   . AC 3t 3 CB 5t 5
2. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Ví dụ 2. Cho đoạn thẳng AB  10cm . a)
Trên đoạn thẳng AB lấy điểm C sao cho CA 3  . Tính độ dài CB . CB 2 b)
Trên tia đối của tia BA lấy điểm D sao cho DA 3  . Tính độ dài CD . DB 2 Lời giải (hình 261) A C B Hình 261 a) Cách 1: Từ giả thiết: CA 3 C  A  3t    với t  0 ; CB 2 C  B  2t 
Nên AB  10cm  CA CB  5t  t  2cm . Vậy CB  4cm . Cách 2: Từ giả thiết CA 3 CA CB CA CB AB 10        2 . CB 2 3 2 3  2 5 5 Vậy CB  4(cm) .
Cách 3: Đặt CB  x thì CA  10  x .
Từ giả thiết và tính chất cơ bản của tỉ lệ thức ta có 3CB  2CA hay
3x  2(10  x)  5x  20  x  4(cm) .  b) Từ giả thiết DA 3 DA  3t    . DB 2 D  B  2t 
Mặt khác D thuộc tia đối của tia BA nên DA  DB .
Do đó AB  10cm  DA  DB  3t  2t  t  10cm , suy ra DB  20cm .
Vậy CD  20  4  24(cm) .
Ví dụ 3. Đoạn thẳng AB  44dm được chia thành các đoạn thẳng liên tiếp AM,MN,NP và
PB lần lượt tỉ lệ với 10,2, 3 và 5 . a)
Tính độ dài mỗi đoạn thẳng đó. b)
Chứng minh rằng hai điểm M và P chia đoạn AN theo cùng một tỉ số k và tính k . c)
Còn hai điểm nào chia đoạn thẳng nào theo cùng một tỉ số nữa không?
3. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Lời giải a)
Từ giả thiết và tính chất của dãy tỉ số bằng nhau ta có: AM MN NP PB AM  MN  NP  PB 44       2,2 . 10 2 3 5 10  2  3  5 20 Vậy AM  22d , m MN  4,4d , m NP  6,6d , m PB  11dm . b) Từ câu a) ta có MA 22 PA 33   5;   5 . MN 4,4 PN 6,6
Điều này chứng tỏ M và P chia đoạn AN theo cùng một tỉ số k  5 . c) Vì AM 22 2 NM 4, 4 2   ,   ; AP 33 3 NP 6,6 3
Nên còn hai điểm A và N chia đoạn MP theo cùng một tỉ số 2 . 3
DẠNG 2.Tính độ dài đoạn thẳng, dựng đoạn thẳng tỉ lệ thứ tư I. PHƯƠNG PHÁP GIẢI 1.
Tính độ dài đoạn thẳng: 
Áp dụng định lí Ta-lét để lập hệ thức của các đoạn thẳng tỉ lệ. 
Xác định đường thẳng song song với một cạnh của tam giác. 
Thay số vào hệ thức rồi giải phương trình. 2.
Trong bốn đoạn thẳng tỉ lệ, dựng đoạn thẳng thứ tự khi biết độ dài của ba đoạn kia: 
Đặt ba đoạn thẳng trên hai cạnh của một góc. 
Dựng đường thẳng song song để xác định đoạn thẳng thứ tư. II. VÍ DỤ
Ví dụ 1. Tính x trong các trường hợp sau (h. 262), biết rằng các số trên hình có cùng đơn vị đo là cm . Lời giải (hình 262) A D x 4 5 8,5 24 P Q 10,5 9 M N x B C E F a) MN BC b) PQ EF
4. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Hình 262 a)
Áp dụng định lí Ta-lét vào A
 BC có MN  BC , ta được: BM CN  hay x 8,5  5 4.3,5   x   2, 8 . MA NA 4 5 5 b)
Áp dụng định lí Ta-lét vào D
 FE có PQ  EF , ta được: DP DQ  hay x 24  9 10,5.15   x   17,5 . O PE QF 10,5 9 9 16 20 x
Ví dụ 2. Tính x trên hình 263. P Q 15 Lời giải (hình 263). M N Hình 263
Áp dụng định lí Ta-lét vào O
 MN có PQ  MN , ta được: MP NQ  hay x 16 15 3 
  x 16  12  x  28 . PO QO 16 20 4
Ví dụ 3. Cho ba đoạn thẳng có độ dài là ,
m n, p (cùng đơn vị đo). Hãy dựng đoạn thẳng có z độ dài x sao cho m n  . x p B p Lời giải (hình 264) A n m  Vẽ góc C t zOt bất kì. O D x 
Trên tia Oz đặt các đoạn OA  n,OB  p . Hình 264 
Trên tia Ot đặt OC  m . 
Vẽ BD  AC thì OD  x là đoạn thẳng cần dựng.
Thật vậy, áp dụng định lí Ta-lét vào O
 BD có AC  BD , ta được: OA OC  hay m n  . OB OD x p
DẠNG 3. Chứng minh các hệ thức hình học I. PHƯƠNG PHÁP GIẢI 1.
Xác định đường thẳng song song với một cạnh của tam giác. 2.
Áp dụng định lí Ta-lét để lập hệ thức của các đoạn thẳng tỉ lệ. 3.
Sử dụng các tính chất của tỉ lệ thức hoặc cộng theo vế các đẳng thức hình học.
5. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com II. VÍ DỤ
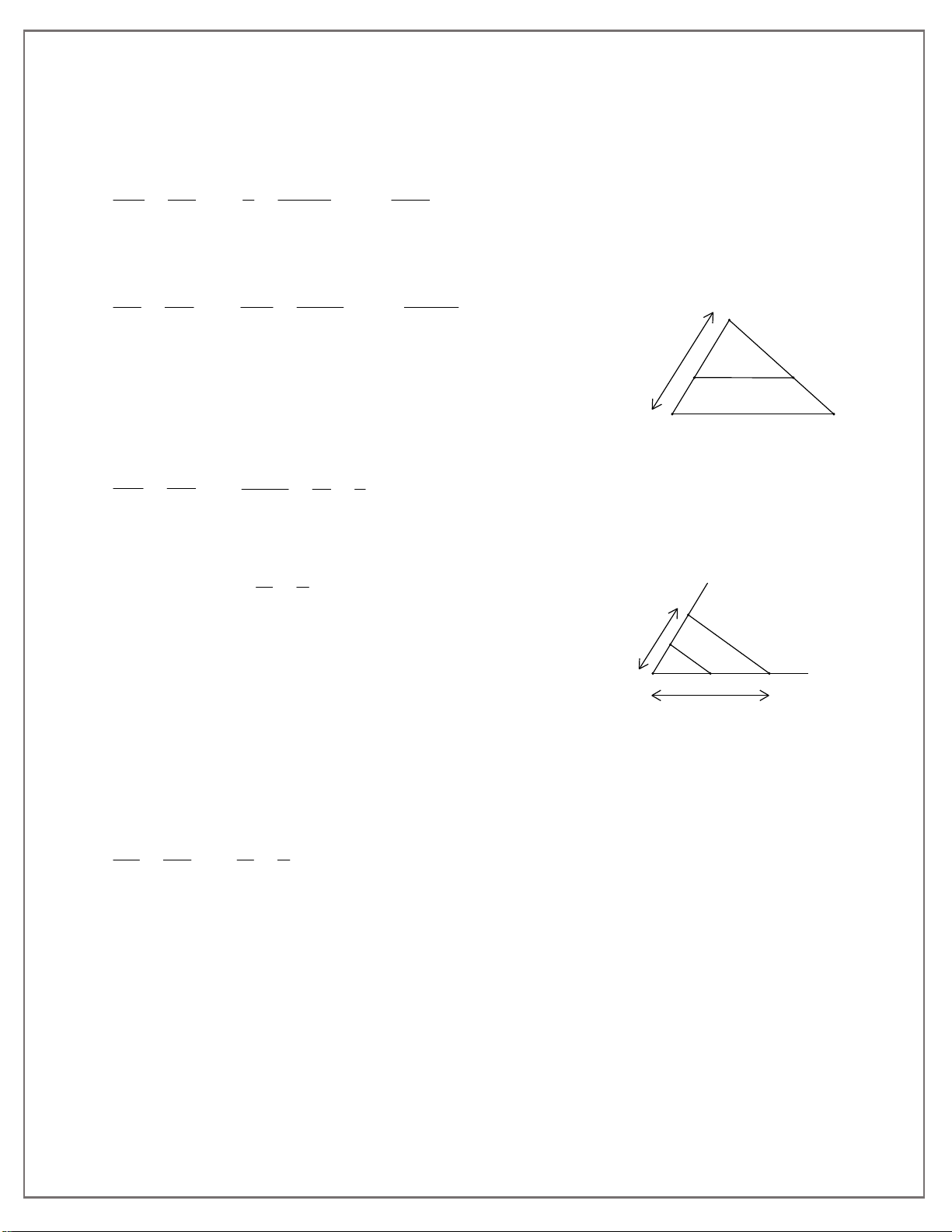
Ví dụ 1. Cho hình thang ABCD (AB CD) . Một đường thẳng song song với hai đáy, cắt
các cạnh bên AD và BC theo thứ tự ở M và N . Chứng minh rằng: a) AM BN  b) AM CN   1 . MD NC AD CB Lời giải (hình 265) A B a)
Gọi I là giao điểm của đường chéo AC với MN . M I N
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB
có MI CD,IN  AB , ta được: D C Hình 265 AM AI  (1); BN AI  (2). MD IC NC IC Từ (1) và (2) suy ra: AM BN  . MD NC b)
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB ta có MI CD,IN  AB ta được AM AI  (3); CN CI  (4). AD AC CB CA
Cộng theo vế các đẳng thức (3) và (4), thu được: AM CN CI  AI CA     1. AD CB CA CA
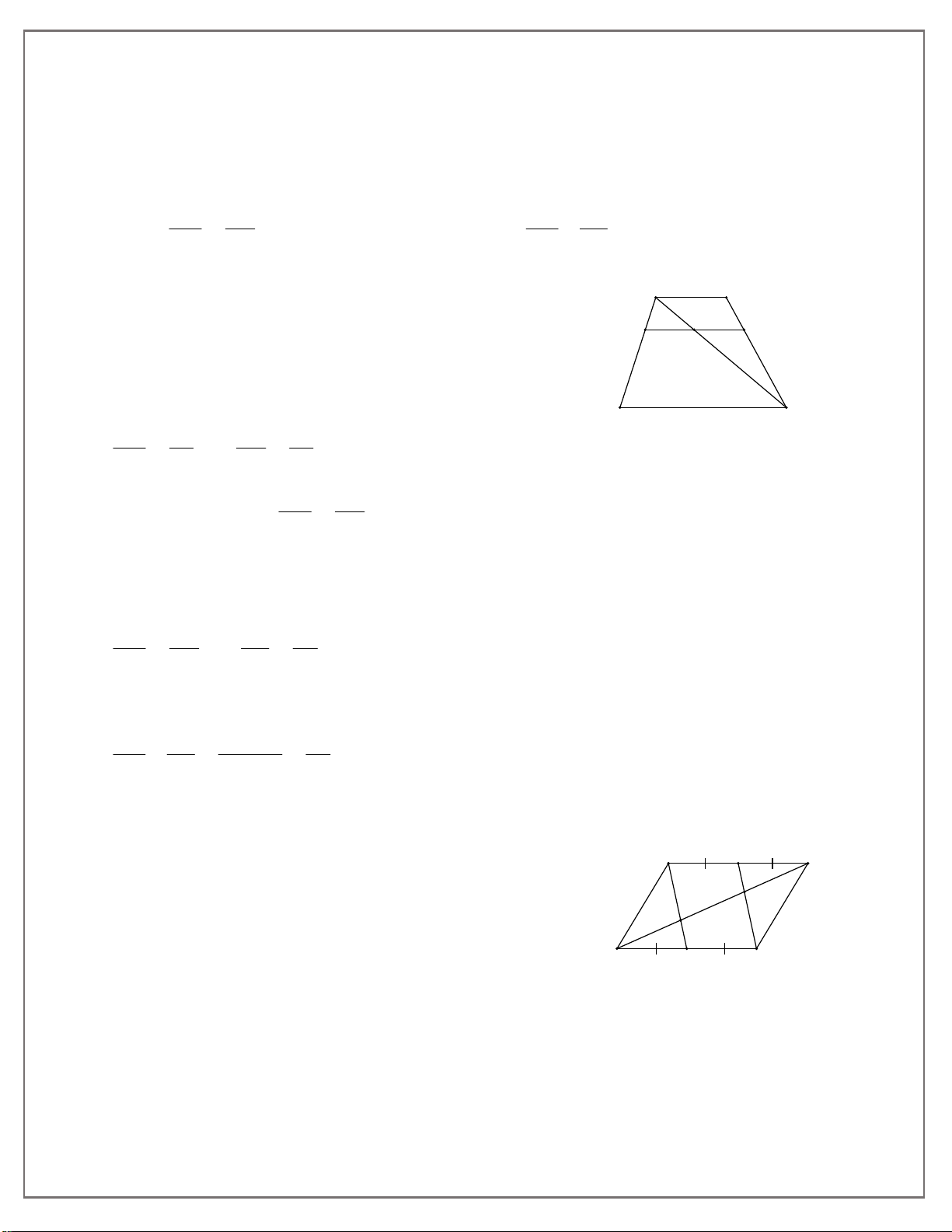
Ví dụ 2. Cho hình bình hành ABCD có M,N lần lượt là trung điểm của AB và CD . Gọi
P,Q thứ tự là giao điểm của AN và CM với đường chéo BD . Chứng minh rằng: A M B DP  PQ  QB . Q Lời giải (hình 266) P
Áp dụng định nghĩa và giả thiết vào hình bình hành ABC D D , N C Hình 266 ta được: AM  NC,AM  NC .
Tứ giác AMCN có hai cạnh đối song song và bằng nhau nên
nó là hình bình hành, do đó MC  AN , suy ra
6. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com MQ  AP,PN QC .
Áp dụng định lí Ta-lét vào hai tam giác APB và DQC có MQ  AP,PN QC , ta được: BQ BM   1  BQ  QP (1). QP MA DP DN   1  DP  PQ (2) PQ NC
Từ (1) và (2) ta có: DP  PQ  QB .
DẠNG 4*. Vẽ thêm đường thẳng song song để tính tỉ số hai đoạn thẳng I. PHƯƠNG PHÁP GIẢI 1.
Vẽ thêm đường thẳng song song. 2.
Sử dụng kĩ thuật đại số hóa hình học. 3.
Áp dụng định lí Ta-lét. II. VÍ DỤ
Ví dụ 1. Cho tam giác ABC . Trên cạnh BC lấy điểm D sao cho BC 4  . Điểm I thuộc BD 1 đoạn AD sao cho AI 1
 . Gọi K là giao điểm của BI và AC . Tính tỉ số AK . ID 2 KC Lời giải (hình 267) A K
Kẻ thêm DE  BK thì DE  IK . E I
Áp dụng định lí Ta-lét vào tam giác ADE có IK  DE , ta được: AK AI 1 A  K  1t      (với ).  t  0 B D C KE ID 2 KE  2t  Hình 267
Áp dụng định lí Ta-lét vào tam giác BCK có DE  BK , ta được: KC BC 4    KC  4KE  8t KE BD 1 Vậy AK 1t 1   . KC 8t 8
7. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Ví dụ 2. Cho tam giác ABC . Trên cạnh BC lấy điểm D sao cho BC  2BD . Trên đoạn AD lấy điểm O sao cho AO 3
 . Gọi I là giao điểm của CO và AB . Tính tỉ số AI . OD 2 IB Lời giải (hình 268) A
Kẻ thêm DH CI thì DH  IO .
Áp dụng định lí Ta-lét vào tam giác ADH có DH  IO , ta được: I O H AI AO 3 A  I  3t      (với t  0 ); B D C IH OD 2 I  H  2t  Hình 268
Áp dụng định lí Ta-lét vào tam giác BIC có DH  IC , ta được: BI BC 2 
  BI  2IH  2.2t  4t . Vậy AI 3t 3   . IH CD 1 IB 4t 4
C.PHIẾU BÀI TỰ LUYỆN DẠNG BÀI CƠ BẢN
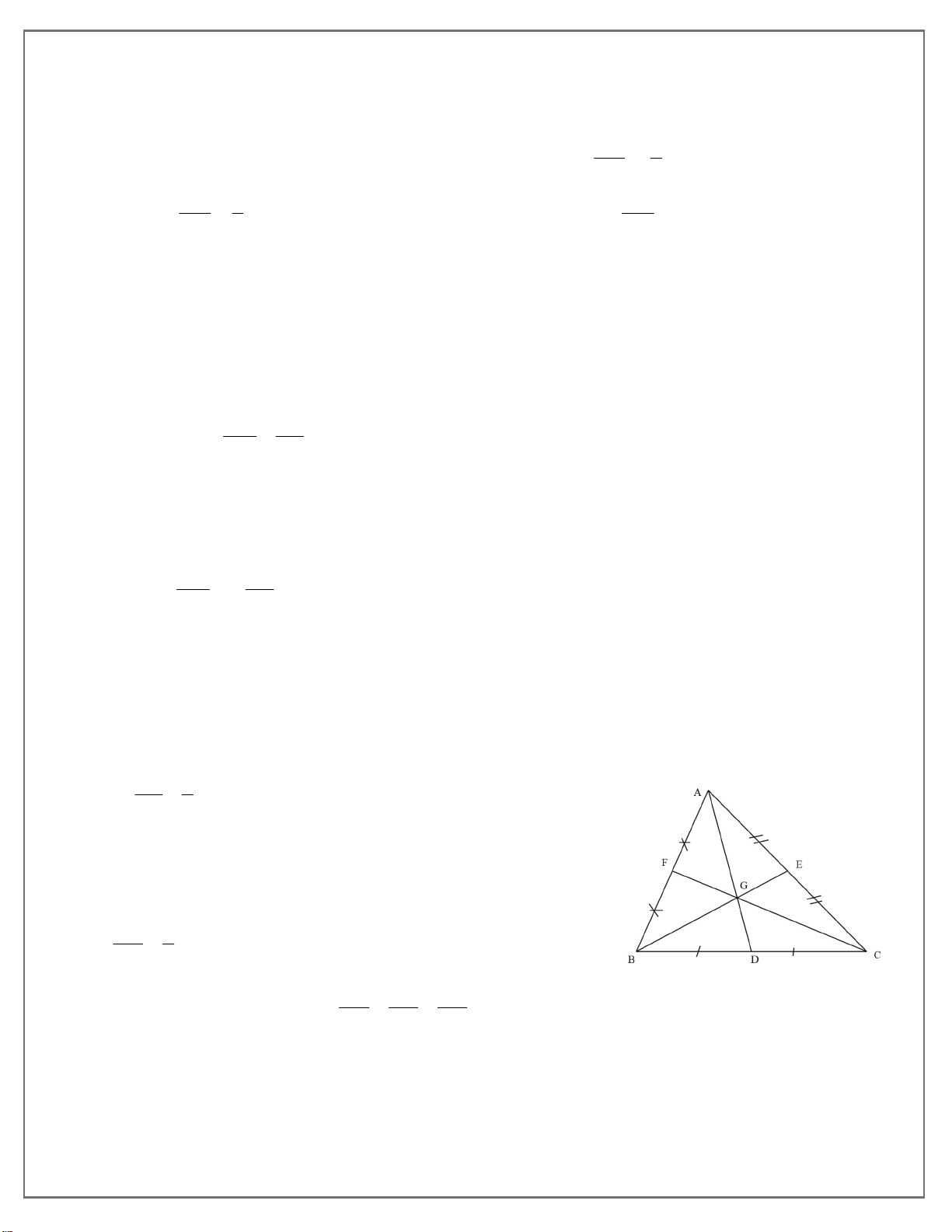
Bài 1: Cho tam giác ABC, các trung tuyến AD,BE,CF cắt nhau tại G . a) Tính AE b) Tính AG AC GD
b) Kể hai cặp đoạn thẳng tỉ lệ với AG và GD .
Bài 2: Cho đoạn thẳng AM , M là một điểm trên đoạn AB . Tính các tỉ số AM và MB AB AB nếu: MA 1 a)  MA 7 b)  c) MA m  MB 2 MB 4 MB n
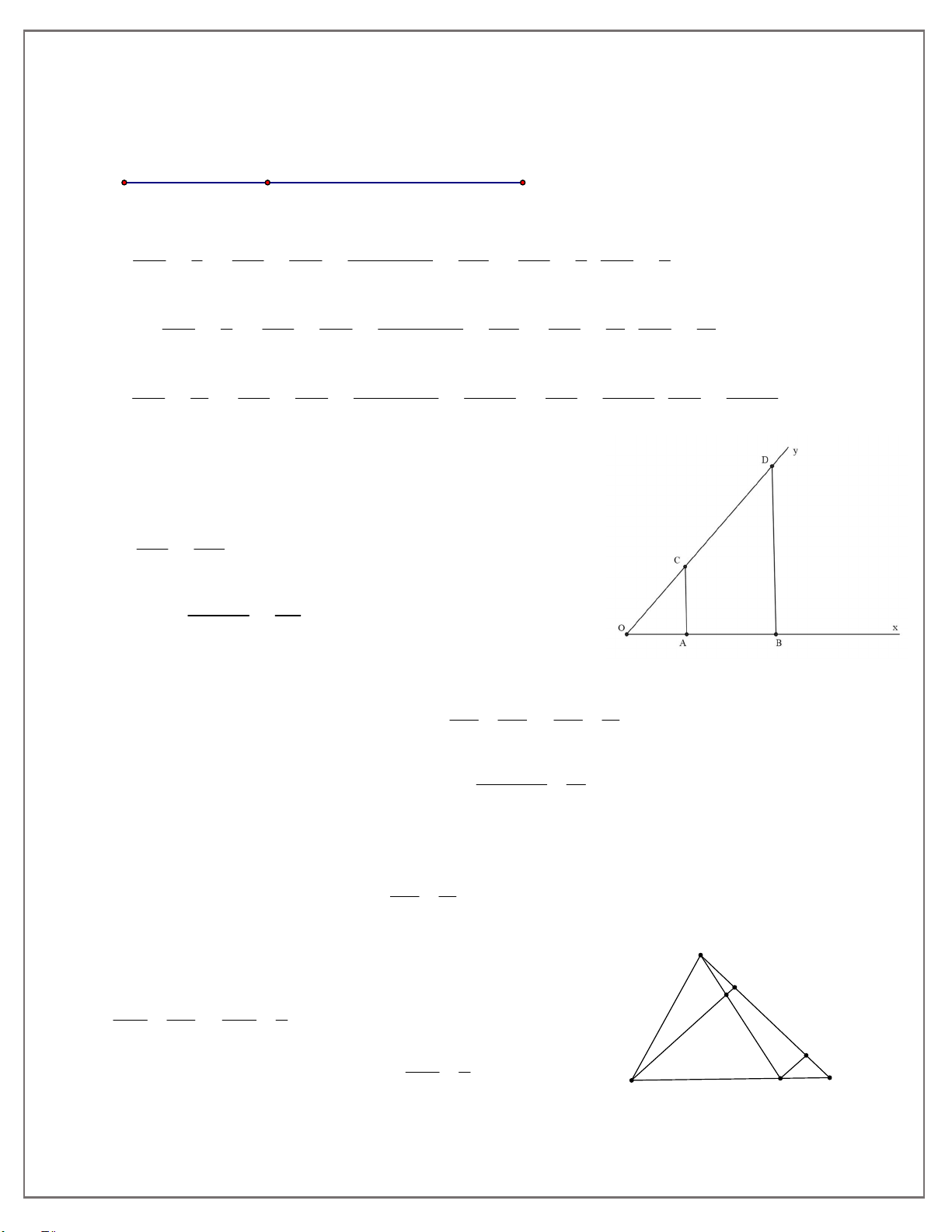
Bài 3: Cho góc xOy . Trên tia Ox , lấy theo thứ tự 2 điểm A,B sao cho
OA  2cm, AB  3cm. Trên tia Oy , lấy điểm C với OC  3cm . Từ B , kẻ đường thẳng song
song với AC cắt Oy tại D . Tính độ dài CD .
Bài 4: Cho tam giác ACE có AC  11cm. Lấy điểm B trên cạnh AC sao cho BC  6cm . Lấy
điểm D trên cạnh AE sao cho DB  EC . Giả sử AE  ED  25,5cm . Hãy tính: a) Tỉ số DE ; AE
8. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
b) Độ dài các đoạn thẳng AE,DE và AD.
Bài 5: Cho tam giác ABC và điểm D trên cạnh BC sao cho BD 3
 , điểm E trên đoạn AD BC 4 sao cho AE 1
 . Gọi K là giao điểm của BE và AC. Tính tỉ số AK . AD 3 KC
Bài 6: Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ
đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song
song với AB, cắt AC ở F. Chứng minh CF  DK. Bài 7: Cho A
 BC. Từ D trên cạnh AB , kẻ đường thẳng song song với BC cắt AC tại E .
Trên tia đối của tia CA , lấy điểm F sao cho CF  DB. Gọi M là giao điểm của DF và BC . Chứng minh DM AC  MF AB
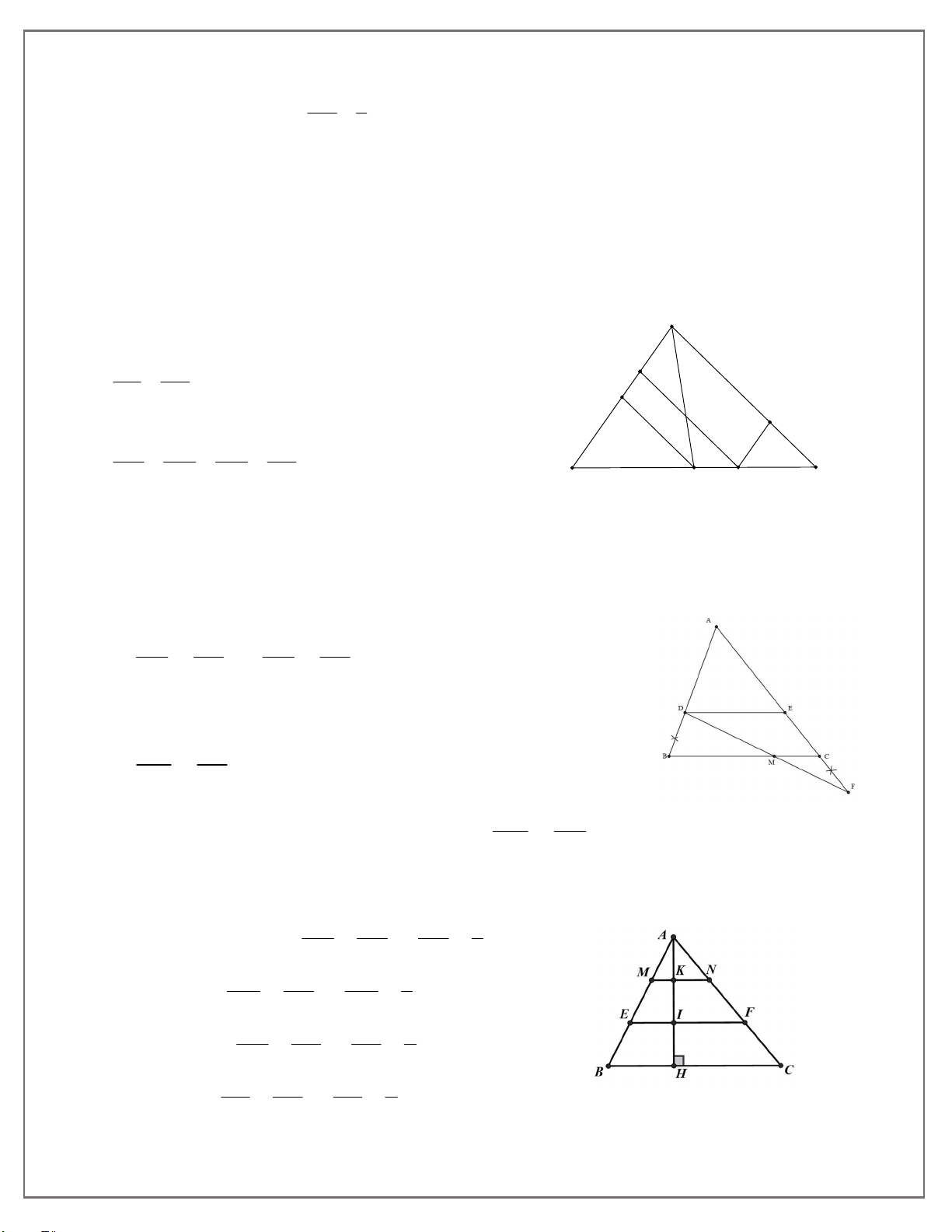
Bài 8: Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho
AK  KI  IH . Qua I, K lần lượt vẽ các đường thẳng EF//BC , MN//BC ( E, M AB, F, N AC). a) Tính MN và EF . BC BC
b) Cho biết diện tích của tam giác ABC là 90 cm2. Tính diện tích tứ giác MNFE .
LỜI GIẢI PHIẾU BÀI TỰ LUYỆN DẠNG CƠ BẢN Bài 1:
a) Có E là trung điểm của AC (vì BE là trung tuyến) AE 1 
 (tính chất trung điểm của đoạn thẳng) AC 2 b) A
 BC có các trung tuyến AD, BE,CF cắt nhau tại G  G là trọng tâm A  BC AG 2
  2 ( G là trọng tâm A  BC) GD 1 c) G là trọng tâm A  BC  AG BG CG   GD GE GF
 BG và GE là cặp đoạn thẳng tỉ lệ với AG và GD .
 CG và GF là cặp đoạn thẳng tỉ lệ với AG và GD .
9. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Bài 2: B A M a) MA 1 MA MB MA  MB AB MA 1 MB 2        ;  MB 2 1 2 1  2 3 AB 3 AB 3 b) Có MA 7 MA MB MA  MB AB MA 7 MB 4        ;  MB 4 7 4 7  4 11 AB 11 AB 11 c) MA m MA MB MA  MB AB MA m        ; MB n  MB n m n m  n m  n AB m  n AB m  n Bài 3: Xét O  BDcó: AC / /BD (gt) AO OC  
(định lí Ta-let trong tam giác) AB CD AB.OC 3.3  CD    4,5(cm) OA 2 Bài 4:
a) Theo định lý Ta-lét trong  DE BC DE ACE , ta có: 6    . AE AC AE 11
b) Cách 1. Theo tính chất của tỉ lệ thức ta có: DE  AE 17  AE 11
Từ đó tính được AE 16,5cm; DE  9cm và AD  7,5cm .
Cách 2. Áp dụng tính chất của dãy tỉ số bằng nhau Cách 3. Thay DE DE  25,5  AE vào 6  AE 11
Bài 5: Kẻ DM / /BK(M  AC) A
Áp dụng định lý Ta-lét trong CBK , ta có: K E KM BD KM 3    (1) KC BC KC 4 M Tương tự với  AK ADM ADM , ta có: 1  (2) KM 2 B C D
10. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Từ (1) và (2), tìm được: AK 3  KC 8
Bài 6: Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ
đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song
song với AB, cắt AC ở F. Chứng minh CF  DK. Hướng dẫn giải
Chứng minh được ADEF là hình bình hành, từ đó: EF  AD (1)
Kẻ MG//AC (G AB), ta được G là trung điểm A
của AB. Áp dụng định lý Ta-lét trong ABC , ta có: CF D  AC (2) EF AB G
Tương tự với AGM và ABC , ta có: F DK  MG  MG  AC (3) AD AG BG AB B C M E
Từ (1), (2), (3) ta suy ra CF  DK Bài 7: Xét A  BC có: DE / /BC AC AB AC EC   hay 
(định lí Ta-let trong tam giác)   1 EC BD AB BD
Xét DEF có: DE / /MC (vì DE / /BC ) DM EC  
(định lí Ta-let trong tam giác) 2 MF CF
Mà CF  DB (gt)3 nên từ   1 , 2 và 3  DM AC  MF AB Bài 8: AK AN AN 1 a) +) NK//CH     AH AC AC 3 MN AN MN 1 MN//BC     BC AC BC 3 AI AF AF 2 +) IF//CH     AH AC AC 3 EF AF EF 2 EF//BC     BC AC BC 3
11. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
b) MNFE có MN//FE và KI  MN . Do đó MNEF là hình thang có 2 đáy MN, FE, chiều cao KI. 1 2    1  BC  BC. AH (MN FE).KI 3 3  3 1 2  S    .S  30(cm ) MNEF 2 2 3 ABC
========== TOÁN HỌC SƠ ĐỒ ==========
12. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com