Chuyên đề hàm số và các bài toán liên quan – Đặng Thành Nam Toán 12

Chuyên đề hàm số và các bài toán liên quan – Đặng Thành Nam Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

104 52 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

LỜI NÓI ĐẦU

Cuốn CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC được viết dựa trên tinh thần

mong muốn có một cuốn tài liệu ôn thi hữu ích tổng hợp và đẩy đủ các phương pháp giải các

dạng toán trong cấu trúc đề thi TSĐH của Bộ giáo dục và đào tào đồng thời phát triển tư duy

giải toán của học sinh. Đây là tâm huyết của tác giả và là mong muốn thời học sinh của tác

giả. Mục tiêu của cuốn tài liệu là cung cấp các dạng toán thông qua các chuyên đề, mỗi dạng

toán sẽ được tác giả tóm lược phương pháp giải kèm theo hệ thống bài tập mẫu và bài tập đề

nghị hay và phong phú , mỗi bài toán đều chứa tính sáng tạo chắc chắn sẽ làm bạn đọc thấy

thú vị và đam mê. Vì thế không đòi hỏi các bạn phải nhớ phương pháp giải mỗi dạng toán mà

phát triển tư duy toán học của bạn đọc, với bài toán cụ thể bạn đọc sẽ tìm được cách giải

nào. Mong muốn đây sẽ là tài liệu hữu ích cho bạn đọc những ai thực sự đang ước mơ bước

chân vào cánh cửa giảng đường đại học. Cuốn tài liệu này được viết theo 15 chuyên đề:

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan.

Chuyên đề 2: Điều kiện để phương trình – hệ phương trình có nghiệm.

Chuyên đề 3: Phương trình lượng giác.

Chuyên đề 4: Phương trình, bất phương trình vô tỷ.

Chuyên đề 5: Hệ phương trình.

Chuyên đề 6: Phương trình, bất phương trình, hệ phương trình mũ, logarit.

Chuyên đề 7: Tích phân và ứng dụng.

Chuyên đề 8: Hình học không gian.

Chuyên đề 9: Giá trị lớn nhất, giá trị nhỏ nhất và chứng minh bất đẳng thức.

Chuyên đề 10: Hình học giải tích trong mặt phẳng.

Chuyên đề 11: Hình học giải tích trong không gian.

Chuyên đề 12: Ba đường Cônic.

Chuyên đề 13: Các bài toán về số phức.

Chuyên đề 14: Nhị thức Newton và ứng dụng.

Chuyên đề 15: Các bài toán đếm và số cách chọn tổ hợp.

Xin được bày tỏ lòng cảm ơn sâu sắc tới sự giúp đỡ và động viên tinh thần của thầy cô, bạn

bè và gia đình trong thời gian hoàn thiện cuốn sách.

Dù đã rất cố gắng nhưng do hạn chế về thời gian và kiến thức hạn chế của tác giả, cộng với

phạm vi rộng của cuốn sách nên thật khó tránh khỏi các thiếu sót, tác giả rất mong nhận

được những ý kiến đóng góp của bạn đọc để trong thời gian tới có thể hoàn thiện cuốn tài

liệu một cách tổng hợp và đầy đủ, dễ hiểu nhất.

Hà nội, ngày 31 tháng 5 năm 2012

ĐẶNG THÀNH NAM

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

MỤC LỤC

LỜI NÓI ĐẦU:……………………………………………………………………….….0

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan…………………………4

Chuyên đề 2: Điều kiện để phương trình, hệ phương trình có nghiệm………..102

Chuyên đề 3: Phương trình lượng giác ………………………………………..…142

Chuyên đề 4: Phương trình, bất phương trình vô tỷ………………………….….196

Chuyên đề 5: Hệ phương trình……………………………………………………..288

Chuyên đề 6: Phương trình, bất phương trình, hệ phương trình mũ,

logarit................................................................................................................402

Chuyên đề 7: Tích phân và ứng dụng………………………………………..........448

Chuyên đề 8: Hình học không gian………………………………………………..554

Chuyên đề 9: Giá trị lớn nhất, giá trị nhỏ nhất và chứng minh bất đẳng

thức…………………………………………………………………………................590

Chuyên đề 10: Hình học giải tích trong mặt phẳng……………………………..648

Chuyên đề 11: Ba đường Cônic……………………………………………...........678

Chuyên đề 12: Hình học giải tích trong không gian…………………………….690

Chuyên đề 13: Các bài toán vế số phức……………………………………..........732

Chuyên đề 14: Nhị thức NEWTON và ứng dụng…………………………..........754

Chuyên đề 15: Các bài toán đếm và số cách chọn tổ hợp…………………......784

TÀI LIỆU THAM KHẢO:……………………………………………………………798

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Email : dangnamneu@gmail.com

Yahoo: changtraipkt

Mobile: 0976266202

CHUYÊN ĐỀ 1:

KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN

LIÊN QUAN

Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Email : dangnamneu@gmail.com

Yahoo: changtraipkt

Mobile: 0976266202

Bài toán hàm số và các vấn đề liên quan thuộc loại cơ bản, để giải quyết tốt phần này các em

nên lưu ý đến các bước của một bài toán khảo sát và vẽ đồ thị hàm số. Trong chương trình thi

Tuyển Sinh đại học chỉ đề cập đến ba dạng hàm số cơ bản đó là hàm số bậc ba, hàm trùng

phương và phân thức bậc nhất trên bậc nhất. Cuốn tài liệu này trình bày mẫu các bước của một

bài toán khảo sát, ngoài ra các bài toán liên quan được phân theo từng dạng. Đó là các bài

toán:

- Bài toán khảo sát sự biến thiên và vẽ đồ thị của hàm số

- Bài toán về tính đơn điệu của hàm số

- Bài toán về điều kiện nghiệm của phương trình, hệ phương trình( được trình bày chi tiết

trong chương 2)

- Bài toán về sự tương giao của đồ thị hàm số

- Bài toán về cực trị hàm số

- Bài toán về tiếp tuyến với đồ thị hàm số

- Bài toán về các điểm đặc biệt

BÀI TOÁN KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ

Dưới đây trình bày mẫu cách khảo sát sự biến thiên và vẽ đồ thị hàm số của ba dạng hàm số là

hàm đa thức bậc ba, hàm trùng phương và hàm phân thức bậc nhất trên bậc nhất.

Hàm đa thức bậc ba

Cho hàm số





3 2

2 1

y x x m x m

    

là tham số thực.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi



Trình bày:

Khi



ta có hàm số

3 2

2 1

y x x

  

+ Tập xác định:



+ Sự biến thiên:

- Chiều biến thiên:

' 3 4 ;

y x x

 

'( ) 0 0

y x x

  

hoặc



Hàm số đồng biến trên các khoảng





 và

;

 



 

 

; nghịch biến trên khoảng

 

 

 

- Cực trị: Hàm số đạt cực đại tại

0; 1

CÐ

x y

 

, đạt cực tiểu tại

4 5

;

3 27

x y   .

- Giới hạn:

lim ;



 

lim



 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

- Bảng biến thiên:

+ Đồ thị:

 

1;0

 

0;1 .

Hàm trùng phương

Cho hàm số

 

4 2

2 1y x m x m    ,

là tham số thực.

Khảo sát sự biến thiên và vẽ đồ thị hàm số khi

1m 

Trình bày:

Khi

1m 

, ta có hàm số

4 2

4 1.y x x  

+ Tập xác định D  

+ Sự biến thiên:

- Chiều biến thiên:

4 8 ; ' 0 0y x x y x     hoặc

2x  

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Hàm số nghịch biến trên các khoảng

 

; 2 

và

 

0; 2 ;

đồng biến trên các khoảng

 

2;0

và

 

2;

- Cực trị: Hàm số đạt cực tiểu tại 2; 3,

x y    đạt cực đại tại 0; 1.

CÐ

x y 

- Giới hạn: lim lim .

x x

y y

 

  

- Bảng biến thiên:

+ Đồ thị:

 

0;1









2 3;0 ; 2 3;0

    .

Hàm bậc nhất trên bậc nhất

Cho hàm số

2 1







Khảo sát sự biến thiên và vẽ đồ thị

 

C của hàm số đã cho.

Trình bày:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

+ Tập xác định:

 

1\D  

+ Sự biến thiên:

- Chiều biến thiên:

 

y x D

   



Hàm số đồng biến trên các khoảng

 

; 1  và

 

1;  .

- Giới hạn và tiệm cận: lim lim 2;

x x

y y

 

  tiệm cận ngang 2y  .

 

lim ,



 

 

 

lim ;



 

 

tiệm cận đứng

1x  

- Bảng biến thiên:

+ Đồ thị:

 



 

 

 

0;1 .

BÀI TOÁN VỀ TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

Phương pháp:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Hàm số

( )

f x

đồng biến trên khoảng





;

a b

khi và chỉ khi





'( ) 0, ;

f x x a b

   .

Hàm số

( )

f x

nghịch biến trên khoảng





;

a b

khi và chỉ khi





'( ) 0, ;

f x x a b

   .

Ta thường biến đổi bất phương trình

'( ) 0

f x



thành hai vế một vế là hàm của

còn một vế chứa

tham số

Có hai dạng bất phương trình sau





 

;

( ) ( ), ; ( ) min ( )

x a b

f x g m x a b g m f x



     .





 

;

( ) ( ), ; ( ) max ( )

x a b

f x g m x a b g m f x



     .

Trong đó

( )

g m

là hàm số theo tham số

BÀI TẬP MẪU

Bài 1. Cho hàm số

   

3 2

1 3 2

y m x mx m x

     .

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên tập xác định.

Lời giải:

+ Tập xác định





Ta có





' 1 2 3 2

y m x mx m

    

Vậy hàm số đồng biến trên tập xác định khi và chỉ khi

  

1 0

' 0, 2

2 1 2 0

' 1 3 2 0

y x m

m m

m m m

 





 

     

 

  

     





Vậy



là những giá trị cần tìm.

Bài 2.Cho hàm số

x m







Tìm tất cả các giá trị của tham số

để hàm số nghịch biến trên khoảng







Lời giải:

+ Tập xác định





D m

 



Ta có

 

x m







Hàm số nghịch biến trên từng khoảng xác định khi và chỉ khi

' 0 4 0 2 2

y m m

       

Để hàm số nghịch biến trên khoảng







thì ta phải có

1 1

m m

   

Kết hợp 2 điều kiện trên suy ra

2 1

  

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 3. Cho hàm số

3 2

3 4

y x x mx

   

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên khoảng





 .

Lời giải:

+ Tập xác định





Ta có

' 3 6

y x x m

  

Hàm số đồng biến trên khoảng





 khi và chỉ khi









 

' 0, ;0 ( ) 3 6 , ;0 min ( )

y x m f x x x x m f x

 

            

Ta có

'( ) 6 6, '( ) 0 1

f x x f x x

     

. Lập bảng biến thiên của hàm số

( )

f x

suy ra

 

min ( ) ( 1) 3

f x f

 

   

Vậy giá trị cần tìm của

là

 

Bài 4.Cho hàm số









3 2

2 3 2 1 6 1 1

y x m x m m x

     

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên khoảng







Lời giải:

+ Tập xác định





Ta có









' 6 6 2 1 6 1

y x m x m m

    

có

   

2 1 4 1 1

m m m

     

' 0 .

x m





 



 



Suy ra hàm số đồng biến trên mỗi khoảng





;

 và





1;m

 

Vậy hàm số đồng biến trên khoảng







khi và chỉ khi

1 2 1

m m

   

Bài 5. Cho hàm số

4 2

2 3 1

y x mx m

   

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên khoảng





1;2

Lời giải:

+ Tập xác định





Ta có





3 2

' 4 4 4

y x mx x x m

   

+ Nếu





0 ' 0, 1;2 0

m y x m

      

thỏa mãn.

+ Nếu

0 ' 0

m y

  

có nghiệm phân biệt , 0,

x m x x m

    .

Hàm số đồng biến trên mỗi khoảng









;0 , ;m m

 

. Vậy hàm số đồng biến trên khoảng





1;2

khi và chỉ khi

1 1

m m

  

Vậy giá trị cần tìm của

là







HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 6.Cho hàm số









3 2

1 2 2 2

y x m x m x m

      

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên khoảng







Lời giải:

+ Tập xác định





Ta có





' 3 2 1 2 2

y x m x m

    

Hàm số đồng biến trên khoảng







khi và chỉ khi









' 3 2 1 2 2 0, 0;y x m x m x

        









3 2 2 1 4 0, 0;x x m x x

        

 

3 2 2

( ) , 0; min ( )

1 4

x x

f x m x m f x

 

 

       



Ta có





 

2 6 3

1 73

'( ) 0 6 3 0

4 1

x x

f x x x x

 

 

       



Lập bảng biến thiên của hàm số

( )

f x

trên







suy ra

 

1 73 3 73

min ( )

12 8

f x f

 

 

  

 

 

 

Vậy

3 73



 là giá trị cần tìm.

Bài 7. Cho hàm số

3 2

2 2

y x x mx

   

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên khoảng







Lời giải:

+ Tập xác định





Ta có

' 4

y x x m

  

Vậy hàm số đồng biến trên khoảng







khi và chỉ khi





' 4 0, ;1

y x x m x

      





 

( ) 4 , ;1 max ( )

m f x x x x m f x

 

         

Ta có





 

'( ) 4 2 0, ;1 max ( ) (1) 3

f x x x f x f

 

        

Vậy



là giá trị cần tìm.

Bài 8. Cho hàm số

3 2

3 3 3 4

y x mx x m

    

Tìm tất cả các giá trị của tham số

để hàm số nghịch biến trên đoạn có độ dài đúng bằng 1.

Lời giải:

+ Tập xác định





HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Ta có





' 3 2 1

y x mx

  

Vậy hàm số nghịch biến trên đoạn có độ dài đúng bằng 1 khi và chỉ khi phương trình

' 0



có 2

nghiệm

1 2

x x

thỏa mãn

1 2

x x

 

Điều này tương đương với

 

1 2

1 2 1 2

' 1 0

(*)

4 1

x x

x x x x







   

 



 

 

  





Theo định lý Vi – ét ta có

1 2

x x m

x x

 









, thay vào (*) ta dược

4 4 1







  



 





Vậy

 

 

 

 

 

 

là giá trị cần tìm.

Bài 9. Cho hàm số













3 2 2

1 2 3 2 2 1

y x m x m m x m m

       

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên







Lời giải:

+ Tập xác định





Ta có









2 2

' 3 2 1 2 3 2 .

y x m x m m     

Hàm số đồng biến trên







khi và chỉ khi

' 0, 2

y x

  













2 2

( ) 3 2 1 2 3 2 0, 2;f x x m x m m x

          

Vì tam thức

( )

f x

có

' 7 7 7 0,

m m m

     

Nên

( )

f x

có hai nghiệm phân biệt:

1 2

1 ' 1 '

;

3 3

m m

x x

     

  .

Vậy

( ) 0

x x

f x

x x





 







Vậy hàm số đồng biến trên mỗi khoảng









1 2

; , ;x x

 

. Vậy hàm số đồng biến

trên đoạn







khi và chỉ khi

 

5 0

2 ' 5 2 .

2 6 0

' 5

x m m

m m

 









          

 

  

  





Vậy

 

 

 

 

là giá trị cần tìm.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 10.Cho hàm số

   

3 2

1 3 2 1

y mx m x m x

     

Tìm tất cả các giá trị của tham số

để hàm số đồng biến trên







Lời giải:

+ Tập xác định





Ta có









' 2 1 3 2

y mx m x m

    

Vậy hàm số đồng biến trên khoảng







khi và chỉ khi













' 2 1 3 2 0, 2;y mx m x m x

        

 

6 2

( ), 2; max ( )

2 3

m f x x m f x

x x

 



       

 

Ta có





 

2 6 3

'( ) 0 6 3 0 3 6 2

2 3

x x

f x x x x

x x

 

         

 

Lập bảng biến thiên của hàm số

( )

f x

trên







ta suy ra

 

max ( ) (2) .

f x f

 

 

Vậy



là giá trị cần tìm.

BÀI TẬP ĐỀ NGHỊ

1.1. Cho hàm số

     

3 2 2

2 2 3 1

y m x m x m x m

      

Tìm các giá trị của tham số

để hàm số đồng biến trên tập xác định.

1.2. Cho hàm số

x m







. Tìm các giá trị của tham số

để hàm số nghịch biến trên

khoảng







1.3. Tìm các giá trị của tham số

để hàm số





3 2

1 4 3

y x m x x

    

nghịch biến trên tập

xác định.

1.4. Cho hàm số

3 2

3 4

y x x mx

    

. Tìm tất cả các giá trị của tham số m để hàm số

nghịch biến trên khoảng







1.5. Cho hàm số









3 2

3 2 1 12 5 2

y x m x m x

     

đồng biến trên cả hai khoảng





; 1

 

và







1.6. Cho hàm số

3 2

y x x mx m

   

. Tìm m để hàm số nghịch biến trên đoạn có độ dài

bằng 1.

1.7. Cho hàm số





3 2

4 3

y x m x mx

    . Tìm m để

a. Hàm số đồng biến trên



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

b. Hàm số đồng biến trên







c. Hàm số nghịch biến trên đoạn

1 1

;

2 2

 



 

 

d. Hàm số đồng biến trên đoạn có độ dài bằng 1.

1.8. Tìm m để hàm số

   

3 2

1 1

1 3 2

3 3

y mx m x m x

     

đồng biến trên khoảng







1.9. Tìm để hàm số





3 2

3 1 4

y x x m x m

     nghịch biến trên khoảng





1,1

 .

1.10. Tìm m để hàm số

 

3 2

y x mx m x



    đồng biến trên



1.11. Tìm m để hàm số

   

3 2

2 1 1

y mx m x m x m

     

đồng biến trên khoảng









,0 2,

 



1.12. Cho hàm số

4 2 2

y x mx m

   

. Tìm m để

a. Hàm số nghịch biến trên







b. Hàm số nghịch biến trên khoảng









1,0 2,3





1.13. Cho hàm số

x m







. Tìm m để

a. Hàm số nghịch biến trên mỗi khoảng xác định của nó.

b. Hàm số đồng biến trên khoảng







KHẢO SÁT SỰ TỒN TẠI NGHIỆM CỦA PT, HPT

Phương pháp:

Xét hàm số

( )

f x

liên tục trên miền

- Nếu

( )

f x

đơn điệu tăng hoặc đơn điệu giảm trên

khi đó phương trình

( ) 0

f x



nếu có

nghiệm thì đó là nghiệm duy nhất.

- Nếu tồn tại ,

a b D



thỏa mãn

( ) ( ) 0

f a f b



khi đó phương trình

( ) 0

f x



có nghiệm





x a b

 .

BÀI TẬP MẪU

Bài 1. Chứng minh rằng phương trình

5 2

2 1 0

x x x

   

có đúng 1 nghiệm thực.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Phương trình tương đương với :

 

1 0 0

x x x

    

. Với

 

0 1 1

x x

   

. Khi đó để

phương trình có nghiệm thì

1 1

x x

  

Vậy ta xét nghiệm của phương trình trên khoảng







Ta xét hàm số

5 2

( ) 2 1

f x x x x

   

liên tục trên



Ta có













4 4 4

'( ) 5 2 2 2 2 3 2 0, 1,f x x x x x x x

          

Do đó hàm số

( )

f x

đơn điệu tăng trên







. Do đó nếu có nghiệm thì phương trình đã cho sẽ

có nghiệm duy nhất.

Mặt khác ta lại có

(1) 3; (2) 23 (1) (2) 0

f f f f

    

. Vậy phương trình đã cho có nghiệm thực duy nhất.



Bài 2. Chứng minh rằng phương trình

.2 1



có nghiệm thực duy nhất trong khoảng





0,1

Lời giải :

Xét hàm số

( ) .2 1

f x x

 

trên khoảng





0,1

Ta có









'( ) 2 2 ln 2 2 1 ln 2 0, 0,1

x x x

f x x x x       . Nên hàm số

( )

f x

đơn điệu tăng trong

khoảng





0,1

Mặt khác ta lại có

(0) 1; (1) 1 (0). (1) 1 0

f f f f

      

. Từ đó suy ra phương trình đã cho có

nghiệm duy nhất trên khoảng





0,1

Bài 3. Chứng minh rằng phương trình

 





có nghiệm thực duy nhất trên đoạn

 

 

 

Lời giải :

Phương trình tương đương với :

 

e x x

 

Với

 



 

 

ta lấy logarit tự nhiên hai vế của phương trình trên ta được





ln 2ln 1 0 (*)

x x x    .

Ta xét hàm số





( ) ln 2ln 1

f x x x x

   

liên tục trên đoạn

 

 

 

Ta có

 

1 2 2 1 1

'( ) 1 0, ,1

1 1 2

x x

f x x

x x x x

 

 

      

 

 

 

. Nên

( )

f x

đơn điệu giảm trên doạn

 

 

 

. Mặt khác ta có

1 1 3

(1) 1 2ln 2 0; ln 2 2ln 0

2 2 2

f f

 

      

 

 

Từ đó suy ra phương trình (*) có nghiệm duy nhất trên

 

 

 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 4. Chứng minh rằng phương trình

 

x x



 

có nghiệm thực dương duy nhất.

Lời giải :

Điều kiện :



Lấy logarit tự nhiên hai vế của phương trình ta được :









1 ln ln 1 0

x x x x

   

Xét hàm số









( ) 1 ln ln 1

f x x x x x

   

trên khoảng







Ta có

 

1 2 1

'( ) ln ln( 1) ln

1 1 1

x x x x

f x x x

x x x x x

 

 

      

 

  

 

Xét hàm số

 

2 1

( ) ln , 0;

1 1

x x

g x x

x x x



 

   

 

 

 

Ta có

'( ) 0

g x



 

, nên hàm số

( )

g x

đơn điệu giảm trên khoảng







Mặt khác ta có

 

2 1

lim ( ) lim ln 0

1 1

x x

g x

x x x

 

 



 

  

 

 

 

. Vậy





( ) 0, 0,g x x

   

. Từ đó

suy ra





'( ) 0, 0,f x x

   

. Vậy

( )

f x

là hàm đơn điệu tăng trên khoảng







Mặt khác ta có (1) ln 2 0, lim ( ) lim ln .

x x

f f x x

 

 

 

     

 

 



 

 

 

Từ đó suy ra phương trình

( ) 0

f x



có nghiệm duy nhất





1,x

 

. Ta có đpcm.

BÀI TẬP ĐỀ NGHỊ

1.1. Chứng minh rằng phương trình

5 3

10 9 1 0

x x x

   

có 5 nghiệm thực phân biệt.

1.2. Chứng minh rằng phương trình





4 4 1 1

 

có đúng ba nghiệm thực phân biệt.

1.3. Chứng minh rằng với mỗi nguyên dương n thì phương trình

2 3 2 2 1

... 2012 2004

n n

x x x x x



      có nghiệm thực duy nhất.

1.4. Chứng minh rằng phương trình :





 

2011

3 2

1 2 1 1 3 3 2 0

x x x x x x

        

có nghiệm thực duy nhất.

1.5. Chứng minh rằng phương trình :

1 1 1 1

... 0,

1 2

x x x x n

     

  



luôn có nghiệm thực duy nhất thuộc khoảng





0,1

1.6. Chứng minh rằng phương trình :

lg sin

x x



có đúng một nghiệm thực trên đoạn

3 5

2 2

 

 

 

 

1.7. Chứng minh rằng với mỗi n nguyên dương,



thì phương trình

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

tan tan ... tan 0

2 2 2

x x x

  

     

      

     

     

có nghiệm thực duy nhất trong khoảng





0,4

1.8. Cho 2 ,n k k

 



. Chứng minh rằng phương trình :









2 1 2

1 3 2 2012 0

n n n

n x n x

  

    

1.9. Chứng minh rằng với mọi m thì phương trình sau luôn có nghiệm duy nhất









3 2 2 3

3 1 3 1 1 0

x m x m x m

      

1.10. Chứng minh rằng phương trình

3 2

3 1 0

x x

  

có ba nghiệm phân biệt

1 2 3

x x x

 

thỏa mãn

   

1 2

1 2 3

2 2 2 27

x x

x x x

 





   





1.11. Chứng minh rằng với

, ,

A B C

là ba góc của một tam giác thì phương trình sau luôn có 4

nghiệm phân biệt

3 sin sin sin

2 2 2

x x

A B C



  

1.12. Chứng minh rằng với mọi m thì hệ sau luôn có nghiệm

   

 

2008 2008

( ) ( ) 0

4 1

f x f y

x m y



 





  





, trong đó





2 2

( ) 3 2 2 3

f x x x x x

    

BÀI TOÁN VỀ SỰ TƯƠNG GIAO

Phương trình hoành độ giao điểm của hai đường cong

( )

y f x



và

( )

y g x



Khi đó số giao điểm của hai đường cong chính là số nghiệm của phương trình (*).

Trong kì thi Tuyển sinh Đại học và Cao đẳng chỉ xét bài toán giao điểm của đường thẳng với đồ

thị của hàm số bậc ba, hàm trùng phương và đồ thị của hàm phân thức bậc nhất trên bậc nhất.

Kiến thức cần vận dụng:

Hai đường cong tiếp xúc nhau:

Hai đường cong





: ( )

C y f x

 và





' : ( )

C y g x

 tiếp xúc nhau khi và chỉ khi hệ phương trình:

0 0

( ) ( )

'( ) '( )

f x g x











có nghiệm

Tương giao với hàm đa thức bậc ba:

(i). Xét phương trình:

3 2

0 (*), 0.

y ax bx cx d a

     

Khi đó phương trình (*) có ba nghiệm phân biệt khi và chỉ khi đồ thị hàm số

( ) ( ) 0 (*)

f x g x

 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

3 2

y ax bx cx d

    

có hai điểm cực trị thỏa mãn

CD CT

y y



i.1- Nếu phân tích phương trình (*) thành

 

( ) (1)

x x

a x x x px q

g x x px q





    



  



Khi đó phương trình (*) có ba nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm

phân biệt khác

4 0

( ) 0

p q

g x







    









i.2- Định lý Vi-ét

1 2 3

1 2 2 3 3 1

1 2 3

(1)

(2)

(3)

x x x

x x x x x x

x x x



   



  











Một số biến đổi thường dùng:

   

2 2 2

1 2 3 1 2 3 1 2 2 3 3 1

x x x x x x x x x x x x

       

    

3 3 3

1 2 3 1 2 3 3 1 2 1 2 3

x x x x x x x x x x x x

        

i.3- Phương trình (*) có ba nghiệm lập thành cấp cố cộng khi

1 3 2

x x x

  thay vào (1) suy ra

 

, lúc này thay ngược vào phương trình (*) ban đầu sẽ tìm ra giá trị của tham số cần tìm.

Tuy nhiên đây chưa phải là điều kiện cần và đủ do đó với mỗi giá trị của tham số tìm được cần

giải lại phương trình xem phương trình có ba nghiệm lập thành cấp số cộng hay không. Lúc đó

mới chấp nhận giá trị của tham số đó hay không.

i.4- Một cách tương tự phương trình (*) có ba nghiệm lập thành cấp số nhân thì

1 3 2

x x x

 , lúc

này ta thay vào (3),…

(ii). Xét với



, ta có:

ii.1- Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt biệt có hoành độ





, khi và chỉ khi

phương trình

' 0



có hai nghiệm phân biệt

1 2

x x



 

và thỏa mãn

1 2

( ) 0

( ). ( ) 0

y x y x













HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

ii.2- Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt biệt có hoành độ





, khi và chỉ khi

phương trình

' 0



có hai nghiệm phân biệt

1 2

x x



 

và thỏa mãn

1 2

( ) 0

( ). ( ) 0

y x y x













Với



, ta biến đổi phương trình hoành độ giao điểm về phương trình có hệ số

dương và áp

dụng với trường hợp



Tương giao với hàm trùng phương :

(i). Xét phương trình:

4 2

, 0 (*)

ax bx c a  

Đặt

t x

 

, khi đó phương trình trở thành

( ) 0 (1)

g t at bt c   

i.1- Phương trình (*) có bốn nghiệm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân

biệt đều dương

4 0

b ac







   







  



 





Khi đó phương trình (1) có 2 nghiệm

1 2

t t

 

. Lúc này phương trình (*) sẽ có bốn nghiệm là:

1 2 2 1 3 1 4 2

, , ,

x t x t x t x t

     

i.2- Vậy phương trình (*) có bốn nghiệm lập thành cấp số cộng khi và chỉ khi

2 1 3 2 4 3 2 1 1 2 1

2 9

x x x x x x t t t t t

         

Định lí Vi-ét với phương trình (1) ta lại có:

1 2

t t



  













Lưu ý: Dạng toán này luôn cần thiết sử dụng đến định lí Vi-ét.

BÀI TẬP MẪU

Bài 1. Cho hàm số





3 2

2 1

y x x m x m

    

(1),

là tham số thực

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Tìm

để đồ thị hàm số (1) cắt trục hoành tại ba điểm phân biệt có hoành độ

1 2 3

, ,

x x x

thỏa mãn

điều kiện

2 2 2

1 2 3

x x x

  

Lời giải:

Phương trình hoành độ giao điểm:





3 2

2 1 0

x x m x m

    









1 0 1

x x x m x

      

hoặc

0 (*)

x x m  

Đồ thị của hàm số (1) cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình (*) có hai

nghiệm phân biệt, khác 1.

Kí hiệu

1 2

( ) ; 1,

g x x x m x x

    và

là các nghiệm của (*).

Yêu cầu bài toán thỏa mãn khi và chỉ khi

2 2

2 3

0 1 4 0

(1) 0 0 1

1 2 3

g m m

x x



   



 

       

 

 

 



và



Vậy

 

1 0

 

 

 

 

là giá trị càn tìm.

Bài 2.Cho hàm số

4 2

y x mx m

   

(1)

Tìm

để đồ thị hàm số

(1)

cắt trục hoành tại bốn điểm phân biệt.

Lời giải:

Phương trình hoành độ giao điểm:

4 2

1 0

x mx m

   

Đặt

t x

 

, khi đó phương trình trở thành

1 0 (*)

t mt m    .

Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt đều dương

 

2 0

0 0 1 2

0 1 0

S m m

P m



 

 





 

      

 

 

  







Bài 3. Cho hàm số

3 2

3 1

y x x mx

   

(1)

(

là tham số

)

Tìm

để đường thẳng

: 1

d y



cắt đồ thị hàm số (1) tại ba điểm phân biệt





0;1 ,

B C

sao cho

các tiếp tuyến của đồ thị hàm số (1) tại

và

vuông góc với nhau.

Lời giải:

Phương trình hoành độ giao điểm:

3 2

3 1 1

x x mx

   

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam





3 0 0

x x x m x

     

hoặc

3 0(*)

x x m  

Kí hiệu

( ) 3

g x x x m

  

Đường thẳng

cắt đồ thị hàm số (1) tại ba điểm phân biệt khi và chỉ khi phương trình (*) có hai

nghiệm phân biệt, khác 0.

9 4 0

, 0.

(0) 0

m m

g m

   



   



 



Khi đó hoành độ của

B C

là nghiệm của phương trình (*)

Hệ số góc của tiếp tuyến tại

B C

lần lượt là

2 2

1 2

3 6 ; 3 6

B B C C

k x x m k x x m

     

Tiếp tuyến tại

B C

vuông góc với nhau khi và chỉ khi









2 2

1 2

1 3 6 3 6 1

B B C C

k k x x m x x m

        

















2 2

3 3 2 3 3 3 2 3 1

B B B C C C

x x m m x x x m m x

          













2 3 2 3 1 4 6 9 1(2)

B C B C B C

m x m x m m x x x x          

Theo định lí Vi-ét ta có

B C

x x

x x m

  









, khi đó (2) trở thành

9 65

4 9 1 0

m m m



     

Bài 4.Cho hàm số

3 2

y x m x m

  

(1)

Tìm

để đồ thị hàm số (1) cắt trục hoành tại đúng 2 điểm phân biệt.

Lời giải:

Đồ thị hàm số (1) cắt trục hoành tại 2 điểm phân biệt thì đồ thị hàm số (1) phải có hai điểm cực

trị

2 2

' 3 3 0

y x m

   

có hai nghiệm phân biệt khi và chỉ khi

0 (*)



Khi đó ' 0

y x m

   

Để đồ thị hàm số (1) cắt trục hoành tại đúng hai điểm khi và chỉ khi hoặc



hoặc



( ) 2 2 0 0 1

y m m m m m

        

( ) 2 2 0 0

y m m m m

      

Chỉ có

 

thỏa mãn điều kiện (*). Vậy giá trị cần tìm của m là

 

hoặc



Bài 5. Cho hàm số





4 2

2 1 2 1

y x m x m

    

(1)

Tìm

để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ lập thành cấp số

cộng.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Phương trình hoành độ giao điểm:





4 2

2 1 2 1 0

x m x m

    

Đặt

t x

 

, khi đó phương trình trở thành





2 1 2 1 0 (*)

t m t m    

Để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt khi và chỉ khi phương trình (*) có 2

nghiệm đều dương

 

' 0

0 2 1 0 0 (2)

2 1 0

S m m





 





        

 

 



 



Khi đó (*) có hai nghiệm là

1 2

t t

 

. Suy ra hoành độ bốn giao điểm lần lượt là

1 2 2 1 3 1 4 2

; ; ;

x t x t x t x t

      . Bốn điểm này lập thành cấp số cộng khi và chỉ khi

2 1 3 2 4 3 2 1 1 2 1

2 9

x x x x x x t t t t t

         

 

1 9 1 5 4 1

m m m m m m







         



 



thỏa mãn (2)

Vậy giá trị cần tìm của

là

 

 

 

 

Bài 6.Cho hàm số





3 2

6 9 6

y x x x C

    .

Tìm

để đường thẳng





: 2 4

d y mx m

  

cắt đồ thị





tại ba điểm phân biệt.

Lời giải:

Phương trình hoành độ giao điểm:

3 2

6 9 6 2 4

x x x mx m

     













3 2 2

6 9 2 2 0 2 4 1 0

x x m x m x x x m

            

 

hoặc

4 1 0 (*)

x x m   

Kí hiệu

( ) 4 1

g x x x m

   

. Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có hai

nghiệm phân biệt, khác 2

' 0 3 0

(2) 0 3 0

g m

   

 

    

 

   

 

Bài 7. Cho hàm số









3 2

2 3 1 6 2

y x m x mx C

     .

Tìm

để đồ thị





cắt trục hoành tại một điểm duy nhất.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Phương trình hoành độ giao điểm:





3 2

2 3 1 6 2 0

x m x mx

    





3 2 2

2 3 2 3 2 (*)

x x m x x    

Nhận thấy

0, 2

x x

 

không là nghiệm của phương trình (*), khi đó phương trình (*) tương

đương với:

3 2

2 3 2

3 (1)

x x

 





Xét hàm số

3 2

2 3 2

( )

x x

g x

x x

 





, ta có bảng biến thiên:

Từ bảng biến thiên suy ra để phương trình (1) có nghiệm duy nhất khi và chỉ khi

3 3 3 3 3 3 3 1 3 1 3

m m         .

Vậy

1 3,1 3

 

  

 

là những giá trị cần tìm.

Cách 2: Để đồ thị hàm số cắt trục hoành tại duy nhất một điểm thì xảy ra một trong hai khả

năng

1. Hàm số luôn đồng biến hoặc luôn nghịch biến.

2. Hàm số có cực đại, cực tiểu nhưng

CÐ

y y



Bạn đọc tự làm theo hướng này và so sánh với kết quả trên.

Bài 8. Cho hàm số





y x mx C

   .

Tìm

để đồ thị





cắt trục hoành tại một điểm duy nhất.

Lời giải:

Phương trình hoành độ giao điểm:

2 0

x mx

  

 

m x x

    

, do



không là nghiệm của phương trình

Xét hàm số

( )f x x

  

. Ta có

2 2

'( ) 0 1.

f x x



   

Ta có bảng biến thiên:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Từ bảng biến thiên của hàm số

( )

f x

ta suy ra để phương trình có một nghiệm duy nhất khi và

chỉ khi

 

Bài 9. Cho hàm số





3 2

3 4

y x x C

   .

Gọi

là đường thẳng đi qua điểm





1;0

A  với hệ số góc là

. Tìm

để đường thẳng

cắt đồ

thị





của hàm số tại ba điểm phân biệt

, ,

A B C

và 2 giao điểm

B C

cùng với gốc tọa độ tạo

thành tam giác có diện tích bằng 1.

Lời giải:

+ Phương trình đường thẳng





: 1

d y k x

 

+ Phương trình hoành độ giao điểm:





3 2

3 4 1

x x k x

   









1 4 4 0 1

x x x k x

        

hoặc

 

2 (*)

x k 

+ Đường thẳng

cắt





tại ba điểm phân biệt khi và chỉ khi

0 9(**)

 

Khi đó các giao điểm của

và





là

 









1;0 , 2 ;3 , 2 ;3

A B k k k k C k k k k

    

Ta có

   

2 1 , ; ;

BC k k d O BC d O d

   



+ Diện tích tam giác

OBC

là

 

. ; 1 1

OBC

S BC d O BC k k k

    

( thỏa mãn điều kiện **).

Vậy



là giá trị cần tìm.

Bài 10. Cho hàm số









3 2

2 3 4

y x mx m x C

    

Tìm giá trị của

để đường thẳng

: 4

d y x

 

cắt đồ thị





của hàm số tại ba điểm phân biệt





0;4 , ,

A B C

sao cho tam giác

KBC

có diện tích bằng

8 2

, biết





1;3

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải:

Phương trình hoành độ giao điểm:





3 2

2 3 4 4

x mx m x x

     









3 2 2

2 2 0 2 2 0

x mx m x x x mx m

         

 

hoặc

2 2 0(*)

x mx m   

Kí hiệu

( ) 2 2

g x x mx m

   

. Khi đó đường thẳng

cắt đồ thị





tại ba điểm phân biệt khi

và chỉ khi phương trình (*) có hai nghiệm phân biệt, khác 0.

2 1

' 2 0

(1)

(0) 2 0

m m

g m

   



    



 

 

 

  



, 4; 4

B B C C

B C d y x y x

     

và ta có









; ; 2

d K BC d K d  .

Vậy

 

. ; 8 2 16 256

KBC

S BC d K BC BC BC     

       

2 2 2 2

256 2 256 4 128(2)

B C B C B C B C B C

x x y y x x x x x x           

Theo định

lí Vi-ét ta có:

2 ; 2

B C B C

x x m x x m

    

 

2 2

1 137

(2) 4 4 2 128 34 0

m m m m m



           thỏa mãn (1).

Vậy

1 137



 là giá trị cần tìm.

Bài 11. Cho hàm số









3 2 2 2

3 3 1 1 (1)

y x mx m x m     

Tìm các giá trị của

để đồ thị hàm số

(1)

cắt trục hoành tại ba điểm phân biệt có hoành độ

dương.

Lời giải:

Ta có





2 2

' 3 6 3 1

y x mx m

   

2 2

' 0 2 1 0

x m x

y x mx m

x m x

  



      



  



Đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ dương khi và chỉ khi

   

 

2 2 2

1 0

0, 0 3 1 2

1 3 2 1 0

. (0) 0

1 0

CD CT

y y

x x m

m m m m

a y



 







 



      

 

    

 







  



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 12. Cho hàm số





3 2

3 4

y x x C

  

Gọi

là đường thẳng đi qua điểm





2;0

A có hệ số góc

. Tìm

để đường thẳng

cắt đồ thị





của hàm số tại 3 điểm phân biệt

, ,

A B C

sao cho tiếp tuyến của





tại

B C

vuông góc với

nhau.

Lời giải:

+ Phương trình đường thẳng





: 2

d y k x

 

+ Phương trình hoành độ giao điểm:





3 2

3 4 2

x x k x

   









2 2 0 2

x x x k x

       

hoặc

2 0(*)

x x k   

Kí hiệu

( ) 2

g x x x k

   

cắt





tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2

nghiệm phân biệt khác 2.

9 4 0

0 (1)

(2) 0

g k

   



    



  



Các tiếp tuyến tại

B C

vuông góc với nhau khi và chỉ khi









' . ' 1

B C

y x y x

 









2 2

3 6 3 6 1 (2)

B B C C

x x x x    

Theo định lí Vi-ét ta có

B C

x x

x x k

 





  



Kết hợp với (1) và (2) ta suy ra:

3 2 2

(2) 9 18 1 0

k k k

 

      ( thỏa mãn (1)).

Vậy

3 2 2

 

 là giá trị cần tìm.

Bài 13. Cho hàm số





y x x C

 

Chứng minh rằng khi

thay đổi đường thẳng





: 1 2

d y m x

  

luôn cắt đồ thị





tại một

điểm cố định

và xác định các giá trị

để

cắt





tại ba điểm phân biệt

, ,

M N P

sao cho

tiếp tuyến của





tại

N P

vuông góc với nhau.

Lời giải:

+ Phương trình hoành độ giao điểm:





3 1 2

x x m x

   









1 2 0 1

x x x m x

        

hoặc

2 0(*)

x x m   

Do đó

luôn cắt





tại điểm





1;2

M  .

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

cắt





tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt, khác -1.

9 4 0

0 (1)

   



    



 



Tiếp tuyến tại

N P

vuông góc với nhau khi và chỉ khi









' . ' 1

N P

y x y x

 









2 2

3 3 3 3 1 (2)

N P

x x    

Theo định lí Vi-ét ta có

B C

x x

x x m

 





  



3 2 2

(2) 9 18 1 0

k k k

 

       ( thỏa (1)).

Vậy

3 2 2

 

 là giá trị cần tìm.

Bài 14. Cho hàm số

 

3 2

1 2

3 3

y x mx x m C

    

Tìm

để đồ thị hàm số





cắt trục hoành tại ba điểm phân biệt có tổng bình phương các

hoành độ lớn hơn 15.

Bài 15. Cho hàm số









4 2

3 2 3 1

y x m x m C

    

Tìm

để đường thẳng

: 1

d y

 

cắt đồ thị





tại bốn điểm phân biệt có hoành độ nhỏ hơn 2.

Lời giải:

+ Phương trình hoành độ giao điểm:





4 2

3 2 3 1 0

x m x m

    









2 2 2

1 3 1 0 1

x x m x

      

hoặc

3 1(*)

x m 

Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác



và

nhỏ hơn 2

0 3 1 4

3 1 1



  

  





 

 

 









Vậy giá trị cần tìm của

là

 

;1 0

 



 

 

Bài 16. Cho hàm số





4 2 2 4

2 2

y x m x m m C

   

Chứng minh rằng đồ thị hàm số





luôn cắt trục hoành tại ít nhất 2 điểm phân biệt với mọi



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải:

+ Phương trình hoành độ giao điểm:

4 2 2 4

2 2 0(*)

x m x m m   

Đặt

t x

 

, khi đó phương trình (*) trở thành

2 2 4

2 2 0(1)

t m t m m   

Ta có

' 2 0

2 0

S m

   



  



 



phương trình (1) luôn có ít nhất một nghiệm dương

Từ đó suy ra phương trình (*) có ít nhất 2 nghiệm phân biệt.Đó là đpcm.

Bài 17. Tìm m sao cho đồ thị hàm số





4 2

y x x m C

   cắt trục hoành tại 4 điểm phân biệt sao

cho hình phẳng giới hạn bởi





và trục hoành có phần trên bằng phần dưới trục hoành.

Lời giải:

Phương trình hoành độ giao điểm:

4 2

4 0

x x m

  

Đặt

t x

  

phương trình trở thành

4 0(1)

t t m  

Vậy





cắt

tại 4 điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt

dương

1 2

t t

 

' 4 0

4 0 0 4 ( )

S m i

P m

   





     





 



Khi đó hoành độ 4 giao điểm của





và

là

1 2 2 1 3 1 4 2

x t x t x t x t

        

Yêu cầu bài toán tương đương với

       

34 4

2 3 3

4 2 4 2 4 2 4 2

4 2 4 2 4 2 4

x x

x x x

x x m dx x x m dx x x m dx x x m dx

            

   

5 3 4 2

4 4 4 4 4

1 4 1 4

0 0(2)

5 3 5 3

x x mx x x m       

Ta lại có

4 2

4 4

4 0(3)

x x m   . Từ (2) và (3) suy ra

5 0 0

m m m

   

(loại)

Hoặc

m  (thỏa (i)).

Vậy

m  là giá trị cần tìm.

Bài 18. Cho hàm số









4 2

2 1 2 1

y x m x m C

     . Tìm tất cả các giá trị thực của tham số

để





cắt trục hoành tại bốn điểm phân biệt

, , ,

A B C D

có hoành độ lần lượt là

1 2 3 4

x x x x

  

sao cho tam giác

ACK

có diện tích bằng 4. Biết rằng





3, 2



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải :

Phương trình hoành độ giao điểm :





4 2

2 1 2 1 0

x m x m

    

, đặt





t x t

 

khi đó phương

trình trở thành :





2 1 2 1 0(*)

t m t m     . Để đồ thị





cắt trục hoành tại bốn điểm phân biệt thì phương

trình (*) có hai nghiệm dương phân biệt

2 1

t t

 

 

' 0

2 1 0 0 ( )

2 1 0

S m m i

P m



  



       





  



Khi đó hoành độ bốn giao điểm lần lượt là

2 1 1 2

, , ,

t t t t

  .

Ta có

 





1 2 1 2 1 2 1 2

1 1

, . 2 4 4 2 16

2 2

ACK

S d K AC AC t t t t t t t t

           

Theo định lý Viét ta có :





1 2 1 2

2 1 ; 2 1

t t m t t m

    

, từ đó suy ra :

 

7 0

2 1 2 2 1 16 2 1 7 4

2 1 7

m m m m m

m m

 





          



  





thỏa mãn điều kiện

(i).

Vậy



là giá trị cần tìm.

Bài 19. Biết rằng đường thẳng

đi qua điểm





2;0

M và có hệ số góc k cắt đồ thị hàm số

3 2

y x x

  

tại bốn điểm phân biệt. Tìm giá trị của k.

Lời giải:

Đường thẳng





: 2

d y k x

 

, ta dùng trực quan đồ thị để biện luận số giao điểm của đường

thẳng

và đồ thị hàm số

 

3 2

y x x C

  

Xét hàm số





( ) 3 2

y f x x x C

    có đồ thị như sau:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Ta có

( ) 3 2, 0

3 2

( ) 3 2, 0

f x x x x

y x x

f x x x x



   



   



     





Do đó đồ thị





gồm hai phần

Phần 1: Giữ nguyên phần đồ thị





bên phải trục tung.

Phần 2: Lấy đối xứng phần 1 qua trục tung.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Để đường thẳng

cắt





tại bốn điểm phân biệt thì

phải nằm trong miền giới hạn bởi hai

đường thẳng trên.

- Đường thẳng thứ nhất đi qua điểm





2;0

M và





0; 2



có hệ số góc là



- Đường thẳng thứ hai là tiếp tuyến với





ứng với



, ta xác định

Ta có





3 2 2

1 3

3 3

6 3 9

x x k x

x k



    





 

 

   

 

 











Vậy để

cắt





tại bốn điểm phân biệt, khi và chỉ khi

1 2

1 6 3 9

k k k k

     

Vậy





1;6 3 9

 

là giá trị cần tìm.

BÀI TẬP ĐỀ NGHỊ

1.1. Tìm các giá trị thực của tham số

để đồ thị





của hàm số tiếp xúc với trục hoành.





3 2

3 3 3 4

y x x mx m C

     .

















3 2 2

1 2 3 2 2 2 1

y x m x m m x m m C

       













3 2

1 4 3 6

y mx m x m x m C

     

1.2. Tìm tất cả các giá trị của tham số m để đường thẳng





: 3

d y m x

 

tiếp xúc với đường

cong

y x x

  

1.3. Tìm những giá trị của tham số m để hai đường cong sau tiếp xúc nhau













3 2

: 1 1 1

C y mx m x m x

     

và









: 1

C y mx m x m

    

1.4. Tìm m để đồ thị hàm số









3 2 2 3

3 1 3 1 1 0

y x m x m x m

       

cắt trục hoành tại

duy nhất một điểm.

1.5. Tìm m để đồ thị hàm số

4 2

y x mx m

   

cắt trục hoành tại bốn điểm phân biệt có

hoành độ lớn hơn



1.6. Viết phương trình đường thẳng

cắt đồ thị hàm số

3 2

y x x

  

tại ba điểm phân biệt

, ,

A B C

sao cho



và

2 2

BC 

1.7. Viết phương trình đường thẳng

song song với trục hoành và cắt đồ thị hàm số

3 2

1 8

3 3

y x x x

   

tại hai điểm phân biệt

A B

sao cho tam giác

OAB

cân tại gốc tọa

độ

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.8. Tìm tất cả các giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số

3 2

3 3 3 4

y x x mx m

    

và trục hoành có phần nằm phía trên trục hoành bằng phần

nằm phía dưới trục hoành.

1.9. Tìm tất cả các giá trị của tham số m để tiếp tuyến của đồ thị hàm số

     

3 2

4 1

2 1 2

3 3

y x m x m x C

      tại giao điểm

của





với trục tung tạo

với hai trục tọa độ một tam giác có diện tích bằng

1.10. Tìm m để đường thẳng :

d y m



cắt đồ thị hàm số

4 2

2 3

y x x

  

tại bốn điểm phân

biệt

, , ,

M N P Q

có hoành độ lần lượt

1 2 3 4

x x x x

  

sao cho

, ,

MN NP PQ

là độ dài ba

cạnh tam giác.

1.11. Giả sử đồ thị hàm số





4 2

3 1 3 2

y x m x m

    

cắt trục hoành tại bốn điểm phân biệt,

khi



gọi

là giao điểm có hoành độ lớn nhất ; tiếp tuyến với đồ thị hàm số tại

cắt

trục tung tại

. Tìm m để tam giác

OAB

có diện tích bằng 24.

1.12. Tìm m để đồ thị hàm số













3 2 2

3 1 2 4 1 4 1

y x m x m m x m m

       

cắt trục hoành

tại ba điểm phân biệt có hoành độ lớn hơn 1.

1.13. Chứng minh rằng đồ thị hàm số

3 2

6 9

y x x x m

   

cắt trục hoành tại ba điểm phân

biệt

1 2 3

x x x

 

thỏa mãn

1 2 4

0 1 3 4

x x x

     

1.14. Tìm m để đồ thị hàm số













3 2

2 2 7 1 3 4

y x m x m x m

      

cắt trục hoành tại 3

điểm phân biệt có hoành độ

1 2 3

, ,

x x x

hỏa mãn

2 2 2

1 2 3 1 2 3

3 53

x x x x x x

   

1.15. Chứng minh rằng khi m thay đổi đường thẳng

d y mx m

 

luôn cắt













3 2 2

: 3 1 2 1

C y x m x m m x m

     

tại một điểm

có hoành độ không đổi. Tìm

m để

cắt





tại một điểm nữa khác

mà tiếp tuyến của





tại hai điểm đó song

song với nhau.

1.16. Tìm m để đường thẳng

: 1

d y x

  

cắt





3 2

: 4 6 1

C y x mx

  

tại 3 điểm





0;1 , ,

A B C

biết

B C

đối xứng với nhau qua đường phân giác thứ nhất.

1.17. Tìm m để đồ thị





4 2

: 4

C y x x m

  

cắt trục hoành tại 4 điểm phân biệt sao cho diện

tích hình phẳng giới hạn bởi





và trục hoành có phần trên bằng phần dưới.

1.18. Cho hàm số









4 2

2 2 2 3

y x m x m C

      . Tìm tất cả các giá trị của tham số

để





cắt trục hoành tại bốn điểm cách đều nhau.

1.19. Tìm m để đồ thị hàm số





3 2

2 1 2 1

y x m x m

    

cắt trục hoành tại ba điểm phân biệt

đều có hoành độ nhỏ hơn 3.

1.20. Chứng minh rằng với



thì đồ thị hàm số

4 2 2 4

2 2

y x m x m m

   

luôn cắt trục

hoành tại ít nhất hai điểm phân biệt.

1.21. Tìm tất cả các giá trị củ tham số m để đường thẳng

: 2 4

d y mx m

  

cắt đồ thị hàm số

3 2

6 9 6

y x x x

   

tại ba điểm phân biệt.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.22. Tìm m để đồ thị hàm số

3 2

y x x mx m

    

cắt trục hoành tại ba điểm phân biệt

, ,

A B C

sao cho tổng hệ số góc các tiếp tuyến với đồ thị hàm số tại

, ,

A B C

bằng 3.

1.23. Tìm tất cả các cặp số





m n

sao cho trong các giao điểm của đồ thị hàm số





3 2

y mx nx mx n C

    có hai điểm cách nhau

2011

và khoảng cách từ tâm đối xứng

của





đến trục hoành bằng

2012

1.24. Tìm tất cả các giá trị của tham số m để đường thẳng : 3

d y x

 

cắt đồ thị hàm số





3 2

3 4

y x x mx m C

     tại ba điểm phân biệt





1;2 , ,

A B C

sao cho tiếp tuyến với





tại

B C

lần lượt cắt





tại

M N

và tứ giác

BMNC

là hình thoi.

1.25. Tìm tất cả các cặp giá trị





m n

để đường thẳng :

d y mx n

 

cắt đồ thị hàm số

4 2

4 3

y x x

   

tại bốn điểm phân biệt

, , ,

A B C D

có hoành độ lần lượt là

1 2 3 4

x x x x

  

sao cho

AB CD BC

 

1.26. Cho hàm số

     

3 2

2 3 2 3

y x m x m x m C

      . Tìm những giá trị của tham số

m để đường thẳng :

d y x m

  

cắt





tại ba điểm phân biệt





0, , ,

A m B C

, đồng thời

là phân giác trong góc



BOC

1.27. Tìm những giá trị của tham số m để đồ thị hàm số

3 2

3 3

y x x mx m

   

cắt trục hoành

tại ba điểm phân biệt

, ,

A B C

có hoành độ tương ứng thỏa mãn

     

3 3 3

2 2 2 3

A B C

x x x

     

1.28. Tìm m để đồ thị hàm số

3 2

3 1

y x mx m

   

cắt đồ thị hàm số tại ba điểm phân biệt

, ,

A B C

sao cho

AB BC



Tương giao với hàm phân thức bậc nhất trên bậc nhất :

BÀI TẬP MẪU

Bài 1.Cho hàm số

 

2 1

y C

 





Chứng minh rằng với mọi

đường thẳng

y x m

 

luôn cắt đồ thị





tại hai điểm phân biệt

và

. Gọi

1 2

k k

lần lượt là hệ số góc của các tiếp tuyến với





tại

và

. Tìm

để tổng

1 2

k k



lớn nhất.

Lời giải:

Hoành độ giao điểm của :

d y x m

 

và





là nghiệm phương trình:

2 1

x m

 

 



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam









2 1 1

x m x x

     

( do



không là nghiệm)

2 2 1 0(*)

x mx m    

Ta có

' 2 2 0,

m m m

     

. Suy ra

luôn cắt





tại hai điểm phân biệt với mọi

Gọi

1 2

x x

là nghiệm của (*), ta có

   

 

1 2 1 2 1 2

1 2

2 2 2

1 2

1 2 1 2

4 8 4 2

1 1

2 1 2 1

4 2 1

x x x x x x

k k

x x

x x x x

    

     

 

  

Theo định lí Vi-ét ta có

1 2 1 2

;

x x m x x



     .

Từ đó suy ra

 

1 2

4 8 6 4 1 2 2

k k m m m

          

. Dấu bằng xảy ra khi và chỉ khi

 

Vậy giá trị lớn nhất của

1 2

k k

  

khi và chỉ khi

 

Bài 2.Cho hàm số

 

2 1

y C







Chứng minh rằng với mọi

đường thẳng

y x m

  

luôn cắt đồ thị





tại hai điểm phân biệt

và

. Gọi

1 2

k k

lần lượt là hệ số góc của các tiếp tuyến với





tại

và

. Tìm

để tổng

1 2

k k



nhỏ nhất.

Lời giải:

Hoành độ giao điểm của :

d y x m

  

và





là nghiệm phương trình:

2 1

x m



  











2 1 1

x m x x

     

( do



không là nghiệm)

2 2 1 0(*)

x mx m    

Ta có

' 2 2 0,

m m m

     

. Suy ra

luôn cắt





tại hai điểm phân biệt với mọi

Gọi

1 2

x x

là nghiệm của (*), ta có

   

 

1 2 1 2 1 2

1 2

2 2 2

1 2

1 2 1 2

4 8 4 2

1 1

2 1 2 1

4 2 1

x x x x x x

k k

x x

x x x x

    

   

 

  

Theo định lí Vi-ét ta có

1 2 1 2

;

x x m x x



     .

Từ đó suy ra

 

1 2

4 8 6 4 1 2 2

k k m m m

       

. Dấu bằng xảy ra khi và chỉ khi

 

Vậy giá trị nhỏ nhất của

1 2

k k

 

khi và chỉ khi

 

Bài 3. Cho hàm số

 

2 1

y C







HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Chứng minh rằng đường thẳng :

d y x m

  

luôn cắt đồ thị hàm số





tại 2 điểm phân biệt

và

. Tìm

để đoạn

có độ dài nhỏ nhất.

Lời giải:

Hoành độ giao điểm của

và





là nghiệm phương trình:

2 1

x m



  











2 2 1

x m x x

     

( do

 

không là nghiệm)





4 1 2 0 (*)

x m x m     

Ta có

   

4 4 1 2 12 0,

m m m m

        

. Suy ra

luôn cắt





tại hai điểm phân biệt

A B

Do , ;

A A B B

A B d y x m y x m

       

. Từ đó suy ra

       

2 2 2 2

2 2 8

A B A B A B A B A B

AB x x y y x x x x x x

        

Theo định lí Vi-ét ta có:

4; 1 2

A B A B

x x m x x m

     . Từ đó suy ra





2 2

2 12 2 2

AB m AB    

. Dấu bằng xảy ra khi và chỉ khi



Vậy giá trị nhỏ nhất của

AB 

khi và chỉ khi



Bài 4.Cho hàm số

 

y C







Đường thẳng

có hệ số góc

đi qua điểm





1;1

I  và cắt





tại hai điểm phân biệt

và

sao cho

là trung điểm của

Tìm

Lời giải:

+ Phương trình đường thẳng





: 1 1

d y k x

  

+ Hoành độ giao điểm của

và





là nghiệm phương trình:

 

1 1

k x



  



2 4 0(*)

kx kx k     (do

 

không là nghiệm).

Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có hai nghiệm phân biệt

1 2

x x

thỏa

mãn

1 2

' 4 0 0

2 2

k k

x x x







     





   



Vậy giá trị cần tìm của

là







Bài 5.Cho hàm số

 

2 4

y C







HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Gọi

là đường thẳng đi qua





1;1

I có hệ số góc

. Tìm

để

cắt





tại hai điểm phân biệt

và

sao cho độ dài

bằng

3 10

Lời giải:

+ Phương trình đường thẳng





: 1 1

d y k x

  

+ Hoành độ giao điểm của

và





là nghiệm phương trình:

 

2 4

1 1

k x



  





không là nghiệm nên phương trình tương đương với





2 3 3 0(*)

kx k x k    

cắt





tại hai điểm phân biệt

M N

khi và chỉ khi phương trình (*) có hai nghiệm phân biệt

0 (1)

9 24 0





   



   











, 1 1; 1 1

M M N N

M N d y k x y k x

       

. Suy ra

   





 





 

2 2 2 2

2 2 2

1 1 4 90

M N M N M N M N M N

MN x x y y k x x k x x x x

 

           

 

Theo định lí Vi-ét ta có:

2 3 3

;

M N M N

k k

x x x x

k k

 

   . Từ đó suy ra









3 2 2

8 27 8 3 0 3 8 3 1 0 3

k k k k k k k

           

hoặc

3 41

 

 ( thỏa mãn (1)).

Vậy giá trị cần tìm của

là

3 41

 

 

 



 

 

 

Bài 6. Cho hàm số

 

2 1

y C







Tìm

để đường thẳng :

d y x m

 

cắt





tại hai điểm phân biệt

và

sao cho

và

cùng

với gốc tọa độ tạo thành tam giác vuông tại

Lời giải:

+ Hoành độ giao điểm của

và





là nghiệm phương trình:

2 1

x m



 











1 2 1

x m x x

    

( do

 

không là nghiệm)





3 1 0(*)

x m x m      . Ta có

2 5 0,

m m m

     

. Từ đó suy ra

luôn cắt





tại hai điểm phân biệt

A B

Do hai điểm , ;

A A B B

A B d y x m y x m

     

Suy ra tọa độ của









; , ;

A A B B

A x x m B x x m

 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Và









; , ;

A A B B

OA x x m OB x x m

   

 

Tam giác

OAB

vuông tại

khi và chỉ khi













. 0 0 2 0(1)

A B A B A B A B

OAOB x x x m x m x x m x x m          

 

Theo định lí Vi-ét ta có: 3 ; 1

A B A B

x x m x x m

    

. Khi đó (1) trở thành









3 2 1 0 2

m m m m m

       

Vậy

 

là giá trị cần tìm.

Bài 7. Cho hàm số

 

y C







Chứng minh rằng với mọi giá trị của

thì trên





luôn có các cặp điểm

và

nằm về hai

nhánh của





và thỏa mãn

A A

B B

x y m

  





  



Lời giải:

+ Ta có

, :

A A A A

B B B B

x y m y x m

A B d y x m

x y m y x m

    

 

    

 

    

 

Khi đó yêu cầu bài toán trở thành chứng minh

luôn cắt





tại hai điểm thuộc về hai nhánh của





+ Hoành độ giao điểm của

và





là nghiệm phương trình:

x m



 











2 2

x m x x

    

(do



không là nghiệm)









3 2 2 0(*)

x m x m      . Ta có

2 17 0,

m m m

     

. Từ đó suy ra

luôn cắt





tại hai điểm phân biệt với mọi

Mặt khác, kí hiệu













( ) 3 2 2 1. 2 4 0 2

g x x m x m g

         

nằm giữa hai nghiệm

của (*). Ta có đpcm.

Bài 8. Cho hàm số

 

2 2

y C







. Tìm tất cả các giá trị thực của tham số

để đường thẳng





d y x m

 

cắt đồ thị





tại hai điểm phân biệt

A B

sao cho

2 2

OA OB  .

Lời giải :

Hoành độ giao điểm của









d C

là nghiệm của phương trình :

2 2

x m



 





, không là nghiệm của phương trình nên phương trình tương đương với

















2 2 2 2 2 3 2 1 0(*)

x x x m x m x m          .

 

4 4 25 2 1 24 0,m m m m

         



. Nên phương trình (*) luôn có hai nghiệm

phân biệt.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Gọi









1 1 2 2

, ; ,

A x x m B x x m

 

là tọa độ giao điểm của





và





, khi đó theo định lý viét, ta

có :

 

1 2 1 2

2 3

; 1

x x x x m



     

Từ đó suy ra :

   

2 2

2 2 2 2

1 1 2 2

OA OB x x m x x m

      

   

1 2 1 2 1 2

2 4 2 2

x x x x m x x m

     

 

2 3 2 3

2 4 1 2 2

2 2

m m

m m m

 

   

     

   

   

 

4 2 17

m m  

Vậy

 

2 2 2

37 1 37 5

4 2 17 2

2 2 2 2

OA OB m m m m

          

Vậy

; 2

m m

  

là hai giá trị cần tìm.

BÀI TẬP ĐỀ NGHỊ

1.1. Cho hàm số

 

x m

y C







. Chứng minh rằng với mọi







cắt đường thẳng





: 2

d y x m

 

tại hai điểm phân biệt

A B

thuộc một đường





cố định. Dường thẳng

cắt trục hoành tại hai điểm

M N

. Tìm những giá trị của m để 3

OAB OMN

S S .

1.2. Cho hàm số

 

y C





. Tìm tất cả các giá trị của tham số

để đường thẳng

y mx m

  

cắt đồ thị





tại hai điểm phân biệt

và

sao cho

2 2

MA MB



đạt giá trị

nhỏ nhất, biết điểm





1,1

M  .

1.3. Cho hàm số

 

2 2

y C







. Tìm

để đường thẳng : 2

d y x m

 

cắt





tại hai điểm

phân biệt

A B

sao cho

AB 

1.4.

Cho hàm số

 

y C

x m







. Tìm

để đường thẳng

y x

 

cắt





tại hai điểm

phân biệt

và

sao cho

2 2

AB 

1.5. Với mỗi giá trị của tham số

để đường thẳng

: 1

d y mx

 

cắt đồ thị hàm số

2 1







tại hai điểm phân biệt

M N

và cắt hai đường tiệm cận lần lượt tại

A B

. Chứng minh

rằng

MA NB



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.6. Cho đường thẳng

 

2 1

y C







và điểm





2;4

A  . Viết phương trình đường thẳng

cắt đồ thị hàm số





tại hai điểm phân biệt

B C

sao cho tam giác

ABC

đều.

1.7. Tìm m để đường thẳng

: 2

d y x m

 

cắt đồ thị hàm số

2 1







tại hai điểm phân biệt

A B

sao cho

4 2

AB 

1.8. Tìm m để đường thẳng

y x m

 

cắt đồ thị hàm số

 

2 1







tại hai điểm phân biệt

A B

sao cho

2 2

OA OB  .

CÁC BÀI TOÁN VỀ CỰC TRỊ HÀM SỐ

Loại 1 : Điều kiện hàm số

( )

y f x



có cực trị .

Phương trình

'( ) 0

f x



có ít nhất 2 nghiệm phân biệt trở lên.

Loại 2 : Điều kiện để một điểm là cực trị của hàm số.

Cho hàm số

( )

y f x



điểm









0 0

;

M x y C

 là điểm cực trị của hàm số khi đó

'( ) 0

f x



(i). Nếu

'( ) 0

''( ) 0

f x













là điểm cực đại của đồ thị hàm số

(ii). Nếu

'( ) 0

''( ) 0

f x













là điểm cực tiểu của đồ thị hàm số

Loại 3 : Đường thẳng đi qua các điểm cực trị của hàm số.

Xét với hàm số đa thức bậc 3 :

3 2

y ax bx cx d

   

có đạo hàm

' 3 2

y ax bx c

  

Lấy

chia cho

ta được

1 2

' 2

3 9 3 9 9

b c b bc

y x y x d

a a a

 

     

 

 

Hàm số đạt cực trị tại

1 2

x x

thì khi đó

1 2

'( ) '( ) 0

y x y x

 

nên

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1 1

2 2

( ) 2

3 9 9

( ) 2

3 9 9

c b bc

y x x d

a a

c b bc

y x x d

a a



 

   



 

  





 



   

 



 



Hai điểm cực trị của hàm số nằm trên đường thẳng

3 9 9

c b bc

y x d

a a

 

   

 

 

Lưu ý : Với các hoành độ cực trị không phụ thuộc tham số thì ta không cần thiết phải làm theo

cách này, nhưng có chứa tham số thì đây là lựa chọn khôn ngoan.

Loại 4 : Các điểm cực trị thỏa mãn một điều kiện chẳng hạn lập thành tam giác vuông, tam giác

đều,…Lúc này chúng ta dựa vào tính chất của tam giác.

Dạng toán : Liên quan đến điều kiện tồn tại cực, cực tiểu- tọa độ cực trị.

Phương pháp :

- Để hàm số có cực trị khi và chỉ khi phương trình

' 0



có hai nghiệm phân biệt.

- Một điểm

là điểm cực tiểu của hàm số thì





 

' 0

'' 0

y x















cần phải thử lại xem

có đổi

dấu từ âm sang dương khi đi qua

hay không.

- Một điểm

là điểm cực đại của hàm số thì





 

' 0

'' 0

y x















cần phải thử lại xem

có đổi

dấu từ dương sang âm khi đi qua

hay không.

- Cho hai điểm









1 1 2 2

; ; ;

A x y B x y

và đường thẳng

: 0

d Ax By C

  

hoặc đường tròn

     

2 2

C x a y b R

   

Xét









   

 

   

 

1 1 2 2

2 2 2 2

2 2

1 1 2 2

T Ax By C Ax By C

V x a y b R x a y b R

     





        





Khi đó hai điểm

A B

nằm cùng phía với

hoặc





khi và chỉ khi



hoặc



Hai điểm

A B

nằm khác phía đối với

hoặc





khi và chỉ khi



hoặc



Đặc biệt :

Hai điểm cực trị nằm khác phía với trục tung thì pt

' 0



có hai nghiệm trái dấu.

Hai điểm cực trị nằm khác phía đối với trục hoành thì

CÐ CT

y y



hoặc phương trình



có

ba nghiệm phân biệt.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

BÀI TẬP MẪU

Bài 1. Tìm m để hàm số sau có cực trị

 

3 2 2

2 3 2 8

y x mx m m x

     

Lời giải :

Ta có

2 2

' 2 2 3 2

y x mx m m

    

Hàm số có cực trị khi và chỉ khi phương trình

' 0



có hai nghiệm phân biệt

' 3 2 0 1 2

m m m

        

Bài 2. Tìm m để hàm số





4 2 2

9 10

y mx m x

   

có 3 cực trị.

Lời giải :

Ta có





3 2 2 2

' 4 2 9 2 (2 9)

y mx m x x mx m

     

Hàm số có 3 cực trị khi và chỉ khi phương trình

' 0



có 3 nghiệm phân biệt, điều này tương

đương với

0 3 3

m m





 



     









Bài 3. Tìm m để hàm số

4 2

1 3

4 2

y x mx

  

chỉ có cực tiểu mà không có cực đại.

Lời giải :

Ta có





3 2

' 2 2

y x mx x x m

   

+ Nếu

 

hàm số chỉ có cực tiểu tại



+ Nếu



thì hàm số chỉ có cực tiểu tại



+ Nếu



thì hàm số có 3 cực trị, nên không thỏa mãn.

Vậy



là những giá trị cần tìm.

Bài 4. Tìm m để hàm số

 

y x m x

  

đạt cực tiểu tại



Lời giải :

Ta có

   

' 3 3; '' 6

y x m y x m

    

Hàm số đạt cực tiểu tại



thì

'(0) 0

3 3 0

''(0) 0

6 0





 



   

 



 



Thử lại với

 

thì hàm số

 

1 3

y x x

  

có

   

' 3 1 3 3 2

y x x x

    

đổi dấu từ âm sang dương khi đi qua

. Vậy nên hàm số đạt cực tiểu tại



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Vậy

 

là giá trị cần tìm.

Bình luận : Rất nhiều học sinh cũng như cả các thầy cô không hiểu rõ điều kiện để hàm số đạt

cực trị tại một điểm ; và tất nhiên như trên khi nói điều kiện để hàm số đạt cực tiểu tại



thì

học sinh lại viết :

Để hàm số đạt cực tiểu tại



khi và chỉ khi

'(0) 0

''(0) 0











Lưu ý : Sẽ không có điều tương đương trên, mà chỉ có là nếu đạt cực tiểu tại



thì

'(0) 0

''(0) 0











chứ không có điều ngược lại

Do đó khi tìm được giá trị của tham số m thì ta phải thử lại xem có thỏa mãn điều kiện đổi dấu

của

hay không.

Bài 5. Tìm m để hàm số

   

3 2 2 2

2 3 1 5

y x m m x m x m

       

đạt cực tiểu tại

 

Lời giải :

Ta có





 

2 2 2

' 2 2 3 1

'' 2 2 2

y x m m x m

y x m m



     





   





Hàm số đạt cực tiểu tại

 

thì

'( 2) 0 2 2 0

''( 2) 0

4 0

y m m

m m



   





  

 

 

 





Thử lại với



thỏa mãn.

Vậy



là giá trị cần tìm.

Bài 6. Tìm m để hàm số









3 1

y x m x x m

    

có cực đại và cực tiểu thỏa mãn

. 1

C CT

x x



Lời giải :

Ta có





' 3 2 3 2 1

y x m x m

    

Hàm số có cực đại và cực tiểu thỏa mãn

. 1

C CT

x x



khi và chỉ khi phương trình

' 0



có hai

nghiệm phân biệt

1 2

x x

thỏa mãn

1 2

x x



, điều này tương đương với

2 2

1 2

' 7 0

2 1

x x



   















 

 

 





 

 



là những giá trị cần tìm.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 7. Tìm các giá trị của tham số

để đồ thị hàm số

   

3 2

1 1

3 2 1 1

3 2

y x m x m x

     

có

hai điểm cực trị với hoành độ lớn hơn 1.

Lời giải :

Ta có









' 3 2 1

y x m x m

    









' 0 3 2 1 0(*)

y x m x m      

Hàm số có 2 cực trị khi và chỉ khi phương trình (*) có hai nghiệm phân biệt

2 1 0 1( )

m m m i

       

Yêu cầu bài toán tương đương với (*) có 2 nghiệm

1 2

x x

thỏa mãn

  

 

1 2

1 22

3 2

2 1 3 1 01 1 01

x x

m mx xx

 





 

   

  

      







Kết hợp với điều kiện (i) suy ra

0 1

 

là giá trị cần tìm.

Bài 7. Cho hàm số





3 2

2 12 13

y x mx x C

    .

Tìm m để





có cực đại và cực tiểu và các điểm này cách đều trục tung.

Lời giải :

Ta có





' 2 3 6

y x mx

  

Phương trình

' 0



có

72 0

   

nên hàm số luôn đạt cực trị tại hai điểm

1 2

x x

Điểm cực đại và điểm cực tiểu của hàm số cách đều trục tung khi và chỉ khi

1 2 1 2 1 2

0 0

x x x x x x m



         

Vậy



là giá trị cần tìm.

Bài 8. Cho hàm số

 

3 2 2

1 1

3 2

y x mx m x

    . Tìm tất cả các giá trị của tham số m để hàm số

có cực đại, cực tiểu sao cho

CÐ

x x

là độ dài các cạnh góc vuông của một tam giác vuông có độ

dài cạnh huyền bằng

Lời giải :

Ta có

2 2

' 3

y x mx m

   

Yêu cầu bài toán tương đương với phương trình

' 0



có hai nghiệm dương phân biệt

1 2

x x

và

thỏa mãn

2 2

1 2

x x

 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

 

2 2 2

2 2

4 0

3 3

3 0

2 2 3

S m

m m

P m

S P m m

  



   





 



 

   

     

  

 

    

 

 



Vậy

m  là giá trị cần tìm.

Bài 9. Tìm tất cả các giá trị của tham số m để các điểm cực đại, cực tiểu của đồ thị hàm số









3 2 2

2 1 3 2 4

y x m x m m x

       

nằm về hai phía trục tung.

Lời giải :

Để đồ thị hàm số có cực đại, cực tiểu nằm về hai phía đối với trục tung khi và chỉ khi phương

trình

' 0



có hai nghiệm trái dấu









2 2

3 2 2 1 3 2

x m x m m

      

có hai nghiệm trái dấu





3 3 2 0 1 2

m m m

      

Vậy





1;2

m là giá trị cần tìm.

Bài 10. Tìm m để đồ thị hàm số

3 2

y x x mx

   

có cực đại, cực tiểu cách đều đường

thẳng

y x

 

Lời giải :

Hàm số có cực trị khi và chỉ phương trình

' 3 6 0

y x x m

   

có hai nghiệm phân biệt

' 9 3 0 3

m m

       

Khi đó gọi tọa độ hai điểm cực trị là









1 1 2 2

; ; ;

A x y B x y

Lấy

chia cho

ta được :

1 2

' 2 2

3 3 3 3

x m m

y y x

   

     

   

   

   

1 1

1 2

2 2

3 3

' ' 0

2 2

3 3

m m

y x

y x y x

m m

y x



 

    

 



  

  



 



    

 



 



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Suy ra đường thẳng đi qua hai điểm cực trị là

: 2 2

3 3

m m

d y x

 

    

 

 

Vậy để hai điểm cực trị cách đều đường thẳng

y x

 

thì hoặc

song song với đường thẳng

y x

 

hoặc trung điểm của

thuộc đường thẳng

y x

 

Trường hợp 1 :

2 3

2 1

3 2

 

      

 

 

Trường hợp 2 :

 

1 2 1 2 1 2

1 2

1 2 2 1

2 2 2 3 3 2

y y x x m m x x

x x

  

 

         

 

 

Theo định lý vi-ét ta có :

1 2

2 2 2 1 1 0

3 3

m m

x x m

 

          

 

 

Cả hai giá trị này đều thỏa mãn điều kiện

Vậy

 

 

 

 

là giá trị cần tìm.

Bài 11. Tìm m để cực đại, cực tiểu của đồ thị hàm số

3 2 3

3 4

y x mx m

   đối xứng nhau qua

đường thẳng

y x



Lời giải :

Ta có

' 3 6 0

y x mx

x m





   







, vậy để hàm số có cực trị khi và chỉ khi



Khi đó gọi tọa độ hai điểm cực trị là













3 3

0;4 ; 2 ;0 2 ; 4

A m B m AB m m

  



và trung

điểm của

là





I m m

Vậy

A B

đối xứng nhau qua đường thẳng

d y x



khi và chỉ khi

AB d

I d











2 4 0

m m



 



   











Vậy

m   là giá trị cần tìm.

Bài 12. Tìm m để hàm số





3 2 2 3

3 3 1

y x mx m x m m

     

có cực trị đồng thời khoảng cách

từ điểm cực đại đến gốc tọa độ bằng

lần khoảng cách từ điểm cực tiểu đến gốc tọa độ.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải :

Hàm số có cực trị khi và chỉ khi pt





2 2

' 3 6 3 1 0

y x mx m

    

có hai nghiệm phân biệt

1 0,

    

Từ đó suy ra tọa độ các điểm cực trị là điểm cực đại





1;2 2

A m m

  và điểm cực tiểu





1; 2 2

B m m

   .

Yêu cầu bài toán tương đương với :

OA OB



6 1 0 3 2 2

m m m       

Bài 13. Tìm m để hàm số









3 2

1 2 2 2

y x m x m x m

      

có cực trị đồng thời hoành độ

cực tiểu nhỏ hơn 1.

Lời giải :

Yêu cầu bài toán tương đương với pt





' 3 2 1 2 2 0

y x m x m

     

có hai nghiệm phân biệt

1 2

x x

 

Cách 1 :

ycbt tương đương với :

' 4 5 0

5 7

2 1 4 5

4 5

m m

m m m



    



  



   

 





Cách 2 :

Đặt





( ) 3 2 1 2 2

g x x m x m

    

Vậy yêu cầu bài toán tương đương với :

' 4 5 0

5 7

(1) 5 7 0

4 5

2 1

2 3

m m

g m m

S m





    



      









 



Vậy

5 7

;

4 5

 



 

 

là giá trị cần tìm.

Bài 14. Tìm m để hàm số









3 2

3 1 3 2 2

y x m x m m x m

      

có cực trị, đồng thời khoảng

cách từ điểm cực đại đến trục hoành bằng khoảng cách từ điểm cực tiểu đến trục tung.

Lời giải :

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Ta có

   

' 3 6 1 3 2 0

x m

y x m x m m

x m





      



 



Suy ra hàm số luôn có cực trị

Khi đó tọa độ điểm cực đại





3 2

; 3 2

A m m m m

  

và điểm cực tiếu





3 2

2; 3 6

B m m m m

   

Yêu cầu bài toán tương đương với

 





3 2 2

3 2 2 2 1 2

m m m m m m m m

          

2 0

1 1

m m

 



 





 



    







   









Vậy có 4 giá trị cần tìm của m là





2; 1;0;1

 

Bài 15. Tìm các giá trị thực của tham số m để điểm cực đại, cực tiểu của hàm số

   

3 2

1 4

1 1

3 3

y x m x m

    

nằm khác phía với đường tròn





2 2

: 4 3 0

T x y x

   

Lời giải:

Ta có

 

' 2 1 0

2 1

y x m x

x m





    



 



Hàm số có cực đại, cực tiểu khi và chỉ khi

 

Khi đó tọa độc hai điểm cực trị là

   

 

0; 1 ; 2 1 ;0

A m B m

 

 

 

 

Đường tròn





có tâm





2;0

I bán kính





Hai điểm

A B

nằm khác phía với đường tròn





khi và chỉ khi

  

 

2 2 2 2 2

0 3 1 4 1 0

IA R IB R m m

 

       

 

 

1 1

4 1 0

2 2

m m

      

thỏa mãn điều kiện

Vậy

1 1

;

2 2

 

 

 

 

là những giá trị cần tìm.

BÀI TẬP ĐỀ NGHỊ

1.1. Tìm m để hàm số





3 2

3 1 1

y mx mx m x

    

có cực trị.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.2. Tìm m để hàm số

4 2 2

y x mx m m

   

đạt cực tiểu tại



1.3. Tìm m để hàm số









3 2

3 2 4 2 1

y x m x m x m

       

đạt cực đại tại

 

1.4. Cho hàm số





4 3 2

4 3 1 1

y x mx m x

    

. Với giá trị nào của tham số m để hàm số chỉ

có cực tiểu mà không có cực đại.

1.5. Cho hàm số









4 3 2

3 2 1

y x m x m x

     . Chứng minh rằng với mọi

 

hàm số

luôn có cực đại mà hoành độ không dương.

1.6. Cho hàm số

4 2

1 1

2 2

y x mx

  

. Xác định m để hàm số có cực tiểu mà không có cực đại.

1.7. Chứng minh rằng với mọi tham số m hàm số

4 3 2

y x mx mx mx

    

không đồng thời

có cực đại và cực tiểu.

1.8. Tìm m để hàm số





4 2

1 1 2

y mx m x m

     chỉ có đúng 1 cực trị.

1.9. Tìm m để hàm số









3 2

2 3 1 6 2 1

y x m x m x

     

có cực đại

và cực tiểu

thỏa

mãn

1 2

x x

 

Đáp số :

 

1.10. Chứng minh rằng với mọi giá trị của tham số m thì hàm số









3 2

2 3 2 1 6 1 1

y x m x m m x

     

luôn có cực đại, cực tiểu đồng thời khoảng cách

giữa cực đại, cực tiểu không đổi.

1.11. Tìm m để hàm số





3 2

3 2 9 1

y x m x x m

     

đạt cực trị tại các điểm

1 2

x x

sao cho

1 2

x x

 

1.12. Cho hàm số













3 2 3

2 3 2 6 5 1 4 2

y x m x m x m

      

. Tìm những giá trị của tham

số m để hàm số đạt cực tiểu tại điểm





1;2

x  .

Đáp số:

 

 





 

1.13. Tìm m để đồ thị hàm số

3 2

y x x mx m

    

có hai điểm cực trị nằm về hai phía của

trục hoành.

Đáp số :





m  .

1.14. Cho hàm số

 

3 2 2

1 1

3 2

y x mx m x

    . Tìm tất cả các giá trị của tham số m để hàm số

có cực đại, cực tiểu sao cho

CÐ

x x

là độ dài các cạnh góc vuông của một tam giác

vuông có độ dài cạnh huyền bằng

1.15. Tìm m để đồ thị hàm số

3 2

y x x m

  

có cực đại, cực tiểu nằm vế hai phía đối

với đường thẳng

x y

 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.16. Tìm m để đồ thị hàm số





3 2

3 1 9 2

y x m x x m

     

có cực đại, cực tiểu đối

xứng nhau qua đường thẳng

y x



1.17. Tìm điểm

trên đường thẳng

y x

 

sao cho tổng khoảng cách từ

đến hai điểm

cực trị của đồ thị hàm số

3 2

y x x

  

đạt giá trị nhỏ nhất.

1.18. Tìm tất cả các giá trị của tham số m để hoành độ các đểm cực đại, cực tiểu của đồ thị hàm

số





3 2

2 3 5

y m x x mx

    

là các số dương.

1.19. Tìm tất cả các giá trị của tham số m để hoành độ các điểm cực trị

1 2

x x

của đồ thị hàm số

3 2

4 3

y x mx x

  

thỏa mãn

1 2

x x

 

1.20. Xác định m để hàm số









3 2

1 2 2 2

y x m x m x m

      

đạt cực trị tại

1 2

x x

sao cho

1 2

x x

 

1.21. Tìm m để hàm số

   

3 2

2 5 4 3 1

y x m x m x m

      

đạt cực tại

1 2

x x



sao cho

1 2

x x

 

1.22. Tìm m để hàm số

   

3 2

1 1

1 3 2

3 3

y mx m x m x

     

đạt cực trị tại

1 2

x x

thỏa mãn

1 2

2 1

x x

 

1.23. Tìm m để hàm số













3 2 2 2

2 1 4 1 2 1

y x m x m m x m

       

đạt cực đại, cực tiểu

tại

1 2

x x

thỏa mãn

1 2

1 1

x x



  .

1.24. Tìm m để đồ thị hàm số

3 2 2

2 9 12 1

y x mx m x

   

có cực đại, cực tiểu đồng thời

CÐ

x x

 

1.25. Tìm m để hàm số

 

3 2 2

1 4 3 1

y x m x m m x

      

đạt cực trị tại hai điểm

1 2

x x

sao cho





1 2 1 2

A x x x x

  

đạt giá trị lớn nhất.

1.26. Tìm m để hàm số

3 2

1 5

4 4

3 2

y x x mx

   

đạt cực trị tại

1 2

x x

sao cho biểu thức

2 1

2 2

1 2

5 12

x mx m

x mx m m

 

 

 

đạt giá trị nhỏ nhất.

1.27. Tìm m để hàm số









3 2

2 3 2 1 6 1 1

y x m x m m x

     

có cực trị, khi đó tìm quỹ tích

trung điểm của đoạn thẳng nối điểm cực đại và cực tiểu.

1.28. Tìm m để các điểm cực trị của đồ thị hàm số

3 2

y x x

  

nằm về hai phía đối với

đường tròn

2 2 2

2 4 5 1 0

x y mx my m

     

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.29. Tìm m để đồ thị hàm số









3 2

3 1 3 2 12 8

y x m x m m x m

      

có hai điểm cực trị

;

A B

sao cho tổng độ dài

MA MB



nhỏ nhất với





3;2

M .

1.30. Chứng minh rằng với mọi giá trị thực của tham sốm thì đồ thị hàm số









3 2 3 2

3 1 3 2 3

y x m x m m m m

       luôn có hai điểm cực trị ; đồng thời khoảng

cách giữa hai điểm cực trị không đổi.

Dạng toán : Đường thẳng đi qua điểm cực đại cực tiểu

BÀI TẬP MẪU

Bài 1. Tìm m để điểm





3;5

A nằm trên đường thẳng nối hai điểm cực trị của đồ thị hàm số





3 2

3 3 6 1

y x mx m x

    

Lời giải :

Hàm số có cực trị khi và chỉ khi phương trình

' 0



có hai nghiệm phân biệt

2 6 0

x mx m

    

có hai nghiệm phân biệt

' 6 0 (*)

m m





      



 



Khi đó tọa độ hai điểm cực trị là









1 1 2 2

; ; ;

M x y N x y

Lấy

chia cho

ta được :

 

2 2

' 2 6 6 1

3 3

x m

y y m m x m m

 

        

 

 

   





 

2 2

1 1

1 2

2 2

2 6 6 1

' ' 0

2 6 6 1

y m m x m m

y x y x

y m m x m m



      



  



      





Suy ra đường thẳng đi qua hai điểm cực trị là





2 2

: 2 6 6 1

d y m m x m m

      

, theo đề bài





3;5

A d



nên

 

2 2

5 6 6 6 1

m m m m







       



 



đối chiếu với điều kiện (*) suy ra chỉ nhận giá trị



Vậy



là giá trị cần tìm.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 2. Cho hàm số

 

3 2

1 1

3 2

y x m x mx

    . Tìm m để đồ thị hàm số có cực đại, cực tiểu đối

xứng nhau qua đường thẳng

:72 12 35 0

x y

   

Lời giải :

Hàm số có cực trị khi và chỉ khi pt





' 1 0

y x m x m

    

có hai nghiệm phân biệt

 

1 4 0 1

m m m

       

Khi đó tọa độ hai điểm cực trị là









1 1 2 2

; ; ;

M x y N x y

Lấy

chia cho

, ta được :

   

1 1 1

' 1 1

3 6 6 6

x m

y y m x m m



 

     

 

 

   

1 1

1 2

2 2

1 1

6 6

' ' 0

1 1

6 6

y m x m m

y x y x

y m x m m



    



  





    





Suy ra đường thẳng đi qua hai điểm cực trị là

   

1 1

: 1 1

6 6

d y m x m m

    

Để

M N

đối xứng nhau qua



thì trước tiên phải có

 

1 .6 1

d m





       







 Với

 

0 0;0 ; 1;

m M N

 

   

 

 

trung điểm của

là

1 1

;

2 12

 

 

 

 

. Nên loại



 Với

5 2

2 1; ; 2;

6 3

m M N

   

  

   

   

trung điểm của

là

3 9

;

2 12

 



 

 

. Nên loại



Vậy không có giá trị nào của m thỏa mãn.

Bài 3. Chứng minh rằng với mọi giá trị của tham số m thì đồ thị hàm số





3 2 2 3 2

3 3 1

y x mx m x m m

      

luôn có cực đại, cực tiểu đồng thời gọi





;

x y

là hoành độ,

tung độ các điểm cực trị thì ta luôn có

2 0

x y

  

Lời giải :

Ta có





2 2

' 3 6 3 1 0

y x mx m

     

, có

1 m

  

. Nên luôn có hai nghiệm phân biệt hay hàm

số luôn có cực trị với mọi m.

Khi đó gọi tọa độ hai điểm cực trị là









1 1 2 2

; ; ;

A x y B x y

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lấy

chia cho

, ta được :

' 2

3 3

x m

y y x m m

 

    

 

 

   

1 1

1 2

2 2

' ' 0

y x m m

y x y x

y x m m



  



  



  





Nên đường thẳng đi qua hai điểm cực trị là

y x m m

  

Từ đó suy ra hoành độ, tung độ các điểm cực trị thỏa mãn

1 1 1

2 0

4 4 2

x y m m m

 

       

 

 

. Từ đó ta có đpcm.

Bài 4. Chứng minh rằng với những giá trị thực của tham số m để đồ thị hàm số

   

3 2

3 1

1 3 1

2 2

y x m x mx m m

     

có cực đại, cực tiểu ; đồng thời gọi





;

x y

là tọa độ các

điểm cực đại, cực tiểu thì ta luôn có





x y x

 

Lời giải :

Ta có

 

' 3 3 1 3 0

x m

y x m x m





     







Để hàm số có cực trị khi và chỉ khi



Khi đó gọi tọa độ hai điểm cực trị là









1 1 2 2

; ; ;

A x y B x y

Lấy

chia cho

, ta được :

   

1 1

1 ' 1

3 6 2

y m y m x

 

    

 

 

   

 

1 1

1 2

2 2

' ' 0

y m x

y x y x

y m x



  



  





  





Nên đường thẳng đi qua hai điểm cực trị là

 

y m x

  

Từ đó suy ra hoành độ, tung độ các điểm cực trị thỏa mãn

 

3 4 2

1 0

x y x x m x

    

. Từ

đó ta có đpcm.

Bài 5. Với mỗi giá trị thực của tham số m để đồ thị hàm số

3 2 2

y x x m x   

có cực đại,

cực tiểu ; đồng thời gọi





;

x y

là tọa độ các điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức

y x

x y







HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải :

Hàm số có cực trị khi và chỉ khi phương trình

2 2

' 3 2 0

y x x m

   

có hai nghiệm phân biệt, khi

và chỉ khi

2 2

' 1 3 0 0

m m

      

Khi đó gọi tọa độ hai điểm cực trị là









1 1 2 2

; ; ;

A x y B x y

Lấy

chia cho

, ta được :

1 2 2

3 9 3 9

y y m x

   

   

   

   

   

1 1

1 2

2 2

3 9

' ' 0

2 2

3 9

y m x

y x y x

y m x



 

 

 



  

  



 



 

 



 



Nên đường thẳng đi qua hai điểm cực trị là

2 2

3 9

y m x

 

 

 

 

Vậy

2 2

2 11

3 9

2 7

2 2

3 9

m x x

y x

x y

m x x

 

 



 



 

  



 



 

 

 

Xét hàm số

2 11

3 9

( )

2 7

3 9

f t







, với

t m

 

 





 

Ta có

( )

f t

là hàm đơn điệu tăng trên

 





 

, nên suy ra

( ) (0)

P f t f

   

Vậy giá trị nhỏ nhất của

bằng



khi



Bài 6. Tìm các giá trị thực của m để đường thẳng đi qua cực đại, cực tiểu của đồ thị hàm số

3 2

3 1

y x x

  

tiếp xúc với đường tròn

     

2 2

: 1 5

T x m y m

    

Lời giải :

Dễ thấy hai điểm cực trị là









0;1 ; 2; 3

A B



, suy ra phương trình đi qua hai điểm cực trị của

hàm số là

:2 1 0

d x y

  

Đường tròn





có tâm





; 1

I m m



và bán kính





Yêu cầu bài toán tương đương với

 

2 2

2 1 1

; 5 5

2 1

m m

d I d m

  

     



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

BÀI TẬP ĐỀ NGHỊ

1.1. Tìm tất cả các giá trị của tham số m để đường thẳng đi qua cực đại, cực tiểu của đồ thị

hàm số

3 2

y x mx

  

cắt đường tròn tâm





1;1

I bán kính bằng 1 tại hai điểm phân biệt

A B

sao cho diện tích tam giác

IAB

lớn nhất.

Đáp số :

2 3





1.2. Tìm m để đồ thị hàm số









3 2

2 3 1 6 1 2

y x m x m m x

    

có cực đại, cực tiểu

nằm trên đường thẳng

4 0

x y

 

1.3. Tìm m để đường thẳng nối hai điểm cực trị của đồ thị hàm số

3 2

7 3

y x mx x

   

vuông góc với đường thẳng

3 7 0

x y

  

1.4. Tìm những giá trị của tham số m để đường thẳng nối hai điểm cực trị của đồ thị hàm số













3 2 2

3 1 2 3 2 1

y x m x m m x m m

       

tạo với đường thẳng

4 20 0

x y

  

một góc bằng

1.5. Tìm tất cả các giá trị của tham số m để hai điểm cực trị của đồ thị hàm số

3 2 2

y x x m x m

   

đối xứng nhau qua đường thẳng

2 5 0

x y

  

1.6. Tìm tất cả các giá trị của tham số m để khoảng cách giữa hai điểm cực trị của đồ thị hàm

số

3 2

y x mx x m

    

là nhỏ nhất.

1.7. Chứng minh rằng với mọi giá trị của tham số m thì đồ thị hàm số





3 2 2 3

3 3 1

y x mx m x m

    

có cực đại, cực tiểu chạy trên một đường thẳng cố

định.

1.8. Tìm tất cả các giá trị của tham số m để đường thẳng nối hai điểm cực trị của đồ thị hàm

số

3 2

y x x mx

   

song song với đường thẳng

4 3

y x

  

1.9. Chứng minh rằng với mọi giá trị của tham số m thì đồ thị hàm số





3 2 2 3 2

3 3 1

y x mx m x m m

      

luôn có cực đại, cực tiểu đồng thời gọi





;

x y

là

hoành độ, tung độ các điểm cực trị thì ta luôn có

2 0

x y

  

1.10. Chứng minh rằng với những giá trị thực của tham số m để đồ thị hàm số

   

3 2

3 1

1 3 1

2 2

y x m x mx m m

     

có cực đại, cực tiểu ; đồng thời gọi





;

x y

là tọa

độ các điểm cực đại, cực tiểu thì ta luôn có





x y x

 

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.11. Tìm m để đồ thị hàm số

   

3 2

3 1

1 3 1

2 2

y x m x mx m m

     

có cực đại, cực tiểu ;

đồng thời hoành độ, tung độ các điểm cực trị thỏa mãn

1 1

2 2

x y y x

  

  

  

  

; trong đó





;

x y

là tọa độ các điểm cực trị.

1.12. Chứng minh rằng với những giá trị thực của tham số m để đồ thị hàm số

   

3 2

3 1

1 3 1

2 2

y x m x mx m m

     

có cực đại, cực tiểu ; đồng thời gọi





;

x y

là tọa

độ các điểm cực đại, cực tiểu thì ta luôn có

x y





1.13. Với mỗi giá trị thực của tham số m để đồ thị hàm số

3 2 2

y x x m x   

có cực đại,

cực tiểu ; đồng thời gọi





;

x y

là tọa độ các điểm cực trị. Tìm giá trị nhỏ nhất của biểu

thức

y x

x y







Dạng toán: Ba điểm cực trị của đồ thị hàm số tạo thành một tam giác

Bài 1. Tìm m để đồ thị hàm số

4 2 2

2 1

y x m x

  

có ba điểm cực trị là ba điểm của một tam giác

vuông cân.

Lời giải:

Ta có

 

3 2 2 2

2 2

' 4 4 4 0

y x m x x x m

x m





     







, vậy với



thì đồ thị hàm số có 3 cực

trị.

Khi đó tọa độ ba điểm cực trị là













4 4

0;1 ; ;1 ; ;1

A B m m C m m

  

, ta thấy

B C

đối xứng với

nhau qua trục tung. Vậy ba điểm cực trị tạo thành tam giác vuông cân thì sẽ vuông tại

Ta có









4 4

; ; ;

AB m m AC m m

    

 

Vậy

2 8

. 0 0 1

AB AC m m m

       

 

, do



Vậy

 

là những giá trị cần tìm.

Bài 2. Tìm m để đồ thị hàm số

4 2

2 1

y x mx

  

có ba điểm cực trị và đường tròn đi qua ba điểm

cực trị có bán kính bằng 1.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Ta có

 

3 2

' 4 4 4

y x mx x x m

x m





    







, vậy đồ thị hàm số có ba điểm cực trị khi và chỉ

khi



Khi đó tọa độ ba điểm cực trị là

 









2 2

0;1 ; ;1 ; ;1

A B m m C m m

  

Gọi

là tâm và

là bán kính đường tròn ngoại tiếp tam giác

ABC

B C

đối xứng với nhau qua trục tung nên tam giác

ABC

cân tại

, do đó tâm

nằm trên

, giả sử :

       

1 2

0; 1 1 1 0;0 ; 0;2

I y IA R y I I





       







Với

 

1 1

0;0 1 1 1 1

1 5

I I B R m m m









        



 









, do



nên chỉ nhận

1 5

m m

 

  .

Với

 

2 2

0;2 1 1 1

I I B R m m

      

, phương trình này vô nghiệm do





0 1 1

m m m

    

Vậy

1 5

m m

 

  là hai giá trị cần tìm.

Bài 3. Cho hàm số

   

4 2

3 1 2 1

y x m x m

    

. Tìm m để hàm số có 3 điểm cực trị tạo

thành một tam giác có trọng tâm là

Lời giải:

Ta có

 

' 2 3 1 ' 0

2 3 1

y x m x y

x m





     



 



Hàm số có 3 cực trị khi và chỉ khi

3 1 0 ( )

m m i

    

Khi đó tọa độ 3 điểm cực trị là:

 









2 2

0;2 2 , 6 2; 9 4 1 , 6 2; 9 4 1

A m B m m m C m m m

         

Yêu cầu bài toán tương đương với:

1 2

0 18 6 4 0 ;

3 3

A B C

y y y m m m m

           

. Chỉ giá trị



thỏa mãn điều kiện.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Vậy



là giá trị cần tìm.

Bài 4. Cho hàm số





4 2

2 2

y x mx C

   . Tìm tất cả các giá trị của tham số

để





có 3

điểm cực trị tạo thành một tam giác có đường tròn ngoại tiếp đi qua điểm

3 9

;

5 5

 

 

 

Lời giải :

Ta có

' 4 4 ' 0

y x mx y

x m





    







Hàm số có 3 cực trị khi và chỉ khi



Khi đó tọa độ 3 điểm cực trị là

 









2 2

0;2 , ; 2 , ; 2

A B m m C m m

    

Gọi





;

I x y

là tâm đường tròn ngoại tiếp tam giác

ABC

, khi đó

 

2 2

2 2 2

2 2

3 1 0

0; 1

2 2

x y

IA ID

x y

IB IC x m x m

IA IB

x m y m x y



  





 





 

    





  



  







      







nên chỉ có



thỏa mãn. Vậy



là giá trị cần tìm.

Bài 5. Tìm m để đồ thị hàm số





4 2 2

2 1 1

y x m x m

    

có 3 điểm cực trị lập thành một tam

giác có diện tích lớn nhất.

Lời giải :

Ta có









3 2 2 2

' 4 4 1 4 1

y x x m x x m

     

. Hàm số có 3 cực trị khi và chỉ khi phương trình

' 0



có 3 nghiệm phân biệt

1 0 1 1( )

m m i

      

Khi đó tọa độ 3 điểm cực trị là :

 









2 2 2 2

0;1 ; 1 ; 1 ; 1 ; 1

A m B m m C m m

     

Ta có

2 1

BC m

 

, phương trình đường thẳng

: 1

BC y m

 

Diện tích tam giác

ABC

là

 

2 2

; . 1 1 1

ABC

S d A BC BC m m

    

Dấu bằng xảy ra khi và chỉ khi



(thỏa mãn (i)).

Vậy



là giá trị cần tìm.

Bài 6. Cho hàm số

4 2 2

2 2 4

y x mx m

   

. Xác định m để đồ thị hàm số có 3 điểm cực trị tạo

thành tam giác có diện tích bằng 1.

Lời giải :

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Ta có

' 4 4

y x mx

 





3 2

' 0 4 4 0 0

y x mx x x m

      

. Hàm số có 3 cực trị

 

(*)

Khi đó tọa độ 3 điểm cực trị của hàm số l :













2 2 2

0;2 4 , ; 4 , ; 4

A m B m m C m m

   

Nhận thấy

; ,

A Oy B C



đối xứng với nhau qua trục tung nên tam giác

ABC

cân tại

Kẻ

AH BC



khi đó

1 1 1

. 2 .2 1 1

2 2 2

ABC A B B

S AH BC y y x m m m

      

( thỏa mãn (*)

Vậy



là giá trị cần tìm.

Bài 7. Tìm m để hàm số





4 2

3 1 3

y x m x

   

có ba cực trị, đồng thời ba điểm cực trị tạo thành

một tam giác cân có độ dài cạnh đáy bằng

độ dài cạnh bên.

Lời giải :

Ta có

 

' 4 2 3 1 0

3 1

y x m x







    





 



Hàm số có ba cực trị khi và chỉ khi

3 1 1

2 3



    

(*)

Khi đó tọa độ ba điểm cực trị là

 

   

2 2

3 1 3 1

0; 3 ; ; 3 ; ; 3

2 4 2 4

m m

A B C

   

 

   

     

   

   

Tam giác

ABC

cân tại

, vậy nên yêu cầu bài toán tương đương với

BC AB



 

3 1

3 1 3 1 5

9.4 4.

2 2 16 3

m m

 



   

 

     

 

 

thỏa (*)

Vậy

 

là gía trị cần tìm của tham số m.

BÀI TẬP ĐỀ NGHỊ

1.1. Tìm m để đồ thị hàm số

4 2

2 1

y x mx m

   

có ba điểm cực trị tạo thành một tam giác

có diện tích bằng

4 2

1.2. Tìm m để đồ thị hàm số

4 2 2

2 1

y x m x

  

có ba điểm cực trị tạo thành một tam giác có

diện tích bằng

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.3. Tìm m để đồ thị hàm số

4 2 2

y x mx m m

   

có ba điểm cực trị tạo thành một tam giác

có một góc bằng

120

1.4. Tìm m để đồ thị hàm số

4 2 2

2 1

y x m x

  

có ba điểm cực trị tạo thành một tam giác

vuông cân.

1.5. Tìm m để đồ thị hàm số

4 2

2 1

y x mx m

   

có ba điểm cực trị tạo thành một tam giác

có bán kính đường tròn ngoại tiếp bằng 1.

1.6. Tìm m để đồ thị hàm số

4 2 4

2 2

y x mx m m

   

có ba điểm cực trị tạo thành một tam

giác đều.

1.7. Tìm tất cả các giá trị của tham số m để đồ thị hàm số

4 2

2 2

y x mx

  

có ba điểm cực trị

tạo thành một tam giác nhận gốc tọa độ làm trực tâm.

1.8. Tìm m để đồ thị hàm số





4 2 2

2 2 5 5

y x m x m m

     

có ba điểm cực trị tạo thành

một tam giác đều.

1.9. Cho hàm số

4 2

2 2

y x mx m

   . Xác định giá trị của tham số m để đồ thị hàm số trên có

cực đại, cực tiểu tạo thành.

1. Một tam giác đều.

2. Một tam giác vuông.

3. Một tam giác có diện tích bằng 16.

1.10. Tìm tất cả các cặp số





m n

sao cho đồ thị hàm số

4 2 2

y x m x n

  

có ba điểm cực trị

là ba đỉnh của một tam giác đều ngoại tiếp đường tròn có tâm là gốc tọa độ.

1.11. Tìm các giá trị của tham số m để đồ thị hàm số

4 2

2 1

y x mx

  

có ba cực trị và đường

tròn đi qua ba điểm này có bán kính bằng 1.

1.12. Tìm m để đồ thị hàm số





4 2

2 1

y x m x m

   

có ba điểm cực trị

, ,

A B C

sao cho

OA BC



với

là gốc tọa độ,

là điểm trên trục tung.

1.13. Tìm m để đồ thị hàm số

   

4 2

3 1 2 1

y x m x m

    

có ba điểm cực trị tạo thành tam

giác có trọng tâm là gốc tọa độ.

Dạng toán: Hai điểm cực trị và một điểm khác tạo thành một tam giác

BÀI TẬP MẪU

Bài 1. Tìm m để đồ thị hàm số





3 2 2 2

3 3 1 3 1

y x x m x m

      

có cực đại, cực tiểu đồng thời

các điểm cực đại, cực tiểu và gốc tọa độ tạo thành vuông tại

Lời giải:

Ta có





2 2

' 3 6 3 1

y x x m

    

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Để hàm số có cực đại, cực tiểu thì phương trình

' 0



phải có hai nghiệm phân biệt





' 9 9 1 0 0

m m

       

Khi đó gọi









1 1 2 2

; ; ;

A x y B x y

là tọa độ hai điểm cực trị.

Lấy

chia cho

, ta được:

 

2 2

' 2 2 1

3 3

y y m x m

 

    

 

 

. Do

   





 

2 2

1 1

1 2

2 2

2 2 1

' ' 0

2 2 1

y m x m

y x y x

y m x m



  



  



  





Vậy tam giác

OAB

vuông tại

. 0

OAOB

 

 

















2 2 2 2

1 2 1 2

2 2 1 2 2 1 0

x x m x m m x m

      





 





 

4 2 2

1 2 1 2 1 2

4 4 1 4 1 0 *

x x m x x m x x m       

Nhưng theo định lý vi-ét ta có:

1 2

x x

x x m

 





 



, khi đó (*) trở thành

  

2 2 4

1 3 4 4 0

m m m

 





    



 





tất cả các giá trị này đều thỏa mãn điều kiện



Vậy

 

 

  

 

 

 

là những giá trị cần tìm.

Bài 2. Tìm m để đồ thị hàm số





3 2

3 3 1 1 3

y x x m x m

      có cực đại, cực tiểu đồng thời

các điểm cực đại, cực tiểu cùng với gốc tọa độ tạo thành tam giác có diện tích bằng 4.

Lời giải:

Hàm số có cực đại, cực tiểu khi và chỉ khi phương trình

' 0



có hai nghiệm phân biệt

2 1 0

x x m

    

có hai nghiệm phân biệt

' 0

   

Khi đó gọi









1 1 2 2

; ; ;

A x y B x y

là tọa độ hai điểm cực trị.

Lấy

chia cho

ta được:

' 2 2 2

3 3

y y mx m

 

    

 

 

, do









1 2

' ' 0

y x y x

 

1 1

2 2

2 2 2

: 2 2 2

2 2 2

y mx m

AB y mx m

y mx m

   



     



   



Ta có

   

2 2

1 2 1 2 1 2

4 4 1

AB x x m x x x x m

      

;

 

2 2

;

1 4

d O AB







Vậy

 

1 2

. ; . . 1 4

OAB

S d O AB AB x x m

    

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

   





2 2

1 2 1 2

16 1 4 (*)

m x x x x    

Theo định lý vi-ét ta có:

1 2

x x

x x m

 





 



, khi đó (*) trở thành

   





1 4 1 3 4 0 1

m m m m m m

        

thỏa mãn điều kiện



Vậy



là giá trị cần tìm.

Bài 3. Cho hàm số

3 2

y x x m

  

. Tìm m để đồ thị hàm số có 2 điểm cực trị

A B

sao cho



120

AOB  .

Lời giải :

Ta có

' 3 6 ' 0 0 2

y x x y x x

        

Tọa độ 2 điểm cực trị là









0; ; 2; 4

A m B m

 

Yêu cầu bài toán tương đương với :



. 2

OAOB

c AOB

OAOB

  



 

2 4 8 20

12 132

m m m m m







      

 









Bài 4. Cho hàm số





3 2 2 2

3 3 1 3 1

y x x m x m

      

. Tìm m để đồ thị hàm số có hai điểm cực

trị cách đều gốc tọa độ.

Lời giải :

Ta có





2 2

' 3 6 3 1

y x x m

    

Hàm số có cực đại, cực tiểu khi và chỉ khi phương trình

' 0



có hai nghiệm phân biệt, điều này

tương đương với

' 9 0 0

m m

    

Giả sử A, B là hai điểm cực trị của hàm số, khi đó tọa độ hai điểm cực trị là









3 3

1 ; 2 2 , 1 ; 2 2

A m m B m m

     

A và B cách đều gốc tọa độ khi và chỉ khi

 

8 2 0

OA OB m m m m

      

Vậy

 

là giá trị cần tìm.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 5. Tìm m để đồ thi hàm số

   

3 2

1 1

1 2 1

3 2

y x m x m x

     

có hai điểm cực trị

và

đồng thời tứ giác

OADB

là hình bình hành, với

là gốc tọa độ và

 

 

 

Lời giải :

Để hàm số có hai cực trị thì phương trình





' 1 2 0

y x m x m

     

có hai nghiệm phân biệt

     

2 2

1 4 2 3 0 3

m m m m

          

Khi đó hoành độ hai điểm cực trị

1; 2

A B

x x m

  

Vì tứ giác

OADB

là hình bình hành nên trung điểm của

cũng là trung điểm của

, từ đó

suy ra

1 3

A B D

x x x m

y y y

   

 



 

 



Suy ra

11 5 11 5 7

4 1; ; 2;

6 3 6 3 2

m A B

   

    

   

   

thỏa mãn

A B D

y y y

 

Vậy



là giá trị cần tìm.

Bài 6. Tìm m để đồ thị hàm số





3 2

3 1 12 3 4

y x m x mx m

     

có hai điểm cực trị là

A B

sao cho hai điểm này cùng với điểm

 

 

 

 

lập thành tam giác nhận gốc tọa độ làm trọng

tâm.

Lời giải :

Ta có





' 3 6 1 12

y x m x m

   

Hàm số có cực trị khi và chỉ khi phương trình

' 0



có hai nghiệm phân biệt

Tương đương với

 

' 1 4 0 1

m m m

      

Khi đó tọa độ hai điểm cực trị là









3 2

2;9 ; 2 ; 4 12 3 4

A m B m m m m

   

Yêu cầu bài toan tương đương với

3 2

2 2 1 0

9 4 12 3 4 0

m m m

  





  



      





thỏa mãn

Vậy

 

là giá trị cần tìm

BÀI TẬP ĐỀ NGHỊ

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.1. Tìm m để đồ thị hàm số

3 2

y x x m

  

có cực đại, cực tiểu và các điểm cực đại, cực

tiểu cùng với gốc tọa độ tạo thành một tam giác có diện tích bằng

1.2. Tìm m để đồ thị hàm số





3 2 2 3

3 3 1

y x mx m x m m

     

có cực trị đồng thời các

điểm cực trị cùng với gốc tọa độ tạo thành một tam giác vuông tại

1.3. Gọi

A B

là các điểm cực trị của đồ thị hàm số

3 2

2 3

y x x x

  

. Tìm điểm

thuộc

trục hoành sao cho diện tích tam giác

MAB

bằng 2.

1.4. Tìm m để đường thẳng đi qua các điểm cực trị của đồ thị hàm số

3 2

y x x mx

   

tạo

với hai trục tọa độ một tam giác vuông cân.

1.5. Cho hàm số









3 2

3 1 3 2 12 8

y x m x m m x m

      

và điểm





3;2

M . Tìm tất cả các

giá trị của tham số m để đồ thị hàm số có hai điểm cực trị

A B

sao cho

MA MB



nhỏ

nhất.

1.6. Tìm m để đồ thị hàm số





3 2 2 2

3 3 1 3 1

y x x m x m

     

có hai điểm cực trị

A B

cùng

với điểm





2;1

C tạo thành một tam giác có diện tích bằng 1.

MỘT SỐ BÀI TẬP TỔNG HỢP VỀ CỰC TRỊ HÀM SỐ

1.1. Cho hàm số

3 1

y x mx

  

. Tìm m để đồ thị hàm số có hai điểm cực trị

A B

sao cho

diện tích tam giác

IAB

bằng

4 2

, biết rằng





1;1

I .

1.2. Tìm tất các giá trị của tham số m để đồ thị hàm số





3 2

3 3 1 1

y x x m m x

    

có 2 cực

trị cùng dấu.

1.3. Tìm m để đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số

3 2

3 1

y x x

  

cắt đường

tròn





2 2

: 4 2 0

T x y x y m

    

theo một dây cung có độ dài bằng

4 30

1.4. Tìm



để đồ thị hàm số

3 2 3

3 4

y x mx m

   có 2 điểm cực trị và khoảng các từ điểm

cực tiểu đến đường thẳng

bằng 2 lần khoảng cách từ điểm cực đại tới

, biết rằng

d y x



1.5. Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số

3 1

y x x m

   

luôn có hai

điểm cực trị, đồng thời đường thẳng nối hai điểm cực trị tạo với trục hoành một góc

không đổi.

CÁC BÀI TOÁN VỀ TIẾP TUYẾN

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Xét hai bài toán cơ bản :

Bài toán 1: Tiếp tuyến tại một điểm.

Tiếp tuyến với đồ thị hàm số

( )

y f x



tại điểm





0 0

; ( )

M x f x

có dạng là













0 0 0

: '

d y f x x x f x

  

Bài toán 2: Tiếp tuyến đi qua một điểm.

Tiếp tuyến với đồ thị hàm số đi qua điểm





0 0

;

M x y

có hệ số góc

có dạng là





0 0

d y k x x y

  

Khi đó hệ









0 0

'( )

f x k x x y

f x k

  













có nghiệm, giải hệ này suy ra

. Từ đó viết phương trình của

tiếp tuyến.

Bài toán 3 : Cho hai đường cong





: ( )

C y f x

 và





: ( )

d y g x

 . Hãy tìm tất cả các tiếp tuyến

chung của









d C

Giả sử







là tiếp tuyến chung của









d C

. Và







tiếp xúc với









C d

lần lượt tại các điểm

có hoành độ

1 2

x x

Khi đó









   

1 1 1

2 2 2

: '( ) ( )

y f x x x f x

y g x x x g x

   



   





từ đó ta có hệ phương trình

1 2

1 1 1 2 2 2

'( ) '( )

( ) '( ) ( ) '( )

f x g x

f x x f x g x x g x







  



giải hệ này ra nghiệm

1 2

x x

Từ đó viết phương trình tiếp tuyến chung:









: '( ) ( )

i i i

y f x x x f x

    .

Một số kiến thức bổ sung :

Hai đường thẳng





1 1

d y k x m

 

và





2 2

d y k x n

 

Khi đó :

   

1 2

/ /

k k

d d

m n





















1 2 1 2

d d k k

   

3. Góc tạo bởi hai đường thẳng này là :

2 1

1 2

tan

k k









HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lưu ý : Tại một điểm

thuộc đồ thị hàm số thì có thể tồn tại tiếp tuyến tại điểm hoặc tiếp

tuyến đi qua điểm nó, vì vậy cần xem kỹ đề bài yêu cầu tìm loại tiếp tuyến nào để không bỏ sót

tiếp tuyến.

BÀI TẬP MẪU

Dạng toán : Viết phương trình tiếp tuyến thỏa mãn một số điều kiện cơ bản

- Tiếp tuyến tại điểm thuộc đồ thị hàm số.

- Tiếp tuyến đi qua một điểm

cho trước.

- Tiếp tuyến song song(có cùng hệ số góc), vuông góc( tích hệ số góc bằng -1) hoặc tạo với

một đường thẳng cho trước một góc



Bài 1. Cho hàm số

 

3 2

1 1

3 2 3

y x x C

   .

Gọi

là điểm có hoành độ bằng



thuộc





. Tìm

để tiếp tuyến với





tại

song song

với đường thẳng

5 0.

x y

 

Viết phương trình tiếp tuyến đó.

Lời giải:

+ Hệ số góc của đường thẳng

5 0

x y

 

là



. Để tiếp tuyến tại

song song với

:5 0

d x y

 

suy ra

'( 1) 1 5 4

y m m

     

. Suy ra

( 1) 2.

  

Vậy tiếp tuyến cần tìm là





: 5 1 2 : 5 3

y x y x

       

Vậy tiếp tuyến cần tìm là

5 3 0

x y

  

Bài 2. Cho hàm số

 

3 2

2 3

y x x x C

   .

Viết phương trình tiếp tuyến



của





tại điểm uốn và chứng minh



là tiếp tuyến có hệ số góc

nhỏ nhất.

Lời giải:

Ta có

' 4 3

y x x

  

và

'' 2 4 ''( ) 0 2

y x y x x

     

. Suy ra điểm

 

 

 

là điểm uốn

của





. Ta có

'(2) 1

 

. Vậy tiếp tuyến của





tại điểm uốn có phương trình là

 

2 8

2 .

3 3

y x y x

       

Hệ số góc tiếp tuyến của





tại điểm bất kì là

 

4 3 2 1 1

k x x x

       

Từ đó suy ra đpcm.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 3. Cho hàm số





3 2

3 1 .

y x x C

  

Chứng minh rằng trên





tồn tại vô số cặp điểm mà mà hai tiếp tuyến với





tại từng cặp điểm

song song với nhau.

Lời giải:

Ta có

' 3 6

y x x

 

. Bài toán trở thành chứng minh tồn tại vô số số

để phương trình

3 6 (*)

x x k

  có hai nghiệm phân biệt.

Xét phương trình (*), có

' 9 3 0 3

k k

      

. Do đó mọi

 

thì phương trình (*) có 2

nghiệm phân biệt. Ta có đpcm.

Bài 4.Cho hàm số





3 2

2 8 5

y x x x C

    .

Chứng minh rằng không tồn tại tiếp tuyến tại hai điểm thuộc đồ thị hàm số mà vuông góc với

nhau.

Lời giải:

Ta có

2 20

' 3 4 8 3 0, (*).

3 3

y x x x x

 

       

 

 

+ Giả sử ngược lại tồn tại hai điểm có hoành độ

1 2

x x

thuộc đồ thị hàm số sao cho tiếp với đồ thị

hàm số tại hai điểm đó vuông góc với nhau. Khi đó









2 2

1 2 1 1 2 2

'( ) '( ) 1 3 4 8 3 4 8 1

y x y x x x x x

        

, mâu thuẫn với (*).

Vậy ta có đpcm.

Bài 5.Cho hàm số









3 2

1 2 2 2(1)

y x m x m x m       .

Tìm

để đồ thị hàm số (1) có tiếp tuyến tạo với đường thẳng

: 7 0

d x y

  

một góc

, os = .

 

Lời giải:

+ Gọi hệ số góc của tiếp tuyến là

suy ra tiếp tuyến có véc tơ pháp tuyến





; 1

n k

 



, véc tơ

pháp tuyến của

là





1;1

n 



Từ đó suy ra :

 

1 3 2

cos 12 26 12 0 .

2 3

2 1

n n

k k k k

n n





          



 

Khi đó yêu cầu bài toán thỏa mãn khi và chỉ khi ít nhất một trong hai phương trình sau có

nghiệm

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

 

3 3

' 3 2 1 2 2

2 2

' 3 2 1 2 2

3 3

y x m x m

 

     

 



 

     

 

 

có nghiệm

' 0

8 2 1 0

1 1

' 0

2 4

4 3 0

m m



 

  



      



 

  



Vậy giá trị cần tìm của

là

1 1

; ; .

4 2

   

   

 

 

   

Bài 6. Cho hàm số

     

3 2

1 4 3 1

y mx m x m x C

      . Tìm các giá trị của

sao cho tồn

tại duy nhất một điểm có hoành độ âm mà tiếp tuyến tại đó vuông góc với đường thẳng

2 3 0

x y

  

Lời giải:

+ Đường thẳng

2 3 0

x y

  

có hệ số góc bằng



nên tiếp tuyến vuông góc với nó có hệ số

góc bằng

, khi đó ta có

















2 2

2 1 4 3 2 2 1 2 3 0(*)

mx m x m mx m x m          

Khi đó yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có duy nhất một nghiệm âm.

+ Nếu

0 (*) 2 2 0 1

m x x

       

(loại).

+ Nếu

0 (*)

2 3







  









Vậy (*) có duy nhất một nghiệm âm khi và chỉ khi

2 3









 







là những giá trị cần

tìm.

Bài 7. Cho hàm số

 

y C





Tìm điểm những điểm thuộc đồ thị hàm số





sao cho khoảng cách từ giao điểm hai đường

tiệm cận đến tiếp tuyến với





tại điểm đó có khoảng cách lớn nhất.

Lời giải:

+ Giao điểm hai đường tiệm cận





2;2

I  .

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

+ Giả sử điểm

;

A a

 

 



 

là điểm cần tìm, khi đó tiếp tuyến với





tại

là

 

   

4 2

: :4 2 2 0

d y x a d x a y a

       



Ta có

 

   

4 2

8 2 8 2

; 2 2

16 2 2.4. 2

a a

d I d

a a

 

  

  

Dấu bằng xảy ra khi và chỉ khi

 

2 16 0 4

a a a

      

Vậy có hai điểm thỏa mãn









0;0 , 4;4

A A  .

Bài 8. Tìm tất cả các giá trị của tham số m để trên đồ thị hàm số

   

3 2

1 4 3 1

y mx m x m x

     

tồn tại đúng hai điểm có hoành độ dương mà tiếp tuyến tại

đó vuông góc với đường thẳng

2 3 0

x y

  

Lời giải :

Ta có





' 2 1 4 3

y mx m x m

    

Yêu cầu bài toán tương đương với phương trình

'. 1

 

  

 

 

có đúng hai nghiệm dương phân

biệt





2 1 4 3 2

mx m x m

     

có đúng hai nghiệm dương phân biệt





2 1 2 3 0

mx m x m

     

có đúng hai nghiệm dương phân biệt

 

' 4 4 1 0

2 1

1 2

2 3

m m







    





 







 





 





 









 



Vậy

1 1 2

0; ;

2 2 3

   

 

   

   

là giá trị cần tìm.

Bài 9. Tìm điểm

thuộc đồ thị hàm số

 

2 2

y x C

  

sao cho tiếp tuyến với





tại

cắt





tại hai điểm phân biệt

B C

khác

sao cho

AC AB



( B nằm giữa

và

Lời giải :

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Xét điểm

 

, 3

2 2

A a a C

 

  

 

 

Tiếp tuyến với





tại

có phương trình là :

 

3 2

: 2 6 3

2 2

d y a a x a a

     

, khi đó hoành độ giao điểm của

và





là

 

4 4

3 2 2

5 5

2 6 3 3

2 2 2 2

a x

a a x a a x

       

 





2 2

2 3 6 0

x a x ax a

     

Để





d C

 tại hai điểm phân biệt khác

thì phương trình :

2 2

2 3 6 0

x ax a

   

có hai nghiệm

phân biệt khác

2 2 2

2 3 6 0

3 3

' 6 2 0

a a a



   

  

 

 

 

 

   





Khi đó gọi









; ; ;

B B C C

B x y C x y

, có

AC AB



(B nằm giữa

A C

) nên

AC AB



 

3 2

C B

x x a

   

, kết hợp với định lý vi-ét ta có hệ

3 2

2 2

3 6

C B B

C B C

C B

x x a x

x x a x a

x x a



   



     

 

 

 

 



thỏa mãn điều kiện, suy ra có hai điểm

1 2

3 3

2; ; 2;

2 2

A A

   

  

   

   

cần tìm.

Bài 10. Viết phương trình tiếp tuyến với đồ thị hàm số

 

y C







tại điểm

thuộc





, biết

tiếp tuyến cắt trục hoành tại

và tam giác

OAB

vuông(

là gốc tọa độ).

Lời giải:

Xét điểm

 

1; , 0

A a C a



 

  

 

 

. Tiếp tuyến với đồ thị hàm số tại điểm

có phương trình:

 

2 2

: 1

d y x a

a a



    

Hệ số góc của

là

 

Tam giác

OAB

vuông nên chỉ có thể vuông tại

hoặc

Trường hợp 1: Tam giác

OAB

vuông tại



thuộc trục tung hay tiếp điểm





0;3

A . Suy ra

tiếp tuyến

: 2 3

d y x

  

Trường hợp 2: Tam giác

OAB

vuông tại

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Hệ số góc của đường thẳng

 

1 0 1

OA k

a a a







 

  

Vậy

 

  

 

1 2

2 2

1 . 1 1 2 2 0

k k a a a

a a a

 



 

          









Với

1 : 2 5

a d y x

     

Với

1 5

2 :

2 2

a d y x

    

Vậy tất cả có ba tiếp tuyến cần tìm là

1 2 3

1 5

: 2 3; : 2 5; :

2 2

d y x d y x d y x

        

BÀI TẬP ĐỀ NGHỊ

1.1. Tìm m để khoảng cách từ điểm

 

 

 

đến tiếp tuyến của đồ thị hàm số





4 2

y x mx m C

   tại điểm

có hoành độ bằng 1 thuộc





đạt giá trị lớn nhất.

Đáp số:



1.2. Chứng minh rằng đồ thị hàm số





4 2

2 2 1

y x mx m C

     luôn đi qua hai điểm cố

định

A B

với mọi m. Tìm m để tiếp tuyến với





tại

và

vuông góc với nhau.

1.3. Tìm m để trên đồ thị hàm số









3 2

1 4 2 1

y x m x m x

     

tồn tại đúng một điểm mà

tiếp tuyến tại điểm đó vuông góc với đường thẳng

10 30 0

x y

  

Đáp số:



1.4. Đường thẳng 3

y x

 

cắt đồ thị hàm số





3 2

3 4

y x x mx m C

     tại

. Tìm m để

tiếp tuyến với





tại

cắt





tại điểm

khác

thỏa mãn tam giác

AIB

vuông, với





1;2

I .

Dạng toán : Tiếp tuyến cùng với hai trục tọa độ tạo thành tam giác

Bài 1. Cho hàm số





1 .

y x mx m C   

Tìm

để tiếp tuyến với





tại giao điểm của





với trục tung, tạo với hai trục tọa độ một

tam giác có diện tích bằng 8.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

+ Tọa độ giao điểm

của





với trục tung là nghiệm của hệ

 

0;1 '(0) .

M m y m

y x mx m





    



   



Vậy phương trình tiếp tuyến với





tại

điểm

là: : 1

d y mx m

   

. Khi đó

cắt các trục tọa độ tại các điểm

 

0;1 , ;0

M m N



 



 

 

. Yêu cầu bài toán tương đương với

 

9 4 5

1 1

. 8 1 16 1 16

7 4 3

OMN

S OM ON m m m



 



        



  





Vậy có 4 giá trị của

như trên thỏa mãn đề bài.

Bài 2.Cho hàm số

 

2 3

y C







Viết phương trình tiếp tuyến với





biết rằng tiếp tuyến cắt trục hoành tại

, trục tung tại

sao cho

OAB

là tam giác vuông cân, ở đây

là gốc tọa độ.

Lời giải:

Ta có

 

2 3







. Vì tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân nên tiếp tuyến

song song với đường thẳng

y x

 

. Vậy hệ số góc của tiếp tuyến bằng



Suy ra

 

2 3

 



   



 





+ Khi

2 ( 2) 0

x y

    

, lúc đó tiếp tuyến là





: 2 : 2.

d y x d y x

      

+ Khi

1 ( 1) 1

x y

    

, lúc đó tiếp tuyến là

y x

 

, không cắt các trục tọa độ tại hai điểm

nên loại.

Vậy tiếp tuyến cần tìm là

: 2.

d y x

  

Bài 3. Cho hàm số

 

y C





Tìm điểm

thuộc





sao cho tiếp tuyến tại

của





cắt

Ox Oy

lần lượt tại

A B

sao cho

diện tích tam giác

OAB

bằng

, ở đây

là gốc tọa độ.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

+ Gọi

 

;

M x C

 



 



 

là điểm cần tìm. Khi đó tiếp tuyến của





tại

có phương trình là:

 

   

0 0

2 2 2

0 0 0

2 2

: :

1 1 1

x x

d y x x d y x

x x x

     



  

Từ đó suy ra

 

;0 , 0;

A x B

 



 



 

Ta có

 

2 0

1 1 1 1

. .

2 4 2 2

OAB

S OAOB OAOB x







      



 





+ Với





0 1

1 1;1

x M  .

+ Với

0 2

1 1

; 2

2 2

x M

 

    

 

 

Vậy có hai điểm

 

1 2

1;1 , ; 2

M M

 

 

 

 

cần tìm.

Bài 4. Viết phương trình tiếp tuyến với đồ thị hàm số

3 2

y x x

  

biết tiếp tuyến cắt các trục

tọa độ tại

A B

sao cho tam giác

OAB

cân tại

( với

là gốc tọa độ).

Lời giải :

Phương trình tiếp tuyến tại điểm





3 2

0 0 0

; 1

M x x x

 

thuộc đồ thị hàm số









2 3 2

0 0 0 0 0

: 3 2 1

d y x x x x x x

     

Khi đó giao điểm của

với

là

3 2

0 0

2 1

3 2

x x

 

 

 



 

, giao điểm của

với

là





3 2

0 0

0; 2 1

B x x

  

Tam giác

OAB

cân tại

nên

OA OB



3 2

0 0

2 1

3 2

x x

 

    



3 2

0 0

3 2

03 2

0 0

2 1

3 2

2 1

3 2

x x



 

   













 





 

 





  









Với

1x A B O

    

loại trường hợp này.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Với

 

ta có tiếp tuyến

d y x  .

Bài 5. Tìm tất cả các giá trị của tham số m để tiếp tuyến tại điểm có hoành độ bằng 1 của đồ thị

hàm số

3 2

y x x m

  

tạo với hai trục tọa độ một tam giác có diện tích bằng

Lời giải :

- Tiếp tuyến tại điểm có hoành độ bằng 1 là

: 3 2

d y x m

   

- Khi đó

cắt

tại



 

 

 

và cắt

tại





0; 2

B m



- Vậy

 

1 2 3

2 2 9

2 3 2

OAB

S m m







      



 



BÀI TẬP ĐỀ NGHỊ

1.1. Viết phương trình tiếp tuyến đến đồ thị hàm số

2 1







biết rằng tiếp tuyến này tạo với

hai trục tọa độ một tam giác cân.

1.2. Viết phương trình tiếp tuyến đến đồ thị hàm số







biết rằng tiếp tuyến này tạo với

hai trục tọa độ một tam giác có diện tích bằng

1.3. Viết phương trình tiếp tuyến đến đồ thị hàm số

 

2 1







biêt rằng tiếp tuyến tạo với

hai trục tọa một tam giác có trọng tâm nằm trên đường thẳng

4 0

x y

 

1.4. Tìm m để tiếp tuyến của đồ thị hàm số

   

3 2

4 1

2 1 2

3 3

y x m x m x

     

tại giao điểm

đồ thị hàm số với trục tung tạo với hai trục tọa độ một tam giác có diện tích bằng

Dạng toán : Số tiếp tuyến đi qua một điểm đến đồ thị hàm số

- Viết phương trình tiếp tuyến đi qua một điểm cho trước đến đồ thị hàm số.

- Tìm những điểm trên mặt phẳng tọa độ kẻ được một, hai, ba hoặc không có tiếp tuyến

nào đi qua đến đồ thị hàm số.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 1. Cho hàm số





3 2

4 6 1 .

y x x C

  

Viết phương trình tiếp tuyến với





biết tiếp tuyến đi qua điểm





1; 9 .

 

Lời giải:

+ Phương trình tiếp tuyến với





đi qua điểm





1; 9

 

có hệ số góc

là





: 1 9

d y k x

  

gọi

là hoành độ tiếp điểm, khi đó ta có hệ





3 2

4 6 1 1 9(1)

12 12 (2)

x x k x

x x k



    





 





Thay (2) vào (1) ta được:

3 2

4 3 6 5 0

x x x

   

   

1 4 5 0 1

x x x x

        

+ Với

1 24

x k

    

phương trình tiếp tuyến là

: 24 15.

d y x

 

+ Với

5 15

4 4

x k

   

phương trình tiếp tuyến là

15 21

: .

4 4

d y x 

Vậy hai tiếp tuyến cần tìm là

:24 15 0

d x y

  

và

:15 4 21 0

d x y

  

Bài 2. Cho hàm số

 

4 2

1 3

3 .

2 2

y x x C

  

Viết phương trình tiếp tuyến với





biết rằng tiếp tuyến đi qua điểm

0; .

 

 

 

Lời giải:

+ Phương trình tiếp tuyến với





đi qua điểm

 

 

 

có hệ số góc

là

d y kx

 

, gọi

là

hoành độ tiếp điểm, khi đó ta có hệ

4 2

1 3 3

3 (1)

2 2 2

2 3 (2)

x x kx

x x k



   







 



Thay (2) vào (1) ta được:





2 2

2 0 0 2.

x x x x      

+ Với

0 0

x k

   

phương trình tiếp tuyến là

: .

d y



+ Với

2 2

x k

   

phương trình tiếp tuyến là

: 2 .

d y x

 

+ Với

2 2

x k

     

phương trình tiếp tuyến là

: 2 .

d y x

  

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bài 3. Viết phương trình tiếp tuyến với đồ thị hàm số

 

3 2

y x x C

  

kẻ từ điểm





0;2

A .

Lời giải:

+ Nhận thấy









0;2

A C

 .

+ Xét tiếp tuyến với





tại

, ta có

 





 

0 0

3 0

( ) (0)

lim lim 3

3 0

x x

f x f

x x





 



 





   





 





không tồn tại

'(0)

y . Vậy không có tiếp

tuyến với





tại

+ Xét tiếp tuyến có hệ số góc

đi qua

có phương trình là

: 2

d y kx

 





đối xứng qua trục tung nên chỉ cần xét trên khoảng







, khi đó

3 2

y x x

  

và ta

có hệ

3 2 2

3 3

x x kx

x k



   





 





có nghiệm

Hệ này vô nghiệm trên







. Vậy không có tiếp tuyến nào của





đi qua

Kết luận: Không có tiếp tuyến nào kẻ từ

đến





Bài 4. Cho hàm số





3 2 .

y x x C

  

Tìm điểm

trên





sao cho chỉ có một tiếp tuyến với





đi qua

Lời giải:

Giả sử điểm









0 0 0

; 3 2

M x x x C

  

. Phương trình tiếp tuyến với





đi qua

có dạng





0 0 0

3 2

y k x x x x

    

, khi đó ta có hệ





3 3

0 0 0

3 2 3 2(1)

3 3 (2)

x x k x x x x

x k



      





 





Thay (2) vào (1) ta được:

   

3 2 3

0 0 0 0

2 3 0 2 0(*)

x x x x x x x x      

Yêu cầu bài toán tương đương với phương trình (*) có nghiệm duy nhất

 

0 0 0

0 0;2 .

x x x M



    

Bài 5. Tìm các điểm trên trục hoành sao cho từ đó vẽ được ba tiếp tuyến đến đồ thị





của hàm

số

3 2

y x x

  , trong đó có hai tiếp tuyến vuông góc với nhau.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải:

Giả sử





M x là điểm cần tìm, khi đó tiếp tuyến với





đi qua

có dạng là





d y k x x

 

, khi đó ta có hệ





3 2

3 (1)

3 6 (2)

x x k x x

x x k



  





 





Thay (2) vào (1) ta được:





3 2

0 0

2 3 1 6 0 0

x x x xx x

     

hoặc





0 0

2 3 1 6 0(*)

x x x x   

Kí hiệu,





0 0

( ) 2 3 1 6

g x x x x x

   

Từ

kẻ được 3 tiếp tuyến đến





khi và chỉ khi phương trình (*) có hai nghiệm phân biệt,

khác không.

0 0

9 30 9 0

(1)

(0) 6 0

x x

xg x

 





    





 





    









Tại điểm





0;0

M tiếp tuyến với đồ thị hàm số chính là trục hoành, dễ thấy không có tiếp tuyến

nào vuông góc với tiếp tuyến này.Khi đó yêu cầu bài toán trở thành tiếp tuyến với đồ thị hàm số

tại các điểm có hoành độ

1 2

x x

(

1 2

x x

là nghiệm của (*)) vuông góc với nhau.

Hệ số góc của các tiếp tuyến này là

2 2

1 1 1 2 2 2

3 6 ; 3 6

k x x k x x

   

Yêu cầu bài toán thỏa mãn khi và chỉ khi









   

2 2

1 2 1 1 2 2 1 2 1 2 1 2 1 2

. 1 3 6 3 6 1 9 18 36 1(2)

k k x x x x x x x x x x x x             Theo

định lí Vi-ét ta có:





1 2 1 2 0

3 1

; 3

x x x x x



   

, khi đó (2) trở thành

0 0

1 1

27 1 0 ;0

27 27

x x M

 

     

 

 

là điểm duy nhất cần tìm.

Bài 6. Cho hàm số

 

y C







. Tìm những điểm trên trục tung kẻ được hai tiếp tuyến đến





sao cho hai tiếp điểm nằm về hai phía với trục hoành.

Lời giải:

+ Giả sử





A a

là điểm cần tìm, đường thẳng đi qua

với hệ số góc

là :

d y kx a

 

tiếp xúc với

 

kx a





 





















có nghiệm













: 1 2 2 2 0(*)

PT a x a x a       có nghiệm



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Kí hiệu:













( ) 1 2 2 2

g x a x a x a

     

, từ

kẻ được hai tiếp tuyến đến





khi và chỉ

khi phương trình (*) có 2 nghiệm phân biệt

1 2

x x

, khác 1.

1 0

' 3 6 0 1(1)

(1) 3 0

a a

 





        





 



Khi đó ta có

1 2

3 3

1 , 1

1 1

y y

x x

   

 

. Để hai tiếp điểm nằm về hai phía với trục hoành khi

và chỉ khi





 

1 2 1 2

1 2

1 2 1 2 1 2

2 4

3 3

0 1 1 0 0(2)

1 1 1

x x x x

y y

x x x x x x

  

  

      

  

    

  

Theo định lí Vi-ét ta có:





1 2 1 2

2 2

;

1 1

x x x x

a a



  

 

, khi đó (2) trở thành

3 2 0

a a

    

. Kết hợp với điều kiện (1) suy ra

  

Vậy những điểm trên trục tung có hoành độ

thỏa mãn

  

thỏa mãn điều kiện bài toán.

BÀI TẬP ĐỀ NGHỊ

1.1. Cho hàm số

 

x m

y C







và hai điểm

 

9 3

4;2 ; ;

2 2

A B

 

 

 

. Tìm tất cả các giá trị của

tham số m để từ

kẻ được hai tiếp tuyến ,

AM AN

đến





(

M N

là các tiếp điểm) sao

cho bán kính đường tròn ngoại tiếp tam giác

BMN

bằng

1.2.

Dạng toán: Tiếp tuyến cắt hai đường tiệm cận

Bài 1. Cho hàm số

 

2 3

y C







. Tìm những điểm trên





sao cho tiếp tuyến với





tại điểm

đó cắt hai tiệm cận của





tại hai điểm

A B

sao cho độ dài

nhỏ nhất.

Lời giải:

+ Giả sử điểm

M m

 



 



 

là điểm cần tìm, khi đó tiếp tuyến với





tại

có phương

trình là:

 

1 1

: 2

d y x m

    



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

+ Giao điểm của

với tiệm cận đứng là

2;2

 



 



 

+ Giao điểm của

với tiệm cận ngang là





2 2;2

B m  .

Ta có

 

2 2

1 1

4 2 8 2 . 8

2 2

AB m m

m m

 

     

 

 

 

 

Dấu bằng xảy ra khi và chỉ khi

 





  









Vậy có hai điểm cần tìm là









1 2

1;1 , 3;3

M M .

Bài 2. Cho hàm số

 

2 1

y C







Tìm trên





những điểm mà tiếp tuyến với





tại điểm đó cắt các đường tiệm cận của





tại

A B

sao cho tam giác

IAB

có chu vi nhỏ nhất(

là giao điểm của hai đường tiệm cận hàm số).

Lời giải:

+ Giả sử điểm

 

M m C

 

 

 



 

là điểm cần tìm, tọa độ





1;2

I .

+ Phương trình tiếp tuyến với





tại

là

 

3 3

: 2

d y x m



   



+ Tọa độ giao điểm của

với các tiệm cận của





là

 

1;2 , 2 1;2

A B m

 

 

 



 

+ Tam giác

IAB

vuông tại

, ta có

; 2 1 . 12.

IA IB m IA IB

    



Chu vi tam giác

IAB

bằng :

2 2

2 . 2 . 4 3 2 6

p IA IB IA IB IA IB IA IB       

Đẳng thức xảy ra khi và chỉ khi





1 3 1 3

IA IB m m      

Vậy có hai điểm









1 2

1 3;2 3 , 1 3;2 3

M M   

cần tìm.

BÀI TẬP ĐỀ NGHỊ

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của đồ thị hàm số





3 2

3 1 1

y x mx m x

    

tại điểm có hoành độ

 

đi qua điểm





1;2

A .

1.2. Tìm tất cả các giá trị của tham số m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số





3 2

2 2 3

y x x m x m

    

đi qua điểm

 



 

 

1.3. Tìm tất cả các giá trị của tham số m để tiếp tuyến tại hai điểm cố định thuộc đồ thị hàm

số

4 2

2 2 1

y x mx m

    

vuông góc với nhau.

1.4. Cho hàm số





3 2

3 1

y x x C

  

. Tìm hai điểm

A B

thuộc





sao cho tiếp tuyến

với





tại

A B

song song với nhau và

4 2

AB  .

1.5. Tìm

để tiếp tuyến của đồ thị hàm số

y x mx m

   

tại điểm có hoành độ bằng

1 cắt đường tròn

     

2 2

: 2 3

C x y

   

theo một dây cung có độ dài nhỏ nhất.

1.6. Tìm các giá trị thực của tham số

để từ điểm





1,2

M kẻ được hai tiếp tuyến đến đồ thị

hàm số





3 2

2 1 2

y x x m x m

    

1.7. Tìm tất cả các giá trị của

để tồn tại hai tiếp tuyến phân biệt với đồ thị hàm số

3 2

6 9 3

y x x x

   

có cùng hệ số góc

, sao cho đường thẳng đi qua các tiếp điểm

của hai tiếp tuyến cắt các trục tọa độ

Ox Oy

lần lượt tại

A B

thỏa mãn

2012

OA OB



1.8. Tìm m để tiếp tuyến của đồ thị hàm số

y x mx m

   

tại điểm có hoành độ

 

cắt đường tròn













2 2

: 2 3 4

C x y

   

theo một dây cung có độ dài nhỏ

nhất.

1.9. Tìm m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số









3 2

: 2 2 3

C y x x m x m

    

đi qua điểm

 



 

 

1.10. Tìm tất cả các giá trị của tham số

để trên đồ thị hàm số

 

   

3 2

: 1 4 3

C y x m x m x

     tồn tại đúng hai điểm có hoành độ dương

sao cho tiếp tuyến của đồ thị tại đó vuông góc với đường thẳng

1 3

2 2

y x

  

1.11. Tìm những điểm trên trục hoành kẻ được ba tiếp tuyến đến đồ thị hàm số





: 3 2

C y x x

   

Tương tự :

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1. Tìm tất cả các điểm trên trục hoành kẻ được 3 tiếp tuyến đến đồ thị hàm số





3 2

: 3

C y x x

 

biết có hai tiếp tuyến vuông góc với nhau.

2. Tìm trên đường thẳng



các điểm kẻ được ba tiếp tuyến đến đồ thị hàm số





y x x C

 

3. Cho hàm số





y x x C

 

. Tìm trên đường thẳng

y x

 

các điểm mà từ đó kẻ

được đúng 2 tiếp tuyến phân biệt đến





4. Cho hàm số





3 2

y x x C

   

. Tìm những điểm thuộc đường thẳng



mà từ

đó kẻ được 3 tiếp tuyến phân biệt đến





5. Cho hàm số





4 2

2 1

y x x C

  

. Tìm những điểm trên trục hoành kẻ được 3 tiếp

tuyến phân biệt đến





6. Tìm những điểm trên trục tung kẻ được ba tiếp tuyến đến đồ thị hàm số





4 2

: 1

C y x x

  

1.12. Tìm hai điểm

A B

phân biệt thuộc đồ thì hàm số





: 3 2

C y x x

  

sao cho tiếp

tuyến tại

A B

song song vơi nhau và đường thẳng đi qua hai điểm đó vuông góc với

đường thẳng

2012 0

x y

  

1.13. Cho hàm số





2011

y x x C

 

. Tiếp tuyến của





tại điểm

( có hoành độ bằng



) cắt





tại điểm

2 1

M M



, tiếp theo tiếp tuyến của





tại

cắt





ở

điểm

3 2

M M



và cứ như vậy tiếp tuyến của





tại



cắt





ở điểm





n n

M M n



  



. Giả sử điểm





n n n

M x y

, hãy tìm

để

2012

2011 2

n n

x y  .

1.14. Chứng minh rằng đồ thị hàm số





4 2

: 2 2 1

C y x mx m

    

luôn đi qua hai điểm

cố định. Tìm m để tiếp tuyến tại hai điểm cố định đó vuông góc với nhau.

1.15. Cho hàm số





4 2

y x x C

 

. Trên





lấy hai điểm

A B

có hoành độ tương ứng là

a b

. Tìm điều kiện của

và

sao cho tiếp tuyến với





tại

A B

song song với nhau.

1.16. Tìm điểm

 

4 2

1 5

: 3

2 2

A C y x x

   

sao cho tiếp tuyến của





tại

cắt





tại

hai điểm phân biệt

B C

khác

sao cho

AC AB



(

nằm giữa

A C

1.17. Viết phương trình tiếp tuyến của đồ thị hàm số

 

y C





biết tiếp tuyến cắt trục

hoành, trục tung lần lượt tại hai điểm

M N

sao cho

MN OM với

là gốc tọa

độ.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.18. Viết phương trình tiếp tuyến với đồ thị hàm số

 

y C







biết tiếp tuyến cắt các

trục tọa độ tại

A B

sao cho bán kính đường tròn nội tiếp tam giác

OAB

lớn nhất.

1.19. Cho hàm số

 

2 3

y C

x m







. Tìm những giá trị thực của tham số

để tiếp tuyến

của





cắt hai đường tiệm cận của





tại

A B

sao cho tam giác

IAB

có diện tích

bằng 64(

là giao điểm của hai đường tiệm cận).

1.20. Viết phương trình tiếp tuyến với đồ thị hàm số

 

y C





biết tiếp tuyến tạo với hai

đường tiệm cận một giác có chu vi bằng

4 2 2

 .

1.21. Viết phương trình tiếp tuyến với đồ thị hàm số

 

y C





biết tiếp tuyến cắt hai trục

tọa độ tại

A B

sao cho đường trung trực của

đi qua gốc tọa độ.

1.22. Tìm trên đồ thị hàm số

2 1







hai điểm

A B

phân biệt sao cho tiếp tuyến tại hai

điểm có song song với nhau và độ dài đoạn

lớn nhất.

1.23. Tìm giá trị nhỏ nhất của tham số

để tồn tại ít nhất một điểm thuộc đồ thị hàm

số

 

2 1

C y







biêt tiếp tuyến tại điểm số tạo với hai trục tọa độ một tam giác có

trọng tâm nằm trên đường thẳng

2 1

y m

 

1.24. Tìm trên hai nhánh của đồ thị hàm số

 

2 1

C y







hai điểm

M N

sao cho tiếp

tuyến tại hai điểm đó cắt các đường tiệm cận tạo thành một hình thang.

1.25. Cho hàm số

 

2 1

C y







và điểm

bất kỳ thuộc





, gọi

là giao điểm của hai

đường tiệm cận. tiếp tuyến tại

cắt hai đường tiệm cận tại

A B

1. Chứng minh

là trung điểm của

2. Chứng minh diện tích tam giác

IAB

không đổi.

3. Tìm m để chu vi tam giác

IAB

nhỏ nhất.

1.26. Lập phương trình tiếp tuyến của đồ thị hàm số

2 3







tại điểm thuộc đồ thị mà có

khoảng cách đến đường thẳng

3 4 2 0

x y

  

bằng 2.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.27. Cho hàm số

 

2 3

y C







. Gọi

là giao điểm của hai đường tiệm cận của





Tìm trên





những điểm mà tiếp tuyến với





tại điểm đó cắt các đường tiệm cận của





tại

A B

sao cho bán kính đường tròn ngoại tiếp tam giác

IAB

nhỏ nhất.

1.28. Cho hàm số

 

y C







. Tìm trên





những điểm mà tiếp tuyến với





tại điểm

đó cắt các đường tiệm cận của





tại hai điểm

A B

sao cho bán kính đường tròn nội

tiếp tam giác

IAB

lớn nhất(

là giao điểm hai đường tiệm cận của





1.29. Cho hàm số

 

y C







. Chứng minh rằng tiếp tuyến với





tại điểm

bất kỳ

trên





luôn cắt các đường tiệm cận của





tại hai điểm

A B

và

là trung điểm của

1.30. Cho hàm số

 

y C







. Chứng minh rằng mọi tiếp tuyến của





tại điểm bất kỳ

thuộc





luôn tạo với hai đường tiệm cận một tam giác có diện tích không đổi.

1.31. Cho hàm số

 

y C







. Gọi

là một tiếp tuyến bất kỳ của





là giao điểm

của hai đường tiệm cận . Viết phương trình đường thẳng

biết khoảng cách từ

đến

là lớn nhất.

1.32. Cho hàm số

 

y C







. Tìm những điểm trên trục tung những điểm kẻ được duy

nhất một tiếp tuyến đến





1.33. Cho hàm số

 

2 1

y C







. Viết phương trình tiếp tuyến với





biết tiếp tuyến đó

cách đều hai điểm









2;4 , 4; 2

A B

 

1.34. Cho hàm số

 

2 3

y C







. Viết phương trình tiếp tuyến tại điểm





M C

 biết

rằng tiếp tuyến đó cắt các tiệm cận đứng, tiệm cận ngang lần lượt tại

A B

sao cho côsin

góc



ABI

bằng

, với

là giao điểm hai đường tiệm cận.

1.35. Viết phương trình tiếp tuyến

với đồ thị hàm số

 

y C







, biết

cắt hai đường

tiệm cận của





tại

A B

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1. Diện tích tam giác

IAB

lớn nhất( với

là giao điểm của hai đường tiệm cận).

2. Độ dài đoạn thẳng

2 10

AB 

1.36. Viết phương trình tiếp tuyến với đồ thị hàm số

2 1







biết tiếp tuyến cách đều hai

điểm





2;4

A và





4; 2

 

1.37. Viết phương trình tiếp tuyến với đồ thị hàm số

2 3







, biết tiếp tuyến cắt các trục

tọa độ

Ox Oy

lần lượt tại

A B

sao cho trung trục của

đi qua gốc tọa độ.

CÁC ĐIỂM ĐẶC BIỆT THUỘC ĐỒ THỊ HÀM SỐ

Xác định các điểm thuộc đồ thị hàm số có tính chất đặc biệt:

Lưu ý:

- Tâm đối xứng của hàm bậc ba là điểm uốn, tâm đối xứng của hàm phân thức là giao điểm

của hai đường tiệm cận.

Các bài toán:

- Tìm điểm cố định thuộc đồ thị hàm số hoặc quỹ tích các điểm cố định.

- Tìm những điểm thuộc đồ thị hàm số sao cho chúng đối xứng qua một điểm hoặc qua

một đường thẳng cho trước.

- Tìm điểm thuộc đồ thị hàm số có tổng khoảng cách đến hai tiệm cận hoặc đến hai trục tọa

độ là nhỏ nhất.

- Tìm điểm thuộc hai nhánh của đồ thị hàm số sao cho khoảng cách giữa chúng nhỏ nhất.

- Tìm những điểm có tọa độ nguyên thuộc đồ thị hàm số( với hàm phân thức).

- Chứng minh rằng đồ thị hàm số luôn tiếp xúc với một đường thẳng cố định.

BÀI TẬP MẪU

Bài 1. Cho hàm số

 

3 2

1 11

3 3

y x x x C

     . Tìm trên





hai điểm phân biệt

M N

đối

xứng với nhau qua trục tung.

Lời giải:

+ giả sử điểm













1 1 2 2

; , ;

M x y N x y C

 . Khi đó

M N

đối xứng với nhau qua trục tung

khi và chỉ khi

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1 2

1 2 1 1

3 2 3 2

1 2 2 2

1 1 1 2 2 2

0 3 3

1 11 1 11

3 3

3 3 3 3

x x

x x x x

y y x x

x x x x x x

 



     

  



  

   

   

        

  





vậy có hai điểm cần tìm là

16 16

3; , 3;

3 3

M N

   



   

   

Bài 2. Cho hàm số

 

4 2

1 5

2 2

y x x C

  

. Lập phương trình đường cong





đối xứng với





qua điểm





0;2

I .

Lời giải:

Lấy điểm

   

4 2

1 5

; 3 ( )

2 2

M x y C y x x i

    

Điểm





' '; '

M x y

đối xứng với

qua điểm





0;2

I nên

4 '

x x

y y

 





 



thay vào (i) ta được

 

4 2 4 2

1 5 1 3

4 ' ' 3 ' ' ' 3 ' '

2 2 2 2

y x x y x x C

        

Bài 3. Cho hàm số





3 2

3 3 3 4

y x x mx m C

    

. Tìm m để





nhận điểm





1;2

làm tâm đối xứng.

Lời giải:

Ta có

' 3 6 3 '' 6 6 '' 0

6 2

y x x m y x y

y m





        



 



Điểm uốn của đồ thị hàm số là tâm đối xứng





1;6 2

U m



Yêu cầu bài toán tương đương với

6 2 2 0

m m

   

là giá trị cần tìm.

Bài 4. Cho hàm số













2 3 2 7

y m x m x m C

     

. Chứng minh rằng với mọi m

đường cong





luôn đi qua 3 điểm cố định thuộc một đường thẳng.

Lời giải:

Gọi





0 0

;

M x y

là điểm cố định thuộc đường cong





. Khi đó ta có









0 0 0

2 3 2 7,

y m x m x m m

      

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam





3 3

0 0 0 0 0

3 1 2 6 7 0,

m x x x x y m

        

 

0 0

0 0 0 0

0 0 0

3 1 0(1)

3 1 0

2 3 1 6 7 12 5(2)

2 6 7 0

x x

y x x x

x x y



  

 

 

 

     

   





Xét hàm số

( ) 3 1

f x x x

  

liên tục trên



Ta có

(0) 1 0; (1) 3 0; lim ( ) ; lim ( )

x x

f f f x f x

 

        

từ đó suy ra phương trình (1) luôn có 3 nghiệm phân biệt.

Và từ (2) suy ra cả 3 nghiệm này đều thuộc đường thẳng

12 5

y x

 

. Ta có đpcm.

Bài 5. Tìm hai điểm trên đồ thị hàm số

3 2

y x x

   

đối xứng nhau qua điểm





1;3

M 

Lời giải:

Giả sử điểm









0 0

;

A x y C

 , điểm

đối xứng với

qua





1;3

M  nên





0 0

2 ;6

B x y

  

Nhưng do





A B C

 nên:

   

0 0 0

3 2

1;0 ; 1;6

6 2 3 2 2

y x x

A B

y x x

   



 





   

 



        







Vậy





1;0

A  và





1;6

B  là hai điểm cần tìm.

Bài 6. Tìm trên đồ thị hàm số

3 2

y x x

   

hai điểm đối xứng qua đường thẳng

:2 2 0

d x y

  

Lời giải:

Giả sử hai điểm









1 1 2 2

; ; ;

M x y N x y

thuộc đồ thị hàm số đối xứng nhau qua đường thẳng

:2 2 0

d x y

  

Khi đó trung điểm

của

cũng thuộc

1 2 1 2

;

2 2

x x y y

I d

MN d

  

 





 

 

















2 1 2 1

3 3

1 2 1 1 2 2 1 2

2 0

3 2 3 2

2. 2

2 2 2

x x y y

y y x x x x x x

    







        

  

















       

2 2

2 1 2 1 1 1 2 2

2 1 1 2 2 1 2 1 2 1

7 2 0

3 3 2

x x x x x x x x

x x x x x x x x x x



     







       





HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

2 2

1 1 2 2

1 1

2 1

2 2

1 1 2 2

7 1 7

2 2 2

7 1 7

2 2 2

x x x x

x y

x x

x y

x x x x

  

  

  

  

  

  

 



  



  

  

  



 





Vậy có hai điểm cần tìm là

7 1 7 7 1 7

;2 ; ;2

2 2 2 2 2 2

M N

   

  

   

   

Bài 7. Tìm những điểm thuộc đồ thị hàm số

 

3 4

y C







cách đều hai đường tiệm cận của

đồ thị hàm số.

Lời giải:

Giả sử điểm

 

3 4

;

M x C



 



 



 

, vậy

cách đều hai đường tiệm cận của





khi và chỉ

khi:

 

1;1

3 4

2 3 2

2 2

4;6

x x



 











        





 







 







Vậy có hai điểm cần tìm









1 2

1;1 ; 4;6

M M .

Bài 8. Tìm những điểm thuộc đồ thị hàm số

2 1







cách đều hai điểm









2;0 ; 0;2

A B .

Lời giải:

Phương trình đường trung trực của

là

d y x



Khi đó điểm

thuộc đồ thị hàm số cách đều hai điểm

A B

có tọa độ là nghiệm của phương

trình:

2 1 5 1 5

2 2 2 0

2 1 2 2

x x x x y

  

        



Vậy có hai điểm thỏa mãn là

1 2

1 5 1 5 1 5 1 5

; ; ;

2 2 2 2

M M

   

   

   

   

Bài 9. Tìm những điểm thuộc đồ thị hàm số

 

y C





sao cho tổng khoảng cách từ điểm

đó đến hai đường tiệm cận của





là nhỏ nhất.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Giả sử điểm

 

;

M x C

 



 



 

, khi đó tổng khoảng cách từ

đến hai đường tiệm cận của





là:

0 0 0

2 2 2

1 2 1 2 1. 2 2

1 1 1

x x x

        

  

Dấu bằng xảy ra khi và chỉ khi

 





 

0 0

1 2;2 2

1 2

1 1 2

1 2

1 2 2 2

x x



  



  



      





  



   







Vậy có hai điểm cần tìm là









1 2

1 2;2 2 ; 1 2; 2 2

M M      

Bài 10. Tìm những điểm thuộc đồ thị hàm số





sao cho khoảng cách từ điểm





1;2

I 

đến tiếp tuyến với đồ thị hàm số tại điểm đó đạt giá trị lớn nhất.

Lời giải:

Giả sử điểm

 

;

M x C

 



 



 

, phương trình tiếp tuyến với đồ thị hàm số tại

là:

 

   

0 0 0

2 2

: 2 1 2 0

y x x x x y x

        



Khi đó khoảng cách từ





1;2

I  đến



là

 

0 0 0

4 4

0 0

2 2 1 2 4 1

4 1 4 1

x x x

x x

    

   

   

 



Dấu bằng xảy ra khi và chỉ khi

 

0 0

1 1 2

x x

     



Vậy có hai điểm cần tìm là









1 2

1 2;2 2 ; 1 2; 2 2

M M      

Bài 11. Tìm hai điểm thuộc hai nhánh của đồ thị hàm số





sao cho khoảng cách giữa

chúng đạt giá trị nhỏ nhất.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Lời giải:

Giả sử điểm

 

2 2

1 ,2 ; 1,2

A a B b C

a b

   

     

   

   

với

, 0

a b



Khi đó ta có

   

     

2 2

2 2 2

1 1 4 4 4

4 1 4 1 8 1. 16

AB a b a b ab ab

a b

ab ab ab

   

 

          

   

 

   

 

   

Dấu bằng xảy ra khi và chỉ khi

 

   

2 1 2; 2 2 ; 2 1;2 2

a b

a b A B







         









Vậy hai điểm cần tìm là









1 2; 2 2 ; 2 1;2 2

A B     

Bài 12. Tìm hai điểm thuộc hai nhánh của đồ thị hàm số





, biết rằng hai điểm đó tạo

với điểm





2;0

A một tam giác vuông cân tại

Lời giải:

Giả sử điểm

2 2

,2 ; ,2

1 1

B b C c

b c

   

 

   

 

   

với

b c

 

Gọi

H K

lần lượt là hình chiếu vuông góc của

B C

trên trục hoành

Từ điều kiện

AB AC

ABH CAK

AB AC





 







 

Từ đó suy ra:

2 2

AH CK b

BH AK c



  



  

 



 

  

 

 



  







Vậy hai điểm cần tìm là









1;1 ; 3;3

B C

Bài 13. Chứng minh rằng với mọi



đồ thị hàm số





m x m

x m

 





luôn tiếp xúc với

một đường thẳng cố định.

Lời giải:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Giả sử đồ thị hàm số tiếp xúc với đường thẳng

d y kx l

 

với mọi

 

   

2 2 2

, ,

1 2 0

x m

m m

m x m

m l x m lx x lx x

kx l

x m















   

 

 

 

      

 









 

2 2

1 0

x m

l x

lx x















 

  

  

 

 



 





 



Vậy đồ thị hàm số luốn tiếp xúc với đường thẳng

: 1

d y x

 

BÀI TẬP ĐỀ NGHỊ

1.1. Tìm m để đồ thị hàm số

 

3 2 , 0

y mx C m

    

nhận điểm





1;0

I làm tâm

đối xứng.

1.2. Cho hàm số





3 2

y x x C

   

. Tìm trên





hai điểm phân biệt đối xứng với nhau

qua đường thẳng

2 2 0

x y

  

1.3. Cho hàm số

 

2 1

y C







. Tìm trên





những điểm có tổng khoảng cách đến hai

tiệm cận của





nhỏ nhất.

1.4. Cho hàm số

 

3 4

y C







. Tìm trên





các điểm cách đều hai đường tiệm cận của





1.5. Cho hàm số

2 4







. Tìm trên đồ thị hàm số hai điểm đối xứng với nhau qua đường

thẳng

biết









3;0 , 1; 1

M N

  

1.6. Cho hàm số

 

2 1

y C







. Tìm trên





điểm

sao cho tiếp tuyến của





tại

và đường thẳng đi qua

và giao điểm của hai đường tiệm cận của





có tích hệ số

góc bằng



HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.7. Cho hàm số

 

2 2

y C







Tìm trên





các điểm có hoành độ là các số nguyên.

1.8. Tìm điểm cố định của













3 2

: 4 4

C y x m m x x m m

     

1.9. Với mỗi giá trị của tham số

để đường thẳng

: 1

d y mx

 

cắt đồ thị hàm số

2 1







tại hai điểm phân biệt

M N

và cắt hai đường tiệm cận lần lượt tại

A B

Chứng minh rằng

MA NB



1.10. Tìm m để trên đồ thị hàm số









3 2 2 2 3

3 2 1 3 1 1

y x m x m x m

      

có hai

điểm phân biệt đối xứng nhau qua gốc tọa độ.

1.11. Tìm những điểm thuộc đồ thị hàm số







biết rằng tổng khoảng cách từ điểm đó

đến đường thẳng

:2 2 0

d x y

  

đạt giá trị nhỏ nhất.

1.12. Tìm nhứng điểm thuộc hai nhánh của đồ thị hàm số





sao cho khoảng cách giữa

chúng đạt giá trị nhỏ nhất.

1.13. Tìm những điểm thuộc đồ thị hàm số







sao cho khoảng cách từ điểm đó đến

trục hoành bằng hai lần khoảng cách từ điểm đó đến trục tung.

1.14. Tìm những điểm thuộc đồ thị hàm số





sao cho tổng khoảng cách từ điểm đó

đến các trục tọa độ đạt giá trị nhỏ nhất.

1.15. Tìm hai điểm thuộc hai nhánh của đồ thị hàm số





, biết rằng hai điểm đó tạo với

điểm





2;0

A một tam giác vuông cân tại

1.16. Tìm trên đồ thị hàm số

 





hai điểm

A B

có độ dài đoạn



và đường

thẳng

vuông góc với đường thẳng

y x

 

1.17. Tìm trên đồ thị hàm số

 





các điểm

A B

biết rằng tiếp tuyến với đồ thị hàm số

tại

A B

song song với nhau và độ dài đoạn

bằng

2 2

1.18. Tìm trên đồ thị

y x x

  

bốn điểm

, , ,

A B C D

sao cho tứ giác

ABCD

là hình

vuông tâm

VẼ ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Dạng 1: Dựa vào đồ thị hàm số

 

C : ( )y f x suy ra đồ thị hàm số

 

: ( )C y f x .

Phương pháp:

Ta có

 

( ), ( ) 0

: ( )

( ), ( ) 0

f x f x

C y f x

f x f x





 



 



Do đó đồ thị

 

C gồm hai phần

Phần 1: Giữ nguyên phần đồ thị

 

C nằ trên trục hoành.

Phần 2: Lấy đối xứng phần đồ thị





nằm phái dưới trục hoành qua trục hoành.

 

3 2

2 9 12 4y x x x C   

 

3 2

2 9 12 4y x x x C   





Dạng 2: Dựa vào đồ thị hàm số





: ( )

C y f x

 suy ra đồ thị hàm số

 

: .C y f x

Phương pháp:

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Ta có

 

( ), 0

f x x

C y f x

f x x





 



 



Do đó đồ thị

 

C gồm hai phần

Phần 1: Giữ nguyên phần đồ thị

 

C bên phải trục tung.

Phần 2: Lấy đối xứng phần 1 qua trục tung.

 

3 2

2 9 12 4y x x x C   

 

2 9 12 4y x x x C   





Dạng 3: Dựa vào đồ thị hàm số

 

: ( )C y f x suy ra đồ thị hàm số









: .

C y f x



Phương pháp:

Đồ thị hàm số ( )y f x đối xứng qua trục hoành.

Ta có

 

, 0

: ( )

, 0

y y

C y f x f x

y y





  



 



Do đó đồ thị nhận trục hoành làm trục đối xứng, nên đồ thị gồm hai phần

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Phần 1: Giữ nguyên phần đồ thị

 

C phía trên trục hoành

Phần 2: Lấy đối xứng phần 1 qua trục hoành

Dạng 4: Dựa vào đồ thị hàm số

 

: ( ) ( ). ( )C y f x u x v x  suy ra đồ thị hàm số

 

: ( ) ( )C y u x v x .

Phương pháp:

Ta có

 

( ) ( ) ( ), ( ) 0

: ( ) ( )

( ) ( ) ( ), ( ) 0

u x v x f x u x

C y u x v x

u x v x f x u x

 



 



   



Do đó đồ thị





gồm hai phần

Phần 1: Giữ nguyên phần đồ thị

 

C nằm trên miền ( ) 0u x  .

Phần 2: Lấy đối xứng phần đồ thị

 

C qua trục hoành nằm trên miền ( ) 0u x  .

 

3 2

2 9 12 4y x x x C   









2 2 5 2

y x x x C

   

 

Trên đây là 4 dạng bài hay gặp trong kỳ thi TSĐH, một số dạng khác phức tạp hơn như sau

Dạng 5: Dựa vào đồ thị hàm số

 

: ( )C y f x suy ra đồ thị hàm số

 

: ( )C y f x .

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Dạng 6: Dựa vào đồ thị hàm số





: ( )

C y f x

 suy ra đồ thị hàm số





: ( )

C y f x

 .

Dạng 7: Dựa vào đồ thị hàm số





: ( )

C y f x

 suy ra đồ thị hàm số





: ( )

C y f x

 .

Dạng toán: Biện luận số nghiệm của phương trình dựa vào đồ thị

Phương pháp:

Dùng trực quan đồ thị để biện luận số nghiệm của phương trình

( ) ( )

f x g m



, trong đó m là

tham số. Coi

( )

y g m



là đường thẳng và

( )

y f x



là đường cong

Ta phải vẽ được đồ thị hàm số

( )

y f x



, khi đó số giao điểm của đường thẳng

( )

y g m



và

đường cong

( )

y f x



chính là số nghiệm của phương trình.

Như vậy điểm mấu chốt của bài toán là vẽ được đồ thị hàm số

( )

y f x



BÀI TẬP MẪU

Lưu ý:

Tài liệu này quan niệm:

- Đồ thị hàm số lúc đầu quan niệm là đồ thị hàm số cơ bản.

- Đồ thị hàm số được suy ra từ đồ thị hàm số cơ bản gọi là đồ thị hàm số mới.

Với các bài toán mẫu ở đây, ta giả sử là đã có đồ thị hàm số cơ bản và ở đây chỉ nên ra cách suy

ra ra đồ thị hàm số mới. Khi làm bài các em phải xuất phát từ đồ thị hàm số cơ bản xong mới

được suy ra đồ thị hàm số mới( thường thì đề ra câu 1, ý một khảo sát sự biến thiên và vẽ đồ thị

hàm số các em đã có đồ thị hàm sô cơ bản).

Bài 1. Tìm m để phương trình sau có 6 nghiệm phân biệt

2 9 12

x x x m

  

Lời giải:

Hàm số cơ bản





3 2

( ) 2 9 12

y f x x x x C

   

Số nghiệm của phương trình chính là số giao điểm của đường thẳng

y m



và đồ thị hàm số





2 9 12

y x x x C

  

Ta có

3 2

( ) 2 9 12 , 0

2 9 12

( ) 2 9 12 , 0

f x x x x x

y x x x

f x x x x x



   



   



     





Do đó đồ thị





gồm hai phần:

Phần 1: giữ nguyên phần đồ thị





bên phải trục tung.

Phần 2: Lấy đối xứng phần 1 qua trục tung.

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Đồ thị hàm số





là phần liền nét trên hình vẽ

Dựa vào đồ thị hàm số suy ra để phương trình có bốn nghiệm phân biệt khi và chỉ khi đường

thẳng

y m



cắt





tại bốn điểm phân biệt

4 5

  

Bài 2. Tìm m để phương trình

4 2

3 2

2 1

x x

 

 

có tám nghiệm phân biệt.

Lời giải:

Điều kiện:



, khi đó phương trình tương đương với:





4 2

3 2 log 1

x x m

   

Đồ thị hàm số

4 2

3 2

y x x

  

như trên hình vẽ

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Dựa vào đồ thị hàm số suy ra để phương trình có tám nghiệm phân biệt khi và chỉ khi đường

thẳng





log 1

y k m

  

cắt đồ thị hàm số tại tám điểm phân biệt

 

0 log 1 2 1 2

m m       

BÀI TẬP ĐỀ NGHỊ

Bài 1. Cho hàm số





3 2

2 9 12 4

y x x x C

   

a. Khảo sát sự biến thiên và vẽ đồ thị hàm số





b. Tìm m để phương trình sau có 6 nghiệm phân biệt

2 9 12

x x x m

  

Bài 2. Cho hàm số





4 2

2 4

y x x C

  .

a. Khảo sát sự biến thiên và vẽ đồ thị





của hàm số.

b. Với giá trị nào của m, phương trình

2 2

x x m

 

có đúng 6 nghiệm phân biệt.

Bài 3. Gọi d là đường thẳng đi qua điểm





2;0

A với hệ số góc

. Tìm k để d cắt đồ thị hàm số

3 2

y x x

  

tại 4 điểm phân biệt.

Bài 4. Cho hàm số





3 2

y x x x C

   

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

a. Khảo sát sự biến thiên và vẽ đồ thị hàm số





b. Tìm những giá trị của tham số m để phương trình sau có 6 nghiệm phân biệt

1 2 1

x x x x m

     

Bài 5. Cho hàm số

 

2 1

y C







a. Khảo sát sự biến thiên và vẽ đồ thị





của hàm số.

b. Tìm m để phương trình sau có nghiều nghiệm nhất

2 1







MỘT SỐ BÀI TẬP TỔNG HỢP

1.1. Cho hàm số









3 2

2 3 3 18 8

y x m x mx C

    

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi



2. Tìm m để





tiếp xúc với trục hoành.

3. Chứng minh rằng tồn tại điểm

sao cho tiếp tuyến với đồ thị hàm số tại điểm đó song

song với nhau với mọi m.

4. Chứng minh rằng trên parabol





P y x



có hai điểm không thuộc đồ thị hàm số với

mọi m.

1.2. Cho hàm số

 

y C







là tham số thực.

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi



2. Cho hai điểm





3;4

A  và





3; 2



. Tìm

để trên đồ thị





có hai điểm

P Q

cách đều hai điểm

A B

và diện tích tứ giác

APBQ

bằng 24.

1.3. Cho hàm số









3 2

3 2 1 3

y mx mx m x m C

      ,

là tham số thực.

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi



2. Tìm

để hàm số





có cực đại, cực tiểu và khoảng cách từ điểm

 

 

 

đến

đường thẳng đi qua điểm cực đại, cực tiểu của hàm số là lớn nhất.

1.4. Cho hàm số





3 2

y x x C

  

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số.

2. Tìm tất cả các giá trị của

để trên đồ thị hàm số





tồn tại đúng hai tiếp tuyến có cùng

hệ số góc

đồng thời đường thẳng đi qua hai tiếp điểm cắt các trục tọa độ

Ox Oy

lần

lượt tại

và

sao cho

AB  .

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1.5. Cho hàm số

 

y m

x m



  



1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi

 

2. Lấy

A B

lần lượt thuộc đồ thị hàm số có hoành độ

1; 1

A B

x x

  

. Xác định

biết

tiếp tuyến với đồ thị hàm số tại

A B

cắt nhau tại

sao cho tam giác

ABC

là tam giác

đều.

1.6. Cho hàm số









3 2

3 1 6 3 4

y x m x mx m C

     

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi



2. Gọi



là tiếp tuyến của đồ thị hàm số





tại điểm có hoành độ bằng

. Tìm m để

tiếp tuyến cắt đồ thị hàm số





tại điểm

khác

, sao cho tam giác

OAB

cân tại

1.7. Cho hàm số









3 2

2 1 1

y x m x m C

     

1. Với



, khảo sát sự biến thiên và vẽ đồ thị hàm số.

2. Tìm m để đường thẳng

2 1

y mx m

  

cắt đồ thị





tại 3 điểm phân biệt

, ,

A B C

sao cho

2 2 2

OA OB OC

  đạt giá trị nhỏ nhất.

1.8. Cho hàm số









4 2

2 2 1 3

y x m x m C

   

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số với



2. Tìm

để





cắt trục hoành tại 4 điểm tạo thành 3 đoạn thẳng bằng nhau.

1.9. Cho hàm số





3 2

3 4

y x x C

  

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.

2. Cho hai điểm

1 7

;2 ; ;2

2 2

M N

   

   

   

. Viết phương trình đường thẳng

cắt đồ thị





tại hai điểm phân biệt

P Q

sao cho tứ giác

MNPQ

là hình bình hành.

1.10. Cho hàm số

 

m x

y C







1. Khảo sát sự biến thiên và vẽ đồ thị hàm số với



2. Tìm m để đường thẳng

:2 2 1 0

d x y

  

cắt





tại hai điểm phân biệt và cùng

với gốc tọa độ tạo thành tam giác có diện tích bằng

1.11. Cho hàm số

   

 

3 2

2 5

1 3 2

3 3

y x m x m x C

      

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

100

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số với



2. Tìm trên đồ thị





hai điểm phân biệt có hoành độ

1 2

x x

thỏa mãn

1 2

x x



sao

cho tiếp tuyến tại mỗi điểm đó vuông góc với đường thẳng

3 1 0

x y

  

1.12. Với





0;4

m tìm điểm thuộc đồ thị hàm số





m x m

x m

 





có hoành độ dương ;

tung độ lớn nhất, biết rằng khoảng cách từ điểm đó đến tiếp tuyến cố định của đồ thị hàm

số bằng

HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN

101

Dang Thanh Nam

Auditing 51a, National economics University, Ha Noi, Viet Nam

Bấm Tải xuống để xem toàn bộ.

| 1/102

| | Tải xuống

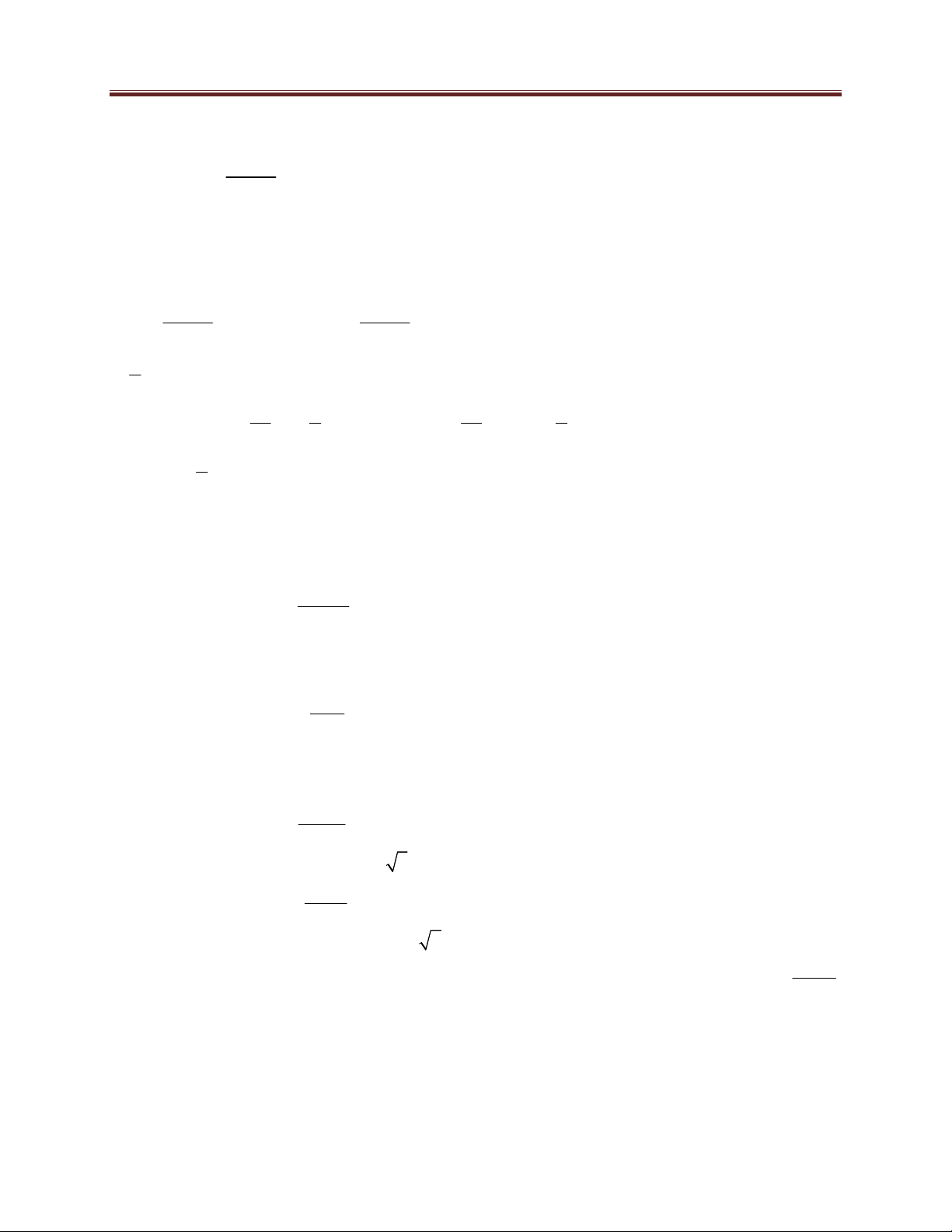
Preview text:

LỜI NÓI ĐẦU
Cuốn CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC được viết dựa trên tinh thần
mong muốn có một cuốn tài liệu ôn thi hữu ích tổng hợp và đẩy đủ các phương pháp giải các
dạng toán trong cấu trúc đề thi TSĐH của Bộ giáo dục và đào tào đồng thời phát triển tư duy
giải toán của học sinh. Đây là tâm huyết của tác giả và là mong muốn thời học sinh của tác
giả. Mục tiêu của cuốn tài liệu là cung cấp các dạng toán thông qua các chuyên đề, mỗi dạng
toán sẽ được tác giả tóm lược phương pháp giải kèm theo hệ thống bài tập mẫu và bài tập đề
nghị hay và phong phú , mỗi bài toán đều chứa tính sáng tạo chắc chắn sẽ làm bạn đọc thấy
thú vị và đam mê. Vì thế không đòi hỏi các bạn phải nhớ phương pháp giải mỗi dạng toán mà
phát triển tư duy toán học của bạn đọc, với bài toán cụ thể bạn đọc sẽ tìm được cách giải
nào. Mong muốn đây sẽ là tài liệu hữu ích cho bạn đọc những ai thực sự đang ước mơ bước
chân vào cánh cửa giảng đường đại học. Cuốn tài liệu này được viết theo 15 chuyên đề:
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan.
Chuyên đề 2: Điều kiện để phương trình – hệ phương trình có nghiệm.
Chuyên đề 3: Phương trình lượng giác.
Chuyên đề 4: Phương trình, bất phương trình vô tỷ.
Chuyên đề 5: Hệ phương trình.
Chuyên đề 6: Phương trình, bất phương trình, hệ phương trình mũ, logarit.
Chuyên đề 7: Tích phân và ứng dụng.
Chuyên đề 8: Hình học không gian.
Chuyên đề 9: Giá trị lớn nhất, giá trị nhỏ nhất và chứng minh bất đẳng thức.
Chuyên đề 10: Hình học giải tích trong mặt phẳng.
Chuyên đề 11: Hình học giải tích trong không gian.
Chuyên đề 12: Ba đường Cônic.
Chuyên đề 13: Các bài toán về số phức.
Chuyên đề 14: Nhị thức Newton và ứng dụng.
Chuyên đề 15: Các bài toán đếm và số cách chọn tổ hợp.
Xin được bày tỏ lòng cảm ơn sâu sắc tới sự giúp đỡ và động viên tinh thần của thầy cô, bạn
bè và gia đình trong thời gian hoàn thiện cuốn sách.
Dù đã rất cố gắng nhưng do hạn chế về thời gian và kiến thức hạn chế của tác giả, cộng với
phạm vi rộng của cuốn sách nên thật khó tránh khỏi các thiếu sót, tác giả rất mong nhận 0
được những ý kiến đóng góp của bạn đọc để trong thời gian tới có thể hoàn thiện cuốn tài
liệu một cách tổng hợp và đầy đủ, dễ hiểu nhất.
Hà nội, ngày 31 tháng 5 năm 2012 ĐẶNG THÀNH NAM 1 MỤC LỤC
LỜI NÓI ĐẦU:……………………………………………………………………….….0
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan…………………………4
Chuyên đề 2: Điều kiện để phương trình, hệ phương trình có nghiệm………..102
Chuyên đề 3: Phương trình lượng giác ………………………………………..…142
Chuyên đề 4: Phương trình, bất phương trình vô tỷ………………………….….196
Chuyên đề 5: Hệ phương trình……………………………………………………..288
Chuyên đề 6: Phương trình, bất phương trình, hệ phương trình mũ,
logarit................................................................................................................402
Chuyên đề 7: Tích phân và ứng dụng………………………………………..........448
Chuyên đề 8: Hình học không gian………………………………………………..554
Chuyên đề 9: Giá trị lớn nhất, giá trị nhỏ nhất và chứng minh bất đẳng
thức…………………………………………………………………………................590
Chuyên đề 10: Hình học giải tích trong mặt phẳng……………………………..648
Chuyên đề 11: Ba đường Cônic……………………………………………...........678
Chuyên đề 12: Hình học giải tích trong không gian…………………………….690
Chuyên đề 13: Các bài toán vế số phức……………………………………..........732
Chuyên đề 14: Nhị thức NEWTON và ứng dụng…………………………..........754
Chuyên đề 15: Các bài toán đếm và số cách chọn tổ hợp…………………......784
TÀI LIỆU THAM KHẢO:……………………………………………………………798 2 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam 3 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam Email : dangnamneu@gmail.com Yahoo: changtraipkt Mobile: 0976266202 CHUYÊN ĐỀ 1:
KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 4 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Chuyên đề 1: Khảo sát hàm số và các bài toán liên quan 5 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam Email : dangnamneu@gmail.com Yahoo: changtraipkt Mobile: 0976266202
Bài toán hàm số và các vấn đề liên quan thuộc loại cơ bản, để giải quyết tốt phần này các em
nên lưu ý đến các bước của một bài toán khảo sát và vẽ đồ thị hàm số. Trong chương trình thi
Tuyển Sinh đại học chỉ đề cập đến ba dạng hàm số cơ bản đó là hàm số bậc ba, hàm trùng
phương và phân thức bậc nhất trên bậc nhất. Cuốn tài liệu này trình bày mẫu các bước của một
bài toán khảo sát, ngoài ra các bài toán liên quan được phân theo từng dạng. Đó là các bài toán:
- Bài toán khảo sát sự biến thiên và vẽ đồ thị của hàm số
- Bài toán về tính đơn điệu của hàm số
- Bài toán về điều kiện nghiệm của phương trình, hệ phương trình( được trình bày chi tiết trong chương 2)
- Bài toán về sự tương giao của đồ thị hàm số
- Bài toán về cực trị hàm số
- Bài toán về tiếp tuyến với đồ thị hàm số
- Bài toán về các điểm đặc biệt
BÀI TOÁN KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
Dưới đây trình bày mẫu cách khảo sát sự biến thiên và vẽ đồ thị hàm số của ba dạng hàm số là
hàm đa thức bậc ba, hàm trùng phương và hàm phân thức bậc nhất trên bậc nhất.
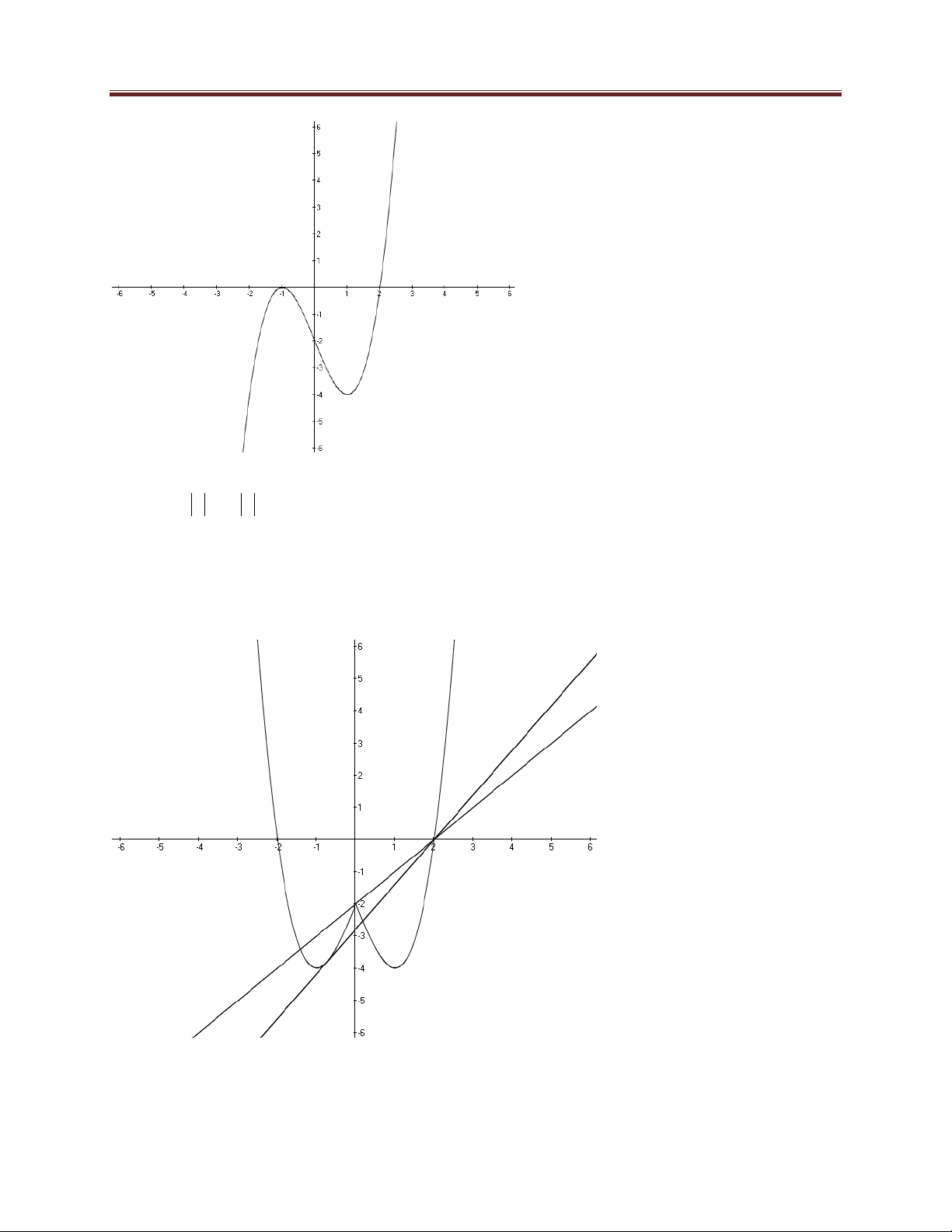
Hàm đa thức bậc ba Cho hàm số 3 2
y  x  2x  1 m x  m , m là tham số thực.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m  1. Trình bày:
Khi m  1ta có hàm số 3 2
y  x  2x 1. + Tập xác định:  + Sự biến thiên: 4 - Chiều biến thiên: 2
y '  3x  4 ; x
y '(x)  0  x  0 hoặc x  . 3  4   4 
Hàm số đồng biến trên các khoảng  ;  0 và ;  
 ; nghịch biến trên khoảng 0;   .  3   3  4 5 -
Cực trị: Hàm số đạt cực đại tại x  0; y
 1, đạt cực tiểu tại x  ; y   . CÐ 3 CT 27 -
Giới hạn: lim y   ;  lim y   . x x 6 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN - Bảng biến thiên: + Đồ thị: 1;0 0;  1 . Hàm trùng phương Cho hàm số 4
y  x  m   2 2
1 x  m , m là tham số thực.
Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m  1. Trình bày:
Khi m  1, ta có hàm số 4 2
y  x  4x 1.
+ Tập xác định D   + Sự biến thiên: - Chiều biến thiên: 3 y  4x  8 ;
x y '  0  x  0 hoặc x   2 7 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Hàm số nghịch biến trên các khoảng  ;
  2  và 0; 2; đồng biến trên các khoảng
 2;0và  2; -
Cực trị: Hàm số đạt cực tiểu tại x   2; y
 3, đạt cực đại tại x  0; y  1. CT CÐ -
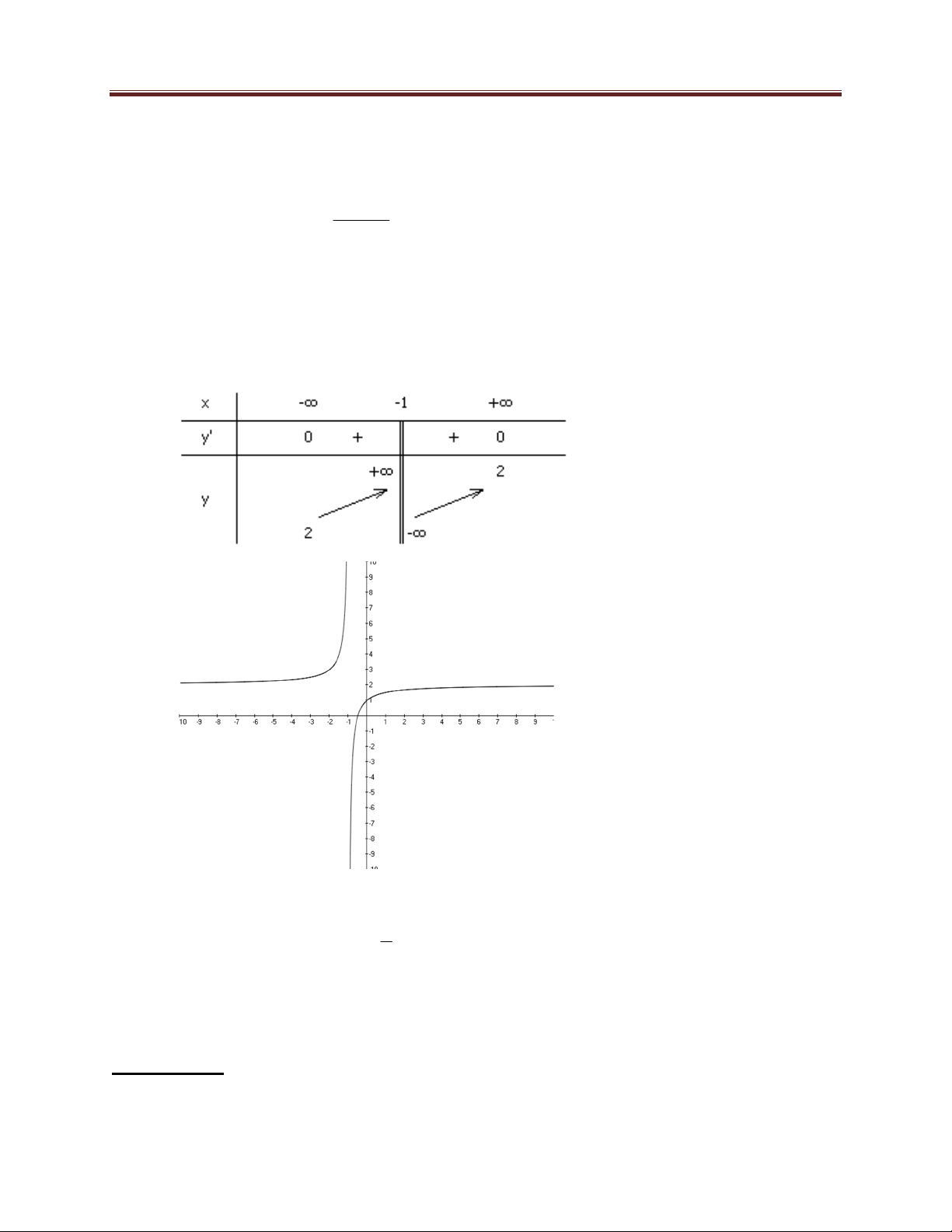
Giới hạn: lim y  lim y   .  x x - Bảng biến thiên: + Đồ thị: Đ 0;  1
 2 3;0; 2 3;0.
Hàm bậc nhất trên bậc nhất 2x 1 Cho hàm số y  . x 1
Khảo sát sự biến thiên và vẽ đồ thị C  của hàm số đã cho. Trình bày: 8 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
+ Tập xác định: D  \  1 + Sự biến thiên: 1 -
Chiều biến thiên: y   0, x   D  x  2 1
Hàm số đồng biến trên các khoảng  ;    1 và  1  ;  . -
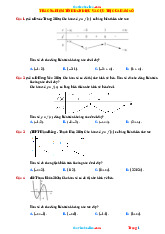
Giới hạn và tiệm cận: lim y  lim y  2; tiệm cận ngang y  2 . x x
lim y  , lim y   ;
 tiệm cận đứng x  1 .   x  1 x  1 - Bảng biến thiên: + Đồ thị:  1   ; 0   0;  1 .  2 
BÀI TOÁN VỀ TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ Phương pháp: 9 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Hàm số f (x) đồng biến trên khoảng a;b khi và chỉ khi f '(x)  0,x a;b .
Hàm số f (x) nghịch biến trên khoảng a;b khi và chỉ khi f '(x)  0,x a;b .
Ta thường biến đổi bất phương trình f '(x)  0 thành hai vế một vế là hàm của x còn một vế chứa tham số m .
Có hai dạng bất phương trình sau
f (x)  g(m),x  ;
a b  g(m)  min f (x). x   a;b
f (x)  g(m),x  ;
a b  g(m)  m ax f (x). x   a;b
Trong đó g(m) là hàm số theo tham số m . BÀI TẬP MẪU 1
Bài 1. Cho hàm số y  m   3 2
1 x  mx  3m  2 x . 3
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên tập xác định. Lời giải:
+ Tập xác định D  
Ta có y  m   2 '
1 x  2mx  3m  2 Vậy hàm số đồng biến trên tập xác định khi và chỉ khi m 1  0  m  1  y '  0, x       m  2 . 2
 '  m   m   1 3m  2  0 
 2  m 1 2m  0 
Vậy m  2 là những giá trị cần tìm. mx  4
Bài 2.Cho hàm số y  . x  m
Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng  ;   1 . Lời giải:
+ Tập xác định D  \  m . 2 m  4 Ta có y '   x  m2
Hàm số nghịch biến trên từng khoảng xác định khi và chỉ khi 2
y '  0  m  4  0  2   m  2 .
Để hàm số nghịch biến trên khoảng  ;  
1 thì ta phải có m  1  m  1
Kết hợp 2 điều kiện trên suy ra 2  m  1. 10 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Bài 3. Cho hàm số 3 2
y  x  3x  mx  4 .
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng  ;  0 . Lời giải:
+ Tập xác định D   . Ta có 2
y '  3x  6x  m
Hàm số đồng biến trên khoảng  ;  0 khi và chỉ khi y '  0, x  ;0 2
 m  f (x)  3x  6x, x    ;
 0  m  min f (x) x   ;0
Ta có f '(x)  6x  6, f '(x)  0  x  1. Lập bảng biến thiên của hàm số f (x) suy ra
min f (x)  f (1)  3 . x   ;0
Vậy giá trị cần tìm của m là m  3 . Bài 4.Cho hàm số 3
y  x   m   2 2 3 2
1 x  6m m   1 x  1.
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng 2;  . Lời giải:
+ Tập xác định D   . 2 Ta có 2
y '  6x  6 2m  
1 x  6m  m  
1 có   2m  
1  4m m   1  1  x  m y '  0  . 
Suy ra hàm số đồng biến trên mỗi khoảng  ;
 m và m 1;  . x  m 1 
Vậy hàm số đồng biến trên khoảng 2;  khi và chỉ khi m 1  2  m  1. Bài 5. Cho hàm số 4 2
y  x  2mx  3m 1.
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng 1; 2 . Lời giải:
+ Tập xác định D  .  Ta có 3
y  x  mx  x  2 ' 4 4 4 x  m .
+ Nếu m  0  y '  0, x  1; 2  m  0 thỏa mãn.
+ Nếu m  0  y '  0 có nghiệm phân biệt x   m, x  0, x  m .
Hàm số đồng biến trên mỗi khoảng  m;0, m;  . Vậy hàm số đồng biến trên khoảng
1; 2 khi và chỉ khi m  1  m  1.
Vậy giá trị cần tìm của m là  ;   1 . 11 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Bài 6.Cho hàm số 3
y  x    m 2 1 2
x  2  m x  m  2 .
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng 0;  . Lời giải:
+ Tập xác định D   . Ta có 2
y '  3x  21 2m x  2  m
Hàm số đồng biến trên khoảng 0;  khi và chỉ khi 2
y '  3x  2 1 2m x  2  m  0,x 0;  2
 3x  2x  2  m 1 4x  0, x  0;  2 3x  2x  2  f (x)   , m x
 0;  m  min f (x) 0;  1 4 x x   2  2
6x  x  3 1   73 Ta có 2 f '(x) 
 0  6x  x  3  x   0 . 4x  2 1 12  1 73  3  73
Lập bảng biến thiên của hàm số f (x) trên 0;  suy ra min f (x)  f    . x   0;  12  8   3  73 Vậy m  là giá trị cần tìm. 8 1 Bài 7. Cho hàm số 3 2 y 
x  2x  mx  2 . 3
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng  ;   1 . Lời giải:
+ Tập xác định D   . Ta có 2
y '  x  4x  m
Vậy hàm số đồng biến trên khoảng  ;   1 khi và chỉ khi 2
y '  x  4x  m  0, x  ;  1 2
 m  f (x)  x  4 , x x    
;1  m  max f (x) x   ;  1
Ta có f '(x)  4  2x  0, x    
;1  max f (x)  f (1)  3 . x   ;  1
Vậy m  3 là giá trị cần tìm. Bài 8. Cho hàm số 3 2
y  x  3mx  3x  3m  4 .
Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên đoạn có độ dài đúng bằng 1. Lời giải:
+ Tập xác định D   . 12 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Ta có y   2 '
3 x  2mx   1
Vậy hàm số nghịch biến trên đoạn có độ dài đúng bằng 1 khi và chỉ khi phương trình y '  0 có 2
nghiệm x , x thỏa mãn x  x  1 . 1 2 1 2 2 2 
 '  m 1  0 m  1 
Điều này tương đương với    (*)
 x  x  1 
 x  x 2   1 2 4x x 1 1 2 1 2 
x  x  2m
Theo định lý Vi – ét ta có 1 2  , thay vào (*) ta dược x x  1  1 2 2  m  1 5   m   . 2 4m  4  1 2   5    Vậy m  
 là giá trị cần tìm.  2    Bài 9. Cho hàm số 3
y  x  m   2 x   2 1
2m  3m  2 x  m2m   1 .
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên 2; Lời giải:
+ Tập xác định D   . Ta có 2
y  x  m   x   2 ' 3 2 1
2m  3m  2.
Hàm số đồng biến trên 2; khi và chỉ khi y '  0, x   2 . 2
 f x  x  m   x   2 ( ) 3 2 1
2m  3m  2  0, x  2; 
Vì tam thức f (x) có 2
 '  7m  7m  7  0, m  m 1  ' m 1  '
Nên f (x) có hai nghiệm phân biệt: x  ; x  . 1 2 3 3  x  x Vậy 2
f (x)  0   x  x  1
Vậy hàm số đồng biến trên mỗi khoảng  ;
 x , x ;  . Vậy hàm số đồng biến 1   2 
trên đoạn 2; khi và chỉ khi 5  m  0  m  5 3 x  2 
 '  5  m      2   m  . 2  '   5  m2 2
2m  m  6  0 2    3  Vậy m  2  ;  là giá trị cần tìm. 2    13 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1 Bài 10.Cho hàm số 3 y 
mx  m   2
1 x  3m  2 x 1 3
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên 2;  . Lời giải:
+ Tập xác định D   . Ta có 2
y '  mx  2m  
1 x  3 m  2 Vậy hàm số đồng biến trên khoảng 2; khi và chỉ khi 2
y '  mx  2 m  
1 x  3 m  2  0,x  2;  6  2x  m 
 f ( x), x
  2;   m  m ax f ( x) 2   2; x  2x  3 x 2  2
x  6x  3 Ta có 2 f '(x) 
 0  x  6x  3  0  x  3  6  2 .
x  2x  32 2 2
Lập bảng biến thiên của hàm số f (x) trên 2;  ta suy ra m ax f (x)  f (2)  . x   2; 3 2 Vậy m  là giá trị cần tìm. 3
BÀI TẬP ĐỀ NGHỊ 1 1.1. Cho hàm số y  m  2 3
x  m  2 2
x  3m   2 1 x  m . 3
Tìm các giá trị của tham số m để hàm số đồng biến trên tập xác định. x  m 1.2. Cho hàm số y 
. Tìm các giá trị của tham số m để hàm số nghịch biến trên x  4m khoảng 1;  1.3.
Tìm các giá trị của tham số m để hàm số 3
y  x  m   2
1 x  4x  3 nghịch biến trên tập xác định. 1.4. Cho hàm số 3 2
y  x  3x  mx  4 . Tìm tất cả các giá trị của tham số m để hàm số
nghịch biến trên khoảng 0;  . 1.5. Cho hàm số 3
y  x   m   2 3 2
1 x  12m  5 x  2 đồng biến trên cả hai khoảng  ;    1 và 2;  . 1.6. Cho hàm số 3 2
y  x  3x  mx  m . Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 1. 1.7. Cho hàm số 3
y  x  m   2 4
3 x  mx . Tìm m để
a. Hàm số đồng biến trên  14 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
b. Hàm số đồng biến trên 0;   1 1 
c. Hàm số nghịch biến trên đoạn  ;  2 2   
d. Hàm số đồng biến trên đoạn có độ dài bằng 1. 1 1 1.8. Tìm m để hàm số 3 y 
mx  m   2
1 x  3m  2 x  đồng biến trên khoảng 2,  3 3 1.9. Tìm để hàm số 3 2
y  x  3x   m  
1 x  4m nghịch biến trên khoảng 1,  1 . m 1
1.10. Tìm m để hàm số 3 2 y 
x  mx  3m  2 x đồng biến trên  3 1
1.11. Tìm m để hàm số 3 y 
mx  2 m   2
1 x   m  
1 x  m đồng biến trên khoảng 3
,0 2,  1.12. Cho hàm số 4 2 2
y  x  2mx  m . Tìm m để
a. Hàm số nghịch biến trên 1, 
b. Hàm số nghịch biến trên khoảng  1  , 0  2,3 x 1
1.13. Cho hàm số y  . Tìm m để x  m
a. Hàm số nghịch biến trên mỗi khoảng xác định của nó.
b. Hàm số đồng biến trên khoảng 0, 
KHẢO SÁT SỰ TỒN TẠI NGHIỆM CỦA PT, HPT Phương pháp:
Xét hàm số f (x) liên tục trên miền D -
Nếu f (x) đơn điệu tăng hoặc đơn điệu giảm trên D khi đó phương trình f (x)  0 nếu có
nghiệm thì đó là nghiệm duy nhất. - Nếu tồn tại ,
a b  D thỏa mãn f (a) f (b)  0 khi đó phương trình f (x)  0 có nghiệm
x  a, b . 0   BÀI TẬP MẪU
Bài 1. Chứng minh rằng phương trình 5 2
x  x  2x 1  0 có đúng 1 nghiệm thực. Lời giải: 15 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Phương trình tương đương với : x   x  2 5 1
 0  x  0 . Với x    x  2 0 1  1. Khi đó để
phương trình có nghiệm thì 5
x  1  x  1.
Vậy ta xét nghiệm của phương trình trên khoảng 1,  . Ta xét hàm số 5 2
f (x)  x  x  2x 1 liên tục trên  . Ta có 4
f x  x  x    4
x  x   4 '( ) 5 2 2 2 2
3x  2  0, x  1, 
Do đó hàm số f (x) đơn điệu tăng trên 1,  . Do đó nếu có nghiệm thì phương trình đã cho sẽ có nghiệm duy nhất. Mặt khác ta lại có f (1)  3
 ; f (2)  23  f (1) f (2)  0 . Vậy phương trình đã cho có nghiệm thực duy nhất.
Bài 2. Chứng minh rằng phương trình .2x x
 1có nghiệm thực duy nhất trong khoảng 0,  1 . Lời giải :
Xét hàm số ( )  .2x f x x 1 trên khoảng 0,  1 Ta có
'( )  2x  2x ln 2  2x f x x
1 x ln 2  0,x 0, 
1 . Nên hàm số f (x) đơn điệu tăng trong khoảng 0,  1 .
Mặt khác ta lại có f (0)  1; f (1)  1  f (0). f (1)  1  0 . Từ đó suy ra phương trình đã cho có
nghiệm duy nhất trên khoảng 0,  1 . x e  1 
Bài 3. Chứng minh rằng phương trình
 x có nghiệm thực duy nhất trên đoạn ,1 .    x  2 1  2  Lời giải :
Phương trình tương đương với : x
e  x  x  2 1  1  Với x  ,1 
ta lấy logarit tự nhiên hai vế của phương trình trên ta được 2   
x  ln x  2 ln  x   1  0 (*) .  1 
Ta xét hàm số f (x)  x  ln x  2 ln  x   1 liên tục trên đoạn ,1  2    2 1 2 x  2x 1  1 
Ta có f '(x)  1    0, x  
,1 . Nên f (x) đơn điệu giảm trên doạn x x 1 x  x  1  2       1   1  1 3 ,1 
. Mặt khác ta có f (1)  1 2 ln 2  0; f   ln 2  2 ln  0   2     2  2 2  1 
Từ đó suy ra phương trình (*) có nghiệm duy nhất trên ,1  . 2    16 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN x
Bài 4. Chứng minh rằng phương trình x 1
x    x  
1 có nghiệm thực dương duy nhất. Lời giải :
Điều kiện : x  0 .
Lấy logarit tự nhiên hai vế của phương trình ta được :  x  
1 ln x  x ln  x   1  0 .
Xét hàm số f (x)   x  
1 ln x  x ln  x  
1 trên khoảng 0,  . x 1 x  x  2x  1
Ta có f '(x)  ln x   ln(x 1)   ln    x x  1  x 1  x  x   1  x  2x 1
Xét hàm số g(x)  ln  , x  0;     .  x 1  x  x   1 1
Ta có g '(x) 
 0 , nên hàm số g(x) đơn điệu giảm trên khoảng 0,  . 2 x   x  2x 1 
Mặt khác ta có lim g(x)  lim  ln   
  0 . Vậy g(x)  0,x  0,  . Từ đó x x   x 1  x  x  1     
suy ra f '( x)  0, x  0,  . Vậy f (x) là hàm đơn điệu tăng trên khoảng 0,  . x  x   
Mặt khác ta có f (1)   ln 2  0, lim f (x)  lim ln  .x      x x  x 1   
Từ đó suy ra phương trình f (x)  0 có nghiệm duy nhất x  1,  . Ta có đpcm. 0  
BÀI TẬP ĐỀ NGHỊ 1.1.
Chứng minh rằng phương trình 5 3
x 10x  9x 1  0 có 5 nghiệm thực phân biệt. 1.2.
Chứng minh rằng phương trình x  2 4 4x  
1  1có đúng ba nghiệm thực phân biệt. 1.3.
Chứng minh rằng với mỗi nguyên dương n thì phương trình 2 3 2n 2n 1 x x x ... x 2012x      
 2004 có nghiệm thực duy nhất. 1.4.
Chứng minh rằng phương trình :
 x  2011  x   3 2 1 2 1
x 1  x  3x  3x  2  0 có nghiệm thực duy nhất. 1.5.
Chứng minh rằng phương trình : 1 1 1 1 *    ... 
 0, n   luôn có nghiệm thực duy nhất thuộc khoảng 0,  1 . 2 x x 1 x  2 n x  n 1.6.
Chứng minh rằng phương trình : lg x  sin x có đúng một nghiệm thực trên đoạn
 3 5  ,  . 2 2    1.7.
Chứng minh rằng với mỗi n nguyên dương, n  2 thì phương trình 17 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN          tan x   tan x   ...  tan x   0   
có nghiệm thực duy nhất trong khoảng 0, 4 . 2     2   2   2n  1.8.
Cho n  2k, k   . Chứng minh rằng phương trình :
n   n2 x
 n   n 1  n2 1 3 2 x  2012  0 . 1.9.
Chứng minh rằng với mọi m thì phương trình sau luôn có nghiệm duy nhất 3
x  m   2 x   2 m   3 3 1 3
1 x  m 1  0 .
1.10. Chứng minh rằng phương trình 3 2
x  3x 1  0 có ba nghiệm phân biệt  x  x  1 2
x  x  x thỏa mãn 1 2 3
2 x 2 x 2 x  27   1   2   3 
1.11. Chứng minh rằng với ,
A B,C là ba góc của một tam giác thì phương trình sau luôn có 4 nghiệm phân biệt 2 x 2 x A B C 3  sin  sin  sin 2 2 2
1.12. Chứng minh rằng với mọi m thì hệ sau luôn có nghiệm 2008 2008   f (x)  f ( y)  0 2 2 
, trong đó f (x)   x  3x  2 x  2x  3 2
x  4  m  y    1 
BÀI TOÁN VỀ SỰ TƯƠNG GIAO
Phương trình hoành độ giao điểm của hai đường cong y  f (x) và y  g(x)
f (x)  g(x)  0 (*)
Khi đó số giao điểm của hai đường cong chính là số nghiệm của phương trình (*).
Trong kì thi Tuyển sinh Đại học và Cao đẳng chỉ xét bài toán giao điểm của đường thẳng với đồ
thị của hàm số bậc ba, hàm trùng phương và đồ thị của hàm phân thức bậc nhất trên bậc nhất.
Kiến thức cần vận dụng:
Hai đường cong tiếp xúc nhau:
Hai đường cong C  : y  f (x) và C ' : y  g(x) tiếp xúc nhau khi và chỉ khi hệ phương trình:
 f (x )  g(x ) 0 0  có nghiệm x .
f '(x )  g '(x ) 0  0 0
Tương giao với hàm đa thức bậc ba:
(i). Xét phương trình: 3 2
y  ax  bx  cx  d  0 (*), a  0.
Khi đó phương trình (*) có ba nghiệm phân biệt khi và chỉ khi đồ thị hàm số 18 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 3 2
y  ax  bx  cx  d  0 có hai điểm cực trị thỏa mãn y y  0. CD CT
i.1- Nếu phân tích phương trình (*) thành  x  x
a  x  x  2
x  px  q  0  1  1  2
g(x)  x  px  q (1) 
Khi đó phương trình (*) có ba nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác x . 1 a  0  2
   p  4q  0 g(x )  0 1 
i.2- Định lý Vi-ét  b
x  x  x   (1) 1 2 3  a   c
x x  x x  x x  (2) 1 2 2 3 3 1 a   d x x x  (3) 1 2 3   a
Một số biến đổi thường dùng:
x  x  x   x  x  x 2 2 2 2
 2 x x  x x  x x 1 2 3 1 2 3  1 2 2 3 3 1 
x  x  x   x  x  x 3 3 3 3  3x x  x
x  x  x 1 2 3 1 2 3 3  1 2   1 2 3 
i.3- Phương trình (*) có ba nghiệm lập thành cấp cố cộng khi x  x  2x thay vào (1) suy ra 1 3 2 b x  
, lúc này thay ngược vào phương trình (*) ban đầu sẽ tìm ra giá trị của tham số cần tìm. 2 3a
Tuy nhiên đây chưa phải là điều kiện cần và đủ do đó với mỗi giá trị của tham số tìm được cần
giải lại phương trình xem phương trình có ba nghiệm lập thành cấp số cộng hay không. Lúc đó
mới chấp nhận giá trị của tham số đó hay không.
i.4- Một cách tương tự phương trình (*) có ba nghiệm lập thành cấp số nhân thì 2
x x  x , lúc 1 3 2 này ta thay vào (3),…
(ii). Xét với a  0 , ta có:
ii.1- Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt biệt có hoành độ   , khi và chỉ khi
phương trình y '  0 có hai nghiệm phân biệt   x  x và thỏa mãn 1 2
 y( )  0 
y(x ).y(x )  0  1 2 19 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
ii.2- Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt biệt có hoành độ   , khi và chỉ khi
phương trình y '  0 có hai nghiệm phân biệt x  x   và thỏa mãn 1 2
 y( )  0 
y(x ).y(x )  0  1 2
Với a  0 , ta biến đổi phương trình hoành độ giao điểm về phương trình có hệ số a dương và áp
dụng với trường hợp a  0 .
Tương giao với hàm trùng phương :
(i). Xét phương trình: 4 2
ax  bx  c, a  0 (*) Đặt 2
t  x  0 , khi đó phương trình trở thành 2
g(t)  at  bt  c  0 (1)
i.1- Phương trình (*) có bốn nghiệm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt đều dương a  0  2
  b  4ac  0   b  S    0  a  c P   0  a
Khi đó phương trình (1) có 2 nghiệm 0  t  t . Lúc này phương trình (*) sẽ có bốn nghiệm là: 1 2
x   t , x   t , x  t , x  t 1 2 2 1 3 1 4 2
i.2- Vậy phương trình (*) có bốn nghiệm lập thành cấp số cộng khi và chỉ khi
x  x  x  x  x  x  t  t  2 t  t  9t 2 1 3 2 4 3 2 1 1 2 1
Định lí Vi-ét với phương trình (1) ta lại có:  b t  t   1 2   a  c t  t  1 2   a
Lưu ý: Dạng toán này luôn cần thiết sử dụng đến định lí Vi-ét. BÀI TẬP MẪU Bài 1. Cho hàm số 3 2
y  x  2x  1 m x  m (1), m là tham số thực 20 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Tìm m để đồ thị hàm số (1) cắt trục hoành tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn 1 2 3 điều kiện 2 2 2
x  x  x  4 1 2 3 Lời giải:
Phương trình hoành độ giao điểm: 3 2
x  2x  1 m x  m  0   x    2
1 x  x  m  0  x  1hoặc 2
x  x  m  0 (*)
Đồ thị của hàm số (1) cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình (*) có hai
nghiệm phân biệt, khác 1. Kí hiệu 2
g(x)  x  x  ;
m x  1, x và x là các nghiệm của (*). 1 2 3
Yêu cầu bài toán thỏa mãn khi và chỉ khi   0 1   4m  0   1 g(1)  0  m  0  
 m  1 và m  0 4  2 2  x  x  3 1 2m  3  2 3   1  Vậy m   ,1 \     0 là giá trị càn tìm.  4  Bài 2.Cho hàm số 4 2
y  x  mx  m 1 (1)
Tìm m để đồ thị hàm số (1) cắt trục hoành tại bốn điểm phân biệt. Lời giải:
Phương trình hoành độ giao điểm: 4 2
x  mx  m 1  0 Đặt 2
t  x  0 , khi đó phương trình trở thành 2
t  mt  m 1  0 (*) .
Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt đều dương   0   m  2 2  0   
 S  0  m  0  1  m  2 P 0   m 1  0    Bài 3. Cho hàm số 3 2
y  x  3x  mx 1 (1) (m là tham số )
Tìm m để đường thẳng d : y  1cắt đồ thị hàm số (1) tại ba điểm phân biệt A0;  1 , B,C sao cho
các tiếp tuyến của đồ thị hàm số (1) tại B và C vuông góc với nhau. Lời giải:
Phương trình hoành độ giao điểm: 3 2
x  3x  mx 1  1 21 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  x  2
x  3x  m  0  x  0 hoặc 2
x  3x  m  0(*) Kí hiệu 2
g(x)  x  3x  m
Đường thẳng d cắt đồ thị hàm số (1) tại ba điểm phân biệt khi và chỉ khi phương trình (*) có hai
nghiệm phân biệt, khác 0.
  9  4m  0 9    m  , m  0. g(0)  m  0 4 
Khi đó hoành độ của B,C là nghiệm của phương trình (*)
Hệ số góc của tiếp tuyến tại B,C lần lượt là 2 2 k  3x  6x  ;
m k  3x  6x  m 1 B B 2 C C
Tiếp tuyến tại B,C vuông góc với nhau khi và chỉ khi k k  1    2 3x  6x  m x
 x  m   B B  2 3 6 1 1 2 C C     2 x
 x  m  m  x   2 3 3 2 3 3 x
 3x  m  2m  3x   1 B B B C C C
  m  x  m  x  2 2 3 2 3  1
  4m  6m  x  x   9x x  1  (2) B C B C B C
x  x  3
Theo định lí Vi-ét ta có B C  , khi đó (2) trở thành x x  m  B C 9  65 2
 4m  9m 1  0  m  8 Bài 4.Cho hàm số 3 2
y  x  3m x  2m (1)
Tìm m để đồ thị hàm số (1) cắt trục hoành tại đúng 2 điểm phân biệt. Lời giải:
Đồ thị hàm số (1) cắt trục hoành tại 2 điểm phân biệt thì đồ thị hàm số (1) phải có hai điểm cực trị 2 2
 y '  3x  3m  0 có hai nghiệm phân biệt khi và chỉ khi m  0 (*)
Khi đó y '  0  x  m
Để đồ thị hàm số (1) cắt trục hoành tại đúng hai điểm khi và chỉ khi hoặc y  0 hoặc y  0 CT CD 3
 y(m)  2m  2m  0  m  0  m  1  3
 y(m)  2m  2m  0  m  0
Chỉ có m  1thỏa mãn điều kiện (*). Vậy giá trị cần tìm của m là m  1hoặc m  1 Bài 5. Cho hàm số 4
y  x  m   2 2 1 x  2m 1 (1)
Tìm m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng. Lời giải: 22 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Phương trình hoành độ giao điểm: 4
x  m   2 2
1 x  2m  1  0 Đặt 2
t  x  0 , khi đó phương trình trở thành 2
t  2 m  
1 t  2m  1  0 (*)
Để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm đều dương 2  '  0 m  0   1
 S  0  2m   1  0    m  0 (2) . 2 P 0    2m 1  0 
Khi đó (*) có hai nghiệm là 0  t  t . Suy ra hoành độ bốn giao điểm lần lượt là 1 2
x   t ; x   t ; x  t ; x  t . Bốn điểm này lập thành cấp số cộng khi và chỉ khi 1 2 2 1 3 1 4 2
x  x  x  x  x  x  t  t  2 t  t  9t 2 1 3 2 4 3 2 1 1 2 1 m  4 m 1 m 9m 1 m  5 m 4 m  1            4 thỏa mãn (2) m    9  4 
Vậy giá trị cần tìm của m là m   ;4  9  Bài 6.Cho hàm số 3 2
y  x  6x  9x  6 C  .
Tìm m để đường thẳng d  : y  mx  2m  4 cắt đồ thị C  tại ba điểm phân biệt. Lời giải:
Phương trình hoành độ giao điểm: 3 2
x  6x  9x  6  mx  2m  4 3 2
 x  x    m x  m     x   2 6 9 2 2 0 2
x  4x 1 m  0  x  2 hoặc 2
x  4x 1 m  0 (*) Kí hiệu 2
g(x)  x  4x 1 m . Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có hai
nghiệm phân biệt, khác 2  '  0 m  3  0      m  3  g(2)  0 3  m  0   Bài 7. Cho hàm số 3
y  x  m   2 2 3
1 x  6mx  2C . m 
Tìm m để đồ thị C
cắt trục hoành tại một điểm duy nhất. m  Lời giải: 23 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Phương trình hoành độ giao điểm: 3
x  m   2 2 3
1 x  6mx  2  0 3 2
 x  x   m 2 2 3 2 3 x  2x (*)
Nhận thấy x  0, x  2 không là nghiệm của phương trình (*), khi đó phương trình (*) tương 3 2 2x  3x  2 đương với: 3m  (1) 2 x  2x 3 2 2x  3x  2
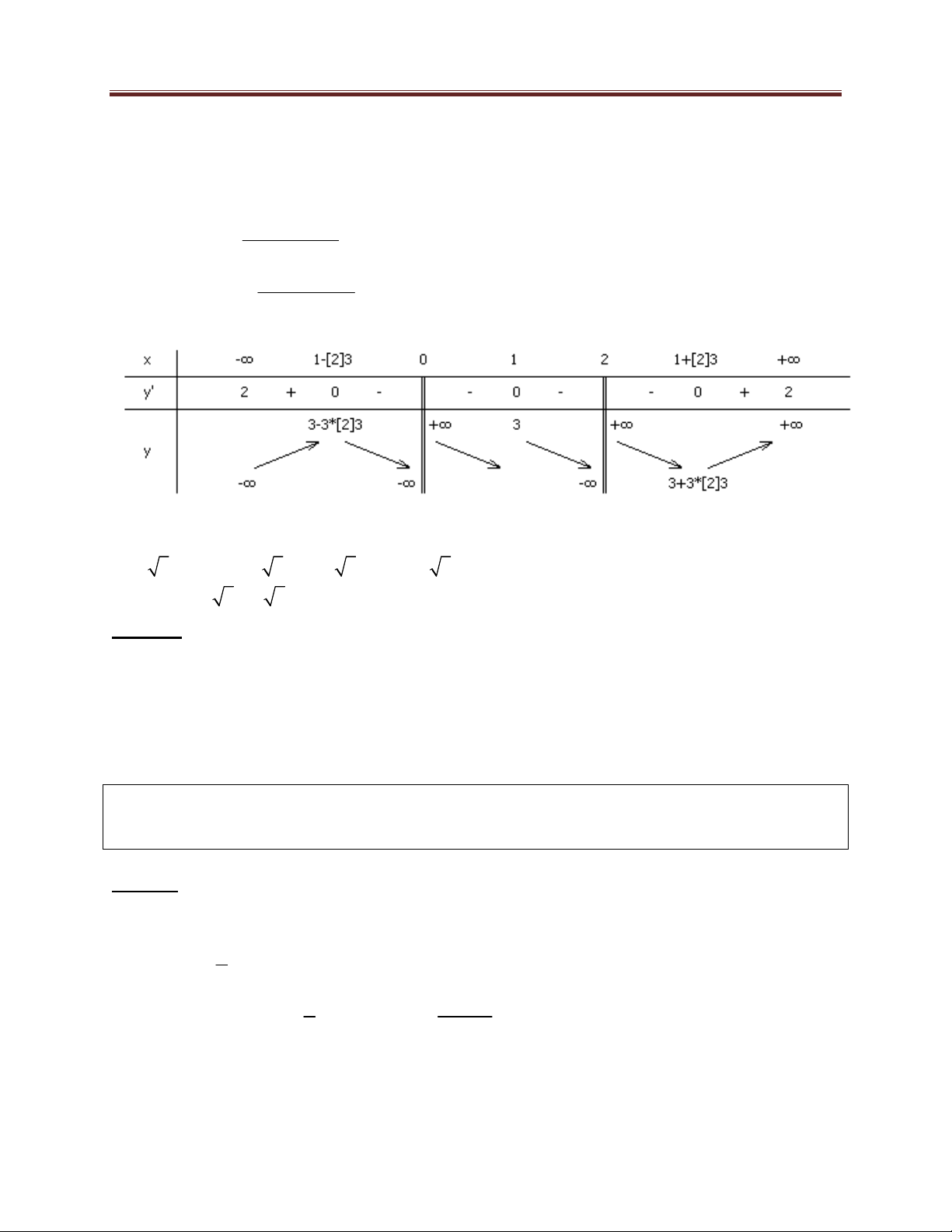
Xét hàm số g(x) 
, ta có bảng biến thiên: 2 x  2x
Từ bảng biến thiên suy ra để phương trình (1) có nghiệm duy nhất khi và chỉ khi
3  3 3  3m  3  3 3  1 3  m  1 3 . Vậy m  1
  3,1 3 là những giá trị cần tìm.  
Cách 2: Để đồ thị hàm số cắt trục hoành tại duy nhất một điểm thì xảy ra một trong hai khả năng
1. Hàm số luôn đồng biến hoặc luôn nghịch biến.
2. Hàm số có cực đại, cực tiểu nhưng y y  0 . CÐ CT
Bạn đọc tự làm theo hướng này và so sánh với kết quả trên. Bài 8. Cho hàm số 3
y  x  mx  2 C . m 
Tìm m để đồ thị C
cắt trục hoành tại một điểm duy nhất. m  Lời giải:
Phương trình hoành độ giao điểm: 3
x  mx  2  0 2 2
 m  x 
 x  0 , do x  0 không là nghiệm của phương trình x 2 3 2  2x Xét hàm số 2
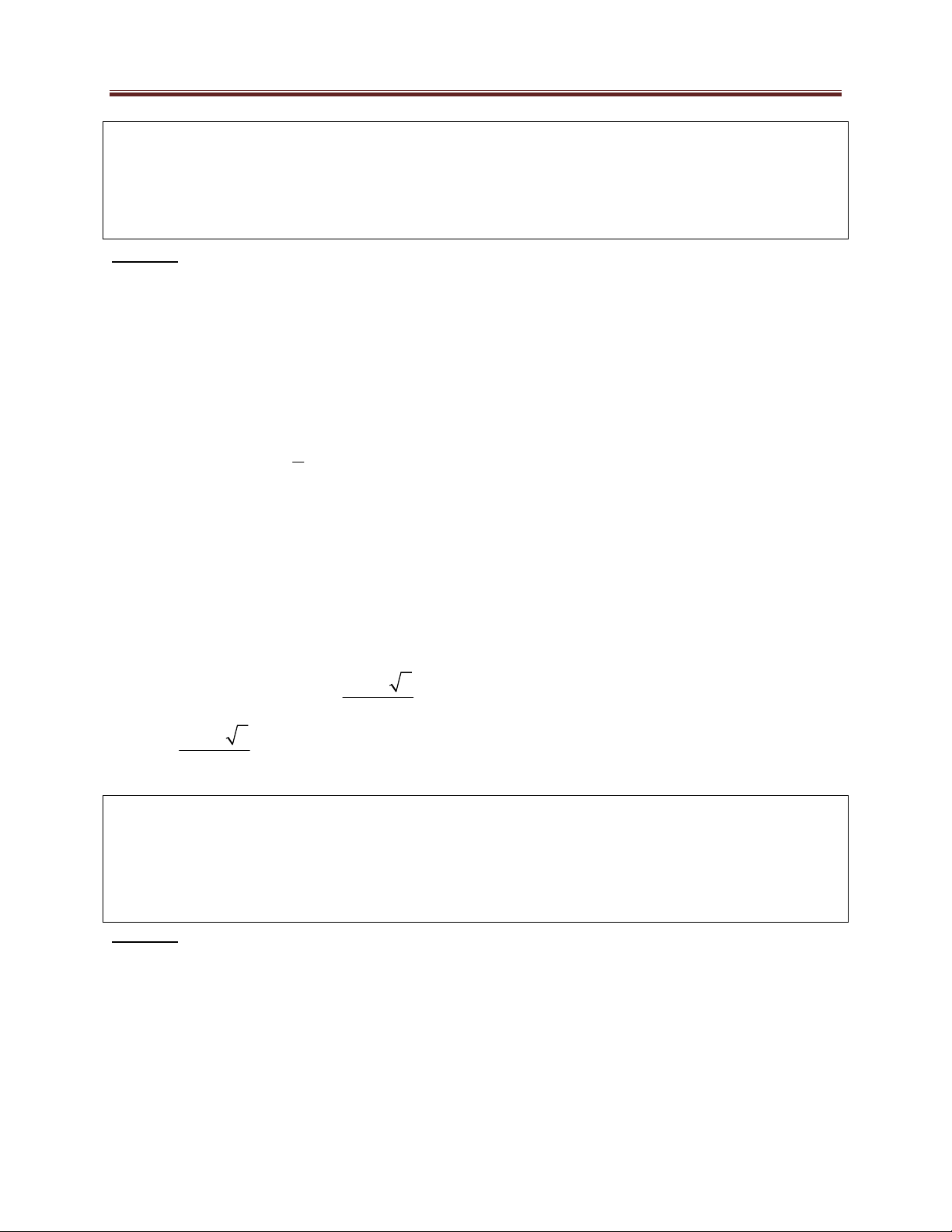
f (x)  x 
. Ta có f '(x)   0  x  1. x 2 x Ta có bảng biến thiên: 24 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Từ bảng biến thiên của hàm số f (x) ta suy ra để phương trình có một nghiệm duy nhất khi và chỉ khi m  3 Bài 9. Cho hàm số 3 2
y  x  3x  4 C  .
Gọi d là đường thẳng đi qua điểm A 1
 ; 0 với hệ số góc là k . Tìm k để đường thẳng d cắt đồ
thị C  của hàm số tại ba điểm phân biệt ,
A B,C và 2 giao điểm B,C cùng với gốc tọa độ tạo
thành tam giác có diện tích bằng 1. Lời giải:
+ Phương trình đường thẳng d : y  k  x   1 .
+ Phương trình hoành độ giao điểm: 3 2
x  3x  4  k  x   1   x   2
1 x  4x  4  k   0  x  1
 hoặc  x  2 2  k (*)
+ Đường thẳng d cắt C  tại ba điểm phân biệt khi và chỉ khi 0  k  9(**)
Khi đó các giao điểm của d và C  là
A 1; 0, B 2  k ;3k  k k ,C 2  k ;3k  k k  k Ta có 2
BC  2 k 1 k , d  ;
O BC   d  ; O d   2 1 k 1
+ Diện tích tam giác OBC là S 
BC.d O BC  k k   k  ( thỏa mãn điều kiện **). OBC  ;  1 1 2
Vậy k  1là giá trị cần tìm. Bài 10. Cho hàm số 3 2
y  x  2mx   m  3 x  4C m 
Tìm giá trị của m để đường thẳng d : y  x  4 cắt đồ thị C
của hàm số tại ba điểm phân biệt m 
A 0; 4 , B,C sao cho tam giác KBC có diện tích bằng 8 2 , biết K 1;3 25 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải:
Phương trình hoành độ giao điểm: 3 2
x  2mx  m  3 x  4  x  4 3 2
 x  mx  m   x   x 2 2 2 0
x  2mx  m  2  0  x  0 hoặc 2
x  2mx  m  2  0(*) Kí hiệu 2
g(x)  x  2mx  m  2 . Khi đó đường thẳng d cắt đồ thị C
tại ba điểm phân biệt khi m 
và chỉ khi phương trình (*) có hai nghiệm phân biệt, khác 0. 2
 '  m  m  2  0
m  2  m  1      (1)
g(0)  m  2  0 m  2   
B, C  d  y  x  4; y  x  4 và ta có d  K; BC   d  K;d   2 . B B C C 1 Vậy S  BC.d K BC   BC   BC  KBC  ;  2 8 2 16 256 2
  x  x 2   y  y 2 
  x  x 2 
  x  x 2 256 2 256
 4x x  128(2) Theo định B C B C B C B C B C
lí Vi-ét ta có: x  x  2  ;
m x x  m  2 . B C B C 1 137 2
 (2)  4m  4m  2 2
 128  m  m  34  0  m  thỏa mãn (1). 2 1 137 Vậy m  là giá trị cần tìm. 2 Bài 11. Cho hàm số 3 2
y  x  mx   2
m   x   2 3 3 1 m   1 (1)
Tìm các giá trị của m để đồ thị hàm số (1) cắt trục hoành tại ba điểm phân biệt có hoành độ dương. Lời giải: Ta có 2
y  x  mx   2 ' 3 6 3 m   1
 x  m 1  x 2 2
y '  0  x  2mx  m 1  0 CD  
x  m 1  x  CT
Đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ dương khi và chỉ khi m 1  0  y y  CD CT 0 m 1  0   x  0, x  0     m   . CD CT  2 m   2 m   2 m  m   3 1 2 1 3 2 1  0  . a y(0) 0     2 m   1  0  26 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Bài 12. Cho hàm số 3 2
y  x  3x  4 C 
Gọi d là đường thẳng đi qua điểm A2; 0 có hệ số góc k . Tìm k để đường thẳng d cắt đồ thị
C  của hàm số tại 3 điểm phân biệt ,
A B,C sao cho tiếp tuyến của C  tại B,C vuông góc với nhau. Lời giải:
+ Phương trình đường thẳng d : y  k  x  2
+ Phương trình hoành độ giao điểm: 3 2
x  3x  4  k  x  2   x    2 2
x  x  k  2  0  x  2hoặc 2
x  x  k  2  0(*) Kí hiệu 2
g(x)  x  x  k  2 . d cắt C  tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2
nghiệm phân biệt khác 2.
  9  4k  0 9      k  0 (1)
g(2)  k  0 4 
Các tiếp tuyến tại B,C vuông góc với nhau khi và chỉ khi y ' x .y ' x   1 B C   2 x  x  2 3 6 3x  6x   1  (2) B B C C
Theo định lí Vi-ét ta có x  x  1 B C
x x  k 2  B C
Kết hợp với (1) và (2) ta suy ra: 3   2 2 2
(2)  9k 18k 1  0  k  ( thỏa mãn (1)). 3 3   2 2 Vậy k  là giá trị cần tìm. 3 Bài 13. Cho hàm số 3
y  x  3x C 
Chứng minh rằng khi m thay đổi đường thẳng d : y  m  x  
1  2 luôn cắt đồ thị C  tại một
điểm cố định M và xác định các giá trị m để d cắt C  tại ba điểm phân biệt M , N, P sao cho
tiếp tuyến của C  tại N, P vuông góc với nhau. Lời giải:
+ Phương trình hoành độ giao điểm: 3
x  3x  m  x   1  2   x   2
1 x  x  2  m  0  x  1  hoặc 2
x  x  2  m  0(*)
Do đó d luôn cắt C  tại điểm M  1  ; 2 . 27 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
+ d cắt C  tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt, khác -1.
  9  4m  0 9      m  0 (1) m  0 4 
Tiếp tuyến tại N, P vuông góc với nhau khi và chỉ khi y ' x .y ' x   1 N P   2 x   2 3 3 3x  3  1  (2) N P
Theo định lí Vi-ét ta có x  x  1 B C 
x x  m  2  B C 3  2 2 2
 (2)  9k 18k 1  0  k  ( thỏa (1)). 3 3   2 2 Vậy k  là giá trị cần tìm. 3 1 2 Bài 14. Cho hàm số 3 2 y 
x  mx  x  m  C  3 3 m
Tìm m để đồ thị hàm số C
cắt trục hoành tại ba điểm phân biệt có tổng bình phương các m  hoành độ lớn hơn 15. Bài 15. Cho hàm số 4
y  x   m   2 3
2 x  3m 1C m 
Tìm m để đường thẳng d : y  1
 cắt đồ thị C
tại bốn điểm phân biệt có hoành độ nhỏ hơn 2. m  Lời giải:
+ Phương trình hoành độ giao điểm: 4
x   m   2 3
2 x  3m 1  0   2 x   2 x  m   2 1 3
1  0  x  1hoặc 2
x  3m 1(*)
Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác 1  và nhỏ hơn 2  1 0  3m 1  4   m  1     3 3m 1  1  m  0   1 
Vậy giá trị cần tìm của m là  ;1 \     0  3  Bài 16. Cho hàm số 4 2 2 4
y  x  2m x  m  2m C m 
Chứng minh rằng đồ thị hàm số C
luôn cắt trục hoành tại ít nhất 2 điểm phân biệt với mọi m  m  0 28 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải:
+ Phương trình hoành độ giao điểm: 4 2 2 4
x  2m x  m  2m  0(*) Đặt 2
t  x  0 , khi đó phương trình (*) trở thành 2 2 4
t  2m t  m  2m  0(1)  '  2  m  0 Ta có  m 
 0  phương trình (1) luôn có ít nhất một nghiệm dương 2 S  2m  0 
Từ đó suy ra phương trình (*) có ít nhất 2 nghiệm phân biệt.Đó là đpcm.
Bài 17. Tìm m sao cho đồ thị hàm số 4 2
y  x  4x  m C  cắt trục hoành tại 4 điểm phân biệt sao
cho hình phẳng giới hạn bởi C  và trục hoành có phần trên bằng phần dưới trục hoành. Lời giải:
Phương trình hoành độ giao điểm: 4 2
x  4x  m  0 Đặt 2
t  x  0  phương trình trở thành 2
t  4t  m  0(1)
Vậy C  cắt Ox tại 4 điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt
dương 0  t  t 1 2
 '  4  m  0   S  4  0
 0  m  4 (i) P  m  0 
Khi đó hoành độ 4 giao điểm của C  và Ox là
x   t  x   t  x  t  x  t 1 2 2 1 3 1 4 2
Yêu cầu bài toán tương đương với 3 x x 4 3 4 x   4 2
x  4x  m dx  2    4 2
x  4x  mdx  2  4 2
x  4x  m dx  2  4 2
x  4x  mdx x x 0 x 2 3 3 1 4 1 4 5 3 4 2  x 
x  mx  0  x 
x  m  0(2) 4 4 4 4 4 5 3 5 3 9 Ta lại có 4 2
x  4x  m  0(3) . Từ (2) và (3) suy ra 2
m  5m  0  m  0 (loại) 4 4 4 20 Hoặc m  (thỏa (i)). 9 20 Vậy m  là giá trị cần tìm. 9 Bài 18. Cho hàm số 4
y  x  m   2 2
1 x  2m  1C
. Tìm tất cả các giá trị thực của tham số m m  để C
cắt trục hoành tại bốn điểm phân biệt , A ,
B C, D có hoành độ lần lượt là x  x  x  x m  1 2 3 4
sao cho tam giác ACK có diện tích bằng 4. Biết rằng K 3, 2 . 29 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải :
Phương trình hoành độ giao điểm : 4
x  m   2 2
1 x  2m  1  0 , đặt 2
t  x t  0 khi đó phương trình trở thành : 2
t  2 m  
1 t  2m 1  0(*) . Để đồ thị C
cắt trục hoành tại bốn điểm phân biệt thì phương m 
trình (*) có hai nghiệm dương phân biệt t  t  0 . 2 1 2  '  m  0  1
 S  2m   1  0    m  0 (i) 2
P  2m 1  0 
Khi đó hoành độ bốn giao điểm lần lượt là  t ,  t , t , t . 2 1 1 2 1 1 Ta có S  d K AC AC   t  t   t  t   t  t  t t  ACK  , . 2  4 4 2 16 1 2  1 2 1 2 1 2 2 2
Theo định lý Viét ta có : t  t  2 m 1 ;t t  2m 1 , từ đó suy ra : 1 2   1 2 7  m  0  2m  
1  2 2m  1  16 
2m 1  7  m  
 m  4thỏa mãn điều kiện 2m 1   7  m2  (i).
Vậy m  4 là giá trị cần tìm.
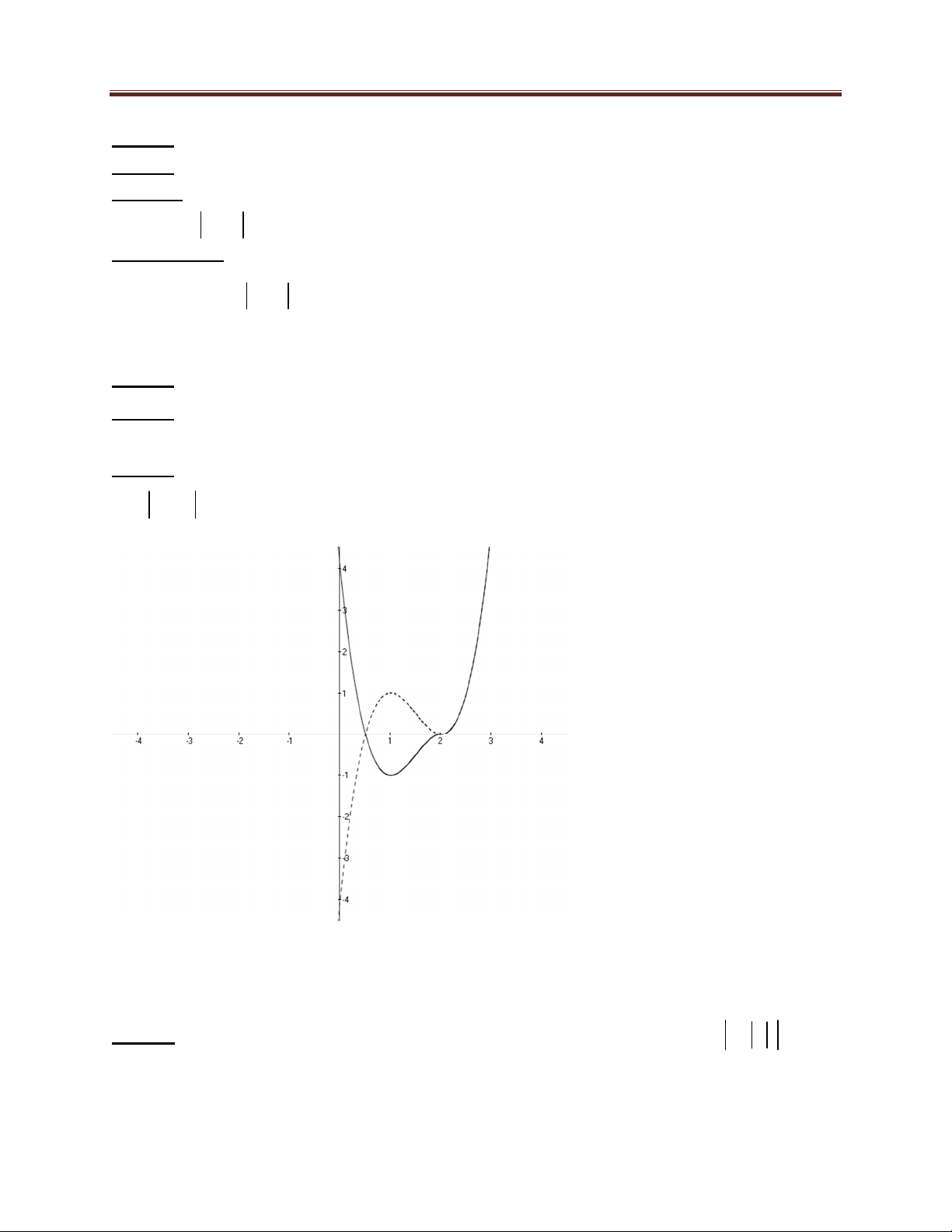
Bài 19. Biết rằng đường thẳng d đi qua điểm M 2; 0 và có hệ số góc k cắt đồ thị hàm số 3
y  x  3 x  2 tại bốn điểm phân biệt. Tìm giá trị của k. Lời giải:
Đường thẳng d : y  k  x  2 , ta dùng trực quan đồ thị để biện luận số giao điểm của đường 3
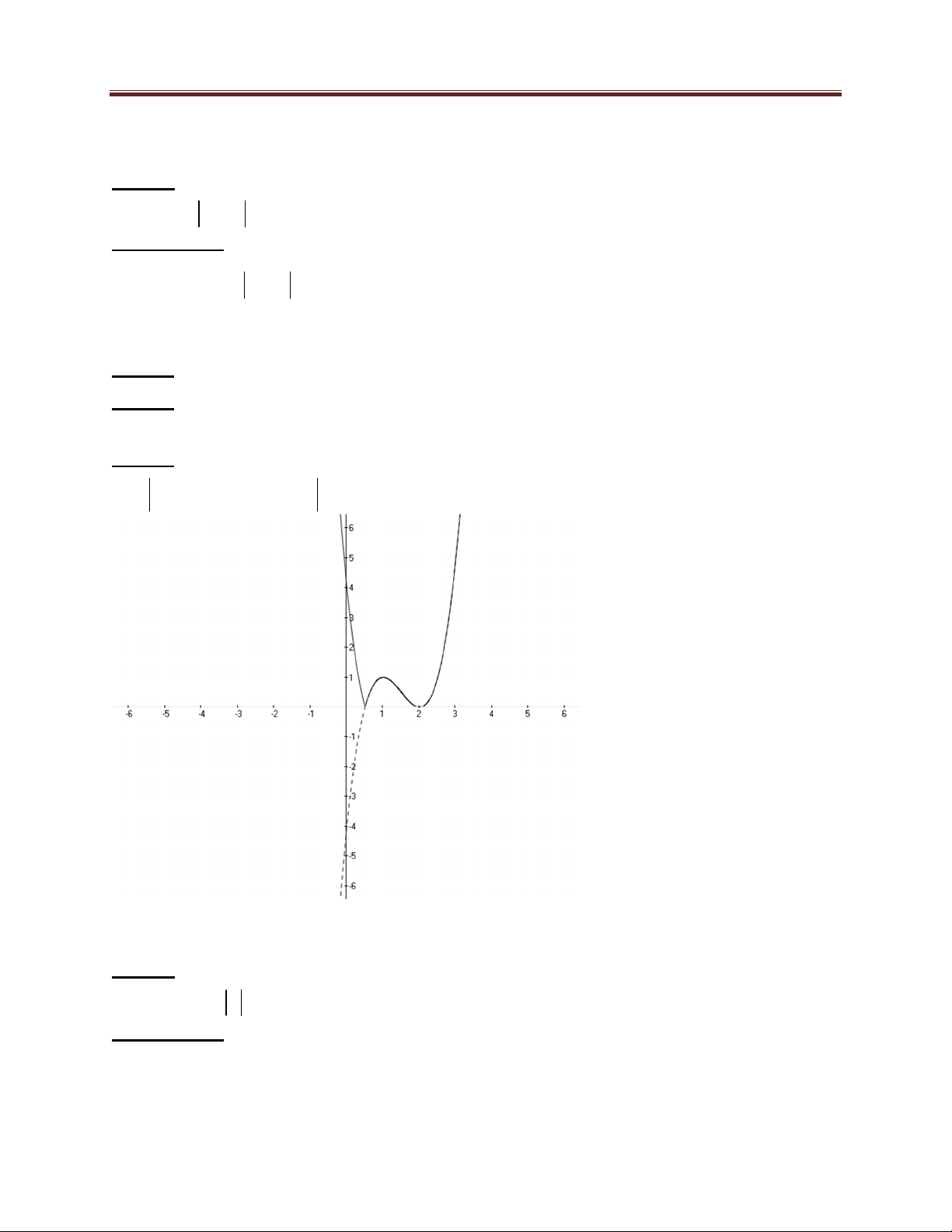
thẳng d và đồ thị hàm số y  x  3 x  2 C . 1  Xét hàm số 3
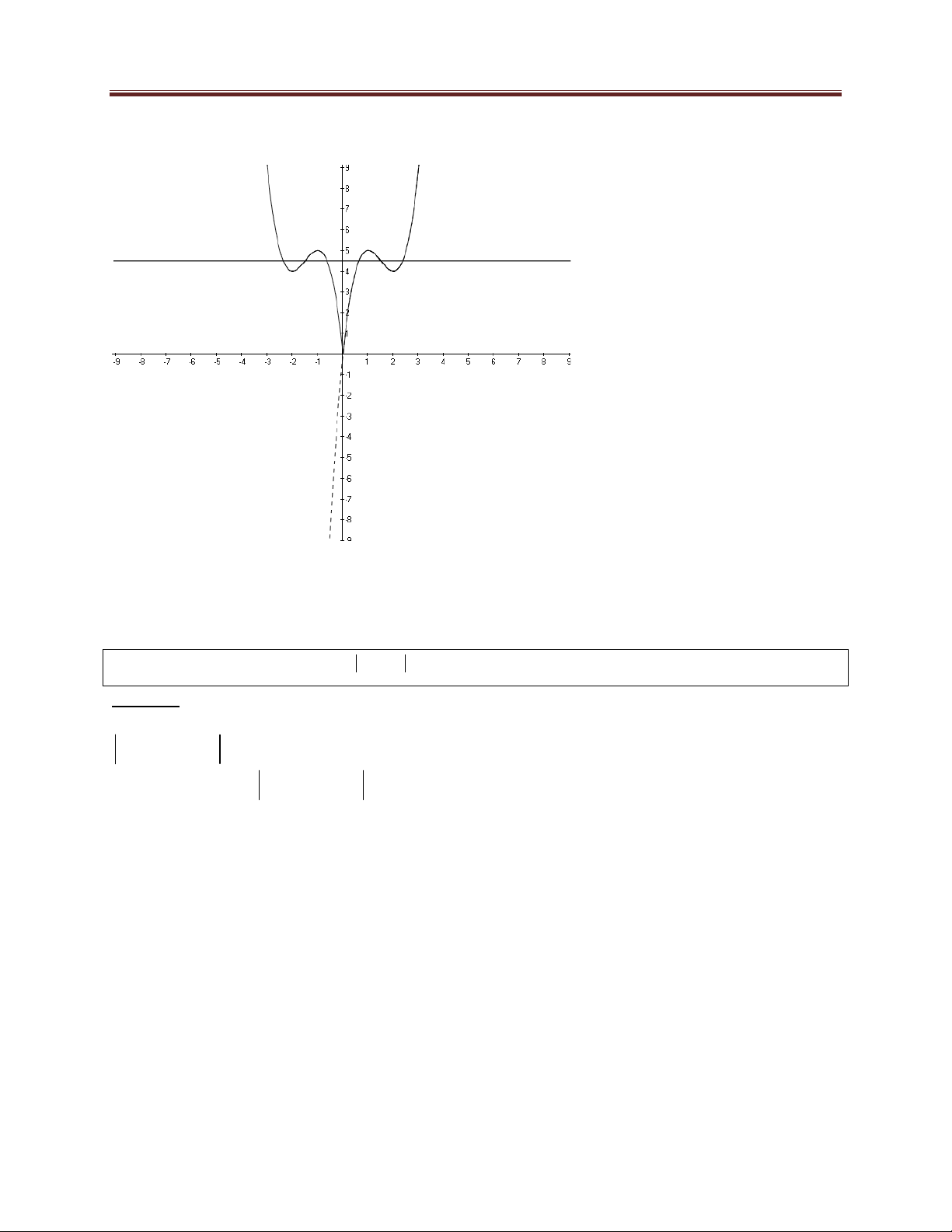
y  f (x)  x  3x  2 C  có đồ thị như sau: 30 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 3  3
 f (x)  x  3x  2, x  0
Ta có y  x  3 x  2   3
 f ( x)   x  3x  2, x  0 
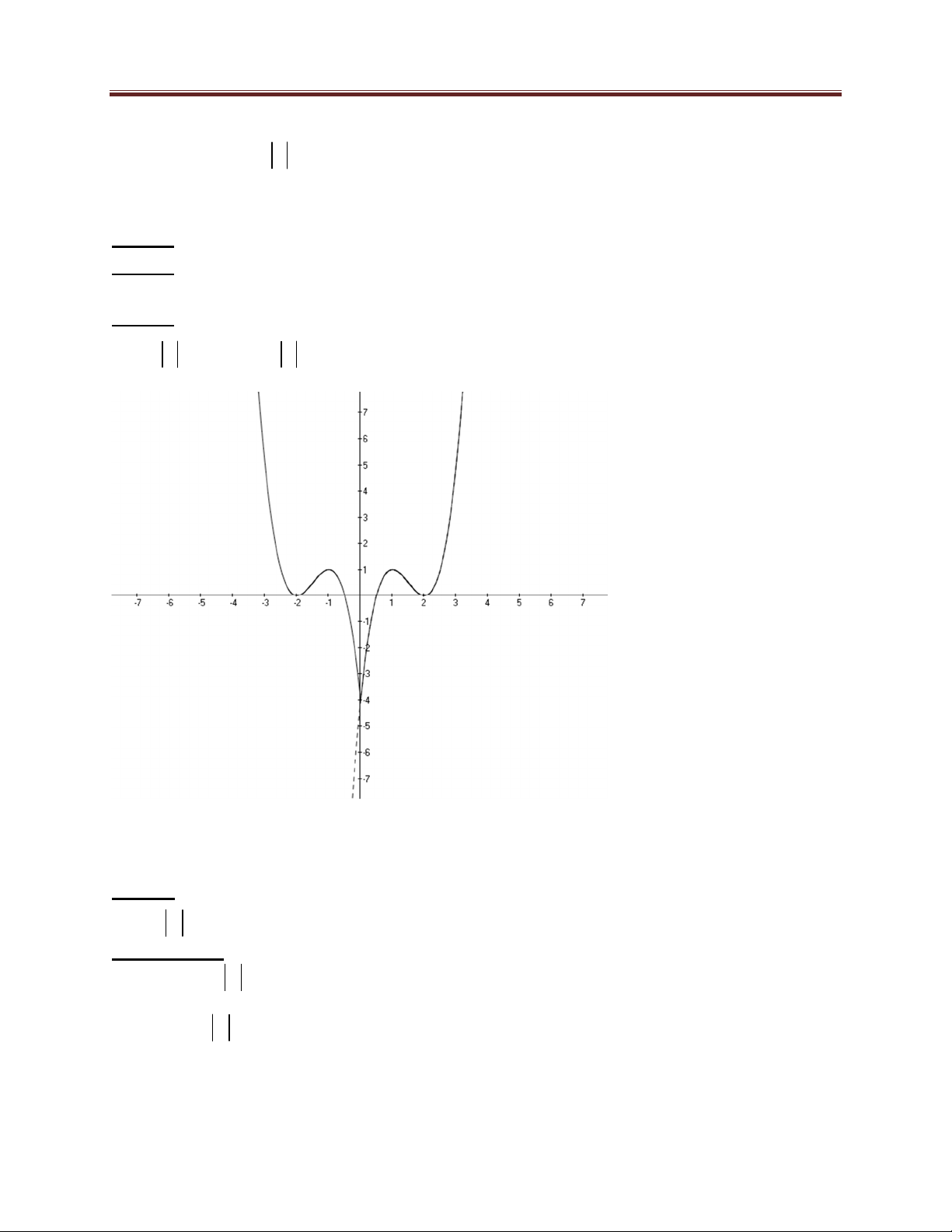
Do đó đồ thị C gồm hai phần 1 
Phần 1: Giữ nguyên phần đồ thị C  bên phải trục tung.
Phần 2: Lấy đối xứng phần 1 qua trục tung. 31 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
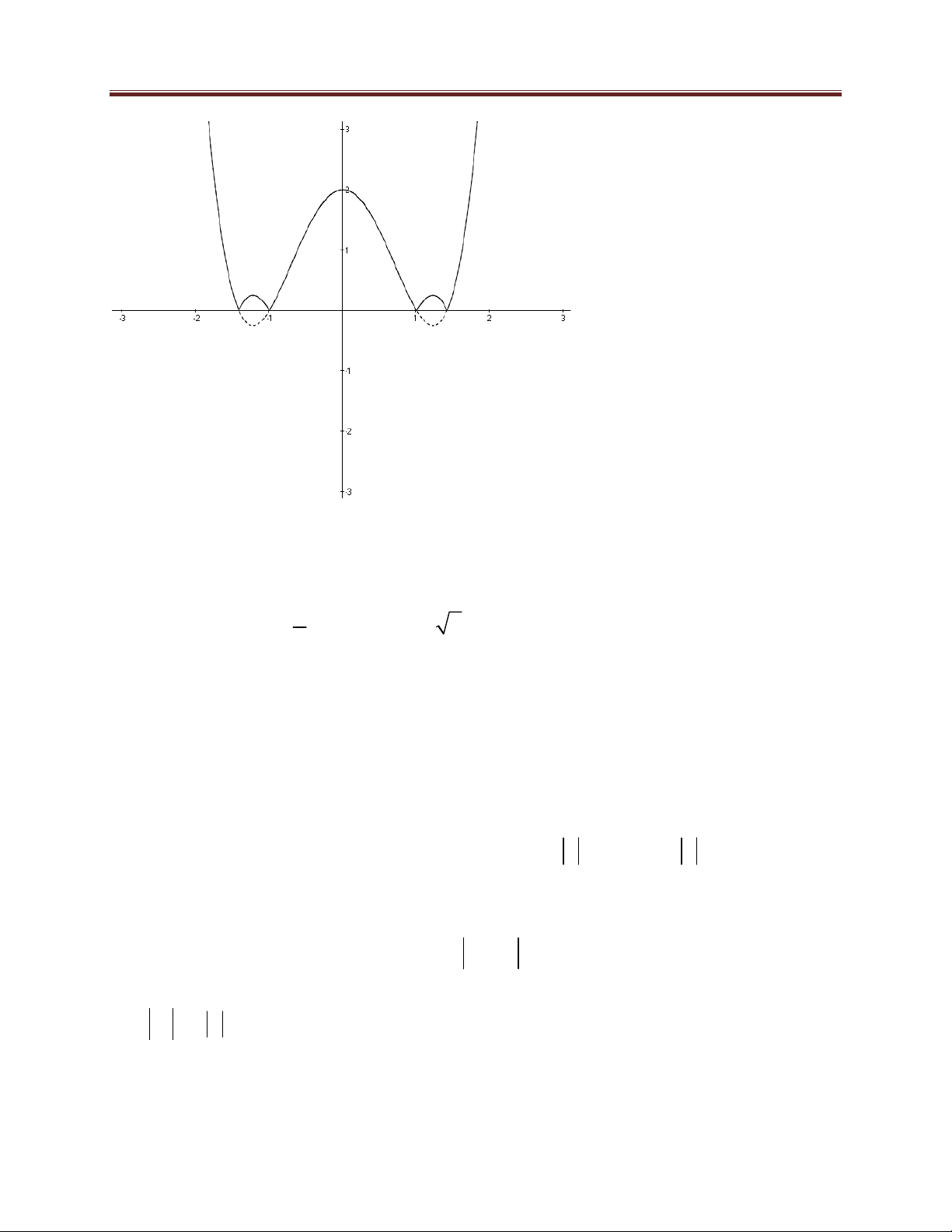
Để đường thẳng d cắt C tại bốn điểm phân biệt thì d phải nằm trong miền giới hạn bởi hai 1  đường thẳng trên. -
Đường thẳng thứ nhất đi qua điểm M 2; 0 và A0;2 có hệ số góc là k 1 1 -
Đường thẳng thứ hai là tiếp tuyến với C ứng với x  0 , ta xác định k 1  2 3
x  3x  2  k x  2 2      x  1 3 Ta có 2  3
 x  3  k  2   k  6 3  9  2 x  0  
Vậy để d cắt C tại bốn điểm phân biệt, khi và chỉ khi 1 
k  k  k  1  k  6 3  9 . 1 2
Vậy k  1;6 3  9 là giá trị cần tìm.
BÀI TẬP ĐỀ NGHỊ 1.1.
Tìm các giá trị thực của tham số m để đồ thị C
của hàm số tiếp xúc với trục hoành. m  1. 3 2
y  x  3x  3mx  3m  4 C . m  2. 3
y  x  m   2 x   2 1
2m  3m  2 x  2m2m   1 C m  3. 3
y  mx  m   2
1 x  4m  3 x  6m C m  1.2.
Tìm tất cả các giá trị của tham số m để đường thẳng d : y  m  x  3 tiếp xúc với đường 1 cong 3 y   x  3x . 3 1.3.
Tìm những giá trị của tham số m để hai đường cong sau tiếp xúc nhau C  3
: y  mx  m   2
1 x  m 1 x  1và C  2
: y  mx  m 1 x  m 2   1   1.4.
Tìm m để đồ thị hàm số 3
y  x  m   2 x   2 m   3 3 1 3
1 x  m 1  0 cắt trục hoành tại duy nhất một điểm. 1.5.
Tìm m để đồ thị hàm số 4 2
y  x  mx  m 1 cắt trục hoành tại bốn điểm phân biệt có
hoành độ lớn hơn 2 . 1.6.
Viết phương trình đường thẳng d cắt đồ thị hàm số 3
y  x  3x  2 tại ba điểm phân biệt ,
A B,C sao cho x  2 và BC  2 2 . A 1.7.
Viết phương trình đường thẳng d song song với trục hoành và cắt đồ thị hàm số 1 8 3 2 y 
x  x  3x 
tại hai điểm phân biệt ,
A B sao cho tam giác OAB cân tại gốc tọa 3 3 độ O . 32 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1.8.
Tìm tất cả các giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y  x  3x  3mx  3m  4 và trục hoành có phần nằm phía trên trục hoành bằng phần
nằm phía dưới trục hoành. 1.9.
Tìm tất cả các giá trị của tham số m để tiếp tuyến của đồ thị hàm số 4 1 3 y 
x  2m   2
1 x   m  2 x  C  tại giao điểm A của C với trục tung tạo m  3 3 m 1
với hai trục tọa độ một tam giác có diện tích bằng . 3
1.10. Tìm m để đường thẳng d : y  m cắt đồ thị hàm số 4 2
y  x  2x  3 tại bốn điểm phân biệt M , N, ,
P Q có hoành độ lần lượt x  x  x  x sao cho MN, ,
NP PQ là độ dài ba 1 2 3 4 cạnh tam giác.
1.11. Giả sử đồ thị hàm số 4
y  x  m   2 3
1 x  3m  2 cắt trục hoành tại bốn điểm phân biệt,
khi m  0 gọi A là giao điểm có hoành độ lớn nhất ; tiếp tuyến với đồ thị hàm số tại A cắt
trục tung tại B . Tìm m để tam giác OAB có diện tích bằng 24.
1.12. Tìm m để đồ thị hàm số 3
y  x  m   2 x   2 3 1
2 m  4m  
1 x  4m m   1 cắt trục hoành
tại ba điểm phân biệt có hoành độ lớn hơn 1.
1.13. Chứng minh rằng đồ thị hàm số 3 2
y  x  6x  9x  m cắt trục hoành tại ba điểm phân
biệt x  x  x thỏa mãn 0  x  1  x  3  x  4 . 1 2 3 1 2 4
1.14. Tìm m để đồ thị hàm số 3
y  x  m   2 2
2 x  7 m  
1 x  3 m  4 cắt trục hoành tại 3
điểm phân biệt có hoành độ x , x , x hỏa mãn 2 2 2
x  x  x  3x x x  53 . 1 2 3 1 2 3 1 2 3
1.15. Chứng minh rằng khi m thay đổi đường thẳng 2
d : y  mx  m luôn cắt m C  3
y  x   m   2
x  m  m   2 : 3 1 2
1 x  m tại một điểm A có hoành độ không đổi. Tìm m
m để d cắt C
tại một điểm nữa khác A mà tiếp tuyến của C tại hai điểm đó song m  m  m song với nhau.
1.16. Tìm m để đường thẳng d : y  x 1cắt C  3 2
: y  4x  6mx 1tại 3 điểm A0;  1 , B, C m
biết B,C đối xứng với nhau qua đường phân giác thứ nhất.
1.17. Tìm m để đồ thị C  4 2
: y  x  4x  m cắt trục hoành tại 4 điểm phân biệt sao cho diện m
tích hình phẳng giới hạn bởi C
và trục hoành có phần trên bằng phần dưới. m  1.18. Cho hàm số 4
y  x  m   2 2
2 x  2m  3C
. Tìm tất cả các giá trị của tham số m để m 
C cắt trục hoành tại bốn điểm cách đều nhau. m 
1.19. Tìm m để đồ thị hàm số 3
y  x  m   2 2
1 x  2m 1 cắt trục hoành tại ba điểm phân biệt
đều có hoành độ nhỏ hơn 3.
1.20. Chứng minh rằng với m  0 thì đồ thị hàm số 4 2 2 4
y  x  2m x  2m  m luôn cắt trục
hoành tại ít nhất hai điểm phân biệt.
1.21. Tìm tất cả các giá trị củ tham số m để đường thẳng d : y  mx  2m  4 cắt đồ thị hàm số 3 2
y  x  6x  9x  6 tại ba điểm phân biệt. 33 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
1.22. Tìm m để đồ thị hàm số 3 2
y  x  3x  mx  2  m cắt trục hoành tại ba điểm phân biệt ,
A B,C sao cho tổng hệ số góc các tiếp tuyến với đồ thị hàm số tại , A B,C bằng 3.
1.23. Tìm tất cả các cặp số m, n sao cho trong các giao điểm của đồ thị hàm số 3 2
y  mx  nx  mx  n C  có hai điểm cách nhau 2011 và khoảng cách từ tâm đối xứng
của C  đến trục hoành bằng 2012 .
1.24. Tìm tất cả các giá trị của tham số m để đường thẳng d : y  3  x cắt đồ thị hàm số 3 2
y  x  3x  mx  4  m C  tại ba điểm phân biệt A1; 2, B,C sao cho tiếp tuyến với
C  tại B,C lần lượt cắt C  tại M , N và tứ giác BMNC là hình thoi.
1.25. Tìm tất cả các cặp giá trị m, n để đường thẳng d : y  mx  n cắt đồ thị hàm số 4 2
y  x  4x  3 tại bốn điểm phân biệt , A ,
B C, D có hoành độ lần lượt là 1
x  x  x  x sao cho AB  CD  BC 1 2 3 4 2 1 1.26. Cho hàm số 3 y 
x  2  m 2
x  32m  3 x  m C  . Tìm những giá trị của tham số 3 m
m để đường thẳng d : y  x  m cắt C
tại ba điểm phân biệt A 0, m, B,C , đồng thời m  
OA là phân giác trong góc BOC .
1.27. Tìm những giá trị của tham số m để đồ thị hàm số 3 2
y  x  3x  3mx  m cắt trục hoành tại ba điểm phân biệt , A B,C có hoành độ tương ứng thỏa mãn
 x  3   x  3   x  3 2 2 2  3 . A B C
1.28. Tìm m để đồ thị hàm số 3 2
y  x  3mx  m 1 cắt đồ thị hàm số tại ba điểm phân biệt ,
A B,C sao cho AB  BC .
Tương giao với hàm phân thức bậc nhất trên bậc nhất : BÀI TẬP MẪU x 1
Bài 1.Cho hàm số y  C 2x 1
Chứng minh rằng với mọi m đường thẳng y  x  m luôn cắt đồ thị C  tại hai điểm phân biệt A
và B . Gọi k , k lần lượt là hệ số góc của các tiếp tuyến với C  tại A và B . Tìm m để tổng 1 2
k  k lớn nhất. 1 2 Lời giải: x 1
Hoành độ giao điểm của d : y  x  m và C  là nghiệm phương trình: x  m  2x 1 34 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1
  x  m2x  
1  x 1( do x  không là nghiệm) 2
 2x  2mx  m 1  0(*) 2 Ta có 2
 '  m  2m  2  0, m
 . Suy ra d luôn cắt C  tại hai điểm phân biệt với mọi . m
Gọi x , x là nghiệm của (*), ta có 1 2 1 1
4  x  x 2  8x x  4 x  x  2 1 2 1 2  1 2  k  k      . 1 2 2x  2 1 2x  2 1
4x x  2 x  x   2 1 1 2 1 2 1 2 m 1
Theo định lí Vi-ét ta có x  x   ; m x x   . 1 2 1 2 2
Từ đó suy ra k  k  4
 m  8m  6  4   m  2 2 1  2  2
 . Dấu bằng xảy ra khi và chỉ khi 1 2 m  1.
Vậy giá trị lớn nhất của k  k  2
 khi và chỉ khi m  1 1 2 x 1
Bài 2.Cho hàm số y  C 2x 1
Chứng minh rằng với mọi m đường thẳng y   x  m luôn cắt đồ thị C  tại hai điểm phân biệt
A và B . Gọi k , k lần lượt là hệ số góc của các tiếp tuyến với C  tại A và B . Tìm m để tổng 1 2
k  k nhỏ nhất. 1 2 Lời giải: x 1
Hoành độ giao điểm của d : y  x  m và C  là nghiệm phương trình: x  m  2x 1 1
  x  m2x  
1  x 1( do x  không là nghiệm) 2
 2x  2mx  m 1  0(*) 2 Ta có 2
 '  m  2m  2  0, m
 . Suy ra d luôn cắt C  tại hai điểm phân biệt với mọi m
Gọi x , x là nghiệm của (*), ta có 1 2 1 1
4 x  x 2  8x x  4 x  x  2 1 2 1 2  1 2  k  k    1 2 2x  2 1 2x  2 1
4x x  2 x  x   2 1 1 2 1 2 1 2 m 1
Theo định lí Vi-ét ta có x  x   ; m x x   . 1 2 1 2 2
Từ đó suy ra k  k  4m  8m  6  4 m  2 2
1  2  2 . Dấu bằng xảy ra khi và chỉ khi m  1. 1 2
Vậy giá trị nhỏ nhất của k  k  2 khi và chỉ khi m  1 1 2 2x 1
Bài 3. Cho hàm số y  C x  2 35 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Chứng minh rằng đường thẳng d : y  x  m luôn cắt đồ thị hàm số C  tại 2 điểm phân biệt A
và B . Tìm m để đoạn AB có độ dài nhỏ nhất. Lời giải: 2x 1
Hoành độ giao điểm của d và C  là nghiệm phương trình: x  m  x 2
 x  m  x  2  2x 1
( do x  2 không là nghiệm) 2
 x  4  m x 1 2m  0 (*) 2
Ta có     m    m 2 4 4 1 2
 m 12  0, m
 . Suy ra d luôn cắt C  tại hai điểm phân biệt , A B Do ,
A B  d  y  x  ;
m y  x  m . Từ đó suy ra A A B B
AB   x  x 2   y  y 2   x  x 2   x  x 2 2 2 2 8x x A B A B A B A B A B
Theo định lí Vi-ét ta có: x  x  m  4; x x  1 2m . Từ đó suy ra A B A B 2 AB   2
2 m 12  2  AB  2 . Dấu bằng xảy ra khi và chỉ khi m  0
Vậy giá trị nhỏ nhất của AB  2 khi và chỉ khi m  0 x  3
Bài 4.Cho hàm số y  C x 1
Đường thẳng d có hệ số góc k đi qua điểm I 1; 
1 và cắt C  tại hai điểm phân biệt M và N
sao cho I là trung điểm của MN. Tìm k . Lời giải:
+ Phương trình đường thẳng d : y  k  x   1 1. x  3
+ Hoành độ giao điểm của d và C  là nghiệm phương trình:
 k  x   1 1 x 1 2
 kx  2kx  k  4  0(*) (do x  1 không là nghiệm).
Yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có hai nghiệm phân biệt x , x thỏa 1 2 mãn k  0   '  4  k  0  k  0 x  x  2   2x  1 2 I
Vậy giá trị cần tìm của k là  ;  0 2x  4
Bài 5.Cho hàm số y  C . 1 x 36 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Gọi d là đường thẳng đi qua I 1; 
1 có hệ số góc k . Tìm k để d cắt C  tại hai điểm phân biệt
M và N sao cho độ dài MN bằng 3 10 Lời giải:
+ Phương trình đường thẳng d : y  k  x   1 1 2x  4
+ Hoành độ giao điểm của d và C  là nghiệm phương trình:
 k  x   1 1 1 x
Do x  1 không là nghiệm nên phương trình tương đương với 2
kx  2k  3 x  k  3  0(*)
d cắt C  tại hai điểm phân biệt M , N khi và chỉ khi phương trình (*) có hai nghiệm phân biệt k  0 3    0  k  (1)   9  24k  0 8 
Do M , N  d  y
 k  x  
1 1; y  k  x   1 1. Suy ra M M N N MN  x x 2  y y 2  k  x x 2
 k  x x 2 2 2 2 1 1 4 x x              90 M N M N M N M N M N   2k  3 k  3
Theo định lí Vi-ét ta có: x  x  ; x x  . Từ đó suy ra M N M N k k 3 2 3  41 k  k  k     k    2 8 27 8 3 0
3 8k  3k   1  0  k  3  hoặc k  ( thỏa mãn (1)). 16   3  41  
Vậy giá trị cần tìm của k là  3  ;   16    2x 1
Bài 6. Cho hàm số y  C x 1
Tìm m để đường thẳng d : y  x  m cắt C  tại hai điểm phân biệt A và B sao cho A và B cùng
với gốc tọa độ tạo thành tam giác vuông tại O . Lời giải: 2x 1
+ Hoành độ giao điểm của d và C  là nghiệm phương trình: x  m  x 1
  x  m x  
1  2x 1( do x  1 không là nghiệm) 2
 x  m  3 x 1 m  0(*) . Ta có 2
  m  2m  5  0, m
 . Từ đó suy ra d luôn cắt C  tại hai điểm phân biệt , A B . Do hai điểm ,
A B  d  y  x  ;
m y  x  m . A A B B
Suy ra tọa độ của A x ; x  m, B  x ; x  m A A B B  37 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  
Và OA   x ; x  m,OB   x ; x  m Tam giác OAB vuông tại O khi và chỉ khi A A B B    OA OB 
 x x   x  m x  m   x x  m x  x  2 . 0 0 2  m  0(1) A B A B A B A B
Theo định lí Vi-ét ta có: x  x  3  ;
m x x  1 m . Khi đó (1) trở thành A B A B 2
m  m 3  m  21 m  0  m  2 .
Vậy m  2 là giá trị cần tìm. x  2
Bài 7. Cho hàm số y  C  . x  2
Chứng minh rằng với mọi giá trị của m thì trên C  luôn có các cặp điểm A và B nằm về hai
x  y  m  0
nhánh của C  và thỏa mãn A A 
x  y  m  0  B B Lời giải:
x  y  m  0
 y  x  m + Ta có A A A A     ,
A B  d : y  x  m
x  y  m  0
y  x  m  B B  B B
Khi đó yêu cầu bài toán trở thành chứng minh d luôn cắt C  tại hai điểm thuộc về hai nhánh của C  . x  2
+ Hoành độ giao điểm của d và C  là nghiệm phương trình: x  m  x  2
  x  m x  2  x  2 (do x  2 không là nghiệm) 2
 x  m  3 x  2m  2  0(*) . Ta có 2
  m  2m 17  0, m
 . Từ đó suy ra d luôn cắt C  tại hai điểm phân biệt với mọi m . Mặt khác, kí hiệu 2
g(x)  x  m  3 x  2m  2  1.g 2  4  0  2 nằm giữa hai nghiệm của (*). Ta có đpcm. x  2
Bài 8. Cho hàm số y 
C . Tìm tất cả các giá trị thực của tham số m để đường thẳng 2x  2 37
d  : y  x  m cắt đồ thị C  tại hai điểm phân biệt , A B sao cho 2 2 OA  OB  . 2 Lời giải : x  2
Hoành độ giao điểm của d  ,C  là nghiệm của phương trình :  x  m 2x  2
Do x  1 , không là nghiệm của phương trình nên phương trình tương đương với x 
  x   x  m 2 2 2 2
 2x   2m  3 x  2 m   1  0(*) .
Do   m  m    m  2 2 4 4 25 2 1  24  0, m
  . Nên phương trình (*) luôn có hai nghiệm phân biệt. 38 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Gọi A  x , x  m ; B x , x  m là tọa độ giao điểm của d  và C  , khi đó theo định lý viét, ta 1 1   2 2  2m  3
có : x  x  
; x x   m 1 1 2 1 2   2 Từ đó suy ra :
OA  OB  x   x  m2  x   x  m2 2 2 2 2 1 1 2 2
 2  x  x 2  4x x  2m x  x  2  2m 1 2 1 2 1 2 2  2m  3   2m  3   2   4   m   2 1  2m  2m    2   2  1   2
4m  2m 17 2 37 1 37 5 Vậy 2 2 OA  OB    2
4m  2m 17   m    m  2 . 2 2 2 2 5
Vậy m   ; m  2 là hai giá trị cần tìm. 2
BÀI TẬP ĐỀ NGHỊ 2x  m 1.1. Cho hàm số y 
C  . Chứng minh rằng với mọi m  0 , C cắt đường thẳng m  mx 1 m
d : y  2  x  m tại hai điểm phân biệt ,
A B thuộc một đường  H  cố định. Dường thẳng
d cắt trục hoành tại hai điểm M , N . Tìm những giá trị của m để S  3S . OAB OMN x 1.2. Cho hàm số y 
C  . Tìm tất cả các giá trị của tham số m để đường thẳng 1 x
y  mx  m 1 cắt đồ thị C  tại hai điểm phân biệt A và B sao cho 2 2
MA  MB đạt giá trị
nhỏ nhất, biết điểm M  1  ,  1 . 2x  2 1.3. Cho hàm số y 
C  . Tìm m để đường thẳng d : y  2x  m cắt C  tại hai điểm x 1 phân biệt ,
A B sao cho AB  5 x 1 1.4. Cho hàm số y  C
. Tìm m để đường thẳng y  x  2 cắt C tại hai điểm m  m  x  m
phân biệt A và B sao cho AB  2 2 2x 1 1.5.
Với mỗi giá trị của tham số m để đường thẳng d : y  mx 1 cắt đồ thị hàm số y  x 1
tại hai điểm phân biệt M , N và cắt hai đường tiệm cận lần lượt tại , A B . Chứng minh
rằng MA  NB . 39 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 2x 1 1.6.
Cho đường thẳng y 
C  và điểm A2; 4 . Viết phương trình đường thẳng d x 1
cắt đồ thị hàm số C  tại hai điểm phân biệt B,C sao cho tam giác ABC đều. 2x 1 1.7.
Tìm m để đường thẳng d : y  x  2m cắt đồ thị hàm số y 
tại hai điểm phân biệt x  2 ,
A B sao cho AB  4 2 . x  2 1.8.
Tìm m để đường thẳng y  x  m cắt đồ thị hàm số y 
tại hai điểm phân biệt 2  x   1 37 , A B sao cho 2 2 OA  OB  . 2
CÁC BÀI TOÁN VỀ CỰC TRỊ HÀM SỐ
Loại 1 : Điều kiện hàm số y  f (x) có cực trị .
Phương trình f '(x)  0 có ít nhất 2 nghiệm phân biệt trở lên.
Loại 2 : Điều kiện để một điểm là cực trị của hàm số.
Cho hàm số y  f (x) điểm M  x ; y  C là điểm cực trị của hàm số khi đó f '(x )  0 . 0 0    0
 f '(x )  0 (i). Nếu 0 
 M là điểm cực đại của đồ thị hàm số f ' (x )  0  0
 f '(x )  0 (ii). Nếu 0 
 M là điểm cực tiểu của đồ thị hàm số f ' (x )  0  0
Loại 3 : Đường thẳng đi qua các điểm cực trị của hàm số.
Xét với hàm số đa thức bậc 3 : 3 2
y  ax  bx  cx  d có đạo hàm 2
y '  3ax  2bx  c .
Lấy y chia cho y ' ta được 2  1 b   2c b  bc y  x  y '  2 x  d       3 9a  3 9a 9a  
Hàm số đạt cực trị tại x , x thì khi đó y '(x )  y '(x )  0 nên 1 2 1 2 40 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 2   2c b  bc y(x )   2 x  d   1   1 3 9a 9a    
 Hai điểm cực trị của hàm số nằm trên đường thẳng 2  2c b   bc y(x )   2 x  d  2   2  3 9a 9a    2  2c b  bc y   2 x  d    3 9a 9a  
Lưu ý : Với các hoành độ cực trị không phụ thuộc tham số thì ta không cần thiết phải làm theo
cách này, nhưng có chứa tham số thì đây là lựa chọn khôn ngoan.
Loại 4 : Các điểm cực trị thỏa mãn một điều kiện chẳng hạn lập thành tam giác vuông, tam giác
đều,…Lúc này chúng ta dựa vào tính chất của tam giác.
Dạng toán : Liên quan đến điều kiện tồn tại cực, cực tiểu- tọa độ cực trị. Phương pháp : -
Để hàm số có cực trị khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt.  y '   x  0 0  -
Một điểm x là điểm cực tiểu của hàm số thì
cần phải thử lại xem y ' có đổi 0  y'   x  0  0 
dấu từ âm sang dương khi đi qua x hay không. 0  y '   x  0 0  -
Một điểm x là điểm cực đại của hàm số thì
cần phải thử lại xem y ' có đổi 0  y'   x  0  0 
dấu từ dương sang âm khi đi qua x hay không. 0 -
Cho hai điểm A x ; y ; B x ; y và đường thẳng d : Ax  By  C  0 hoặc đường tròn 1 1   2 2 
C  x  a2   y  b2 2 :  R . T
   Ax  By  C Ax  By  C 1 1  2 2   Xét  V  
x a2  y b2  R x a2  y b2 2 2  R 1 1 2 2   Khi đó hai điểm ,
A B nằm cùng phía với d hoặc C khi và chỉ khi T  0 hoặc V  0 . Hai điểm ,
A B nằm khác phía đối với d hoặc C khi và chỉ khi T  0 hoặc V  0 . Đặc biệt :
Hai điểm cực trị nằm khác phía với trục tung thì pt y '  0có hai nghiệm trái dấu.
Hai điểm cực trị nằm khác phía đối với trục hoành thì y y
 0 hoặc phương trình y  0 có CÐ CT ba nghiệm phân biệt. 41 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN BÀI TẬP MẪU 1
Bài 1. Tìm m để hàm số sau có cực trị 3 2 y  x  mx   2
2m  3m  2 x  8 . 3 Lời giải : Ta có 2 2
y '  x  2mx  2m  3m  2
Hàm số có cực trị khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt 2
 '  m  3m  2  0  1  m  2 .
Bài 2. Tìm m để hàm số 4
y  mx   2 m   2
9 x 10 có 3 cực trị. Lời giải : Ta có 3
y  mx   2 m   2 2 ' 4 2
9 x  2x(2mx  m  9)
Hàm số có 3 cực trị khi và chỉ khi phương trình y '  0 có 3 nghiệm phân biệt, điều này tương đương với 2  m  9   0  m
 0  m  3  m  3  m  0  1 3
Bài 3. Tìm m để hàm số 4 2 y  x  mx 
chỉ có cực tiểu mà không có cực đại. 4 2 Lời giải : Ta có 3
y  x  mx  x  2 ' 2 x  2m
+ Nếu m  0  hàm số chỉ có cực tiểu tại x  0 .
+ Nếu m  0 thì hàm số chỉ có cực tiểu tại x  0 .
+ Nếu m  0 thì hàm số có 3 cực trị, nên không thỏa mãn.
Vậy m  0 là những giá trị cần tìm.
Bài 4. Tìm m để hàm số y   x  m3  3x đạt cực tiểu tại x  0 . Lời giải : 2
Ta có y '  3 x  m  3; y '  6 x  m 2  y '(0)  0 3m  3  0
Hàm số đạt cực tiểu tại x  0 thì     m  1  . y ' (0)  0  6m  0  2
Thử lại với m  1thì hàm số y   x  3
1  3x có y '  3 x  
1  3  3x  x  2
đổi dấu từ âm sang dương khi đi qua 0 . Vậy nên hàm số đạt cực tiểu tại x  0 . 42 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Vậy m  1là giá trị cần tìm.
Bình luận : Rất nhiều học sinh cũng như cả các thầy cô không hiểu rõ điều kiện để hàm số đạt
cực trị tại một điểm ; và tất nhiên như trên khi nói điều kiện để hàm số đạt cực tiểu tại x  0 thì học sinh lại viết :  y '(0)  0
Để hàm số đạt cực tiểu tại x  0 khi và chỉ khi  y ' (0)  0 
Lưu ý : Sẽ không có điều tương đương trên, mà chỉ có là nếu đạt cực tiểu tại x  0 thì  y '(0)  0 
chứ không có điều ngược lại y ' (0)  0 
Do đó khi tìm được giá trị của tham số m thì ta phải thử lại xem có thỏa mãn điều kiện đổi dấu của y ' hay không. 1
Bài 5. Tìm m để hàm số 3 y  x   2
m  m  2 2 x   2 3m  
1 x  m  5 đạt cực tiểu tại x  2 . 3 Lời giải : 2
 y '  x  2   2 m  m  2 2 x  3m 1 Ta có 
 y '  2x  2  2 m  m  2  2  y '( 2)   0 
2m  2m  0
Hàm số đạt cực tiểu tại x  2 thì     m  4 . 2 y ' ( 2)   0 
4m  m  0 
Thử lại với m  4 thỏa mãn.
Vậy m  4 là giá trị cần tìm.
Bài 6. Tìm m để hàm số y   x  m 2
x  3x  m  
1 có cực đại và cực tiểu thỏa mãn x .x  1. CD CT Lời giải : Ta có 2
y '  3x  2 m  3 x  2m 1
Hàm số có cực đại và cực tiểu thỏa mãn x .x
 1 khi và chỉ khi phương trình y '  0 có hai CD CT
nghiệm phân biệt x , x thỏa mãn x x  1 , điều này tương đương với 1 2 1 2 2
 '  m  7  0  m  2 2   2m 1   
là những giá trị cần tìm. 2 2 x x   1 m  1     1 2   3  43 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1 1
Bài 7. Tìm các giá trị của tham số m để đồ thị hàm số 3 y 
x  m  3 2
x  2 m   1 x 1có 3 2
hai điểm cực trị với hoành độ lớn hơn 1. Lời giải : Ta có 2
y '  x  m  3 x  2 m   1 2
y '  0  x  m  3 x  2 m   1  0(*)
Hàm số có 2 cực trị khi và chỉ khi phương trình (*) có hai nghiệm phân biệt 2
   m  2m 1  0  m  1(i)
Yêu cầu bài toán tương đương với (*) có 2 nghiệm x , x thỏa mãn 1 2 x  1 x  x  2  m  3  2 1 1 2        m  0 x  1
x 1 x 1  0   
2 m 1  m  3 1  0 2  1  2    
Kết hợp với điều kiện (i) suy ra 0  m  1là giá trị cần tìm. Bài 7. Cho hàm số 3 2
y  2x  mx 12x 13C . m  Tìm m để C
có cực đại và cực tiểu và các điểm này cách đều trục tung. m  Lời giải : Ta có y   2 '
2 3x  mx  6
Phương trình y '  0 có 2
  m  72  0 nên hàm số luôn đạt cực trị tại hai điểm x , x . 1 2
Điểm cực đại và điểm cực tiểu của hàm số cách đều trục tung khi và chỉ khi m
x  x  x  x  x  x   0  m  0 . 1 2 1 2 1 2 3
Vậy m  0 là giá trị cần tìm. 1 1 Bài 8. Cho hàm số 3 2 y  x  mx   2
m  3 x . Tìm tất cả các giá trị của tham số m để hàm số 3 2
có cực đại, cực tiểu sao cho x , x
là độ dài các cạnh góc vuông của một tam giác vuông có độ CÐ CT 5 dài cạnh huyền bằng . 2 Lời giải : Ta có 2 2
y '  x  mx  m  3
Yêu cầu bài toán tương đương với phương trình y '  0 có hai nghiệm dương phân biệt x , x và 1 2 5 thỏa mãn 2 2 x  x  1 2 2 44 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 2      2   m  2 4 m 0  m  0 S  m  0     14 2
 P  m  3  0    3    3  m m m  2   5 2 2 S P m  2 m  14 2 2 3       m     2   2 14 Vậy m  là giá trị cần tìm. 2
Bài 9. Tìm tất cả các giá trị của tham số m để các điểm cực đại, cực tiểu của đồ thị hàm số 3
y  x   m   2 x   2 2 1
m  3m  2 x  4 nằm về hai phía trục tung. Lời giải :
Để đồ thị hàm số có cực đại, cực tiểu nằm về hai phía đối với trục tung khi và chỉ khi phương
trình y '  0có hai nghiệm trái dấu 2
  x   m   x   2 3 2 2 1
m  3m  2 có hai nghiệm trái dấu   2
3 m  3m  2  0 1 m  2
Vậy m  1;2 là giá trị cần tìm.
Bài 10. Tìm m để đồ thị hàm số 3 2
y  x  3x  mx  2 có cực đại, cực tiểu cách đều đường
thẳng y  x 1. Lời giải :
Hàm số có cực trị khi và chỉ phương trình 2
y '  3x  6x  m  0 có hai nghiệm phân biệt
  '  9  3m  0  m  3.
Khi đó gọi tọa độ hai điểm cực trị là A x ; y ; B x ; y 1 1   2 2   x 1   2m  m
Lấy y chia cho y ' ta được : y   y '  2 x  2       3 3   3  3   2m  m y    2 x  2   1   1   3  3
Do y ' x  y ' x  0  1   2    2m  m  y    2 x  2  2   2    3  3 45 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  2m  m
Suy ra đường thẳng đi qua hai điểm cực trị là d : y    2 x  2    .  3  3
Vậy để hai điểm cực trị cách đều đường thẳng y  x 1thì hoặc d song song với đường thẳng
y  x 1hoặc trung điểm của AB thuộc đường thẳng y  x 1.  2m  3 Trường hợp 1 :   2  1   m      3  2 y  y x  x 1  2m  m x  x Trường hợp 2 : 1 2 1 2  1    2 
 x  x  1 2  2   1 1 2 2 2 2  3  3 2  2m  m
Theo định lý vi-ét ta có : x  x  2    2  2 
 1  1  m  0 1 2    3  3
Cả hai giá trị này đều thỏa mãn điều kiện  3 
Vậy m  0; là giá trị cần tìm.  2 
Bài 11. Tìm m để cực đại, cực tiểu của đồ thị hàm số 3 2 3
y  x  3mx  4m đối xứng nhau qua
đường thẳng y  x . Lời giải :  x  0 2
Ta có y '  3x  6mx  0  
, vậy để hàm số có cực trị khi và chỉ khi m  0 x  2m   3 3
Khi đó gọi tọa độ hai điểm cực trị là A0;4m ; B2 ;
m 0  AB  2 ; m 4  m  và trung 3
điểm của AB là I  ; m 2m  .  AB  d Vậy ,
A B đối xứng nhau qua đường thẳng d : y  x khi và chỉ khi  I  d  3 
2m  4m  0 2    m   do m  0 . 3 2m  m 2  2 Vậy m   là giá trị cần tìm. 2
Bài 12. Tìm m để hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m  m có cực trị đồng thời khoảng cách
từ điểm cực đại đến gốc tọa độ bằng 2 lần khoảng cách từ điểm cực tiểu đến gốc tọa độ. 46 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải :
Hàm số có cực trị khi và chỉ khi pt 2
y  x  mx   2 ' 3 6 3 m  
1  0 có hai nghiệm phân biệt    1  0, m  .
Từ đó suy ra tọa độ các điểm cực trị là điểm cực đại A m 1; 2  2m và điểm cực tiểu
B m 1; 2  2m .
Yêu cầu bài toán tương đương với : OA  2OB 2
 m  6m 1  0  m  3   2 2 .
Bài 13. Tìm m để hàm số 3
y  x    m 2 1 2
x  2  m x  m  2 có cực trị đồng thời hoành độ cực tiểu nhỏ hơn 1. Lời giải :
Yêu cầu bài toán tương đương với pt 2
y '  3x  2 1 2m x  2  m  0 có hai nghiệm phân biệt x  x  1. 1 2 Cách 1 : 2
 '  4m  m  5  0  5 7 ycbt tương đương với : 2  2 1 4   5   m m m m  4 5 x   1 CT  3 Cách 2 : Đặt 2
g(x)  3x  21 2m x  2  m
Vậy yêu cầu bài toán tương đương với :  2
 '  4m  m  5  0  5 7
g(1)  5m  7  0   m  4 5  S 2m 1    1  2 3  5 7  Vậy m  ; 
 là giá trị cần tìm.  4 5 
Bài 14. Tìm m để hàm số 3
y  x  m   2 3
1 x  3m  m  2 x  2  m có cực trị, đồng thời khoảng
cách từ điểm cực đại đến trục hoành bằng khoảng cách từ điểm cực tiểu đến trục tung. Lời giải : 47 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN x  m Ta có 2
y '  3x  6 m  
1 x  3m m  2  0   x  m  2 
Suy ra hàm số luôn có cực trị
Khi đó tọa độ điểm cực đại A 3 2 ;
m m  3m  m  2 và điểm cực tiếu B  3 2
m  2; m  3m  m  6
Yêu cầu bài toán tương đương với 3 2
m  m  m   m    m   2 3 2 2
2 m  m   1  m  2 m  2  m  2  0   m  1  2 m m 1 1        m  1 2
m  m 1  1    m  0 
Vậy có 4 giá trị cần tìm của m là 2; 1; 0;  1
Bài 15. Tìm các giá trị thực của tham số m để điểm cực đại, cực tiểu của hàm số 1 4 y 
x  m   1 x  m  3 3 2
1 nằm khác phía với đường tròn T  2 2
: x  y  4x  3  0 3 3 Lời giải:  x  0 Ta có 2
y '  x  2m   1 x  0  
x  2 m   1 
Hàm số có cực đại, cực tiểu khi và chỉ khi m  1  4 3 
Khi đó tọa độc hai điểm cực trị là A 0; m   1 ; B 2m     1 ;0  3 
Đường tròn T  có tâm I 2;0 bán kính   1 Hai điểm , A B nằm khác phía với đường tròn
T  khi và chỉ khi   
IA  R  IB  R  16  0  3   m  6 2 2 2 2 1  2 4m   1  0  9  1 1 2
 4m 1  0    m  thỏa mãn điều kiện 2 2  1 1  Vậy m   ; 
 là những giá trị cần tìm.  2 2 
BÀI TẬP ĐỀ NGHỊ 1.1. Tìm m để hàm số 3 2
y  mx  3mx   m  
1 x 1 có cực trị. 48 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1.2. Tìm m để hàm số 4 2 2
y  x  3mx  m  m đạt cực tiểu tại x  0 . 1.3. Tìm m để hàm số 3
y  x  m   2 3
2 x   m  4 x  2m 1 đạt cực đại tại x  1 . 1.4. Cho hàm số 4 3
y  x  mx  m   2 4 3
1 x 1 . Với giá trị nào của tham số m để hàm số chỉ
có cực tiểu mà không có cực đại. 1.5. Cho hàm số 4
y  x  m   3
x  m   2 3 2
1 x . Chứng minh rằng với mọi m  1hàm số
luôn có cực đại mà hoành độ không dương. 1 1 1.6. Cho hàm số 4 2 y  x  mx 
. Xác định m để hàm số có cực tiểu mà không có cực đại. 2 2 1.7.
Chứng minh rằng với mọi tham số m hàm số 4 3 2
y  x  mx  mx  mx 1không đồng thời
có cực đại và cực tiểu. 1.8. Tìm m để hàm số 4
y  mx  m   2
1 x  1 2m chỉ có đúng 1 cực trị. 1.9. Tìm m để hàm số 3
y  x  m   2 2 3
1 x  6  m  2 x 1 có cực đại x và cực tiểu x thỏa 1 2 mãn 3 x  x  26 . 1 2
Đáp số : m  1. 1.10. Chứng minh rằng với mọi giá trị của tham số m thì hàm số 3
y  x   m   2 2 3 2
1 x  6m m  
1 x  1luôn có cực đại, cực tiểu đồng thời khoảng cách
giữa cực đại, cực tiểu không đổi.
1.11. Tìm m để hàm số 3
y  x  m   2 3
2 x  9x  m 1đạt cực trị tại các điểm x , x sao cho 1 2 x  x  2 . 1 2 1.12. Cho hàm số 3
y  x  m   2
x   m   x  3 2 3 2 6 5 1
4m  2 . Tìm những giá trị của tham
số m để hàm số đạt cực tiểu tại điểm x  1; 2 . 0    1 
Đáp số: m   ; 0   .  3 
1.13. Tìm m để đồ thị hàm số 3 2
y  x  3x  mx  m  2 có hai điểm cực trị nằm về hai phía của trục hoành.
Đáp số : m  ;3 . 1 1 1.14. Cho hàm số 3 2 y  x  mx   2
m  3 x . Tìm tất cả các giá trị của tham số m để hàm số 3 2
có cực đại, cực tiểu sao cho x , x
là độ dài các cạnh góc vuông của một tam giác CÐ CT 5
vuông có độ dài cạnh huyền bằng . 2 3m
1.15. Tìm m để đồ thị hàm số 3 2 y  x 
x  m có cực đại, cực tiểu nằm vế hai phía đối 2
với đường thẳng x  y  0 . 49 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 3 2
1.16. Tìm m để đồ thị hàm số y  x  3 m  
1 x  9x  m  2 có cực đại, cực tiểu đối 1
xứng nhau qua đường thẳng y  x . 2
1.17. Tìm điểm M trên đường thẳng y  x  2 sao cho tổng khoảng cách từ M đến hai điểm
cực trị của đồ thị hàm số 3 2
y  x  3x  2 đạt giá trị nhỏ nhất.
1.18. Tìm tất cả các giá trị của tham số m để hoành độ các đểm cực đại, cực tiểu của đồ thị hàm
số y  m   3 2
2 x  3x  mx  5 là các số dương.
1.19. Tìm tất cả các giá trị của tham số m để hoành độ các điểm cực trị x , x của đồ thị hàm số 1 2 3 2
y  4x  mx  3x thỏa mãn x  4  x . 1 2
1.20. Xác định m để hàm số 3
y  x    m 2 1 2
x  2  m x  m  2 đạt cực trị tại x , x sao cho 1 2 1 x  x  . 1 2 3 1
1.21. Tìm m để hàm số 3 y 
x  m  2 2
x  5m  4 x  3m 1đạt cực tại x  x sao cho 3 1 2 x  2  x . 1 2 1 1
1.22. Tìm m để hàm số 3 y 
mx  m   2
1 x  3m  2 x  đạt cực trị tại x , x thỏa mãn 3 3 1 2 x  2x  1. 1 2
1.23. Tìm m để hàm số 3
y  x  m   2 x   2
m  m   x   2 2 1 4 1 2 m  
1 đạt cực đại, cực tiểu 1 1 x  x
tại x , x thỏa mãn 1 2   . 1 2 x x 2 1 2
1.24. Tìm m để đồ thị hàm số 3 2 2
y  2x  9mx 12m x 1có cực đại, cực tiểu đồng thời 2 x  x  0 . CÐ CT 2
1.25. Tìm m để hàm số 3 y 
x  m   2 1 x   2
m  4m  3 x 1 đạt cực trị tại hai điểm x , x 3 1 2
sao cho A  x x  2 x  x
đạt giá trị lớn nhất. 1 2  1 2  1 5m
1.26. Tìm m để hàm số 3 2 y  x 
x  4mx  4 đạt cực trị tại x , x sao cho biểu thức 3 2 1 2 2 2 m
x  5mx  12m 2 1 A  
đạt giá trị nhỏ nhất. 2 2
x  5mx 12m m 1 2
1.27. Tìm m để hàm số 3
y  x   m   2 2 3 2
1 x  6m m  
1 x  1có cực trị, khi đó tìm quỹ tích
trung điểm của đoạn thẳng nối điểm cực đại và cực tiểu.
1.28. Tìm m để các điểm cực trị của đồ thị hàm số 3 2
y  x  3x  2 nằm về hai phía đối với đường tròn 2 2 2
x  y  2mx  4my  5m 1  0 . 50 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
1.29. Tìm m để đồ thị hàm số 3
y  x  m   2 3
1 x  3m  m  2 x 12m  8 có hai điểm cực trị ;
A B sao cho tổng độ dài MA  MB nhỏ nhất với M 3; 2 .
1.30. Chứng minh rằng với mọi giá trị thực của tham sốm thì đồ thị hàm số 3
y  x  m   2
x  m  m   3 2 3 1 3
2  m  3m luôn có hai điểm cực trị ; đồng thời khoảng
cách giữa hai điểm cực trị không đổi.
Dạng toán : Đường thẳng đi qua điểm cực đại cực tiểu BÀI TẬP MẪU
Bài 1. Tìm m để điểm A3;5 nằm trên đường thẳng nối hai điểm cực trị của đồ thị hàm số 3 2
y  x  3mx  3 m  6 x 1 Lời giải :
Hàm số có cực trị khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt 2
 x  2mx  m  6  0 có hai nghiệm phân biệt m  3 2
  '  m  m  6  0  (*)  m  2 
Khi đó tọa độ hai điểm cực trị là M  x ; y ; N x ; y 1 1   2 2   x m 
Lấy y chia cho y ' ta được : y   y     2
m  m   2 ' 2
6 x  m  6m 1  3 3   y  2   2
m  m  6 2
x  m  6m 1 1 1
Do y ' x  y ' x  0  1   2    y  2  2
m  m  6 2
x  m  6m 1 2 2 
Suy ra đường thẳng đi qua hai điểm cực trị là d y   2
m  m   2 : 2
6 x  m  6m 1, theo đề bài A 3;5  d nên m  4 5 6  2 m m 6 2 m 6m 1         
8 đối chiếu với điều kiện (*) suy ra chỉ nhận giá trị m    5 m  4 .
Vậy m  4 là giá trị cần tìm. 51 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1 1 Bài 2. Cho hàm số 3 y 
x  m   2
1 x  mx . Tìm m để đồ thị hàm số có cực đại, cực tiểu đối 3 2
xứng nhau qua đường thẳng  : 72x 12 y  35  0 . Lời giải :
Hàm số có cực trị khi và chỉ khi pt 2
y '  x  m  
1 x  m  0 có hai nghiệm phân biệt
   m  2
1  4m  0  m  1.
Khi đó tọa độ hai điểm cực trị là M  x ; y ; N x ; y 1 1   2 2   x m 1  1 2 1
Lấy y chia cho y ' , ta được : y  
y '  m   1 x  m m     1  3 6  6 6  1 1
y   m  2 1 x  m m 1 1 1     6 6
Do y ' x  y ' x  0  1   2   1 1
 y   m  2 1 x  m m 1 2 2     6 6 1 2 1
Suy ra đường thẳng đi qua hai điểm cực trị là d : y   m   1 x  m m   1 6 6
Để M , N đối xứng nhau qua  thì trước tiên phải có 1 m 
d     m  2 0 1 .6  1    6 m  2   1   1 1  
Với m  0  M 0;0; N 1;    
trung điểm của MN là I ;      . Nên loại  6   2 12  m  0 .  5   2   3 9  
Với m  2  M 1; ; N 2;     
trung điểm của MN là I ;    
. Nên loại m  2 .  6   3   2 12 
Vậy không có giá trị nào của m thỏa mãn.
Bài 3. Chứng minh rằng với mọi giá trị của tham số m thì đồ thị hàm số 3 2
y  x  mx   2  m  3 2 3 3 1
x  m  m luôn có cực đại, cực tiểu đồng thời gọi  x; y là hoành độ, 1
tung độ các điểm cực trị thì ta luôn có 2x  y   0 . 4 Lời giải : Ta có 2
y   x  mx   2 ' 3 6
3 1 m   0 , có  1 m 
. Nên luôn có hai nghiệm phân biệt hay hàm
số luôn có cực trị với mọi m.
Khi đó gọi tọa độ hai điểm cực trị là A x ; y ; B x ; y 1 1   2 2  52 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  x m 
Lấy y chia cho y ' , ta được : 2 y  
y ' 2x  m  m    3 3  2 
 y  2x  m  m
Do y ' x   y ' x  1 1  0  1 2  2
 y  2x  m  m  2 2
Nên đường thẳng đi qua hai điểm cực trị là 2
y  2x  m  m Từ đó suy ra hoành độ, tung độ các điểm cực trị thỏa mãn 2 1 1  1 2  2x  y   m  m   m   0   . Từ đó ta có đpcm. 4 4  2 
Bài 4. Chứng minh rằng với những giá trị thực của tham số m để đồ thị hàm số 3 1 3
y  x  m   2 1 x  3mx  m m  
1 có cực đại, cực tiểu ; đồng thời gọi  x; y là tọa độ các 2 2
điểm cực đại, cực tiểu thì ta luôn có  3
x  y x  0. Lời giải :  x  m Ta có 2
y '  3x  3m  
1 x  3m  0   x  1 
Để hàm số có cực trị khi và chỉ khi m  1.
Khi đó gọi tọa độ hai điểm cực trị là A x ; y ; B x ; y 1 1   2 2   x 1  1
Lấy y chia cho y ' , ta được : y   m   1 y '  m    2 1 x  3 6  2  1
y   m  2 1 x 1 1   2
Do y ' x  y ' x  0  1   2   1
 y   m  2 1 x 2 2   2 1
Nên đường thẳng đi qua hai điểm cực trị là y   m  2 1 x 2 1
Từ đó suy ra hoành độ, tung độ các điểm cực trị thỏa mãn  x  y x  x  m  2 3 4 2 1 x  0 . Từ 2 đó ta có đpcm. 2 m
Bài 5. Với mỗi giá trị thực của tham số m để đồ thị hàm số 3 2 2
y  x  x  m x  có cực đại, 9
cực tiểu ; đồng thời gọi  x; y là tọa độ các điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức y  x P  . x  y 53 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải :
Hàm số có cực trị khi và chỉ khi phương trình 2 2
y '  3x  2x  m  0 có hai nghiệm phân biệt, khi 1 và chỉ khi 2 2
 '  1 3m  0  0  m  3
Khi đó gọi tọa độ hai điểm cực trị là A x ; y ; B x ; y 1 1   2 2   x 1   2 2 
Lấy y chia cho y ' , ta được : 2 y   y ' m  x      3 9   3 9    2 2 2  y  m  x  1   1   3 9 
Do y ' x  y ' x  0  1   2    2 2 2   y  m  x 2   2    3 9   2 2 
Nên đường thẳng đi qua hai điểm cực trị là 2 y  m  x    3 9   2 2 2  2 11 2 m  x  x   m  y  x  3 9 Vậy  3 9 P    x  y  2 2  2 7 2 2 m  x  x m     3 9 3 9  2 11 t   1  Xét hàm số 3 9 f (t)  , với 2 t  m  0; 2 7    3 t   3 9  1  11
Ta có f (t) là hàm đơn điệu tăng trên 0; 
 , nên suy ra P  f (t)  f (0)   .  3  7 11
Vậy giá trị nhỏ nhất của P bằng  khi m  0 . 7
Bài 6. Tìm các giá trị thực của m để đường thẳng đi qua cực đại, cực tiểu của đồ thị hàm số 3 2 2 2
y  x  3x 1 tiếp xúc với đường tròn T  :  x  m   y  m   1  5 Lời giải :
Dễ thấy hai điểm cực trị là A 0; 
1 ; B 2;3 , suy ra phương trình đi qua hai điểm cực trị của
hàm số là d : 2x  y 1  0
Đường tròn T  có tâm I m; m   1 và bán kính   5
Yêu cầu bài toán tương đương với
2m  m 11 d  5
I;d   5   5  m   2 2 3 2 1 54 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
BÀI TẬP ĐỀ NGHỊ 1.1.
Tìm tất cả các giá trị của tham số m để đường thẳng đi qua cực đại, cực tiểu của đồ thị hàm số 3
y  x  3mx  2 cắt đường tròn tâm I 1; 
1 bán kính bằng 1 tại hai điểm phân biệt ,
A B sao cho diện tích tam giác IAB lớn nhất. 2  3 Đáp số : m  2 3 2 1.2.
Tìm m để đồ thị hàm số y  2x  3 m  
1 x  6m1 2m x có cực đại, cực tiểu
nằm trên đường thẳng 4x  y  0 . 1.3.
Tìm m để đường thẳng nối hai điểm cực trị của đồ thị hàm số 3 2
y  x  mx  7 x  3
vuông góc với đường thẳng 3x  y  7  0 . 1.4.
Tìm những giá trị của tham số m để đường thẳng nối hai điểm cực trị của đồ thị hàm số 3
y  x  m   2 x   2 3 1
2m  3m  2 x  m m   1 tạo với đường thẳng
x  4 y  20  0 một góc bằng 0 45 . 1.5.
Tìm tất cả các giá trị của tham số m để hai điểm cực trị của đồ thị hàm số 3 2 2
y  x  3x  m x  m đối xứng nhau qua đường thẳng x  2 y  5  0 . 1.6.
Tìm tất cả các giá trị của tham số m để khoảng cách giữa hai điểm cực trị của đồ thị hàm 1 số 3 2 y 
x  mx  x  m 1là nhỏ nhất. 3 1.7.
Chứng minh rằng với mọi giá trị của tham số m thì đồ thị hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m có cực đại, cực tiểu chạy trên một đường thẳng cố định. 1.8.
Tìm tất cả các giá trị của tham số m để đường thẳng nối hai điểm cực trị của đồ thị hàm số 3 2
y  x  3x  mx  2 song song với đường thẳng y  4x  3 . 1.9.
Chứng minh rằng với mọi giá trị của tham số m thì đồ thị hàm số 3 2
y  x  mx   2  m  3 2 3 3 1
x  m  m luôn có cực đại, cực tiểu đồng thời gọi  ; x y  là 1
hoành độ, tung độ các điểm cực trị thì ta luôn có 2x  y   0 . 4
1.10. Chứng minh rằng với những giá trị thực của tham số m để đồ thị hàm số 3 1 3
y  x  m   2 1 x  3mx  m m  
1 có cực đại, cực tiểu ; đồng thời gọi  x; y là tọa 2 2
độ các điểm cực đại, cực tiểu thì ta luôn có  3
x  y x  0. 55 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 3 1
1.11. Tìm m để đồ thị hàm số 3
y  x  m   2 1 x  3mx  m m  
1 có cực đại, cực tiểu ; 2 2  1   1 
đồng thời hoành độ, tung độ các điểm cực trị thỏa mãn x  y y  x  0     ; trong đó  2  2 
 x; y là tọa độ các điểm cực trị.
1.12. Chứng minh rằng với những giá trị thực của tham số m để đồ thị hàm số 3 1 3
y  x  m   2 1 x  3mx  m m  
1 có cực đại, cực tiểu ; đồng thời gọi  x; y là tọa 2 2 x  y
độ các điểm cực đại, cực tiểu thì ta luôn có  1. x 2 m
1.13. Với mỗi giá trị thực của tham số m để đồ thị hàm số 3 2 2
y  x  x  m x  có cực đại, 9
cực tiểu ; đồng thời gọi  x; y là tọa độ các điểm cực trị. Tìm giá trị nhỏ nhất của biểu y  x thức P  . x  y
Dạng toán: Ba điểm cực trị của đồ thị hàm số tạo thành một tam giác
Bài 1. Tìm m để đồ thị hàm số 4 2 2
y  x  2m x 1 có ba điểm cực trị là ba điểm của một tam giác vuông cân. Lời giải:  x  0 Ta có 3 2
y '  4x  4m x  4x  2 2
x  m   0  
, vậy với m  0 thì đồ thị hàm số có 3 cực 2 2 x  m  trị.
Khi đó tọa độ ba điểm cực trị là A  B 4
m  m  C  4 0;1 ; ;1 ; ;
m 1 m  , ta thấy B,C đối xứng với
nhau qua trục tung. Vậy ba điểm cực trị tạo thành tam giác vuông cân thì sẽ vuông tại A .   Ta có AB   4
m m  AC   4 ; ; ; m m    Vậy 2 8 A .
B AC  0  m  m  0  m  1  , do m  0 .
Vậy m  1là những giá trị cần tìm.
Bài 2. Tìm m để đồ thị hàm số 4 2
y  x  2mx 1có ba điểm cực trị và đường tròn đi qua ba điểm
cực trị có bán kính bằng 1. Lời giải: 56 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  x  0 Ta có 3
y '  4x  4mx  4x  2
x  m  
, vậy đồ thị hàm số có ba điểm cực trị khi và chỉ 2 x  m  khi m  0 .
Khi đó tọa độ ba điểm cực trị là A   B  2  m  m  C  2 0;1 ; ;1 ; m;1 m 
Gọi I là tâm và R là bán kính đường tròn ngoại tiếp tam giác ABC .
Do B,C đối xứng với nhau qua trục tung nên tam giác ABC cân tại A , do đó tâm I nằm trên Oy , giả sử :  y  2
I 0; y  IA  R  1   y  2 1  1   I 0; 0 ; I 0; 2  1   2   y  0   m  0 
Với I 0;0  I B  R  1  m  1 m 2 2  1  m  1
, do m  0 nên chỉ nhận 1 1  1 5 m   2 1   5 m  1; m  . 2 Với
I 0;2  I B  R  1  m  1 m 2 2
 1, phương trình này vô nghiệm do 2 2 m 
 m    m 2 2 0 1  1. 1   5
Vậy m  1; m 
là hai giá trị cần tìm. 2 1 Bài 3. Cho hàm số 4 y 
x  3m   2
1 x  2 m  
1 . Tìm m để hàm số có 3 điểm cực trị tạo 4
thành một tam giác có trọng tâm là O . Lời giải:  x  0 Ta có 3
y '  x  2 3m  
1 x  y '  0   2
x  2 3m   1  1
Hàm số có 3 cực trị khi và chỉ khi 3m 1  0  m   (i) 3
Khi đó tọa độ 3 điểm cực trị là: A  m   B  2  m 
 m  m   C  2 0; 2 2 , 6 2; 9 4 1 ,
6m  2; 9m  4m   1
Yêu cầu bài toán tương đương với: 1 2 1 2
y  y  y  0  1
 8m  6m  4  0  m  ; m  
. Chỉ giá trị m  thỏa mãn điều kiện. A B C 3 3 3 57 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1 Vậy m  là giá trị cần tìm. 3 Bài 4. Cho hàm số 4 2
y  x  2mx  2 C . Tìm tất cả các giá trị của tham số m để C có 3 m  m   3 9 
điểm cực trị tạo thành một tam giác có đường tròn ngoại tiếp đi qua điểm D ;   .  5 5  Lời giải :  x  0 Ta có 3
y '  4x  4mx  y '  0   2 x  m 
Hàm số có 3 cực trị khi và chỉ khi m  0
Khi đó tọa độ 3 điểm cực trị là A   B  2
 m m   C  2 0; 2 , ; 2 ,
m; m  2
Gọi I  x; y là tâm đường tròn ngoại tiếp tam giác ABC , khi đó  2 2 IA  ID
3x  y 1  0
x  0; y  1   2 2  
IB  IC  2x m  2  x m    m  0  2 2    IA  IB   
 x  m 2   y   m 2  x   y  2 2 2 m 1 2 2  
Do m  0 nên chỉ có m  1thỏa mãn. Vậy m  1là giá trị cần tìm.
Bài 5. Tìm m để đồ thị hàm số 4 y  x   2  m  2 2 1
x  m 1có 3 điểm cực trị lập thành một tam
giác có diện tích lớn nhất. Lời giải : Ta có 3
y  x  x  2
 m   x 2 2 ' 4 4 1 4
x 1 m  . Hàm số có 3 cực trị khi và chỉ khi phương trình
y '  0 có 3 nghiệm phân biệt 2
 1 m  0  1  m  1(i)
Khi đó tọa độ 3 điểm cực trị là : A  m B  2 2   m  m  C 2 2 0;1 ; 1 ; 1 ;
1 m ; 1 m  Ta có 2
BC  2 1  m , phương trình đường thẳng 2
BC : y  1 m 1
Diện tích tam giác ABC là S  d A BC BC   m  m  ABC  ; . 1 2 2 2 1 1 2
Dấu bằng xảy ra khi và chỉ khi m  1(thỏa mãn (i)).
Vậy m  1là giá trị cần tìm. Bài 6. Cho hàm số 4 2 2
y  x  2mx  2m  4 . Xác định m để đồ thị hàm số có 3 điểm cực trị tạo
thành tam giác có diện tích bằng 1. Lời giải : 58 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Ta có 3
y '  4x  4mx 3 y   x  mx   x 2 ' 0 4 4 0
x  m  0 . Hàm số có 3 cực trị  m  0 (*)
Khi đó tọa độ 3 điểm cực trị của hàm số l : A  2 m   B  2
m m   C  2 0; 2 4 , ; 4 ,
 m; m  4
Nhận thấy A Oy; ,
B C đối xứng với nhau qua trục tung nên tam giác ABC cân tại A . 1 1 1
Kẻ AH  BC khi đó 2 S  AH.BC  y  y 2x 
m .2 m  1  m  1( thỏa mãn (*) ABC 2 2 A B B 2 ).
Vậy m  1là giá trị cần tìm.
Bài 7. Tìm m để hàm số 4
y  x   m   2 3
1 x  3 có ba cực trị, đồng thời ba điểm cực trị tạo thành 2
một tam giác cân có độ dài cạnh đáy bằng độ dài cạnh bên. 3 Lời giải :  x  0 Ta có 3 y ' 4x 2 3m  1 x 0       3m 1 2  x    2 3m 1 1
Hàm số có ba cực trị khi và chỉ khi 
 0  m   (*) 2 3
Khi đó tọa độ ba điểm cực trị là
 3m 1  m 2   3m 1  m 2 3 1 3 1    A0; 3  ; B ;   3;C   ;   3  2 4   2 4      2
Tam giác ABC cân tại A , vậy nên yêu cầu bài toán tương đương với BC  AB 3  3  m 1   3m 1  m 4 3 1   5  9.4  4.    m     thỏa (*) 2  2 16    3   5
Vậy m   là gía trị cần tìm của tham số m. 3
BÀI TẬP ĐỀ NGHỊ 1.1.
Tìm m để đồ thị hàm số 4 2
y  x  2mx  m 1có ba điểm cực trị tạo thành một tam giác có diện tích bằng 4 2 . 1.2.
Tìm m để đồ thị hàm số 4 2 2
y  x  2m x 1 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 32 . 59 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1.3.
Tìm m để đồ thị hàm số 4 2 2
y  x  2mx  m  m có ba điểm cực trị tạo thành một tam giác có một góc bằng 0 120 . 1.4.
Tìm m để đồ thị hàm số 4 2 2
y  x  2m x 1có ba điểm cực trị tạo thành một tam giác vuông cân. 1.5.
Tìm m để đồ thị hàm số 4 2
y  x  2mx  m 1có ba điểm cực trị tạo thành một tam giác
có bán kính đường tròn ngoại tiếp bằng 1. 1.6.
Tìm m để đồ thị hàm số 4 2 4
y  x  2mx  2m  m có ba điểm cực trị tạo thành một tam giác đều. 1.7.
Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 2
y  x  2mx  2 có ba điểm cực trị
tạo thành một tam giác nhận gốc tọa độ làm trực tâm. 1.8.
Tìm m để đồ thị hàm số 4
y  x  m   2 2 2
2 x  m  5m  5 có ba điểm cực trị tạo thành một tam giác đều. 1.9. Cho hàm số 4 2
y  x  2mx  2m . Xác định giá trị của tham số m để đồ thị hàm số trên có
cực đại, cực tiểu tạo thành.
1. Một tam giác đều.
2. Một tam giác vuông.
3. Một tam giác có diện tích bằng 16.
1.10. Tìm tất cả các cặp số m, n sao cho đồ thị hàm số 4 2 2
y  x  2m x  n có ba điểm cực trị
là ba đỉnh của một tam giác đều ngoại tiếp đường tròn có tâm là gốc tọa độ.
1.11. Tìm các giá trị của tham số m để đồ thị hàm số 4 2
y  x  2mx 1có ba cực trị và đường
tròn đi qua ba điểm này có bán kính bằng 1.
1.12. Tìm m để đồ thị hàm số 4
y  x  m   2 2
1 x  m có ba điểm cực trị , A B,C sao cho
OA  BC với O là gốc tọa độ, A là điểm trên trục tung. 1
1.13. Tìm m để đồ thị hàm số 4 y 
x  3m   2
1 x  2 m  
1 có ba điểm cực trị tạo thành tam 4
giác có trọng tâm là gốc tọa độ.
Dạng toán: Hai điểm cực trị và một điểm khác tạo thành một tam giác BÀI TẬP MẪU
Bài 1. Tìm m để đồ thị hàm số 3 2
y  x  x   2 m   2 3 3
1 x  3m 1có cực đại, cực tiểu đồng thời
các điểm cực đại, cực tiểu và gốc tọa độ tạo thành vuông tại O . Lời giải: Ta có 2
y   x  x   2 ' 3 6 3 m   1 60 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Để hàm số có cực đại, cực tiểu thì phương trình y '  0 phải có hai nghiệm phân biệt      2 ' 9 9 m   1  0  m  0 .
Khi đó gọi A x ; y ; B x ; y là tọa độ hai điểm cực trị. 1 1   2 2 
Lấy y chia cho y ' , ta được: 2 2   x 1 
y  2m x  2 m 1 1 1    2 y  
y ' 2m x  2  2 m    
1 . Do y ' x  y ' x  0  1   2    3 3  2
 y  2m x  2 2 m 1 2 2    
Vậy tam giác OAB vuông tại O  O . A OB  0  x x   2 2m x  2  2 m   1  2 2m x  2 2 m  1  0 1 2 1 2 
 x x  4m x x  4 m   2 4 2
1  x  x   4 2 m 1  0 * 1 2 1 2 1 2    x  x  2
Nhưng theo định lý vi-ét ta có: 1 2  , khi đó (*) trở thành 2 x x  1 m  1 2 m  1  2 m  1  2 4 3 4m 4m  0      
6 tất cả các giá trị này đều thỏa mãn điều kiện m  0 . m    2  6    Vậy m   1  ; 
 là những giá trị cần tìm.  2   
Bài 2. Tìm m để đồ thị hàm số 3 2
y  x  3x  31 m x 1 3m có cực đại, cực tiểu đồng thời
các điểm cực đại, cực tiểu cùng với gốc tọa độ tạo thành tam giác có diện tích bằng 4. Lời giải:
Hàm số có cực đại, cực tiểu khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt 2
 x  2x 1 m  0 có hai nghiệm phân biệt   '  m  0 .
Khi đó gọi A x ; y ; B x ; y là tọa độ hai điểm cực trị. 1 1   2 2 
Lấy y chia cho y ' ta được:  x 1  y  
y ' 2mx  2m  2  
, do y ' x  y ' x  0 1   2   3 3 
 y  2mx  2m  2 1 1    AB : y  2
 mx  2m  2 y  2
 mx  2m  2  2 2 2 2 2m  2
Ta có AB   x  x  2
 4m  x  x  2  x  x
4m 1 ; d  ; O AB  1 2 1 2 1 2 2 1 4m 1 Vậy S 
.d O AB AB  x  x m   OAB  ; . . 1 4 1 2 2 61 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
 16  m  2
1  x  x 2  4x x (*) 1 2 1 2  x  x  2 Theo định lý vi-ét ta có: 1 2  , khi đó (*) trở thành x x  1  m  1 2
m m  2    m   2 1 4
1 m  3m  4  0  m  1thỏa mãn điều kiện m  0
Vậy m  1là giá trị cần tìm. Bài 3. Cho hàm số 3 2
y  x  3x  m . Tìm m để đồ thị hàm số có 2 điểm cực trị , A B sao cho  0 AOB  120 . Lời giải : Ta có 2
y '  3x  6x  y '  0  x  0  x  2 
Tọa độ 2 điểm cực trị là A 0; m; B 2; m  4
Yêu cầu bài toán tương đương với :   OAOB 1 os c AOB    O . A OB 2 m  0 2m m 4 2 m m 8m 20         12  132 m   3 Bài 4. Cho hàm số 3 2
y  x  x   2 m   2 3 3
1 x  3m 1. Tìm m để đồ thị hàm số có hai điểm cực
trị cách đều gốc tọa độ. Lời giải : Ta có 2
y   x  x   2 ' 3 6 3 m   1
Hàm số có cực đại, cực tiểu khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt, điều này tương đương với 2
 '  9m  0  m  0 .
Giả sử A, B là hai điểm cực trị của hàm số, khi đó tọa độ hai điểm cực trị là A 3
 m   m  B 3 1 ; 2 2 , 1 ; m 2   2m  1
A và B cách đều gốc tọa độ khi và chỉ khi 3
OA  OB  8m  2m  m    m  0 . 2 1 Vậy m   là giá trị cần tìm. 2 62 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1 1
Bài 5. Tìm m để đồ thi hàm số 3 y  x  m   2
1 x   m  2 x 1có hai điểm cực trị A và B 3 2  7 
đồng thời tứ giác OADB là hình bình hành, với O là gốc tọa độ và D 3;   .  2  Lời giải :
Để hàm số có hai cực trị thì phương trình 2
y '  x  m  
1 x  m  2  0 có hai nghiệm phân biệt
   m  2  m     m  2 1 4 2 3  0  m  3
Khi đó hoành độ hai điểm cực trị x  1; x  m  2 A B
Vì tứ giác OADB là hình bình hành nên trung điểm của AB cũng là trung điểm của OD , từ đó suy ra
x  x  x m 1  3 A B D   
y  y  y
y  y  y  A B D  A B D  11   5  11 5 7
Suy ra m  4  A 1; ; B 2;       
thỏa mãn y  y  y A B D  6   3  6 3 2
Vậy m  4 là giá trị cần tìm.
Bài 6. Tìm m để đồ thị hàm số 3
y  x  m   2 3
1 x 12mx  3m  4 có hai điểm cực trị là , A B  9 
sao cho hai điểm này cùng với điểm C 1  ;  
 lập thành tam giác nhận gốc tọa độ làm trọng  2  tâm. Lời giải : Ta có 2
y '  3x  6 m   1 x  12m
Hàm số có cực trị khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt
Tương đương với   m  2 '
1  4m  0  m  1
Khi đó tọa độ hai điểm cực trị là A m B  3 2 2;9 ; 2 ; m 4
 m 12m  3m  4
Yêu cầu bài toan tương đương với 2  2m 1  0  1  9  m   thỏa mãn 3 2 9  4
 m  12m  3m  4   0 2   2 1 Vậy m   là giá trị cần tìm 2
BÀI TẬP ĐỀ NGHỊ 63 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1.1.
Tìm m để đồ thị hàm số 3 2
y  x  3x  m có cực đại, cực tiểu và các điểm cực đại, cực
tiểu cùng với gốc tọa độ tạo thành một tam giác có diện tích bằng 4 . 1.2.
Tìm m để đồ thị hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m  m có cực trị đồng thời các
điểm cực trị cùng với gốc tọa độ tạo thành một tam giác vuông tại O . 1 1.3. Gọi ,
A B là các điểm cực trị của đồ thị hàm số 3 2 y 
x  2x  3x . Tìm điểm M thuộc 3
trục hoành sao cho diện tích tam giác MAB bằng 2. 1.4.
Tìm m để đường thẳng đi qua các điểm cực trị của đồ thị hàm số 3 2
y  x  3x  mx  2 tạo
với hai trục tọa độ một tam giác vuông cân. 1.5. Cho hàm số 3
y  x  m   2 3
1 x  3m  m  2 x 12m  8 và điểm M 3; 2 . Tìm tất cả các
giá trị của tham số m để đồ thị hàm số có hai điểm cực trị ,
A B sao cho MA  MB nhỏ nhất. 1.6.
Tìm m để đồ thị hàm số 3 2
y  x  x   2 m   2 3 3
1 x  3m 1có hai điểm cực trị , A B cùng
với điểm C 2; 
1 tạo thành một tam giác có diện tích bằng 1.
MỘT SỐ BÀI TẬP TỔNG HỢP VỀ CỰC TRỊ HÀM SỐ 1.1. Cho hàm số 3
y  x  3mx 1. Tìm m để đồ thị hàm số có hai điểm cực trị , A B sao cho
diện tích tam giác IAB bằng 4 2 , biết rằng I 1;  1 . 1.2.
Tìm tất các giá trị của tham số m để đồ thị hàm số 3 2
y  x  3x  3m m   1 x 1 có 2 cực trị cùng dấu. 1.3.
Tìm m để đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3 2
y  x  3x 1 cắt đường 4 30 tròn T  2 2
: x  y  4x  2 y  m  0 theo một dây cung có độ dài bằng . 5 1.4.
Tìm m  0 để đồ thị hàm số 3 2 3
y  x  3mx  4m có 2 điểm cực trị và khoảng các từ điểm
cực tiểu đến đường thẳng d bằng 2 lần khoảng cách từ điểm cực đại tới d , biết rằng
d : y  x . 1.5.
Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số 3
y  x  3x  m 1 luôn có hai
điểm cực trị, đồng thời đường thẳng nối hai điểm cực trị tạo với trục hoành một góc không đổi.
CÁC BÀI TOÁN VỀ TIẾP TUYẾN 64 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Xét hai bài toán cơ bản :
Bài toán 1: Tiếp tuyến tại một điểm. Tiếp tuyến với đồ thị hàm số
y  f (x) tại điểm
M  x ; f (x ) có dạng là 0 0 
d : y  f ' x x  x  f x 0   0   0 
Bài toán 2: Tiếp tuyến đi qua một điểm.
Tiếp tuyến với đồ thị hàm số đi qua điểm M  x ; y có hệ số góc k có dạng là 0 0 
d : y  k  x  x  y 0  0 
 f  x  k  x  x  y 0  Khi đó hệ 0 
có nghiệm, giải hệ này suy ra k . Từ đó viết phương trình của
 f '(x)  k  tiếp tuyến.
Bài toán 3 : Cho hai đường cong C  : y  f (x) và d  : y  g(x) . Hãy tìm tất cả các tiếp tuyến
chung của d  ,C  .
Giả sử  là tiếp tuyến chung của d  ,C  . Và  tiếp xúc với C  ,d  lần lượt tại các điểm
có hoành độ x , x . 1 2 Khi đó
 : y  f '(x ) x  x  f (x ) 1  1  1 
từ đó ta có hệ phương trình
  : y  g '(x ) x  x  g(x )  2  2  2
 f '(x )  g '(x ) 1 2 
giải hệ này ra nghiệm x , x .
f (x )  x f '(x )  g(x )  x g '(x ) 1 2  1 1 1 2 2 2
Từ đó viết phương trình tiếp tuyến chung:  : y  f '(x )  x  x   f (x ) . i i i
Một số kiến thức bổ sung :
Hai đường thẳng d : y  k x  m và d : y  k x  n 2  1  1 2 Khi đó : k  k
1. d  / / d  1 2  1 2 m  n  2. d  d  k k  1. 1   2  1 2 k  k
3. Góc tạo bởi hai đường thẳng này là : 2 1 tan   . 1 k k 1 2 65 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Lưu ý : Tại một điểm M thuộc đồ thị hàm số thì có thể tồn tại tiếp tuyến tại điểm hoặc tiếp
tuyến đi qua điểm nó, vì vậy cần xem kỹ đề bài yêu cầu tìm loại tiếp tuyến nào để không bỏ sót tiếp tuyến. BÀI TẬP MẪU
Dạng toán : Viết phương trình tiếp tuyến thỏa mãn một số điều kiện cơ bản -
Tiếp tuyến tại điểm thuộc đồ thị hàm số. -
Tiếp tuyến đi qua một điểm A cho trước. -
Tiếp tuyến song song(có cùng hệ số góc), vuông góc( tích hệ số góc bằng -1) hoặc tạo với
một đường thẳng cho trước một góc  . 1 m 1 Bài 1. Cho hàm số 3 2 y  x 
x  C  . 3 2 3 m
Gọi M là điểm có hoành độ bằng 1  thuộc C
. Tìm m để tiếp tuyến với C tại M song song m  m 
với đường thẳng 5x  y  0.Viết phương trình tiếp tuyến đó. Lời giải:
+ Hệ số góc của đường thẳng 5x  y  0 là k  5 . Để tiếp tuyến tại M song song với
d : 5x  y  0 suy ra y '( 1
 )  m 1  5  m  4 . Suy ra y( 1  )  2.
Vậy tiếp tuyến cần tìm là  : y  5 x  
1  2   : y  5x  3 .
Vậy tiếp tuyến cần tìm là 5x  y  3  0 . 1 Bài 2. Cho hàm số 3 2 y 
x  2x  3x C  . 3
Viết phương trình tiếp tuyến  của C  tại điểm uốn và chứng minh  là tiếp tuyến có hệ số góc nhỏ nhất. Lời giải:  2  Ta có 2
y '  x  4x  3 và y '  2x  4  y ' (x)  0  x  2 . Suy ra điểm M 2;   là điểm uốn  3 
của C  . Ta có y '(2)  1. Vậy tiếp tuyến của C  tại điểm uốn có phương trình là 2 8
y    x  2 
 y  x  . 3 3
Hệ số góc tiếp tuyến của C  tại điểm bất kì là k  x  x    x  2 2 4 3 2 1  1  . Từ đó suy ra đpcm. 66 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Bài 3. Cho hàm số 3 2
y  x  3x  1C .
Chứng minh rằng trên C  tồn tại vô số cặp điểm mà mà hai tiếp tuyến với C  tại từng cặp điểm song song với nhau. Lời giải: Ta có 2
y '  3x  6x . Bài toán trở thành chứng minh tồn tại vô số số k để phương trình 2
3x  6x  k(*) có hai nghiệm phân biệt.
Xét phương trình (*), có  '  9  3k  0  k  3 . Do đó mọi k  3 thì phương trình (*) có 2
nghiệm phân biệt. Ta có đpcm. Bài 4.Cho hàm số 3 2
y  x  2x  8x  5C  .
Chứng minh rằng không tồn tại tiếp tuyến tại hai điểm thuộc đồ thị hàm số mà vuông góc với nhau. Lời giải: 2  2  20 Ta có 2
y '  3x  4x  8  3 x    0,x(*).    3  3
+ Giả sử ngược lại tồn tại hai điểm có hoành độ x , x thuộc đồ thị hàm số sao cho tiếp với đồ thị 1 2
hàm số tại hai điểm đó vuông góc với nhau. Khi đó
y '(x ) y '(x )  1    2
3x  4x  8 2
3x  4x  8  1  , mâu thuẫn với (*). 1 2 1 1 2 2  Vậy ta có đpcm. Bài 5.Cho hàm số 3
y  x    m 2 1 2
x  2  m x  m  2(1) .
Tìm m để đồ thị hàm số (1) có tiếp tuyến tạo với đường thẳng d : x  y  7  0 một góc 1 , o c s = . 26 Lời giải: 
+ Gọi hệ số góc của tiếp tuyến là k suy ra tiếp tuyến có véc tơ pháp tuyến n  k; 1 , véc tơ 1   
pháp tuyến của d là n  1;1 . 2   Từ đó suy ra :  n n2 1 1 k 1 3 2 2 cos     
 12k  26k 12  0  k   k  . n n 26 2  2 2 3 2 1 k   1
Khi đó yêu cầu bài toán thỏa mãn khi và chỉ khi ít nhất một trong hai phương trình sau có nghiệm 67 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  3  3 2 y ' 
3x  21 2m x  2  m   2  2    có nghiệm 2 2 2  y '  
3x  21 2m x  2  m   3  3 2  '  0 8
 m  2m 1  0 1 1 1      m   m   . 2  '  0 
4m  m  3  0 2 4 2   1  1 
Vậy giá trị cần tìm của m là  ;    ;  .      4   2  1 Bài 6. Cho hàm số 3 y 
mx  m   2
1 x  4  3m x  
1 C  . Tìm các giá trị của m sao cho tồn 3 m
tại duy nhất một điểm có hoành độ âm mà tiếp tuyến tại đó vuông góc với đường thẳng
x  2 y  3  0 . Lời giải: 1
+ Đường thẳng x  2 y  3  0 có hệ số góc bằng 
nên tiếp tuyến vuông góc với nó có hệ số 2
góc bằng 2 , khi đó ta có 2
mx  m   x    m 2 2 1 4 3
 2  mx  2 m  
1 x   2  3m  0(*)
Khi đó yêu cầu bài toán thỏa mãn khi và chỉ khi phương trình (*) có duy nhất một nghiệm âm.
+ Nếu m  0  (*)  2
 x  2  0  x  1(loại).  x  1 + Nếu m 0 (*)     2  3m  x   m m  0 2  3m
Vậy (*) có duy nhất một nghiệm âm khi và chỉ khi 0   
2 là những giá trị cần m m   3 tìm. 2x
Bài 7. Cho hàm số y  C  . x  2
Tìm điểm những điểm thuộc đồ thị hàm số C  sao cho khoảng cách từ giao điểm hai đường
tiệm cận đến tiếp tuyến với C  tại điểm đó có khoảng cách lớn nhất. Lời giải:
+ Giao điểm hai đường tiệm cận I  2  ; 2 . 68 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  2a  + Giả sử điểm A ; a 
 là điểm cần tìm, khi đó tiếp tuyến với C  tại A là  a  2  4 2a d : y  x  a 
 d : 4x  a  2 y  2a  0 2    2 2 a  2 a  2 8 a  2 8 a  2
Ta có d  I; d     2 2 . 16  a  24 2.4.a  22
Dấu bằng xảy ra khi và chỉ khi a  4 2
 16  a  0  a  4 
Vậy có hai điểm thỏa mãn A0; 0 , A 4; 4 . 2  
Bài 8. Tìm tất cả các giá trị của tham số m để trên đồ thị hàm số 1 3 y 
mx  m   2
1 x  4  3m x 1tồn tại đúng hai điểm có hoành độ dương mà tiếp tuyến tại 3
đó vuông góc với đường thẳng x  2 y  3  0 . Lời giải : Ta có 2
y '  mx  2 m  
1 x  4  3m  1 
Yêu cầu bài toán tương đương với phương trình y '.   1   
có đúng hai nghiệm dương phân  2  biệt 2
 mx  2 m  
1 x  4  3m  2 có đúng hai nghiệm dương phân biệt 2
 mx  2 m  
1 x  2  3m  0 có đúng hai nghiệm dương phân biệt m  0  2
 '  4m  4m 1  0  1  0  m    2 1 m 2  S   0   1 2  m   m    2 3 2  3m P   0  m  1   1 2  Vậy m  0;  ;   
 là giá trị cần tìm.  2   2 3  4 x 5
Bài 9. Tìm điểm A thuộc đồ thị hàm số 2 y   3x 
C sao cho tiếp tuyến với C  tại A 2 2
cắt C  tại hai điểm phân biệt B,C khác A sao cho AC  3AB ( B nằm giữa A và C ). Lời giải : 69 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 4  a 5  Xét điểm 2 A a,  3a     C  2 2  
Tiếp tuyến với C  tại A có phương trình là : 4 a d : y   5 3
2a  6a x  a 2   3a 
, khi đó hoành độ giao điểm của d và C  là 2 2 4 4  a 5 x 5 3
2a  6a x  a 2 2   3a    3x  2 2 2 2
  x  a2  2 2
x  2ax  3a  6  0
Để d  C  tại hai điểm phân biệt khác A thì phương trình : 2 2
x  2ax  3a  6  0 có hai nghiệm phân biệt khác a . 2 2 2 
a  2a  3a  6  0   3  a  3     2
 '  6  2a  0  a  1    
Khi đó gọi B  x ; y ;C  x ; y
, có AC  3AB (B nằm giữa ,
A C ) nên AC  3AB B B C C 
 x  3x  2
 a , kết hợp với định lý vi-ét ta có hệ C B
x  3x  2a x  0 C B B  
x  x  2a  x  2  a thỏa mãn điều kiện, suy ra có hai điểm C B C  2  x x  3a  6    C B a 2   3   3  A  2;  ; A 2;  cần tìm. 1   2    2   2  x  3
Bài 10. Viết phương trình tiếp tuyến với đồ thị hàm số y 
C tại điểm A thuộc C  , biết x 1
tiếp tuyến cắt trục hoành tại B và tam giác OAB vuông( O là gốc tọa độ). Lời giải:  a  2  Xét điểm A a 1;  
 C  , a  0 . Tiếp tuyến với đồ thị hàm số tại điểm A có phương trình:  a  2 a  2 d : y  
x  a  1  2   a a 2
Hệ số góc của d là k   1 2 a
Tam giác OAB vuông nên chỉ có thể vuông tại O hoặc A .
Trường hợp 1: Tam giác OAB vuông tại O  A thuộc trục tung hay tiếp điểm A 0;3 . Suy ra
tiếp tuyến d : y  2  x  3 . 1
Trường hợp 2: Tam giác OAB vuông tại A 70 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN a  2 0 a  2
Hệ số góc của đường thẳng : a OA k   2 a 1 0 a a   1 2 a  2 a  1  Vậy k k  1   .
 1   a   1  a  2 2 a  2  0  1 2 2   a a a   1 a  2 
Với a  1  d : y  2x  5 2 1 5
Với a  2  d : y   x  3 2 2
Vậy tất cả có ba tiếp tuyến cần tìm là 1 5 d : y  2
 x  3; d : y  2x  5; d : y   x  1 2 3 2 2
BÀI TẬP ĐỀ NGHỊ  3  1.1.
Tìm m để khoảng cách từ điểm M ;1 
 đến tiếp tuyến của đồ thị hàm số  4  4 2
y  x  2mx  m C  tại điểm A có hoành độ bằng 1 thuộc C  đạt giá trị lớn nhất. Đáp số: m  1. 1.2.
Chứng minh rằng đồ thị hàm số 4 2
y   x  2mx  2m 1 C  luôn đi qua hai điểm cố định ,
A B với mọi m. Tìm m để tiếp tuyến với C  tại A và B vuông góc với nhau. 1.3.
Tìm m để trên đồ thị hàm số 3
y  x  m   2
1 x  4m  2 x 1tồn tại đúng một điểm mà
tiếp tuyến tại điểm đó vuông góc với đường thẳng x 10 y  30  0 . Đáp số: m  5 . 1.4.
Đường thẳng y  3  x cắt đồ thị hàm số 3 2
y  x  3x  mx  4  m C  tại A . Tìm m để
tiếp tuyến với C  tại A cắt C  tại điểm B khác A thỏa mãn tam giác AIB vuông, với I 1; 2 .
Dạng toán : Tiếp tuyến cùng với hai trục tọa độ tạo thành tam giác Bài 1. Cho hàm số 3
y  x  mx 1  m C . m
Tìm m để tiếp tuyến với C
tại giao điểm của C
với trục tung, tạo với hai trục tọa độ một m  m 
tam giác có diện tích bằng 8. Lời giải: 71 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
+ Tọa độ giao điểm M của C
với trục tung là nghiệm của hệ m  x  0 
 M 0;1 m  y '(0)   .
m Vậy phương trình tiếp tuyến với C tại m  3
y  x  mx 1 m  điểm M là:
d : y  mx 1 m . Khi đó
d cắt các trục tọa độ tại các điểm  1 m 
M 0;1 m, N ;0 
 . Yêu cầu bài toán tương đương với  m  1 1 m m   S 
OM .ON  8  1 m  16   m  m   . OMN 1 2 9 4 5 16 2 m m  7  4 3 
Vậy có 4 giá trị của m như trên thỏa mãn đề bài. x  2
Bài 2.Cho hàm số y  C. 2x  3
Viết phương trình tiếp tuyến với C  biết rằng tiếp tuyến cắt trục hoành tại A , trục tung tại B
sao cho OAB là tam giác vuông cân, ở đây O là gốc tọa độ. Lời giải: 1  Ta có y ' 
. Vì tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân nên tiếp tuyến 2x  32
song song với đường thẳng y   x . Vậy hệ số góc của tiếp tuyến bằng 1. 1 x  1  Suy ra 0   1    2x  32 x  2   0 0 + Khi x  2   y( 2
 )  0 , lúc đó tiếp tuyến là d : y    x  2  d : y  x  2. 0 + Khi x  1   y( 1
 )  1, lúc đó tiếp tuyến là y   x , không cắt các trục tọa độ tại hai điểm 0 nên loại.
Vậy tiếp tuyến cần tìm là d : y  x  2. 2x
Bài 3. Cho hàm số y  C. x 1
Tìm điểm M thuộc C  sao cho tiếp tuyến tại M của C  cắt Ox,Oy lần lượt tại , A B sao cho 1
diện tích tam giác OAB bằng
, ở đây O là gốc tọa độ. 4 Lời giải: 72 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  2x  + Gọi 0 M x ;  C 
là điểm cần tìm. Khi đó tiếp tuyến của C  tại M có phương trình là: 0    x  1  0  2 2 2x 2 2x d : y  x  x   d : y  x  2  0  0 0  x   1 x 1  x  2 1  x  2 0 1 0 0 0 2  2x  Từ đó suy ra A 2  x ;0 0 , B  0;  . 0   x 2 1    0   x  1 2 0 1 1 1 2x 1 Ta có 2 0 S O . A OB O . A OB x         OAB 0 1 2 4 2  x 1 2  x   0 2 0  2
+ Với x  1  M 1;1 . 0 1   1  1  + Với x    M  ; 2  . 0 2   2  2   1 
Vậy có hai điểm M 1;1 , M  ; 2  cần tìm. 1   2    2 
Bài 4. Viết phương trình tiếp tuyến với đồ thị hàm số 3 2
y  x  x 1 biết tiếp tuyến cắt các trục tọa độ tại ,
A B sao cho tam giác OAB cân tại O ( với O là gốc tọa độ). Lời giải :
Phương trình tiếp tuyến tại điểm M  3 2
x ; x  x 1 thuộc đồ thị hàm số 0 0 0  d : y   2
3x  2x  x  x  3 2
 x  x 1 0 0 0 0 0 3 2
 2x  x 1 
Khi đó giao điểm của d với Ox là 0 0 A ; 0 
, giao điểm của d với Oy là 2  3x  2x  0 0  B  3 2 0; 2
 x  x 1 . 0 0 
Tam giác OAB cân tại O nên OA  OB 3 2 2x  x 1 0 0 3 2   2
 x  x 1 2 0 0 3x  2x 0 0 3 2
 2x  x 1 0 0 3 2  2  x  x 1  2 0 0  x  1 0  3x  2x 0 0     1 3 2 2x  x 1  x    0 0 3 2 0
 2x  x 1  3 2 0 0  3x  2x  0 0
Với x  1  A  B  O  loại trường hợp này. 0 73 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1 32 Với x  
ta có tiếp tuyến d : y  x  . 0 3 27
Bài 5. Tìm tất cả các giá trị của tham số m để tiếp tuyến tại điểm có hoành độ bằng 1 của đồ thị 3 hàm số 3 2
y  x  3x  m tạo với hai trục tọa độ một tam giác có diện tích bằng . 2 Lời giải : -
Tiếp tuyến tại điểm có hoành độ bằng 1 là d : y  3x  m  2 .  m  2  -
Khi đó d cắt Ox tại A ;0 
 và cắt Oy tại B 0; m  2  3  1 m  2 3 m  - Vậy S  m  2   m    OAB  22 1 9  2 3 2 m  5 
BÀI TẬP ĐỀ NGHỊ 2x 1 1.1.
Viết phương trình tiếp tuyến đến đồ thị hàm số y 
biết rằng tiếp tuyến này tạo với x 1
hai trục tọa độ một tam giác cân. x 1 1.2.
Viết phương trình tiếp tuyến đến đồ thị hàm số y 
biết rằng tiếp tuyến này tạo với x 1 1
hai trục tọa độ một tam giác có diện tích bằng . 6 x 1 1.3.
Viết phương trình tiếp tuyến đến đồ thị hàm số y 
biêt rằng tiếp tuyến tạo với 2  x   1
hai trục tọa một tam giác có trọng tâm nằm trên đường thẳng 4x  y  0 . 4 1 1.4.
Tìm m để tiếp tuyến của đồ thị hàm số 3 y 
x  2m   2
1 x   m  2 x  tại giao điểm 3 3 1
đồ thị hàm số với trục tung tạo với hai trục tọa độ một tam giác có diện tích bằng . 3
Dạng toán : Số tiếp tuyến đi qua một điểm đến đồ thị hàm số -
Viết phương trình tiếp tuyến đi qua một điểm cho trước đến đồ thị hàm số. -
Tìm những điểm trên mặt phẳng tọa độ kẻ được một, hai, ba hoặc không có tiếp tuyến
nào đi qua đến đồ thị hàm số. 74 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Bài 1. Cho hàm số 3 2
y  4 x  6x 1C .
Viết phương trình tiếp tuyến với C  biết tiếp tuyến đi qua điểm M 1; 9. Lời giải:
+ Phương trình tiếp tuyến với C  đi qua điểm M  1  ; 9
  có hệ số góc k là d : y  k  x   1  9 ,
gọi x là hoành độ tiếp điểm, khi đó ta có hệ 3 2
4x  6x 1  k   x   1  9(1)  2 12 
x 12x  k (2) 
Thay (2) vào (1) ta được: 3 2
4x  3x  6x  5  0 2 5   x  
1 4x  5  0  x  1 x  4
+ Với x  1  k  24  phương trình tiếp tuyến là d : y  24x 15. 5 15 15 21 + Với x   k 
 phương trình tiếp tuyến là d : y  x  . 4 4 4 4
Vậy hai tiếp tuyến cần tìm là d : 24x  y 15  0 và d :15x  4 y  21  0 . 1 2 1 3 Bài 2. Cho hàm số 4 2 y  x  3x  C. 2 2  3 
Viết phương trình tiếp tuyến với C  biết rằng tiếp tuyến đi qua điểm M 0; .    2  Lời giải:  3  3
+ Phương trình tiếp tuyến với C  đi qua điểm M 0; 
 có hệ số góc k là d : y  kx  , gọi x là  2  2
hoành độ tiếp điểm, khi đó ta có hệ 1 3 3 4 2  x  3x   kx  (1) 2 2 2 3
2x  3x  k(2) 
Thay (2) vào (1) ta được: 2 x  2
x  2  0  x  0  x   2. 3
+ Với x  0  k  0  phương trình tiếp tuyến là d : y  . 2 3
+ Với x  2  k  2  phương trình tiếp tuyến là d : y  2x  . 2 3
+ Với x   2  k   2  phương trình tiếp tuyến là d : y   2x  . 2 75 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Bài 3. Viết phương trình tiếp tuyến với đồ thị hàm số 3
y  x  3 x  2C  kẻ từ điểm A0; 2 . Lời giải:
+ Nhận thấy A 0; 2  C  .
+ Xét tiếp tuyến với C  tại A , ta có  3  f x  f x   x  0 ( ) (0)  lim  lim  2 x  3  
 không tồn tại y '(0) . Vậy không có tiếp x0 x0 x  0 x
 3 x  0  
tuyến với C  tại A .
+ Xét tiếp tuyến có hệ số góc k đi qua A có phương trình là d : y  kx  2
Do C  đối xứng qua trục tung nên chỉ cần xét trên khoảng 0;  , khi đó 3
y  x  3x  2 và ta 3 
x  3x  2  kx  2 có hệ  có nghiệm 2 3
 x  3  k 
Hệ này vô nghiệm trên 0;  . Vậy không có tiếp tuyến nào của C  đi qua A .
Kết luận: Không có tiếp tuyến nào kẻ từ A đến C  . Bài 4. Cho hàm số 3
y  x  3x  2 C .
Tìm điểm M trên C  sao cho chỉ có một tiếp tuyến với C  đi qua M . Lời giải:
Giả sử điểm M  3
x ; x  3x  2  C . Phương trình tiếp tuyến với C  đi qua M có dạng 0 0 0   
y  k  x  x  3
 x  3x  2 , khi đó ta có hệ 0 0 0 3
x  3x  2  k   x  x  3
 x  3x  2(1) 0 0 0  2 3
 x  3  k (2) 
Thay (2) vào (1) ta được:
2x  3x x  x  0   x  x 2 3 2 3 2x  x  0(*) 0 0 0  0 
Yêu cầu bài toán tương đương với phương trình (*) có nghiệm duy nhất x0 x 
 x  x  0  M 0; 2 . 0 0 0   2
Bài 5. Tìm các điểm trên trục hoành sao cho từ đó vẽ được ba tiếp tuyến đến đồ thị C  của hàm số 3 2
y  x  3x , trong đó có hai tiếp tuyến vuông góc với nhau. 76 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải:
Giả sử M  x ; 0 là điểm cần tìm, khi đó tiếp tuyến với C  đi qua M có dạng là d : y  k  x  x0  0  , khi đó ta có hệ 3 2
x  3x  k   x  x (1) 0   2 3
 x  6x  k (2) 
Thay (2) vào (1) ta được: 3
2x  31 x  2
x  6xx  0  x  0 hoặc 2
2x  31 x x  6x  0(*) 0  0 0 0 Kí hiệu, 2
g(x)  2x  31 x x  6x 0  0
Từ M kẻ được 3 tiếp tuyến đến C  khi và chỉ khi phương trình (*) có hai nghiệm phân biệt, khác không.  x  3 2 0 
  9x  30x  9  0 0 0     1 (1) g(0)  6  x  0   x  0  0 0  3
Tại điểm M 0;0 tiếp tuyến với đồ thị hàm số chính là trục hoành, dễ thấy không có tiếp tuyến
nào vuông góc với tiếp tuyến này.Khi đó yêu cầu bài toán trở thành tiếp tuyến với đồ thị hàm số
tại các điểm có hoành độ x , x ( x , x là nghiệm của (*)) vuông góc với nhau. 1 2 1 2
Hệ số góc của các tiếp tuyến này là 2 2
k  3x  6x ; k  3x  6x 1 1 1 2 2 2 Yêu cầu bài toán thỏa mãn khi và chỉ khi k .k  1
  3x  6x 3x  6x   1   9 x x 2 2 2 18x x x  x  36x x  1  (2) Theo 1 2 1 1 2 2 1 2 1 2  1 2  1 2 3 x 1 0 
định lí Vi-ét ta có: x  x  ; x x  3
 x , khi đó (2) trở thành 1 2 1 2 0 2 1  1  27 
x 1  0  x   M
;0 là điểm duy nhất cần tìm. 0 0   27  27  x  2
Bài 6. Cho hàm số y 
C  . Tìm những điểm trên trục tung kẻ được hai tiếp tuyến đến x 1
C  sao cho hai tiếp điểm nằm về hai phía với trục hoành. Lời giải:
+ Giả sử A0; a là điểm cần tìm, đường thẳng đi qua A với hệ số góc k là d : y  kx  a .
 x  2  kx  a   x 1
d tiếp xúc với C    có nghiệm 3   k  x  2 1 
 PT   a 2 : 1
x  2a  2 x   a  2  0(*) có nghiệm x  1. 77 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Kí hiệu: g x    a 2 ( ) 1
x  2 a  2 x   a  2 , từ A kẻ được hai tiếp tuyến đến C  khi và chỉ
khi phương trình (*) có 2 nghiệm phân biệt x , x , khác 1. 1 2 1   a  0  1
  '  3a  6  0    a  1(1) . 2 g(1)  3  0  3 3
Khi đó ta có y  1 , y  1
. Để hai tiếp điểm nằm về hai phía với trục hoành khi 1 2 x 1 x 1 1 2  3   3 
x x  2 x  x  4 1 2  1 2 
và chỉ khi y y  0  1 1  0   0(2) 1 2     x 1 x 1
x x  x  x 1  1   2  1 2  1 2  2 a  2 a  2
Theo định lí Vi-ét ta có: x  x  ; x x  , khi đó (2) trở thành 1 2 1 2 a 1 a 1 2 2
3a  2  0  a  
. Kết hợp với điều kiện (1) suy ra   a  1. 3 3 2
Vậy những điểm trên trục tung có hoành độ x thỏa mãn 
 x  1 thỏa mãn điều kiện bài toán. 3
BÀI TẬP ĐỀ NGHỊ x  m  9 3  1.1. Cho hàm số y 
C và hai điểm A4;2; B ; 
 . Tìm tất cả các giá trị của x  2  2 2 
tham số m để từ A kẻ được hai tiếp tuyến AM , AN đến C  ( M , N là các tiếp điểm) sao
cho bán kính đường tròn ngoại tiếp tam giác BMN bằng 5 . 1.2.
Dạng toán: Tiếp tuyến cắt hai đường tiệm cận 2x  3
Bài 1. Cho hàm số y 
C  . Tìm những điểm trên C  sao cho tiếp tuyến với C  tại điểm x  2
đó cắt hai tiệm cận của C  tại hai điểm ,
A B sao cho độ dài AB nhỏ nhất. Lời giải:  1  + Giả sử điểm M ; m 2  
 là điểm cần tìm, khi đó tiếp tuyến với C  tại M có phương  m  2  1 1
trình là: d : y  
x  m  2  2   m  2 m  2 78 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  2 
+ Giao điểm của d với tiệm cận đứng là A 2; 2    .  m  2 
+ Giao điểm của d với tiệm cận ngang là B 2m  2; 2 .   2 1 2 1 Ta có 2
AB  4 m  2    8 m  2 .  8 2    m  2  m  22   2 1 m  1
Dấu bằng xảy ra khi và chỉ khi m  2    m  22 m  3 
Vậy có hai điểm cần tìm là M 1;1 , M 3;3 . 1   2   2x 1
Bài 2. Cho hàm số y  C. x 1
Tìm trên C  những điểm mà tiếp tuyến với C  tại điểm đó cắt các đường tiệm cận của C  tại ,
A B sao cho tam giác IAB có chu vi nhỏ nhất( I là giao điểm của hai đường tiệm cận hàm số). Lời giải:  3  + Giả sử điểm M ; m 2   
 C  là điểm cần tìm, tọa độ I 1; 2 .  m  1  3  3
+ Phương trình tiếp tuyến với C  tại M là d : y 
x  m  2  . 2   m   1 m 1  6 
+ Tọa độ giao điểm của d với các tiệm cận của C  là A 1; 2  , B   2m 1;2  m  1  6
+ Tam giác IAB vuông tại I , ta có IA 
; IB  2 m 1  I . A IB  12. m 1
Chu vi tam giác IAB bằng : 2 2
p  IA  IB 
IA  IB  2 I . A IB  2I . A IB  4 3  2 6
Đẳng thức xảy ra khi và chỉ khi IA  IB  m  2 1
 3  m  1  3 .
Vậy có hai điểm M 1 
3;2  3 , M 1  3;2  3 cần tìm. 1   2  
BÀI TẬP ĐỀ NGHỊ 79 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1.1.
Tìm tất cả các giá trị của tham số m để tiếp tuyến của đồ thị hàm số 3 2
y  x  3mx  m  
1 x  1tại điểm có hoành độ x  1đi qua điểm A1;2 . 1.2.
Tìm tất cả các giá trị của tham số m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số 3 2  55 
y  x  2x  m  2 x  3m đi qua điểm A 1;   .  27  1.3.
Tìm tất cả các giá trị của tham số m để tiếp tuyến tại hai điểm cố định thuộc đồ thị hàm số 4 2
y  x  2mx  2m  1vuông góc với nhau. 3 2 1.4.
Cho hàm số y  x  3x 1 C . Tìm hai điểm ,
A B thuộc C  sao cho tiếp tuyến với C  tại ,
A B song song với nhau và AB  4 2 . 1.5.
Tìm m để tiếp tuyến của đồ thị hàm số 3
y  x  mx  m 1tại điểm có hoành độ bằng 2 2 1
1 cắt đường tròn C  :  x  2   y  3  theo một dây cung có độ dài nhỏ nhất. 5 1.6.
Tìm các giá trị thực của tham số m để từ điểm M 1, 2 kẻ được hai tiếp tuyến đến đồ thị 3 2
hàm số y  x  2x   m   1 x  2m. 1.7.
Tìm tất cả các giá trị của k để tồn tại hai tiếp tuyến phân biệt với đồ thị hàm số 3 2
y  x  6x  9x  3có cùng hệ số góc k , sao cho đường thẳng đi qua các tiếp điểm
của hai tiếp tuyến cắt các trục tọa độ Ox,Oy lần lượt tại ,
A B thỏa mãn OA  2012OB . 1.8.
Tìm m để tiếp tuyến của đồ thị hàm số 3
y  x  mx  m 1tại điểm có hoành độ 2 2 x  1
 cắt đường tròn C  :  x  2   y   3
 4 theo một dây cung có độ dài nhỏ 0 nhất. 1.9.
Tìm m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số   55  C  3 2
: y  x  2x  m  2 x  3m đi qua điểm A 1,  . m    27  1.10. Tìm tất cả các giá trị của tham số
m để trên đồ thị hàm số m C y  x  m  x 
 m x tồn tại đúng hai điểm có hoành độ dương m  3   2 : 1 4 3  3 1 3
sao cho tiếp tuyến của đồ thị tại đó vuông góc với đường thẳng y   x  . 2 2
1.11. Tìm những điểm trên trục hoành kẻ được ba tiếp tuyến đến đồ thị hàm số C 3
: y  x  3x  2 . Tương tự : 80 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
1. Tìm tất cả các điểm trên trục hoành kẻ được 3 tiếp tuyến đến đồ thị hàm số C 3 2
: y  x  3x biết có hai tiếp tuyến vuông góc với nhau.
2. Tìm trên đường thẳng y  2 các điểm kẻ được ba tiếp tuyến đến đồ thị hàm số 3
y  x  3xC . 3
3. Cho hàm số y  3x  x C . Tìm trên đường thẳng y  x các điểm mà từ đó kẻ
được đúng 2 tiếp tuyến phân biệt đến C  . 3 2
4. Cho hàm số y  x  3x  2 C . Tìm những điểm thuộc đường thẳng y  2 mà từ
đó kẻ được 3 tiếp tuyến phân biệt đến C  . 4 2
5. Cho hàm số y  x  2x 1 C . Tìm những điểm trên trục hoành kẻ được 3 tiếp
tuyến phân biệt đến C  .
6. Tìm những điểm trên trục tung kẻ được ba tiếp tuyến đến đồ thị hàm số C 4 2
: y  x  x 1. 1.12. Tìm hai điểm ,
A B phân biệt thuộc đồ thì hàm số C 3
: y  x  3x  2 sao cho tiếp tuyến tại ,
A B song song vơi nhau và đường thẳng đi qua hai điểm đó vuông góc với
đường thẳng x  y  2012  0 . 3
1.13. Cho hàm số y  x  2011xC . Tiếp tuyến của C  tại điểm M ( có hoành độ bằng 1
x  1) cắt C  tại điểm M  M , tiếp theo tiếp tuyến của C  tại M cắt C  ở 1 2 1 2
điểm M  M và cứ như vậy tiếp tuyến của C  tại M
cắt C  ở điểm 3 2 n 1  M  M 3  n   . Giả sử điểm
M  x , y , hãy tìm n để n n n  n n 1    2012
2011x  y  2 . n n
1.14. Chứng minh rằng đồ thị hàm số C  4 2
: y  x  2mx  2m 1 luôn đi qua hai điểm m
cố định. Tìm m để tiếp tuyến tại hai điểm cố định đó vuông góc với nhau. 4 2
1.15. Cho hàm số y  x  2x C . Trên C  lấy hai điểm ,
A B có hoành độ tương ứng là
a, b . Tìm điều kiện của a và b sao cho tiếp tuyến với C  tại ,
A B song song với nhau. 1 5
1.16. Tìm điểm AC  4 2 : y  x  3x 
sao cho tiếp tuyến của C  tại A cắt C  tại 2 2
hai điểm phân biệt B,C khác A sao cho AC  3AB ( B nằm giữa , A C ). 2x
1.17. Viết phương trình tiếp tuyến của đồ thị hàm số y 
C biết tiếp tuyến cắt trục x  2
hoành, trục tung lần lượt tại hai điểm M , N sao cho MN  OM
2 với O là gốc tọa độ. 81 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN x  2
1.18. Viết phương trình tiếp tuyến với đồ thị hàm số y 
C biết tiếp tuyến cắt các x 1 trục tọa độ tại ,
A B sao cho bán kính đường tròn nội tiếp tam giác OAB lớn nhất. 2mx  3
1.19. Cho hàm số y 
C . Tìm những giá trị thực của tham số m để tiếp tuyến m  x  m của C
cắt hai đường tiệm cận của C tại ,
A B sao cho tam giác IAB có diện tích m  m 
bằng 64( I là giao điểm của hai đường tiệm cận). x
1.20. Viết phương trình tiếp tuyến với đồ thị hàm số y 
C biết tiếp tuyến tạo với hai x 1
đường tiệm cận một giác có chu vi bằng 4  2 2 . x
1.21. Viết phương trình tiếp tuyến với đồ thị hàm số y 
C biết tiếp tuyến cắt hai trục x 1 tọa độ tại ,
A B sao cho đường trung trực của AB đi qua gốc tọa độ. 2x  1
1.22. Tìm trên đồ thị hàm số y  hai điểm ,
A B phân biệt sao cho tiếp tuyến tại hai x  2
điểm có song song với nhau và độ dài đoạn AB lớn nhất.
1.23. Tìm giá trị nhỏ nhất của tham số m để tồn tại ít nhất một điểm thuộc đồ thị hàm x  1
số C  : y 
biêt tiếp tuyến tại điểm số tạo với hai trục tọa độ một tam giác có 2x 1
trọng tâm nằm trên đường thẳng y  2m 1. 2x  1
1.24. Tìm trên hai nhánh của đồ thị hàm số C  : y 
hai điểm M , N sao cho tiếp x  1
tuyến tại hai điểm đó cắt các đường tiệm cận tạo thành một hình thang. 2x 1
1.25. Cho hàm số C  : y 
và điểm M bất kỳ thuộc C  , gọi I là giao điểm của hai x 1
đường tiệm cận. tiếp tuyến tại M cắt hai đường tiệm cận tại , A B .
1. Chứng minh M là trung điểm của AB .
2. Chứng minh diện tích tam giác IAB không đổi.
3. Tìm m để chu vi tam giác IAB nhỏ nhất. 2x  3
1.26. Lập phương trình tiếp tuyến của đồ thị hàm số y 
tại điểm thuộc đồ thị mà có x 1
khoảng cách đến đường thẳng 3x  4 y  2  0 bằng 2. 82 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 2x  3
1.27. Cho hàm số y 
C  . Gọi I là giao điểm của hai đường tiệm cận của C  . x  2
Tìm trên C  những điểm mà tiếp tuyến với C  tại điểm đó cắt các đường tiệm cận của C  tại ,
A B sao cho bán kính đường tròn ngoại tiếp tam giác IAB nhỏ nhất. x 1
1.28. Cho hàm số y 
C . Tìm trên C  những điểm mà tiếp tuyến với C  tại điểm x 1
đó cắt các đường tiệm cận của C  tại hai điểm ,
A B sao cho bán kính đường tròn nội
tiếp tam giác IAB lớn nhất( I là giao điểm hai đường tiệm cận của C  ). x  3
1.29. Cho hàm số y 
C  . Chứng minh rằng tiếp tuyến với C  tại điểm M bất kỳ x 1
trên C  luôn cắt các đường tiệm cận của C  tại hai điểm ,
A B và M là trung điểm của AB . x  2
1.30. Cho hàm số y 
C . Chứng minh rằng mọi tiếp tuyến của C  tại điểm bất kỳ x 1
thuộc C  luôn tạo với hai đường tiệm cận một tam giác có diện tích không đổi. x  2
1.31. Cho hàm số y 
C . Gọi d là một tiếp tuyến bất kỳ của C  , I là giao điểm x 1
của hai đường tiệm cận . Viết phương trình đường thẳng d biết khoảng cách từ I đến d là lớn nhất. x 1
1.32. Cho hàm số y 
C . Tìm những điểm trên trục tung những điểm kẻ được duy x 1
nhất một tiếp tuyến đến C  . 2x  1
1.33. Cho hàm số y 
C  . Viết phương trình tiếp tuyến với C  biết tiếp tuyến đó x 1
cách đều hai điểm A2;4, B4; 2   . 2x  3
1.34. Cho hàm số y 
C  . Viết phương trình tiếp tuyến tại điểm M C  biết x  2
rằng tiếp tuyến đó cắt các tiệm cận đứng, tiệm cận ngang lần lượt tại , A B sao cho côsin  4 góc ABI bằng
, với I là giao điểm hai đường tiệm cận. 17 x  2
1.35. Viết phương trình tiếp tuyến d với đồ thị hàm số y 
C  , biết d cắt hai đường x 1
tiệm cận của C  tại , A B . 83 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 1.
Diện tích tam giác IAB lớn nhất( với I là giao điểm của hai đường tiệm cận). 2.
Độ dài đoạn thẳng AB  2 10 . 2x  1
1.36. Viết phương trình tiếp tuyến với đồ thị hàm số y 
biết tiếp tuyến cách đều hai x  1
điểm A 2;4 và B  4  ; 2   . x  2
1.37. Viết phương trình tiếp tuyến với đồ thị hàm số y 
, biết tiếp tuyến cắt các trục 2x  3
tọa độ Ox,Oy lần lượt tại ,
A B sao cho trung trục của AB đi qua gốc tọa độ.
CÁC ĐIỂM ĐẶC BIỆT THUỘC ĐỒ THỊ HÀM SỐ
Xác định các điểm thuộc đồ thị hàm số có tính chất đặc biệt: Lưu ý: -
Tâm đối xứng của hàm bậc ba là điểm uốn, tâm đối xứng của hàm phân thức là giao điểm
của hai đường tiệm cận. Các bài toán: -
Tìm điểm cố định thuộc đồ thị hàm số hoặc quỹ tích các điểm cố định. -
Tìm những điểm thuộc đồ thị hàm số sao cho chúng đối xứng qua một điểm hoặc qua
một đường thẳng cho trước. -
Tìm điểm thuộc đồ thị hàm số có tổng khoảng cách đến hai tiệm cận hoặc đến hai trục tọa độ là nhỏ nhất. -
Tìm điểm thuộc hai nhánh của đồ thị hàm số sao cho khoảng cách giữa chúng nhỏ nhất. -
Tìm những điểm có tọa độ nguyên thuộc đồ thị hàm số( với hàm phân thức). -
Chứng minh rằng đồ thị hàm số luôn tiếp xúc với một đường thẳng cố định. BÀI TẬP MẪU 1 11 Bài 1. Cho hàm số 3 2
y   x  x  3x 
C . Tìm trên C  hai điểm phân biệt M , N đối 3 3
xứng với nhau qua trục tung. Lời giải:
+ giả sử điểm M  x ; y , N x ; y  C . Khi đó M , N đối xứng với nhau qua trục tung 1 1   2 2    khi và chỉ khi 84 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN x  x 1 2
x  x  0  x  3 x  3  1 2 1 1    1 11 1 11     3 2 3 2 y  y
 x  x  3x 
  x  x  3x  x  3  x  3  1 2  1 1 1 2 2 2  2  2  3 3 3 3  16   16 
vậy có hai điểm cần tìm là M 3; , N 3;     .  3   3  1 5 4 2
Bài 2. Cho hàm số y  x  3x 
C. Lập phương trình đường cong C 'đối xứng với 2 2
C  qua điểm I 0;2 . Lời giải: 1 5 Lấy điểm M  ;
x y C 4 2  y  x  3x  (i) 2 2 x  x '
Điểm M ' x '; y ' đối xứng với M qua điểm I 0;2 nên  thay vào (i) ta được y  4  y '  1 5 1 3 4 2 4 2 4  y '  x '  3x '   y '   x '  3x '  C ' 2 2 2 2 3 2
Bài 3. Cho hàm số y  x  3x  3mx  3m  4C . Tìm m để C
nhận điểm I 1; 2 m  m  làm tâm đối xứng. Lời giải: x  1 2
Ta có y '  3x  6x  3m  y '  6x  6  y '  0   y  6m  2 
Điểm uốn của đồ thị hàm số là tâm đối xứng U 1;6m  2
Yêu cầu bài toán tương đương với 6m  2  2  m  0 là giá trị cần tìm. 3
Bài 4. Cho hàm số y  m  2 x  3 m  2 x  m  7C
. Chứng minh rằng với mọi m m  đường cong C
luôn đi qua 3 điểm cố định thuộc một đường thẳng. m  Lời giải:
Gọi M  x ; y là điểm cố định thuộc đường cong C . Khi đó ta có m  0 0 
y  m  2 3
x  3 m  2 x  m  7, m  0 0   0 85 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  m  3 x  3x   3
1  2x  6x  7  y  0,m 0 0 0 0 0 3 3 
 x  3x  1  0
 x  3x  1  0(1) 0 0  0 0     3
2 x  6 x  7  y  0
y  2 3x  1  6x  7  12x  5(2)  0 0 0   0  0  0 0 Xét hàm số 3
f (x)  x  3x  1liên tục trên 
Ta có f (0)  1  0; f (1)  3
  0; lim f (x)   ;
 lim f (x)   x x
từ đó suy ra phương trình (1) luôn có 3 nghiệm phân biệt.
Và từ (2) suy ra cả 3 nghiệm này đều thuộc đường thẳng y  12x  5 . Ta có đpcm.
Bài 5. Tìm hai điểm trên đồ thị hàm số 3
y  x  3x  2 đối xứng nhau qua điểm M  1  ;3 Lời giải: Giả sử điểm
A x ; y  C , điểm B đối xứng với A qua M  1  ;3 nên 0 0    B 2
  x ;6  y 0 0  Nhưng do ,
A B C  nên: 3
 y  x  3x  2  x  1  0 0 0 0     A 1  ;0 ; B 1  ;6 3     6  y   
2  x   32  x   2 y  0  0 0 0 0  Vậy A 1  ;0 và B 1
 ;6 là hai điểm cần tìm.
Bài 6. Tìm trên đồ thị hàm số 3
y  x  3x  2 hai điểm đối xứng qua đường thẳng
d : 2x  y  2  0 . Lời giải:
Giả sử hai điểm M  x ; y ; N x ; y thuộc đồ thị hàm số đối xứng nhau qua đường thẳng 1 1   2 2 
d : 2x  y  2  0 .   x  x y  y  1 2 1 2 I ;  d  
Khi đó trung điểm I của MN cũng thuộc d :   2 2  MN  d 
 x  x  2 y  y  0 2 1   2 1   3 3   y  y
 x  3x  2  x  3x  2 x  x 1 2 1 1 2 2 1 2   2.  2   2 2 2
7 x  x   2 x  x    2 2
x  x x  x  0 2 1 2 1 1 1 2 2   
 x  x 3  3x x x  x  3 x  x  2 x  x 2 1 1 2  2 1   2 1   2 1   86 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  7 2 2  7  1 7
x  x x  x   1 1 2 2 x   y  2   1  1 2   2  2 2      x x 0    2 1   7  1 7   2 2 x  y  2  2 2
 x  x x  x 1    1 1 2 2  2  2 2  7 1 7   7 1 7 
Vậy có hai điểm cần tìm là M  ;2  ; N   ;2   . 2 2 2 2 2 2     3x  4
Bài 7. Tìm những điểm thuộc đồ thị hàm số y 
C  cách đều hai đường tiệm cận của x  2 đồ thị hàm số. Lời giải:  3x  4  Giả sử điểm M ; x  
 C  , vậy M cách đều hai đường tiệm cận của C  khi và chỉ  x  2  khi:  x  x  2 3x  4 x    x  1 M 1;  1 x 2 x  2   3  x  2        x  2 x  2 x x  4   M  4;6 2 x     x  2
Vậy có hai điểm cần tìm M 1;1 ; M 4;6 . 1   2   x  2
Bài 8. Tìm những điểm thuộc đồ thị hàm số y 
cách đều hai điểm A2;0; B0;2 . 2x 1 Lời giải:
Phương trình đường trung trực của AB là d : y  x
Khi đó điểm M thuộc đồ thị hàm số cách đều hai điểm ,
A B có tọa độ là nghiệm của phương trình: x  2 1  5 1  5 2
 x  2x  2x  2  0  x   y  2x 1 2 2  1 5 1 5   1 5 1 5 
Vậy có hai điểm thỏa mãn là M  ; ; M  ; 1 2  2 2 2 2     2x
Bài 9. Tìm những điểm thuộc đồ thị hàm số y 
C  sao cho tổng khoảng cách từ điểm x 1
đó đến hai đường tiệm cận của C  là nhỏ nhất. Lời giải: 87 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN  2x  Giả sử điểm 0 M x ;  C 
, khi đó tổng khoảng cách từ M đến hai đường tiệm cận của 0    x  1  0  C là: 2x 2 2 0 x  1   2  x 1   2 x  1 .  2 2 0 0 0 x  1 x  1 x  1 0 0 0 Dấu bằng xảy ra khi và chỉ khi   M 1  2;2  2 2 x  1  2 2   x 1  x  0 1 2          0 0 x  1  0  x  1  2  M 1  2  2  2 0    
Vậy có hai điểm cần tìm là M 1  2;2  2 ; M 1  2;2  2 1   2  2x
Bài 10. Tìm những điểm thuộc đồ thị hàm số y 
sao cho khoảng cách từ điểm I  1  ;2 x 1
đến tiếp tuyến với đồ thị hàm số tại điểm đó đạt giá trị lớn nhất. Lời giải:  2x  Giả sử điểm 0 M x ;  C 
, phương trình tiếp tuyến với đồ thị hàm số tại M là: 0    x  1  0  2 2x  : y   x  x  0 
 2x  x 1 y  2x  0 2 0  0 2 2  x 1 x  1 0  0 0 Khi đó khoảng cách từ I  1  ;2 đến  là 2   2 x  2 2 1  2x 4 x  1 4 0 0  0  d     2   x  4   x  4 4 4 1 4 1  x  1 2  0 2 0 0  x 1 0  2 4
Dấu bằng xảy ra khi và chỉ khi  x 1   x  1   2 0   x  2 0 1 0
Vậy có hai điểm cần tìm là M 1  2;2  2 ; M 1  2;2  2 1   2  2x
Bài 11. Tìm hai điểm thuộc hai nhánh của đồ thị hàm số y 
sao cho khoảng cách giữa x 1
chúng đạt giá trị nhỏ nhất. 88 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Lời giải:  2   2 
Giả sử điểm A 1  a, 2  ; B b 1, 2     
  C  với a,b  0  a   b  Khi đó ta có 2 1 1  4   4    4
AB  a  b2  4     a  b2 2 1    4ab1    8ab 1. 16 a b  ab2   ab2    ab2     Dấu bằng xảy ra khi và chỉ khi a  b  4 
 a  b  2  A 1   2; 2
  2 ; B 2 1;2  2 1   ab2 
Vậy hai điểm cần tìm là A1 2;2  2 ; B 2 1;2  2  2x
Bài 12. Tìm hai điểm thuộc hai nhánh của đồ thị hàm số y 
, biết rằng hai điểm đó tạo x 1
với điểm A 2;0 một tam giác vuông cân tại A . Lời giải:  2   2  Giả sử điểm B , b 2  ;C c, 2    
 với b  1  c  b  1   c  1 
Gọi H , K lần lượt là hình chiếu vuông góc của B,C trên trục hoành  AB  AC Từ điều kiện  ABH  C  AK AB  AC   2 2  b  2   AH CK    c 1 b   1  Từ đó suy ra:      BH  AK 2 c  3   2   c  2   b 1 
Vậy hai điểm cần tìm là B  1  ;  1 ;C 3;3 m   1 x  m
Bài 13. Chứng minh rằng với mọi m  0 đồ thị hàm số y  luôn tiếp xúc với x  m
một đường thẳng cố định. Lời giải: 89 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Giả sử đồ thị hàm số tiếp xúc với đường thẳng d : y  kx  l với mọi m 2  m 2  k  m   2 k x m      , m     x  m2 , m  m   1 x  m  2  kx  l
m l  x  
1  2mlx  x 2 2
 lx  x  0    x  m 2  m k    x  m2 x  0   
 l  x 1  0  l   1
lx  x  0 k 1   2 2
lx  x  0 
Vậy đồ thị hàm số luốn tiếp xúc với đường thẳng d : y  x  1
BÀI TẬP ĐỀ NGHỊ 3 x 2 1.1.
Tìm m để đồ thị hàm số y  
 3mx  2C ,m  0 nhận điểm I 1;0 làm tâm m m đối xứng. 3 1.2.
Cho hàm số y  x  3x  2C . Tìm trên C  hai điểm phân biệt đối xứng với nhau
qua đường thẳng 2x  y  2  0 . 2x  1 1.3. Cho hàm số y 
C. Tìm trên C  những điểm có tổng khoảng cách đến hai x 1
tiệm cận của C  nhỏ nhất. 3x  4 1.4. Cho hàm số y 
C . Tìm trên C  các điểm cách đều hai đường tiệm cận của x  2 C. 2x  4 1.5. Cho hàm số y 
. Tìm trên đồ thị hàm số hai điểm đối xứng với nhau qua đường x  1
thẳng MN biết M  3  ;0, N  1  ;  1 . 2x 1 1.6. Cho hàm số y 
C  . Tìm trên C  điểm M sao cho tiếp tuyến của C  tại x  1
M và đường thẳng đi qua M và giao điểm của hai đường tiệm cận của C  có tích hệ số góc bằng 9 . 90 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 2x  2 1.7. Cho hàm số y 
C. Tìm trên C  các điểm có hoành độ là các số nguyên. x  1 1.8.
Tìm điểm cố định của C  3
y  x  m  m  2 :
x  4x  4 m  m . m   1.9.
Với mỗi giá trị của tham số m để đường thẳng d : y  mx  1cắt đồ thị hàm số 2x 1 y 
tại hai điểm phân biệt M , N và cắt hai đường tiệm cận lần lượt tại , A B . x 1
Chứng minh rằng MA  NB .
1.10. Tìm m để trên đồ thị hàm số 3 y  x   2 m   2 x   2 m   3 3 2 1 3
1 x  1  m có hai
điểm phân biệt đối xứng nhau qua gốc tọa độ. x  2
1.11. Tìm những điểm thuộc đồ thị hàm số y 
biết rằng tổng khoảng cách từ điểm đó x 1
đến đường thẳng d : 2x  y  2  0 đạt giá trị nhỏ nhất. 2x
1.12. Tìm nhứng điểm thuộc hai nhánh của đồ thị hàm số y 
sao cho khoảng cách giữa x 1
chúng đạt giá trị nhỏ nhất. x 1
1.13. Tìm những điểm thuộc đồ thị hàm số y 
sao cho khoảng cách từ điểm đó đến x 1
trục hoành bằng hai lần khoảng cách từ điểm đó đến trục tung. 2x
1.14. Tìm những điểm thuộc đồ thị hàm số y 
sao cho tổng khoảng cách từ điểm đó x 1
đến các trục tọa độ đạt giá trị nhỏ nhất. 2x
1.15. Tìm hai điểm thuộc hai nhánh của đồ thị hàm số y 
, biết rằng hai điểm đó tạo với x 1
điểm A 2;0 một tam giác vuông cân tại A . x  1
1.16. Tìm trên đồ thị hàm số y  hai điểm ,
A B có độ dài đoạn AB  4 và đường x  2
thẳng AB vuông góc với đường thẳng y  x  0 . x 1
1.17. Tìm trên đồ thị hàm số y  các điểm ,
A B biết rằng tiếp tuyến với đồ thị hàm số x  2 tại ,
A B song song với nhau và độ dài đoạn AB bằng 2 2 .
1.18. Tìm trên đồ thị 3
y  x  3x bốn điểm ,
A B,C, D sao cho tứ giác ABCD là hình vuông tâm O .
VẼ ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI 91 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Dạng 1: Dựa vào đồ thị hàm số C  : y  f (x) suy ra đồ thị hàm số
C : y  f (x) . 1  Phương pháp:
 f (x), f (x)  0
Ta có C : y  f (x)  1 
 f (x), f (x)  0 
Do đó đồ thị C gồm hai phần 1 
Phần 1: Giữ nguyên phần đồ thị C  nằ trên trục hoành.
Phần 2: Lấy đối xứng phần đồ thị C  nằm phái dưới trục hoành qua trục hoành. 3 2
y  2x  9x 12x  4C 3 2
y  2x  9x 12x  4 C 1  C 1 
Dạng 2: Dựa vào đồ thị hàm số C  : y  f (x)suy ra đồ thị hàm số
C : y  f x . 2    Phương pháp: 92 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
 f (x), x  0
Ta có C : y  f x  2 
   f (x),x 0 
Do đó đồ thị C gồm hai phần 2 
Phần 1: Giữ nguyên phần đồ thị C  bên phải trục tung.
Phần 2: Lấy đối xứng phần 1 qua trục tung. 3 2
y  2x  9x 12x  4C 3 2
y  2 x  9x  12 x  4C 1  C 1 
Dạng 3: Dựa vào đồ thị hàm số C  : y  f (x)suy ra đồ thị hàm số
C : y  f x . 3    Phương pháp:
Đồ thị hàm số y  f (x) đối xứng qua trục hoành.  y, y  0
Ta có C : y  f x  f (x)  3    y, y  0 
Do đó đồ thị nhận trục hoành làm trục đối xứng, nên đồ thị gồm hai phần 93 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Phần 1: Giữ nguyên phần đồ thị C  phía trên trục hoành
Phần 2: Lấy đối xứng phần 1 qua trục hoành
Dạng 4: Dựa vào đồ thị hàm số C  : y  f (x)  u(x).v(x) suy ra đồ thị hàm số
C : y  u(x) v(x). 4  Phương pháp:
u(x)v(x)  f (x),u(x)  0
Ta có C : y  u(x) v(x)  . 4   u
 (x)v(x)   f (x),u(x)  0 
Do đó đồ thị C gồm hai phần 4 
Phần 1: Giữ nguyên phần đồ thị C  nằm trên miền u(x)  0 .
Phần 2: Lấy đối xứng phần đồ thị C  qua trục hoành nằm trên miền u(x)  0 . 3 2
y  2x  9x 12x  4C
y  x  2  2
2x  5x  2C 1  C 1 
Trên đây là 4 dạng bài hay gặp trong kỳ thi TSĐH, một số dạng khác phức tạp hơn như sau
Dạng 5: Dựa vào đồ thị hàm số C  : y  f (x) suy ra đồ thị hàm số C : y  f ( x ) . 5  94 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Dạng 6: Dựa vào đồ thị hàm số C  : y  f (x) suy ra đồ thị hàm số C : y  f ( x ) . 6 
Dạng 7: Dựa vào đồ thị hàm số C  : y  f (x) suy ra đồ thị hàm số C : y  f ( x ) . 7 
Dạng toán: Biện luận số nghiệm của phương trình dựa vào đồ thị Phương pháp:
Dùng trực quan đồ thị để biện luận số nghiệm của phương trình f (x)  g(m) , trong đó m là
tham số. Coi y  g(m) là đường thẳng và y  f (x) là đường cong
Ta phải vẽ được đồ thị hàm số y  f (x) , khi đó số giao điểm của đường thẳng y  g(m) và
đường cong y  f (x) chính là số nghiệm của phương trình.
Như vậy điểm mấu chốt của bài toán là vẽ được đồ thị hàm số y  f (x) . BÀI TẬP MẪU Lưu ý:
Tài liệu này quan niệm: -
Đồ thị hàm số lúc đầu quan niệm là đồ thị hàm số cơ bản. -
Đồ thị hàm số được suy ra từ đồ thị hàm số cơ bản gọi là đồ thị hàm số mới.
Với các bài toán mẫu ở đây, ta giả sử là đã có đồ thị hàm số cơ bản và ở đây chỉ nên ra cách suy
ra ra đồ thị hàm số mới. Khi làm bài các em phải xuất phát từ đồ thị hàm số cơ bản xong mới
được suy ra đồ thị hàm số mới( thường thì đề ra câu 1, ý một khảo sát sự biến thiên và vẽ đồ thị
hàm số các em đã có đồ thị hàm sô cơ bản). 3 2
Bài 1. Tìm m để phương trình sau có 6 nghiệm phân biệt 2 x  9x 12 x  m . Lời giải: 3 2
Hàm số cơ bản y  f (x)  2x  9x 12x C
Số nghiệm của phương trình chính là số giao điểm của đường thẳng y  m và đồ thị hàm số 3 2
y  2 x  9x  12 x C 1  3 2  3
 f (x)  2x  9x 12x, x  0 Ta có 2
y  2 x  9x 12 x   3 2
 f (x)  2x  9x 12x, x  0 
Do đó đồ thị C gồm hai phần: 1 
Phần 1: giữ nguyên phần đồ thị C  bên phải trục tung.
Phần 2: Lấy đối xứng phần 1 qua trục tung. 95 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Đồ thị hàm số C là phần liền nét trên hình vẽ 1 
Dựa vào đồ thị hàm số suy ra để phương trình có bốn nghiệm phân biệt khi và chỉ khi đường
thẳng y  m cắt C tại bốn điểm phân biệt  4  m  5 . 1  4 2 x 3x 2
Bài 2. Tìm m để phương trình 2
 m 1có tám nghiệm phân biệt. Lời giải:
Điều kiện: m  1, khi đó phương trình tương đương với: 4 2
x  3x  2  log m 1 2   Đồ thị hàm số 4 2
y  x  3x  2 như trên hình vẽ 96 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Dựa vào đồ thị hàm số suy ra để phương trình có tám nghiệm phân biệt khi và chỉ khi đường y  k  log m 1 2   thẳng
cắt đồ thị hàm số tại tám điểm phân biệt 1
 0  log m   4 1   2  m  1  2 2 4
BÀI TẬP ĐỀ NGHỊ Bài 1. Cho hàm số 3 2
y  2x  9x  12x  4C 
a. Khảo sát sự biến thiên và vẽ đồ thị hàm số C  . 3 2
b. Tìm m để phương trình sau có 6 nghiệm phân biệt 2 x  9x 12 x  m . Bài 2. Cho hàm số 4 2
y  2x  4x C .
a. Khảo sát sự biến thiên và vẽ đồ thị C  của hàm số.
b. Với giá trị nào của m, phương trình 2 2
x x  2  m có đúng 6 nghiệm phân biệt.
Bài 3. Gọi d là đường thẳng đi qua điểm A2;0 với hệ số góc k . Tìm k để d cắt đồ thị hàm số 3
y  x  3 x  2 tại 4 điểm phân biệt. 3 2
Bài 4. Cho hàm số y  x  x  x   1 C . 97 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
a. Khảo sát sự biến thiên và vẽ đồ thị hàm số C 
b. Tìm những giá trị của tham số m để phương trình sau có 6 nghiệm phân biệt 3 2
x 1  x  2x  x 1  m. 2x  1
Bài 5. Cho hàm số y  C. x 1
a. Khảo sát sự biến thiên và vẽ đồ thị C  của hàm số. 2 x  1
b. Tìm m để phương trình sau có nghiều nghiệm nhất  m . x  1
MỘT SỐ BÀI TẬP TỔNG HỢP 3 2 1.1.
Cho hàm số y  2x  3 m  
3 x 18mx  8 C m 
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m  1.
2. Tìm m để C
tiếp xúc với trục hoành. m 
3. Chứng minh rằng tồn tại điểm x sao cho tiếp tuyến với đồ thị hàm số tại điểm đó song 0
song với nhau với mọi m.
4. Chứng minh rằng trên parabol  P 2
: y  x có hai điểm không thuộc đồ thị hàm số với mọi m. mx  2 1.2. Cho hàm số y 
C  , m là tham số thực. x 1 m
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m  3 .
2. Cho hai điểm A 3  ;4 và B3; 2
  . Tìm m để trên đồ thị C có hai điểm , P Q m  cách đều hai điểm ,
A B và diện tích tứ giác APBQ bằng 24. 1.3. Cho hàm số 3 2
y  mx  3mx  2m  
1 x  3  mC
, m là tham số thực. m 
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m  2 .  1 
2. Tìm m để hàm số C
có cực đại, cực tiểu và khoảng cách từ điểm N ;4 đến m     2 
đường thẳng đi qua điểm cực đại, cực tiểu của hàm số là lớn nhất. 3 2 1.4.
Cho hàm số y  x  3x  2 C
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số.
2. Tìm tất cả các giá trị của k để trên đồ thị hàm số C  tồn tại đúng hai tiếp tuyến có cùng
hệ số góc k đồng thời đường thẳng đi qua hai tiếp điểm cắt các trục tọa độ Ox,Oy lần
lượt tại A và B sao cho AB  5 . 98 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN mx  1 1.5. Cho hàm số y  m    1 x  m 1
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m   . 2 2. Lấy ,
A B lần lượt thuộc đồ thị hàm số có hoành độ x  1; x  1 . Xác định m biết A B
tiếp tuyến với đồ thị hàm số tại ,
A B cắt nhau tại C sao cho tam giác ABC là tam giác đều. 3 2 1.6.
Cho hàm số y  x  3 m  
1 x  6mx  3m  4 C m 
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m  1.
2. Gọi  là tiếp tuyến của đồ thị hàm số C
tại điểm có hoành độ bằng 1. Tìm m để m 
tiếp tuyến cắt đồ thị hàm số C
tại điểm B khác A , sao cho tam giác OAB cân tại m  O . 3 2 1.7.
Cho hàm số y  x  2m  
1 x  m 1 C m 
1. Với m  1, khảo sát sự biến thiên và vẽ đồ thị hàm số.
2. Tìm m để đường thẳng y  2mx  m 1cắt đồ thị C tại 3 điểm phân biệt , A B,C m  sao cho 2 2 2
OA  OB  OC đạt giá trị nhỏ nhất. 4 2 1.8.
Cho hàm số y  x  22m   1 x  3 m C m  3
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số với m  . 2
2. Tìm m để C
cắt trục hoành tại 4 điểm tạo thành 3 đoạn thẳng bằng nhau. m  3 2 1.9.
Cho hàm số y  x  3x  4 C .
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.  1   7 
2. Cho hai điểm M ;2 ; N ; 2   
 . Viết phương trình đường thẳng d cắt đồ thị C   2   2 
tại hai điểm phân biệt P,Q sao cho tứ giác MNPQ là hình bình hành. m  x
1.10. Cho hàm số y  C  x  2 m
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số với m  1 .
2. Tìm m để đường thẳng d : 2x  2 y 1  0 cắt C
tại hai điểm phân biệt và cùng m  3
với gốc tọa độ tạo thành tam giác có diện tích bằng . 8 2 5 1.11. Cho hàm số 3 y  
x  m   2
1 x  3m  2 x  C  3 3 m 99 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số với m  2 .
2. Tìm trên đồ thị C
hai điểm phân biệt có hoành độ x , x thỏa mãn x x  0 sao m  1 2 1 2
cho tiếp tuyến tại mỗi điểm đó vuông góc với đường thẳng x  3y  1  0 . m   1 x  m
1.12. Với m 0;4 tìm điểm thuộc đồ thị hàm số y  có hoành độ dương ; x  m
tung độ lớn nhất, biết rằng khoảng cách từ điểm đó đến tiếp tuyến cố định của đồ thị hàm số bằng 2 . 100 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN 101 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam

Chuyên đề hàm số và các bài toán liên quan – Đặng Thành Nam Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề khảo sát hàm số – Trung tâm LTĐH Vĩnh Viễn Toán 12

Chuyên đề khảo sát hàm số – Trần Sĩ Tùng Toán 12

Giá trị lớn nhất – nhỏ nhất của hàm nhiều biến – Trần Phương Toán 12

Sử dụng phương pháp đạo hàm để tìm GTLN – GTNN Toán 12

Tuyển chọn bài tập hàm số – Phạm Duy Toán 12