Chuyên đề hệ thức lượng trong tam giác vuông lớp 9 file word

Chuyên đề hệ thức lượng trong tam giác vuông lớp 9 file word
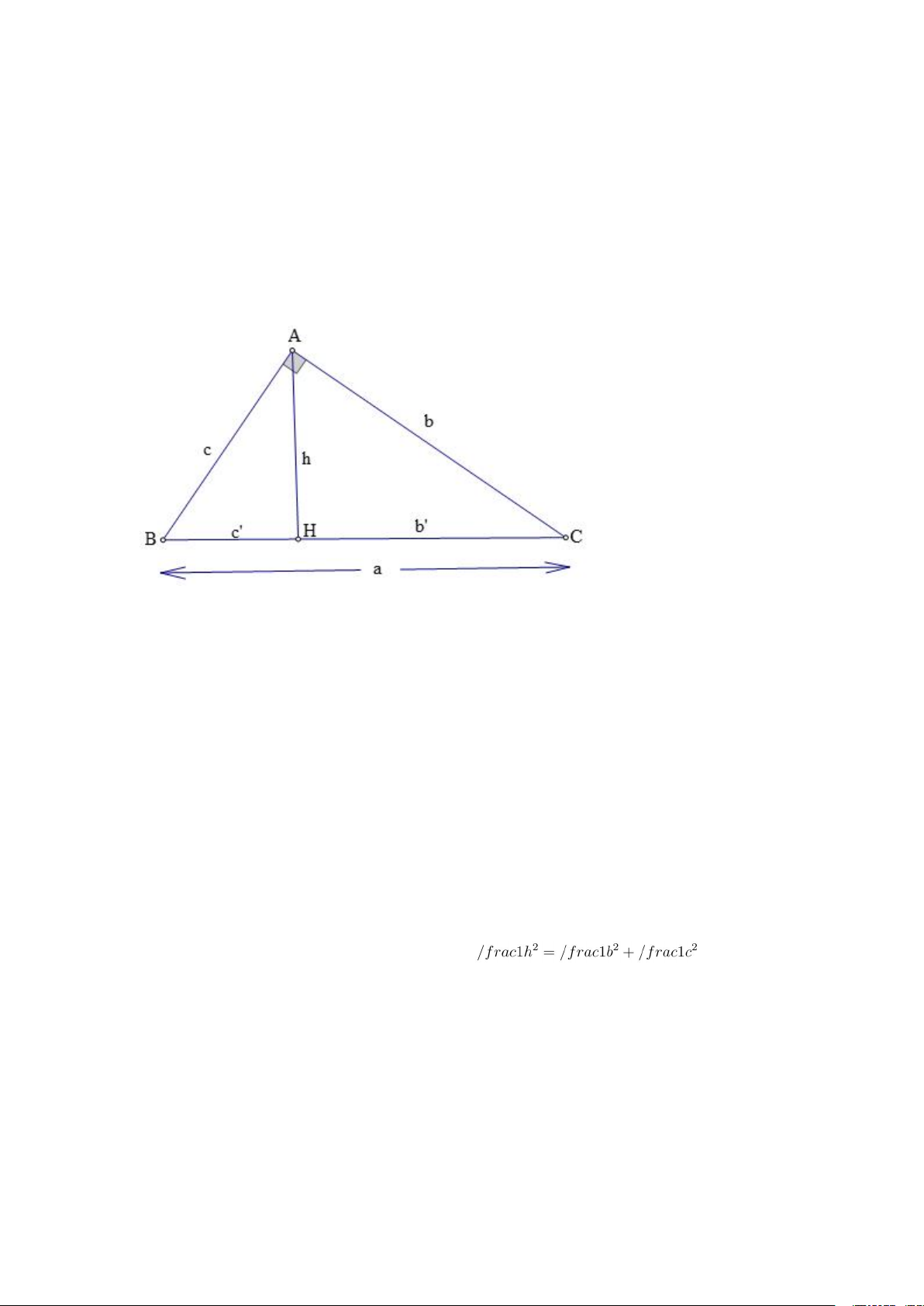
1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh
huyền và hình chiếu của cạnh góc vuông trên cạnh huyền.
Một số hệ thức về cạnh và đường cao trong tam giác vuông: - Định lý 1: 
Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng
tích hai hình chiếu của cạnh góc vuông trên cạnh huyền. 
Trong tam giác vuông ABC vuông tại A, ta có: a.h = h.c - Định lý 2: 
Trong một tam giác vuông, tích của hai cạnh góc vuông bằng tích của cạnh
huyền với đường cao tương ứng. 
Trong tam giác ABC vuông tại A, ta có: a.h = b.c - Định lý 3: 
Trong tam giác vuông, nghịch đảo của bình phương đường cao ứng với
cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông. 
Trong tam giác ABC vuông tại A, ta có:
2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
Tỉ số lượng giác của góc nhọn là tỉ số của góc nhọn và các cạnh tương
ứng xuất hiện trong các tam giác vuông. 
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc a, ký hiệu là: sin a. 
Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc a, ký hiệu là: cos a. 
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc a, ký hiệu là: tan a. 
Tỉ số giữa cạnh kề và cạnh đối được gọi là cotang của góc a, lý hiệu là: cot a.
Tính chất của tỉ số lượng giác của góc nhọn
- Tính chất 1: nếu hai góc phụ nhau (tổng hai góc bằng 90 độ), thì sin góc này
bằng cos góc kia, tan góc này bằng cot góc kia.
- Tính chất 2: Nếu hai góc a = b thì sin a = sin b, cos a = cos b
- Tính chất 3: Nếu a là góc nhọn bất kỳ trong một tam giác vuông, ta có
những công thức sau đây:
3. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c, ta được: Trong một tam giác vuông:
- Cạnh góc vuông = (cạnh huyền) × (sin góc đối) = (cạnh huyền) × (cosin góc kề)
- Cạnh góc vuông = (cạnh góc vuông còn lại) × (tang góc đối) = (cạnh góc
vuông còn lại) × (cotang góc kề)
Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít
nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.
Các dạng toán thường gặp:
- Dạng 1: Giải tam giác vuông 
Phương pháp: Giải tam giác là tính độ dài các cạnh và số đo các góc dựa
vào dữ kiện cho trước của bài toán. Trong tam giác vuông, ta dùng hệ thức
giữa cạnh và các góc của một tam giác vuông để tính toán. 
Bài toán 1: Giải tam giác vuông khi biết độ dài một cạnh và số đo một góc nhọn. 
Bài toán 2: Giải tam giác vuông khi biết độ dài hai cạnh.
- Dạng 2: Tính cạnh và góc của tam giác 
Phương pháp: Bằng cách kẻ thêm đường cao ta làm xuất hiện tam giác
vuông để áp dụng các hệ thức giữa cạnh và góc thích hợp.
4. GIẢI BÀI TOÁN HỆ THỨC LƯỢNG BẰNG PHƯƠNG PHÁP ĐẠI SỐ
Lý thuyết: Thường gọi độ dài một cạnh cần tìm là ẩn, từ đó thiết lập phương
trình, giải phương trình, tính ra kết quả.
Bài tập minh họa: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB =
20cm, HC = 9cm. Tính độ dài AH.
=> Hướng dẫn giải:
Đặt BH = x. Áp dụng hệ thức lượng trong tam giác ABC vuông tại A, có đường cao AH. Ta được: hay .
Giải phương trình này t được: x1 = 16 và x2 = 25 (loại)
Dùng định lý Pithagoras tính được AH = 12cm
Lưu ý: Giải phương trình bậc 2 nên dùng máy tính để giải cho nhanh.
Thuộc một số bộ ba số Pithagoras càng tốt để mau chóng ghi kết quả.
5. BÀI TẬP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Cho tam giác ABC vuông tại A. Biết . Đường cao AH = 15cm. Tính HB và HC.
Bài 2. Cho tam giác ABC vuông tại A, AB = 12cm, AC = 16cm, phân giác AD,
đường cao AH. Tính HD, HB và HC.
Bài 3. Cho biết chu vi của một tam giác bằng 120cm. Độ dài các cạnh tỉ lệ với 8; 15; 17.
a) Chứng minh rằng tam giác đó là một tam giác vuông.
b) Tính khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh.
Bài 4. Cho tam giác ABC có AB = 24cm, AC = 18cm, BC = 30cm
a) Tính đường cao AH, số đo góc B và C.
b) Phân giác của góc A cắt BC tại D. Tính BD và CD.
c) Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình
gì? Tính chu vi và diện tích tứ giác AEDF.
Bài 5. Cho tam giác ABC vuông cân tại A, trung tuyến BD. Gọi I là hình chiếu
của C trên BD, H là hình chiếu của I trên AC. Chứng minh: AH = 3HI.
Bài 6. Một cây cau có chiều cao 6m. Để hái một buồng cau xuống, phải đặt
thang tre sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với
mặt đất là bao nhiêu, biết chiếc thang dài 8m (làm tròn đến phút).
Bài 7. Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5m.
Hãy tính góc BCA (làm tròn đến phút) mà tia nắng mặt trời tạo với mặt đất.
Bài 8. Tia nắng chiếu qua nóc của tòa nhà hợp với mặt đất một góc a. Cho
biết tòa nhà cao 21m và bóng của nó trên mặt đất dài 15m. Tính góc a (làm tròn đến phút).
Bài 9. Một cái thang dài 6m được đặt dựa vào một bức tường sao cho chân
thang cách tường 3m. Tính góc a tạo bởi thang với bức tường.
Bài 10. Một máy bay đang bay ở độ cao 12km. Khi máy bay hạ cánh xuống
mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất. Nếu
cách sân bay 320km, máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?
Bài 11. Một người thợ sử dụng thước ngắm có góc vuông để đo chiều cao
một cây dừa. Khoảng cách từ gốc cây đến chân người thợ là 4,8m và từ vị trí
chân đứng thẳng trên mặt đất đến mắt của người nhắm là 1,6m. Hỏi với các
kích thước trên, người thợ đo được chiều cao của cây dừa đó là bao nhiêu? (làm tròn đến mét).
Bài 12. Hải đăng Kê Gà thuộc xã Tân Thành, huyện Hàm Thuận Nam, Bình
Thuận là ngọn hải đăng được trung tâm sách kỷ luật Việt Nam xác nhận
là ngọn hải đăng cao nhất và nhiều tuổi nhất. Hải đăng Kê Gà được xây dựng
từ năm 1897 - 1899 và toàn bộ bằng đá. Tháp đèn có hình bát giác, cao 66m
so với mực nước biển. Ngọn đèn đặt trong tháp có thể phát sáng xa 22 hải lý (tương đương 40km).
Một người đi thuyền thúng trên biển, muốn đến ngọn hải đăng có độ cao 66m,
người đó đứng trên mũi thuyền và dùng giác kế đo được góc giữa thuyền và
tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là 25 độ. Tính khoảng cách
của thuyền đến ngọn hải đăng (làm tròn đến m).
Bài 13. Tòa nhà Bitexco Financial (hay Tháp Tài chính Bitexco) là một tòa
nhà chọc trời được xây dựng tại trung tâm Quận 1, Thành phố Hồ Chí Minh.
Tòa nhà có 68 tầng (không tính 3 tầng hầm). Biết rằng, khi tòa nhà có bóng in
trên mặt đất dài 47,3 mét, thì cũng thời điểm đó có một cột cờ (được cắm
thẳng đứng trên mặt đất) cao 15 mét có bóng in trên mặt đất dài 2,64 mét.
a) Tính góc tạo bởi tia nắng mặt trời với mặt đất (đơn vị đo góc được làm tròn đến độ).
b) Tính chiều cao của tòa nhà (làm tròn đến hàng đơn vị).
Bài 14. Giông bão thổi mạnh, một cây tre gãy gập xuống làm ngọn cây chạm
đất và ngọn cây tạo với mặt đất một góc 30 độ. Người ta đo được khoảng
cách từ ngọn cây chạm đất đến gốc tre là 8,5m. Giải sử cây tre mọc vuông
góc với mặt đất, hãy tính chiều cao của cây tre đó (làm tròn đến chữ số thập phân thứ hai).
Bài 15. Tính chiều cao của trụ cầu Cần Thơ so với mặt sông Hậu, cho biết tại
hai điểm cách nhau 89 mét trên mặt sông người ta nhìn thấy đỉnh trụ cầu với
góc nâng lần lượt là 40 độ và 30 độ.
Document Outline

• Chuyên đề hệ thức lượng trong tam giác vuông lớp 9
  • 1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔ
  • 2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
  • 3. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VU
  • 4. GIẢI BÀI TOÁN HỆ THỨC LƯỢNG BẰNG PHƯƠNG PHÁP ĐẠ
  • 5. BÀI TẬP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG